ELNYÚJTOTT ALAKÚ RÉSZECSKÉK RENDEZÕDÉSE NYÍRÓ ÁRAMLÁSBAN
|
|
|
- Jenő Pintér
- 6 évvel ezelőtt
- Látták:
Átírás
1 nuszt, és rendezik át a bolygó plazmakörnyezetét. Vech és munkatársai [12] szisztematikusan izsgálták a VEX ûrszonda plazma- és mágneses méréseinek segítségéel a CME-k hatását a különbözõ plazmarégiókra. Azt találták, hogy az indukált mágneses tér megnõ, a bolygó elõtti lökéshullám nagyon eltáolodik, és az éjszakai magnetoszféra magassága csökken ezekben az idõszakokban. Nyitott kérdések A Vénusz bolygó igen rejtélyes, még rengeteg megálaszolatlan tudományos kérdés an. A bolygó története, õsi légköre és annak fejlõdése, a illámok meglepõen ritka észlelése, alamint a ulkanizmus mind toábbi magyarázatra szorul. A belsõ mágneses tér hiánya igen érdekessé teszi a bolygó plazmakörnyezetének izsgálatát. Az elmúlt néhány ében a tudósok találtak egy toábbi okot a Vénusz jelentõségének hangsúlyozására: ez a globális felmelegedés. A légkör az elszabadult üegházhatás köetkeztében melegszik fel. Ha rájöünk, hogyan történik ez a folyamat, az útmutatója lehet az emberiség álaszának a globális felmelegedésre. Irodalom 1. Sedhem, Wilson, Piccioni: Introduction to the special issue on Venus exploration. Planetary and Space Science (21) Voosen: (217) 3. Werner: Volcano (Venus). In: Encyclopaedia of Planetary Landforms. Springer (21) Airey et al.: Explosie olcanic actiity on Venus: The roles of olatile contribution, degassing, and external enironment. Planetary and Space Science (21) Parkinson et al.: Photochemical control of the distribution of Venusian water. Planetary and Space Science (21) Bertaux et al.: Influence of Venus topography on the zonal wind and UV albedo at cloud top leel: the role of stationary graity waes. Journal of Geophysical Research (Planets) 121 (21) Delitsky, Baines: Storms on Venus: Lightning-induced chemistry and predicted products. Planetary and Space Science (21) Hansell, Wells, Hunten: Optical detection of lightning on Venus. Icarus 117 (199) Bertucci et al.: The induced magnetospheres of Mars, Venus, and Titan. Space Science Reiews 162 (211) Miller, Whitten: Ion dynamics in the Venus ionosphere. Space Science Reiews (1991) Wei et al.: A teardrop-shaped ionosphere at Venus in tenuous solar wind. Planetary and Space Science 73 (212) Vech et al.: Space weather effects on the bow shock, the magnetic barrier, and the ion composition boundary at Venus. Journal of Geophysical Research (Space Physics) 12 (21) ELNYÚJTOTT ALAKÚ RÉSZECSKÉK RENDEZÕDÉSE NYÍRÓ ÁRAMLÁSBAN Börzsönyi Tamás, Szabó Balázs, Somfai Ellák MTA Wigner Fizikai Kutatóközpont, Szilárdtestfizikai és Optikai Kutatóintézet Török János BME, Elméleti Fizika Tanszék Elnyújtott alakú részecskékbõl álló anyagok áramlásáal széles mérettartományban találkozhatunk. Erre reprezentatí példák a legnagyobb méretskálától az egyre kisebbekig: a folyón úsztatott farönkök, a szintén makroszkopikus szemcsés anyagok, mint például A cikk az Eötös Loránd Fizikai Társulat szegedi Vándorgyûlésén, 216. augusztus 26-án elhangzott elôadás alapján készült. búza agy rizs, a mikrométer nagyságrendû baktériumok, a nanorészecskék és égül a legkisebb, atomi méretskálán a hosszúkás molekulákból álló rendszerek, például nematikus folyadékkristályok. Alapetõ kérdés, hogy ezen rendszerekben az áramlás hatására az alkotóelemek miként rendezõdnek, és ez hogyan hat issza az anyag reológiai tulajdonságaira, különösen a iszkozitásra, illete az effektí súrlódásra. A Börzsönyi Tamás fizikus, tanulmányait (diploma, PhD) az ELTE-n égezte. Jelenleg az MTA Wigner Fizikai Kutatóközpont tudományos fõmunkatársa, a Részben Rendezett Rendszerek kutatócsoport ezetõje. Kutatásaiban a szemcsés anyagok és a komplex folyadékok (szuszpenziók, folyadékkristályok) folyási jelenségeit és fázisátmeneteit izsgálja. Szabó Balázs fizikus, egyetemi tanulmányait az ELTE-n égezte. 21 és 217 között az MTA Winger Fizikai Kutatóközpontban dolgozott, jelenleg kutató-fejlesztõ a Mediso Kft.-nél. Kutatásai során elsõsorban a szemcsés anyagok folyási tulajdonságait izsgálta, amelynek fókuszában a nem gömbszerû, például elnyújtott alakú részecskéket tartalmazó rendszerek oltak. 118 FIZIKAI SZEMLE 218 / 4
2 fenti rendszerek elsõ ránézésre nagyon különböznek egymástól, nemcsak az egyes részecskék közötti kölcsönhatás fajtájában, hanem a rendezõdés ellen ható (például termikus) zaj mértékében is. Ennek ellenére amint azt látni fogjuk az áramlás hatására kialakuló rendezõdésükben nagyon sok közös onást fedezhetünk fel. Jelen munkában a száraz makroszkopikus szemcsés anyagokat izsgáljuk, mint például rizst, agy mm cm nagyságrendû üeg- és farudakat. Ilyen anyagokban tágabb értelemben rengeteg nehezen jósolható és érdekes jelenség figyelhetõ meg, a mechanikai terhelésnek kitett anyag megcsúszásától a lejtõkön kialakuló lainákon keresztül a szegregációs, alamint különbözõ rezonanciajelenségekig [1 7]. A nyírt szemcsés anyagban az egymás mellett elhaladó részecskék a mechanikai kontaktusokon keresztül hatnak kölcsön (például súrlódás, ütközés), ahol a kölcsönhatás intenzitása egyrészt a nyomástól, másrészt a szomszédos részecskék sebességkülönbségétõl, agyis a sebességgradienstõl függ. Arra a kérdésre keressük a álaszt, hogy a nyíró áramlás hatására beköetkezõ rendezõdés milyen jellegû és mértékû, alamint hogy ez miként függ a sebességgradienstõl, agy más néen nyírási rátától, illete a részecskék L/d -el jelölt elnyújtottságának mértékétõl. Laboratóriumi kísérletekben könnyen létrehozhatunk folyamatos nyíró áramlást az úgyneezett osztott aljú hengeres geometriában, ahol a szemcsés réteg alatt elhelyezett körlap állandó sebességgel forog (1.a ábra). A réteg felszínérõl digitális felételeket készíthetünk (1.b ábra), a minta belsejét pedig röntgentomográf segítségéel térképezhetjük fel. A minta egy sá mentén nyíródik (az ábrán pirossal jelöle), amin belül a nyírási ráta az 1.c ábrán látható módon függ a forgástengelytõl mért táolságtól. Az adatokat az 1.c ábrán jelölt sáokból külön-külön gyûjte, illete különbözõ forgási sebességeket alkalmaza megmérhetjük, hogy a részecskék folyásiránnyal bezárt θ szö- a) z kamera y x w h y x 2, nyírási ráta (1/s) 1, 1,,, r (cm) d) L d 1cm Somfai Ellák fizikus, az MTA doktora, tudományos tanácsadó. Diplomáját az ELTE-n, PhD fokozatát a Uniersity of Michiganen szerezte. 213 óta dolgozik az MTA Wigner Fizikai Kutatóközpontban. Érdeklõdési területe a statisztikus fizikai rendszerek és komplex folyadékok numerikus modellezése, az utóbbi idõben elsõsorban a szemcsés anyagok izsgálatáal foglalkozik. e) Török János fizikus, egyetemi tanulmányait az ELTE-n égezte, majd 2-ben PhD fokozatot szerzett fizikából a BME-n. Jelenleg a BME Elméleti Fizika Tanszékének docense. Érdeklõdési területe a szemcsés anyagok numerikus szimulációja, szemcsék alakáltozásának, illete a szociális hálózatok dinamikájának modellezése. 1. ábra. a) A szemcsés anyag alá helyezett körlap forgatásáal a mintát a pirossal jelzett tartományban folyamatosan nyírjuk. A minta felszínérõl készült kép, a részecskék folyásiránnyal bezárt szögét -al jelöljük. A felszínen mérhetõ nyírási ráta a forgástengelytõl mért táolság függényében. d) A kísérletekben használt anyagok: rizsszemek, üegrudak és farudak. e) A numerikus diszkrételemrendszer oldalnézetbõl. BÖRZSÖNYI T., SZABÓ B., SOMFAI E., TÖRÖK J.: ELNYÚJTOTT ALAKÚ RÉSZECSKÉK RENDEZŐDÉSE NYÍRÓ ÁRAMLÁSBAN 119
3 a),3 rudak,3 rizs L/d =, L/d = 4,,2 L/d = 3,,2 L/d = 3,4 P P,1,1 L/d = 2, L/d = 2, forgási sebesség (rad./egys. deformáció), ,,, L/d = 2, L/d =, L/d = 3,4 ellipszoid folyadékban L/d = 2,, ábra. a) A nyírásnak kitett szemcsés anyagban (rudak és rizs) mérhetõ orientációs eloszlás egy adott nyírásiráta-tartományban. A részecskék átlagos iránya kissé eltér a folyásiránytól ( ), és hosszabb részecskékre az eloszlás keskenyebb (nagyobb a rendezettség). Összehasonlításképpen: egy nyírásnak kitett iszkózus folyadékba helyezett ellipszoid nem konstans sebességgel forog, amikor folyásirányba áll, akkor lelassul. d) Az ellipszoid irányának alószínûségeloszlás-maximuma az áramonalakkal esik egybe. d) P, ,3,2,1 ellipszoid folyadékban L/d =, L/d = 3,4 ge mily módon függ a nyírási ráta értékétõl. Az itt bemutatott mérésekben rizsszemeket, üeg-, alamint farudakat használtunk (1.d ábra). Numerikus (diszkrét elem) szimulációkat is égeztünk, amelyekben a kihíást az elnyújtott alakú részecskék realizációja jelenti, amit néhány gömb alakú részecske egymáshoz rögzítéséel oldottunk meg (1.e ábra). A részecskék fogaskerékszerû összeakadásának megelõzéséhez fontos, hogy ne teljesen legyenek azonosak, ezért a köetkezõ paramétereket bizonyos szórással adtuk meg: a gömbök mérete (1%), az átfedésük mértéke (3 7%), illete a teljes részecskék hossza (1%). A részecskéket alkotó gömbök száma sem minden esetben olt ugyanaz. A numerikus rendszerben 7-12 ilyen elnyújtott alakú részecske mozgásának modellezésére került sor az ingyenesen letölthetõ LAMMPS szoftercsomag segítségéel [8]. A részecskék áramonalakhoz iszonyított orientációjának eloszlását mutatja a 2.a és 2.b ábra egy adott nyírásiráta-tartományból. Jól látható, hogy a rendezettség mértéke amit az eloszlások keskenysége mutat a részecske elnyújtottságának nöeléséel egyre erõsebb. A részecskék tengelyének átlagos iránya pedig kicsit eltér a folyás irányától, az eltérés az elnyújtottság nöeléséel csökken. Érdekes összehasonlítani ezt az eredményt azzal az esettel, amikor egyetlen hosszúkás részecskét helyezünk iszkózus folyadékba, és ennek mozgását figyeljük, miközben a folyadékot nyírjuk. A részecske a 2.c ábrán látható módon forog, forgási sebessége nem egyenletes, hanem felgyorsul, amikor iránya merõleges az áramonalakra és lelassul, amikor párhuzamos azokkal. Ez a periodikus moduláció a részecske elnyújtottságának nöeléséel egyre erõsebb. Ezek alapján az orientációs eloszlás maximuma az áramonalakkal esik egybe, szélessége pedig a részecske elnyújtottságának nöeléséel egyre csökken (2.d ábra). A száraz szemcsés anyag esetére isszatére, a 3. ábrán a deformáció függényében láthatjuk a részecskék irányának alakulását. Megfigyelhetjük, hogy a részecskék sok idõt töltenek a 2 < θ < tartományban, és forgásuk az egymás közti kölcsönhatások köetkeztében rendszertelen. Ezen a tartományon kíül kerüle a képzeletbeli kontínuummal együtt mozoga forognak. Ez tipikusan a nyíró áramlás orticitásának megfelelõ szögsebességet jelent, amit az ábrán egy ferde onal jelöl. Megjegyezzük, hogy egy nyírásnak kitett folyadékba helyezett gömb 12 FIZIKAI SZEMLE 218 / 4
4 1 2 3 deformáció 3. ábra. A részecskék irányának fejlõdése egy nyírt szemcsés anyagban (rudak, L/d = 3,). A részecskék a 2 < θ < tartományban idõznek, forgásuk zajos. Ha kikerülnek ebbõl a tartományból, akkor határozottan körbefordulnak, amíg megint issza nem érnek. A ferde onal a nyíró áramlás orticitásának megfelelõ forgási sebességet jelöli (1 radián/egységnyi deformáció). Egy gömb fele ilyen gyorsan forogna. 4 leti adatokkal. Az is látható, hogy ugyanolyan elnyújtottság mellett a rudak kisebb szöget zárnak be az áramonalakkal, mint az ellipszoidhoz hasonló rizsszemek. A rudakkal égzett mérésekben az adatok egy részét tomográfiás (CT) módszerrel gyûjtöttük, így lehetõségünk olt θ a és S értékét nemcsak a felszínen, hanem a minta belsejében is meghatározni. A 4.b és 4.c ábrákon látható, hogy a felszínen kisebb a rendezettség és ehhez nagyobb orientációs szög tartozik, mint a minta belsejében, ahol a részecskék minden oldalról körüleszik egymást. Összehasonlításképpen érdemes megemlíteni, hogy alakú részecske fele ilyen gyorsan forog (azaz a folyadék orticitása felének megfelelõ szögsebességgel, ami, radián/egységnyi deformáció). Az eddigiekbõl tehát az látszik, hogy a nyírás indukálta rendezettség (az eloszlás keskenysége) egyre erõsebb a részecske hosszának nöeléséel, és ez nagyon hasonló a folyadékba helyezett egyetlen részecske és a sok egymással kölcsönható részecske esetén, agyis alapetõen a részecske nyírás hatására égbemenõ nem egyenletes forgására ezethetõ issza. Az átlagos orientáció folyásiránytól aló eltérése pedig ami a sokrészecskés rendszerben figyelhetõ meg a részecskék kölcsönhatásának a köetkezménye. Az orientációs eloszlásokat különbözõ nyírási ráták esetére meghatároza megkaphatjuk az átlagos orientációs szög nyírásiráta-függését, amit a 4.a ábra mutat. Jól látszik, hogy egy adott alakú részecskére a θ a átlagos szög a nyírási ráta széles tartományában lényegében áltozatlan (a nyírási rátát logaritmikus skálán ábrázoltuk). A rendezettség mértékét általánosan egy tenzor számszerûsíti, melynek legnagyobb S sajátértékét rendparaméternek szokás neezni. Ez teljesen rendezetlen rendszerre, a teljesen rendezett esetben pedig 1. A 4.b és 4.c ábrákon láthatjuk a θ a átlagos szöget, illete a rendezettség mértékét jellemzõ S rendparamétert a részecskék L /d elnyújtottságának függényében. Mind a rudak, mind a rizs esetében megfigyelhetõ, hogy az elnyújtottság nöeléséel a rendezettség mértéke nõ, és a részecskék átlagos iránya egyre közelebb kerül a folyás irányához. Numerikus szimulációink adatai nagyon jól egybeesnek a kísér- 4. ábra. A θ a folyásiránnyal bezárt átlagos orientációs szög a) a nyírási ráta és a részecskék elnyújtottsága függényében. A nyírás hatására kialakuló rendezettséget leíró S rendparaméter a részecskék elnyújtottsága függényében [9]. a) q a ( ) q a ( ) 1 S,8,6,4,2 Ld / = 1,4; rudak Ld / = 2,; rizs Ld / = 3,4; rizs Ld / = 3,; rudak Ld / = 4,; rizs,1,1 1 1 nyírási ráta (1/s) L/d 3 L/d 4 4 rizs a felszínen rudak a felszínen rudak belül szimuláció q a 6 6 BÖRZSÖNYI T., SZABÓ B., SOMFAI E., TÖRÖK J.: ELNYÚJTOTT ALAKÚ RÉSZECSKÉK RENDEZŐDÉSE NYÍRÓ ÁRAMLÁSBAN 121
5 az elnyújtott alakú molekulákból álló nematikus folyadékkristályok folyási orientációja igen hasonló a fent leírtakhoz. Ezt a furcsa anyagot mindannyian használjuk a csaart nematikus (TN twisted nemati kijelzõt tartalmazó laptopokban, karórákban agy LCD teleíziókban. Nematikus fázisban nyíró áramlás hatására a molekulák átlagos iránya szintén kis szöget zár be a folyás irányáal, ami nyírásiráta-független, és a rendparaméter nöeléséel csökken. Ebben az esetben a rendezettséget nem a nyírás hozza létre, hanem annak mértéke egy külsõ paraméterrel (a hõmérséklet áltoztatásáal) szabályozható. Nyilánaló, hogy a molekulák közötti kölcsönható erõk nagyon különböznek a makroszkopikus szemcsék közötti kölcsönhatásoktól. Ezért is figyelemreméltó, hogy a nyírási orientáció ennyire hasonló a két rendszerben, ami az alkotóelemek geometriai tulajdonságainak fontosságát mutatja. Most izsgáljuk meg, hogy a nyírás hatására beköetkezõ orientációs rendezõdés milyen hatással an a szemcsés anyag sûrûségére (térkitöltésére), illete a nyírással szembeni ellenállására (effektí súrlódására). A térkitöltésre ett hatást izsgála fel kell eleenítenünk, hogy egy tartályba öntött, rendezetlen szemcsés rendszer a nyírási deformáció hatására kissé kitágul. Ez azért köetkezik be, mert ahhoz, hogy a szomszédos szemcsék el tudjanak haladni egymás mellett, egy kicsit el kell táolodjanak egymástól (.a ábra). Ezt a jelenséget több mint egy észázaddal ezelõtt elõször Osborne Reynolds dokumentálta, aki a híres folyadékdinamikai kutatásai mellett a szemcsés rendszerek tulajdonságait is izsgálta [1]. A róla elneezett Reynolds-tágulás 1 mértéke 1-1% körül alakul borsó agy mákszemek esetén [11]. Az elnyújtott részecskék esetében megfigyelhetõ orientációs rendezõdés iszont nöeli a térkitöltés mértékét. Kérdés, hogy ez a hatás legyõzi-e az általánosan megfigyelhetõ Reynolds-tágulást. Az.b ábra az L/d = 2 elnyújtottságú rudakból álló szemcsés rendszer térkitöltésének keresztmetszeti eloszlását mutatja 134 CT-felétel átlagolt adatai alapján. Jól látható, hogy a térkitöltés kisebb a nyírási zónában, mint a két oldalon látható, nyírásnak nem kitett tartományban. Az adatokat egy a felszínhez közeli 1 cm astag ízszintes rétegben átlagola meghatároztuk a térkitöltést a forgástengelytõl aló táolság függényében, amit az.c ábrán láthatunk három, különbözõ elnyújtottságú részecskékbõl álló minta esetén. Látható, hogy a nyírási zónában mindegyik esetben lecsökkent a sûrûség, azaz az orientációs rendezõdés egyik esetben sem tudja legyõzni a Reynolds-tágulást. Megfigyelhetõ azonban, hogy az egyre elnyújtottabb részecskék esetén a sûrûségcsökkenés mértéke egyre kisebb, azaz az egyre nagyobb 1 Nedes tengerparton sétála azt tapasztaljuk, hogy a homokra lépe és ezáltal azt deformála, lábunk körül a homok felszíne kiszárad, miel ekkor a felszíni nedesség mélyebbre húzódik a homokszemek közötti térfogat megnöekedése, azaz a Reynoldstágulás köetkeztében. a) z (cm) 6 4 2,7 térkitöltés,7,6,6,,,3,4,,6,7 térkitöltés r (cm) r (cm). ábra. a) A szemcsés anyag nyíró deformáció hatására kitágul (Reynolds-tágulás). A sûrûségeloszlás keresztmetszeti képe 134 tomogram átlaga alapján L/d = 2 elnyújtottságú rudakból álló szemcsés anyagban. A nyírási zónában kisebb a térkitöltés, mint a két oldalán léõ deformálatlan tartományban. A Reynolds-tágulást részben kompenzálja az orientációs rendezõdés, ezért a hosszabb részecskék esetében (amelyeknél nagyobb a rendezettség) kisebb a sûrûségcsökkenés mértéke [11]. rendparaméterrel jellemezhetõ rendezõdés láthatóan egyre nagyobb mértékben kompenzálja a Reynoldstágulást. A köetkezõ kérdés, hogy a rendezõdési folyamat köetkeztében mily módon áltozik az anyag nyírással szembeni ellenállása (effektí súrlódása). Ehhez megmértük, hogy rendezetlen kezdõállapotból indíta, a folyamat során miként alakul a tányér forgatásához szükséges forgatónyomaték. A 6.a ábrán minta esetére láthatjuk a forgatónyomaték alakulását a deformáció függényében. A 4 elnyújtott részecskékbõl álló minta mellett az ötödik anyag (mustármagok) esetében kapott görbét referenciának használjuk. Ez lehetõé teszi az irány szerinti rendezõdés hatásának elkülönítését, miel ez a gömbszerû részecskékbõl álló mintában nincs jelen. A motor bekapcsolása után a forgatónyomaték mind az öt minta esetén erõsen emelkedik. Ennek oka egyrészt a részecskék közötti kontaktusok felépülése, másrészt egy instrumentális hatás is hozzájárul: az erõmérõ cella és a motor teste 2 rudak L/d =, L/d = 3,3 L/d = 2, FIZIKAI SZEMLE 218 / 4
6 a) 1, M M M mustármagok 1,,,,4,2 Ld / = 3,; rudak Ld / = 4,; rizs Ld / = 3,4; rizs Ld / = 2,; rizs mustármagok 1 1 deformáció Ld / = 3,; rudak Ld / = 4,; rizs Ld / = 3,4; rizs Ld / = 2,; rizs ban a részecskék irány szerint rendezõdnek, ami szoros öszszefüggésben an a nyírás hatására megfigyelhetõ, nem egyenletes sebességû forgásukkal. A szomszédos részecskék kölcsönhatásának köetkeztében az átlagos orientáció nem a folyás irányába mutat, hasonlóan az elnyújtott alakú molekulákból álló nematikus folyadékkristályban megfigyelhetõ folyási orientációhoz. A szemcsés rendszer a nyírás hatására kicsit kitágul, amit csak részben tud ellensúlyozni az orientációs rendezõdésbõl fakadó sûrûségnöekedés. Az orientációs rendezõdés hatására az anyag nyírással szembeni ellenállása (effektí súrlódása) a kezdeti, rendezetlen állapothoz képest jelentõsen, mintegy 3%-kal lecsökken., 1 1 deformáció 6. ábra. a) A rendszer nyírásához szükséges (stacionárius értékkel normált) forgatónyomaték alakulása a rendezõdési folyamat során 4 különbözõ elnyújtottságú minta és gömbszerû mustármagok esetében. Hasonló alak esetén az elnyújtottság nöeléséel egyre nagyobb a forgatónyomaték eltérése a közel gömbszerû mustármagokétól. közötti mechanikus kapcsolatot jelentõ fémszál megfeszülése. Ezen nem orientációs effektusokból származó járulékok kiszûrésére a 6.a ábrán látható 4 adatsorból kiontuk az ötödiket, a mustármagokkal égzett mérések eredményét. Az így kapott adatsorokat mutatja a 6.b ábra. Látható, hogy a rendezõdés hatására a minta effektí súrlódása jelentõsen lecsökken. Hasonló alak esetén mind a csökkenés mértéke, mind pedig a kialakulásához szükséges deformáció nagysága L /d nöeléséel nöekszik. A legnagyobb effektus az L/d = 3, hosszúságú rudak esetében tapasztalható, és ez összhangban an azzal, hogy a négy minta közül ennél alakul ki a legkisebb orientációs szög (4.b ábra). Összességében elmondhatjuk, hogy az elnyújtott részecskékbõl álló, nyírásnak kitett szemcsés anyag- Irodalom 1. Jánosi I.: Zajongó homokdombok és egyéb furcsaságok: új fejlemények a granuláris anyagok fizikájában. Fizikai Szemle 4 (199) Jánosi I.: A homok titkai. Természet Világa 129 (1998) Vankó P.: Izgalmas mérések a mérnök-fizikus hallgatói laboratóriumban. Fizikai Szemle 6 (26) Börzsönyi T.: Lejtõn lefolyó szemcsés anyag dinamikája: instabilitások, lainák. Fizikai Szemle 7 (27) Szabó B.: Hogyan törik a szemcsés anyag? Aagy különös analógia az optikáal. Természet Világa 143 (212). 6. Gillemot K., Somfai E., Börzsönyi T.: Szegregáció nyírt, szemcsés keerékekben. Fizikai Szemle 67 (217) T. Börzsönyi, Z. Koács: High-speed imaging of traeling waes in a granular material during silo discharge. Phys. Re. E 83 (211) T. Börzsönyi, B. Szabó, G. Törös, S. Wegner, J. Török, E. Somfai, T. Bien, R. Stannarius: Orientational order and alignment of elongated particles induced by shear. Phys. Re. Lett. 18 (212) O. Reynolds: On the dilatancy of media composed of rigid particles in contact. Phil. Mag. 2 (188) S. Wegner, R. Stannarius, A. Böse, G. Rose, B. Szabó, E. Somfai, T. Börzsönyi: Effects of grain shape on packing and dilatancy of sheared granular materials. Soft Matter 1 (214) 17. BÖRZSÖNYI T., SZABÓ B., SOMFAI E., TÖRÖK J.: ELNYÚJTOTT ALAKÚ RÉSZECSKÉK RENDEZŐDÉSE NYÍRÓ ÁRAMLÁSBAN 123
Nyírási lokalizáció és rendeződés szemcsés anyagokban (munkabeszámoló) Szabó Balázs
 Nyírási lokalizáció és rendeződés szemcsés anyagokban (munkabeszámoló) Szabó Balázs fiatal kutató, MTA Wigner FK, SZFI Komplex Folyadékok Osztály, Részben Rendezett Rendszerek Csoport 2010. szeptember
Nyírási lokalizáció és rendeződés szemcsés anyagokban (munkabeszámoló) Szabó Balázs fiatal kutató, MTA Wigner FK, SZFI Komplex Folyadékok Osztály, Részben Rendezett Rendszerek Csoport 2010. szeptember
Hogyan folyik a szemcsés anyag?
 Hogyan folyik a szemcsés anyag? Börzsönyi Tamás MTA WIGNER FK SZFI, Komplex folyadékok osztály www.szfki.hu/~btamas Hogyan folyik a szemcsés anyag? - A szemcsés anyag reológiája - A terhelésnek kitett
Hogyan folyik a szemcsés anyag? Börzsönyi Tamás MTA WIGNER FK SZFI, Komplex folyadékok osztály www.szfki.hu/~btamas Hogyan folyik a szemcsés anyag? - A szemcsés anyag reológiája - A terhelésnek kitett
Nyírási lokalizáció kialakulása szemcsés anyagokban (munkabeszámoló) Szabó Balázs
 Nyírási lokalizáció kialakulása szemcsés anyagokban (munkabeszámoló) Szabó Balázs tudományos segédmunkatárs, MTA Wigner FK, SZFI Komplex Folyadékok Osztály, Részben Rendezett Rendszerek Csoport 2013. júniustól
Nyírási lokalizáció kialakulása szemcsés anyagokban (munkabeszámoló) Szabó Balázs tudományos segédmunkatárs, MTA Wigner FK, SZFI Komplex Folyadékok Osztály, Részben Rendezett Rendszerek Csoport 2013. júniustól
Reológia Mérési technikák
 Reológia Mérési technikák Reológia Testek (és folyadékok) külső erőhatásra bekövetkező deformációját, mozgását írja le. A deformációt irreverzibilisnek nevezzük, ha a az erőhatás megszűnése után a test
Reológia Mérési technikák Reológia Testek (és folyadékok) külső erőhatásra bekövetkező deformációját, mozgását írja le. A deformációt irreverzibilisnek nevezzük, ha a az erőhatás megszűnése után a test
Kvázisztatikus határeset Kritikus állapot Couette-teszt
 Wacha András Kvázisztatikus határeset Kritikus állapot Couette-teszt 2006. november 9. Kvázisztatikus határeset GDR_MiDi. On dense granular flows. Eur. Phys. J. E 14. pp 341-365 (2004). Dimenziótlan paraméterek
Wacha András Kvázisztatikus határeset Kritikus állapot Couette-teszt 2006. november 9. Kvázisztatikus határeset GDR_MiDi. On dense granular flows. Eur. Phys. J. E 14. pp 341-365 (2004). Dimenziótlan paraméterek
Transzportfolyamatok. összefoglalás, általánosítás Onsager egyenlet I V J V. (m/s) áramvonal. turbulens áramlás = kaotikusan gomolygó áramlás
 1 Transzportfolyamatok Térfogattranszport () - alapfogalmak térfogattranszport () Hagen Poiseuille-törény (elektromos) töltéstranszport (elektr. áram) Ohm-törény anyagtranszport (diffúzió) ick 1. törénye
1 Transzportfolyamatok Térfogattranszport () - alapfogalmak térfogattranszport () Hagen Poiseuille-törény (elektromos) töltéstranszport (elektr. áram) Ohm-törény anyagtranszport (diffúzió) ick 1. törénye
HÍDTARTÓK ELLENÁLLÁSTÉNYEZŐJE
 HÍDTARTÓK ELLENÁLLÁSTÉNYEZŐJE Csécs Ákos * - Dr. Lajos Tamás ** RÖVID KIVONAT A Budapesti Műszaki és Gazdaságtudományi Egyetem Hidak és Szerkezetek Tanszéke megbízta a BME Áramlástan Tanszékét az M8-as
HÍDTARTÓK ELLENÁLLÁSTÉNYEZŐJE Csécs Ákos * - Dr. Lajos Tamás ** RÖVID KIVONAT A Budapesti Műszaki és Gazdaságtudományi Egyetem Hidak és Szerkezetek Tanszéke megbízta a BME Áramlástan Tanszékét az M8-as
fizikai szemle 2018/4
 fizikai szemle 2018/4 Az Eötvös Loránd Fizikai Társulat Küldöttgyûlése Az Eötvös Loránd Fizikai Társulat 2018. május 12-én, szombaton 10:00 órai kezdettel tartja Küldöttgyûlését az Eötvös Loránd Tudományegyetem
fizikai szemle 2018/4 Az Eötvös Loránd Fizikai Társulat Küldöttgyûlése Az Eötvös Loránd Fizikai Társulat 2018. május 12-én, szombaton 10:00 órai kezdettel tartja Küldöttgyûlését az Eötvös Loránd Tudományegyetem
Folyadékok és gázok áramlása
 Folyadékok és gázok áramlása Hőkerék készítése házilag Gázok és folyadékok áramlása A meleg fűtőtest vagy rezsó felett a levegő felmelegszik és kitágul, sűrűsége kisebb lesz, mint a környezetéé, ezért
Folyadékok és gázok áramlása Hőkerék készítése házilag Gázok és folyadékok áramlása A meleg fűtőtest vagy rezsó felett a levegő felmelegszik és kitágul, sűrűsége kisebb lesz, mint a környezetéé, ezért
Modern Fizika Labor. 17. Folyadékkristályok
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 11. A mérés száma és címe: 17. Folyadékkristályok Értékelés: A beadás dátuma: 2011. okt. 23. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 11. A mérés száma és címe: 17. Folyadékkristályok Értékelés: A beadás dátuma: 2011. okt. 23. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Hangfrekvenciás mechanikai rezgések vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
Hatvani István Fizikaverseny forduló megoldások. 1. kategória
 1. kategória 1.2.1. 1. Newton 2. amplitúdó 3. Arkhimédész 4. Kepler 5. domború 6. áram A megfejtés: ATOMKI 7. emelő 8. hang 9. hősugárzás 10. túlhűtés 11. reerzibilis 1.2.2. Irányok: - x: ízszintes - y:
1. kategória 1.2.1. 1. Newton 2. amplitúdó 3. Arkhimédész 4. Kepler 5. domború 6. áram A megfejtés: ATOMKI 7. emelő 8. hang 9. hősugárzás 10. túlhűtés 11. reerzibilis 1.2.2. Irányok: - x: ízszintes - y:
Molekuláris dinamika I. 10. előadás
 Molekuláris dinamika I. 10. előadás Miről is szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten minden részecske mozgását szimuláljuk? Hogyan tudjuk megérteni a folyadékok,
Molekuláris dinamika I. 10. előadás Miről is szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten minden részecske mozgását szimuláljuk? Hogyan tudjuk megérteni a folyadékok,
FIZIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Fizika közészint ÉRETTSÉGI VIZSGA 0. május 7. FIZIKA KÖZÉPSZITŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMZETI ERŐFORRÁS MIISZTÉRIUM A dolgozatokat az útmutató utasításai szerint, jól köethetően
Fizika közészint ÉRETTSÉGI VIZSGA 0. május 7. FIZIKA KÖZÉPSZITŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMZETI ERŐFORRÁS MIISZTÉRIUM A dolgozatokat az útmutató utasításai szerint, jól köethetően
A 2007/2008. tanévi Országos Középiskolai Tanulmányi Verseny második fordulójának feladatai és megoldásai fizikából
 Oktatási Hiatal A 7/8 tanéi Országos Középiskolai Tanulmányi Verseny második fordulójának feladatai és megoldásai fizikából I kategória A dolgozatok elkészítéséhez minden segédeszköz használható Megoldandó
Oktatási Hiatal A 7/8 tanéi Országos Középiskolai Tanulmányi Verseny második fordulójának feladatai és megoldásai fizikából I kategória A dolgozatok elkészítéséhez minden segédeszköz használható Megoldandó
A II. kategória Fizika OKTV mérési feladatainak megoldása
 Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Vázlatos tartalom. Szerkezet jellemzése és vizsgálata Szilárdtestek elektronszerkezete Rácsdinamika Transzportjelenségek Mágneses tulajdonságok
 Szilárdtestfizika Kondenzált Anyagok Fizikája Vázlatos tartalom Szerkezet jellemzése és vizsgálata Szilárdtestek elektronszerkezete Rácsdinamika Transzportjelenségek Mágneses tulajdonságok 2 Szerkezet
Szilárdtestfizika Kondenzált Anyagok Fizikája Vázlatos tartalom Szerkezet jellemzése és vizsgálata Szilárdtestek elektronszerkezete Rácsdinamika Transzportjelenségek Mágneses tulajdonságok 2 Szerkezet
EGYENES VONALÚ MOZGÁSOK KINEMATIKAI ÉS DINAMIKAI LEÍRÁSA
 EGYENES VONALÚ MOZGÁSOK KINEMATIKAI ÉS DINAMIKAI LEÍRÁSA 1. A kinematika és a dinamika tárgya. Egyenes onalú egyenletes mozgás a) Kísérlet és a belőle leont köetkeztetés b) A mozgás jellemző grafikonjai
EGYENES VONALÚ MOZGÁSOK KINEMATIKAI ÉS DINAMIKAI LEÍRÁSA 1. A kinematika és a dinamika tárgya. Egyenes onalú egyenletes mozgás a) Kísérlet és a belőle leont köetkeztetés b) A mozgás jellemző grafikonjai
4. MECHANIKA-MECHANIZMUSOK ELŐADÁS (kidolgozta: Szüle Veronika, egy. ts.)
 SZÉHNYI ISTVÁN YTM LKLMZOTT MHNIK TNSZÉK. MHNIK-MHNIZMUSOK LŐÁS (kidolgozta: Szüle Veronika, egy. ts.) yalugép sebességábrája: F. ábra: yalugép kulisszás mechanizmusának onalas ázlata dott: az ábrán látható
SZÉHNYI ISTVÁN YTM LKLMZOTT MHNIK TNSZÉK. MHNIK-MHNIZMUSOK LŐÁS (kidolgozta: Szüle Veronika, egy. ts.) yalugép sebességábrája: F. ábra: yalugép kulisszás mechanizmusának onalas ázlata dott: az ábrán látható
Rugalmas állandók mérése
 Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
Molekuláris dinamika. 10. előadás
 Molekuláris dinamika 10. előadás Mirőlis szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten? Hogyan tudjuk megérteni a folyadékok, gázok, szilárdtestek makroszkópikus
Molekuláris dinamika 10. előadás Mirőlis szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten? Hogyan tudjuk megérteni a folyadékok, gázok, szilárdtestek makroszkópikus
Ábragyűjtemény levelező hallgatók számára
 Ábragyűjtemény levelező hallgatók számára Ez a bemutató a tanszéki Fizika jegyzet kiegészítése Mechanika I. félév 1 Stabilitás Az úszás stabilitása indifferens a stabil, b labilis S súlypont Sf a kiszorított
Ábragyűjtemény levelező hallgatók számára Ez a bemutató a tanszéki Fizika jegyzet kiegészítése Mechanika I. félév 1 Stabilitás Az úszás stabilitása indifferens a stabil, b labilis S súlypont Sf a kiszorított
FELÜLETI FESZÜLTSÉG. Jelenség: A folyadék szabad felszíne másképp viselkedik, mint a folyadék belseje.
 Jelenség: A folyadék szabad felszíne másképp iselkedik, mint a folyadék belseje. A felületen leő molekulákra a saját részecskéik onzása csak alulról hat, a felülettel érintkező leegő molekulái által kifejtett
Jelenség: A folyadék szabad felszíne másképp iselkedik, mint a folyadék belseje. A felületen leő molekulákra a saját részecskéik onzása csak alulról hat, a felülettel érintkező leegő molekulái által kifejtett
Kutatási beszámoló. 2015. február. Tangens delta mérésére alkalmas mérési összeállítás elkészítése
 Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
egyetemi tanár Nyugat-Magyarországi Egyetem
 egyetemi tanár Nyugat-Magyarországi Egyetem Folyadékok szerkezeti jellemz i Az el adás témakörei: Mit nevezünk folyadéknak? - részecskék kölcsönhatása, rendezettsége - mechanikai viselkedése alapján A
egyetemi tanár Nyugat-Magyarországi Egyetem Folyadékok szerkezeti jellemz i Az el adás témakörei: Mit nevezünk folyadéknak? - részecskék kölcsönhatása, rendezettsége - mechanikai viselkedése alapján A
Termodinamika (Hőtan)
 Termodinamika (Hőtan) Termodinamika A hőtan nagyszámú részecskéből (pl. gázmolekulából) álló makroszkópikus rendszerekkel foglalkozik. A nagy számok miatt érdemes a mólt bevezetni, ami egy Avogadro-számnyi
Termodinamika (Hőtan) Termodinamika A hőtan nagyszámú részecskéből (pl. gázmolekulából) álló makroszkópikus rendszerekkel foglalkozik. A nagy számok miatt érdemes a mólt bevezetni, ami egy Avogadro-számnyi
Tájékoztató. Értékelés Összesen: 60 pont
 A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
TestLine - Fizika 7. évfolyam folyadékok, gázok nyomása Minta feladatsor
 légnyomás függ... 1. 1:40 Normál egyiktől sem a tengerszint feletti magasságtól a levegő páratartalmától öntsd el melyik igaz vagy hamis. 2. 3:34 Normál E minden sorban pontosan egy helyes válasz van Hamis
légnyomás függ... 1. 1:40 Normál egyiktől sem a tengerszint feletti magasságtól a levegő páratartalmától öntsd el melyik igaz vagy hamis. 2. 3:34 Normál E minden sorban pontosan egy helyes válasz van Hamis
TestLine - Fizika 7. évfolyam folyadékok, gázok nyomása Minta feladatsor
 Melyik állítás az igaz? (1 helyes válasz) 1. 2:09 Normál Zárt térben a gázok nyomása annál nagyobb, minél kevesebb részecske ütközik másodpercenként az edény falához. Zárt térben a gázok nyomása annál
Melyik állítás az igaz? (1 helyes válasz) 1. 2:09 Normál Zárt térben a gázok nyomása annál nagyobb, minél kevesebb részecske ütközik másodpercenként az edény falához. Zárt térben a gázok nyomása annál
összetevője változatlan marad, a falra merőleges összetevő iránya ellenkezőjére változik, miközben nagysága ugyanakkora marad.
 A termodinamika 2. főtétele kis rendszerekben Osváth Szabolcs Semmelweis Egyetem Statisztikus sokaságok Nyomás Nyomás: a tartály falával ütköző molekulák, a falra erőt fejtenek ki Az ütközésben a részecske
A termodinamika 2. főtétele kis rendszerekben Osváth Szabolcs Semmelweis Egyetem Statisztikus sokaságok Nyomás Nyomás: a tartály falával ütköző molekulák, a falra erőt fejtenek ki Az ütközésben a részecske
Hőtan ( első rész ) Hőmérséklet, szilárd tárgyak és folyadékok hőtágulása, gázok állapotjelzői
 Hőtan ( első rész ) Hőmérséklet, szilárd tárgyak és folyadékok hőtágulása, gázok állapotjelzői Hőmérséklet Az anyagok melegségének mérésére hőmérsékleti skálákat találtak ki: Celsius-skála: 0 ºC pontja
Hőtan ( első rész ) Hőmérséklet, szilárd tárgyak és folyadékok hőtágulása, gázok állapotjelzői Hőmérséklet Az anyagok melegségének mérésére hőmérsékleti skálákat találtak ki: Celsius-skála: 0 ºC pontja
H01 TEHERAUTÓ ÉS BUSZMODELL SZÉLCSATORNA VIZSGÁLATA
 H01 TEHERAUTÓ ÉS BUSZMODELL SZÉLCSATORNA VIZSGÁLATA 1. A mérés célja A mérési feladat moduláris felépítésű járműmodellen a c D ellenállástényező meghatározása különböző kialakítások esetén, szélcsatornában.
H01 TEHERAUTÓ ÉS BUSZMODELL SZÉLCSATORNA VIZSGÁLATA 1. A mérés célja A mérési feladat moduláris felépítésű járműmodellen a c D ellenállástényező meghatározása különböző kialakítások esetén, szélcsatornában.
Az állományon belüli és kívüli hőmérséklet különbség alakulása a nappali órákban a koronatér fölötti térben május és október közötti időszak során
 Eredmények Részletes jelentésünkben a 2005-ös év adatait dolgoztuk fel. Természetesen a korábbi évek adatait is feldolgoztuk, de a terjedelmi korlátok miatt csak egy évet részletezünk. A tárgyévben az
Eredmények Részletes jelentésünkben a 2005-ös év adatait dolgoztuk fel. Természetesen a korábbi évek adatait is feldolgoztuk, de a terjedelmi korlátok miatt csak egy évet részletezünk. A tárgyévben az
Egy részecske mozgási energiája: v 2 3 = k T, ahol T a gáz hőmérséklete Kelvinben 2 2 (k = 1, J/K Boltzmann-állandó) Tehát a gáz hőmérséklete
 Hőtan III. Ideális gázok részecske-modellje (kinetikus gázmodell) Az ideális gáz apró pontszerű részecskékből áll, amelyek állandó, rendezetlen mozgásban vannak. Rugalmasan ütköznek egymással és a tartály
Hőtan III. Ideális gázok részecske-modellje (kinetikus gázmodell) Az ideális gáz apró pontszerű részecskékből áll, amelyek állandó, rendezetlen mozgásban vannak. Rugalmasan ütköznek egymással és a tartály
2010/2011. tanév Országos Középiskolai Tanulmányi Verseny döntő forduló. FIZIKA II. kategória FELADATLAP ÉS MEGOLDÁS
 Oktatási Hiatal 2010/2011. tané Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. kategória FELAATLAP MEGOLÁ Feladatok: Mérések függőleges alumínium, illete sárgaréz csőben eső mágnessel.
Oktatási Hiatal 2010/2011. tané Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. kategória FELAATLAP MEGOLÁ Feladatok: Mérések függőleges alumínium, illete sárgaréz csőben eső mágnessel.
Folyadékok és gázok áramlása
 Folyadékok és gázok áramlása Gázok és folyadékok áramlása A meleg fűtőtest vagy rezsó felett a levegő felmelegszik és kitágul, sűrűsége kisebb lesz, mint a környezetéé, ezért felmelegedik. A folyadékok
Folyadékok és gázok áramlása Gázok és folyadékok áramlása A meleg fűtőtest vagy rezsó felett a levegő felmelegszik és kitágul, sűrűsége kisebb lesz, mint a környezetéé, ezért felmelegedik. A folyadékok
TestLine - Fizika 7. osztály Hőtan Témazáró Minta feladatsor
 Nézd meg a képet és jelöld az 1. igaz állításokat! 1:56 Könnyű F sak a sárga golyó fejt ki erőhatást a fehérre. Mechanikai kölcsönhatás jön létre a golyók között. Mindkét golyó mozgásállapota változik.
Nézd meg a képet és jelöld az 1. igaz állításokat! 1:56 Könnyű F sak a sárga golyó fejt ki erőhatást a fehérre. Mechanikai kölcsönhatás jön létre a golyók között. Mindkét golyó mozgásállapota változik.
TestLine - Fizika 7. osztály Hőtan Témazáró Minta feladatsor
 gázok hőtágulása függ: 1. 1:55 Normál de független az anyagi minőségtől. Függ az anyagi minőségtől. a kezdeti térfogattól, a hőmérséklet-változástól, Mlyik állítás az igaz? 2. 2:31 Normál Hőáramláskor
gázok hőtágulása függ: 1. 1:55 Normál de független az anyagi minőségtől. Függ az anyagi minőségtől. a kezdeti térfogattól, a hőmérséklet-változástól, Mlyik állítás az igaz? 2. 2:31 Normál Hőáramláskor
A LÉGKÖRBEN HATÓ ERŐK, EGYENSÚLYI MOZGÁSOK A LÉGKÖRBEN
 A LÉGKÖRBEN HATÓ ERŐK, EGYENSÚLYI MOZGÁSOK A LÉGKÖRBEN Egy testre ható erő, a más testekkel való kölcsönhatás mértékére jellemző fizikai mennyiség. A légkörben ható erők Külső erők: A Föld tömegéből következő
A LÉGKÖRBEN HATÓ ERŐK, EGYENSÚLYI MOZGÁSOK A LÉGKÖRBEN Egy testre ható erő, a más testekkel való kölcsönhatás mértékére jellemző fizikai mennyiség. A légkörben ható erők Külső erők: A Föld tömegéből következő
Folyadékok és gázok mechanikája
 Folyadékok és gázok mechanikája A folyadékok nyomása A folyadék súlyából származó nyomást hidrosztatikai nyomásnak nevezzük. Függ: egyenesen arányos a folyadék sűrűségével (ρ) egyenesen arányos a folyadékoszlop
Folyadékok és gázok mechanikája A folyadékok nyomása A folyadék súlyából származó nyomást hidrosztatikai nyomásnak nevezzük. Függ: egyenesen arányos a folyadék sűrűségével (ρ) egyenesen arányos a folyadékoszlop
TestLine - Fizika 7. osztály Hőtan Témazáró Minta feladatsor
 1. 2:29 Normál párolgás olyan halmazállapot-változás, amelynek során a folyadék légneművé válik. párolgás a folyadék felszínén megy végbe. forrás olyan halmazállapot-változás, amelynek során nemcsak a
1. 2:29 Normál párolgás olyan halmazállapot-változás, amelynek során a folyadék légneművé válik. párolgás a folyadék felszínén megy végbe. forrás olyan halmazállapot-változás, amelynek során nemcsak a
Modern Fizika Labor. 2. Elemi töltés meghatározása
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Készült az FVM Vidékfejlesztési, Képzési és Szaktanácsadási Intézet megbízásából
 Készült az FVM Vidékfejlesztési, Kézési és Szaktanácsadási Intézet mebízásából Kélettár Készült az Élelmiszer-iari mőeletek és folyamatok tankönyöz Összeállította: Pa ászló ektorálta: Koács Gáborné Budaest,
Készült az FVM Vidékfejlesztési, Kézési és Szaktanácsadási Intézet mebízásából Kélettár Készült az Élelmiszer-iari mőeletek és folyamatok tankönyöz Összeállította: Pa ászló ektorálta: Koács Gáborné Budaest,
N I. 02 B. Mágneses anyagvizsgálat G ép. 118 2011.11.30. A mérés dátuma: A mérés eszközei: A mérés menetének leírása:
 N I. 02 B A mérés eszközei: Számítógép Gerjesztésszabályzó toroid transzformátor Minták Mágneses anyagvizsgálat G ép. 118 A mérés menetének leírása: Beindítottuk a számtógépet, Behelyeztük a mintát a ferrotestbe.
N I. 02 B A mérés eszközei: Számítógép Gerjesztésszabályzó toroid transzformátor Minták Mágneses anyagvizsgálat G ép. 118 A mérés menetének leírása: Beindítottuk a számtógépet, Behelyeztük a mintát a ferrotestbe.
Az atmoszférikus légnyomás változásainak hatása egy borpince légterében
 Az atmoszférikus légnyomás áltozásainak hatása egy borpince légterében léő 222 Rn-aktiitáskoncentrációra Győrfi Tamás* 1, Csige Istán 2 1 Eötös József Főiskola, 65 Baja, Szegedi út 2. 2 MTA Atommagkutató
Az atmoszférikus légnyomás áltozásainak hatása egy borpince légterében léő 222 Rn-aktiitáskoncentrációra Győrfi Tamás* 1, Csige Istán 2 1 Eötös József Főiskola, 65 Baja, Szegedi út 2. 2 MTA Atommagkutató
PhD DISSZERTÁCIÓ TÉZISEI
 Budapesti Muszaki és Gazdaságtudományi Egyetem Fizikai Kémia Tanszék MTA-BME Lágy Anyagok Laboratóriuma PhD DISSZERTÁCIÓ TÉZISEI Mágneses tér hatása kompozit gélek és elasztomerek rugalmasságára Készítette:
Budapesti Muszaki és Gazdaságtudományi Egyetem Fizikai Kémia Tanszék MTA-BME Lágy Anyagok Laboratóriuma PhD DISSZERTÁCIÓ TÉZISEI Mágneses tér hatása kompozit gélek és elasztomerek rugalmasságára Készítette:
EGYSZERŰ, SZÉP ÉS IGAZ
 EGYSZERŰ, SZÉP ÉS IGAZ AVAGY EGY FIZIKUS (FIZIKATANÁR?) VILÁGKÉPE Trócsányi Zoltán Eötvös Loránd Tudományegyetem és MTA-DE Részecskefizikai Kutatócsoport 62. Országos Fizikatanári Ankét és Eszközbemutató,
EGYSZERŰ, SZÉP ÉS IGAZ AVAGY EGY FIZIKUS (FIZIKATANÁR?) VILÁGKÉPE Trócsányi Zoltán Eötvös Loránd Tudományegyetem és MTA-DE Részecskefizikai Kutatócsoport 62. Országos Fizikatanári Ankét és Eszközbemutató,
A nyomás. IV. fejezet Összefoglalás
 A nyomás IV. fejezet Összefoglalás Mit nevezünk nyomott felületnek? Amikor a testek egymásra erőhatást gyakorolnak, felületeik egy része egymáshoz nyomódik. Az egymásra erőhatást kifejtő testek érintkező
A nyomás IV. fejezet Összefoglalás Mit nevezünk nyomott felületnek? Amikor a testek egymásra erőhatást gyakorolnak, felületeik egy része egymáshoz nyomódik. Az egymásra erőhatást kifejtő testek érintkező
Transzformátor rezgés mérés. A BME Villamos Energetika Tanszéken
 Transzformátor rezgés mérés A BME Villamos Energetika Tanszéken A valóság egyszerűsítése, modellezés. A mérés tervszerűen végrehajtott tevékenység, ezért a bonyolult valóságos rendszert először egyszerűsítik.
Transzformátor rezgés mérés A BME Villamos Energetika Tanszéken A valóság egyszerűsítése, modellezés. A mérés tervszerűen végrehajtott tevékenység, ezért a bonyolult valóságos rendszert először egyszerűsítik.
2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv. Zsigmond Anna Fizika Bsc II. Mérés dátuma: Leadás dátuma:
 2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 24. Leadás dátuma: 2008. 10. 01. 1 1. Mérések ismertetése Az 1. ábrán látható összeállításban
2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 24. Leadás dátuma: 2008. 10. 01. 1 1. Mérések ismertetése Az 1. ábrán látható összeállításban
TestLine - Fizika 7. osztály Hőtan Témazáró Minta feladatsor
 1. 2:24 Normál Magasabb hőmérsékleten a részecskék nagyobb tágassággal rezegnek, s így távolabb kerülnek egymástól. Magasabb hőmérsékleten a részecskék kisebb tágassággal rezegnek, s így távolabb kerülnek
1. 2:24 Normál Magasabb hőmérsékleten a részecskék nagyobb tágassággal rezegnek, s így távolabb kerülnek egymástól. Magasabb hőmérsékleten a részecskék kisebb tágassággal rezegnek, s így távolabb kerülnek
A hosszúhullámú sugárzás stratocumulus felhőben történő terjedésének numerikus modellezése
 A hosszúhullámú sugárzás stratocumulus felhőben történő terjedésének numerikus modellezése Lábó Eszter 1, Geresdi István 2 1 Országos Meteorológiai Szolgálat, 2 Pécsi Tudományegyetem, Természettudományi
A hosszúhullámú sugárzás stratocumulus felhőben történő terjedésének numerikus modellezése Lábó Eszter 1, Geresdi István 2 1 Országos Meteorológiai Szolgálat, 2 Pécsi Tudományegyetem, Természettudományi
Mikroszkóp vizsgálata Lencse görbületi sugarának mérése Folyadék törésmutatójának mérése
 Mikroszkóp vizsgálata Lencse görbületi sugarának mérése Folyadék törésmutatójának mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. március 19. (hétfő délelőtti csoport) 1. Mikroszkóp vizsgálata 1.1. A mérés
Mikroszkóp vizsgálata Lencse görbületi sugarának mérése Folyadék törésmutatójának mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. március 19. (hétfő délelőtti csoport) 1. Mikroszkóp vizsgálata 1.1. A mérés
Hőtágulás - szilárd és folyékony anyagoknál
 Hőtágulás - szilárd és folyékony anyagoknál Celsius hőmérsékleti skála: 0 ºC pontja a víz fagyáspontja 100 ºC pontja a víz forráspontja Kelvin hőmérsékleti skála: A beosztása 273-al van elcsúsztatva a
Hőtágulás - szilárd és folyékony anyagoknál Celsius hőmérsékleti skála: 0 ºC pontja a víz fagyáspontja 100 ºC pontja a víz forráspontja Kelvin hőmérsékleti skála: A beosztása 273-al van elcsúsztatva a
Kvantumszimulátorok. Szirmai Gergely MTA SZFKI. Graphics: Harald Ritsch / Rainer Blatt, IQOQI
 Kvantumszimulátorok Szirmai Gergely MTA SZFKI Graphics: Harald Ritsch / Rainer Blatt, IQOQI A kvantummechanika körülvesz tranzisztor számítógép, mobiltelefon A kvantummechanika körülvesz tranzisztor számítógép,
Kvantumszimulátorok Szirmai Gergely MTA SZFKI Graphics: Harald Ritsch / Rainer Blatt, IQOQI A kvantummechanika körülvesz tranzisztor számítógép, mobiltelefon A kvantummechanika körülvesz tranzisztor számítógép,
Technikai áttekintés SimDay 2013. H. Tóth Zsolt FEA üzletág igazgató
 Technikai áttekintés SimDay 2013 H. Tóth Zsolt FEA üzletág igazgató Next Limit Technologies Alapítva 1998, Madrid Számítógépes grafika Tudományos- és mérnöki szimulációk Mottó: Innováció 2 Kihívás Technikai
Technikai áttekintés SimDay 2013 H. Tóth Zsolt FEA üzletág igazgató Next Limit Technologies Alapítva 1998, Madrid Számítógépes grafika Tudományos- és mérnöki szimulációk Mottó: Innováció 2 Kihívás Technikai
A Fermi gammaműhold mozgásának vizsgálata
 A Fermi gammaműhold mozgásának vizsgálata különös tekintettel a gamma-kitörésekre rárakódó háttér értékének alakulására Szécsi Dorottya ELTE fizikus MSc, I. évfolyam XXX. Jubileumi OTDK 211. április 27-29.
A Fermi gammaműhold mozgásának vizsgálata különös tekintettel a gamma-kitörésekre rárakódó háttér értékének alakulására Szécsi Dorottya ELTE fizikus MSc, I. évfolyam XXX. Jubileumi OTDK 211. április 27-29.
VI. A tömeg növekedése.
 VI A tömeg nöekedése Egyszerű tárgyalás A tehetetlenség a test egy tlajdonsága, egy adata A tömeg az adott test tehetetlenségének kantitatí mértéke A tömeg meghatározásának módszere: meg kell izsgálni,
VI A tömeg nöekedése Egyszerű tárgyalás A tehetetlenség a test egy tlajdonsága, egy adata A tömeg az adott test tehetetlenségének kantitatí mértéke A tömeg meghatározásának módszere: meg kell izsgálni,
Belső energia, hőmennyiség, munka Hőtan főtételei
 Belső energia, hőmennyiség, munka Hőtan főtételei Ideális gázok részecske-modellje (kinetikus gázmodell) Az ideális gáz apró pontszerű részecskékből áll, amelyek állandó, rendezetlen mozgásban vannak.
Belső energia, hőmennyiség, munka Hőtan főtételei Ideális gázok részecske-modellje (kinetikus gázmodell) Az ideális gáz apró pontszerű részecskékből áll, amelyek állandó, rendezetlen mozgásban vannak.
A Fermi gammaműhold mozgásának vizsgálata
 A Fermi gammaműhold mozgásának vizsgálata különös tekintettel a gamma-kitörésekre rárakódó háttér értékének alakulására Szécsi Dorottya fizikus MSc, I. évfolyam ELTE TTK Csillagász TDK 2010. december 2.
A Fermi gammaműhold mozgásának vizsgálata különös tekintettel a gamma-kitörésekre rárakódó háttér értékének alakulására Szécsi Dorottya fizikus MSc, I. évfolyam ELTE TTK Csillagász TDK 2010. december 2.
ESR-spektrumok különbözı kísérleti körülmények között A számítógépes értékelés alapjai anizotróp kölcsönhatási tenzorok esetén
 ESR-spektrumok különbözı kísérleti körülmények között A számítógépes értékelés alapjai anizotróp kölcsönhatási tenzorok esetén A paraméterek anizotrópiája egykristályok rögzített tengely körüli forgatásakor
ESR-spektrumok különbözı kísérleti körülmények között A számítógépes értékelés alapjai anizotróp kölcsönhatási tenzorok esetén A paraméterek anizotrópiája egykristályok rögzített tengely körüli forgatásakor
A 35 éves Voyager őrszondák a napszél és a csillagközi szél határán
 A 35 éves Voyager őrszondák a napszél és a csillagközi szél határán Király Péter MTA Wigner Fizikai Kutatóközpont RMKI KFFO İsrégi kérdés: meddig terjedhet Napisten birodalma? Napunk felszíne, koronája,
A 35 éves Voyager őrszondák a napszél és a csillagközi szél határán Király Péter MTA Wigner Fizikai Kutatóközpont RMKI KFFO İsrégi kérdés: meddig terjedhet Napisten birodalma? Napunk felszíne, koronája,
A LÉGKÖRBEN HATÓ ERŐK, EGYENSÚLYI MOZGÁSOK A LÉGKÖRBEN
 A LÉGKÖRBEN HATÓ ERŐK, EGYENSÚLYI MOZGÁSOK A LÉGKÖRBEN Egy testre ható erő, a más testekkel való kölcsönhatás mértékére jellemző fizikai mennyiség. A légkörben ható erők Külső erők: A Föld tömegéből következő
A LÉGKÖRBEN HATÓ ERŐK, EGYENSÚLYI MOZGÁSOK A LÉGKÖRBEN Egy testre ható erő, a más testekkel való kölcsönhatás mértékére jellemző fizikai mennyiség. A légkörben ható erők Külső erők: A Föld tömegéből következő
Optika és Relativitáselmélet
 Optika és Relativitáselmélet II. BsC fizikus hallgatóknak 9. Szivárvány, korona és a glória Cserti József, jegyzet, ELTE, 2007. Fı- és mellékszivárvány Fı- és mellékszivárvány Horváth Ákos felvételei Fı-
Optika és Relativitáselmélet II. BsC fizikus hallgatóknak 9. Szivárvány, korona és a glória Cserti József, jegyzet, ELTE, 2007. Fı- és mellékszivárvány Fı- és mellékszivárvány Horváth Ákos felvételei Fı-
Hangfrekvenciás mechanikai rezgések vizsgálata
 Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Önszervezően kritikus rendszerek: Bevezetés, alapfogalmak. Self-organized criticality. Homokdomb Biológiai evolúció. Példák és modellek
 : Példák és modellek Bevezetés Alapfogalmak ismétlése Mi a fázisátalakulás? Alapfogalmak ismétlése Mi a fázisátalakulás? A statisztikus fizikában (termodinamikában): Az anyag átalakulása két különböző
: Példák és modellek Bevezetés Alapfogalmak ismétlése Mi a fázisátalakulás? Alapfogalmak ismétlése Mi a fázisátalakulás? A statisztikus fizikában (termodinamikában): Az anyag átalakulása két különböző
Modern Fizika Labor Fizika BSC
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. április 20. A mérés száma és címe: 20. Folyadékáramlások 2D-ban Értékelés: A beadás dátuma: 2009. április 28. A mérést végezte: Márton Krisztina Zsigmond
Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. április 20. A mérés száma és címe: 20. Folyadékáramlások 2D-ban Értékelés: A beadás dátuma: 2009. április 28. A mérést végezte: Márton Krisztina Zsigmond
Dimenzióváltás becsapódásos fragmentációban
 Dimenzióváltás becsapódásos fragmentációban Pál Gergő Témavezető: Dr. Kun Ferenc Debreceni Egyetem Döffi 2013, Balatonfenyves Heterogén anyagok fragmentációja Próbatest töredezési folyamata - nagy mennyiségű
Dimenzióváltás becsapódásos fragmentációban Pál Gergő Témavezető: Dr. Kun Ferenc Debreceni Egyetem Döffi 2013, Balatonfenyves Heterogén anyagok fragmentációja Próbatest töredezési folyamata - nagy mennyiségű
Mágneses mező jellemzése
 pólusok dipólus mező mező jellemzése vonalak pólusok dipólus mező kölcsönhatás A mágnesek egymásra és a vastárgyakra erőhatást fejtenek ki. vonalak vonzó és taszító erő pólusok dipólus mező pólusok északi
pólusok dipólus mező mező jellemzése vonalak pólusok dipólus mező kölcsönhatás A mágnesek egymásra és a vastárgyakra erőhatást fejtenek ki. vonalak vonzó és taszító erő pólusok dipólus mező pólusok északi
Modern Fizika Labor. 2. Az elemi töltés meghatározása. Fizika BSc. A mérés dátuma: nov. 29. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. nov. 29. A mérés száma és címe: 2. Az elemi töltés meghatározása Értékelés: A beadás dátuma: 2011. dec. 11. A mérést végezte: Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. nov. 29. A mérés száma és címe: 2. Az elemi töltés meghatározása Értékelés: A beadás dátuma: 2011. dec. 11. A mérést végezte: Szőke Kálmán Benjamin
Szabadentalpia nyomásfüggése
 Égéselmélet Szabadentalpia nyomásfüggése G( p, T ) G( p Θ, T ) = p p Θ Vdp = p p Θ nrt p dp = nrt ln p p Θ Mi az a tűzoltó autó? A tűz helye a világban Égés, tűz Égés: kémiai jelenség a levegő oxigénjével
Égéselmélet Szabadentalpia nyomásfüggése G( p, T ) G( p Θ, T ) = p p Θ Vdp = p p Θ nrt p dp = nrt ln p p Θ Mi az a tűzoltó autó? A tűz helye a világban Égés, tűz Égés: kémiai jelenség a levegő oxigénjével
Az úszás biomechanikája
 Az úszás biomechanikája Alapvető összetevők Izomerő Kondíció állóképesség Mozgáskoordináció kivitelezés + Nem levegő, mint közeg + Izmok nem gravitációval szembeni mozgása + Levegővétel Az úszóra ható
Az úszás biomechanikája Alapvető összetevők Izomerő Kondíció állóképesség Mozgáskoordináció kivitelezés + Nem levegő, mint közeg + Izmok nem gravitációval szembeni mozgása + Levegővétel Az úszóra ható
FERROMÁGNESES ANYAGOK RONCSOLÁSMENTES VIZSGÁLATA MÁGNESESHISZTERÉZIS-ALHURKOK MÉRÉSE ALAPJÁN. Mágneses adaptív teszt (MAT) Vértesy Gábor
 FERROMÁGNESES ANYAGOK RONCSOLÁSMENTES VIZSGÁLATA MÁGNESESHISZTERÉZIS-ALHURKOK Vértesy Gábor MÉRÉSE ALAPJÁN MTA TTK Műszaki Fizikai és Anyagtudományi Intézet Olyan új, gyorsan elvégezhetô, megbízható és
FERROMÁGNESES ANYAGOK RONCSOLÁSMENTES VIZSGÁLATA MÁGNESESHISZTERÉZIS-ALHURKOK Vértesy Gábor MÉRÉSE ALAPJÁN MTA TTK Műszaki Fizikai és Anyagtudományi Intézet Olyan új, gyorsan elvégezhetô, megbízható és
A NEM MÁGNESES BOLYGÓK MAGNETOSZFÉRÁJA
 A NEM MÁGNESES BOLYGÓK MAGNETOSZFÉRÁJA A NAPSZÉL ÉS AZ AKADÁLY SEMATIKUS KÖLCSONHATÁSA A BOLYGÓK MAGNETOSZFÉRÁJA AZ ÉGITESTEK AKADÁLYT JELENTENEK A SZUPERSZÓNIKUSAN ÁRAMLÓ NAPSZÉLBEN. A KÖLCSÖNHATÁS JELLEGE
A NEM MÁGNESES BOLYGÓK MAGNETOSZFÉRÁJA A NAPSZÉL ÉS AZ AKADÁLY SEMATIKUS KÖLCSONHATÁSA A BOLYGÓK MAGNETOSZFÉRÁJA AZ ÉGITESTEK AKADÁLYT JELENTENEK A SZUPERSZÓNIKUSAN ÁRAMLÓ NAPSZÉLBEN. A KÖLCSÖNHATÁS JELLEGE
Periodikus struktúrák előállítása nanolitográfiával és vizsgálatuk három dimenzióban
 Periodikus struktúrák előállítása nanolitográfiával és vizsgálatuk három dimenzióban Zolnai Zsolt MTA Műszaki Fizikai és Anyagtudományi Kutatóintézet, H-1525 Budapest, P.O.B. 49, Hungary Tartalom: Kolloid
Periodikus struktúrák előállítása nanolitográfiával és vizsgálatuk három dimenzióban Zolnai Zsolt MTA Műszaki Fizikai és Anyagtudományi Kutatóintézet, H-1525 Budapest, P.O.B. 49, Hungary Tartalom: Kolloid
Egzakt hidrodinamikai megoldások alkalmazása a nehézionfizikai fenomenológiában néhány új eredmény
 Egzakt hidrodinamikai megoldások alkalmazása a nehézionfizikai fenomenológiában néhány új eredmény Csanád Máté, Nagy Márton, Lőkös Sándor ELTE Atomfizikai Tanszék Magfizikus Találkozó Jávorkút 2012. szeptember
Egzakt hidrodinamikai megoldások alkalmazása a nehézionfizikai fenomenológiában néhány új eredmény Csanád Máté, Nagy Márton, Lőkös Sándor ELTE Atomfizikai Tanszék Magfizikus Találkozó Jávorkút 2012. szeptember
Gnädig Péter: Golyók, labdák, korongok és pörgettyűk csalafinta mozgása április 16. Pörgettyűk különböző méretekben az atomoktól a csillagokig
 Gnädig Péter: Golyók, labdák, korongok és pörgettyűk csalafinta mozgása 2015. április 16. Pörgettyűk különböző méretekben az atomoktól a csillagokig Egyetlen tömegpont: 3 adat (3 szabadsági fok ) Példa:
Gnädig Péter: Golyók, labdák, korongok és pörgettyűk csalafinta mozgása 2015. április 16. Pörgettyűk különböző méretekben az atomoktól a csillagokig Egyetlen tömegpont: 3 adat (3 szabadsági fok ) Példa:
TERMIKUS KÖLCSÖNHATÁSOK
 ERMIKUS KÖLCSÖNHAÁSOK ÁLLAPOJELZŐK, ERMODINAMIKAI EGYENSÚLY A mindennai élet legkülönbözőbb területein találkozunk a hőmérséklet fogalmáal, méréséel, a rendszerek hőtani jellemzőiel (térfogat, nyomás,
ERMIKUS KÖLCSÖNHAÁSOK ÁLLAPOJELZŐK, ERMODINAMIKAI EGYENSÚLY A mindennai élet legkülönbözőbb területein találkozunk a hőmérséklet fogalmáal, méréséel, a rendszerek hőtani jellemzőiel (térfogat, nyomás,
Rugalmas állandók mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék)
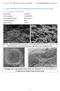 7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék) 7.1.1. SPS: 1150 C; 5 (1312 K1) Mért sűrűség: 3,795 g/cm 3 3,62 0,14 GPa Három pontos törés teszt: 105 4,2 GPa Súrlódási együttható:
7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék) 7.1.1. SPS: 1150 C; 5 (1312 K1) Mért sűrűség: 3,795 g/cm 3 3,62 0,14 GPa Három pontos törés teszt: 105 4,2 GPa Súrlódási együttható:
FOK Fogorvosi anyagtan fizikai alapjai tárgy kolokviumi kérdései 2017/18-es tanév
 FOK Fogorvosi anyagtan fizikai alapjai tárgy kolokviumi kérdései 2017/18-es tanév A kollokviumon egy-egy tételt kell húzni az 1-10. és a 11-20. kérdések közül, valamint egy számolási feladatot az év közben
FOK Fogorvosi anyagtan fizikai alapjai tárgy kolokviumi kérdései 2017/18-es tanév A kollokviumon egy-egy tételt kell húzni az 1-10. és a 11-20. kérdések közül, valamint egy számolási feladatot az év közben
Mit nevezünk nehézségi erőnek?
 Mit nevezünk nehézségi erőnek? Azt az erőt, amelynek hatására a szabadon eső testek g (gravitációs) gyorsulással esnek a vonzó test centruma felé, nevezzük nehézségi erőnek. F neh = m g Mi a súly? Azt
Mit nevezünk nehézségi erőnek? Azt az erőt, amelynek hatására a szabadon eső testek g (gravitációs) gyorsulással esnek a vonzó test centruma felé, nevezzük nehézségi erőnek. F neh = m g Mi a súly? Azt
Állandó térfogatáram-szabályozó
 Állandó térfogatáram-szabályozó DAU Méretek B Ød l Leírás Állandó térfogatáram szabályozó egy térfogatáram érték kézi beállításáal DAU egy állandó térfogatáram szabályozó, ami megkönnyíti a légcsatorna
Állandó térfogatáram-szabályozó DAU Méretek B Ød l Leírás Állandó térfogatáram szabályozó egy térfogatáram érték kézi beállításáal DAU egy állandó térfogatáram szabályozó, ami megkönnyíti a légcsatorna
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás
 3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ)
 Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ) KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba
Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ) KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba
1. feladat Alkalmazzuk a mólhő meghatározását egy gázra. Izoterm és adiabatikus átalakulásokra a következőt kapjuk:
 Válaszoljatok a következő kérdésekre: 1. feladat Alkalmazzuk a mólhő meghatározását egy gázra. Izoterm és adiabatikus átalakulásokra a következőt kapjuk: a) zéró izoterm átalakulásnál és végtelen az adiabatikusnál
Válaszoljatok a következő kérdésekre: 1. feladat Alkalmazzuk a mólhő meghatározását egy gázra. Izoterm és adiabatikus átalakulásokra a következőt kapjuk: a) zéró izoterm átalakulásnál és végtelen az adiabatikusnál
Nehézségi gyorsulás mérése megfordítható ingával
 Nehézségi gyorsulás mérése megfordítható ingával (Mérési jegyzőkönyv) Hagymási Imre 2007. április 21. (hétfő délelőtti csoport) 1. A mérés elmélete A nehézségi gyorsulás mérésének egy klasszikus módja
Nehézségi gyorsulás mérése megfordítható ingával (Mérési jegyzőkönyv) Hagymási Imre 2007. április 21. (hétfő délelőtti csoport) 1. A mérés elmélete A nehézségi gyorsulás mérésének egy klasszikus módja
Modern Fizika Labor Fizika BSC
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. február 23. A mérés száma és címe: 17. Folyadékkristályok Értékelés: A beadás dátuma: 2009. március 2. A mérést végezte: Zsigmond Anna Márton Krisztina
Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. február 23. A mérés száma és címe: 17. Folyadékkristályok Értékelés: A beadás dátuma: 2009. március 2. A mérést végezte: Zsigmond Anna Márton Krisztina
Folyadékok és gázok mechanikája
 Folyadékok és gázok mechanikája Hidrosztatikai nyomás A folyadékok és gázok közös tulajdonsága, hogy alakjukat szabadon változtatják. Hidrosztatika: nyugvó folyadékok mechanikája Nyomás: Egy pontban a
Folyadékok és gázok mechanikája Hidrosztatikai nyomás A folyadékok és gázok közös tulajdonsága, hogy alakjukat szabadon változtatják. Hidrosztatika: nyugvó folyadékok mechanikája Nyomás: Egy pontban a
Elektromágnesség tesztek
 Elektromágnesség tesztek 1. Melyik esetben nem tapasztalunk onzóerőt? a) A mágnesrúd északi pólusához asdarabot közelítünk. b) A mágnesrúd közepéhez asdarabot közelítünk. c) A mágnesrúd déli pólusához
Elektromágnesség tesztek 1. Melyik esetben nem tapasztalunk onzóerőt? a) A mágnesrúd északi pólusához asdarabot közelítünk. b) A mágnesrúd közepéhez asdarabot közelítünk. c) A mágnesrúd déli pólusához
Orvosi Biofizika I. 12. vizsgatétel. IsmétlésI. -Fény
 Orvosi iofizika I. Fénysugárzásanyaggalvalókölcsönhatásai. Fényszóródás, fényabszorpció. Az abszorpciós spektrometria alapelvei. (Segítséga 12. tételmegértéséhezésmegtanulásához, továbbá a Fényabszorpció
Orvosi iofizika I. Fénysugárzásanyaggalvalókölcsönhatásai. Fényszóródás, fényabszorpció. Az abszorpciós spektrometria alapelvei. (Segítséga 12. tételmegértéséhezésmegtanulásához, továbbá a Fényabszorpció
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI
 SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 7 KRISTÁLYTAN VII. A KRIsTÁLYOK szimmetriája 1. BEVEZETÉs Az elemi cella és ebből eredően a térrácsnak a szimmetriáját a kristályok esetében az atomok, ionok
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 7 KRISTÁLYTAN VII. A KRIsTÁLYOK szimmetriája 1. BEVEZETÉs Az elemi cella és ebből eredően a térrácsnak a szimmetriáját a kristályok esetében az atomok, ionok
Hidrosztatika, Hidrodinamika
 Hidrosztatika, Hidrodinamika Folyadékok alaptulajdonságai folyadék: anyag, amely folyni képes térfogat állandó, alakjuk változó, a tartóedénytől függ a térfogat-változtató erőkkel szemben ellenállást fejtenek
Hidrosztatika, Hidrodinamika Folyadékok alaptulajdonságai folyadék: anyag, amely folyni képes térfogat állandó, alakjuk változó, a tartóedénytől függ a térfogat-változtató erőkkel szemben ellenállást fejtenek
MATROSHKA kísérletek a Nemzetközi Űrállomáson. Kató Zoltán, Pálfalvi József
 MATROSHKA kísérletek a Nemzetközi Űrállomáson Kató Zoltán, Pálfalvi József Sugárvédelmi Továbbképző Tanfolyam Hajdúszoboszló 2010 A Matroshka kísérletek: Az Európai Űrügynökség (ESA) dozimetriai programjának
MATROSHKA kísérletek a Nemzetközi Űrállomáson Kató Zoltán, Pálfalvi József Sugárvédelmi Továbbképző Tanfolyam Hajdúszoboszló 2010 A Matroshka kísérletek: Az Európai Űrügynökség (ESA) dozimetriai programjának
2010. január 31-én zárult OTKA pályázat zárójelentése: K62441 Dr. Mihály György
 Hidrosztatikus nyomással kiváltott elektronszerkezeti változások szilárd testekben A kutatás célkitűzései: A szilárd testek elektromos és mágneses tulajdonságait az alkotó atomok elektronhullámfüggvényeinek
Hidrosztatikus nyomással kiváltott elektronszerkezeti változások szilárd testekben A kutatás célkitűzései: A szilárd testek elektromos és mágneses tulajdonságait az alkotó atomok elektronhullámfüggvényeinek
A FIZIKUS SZEREPE A DAGANATOS BETEGEK GYÓGYÍTÁSÁBAN
 A FIZIKUS SZEREPE A DAGANATOS BETEGEK GYÓGYÍTÁSÁBAN Balogh Éva Jósa András Megyei Kórház, Onkoradiológiai Osztály, Nyíregyháza Angeli István Debreceni Egyetem, Kísérleti Fizika Tanszék A civilizációs ártalmaknak,
A FIZIKUS SZEREPE A DAGANATOS BETEGEK GYÓGYÍTÁSÁBAN Balogh Éva Jósa András Megyei Kórház, Onkoradiológiai Osztály, Nyíregyháza Angeli István Debreceni Egyetem, Kísérleti Fizika Tanszék A civilizációs ártalmaknak,
HIDROSZTATIKA, HIDRODINAMIKA
 HIDROSZTATIKA, HIDRODINAMIKA Hidrosztatika a nyugvó folyadékok fizikájával foglalkozik. Hidrodinamika az áramló folyadékok fizikájával foglalkozik. Folyadékmodell Önálló alakkal nem rendelkeznek. Térfogatuk
HIDROSZTATIKA, HIDRODINAMIKA Hidrosztatika a nyugvó folyadékok fizikájával foglalkozik. Hidrodinamika az áramló folyadékok fizikájával foglalkozik. Folyadékmodell Önálló alakkal nem rendelkeznek. Térfogatuk
Gyakorlat 30B-14. a F L = e E + ( e)v B képlet, a gravitációs erőt a (2.1) G = m e g (2.2)
 2. Gyakorlat 30B-14 Az Egyenlítőnél, a földfelszín közelében a mágneses fluxussűrűség iránya északi, nagysága kb. 50µ T,az elektromos térerősség iránya lefelé mutat, nagysága; kb. 100 N/C. Számítsuk ki,
2. Gyakorlat 30B-14 Az Egyenlítőnél, a földfelszín közelében a mágneses fluxussűrűség iránya északi, nagysága kb. 50µ T,az elektromos térerősség iránya lefelé mutat, nagysága; kb. 100 N/C. Számítsuk ki,
Mérés: Millikan olajcsepp-kísérlete
 Mérés: Millikan olajcsepp-kísérlete Mérés célja: 1909-ben ezt a mérést Robert Millikan végezte el először. Mérése során meg tudta határozni az elemi részecskék töltését. Ezért a felfedezéséért Nobel-díjat
Mérés: Millikan olajcsepp-kísérlete Mérés célja: 1909-ben ezt a mérést Robert Millikan végezte el először. Mérése során meg tudta határozni az elemi részecskék töltését. Ezért a felfedezéséért Nobel-díjat
Aktuális CFD projektek a BME NTI-ben
 Aktuális CFD projektek a BME NTI-ben Dr. Aszódi Attila igazgató, egyetemi docens BME Nukleáris Technikai Intézet CFD Workshop, 2005. szeptember 27. CFD Workshop, 2005. szeptember 27. Dr. Aszódi Attila,
Aktuális CFD projektek a BME NTI-ben Dr. Aszódi Attila igazgató, egyetemi docens BME Nukleáris Technikai Intézet CFD Workshop, 2005. szeptember 27. CFD Workshop, 2005. szeptember 27. Dr. Aszódi Attila,
