Populáció-reguláció és niche
|
|
|
- Attila Pap
- 6 évvel ezelőtt
- Látták:
Átírás
1 Magyar Tudomány 2005/4 Populáció-reguláció és niche Meszéna Géza egyetemi docens, ELTE Biológiai Fizika Tanszék A niche (ökológiai fülke) az ökológia gyakran bizonytalan körvonalúnak és bizonytalan létjogosultságúnak érzett kulcsfogalma. Talán nem tévedünk nagyot, ha a következõ két homályos állításban foglaljuk össze azt a képet, amit a szó kezdettõl fogva megjeleníteni hivatott: A fajok felosztják egymás között az ökológiai szerepek, lehetõségek terét a niche teret, és elfoglalják a maguk fülkéjét, niche-ét. Talán épp azért élhetnek együtt békében, s nem darwini háborúban, mert felosztották maguk között ezt a teret. De ha elégedetlenek vagyunk az efféle képes beszéddel, akkor kérdeznünk kell. Mi is az pontosan, amit fel kell osztani? Mi a pontos kapcsolat a felosztás és az együttélés között? Az ökológiai fogalmak bizonytalansága szorosan összefügg a matematikai modellezés bizonytalan helyzetével az ökológiában. Kétféle ökológiai modellt szokás megkülönböztetni (Czárán, 1998, xii.). A taktikai modell egy konkrét ökológiai szituációt igyekszik minél pontosabban leírni. Ekkor értelemszerûen nem cél a konkrétumon túlmenõ általánosság. Ezzel szemben a stratégiai modell lényegkiemelésre hivatott. Erõsen egyszerûsítõ modellek ezek, nincsen bennük más, mint amit alkotójuk a jelenség lényegének gondol. De honnan tudhatnánk, hogy valóban ez a lényeg? Magából a lényegkifejezõ modellbõl biztosan nem. Így azután sem az egyik, sem a másik modellezési mód nem igazít el igazán bennünket abban, szabad-e remélnünk általános képek érvényességét az ökológiai valóság kavalkádjában. Ha például a niche fentebb homályosan megfogalmazott fogalma hozzákapcsolódik egy konkrét stratégiai modellhez (ez a jól ismert Lotka Volterra kompetíciós modell), akkor ezen igen egyszerû modell feltevéseivel kapcsolatos minden kétség megkérdõjelezi a fogalom és a hozzá kapcsolódó kép érvényességét is. Jelen szerzõ abban bízik, hogy az ökológiában is lehetõség van elegendõen általános matematikai elméletek megalkotására. Kollégáival együtt javaslatot tett a fajok együttélési feltételének ilyen igényû megfogalmazására (Gyllenberg Meszéna, 2004; további tanulmányok elbírálás alatt). A jelen írás arra vállalkozik, hogy szembenézzen azzal a kérdéssel, mit is jelent ez az elmélet a nichefogalom vonatkozásában. Malthus Darwin Gause Egy elegendõen robusztus elmélet érdekében elegendõen robusztus gondolatokból kell kiindulnunk. Indulunk tehát a kályhától, az élõlények szaporodóképességétõl. A szaporodóképesség közvetlen következménye az a Robert Malthustól származó felismerés (Malthus, 1798), miszerint egy populáció alapesetben exponenciálisan (régebbi szóhasználattal: mértani haladvány szerint) szaporodik. Ma már matematikailag is teljesen világosan látjuk, hogy az exponenciális növekedés tényén semmi más nem 410
2 Meszéna Géza Populáció-reguláció és niche változtathat, mint az, ha a növekedés korlátba ütközik, azaz ha maga a létszámnövekedés valamilyen úton-módon lelassítja, megállítja a növekedést. Nem számít, mennyire bonyolult, térben-idõben heterogén körülmények között nõ a populáció, e populáció-regulációnak nevezett visszacsatolás nélkül hosszabb távon exponenciálisan fog nõni vagy persze csökkenni. Természetesen nem sok exponenciálisan növekvõ populációt látunk magunk körül. Olyan ez, mint a tehetetlenségi mozgás a mechanikában: nem túl sok erõmentes tárgyat figyelhetünk meg magunk körül, amint éppen egyenes vonalú egyenletes mozgást végeznek. Mégis tudjuk, hogy az egyenes vonalú egyenletes mozgás a referenciaeset, s mindig azt kell kérdezni: mi az az erõ, ami a megfigyelt objektumot eltéríti ettõl a mozgástól? Az analóg ökológiai kérdés: mi az a reguláció, amely a populációt az exponenciális növekedéstõl eltéríti? (Idézet Charles Darwintól: Nézzünk meg egy növényt elterjedésének középsõ területén: vajon miért nincs belõle kétszer vagy négyszer annyi? [Darwin, 2001, 71.]) Az exponenciális növekedés mint nullhipotézis a növényökológus számára egyébként nehezebb absztrakció, mint az állatökológiában. A növények egyik legfontosabb növekedési korlátja a fizikai tér: adott területen csak adott számú növény fér el. Nem könnyû magunkat rávenni annak kijelentésére, hogy a növénypopulációnk exponenciálisan nõne, ha a térbeli korlát nem létezne. De azért nem rosszabb ez annál, mint amikor egy ugráló ember szívének tömegközéppontjáról azt gondoljuk, hogy tehetetlenségi mozgást végezne, ha nem lenne az ugráló ember mellkasába rögzítve. A természetes szelekció darwini elméletét az exponenciális növekedés malthusi képe sugalmazta (Darwin, i. m. 61.). Ha a populációk alapesetben exponenciálisan nõnek, akkor elkerülhetetlen, hogy elég hamar beleütközzenek szaporodásuk valamilyen korlátjába. Ha beleütköznek, akkor az élet többé nem habostorta, hanem kemény küzdelem a létért. S ebben a küzdelemben el is lehet bukni. Ahol a gyõztes jutalma a nulla növekedés, ott a vesztesé a negatív növekedés, vagyis az exponenciális kihalás. Darwin csírájában világosan értette azt is, amit ma a niche-folklór alapvetõ elemének tekintünk: hasonló fajok között erõsebb a verseny, hiszen õk ugyanabba a szaporodási korlátba ütköznek (Darwin, i. m. 70.). A 20. században már a kompetitív kizárás elvének vagy Gause-elvnek nevezik lényegében ugyanennek egy kicsit erõsebb megfogalmazását. (Georgij Francsevics Gause kísérleteivel érdemelte ki a névadó szerepét.) Az elv Garrett Hardin (1960) bevallottan pontatlan megfogalmazását idézve így szól: fajok együttélésének szükséges feltétele az ökológiai differenciálódás. Ez az az alapkép, amelyet pontosítanunk és formalizálnunk kell. Kompetíció, reguláció és niche-tér A kompetíció szónál meg kell állnunk egy pillanatra. A kifejezés Darwinnál még a versenyben lét általános fogalmát takarta, a létért való küzdelemmel egy sorban. A modern ökológiai irodalomban viszont általában az erõforrásért való versengés sokkal specifikusabb értelmében szerepel. A két jelentésárnyalat összemosódása vezet ahhoz a véleményhez (lásd például Begon et al., 1996, 265.), amely a kompetitív kizárás elvét az erõforrás-kompetíció specifikus ökológiai szituációjára korlátozza. Ez egy félrevezetõ gondolat. A dolgok logikája szerint a kompetitív kizárás szókapcsolatban a kompetíció a széles, darwini értelemben szerepel. Az erõforrások korlátozott volta kétségtelenül a legtöbbet emlegetett, és valószínûleg valóban legfontosabb szaporodási korlát. De sok minden más is korlátozhatja a növekedést. A második legfontosabb 411
3 Magyar Tudomány 2005/4 példa talán a predáció: a megnövekedett létszámú populáción elszaporodhatnak ragadozóik, megnövelve a populáció egy egyedére esõ predációs halálozási rátát. A két eset között nincs principális különbség: minden populáció beleütközik valamilyen szaporodási korlátba, s az együttéléshez különbözõ korlátokba kell ütközni, bármik legyenek is azok. Külön kell szólnunk azokról a fajokról, amelyek a környezet változékonyságának köszönhetik megélhetésüket. A ruderális növények bárhol, bármilyen szituációban elveszítik a versenyt a helyi kompetíciót jobban tûrõ versenytársaikkal szemben. Fennmaradásukat annak köszönhetik, hogy a környezetben hol itt, hol ott valamilyen lokális katasztrófa következtében megjelennek üres élõhelyek, amelyeket õk foglalnak el elõször hogy azután onnét ismét kiszoruljanak. A ruderális fajok növekedési korlátja tehát az üres élõhelyek korlátozott száma. S bár a ruderálisokat lokális viselkedésük alapján gyenge kompetítorokként tartja számon a szakma, a szó darwini értelmében vett kompetíciót mégiscsak meg kell nyerniük saját versenyszámukban persze, tehát más ruderálisokkal összevetve. A környezet nem-egyensúlyi mivolta tehát jócskán szaporíthatja a növekedési korlátokat, s így nagymértékben hozzájárulhat a biológiai diverzitáshoz. Nem ad azonban felmentést a kompetitív kizárás, a különbözõ korlátokba ütközés elve alól. Reguláló változónak (Krebs, 2001, 288.) fogjuk nevezni azokat a környezeti változókat, amelyeken keresztül a populáció-reguláció visszacsatolása mûködik: tápanyag-koncentrációk, predációs nyomások stb. Nem reguláló változó viszont az olyasfajta, a visszacsatoló hurokban benne nem lévõ, külsõ paraméter, mint a hõmérséklet. A hideg természetesen növelheti a halálozási rátát és csökkentheti a születésekét, ezzel tehát lassíthatja, vagy fogyásba fordíthatja a populáció növekedését. De a populáció növekedésétõl (általában) nem lesz hidegebb: ha a populáció egy adott hõmérsékleten nõ, akkor növekedési korlát hiányában ez így is marad. Az már más kérdés, hogy az alacsony hõmérséklet csökkentheti a populáció például tápanyaglimitáció miatt beálló egyensúlyi létszámát: hidegben több táplálékra van szükség a populáció szinten tartásához. Ezen a ponton meg tudjuk mondani, mit is kell felosztani. Ha az együttélés feltétele az, hogy a fajok különbözõ szaporodási korlátokba ütközzenek, akkor e korlátok, vagy ha úgy tetszik, a reguláló változók összessége, halmaza az, amit niche-térnek kell tekinteni. Általánosságban ezt a teret kell a fajoknak felosztaniuk. Lakcím és foglalkozás Nyilván két alapmódja van az ökológiai elkülönülésnek, a különbözõ növekedési korlátokba ütközésnek: Különbözõ helyen élõ populációk nyilván nem egymás rovására élnek. S akkor nem élnek egy helyen, ha különböznek környezeti igényeikben. De ütközhetnek különbözõ növekedési korlátokba, például lehetnek különbözõ erõforrások által reguláltak az azonos helyen élõ populációk is. Ennek megfelelõen tehát a faj elhelyezkedését az ökológiai térben lakcímével (address) és foglalkozásával (profession) együtt jellemezhetjük (Miller, 1967). A lakcímet ökológiailag releváns módon természetesen nem a földrajzi koordinátákkal, hanem a faj megélhetését lehetõvé tevõ környezeti paraméterek, kondíciók specifikálásával lehet megadni. Ha egy fafaj egy adott hõmérséklet-tartományban életképes, akkor ez megfelel a tengerszint feletti magasság egy a földrajzi szélességtõl is függõ tartományának. A lakcím-niche lényege tehát egy kapcsolat a környezeti kondíciók tere és a topológiai tér között. 412
4 Meszéna Géza Populáció-reguláció és niche Ha tehát a felosztásra váró niche-tér nem más, mint a növekedési korlátok azaz a reguláló tényezõk halmaza, akkor ezen tényezõket is lakcím és foglalkozás szerint kell számon tartani. Madarak táplálékául szolgáló magokat meg kell különböztetnünk mind méretük (foglalkozás), mind elõfordulásuk helye, ill. az annak megfelelõ környezeti kondíciók (lakcím) szerint. Egy adott hõmérsékleten életképes, adott méretû magokat fogyasztani képes madárpopulációt az adott hõmérséklet alatt elõforduló, adott méretû magok mennyisége regulálja. Ha egy másik madárfaj akár csõrméretében (amely megfelel a fogyasztott magok méretének), akár hõmérsékletigényében (amely meghatározza elterjedési területét) különbözik, akkor olyan magok fognak a rendelkezésére állni, amelyet az elsõ fajunk nem fogyaszt elkerülik tehát a versenyt, és együtt élhetnek. Talán semmi nem okozott annyi konfúziót a niche fogalmával kapcsolatban, mint a lakcím- és foglalkozás-niche közötti különbség. A fogalom bevezetõi közül Joseph Grinnel elsõsorban az elõbbi, míg Charles Elton (1927) elsõsorban az utóbbi jelentést hangsúlyozta. Richard S. Miller (1967) mondta ki világosan a különbséget, és vezette be a lakcím és foglalkozás terminológiát. George Evelyn Hutchinson a niche-tengelyek szintjén tette meg a megfelelõ megkülönböztetést lásd alább. Azóta viszont egyre nagyobb a zavar a szóhasználatban. A kettõ közül a lakcím-niche empirikusan egyszerûen vizsgálható: meg kell nézni, milyen körülmények között életképes a faj, s ehhez nem szükséges azzal foglalkoznunk, mi is regulálja a populációt. Modellezni viszont a foglalkozás-niche-t egyszerûbb, mert nem kell a topográfiai térben való kiterjedéssel bajlódni. (Léteznek azért modellek a lakcím szegregáció leírására is: Czárán, 1989; Mizera Meszéna, 2003) Így azután hol csak az egyik, hol csak a másik niche-fogalom fordul elõ ráadásul az egyik az elméletben, míg a másik az empíriában s majdnem mindig a niche fogalmaként. A lakcím-niche kontextusában szokás beszélni a fundamentális és a realizált niche megkülönböztetésérõl. Az elsõ a környezeti követelmények azon tartományát jelenti, ahol a faj életképes, míg a második azt a szûkebbet, ahonnan a kompetitorok nem szorítják ki. (E vonatkozásban az egyedek mozgékonyságáról, vagyis arról, hogy olyan területeken is jelen lehetnek, ahol nem tudják magukat újratermelni, általában eltekintenek.) Bizonyára nem lenne akadálya megfelelõ modellkontextusban feltenni az analóg kérdést a foglalkozás-niche vonatkozásában. A foglalkozás-niche elválaszthatatlan a kompetitív kizárási problematikától: mindig is az erõforrás-felosztás kontextusában szólnak errõl a fajta niche-fogalomról. Nem így a lakcím-niche; hogy egy faj milyen környezeti körülmények között él meg, a Gause-elvre való hivatkozás nélkül is elmondható. Kõszeghy Kolos (2004) vezeti be következetesen ezt a fajta niche-fogalmat. A tisztán a környezeti követelmények terében elhatárolt niche-nek az eredeti mindenkinek saját fülke képhez már nem lesz köze: természetesen egynél több faj is megélhet ugyanazon környezeti feltételek mellett. Michael Begon, John Harper és Colin Townstead (i. m. 87.) elõször tisztán a környezeti követelmények alapján vezetik be a niche fogalmát, majd egy másik fejezetben (130. oldal) úgy találják, hogy a fogalom az erõforrások kontextusában az igazán erõs. Itt tehát képzavarral állunk szemben. Így keletkezik a mítosz, hogy a niche érthetetlenül kusza fogalom. Pedig valaha ha intuitív kontextusban is értették. Diszkrét és folytonos niche-tér Az ökológiai szituációtól függõen a megkülönböztethetõ reguláló tényezõk száma lehet sok is, kevés is. Speciális esetekben 413
5 Magyar Tudomány 2005/4 a populációt egy-két-három különbözõ erõforrás regulálja például foszfát és nitrát egy tóban. Ekkor az együtt élõ fajok ezt az egy-két-három erõforrást oszthatják fel egymás között. Vagyis a felosztandó niche-tér nem más, mint az erõforrások egy-két-három elemû halmaza. Hasonlóképpen, ha néhány különbözõ élõhely alkotja az osztozkodás tárgyát, akkor ez a véges halmaz a niche-tér. A reguláló tényezõk azonban sokszor egy folytonos sokaságot alkotnak. Erõforrások esetén az alappélda a versengõ madárpopulációk által fogyasztott magok méretének folytonos skálája. Ezt a foglalkozás- (Hutchinson kifejezésével: bionomic) niche-tengelyt kell a madárfajoknak egymás között felosztaniuk. A lakcím- (scenopoetic) niche-tengely alapesete a környezeti gradiens mentén változó környezeti paraméter. A hegyen felfelé folyamatosan csökken a hõmérséklet, és ezt a hõmérsékletskálát osztják fel egymás között a különbözõ fafajok. A folytonos változók által kifeszített niche-tér hutchinsoni képe (1978) olyannyira mélyen beivódott az ökológiai kultúrába, hogy szinte abszurdnak hat egy néhány elemû halmazt niche-térnek nevezni. Mégiscsak ez a jó választás, ha a lényeget nézzük. Van alapvetõ biológiai különbség aközött, amikor néhány fajta magon kell osztozkodni, és aközött, amikor a magok egy kontinuumát kell felosztani? Nyilván nincs túl sok. A biológiailag értelmes fogalom rendkívül egyszerû és általános: a niche-tér az, amit fel kell osztani. Ez lehet diszkrét és lehet folytonos. S persze, az ilyen általános értelemben vett niche-tér lehet valami sokkal komplikáltabb is, mint néhány niche-tengely által meghatározott folytonos tér. Gondoljunk bele, milyen bonyolult felosztanivalót jelent egy térben-idõben heterogén világ. De ezt inkább hagyjuk is most Természetesen nem élhet több faj együtt, mint a niche-tér pontjainak száma azaz az erõforrások száma, ha erõforrás-kompetícióról beszélünk. Ha több élne, nem jutna mindegyiknek más növekedési korlát. Mivel a kompetitív kizárás jelenségének ez a legegyszerûbb esete (és az egyetlen esete, amelynek a matematikája régóta világos), sok helyen a kompetitív kizárás kimondottan ezt a korlátot jelenti. Az nyilván lehetséges, hogy kevesebb faj él együtt, mint a niche-tér pontjainak száma. Folytonos niche-tér esetén ez a szám egyébként is végtelen. Niche mint halmaz és mint erõforrás-hasznosítási függvény Eddig arról esett szó, hogy mi az a tér, amit a fajok felosztanak egymás között. De mit is jelent, hogy felosztják egymás között? Mivel egy fajhoz a niche-tér több pontja tartozhat, a faj niche-ének e pontok vagyis az õt reguláló tényezõk halmazát tekinthetjük. Minden alapvetõ ökológiakönyvben megtalálható az az ábra, amely a niche ezen halmaz interpretációját reprezentálja a hutchinsoni folytonos niche-tér kontextusában. A szokásos állítás az, hogy két együtt élõ faj niche-e nem eshet pontosan egybe. A halmaz-niche kép azonban pontosításra szorul. Valószínûtlen, hogy egyszerû választ lehetne adni arra, hogy egy adott erõforrás az adott fajt regulálja vagy sem, azaz hogy eleme-e a faj niche-ének. A nicheszegregáció szokásos Lotka Volterra-modelljében amely egy erõforrás-tulajdonság jellegû niche-tengely felosztásáról szól egy faj niche-e az erõforrás-hasznosítási függvényével adott. Ez a függvény specifikálja, milyen mértékben hasznosítja a faj a különbözõ erõforrásokat. Az így megadott niche határa nem olyan éles, mint a halmaz-niche esetén: a faj a számára egyre kevésbé alkalmas erõforrásokat egyre kevésbé hasznosítja, azok egyre kisebb mértékben részei a faj niche-ének. Azért persze a halmaz-niche és a függvény-niche közel azonos biológiai tartalmat fejez ki: a niche-tér felosztását. 414
6 Meszéna Géza Populáció-reguláció és niche Az erõforrás-hasznosítási függvénnyel egy baj van: fenomenologikusan bevezetett fogalom, nem tudható pontosan, mit jelent egy adott ökológiai szituációban. A Lotka Volterra-kompetíciós modellben feltételezzük, hogy két adott faj közötti kompetíció arányos a két erõforrás-hasznosítási függvény átfedési integráljával. Noha ez a matematikai feltevés egy józan biológiai intuíciót fejez ki, pontos érvényességét semmi sem garantálja. S mint stratégiai modell, nem is való arra, hogy a valósággal való kvantitatív egyezést várjunk tõle. Impakt és szenzitivitás A következõ két kérdés (v. ö. Chase Leibold, 2003) minden ökológiai szituációban felvethetõ: Mennyivel változik egy adott faj növekedési rátája, ha az egyik reguláló változó értékét kismértékben megváltoztatjuk? Nevezzük ezt a megváltozást az adott fajnak a szóban forgó reguláló tényezõre való érzékenységének, szenzitivitásának. Mennyivel változik a vizsgált reguláló változó értéke, ha egy adott faj létszámát kismértékben megváltoztatjuk? Nevezzük ezt a megváltozást az adott fajnak a vizsgált reguláló tényezõre vonatkozó impaktjának. Egy térben, idõben heterogén szituációban ennél kissé pontosabb elõírásra lenne szükség, de ezt itt nem részletezhetjük. A lényeg, hogy bármelyik faj szerepe jellemezhetõ azzal, ha megadjuk minden reguláló tényezõre vonatkozó impaktját és szenzitivitását. Az impakt és szenzitivitás fogalma az erõforrás-hasznosítási függvény általánosítása pontosítása. Természetesen egy faj nagyjából azokat az erõforrásokat terheli, és nagyjából azoktól függ, amelyeket fogyaszt, hasznosít. Annyi a különbség, hogy az impakt és a szenzitivitás pontosan és általánosan definiált fogalmak. Egy faj niche-ét pontosan azzal határolhatjuk körül, ha megadjuk a rá vonatkozó impakt- és szenzitivitás-függvényeket. Szabályozott együttélés Eddig arról beszéltünk, hogy mit is osztunk fel, és hogyan adjuk meg ezt a felosztást. De mire is jó mindez? Mi a pontos kapcsolat a niche-tér felosztása és az együttélés között? Másképpen fogalmazva: mekkora átfedés engedhetõ meg a niche-ek között? Korlátozott hasonlóság az elnevezése a kompetitív kizárási elv azon finomításának, amely szerint az együttélés megkíván egy meghatározott mértékû minimális különbséget a fajok között. Mi ez a minimális különbség? Nagyjából azt gondoljuk, hogy az erõforrás-hasznosítási függvény szélessége, azaz a niche-szélesség szabja meg ezt a minimális különbséget. A pontosítási-általánosítási kísérletek azonban eredménytelenül végzõdtek: minden modellben más minimum adódik (Abrams, 1983). Ez a kudarc is hozzájárult a kompetíciós elmélet háttérbe szorulásához (Rosenzweig, ). De ha jobban belegondolunk, akkor triviális, hogy nem létezhet a hasonlóságnak egy modellfüggetlen alsó korlátja. Eleve pontosítanunk kell már az eredeti állítást is, miszerint az ugyanazon növekedési korlátba ütközõ fajok nem élhetnek együtt. Bizony élhetnek együtt, ha éppen azonos mértékben sikeresek. Két faj relatív elõnye-hátránya függ a környezeti feltételektõl, tehát a környezeti paramétereknek lehet olyan kombinációja, amely mellett a két faj niche-szegregáció nélkül is élhet együtt. De ehhez valószínûtlen szerencséjüknek kellene lenniük, s a legkisebb környezeti változás lerombolná az együttélést. Nem az tehát a jó kérdés, mikor élhetnek együtt egy meghatározott csoport fajai, hanem az, hogy mikor élhetnek együtt valószínûtlen szerencse, a paraméterek finomhangolása nélkül. Akkor lehet robusztusan tehát a paraméterekre való túlzott érzékenység nélkül együtt élni, ha 415
7 Magyar Tudomány 2005/4 léteznek olyan visszacsatolások (regulációk), amelyek a fitnesskülönbségeket a paraméterek egy széles tartományában semlegesítik. Erõforrások felosztása esetén jól ismert, hogy az ilyen szabályozott együttélés feltétele, hogy a fajok közötti kompetíciónak kisebbnek kell lennie, mint a fajokon belülinek. Ily módon, ha egy faj valamilyen elõnyre tesz szert, és kezd másokat kiszorítani, akkor létszámának növekedése nagyobb hátrányt okoz saját magának, mint a társulás más tagjainak. Ezen a módon a létszámnövekedés egy visszacsatoló mechanizmus keretében kompenzálja az eredeti perturbáció hatását, s a társulás újra stabilizálódik kissé megváltozott létszámarányok mellett. Elmondható ugyanez általánosságban is, azaz az erõforrás-hasznosítási függvény fenomenologikus fogalma nélkül is. Ahhoz, hogy a megfelelõ szabályozómechanizmus mûködjön, arra van szükség, hogy a fajoknak különbözniük kell a reguláló tényezõkhöz való viszonyukban, azaz mind az impakt niche-ükben, mind a szenzitivitás niche-ükben. Ha nem különböznek, akkor a szabályozómechanizmus nem lesz képes specifikusan annak a fajnak a növekedését lassítani, amelyik elõnyre tett szert. S ha nem Irodalom Abrams, Peter A. (1983): The Theory of Limiting Similarity. Annual Review of Ecology and Systematics. 14, Begon, Michael E. Harper, L. John Townstead, Colin. R (1996): Ecology. Blackwell Science Publisher, London Chase, Jonathan M. Leibold, A. Mathew (2003): Ecological Niches: Linking Classical and Contemporary Approaches. The University of Chicago Press, Chicago Czárán Tamás (1989): Coexistence of Competing Populations Along an Environmental Gradient: A Simulation Study. Coenoses. 4, Czárán Tamás (1998): Spatiotemporal Models of Population and Community Dynamics. Population and Community Biology series. Chapman & Hall, London Darvin, Charles (2001): A fajok eredete. Typotex Elektronikus Kiadó Kft. képes, akkor a legkisebb elõny is kompetitív kizáráshoz vezet. Ha a különbség kicsi, akkor a szabályozás gyenge, azaz csak a paraméterek egy szûk tartományában képes a fitnesskülönbségeket kiegyenlíteni. Minél kisebb a niche-különbség, annál szûkebb az együttélést lehetõvé tevõ paraméter-tartomány. S ezek már teljesen általános és pontosan bizonyítható állítások. Nincs tehát a hasonlóságnak abszolút korlátja: hasonló fajok együttélése nem lehetetlen, csak valószínûtlen. Nyilván csak egy konkrét taktikai modell esetében számítható ki pontosan, hogy adott ökológiai különbség mennyire robusztus, mennyire valószínû együttélést tesz lehetõvé. De a kép általános és matematikailag pontosan alátámasztható: túlzottan hasonló fajok együttélése valószínûtlen. S hogy mi a túlzott hasonlóság, azt az impakt- és a szenzitivitás-függvények átfedése szabja meg. Azaz, ökölszabályként mégiscsak elmondhatjuk: nagyjából a niche-szélességek szabják meg az együttéléshez minimálisan szükséges különbségeket. Kulcsszavak: kompetíció, Gause-elv, populáció-reguláció, niche Elton, Charles (1927): Animal Ecology. Sidwick and Jackson, London Gyllenberg, Mats Meszéna Géza (2005): On the Impossibility of Coexistence of Infinitely Many Strategies. Journal of Mathematical Biology (megjelenés alatt) 50, Hardin, Garrett (1960): Competitive Exclusion. Science. 131, Huston, Michael A. (1979): A General Hypothesis of Species Diversity. American Naturalist 113, Hutchinson, George Evelyn (1978): An introduction to population ecology. Yale University Press, New Haven Kõszeghy Kolos (2004): Az ökológiai niche fogalmának egy operatív formalizálása: a niche egzisztencia-tartomány értelmezése. ELTE diplomamunka 416
8 Meszéna Géza Populáció-reguláció és niche Krebs, Charles J. (2001): Ecology. The Experimental Analysis of Distribution and Abundance. Benjamin Cummings, San Francisco, California Malthus, Thomas (1789): An Essay on the Principle of Population. London, printed for J. Johnson in St. Paul s church-yard. edu/~stephan/malthus/malthus.0.html Miller, Richard S. (1967) Pattern and Process in Competition. Advanced Ecological Research. 4, Mizera Ferenc Meszéna Géza (2003): Spatial Niche Packing, Character Displacement and Adaptive Speciation Along an Environmental Gradient. Evolutionary Ecology Research. 5, Rosenzweig, Michael R. (1995) Species Diversity in Space and Time. Cambridge University Press, Cambridge 417
Az ökológia alapjai NICHE
 Az ökológia alapjai NICHE Niche Meghatározás funkció ill. alkalmazkodás szerint a növény- és állatfajok élő és élettelen környezetükbe eltérő módon illeszkednek be ott a többi élőlénytől többé-kevésbé
Az ökológia alapjai NICHE Niche Meghatározás funkció ill. alkalmazkodás szerint a növény- és állatfajok élő és élettelen környezetükbe eltérő módon illeszkednek be ott a többi élőlénytől többé-kevésbé
Niche. Tárgya a fajok koegzisztenciájának problémája A fogalom fejlődése: Toleranciahatárok! A hutchinsoni niche fogalom definíciója:
 Niche Tárgya a fajok koegzisztenciájának problémája A fogalom fejlődése: Grinnell térbeli Elton funkcionális Hutchinson hipertérfogat modell Juhász-Nagy niche értelmezése A hutchinsoni niche fogalom definíciója:
Niche Tárgya a fajok koegzisztenciájának problémája A fogalom fejlődése: Grinnell térbeli Elton funkcionális Hutchinson hipertérfogat modell Juhász-Nagy niche értelmezése A hutchinsoni niche fogalom definíciója:
Fajok közötti kapcsolatok
 Egyedek közötti kölcsönkapcsolatok Környezete = a környék ható tényezôi Fajok közötti kapcsolatok Vadbiológia és ökológia h Az egymásra ható egyedek lehetnek g Fajtársak - interspecifikus kapcsolatok #
Egyedek közötti kölcsönkapcsolatok Környezete = a környék ható tényezôi Fajok közötti kapcsolatok Vadbiológia és ökológia h Az egymásra ható egyedek lehetnek g Fajtársak - interspecifikus kapcsolatok #
Bevezetés az ökológiába Szerkesztette: Vizkievicz András
 Vizsgakövetelmények Ismerje a(z élettelen és élő) környezet fogalmát. Elemezzen tűrőképességi görbéket: minimum, maximum, optimum, szűk és tág tűrés. Legyen képes esettanulmányok alapján a biológiai jelzések
Vizsgakövetelmények Ismerje a(z élettelen és élő) környezet fogalmát. Elemezzen tűrőképességi görbéket: minimum, maximum, optimum, szűk és tág tűrés. Legyen képes esettanulmányok alapján a biológiai jelzések
Populáció A populációk szerkezete
 Populáció A populációk szerkezete Az azonos fajhoz tartozó élőlények egyedei, amelyek adott helyen és időben együtt élnek és egymás között szaporodnak, a faj folytonosságát fenntartó szaporodásközösséget,
Populáció A populációk szerkezete Az azonos fajhoz tartozó élőlények egyedei, amelyek adott helyen és időben együtt élnek és egymás között szaporodnak, a faj folytonosságát fenntartó szaporodásközösséget,
Populációs kölcsönhatások. A populációs kölcsönhatások jelentik az egyedek biológiai környezetének élő (biotikus) tényezőit.
 Populációs kölcsönhatások A populációs kölcsönhatások jelentik az egyedek biológiai környezetének élő (biotikus) tényezőit. A populációk között kialakulhatnak közvetett vagy közvetlen kapcsolatok. Ezek
Populációs kölcsönhatások A populációs kölcsönhatások jelentik az egyedek biológiai környezetének élő (biotikus) tényezőit. A populációk között kialakulhatnak közvetett vagy közvetlen kapcsolatok. Ezek
2. Alapfeltevések és a logisztikus egyenlet
 Populáció dinamika Szőke Kálmán Benjamin - SZKRADT.ELTE 22. május 2.. Bevezetés A populációdinamika az élőlények egyedszámának és népességviszonyainak térbeli és időbeli változásának menetét adja meg.
Populáció dinamika Szőke Kálmán Benjamin - SZKRADT.ELTE 22. május 2.. Bevezetés A populációdinamika az élőlények egyedszámának és népességviszonyainak térbeli és időbeli változásának menetét adja meg.
Az ökológia alapjai. Diverzitás és stabilitás
 Az ökológia alapjai Diverzitás és stabilitás Diverzitás = sokféleség, változatosság a sokféleség kvantitatív megjelenítése biodiverzitás: a biológiai változatosság matematikai (kvantitatív) megjelenítése
Az ökológia alapjai Diverzitás és stabilitás Diverzitás = sokféleség, változatosság a sokféleség kvantitatív megjelenítése biodiverzitás: a biológiai változatosság matematikai (kvantitatív) megjelenítése
Szakmai önéletrajz Meszéna Géza
 Szakmai önéletrajz Meszéna Géza 1. Tanulmányok és tudományos fokozatok Érettségi: 1974, Berzsenyi Dániel Gimnázium, Budapest, matematika II. tagozat Nemzetközi Fizikai Diákolimpia: 1974, Varsó, I. díj
Szakmai önéletrajz Meszéna Géza 1. Tanulmányok és tudományos fokozatok Érettségi: 1974, Berzsenyi Dániel Gimnázium, Budapest, matematika II. tagozat Nemzetközi Fizikai Diákolimpia: 1974, Varsó, I. díj
Populációdinamika és modellezés. A populációk változása populációdinamika. A populáció meghatározása. Modellezés
 Populációdinamika és modellezés Vadbiológia és ökológia Prof. Dr. Csányi Sándor A populáció meghatározása g Ökológia: saz egyed feletti (szupraindividuális) szervezôdés strukturális és funkcionális jelenségeinek
Populációdinamika és modellezés Vadbiológia és ökológia Prof. Dr. Csányi Sándor A populáció meghatározása g Ökológia: saz egyed feletti (szupraindividuális) szervezôdés strukturális és funkcionális jelenségeinek
Dinamikai rendszerek, populációdinamika
 Dinamikai rendszerek, populációdinamika Számítógépes szimulációk 1n4i11/1 Csabai István ELTE Komplex Rendszerek Fizikája Tanszék 5.102 Email: csabaiθcomplex.elte.hu 2009 tavasz Dierenciálegyenletek a zikán
Dinamikai rendszerek, populációdinamika Számítógépes szimulációk 1n4i11/1 Csabai István ELTE Komplex Rendszerek Fizikája Tanszék 5.102 Email: csabaiθcomplex.elte.hu 2009 tavasz Dierenciálegyenletek a zikán
Populációdinamika. Számítógépes szimulációk szamszimf17la
 Populációdinamika Számítógépes szimulációk szamszimf17la Csabai István, Stéger József ELTE Komplex Rendszerek Fizikája Tanszék Email: csabai@complex.elte.hu, steger@complex.elte.hu Bevezetés Dierenciálegyenletek
Populációdinamika Számítógépes szimulációk szamszimf17la Csabai István, Stéger József ELTE Komplex Rendszerek Fizikája Tanszék Email: csabai@complex.elte.hu, steger@complex.elte.hu Bevezetés Dierenciálegyenletek
Területi statisztikai elemzések
 Területi statisztikai elemzések KOTOSZ Balázs, SZTE, kotosz@eco.u-szeged.hu Módszertani dilemmák a statisztikában 2016. november 18. Budapest Apropó Miért különleges a területi adatok elemzése? A számításokhoz
Területi statisztikai elemzések KOTOSZ Balázs, SZTE, kotosz@eco.u-szeged.hu Módszertani dilemmák a statisztikában 2016. november 18. Budapest Apropó Miért különleges a területi adatok elemzése? A számításokhoz
Példa a report dokumentumosztály használatára
 Példa a report dokumentumosztály használatára Szerző neve évszám Tartalomjegyzék 1. Valószínűségszámítás 5 1.1. Események matematikai modellezése.............. 5 1.2. A valószínűség matematikai modellezése............
Példa a report dokumentumosztály használatára Szerző neve évszám Tartalomjegyzék 1. Valószínűségszámítás 5 1.1. Események matematikai modellezése.............. 5 1.2. A valószínűség matematikai modellezése............
Együttélés és versengés: ökológia és evolúció
 . Együttélés és versengés: ökológia és evolúció Meszéna Géza MTA doktori értekezés Budapest, 2006 ii Tartalomjegyzék Előszó: Megy-e a képletek által az ökológia elébb? vii I. Biológiai rész 1 1. Bevezetés:
. Együttélés és versengés: ökológia és evolúció Meszéna Géza MTA doktori értekezés Budapest, 2006 ii Tartalomjegyzék Előszó: Megy-e a képletek által az ökológia elébb? vii I. Biológiai rész 1 1. Bevezetés:
Pedagógiai Kar Tantárgypedagógiai Tanszék. Ökológia. Összeállította: Dávid János. főiskolai docens
 Pedagógiai Kar Tantárgypedagógiai Tanszék Ökológia Összeállította: Dávid János főiskolai docens ÖKOLÓGIAI SZERVEZŐDÉSI SZINTEK biológiai rendszerek: az élő egyedek összessége és az élettelen környezet
Pedagógiai Kar Tantárgypedagógiai Tanszék Ökológia Összeállította: Dávid János főiskolai docens ÖKOLÓGIAI SZERVEZŐDÉSI SZINTEK biológiai rendszerek: az élő egyedek összessége és az élettelen környezet
A leíró statisztikák
 A leíró statisztikák A leíró statisztikák fogalma, haszna Gyakori igény az, hogy egy adathalmazt elemei egyenkénti felsorolása helyett néhány jellemző tulajdonságának megadásával jellemezzünk. Ezeket az
A leíró statisztikák A leíró statisztikák fogalma, haszna Gyakori igény az, hogy egy adathalmazt elemei egyenkénti felsorolása helyett néhány jellemző tulajdonságának megadásával jellemezzünk. Ezeket az
Általános ökológia előadás II. félév Szabó D. Zoltán
 Általános ökológia előadás II. félév Szabó D. Zoltán http://okologia.wordpress.com Felhasznált és javasolt irodalom: Begon, M., Harper, J.L., Townsend, C.R. 2006. Ecology Individuals, populations and communities.
Általános ökológia előadás II. félév Szabó D. Zoltán http://okologia.wordpress.com Felhasznált és javasolt irodalom: Begon, M., Harper, J.L., Townsend, C.R. 2006. Ecology Individuals, populations and communities.
Statisztika - bevezetés Méréselmélet PE MIK MI_BSc VI_BSc 1
 Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Az Állatökológia tárgya
 Információk Szentesi Árpád, egyetemi docens 1. Állatrendszertani és Ökológiai Tanszék 7.727. sz. szoba 8758. sz. tel. mellék e-mail: szentesi@elte.hu 2. MTA Növényvédelmi Kutatóintézete Állattani Osztály
Információk Szentesi Árpád, egyetemi docens 1. Állatrendszertani és Ökológiai Tanszék 7.727. sz. szoba 8758. sz. tel. mellék e-mail: szentesi@elte.hu 2. MTA Növényvédelmi Kutatóintézete Állattani Osztály
Sorozatok határértéke SOROZAT FOGALMA, MEGADÁSA, ÁBRÁZOLÁSA; KORLÁTOS ÉS MONOTON SOROZATOK
 Sorozatok határértéke SOROZAT FOGALMA, MEGADÁSA, ÁBRÁZOLÁSA; KORLÁTOS ÉS MONOTON SOROZATOK Sorozat fogalma Definíció: Számsorozaton olyan függvényt értünk, amelynek értelmezési tartománya a pozitív egész
Sorozatok határértéke SOROZAT FOGALMA, MEGADÁSA, ÁBRÁZOLÁSA; KORLÁTOS ÉS MONOTON SOROZATOK Sorozat fogalma Definíció: Számsorozaton olyan függvényt értünk, amelynek értelmezési tartománya a pozitív egész
biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás
 Kísérlettervezés - biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás A matematikai-statisztika feladata tapasztalati adatok feldolgozásával segítséget nyújtani
Kísérlettervezés - biometria II. foglalkozás előadó: Prof. Dr. Rajkó Róbert Matematikai-statisztikai adatfeldolgozás A matematikai-statisztika feladata tapasztalati adatok feldolgozásával segítséget nyújtani
A mechanika alapjai. A pontszerű testek dinamikája
 A mechanika alapjai A pontszerű testek dinamikája Horváth András SZE, Fizika Tsz. v 0.6 1 / 26 alapi Bevezetés Newton I. Newton II. Newton III. Newton IV. alapi 2 / 26 Bevezetés alapi Bevezetés Newton
A mechanika alapjai A pontszerű testek dinamikája Horváth András SZE, Fizika Tsz. v 0.6 1 / 26 alapi Bevezetés Newton I. Newton II. Newton III. Newton IV. alapi 2 / 26 Bevezetés alapi Bevezetés Newton
Matematikai modellezés
 Matematikai modellezés Bevezető A diasorozat a Döntési modellek című könyvhöz készült. Készítette: Dr. Ábrahám István Döntési folyamatok matematikai modellezése Az emberi tevékenységben meghatározó szerepe
Matematikai modellezés Bevezető A diasorozat a Döntési modellek című könyvhöz készült. Készítette: Dr. Ábrahám István Döntési folyamatok matematikai modellezése Az emberi tevékenységben meghatározó szerepe
I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI
 I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI 1 A digitális áramkörökre is érvényesek a villamosságtanból ismert Ohm törvény és a Kirchhoff törvények, de az elemzés és a tervezés rendszerint nem ezekre épül.
I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI 1 A digitális áramkörökre is érvényesek a villamosságtanból ismert Ohm törvény és a Kirchhoff törvények, de az elemzés és a tervezés rendszerint nem ezekre épül.
Good-Turing lefedés. Lang Zsolt
 Good-Turing lefedés Lang Zsolt 2017.03.24. Bevezetés Fajok közösségét vizsgáljuk. Sok faj van, az egyedek száma gyakorlatilag végtelen. Az egyedekből véletlen mintát veszünk. Kérdés, a mintában van-e,
Good-Turing lefedés Lang Zsolt 2017.03.24. Bevezetés Fajok közösségét vizsgáljuk. Sok faj van, az egyedek száma gyakorlatilag végtelen. Az egyedekből véletlen mintát veszünk. Kérdés, a mintában van-e,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
Adatok statisztikai értékelésének főbb lehetőségei
 Adatok statisztikai értékelésének főbb lehetőségei 1. a. Egy- vagy kétváltozós eset b. Többváltozós eset 2. a. Becslési problémák, hipotézis vizsgálat b. Mintázatelemzés 3. Szint: a. Egyedi b. Populáció
Adatok statisztikai értékelésének főbb lehetőségei 1. a. Egy- vagy kétváltozós eset b. Többváltozós eset 2. a. Becslési problémák, hipotézis vizsgálat b. Mintázatelemzés 3. Szint: a. Egyedi b. Populáció
Szöveg címe: Az ázsiai elefánt Forrás: és Kép forrása: szabadon használható fotók.
 Szöveg címe: Az ázsiai elefánt Forrás: http://hu.wikipedia.org/ és http://www.sulinet.hu/ Kép forrása: http://www.sxc.hu, szabadon használható fotók. Szövegtípus: magyarázó szöveg Szöveg olvashatósága:
Szöveg címe: Az ázsiai elefánt Forrás: http://hu.wikipedia.org/ és http://www.sulinet.hu/ Kép forrása: http://www.sxc.hu, szabadon használható fotók. Szövegtípus: magyarázó szöveg Szöveg olvashatósága:
Demográfia. Def.: A születés, mortalitás, ki- és bevándorlás kvantifikálása. N jelenleg. = N korábban. + Sz M + Be Ki. A szervezetek típusai: UNITER
 Demográfia Def.: A születés, mortalitás, ki- és bevándorlás kvantifikálása N jelenleg = N korábban + Sz M + Be Ki A szervezetek típusai: UNITER MODULÁRIS Ramet Genet 1 Élőlények egyedszámának meghatározása:
Demográfia Def.: A születés, mortalitás, ki- és bevándorlás kvantifikálása N jelenleg = N korábban + Sz M + Be Ki A szervezetek típusai: UNITER MODULÁRIS Ramet Genet 1 Élőlények egyedszámának meghatározása:
Sorozatok, sorok, függvények határértéke és folytonossága Leindler Schipp - Analízis I. könyve + jegyzetek, kidolgozások alapján
 Sorozatok, sorok, függvények határértéke és folytonossága Leindler Schipp - Analízis I. könyve + jegyzetek, kidolgozások alapján Számsorozatok, vektorsorozatok konvergenciája Def.: Számsorozatok értelmezése:
Sorozatok, sorok, függvények határértéke és folytonossága Leindler Schipp - Analízis I. könyve + jegyzetek, kidolgozások alapján Számsorozatok, vektorsorozatok konvergenciája Def.: Számsorozatok értelmezése:
Biomatematika 2 Orvosi biometria
 Biomatematika 2 Orvosi biometria 2017.02.13. Populáció és minta jellemző adatai Hibaszámítás Valószínűség 1 Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza)
Biomatematika 2 Orvosi biometria 2017.02.13. Populáció és minta jellemző adatai Hibaszámítás Valószínűség 1 Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza)
Bevezetés a biometriába Dr. Dinya Elek egyetemi tanár. PhD kurzus. KOKI,
 Bevezetés a biometriába Dr. Dinya Elek egyetemi tanár PhD kurzus. KOKI, 2015.09.17. Mi a statisztika? A sokaság (a sok valami) feletti áttekintés megszerzése, a sokaságról való információszerzés eszköze.
Bevezetés a biometriába Dr. Dinya Elek egyetemi tanár PhD kurzus. KOKI, 2015.09.17. Mi a statisztika? A sokaság (a sok valami) feletti áttekintés megszerzése, a sokaságról való információszerzés eszköze.
A MODELLALKOTÁS ELVEI ÉS MÓDSZEREI
 SZENT ISTVÁN EGYETEM GÖDÖLLŐ MECHANIKAI ÉS GÉPTANI INTÉZET A MODELLALKOTÁS ELVEI ÉS MÓDSZEREI Dr. M. Csizmadia Béla egyetemi tanár, az MMK Gépészeti Tagozatának elnöke Budapest 2013. október. 25. BPMK
SZENT ISTVÁN EGYETEM GÖDÖLLŐ MECHANIKAI ÉS GÉPTANI INTÉZET A MODELLALKOTÁS ELVEI ÉS MÓDSZEREI Dr. M. Csizmadia Béla egyetemi tanár, az MMK Gépészeti Tagozatának elnöke Budapest 2013. október. 25. BPMK
Azonos és egymással nem kölcsönható részecskékből álló kvantumos rendszer makrókanónikus sokaságban.
 Kvantum statisztika A kvantummechanika előadások során már megtanultuk, hogy az anyagot felépítő részecskék nemklasszikus, hullámtulajdonságokkal is rendelkeznek aminek következtében viselkedésük sok szempontból
Kvantum statisztika A kvantummechanika előadások során már megtanultuk, hogy az anyagot felépítő részecskék nemklasszikus, hullámtulajdonságokkal is rendelkeznek aminek következtében viselkedésük sok szempontból
9. Tétel Els - és másodfokú egyenl tlenségek. Pozitív számok nevezetes közepei, ezek felhasználása széls érték-feladatok megoldásában
 9. Tétel Els - és másodfokú egyenl tlenségek. Pozitív számok nevezetes közepei, ezek felhasználása széls érték-feladatok megoldásában Bevezet : A témakörben els - és másodfokú egyenl tlenségek megoldásának
9. Tétel Els - és másodfokú egyenl tlenségek. Pozitív számok nevezetes közepei, ezek felhasználása széls érték-feladatok megoldásában Bevezet : A témakörben els - és másodfokú egyenl tlenségek megoldásának
Evolúció. Dr. Szemethy László egyetemi docens Szent István Egyetem VadVilág Megőrzési Intézet
 Evolúció Dr. Szemethy László egyetemi docens Szent István Egyetem VadVilág Megőrzési Intézet Mi az evolúció? Egy folyamat: az élőlények tulajdonságainak változása a környezethez való alkalmazkodásra Egy
Evolúció Dr. Szemethy László egyetemi docens Szent István Egyetem VadVilág Megőrzési Intézet Mi az evolúció? Egy folyamat: az élőlények tulajdonságainak változása a környezethez való alkalmazkodásra Egy
A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a
 a Matematika mérnököknek I. című tárgyhoz Függvények. Függvények A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a szabadon eső test sebessége az idő függvénye. Konstans hőmérsékleten
a Matematika mérnököknek I. című tárgyhoz Függvények. Függvények A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a szabadon eső test sebessége az idő függvénye. Konstans hőmérsékleten
Tovább nem egyszerűsíthető rendszerek Részletek Az élet rejtélyének megfejtése c. cikkből.
 Tovább nem egyszerűsíthető rendszerek Részletek Az élet rejtélyének megfejtése c. cikkből. Az utóbbi években egyre erősödik egy alternatív tudományos szemléletmód: az intelligens tervezés elmélete. Az
Tovább nem egyszerűsíthető rendszerek Részletek Az élet rejtélyének megfejtése c. cikkből. Az utóbbi években egyre erősödik egy alternatív tudományos szemléletmód: az intelligens tervezés elmélete. Az
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/47/23623719.jpg) [Biomatematika 2] Orvosi biometria 2016.02.15. Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza) alkotja az eseményteret. Esemény: az eseménytér részhalmazai.
[Biomatematika 2] Orvosi biometria 2016.02.15. Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza) alkotja az eseményteret. Esemény: az eseménytér részhalmazai.
Számítógépes döntéstámogatás. Genetikus algoritmusok
 BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
Dobzhansky: In Biology nothing makes sense except in the light of Evolution.
 Dobzhansky: In Biology nothing makes sense except in the light of Evolution. Az Evolúcióbiológia Története Molnár István im54@invitel.hu Mai témák 1. Mi az evolúció? 2. Hogyan alakult ki a mai evolúciós
Dobzhansky: In Biology nothing makes sense except in the light of Evolution. Az Evolúcióbiológia Története Molnár István im54@invitel.hu Mai témák 1. Mi az evolúció? 2. Hogyan alakult ki a mai evolúciós
Biomatematika 2 Orvosi biometria
 Biomatematika 2 Orvosi biometria 2017.02.05. Orvosi biometria (orvosi biostatisztika) Statisztika: tömegjelenségeket számadatokkal leíró tudomány. A statisztika elkészítésének menete: tanulmányok (kísérletek)
Biomatematika 2 Orvosi biometria 2017.02.05. Orvosi biometria (orvosi biostatisztika) Statisztika: tömegjelenségeket számadatokkal leíró tudomány. A statisztika elkészítésének menete: tanulmányok (kísérletek)
2011. szeptember 14. Dr. Vincze Szilvia;
 2011. szeptember 14. Dr. Vincze Szilvia; vincze@fin.unideb.hu https://portal.agr.unideb.hu/oktatok/drvinczeszilvia Első pillantásra hihetetlennek tűnik, hogy egy olyan tiszta és érzelmektől mentes tudomány,
2011. szeptember 14. Dr. Vincze Szilvia; vincze@fin.unideb.hu https://portal.agr.unideb.hu/oktatok/drvinczeszilvia Első pillantásra hihetetlennek tűnik, hogy egy olyan tiszta és érzelmektől mentes tudomány,
Kvantitatív módszerek
 Kvantitatív módszerek szimuláció Kovács Zoltán Szervezési és Vezetési Tanszék E-mail: kovacsz@gtk.uni-pannon.hu URL: http://almos/~kovacsz Mennyiségi problémák megoldása analitikus numerikus szimuláció
Kvantitatív módszerek szimuláció Kovács Zoltán Szervezési és Vezetési Tanszék E-mail: kovacsz@gtk.uni-pannon.hu URL: http://almos/~kovacsz Mennyiségi problémák megoldása analitikus numerikus szimuláció
Az evolúció folyamatos változások olyan sorozata, melynek során bizonyos populációk öröklődő jellegei nemzedékről nemzedékre változnak.
 Evolúció Az evolúció folyamatos változások olyan sorozata, melynek során bizonyos populációk öröklődő jellegei nemzedékről nemzedékre változnak. Latin eredetű szó, jelentése: kibontakozás Időben egymást
Evolúció Az evolúció folyamatos változások olyan sorozata, melynek során bizonyos populációk öröklődő jellegei nemzedékről nemzedékre változnak. Latin eredetű szó, jelentése: kibontakozás Időben egymást
1. Generátorrendszer. Házi feladat (fizikából tudjuk) Ha v és w nem párhuzamos síkvektorok, akkor generátorrendszert alkotnak a sík vektorainak
 1. Generátorrendszer Generátorrendszer. Tétel (Freud, 4.3.4. Tétel) Legyen V vektortér a T test fölött és v 1,v 2,...,v m V. Ekkor a λ 1 v 1 + λ 2 v 2 +... + λ m v m alakú vektorok, ahol λ 1,λ 2,...,λ
1. Generátorrendszer Generátorrendszer. Tétel (Freud, 4.3.4. Tétel) Legyen V vektortér a T test fölött és v 1,v 2,...,v m V. Ekkor a λ 1 v 1 + λ 2 v 2 +... + λ m v m alakú vektorok, ahol λ 1,λ 2,...,λ
Matematikai alapok és valószínőségszámítás. Középértékek és szóródási mutatók
 Matematikai alapok és valószínőségszámítás Középértékek és szóródási mutatók Középértékek A leíró statisztikák talán leggyakrabban használt csoportját a középértékek jelentik. Legkönnyebben mint az adathalmaz
Matematikai alapok és valószínőségszámítás Középértékek és szóródási mutatók Középértékek A leíró statisztikák talán leggyakrabban használt csoportját a középértékek jelentik. Legkönnyebben mint az adathalmaz
JÁTÉKELMÉLETI MAGYARÁZAT A KÖZJÓSZÁGOK LÉTREJÖTTÉNEK ELMARADÁSÁRA
 Szociológiai Szemle 2005/1, 23 40. JÁTÉKELMÉLETI MAGYARÁZAT A KÖZJÓSZÁGOK LÉTREJÖTTÉNEK ELMARADÁSÁRA MÉSZÁROS József Budapesti Mûszaki és Gazdaságtudományi, Egyetem Szociológia és Kommunikáció Tanszék
Szociológiai Szemle 2005/1, 23 40. JÁTÉKELMÉLETI MAGYARÁZAT A KÖZJÓSZÁGOK LÉTREJÖTTÉNEK ELMARADÁSÁRA MÉSZÁROS József Budapesti Mûszaki és Gazdaságtudományi, Egyetem Szociológia és Kommunikáció Tanszék
ÖKOLÓGIA FÖLDRAJZ ALAPSZAK (NAPPALI MUNKAREND) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ
 ÖKOLÓGIA FÖLDRAJZ ALAPSZAK (NAPPALI MUNKAREND) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI FÖLDTUDOMÁNYI KAR FÖLDRAJZ-GEOINFORMATIKA INTÉZET Miskolc, 2019 TARTALOMJEGYZÉK 1. Tantárgyleírás
ÖKOLÓGIA FÖLDRAJZ ALAPSZAK (NAPPALI MUNKAREND) TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI FÖLDTUDOMÁNYI KAR FÖLDRAJZ-GEOINFORMATIKA INTÉZET Miskolc, 2019 TARTALOMJEGYZÉK 1. Tantárgyleírás
Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit.
 2. A VALÓS SZÁMOK 2.1 A valós számok aximómarendszere Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit. 1.Testaxiómák R-ben két művelet van értelmezve, az
2. A VALÓS SZÁMOK 2.1 A valós számok aximómarendszere Az R halmazt a valós számok halmazának nevezzük, ha teljesíti az alábbi 3 axiómacsoport axiómáit. 1.Testaxiómák R-ben két művelet van értelmezve, az
6. Függvények. Legyen függvény és nem üreshalmaz. A függvényt az f K-ra való kiterjesztésének
 6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
Vadbiológia és ökológia II.
 Vadbiológia és ökológia II. Populációk kölcsönhatásai Dr. Szemethy László Az élőlények nem önmagukban, hanem a legkülönbözőbb módokon együtt élve, életközösséget formálva léteznek. számos esetben kölcsönös
Vadbiológia és ökológia II. Populációk kölcsönhatásai Dr. Szemethy László Az élőlények nem önmagukban, hanem a legkülönbözőbb módokon együtt élve, életközösséget formálva léteznek. számos esetben kölcsönös
Bevezetés a biometriába Dr. Dinya Elek egyetemi tanár. PhD kurzus
 Bevezetés a biometriába Dr. Dinya Elek egyetemi tanár PhD kurzus Mi a statisztika? A sokaság (a sok valami) feletti áttekintés megszerzése, a sokaságról való információszerzés eszköze. Célja: - a sokaságot
Bevezetés a biometriába Dr. Dinya Elek egyetemi tanár PhD kurzus Mi a statisztika? A sokaság (a sok valami) feletti áttekintés megszerzése, a sokaságról való információszerzés eszköze. Célja: - a sokaságot
A valószínűségszámítás elemei
 A valószínűségszámítás elemei Kísérletsorozatban az esemény relatív gyakorisága: k/n, ahol k az esemény bekövetkezésének abszolút gyakorisága, n a kísérletek száma. Pl. Jelenség: kockadobás Megfigyelés:
A valószínűségszámítás elemei Kísérletsorozatban az esemény relatív gyakorisága: k/n, ahol k az esemény bekövetkezésének abszolút gyakorisága, n a kísérletek száma. Pl. Jelenség: kockadobás Megfigyelés:
Numerikus integrálás
 Közelítő és szimbolikus számítások 11. gyakorlat Numerikus integrálás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján 1. Határozatlan integrál
Közelítő és szimbolikus számítások 11. gyakorlat Numerikus integrálás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján 1. Határozatlan integrál
Adatbázis rendszerek 6.. 6. 1.1. Definíciók:
 Adatbázis Rendszerek Budapesti Műszaki és Gazdaságtudományi Egyetem Fotogrammetria és Térinformatika 6.1. Egyed relációs modell lényegi jellemzői 6.2. Egyed relációs ábrázolás 6.3. Az egyedtípus 6.4. A
Adatbázis Rendszerek Budapesti Műszaki és Gazdaságtudományi Egyetem Fotogrammetria és Térinformatika 6.1. Egyed relációs modell lényegi jellemzői 6.2. Egyed relációs ábrázolás 6.3. Az egyedtípus 6.4. A
8. Előadás. Megyesi László: Lineáris algebra, , oldal. 8. előadás Mátrix rangja, Homogén lineáris egyenletrendszer
 8. Előadás Megyesi László: Lineáris algebra, 51. 56., 70. 74. oldal. Gondolkodnivalók Elemi bázistranszformáció 1. Gondolkodnivaló Most ne vegyük figyelembe, hogy az elemi bázistranszformáció során ez
8. Előadás Megyesi László: Lineáris algebra, 51. 56., 70. 74. oldal. Gondolkodnivalók Elemi bázistranszformáció 1. Gondolkodnivaló Most ne vegyük figyelembe, hogy az elemi bázistranszformáció során ez
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
Algoritmusok Tervezése. 6. Előadás Algoritmusok 101 Dr. Bécsi Tamás
 Algoritmusok Tervezése 6. Előadás Algoritmusok 101 Dr. Bécsi Tamás Mi az algoritmus? Lépések sorozata egy feladat elvégzéséhez (legáltalánosabban) Informálisan algoritmusnak nevezünk bármilyen jól definiált
Algoritmusok Tervezése 6. Előadás Algoritmusok 101 Dr. Bécsi Tamás Mi az algoritmus? Lépések sorozata egy feladat elvégzéséhez (legáltalánosabban) Informálisan algoritmusnak nevezünk bármilyen jól definiált
1. Magyarországi INCA-CE továbbképzés
 1. Magyarországi INCA rendszer kimenetei. A meteorológiai paraméterek gyakorlati felhasználása, sa, értelmezése Simon André Országos Meteorológiai Szolgálat lat Siófok, 2011. szeptember 26. INCA kimenetek
1. Magyarországi INCA rendszer kimenetei. A meteorológiai paraméterek gyakorlati felhasználása, sa, értelmezése Simon André Országos Meteorológiai Szolgálat lat Siófok, 2011. szeptember 26. INCA kimenetek
Bevezetés. Korlátozott hasonlóság
 Bevezetés A pályázat keretében folytatott munka egy általános keret-elmélet köré szerveződik. Ennek alapgondolatai az előző (T033097 számú) OTKA pályázat futamideje alatt alakultak ki, alapjául szolgáltak
Bevezetés A pályázat keretében folytatott munka egy általános keret-elmélet köré szerveződik. Ennek alapgondolatai az előző (T033097 számú) OTKA pályázat futamideje alatt alakultak ki, alapjául szolgáltak
Arról, ami nincs A nemlétezés elméletei. 10. Mindaz, ami van. Meinong dzsungele: A létezéstől a fennálláson át az adva levésig november 25.
 Arról, ami nincs A nemlétezés elméletei 10. Mindaz, ami van. Meinong dzsungele: A létezéstől a fennálláson át az adva levésig. 2013. november 25. Alexius Meinong ( Ritter von Handschuchsheim) 1853-1920
Arról, ami nincs A nemlétezés elméletei 10. Mindaz, ami van. Meinong dzsungele: A létezéstől a fennálláson át az adva levésig. 2013. november 25. Alexius Meinong ( Ritter von Handschuchsheim) 1853-1920
Függvények növekedési korlátainak jellemzése
 17 Függvények növekedési korlátainak jellemzése A jellemzés jól bevált eszközei az Ω, O, Θ, o és ω jelölések. Mivel az igények általában nemnegatívak, ezért az alábbi meghatározásokban mindenütt feltesszük,
17 Függvények növekedési korlátainak jellemzése A jellemzés jól bevált eszközei az Ω, O, Θ, o és ω jelölések. Mivel az igények általában nemnegatívak, ezért az alábbi meghatározásokban mindenütt feltesszük,
Termodinamika. Belső energia
 Termodinamika Belső energia Egy rendszer belső energiáját az alkotó részecskék mozgási energiájának és a részecskék közötti kölcsönhatásból származó potenciális energiák teljes összegeként határozhatjuk
Termodinamika Belső energia Egy rendszer belső energiáját az alkotó részecskék mozgási energiájának és a részecskék közötti kölcsönhatásból származó potenciális energiák teljes összegeként határozhatjuk
Paleobiológiai módszerek és modellek 11. hét
 Paleobiológiai módszerek és modellek 11. hét A diverzitás fajtái és mérőszámai Nagy őslénytani adatbázisok: Sepkoski The Fossil Record Paleobiology Database A diverzitás fogalma Diverzitás sokféleség az
Paleobiológiai módszerek és modellek 11. hét A diverzitás fajtái és mérőszámai Nagy őslénytani adatbázisok: Sepkoski The Fossil Record Paleobiology Database A diverzitás fogalma Diverzitás sokféleség az
Közgazdasági elméletek. Dr. Karajz Sándor Gazdaságelméleti Intézet
 Közgazdasági elméletek Dr. Karajz Sándor Gazdaságelméleti 3. Előadás A karakterisztikai elmélet Bizonytalan körülmények közötti választás A karakterisztikai elmélet Hagyományos modell a fogyasztó különböző
Közgazdasági elméletek Dr. Karajz Sándor Gazdaságelméleti 3. Előadás A karakterisztikai elmélet Bizonytalan körülmények közötti választás A karakterisztikai elmélet Hagyományos modell a fogyasztó különböző
Környezet és fejlődés 2017 Ellenőrző kérdések
 Környezet és fejlődés 2017 Ellenőrző kérdések A növekedés határai 1. Mit értünk azon, hogy a Föld összetett anyagforgalmi rendszer? 2. Mely kérdésekre keresték a választ a Római Klub által megbízott kutatók,
Környezet és fejlődés 2017 Ellenőrző kérdések A növekedés határai 1. Mit értünk azon, hogy a Föld összetett anyagforgalmi rendszer? 2. Mely kérdésekre keresték a választ a Római Klub által megbízott kutatók,
Tranziens jelenségek rövid összefoglalás
 Tranziens jelenségek rövid összefoglalás Átmenet alakul ki akkor, ha van energiatároló (kapacitás vagy induktivitás) a rendszerben, mert ezeken a feszültség vagy áram nem jelenik meg azonnal, mint az ohmos
Tranziens jelenségek rövid összefoglalás Átmenet alakul ki akkor, ha van energiatároló (kapacitás vagy induktivitás) a rendszerben, mert ezeken a feszültség vagy áram nem jelenik meg azonnal, mint az ohmos
Mi az adat? Az adat elemi ismeret. Az adatokból információkat
 Mi az adat? Az adat elemi ismeret. Tények, fogalmak olyan megjelenési formája, amely alkalmas emberi eszközökkel történő értelmezésre, feldolgozásra, továbbításra. Az adatokból gondolkodás vagy gépi feldolgozás
Mi az adat? Az adat elemi ismeret. Tények, fogalmak olyan megjelenési formája, amely alkalmas emberi eszközökkel történő értelmezésre, feldolgozásra, továbbításra. Az adatokból gondolkodás vagy gépi feldolgozás
f(x) vagy f(x) a (x x 0 )-t használjuk. lim melyekre Mivel itt ɛ > 0 tetszőlegesen kicsi, így a a = 0, a = a, ami ellentmondás, bizonyítva
 6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
Információ megjelenítés Tufte szabályai
 Információ megjelenítés Tufte szabályai Mennyiségi adatok megjelenítése Edward Tufte (Professor, Yale) Mondat: 2, 3 adat összehasonlítására alkalmas Táblázat: sorokba, oszlopokba rendezett adat pontos
Információ megjelenítés Tufte szabályai Mennyiségi adatok megjelenítése Edward Tufte (Professor, Yale) Mondat: 2, 3 adat összehasonlítására alkalmas Táblázat: sorokba, oszlopokba rendezett adat pontos
Fázisátalakulások vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 6. MÉRÉS Fázisátalakulások vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. szeptember 28. Szerda délelőtti csoport 1. A mérés célja A mérés
KLASSZIKUS FIZIKA LABORATÓRIUM 6. MÉRÉS Fázisátalakulások vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. szeptember 28. Szerda délelőtti csoport 1. A mérés célja A mérés
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
Normák, kondíciószám
 Normák, kondíciószám A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris egyenletrendszerek Nagyon sok probléma közvetlenül lineáris egyenletrendszer megoldásával kezelhetı Sok numerikus
Normák, kondíciószám A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris egyenletrendszerek Nagyon sok probléma közvetlenül lineáris egyenletrendszer megoldásával kezelhetı Sok numerikus
10. modul: FÜGGVÉNYEK, FÜGGVÉNYTULAJDONSÁGOK
 MATEMATIK A 9. évfolyam 10. modul: FÜGGVÉNYEK, FÜGGVÉNYTULAJDONSÁGOK KÉSZÍTETTE: CSÁKVÁRI ÁGNES Matematika A 9. évfolyam. 10. modul: FÜGGVÉNYEK, FÜGGVÉNYTULAJDONSÁGOK Tanári útmutató 2 MODULLEÍRÁS A modul
MATEMATIK A 9. évfolyam 10. modul: FÜGGVÉNYEK, FÜGGVÉNYTULAJDONSÁGOK KÉSZÍTETTE: CSÁKVÁRI ÁGNES Matematika A 9. évfolyam. 10. modul: FÜGGVÉNYEK, FÜGGVÉNYTULAJDONSÁGOK Tanári útmutató 2 MODULLEÍRÁS A modul
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/54/33134285.jpg) [Biomatematika 2] Orvosi biometria 2016.02.08. Orvosi biometria (orvosi biostatisztika) Statisztika: tömegjelenségeket számadatokkal leíró tudomány. A statisztika elkészítésének menete: tanulmányok (kísérletek)
[Biomatematika 2] Orvosi biometria 2016.02.08. Orvosi biometria (orvosi biostatisztika) Statisztika: tömegjelenségeket számadatokkal leíró tudomány. A statisztika elkészítésének menete: tanulmányok (kísérletek)
ismertetem, hogy milyen probléma vizsgálatában jelent meg ez az eredmény. A kérdés a következő: Mikor mondhatjuk azt, hogy bizonyos események közül
 A Borel Cantelli lemma és annak általánosítása. A valószínűségszámítás egyik fontos eredménye a Borel Cantelli lemma. Először informálisan ismertetem, hogy milyen probléma vizsgálatában jelent meg ez az
A Borel Cantelli lemma és annak általánosítása. A valószínűségszámítás egyik fontos eredménye a Borel Cantelli lemma. Először informálisan ismertetem, hogy milyen probléma vizsgálatában jelent meg ez az
STATISZTIKUS TÖRVÉNYSZERŰSÉGEK EGYSZERŰ DEMONSTRÁLÁSA GALTON-DESZKÁVAL SIMPLE DEMONSTRATION OF STATISTICAL LAWS WITH GALTON-BOARD
 STATISZTIKUS TÖRVÉNYSZERŰSÉGEK EGYSZERŰ DEMONSTRÁLÁSA GALTON-DESZKÁVAL SIMPLE DEMONSTRATION OF STATISTICAL LAWS WITH GALTON-BOARD Gyertyán Attila 1, Dr. Juhász András 2 1 ELTE Apáczai Csere János Gyakorlóiskola,
STATISZTIKUS TÖRVÉNYSZERŰSÉGEK EGYSZERŰ DEMONSTRÁLÁSA GALTON-DESZKÁVAL SIMPLE DEMONSTRATION OF STATISTICAL LAWS WITH GALTON-BOARD Gyertyán Attila 1, Dr. Juhász András 2 1 ELTE Apáczai Csere János Gyakorlóiskola,
5. Laboratóriumi gyakorlat
 5. Laboratóriumi gyakorlat HETEROGÉN KÉMIAI REAKCIÓ SEBESSÉGÉNEK VIZSGÁLATA A CO 2 -nak vízben történő oldódása és az azt követő egyensúlyra vezető kémiai reakció az alábbi reakcióegyenlettel írható le:
5. Laboratóriumi gyakorlat HETEROGÉN KÉMIAI REAKCIÓ SEBESSÉGÉNEK VIZSGÁLATA A CO 2 -nak vízben történő oldódása és az azt követő egyensúlyra vezető kémiai reakció az alábbi reakcióegyenlettel írható le:
Ha bármi kérdés van, akkor engem elérhettek a en.
 Ha bármi kérdés van, akkor engem elérhettek a kunadam@elte.hu e-mailen. 1 Tanszékünk fizikailag a biológus épület VII. emeletén van a Dunához közeli oldalon. A tanszéki honlap a plantsys.elte.hu (új, de
Ha bármi kérdés van, akkor engem elérhettek a kunadam@elte.hu e-mailen. 1 Tanszékünk fizikailag a biológus épület VII. emeletén van a Dunához közeli oldalon. A tanszéki honlap a plantsys.elte.hu (új, de
Miért van egyes közösségekben több faj és másokban kevesebb? Vannak-e mintázatok és gradiensek a fajgazdagságban? Ha igen, ezeket mi okozza?
 Fajgazdagság Miért van egyes közösségekben több faj és másokban kevesebb? Vannak-e mintázatok és gradiensek a fajgazdagságban? Ha igen, ezeket mi okozza? biodiverzitás a természet változatosságának leírására
Fajgazdagság Miért van egyes közösségekben több faj és másokban kevesebb? Vannak-e mintázatok és gradiensek a fajgazdagságban? Ha igen, ezeket mi okozza? biodiverzitás a természet változatosságának leírására
Geometria 1 normál szint
 Geometria 1 normál szint Naszódi Márton nmarci@math.elte.hu www.math.elte.hu/ nmarci ELTE TTK Geometriai Tsz. Budapest Geometria 1 p.1/4 Vizsga 1. Írásban, 90 perc. 2. Index nélkül nem lehet vizsgázni!
Geometria 1 normál szint Naszódi Márton nmarci@math.elte.hu www.math.elte.hu/ nmarci ELTE TTK Geometriai Tsz. Budapest Geometria 1 p.1/4 Vizsga 1. Írásban, 90 perc. 2. Index nélkül nem lehet vizsgázni!
ETOLÓGIA. A kommunikációs magatartásformák evolúciója - csalás, megtévesztés - Pongrácz Péter
 ETOLÓGIA A kommunikációs magatartásformák evolúciója - csalás, megtévesztés - Pongrácz Péter Őszinteség? Manipuláció? Korai etológia ( információ-megosztás ) Egyértelmű, őszinte, kölcsönösen előnyös Evolúcióbiológia
ETOLÓGIA A kommunikációs magatartásformák evolúciója - csalás, megtévesztés - Pongrácz Péter Őszinteség? Manipuláció? Korai etológia ( információ-megosztás ) Egyértelmű, őszinte, kölcsönösen előnyös Evolúcióbiológia
3/29/12. Biomatematika 2. előadás. Biostatisztika = Biometria = Orvosi statisztika. Néhány egyszerű definíció:
 Biostatisztika = Biometria = Orvosi statisztika Biomatematika 2. előadás Néhány egyszerű definíció: A statisztika olyan tudomány, amely a tömegjelenségekkel kapcsolatos tapasztalati törvényeket megfigyelések
Biostatisztika = Biometria = Orvosi statisztika Biomatematika 2. előadás Néhány egyszerű definíció: A statisztika olyan tudomány, amely a tömegjelenségekkel kapcsolatos tapasztalati törvényeket megfigyelések
A vérképző rendszerben ionizáló sugárzás által okozott mutációk kialakulásának numerikus modellezése
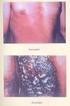 A vérképző rendszerben ionizáló sugárzás által okozott mutációk kialakulásának numerikus modellezése Madas Balázs Gergely XXXIX. Sugárvédelmi Továbbképző Tanfolyam Hajdúszoboszló, Hunguest Hotel Béke 2014.
A vérképző rendszerben ionizáló sugárzás által okozott mutációk kialakulásának numerikus modellezése Madas Balázs Gergely XXXIX. Sugárvédelmi Továbbképző Tanfolyam Hajdúszoboszló, Hunguest Hotel Béke 2014.
Evolúció. Dr. Szemethy László egyetemi docens Szent István Egyetem VadVilág Megőrzési Intézet
 Evolúció Dr. Szemethy László egyetemi docens Szent István Egyetem VadVilág Megőrzési Intézet Mi az evolúció? Egy folyamat: az élőlények tulajdonságainak változása a környezethez való alkalmazkodásra Egy
Evolúció Dr. Szemethy László egyetemi docens Szent István Egyetem VadVilág Megőrzési Intézet Mi az evolúció? Egy folyamat: az élőlények tulajdonságainak változása a környezethez való alkalmazkodásra Egy
Dr. Vincze Szilvia;
 2014. szeptember 17. és 19. Dr. Vincze Szilvia; vincze@agr.unideb.hu https://portal.agr.unideb.hu/oktatok/drvinczeszilvia/oktatas/oktatott_targyak/index/index.html 2010/2011-es tanév I. féléves tematika
2014. szeptember 17. és 19. Dr. Vincze Szilvia; vincze@agr.unideb.hu https://portal.agr.unideb.hu/oktatok/drvinczeszilvia/oktatas/oktatott_targyak/index/index.html 2010/2011-es tanév I. féléves tematika
Predáció szerepe a közösségszerkezet alakításában
 Predáció szerepe a közösségszerkezet alakításában Def.: A populáció méretet és/vagy a fajgazdagságot befolyásoló hatást zavarásnak (diszturbancia) nevezzük A zavarás lehet: predáció/herbivoria/parazitizmus
Predáció szerepe a közösségszerkezet alakításában Def.: A populáció méretet és/vagy a fajgazdagságot befolyásoló hatást zavarásnak (diszturbancia) nevezzük A zavarás lehet: predáció/herbivoria/parazitizmus
5. Állapotegyenletek : Az ideális gáz állapotegyenlet és a van der Waals állapotegyenlet
 5. Állapotegyenletek : Az ideális gáz állapotegyenlet és a van der Waals állapotegyenlet Ideális gáz Az ideális gáz állapotegyenlete pv=nrt empírikus állapotegyenlet, a Boyle-Mariotte (pv=konstans) és
5. Állapotegyenletek : Az ideális gáz állapotegyenlet és a van der Waals állapotegyenlet Ideális gáz Az ideális gáz állapotegyenlete pv=nrt empírikus állapotegyenlet, a Boyle-Mariotte (pv=konstans) és
Molekuláris biológiai módszerek alkalmazása a maláriát okozó paraziták elterjedésének és prevalenciájának vizsgálatában
 TÉMA ÉRTÉKELÉS TÁMOP-4.2.1/B-09/1/KMR-2010-0003 (minden téma külön lapra) 2010. június 1. 2012. május 31. 1. Az elemi téma megnevezése Molekuláris biológiai módszerek alkalmazása a maláriát okozó paraziták
TÉMA ÉRTÉKELÉS TÁMOP-4.2.1/B-09/1/KMR-2010-0003 (minden téma külön lapra) 2010. június 1. 2012. május 31. 1. Az elemi téma megnevezése Molekuláris biológiai módszerek alkalmazása a maláriát okozó paraziták
A ökológia tárgya és alapvető fogalmai, az ökológiai kutatások Krebs (1972): Haeckel (1866): Pianka (1983): Haeckel (1879): Entz (1907):
 Ökológia alapjai Bevezetés az ökológiába A ökológia tárgya és alapvető fogalmai, az ökológiai kutatások Az ökológia meghatározása körül számos vita merült fel Az ember és bioszféra kapcsolatának tapasztalati
Ökológia alapjai Bevezetés az ökológiába A ökológia tárgya és alapvető fogalmai, az ökológiai kutatások Az ökológia meghatározása körül számos vita merült fel Az ember és bioszféra kapcsolatának tapasztalati
Gépi tanulás és Mintafelismerés
 Gépi tanulás és Mintafelismerés jegyzet Csató Lehel Matematika-Informatika Tanszék BabesBolyai Tudományegyetem, Kolozsvár 2007 Aug. 20 2 1. fejezet Bevezet A mesterséges intelligencia azon módszereit,
Gépi tanulás és Mintafelismerés jegyzet Csató Lehel Matematika-Informatika Tanszék BabesBolyai Tudományegyetem, Kolozsvár 2007 Aug. 20 2 1. fejezet Bevezet A mesterséges intelligencia azon módszereit,
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2015. tavasz 1. Diszkrét matematika 2.C szakirány 1. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu Komputeralgebra Tanszék 2015. tavasz Gráfelmélet Diszkrét
Diszkrét matematika 2.C szakirány 2015. tavasz 1. Diszkrét matematika 2.C szakirány 1. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu Komputeralgebra Tanszék 2015. tavasz Gráfelmélet Diszkrét
Predáció populációdinamikai hatása
 Predáció populációdinamikai hatása Def.: olyan szervezet, amely a zsákmányát, annak elfogása után, megöli és elfogyasztja. (Ellentétben: herbivor, parazitoid, ahol késleltetett a hatás, de ezekre is a
Predáció populációdinamikai hatása Def.: olyan szervezet, amely a zsákmányát, annak elfogása után, megöli és elfogyasztja. (Ellentétben: herbivor, parazitoid, ahol késleltetett a hatás, de ezekre is a
A stratégiai menedzsment áttekintése. Máté Domicián
 A stratégiai menedzsment áttekintése Máté Domicián A tantárgy felépítése A stratégia alkotás menete Mi a fő célkitűzés, misszió, vízió Tényezők SWOT elemzése Külső faktorok értékelése Belső faktorok értékelése
A stratégiai menedzsment áttekintése Máté Domicián A tantárgy felépítése A stratégia alkotás menete Mi a fő célkitűzés, misszió, vízió Tényezők SWOT elemzése Külső faktorok értékelése Belső faktorok értékelése
GAZDASÁGSZOCIOLÓGIA I.
 GAZDASÁGSZOCIOLÓGIA I. Készült a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA Közgazdaságtudományi
GAZDASÁGSZOCIOLÓGIA I. Készült a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA Közgazdaságtudományi
A TERMODINAMIKA I. AXIÓMÁJA. Egyszerű rendszerek egyensúlya. Első észrevétel: egyszerű rendszerekről beszélünk.
 A TERMODINAMIKA I. AXIÓMÁJA Egyszerű rendszerek egyensúlya Első észrevétel: egyszerű rendszerekről beszélünk. Második észrevétel: egyensúlyban lévő egyszerű rendszerekről beszélünk. Mi is tehát az egyensúly?
A TERMODINAMIKA I. AXIÓMÁJA Egyszerű rendszerek egyensúlya Első észrevétel: egyszerű rendszerekről beszélünk. Második észrevétel: egyensúlyban lévő egyszerű rendszerekről beszélünk. Mi is tehát az egyensúly?
GAZDASÁGSZOCIOLÓGIA I.
 GAZDASÁGSZOCIOLÓGIA I. GAZDASÁGSZOCIOLÓGIA I. Készült a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázati projekt keretében Tartalomfejlesztés az ELTE TátK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi
GAZDASÁGSZOCIOLÓGIA I. GAZDASÁGSZOCIOLÓGIA I. Készült a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázati projekt keretében Tartalomfejlesztés az ELTE TátK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi
Alkalmazás a makrókanónikus sokaságra: A fotongáz
 Alkalmazás a makrókanónikus sokaságra: A fotongáz A fotonok az elektromágneses sugárzás hordozó részecskéi. Spinkvantumszámuk S=, tehát kvantumstatisztikai szempontból bozonok. Fotonoknak habár a spinkvantumszámuk,
Alkalmazás a makrókanónikus sokaságra: A fotongáz A fotonok az elektromágneses sugárzás hordozó részecskéi. Spinkvantumszámuk S=, tehát kvantumstatisztikai szempontból bozonok. Fotonoknak habár a spinkvantumszámuk,
