MÁTRIXALGEBRAI HIBAFA- ÉRZÉKENYSÉGELEMZÉS
|
|
|
- Enikő Boros
- 6 évvel ezelőtt
- Látták:
Átírás
1 Miskolci Egyetem Multidiszciplináris tudományok. kötet (2). szám pp. 3-. MÁTRIXALGEBRAI HIBAFA- ÉRZÉENYSÉGELEMZÉS Pokorádi László egyetemi tanár Debreceni Egyetem Műszaki ar 428 Debrecen Ótemető u Összefoglalás A tanulmány egy moduláris megközelítésű könnyen algoritmizálható hibafa érzékenység elemzési módszert mutat be mely repülőgép rendszerek és gázturbinás hajtóművek matematikai modellezési eljárásain alapszik. A tanulmány fő célja a lineáris matematikai diagnosztikai modellezési módszerek alkalmazásával a Lineáris Hibafa Érzékenységi Modell (LFTSM) módszertanának kidolgozása és egy példán keresztül az alkalmazási lehetőség szemléltetése ulcsszavak: hibafa elemzés érzékenység vizsgálat LFTSM Abstract In this paper a modular approach easy-useable fault tree sensitivity investigation method using matrix-algebraic method based upon the mathematical modelling of aircraft systems and gas turbine engines has been introduced. The main aim of this study is to show the adaptation of linear mathematical diagnostic modelling methodology for setting-up of LFTSM and its possibility of use to investigate Fault Tree sensitivity by a demonstrative example. eywords: Fault Tree Sensitivity analysis LFTSM. Bevezetés Technikai rendszerek megbízhatósági vizsgálatainak egyik legelterjedtebb módszere a hibafa elemzés (FTA Fault Tree Analysis). A hibafa-elemzés érzékenyvizsgálatának célja annak meghatározása hogy az adott hibafa elemi események bekövetkezési valószínűségeinek változásaira milyen mértékben reagálnak mennyire érzékenyek a hozzá kapcsolódó közbülső események és a főesemény bekövetkezési valószínűségei. A hibafa-elemzés során egy valós vagy feltételezett rendszerhibából az úgynevezett főeseményből (Top Event) indulunk ki és fokozatosan derítjük fel azokat az alkotóelem és részrendszer meghibásodási lehetőségeket melyek az adott nem kívánt esemény bekövetkezéséhez vezetnek vagy vezethetnek. Az elemző munkát fastruktúrájú gráf megjelenítés segíti amit különböző például megbízhatósági számításokkal is ki lehet egészíteni. Módszertanát a [3] és [4] szabványokból tud- 3
2 Pokorádi László juk megismerni. Számítógéppel segített hibafa-elemzés módszertanát ismerteti Ferdous szerzőtársaival a [2] irodalomban. A hibafa-érzékenységelemzések korábban alkalmazott módszere esetén a kiértékelést úgy végezzük el hogy a hibafa egyik elemi eseményéhez nagy majd kis értékű meghibásodási rátát rendelünk. Amennyiben a kiszámított rendszermegbízhatósági paraméter azaz a főesemény bekövetkezési valószínűsége nem változott számottevően akkor ez az elemi esemény nem bír nagy kockázati jelentőséggel. Viszont ha a rendszer-megbízhatósági paraméter változása jelentős mértékűre adódott akkor az adott elemi eseményt további megbízhatósági vizsgálatok alá kell helyezni. Csiba elemzései során az érzékenységi együtthatók meghatározásához a csúcsesemény bekövetkezési valószínűségét leíró teljes függvény elemi események bekövetkezési valószínűségei szerinti parciális differenciál hányadosait képezte []. Ezen eljárás hátránya az hogy egy nagyméretű összetett hibafa esetén viszonylag nagy a hibázás lehetősége. Pokorádi [5] könyvében vizsgálta a technikai rendszerek lineáris érzékenységi modelljeinek felállítási és alkalmazhatósági lehetőségeit. A Szerző a repülőgép gépészeti rendszereinek lineáris diagnosztikai eljárásait alkalmazta a hibafa-elemzés relatív érzékenységvizsgálatára valamint a Lineáris Hibafa Érzékenységi Modell (LFTSM Linear Fault Tree Sensitivity Model) módszerét dolgozta ki [6]. Jelen tanulmány a hibafa-elemzés érzékenységvizsgálatának a fenti eljárástól eltérő moduláris megközelítésű mátrixalgebrai módszerét mutatja be a szerző által kidolgozott LFTSM alkalmazásával. A tanulmány az alábbi részekből áll: A 2. fejezet a Hibafa-elemzést mutatja be röviden. A 3. fejezet az érzékenységvizsgálat teljes derivált módszerét írja le. A 4. fejezet egy egyszerű mintapéldán keresztül szemlélteti az előzőleg ismertetett módszer alkalmazását. Végül az 5. fejezet összegzi a tanulmány elkészítésekor szerzett tapasztalatokat és megfogalmazza a Szerző jövőbeli célkitűzéseit. 2. A Hibafa-elemzés A hibafa-elemzés során egy feltételezett rendszerhibából az úgynevezett főeseményből (Top Event) indulunk ki és fokozatosan derítjük fel azokat az alkotóelem és/vagy részrendszer meghibásodási lehetőségeket melyek az adott nem kívánt esemény bekövetkezéséhez vezetnek vagy vezethetnek. Az elemző munkát fastruktúrájú gráf megjelenítés segíti amit különböző például megbízhatósági számításokkal is ki lehet egészíteni. Egy (nem elemi) esemény bekövetkezési valószínűsége meghatározható az azt kiváltó események melyek lehetnek elemi vagy alacsonyabb szintű közbülső események bekövetkezési valószínűségeinek illetve a kapcsolatot leíró logikai kapu ismeretében azaz: 4
3 Mátrixalgebrai hibafa-érzékenységelemzés ÉS kapu amikor a kimeneti esemény csak akkor következik be hogyha az öszszes bemeneti esemény bekövetkezik esetén: P k P i i () VAGY kapu azaz ha a kimeneti esemény akkor következik be hogyha legalább egy bemeneti esemény bekövetkezik esetén: ahol: k P P i. (2) i P i az i-edik kiváltó esemény bekövetkezési valószínűsége; P i [] i{2...k} k k a kiváltó események száma. 3. Érzékenységi modell felállítása A hibafa-elemzés érzékenyvizsgálatának célja annak meghatározása hogy az elemi események bekövetkezési valószínűségeinek változásaira milyen mértékben reagál mennyire érzékeny a közbülső események és a főesemény bekövetkezési valószínűsége [6]. Az érzékenységi modell felállítása során mindegyik logikai kapuhoz kapcsolódó valószínűségi leírás lásd () és (2) egyenletek alapján a kimenő esemény bekövetkezési valószínűségének érzékenységi függvénye és együtthatói. A Lineáris Hibafa Érzékenységi Modell (LFTSM Linear Fault Tree Sensitivity Model) felállításához a logikai kapukat külön vizsgálva írjuk le azok érzékenységi függvényeit és határozzuk meg együtthatóit. Általánosan egy y kimenő jellemző x i bemenő jellemzővel szembeni érzékenységi együtthatója a f ( x ;x ; x ) x y k i y;x i 2 xi f ( x ;x2; xk ) xi parciális differenciálegyenlettel adható meg amely egyenlet a paraméterek relatív változásai közti kapcsolatot azaz a kimenő jellemző relatív érzékenységét írja le [6]. A hibafa elemzéseknél alkalmazott logikai kapuk érzékenységi együtthatóit az alábbiak szerint határozhatjuk meg: ÉS kapu esetén: xi y (3) 5
4 Pokorádi László i i { 2...k }. (4) VAGY kapu esetén: Pj k j P i i i. (5) P j övetkező lépésként különválasztjuk a vizsgált hibafa eseményeit az elemi és nem-elemi (közbülső és fő-) eseményekre mivel az utóbbiak mindegyike valamelyik logikai kapu kimenő (függő) változója. Az elemi és nem-elemi események bekövetkezési valószínűségeit az x m illetve y n vektorokba rendezzük. Ekkor a bekövetkezési valószínűségek relatív változásai közti kapcsolat az dy y y y y A y Bx (6) mátrixegyenlettel tudjuk leírni ahol: A nn nem elemi események együttható mátrixa; B nm elemi események együttható mátrixa; n nem elemi események száma m elemi események száma. A D A B nm (7) mátrixalgebrai összefüggést felhasználva a hibafa-elemzés D relatív érzékenységi mátrixát kapjuk meg és a (6) egyenlet a 6 y Dx (8) alakúra módosul. A relatív érzékenységi mátrix i-edik sorának j-edik eleme azt mutatja meg hogy az i-edik nem elemi esemény bekövetkezési valószínűségének relatív változását milyen mértékben befolyásolja a j-edik elemi esemény bekövetkezési valószínűségének relatív változása. A mátrix első sora különösen fontos lehet mivel az a főesemény bekövetkezési valószínűségének az elemi események bekövetkezési valószínűségeivel szembeni érzékenységi együtthatókat adja meg. A D mátrix ezen sorát mint relatív érzékenységi (sor)vektort kezelhetjük és d T -vel jelöljük.
5 4. Érzékenységvizsgálat (Mintapélda) Az. ábra az elemzéseink során alkalmazott hibafát szemlélteti. Mátrixalgebrai hibafa-érzékenységelemzés. ábra Hibafa (mintapélda) Az ábrából leolvasható hogy az ; 2; és 22 kódú események a közbülső események míg a 2; 2; ; 2; 22 és 222 számú események pedig elemi események. A vizsgált hibafa valószínűségi modellje: P TE P P 2 (9) P P P2 PP2 () P2 P2P22 () P PP2 (2) P22 P22 P222 P22P222 (3) További vizsgálatunkhoz először az elemi események névleges (átlagos jellemző) bekövetkezési valószínűségeit kell meghatároznunk melyeket az. táblázat tartalmazza. Ezek alapján a (3) (9) egyenletek felhasználásával (visszafelé haladva) meghatározhatók a közbülső események valamint a főesemény névleges bekövetkezési valószínűsége (2. táblázat). 7
6 Pokorádi László. táblázat iinduló adatok P 2 = P 2 = 2 P = 5 P 2 = 25 P 22 = 3 P 222 = 2. táblázat Számított (névleges) valószínűségi értékek P 22 = 37 P = 375 P 2 = 74 P = 375 P TE = Az. ábrán szemléltetett hiba-fa a (9) (3) egyenletekkel leírt valószínűségi elemzésének érzékenységi függvényei és együtthatói a következők: 8 P TE P 2P2 2 P P 2P2 P 2 P P 2 P P 525 P P2 2P2 22P P P 2P2 2 P22 22P22 222P222 P P22 P P22 P P övetkező lépésként külön kell választanunk vizsgált hibafa eseményeit a 2; 2; ; 2; 22 és 222 elemi és TE; ; 2; és 22 nem-elemi (fő- és közbülső) eseményekre és ezek bekövetkezési valószínűségeit a (4) (5) (6) (7) (8) x T P2;P2;P;P2;P22; P222 (9) y T P TE ;P ;P2 ;P; P22 (2) vektorokba rendezzük.
7 Mátrixalgebrai hibafa-érzékenységelemzés 9 A fenti vektorok ismeretében valamint a (4) (8) egyenletek alapján meghatározzuk a bekövetkezési valószínűségek relatív változásainak együttható mátrixait: A ; (2) B (22) A relatív érzékenységi együttható mátrix: D (23) illetve a relatív érzékenységi vektor: d T. (24) Matematikailag megfogalmazva a relatív érzékenység vektor elemei megmutatják hogy az elemi események bekövetkezési valószínűségeinek relatív értékcsökkenése vagy növekedése a főesemény bekövetkezési valószínűségének milyen mértékű relatív csökkenését illetve növekedését okozzák. Másképpen értelmezve: mely elemi esemény bekövetkezési valószínűségének változása bír a legnagyobb hatással a főesemény bekövetkezési valószínűségére. Mérnöki szempontból ez azt mutatja meg mely elemi eseményt létrehozó rendszerelem megbízhatóságának növelésével tudjuk a legnagyobb mértékben javítani a teljes rendszer megbízhatóságát. Azaz mely elemi események bekövetkezési valószínűségének csökkentését (például a konstrukciójának változtatását) célszerű elvégezni. A fenti eredmények műszaki szakmai elemzése (például Pareto-elemzés alkalmazása) már túlmutat jelen tanulmány keretein.
8 Pokorádi László 5. Összefoglalás A Szerző az utóbbi években kutatómunkát folytat annak feltárására hogy a széles értelemben vett modellezési és rendszer bizonytalanság valamint rendszerérzékenység elemzés és kezelés milyen módon oldható meg a leghatékonyabb formában. A kutatási program keretében készült ez a tanulmány is mely egy új könnyen algoritmizálható mátrixalgebrai módszert mutat be a hibafák érzékenységi elemzéséhez. A cikk egy egyszerű mintapéldán keresztül szemlélteti és igazolja az LFTSM (Linear Fault Tree Sensitivity Model Lineáris Hibafa Érzékenységi Modell) eljárás használhatóságát. Az elemzőmunka egyértelműen bizonyította hogy a repülőgépészeti rendszerek diagnosztikai elemzéseinél alkalmazott rendszerérzékenységi modellvizsgálati eljárások jól alkalmazhatóak a hibafa elemzések érzékenységvizsgálatához. A Szerző további tudományos kutatómunkája során olyan tanulmányok elkészítését tűzte ki célként amelyek leírják a modell- és rendszerbizonytalanságokat illetve rendszer érzékenységeket értelmezik vizsgálják és szemléltetik azok elemzési módszereit. 6. Felhasznált irodalom [] Csiba J.: Sensitivity Analysis of the Reliability Computed by Using the Failure Tree Method Proc. Of the th Mini Conference on Vehicle System Dynamics Identification and Anomalies 28. Budapest [2] Ferdous R. et al. Methodology for Computer-Aided Fault Tree Analysis Trans IChemE Part B Process Safety and Environmental Protection (B): 7-8. [3] IEC (99) Standard IEC 25 Fault tree analysis (FTA) International Electrotechnical Commission 39. [4] MSZ EN Gépek biztonsága. A kockázatértékelés elvei Magyar Szabványügyi Testület Budapest 999. pp. 22. [5] Pokorádi L.: Rendszerek és folyamatok modellezése Campus iadó Debrecen [6] Pokorádi L.: Sensitivity Investigation of Fault Tree Analysis with Matrix- Algebraic Method Theory and Applications of Mathematics & Computer Science (ISSN: ) 2 Spring (April) Volume Number p
MISKOLCI EGYETEM KÖZLEMÉNYEI
 HU ISSN 262-9737 MISOLCI EGYETEM ÖZLEMÉNYEI Interdiszciplináris tudományok. kötet (2). szám MISOLCI EGYETEMI IADÓ Miskolc 2 SZERESZTŐ BIZOTTSÁG TISZA Miklós főszerkesztő GÁCSI Zoltán GINSZTLER János ILLÉS
HU ISSN 262-9737 MISOLCI EGYETEM ÖZLEMÉNYEI Interdiszciplináris tudományok. kötet (2). szám MISOLCI EGYETEMI IADÓ Miskolc 2 SZERESZTŐ BIZOTTSÁG TISZA Miklós főszerkesztő GÁCSI Zoltán GINSZTLER János ILLÉS
HIBAFA ÉRZÉKENYSÉG ELEMZÉSE 2 1. BEVEZETÉS
 oorádi László Szolnoi Tudományos Közleménye XVI. Szolno, 202 HIBAFA ÉRZÉKENYSÉG ELEMZÉSE 2 A tanulmány egy önnyen algoritmizálható hibafa érzéenység elemzési módszert mutat be, mely a gázturbinás hajtóműve
oorádi László Szolnoi Tudományos Közleménye XVI. Szolno, 202 HIBAFA ÉRZÉKENYSÉG ELEMZÉSE 2 A tanulmány egy önnyen algoritmizálható hibafa érzéenység elemzési módszert mutat be, mely a gázturbinás hajtóműve
MŰSZAKI TUDOMÁNY AZ ÉSZAK-ALFÖLDI RÉGIÓBAN 2010
 MŰSZAKI TUDOMÁNY AZ ÉSZAK-ALFÖLDI RÉGIÓBAN 2010 KONFERENCIA ELŐADÁSAI Nyíregyháza, 2010. május 19. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
MŰSZAKI TUDOMÁNY AZ ÉSZAK-ALFÖLDI RÉGIÓBAN 2010 KONFERENCIA ELŐADÁSAI Nyíregyháza, 2010. május 19. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
MŰSZAKI TUDOMÁNY AZ ÉSZAK-ALFÖLDI RÉGIÓBAN 2010
 MŰSZAKI TUDOMÁNY AZ ÉSZAK-ALFÖLDI RÉGIÓBAN 2010 KONFERENCIA ELŐADÁSAI Nyíregyháza, 2010. május 19. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
MŰSZAKI TUDOMÁNY AZ ÉSZAK-ALFÖLDI RÉGIÓBAN 2010 KONFERENCIA ELŐADÁSAI Nyíregyháza, 2010. május 19. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
MŰSZAKI TUDOMÁNY AZ ÉSZAK-KELET MAGYARORSZÁGI RÉGIÓBAN 2012
 MŰSZAKI TUDOMÁNY AZ ÉSZAK-KELET MAGYARORSZÁGI RÉGIÓBAN 2012 KONFERENCIA ELŐADÁSAI Szolnok, 2012. május 10. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
MŰSZAKI TUDOMÁNY AZ ÉSZAK-KELET MAGYARORSZÁGI RÉGIÓBAN 2012 KONFERENCIA ELŐADÁSAI Szolnok, 2012. május 10. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
Hibafaelemzés a hibátlan tervezés érdekében
 Hibafaelemzés a hibátlan tervezés érdekében Johanyák Zsolt Csaba A minõségbiztosítás hagyományos módszerei legtöbbször csak a gyártásközi és végellenõrzésre szorítkoznak. Ez azonban nem elégíti ki a termékfejlesztéssel
Hibafaelemzés a hibátlan tervezés érdekében Johanyák Zsolt Csaba A minõségbiztosítás hagyományos módszerei legtöbbször csak a gyártásközi és végellenõrzésre szorítkoznak. Ez azonban nem elégíti ki a termékfejlesztéssel
A GÉPIPARI TUDOMÁNYOS EGYESÜLET MŰSZAKI FOLYÓIRATA 2009/4 5. 128 oldal LX. évfolyam
 A GÉPIPARI TUDOMÁNYOS EGYESÜLET MŰSZAKI FOLYÓIRATA 2009/4 5. 128 oldal LX. évfolyam GÉP A GÉPIPARI TUDOMÁNYOS EGYESÜLET műszaki, vállalkozási, befektetési, értékesítési, kutatás-fejlesztési, piaci információs
A GÉPIPARI TUDOMÁNYOS EGYESÜLET MŰSZAKI FOLYÓIRATA 2009/4 5. 128 oldal LX. évfolyam GÉP A GÉPIPARI TUDOMÁNYOS EGYESÜLET műszaki, vállalkozási, befektetési, értékesítési, kutatás-fejlesztési, piaci információs
LÉTRADIAGRAM FORDÍTÓK ELMÉLETE PLC VEZÉRLÉSEK SZÁMÁRA II.
 V. Évfolyam 1. szám - 2010. március Deák Ferenc deak@nct.hu LÉTRADIAGRAM FORDÍTÓK ELMÉLETE PLC VEZÉRLÉSEK SZÁMÁRA II. Absztrakt A létradiagram egyszerű, programozási képzettséggel nem rendelkező szakemberek
V. Évfolyam 1. szám - 2010. március Deák Ferenc deak@nct.hu LÉTRADIAGRAM FORDÍTÓK ELMÉLETE PLC VEZÉRLÉSEK SZÁMÁRA II. Absztrakt A létradiagram egyszerű, programozási képzettséggel nem rendelkező szakemberek
Elemzési módszerek. Egyes módszerek ágazat-specifikusak, mások teljesen általánosan használatosak. A leggyakoribb veszélyelemző módszerek:
 Elemzési módszerek Egyes módszerek ágazat-specifikusak, mások teljesen általánosan használatosak. A leggyakoribb veszélyelemző módszerek: Hibamód és -hatás elemzés - failure modes and effects analysis
Elemzési módszerek Egyes módszerek ágazat-specifikusak, mások teljesen általánosan használatosak. A leggyakoribb veszélyelemző módszerek: Hibamód és -hatás elemzés - failure modes and effects analysis
SÚLYOS BALESETEK ELEMZÉSE. 3. téma: Kvalitatív módszerek - Hibafa
 Az oktatási anyag a szerzők szellemi terméke. Az anyag kizárólag a 2014.01.22-23 23-i OKF Továbbképzés céljaira használható. Sokszorosítás, utánközlés és mindennemű egyéb felhasználás a szerzők engedélyéhez
Az oktatási anyag a szerzők szellemi terméke. Az anyag kizárólag a 2014.01.22-23 23-i OKF Továbbképzés céljaira használható. Sokszorosítás, utánközlés és mindennemű egyéb felhasználás a szerzők engedélyéhez
A kockázatelemzés menete
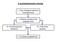 A kockázatelemzés menete 1. Üzem (folyamat) jellemzői Veszélyforrások 2. Baleseti sorok meghatározása 3a. Következmények felmérése 3b. Gyakoriság becslése 4. Kockázat meghatározás Balesetek Gyakoriság
A kockázatelemzés menete 1. Üzem (folyamat) jellemzői Veszélyforrások 2. Baleseti sorok meghatározása 3a. Következmények felmérése 3b. Gyakoriság becslése 4. Kockázat meghatározás Balesetek Gyakoriság
BIZONYTALANSÁG A KOCKÁZATBECSLÉSBEN 1. BEVEZETÉS
 Pokorádi László BIZONYTALANSÁG A KOCKÁZATBECSLÉSBEN A műszaki menedzsment döntései különböző pozitív vagy negatív előjelű eredményeket eredményezhetnek. A döntéshozóknak mind morális, mind szakmai szempontokat
Pokorádi László BIZONYTALANSÁG A KOCKÁZATBECSLÉSBEN A műszaki menedzsment döntései különböző pozitív vagy negatív előjelű eredményeket eredményezhetnek. A döntéshozóknak mind morális, mind szakmai szempontokat
A KUTATÁS EREDMÉNYEI ZÁRÓJELENTÉS 2004-2006.
 ÖNELLENŐRZÉS ÉS FUTÁSIDEJŰ VERIFIKÁCIÓ SZÁMÍTÓGÉPES PROGRAMOKBAN OTKA T-046527 A KUTATÁS EREDMÉNYEI ZÁRÓJELENTÉS 2004-2006. Témavezető: dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem
ÖNELLENŐRZÉS ÉS FUTÁSIDEJŰ VERIFIKÁCIÓ SZÁMÍTÓGÉPES PROGRAMOKBAN OTKA T-046527 A KUTATÁS EREDMÉNYEI ZÁRÓJELENTÉS 2004-2006. Témavezető: dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem
AKTUÁTOR MODELLEK KIVÁLASZTÁSA ÉS OBJEKTÍV ÖSSZEHASONLÍTÁSA
 AKTUÁTOR MODELLEK KIVÁLASZTÁSA ÉS OBJEKTÍV ÖSSZEHASONLÍTÁSA Kovács Ernő 1, Füvesi Viktor 2 1 Egyetemi docens, PhD; 2 tudományos segédmunkatárs 1 Eletrotechnikai és Elektronikai Tanszék, Miskolci Egyetem
AKTUÁTOR MODELLEK KIVÁLASZTÁSA ÉS OBJEKTÍV ÖSSZEHASONLÍTÁSA Kovács Ernő 1, Füvesi Viktor 2 1 Egyetemi docens, PhD; 2 tudományos segédmunkatárs 1 Eletrotechnikai és Elektronikai Tanszék, Miskolci Egyetem
Modellezés és szimuláció a tervezésben
 Modellezés és szimuláció a tervezésben Szimuláció: egy másik rendszerrel - amely bizonyos vonatkozásokban hasonló az eredeti rendszerhez - utánozzuk egy rendszer viselkedését, vagyis az eredeti rendszer
Modellezés és szimuláció a tervezésben Szimuláció: egy másik rendszerrel - amely bizonyos vonatkozásokban hasonló az eredeti rendszerhez - utánozzuk egy rendszer viselkedését, vagyis az eredeti rendszer
Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével
 Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével Pekárdy Milán, Baumgartner János, Süle Zoltán Pannon Egyetem, Veszprém XXXII. Magyar Operációkutatási
Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével Pekárdy Milán, Baumgartner János, Süle Zoltán Pannon Egyetem, Veszprém XXXII. Magyar Operációkutatási
Egy gazdasa gmatematikai modell An economical mathematics model
 Egy gazdasa gmatematikai modell An economical mathematics model KÉZI CS. University of Debrecen, kezicsaba@science.unideb.hu Absztrakt. Az NTP-NFTÖ-17-C-159 azonosítószámú pályázat keretében az egyik fő
Egy gazdasa gmatematikai modell An economical mathematics model KÉZI CS. University of Debrecen, kezicsaba@science.unideb.hu Absztrakt. Az NTP-NFTÖ-17-C-159 azonosítószámú pályázat keretében az egyik fő
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
Városi légszennyezettség vizsgálata térinformatikai és matematikai statisztikai módszerek alkalmazásával
 Pannon Egyetem Vegyészmérnöki Tudományok és Anyagtudományok Doktori Iskola Városi légszennyezettség vizsgálata térinformatikai és matematikai statisztikai módszerek alkalmazásával DOKTORI (Ph.D.) ÉRTEKEZÉS
Pannon Egyetem Vegyészmérnöki Tudományok és Anyagtudományok Doktori Iskola Városi légszennyezettség vizsgálata térinformatikai és matematikai statisztikai módszerek alkalmazásával DOKTORI (Ph.D.) ÉRTEKEZÉS
Hidraulikus hálózatok robusztusságának növelése
 Dr. Dulovics Dezső Junior Szimpózium 2018. Hidraulikus hálózatok robusztusságának növelése Előadó: Huzsvár Tamás MSc. Képzés, II. évfolyam Témavezető: Wéber Richárd, Dr. Hős Csaba www.hds.bme.hu Az előadás
Dr. Dulovics Dezső Junior Szimpózium 2018. Hidraulikus hálózatok robusztusságának növelése Előadó: Huzsvár Tamás MSc. Képzés, II. évfolyam Témavezető: Wéber Richárd, Dr. Hős Csaba www.hds.bme.hu Az előadás
Matematika III. harmadik előadás
 Matematika III. harmadik előadás Kézi Csaba Debreceni Egyetem, Műszaki Kar Debrecen, 2013/14 tanév, I. félév Kézi Csaba (DE) Matematika III. harmadik előadás 2013/14 tanév, I. félév 1 / 13 tétel Az y (x)
Matematika III. harmadik előadás Kézi Csaba Debreceni Egyetem, Műszaki Kar Debrecen, 2013/14 tanév, I. félév Kézi Csaba (DE) Matematika III. harmadik előadás 2013/14 tanév, I. félév 1 / 13 tétel Az y (x)
A mérési eredmény megadása
 A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
ÉS TESZTEK A DEFINITSÉG
 MÁTRIX DEFINITSÉGÉNEK FOGALMA ÉS TESZTEK A DEFINITSÉG ELDÖNTÉSÉRE DR. NAGY TAMÁS egyetemi docens Miskolci Egyetem Alkalmazott Matematikai Tanszék A bemutatott kutató munka a TÁMOP-..1.B-10//KONV-010-0001
MÁTRIX DEFINITSÉGÉNEK FOGALMA ÉS TESZTEK A DEFINITSÉG ELDÖNTÉSÉRE DR. NAGY TAMÁS egyetemi docens Miskolci Egyetem Alkalmazott Matematikai Tanszék A bemutatott kutató munka a TÁMOP-..1.B-10//KONV-010-0001
A MEGBÍZHATÓSÁGI ELEMZŐ MÓDSZEREK
 1. Elemző módszerek A MEGBÍZHATÓSÁGI ELEMZŐ MÓDSZEREK Ebben a fejezetben röviden összefoglaljuk azokat a módszereket, amelyekkel a technikai, technológiai és üzemeltetési rendszerek megbízhatósági elemzései
1. Elemző módszerek A MEGBÍZHATÓSÁGI ELEMZŐ MÓDSZEREK Ebben a fejezetben röviden összefoglaljuk azokat a módszereket, amelyekkel a technikai, technológiai és üzemeltetési rendszerek megbízhatósági elemzései
Diagnosztikai szemléletű talajtérképek szerkesztése korrelált talajtani adatrendszerek alapján
 Diagnosztikai szemléletű talajtérképek szerkesztése korrelált talajtani adatrendszerek alapján Bakacsi Zsófia 1 - Szabó József 1 Waltner István 2 Michéli Erika 2 Fuchs Márta 2 - Laborczi Annamária 1 -
Diagnosztikai szemléletű talajtérképek szerkesztése korrelált talajtani adatrendszerek alapján Bakacsi Zsófia 1 - Szabó József 1 Waltner István 2 Michéli Erika 2 Fuchs Márta 2 - Laborczi Annamária 1 -
Süle Zoltán publikációs listája
 Süle Zoltán publikációs listája Statisztikai összegzés Referált nemzetközi folyóiratcikkeim száma: 3 (+1) Nemzetközi konferenciakiadványban megjelent publikációim száma: 14 Hazai konferenciakiadványban
Süle Zoltán publikációs listája Statisztikai összegzés Referált nemzetközi folyóiratcikkeim száma: 3 (+1) Nemzetközi konferenciakiadványban megjelent publikációim száma: 14 Hazai konferenciakiadványban
DIFFERENCIÁLEGYENLETEK. BSc. Matematika II. BGRMA2HNND, BGRMA2HNNC
 016.03.1. BSC MATEMATIKA II. ELSŐ ÉS MÁSODRENDŰ LINEÁRIS DIFFERENCIÁLEGYENLETEK BSc. Matematika II. BGRMAHNND, BGRMAHNNC AZ ELSŐRENDŰ LINEÁRIS DIFFERENCIÁLEGYENLET FOGALMA Az elsőrendű közönséges differenciálegyenletet
016.03.1. BSC MATEMATIKA II. ELSŐ ÉS MÁSODRENDŰ LINEÁRIS DIFFERENCIÁLEGYENLETEK BSc. Matematika II. BGRMAHNND, BGRMAHNNC AZ ELSŐRENDŰ LINEÁRIS DIFFERENCIÁLEGYENLET FOGALMA Az elsőrendű közönséges differenciálegyenletet
SZOFTVEREK A SORBANÁLLÁSI ELMÉLET OKTATÁSÁBAN
 SZOFTVEREK A SORBANÁLLÁSI ELMÉLET OKTATÁSÁBAN Almási Béla, almasi@math.klte.hu Sztrik János, jsztrik@math.klte.hu KLTE Matematikai és Informatikai Intézet Abstract This paper gives a short review on software
SZOFTVEREK A SORBANÁLLÁSI ELMÉLET OKTATÁSÁBAN Almási Béla, almasi@math.klte.hu Sztrik János, jsztrik@math.klte.hu KLTE Matematikai és Informatikai Intézet Abstract This paper gives a short review on software
Méréselmélet MI BSc 1
 Mérés és s modellezés 2008.02.15. 1 Méréselmélet - bevezetés a mérnöki problémamegoldás menete 1. A probléma kitűzése 2. A hipotézis felállítása 3. Kísérlettervezés 4. Megfigyelések elvégzése 5. Adatok
Mérés és s modellezés 2008.02.15. 1 Méréselmélet - bevezetés a mérnöki problémamegoldás menete 1. A probléma kitűzése 2. A hipotézis felállítása 3. Kísérlettervezés 4. Megfigyelések elvégzése 5. Adatok
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011.
 BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
Problémás regressziók
 Universitas Eotvos Nominata 74 203-4 - II Problémás regressziók A közönséges (OLS) és a súlyozott (WLS) legkisebb négyzetes lineáris regresszió egy p- változós lineáris egyenletrendszer megoldása. Az egyenletrendszer
Universitas Eotvos Nominata 74 203-4 - II Problémás regressziók A közönséges (OLS) és a súlyozott (WLS) legkisebb négyzetes lineáris regresszió egy p- változós lineáris egyenletrendszer megoldása. Az egyenletrendszer
Normák, kondíciószám
 Normák, kondíciószám A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris egyenletrendszerek Nagyon sok probléma közvetlenül lineáris egyenletrendszer megoldásával kezelhetı Sok numerikus
Normák, kondíciószám A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris egyenletrendszerek Nagyon sok probléma közvetlenül lineáris egyenletrendszer megoldásával kezelhetı Sok numerikus
B/16. számú melléklet Önéletrajz sablon
 Europass Önéletrajz Személyi adatok Vezetéknév / Utónév(ek) Tímea Fülep Cím(ek) 3, Törökugrató u. 3., 1118, Budapest, Magyarország Telefonszám(ok) +36 96 50 3308 Mobil: +36 70 210 4319 Fax(ok) +36 1 436
Europass Önéletrajz Személyi adatok Vezetéknév / Utónév(ek) Tímea Fülep Cím(ek) 3, Törökugrató u. 3., 1118, Budapest, Magyarország Telefonszám(ok) +36 96 50 3308 Mobil: +36 70 210 4319 Fax(ok) +36 1 436
9. Előadás. Megyesi László: Lineáris algebra, oldal. 9. előadás Mátrix inverze, mátrixegyenlet
 9. Előadás Megyesi László: Lineáris algebra, 75. 84. oldal. Gondolkodnivalók Mátrix rangja 1. Gondolkodnivaló Határozzuk meg a p valós paraméter értékétől függően a következő mátrix rangját: p 3 1 2 2
9. Előadás Megyesi László: Lineáris algebra, 75. 84. oldal. Gondolkodnivalók Mátrix rangja 1. Gondolkodnivaló Határozzuk meg a p valós paraméter értékétől függően a következő mátrix rangját: p 3 1 2 2
Az informatikai biztonsági kockázatok elemzése
 ROBOTHADVISELÉS S 2009 Az informatikai biztonsági kockázatok elemzése Muha Lajos PhD, CISM főiskolai tanár, mb. tanszékvezet kvezető ZMNE BJKMK IHI Informatikai Tanszék 1 Az informatikai biztonság Az informatikai
ROBOTHADVISELÉS S 2009 Az informatikai biztonsági kockázatok elemzése Muha Lajos PhD, CISM főiskolai tanár, mb. tanszékvezet kvezető ZMNE BJKMK IHI Informatikai Tanszék 1 Az informatikai biztonság Az informatikai
Bázistranszformáció és alkalmazásai 2.
 Bázistranszformáció és alkalmazásai 2. Lineáris algebra gyakorlat Összeállította: Bogya Norbert Tartalomjegyzék 1 Mátrix rangja 2 Mátrix inverze 3 Mátrixegyenlet Mátrix rangja Tartalom 1 Mátrix rangja
Bázistranszformáció és alkalmazásai 2. Lineáris algebra gyakorlat Összeállította: Bogya Norbert Tartalomjegyzék 1 Mátrix rangja 2 Mátrix inverze 3 Mátrixegyenlet Mátrix rangja Tartalom 1 Mátrix rangja
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 6. Differenciálegyenletekről röviden Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés 2 Elsőrendű differenciálegyenletek Definíciók Kezdetiérték-probléma
BIOMATEMATIKA ELŐADÁS 6. Differenciálegyenletekről röviden Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés 2 Elsőrendű differenciálegyenletek Definíciók Kezdetiérték-probléma
3. Lineáris differenciálegyenletek
 3. Lineáris differenciálegyenletek A közönséges differenciálegyenletek két nagy csoportba oszthatók lineáris és nemlineáris egyenletek csoportjába. Ez a felbontás kicsit önkényesnek tűnhet, a megoldásra
3. Lineáris differenciálegyenletek A közönséges differenciálegyenletek két nagy csoportba oszthatók lineáris és nemlineáris egyenletek csoportjába. Ez a felbontás kicsit önkényesnek tűnhet, a megoldásra
Hurokegyenlet alakja, ha az áram irányával megegyező feszültségeséseket tekintjük pozitívnak:
 Első gyakorlat A gyakorlat célja, hogy megismerkedjünk Matlab-SIMULINK szoftverrel és annak segítségével sajátítsuk el az Automatika c. tantárgy gyakorlati tananyagát. Ezen a gyakorlaton ismertetésre kerül
Első gyakorlat A gyakorlat célja, hogy megismerkedjünk Matlab-SIMULINK szoftverrel és annak segítségével sajátítsuk el az Automatika c. tantárgy gyakorlati tananyagát. Ezen a gyakorlaton ismertetésre kerül
DINAMIKAI VIZSGÁLAT ÁLLAPOTTÉRBEN. 2003.11.06. Dr. Aradi Petra, Dr. Niedermayer Péter: Rendszertechnika segédlet 1
 DINAMIKAI VIZSGÁLAT ÁLLAPOTTÉRBEN 2003..06. Dr. Aradi Petra, Dr. Niedermayer Péter: Rendszertechnika segédlet Egy bemenetű, egy kimenetű rendszer u(t) diff. egyenlet v(t) zárt alakban n-edrendű diff. egyenlet
DINAMIKAI VIZSGÁLAT ÁLLAPOTTÉRBEN 2003..06. Dr. Aradi Petra, Dr. Niedermayer Péter: Rendszertechnika segédlet Egy bemenetű, egy kimenetű rendszer u(t) diff. egyenlet v(t) zárt alakban n-edrendű diff. egyenlet
Mérés és modellezés Méréstechnika VM, GM, MM 1
 Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
MŰSZAKI TUDOMÁNY AZ ÉSZAK-KELET MAGYARORSZÁGI RÉGIÓBAN 2012
 MŰSZAKI TUDOMÁNY AZ ÉSZAK-KELET MAGYARORSZÁGI RÉGIÓBAN 0 KONFERENCIA ELŐADÁSAI Szolnok 0. május 0. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
MŰSZAKI TUDOMÁNY AZ ÉSZAK-KELET MAGYARORSZÁGI RÉGIÓBAN 0 KONFERENCIA ELŐADÁSAI Szolnok 0. május 0. Szerkesztette: Edited by Pokorádi László Kiadja: Debreceni Akadémiai Bizottság Műszaki Szakbizottsága
Alap-ötlet: Karl Friedrich Gauss ( ) valószínűségszámítási háttér: Andrej Markov ( )
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel: 463-6-80 Fa: 463-30-9 http://www.vizgep.bme.hu Alap-ötlet:
IKR Agrár Kft. biztonsági elemzése Füzesabony Területi Központ
 2016. IKR Agrár Kft. biztonsági elemzése Füzesabony Területi Központ 5. számú melléklet Kockázat csökkentő intézkedés tervezete AGEL-CBI Kft. Verzió: 1.0 2016.04.30. IKR Agrár Kft. biztonsági elemzése
2016. IKR Agrár Kft. biztonsági elemzése Füzesabony Területi Központ 5. számú melléklet Kockázat csökkentő intézkedés tervezete AGEL-CBI Kft. Verzió: 1.0 2016.04.30. IKR Agrár Kft. biztonsági elemzése
Dinamikus modellek szerkezete, SDG modellek
 Diagnosztika - 3. p. 1/2 Modell Alapú Diagnosztika Diszkrét Módszerekkel Dinamikus modellek szerkezete, SDG modellek Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék Diagnosztika - 3.
Diagnosztika - 3. p. 1/2 Modell Alapú Diagnosztika Diszkrét Módszerekkel Dinamikus modellek szerkezete, SDG modellek Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék Diagnosztika - 3.
Irányítási struktúrák összehasonlító vizsgálata. Tóth László Richárd. Pannon Egyetem Vegyészmérnöki és Anyagtudományok Doktori Iskola
 Doktori (PhD) értekezés tézisei Irányítási struktúrák összehasonlító vizsgálata Tóth László Richárd Pannon Egyetem Vegyészmérnöki és Anyagtudományok Doktori Iskola Témavezetők: Dr. Szeifert Ferenc Dr.
Doktori (PhD) értekezés tézisei Irányítási struktúrák összehasonlító vizsgálata Tóth László Richárd Pannon Egyetem Vegyészmérnöki és Anyagtudományok Doktori Iskola Témavezetők: Dr. Szeifert Ferenc Dr.
Anyagjellemzők változásának hatása a fúróiszap hőmérsékletére
 Anyagjellemzők változásának hatása a fúróiszap hőmérsékletére Kis László, PhD. hallgató, okleveles olaj- és gázmérnök Miskolci Egyetem, Műszaki Földtudományi Kar Kőolaj és Földgáz Intézet Kulcsszavak:
Anyagjellemzők változásának hatása a fúróiszap hőmérsékletére Kis László, PhD. hallgató, okleveles olaj- és gázmérnök Miskolci Egyetem, Műszaki Földtudományi Kar Kőolaj és Földgáz Intézet Kulcsszavak:
Bozóki Sándor február 16. Érzékenységvizsgálat a Promethee módszertanban p. 1/18
 Érzékenységvizsgálat a Promethee módszertanban Bozóki Sándor 2011. február 16. Érzékenységvizsgálat a Promethee módszertanban p. 1/18 Vázlat PROMETHEE Parciális érzékenységvizsgálat egy szempontsúly változhat
Érzékenységvizsgálat a Promethee módszertanban Bozóki Sándor 2011. február 16. Érzékenységvizsgálat a Promethee módszertanban p. 1/18 Vázlat PROMETHEE Parciális érzékenységvizsgálat egy szempontsúly változhat
Publikációs lista. Gódor Győző. 2008. július 14. Cikk szerkesztett könyvben... 2. Külföldön megjelent idegen nyelvű folyóiratcikk...
 Publikációs lista Gódor Győző 2008. július 14. Cikk szerkesztett könyvben... 2 Külföldön megjelent idegen nyelvű folyóiratcikk... 2 Nemzetközi konferencia-kiadványban megjelent idegen nyelvű előadások...
Publikációs lista Gódor Győző 2008. július 14. Cikk szerkesztett könyvben... 2 Külföldön megjelent idegen nyelvű folyóiratcikk... 2 Nemzetközi konferencia-kiadványban megjelent idegen nyelvű előadások...
Mérnök informatikus (BSc) alapszak levelező tagozat (BIL) / BSc in Engineering Information Technology (Part Time)
 Mérnök informatikus (BSc) alapszak levelező tagozat (BIL) / BSc in Engineering Information Technology (Part Time) (specializáció választás a 4. félévben, specializációra lépés feltétele: az egyik szigorlat
Mérnök informatikus (BSc) alapszak levelező tagozat (BIL) / BSc in Engineering Information Technology (Part Time) (specializáció választás a 4. félévben, specializációra lépés feltétele: az egyik szigorlat
Határozatlan integrál (2) First Prev Next Last Go Back Full Screen Close Quit
 Határozatlan integrál () First Prev Next Last Go Back Full Screen Close Quit 1. Az összetett függvények integrálására szolgáló egyik módszer a helyettesítéssel való integrálás. Az idevonatkozó tétel pontos
Határozatlan integrál () First Prev Next Last Go Back Full Screen Close Quit 1. Az összetett függvények integrálására szolgáló egyik módszer a helyettesítéssel való integrálás. Az idevonatkozó tétel pontos
Konvexitás, elaszticitás
 DIFFERENCIÁLSZÁMÍTÁS ALKALMAZÁSAI Konveitás, elaszticitás Tanulási cél A másodrendű deriváltat vizsgálva milyen következtetéseket vonhatunk le a üggvény konveitására vonatkozóan. Elaszticitás ogalmának
DIFFERENCIÁLSZÁMÍTÁS ALKALMAZÁSAI Konveitás, elaszticitás Tanulási cél A másodrendű deriváltat vizsgálva milyen következtetéseket vonhatunk le a üggvény konveitására vonatkozóan. Elaszticitás ogalmának
Rugalmas láncgörbe alapvető összefüggések és tudnivalók I. rész
 Rugalmas láncgörbe alapvető összefüggések és tudnivalók I rész evezetés rugalmas láncgörbe magyar nyelvű szakirodalma nem túl gazdag Egy viszonylag rövid ismertetés található [ 1 ] - ben közönséges ( azaz
Rugalmas láncgörbe alapvető összefüggések és tudnivalók I rész evezetés rugalmas láncgörbe magyar nyelvű szakirodalma nem túl gazdag Egy viszonylag rövid ismertetés található [ 1 ] - ben közönséges ( azaz
I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE
 I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE Komplex termékek gyártására jellemző, hogy egy-egy termékbe akár több ezer alkatrész is beépül. Ilyenkor az alkatrészek általában sok különböző beszállítótól érkeznek,
I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE Komplex termékek gyártására jellemző, hogy egy-egy termékbe akár több ezer alkatrész is beépül. Ilyenkor az alkatrészek általában sok különböző beszállítótól érkeznek,
Tanulási cél Szorzatfüggvényekre vonatkozó integrálási technikák megismerése és különböző típusokra való alkalmazása. 5), akkor
 Integrálszámítás Integrálási szabályok Tanulási cél Szorzatfüggvényekre vonatkozó integrálási technikák megismerése és különböző típusokra való alkalmazása Motivációs feladat Valószínűség-számításnál találkozhatunk
Integrálszámítás Integrálási szabályok Tanulási cél Szorzatfüggvényekre vonatkozó integrálási technikák megismerése és különböző típusokra való alkalmazása Motivációs feladat Valószínűség-számításnál találkozhatunk
3. Előadás. Megyesi László: Lineáris algebra, oldal. 3. előadás Lineáris egyenletrendszerek
 3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
Függvények növekedési korlátainak jellemzése
 17 Függvények növekedési korlátainak jellemzése A jellemzés jól bevált eszközei az Ω, O, Θ, o és ω jelölések. Mivel az igények általában nemnegatívak, ezért az alábbi meghatározásokban mindenütt feltesszük,
17 Függvények növekedési korlátainak jellemzése A jellemzés jól bevált eszközei az Ω, O, Θ, o és ω jelölések. Mivel az igények általában nemnegatívak, ezért az alábbi meghatározásokban mindenütt feltesszük,
11. Előadás. 11. előadás Bevezetés a lineáris programozásba
 11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
SZÁMÍTÓGÉPES VIZUALIZÁCIÓ A MATEMATIKA TANÍTÁSÁBAN: ESZKÖZÖK, FEJLESZTÉSEK, TAPASZTALATOK
 SZÁMÍTÓGÉPES VIZUALIZÁCIÓ A MATEMATIKA TANÍTÁSÁBAN: ESZKÖZÖK, FEJLESZTÉSEK, TAPASZTALATOK Karsai János, karsai@silver.szote.u-szeged.hu, Forczek Erzsébet, forczek@dmi.szote.u-szeged.hu, Nyári Tibor, nyari@dmi.szote.u-szeged.hu
SZÁMÍTÓGÉPES VIZUALIZÁCIÓ A MATEMATIKA TANÍTÁSÁBAN: ESZKÖZÖK, FEJLESZTÉSEK, TAPASZTALATOK Karsai János, karsai@silver.szote.u-szeged.hu, Forczek Erzsébet, forczek@dmi.szote.u-szeged.hu, Nyári Tibor, nyari@dmi.szote.u-szeged.hu
Dr. Kalló Noémi. Termelés- és szolgáltatásmenedzsment. egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék. Dr.
 Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Ismertesse a legfontosabb előrejelzési módszereket és azok gyakorlati
Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Ismertesse a legfontosabb előrejelzési módszereket és azok gyakorlati
Optimális mérési elrendezés hidraulikus hálózatokon
 Optimális mérési elrendezés hidraulikus hálózatokon MaSzeSz Juniuor Szimpózium Wéber Richárd PhD hallgató, III. félév BME, GPK, Hidrodinamikai Rendszerek Tanszék Budapest, 2018, egyetemi docens Tartalom
Optimális mérési elrendezés hidraulikus hálózatokon MaSzeSz Juniuor Szimpózium Wéber Richárd PhD hallgató, III. félév BME, GPK, Hidrodinamikai Rendszerek Tanszék Budapest, 2018, egyetemi docens Tartalom
Matematikai geodéziai számítások 5.
 Matematikai geodéziai számítások 5 Hibaterjedési feladatok Dr Bácsatyai László Matematikai geodéziai számítások 5: Hibaterjedési feladatok Dr Bácsatyai László Lektor: Dr Benedek Judit Ez a modul a TÁMOP
Matematikai geodéziai számítások 5 Hibaterjedési feladatok Dr Bácsatyai László Matematikai geodéziai számítások 5: Hibaterjedési feladatok Dr Bácsatyai László Lektor: Dr Benedek Judit Ez a modul a TÁMOP
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
Publikációs jegyzék. Sitkuné Görömbei Cecília PKK, Tanítóképző Intézet
 Publikációs jegyzék Sitkuné Görömbei Cecília PKK, Tanítóképző Intézet Referált cikk nemzetközi folyóiratban 1. Sitkuné Görömbei Cecília: Shall we use one more representation? Suggestions about establishing
Publikációs jegyzék Sitkuné Görömbei Cecília PKK, Tanítóképző Intézet Referált cikk nemzetközi folyóiratban 1. Sitkuné Görömbei Cecília: Shall we use one more representation? Suggestions about establishing
Sportberuházások pénzügyi és közgazdasági érzékenységvizsgálata kockázatok egy sportlétesítmény életében
 Sportberuházások pénzügyi és közgazdasági érzékenységvizsgálata kockázatok egy sportlétesítmény életében Vörös Tünde Széchenyi István Egyetem Nyerges Mihály Emlékkonferencia 2017.01.26. Probléma felvetés
Sportberuházások pénzügyi és közgazdasági érzékenységvizsgálata kockázatok egy sportlétesítmény életében Vörös Tünde Széchenyi István Egyetem Nyerges Mihály Emlékkonferencia 2017.01.26. Probléma felvetés
Publikációk. Libor Józsefné dr.
 Publikációk Libor Józsefné dr. Referált publikációk/ Refereed publications 1, Libor Józsefné, Tómács Tibor: Rényi-Hajek inequality and its applications. ( Annales Mathematicae et Informaticae, 33. Eger,
Publikációk Libor Józsefné dr. Referált publikációk/ Refereed publications 1, Libor Józsefné, Tómács Tibor: Rényi-Hajek inequality and its applications. ( Annales Mathematicae et Informaticae, 33. Eger,
MŰSZAKI MEGBÍZHATÓSÁGÁNAK VIZSGÁLATI MÓDSZEREI EXAMINATION METHODS FOR EVALUATING RELIABILITY IN COMPLEX MILITARY RECONNAISSANCE SYSTEMS.
 BÁRKÁNYI PÁL KOMPLEX KATONAI FELDERÍTŐ RENDSZEREK MŰSZAKI MEGBÍZHATÓSÁGÁNAK VIZSGÁLATI MÓDSZEREI EXAMINATION METHODS FOR EVALUATING RELIABILITY IN COMPLEX MILITARY RECONNAISSANCE SYSTEMS A cikk a komplex
BÁRKÁNYI PÁL KOMPLEX KATONAI FELDERÍTŐ RENDSZEREK MŰSZAKI MEGBÍZHATÓSÁGÁNAK VIZSGÁLATI MÓDSZEREI EXAMINATION METHODS FOR EVALUATING RELIABILITY IN COMPLEX MILITARY RECONNAISSANCE SYSTEMS A cikk a komplex
Ensemble előrejelzések: elméleti és gyakorlati háttér HÁGEL Edit Országos Meteorológiai Szolgálat Numerikus Modellező és Éghajlat-dinamikai Osztály 34
 Ensemble előrejelzések: elméleti és gyakorlati háttér HÁGEL Edit Országos Meteorológiai Szolgálat Numerikus Modellező és Éghajlat-dinamikai Osztály 34. Meteorológiai Tudományos Napok Az előadás vázlata
Ensemble előrejelzések: elméleti és gyakorlati háttér HÁGEL Edit Országos Meteorológiai Szolgálat Numerikus Modellező és Éghajlat-dinamikai Osztály 34. Meteorológiai Tudományos Napok Az előadás vázlata
Dinamikus rendszerek identifikációja genetikus programozással
 Dinamikus rendszerek identifikációja genetikus programozással Madár János, Abonyi János, Szeifert Ferenc Veszprémi Egyetem, Folyamatmérnöki Tanszék www.fmt.vein.hu/softcomp, abonyij@fmt.vein.hu Kulcsszavak:
Dinamikus rendszerek identifikációja genetikus programozással Madár János, Abonyi János, Szeifert Ferenc Veszprémi Egyetem, Folyamatmérnöki Tanszék www.fmt.vein.hu/softcomp, abonyij@fmt.vein.hu Kulcsszavak:
Quadkopter szimulációja LabVIEW környezetben Simulation of a Quadcopter with LabVIEW
 Quadkopter szimulációja LabVIEW környezetben Simulation of a Quadcopter with LabVIEW T. KISS 1 P. T. SZEMES 2 1University of Debrecen, kiss.tamas93@gmail.com 2University of Debrecen, szemespeter@eng.unideb.hu
Quadkopter szimulációja LabVIEW környezetben Simulation of a Quadcopter with LabVIEW T. KISS 1 P. T. SZEMES 2 1University of Debrecen, kiss.tamas93@gmail.com 2University of Debrecen, szemespeter@eng.unideb.hu
ICT ÉS BP RENDSZEREK HATÉKONY TELJESÍTMÉNY SZIMULÁCIÓJA DR. MUKA LÁSZLÓ
 ICT ÉS BP RENDSZEREK HATÉKONY TELJESÍTMÉNY SZIMULÁCIÓJA DR. MUKA LÁSZLÓ 1 TARTALOM 1.1 A MODELLEZÉS ÉS SZIMULÁCIÓ META-SZINTŰ HATÉKONYSÁGÁNAK JAVÍTÁSA A. Az SMM definiálása, a Jackson Keys módszer kiterjesztése
ICT ÉS BP RENDSZEREK HATÉKONY TELJESÍTMÉNY SZIMULÁCIÓJA DR. MUKA LÁSZLÓ 1 TARTALOM 1.1 A MODELLEZÉS ÉS SZIMULÁCIÓ META-SZINTŰ HATÉKONYSÁGÁNAK JAVÍTÁSA A. Az SMM definiálása, a Jackson Keys módszer kiterjesztése
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
Generátor differenciálvédelmi funkció blokk leírása
 Generátor differenciálvédelmi funkció blokk leírása Dokumentum azonosító: V1.2 Budapest, 2015. május A leírás verzió-információja Verzió Dátum Változás Szerkesztette 1.1 2015-05-25 Első verzió, angolból
Generátor differenciálvédelmi funkció blokk leírása Dokumentum azonosító: V1.2 Budapest, 2015. május A leírás verzió-információja Verzió Dátum Változás Szerkesztette 1.1 2015-05-25 Első verzió, angolból
BME Szilárdságtani és Tartószerkezeti Tanszék. Tartószerkezet-rekonstrukciós Szakmérnöki Képzés. Dr. Móczár Balázs
 Dr. Móczár Balázs 1 Az előadás célja MSZ EN 1997 1 szabvány 6. fejezetében és egyes mellékleteiben leírt síkalapozással kapcsolatos előírások lényegesebb elemeinek, a szabvány elveinek bemutatása Az eddig
Dr. Móczár Balázs 1 Az előadás célja MSZ EN 1997 1 szabvány 6. fejezetében és egyes mellékleteiben leírt síkalapozással kapcsolatos előírások lényegesebb elemeinek, a szabvány elveinek bemutatása Az eddig
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
(kidolgozta: Dr. Nagy Zoltán egyetemi adjunktus)
 Széchenyi István Egyetem Műszaki Tudományi Kar Alkalmazott Mechanika Tanszék GÉPEK DINAMIKÁJA 2.gyak.hét 1. és 2. Feladat (kidolgozta: Dr. Nagy Zoltán egyetemi adjunktus) Gépek dinamikája - 2. gyakorlat
Széchenyi István Egyetem Műszaki Tudományi Kar Alkalmazott Mechanika Tanszék GÉPEK DINAMIKÁJA 2.gyak.hét 1. és 2. Feladat (kidolgozta: Dr. Nagy Zoltán egyetemi adjunktus) Gépek dinamikája - 2. gyakorlat
Nem teljesen kitöltött páros összehasonlítás mátrixok sajátérték optimalizálása Newton-módszerrel p. 1/29. Ábele-Nagy Kristóf BCE, ELTE
 Nem teljesen kitöltött páros összehasonlítás mátrixok sajátérték optimalizálása Newton-módszerrel Ábele-Nagy Kristóf BCE, ELTE Bozóki Sándor BCE, MTA SZTAKI 2010. november 4. Nem teljesen kitöltött páros
Nem teljesen kitöltött páros összehasonlítás mátrixok sajátérték optimalizálása Newton-módszerrel Ábele-Nagy Kristóf BCE, ELTE Bozóki Sándor BCE, MTA SZTAKI 2010. november 4. Nem teljesen kitöltött páros
ZRÍNYI MIKLÓS NEMZETVÉDELMI EGYETEM BOLYAI JÁNOS KATONAI MŰSZAKI KAR AUTOMATIZÁLÁSI ÉS ROBOTIKAI INTÉZET
 ZRÍNYI MIKLÓS NEMZETVÉDELMI EGYETEM BOLYAI JÁNOS KATONAI MŰSZAKI KAR AUTOMATIZÁLÁSI ÉS ROBOTIKAI INTÉZET Prof. Dr. Szabolcsi Róbert okl. ml. ezredes egyetemi tanár tudományos és nemzetközi kapcsolatok
ZRÍNYI MIKLÓS NEMZETVÉDELMI EGYETEM BOLYAI JÁNOS KATONAI MŰSZAKI KAR AUTOMATIZÁLÁSI ÉS ROBOTIKAI INTÉZET Prof. Dr. Szabolcsi Róbert okl. ml. ezredes egyetemi tanár tudományos és nemzetközi kapcsolatok
Regresszió. Fő cél: jóslás Történhet:
 Fő cél: jóslás Történhet: Regresszó 1 változó több változó segítségével Lépések: Létezk-e valamlyen kapcsolat a 2 változó között? Kapcsolat természetének leírása (mat. egy.) A regresszós egyenlet alapján
Fő cél: jóslás Történhet: Regresszó 1 változó több változó segítségével Lépések: Létezk-e valamlyen kapcsolat a 2 változó között? Kapcsolat természetének leírása (mat. egy.) A regresszós egyenlet alapján
Mérés és modellezés 1
 Mérés és modellezés 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni kell
Mérés és modellezés 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni kell
Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel
 Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel Segédlet az A végeselem módszer alapjai tárgy 4. laborgyakorlatához http://www.mm.bme.hu/~kossa/vemalap4.pdf Kossa Attila (kossa@mm.bme.hu)
Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel Segédlet az A végeselem módszer alapjai tárgy 4. laborgyakorlatához http://www.mm.bme.hu/~kossa/vemalap4.pdf Kossa Attila (kossa@mm.bme.hu)
Kétdimenziós mesterséges festési eljárások. Hatások és alkalmazások
 Pannon Egyetem Informatikai Tudományok Doktori Iskola Tézisfüzet Kétdimenziós mesterséges festési eljárások. Hatások és alkalmazások Kovács Levente Képfeldolgozás és Neuroszámítógépek Tanszék Témavezet
Pannon Egyetem Informatikai Tudományok Doktori Iskola Tézisfüzet Kétdimenziós mesterséges festési eljárások. Hatások és alkalmazások Kovács Levente Képfeldolgozás és Neuroszámítógépek Tanszék Témavezet
EGYÜTTMŰKÖDŐ ÉS VERSENGŐ ERŐFORRÁSOK SZERVEZÉSÉT TÁMOGATÓ ÁGENS RENDSZER KIDOLGOZÁSA
 infokommunikációs technológiák EGYÜTTMŰKÖDŐ ÉS VERSENGŐ ERŐFORRÁSOK SZERVEZÉSÉT TÁMOGATÓ ÁGENS RENDSZER KIDOLGOZÁSA Témavezető: Tarczali Tünde Témavezetői beszámoló 2015. január 7. TÉMAKÖR Felhő technológián
infokommunikációs technológiák EGYÜTTMŰKÖDŐ ÉS VERSENGŐ ERŐFORRÁSOK SZERVEZÉSÉT TÁMOGATÓ ÁGENS RENDSZER KIDOLGOZÁSA Témavezető: Tarczali Tünde Témavezetői beszámoló 2015. január 7. TÉMAKÖR Felhő technológián
Irányítástechnika 2. előadás
 Irányítástechnika 2. előadás Dr. Kovács Levente 2013. 03. 19. 2013.03.19. Tartalom Tipikus vizsgálójelek és azok információtartalma Laplace transzformáció, állapotegyenlet, átviteli függvény Alaptagok
Irányítástechnika 2. előadás Dr. Kovács Levente 2013. 03. 19. 2013.03.19. Tartalom Tipikus vizsgálójelek és azok információtartalma Laplace transzformáció, állapotegyenlet, átviteli függvény Alaptagok
A matematikai feladatok és megoldások konvenciói
 A matematikai feladatok és megoldások konvenciói Kozárné Fazekas Anna Kántor Sándor Matematika és Informatika Didaktikai Konferencia - Szatmárnémeti 2011. január 28-30. Konvenciók Mindenki által elfogadott
A matematikai feladatok és megoldások konvenciói Kozárné Fazekas Anna Kántor Sándor Matematika és Informatika Didaktikai Konferencia - Szatmárnémeti 2011. január 28-30. Konvenciók Mindenki által elfogadott
A szimplex algoritmus
 A szimplex algoritmus Ismétlés: reprezentációs tétel, az optimális megoldás és az extrém pontok kapcsolata Alapfogalmak: bázisok, bázismegoldások, megengedett bázismegoldások, degenerált bázismegoldás
A szimplex algoritmus Ismétlés: reprezentációs tétel, az optimális megoldás és az extrém pontok kapcsolata Alapfogalmak: bázisok, bázismegoldások, megengedett bázismegoldások, degenerált bázismegoldás
1. Oldja meg a z 3 (5 + 3j) (8 + 2j) 2. Adottak az A(1,4,3), B(3,1, 1), C( 5,2,4) pontok a térben.
 Szak: Műszaki menedzser I. Dátum: 006. június. MEGOLDÓKULCS Tárgy: Matematika szigorlat Idő: 0 perc Neptun kód: Előadó: Berta Gábor szig 06 06 0 Pontszám: /00p. Oldja meg a z (5 + j (8 + j + = (+5j (7
Szak: Műszaki menedzser I. Dátum: 006. június. MEGOLDÓKULCS Tárgy: Matematika szigorlat Idő: 0 perc Neptun kód: Előadó: Berta Gábor szig 06 06 0 Pontszám: /00p. Oldja meg a z (5 + j (8 + j + = (+5j (7
Elektro-pneumatikus tengelykapcsoló rendszerek megfigyelő alapú előrecsatolt/visszacsatolt irányítása. Szimandl Barna
 Elektro-pneumatikus tengelykapcsoló rendszerek megfigyelő alapú előrecsatolt/visszacsatolt irányítása Tézisek Szimandl Barna Témavezető: Németh Huba Kandó Kálmán Doktori Iskola Közlekedés- és járműtudományok
Elektro-pneumatikus tengelykapcsoló rendszerek megfigyelő alapú előrecsatolt/visszacsatolt irányítása Tézisek Szimandl Barna Témavezető: Németh Huba Kandó Kálmán Doktori Iskola Közlekedés- és járműtudományok
Matematikai geodéziai számítások 9.
 Matematikai geodéziai számítások 9 Szabad álláspont kiegyenlítése Dr Bácsatyai, László Created by XMLmind XSL-FO Converter Matematikai geodéziai számítások 9: Szabad álláspont kiegyenlítése Dr Bácsatyai,
Matematikai geodéziai számítások 9 Szabad álláspont kiegyenlítése Dr Bácsatyai, László Created by XMLmind XSL-FO Converter Matematikai geodéziai számítások 9: Szabad álláspont kiegyenlítése Dr Bácsatyai,
Bevezetés az állapottér-elméletbe Dinamikus rendszerek állapottér reprezentációi
 Tartalom Bevezetés az állapottér-elméletbe Irányítható alak Megfigyelhetőségi alak Diagonális alak Állapottér transzformáció 2018 1 A szabályozáselmélet klasszikus, BODE, NICHOLS, NYQUIST nevéhez kötődő,
Tartalom Bevezetés az állapottér-elméletbe Irányítható alak Megfigyelhetőségi alak Diagonális alak Állapottér transzformáció 2018 1 A szabályozáselmélet klasszikus, BODE, NICHOLS, NYQUIST nevéhez kötődő,
Lövedékálló védőmellény megfelelőségének elemzése lenyomatmélységek (traumahatás) alapján
 Lövedékálló védőmellény megfelelőségének elemzése lenyomatmélységek (traumahatás) alapján Eur.Ing. Frank György c. docens az SzVMSzK Szakmai Kollégium elnöke SzVMSzK mérnök szakértő (B5) A lövedékálló
Lövedékálló védőmellény megfelelőségének elemzése lenyomatmélységek (traumahatás) alapján Eur.Ing. Frank György c. docens az SzVMSzK Szakmai Kollégium elnöke SzVMSzK mérnök szakértő (B5) A lövedékálló
A katasztrófavédelemben is alkalmazható (determinisztikus) logikai kockázatelemzési módszer
 Dr Károlyi László A katasztrófavédelemben is alkalmazható (determinisztikus) logikai kockázatelemzési módszer A kockázatkezelés ún. hibafa-módszere alapján el lehet eljutni egy egyedi eseményeket kezelni
Dr Károlyi László A katasztrófavédelemben is alkalmazható (determinisztikus) logikai kockázatelemzési módszer A kockázatkezelés ún. hibafa-módszere alapján el lehet eljutni egy egyedi eseményeket kezelni
Pacemaker készülékek szoftverének verifikációja. Hesz Gábor
 Pacemaker készülékek szoftverének verifikációja Hesz Gábor A szív felépítése http://hu.wikipedia.org/w/index.php?title=fájl:diagram_of_the_human_heart_hu.svg http://en.wikipedia.org/wiki/file:conductionsystemoftheheartwithouttheheart.png
Pacemaker készülékek szoftverének verifikációja Hesz Gábor A szív felépítése http://hu.wikipedia.org/w/index.php?title=fájl:diagram_of_the_human_heart_hu.svg http://en.wikipedia.org/wiki/file:conductionsystemoftheheartwithouttheheart.png
Bevezetés az informatikába
 Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
DR. KOKOVAY ÁGNES. Személyes információk. Születési hely, idő: 1956. május 30. Várpalota. Képzettség
 DR. KOKOVAY ÁGNES Személyes információk Születési hely, idő: 1956. május 30. Várpalota Képzettség Középiskolai testnevelő tanár (1978) Aerobic oktató (1983) Kézilabda szakedző (1989) C kategóriás néptáncoktató
DR. KOKOVAY ÁGNES Személyes információk Születési hely, idő: 1956. május 30. Várpalota Képzettség Középiskolai testnevelő tanár (1978) Aerobic oktató (1983) Kézilabda szakedző (1989) C kategóriás néptáncoktató
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
LINEÁRIS EGYENLETRENDSZEREK október 12. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak
 LINEÁRIS EGYENLETRENDSZEREK 004. október. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László:
LINEÁRIS EGYENLETRENDSZEREK 004. október. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László:
FELADATMEGOLDÁSI SZOKÁSAINAK VIZSGÁLATA. Baranyai Tünde
 Volume 3, Number 1, 2013 3. kötet, 1. szám, 2013 A SZATMÁRNÉMETI TANÍTÓ- ÉS ÓVÓKÉPZŐS HALLGATÓK FELADATMEGOLDÁSI SZOKÁSAINAK VIZSGÁLATA THE EXAMINATION OF TEACHER TRAINING COLLEGE STUDENTS PROBLEM-SOLVING
Volume 3, Number 1, 2013 3. kötet, 1. szám, 2013 A SZATMÁRNÉMETI TANÍTÓ- ÉS ÓVÓKÉPZŐS HALLGATÓK FELADATMEGOLDÁSI SZOKÁSAINAK VIZSGÁLATA THE EXAMINATION OF TEACHER TRAINING COLLEGE STUDENTS PROBLEM-SOLVING
9. Előadás. Megyesi László: Lineáris algebra, oldal. 9. előadás Mátrix inverze, Leontyev-modell
 9. Előadás Megyesi László: Lineáris algebra, 75. 84. oldal. Gondolkodnivalók Mátrix rangja 1. Gondolkodnivaló Tegyük fel, hogy egy elemi bázistranszformáció kezdetekor a sor- és oszlopindexek sorban helyezkednek
9. Előadás Megyesi László: Lineáris algebra, 75. 84. oldal. Gondolkodnivalók Mátrix rangja 1. Gondolkodnivaló Tegyük fel, hogy egy elemi bázistranszformáció kezdetekor a sor- és oszlopindexek sorban helyezkednek
1. ábra Modell tér I.
 1 Veres György Átbocsátó képesség vizsgálata számítógépes modell segítségével A kiürítés szimuláló számítógépes modellek egyes apró, de igen fontos részletek vizsgálatára is felhasználhatóak. Az átbocsátóképesség
1 Veres György Átbocsátó képesség vizsgálata számítógépes modell segítségével A kiürítés szimuláló számítógépes modellek egyes apró, de igen fontos részletek vizsgálatára is felhasználhatóak. Az átbocsátóképesség
