Elektromos vezetési tulajdonságok Fémek, szupravezetők
|
|
|
- Attila Szőke
- 7 évvel ezelőtt
- Látták:
Átírás
1 Elektromos tulajdonságok Fémek, szupravezetők Roncsolásmentes anyagvizsgálat tárgy Dr. Mészáros István BME, Anyagtudomány és Technológia Tanszék Elektromos vezetési tulajdonságok Fémek, szupravezetők Vezetési jelenségek (transzportfolyamatok) fenomenologikus leírása Elektromos vezetés: külső E Þ töltéstranszport j = s grad U = s E 1
2 j j du = s dx = s gradu 1 dw - s q dx F -s S 1 - s gradw q dt dx F -s S gradt Diff. Ohm törvény Kontakt potenciál Peltier-hatás Seebeck-hatás Potenciál gradiens Fermi-szint gradiens Hőmérséklet grad (anyagminőség változás) fém-fém (hőelem) pn-átmenet Schottky-átmenet Elektromos- és hővezetés kapcsolata k L = Franz - Wiedmann törvény s T (főként egyvegyértékű fémekre) k = LsT L = 2, WW/K 2 Lorentz-szám Transzportban részvevő részecskék: Elektromos vezetés: Hővezetés: Szabad elektronok T = állandó k = konst s Szabad elektronok Fononok (rácsrezgés kvantum) Kivételek! pl. gyémánt 2
3 Elektromos vezetési folyamatban töltést továbbító (elmozdulni képes) részecskék: Vezetők fémek szabad elektron ötvözetek szabad elektron elektrolitok + és - ionok plazma áll. gázok + és - ionok Félvezetők elemi szabad elektronok, lyukak vegyület szabad elektronok, lyukak Szigetelők kovalens kristályok szabad elektronok, lyukak ionos kristályok szabad elektronok, lyukak folyadékok gázok + és - ionok + és - ionok Vezető anyagok klasszikus csoportosítása s (fajlagos vezetőképesség) Siemens/m, 1/Ohm m < 10-8 S/m szigetelő S/m félvezető > 10 6 S/m fémes vezető l R = r A 1 s = r r é s ê ë [ Wm] S m ù ú û 3
4 Fajlagos ellenállás irányfüggése izotróp (köbös szerezetű egykristályok, polikristályok) anizotróp (alacsony szimmetriájú kristályok: hex., tetragonális ) pl: Cd, Mg, Zn, C (grafit): r r párhuzamos meroleges» 1000 Matematikai leírása: tenzor mennyiség Vezetési mechanizmusok leírása Klasszikus (Sommerfeld-féle, szabad-elektron modell) Feltételezés: elektromok között nincs kölcsönhatás (ideális gáz) Elektron mozgása: Rendezetlen termikus mozgás + sodródás (drift) Kvantummechanikai leírás Elektronhoz rendelt síkhullám mozgása a rácsperiodikus potenciáltérben. Vezető test: potenciálgödör. 4
5 v (sebesség) j = q n v d t (idő) q E vd = t m 2 n q t j = E = s E m v drift t: átl. élettartam l: átl. szabad úthossz v d = µ E µ n : elektron mozg. µ p : lyuk mozg. anizotróp, [cm 2 /Vs] Mérése: Hall - effektus C- V mérés Eredmények: Differenciális Ohm-törvény 1-2 vegyértékű fémekre jó fajlagos ellenállás értékek Problémák: azonos fém allotróp módosulatai többvegyértékű fémek (számított fajlagos ellenállás hibás) Félvezetők, szigetelők (hőmérsékletfüggés nem magyarázható) s (T, megvilágítás, külső E, sugárzás ) s = const e - E kt 5
6 Elektron kettős természete: korpuszkuláris, hullám de Broglie: h l = mv -34 6,6 10 Js l = -31 9,1 10 kg 10 5 m s 25 C, szabad e - : E=26meV ß 10 5 m/s termikus sebesség = 7,3nm Û rácsállandó» 0,3-0,4 nm ß csak kvantummechanikai leírás lehetséges Probléma: elektronhoz rendelt síkhullám terjedése rácsperiodokus potenciáltérben 2p 2p 1 k = k = = mv = mv l h! 1 E = mv 2 2! E = k 2m æ k! ö = mç 2 è m ø p ± 2a p ± 3 2a Szabad elektronok esetén Kristály: Brillouin zónák Þ zónahatárok E(k) szintfelületek (4dim Þ célszerű síkmetszetek) 6
7 Fémek fajlagos ellenállását befolyásoló tényezők periodikus pot. tér torzulása Þ r növekedése rácsrendezetlenség termikus rácsrezgések ponthibák diszlokációk (alakítás) felületszerű hibák (szemcseméret) térfogati hibák (kiválások, új fázis) rácstorzulás (szilárd oldatos ötvözés)... Matthiesen-szabály (szeparálható fv.) ( T, c, e ) = r ( T ) + r ( c) + r ( e ) + r r hőmérsékletfüggése (fémes vezető) r r r 2 n ( T ) = r ( 1+ adt + bdt + + µ DT ) ( T ) = r ( 1+ adt ) 1 Dr ar = r DT Maradó ellenállás m * m * æ 1 r = = nq t nq ç 2 2 èt R 1 ö + = rr + rt t T ø» 100K 2/3OP OP T (K) kr. hibák Þ maradó ellenállás Szupravezető: maradó ellenállás nulla Lineáris viselkedéstől eltér ha van: ferro-paramágneses átmenet allotróp átalakulás fázis átalakulás 7
8 Ötvözés hatása ötvöző perturbálja a potenciál teret Þ növeli a r-t szilárd oldat esetén második fázis (vegyület) Dr ññd 1 r 2 T olvadék T olvadék olvadék + a olv. + A olv. + B T 1 szilárd oldat (a) A + B T 1 a. A C B B a. A B r, a r T 1 r T 1 r r B b. A r A a r rb C B ( c) Drötv = Ac 1- B b. A r A r = r V + r V ötv A A B B B 8
9 Nordheim-szabály Dr ötv = A ( 1- c) ( r - r ) c + Ac( 1- c) Ac r = r + A B Mott-szabály Dr = Ac Þ Dr AB = Dr BA Rendezett rácsú szilárd oldat Ni 3 Al superalloy Képlékeny alakítás, hőkezelés hatása Fajlagos-ellenállás növekmény Alakítás mértéke Képlékeny alakítás Þ vakanciák, diszlokációk n Dr = k e e ln Dr = n lne + lnk e Egyensúly felé tart a rendszer r csökken. 9
10 Szupravezetés Kamerlingh 1911 (Hg) 28 elem és több mint 1000 vegyület Nb 7,5K Hg 4.15 K Nb 3 Sn 18,1K Nb 3 Al 17,5K V 3 Si 17K V 3 Ga 16,8K Elem nem lehet szupravezető ha: egy vegyértékű rendezett mágneses szerkezete van Higany ellenállásának hőmérsékletfüggése Kammerlingh-Onnes mérése,
11 Bardeen-Cooper-Schrieffer BCS-elmélet Szupravezető állapotban: Cooper-párok (2e - töltés) (+1/2) - (-1/2) spínű elektron párok a töltéshordozók ß nincs taszító kölcsönhatás Cooper-pár: elektron-fonon-elektron kölcsönhatás Elektron hullám terjed rácsrezgést (fonon) kelthet pályája megváltozik Másik terjedő elektron a rezgő rácsot érzi a rácsrezgést megszüntetheti (a fonont elnyelheti) pályája megváltozik A rács közvetítésével tehát a két elektron egymás pályáját befolyásolja. Ha ez elég erős, a két elektronból kötött pár alakulhat ki. Ezt nevezzük Cooper-párnak. Nem érvényes rájuk a Pauli elv betöltött szintet is elfoglalhatnak. Josephson-jelenség 11
12 Elektronok alagutazása M-I-M átmenetben Alagút effektus (fölötte nem de keresztül igen) A hullámfüggvény mindkét oldalról belóg a szigetelőbe. Az elektronok csak akkor juthatnak át a szigetelőn ha a túloldalon van betöltetlen energiaszint. Azaz, ha van feszültség különbség. Cooper-párok alagutazása S-I-S átmenetben Josephson-jelenség A Cooper-pár akkor is átalagutazhat a másik oldalra ha nincs feszültségkülönbség. Nem érvényes a Pauli-elv. 12
13 Josephsoninterferencia SQUID elve Két párhuzamosan kapcsolt Josephson-átmenet (szupra-szigetelő-szupra) A gyűrű belsejében haladó mágneses erővonalak megváltoztatják a Cooperpárok fázisviszonyait interferencia áram erőssége függ a B-től. SQUID (szupravezető kvantum interferométer) Érzékenység: fempto T (10-15 T) Meissner-effektus Mágneses tér erővonalai kiszorulnak Szupravezető: ideális diamágnes (I. fajú) B = µ 0 M = kh ( H + M ) B = 0 Þ H = -M Þ k = -1 13
14 Szupravezető I. fajú II. fajú Behatoló B vonalak a II. fajú szupravezetőbe Vortex vonalak I. és II. fajú szupravezetők M mágnesezettségének alakulása a külső tér függvényében Hc1: alsó kritikus térerő Hc2: felső kritikus térerő Hc1 alatt: ideális diamágnes Hc1-Hc2: H tér behatol Meissner-Higgs effektus Szupravezető állaptban T<T c I. fajú: (Pb) a B-vonalak kiszorulnak a mintából (B belül =0) (A szupravezetőben belül indukálódó áramok tere kompenzálja a külső tér indukcióját.) II. fajú: (Nb) a B a minta nagyrészéből kiszorul (B=0) csak a hiba ún. vortex vonalak mentén sűrűsödik. A B-vonalak a minta felületébe (és a vortexek környezetében) ~10 nm mélységben behatolnak a szupravezetőbe. 14
15 Szupravezető Elem Ötvözet Vegyület (intermetallikus) Kerámia (rideg, törékeny, magas Tc) Többkomponensű Magas hőmérsékletű szupravezető: T c > 77 K (-196 ºC) folyékony nitrogén/levegő Szupravezető elemek a periódusos rendszerben 15
16 Ismertebb I. és II. fajú szupravezető elemek és T c (K) Ti 0,39 Zr 0,55 V 5,03 Nb 9,5 Ta 4,48 *** Zn 0,86 Cd 0,52 Hg 4,15 Al 1,18 Ga 1,09 In 3,41 Tl 2,37 Sn 3,72 Pb 7,19 Néhány többkomponensű szupravezető ( Több ezer ismert. Hg 0.8 Tl 0.2 Ba 2 Ca 2 Cu 3 O K (Rekord tartó) TET HgBa 2 Ca 2 Cu 3 O K TET Tl 0.5 Pb 0.5 Sr 2 Ca 2 Cu 3 O K TET Bi 2 Sr 2 Ca 2 Cu 3 O K ORTR Ca 1-x Sr x CuO K (legmagasabb Tc 4 komp.) GdBa 2 Cu 3 O 7 94 K TET YBa 2 Cu 3 O 7 93 K TET Nb 3 Ge 23,2 K Perovszkit (β-volfram) Nb 3 Si 19 K Perovszkit (β-volfram) Nb 3 Al 18 K Perovszkit (β-volfram) 16
17 Perovskit-szerkezet b-volfram pl: Nb 3 Sn A Perovszkit szerkezet Az A 3 B képletű (vegyületfázis) szupravezetők szerkezete többségében ilyen. T C, H C, (J C ) H = H C é æ T ê1 - ç êë è TC ö ø 2 ù ú úû j H = 2 rp 17
18 Fejlesztési irányok: T c, H c, technológia Alkalmazások: Tekercs (nagy indukciójú terek előállítása) SQUID (kis indukciók mérése B < 0,01 nt) Lebegtetés (vasút) Energiatárolás (szupravezető csapágy, lendkerék) Távvezeték (vesztesség nélküli áramtovábbítás) Technológiai problémák Rideg, törékeny alakos testek (pl. tekercs gyártása) Szupravezető tekercs (Nb 3 Sn) Nb(tkk) + Sn(tetragonális) porkeverék Cu csőben + hőkezelés típusú szupravezetők (T c =80-90 K) Y-X 2 -Cu 3 -O 7 Y: ritkaföldfém: Ittrium (Y), Gadolinium (Gd), Túlium (Tm) X: Ba, Ca, K Például: Y-Ba 2 -Cu 3 -O 7 YBCO, T c =93 K, tetragonális Valós szerkezet: Cu-Ba 2 -Y-Cu 2 -O 7 azaz: Előállítás: Y 2 O 3 + Ba(OH) 2 x 8 H 2 O + CuO YBa 2 Cu 3 O 7 Porok préselése + hőkezelés 18
19 Y 2 BaCu zöld fázis nem szupravezető fázis pinning centrum, hiba amely segít az erővonalak befogásában (vortex). Hibák előnyösek szándékosan bevitt pinning centerek. Szupravezető felmágnesezése (csak II. fajú esetén) FC: field cooled (sok erővonalat fog be, erős felmágnesezés) ZFC: zero field cooled (kevés befogott erővonal, gyenge) Szupravezetők alkalmazási példái Lebegtetés 19
20 SmCo permanens mágnes lebegése YBCO szupravezető fölött. Video: Lebegés MAGLEV vonat Japán > 500 km/h 20
21 Extrém kis mágneses terek mérése SQUID-detektorral Orvosi alkalmazások 21
Szupravezetés. Mágneses tér mérő szenzorok (DC, AC) BME, Anyagtudomány és Technológia Tanszék. Dr. Mészáros István. Előadásvázlat 2013.
 BME, Anyagtudomány és Technológia Tanszék Dr. Mészáros István Szupravezetés Előadásvázlat 2013. Mágneses tér mérő szenzorok (DC, AC) Erő ill. nyomaték mérésen alapuló eszközök Tekercs (induktív) Magnetorezisztív
BME, Anyagtudomány és Technológia Tanszék Dr. Mészáros István Szupravezetés Előadásvázlat 2013. Mágneses tér mérő szenzorok (DC, AC) Erő ill. nyomaték mérésen alapuló eszközök Tekercs (induktív) Magnetorezisztív
Vezetési jelenségek, vezetőanyagok
 Anyagszerkezettan és anyagvizsgálat 2015/16 Vezetési jelenségek, vezetőanyagok Dr. Szabó Péter János szpj@eik.bme.hu Elektromos vezetési folyamatban töltést továbbító (elmozdulni képes) részecskék: Vezetők
Anyagszerkezettan és anyagvizsgálat 2015/16 Vezetési jelenségek, vezetőanyagok Dr. Szabó Péter János szpj@eik.bme.hu Elektromos vezetési folyamatban töltést továbbító (elmozdulni képes) részecskék: Vezetők
Elektromos vezetési tulajdonságok
 Elektromos vezetési tulajdonságok Vezetési jelenségek (transzportfolyamatok) fenomenologikus leírása Termodinamikai hajtóerő: kémiai potenciál különbség: Egyensúlyban lévő rendszer esetén: = U TS δ = δx
Elektromos vezetési tulajdonságok Vezetési jelenségek (transzportfolyamatok) fenomenologikus leírása Termodinamikai hajtóerő: kémiai potenciál különbség: Egyensúlyban lévő rendszer esetén: = U TS δ = δx
Vezetési jelenségek, vezetőanyagok. Elektromos vezetési folyamatban töltést továbbító (elmozdulni képes) részecskék:
 nyagtudomány 2014/15 Vezetési jelenségek, vezetőanyagok Dr. Szabó Péter János szpj@eik.bme.hu Elektromos vezetési folyamatban töltést továbbító (elmozdulni képes) részecskék: Vezetők fémek ötvözetek elektrolitok
nyagtudomány 2014/15 Vezetési jelenségek, vezetőanyagok Dr. Szabó Péter János szpj@eik.bme.hu Elektromos vezetési folyamatban töltést továbbító (elmozdulni képes) részecskék: Vezetők fémek ötvözetek elektrolitok
Vezetési jelenségek, vezetőanyagok
 Anyagtudomány 2018/19 Vezetési jelenségek, vezetőanyagok Dr. Szabó Péter János szpj@eik.bme.hu Elektromos vezetési folyamatban töltést továbbító (elmozdulni képes) részecskék: Vezetők fémek szabad elektron
Anyagtudomány 2018/19 Vezetési jelenségek, vezetőanyagok Dr. Szabó Péter János szpj@eik.bme.hu Elektromos vezetési folyamatban töltést továbbító (elmozdulni képes) részecskék: Vezetők fémek szabad elektron
BME, Anyagtudomány és Technológia Tanszék. Trendek az anyagtudományban Vezetési jelenségek Dr. Mészáros István 2013.
 BME, nyagtudomány és Technológia Tanszék Trendek az anyagtudományban Vezetési jelenségek Dr. Mészáros István 03. Elektromos vezetési tulajdonságok Vezetési jelenségek (transzportfolyamatok) fenomenologikus
BME, nyagtudomány és Technológia Tanszék Trendek az anyagtudományban Vezetési jelenségek Dr. Mészáros István 03. Elektromos vezetési tulajdonságok Vezetési jelenségek (transzportfolyamatok) fenomenologikus
Anyagszerkezettan és anyagvizsgálat 2015/16. Mágneses anyagok. Dr. Szabó Péter János
 Anyagszerkezettan és anyagvizsgálat 2015/16 Mágneses anyagok Dr. Szabó Péter János szpj@eik.bme.hu Mágneses tér anyag kölcsönhatás leírása B H B M r 0 H r H 1 1 V 0 ( P H i M ) 1 P V H : az anyagra ható
Anyagszerkezettan és anyagvizsgálat 2015/16 Mágneses anyagok Dr. Szabó Péter János szpj@eik.bme.hu Mágneses tér anyag kölcsönhatás leírása B H B M r 0 H r H 1 1 V 0 ( P H i M ) 1 P V H : az anyagra ható
Diffúzió. Diffúzió sebessége: gáz > folyadék > szilárd (kötőerő)
 Diffúzió Diffúzió - traszportfolyamat (fonon, elektron, atom, ion, hőmennyiség...) Elektromos vezetés (Ohm) töltés áram elektr. potenciál grad. Hővezetés (Fourier) energia áram hőmérséklet különbség Kémiai
Diffúzió Diffúzió - traszportfolyamat (fonon, elektron, atom, ion, hőmennyiség...) Elektromos vezetés (Ohm) töltés áram elektr. potenciál grad. Hővezetés (Fourier) energia áram hőmérséklet különbség Kémiai
Fizika M1 - A szilárdtestfizika alapjai. Gépészmérnök és Energetikai mérnök mesterszak
 Fizika M1 - A szilárdtestfizika alapjai Gépészmérnök és Energetikai mérnök mesterszak Kondenzált anyagok fizikája Tematika: Szerkezet jellemzése, vizsgálata A kristályrácsot összetartó erők Rácsdinamika
Fizika M1 - A szilárdtestfizika alapjai Gépészmérnök és Energetikai mérnök mesterszak Kondenzált anyagok fizikája Tematika: Szerkezet jellemzése, vizsgálata A kristályrácsot összetartó erők Rácsdinamika
Anyagismeret 2016/17. Diffúzió. Dr. Mészáros István Diffúzió
 Anyagismeret 6/7 Diffúzió Dr. Mészáros István meszaros@eik.bme.hu Diffúzió Különféle anyagi részecskék anyagon belüli helyváltoztatása Az anyag lehet gáznemű, folyékony vagy szilárd Diffúzió Diffúzió -
Anyagismeret 6/7 Diffúzió Dr. Mészáros István meszaros@eik.bme.hu Diffúzió Különféle anyagi részecskék anyagon belüli helyváltoztatása Az anyag lehet gáznemű, folyékony vagy szilárd Diffúzió Diffúzió -
Diffúzió. Diffúzió. Diffúzió. Különféle anyagi részecskék anyagon belüli helyváltoztatása Az anyag lehet gáznemű, folyékony vagy szilárd
 Anyagszerkezettan és anyagvizsgálat 5/6 Diffúzió Dr. Szabó Péter János szpj@eik.bme.hu Diffúzió Különféle anyagi részecskék anyagon belüli helyváltoztatása Az anyag lehet gáznemű, folyékony vagy szilárd
Anyagszerkezettan és anyagvizsgálat 5/6 Diffúzió Dr. Szabó Péter János szpj@eik.bme.hu Diffúzió Különféle anyagi részecskék anyagon belüli helyváltoztatása Az anyag lehet gáznemű, folyékony vagy szilárd
Szigetelők Félvezetők Vezetők
 Dr. Báder Imre: AZ ELEKTROMOS VEZETŐK Az anyagokat elektromos erőtérben tapasztalt viselkedésük alapján két alapvető csoportba soroljuk: szigetelők (vagy dielektrikumok) és vezetők (vagy konduktorok).
Dr. Báder Imre: AZ ELEKTROMOS VEZETŐK Az anyagokat elektromos erőtérben tapasztalt viselkedésük alapján két alapvető csoportba soroljuk: szigetelők (vagy dielektrikumok) és vezetők (vagy konduktorok).
ANYAGTUDOMÁNY ÉS TECHNOLÓGIA TANSZÉK. Anyagismeret 2016/17. Szilárdságnövelés. Dr. Mészáros István Az előadás során megismerjük
 ANYAGTUDOMÁNY ÉS TECHNOLÓGIA TANSZÉK Anyagismeret 2016/17 Szilárdságnövelés Dr. Mészáros István meszaros@eik.bme.hu 1 Az előadás során megismerjük A szilárságnövelő eljárásokat; Az eljárások anyagszerkezeti
ANYAGTUDOMÁNY ÉS TECHNOLÓGIA TANSZÉK Anyagismeret 2016/17 Szilárdságnövelés Dr. Mészáros István meszaros@eik.bme.hu 1 Az előadás során megismerjük A szilárságnövelő eljárásokat; Az eljárások anyagszerkezeti
A SZUPRAVEZETÉS. Fizika. A mágneses tér hatása a szupravezető állapotra
 Fizika A SZUPRAVEZETÉS A szupravezetés jelenségét 80 évvel ezelőtt fedezték fel, de az azóta eltelt idő alatt semmivel sem lankadt a fizikusok érdeklődése e témakör iránt. A szupravezetők tanulmányozása
Fizika A SZUPRAVEZETÉS A szupravezetés jelenségét 80 évvel ezelőtt fedezték fel, de az azóta eltelt idő alatt semmivel sem lankadt a fizikusok érdeklődése e témakör iránt. A szupravezetők tanulmányozása
Szilárdtestek mágnessége. Mágnesesen rendezett szilárdtestek
 Szilárdtestek mágnessége Mágnesesen rendezett szilárdtestek 2 Mágneses anyagok Permanens atomi mágneses momentumok: irány A kétféle spin-beállású elektronok betöltöttsége különbözik (spin-polarizáció)
Szilárdtestek mágnessége Mágnesesen rendezett szilárdtestek 2 Mágneses anyagok Permanens atomi mágneses momentumok: irány A kétféle spin-beállású elektronok betöltöttsége különbözik (spin-polarizáció)
Diffúzió 2003 március 28
 Diffúzió 3 március 8 Diffúzió: különféle anyagi részecskék (szilárd, folyékony, gáznemű) anyagon belüli helyváltozása. Szilárd anyagban való mozgás Öndiffúzió: a rácsot felépítő saját atomok energiaszint-különbség
Diffúzió 3 március 8 Diffúzió: különféle anyagi részecskék (szilárd, folyékony, gáznemű) anyagon belüli helyváltozása. Szilárd anyagban való mozgás Öndiffúzió: a rácsot felépítő saját atomok energiaszint-különbség
2010. január 31-én zárult OTKA pályázat zárójelentése: K62441 Dr. Mihály György
 Hidrosztatikus nyomással kiváltott elektronszerkezeti változások szilárd testekben A kutatás célkitűzései: A szilárd testek elektromos és mágneses tulajdonságait az alkotó atomok elektronhullámfüggvényeinek
Hidrosztatikus nyomással kiváltott elektronszerkezeti változások szilárd testekben A kutatás célkitűzései: A szilárd testek elektromos és mágneses tulajdonságait az alkotó atomok elektronhullámfüggvényeinek
Mágneses tér anyag kölcsönhatás leírása
 Anyagszerkezettan és anyagvizsgálat 2014/15 Mágneses anyagok Dr. Szabó Péter János szpj@eik.bme.hu Mágneses tér anyag kölcsönhatás leírása B H B H H M ) 0 1 M H V 1 r r 0 ( 1 Pi P V H : az anyagra ható
Anyagszerkezettan és anyagvizsgálat 2014/15 Mágneses anyagok Dr. Szabó Péter János szpj@eik.bme.hu Mágneses tér anyag kölcsönhatás leírása B H B H H M ) 0 1 M H V 1 r r 0 ( 1 Pi P V H : az anyagra ható
dinamikai tulajdonságai
 Szilárdtest rácsok statikus és dinamikai tulajdonságai Szilárdtestek osztályozása kötéstípusok szerint Kötések eredete: elektronszerkezet k t ionok (atomtörzsek) tö Coulomb- elektronok kölcsönhatás lokalizáltak
Szilárdtest rácsok statikus és dinamikai tulajdonságai Szilárdtestek osztályozása kötéstípusok szerint Kötések eredete: elektronszerkezet k t ionok (atomtörzsek) tö Coulomb- elektronok kölcsönhatás lokalizáltak
Mágneses tér anyag kölcsönhatás leírása
 Anyagszerkezettan és anyagvizsgálat 2012/13 Mágneses anyagok Dr. Szabó Péter János szpj@eik.bme.hu Mágneses tér anyag kölcsönhatás leírása B = µ H B = µ µ H = µ H + M ) 0 r 0 ( 1 1 M = κh = Pi = P V V
Anyagszerkezettan és anyagvizsgálat 2012/13 Mágneses anyagok Dr. Szabó Péter János szpj@eik.bme.hu Mágneses tér anyag kölcsönhatás leírása B = µ H B = µ µ H = µ H + M ) 0 r 0 ( 1 1 M = κh = Pi = P V V
3. (b) Kereszthatások. Utolsó módosítás: április 1. Dr. Márkus Ferenc BME Fizika Tanszék
 3. (b) Kereszthatások Utolsó módosítás: 2013. április 1. Vezetési együtthatók fémekben (1) 1 Az elektrongáz hővezetési együtthatója A levezetésben alkalmazott feltételek: 1. Minden elektron ugyanazzal
3. (b) Kereszthatások Utolsó módosítás: 2013. április 1. Vezetési együtthatók fémekben (1) 1 Az elektrongáz hővezetési együtthatója A levezetésben alkalmazott feltételek: 1. Minden elektron ugyanazzal
Szupravezetés Vajda István: A szupravezetők alkalmazásai "Fizikus Napok", Debrecen, 2008. március 6.
 A szupravezetés elmélete és alkalmazásai Előadás a Fizikus napok látogatói számára Dr Vajda István egyetemi tanár Budapest Műszaki és Gazdaságtudományi Egyetem Supertech Laboratórium vajda@supertech.vgt.bme.hu
A szupravezetés elmélete és alkalmazásai Előadás a Fizikus napok látogatói számára Dr Vajda István egyetemi tanár Budapest Műszaki és Gazdaságtudományi Egyetem Supertech Laboratórium vajda@supertech.vgt.bme.hu
Szilárdtestek sávelmélete. Sávelmélet a szabadelektron-modell alapján
 Szilárdtestek sávelmélete Sávelmélet a szabadelektron-modell alapján A Fermi Dirac statisztika alapjai Nagy részecskeszámú rendszerek fizikai jellemzéséhez statisztikai leírást kell alkalmazni. (Pl. gázokra
Szilárdtestek sávelmélete Sávelmélet a szabadelektron-modell alapján A Fermi Dirac statisztika alapjai Nagy részecskeszámú rendszerek fizikai jellemzéséhez statisztikai leírást kell alkalmazni. (Pl. gázokra
American Society of Materials. Szilárdtestek. Fullerének (C atomok, sokszögek) zárt gömb, tojás cső (egy és többrétegű)
 Szilárdtestek Fullerének (C atomok, sokszögek) zárt gömb, tojás cső (egy és többrétegű) csavart alakzatok (spirál, tórusz, stb.) egyatomos vastagságú sík, grafén (0001) Amorf (atomok geometriai rend nélkül)
Szilárdtestek Fullerének (C atomok, sokszögek) zárt gömb, tojás cső (egy és többrétegű) csavart alakzatok (spirál, tórusz, stb.) egyatomos vastagságú sík, grafén (0001) Amorf (atomok geometriai rend nélkül)
Az elektronpályák feltöltődési sorrendje
 3. előadás 12-09-17 2 12-09-17 Az elektronpályák feltöltődési sorrendje 3 Az elemek rendszerezése, a periódusos rendszer Elsőként Dimitrij Ivanovics Mengyelejev és Lothar Meyer vette észre az elemek halmazában
3. előadás 12-09-17 2 12-09-17 Az elektronpályák feltöltődési sorrendje 3 Az elemek rendszerezése, a periódusos rendszer Elsőként Dimitrij Ivanovics Mengyelejev és Lothar Meyer vette észre az elemek halmazában
Elektrodinamika. Maxwell egyenletek: Kontinuitási egyenlet: div n v =0. div E =4 div B =0. rot E = rot B=
 Elektrodinamika Maxwell egyenletek: div E =4 div B =0 rot E = rot B= 1 B c t 1 E c t 4 c j Kontinuitási egyenlet: n t div n v =0 Vektoranalízis rot rot u=grad divu u rot grad =0 div rotu=0 udv= ud F V
Elektrodinamika Maxwell egyenletek: div E =4 div B =0 rot E = rot B= 1 B c t 1 E c t 4 c j Kontinuitási egyenlet: n t div n v =0 Vektoranalízis rot rot u=grad divu u rot grad =0 div rotu=0 udv= ud F V
Fogorvosi anyagtan fizikai alapjai 9. Hőtani, elektromos és kémiai tulajdonságok
 Fogorvosi anyagtan fizikai alapjai 9. Hőtani, elektromos és kémiai tulajdonságok Kiemelt témák: Elektromosságtan alapfogalmai Szilárdtestek energiasáv modelljei Félvezetők és alkalmazásaik Tankönyv fej.:
Fogorvosi anyagtan fizikai alapjai 9. Hőtani, elektromos és kémiai tulajdonságok Kiemelt témák: Elektromosságtan alapfogalmai Szilárdtestek energiasáv modelljei Félvezetők és alkalmazásaik Tankönyv fej.:
2. (d) Hővezetési problémák II. főtétel - termoelektromosság
 2. (d) Hővezetési problémák II. főtétel - termoelektromosság Utolsó módosítás: 2015. március 10. Kezdeti érték nélküli problémák (1) 1 A fél-végtelen közeg a Az x=0 pontban a tartományban helyezkedik el.
2. (d) Hővezetési problémák II. főtétel - termoelektromosság Utolsó módosítás: 2015. március 10. Kezdeti érték nélküli problémák (1) 1 A fél-végtelen közeg a Az x=0 pontban a tartományban helyezkedik el.
Transzportfolyamatok. Alapfogalmak. Lokális mérlegegyenlet. Transzportfolyamatok 15/11/2015
 Alapfogalmak Transzportfolyamatok Diffúzió, Hővezetés Viszkozitás Önként végbemenő folyamat: Egyensúlyi állapot irányába Intenzív paraméterek kiegyenlítődése (p, T, µ) Extenzív paraméterek áramlása (V,
Alapfogalmak Transzportfolyamatok Diffúzió, Hővezetés Viszkozitás Önként végbemenő folyamat: Egyensúlyi állapot irányába Intenzív paraméterek kiegyenlítődése (p, T, µ) Extenzív paraméterek áramlása (V,
Villamos tulajdonságok
 Villamos tulajdonságok A vezetés s magyarázata Elektron függıleges falú potenciálgödörben: állóhullámok alap és gerjesztett állapotok Több elektron: Pauli-elv Sok elektron: Energia sávok Sávelméletlet
Villamos tulajdonságok A vezetés s magyarázata Elektron függıleges falú potenciálgödörben: állóhullámok alap és gerjesztett állapotok Több elektron: Pauli-elv Sok elektron: Energia sávok Sávelméletlet
 Egzotikus elektromágneses jelenségek alacsony hőmérsékleten Mihály György BME Fizikai Intézet Hall effektus Edwin Hall és az összenyomhatatlan elektromosság Kvantum Hall effektus Mágneses áram anomális
Egzotikus elektromágneses jelenségek alacsony hőmérsékleten Mihály György BME Fizikai Intézet Hall effektus Edwin Hall és az összenyomhatatlan elektromosság Kvantum Hall effektus Mágneses áram anomális
Periódusosság. Általános Kémia, Periódikus tulajdonságok. Slide 1 of 35
 Periódusosság 3-1 Az elemek csoportosítása: a periódusos táblázat 3-2 Fémek, nemfémek és ionjaik 3-3 Az atomok és ionok mérete 3-4 Ionizációs energia 3-5 Elektron affinitás 3-6 Mágneses 3-7 Az elemek periodikus
Periódusosság 3-1 Az elemek csoportosítása: a periódusos táblázat 3-2 Fémek, nemfémek és ionjaik 3-3 Az atomok és ionok mérete 3-4 Ionizációs energia 3-5 Elektron affinitás 3-6 Mágneses 3-7 Az elemek periodikus
ELSŐ ZH-kédések kidolgozása: BY HENTES
 ELSŐ ZH-kédések kidolgozása: BY HENTES A1) Bevezetés 1. Történeti áttekintés. A villamosság, mint jel- és energiahordozó. Történet Mo-n: Jedlik Ányos (Villamdelejes forgony, dinamó elv) 1880: Ganz Gyár
ELSŐ ZH-kédések kidolgozása: BY HENTES A1) Bevezetés 1. Történeti áttekintés. A villamosság, mint jel- és energiahordozó. Történet Mo-n: Jedlik Ányos (Villamdelejes forgony, dinamó elv) 1880: Ganz Gyár
Vezetékek. Fizikai alapok
 Vezetékek Fizikai alapok Elektromos áram A vezetékeket az elektromos áram ill. elektromos jelek vezetésére használják. Az elektromos áramot töltéshordozók (elektromos töltéssel rendelkező részecskék: elektronok,
Vezetékek Fizikai alapok Elektromos áram A vezetékeket az elektromos áram ill. elektromos jelek vezetésére használják. Az elektromos áramot töltéshordozók (elektromos töltéssel rendelkező részecskék: elektronok,
Folyadékok. Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok.
 Folyadékok folyékony nincs saját alakja szilárd van saját alakja (deformálás után úgy marad, nem (deformálás után visszaalakul, mert ébrednek benne visszatérítő nyíróerők) visszatérítő nyíróerők léptek
Folyadékok folyékony nincs saját alakja szilárd van saját alakja (deformálás után úgy marad, nem (deformálás után visszaalakul, mert ébrednek benne visszatérítő nyíróerők) visszatérítő nyíróerők léptek
Az anyagok mágneses tulajdonságai
 BME, Anyagtudomány és Technológia Tanszék Dr. Mészáros István Mágneses tulajdonságok, mágneses anyagok Előadásvázlat 2013. 1 Az anyagok mágneses tulajdonságai Alkalmazási területek Jelentőségük (lágy:
BME, Anyagtudomány és Technológia Tanszék Dr. Mészáros István Mágneses tulajdonságok, mágneses anyagok Előadásvázlat 2013. 1 Az anyagok mágneses tulajdonságai Alkalmazási területek Jelentőségük (lágy:
Periódusosság. Általános Kémia, Periódikus tulajdonságok. Slide 1 of 35
 Periódusosság 11-1 Az elemek csoportosítása: a periódusos táblázat 11-2 Fémek, nemfémek és ionjaik 11-3 Az atomok és ionok mérete 11-4 Ionizációs energia 11-5 Elektron affinitás 11-6 Mágneses 11-7 Az elemek
Periódusosság 11-1 Az elemek csoportosítása: a periódusos táblázat 11-2 Fémek, nemfémek és ionjaik 11-3 Az atomok és ionok mérete 11-4 Ionizációs energia 11-5 Elektron affinitás 11-6 Mágneses 11-7 Az elemek
Fogorvosi anyagtan fizikai alapjai 2.
 Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok Kiemelt témák: Viszkozitás Víz és nyál Kristályok - apatit Polimorfizmus Kristályhibák
Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok Kiemelt témák: Viszkozitás Víz és nyál Kristályok - apatit Polimorfizmus Kristályhibák
Kémiai fizikai alapok I. Vízminőség, vízvédelem 2009-2010. tavasz
 Kémiai fizikai alapok I. Vízminőség, vízvédelem 2009-2010. tavasz 1. A vízmolekula szerkezete Elektronegativitás, polaritás, másodlagos kötések 2. Fizikai tulajdonságok a) Szerkezetből adódó különleges
Kémiai fizikai alapok I. Vízminőség, vízvédelem 2009-2010. tavasz 1. A vízmolekula szerkezete Elektronegativitás, polaritás, másodlagos kötések 2. Fizikai tulajdonságok a) Szerkezetből adódó különleges
Szilárdságnövelés. Az előkészítő témakörei
 ANYAGTUDOMÁNY ÉS TECHNOLÓGIA TANSZÉK Alapképzés Anyagszerkezettan és anyagvizsgálat 2007/08 Szilárdságnövelés Dr. Palotás Béla palotasb@eik.bme.hu Dr. Németh Árpád arpinem@eik.bme.hu Szilárdság növelés
ANYAGTUDOMÁNY ÉS TECHNOLÓGIA TANSZÉK Alapképzés Anyagszerkezettan és anyagvizsgálat 2007/08 Szilárdságnövelés Dr. Palotás Béla palotasb@eik.bme.hu Dr. Németh Árpád arpinem@eik.bme.hu Szilárdság növelés
Szilárdság (folyáshatár) növelési eljárások
 Képlékeny alakítás Szilárdság (folyáshatár) növelési eljárások Szemcseméret csökkentés Hőkezelés Ötvözés allotróp átalakulással rendelkező ötvözetek kiválásos nemesítés diszperziós keményítés interstíciós
Képlékeny alakítás Szilárdság (folyáshatár) növelési eljárások Szemcseméret csökkentés Hőkezelés Ötvözés allotróp átalakulással rendelkező ötvözetek kiválásos nemesítés diszperziós keményítés interstíciós
XLVI. Irinyi János Középiskolai Kémiaverseny 2014. február 6. * Iskolai forduló I.a, I.b és III. kategória
 Tanuló neve és kategóriája Iskolája Osztálya XLVI. Irinyi János Középiskolai Kémiaverseny 201. február 6. * Iskolai forduló I.a, I.b és III. kategória Munkaidő: 120 perc Összesen 100 pont A periódusos
Tanuló neve és kategóriája Iskolája Osztálya XLVI. Irinyi János Középiskolai Kémiaverseny 201. február 6. * Iskolai forduló I.a, I.b és III. kategória Munkaidő: 120 perc Összesen 100 pont A periódusos
Orvosi jelfeldolgozás. Információ. Információtartalom. Jelek osztályozása De, mi az a jel?
 Orvosi jelfeldolgozás Információ De, mi az a jel? Jel: Információt szolgáltat (információ: új ismeretanyag, amely csökkenti a bizonytalanságot).. Megjelent.. Panasza? információ:. Egy beteg.. Fáj a fogam.
Orvosi jelfeldolgozás Információ De, mi az a jel? Jel: Információt szolgáltat (információ: új ismeretanyag, amely csökkenti a bizonytalanságot).. Megjelent.. Panasza? információ:. Egy beteg.. Fáj a fogam.
Elektron mozgása kristályrácsban Drude - féle elektrongáz
 Elektron mozgása kristályrácsban Drude - féle elektrongáz Dr. Berta Miklós bertam@sze.hu 2017. október 13. 1 / 24 Drude - féle elektrongáz Tapasztalat alapján a fémekben vannak szabad töltéshordozók. Szintén
Elektron mozgása kristályrácsban Drude - féle elektrongáz Dr. Berta Miklós bertam@sze.hu 2017. október 13. 1 / 24 Drude - féle elektrongáz Tapasztalat alapján a fémekben vannak szabad töltéshordozók. Szintén
 Anyagos rész: Lásd: állapotábrás pdf. Ha többet akarsz tudni a metallográfiai vizsgálatok csodáiról, akkor: http://testorg.eu/editor_up/up/egyeb/2012_01/16/132671554730168934/metallografia.pdf
Anyagos rész: Lásd: állapotábrás pdf. Ha többet akarsz tudni a metallográfiai vizsgálatok csodáiról, akkor: http://testorg.eu/editor_up/up/egyeb/2012_01/16/132671554730168934/metallografia.pdf
Az anyagok vezetési tulajdonságai (segédanyag a "Vezetési jelenségek" című gyakorlathoz)
 udapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar nyagtudomány és Technológia Tanszék z anyagok vezetési tulajdonságai (segédanyag a "Vezetési jelenségek" című gyakorlathoz) evezetés fémek
udapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar nyagtudomány és Technológia Tanszék z anyagok vezetési tulajdonságai (segédanyag a "Vezetési jelenségek" című gyakorlathoz) evezetés fémek
9. évfolyam. Osztályozóvizsga tananyaga FIZIKA
 9. évfolyam Osztályozóvizsga tananyaga A testek mozgása 1. Egyenes vonalú egyenletes mozgás 2. Változó mozgás: gyorsulás fogalma, szabadon eső test mozgása 3. Bolygók mozgása: Kepler törvények A Newtoni
9. évfolyam Osztályozóvizsga tananyaga A testek mozgása 1. Egyenes vonalú egyenletes mozgás 2. Változó mozgás: gyorsulás fogalma, szabadon eső test mozgása 3. Bolygók mozgása: Kepler törvények A Newtoni
Periódusosság. 9-1 Az elemek csoportosítása: a periódusostáblázat
 Periódusosság 9-1 Az elemek csoportosítása: aperiódusos táblázat 9-2 Fémek, nemfémek és ionjaik 9-3 Az atomok és ionok mérete 9-4 Ionizációs energia 9-5 Elektron affinitás 9-6 Mágneses 9-7 Az elemek periódikus
Periódusosság 9-1 Az elemek csoportosítása: aperiódusos táblázat 9-2 Fémek, nemfémek és ionjaik 9-3 Az atomok és ionok mérete 9-4 Ionizációs energia 9-5 Elektron affinitás 9-6 Mágneses 9-7 Az elemek periódikus
Fázisátalakulás Fázisátalakulások diffúziós (egyedi atomi mozgás) martenzites (kollektív atomi mozgás, diffúzió nélkül)
 ázisátalakulások, P, C változása új (egyensúlyi) állapot Új fázis(ok): stabil, metastabil ázisátalakulás: folyamat, amelynek során a régi fázis(ok)ból új, más szerkezetű (rács, szövet) vagy halmazállapotú
ázisátalakulások, P, C változása új (egyensúlyi) állapot Új fázis(ok): stabil, metastabil ázisátalakulás: folyamat, amelynek során a régi fázis(ok)ból új, más szerkezetű (rács, szövet) vagy halmazállapotú
FÉLVEZETŐ ESZKÖZÖK I. Elektrotechnika 4. előadás
 FÉLVEZETŐ ESZKÖZÖK I. Elektrotechnika 4. előadás FÉLVEZETŐ ESZKÖZÖK A leggyakrabban használt félvezető anyagok a germánium (Ge), és a szilícium (Si). Félvezető tulajdonsággal rendelkező elemek: szén (C),
FÉLVEZETŐ ESZKÖZÖK I. Elektrotechnika 4. előadás FÉLVEZETŐ ESZKÖZÖK A leggyakrabban használt félvezető anyagok a germánium (Ge), és a szilícium (Si). Félvezető tulajdonsággal rendelkező elemek: szén (C),
BŐVÍTETT TEMATIKA a Kondenzált anyagok fizikája c. tárgyhoz
 BŐVÍTETT TEMATIKA a Kondenzált anyagok fizikája c. tárgyhoz Az anyag szerveződési formái Ebben a részben bemutatjuk az anyag elemi építőköveinek sokszerű kapcsolódási formáit, amelyek makroszkopikusan
BŐVÍTETT TEMATIKA a Kondenzált anyagok fizikája c. tárgyhoz Az anyag szerveződési formái Ebben a részben bemutatjuk az anyag elemi építőköveinek sokszerű kapcsolódási formáit, amelyek makroszkopikusan
1. SI mértékegységrendszer
 I. ALAPFOGALMAK 1. SI mértékegységrendszer Alapegységek 1 Hosszúság (l): méter (m) 2 Tömeg (m): kilogramm (kg) 3 Idő (t): másodperc (s) 4 Áramerősség (I): amper (A) 5 Hőmérséklet (T): kelvin (K) 6 Anyagmennyiség
I. ALAPFOGALMAK 1. SI mértékegységrendszer Alapegységek 1 Hosszúság (l): méter (m) 2 Tömeg (m): kilogramm (kg) 3 Idő (t): másodperc (s) 4 Áramerősség (I): amper (A) 5 Hőmérséklet (T): kelvin (K) 6 Anyagmennyiség
Folyadékok. Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok.
 Folyadékok folyékony szilárd Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok Kiemelt témák: Viszkozitás Apatit Kristályhibák és
Folyadékok folyékony szilárd Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok Kiemelt témák: Viszkozitás Apatit Kristályhibák és
Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Molekulák, folyadékok, szilárd anyagok, folyadékkristályok
 Molekulák energiaállapotai E molekula E elektron E (A tankönyvben nem található téma!) vibráció E rotáció pl. vibráció 1 ev 0,1 ev 0,01 ev Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti
Molekulák energiaállapotai E molekula E elektron E (A tankönyvben nem található téma!) vibráció E rotáció pl. vibráció 1 ev 0,1 ev 0,01 ev Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti
A SZILÁRDTEST FOGALMA. Szilárdtest: makroszkópikus, szilárd, rendezett anyagdarab. molekula klaszter szilárdtest > σ λ : rel.
 A SZILÁRDTEST FOGALMA Szilárdtest: makroszkópikus, szilárd, rendezett anyagdarab. a) Méret: b) Szilárdság: molekula klaszter szilárdtest > ~ 100 Å ideálisan rugalmas test: λ = 1 E σ λ : rel. megnyúlás
A SZILÁRDTEST FOGALMA Szilárdtest: makroszkópikus, szilárd, rendezett anyagdarab. a) Méret: b) Szilárdság: molekula klaszter szilárdtest > ~ 100 Å ideálisan rugalmas test: λ = 1 E σ λ : rel. megnyúlás
Anyagtudomány: hagyományos szerkezeti anyagok és polimerek
 Anyagtudomány: hagyományos szerkezeti anyagok és polimerek Anyagok termikus tulajdonságai és egyedi jellegzetességei Fizikai Kémia és Anyagtudományi Tanszék BME Műanyag- és Gumiipari Laboratórium H ép.
Anyagtudomány: hagyományos szerkezeti anyagok és polimerek Anyagok termikus tulajdonságai és egyedi jellegzetességei Fizikai Kémia és Anyagtudományi Tanszék BME Műanyag- és Gumiipari Laboratórium H ép.
Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások
 Miskolci Egyetem Műszaki Anyagtudományi Kar Anyagtudományi Intézet Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások Dr.Krállics György krallics@eik.bme.hu
Miskolci Egyetem Műszaki Anyagtudományi Kar Anyagtudományi Intézet Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások Dr.Krállics György krallics@eik.bme.hu
Az elemek rendszerezése, a periódusos rendszer
 Az elemek rendszerezése, a periódusos rendszer 12-09-16 1 A rendszerezés alapja, az elektronszerkezet kiépülése 12-09-16 2 Csoport 1 2 3 II III IA A B 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 IV V VI VII
Az elemek rendszerezése, a periódusos rendszer 12-09-16 1 A rendszerezés alapja, az elektronszerkezet kiépülése 12-09-16 2 Csoport 1 2 3 II III IA A B 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 IV V VI VII
Bevezetés a lézeres anyagmegmunkálásba
 Bevezetés a lézeres anyagmegmunkálásba FBN332E-1 Dr. Geretovszky Zsolt 2010. október 13. A lézeres l anyagmegmunkálás szempontjából l fontos anyagi tulajdonságok Optikai tulajdonságok Mechanikai tulajdonságok
Bevezetés a lézeres anyagmegmunkálásba FBN332E-1 Dr. Geretovszky Zsolt 2010. október 13. A lézeres l anyagmegmunkálás szempontjából l fontos anyagi tulajdonságok Optikai tulajdonságok Mechanikai tulajdonságok
Folyadékok. Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok
 Folyadékok víz Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok 1 saját térfogat nincs saját alak/folyékony nincsenek belső nyíróerők
Folyadékok víz Fogorvosi anyagtan fizikai alapjai 2. Általános anyagszerkezeti ismeretek Folyadékok, szilárd anyagok, folyadékkristályok 1 saját térfogat nincs saját alak/folyékony nincsenek belső nyíróerők
MIKROELEKTRONIKA, VIEEA306
 Budaesti Műszaki és Gazdaságtudomáyi Egyetem Elektroikus Eszközök Taszéke MIKROELEKTRONIKA, VIEEA306 Félvezető fizikai alaok htt://www.eet.bme.hu/~oe/miel/hu/03-felvez-fiz.tx htt://www.eet.bme.hu Budaesti
Budaesti Műszaki és Gazdaságtudomáyi Egyetem Elektroikus Eszközök Taszéke MIKROELEKTRONIKA, VIEEA306 Félvezető fizikai alaok htt://www.eet.bme.hu/~oe/miel/hu/03-felvez-fiz.tx htt://www.eet.bme.hu Budaesti
Szilárdságnövelés. Az előadás során megismerjük. Szilárdságnövelési eljárások
 Anyagszerkezettan és anyagvizsgálat 2015/16 Szilárdságnövelés Dr. Szabó Péter János szpj@eik.bme.hu Az előadás során megismerjük A szilárságnövelő eljárásokat; Az eljárások anyagszerkezeti alapjait; Technológiai
Anyagszerkezettan és anyagvizsgálat 2015/16 Szilárdságnövelés Dr. Szabó Péter János szpj@eik.bme.hu Az előadás során megismerjük A szilárságnövelő eljárásokat; Az eljárások anyagszerkezeti alapjait; Technológiai
Fémek és ötvözetek termikus viselkedése
 Anyagtudomány és Technológia Tanszék Fémek és ötvözetek termikus viselkedése Dr. Szabó Péter János szpj@eik.bme.hu Anyagszerkezettan és anyagvizsgálat BMEGEMTBGA1 2018/2019/2 Az előadás során megismerjük
Anyagtudomány és Technológia Tanszék Fémek és ötvözetek termikus viselkedése Dr. Szabó Péter János szpj@eik.bme.hu Anyagszerkezettan és anyagvizsgálat BMEGEMTBGA1 2018/2019/2 Az előadás során megismerjük
Gyakorlat 30B-14. a F L = e E + ( e)v B képlet, a gravitációs erőt a (2.1) G = m e g (2.2)
 2. Gyakorlat 30B-14 Az Egyenlítőnél, a földfelszín közelében a mágneses fluxussűrűség iránya északi, nagysága kb. 50µ T,az elektromos térerősség iránya lefelé mutat, nagysága; kb. 100 N/C. Számítsuk ki,
2. Gyakorlat 30B-14 Az Egyenlítőnél, a földfelszín közelében a mágneses fluxussűrűség iránya északi, nagysága kb. 50µ T,az elektromos térerősség iránya lefelé mutat, nagysága; kb. 100 N/C. Számítsuk ki,
Nanoelektronikai eszközök III.
 Nanoelektronikai eszközök III. Dr. Berta Miklós bertam@sze.hu 2017. november 23. 1 / 10 Kvantumkaszkád lézer Tekintsünk egy olyan, sok vékony rétegbõl kialakított rendszert, amelyre ha külsõ feszültséget
Nanoelektronikai eszközök III. Dr. Berta Miklós bertam@sze.hu 2017. november 23. 1 / 10 Kvantumkaszkád lézer Tekintsünk egy olyan, sok vékony rétegbõl kialakított rendszert, amelyre ha külsõ feszültséget
Anyagtudomány MÁGNESES ANYAGOK GERZSON MIKLÓS
 Anyagtudomány MÁGNESES ANYAGOK GERZSON MIKLÓS 1 mágneses pólusok (Föld, állandó mágnesek) pólusok nem szétválaszthatók történetük: Magnetosz Kréta Ókori Kína iránytű Gilbert: On the Magnet (1600) Oersted:
Anyagtudomány MÁGNESES ANYAGOK GERZSON MIKLÓS 1 mágneses pólusok (Föld, állandó mágnesek) pólusok nem szétválaszthatók történetük: Magnetosz Kréta Ókori Kína iránytű Gilbert: On the Magnet (1600) Oersted:
Átmenetifém-komplexek ESR-spektrumának jellemzıi
 Átmenetifém-komplexek ESR-spektrumának jellemzıi A párosítatlan elektron d-pályán van. Kevéssé delokalizálódik a fémionról, a fém-donoratom kötések meglehetısen ionos jellegőek. A spin-pálya csatolás viszonylag
Átmenetifém-komplexek ESR-spektrumának jellemzıi A párosítatlan elektron d-pályán van. Kevéssé delokalizálódik a fémionról, a fém-donoratom kötések meglehetısen ionos jellegőek. A spin-pálya csatolás viszonylag
Szupravezetők a mindennapokban
 Szupravezetők a mindennapokban Szupravezetők az elektrotechnikában Jelen és jövő Dr Vajda István egyetemi tanár Budapest Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék, Supertech Laboratórium
Szupravezetők a mindennapokban Szupravezetők az elektrotechnikában Jelen és jövő Dr Vajda István egyetemi tanár Budapest Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék, Supertech Laboratórium
Munkagázok hatása a hegesztési technológiára és a hegesztési kötésre a CO 2 és a szilárdtest lézersugaras hegesztéseknél
 Munkagázok hatása a hegesztési technológiára és a hegesztési kötésre a CO 2 és a szilárdtest lézersugaras hegesztéseknél Fémgőz és plazma Buza Gábor, Bauer Attila Messer Innovation Forum 2016. december
Munkagázok hatása a hegesztési technológiára és a hegesztési kötésre a CO 2 és a szilárdtest lézersugaras hegesztéseknél Fémgőz és plazma Buza Gábor, Bauer Attila Messer Innovation Forum 2016. december
Anyagtudomány. Ötvözetek egyensúlyi diagramjai (állapotábrák)
 Anyagtudomány Ötvözetek egyensúlyi diagramjai (állapotábrák) Kétkomponensű fémtani rendszerek fázisai és szövetelemei Folyékony, olvadék fázis Színfém (A, B) Szilárd oldat (α, β) (szubsztitúciós, interstíciós)
Anyagtudomány Ötvözetek egyensúlyi diagramjai (állapotábrák) Kétkomponensű fémtani rendszerek fázisai és szövetelemei Folyékony, olvadék fázis Színfém (A, B) Szilárd oldat (α, β) (szubsztitúciós, interstíciós)
Bevezetés a lézeres anyagmegmunkálásba
 Bevezetés a lézeres anyagmegmunkálásba FBN332E-1 Dr. Geretovszky Zsolt 2010. október 6. Anyagcsaládok Fémek Kerámiák, üvegek Műanyagok Kompozitok A családok közti különbségek tárgyalhatóak: atomi szinten
Bevezetés a lézeres anyagmegmunkálásba FBN332E-1 Dr. Geretovszky Zsolt 2010. október 6. Anyagcsaládok Fémek Kerámiák, üvegek Műanyagok Kompozitok A családok közti különbségek tárgyalhatóak: atomi szinten
Egyenáram. Áramkörök jellemzése Fogyasztók és áramforrások kapcsolása Az áramvezetés típusai
 Egyenáram Áramkörök jellemzése Fogyasztók és áramforrások kapcsolása Az áramvezetés típusai Elektromos áram Az elektromos töltéshordozók meghatározott irányú rendezett mozgását elektromos áramnak nevezzük.
Egyenáram Áramkörök jellemzése Fogyasztók és áramforrások kapcsolása Az áramvezetés típusai Elektromos áram Az elektromos töltéshordozók meghatározott irányú rendezett mozgását elektromos áramnak nevezzük.
Fázisátalakulások, avagy az anyag ezer arca. Sasvári László ELTE Fizikai Intézet ELTE Bolyai Kollégium
 Fázisátalakulások, avagy az anyag ezer arca Sasvári László ELTE Fizikai Intézet ELTE Bolyai Kollégium Atomoktól a csillagokig, Budapest, 2016. december 8. Fázisátalakulások Csak kondenzált anyag? A kondenzált
Fázisátalakulások, avagy az anyag ezer arca Sasvári László ELTE Fizikai Intézet ELTE Bolyai Kollégium Atomoktól a csillagokig, Budapest, 2016. december 8. Fázisátalakulások Csak kondenzált anyag? A kondenzált
A szilárd testek alakja és térfogata észrevehetően csak nagy erő hatására változik meg. A testekben a részecskék egymáshoz közel vannak, kristályos
 Az anyagok lehetséges állapotai, a fizikai körülményektől (nyomás, hőmérséklet) függően. Az anyagokat általában a normál körülmények között jellemző állapotuk alapján soroljuk be szilád, folyékony vagy
Az anyagok lehetséges állapotai, a fizikai körülményektől (nyomás, hőmérséklet) függően. Az anyagokat általában a normál körülmények között jellemző állapotuk alapján soroljuk be szilád, folyékony vagy
József Cserti. ELTE, TTK Komplex Rendszerek Fizikája Tanszék. A évi fizikai Nobel-díj. a topológikus fázisokért...
 József Cserti ELTE, TTK Komplex Rendszerek Fizikája Tanszék A 2016. évi fizikai Nobel-díj a topológikus fázisokért... Atomcsill, 2016. október 6., ELTE, Budapest Svéd Királyi Tudományos Akadémia A 2016.
József Cserti ELTE, TTK Komplex Rendszerek Fizikája Tanszék A 2016. évi fizikai Nobel-díj a topológikus fázisokért... Atomcsill, 2016. október 6., ELTE, Budapest Svéd Királyi Tudományos Akadémia A 2016.
Elektromos áram. Vezetési jelenségek
 Elektromos áram. Vezetési jelenségek Emlékeztető Elektromos áram: töltéshordozók egyirányú áramlása Áramkör részei: áramforrás, vezető, fogyasztó Áramköri jelek Emlékeztető Elektromos áram hatásai: Kémiai
Elektromos áram. Vezetési jelenségek Emlékeztető Elektromos áram: töltéshordozók egyirányú áramlása Áramkör részei: áramforrás, vezető, fogyasztó Áramköri jelek Emlékeztető Elektromos áram hatásai: Kémiai
Elektromos ellenállás, az áram hatásai, teljesítmény
 Elektromos ellenállás, az áram hatásai, teljesítmény Elektromos ellenállás Az anyag részecskéi akadályozzák a töltések mozgását. Ezt a tulajdonságot nevezzük elektromos ellenállásnak. Annak a fogyasztónak
Elektromos ellenállás, az áram hatásai, teljesítmény Elektromos ellenállás Az anyag részecskéi akadályozzák a töltések mozgását. Ezt a tulajdonságot nevezzük elektromos ellenállásnak. Annak a fogyasztónak
Tematika. Az atomok elrendeződése Kristályok, rácshibák
 Anyagtudomány 2013/14 Kristályok, rácshibák Dr. Szabó Péter János szpj@eik.bme.hu Tematika 1. hét: Bevezetés. 2. hét: Kristályok, rácshibák. 3. hét: Ötvözetek. 4. hét: Mágneses és elektromos anyagok. 5.
Anyagtudomány 2013/14 Kristályok, rácshibák Dr. Szabó Péter János szpj@eik.bme.hu Tematika 1. hét: Bevezetés. 2. hét: Kristályok, rácshibák. 3. hét: Ötvözetek. 4. hét: Mágneses és elektromos anyagok. 5.
Kerámia, üveg és fém-kerámia implantátumok
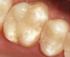 Kerámia, üveg és fém-kerámia implantátumok Bagi István BME MTAT Bevezetés Kerámiák csoportosítása teljesen tömör bioinert porózus bioinert teljesen tömör bioaktív oldódó Definíciók Bioinert a szomszédos
Kerámia, üveg és fém-kerámia implantátumok Bagi István BME MTAT Bevezetés Kerámiák csoportosítása teljesen tömör bioinert porózus bioinert teljesen tömör bioaktív oldódó Definíciók Bioinert a szomszédos
Elektrotechnika. Ballagi Áron
 Elektrotechnika Ballagi Áron Mágneses tér Elektrotechnika x/2 Mágneses indukció kísérlet Állandó mágneses térben helyezzünk el egy l hosszúságú vezetőt, és bocsássunk a vezetőbe I áramot! Tapasztalat:
Elektrotechnika Ballagi Áron Mágneses tér Elektrotechnika x/2 Mágneses indukció kísérlet Állandó mágneses térben helyezzünk el egy l hosszúságú vezetőt, és bocsássunk a vezetőbe I áramot! Tapasztalat:
N I. 02 B. Mágneses anyagvizsgálat G ép. 118 2011.11.30. A mérés dátuma: A mérés eszközei: A mérés menetének leírása:
 N I. 02 B A mérés eszközei: Számítógép Gerjesztésszabályzó toroid transzformátor Minták Mágneses anyagvizsgálat G ép. 118 A mérés menetének leírása: Beindítottuk a számtógépet, Behelyeztük a mintát a ferrotestbe.
N I. 02 B A mérés eszközei: Számítógép Gerjesztésszabályzó toroid transzformátor Minták Mágneses anyagvizsgálat G ép. 118 A mérés menetének leírása: Beindítottuk a számtógépet, Behelyeztük a mintát a ferrotestbe.
Orvosi Fizika 13. Bari Ferenc egyetemi tanár SZTE ÁOK-TTIK Orvosi Fizikai és Orvosi Informatikai Intézet
 Orvosi Fizika 13. Elektromosságtan és mágnességtan az életfolyamatokban 2. Bari Ferenc egyetemi tanár SZTE ÁOK-TTIK Orvosi Fizikai és Orvosi Informatikai Intézet Szeged, 2011. december 5. Egyenáram Vezető
Orvosi Fizika 13. Elektromosságtan és mágnességtan az életfolyamatokban 2. Bari Ferenc egyetemi tanár SZTE ÁOK-TTIK Orvosi Fizikai és Orvosi Informatikai Intézet Szeged, 2011. december 5. Egyenáram Vezető
DR. KOVÁCS ERNŐ ELEKTRONIKA II. (DISZKRÉT FÉLVEZETŐK, ERŐSÍTŐK) ELŐADÁS JEGYZET
 MISKOLCI EGYETEM VILLAMOSMÉRNÖKI INTÉZET ELEKTROTECHNIKAI- ELEKTRONIKAI TANSZÉK DR. KOVÁCS ERNŐ ELEKTRONIKA II. (DISZKRÉT FÉLVEZETŐK, ERŐSÍTŐK) ELŐADÁS JEGYZET 2003. 2.0. Diszkrét félvezetők és alkalmazásaik
MISKOLCI EGYETEM VILLAMOSMÉRNÖKI INTÉZET ELEKTROTECHNIKAI- ELEKTRONIKAI TANSZÉK DR. KOVÁCS ERNŐ ELEKTRONIKA II. (DISZKRÉT FÉLVEZETŐK, ERŐSÍTŐK) ELŐADÁS JEGYZET 2003. 2.0. Diszkrét félvezetők és alkalmazásaik
Osztályozó vizsga anyagok. Fizika
 Osztályozó vizsga anyagok Fizika 9. osztály Kinematika Mozgás és kölcsönhatás Az egyenes vonalú egyenletes mozgás leírása A sebesség fogalma, egységei A sebesség iránya Vektormennyiség fogalma Az egyenes
Osztályozó vizsga anyagok Fizika 9. osztály Kinematika Mozgás és kölcsönhatás Az egyenes vonalú egyenletes mozgás leírása A sebesség fogalma, egységei A sebesség iránya Vektormennyiség fogalma Az egyenes
 Név:............................ Helység / iskola:............................ Beküldési határidő: Kémia tanár neve:........................... 2013.feb.18. TAKÁCS CSABA KÉMIA EMLÉKVERSENY, IX. osztály,
Név:............................ Helység / iskola:............................ Beküldési határidő: Kémia tanár neve:........................... 2013.feb.18. TAKÁCS CSABA KÉMIA EMLÉKVERSENY, IX. osztály,
Fogorvosi anyagtan fizikai alapjai 5. Általános anyagszerkezeti ismeretek Fémek, ötvözetek
 Fémek törékeny/képlékeny nemesémek magas/alacsony o.p. Fogorvosi anyagtan izikai alapjai 5. Általános anyagszerkezeti ismeretek Fémek, ötvözetek ρ < 5 g cm 3 könnyűémek 5 g cm3 < ρ nehézémek 2 Fémek tulajdonságai
Fémek törékeny/képlékeny nemesémek magas/alacsony o.p. Fogorvosi anyagtan izikai alapjai 5. Általános anyagszerkezeti ismeretek Fémek, ötvözetek ρ < 5 g cm 3 könnyűémek 5 g cm3 < ρ nehézémek 2 Fémek tulajdonságai
Vezető anyagok. Vezető anyagok. Villamos anyagok, villamos tulajdonságok. Fontosabb fémek vezetőképessége 15/11/2015
 Villamos anyagok, villamos tulajdonságok Emlékeztető: Sávelmélet alapjai Femi-Dirac statisztika, Fermi energia Vegyérték sáv, vezetési sáv, tilos sáv Vezetőképesség értelmezés az elektronok hullámterjedése
Villamos anyagok, villamos tulajdonságok Emlékeztető: Sávelmélet alapjai Femi-Dirac statisztika, Fermi energia Vegyérték sáv, vezetési sáv, tilos sáv Vezetőképesség értelmezés az elektronok hullámterjedése
Az elektromágneses tér energiája
 Az elektromágneses tér energiája Az elektromos tér energiasűrűsége korábbról: Hasonlóképpen, a mágneses tér energiája: A tér egy adott pontjában az elektromos és mágneses terek együttes energiasűrűsége
Az elektromágneses tér energiája Az elektromos tér energiasűrűsége korábbról: Hasonlóképpen, a mágneses tér energiája: A tér egy adott pontjában az elektromos és mágneses terek együttes energiasűrűsége
Villamos anyagok, villamos tulajdonságok
 Villamos anyagok, villamos tulajdonságok Emlékeztető: Sávelmélet alapjai Femi-Dirac statisztika, Fermi energia Vegyérték sáv, vezetési sáv, tilos sáv Vezetőképesség értelmezés az elektronok hullámterjedése
Villamos anyagok, villamos tulajdonságok Emlékeztető: Sávelmélet alapjai Femi-Dirac statisztika, Fermi energia Vegyérték sáv, vezetési sáv, tilos sáv Vezetőképesség értelmezés az elektronok hullámterjedése
Fizika. Fizika. Nyitray Gergely (PhD) PTE PMMIK április 3.
 Fizika Nyitray Gergely (PhD) PTE PMMIK 2017. április 3. Kriogenika A gázcseppfolyósítások korszaka Az elektronrendszer adiabatikus lemágnesezése Az atommagok demagnetizációja Lézeres hűtés Nagy eredmények:
Fizika Nyitray Gergely (PhD) PTE PMMIK 2017. április 3. Kriogenika A gázcseppfolyósítások korszaka Az elektronrendszer adiabatikus lemágnesezése Az atommagok demagnetizációja Lézeres hűtés Nagy eredmények:
KRISTÁLYOK GEOMETRIAI LEÍRÁSA
 KRISTÁLYOK GEOMETRIAI LEÍRÁSA Kristály Bázis Pontrács Ideális Kristály: hosszútávúan rendezett hibamentes, végtelen szilárd test Kristály Bázis: a kristály legkisebb, ismétlœdœ atomcsoportja Rácspont:
KRISTÁLYOK GEOMETRIAI LEÍRÁSA Kristály Bázis Pontrács Ideális Kristály: hosszútávúan rendezett hibamentes, végtelen szilárd test Kristály Bázis: a kristály legkisebb, ismétlœdœ atomcsoportja Rácspont:
RÖNTGEN-FLUORESZCENCIA ANALÍZIS
 RÖNTGEN-FLUORESZCENCIA ANALÍZIS 1. Mire jó a röntgen-fluoreszcencia analízis? A röntgen-fluoreszcencia analízis (RFA vagy angolul XRF) roncsolás-mentes atomfizikai anyagvizsgálati módszer. Rövid idõ alatt
RÖNTGEN-FLUORESZCENCIA ANALÍZIS 1. Mire jó a röntgen-fluoreszcencia analízis? A röntgen-fluoreszcencia analízis (RFA vagy angolul XRF) roncsolás-mentes atomfizikai anyagvizsgálati módszer. Rövid idõ alatt
1. Prefix jelentések. 2. Mi alapján definiáljuk az 1 másodpercet? 3. Mi alapján definiáljuk az 1 métert? 4. Mi a tömegegység definíciója?
 1. Prefix jelentések. 10 1 deka 10-1 deci 10 2 hektó 10-2 centi 10 3 kiló 10-3 milli 10 6 mega 10-6 mikró 10 9 giga 10-9 nano 10 12 tera 10-12 piko 10 15 peta 10-15 fento 10 18 exa 10-18 atto 2. Mi alapján
1. Prefix jelentések. 10 1 deka 10-1 deci 10 2 hektó 10-2 centi 10 3 kiló 10-3 milli 10 6 mega 10-6 mikró 10 9 giga 10-9 nano 10 12 tera 10-12 piko 10 15 peta 10-15 fento 10 18 exa 10-18 atto 2. Mi alapján
Az anyagok lehetséges állapotai, a fizikai körülményektől (nyomás, hőmérséklet) függően. Az anyagokat általában a normál körülmények között jellemző
 Az anyagok lehetséges állapotai, a fizikai körülményektől (nyomás, hőmérséklet) függően. Az anyagokat általában a normál körülmények között jellemző állapotuk alapján soroljuk be szilárd, folyékony vagy
Az anyagok lehetséges állapotai, a fizikai körülményektől (nyomás, hőmérséklet) függően. Az anyagokat általában a normál körülmények között jellemző állapotuk alapján soroljuk be szilárd, folyékony vagy
Fizika 1 Elektrodinamika beugró/kis kérdések
 Fizika 1 Elektrodinamika beugró/kis kérdések 1.) Írja fel a 4 Maxwell-egyenletet lokális (differenciális) alakban! rot = j+ D rot = B div B=0 div D=ρ : elektromos térerősség : mágneses térerősség D : elektromos
Fizika 1 Elektrodinamika beugró/kis kérdések 1.) Írja fel a 4 Maxwell-egyenletet lokális (differenciális) alakban! rot = j+ D rot = B div B=0 div D=ρ : elektromos térerősség : mágneses térerősség D : elektromos
Bevezetés az anyagtudományba III. előadás
 Bevezetés az anyagtudományba III. előadás 2010. február 18. Kristályos és s nem-krist kristályos anyagok A kristályos anyag atomjainak elrendeződése sok atomnyi távolságig, a tér mindhárom irányában periodikusan
Bevezetés az anyagtudományba III. előadás 2010. február 18. Kristályos és s nem-krist kristályos anyagok A kristályos anyag atomjainak elrendeződése sok atomnyi távolságig, a tér mindhárom irányában periodikusan
TANULÁSTÁMOGATÓ KÉRDÉSEK AZ 2.KOLLOKVIUMHOZ
 TANULÁSTÁMOGATÓ KÉRDÉSEK AZ 2.KOLLOKVIUMHOZ Vas-karbon diagram: A vas olvadáspontja: a) 1563 C. b) 1536 C. c) 1389 C. Mennyi a vas A1-el jelölt hőmérséklete? b) 1538 C. Mennyi a vas A2-el jelölt hőmérséklete?
TANULÁSTÁMOGATÓ KÉRDÉSEK AZ 2.KOLLOKVIUMHOZ Vas-karbon diagram: A vas olvadáspontja: a) 1563 C. b) 1536 C. c) 1389 C. Mennyi a vas A1-el jelölt hőmérséklete? b) 1538 C. Mennyi a vas A2-el jelölt hőmérséklete?
Mikrohullámú abszorbensek vizsgálata
 Óbudai Egyetem Anyagtudományok és Technológiák Doktori Iskola Mikrohullámú abszorbensek vizsgálata Balla Andrea Témavezetők: Dr. Klébert Szilvia, Dr. Károly Zoltán MTA Természettudományi Kutatóközpont
Óbudai Egyetem Anyagtudományok és Technológiák Doktori Iskola Mikrohullámú abszorbensek vizsgálata Balla Andrea Témavezetők: Dr. Klébert Szilvia, Dr. Károly Zoltán MTA Természettudományi Kutatóközpont
ü ü ű ű ü ü ü Á ű ü ü ü ű Ü
 ü ű ü ű ü ü ü ü Á ü ü ű ű ü ü ü Á ű ü ü ü ű Ü É É Á Á Á Á É Á Á Ő É É É Á É Á É Á É Á ű É É Á Á É É É Á É Á É Á É Á Á ü ű ű ü ü ü ü ü üü ü ü ü ü ü ü ű ü ü ű ü ü ü ü ű ü ü ü ű ü ü ü ü ü ü ü ü ü ü ü ű ü
ü ű ü ű ü ü ü ü Á ü ü ű ű ü ü ü Á ű ü ü ü ű Ü É É Á Á Á Á É Á Á Ő É É É Á É Á É Á É Á ű É É Á Á É É É Á É Á É Á É Á Á ü ű ű ü ü ü ü ü üü ü ü ü ü ü ü ű ü ü ű ü ü ü ü ű ü ü ü ű ü ü ü ü ü ü ü ü ü ü ü ű ü
Fizika minta feladatsor
 Fizika minta feladatsor 10. évf. vizsgára 1. A test egyenes vonalúan egyenletesen mozog, ha A) a testre ható összes erő eredője nullával egyenlő B) a testre állandó értékű erő hat C) a testre erő hat,
Fizika minta feladatsor 10. évf. vizsgára 1. A test egyenes vonalúan egyenletesen mozog, ha A) a testre ható összes erő eredője nullával egyenlő B) a testre állandó értékű erő hat C) a testre erő hat,
