Magasabbrendű funkcionális programozás
|
|
|
- Ákos Török
- 8 évvel ezelőtt
- Látták:
Átírás
1 1 Magasabbrendű funkcionális programozás Hanák Péter Irányítástechnika és Informatika Tanszék OM Kutatás-Fejlesztési Helyettes Államtitkárság Hanák Dávid Számítástudományi és Információelméleti Tanszék Csala Viktor AAM Technologies Kft.
2 BEVEZETÉS
3 Bevezetés 3 Az előadás felépítése 1. alkalom: a alapjai 2. alkalom: a, mint programozási nyelv 3. alkalom: Típusok bevezetése A Caml nyelvcsalád bevezetése a on keresztül
4 Felhasznált irodalom 4 A jelentős irodalommal bír, az előadás alapját a következő bevezető cikkek képezték: Greg Michaelson: An Introduction to Functional Programming Through Lambda Calculus John Harisson: Intorduction to Functional Programming (A cikk a lambda kalkuluson keresztűl vezeti le a Caml alapjait, így a továbbiakban is hasznos lehet, emellett az előadás szerkezete a cikk szerkezetéhez illeszkedik) Henk Barendregt, Erik Barendsen: Introduction to Lambda Calculus (erősen matematikai tárgyalás) További elolvasásra érdemes még Csörnyei Zoltán: A lambda-kalkulus (magyar nyelvű, az ELTE-n használt jogvédett oktatási anyag)
5 A λ-kalkulus ALAPJAI
6 A története Leibniz Univerzális nyelv, amelyen minden probléma megfogalmazható Általános megoldási metódus, amely minden univerzális nyelven megfogalmazott problémára megoldást talál Entscheidungsproblem Hilbert 2. kérdése: Létezik-e teljes és konzisztens matematikai axióma rendszer? Russell, Whitehead: Principia Mathematica A matematika logikai leírásának kísérlete Gödel (1931): Modellelmélet segítségével bebizonyította, hogy Hilbert kérdésére a válasz nemleges!
7 A története Gödel negatív eredménye ellenére az univerzális megoldó eszköz keresése nyomán megszületett a kiszámíthatóság elmélete (theory of computability) Turing: Turing-gép (többé-kevésbé a mai számítógépek őse, a Neumann architektúra lényegében véges Turing-gép közvetlen elérésű memóriával szalag helyett) Kleene: Rekurzív függvények elmélete Church: Church tézise szerint a három metódus ekvivalens és minden probléma leírható velük (ezt mai napig nem bizonyították formálisan). Kleene és Church munkája tekinthető a funkcionális paradigma alapjának.
8 A formális leírása 8 A formális szintaxis a következőképp néz ki: < λ-kifejezés > < változó > <konstans> < λ-absztrakció > < applikáció > < λ-absztrakció > ( λ < változó >. < λ-kifejezés > ) < applikáció > ( < λ-kifejezés > < λ-kifejezés > ) Az előadás során alkalmazott szabályok Függvény alkalmazás jelölése: f(x), vagy f x A függvény applikáció balra köt: f x y jelentése (f(x))(y) λ x.λ y.t[x, y] helyett λ x y.t[x,y]-t írunk A λ-absztrakciót minden esetben a lehető leghosszabban kiterjesztjük jobbra, vagyis λ x.x y jelentése λ x.(x y) (ezt sok szerző nem teszi meg).
9 Mit jelent a λ? 9 Gyakorlatilag semmit A λ csak jelölési konvenció (pl. jellemzően francia szövegekben mai napig használják a [a] t[a] jelölést), létét egy evolúciós folyamatnak köszönheti: 1. Russell és Whitehead a Principia Mathematica-ban a kalap jelölést használta: t[â]. 2. Church módosította a jelölést: â.t[a], de ezt csak a.t[a] formában tudták az akkori nyomdászok megjeleníteni. 3. Végül egy újabb nyomdász kezében, valószínűleg tévedésből kialakult a végleges forma: λa.t[a]
10 A λ jelölés előnyei 10 Nagyon egyszerű eszközrendszerrel gyakorlatilag tetszőleges bonyolultságú matematikai elemek leírhatók és jellemezhetők (persze idővel az egyszerűségért az átláthatóság csökkenésével fizetünk, de mindez javítható szintaktikus édesítőszerek alkalmazásával, ld. Michaelson könyv). Matematikai szövegekben jellemzően az f(x) jelölést használják mind magára az f függvényre való hivatkozásra, mind az f x-re való alkalmazására. Ezt a kétértelműséget teljesen megszűnteti a λ jelölés. Erősen megkönnyíti a változók kezelését (bevezethetővé válik a kötött és a szabad változók fogalma, illetve a programozási nyelveknél jól ismert láthatóság (scoping)).
11 A ereje 11 Számítási képességét tekintve valószínűleg ekvivalens a Turing-géppel (Church tézis) Ennek megfelelően léteznek a Turing-gép problémáival (pl. megállási probléma) ekvivalens problémák. Russell paradoxon: az önmagát nem tartalmazó halmazok halmaza tartalmazza és nem is tartalmazza önmagát: (R = {x x x} R R R R) megfelelője: R = λ x. (x x), így R R = (R R), már pedig ez pont ellentétes a negálás természetes jelentésével. Church ezt felismerve vezette be a típusokat a ba, ami kiküszöbölte az ellentmondást (ld. a 3. alkalom anyagát).
12 Szabad és kötött változók 12 Szabad változók: FV(x) = {x} változó FV(c) = Ø konstans FV(s t) = FV(s) FV(t) applikáció FV(λ x.s) = FV(s) {x} λ-absztrakció Kötött változók: BV(x) = Ø változó BV(c) = Ø konstans BV(s t) = BV(s) BV(t) applikáció BV(λ x.s) = BV(s) {x} λ-absztrakció pl. s = (λ x y.x)(λ x.z x), akkor FV(s) = {z} és BV(s) = {x, y}
13 Helyettesítés 13 Intuitív megközelítésben egyszerű a helyettesítés, de nekünk most gépies metódust kell megalkotnunk. Pl. (λ y.x+y)[y/x] = λ y.y + y, márpedig nem ez az elvárt működés. Helyes szabályok: x[t/x] = t y[t/x] = y if x y c[t/x] = c (s 1 s 2 )[t/x] = s 1 [t/x] s 2 [t/x] (λ x.s) [t/x] = λ x.s (λ y.s) [t/x] = λ y.(s[t/x]), ha x y és x FV(s) vagy y FV(t) (λ y.s) [t/x] = λ z.(s[z/y][t/x]) egyébként, ahol z FV(s) FV(t)
14 Konverziók 14 A három konverziós szabályon alapul: α-konverzió: λ x.s α λ y.s[y/s] feltéve, hogy y FV(s) β-konverzió: (λ x.s) t β s[t/x] η-konverzió: λ x.t x η t feltéve, hogy x FV(t) (pl. λ u.v u η v, de λ u.u u / η u)
15 A λ-azonosság 15 Két λ-kifejezés azonos (=), ha létezik az előző konverziók olyan véges sorozata, amely az egyiket a másikba viszi át: s α t vagy s β t vagy s η t s = t T t = t s = t t = s s = t és t = u s = u s = t s u = t u s = t u s = u t s = t λ x.s = λ x.t Két λ-kifejezés szintaktikailag megegyezik ( ), ha teljesen azonos (vagyis λ x.x λx.x, de a λ y.y λx.x már nem igaz, annak ellenére, hogy λ y.y = λ x.x) A szintaktikai egyezőség gyengített, de sokkal hasznosabb változata az, ahol a szintaktikai egyezőség elérhető kizárólag α-konverzióval ( α ). Pl. λ x.x α λ y.y
16 λ-redukció A λ-azonosság fontos, de nem túl hasznos reláció, sokkal hasznosabb az aszimmetrikus változata a λ-redukció ( ): s α t vagy s β t vagy s η t s t T t t s t és t u s u s t s u t u s t u s u t s t λ x.s λ x.t A redukció (bár nevével ellentétben néha méret növekedéssel jár együtt) a λ-kifejezések szisztematikus kiértékelését jelenti. Amennyiben egy kifejezés redukciója α-konverziók kivételével tovább már nem folytatható, úgy a kifejezés elérte a normál formáját.
17 λ-redukció Kézenfekvő, hogy egy összetett λ-kifejezés redukálása többféleképp is elvégezhető, amelyek között lehet végtelen redukciós sorozat is. Pl. (λ x.y)(λ x.x x x)(λ x.x x x) (λ x.y)(λ x.x x x)(λ x.x x x) (λ x.x x x) (λ x.y)(λ x.x x x)(λ x.x x x) (λ x.x x x)(λ x.x x x) de (λ x.y)(λ x.x x x)(λ x.x x x) y Tétel: ha s t és t normál fomájú, akkor az a stratégia, amely minden esetben s legkülső, legbaloldalibb redukálható részkifejezését redukálja véges redukciós sorozathoz vezet és normál formájú kifejezésben ér véget.
18 Church-Rosser tétel 18 Tétel: ha t s 1 és t s 2, akkor létezik olyan u kifejezés, hogy s 1 u és s 2 u. Következmény1: ha t 1 = t 2, akkor létezik u kifejezés, hogy t 1 u és t 2 u. Következmény2: ha t = t 1 és t = t 2, és t 1 és t 2 normál formájú, akkor t 1 α t 2.
19 Kombinátorok 19 A kombinátorok elmélete a hoz hasonló elmélet, azonos számítási képességekkel: Kombinátornak tekinthető minden szabad változótól mentes λ-kifejezés. Ezeket zárt kifejezéseknek is nevezzük. 3 alap kombinátorral minden kifejezés kifejthető: I = λ x.x ( identity azonosság) K = λ x y.x (konstans) S = λ f g x.(f x)(g x) ( sharing megosztás) Sőt: I = S K A, ahol A bármilyen kombinátor lehet (rendszerint A-nak K-t választják, így I = S K K). A kombinátorok kicsit a gépi kód analógiájának felelnek meg a funkcionális világban.
20 A λ-kalkulus, MINT PROGRAMOZÁSI NYELV
21 Első lépések 21 Egy valós programozási nyelv elképzelhetetlen adatok nélkül. Az első lépésnek valamiféle adatreprezentáció kialakításának és az adatok végezhető alapvető műveleteknek kell lennie. Meg kell teremteni a programvezérlés valamilyen módját. Alapvető elemek: igazságértékek feltételes kifejezés logikai operátorok valamiféle számábrázolás, és a számokon végezhető műveletek ismételt végrehajtás lehetősége Továbbiakban a definíció jelölése: s s, ami annyit jelent, hogy s = s definíció szerint.
22 Igazságértékek 22 A cél valamiképp a true és a false értékek definiálása λ-kifejezések segítségével. Természetes, hogy erre a célra elvben bármely két egymással nem egyenlő (λ-azonosságot tekintve) λ-kifejezés megfelelne. Célszerűségi okokból a következő definíciót használjuk: true λxy. x false λxy. y A fenti kifejezéseknek még nagyon fontos szerepe lesz a továbbiakban Bebizonyítható, hogy ez a két λ-kifejezés semmilyen redukciós sorozattal sem vihető át egymásba (mindez intuitív úton is belátható, lévén egy pár első elemét kiválasztó függvény soha nem fog ugyanúgy viselkedni, mint a második elemet visszaadó kifejezés).
23 Feltételes kifejezés 23 A C c? x : y konstrukcióját akarjuk megalkotni. Fontos, hogy nem feltételes utasításról, hanem tényleges kifejezésről beszélünk, így az else ág nem elhagyható (ez a legtöbb funkcionális nyelvben tényleg így is van). Ennek megfelelően: if E then E1 else E2 E E1 E2 (vagyis (E(E1))(E2)) Például: if true then E1 else E2 = true E1 E2 = (λx y. x) E1 E2 = E1 if false then E1 else E2 = false E1 E2 = (λx y. y) E1 E2 = E2
24 Logikai operátorok 24 Az igazságértékek logikai operátorok nélkül nem igazán használhatóak, de a feltételes kifejezés megteremtette a definiálásuk lehetőségét: not p if p then false else true p and q if p then q else false p or q if p then true else q Az igazságtáblák ellenőrzésével formálisan is bizonyítható ezek helyessége, de szükségtelen.
25 Párok és többesek 25 Minden felsorolás (lista vagy többes) tekinthető párok egymásba ágyazásának a következő módon: (E 1, (E 2, (E 3, ))) (ez egyfajta rekurzív konstrukció, ami az egyik legalapvetőbb funkcionális eszköz) Alapvető a párok ábrázolásának és kezelésének a képessége. Párok ábrázolása: (E 1, E 2 ) λf.f E1 E2 Destruktorok: fst p p true snd p p false hiszen például: fst (p, q) = (p, q) true = (λf.f p q) (λxy. x) = (λx y. x) p q = p Többesekre (jelölés): (p) 1 fst p (p) i fst (snd i-1 p)
26 Curry-ing 26 A párok kezelése lehetővé teszi a függvények hagyományos meghívását (f x y z helyett f(x, y, z, )) Az ehhez szükséges eszközök párokra: CURRY f λx y.f(x, y) UNCURRY g λp.g (fst p) (snd p) Többesekre: CURRY n f λx 1 x n.f(x 1,..., x n ) UNCURRY n g λp.g (p) 1 (p) n Ezután λ(x 1,, x n ).t írható az UNCURRY n (λx 1 x n.t) rövidítéseként
27 Természetes számok 27 Számábrázoláshoz a Chruch-számábrázolást használjuk, ami gyakorlatilag megegyezik a Turing-gépeknél tanulthoz, vagyis az unáris számokról van szó: 1, 11, 111, (ez nem túl hatékony, de rendelkezik néhány nagyon kellemes tulajdonsággal). Ennek megfelelően: n λf x.f n x, Például: 0 λf x.x 1 λf x.fx 2 λf x.f(f x) A számok ilyetén ábrázolásának megválasztása bár nem önkényes, de nem is kötelező, gyakorlatilag alkalmazható bármilyen hasonló tulajdonságokkal rendelkező λ-kifejezés (pl. a 0 lehet az azonosság függvény λx.x és a minden egyes szám a λns.(sfalse) nnövekmény függvény megfelelő számú alkalmazásával definiálható).
28 Műveletek természetes számokon Nulla vizsgálat: ISZERO n n (λx.false) true vagyis ISZERO 0 = (λf x.x) (λx.false) true = true és ISZERO (n + 1) = (λf x.f n+1 x) (λx.false) true = (λx.false) n+1 true = (λx.false)((λx.false) n true) = false
29 Műveletek természetes számokon Következő szám: SUC λnf x.nf (f x) vagyis SUC n = (λn f x.n f (f x)) (λf x.f n x) = λf x.(λfx.f n x)f (f x) = λf x.(λfx.f n x)(f x) = λf x.f n (f x) = λf x.f n+1 x = n + 1
30 Műveletek természetes számokon Az előző szám már nehezebb (cél: PRE 0 = 0 és PRE (n + 1) = n) Trükk a párokra értelmezett PREFN deklarálása, ami eldobja f egy példányát f n -ből a következőképp: PREFN f (true, x) = (false, x) és PREFN f (false, x) = (false, f x) vagyis PREFN λf p.(false, if fst p then snd p else f (snd p)) Majd ezzel: PRE λf x.snd(n (PREFN f) (true, x)) (a helyhiány miatt eltekintek a levezetéstől, mivel viszonylag hosszú, de mindenki kipróbálhatja).
31 Műveletek természetes számokon Összeadás: m + n λf x.m f (n f x) vagyis m + n = λf x.m f (n f x) = λf x.(λfx.f m x)(n f x) = λf x.f m (n f x) = λf x.f m ((λf x.f n x) f x) = λf x.f m ((λx.f n x) x) = λf x.f m (f n x) = λf x.f m+n x
32 Műveletek természetes számokon Szorzás: m * n λf x.m(n f) x vagyis m * n = λf x.m(n f) x = λf x.(λfx.f m x) (n f) x = λf x.(λx.(n f) m x) x = λfx.(nf) m x = λf x.((λfx.f n x) f) m x = λf x.(λx.f n x) m x = λf x.(f n ) m x = λf x.f n*m x
33 Rekurzív függvények bevezető 33 Az ismételt végrehajtás alapvető programozási elem, erre a célra a funkcionális programozáson belül a rekurzió szolgál. Lévén a név nélküli függvényekkel dolgozik első gondolatra lehetetlennek tűnik a rekurzív kifejezések definiálása. Szerencsére ezt nem minden matematikus gondolta így és nem kis erőfeszítéssel megtalálták a megoldást (Curry publikálta először), ami egy előtét függvény alkalmazásával lehetővé teszi a rekurzió alkalmazását a λ- kalkulusban. Az előtét függvény neve fix pont kombinátor: Az Y zárt λ-kifejezést akkor nevezzük fix pont kombinátornak, ha minden f λ-kifejezésre f (Y f) = Y f A fix pont kombinátor egy f kifejezésre alkalmazva azt az x értéket adja vissza, amelyre f(x) = x.
34 Rekurzív függvények fix pont kombinátor 34 Russell-paradoxon: R = λx. (x x) és R R = (R R) vagyis R a operátor fix pont kombinátora. Általánosítsuk R-t: Y λf.(λx.f (x x)) (λx.f (x x)) amire Y f = (λf.(λx.f (x x)) (λx.f (x x))) f = (λx.f (x x)) (λx.f (x x)) = f (λx.f (x x)) (λx.f (x x)) = f (Y f) Mivel az utolsó lépésben egy fordított β-redukciót hajtottunk végre, a fenti kifejezés programozási szempontból nem megfelelő (mivel ott csak a normális redukciós lépések megengedettek), így gyakorlati alkalmazásokban Turing után: T (λx y. y (x x y)) (λx y. y (x x y)). Továbbiakban Y-t használjuk, de a helyére bármelyik fix pont kombinátor használható (pl., ahol = λabcdefghijklmnopqstuvwxyzr.r(thisisafixedpointcombinator))
35 Rekurzív függvények definiálása 35 Példaként definiáljuk a faktoriális függvényt a következőképp: fact(n) = if ISZERO n then 1 else n * fact(pre n) Írjuk át λ-kifejezésszerű formára: fact = λn. if ISZERO n then 1 else n * fact(pre n) = (λf n. if ISZERO n then 1 else n * f(pre n)) fact Ha jól megnézzük látszik, hogy fact a F = λf n. if ISZERO n then 1 else n * f(pre n) függvény fix pontja, vagyis fact = Y F. Hasonlóan megoldható a kölcsönösen rekurzív függvények definiálása is.
36 TÍPUSOK BEVEZETÉSE
37 Típusok 37 Mind logikai, mind programozási szempontból indokolt a típusok bevezetése. A logikai szempontot a Russell paradoxon megléte adja, ami gyakorlatilag azért fordulhat elő, mert megengedett a függvények önmagukra való alkalmazása ennek kiküszöbölése megszünteti a paradoxont, emiatt vezette be eredetileg Russell a típusokat a Principia Mathematica-ban. Programozási szempont összetettebb: Már a FORTRAN is megkülönböztet típusokat, mert így hatékonyabb kódot tud előállítani (ugyanez igaz pl. a C mutató aritmetikájára). A típusok megléte segít kiküszöbölni a programozási hibák jelentős részét. A típusok használata több féle lehet: nincsenek típusok (BCPL, ISWIM, SASL, Erlang), gyenge típizálás (PL/I), futásidejű dinamikus típusellenőrzés (LISP), fordítás idejű erős tipizálás polimorfizmussal (ML).
38 Típusos 38 Típusok bevezetése a ba viszonylag kézenfekvő dolognak tűnik, de az eredménye nagyon messzire visz. Alapötlet: minden λ-kifejezésnek legyen típusa, így s csak akkor alkalmazható t-re (s t), ha a típusok megfelelően illeszkednek. Vagyis, ha s típusa σ τ és t típusa σ, akkor s t típusa τ. Programozási nyelvek között ezt hívják erős tipizálásnak, vagyis t-nek σ típusúnak kell lennie, nincs szó altípusokról vagy megfeleltetésről (ezzel szemben pl. a C nyelvben egy függvény double típusú paramétert vár, akkor elfogad float típusút is). Jelölésmód: t : σ jelentése t típusa σ (ez teljesen összhangban van a matematikában használt jelölésmóddal). A típusokra úgy tekintünk, mint értékhalmazokra, vagyis t : σ t σ.
39 Típusok halmaza 39 A formális tárgyalás első lépéseként meg kell határoznunk, hogy pontosan mit értűnk típusokon. Feltételezzük, hogy rendelkezünk néhány primitív típussal (pl. bool, int, stb.). Vannak típus konstruktoraink, amelyekkel a primitív típusokból összetett típusokat hozhatunk létre, jelölésük (α 1,, α n )con (pl., vagy list). Ennek megfelelően Ty C típus halmaza a C típushalmazból a következő induktív szabályokkal állítható elő (α i tetszőleges típust jelöl): σ C σ Ty C i [1..n] : α i Ty C (α i,, α n )con Ty C
40 Church megközelítése 40 Church a típusok bevezetésénél az explicit típusjelölést alkalmazta, vagyis minden kifejezéshez hozzárendelte a megfelelő típust. Az explicit típusmegadás szabályai a következők: v : σ A c konstans típusa σ c : σ s : σ τ és t : σ s t : τ v : σ és t : τ λv.t : σ τ
41 Curry megközelítése 41 Curry a típusok kezelésére a teljesen implicit megoldást választotta, vagyis a kifejezések teljesen megegyeznek a nem típusos kifejezéseivel, vagy nincs egyáltalán típusuk, vagy van és akár többféle is lehet. Pl. a λx.x függvény típusa σ σ, ahol σ tetszőleges típus lehet (mindig az adott környezet dönti el). Ebben az esetben a tipizálás mindig a környezettől függ, ami a változók típus hozzárendelésének véges halmaza. Formálisan: Γ t : σ, ahol Γ elemei v : σ változó típus összerendelések. Γ lehet üres, akkor t : σ-t írunk. Feltételezzük, hogy Γ nem tartalmaz ugyanarra a változóra ellentmondó típus hozzárendelést (tekinthető a változók halmaza és a típusok halmaza közötti függvénykapcsolatnak is). A továbbiakban ezt a tipizálást használjuk, mivel az ML nyelvek is ezt a fajta megoldást követik.
42 Formális típus szabályok 42 Az általunk használt tipizálás szabályai a következők: v : σ Γ Γ v : σ A c konstans típusa σ c : σ Γ s : σ τ és Γ t : σ Γ s t : τ Γ {v : σ} t : τ Γ λv.t : σ τ Pl. az azonosság függvény levezetése: a változók szabályából {x : σ} x : σ, majd az utolsó szabályból Ø λx.x : σ σ. Churchnél ugyanez lehet λx: σ.(x : τ) : σ τ...
43 Típus megőrzés 43 A típusok bevezetésének csak akkor van értelme, ha a redukció megőrzi egy kifejezés típusát. Ez bizonyíthatóan így van, most röviden felvázoljuk az η-redukcióra: Lemma 1: ha Γ t : σ és Γ, akkor t : σ. Bizonyítás strukturális indukcióval mehet. Lemma 2: ha Γ t : σ, akkor Γ t t : σ, ahol Γ t csak azokra a változókra tartalmaz hozzárendeléseket, amik szabadok t-ben (formálisan Γ t = {x : α x : α Γ és x FV(t)}). Ismét strukturális indukcióval bizonyítható. Tétel: ha Γ t : σ és t η t, akkor Γ t : σ is fennáll. A két lemma segítségével bizonyítható. Ugyanilyen módon belátható az α és a β-redukció is.
44 Polimorfizmus 44 A polimorfizmus és a túlterhelés (overloading) hasonló jelentésű fogalmak, mind a kettő nagy vonalakban azt jelenti, hogy egy kifejezésnek több típusa is lehet. A polimorfizmus pontos jelentése, hogy a kifejezés típusa minden olyan típus lehet, ami megfelel a megadott mintának (paraméteres polimorfizmus). A túlterhelés ugyanahhoz a kifejezéshez több strukturálisan nem összefüggő típust rendel hozzá (ad-hoc polimorfizmus).
45 Let utasítás - előtekintés 45 A kifejezések átláthatóságának érdekében érdemes bevezetni a lokális értékadásnak megfelelő szintaktikai édesítőszert. Ennek megfelelően: let x = s in t (λx.t) s A fenti forma az ML nyelvek alapvető eleme, sőt a CAML alapvető definíciós eszköze (az SML val és fun utasításainak a CAML-ben a let felel meg).
46 A let utasítás polimorfizmusa 46 Tekintsük a if (λx.x) true then (λx.x) 1 else 0 kifejezést: {x : bool} x : bool {x : int} x : int λx.x : bool bool true : bool λx.x : int int 1 : int (λx.x) true : bool (λx.x) 1 : int 0 : int if (λx.x) true then (λx.x) 1 else 0 : int De let I = λx.x in if I true then I 1 else 0 kifejezéshez, ami a (λi.if I true then I 1 else 0) λx.x kifejezésnek felel meg, nem rendelhető típus, mivel I típusa már a λ-absztrakcióban eldől. Emiatt a let-et, mint primitív utasítást vezetjük be: Γ s : σ Γ t[s/x] : τ Γ let x = s in t : τ
47 A legáltalánosabb típus 47 A Curry-féle típus megállapításra a polimorfizmusnál erősebb állítás is igaz, azaz minden kifejezéshez létezik egy legáltalánosabb típus (principal type), és a kifejezés minden lehetséges típusa ennek egyede. A tétel megfogalmazásához bevezetjűk a típusváltozókat és az azokon értelmezett helyettesítést: α i [τ 1 / α 1,, τ n / α n ] = τ i β[τ 1 / α 1,, τ n / α n ] = β, ha α i β (1 i k) (α 1,, α n )con[θ] = (α 1 [θ],, α n [θ])con Az alaptípusokat nullargumentumos konstruktorként kezeljük, pl. ()int. Jelölés: σ σ jelentése σ általánosabb típus, mint σ. Tétel: Minden típusos kifejezéshez létezik egy legáltalánosabb típus, vagyis ha t : τ, akkor létezik σ, hogy t : σ és bármely σ -re, ha t : σ, akkor σ σ. A bizonyítás a Milner (v. Hindley-Milner) algoritmuson alapszik, amire az MLekben alkalmazott típus-meghatározás is épül.
48 Erős normalizáció 48 Tekintsük a korábban már mutatott példát: ((λx.x x x)(λx.x x x)) ((λx.x x x)(λx.x x x)(λx.x x x)) ( ) A típusos kifejezések világában ez a fajta viselkedés nem létezik, ahogy azt a következő tétel kimondja. Tétel: minden tipizálható kifejezésnek létezik normál formája (ha itt vége lenne, akkor beszélnénk gyenge normalizációról) és minden lehetséges redukciós sorozat terminál.
49 A típusos korlátai 49 Az erős normalizáció jól hangzik, de ára van, mivel nagyon korlátozott azoknak a függvényeknek a száma, amit a típusos ki tud fejezni (sőt bebizonyítható, hogy a leírható kifejezések köre nagyban függ a választott számábrázolástól). Pl. nem termináló kifejezés írása alapvető feltétele a Turing-teljesség elérésének. A rekurzió sem megvalósítható a korábban felvázolt módon, mert a fix pont kombinátorok jellemzően nem tipizálhatóak. A Turing-teljesség érdekében bevezetünk egy polimorf rekurziós operátort: Rec : ((σ τ) (σ τ)) σ τ és az ehhez tartozó redukciós szabályt: Rec F F (Rec F)
50 A CAML NYELVCSALÁD BEVEZETÉSE A λ-kalkuluson KERESZTÜL
51 Rövid ismertető 51 A Caml Light és az OCaml (az utóbbi objektum orientált) az Edinborough ML-ből alakult ki, az ML nyelvjárásának tekinthető (a Standard ML csak nevében szabványos, ténylegesen még nem szabványosították). Keletkezési helye a francia INRIA. Teljesítményében összemérhető a C++-szal, köszönhetően a hatékony megvalósításának (a nyelv megvalósításának alapja Category Abstract Machine-nek nevezett eszköz innen kapta a nevét is megfelelően hangolt garbage collectionnal kiegészítve). Bővebben a Caml előadáson
52 A megfelelői a Caml-ben 52 Névadás: let <név> = <kifejezés> Helyi értékadás: let <név> = <kifejezés> in <kifejezés> (ld. korábban) Rekurzív definíció: let rec <név> = <rekurzív kifejezés> Kölcsönösen rekuzív definíció: let rec <név> = <kölcsönösen rekurzív kifejezés> and <név> = <kölcsönösen rekurzív kifejezés> and A λ-absztrakció: function <paraméter> -> <kifejezés> vagy fun <paraméter> <paraméter> -> <kifejezés>...
Nyelvek típusrendszere (IPM-08sztNYTRE, IPM-08EsztNYTRE)
 Nyelvek típusrendszere (IPM-08sztNYTRE, IPM-08EsztNYTRE) http://people.inf.elte.hu/pgj/nytr_msc/ Páli Gábor János pgj@elte.hu Eötvös Loránd Tudományegyetem, Informatikai Kar Programozási Nyelvek és Fordítóprogramok
Nyelvek típusrendszere (IPM-08sztNYTRE, IPM-08EsztNYTRE) http://people.inf.elte.hu/pgj/nytr_msc/ Páli Gábor János pgj@elte.hu Eötvös Loránd Tudományegyetem, Informatikai Kar Programozási Nyelvek és Fordítóprogramok
FUNKCIONÁLIS PROGRAMOZÁS
 FUNKCIONÁLIS PROGRAMOZÁS A funkcionális programozás néhány jellemzője Funkcionális programozás 1-2 Funkcionális, más néven applikatív programozás Funkcionális = függvényalapú, függvényközpontú Applikatív
FUNKCIONÁLIS PROGRAMOZÁS A funkcionális programozás néhány jellemzője Funkcionális programozás 1-2 Funkcionális, más néven applikatív programozás Funkcionális = függvényalapú, függvényközpontú Applikatív
Kaposi Ambrus. University of Nottingham Functional Programming Lab. Hackerspace Budapest 2015. január 6.
 Bizonyítás és programozás Kaposi Ambrus University of Nottingham Functional Programming Lab Hackerspace Budapest 2015. január 6. Bizonyítás, érvelés Példa: sáros a csizmám ha vizes a föld, esett az eső
Bizonyítás és programozás Kaposi Ambrus University of Nottingham Functional Programming Lab Hackerspace Budapest 2015. január 6. Bizonyítás, érvelés Példa: sáros a csizmám ha vizes a föld, esett az eső
Kaposi Ambrus. Informatikai Kar. Pannonhalmi Bencés Gimnázium november 24.
 Bizonyítás és programozás Kaposi Ambrus Eötvös Loránd Tudományegyetem Informatikai Kar Pannonhalmi Bencés Gimnázium 2017. november 24. A tökéletes operációs rendszer (i) BeOS Plan9 2 / 22 A tökéletes operációs
Bizonyítás és programozás Kaposi Ambrus Eötvös Loránd Tudományegyetem Informatikai Kar Pannonhalmi Bencés Gimnázium 2017. november 24. A tökéletes operációs rendszer (i) BeOS Plan9 2 / 22 A tökéletes operációs
Kiterjesztések sek szemantikája
 Kiterjesztések sek szemantikája Példa D Integer = {..., -1,0,1,... }; D Boolean = { true, false } D T1... T n T = D T 1... D Tn D T Az összes függvf ggvény halmaza, amelyek a D T1,..., D Tn halmazokból
Kiterjesztések sek szemantikája Példa D Integer = {..., -1,0,1,... }; D Boolean = { true, false } D T1... T n T = D T 1... D Tn D T Az összes függvf ggvény halmaza, amelyek a D T1,..., D Tn halmazokból
Programok értelmezése
 Programok értelmezése Kód visszafejtés. Izsó Tamás 2016. szeptember 22. Izsó Tamás Programok értelmezése/ 1 Section 1 Programok értelmezése Izsó Tamás Programok értelmezése/ 2 programok szemantika értelmezése
Programok értelmezése Kód visszafejtés. Izsó Tamás 2016. szeptember 22. Izsó Tamás Programok értelmezése/ 1 Section 1 Programok értelmezése Izsó Tamás Programok értelmezése/ 2 programok szemantika értelmezése
Logika és informatikai alkalmazásai kiskérdések február Mikor mondjuk, hogy az F formula a G-nek részformulája?
 ,,Alap kiskérdések Logika és informatikai alkalmazásai kiskérdések 2012. február 19. 1. Hogy hívjuk a 0 aritású függvényjeleket? 2. Definiálja a termek halmazát. 3. Definiálja a formulák halmazát. 4. Definiálja,
,,Alap kiskérdések Logika és informatikai alkalmazásai kiskérdések 2012. február 19. 1. Hogy hívjuk a 0 aritású függvényjeleket? 2. Definiálja a termek halmazát. 3. Definiálja a formulák halmazát. 4. Definiálja,
... S n. A párhuzamos programszerkezet két vagy több folyamatot tartalmaz, melyek egymással közös változó segítségével kommunikálnak.
 Párhuzamos programok Legyen S parbegin S 1... S n parend; program. A párhuzamos programszerkezet két vagy több folyamatot tartalmaz, melyek egymással közös változó segítségével kommunikálnak. Folyamat
Párhuzamos programok Legyen S parbegin S 1... S n parend; program. A párhuzamos programszerkezet két vagy több folyamatot tartalmaz, melyek egymással közös változó segítségével kommunikálnak. Folyamat
Alapok. tisztán funkcionális nyelv, minden függvény (a konstansok is) nincsenek hagyományos változók, az első értékadás után nem módosíthatók
 Haskell 1. Alapok tisztán funkcionális nyelv, minden függvény (a konstansok is) nincsenek hagyományos változók, az első értékadás után nem módosíthatók elég jól elkerülhetők így a mellékhatások könnyebben
Haskell 1. Alapok tisztán funkcionális nyelv, minden függvény (a konstansok is) nincsenek hagyományos változók, az első értékadás után nem módosíthatók elég jól elkerülhetők így a mellékhatások könnyebben
Bonyolultságelmélet. Monday 26 th September, 2016, 18:27. Bonyolultságelmélet
 Monday 26 th September, 2016, 18:27 A kurzus teljesítési követelményei Gyakorlat Három kisdolgozat 6 6 pontért kb. a 4., 7. és 10. gyakorlaton Egy nagydolgozat 28 pontért utolsó héten előadáson Pontszám:
Monday 26 th September, 2016, 18:27 A kurzus teljesítési követelményei Gyakorlat Három kisdolgozat 6 6 pontért kb. a 4., 7. és 10. gyakorlaton Egy nagydolgozat 28 pontért utolsó héten előadáson Pontszám:
Bonyolultságelmélet. Monday 26 th September, 2016, 18:28
 Bonyolultságelmélet Monday 26 th September, 2016, 18:28 A kurzus teljesítési követelményei 2 Gyakorlat Három kisdolgozat 6 6 pontért kb. a 4., 7. és 10. gyakorlaton Egy nagydolgozat 28 pontért utolsó héten
Bonyolultságelmélet Monday 26 th September, 2016, 18:28 A kurzus teljesítési követelményei 2 Gyakorlat Három kisdolgozat 6 6 pontért kb. a 4., 7. és 10. gyakorlaton Egy nagydolgozat 28 pontért utolsó héten
1. Példa. A gamma függvény és a Fubini-tétel.
 . Példa. A gamma függvény és a Fubini-tétel.. Az x exp x + t )) függvény az x, t tartományon folytonos, és nem negatív, ezért alkalmazható rá a Fubini-tétel. I x exp x + t )) dxdt + t dt π 4. [ exp x +
. Példa. A gamma függvény és a Fubini-tétel.. Az x exp x + t )) függvény az x, t tartományon folytonos, és nem negatív, ezért alkalmazható rá a Fubini-tétel. I x exp x + t )) dxdt + t dt π 4. [ exp x +
2016, Funkcionális programozás
 Funkcionális programozás 2. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2016, tavaszi félév Miről volt szó? Programozási paradigmák: imperatív,
Funkcionális programozás 2. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2016, tavaszi félév Miről volt szó? Programozási paradigmák: imperatív,
TÍPUSKIKÖVETKEZTETÉSI MÓDSZEREK
 TÍPUSKIKÖVETKEZTETÉSI MÓDSZEREK THE METHODS OF TYPE INFERENCE Csörnyei Zoltán 1, Nagy Sára 2 ELTE Informatikai Kar, Programozási Nyelvek és Fordítóprogramok Tanszék 1 ELTE Informatikai Kar, Algoritmusok
TÍPUSKIKÖVETKEZTETÉSI MÓDSZEREK THE METHODS OF TYPE INFERENCE Csörnyei Zoltán 1, Nagy Sára 2 ELTE Informatikai Kar, Programozási Nyelvek és Fordítóprogramok Tanszék 1 ELTE Informatikai Kar, Algoritmusok
Kifejezések. Kozsik Tamás. December 11, 2016
 Kifejezések Kozsik Tamás December 11, 2016 Kifejezések Lexika Szintaktika Szemantika Lexika azonosítók (változó-, metódus-, típus- és csomagnevek) literálok operátorok, pl. + zárójelek: (), [], {},
Kifejezések Kozsik Tamás December 11, 2016 Kifejezések Lexika Szintaktika Szemantika Lexika azonosítók (változó-, metódus-, típus- és csomagnevek) literálok operátorok, pl. + zárójelek: (), [], {},
A digitális számítás elmélete
 A digitális számítás elmélete 8. előadás ápr. 16. Turing gépek és nyelvtanok A nyelvosztályok áttekintése Turing gépek és a természetes számokon értelmezett függvények Áttekintés Dominó Bizonyítások: L
A digitális számítás elmélete 8. előadás ápr. 16. Turing gépek és nyelvtanok A nyelvosztályok áttekintése Turing gépek és a természetes számokon értelmezett függvények Áttekintés Dominó Bizonyítások: L
5. előadás. Programozás-elmélet. Programozás-elmélet 5. előadás
 Elemi programok Definíció Az S A A program elemi, ha a A : S(a) { a, a, a, a,..., a, b b a}. A definíció alapján könnyen látható, hogy egy elemi program tényleg program. Speciális elemi programok a kövekezők:
Elemi programok Definíció Az S A A program elemi, ha a A : S(a) { a, a, a, a,..., a, b b a}. A definíció alapján könnyen látható, hogy egy elemi program tényleg program. Speciális elemi programok a kövekezők:
A következő feladat célja az, hogy egyszerű módon konstruáljunk Poisson folyamatokat.
 Poisson folyamatok, exponenciális eloszlások Azt mondjuk, hogy a ξ valószínűségi változó Poisson eloszlású λ, 0 < λ
Poisson folyamatok, exponenciális eloszlások Azt mondjuk, hogy a ξ valószínűségi változó Poisson eloszlású λ, 0 < λ
2. Rekurzió. = 2P2(n,n) 2 < 2P2(n,n) 1
 2. Rekurzió Egy objektum definícióját rekurzívnak nevezünk, ha a definíció tartalmazza a definiálandó objektumot. Egy P eljárást (vagy függvényt) rekurzívnak nevezünk, ha P utasításrészében előfordul magának
2. Rekurzió Egy objektum definícióját rekurzívnak nevezünk, ha a definíció tartalmazza a definiálandó objektumot. Egy P eljárást (vagy függvényt) rekurzívnak nevezünk, ha P utasításrészében előfordul magának
FUNKCIONÁLIS PROGRAMOZÁS ELŐADÁS JEGYZET
 FUNKCIONÁLIS PROGRAMOZÁS ELŐADÁS JEGYZET Szerkesztette: Balogh Tamás 2013. május 30. Ha hibát találsz, kérlek jelezd a info@baloghtamas.hu e-mail címen! Ez a Mű a Creative Commons Nevezd meg! - Ne add
FUNKCIONÁLIS PROGRAMOZÁS ELŐADÁS JEGYZET Szerkesztette: Balogh Tamás 2013. május 30. Ha hibát találsz, kérlek jelezd a info@baloghtamas.hu e-mail címen! Ez a Mű a Creative Commons Nevezd meg! - Ne add
Analízis előadás és gyakorlat vázlat
 Analízis előadás és gyakorlat vázlat Készült a PTE TTK GI szakos hallgatóinak Király Balázs 2010-11. I. Félév 2 1. fejezet Számhalmazok és tulajdonságaik 1.1. Nevezetes számhalmazok ➀ a) jelölése: N b)
Analízis előadás és gyakorlat vázlat Készült a PTE TTK GI szakos hallgatóinak Király Balázs 2010-11. I. Félév 2 1. fejezet Számhalmazok és tulajdonságaik 1.1. Nevezetes számhalmazok ➀ a) jelölése: N b)
Formális szemantika. Kifejezések szemantikája. Horpácsi Dániel ELTE Informatikai Kar
 Formális szemantika Kifejezések szemantikája Horpácsi Dániel ELTE Informatikai Kar 2016-2017-2 Az előadás témája Egyszerű kifejezések formális szemantikája Az első lépés a programozási nyelvek szemantikájának
Formális szemantika Kifejezések szemantikája Horpácsi Dániel ELTE Informatikai Kar 2016-2017-2 Az előadás témája Egyszerű kifejezések formális szemantikája Az első lépés a programozási nyelvek szemantikájának
2019, Funkcionális programozás. 2. el adás. MÁRTON Gyöngyvér
 Funkcionális programozás 2. el adás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2019, tavaszi félév Mir l volt szó? Követelmények, osztályozás Programozási
Funkcionális programozás 2. el adás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2019, tavaszi félév Mir l volt szó? Követelmények, osztályozás Programozási
Bánsághi Anna 2014 Bánsághi Anna 1 of 33
 IMPERATÍV PROGRAMOZÁS Bánsághi Anna anna.bansaghi@mamikon.net 7. ELŐADÁS - ABSZTRAKT ADATTÍPUS 2014 Bánsághi Anna 1 of 33 TEMATIKA I. ALAPFOGALMAK, TUDOMÁNYTÖRTÉNET II. IMPERATÍV PROGRAMOZÁS Imperatív
IMPERATÍV PROGRAMOZÁS Bánsághi Anna anna.bansaghi@mamikon.net 7. ELŐADÁS - ABSZTRAKT ADATTÍPUS 2014 Bánsághi Anna 1 of 33 TEMATIKA I. ALAPFOGALMAK, TUDOMÁNYTÖRTÉNET II. IMPERATÍV PROGRAMOZÁS Imperatív
f(x) vagy f(x) a (x x 0 )-t használjuk. lim melyekre Mivel itt ɛ > 0 tetszőlegesen kicsi, így a a = 0, a = a, ami ellentmondás, bizonyítva
 6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
6. FÜGGVÉNYEK HATÁRÉRTÉKE ÉS FOLYTONOSSÁGA 6.1 Függvény határértéke Egy D R halmaz torlódási pontjainak halmazát D -vel fogjuk jelölni. Definíció. Legyen f : D R R és legyen x 0 D (a D halmaz torlódási
Kifejezések. Kozsik Tamás. December 11, 2016
 Kifejezések Kozsik Tamás December 11, 2016 Kifejezés versus utasítás C/C++: kifejezés plusz pontosvessző: utasítás kiértékeli a kifejezést jellemzően: mellékhatása is van például: értékadás Ada: n = 5;
Kifejezések Kozsik Tamás December 11, 2016 Kifejezés versus utasítás C/C++: kifejezés plusz pontosvessző: utasítás kiértékeli a kifejezést jellemzően: mellékhatása is van például: értékadás Ada: n = 5;
Programozási nyelvek Java
 Programozási nyelvek Java Kozsik Tamás előadása alapján Készítette: Nagy Krisztián 9. előadás Interface - típust vezet be, de osztálypéldány nem készíthető belőle (statikus típust ad) - több osztály is
Programozási nyelvek Java Kozsik Tamás előadása alapján Készítette: Nagy Krisztián 9. előadás Interface - típust vezet be, de osztálypéldány nem készíthető belőle (statikus típust ad) - több osztály is
Modellellenőrzés. dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék
 Modellellenőrzés dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális vagy félformális tervek Informális követelmények Formális modell: KS, LTS, TA
Modellellenőrzés dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális vagy félformális tervek Informális követelmények Formális modell: KS, LTS, TA
FUNKCIONÁLIS PROGRAMNYELVEK IMPLEMENTÁCIÓJA
 CSÖRNYEI ZOLTÁN FUNKCIONÁLIS PROGRAMNYELVEK IMPLEMENTÁCIÓJA I. rész BUDAPEST, 2010 ii c Csörnyei Zoltán, 2010. Minden jog fenntartva. Jelen könyvet, illetve annak részeit tilos reprodukálni, adatrögzítő
CSÖRNYEI ZOLTÁN FUNKCIONÁLIS PROGRAMNYELVEK IMPLEMENTÁCIÓJA I. rész BUDAPEST, 2010 ii c Csörnyei Zoltán, 2010. Minden jog fenntartva. Jelen könyvet, illetve annak részeit tilos reprodukálni, adatrögzítő
Java II. I A Java programozási nyelv alapelemei
 Java II. I A Java programozási nyelv alapelemei Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2008. 02. 19. Java II.: Alapelemek JAVA2 / 1 A Java formalizmusa A C, illetve az annak
Java II. I A Java programozási nyelv alapelemei Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2008. 02. 19. Java II.: Alapelemek JAVA2 / 1 A Java formalizmusa A C, illetve az annak
A szemantikus elemzés helye. A szemantikus elemzés feladatai. A szemantikus elemzés feladatai. Deklarációk és láthatósági szabályok
 A szemantikus elemzés helye Forrásprogram Forrás-kezelő (source handler) Lexikális elemző (scanner) A szemantikus elemzés feladatai Fordítóprogramok előadás (A, C, T szakirány) Szintaktikus elemző (parser)
A szemantikus elemzés helye Forrásprogram Forrás-kezelő (source handler) Lexikális elemző (scanner) A szemantikus elemzés feladatai Fordítóprogramok előadás (A, C, T szakirány) Szintaktikus elemző (parser)
Komputeralgebra Rendszerek
 Komputeralgebra Rendszerek Programozás Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2014. február 23. TARTALOMJEGYZÉK 1 of 28 TARTALOMJEGYZÉK I 1 TARTALOMJEGYZÉK 2 Értékadás MAPLE -ben SAGE -ben 3
Komputeralgebra Rendszerek Programozás Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2014. február 23. TARTALOMJEGYZÉK 1 of 28 TARTALOMJEGYZÉK I 1 TARTALOMJEGYZÉK 2 Értékadás MAPLE -ben SAGE -ben 3
NP-teljesség röviden
 NP-teljesség röviden Bucsay Balázs earthquake[at]rycon[dot]hu http://rycon.hu 1 Turing gépek 1/3 Mi a turing gép? 1. Definíció. [Turing gép] Egy Turing-gép formálisan egy M = (K, Σ, δ, s) rendezett négyessel
NP-teljesség röviden Bucsay Balázs earthquake[at]rycon[dot]hu http://rycon.hu 1 Turing gépek 1/3 Mi a turing gép? 1. Definíció. [Turing gép] Egy Turing-gép formálisan egy M = (K, Σ, δ, s) rendezett négyessel
Deníciók és tételek a beugró vizsgára
 Deníciók és tételek a beugró vizsgára (a szóbeli viszgázás jogáért) Utolsó módosítás: 2008. december 2. 2 Bevezetés Számítási problémának nevezünk egy olyan, a matematika nyelvén megfogalmazott kérdést,
Deníciók és tételek a beugró vizsgára (a szóbeli viszgázás jogáért) Utolsó módosítás: 2008. december 2. 2 Bevezetés Számítási problémának nevezünk egy olyan, a matematika nyelvén megfogalmazott kérdést,
Halmazelmélet. 1. előadás. Farkas István. DE ATC Gazdaságelemzési és Statisztikai Tanszék. Halmazelmélet p. 1/1
 Halmazelmélet 1. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Halmazelmélet p. 1/1 A halmaz fogalma, jelölések A halmaz fogalmát a matematikában nem definiáljuk, tulajdonságaival
Halmazelmélet 1. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Halmazelmélet p. 1/1 A halmaz fogalma, jelölések A halmaz fogalmát a matematikában nem definiáljuk, tulajdonságaival
Diszkrét matematika II., 8. előadás. Vektorterek
 1 Diszkrét matematika II., 8. előadás Vektorterek Dr. Takách Géza NyME FMK Informatikai Intézet takach@inf.nyme.hu http://inf.nyme.hu/ takach/ 2007.??? Vektorterek Legyen T egy test (pl. R, Q, F p ). Definíció.
1 Diszkrét matematika II., 8. előadás Vektorterek Dr. Takách Géza NyME FMK Informatikai Intézet takach@inf.nyme.hu http://inf.nyme.hu/ takach/ 2007.??? Vektorterek Legyen T egy test (pl. R, Q, F p ). Definíció.
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 4 IV. FÜGGVÉNYEk 1. LEkÉPEZÉSEk, függvények Definíció Legyen és két halmaz. Egy függvény -ből -ba egy olyan szabály, amely minden elemhez pontosan egy elemet rendel hozzá. Az
KOVÁCS BÉLA, MATEmATIkA I. 4 IV. FÜGGVÉNYEk 1. LEkÉPEZÉSEk, függvények Definíció Legyen és két halmaz. Egy függvény -ből -ba egy olyan szabály, amely minden elemhez pontosan egy elemet rendel hozzá. Az
2018, Diszkrét matematika
 Diszkrét matematika 3. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? számtartományok: természetes
Diszkrét matematika 3. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? számtartományok: természetes
A programozás alapjai előadás. Amiről szólesz: A tárgy címe: A programozás alapjai
 A programozás alapjai 1 1. előadás Híradástechnikai Tanszék Amiről szólesz: A tárgy címe: A programozás alapjai A számítógép részegységei, alacsony- és magasszintű programnyelvek, az imperatív programozási
A programozás alapjai 1 1. előadás Híradástechnikai Tanszék Amiről szólesz: A tárgy címe: A programozás alapjai A számítógép részegységei, alacsony- és magasszintű programnyelvek, az imperatív programozási
Leképezések. Leképezések tulajdonságai. Számosságok.
 Leképezések Leképezések tulajdonságai. Számosságok. 1. Leképezések tulajdonságai A továbbiakban legyen A és B két tetszőleges halmaz. Idézzünk fel néhány definíciót. 1. Definíció (Emlékeztető). Relációknak
Leképezések Leképezések tulajdonságai. Számosságok. 1. Leképezések tulajdonságai A továbbiakban legyen A és B két tetszőleges halmaz. Idézzünk fel néhány definíciót. 1. Definíció (Emlékeztető). Relációknak
BASH script programozás II. Vezérlési szerkezetek
 06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
3. előadás. Programozás-elmélet. A változó fogalma Kiterjesztések A feladat kiterjesztése A program kiterjesztése Kiterjesztési tételek Példa
 A változó fogalma Definíció Legyen A = A 1 A 2... A n állapottér. A pr Ai projekciós függvényeket változóknak nevezzük: : A A i pr Ai (a) = a i ( a = (a 1, a 2,..., a n ) A). A változók jelölése: v i =
A változó fogalma Definíció Legyen A = A 1 A 2... A n állapottér. A pr Ai projekciós függvényeket változóknak nevezzük: : A A i pr Ai (a) = a i ( a = (a 1, a 2,..., a n ) A). A változók jelölése: v i =
FFT. Második nekifutás. Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék október 2.
 TARTALOMJEGYZÉK Polinomok konvolúviója A DFT és a maradékos osztás Gyűrűk támogatás nélkül Második nekifutás Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2015. október 2. TARTALOMJEGYZÉK Polinomok
TARTALOMJEGYZÉK Polinomok konvolúviója A DFT és a maradékos osztás Gyűrűk támogatás nélkül Második nekifutás Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2015. október 2. TARTALOMJEGYZÉK Polinomok
A Számítástudomány alapjai
 Mechatronika, Optika és Gépészeti Informatika Tanszék A Számítástudomány alapjai Szemelvények az Elméleti Számítástudomány területéről Fogalmak: Számítástechnika Realizáció, technológia Elméleti számítástudomány
Mechatronika, Optika és Gépészeti Informatika Tanszék A Számítástudomány alapjai Szemelvények az Elméleti Számítástudomány területéről Fogalmak: Számítástechnika Realizáció, technológia Elméleti számítástudomány
Automaták és formális nyelvek
 Automaták és formális nyelvek Bevezetés a számítástudomány alapjaiba 1. Formális nyelvek 2006.11.13. 1 Automaták és formális nyelvek - bevezetés Automaták elmélete: információs gépek általános absztrakt
Automaták és formális nyelvek Bevezetés a számítástudomány alapjaiba 1. Formális nyelvek 2006.11.13. 1 Automaták és formális nyelvek - bevezetés Automaták elmélete: információs gépek általános absztrakt
ködös határ (félreértés, hiba)
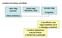 probléma formálisan specifikált: valós világ (domain) (hibás eredmény) ködös határ (félreértés, hiba) formális világ (megoldás) A szoftver fejlesztőnek meg kell értenie a felhasználó problémáját. A specifikáció
probléma formálisan specifikált: valós világ (domain) (hibás eredmény) ködös határ (félreértés, hiba) formális világ (megoldás) A szoftver fejlesztőnek meg kell értenie a felhasználó problémáját. A specifikáció
Nyelvek típusrendszere (jegyzet)
 Nyelvek típusrendszere (jegyzet) Kaposi Ambrus Eötvös Loránd Tudományegyetem akaposi@inf.elte.hu 2017. november 6. Lektorálta: Csörnyei Zoltán Az ELTE tankönyv- és jegyzettámogatási pályázatán elnyert
Nyelvek típusrendszere (jegyzet) Kaposi Ambrus Eötvös Loránd Tudományegyetem akaposi@inf.elte.hu 2017. november 6. Lektorálta: Csörnyei Zoltán Az ELTE tankönyv- és jegyzettámogatási pályázatán elnyert
Rekurzió. Dr. Iványi Péter
 Rekurzió Dr. Iványi Péter 1 Függvényhívás void f3(int a3) { printf( %d,a3); } void f2(int a2) { f3(a2); a2 = (a2+1); } void f1() { int a1 = 1; int b1; b1 = f2(a1); } 2 Függvényhívás void f3(int a3) { printf(
Rekurzió Dr. Iványi Péter 1 Függvényhívás void f3(int a3) { printf( %d,a3); } void f2(int a2) { f3(a2); a2 = (a2+1); } void f1() { int a1 = 1; int b1; b1 = f2(a1); } 2 Függvényhívás void f3(int a3) { printf(
Segédanyagok. Formális nyelvek a gyakorlatban. Szintaktikai helyesség. Fordítóprogramok. Formális nyelvek, 1. gyakorlat
 Formális nyelvek a gyakorlatban Formális nyelvek, 1 gyakorlat Segédanyagok Célja: A programozási nyelvek szintaxisának leírására használatos eszközök, módszerek bemutatása Fogalmak: BNF, szabály, levezethető,
Formális nyelvek a gyakorlatban Formális nyelvek, 1 gyakorlat Segédanyagok Célja: A programozási nyelvek szintaxisának leírására használatos eszközök, módszerek bemutatása Fogalmak: BNF, szabály, levezethető,
Tömbök kezelése. Példa: Vonalkód ellenőrzőjegyének kiszámítása
 Tömbök kezelése Példa: Vonalkód ellenőrzőjegyének kiszámítása A számokkal jellemzett adatok, pl. személyi szám, adószám, taj-szám, vonalkód, bankszámlaszám esetében az elírásból származó hibát ún. ellenőrző
Tömbök kezelése Példa: Vonalkód ellenőrzőjegyének kiszámítása A számokkal jellemzett adatok, pl. személyi szám, adószám, taj-szám, vonalkód, bankszámlaszám esetében az elírásból származó hibát ún. ellenőrző
Occam 1. Készítette: Szabó Éva
 Occam 1. Készítette: Szabó Éva Párhuzamos programozás Egyes folyamatok (processzek) párhuzamosan futnak. Több processzor -> tényleges párhuzamosság Egy processzor -> Időosztásos szimuláció Folyamatok közötti
Occam 1. Készítette: Szabó Éva Párhuzamos programozás Egyes folyamatok (processzek) párhuzamosan futnak. Több processzor -> tényleges párhuzamosság Egy processzor -> Időosztásos szimuláció Folyamatok közötti
II. Két speciális Fibonacci sorozat, szinguláris elemek, természetes indexelés
 II. Két speciális Fibonacci sorozat, szinguláris elemek, természetes indexelés Nagyon könnyen megfigyelhetjük, hogy akármilyen két számmal elindítunk egy Fibonacci sorozatot, a sorozat egymást követő tagjainak
II. Két speciális Fibonacci sorozat, szinguláris elemek, természetes indexelés Nagyon könnyen megfigyelhetjük, hogy akármilyen két számmal elindítunk egy Fibonacci sorozatot, a sorozat egymást követő tagjainak
Fraktálok. Kontrakciók Affin leképezések. Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék. TARTALOMJEGYZÉK Kontrakciók Affin transzformációk
 Fraktálok Kontrakciók Affin leképezések Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék TARTALOMJEGYZÉK 1 of 71 A Lipschitz tulajdonság ÁTMÉRŐ, PONT ÉS HALMAZ TÁVOLSÁGA Definíció Az (S, ρ) metrikus tér
Fraktálok Kontrakciók Affin leképezések Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék TARTALOMJEGYZÉK 1 of 71 A Lipschitz tulajdonság ÁTMÉRŐ, PONT ÉS HALMAZ TÁVOLSÁGA Definíció Az (S, ρ) metrikus tér
minden x D esetén, akkor x 0 -at a függvény maximumhelyének mondjuk, f(x 0 )-at pedig az (abszolút) maximumértékének.
 Függvények határértéke és folytonossága Egy f: D R R függvényt korlátosnak nevezünk, ha a függvényértékek halmaza korlátos. Ha f(x) f(x 0 ) teljesül minden x D esetén, akkor x 0 -at a függvény maximumhelyének
Függvények határértéke és folytonossága Egy f: D R R függvényt korlátosnak nevezünk, ha a függvényértékek halmaza korlátos. Ha f(x) f(x 0 ) teljesül minden x D esetén, akkor x 0 -at a függvény maximumhelyének
OOP #14 (referencia-elv)
 OOP #14 (referencia-elv) v1.0 2003.03.19. 21:22:00 Eszterházy Károly Főiskola Információtechnológia tsz. Hernyák Zoltán adj. e-mail: aroan@ektf.hu web: http://aries.ektf.hu/~aroan OOP OOP_14-1 - E jegyzet
OOP #14 (referencia-elv) v1.0 2003.03.19. 21:22:00 Eszterházy Károly Főiskola Információtechnológia tsz. Hernyák Zoltán adj. e-mail: aroan@ektf.hu web: http://aries.ektf.hu/~aroan OOP OOP_14-1 - E jegyzet
Java II. I A Java programozási nyelv alapelemei
 Java2 / 1 Java II. I A Java programozási nyelv alapelemei Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2009. 02. 09. Java II.: Alapelemek JAVA2 / 1 A Java formalizmusa A C, illetve
Java2 / 1 Java II. I A Java programozási nyelv alapelemei Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2009. 02. 09. Java II.: Alapelemek JAVA2 / 1 A Java formalizmusa A C, illetve
Logika és informatikai alkalmazásai
 Logika és informatikai alkalmazásai 4. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Logika és informatikai alkalmazásai 4. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Hadamard-mátrixok Előadó: Hajnal Péter február 23.
 Szimmetrikus kombinatorikus struktúrák MSc hallgatók számára Hadamard-mátrixok Előadó: Hajnal Péter 2012. február 23. 1. Hadamard-mátrixok Ezen az előadáson látásra a blokkrendszerektől független kombinatorikus
Szimmetrikus kombinatorikus struktúrák MSc hallgatók számára Hadamard-mátrixok Előadó: Hajnal Péter 2012. február 23. 1. Hadamard-mátrixok Ezen az előadáson látásra a blokkrendszerektől független kombinatorikus
Programozási nyelvek a közoktatásban alapfogalmak II. előadás
 Programozási nyelvek a közoktatásban alapfogalmak II. előadás Szintaxis, szemantika BNF szintaxisgráf absztrakt értelmező axiomatikus (elő- és utófeltétel) Pap Gáborné. Szlávi Péter, Zsakó László: Programozási
Programozási nyelvek a közoktatásban alapfogalmak II. előadás Szintaxis, szemantika BNF szintaxisgráf absztrakt értelmező axiomatikus (elő- és utófeltétel) Pap Gáborné. Szlávi Péter, Zsakó László: Programozási
Programozás I. 3. gyakorlat. Szegedi Tudományegyetem Természettudományi és Informatikai Kar
 Programozás I. 3. gyakorlat Szegedi Tudományegyetem Természettudományi és Informatikai Kar Antal Gábor 1 Primitív típusok Típus neve Érték Alap érték Foglalt tár Intervallum byte Előjeles egész 0 8 bit
Programozás I. 3. gyakorlat Szegedi Tudományegyetem Természettudományi és Informatikai Kar Antal Gábor 1 Primitív típusok Típus neve Érték Alap érték Foglalt tár Intervallum byte Előjeles egész 0 8 bit
C++ programozási nyelv Konstruktorok-destruktorok
 C++ programozási nyelv Konstruktorok-destruktorok Nyugat-Magyarországi Egyetem Faipari Mérnöki Kar Informatikai Intézet Soós Sándor 2004. szeptember A C++ programozási nyelv Soós Sándor 1/20 Tartalomjegyzék
C++ programozási nyelv Konstruktorok-destruktorok Nyugat-Magyarországi Egyetem Faipari Mérnöki Kar Informatikai Intézet Soós Sándor 2004. szeptember A C++ programozási nyelv Soós Sándor 1/20 Tartalomjegyzék
Már megismert fogalmak áttekintése
 Interfészek szenasi.sandor@nik.bmf.hu PPT 2007/2008 tavasz http://nik.bmf.hu/ppt 1 Témakörök Polimorfizmus áttekintése Interfészek Interfészek kiterjesztése Eseménykezelési módszerek 2 Már megismert fogalmak
Interfészek szenasi.sandor@nik.bmf.hu PPT 2007/2008 tavasz http://nik.bmf.hu/ppt 1 Témakörök Polimorfizmus áttekintése Interfészek Interfészek kiterjesztése Eseménykezelési módszerek 2 Már megismert fogalmak
Adatbázisok elmélete 12. előadás
 Adatbázisok elmélete 12. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu http://www.cs.bme.hu/ kiskat 2005 ADATBÁZISOK ELMÉLETE
Adatbázisok elmélete 12. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu http://www.cs.bme.hu/ kiskat 2005 ADATBÁZISOK ELMÉLETE
Bevezetés az informatikába
 Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Logika és informatikai alkalmazásai
 Logika és informatikai alkalmazásai 4. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Logika és informatikai alkalmazásai 4. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás
Programozás. (GKxB_INTM021) Dr. Hatwágner F. Miklós március 3. Széchenyi István Egyetem, Gy r
 Programozás (GKxB_INTM021) Széchenyi István Egyetem, Gy r 2018. március 3. Függvények Mi az a függvény (function)? Programkód egy konkrét, azonosítható, paraméterezhet, újrahasznosítható blokkja Miért
Programozás (GKxB_INTM021) Széchenyi István Egyetem, Gy r 2018. március 3. Függvények Mi az a függvény (function)? Programkód egy konkrét, azonosítható, paraméterezhet, újrahasznosítható blokkja Miért
5. SOR. Üres: S Sorba: S E S Sorból: S S E Első: S E
 5. SOR A sor adatszerkezet is ismerős a mindennapokból, például a várakozási sornak számos előfordulásával van dolgunk, akár emberekről akár tárgyakról (pl. munkadarabokról) legyen szó. A sor adattípus
5. SOR A sor adatszerkezet is ismerős a mindennapokból, például a várakozási sornak számos előfordulásával van dolgunk, akár emberekről akár tárgyakról (pl. munkadarabokról) legyen szó. A sor adattípus
Informatika terméktervezőknek
 Informatika terméktervezőknek C# alapok Névterület (namespace) using Osztály (class) és Obejtumok Metódus (function, procedure, method) main() static void string[] arg Szintaxis // /* */ \n \t Névadások
Informatika terméktervezőknek C# alapok Névterület (namespace) using Osztály (class) és Obejtumok Metódus (function, procedure, method) main() static void string[] arg Szintaxis // /* */ \n \t Névadások
Előfeltétel: legalább elégséges jegy Diszkrét matematika II. (GEMAK122B) tárgyból
 ÜTEMTERV Programozás-elmélet c. tárgyhoz (GEMAK233B, GEMAK233-B) BSc gazdaságinformatikus, programtervező informatikus alapszakok számára Óraszám: heti 2+0, (aláírás+kollokvium, 3 kredit) 2019/20-es tanév
ÜTEMTERV Programozás-elmélet c. tárgyhoz (GEMAK233B, GEMAK233-B) BSc gazdaságinformatikus, programtervező informatikus alapszakok számára Óraszám: heti 2+0, (aláírás+kollokvium, 3 kredit) 2019/20-es tanév
Differenciálegyenletek numerikus megoldása
 a Matematika mérnököknek II. című tárgyhoz Differenciálegyenletek numerikus megoldása Fokozatos közeĺıtés módszere (1) (2) x (t) = f (t, x(t)), x I, x(ξ) = η. Az (1)-(2) kezdeti érték probléma ekvivalens
a Matematika mérnököknek II. című tárgyhoz Differenciálegyenletek numerikus megoldása Fokozatos közeĺıtés módszere (1) (2) x (t) = f (t, x(t)), x I, x(ξ) = η. Az (1)-(2) kezdeti érték probléma ekvivalens
Programozás BMEKOKAA146. Dr. Bécsi Tamás 2. előadás
 Programozás BMEKOKAA146 Dr. Bécsi Tamás 2. előadás Szintaktikai alapok Alapvető típusok, ismétlés C# típus.net típus Méret (byte) Leírás byte System.Byte 1Előjel nélküli 8 bites egész szám (0..255) char
Programozás BMEKOKAA146 Dr. Bécsi Tamás 2. előadás Szintaktikai alapok Alapvető típusok, ismétlés C# típus.net típus Méret (byte) Leírás byte System.Byte 1Előjel nélküli 8 bites egész szám (0..255) char
Alap fatranszformátorok II
 Alap fatranszformátorok II Vágvölgyi Sándor Fülöp Zoltán és Vágvölgyi Sándor [2, 3] közös eredményeit ismertetjük. Fogalmak, jelölések A Σ feletti alaptermek TA = (T Σ, Σ) Σ algebráját tekintjük. Minden
Alap fatranszformátorok II Vágvölgyi Sándor Fülöp Zoltán és Vágvölgyi Sándor [2, 3] közös eredményeit ismertetjük. Fogalmak, jelölések A Σ feletti alaptermek TA = (T Σ, Σ) Σ algebráját tekintjük. Minden
17. előadás: Vektorok a térben
 17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
Funkcionális és logikai programozás. { Márton Gyöngyvér, 2012} { Sapientia, Erdélyi Magyar Tudományegyetem }
 Funkcionális és logikai programozás { Márton Gyöngyvér, 2012} { Sapientia, Erdélyi Magyar Tudományegyetem } http://www.ms.sapientia.ro/~mgyongyi ` 1 Jelenlét: Követelmények, osztályozás Az első 4 előadáson
Funkcionális és logikai programozás { Márton Gyöngyvér, 2012} { Sapientia, Erdélyi Magyar Tudományegyetem } http://www.ms.sapientia.ro/~mgyongyi ` 1 Jelenlét: Követelmények, osztályozás Az első 4 előadáson
Programozás alapjai (ANSI C)
 Programozás alapjai (ANSI C) 1. Előadás vázlat A számítógép és programozása Dr. Baksáné dr. Varga Erika adjunktus Miskolci Egyetem, Informatikai Intézet Általános Informatikai Intézeti Tanszék www.iit.uni-miskolc.hu
Programozás alapjai (ANSI C) 1. Előadás vázlat A számítógép és programozása Dr. Baksáné dr. Varga Erika adjunktus Miskolci Egyetem, Informatikai Intézet Általános Informatikai Intézeti Tanszék www.iit.uni-miskolc.hu
Programkonstrukciók A programkonstrukciók programfüggvényei Levezetési szabályok. 6. előadás. Programozás-elmélet. Programozás-elmélet 6.
 Programkonstrukciók Definíció Legyen π feltétel és S program A-n. A DO A A relációt az S-ből a π feltétellel képezett ciklusnak nevezzük, és (π, S)-sel jelöljük, ha 1. a / [π] : DO (a) = { a }, 2. a [π]
Programkonstrukciók Definíció Legyen π feltétel és S program A-n. A DO A A relációt az S-ből a π feltétellel képezett ciklusnak nevezzük, és (π, S)-sel jelöljük, ha 1. a / [π] : DO (a) = { a }, 2. a [π]
A Formális nyelvek vizsga teljesítése. a) Normál A vizsgán 60 pont szerezhet, amely két 30 pontos részb l áll össze az alábbi módon:
 A Formális nyelvek vizsga teljesítése a) Normál A vizsgán 60 pont szerezhet, amely két 30 pontos részb l áll össze az alábbi módon: 1. Öt rövid kérdés megválaszolása egyenként 6 pontért, melyet minimum
A Formális nyelvek vizsga teljesítése a) Normál A vizsgán 60 pont szerezhet, amely két 30 pontos részb l áll össze az alábbi módon: 1. Öt rövid kérdés megválaszolása egyenként 6 pontért, melyet minimum
Algoritmuselmélet 12. előadás
 Algoritmuselmélet 12. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu 2002 Április 9. ALGORITMUSELMÉLET 12. ELŐADÁS 1 Turing-gépek
Algoritmuselmélet 12. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu 2002 Április 9. ALGORITMUSELMÉLET 12. ELŐADÁS 1 Turing-gépek
Programozás II. 2. Dr. Iványi Péter
 Programozás II. 2. Dr. Iványi Péter 1 C++ Bjarne Stroustrup, Bell Laboratórium Első implementáció, 1983 Kezdetben csak precompiler volt C++ konstrukciót C-re fordította A kiterjesztés alapján ismerte fel:.cpp.cc.c
Programozás II. 2. Dr. Iványi Péter 1 C++ Bjarne Stroustrup, Bell Laboratórium Első implementáció, 1983 Kezdetben csak precompiler volt C++ konstrukciót C-re fordította A kiterjesztés alapján ismerte fel:.cpp.cc.c
2014. szeptember 24. és 26. Dr. Vincze Szilvia
 2014. szeptember 24. és 26. Dr. Vincze Szilvia Mind a hétköznapi, mind a tudományos életben gyakran előfordul, hogy bizonyos halmazok elemei között kapcsolat figyelhető meg. A kapcsolat fogalmának matematikai
2014. szeptember 24. és 26. Dr. Vincze Szilvia Mind a hétköznapi, mind a tudományos életben gyakran előfordul, hogy bizonyos halmazok elemei között kapcsolat figyelhető meg. A kapcsolat fogalmának matematikai
I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI
 I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI 1 A digitális áramkörökre is érvényesek a villamosságtanból ismert Ohm törvény és a Kirchhoff törvények, de az elemzés és a tervezés rendszerint nem ezekre épül.
I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI 1 A digitális áramkörökre is érvényesek a villamosságtanból ismert Ohm törvény és a Kirchhoff törvények, de az elemzés és a tervezés rendszerint nem ezekre épül.
Matematika alapjai; Feladatok
 Matematika alapjai; Feladatok 1. Hét 1. Tekintsük a,, \ műveleteket. Melyek lesznek a.) kommutativok b.) asszociativak c.) disztributívak-e a, műveletek? Melyik melyikre? 2. Fejezzük ki a műveletet a \
Matematika alapjai; Feladatok 1. Hét 1. Tekintsük a,, \ műveleteket. Melyek lesznek a.) kommutativok b.) asszociativak c.) disztributívak-e a, műveletek? Melyik melyikre? 2. Fejezzük ki a műveletet a \
Véletlenszám generátorok és tesztelésük. Tossenberger Tamás
 Véletlenszám generátorok és tesztelésük Tossenberger Tamás Érdekességek Pénzérme feldobó gép: $0,25-os érme 1/6000 valószínűséggel esik az élére 51% eséllyel érkezik a felfelé mutató oldalára Pörgetésnél
Véletlenszám generátorok és tesztelésük Tossenberger Tamás Érdekességek Pénzérme feldobó gép: $0,25-os érme 1/6000 valószínűséggel esik az élére 51% eséllyel érkezik a felfelé mutató oldalára Pörgetésnél
definiálunk. Legyen egy konfiguráció, ahol és. A következő három esetet különböztetjük meg. 1. Ha, akkor 2. Ha, akkor, ahol, ha, és egyébként.
 Számításelmélet Kiszámítási problémának nevezünk egy olyan, a matematika nyelvén megfogalmazott kérdést, amire számítógéppel szeretnénk megadni a választ. (A matematika nyelvén precízen megfogalmazott
Számításelmélet Kiszámítási problémának nevezünk egy olyan, a matematika nyelvén megfogalmazott kérdést, amire számítógéppel szeretnénk megadni a választ. (A matematika nyelvén precízen megfogalmazott
Algoritmusok helyességének bizonyítása. A Floyd-módszer
 Algoritmusok helyességének bizonyítása A Floyd-módszer Algoritmusok végrehajtása Egy A algoritmus esetében a változókat három változótípusról beszélhetünk, melyeket az X, Y és Z vektorokba csoportosítjuk
Algoritmusok helyességének bizonyítása A Floyd-módszer Algoritmusok végrehajtása Egy A algoritmus esetében a változókat három változótípusról beszélhetünk, melyeket az X, Y és Z vektorokba csoportosítjuk
Gráfelmélet. I. Előadás jegyzet (2010.szeptember 9.) 1.A gráf fogalma
 Készítette: Laczik Sándor János Gráfelmélet I. Előadás jegyzet (2010.szeptember 9.) 1.A gráf fogalma Definíció: a G=(V,E) párt egyszerű gráfnak nevezzük, (V elemeit a gráf csúcsainak/pontjainak,e elemeit
Készítette: Laczik Sándor János Gráfelmélet I. Előadás jegyzet (2010.szeptember 9.) 1.A gráf fogalma Definíció: a G=(V,E) párt egyszerű gráfnak nevezzük, (V elemeit a gráf csúcsainak/pontjainak,e elemeit
Csima Judit október 24.
 Adatbáziskezelés Funkcionális függőségek Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2018. október 24. Csima Judit Adatbáziskezelés Funkcionális függőségek 1 / 1 Relációs sémák
Adatbáziskezelés Funkcionális függőségek Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2018. október 24. Csima Judit Adatbáziskezelés Funkcionális függőségek 1 / 1 Relációs sémák
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 1 I. HALmAZOk 1. JELÖLÉSEk A halmaz fogalmát tulajdonságait gyakran használjuk a matematikában. A halmazt nem definiáljuk, ezt alapfogalomnak tekintjük. Ez nem szokatlan, hiszen
KOVÁCS BÉLA, MATEmATIkA I. 1 I. HALmAZOk 1. JELÖLÉSEk A halmaz fogalmát tulajdonságait gyakran használjuk a matematikában. A halmazt nem definiáljuk, ezt alapfogalomnak tekintjük. Ez nem szokatlan, hiszen
OOP. Alapelvek Elek Tibor
 OOP Alapelvek Elek Tibor OOP szemlélet Az OOP szemlélete szerint: a valóságot objektumok halmazaként tekintjük. Ezen objektumok egymással kapcsolatban vannak és együttműködnek. Program készítés: Absztrakciós
OOP Alapelvek Elek Tibor OOP szemlélet Az OOP szemlélete szerint: a valóságot objektumok halmazaként tekintjük. Ezen objektumok egymással kapcsolatban vannak és együttműködnek. Program készítés: Absztrakciós
Hardver leíró nyelvek (HDL)
 Hardver leíró nyelvek (HDL) Benesóczky Zoltán 2004 A jegyzetet a szerzıi jog védi. Azt a BME hallgatói használhatják, nyomtathatják tanulás céljából. Minden egyéb felhasználáshoz a szerzı belegyezése szükséges.
Hardver leíró nyelvek (HDL) Benesóczky Zoltán 2004 A jegyzetet a szerzıi jog védi. Azt a BME hallgatói használhatják, nyomtathatják tanulás céljából. Minden egyéb felhasználáshoz a szerzı belegyezése szükséges.
S0-02 Típusmodellek (Programozás elmélet)
 S0-02 Típusmodellek (Programozás elmélet) Tartalom 1. Absztrakt adattípus 2. Adattípus specifikációja 3. Adattípus osztály 4. Paraméterátadás 5. Reprezentációs függvény 6. Öröklődés és polimorfizmus 7.
S0-02 Típusmodellek (Programozás elmélet) Tartalom 1. Absztrakt adattípus 2. Adattípus specifikációja 3. Adattípus osztály 4. Paraméterátadás 5. Reprezentációs függvény 6. Öröklődés és polimorfizmus 7.
1. A polinom fogalma. Számolás formális kifejezésekkel. Feladat Oldjuk meg az x2 + x + 1 x + 1. = x egyenletet.
 1. A polinom fogalma Számolás formális kifejezésekkel. Feladat Oldjuk meg az x2 + x + 1 x + 1 = x egyenletet. Megoldás x + 1-gyel átszorozva x 2 + x + 1 = x 2 + x. Innen 1 = 0. Ez ellentmondás, így az
1. A polinom fogalma Számolás formális kifejezésekkel. Feladat Oldjuk meg az x2 + x + 1 x + 1 = x egyenletet. Megoldás x + 1-gyel átszorozva x 2 + x + 1 = x 2 + x. Innen 1 = 0. Ez ellentmondás, így az
2. Logika gyakorlat Függvények és a teljes indukció
 2. Logika gyakorlat Függvények és a teljes indukció Folláth János Debreceni Egyetem - Informatika Kar 2012/13. I. félév Áttekintés 1 Függvények Relációk Halmazok 2 Természetes számok Formulák Definíció
2. Logika gyakorlat Függvények és a teljes indukció Folláth János Debreceni Egyetem - Informatika Kar 2012/13. I. félév Áttekintés 1 Függvények Relációk Halmazok 2 Természetes számok Formulák Definíció
Térinformatikai algoritmusok Elemi algoritmusok
 Cserép Máté Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot oldottuk meg korábban,
Cserép Máté Analóg programozásnak nevezzük azt, amikor egy feladat megoldásához egy már ismert és megoldott feladat megoldását használjuk fel. Általában nem pontosan ugyanazt a feladatot oldottuk meg korábban,
Matematikai logika és halmazelmélet
 Matematikai logika és halmazelmélet Wettl Ferenc előadása alapján 2015-09-07 Wettl Ferenc előadása alapján Matematikai logika és halmazelmélet 2015-09-07 1 / 21 Tartalom 1 Matematikai kijelentések szerkezete
Matematikai logika és halmazelmélet Wettl Ferenc előadása alapján 2015-09-07 Wettl Ferenc előadása alapján Matematikai logika és halmazelmélet 2015-09-07 1 / 21 Tartalom 1 Matematikai kijelentések szerkezete
Logika es sz am ıt aselm elet I. r esz Logika 1/36
 1/36 Logika és számításelmélet I. rész Logika 2/36 Elérhetőségek Tejfel Máté Déli épület, 2.606 matej@inf.elte.hu http://matej.web.elte.hu Tankönyv 3/36 Tartalom 4/36 Bevezető fogalmak Ítéletlogika Ítéletlogika
1/36 Logika és számításelmélet I. rész Logika 2/36 Elérhetőségek Tejfel Máté Déli épület, 2.606 matej@inf.elte.hu http://matej.web.elte.hu Tankönyv 3/36 Tartalom 4/36 Bevezető fogalmak Ítéletlogika Ítéletlogika
Programozás alapjai. 5. előadás
 5. előadás Wagner György Általános Informatikai Tanszék Cserélve kiválasztásos rendezés (1) A minimum-maximum keresés elvére épül. Ismétlés: minimum keresés A halmazból egy tetszőleges elemet kinevezünk
5. előadás Wagner György Általános Informatikai Tanszék Cserélve kiválasztásos rendezés (1) A minimum-maximum keresés elvére épül. Ismétlés: minimum keresés A halmazból egy tetszőleges elemet kinevezünk
Programozás alapjai. (GKxB_INTM023) Dr. Hatwágner F. Miklós október 11. Széchenyi István Egyetem, Gy r
 Programozás alapjai (GKxB_INTM023) Széchenyi István Egyetem, Gy r 2018. október 11. Függvények Mi az a függvény (function)? Programkód egy konkrét, azonosítható, paraméterezhet, újrahasznosítható blokkja
Programozás alapjai (GKxB_INTM023) Széchenyi István Egyetem, Gy r 2018. október 11. Függvények Mi az a függvény (function)? Programkód egy konkrét, azonosítható, paraméterezhet, újrahasznosítható blokkja
1. Interpoláció. Egyértelműség Ha f és g ilyen polinomok, akkor n helyen megegyeznek, így a polinomok azonossági tétele miatt egyenlők.
 1. Interpoláció Az interpoláció alapproblémája. Feladat Olyan polinomot keresünk, amely előre megadott helyeken előre megadott értékeket vesz fel. A helyek: páronként különböző a 1, a,...,a n számok. Az
1. Interpoláció Az interpoláció alapproblémája. Feladat Olyan polinomot keresünk, amely előre megadott helyeken előre megadott értékeket vesz fel. A helyek: páronként különböző a 1, a,...,a n számok. Az
7.4. A programkonstrukciók és a kiszámíthatóság
 H @ tj 68 7 PROGRAMKONSTRUKCIÓK 74 A programkonstrukciók és a kiszámíthatóság Ebben az alfejezetben kis kitérőt teszünk a kiszámíthatóság-elmélet felé, és megmutatjuk, hog az imént bevezetett három programkonstrukció
H @ tj 68 7 PROGRAMKONSTRUKCIÓK 74 A programkonstrukciók és a kiszámíthatóság Ebben az alfejezetben kis kitérőt teszünk a kiszámíthatóság-elmélet felé, és megmutatjuk, hog az imént bevezetett három programkonstrukció
