A szolgáltatásbiztonság analízise
|
|
|
- Lídia Lakatos
- 8 évvel ezelőtt
- Látták:
Átírás
1 A szolgáltatásbiztonság analízise Előadásvázlat Szolgáltatásbiztonságra tervezés tárgyból Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Tartalomjegyzék: 1 Bevezetés Kvalitatív analízis technikák Ellenőrző lista (Checklist) Hibafa analízis (Fault Tree Analysis, FTA) Eseményfa analízis (Event Tree Analysis, ETA) Ok-következmény analízis (Cause-Consequence Analysis, CCA) Veszély és működőképesség analízis (Hazards and Operability Analysis, HAZOP) Hibamód és -hatás analízis (Failure Modes and Effects Analysis, FMEA) Állapot alapú veszély analízis (State Machine Hazard Analysis) Emberi hibák analízise (Human Error Analysis) Kvantitatív megbízhatósági modellezés és analízis technikák Boole modellek Markov modellek Sztochasztikus Petri-háló modellek
2 1 Bevezetés Az analízis célja: A komponens szintű hibák (hibaállapotok, események) és a rendszerszintű hibajelenség kapcsolatának kiderítése: Mihez vezet rendszerszinten egy vagy több komponens hibája? Mik lehetnek egy rendszerszintű hibajelenség okai? Milyen valószínűségi és időadatok jellemzik a rendszerszintű hibajelenséget, ha adottak a komponensek hibavalószínűségei, illetve meghibásodási tényezői? Az analízis által vizsgált illetve használt jellemzők: Valószínűségi időfüggvények: megbízhatóság, rendelkezésre állás, biztonságosság Aszimptotikus valószínűség: Készenlét Várható értékek: MTFF, MTTF (MUT), MTTR (MDT), MTBF Paraméterek: meghibásodási tényező, hibaterjedési valószínűség Az analízis típusai ok-okozati szempontból: Előrelépő (induktív) keresés: Kiindulási hiba hatásainak továbbkövetése a rendszerben; időbeli és oksági továbblépés. Visszalépő (deduktív) keresés: A rendszerszintű hiba okainak visszavezetése komponens hibákra. Az analízis típusai a rendszer struktúrája szempontjából: Alulról felfelé (bottom-up) történő keresés: Alrendszerek (komponensek) felől a teljes rendszer felé. Felülről lefelé (top-down) történő keresés: Magasabb szintű absztrakciók finomítása (rendszer felől az alrendszerek felé). Módszerek: Kvalitatív technikák: Szisztematikus módszert adnak az elemzéshez, azonosítják a beavatkozás helyét (pl. egyszeres hibaok, kritikus hibák). Kvantitatív technikák: A komponensek paraméterei alapján kiszámítják a rendszerszintű hiba jellemzőit (valószínűségi és időadatok) a komponens szintű jellemzők alapján. 2 Kvalitatív analízis technikák 2.1 Ellenőrző lista (Checklist) Tapasztalatok (ökölszabályok) összegyűjtése és alkalmazása/ellenőrzése újabb rendszerek esetén: ismert hibaforrások (tapasztalatok) ki ne maradjanak létező szabványokhoz, megoldásokhoz való illeszkedés biztosított legyen Rendszeres frissítés alapkövetelmény Probléma: Nagy méretűvé válhat (alkalmazása nehézkes); téves biztonságérzetet adhat. 2
3 2.2 Hibafa analízis (Fault Tree Analysis, FTA) Rendszerszintű hiba okainak vizsgálata (az elektronikai és repülőgépiparból elterjedt technika) Az elemzés célja Legfelső szintű események (hibák) meghatározása (rendszerterv, szolgáltatások alapján) Felülről lefelé haladó (egyben deduktív) elemzés: Legfelső szintű esemény: azonosított rendszerszintű hibajelenség Közbenső események: amelyek a legfelső szintű esemény kialakulásához vezetnek (szükséges vagy elégséges) Pszeudo-események: események kombinációi (Boole relációk: AND, OR, NOT) Elsődleges (vagy alapszintű) események: nincs további felbontás alacsonyabb szintű eseményekre Hibafa konstrukció Specifikáció (legfelső szintű esemény) architektúra (közbenső események, pszeudo-esemény) cserélhető komponensek (alapszintű események) bejárása Grafikus reprezentáció: Szabványos szimbólumkészlet (igazságtábla helyett áttekinthetőbb): AND, OR, INHIBIT kapuk Hardver esetén: automatizált technikák léteznek a hibafa konstrukcióra (jól megfogható struktúra és hibamódok) Szoftver esetén: vezérlési struktúrák vizsgálatán alapul Kvalitatív analízis A hibafa szokásos elemei Hibafa redukciója (közbenső események feloldása): Diszjunktív normál forma kialakítása; a legfelső szintű esemény kifejezése az alapszintű eseményekkel. Vágat: AND kapcsolatban lévő események halmaza a legfelső OR alatt a diszjunktív normál forma szerinti alakban Redukálható vágat: Eseményeinek részhalmaza is vágatot képez 3
4 Minimális vágathalmaz: tovább nem redukálható vágatok Azonosítható: rendszerszintű hibához vezető kombinációk Egyszeres hibaok (SPOF): Önmagában is a rendszerszintű hibához vezet (egy vágatot képez) Több vágathalmazban szereplő esemény: kiküszöbölése hatásosan redukálja a hibafát Alkalmazási korlátok: Részletes tervezés után használható Csak statikus kombinációkat ad meg: nincs sorrendbeli függőség, dinamikus viselkedés leírása, eseményszekvenciák kezelése Mintapéldák: NVP hibafa: SPOF azonosítható (szavazó), közös módusú hiba felveendő. RB hibafa: A hibafa nem tükrözi a működési módot, mivel csak egy snapshot. Hardver struktúra: Minimális vágathalmazok meghatározása Kvantitatív analízis Alapszintű eseményekhez rendelt valószínűségek alapján a rendszerszintű esemény valószínűsége számítható. A hibafa kapuinak szerepe: AND kapu: valószínűségek szorzata:, itt ha függetlenek OR kapu: valószínűségek összege: felülbecslés szokásos Probléma: Közös módusú hibák, paraméterértékek forrása (elsődleges események valószínűségei). 2.3 Eseményfa analízis (Event Tree Analysis, ETA) Előrelépő analízis elsődleges események következményeinek kiderítésére Analízis: Előnyök: kezdeti esemény: egy komponens hibája/veszélyes helyzete következő események: más rendszerkomponensek származtatott vagy rákövetkező hibái sorrendezés: időbeli/oksági viszony, balról jobbra haladva esemény (komponens hiba) bekövetkezése vagy nem bekövetkezése mint elágazás jelenik meg a diagramon. Egy útvonal valószínűsége: események valószínűségeinek szorzata Használatos: többszintű védelmi rendszerek analízise esetén Események sorrendje vizsgálható Hibajelenség (baleset) forgatókönyvek származtathatók 4
5 Korlátok: komplexitás, többszörös események kezelése, sorrendezés kritikus Mintapélda: Tartály túlhevülés, RB séma megadása. 2.4 Ok-következmény analízis (Cause-Consequence Analysis, CCA) Eseményszekvencia és oksági függések egyidejű ábrázolása Következmény fa: egy elsődleges esemény következményei (esemény szekvencia) Csatolt hibafák: az egyes eseményekhez tartozó döntés (bekövetkezik vagy nem) indokainak felderítésére Szimbólumok a grafikus reprezentációban: ld. hibafa és eseményfa Előnyök: a hibafa és eseményfa előnyeit ötvözi Korlátok: minden kezdeti eseményhez külön diagram szükséges 2.5 Veszély és működőképesség analízis (Hazards and Operability Analysis, HAZOP) Kémiai folyamatok esetén elterjedt: balesetet az anyagáramlás tervezettől való eltérése okozza; ezeket a lehetséges eltéréseket néhány jellemző kulcsszó alapján át lehet tekinteni: NO, NONE: nincs működés (pl. nincs anyagáramlás) MORE: több eredmény (pl. több anyag áramlik) LESS: kevesebb eredmény (pl. kevesebb anyag) AS WELL AS: más, nem tervezett aktivitás PART OF: csak részben valósul meg REVERSE: az előírtak ellenkezője történik OTHER THAN: egészen más történik, mint az előírt Alkalmazás informatikai rendszerekben: az információ áramlásának vizsgálata lehetséges eltérések azonosítása (szisztematikus keresés a folyamatdiagramok alapján) az eltérésekhez tartozó veszélyek azonosítása okok azonosítása, kiküszöbölés Előny: a tervezési dokumentáció alapján elvégezhető Hátrány: a folyamat szakértőit igényli, munkaigényes 2.6 Hibamód és -hatás analízis (Failure Modes and Effects Analysis, FMEA) Alkalmazás: Komponensek, hibamódok felsorolása, valószínűségekkel illetve gyakoriságokkal Más komponensekre illetve a rendszerre gyakorolt hatások azonosítása (előrelépő analízis) 5
6 FMEA táblázat: Komponens Hibamód Hiba valószínűség vagy gyakoriság Hatás Előnyök: egyszeres hibapontok (SPOF) felismerhetők Hátrányok: hibamódok ismertek kell legyenek, többszörös hibák nem vizsgálhatók Kiegészítés: Hibamód, -hatás és kritikusság vizsgálat (Failure Modes, Effects and Criticality Analysis, FMECA) FMEA kiegészítése a hiba kritikusság jellemzésével (rangsorolás kategóriákba) Megelőző/korrigáló akciók szintén felsorolhatók 2.7 Állapot alapú veszély analízis (State Machine Hazard Analysis) Állapotgép alapú modell: állapotok, átmenetek, feltételek, trigger események és akciók Biztonsági analízis: meghatározni, a rendszer beléphet-e veszélyes állapotba (a veszélyes állapotokat tartalmazó állapotpartícióba) elméleti megoldás: kezdeti állapotból az állapottér felderítése gyakorlati megközelítés: visszafelé keresés a veszélyes állapotból (hogyan kerülhető el) Előnyök: automatizálható, tervezési modell használható Hátrányok: veszélyes állapot formális specifikációja nehéz, állapottér-robbanás (konkurens rendszerek esetén) 2.8 Emberi hibák analízise (Human Error Analysis) Kvalitatív módszerek: az emberi tevékenységek/műveletek esetén megvizsgálni: lehetséges funkcionális hibák (pl. kihagyás, összecserélés) illetve teljesítményhibák (pl. lassú, túl gyors) a hibák (veszélyek) hatása, ezek kritikussága okok elemzése: pl. fizikai és mentális elvárások a hibák elkerülésének módszerei Táblázatos forma: Művelet Veszély Hatások Okok Elkerülés Kvantitatív technikák: emberi hibákhoz valószínűséget rendelni; befolyásol: pszichológiai hatások (stressz), ember-gép interfész, betanítás, utasítások, függőség más műveletektől mérés: dokumentált környezetben (nehézkes); személyenként eltérő lehet a veszélyhelyzetben való viselkedés 6
7 3 Kvantitatív megbízhatósági modellezés és analízis technikák A formális megbízhatósági modellek készítésének és megoldásának (az állapot alapú, kvantitatív módszereknek) célja: A komponensek meghibásodási jellemzői alapján a rendszerszintű jellemzőket kiszámítani; ezek alapján architektúra változatokat összehasonlítani, érzékenységvizsgálatot végezni (melyik komponens tulajdonságaira érzékenyek a rendszerszintű jellemzők), megbízhatóság szempontjából szűk keresztmetszetet azonosítani (mit érdemes kicserélni). Jellemzők: A komponens szintű paraméterek nehezen mérhetők, sokszor csak becslések vannak. Egyszerűsítő hipotézisek kellenek (magas absztrakciós szint, a meghibásodás illetve javítás egyszerűsített modellje). Modell validációjára lehet szükség (log elemzés, hibainjektálás). Ismétlés a szolgáltatásbiztonság jellemzőiről: Rendszer állapottér partíciók: (hibamentes, U-val is jelölhető), (hibás, D-vel is jelölhető) Rendszerállapot: Megbízhatóság: (folyamatos szolgáltatás) Rendelkezésre állás: (javítva szolgáltatásra kész) Meghibásodási tényező: (a időpillanatban következik be a meghibásodás) A definíció alapján: Kádgörbe: Középső szakaszán konstans, így (egyébként ) Megbízhatóság: Hibamentes állapotban maradás valószínűsége egy komponens esetén, ha a meghibásodási tényező: 3.1 Boole modellek Használat: Egyszerű architektúrák esetén a megbízhatóság számítására (nincsenek függőségek a komponensek között). Alapmodell: Komponensek független hibás vagy hibamentes állapota. Soros architektúra: Bármely komponens hibája esetén rendszerhiba (OR hibafa). komponens esetén: Párhuzamos architektúra: A komponensek egymást helyettesíthetik (tartalékok, AND hibafa). egyforma komponens esetén: Ugyanitt MTFF (levezetését ld. később, Markov-láncok segítségével); egy-egy újabb komponens egyre kevesebb pluszt jelent. 7
8 Kanonikus rendszer: Soros és párhuzamos komponensekből áll: Megbízhatósági blokk diagram: Komponensek a blokkok, a soros vagy párhuzamos kapcsolat jelenik meg a diagramon a kapcsolásuk formájában. A rendszer hibamentes, ha van út a kiindulási és a végpont között. Ez nem az áramköri kapcsolás, hanem a megbízhatósági modell; ld. két párhuzamosan kapcsolt dióda rövidzár hibára soros, szakadás hibára párhuzamos megbízhatósági modellel jellemezhető. egyforma egység; komponens hiba esetén rendszerhiba: Ideális többségi szavazás (TMR): hiba van ; összegzés kell -re. Itt MTFF=, rosszabb, mint egy komponens esetén! De az görbe a kezdeti szakaszán magasabb, így missziókritikus rendszerekben jól alkalmazható. Készenlét összevetése: Soros rendszer:, párhuzamos rendszer: Példák: (1) párhuzamos rendszer, (2) stand-by rendszer nem-ideális kapcsolóval, (3) ideális többségi szavazás, (4) többségi szavazás nem-ideális szavazóval; szavazó határmegbízhatósága. 3.2 Markov modellek Használat: Modellezhetők a javított rendszerek, degradált állapotok illetve függőségben lévő komponensek. Ismétlés a Markov láncokról: Diszkrét állapotok és átmenetek ezek között Emlékezetnélküliség Állapotátmenet valószínűsége: Homogén Markov-folyamat: Állapotátmeneti intenzitás: azaz Állapot elhagyásának összesített rátája állapotban: CTMC: Folytonos idejű Markov-lánc, itt értékek -be rendezve Állapotvalószínűségek: -ből indulva idő elteltével -ben lesz a rendszer CTMC tranziens megoldása: Állapotvalószínűség időfüggvények kiszámítása kezdőállapotra: Minden állapotra, azaz a sorvektor; hasonlóan értékek -be rendezve 8
9 Megoldás alapja: infinitezimális generátormátrix A differenciál-egyenletrendszer megoldás módja: Laplace-transzformáció vagy idősorok: Egyszerű eredmények: -ből -be megy időn belül, ahol Tartózkodási idő: -ben marad ideig állapotban tartózkodás ideje negatív exponenciális eloszlású valószínűségi változó CTMC állandósult állapotbeli megoldása: Állapotvalószínűségek kiszámítása létezik, ha a CTMC véges állapotú és irreducibilis; itt kb: minden állapotból van javítás nincs időfüggés Megoldás alapja: Analógia a szolgáltatásbiztonság és a CTMC alapfogalmai között: Szolgáltatásbiztonság CTMC állapotok, állapotok konstans, homogén a Markov-folyamat -ben marad ideig hibamentes állapotban maradás állapotban tartózkodás ideje (itt ) CTMC modell alapelemei: Kezdőállapot ( része), degradált állapotok, hibajelenség ( része) Komponens meghibásodás: Ráta a meghibásodási tényező Komponens hibamentes állapotának tartási ideje : Több komponens állapotának összevont modellezése: ráta; exp. eloszlású valószínűségi változók minimuma: exp. eloszlású, a paraméterek összegződnek. Állapotok összevonása: Feltétel: Átmenetek azonos kimenő rátákkal azonos állapot(ok)ba. Kimenő ráta ugyanaz marad a közös cél állapotba, bemenő ráták azonos állapotból összegezve lesznek. Javítás: javítási tényező (exponenciális eloszlás paramétere; matematikai kezelhetőség érdekében feltételezve) 9
10 Teljes javítás (hibamentes állapotba), részleges javítás (degradált állapotba), megelőző javítás (degradált állapotból) Eredmények egy és állapot-partíciókra osztott, kezdőállapottal rendelkező CTMC alapján: a javítási élek elhagyásával kapott CTMC alapján számolva a javítási élek bennhagyásával számolva állandósult állapotban (létezik, ha minden hibaállapotból van javítás) A CTMC állandósult állapotbeli megoldásának nehézségei: Kiegyenlítetlenség a numerikus értékekben A javítási tényező nagy (gyors javítás) A meghibásodási tényező kicsi (ritka meghibásodás) jellegű összegek számítógépes ábrázolása nehéz ( jellegű értékekkel műveletek; pl. kivonás után nem elhanyagolható lesz a ) Mintapéldák felrajzolása: Nem javított rendszerek: (1) meleg tartalék, (2) csökkentett terhelésű tartalék, (3) hideg tartalék Stand-by rendszer: (1) ideális kapcsolóval, (2) nem ideális kapcsolóval, hibára kikapcsol illetve (3) hibára bekapcsolva maradó komponensekkel Javított rendszerek: (1) TMR preventív és teljes javítással, (2) egyszerelős rendszer (egyszerre csak egy elem javítható; egyszerűsödő állandósult állapotbeli megoldás) számú meleg tartalék komponensből álló rendszer MTFF számítása Markov-láncokkal:, mivel minden állapotban a várható tartózkodási idő. 3.3 Sztochasztikus Petri-háló modellek CTMC-nél magasabb szintű formalizmus (konkurens folyamatok jól modellezhetők), jó eszköztámogatással Formalizmusok Petri-háló: PN=(P,T,I,O), ahol P helyek, T átmenetek, I input élek, O output élek. Sztochasztikus Petri-háló:, ahol a kezdeti jelölés átmenetekhez rendelt időzítés, a negatív exponenciális valószínűségi eloszlásfüggvény paramétere. Az időzített átmenet engedélyezetté válásakor sorsol egy időzítést ebből a paraméterű eloszlásból, aminek letelte után tüzel: SPN elérhetőségi gráfja alkot CTMC-t (jelölések valószínűsége számítható). Általánosított sztochasztikus Petri-háló:, ahol tiltó élek prioritások 10
11 0 az időzített átmenetek prioritása >0 az azonnali átmenetek priortása; ez alapján feloldhatók a konfliktusok közöttük. paraméter: időzített átmenetek esetén: az időzítés negatív exponenciális valószínűség eloszlásfv. paramétere, azonnali átmenetek esetén: súlyok az azonos prioritású, konfliktusban lévő engedélyezett átmenetek közötti véletlenszerű választáshoz. Boole-fv.; őrfeltétel, az adott átmenet engedélyezetté válásához igaznak kell lennie; a Boole-fv. a jelöléseken értelmezett (pl. m(p)>2, ahol m(p) a P hely jelölését jelenti. Sztochasztikus reward hálózatok: Kiterjesztés a reward (haszon, jutalom) függvényekkel. rate reward: állapotokon (jelöléseken) értelmezett, időintervallumra összegezhető integrálva a rátát (a ráta időpillanatra vonatkozik). Példa: if (m(premium)==1) or m(minimum)==1) then ra=1 else ra=0. impulse reward: egy-egy eseményhez rendelhető (pl. tüzelés), időintervallumra összegezhető az impulzusok összeadásával. Példa: if (fire(repair)) then ri=12 (egy-egy javítás költsége 12 egység). Időzített Petri-háló (Timed Petri Net): tetszőleges valószínűségi eloszlásfv. az időzítés sorsolásához. Itt már nem CTMC az alapszintű modell, analitikus megoldás helyett szimulációra lehet szükség. Pontos időzítési szemantika kell (ha a tüzelés megtörténte előtt megszűnik az átmenet engedélyezettsége, majd újra engedélyezett lesz, mi lesz az időzítés értéke: új időzítést sorsol az eredeti eloszlásfüggvény alapján, vagy az eredeti időzítésből maradt időt várja ki tüzelésig) Részhálók a megbízhatósági modellezéshez A GSPN formalizmust használva modellezzük a meghibásodási, hibaterjedési és javítási folyamatot. Az alapértelmezett részhálók adaptíven finomíthatók (az interfész helyek megtartásával). Komponens meghibásodási folyamat: Hibamentes hibaállapot hibajelenség. Jellemzi a meghibásodási tényező és a hiba késleltetése (lappangási idő). Különböző lesz állapottal rendelkező vagy nem rendelkező komponensek esetén. Különböző, ha van/nincs kezdeti hiba, vagy ha a meghibásodás nem időfüggő. Interfész helyek: H (hibamentes), E (hibaállapot), F (hibajelenség). Hibaterjedési folyamat: Jellemzi a hibaterjedési valószínűség illetve a komponens hiba és rendszerhiba közötti logikai kapcsolat (hibafa). Nem-redundáns rendszerek: Hibaterjedési részháló az interfész helyek között. Komponens (rész)rendszer állapotok közötti kapcsolatok: Nemredundáns komponens - részrendszer - rendszer hierarchia: H és F interfész helyek a (rész)rendszerekhez rendelve, OR hibafa alapján terjed a hiba felfelé. 11
12 Redundáns komponensek és részrendszer: A hibaterjedést egy általános hibafa írja el, ezt valósítjuk meg a kapukhoz tartozó GSPN alhálók segítségével. A javítás terjedésének modellezésére a meghibásodáshoz felvett hibafa duálisát kel használni. Javítási folyamat: Tranziens hiba implicit javítása: (csaknem) azonnali, de hibaterjedésre lehetőséget ad. Állandósult hiba explicit javítása: időzített átmenettel modellezhető. Javítási stratégiák modellezhetők: pl. nempreemtív prioritásos javítás közös javítóval, preemptív javítás stb. Feltételes javítás: Tiltó éllel modellezhető. 12
Szolgáltatásbiztonság verifikációja: Megbízhatósági analízis
 Szolgáltatásbiztonság verifikációja: Megbízhatósági analízis Rendszer- és szoftverellenőrzés előadás dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek
Szolgáltatásbiztonság verifikációja: Megbízhatósági analízis Rendszer- és szoftverellenőrzés előadás dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek
Sztochasztikus temporális logikák
 Sztochasztikus temporális logikák Teljesítmény és szolgáltatásbiztonság jellemzők formalizálása és ellenőrzése Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs
Sztochasztikus temporális logikák Teljesítmény és szolgáltatásbiztonság jellemzők formalizálása és ellenőrzése Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs
Megbízhatósági analízis
 Megbízhatósági analízis Rendszertervezés és -integráció előadás dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT Célkitűzések BME-MIT
Megbízhatósági analízis Rendszertervezés és -integráció előadás dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT Célkitűzések BME-MIT
Szoftver architektúra tervek ellenőrzése
 Szoftver architektúra tervek ellenőrzése Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/~majzik/ Tartalomjegyzék A fázis
Szoftver architektúra tervek ellenőrzése Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/~majzik/ Tartalomjegyzék A fázis
Veszély analízis. Rendszertervezés és -integráció előadás dr. Majzik István
 Veszély analízis Rendszertervezés és -integráció előadás dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT Célkitűzések BME-MIT 2.
Veszély analízis Rendszertervezés és -integráció előadás dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT Célkitűzések BME-MIT 2.
Sztochasztikus Petri-hálók
 Sztochasztikus Petri-hálók Teljesítmény és megbízhatóság modellezés dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Áttekintés Motiváció Sztochasztikus folyamatok és modellek Folytonos
Sztochasztikus Petri-hálók Teljesítmény és megbízhatóság modellezés dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Áttekintés Motiváció Sztochasztikus folyamatok és modellek Folytonos
Elemzési módszerek. Egyes módszerek ágazat-specifikusak, mások teljesen általánosan használatosak. A leggyakoribb veszélyelemző módszerek:
 Elemzési módszerek Egyes módszerek ágazat-specifikusak, mások teljesen általánosan használatosak. A leggyakoribb veszélyelemző módszerek: Hibamód és -hatás elemzés - failure modes and effects analysis
Elemzési módszerek Egyes módszerek ágazat-specifikusak, mások teljesen általánosan használatosak. A leggyakoribb veszélyelemző módszerek: Hibamód és -hatás elemzés - failure modes and effects analysis
Biztonságkritikus rendszerek Gyakorlat: Megbízhatósági analízis
 Biztonságkritikus rendszerek Gyakorlat: Megbízhatósági analízis Rendszertervezés és -integráció dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek
Biztonságkritikus rendszerek Gyakorlat: Megbízhatósági analízis Rendszertervezés és -integráció dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek
Elérhetőségi probléma egyszerűsítése: Állapottér és struktúra redukció Petri-háló alosztályok
 Elérhetőségi probléma egyszerűsítése: Állapottér és struktúra redukció Petri-háló alosztályok dr. Bartha Tamás Dr. Pataricza András BME Méréstechnika és Információs Rendszerek Tanszék Elérhetőségi probléma
Elérhetőségi probléma egyszerűsítése: Állapottér és struktúra redukció Petri-háló alosztályok dr. Bartha Tamás Dr. Pataricza András BME Méréstechnika és Információs Rendszerek Tanszék Elérhetőségi probléma
Méréselmélet MI BSc 1
 Mérés és s modellezés 2008.02.15. 1 Méréselmélet - bevezetés a mérnöki problémamegoldás menete 1. A probléma kitűzése 2. A hipotézis felállítása 3. Kísérlettervezés 4. Megfigyelések elvégzése 5. Adatok
Mérés és s modellezés 2008.02.15. 1 Méréselmélet - bevezetés a mérnöki problémamegoldás menete 1. A probléma kitűzése 2. A hipotézis felállítása 3. Kísérlettervezés 4. Megfigyelések elvégzése 5. Adatok
A kockázatelemzés menete
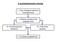 A kockázatelemzés menete 1. Üzem (folyamat) jellemzői Veszélyforrások 2. Baleseti sorok meghatározása 3a. Következmények felmérése 3b. Gyakoriság becslése 4. Kockázat meghatározás Balesetek Gyakoriság
A kockázatelemzés menete 1. Üzem (folyamat) jellemzői Veszélyforrások 2. Baleseti sorok meghatározása 3a. Következmények felmérése 3b. Gyakoriság becslése 4. Kockázat meghatározás Balesetek Gyakoriság
Rendszermodellezés. Modellellenőrzés. Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék
 Rendszermodellezés Modellellenőrzés Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Ismétlés: Mire használunk modelleket? Kommunikáció, dokumentáció Gondolkodás,
Rendszermodellezés Modellellenőrzés Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Ismétlés: Mire használunk modelleket? Kommunikáció, dokumentáció Gondolkodás,
Valószínűségi modellellenőrzés Markov döntési folyamatokkal
 Valószínűségi modellellenőrzés Markov döntési folyamatokkal Hajdu Ákos Szoftver verifikáció és validáció 2015.12.09. Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek
Valószínűségi modellellenőrzés Markov döntési folyamatokkal Hajdu Ákos Szoftver verifikáció és validáció 2015.12.09. Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek
Alapszintű formalizmusok
 Alapszintű formalizmusok dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális tervek Informális követelmények Formális modell Formalizált követelmények
Alapszintű formalizmusok dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális tervek Informális követelmények Formális modell Formalizált követelmények
Mérés és modellezés Méréstechnika VM, GM, MM 1
 Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
SÚLYOS BALESETEK ELEMZÉSE. 3. téma: Kvalitatív módszerek - Hibafa
 Az oktatási anyag a szerzők szellemi terméke. Az anyag kizárólag a 2014.01.22-23 23-i OKF Továbbképzés céljaira használható. Sokszorosítás, utánközlés és mindennemű egyéb felhasználás a szerzők engedélyéhez
Az oktatási anyag a szerzők szellemi terméke. Az anyag kizárólag a 2014.01.22-23 23-i OKF Továbbképzés céljaira használható. Sokszorosítás, utánközlés és mindennemű egyéb felhasználás a szerzők engedélyéhez
Elérhetőségi analízis Petri hálók dinamikus tulajdonságai
 Elérhetőségi analízis Petri hálók dinamikus tulajdonságai dr. Bartha Tamás Dr. Pataricza András BME Méréstechnika és Információs Rendszerek Tanszék Petri hálók vizsgálata Az elemzés mélysége szerint: Vizsgálati
Elérhetőségi analízis Petri hálók dinamikus tulajdonságai dr. Bartha Tamás Dr. Pataricza András BME Méréstechnika és Információs Rendszerek Tanszék Petri hálók vizsgálata Az elemzés mélysége szerint: Vizsgálati
Modell alapú tesztelés mobil környezetben
 Modell alapú tesztelés mobil környezetben Micskei Zoltán Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék A terület behatárolása Testing is an activity performed
Modell alapú tesztelés mobil környezetben Micskei Zoltán Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék A terület behatárolása Testing is an activity performed
Mérés és modellezés 1
 Mérés és modellezés 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni kell
Mérés és modellezés 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni kell
A szolgáltatásbiztonság alapfogalmai
 A szolgáltatásbiztonság alapfogalmai Majzik István majzik@mit.bme.hu http://www.inf.mit.bme.hu/edu/courses/szbt 1 Tartalomjegyzék A szolgáltatásbiztonság fogalma A szolgáltatásbiztonságot befolyásoló tényezők
A szolgáltatásbiztonság alapfogalmai Majzik István majzik@mit.bme.hu http://www.inf.mit.bme.hu/edu/courses/szbt 1 Tartalomjegyzék A szolgáltatásbiztonság fogalma A szolgáltatásbiztonságot befolyásoló tényezők
MŰSZAKI MEGBÍZHATÓSÁGÁNAK VIZSGÁLATI MÓDSZEREI EXAMINATION METHODS FOR EVALUATING RELIABILITY IN COMPLEX MILITARY RECONNAISSANCE SYSTEMS.
 BÁRKÁNYI PÁL KOMPLEX KATONAI FELDERÍTŐ RENDSZEREK MŰSZAKI MEGBÍZHATÓSÁGÁNAK VIZSGÁLATI MÓDSZEREI EXAMINATION METHODS FOR EVALUATING RELIABILITY IN COMPLEX MILITARY RECONNAISSANCE SYSTEMS A cikk a komplex
BÁRKÁNYI PÁL KOMPLEX KATONAI FELDERÍTŐ RENDSZEREK MŰSZAKI MEGBÍZHATÓSÁGÁNAK VIZSGÁLATI MÓDSZEREI EXAMINATION METHODS FOR EVALUATING RELIABILITY IN COMPLEX MILITARY RECONNAISSANCE SYSTEMS A cikk a komplex
A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel
 A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel Majzik István Micskei Zoltán BME Méréstechnika és Információs Rendszerek Tanszék 1 Modell alapú fejlesztési folyamat (részlet)
A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel Majzik István Micskei Zoltán BME Méréstechnika és Információs Rendszerek Tanszék 1 Modell alapú fejlesztési folyamat (részlet)
Az UPPAAL egyes modellezési lehetőségeinek összefoglalása. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék
 Az UPPAAL egyes modellezési lehetőségeinek összefoglalása Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Résztvevők együttműködése (1) Automaták interakciói üzenetküldéssel Szinkron
Az UPPAAL egyes modellezési lehetőségeinek összefoglalása Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Résztvevők együttműködése (1) Automaták interakciói üzenetküldéssel Szinkron
A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel
 A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel Majzik István Micskei Zoltán BME Méréstechnika és Információs Rendszerek Tanszék 1 Modell alapú fejlesztési folyamat (részlet)
A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel Majzik István Micskei Zoltán BME Méréstechnika és Információs Rendszerek Tanszék 1 Modell alapú fejlesztési folyamat (részlet)
Logikai hálózatok. Dr. Bede Zsuzsanna St. I. em. 104.
 Logikai hálózatok Dr. Bede Zsuzsanna bede.zsuzsanna@mail.bme.hu St. I. em. 04. Tanszéki honlap: www.kjit.bme.hu/hallgatoknak/bsc-targyak-3/logikai-halozatok Gyakorlatok: hétfő + 08:5-0:00 J 208 HF: 4.
Logikai hálózatok Dr. Bede Zsuzsanna bede.zsuzsanna@mail.bme.hu St. I. em. 04. Tanszéki honlap: www.kjit.bme.hu/hallgatoknak/bsc-targyak-3/logikai-halozatok Gyakorlatok: hétfő + 08:5-0:00 J 208 HF: 4.
Autóipari beágyazott rendszerek. Kockázatelemzés
 Autóipari beágyazott rendszerek Kockázatelemzés 1 Biztonságkritikus rendszer Beágyazott rendszer Aminek hibája Anyagi vagyont, vagy Emberéletet veszélyeztet Tipikus példák ABS, ESP, elektronikus szervokormány
Autóipari beágyazott rendszerek Kockázatelemzés 1 Biztonságkritikus rendszer Beágyazott rendszer Aminek hibája Anyagi vagyont, vagy Emberéletet veszélyeztet Tipikus példák ABS, ESP, elektronikus szervokormány
Diszkrét állapotú rendszerek modellezése. Petri-hálók
 Diszkrét állapotú rendszerek modellezése Petri-hálók Diszkrét eseményű rendszerek Discret Event (Dynamic) Systems DES, DEDS állapotterük diszkrét halmaz állapotváltozásuk kizárólag az időben aszinkron
Diszkrét állapotú rendszerek modellezése Petri-hálók Diszkrét eseményű rendszerek Discret Event (Dynamic) Systems DES, DEDS állapotterük diszkrét halmaz állapotváltozásuk kizárólag az időben aszinkron
Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével
 Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével Pekárdy Milán, Baumgartner János, Süle Zoltán Pannon Egyetem, Veszprém XXXII. Magyar Operációkutatási
Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével Pekárdy Milán, Baumgartner János, Süle Zoltán Pannon Egyetem, Veszprém XXXII. Magyar Operációkutatási
Diszkrét állapotú rendszerek modellezése. Petri-hálók
 Diszkrét állapotú rendszerek modellezése Petri-hálók Diszkrét eseményű rendszerek Discret Event (Dynamic) Systems DES, DEDS állapotterük diszkrét halmaz állapotváltozásuk kizárólag az időben aszinkron
Diszkrét állapotú rendszerek modellezése Petri-hálók Diszkrét eseményű rendszerek Discret Event (Dynamic) Systems DES, DEDS állapotterük diszkrét halmaz állapotváltozásuk kizárólag az időben aszinkron
folyamatrendszerek modellezése
 Diszkrét eseményű folyamatrendszerek modellezése Hangos Katalin Számítástudomány Alkalmazása Tanszék Veszprémi Egyetem Haladó Folyamatmodellezés és modell analízis PhD kurzus p. 1/36 Tartalom Diszkrét
Diszkrét eseményű folyamatrendszerek modellezése Hangos Katalin Számítástudomány Alkalmazása Tanszék Veszprémi Egyetem Haladó Folyamatmodellezés és modell analízis PhD kurzus p. 1/36 Tartalom Diszkrét
Veszély analízis. Rendszertervezés és -integráció előadás dr. Majzik István
 Veszély analízis Rendszertervezés és -integráció előadás dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT Célkitűzések BME-MIT 2.
Veszély analízis Rendszertervezés és -integráció előadás dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT Célkitűzések BME-MIT 2.
Az informatikai biztonsági kockázatok elemzése
 ROBOTHADVISELÉS S 2009 Az informatikai biztonsági kockázatok elemzése Muha Lajos PhD, CISM főiskolai tanár, mb. tanszékvezet kvezető ZMNE BJKMK IHI Informatikai Tanszék 1 Az informatikai biztonság Az informatikai
ROBOTHADVISELÉS S 2009 Az informatikai biztonsági kockázatok elemzése Muha Lajos PhD, CISM főiskolai tanár, mb. tanszékvezet kvezető ZMNE BJKMK IHI Informatikai Tanszék 1 Az informatikai biztonság Az informatikai
Kritikus Beágyazott Rendszerek
 Kritikus Beágyazott Rendszerek Megbízhatósági modellezés Gyakorlat Készítette: Vörös András Utolsó módosítás: 015-09- Verzió: 1.0 Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs
Kritikus Beágyazott Rendszerek Megbízhatósági modellezés Gyakorlat Készítette: Vörös András Utolsó módosítás: 015-09- Verzió: 1.0 Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs
Szoftver értékelés és karbantartás
 Szoftver értékelés és karbantartás Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/~majzik/ Emlékeztető: Biztonsági követelmények
Szoftver értékelés és karbantartás Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/~majzik/ Emlékeztető: Biztonsági követelmények
Szoftverminőségbiztosítás
 NGB_IN003_1 SZE 2014-15/2 (13) Szoftverminőségbiztosítás Szoftverminőség és formális módszerek Formális módszerek Formális módszer formalizált módszer(tan) Formális eljárások alkalmazása a fejlesztésben
NGB_IN003_1 SZE 2014-15/2 (13) Szoftverminőségbiztosítás Szoftverminőség és formális módszerek Formális módszerek Formális módszer formalizált módszer(tan) Formális eljárások alkalmazása a fejlesztésben
Programfejlesztési Modellek
 Programfejlesztési Modellek Programfejlesztési fázisok: Követelmények leírása (megvalósíthatósági tanulmány, funkcionális specifikáció) Specifikáció elkészítése Tervezés (vázlatos és finom) Implementáció
Programfejlesztési Modellek Programfejlesztési fázisok: Követelmények leírása (megvalósíthatósági tanulmány, funkcionális specifikáció) Specifikáció elkészítése Tervezés (vázlatos és finom) Implementáció
Szoftver karbantartás
 Szoftver karbantartás Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/~majzik/ Áttekintés Követelményspecifikálás Architektúra
Szoftver karbantartás Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/~majzik/ Áttekintés Követelményspecifikálás Architektúra
Diagnosztika Petri háló modellek felhasználásával
 Diagnosztika - Ea9. p. 1/2 Modell Alapú Diagnosztika Diszkrét Módszerekkel Diagnosztika Petri háló modellek felhasználásával Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék Diagnosztika
Diagnosztika - Ea9. p. 1/2 Modell Alapú Diagnosztika Diszkrét Módszerekkel Diagnosztika Petri háló modellek felhasználásával Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék Diagnosztika
Gyakorló feladatok: Formális modellek, temporális logikák, modellellenőrzés. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék
 Gyakorló feladatok: Formális modellek, temporális logikák, modellellenőrzés Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Formális modellek használata és értelmezése Formális modellek
Gyakorló feladatok: Formális modellek, temporális logikák, modellellenőrzés Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Formális modellek használata és értelmezése Formális modellek
Szoftverminőségbiztosítás
 NGB_IN003_1 SZE 2014-15/2 (8) Szoftverminőségbiztosítás Szoftvertesztelési folyamat (folyt.) Szoftvertesztelési ráfordítások (Perry 1995) Tesztelésre fordítódik a projekt költségvetés 24%-a a projekt menedzsment
NGB_IN003_1 SZE 2014-15/2 (8) Szoftverminőségbiztosítás Szoftvertesztelési folyamat (folyt.) Szoftvertesztelési ráfordítások (Perry 1995) Tesztelésre fordítódik a projekt költségvetés 24%-a a projekt menedzsment
Hibatűrés. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék
 Hibatűrés Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/ 1 Hibatűrés különféle hibák esetén Hardver tervezési hibák
Hibatűrés Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/ 1 Hibatűrés különféle hibák esetén Hardver tervezési hibák
Formális módszerek GM_IN003_1 Program verifikálás, formalizmusok
 Formális módszerek GM_IN003_1 Program verifikálás, formalizmusok Program verifikálás Konkurens programozási megoldások terjedése -> verifikálás szükséges, (nehéz) logika Legszélesebb körben alkalmazott
Formális módszerek GM_IN003_1 Program verifikálás, formalizmusok Program verifikálás Konkurens programozási megoldások terjedése -> verifikálás szükséges, (nehéz) logika Legszélesebb körben alkalmazott
A szolgáltatásbiztonság alapfogalmai
 A szolgáltatásbiztonság alapfogalmai Majzik István majzik@mit.bme.hu http://www.mit.bme.hu/oktatas/targyak/vimim146/ 1 Tartalomjegyzék A szolgáltatásbiztonság fogalma A szolgáltatásbiztonságot befolyásoló
A szolgáltatásbiztonság alapfogalmai Majzik István majzik@mit.bme.hu http://www.mit.bme.hu/oktatas/targyak/vimim146/ 1 Tartalomjegyzék A szolgáltatásbiztonság fogalma A szolgáltatásbiztonságot befolyásoló
Modellezés és szimuláció a tervezésben
 Modellezés és szimuláció a tervezésben Szimuláció: egy másik rendszerrel - amely bizonyos vonatkozásokban hasonló az eredeti rendszerhez - utánozzuk egy rendszer viselkedését, vagyis az eredeti rendszer
Modellezés és szimuláció a tervezésben Szimuláció: egy másik rendszerrel - amely bizonyos vonatkozásokban hasonló az eredeti rendszerhez - utánozzuk egy rendszer viselkedését, vagyis az eredeti rendszer
Ellenőrző kérdések. 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t
 Ellenőrző kérdések 2. Kis dolgozat kérdései 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t 37. Ha t szintű indexet használunk,
Ellenőrző kérdések 2. Kis dolgozat kérdései 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t 37. Ha t szintű indexet használunk,
Az előadásdiák gyors összevágása, hogy legyen valami segítség:
 Az előadásdiák gyors összevágása, hogy legyen valami segítség: Az elektronikai gyártás ellenőrző berendezései (AOI, X-RAY, ICT) 1. Ismertesse az automatikus optikai ellenőrzés alapelvét (a), megvilágítási
Az előadásdiák gyors összevágása, hogy legyen valami segítség: Az elektronikai gyártás ellenőrző berendezései (AOI, X-RAY, ICT) 1. Ismertesse az automatikus optikai ellenőrzés alapelvét (a), megvilágítási
Szoftverminőségbiztosítás
 NGB_IN003_1 SZE 2017-18/2 (9) Szoftverminőségbiztosítás Specifikáció alapú (black-box) technikák A szoftver mint leképezés Szoftverhiba Hibát okozó bement Hibás kimenet Input Szoftver Output Funkcionális
NGB_IN003_1 SZE 2017-18/2 (9) Szoftverminőségbiztosítás Specifikáció alapú (black-box) technikák A szoftver mint leképezés Szoftverhiba Hibát okozó bement Hibás kimenet Input Szoftver Output Funkcionális
Szoftver-modellellenőrzés absztrakciós módszerekkel
 Szoftver-modellellenőrzés absztrakciós módszerekkel Hajdu Ákos Formális módszerek 2017.03.22. Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék 1 BEVEZETŐ 2
Szoftver-modellellenőrzés absztrakciós módszerekkel Hajdu Ákos Formális módszerek 2017.03.22. Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék 1 BEVEZETŐ 2
Szoftver karbantartási lépések ellenőrzése
 Szoftverellenőrzési technikák (vimim148) Szoftver karbantartási lépések ellenőrzése Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.inf.mit.bme.hu/
Szoftverellenőrzési technikák (vimim148) Szoftver karbantartási lépések ellenőrzése Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.inf.mit.bme.hu/
Zárthelyi mintapéldák. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék
 Zárthelyi mintapéldák Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Elméleti kérdések Indokolja meg, hogy az A (X Stop F Start) kifejezés szintaktikailag helyes kifejezés-e CTL illetve
Zárthelyi mintapéldák Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Elméleti kérdések Indokolja meg, hogy az A (X Stop F Start) kifejezés szintaktikailag helyes kifejezés-e CTL illetve
Szoftverminőségbiztosítás
 NGB_IN003_1 SZE 2014-15/2 (4) Szoftverminőségbiztosítás Biztonság kritikus szoftverek Hibatűrés Szoftver-diverzitás Biztonság, biztonságosság Mentesség azoktól a feltételektől, melyek halált, sérülést,
NGB_IN003_1 SZE 2014-15/2 (4) Szoftverminőségbiztosítás Biztonság kritikus szoftverek Hibatűrés Szoftver-diverzitás Biztonság, biztonságosság Mentesség azoktól a feltételektől, melyek halált, sérülést,
Modulzáró ellenőrző kérdések és feladatok (2)
 Modulzáró ellenőrző kérdések és feladatok (2) 1. Definiálja az alábbi, technikai eszközök üzemi megbízhatóságával kapcsolatos fogalmakat (1): Megbízhatóság. Használhatóság. Hibamentesség. Fenntarthatóság.
Modulzáró ellenőrző kérdések és feladatok (2) 1. Definiálja az alábbi, technikai eszközök üzemi megbízhatóságával kapcsolatos fogalmakat (1): Megbízhatóság. Használhatóság. Hibamentesség. Fenntarthatóság.
A fejlesztési szabványok szerepe a szoftverellenőrzésben
 A fejlesztési szabványok szerepe a szoftverellenőrzésben Majzik István majzik@mit.bme.hu http://www.inf.mit.bme.hu/ 1 Tartalomjegyzék Biztonságkritikus rendszerek A biztonságintegritási szint Az ellenőrzés
A fejlesztési szabványok szerepe a szoftverellenőrzésben Majzik István majzik@mit.bme.hu http://www.inf.mit.bme.hu/ 1 Tartalomjegyzék Biztonságkritikus rendszerek A biztonságintegritási szint Az ellenőrzés
A szolgáltatásbiztonság alapfogalmai
 A szolgáltatásbiztonság alapfogalmai Majzik István majzik@mit.bme.hu http://www.mit.bme.hu/oktatas/targyak/vimim146/ 1 Tartalomjegyzék A szolgáltatásbiztonság fogalma A szolgáltatásbiztonságot befolyásoló
A szolgáltatásbiztonság alapfogalmai Majzik István majzik@mit.bme.hu http://www.mit.bme.hu/oktatas/targyak/vimim146/ 1 Tartalomjegyzék A szolgáltatásbiztonság fogalma A szolgáltatásbiztonságot befolyásoló
0,424 0,576. f) P (X 2 = 3) g) P (X 3 = 1) h) P (X 4 = 1 vagy 2 X 2 = 2) i) P (X 7 = 3, X 4 = 1, X 2 = 2 X 0 = 2) j) P (X 7 = 3, X 4 = 1, X 2 = 2)
 Legyen adott a P átmenetvalószín ség mátrix és a ϕ 0 kezdeti eloszlás Kérdés, hogy miként lehetne meghatározni az egyes állapotokban való tartózkodás valószín ségét az n-edik lépés múlva Deniáljuk az n-lépéses
Legyen adott a P átmenetvalószín ség mátrix és a ϕ 0 kezdeti eloszlás Kérdés, hogy miként lehetne meghatározni az egyes állapotokban való tartózkodás valószín ségét az n-edik lépés múlva Deniáljuk az n-lépéses
Kiterjesztések sek szemantikája
 Kiterjesztések sek szemantikája Példa D Integer = {..., -1,0,1,... }; D Boolean = { true, false } D T1... T n T = D T 1... D Tn D T Az összes függvf ggvény halmaza, amelyek a D T1,..., D Tn halmazokból
Kiterjesztések sek szemantikája Példa D Integer = {..., -1,0,1,... }; D Boolean = { true, false } D T1... T n T = D T 1... D Tn D T Az összes függvf ggvény halmaza, amelyek a D T1,..., D Tn halmazokból
E.4 Markov-láncok E.4 Markov-láncok. Sok sorbanállási hálózat viselkedése leírható "folytonos idejű Markovláncok " segítségével.
 E.4 Markov-láncok Sok sorbanállási hálózat viselkedése leírható "folytonos idejű Markovláncok " segítségével. Egy Markov-láncot (MC) meghatároznak az alapját adó sorbanállási hálózat állapotai és az ezek
E.4 Markov-láncok Sok sorbanállási hálózat viselkedése leírható "folytonos idejű Markovláncok " segítségével. Egy Markov-láncot (MC) meghatároznak az alapját adó sorbanállási hálózat állapotai és az ezek
Magasabb szintű formalizmus: Állapottérképek (statecharts) dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék
 Magasabb szintű formalizmus: Állapottérképek (statecharts) dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Modellek a formális ellenőrzéshez Mivel nyújt többet egy magasabb szintű
Magasabb szintű formalizmus: Állapottérképek (statecharts) dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Modellek a formális ellenőrzéshez Mivel nyújt többet egy magasabb szintű
FMEA tréning OKTATÁSI SEGÉDLET
 FMEA tréning OKTATÁSI SEGÉDLET 1. Hibamód és hatás elemzés : FMEA (Failure Mode and Effects Analysis) A fejlett nyugati piacokon csak azok a vállalatok képesek hosszabbtávon megmaradni, melyek gazdaságosan
FMEA tréning OKTATÁSI SEGÉDLET 1. Hibamód és hatás elemzés : FMEA (Failure Mode and Effects Analysis) A fejlett nyugati piacokon csak azok a vállalatok képesek hosszabbtávon megmaradni, melyek gazdaságosan
Modulzáró ellenőrző kérdések és feladatok (2)
 Modulzáró ellenőrző kérdések és feladatok (2) 1. Definiálja az alábbi, technikai eszközök üzemi megbízhatóságával kapcsolatos fogalmakat (1): Megbízhatóság. Használhatóság. Hibamentesség. Fenntarthatóság.
Modulzáró ellenőrző kérdések és feladatok (2) 1. Definiálja az alábbi, technikai eszközök üzemi megbízhatóságával kapcsolatos fogalmakat (1): Megbízhatóság. Használhatóság. Hibamentesség. Fenntarthatóság.
Tranziens jelenségek rövid összefoglalás
 Tranziens jelenségek rövid összefoglalás Átmenet alakul ki akkor, ha van energiatároló (kapacitás vagy induktivitás) a rendszerben, mert ezeken a feszültség vagy áram nem jelenik meg azonnal, mint az ohmos
Tranziens jelenségek rövid összefoglalás Átmenet alakul ki akkor, ha van energiatároló (kapacitás vagy induktivitás) a rendszerben, mert ezeken a feszültség vagy áram nem jelenik meg azonnal, mint az ohmos
Mérési hibák 2006.10.04. 1
 Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
Mérési hibák 2006.10.04. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák_labor/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
Verifikáció és validáció Általános bevezető
 Verifikáció és validáció Általános bevezető Általános Verifikáció és validáció verification and validation - V&V: ellenőrző és elemző folyamatok amelyek biztosítják, hogy a szoftver megfelel a specifikációjának
Verifikáció és validáció Általános bevezető Általános Verifikáció és validáció verification and validation - V&V: ellenőrző és elemző folyamatok amelyek biztosítják, hogy a szoftver megfelel a specifikációjának
Mintavétel fogalmai STATISZTIKA, BIOMETRIA. Mintavételi hiba. Statisztikai adatgyűjtés. Nem véletlenen alapuló kiválasztás
 STATISZTIKA, BIOMETRIA. Előadás Mintavétel, mintavételi technikák, adatbázis Mintavétel fogalmai A mintavételt meg kell tervezni A sokaság elemei: X, X X N, lehet véges és végtelen Mintaelemek: x, x x
STATISZTIKA, BIOMETRIA. Előadás Mintavétel, mintavételi technikák, adatbázis Mintavétel fogalmai A mintavételt meg kell tervezni A sokaság elemei: X, X X N, lehet véges és végtelen Mintaelemek: x, x x
Mechatronika alapjai órai jegyzet
 - 1969-ben alakult ki a szó - Rendszerek és folyamatok, rendszertechnika - Automatika, szabályozás - számítástechnika Cd olvasó: Dia Mechatronika alapjai órai jegyzet Minden mechatronikai rendszer alapstruktúrája
- 1969-ben alakult ki a szó - Rendszerek és folyamatok, rendszertechnika - Automatika, szabályozás - számítástechnika Cd olvasó: Dia Mechatronika alapjai órai jegyzet Minden mechatronikai rendszer alapstruktúrája
Biztonságkritikus rendszerek
 Biztonságkritikus rendszerek Rendszertervezés és -integráció dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT Mik azok a biztonságkritikus
Biztonságkritikus rendszerek Rendszertervezés és -integráció dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT Mik azok a biztonságkritikus
Modellellenőrzés. dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék
 Modellellenőrzés dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális vagy félformális tervek Informális követelmények Formális modell: KS, LTS, TA
Modellellenőrzés dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális vagy félformális tervek Informális követelmények Formális modell: KS, LTS, TA
Digitális technika (VIMIAA02) Laboratórium 4
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika (VIMIAA02) Laboratórium 4 Fehér Béla Raikovich Tamás,
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika (VIMIAA02) Laboratórium 4 Fehér Béla Raikovich Tamás,
BASH script programozás II. Vezérlési szerkezetek
 06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
Adatfolyam hálók Dr. Bartha Tamás, Dr. Pataricza András fóliái
 Adatfolyam hálók Dr. Bartha Tamás, Dr. Pataricza András fóliái Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Adatfolyam modellezés Nem determinisztikus
Adatfolyam hálók Dr. Bartha Tamás, Dr. Pataricza András fóliái Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Adatfolyam modellezés Nem determinisztikus
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék
 Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék 06/7. félév 7. Előadás Dr. Kulcsár Gyula egyetemi docens Tartalom. A projektütemezés alapjai..
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék 06/7. félév 7. Előadás Dr. Kulcsár Gyula egyetemi docens Tartalom. A projektütemezés alapjai..
A MEGBÍZHATÓSÁGI ELEMZŐ MÓDSZEREK
 1. Elemző módszerek A MEGBÍZHATÓSÁGI ELEMZŐ MÓDSZEREK Ebben a fejezetben röviden összefoglaljuk azokat a módszereket, amelyekkel a technikai, technológiai és üzemeltetési rendszerek megbízhatósági elemzései
1. Elemző módszerek A MEGBÍZHATÓSÁGI ELEMZŐ MÓDSZEREK Ebben a fejezetben röviden összefoglaljuk azokat a módszereket, amelyekkel a technikai, technológiai és üzemeltetési rendszerek megbízhatósági elemzései
Statisztika - bevezetés Méréselmélet PE MIK MI_BSc VI_BSc 1
 Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Statisztika - bevezetés 00.04.05. Méréselmélet PE MIK MI_BSc VI_BSc Bevezetés Véletlen jelenség fogalma jelenséget okok bizonyos rendszere hozza létre ha mindegyik figyelembe vehető egyértelmű leírás általában
Részletes szoftver tervek ellenőrzése
 Részletes szoftver tervek ellenőrzése Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/~majzik/ Tartalomjegyzék A részletes
Részletes szoftver tervek ellenőrzése Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/~majzik/ Tartalomjegyzék A részletes
Dr. Kalló Noémi. Termelés- és szolgáltatásmenedzsment. egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék. Dr.
 Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Ismertesse a legfontosabb előrejelzési módszereket és azok gyakorlati
Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Ismertesse a legfontosabb előrejelzési módszereket és azok gyakorlati
Modellek ellenőrzése és tesztelése
 Modellek ellenőrzése és tesztelése Rendszermodellezés imsc gyakorlat Budapesti Műszaki és Gazdaságtudományi Egyetem Hibatűrő Rendszerek Kutatócsoport Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika
Modellek ellenőrzése és tesztelése Rendszermodellezés imsc gyakorlat Budapesti Műszaki és Gazdaságtudományi Egyetem Hibatűrő Rendszerek Kutatócsoport Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika
Operációs rendszerek II. Folyamatok ütemezése
 Folyamatok ütemezése Folyamatok modellezése az operációs rendszerekben Folyamatok állapotai alap állapotok futásra kész fut és várakozik felfüggesztett állapotok, jelentőségük Állapotátmeneti diagram Állapotátmenetek
Folyamatok ütemezése Folyamatok modellezése az operációs rendszerekben Folyamatok állapotai alap állapotok futásra kész fut és várakozik felfüggesztett állapotok, jelentőségük Állapotátmeneti diagram Állapotátmenetek
1. Egy lineáris hálózatot mikor nevezhetünk rezisztív hálózatnak és mikor dinamikus hálózatnak?
 Ellenörző kérdések: 1. előadás 1/5 1. előadás 1. Egy lineáris hálózatot mikor nevezhetünk rezisztív hálózatnak és mikor dinamikus hálózatnak? 2. Mit jelent a föld csomópont, egy áramkörben hány lehet belőle,
Ellenörző kérdések: 1. előadás 1/5 1. előadás 1. Egy lineáris hálózatot mikor nevezhetünk rezisztív hálózatnak és mikor dinamikus hálózatnak? 2. Mit jelent a föld csomópont, egy áramkörben hány lehet belőle,
UML (Unified Modelling Language)
 UML (Unified Modelling Language) UML (+ Object Constraint Language) Az objektum- modellezés egy szabványa (OMG) UML A 80-as, 90-es években egyre inkább terjedő objektum-orientált analízis és tervezés (OOA&D)
UML (Unified Modelling Language) UML (+ Object Constraint Language) Az objektum- modellezés egy szabványa (OMG) UML A 80-as, 90-es években egyre inkább terjedő objektum-orientált analízis és tervezés (OOA&D)
A BIZTONSÁGINTEGRITÁS ÉS A BIZTONSÁGORIENTÁLT ALKALMAZÁSI FELTÉTELEK TELJESÍTÉSE A VASÚTI BIZTOSÍTÓBERENDEZÉSEK TERVEZÉSE ÉS LÉTREHOZÁSA SORÁN
 A BIZTONSÁGINTEGRITÁS ÉS A BIZTONSÁGORIENTÁLT ALKALMAZÁSI FELTÉTELEK TELJESÍTÉSE A VASÚTI BIZTOSÍTÓBERENDEZÉSEK TERVEZÉSE ÉS LÉTREHOZÁSA SORÁN Szabó Géza Bevezetés Az előadás célja, vasúti alrendszerekre
A BIZTONSÁGINTEGRITÁS ÉS A BIZTONSÁGORIENTÁLT ALKALMAZÁSI FELTÉTELEK TELJESÍTÉSE A VASÚTI BIZTOSÍTÓBERENDEZÉSEK TERVEZÉSE ÉS LÉTREHOZÁSA SORÁN Szabó Géza Bevezetés Az előadás célja, vasúti alrendszerekre
Szimuláció. Fault Tolerant Systems Research Group. Budapest University of Technology and Economics. Department of Measurement and Information Systems
 Szimuláció Budapest University of Technology and Economics Fault Tolerant Systems Research Group Budapest University of Technology and Economics Department of Measurement and Information Systems 1 Mérés:
Szimuláció Budapest University of Technology and Economics Fault Tolerant Systems Research Group Budapest University of Technology and Economics Department of Measurement and Information Systems 1 Mérés:
Modellezés Petri hálókkal. dr. Bartha Tamás dr. Majzik István dr. Pataricza András BME Méréstechnika és Információs Rendszerek Tanszék
 Modellezés Petri hálókkal dr. Bartha Tamás dr. Majzik István dr. Pataricza András BME Méréstechnika és Információs Rendszerek Tanszék Modellező eszközök: DNAnet, Snoopy, PetriDotNet A DNAnet modellező
Modellezés Petri hálókkal dr. Bartha Tamás dr. Majzik István dr. Pataricza András BME Méréstechnika és Információs Rendszerek Tanszék Modellező eszközök: DNAnet, Snoopy, PetriDotNet A DNAnet modellező
Készítette: Trosztel Mátyás Konzulens: Hajós Gergely
 Készítette: Trosztel Mátyás Konzulens: Hajós Gergely Monte Carlo Markov Chain MCMC során egy megfelelően konstruált Markov-lánc segítségével mintákat generálunk. Ezek eloszlása követi a céleloszlást. A
Készítette: Trosztel Mátyás Konzulens: Hajós Gergely Monte Carlo Markov Chain MCMC során egy megfelelően konstruált Markov-lánc segítségével mintákat generálunk. Ezek eloszlása követi a céleloszlást. A
Biztonságkritikus rendszerek Gyakorlat: Architektúrák
 Biztonságkritikus rendszerek Gyakorlat: Architektúrák Rendszertervezés és -integráció dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT
Biztonságkritikus rendszerek Gyakorlat: Architektúrák Rendszertervezés és -integráció dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT
A kockázat fogalma. A kockázat fogalma. Fejezetek a környezeti kockázatok menedzsmentjéből 2 Bezegh András
 Fejezetek a környezeti kockázatok menedzsmentjéből 2 Bezegh András A kockázat fogalma A kockázat (def:) annak kifejezése, hogy valami nem kívánt hatással lesz a valaki/k értékeire, célkitűzésekre. A kockázat
Fejezetek a környezeti kockázatok menedzsmentjéből 2 Bezegh András A kockázat fogalma A kockázat (def:) annak kifejezése, hogy valami nem kívánt hatással lesz a valaki/k értékeire, célkitűzésekre. A kockázat
Működésbiztonsági veszélyelemzés (Hazard and Operability Studies, HAZOP) MSZ
 Működésbiztonsági veszélyelemzés (Hazard and Operability Studies, HAZOP) MSZ-09-960614-87 Célja: a szisztematikus zavar-feltárás, nyomozás. A tervezett működési körülményektől eltérő állapotok azonosítása,
Működésbiztonsági veszélyelemzés (Hazard and Operability Studies, HAZOP) MSZ-09-960614-87 Célja: a szisztematikus zavar-feltárás, nyomozás. A tervezett működési körülményektől eltérő állapotok azonosítása,
Miskolci Egyetem Általános Informatikai Tanszék
 Software tesztelés Miskolci Egyetem Általános Informatikai Tanszék Software tesztelés SWTESZT / 1 A tesztelés feladata Két alapvető cél rendszerben található hibák felderítése annak ellenőrzése, hogy a
Software tesztelés Miskolci Egyetem Általános Informatikai Tanszék Software tesztelés SWTESZT / 1 A tesztelés feladata Két alapvető cél rendszerben található hibák felderítése annak ellenőrzése, hogy a
A tesztelés feladata. Verifikáció
 Software tesztelés Miskolci Egyetem Általános Informatikai Tanszék Software tesztelés SWTESZT / 1 A tesztelés feladata Két alapvető cél rendszerben található hibák felderítése annak ellenőrzése, hogy a
Software tesztelés Miskolci Egyetem Általános Informatikai Tanszék Software tesztelés SWTESZT / 1 A tesztelés feladata Két alapvető cél rendszerben található hibák felderítése annak ellenőrzése, hogy a
STATISZTIKA ELŐADÁS ÁTTEKINTÉSE. Matematikai statisztika. Mi a modell? Binomiális eloszlás sűrűségfüggvény. Binomiális eloszlás
 ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
Logisztikai szimulációs módszerek
 Üzemszervezés Logisztikai szimulációs módszerek Dr. Juhász János Integrált, rugalmas gyártórendszerek tervezésénél használatos szimulációs módszerek A sztochasztikus külső-belső tényezőknek kitett folyamatok
Üzemszervezés Logisztikai szimulációs módszerek Dr. Juhász János Integrált, rugalmas gyártórendszerek tervezésénél használatos szimulációs módszerek A sztochasztikus külső-belső tényezőknek kitett folyamatok
Adaptív menetrendezés ADP algoritmus alkalmazásával
 Adaptív menetrendezés ADP algoritmus alkalmazásával Alcím III. Mechwart András Ifjúsági Találkozó Mátraháza, 2013. szeptember 10. Divényi Dániel Villamos Energetika Tanszék Villamos Művek és Környezet
Adaptív menetrendezés ADP algoritmus alkalmazásával Alcím III. Mechwart András Ifjúsági Találkozó Mátraháza, 2013. szeptember 10. Divényi Dániel Villamos Energetika Tanszék Villamos Művek és Környezet
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011.
 BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
2. gyakorlat RENDSZEREK MEGBÍZHATÓSÁGA: SOROS RENDSZEREK, REDUNDANCIA. Összeállította: Farkas Balázs
 2. gyakorlat RENDSZEREK MEGBÍZHATÓSÁGA: SOROS RENDSZEREK, REDUNDANCIA Összeállította: Farkas Balázs BEVEZETÉS RENDSZERTULAJDONSÁGOK Egy rendszer megbízhatósága függ: elemeinek megbízhatóságától és az elemek
2. gyakorlat RENDSZEREK MEGBÍZHATÓSÁGA: SOROS RENDSZEREK, REDUNDANCIA Összeállította: Farkas Balázs BEVEZETÉS RENDSZERTULAJDONSÁGOK Egy rendszer megbízhatósága függ: elemeinek megbízhatóságától és az elemek
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
IRÁNYÍTÁSTECHNIKA I.
 IRÁNÍTÁSTEHNIK I. 5 éves Sc kurzus Összeállította: Dr. Tarnai Géza egetemi tanár udapest, 8. Rendszer- és iránításelméleti ismeretek. félév. félév Diszkrét állapotú rendszerek, logikai hálózatok Foltonos
IRÁNÍTÁSTEHNIK I. 5 éves Sc kurzus Összeállította: Dr. Tarnai Géza egetemi tanár udapest, 8. Rendszer- és iránításelméleti ismeretek. félév. félév Diszkrét állapotú rendszerek, logikai hálózatok Foltonos
Termelés- és szolgáltatásmenedzsment
 Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Előrejelzési módszerek 14. Az előrejelzési modellek felépítése
Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Előrejelzési módszerek 14. Az előrejelzési modellek felépítése
Miskolci Egyetem Alkalmazott Informatikai Intézeti Tanszék A minőségbiztosítás informatikája. Készítette: Urbán Norbert
 Miskolci Egyetem Alkalmazott Informatikai Intézeti Tanszék A minőségbiztosítás informatikája Készítette: Urbán Norbert Szoftver-minőség A szoftver egy termelő-folyamat végterméke, A minőség azt jelenti,
Miskolci Egyetem Alkalmazott Informatikai Intézeti Tanszék A minőségbiztosítás informatikája Készítette: Urbán Norbert Szoftver-minőség A szoftver egy termelő-folyamat végterméke, A minőség azt jelenti,
Jelek és rendszerek 1. 10/9/2011 Dr. Buchman Attila Informatikai Rendszerek és Hálózatok Tanszék
 Jelek és rendszerek 1 10/9/2011 Dr. Buchman Attila Informatikai Rendszerek és Hálózatok Tanszék 1 Ajánlott irodalom: FODOR GYÖRGY : JELEK ÉS RENDSZEREK EGYETEMI TANKÖNYV Műegyetemi Kiadó, Budapest, 2006
Jelek és rendszerek 1 10/9/2011 Dr. Buchman Attila Informatikai Rendszerek és Hálózatok Tanszék 1 Ajánlott irodalom: FODOR GYÖRGY : JELEK ÉS RENDSZEREK EGYETEMI TANKÖNYV Műegyetemi Kiadó, Budapest, 2006
