Megbízhatósági analízis
|
|
|
- Zoltán Kiss
- 6 évvel ezelőtt
- Látták:
Átírás
1 Megbízhatósági analízis Rendszertervezés és -integráció előadás dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT
2 Célkitűzések BME-MIT 2.
3 Áttekintés Kvalitatív analízis (ismétlés): o Hibahatás analízis: Mik azok a komponens szintű hibák, amik rendszerszintű veszélyt, hibajelenséget okoznak? Egyszeres hibapontok meghatározása Kritikus hibák meghatározása o Szisztematikus módszerek: Hibafa, eseményfa, ok-következmény analízis, hibamód és hatás analízis Kvantitatív analízis: o Megbízhatósági analízis: Hogyan számszerűsíthető a komponens meghibásodások jellemzői alapján a rendszer megbízhatósága? Rendszerszintű megbízhatóság, rendelkezésre állás, MTTF, o Módszerek: Matematikai modell készítése a számításokhoz Megbízhatósági blokkdiagram Markov-lánc (folytonos idejű) BME-MIT 3.
4 Ismétlés: Megbízhatósági mértékek I. Állapot particionálás s(t) rendszerállapot esetén o Hibamentes (Up) illetve Hibás (Down) állapotpartíció s(t) U D u1 d1 u2 d2 u3 d3 u4 d4 u5 d5... Várható értékek: o Első hiba bekövetkezése: (Mean Time to First Failure) o Hibamentes működési idő: (Mean Up Time, Mean Time To Failure) o Hibás működési idő: (Mean Down Time, Mean Time To Repair) o Hibák közötti idő: (Mean Time Between Failures) MTFF = E{u1} Javított rendszer esetén MUT = MTTF = E{ui} MDT = MTTR = E{di} MTBF = MUT + MDT BME-MIT 4. t
5 Ismétlés: Megbízhatósági mértékek II. Valószínűség időfüggvények: o Rendelkezésre állás: a(t) = P{ s(t) U } o Megbízhatóság: r(t) = P{ s(t ) U, t <t}, Aszimptotikus értékek: o Készenlét: K= lim at ( ) t MUT MTTF K= MUT+MDT MTTF+MTTR (közben meghibásodhat) (nem hibásodhat meg t-ig) Biztonságosság analíziséhez: Biztonságos állapotpartícióban tartózkodás valószínűsége Aszimptotikus rendelkezésre állás (szokás az A jelölés is) Rendszeresen javított rendszer: K>0 BME-MIT 5.
6 Ismétlés: Megbízhatósági mértékek II. Valószínűség időfüggvények: o Rendelkezésre állás: a(t) = P{ s(t) U } o Megbízhatóság: r(t) = P{ s(t ) U, t <t}, Aszimptotikus értékek: 1.0 o Készenlét: K= lim a(t) at ( ) A 0 t MUT MTTF K= MUT+MDT MTTF+MTTR (közben meghibásodhat) (nem hibásodhat meg t-ig) Rendszeresen javított rendszer: A=K > 0 r(t) t BME-MIT 6.
7 Korábbi példa: DMI megbízhatósági követelmények Biztonság: o Biztonsági funkció elviselhető hibája óránként (Tolerable Hazard Rate): 10-7 <= THR < 10-6 o Biztonságintegritási szint: SIL 2 Megbízhatóság: o Mean Time To Failure: MTTF > 5000 óra (5000 óra: ~ 7 hónap) Rendelkezésre állás (készenlét): o A = MTTF / (MTTF+MTTR), A > Hibás állapot: évenként kevesebb, mint 42 óra MTTR < 24 óra esetén teljesíthető, ha a fenti MTTF adott BME-MIT 7.
8 Ismétlés: Komponens jellemző Meghibásodási tényező (gyakoriság): (t) o A komponens mekkora valószínűséggel fog éppen t időpont t környezetében elromlani, feltéve, hogy t-ig jól működött: (t)t = P{ s(t+t) D s(t) U }, miközben t0 o A megbízhatóság definíciója alapján: 1 dr( t) ( t), így r( t) e r() t dt o Elektronikai alkatrészekre: (t) t () t dt Itt r( t) e t 0 MTFF E U r() t dt Kezdeti hibák (gyártás utáni kiesés) Használati tartomány élettartam Öregedési tartomány (elavulás) BME-MIT 8. t
9 Hogyan becsülhetők a komponens adatok? Alkatrész szintű adatok: Megbízhatósági kézikönyvek o MIL-HDBK-217: The Military Handbook Reliability Prediction of Electronic Equipment (katonai alkalmazásokhoz, pesszimista) o Telcordia SR-332: Reliability Prediction Procedure for Electronic Equipment (telco alkalmazásokhoz, kevésbé pesszimista) o IEC TR 62380: Reliability Data Handbook - Universal Model for Reliability Prediction of Electronic Components, PCBs, and Equipment Alkatrész szintű meghibásodási gyakoriság függőségei: o Hőmérséklet, időjárási kitettség, rázkódás (pl. jármű fedélzet), magasság, o Jellegzetes felhasználási profilok Ground; stationary; weather protected / non weather protected Ground; non stationary; moderate / severe BME-MIT 9.
10 Komponens meghibásodási adatok adatbázisa BME-MIT 10.
11 Komponens meghibásodási adatok adatbázisa BME-MIT 11.
12 Élettartam becslése Milyen élettartam figyelembe vételével használhatók az elektronikai komponensek? o Mikortól kezd nőni a meghibásodási tényező? o Ekkorra ütemezett karbantartás (csere) előírható IEC 62380: Life expectancy definiált Példa: Elektrolit kondenzátorok (kiszáradás miatt leginkább korlátozott élettartam) o Hőmérsékletfüggő o Kezdeti bevizsgálástól is függ o Példa: 25C esetén ~ óra (~ 11 év) BME-MIT 12.
13 Komponens jellemzők Célkitűzés o meghibásodási tényező (folyamatos üzemben) o hibázási valószínűség (igény szerinti végrehajtás esetén) o megbízhatósági időfüggvény alapján rendszerszintű jellemzők o megbízhatósági időfüggvény o biztonságosság időfüggvény o rendelkezésre állás időfüggvény o készenlét o MTFF számítása A biztonságos állapotpartícióra vonatkoztatva: r(t)-hez hasonlóan a rendszerbiztonságosság is számolható A számítás az architektúra és a hibamódok alapján történik BME-MIT 13.
14 Kombinatorikus (Boole) modellek a megbízhatóság számítására BME-MIT 14.
15 Boole-modellek Komponensek kétféle állapota: o Hibamentes (jó) vagy hibás (rossz) Nincsenek függőségek a komponensek között o sem meghibásodás, o sem javítás szempontjából Komponensek kapcsolata a megbízhatóság szempontjából: Milyen a redundancia séma? o Soros kapcsolat: A komponensek nem redundánsak A komponensek egyaránt szükségesek a rendszer működéséhez o Párhuzamos kapcsolat: A komponensek redundánsak A komponensek egymást kiválthatják hiba esetén A kapcsolat (redundancia séma) a hibamódoktól is függhet BME-MIT 15.
16 Blokkok: Kapcsolat: Utak: Megbízhatósági blokkdiagram Komponensek (hibamódjai) Soros vagy párhuzamos (redundancia) Működőképes rendszerkonfigurációk o Működőképes a rendszer, ha van út a megbízhatósági blokkdiagramon a kezdőponttól a végpontig hibamentes komponenseken keresztül (komponens hibák ezt megszakítják ) Soros (nem redundáns komponensek): Párhuzamos (redundáns komponensek): K 1 K 1 K 2 K 3 K 2 K 3 BME-MIT 16.
17 Megbízhatósági blokkdiagram példák R1 R2 Átkapcsoló R3 BME-MIT 17.
18 Leggyakoribb rendszerek (áttekintés) Soros rendszer: Nincs redundancia Párhuzamos rendszer: Redundáns komponensek Összetett kanonikus rendszer: Soros és párhuzamos alrendszerek Ideális többségi szavazás: Bemenet TMR, NMR TMR/simplex rendszer Hidegtartalékolás Bemenet Normál modul Tartalék modul 1. modul 2. modul 3. modul Diagnosztikai egység Átkapcsoló egység Szavazó egység Kimenet Hibajel Kimenet Hibajel (Többségi szavazás) BME-MIT 18.
19 Soros rendszer K 1 K 2 K... N Rendszer hibátlan K 1 hibátlan... K N hibátlan P(AB)=P(A)P(B) ha függetlenek BME-MIT 19.
20 Soros rendszer K 1 K 2 K... N Rendszer hibátlan Megbízhatóság: N r ( t) r( t) R A rendszer megbízhatósága i1 i A komponensek megbízhatósága K 1 hibátlan... K N hibátlan P(AB)=P(A)P(B) ha függetlenek MTFF: R N i i1 MTFF N 1 i1 i BME-MIT 20.
21 Példa: Egy modul analízise (soros rendszer) Component name Type Additional data IEC reference Fault rate Quantity Panduit D Connector Rectangular Default value 0, Panduit D Connector Rectangular Default value 0, AHCT14 IC-Digital Standard Substituted with - 0, SN74AHCT14D 74HC/HCT540 IC-Digital Standard Substituted with - 0, CD74HC540E 74HC/HCT541 IC-Digital Standard Substituted with - 0, SN74AHCT541DW PALCE16V8 IC-Digital PAL Exact matching 0, HMA124 Optoelectronic Optocoupler Default value 0, MB6S IC-Digital Standard Default value 0, Resistor Resistor General purpose Default value 0, Resistor Resistor Fixed, high Default value 0, dissipation film Capacitor Capacitor Tantalum - solid Default value 0, electrolyte Capacitor Capacitor Ceramic class II. Default value 0, SMD led Optoelectronic Solid State Lamp Default value 0, U22-DI016-C3 PWB Default value 0, SOD80 BZV55C LF Diode Zener Default value 0, Module: 1, failure per million hours BME-MIT 21.
22 Párhuzamos rendszer K 1 K 2... K N Rendszer hibás K 1 hibás... K N hibás P(AB)=P(A)P(B) ha függetlenek BME-MIT 22.
23 Párhuzamos rendszer K 1 K 2... K N Megbízhatóság: 1 r ( t) (1 r ( t)) R Egyforma N komponens: N i1 i Rendszer hibás r ( t) 1 (1 r ( t)) N R K K 1 hibás... K N hibás P(AB)=P(A)P(B) ha függetlenek Itt MTFF (levezetés nélkül): MTFF 1 N 1 i1 i BME-MIT 23.
24 Összetett kanonikus rendszer Soros és párhuzamos alrendszerek Példa: Számítás készenlétek esetén: 0,7 0,75 0,95 0,99 0,7 0,9 0,7 0,75 A rendszer készenlét: 3 2 K R 0,95 0, , , 75 0,9 BME-MIT 24.
25 N-ből M hibás komponens N egyforma komponens; M vagy több komponens hiba esetén a rendszer is hibás r R M 1 i0 P "éppen i hiba van " M 1N rr (1 r) r i0 i i N i Itt egyszerűen r jelöli a komponens r(t) megbízhatóságot BME-MIT 25.
26 N-ből M hibás komponens és TMR N egyforma komponens; M vagy több komponens hiba esetén a rendszer is hibás r R M 1 i0 P "éppen i hiba van " M 1N rr (1 r) r i0 i i N i Alkalmazás: Ideális többségi szavazás (TMR): N=3, M=2 1 3 i 3 3 rr (1 r) r (1 r) r (1 r) r 3r 2r i0 i 0 1 3i R ( ) (3 2 ) 0 0 MTFF r t dt r r dt Kisebb, mintha csak 1 komponens lenne! BME-MIT 26.
27 TMR/simplex rendszer Alapeset: TMR működés Hiba esetén: Átkapcsolás simplex konfigurációra o Ha a TMR egy komponense meghibásodik (ezt a szavazó logika azonosítja) o A továbbiakban csak az egyik megmaradó hibátlan komponens működik tovább (de már hibadetektálás nélkül) MTFF rr r r BME-MIT 27.
28 Hidegtartalékolás Meghibásodó komponens helyébe új komponens lép (ami nem volt üzemben) MTFF N i1 MTFF Megbízhatóság általános felírása zárt alakban bonyolult (valószínűségi változók összegének sűrűségfüggvénye) o Azonos komponensek, exp. eloszlású komponens megbízhatósági függvény esetén: N 1 t rr () t e i! i0 i i t BME-MIT 28.
29 Architektúra változatok összevetése Analízis: Hogyan változik a rendszer rendelkezésre állása (itt: készenléte) o Különféle architektúrák esetén o A komponensek készenlétének növelésével Vizsgált architektúrák: o Referencia: Simplex rendszer (egy komponens) o Soros rendszer o Párhuzamos rendszer o Párhuzamos rendszer nem tökéletes átkapcsolóval o Többségi szavazás ideális szavazóval o Többségi szavazás nem ideális szavazóval BME-MIT 29.
30 Összefoglalás Megbízhatósági blokkdiagram Boole-modellek kanonikus rendszerekhez o Soros o Párhuzamos o N-ből M o TMR Architektúra változatok összevetése BME-MIT 30.
31 Kiegészítés: Markov modellek megbízhatósági analízisre BME-MIT 31.
32 Markov modellek A modell elemei o Állapotok o Állapotátmenetek Rendszerállapot: Komponens állapotok (jó/hibás) kombinációi Komponens meghibásodás, javítás o Állapotátmenet gyakoriság Meghibásodási tényező, javítási tényező (javítási idő reciproka) Analízis o Tranziens: Állapotok valószínűségi időfüggvénye o Állandósult: Állapotok valószínűsége (határérték) Megbízhatósági analízis o Rendelkezésre állás: Hibamentes (U) állapotpartícióban lévő állapotok valószínűségeinek összege BME-MIT 32.
33 Példa: CTMC megbízhatósági modell Két szerverből (A, B) álló rendszer: o Bármelyik szerver meghibásodhat o A szerverek külön-külön vagy együtt is javíthatók Rendszerszintű állapotok: Szerverek állapotai (jó / hibás) alapján Állapotátmenetek és gyakoriságok: o Az A szerver meghibásodása: o A B szerver meghibásodása: o Egy szerver javítása: o Teljes rendszer javítása: A meghibásodási tényező B meghibásodási tényező 1 javítási tényező 2 javítási tényező U partíció B jó B D partíció A,B jó A 1 2 Nincs jó B 1 A jó A BME-MIT 33.
34 Példa: CTMC megbízhatósági modell Állapotpartíciók: o U = {s AB, s A, s B }, s 0 = s AB o D = {s N } Markov-lánc megoldása: o Tranziens: (s i, t) o Állandósult állapot: (s i ) Rendelkezésre állás: a(t) = (s AB, t) + (s A, t) + (s B, t) Készenlét: K = A = (s AB ) + (s A ) + (s B ) Megbízhatóság: o Modell módosítása: D partícióból U partícióba vezető élek törlése o Módosított modell megoldásából: r(t) = (s AB, t) + (s A, t) + (s B, t) U partíció A B 1 AB 2 1 B A A B 1 AB 1 B A D partíció B A B A N N BME-MIT 34.
Biztonságkritikus rendszerek Gyakorlat: Megbízhatósági analízis
 Biztonságkritikus rendszerek Gyakorlat: Megbízhatósági analízis Rendszertervezés és -integráció dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek
Biztonságkritikus rendszerek Gyakorlat: Megbízhatósági analízis Rendszertervezés és -integráció dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek
Szolgáltatásbiztonság verifikációja: Megbízhatósági analízis
 Szolgáltatásbiztonság verifikációja: Megbízhatósági analízis Rendszer- és szoftverellenőrzés előadás dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek
Szolgáltatásbiztonság verifikációja: Megbízhatósági analízis Rendszer- és szoftverellenőrzés előadás dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek
A szolgáltatásbiztonság alapfogalmai
 A szolgáltatásbiztonság alapfogalmai Majzik István majzik@mit.bme.hu http://www.inf.mit.bme.hu/edu/courses/szbt 1 Tartalomjegyzék A szolgáltatásbiztonság fogalma A szolgáltatásbiztonságot befolyásoló tényezők
A szolgáltatásbiztonság alapfogalmai Majzik István majzik@mit.bme.hu http://www.inf.mit.bme.hu/edu/courses/szbt 1 Tartalomjegyzék A szolgáltatásbiztonság fogalma A szolgáltatásbiztonságot befolyásoló tényezők
A szolgáltatásbiztonság alapfogalmai
 A szolgáltatásbiztonság alapfogalmai Majzik István majzik@mit.bme.hu http://www.mit.bme.hu/oktatas/targyak/vimim146/ 1 Tartalomjegyzék A szolgáltatásbiztonság fogalma A szolgáltatásbiztonságot befolyásoló
A szolgáltatásbiztonság alapfogalmai Majzik István majzik@mit.bme.hu http://www.mit.bme.hu/oktatas/targyak/vimim146/ 1 Tartalomjegyzék A szolgáltatásbiztonság fogalma A szolgáltatásbiztonságot befolyásoló
Biztonságkritikus rendszerek
 Biztonságkritikus rendszerek Rendszertervezés és -integráció dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT Mik azok a biztonságkritikus
Biztonságkritikus rendszerek Rendszertervezés és -integráció dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT Mik azok a biztonságkritikus
A szolgáltatásbiztonság alapfogalmai
 A szolgáltatásbiztonság alapfogalmai Majzik István majzik@mit.bme.hu http://www.mit.bme.hu/oktatas/targyak/vimim146/ 1 Tartalomjegyzék A szolgáltatásbiztonság fogalma A szolgáltatásbiztonságot befolyásoló
A szolgáltatásbiztonság alapfogalmai Majzik István majzik@mit.bme.hu http://www.mit.bme.hu/oktatas/targyak/vimim146/ 1 Tartalomjegyzék A szolgáltatásbiztonság fogalma A szolgáltatásbiztonságot befolyásoló
Biztosítóberendezések biztonságának értékelése
 Žilinská univerzita v Žiline Elektrotechnická fakulta Univerzitná 1, 010 26 Žilina tel: +421 41 5133301 e mail: kris@fel.uniza.sk Téma: Biztosítóberendezések ának értékelése prof. Ing. Karol Rástočný,
Žilinská univerzita v Žiline Elektrotechnická fakulta Univerzitná 1, 010 26 Žilina tel: +421 41 5133301 e mail: kris@fel.uniza.sk Téma: Biztosítóberendezések ának értékelése prof. Ing. Karol Rástočný,
Biztonságkritikus rendszerek Gyakorlat: Architektúrák
 Biztonságkritikus rendszerek Gyakorlat: Architektúrák Rendszertervezés és -integráció dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT
Biztonságkritikus rendszerek Gyakorlat: Architektúrák Rendszertervezés és -integráció dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT
A szolgáltatásbiztonság analízise
 A szolgáltatásbiztonság analízise Előadásvázlat Szolgáltatásbiztonságra tervezés tárgyból Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Tartalomjegyzék: 1 Bevezetés...2 2 Kvalitatív
A szolgáltatásbiztonság analízise Előadásvázlat Szolgáltatásbiztonságra tervezés tárgyból Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Tartalomjegyzék: 1 Bevezetés...2 2 Kvalitatív
Szoftverminőségbiztosítás
 NGB_IN003_1 SZE 2014-15/2 (4) Szoftverminőségbiztosítás Biztonság kritikus szoftverek Hibatűrés Szoftver-diverzitás Biztonság, biztonságosság Mentesség azoktól a feltételektől, melyek halált, sérülést,
NGB_IN003_1 SZE 2014-15/2 (4) Szoftverminőségbiztosítás Biztonság kritikus szoftverek Hibatűrés Szoftver-diverzitás Biztonság, biztonságosság Mentesség azoktól a feltételektől, melyek halált, sérülést,
Szoftver architektúra tervek ellenőrzése
 Szoftver architektúra tervek ellenőrzése Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/~majzik/ Tartalomjegyzék A fázis
Szoftver architektúra tervek ellenőrzése Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/~majzik/ Tartalomjegyzék A fázis
A BIZTONSÁGINTEGRITÁS ÉS A BIZTONSÁGORIENTÁLT ALKALMAZÁSI FELTÉTELEK TELJESÍTÉSE A VASÚTI BIZTOSÍTÓBERENDEZÉSEK TERVEZÉSE ÉS LÉTREHOZÁSA SORÁN
 A BIZTONSÁGINTEGRITÁS ÉS A BIZTONSÁGORIENTÁLT ALKALMAZÁSI FELTÉTELEK TELJESÍTÉSE A VASÚTI BIZTOSÍTÓBERENDEZÉSEK TERVEZÉSE ÉS LÉTREHOZÁSA SORÁN Szabó Géza Bevezetés Az előadás célja, vasúti alrendszerekre
A BIZTONSÁGINTEGRITÁS ÉS A BIZTONSÁGORIENTÁLT ALKALMAZÁSI FELTÉTELEK TELJESÍTÉSE A VASÚTI BIZTOSÍTÓBERENDEZÉSEK TERVEZÉSE ÉS LÉTREHOZÁSA SORÁN Szabó Géza Bevezetés Az előadás célja, vasúti alrendszerekre
BME Járműgyártás és -javítás Tanszék. Javítási ciklusrend kialakítása
 BME Járműgyártás és -javítás Tanszék Javítási ciklusrend kialakítása A javítási ciklus naptári napokban, üzemórákban vagy más teljesítmény paraméterben meghatározott időtartam, amely a jármű, gép új állapotától
BME Járműgyártás és -javítás Tanszék Javítási ciklusrend kialakítása A javítási ciklus naptári napokban, üzemórákban vagy más teljesítmény paraméterben meghatározott időtartam, amely a jármű, gép új állapotától
Sztochasztikus temporális logikák
 Sztochasztikus temporális logikák Teljesítmény és szolgáltatásbiztonság jellemzők formalizálása és ellenőrzése Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs
Sztochasztikus temporális logikák Teljesítmény és szolgáltatásbiztonság jellemzők formalizálása és ellenőrzése Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs
A fejlesztési szabványok szerepe a szoftverellenőrzésben
 A fejlesztési szabványok szerepe a szoftverellenőrzésben Majzik István majzik@mit.bme.hu http://www.inf.mit.bme.hu/ 1 Tartalomjegyzék Biztonságkritikus rendszerek A biztonságintegritási szint Az ellenőrzés
A fejlesztési szabványok szerepe a szoftverellenőrzésben Majzik István majzik@mit.bme.hu http://www.inf.mit.bme.hu/ 1 Tartalomjegyzék Biztonságkritikus rendszerek A biztonságintegritási szint Az ellenőrzés
Hibatűrés. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék
 Hibatűrés Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/ 1 Hibatűrés különféle hibák esetén Hardver tervezési hibák
Hibatűrés Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/ 1 Hibatűrés különféle hibák esetén Hardver tervezési hibák
Architektúra tervezési példák: Architektúrák biztonságkritikus rendszerekben
 Architektúra tervezési példák: Architektúrák biztonságkritikus rendszerekben Majzik István majzik@mit.bme.hu Biztonságos állapotok Működésmód Fail-stop működés A megállás (lekapcsolás) biztonságos állapot
Architektúra tervezési példák: Architektúrák biztonságkritikus rendszerekben Majzik István majzik@mit.bme.hu Biztonságos állapotok Működésmód Fail-stop működés A megállás (lekapcsolás) biztonságos állapot
TERMÉKEK MŐSZAKI TERVEZÉSE Megbízhatóságra, élettartamra tervezés I.
 TERMÉKEK MŐSZAKI TERVEZÉSE Megbízhatóságra, élettartamra tervezés I. Dr. Kovács Zsolt egyetemi tanár Megbízhatóság-elméleti alapok A megbízhatóságelmélet az a komplex tudományág, amely a meghibásodási
TERMÉKEK MŐSZAKI TERVEZÉSE Megbízhatóságra, élettartamra tervezés I. Dr. Kovács Zsolt egyetemi tanár Megbízhatóság-elméleti alapok A megbízhatóságelmélet az a komplex tudományág, amely a meghibásodási
Modulzáró ellenőrző kérdések és feladatok (2)
 Modulzáró ellenőrző kérdések és feladatok (2) 1. Definiálja az alábbi, technikai eszközök üzemi megbízhatóságával kapcsolatos fogalmakat (1): Megbízhatóság. Használhatóság. Hibamentesség. Fenntarthatóság.
Modulzáró ellenőrző kérdések és feladatok (2) 1. Definiálja az alábbi, technikai eszközök üzemi megbízhatóságával kapcsolatos fogalmakat (1): Megbízhatóság. Használhatóság. Hibamentesség. Fenntarthatóság.
Autóipari beágyazott rendszerek. Kockázatelemzés
 Autóipari beágyazott rendszerek Kockázatelemzés 1 Biztonságkritikus rendszer Beágyazott rendszer Aminek hibája Anyagi vagyont, vagy Emberéletet veszélyeztet Tipikus példák ABS, ESP, elektronikus szervokormány
Autóipari beágyazott rendszerek Kockázatelemzés 1 Biztonságkritikus rendszer Beágyazott rendszer Aminek hibája Anyagi vagyont, vagy Emberéletet veszélyeztet Tipikus példák ABS, ESP, elektronikus szervokormány
Modulzáró ellenőrző kérdések és feladatok (2)
 Modulzáró ellenőrző kérdések és feladatok (2) 1. Definiálja az alábbi, technikai eszközök üzemi megbízhatóságával kapcsolatos fogalmakat (1): Megbízhatóság. Használhatóság. Hibamentesség. Fenntarthatóság.
Modulzáró ellenőrző kérdések és feladatok (2) 1. Definiálja az alábbi, technikai eszközök üzemi megbízhatóságával kapcsolatos fogalmakat (1): Megbízhatóság. Használhatóság. Hibamentesség. Fenntarthatóság.
Biztonságkritikus rendszerek architektúrája (2. rész)
 Biztonságkritikus rendszerek architektúrája (2. rész) Rendszertervezés és -integráció előadás dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék
Biztonságkritikus rendszerek architektúrája (2. rész) Rendszertervezés és -integráció előadás dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék
Az előadásdiák gyors összevágása, hogy legyen valami segítség:
 Az előadásdiák gyors összevágása, hogy legyen valami segítség: Az elektronikai gyártás ellenőrző berendezései (AOI, X-RAY, ICT) 1. Ismertesse az automatikus optikai ellenőrzés alapelvét (a), megvilágítási
Az előadásdiák gyors összevágása, hogy legyen valami segítség: Az elektronikai gyártás ellenőrző berendezései (AOI, X-RAY, ICT) 1. Ismertesse az automatikus optikai ellenőrzés alapelvét (a), megvilágítási
Szoftver értékelés és karbantartás
 Szoftver értékelés és karbantartás Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/~majzik/ Emlékeztető: Biztonsági követelmények
Szoftver értékelés és karbantartás Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/~majzik/ Emlékeztető: Biztonsági követelmények
MŰSZAKI MEGBÍZHATÓSÁGÁNAK VIZSGÁLATI MÓDSZEREI EXAMINATION METHODS FOR EVALUATING RELIABILITY IN COMPLEX MILITARY RECONNAISSANCE SYSTEMS.
 BÁRKÁNYI PÁL KOMPLEX KATONAI FELDERÍTŐ RENDSZEREK MŰSZAKI MEGBÍZHATÓSÁGÁNAK VIZSGÁLATI MÓDSZEREI EXAMINATION METHODS FOR EVALUATING RELIABILITY IN COMPLEX MILITARY RECONNAISSANCE SYSTEMS A cikk a komplex
BÁRKÁNYI PÁL KOMPLEX KATONAI FELDERÍTŐ RENDSZEREK MŰSZAKI MEGBÍZHATÓSÁGÁNAK VIZSGÁLATI MÓDSZEREI EXAMINATION METHODS FOR EVALUATING RELIABILITY IN COMPLEX MILITARY RECONNAISSANCE SYSTEMS A cikk a komplex
Szoftver karbantartás
 Szoftver karbantartás Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/~majzik/ Áttekintés Követelményspecifikálás Architektúra
Szoftver karbantartás Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/~majzik/ Áttekintés Követelményspecifikálás Architektúra
SZOLGÁLTATÁS BIZTOSÍTÁS
 6. óra SZOLGÁLTATÁS BIZTOSÍTÁS Tárgy: Szolgáltatás menedzsment Kód: NIRSM1MMEM Kredit: 5 Szak: Mérnök Informatikus MSc (esti) Óraszám: Előadás: 2/hét Laborgyakorlat: 2/hét Számonkérés: Vizsga, (félévi
6. óra SZOLGÁLTATÁS BIZTOSÍTÁS Tárgy: Szolgáltatás menedzsment Kód: NIRSM1MMEM Kredit: 5 Szak: Mérnök Informatikus MSc (esti) Óraszám: Előadás: 2/hét Laborgyakorlat: 2/hét Számonkérés: Vizsga, (félévi
Kecskeméti Fıiskola GAMF Kar Informatika Tanszék. Johanyák Zsolt Csaba
 Kecskeméti Fıiskola GAMF Kar Informatika Tanszék Johanyák Zsolt Csaba 003 Tartalomjegyzék. Bevezetés.... A megbízhatóság fogalmai..... A termék idıtıl függı képességei...... Használhatóság /Üzemkészség/
Kecskeméti Fıiskola GAMF Kar Informatika Tanszék Johanyák Zsolt Csaba 003 Tartalomjegyzék. Bevezetés.... A megbízhatóság fogalmai..... A termék idıtıl függı képességei...... Használhatóság /Üzemkészség/
Fejlesztés kockázati alapokon
 Fejlesztés kockázati alapokon Az IEC61508 és az IEC61511 Szabó Géza Szabo.geza@mail.bme.hu 1 A blokk célja Áttekintő kép a 61508-ról és a 61511-ről, A filozófia megismertetése, Nem cél a követelmények
Fejlesztés kockázati alapokon Az IEC61508 és az IEC61511 Szabó Géza Szabo.geza@mail.bme.hu 1 A blokk célja Áttekintő kép a 61508-ról és a 61511-ről, A filozófia megismertetése, Nem cél a követelmények
Szoftverminőségbiztosítás
 NGB_IN003_1 SZE 2017-18/2 (4) Szoftverminőségbiztosítás Biztonság kritikus szoftverek Hibatűrés Szoftver-diverzitás Biztonság, biztonságosság Mentesség azoktól a feltételektől, melyek halált, sérülést,
NGB_IN003_1 SZE 2017-18/2 (4) Szoftverminőségbiztosítás Biztonság kritikus szoftverek Hibatűrés Szoftver-diverzitás Biztonság, biztonságosság Mentesség azoktól a feltételektől, melyek halált, sérülést,
1002D STRUKTÚRÁJÚ, KRITIKUS ÜZEMBIZTONSÁGÚ RENDSZER (SCS 1 ) ELEMZÉSE DISZKRÉT-DISZKRÉT MARKOV MODELLEL
 Dr. Forgon Miklós mk. ezredes ZMNE olyai János Katonai Műszaki Kar Katonai Elektronikai Tanszék forgon.miklos@zmne.hu Neszveda József főiskolai docens, irányítástechnikai szakmérnök MF Kandó Villamosmérnöki
Dr. Forgon Miklós mk. ezredes ZMNE olyai János Katonai Műszaki Kar Katonai Elektronikai Tanszék forgon.miklos@zmne.hu Neszveda József főiskolai docens, irányítástechnikai szakmérnök MF Kandó Villamosmérnöki
biztonságkritikus rendszerek
 Kockázat, biztonság, biztonságkritikus rendszerek Dr. Sághi Balázs BME Közlekedés- és Járműirányítási Tanszék Tartalom A közlekedéssel szembeni elvárások A kockázat fogalma Kockázatcsökkentés Követelmények
Kockázat, biztonság, biztonságkritikus rendszerek Dr. Sághi Balázs BME Közlekedés- és Járműirányítási Tanszék Tartalom A közlekedéssel szembeni elvárások A kockázat fogalma Kockázatcsökkentés Követelmények
A kockázatelemzés menete
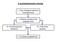 A kockázatelemzés menete 1. Üzem (folyamat) jellemzői Veszélyforrások 2. Baleseti sorok meghatározása 3a. Következmények felmérése 3b. Gyakoriság becslése 4. Kockázat meghatározás Balesetek Gyakoriság
A kockázatelemzés menete 1. Üzem (folyamat) jellemzői Veszélyforrások 2. Baleseti sorok meghatározása 3a. Következmények felmérése 3b. Gyakoriság becslése 4. Kockázat meghatározás Balesetek Gyakoriság
Veszély analízis. Rendszertervezés és -integráció előadás dr. Majzik István
 Veszély analízis Rendszertervezés és -integráció előadás dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT Célkitűzések BME-MIT 2.
Veszély analízis Rendszertervezés és -integráció előadás dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék BME-MIT Célkitűzések BME-MIT 2.
SÚLYOS BALESETEK ELEMZÉSE. 3. téma: Kvalitatív módszerek - Hibafa
 Az oktatási anyag a szerzők szellemi terméke. Az anyag kizárólag a 2014.01.22-23 23-i OKF Továbbképzés céljaira használható. Sokszorosítás, utánközlés és mindennemű egyéb felhasználás a szerzők engedélyéhez
Az oktatási anyag a szerzők szellemi terméke. Az anyag kizárólag a 2014.01.22-23 23-i OKF Továbbképzés céljaira használható. Sokszorosítás, utánközlés és mindennemű egyéb felhasználás a szerzők engedélyéhez
Alapvető karbantartási stratégiák
 Alapvető karbantartási stratégiák MBA képzés 2009 Erdei János 4. Tervszerű karbantartás teljesítőképess pesség 00% Teljesítm tménytartalék-diagram kiesési si ciklikus állapotfüggő teljesítménymaradék t
Alapvető karbantartási stratégiák MBA képzés 2009 Erdei János 4. Tervszerű karbantartás teljesítőképess pesség 00% Teljesítm tménytartalék-diagram kiesési si ciklikus állapotfüggő teljesítménymaradék t
Autóipari beágyazott rendszerek. Funkcionális biztonságossági koncepció
 Autóipari beágyazott rendszerek Funkcionális biztonságossági koncepció 1 Funkcionális biztonsági koncepció Functional safety concept Cél A funkcionális biztonsági követelmények levezetése A biztonsági
Autóipari beágyazott rendszerek Funkcionális biztonságossági koncepció 1 Funkcionális biztonsági koncepció Functional safety concept Cél A funkcionális biztonsági követelmények levezetése A biztonsági
Kedvenc rejtvényeim Mit tudok és mit hiszek el?
 Kedvenc rejtvényeim Mit tudok és mit hiszek el? Mottó A matematikus azt old meg, amit tud A mérnök azt old meg, amit kell Ebből következik, hogy Nem tudunk minden részletében tökéleteset csinálni Sok mindent
Kedvenc rejtvényeim Mit tudok és mit hiszek el? Mottó A matematikus azt old meg, amit tud A mérnök azt old meg, amit kell Ebből következik, hogy Nem tudunk minden részletében tökéleteset csinálni Sok mindent
PCS100 UPS-I Ipari felhasználási célú UPS
 DMPC LV Power Conditioning, 09/2015 PCS100 UPS-I Ipari felhasználási célú UPS 2UCD120000E028 rev A September 25, 2015 Slide 1 PCS100 UPS-I, Ipari felhasználási célú UPS A létesítményét tápláló energiaellátás
DMPC LV Power Conditioning, 09/2015 PCS100 UPS-I Ipari felhasználási célú UPS 2UCD120000E028 rev A September 25, 2015 Slide 1 PCS100 UPS-I, Ipari felhasználási célú UPS A létesítményét tápláló energiaellátás
Hálózatba kapcsolt adatbázisok. Erős Levente, TMIT eros@tmit.bme.hu 2011.
 Hálózatba kapcsolt adatbázisok Magas rendelkezésreállás Erős Levente, TMIT eros@tmit.bme.hu 2011. Tartalom Mi az, hogy rendelkezésreállás? Miért fontos? Hogyan mérjük? Mitől sérül? Védelmi szintek Rendelkezésreállási
Hálózatba kapcsolt adatbázisok Magas rendelkezésreállás Erős Levente, TMIT eros@tmit.bme.hu 2011. Tartalom Mi az, hogy rendelkezésreállás? Miért fontos? Hogyan mérjük? Mitől sérül? Védelmi szintek Rendelkezésreállási
62. MEE Vándorgyűlés, Síófok 2015 Szetember Csernoch Viktor, ABB Components. Vacuum Tap-Changers Minősítése
 62. MEE Vándorgyűlés, Síófok 2015 Szetember Csernoch Viktor, ABB Components Vacuum Tap-Changers Minősítése Tartalomjegyzék Fokozatkapcsoló design Technológiai áttekintés Áttétel váltás folyamata Tipikus
62. MEE Vándorgyűlés, Síófok 2015 Szetember Csernoch Viktor, ABB Components Vacuum Tap-Changers Minősítése Tartalomjegyzék Fokozatkapcsoló design Technológiai áttekintés Áttétel váltás folyamata Tipikus
Szoftverminőségbiztosítás
 NGB_IN003_1 SZE 2017-18/2 (9) Szoftverminőségbiztosítás Specifikáció alapú (black-box) technikák A szoftver mint leképezés Szoftverhiba Hibát okozó bement Hibás kimenet Input Szoftver Output Funkcionális
NGB_IN003_1 SZE 2017-18/2 (9) Szoftverminőségbiztosítás Specifikáció alapú (black-box) technikák A szoftver mint leképezés Szoftverhiba Hibát okozó bement Hibás kimenet Input Szoftver Output Funkcionális
Elemzési módszerek. Egyes módszerek ágazat-specifikusak, mások teljesen általánosan használatosak. A leggyakoribb veszélyelemző módszerek:
 Elemzési módszerek Egyes módszerek ágazat-specifikusak, mások teljesen általánosan használatosak. A leggyakoribb veszélyelemző módszerek: Hibamód és -hatás elemzés - failure modes and effects analysis
Elemzési módszerek Egyes módszerek ágazat-specifikusak, mások teljesen általánosan használatosak. A leggyakoribb veszélyelemző módszerek: Hibamód és -hatás elemzés - failure modes and effects analysis
Rendszermodellezés. Hibamodellezés (dr. Majzik István és Micskei Zoltán fóliái alapján) Fault Tolerant Systems Research Group
 Rendszermodellezés Hibamodellezés (dr. Majzik István és Micskei Zoltán fóliái alapján) Budapest University of Technology and Economics Fault Tolerant Systems Research Group Budapest University of Technology
Rendszermodellezés Hibamodellezés (dr. Majzik István és Micskei Zoltán fóliái alapján) Budapest University of Technology and Economics Fault Tolerant Systems Research Group Budapest University of Technology
2. gyakorlat RENDSZEREK MEGBÍZHATÓSÁGA: SOROS RENDSZEREK, REDUNDANCIA. Összeállította: Farkas Balázs
 2. gyakorlat RENDSZEREK MEGBÍZHATÓSÁGA: SOROS RENDSZEREK, REDUNDANCIA Összeállította: Farkas Balázs BEVEZETÉS RENDSZERTULAJDONSÁGOK Egy rendszer megbízhatósága függ: elemeinek megbízhatóságától és az elemek
2. gyakorlat RENDSZEREK MEGBÍZHATÓSÁGA: SOROS RENDSZEREK, REDUNDANCIA Összeállította: Farkas Balázs BEVEZETÉS RENDSZERTULAJDONSÁGOK Egy rendszer megbízhatósága függ: elemeinek megbízhatóságától és az elemek
Túlélés analízis. Probléma:
 1 Probléma: Túlélés analízis - Túlélési idő vizsgálata speciális vizsgálati módszereket igényel (pl. két csoport között az idők átlagait nem lehet direkt módon összehasonlítani) - A túlélési idő nem normális
1 Probléma: Túlélés analízis - Túlélési idő vizsgálata speciális vizsgálati módszereket igényel (pl. két csoport között az idők átlagait nem lehet direkt módon összehasonlítani) - A túlélési idő nem normális
Kockázat alapú karbantartás kialakítása a TPM rendszerben
 Kockázat alapú karbantartás kialakítása a TPM rendszerben Előadásanyag Összeállította: Fekete Gábor A.A. Stádium Kft. 6723 Szeged, József Attila sgt. 130. Tel.: 62/431-927 aastadium@aastadium.hu www.aastadium.hu
Kockázat alapú karbantartás kialakítása a TPM rendszerben Előadásanyag Összeállította: Fekete Gábor A.A. Stádium Kft. 6723 Szeged, József Attila sgt. 130. Tel.: 62/431-927 aastadium@aastadium.hu www.aastadium.hu
Biomatematika 2 Orvosi biometria
 Biomatematika 2 Orvosi biometria 2017.02.13. Populáció és minta jellemző adatai Hibaszámítás Valószínűség 1 Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza)
Biomatematika 2 Orvosi biometria 2017.02.13. Populáció és minta jellemző adatai Hibaszámítás Valószínűség 1 Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza)
Biztonságkritikus rendszerek
 Biztonságkritikus rendszerek Biztonságkritikusnak nevezzük azon rendszereket, melyek hibás működése jelentős anyagi kárt okoz, vagy emberek testi épségét, életét veszélyezteti. Autóipari rendszerek esetében
Biztonságkritikus rendszerek Biztonságkritikusnak nevezzük azon rendszereket, melyek hibás működése jelentős anyagi kárt okoz, vagy emberek testi épségét, életét veszélyezteti. Autóipari rendszerek esetében
Közlekedési automatika Biztonsági architektúrák
 Közlekedési automatika Biztonsági architektúrák Dr. Sághi Balázs diasora alapján összeállította, kiegészítette: Lövétei István Ferenc BME Közlekedés- és Járműirányítási Tanszék 2019 Tartalomjegyzék Bevezetés
Közlekedési automatika Biztonsági architektúrák Dr. Sághi Balázs diasora alapján összeállította, kiegészítette: Lövétei István Ferenc BME Közlekedés- és Járműirányítási Tanszék 2019 Tartalomjegyzék Bevezetés
Kritikus Beágyazott Rendszerek
 Kritikus Beágyazott Rendszerek Megbízhatósági modellezés Gyakorlat Készítette: Vörös András Utolsó módosítás: 015-09- Verzió: 1.0 Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs
Kritikus Beágyazott Rendszerek Megbízhatósági modellezés Gyakorlat Készítette: Vörös András Utolsó módosítás: 015-09- Verzió: 1.0 Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs
Folyamatmodellezés és eszközei. Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék
 Folyamatmodellezés és eszközei Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Folyamat, munkafolyamat Munkafolyamat (Workflow): azoknak a lépéseknek a sorozata,
Folyamatmodellezés és eszközei Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Folyamat, munkafolyamat Munkafolyamat (Workflow): azoknak a lépéseknek a sorozata,
Kihívások és tendenciák a vasúti járművek karbantartásával kapcsolatban
 Kihívások és tendenciák a vasúti járművek karbantartásával kapcsolatban Dr. Csiba József igazgató, MÁV Zrt. Vasúti Mérnöki és Mérésügyi Szolg. Központ Kiss Csaba fejlesztőmérnök, Vasúti Mérnöki és Mérésügyi
Kihívások és tendenciák a vasúti járművek karbantartásával kapcsolatban Dr. Csiba József igazgató, MÁV Zrt. Vasúti Mérnöki és Mérésügyi Szolg. Központ Kiss Csaba fejlesztőmérnök, Vasúti Mérnöki és Mérésügyi
LOGIT-REGRESSZIÓ a függő változó: névleges vagy sorrendi skála
 LOGIT-REGRESSZIÓ a függő változó: névleges vagy sorrendi skála a független változó: névleges vagy sorrendi vagy folytonos skála BIOMETRIA2_NEMPARAMÉTERES_5 1 Y: visszafizeti-e a hitelt x: fizetés (életkor)
LOGIT-REGRESSZIÓ a függő változó: névleges vagy sorrendi skála a független változó: névleges vagy sorrendi vagy folytonos skála BIOMETRIA2_NEMPARAMÉTERES_5 1 Y: visszafizeti-e a hitelt x: fizetés (életkor)
Diagnosztika Petri háló modellek felhasználásával
 Diagnosztika - Ea9. p. 1/2 Modell Alapú Diagnosztika Diszkrét Módszerekkel Diagnosztika Petri háló modellek felhasználásával Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék Diagnosztika
Diagnosztika - Ea9. p. 1/2 Modell Alapú Diagnosztika Diszkrét Módszerekkel Diagnosztika Petri háló modellek felhasználásával Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék Diagnosztika
Valószínűségi változók. Várható érték és szórás
 Matematikai statisztika gyakorlat Valószínűségi változók. Várható érték és szórás Valószínűségi változók 2016. március 7-11. 1 / 13 Valószínűségi változók Legyen a (Ω, A, P) valószínűségi mező. Egy X :
Matematikai statisztika gyakorlat Valószínűségi változók. Várható érték és szórás Valószínűségi változók 2016. március 7-11. 1 / 13 Valószínűségi változók Legyen a (Ω, A, P) valószínűségi mező. Egy X :
Architektúra tervek ellenőrzése
 Szoftverellenőrzési technikák Architektúra tervek ellenőrzése Majzik István http://www.inf.mit.bme.hu/ 1 Tartalomjegyzék Motiváció Mit határoz meg az architektúra? Milyen vizsgálati módszerek vannak? Követhetőség
Szoftverellenőrzési technikák Architektúra tervek ellenőrzése Majzik István http://www.inf.mit.bme.hu/ 1 Tartalomjegyzék Motiváció Mit határoz meg az architektúra? Milyen vizsgálati módszerek vannak? Követhetőség
Fejlesztés kockázati alapokon 2.
 Fejlesztés kockázati alapokon 2. Az IEC61508 és az IEC61511 Szabó Géza Szabo.geza@mail.bme.hu 1 A blokk célja Áttekintő kép a 61508-ról és a 61511-ről, A filozófia megismertetése, Nem cél a követelmények
Fejlesztés kockázati alapokon 2. Az IEC61508 és az IEC61511 Szabó Géza Szabo.geza@mail.bme.hu 1 A blokk célja Áttekintő kép a 61508-ról és a 61511-ről, A filozófia megismertetése, Nem cél a követelmények
A kockázat fogalma. A kockázat fogalma. Fejezetek a környezeti kockázatok menedzsmentjéből 2 Bezegh András
 Fejezetek a környezeti kockázatok menedzsmentjéből 2 Bezegh András A kockázat fogalma A kockázat (def:) annak kifejezése, hogy valami nem kívánt hatással lesz a valaki/k értékeire, célkitűzésekre. A kockázat
Fejezetek a környezeti kockázatok menedzsmentjéből 2 Bezegh András A kockázat fogalma A kockázat (def:) annak kifejezése, hogy valami nem kívánt hatással lesz a valaki/k értékeire, célkitűzésekre. A kockázat
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 3 III. VÉLETLEN VEKTOROK 1. A KÉTDIMENZIÓs VÉLETLEN VEKTOR Definíció: Az leképezést (kétdimenziós) véletlen vektornak nevezzük, ha Definíció:
Valószínűségi modellellenőrzés Markov döntési folyamatokkal
 Valószínűségi modellellenőrzés Markov döntési folyamatokkal Hajdu Ákos Szoftver verifikáció és validáció 2015.12.09. Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek
Valószínűségi modellellenőrzés Markov döntési folyamatokkal Hajdu Ákos Szoftver verifikáció és validáció 2015.12.09. Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek
R-KORD Kft Präsentation LED.pptx - Fordította: Nikli Barbara
 1 2 izzószálas lámpa hosszútávon már nem áll rendelkezésre a világítástechnikában jelentkező műszaki innovációt a vasúton is követni kell (élettartam, alacsonyabb energiaszükséglet, rezgésállóság) 3 L1
1 2 izzószálas lámpa hosszútávon már nem áll rendelkezésre a világítástechnikában jelentkező műszaki innovációt a vasúton is követni kell (élettartam, alacsonyabb energiaszükséglet, rezgésállóság) 3 L1
Modellezés és szimuláció a tervezésben
 Modellezés és szimuláció a tervezésben Szimuláció: egy másik rendszerrel - amely bizonyos vonatkozásokban hasonló az eredeti rendszerhez - utánozzuk egy rendszer viselkedését, vagyis az eredeti rendszer
Modellezés és szimuláció a tervezésben Szimuláció: egy másik rendszerrel - amely bizonyos vonatkozásokban hasonló az eredeti rendszerhez - utánozzuk egy rendszer viselkedését, vagyis az eredeti rendszer
Valószínűségszámítás összefoglaló
 Statisztikai módszerek BMEGEVGAT Készítette: Halász Gábor Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
Statisztikai módszerek BMEGEVGAT Készítette: Halász Gábor Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Hidrodinamikai Rendszerek Tanszék, Budapest, Műegyetem rkp. 3. D ép. 334. Tel:
STATISZTIKA ELŐADÁS ÁTTEKINTÉSE. Matematikai statisztika. Mi a modell? Binomiális eloszlás sűrűségfüggvény. Binomiális eloszlás
 ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 9. Előadás Binomiális eloszlás Egyenletes eloszlás Háromszög eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell 2/62 Matematikai statisztika
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/47/23623719.jpg) [Biomatematika 2] Orvosi biometria 2016.02.15. Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza) alkotja az eseményteret. Esemény: az eseménytér részhalmazai.
[Biomatematika 2] Orvosi biometria 2016.02.15. Esemény Egy kísérlet vagy megfigyelés (vagy mérés) lehetséges eredményeinek összessége (halmaza) alkotja az eseményteret. Esemény: az eseménytér részhalmazai.
Megbízhatóságra alapozott program a berendezések értékelésére
 AZ ÜZEMFENNTARTÁS ÁLTALÁNOS KÉRDÉSEI 1.02 Megbízhatóságra alapozott program a berendezések értékelésére Tárgyszavak: megbízhatóság; MTBF; adatgyűjtés; hibaelemzés; állapotfelmérés; kőolajipar. A szénhidrogént
AZ ÜZEMFENNTARTÁS ÁLTALÁNOS KÉRDÉSEI 1.02 Megbízhatóságra alapozott program a berendezések értékelésére Tárgyszavak: megbízhatóság; MTBF; adatgyűjtés; hibaelemzés; állapotfelmérés; kőolajipar. A szénhidrogént
Szoftver karbantartási lépések ellenőrzése
 Szoftverellenőrzési technikák (vimim148) Szoftver karbantartási lépések ellenőrzése Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.inf.mit.bme.hu/
Szoftverellenőrzési technikák (vimim148) Szoftver karbantartási lépések ellenőrzése Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.inf.mit.bme.hu/
MUST 30-120. Három fázisú Moduláris UPS. A moduláris UPS előnyei már mindenki számára elérhetőek
 MUST 30-120 Három fázisú Moduláris UPS A moduláris UPS előnyei már mindenki számára elérhetőek MUST30-120 A MUST 30/120 termékcsalád egy szünetmentes áramellátó rendszer, három fázisú be- illetve kimenettel,
MUST 30-120 Három fázisú Moduláris UPS A moduláris UPS előnyei már mindenki számára elérhetőek MUST30-120 A MUST 30/120 termékcsalád egy szünetmentes áramellátó rendszer, három fázisú be- illetve kimenettel,
Biztonsági folyamatirányító. rendszerek szoftvere
 Biztonsági folyamatirányító rendszerek szoftvere 1 Biztonsági folyamatirányító rendszerek szoftvere Tartalom Szoftverek szerepe a folyamatirányító rendszerekben Szoftverek megbízhatósága Szoftver életciklus
Biztonsági folyamatirányító rendszerek szoftvere 1 Biztonsági folyamatirányító rendszerek szoftvere Tartalom Szoftverek szerepe a folyamatirányító rendszerekben Szoftverek megbízhatósága Szoftver életciklus
Dr. BALOGH ALBERT: MEGBÍZHATÓSÁGI ÉS KOCKÁZATKEZELÉSI SZAKKIFEJEZÉSEK FELÜLVIZSGÁLATÁNAK HELYZETE
 Dr. BALOGH ALBERT: MEGBÍZHATÓSÁGI ÉS KOCKÁZATKEZELÉSI SZAKKIFEJEZÉSEK FELÜLVIZSGÁLATÁNAK HELYZETE 1 Megbízhatósági terminológia: IEC 50(191):2007 változat (tervezet) Kockázatkezelő irányítási terminológia:
Dr. BALOGH ALBERT: MEGBÍZHATÓSÁGI ÉS KOCKÁZATKEZELÉSI SZAKKIFEJEZÉSEK FELÜLVIZSGÁLATÁNAK HELYZETE 1 Megbízhatósági terminológia: IEC 50(191):2007 változat (tervezet) Kockázatkezelő irányítási terminológia:
Használati alapú és modell alapú tesztelés kombinálása szolgáltatásorientált architektúrák teszteléséhez az ipari gyakorlatban
 Használati alapú és modell alapú tesztelés kombinálása szolgáltatásorientált architektúrák teszteléséhez az ipari gyakorlatban Nagy Attila Mátyás 2016.12.07. Áttekintés Bevezetés Megközelítés Pilot tanulmányok
Használati alapú és modell alapú tesztelés kombinálása szolgáltatásorientált architektúrák teszteléséhez az ipari gyakorlatban Nagy Attila Mátyás 2016.12.07. Áttekintés Bevezetés Megközelítés Pilot tanulmányok
ISO A bevezetés néhány gyakorlati lépése
 ISO 9001-2015 A bevezetés néhány gyakorlati lépése 115 30 20 Fö tevékenységünk: Felületkezelés Horganyzás, ZnNi, ZnFe bevonatok Folyamatalapú szabályozás SPC bevezetése FMEA bevezetése Elsődarabos folyamat
ISO 9001-2015 A bevezetés néhány gyakorlati lépése 115 30 20 Fö tevékenységünk: Felületkezelés Horganyzás, ZnNi, ZnFe bevonatok Folyamatalapú szabályozás SPC bevezetése FMEA bevezetése Elsődarabos folyamat
Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével
 Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével Pekárdy Milán, Baumgartner János, Süle Zoltán Pannon Egyetem, Veszprém XXXII. Magyar Operációkutatási
Ellátási lánc optimalizálás P-gráf módszertan alkalmazásával mennyiségi és min ségi paraméterek gyelembevételével Pekárdy Milán, Baumgartner János, Süle Zoltán Pannon Egyetem, Veszprém XXXII. Magyar Operációkutatási
STATISZTIKA ELŐADÁS ÁTTEKINTÉSE. Mi a modell? Matematikai statisztika. 300 dobás. sűrűségfüggvénye. Egyenletes eloszlás
 ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 7. Előadás Egyenletes eloszlás Binomiális eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell /56 Matematikai statisztika Reprezentatív mintavétel
ELŐADÁS ÁTTEKINTÉSE STATISZTIKA 7. Előadás Egyenletes eloszlás Binomiális eloszlás Normális eloszlás Standard normális eloszlás Normális eloszlás mint modell /56 Matematikai statisztika Reprezentatív mintavétel
Zárthelyi mintapéldák. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék
 Zárthelyi mintapéldák Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Elméleti kérdések Indokolja meg, hogy az A (X Stop F Start) kifejezés szintaktikailag helyes kifejezés-e CTL illetve
Zárthelyi mintapéldák Majzik István BME Méréstechnika és Információs Rendszerek Tanszék Elméleti kérdések Indokolja meg, hogy az A (X Stop F Start) kifejezés szintaktikailag helyes kifejezés-e CTL illetve
Digitális jelfeldolgozás
 Digitális jelfeldolgozás Kvantálás Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2010. szeptember 15. Áttekintés
Digitális jelfeldolgozás Kvantálás Magyar Attila Pannon Egyetem Műszaki Informatikai Kar Villamosmérnöki és Információs Rendszerek Tanszék magyar.attila@virt.uni-pannon.hu 2010. szeptember 15. Áttekintés
Túlélés elemzés október 27.
 Túlélés elemzés 2017. október 27. Néhány példa Egy adott betegség diagnózisától kezdve mennyi ideje van hátra a páciensnek? Tipikusan mennyi ideig élhet túl? Bizonyos ráktípus esetén mennyi idő telik el
Túlélés elemzés 2017. október 27. Néhány példa Egy adott betegség diagnózisától kezdve mennyi ideje van hátra a páciensnek? Tipikusan mennyi ideig élhet túl? Bizonyos ráktípus esetén mennyi idő telik el
Szolgáltatásbiztos rendszerek: Architektúra tervezési példák
 Szolgáltatásbiztos rendszerek: Architektúra tervezési példák Majzik István majzik@mit.bme.hu Feladatátvételi fürtök (Failover clustering, High availability clustering) Hardver architektúra Egyszeres hibapont
Szolgáltatásbiztos rendszerek: Architektúra tervezési példák Majzik István majzik@mit.bme.hu Feladatátvételi fürtök (Failover clustering, High availability clustering) Hardver architektúra Egyszeres hibapont
Rendelkezésre állás modellek. Dr. Tapolcai János tapolcai@tmit.bme.hu http://opti.tmit.bme.hu/~tapolcai/
 Rendelkezésre állás odellek Dr. Tapolcai János tapolcai@tit.be.hu http://opti.tit.be.hu/~tapolcai/ 1 Hiba források hardware hibák Hálózati eszközök eghibásodása (hardware failures) Típushibák gyártás és
Rendelkezésre állás odellek Dr. Tapolcai János tapolcai@tit.be.hu http://opti.tit.be.hu/~tapolcai/ 1 Hiba források hardware hibák Hálózati eszközök eghibásodása (hardware failures) Típushibák gyártás és
Szolgáltatás mérés/riportolás magas fokon Egy valós megoldás Pepsi berkekben
 Szolgáltatás mérés/riportolás magas fokon Egy valós megoldás Pepsi berkekben Mérő Gábor PepsiAmericas Kft Technikai szolgáltatási Vezető Hajdú Miklós ICON Számítástechnikai Rt Alkalmazás- és Rendszerfelügyeleti
Szolgáltatás mérés/riportolás magas fokon Egy valós megoldás Pepsi berkekben Mérő Gábor PepsiAmericas Kft Technikai szolgáltatási Vezető Hajdú Miklós ICON Számítástechnikai Rt Alkalmazás- és Rendszerfelügyeleti
A statisztikai élettartam elemzés alkalmazása és korlátai a villamosenergia hálózat eszközgazdálkodásában
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék A statisztikai élettartam elemzés alkalmazása és korlátai a villamosenergia hálózat eszközgazdálkodásában Cselkó Richárd, Németh
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék A statisztikai élettartam elemzés alkalmazása és korlátai a villamosenergia hálózat eszközgazdálkodásában Cselkó Richárd, Németh
Folyamatmodellezés és eszközei. Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék
 Folyamatmodellezés és eszközei Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Folyamat, munkafolyamat Ez vajon egy állapotgép-e? Munkafolyamat (Workflow):
Folyamatmodellezés és eszközei Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Folyamat, munkafolyamat Ez vajon egy állapotgép-e? Munkafolyamat (Workflow):
Karbantartási filozófiák. a karbantartás szervezetére és a folyamat teljes végrehajtására vonatkozó alapelvek rendszere.
 Karbantartási filozófiák a karbantartás szervezetére és a folyamat teljes végrehajtására vonatkozó alapelvek rendszere. TPM Total Productive Maintanance Teljeskörű hatékony karbantartás, Termelésbe integrált
Karbantartási filozófiák a karbantartás szervezetére és a folyamat teljes végrehajtására vonatkozó alapelvek rendszere. TPM Total Productive Maintanance Teljeskörű hatékony karbantartás, Termelésbe integrált
The modular mitmót system. DPY kijelző kártya C API
 The modular mitmót system DPY kijelző kártya C API Dokumentációkód: -D 01.0.0.0 Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Beágyazott Információs Rendszerek
The modular mitmót system DPY kijelző kártya C API Dokumentációkód: -D 01.0.0.0 Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Beágyazott Információs Rendszerek
Alapszintű formalizmusok
 Alapszintű formalizmusok dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális tervek Informális követelmények Formális modell Formalizált követelmények
Alapszintű formalizmusok dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális tervek Informális követelmények Formális modell Formalizált követelmények
A megtervezés folyamata 1. Vázlatos kialakítás
 A megtervezés folyamata 1. Vázlatos kialakítás 1 / 15 A megtervezés folyamata 2. Részletes kialakítás 2 / 15 A megtervezés folyamata 3. Tökéletesítés és ellenőrzés 3 / 15 A kialakítás (megtervezés) folyamata
A megtervezés folyamata 1. Vázlatos kialakítás 1 / 15 A megtervezés folyamata 2. Részletes kialakítás 2 / 15 A megtervezés folyamata 3. Tökéletesítés és ellenőrzés 3 / 15 A kialakítás (megtervezés) folyamata
Gyártórendszerek irányítási struktúrái
 GyRDin-10 p. 1/2 Gyártórendszerek Dinamikája Gyártórendszerek irányítási struktúrái Hangos Katalin Villamosmérnöki és Információs Rendszerek Tanszék e-mail: hangos@scl.sztaki.hu GyRDin-10 p. 2/2 Tartalom
GyRDin-10 p. 1/2 Gyártórendszerek Dinamikája Gyártórendszerek irányítási struktúrái Hangos Katalin Villamosmérnöki és Információs Rendszerek Tanszék e-mail: hangos@scl.sztaki.hu GyRDin-10 p. 2/2 Tartalom
Szoftver újrafelhasználás
 Szoftver újrafelhasználás Szoftver újrafelhasználás Szoftver fejlesztésekor korábbi fejlesztésekkor létrehozott kód felhasználása architektúra felhasználása tudás felhasználása Nem azonos a portolással
Szoftver újrafelhasználás Szoftver újrafelhasználás Szoftver fejlesztésekor korábbi fejlesztésekkor létrehozott kód felhasználása architektúra felhasználása tudás felhasználása Nem azonos a portolással
Dr. Kalló Noémi. Termelés- és szolgáltatásmenedzsment. egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék. Dr.
 Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Ismertesse a legfontosabb előrejelzési módszereket és azok gyakorlati
Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Ismertesse a legfontosabb előrejelzési módszereket és azok gyakorlati
Közlekedési automatika Biztonságintegritás, életciklus modellek
 Közlekedési automatika Biztonságintegritás, életciklus modellek Dr. Sághi Balázs diasora alapján összeállította, kiegészítette: Lövétei István Ferenc BME Közlekedés- és Járműirányítási Tanszék 2019 Tartalomjegyzék
Közlekedési automatika Biztonságintegritás, életciklus modellek Dr. Sághi Balázs diasora alapján összeállította, kiegészítette: Lövétei István Ferenc BME Közlekedés- és Járműirányítási Tanszék 2019 Tartalomjegyzék
Sztochasztikus Petri-hálók
 Sztochasztikus Petri-hálók Teljesítmény és megbízhatóság modellezés dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Áttekintés Motiváció Sztochasztikus folyamatok és modellek Folytonos
Sztochasztikus Petri-hálók Teljesítmény és megbízhatóság modellezés dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Áttekintés Motiváció Sztochasztikus folyamatok és modellek Folytonos
Biostatisztika VIII. Mátyus László. 19 October
 Biostatisztika VIII Mátyus László 19 October 2010 1 Ha σ nem ismert A gyakorlatban ritkán ismerjük σ-t. Ha kiszámítjuk s-t a minta alapján, akkor becsülhetjük σ-t. Ez további bizonytalanságot okoz a becslésben.
Biostatisztika VIII Mátyus László 19 October 2010 1 Ha σ nem ismert A gyakorlatban ritkán ismerjük σ-t. Ha kiszámítjuk s-t a minta alapján, akkor becsülhetjük σ-t. Ez további bizonytalanságot okoz a becslésben.
Tantárgy: TELJESÍTMÉNYELEKTRONIKA Tanár: Dr. Burány Nándor Tanársegéd: Mr. Divéki Szabolcs 3. FEJEZET
 Tantárgy: TELJESÍTMÉNYELEKTRONIKA Tanár: Dr. Burány Nándor Tanársegéd: Mr. Divéki Szabolcs 5. félév Óraszám: 2+2 1 3. FEJEZET TÁPEGYSÉGEK A tápegységek építése, üzemeltetése és karbantartása a teljesítményelektronika
Tantárgy: TELJESÍTMÉNYELEKTRONIKA Tanár: Dr. Burány Nándor Tanársegéd: Mr. Divéki Szabolcs 5. félév Óraszám: 2+2 1 3. FEJEZET TÁPEGYSÉGEK A tápegységek építése, üzemeltetése és karbantartása a teljesítményelektronika
Hibatűrés. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék
 Hibatűrés Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/ 1 Hibatűrés különféle hibák esetén Hardver tervezési hibák
Hibatűrés Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék http://www.mit.bme.hu/ 1 Hibatűrés különféle hibák esetén Hardver tervezési hibák
Spotlámpák Mélysugárzók Lineáris lámpa Térvilágítók Padló fali lámpák Szabadonsugárzók Dekor. lámpák Csarnokvilágítók
 T LED Tconverter Spotlámpák Mélysugárzók Lineáris lámpa Térvilágítók Padló fali lámpák Szabadonsugárzók Dekor. lámpák Csarnokvilágítók 1 www.tridonic.com Tconverter Okos lépés A szituáció tökéletes. Akármilyen
T LED Tconverter Spotlámpák Mélysugárzók Lineáris lámpa Térvilágítók Padló fali lámpák Szabadonsugárzók Dekor. lámpák Csarnokvilágítók 1 www.tridonic.com Tconverter Okos lépés A szituáció tökéletes. Akármilyen
Architektúra tervek ellenőrzése
 Szoftverellenőrzési technikák Architektúra tervek ellenőrzése Majzik István http://www.inf.mit.bme.hu/ 1 Tartalomjegyzék Motiváció Mit határoz meg az architektúra? Milyen vizsgálati módszerek vannak? Követhetőség
Szoftverellenőrzési technikák Architektúra tervek ellenőrzése Majzik István http://www.inf.mit.bme.hu/ 1 Tartalomjegyzék Motiváció Mit határoz meg az architektúra? Milyen vizsgálati módszerek vannak? Követhetőség
Mi az adat? Az adat elemi ismeret. Az adatokból információkat
 Mi az adat? Az adat elemi ismeret. Tények, fogalmak olyan megjelenési formája, amely alkalmas emberi eszközökkel történő értelmezésre, feldolgozásra, továbbításra. Az adatokból gondolkodás vagy gépi feldolgozás
Mi az adat? Az adat elemi ismeret. Tények, fogalmak olyan megjelenési formája, amely alkalmas emberi eszközökkel történő értelmezésre, feldolgozásra, továbbításra. Az adatokból gondolkodás vagy gépi feldolgozás
Az ellátási láncok algoritmikus szintézise
 Az ellátási láncok algoritmikus szintézise Bertók Botond, Adonyi Róbert, Kovács Zoltán, Friedler Ferenc Pannon Egyetem Műszaki Informatikai Kar XXVII. Magyar Operációkutatási Konferencia 2007. június 7.
Az ellátási láncok algoritmikus szintézise Bertók Botond, Adonyi Róbert, Kovács Zoltán, Friedler Ferenc Pannon Egyetem Műszaki Informatikai Kar XXVII. Magyar Operációkutatási Konferencia 2007. június 7.
Java-ról Kotlinra. Ekler Péter AutSoft BME AUT. AutSoft
 Java-ról Kotlinra Ekler Péter peter.ekler@aut.bme.hu BME AUT Tartalom Java és Kotlin kapcsolata Hogyan próbálhatjuk ki? Kotlin kultúra kialakítása cégen belül Milyen a Kotlin a Java-hoz képest? Történet
Java-ról Kotlinra Ekler Péter peter.ekler@aut.bme.hu BME AUT Tartalom Java és Kotlin kapcsolata Hogyan próbálhatjuk ki? Kotlin kultúra kialakítása cégen belül Milyen a Kotlin a Java-hoz képest? Történet
