SZEMCSÉS ANYAGOK TERMÉSZETES BOLTOZÓDÁSA
|
|
|
- Gábor Róbert Orbán
- 9 évvel ezelőtt
- Látták:
Átírás
1 Szent István Egyetem SZEMCSÉS ANYAGOK TERMÉSZETES BOLTOZÓDÁSA Doktori (Ph.D.) értekezés Keppler István Gödöllő 2006.
2 Adoktoriiskola megnevezése: tudományága: vezetője: Témavezető: Műszaki Tudományi Doktori Iskola Agrárműszaki Tudomány Dr. Szendrő Péter egyetemi tanár, az MTA doktora Szent István Egyetem, Gépészmérnöki Kar Mechanikai és Géptani Intézet Gödöllő Dr.M.CsizmadiaBéla egyetemi tanár, a műszaki tudomány kandidátusa Szent István Egyetem, Gépészmérnöki Kar Mechanikai és Géptani Intézet Gödöllő Az iskolavezető jóváhagyása A témavezető jóváhagyása
3 Tartalom BEVEZETÉS 1 1. IRODALMI ÁTTEKINTÉS Szemcsés halmazok kontinuum modellje Anyag- és tönkremeneteli jellemzők Anyagjellemzők Tönkremeneteli jellemzők Nyírási tönkremenetel Tönkremenetel kéttengelyű feszültségállapotban Feszültségviszonyok szemcsés halmazokban Feszültségek asilóban Janssenmodellje Enstad modellje Csizmadiamodellje Feszültségek agaratban Jenikemodellje Enstad modellje Feszültségek amodellsilóban Boltozódás Jenike modellje Enstad modellje Drescher kísérletivizsgálatai I
4 TARTALOM Onoés Yamadamodellje KÍSÉRLETI VIZSGÁLATOK Anyagjellemzőkmérése Anyag és tönkremeneteli jellemzők mérőeszközei. 48 Nyírókészülék Valódi triaxiális berendezés Anyag- és tönkremeneteli jellemzőkmérése Anyagállandók meghatározása Nyírási tönkremenetel vizsgálata Tönkremenetel kéttengelyű feszültségállapotban A boltozódásifolyamatkísérletivizsgálata Boltozódásvizsgáló berendezés Boltozat kialakulás és tönkremenetel A TERMÉSZETES BOLTOZÓDÁS MODELLJE Boltozódás lapos fenekű tartályokban Atermészetes boltozatkialakulása A természetes boltozat összeomlása Boltozódási algoritmus Boltozódásgaratban ÖSSZEFOGLALÁS A kutatási tevékenység összefoglalása Új tudományos eredmények SUMMARY Summary of the research activity Newscientificresults IRODALOM 111 II
5 Ábrák jegyzéke 1.1. Rugalmas test egy kontinuumelemmel Nyírási tönkremenetel a Δy vastagságú szelet egyensúlya Janssen szerint Csizmadiasilómodellje a dy vastagságú szelet egyensúlya a garatban, Jenike szerint Egy anyagréteg egyensúlya a garatban, Enstad szerint Drescher modellsilójánakméretei Feszültségek amodellsilóban Boltozat agaratban Folyásifaktorértékei Tönkremeneteli határgörbék gipsz esetén Ono és Yamadaboltozódásimodellje Az A és R tartományokpereme Nyíródoboz vázlata Nyíródoboz mechanikai modellje Csúsztatófeszültség eloszlás a nyíródoboz középvonalában A valódi triaxiális berendezés vázlata Triaxiálisvizsgálat Gipsz por látszólagos rugalmassági modulusának függése a por tömörödésétől Gipsz por Poisson tényezőjének függése a por tömörödésétől. 56 III
6 ÁBRÁK JEGYZÉKE % nedvességtartalmúhomokcsúsztatófeszültség elmozdulásdiagramja Belső súrlódás és kohézió mérése nyíródobozzal Kéttengelyű feszültségállapothoz tartozó tönkremeneteli határgörbefelvétele % nedvességtartalmú homok kéttengelyű feszültségállapothoz tartozó tönkremeneteli határfeszültségének mérése Kéttengelyű feszültségállapothoz tartozó tönkremeneteli határfeszültségmérése % nedvességtartalmú homok kéttengelyű feszültségállapothoztartozóhatárfeszültsége Boltozódásvizsgáló berendezés Különböző kifolyónyílás méretekhez tartozó természetes boltozatokalakja Fényképfelvételek a boltozat létrejöttéről és tönkremeneteléről mm-es kiömlőnyílásnál megjelenő első stabil boltozat alakja mm-es kiömlőnyíláshoz tartozó boltozat alakja Modellsiló rajza Fajlagos első főfeszültség a modellsiló nyitott kiömlőnyílásafelett A kéttengelyű feszültségállapothoz tartozó kritikus nyomófeszültség és a főfeszültségek viszonya A hidrosztatikus feszültséggel osztott harmadik főfeszültségek eloszlása a boltív mentén, talpponttól a tetőpontig A boltozat tönkremenetelét előidéző repedések a talppont környezetéből indulnak A nyírókészülékben elhelyezett anyagmintára ható erők munkája Természetes boltozat kialakulása lapos fenekű tartályban Silómodellgarattal IV
7 ÁBRÁK JEGYZÉKE 3.9. Fajlagos feszültségek a modellsiló szimmetriatengelyében zárt ésnyitottkifolyónyílásesetén Fajlagos harmadik főfeszültségek a modellsiló kifolyónyílásánál Fajlagos harmadik főfeszültségek a modellsiló fala mentén, nyitottkifolyónyílásnál Az előtömörítő feszültség és a garatban mért minimális feszültség hányadosa a kifolyónyílás-méret függvényében A feszültséghányados értékek és a tönkrementeli határgörbeviszonyagipszesetén A garat falánál számított maximális és minimális fajlagos alakváltozási energiasűrűség Kritikuskifolyónyílásmért ésszámítottértékei A feszültséghányados értékének kapcsolata a töltet és silófal közötti súrlódási tényezővel A feszültséghányados értékének kapcsolata a töltet látszólagos rugalmassági modulusával A feszültséghányados értékének kapcsolata a töltet Poissontényezőjével A töltetmagasság növelésének hatása a szemcsés halmaz boltozódási tulajdonságaira V
8 VI
9 JELÖLÉSEK a állandó A állandó A alakváltozási tenzor A I alakváltozási tenzor első skalárinvariánsa b állandó B siló szélessége c kohézió C konstans c 0 a siló oldalfalának merevsége C rugalmas együtthatók tenzora d állandó D k kritikus nyílásméret E rugalmassági modulus e állandó F állandó F F folyási függvény f f folyási faktor F I feszültségi tenzor első skalárinvariánsa F K kéttengelyű feszültségállapotban az anyagmintára felvihető maximális terhelő erő F max háromtengelyű feszültségállapothoz tartozó maximális terhelő erő F feszültségi tenzor G csúsztató rugalmassági modulus g nehézségi gyorsulás H a siló magassága h a garat magassága K Janssen konstans VII
10 JELÖLÉSEK K 0 nyugalmi talajnyomás tényező K 1 konstans Janssen modelljében m konstans σ y számításához, téglatest alakú silóra m =1, hengeres silóra m =2 n felületelem normálvektora N konstans Jenike modelljében p 0 felületelemre ható külső erő q állandó q kontinuumelemre ható térfogati erő r távolság a garat csúcsától R távolság a garat csúcsától a garat tetőpontjáig s a siló oldalfala mentén mért távolság T a szemcsés anyaggal kitöltött tartomány u fajlagos alakváltozási energia u K kritikus energiasűrűség u elmozdulásvektor X konstans Enstad modelljében X b konstans Enstad modelljében Y konstans Enstad modelljében Y b konstans Enstad modelljében α garat félkúpszöge α K kritikus félkúpszög γ fajsúly γ = ρg ζ a boltozat középvonala és a garat falának normálvektora által közrezárt szög κ konstans K számításához, aktív állapotban κ=1, passzív állapotban κ =2 λ konstans, K számításához μ silófal és szemcsehalmaz közötti súrlódási együttható ν Poisson tényező ρ sűrűség τ nm csúsztatófeszültség az n normálvektorú felületelemen, m irányban σ 1 legnagyobb főfeszültség σ 1,a legnagyobb főfeszültség a garat fala mellett σ 3 legkisebb főfeszültség σ K kéttengelyű feszültségállapothoz tartozó tönkremeneteli határfeszültség VIII
11 σ +min az összetömörített anyag által szakadás nélkül elviselt húzófeszültség értéke σ n n irányú normálfeszültség σ t σ K meghatározása során alkalmazott előtömörítő feszültség φ belső súrlódási szög φ w silófal szemcsehalmaz súrlódási félkúpszög Φ feszültségfüggvény ω konstans közötti IX
12 X
13 BEVEZETÉS Amezőgazdaság, az élelmiszeripar, a gyógyszeripar, valamint az építészet területén dolgozó mérnökök gyakran találkoznak a szemcsés anyaghalmazok különleges mechanikai tulajdonságaiból eredő problémákkal. Szemcsés anyaghalmazok bizonyos körülmények között szilárd anyagokhoz hasonlóan viselkednek. Teherviselésre képesek, megőrzik alakjukat. Más körülmények között ugyanaz a szemcsehalmaz, amely korábban szilárd testként volt modellezhető, folyadékhoz hasonló tulajdonságokat mutat. Silóban tárolhatjuk, amelyből gravitációs ürítéssel eltávolíthatjuk. Bizonyos feltételek teljesülése esetén ugyanez a halmaz ismét szilárd testként kezd viselkedni, képessé válik a felette lévő anyagtömeg súlyából adódó terhelések elviselésére, a tárolóból történőkiáramlásamegszűnik, mivel a nyílás felett boltozat jön létre. Aműszaki élet sok területén felvetődő jelentős probléma a szemcsés halmazok természetes boltozódása. 1. definíció. Természetes boltozódásnak nevezi a szakirodalom azt a jelenséget, amely során a szemcsés halmazban a terhelések hatására kialakul egy anyagréteg, amely képes a felette lévő anyagtömeg súlyából eredőterhelések elviselésére. Dolgozatomban megmutatom, hogy a természetes boltozódás jelenségét helyesebb a teljes szemcsehalmazra vonatkozó egyensúlyi állapotként kezelnünk, ezért a későbbiekben megadom a természetes boltozódás egy új definícióját. 1
14 BEVEZETÉS Bizonyos esetekben a szerkezeteket úgy kell kialakítani, hogy a boltozat ne jöjjön létre. A természetes boltozat megjelenése ugyanis egyrészt akadályozza a szemcsés anyaghalmazok áramlását (pl. a tároló kiürítését), másrészt a boltozatok megjelenése jelentős mértékben módosítjaa halmazbeli feszültségviszonyokat. A feszültségviszonyok módosulása pedig a tároló falának többletterhelését, esetleg a tároló károsodását, tönkremenetelét okozhatja. Más esetekben a kialakuló természetes boltozat teherhordó szerkezetként vehető figyelembe, azaz itt a viszonyokat úgy célszerű kialakítani, hogy a boltozat létrejöjjön. Ilyen esetekkel a bányászatban valamint föld alatti építmények (alagutak, csővezetékek) terhelésviszonyainak vizsgálata során találkozhatunk. A szemcsés anyagok mechanikájának területén végzett elméleti vizsgálatok olyan erőteljes közelítéseket és elhanyagolásokat hordoznak magukban, hogy az ezekből származó becslések és a mérési eredmények között jelentős az eltérés 1. Jelen munka célja a szemcsés anyaghalmazok természetes boltozódásának olyan új modelljét létrehozni, amelynek felhasználásával a jelenséggel kapcsolatos előrejelzéseink, becsléseink a mérésekkel meghatározható értékekhez közelebb álló eredményekre vezetnek. Ennek elérése érdekében: I. Dolgozatomban bemutatom a szemcsés halmazok kontinuum modelljében felhasznált anyag- és tönkremeneteli jellemzőket. II. Összefoglalom a szemcsés halmazokban kialakuló feszültségviszonyok, valamint a természetes boltozódás jelenségének modellezésével kapcsolatos eddigi eredményeket. III. Bemutatom a szemcsés halmazok anyagtulajdonságainakvalaminta boltozódás jelenségének vizsgálatára szolgáló kísérleti módszereket. 1 Például silóknál a boltozódás szempontjából kritikus nyílásméret elméleti úton becsült, és mérésekkel meghatározott értéke között az eltérés gyakran a kétszeres értéket is meghaladja [9]. 2
15 IV. Bemutatom az általam létrehozott új boltozódásvizsgáló berendezést valamint a triaxiális berendezésen általam végzett módosításokat. V. A boltozódással kapcsolatos kísérleti vizsgálataim alapján bevezetek egy új boltozat kialakulási és tönkremeneteli modellt. VI. Bemutatomaboltozatkialakulás és tönkremenetel numerikusszimulációjában az új modell felhasználásával elért eredményeimet. 3
16 4
17 1. IRODALMI ÁTTEKINTÉS Szemcsés anyaghalmazokkal kapcsolatos vizsgálatok során a mechanikai modell megválasztása jelenti a legnehezebb feladatot. Bármennyire is időnként úgy viselkednek a szemcsés halmazok, mint a folyékony halmazállapotú anyagok, bizonyos tulajdonságaik modellezésére a folyadékmechanika nem alkalmas. Ugyanez igaz a szilárd testek mechanikájának műszaki gyakorlatban megszokott módszereire is. A későbbiekben látni fogjuk, hogy a szilárd testek mechanikájának megszokott eszközein túlmutató további meggondolásokat kell alkalmaznunk egyes jelenségek leírására Szemcsés halmazok kontinuum modellje A szakirodalmi források az anyagmodell alapján két fő csoportra oszthatók. Túlnyomó többségük a klasszikus kontinuummechanika eszközrendszerét alkalmazva folytatja vizsgálatait. Másik kisebb részük az egyes szemcsék mozgásegyenleteit felírva, a szemcsék közötti kölcsönhatásokat leírva próbálja modellezni a szemcsehalmaz viselkedését. Ez az úgynevezett diszkrét elemes modell manapság egyre több kutatásban teret nyer, eredményei azonban jelenleg néhány alapvető jelenség szimulációjára korlátozódnak. Nemzetközi szinten is kiemelkedő eredményeket ért el ezen a területen Bagi [4]. Az irodalmi források különösen [34] alapján véleményem szerint a diszkrét elemes módszer jelenlegi állapotában nem alkalmas a természetes 5
18 1. IRODALMI ÁTTEKINTÉS boltozódás folyamatának általános vizsgálatára. Amennyiben a műszaki gyakorlat számára könnyen alkalmazható, ismert fogalmakon alapuló eljárást kívánunk kifejleszteni, célszerű a klasszikus kontinuum modell alkalmazása. Dolgozatomban én is ezt az utat kívánom követni. Kontinuum modell alkalmazása esetén a halmaz szerkezetére semmilyen feltevést nem teszünk, hanem annak sajátságait mérésekkel meghatározott anyagi állandók segítségével jellemezzük. Feltételezzük, hogy a szemcsés halmaz folytonosan tölti ki a rendelkezésére álló térfogatot 1.A szemcsehalmazra jellemző mechanikai mennyiségeket folytonos függvények segítségével adjuk meg. A halmaz állapotának leírására is folytonos függvényeket alkalmazunk, az állapotváltozást pedig differenciálegyenletek alakjában írjuk fel. z dv da n p 0 f A p x y A u 1.1. ábra. Rugalmas test egy kontinuumelemmel. A kontinuumelemre ható térfogati erő f, egy felületelemre ható külsőerő p 0. A legegyszerűbb és a boltozódással foglalkozó szakirodalmi forrá- 1 Ez a kikötés maga után vonja, hogy a kontinuumelemek méretét legalább olyan nagynak kell feltételeznünk, hogy a halmaz finomszerkezetének hatásai kiátlagolódjanak, és legfeljebb akkorának, hogy a differenciálegyenletek felírása során végrehajtott határátmenetek még elfogadható közelítését jelentsék a valóságban lejátszódó jelenségeknek. 6
19 1.1. SZEMCSÉS HALMAZOK KONTINUUM MODELLJE sok által leggyakrabban használt modell a homogén, izotróp, lineárisan rugalmas anyagmodell. Az így modellezett szemcsehalmaz állapotát az F (x, y, z) feszültségi tenzormező, az A(x, y, z) alakváltozási tenzormező és az u(x, y, z) elmozdulási vektormező határozza meg. Szilárd testek rugalmas deformációjának lineáris közelítésben történő modellezése esetén a test bármely pontjában a feszültségi és az alakváltozási tenzormező közötti kapcsolatot legáltalánosabb formában egy negyedrendű tenzor, C segítségével írhatjuk fel. C összetevői a test rugalmas együtthatói, értékük elméletileg a test minden egyes pontjában, minden időpillanatban más és más lehet. A szemcsehalmaz mechanikai állapotára jellemző mennyiségek kapcsolatát és a kontinuum környezetével való kölcsönhatását a rugalmasságtani egyenletek és azok peremfeltételei írják le (1.1. ábra): F +f = 0, (1.1) 1 (u + u) 2 = A, (1.2) C A = F, (1.3) u Au = u 0, (1.4) F n Ap = p 0. (1.5) A fenti egyenletrendszer analitikus úton történő egzakt megoldása a gyakorlati problémák túlnyomó többségénél és a mi esetünkben is reménytelen feladat. Alagutak környezetében kialakuló feszültségviszonyok analitikus úton történő tárgyalása során [31] komplex változók alkalmazásával kialakított módszere alkalmazható a legnagyobb hatékonysággal. Ennek a módszernek is erősen korlátozott azonban az alkalmazhatósága. [46] jelentős eredményeket ért el ezen a területen. Természetes boltozatok vizsgálata során azonban nem ismert a boltozat alakja, így a komplex változós módszer sem alkalmazható erre az esetre. A gyakorlatban közelítő megoldásokat keresünk numerikus módsze- 7
20 1. IRODALMI ÁTTEKINTÉS rekkel. Különösen a végeselem módszer ad kiválóan használható numerikus eljárást, amelyet a későbbiekben fel is fogunk használni a boltozódási jelenség vizsgálatára Anyag- és tönkremeneteli jellemzők A szemcsés halmazok kontinuum modelljében az anyagegyenletek teremtenek kapcsolatot a feszültségi tenzormező F (x, y, z) és az alakváltozási tenzormező A(x, y, z) között. Az (1.3) összefüggésben jelennek meg azok a mennyiségek, amelyek a test anyagától függő tulajdonságokat kifejezik, ezeket szokás anyagjellemzőnek nevezni. A testek anyagától függő tulajdonságokat háromféleképpen határozhatjuk meg [41]: deduktív módon, elméleti megfontolások alapján, induktív úton, elsősorban kísérletekre támaszkodva, reológiai modellek segítségével. Dolgozatomban a szemcsés anyagok mechanikai viselkedésének leírásához szükséges anyagjellemzőket kísérleti úton kívánom meghatározni. A tönkremenetelt a gépészmérnöki gyakorlatban úgy definiáljuk, mint a szerkezet valamely méretének egy megengedett értéket meghaladó változását. Egy szemcsés anyaghalmaz tönkremenetele jóval bonyolultabb folyamat, mint egy acél próbatest maradó alakváltozása. Maga a tönkremenetel fogalmasem olyan egyértelmű ilyen anyagok esetén, mint a műszaki gyakorlatban általában használt anyagoknál. 2. definíció. Szemcsés anyaghalmaz tönkremenetelének nevezem azt a jelenséget, amely során a halmaz anyagjellemzői olyan mértékben megváltoznak (esetenként értelmezhetetlenné válnak), hogy ennek következtében ahalmazmechanikai viselkedése jelentős mértékben módosul. 8
21 1.2. ANYAG- ÉS TÖNKREMENETELI JELLEMZŐK 3. definíció. Tönkremeneteli jellemzőnek nevezem azokat a mennyiségeket, melyek a szemcsés halmaz tönkremeneteli tulajdonságait egyértelműen meghatározzák. A szemcsehalmazok tönkremeneteli tulajdonságait ugyancsak kísérletekre támaszkodva vizsgálom Anyagjellemzők Homogén, izotróp, lineárisan rugalmas szilárd test esetén a C negyedrendű tenzor helyett elég két független rugalmas együtthatót például a ν Poisson tényezőt és a G csúsztató rugalmassági modulust alkalmaznunk [32]. Ekkor a feszültségi és alakváltozási tenzormező kapcsolatát kifejező egyenlet az általános Hooke-törvényre egyszerűsödik: A = 1 ( F ν ) 2G 1+ν F IE, vagy megfordítva (1.6) ( F = 2G A+ ν ) 1 2ν A IE. (1.7) ahol F I a feszültségi tenzor-, A I pedig az alakváltozási tenzor első skalárinvariánsa. A G csúsztató rugalmassági modulus és az E rugalmassági modulus közötti kapcsolatot az ismert G = E összefüggés fejezi ki. 2(1+ν) Az általános Hooke-törvényben szereplő, a szemcsés halmazra jellemző ν Poisson tényező ésg csúsztató rugalmassági modulus méréséről a későbbiekben lesz szó. A lineárisan rugalmas anyagmodell a lehető legegyszerűbb, a műszaki mechanika más területein sikerrel alkalmazott közelítés. A természetes boltozódás vizsgálatával foglalkozó kutatók döntő többsége is lineárisan rugalmas, homogén, izotróp anyagmodellt alkalmaz. 9
22 1. IRODALMI ÁTTEKINTÉS Tönkremeneteli jellemzők A gépészmérnöki gyakorlatban ahol az esetek döntő többségében acélvagy ahhoz hasonló mechanikai tulajdonságú anyagokkal találkozunk a tönkremenetel fogalmát a legtöbbször úgy definiálják, mint a szerkezet valamely méretének egy megengedett értéket meghaladó változását. A vizsgált anyagokból megfelelő gondossággal kiválasztott próbatestek szakítóvizsgálatával meghatározott kritikus feszültségek és a valódi terhelésbőladódó esetlegtöbbtengelyűigénybevételekáltal létrehozott terhelések között pedig a redukált feszültség fogalmának alkalmazásával teremtenek kapcsolatot. A szakítóvizsgálatból nyert kritikus feszültség és az anyagra megengedhető maximális redukált feszültség összehasonlítására tönkremeneteli kritériumokat alkalmaznak. Ezek közül a legegyszerűbb a Mohr féle hipotézis, amely a feszültségállapotra jellemző Mohr körök és az ún. tönkremeneteli határgörbék között vizsgál egyszerű geometriai kapcsolatokat. A Mohr féle kritériumnál léteznek jóval több fizikai alapot tartalmazó (pl. torzítási munkák azonosságát vizsgáló) tönkremeneteli kritériumok is. Az egyes törési elméletek között a végeredményt tekintve a legtöbb esetben nem túl nagy az eltérés, ezért gyakran megelégednek a Mohr féle törési elmélet felhasználásával kapott eredményekkel. A szemcsés anyaghalmazok tönkremenetele azonban az előbbinél sokkal összetettebb folyamat. Nyírási tönkremenetel 4. definíció. A szemcsehalmaz egy elemi tartományában akkor következik be nyírási tönkremenetel, ha található a tartományon átmenő olyan n normálisú sík, amelyiken a nyírófeszültségek túllépik a σ n normálfeszültség értékének egy meghatározott hányadát (Mohr Coulomb-féle tönkremeneteli kritérium): τ nm σ n tan φ, (1.8) 10
23 1.2. ANYAG- ÉS TÖNKREMENETELI JELLEMZŐK ahol φ a halmaz belső súrlódási szöge. Amennyiben a szemcsehalmazon belüli c kohézió is létezik, az előbbi összefüggés módosul: τ nm σ n tan φ+c. (1.9) Tönkremeneteli határgörbe τ c φ σ 3 σ 2 σ 1 σ Mohr kör 1.2. ábra. Nyírási tönkremenetel. A nyírási tönkremenetelhez tartozó Mohr-körök burkológörbéjét tönkremeneteli határgörbének nevezzük. Az 1.2. ábrán vázolt tönkremeneteli határgörbe linearitása természetesen csak közelítés. Ennek a közelítésnek a jóságát méréseinknek kell eldönteniük, mint ahogy a tönkremeneteli határgörbe φ és c paramétereinek meghatározása is mérések útján történik. Tönkremenetel kéttengelyű feszültségállapotban Szemcsés anyagok tönkremeneteli tulajdonságai nem csak tömörítő erőktől, hanem a feszültségállapottól is függenek. Szemcsés anyaghalmazok 11
24 1. IRODALMI ÁTTEKINTÉS kéttengelyű feszültségállapotban a háromtengelyűhöz tartozó értéknél csak jóval kisebb nyomófeszültséget képesek elviselni. 5. definíció. Kéttengelyű feszültségállapothoz tartozó tönkremenetelről beszélünk abban az esetben, amikor a kéttengelyű feszültségállapotban levő anyaghalmaz a rá ható terhelések következtében elveszíti terhelhetőségét. Kéttengelyű feszültségállapothoz tartozó határfeszültségnek nevezzük azt a nyomófeszültséget, amelynek hatására a kéttengelyű feszültségállapotban levő anyaghalmaz elveszíti terhelhetőségét A természetes boltozatok szabad felületének környezetében a szemcsés anyag kéttengelyű feszültségállapotban van. Szükséges tehát, hogy a kéttengelyű feszültségállapothoz tartozó tönkremeneteli jellemzőket meghatározzuk, és a boltozódási folyamat során a boltív peremének mechanikai tulajdonságait a kéttengelyű feszültségállapot figyelembevételével vizsgáljuk. * Az itt felsorolt anyag- és tönkremeneteli jellemzőket mérésekkel kell meghatároznunk. A mérőeszközöket, mérési módszereket, valamint mérési eredményeimet a későbbiekben ismertetem Feszültségviszonyok szemcsés halmazokban A természetes boltozódás jelenségének vizsgálatához elengedhetetlenül fontos a szemcsés anyaghalmazokban kialakuló feszültségviszonyok tisztázása. A feszültségviszonyok pontos ismerete nélkül nem adható becslés a természetes boltozatok várható alakjára, a boltozatban kialakuló feszültségviszonyokra, a boltozat által átívelhető maximális nyílásméretre. A feszültségviszonyok nyomonkövetésére szolgáló elsődleges információ forrásunk a feszültségek mérések útján történő meghatározása lehetne. Silónyomás méréssel sok szerző foglalkozott Janssen cikkének megjelenése óta [18]. A méréssel kapcsolatban néhány probléma napjainkig sem 12
25 1.3. FESZÜLTSÉGVISZONYOK SZEMCSÉS HALMAZOKBAN került megoldásra. Stroppel [40] foglalkozik a silónyomás mérésnek azzal az érdekes problémájával, hogy a silófalhoz rögzített nyomásmérő érzékelő elmozdulásának igen kis értéke is jelentősen befolyásolja a mért nyomásértéket. [45] a kísérleti eredmények és a silónyomás modellek összehasonlítását kísérli meg. Sajnálatos módon a szemcsehalmazbeli feszültségviszonyok mérésére jelenleg nem áll a kutatók rendelkezésére kellő pontosságú eredményeket szolgáltató eszköz. Nagy feszültség (nyomás) értékek mérése többékevésbé elfogadható pontossággal megoldható a halmazba helyezett különféle nyomás érzékelők segítségével. Ezek az érzékelők azonban egyrészt jelentős mértékben módosíthatják a környezetükben kialakult nyomásviszonyokat, másrészt elsősorban a szemcsés anyaghalmazok belső súrlódásának következtében sokszor jelentős hibával terhelten működnek. A szemcsehalmazbeli feszültségviszonyok mérésére optikai feszültség analízist is felhasználhatunk [1]. A szemcsés halmaznak optikailag érzékeny anyagszemcsékből kell állnia, és a szemcsék közötti részt olajjal kell kitölteni. A szemcsék közötti olaj miatt a boltozódás vizsgálatokhoz használt nyitott kifolyónyílású tartályban elhelyezett anyaghalmaz feszültségviszonyainak optikai úton történő vizsgálata nem kivitelezhető. Egyedül természetes boltozattal átívelhetőkritikusnyílásméret meghatározására van lehetőségünk, és minden, a továbbiakban következő feltételezés helyességét csupán ennek a mennyiségnek a mérésével dönthetjük el Feszültségek a silóban Janssen modellje Az ideális folyadékokkal ellentétben a szemcsés anyaghalmazok képesek nyírófeszültségekfelvételére. A falsúrlódás miatt a töltet tömegét részben a 13
26 1. IRODALMI ÁTTEKINTÉS siló fala hordozza, ezért a függőleges feszültségösszetevő értéke nem lineárisan növekszik a mélység függvényében. Ennek a változásnak a jellegét Janssen vizsgálta elsőként. A XIX. század végén alkotta meg Janssen a silókban kialakuló nyomásviszonyokat leíró differenciálegyenletét [18]. Annak ellenére, hogy az elmúlt több, mint száz év alatt az elmélet jónéhány hiányosságára rámutattak a témával foglakozó kutatók, az Európai Únió szabványgyűjteményében (EUROCODE 1, Part IV.: Actions in silos and tanks) megfogalmazottak tulajdonképpen Janssen 1895-ben elért eredményeinek alkalmazásai [49]. 6. definíció. Janssen féle feltételek: I. A szemcsés anyag homogén, izotróp lineárisan rugalmas kontinuumként modellezhető, II. a terhelés az anyag önsúlyából származik, III. a szemcsehalmaz megcsúszása a fal mellett következik be, IV. a függőleges (σ y ) feszültség értéke egy adott magasságban állandó (1.3. ábra), V. a σx σ y hányados az y mentén állandó, VI. az anyaghalmaz sík-alakváltozási állapotban van, VII. a silófal végtelen merevségű, VIII. E és ν a feszültségviszonyokra nincs hatással, IX. a halmazban kijelölt Δy magasságú töltetrész merev testként mozog a silóban. 14
27 1.3. FESZÜLTSÉGVISZONYOK SZEMCSÉS HALMAZOKBAN 1. tétel. A Janssen féle feltételek teljesülése esetén a silóban tárolt szemcsés halmazban kialakuló σ y függőleges feszültségek meghatározhatók a σ y = Bρg 2K összefüggés segítségével [18]. x (1 e 2K B y ) (1.10) σ y σ x τ xy Δy σ x τ xy σ y +Δσ y ρg y B 1.3. ábra. a Δy vastagságú szelet egyensúlya Janssen szerint. Bizonyítás. Az 1.3. ábrán vázolt, z irányban egységnyi méretű szelet egyensúlyát kifejező egyenlet: Bσ y B(σ y +Δσ y )+BρgΔy 2Δyτ xy =0. (1.11) BΔy-nal végigosztva, elvégezve a Δy 0 határátmenetet, majd egyszerűsítve a dσ y dy +2τ xy ρg =0 (1.12) B 15
28 1. IRODALMI ÁTTEKINTÉS differenciálegyenlet adódik. Mivel τ xy = μσ x = μk 1 σ x (a III. és az V. feltételt felhasználva), ezért írható, hogy τ xy = Kσ y, (1.13) ezzel dσ y dy +2K B σ y ρg =0. (1.14) A differenciálegyenlet megoldása: σ y = Bρg 2K (1 e 2K B y ). (1.15) 7. definíció. Az előbbi bizonyításban szereplő, σ x és σ y közötti kapcsolatot kifejező K állandót a szakirodalom Janssen konstansnak nevezi. A Janssen kontans kezelése nem egységes az irodalomban. Néhány szerző ugyanis a K 1 = K értéket nevezi Janssen konstansnak. μ Janssen modelljét [47] és [9] is finomította. Módszereik és eredményeik a lényeget tekintve nem sokban különböznek az előzőekben leírtaktól. Felírható a silónyomásmagasságtólfüggő változására egy általánosabb összefüggés is, mely hengeres silóra is alkalmazható [43]: σ y = Bρg ( ) 1 e m2k B y, (1.16) m2k ahol m =1adja az előbbiekben tárgyalt esetet, m =2pedig a hengeres silóra vonatkozó megoldást. 16
29 1.3. FESZÜLTSÉGVISZONYOK SZEMCSÉS HALMAZOKBAN Enstad modellje [10] a párhuzamos falú részben található szemcsés anyaghalmazban kialakuló feszültségállapot modellezésére a [18]-ben leírt módszert használja. Ezt azonban kiegészíti azzal, hogy meghatározza a K konstans értékét, bizonyos feltételezések mellett. Amennyiben a szemcsés anyag a silófal mentén mindenütt megcsúszási határhelyzetben van, akkor a Janssen konstans [10] szerint a K = 1+sinφ cos 2λ 1 sin φ cos 2λ (1.17) összefüggéssel számítható, ahol λ = 1 2 (φ w +ω), (1.18) sin ω = sin φ w sin φ. (1.19) A szemcsehalmazban ébredő függőleges (y) irányú feszültségek pedig meghatározhatók az (1.10) Janssen-féle egyenlettel. 8. definíció. Aktív Rankine féle állapotnak nevezzük azt az esetet, amikor a szemcsés anyaghalmaz minden pontjában a csúszás határállapotában van [23]. 9. definíció. Passzív állapotról beszélünk abban az esetben, amikor a szemcsés halmaz képes a rá ható erőkkel szemben ellenállás kifejtésére. [9] szerint a Janssen egyenletben szereplő K konstans értéke a siló függőleges falakkal határolt tartományában: K = 1 κ sin φ 1+κ sin φ tan φ w, (1.20) 17
30 1. IRODALMI ÁTTEKINTÉS a kúpos szakaszon pedig K = 1 κ sin φ cos 2φ w 1+κ sin φ Itt κ =1aktív, κ = 1 passzív feszültségi állapot esetén. tan φ w. (1.21) Csizmadia modellje Önsúlyával terhelt, függőleges falak közé helyezett szemcsés anyaghalmazban kialakuló feszültségek meghatározásának általánosabb módszerét vizsgálja [8]. 10. definíció. Csizmadia féle feltételek: I. A szemcsehalmaz homogén, izotróp kontinuum. II. A terhelés csak az anyaghalmaz önsúlyából származik. III. Az anyagtulajdonságok lineáris függvénnyel modellezhetők. IV. A halmaz belső súrlódása és kohéziója valamint a fal és a szemcsehalmaz közötti súrlódás nem hagyható figyelmen kívül. V. A silófal megtámasztása rugalmas (C felület) (1.4. ábra). VI. A szemcsehalmaz a fal mellett csúszási határhelyzetben van. VII. A siló alján nincs súrlódás (D felület). VIII. A halmaz síkalakváltozási állapotban van. IX. A felső részen σ y = állandó (B felület). 18
31 1.3. FESZÜLTSÉGVISZONYOK SZEMCSÉS HALMAZOKBAN B z B A C H D y 1.4. ábra. Csizmadia silómodellje. 1. állítás. A Csizmadia féle feltételek teljesülése esetén a modellsilóban kialakuló feszültségviszonyok leírhatók egy Φ(y, z) feszültségfüggvény segítségével, melyre: σ y = 2 Φ z 2 ; σ z = 2 Φ y 2 +ρgz; τ yz = 2 Φ y z, (1.22) σ x = ν(σ y +σ z ). (1.23) 4 Φ y +2 4 Φ 4 y 2 z + 4 Φ =0. (1.24) 2 z4 Csizmadia a silóban kialakuló feszültségviszonyok vizsgálatát a (1.24) biharmonikus egyenlet megoldására vezette vissza. A peremfeltételekre és 19
32 1. IRODALMI ÁTTEKINTÉS megoldási módszerekre részletesebben itt nem térek ki [8]. A biharmonikus egyenlet megoldásáta szerző a véges differenciák módszerével kereste. Csizmadia modelljét használva lehetőség nyílik a siló oldalfal merevségének figyelembevételére, amely [25] szerint a betonénál rugalmasabb (pl. acéllemez) oldalfalú silók esetén nagy fontossággal bír Feszültségek a garatban Jenike modellje [19] vizsgálataihoz a garatban található szemcsés anyagot a függőleges falakkal határolt résznél alkalmazottakhoz hasonlóan vízszintes síkokkal bontotta szeletekre, és egy ilyen szelet egyensúlyának vizsgálatával vezette le a feszültségeloszlást meghatározó differenciálegyenletet. 2. tétel. A Janssen féle feltételek teljesülése esetén a σ y = ρgy 1+N +Cy N (1.25) összefüggés adja a garat középvonalában, függőleges irányban kialakuló feszültségeloszlást [19]. Bizonyítás. A 1.5. ábrán vázolt szelet egyensúlyát kifejező egyenlet: 2y tan ασ y 2(y+dy)(σ y +dσ y )tanα+2dy(σ n tan α+τ n ) 2yρgdy tan α=0. (1.26) Az egyenletet rendezve és a másodrendűen kicsiny mennyiségeket elhanyagolva a dσ y dy + 1 ( σ y σ n y τ ) n +ρg =0 (1.27) tan α differenciálegyenlet adódik. Helyettesítve τ n = K σ y és σ n = K tan φ w σ y értékeket Jenike a dσ y dy +N σ y +ρg =0 (1.28) y 20
33 1.3. FESZÜLTSÉGVISZONYOK SZEMCSÉS HALMAZOKBAN y σ y +dσ y σ n dy σ n τ n τ n σ y ρg y α x O 1.5. ábra. a dy vastagságú szelet egyensúlya a garatban, Jenike szerint. differenciálegyenletet kapja, ahol N =1 K (ctgφ w + ctgα). Ennek általános megoldása σ y = ρgy 1+N +Cy N. (1.29) 21
34 1. IRODALMI ÁTTEKINTÉS K szerepe hasonlít a K konstanséhoz, azonban K K. 11. definíció. Átmeneti tartománynak nevezem függőleges falakkal határolt rész és a garat találkozásának környezetét. C meghatározásához a függőleges és a kúpos rész közötti átmenet tartományában ismerni kell σ y értékét. A feszültségfüggvény azonban az átmeneti tartományban nem folytonos a mérések szerint [44]. A differenciálegyenlet megoldását vizsgálva Jenike megállapítja, hogy a kúpos rész bemeneti oldalán ébredő feszültségek nagysága nincs nagy hatással a kifolyónyílás környezetében keletkező feszültségekre. Végeselem módszerrel végzett számításaim szerint Jenike előbbi feltételezése nem állja meg a helyét. Vizsgálataim során azt tapasztaltam, hogy az átmeneti tartományban kialakult feszültségviszonyok kismértékű megváltozása is komoly hatással van a talppontban számított feszültségek értékére. Amennyiben csak a kúp csúcsának környezetében kialakuló feszültségviszonyokat vizsgáljuk, akkor a C =0feltételt alkalmazhatjuk. Ezzel a σ y = ρg 1+N y (1.30) összefüggést nyerjük a garat középvonalában keletkező feszültségekre. 12. definíció. Radiális megoldásnak nevezi a szakirodalom a összefüggéssel nyert feszültségeloszlást 2. σ y = ρg 1+N y (1.31) 2 Esetenként a megoldás tényleges alakja kismértékben eltér a definícióban szereplőtől, de a linearitás, és a monoton csökkenés (!) minden esetben megmarad 22
35 1.3. FESZÜLTSÉGVISZONYOK SZEMCSÉS HALMAZOKBAN A σ y feszültség ismeretében meghatározható a másik két feszültség: τ n = ρgk y, 1+N (1.32) ρgk σ n = y. (1+N)tanφ w (1.33) Enstad modellje A garatban kialakuló feszültségviszonyok vizsgálatához Enstad az alábbi feltételezésekkel él [10]. 13. definíció. Enstad féle feltételek: I. A szemcsés anyag a függőlegesfalakkal határolt tartománybanaktív feszültségállapotban van. II. A garatban található anyaghalmaz passzív feszültségállapotban van. III. Az azonos feszültségállapotban lévő anyagrészek a garatban olyan tartományokban helyezkednek el, amelynek határait a szimmetriatengelyen elhelyezkedő középpontú, excentrikus körök alkotják. IV. Anagyobb főfeszültség az előbbi körívekérintőjének irányában hat. 3. tétel. Az Enstad féle feltételek teljesülése esetén a garat középvonalában kialakuló feszültségviszonyokat a σ(r)= ρgy r ( X 1 + σ(r) ρgy R ) ( r ) X (1.34) X 1 R egyenlet írja le. 23
36 1. IRODALMI ÁTTEKINTÉS Bizonyítás. Az 1.6. ábrán látható szelet egyensúlyánakvizsgálatából (Enstad jelöléseivel) a következő differenciálegyenlet adódik: r dσ Xσ = ρgy r. (1.35) dr Az állítás bizonyítása a fenti differenciálegyenlet megoldásával történik. Ennek részleteire itt nem térek ki, lásd [10]. Enstad szerint passzív feszültségállapot esetén X = sin φ ( 1+ sin (2β ) p +α), 1 sin φ sin α (1.36) Y = sin α (β p +α)+sinβ p sin (β p +α) (1 sin φ)sin 2, (β p +α) (1.37) míg aktív feszültségállapotban a a differenciálegyenletben szereplő konstansok meghatározásának módja: X = sin φ ( ) sin (2βa +α) 1, (1.38) 1+sinφ sin α Y = sin α ( ) β a +α π +cosβa cos (β 2 a +α). (1.39) (1+sin φ)cos 2 (β a +α) Aktív feszültségállapot a garatban csak akkor jöhet létre [10], ha α π 2 β a. (1.40) Az (1.34) egyenletet megvizsgálva láthatjuk, hogy mivel X egy körülbelül 10 nagyságrendű szám az egyenlet első tagja fog dominálni a garat csúcsánál, a kifolyónyílás közelében. Ez azt jelenti, hogy ebben a tartományban a feszültségek értéke Enstad szerint is r-rel arányos, ugyanúgy, mint ahogyan azt Jenike modelljénél is tapasztaltuk. 24
37 1.3. FESZÜLTSÉGVISZONYOK SZEMCSÉS HALMAZOKBAN y σ 2 (r +Δr) ΔF β σ 2 (r +Δr) α β σ 1 σ 2 (r) β ρg dr 1 ΔF 2 r α x 1.6. ábra. Egy anyagréteg egyensúlya a garatban, Enstad szerint. O Enstad módszere tehát gyakorlati szemszögbőlnem ad számunkra többet, mint Jenike modellje, hiszen a természetes boltozat környezetében 25
38 1. IRODALMI ÁTTEKINTÉS mindkét gondolatmenet lineáris feszültségeloszlást (az úgynevezett radiális feszültségmezőt) eredményez. A radiális feszültségmező alkalmazásánál mindkét szerző abból a hibás feltételezésből indul ki, hogy a radiális feszültségmező hipotézis zárt kiömlőnyílás esetén is érvényes. Ha végeselem módszerrel megvizsgáljuk a silóban kialakult feszültségviszonyokat, akkor láthatjuk, hogy a radiális feszültségmező csak nyitott kiömlőnyílásnál jelentkezik (3.9. ábra) Feszültségek a modellsilóban A [9] által boltozódási vizsgálatokra alkalmazott modellsiló adatait felhasználva meghatároztam (Janssen módszerével) a silóban függőleges irányban keletkező feszültségeket. Janssen szerint σ y = Bρg 2K (1 e 2K B y ). (1.41) A garatbeli feszültségviszonyokat pedig a Jenike által levezetett σ y = ρg 1+N y (1.42) egyenlet segítségével határoztam meg. A modellsiló (1.7. ábra) geometriai adatai: H =1.7m magas, a garat magassága h =0.7m, a siló szélessége B =1.3m, a garat félkúpszöge α = =40. A töltet anyaga gipsz, melynek fajsúlya γ=12.85 kn, a falsúrlódási szög m 3 φ w =38.2,belső súrlódása φ =54.1. Az (1.41) összefüggésben szerepel a K tényező, melynek meghatározása [9] szerint a K = 1 κ sin φ 1+κ sin φ tan φ w (1.43) 26
39 1.3. FESZÜLTSÉGVISZONYOK SZEMCSÉS HALMAZOKBAN s B H α h D y 1.7. ábra. Drescher modellsilójának méretei. egyenlettel határozható meg. Tételezzük fel, hogy esetünkben κ =1eset aktív állapot valósul meg, ezért K értéke: K = 1 sin sin54.1 tan 38.2 =0.08. (1.44) K -t felhasználva meghatározhatjuk a függőleges irányban feltételezett σ y feszültségeloszlást (1.41) felhasználásával: σ y = ( 1 e 0.12y). (1.45) Az így számolt feszültségeloszlás látható a 1.8. ábrán. Láthatjuk, hogy ez exponenciális tag hatása ilyen kis (y =1m) mélységben még nem számottevő. Természetesen nagy silómagasság esetén az eltérés a hidrosztatikus megoldástól igen jelentős lehet [39]. 27
40 1. IRODALMI ÁTTEKINTÉS σ y ρgh 1 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0 σ y = Bρg 2K (1 e 2KB y ) 0 0,2 0,4 0,6 0,8 1 y [m] 1.8. ábra. Feszültségek a modellsilóban. Szaggatott vonallal a hidrosztatikus modellhez tartozó feszültség értékeket rajzoltam meg. A garatbeli feszültségeloszlásra felírt (1.42) összefüggésben szerepel az N =1 K (ctgφ w +ctgα) konstans, amelynek értéke esetünkben: N =1 0.08(ctg38.2 +ctg40 )=0.8. (1.46) N értékét felhasználva σ y = ρg y =7.14y, (1.47) 1+N ha y értékét a garatot alkotó kúp csúcsától felfelé mérjük. A fentről lefelé és lentről felfelé meghatározott feszültség értékek a függőleges falakkal határolt rész és a garat találkozási pontjánál nem ugyanazt az értéket adják. A mérések [44] szerint is létezik ez a feszültségugrás. 28
41 1.4. BOLTOZÓDÁS 1.4. Boltozódás A természetes boltozódás vizsgálata során a kutatók a silókkal kapcsolatos boltozódásvizsgálatoknál két lényeges kérdés megválaszolására törekednek [9] összefoglaló munkája szerint: I. Azon feszültségek meghatározására, amelyek a szemcsés anyag tömörödését okozzák. A tömörödés hatására létrejövő anyagtulajdonság változások következtében a szemcsés anyag képessé válik önsúlyának és esetleg a felette elhelyezkedő anyagréteg súlyából adódó terhelések elviselésére. II. A természetes boltozatot alkotó szemcsehalmazban keletkező feszültségek meghatározására. A feszültségek és a tönkremeneteli kritériumoknak az ismeretében kívánják meghatározni a boltív teherbírását és ebből a kritikus nyílásméretet. Itt először a boltozódási folyamat vizsgálatának általános leírását kívánom megadni, a későbbiekben részletezem az egyes szerzők munkáit. [19] és [9] feltételezik, hogy a tömörödést okozó feszültségek nagysága egyenesen arányos a siló kúpos részének csúcsától mért távolsággal (radiális feszültségmező hipotézis). Feltételezéseik szerint ez a radiális feszültségmező okozza a szemcsehalmaz olyan mértékű deformációját, melynek hatására a tönkremenetel lezajlik, a boltozat összeomlik. A tömörödés okozójának a fal mellett kialakuló legnagyobb főfeszültséget tekintik. A tömörödést okozó σ t feszültséget σ t = ρgrf(φ, α, φ w ) (1.48) alakban határozzák meg a szerzők, ahol r a garat csúcsától mért távolság. A boltívbenkialakuló feszültségek meghatározása során a szerzők előzetesen feltételezik, hogy milyen alakú az adott boltív, és ezen feltételezés felhasználásával számítják ki a boltívben ébredő feszültségeket. 29
42 1. IRODALMI ÁTTEKINTÉS A fal melletti legnagyobb főfeszültség értéke [19]: σ 1,a = ρgrg(φ w,α) (1.49) alakú. Az egyes elméletek a boltív alakjával, valamint a tönkremenetellel kapcsolatos feltételezésekben különböznek. Természetesen az egyes modellekben az f(φ, α, φ w ) és g(φ w,α) függvények alakja is különböző. A kapott σ 1,a feszültséget ezután összehasonlítják a nyíródobozos vagy atriaxiálisvizsgálatbólszármazó tönkremenetelihatárfeszültséggel, amelynek meghatározásáról a későbbiekben lesz szó. A természetes boltozat kialakulásának szükséges feltétele: ahol σ K a tönkremeneteli határfeszültség. σ 1,a σ K, (1.50) 14. definíció. Kritikus nyílásméretnek nevezzük a siló kifolyónyílásának azt a legkisebb méretét, amelynél az anyag akadálytalanul ki tud folyni a silóból. σ 1,a ismeretében a kritikus nyílásméret meghatározható: D k = 2σ 1,a sin α ρgg(α, φ w ). (1.51) Ag(α, φ w ) függvény típusa a boltozat alakjára tett feltételezésektől függ. A garatbeli radiális feszültségmező kialakulásának szükséges feltétele az anyag sűrűségének állandósága [9]. Ha a sűrűséget állandónak tekintjük a teljes vizsgálat során, akkor nincs tömörödés, azaz éppen az a hatás nem jelentkezhet, ami a fenti modell szerint a boltozódást okozza. A silóban tárolt szemcsés anyag anyagjellemzőit a garatbeli, tömörített állapotra vonatkozóan kell megadnunk. A garatbeli szemcsehalmazt sokan különálló, önkényesen kijelölt alakú és kiterjedésű boltívekre osztják, majd ezek teherbírására vonatkozó 30
43 1.4. BOLTOZÓDÁS feltételezésekből kívánják a kritikus kiömlőnyílás méretét meghatározni. Ennek semmilyen mechanikai alapja nincs. A garatbeli anyaghalmazban nem alakulnak ki ilyesféle egymásra támaszkodó öntartó ívek. A radiális feszültségmező hipotézis csak nyitott kifolyónyílás esetén jelent elfogadható közelítést. Jenike és Enstad a radiális feszültségmező hipotézisét alkalmazza a boltozat terhelhetőségének meghatározása során, azaz kimondatlanul a boltozódást az anyag kiáramlási folyamatának megszakadásaként modellezi. A feszültségviszonyok elemzése során viszont az anyaghalmaz mozgásából eredő határokat teljesen figyelmen kívül hagyják. A halmaz a természetes boltozatok környezetében kéttengelyű feszültségállapotban van. A tönkremenetelhez tartozó kritikus nyomófeszültség értékét egytengelyű feszültségállapotban vizsgálják. A kéttengelyű és egytengelyű feszültségállapotban mérhető kritikus nyomófeszültség értéke nem ugyanakkora. A fejezet további részében található elméleti eredmények és a mérési eredmények összehasonlítása azt mutatja, hogy a napjainkban alkalmazott az előbbiekben általánosan összefoglalt elméletek jelentős túlméretezéshez vezetnek és feltételezhetőencsak durvaközelítését jelentika valóságos folyamatoknak Jenike modellje [19] szerint a szemcsehalmaz a kifolyás során olyan öntartó boltíveket alkot, amelyek képesek az anyag kiömlésének megakadályozására. Jenike feltételezése szerint a szemcsehalmazban kialakuló boltozatnak csak a saját súlyát kell megtartania. Jenike szerint a garatban lefelé haladva a szemcsehalmazra ható nyomóerő értéke csökken. Jenike állítása nem igaz akiömlőnyílás kinyitásának pillanatában, amikor nincs anyagkiáramlás mint azt végeselem módszerrel végzett számításaim mutatják hanem csak a kiáramlási folyamat során élhetünk ilyen 31
44 1. IRODALMI ÁTTEKINTÉS feltételezéssel. Mivel a párhuzamos tartomány alján jelentkező nagy nyomás hatására az anyag tömörsége megnövekedett, elképzelhető, hogy a kifolyónyílás környezetében képes a saját súlyából adódó terhelés elviselésére. Ekkor a kifolyás megszűnik, az anyag boltozódik. D r α L 1.9. ábra. Boltozat a garatban. A boltívben ébredő maximális feszültség arányos a boltív szélességével, a maximális feszültség pedig a fal melletti érintkezési pontban ébred. Közelítőértéke: σ 1,a ρgd =2rρg sin α. (1.52) A boltozat összeomlásának feltétele Jenike szerint a σ 1,a σ K (1.53) egyenlőtlenség teljesülése. A kritikus nyílásméret meghatározásához meg kell találni r-nek azt az értékét, melyre F F (σ t )=σ K = σ 1,a =2rρg sin α (1.54) 32
45 1.4. BOLTOZÓDÁS teljesül. Kritikus nyílásméretnek nevezi azt a D k =2r sin α értéket, melynél az (1.53) egyenlőtlenségből egyenlőség lesz. Tehát a σ 1,a =2rρg sin α = D k ρg = σ K = F F (σ t ) (1.55) egyenlőséghez tartozó D k kritikus nyílásméretet keresi. Nehézséget okoz azonban az, hogy az F F (σ t ) folyási függvény értékének nem ismert explicit alakja, értékét általában grafikus úton szokták meghatározni. E nehézség leküzdésére Jenike bevezette a folyási faktor fogalmát. 15. definíció. Folyási faktornak nevezi Jenike a garat fala mellett keletkező legnagyobb főfeszültség (σ 1,a ) és az előtömörítő (σ t ) feszültség hányadosát: f f = σ t. (1.56) σ 1,a A folyási faktor felhasználásával az σ K = F F (σ t ); σ 1,a = 1 f f σ t (1.57) egyenletrendszert kell megoldani. Ennek közelítő megoldása általában grafikus eljárással történik. Az F F függvény grafikonját metszik el egy 1 f f meredekségű egyenessel. Az ábrán látható diagramhoz hasonlók valamelyikének segítségével határozható meg f f értéke. Jenike a halmaz garatbeli feszültségviszonyait leíró differenciálegyenlet numerikus megoldásának felhasználásával alkotta meg az és az ehhez hasonló jellegű, további diagramokat [44]. A silótervezéssel foglalkozó szakemberek gyakran használják ezeket az ú.n. Jenike diagramokat. Kohéziós anyagok esetén σ K =F F (σ t ) esetenként meghatározható analitikus úton is, a Warren Spring egyenlet felhasználásával [44]: [ (σt ) ] 1 σ K = A F +1 q 1, (1.58) 33
46 1. IRODALMI ÁTTEKINTÉS 40 φ w [ ] α[ ] ábra. Folyási faktor értékei a falsúrlódás φ w és a garat félkúpszögének α függvényében, (φ =40 ). [20]. itt A, F és q anyagra jellemző állandók. Az állandók értékei az 1.2. táblázatban láthatók néhány anyagra. A folyási függvény lineáris alakja: σ K = Mσ t +Q, (1.59) ahol M és Q anyagfüggő állandók. A tönkremeneteli határgörbék jellegzetes alakja látható az ábrán. Az ábrát megfigyelve szembetűnő az eltérés a lineáris és nemlineáris tönkremeneteli határgörbe között (más anyagok esetén is). Nehezen valószínűsíthető, hogy mindkét görbe elfogadható pontossággal leírná a valóságban lezajló tönkremeneteli folyamatot. Az egyes tönkremeneteli határgörbék alkalmazhatóságával kapcsolatos 34
47 1.4. BOLTOZÓDÁS σ K [kpa] σ t [kpa] ábra. Tönkremeneteli határgörbék gipsz esetén. [9]. információkat a szakirodalom áttanulmányozása során nem találtam. Kísérleti vizsgálataim a lineáris határgörbe alkalmazhatóságát erősítik meg. Jenike azon feltevése, amely szerint a boltívnek csupán saját súlyát kell elviselnie, valamint a boltozat alakjának önkényes, minden mechanikai alapot nélkülöző kijelölése következtében és a folyási faktor méréssel meghatározott értékében rejlő bizonytalanságok együttes hatásaként ajenike módszerével meghatározott kritikus kiömlőnyílás-méret kettő négyszerese a méréssel meghatározható értéknek Enstad modellje A boltozódás szempontjából kritikus kifolyónyílás méret Jenike módszerével történő meghatározása jelentős túlméretezéshez vezet. A túlméretezés két fő oka [10]: Jenike nem vette figyelembe annak lehetőségét, hogy a boltozatot 35
48 1. IRODALMI ÁTTEKINTÉS alkotó szemcsehalmaz megcsúszhat a fal mentén, valamint a boltívet alkotó szemcsés anyagnak a saját súlya mellett a felette lévő anyagtömeg egy részének súlyát is meg kell tartania. Enstad e két dolgot próbálja elméletében figyelembe venni, és így kíván pontosabb modellel szolgálni a boltozódási folyamat vizsgálatához. Az Enstad által a garatbeli feszültségek eloszlására levezetett egyenlet, (lásd a 1.6. ábrát is) a σ(r)= ρgy r ( X 1 + σ(r) ρgy R ) ( r ) X (1.60) X 1 R összefüggés csak abban az esetben érvényes a feszültségekre, amelyben a szemcsés anyag szabadon áramlik kifelé a garatból, vagy ha a kifolyónyílás zárva van. A feszültségeloszlás nagymértékben megváltozik a kifolyónyílás megnyitásának pillanatában ha a szemcsehalmaz boltozódik. A boltozat kialakulásához szükséges kritikus nyílásméret meghatározásához Enstad feltételezi, hogy a garatban található szemcsés anyagban ébredő feszültség mindenütt elérte a kritikus állapothoz szükséges értéket. Ez a feltételezés véleményem szerint csak igen speciális esetben felel meg a valóságnak. Esetleg a szemcsés anyag kiömlése során elfogadható, de a tároló kinyitásának pillanatában nem. A szemcsehalmazt továbbra is ugyanolyan körívekkel határolt tartományokra osztja, mint amelyeket a feszültségeloszlás meghatározásához alkalmazott. Ez esetben azonban a tartományok a boltozatok oldalfallal érintkező részének középvonala a falra bocsátott normálvektorral ζ szöget zár be, és ez a ζ szög akkora érétket vesz fel, hogy a lehetséges legnagyobb támasztóerők jelentkezzenek a boltívek talapzatánál a megcsúszás határhelyzetében: ahol ζ = { φ ha φ ζm, ζ m ha φ>ζ m. (1.61) ζ m = π 4 α 2. (1.62) 36
[MECHANIKA- HAJLÍTÁS]
![[MECHANIKA- HAJLÍTÁS] [MECHANIKA- HAJLÍTÁS]](/thumbs/39/20428431.jpg) 2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
Mágneses szuszceptibilitás vizsgálata
 Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
VASÚTI PÁLYA DINAMIKÁJA
 VASÚTI PÁLYA DINAMIKÁJA Dynamics of the railway track Liegner Nándor BME Út és Vasútépítési Tanszék A vasúti felépítmény szerkezeti elemeiben ébredő igénybevételek A Zimmermann Eisenmann elmélet alapján
VASÚTI PÁLYA DINAMIKÁJA Dynamics of the railway track Liegner Nándor BME Út és Vasútépítési Tanszék A vasúti felépítmény szerkezeti elemeiben ébredő igénybevételek A Zimmermann Eisenmann elmélet alapján
BETONACÉLOK HAJLÍTÁSÁHOZ SZÜKSÉGES l\4"yomaték MEGHATÁROZÁSÁNAK EGYSZERŰ MÓDSZERE
 BETONACÉLOK HAJLÍTÁSÁHOZ SZÜKSÉGES l\4"yomaték MEGHATÁROZÁSÁNAK EGYSZERŰ MÓDSZERE BACZY"SKI Gábor Budape?ti 1Iűszaki Egyetem, Közlekedésmérnöki Kar Epítő- és Anyagmozgató Gépek Tanszék Körkeresztmetszet{Í
BETONACÉLOK HAJLÍTÁSÁHOZ SZÜKSÉGES l\4"yomaték MEGHATÁROZÁSÁNAK EGYSZERŰ MÓDSZERE BACZY"SKI Gábor Budape?ti 1Iűszaki Egyetem, Közlekedésmérnöki Kar Epítő- és Anyagmozgató Gépek Tanszék Körkeresztmetszet{Í
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
Fa- és Acélszerkezetek I. 5. Előadás Stabilitás I. Dr. Szalai József Főiskolai adjunktus
 Fa- és Acélszerkezetek I. 5. Előadás Stabilitás I. Dr. Szalai József Főiskolai adjunktus Tartalom Egyensúly elágazási határállapot Rugalmas nyomott oszlop kritikus ereje (Euler erő) Valódi nyomott oszlopok
Fa- és Acélszerkezetek I. 5. Előadás Stabilitás I. Dr. Szalai József Főiskolai adjunktus Tartalom Egyensúly elágazási határállapot Rugalmas nyomott oszlop kritikus ereje (Euler erő) Valódi nyomott oszlopok
Épületvillamosság laboratórium. Villámvédelemi felfogó-rendszer hatásosságának vizsgálata
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
Tartószerkezetek I. (Vasbeton szilárdságtan)
 Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.09.27. Hajlított vasbeton keresztmetszetek vizsgálata 2 3 Jelölések, elnevezések b : a keresztmetszet szélessége h : a keresztmetszet magassága
Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.09.27. Hajlított vasbeton keresztmetszetek vizsgálata 2 3 Jelölések, elnevezések b : a keresztmetszet szélessége h : a keresztmetszet magassága
TRANZISZTOROS KAPCSOLÁSOK KÉZI SZÁMÍTÁSA
 TRNZSZTOROS KPSOLÁSOK KÉZ SZÁMÍTÁS 1. gyenáramú számítás kézi számításokhoz az ábrán látható egyszerű közelítést használjuk: = Normál aktív tartományban a tranzisztort bázis-emitter diódáját az feszültségforrással
TRNZSZTOROS KPSOLÁSOK KÉZ SZÁMÍTÁS 1. gyenáramú számítás kézi számításokhoz az ábrán látható egyszerű közelítést használjuk: = Normál aktív tartományban a tranzisztort bázis-emitter diódáját az feszültségforrással
Lineáris algebra gyakorlat
 Lineáris algebra gyakorlat 3 gyakorlat Gyakorlatvezet : Bogya Norbert 2012 február 27 Bogya Norbert Lineáris algebra gyakorlat (3 gyakorlat) Tartalom Egyenletrendszerek Cramer-szabály 1 Egyenletrendszerek
Lineáris algebra gyakorlat 3 gyakorlat Gyakorlatvezet : Bogya Norbert 2012 február 27 Bogya Norbert Lineáris algebra gyakorlat (3 gyakorlat) Tartalom Egyenletrendszerek Cramer-szabály 1 Egyenletrendszerek
A mérések eredményeit az 1. számú táblázatban tüntettük fel.
 Oktatási Hivatal A Mérések függőleges, vastag falú alumínium csőben eső mágnesekkel 2011/2012. tanévi Fizika Országos Középiskolai Tanulmányi Verseny döntő feladatának M E G O L D Á S A I. kategória. A
Oktatási Hivatal A Mérések függőleges, vastag falú alumínium csőben eső mágnesekkel 2011/2012. tanévi Fizika Országos Középiskolai Tanulmányi Verseny döntő feladatának M E G O L D Á S A I. kategória. A
1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi
 1 Mélyhúzott edény teríték méretének meghatározása 1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi A mélyhúzott edény kiindulási teríték átmérőjének meghatározása a térfogat-állandóság alapján
1 Mélyhúzott edény teríték méretének meghatározása 1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi A mélyhúzott edény kiindulási teríték átmérőjének meghatározása a térfogat-állandóság alapján
Párhuzamos programozás
 Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
Programozható irányítóberendezések és szenzorrendszerek ZH. Távadók. Érdemjegy
 Név Neptun-kód Hallgató aláírása 0-15 pont: elégtelen (1) 16-21 pont: elégséges (2) 22-27 pont: közepes (3) 28-33 pont: jó (4) 34-40 pont: jeles (5) Érzékelők jellemzése Hőmérsékletérzékelés Erő- és nyomásmérés
Név Neptun-kód Hallgató aláírása 0-15 pont: elégtelen (1) 16-21 pont: elégséges (2) 22-27 pont: közepes (3) 28-33 pont: jó (4) 34-40 pont: jeles (5) Érzékelők jellemzése Hőmérsékletérzékelés Erő- és nyomásmérés
Kooperáció és intelligencia
 Kooperáció és intelligencia Tanulás többágenses szervezetekben/2 Tanulás több ágensből álló környezetben -a mozgó cél tanulás problémája (alapvetően megerősítéses tanulás) Legyen az ágens közösség formalizált
Kooperáció és intelligencia Tanulás többágenses szervezetekben/2 Tanulás több ágensből álló környezetben -a mozgó cél tanulás problémája (alapvetően megerősítéses tanulás) Legyen az ágens közösség formalizált
A döntő feladatai. valós számok!
 OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
Az aktiválódásoknak azonban itt még nincs vége, ugyanis az aktiválódások 30 évenként ismétlődnek!
 1 Mindannyiunk életében előfordulnak jelentős évek, amikor is egy-egy esemény hatására a sorsunk új irányt vesz. Bár ezen események többségének ott és akkor kevésbé tulajdonítunk jelentőséget, csak idővel,
1 Mindannyiunk életében előfordulnak jelentős évek, amikor is egy-egy esemény hatására a sorsunk új irányt vesz. Bár ezen események többségének ott és akkor kevésbé tulajdonítunk jelentőséget, csak idővel,
Egységes jelátalakítók
 6. Laboratóriumi gyakorlat Egységes jelátalakítók 1. A gyakorlat célja Egységes feszültség és egységes áram jelformáló áramkörök tanulmányozása, átviteli karakterisztikák felvétele, terhelésfüggőségük
6. Laboratóriumi gyakorlat Egységes jelátalakítók 1. A gyakorlat célja Egységes feszültség és egységes áram jelformáló áramkörök tanulmányozása, átviteli karakterisztikák felvétele, terhelésfüggőségük
Jelek tanulmányozása
 Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria
 005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
Lécgerenda. 1. ábra. 2. ábra
 Lécgerenda Egy korábbi dolgozatunkban melynek címe: Karimás csőillesztés már szóltunk arról, hogy a szeezetek számításaiban néha célszerű lehet a diszkrét mennyiségeket folyto - nosan megoszló mennyiségekkel
Lécgerenda Egy korábbi dolgozatunkban melynek címe: Karimás csőillesztés már szóltunk arról, hogy a szeezetek számításaiban néha célszerű lehet a diszkrét mennyiségeket folyto - nosan megoszló mennyiségekkel
Osztályozó és Javító vizsga témakörei matematikából 9. osztály 2. félév
 Osztályozó és Javító vizsga témakörei matematikából 9. osztály 2. félév IV. Háromszögek, négyszögek, sokszögek Pontok, egyenesek, síkok és ezek kölcsönös helyzete Néhány alapvető geometriai fogalom A háromszögekről.
Osztályozó és Javító vizsga témakörei matematikából 9. osztály 2. félév IV. Háromszögek, négyszögek, sokszögek Pontok, egyenesek, síkok és ezek kölcsönös helyzete Néhány alapvető geometriai fogalom A háromszögekről.
Azonosító jel: Matematika emelt szint
 I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
A MŰSZAKI MECHANIKA TANTÁRGY JAVÍTÓVIZSGA KÖVETELMÉNYEI 20150. AUGUSZTUS
 A MŰSZAKI MECHANIKA TANTÁRGY JAVÍTÓVIZSGA KÖVETELMÉNYEI 20150. AUGUSZTUS 1., Merev testek általános statikája mértékegységek a mechanikában a számító- és szerkesztő eljárások parallel alkalmazása Statikai
A MŰSZAKI MECHANIKA TANTÁRGY JAVÍTÓVIZSGA KÖVETELMÉNYEI 20150. AUGUSZTUS 1., Merev testek általános statikája mértékegységek a mechanikában a számító- és szerkesztő eljárások parallel alkalmazása Statikai
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2007. május 25. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
ÉRETTSÉGI VIZSGA 2007. május 25. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
Reológia 2. Bányai István DE Kolloid- és Környezetkémiai Tanszék
 Reológia 2 Bányai István DE Kolloid- és Környezetkémiai Tanszék Mérése nyomásesés áramlásra p 1 p 2 v=0 folyás csőben z r p 1 p 2 v max I V 1 p p t 8 l 1 2 r 2 x Höppler-típusú viszkoziméter v 2g 9 2 testgömb
Reológia 2 Bányai István DE Kolloid- és Környezetkémiai Tanszék Mérése nyomásesés áramlásra p 1 p 2 v=0 folyás csőben z r p 1 p 2 v max I V 1 p p t 8 l 1 2 r 2 x Höppler-típusú viszkoziméter v 2g 9 2 testgömb
Analízis elo adások. Vajda István. 2012. október 3. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
1. Feladatok a dinamika tárgyköréből
 1. Feladatok a dinamika tárgyköréből Newton három törvénye 1.1. Feladat: Órai kidolgozásra: 1. feladat Három azonos m tömegű gyöngyszemet fonálra fűzünk, egymástól kis távolságokban a fonálhoz rögzítünk,
1. Feladatok a dinamika tárgyköréből Newton három törvénye 1.1. Feladat: Órai kidolgozásra: 1. feladat Három azonos m tömegű gyöngyszemet fonálra fűzünk, egymástól kis távolságokban a fonálhoz rögzítünk,
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (13. fejezet)
 Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
A jelenség magyarázata. Fényszórás mérése. A dipólus keletkezése. Oszcilláló dipólusok. A megfigyelhető jelenségek. A fény elektromágneses hullám.
 Fényszórás mérése A jelenség magyarázata A megfigyelhető jelenségek A fény elektromágneses hullám. Az elektromos tér töltésekre erőhatást fejt ki. A dipólus keletkezése Dipólusok: a pozitív és a negatív
Fényszórás mérése A jelenség magyarázata A megfigyelhető jelenségek A fény elektromágneses hullám. Az elektromos tér töltésekre erőhatást fejt ki. A dipólus keletkezése Dipólusok: a pozitív és a negatív
A nyugalomban levő levegő fizikai jellemzői. Dr. Lakotár Katalin
 A nyugalomban levő levegő fizikai jellemzői Dr. Lakotár Katalin Száraz, nyugalomban levő levegő légköri jellemzői egyszerűsített légkör modell állapotjelzői: sűrűség vagy fajlagos térfogat térfogategységben
A nyugalomban levő levegő fizikai jellemzői Dr. Lakotár Katalin Száraz, nyugalomban levő levegő légköri jellemzői egyszerűsített légkör modell állapotjelzői: sűrűség vagy fajlagos térfogat térfogategységben
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI
 SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 12 KRISTÁLYkÉMIA XII. KÖTÉsTÍPUsOK A KRIsTÁLYOKBAN 1. KÉMIAI KÖTÉsEK Valamennyi kötéstípus az atommag és az elektronok, illetve az elektronok egymás közötti
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 12 KRISTÁLYkÉMIA XII. KÖTÉsTÍPUsOK A KRIsTÁLYOKBAN 1. KÉMIAI KÖTÉsEK Valamennyi kötéstípus az atommag és az elektronok, illetve az elektronok egymás közötti
Koordináta - geometria I.
 Koordináta - geometria I. DEFINÍCIÓ: (Helyvektor) A derékszögű koordináta - rendszerben a pont helyvektora az origóból a pontba mutató vektor. TÉTEL: Ha i az (1; 0) és j a (0; 1) pont helyvektora, akkor
Koordináta - geometria I. DEFINÍCIÓ: (Helyvektor) A derékszögű koordináta - rendszerben a pont helyvektora az origóból a pontba mutató vektor. TÉTEL: Ha i az (1; 0) és j a (0; 1) pont helyvektora, akkor
[GVMGS11MNC] Gazdaságstatisztika
![[GVMGS11MNC] Gazdaságstatisztika [GVMGS11MNC] Gazdaságstatisztika](/thumbs/40/21500887.jpg) [GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
[GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
Analízis elo adások. Vajda István. 2012. szeptember 24. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem 1/8 A halmaz alapfogalom, tehát nem definiáljuk. Jelölés: A halmazokat általában nyomtatott nagybetu vel jelöljük Egy H halmazt akkor tekintünk
Vajda István Neumann János Informatika Kar Óbudai Egyetem 1/8 A halmaz alapfogalom, tehát nem definiáljuk. Jelölés: A halmazokat általában nyomtatott nagybetu vel jelöljük Egy H halmazt akkor tekintünk
Bevezetés a lágy számítás módszereibe
 BLSZM-07 p. 1/10 Bevezetés a lágy számítás módszereibe Nem fuzzy halmaz kimenetű fuzzy irányítási rendszerek Egy víztisztító berendezés szabályozását megvalósító modell Viselkedésijósló tervezési példa
BLSZM-07 p. 1/10 Bevezetés a lágy számítás módszereibe Nem fuzzy halmaz kimenetű fuzzy irányítási rendszerek Egy víztisztító berendezés szabályozását megvalósító modell Viselkedésijósló tervezési példa
1. Nyomásmérővel mérjük egy gőzvezeték nyomását. A hőmérő méréstartománya 0,00 250,00 kpa,
 1. Nyomásmérővel mérjük egy gőzvezeték nyomását. A hőmérő méréstartománya 0,0 250,0 kpa, pontossága 3% 2 osztás. Mekkora a relatív hibája a 50,0 kpa, illetve a 210,0 kpa értékek mérésének? rel. hiba_tt
1. Nyomásmérővel mérjük egy gőzvezeték nyomását. A hőmérő méréstartománya 0,0 250,0 kpa, pontossága 3% 2 osztás. Mekkora a relatív hibája a 50,0 kpa, illetve a 210,0 kpa értékek mérésének? rel. hiba_tt
Osztályozó vizsga kérdések. Mechanika. I.félév. 2. Az erőhatás jellege, jelölések, mértékegységek
 Osztályozó vizsga kérdések Mechanika I.félév 1. Az erő fogalma, jellemzői, mértékegysége 2. Az erőhatás jellege, jelölések, mértékegységek 4 A 4. 4 3. A statika I., II. alaptörvénye 4. A statika III. IV.
Osztályozó vizsga kérdések Mechanika I.félév 1. Az erő fogalma, jellemzői, mértékegysége 2. Az erőhatás jellege, jelölések, mértékegységek 4 A 4. 4 3. A statika I., II. alaptörvénye 4. A statika III. IV.
Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 2005. november. I. rész
 Szászné Simon Judit, 005. november Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 005. november. feladat I. rész Oldjuk meg a valós számok halmazán a x 5x
Szászné Simon Judit, 005. november Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 005. november. feladat I. rész Oldjuk meg a valós számok halmazán a x 5x
GENERÁTOR FORGÓRÉSZ ELLENŐRZÉS A FLUXUS SZONDA FELÉPÍTÉSE, MŰKÖDÉSE
 GENERÁTOR FORGÓRÉSZ ELLENŐRZÉS A FLUXUS SZONDA FELÉPÍTÉSE, MŰKÖDÉSE Készítette: Ács György RTO FORRÁS: FLUXUS SZONDA ÉS ALKALMAZÁSA KTT MÉRNÖKI IRODA 11SP mérési eredményei A forgórész menetzárlat okozta
GENERÁTOR FORGÓRÉSZ ELLENŐRZÉS A FLUXUS SZONDA FELÉPÍTÉSE, MŰKÖDÉSE Készítette: Ács György RTO FORRÁS: FLUXUS SZONDA ÉS ALKALMAZÁSA KTT MÉRNÖKI IRODA 11SP mérési eredményei A forgórész menetzárlat okozta
Egyszerű áramkörök vizsgálata
 A kísérlet célkitűzései: Egyszerű áramkörök összeállításának gyakorlása, a mérőműszerek helyes használatának elsajátítása. Eszközszükséglet: Elektromos áramkör készlet (kapcsolótábla, áramköri elemek)
A kísérlet célkitűzései: Egyszerű áramkörök összeállításának gyakorlása, a mérőműszerek helyes használatának elsajátítása. Eszközszükséglet: Elektromos áramkör készlet (kapcsolótábla, áramköri elemek)
Alagútépítés Ideiglenes megtámasztás tervezése Példafeladat TÓTH Ákos
 Alagútépítés Ideiglenes megtámasztás tervezése Példafeladat TÓTH Ákos 2015.05.14 1 RMR Geomechanikai Osztályozás, RMR Az RMR rendszer 6 paraméterre alapul: 1. A kőzet egyirányú nyomószilárdsága; (r σ )
Alagútépítés Ideiglenes megtámasztás tervezése Példafeladat TÓTH Ákos 2015.05.14 1 RMR Geomechanikai Osztályozás, RMR Az RMR rendszer 6 paraméterre alapul: 1. A kőzet egyirányú nyomószilárdsága; (r σ )
Használható segédeszköz: szabványok, táblázatok, gépkönyvek, számológép
 A 27/2012 (VIII. 27.) NGM rendelet (12/2013 (III.28) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 34 522 02 Elektromos gép és készülékszerelő
A 27/2012 (VIII. 27.) NGM rendelet (12/2013 (III.28) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 34 522 02 Elektromos gép és készülékszerelő
Radon, Toron és Aeroszol koncentráció viszonyok a Tapolcai Tavas-barlangban
 Radon, Toron és Aeroszol koncentráció viszonyok a Tapolcai Tavas-barlangban Kutatási jelentés Veszprém 29. november 16. Dr. Kávási Norbert ügyvezetı elnök Mérési módszerek, eszközök Légtéri radon és toron
Radon, Toron és Aeroszol koncentráció viszonyok a Tapolcai Tavas-barlangban Kutatási jelentés Veszprém 29. november 16. Dr. Kávási Norbert ügyvezetı elnök Mérési módszerek, eszközök Légtéri radon és toron
Földrajzi helymeghatározás
 A mérés megnevezése, célkitűzései: Földrajzi fokhálózat jelentősége és használata a gyakorlatban Eszközszükséglet: Szükséges anyagok: narancs Szükséges eszközök: GPS készülék, földgömb, földrajz atlasz,
A mérés megnevezése, célkitűzései: Földrajzi fokhálózat jelentősége és használata a gyakorlatban Eszközszükséglet: Szükséges anyagok: narancs Szükséges eszközök: GPS készülék, földgömb, földrajz atlasz,
A mérés célkitűzései: Kaloriméter segítségével az étolaj fajhőjének kísérleti meghatározása a Joule-féle hő segítségével.
 A mérés célkitűzései: Kaloriméter segítségével az étolaj fajhőjének kísérleti meghatározása a Joule-féle hő segítségével. Eszközszükséglet: kaloriméter fűtőszállal digitális mérleg tanulói tápegység vezetékek
A mérés célkitűzései: Kaloriméter segítségével az étolaj fajhőjének kísérleti meghatározása a Joule-féle hő segítségével. Eszközszükséglet: kaloriméter fűtőszállal digitális mérleg tanulói tápegység vezetékek
1. Írja fel prímszámok szorzataként a 420-at! 2. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen!
 1. Írja fel prímszámok szorzataként a 40-at! 40 =. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen! A részek: 3. Egy sejttenyészetben naponta kétszereződik meg a sejtek száma.
1. Írja fel prímszámok szorzataként a 40-at! 40 =. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen! A részek: 3. Egy sejttenyészetben naponta kétszereződik meg a sejtek száma.
xdsl Optika Kábelnet Mért érték (2012. II. félév): SL24: 79,12% SL72: 98,78%
 Minőségi mutatók Kiskereskedelmi mutatók (Internet) Megnevezés: Új hozzáférés létesítési idő Meghatározás: A szolgáltatáshoz létesített új hozzáféréseknek, az esetek 80%ban teljesített határideje. Mérési
Minőségi mutatók Kiskereskedelmi mutatók (Internet) Megnevezés: Új hozzáférés létesítési idő Meghatározás: A szolgáltatáshoz létesített új hozzáféréseknek, az esetek 80%ban teljesített határideje. Mérési
2011. március 9. Dr. Vincze Szilvia
 . márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
. márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
EPER E-KATA integráció
 EPER E-KATA integráció 1. Összhang a Hivatalban A hivatalban használt szoftverek összekapcsolása, integrálása révén az egyes osztályok, nyilvántartások között egyezőség jön létre. Mit is jelent az integráció?
EPER E-KATA integráció 1. Összhang a Hivatalban A hivatalban használt szoftverek összekapcsolása, integrálása révén az egyes osztályok, nyilvántartások között egyezőség jön létre. Mit is jelent az integráció?
BOLYAI MATEMATIKA CSAPATVERSENY FŐVÁROSI DÖNTŐ SZÓBELI (2005. NOVEMBER 26.) 5. osztály
 5. osztály Írd be az ábrán látható hat üres körbe a 10, 30, 40, 60, 70 és 90 számokat úgy, hogy a háromszög mindhárom oldala mentén a számok összege 200 legyen! 50 20 80 Egy dobozban háromféle színű: piros,
5. osztály Írd be az ábrán látható hat üres körbe a 10, 30, 40, 60, 70 és 90 számokat úgy, hogy a háromszög mindhárom oldala mentén a számok összege 200 legyen! 50 20 80 Egy dobozban háromféle színű: piros,
Korszerű geodéziai adatfeldolgozás Kulcsár Attila
 Korszerű geodéziai adatfeldolgozás Kulcsár Attila Nyugat-Magyarországi Egyetem Geoinformatikai Főiskolai Kar Térinformatika Tanszék 8000 Székesfehérvár, Pirosalma -3 Tel/fax: (22) 348 27 E-mail: a.kulcsar@geo.info.hu.
Korszerű geodéziai adatfeldolgozás Kulcsár Attila Nyugat-Magyarországi Egyetem Geoinformatikai Főiskolai Kar Térinformatika Tanszék 8000 Székesfehérvár, Pirosalma -3 Tel/fax: (22) 348 27 E-mail: a.kulcsar@geo.info.hu.
Ablakok használata. 1. ábra Programablak
 Ha elindítunk egy programot, az egy Ablakban jelenik meg. A program az üzeneteit szintén egy újabb ablakban írja ki számunkra. Mindig ablakokban dolgozunk. Az ismertetett operációs rendszer is az Ablakok
Ha elindítunk egy programot, az egy Ablakban jelenik meg. A program az üzeneteit szintén egy újabb ablakban írja ki számunkra. Mindig ablakokban dolgozunk. Az ismertetett operációs rendszer is az Ablakok
Teherbíró-képesség meghatározásának lehetőségei
 Teherbíró-képesség meghatározásának lehetőségei H-TPA Kft. technológus, BME PhD hallgató 11. Útépítési Akadémia A dinamikus teherbírás adatainak felhasználása az útpályaszerkezetek korszerűsítésében 1
Teherbíró-képesség meghatározásának lehetőségei H-TPA Kft. technológus, BME PhD hallgató 11. Útépítési Akadémia A dinamikus teherbírás adatainak felhasználása az útpályaszerkezetek korszerűsítésében 1
Homlokzati tűzterjedés vizsgálati módszere
 Homlokzati tűzterjedés vizsgálati módszere Siófok 2008. április 17. Dr. Bánky Tamás Nyílásos homlokzatok esetén a tűzterjedési gát kritériumait nem kielégítő homlokzati megoldásoknál továbbá nyílásos homlokzatokon
Homlokzati tűzterjedés vizsgálati módszere Siófok 2008. április 17. Dr. Bánky Tamás Nyílásos homlokzatok esetén a tűzterjedési gát kritériumait nem kielégítő homlokzati megoldásoknál továbbá nyílásos homlokzatokon
Vektorok összeadása, kivonása, szorzás számmal, koordináták, lineáris függetlenség
 Vektoralgebra Vektorok összeadása, kivonása, szorzás számmal, koordináták, lineáris függetlenség Feladatok: 1) A koordinátarendszerben úgy helyezzük el az egységkockát, hogy az origó az egyik csúcsba essék,
Vektoralgebra Vektorok összeadása, kivonása, szorzás számmal, koordináták, lineáris függetlenség Feladatok: 1) A koordinátarendszerben úgy helyezzük el az egységkockát, hogy az origó az egyik csúcsba essék,
Henger körüli áramlás. Henger körüli áramlás. Henger körüli áramlás 2015.03.02. ρ 2. R z. R z = 2 2. c A. = 4c. c p. = 2c. y/r 1.5.
 5.3.. Henger körüli áramlás y/r.5.5.5 x/r.5 3 3 R w z + z R R iϑ e r R R z ( os ϑ + i sin ϑ ) Henger körüli áramlás ( os ϑ i sin ϑ ) r R + [ ϑ + sin ϑ ] ( ) ( os ) r R r R os ϑ + os ϑ + sin ϑ 444 3 r R
5.3.. Henger körüli áramlás y/r.5.5.5 x/r.5 3 3 R w z + z R R iϑ e r R R z ( os ϑ + i sin ϑ ) Henger körüli áramlás ( os ϑ i sin ϑ ) r R + [ ϑ + sin ϑ ] ( ) ( os ) r R r R os ϑ + os ϑ + sin ϑ 444 3 r R
Térfogatáram mérési módszerek 2.: Térfogatáram mérés csőívben (K)
 Térfogatáram mérési módszerek.: Térfogatáram mérés csőívben (K) A mérés célja: meghatározandó egy csőkönyök nyomásesése és ellenállástényezője, illetve a csőkönyök legkisebb és legnagyobb görbületi sugarú
Térfogatáram mérési módszerek.: Térfogatáram mérés csőívben (K) A mérés célja: meghatározandó egy csőkönyök nyomásesése és ellenállástényezője, illetve a csőkönyök legkisebb és legnagyobb görbületi sugarú
HÁLÓZATSEMLEGESSÉG - EGYSÉGES INTERNET SZOLGÁLTATÁS-LEÍRÓ TÁBLÁZAT
 HÁLÓZATSEMLEGESSÉG - EGYSÉGES INTERNET SZOLGÁLTATÁS-LEÍRÓ TÁBLÁZAT - 2016.04.01 után kötött szerződésekre Díjcsomag neve Go Go+ Go EU Go EU+ Kínált letöltési sebesség - 3G 42 Mbit/s 42 Mbit/s 42 Mbit/s
HÁLÓZATSEMLEGESSÉG - EGYSÉGES INTERNET SZOLGÁLTATÁS-LEÍRÓ TÁBLÁZAT - 2016.04.01 után kötött szerződésekre Díjcsomag neve Go Go+ Go EU Go EU+ Kínált letöltési sebesség - 3G 42 Mbit/s 42 Mbit/s 42 Mbit/s
Vezetőtárs értékelő kérdőív
 Vezetőtárs értékelő kérdőív Kérdőív megnevezése Jele, kódja Vezetőtárs értékelő kérdőív 11_Ovodavezetőtárs_Ért Önértékelés Értékelés Kérjük a megfelelőt aláhúzni! sorsz Megnevezés Adat 1. Óvodavezető neve
Vezetőtárs értékelő kérdőív Kérdőív megnevezése Jele, kódja Vezetőtárs értékelő kérdőív 11_Ovodavezetőtárs_Ért Önértékelés Értékelés Kérjük a megfelelőt aláhúzni! sorsz Megnevezés Adat 1. Óvodavezető neve
ELEKTRONIKAI ALAPISMERETEK
 Elektronikai alapismeretek középszint 080 ÉETTSÉGI VIZSG 009. május. ELEKTONIKI LPISMEETEK KÖZÉPSZINTŰ ÍÁSBELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMTTÓ OKTTÁSI ÉS KLTÁLIS MINISZTÉIM Egyszerű, rövid feladatok
Elektronikai alapismeretek középszint 080 ÉETTSÉGI VIZSG 009. május. ELEKTONIKI LPISMEETEK KÖZÉPSZINTŰ ÍÁSBELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMTTÓ OKTTÁSI ÉS KLTÁLIS MINISZTÉIM Egyszerű, rövid feladatok
Javítóvizsga témakörei matematika tantárgyból
 9.osztály Halmazok: - ismerje és használja a halmazok megadásának különböző módjait, a halmaz elemének fogalmát - halmazműveletek : ismerje és alkalmazza gyakorlati és matematikai feladatokban a következő
9.osztály Halmazok: - ismerje és használja a halmazok megadásának különböző módjait, a halmaz elemének fogalmát - halmazműveletek : ismerje és alkalmazza gyakorlati és matematikai feladatokban a következő
2004. december 1. Irodalom
 LINEÁRIS LEKÉPEZÉSEK I. 2004. december 1. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László:
LINEÁRIS LEKÉPEZÉSEK I. 2004. december 1. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László:
Ipari és vasúti szénkefék
 www.schunk-group.com Ipari és vasúti szénkefék A legjelentősebb anyagminőségek fizikai tulajdonságai A legjelentősebb anyagminőségek fizikai tulajdonságai A szénkefetestként használt szén és grafit anyagminőségek
www.schunk-group.com Ipari és vasúti szénkefék A legjelentősebb anyagminőségek fizikai tulajdonságai A legjelentősebb anyagminőségek fizikai tulajdonságai A szénkefetestként használt szén és grafit anyagminőségek
Algebra es sz amelm elet 3 el oad as Rel aci ok Waldhauser Tam as 2014 oszi f el ev
 Algebra és számelmélet 3 előadás Relációk Waldhauser Tamás 2014 őszi félév Relációk reláció lat. 1. kapcsolat, viszony; összefüggés vmivel 2. viszonylat, vonatkozás reláció lat. 3. mat halmazok elemei
Algebra és számelmélet 3 előadás Relációk Waldhauser Tamás 2014 őszi félév Relációk reláció lat. 1. kapcsolat, viszony; összefüggés vmivel 2. viszonylat, vonatkozás reláció lat. 3. mat halmazok elemei
Sz ekelyhidi L aszl o Val osz ın us egsz am ıt as es matematikai statisztika *************** Budapest, 1998
 Székelyhidi László Valószínűségszámítás és matematikai statisztika *************** Budapest, 1998 Előszó Ez a jegyzet a valószínűségszámításnak és a matematikai statisztikának azokat a fejezeteit tárgyalja,
Székelyhidi László Valószínűségszámítás és matematikai statisztika *************** Budapest, 1998 Előszó Ez a jegyzet a valószínűségszámításnak és a matematikai statisztikának azokat a fejezeteit tárgyalja,
ELLENÁLLÁSOK PÁRHUZAMOS KAPCSOLÁSA, KIRCHHOFF I. TÖRVÉNYE, A CSOMÓPONTI TÖRVÉNY ELLENÁLLÁSOK PÁRHUZAMOS KAPCSOLÁSA. 1. ábra
 ELLENÁLLÁSOK PÁRHUZAMOS KAPCSOLÁSA Három háztartási fogyasztót kapcsoltunk egy feszültségforrásra (hálózati feszültségre: 230V), vagyis közös kapocspárra, tehát párhuzamosan. A PÁRHUZAMOS KAPCSOLÁS ISMÉRVE:
ELLENÁLLÁSOK PÁRHUZAMOS KAPCSOLÁSA Három háztartási fogyasztót kapcsoltunk egy feszültségforrásra (hálózati feszültségre: 230V), vagyis közös kapocspárra, tehát párhuzamosan. A PÁRHUZAMOS KAPCSOLÁS ISMÉRVE:
Programozás I. - 9. gyakorlat
 Programozás I. - 9. gyakorlat Mutatók, dinamikus memóriakezelés Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 9, 2009 1 tar@dcs.vein.hu
Programozás I. - 9. gyakorlat Mutatók, dinamikus memóriakezelés Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 9, 2009 1 tar@dcs.vein.hu
A táblázatkezelő felépítése
 A táblázatkezelés A táblázatkezelő felépítése A táblázatkezelő felépítése Címsor: A munkafüzet címét mutatja, és a program nevét, amivel megnyitottam. Menüszalag: A menüsor segítségével használhatjuk az
A táblázatkezelés A táblázatkezelő felépítése A táblázatkezelő felépítése Címsor: A munkafüzet címét mutatja, és a program nevét, amivel megnyitottam. Menüszalag: A menüsor segítségével használhatjuk az
A TŰZVÉDELMI TERVEZÉS FOLYAMATA. Dr. Takács Lajos Gábor okl. építészmérnök BME Építészmérnöki Kar Épületszerkezettani Tanszék
 A TŰZVÉDELMI TERVEZÉS FOLYAMATA Dr. Takács Lajos Gábor okl. építészmérnök BME Építészmérnöki Kar Épületszerkezettani Tanszék BME Épít Épületsze TŰZVÉDELMI TERVEZÉSI FELADATOK A tűzvédelmi tervezési tevékenység
A TŰZVÉDELMI TERVEZÉS FOLYAMATA Dr. Takács Lajos Gábor okl. építészmérnök BME Építészmérnöki Kar Épületszerkezettani Tanszék BME Épít Épületsze TŰZVÉDELMI TERVEZÉSI FELADATOK A tűzvédelmi tervezési tevékenység
Előterjesztés. (ifj. Kovács Róbert kérelme)
 (ifj. Kovács Róbert kérelme) Kérelem: Az 1901/10, 1901/11, 1901/12 hrsz-ú területek jelenleg Mk (mezőgazdasági kert) övezeti besorolású részben külterületi részben belterületi telkek. A tulajdonos három
(ifj. Kovács Róbert kérelme) Kérelem: Az 1901/10, 1901/11, 1901/12 hrsz-ú területek jelenleg Mk (mezőgazdasági kert) övezeti besorolású részben külterületi részben belterületi telkek. A tulajdonos három
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 5 V. BECsLÉsELMÉLET 1. STATIsZTIKAI becslés A becsléselméletben gyakran feltesszük, hogy a megfigyelt mennyiségek független valószínűségi
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 5 V. BECsLÉsELMÉLET 1. STATIsZTIKAI becslés A becsléselméletben gyakran feltesszük, hogy a megfigyelt mennyiségek független valószínűségi
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN
 GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten RACIONÁLIS TÖRTFÜGGVÉNYEK INTEGRÁLJA Készítette: Gábor Szakmai felel s: Gábor Vázlat
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten RACIONÁLIS TÖRTFÜGGVÉNYEK INTEGRÁLJA Készítette: Gábor Szakmai felel s: Gábor Vázlat
A mérés célja: Példák a műveleti erősítők lineáris üzemben történő felhasználására, az előadásokon elhangzottak alkalmazása a gyakorlatban.
 E II. 6. mérés Műveleti erősítők alkalmazása A mérés célja: Példák a műveleti erősítők lineáris üzemben történő felhasználására, az előadásokon elhangzottak alkalmazása a gyakorlatban. A mérésre való felkészülés
E II. 6. mérés Műveleti erősítők alkalmazása A mérés célja: Példák a műveleti erősítők lineáris üzemben történő felhasználására, az előadásokon elhangzottak alkalmazása a gyakorlatban. A mérésre való felkészülés
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2005. május 20. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI MINISZTÉRIM Elektronikai alapismeretek
ÉRETTSÉGI VIZSGA 2005. május 20. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI MINISZTÉRIM Elektronikai alapismeretek
2010.05.12. 1300 Infó Rádió. Hírek
 2010.05.12. 1300 Infó Rádió Hírek 100512 1303 [1127h GAZ MKIK - pozitív index MTI km 100512] Jelentősen javultak a magyar vállalatok várakozásai a következő félévre a Magyar Kereskedelmi és Iparkamara
2010.05.12. 1300 Infó Rádió Hírek 100512 1303 [1127h GAZ MKIK - pozitív index MTI km 100512] Jelentősen javultak a magyar vállalatok várakozásai a következő félévre a Magyar Kereskedelmi és Iparkamara
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
GÉPJÁRMŰ ÉRTÉKELŐ SZAKÉRTŐI VÉLEMÉNY
 Havas Szakértői Iroda Kft. Budapest GÉPJÁRMŰ ÉRTÉKELŐ SZAKÉRTŐI VÉLEMÉNY A Hungero-Mobil Kft. f. a. tehergépjárművének forgalmi értékelése Budapest, 2015. szeptember SZAKÉRTŐI VÉLEMÉNY I. Megbízás: A Hungero-Mobil
Havas Szakértői Iroda Kft. Budapest GÉPJÁRMŰ ÉRTÉKELŐ SZAKÉRTŐI VÉLEMÉNY A Hungero-Mobil Kft. f. a. tehergépjárművének forgalmi értékelése Budapest, 2015. szeptember SZAKÉRTŐI VÉLEMÉNY I. Megbízás: A Hungero-Mobil
Házi dolgozat. Minta a házi dolgozat formai és tartalmi követelményeihez. Készítette: (név+osztály) Iskola: (az iskola teljes neve)
 Házi dolgozat Minta a házi dolgozat formai és tartalmi követelményeihez Készítette: (név+osztály) Iskola: (az iskola teljes neve) Dátum: (aktuális dátum) Tartalom Itt kezdődik a címbeli anyag érdemi kifejtése...
Házi dolgozat Minta a házi dolgozat formai és tartalmi követelményeihez Készítette: (név+osztály) Iskola: (az iskola teljes neve) Dátum: (aktuális dátum) Tartalom Itt kezdődik a címbeli anyag érdemi kifejtése...
ADATBÁZIS-KEZELÉS. Funkcionális függés, normál formák
 ADATBÁZIS-KEZELÉS Funkcionális függés, normál formák KARBANTARTÁSI ANOMÁLIÁK beszúrási anomáliák törlési anomáliák módosítási anomáliák DOLG_PROJ(Dszsz, Pszám, Dnév, Pnév, Órák) 2 MÓDOSÍTÁSI ANOMÁLIÁK
ADATBÁZIS-KEZELÉS Funkcionális függés, normál formák KARBANTARTÁSI ANOMÁLIÁK beszúrási anomáliák törlési anomáliák módosítási anomáliák DOLG_PROJ(Dszsz, Pszám, Dnév, Pnév, Órák) 2 MÓDOSÍTÁSI ANOMÁLIÁK
MATEMATIKA HETI 3 ÓRA
 EURÓPAI ÉRETTSÉGI 010 MATEMATIKA HETI 3 ÓRA IDŐPONT : 010. június 4. A VIZSGA IDŐTARTAMA : 3 óra (180 perc) MEGENGEDETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
EURÓPAI ÉRETTSÉGI 010 MATEMATIKA HETI 3 ÓRA IDŐPONT : 010. június 4. A VIZSGA IDŐTARTAMA : 3 óra (180 perc) MEGENGEDETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
A mechanika alapjai. A pontszerű testek dinamikája. Horváth András SZE, Fizika és Kémia Tsz. 2006. szeptember 29.
 A mechanika alapjai A pontszerű testek dinamikája Horváth András SZE, Fizika és Kémia Tsz. 2006. szeptember 29. Bevezetés Newton I. Newton II. Newton III. Newton IV. 2 / 27 Bevezetés Bevezetés Newton I.
A mechanika alapjai A pontszerű testek dinamikája Horváth András SZE, Fizika és Kémia Tsz. 2006. szeptember 29. Bevezetés Newton I. Newton II. Newton III. Newton IV. 2 / 27 Bevezetés Bevezetés Newton I.
Adatgyőjtés, mérési alapok, a környezetgazdálkodás fontosabb mőszerei
 GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ. Orvosi laboratóriumi technikai asszisztens szakképesítés. 2449-06 Mikrobiológiai vizsgálatok modul. 1.
 Emberi Erőforrások Minisztériuma Korlátozott terjesztésű! Érvényességi idő: az írásbeli vizsgatevékenység befejezésének időpontjáig A minősítő neve: Rauh Edit A minősítő beosztása: mb. főigazgató-helyettes
Emberi Erőforrások Minisztériuma Korlátozott terjesztésű! Érvényességi idő: az írásbeli vizsgatevékenység befejezésének időpontjáig A minősítő neve: Rauh Edit A minősítő beosztása: mb. főigazgató-helyettes
JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ. Foglalkozásegészségügyi szakápoló szakképesítés. 2379-06 Foglalkozásegészségügyi felmérés modul. 1.
 Emberi Erőforrások Minisztériuma Korlátozott terjesztésű! Érvényességi idő: az írásbeli vizsgatevékenység befejezésének időpontjáig A minősítő neve: Rauh Edit A minősítő beosztása: mb. főigazgató-helyettes
Emberi Erőforrások Minisztériuma Korlátozott terjesztésű! Érvényességi idő: az írásbeli vizsgatevékenység befejezésének időpontjáig A minősítő neve: Rauh Edit A minősítő beosztása: mb. főigazgató-helyettes
Szerb középszintű szóbeli vizsga értékelési útmutató
 Szerb középszintű szóbeli vizsga értékelési útmutató Ez az értékelési eljárás meghatározott értékelési szempontokon, valamint az egyes szempontokhoz tartozó szintleírásokon alapul. Minden feleletet ezen
Szerb középszintű szóbeli vizsga értékelési útmutató Ez az értékelési eljárás meghatározott értékelési szempontokon, valamint az egyes szempontokhoz tartozó szintleírásokon alapul. Minden feleletet ezen
MATEMATIKA ÍRÁSBELI VIZSGA 2011. május 3.
 MATEMATIKA ÍRÁSBELI VIZSGA I. rész Fontos tudnivalók A megoldások sorrendje tetszőleges. A feladatok megoldásához szöveges adatok tárolására és megjelenítésére nem alkalmas zsebszámológépet és bármelyik
MATEMATIKA ÍRÁSBELI VIZSGA I. rész Fontos tudnivalók A megoldások sorrendje tetszőleges. A feladatok megoldásához szöveges adatok tárolására és megjelenítésére nem alkalmas zsebszámológépet és bármelyik
FENNTARTHATÓ FEJLŐDÉS
 FENNTARTHATÓ FEJLŐDÉS Kump Edina ÖKO-Pack Nonprofit Kft. E-mail: edina@okopack.hu Web: www.okopack.hu Dunaújváros, 2014. november 07. A FENNTARTHATÓ FEJLŐDÉS FOGALMA A fenntartható fejlődés a fejlődés
FENNTARTHATÓ FEJLŐDÉS Kump Edina ÖKO-Pack Nonprofit Kft. E-mail: edina@okopack.hu Web: www.okopack.hu Dunaújváros, 2014. november 07. A FENNTARTHATÓ FEJLŐDÉS FOGALMA A fenntartható fejlődés a fejlődés
Arany Dániel Matematikai Tanulóverseny 2011/2012-es tanév első (iskolai) forduló haladók I. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 011/01-es tanév első (iskolai) forduló haladók I. kategória Megoldások és javítási útmutató 1. Az ábrán látható ABC derékszögű háromszög
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 011/01-es tanév első (iskolai) forduló haladók I. kategória Megoldások és javítási útmutató 1. Az ábrán látható ABC derékszögű háromszög
KOMPLEX TERVEZÉS TERVEZÉSI SZAKIRÁNY TARTÓSZERKEZETI FELADATRÉSZ 1. félév
 KOMPLEX TERVEZÉS TERVEZÉSI SZAKIRÁNY 1. félév engedélyezési terv szintű dokumentáció tartószerkezeti munkarészének elkészítése folyamatos konzultáció, az első konzultációnak a vázlatterv beadás előtt meg
KOMPLEX TERVEZÉS TERVEZÉSI SZAKIRÁNY 1. félév engedélyezési terv szintű dokumentáció tartószerkezeti munkarészének elkészítése folyamatos konzultáció, az első konzultációnak a vázlatterv beadás előtt meg
54 481 01 1000 00 00 CAD-CAM
 Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
31 521 09 1000 00 00 Gépi forgácsoló Gépi forgácsoló
 Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Conjoint-analízis példa (egyszerűsített)
 Conjoint-analízis példa (egyszerűsített) Az eljárás meghatározza, hogy a fogyasztók a vásárlás szempontjából lényeges terméktulajdonságoknak mekkora relatív fontosságot tulajdonítanak és megadja a tulajdonságok
Conjoint-analízis példa (egyszerűsített) Az eljárás meghatározza, hogy a fogyasztók a vásárlás szempontjából lényeges terméktulajdonságoknak mekkora relatív fontosságot tulajdonítanak és megadja a tulajdonságok
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2010. május 1. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2010. május 1. 8:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
ÉRETTSÉGI VIZSGA 2010. május 1. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2010. május 1. 8:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
SZOLGÁLATI TITOK! KORLÁTOZOTT TERJESZTÉSŰ!
 A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata. Az r-time és a TNS Hoffmann által végzett kutatás
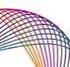 Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata Az r-time és a TNS Hoffmann által végzett kutatás 2002-2010: stabil szponzorációs részarány Televíziós reklámbevételek
Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata Az r-time és a TNS Hoffmann által végzett kutatás 2002-2010: stabil szponzorációs részarány Televíziós reklámbevételek
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló gimnáziuma) Térgeometria III.
 Térgeometria III. 1. Szabályos háromoldalú gúla alapéle 1 cm, oldaléle 1 cm. Milyen magas a gúla? Tekintsük a következő ábrát: Az alaplap szabályos ABC, így a D csúcs merőleges vetülete a háromszög S súlypontja.
Térgeometria III. 1. Szabályos háromoldalú gúla alapéle 1 cm, oldaléle 1 cm. Milyen magas a gúla? Tekintsük a következő ábrát: Az alaplap szabályos ABC, így a D csúcs merőleges vetülete a háromszög S súlypontja.
Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között
 Dr. Nyári Tibor Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között tökéletes színeket visszaadni. A digitális
Dr. Nyári Tibor Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között tökéletes színeket visszaadni. A digitális
Kombinatorika. 9. előadás. Farkas István. DE ATC Gazdaságelemzési és Statisztikai Tanszék. Kombinatorika p. 1/
 Kombinatorika 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Kombinatorika p. 1/ Permutáció Definíció. Adott n különböző elem. Az elemek egy meghatározott sorrendjét az adott
Kombinatorika 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Kombinatorika p. 1/ Permutáció Definíció. Adott n különböző elem. Az elemek egy meghatározott sorrendjét az adott
