A Feldmann ~ Sapiro - elv igazolása
|
|
|
- Lilla Illésné
- 9 évvel ezelőtt
- Látták:
Átírás
1 A Feldmann ~ Sapiro - elv igazolása Bevezetés Már középiskolás koromban is érdekelt, hogy mi lehet az a borzasztó nehéz számítás, aminek csak a végeredményét közölték velünk, s amit Feldmann ~ Sapiro - elv -nek ( röviden: FSE ) neveztek. Aztán sokkal később [ ] - ben találkoztam hasonló mondatokkal: Hosszas matematikai levezetés után a következő eredmény született Aztán még később megtudtam, hogy az elv alkalmazását megkönnyíteni szánt mozgatható skálákkal bíró számolóeszközből tolótáblázatból már csak néhány működő darab van, ezek is már szinte muzeális értékek. Szóval, ez kész rejtély! Elérkezettnek látszott az idő: fel kellene már lebbenteni erről a fátylat! Hiszen a számítógépek korát éljük! Vagy nem? Az FSE kimondása és bizonyítása Az FSE a fűrészáru - kihozatali számítások kapcsán merül fel. Az a cél, hogy az adott átmérőjű fűrészrönk feldolgozása során a lehető legkisebb veszteséget, azaz a legnagyobb kihozatali % - ot érjük el. Utóbbi meghatározása: v K 00 ( % ), ( ) V ahol K: a mennyiségi kihozatali %; v: a termelt fűrészáru mennyisége ( m 3 ); V: a feldolgozott rönk mennyisége ( m 3 ). Továbbá: v = t h, ( ) V = T h, ( 3 ) így ( ), ( ), ( 3 ) - mal: t K= 00 ( % ). T ( 4 ) Itt t: a termelt fűrészáru keresztmetszeti területe ( m ); T: a feldolgozott rönk - mennyiség keresztmetszeti területe ( m ); h: a rönk, ill. a belőle termelt fűrészáru hossza ( m ). ( 4 ) szerint a kihozatali % annál nagyobb, minél nagyobb az adott bütüre rárajzolható fűrészáru keresztmetszeti területe. A FSE azt állítja, hogy a rárajzolást, vagy másként mondva a fűrészpenge - elrendezést bizonyos módon végezve, K max 85 % érhető el. A munkát úgy szervezzük, hogy először tételként kimondjuk a FSE - t, majd bebizonyítjuk azt. Ennek során nem csak a szokásos középiskolai matematikát alkalmazzuk, de igyekszünk megmutatni, vagy ötletet adni, hogy hogyan lehetne a tételt, ill. egyes részeit magasabb matematika alkalmazása nélkül is belátni.
2 Tétel: A d átmérőjű rönkből kivágható fűrészáru - keresztmetszet legnagyobb hasznos területe ld. az. ábrát is! : max t t 4 t 0,707 d 4 0,d 0,43 d.. ábra A tétel igazolása két lépésben történik:.) Igazoljuk, hogy a d átmérőjű körbe írható legnagyobb területű téglalap egy a = 0,707 d oldalú négyzet, amelyre: t a 0,707 d..) Igazoljuk, hogy a d átmérőjű körben a fennmaradó 4 darab körszeletbe írható legnagyobb területű téglalapok kereken 0,0 d x 0,43 d méretűek, így ezek területe: t 0, d 0,43 d. Ha e két állítás igazságát beláttuk, akkor a tétel állítása már a szemlélet alapján adódik..) Lépés Ehhez tekintsük a. ábrát is! A téglalap területe: T 4 x y. ( 5 ) Pitagorász - tétellel: y r x. ( 6 ) Most ( 5 ) és ( 6 ) - tal: T (x) 4 x r x.. ábra ( 7 )
3 3 A T (x) területfüggvény szélső értékének szükséges feltétele: dt (x) 0. ( 8 ) dx Elvégezve a deriválást: dt (x) x 4 r x x 0; dx r x ( 9 ) Majd ( 9 ) - ből: r x 0; ( 0 ) r x minthogy ( 0 ) nevezője ( 6 ) szerint y, ez pedig nem lehet végtelen nagy, ezért a számlálónak kell zérusnak lennie, amiből: r x*. ( ) Most ( 6 ) és ( ) - ből: r y*. ( ) Az utóbbi két képlet szerint a keresett téglalap valójában négyzet. Ennek oldalai: d a b x* r 0,707 d, tehát a b 0,707 d. ( 3 ) A négyzet területe: t a 0,707 d. ( 4 ) Annak további igazolása, hogy a vizsgált szélsőérték maximum, és nem minimum, nem szükséges, mert a terület minimuma éppen zéró lenne. Ezzel a tétel igazolásának első lépését elvégeztük.. Lépés Ehhez tekintsük a 3. ábrát is! Pitagorász - tétellel: y * r, innen r y*. ( 5 ) A kis téglalap területe:
4 4 3. ábra T. ( 6 ) Most ( 5 ) és ( 6 ) - tal: T r y * ; ( 7 ) majd ( ) és ( 7 ) - tel: r T r ; ( 8 ) most ( 8 ) - at r - tel osztva: T ; r r r ( 9 ) bevezetve a T, u = r r ( 0 ) rövidítő jelöléseket, ( 9 ) és ( 0 ) szerint: (u) u u. ( ) A kis téglalap területe maximális, ha d (u) 0. ( ) du Elvégezve a deriválást: d (u) u u u 0; du u rendezve:
5 5 u u u 0. Innen: Rendezve: u u u 0. u u. Négyzetre emeléssel: u u. A bal oldalon elvégezve a kijelölt műveletet: 4 u 4 u 4 u. Rendezve: 4 8u 8 u u, majd a 4 8 u 7 u 0 u - ben másodfokú egyenletre jutunk. Megoldása gyökképlettel: u,, 8 6 innen u 0, u 0, ; r majd u 0, u 0, r Itt az u - kat csak pozitív előjellel vettük, mert a 3. ábra szerint ezt használtuk a területszámításhoz. Most el kell döntenünk, hogy a két u - érték közül melyik adhatja a feladatunk megoldását. A 3. ábra szerint a pozitív értelmezési tartományban maradva 0 x*, azaz 0 0, 707 r. Eszerint u adja a megoldást: u* 0,440 * 0,440 r. ( 3 ) Felfelé (! ) kerekítéssel: * 0,43 r. ( 4 ) Most ( 5 ) és ( 3 ) - mal:
6 6 * u * 0,985, r innen * 0,0 r. ( 5 ) Most ( 6 ), ( 4 ), ( 5 ) - tel: T * * * 0,43 r 0,0 r d d 0,43 0,0 0,43d0,0d. T * t jelöléssel, ( 6 ) szerint: A ( 6 ) t 0,43d 0,0 d. ( 7 ) Ezzel a tétel. részét is igazoltuk. Eddig beláttuk, hogy a helyzet az. ábra szerinti, amelynek megfelelően a legnagyobb kifűrészelhető keresztmetszeti terület: t t 4 t, ( 8 ) max így ( 4 ), ( 7 ) és ( 8 ) képletekkel kapjuk, hogy tmax t 4 t 0,707d 4 0, 43d 0,0 d, ( 9 ) a tétel állításának megfelelően. Ezzel a tételt teljesen igazoltuk. A maximális kihozatali százalék értékének meghatározása A ( 4 ) meghatározás és ( 9 ) szerint, felhasználva a T d ( 30 Ö 4 összefüggést is: 0,707 d 40,43d0,0 d t max K max 00 85,6%. T 0,785 d Megjegyezzük, hogy ezt pontosabban számolva mintegy 85% - ot kapunk.
7 7 Azt is érdemes megemlíteni, hogy a FSE egy geometriai természetű szélsőérték - számításon alapul, amely nincs tekintettel a felhasználók egyéb feltételekre alapozott igényeire. Ilyen egyéb feltétel lehet pl. az, hogy az ácsok által felhasznált építőfa / gerenda keresztmetszetének oldalarányára ajánlott érték az 5:7, stb. Ez azt is jelenti, hogy a FSE csak segédeszköz, nem pedig alapszabály! Az. ábra szerinti eredeti FSE kis átalakításával jutunk a módosított FSE - hez ld.: 4. ábra. 4. ábra Látható, hogy a rárajzolt területek aránya a teljes kör területéhez mindkét esetben ugyanaz, vagyis az elméleti mennyiségi kihozatali százalékok megegyeznek. Az FSE alkalmazásáról Az alábbi idézetet [ ] - ben olvashatjuk. A Feldmann Sapiro - féle vágáselmélet gyakorlati alkalmazása nem terjedt el a várt mértékben. Ennek oka, hogy a számítások túlságosan bonyolultak, hosszadalmasak, a termelés üteméhez képest lassúak. A számítás azonban tolótáblázatokkal gyorsítható. A több mint három évtizede leírt fenti sorok ma már nyilván nem időszerűek, hiszen a fűrészipari technológiák is erősen számítógépesítettek, vagy egyre inkább azok lesznek. Hogy az elv a faiparban nem teljesen haszontalan, azt az is jelzi, hogy ma is része a faipari szakképzés tananyagának, főként a technikus - képzésben. Bár a faipari mérnökök, ill. üzemmérnökök számára a számítások sosem lehettek túl nehezek és hosszadalmasak, az tény, hogy a mai matematika érettségi tananyag ismeretében nem
8 8 várható el, hogy a fenti levezetést a tanuló minden részletében megértse. Megjegyzendő, hogy a [ ] mű keletkezésének idején a szakközépiskolai matematika érettségi tananyaga tartalmazta az egyváltozós függvények szélsőérték számításának alapvető ismereteit e sorok írója is tanulta azokat, így aztán végképp nem világos, hogy az akkori technikusoknak vajon miért volt ez a levezetés és az eredmények alkalmazása túl nehéz. Talán mert nem publikálták? A levezetés ha a tanórán sor kerülne rá ma bizonyára másképpen történne. Ennek az lenne a lényege, hogy a szóban forgó területek maximumát más, a deriválás alkalmazását elkerülő módon állítanánk elő. Ennek egy - egy lehetséges módját alább részletezzük. A szélsőértékek elemi meghatározási módjáról Foglalkozzunk először a T terület - függvénnyel! Ennek szélsőérték - helyét a másodfokú egyenlet megoldásának ismereteire alapozva állítjuk elő ld. pl.: [ 3 ]. Fejezzük ki x - et T - gyel! ( 7 ) átalakítását részletezve: T x r x ; 4 négyzetre emelve: T x r x ; 4 kifejtve: T 4 r x x ; 4 rendezve: 4 T x r x 0. 4 Ez utóbbi egy másodfokú egyenlet, x - re. Megoldása a gyökképlettel: 4 T r r 4 4 x,. ( ) Tudjuk, hogy a T terület lehető legnagyobb értékét keressük. Minthogy azonban a ( ) egyenletben a négyzetgyök alatt nem állhat negatív szám, ezért T legfeljebb akkora lehet, hogy a gyök alatti mennyiség éppen 0 legyen: 4 T * r ( ) Most ( ) és ( ) képletekkel:
9 9 r r x * x*. ( $ ) Majd ( 6 ) és ( $ ) képletekkel: r r r y* r x * r x*, tehát y* r. ( $$) A legnagyobb terület: r r ( $$$ ) T * T (x*, y*) 4 x * y* 4 r. Ellenőrzés : ( ) szerint T * T * r T * r, egyezésben a ( $$$ ) eredménnyel. 4 Látjuk, hogy deriválás nélkül is megkaptuk az alapvető ( $ ) és ( $$), ill. a ( ) és ( ) eredményeket. Térjünk át most a T, ill. a τ területfüggvény szélsőértékének keresésére! Sajnos, az előbbi fogást itt nem tudjuk alkalmazni, mert olyan hiányos negyedfokú egyenletet kapunk, amely már nem redukálható másodfokúra. Itt azt a megkerülő manővert választhatjuk, hogy a ( ) képlettel leírt függvényt ábrázoljuk számítógéppel ez könnyen és gyorsan mehet, majd leolvassuk a legnagyobb függvényértékekhez ( a helyi szélső - értékekhez ) tartozó u és u értékeket, végül ezekkel a már leírt módon nyerjük az eredményeket. Zárszó A fentiekben pótoltuk a magyar faipari szakképzés egy évtizedek óta fennálló hiányosságát: részletesen levezettük a Feldmann ~ Sapiro - elvként ismert, egy bizonyos értelemben optimális fűrészpenge - elrendezési esetet leíró összefüggéseket. Ennek során az érdeklődő Olvasó képet alkothatott a szükséges számítások hosszadalmasságáról, bonyolultságáról, valamint ötleteket kaphatott az eredmények elemi úton történő előállításához. Fontosnak tartjuk, hogy a szakmailag értékes mozzanatok legyenek azok bármely kor és nép eredményei fennmaradjanak, és a következő generációk tudását gyarapítsák, szemléletét formálják. Úgy is fogalmazhatunk, hogy kár lenne kiönteni a fürdővízzel együtt a gyereket is.
10 0 Irodalomjegyzék: [ ] Bálint László: Faipari technológia I. Műszaki Könyvkiadó, Budapest, 983. [ ] Szerk. Lugosi Armand: Faipari Kézikönyv Műszaki Könyvkiadó, Budapest, 976. [ 3 ] Johannes Gabler: Mathematik und Leben, Band I. VEB Fachbuchverlag Leipzig, 966. Sződliget, 008. október 8. Összeállította: Galgóczi Gyula mérnöktanár
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 5 V ELEmI ALGEbRA 1 BINÁRIS műveletek Definíció Az halmazon definiált bináris művelet egy olyan függvény, amely -ből képez -be Ha akkor az elempár képét jelöljük -vel, a művelet
KOVÁCS BÉLA, MATEmATIkA I 5 V ELEmI ALGEbRA 1 BINÁRIS műveletek Definíció Az halmazon definiált bináris művelet egy olyan függvény, amely -ből képez -be Ha akkor az elempár képét jelöljük -vel, a művelet
MATEMATIKA. 5 8. évfolyam
 MATEMATIKA 5 8. évfolyam Célok és feladatok A matematikatanítás célja és ennek kapcsán feladata: megismertetni a tanulókat az őket körülvevő konkrét környezet mennyiségi és térbeli viszonyaival, megalapozni
MATEMATIKA 5 8. évfolyam Célok és feladatok A matematikatanítás célja és ennek kapcsán feladata: megismertetni a tanulókat az őket körülvevő konkrét környezet mennyiségi és térbeli viszonyaival, megalapozni
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika emelt szint 1613 ÉRETTSÉGI VIZSGA 016. május 3. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos tudnivalók Formai előírások:
Matematika emelt szint 1613 ÉRETTSÉGI VIZSGA 016. május 3. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos tudnivalók Formai előírások:
Az indukció. Azáltal, hogy ezt az összefüggést felírtuk, ezúttal nem bizonyítottuk, ez csak sejtés!
 Az indukció A logikában indukciónak nevezzük azt a következtetési módot, amelyek segítségével valamely osztályon belül az egyes esetekb l az általánosra következtetünk. Például: 0,, 804, 76, 48 mind oszthatóak
Az indukció A logikában indukciónak nevezzük azt a következtetési módot, amelyek segítségével valamely osztályon belül az egyes esetekb l az általánosra következtetünk. Például: 0,, 804, 76, 48 mind oszthatóak
MATEMATIKA TANTERV Bevezetés Összesen: 432 óra Célok és feladatok
 MATEMATIKA TANTERV Bevezetés A matematika tanítását minden szakmacsoportban és minden évfolyamon egységesen heti három órában tervezzük Az elsı évfolyamon mindhárom órát osztálybontásban tartjuk, segítve
MATEMATIKA TANTERV Bevezetés A matematika tanítását minden szakmacsoportban és minden évfolyamon egységesen heti három órában tervezzük Az elsı évfolyamon mindhárom órát osztálybontásban tartjuk, segítve
A hagyományos fa tartógerendák keresztmetszeti méreteinek arányairól
 Bevezetés A hagyományos fa tartógerenák keresztmetszeti méreteinek arányairól Az iők során figyelve az ács, ill. a fás szakmai tananyag alakulását, feltűnt, hogy bizonyos kérések nem, vagy csak alig kerülnek
Bevezetés A hagyományos fa tartógerenák keresztmetszeti méreteinek arányairól Az iők során figyelve az ács, ill. a fás szakmai tananyag alakulását, feltűnt, hogy bizonyos kérések nem, vagy csak alig kerülnek
MATEMATIKA ÉRETTSÉGI 2012. május 8. EMELT SZINT I.
 MATEMATIKA ÉRETTSÉGI 01. május 8. EMELT SZINT I. 1) Egy 011-ben készült statisztikai összehasonlításban az alábbiakat olvashatjuk: Ha New York-ban az átlagfizetést és az átlagos árszínvonalat egyaránt
MATEMATIKA ÉRETTSÉGI 01. május 8. EMELT SZINT I. 1) Egy 011-ben készült statisztikai összehasonlításban az alábbiakat olvashatjuk: Ha New York-ban az átlagfizetést és az átlagos árszínvonalat egyaránt
A távmunka és a távdolgozók jellemzői
 MAKROGAZDASÁGI HELYZETKÉP A távmunka és a távdolgozók jellemzői A távmunka képlékeny meghatározása arra enged következtetni, hogy elterjedtebb, mint általában gondolják. A cikk szerzői hat ország adatai
MAKROGAZDASÁGI HELYZETKÉP A távmunka és a távdolgozók jellemzői A távmunka képlékeny meghatározása arra enged következtetni, hogy elterjedtebb, mint általában gondolják. A cikk szerzői hat ország adatai
2. Halmazelmélet (megoldások)
 (megoldások) 1. A pozitív háromjegy páros számok halmaza. 2. Az olyan, 3-mal osztható egész számok halmaza, amelyek ( 100)-nál nagyobbak és 100-nál kisebbek. 3. Az olyan pozitív egész számok halmaza, amelyeknek
(megoldások) 1. A pozitív háromjegy páros számok halmaza. 2. Az olyan, 3-mal osztható egész számok halmaza, amelyek ( 100)-nál nagyobbak és 100-nál kisebbek. 3. Az olyan pozitív egész számok halmaza, amelyeknek
Analízisfeladat-gyűjtemény IV.
 Oktatási segédanyag a Programtervező matematikus szak Analízis. című tantárgyához (003 004. tanév tavaszi félév) Analízisfeladat-gyűjtemény IV. (Függvények határértéke és folytonossága) Összeállította
Oktatási segédanyag a Programtervező matematikus szak Analízis. című tantárgyához (003 004. tanév tavaszi félév) Analízisfeladat-gyűjtemény IV. (Függvények határértéke és folytonossága) Összeállította
Ady Endre Líceum Nagyvárad XII.C. Matematika Informatika szak ÉRINTVE A GÖRBÉT. Készítette: Szigeti Zsolt. Felkészítő tanár: Báthori Éva.
 Ady Endre Líceum Nagyvárad XII.C. Matematika Informatika szak ÉRINTVE A GÖRBÉT Készítette: Szigeti Zsolt Felkészítő tanár: Báthori Éva 2010 október Dolgozatom témája a különböző függvények, illetve mértani
Ady Endre Líceum Nagyvárad XII.C. Matematika Informatika szak ÉRINTVE A GÖRBÉT Készítette: Szigeti Zsolt Felkészítő tanár: Báthori Éva 2010 október Dolgozatom témája a különböző függvények, illetve mértani
Matematika tanmenet/4. osztály
 Comenius Angol-Magyar Két Tanítási Nyelvű Iskola 2015/2016. tanév Matematika tanmenet/4. osztály Tanító: Fürné Kiss Zsuzsanna és Varga Mariann Tankönyv: C. Neményi Eszter Wéber Anikó: Matematika 4. (Nemzeti
Comenius Angol-Magyar Két Tanítási Nyelvű Iskola 2015/2016. tanév Matematika tanmenet/4. osztály Tanító: Fürné Kiss Zsuzsanna és Varga Mariann Tankönyv: C. Neményi Eszter Wéber Anikó: Matematika 4. (Nemzeti
43. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ NYOLCADIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ
 43. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ NYOLCADIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ 1. Az apa, az anya és a három lányuk együtt 118 évesek. Az anya 10 évvel idősebb, mint a három lány együtt.
43. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ NYOLCADIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ 1. Az apa, az anya és a három lányuk együtt 118 évesek. Az anya 10 évvel idősebb, mint a három lány együtt.
Tető nem állandó hajlású szarufákkal
 1 Tető nem állandó hajlású szarufákkal Már korábbi dolgozatainkban is szó volt a címbeli témáról. Most azért vettük újra elő, mert szép és érdekes ábrákat találtunk az interneten, ezzel kapcsolatban, és
1 Tető nem állandó hajlású szarufákkal Már korábbi dolgozatainkban is szó volt a címbeli témáról. Most azért vettük újra elő, mert szép és érdekes ábrákat találtunk az interneten, ezzel kapcsolatban, és
Egy kétszeresen aszimmetrikus kontytető főbb geometriai adatainak meghatározásáról
 1 Egy kétszeresen aszimmetrikus kontytető főbb geometriai adatainak meghatározásáról Korábban már több egyszerűbb tető - alak geometriáját leírtuk. Most egy kicsit nehezebb feladat megoldását tűzzük ki
1 Egy kétszeresen aszimmetrikus kontytető főbb geometriai adatainak meghatározásáról Korábban már több egyszerűbb tető - alak geometriáját leírtuk. Most egy kicsit nehezebb feladat megoldását tűzzük ki
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 9 IX MÁTRIxOk 1 MÁTRIx FOGALmA, TULAJDONSÁGAI A mátrix egy téglalap alakú táblázat, melyben az adatok, a mátrix elemei, sorokban és oszlopokban vannak elhelyezve Az (1) mátrixnak
KOVÁCS BÉLA, MATEmATIkA I 9 IX MÁTRIxOk 1 MÁTRIx FOGALmA, TULAJDONSÁGAI A mátrix egy téglalap alakú táblázat, melyben az adatok, a mátrix elemei, sorokban és oszlopokban vannak elhelyezve Az (1) mátrixnak
Seite 1. Térfogatalakító eljárások. Zömítés. Térfogatalakító eljárások. Prof. Dr. Tisza Miklós Miskolci Egyetem
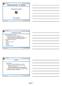 10. előad adás Térfogatalakító eljárások Prof. Dr. Tisza Miklós 1 Térfogatalakító eljárások A térfogatalakító eljárások definíciója olyan képlékenyalakító eljárások, amelyeknél» az alakváltozó zóna egy
10. előad adás Térfogatalakító eljárások Prof. Dr. Tisza Miklós 1 Térfogatalakító eljárások A térfogatalakító eljárások definíciója olyan képlékenyalakító eljárások, amelyeknél» az alakváltozó zóna egy
Miskolci Egyetem GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR. Analízis I. példatár. (kidolgozott megoldásokkal) elektronikus feladatgyűjtemény
 Miskolci Egyetem GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR Analízis I. példatár kidolgozott megoldásokkal) elektronikus feladatgyűjtemény Összeállította: Lengyelné Dr. Szilágyi Szilvia Miskolc, 013. Köszönetnyilvánítás
Miskolci Egyetem GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR Analízis I. példatár kidolgozott megoldásokkal) elektronikus feladatgyűjtemény Összeállította: Lengyelné Dr. Szilágyi Szilvia Miskolc, 013. Köszönetnyilvánítás
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika emelt szint 05 ÉRETTSÉGI VIZSGA 006. május 9. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI MINISZTÉRIUM Formai előírások: Fontos tudnivalók A dolgozatot
Matematika emelt szint 05 ÉRETTSÉGI VIZSGA 006. május 9. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI MINISZTÉRIUM Formai előírások: Fontos tudnivalók A dolgozatot
MATEMATIKA 1-12. ÉVFOLYAM
 MATEMATIKA 1-12. ÉVFOLYAM SZERZŐK: Veppert Károlyné, Ádám Imréné, Heibl Sándorné, Rimainé Sz. Julianna, Kelemen Ildikó, Antalfiné Kutyifa Zsuzsanna, Grószné Havasi Rózsa 1 1-2. ÉVFOLYAM Gondolkodási, megismerési
MATEMATIKA 1-12. ÉVFOLYAM SZERZŐK: Veppert Károlyné, Ádám Imréné, Heibl Sándorné, Rimainé Sz. Julianna, Kelemen Ildikó, Antalfiné Kutyifa Zsuzsanna, Grószné Havasi Rózsa 1 1-2. ÉVFOLYAM Gondolkodási, megismerési
BESZÁMOLÓ. a hajléktalanok átmeneti szállásainak körében végzett kutatásról. 2008. március
 BESZÁMOLÓ a hajléktalanok átmeneti szállásainak körében végzett kutatásról 2008. március A Hajléktalanokért Közalapítvány megbízásából készülő kutatás keretében a hajléktalan embereket ellátó intézmények
BESZÁMOLÓ a hajléktalanok átmeneti szállásainak körében végzett kutatásról 2008. március A Hajléktalanokért Közalapítvány megbízásából készülő kutatás keretében a hajléktalan embereket ellátó intézmények
HITELESÍTÉSI ELŐÍRÁS TARTÁLYOK
 HITELESÍTÉSI ELŐÍRÁS TARTÁLYOK GEOMETRIAI TARTÁLYHITELESÍTÉS HE 31/4-2000 TARTALOMJEGYZÉK 1. AZ ELŐÍRÁS HATÁLYA 2. MÉRTÉKEGYSÉGEK, JELÖLÉSEK 3. ALAPFOGALMAK 3.1 Tartályhitelesítés 3.2 Folyadékos (volumetrikus)
HITELESÍTÉSI ELŐÍRÁS TARTÁLYOK GEOMETRIAI TARTÁLYHITELESÍTÉS HE 31/4-2000 TARTALOMJEGYZÉK 1. AZ ELŐÍRÁS HATÁLYA 2. MÉRTÉKEGYSÉGEK, JELÖLÉSEK 3. ALAPFOGALMAK 3.1 Tartályhitelesítés 3.2 Folyadékos (volumetrikus)
E E E W. Előszó. Kifejtés
 Géptan HF - Előszó A fenti feladatot a http://wwwuni-miskolchu/~gtbweb/tantargyak/geptanfeladat04pdfa internet - címen találtam Alább megkísérlem megoldani A feladat összetett az egyes részek külön előadás
Géptan HF - Előszó A fenti feladatot a http://wwwuni-miskolchu/~gtbweb/tantargyak/geptanfeladat04pdfa internet - címen találtam Alább megkísérlem megoldani A feladat összetett az egyes részek külön előadás
LÁNG CSABÁNÉ SZÁMELMÉLET. Példák és feladatok. ELTE IK Budapest 2010-10-24 2. javított kiadás
 LÁNG CSABÁNÉ SZÁMELMÉLET Példák és feladatok ELTE IK Budapest 2010-10-24 2. javított kiadás Fels oktatási tankönyv Lektorálták: Kátai Imre Bui Minh Phong Burcsi Péter Farkas Gábor Fülöp Ágnes Germán László
LÁNG CSABÁNÉ SZÁMELMÉLET Példák és feladatok ELTE IK Budapest 2010-10-24 2. javított kiadás Fels oktatási tankönyv Lektorálták: Kátai Imre Bui Minh Phong Burcsi Péter Farkas Gábor Fülöp Ágnes Germán László
MATEMATIKA ÉRETTSÉGI 2006. május 9. EMELT SZINT
 ) A PQRS négyszög csúcsai: MATEMATIKA ÉRETTSÉGI 006. május 9. EMELT SZINT P 3; I., Q ;3, R 6; és S 5; 5 Döntse el, hogy az alábbi három állítás közül melyik igaz és melyik hamis! Tegyen * jelet a táblázat
) A PQRS négyszög csúcsai: MATEMATIKA ÉRETTSÉGI 006. május 9. EMELT SZINT P 3; I., Q ;3, R 6; és S 5; 5 Döntse el, hogy az alábbi három állítás közül melyik igaz és melyik hamis! Tegyen * jelet a táblázat
Sztojka Miroszláv LINEÁRIS ALGEBRA Egyetemi jegyzet Ungvár 2013
 UKRAJNA OKTATÁSI ÉS TUDOMÁNYÜGYI MINISZTÉRIUMA ÁLLAMI FELSŐOKTATÁSI INTÉZMÉNY UNGVÁRI NEMZETI EGYETEM MAGYAR TANNYELVŰ HUMÁN- ÉS TERMÉSZETTUDOMÁNYI KAR FIZIKA ÉS MATEMATIKA TANSZÉK Sztojka Miroszláv LINEÁRIS
UKRAJNA OKTATÁSI ÉS TUDOMÁNYÜGYI MINISZTÉRIUMA ÁLLAMI FELSŐOKTATÁSI INTÉZMÉNY UNGVÁRI NEMZETI EGYETEM MAGYAR TANNYELVŰ HUMÁN- ÉS TERMÉSZETTUDOMÁNYI KAR FIZIKA ÉS MATEMATIKA TANSZÉK Sztojka Miroszláv LINEÁRIS
ÍRÁSBELI KIVONÁS. 31. modul. Készítette: KONRÁD ÁGNES
 Matematika A 3. évfolyam ÍRÁSBELI KIVONÁS 31. modul Készítette: KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 31. modul ÍRÁSBELI KIVONÁS MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
Matematika A 3. évfolyam ÍRÁSBELI KIVONÁS 31. modul Készítette: KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 31. modul ÍRÁSBELI KIVONÁS MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
MATEMATIKA A és B variáció
 MATEMATIKA A és B variáció A Híd 2. programban olyan fiatalok vesznek részt, akik legalább elégséges érdemjegyet kaptak matematikából a hatodik évfolyam végén. Ezzel együtt az adatok azt mutatják, hogy
MATEMATIKA A és B variáció A Híd 2. programban olyan fiatalok vesznek részt, akik legalább elégséges érdemjegyet kaptak matematikából a hatodik évfolyam végén. Ezzel együtt az adatok azt mutatják, hogy
43. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ HETEDIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ
 43. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ HETEDIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ 1. Alfa tanár úr 5 tanulót vizsgáztatott matematikából. Az elért pontszámokat véletlen sorrendben írta
43. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ HETEDIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ 1. Alfa tanár úr 5 tanulót vizsgáztatott matematikából. Az elért pontszámokat véletlen sorrendben írta
TIMSS 2011. Tanári kérdőív Matematika. online. 8. évfolyam. Azonosító címke
 Azonosító címke TIMSS 2011 Tanári kérdőív Matematika online 8. évfolyam Oktatási Hivatal Közoktatási Mérési és Értékelési Osztály 1054 Budapest, Báthory u. 10. IEA, 2011 Tanári kérdőív Az Önök iskolája
Azonosító címke TIMSS 2011 Tanári kérdőív Matematika online 8. évfolyam Oktatási Hivatal Közoktatási Mérési és Értékelési Osztály 1054 Budapest, Báthory u. 10. IEA, 2011 Tanári kérdőív Az Önök iskolája
8. előadás EGYÉNI KERESLET
 8. előadás EGYÉNI KERESLET Kertesi Gábor Varian 6. fejezete, enyhe változtatásokkal 8. Bevezető megjegyzések Az elmúlt héten az optimális egyéni döntést elemeztük grafikus és algebrai eszközökkel: a preferenciatérkép
8. előadás EGYÉNI KERESLET Kertesi Gábor Varian 6. fejezete, enyhe változtatásokkal 8. Bevezető megjegyzések Az elmúlt héten az optimális egyéni döntést elemeztük grafikus és algebrai eszközökkel: a preferenciatérkép
DT9541. Környezeti hőmérséklet érzékelő. Kezelési útmutató
 Környezeti hőmérséklet érzékelő Kezelési útmutató Tartalomjegyzék 1. Kezelési útmutató...3 1.1. Rendeltetése... 3 1.2. Célcsoport... 3 1.3. Az alkalmazott szimbólumok... 3 2. Biztonsági útmutató...4 2.1.
Környezeti hőmérséklet érzékelő Kezelési útmutató Tartalomjegyzék 1. Kezelési útmutató...3 1.1. Rendeltetése... 3 1.2. Célcsoport... 3 1.3. Az alkalmazott szimbólumok... 3 2. Biztonsági útmutató...4 2.1.
4. A GYÁRTÁS ÉS GYÁRTÓRENDSZER TERVEZÉSÉNEK ÁLTALÁNOS MODELLJE (Dudás Illés)
 4. A GYÁRTÁS ÉS GYÁRTÓRENDSZER TERVEZÉSÉNEK ÁLTALÁNOS MODELLJE (Dudás Illés) ). A gyártás-előkészítés-irányítás funkcióit, alrendszereit egységbe foglaló (általános gyártási) modellt a 4.1. ábra szemlélteti.
4. A GYÁRTÁS ÉS GYÁRTÓRENDSZER TERVEZÉSÉNEK ÁLTALÁNOS MODELLJE (Dudás Illés) ). A gyártás-előkészítés-irányítás funkcióit, alrendszereit egységbe foglaló (általános gyártási) modellt a 4.1. ábra szemlélteti.
Élesmenetű csavar egyensúlya másként
 Élesmenetű csavar egyensúlya másként A szakirodalom ld pl: [ 1 ], [ 2 ], [ 3 ], [ 4 ], [ 5 ] tanulmányozása során feltűnt, hogy ~ leginkább a laposmenetű csavar erőjátékának vizsgálatát közlik, annak egyensúlyi
Élesmenetű csavar egyensúlya másként A szakirodalom ld pl: [ 1 ], [ 2 ], [ 3 ], [ 4 ], [ 5 ] tanulmányozása során feltűnt, hogy ~ leginkább a laposmenetű csavar erőjátékának vizsgálatát közlik, annak egyensúlyi
Gráfokkal megoldható hétköznapi problémák
 Eötvös Loránd Tudományegyetem Természettudományi Kar Gráfokkal megoldható hétköznapi problémák Szakdolgozat Készítette Vincze Ágnes Melitta Konzulens Héger Tamás Budapest, 2015 Tartalomjegyzék Bevezetés
Eötvös Loránd Tudományegyetem Természettudományi Kar Gráfokkal megoldható hétköznapi problémák Szakdolgozat Készítette Vincze Ágnes Melitta Konzulens Héger Tamás Budapest, 2015 Tartalomjegyzék Bevezetés
Tanmenetjavaslat 5. osztály
 Tanmenetjavaslat 5. osztály 1. A természetes számok A tanmenetjavaslatokban dőlt betűvel szedtük a tananyag legjellemzőbb részét (amelyet a naplóba írunk). Kisebb betűvel jelezzük a folyamatos ismétléssel
Tanmenetjavaslat 5. osztály 1. A természetes számok A tanmenetjavaslatokban dőlt betűvel szedtük a tananyag legjellemzőbb részét (amelyet a naplóba írunk). Kisebb betűvel jelezzük a folyamatos ismétléssel
Számelméleti feladatok az általános iskolai versenyek tükrében dr. Pintér Ferenc, Nagykanizsa
 Számelméleti feladatok az általános iskolai versenyek tükrében dr. Pintér Ferenc, Nagykanizsa 1. Mutasd meg, hogy a tízes számrendszerben felírt 111111111111 tizenhárom jegyű szám összetett szám, azaz
Számelméleti feladatok az általános iskolai versenyek tükrében dr. Pintér Ferenc, Nagykanizsa 1. Mutasd meg, hogy a tízes számrendszerben felírt 111111111111 tizenhárom jegyű szám összetett szám, azaz
A Közbeszerzési Döntőbizottság (a továbbiakban: Döntőbizottság) a Közbeszerzési Hatóság nevében meghozta az alábbi. H A T Á R O Z A T ot.
 Ikt.sz.: D.696/8/2014. KÖZBESZERZÉSI HATÓSÁG KÖZBESZERZÉSI DÖNTŐBIZOTTSÁG 1026 Budapest, Riadó u. 5. 1525 Pf.: 166. Tel.: 06-1/882-8594, fax: 06-1/882-8593 E-mail: [email protected] A Közbeszerzési
Ikt.sz.: D.696/8/2014. KÖZBESZERZÉSI HATÓSÁG KÖZBESZERZÉSI DÖNTŐBIZOTTSÁG 1026 Budapest, Riadó u. 5. 1525 Pf.: 166. Tel.: 06-1/882-8594, fax: 06-1/882-8593 E-mail: [email protected] A Közbeszerzési
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Kombinatorika
 Kombinatorika Modulok: A kombinatorikai feladatok megoldásához három modult használunk: Permutáció (Sorba rendezés) Kombináció (Kiválasztás) Variáció (Kiválasztás és sorba rendezés) DEFINÍCIÓ: (Ismétlés
Kombinatorika Modulok: A kombinatorikai feladatok megoldásához három modult használunk: Permutáció (Sorba rendezés) Kombináció (Kiválasztás) Variáció (Kiválasztás és sorba rendezés) DEFINÍCIÓ: (Ismétlés
közti kapcsolatok, Ellenőrzés, Játék 21. modul
 Matematika A 4. évfolyam MŰVELETi tulajdonságok, a műveletek közti kapcsolatok, Ellenőrzés, Játék 21. modul Készítette: KONRÁD ÁGNES matematika A 4. ÉVFOLYAM 21. modul Műveleti tulajdonságok, a műveletek
Matematika A 4. évfolyam MŰVELETi tulajdonságok, a műveletek közti kapcsolatok, Ellenőrzés, Játék 21. modul Készítette: KONRÁD ÁGNES matematika A 4. ÉVFOLYAM 21. modul Műveleti tulajdonságok, a műveletek
Kő, papír, olló és a snóbli
 Matematika C 3. évfolyam Kő, papír, olló és a snóbli 1. modul Készítette: Köves Gabriella Matematika C 3. évfolyam 1. modul kő, papír, olló és A snóbli MODULLEÍRÁS A modul célja Szabály megértése, követése,
Matematika C 3. évfolyam Kő, papír, olló és a snóbli 1. modul Készítette: Köves Gabriella Matematika C 3. évfolyam 1. modul kő, papír, olló és A snóbli MODULLEÍRÁS A modul célja Szabály megértése, követése,
ELŐTERJESZTÉS a KÉPVISELŐTESTÜLET 2012. május 17-i ülésére
 Budapest Főváros IX. Kerület Ferencváros Önkormányzata Iktató szám: 141/2012. ELŐTERJESZTÉS a KÉPVISELŐTESTÜLET 2012. május 17-i ülésére Tárgy: Előterjesztő: Készítette: Térfelügyeleti rendszer üzemeltetése
Budapest Főváros IX. Kerület Ferencváros Önkormányzata Iktató szám: 141/2012. ELŐTERJESZTÉS a KÉPVISELŐTESTÜLET 2012. május 17-i ülésére Tárgy: Előterjesztő: Készítette: Térfelügyeleti rendszer üzemeltetése
0653. MODUL TÖRTEK. Szorzás törttel, osztás törttel KÉSZÍTETTE: BENCZÉDY LACZKA KRISZTINA, MALMOS KATALIN
 06. MODUL TÖRTEK Szorzás törttel, osztás törttel KÉSZÍTETTE: BENCZÉDY LACZKA KRISZTINA, MALMOS KATALIN 06. Törtek Szorzás törttel, osztás törttel Tanári útmutató MODULLEÍRÁS A modul célja Időkeret Ajánlott
06. MODUL TÖRTEK Szorzás törttel, osztás törttel KÉSZÍTETTE: BENCZÉDY LACZKA KRISZTINA, MALMOS KATALIN 06. Törtek Szorzás törttel, osztás törttel Tanári útmutató MODULLEÍRÁS A modul célja Időkeret Ajánlott
Ügyszám: FVO-1848-16(2009) Ügyintéző: Jarabek Péter Telefon: 06-1-459-7719 Telefax: 06-1-459-7739 E-mail: [email protected]
 Ügyszám: FVO-1848-16(2009) Ügyintéző: Jarabek Péter Telefon: 06-1-459-7719 Telefax: 06-1-459-7739 E-mail: jarabekp@ehgovhu HATÁROZAT SZÁMA: 711/2009 Tárgy: EON Tiszántúli Áramhálózati Zrt (4024 Debrecen,
Ügyszám: FVO-1848-16(2009) Ügyintéző: Jarabek Péter Telefon: 06-1-459-7719 Telefax: 06-1-459-7739 E-mail: jarabekp@ehgovhu HATÁROZAT SZÁMA: 711/2009 Tárgy: EON Tiszántúli Áramhálózati Zrt (4024 Debrecen,
AZ ÉLELMISZERPIACI KUTATÓMUNKÁLATOK SZOCIÁLIS VONATKOZÁSAI ÍRTA:
 AZ ÉLELMISZERPIACI KUTATÓMUNKÁLATOK SZOCIÁLIS VONATKOZÁSAI ÍRTA: BENE LAJOS A PIACKUTATÁS MUNKAKÖRE. Az emberi haladás jellemző sajátsága, hogy a jólétét egészen közvetlenül érintő kérdésekre legkésőbben
AZ ÉLELMISZERPIACI KUTATÓMUNKÁLATOK SZOCIÁLIS VONATKOZÁSAI ÍRTA: BENE LAJOS A PIACKUTATÁS MUNKAKÖRE. Az emberi haladás jellemző sajátsága, hogy a jólétét egészen közvetlenül érintő kérdésekre legkésőbben
ELLENŐRZÉSI JELENTÉS
 ELLENŐRZÉSI JELENTÉS Az Európai Uniós pályázatok vizsgálata A vizsgálatot végezte: Az ellenőrzött szervezeti egység: Fővárosi Bíróság Belső Ellenőrzési Osztály Fővárosi Bíróság Gazdasági Hivatala Hivatkozási
ELLENŐRZÉSI JELENTÉS Az Európai Uniós pályázatok vizsgálata A vizsgálatot végezte: Az ellenőrzött szervezeti egység: Fővárosi Bíróság Belső Ellenőrzési Osztály Fővárosi Bíróság Gazdasági Hivatala Hivatkozási
A rögzített tengely körül forgó testek kiegyensúlyozottságáról kezdőknek
 A rögzített tengely körül forgó tetek kiegyenúlyozottágáról kezdőknek Bevezeté A faiparban nagyon ok forgó mozgát végző gépelem, zerzám haználato, melyek rende működéének feltétele azok kiegyenúlyozottága.
A rögzített tengely körül forgó tetek kiegyenúlyozottágáról kezdőknek Bevezeté A faiparban nagyon ok forgó mozgát végző gépelem, zerzám haználato, melyek rende működéének feltétele azok kiegyenúlyozottága.
BARANYA MEGYEI TANULÓK TUDÁSSTRUKTÚRÁI. Takács Viola
 BARANYA MEGYEI TANULÓK TUDÁSSTRUKTÚRÁI Takács Viola Iskolakultúra könyvek 20. Sorozatszerkesztõ: Géczi János Szerkesztõ: Sz. Molnár Szilvia BARANYA MEGYEI TANULÓK TUDÁSSTRUKTÚRÁI TAKÁCS VIOLA iskolakultúra
BARANYA MEGYEI TANULÓK TUDÁSSTRUKTÚRÁI Takács Viola Iskolakultúra könyvek 20. Sorozatszerkesztõ: Géczi János Szerkesztõ: Sz. Molnár Szilvia BARANYA MEGYEI TANULÓK TUDÁSSTRUKTÚRÁI TAKÁCS VIOLA iskolakultúra
4. modul Poliéderek felszíne, térfogata
 Matematika A 1. évfolyam 4. modul Poliéderek felszíne, térfogata Készítette: Vidra Gábor Matematika A 1. évfolyam 4. modul: POLIÉDEREK FELSZÍNE, TÉRFOGATA Tanári útmutató A modul célja Időkeret Ajánlott
Matematika A 1. évfolyam 4. modul Poliéderek felszíne, térfogata Készítette: Vidra Gábor Matematika A 1. évfolyam 4. modul: POLIÉDEREK FELSZÍNE, TÉRFOGATA Tanári útmutató A modul célja Időkeret Ajánlott
Pap Nárcisz 1 Pap János 2 A termésbecslés és terméselemzés jelentősége a precíziós kukoricatermesztésben
 Pap Nárcisz 1 Pap János 2 A termésbecslés és terméselemzés jelentősége a precíziós kukoricatermesztésben The importance of yield estimation and yield analysis in precision corn production [email protected]
Pap Nárcisz 1 Pap János 2 A termésbecslés és terméselemzés jelentősége a precíziós kukoricatermesztésben The importance of yield estimation and yield analysis in precision corn production [email protected]
Bánhalmi Árpád * Bakos Viktor ** MIÉRT BUKNAK MEG STATISZTIKÁBÓL A JÓ MATEKOSOK?
 Bánhalmi Árpád * Bakos Viktor ** MIÉRT BUKNAK MEG STATISZTIKÁBÓL A JÓ MATEKOSOK? A BGF KKFK Nemzetközi gazdálkodás és Kereskedelem és marketing szakjain a hallgatók tanrendjében statisztikai és matematikai
Bánhalmi Árpád * Bakos Viktor ** MIÉRT BUKNAK MEG STATISZTIKÁBÓL A JÓ MATEKOSOK? A BGF KKFK Nemzetközi gazdálkodás és Kereskedelem és marketing szakjain a hallgatók tanrendjében statisztikai és matematikai
PÁLYÁZAT. Program neve: Támogatás szakmai iránya: Program kódja:
 PÁLYÁZAT Program neve: Támogatás szakmai iránya: Program kódja: Megvalósítandó cél: Kedvezményezettek Környezet és Energia Operatív Program Épületenergetikai fejlesztések megújuló energiaforrás hasznosítással
PÁLYÁZAT Program neve: Támogatás szakmai iránya: Program kódja: Megvalósítandó cél: Kedvezményezettek Környezet és Energia Operatív Program Épületenergetikai fejlesztések megújuló energiaforrás hasznosítással
3. Konzultáció: Kondenzátorok, tekercsek, RC és RL tagok, bekapcsolási jelenségek (még nagyon Béta-verzió)
 3. Konzultáció: Kondenzátorok, tekercsek, R és RL tagok, bekapcsolási jelenségek (még nagyon Béta-verzió Zoli 2009. október 28. 1 Tartalomjegyzék 1. Frekvenciafüggő elemek, kondenzátorok és tekercsek:
3. Konzultáció: Kondenzátorok, tekercsek, R és RL tagok, bekapcsolási jelenségek (még nagyon Béta-verzió Zoli 2009. október 28. 1 Tartalomjegyzék 1. Frekvenciafüggő elemek, kondenzátorok és tekercsek:
Ellipszis átszelése. 1. ábra
 1 Ellipszis átszelése Adott egy a és b féltengely - adatokkal bíró ellipszis, melyet a befoglaló téglalapjának bal alsó sarkában csuklósan rögzítettnek képzelünk. Az ellipszist e C csukló körül forgatva
1 Ellipszis átszelése Adott egy a és b féltengely - adatokkal bíró ellipszis, melyet a befoglaló téglalapjának bal alsó sarkában csuklósan rögzítettnek képzelünk. Az ellipszist e C csukló körül forgatva
Újdonságok az extruderszerszámok kialakításában
 A MÛANYAGOK FELDOLGOZÁSA 3.3 3.16 3.17 Újdonságok az extruderszerszámok kialakításában Tárgyszavak: extrudálás; extruderszerszám; profil; lemez; cső; műanyag betét; ömledéktörés; szerszámtervezés; matematikai
A MÛANYAGOK FELDOLGOZÁSA 3.3 3.16 3.17 Újdonságok az extruderszerszámok kialakításában Tárgyszavak: extrudálás; extruderszerszám; profil; lemez; cső; műanyag betét; ömledéktörés; szerszámtervezés; matematikai
Bevezetés és gyakorlati tanácsok Az első lépés minden tudomány elsajátítása felé az, hogy megértjük az alapjait, és megbízható tudást szerzünk
 Bevezetés és gyakorlati tanácsok Az első lépés minden tudomány elsajátítása felé az, hogy megértjük az alapjait, és megbízható tudást szerzünk belőle. A következő az, hogy a megszerzett tudást elmélyítjük.
Bevezetés és gyakorlati tanácsok Az első lépés minden tudomány elsajátítása felé az, hogy megértjük az alapjait, és megbízható tudást szerzünk belőle. A következő az, hogy a megszerzett tudást elmélyítjük.
4. sz. Füzet. A hibafa számszerű kiértékelése 2002.
 M Ű S Z A K I B I Z O N S Á G I F Ő F E L Ü G Y E L E 4. sz. Füzet A hibafa számszerű kiértékelése 00. Sem a Műszaki Biztonsági Főfelügyelet, sem annak nevében, képviseletében vagy részéről eljáró személy
M Ű S Z A K I B I Z O N S Á G I F Ő F E L Ü G Y E L E 4. sz. Füzet A hibafa számszerű kiértékelése 00. Sem a Műszaki Biztonsági Főfelügyelet, sem annak nevében, képviseletében vagy részéről eljáró személy
10.3. A MÁSODFOKÚ EGYENLET
 .. A MÁSODFOKÚ EGYENLET A másodfokú egenlet és függvén megoldások w9 a) ( ) + ; b) ( ) + ; c) ( + ) ; d) ( 6) ; e) ( + 8) 6; f) ( ) 9; g) (,),; h) ( +,),; i) ( ) + ; j) ( ) ; k) ( + ) + 7; l) ( ) + 9.
.. A MÁSODFOKÚ EGYENLET A másodfokú egenlet és függvén megoldások w9 a) ( ) + ; b) ( ) + ; c) ( + ) ; d) ( 6) ; e) ( + 8) 6; f) ( ) 9; g) (,),; h) ( +,),; i) ( ) + ; j) ( ) ; k) ( + ) + 7; l) ( ) + 9.
KÖZBESZERZÉSI DOKUMENTUMOK
 DEPÓNIA Hulladékkezelő és Településtisztasági Nonprofit Korlátolt Felelősségű Társaság 8000 Székesfehérvár, Sörház tér 3. KÖZBESZERZÉSI DOKUMENTUMOK Tolólapos kompaktor beszerzése adásvételi szerződés
DEPÓNIA Hulladékkezelő és Településtisztasági Nonprofit Korlátolt Felelősségű Társaság 8000 Székesfehérvár, Sörház tér 3. KÖZBESZERZÉSI DOKUMENTUMOK Tolólapos kompaktor beszerzése adásvételi szerződés
2.3.2.2.1.2.1 Visszatérítő nyomaték és visszatérítő kar
 2.3.2.2.1.2 Keresztirányú stabilitás nagy dőlésszögeknél A keresztirányú stabilitás számszerűsítésénél, amint korábban láttuk, korlátozott a metacentrikus magasságra való támaszkodás lehetősége. Csak olyankor
2.3.2.2.1.2 Keresztirányú stabilitás nagy dőlésszögeknél A keresztirányú stabilitás számszerűsítésénél, amint korábban láttuk, korlátozott a metacentrikus magasságra való támaszkodás lehetősége. Csak olyankor
FOGYASZTÓ ELÉGEDETTSÉGI FELMÉRÉS A FŐTÁV ZRT. SZÁMÁRA 2012.
 FOGYASZTÓ ELÉGEDETTSÉGI FELMÉRÉS A FŐTÁV ZRT. SZÁMÁRA 2012. 2 Szerkesztette: Dr. Ács Ferenc A munkában részt vevők: Dr. Ács Ferenc Dr. Sárkány Péterné A mű szerzői jogilag védett. A M.Á.S.T. Kft. és a
FOGYASZTÓ ELÉGEDETTSÉGI FELMÉRÉS A FŐTÁV ZRT. SZÁMÁRA 2012. 2 Szerkesztette: Dr. Ács Ferenc A munkában részt vevők: Dr. Ács Ferenc Dr. Sárkány Péterné A mű szerzői jogilag védett. A M.Á.S.T. Kft. és a
összeadás, kivonás 9-ig
 Matematika A 1. évfolyam összeadás, kivonás 9-ig 27. modul Készítették: Bóta Mária Kőkúti Ágnes matematika A 1. ÉVFOLYAM 27. modul összeadás, kivonás 9-ig modulleírás A modul célja Időkeret Ajánlott korosztály
Matematika A 1. évfolyam összeadás, kivonás 9-ig 27. modul Készítették: Bóta Mária Kőkúti Ágnes matematika A 1. ÉVFOLYAM 27. modul összeadás, kivonás 9-ig modulleírás A modul célja Időkeret Ajánlott korosztály
Kosztolányi József Kovács István Pintér Klára Urbán János Vincze István. tankönyv. Mozaik Kiadó Szeged, 2013
 Kosztolányi József Kovács István Pintér Klára Urbán János Vincze István tankönyv 0 Mozaik Kiadó Szeged, 03 TARTALOMJEGYZÉK Gondolkodási módszerek. Mi következik ebbõl?... 0. A skatulyaelv... 3. Sorba rendezési
Kosztolányi József Kovács István Pintér Klára Urbán János Vincze István tankönyv 0 Mozaik Kiadó Szeged, 03 TARTALOMJEGYZÉK Gondolkodási módszerek. Mi következik ebbõl?... 0. A skatulyaelv... 3. Sorba rendezési
Algebrai és transzcendens számok
 MATEMATIKA Szakköri füzet Algebrai és transzcenens számok Készítette: Klement Anrás 00 SZAKKÖRI FÜZET Algebrai és transzcenens számok Bevezetés A szakköri füzetben áttekintjük a számhalmazokat és új szempont
MATEMATIKA Szakköri füzet Algebrai és transzcenens számok Készítette: Klement Anrás 00 SZAKKÖRI FÜZET Algebrai és transzcenens számok Bevezetés A szakköri füzetben áttekintjük a számhalmazokat és új szempont
54 544 01 0010 54 02 Külszíni bányaipari technikus Bányaipari technikus 54 544 01 0010 54 03 Mélyművelési bányaipari Bányaipari technikus
 A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
Szimplex módszer, szimplex tábla Példaként tekintsük a következ LP feladatot:
 Szimplex módszer, szimplex tábla Példaként tekintsük a következ LP feladatot: z = 5x 1 + 4x 2 + 3x 3 2x 1 + 3x 2 + x 3 5 4x 1 + x 2 + 2x 3 11 3x 1 + 4x 2 + 2x 3 8 x 1, x 2, x 3 0 = maximum, feltéve, hogy
Szimplex módszer, szimplex tábla Példaként tekintsük a következ LP feladatot: z = 5x 1 + 4x 2 + 3x 3 2x 1 + 3x 2 + x 3 5 4x 1 + x 2 + 2x 3 11 3x 1 + 4x 2 + 2x 3 8 x 1, x 2, x 3 0 = maximum, feltéve, hogy
5. Trigonometria. 2 cos 40 cos 20 sin 20. BC kifejezés pontos értéke?
 5. Trigonometria I. Feladatok 1. Mutassuk meg, hogy cos 0 cos 0 sin 0 3. KöMaL 010/október; C. 108.. Az ABC háromszög belsejében lévő P pontra PAB PBC PCA φ. Mutassuk meg, hogy ha a háromszög szögei α,
5. Trigonometria I. Feladatok 1. Mutassuk meg, hogy cos 0 cos 0 sin 0 3. KöMaL 010/október; C. 108.. Az ABC háromszög belsejében lévő P pontra PAB PBC PCA φ. Mutassuk meg, hogy ha a háromszög szögei α,
Szekeres Bernadett * A MAGYAR ÉS A NÉMET KÖNYVVIZSGÁLÓI KAMARA MINİSÉG-ELLENİRZÉSI SZABÁLYZATÁNAK ÖSSZEHASONLÍTÓ ELEMZÉSE
 Szekeres Bernadett * A MAGYAR ÉS A NÉMET KÖNYVVIZSGÁLÓI KAMARA MINİSÉG-ELLENİRZÉSI SZABÁLYZATÁNAK ÖSSZEHASONLÍTÓ ELEMZÉSE BEVEZETÉS A könyvvizsgálati munka minıségbiztosításának folyamatos fejlıdését napjainkban
Szekeres Bernadett * A MAGYAR ÉS A NÉMET KÖNYVVIZSGÁLÓI KAMARA MINİSÉG-ELLENİRZÉSI SZABÁLYZATÁNAK ÖSSZEHASONLÍTÓ ELEMZÉSE BEVEZETÉS A könyvvizsgálati munka minıségbiztosításának folyamatos fejlıdését napjainkban
A.26. Hagyományos és korszerű tervezési eljárások
 A.26. Hagyományos és korszerű tervezési eljárások A.26.1. Hagyományos tervezési eljárások A.26.1.1. Csuklós és merev kapcsolatú keretek tervezése Napjainkig a magasépítési tartószerkezetek tervezése a
A.26. Hagyományos és korszerű tervezési eljárások A.26.1. Hagyományos tervezési eljárások A.26.1.1. Csuklós és merev kapcsolatú keretek tervezése Napjainkig a magasépítési tartószerkezetek tervezése a
5. Mérés Transzformátorok
 5. Mérés Transzformátorok A transzformátor a váltakozó áramú villamos energia, feszültség, ill. áram értékeinek megváltoztatására (transzformálására) alkalmas villamos gép... Működési elv A villamos energia
5. Mérés Transzformátorok A transzformátor a váltakozó áramú villamos energia, feszültség, ill. áram értékeinek megváltoztatására (transzformálására) alkalmas villamos gép... Működési elv A villamos energia
A beszerzési logisztikai folyamat tervezésének és működtetésének stratégiái II.
 A beszerzési logisztikai folyamat tervezésének és működtetésének stratégiái II. Prof. Dr. Cselényi József Dr. Illés Béla PhD. egyetemi tanár tanszékvezető egyetemi docens MISKOLCI EGYETEM Anyagmozgatási
A beszerzési logisztikai folyamat tervezésének és működtetésének stratégiái II. Prof. Dr. Cselényi József Dr. Illés Béla PhD. egyetemi tanár tanszékvezető egyetemi docens MISKOLCI EGYETEM Anyagmozgatási
EGYENLŐ BÁNÁSMÓD HATÓSÁG Elnök
 EGYENLŐ BÁNÁSMÓD HATÓSÁG Elnök Ügyiratszám: EBH/ / /2009 Ügyintéző: dr. Kegye Adél Az Egyenlő Bánásmód Hatóság (1024 Budapest, Margit krt. 85.) Dr. X.Y (továbbiakban, mint Kérelmező) által az egyenlő bánásmód
EGYENLŐ BÁNÁSMÓD HATÓSÁG Elnök Ügyiratszám: EBH/ / /2009 Ügyintéző: dr. Kegye Adél Az Egyenlő Bánásmód Hatóság (1024 Budapest, Margit krt. 85.) Dr. X.Y (továbbiakban, mint Kérelmező) által az egyenlő bánásmód
A SZENT ISTVÁN EGYETEM. T a n á c s á n a k. 16/2002/2003.ET. számú
 A SZENT ISTVÁN EGYETEM T a n á c s á n a k 16/2002/2003.ET. számú h a t á r o z a t a a Rendészeti és Vagyonvédelmi Szabályzatról 1 I. A RENDÉSZETI ÉS VAGYONVÉDELMI TEVÉKENYSÉG CÉLJA A vagyonvédelmi és
A SZENT ISTVÁN EGYETEM T a n á c s á n a k 16/2002/2003.ET. számú h a t á r o z a t a a Rendészeti és Vagyonvédelmi Szabályzatról 1 I. A RENDÉSZETI ÉS VAGYONVÉDELMI TEVÉKENYSÉG CÉLJA A vagyonvédelmi és
A szőlőtermesztés és borkészítés számviteli sajátosságai
 A szőlőtermesztés és borkészítés számviteli sajátosságai KÁNTOR Béla, TÓTH Zsuzsanna Miskolci Egyetem, Gazdaságtudományi Kar, Miskolc [email protected], [email protected] A borkészítésnek Magyarországon
A szőlőtermesztés és borkészítés számviteli sajátosságai KÁNTOR Béla, TÓTH Zsuzsanna Miskolci Egyetem, Gazdaságtudományi Kar, Miskolc [email protected], [email protected] A borkészítésnek Magyarországon
TARTALOM. Ismétlő tesztek...248 ÚTMUTATÁSOK ÉS EREDMÉNYEK...255
 TARTALOM. SZÁMHALMAZOK...5.. Természetes kitevőjű hatványok...5.. Negatív egész kitevőjű hatványok...6.. Racionális kitevőjű hatványok...7.4. Irracionális kitevőjű hatványok...0.5. Négyzetgyök és köbgyök...
TARTALOM. SZÁMHALMAZOK...5.. Természetes kitevőjű hatványok...5.. Negatív egész kitevőjű hatványok...6.. Racionális kitevőjű hatványok...7.4. Irracionális kitevőjű hatványok...0.5. Négyzetgyök és köbgyök...
A.11. Nyomott rudak. A.11.1. Bevezetés
 A.. Nyomott rudak A... Bevezetés A nyomott szerkezeti elem fogalmat általában olyan szerkezeti elemek jelölésére használjuk, amelyekre csak tengelyirányú nyomóerő hat. Ez lehet speciális terhelésű oszlop,
A.. Nyomott rudak A... Bevezetés A nyomott szerkezeti elem fogalmat általában olyan szerkezeti elemek jelölésére használjuk, amelyekre csak tengelyirányú nyomóerő hat. Ez lehet speciális terhelésű oszlop,
HIRDETMÉNY. Az FHB JELZÁLOGBANK NYRT. hivatalos tájékoztatója a forintosítással érintett lakossági jelzáloghitelek esetén alkalmazott kondíciókról
 HIRDETMÉNY Lakossági Jelzáloghitel Hirdetmény Az FHB JELZÁLOGBANK NYRT. hivatalos tájékoztatója a forintosítással érintett lakossági jelzáloghitelek alkalmazott kondíciókról Közzététel napja: 2016. április
HIRDETMÉNY Lakossági Jelzáloghitel Hirdetmény Az FHB JELZÁLOGBANK NYRT. hivatalos tájékoztatója a forintosítással érintett lakossági jelzáloghitelek alkalmazott kondíciókról Közzététel napja: 2016. április
Keresztmetszeti megmunkálás egyengető-, vastagoló-, és kombinált gyalugépekkel
 Pagonyné Mezősi Marietta Keresztmetszeti megmunkálás egyengető-, vastagoló-, és kombinált gyalugépekkel A követelménymodul megnevezése: Alapvető tömörfa megmunkálási feladatok A követelménymodul száma:
Pagonyné Mezősi Marietta Keresztmetszeti megmunkálás egyengető-, vastagoló-, és kombinált gyalugépekkel A követelménymodul megnevezése: Alapvető tömörfa megmunkálási feladatok A követelménymodul száma:
BESZÁMOLÓ. a hajléktalan emberek számára fenntartott, nappali ellátást nyújtó intézmények körében végzett kutatásról. 2008.
 BESZÁMOLÓ a hajléktalan emberek számára fenntartott, nappali ellátást nyújtó intézmények körében végzett kutatásról 2008. március A Hajléktalanokért Közalapítvány megbízásából készülő kutatás keretében
BESZÁMOLÓ a hajléktalan emberek számára fenntartott, nappali ellátást nyújtó intézmények körében végzett kutatásról 2008. március A Hajléktalanokért Közalapítvány megbízásából készülő kutatás keretében
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika emelt szint 0613 ÉRETTSÉGI VIZSGA 007. május 8. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Formai előírások: Fontos tudnivalók
Matematika emelt szint 0613 ÉRETTSÉGI VIZSGA 007. május 8. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Formai előírások: Fontos tudnivalók
ÍRÁSBELI SZORZÁS ELŐKÉSZÍTÉSE; TÖBBTAGÚ ÖSSZEADÁSOK, TÖBBSZÖRÖZÉSEK. 37. modul
 Matematika A 3. évfolyam ÍRÁSBELI SZORZÁS ELŐKÉSZÍTÉSE; TÖBBTAGÚ ÖSSZEADÁSOK, TÖBBSZÖRÖZÉSEK 37. modul Készítette: KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 37. modul ÍRÁSBELI SZORZÁS ELŐKÉSZÍTÉSE; TÖBBTAGÚ
Matematika A 3. évfolyam ÍRÁSBELI SZORZÁS ELŐKÉSZÍTÉSE; TÖBBTAGÚ ÖSSZEADÁSOK, TÖBBSZÖRÖZÉSEK 37. modul Készítette: KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 37. modul ÍRÁSBELI SZORZÁS ELŐKÉSZÍTÉSE; TÖBBTAGÚ
H A T Á R O Z A T. Szám: 36610/2070-3/2015.ált. Tárgy:
 Szám: 36610/2070-3/2015.ált. Tárgy: A MODIVI-Aqua Korlátolt Felelősségű Társaság terhére bírság kiszabása a veszélyes áruk közúti szállításra vonatkozó rendelkezések megsértése miatt H A T Á R O Z A T
Szám: 36610/2070-3/2015.ált. Tárgy: A MODIVI-Aqua Korlátolt Felelősségű Társaság terhére bírság kiszabása a veszélyes áruk közúti szállításra vonatkozó rendelkezések megsértése miatt H A T Á R O Z A T
EPERJES KRISZTIÁN HAUTZINGER ZOLTÁN A KATONAI RENDÉSZET. 1. Bevezetı gondolatok
 EPERJES KRISZTIÁN HAUTZINGER ZOLTÁN A KATONAI RENDÉSZET 1. Bevezetı gondolatok Senki nem szólt, és Fleur de Bac indítványt tett, hogy a legerısebb katonák, az ırvezetıvel az élükön alapítsanak tábori csendırséget,
EPERJES KRISZTIÁN HAUTZINGER ZOLTÁN A KATONAI RENDÉSZET 1. Bevezetı gondolatok Senki nem szólt, és Fleur de Bac indítványt tett, hogy a legerısebb katonák, az ırvezetıvel az élükön alapítsanak tábori csendırséget,
ALAPFOKÚ HIDRAULIKA LABORATÓRIUMI GYAKORLATOK
 ALAPFOKÚ HIDRAULIKA LABORATÓRIUMI GYAKORLATOK (Hallgatói példány) 1. KÖZVETLEN VEZÉRLÉS ÉS EL VEZÉRELT NYOMÁSIRÁNYÍTÓK JELLEGGÖRBÉI, SZELEPÁLLANDÓ MEGHATÁROZÁSA MÉRÉSSEL 2. FOJTÓ ÉS TÉRFOGATÁRAM-IRÁNYÍTÓ
ALAPFOKÚ HIDRAULIKA LABORATÓRIUMI GYAKORLATOK (Hallgatói példány) 1. KÖZVETLEN VEZÉRLÉS ÉS EL VEZÉRELT NYOMÁSIRÁNYÍTÓK JELLEGGÖRBÉI, SZELEPÁLLANDÓ MEGHATÁROZÁSA MÉRÉSSEL 2. FOJTÓ ÉS TÉRFOGATÁRAM-IRÁNYÍTÓ
LINEÁRIS ALGEBRA PÉLDATÁR MÉRNÖK INFORMATIKUSOKNAK
 Írta: LEITOLD ADRIEN LINEÁRIS ALGEBRA PÉLDATÁR MÉRNÖK INFORMATIKUSOKNAK Egyetemi tananyag COPYRIGHT: Dr. Leitold Adrien Pannon Egyetem Műszaki Informatika Kar Matematika Tanszék LEKTORÁLTA: Dr. Buzáné
Írta: LEITOLD ADRIEN LINEÁRIS ALGEBRA PÉLDATÁR MÉRNÖK INFORMATIKUSOKNAK Egyetemi tananyag COPYRIGHT: Dr. Leitold Adrien Pannon Egyetem Műszaki Informatika Kar Matematika Tanszék LEKTORÁLTA: Dr. Buzáné
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 11 XI LINEÁRIS EGYENLETRENDSZEREk 1 LINEÁRIS EGYENLETRENDSZER A lineáris egyenletrendszer általános alakja: (1) Ugyanez mátrix alakban: (2), ahol x az ismeretleneket tartalmazó
KOVÁCS BÉLA, MATEmATIkA I 11 XI LINEÁRIS EGYENLETRENDSZEREk 1 LINEÁRIS EGYENLETRENDSZER A lineáris egyenletrendszer általános alakja: (1) Ugyanez mátrix alakban: (2), ahol x az ismeretleneket tartalmazó
NYUGAT-MAGYARORSZÁGI EGYETEM Faipari Mérnöki Kar. Mőszaki Mechanika és Tartószerkezetek Intézet. Dr. Hajdu Endre egyetemi docens MECHANIKA I.
 NYUGAT-MAGYARORSZÁGI EGYETEM aipari Mérnöki Kar Mőszaki Mechanika és Tartószerkezetek Intézet Dr Hajdu Endre egyetemi docens MECHANIKA I Sopron 9 javított kiadás TARTALOMJEGYZÉK I Bevezetés a mőszaki mechanika
NYUGAT-MAGYARORSZÁGI EGYETEM aipari Mérnöki Kar Mőszaki Mechanika és Tartószerkezetek Intézet Dr Hajdu Endre egyetemi docens MECHANIKA I Sopron 9 javított kiadás TARTALOMJEGYZÉK I Bevezetés a mőszaki mechanika
Matematika A 1. évfolyam. páros, páratlan. 22. modul. Készítették: Szabóné Vajna Kinga Harzáné Kälbli Éva Molnár Éva
 Matematika A 1. évfolyam páros, páratlan 22. modul Készítették: Szabóné Vajna Kinga Harzáné Kälbli Éva Molnár Éva matematika A 1. ÉVFOLYAM 22. modul Páros, páratlan modulleírás A modul célja Időkeret Ajánlott
Matematika A 1. évfolyam páros, páratlan 22. modul Készítették: Szabóné Vajna Kinga Harzáné Kälbli Éva Molnár Éva matematika A 1. ÉVFOLYAM 22. modul Páros, páratlan modulleírás A modul célja Időkeret Ajánlott
PÁLYÁZATI FELHÍVÁS a Társadalmi Megújulás Operatív Program keretében
 PÁLYÁZATI FELHÍVÁS a Társadalmi Megújulás Operatív Program keretében Egészségre nevelő és szemléletformáló életmódprogramok a leghátrányosabb helyzetű kistérségekben Kódszám: TÁMOP-6.1.2/LHH/11/A Tartalom
PÁLYÁZATI FELHÍVÁS a Társadalmi Megújulás Operatív Program keretében Egészségre nevelő és szemléletformáló életmódprogramok a leghátrányosabb helyzetű kistérségekben Kódszám: TÁMOP-6.1.2/LHH/11/A Tartalom
2.3. A rendez pályaudvarok és rendez állomások vonat-összeállítási tervének kidolgozása...35 2.3.1. A vonatközlekedési terv modellje...37 2.3.2.
 TARTALOMJEGYZÉK BEVEZETÉS...5 1. ÁRU ÉS KOCSIÁRAMLATOK TERVEZÉSE...6 1.1. A vonatközlekedési terv fogalma, jelent sége és kidolgozásának fontosabb elvei...6 1.2. A kocsiáramlatok és osztályozásuk...7 1.2.1.
TARTALOMJEGYZÉK BEVEZETÉS...5 1. ÁRU ÉS KOCSIÁRAMLATOK TERVEZÉSE...6 1.1. A vonatközlekedési terv fogalma, jelent sége és kidolgozásának fontosabb elvei...6 1.2. A kocsiáramlatok és osztályozásuk...7 1.2.1.
Általános statisztika II. Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László
 Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Publication
Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Publication
Szabad a vásár! múzeumpedagógiai forgatókönyv. írta: Geiszt Elina 2016.
 Szabad a vásár! múzeumpedagógiai forgatókönyv írta: Geiszt Elina 2016. A múzeumi óra címe: Szabad a vásár! - forgatókönyv a Magyar Kereskedelmi és Vendéglátóipari Múzeum állandó kiállításához Helyszín:
Szabad a vásár! múzeumpedagógiai forgatókönyv írta: Geiszt Elina 2016. A múzeumi óra címe: Szabad a vásár! - forgatókönyv a Magyar Kereskedelmi és Vendéglátóipari Múzeum állandó kiállításához Helyszín:
A Rendeletet a Bizottsági rendelet hatálya alá tartozó támogatásokra vonatkozóan 2013. december 31-ig lehet alkalmazni.
 Útmutató a saját munkavállalók részére szervezett képzés költségeinek a szakképzési hozzájárulás terhére történő elszámolásáról szóló 15/2009. (VII. 24.) SZMM rendelet alkalmazásáról A Rendelet a kihirdetését
Útmutató a saját munkavállalók részére szervezett képzés költségeinek a szakképzési hozzájárulás terhére történő elszámolásáról szóló 15/2009. (VII. 24.) SZMM rendelet alkalmazásáról A Rendelet a kihirdetését
A 2011/2012. tanévi FIZIKA Országos Középiskolai Tanulmányi Verseny első fordulójának feladatai és megoldásai fizikából. I.
 Oktatási Hivatal A 11/1. tanévi FIZIKA Országos Középiskolai Tanulmányi Verseny első fordulójának feladatai és megoldásai fizikából I. kategória A dolgozatok elkészítéséhez minden segédeszköz használható.
Oktatási Hivatal A 11/1. tanévi FIZIKA Országos Középiskolai Tanulmányi Verseny első fordulójának feladatai és megoldásai fizikából I. kategória A dolgozatok elkészítéséhez minden segédeszköz használható.
AZ MKB BANK ZRT. ÜZLETSZABÁLYZATA A HITELMŰVELETEK VÉGZÉSÉRŐL. Budapest, 2010. június 28.
 AZ MKB BANK ZRT. ÜZLETSZABÁLYZATA A HITELMŰVELETEK VÉGZÉSÉRŐL Budapest, 2010. június 28. TARTALOMJEGYZÉK 1. Az üzletszabályzat hatálya... 3 2. Hitelműveletek...3 3. A hitelműveletek általános feltételei...
AZ MKB BANK ZRT. ÜZLETSZABÁLYZATA A HITELMŰVELETEK VÉGZÉSÉRŐL Budapest, 2010. június 28. TARTALOMJEGYZÉK 1. Az üzletszabályzat hatálya... 3 2. Hitelműveletek...3 3. A hitelműveletek általános feltételei...
HASZNOS TUDNIVALÓK. a 2016. január 1-től érvényes egyes fixösszegű ellátásokról, adó- és tb-törvények fontosabb változásairól
 HASZNOS TUDNIVALÓK a 2016. január 1-től érvényes egyes fixösszegű ellátásokról, adó- és tb-törvények fontosabb változásairól A munkajog területén 2014 2015 2016 Minimálbér (Ft/hó) bruttó összege 101.500,-
HASZNOS TUDNIVALÓK a 2016. január 1-től érvényes egyes fixösszegű ellátásokról, adó- és tb-törvények fontosabb változásairól A munkajog területén 2014 2015 2016 Minimálbér (Ft/hó) bruttó összege 101.500,-
