Általános statisztika II. Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László
|
|
|
- Emil Pap
- 9 évvel ezelőtt
- Látták:
Átírás
1 Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László
2 Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Publication date 1997 Szerzői jog 1997 dr. Korpás Attiláné, Sándorné dr. Kriszt Éva, Varga Edit, Veitzné Kenyeres Erika, Nemzeti Tankönyvkiadó Rt. Dr. Korpás Attiláné- főiskolai docens Sándorné Dr. Kriszt Éva - főiskolai docens (9. és 10. fejezet) Varga Edit - főiskolai adjunktus (11. fejezet) Veitzné Kenyeres Erika - főiskolai tanársegéd (6., 7. és 8. fejezet) A gyakorlófeladatokat: Dr. Korpás Attiláné állította össze. Szakmai lektor: Dr. Csernyák László - egyetemi tanár, tanszékvezető, a matematikatudomány kandidátusa A mű más kiadványban való részleges vagy teljes felhasználása, illetve utánközlése a kiadó engedélye nélkül tilos!
3 Tartalom 6. Mintavétel Alapfogalmak, jelölések Véletlen mintavételi eljárások Független, azonos eloszlású minta kiválasztása Egyszerű véletlen mintavétel Szisztematikus mintavétel Rétegzett mintavétel Csoportos mintavétel Többlépcsős mintavétel Kombinált eljárások Nem véletlen mintavételi eljárások A mintajellemzők fontosabb tulajdonságai Gyakorlófeladatok Statisztikai becslések Alapfogalmak A becslőfüggvényekkel szemben támasztott követelmények Torzítatlanság Konzisztencia Hatásosság Elégségesség Intervallumbecslés A sokaság várható értékének becslése A sokasági értékösszeg becslése A sokasági arány becslése A sokasági szórásnégyzet becslése A konfidenciaintervallum meghatározása rétegzett mintavétel esetén A minta elemszámának meghatározása Gyakorlófeladatok Hipotézisvizsgálat A hipotézisvizsgálat alapfogalmai A hipotézisvizsgálat során elkövethető hibák A statisztikai hipotézisvizsgálat menete Egymintás statisztikai próbák A várható értékkel kapcsolatos próbák A sokasági szórásra vonatkozó próba iii
4 Általános statisztika II A sokasági arányszámmal (valószínűséggel) kapcsolatos próba Kétmintás statisztikai próbák Két sokasági várható érték különbségének vizsgálata Két sokasági arányra (valószínűségre) vonatkozó próba Két sokasági szórás egyezőségére vonatkozó statisztikai próba Egyéb hipotézisvizsgálatok Illeszkedésvizsgálat Függetlenségvizsgálat Varianciaanalízis Gyakorlófeladatok Kétváltozós korreláció- és regressziószámítás Kétváltozós korrelációszámítás A kovariancia A lineáris korrelációs együttható A rangkorrelációs együttható Kétváltozós regressziószámítás Az elméleti regresszió A tapasztalati regresszió A regressziófüggvény paramétereinek meghatározása A változók felcserélhetősége A rugalmassági együttható Statisztikai következtetések a kétváltozós lineáris regresszió alapján A regressziós modell feltételrendszere A regressziós becslés pontosságának mérése A regressziófüggvény paramétereinek intervallumbecslése Regressziós becslések és prognózisok A regressziófüggvény eredményeinek hipotézis-ellenőrzése A reziduális változó vizsgálata A paraméterek robusztus becslése Nemlineáris regresszió Gyakorlófeladatok Többváltozós korreláció- és regressziószámítás A lineáris regressziófüggvény meghatározása A háromváltozós lineáris regressziófüggvény A legkisebb négyzetek módszere és tulajdonságai A regressziófüggvény paramétereinek intervallumbecslése A regressziófüggvény eredményeinek ellenőrzése iv
5 Általános statisztika II A varianciaanalízis alkalmazása a többváltozós regressziószámításban Többváltozós korrelációszámítás Páronkénti korrelációs együttható Parciális korrelációs együttható Többszörös korrelációs és determinációs együttható A multikollinearitás és mérése Néhány kiegészítés a regressziószámításhoz Minőségi ismérvek kezelése a regressziós modellben A tényezőváltozók kiválasztása Gyakorlófeladatok Az idősorok összetevőinek vizsgálata Az idősorok összetevői Additív és multiplikatív komponensek Trendszámítás Trendszámítás mozgóátlagolással Analitikus trendszámítás A szezonalitás vizsgálata Szezonális eltérések számítása Szezonindexek számítása Előrejelzés az eredmények alapján Gyakorlófeladatok A. Függelék B. Tárgymutató v
6 Az ábrák listája 6,1. A képviselők életkor szerinti megoszlásának hisztogramja ,2. A mintaátlagok megoszlásának hisztogramja 100 db 30 elemű minta alapján ,3. A mintaátlagok megoszlásának hisztogramja 100 db 100 elemű minta alapján ,1. 7,2. 7,3. 7,4. A és becslőfüggvény eloszlás... A konfidenciaintervallum ábrázolása... A konfidenciaintervallum elhelyezkedése a mintavétel többszöri végrehajtása esetén... A standard normális és a Student-féle t-eloszlás ,5. A sűrűségfüggvénye különböző szabadságfokok esetén ,1. Az elfogadási és a kritikus tartomány lehetséges elhelyezkedés ,2. ábra a. Az elfogadási és a kritikus tartomány elhelyezkedés a z próbafüggvénynél ,2. ábra b. Az elfogadási és a kritikus tartomány elhelyezkedés a z próbafüggvénynél ,2. ábra c. Az elfogadási és a kritikus tartomány elhelyezkedés a z próbafüggvénynél ,3. Az elfogadási és a kritikus tartomány elhelyezkedés ,4. Az α és a β grafikus meghatározása különböző alternatívhipotézisek esetén ,5. Az α és a β grafikus meghatározása különböző kritikus értékek esetén ,6. Az F-eloszlás sűrűségfüggvénye különböző szabadságfokok esetén ,1. Pontdiagramok különböző korrelációs együtthatókkal ,2. Rangszámpárok ábrázolása ,3. A munkában töltött évek számának és a bruttó kereseteknek megfelelő pontok ,4. A bruttó átlagkereset a munkában töltött évek számának függvényében a középfokú végzettségű nőknél ,5. Korrrelálatlanság ,6. Függvényszerű kapcsolat ,7. A függvénytípus kiválasztását segítő grafikus ábrák ,8. A legkisebb négyzetek módszere ,9. A megfigyelt adatok és a különböző módon számolt regressziófüggvények ,10. A szállítási távolság és a szállítás időtartamának pontdiagramja ,11. A koordináta-rendszer transzformációja ,12. A változók felcserélése ,13. A hibatényező eloszlásának vizsgálata ,14. A mérési hiba hatása a regressziófüggvényre ,1. A regressziós együtthatók közötti összefüggések ,2. Útdiagram ,1. Az idősorok komponensei vi
7 Általános statisztika II 11,2. 11,3. 11,4. 11,5. 11,6. A háztartások gázfelhasználásának alakulása Nógrád megyében 1990 és 1994 között... A népesség természetes fogyásának alakulása Nógrád megyében... Az ellátatlan munkanélküliek létszámának alakulása... A kiemelt üdülőövezet vendéglétszámának idősora és exponenciális trendje... Az urántermelés parabolikus trendje... vii
8 A táblázatok listája A sokaság típusa, a mintavétel módja és a mintaelemek kapcsolata elemű minták mintaátlagainak megoszlása A 100 elemű minták átlagai elemű minták mintaátlagainak megoszlása A mintába került üvegek nettó töltési tömeg szerinti megoszlása A mintába került kávécsomagok megoszlása A rétegzett mintából történő becslés jelölésrendszere A számításhoz szükséges adatok A sokaság és a minta elemszámának megoszlása elemű minta adatai A hipotézisvizsgálat során hozott döntések és bekövetkezésük valószínűsége A másodfajú hiba elkövetésének valószínűsége különböző ellenhipotézisek esetén Az z-próba elfogadási tartományának határai szignifikanciaszint mellett A t-próba elfogadási tartományának határai α szignifikanciaszint mellett A elfogadási tartományának határai α szignifikanciaszint mellett Két mintát igénylő próbák esetén alkalmazott jelölések A 10 elemű minta mérési eredményei Az F-próba elfogadási tartományai α szignifikanciaszint mellett A minta valamilyen ismérv szerinti megoszlása A kiválasztott vendégek kiszolgálási idő szerinti megoszlása A próbafüggvény számított értékének meghatározására szolgáló munkatábla A megkérdezett személyek nemhez való tartozás és beosztás szerinti megoszlása Munkatábla a próbafüggvény aktuális értékének meghatározásához Varianciaanalízis-tábla sémája Az egyes dolgozók teljesítményadatai Az olvasók megoszlása kölcsönzési idő és a kölcsönzött kötetek szerint Az olvasók megoszlása kölcsönzési idő és a kölcsönzött kötetek szerint Munkatábla a lineáris korrelációs együttható kiszámításához A versenyen elért helyezések Munkatábla a rangkorrelációs együttható kiszámításához Munkatábla a rangkorrelációs együttható kiszámításához A hallgatók létszámmegoszlása A hallgatók matematika- és statisztika-vizsgaeredményei közötti kapcsolat tapasztalati regressziófüggvénye viii
9 Általános statisztika II A munkában töltött évek száma és a havi átlagkereset tapasztalati regressziófüggvénye a középfokú végzettségű nőknél Munkatábla az analitikus regressziófüggvény meghatározásához Munkatábla a normálegyenletekkel történő megoldáshoz Munkatábla a transzformált normálegyenletekkel történő megoldáshoz A maradék-négyzetösszeg kiszámításának táblázata Varianciaanalízis-tábla Varianciaanalízis-tábla Eredménytábla a szállítási távolság és a szállítási idő közötti összefüggés vizsgálatához A feljegyzett adatok táblázata Munkatábla a reziduumok számítására A megmaradó adatok táblázata a Munkatábla a hatványkitevős regressziófüggvény meghatározásához A tokaji aszú életkora és eladási ára közötti összefüggés Munkatábla az exponenciális regressziófüggvény meghatározásához A szállítási idő vizsgálatára vonatkozó adatok Számítások a transzformált változók alapján A maradéktag négyzetösszegének kiszámítása Az eddigi részeredmények A regressziófüggvény paramétereinek ellenőrzéséhez szükséges részeredmények A varianciaanalízis-tábla többváltozós regressziószámítás esetén A varianciaanalízis-tábla A 20 elemű minta adatai Az felbontása Az felbontása Háromtagú mozgóátlagok számítása ( ) Négytagú mozgóátlagok számítása ( ) A háztartások számára értékesített gázmennyiség Nógrád megyében 1990 és 1994 között negyedéves bontásban A mozgóátlagolású trendszámítás munkatáblája ( ) A népesség természetes fogyásának alakulása Nógrád megyében Munkatábla a paraméterek meghatározásához Munkatábla a paraméterek meghatározásához A legkisebb négyzetek módszerének megfelelő négyzetösszeg kiszámítása Az ellátatlan munkanélküliek létszámának alakulása Nógrád megyében 1991 és 1994 között (ezer fő) Munkatábla az ellátatlan munkanélküliek létszámának alakulását kifejező lineáris trendfüggvény kiszámításához A legkisebb négyzetek módszerének megfelelő négyzetösszeg kiszámításának munkatáblája... ix
10 Általános statisztika II Egy kiemelt üdülőövezet vendégeinek létszáma 1982 és 1992 között A legkisebb négyzetek módszerének megfelelő négyzetösszeg számítása A trendtől való eltérések összehasonlítása Az urántermelés alakulása Magyarországon Az egyedi szezonális eltérések számítási táblázata Egy márkakereskedő személygépkocsi-értékesítésének adatai Munkatábla az egyedi szezonindexek kiszámításához A személygépkocsi-értékesítés szezonalitását jellemző szezonindexek A trend és a szezonhatás előrejezése A standard normális eloszlású valószínűségi változó eloszlásfüggvényének táblázata A standard normális eloszlású valószínűségi változó eloszlásfüggvényének táblázata (folytatás) A -eloszlás táblázata A -eloszlás táblázata (folytatás) AzF-eloszlás táblázata Az F-eloszlás táblázata (folytatás) Az F-eloszlás táblázata (folytatás) Az F-eloszlás táblázata (folytatás) Az F-eloszlás táblázata (folytatás) Az F-eloszlás táblázata (folytatás) A Student-féle t-eloszlás táblázata x
11 6. fejezet - Mintavétel 6.1. Alapfogalmak, jelölések Tankönyvünk első kötetében a megfigyelt statisztikai sokaság elemzésére szolgáló különböző eszközökkel, mutatószámokkal ismerkedtünk meg. A sokaságot ismertnek feltételezve, figyelmünket csak arra fordítottuk, hogyan lehet annak összetételét, változását, törvényszerűségeit megvizsgálni. Nem tértünk ki részletesen arra, hogy az alapadatokhoz teljes körű vagy részleges felvétellel jutottunk. Utólag azt mondhatjuk, hogy az eddigiek során megfigyelésünk a sokaság minden elemére kiterjedt, tehát elemzéseink a sokaság teljes körű megfigyelésén alapultak. Ebben a kötetben olyan módszerekkel ismerkedünk meg, amelyekhez nem szükséges a sokaság minden egyes elemének megfigyelése, mivel erre gyakran nincs is lehetőségünk. A társadalmi-gazdasági statisztikában azonban az adatokhoz való hozzájutás gyakori formája a részleges adatgyűjtés, melynek egyik módja a reprezentatív megfigyelés. Reprezentatív megfigyelésre vagy más néven mintavételes megfigyelésre van szükség pl. a lakosság életkörülményeivel kapcsolatos kérdések (jövedelem, fogyasztási szokások stb.) megválaszolásához, a tömegtermelés minőség-ellenőrzési eljárásaihoz vagy a közvélemény-kutatásokhoz. Ily módon becsüljük pl. a várható termés mennyiségét a mezőgazdaságban vagy a kisvállalkozások tevékenységének eredményeit is. (Ilyen jellegű kérdésekkel már a Valószínűségszámítás c. tárgyban is foglalkoztunk.) A reprezentatív megfigyelés, röviden szólva a mintavétel célja, hogy valamely sokaság egy részének megfigyelése révén következtetéseket tudjunk levonni a sokaság egészére, annak jellemzőire, összetételére vonatkozóan. Azt a sokaságot, amelyre a mintavétel segítségével következtetni szeretnénk, alapsokaságnak, az alapsokaság azon részét, amely alapján a következtetéseket levonjuk, mintasokaságnak nevezzük. A továbbiakban az alapsokaságot röviden sokaságnak, a mintasokaságot pedig mintának fogjuk nevezni. Tekintsük át először a sokaság megadásának módjait és a legfontosabb sokasági jellemzőket. A sokaság elemszáma lehet véges vagy végtelen. Legyen Xa sokaság egy ismérve. Ha a sokaságból véletlenszerűen kiemelünk egy egyedet, ennek ismérvértéke a véletlentől függ, ezért valószínűségi változó, ezt a véletlentől függő ismérvértéket jelölje Ekkor eloszlásfüggvénye Véges sokaság esetén az egyedeket, illetve azok ismérvértékeit nagyság szerint sorba rendezhetjük. Az ismérvértékek legyenek (N az egyedek száma). Ekkor 1
12 Mintavétel A várható értéke, vagy másképpen a sokaság ismérvértékének várható értéke véges sokaság esetén mint ismeretes az átlaggal egyenlő: szórásnégyzete Végtelen elemszámú sokaság esetén két esetet különböztetünk meg. Ha diszkrét valószínűségi változó, ami azt jelenti, hogy az ismérvértékek véges vagy megszámlálhatóan végtelen halmazt alkotnak, akkor az F eloszlásfüggvény szintén egy lépcsősfüggvény (az intervallumban állandó), várható értéke Ha folytonos és létezik a sűrűségfüggvénye, akkor a várható értéke (ha ez az improprius integrál is létezik). A szórásnégyzetet a szokásos módon kapjuk: (A jobb oldalon szereplő várható értékeknek is létezniük kell.) 2
13 Mintavétel A gyakorlatban a mintavétel általában véges sokaságból történik. Ugyanakkor a nagy elemszámú sokaságokat tekinthetjük végtelennek, így a végtelen elemszámú sokaságra kidolgozott eszközök jól használhatók ezen sokaságok esetén is. Ezek után tekintsük át a mintával kapcsolatos alapfogalmakat. A minta elemszáma, tekintet nélkül arra, hogy véges vagy végtelen sokaságból származik, mindig véges. Elemszámát n-nel jelöljük. Az egyes mintaelemek valószínűségi változók, értékük mintáról mintára változhat. Ezeket célszerű -nel jelölni. A minta elemei csak addig tekinthetők változóknak, míg a mintavétel nem történt meg, a minta elemeinek kiválasztása után konkrét számértékek lesznek: A mintából különböző mintajellemzők (átlag, szórás, értékösszeg, arány stb.) számíthatók. Miután a minta elemei valószínűségi változók, az ezekből számított mintajellemzők is valószínűségi változók lesznek, értékük mintáról mintára változhat attól függően, hogy mely sokasági elemek kerültek a mintába. Ez a mintajellemzőknek nagyon fontos tulajdonsága. A véges elemszámú sokaságból történő mintavételnél alapvető fontosságú, hogy rendelkezésre álljon egy ún. mintavételi keret, amely egyenként tartalmazza a vizsgálni kívánt sokaság elemeit, mégpedig mindegyiket, és mindegyiket csak egyszer. Egy ilyen teljes keret biztosítása sokszor nem könnyű feladat, mert vannak olyan sokaságok, amelyeknél az elemek száma és összetétele napról napra változik, s bármilyen jó is a megszűnő és az újonnan létrejövő egységek nyilvántartása, ez szükségszerűen különbözik a mintavételi keret összeállításakor létező sokaságtól. (Ilyen nehézség léphet fel a mintavételi keret összeállításánál, ha a sokaságot pl. Magyarország népessége vagy a Magyarországon működő kisvállalkozások stb. képezik.) A mintavétel tervezése, a mintavételi eljárás megválasztása során két egymásnak ellentmondó követelményt kell figyelembe vennünk. Az egyik követelmény a pontosság, a másik az olcsóság. Mivel az egyik követelmény előtérbe helyezése a másik háttérbe szorulását jelenti, lényeges a mintavétel tervezése során az elvárt célok és a lehetséges eszközök pontos megfogalmazása, számbavétele. Az, hogy ezen követelményeket mennyire vesszük figyelembe a mintavétel tervezése során, lényegesen befolyásolja a mintaelemek kiválasztási eljárását. A következőkben a mintaelemek kiválasztási módjait tekintjük át. A mintaelemek kiválasztása visszatevéssel vagy visszatevés nélkül történhet. Végtelen (vagy végtelennek tekintett) elemszámú sokaságból akár visszatevéssel, akár visszatevés nélkül választjuk ki a minta elemeit, azok mint valószínűségi változók minden esetben függetlenek lesznek egymástól. Véges sokaság esetén csak a visszatevéses mintavétel eredményez független mintaelemeket. A mintaelemek ezen tulajdonságára a későbbiek során még visszatérünk. Az elmondottakat a 6.1. táblázatban foglaltuk össze táblázat - A sokaság típusa, a mintavétel módja és a mintaelemek kapcsolata A sokaság elemszáma A mintavétel módja végtelen visszatevéses A mintaelemek 3
14 Mintavétel visszatevés nélküli véges függetlenek visszatevéses visszatevés nélküli nem függetlenek Az elmondottak alapján különbséget teszünk független mintavételi eljárások és nem független mintavételi eljárások között. Véges sokaság esetén a minta fontos jellemzője a kiválasztási arány, amely azt mutatja meg, hogy a sokaság elemeinek mekkora hányada kerül a mintába. Adott N mellett annál nagyobb valószínűséggel lehet a mintából a sokaságra következtetni, minél nagyobb a kiválasztási arány. Az n-nek, a minta elemszámának azonban nagyobb jelentősége van a kiválasztási aránynál, mert ez határozza meg a mintából való következtetésnél használható módszereket. A mintavétel során és a mintából történő következtetésnél meg kell különböztetnünk a kis és a nagy minta fogalmát. Ennek jelentőségét az adja, hogy a mintából számított jellemzők nagy részének (pl. mintaátlag, mintabeli arány) eloszlása nagy minta esetén közelítőleg normális eloszlásúvá válik, ennélfogva kezelésük egyszerűsödik. (Ezen megállapításra a későbbiek során még visszatérünk.) Felvetődik a kérdés, hogy mi tekinthető kis, illetve nagy mintának. Azt mondhatjuk, hogy már nagy mintának tekinthető, azaz egyes mintajellemzők eloszlásfüggvényei ezen mintaelemszám fölött már közelítőleg normális eloszlásúvá válnak. A mintanagysághoz szorosan kapcsolódik a mintavételi hiba fogalma. A mintavételi hiba abból adódik, hogy a sokaság egy részéből következtetünk az egészre. Meghatározásának módszerei matematikailag kidolgozottak. Nagysága, illetve annak valószínűsége a sokaság jellege, az alkalmazott mintavételi eljárás és a mutató fajtája mellett alapvetően a mintanagyságtól függ, hiszen a mintanagyság növelésével a sokaság egyre nagyobb részét vizsgáljuk meg, s így egyre kisebbé válik a mintavételből eredő nagy hiba valószínűsége. A mintaelemek kiválasztása során elkövethetünk ún. nem mintavételi hibát is, amely több forrásból adódhat: többek között a sokaságot nem tökéletesen fedi le a mintavételi keret (pl. ilyen fordulhat elő, ha a megfigyelt sokaság a Magyarországon működő kisvállalkozások), nem sikerül a megfigyeléseket a terv szerint végrehajtani, válaszmegtagadás vagy egyéb okok miatt hiányoznak adatok. Hiba adódhat abból is, hogy a kérdésekre kapott válaszok nem egészen pontosak (tudatosan vagy önhibáján kívül téves adatot szolgáltat a válaszadó), vagy hibákat követhetnek el a kódolás, táblázás stb. során. Az ilyen típusú hibák nagyságát nehéz meghatározni. Vizsgálatuknak, feltárásuknak elsődlegesen az a célja, hogy a mintavétel tervezésének és végrehajtásának különböző fázisaiban hatásukat csökkenteni lehessen. Egy mintából csak akkor lehet számítható megbízhatóságú következtetéseket levonni a sokaságra vonatkozóan, ha a minta elemeit nem önkényesen, hanem véletlenszerűen választjuk ki. A véletlenszerűség nem feltétlenül jelenti azt, hogy a sokaság minden egyes elemének egyenlő esélye van a mintába történő kerülésre, hanem csak azt jelenti, hogy minden elemhez egy előre meghatározott ismert valószínűség tartozik, és biztosítjuk, hogy ezzel a valószínűséggel kerüljön be a mintába az adott elem, továbbá azt, hogy a mintaelemek kiválasztási eljárásának előre meghatározottnak és egyértelműnek kell lennie. 4
15 Mintavétel Ha a minta elemeit véletlenszerűen választjuk ki a sokaságból, véletlen (vagy valószínűségi) mintát kapunk. Attól függően, hogy a mintavétel során biztosítjuk-e a véletlenszerűséget vagy sem, különböző mintavételi eljárásokról beszélhetünk Véletlen mintavételi eljárások Független, azonos eloszlású minta kiválasztása Független, azonos eloszlású mintát akkor kapunk, ha homogén és végtelen (vagy nagyon nagy) sokaságból veszünk véletlen (visszatevéses vagy visszatevés nélküli) mintát, illetve amikor véges sokaságból visszatevéssel választjuk ki a minta elemeit. Tehát független mintát veszünk. Ilyenkor a minta elemei független (vagy függetlennek tekinthető), azonos eloszlású valószínűségi változók lesznek. Ugyanis az i-edik mintaelem ismérvértékére nyilvánvalóan igaz, hogy valószínűségi változók eloszlása a tehát az egyes mintaelemek mint ismérvérték sokaságbeli eloszlásával azonos. Alkalmazása elsősorban a tömegtermelés minőség-ellenőrzésénél célszerű. Például azonos eloszlású, független mintához jutunk, ha az 1 kg-os liszt töltési tömegének ellenőrzéséhez mintát veszünk. Ekkor a sokaság végtelennek tekinthető, így a minta elemei minden esetben függetlenek lesznek. A gyakorlatban azonban nem túl gyakran jutunk független, azonos eloszlású mintához, mivel a valóságban ritkán áll rendelkezésünkre végtelen vagy végtelennek tekinthető sokaság, vagy véges sokaság esetén nem minden esetben van lehetőség a mintaelemek megvizsgálása után a sokaságba történő visszatevésre (pl. egy adott cégtől vásárolt gumiabroncsok elhasználódásának minőségi vizsgálatakor). Ennek ellenére ez a mintavételi eljárás későbbi vizsgálataink során kiemelt szerepet kap, mert matematikailag rendkívül könnyen kezelhető, és ezen a mintatípuson keresztül lehet a legkönnyebben megmutatni a sokasági és a mintajellemzők kapcsolatát Egyszerű véletlen mintavétel Egyszerű véletlen mintavételt hajtunk végre homogén, véges elemszámú sokaság esetén, amikor a mintát visszatevés nélkül választjuk ki, elemenként egyenlő valószínűséggel. (Ezt az esetet a valószínűségszámításban is vizsgáltuk.) A végrehajtásához egy, a mintavételi keret minden elemét, de mindegyiket csak egyszer tartalmazó komplex lista szükséges. Ezen listából a mintaelemek kiválasztása történhet sorsolással, ún. véletlenszám-táblázattal, illetve számítógépes véletlenszám-generálással. A visszatevés nélküliség követelményét a sorsolásnál oly módon biztosíthatjuk, hogy a kihúzott cédulákat nem tesszük vissza az urnába, míg a véletlenszámtáblázatnál, illetve a számítógépes véletlenszám-generálásnál az ismételten előforduló sorszámot átugorjuk, és haladunk tovább a táblázatban, illetve a számítógép által előállított listában. 5
16 Mintavétel Az egyszerű véletlen mintavétel során különböző összetételű mintát kaphatunk. Minden n elemű minta előfordulásának a valószínűsége ugyanakkora. Természetesen a mintavétel végrehajtása után csak egyetlenegy mintánk lesz, s ebből következtetünk a sokaság jellemzőire. A gyakorlatban a sokaságok ritkán homogének, ezért az egyszerű véletlen mintavétel tiszta alkalmazása sem fordul elő gyakran, de ugyanakkor kiindulópontként szolgál a bonyolultabb eljárásokhoz Szisztematikus mintavétel A gyakorlatban a véletlen kiválasztást a szisztematikus mintavétellel lehet legegyszerűbben megvalósítani. Az eljárás lényege a következő: egy n elemű mintát kívánunk venni egy N elemű sokaságból. Ehhez először a sokaságot valamely szempont szerint sorba rendezzük általában eleve adott egy sorrend, majd meghatározzuk a kiválasztjuk a számértéket, ahol a szám egész részét jelenti. Az első k elem közül egyenlő valószínűséggel kiindulópontot, s ezután szisztematikusan az erre következő minden k-adik elem kerül be a mintába. A szisztematikus mintavétel végrehajtása rendkívül egyszerű, nem igényel szakismeretet, ellenőrzése is könnyű. Ezen mintavételi eljárás azonban csak akkor eredményez véletlen mintát, ha a listaképző ismérv és a megfigyelt ismérv között nincs sztochasztikus kapcsolat. Súlyos torzítást okozhat az is, ha a lista rejtett trendet vagy periodicitást tartalmaz. Tekintsük a következő példát. Valamely főiskola hallgatóinak akikről rendelkezésre áll egy ábécé szerinti lista a tandíjfizetéssel kapcsolatos véleményére vagyunk kíváncsiak. Ekkor a szisztematikus mintavétel nagy valószínűséggel véletlen mintát fog eredményezni, hiszen nagyon valószínű, hogy a hallgató nevének kezdőbetűje és a tandíj fizetéséről alkotott véleménye között nincs sztochasztikus kapcsolat. Ebben az esetben a szisztematikus kiválasztás egyszerűsíti a munkát Rétegzett mintavétel Minden mintavételnél felmerül az a kérdés, hogyan lehet a mintaelemek kiválasztását úgy végrehajtani, hogy az meghatározott mintanagyság mellett minél jobban reprezentálja a vizsgálni kívánt sokaságot. Célszerű továbbá olyan becslési eljárásokat alkalmazni, amelyek minél kisebb hibával becsülik az ismeretlen sokasági jellemzőt. A leggyakrabban alkalmazott ilyen eljárás az ún. rétegzett mintavétel. A rétegzett mintavétel során a vizsgált ismérv szempontjából heterogén sokaságot több homogén (minél kisebb szórású) részsokaságra (rétegekre) bontjuk úgy, hogy a csoportok kiadják a teljes sokaságot, továbbá egyetlen sokasági elem se tartozzon két vagy több csoportba. Az egyes rétegeken belül a minta elemeinek a kiválasztása egyszerű véletlen mintavétellel történik. A rétegzett mintavétel eredményeként egyrészt jobb keresztmetszetet kapunk a vizsgált sokaság összetételéről, másrészt az egyes rétegek nagyobb homogenitása miatt ezeken belüli kisebb mintákból is megfelelő pontosságú következtetést vonhatunk le. Ilyen módon az eredetileg heterogén 6
17 Mintavétel sokaságra ugyanakkora minta esetén pontosabb következtetést tudunk levonni rétegzett mintából, mint ha egyszerű véletlen mintavételt alkalmaztunk volna. A rétegzés nem csupán pontosságnövelő hatása miatt elterjedt mintavételi eljárás. A rétegzett kiválasztást arra is felhasználhatjuk, hogy az egyes rétegek sokasági jellemzőire megbízható becslést adjunk. Pl. az egyik kisvárosunkban a háztartások jövedelemviszonyait szeretnénk megvizsgálni. Ehhez a város háztartásait a gyermekszám alapján rétegekbe soroljuk. A mintavétel végrehajtása után lehetőség van egyrészt a kisvárosban lévő háztartások egy főre jutó jövedelmének, másrészt az egyes rétegek tehát a gyermektelen, az 1 gyermekes, a 2 gyermekes stb. háztartások esetén az egy főre jutó jövedelemnek a becslésére. Rétegzett mintavételt alkalmaz többek között a Központi Statisztikai Hivatal negyedéves rendszerességgel az 50 vagy kevesebb főt foglalkoztató iparba és a kivitelező építőiparba sorolt kisszervezetek reprezentatív megfigyelésére. (Az 50 főt meghaladó létszámú szervezetek megfigyelése teljes körű és folyamatos.) A rétegzés során több szempontot is figyelembe vettek: jogi személyiségű-e a gazdasági társaság; a jogi személyiségű társaságokon belül 21 és 50 fő közötti vagy 21 fő alatti létszámkategóriába tartozik-e; budapesti vagy vidéki székhelyű-e, illetve azt, hogy mikor 1 alakult meg a gazdasági társaság. Ezen szempontok alapján a feldolgozóiparban 16, a kivitelező építőiparban 12 réteget alakítottak ki a vizsgálat végrehajtásához. A továbbiak megértéséhez néhány újabb jelölés bevezetésére van szükség. A sokaság rétegeinek számát M-mel jelöljük, az egyes rétegeken belül a sokaság elemszáma pedig: ekkor: Rétegenként elemű mintákat veszünk, és a mintákra igaz, hogy Felvetődik a kérdés, hogy hogyan osszuk el a minta elemeit az egyes rétegek között. A mintaelemek szétosztása történhet arányos elosztással, illetve nem arányos elosztással. 1 A módszer részletes leírása Dr. Telegdi László: Az ipari és építőipari kisszervezetek reprezentatív megfigyelése (Statisztikai Szemle március) c. tanulmányában olvasható. 7
18 Mintavétel a) Az arányos elosztás lényege, hogy a mintában a sokasági rétegarányoknak megfelelően választjuk meg a minta elemszámát, tehát adott réteg aránya a mintában és a sokaságban megegyezik, azaz Ezt a kedvező tulajdonságot a későbbi számításoknál fogjuk felhasználni. A j-edik réteg mintaelemszámát ekkor a következő összefüggéssel állapíthatjuk meg: b) A nem arányos elosztás során a mintában a rétegarányok nem egyeznek meg a sokaságbeli arányokkal. Tehát A következőkben a nem arányos elosztáshoz tartozó néhány, a statisztikai gyakorlatban legtöbbször előforduló eljárást mutatunk be. Egyenletes elosztás során minden egyes rétegbe azonos számú mintaelem kerül. Így a j-edik réteg mintaelemszáma lesz. Előnyös tulajdonsága, hogy egyszerű, semmilyen tervezési előkészítést nem igényel, végrehajtása kényelmes. Hátránya pedig, hogy az egyes rétegek nagyságát, szórását stb. nem veszi figyelembe a szükséges mintaelemszám meghatározásához. Így nagyfokú torzítást okozhat. A Neyman-féle optimális elosztás végrehajtásához szükséges, hogy előre ismerjük (vagy legalább hozzávetőlegesen becsülni tudjuk) a sokaság rétegenkénti szórásait. Ekkor rögzített mintaelemszám mellett kedvezőbb tulajdonságú mintát kapunk, ha nagyobb szórású rétegből aránylag nagyobb, kisebb szórásúból pedig kisebb mintát veszünk. Ezt az eljárást a rendszeres időközönként megismétlődő megfigyeléseknél alkalmazzák. Így a megelőző időszak eredményei felhasználhatók az egyes rétegek mintaelemszámának meghatározásához. A j-edik réteg mintaelemszáma az alábbi összefüggés alapján határozható meg: ahol a j-edik réteg elemszáma a sokaságban, 8
19 Mintavétel a j-edik réteg szórása a sokaságban, n: a minta elemszáma Csoportos mintavétel Az egyszerű véletlen, a szisztematikus és a rétegzett mintavétel során feltételeztük, hogy rendelkezésünkre áll egy olyan lista a mintavételi keret, amely a sokaság összes elemét tartalmazza, s ebből választjuk ki a mintát. A gyakorlati feladatok egy részénél azonban ilyen lista nem áll rendelkezésre, bár elkészíthető volna, de előállítása költséges és munkaigényes lenne. Más esetekben rendelkezésre áll ugyan a lista, de ha abból választanánk ki közvetlenül a mintaelemeket, a felvétel végrehajtása rendkívül költséges lenne. Ezen feladatoknál célszerű a sokaság elemeit nem közvetlenül kiválasztani, hanem ezek természetes vagy mesterséges csoportjait megfigyelni. A csoportos mintavétel során a homogén sokaság elemeinek (természetes vagy mesterséges) csoportjai közül egyszerű véletlen mintát veszünk, majd a kiválasztott csoportokon belül minden egyes egyedet megfigyelünk. A csoportos mintavétel esetén a költségtakarékosságot tartjuk elsődleges szempontnak, míg a megfigyelés megbízhatósága némileg háttérbe szorul. Bizonyos esetekben a csoportos mintavétel segítségével, ugyanazon költségkeret mellett lényegesen nagyobb mintához juthatunk, mint egyszerű véletlen mintavétellel. Nézzünk néhány példát a csoportos mintavétel alkalmazására. Egy adott évben vizsgálni kívánjuk a szakközépiskolában végzettek továbbtanulását, illetve munkába állását az érettségi után 3 hónappal. Ha egyszerű véletlen mintavételt hajtanánk végre, akkor az országban található valamennyi szakközépiskola végzős évfolyamának tanulóiról teljes körű listát kellene összeállítani. A mintát ebből a listából kellene kiválasztani. Egy ilyen lista összeállítása rendkívül nehézkes és költséges lenne. További jelentős költséget jelentene, hogy az így kiválasztott diákok területileg is rendkívül szétszórtan helyezkednek el, így az információk begyűjtése is hosszadalmas lenne. Ha azonban csoportos mintavételt végzünk, akkor a középiskolák rendelkezésre álló országos listájából egyszerű véletlen mintavétellel kiválaszthatunk néhány középiskolát. Ilyenkor a kiválasztott iskola végzős évfolyamának valamennyi hallgatója belekerül a mintába, s a felvétel során mindannyiukat meg kell kérdezni. Ebben az esetben a csoportok területi koncentráltsága miatt a csoportos mintavétel olcsóbb, mint az egyszerű véletlen mintavétel. Az egyik nagy országos politikai párt valamely döntés meghozatala előtt kíváncsi a tagság véleményére. Ekkor egyszerűbb és olcsóbb a helyi pártszervezetek közül néhányat egyszerű véletlen mintavétellel kiválasztani, s ezeknél minden párttagot megkérdezni, mint egy részletes címlistát összeállítani a párt tagságáról. Csak akkor célszerű a csoportos mintavétel alkalmazása, ha a helyi szervezeteken belül a párt tagjainak véleménye nem azonos a vizsgált kérdésről. Ellenkező esetben a csoportos mintavétel torz eredményre vezethet. A fenti példákból is kitűnik, hogy a csoportos mintavétel során kétféle egység különül el: elsődleges mintavételi egység, amelyre a felvétel közvetlenül irányul (iskolák, helyi szervezetek), végső mintavételi egység, amelyre vonatkozóan következtetéseket akarunk levonni a kapott mintából (tanulók, párttagok). 9
20 Mintavétel Többlépcsős mintavétel A többlépcsős mintavételt hasonló esetekben alkalmazzuk, mint a csoportos mintavételt amelyet egylépcsősnek is szoktak nevezni, azzal a különbséggel, hogy többször ismételjük meg egymás után az egyszerű véletlen mintavételt, tehát a mintaelemek kiválasztása több fokozatban, több lépcsőben történik. A mintavétel végrehajtása során először kiválasztjuk az elsődleges mintavételi egységeket. Attól függően, hogy hányszor ismételjük meg egymás után az egyszerű véletlen kiválasztást, két-, három- vagy többlépcsős mintavételről beszélhetünk. Ha az elsődleges mintavételi egységeken belül rögtön a megfigyelni kívánt elemeket választjuk ki (egyszerű véletlen mintavétellel), akkor kétlépcsős a mintavétel. Ha az elsődleges mintavételi egységeken belül először újabb nagyobb csoportokat választunk ki, majd az így képzett csoportokból választjuk ki a mintaelemeket, akkor a mintavétel három- (vagy több-) lépcsős lesz. A többlépcsős mintavétel előnye a csoportos kiválasztással szemben, hogy homogén elsődleges mintavételi egységek homogenitása esetén a teljes körű megfigyelés helyett mintára támaszkodik, s ezáltal csökken a fölösleges adatfelvételek száma, s így ugyanakkora elemszámú minta esetén kisebb a mintavételi hiba valószínűsége, mint a csoportos mintavételnél. Előző példánkat folytatva, ha a helyi szervezetekben nem kérdeznek meg minden párttagot, hanem egyszerű véletlen mintavétellel kiválasztanak néhányat, s csak ezeknek teszik fel a megfelelő kérdéseket, akkor kétlépcsős mintavételi eljárást hajtanak végre. Ebben az esetben az első lépcső a helyi szervezetek (elsődleges mintavételi egységek) kiválasztása, a második lépcső pedig a megkérdezésre kerülő tagok (végső mintavételi egységek) kiválasztása Kombinált eljárások A kombinált eljárások gyakorta egy lépésben alkalmaznak több, eddig megismert mintavételi módszert. Ily módon ötvözhető például a rétegzés pontosságnövelő előnye a csoportos vagy többlépcsős mintavétel költségmegtakarításával. A KSH pl. az egységes lakossági adatfelvételi rendszerben (ELAR) egyszerre alkalmaz rétegzést és lépcsőzést. A kombinált eljárások külön csoportját képezik a ismétlődő felvételek, illetve panelfelvételek. Ezen felvételek alkalmazására akkor van szükség, ha a vizsgált sokaság szerkezetét vagy az egyes egyedek jellemzőinek időbeni változását akarjuk vizsgálni. Az ismétlődő felvételek esetén nem szükséges, hogy a mintában szereplő egyedek azonosak legyenek. E módszer legfőbb erénye, hogy egy-egy időpontban a vizsgált sokaság keresztmetszetéről megbízható képet ad. Az ismétlődő felvételek általában úgy történnek (például a legtöbb országban a munkaerő-felvételek), hogy a minta elemei néhány egymás után következő megkérdezéskor azonosak, majd előírt rend szerint cserélődnek. A panelfelvételeknél a minta elemeinek a lehetőségek keretei között azonosaknak kell lenniük, s ezáltal alkalmasak az egyes egyedek jellemzőinek időbeni vizsgálatára. A panelfelvétel előnye, hogy számos társadalmi jelenségre vonatkozóan pontosabb információkat ad, mint a szerkezeti változásokból levonható következtetések. Ezeket az előnyöket már az 1940-es években felismerték, és törekedtek a panelfelvételek alkalmazására. 10
21 Mintavétel Az eljárás hátránya, hogy a mintába került egyedek nyomon követése nehéz, és a válasz megtagadása miatti torzítás gyorsan növekszik. Ilyen panelfelvételnek tekinthető például a KSH háztartás-statisztikája, amelyben ELAR mintára támaszkodva nyernek kétévenként összehasonlító adatokat a lakosság jövedelmére és fogyasztási szokásaira vonatkozóan. A gyakorlatban sokszor előfordul a teljes körű felvétel és a mintavétel összekapcsolása. Pl. Magyarországon jelenleg 3-4 évente tartanak teljes körű állatszámlálást, amikor a kisgazdaságok teljes állatállományát összeírják. Ezen információ kiegészítéseként negyedévente reprezentatív felvételt végeznek egyes fontosabb állatfajták állományának becslése érdekében. A teljes körű felvételek közötti időszakban a reprezentatív felvételből és a megelőző teljes körű felvételből következtetnek a sokaság állapotára, a teljes állatállományra. Ez úgy történik, hogy kiválasztják a sokaságnak a reprezentatív felvétel során a mintába került egyedeit, majd ezeknél a teljes körű és a reprezentatív megfigyelés során nyert eredményeket összehasonlítják. A tapasztalt változásokat a sokaságra matematikai módszerek segítségével általánosítják Nem véletlen mintavételi eljárások Az eddigiek során áttekintettük a véletlenen alapuló mintavételi eljárásokat. Vannak azonban olyan mintavételi eljárások, amelyekre a véletlen kiválasztás nem jellemző, így ezen eljárásokkal létrejövő minták nem tekinthetők véletlen avagy valószínűségi mintáknak. Az eddig ismertetett mintavételi eljárásoknak számtalan hátrányos tulajdonsága van. Ezek közül a leglényegesebb, hogy nincs biztosítva, a minta a sokaságra valóban jellemző legyen, így félrevezető következtetések forrása lehet. Továbbá a nem véletlen minták esetén nem lehetséges a mintából számított jellemzők hibájának a meghatározása, tehát nem tudjuk a bizonytalanság, a tévedés várható hibáját becsülni. Ennek ellenére a nem véletlen mintavételi eljárásokat széles körben alkalmazzák, mivel végrehajtásuk egyszerűbb és esetenként lényegesen olcsóbb, mint a korrektül megtervezett és végrehajtott véletlen mintavétel. Főleg igénytelen felvételeknél (gyors elővizsgálatoknál) használják, korlátozott következtetési lehetőségekkel. A szisztematikus kiválasztásról a véletlen mintavételi eljárások között már esett szó. Láttuk, ha a listaképző ismérv és a megfigyelt ismérv között nincs sztochasztikus kapcsolat, akkor ez az eljárás véletlen mintát eredményez. Ellenkező esetben a kapott mintaelemek nem lesznek függetlenek egymástól, így a következtetések levonása során figyelembe kell venni a mintaelemek függőségéből adódó torzítást is. Időbeni megfigyeléseknél a periodicitás veszélye miatt alkalmazása nem célszerű. Eléggé elterjedt mintavételi eljárás a kvóta szerinti kiválasztás. Ennek lényege, hogy a felvételt végző személyek (kérdezőbiztosok) előre megkapják, hogy milyen összetételű mintához kell jutniuk, de az előre adott kereteken belül rájuk van bízva a véletlenszerű kitöltés. A kvóta szerinti kiválasztás legnagyobb hátránya, hogy a kapott minta a kérdezőbiztosok szimpátiája, illetve ítélőképessége szerint áll össze. Ez a statisztikailag nem számszerűsíthető szubjektivitás jelentős mértékben befolyásolja a kapott eredményeket. Az önkormányzati választások várható eredményét mintavételes eljárással kívánják meghatározni. Kvóta szerinti kiválasztás esetén a kérdezőbiztos úgy kapja meg a feladatát, hogy kérdezzen meg az adott választókörzetben öt 18 és 30 év, tíz 31 és 40 év közötti férfit, három 18 és 30 közötti nőt stb. Ezeken a határokon belül saját maga választja ki a megkérdezett személyeket, elvben véletlenszerűen, gyakorlatban azonban szubjektíven, ötletszerűen. Annak ellenére, hogy a kérdezőbiztos korrektül jár el, előfordulhat, ha kora délutáni órában végzi a felmérést, hogy a felvett mintában nagyobb lesz pl. a munkanélküliek aránya, mint a sokaságban. Továbbá gyakori, hogy a kérdezőbiztos saját ismeretségi köréből igyekszik véletlen mintát biztosítani, ez viszont bizonyos szempontból homogén csoportok megfigyelését jelenti. 11
22 Mintavétel Az önkényes kiválasztás során a felvételt végző személy szakmai ismereteire támaszkodva a véletlent figyelmen kívül hagyva választja ki a sokaságra jellemző (vagy legalábbis általa jellemzőnek tartott) mintát. Sokéves tapasztalatok mutatják, hogy az ilyen kiválasztáson alapuló megfigyelés sokszor erősen torzított eredményt ad. Meg kell említenünk, hogy az önkényes kiválasztás a mintavétel történelmileg elsőként alkalmazott módszere volt, mára azonban eléggé visszaszorult. Az utóbbi időben elterjedt az ún. exit pool eljárás, amelyet elsősorban a választási eredmények előrejelzésére alkalmaznak. A módszer lényege, hogy a szavazóhelyiségből kijövő választót megkérdezik arról, hogy kire adta a voksát, s az így kapott minta alapján következtetnek a választási eredményekre A mintajellemzők fontosabb tulajdonságai Ha a minta elemeit véletlen mintavételi eljárással választjuk ki, akkor a mintaelemek ismérvértékei változók lesznek. és a mintajellemzők valószínűségi A következőkben a mintajellemzők közül a minta átlagával foglalkozunk részletesen. Kiszámítása a összefüggéssel történik, ahol az i-edik mintaelem ismérvértéke. Egy konkrét mintavételnél, ha adódik, akkor a mintaátlag A mintaátlag tulajdonságait független, azonos eloszlású minta esetén mutatjuk be, mivel ezen mintavételi mód kezelése matematikailag egyszerűbb. Néhány esetben gyakorlati jelentősége miatt kitérünk az egyszerű véletlen mintavétel esetére is. Tekintsük először a mintaelemek eloszlását. A független, azonos eloszlású minta esetén a minta elemeinek eloszlása megegyezik a sokaság eloszlásával. A mintaelemek várható értéke és szórása pedig a sokaság várható értékével és szórásával fog megegyezni. Hiszen és Feladatunk azonban a mintaátlag vizsgálata. A mintaátlagot mint valószínűségi változót várható értékével, szórásával és eloszlásával jellemezhetjük. 12
23 Mintavétel Vizsgáljuk meg először a mintaátlag mint valószínűségi változó várható értékét. Valószínűségszámításból ismeretes, hogy Így a minta átlagának várható értéke: vagyis megegyezik a sokaságra vonatkozó várható értékkel. A mintaátlag szórásnégyzete a mintaelemek függetlensége miatt Így a mintaátlag szórásnégyzete azaz a mintaátlag szórása A mintaátlag szórását, a -ot a mintaátlag standard hibájának nevezzük. A standard hiba megmutatja, hogy mekkora a mintaátlagok sokasági várható értéktől való átlagos (négyzetes) eltérésének várható értéke. Nagysága a sokasági szórástól és a mintanagyságtól (n) függ. Egyszerűbben fogalmazva a standard hiba arra ad választ, hogy egyetlen mintavétel esetén mekkora hibát követünk el átlagosan. Mivel a hiba elkövetésének oka maga a reprezentatív mintavétel, szokásos ezt a hibát a reprezentatív megfigyelés hibájának is nevezni. Ha a mintaelemek kiválasztása egyszerű véletlen mintavétellel történt, akkor a mintaátlag standard hibájának meghatározása (bizonyítás nélkül) a következő összefüggéssel történik: 13
24 Mintavétel ahol a -t korrekciós tényezőnek vagy véges szorzónak nevezzük. A fenti összefüggésben a korrekciós tényező alkalmazása egyszerű véletlen mintavételnél abból következik, hogy ezen eljárás esetén a mintaelemek nem függetlenek, és ezért a standard hiba levezetésekor a mintaelemek közötti kapcsolatszorosságról tájékoztató kovarianciát is figyelembe kell venni. Az összefüggésből jól látható, hogy egyszerű véletlen mintavétel esetén a mintaátlag szórása jelentős mértékben függhet a kiválasztási aránytól. A korrekciós tényező értéke 0 és 1 között lehet. Alacsony (pl. 1% alatti) kiválasztási arány esetén értéke közel esik 1-hez, ezért elhagyása lényegesen nem befolyásolja a kapott eredményt. Ha viszonylag magas a kiválasztási arány (5 és 10% közötti vagy ennél nagyobb), akkor a korrekciós tényező alkalmazására feltétlenül szükség van. Konkrét mintavételnél a standard hibát -gal fogjuk jelölni, és a összefüggéssel határozzuk meg. Végül vizsgáljuk meg a mintaátlag eloszlását. Független, azonos eloszlású minta esetén a mintaátlag ( ) eloszlásáról a következők mondhatók (a bizonyításokat nem részletezzük, de felhívjuk a figyelmet arra, hogy a a valószínűségi változók összegének konstansszorosa): 1. Normális eloszlású sokaság esetén a mintaátlag is normális eloszlású, függetlenül a minta nagyságától. (Normális eloszlású valószínűségi változók összege is normális eloszlású.) 2. Ha a sokaság eloszlása nem ismert, de nagy mintát veszünk, akkor a mintaátlag közelítőleg normális eloszlású lesz, a centrális határeloszlás2 tétel következményeként. 3. Ha a sokaság eloszlása nem ismert és kis mintát veszünk, akkor a mintaátlag eloszlása függ a sokaság eloszlásától, ezért általánosan semmit sem tudunk mondani. A mintaátlag egy-egy mintavételnél megvalósuló konkrét értékeinek eloszlását is szemléltethetjük. Erre vonatkozóan nézzük a következő példát. 2 Matematika üzemgazdászoknak. Valószínűségszámítás. (Szerk: dr. Csernyák László.) Nemzeti Tankönyvkiadó, Budapest, oldal. (A további hivatkozásoknál: Valószínűségszámítás.) 14
25 Mintavétel 3 Az 1994-ben megválasztott 371 országgyűlési képviselő életkor szerinti megoszlása a következő hisztogrammal szemléltethető (6.1. ábra): 6,1. ábra - A képviselők életkor szerinti megoszlásának hisztogramja A mintaátlag eloszlásának vizsgálatához a 371 elemű sokaságból először 30, majd 100 elemű mintákat vettünk számítógépes véletlenszámgenerálás segítségével, visszatevéssel, így független, azonos eloszlású mintához jutottunk. A mintavételt mindkét esetben 100-szor ismételtük meg, majd minden egyes mintára vonatkozóan kiszámítottuk a mintaátlagot. A 30 elemű minták mintaátlagainak megoszlása a következő volt (6.2. táblázat): 6.2. táblázat - 30 elemű minták mintaátlagainak megoszlása 3 A mintaátlag értéke (év) A mintaátlagok megoszlása (%) 43, ,91 45, ,01 46, ,11 47, ,21 48, ,31 49,40 25 Az alapadatokat nem közöljük. 15
26 Mintavétel 49,41 50, ,51 51, ,61 52, ,71 53,80 1 Összesen 100 Ezt követően a 100 elemű mintákat választottuk ki a 30 elemű mintákhoz hasonló módon. A kiszámított mintaátlagokat a 6.3. táblázat tartalmazza: 6.3. táblázat - A 100 elemű minták átlagai 47,08 48,64 48,38 46,54 48,68 47,74 46,29 47,52 48,46 48,02 49,51 47,78 46,94 49,34 46,25 47,48 48,21 47,71 46,78 46,03 51,25 47,71 47,55 47,57 47,21 47,78 47,82 46,13 48,58 48,32 48,99 46,74 46,62 47,83 46,70 48,04 47,33 45,68 48,13 47,39 49,45 48,71 46,08 47,16 47,14 48,52 49,47 47,06 48,33 47,65 49,34 47,05 48,13 47,14 50,17 47,54 48,07 48,45 47,98 48,37 46,09 47,87 46,07 47,69 47,79 50,11 47,89 48,68 46,99 47,80 47,97 46,88 47,92 47,48 46,77 47,91 47,35 47,32 46,70 46,73 48,27 49,10 46,17 47,77 48,14 47,16 49,45 46,86 48,96 48,49 48,49 48,44 46,66 50,24 48,05 48,64 47,22 48,17 46,08 46,94 A kapott mintaátlagokat osztályközös relatív gyakorisági sorba rendeztük (6.4. táblázat) táblázat elemű minták mintaátlagainak megoszlása A mintaátlag értéke (év) A mintaátlagok megoszlása (%) 16
27 Mintavétel 46, ,11 47, ,21 48, ,31 49, ,41 50, ,51 51,60 1 Összesen 100 A mintaátlagok megoszlásait hisztogrammal szemléltethetjük (6.2. és 6.3. ábra). 6,2. ábra - A mintaátlagok megoszlásának hisztogramja 100 db 30 elemű minta alapján 17
AZ ÉPÍTÉSI MUNKÁK IDŐTERVEZÉSE
 UDPESTI MŰSZKI ÉS GZDSÁGTUDOMÁNYI EGYETEM ÉPÍTÉSZMÉRNÖKI KR ÉPÍTÉSKIVITELEZÉSI és SZERVEZÉSI TNSZÉK dr. Neszmélyi László Z ÉPÍTÉSI MUNKÁK IDŐTERVEZÉSE - 2015. - Tartalom 1. EVEZETÉS... 4 2. Z ÉPÍTÉSEN
UDPESTI MŰSZKI ÉS GZDSÁGTUDOMÁNYI EGYETEM ÉPÍTÉSZMÉRNÖKI KR ÉPÍTÉSKIVITELEZÉSI és SZERVEZÉSI TNSZÉK dr. Neszmélyi László Z ÉPÍTÉSI MUNKÁK IDŐTERVEZÉSE - 2015. - Tartalom 1. EVEZETÉS... 4 2. Z ÉPÍTÉSEN
Az informatika tárgy oktatásának folyamata. Dr. Nyéki Lajos 2015
 Az informatika tárgy oktatásának folyamata Dr. Nyéki Lajos 2015 Az oktatási folyamat fogalma Oktatási folyamat - az a folyamat, amelynek során az egyes tantárgyak éves vagy több éves tananyagának feldolgozására
Az informatika tárgy oktatásának folyamata Dr. Nyéki Lajos 2015 Az oktatási folyamat fogalma Oktatási folyamat - az a folyamat, amelynek során az egyes tantárgyak éves vagy több éves tananyagának feldolgozására
Hajdúsági Kistérség Területfejlesztési Koncepciója és Programja HELYZETÉRTÉKELÉS 2005.
 Hajdúsági Kistérség Területfejlesztési Koncepciója és Programja HELYZETÉRTÉKELÉS 2005. Tartalomjegyzék BEVEZETÉS I. A PROGRAMOZÁS MÓDSZERTANI MEGFONTOLÁSAI... 4 II. GAZDASÁG- ÉS IPARFEJLESZTÉS... 14 III.
Hajdúsági Kistérség Területfejlesztési Koncepciója és Programja HELYZETÉRTÉKELÉS 2005. Tartalomjegyzék BEVEZETÉS I. A PROGRAMOZÁS MÓDSZERTANI MEGFONTOLÁSAI... 4 II. GAZDASÁG- ÉS IPARFEJLESZTÉS... 14 III.
Tantárgyi útmutató. 1. A tantárgy helye a szaki hálóban. 2. A tantárgyi program általános célja. Statisztika 1.
 Tantárgyi útmutató 1. A tantárgy helye a szaki hálóban Gazdálkodási és menedzsment szakirány áttekintő tanterv Nagyításhoz kattintson a képre! Turizmus - vendéglátás szakirány áttekintő tanterv Nagyításhoz
Tantárgyi útmutató 1. A tantárgy helye a szaki hálóban Gazdálkodási és menedzsment szakirány áttekintő tanterv Nagyításhoz kattintson a képre! Turizmus - vendéglátás szakirány áttekintő tanterv Nagyításhoz
TARTALOM AZ INFORMATIKA FOGALMA... 3 1. A fogalom kialakítása... 3 2. Az informatika tárgyköre és fogalma... 3 3. Az informatika kapcsolata egyéb
 TARTALOM AZ INFORMATIKA FOGALMA... 3 1. A fogalom kialakítása... 3 2. Az informatika tárgyköre és fogalma... 3 3. Az informatika kapcsolata egyéb tudományterületekkel... 4 4. Az informatika ágai... 5 AZ
TARTALOM AZ INFORMATIKA FOGALMA... 3 1. A fogalom kialakítása... 3 2. Az informatika tárgyköre és fogalma... 3 3. Az informatika kapcsolata egyéb tudományterületekkel... 4 4. Az informatika ágai... 5 AZ
Pongrácz Tiborné S. Molnár Edit: A gyermekvállalási magatartás alakulása
 Pongrácz Tiborné S. Molnár Edit: A gyermekvállalási magatartás alakulása (elektronikus verzió, készült 2006-ban) A tanulmány eredetileg nyomtatásban megjelent: Pongrácz Tiborné S. Molnár Edit (1997): A
Pongrácz Tiborné S. Molnár Edit: A gyermekvállalási magatartás alakulása (elektronikus verzió, készült 2006-ban) A tanulmány eredetileg nyomtatásban megjelent: Pongrácz Tiborné S. Molnár Edit (1997): A
MUNKAERŐ-PIACI ESÉLYEK, MUNKAERŐ-PIACI STRATÉGIÁK 1
 GYÖRGYI ZOLTÁN MUNKAERŐ-PIACI ESÉLYEK, MUNKAERŐ-PIACI STRATÉGIÁK 1 Bevezetés Átfogó statisztikai adatok nem csak azt jelzik, hogy a diplomával rendelkezők viszonylag könynyen el tudnak helyezkedni, s jövedelmük
GYÖRGYI ZOLTÁN MUNKAERŐ-PIACI ESÉLYEK, MUNKAERŐ-PIACI STRATÉGIÁK 1 Bevezetés Átfogó statisztikai adatok nem csak azt jelzik, hogy a diplomával rendelkezők viszonylag könynyen el tudnak helyezkedni, s jövedelmük
SZENT ISTVÁN EGYETEM
 SZENT ISTVÁN EGYETEM A magyar mezőgazdasági gépgyártók innovációs aktivitása Doktori (PhD) értekezés tézisei Bak Árpád Gödöllő 2013 A doktori iskola Megnevezése: Műszaki Tudományi Doktori Iskola Tudományága:
SZENT ISTVÁN EGYETEM A magyar mezőgazdasági gépgyártók innovációs aktivitása Doktori (PhD) értekezés tézisei Bak Árpád Gödöllő 2013 A doktori iskola Megnevezése: Műszaki Tudományi Doktori Iskola Tudományága:
Biztosítási ügynökök teljesítményének modellezése
 Eötvös Loránd Tudományegyetem Természettudományi Kar Budapest Corvinus Egyetem Közgazdaságtudományi Kar Biztosítási ügynökök teljesítményének modellezése Szakdolgozat Írta: Balogh Teréz Biztosítási és
Eötvös Loránd Tudományegyetem Természettudományi Kar Budapest Corvinus Egyetem Közgazdaságtudományi Kar Biztosítási ügynökök teljesítményének modellezése Szakdolgozat Írta: Balogh Teréz Biztosítási és
Regressziószámítás alkalmazása kistérségi adatokon
 Lengyel I. Lukovics M. (szerk.) 2008: Kérdıjelek a régiók gazdasági fejlıdésében. JATEPress, Szeged, 264-287. o. Regressziószámítás alkalmazása kistérségi adatokon Szakálné Kanó Izabella 1 A lokális térségek
Lengyel I. Lukovics M. (szerk.) 2008: Kérdıjelek a régiók gazdasági fejlıdésében. JATEPress, Szeged, 264-287. o. Regressziószámítás alkalmazása kistérségi adatokon Szakálné Kanó Izabella 1 A lokális térségek
TÁMOP 4.1.1 VIR alprojekt VIR felhasználói kézikönyv
 1. sz. melléklet TÁMOP 4.1.1 VIR alprojekt Készítette: Aloha Informatika Kft. Tartalomjegyzék 1. A Vezetői Információs Rendszer, mint a stratégiai gondolkodás eszköze...4 1.1 Elméleti háttér...4 1.2 VIR
1. sz. melléklet TÁMOP 4.1.1 VIR alprojekt Készítette: Aloha Informatika Kft. Tartalomjegyzék 1. A Vezetői Információs Rendszer, mint a stratégiai gondolkodás eszköze...4 1.1 Elméleti háttér...4 1.2 VIR
IDŐSOROS ROMA TANULÓI ARÁNYOK ÉS KIHATÁSUK A KOMPETENCIAEREDMÉNYEKRE*
 CIGÁNY KISEBBSÉG: OKTATÁS, EGYHÁZ, KULTÚRA PAPP Z. ATTILA IDŐSOROS ROMA TANULÓI ARÁNYOK ÉS KIHATÁSUK A KOMPETENCIAEREDMÉNYEKRE* Tanulmányunkban két témakört szeretnénk körüljárni. Egyrészt megvizsgáljuk,
CIGÁNY KISEBBSÉG: OKTATÁS, EGYHÁZ, KULTÚRA PAPP Z. ATTILA IDŐSOROS ROMA TANULÓI ARÁNYOK ÉS KIHATÁSUK A KOMPETENCIAEREDMÉNYEKRE* Tanulmányunkban két témakört szeretnénk körüljárni. Egyrészt megvizsgáljuk,
A HÁZTARTÁSI TERMELÉS PÉNZÉRTÉKE
 A HÁZTARTÁSI TERMELÉS PÉNZÉRTÉKE SZÉP KATALIN SIK ENDRE A háztartási termelés pénzértékének becslésekor két alapvető elméleti és mérési kérdést kell megoldani: a háztartási termelés volumenének mérését
A HÁZTARTÁSI TERMELÉS PÉNZÉRTÉKE SZÉP KATALIN SIK ENDRE A háztartási termelés pénzértékének becslésekor két alapvető elméleti és mérési kérdést kell megoldani: a háztartási termelés volumenének mérését
Ingatlanvagyon értékelés
 Nyugat-Magyarországi Egyetem Geoinformatikai Kar Ingatlanfejlesztı 8000 Székesfehérvár, Pirosalma u. 1-3. Szakirányú Továbbképzési Szak Ingatlanvagyon értékelés 4. A vagyon elemzése Szerzı: Harnos László
Nyugat-Magyarországi Egyetem Geoinformatikai Kar Ingatlanfejlesztı 8000 Székesfehérvár, Pirosalma u. 1-3. Szakirányú Továbbképzési Szak Ingatlanvagyon értékelés 4. A vagyon elemzése Szerzı: Harnos László
A NŐK GAZDASÁGI AKTIVITÁSA ÉS FOGLALKOZTATOTTSÁGA*
 A NŐK GAZDASÁGI AKTIVITÁSA ÉS FOGLALKOZTATOTTSÁGA* NAGY GYULA A tanulmány a magyarországi gazdasági átalakulás nyomán a nők és a férfiak munkaerőpiaci részvételében és foglalkoztatottságában bekövetkezett
A NŐK GAZDASÁGI AKTIVITÁSA ÉS FOGLALKOZTATOTTSÁGA* NAGY GYULA A tanulmány a magyarországi gazdasági átalakulás nyomán a nők és a férfiak munkaerőpiaci részvételében és foglalkoztatottságában bekövetkezett
Energiaipar: a jég hátán is megél?
 OTDK-dolgozat 2015 Energiaipar: a jég hátán is megél? A szektor kereskedelmi engedélyes vállalkozásainak beszámolóelemzése az elmúlt évek tükrében Energy industry: can he always make do? The recent year
OTDK-dolgozat 2015 Energiaipar: a jég hátán is megél? A szektor kereskedelmi engedélyes vállalkozásainak beszámolóelemzése az elmúlt évek tükrében Energy industry: can he always make do? The recent year
A határmenti vállalkozások humáner forrás ellátottsága és -gazdálkodása
 Magyarország-Szlovákia Phare CBC 2003 Program Üzleti infrastruktúra, innováció és humáner forrás-fejlesztés a határ mentén Regionális Vállalkozói Együttm ködés HU2003/004-628-01-21 A határmenti vállalkozások
Magyarország-Szlovákia Phare CBC 2003 Program Üzleti infrastruktúra, innováció és humáner forrás-fejlesztés a határ mentén Regionális Vállalkozói Együttm ködés HU2003/004-628-01-21 A határmenti vállalkozások
KUTATÁSI BESZÁMOLÓ. A terület alapú gazdaságméret és a standard fedezeti hozzájárulás (SFH) összefüggéseinek vizsgálata a Nyugat-dunántúli régióban
 KUTATÁSI BESZÁMOLÓ A terület alapú gazdaságméret és a standard fedezeti hozzájárulás (SFH) összefüggéseinek vizsgálata a Nyugat-dunántúli régióban OTKA 48960 TARTALOMJEGYZÉK 1. A KUTATÁST MEGELŐZŐ FOLYAMATOK
KUTATÁSI BESZÁMOLÓ A terület alapú gazdaságméret és a standard fedezeti hozzájárulás (SFH) összefüggéseinek vizsgálata a Nyugat-dunántúli régióban OTKA 48960 TARTALOMJEGYZÉK 1. A KUTATÁST MEGELŐZŐ FOLYAMATOK
Matematikai statisztikai elemzések 6.
 Matematikai statisztikai elemzések 6. Regressziószámítás: kétváltozós lineáris és nemlineáris regresszió, többváltozós regresszió Prof. Dr. Závoti, József Matematikai statisztikai elemzések 6.: Regressziószámítás:
Matematikai statisztikai elemzések 6. Regressziószámítás: kétváltozós lineáris és nemlineáris regresszió, többváltozós regresszió Prof. Dr. Závoti, József Matematikai statisztikai elemzések 6.: Regressziószámítás:
NYUGAT-MAGYARORSZÁGI EGYETEM Faipari Mérnöki Kar. Mőszaki Mechanika és Tartószerkezetek Intézet. Dr. Hajdu Endre egyetemi docens MECHANIKA I.
 NYUGAT-MAGYARORSZÁGI EGYETEM aipari Mérnöki Kar Mőszaki Mechanika és Tartószerkezetek Intézet Dr Hajdu Endre egyetemi docens MECHANIKA I Sopron 9 javított kiadás TARTALOMJEGYZÉK I Bevezetés a mőszaki mechanika
NYUGAT-MAGYARORSZÁGI EGYETEM aipari Mérnöki Kar Mőszaki Mechanika és Tartószerkezetek Intézet Dr Hajdu Endre egyetemi docens MECHANIKA I Sopron 9 javított kiadás TARTALOMJEGYZÉK I Bevezetés a mőszaki mechanika
Hosszú Zsuzsanna Körmendi Gyöngyi Tamási Bálint Világi Balázs: A hitelkínálat hatása a magyar gazdaságra*
 Hosszú Zsuzsanna Körmendi Gyöngyi Tamási Bálint Világi Balázs: A hitelkínálat hatása a magyar gazdaságra* A hitelkínálat elmúlt évekbeli alakulását, szerepének jelentőségét vizsgáljuk különböző megközelítésekben,
Hosszú Zsuzsanna Körmendi Gyöngyi Tamási Bálint Világi Balázs: A hitelkínálat hatása a magyar gazdaságra* A hitelkínálat elmúlt évekbeli alakulását, szerepének jelentőségét vizsgáljuk különböző megközelítésekben,
A megváltozott munkaképességű személyek foglalkoztatási helyzete
 VÉDETT SZERVEZETEK ORSZÁGOS SZÖVETSÉGE A megváltozott munkaképességű személyek foglalkoztatási helyzete Felmérés az Országos Foglalkoztatási Közalapítvány támogatásával Készítette: Balogh Zoltán, Dr. Czeglédi
VÉDETT SZERVEZETEK ORSZÁGOS SZÖVETSÉGE A megváltozott munkaképességű személyek foglalkoztatási helyzete Felmérés az Országos Foglalkoztatási Közalapítvány támogatásával Készítette: Balogh Zoltán, Dr. Czeglédi
Dr. Saxné Dr. Andor Ágnes Márta. Immateriális javak a számviteli gyakorlatban
 Dr. Saxné Dr. Andor Ágnes Márta egyetemi tanársegéd, Budapesti Corvinus Egyetem Immateriális javak a számviteli gyakorlatban A szerző a SZAKma 2012. novemberi számában a szellemi tőkével kapcsolatos hazai
Dr. Saxné Dr. Andor Ágnes Márta egyetemi tanársegéd, Budapesti Corvinus Egyetem Immateriális javak a számviteli gyakorlatban A szerző a SZAKma 2012. novemberi számában a szellemi tőkével kapcsolatos hazai
A teljesítményértékelés és minősítés a közigazgatási szervek vezetésében
 Kormányzati Személyügyi Szolgáltató és Közigazgatási Képzési Központ ROP.. Programigazgatóság A teljesítményértékelés és minősítés a közigazgatási szervek vezetésében Tankönyv a köztisztviselők továbbképzéséhez
Kormányzati Személyügyi Szolgáltató és Közigazgatási Képzési Központ ROP.. Programigazgatóság A teljesítményértékelés és minősítés a közigazgatási szervek vezetésében Tankönyv a köztisztviselők továbbképzéséhez
Budapest 2011. április
 TÁMOP - 5.5.5/08/1 A diszkrimináció elleni küzdelem a társadalmi szemléletformálás és hatósági munka erősítése A férfiak és nők közötti jövedelemegyenlőtlenség és a nemi szegregáció a mai Magyarországon
TÁMOP - 5.5.5/08/1 A diszkrimináció elleni küzdelem a társadalmi szemléletformálás és hatósági munka erősítése A férfiak és nők közötti jövedelemegyenlőtlenség és a nemi szegregáció a mai Magyarországon
NÓGRÁD MEGYE SZAKKÉPZÉS-FEJLESZTÉSI KONCEPCIÓJA (2013-2020)
 NÓGRÁD MEGYE SZAKKÉPZÉS-FEJLESZTÉSI KONCEPCIÓJA (2013-2020) 2013. NÓGRÁD MEGYEI FEJLESZTÉSI ÉS KÉPZÉSI BIZOTTSÁG I. Tartalom II. BEVEZETÉS... 3 III. HELYZETELEMZÉS... 6 1. Jogszabályi környezet vizsgálata,
NÓGRÁD MEGYE SZAKKÉPZÉS-FEJLESZTÉSI KONCEPCIÓJA (2013-2020) 2013. NÓGRÁD MEGYEI FEJLESZTÉSI ÉS KÉPZÉSI BIZOTTSÁG I. Tartalom II. BEVEZETÉS... 3 III. HELYZETELEMZÉS... 6 1. Jogszabályi környezet vizsgálata,
Aranyszárny CLaVis. Nysz.: 17386
 Aranyszárny CLaVis rendszeres díjas, befektetési egységekhez kötött, élethosszig tartó életbiztosítás különös feltételei (G75/014) Hatályos: 014. március 15. Módosítva: 014. november 1. Nysz.: 1786 Tartalomjegyzék
Aranyszárny CLaVis rendszeres díjas, befektetési egységekhez kötött, élethosszig tartó életbiztosítás különös feltételei (G75/014) Hatályos: 014. március 15. Módosítva: 014. november 1. Nysz.: 1786 Tartalomjegyzék
A közvetett hatások értékelésének lehetőségei
 A közvetett hatások értékelésének lehetőségei Összefoglaló jelentés Készült A VKI végrehajtásának elősegítése II. fázis című projekt keretében Készítették: Marjainé Dr. Szerényi Zsuzsanna Harangozó Gábor
A közvetett hatások értékelésének lehetőségei Összefoglaló jelentés Készült A VKI végrehajtásának elősegítése II. fázis című projekt keretében Készítették: Marjainé Dr. Szerényi Zsuzsanna Harangozó Gábor
A mezõgazdaság gazdaságstruktúrája és jövedeleminformációs rendszerei
 A mezõgazdaság gazdaságstruktúrája és jövedeleminformációs rendszerei Dr. Kapronczai István PhD, az Agrárgazdasági Kutató Intézet főigazgató-helyettese E-mail: kapronczai@akii.hu Az EU-csatlakozást megelőző-,
A mezõgazdaság gazdaságstruktúrája és jövedeleminformációs rendszerei Dr. Kapronczai István PhD, az Agrárgazdasági Kutató Intézet főigazgató-helyettese E-mail: kapronczai@akii.hu Az EU-csatlakozást megelőző-,
SZOMBATHELY MEGYEI JOGÚ VÁROS
 SZOMBATHELY MEGYEI JOGÚ VÁROS ÁLTAL FENNTARTOTT INTÉZMÉNYEK ÉS 100% TULAJDONÚ GAZDASÁGI TÁRSASÁGOK SZOCIÁLIS ALAPELLÁTÁSÁNAK VIZSGÁLATA Készítette: Kanyik Csaba Szollár Zsuzsa Dr. Szántó Tamás Szombathely,
SZOMBATHELY MEGYEI JOGÚ VÁROS ÁLTAL FENNTARTOTT INTÉZMÉNYEK ÉS 100% TULAJDONÚ GAZDASÁGI TÁRSASÁGOK SZOCIÁLIS ALAPELLÁTÁSÁNAK VIZSGÁLATA Készítette: Kanyik Csaba Szollár Zsuzsa Dr. Szántó Tamás Szombathely,
KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZET KUTATÁSI JELENTÉSEI 51.
 KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZET KUTATÁSI JELENTÉSEI 51. KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZET Igazgató: Dr. Miltényi Károly ISSN 0236-736-X írta:
KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZET KUTATÁSI JELENTÉSEI 51. KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZET Igazgató: Dr. Miltényi Károly ISSN 0236-736-X írta:
BUDAPESTI GAZDASÁGI FŐISKOLA KÜLKERESKEDELMI FŐISKOLAI KAR NEMZETKÖZI GAZDÁLKODÁS SZAK
 BUDAPESTI GAZDASÁGI FŐISKOLA KÜLKERESKEDELMI FŐISKOLAI KAR NEMZETKÖZI GAZDÁLKODÁS SZAK Nappali tagozat Külgazdasági vállalkozás szakirány SZÁRMAZÁSI SZABÁLYOK ALKALMAZÁSA A KUMULÁCIÓ JELENTŐSÉGE NEMZETKÖZI
BUDAPESTI GAZDASÁGI FŐISKOLA KÜLKERESKEDELMI FŐISKOLAI KAR NEMZETKÖZI GAZDÁLKODÁS SZAK Nappali tagozat Külgazdasági vállalkozás szakirány SZÁRMAZÁSI SZABÁLYOK ALKALMAZÁSA A KUMULÁCIÓ JELENTŐSÉGE NEMZETKÖZI
DOKTORI (PhD) ÉRTEKEZÉS TÉZISEI NYUGAT-MAGYARORSZÁGI EGYETEM
 DOKTORI (PhD) ÉRTEKEZÉS TÉZISEI NYUGAT-MAGYARORSZÁGI EGYETEM MEZŐGAZDASÁG- ÉS ÉLELMISZERTUDOMÁNYI KAR AGRÁRGAZDASÁGTANI ÉS MARKETING TANSZÉK Programvezető: Dr. Dr. hc. Iváncsics János egyetemi tanár az
DOKTORI (PhD) ÉRTEKEZÉS TÉZISEI NYUGAT-MAGYARORSZÁGI EGYETEM MEZŐGAZDASÁG- ÉS ÉLELMISZERTUDOMÁNYI KAR AGRÁRGAZDASÁGTANI ÉS MARKETING TANSZÉK Programvezető: Dr. Dr. hc. Iváncsics János egyetemi tanár az
Ingatlanvagyon értékelés
 Nyugat-Magyarországi Egyetem Geoinformatikai Kar Ingatlanfejlesztı 8000 Székesfehérvár, Pirosalma u. 1-3. Szakirányú Továbbképzési Szak Ingatlanvagyon értékelés 2. Számviteli alapok Szerzı: Harnos László
Nyugat-Magyarországi Egyetem Geoinformatikai Kar Ingatlanfejlesztı 8000 Székesfehérvár, Pirosalma u. 1-3. Szakirányú Továbbképzési Szak Ingatlanvagyon értékelés 2. Számviteli alapok Szerzı: Harnos László
1 Rendszer alapok. 1.1 Alapfogalmak
 ÉRTÉKTEREMTŐ FOLYAM ATOK MENEDZSMENTJE II. RENDSZEREK ÉS FOLYAMATOK TARTALOMJEGYZÉK 1 Rendszer alapok 1.1 Alapfogalmak 1.2 A rendszerek csoportosítása 1.3 Rendszerek működése 1.4 Rendszerek leírása, modellezése,
ÉRTÉKTEREMTŐ FOLYAM ATOK MENEDZSMENTJE II. RENDSZEREK ÉS FOLYAMATOK TARTALOMJEGYZÉK 1 Rendszer alapok 1.1 Alapfogalmak 1.2 A rendszerek csoportosítása 1.3 Rendszerek működése 1.4 Rendszerek leírása, modellezése,
Az őrültek helye a 21. századi magyar társadalomban
 Az őrültek helye a 21. századi magyar társadalomban Ez a címe annak a kutatási programnak, amely az MTA Társadalomtudományi Kutatóközpontban, Légmán Anna szociológus vezetésével mutatja be, hogyan jelennek
Az őrültek helye a 21. századi magyar társadalomban Ez a címe annak a kutatási programnak, amely az MTA Társadalomtudományi Kutatóközpontban, Légmán Anna szociológus vezetésével mutatja be, hogyan jelennek
A népesség iskolázottságának előrejelzése 2020-ig
 Közgazdasági Szemle, LIX. évf., 2012. július augusztus (854 891. o.) Hermann Zoltán Varga Júlia A népesség iskolázottságának előrejelzése 2020-ig Iskolázási mikroszimulációs modell (ISMIK) Tanulmányunkban
Közgazdasági Szemle, LIX. évf., 2012. július augusztus (854 891. o.) Hermann Zoltán Varga Júlia A népesség iskolázottságának előrejelzése 2020-ig Iskolázási mikroszimulációs modell (ISMIK) Tanulmányunkban
Speciális ingatlanok értékelése
 Nyugat-Magyarországi Egyetem Geoinformatikai Kar Ingatlanfejlesztı 8000 Székesfehérvár, Pirosalma u. 1-3. Szakirányú Továbbképzési Szak Speciális ingatlanok értékelése 3. Speciális lakóingatlanok értékelése
Nyugat-Magyarországi Egyetem Geoinformatikai Kar Ingatlanfejlesztı 8000 Székesfehérvár, Pirosalma u. 1-3. Szakirányú Továbbképzési Szak Speciális ingatlanok értékelése 3. Speciális lakóingatlanok értékelése
Útközben Hírlevél. 1. Az együttműködés dimenziói. Az nyolcadik szám tartalmából:
 Útközben Hírlevél 1. Az együttműködés dimenziói Az Igazságügyi Hivatal Pártfogó Felügyelői Szolgálata az idei évben valósítja meg nyertes pályázatát - TÁMOP 1. 4. 3. Innovatív kísérleti foglalkoztatási
Útközben Hírlevél 1. Az együttműködés dimenziói Az Igazságügyi Hivatal Pártfogó Felügyelői Szolgálata az idei évben valósítja meg nyertes pályázatát - TÁMOP 1. 4. 3. Innovatív kísérleti foglalkoztatási
KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZETÉNEK KUTATÁSI JELENTÉSEI 41.
 KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZETÉNEK KUTATÁSI JELENTÉSEI 41. KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZET Igazgató: Dr. Miltényi Károly ISSN 0236 736 X írták:
KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZETÉNEK KUTATÁSI JELENTÉSEI 41. KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZET Igazgató: Dr. Miltényi Károly ISSN 0236 736 X írták:
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 5 V ELEmI ALGEbRA 1 BINÁRIS műveletek Definíció Az halmazon definiált bináris művelet egy olyan függvény, amely -ből képez -be Ha akkor az elempár képét jelöljük -vel, a művelet
KOVÁCS BÉLA, MATEmATIkA I 5 V ELEmI ALGEbRA 1 BINÁRIS műveletek Definíció Az halmazon definiált bináris művelet egy olyan függvény, amely -ből képez -be Ha akkor az elempár képét jelöljük -vel, a művelet
A kereslet elırejelzésének módszerei ÚTMUTATÓ 1
 A kereslet elırejelzésének módszerei ÚTMUTATÓ 1 A programozást elvégezték és a hozzá tartozó útmutatót készítették: dr. Gelei Andrea és dr. Dobos Imre, egyetemi docensek, Budapesti Corvinus Egyetem, Logisztika
A kereslet elırejelzésének módszerei ÚTMUTATÓ 1 A programozást elvégezték és a hozzá tartozó útmutatót készítették: dr. Gelei Andrea és dr. Dobos Imre, egyetemi docensek, Budapesti Corvinus Egyetem, Logisztika
Tartalomjegyzék. 5. A közbeszerzési eljárás főbb eljárási cselekményei. 6. Eljárási időkedvezmények a közbeszerzési törvényben
 Magyar Terület- és Regionális Fejlesztési Hivatal Regionális Fejlesztés Operatív Program Irányító Hatósága INFORMÁCIÓS CSOMAG a Strukturális Alapokból és a Kohéziós Alapból származó támogatásokat felhasználó
Magyar Terület- és Regionális Fejlesztési Hivatal Regionális Fejlesztés Operatív Program Irányító Hatósága INFORMÁCIÓS CSOMAG a Strukturális Alapokból és a Kohéziós Alapból származó támogatásokat felhasználó
OTDK-DOLGOZAT 2015 1
 OTDK-DOLGOZAT 2015 1 Környezeti vezetői számvitel alkalmazhatóságának kérdései a szarvasmarha tenyésztés területén, kiemelten az önköltségszámításban Questions of applicability of environmental management
OTDK-DOLGOZAT 2015 1 Környezeti vezetői számvitel alkalmazhatóságának kérdései a szarvasmarha tenyésztés területén, kiemelten az önköltségszámításban Questions of applicability of environmental management
A beszerzési logisztikai folyamat tervezésének és működtetésének stratégiái II.
 A beszerzési logisztikai folyamat tervezésének és működtetésének stratégiái II. Prof. Dr. Cselényi József Dr. Illés Béla PhD. egyetemi tanár tanszékvezető egyetemi docens MISKOLCI EGYETEM Anyagmozgatási
A beszerzési logisztikai folyamat tervezésének és működtetésének stratégiái II. Prof. Dr. Cselényi József Dr. Illés Béla PhD. egyetemi tanár tanszékvezető egyetemi docens MISKOLCI EGYETEM Anyagmozgatási
Elemzések a gazdasági és társadalompolitikai döntések előkészítéséhez 27. 2001. július. Budapest, 2002. április
 Elemzések a gazdasági és társadalompolitikai döntések előkészítéséhez 27. 2001. július Budapest, 2002. április Az elemzés a Miniszterelnöki Hivatal megrendelésére készült. Készítette: Gábos András TÁRKI
Elemzések a gazdasági és társadalompolitikai döntések előkészítéséhez 27. 2001. július Budapest, 2002. április Az elemzés a Miniszterelnöki Hivatal megrendelésére készült. Készítette: Gábos András TÁRKI
KUTATÁS, FEJLESZTÉS, PÁLYÁZATOK ÉS PROGRAMOK A FELSŐOKTATÁSBAN AZ OKTATÁSI MINISZTÉRIUM FELSŐOKTATÁS-FEJLESZTÉSI ÉS TUDOMÁNYOS ÜGYEK FŐOSZTÁLYÁNAK
 KUTATÁS, FEJLESZTÉS, PÁLYÁZATOK ÉS PROGRAMOK A FELSŐOKTATÁSBAN AZ OKTATÁSI MINISZTÉRIUM FELSŐOKTATÁS-FEJLESZTÉSI ÉS TUDOMÁNYOS ÜGYEK FŐOSZTÁLYÁNAK 2005. ÉVI JELENTÉSE Jel2005.rtf A kiadványt összeállította
KUTATÁS, FEJLESZTÉS, PÁLYÁZATOK ÉS PROGRAMOK A FELSŐOKTATÁSBAN AZ OKTATÁSI MINISZTÉRIUM FELSŐOKTATÁS-FEJLESZTÉSI ÉS TUDOMÁNYOS ÜGYEK FŐOSZTÁLYÁNAK 2005. ÉVI JELENTÉSE Jel2005.rtf A kiadványt összeállította
J/9457. B E S Z Á M O L Ó
 KÖZBESZERZÉSEK TANÁCSA J/9457. B E S Z Á M O L Ó az Országgyűlés részére a Közbeszerzések Tanácsának a közbeszerzések tisztaságával és átláthatóságával kapcsolatos tapasztalatairól, valamint a 2008. január
KÖZBESZERZÉSEK TANÁCSA J/9457. B E S Z Á M O L Ó az Országgyűlés részére a Közbeszerzések Tanácsának a közbeszerzések tisztaságával és átláthatóságával kapcsolatos tapasztalatairól, valamint a 2008. január
2.3. A rendez pályaudvarok és rendez állomások vonat-összeállítási tervének kidolgozása...35 2.3.1. A vonatközlekedési terv modellje...37 2.3.2.
 TARTALOMJEGYZÉK BEVEZETÉS...5 1. ÁRU ÉS KOCSIÁRAMLATOK TERVEZÉSE...6 1.1. A vonatközlekedési terv fogalma, jelent sége és kidolgozásának fontosabb elvei...6 1.2. A kocsiáramlatok és osztályozásuk...7 1.2.1.
TARTALOMJEGYZÉK BEVEZETÉS...5 1. ÁRU ÉS KOCSIÁRAMLATOK TERVEZÉSE...6 1.1. A vonatközlekedési terv fogalma, jelent sége és kidolgozásának fontosabb elvei...6 1.2. A kocsiáramlatok és osztályozásuk...7 1.2.1.
A KÖZPONTI KÖLTSÉGVETÉSI SZERVEK ELEMI BESZÁMOLÓJÁNAK PÉNZÜGYI (SZABÁLYSZERŰSÉGI) ELLENŐRZÉSÉNEK MÓDSZERTANA. 2003. május 001-1
 A KÖZPONTI KÖLTSÉGVETÉSI SZERVEK ELEMI BESZÁMOLÓJÁNAK PÉNZÜGYI (SZABÁLYSZERŰSÉGI) ELLENŐRZÉSÉNEK MÓDSZERTANA 2003. május 001-1 2. Államháztartás Központi Szintjét Ellenőrző Igazgatóság A központi költségvetési
A KÖZPONTI KÖLTSÉGVETÉSI SZERVEK ELEMI BESZÁMOLÓJÁNAK PÉNZÜGYI (SZABÁLYSZERŰSÉGI) ELLENŐRZÉSÉNEK MÓDSZERTANA 2003. május 001-1 2. Államháztartás Központi Szintjét Ellenőrző Igazgatóság A központi költségvetési
BMEEOUVAI01 segédlet a BME Építőmérnöki Kar hallgatói részére. Az építész- és az építőmérnök képzés szerkezeti és tartalmi fejlesztése
 EURÓPAI UNIÓ STRUKTURÁLIS ALAPOK Az építész- és az építőmérnök képzés szerkezeti és tartalmi fejlesztése HEFOP/2004/3.3.1/0001.01 I N F R A S T R U K T Ú R A L É T E S Í T M É N Y E K K I V I T E L E Z
EURÓPAI UNIÓ STRUKTURÁLIS ALAPOK Az építész- és az építőmérnök képzés szerkezeti és tartalmi fejlesztése HEFOP/2004/3.3.1/0001.01 I N F R A S T R U K T Ú R A L É T E S Í T M É N Y E K K I V I T E L E Z
J/55. B E S Z Á M O L Ó
 KÖZBESZERZÉSEK TANÁCSA J/55. B E S Z Á M O L Ó az Országgyűlés részére a Közbeszerzések Tanácsának a közbeszerzések tisztaságával és átláthatóságával kapcsolatos tapasztalatairól, valamint a 2005. január
KÖZBESZERZÉSEK TANÁCSA J/55. B E S Z Á M O L Ó az Országgyűlés részére a Közbeszerzések Tanácsának a közbeszerzések tisztaságával és átláthatóságával kapcsolatos tapasztalatairól, valamint a 2005. január
Magyarajkú, nem-magyar állampolgárságú tanulók nevelésének, oktatásának helyzete a magyar közoktatásban. Készítette: Kováts András és Medjesi Anna
 Magyarajkú, nem-magyar állampolgárságú tanulók nevelésének, oktatásának helyzete a magyar közoktatásban Készítette: Kováts András és Medjesi Anna Budapest, 2005 1 Összefoglaló A magyar nemzetiségű külföldi
Magyarajkú, nem-magyar állampolgárságú tanulók nevelésének, oktatásának helyzete a magyar közoktatásban Készítette: Kováts András és Medjesi Anna Budapest, 2005 1 Összefoglaló A magyar nemzetiségű külföldi
Aronic Főkönyv kettős könyvviteli programrendszer
 6085 Fülöpszállás, Kiskunság tér 4. Internet: www.cin.hu E-mail: software@cin.hu Tel: 78/435-081, 30/9-573-673, 30/9-593-167 kettős könyvviteli programrendszer v2.0 Szoftverdokumentáció Önnek is jár egy
6085 Fülöpszállás, Kiskunság tér 4. Internet: www.cin.hu E-mail: software@cin.hu Tel: 78/435-081, 30/9-573-673, 30/9-593-167 kettős könyvviteli programrendszer v2.0 Szoftverdokumentáció Önnek is jár egy
A KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZETÉNEK KUTATÁSI JELENTÉSEI 43.
 A KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZETÉNEK KUTATÁSI JELENTÉSEI 43. KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZET Igazgató: Dr. Miltényi Károly ISSN 0236-736-X
A KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZETÉNEK KUTATÁSI JELENTÉSEI 43. KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZET Igazgató: Dr. Miltényi Károly ISSN 0236-736-X
Készült: Készítette: IBS Kutató és Tanácsadó Kft
 A feldolgozott interjúk alapján készült áttekintő értékelő tanulmány Készült: A szlovák-magyar határmenti migráció/slovensko-maďarská pohraničná migrácia HUSK 1101/1.2.1/0171 számú projekt keretében a
A feldolgozott interjúk alapján készült áttekintő értékelő tanulmány Készült: A szlovák-magyar határmenti migráció/slovensko-maďarská pohraničná migrácia HUSK 1101/1.2.1/0171 számú projekt keretében a
Nyugat-magyarországi Egyetem Geoinformatikai Kara. Prof. Dr. Závoti József. Matematika III. 6. MA3-6 modul. A statisztika alapfogalmai
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof. Dr. Závoti József Matematika III. 6. MA3-6 modul A statisztika alapfogalmai SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról szóló 1999.
Nyugat-magyarországi Egyetem Geoinformatikai Kara Prof. Dr. Závoti József Matematika III. 6. MA3-6 modul A statisztika alapfogalmai SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról szóló 1999.
A szakképző iskolát végzettek iránti kereslet és kínálat várható alakulása 2011
 A szakképző iskolát végzettek iránti kereslet és kínálat várható alakulása 2011 Az elemzés a Szakiskolai férőhelyek meghatározása 2011, a regionális fejlesztési és képzési bizottságok (RFKB-k) részére
A szakképző iskolát végzettek iránti kereslet és kínálat várható alakulása 2011 Az elemzés a Szakiskolai férőhelyek meghatározása 2011, a regionális fejlesztési és képzési bizottságok (RFKB-k) részére
EGÉSZTESTSZÁMLÁLÁS. Mérésleírás Nukleáris környezetvédelem gyakorlat környezetmérnök hallgatók számára
 EGÉSZTESTSZÁMLÁLÁS Mérésleírás Nukleáris környezetvédelem gyakorlat környezetmérnök hallgatók számára Zagyvai Péter - Osváth Szabolcs Bódizs Dénes BME NTI, 2008 1. Bevezetés Az izotópok stabilak vagy radioaktívak
EGÉSZTESTSZÁMLÁLÁS Mérésleírás Nukleáris környezetvédelem gyakorlat környezetmérnök hallgatók számára Zagyvai Péter - Osváth Szabolcs Bódizs Dénes BME NTI, 2008 1. Bevezetés Az izotópok stabilak vagy radioaktívak
AZ EU KÖZÖS ÁRUSZÁLLÍTÁSI LOGISZTIKAI POLITIKÁJA
 DR. RIXER ATTILA * DR. TÓTH LAJOS ** AZ EU KÖZÖS ÁRUSZÁLLÍTÁSI LOGISZTIKAI POLITIKÁJA 1. BEVEZETÉS Az EU közös áruszállítási logisztikai politikája önállóan nem létezik, de az EU közös közlekedéspolitikájának
DR. RIXER ATTILA * DR. TÓTH LAJOS ** AZ EU KÖZÖS ÁRUSZÁLLÍTÁSI LOGISZTIKAI POLITIKÁJA 1. BEVEZETÉS Az EU közös áruszállítási logisztikai politikája önállóan nem létezik, de az EU közös közlekedéspolitikájának
Innováció és együttm ködési hálózatok Magyarországon
 Bajmócy Zoltán Lengyel Imre Málovics György (szerk.) 2012: Regionális innovációs képesség, versenyképesség és fenntarthatóság. JATEPress, Szeged, 52-73. o. Innováció és együttm ködési hálózatok Magyarországon
Bajmócy Zoltán Lengyel Imre Málovics György (szerk.) 2012: Regionális innovációs képesség, versenyképesség és fenntarthatóság. JATEPress, Szeged, 52-73. o. Innováció és együttm ködési hálózatok Magyarországon
Egy helytelen törvényi tényállás az új Büntető törvénykönyv rendszerében
 6 Dr. Fá z si Lá sz l ó PhD * Egy helytelen törvényi tényállás az új Büntető törvénykönyv rendszerében 1. Miről van szó A 2012. évi C. törvénnyel elfogadott új Büntető Törvénykönyv [Btk.] Különös Részének
6 Dr. Fá z si Lá sz l ó PhD * Egy helytelen törvényi tényállás az új Büntető törvénykönyv rendszerében 1. Miről van szó A 2012. évi C. törvénnyel elfogadott új Büntető Törvénykönyv [Btk.] Különös Részének
Hallgatói szemmel: a HÖK. A Politológus Műhely közvélemény-kutatásának eredményei
 Hallgatói szemmel: a HÖK A Politológus Műhely közvélemény-kutatásának eredményei Tartalomjegyzék Elnöki köszöntő... 3 Bevezetés... 4 Évfolyamképviselők és megítélésük... 7 A Hallgatói Önkormányzat és a
Hallgatói szemmel: a HÖK A Politológus Műhely közvélemény-kutatásának eredményei Tartalomjegyzék Elnöki köszöntő... 3 Bevezetés... 4 Évfolyamképviselők és megítélésük... 7 A Hallgatói Önkormányzat és a
Munkaügyi Központja 2014. I. NEGYEDÉV
 Munkaügyi Központja A MUNKAERİ-GAZDÁLKODÁSI FELMÉRÉS ÖSSZEFOGLALÓJA 2014. I. NEGYEDÉV Pápa Zirc Devecser Ajka Veszprém Várpalota Sümeg Balatonalmádi Tapolca Balatonfüred Veszprém megye 8200 Veszprém, Megyeház
Munkaügyi Központja A MUNKAERİ-GAZDÁLKODÁSI FELMÉRÉS ÖSSZEFOGLALÓJA 2014. I. NEGYEDÉV Pápa Zirc Devecser Ajka Veszprém Várpalota Sümeg Balatonalmádi Tapolca Balatonfüred Veszprém megye 8200 Veszprém, Megyeház
Szakmai beszámoló és elemzés a békéltető testületek 2010. évi tevékenységéről
 Szakmai beszámoló és elemzés a békéltető testületek 2010. évi tevékenységéről Budapest, 2011. február Az MKIK Gazdaság- és Vállalkozáskutató Intézet olyan nonprofit kutatóműhely, amely elsősorban alkalmazott
Szakmai beszámoló és elemzés a békéltető testületek 2010. évi tevékenységéről Budapest, 2011. február Az MKIK Gazdaság- és Vállalkozáskutató Intézet olyan nonprofit kutatóműhely, amely elsősorban alkalmazott
Szegény gazdagok és gazdag szegények ( Vizsgálódások a személyi jövedelmek körében)
 Közgazdasági Szemle, XXXI.évf.1984.6.sz. (664-678.l.) Szegény gazdagok és gazdag szegények ( Vizsgálódások a személyi jövedelmek körében) Práger László A társadalomtudományi kutatások, a közgazdasági elemzések
Közgazdasági Szemle, XXXI.évf.1984.6.sz. (664-678.l.) Szegény gazdagok és gazdag szegények ( Vizsgálódások a személyi jövedelmek körében) Práger László A társadalomtudományi kutatások, a közgazdasági elemzések
I. FEJEZET BEVEZETİ. I.1. A koncepció szükségessége
 I. FEJEZET BEVEZETİ A Magyar Köztársaság Alkotmányáról szóló 1949. évi XX. törvény 70/E. -a deklarálja alapvetı állampolgári jogként a szociális biztonsághoz való jogot, amely szerint az állampolgárok
I. FEJEZET BEVEZETİ A Magyar Köztársaság Alkotmányáról szóló 1949. évi XX. törvény 70/E. -a deklarálja alapvetı állampolgári jogként a szociális biztonsághoz való jogot, amely szerint az állampolgárok
Felkészülést segítő kérdések Gépszerkesztés alapjai tárgyból
 Felkészülést segítő kérdések Gépszerkesztés alapjai tárgyból - Ismertesse a kézi rajzkészítési technikát (mikor használjuk, előny-hátrány stb.)! Kézi technikák közül a gondolatrögzítés leggyorsabb, praktikus
Felkészülést segítő kérdések Gépszerkesztés alapjai tárgyból - Ismertesse a kézi rajzkészítési technikát (mikor használjuk, előny-hátrány stb.)! Kézi technikák közül a gondolatrögzítés leggyorsabb, praktikus
Önértékelési kézikönyv KOLLÉGIUMOK SZÁMÁRA
 Önértékelési kézikönyv KOLLÉGIUMOK SZÁMÁRA Szerzők: Barcsák Marianna, Barlai Róbertné, Bot Szilvia, Farkasné Egyed Zsuzsanna, Horváthné Moldvay Ilona, Járainé dr. Bődi Györgyi, Jurecz Emil, Molnárné Stadler
Önértékelési kézikönyv KOLLÉGIUMOK SZÁMÁRA Szerzők: Barcsák Marianna, Barlai Róbertné, Bot Szilvia, Farkasné Egyed Zsuzsanna, Horváthné Moldvay Ilona, Járainé dr. Bődi Györgyi, Jurecz Emil, Molnárné Stadler
Terület- és településrendezési ismeretek
 Terület- és településrendezési ismeretek Tankönyv a köztisztviselők továbbképzéséhez Szerkesztette: László László Budapest 006. október A TANANYAGOT MEGALAPOZÓ TANULMÁNYOK SZERZŐI: DR. KÖKÉNYESI JÓZSEF
Terület- és településrendezési ismeretek Tankönyv a köztisztviselők továbbképzéséhez Szerkesztette: László László Budapest 006. október A TANANYAGOT MEGALAPOZÓ TANULMÁNYOK SZERZŐI: DR. KÖKÉNYESI JÓZSEF
SZÜKSÉGLETFELMÉRÉS SZOLGÁLTATÁSTERVEZÉS MÓDSZERTANI AJÁNLÁS
 SZÜKSÉGLETFELMÉRÉS SZOLGÁLTATÁSTERVEZÉS MÓDSZERTANI AJÁNLÁS Készítette: Mártháné Megyesi Mária SZKTT Egyesített Szociális Intézmény Tabán Családsegítő Közösségi Ház és Dél-alföldi Regionális Módszertani
SZÜKSÉGLETFELMÉRÉS SZOLGÁLTATÁSTERVEZÉS MÓDSZERTANI AJÁNLÁS Készítette: Mártháné Megyesi Mária SZKTT Egyesített Szociális Intézmény Tabán Családsegítő Közösségi Ház és Dél-alföldi Regionális Módszertani
A vállalkozások tevékenységének komplex elemzése
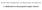 Dr. Bíró Tibor Kresalek Péter Dr. Pucsek József Dr. Sztanó Imre A vállalkozások tevékenységének komplex elemzése Dr. Bíró Tibor Kresalek Péter Dr. Pucsek József Dr. Sztanó Imre A vállalkozások tevékenységének
Dr. Bíró Tibor Kresalek Péter Dr. Pucsek József Dr. Sztanó Imre A vállalkozások tevékenységének komplex elemzése Dr. Bíró Tibor Kresalek Péter Dr. Pucsek József Dr. Sztanó Imre A vállalkozások tevékenységének
A TÖMEGKÖZLEKEDÉSI KÖZSZOLGÁLTATÁS SZOLGÁLTATÓ JELLEGÉNEK MEGALAPOZÁSA: MEGÁLLÓHELY ELLÁTOTTSÁG BUDAPESTEN. Összefoglaló
 RUZSÁNYI TIVADAR A TÖMEGKÖZLEKEDÉSI KÖZSZOLGÁLTATÁS SZOLGÁLTATÓ JELLEGÉNEK MEGALAPOZÁSA: MEGÁLLÓHELY ELLÁTOTTSÁG BUDAPESTEN Összefoglaló A tanulmányban a tömegközlekedés igénybevételének alapvető feltételét,
RUZSÁNYI TIVADAR A TÖMEGKÖZLEKEDÉSI KÖZSZOLGÁLTATÁS SZOLGÁLTATÓ JELLEGÉNEK MEGALAPOZÁSA: MEGÁLLÓHELY ELLÁTOTTSÁG BUDAPESTEN Összefoglaló A tanulmányban a tömegközlekedés igénybevételének alapvető feltételét,
A növénytermesztési technológiák élelmiszerbiztonsági kérdései. 2014. július 9.
 A növénytermesztési technológiák élelmiszerbiztonsági kérdései 2014. július 9. 2 Készült a TÁMOP-4.1.1.C- 12/1/KONV-2012-0014: Élelmiszerbiztonság és gasztronómia vonatkozású egyetemi együttműködés, DE-SZTE-EKF-NYME
A növénytermesztési technológiák élelmiszerbiztonsági kérdései 2014. július 9. 2 Készült a TÁMOP-4.1.1.C- 12/1/KONV-2012-0014: Élelmiszerbiztonság és gasztronómia vonatkozású egyetemi együttműködés, DE-SZTE-EKF-NYME
2013.03.11. Az SPC alapjai. Az SPC alapjai SPC 5. 5. Az SPC (Statistic Process Control) módszer. Dr. Illés Balázs
 SPC 5 5. Az SPC (Statistic Process Control) módszer Dr. Illés Balázs BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM ELEKTRONIKAI TECHNOLÓGIA TANSZÉK Az SPC alapjai SPC (Statistical Process Controll) =
SPC 5 5. Az SPC (Statistic Process Control) módszer Dr. Illés Balázs BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM ELEKTRONIKAI TECHNOLÓGIA TANSZÉK Az SPC alapjai SPC (Statistical Process Controll) =
A kamara ahol a gazdaság terem. Beszámoló a Tolna Megyei Kereskedelmi és Iparkamara 2013. évi tevékenységéről
 A kamara ahol a gazdaság terem Beszámoló a Tolna Megyei Kereskedelmi és Iparkamara 2013. évi tevékenységéről 1 Bevezetés Jelen beszámoló elkészítésének célja a kamarai küldöttek tájékoztatása a szervezet
A kamara ahol a gazdaság terem Beszámoló a Tolna Megyei Kereskedelmi és Iparkamara 2013. évi tevékenységéről 1 Bevezetés Jelen beszámoló elkészítésének célja a kamarai küldöttek tájékoztatása a szervezet
Időtervek: III./1.Hálóterv (CPM) szerkesztése
 Faicsiné Adorján Edit Időtervek: III./1.Hálóterv (CPM) szerkesztése A követelménymodul megnevezése: Építőipari kivitelezés tervezése A követelménymodul száma: 0688-06 A tartalomelem azonosító száma és
Faicsiné Adorján Edit Időtervek: III./1.Hálóterv (CPM) szerkesztése A követelménymodul megnevezése: Építőipari kivitelezés tervezése A követelménymodul száma: 0688-06 A tartalomelem azonosító száma és
A MUNKÁLTATÓKAT TÁMOGATÓ SZOLGÁLTATÁSI RENDSZER MÓDSZERTANI ÉS DOKUMENTÁCIÓS FOLYAMATA
 A MUNKÁLTATÓKAT TÁMOGATÓ SZOLGÁLTATÁSI RENDSZER MÓDSZERTANI ÉS DOKUMENTÁCIÓS FOLYAMATA 1 Tartalom BEVEZETŐ... 4 MUNKAERŐ KERESLET, MUNKAERŐPIACI IGÉNYEK... 7 Munkaerő-piaci kereslet - prognózis 2013...
A MUNKÁLTATÓKAT TÁMOGATÓ SZOLGÁLTATÁSI RENDSZER MÓDSZERTANI ÉS DOKUMENTÁCIÓS FOLYAMATA 1 Tartalom BEVEZETŐ... 4 MUNKAERŐ KERESLET, MUNKAERŐPIACI IGÉNYEK... 7 Munkaerő-piaci kereslet - prognózis 2013...
I: Az értékteremtés lehetőségei a vállalaton belüli megközelítésben és piaci szempontokból
 16. Tétel Az értékteremtés lehetőségei a vállalaton belüli megközelítésben és piaci szempontokból. Az értékteremtő folyamatok a vállalat működésében, az értéklánc elemei. A teljesítmény és menedzsmentje,
16. Tétel Az értékteremtés lehetőségei a vállalaton belüli megközelítésben és piaci szempontokból. Az értékteremtő folyamatok a vállalat működésében, az értéklánc elemei. A teljesítmény és menedzsmentje,
Tűgörgős csapágy szöghiba érzékenységének vizsgálata I.
 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Tudományos Diákköri Konferencia Tűgörgős csapágy szöghiba érzékenységének vizsgálata I. Szöghézag és a beépítésből adódó szöghiba vizsgálata
Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Tudományos Diákköri Konferencia Tűgörgős csapágy szöghiba érzékenységének vizsgálata I. Szöghézag és a beépítésből adódó szöghiba vizsgálata
Az AXA megoldásai a pénzügyi biztonságért
 BI001 / 20100501 Az AXA megoldásai a pénzügyi biztonságért Mindannyiunk igénye az, hogy életünk biztos alapokra épüljön és magabiztosan készülhessünk a jövőre. A mi feladatunk, hogy ehhez olyan biztosítási,
BI001 / 20100501 Az AXA megoldásai a pénzügyi biztonságért Mindannyiunk igénye az, hogy életünk biztos alapokra épüljön és magabiztosan készülhessünk a jövőre. A mi feladatunk, hogy ehhez olyan biztosítási,
Részidős hallgatók intézményválasztási döntései határokon innen és túl
 TŐZSÉR Zoltán Debreceni Egyetem Részidős hallgatók intézményválasztási döntései határokon innen és túl Bevezetés Ebben az esettanulmányban a Partium történelmi régió magyar tannyelvű felsőoktatási intézményében
TŐZSÉR Zoltán Debreceni Egyetem Részidős hallgatók intézményválasztási döntései határokon innen és túl Bevezetés Ebben az esettanulmányban a Partium történelmi régió magyar tannyelvű felsőoktatási intézményében
A.26. Hagyományos és korszerű tervezési eljárások
 A.26. Hagyományos és korszerű tervezési eljárások A.26.1. Hagyományos tervezési eljárások A.26.1.1. Csuklós és merev kapcsolatú keretek tervezése Napjainkig a magasépítési tartószerkezetek tervezése a
A.26. Hagyományos és korszerű tervezési eljárások A.26.1. Hagyományos tervezési eljárások A.26.1.1. Csuklós és merev kapcsolatú keretek tervezése Napjainkig a magasépítési tartószerkezetek tervezése a
Aronic Bér Bérszámfejtés és munkaügyi nyilvántartás program
 CIN Számítástechnika és Szoftverház 6085 Fülöpszállás, Kiskunság tér 4. Internet: www.cin.hu E-mail: software@cin.hu Tel: 78/435-081, 30/9-573-673 Aronic Bér Bérszámfejtés és munkaügyi nyilvántartás program
CIN Számítástechnika és Szoftverház 6085 Fülöpszállás, Kiskunság tér 4. Internet: www.cin.hu E-mail: software@cin.hu Tel: 78/435-081, 30/9-573-673 Aronic Bér Bérszámfejtés és munkaügyi nyilvántartás program
Dr. Göndöcs Balázs, BME Közlekedésmérnöki Kar. Tárgyszavak: szerelés; javíthatóság; cserélhetőség; karbantartás.
 JELLEGZETES ÜZEMFENNTARTÁS-TECHNOLÓGIAI ELJÁRÁSOK 4.06 Javításhelyes szerelés 1 Dr. Göndöcs Balázs, BME Közlekedésmérnöki Kar Tárgyszavak: szerelés; javíthatóság; cserélhetőség; karbantartás. A mai termékek
JELLEGZETES ÜZEMFENNTARTÁS-TECHNOLÓGIAI ELJÁRÁSOK 4.06 Javításhelyes szerelés 1 Dr. Göndöcs Balázs, BME Közlekedésmérnöki Kar Tárgyszavak: szerelés; javíthatóság; cserélhetőség; karbantartás. A mai termékek
Módszertani megjegyzések
 Módszertani megjegyzések Az adatok forrása amennyiben nincs hivatkozás más adatforrásra a Központi Statisztikai Hivatal (KSH) adatgyűjtése. 2009-től az adatok publikálása az európai uniós szabályozásoknak
Módszertani megjegyzések Az adatok forrása amennyiben nincs hivatkozás más adatforrásra a Központi Statisztikai Hivatal (KSH) adatgyűjtése. 2009-től az adatok publikálása az európai uniós szabályozásoknak
9. A FORGÁCSOLÁSTECHNOLÓGIAI TERVEZŐ-RENDSZER FUNKCIONÁLIS STRUKTÚRÁJA
 9. A FORGÁCSOLÁSTECHNOLÓGIAI TERVEZŐ-RENDSZER FUNKCIONÁLIS STRUKTÚRÁJA Egy-egy konkrét forgácsolástechnológiai tervezőrendszer saját, a fejlesztő által megfogalmazott struktúrát testesít meg. Az itt tárgyalt
9. A FORGÁCSOLÁSTECHNOLÓGIAI TERVEZŐ-RENDSZER FUNKCIONÁLIS STRUKTÚRÁJA Egy-egy konkrét forgácsolástechnológiai tervezőrendszer saját, a fejlesztő által megfogalmazott struktúrát testesít meg. Az itt tárgyalt
A nemzetközi vándorlás hatása a magyarországi népesség számának alakulására 1994 2010 között 1
 Hablicsek László Tóth Pál Péter A nemzetközi vándorlás hatása a magyarországi népesség számának alakulására 1994 2010 között 1 A magyarországi népesség-előreszámítások eddig a zárt népesség elvén készültek,
Hablicsek László Tóth Pál Péter A nemzetközi vándorlás hatása a magyarországi népesség számának alakulására 1994 2010 között 1 A magyarországi népesség-előreszámítások eddig a zárt népesség elvén készültek,
Felhívás észrevételek benyújtására az állami támogatások kérdéskörében a Bizottság általános csoportmentességi rendelettervezetére vonatkozóan
 C 210/14 Felhívás észrevételek benyújtására az állami támogatások kérdéskörében a Bizottság általános csoportmentességi rendelettervezetére vonatkozóan (2007/C 210/10) Az érdekelt felek észrevételeiket
C 210/14 Felhívás észrevételek benyújtására az állami támogatások kérdéskörében a Bizottság általános csoportmentességi rendelettervezetére vonatkozóan (2007/C 210/10) Az érdekelt felek észrevételeiket
Matematikai és matematikai statisztikai alapismeretek
 Kézirat a Matematikai és matematikai statisztikai alapismeretek című előadáshoz Dr. Győri István NEVELÉSTUDOMÁNYI PH.D. PROGRM 1999/2000 1 1. MTEMTIKI LPOGLMK 1.1. Halmazok Halmazon mindig bizonyos dolgok
Kézirat a Matematikai és matematikai statisztikai alapismeretek című előadáshoz Dr. Győri István NEVELÉSTUDOMÁNYI PH.D. PROGRM 1999/2000 1 1. MTEMTIKI LPOGLMK 1.1. Halmazok Halmazon mindig bizonyos dolgok
AZ ELSŐ ÉS MÁSODIK DEMOGRÁFIAI ÁTMENET MAGYARORSZÁGON ÉS KÖZÉP-KELET-EURÓPÁBAN
 AZ ELSŐ ÉS MÁSODIK DEMOGRÁFIAI ÁTMENET MAGYARORSZÁGON ÉS KÖZÉP-KELET-EURÓPÁBAN Készült az ОТKA 400 kutatási program keretében BUDAPEST 1995/1 KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZET
AZ ELSŐ ÉS MÁSODIK DEMOGRÁFIAI ÁTMENET MAGYARORSZÁGON ÉS KÖZÉP-KELET-EURÓPÁBAN Készült az ОТKA 400 kutatási program keretében BUDAPEST 1995/1 KÖZPONTI STATISZTIKAI HIVATAL NÉPESSÉGTUDOMÁNYI KUTATÓ INTÉZET
ELEMI BÁZISTRANSZFORMÁCIÓ LÉPÉSEI 2.NEHEZÍTETT VÁLTOZAT 2.a) Paramétert nem tartalmazó eset
 ELEMI BÁZISTRANSZFORMÁCIÓ LÉPÉSEI 2.NEHEZÍTETT VÁLTOZAT 2.a) Paramétert nem tartalmazó eset A bázistranszformáció nehezített változatában a bázison kívül elhelyezkedő vektorokból amennyit csak lehetséges
ELEMI BÁZISTRANSZFORMÁCIÓ LÉPÉSEI 2.NEHEZÍTETT VÁLTOZAT 2.a) Paramétert nem tartalmazó eset A bázistranszformáció nehezített változatában a bázison kívül elhelyezkedő vektorokból amennyit csak lehetséges
A migrációs statisztika fejlesztésének lehetőségei
 A migrációs statisztika fejlesztésének lehetőségei Megvalósíthatósági tanulmány Összeállította Tóth Pál Péter Készült a A migrációs statisztika fejlesztésének lehetőségei c. projekt (EIA/2010/3.2.1.1.)
A migrációs statisztika fejlesztésének lehetőségei Megvalósíthatósági tanulmány Összeállította Tóth Pál Péter Készült a A migrációs statisztika fejlesztésének lehetőségei c. projekt (EIA/2010/3.2.1.1.)
Költségvetés és árképzés az építőiparban TERC Kft., Budapest, 2013.
 Dr. Neszmélyi László Költségvetés és árképzés az építőiparban TERC Kft., Budapest, 2013. Dr. Neszmélyi László, 2013 TERC Kft., 2013 A könyv részeit vagy egészét közölni a szerzőre és a kiadóra vonatkozó
Dr. Neszmélyi László Költségvetés és árképzés az építőiparban TERC Kft., Budapest, 2013. Dr. Neszmélyi László, 2013 TERC Kft., 2013 A könyv részeit vagy egészét közölni a szerzőre és a kiadóra vonatkozó
FELCSÚTI KÖZÖS ÖNKORMÁNYZATI HIVATAL
 FELCSÚTI KÖZÖS ÖNKORMÁNYZATI HIVATAL BIZONYLATI RENDJE Hatályos: 2013. március 1-jétől. BIZONYLATI REND A Felcsúti Közös Önkormányzati Hivatal (továbbiakban: Hivatal) Bizonylati rendjét a számvitelről
FELCSÚTI KÖZÖS ÖNKORMÁNYZATI HIVATAL BIZONYLATI RENDJE Hatályos: 2013. március 1-jétől. BIZONYLATI REND A Felcsúti Közös Önkormányzati Hivatal (továbbiakban: Hivatal) Bizonylati rendjét a számvitelről
MAGYARORSZÁG NYUGDÍJRENDSZERE (1997-2013) 2013. Október 5-7.
 MAGYARORSZÁG NYUGDÍJRENDSZERE (1997-2013) 2013. Október 5-7. 1 TARTALOM: I. Előzmény 1997-(röviden) 1. MAGÁNNYUGDÍJ RENDSZER II. NYUGDÍJREFORM FOLYAMATOK MAGYARORSZÁGON 2009-2013 1. KORHATÁREMELÉS 2. MAGÁNNYUGDÍJ
MAGYARORSZÁG NYUGDÍJRENDSZERE (1997-2013) 2013. Október 5-7. 1 TARTALOM: I. Előzmény 1997-(röviden) 1. MAGÁNNYUGDÍJ RENDSZER II. NYUGDÍJREFORM FOLYAMATOK MAGYARORSZÁGON 2009-2013 1. KORHATÁREMELÉS 2. MAGÁNNYUGDÍJ
Az Idősügyi Nemzeti Stratégia nem tárgyalja
 NYUGDÍJ a nyugdíjrendszer jövőjéről a kötelező nyugdíjbiztosítás öregségi nyugdíj korhatár korkedvezmény; korengedmény korrekció nyugdíjemelés nyugdíjprémium rokkantsági nyugdíj hátramaradotti ellátások
NYUGDÍJ a nyugdíjrendszer jövőjéről a kötelező nyugdíjbiztosítás öregségi nyugdíj korhatár korkedvezmény; korengedmény korrekció nyugdíjemelés nyugdíjprémium rokkantsági nyugdíj hátramaradotti ellátások
ÜZLETSZABÁLYZAT. ALFA-NOVA Energetikai, Fejlesztő, Tervező és Vállalkozó Korlátolt Felelősségű Társaság SZEKSZÁRD
 ÜZLETSZABÁLYZAT ALFA-NOVA Energetikai, Fejlesztő, Tervező és Vállalkozó Korlátolt Felelősségű Társaság SZEKSZÁRD Hatálybalépés időpontja: 2013. február 01. Szekszárd, 2013. február 01. 1 Tartalomjegyzék
ÜZLETSZABÁLYZAT ALFA-NOVA Energetikai, Fejlesztő, Tervező és Vállalkozó Korlátolt Felelősségű Társaság SZEKSZÁRD Hatálybalépés időpontja: 2013. február 01. Szekszárd, 2013. február 01. 1 Tartalomjegyzék
Az ipari parkok megjelenése
 Az ipari parkok megjelenése Tartalomjegyzék: 1. Bevezetés 4 2. Logisztika 5 2.1 A logisztika fogalma és rövid története 5 2.2 A logisztika feladata 6 2.3 A logisztika céljai 6 2.4 A logisztika legfıbb
Az ipari parkok megjelenése Tartalomjegyzék: 1. Bevezetés 4 2. Logisztika 5 2.1 A logisztika fogalma és rövid története 5 2.2 A logisztika feladata 6 2.3 A logisztika céljai 6 2.4 A logisztika legfıbb
Segédlet a lakásszövetkezetek tisztségviselőinek megválasztásához
 Segédlet a lakásszövetkezetek tisztségviselőinek megválasztásához A lakásszövetkezetek törvényes működésének elengedhetetlen feltétele a tisztségviselők szabályszerű választása. Az alábbiakban áttekintjük
Segédlet a lakásszövetkezetek tisztségviselőinek megválasztásához A lakásszövetkezetek törvényes működésének elengedhetetlen feltétele a tisztségviselők szabályszerű választása. Az alábbiakban áttekintjük
