2.2. Alapfogalmak, alapjelenségek
|
|
|
- Gréta Boros
- 6 évvel ezelőtt
- Látták:
Átírás
1 .. Alapfogalmak, alapjelenségek Az irodalomban nem teljesen egyértelműek a használt definíciók, ezért itt rögzítjük azokat és az angol megfelelőiket, továbbá több, felhasznált jelölést, rövidítést. Ion: töltéssel rendelkező atom, molekula, atomfürt. Ha meghatározott töltésállapotban van, felső indexszel jelöljük, ha ez nem lényeges, vagy nem ismert "ion"-t írunk. Ionnyaláb (ion beam). Gyorsított és valamilyen ionoptikával formált ionnyaláb, tartalmazhat neutrálizálódott ionokat, azaz gyorsított atomokat is. Áram (current), itt szokásos egysége a µa, megfelel ion/s-nak. Áramsűrűség (flux, current density), egységnyi felületre érkező ionáram, µa/cm. Dózis (fluence), az egységnyi felületre érkezett ionok száma, ion/cm. Ionenergia (ion energy), elektronvolt és többszörösei (kev, MeV). Esetenként atomi tömegegységre vonatkoztatjuk, ekkor MeV/amu (atomic mass unit) az egysége. Az implantáció hőmérséklete: T i, a hőkezelésé T h, az éppen kérdéses anyag olvadáspontja T m, a szobahőmérséklet T sz, a folyékony nitrogéné T LN. D, 3D: a két-, ill. háromdimenzió(s) rövidítése...1. Az ionok behatolása, fékeződése 1 Az ionok behatolása és fékeződési folyamatai kettős értelemben is statisztikus jellegűek: előszöris az ionok becsapódása véletlenszerű, másrészt a fékeződési folyamatot független ütközések sorozataként tekintjük. Már a XX. század elején megszülettek azok az elméletek, amelyek ugyan változtatásokkal, de mindmáig alkalmazhatók a 1 Részben követjük J.F: Ziegler: "Ion implantation Physics" fejezetét [Handbook of Ion Implantation Technology, Ed. J.F. Ziegler (North-Holland, Amsterdam, 199)] p
2 folyamatok általános jellemzésére. Bohr [1940] kidolgozott egy "effektív töltés" (Z*) leírást, amelynek alapfeltevése, hogy a v sebességgel mozgó ion minden olyan elektronját elveszti, amelyek v-nél kisebb sebességgel mozognak: 90
3 .4. ábra. A szórás geometriája laboratóriumi és tömegközépponti koordináta-rendszerben. Az ion tömege és sebssége ütközás előtt M 1 és v 0, utána v 1. Az atomé M és meglökés utáni sebssége v. A P az impakt faktor. v c sebesség a tömegközépponti rendszerben. A szögeket értelemszerűen jelöltük. * 13 / Z = Z v/ v,
4 ahol az "1" index az ionra vonatkozik és v 0 a Bohr-sebesség (, m/s). Ez az effektív töltés szerepel a fékezésben (l...7 egyenlet). Ugyancsak ekkor definiálta Bohr az a 1 árnyékolási távolságot, amely jellemzi két semleges atom kölcsönhatását: 3 / / ( ) a = a / Z + Z /,.. ahol a "" index a tárgyatomot jelzi és a 0 a Bohr sugár (0,059 nm). Bohr [1948] a Thomas-Fermi potenciált használta az árnyékolt Coulomb potenciál becslésére: 1 () = ( r a ) Vr ZZ r exp /,..3 ahol Z 1 és Z a rendszám, r a magok távolsága és a 1 az árnyékolási paraméter. Firsov [1958] numerikus számításokkal mutatta meg, hogy a.. árnyékolási paraméter adja a legjobb közelítést az atom statisztikus elméletének keretei között. A nagy lépés a fékezés és a behatolás egységes leírására 1963 után következett be Lindhard, Scharff és Schiøtt munkái nyomán (LSS elmélet) [1963]. Az elmélet a Thomas-Fermi atomra vonatkozik, ezért főleg a nagyobb rendszámokra és közepes energiákra pontos. Ekkor kettes faktoron belül helyesen írja le az energiaveszteség kísérleti értékeit. Klasszikus kétrészecske szórás. Felírjuk a mozgó ionra ("ion") és a tárgyatomra ("atom") a rugalmas szórásban az energiamegmaradás, valamint az impulzusmegmaradás egyenleteit a.4. ábra szerinti geometriában. Az ábrán M 1, M a tömegeket jelöli, P az impakt (ütközési) faktor. A szóródás után az ion v 1 sebességgel, ϑ irányban folytatja az útját, míg az atom v sebességgel, φ irányba lökődik: E0 = M1v0 = M1v1 + Mv,..4 ebből két komponens, a longitudinális Mv = Mv cosϑ + Mv cos φ, és a transzverzális 0 = Mv 1 1 sin ϑ + Mv sin φ..6 számítható. Ez az egyenlet több változóra is megoldható. Pl. a φ kiküszöbölésével 9
5 v v 1 v1 v M 0 M 1 + M 1 M M1 cosϑ = 0..7 M + M 1 adódik. Az összefüggések transzformálhatók a tömegközépponti rendszerbe, amikoris a kétrészecske mozgás egyetlen részecskének egy központi potenciáltérben való mozgására redukálódik. Válasszuk a rendszer v c sebességét úgy, hogy ebben a rendszerben az impulzus eltűnjék: ( ) Mv 1 0 = M 1 + M v c...8 Bevezetve az M c redukált tömeget, M = M M ( M + c 1 1 M )..9 adódik, ahol a v c rendszersebesség állandó és nem függ a szögektől: v v M / M...10 c = 0 c Ezekkel az ütközéskor fellépő T r energiaátadás: 1 M v0mc cosφ T M v ( ) M M vm r = = = 0 c cosφ...11 Felhasználva, hogy a tömegközépponti rendszerben definiált Θ szórási szögre φ = π -Θ, az energiaátadás pl. a következő alakba írható: T r = 4E M M ( M + M ) 93 sin Θ...1 Frontális ütközésnél Θ = π, ekkor a transzfer maximális (T r,max ). Atomközi potenciálok. Különféle potenciál-közelítések használatosak. A Thomas-Fermi atom Sommerfeld-féle [193] közelítése a legelterjedtebb. Emellett a Lenz-Jensen [193], valamint a Moliérepotenciál [1947] alkalmazása közkeletű. Valamennyi V(r) potenciálra igaz, hogy egy 1/r-es távolságfüggő Coulomb tagot, továbbá egy árnyékoló faktort tartalmaz: V ( r) Φ ) =,..13 ( Ze r) ahol Φ ) az árnyékolási függvény, e az elektron töltése. A kiszámításának legkezelhetőbb módszerét Gombás [1949] ajánlotta és ) Φ
6 újabban Ziegler et al. [1984]számított ki annak alapján egy "univerzális" árnyékoló potenciált, ) Φ U = 0,1818e x = r a U, 3, x a U + 0,5099e = 0,8854a 0,943x 1 + 0,80e = 0,8854a 0 0,408x / 3 /3 /( Z + Z ) ,817e 0,016x, ahol..14 Energiaátadás az ion és az atom között...1 alakja a tömegközépponti rendszerben: T r EM c c = 4 sin Θ...15 M Univerzális nukleáris fékeződés. A teljes fékeződés két részből összetettnek tekintjük: az atom elektronfelhőjének (elektronfékeződés), illetve az atommagoknak (nukleáris fékeződés) átadott energia. A nukleáris fékeződés függetlenül tárgyalható, mert az ionsebességek miatt a folyamat során az atom "lecsatolódik" a rácsról, tehát tárgyalható két szabad (bár árnyékolt töltéssel rendelkező) részecske rugalmas kinetikai szórásaként. Ez a közelítés nem veszi figyelembe az esetleges korrelációt a "kemény" nukleáris ütközések és az elektronfelhővel való rugalmatlan kölcsönhatás között. Ezt a korrelációt a szilárd testben kicsinynek vesszük a kollektív hatások feltehető átlagoló hatása miatt. A korreláció azonban nem elhanyagolható, ha egyedi atomok ütközéseit, vagy ionoknak vékony rétegekben létrejövő ütközéseit tárgyaljuk. A fékeződés jellemzője tehát az egységnyi úton leadott energia de/dr (másutt de/dx). Ennek az S n (E) fékezési keresztmetszettel való kapcsolatát az anyag N atomi sűrűsége teremti meg: de/dr = NS n (E). Maga az S n (E) átlagos átadott energia a P impaktparaméter valamennyi értékére való összegzéssel számítható ki: max Θ S n ( E) = T( E, p) πpdp = πγe 0 sin PdP,..16 ahol γ MM ( M + M ) / 1, a tömegközépponti rendszerben a transzformációs egység. Ezzel az LSS elmélet "redukált energiáját" p 0 ( ) ε a M E / Z Z e M + M..17 U 0 1 bevezetve, a nukleáris fékeződés értéke: 1 94
7 S n ε a E S E n π γ ( ε) ( ) = U Gyakorlati alkalmazások számára ezen univerzális fékeződés a következő konkrét alakba írható: S n ( E ) 0 846, 10 = 15 ZZMS 1 1 ( ε) 03, 03, ( M1 + M)( Z1 + Z ) Az ε redukált energia numerikus alakjában a következő ε 3, 53M E 0 ZZ M M Z Z n 03, ( + )( + 03, ) ev /( atom / cm ) Mindezekkel a redukált nukleáris fékeződés a következőképpen számítható: ( ε) ln, ε 30 S n ( ε) = , 16 0, 5 ( ε +, ε +, ε ) ( ε) ε> 30 S = n ln [ ε] ε...1a-b Elektronos fékeződés és hatáskeresztmetszet. Bohr [1913] az atomok kötött elektronjait harmonikus potenciáltérben mozgó töltésként kezelte, amelyeknek a frekvenciája optikai abszorpciós adatokból származtatható. Kimutatta, hogy az energiaveszteségben egy levágásos határ jön létre, ha feltette, hogy a P/v ütközési időtartamot az elektron "keringési" idejénél, azaz 1/ν-nél kisebbnek veszi. A ν egyébként a harmonikus oszcillátor frekvenciája. A levágás azt jelenti, hogy hosszabb kölcsönhatásokat feltételezve az ion egyáltalán nem ad át energiát az elektronfelhőnek. A ma használt elméletet Bethe-Bloch [1930, 33] elméletként ismerjük. Ez az elmélet kvantummechanikai úton, első Born közelítésben oldotta meg a töltött részecske-atom energiaátadást. A céltárgy atomos jellegét az elektronfelhőnek egy átlagos gerjesztésével veszik figyelembe. Bohr "távoli kölcsönhatás" elmélete akkor lesz azonos a "közeli kölcsönhatás" Bethe- elméletével, ha az átlagos energiaveszteséget valamennyi elektronátmenetre átlagoljuk. Bloch szintetizálta a két elméletet olymódon, hogy az "kemény" ütközések 95
8 esetén a Bohr-közelítésre redukálódik, gyenge kölcsönhatásokra pedig közelítőleg megegyezik Bethe megoldásával. Mindez akkor igaz, ha az ionsebesség sokkal nagyobb, mint az elektron "pályasebessége". (Vannak közelítések a belső héjak energikus elektronjainak figyelembevételére is.) Az ionimplantáció tárgyalásakor - kivéve egyetlen fejezetet - az ionenergiák kisebbek 10 MeV/amu-nál, amikoris nincs szükség relativisztikus korrekciókra. Ma annyiban egzaktabb a tárgyalás, hogy a céltárgy elektronjait plazmának fogjuk fel és az energiaveszteség is kollektív folyamatokban, úm. a dinamikus polarizációban zajlik és a plazmonoknak átadott energiában valósul meg (Fermi [1940], Fermi és Teller [1947]). Ebben a közelítésben a tipikus energiaveszteség de dx = vρ 13 /,.. ahol ρ az elektronsűrűség. (Felhívjuk a figyelmet arra, hogy az elektron-, ill. nukleáris fékeződés eredeti irodalmi tárgyalásaiban az ionsebességet eltérően definiálják.) Lindhard [1954] tárgyalása vezetett explicit leíráshoz, amely az ionimplantáció során fellépő ion-elektronfelhő kölcsönhatás tárgyalására a legalkalmasabb. A feltételezések itt: 1) az elektronfelhő 0 K hőmérsékletű (síkhullám) és egy egyenletes pozitív töltésfelhőben foglal helyet, amelyre igaz a töltéssemlegesség, ) az elektronfelhő kezdetben konstans sűrűségű, 3) az ion hatása az elektronfelhő perturbációjaként jelentkezik, 4) a közelítés nemrelativisztikus. Ekkor az elektronos fékeződés a következőképpen közelíthető: ( ) Se = I v,ρ Z 1 ρdv,..3 ahol S e az elektronfékeződés keresztmetszete, I(v,ρ) egy egységtöltésre vonatkoztatott fékeződési kölcsönhatási függvény, az egységtöltés sebessége v, Z 1 az ion töltése és az integrálást a teljes térfogatra kell kiterjeszteni. A pozitív háttértöltést Z = ρ dv felhasználásával normáljuk. Mindezekkel Lindhard a következő kölcsönhatási függvényt vezette le: I 4πe = mv 4 i πω 0 + kv 0 dk k kv ωdω l ε 1, ( k ω) 1,..4 96
9 ahol az ε l "longitudiális" dielektromos állandót egy bonyolult összefüggés adja: l ε ( k, ω) = m ω0 f ( En ) = 1+, h k rr k + kkn n m h N 1 rr m h ( ω iδ ) + k kk + ( ω iδ )...5 ahol m az elektron tömege, ω 0 a plazmafrekvencia, ω az átadott energia és ω = 4πe ρ/ m, E n az elektron energiája, k r n a hullámszáma az n-edik állapotban, f(e n ) az eloszlásfüggvény (a hullámszám páros függvénye) és δ egy (kis) csillapítási faktor. A..5 formulát rendszerint polinomiális közelítésben használják (Iafrate és Ziegler [1979]). n 1.5. ábra. Fékeződési erő az elektronsűrűség függvényében három ionenergiára. az abszcisszán a v F Fermi-sebességeket is bejelöltük, ez összeesik azzal a ponttal, ahol a folyamat adiabatikussá alakul és az atom nem vesz át energiát. 97
10 .6. ábra. Töltéssűrűség mint az atomi sugár függvénye 9 Cu atomra. Thomas-Fermi atom esetén - amelynek nincs héjszerkezete, emiatt analitikusan kezelhető -, ill. Hartree-Fock atomra, amely viszont pontosabb numerikus élertékeket szolgáltat. A.5. ábra szemlélteti az I-függvény futását. Az alacsony elektronkoncentrációjú részben a lineáris rész felel meg annak a tartománynak, ahol az ion sokkalta gyorsabban mozog, mint az elektronok átlagos sebessége. A lehajlás ott kezdődik, ahol az ionsebesség a szabad elektrongáz v F Fermi-sebességével egyezik meg: v = F ( ) h 3 13 πρ / m Pl. a 100 kev/amu ion sebessége 6x10 10 m/s (az ábrán a folytonos vonal), a /m 3 elektronsűrűséghez v F = 3,5x10 10 m/s tartozik - itt konyul le a görbe. Nagy elektronsűrűségeknél az elektronfelhő adiabatikusan reagál a nagyobb sebessége miatt, ezért a kölcsönhatás gyengül. A kölcsönhatás erősségének maximuma minden elektronsűrűségnél más és más és egybeesik az ahhoz tartozó v F -fel. 98
11 A fékeződési elmélet lokális sűrűség közelítése. Foglalkozzunk először a legkönnyebb ionnal. Ezen közelítésben úgy számoljuk ki a proton energiaveszteségét, hogy feltételezzük, minden térfogatelem önálló elektronplazma és a fékeződési erő ezeknek az eloszlásával súlyozott átlaga, azaz..1.3 alapján ( 1 ) * ( ρ) ( ) Se = I v, Z v ρdv,..7 ahol a * azt jelenti, hogy a proton nincs feltétlenül teljesen megfosztva az elektronjától. A számítások közelítőleg leírják a He esetét is. A.6-7 ábrák a réz példáján mutatja be az atom sugarát különböző közelítésekben, másrészt a..4-5 egyenletek integranduszait grafikusan (szaggatott vonal). Az ábrán az ion sebesssége mintegy hússzorosa a Bohr sebsségnek, ezért sokkal gyorsabban mozog, mint az elektronok, tehát a kölcsönhatás viszonylag független az elektronok sebességétől (a.5. ábra menedékes részére esik). Elektronikus fékeződési erő nehéz ionok esetében. A leírást három sebesség-tartományra adjuk meg: a) kis sebességű ionok, azaz v 1 < v F, ahol kiderül, hogy az energiaveszteség arányos a az ionok sebsségével, 99
12 b) nagysebességű ionok, ahol v 1 > 3v F, ahol a protonokra érvényes fékeződés skálázható a nehéz ionra, végül egy bonyolultabb elmélettel áthidalható a két tartomány, azaz ahol v F < v 1 < 3v F..7. ábra. A 9 Cu atom fékeződési erő értékei az atomsugár függvényében (a..4-5 egyenletek integranduszai). A pontozott vonal a ρ töltés-sűrűség, a szaggatott vonal az I kölcsönhatási súly egy nagyenergiájú 10 4 kev/amu részecskére (a belső héj elektronjaira kis értéket vesz fel). A fékeződési erő integrandusza, I p a folytonos vonal (l. a..7 egyenletet). Mivel szilárd testekben v F v B (Bohr sebesség), a három tartomány közötti válaszvonalat a 5 kev/amu és a 00 kev/amu energiák jelentik. Kis energiák esetén az elektronok sokkalta gyorsabban mozognak, mint az ion, ezért az ütközések adiabatikusak és nem járnak energiaveszteséggel. Erre az esetre dolgozott ki Firsov [1958] egy kváziklasszikus modellt. Ebben a két ion torzítatlan elektronhéjai összemerülnek és a gerjesztési energia egyenletesen oszlik el az elektronok között. Az elektronikus fékeződés végülis az atom ionizációjára fordítódik. A sebességgel arányos fékeződés eléggé jól teljesül fémekre, de a fontos kovalens kristályokban (Si, Ge) jelentős az eltérés ettől. Szilíciumra és Z 19-ig a keskeny tiltott sávú anyagokra 300
13 sikerült kísérleti formulát találni, amikoris az arányosság a következőképpen alakul: S v e ,...8 Nagysebességű ionoknál skálázással lehet továbblépni: S S H H ( v1z) ( v Z ) ( v1z) ( v Z ) Sni =,..9 S ahol az S H egységnyi iontöltésre vonatkozó protonfékeződés, a "ni" index "nehéz ion"-t jelöl. A kifejezés tovább egyszerűsíthető a γ effektív relatív töltés bevezetésével: * ( ) ni ni H ni H ni S = S Z = S Z γ,..30 ahol Z ni a nehéz ion atomszáma. A γ becsülhető a Thomas-Fermi elméletből abban a tartományban, ahol a Thomas-Fermi atomok és a Hartree-Fock atomok közelítőleg azonos módon viselkednak, azaz 0,3 γ 0,8 esetre. A skálafaktorok a Thomas-Fermi által definiált Z magtöltésre a következők: töltéssűrűség, ρ Z, a teljes elektronrendszer kötési energiája, E k Z 7/3, egy elektronra vonatkoztatott kötési energia, e k Z 4/3, elektron-sebesség, v Z /3. Az eredeti Bohr-feltevés szerint, azaz minden olyan elektron távozik az atomról, amelyek klasszikus sebessége kisebb v-nél, a következő explicit formulához vezet (Northcliffe [1960]): 3 / [ ] γ = 1 exp 1 / 0 1 v v Z...31 Közepes energiák esetét Brandt és Kitagawa [198] számításainak rövid elemzésével tárgyaljuk. Ekkor az ionizáció feltétele nem v 1 -nek v 0 - hoz való viszonyításából, hanem v 1 és a közeg elektronjainak sebességarányától függ, amely a kisebb v 1 -ek esetén jelent eltérést. A kisebb sebességekre, azaz 1 v 1 /v 0 5-nél, v 1 v F és a belső elektronok már nem tudnak gerjesztődni és a fékeződés a vezetési elektronokon következik be. A Brandt -Kitagawa model szerint [ F ] ( ) ln ( / ) γ= q + C 1 q 1+ Λ v a0v0,..3
14 ahol q = 1 - N/Z 1 részleges ionizáció (N a még kötött elektronok száma a Z 1 atomon), Λ egy árnyékoló faktor, mely összekapcsolja az ion.8. ábra. Az ionok ionizációs hányada mint a v r "effektív" ionsebesség függvénye. Kísérlet és Northcliffe becslés (..33. egyenlet). A v r bevezetése pontosítja a Thomas-Fermi ionvesztés kritériumot a Brandt- Kitigawa közelítéssel (az elektron leszakadásának küszöbét az ion és a szilárd test kollektív elektronjainak relatív sebességére vonatkoztatja. töltésállapotát a sebességével, C egy az anyagtól alig függő állandó, 1 amelynek értéke - kísérleti adatok elemzésével - közelítőleg ( v0 / v F ). Bevezetve az ionnak az elektronokhoz viszonyított v r relatív sebességének fogalmát 3 3 r r v ( v ve ) v v e 1 / / e 1 ( vr < v1 ve >= ), v / v 6 1 e 30
15 továbbá..31 figyelembe vételével, a Brandt és Kitigawa számítások nehéz ionok ionizációjára a következő közelítő formulához vezetnek (az illeszkedés minőségét a.8. ábra mutatja): 09, v r q = 1 exp / vz 0 1 Megszokott, hogy első közelítésben a két fékeződési.9. ábra. Az (de/dx) n és (de/dx) e futása, sematikusan. E' és E'' két karakterisz-tikus energia: E 1 az (de/dx) n maximuma, E az az energia, ahol - a fékeződés során - az (de/dx) n veszi át a fő szerepet. E' és E'' értékeit - néhány fontos anyagpárra - a Táblázat tartalmazza (Mayer és Lau [1990] nyomán) mechanizmust függetlennek tekintsük. Bevezetve az S tot teljes fékeződési erőt, ezzel Stot = Sn + Se A fejezet végén összefoglaljuk és egy közös ábrán (.9) világítjuk meg a kétféle fékeződés jellegét. Az egyes ionok fékeződésük során egyidejűleg végigfutják - valamilyen induló energiától kezdődően - mindkét görbét. 303
16 Minden pillanatnyi ionenergián egyszerrre van jelen mindkét fékeződési mechanizmus. Szerepük azonban pillanatról pillanatra változik..10. ábra. Az (de/dx) n és (de/dx) e futása arzén, foszfor és bór ionokra. (Mayer és Lau [1990] nyomán) A.9 ábrán feltüntettük azokat a karakterisztikus energiákat, E'' és E', amelyek az (de/dx) e = (de/dx) n -hez, ill. ahhoz az energiához tartoznak, ahol (de/dx) n maximális. 304
17 A..1. Táblázatban adjuk meg ezen energia-értékeket néhány fontos anyagpárra. Ion \ Energia (kev) E' (Si) E'' (Si) E' (GaAs) E'' (GaAs) B P As Sb Bi Mivel jó közelítéssel igaz az, hogy ha az elektronos fékeződés - rugalmatlan lévén - főleg pl. röntgen-emissziót és legfeljebb ponthibákat okoz, és a rugalmas folyamatokat okozó nukleáris fékeződés felelős az atomok tényleges kimozdításáért, a görbékből kvalitatív következtetés is levonható a rácshibák eloszlásának jellegére. Eszerint, ahol az ion energiája E > E'', ott döntően ponthibákat találunk, ahogy csökken E < E'' ( de E > E') érték alá, ott egyre nő a komplexebb rácshibák száma. A hibakoncentráció maximuma E = E'-nél található, azaz ott, ahol az ionnak még van némi energiája, hogy beljebb hatoljon. Emiatt a hibaeloszlás maximuma közelebb található a felülethez, mint az implantált atomok eloszlása. A magfékezés során zajló hibakeltés diszkrét energiaátadason alapul, jó közelítéssel tekinthető úgy, mint két-részecske ütközések sorozatából felépülő folyamat, amelynek során az ion, vagy a helyéről kilökött céltárgy atom biliárdgolyószerűen (rugalmasan) ütközik az álló céltárgy atomokkal. Ezzel szemben, úgy tekintjük, hogy az elektronfékezés során (rugalmatlan ütközések) az ion folyamatosan adja le energiáját a céltárgy elektronjainak. Az egy elektronra jutó energia nem csak arra elég, hogy kiemelje az elektront a mag potenciálgödréből (ionizáció), hanem jelentős mértékű mozgási energiát is biztosít az elektronnak. A nagyenergiájú elektronok rövid idő alatt, s, elhagyják a gyors részecske pályájának közvetlen környezetét. Attól függően, hogy az elektronfékezés értéke meghaladja, vagy sem a küszöbértéket, képződik, vagy nem képződik maradandó roncsolódás, ún. 305
18 nyom (track) a gyors részecske pályája körül. A (de/dx) e értéktől függ az is, hogy milyen lesz a nyom szerkezete, folyamatos, vagy szaggatott (Meftah [1993]). A nyom kialakulásának folyamatára két modellt dolgoztak ki: az elektron-termikus spike (Chadderton [1969]) modellt, és a Coulomb robbanás (Fleischer [1965]) modellt. Az elektron-termikus spike modell abból a feltevésből indul ki, hogy az ionizáció során keltett gyors elektronok energiája rácsrezgésekké alakul, ennek következtében, a nyomot keltő részecske pályájának néhány nm-es környezetében a hőmérséklet akar többszörösen is meghaladhatja a céltárgy olvadáspontját. A gyors hőmérsékletnövekedést, gyors lehülés követi, ami az "olvadt" állapot befagyásához, ún. kvencseléshez vezet. A coulomb robbanás modell azon a feltevésen alapul, hogy a gyors elektronok távozása nyomán, pozitív magokat tartalmazó henger marad vissza a nyomot keltő részecske pályája körül. A fellépő elektrosztatikus taszítás arra kényszeríti a magokat, hogy egyszerre (kollektív módon) kimozduljanak helyükről. A folyamat kollektív voltából következik, hogy az amorf szerkezet kialakulása akkor is bekövetkezhet, ha a magok között páronként felhalmozódó elektrosztatikus helyzeti energia nem éri el a hibakeltési küszöböt. Mindkét folyamat azt eredményezi, hogy a gyors részecske pályája körül egy amorfizálódott henger alakul ki. 1.,. Példa 1. Számolja ki 1) milyen távol vannak az "aktív" kaszkádok különféle ionáramsűrűségek esetén, ) milyen ionáramsűrűségeknél kell pl. a felület megolvadásával számolni.. Számítsa ki a direkt ütközéskor átadott energiát Si-ba becsapódó 100 kev-es bór, foszfor és arzén ionokra! Megoldás. A tömegközépponti rendszerben számítsuk ki az ionok sebességét. Pl. M 1 = 11 és M = 8-ra v 1 = 0,7v 0 és v = 0,8v 0. Ezzel számítható az ionok energiája a tömegközépponti rendszerben (5, ill.0 kev). T max ezután 81 kev, é.i.t. 306
2. IONIMPLANTÁCIÓ 282
 2. IONIMPLANTÁCIÓ 282 2.1. Bevezetés, történeti áttekintés 282 2.2. Alapfogalmak, alapjelenségek 293 2.2.1. Az ionok behatolása, fékeződése 293 2.2.2. A porlódás jelensége 310 2.2.3. Az atomok és defektek
2. IONIMPLANTÁCIÓ 282 2.1. Bevezetés, történeti áttekintés 282 2.2. Alapfogalmak, alapjelenségek 293 2.2.1. Az ionok behatolása, fékeződése 293 2.2.2. A porlódás jelensége 310 2.2.3. Az atomok és defektek
 http://www.nature.com 1) Magerő-sugár: a magközéppontból mért távolság, ameddig a magerők hatótávolsága terjed. Rutherford-szórásból határozható meg. R=1,4 x 10-13 A 1/3 cm Az atommag terének potenciálja
http://www.nature.com 1) Magerő-sugár: a magközéppontból mért távolság, ameddig a magerők hatótávolsága terjed. Rutherford-szórásból határozható meg. R=1,4 x 10-13 A 1/3 cm Az atommag terének potenciálja
Atomok és molekulák elektronszerkezete
 Atomok és molekulák elektronszerkezete Szabad atomok és molekulák Schrödinger egyenlete Tekintsünk egy kvantummechanikai rendszert amely N n magból és N e elektronból áll. Koordinátáikat jelölje rendre
Atomok és molekulák elektronszerkezete Szabad atomok és molekulák Schrödinger egyenlete Tekintsünk egy kvantummechanikai rendszert amely N n magból és N e elektronból áll. Koordinátáikat jelölje rendre
A kvantummechanika kísérleti előzményei A részecske hullám kettősségről
 A kvantummechanika kísérleti előzményei A részecske hullám kettősségről Utolsó módosítás: 2016. május 4. 1 Előzmények Franck-Hertz-kísérlet (1) A Franck-Hertz-kísérlet vázlatos elrendezése: http://hyperphysics.phy-astr.gsu.edu/hbase/frhz.html
A kvantummechanika kísérleti előzményei A részecske hullám kettősségről Utolsó módosítás: 2016. május 4. 1 Előzmények Franck-Hertz-kísérlet (1) A Franck-Hertz-kísérlet vázlatos elrendezése: http://hyperphysics.phy-astr.gsu.edu/hbase/frhz.html
3. (b) Kereszthatások. Utolsó módosítás: április 1. Dr. Márkus Ferenc BME Fizika Tanszék
 3. (b) Kereszthatások Utolsó módosítás: 2013. április 1. Vezetési együtthatók fémekben (1) 1 Az elektrongáz hővezetési együtthatója A levezetésben alkalmazott feltételek: 1. Minden elektron ugyanazzal
3. (b) Kereszthatások Utolsó módosítás: 2013. április 1. Vezetési együtthatók fémekben (1) 1 Az elektrongáz hővezetési együtthatója A levezetésben alkalmazott feltételek: 1. Minden elektron ugyanazzal
Sugárzások és anyag kölcsönhatása
 Sugárzások és anyag kölcsönhatása Az anyaggal kölcsönhatásba lépő részecskék Töltött részecskék Semleges részecskék Nehéz Könnyű Nehéz Könnyű T D p - + n Radioaktív sugárzás + anyag energia- szóródás abszorpció
Sugárzások és anyag kölcsönhatása Az anyaggal kölcsönhatásba lépő részecskék Töltött részecskék Semleges részecskék Nehéz Könnyű Nehéz Könnyű T D p - + n Radioaktív sugárzás + anyag energia- szóródás abszorpció
dinamikai tulajdonságai
 Szilárdtest rácsok statikus és dinamikai tulajdonságai Szilárdtestek osztályozása kötéstípusok szerint Kötések eredete: elektronszerkezet k t ionok (atomtörzsek) tö Coulomb- elektronok kölcsönhatás lokalizáltak
Szilárdtest rácsok statikus és dinamikai tulajdonságai Szilárdtestek osztályozása kötéstípusok szerint Kötések eredete: elektronszerkezet k t ionok (atomtörzsek) tö Coulomb- elektronok kölcsönhatás lokalizáltak
A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld ábra ábra
 . Gyakorlat 4B-9 A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld. 4-6 ábra.). Számítsuk ki az E elektromos térerősséget a vonal irányában lévő, annak.. ábra. 4-6 ábra végpontjától
. Gyakorlat 4B-9 A +Q töltés egy L hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld. 4-6 ábra.). Számítsuk ki az E elektromos térerősséget a vonal irányában lévő, annak.. ábra. 4-6 ábra végpontjától
Alkalmazás a makrókanónikus sokaságra: A fotongáz
 Alkalmazás a makrókanónikus sokaságra: A fotongáz A fotonok az elektromágneses sugárzás hordozó részecskéi. Spinkvantumszámuk S=, tehát kvantumstatisztikai szempontból bozonok. Fotonoknak habár a spinkvantumszámuk,
Alkalmazás a makrókanónikus sokaságra: A fotongáz A fotonok az elektromágneses sugárzás hordozó részecskéi. Spinkvantumszámuk S=, tehát kvantumstatisztikai szempontból bozonok. Fotonoknak habár a spinkvantumszámuk,
Atomfizika. Az atommag szerkezete. Radioaktivitás Biofizika, Nyitrai Miklós
 Atomfizika. Az atommag szerkezete. Radioaktivitás. 2010. 10. 13. Biofizika, Nyitrai Miklós Összefoglalás Atommag alkotói, szerkezete; Erős vagy magkölcsönhatás; Tömegdefektus. A kölcsönhatások világképe
Atomfizika. Az atommag szerkezete. Radioaktivitás. 2010. 10. 13. Biofizika, Nyitrai Miklós Összefoglalás Atommag alkotói, szerkezete; Erős vagy magkölcsönhatás; Tömegdefektus. A kölcsönhatások világképe
Atomfizika. A hidrogén lámpa színképei. Elektronok H atom. Fényképlemez. emisszió H 2. gáz
 Atomfizika A hidrogén lámpa színképei - Elektronok H atom emisszió Fényképlemez V + H 2 gáz Az atom és kvantumfizika fejlődésének fontos szakasza volt a hidrogén lámpa színképeinek leírása, és a vonalas
Atomfizika A hidrogén lámpa színképei - Elektronok H atom emisszió Fényképlemez V + H 2 gáz Az atom és kvantumfizika fejlődésének fontos szakasza volt a hidrogén lámpa színképeinek leírása, és a vonalas
1. ábra. 24B-19 feladat
 . gyakorlat.. Feladat: (HN 4B-9) A +Q töltés egy hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld.. ábra.). Számítsuk ki az E elektromos térerősséget a vonal. ábra. 4B-9 feladat irányában lévő,
. gyakorlat.. Feladat: (HN 4B-9) A +Q töltés egy hosszúságú egyenes szakasz mentén oszlik el egyenletesen (ld.. ábra.). Számítsuk ki az E elektromos térerősséget a vonal. ábra. 4B-9 feladat irányában lévő,
Radiokémia vegyész MSc radiokémia szakirány Kónya József, M. Nagy Noémi: Izotópia I és II. Debreceni Egyetemi Kiadó, 2007, 2008.
 Radiokémia vegyész MSc radiokémia szakirány Kónya József, M. Nagy Noémi: Izotópia I és II. Debreceni Egyetemi Kiadó, 2007, 2008. Kiss István,Vértes Attila: Magkémia (Akadémiai Kiadó) Nagy Lajos György,
Radiokémia vegyész MSc radiokémia szakirány Kónya József, M. Nagy Noémi: Izotópia I és II. Debreceni Egyetemi Kiadó, 2007, 2008. Kiss István,Vértes Attila: Magkémia (Akadémiai Kiadó) Nagy Lajos György,
Theory hungarian (Hungary)
 Q3-1 A Nagy Hadronütköztető (10 pont) Mielőtt elkezded a feladat megoldását, olvasd el a külön borítékban lévő általános utasításokat! Ez a feladat a CERN-ben működő részecskegyorsító, a Nagy Hadronütköztető
Q3-1 A Nagy Hadronütköztető (10 pont) Mielőtt elkezded a feladat megoldását, olvasd el a külön borítékban lévő általános utasításokat! Ez a feladat a CERN-ben működő részecskegyorsító, a Nagy Hadronütköztető
A kémiai kötés eredete; viriál tétel 1
 A kémiai kötés ereete; viriál tétel 1 Probléma felvetés Ha egy molekula atommagjai közötti távolság csökken, akkor a közöttük fellép elektrosztatikus taszításhoz tartozó energia n. Ugyanez igaz az elektronokra
A kémiai kötés ereete; viriál tétel 1 Probléma felvetés Ha egy molekula atommagjai közötti távolság csökken, akkor a közöttük fellép elektrosztatikus taszításhoz tartozó energia n. Ugyanez igaz az elektronokra
Sugárzások kölcsönhatása az anyaggal
 Radioaktivitás Biofizika előadások 2013 december Sugárzások kölcsönhatása az anyaggal PTE ÁOK Biofizikai Intézet, Orbán József Összefoglaló radioaktivitás alapok Nukleononkénti kötési energia (MeV) Egy
Radioaktivitás Biofizika előadások 2013 december Sugárzások kölcsönhatása az anyaggal PTE ÁOK Biofizikai Intézet, Orbán József Összefoglaló radioaktivitás alapok Nukleononkénti kötési energia (MeV) Egy
2, = 5221 K (7.2)
 7. Gyakorlat 4A-7 Az emberi szem kb. 555 nm hullámhossznál a Iegnagyobb érzékenységű. Adjuk meg annak a fekete testnek a hőmérsékletét, amely sugárzásának a spektrális teljesitménye ezen a hullámhosszon
7. Gyakorlat 4A-7 Az emberi szem kb. 555 nm hullámhossznál a Iegnagyobb érzékenységű. Adjuk meg annak a fekete testnek a hőmérsékletét, amely sugárzásának a spektrális teljesitménye ezen a hullámhosszon
Folyadékszcintillációs spektroszkópia jegyz könyv
 Folyadékszcintillációs spektroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc I. Mérés vezet je: Horváth Ákos Mérés dátuma: 2010. október 21. Leadás dátuma: 2010. november 8. 1 1. Bevezetés A mérés
Folyadékszcintillációs spektroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc I. Mérés vezet je: Horváth Ákos Mérés dátuma: 2010. október 21. Leadás dátuma: 2010. november 8. 1 1. Bevezetés A mérés
Compton-effektus. Zsigmond Anna. jegyzıkönyv. Fizika BSc III.
 Compton-effektus jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Csanád Máté Mérés dátuma: 010. április. Leadás dátuma: 010. május 5. Mérés célja A kvantumelmélet egyik bizonyítékának a Compton-effektusnak
Compton-effektus jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Csanád Máté Mérés dátuma: 010. április. Leadás dátuma: 010. május 5. Mérés célja A kvantumelmélet egyik bizonyítékának a Compton-effektusnak
Abszorpciós spektrumvonalak alakja. Vonalak eredete (ld. előző óra)
 Abszorpciós spektrumvonalak alakja Vonalak eredete (ld. előző óra) Nagysága Kiszélesedése Elem mennyiségének becslése a vonalerősségből Elemi statfiz Boltzmann-faktor: Megadja egy állapot súlyát a sokaságban
Abszorpciós spektrumvonalak alakja Vonalak eredete (ld. előző óra) Nagysága Kiszélesedése Elem mennyiségének becslése a vonalerősségből Elemi statfiz Boltzmann-faktor: Megadja egy állapot súlyát a sokaságban
Hangfrekvenciás mechanikai rezgések vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
Q 1 D Q 2 (D x) 2 (1.1)
 . Gyakorlat 4B-9 Két pontszerű töltés az x tengelyen a következőképpen helyezkedik el: egy 3 µc töltés az origóban, és egy + µc töltés az x =, 5 m koordinátájú pontban van. Keressük meg azt a helyet, ahol
. Gyakorlat 4B-9 Két pontszerű töltés az x tengelyen a következőképpen helyezkedik el: egy 3 µc töltés az origóban, és egy + µc töltés az x =, 5 m koordinátájú pontban van. Keressük meg azt a helyet, ahol
Elektrodinamika. Maxwell egyenletek: Kontinuitási egyenlet: div n v =0. div E =4 div B =0. rot E = rot B=
 Elektrodinamika Maxwell egyenletek: div E =4 div B =0 rot E = rot B= 1 B c t 1 E c t 4 c j Kontinuitási egyenlet: n t div n v =0 Vektoranalízis rot rot u=grad divu u rot grad =0 div rotu=0 udv= ud F V
Elektrodinamika Maxwell egyenletek: div E =4 div B =0 rot E = rot B= 1 B c t 1 E c t 4 c j Kontinuitási egyenlet: n t div n v =0 Vektoranalízis rot rot u=grad divu u rot grad =0 div rotu=0 udv= ud F V
Az Ampère-Maxwell-féle gerjesztési törvény
 Az Ampère-Maxwell-féle gerjesztési törvény Maxwell elméleti meggondolások alapján feltételezte, hogy a változó elektromos tér örvényes mágneses teret kelt (hasonlóan ahhoz ahogy a változó mágneses tér
Az Ampère-Maxwell-féle gerjesztési törvény Maxwell elméleti meggondolások alapján feltételezte, hogy a változó elektromos tér örvényes mágneses teret kelt (hasonlóan ahhoz ahogy a változó mágneses tér
Szilárdtestek el e ek e tr t o r n o s n zer e k r ez e et e e t
 Szilárdtestek elektronszerkezete Kvantummechanikai leírás Ismétlés: Schrödinger egyenlet, hullámfüggvény, hidrogén-atom, spin, Pauli-elv, periódusos rendszer 2 Szilárdtestek egyelektron-modellje a magok
Szilárdtestek elektronszerkezete Kvantummechanikai leírás Ismétlés: Schrödinger egyenlet, hullámfüggvény, hidrogén-atom, spin, Pauli-elv, periódusos rendszer 2 Szilárdtestek egyelektron-modellje a magok
Radioaktív sugárzások tulajdonságai és kölcsönhatásuk az elnyelő közeggel. A radioaktív sugárzások detektálása.
 Különböző sugárzások tulajdonságai Típus töltés Energia hordozó E spektrum Radioaktí sugárzások tulajdonságai és kölcsönhatásuk az elnyelő közeggel. A radioaktí sugárzások detektálása. α-sugárzás pozití
Különböző sugárzások tulajdonságai Típus töltés Energia hordozó E spektrum Radioaktí sugárzások tulajdonságai és kölcsönhatásuk az elnyelő közeggel. A radioaktí sugárzások detektálása. α-sugárzás pozití
Hangfrekvenciás mechanikai rezgések vizsgálata
 Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Z bozonok az LHC nehézion programjában
 Z bozonok az LHC nehézion programjában Zsigmond Anna Julia MTA Wigner FK Max Planck Institut für Physik Fizikus Vándorgyűlés Szeged, 2016 augusztus 24-27. Nehézion-ütközések az LHC-nál A-A és p-a ütközések
Z bozonok az LHC nehézion programjában Zsigmond Anna Julia MTA Wigner FK Max Planck Institut für Physik Fizikus Vándorgyűlés Szeged, 2016 augusztus 24-27. Nehézion-ütközések az LHC-nál A-A és p-a ütközések
Szilárd testek sugárzása
 A fény keletkezése Szilárd testek sugárzása A szilárd test melegítés hatására fényt bocsát ki A sugárzás forrása a közelítőleg termikus egyensúlyban lévő kibocsátó test atomi részecskéinek véletlenszerű
A fény keletkezése Szilárd testek sugárzása A szilárd test melegítés hatására fényt bocsát ki A sugárzás forrása a közelítőleg termikus egyensúlyban lévő kibocsátó test atomi részecskéinek véletlenszerű
Röntgensugárzás az orvostudományban. Röntgen kép és Komputer tomográf (CT)
 Röntgensugárzás az orvostudományban Röntgen kép és Komputer tomográf (CT) Orbán József, Biofizikai Intézet, 2008 Hand mit Ringen: print of Wilhelm Röntgen's first "medical" x-ray, of his wife's hand, taken
Röntgensugárzás az orvostudományban Röntgen kép és Komputer tomográf (CT) Orbán József, Biofizikai Intézet, 2008 Hand mit Ringen: print of Wilhelm Röntgen's first "medical" x-ray, of his wife's hand, taken
A sugárzás és az anyag kölcsönhatása. A béta-sugárzás és anyag kölcsönhatása
 A sugárzás és az anyag kölcsönhatása A béta-sugárzás és anyag kölcsönhatása Cserenkov-sugárzás v>c/n, n törésmutató cos c nv Cserenkov-sugárzás Pl. vízre (n=1,337): 0,26 MeV c 8 m / s 2. 2* 10 A sugárzás
A sugárzás és az anyag kölcsönhatása A béta-sugárzás és anyag kölcsönhatása Cserenkov-sugárzás v>c/n, n törésmutató cos c nv Cserenkov-sugárzás Pl. vízre (n=1,337): 0,26 MeV c 8 m / s 2. 2* 10 A sugárzás
8. AZ ATOMMAG FIZIKÁJA
 8. AZ ATOMMAG FIZIKÁJA Az atommag szerkezete (40-44 oldal) A tömegspektrométer elve Az atommag komponensei Izotópok Tömeghiány, kötési energia, stabilitás Magerők Magmodellek Az atommag stabilitásának
8. AZ ATOMMAG FIZIKÁJA Az atommag szerkezete (40-44 oldal) A tömegspektrométer elve Az atommag komponensei Izotópok Tömeghiány, kötési energia, stabilitás Magerők Magmodellek Az atommag stabilitásának
Elektrosztatikai alapismeretek
 Elektrosztatikai alapismeretek THALÉSZ: a borostyánt (élektron) megdörzsölve az a könnyebb testeket magához vonzza. Az egymással szorosan érintkező anyagok elektromosan feltöltődnek, elektromos állapotba
Elektrosztatikai alapismeretek THALÉSZ: a borostyánt (élektron) megdörzsölve az a könnyebb testeket magához vonzza. Az egymással szorosan érintkező anyagok elektromosan feltöltődnek, elektromos állapotba
Beugró kérdések. Elektrodinamika 2. vizsgához. Számítsa ki a gradienst, divergenciát és a skalár Laplace operátort henger koordinátákban!
 Beugró kérdések Elektrodinamika 2. vizsgához. Görbült koordináták Henger koordináták: r=(ρ cos φ, ρ sin φ, z) Számítsa ki a gradienst, divergenciát és a skalár Laplace operátort henger koordinátákban!
Beugró kérdések Elektrodinamika 2. vizsgához. Görbült koordináták Henger koordináták: r=(ρ cos φ, ρ sin φ, z) Számítsa ki a gradienst, divergenciát és a skalár Laplace operátort henger koordinátákban!
Milyen simaságú legyen a minta felülete jó minőségű EBSD mérésekhez
 1 Milyen simaságú legyen a minta felülete jó minőségű EBSD mérésekhez Havancsák Károly Dankházi Zoltán Ratter Kitti Varga Gábor Visegrád 2012. január Elektron diffrakció 2 Diffrakció - kinematikus elmélet
1 Milyen simaságú legyen a minta felülete jó minőségű EBSD mérésekhez Havancsák Károly Dankházi Zoltán Ratter Kitti Varga Gábor Visegrád 2012. január Elektron diffrakció 2 Diffrakció - kinematikus elmélet
ELEKTROSZTATIKA. Ma igazán feltöltődhettek!
 ELEKTROSZTATIKA Ma igazán feltöltődhettek! Elektrosztatikai alapismeretek THALÉSZ: a borostyánt (élektron) megdörzsölve az a könnyebb testeket magához vonzza. Elektrosztatikai alapjelenségek Az egymással
ELEKTROSZTATIKA Ma igazán feltöltődhettek! Elektrosztatikai alapismeretek THALÉSZ: a borostyánt (élektron) megdörzsölve az a könnyebb testeket magához vonzza. Elektrosztatikai alapjelenségek Az egymással
Atommagok alapvető tulajdonságai
 Atommagok alapvető tulajdonságai Mag és részecskefizika 5. előadás 017. március 17. Áttekintés Atommagok szerkezete a kvarkképben proton szerkezete, atommagok szerkezete, magerő Atommagok összetétele izotópok,
Atommagok alapvető tulajdonságai Mag és részecskefizika 5. előadás 017. március 17. Áttekintés Atommagok szerkezete a kvarkképben proton szerkezete, atommagok szerkezete, magerő Atommagok összetétele izotópok,
 http://www.nucleonica.net Az atommag tömege A hidrogénre vonatkoztatott relatív atomtömeg (=atommag tömegével, ha az e - tömegét elhanyagoljuk) a hidrogénnek nem egész számú többszöröse. Az elemek különböző
http://www.nucleonica.net Az atommag tömege A hidrogénre vonatkoztatott relatív atomtömeg (=atommag tömegével, ha az e - tömegét elhanyagoljuk) a hidrogénnek nem egész számú többszöröse. Az elemek különböző
Kirchhoff 2. törvénye (huroktörvény) szerint az áramkörben levő elektromotoros erők. E i = U j (3.1)
 3. Gyakorlat 29A-34 Egy C kapacitású kondenzátort R ellenálláson keresztül sütünk ki. Mennyi idő alatt csökken a kondenzátor töltése a kezdeti érték 1/e 2 ed részére? Kirchhoff 2. törvénye (huroktörvény)
3. Gyakorlat 29A-34 Egy C kapacitású kondenzátort R ellenálláson keresztül sütünk ki. Mennyi idő alatt csökken a kondenzátor töltése a kezdeti érték 1/e 2 ed részére? Kirchhoff 2. törvénye (huroktörvény)
Atomenergetikai alapismeretek
 Atomenergetikai alapismeretek 2. előadás Dr. Szieberth Máté Dr. Sükösd Csaba előadásanyagának felhasználásával Négyfaktor formula (végtelen kiterjedésű n-sokszorozó közeg) n Maghasadás (gyors neutronok)
Atomenergetikai alapismeretek 2. előadás Dr. Szieberth Máté Dr. Sükösd Csaba előadásanyagának felhasználásával Négyfaktor formula (végtelen kiterjedésű n-sokszorozó közeg) n Maghasadás (gyors neutronok)
Thomson-modell (puding-modell)
 Atommodellek Thomson-modell (puding-modell) A XX. század elejére világossá vált, hogy az atomban található elektronok ugyanazok, mint a katódsugárzás részecskéi. Magyarázatra várt azonban, hogy mi tartja
Atommodellek Thomson-modell (puding-modell) A XX. század elejére világossá vált, hogy az atomban található elektronok ugyanazok, mint a katódsugárzás részecskéi. Magyarázatra várt azonban, hogy mi tartja
Atomfizika. Fizika kurzus Dr. Seres István
 Atomfizika Fizika kurzus Dr. Seres István Történeti áttekintés J.J. Thomson (1897) Katódsugárcsővel végzett kísérleteket az elektron fajlagos töltésének (e/m) meghatározására. A katódsugarat alkotó részecskét
Atomfizika Fizika kurzus Dr. Seres István Történeti áttekintés J.J. Thomson (1897) Katódsugárcsővel végzett kísérleteket az elektron fajlagos töltésének (e/m) meghatározására. A katódsugarat alkotó részecskét
Szilárdtestek sávelmélete. Sávelmélet a szabadelektron-modell alapján
 Szilárdtestek sávelmélete Sávelmélet a szabadelektron-modell alapján A Fermi Dirac statisztika alapjai Nagy részecskeszámú rendszerek fizikai jellemzéséhez statisztikai leírást kell alkalmazni. (Pl. gázokra
Szilárdtestek sávelmélete Sávelmélet a szabadelektron-modell alapján A Fermi Dirac statisztika alapjai Nagy részecskeszámú rendszerek fizikai jellemzéséhez statisztikai leírást kell alkalmazni. (Pl. gázokra
azonos sikban fekszik. A vezetőhurok ellenállása 2 Ω. Számítsuk ki a hurok teljes 4.1. ábra ábra
 4. Gyakorlat 31B-9 A 31-15 ábrán látható, téglalap alakú vezetőhurok és a hosszúságú, egyenes vezető azonos sikban fekszik. A vezetőhurok ellenállása 2 Ω. Számítsuk ki a hurok teljes 4.1. ábra. 31-15 ábra
4. Gyakorlat 31B-9 A 31-15 ábrán látható, téglalap alakú vezetőhurok és a hosszúságú, egyenes vezető azonos sikban fekszik. A vezetőhurok ellenállása 2 Ω. Számítsuk ki a hurok teljes 4.1. ábra. 31-15 ábra
Modern fizika laboratórium
 Modern fizika laboratórium 11. Az I 2 molekula disszociációs energiája Készítette: Hagymási Imre A mérés dátuma: 2007. október 3. A beadás dátuma: 2007. október xx. 1. Bevezetés Ebben a mérésben egy kétatomos
Modern fizika laboratórium 11. Az I 2 molekula disszociációs energiája Készítette: Hagymási Imre A mérés dátuma: 2007. október 3. A beadás dátuma: 2007. október xx. 1. Bevezetés Ebben a mérésben egy kétatomos
Az ionizáló sugárzások fajtái, forrásai
 Az ionizáló sugárzások fajtái, forrásai magsugárzás Magsugárzások Röntgensugárzás Függelék. Intenzitás 2. Spektrum 3. Atom Repetitio est mater studiorum. Röntgen Ionizációnak nevezzük azt a folyamatot,
Az ionizáló sugárzások fajtái, forrásai magsugárzás Magsugárzások Röntgensugárzás Függelék. Intenzitás 2. Spektrum 3. Atom Repetitio est mater studiorum. Röntgen Ionizációnak nevezzük azt a folyamatot,
Elektrosztatikus számítások. Elektrosztatikus számítások. Elektrosztatikus számítások. Elektrosztatikus számítások Definíciók
 Jelentősége szubsztrát kötődés szolvatáció ionizációs állapotok (pka) mechanizmus katalízis ioncsatornák szimulációk (szerkezet) all-atom dipolar fluid dipolar lattice continuum Definíciók töltéseloszlás
Jelentősége szubsztrát kötődés szolvatáció ionizációs állapotok (pka) mechanizmus katalízis ioncsatornák szimulációk (szerkezet) all-atom dipolar fluid dipolar lattice continuum Definíciók töltéseloszlás
Mechanika I-II. Példatár
 Budapesti Műszaki és Gazdaságtudományi Egyetem Műszaki Mechanika Tanszék Mechanika I-II. Példatár 2012. május 24. Előszó A példatár célja, hogy támogassa a mechanika I. és mechanika II. tárgy oktatását
Budapesti Műszaki és Gazdaságtudományi Egyetem Műszaki Mechanika Tanszék Mechanika I-II. Példatár 2012. május 24. Előszó A példatár célja, hogy támogassa a mechanika I. és mechanika II. tárgy oktatását
A Hamilton-Jacobi-egyenlet
 A Hamilton-Jacobi-egyenlet Ha sikerül olyan kanonikus transzformációt találnunk, amely a Hamilton-függvényt zérusra transzformálja akkor valamennyi új koordináta és impulzus állandó lesz: H 0 Q k = H P
A Hamilton-Jacobi-egyenlet Ha sikerül olyan kanonikus transzformációt találnunk, amely a Hamilton-függvényt zérusra transzformálja akkor valamennyi új koordináta és impulzus állandó lesz: H 0 Q k = H P
A II. kategória Fizika OKTV mérési feladatainak megoldása
 Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
A spin. November 28, 2006
 A spin November 28, 2006 1 A spin a kvantummechanikában Az elektronnak és sok más kvantummechanikai részecskének is van egy saját impulzusnyomatéka amely független a mozgásállapottól. (Úgy is mondhatjuk,
A spin November 28, 2006 1 A spin a kvantummechanikában Az elektronnak és sok más kvantummechanikai részecskének is van egy saját impulzusnyomatéka amely független a mozgásállapottól. (Úgy is mondhatjuk,
Reakciókinetika és katalízis
 Reakciókinetika és katalízis k 4. előadás: 1/14 Különbségek a gázfázisú és az oldatreakciók között: 1 Reaktáns molekulák által betöltött térfogat az oldatreakciónál jóval nagyobb. Nincs akadálytalan mozgás.
Reakciókinetika és katalízis k 4. előadás: 1/14 Különbségek a gázfázisú és az oldatreakciók között: 1 Reaktáns molekulák által betöltött térfogat az oldatreakciónál jóval nagyobb. Nincs akadálytalan mozgás.
Jegyzet. Kémia, BMEVEAAAMM1 Műszaki menedzser hallgatók számára Dr Csonka Gábor, egyetemi tanár Dr Madarász János, egyetemi docens.
 Kémia, BMEVEAAAMM Műszaki menedzser hallgatók számára Dr Csonka Gábor, egyetemi tanár Dr Madarász János, egyetemi docens Jegyzet dr. Horváth Viola, KÉMIA I. http://oktatas.ch.bme.hu/oktatas/konyvek/anal/
Kémia, BMEVEAAAMM Műszaki menedzser hallgatók számára Dr Csonka Gábor, egyetemi tanár Dr Madarász János, egyetemi docens Jegyzet dr. Horváth Viola, KÉMIA I. http://oktatas.ch.bme.hu/oktatas/konyvek/anal/
3.1. ábra ábra
 3. Gyakorlat 28C-41 A 28-15 ábrán két, azonos anyagból gyártott ellenállás látható. A véglapokat vezető 3.1. ábra. 28-15 ábra réteggel vonták be. Tételezzük fel, hogy az ellenállások belsejében az áramsűrűség
3. Gyakorlat 28C-41 A 28-15 ábrán két, azonos anyagból gyártott ellenállás látható. A véglapokat vezető 3.1. ábra. 28-15 ábra réteggel vonták be. Tételezzük fel, hogy az ellenállások belsejében az áramsűrűség
Elektronok, atomok. Általános Kémia - Elektronok, Atomok. Dia 1/61
 Elektronok, atomok 2-1 Elektromágneses sugárzás 2-2 Atomi Spektrum 2-3 Kvantumelmélet 2-4 A Bohr Atom 2-5 Az új Kvantummechanika 2-6 Hullámmechanika 2-7 Kvantumszámok Dia 1/61 Tartalom 2-8 Elektronsűrűség
Elektronok, atomok 2-1 Elektromágneses sugárzás 2-2 Atomi Spektrum 2-3 Kvantumelmélet 2-4 A Bohr Atom 2-5 Az új Kvantummechanika 2-6 Hullámmechanika 2-7 Kvantumszámok Dia 1/61 Tartalom 2-8 Elektronsűrűség
1. fejezet. Gyakorlat C-41
 1. fejezet Gyakorlat 3 1.1. 28C-41 A 1.1 ábrán két, azonos anyagból gyártott ellenállás látható. A véglapokat vezető réteggel vonták be. Tételezzük fel, hogy az ellenállások belsejében az áramsűrűség bármely,
1. fejezet Gyakorlat 3 1.1. 28C-41 A 1.1 ábrán két, azonos anyagból gyártott ellenállás látható. A véglapokat vezető réteggel vonták be. Tételezzük fel, hogy az ellenállások belsejében az áramsűrűség bármely,
Röntgensugárzás. Röntgensugárzás
 Röntgensugárzás 2012.11.21. Röntgensugárzás Elektromágneses sugárzás (f=10 16 10 19 Hz, E=120eV 120keV (1.9*10-17 10-14 J), λ
Röntgensugárzás 2012.11.21. Röntgensugárzás Elektromágneses sugárzás (f=10 16 10 19 Hz, E=120eV 120keV (1.9*10-17 10-14 J), λ
A hőmérsékleti sugárzás
 A hőmérsékleti sugárzás Alapfogalmak 1. A hőmérsékleti sugárzás Értelmezés (hőmérsékleti sugárzás): A testek hőmérsékletével kapcsolatos, a teljes elektromágneses spektrumra kiterjedő sugárzást hőmérsékleti
A hőmérsékleti sugárzás Alapfogalmak 1. A hőmérsékleti sugárzás Értelmezés (hőmérsékleti sugárzás): A testek hőmérsékletével kapcsolatos, a teljes elektromágneses spektrumra kiterjedő sugárzást hőmérsékleti
Molekuláris dinamika I. 10. előadás
 Molekuláris dinamika I. 10. előadás Miről is szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten minden részecske mozgását szimuláljuk? Hogyan tudjuk megérteni a folyadékok,
Molekuláris dinamika I. 10. előadás Miről is szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten minden részecske mozgását szimuláljuk? Hogyan tudjuk megérteni a folyadékok,
January 16, ψ( r, t) ψ( r, t) = 1 (1) ( ψ ( r,
 Közelítő módszerek January 16, 27 1 A variációs módszer A variációs módszer szintén egy analitikus közelítő módszer. Olyan esetekben alkalmazzuk mikor ismert az analitikus alak amelyben keressük a sajátfüggvényt,
Közelítő módszerek January 16, 27 1 A variációs módszer A variációs módszer szintén egy analitikus közelítő módszer. Olyan esetekben alkalmazzuk mikor ismert az analitikus alak amelyben keressük a sajátfüggvényt,
Gázok. 5-7 Kinetikus gázelmélet 5-8 Reális gázok (limitációk) Fókusz Légzsák (Air-Bag Systems) kémiája
 Gázok 5-1 Gáznyomás 5-2 Egyszerű gáztörvények 5-3 Gáztörvények egyesítése: Tökéletes gáz egyenlet és általánosított gáz egyenlet 5-4 A tökéletes gáz egyenlet alkalmazása 5-5 Gáz halmazállapotú reakciók
Gázok 5-1 Gáznyomás 5-2 Egyszerű gáztörvények 5-3 Gáztörvények egyesítése: Tökéletes gáz egyenlet és általánosított gáz egyenlet 5-4 A tökéletes gáz egyenlet alkalmazása 5-5 Gáz halmazállapotú reakciók
11. tétel - Elektromágneses sugárzás és ionizáló sugárzás kölcsönhatása kondenzált anyaggal, áthatolóképesség, záporjelenségek.
 11. tétel - Elektromágneses sugárzás és ionizáló sugárzás kölcsönhatása kondenzált anyaggal, áthatolóképesség, záporjelenségek. Ionizáció Bevezetés Ionizációra minden töltött részecske képes, de az elektront
11. tétel - Elektromágneses sugárzás és ionizáló sugárzás kölcsönhatása kondenzált anyaggal, áthatolóképesség, záporjelenségek. Ionizáció Bevezetés Ionizációra minden töltött részecske képes, de az elektront
Diffúzió. Diffúzió. Diffúzió. Különféle anyagi részecskék anyagon belüli helyváltoztatása Az anyag lehet gáznemű, folyékony vagy szilárd
 Anyagszerkezettan és anyagvizsgálat 5/6 Diffúzió Dr. Szabó Péter János szpj@eik.bme.hu Diffúzió Különféle anyagi részecskék anyagon belüli helyváltoztatása Az anyag lehet gáznemű, folyékony vagy szilárd
Anyagszerkezettan és anyagvizsgálat 5/6 Diffúzió Dr. Szabó Péter János szpj@eik.bme.hu Diffúzió Különféle anyagi részecskék anyagon belüli helyváltoztatása Az anyag lehet gáznemű, folyékony vagy szilárd
Orvosi Biofizika I. 12. vizsgatétel. IsmétlésI. -Fény
 Orvosi iofizika I. Fénysugárzásanyaggalvalókölcsönhatásai. Fényszóródás, fényabszorpció. Az abszorpciós spektrometria alapelvei. (Segítséga 12. tételmegértéséhezésmegtanulásához, továbbá a Fényabszorpció
Orvosi iofizika I. Fénysugárzásanyaggalvalókölcsönhatásai. Fényszóródás, fényabszorpció. Az abszorpciós spektrometria alapelvei. (Segítséga 12. tételmegértéséhezésmegtanulásához, továbbá a Fényabszorpció
Magszerkezet modellek. Folyadékcsepp modell
 Magszerkezet modellek Folyadékcsepp modell Az atommag összetevői (emlékeztető) atommag Z proton + (A-Z) neutron (nukleonok) szorosan kötve Állapot leírása: kvantummechanika + kölcsönhatások Nem relativisztikus
Magszerkezet modellek Folyadékcsepp modell Az atommag összetevői (emlékeztető) atommag Z proton + (A-Z) neutron (nukleonok) szorosan kötve Állapot leírása: kvantummechanika + kölcsönhatások Nem relativisztikus
Gyakorlati útmutató a Tartók statikája I. tárgyhoz. Fekete Ferenc. 5. gyakorlat. Széchenyi István Egyetem, 2015.
 Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
Zárthelyi dolgozat I. /A.
 Zárthelyi dolgozat I. /A. 1. Az FCC rács és reciprokrácsa (és tudjuk, hogy: V W.S. * V B.z. /() 3 = 1 / mindig!/) a 1 = ½ a (0,1,1) ; a = ½ a (1,0,1) ; a 3 = ½ a (1,1,0) b 1 = (/a) (-1,1,1); b = (/a) (1,-1,1);
Zárthelyi dolgozat I. /A. 1. Az FCC rács és reciprokrácsa (és tudjuk, hogy: V W.S. * V B.z. /() 3 = 1 / mindig!/) a 1 = ½ a (0,1,1) ; a = ½ a (1,0,1) ; a 3 = ½ a (1,1,0) b 1 = (/a) (-1,1,1); b = (/a) (1,-1,1);
MTA Atommagkutató Intézet, 4026 Debrecen, Bem tér 18/c.
 Negatív hidrogénionok keletkezése 7 kev-es OH + + Ar és OH + + aceton ütközésekben: Egy általános mechanizmus hidrogént tartalmazó molekuláris rendszerekre JUHASZ Zoltán a), BENE Erika a), RANGAMA Jimmy
Negatív hidrogénionok keletkezése 7 kev-es OH + + Ar és OH + + aceton ütközésekben: Egy általános mechanizmus hidrogént tartalmazó molekuláris rendszerekre JUHASZ Zoltán a), BENE Erika a), RANGAMA Jimmy
Vezetők elektrosztatikus térben
 Vezetők elektrosztatikus térben Vezető: a töltések szabadon elmozdulhatnak Ha a vezető belsejében a térerősség nem lenne nulla akkor áram folyna. Ha a felületen a térerősségnek lenne tangenciális (párhuzamos)
Vezetők elektrosztatikus térben Vezető: a töltések szabadon elmozdulhatnak Ha a vezető belsejében a térerősség nem lenne nulla akkor áram folyna. Ha a felületen a térerősségnek lenne tangenciális (párhuzamos)
Rádl Attila december 11. Rádl Attila Spalláció december / 21
 Spalláció Rádl Attila 2018. december 11. Rádl Attila Spalláció 2018. december 11. 1 / 21 Definíció Atommagok nagyenergiás részecskével történő ütközése során másodlagos részecskéket létrehozó rugalmatlan
Spalláció Rádl Attila 2018. december 11. Rádl Attila Spalláció 2018. december 11. 1 / 21 Definíció Atommagok nagyenergiás részecskével történő ütközése során másodlagos részecskéket létrehozó rugalmatlan
Radioaktív sugárzások tulajdonságai és kölcsönhatásuk az elnyelő közeggel. A radioaktív sugárzások detektálása.
 Radioaktív sugárzások tulajdonságai és kölcsönhatásuk az elnyelő közeggel. A radioaktív sugárzások detektálása. Magsugárzások (α, β, γ) kölcsönhatása atomi rendszerekkel (170-174, 540-545 o.) Direkt és
Radioaktív sugárzások tulajdonságai és kölcsönhatásuk az elnyelő közeggel. A radioaktív sugárzások detektálása. Magsugárzások (α, β, γ) kölcsönhatása atomi rendszerekkel (170-174, 540-545 o.) Direkt és
a térerősség mindig az üreg falára merőleges, ezért a tér ott nem gömbszimmetrikus.
 2. Gyakorlat 25A-0 Tekintsünk egy l0 cm sugarú üreges fémgömböt, amelyen +0 µc töltés van. Legyen a gömb középpontja a koordinátarendszer origójában. A gömb belsejében az x = 5 cm pontban legyen egy 3
2. Gyakorlat 25A-0 Tekintsünk egy l0 cm sugarú üreges fémgömböt, amelyen +0 µc töltés van. Legyen a gömb középpontja a koordinátarendszer origójában. A gömb belsejében az x = 5 cm pontban legyen egy 3
Fizika 1 Elektrodinamika beugró/kis kérdések
 Fizika 1 Elektrodinamika beugró/kis kérdések 1.) Írja fel a 4 Maxwell-egyenletet lokális (differenciális) alakban! rot = j+ D rot = B div B=0 div D=ρ : elektromos térerősség : mágneses térerősség D : elektromos
Fizika 1 Elektrodinamika beugró/kis kérdések 1.) Írja fel a 4 Maxwell-egyenletet lokális (differenciális) alakban! rot = j+ D rot = B div B=0 div D=ρ : elektromos térerősség : mágneses térerősség D : elektromos
Nehézségi gyorsulás mérése megfordítható ingával
 Nehézségi gyorsulás mérése megfordítható ingával (Mérési jegyzőkönyv) Hagymási Imre 2007. április 21. (hétfő délelőtti csoport) 1. A mérés elmélete A nehézségi gyorsulás mérésének egy klasszikus módja
Nehézségi gyorsulás mérése megfordítható ingával (Mérési jegyzőkönyv) Hagymási Imre 2007. április 21. (hétfő délelőtti csoport) 1. A mérés elmélete A nehézségi gyorsulás mérésének egy klasszikus módja
Axiomatikus felépítés az axiómák megalapozottságát a felépített elmélet teljesítképessége igazolja majd!
 Hol vagyunk most? Definiáltuk az alapvet fogalmakat! - TD-i rendszer, fajtái - Környezet, fal - TD-i rendszer jellemzi - TD-i rendszer leírásához szükséges változók, állapotjelzk, azok csoportosítása -
Hol vagyunk most? Definiáltuk az alapvet fogalmakat! - TD-i rendszer, fajtái - Környezet, fal - TD-i rendszer jellemzi - TD-i rendszer leírásához szükséges változók, állapotjelzk, azok csoportosítása -
Atomfizika. Fizika kurzus Dr. Seres István
 Atomfizika Fizika kurzus Dr. Seres István Történeti áttekintés 440 BC Democritus, Leucippus, Epicurus 1660 Pierre Gassendi 1803 1897 1904 1911 19 193 John Dalton Joseph John (J.J.) Thomson J.J. Thomson
Atomfizika Fizika kurzus Dr. Seres István Történeti áttekintés 440 BC Democritus, Leucippus, Epicurus 1660 Pierre Gassendi 1803 1897 1904 1911 19 193 John Dalton Joseph John (J.J.) Thomson J.J. Thomson
FIZIKA ZÁRÓVIZSGA 2015
 FIZIKA ZÁRÓVIZSGA 2015 TESZT A következő feladatokban a három vagy négy megadott válasz közül pontosan egy helyes. Írd be az általad helyesnek vélt válasz betűjelét a táblázat megfelelő cellájába! Indokolni
FIZIKA ZÁRÓVIZSGA 2015 TESZT A következő feladatokban a három vagy négy megadott válasz közül pontosan egy helyes. Írd be az általad helyesnek vélt válasz betűjelét a táblázat megfelelő cellájába! Indokolni
Az időtől független Schrödinger-egyenlet (energia sajátértékegyenlet), A Laplace operátor derékszögű koordinátarendszerben
 Atomfizika ψ ψ ψ ψ ψ E z y x U z y x m = + + + ),, ( h ) ( ) ( ) ( ) ( r r r r ψ ψ ψ E U m = + Δ h z y x + + = Δ ),, ( ) ( z y x ψ =ψ r Az időtől független Schrödinger-egyenlet (energia sajátértékegyenlet),
Atomfizika ψ ψ ψ ψ ψ E z y x U z y x m = + + + ),, ( h ) ( ) ( ) ( ) ( r r r r ψ ψ ψ E U m = + Δ h z y x + + = Δ ),, ( ) ( z y x ψ =ψ r Az időtől független Schrödinger-egyenlet (energia sajátértékegyenlet),
Ütközések elemzése energia-impulzus diagramokkal II. A relativisztikus rakéta
 Ütközések elemzése energia-impulzus diagramokkal II. A relativisztikus rakéta Bokor Nándor Budapesti Műszaki és Gazdaságtudományi Egyetem, Fizika Tanszék 1111 Budapest, Budafoki u. 8. Ebben a cikkben olyan
Ütközések elemzése energia-impulzus diagramokkal II. A relativisztikus rakéta Bokor Nándor Budapesti Műszaki és Gazdaságtudományi Egyetem, Fizika Tanszék 1111 Budapest, Budafoki u. 8. Ebben a cikkben olyan
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Gázok. 5-7 Kinetikus gázelmélet 5-8 Reális gázok (korlátok) Fókusz: a légzsák (Air-Bag Systems) kémiája
 Gázok 5-1 Gáznyomás 5-2 Egyszerű gáztörvények 5-3 Gáztörvények egyesítése: Tökéletes gázegyenlet és általánosított gázegyenlet 5-4 A tökéletes gázegyenlet alkalmazása 5-5 Gáz reakciók 5-6 Gázkeverékek
Gázok 5-1 Gáznyomás 5-2 Egyszerű gáztörvények 5-3 Gáztörvények egyesítése: Tökéletes gázegyenlet és általánosított gázegyenlet 5-4 A tökéletes gázegyenlet alkalmazása 5-5 Gáz reakciók 5-6 Gázkeverékek
Azonos és egymással nem kölcsönható részecskékből álló kvantumos rendszer makrókanónikus sokaságban.
 Kvantum statisztika A kvantummechanika előadások során már megtanultuk, hogy az anyagot felépítő részecskék nemklasszikus, hullámtulajdonságokkal is rendelkeznek aminek következtében viselkedésük sok szempontból
Kvantum statisztika A kvantummechanika előadások során már megtanultuk, hogy az anyagot felépítő részecskék nemklasszikus, hullámtulajdonságokkal is rendelkeznek aminek következtében viselkedésük sok szempontból
A gradiens törésmutatójú közeg I.
 10. Előadás A gradiens törésmutatójú közeg I. Az ugrásszerű törésmutató változással szemben a TracePro-ban lehetőség van folytonosan változó törésmutatójú közeg definiálására. Ilyen érdekes típusú közegek
10. Előadás A gradiens törésmutatójú közeg I. Az ugrásszerű törésmutató változással szemben a TracePro-ban lehetőség van folytonosan változó törésmutatójú közeg definiálására. Ilyen érdekes típusú közegek
Mágneses monopólusok?
 1 Mágneses monopólusok? (Atomcsill 2015 február) Palla László ELTE Elméleti Fizikai Tanszék 2 Maxwell egyenletek potenciálok, mértéktranszformáció legegyszerűbb e.m. mezők A klasszikus e g rendszer A monopólus
1 Mágneses monopólusok? (Atomcsill 2015 február) Palla László ELTE Elméleti Fizikai Tanszék 2 Maxwell egyenletek potenciálok, mértéktranszformáció legegyszerűbb e.m. mezők A klasszikus e g rendszer A monopólus
Megoldás: A feltöltött R sugarú fémgömb felületén a térerősség és a potenciál pontosan akkora, mintha a teljes töltése a középpontjában lenne:
 3. gyakorlat 3.. Feladat: (HN 27A-2) Becsüljük meg azt a legnagyo potenciált, amelyre egy 0 cm átmérőjű fémgömöt fel lehet tölteni, anélkül, hogy a térerősség értéke meghaladná a környező száraz levegő
3. gyakorlat 3.. Feladat: (HN 27A-2) Becsüljük meg azt a legnagyo potenciált, amelyre egy 0 cm átmérőjű fémgömöt fel lehet tölteni, anélkül, hogy a térerősség értéke meghaladná a környező száraz levegő
Ejtési teszt modellezése a tervezés fázisában
 Antal Dániel, doktorandusz, Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szabó Tamás, egyetemi docens, Ph.D., Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szilágyi Attila, egyetemi adjunktus,
Antal Dániel, doktorandusz, Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szabó Tamás, egyetemi docens, Ph.D., Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szilágyi Attila, egyetemi adjunktus,
Bevezetés a lézeres anyagmegmunkálásba
 Bevezetés a lézeres anyagmegmunkálásba FBN332E-1 Dr. Geretovszky Zsolt 2010. október 13. A lézeres l anyagmegmunkálás szempontjából l fontos anyagi tulajdonságok Optikai tulajdonságok Mechanikai tulajdonságok
Bevezetés a lézeres anyagmegmunkálásba FBN332E-1 Dr. Geretovszky Zsolt 2010. október 13. A lézeres l anyagmegmunkálás szempontjából l fontos anyagi tulajdonságok Optikai tulajdonságok Mechanikai tulajdonságok
Bevezetés a modern fizika fejezeteibe. 4. (a) Kvantummechanika. Utolsó módosítás: november 15. Dr. Márkus Ferenc BME Fizika Tanszék
 Bevezetés a modern fizika fejezeteibe 4. (a) Kvantummechanika Utolsó módosítás: 2015. november 15. 1 Előzmények Az atomok színképe (1) A fehér fény komponensekre bontható: http://en.wikipedia.org/wiki/spectrum
Bevezetés a modern fizika fejezeteibe 4. (a) Kvantummechanika Utolsó módosítás: 2015. november 15. 1 Előzmények Az atomok színképe (1) A fehér fény komponensekre bontható: http://en.wikipedia.org/wiki/spectrum
Diffúzió 2003 március 28
 Diffúzió 3 március 8 Diffúzió: különféle anyagi részecskék (szilárd, folyékony, gáznemű) anyagon belüli helyváltozása. Szilárd anyagban való mozgás Öndiffúzió: a rácsot felépítő saját atomok energiaszint-különbség
Diffúzió 3 március 8 Diffúzió: különféle anyagi részecskék (szilárd, folyékony, gáznemű) anyagon belüli helyváltozása. Szilárd anyagban való mozgás Öndiffúzió: a rácsot felépítő saját atomok energiaszint-különbség
Kvantumos jelenségek lézertérben
 Kvantumos jelenségek lézertérben Atomfizika Benedict Mihály SZTE Elméleti Fizikai Tanszék Az előadást támogatta a TÁMOP-4.2.1/B-09/1/KONV-2010-0005 sz. Kutatóegyetemi Kiválósági Központ létrehozása a Szegedi
Kvantumos jelenségek lézertérben Atomfizika Benedict Mihály SZTE Elméleti Fizikai Tanszék Az előadást támogatta a TÁMOP-4.2.1/B-09/1/KONV-2010-0005 sz. Kutatóegyetemi Kiválósági Központ létrehozása a Szegedi
Elektromos alapjelenségek
 Elektrosztatika Elektromos alapjelenségek Dörzselektromos jelenség: egymással szorosan érintkező, vagy egymáshoz dörzsölt testek a szétválasztásuk után vonzó, vagy taszító kölcsönhatást mutatnak. Ilyenkor
Elektrosztatika Elektromos alapjelenségek Dörzselektromos jelenség: egymással szorosan érintkező, vagy egymáshoz dörzsölt testek a szétválasztásuk után vonzó, vagy taszító kölcsönhatást mutatnak. Ilyenkor
Röntgendiagnosztikai alapok
 Röntgendiagnosztikai alapok Dr. Voszka István A röntgensugárzás keltésének alternatív lehetőségei (röntgensugárzás keletkezik nagy sebességű, töltéssel rendelkező részecskék lefékeződésekor) Röntgencső:
Röntgendiagnosztikai alapok Dr. Voszka István A röntgensugárzás keltésének alternatív lehetőségei (röntgensugárzás keletkezik nagy sebességű, töltéssel rendelkező részecskék lefékeződésekor) Röntgencső:
A gamma-sugárzás kölcsönhatásai
 Ref. [3] A gamma-sugárzás kölcsönhatásai Az anyaggal való kölcsönhatás kis valószínűségű hatótávolság nagy A sugárzás gyengülését 3 féle kölcsönhatás okozza. fotoeffektus Compton-szórás párkeltés A gamma-fotonok
Ref. [3] A gamma-sugárzás kölcsönhatásai Az anyaggal való kölcsönhatás kis valószínűségű hatótávolság nagy A sugárzás gyengülését 3 féle kölcsönhatás okozza. fotoeffektus Compton-szórás párkeltés A gamma-fotonok
Kvantummechanika gyakorlat Beadandó feladatsor Határid : 4. heti gyakorlatok eleje
 Kvantummechanika gyakorlat 015 1. Beadandó feladatsor Határid : 4. heti gyakorlatok eleje 1. Mutassuk meg, hogy A és B tetsz leges operátorokra igaz, hogy e B A e B = A + [B, A] + 1![ B, [B, A] ] +....
Kvantummechanika gyakorlat 015 1. Beadandó feladatsor Határid : 4. heti gyakorlatok eleje 1. Mutassuk meg, hogy A és B tetsz leges operátorokra igaz, hogy e B A e B = A + [B, A] + 1![ B, [B, A] ] +....
Elektronegativitás. Elektronegativitás
 Általános és szervetlen kémia 3. hét Elektronaffinitás Az az energiaváltozás, ami akkor következik be, ha 1 mól gáz halmazállapotú atomból 1 mól egyszeresen negatív töltésű anion keletkezik. Mértékegysége:
Általános és szervetlen kémia 3. hét Elektronaffinitás Az az energiaváltozás, ami akkor következik be, ha 1 mól gáz halmazállapotú atomból 1 mól egyszeresen negatív töltésű anion keletkezik. Mértékegysége:
alapvető tulajdonságai
 A z a to m m a g o k alapvető tulajdonságai Mérhető mennyiségek Az atommagok mérete, tömege, töltése, spinje, mágneses momentuma, elektromos kvadrupól momentuma Az atommag töltés- és nukleon-eloszlása
A z a to m m a g o k alapvető tulajdonságai Mérhető mennyiségek Az atommagok mérete, tömege, töltése, spinje, mágneses momentuma, elektromos kvadrupól momentuma Az atommag töltés- és nukleon-eloszlása
Általános Kémia, BMEVESAA101
 Általános Kémia, BMEVESAA101 Dr Csonka Gábor, egyetemi tanár Az anyag Készítette: Dr. Csonka Gábor egyetemi tanár, csonkagi@gmail.com 1 Jegyzet Dr. Csonka Gábor http://web.inc.bme.hu/csonka/ Óravázlatok:
Általános Kémia, BMEVESAA101 Dr Csonka Gábor, egyetemi tanár Az anyag Készítette: Dr. Csonka Gábor egyetemi tanár, csonkagi@gmail.com 1 Jegyzet Dr. Csonka Gábor http://web.inc.bme.hu/csonka/ Óravázlatok:
A kémiai kötés magasabb szinten
 A kémiai kötés magasabb szinten 11-1 Mit kell tudnia a kötéselméletnek? 11- Vegyérték kötés elmélet 11-3 Atompályák hibridizációja 11-4 Többszörös kovalens kötések 11-5 Molekulapálya elmélet 11-6 Delokalizált
A kémiai kötés magasabb szinten 11-1 Mit kell tudnia a kötéselméletnek? 11- Vegyérték kötés elmélet 11-3 Atompályák hibridizációja 11-4 Többszörös kovalens kötések 11-5 Molekulapálya elmélet 11-6 Delokalizált
ahol m-schmid vagy geometriai tényező. A terhelőerő növekedésével a csúszó síkban fellép az un. kritikus csúsztató feszültség τ
 Egykristály és polikristály képlékeny alakváltozása A Frenkel féle modell, hibátlan anyagot feltételezve, nagyon nagy folyáshatárt eredményez. A rácshibák, különösen a diszlokációk jelenléte miatt a tényleges
Egykristály és polikristály képlékeny alakváltozása A Frenkel féle modell, hibátlan anyagot feltételezve, nagyon nagy folyáshatárt eredményez. A rácshibák, különösen a diszlokációk jelenléte miatt a tényleges
Sugárterápia. Ionizáló sugárzások elnyelődésének következményei. Konzultáció: minden hétfőn 15 órakor. 1. Fizikai történések
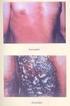 Sugárterápia 40% 35% 30% 25% 20% 15% % 5% 0% 2014/2015. tanév FOK biofizika kollokvium jegyspektruma 5 4,5 4 3,5 3 2,5 2 1,5 1 Konzultáció: minden hétfőn 15 órakor Ionizáló sugárzások elnyelődésének következményei
Sugárterápia 40% 35% 30% 25% 20% 15% % 5% 0% 2014/2015. tanév FOK biofizika kollokvium jegyspektruma 5 4,5 4 3,5 3 2,5 2 1,5 1 Konzultáció: minden hétfőn 15 órakor Ionizáló sugárzások elnyelődésének következményei
