2. ábra Változó egyenfeszültségek
|
|
|
- Marcell Hegedüs
- 9 évvel ezelőtt
- Látták:
Átírás
1 3.5.. Váltakozó feszültségek és áramok Időben változó feszültségek és áramok Az (ideális) galvánelem által szolgáltatott feszültség iránya és nagysága az idő múlásával nem változik. Ha az áramkörben az ellenállás sem változik, az áram is állandó értékű. Az ilyen áramkört nevezik egyenáramú áramkörnek. Ha a generátor feszültsége, vagy a terhelő ellenállás nem állandó értékű, az áramerősség is változik. Ha az áram (ill. feszültség) iránya állandó, csak az erőssége változik, változó áramú (változó feszültségű) áramkörről beszélünk. Az áram (feszültség) idő függvényében történő változását grafikonon ábrázolhatjuk. Az. ábra különböző lefolyású változó feszültségeket ill. áramot mutat.. ábra Változó egyenfeszültségek Az olyan feszültséget vagy áramot, amelynek nem csak a nagysága, hanem iránya is változik, váltakozó feszültségnek (váltakozó áramnak) nevezik (. ábra).. ábra Váltakozó áramok és feszültség
2 A váltakozó feszültség (áram) periodikus, ha az időbeli lefolyását leíró görbe szakaszai szabályszerűen ismétlődnek. A. ábra ilyen jelalakokat mutat. A görbe egymás után azonosan megismétlődő szakasza a periódus. Egy periódus lejátszódásának az idejét periódusidőnek nevezik, és T-vel jelölik. Az egy másodperc alatt lejátszódó periódusok száma a frekvencia, melynek jele: f. Ezt az értéket úgy számíthatjuk ki, hogy megvizsgáljuk, másodpercben hányszor van meg a periódusidő: f T A frekvencia mértékegysége f [ ] Hz [ T ] s azaz a hertz. (Az angolszász szakirodalomban használatos a cps vagy c/s [cycle per secundum], vagy röviden c [cycle]). A híradástechnikában a frekvencia nagyobb egységei is használatosak: khz 0 3 Hz ( kc/s vagy kc ) MHz 0 6 Hz ( Mc/s vagy Mc ) GHz 0 9 Hz ( Gc/s vagy Gc ) Szinuszos váltakozó feszültség Az elektrotechnikában, híradástechnikában legnagyobb jelentősége a szinuszos lefolyású váltakozó feszültségnek van. Ilyen feszültség indukálódik abban a vezetőkeretben, amelyet homogén mágneses térben állandó szögsebességgel forgatunk (3. ábra). 3. ábra Ha a kiindulási helyzetben a keret függőlegesen áll, forgatásának első pillanatában az indukcióvonalakkal párhuzamosan halad (ld. az ábra jobb oldalát), nem metszi azokat, így nem indukálódik feszültség. Tovább fordulva a keret vízszintes helyzetéig - azonos idő alatt egyre nagyobb számú indukcióvonalat metsz, így egyre nagyobb feszültség indukálódik a keretben. Az indukált feszültség a csúcsértékét ( max ) akkor éri el, amikor a keret vízszintes helyzetben van, és ekkor egy rövid ideig az indukcióvonalakra merőlegesen halad. Ez után az indukált feszültség ismét csökken, amíg a keret 80 fokkal (radiánban kifejezve Π-vel) el nem fordul; ekkor ismét egy pillanatra nem metsz indukcióvonalat, így az indukált feszültség 0 lesz. A keretet tovább forgatva az indukált feszültség a keret vízszintes helyzetéig ismét növekszik, de (mivel a keret vezetői az előzővel ellentétes irányban metszik az indukcióvonalakat), most az indukálódott feszültség iránya megfordul. Amikor a keret kiindulási állapotába tér vissza, az indukált feszültség egy pillanatra megint 0 lesz (ekkor ért véget az első periódus), majd a folyamat ciklikusan ismétlődik.
3 Az indukált feszültség időbeli lefolyását a 4. ábra mutatja. 4. ábra Kimutatható, hogy valamely t időpontban az indukált feszültség pillanatértéke u max sin ωt függvény szerint alakul, ezért az ilyen lefolyású jelet szinuszjelnek nevezik. A képletben u max ω t az indukált feszültség pillanatértéke (V) az indukált feszültség maximális értéke (csúcsértéke) (V) a keret szögsebességével megegyező ún. körfrekvencia, ω Πf Π/T (rad/s) a kiindulástól számított idő (s) Megjegyzés: A váltakozó áramokat és feszültségeket az egyenfeszültségtől való megkülönböztetésül kis betűkkel (u, i) szokás jelölni. A szinuszos jel max maximális értékét, 0-tól való maximális kitérését a jel amplitudójának nevezik. Tekintettel arra, hogy villamos hálózatban is forgó gépekkel állítják elő a villamos energiát, a hálózati feszültség szintén szinuszos lefolyású. Európában a hálózati frekvencia 50 Hz (viszont pl. az SA-ban 60 Hz!). Példa: Az 50 Hz-es hálózati feszültség csúcsértéke 30V. Mekkora a feszültség pillanatértéke a nullátmenettől számítva 4 ms időpontban? Megoldás: (minden adatot a képletben megadott mértékegységben írunk be, így az eredményt is abban kapjuk. 4ms 0,004s) A körfrekvencia ω Πf 3, rad/s. u max sin ωt 30 sin 34 0, sin, ,95 94,7V A szinuszos váltakozó feszültség középértékei Ha szinuszos feszültséget szolgáltató feszültségforrásra fogyasztót kapcsolunk, azon szintén szinuszos lefolyású áram alakul ki. Tekintettel arra, hogy e váltakozó mennyiségek pillanatértékei negatív és pozitív csúcsértékei között folyamatosan változnak, különféle (hő, vegyi) hatásai sem a csúcsértékkel, hanem valamilyen középértékkel arányosak. A villamos áram effektív értéke (vagy négyzetes középértéke) az áram hőhatására ad útmutatást. Az effektív érték annak az egyenáramnak az értékével egyenlő, amely azonos idő alatt ugyanakkora munkát végez (hőt termel), mint a vizsgált váltakozóáram. (Az effektív értéket azért hívják négyzetes középértéknek, mert ha ellenálláson I áram folyik keresztül, azon I feszültség esik, és P I I I I teljesítmény alakul hővé; így az effektív érték az áram négyzetével arányos középérték.) Kimutatható, hogy szinuszos jel esetén
4 I I max eff illetve max eff Megállapodás szerint a szinuszos váltakozó feszültség (vagy váltakozó áram) értékeként az effektív értéket adják meg. (Pl. a 30V-os hálózati feszültség effektív értéke 30V.) A szinuszos feszültséget vagy áramot mérő műszerek is az effektív értéket mutatják. Az áram elektrolitikus középértéke (vagy számtani, vagy egyenirányított középértéke) az áram vegyi hatása alapján számítható. Az elektrolízis során ui. az áram hatására az elektrolitba merülő elektródákon anyag választódik ki. Az elektrolitikus középérték annak az egyenáramnak az értékével egyenlő, amely azonos idő alatt ugyanakkora anyagmennyiséget választ ki, mint az egyenirányított váltakozóáram. Kimutatható, hogy szinuszos jel esetén I max I el illetve Π el max Π Példa:. Mekkora a 00V csúcsértékű szinuszos feszültség effektív értéke, ill. elektrolitikus középértéke? Megoldás: max 00 eff 70, 7V,4 00 el max 63, 6V Π 3,4. Mekkora a csúcsértéke a 30V-os hálózati feszültségnek? Megoldás: A megadott 30V a szinuszos hálózati feszültség effektív értéke. Az effektív értékre vonatkozó képlet átrendezésével max eff, , V A szinuszos váltakozó feszültség ábrázolása forgó vektorral Az 5. ábra bal oldalán egy vízszintes és függőleges egyenes a 0 pontban metszi egymást. A 0 pont körül ω szögsebességgel körbe forog az A amplitudójú vektor. Ha a vektor kiinduláskor (t 0) vízszintes helyzetben van, t t időpontban ωt szöggel fordul el, és a függőleges tengelyre való vetülete a A sin ωt. A forgó vektor függőleges tengelyre való vetületének időfüggvénye (ld. ábra jobb oldalán) ugyanolyan szinuszos lefolyású, mint az u max sin ωt váltakozófeszültség. 5. ábra
5 A szinuszosan váltakozó mennyiséget (feszültséget, áramot) tehát felfoghatjuk úgy, mint egy, a jel max csúcsértékével (amplitudójával) megegyező nagyságú, és ω Π f körfrekvenciájával forgó vektornak a függőleges tengelyre való vetületét. A forgó vektornak a periódus kezdetétől a vizsgált pillanatig megtett szögelfordulása a fázisszög. Fázishelyzet, fáziskülönbség Elképzelhető, hogy két szinuszos lefolyású mennyiség ugyanolyan frekvenciájú, de nullátmeneteik nem azonos időpontra esnek. Ilyen jeleket láthatunk a 6. ábrán. 6. ábra Mindkét jel 50 Hz-es frekvenciájú (T0 ms), de az. görbe szerinti áram maximuma a t 0 (ill. 0, 40 stb.) ms pillanatra esik, a. görbe szerinti áram pedig maximális értékét a t5 (ill. 5, 45, stb.) ms pillanatokban veszi fel. A. görbe szerinti áram időfüggvénye megegyezik a korábban bemutatottakkal, behelyettesítve az ω Π f Π rad/s értéket: i I max sin 34 t Az. görbe szerinti áramnak azonban a t0 időpillanatban van maximuma, és minimális értékét csak egy negyed periódus lezajlása után, t5 ms időpontban éri el. Az ábra jobb oldalán látható, hogy ez az áram is megfeleltethető egy forgó vektor függőleges tengelyre való vetületének, csak ez a vektor t 0 időpontban nem vízszintesen áll, hanem függőlegesen, azaz (ω az óramutató járásával ellentétes forgásirányát tekintve) I áram vektorához képest 90 -al (ívszögben kifejezve Π/ radiánnal) siet. I időfüggvénye ennek értelmében: i I max sin (34t + Π/) A két, azonos frekvenciájú áram időbeli lefolyásának különbségét fázisszögük különbségével, a fáziskülönbségükkel jellemezhetjük. A fáziskülönbség a két áramot jelképező vektor egymáshoz viszonyított szögével azonos (a fenti példában ez 90, azaz Π/ radián ) Váltakozóáramú körök elemei A váltakozófeszültségre kapcsolt ellenállás Ha (ideális) ellenállásra u váltakozófeszültséget kapcsolunk, azon i áram indul meg. Az Ohm-törvény a pillanatértékekre is érvényes, ezért i azaz az áram a feszültség ütemében változik, a két mennyiségnek egyszerre van a nullátmenete, a maximális és a minimális értéke: az ellenálláson átfolyó áram és a rajta eső feszültség között nincs fáziskülönbség (7. ábra). u
6 7.ábra Az ellenállást váltakozóáramú áramkörökben ohmos vagy hatásos ellenállásnak nevezik. A sorosan ill. párhuzamosan kapcsolt ellenállások eredőjét ugyanolyan módon számíthatjuk ki, mint egyenáram esetén. Kondenzátor töltési folyamata Kapcsoljunk G egyenfeszültségű generátorra a 8. ábrán látható módon sorba kapcsolt ellenállást és C kondenzátort. A K kapcsoló nyitott állásában a töltetlen kondenzátor kapocsfeszültsége 0, a kapcsolóval megszakított áramkörben áram nem folyik. 8. ábra A kapcsoló zárásának pillanatában (t 0) a kondenzátor kapocsfeszültsége 0. Kirchhoff huroktörvénye értelmében a kondenzátorra és az ellenállásra jutó feszültség együttesen adja ki a generátor feszültségét. Most C 0, ezért a teljes G feszültség ellenállásra kapcsolódik, és azon I 0 áram indul meg. Ez az áram tölti C kondenzátort, ezért C kapocsfeszültsége növekszik. Viszont a már említett huroktörvény értelmében minél nagyobb C, annál kevesebb lesz, így a hurokban I töltő áram annál jobban csökken. Ha a töltő áram csökken, a kondenzátor kapocsfeszültsége egyre kisebb mértékben emelkedik (9. ábra). A töltési folyamat végén C megegyezik G -vel, I 0, az ellenálláson nem esik feszültség. Kimutatható, hogy a kondenzátor feszültségének időbeli lefolyása exponenciális görbe szerint megy végbe. A kondenzátor kapacitásának (C) és az ellenállás értékének () szorzata egy τ (tau) val jelölt időállandót ad meg: G ahol τ C az időállandó (s) az ellenállás (Ω) a kondenzátor kapacitása (F) τ C τ idő alatt a kondenzátor a generátor feszültségének kb. 63%-ára töltődik, ugyanennyi idő alatt a töltőáram kb. 37%-ára csökken. Gyakorlatilag 3-5 τ idő alatt a kondenzátor teljesen feltöltődik.
7 9. ábra Figyeljük meg, hogy a töltődő kondenzátoron a töltés megkezdésekor a feszültség ( C ) 0, ugyanekkor a töltőáram maximális értékű. A töltődés befejezésekor viszont a töltőáram 0, ekkor viszont C maximális. A váltakozófeszültségre kapcsolt kondenzátor Ha a 0. ábra szerinti kapcsolásban egy kondenzátort váltakozóáramú generátorra kapcsolunk, a generátor feszültségének állandó változása következtében a kondenzátor mintegy folyamatosan áttöltődik, így rajta folyamatosan váltakozó áram folyik. Matematikai eszközökkel kimutatható, hogy az így kialakuló áram és a kondenzátor kapocsfeszültsége között hasonló jellegű a kapcsolat, mint az egyenfeszültségről, ellenálláson keresztül töltött kondenzátor esetében: amikor a kondenzátor kapocsfeszültsége 0, akkor folyik a legnagyobb töltőáram, és amikor kapocsfeszültsége a maximális, a töltő áramnak épp akkor van a 0-átmenete (0. ábra). 0. ábra
8 Megállapíthatjuk, hogy (szinuszos áramú áramkörben) a kondenzátoron az átfolyó áram és a kapocsfeszültség között 90 (Π/ radián) fáziseltérés mutatkozik, és pedig - ω irányát figyelembe véve - az áram siet a feszültséghez képest. Kimutatható, hogy a kialakuló áram nagysága i u ω C A kondenzátorra kapcsolt váltakozó feszültség és az ennek hatására kialakuló áram hányadosa Ohm törvénye értelmében egy ellenállás dimenziójú mennyiséget határoz meg, melyet a kondenzátor reaktanciájának vagy meddő ellenállásának neveznek és X C -vel jelölnek. A képlet átrendezésével: u X C i ω C ahol X C ω C a kondenzátor reaktanciája vagy meddő ellenállása (Ω) a körfrekvencia, ω Π f (rad/s) a kondenzátor kapacitása (F) A reaktancia vagy meddő ellenállás kifejezés arra utal, hogy ellentétben az ohmos vagy hatásos ellenállással az áram és a feszültség között 90 -os fáziskülönbség van. A kondenzátor reaktanciáját szokás kapacitív reaktanciának nevezni. Példa Határozzuk meg egy 7 nf kapacitású kondenzátor raktanciáját f 00 khz frekvencián! Megoldás: (a képletbe minden mennyiséget az ott megadott alapegységben helyettesítünk be) X C 5894, 6Ω ωc 3 9 Π f C Π Tekercs (induktivítás) bekapcsolás folyamata egyenáramú áramkörben A. ábra szerinti áramkörben G egyenfeszültségű generátorra a sorosan kapcsolt ellenállás és L induktivitás kapcsolódik. K kapcsoló nyitott állásában az áramkörben nem folyik áram, az ellenálláson eső és a tekercsen mérhető L feszültség egyaránt 0.. ábra A kapcsoló zárásakor az áramkörben áram indul meg. Ennek nagysága (mivel az ellenállásra - Kirchhoff huroktörvénye értelmében - G generátorfeszültség és L feszültség különbsége jut) lesz. I G L
9 A tekercsen eső L feszültség nem más, mint az áramváltozás hatására a tekercsben indukálódott feszültség (hiszen az ideális tekercsnek 0 az ohmos ellenállása, így azon a kialakuló áramtól függetlenül nem eshet feszültség). Az indukálódott ΔI i L Δt feszültség iránya Lenz törvénye értelmében olyan, hogy akadályozza az áram kialakulását, mintegy szembekapcsolódik a generátor feszültségével. A bekapcsolás pillanatában I 0, ami azt jelenti, hogy az ellenálláson nem esik feszültség: ekkor a tekercsben indukálódott feszültség megegyezik a generátor feszültségével. Az áram azonban folyamatosan növekszik (hiszen a tekercsben a feszültséget éppen az áram változása indukálja), így az ellenálláson egyre nagyobb feszültség esik, és egyre kisebb feszültség jut a tekercsre. Így egyre kevesebb lesz a tekercsre jutó ΔI L Δ t indukált feszültség is, azaz az áram növekedésének az üteme (ΔI/Δt) is. Végül az áram I G értéken stabilizálódik, ΔI/Δt 0 lesz, így a tekercsen nem indukálódik feszültség. Kimutatható, hogy az áram kialakulása (illetve a tekercsen a feszültség csökkenése) exponenciális lefolyású (. ábra).. ábra Az ábrán τ-val jelölt időállandó értéke L/ (ha L-t H-ban, -t Ω-ban helyettesítjük be, τ-t s-ban kapjuk). Ennyi idő alatt csökken a tekercs feszültsége a generátor feszültségének megközelítőleg 37%-ára, illetve nő az áram a végleges érték kb. 63%-ára. 3-5 τ idő alatt gyakorlatilag kialakul a végleges áramerősség, és a tekercsen indukálódott feszültség 0-ra csökken.
10 Figyeljük meg, hogy a tekercsen a bekapcsoláskor az áram 0, a feszültség maximális értékű volt, a végleges állapot kialakulásakor pedig a feszültség 0, és az áram maximális. A váltakozó feszültségre kapcsolt tekercs (induktivitás) A 3. ábra szerinti kapcsolásban a szinuszos váltakozó feszültségű generátorra L induktivitás kapcsolódik. A generátor feszültségének állandó változása következtében a tekercsen indukálódó feszültség (és így a kialakuló áram is) folyamatosan változik, az áramkörben váltakozó áram folyik. 3. ábra A tekercsben önindukció útján keletkező feszültség mindig megegyezik a generátor feszültségével. Az i ΔI L Δt összefüggés alapján belátható, hogy ez a feszültség akkor a legnagyobb, amikor az áram változási sebessége a legnagyobb: az áram nullátmeneténél. Amikor viszont az áram változási sebessége 0 (a pozitív ill. negatív csúcsértékénél), akkor az indukált feszültség értéke 0. Tehát a tekercsen kialakuló áram és feszültség között hasonló a kapcsolat, mint az egyenfeszültségre kapcsolt tekercs bekapcsolási folyamatánál: a feszültség maximális értékénél az áram 0, az árammaximum időpontjában pedig a feszültségé. Megállapítható, hogy (szinuszos áramú áramkörben) a tekercsen az átfolyó áram és a kapocsfeszültség között 90 (Π/ radián) fáziseltérés mutatkozik, és pedig a feszültség siet az áramhoz képest. Kimutatható, hogy a kialakuló áram nagysága i u ωl A feszültség és az áram hányadosa itt is ellenállás dimenziójú mennyiséget (az áram és a feszültség közötti 90 (Π/ radián) fáziskülönbség figyelembe vételével reaktanciát) határoz meg, melynek értéke a képlet átrendezésével: ahol X L ω L X L u i ωl a tekercs (induktivitás) reaktanciája, meddő ellenállása (Ω) a körfrekvencia (ω Π f) (rad/s) a tekercs induktivitása (H) A tekercs reaktanciáját induktív raktanciának nevezik. Példa:. Mekkora reaktanciát tanúsít khz frekvencián egy L50 mh induktivitású tekercs? Megoldás: (az adatokat Hz-ben, H-ban helyettesítjük be, így az eredményt Ω-ban kapjuk) X L ωl ΠfL 3, ,5 94,47 Ω
11 . Hogyan alakul a frekvencia függvényében az ohmos ellenállás, az induktivitás illetve a kondenzátor ellenállása ill. reaktanciája? Válasz: ld. a 4.ábrát. 4. ábra Váltakozóáramú körök számításai Az impedancia fogalma A 5. ábra szerinti kapcsolásban a soros ellenállásból és C kondenzátorból álló áramkört kapcsoljuk a szinuszjelet szolgáltató generátorra. A kialakuló I áram mindkét sorba kapcsolt áramköri elemen azonos lesz. Az ellenálláson eső feszültség fázisban van az átfolyó árammal (a kettő hányadosa adja az ellenállás értéket), a kondenzátoron a feszültséghez képest az áram 90 fokot siet (e kettő hányadosa pedig X C reaktancia). 5. ábra Az ábra középső részén láthatjuk a fázisviszonyokat. Az I áramot képviselő vektor vízszintesen jobbra mutat. Az ellenálláson eső feszültség fázisban van az átfolyó árammal, ezért feszültséget jelképező vektor szintén vízszintes, jobbra mutató. A kondenzátoron a feszültség 90 fokot késik I áramhoz képest, ezért (ω forgásirányát is figyelembe véve) az C -t jelképező vektor függőlegesen lefelé irányul. A generátor feszültsége és C vektorok eredőjeként adódik. Látható, hogy a generátor feszültsége és a kialakuló I áram között ϕ fáziskülönbség van: az áram siet a feszültséghez képest. E két mennyiség hányadosa ellenállás jellegű értéket ad, amelyet impedanciának (váltakozóáramú ellenállásnak) neveznek, és Z-vel jelölnek (mértékegysége: Ω). Ha az ábra középső részén látható vektorábra feszültségeinek értékét osztjuk I-vel, /I, C /IX C, /IZ összefüggéseket kapjuk, ezt ábrázoltuk az ábra jobb oldalán. Z az átfogója egy derékszögű háromszögnek, melynek és X C a befogói. Így Z abszolút értéke fázisszöge pedig Z + X C X ϕ arctan C Az impedancia tehát az áramkörben kialakuló feszültség és áram értékének hányadosa, amelynek része lehet ohmos ellenállás és reaktancia. Az ohmos és reaktáns komponenseket a fázisviszonyok figyelembe vételével, vektori összegzéssel kell összevonni. Határfrekvencia Az ohmos ellenállásból és reaktáns elemből álló áramkörben gyakran van szükség annak a frekvenciának (f h határfrekvenciának) a meghatározására, amikor az áramkör ohmosból reaktáns
12 jellegűvé válik. Ez azon a frekvencián következik be, amikor az ohmos ellenállás megegyezik a reaktancia értékével. Pl. a 5. ábra szerinti áramkörben ekkor X C ω C Πf C amiből f h illetve ω h kifejezhető: h h ω h C f h ΠC Ezen a frekvencián a összefüggés szerint az impedancia értékű. Z + X C Teljesítmény számítása váltakozóáramú áramkörben Ha az áramkörben nem csak ellenállás, hanem reaktáns elem (tekercs vagy kondenzátor) is jelen van, a feszültség és a kialakuló áram között fáziskülönbség lehet. A teljesítmény kiszámításánál azt kell figyelembe vennünk, hogy amikor az áramkör valamely elemén a feszültség és az áram azonos irányú, akkor az adott elem teljesítményt vesz fel (azaz fogyasztó), amikor pedig a feszültség és az áram ellentétes irányú, akkor teljesítményt ad le, (azaz generátor). A 6. ábra a feszültség és áram alakulását ohmos ellenálláson mutatja. A fáziskülönbség 0, a feszültség és az áram iránya a teljes T periódusidő alatt megegyezik, így az ellenállás mindig fogyasztó: a felvett P I (az effektív értékeket kell figyelembe venni, az eredmény mértékegysége: W) hatásos teljesítményt hővé alakítja. 6. ábra Kapacitív illetve induktív reaktancián a feszültség és az áram között 90 fok fáziseltérés van. A 7. ábrából láthatjuk, hogy ilyenkor a reaktáns elemen egy negyed periódusideig az áram és feszültség azonos, majd egy negyed periódusideig ellentétes irányú, azaz ez egyik negyed periódusidő alatt felvett teljesítményt a következő negyed periódusidő alatt leadja. Ilyen formán a reaktáns elem valóságos teljesítményt nem vesz fel (P 0 W, az I szorzat ebben az esetben az ún. meddő (vagy reaktáns) teljesítményt adja, melynek mértékegysége: VAr).
13 7. ábra A 8. ábrán 0 90 fok közötti fázistolású hálózat feszültség és áram görbéit láthatjuk. A hálózat hosszabb ideig vesz fel energiát, mint ameddig lead, tehát összességében fogyasztó. 8. ábra Ekkor az áramkör által fogyasztott un. hatásos teljesítmény a meddő teljesítmény pedig P I cos ϕ (W), Q I sin ϕ (VAr). A feszültség és az áram szorzatát látszólagos teljesítménynek nevezik, és S-el jelölik, mértékegysége: VA (voltamper): S I ezgőkörök Soros LC kör Az ohmos és reaktáns elemekből összeállított áramkörök között kitüntetett szerepe van a kondenzátorból, tekercsből (és ellenállásból) álló áramkörnek. (Az ellenállást gyakorlati számításokban nem célszerű kihagyni, így vehetjük figyelembe a valóságos tekercs veszteségi ellenállását.) A soros áramkört és a fázisviszonyokat a 9. ábrán láthatjuk (A soros LC kört később tisztázandó okból soros rezgőkörnek nevezik.)
14 9. ábra Mindhárom sorba kapcsolt elemen ugyanaz az I áram folyik keresztül, a vektorábrán ezt a vízszintesen jobbra mutató I vektor jelzi. Az ellenálláson eső feszültség fázisban van az árammal, ezért azzal azonos irányú. A tekercsen indukálódó L feszültség az áramhoz képest 90 fokkal siet, ezért függőleges, felfelé irányított vektor jelzi. A kondenzátoron eső C feszültség az átfolyó áramhoz képest 90 fokkal késik, ezért az ennek megfelelő vektor lefelé irányul (bal oldali vektorábra). A generátor feszültsége e három feszültség (, L, C ) vektori eredője. Mivel L és C ellentétes irányú, e két feszültség eredője a két feszültség különbsége; a példában L a nagyobb értékű, ezért a különbségi feszültség ( L C ) vektora felfelé irányul. Ezt a feszültséget kell vektori módon összegezni el (középső vektorábra), az eredő feszültséggel egyezik meg. Az impedancia kiszámításához (jobb oldali vektorábra) valamennyi feszültséget elosztottuk I árammal, így olyan derékszögű háromszög adódik, melynek átfogója Z, befogói és (X L X C ). Ebből adódik, hogy és Z ϕ arctan + ( X L X C ) X X L C Tekintettel arra, hogy X L és X C a frekvencia függvényében változik, Z értéke is a frekvenciától függ (0. ábra). A képletből kiolvasható, hogy azon a frekvencián, ahol X L X C, a két mennyiség különbsége 0, és itt Z, azaz az áramkör -el megegyező ohmos ellenállást tanúsít. Ezt a frekvenciát rezonanciafrekvenciának nevezik és f 0 - al (az ennek megfelelő körfrekvenciát ω 0 -al) jelölik. Mivel X L ωl, és X C, és a rezonanciafrekvencián e két mennyiség egyenlő, ω C ω0l ω0c ω0 LC ω0 LC ω0 f 0 Π Π LC Ez, a rezonanciafrekvencia meghatározására szolgáló képlet az ún. Thomson-képlet.
15 0. ábra A 0. ábrán Z impedanciát (és annak komponenseit) ill. ϕ fázisszöget ábrázoltuk a frekvencia függvényében. Z komponensei: -, melynek ellenállása a frekvencia függvényében nem változik, -X L ωl Π f L a frekvenciával arányosan nő, -X C /ωc / Π f C a frekvencia növekedtével a görbe szerint csökken. Kis frekvenciákon (f << f 0 ) a három komponens közül X C a domináns, a soros LC kör mint sorosan kapcsolt ellenállás és kondenzátor viselkedik, ennek megfelelően a fázisszög is a kapacitív reaktancia 90 fokos szögéhez közelít. ezonanciafrekvencián (f f 0 ) a kapacitív és induktív reaktancia megegyezik, de ellentétes fázisszögüknél fogva kiejtik egymást, és a rezgőkör csak ellenállást mutatja. A frekvencia növekedtével (f >>f 0 ) egyre inkább az induktív reaktancia válik dominánssá, a soros LC kör mint ellenállás és sorba kapcsolt tekercs viselkedik, e szerint alakul a +90 fokhoz közelítő fázisszög is (ilyen a viszonyokat mutatnak be a 9. ábra vektordiagramjai is). Nagy jelentősége van annak a két frekvenciának, amelynél a rezgőkör impedanciájának valós és képzetes része megegyezik (f h, f h ). Ezeken a frekvenciákon (X L X C ) vagy (X C X L ), így Z + ( X X + L C ) Az f h - f h frekvenciakülönbséget a rezgőkör sávszélességének nevezik, és B vel jelölik (mértékegysége: Hz): B f h - f h A rezonanciafrekvencia és a sávszélesség hányadosa a rezgőkör jósága, jele: Q (mértékegység nélküli viszonyszám). Q f 0 B
16 A képlet átrendezésével megkaphatjuk a rezgőkör sávszélességét, ha ismert a rezonanciafrekvencia és a kör jósága: B f 0 Q A soros rezgőkör jósága a képlet segítségével határozható meg. Q ω 0 L Párhuzamos rezgőkör ellenállás, C kondenzátor és L tekercs párhuzamos kapcsolásával párhuzamos rezgőkörhöz jutunk (. ábra).. ábra A párhuzamos áramköri elemek mindegyikére szinuszos váltakozó feszültség kapcsolódik (a bal oldali vektorábrán a feszültség vektora vízszintesen, jobbra irányul). Az ellenálláson átfolyó I áram a feszültséggel fázisban van, vektora ugyanebbe az irányba mutat. A kondenzátoron I C áram a feszültséghez képest 90 fokkal siet, vektora függőlegesen felfelé irányul. A tekercs I L árama 90 fokkal késik, vektora függőlegesen lefelé mutat. A rezgőkörön kialakuló I áram I, I L és I C vektori összegeként adódik. I L és I C ellenfázisú, egymásból kivonódnak. Az ábrán I C a nagyobb, ezért eredőjük I C irányú, nagysága I C I L (középső ábrarész). Ha most mindegyik áramot elosztjuk a közös feszültséggel, az ellenállás ill. a reaktanciák reciprokát kapjuk (az ábra jobb oldalán). /Z egy derékszögű háromszög átfogója, / és (/X C -/X L ) a befogói, így ebből illetve Z Z + X C X L + X C X L
17 ϕ arctan X L X C gyanúgy mint a soros rezgőkörnél, azt az f 0 frekvenciát, ahol X C X L rezonanciafrekvenciának nevezik. (Meghatározása a Thomson-képlet segítségével: f 0 Π LC történik). Ezen a frekvencián a kondenzátoron és a tekercsen ellentétes irányú, azonos nagyságú áram folyik, ezek egymást kiegyenlítik, és a rezgőkör ohmos ellenállást tanúsít. Minden más frekvencián reaktáns áram is folyik, ezért a rezgőkör impedanciája csökken (. ábra). Kisebb frekvenciákon a tekercs jelenti a kisebb reaktanciát, így a rezgőkör impedanciája induktív jellegű, míg a rezonanciafrekvencia felett a kapacitív reaktancia a kisebb, ezért az impedancia kapacitív jellegű..ábra A sávszélesség annak a két frekvenciának (f h és f h ) a különbsége, ahol a párhuzamos rezgőkör impedanciája a rezonanciafrekvencián mért érték / részére csökken: B f h - f h A párhuzamos rezgőkör jósága a összefüggésből számítható ki. Q ω C 0
18 Hogyan rezeg a rezgőkör? Töltsük fel a 3. ábrán látható C kondenzátort 0 feszültségre, majd zárjuk a K kapcsolót. 3. ábra Az összekapcsolás pillanatától mindkét elemen ugyanakkora áram folyik, és ugyanakkora a feszültség is. A t 0 időpontban a kondenzátor 0 feszültségre van feltöltve, áram nem folyik. A feszültség hatására a tekercsen egyre nagyobb áram indul meg, amely a kondenzátort fokozatosan kisüti. Amikor a kondenzátor teljesen kisült, a feszültség 0, ugyanekkor folyik a legnagyobb áram (a feltöltött kondenzátorban tárolt energia ekkor teljes egészében mágneses energiává alakul). Ennek az energiának a hatására a tekercsen az áram tovább folyik, és az előzővel ellentétes polaritással tölteni kezdi a kondenzátort. Amikor a kondenzátor 0 feszültségre töltődött, az áram ismét 0-ra csökken: a mágneses energia teljes egészében elektrosztatikus energiává alakult vissza. A folyamat ciklikusan ismétlődik, a feszültség és az áram lefolyását az ábra jobb oldalán láthatjuk. (Mindkét elemen az ismert 90 fokos fáziseltérés van a feszültség és az áram között.) Tehát a magára hagyott LC körben szinuszos rezgés alakult ki, az ilyen elrendezést ezért nevezik rezgőkörnek Ha a rezgőkör ideális (veszteség nélküli) kondenzátorból és tekercsből áll, a rezgés az idők végeztéig fennmarad. A valóságban a rezgőkör elemei veszteségesek, ezt gyakorlati számításokkor a rezgőkörbe helyezett ellenállással vesszük figyelembe. A veszteségek miatt a rezgés amplitúdója folyamatosan csökken (4. ábra). 4. ábra Minél nagyobb a rezgőkör jósága (Q-ja), annál hosszabb idő alatt csillapodnak a rezgőkör rezgései. Csekély jóságú rezgőkörnél egy teljes rezgési periódus sem zajlik le (aperiodikus csillapítás).
19 Példa Egy párhuzamos rezgőkörben L 00μH, C 0 pf, a veszteségeket 47 kω ellenállással vesszük figyelembe. Mekkora a rezgőkör rezonanciafrekvenciája, jósága, sávszélessége? Megoldás: (00μH H, 0 pf F, 47 kω Ω) A rezonanciafrekvencia a Thomson-képlet szerint f, Π LC Π Π, 0 6,8, (azaz,073 MHz). A rezgőkör jósága a sávszélesség pedig Q ω 0 C Π, ,7 6 f 0, B 5,39 0 Hz 5, 39kHz Q 69,7 6 Hz Transzformátor A 3... pontban említettük, hogy amíg a csatolás egymástól független tekercsek esetében általában nem kívánatos, egyes alkalmazásokban szándékosan hoznak létre csatolást tekercsek között. Ilyen alkalmazás a transzformátor. A transzformátort általában zárt ferromágneses magon elhelyezett tekercsek formájában alakítják ki (5. ábra). 5. ábra Az ún. primer tekercsre szinuszos feszültséget szolgáltató generátort kapcsolunk. Abban az esetben, ha a szekunder tekercsre még nem kapcsoljuk rá terhelést, a primer tekercsben induktív reaktanciájának megfelelő csekély I ü üresjárási áram indul meg. Ez az áram mágneses indukciót hoz létre. Az indukcióvonalak a szoros csatolást biztosító ferromágneses magon mindkét tekercsen áthaladnak, és mindkét tekercsben feszültséget indukálnak. A primer és a szekunder tekercs egy - egy menetében ugyanakkora feszültség indukálódik. Így primer feszültség és szekunder feszültség aránya a két tekercs N ill. N menetszámának arányával egyezik meg, melyet áttételnek neveznek és a-val jelölnek: a N N Ha a szekunder tekercsre terhelést kapcsoljuk, feszültség hatására azon I áram indul meg, ellenálláson P I teljesítmény disszipálódik. Ezt a teljesítményt a transzformátor az
2. ábra Változó egyenfeszültségek
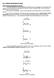 3.5.. Váltakozó feszültségek és áramok Időben változó feszültségek és áramok Az (ideális) galvánelem által szolgáltatott feszültség iránya és nagysága az idő múlásával nem változik. Ha az áramkörben az
3.5.. Váltakozó feszültségek és áramok Időben változó feszültségek és áramok Az (ideális) galvánelem által szolgáltatott feszültség iránya és nagysága az idő múlásával nem változik. Ha az áramkörben az
Számítási feladatok megoldással a 6. fejezethez
 Számítási feladatok megoldással a 6. fejezethez. Egy szinuszosan változó áram a polaritás váltás után μs múlva éri el első maximumát. Mekkora az áram frekvenciája? T = 4 t = 4 = 4ms 6 f = = =,5 Hz = 5
Számítási feladatok megoldással a 6. fejezethez. Egy szinuszosan változó áram a polaritás váltás után μs múlva éri el első maximumát. Mekkora az áram frekvenciája? T = 4 t = 4 = 4ms 6 f = = =,5 Hz = 5
Számítási feladatok a 6. fejezethez
 Számítási feladatok a 6. fejezethez 1. Egy szinuszosan változó áram a polaritás váltás után 1 μs múlva éri el első maximumát. Mekkora az áram frekvenciája? 2. Egy áramkörben I = 0,5 A erősségű és 200 Hz
Számítási feladatok a 6. fejezethez 1. Egy szinuszosan változó áram a polaritás váltás után 1 μs múlva éri el első maximumát. Mekkora az áram frekvenciája? 2. Egy áramkörben I = 0,5 A erősségű és 200 Hz
1. Milyen módszerrel ábrázolhatók a váltakozó mennyiségek, és melyiknek mi az előnye?
 .. Ellenőrző kérdések megoldásai Elméleti kérdések. Milyen módszerrel ábrázolhatók a váltakozó mennyiségek, és melyiknek mi az előnye? Az ábrázolás történhet vonaldiagramban. Előnye, hogy szemléletes.
.. Ellenőrző kérdések megoldásai Elméleti kérdések. Milyen módszerrel ábrázolhatók a váltakozó mennyiségek, és melyiknek mi az előnye? Az ábrázolás történhet vonaldiagramban. Előnye, hogy szemléletes.
EGYFÁZISÚ VÁLTAKOZÓ ÁRAM
 VANYSEEŐ KÉPÉS 0 5 EGYFÁSÚ VÁTAKOÓ ÁAM ÖSSEÁÍTOTTA NAGY ÁSÓ MÉNÖKTANÁ - - Tartalomjegyzék Váltakozó áram fogalma és jellemzői...3 Szinuszos lefolyású váltakozó feszültség előállítása...3 A szinuszos lefolyású
VANYSEEŐ KÉPÉS 0 5 EGYFÁSÚ VÁTAKOÓ ÁAM ÖSSEÁÍTOTTA NAGY ÁSÓ MÉNÖKTANÁ - - Tartalomjegyzék Váltakozó áram fogalma és jellemzői...3 Szinuszos lefolyású váltakozó feszültség előállítása...3 A szinuszos lefolyású
VÁLTAKOZÓ ÁRAMÚ KÖRÖK
 Számítsuk ki a 80 mh induktivitású ideális tekercs reaktanciáját az 50 Hz, 80 Hz, 300 Hz, 800 Hz, 1200 Hz és 1,6 khz frekvenciájú feszültséggel táplált hálózatban! Sorosan kapcsolt C = 700 nf, L=600 mh,
Számítsuk ki a 80 mh induktivitású ideális tekercs reaktanciáját az 50 Hz, 80 Hz, 300 Hz, 800 Hz, 1200 Hz és 1,6 khz frekvenciájú feszültséggel táplált hálózatban! Sorosan kapcsolt C = 700 nf, L=600 mh,
ALAPFOGALMIKÉRDÉSEK VILLAMOSSÁGTANBÓL 1. EGYENÁRAM
 ALAPFOGALMIKÉRDÉSEK VILLAMOSSÁGTANBÓL INFORMATIKUS HALLGATÓK RÉSZÉRE 1. EGYENÁRAM 1. Vezesse le a feszültségosztó képletet két ellenállás (R 1 és R 2 ) esetén! Az összefüggésben szerepl mennyiségek jelölését
ALAPFOGALMIKÉRDÉSEK VILLAMOSSÁGTANBÓL INFORMATIKUS HALLGATÓK RÉSZÉRE 1. EGYENÁRAM 1. Vezesse le a feszültségosztó képletet két ellenállás (R 1 és R 2 ) esetén! Az összefüggésben szerepl mennyiségek jelölését
2.11. Feladatok megoldásai
 Elektrotechnikai alaismeretek.. Feladatok megoldásai. feladat: Egy szinuszosan változó áram a olaritás váltás után μs múlva éri el első maximumát. Mekkora az áram frekvenciája? T 4 t 4 4µ s f,5 Hz 5 khz
Elektrotechnikai alaismeretek.. Feladatok megoldásai. feladat: Egy szinuszosan változó áram a olaritás váltás után μs múlva éri el első maximumát. Mekkora az áram frekvenciája? T 4 t 4 4µ s f,5 Hz 5 khz
A soros RC-kör. t, szög [rad] feszültség áramerősség. 2. ábra a soros RC-kör kapcsolási rajza. a) b) 3. ábra
![A soros RC-kör. t, szög [rad] feszültség áramerősség. 2. ábra a soros RC-kör kapcsolási rajza. a) b) 3. ábra A soros RC-kör. t, szög [rad] feszültség áramerősség. 2. ábra a soros RC-kör kapcsolási rajza. a) b) 3. ábra](/thumbs/54/33962402.jpg) A soros RC-kör Az átmeneti jelenségek vizsgálatakor soros RC-körben egyértelművé vált, hogy a kondenzátoron a késik az áramhoz képest. Váltakozóáramú körökben ez a késés, pontosan 90 fok. Ezt figyelhetjük
A soros RC-kör Az átmeneti jelenségek vizsgálatakor soros RC-körben egyértelművé vált, hogy a kondenzátoron a késik az áramhoz képest. Váltakozóáramú körökben ez a késés, pontosan 90 fok. Ezt figyelhetjük
7. L = 100 mh és r s = 50 Ω tekercset 12 V-os egyenfeszültségű áramkörre kapcsolunk. Mennyi idő alatt éri el az áram az állandósult értékének 63 %-át?
 1. Jelöld H -val, ha hamis, I -vel ha igaz szerinted az állítás!...két elektromos töltés között fellépő erőhatás nagysága arányos a két töltés nagyságával....két elektromos töltés között fellépő erőhatás
1. Jelöld H -val, ha hamis, I -vel ha igaz szerinted az állítás!...két elektromos töltés között fellépő erőhatás nagysága arányos a két töltés nagyságával....két elektromos töltés között fellépő erőhatás
1 kérdés. Személyes kezdőlap Villamos Gelencsér Géza Simonyi teszt május 13. szombat Teszt feladatok 2017 Előzetes megtekintés
 Személyes kezdőlap Villamos Gelencsér Géza Simonyi teszt 2017. május 13. szombat Teszt feladatok 2017 Előzetes megtekintés Kezdés ideje 2017. május 9., kedd, 16:54 Állapot Befejezte Befejezés dátuma 2017.
Személyes kezdőlap Villamos Gelencsér Géza Simonyi teszt 2017. május 13. szombat Teszt feladatok 2017 Előzetes megtekintés Kezdés ideje 2017. május 9., kedd, 16:54 Állapot Befejezte Befejezés dátuma 2017.
A soros RL-kör. t, szög [rad] áram feszültség. 1. ábra Feszültség és áramviszonyok az ellenálláson, illetve a tekercsen
![A soros RL-kör. t, szög [rad] áram feszültség. 1. ábra Feszültség és áramviszonyok az ellenálláson, illetve a tekercsen A soros RL-kör. t, szög [rad] áram feszültség. 1. ábra Feszültség és áramviszonyok az ellenálláson, illetve a tekercsen](/thumbs/89/97648728.jpg) A soros L-kör Mint ismeretes, a tekercsen az áram 90 fokot késik a hez képest, ahogyan az az 1. ábrán látható. A valós terhelésen a és az áramerősség azonos fázisú. Lényegében viszonyítás kérdése, de lássuk
A soros L-kör Mint ismeretes, a tekercsen az áram 90 fokot késik a hez képest, ahogyan az az 1. ábrán látható. A valós terhelésen a és az áramerősség azonos fázisú. Lényegében viszonyítás kérdése, de lássuk
FIZIKA. Váltóáramú hálózatok, elektromágneses hullámok
 Váltóáramú hálózatok, elektromágneses Váltóáramú hálózatok Maxwell egyenletek Elektromágneses Váltófeszültség (t) = B A w sinwt = sinwt maximális feszültség w= pf körfrekvencia 4 3 - - -3-4,5,,5,,5,3,35
Váltóáramú hálózatok, elektromágneses Váltóáramú hálózatok Maxwell egyenletek Elektromágneses Váltófeszültség (t) = B A w sinwt = sinwt maximális feszültség w= pf körfrekvencia 4 3 - - -3-4,5,,5,,5,3,35
A soros RC-kör. t, szög [rad]
![A soros RC-kör. t, szög [rad] A soros RC-kör. t, szög [rad]](/thumbs/91/105121094.jpg) A soros C-kör Az átmeneti jelenségek vizsgálatakor soros C-körben egyértelművé vált, hogy a kondenzátoron a késik az áramhoz képest. Váltakozóáramú körökben ez a késés, pontosan 90 fok. Ezt figyelhetjük
A soros C-kör Az átmeneti jelenségek vizsgálatakor soros C-körben egyértelművé vált, hogy a kondenzátoron a késik az áramhoz képest. Váltakozóáramú körökben ez a késés, pontosan 90 fok. Ezt figyelhetjük
Gyakorlat 34A-25. kapcsolunk. Mekkora a fűtőtest teljesítménye? I o = U o R = 156 V = 1, 56 A (3.1) ezekkel a pillanatnyi értékek:
 3. Gyakorlat 34-5 Egy Ω ellenállású elektromos fűtőtestre 56 V amplitúdójú váltakozó feszültséget kapcsolunk. Mekkora a fűtőtest teljesítménye? Jelölések: R = Ω, U o = 56 V fűtőtestben folyó áram amplitudója
3. Gyakorlat 34-5 Egy Ω ellenállású elektromos fűtőtestre 56 V amplitúdójú váltakozó feszültséget kapcsolunk. Mekkora a fűtőtest teljesítménye? Jelölések: R = Ω, U o = 56 V fűtőtestben folyó áram amplitudója
a) Valódi tekercs b) Kondenzátor c) Ohmos ellenállás d) RLC vegyes kapcsolása
 Bolyai Farkas Országos Fizika Tantárgyverseny 2016 Bolyai Farkas Elméleti Líceum, Marosvásárhely XI. Osztály 1. Adott egy alap áramköri elemen a feszültség u=220sin(314t-30 0 )V és az áramerősség i=2sin(314t-30
Bolyai Farkas Országos Fizika Tantárgyverseny 2016 Bolyai Farkas Elméleti Líceum, Marosvásárhely XI. Osztály 1. Adott egy alap áramköri elemen a feszültség u=220sin(314t-30 0 )V és az áramerősség i=2sin(314t-30
2.) Fajlagos ellenállásuk nagysága alapján állítsd sorrendbe a következő fémeket! Kezd a legjobban vezető fémmel!
 1.) Hány Coulomb töltést tartalmaz a 72 Ah ás akkumulátor? 2.) Fajlagos ellenállásuk nagysága alapján állítsd sorrendbe a következő fémeket! Kezd a legjobban vezető fémmel! a.) alumínium b.) ezüst c.)
1.) Hány Coulomb töltést tartalmaz a 72 Ah ás akkumulátor? 2.) Fajlagos ellenállásuk nagysága alapján állítsd sorrendbe a következő fémeket! Kezd a legjobban vezető fémmel! a.) alumínium b.) ezüst c.)
1. feladat R 1 = 2 W R 2 = 3 W R 3 = 5 W R t1 = 10 W R t2 = 20 W U 1 =200 V U 2 =150 V. Megoldás. R t1 R 3 R 1. R t2 R 2
 1. feladat = 2 W R 2 = 3 W R 3 = 5 W R t1 = 10 W R t2 = 20 W U 1 =200 V U 2 =150 V U 1 R 2 R 3 R t1 R t2 U 2 R 2 a. Számítsd ki az R t1 és R t2 ellenállásokon a feszültségeket! b. Mekkora legyen az U 2
1. feladat = 2 W R 2 = 3 W R 3 = 5 W R t1 = 10 W R t2 = 20 W U 1 =200 V U 2 =150 V U 1 R 2 R 3 R t1 R t2 U 2 R 2 a. Számítsd ki az R t1 és R t2 ellenállásokon a feszültségeket! b. Mekkora legyen az U 2
MÁGNESES INDUKCIÓ VÁLTÓÁRAM VÁLTÓÁRAMÚ HÁLÓZATOK
 MÁGNESES NDUKCÓ VÁLTÓÁRAM VÁLTÓÁRAMÚ HÁLÓZATOK Mágneses indukció Mozgási indukció v B Vezetőt elmozdítunk mágneses térben B-re merőlegesen, akkor a vezetőben áram keletkezik, melynek iránya az őt létrehozó
MÁGNESES NDUKCÓ VÁLTÓÁRAM VÁLTÓÁRAMÚ HÁLÓZATOK Mágneses indukció Mozgási indukció v B Vezetőt elmozdítunk mágneses térben B-re merőlegesen, akkor a vezetőben áram keletkezik, melynek iránya az őt létrehozó
Négypólusok helyettesítő kapcsolásai
 Transzformátorok Magyar találmány: Bláthy Ottó Titusz (1860-1939), Déry Miksa (1854-1938), Zipernovszky Károly (1853-1942), Ganz Villamossági Gyár, 1885. Felépítés, működés Transzformátor: négypólus. Működési
Transzformátorok Magyar találmány: Bláthy Ottó Titusz (1860-1939), Déry Miksa (1854-1938), Zipernovszky Károly (1853-1942), Ganz Villamossági Gyár, 1885. Felépítés, működés Transzformátor: négypólus. Működési
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2015. október 12. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2015. október 12. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2015. október 12. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2015. október 12. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
2. Ideális esetben az árammérő belső ellenállása a.) nagyobb, mint 1kΩ b.) megegyezik a mért áramkör eredő ellenállásával
 Teszt feladatok A választásos feladatoknál egy vagy több jó válasz lehet! Számításos feladatoknál csak az eredményt és a mértékegységet kell megadni. 1. Mitől függ a vezetők ellenállása? a.) a rajta esett
Teszt feladatok A választásos feladatoknál egy vagy több jó válasz lehet! Számításos feladatoknál csak az eredményt és a mértékegységet kell megadni. 1. Mitől függ a vezetők ellenállása? a.) a rajta esett
(Az 1. példa adatai Uray-Szabó: Elektrotechnika c. (Nemzeti Tankönyvkiadó) könyvéből vannak.)
 Egyenáramú gépek (Az 1. példa adatai Uray-Szabó: Elektrotechnika c. (Nemzeti Tankönyvkiadó) könyvéből vannak.) 1. Párhuzamos gerjesztésű egyenáramú motor 500 V kapocsfeszültségű, párhuzamos gerjesztésű
Egyenáramú gépek (Az 1. példa adatai Uray-Szabó: Elektrotechnika c. (Nemzeti Tankönyvkiadó) könyvéből vannak.) 1. Párhuzamos gerjesztésű egyenáramú motor 500 V kapocsfeszültségű, párhuzamos gerjesztésű
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2014. október 13. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2014. október 13. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2014. október 13. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2014. október 13. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
Egyszerű áramkörök árama, feszültsége, teljesítménye
 Egyszerű árakörök áraa, feszültsége, teljesíténye A szokásos előjelek Általában az ún fogyasztói pozitív irányokat használják, ezek szerint: - a ϕ fázisszög az ára helyzete a feszültség szinusz hullá szöghelyzetéhez
Egyszerű árakörök áraa, feszültsége, teljesíténye A szokásos előjelek Általában az ún fogyasztói pozitív irányokat használják, ezek szerint: - a ϕ fázisszög az ára helyzete a feszültség szinusz hullá szöghelyzetéhez
A váltakozó áramú hálózatok
 A váltakozó áramú hálózatok Az egyenáramú hálózatokkal foglalkozó fejezeteinkben a vizsgált áramkörökben minden ág árama és feszültsége az idő függvényében állandó volt, vagyis sem az irányuk, sem a nagyságuk
A váltakozó áramú hálózatok Az egyenáramú hálózatokkal foglalkozó fejezeteinkben a vizsgált áramkörökben minden ág árama és feszültsége az idő függvényében állandó volt, vagyis sem az irányuk, sem a nagyságuk
1. Feladat. Megoldás. Számítsd ki az ellenállás-hálózat eredő ellenállását az A B az A C és a B C pontok között! Mindegyik ellenállás értéke 100 Ω.
 1. Feladat Számítsd ki az ellenállás-hálózat eredő ellenállását az A B az A C és a B C pontok között! Mindegyik ellenállás értéke 100 Ω. A 1 2 B 3 4 5 6 7 A B pontok között C 13 = 1 + 3 = 2 = 200 Ω 76
1. Feladat Számítsd ki az ellenállás-hálózat eredő ellenállását az A B az A C és a B C pontok között! Mindegyik ellenállás értéke 100 Ω. A 1 2 B 3 4 5 6 7 A B pontok között C 13 = 1 + 3 = 2 = 200 Ω 76
MUNKAANYAG. Danás Miklós. Váltakozó áramú hálózatok. A követelménymodul megnevezése: Elektronikai áramkörök tervezése, dokumentálása
 Danás Miklós Váltakozó áramú hálózatok A követelménymodul megnevezése: Elektronikai áramkörök tervezése, dokumentálása A követelménymodul száma: 0917-06 A tartalomelem azonosító száma és célcsoportja:
Danás Miklós Váltakozó áramú hálózatok A követelménymodul megnevezése: Elektronikai áramkörök tervezése, dokumentálása A követelménymodul száma: 0917-06 A tartalomelem azonosító száma és célcsoportja:
= Φ B(t = t) Φ B (t = 0) t
 4. Gyakorlat 32B-3 Egy ellenállású, r sugarú köralakú huzalhurok a B homogén mágneses erőtér irányára merőleges felületen fekszik. A hurkot gyorsan, t idő alatt 180 o -kal átforditjuk. Számitsuk ki, hogy
4. Gyakorlat 32B-3 Egy ellenállású, r sugarú köralakú huzalhurok a B homogén mágneses erőtér irányára merőleges felületen fekszik. A hurkot gyorsan, t idő alatt 180 o -kal átforditjuk. Számitsuk ki, hogy
Teljesítm. ltség. U max
 1 tmény a váltakozó áramú körben A váltakozv ltakozó feszülts ltség Áttekinthetően szemlélteti a feszültség pillanatnyi értékét a forgóvektoros ábrázolás, mely szerint a forgó vektor y-irányú vetülete
1 tmény a váltakozó áramú körben A váltakozv ltakozó feszülts ltség Áttekinthetően szemlélteti a feszültség pillanatnyi értékét a forgóvektoros ábrázolás, mely szerint a forgó vektor y-irányú vetülete
Fizika II. feladatsor főiskolai szintű villamosmérnök szak hallgatóinak. Levelező tagozat
 Fizika. feladatsor főiskolai szintű villamosmérnök szak hallgatóinak Levelező tagozat 1. z ábra szerinti félgömb alakú, ideális vezetőnek tekinthető földelőbe = 10 k erősségű áram folyik be. föld fajlagos
Fizika. feladatsor főiskolai szintű villamosmérnök szak hallgatóinak Levelező tagozat 1. z ábra szerinti félgömb alakú, ideális vezetőnek tekinthető földelőbe = 10 k erősségű áram folyik be. föld fajlagos
4. /ÁK Adja meg a villamos áramkör passzív építő elemeit!
 Áramkörök 1. /ÁK Adja meg a mértékegységek lehetséges prefixumait (20db)! 2. /ÁK Értelmezze az ideális feszültség generátor fogalmát! 3. /ÁK Mit ért valóságos feszültség generátor alatt? 4. /ÁK Adja meg
Áramkörök 1. /ÁK Adja meg a mértékegységek lehetséges prefixumait (20db)! 2. /ÁK Értelmezze az ideális feszültség generátor fogalmát! 3. /ÁK Mit ért valóságos feszültség generátor alatt? 4. /ÁK Adja meg
Elektrotechnika. Ballagi Áron
 Elektrotechnika Ballagi Áron Mágneses tér Elektrotechnika x/2 Mágneses indukció kísérlet Állandó mágneses térben helyezzünk el egy l hosszúságú vezetőt, és bocsássunk a vezetőbe I áramot! Tapasztalat:
Elektrotechnika Ballagi Áron Mágneses tér Elektrotechnika x/2 Mágneses indukció kísérlet Állandó mágneses térben helyezzünk el egy l hosszúságú vezetőt, és bocsássunk a vezetőbe I áramot! Tapasztalat:
Oszcillátorok. Párhuzamos rezgőkör L C Miért rezeg a rezgőkör?
 Oszcillátorok Párhuzamos rezgőkör L C Miért rezeg a rezgőkör? Töltsük fel az ábrán látható kondenzátor egy megadott U feszültségre, majd zárjuk az áramkört az ábrán látható módon. Mind a tekercsen, mind
Oszcillátorok Párhuzamos rezgőkör L C Miért rezeg a rezgőkör? Töltsük fel az ábrán látható kondenzátor egy megadott U feszültségre, majd zárjuk az áramkört az ábrán látható módon. Mind a tekercsen, mind
Elektrotechnika 11/C Villamos áramkör Passzív és aktív hálózatok
 Elektrotechnika 11/C Villamos áramkör A villamos áramkör. A villamos áramkör részei. Ideális feszültségforrás. Fogyasztó. Vezeték. Villamos ellenállás. Ohm törvénye. Részfeszültségek és feszültségesés.
Elektrotechnika 11/C Villamos áramkör A villamos áramkör. A villamos áramkör részei. Ideális feszültségforrás. Fogyasztó. Vezeték. Villamos ellenállás. Ohm törvénye. Részfeszültségek és feszültségesés.
Tekercsek. Induktivitás Tekercs: induktivitást megvalósító áramköri elem. Az induktivitás definíciója: Innen:
 Tekercsek Induktivitás Tekercs: induktivitást megvalósító áramköri elem. Az induktivitás definíciója: u i =-N dφ/dt=-n dφ/di di/dt=-l di/dt Innen: L=N dφ/di Ezt integrálva: L=N Φ/I A tekercs induktivitása
Tekercsek Induktivitás Tekercs: induktivitást megvalósító áramköri elem. Az induktivitás definíciója: u i =-N dφ/dt=-n dφ/di di/dt=-l di/dt Innen: L=N dφ/di Ezt integrálva: L=N Φ/I A tekercs induktivitása
4. /ÁK Adja meg a villamos áramkör passzív építő elemeit!
 Áramkörök 1. /ÁK Adja meg a mértékegységek lehetséges prefixumait (20db)! 2. /ÁK Értelmezze az ideális feszültség generátor fogalmát! 3. /ÁK Mit ért valóságos feszültség generátor alatt? 4. /ÁK Adja meg
Áramkörök 1. /ÁK Adja meg a mértékegységek lehetséges prefixumait (20db)! 2. /ÁK Értelmezze az ideális feszültség generátor fogalmát! 3. /ÁK Mit ért valóságos feszültség generátor alatt? 4. /ÁK Adja meg
Az elektromágneses indukció jelensége
 Az elektromágneses indukció jelensége Korábban láttuk, hogy az elektromos áram hatására mágneses tér keletkezik (Ampère-féle gerjesztési törvény) Kérdés, hogy vajon ez megfordítható-e, és a mágneses tér
Az elektromágneses indukció jelensége Korábban láttuk, hogy az elektromos áram hatására mágneses tér keletkezik (Ampère-féle gerjesztési törvény) Kérdés, hogy vajon ez megfordítható-e, és a mágneses tér
TARTALOMJEGYZÉK. Előszó 9
 TARTALOMJEGYZÉK 3 Előszó 9 1. Villamos alapfogalmak 11 1.1. A villamosság elő for d u lá s a é s je le n t ősége 12 1.1.1. Történeti áttekintés 12 1.1.2. A vil la mos ság tech ni kai, tár sa dal mi ha
TARTALOMJEGYZÉK 3 Előszó 9 1. Villamos alapfogalmak 11 1.1. A villamosság elő for d u lá s a é s je le n t ősége 12 1.1.1. Történeti áttekintés 12 1.1.2. A vil la mos ság tech ni kai, tár sa dal mi ha
A kísérlet, mérés megnevezése célkitűzései: Váltakozó áramú körök vizsgálata, induktív ellenállás mérése, induktivitás értelmezése.
 A kísérlet, mérés megnevezése célkitűzései: Váltakozó áramú körök vizsgálata, induktív ellenállás mérése, induktivitás értelmezése. Eszközszükséglet: tanulói tápegység funkcionál generátor tekercsek digitális
A kísérlet, mérés megnevezése célkitűzései: Váltakozó áramú körök vizsgálata, induktív ellenállás mérése, induktivitás értelmezése. Eszközszükséglet: tanulói tápegység funkcionál generátor tekercsek digitális
Hálózatok számítása egyenáramú és szinuszos gerjesztések esetén. Egyenáramú hálózatok vizsgálata Szinuszos áramú hálózatok vizsgálata
 Hálózatok számítása egyenáramú és szinuszos gerjesztések esetén Egyenáramú hálózatok vizsgálata Szinuszos áramú hálózatok vizsgálata Egyenáramú hálózatok vizsgálata ellenállások, generátorok, belső ellenállások
Hálózatok számítása egyenáramú és szinuszos gerjesztések esetén Egyenáramú hálózatok vizsgálata Szinuszos áramú hálózatok vizsgálata Egyenáramú hálózatok vizsgálata ellenállások, generátorok, belső ellenállások
Elektromágnesség tesztek
 Elektromágnesség tesztek 1. Melyik esetben nem tapasztalunk vonzóerőt? a) A mágnesrúd északi pólusához vasdarabot közelítünk. b) A mágnesrúd közepéhez vasdarabot közelítünk. c) A mágnesrúd déli pólusához
Elektromágnesség tesztek 1. Melyik esetben nem tapasztalunk vonzóerőt? a) A mágnesrúd északi pólusához vasdarabot közelítünk. b) A mágnesrúd közepéhez vasdarabot közelítünk. c) A mágnesrúd déli pólusához
1. konferencia: Egyenáramú hálózatok számítása
 1. konferencia: Egyenáramú hálózatok számítása 1.feladat: 20 1 kω Határozzuk meg az R jelű ellenállás értékét! 10 5 kω R z ellenállás értéke meghatározható az Ohm-törvény alapján. Ehhez ismernünk kell
1. konferencia: Egyenáramú hálózatok számítása 1.feladat: 20 1 kω Határozzuk meg az R jelű ellenállás értékét! 10 5 kω R z ellenállás értéke meghatározható az Ohm-törvény alapján. Ehhez ismernünk kell
Elektromechanika. 6. mérés. Teljesítményelektronika
 Elektromechanika 6. mérés Teljesítményelektronika 1. Rajzolja fel az ideális és a valódi dióda feszültségáram jelleggörbéjét! Valódi dióda karakterisztikája: Ideális dióda karakterisztikája (3-as jelű
Elektromechanika 6. mérés Teljesítményelektronika 1. Rajzolja fel az ideális és a valódi dióda feszültségáram jelleggörbéjét! Valódi dióda karakterisztikája: Ideális dióda karakterisztikája (3-as jelű
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2012. október 15. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2012. október 15. 1:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2012. október 15. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2012. október 15. 1:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
AUTOMATIKAI ÉS ELEKTRONIKAI ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ
 ATOMATKA ÉS ELEKTONKA SMEETEK KÖZÉPSZNTŰ ÍÁSBEL VZSGA JAVÍTÁS-ÉTÉKELÉS ÚTMTATÓ A MNTAFELADATOKHOZ Egyszerű, rövid feladatok Maximális pontszám: 40. Egy A=,5 mm keresztmetszetű alumínium (ρ= 0,08 Ω mm /m)
ATOMATKA ÉS ELEKTONKA SMEETEK KÖZÉPSZNTŰ ÍÁSBEL VZSGA JAVÍTÁS-ÉTÉKELÉS ÚTMTATÓ A MNTAFELADATOKHOZ Egyszerű, rövid feladatok Maximális pontszám: 40. Egy A=,5 mm keresztmetszetű alumínium (ρ= 0,08 Ω mm /m)
11-12. évfolyam. A tantárgy megnevezése: elektrotechnika. Évi óraszám: 69. Tanítási hetek száma: 37 + 32. Tanítási órák száma: 1 óra/hét
 ELEKTROTECHNIKA (VÁLASZTHATÓ) TANTÁRGY 11-12. évfolyam A tantárgy megnevezése: elektrotechnika Évi óraszám: 69 Tanítási hetek száma: 37 + 32 Tanítási órák száma: 1 óra/hét A képzés célja: Választható tantárgyként
ELEKTROTECHNIKA (VÁLASZTHATÓ) TANTÁRGY 11-12. évfolyam A tantárgy megnevezése: elektrotechnika Évi óraszám: 69 Tanítási hetek száma: 37 + 32 Tanítási órák száma: 1 óra/hét A képzés célja: Választható tantárgyként
5. VÁLTAKOZÓ ÁRAM. A mérés leírása előtt összefoglaljuk a váltóáramú hálózatszámításhoz szükséges alapismereteket.
 5. VÁLTAKOZÓ ÁAM A mérés leírása előtt összefoglaljuk a váltóáramú hálózatszámításhoz szükséges alapismereteket. 5.. VÁLTÓÁAMÚ HÁLÓZATSZÁMÍTÁS Ha a feszültség, illetve az áramerősség időfüggése harmonikus,
5. VÁLTAKOZÓ ÁAM A mérés leírása előtt összefoglaljuk a váltóáramú hálózatszámításhoz szükséges alapismereteket. 5.. VÁLTÓÁAMÚ HÁLÓZATSZÁMÍTÁS Ha a feszültség, illetve az áramerősség időfüggése harmonikus,
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2007. május 25. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
ÉRETTSÉGI VIZSGA 2007. május 25. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
 Marcsa Dániel Transzformátor - példák 1. feladat : Egyfázisú transzformátor névleges teljesítménye 125kVA, a feszültsége U 1 /U 2 = 5000/400V. A névleges terheléshez tartozó tekercsveszteség 0,06S n, a
Marcsa Dániel Transzformátor - példák 1. feladat : Egyfázisú transzformátor névleges teljesítménye 125kVA, a feszültsége U 1 /U 2 = 5000/400V. A névleges terheléshez tartozó tekercsveszteség 0,06S n, a
Egyenáram tesztek. 3. Melyik mértékegység meghatározása nem helyes? a) V = J/s b) F = C/V c) A = C/s d) = V/A
 Egyenáram tesztek 1. Az alábbiak közül melyik nem tekinthető áramnak? a) Feltöltött kondenzátorlemezek között egy fémgolyó pattog. b) A generátor fémgömbje és egy földelt gömb között szikrakisülés történik.
Egyenáram tesztek 1. Az alábbiak közül melyik nem tekinthető áramnak? a) Feltöltött kondenzátorlemezek között egy fémgolyó pattog. b) A generátor fémgömbje és egy földelt gömb között szikrakisülés történik.
EGYENÁRAMÚ TÁPEGYSÉGEK
 dátum:... a mérést végezte:... EGYENÁRAMÚ TÁPEGYSÉGEK m é r é s i j e g y z k ö n y v 1/A. Mérje meg az adott hálózati szabályozható (toroid) transzformátor szekunder tekercsének minimálisan és maximálisan
dátum:... a mérést végezte:... EGYENÁRAMÚ TÁPEGYSÉGEK m é r é s i j e g y z k ö n y v 1/A. Mérje meg az adott hálózati szabályozható (toroid) transzformátor szekunder tekercsének minimálisan és maximálisan
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2014. május 20. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2014. május 20. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2014. május 20. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2014. május 20. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
Elektrotechnika 9. évfolyam
 Elektrotechnika 9. évfolyam Villamos áramkörök A villamos áramkör. A villamos áramkör részei. Ideális feszültségforrás. Fogyasztó. Vezeték. Villamos ellenállás. Ohm törvénye. Részfeszültségek és feszültségesés.
Elektrotechnika 9. évfolyam Villamos áramkörök A villamos áramkör. A villamos áramkör részei. Ideális feszültségforrás. Fogyasztó. Vezeték. Villamos ellenállás. Ohm törvénye. Részfeszültségek és feszültségesés.
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2009. október 19. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2009. október 19. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS
ÉRETTSÉGI VIZSGA 2009. október 19. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2009. október 19. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS
Mérési útmutató Periodikus, nem szinusz alakú jelek értékelése, félvezetős egyenirányítók
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁYI EGYETEM VILLAMOSMÉRÖKI ÉS IFORMATIKAI KAR VILLAMOS EERGETIKA TASZÉK Mérési útmutató Periodikus, nem szinusz alakú jelek értékelése, félvezetős egyenirányítók vizsgálata
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁYI EGYETEM VILLAMOSMÉRÖKI ÉS IFORMATIKAI KAR VILLAMOS EERGETIKA TASZÉK Mérési útmutató Periodikus, nem szinusz alakú jelek értékelése, félvezetős egyenirányítók vizsgálata
Átmeneti jelenségek egyenergiatárolós áramkörökben
 TARTALOM JEGYZÉK 1. Egyenergiatárolós áramkörök átmeneti függvényeinek meghatározása Példák az egyenergiatárolós áramkörök átmeneti függvényeinek meghatározására 1.1 feladat 1.2 feladat 1.3 feladat 1.4
TARTALOM JEGYZÉK 1. Egyenergiatárolós áramkörök átmeneti függvényeinek meghatározása Példák az egyenergiatárolós áramkörök átmeneti függvényeinek meghatározására 1.1 feladat 1.2 feladat 1.3 feladat 1.4
A 27/2012 (VIII. 27.) NGM rendelet (12/2013 (III.28) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján.
 A 27/2012 (VIII. 27.) NGM rendelet (12/2013 (III.28) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 54 522 01 Erősáramú elektrotechnikus
A 27/2012 (VIII. 27.) NGM rendelet (12/2013 (III.28) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 54 522 01 Erősáramú elektrotechnikus
A 27/2012 (VIII. 27.) NGM rendelet (12/2013 (III.28) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján.
 A 27/2012 (VIII. 27.) NGM rendelet (12/2013 (III.28) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 54 523 02 Elektronikai technikus
A 27/2012 (VIII. 27.) NGM rendelet (12/2013 (III.28) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 54 523 02 Elektronikai technikus
II. Szakmai alap- és szakismeretek, gyakorlati alkalmazásuk 4. Villamosságtani alapismeretek Hunyadi Sándor
 A 2015. LVII-es energiahatékonysági törvényben meghatározott auditori és energetikai szakreferens vizsga felkészítő anyaga II. Szakmai alap- és szakismeretek, gyakorlati alkalmazásuk 4. Villamosságtani
A 2015. LVII-es energiahatékonysági törvényben meghatározott auditori és energetikai szakreferens vizsga felkészítő anyaga II. Szakmai alap- és szakismeretek, gyakorlati alkalmazásuk 4. Villamosságtani
Mérés és adatgyűjtés
 Mérés és adatgyűjtés 4. óra - levelező Mingesz Róbert Szegedi Tudományegyetem 2011. március 18. MA lev - 4. óra Verzió: 1.3 Utolsó frissítés: 2011. május 15. 1/51 Tartalom I 1 A/D konverterek alkalmazása
Mérés és adatgyűjtés 4. óra - levelező Mingesz Róbert Szegedi Tudományegyetem 2011. március 18. MA lev - 4. óra Verzió: 1.3 Utolsó frissítés: 2011. május 15. 1/51 Tartalom I 1 A/D konverterek alkalmazása
Áram mágneses hatása, elektromágnes, váltakozó áram előállítása, transzformálása
 Áram mágneses hatása, elektromágnes, váltakozó áram előállítása, transzformálása A feltekercselt vezeték; tekercs, amelyben áram folyik, rúdmágnesként viselkedik, olyan mágneses tere lesz, mint a rúdmágnesnek.
Áram mágneses hatása, elektromágnes, váltakozó áram előállítása, transzformálása A feltekercselt vezeték; tekercs, amelyben áram folyik, rúdmágnesként viselkedik, olyan mágneses tere lesz, mint a rúdmágnesnek.
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI ÉRETTSÉGI VIZSGA VIZSGA 2006. október 2006. 24. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2006. október 24. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati
ÉRETTSÉGI ÉRETTSÉGI VIZSGA VIZSGA 2006. október 2006. 24. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2006. október 24. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI ÉRETTSÉGI VIZSGA VIZSGA 2009. 2006. május 22. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2009. május 22. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati
ÉRETTSÉGI ÉRETTSÉGI VIZSGA VIZSGA 2009. 2006. május 22. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2009. május 22. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati
Mágnesesség, elektromágnes, indukció Tudománytörténeti háttér Már i. e. 600 körül Thalész felfedezte, hogy Magnesia város mellett vannak olyan talált
 Mágnesesség, elektromágnes, indukció Tudománytörténeti háttér Már i. e. 600 körül Thalész felfedezte, hogy Magnesia város mellett vannak olyan talált ércek, amelyek vonzzák a vasat. Ezeket mágnesnek nevezték
Mágnesesség, elektromágnes, indukció Tudománytörténeti háttér Már i. e. 600 körül Thalész felfedezte, hogy Magnesia város mellett vannak olyan talált ércek, amelyek vonzzák a vasat. Ezeket mágnesnek nevezték
Bevezető fizika (infó), 8. feladatsor Egyenáram, egyenáramú áramkörök 2.
 evezető fizika (infó), 8 feladatsor Egyenáram, egyenáramú áramkörök 04 november, 3:9 mai órához szükséges elméleti anyag: Kirchhoff törvényei: I Minden csomópontban a befolyó és kifolyó áramok előjeles
evezető fizika (infó), 8 feladatsor Egyenáram, egyenáramú áramkörök 04 november, 3:9 mai órához szükséges elméleti anyag: Kirchhoff törvényei: I Minden csomópontban a befolyó és kifolyó áramok előjeles
Hálózati egyenirányítók, feszültségsokszorozók Egyenirányító kapcsolások
 Hálózati egyenirányítók, feszültségsokszorozók Egyenirányító kapcsolások Egyenirányítás: egyenáramú komponenst nem tartalmazó jelből egyenáramú összetevő előállítása. Nemlineáris áramköri elemet tartalmazó
Hálózati egyenirányítók, feszültségsokszorozók Egyenirányító kapcsolások Egyenirányítás: egyenáramú komponenst nem tartalmazó jelből egyenáramú összetevő előállítása. Nemlineáris áramköri elemet tartalmazó
Budapesti Műszaki- és Gazdaságtudományi Egyetem. Gazdaság- és Társadalomtudományi Kar. Fizika dolgozat. Kovács Emese. 4-es tankör április 30.
 Budapesti Műszaki- és Gazdaságtudományi Egyetem Gazdaság- és ársadalomtudományi Kar Fizika dolgozat 4. Váltakozó áramú áramkörök munkája és teljesítménye Kovács Emese Műszaki szakoktató hallgató 4-es tankör
Budapesti Műszaki- és Gazdaságtudományi Egyetem Gazdaság- és ársadalomtudományi Kar Fizika dolgozat 4. Váltakozó áramú áramkörök munkája és teljesítménye Kovács Emese Műszaki szakoktató hallgató 4-es tankör
A 27/2012 (VIII. 27.) NGM rendelet 29/2016 (VIII.26) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján.
 A 27/2012 (VIII. 27.) NGM rendelet 29/2016 (VIII.26) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 54 522 01 Erősáramú elektrotechnikus
A 27/2012 (VIII. 27.) NGM rendelet 29/2016 (VIII.26) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 54 522 01 Erősáramú elektrotechnikus
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2016. május 18. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2016. május 18. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2016. május 18. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2016. május 18. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2015. május 19. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2015. május 19. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2015. május 19. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2015. május 19. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
MÉRÉSI GYAKORLATOK (ELEKTROTECHNIKA) 10. évfolyam (10.a, b, c)
 MÉRÉSI GYAKORLATOK (ELEKTROTECHNIKA) 10. évfolyam (10.a, b, c) 1. - Mérőtermi szabályzat, a mérések rendje - Balesetvédelem - Tűzvédelem - A villamos áram élettani hatásai - Áramütés elleni védelem - Szigetelési
MÉRÉSI GYAKORLATOK (ELEKTROTECHNIKA) 10. évfolyam (10.a, b, c) 1. - Mérőtermi szabályzat, a mérések rendje - Balesetvédelem - Tűzvédelem - A villamos áram élettani hatásai - Áramütés elleni védelem - Szigetelési
Háromfázisú aszinkron motorok
 Háromfázisú aszinkron motorok 1. példa Egy háromfázisú, 20 kw teljesítményű, 6 pólusú, 400 V/50 Hz hálózatról üzemeltetett aszinkron motor fordulatszáma 950 1/min. Teljesítmény tényezője 0,88, az állórész
Háromfázisú aszinkron motorok 1. példa Egy háromfázisú, 20 kw teljesítményű, 6 pólusú, 400 V/50 Hz hálózatról üzemeltetett aszinkron motor fordulatszáma 950 1/min. Teljesítmény tényezője 0,88, az állórész
Orvosi jelfeldolgozás. Információ. Információtartalom. Jelek osztályozása De, mi az a jel?
 Orvosi jelfeldolgozás Információ De, mi az a jel? Jel: Információt szolgáltat (információ: új ismeretanyag, amely csökkenti a bizonytalanságot).. Megjelent.. Panasza? információ:. Egy beteg.. Fáj a fogam.
Orvosi jelfeldolgozás Információ De, mi az a jel? Jel: Információt szolgáltat (információ: új ismeretanyag, amely csökkenti a bizonytalanságot).. Megjelent.. Panasza? információ:. Egy beteg.. Fáj a fogam.
MÉSZÁROS GÉZA okl. villamosmérnök villamos biztonsági szakértő
 MÉSZÁOS GÉZA okl. villamosmérnök villamos biztonsági szakértő VLLAMOS ALAPSMEETEK villamos ----------- elektromos villamos áram villamos készülék villamos hálózat villamos tér villamos motor villamos
MÉSZÁOS GÉZA okl. villamosmérnök villamos biztonsági szakértő VLLAMOS ALAPSMEETEK villamos ----------- elektromos villamos áram villamos készülék villamos hálózat villamos tér villamos motor villamos
Fizika II. tantárgy 4. előadásának vázlata MÁGNESES INDUKCIÓ, VÁLTÓÁRAM, VÁLTÓÁRAMÚ HÁLÓZATOK 1. Mágneses indukció: Mozgási indukció
 Fizika. tatárgy 4. előadásáak vázlata MÁGNESES NDKÓ, VÁLÓÁAM, VÁLÓÁAMÚ HÁLÓAOK. Mágeses idukció: Mozgási idukció B v - Vezetőt elmozdítuk mágeses térbe B-re merőlegese, akkor a vezetőbe áram keletkezik,
Fizika. tatárgy 4. előadásáak vázlata MÁGNESES NDKÓ, VÁLÓÁAM, VÁLÓÁAMÚ HÁLÓAOK. Mágeses idukció: Mozgási idukció B v - Vezetőt elmozdítuk mágeses térbe B-re merőlegese, akkor a vezetőbe áram keletkezik,
azonos sikban fekszik. A vezetőhurok ellenállása 2 Ω. Számítsuk ki a hurok teljes 4.1. ábra ábra
 4. Gyakorlat 31B-9 A 31-15 ábrán látható, téglalap alakú vezetőhurok és a hosszúságú, egyenes vezető azonos sikban fekszik. A vezetőhurok ellenállása 2 Ω. Számítsuk ki a hurok teljes 4.1. ábra. 31-15 ábra
4. Gyakorlat 31B-9 A 31-15 ábrán látható, téglalap alakú vezetőhurok és a hosszúságú, egyenes vezető azonos sikban fekszik. A vezetőhurok ellenállása 2 Ω. Számítsuk ki a hurok teljes 4.1. ábra. 31-15 ábra
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2016. október 17. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2016. október 17. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2016. október 17. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2016. október 17. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
Az elektromágneses indukció jelensége
 Az elektromágneses indukció jelensége Korábban láttuk, hogy az elektromos áram hatására mágneses tér keletkezik (Ampère-féle gerjesztési törvény) Kérdés, hogy vajon ez megfordítható-e, és a mágneses tér
Az elektromágneses indukció jelensége Korábban láttuk, hogy az elektromos áram hatására mágneses tér keletkezik (Ampère-féle gerjesztési törvény) Kérdés, hogy vajon ez megfordítható-e, és a mágneses tér
Fizika A2E, 8. feladatsor
 Fizika AE, 8. feladatsor ida György József vidagyorgy@gmail.com. feladat: Az ábrán látható áramkörben határozzuk meg az áramer sséget! 4 5 Utolsó módosítás: 05. április 4., 0:9 El ször ki kell számolnunk
Fizika AE, 8. feladatsor ida György József vidagyorgy@gmail.com. feladat: Az ábrán látható áramkörben határozzuk meg az áramer sséget! 4 5 Utolsó módosítás: 05. április 4., 0:9 El ször ki kell számolnunk
Gépészmérnöki alapszak, Mérnöki fizika 2. ZH, december 05. Feladatok (maximum 3x6 pont=18 pont)
 1. 2. 3. Mondat E1 E2 NÉV: Gépészmérnöki alapszak, Mérnöki fizika 2. ZH, 2017. december 05. Neptun kód: Aláírás: g=10 m/s 2 ; ε 0 = 8.85 10 12 F/m; μ 0 = 4π 10 7 Vs/Am; c = 3 10 8 m/s Előadó: Márkus /
1. 2. 3. Mondat E1 E2 NÉV: Gépészmérnöki alapszak, Mérnöki fizika 2. ZH, 2017. december 05. Neptun kód: Aláírás: g=10 m/s 2 ; ε 0 = 8.85 10 12 F/m; μ 0 = 4π 10 7 Vs/Am; c = 3 10 8 m/s Előadó: Márkus /
Váltakozó áram (Vázlat)
 Váltakozó áram (Vázlat) 1. Váltakozó áram fogalma és előállítása. A váltakozó áram pillanatnyi és effektív értékei 3. Ellenállások váltakozó áramú áramkörben a) Ohmos ellenállás b) Induktív ellenállás
Váltakozó áram (Vázlat) 1. Váltakozó áram fogalma és előállítása. A váltakozó áram pillanatnyi és effektív értékei 3. Ellenállások váltakozó áramú áramkörben a) Ohmos ellenállás b) Induktív ellenállás
LI 2 W = Induktív tekercsek és transzformátorok
 Induktív tekercsek és transzformátorok A tekercsek olyan elektronikai alkatrészek, amelyek mágneses terükben jelentős elektromos energiát képesek felhalmozni. A mágneses tér a tekercset alkotó vezetéken
Induktív tekercsek és transzformátorok A tekercsek olyan elektronikai alkatrészek, amelyek mágneses terükben jelentős elektromos energiát képesek felhalmozni. A mágneses tér a tekercset alkotó vezetéken
5. VÁLTAKOZÓ ÁRAM. A mérés leírása előtt összefoglaljuk a váltóáramú hálózatszámításhoz szükséges alapismereteket.
 5. VÁTAKOZÓ ÁAM A mérés leírása előtt összefoglaljuk a váltóáramú hálózatszámításhoz szükséges alapismereteket. 5.. VÁTÓÁAMÚ HÁÓZATSZÁMÍTÁS Ha a feszültség, illetve az áramerősség időfüggése harmonikus,
5. VÁTAKOZÓ ÁAM A mérés leírása előtt összefoglaljuk a váltóáramú hálózatszámításhoz szükséges alapismereteket. 5.. VÁTÓÁAMÚ HÁÓZATSZÁMÍTÁS Ha a feszültség, illetve az áramerősség időfüggése harmonikus,
ELEKTRONIKAI ALAPISMERETEK
 zonosító ÉRETTSÉGI VIZSG 2016. május 18. ELEKTRONIKI LPISMERETEK EMELT SZINTŰ ÍRÁSELI VIZSG 2016. május 18. 8:00 z írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMERI ERŐFORRÁSOK
zonosító ÉRETTSÉGI VIZSG 2016. május 18. ELEKTRONIKI LPISMERETEK EMELT SZINTŰ ÍRÁSELI VIZSG 2016. május 18. 8:00 z írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMERI ERŐFORRÁSOK
ÁGAZATI SZAKMAI ÉRETTSÉGI VIZSGA VILLAMOSIPAR ÉS ELEKTRONIKA ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ
 VILLAMOSIPAR ÉS ELEKTRONIKA ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ I. feladatlap Egyszerű, rövid feladatok megoldása Maximális pontszám: 40. feladat 4 pont
VILLAMOSIPAR ÉS ELEKTRONIKA ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ I. feladatlap Egyszerű, rövid feladatok megoldása Maximális pontszám: 40. feladat 4 pont
MÁGNESES TÉR, INDUKCIÓ
 Egy vezetéket 2 cm átmérőjű szigetelő testre 500 menettel tekercselünk fel, 25 cm hosszúságban. Mekkora térerősség lép fel a tekercs belsejében, ha a vezetékben 5 amperes áram folyik? Mekkora a mágneses
Egy vezetéket 2 cm átmérőjű szigetelő testre 500 menettel tekercselünk fel, 25 cm hosszúságban. Mekkora térerősség lép fel a tekercs belsejében, ha a vezetékben 5 amperes áram folyik? Mekkora a mágneses
Az elektromos töltések eloszlása atomokban, molekulákban, ionokon belül és a vegyületekben. Vezetők, félvezetők és szigetelők molekuláris szerkezete.
 Szakképesítés: Log Autószerelő - 54 525 02 iszti Tantárgy: Elektrotechnikaelektronika Modul: 10416-12 Közlekedéstechnikai alapok Osztály: 11.a Évfolyam: 11. 36 hét, heti 2 óra, évi 72 óra Ok Dátum: 2013.09.21
Szakképesítés: Log Autószerelő - 54 525 02 iszti Tantárgy: Elektrotechnikaelektronika Modul: 10416-12 Közlekedéstechnikai alapok Osztály: 11.a Évfolyam: 11. 36 hét, heti 2 óra, évi 72 óra Ok Dátum: 2013.09.21
Használható segédeszköz: szabványok, táblázatok, gépkönyvek, számológép
 A 27/2012 (VIII. 27.) NGM rendelet (12/2013 (III.28) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 34 522 02 Elektromos gép- és készülékszerelő
A 27/2012 (VIII. 27.) NGM rendelet (12/2013 (III.28) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 34 522 02 Elektromos gép- és készülékszerelő
Áramköri elemek mérése ipari módszerekkel
 3. aboratóriumi gyakorlat Áramköri elemek mérése ipari módszerekkel. dolgozat célja oltmérők, ampermérők használata áramköri elemek mérésénél, mérési hibák megállapítása és azok függősége a használt mérőműszerek
3. aboratóriumi gyakorlat Áramköri elemek mérése ipari módszerekkel. dolgozat célja oltmérők, ampermérők használata áramköri elemek mérésénél, mérési hibák megállapítása és azok függősége a használt mérőműszerek
Tranziens jelenségek rövid összefoglalás
 Tranziens jelenségek rövid összefoglalás Átmenet alakul ki akkor, ha van energiatároló (kapacitás vagy induktivitás) a rendszerben, mert ezeken a feszültség vagy áram nem jelenik meg azonnal, mint az ohmos
Tranziens jelenségek rövid összefoglalás Átmenet alakul ki akkor, ha van energiatároló (kapacitás vagy induktivitás) a rendszerben, mert ezeken a feszültség vagy áram nem jelenik meg azonnal, mint az ohmos
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2014. október 13. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2014. október 13. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2014. október 13. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2014. október 13. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
VILLAMOSIPAR ÉS ELEKTRONIKA ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Villamosipar és elektronika ismeretek középszint 7 ÉRETTSÉGI VIZSG 07. október 0. VILLMOSIPR ÉS ELEKTRONIK ISMERETEK KÖZÉPSZINTŰ ÍRÁSELI VIZSG JVÍTÁSI-ÉRTÉKELÉSI ÚTMUTTÓ EMERI ERŐFORRÁSOK MINISZTÉRIUM
Villamosipar és elektronika ismeretek középszint 7 ÉRETTSÉGI VIZSG 07. október 0. VILLMOSIPR ÉS ELEKTRONIK ISMERETEK KÖZÉPSZINTŰ ÍRÁSELI VIZSG JVÍTÁSI-ÉRTÉKELÉSI ÚTMUTTÓ EMERI ERŐFORRÁSOK MINISZTÉRIUM
1. Adja meg az áram egységének mértékrendszerünkben (m, kg, s, A) érvényes definícióját!
 1. Adja meg az áram egységének mértékrendszerünkben (m, kg, s, A) érvényes definícióját! A villamos áram a villamos töltések rendezett mozgása. A villamos áramerősség egységét az áramot vivő vezetők közti
1. Adja meg az áram egységének mértékrendszerünkben (m, kg, s, A) érvényes definícióját! A villamos áram a villamos töltések rendezett mozgása. A villamos áramerősség egységét az áramot vivő vezetők közti
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2010. október 18. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2010. október 18. 1:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
ÉRETTSÉGI VIZSGA 2010. október 18. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2010. október 18. 1:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
VILLAMOS ENERGETIKA VIZSGA DOLGOZAT - A csoport
 VILLAMOS ENERGETIKA VIZSGA DOLGOZAT - A csoport MEGOLDÁS 2013. június 3. 1.1. Mekkora áramot (I w, I m ) vesz fel az a fogyasztó, amelynek adatai: U n = 0,4 kv (vonali), S n = 0,6 MVA (3 fázisú), cosφ
VILLAMOS ENERGETIKA VIZSGA DOLGOZAT - A csoport MEGOLDÁS 2013. június 3. 1.1. Mekkora áramot (I w, I m ) vesz fel az a fogyasztó, amelynek adatai: U n = 0,4 kv (vonali), S n = 0,6 MVA (3 fázisú), cosφ
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2012. május 25. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2012. május 25. 8:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐORRÁS
ÉRETTSÉGI VIZSGA 2012. május 25. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2012. május 25. 8:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐORRÁS
A szinuszosan váltakozó feszültség és áram
 A szinszosan váltakozó feszültség és ára. A szinszos feszültség előállítása: Egy téglalap alakú vezető keretet egyenletesen forgatnk szögsebességgel egy hoogén B indkciójú ágneses térben úgy, hogy a keret
A szinszosan váltakozó feszültség és ára. A szinszos feszültség előállítása: Egy téglalap alakú vezető keretet egyenletesen forgatnk szögsebességgel egy hoogén B indkciójú ágneses térben úgy, hogy a keret
A 27/2012 (VIII. 27.) NGM rendelet (12/2013 (III.28) és a 29/2016 (VIII.26) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján.
 A 27/2012 (VIII. 27.) NGM rendelet (12/2013 (III.28) és a 29/2016 (VIII.26) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 54 522 01
A 27/2012 (VIII. 27.) NGM rendelet (12/2013 (III.28) és a 29/2016 (VIII.26) NGM rendelet által módosított) szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 54 522 01
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2009. május 22. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2009. május 22. 8:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KLTRÁLIS
ÉRETTSÉGI VIZSGA 2009. május 22. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2009. május 22. 8:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KLTRÁLIS
