A második katonai felmérés térképeinek közelítõ vetületi és alapfelületi leírása a térinformatikai alkalmazások számára
|
|
|
- Dezső Molnár
- 9 évvel ezelőtt
- Látták:
Átírás
1 A második katonai felmérés térképeinek közelítõ vetületi és alapfelületi leírása a térinformatikai alkalmazások számára Timár Gábor Molnár Gábor ELTE Geofizikai Tanszék Ûrkutató Csoport 1. Bevezetés A Habsburg Monarchia második katonai felmérése részletes (1:28800 méretarányú, vagyis felmérési) térképei tekinthetõk az elsõ olyan térképmûnek, amely Magyarország területét topográfiai céllal és valamilyen vetület szerint ábrázolja. Bár Strenk (1985) felveti, hogy az elsõ, avagy jozefiánus felmérés térképeinek szerkezete is a ferdetengelyû négyzetes hengervetület (tehát a Cassinivetület) szerinti, az elsõ felmérést a szakirodalom gyakorlatilag egységesen vetületi és geodéziai alap nélküli térképrendszerként ismeri (Bod, 1982; Stegena, 1986; Vagács, 1999). A második, avagy franciskánus felmérés vetületeként, pl. Stegena (1986) és Jankó (2001) a Cassini-Soldner vetületet adja meg. Mivel a felmérésnek nem pontosan ez a vetülete, azt vetületnélküli rendszer néven is említik (Varga, 2002). A környezet- és településtudomány fejlõdése kapcsán egyre gyakoribb igény, hogy a vizsgált területek régebbi sok esetben természetközeli vagy korabeli gazdálkodást, illetve településszerkezetet tükrözõ állapota mai térképekre vetítve vagy ma használatos vetületi rendszerekben legyen megjeleníthetõ. A fent említett elsõség miatt Magyarország és a történelmi Monarchia területén a második katonai felmérés térképei kínálják ehhez a legjobb alapot az elsõ katonai felmérés térképeinek transzformációja ugyanis illesztõpontok segítségével is nagyon bonyolult feladat, a biztosan azonosítható pontok ritkasága miatt. A térinformatikai gyakorlatban emiatt egyre sûrûbben jelentkezik az a feladat, hogy e térképeket vagy információtartalmuk egy részét azonosítható illesztõpontok segítségével vagy bárhogy a ma használatos vetületi rendszerekbe transzformáljuk. Illesztõpontok segítségével a feladat nem igényel különösebb térképészeti vagy geodéziai ismereteket, feltétlenül gondot jelent azonban az alkalmas illesztõpontok változó sûrûsége, sok szelvény esetén a hiánya. Nyilvánvaló, hogy kis számú és/vagy bizonytalan referenciapont az illesztés pontosságának csökkenését eredményezi, s az ebbõl származó hiba, tapasztalataink szerint, a második felmérés esetén akár a 200 métert is elérheti. A jelen dolgozatban megkíséreljük a második katonai felmérés térképeinek minél pontosabb vetületi és alapfelületi definícióját megadni, amelynek segítségével e szelvények illesztõpontok nélkül (vagy még nagyobb lokális pontosságigény esetén szelvényenként egyetlen illesztõponttal) transzformálhatók bármilyen ismert vetületi rendszerbe. 2. A második katonai felmérés térképészeti adatai Mivel a második felmérés térképezési munkáinak történeti részletei nálunk avatottabb szerzõk tollából már ismertek (Strenk, 1992; Jankó, 2001; illetve az osztrák irodalomban Hofstätter, 1989), itt csak a térképmû olyan tulajdonságait részletezzük, amelyek a vetületi számítások szempontjából fontosak. Ilyenek a szelvényezés adatai, illetve a vetületi kezdõpont(ok). A térképmû keretében több méretarányban készültek szelvénysorozatok. A felmérési szelvények méretaránya 1:28800, a részletes térképeké (Spezialkarte) pedig Magyarországon 1: Két, ennél kisebb méretarányú sorozat is készült, ezekkel azonban a jelen dolgozatban nem foglalkozunk. A részletes térképek 3x3, tehát összesen 9 27
2 felmérési szelvény által mutatott területet ábrázolnak. Georeferenciát csak a részletes térképeken találunk, a kereten a földrajzi fokhálózat fok-perc pontossággal van feltüntetve, a földrajzi hosszúság a ferroi kezdõmeridiántól értendõ (a ferroi és a greenwichi kezdõmeridiánok Albrecht-féle különbsége 17º 39' 46,02" [Homoródi, 1952], a katonai térképészetben ennél néhány század-szögmásodperccel kisebb értéket alkalmaztak, míg a jelen dolgozatban a fenti kezdõmeridiánok távolságát 17º 39' 46"-nek vettük). A fokhálózati adatok értelmezésével, alapfelületével a 4. pontban foglalkozunk. A felmérési szelvényeken fokhálózati adatok nincsenek feltüntetve. A Monarchia területén az alkalmazott vetületnek a középmeridiántól távolodóan növekvõ torzítása miatt több vetületi kezdõpontot, illetve középmeridiánt vettek fel. A Magyar Királyság területének térképein a bécsi Stephansdom legmagasabb, ún. déli tornya szolgált vetületi középpontként Megjegyezzük, hogy ugyanez a vetületi középponja Vorarlberg, Tirol, Salzburg, Alsó- és Felsõ-Ausztria térképeinek. A felsorolt tartományok esetén a szelvényezés is a magyarországival azonos, míg Morvaország, Szilézia valamint Dalmácia esetén is ez a vetületi középpont, de a szelvényezés itt eltérõ (Jankó, 2001). Az Erdélyi Fejedelemség (a térképezés megkezdésekor külön közigazgatási egység) térképein Vízakna, a bánsági határõrvidékéin (a történeti Torontál, Temes és Krassó-Szörény vármegyék déli, al-dunai peremén) pedig a gellérthegyi csillagda keleti tornya volt a vetületi középpont. Megjegyezzük, hogy Mugnier (1999) közlésével ellentétben a gellérthegyi csillagda a korabeli Magyarország területének csak ezen a kis részén volt vetületi középpont; a félreértés oka az lehet, hogy a Gellérthegy tõl a magyarországi koordinátarendszer kezdõpontja lett (Homoródi, 1953), ez azonban a geodéziai alapfelületre, és nem a vetületi rendszerre vonatkozik. A bécsi Stephansdom alapfelületi földrajzi koordinátái Mugnier (1999) adata szerint: Φ=48º 12' 34"; Λ F =34º 02' 15" (Ferrotól), vagyis Λ G =16º 22' 29" (Greenwichtõl), a felmérésnek a 4. pontban leírt alapfelületén értelmezve. A részletes (M=1:144000) térképek szelvényezése és számozása a következõ: az oszlopokat betûkkel, a sorokat számokkal jelezték, a vetületi kezdõpont pedig a C5-ös jelzetû szelvény geometriai középpontja (Jankó, 2001). Megjegyezzük, hogy e szelvény középpontjának koordinátái a leolvasási pontosság szintjén alátámasztják Mugnier (1999) fenti adatait. A szelvényoszlopok betûjele nyugatról keletre az abc-nek megfelelõen, a szelvénysorok számozása pedig északról délre növekszik. A felmérési (M=1:28800) szelvények szintén sorokba (Sectio) és oszlopokba (Colonne) rendezettek. A vetületi kezdõpont a 44. sor 21. oszlopában levõ szelvény geometriai középpontja (az oszlopokat római számok jelzik a szelvények tetején, így az említett lapnak megfelelõ jelzet: Sectio 44 Colonne XXI ). E szelvények mérete az elsõ katonai felmérés szelvényméretével megegyezõ (Jankó, 2001), tehát a terepen 9600 öl x 6400 öl, a térképen pedig 63,21 cm x 42,14 cm (Vagács, 1999). Mivel 1 bécsi öl 1,89648 m, a terepi méret 18206,2 m x 12137,5 m. A kisebb méretarányú részletes térképek által ábrázolt terület kiterjedése ennek mindkét irányban a háromszorosa: a szelvény a nagyobb méretarányú felmérési szelvények közül 3x3-nak, tehát összesen kilencnek a területére terjed ki. Fel kell hívjuk a figyelmet arra, hogy a felmérési szelvények Hadtudományi Térképtárban fellelhetõ másolatain a térképi tartalom bal és alsó szegélyei bizonytalanok, nyilvánvalóan az eredeti szelvények manuális összeillesztésekor szükséges hajtogatások következtében. Így az automatikus vagy félautomatikus illesztés során csak a szelvények jobb felsõ (északkeleti) sarokpontja használható referenciapontként. 3. A térképmû vetülete Mint a bevezetõben már említettük a térképmû vetületét az irodalomban általában Cassini-Soldner vetületként adják meg. Jankó (2001) megemlíti továbbá, hogy egyes tartományok, illetve felmérési körzetek esetén ezt nem követték következetesen, ezért a térképmûnek e helyeken nincs vetülete. A térképmû feltételezett vetületének bemutatását a Soldner-koordináták értelmezésével kezdjük. Jelölje K a vetület kezdõpontját az alapfelületen, P pedig azt a pontot, amelynek koordinátáit keressük. A K ponton áthaladó meridiánra bocsássunk a P pontból merõleges ellipszoidi geodéziai vonalat: a középmeridián és e vonal metszéspontját jelölje M. A P pont Soldner koordinátái ez esetben a PM, illetve KM ívhosszak (Varga, 2000). A Cassini-vetület a Soldner-koordináták derékszögû síkkoordinátákként történõ ábrázolása. Mivel az azonos X vagy Y Soldner-koordinátájú pontok a síkon a kezdõmeridiánnal párhuzamos vagy arra merõleges vonalakat alkotnak, a Cassini-Soldner 28
3 vetületet az irodalomban (pl. Jankó, 2001), némileg talán félrevezetõ módon, négyzetes hengervetületnek is nevezik. Amennyiben tehát a térképmû Cassini-Soldner vetületben készült, és középmeridiánja egybeesik a XXI. (illetve a részletes térképeken a C) oszlop középvonalával, akkor a szelvényhatárok úgy írhatók le, mint e vetületben azonos X- vagy Y-koordinátájú vonalak. Meg kell említsük azonban, hogy a térképmû vetülete nem felel meg pontosan a Cassini-Soldner-féle definíciónak. Varga (2002) szerint ugyanis a háromszögelési pontok síkkoordinátáit úgy számították, hogy a pontokat a kezdõpontból kiinduló sokszögvonalakba foglalták, azután a síkhosszakból és az azimutokból számították az oldalak meridián irányú és arra merõleges összetevõinek hosszát. Ezeknek az összegzésével nyerték az egyes pontok M-mel (Meridiane) és P-vel (Perpendickel) jelölt síkkoordinátáit. Mivel a hosszakat minden irányban redukció nélkül vitték át a síkra, az ábrázolásnak ez a módja nem tekinthetõ Cassini-féle vetületnek, és nem is egyértelmû, mert a különbözõ útvonalakon számított koordináták között igen jelentõs ellentmondások adódtak. Egy 600 km hosszú geodéziai vonal bizonytalansága kereken 1 km volt. A fentiek miatt jelentkezik a térképek helyenként 200 métert is elérõ torzulási hibájának nagy része. 4. A térképmû geodéziai alapfelülete A térképmû elkészítését támogatandó, Ferenc császár 1806-ban kelt kabinetparancsát követõen, Magyaroszág területén feltehetõen 1821-gyel kezdõdõen, 1861-ig elkészült a birodalom második háromszögelése (Homoródi, 1953). A vonatkozó irodalomban (Homoródi, 1953; Bod, 1982; Mugnier, 1999) az alapfelületként használt ellipszoid paramétereire különféle adatok találhatók. Varga (2002) választását elfogadva e munkában Bod (1982) adatait használjuk, amely a Zach-Oriani hibrid ellipszoidot tekinti érvényesnek, amelynek fél nagytengelye a Zach szerinti a= m, míg lapultsága az Oriani-ellipszoidnak megfelelõ f=1/310. A geodéziai gyakorlatban szokásos, hogy a relatív elhelyezésû alapfelületeket egy vagy több pont alapfelületi és csillagászati koordinátáival, illetve ezen pont(ok)ról más pont(ok)ba vezetett azimutokkal adják meg. A térinformatikai gyakorlatban az alapfelületek (dátumok) meghatározása a nagytengely és a lapultság megadása mellett az ellipszoidnak a WGS84 földi ellipszoidhoz képesti helyzetének megadását jelenti, legtöbbször három- vagy hétparaméteres transzformációval. A három- és hétparaméteres transzformációkat itt nem részletezzük (leírásukat lásd, pl. Biró, 2000), csak megemlítjük, hogy a háromparaméteres transzformáció a vizsgált ellipszoidok geometriai középpontjának egymáshoz képesti eltolását jelenti, a valamivel nagyobb pontosságot eredményezõ hétparaméteres pedig emellett három tengely körüli (kismértékû) elforgatást és a méretarányok kicsiny megváltozását is lehetõvé teszi. E transzformációk pontossága nem éri el a geodéziában elvárt mértéket, azonban a GPS-navigációban és a térinformatikában általánosan elterjedtek. Pontosságuk alapvetõen a bemenõ adatok (háromszögelési alapadatok vagy térképrõl leolvasott koordináták) konzisztenciájának függvénye. A második felmérés térképeinek mai rendszerekbe történõ transzformációjához az alapfelület definiálására is szükség van. A második felmérés alapfelületét Mugnier (1999), eredeti elnevezés híján Vienna Datum 1806 néven említi, amelynek középpontja a Stephansdom, a 2. pontban leírt ellipszoidi koordinátákkal és a leopoldsbergi azimuttal. Az 1806 évszámot úgy értelmezzük, hogy az évszám a második felmérés céljára létrehozott háromszögelési hálózatot jelenti. Amint már leírtuk, a magyarországi háromszögelési hálózat középpontja 1821 után a gellérthegyi csillagda keleti pillére volt, így a továbbiakban a dátumot Buda-1821 néven említjük. A kezdõpont földrajzi hosszúságát Bécsbõl levezetve; Λ 0,F =36º 42' 51.57" (Ferrotól), vagyis Λ 0,G =19 o 3' 5.55" (Greenwichtõl) értéknek, szélességét csillagászati mérések alapján Φ=47º 29' 15.97"-nek vették (Homoródi, 1953). Az imént említett munka azonban több koordináta-értéket is közöl a kezdõpontra, ugyanazon Marek-féle forrásmû alapján, ezért a dátumparaméterekben ennek megfelelõ bizonytalanság mindenképp mutatkozni fog. A gellérthegyi csillagda Buda évi ostromakor elpusztult, azonban a keleti torony egészen ig állt (lásd a hátsó belsõ borítón), így a felmérés geodéziai munkái alatt végig látható volt. A WGS84 dátumhoz képest érvényes eltolási paraméterek megbecsléséhez szükség van a középpont WGS84 koordinátáira és ellipszoidi magasságára is. A ma harmadrendûnek számító sz. (Gellérthegy) pont EOV-koordinátáiból korábbi cikkünkben (Timár et al., 2002) leírt eljárással megkaptuk a pont WGS84 ellipszoidi koor- 29
4 dinátáit, az EGM96 geoidmodell (NIMA, 1997) alkalmazásával pedig megbecsültük a pont WGS84 ellipszoid feletti magasságát. Így a Gellérthegy pont WGS84 geocentrikus koordinátái: X WGS84,Gellérthegy = m; Y WGS84,Gellérthegy = m; Z WGS84,Gellérthegy = m; maximum 1,5 méter hibával terhelve. Feltételezve, hogy a pont Buda-1821 dátum feletti magassága megegyezik a tengerszint feletti magassággal, a lokális dátumhoz képest érvényes geocentrikus koordináták: X Buda1821,Gellérthegy = m; Y Buda1821,Gellérthegy = m; Z Buda1821,Gellérthegy = m; a pont nem-egyértelmûségébõl adódó hiba itt méter is lehet. A két adatrendszer különbségébõl adódnak az eltolási paraméterek: dx Buda-1821 = XW GS84,Gellérthegy -X Buda-1821,Gellérthegy m; dy Buda-1821 = YW GS84,Gellérthegy -Y Buda-1821,Gellérthegy +283 m; dz Buda-1821 = ZW GS84,Gellérthegy -Z Buda-1821,Gellérthegy +569 m. 5. A térképmû GIS-integrációjának lépései és a fellépõ hibák Az eddig felsorolt adatok alapján a második felmérés térképeinek integrálása GIS rendszerekbe, illetve ezt követõen transzformációjuk más, pl. EOV vetületbe a következõ lépésekben történhet. A Stephansdom-középpontú és a Zach-Oriani hibrid ellipszoidon értelmezett Cassini-vetület és a Buda-1821 dátum definiálása az alkalmazott GIS szoftverben. A szelvény északkeleti sarokpontja Cassinikoordinátáinak meghatározása a szelvény sor- (Sectio: S) és oszlopszámából (Colonne: C), a következõ összefüggéssel: X (Easting) = (C-20,5) x 18206,2 méter; Y (Northing) = (44,5-S) x 12137,5 méter. A szkennelt térképi tartalom elforgatása (illetve az esetleges paralelogrammáról téglalap alakra torzítása) képfeldolgozó szoftverrel oly módon, hogy a térkép felsõ szegélye a pixelsorokkal, a jobb szegély pedig a pixeloszlopokkal párhuzamos legyen. Az északkeleti sarokpont definiálása illesztõpontként, képi és vetületi koordinátáinak felhasználásával. A pixelméret beállítása a szkennelési felbontás és a térképi méretarány ismeretében. A térkép átmintavételezése más vetületbe. Az 1: méretarányú részletes térképek illesztése egyszerûbb: itt mind a négy sarokpont használható referenciapontként. Ezek koordinátáinak meghatározásakor figyelemmel kell lenni arra, hogy a szelvényezésben J oszlop nincs, az I oszlopot a K követi. A felmérési szelvények fenti módszerrel történt illesztését érdemi hiba terheli, amelynek összetevõi: a dátumparaméterek hibája és a koordinátarendszer eltérõ tájékozásának figyelmen kívül hagyása; a korabeli háromszögelési hálózat nem szabványos kiegyenlítése; az eredeti felvételezés eltérései a szabványos Cassini-vetülettõl; a térképek papíranyagának száradás miatti méretváltozása és a (többszöri) másolás eredményeképp fellépõ torzulások. Összességében a fenti hibaforrások akár 200 méter eltérést is okozhatnak az illesztéskor. Ezért célszerû az illesztett (transzformált) térkép forgatás nélküli eltolása egy (és csak egy!) biztos illesztõpont alapján. Tapasztalataink szerint a hibák az alföldi területeteken kisebbek, domb- és hegyvidékeken pedig nagyobbak. Köszönetnyilvánítás A szerzõk köszönettel tartoznak a Hadtörténeti Intézet és Múzeum Térképtára munkatársainak, illetve dr. Jankó Annamáriának, a Térképtár vezetõjének a munka elkészítéséhez nyújtott sokoldalú segítségükért. IRODALOM Biró Péter (2000): Felsõgeodézia. Mûegyetemi Kiadó, Bp, 196 o. Bod Emil (1982): A magyar asztrogeodézia rövid története 1730-tól napjainkig, I. rész. Geodézia és Kartográfia 34: Gönczi Ambrus, Winkelmayer Zoltán (2002): Ferencváros metszeteken. Ferencvárosi Önkormányzat, Bp., 52 o. Hofstätter, Ernst (1989): Beiträge zur Geschichte der österreichischen Landesaufnahmen, I. Teil, Bundesamt für Eich- und Vermessungwesen, Wien, 196 p. Homoródi Lajos (1952): Vizsgálatok új háromszögelési hálózatunk elhelyezésére és tájékozására. Földméréstani Közlemények 4: Homoródi Lajos (1953): Régi háromszögelési 30
5 hálózataink elhelyezése és tájékozása. Földméréstani Közlemények 5: Jankó Annamária (2001): A második katonai felmérés. Hadtörténeti Közlemények 114: Mugnier, Clifford J. (1999): Grids & Datums Republic of Hungary. Photogrammetric Engineering & Remote Sensing 65: 423 & p NIMA, National Imagery and Mapping Agency, National Aeronautics and Space Administration GSFC (1997): WGS84 EGM96 (complete to degree and order 360) 1st Edition. NIMA NASA GSFC, St. Louis, Missouri, USA Stegena Lajos (1986): Vetülettan. Tankönyvkiadó, Budapest Strenk Tamás (1985): The stucture of maps covering Hungary from the first military topographic survey. Ann. Univ. Sci. Bud. de Roland Eötvös., Tom. I II: Strenk Tamás (1992): A II. katonai felvételek. In: Joó István, Raum Frigyes (eds): A magyar földmérés és térképészet története, I. kötet, Bp., Timár Gábor Molnár Gábor Pásztor Szilárd (2002): A WGS84 és HD72 alapfelületek közötti transzformáció Molodensky-Badekas-féle (3 paraméteres) meghatározása a gyakorlat számára. Geodézia és Kartográfia 54(1): Vagács Géza (1999): Téves nézetek az elsõ katonai felméréssel kapcsolatban. Geodézia és Kartográfia 51(10): Varga József (2000): Vetülettan. Mûegyetemi Kiadó, Bp. 296 o. Varga József (2002): A vetületnélküli rendszerektõl az UTM-ig. Kézirat, internetes elérhetõséggel. (URL: Dok3uj.htm) Approximative projection and datum description of the second military survey of the Hungarian part of the Habsburg Empire, for the GIS applications G. Timár G. Molnár Summary The second military survey of the Habsburg Empire has been taken between 1806 and 1869 in Hungary. Detailed map sheets (Spezialkarte) with the scale of 1: and survey map sheets with the scale of 1:28800 are available offering fair tool for the research of the natural and built environment of the 19 th century. The maps are without indicated grid lines moreover the survey maps have no any indicated coordinates. On the detailed sheets, geodetic longitude (from the nullmeridian of Ferro) and latutide values are given. Knowing that for Hungary the projection centre was the Stephansdom, Vienna, which signs the centre of the detailed sheet 'C5' and the survey sheet 'Sectio 44 Colonne XXI', and also that the extents of the terrain depicted on a detailed sheet is m * m (in case of the survey sheets: m * m), projection coordinates of the map corners can be achieved by simple multiplication. The 'Zach-Oriani' hybrid ellipsoid has been used for the geodetic and mapping measures, with the semimajor axis of the Zach ellipsoid (a= m) and the flattening of the one of Oriani (f=1/310). The projection of the map system can be approximated by the Cassini one and the projection centre is the Stephansdom (Φ=48º 12' 34"; Λ F =34º 02' 15" from Ferro; therefore Λ G =16º 22' 29" from Greenwich). The fundamental point of the datum had been the Eastern tower of the Gellérthegy observatory since 1821 so we propose to refer it as Buda-1821 (Mugnier, 1999, calls it as 'Vienna1806'). The approximate datum shift parameters from the Buda to the WGS84 are: dx m; dy +283 m; dz +569 m. Note that this datum hasn't been equalized with standard method, and the local coordinates of the origin are a subject of historical debate so these numbers are burdened with an error of at least 30 meters. Besides, as the projection is not exactly the Cassini one, the projection approximation causes an error up to even 200 meters. In the practice it is worth to notice that the left and the lower edges of the survey sheets are uncertain because of several previous folding. A possible processing method could be based on the following steps: 1. setting the projection and datum parameters in the GIS; 2. determination of the Cassini coordinates of the upper-right (NE) corner from the row and column numbers of the sheet; 3. rotation of the scanned map content to a position where the upper and the right map edges are parallel to the pixel rows and columns; 4. marking the NE corner by its coordinates and setting the exact pixel size from the known scan resolution and the known map scale of 1:28800; 5. rectification the map to a selected projection; 6. using only one control point, shift the map content horizontally but without any further rotation. 31
A második és harmadik katonai felmérés erdélyi szelvényeinek vetületiés dátumparaméterei
 geos-majus.qxd 9/1/04 9:35 PM Page 1 A második és harmadik katonai felmérés erdélyi szelvényeinek vetületiés dátumparaméterei Timár Gábor 1 Molnár Gábor 1 Păunescu Cornel Pendea Florin 3 1 ELTE Geofizikai
geos-majus.qxd 9/1/04 9:35 PM Page 1 A második és harmadik katonai felmérés erdélyi szelvényeinek vetületiés dátumparaméterei Timár Gábor 1 Molnár Gábor 1 Păunescu Cornel Pendea Florin 3 1 ELTE Geofizikai
Az ivanicsi (ivanići) rendszer paraméterezése a térinformatikai alkalmazásokban Dr. Timár Gábor 1, Markovinović Danko 2, Kovács Béla 3
 Az ivanicsi (ivanići) rendszer paraméterezése a térinformatikai alkalmazásokban Dr. Timár Gábor 1, Markovinović Danko 2, Kovács Béla 3 1 ELTE Geofizikai Tanszék Űrkutató Csoport 2 Zágrábi Egyetem, Geodéziai
Az ivanicsi (ivanići) rendszer paraméterezése a térinformatikai alkalmazásokban Dr. Timár Gábor 1, Markovinović Danko 2, Kovács Béla 3 1 ELTE Geofizikai Tanszék Űrkutató Csoport 2 Zágrábi Egyetem, Geodéziai
A magyarországi Gauss-Krüger-vetületû katonai topográfiai térképek dátumparaméterei
 A magyarországi Gauss-Krüger-vetületû katonai topográfiai térképek dátumparaméterei Timár Gábor 1 Kubány Csongor 2 Molnár Gábor 1 1ELTE Geofizikai Tanszék, Ûrkutató Csoport 2Honvédelmi Minisztérium, Térképészeti
A magyarországi Gauss-Krüger-vetületû katonai topográfiai térképek dátumparaméterei Timár Gábor 1 Kubány Csongor 2 Molnár Gábor 1 1ELTE Geofizikai Tanszék, Ûrkutató Csoport 2Honvédelmi Minisztérium, Térképészeti
A budapesti sztereografikus, illetve a régi magyarországi hengervetületek és geodéziai dátumaik paraméterezése a térinformatikai gyakorlat számára
 A budapesti sztereografikus, illetve a régi magyarországi hengervetületek és geodéziai dátumaik paraméterezése a térinformatikai gyakorlat számára Timár Gábor 1, Molnár Gábor 1, Márta Gergely 2 1ELTE Geofizikai
A budapesti sztereografikus, illetve a régi magyarországi hengervetületek és geodéziai dátumaik paraméterezése a térinformatikai gyakorlat számára Timár Gábor 1, Molnár Gábor 1, Márta Gergely 2 1ELTE Geofizikai
Koordináta-rendszerek
 Koordináta-rendszerek Térkép: a Föld felszín (részletének) ábrázolása síkban Hogyan határozható meg egy pont helyzete egy síkon? Derékszögű koordináta-rendszer: a síkban két, egymást merőlegesen metsző
Koordináta-rendszerek Térkép: a Föld felszín (részletének) ábrázolása síkban Hogyan határozható meg egy pont helyzete egy síkon? Derékszögű koordináta-rendszer: a síkban két, egymást merőlegesen metsző
A második katonai felmérés horvátországi szelvényeinek georeferálása Bevezetés
 A második katonai felmérés horvátországi szelvényeinek georeferálása Timár Gábor 1, Molnár Gábor 1, Székely Balázs 1, Biszak Sándor 2, Kovács Béla 3, Markovinović Danko 4, Kuhar Miran 5 1 ELTE Földrajz-
A második katonai felmérés horvátországi szelvényeinek georeferálása Timár Gábor 1, Molnár Gábor 1, Székely Balázs 1, Biszak Sándor 2, Kovács Béla 3, Markovinović Danko 4, Kuhar Miran 5 1 ELTE Földrajz-
3. Vetülettan (3/6., 8., 10.) Unger János. @geo.u-szeged.hu www.sci.u-szeged.hu/eghajlattan
 Kartográfia (GBN309E) Térképészet (GBN317E) előadás 3. Vetülettan (3/6., 8., 10.) Unger János unger@geo.u @geo.u-szeged.hu www.sci.u-szeged.hu/eghajlattan szeged.hu/eghajlattan SZTE Éghajlattani és Tájföldrajzi
Kartográfia (GBN309E) Térképészet (GBN317E) előadás 3. Vetülettan (3/6., 8., 10.) Unger János unger@geo.u @geo.u-szeged.hu www.sci.u-szeged.hu/eghajlattan szeged.hu/eghajlattan SZTE Éghajlattani és Tájföldrajzi
RÉGI TÉRKÉPEK DIGITÁLIS FELDOLGOZÁSA. Bartos-Elekes Zsombor BBTE Magyar Földrajzi Intézet, Kolozsvár
 RÉGI TÉRKÉPEK DIGITÁLIS FELDOLGOZÁSA Bartos-Elekes Zsombor BBTE Magyar Földrajzi Intézet, Kolozsvár arcanum.hu (I., II., III. katonai felmérés) http://mapire.staatsarchiv.at/en/ (II. felm.) Románia Lambert
RÉGI TÉRKÉPEK DIGITÁLIS FELDOLGOZÁSA Bartos-Elekes Zsombor BBTE Magyar Földrajzi Intézet, Kolozsvár arcanum.hu (I., II., III. katonai felmérés) http://mapire.staatsarchiv.at/en/ (II. felm.) Románia Lambert
Űrfelvételek térinformatikai rendszerbe integrálása
 Budapest, 2005. október 18. Űrfelvételek térinformatikai rendszerbe integrálása Molnár Gábor ELTE Geofizikai Tanszék Űrkutató Csoport Témavezető: Dr. Ferencz Csaba Eötvös Loránd Tudományegyetem Geofizikai
Budapest, 2005. október 18. Űrfelvételek térinformatikai rendszerbe integrálása Molnár Gábor ELTE Geofizikai Tanszék Űrkutató Csoport Témavezető: Dr. Ferencz Csaba Eötvös Loránd Tudományegyetem Geofizikai
Budapest 1938 előtti nagyméretarányú térképeinek georeferálása Dr. Timár Gábor 1, Biszak Sándor 2,1
 Budapest 1938 előtti nagyméretarányú térképeinek georeferálása Dr. Timár Gábor 1, Biszak Sándor 2,1 1 ELTE Geofizikai Tanszék Űrkutató Csoport 2 Arcanum Adatbázis Kft. Bevezetés Az 1850-es években, a szabadságharc
Budapest 1938 előtti nagyméretarányú térképeinek georeferálása Dr. Timár Gábor 1, Biszak Sándor 2,1 1 ELTE Geofizikai Tanszék Űrkutató Csoport 2 Arcanum Adatbázis Kft. Bevezetés Az 1850-es években, a szabadságharc
Átszámítások különböző alapfelületek koordinátái között
 Átszámítások különböző alapfelületek koordinátái között A különböző időpontokban, különböző körülmények között rögzített pontok földi koordinátái különböző alapfelületekre (ellipszoidokra geodéziai dátumokra)
Átszámítások különböző alapfelületek koordinátái között A különböző időpontokban, különböző körülmények között rögzített pontok földi koordinátái különböző alapfelületekre (ellipszoidokra geodéziai dátumokra)
GEODÉZIA ÉS KARTOGRÁFIA
 GEODÉZIA ÉS KARTOGRÁFIA 55. ÉVFOLYAM 2003 10. SZÁM Az EOV-alapfelületek térbeli helyzetének vizsgálata Kratochvilla Krisztina doktorandusz BME Általános- és Felsõgeodézia Tanszék Bevezetés Az 1975-ben
GEODÉZIA ÉS KARTOGRÁFIA 55. ÉVFOLYAM 2003 10. SZÁM Az EOV-alapfelületek térbeli helyzetének vizsgálata Kratochvilla Krisztina doktorandusz BME Általános- és Felsõgeodézia Tanszék Bevezetés Az 1975-ben
Vetületi rendszerek és átszámítások
 Vetületi rendszerek és átszámítások PhD értekezés tézisei Dr. Varga József egyetemi adjunktus Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki Kar Általános- és Felsőgeodézia Tanszék Budapest,
Vetületi rendszerek és átszámítások PhD értekezés tézisei Dr. Varga József egyetemi adjunktus Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki Kar Általános- és Felsőgeodézia Tanszék Budapest,
A Föld alakja TRANSZFORMÁCIÓ. Magyarországon még használatban lévő vetületi rendszerek. Miért kell transzformálni? Főbb transzformációs lehetőségek
 TRANSZFORMÁCIÓ A Föld alakja -A föld alakja: geoid (az a felület, amelyen a nehézségi gyorsulás értéke állandó) szabálytalan alak, kezelése nehéz -A geoidot ellipszoiddal közelítjük -A földfelszíni pontokat
TRANSZFORMÁCIÓ A Föld alakja -A föld alakja: geoid (az a felület, amelyen a nehézségi gyorsulás értéke állandó) szabálytalan alak, kezelése nehéz -A geoidot ellipszoiddal közelítjük -A földfelszíni pontokat
A harmadik katonai felmérés térképszelvényeinek georeferálása Dr. Timár Gábor 1, dr. Molnár Gábor 1,2
 A harmadik katonai felmérés térképszelvényeinek georeferálása Dr. Timár Gábor 1, dr. Molnár Gábor 1,2 1 ELTE Geofizikai és Űrtudományi Tanszék 2 Bécsi Műszaki Egyetem, Távérzékelési és Fotogrammetriai
A harmadik katonai felmérés térképszelvényeinek georeferálása Dr. Timár Gábor 1, dr. Molnár Gábor 1,2 1 ELTE Geofizikai és Űrtudományi Tanszék 2 Bécsi Műszaki Egyetem, Távérzékelési és Fotogrammetriai
Matematikai geodéziai számítások 3.
 Matematikai geodéziai számítások 3 Kettős vetítés és EOV szelvényszám keresése koordinátákból Dr Bácsatyai, László Matematikai geodéziai számítások 3: Kettős vetítés és EOV szelvényszám keresése koordinátákból
Matematikai geodéziai számítások 3 Kettős vetítés és EOV szelvényszám keresése koordinátákból Dr Bácsatyai, László Matematikai geodéziai számítások 3: Kettős vetítés és EOV szelvényszám keresése koordinátákból
II. A TÉRKÉPVETÜLETEK RENDSZERES LEÍRÁSA 83
 T A R T A L O M J E G Y Z É K I. A TÉRKÉPVETÜLETEKRŐL ÁLTALÁBAN 13 VETÜLETTANI ALAPFOGALMAK 15 A térkép mint matematikai leképezés eredménye 15 Az alapfelület paraméterezése földrajzi koordinátákkal 18
T A R T A L O M J E G Y Z É K I. A TÉRKÉPVETÜLETEKRŐL ÁLTALÁBAN 13 VETÜLETTANI ALAPFOGALMAK 15 A térkép mint matematikai leképezés eredménye 15 Az alapfelület paraméterezése földrajzi koordinátákkal 18
Matematikai geodéziai számítások 3.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr Bácsatyai László Matematikai geodéziai számítások 3 MGS3 modul Kettős vetítés és EOV szelvényszám keresése koordinátákból SZÉKESFEHÉRVÁR 2010 Jelen
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr Bácsatyai László Matematikai geodéziai számítások 3 MGS3 modul Kettős vetítés és EOV szelvényszám keresése koordinátákból SZÉKESFEHÉRVÁR 2010 Jelen
Matematikai geodéziai számítások 4.
 Matematikai geodéziai számítások 4. Vetületi átszámítások Dr. Bácsatyai, László Matematikai geodéziai számítások 4.: Vetületi átszámítások Dr. Bácsatyai, László Lektor: Dr. Benedek, Judit Ez a modul a
Matematikai geodéziai számítások 4. Vetületi átszámítások Dr. Bácsatyai, László Matematikai geodéziai számítások 4.: Vetületi átszámítások Dr. Bácsatyai, László Lektor: Dr. Benedek, Judit Ez a modul a
Magyarország georeferált történelmi helységnévtára készítésének helyzete Biszak Sándor Arcanum Adatbázis Kft. doktorandusz, ELTE FFI Űrkutató Csoport
 Magyarország georeferált történelmi helységnévtára készítésének helyzete Biszak Sándor Arcanum Adatbázis Kft. doktorandusz, ELTE FFI Űrkutató Csoport Bevezetés: mit tekintünk helységnévtárnak Az elmúlt
Magyarország georeferált történelmi helységnévtára készítésének helyzete Biszak Sándor Arcanum Adatbázis Kft. doktorandusz, ELTE FFI Űrkutató Csoport Bevezetés: mit tekintünk helységnévtárnak Az elmúlt
Bevezetés. A Lipszky-térkép alapfelülete
 Lipszky János térképének (Magyarország és társországai, 1804 1810) georeferálása térinformatikai alkalmazásokban Dr. Timár Gábor 1 dr. Székely Balázs 1 dr. Molnár Gábor 1 Biszak Sándor 2 1 ELTE Földrajz-
Lipszky János térképének (Magyarország és társországai, 1804 1810) georeferálása térinformatikai alkalmazásokban Dr. Timár Gábor 1 dr. Székely Balázs 1 dr. Molnár Gábor 1 Biszak Sándor 2 1 ELTE Földrajz-
Folyószabályozási térképek geodéziai alapja
 Eötvös Loránd Tudományegyetem Informatikai Kar Térképtudományi és Geoinformatikai Tanszék Mészáros János Folyószabályozási térképek geodéziai alapja Doktori értekezés tézisei Eötvös Loránd Tudományegyetem
Eötvös Loránd Tudományegyetem Informatikai Kar Térképtudományi és Geoinformatikai Tanszék Mészáros János Folyószabályozási térképek geodéziai alapja Doktori értekezés tézisei Eötvös Loránd Tudományegyetem
Egy pont földfelszíni helyzetét meghatározzák: a pont alapfelületi földrajzi koordinátái a pont tengerszint feletti magassága
 Földrajzi koordináták Egy pont földfelszíni helyzetét meghatározzák: a pont alapfelületi földrajzi koordinátái a pont tengerszint feletti magassága Topo-Karto-2 1 Földrajzi koordináták pólus egyenlítő
Földrajzi koordináták Egy pont földfelszíni helyzetét meghatározzák: a pont alapfelületi földrajzi koordinátái a pont tengerszint feletti magassága Topo-Karto-2 1 Földrajzi koordináták pólus egyenlítő
A második világháború német katonai térképeinek koordinátarendszere
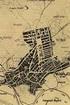 geos-junius.qxd 9/1/04 9:52 PM Page 28 A második világháború német katonai térképeinek koordinátarendszere Dr. Timár Gábor 1, Lévai Pál 2, dr. Molnár Gábor 1, dr. Varga József 3 1ELTE Geofizikai Tanszék
geos-junius.qxd 9/1/04 9:52 PM Page 28 A második világháború német katonai térképeinek koordinátarendszere Dr. Timár Gábor 1, Lévai Pál 2, dr. Molnár Gábor 1, dr. Varga József 3 1ELTE Geofizikai Tanszék
2. fejezet. Vetületi alapfogalmak. Dr. Mélykúti Gábor
 2. fejezet Dr. Mélykúti Gábor Nyugat-magyarországi Egyetem Geoinformatikai Kar 2010 2.1 Bevezetés A modul a Térképtan és a Topográfia c. tantárgyak részét képezi. A modul a térképek készítése és használata
2. fejezet Dr. Mélykúti Gábor Nyugat-magyarországi Egyetem Geoinformatikai Kar 2010 2.1 Bevezetés A modul a Térképtan és a Topográfia c. tantárgyak részét képezi. A modul a térképek készítése és használata
Magyarország katonai felmérései
 Jankó A nnamária Magyarország katonai felmérései 1763-1950 2007 TARTALOM E lő sz ó... 9 I. Az első katonai felmérés (1763-1787)... 13 1. 1. Az 1. katonai felmérés előzményei... 13 1. 2. Az 1. katonai felm
Jankó A nnamária Magyarország katonai felmérései 1763-1950 2007 TARTALOM E lő sz ó... 9 I. Az első katonai felmérés (1763-1787)... 13 1. 1. Az 1. katonai felmérés előzményei... 13 1. 2. Az 1. katonai felm
Topográfia 2. Vetületi alapfogalmak Mélykúti, Gábor
 Topográfia 2. Vetületi alapfogalmak Mélykúti, Gábor Topográfia 2. : Vetületi alapfogalmak Mélykúti, Gábor Lektor : Alabér, László Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027 Tananyagfejlesztéssel a GEO-ért
Topográfia 2. Vetületi alapfogalmak Mélykúti, Gábor Topográfia 2. : Vetületi alapfogalmak Mélykúti, Gábor Lektor : Alabér, László Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027 Tananyagfejlesztéssel a GEO-ért
Az EOV-koordináták nagypontosságú közelítése Hotine-féle ferdetengelyû Mercator-vetülettel
 Az EOV-koordináták nagypontosságú közelítése Hotine-féle ferdetengelyû Mercator-vetülettel Molnár Gábor Timár Gábor ELTE Geofizikai Tanszék, Ûrkutató Csoport 1 Hotine (1947) vetületi leírása a Gauss-gömböt
Az EOV-koordináták nagypontosságú közelítése Hotine-féle ferdetengelyû Mercator-vetülettel Molnár Gábor Timár Gábor ELTE Geofizikai Tanszék, Ûrkutató Csoport 1 Hotine (1947) vetületi leírása a Gauss-gömböt
A méretaránytényező kérdése a földmérésben és néhány szakmai következménye
 A méretaránytényező kérdése a földmérésben és néhány szakmai következménye Dr. Busics György c. egyetemi tanár Óbudai Egyetem Alba Regia Műszaki Kar Székesfehérvár MFTTT Vándorgyűlés, Békéscsaba, 2019.
A méretaránytényező kérdése a földmérésben és néhány szakmai következménye Dr. Busics György c. egyetemi tanár Óbudai Egyetem Alba Regia Műszaki Kar Székesfehérvár MFTTT Vándorgyűlés, Békéscsaba, 2019.
(térképi ábrázolás) Az egész térképre érvényes meghatározása: Definíció
 Az egész térképre érvényes meghatározása: A térkép hossztartó vonalain mért távolságnak és a valódi redukált vízszintes távolságnak a hányadosa. M = 1 / m, vagy M = 1 : m (m=méretarányszám) A méretarány
Az egész térképre érvényes meghatározása: A térkép hossztartó vonalain mért távolságnak és a valódi redukált vízszintes távolságnak a hányadosa. M = 1 / m, vagy M = 1 : m (m=méretarányszám) A méretarány
A DIGITÁLIS TÉRKÉP ADATAINAK ELŐÁLLÍTÁSA, ADATNYERÉSI ELJÁRÁSOK
 A DIGITÁLIS TÉRKÉP ADATAINAK ELŐÁLLÍTÁSA, ADATNYERÉSI ELJÁRÁSOK - két féle adatra van szükségünk: térbeli és leíró adatra - a térbeli adat előállítása a bonyolultabb. - a költségek nagyjából 80%-a - munkaigényes,
A DIGITÁLIS TÉRKÉP ADATAINAK ELŐÁLLÍTÁSA, ADATNYERÉSI ELJÁRÁSOK - két féle adatra van szükségünk: térbeli és leíró adatra - a térbeli adat előállítása a bonyolultabb. - a költségek nagyjából 80%-a - munkaigényes,
A ferdetengelyű szögtartó hengervetület és magyarországi alkalmazásai
 A ferdetengelyű szögtartó hengervetület magyarországi alkalmazásai Perspektív hengervetületek A perspektív hengervetületek a gömb alapfelületet egy forgáshenger palástjára képezik le középpontos geometriai
A ferdetengelyű szögtartó hengervetület magyarországi alkalmazásai Perspektív hengervetületek A perspektív hengervetületek a gömb alapfelületet egy forgáshenger palástjára képezik le középpontos geometriai
Matematikai geodéziai számítások 1.
 Matematikai geodéziai számítások 1 Ellipszoidi számítások, ellipszoid, geoid és terep metszete Dr Bácsatyai, László Created by XMLmind XSL-FO Converter Matematikai geodéziai számítások 1: Ellipszoidi számítások,
Matematikai geodéziai számítások 1 Ellipszoidi számítások, ellipszoid, geoid és terep metszete Dr Bácsatyai, László Created by XMLmind XSL-FO Converter Matematikai geodéziai számítások 1: Ellipszoidi számítások,
Magyarországi topográfiai térképek
 Eötvös Loránd Tudományegyetem, Természettudományi Kar Juhász Péter MTA SZTAKI Magyarországi topográfiai térképek vetületének torzulási vizsgálata doktori értekezés tézisei Budapest, 2008. Témavezető: Györffy
Eötvös Loránd Tudományegyetem, Természettudományi Kar Juhász Péter MTA SZTAKI Magyarországi topográfiai térképek vetületének torzulási vizsgálata doktori értekezés tézisei Budapest, 2008. Témavezető: Györffy
7. előadás: Lineármodulus a vetületi főirányokban és a területi modulus az azimutális vetületeken
 7 előadás: Lineármodulus a vetületi főirányokban és a területi modulus az azimutális vetületeken Mivel az azimutális vetületeken normális elhelyezésben a meridiánok és a paralelkörök, más elhelyezésben
7 előadás: Lineármodulus a vetületi főirányokban és a területi modulus az azimutális vetületeken Mivel az azimutális vetületeken normális elhelyezésben a meridiánok és a paralelkörök, más elhelyezésben
GPS-navigáció történeti topográfiai és kataszteri térképeken Dr. Timár Gábor ELTE Földrajz- és Földtudományi Intézet, Űrkutató Csoport
 GPS-navigáció történeti topográfiai és kataszteri térképeken Dr. Timár Gábor ELTE Földrajz- és Földtudományi Intézet, Űrkutató Csoport Bevezetés Az elmúlt évtizedben, különösen a GPS-rendszer pontosságát
GPS-navigáció történeti topográfiai és kataszteri térképeken Dr. Timár Gábor ELTE Földrajz- és Földtudományi Intézet, Űrkutató Csoport Bevezetés Az elmúlt évtizedben, különösen a GPS-rendszer pontosságát
A legjobb vízszintes illeszkedést. azonos pontok adatai alapján
 legjobb vízszintes illeszkedést biztosító Molodenskyparaméterek meghatározása azonos pontok adatai alapján Molnár Gábor dr. Timár Gábor ELTE Geofizikai Tanszék, Ûrkutató Csoport. Bevezetés térinformatika
legjobb vízszintes illeszkedést biztosító Molodenskyparaméterek meghatározása azonos pontok adatai alapján Molnár Gábor dr. Timár Gábor ELTE Geofizikai Tanszék, Ûrkutató Csoport. Bevezetés térinformatika
TÉRINFORMATIKA I. Dr. Kulcsár Balázs egyetemi docens. Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék
 TÉRINFORMATIKA I. Dr. Kulcsár Balázs egyetemi docens Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék TÁJÉKOZTATÁS TANTÁRGYI TEMATIKA 1 Előadás 1. Bevezetés a térinformatikába. Kartográfia történet.
TÉRINFORMATIKA I. Dr. Kulcsár Balázs egyetemi docens Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék TÁJÉKOZTATÁS TANTÁRGYI TEMATIKA 1 Előadás 1. Bevezetés a térinformatikába. Kartográfia történet.
3. Vetülettan (3/3-5.) Unger szeged.hu/eghajlattan SZTE Éghajlattani és Tájföldrajzi Tanszék
 Kartográfia (GBN309E) Térképészet (GBN317E) előadás 3. Vetülettan (3/3-5.) Unger János unger@geo.u @geo.u-szeged.hu www.sci.u-szeged.hu/eghajlattan szeged.hu/eghajlattan SZTE Éghajlattani és Tájföldrajzi
Kartográfia (GBN309E) Térképészet (GBN317E) előadás 3. Vetülettan (3/3-5.) Unger János unger@geo.u @geo.u-szeged.hu www.sci.u-szeged.hu/eghajlattan szeged.hu/eghajlattan SZTE Éghajlattani és Tájföldrajzi
A FÖLDMINŐSÍTÉS GEOMETRIAI ALAPJAI
 A FÖLDMINŐSÍTÉS GEOMETRIAI ALAPJAI Detrekői Ákos Keszthely, 2003. 12. 11. TARTALOM 1 Bevezetés 2 Milyen geometriai adatok szükségesek? 3 Néhány szó a referencia rendszerekről 4 Geometriai adatok forrásai
A FÖLDMINŐSÍTÉS GEOMETRIAI ALAPJAI Detrekői Ákos Keszthely, 2003. 12. 11. TARTALOM 1 Bevezetés 2 Milyen geometriai adatok szükségesek? 3 Néhány szó a referencia rendszerekről 4 Geometriai adatok forrásai
Bevezetés a geodéziába
 Bevezetés a geodéziába 1 Geodézia Definíció: a földmérés a Föld alakjának és méreteinek, a Föld fizikai felszínén, ill. a felszín alatt lévő természetes és mesterséges alakzatok geometriai méreteinek és
Bevezetés a geodéziába 1 Geodézia Definíció: a földmérés a Föld alakjának és méreteinek, a Föld fizikai felszínén, ill. a felszín alatt lévő természetes és mesterséges alakzatok geometriai méreteinek és
9. előadás: A gömb valós hengervetületei
 A valós hengervetületek általános tulajdonságai A hengervetületek (cilindrikus vetületek) jellemzője hogy normális elhelyezésben az egyenlítő és a paralelkörök képei párhuzamos egyenesek. A valós hengervetületnek
A valós hengervetületek általános tulajdonságai A hengervetületek (cilindrikus vetületek) jellemzője hogy normális elhelyezésben az egyenlítő és a paralelkörök képei párhuzamos egyenesek. A valós hengervetületnek
A GEOMETRIAI ADATOK VONATKOZÁSI RENDSZEREI A TÉRINFORMATIKÁBAN
 MIHALIK JÓZSEF A téma aktualitása A GEOMETRIAI ADATOK VONATKOZÁSI RENDSZEREI A TÉRINFORMATIKÁBAN A térinformatikai rendszerek alkalmazása ma már sok területen, így a honvédelem területén is nélkülözhetetlen
MIHALIK JÓZSEF A téma aktualitása A GEOMETRIAI ADATOK VONATKOZÁSI RENDSZEREI A TÉRINFORMATIKÁBAN A térinformatikai rendszerek alkalmazása ma már sok területen, így a honvédelem területén is nélkülözhetetlen
A sztereografikus vetület és magyarországi alkalmazása
 A sztereografikus vetület és magyarországi alkalmazása Perspektív síkvetületek A perspektív síkvetületek a gömb alapfelületet síkra képezik le középpontos geometriai vetítéssel. A vetítés Q középpontja
A sztereografikus vetület és magyarországi alkalmazása Perspektív síkvetületek A perspektív síkvetületek a gömb alapfelületet síkra képezik le középpontos geometriai vetítéssel. A vetítés Q középpontja
3. Nemzetközi talajinformációs rendszerek
 Magyar Tudományos Akadémia Agrártudományi Kutatóközpont Talajtani és Agrokémiai Intézet Környezetinformatikai Osztály Pásztor László: Térbeli Talajinformációs Rendszerek/ Bevezetés a digitális talajtérképezésbe
Magyar Tudományos Akadémia Agrártudományi Kutatóközpont Talajtani és Agrokémiai Intézet Környezetinformatikai Osztály Pásztor László: Térbeli Talajinformációs Rendszerek/ Bevezetés a digitális talajtérképezésbe
MIKOVINY SÁMUEL TÉRINFORMATIKAI EMLÉKVERSENY
 FVM VIDÉKFEJLESZTÉSI, KÉPZÉSI ÉS SZAKTANÁCSADÁSI INTÉZET NYUGAT MAGYARORSZÁGI EGYETEM GEOINFORMATIKAI KAR MIKOVINY SÁMUEL TÉRINFORMATIKAI EMLÉKVERSENY 2008/2009. TANÉV Az I. FORDULÓ FELADATAI NÉV:... Tudnivalók
FVM VIDÉKFEJLESZTÉSI, KÉPZÉSI ÉS SZAKTANÁCSADÁSI INTÉZET NYUGAT MAGYARORSZÁGI EGYETEM GEOINFORMATIKAI KAR MIKOVINY SÁMUEL TÉRINFORMATIKAI EMLÉKVERSENY 2008/2009. TANÉV Az I. FORDULÓ FELADATAI NÉV:... Tudnivalók
TÉRINFORMATIKA I. Dr. Kulcsár Balázs egyetemi docens. Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék
 TÉRINFORMATIKA I. Dr. Kulcsár Balázs egyetemi docens Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék 3. előadás MAGYARORSZÁGON ALKALMAZOTT MODERN TÉRKÉPRENDSZEREK Magyarország I. katonai felmérése
TÉRINFORMATIKA I. Dr. Kulcsár Balázs egyetemi docens Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék 3. előadás MAGYARORSZÁGON ALKALMAZOTT MODERN TÉRKÉPRENDSZEREK Magyarország I. katonai felmérése
INFORMATIKA ÁGAZATI ALKALMAZÁSAI. Az Agrármérnöki MSc szak tananyagfejlesztése TÁMOP-4.1.2-08/1/A-2009-0010
 INFORMATIKA ÁGAZATI ALKALMAZÁSAI Az Agrármérnöki MSc szak tananyagfejlesztése TÁMOP-4.1.2-08/1/A-2009-0010 7. Digitális térképezés, georeferálás, vektorizálás Digitális térkép Fogalma Jellemzői Georeferálás
INFORMATIKA ÁGAZATI ALKALMAZÁSAI Az Agrármérnöki MSc szak tananyagfejlesztése TÁMOP-4.1.2-08/1/A-2009-0010 7. Digitális térképezés, georeferálás, vektorizálás Digitális térkép Fogalma Jellemzői Georeferálás
GPS-navigáció történeti és modern földtani térképeken
 139/1, 93 100., Budapest, 2009 GPS-navigáció történeti és modern földtani térképeken GALAMBOS Csilla 1, TIMÁR Gábor 2, SZÉKELY Balázs 3, 2 1 Magyar Állami Földtani Intézet Geoinformatikai Osztály, 1143
139/1, 93 100., Budapest, 2009 GPS-navigáció történeti és modern földtani térképeken GALAMBOS Csilla 1, TIMÁR Gábor 2, SZÉKELY Balázs 3, 2 1 Magyar Állami Földtani Intézet Geoinformatikai Osztály, 1143
RTCM alapú VITEL transzformáció felhasználó oldali beállítása Spectra Precision Survey Pro Recon szoftver használata esetén
 RTCM alapú VITEL transzformáció felhasználó oldali beállítása Spectra Precision Survey Pro Recon szoftver használata esetén A http://www.gnssnet.hu/valos_trafo.php weboldalon található, Spectra Precision
RTCM alapú VITEL transzformáció felhasználó oldali beállítása Spectra Precision Survey Pro Recon szoftver használata esetén A http://www.gnssnet.hu/valos_trafo.php weboldalon található, Spectra Precision
SZLOVÁKIA ÁLLAMHATÁRA
 SZLOVÁKIA ÁLLAMHATÁRA Hedviga Májovská okleveles földmérő mérnök Szlovák Köztársaság Honvédelmi Minisztériuma IX. TAVASZI MÉRNÖKNAP, NÓGRÁD - 2017 Salgótarján, 2017. április 4. Az államhatár 1918-1920
SZLOVÁKIA ÁLLAMHATÁRA Hedviga Májovská okleveles földmérő mérnök Szlovák Köztársaság Honvédelmi Minisztériuma IX. TAVASZI MÉRNÖKNAP, NÓGRÁD - 2017 Salgótarján, 2017. április 4. Az államhatár 1918-1920
Térinformatika. A vonatkozási és koordináta rendszerek szerepe. Vonatkozási és koordináta rendszerek. Folytonos vonatkozási rendszer
 Térinformatika Vonatkozási és koordináta rendszerek Dr. Szabó György BME Fotogrammetria és Térinformatika Tanszék A vonatkozási és koordináta rendszerek szerepe Heterogén jelenségek közös referencia kerete
Térinformatika Vonatkozási és koordináta rendszerek Dr. Szabó György BME Fotogrammetria és Térinformatika Tanszék A vonatkozási és koordináta rendszerek szerepe Heterogén jelenségek közös referencia kerete
3. fejezet. Térképek jellemző tulajdonságai. Dr. Mélykúti Gábor
 3. fejezet Dr. Mélykúti Gábor Nyugat-magyarországi Egyetem Geoinformatikai Kar 3.1 Bevezetés A Térképek jellemzői modul a Térképtan és a Topográfia c. tantárgyak részét képezi. A modul a térképek készítése
3. fejezet Dr. Mélykúti Gábor Nyugat-magyarországi Egyetem Geoinformatikai Kar 3.1 Bevezetés A Térképek jellemzői modul a Térképtan és a Topográfia c. tantárgyak részét képezi. A modul a térképek készítése
Magasságos GPS. avagy továbbra is
 Magasságos GPS avagy továbbra is Tisztázatlan kérdések az RTK-technológiával végzett magasságmeghatározás területén? http://www.sgo.fomi.hu/files/magassagi_problemak.pdf Takács Bence BME Általános- és
Magasságos GPS avagy továbbra is Tisztázatlan kérdések az RTK-technológiával végzett magasságmeghatározás területén? http://www.sgo.fomi.hu/files/magassagi_problemak.pdf Takács Bence BME Általános- és
Regresszió számítás. Tartalomjegyzék: GeoEasy V2.05+ Geodéziai Kommunikációs Program
 Regresszió számítás GeoEasy V2.05+ Geodéziai Kommunikációs Program DigiKom Kft. 2006-2010 Tartalomjegyzék: Egyenes x változik Egyenes y változik Egyenes y és x változik Kör Sík z változik Sík y, x és z
Regresszió számítás GeoEasy V2.05+ Geodéziai Kommunikációs Program DigiKom Kft. 2006-2010 Tartalomjegyzék: Egyenes x változik Egyenes y változik Egyenes y és x változik Kör Sík z változik Sík y, x és z
Lázár térképe és a ptolemaioszi vetület
 Lázár térképe és a ptolemaioszi vetület Dr. Timár Gábor 1 dr. Molnár Gábor 2,1 dr. Székely Balázs 2,1 dr. Plihál Katalin 3 1 ELTE Geofizikai és Űrtudományi Tanszék 2 Bécsi Műszaki Egyetem, Fotogrammetriai
Lázár térképe és a ptolemaioszi vetület Dr. Timár Gábor 1 dr. Molnár Gábor 2,1 dr. Székely Balázs 2,1 dr. Plihál Katalin 3 1 ELTE Geofizikai és Űrtudományi Tanszék 2 Bécsi Műszaki Egyetem, Fotogrammetriai
Eötvös Loránd Tudományegyetem Informatikai Kar Térképtudományi és Geoinformatikai Tanszék. Kovács Béla
 Eötvös Loránd Tudományegyetem Informatikai Kar Térképtudományi és Geoinformatikai Tanszék Kovács Béla A műholdas helymeghatározó rendszer (GPS) és a délszláv térség történeti és modern térképeinek kapcsolata
Eötvös Loránd Tudományegyetem Informatikai Kar Térképtudományi és Geoinformatikai Tanszék Kovács Béla A műholdas helymeghatározó rendszer (GPS) és a délszláv térség történeti és modern térképeinek kapcsolata
Koordinátarendszerek, dátumok, GPS
 Koordinátarendszerek, dátumok, GPS KOORDINÁTARENDSZEREK A SPATIAL-BEN Koordinátarendszer típusok 1. Descartes-féle koordinátarendszer: egy adott pontból (origó) kiinduló, egymásra merőleges egyenesek alkotják,
Koordinátarendszerek, dátumok, GPS KOORDINÁTARENDSZEREK A SPATIAL-BEN Koordinátarendszer típusok 1. Descartes-féle koordinátarendszer: egy adott pontból (origó) kiinduló, egymásra merőleges egyenesek alkotják,
AZ ERDÕ NÖVEKEDÉSÉNEK VIZSGÁLATA TÉRINFORMATIKAI ÉS FOTOGRAMMETRIAI MÓDSZEREKKEL KARSZTOS MINTATERÜLETEN
 Tájökológiai Lapok 5 (2): 287 293. (2007) 287 AZ ERDÕ NÖVEKEDÉSÉNEK VIZSGÁLATA TÉRINFORMATIKAI ÉS FOTOGRAMMETRIAI MÓDSZEREKKEL KARSZTOS MINTATERÜLETEN ZBORAY Zoltán Honvédelmi Minisztérium Térképészeti
Tájökológiai Lapok 5 (2): 287 293. (2007) 287 AZ ERDÕ NÖVEKEDÉSÉNEK VIZSGÁLATA TÉRINFORMATIKAI ÉS FOTOGRAMMETRIAI MÓDSZEREKKEL KARSZTOS MINTATERÜLETEN ZBORAY Zoltán Honvédelmi Minisztérium Térképészeti
5. előadás: Földi vonatkoztatási rendszerek
 5. előadás: Földi vonatkoztatási rendszerek 5. előadás: Földi vonatkoztatási rendszerek A Nemzetközi Földi Vonatkoztatási Rendszer A csillagászati geodézia története során egészen a XX. század kezdetéig
5. előadás: Földi vonatkoztatási rendszerek 5. előadás: Földi vonatkoztatási rendszerek A Nemzetközi Földi Vonatkoztatási Rendszer A csillagászati geodézia története során egészen a XX. század kezdetéig
Geodézia terepgyakorlat számítási feladatok ismertetése 1.
 A Geodézia terepgyakorlaton Sukorón mért geodéziai hálózat új pontjainak koordináta-számításáról Geodézia terepgyakorlat számítási feladatok ismertetése 1. Dr. Busics György 1 Témák Cél, feladat Iránymérési
A Geodézia terepgyakorlaton Sukorón mért geodéziai hálózat új pontjainak koordináta-számításáról Geodézia terepgyakorlat számítási feladatok ismertetése 1. Dr. Busics György 1 Témák Cél, feladat Iránymérési
A PPP. a vonatkoztatási rendszer, az elmélet és gyakorlat összefüggése egy Fehérvár környéki kísérleti GNSS-mérés tapasztalatai alapján
 GISopen konferencia, Székesfehérvár, 2017. 04. 11-13. A PPP a vonatkoztatási rendszer, az elmélet és gyakorlat összefüggése egy Fehérvár környéki kísérleti GNSS-mérés tapasztalatai alapján Busics György
GISopen konferencia, Székesfehérvár, 2017. 04. 11-13. A PPP a vonatkoztatási rendszer, az elmélet és gyakorlat összefüggése egy Fehérvár környéki kísérleti GNSS-mérés tapasztalatai alapján Busics György
Milyen északi irány található a tájfutótérképen?
 Milyen északi irány található a tájfutótérképen? A felmérést a Hárshegy :000 méretarányú tájfutótérképén végeztem. Olyan pontokat választottam ki, amik a terepen és a térképen is jól azonosíthatók. ezeket
Milyen északi irány található a tájfutótérképen? A felmérést a Hárshegy :000 méretarányú tájfutótérképén végeztem. Olyan pontokat választottam ki, amik a terepen és a térképen is jól azonosíthatók. ezeket
A PANNON-MEDENCE MEANDEREZŐ VÍZFOLYÁSAINAK KANYARFEJLETTSÉG-ELEMZÉSE
 KDI. Beszámoló 2010. 06. 07. Petrovszki Judit: A PANNON-MEDENCE MEANDEREZŐ VÍZFOLYÁSAINAK KANYARFEJLETTSÉG-ELEMZÉSE Témavezető: dr. Timár Gábor Szárazföldi szeizmikus szelvény: TWT 0 500 1000 1500 2000
KDI. Beszámoló 2010. 06. 07. Petrovszki Judit: A PANNON-MEDENCE MEANDEREZŐ VÍZFOLYÁSAINAK KANYARFEJLETTSÉG-ELEMZÉSE Témavezető: dr. Timár Gábor Szárazföldi szeizmikus szelvény: TWT 0 500 1000 1500 2000
Matematikai geodéziai számítások 2.
 Matematikai geodéziai számítások 2. Geodéziai vonal és ábrázolása gömbön és vetületben Dr. Bácsatyai, László Matematikai geodéziai számítások 2.: Geodéziai vonal és ábrázolása Dr. Bácsatyai, László Lektor:
Matematikai geodéziai számítások 2. Geodéziai vonal és ábrázolása gömbön és vetületben Dr. Bácsatyai, László Matematikai geodéziai számítások 2.: Geodéziai vonal és ábrázolása Dr. Bácsatyai, László Lektor:
Construction of a cube given with its centre and a sideline
 Transformation of a plane of projection Construction of a cube given with its centre and a sideline Exercise. Given the center O and a sideline e of a cube, where e is a vertical line. Construct the projections
Transformation of a plane of projection Construction of a cube given with its centre and a sideline Exercise. Given the center O and a sideline e of a cube, where e is a vertical line. Construct the projections
Matematikai geodéziai számítások 4.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 4. MGS4 modul Vetületi átszámítások SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 4. MGS4 modul Vetületi átszámítások SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról
Az alap- és a képfelület fogalma, megadási módjai és tulajdonságai
 A VETÜLETEK ALAP- ÉS KÉPFELÜLETE Az alap- és a képfelület fogalma, megadási módjai és tulajdonságai A geodézia, a térinformatika és a térképészet a görbült földfelületen elhelyezkedő geometriai alakzatokat
A VETÜLETEK ALAP- ÉS KÉPFELÜLETE Az alap- és a képfelület fogalma, megadási módjai és tulajdonságai A geodézia, a térinformatika és a térképészet a görbült földfelületen elhelyezkedő geometriai alakzatokat
Matematikai geodéziai számítások 2.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 2. MGS2 modul Geodéziai vonal és ábrázolása gömbön és vetületben SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 2. MGS2 modul Geodéziai vonal és ábrázolása gömbön és vetületben SZÉKESFEHÉRVÁR 2010 Jelen szellemi
NYOMÁSOS ÖNTÉS KÖZBEN ÉBREDŐ NYOMÁSVISZONYOK MÉRÉTECHNOLÓGIAI TERVEZÉSE DEVELOPMENT OF CAVITY PRESSURE MEASUREMENT FOR HIGH PRESURE DIE CASTING
 Anyagmérnöki Tudományok, 39/1 (2016) pp. 82 86. NYOMÁSOS ÖNTÉS KÖZBEN ÉBREDŐ NYOMÁSVISZONYOK MÉRÉTECHNOLÓGIAI TERVEZÉSE DEVELOPMENT OF CAVITY PRESSURE MEASUREMENT FOR HIGH PRESURE DIE CASTING LEDNICZKY
Anyagmérnöki Tudományok, 39/1 (2016) pp. 82 86. NYOMÁSOS ÖNTÉS KÖZBEN ÉBREDŐ NYOMÁSVISZONYOK MÉRÉTECHNOLÓGIAI TERVEZÉSE DEVELOPMENT OF CAVITY PRESSURE MEASUREMENT FOR HIGH PRESURE DIE CASTING LEDNICZKY
A Föld alakjának ismerettörténete az archív térképek georeferálásának geofizikai alapja
 A Föld alakjának ismerettörténete az archív térképek georeferálásának geofizikai alapja MTA doktori értekezés tézisei Timár Gábor Budapest 018 A feladat megfogalmazása A doktori dolgozatban szélesebb történeti
A Föld alakjának ismerettörténete az archív térképek georeferálásának geofizikai alapja MTA doktori értekezés tézisei Timár Gábor Budapest 018 A feladat megfogalmazása A doktori dolgozatban szélesebb történeti
TÉRKÉPTAN óravázlat 2006/07. I.félév Dr. Mélykúti Gábor
 TÉRKÉPTAN óravázlat 2006/07. I.félév Dr. Mélykúti Gábor TARTALOMJEGYZÉK I. A FÖLD ALAKJA 1. A föld főbb geometriai paraméterei 2. A föld fizikai és elméleti alakja 3. Alapszintfelületek 4. A föld elméleti
TÉRKÉPTAN óravázlat 2006/07. I.félév Dr. Mélykúti Gábor TARTALOMJEGYZÉK I. A FÖLD ALAKJA 1. A föld főbb geometriai paraméterei 2. A föld fizikai és elméleti alakja 3. Alapszintfelületek 4. A föld elméleti
Digitális topográfiai adatok többcélú felhasználása
 Digitális topográfiai adatok többcélú felhasználása Iván Gyula Földmérési és Távérzékelési Intézet GIS OPEN 2003. Székesfehérvár, 2003. március 10-12. Tartalom A FÖMI digitális topográfiai adatai Minőségbiztosítás
Digitális topográfiai adatok többcélú felhasználása Iván Gyula Földmérési és Távérzékelési Intézet GIS OPEN 2003. Székesfehérvár, 2003. március 10-12. Tartalom A FÖMI digitális topográfiai adatai Minőségbiztosítás
4/2013. (II. 27.) BM rendelet
 4/2013. (II. 27.) BM rendelet Magyarország, Románia és Ukrajna államhatárai találkozási pontjának megjelölésére felállított TÚR határjelről készült Jegyzőkönyv jóváhagyásáról Az államhatárról szóló 2007.
4/2013. (II. 27.) BM rendelet Magyarország, Románia és Ukrajna államhatárai találkozási pontjának megjelölésére felállított TÚR határjelről készült Jegyzőkönyv jóváhagyásáról Az államhatárról szóló 2007.
A Kozmikus Geodéziai Obszervatórium
 Földmérési és Távérzékelési Intézet Kozmikus Geodéziai Obszervatórium Nagy Sándor A Kozmikus Geodéziai Obszervatórium mint komplex geodinamikai állomás leírása Penc AD 2000. Dokumentum kísérõ ûrlap A dokumentum
Földmérési és Távérzékelési Intézet Kozmikus Geodéziai Obszervatórium Nagy Sándor A Kozmikus Geodéziai Obszervatórium mint komplex geodinamikai állomás leírása Penc AD 2000. Dokumentum kísérõ ûrlap A dokumentum
Using the CW-Net in a user defined IP network
 Using the CW-Net in a user defined IP network Data transmission and device control through IP platform CW-Net Basically, CableWorld's CW-Net operates in the 10.123.13.xxx IP address range. User Defined
Using the CW-Net in a user defined IP network Data transmission and device control through IP platform CW-Net Basically, CableWorld's CW-Net operates in the 10.123.13.xxx IP address range. User Defined
A loxodrómáról. Előző írásunkban melynek címe: A Gudermann - függvényről szó esett a Mercator - vetületről,illetve az ezen alapuló térképről 1. ábra.
 1 A loxodrómáról Előző írásunkban melynek címe: A Gudermann - függvényről szó esett a Mercator - vetületről,illetve az ezen alapuló térképről 1. ábra. 1. ábra forrása: [ 1 ] Ezen a térképen a szélességi
1 A loxodrómáról Előző írásunkban melynek címe: A Gudermann - függvényről szó esett a Mercator - vetületről,illetve az ezen alapuló térképről 1. ábra. 1. ábra forrása: [ 1 ] Ezen a térképen a szélességi
UAS rendszerekkel végzett légi felmérés kiértékelési és pontossági kérdései
 UAS rendszerekkel végzett légi felmérés kiértékelési és pontossági kérdései DR. HABIL. JANCSÓ TAMÁS ÓBUDAI EGYETEM, ALBA REGIA MŰSZAKI KAR, GEOINFORMATIKAI INTÉZET FÖLDMÉRŐK VILÁGNAPJA ÉS AZ EURÓPAI FÖLDMÉRŐK
UAS rendszerekkel végzett légi felmérés kiértékelési és pontossági kérdései DR. HABIL. JANCSÓ TAMÁS ÓBUDAI EGYETEM, ALBA REGIA MŰSZAKI KAR, GEOINFORMATIKAI INTÉZET FÖLDMÉRŐK VILÁGNAPJA ÉS AZ EURÓPAI FÖLDMÉRŐK
Magyarországi geodéziai vonatkozási rendszerek és vetületi síkkoordináta-rendszerek vizsgálata
 Magyarországi geodéziai vonatkozási rendszerek és vetületi síkkoordináta-rendszerek vizsgálata Az elmúlt 150 év során Magyarországon a történelmi helyzet sajátos alakulása következtében több alkalommal
Magyarországi geodéziai vonatkozási rendszerek és vetületi síkkoordináta-rendszerek vizsgálata Az elmúlt 150 év során Magyarországon a történelmi helyzet sajátos alakulása következtében több alkalommal
UAV felmérés tapasztalatai
 Mérnökgeodézia Konferencia 2018. UAV felmérés tapasztalatai Multikopteres térképezés kis méretű munkaterületeken Felmérések pontossága, megbízhatósága Budapest, 2018. 10. 27. Lennert József - Lehoczky
Mérnökgeodézia Konferencia 2018. UAV felmérés tapasztalatai Multikopteres térképezés kis méretű munkaterületeken Felmérések pontossága, megbízhatósága Budapest, 2018. 10. 27. Lennert József - Lehoczky
Infokommunikáció a közlekedésben (VITMJV27)
 (VITMJV27) Hely fogalma, pozícionálási alapok, cellás pozícionálási technikák Heszberger Zalán Pozícionálási technológiák A pozícionálás fő elvei: bázispontok/állomások pontos helye ismert mért jel konverziója
(VITMJV27) Hely fogalma, pozícionálási alapok, cellás pozícionálási technikák Heszberger Zalán Pozícionálási technológiák A pozícionálás fő elvei: bázispontok/állomások pontos helye ismert mért jel konverziója
Tervezési célú geodéziai feladatok és az állami térképi adatbázisok kapcsolata, azok felhasználhatósága III. rész
 Tervezési célú geodéziai feladatok és az állami térképi adatbázisok kapcsolata, azok felhasználhatósága III. rész Herczeg Ferenc Székesfehérvár, 2016. szeptember 16. HATÁLYON KÍVÜLI UTASÍTÁSOK száma típusa
Tervezési célú geodéziai feladatok és az állami térképi adatbázisok kapcsolata, azok felhasználhatósága III. rész Herczeg Ferenc Székesfehérvár, 2016. szeptember 16. HATÁLYON KÍVÜLI UTASÍTÁSOK száma típusa
Hengervetületek alkalmazása a magyar topográfiában
 EÖTVÖS LORÁND TUDOMÁNYEGYETEM TERMÉSZETTUDOMÁNYI KAR Hengervetületek alkalmazása a magyar topográfiában SZAKDOLGOZAT FÖLDTUDOMÁNYI ALAPSZAK Készítette: Szántó Henriett térképész és geoinformatikus szakirányú
EÖTVÖS LORÁND TUDOMÁNYEGYETEM TERMÉSZETTUDOMÁNYI KAR Hengervetületek alkalmazása a magyar topográfiában SZAKDOLGOZAT FÖLDTUDOMÁNYI ALAPSZAK Készítette: Szántó Henriett térképész és geoinformatikus szakirányú
100 év a katonai topográfiai térképeken
 100 év a katonai topográfiai térképeken MFTTT vándorgyűlés 2019. július 04-05. Békéscsaba Koós Tamás alezredes MH Geoinformációs Szolgálat főmérnök (szolgálatfőnök-helyettes) 100 éves az Önálló Magyar
100 év a katonai topográfiai térképeken MFTTT vándorgyűlés 2019. július 04-05. Békéscsaba Koós Tamás alezredes MH Geoinformációs Szolgálat főmérnök (szolgálatfőnök-helyettes) 100 éves az Önálló Magyar
Matematikai geodéziai számítások 11.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 11. MGS11 modul Geoidkép meghatározása csillagászati szintezéssel SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 11. MGS11 modul Geoidkép meghatározása csillagászati szintezéssel SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Fotogrammetriai munkaállomások szoftvermoduljainak tervezése. Dr. habil. Jancsó Tamás Óbudai Egyetem, Alba Regia Műszaki Kar
 Fotogrammetriai munkaállomások szoftvermoduljainak tervezése Dr. habil. Jancsó Tamás Óbudai Egyetem, Alba Regia Műszaki Kar Témakörök DPW szoftvermodulok Szoftverek funkciói Pár példa Mi hiányzik gyakran?
Fotogrammetriai munkaállomások szoftvermoduljainak tervezése Dr. habil. Jancsó Tamás Óbudai Egyetem, Alba Regia Műszaki Kar Témakörök DPW szoftvermodulok Szoftverek funkciói Pár példa Mi hiányzik gyakran?
b) Ábrázolja ugyanabban a koordinátarendszerben a g függvényt! (2 pont) c) Oldja meg az ( x ) 2
 1) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) b) c) ( ) ) Határozza meg az 1. feladatban megadott, ; intervallumon
1) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) b) c) ( ) ) Határozza meg az 1. feladatban megadott, ; intervallumon
TÉRINFORMATIKA II. Dr. Kulcsár Balázs főiskolai docens. Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék
 TÉRINFORMATIKA II. Dr. Kulcsár Balázs főiskolai docens Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék TÁJÉKOZTATÁS TANTÁRGYI TEMATIKA 1 Előadás 1. GPS műszerek és kapcsolódó szoftvereik bemutatása
TÉRINFORMATIKA II. Dr. Kulcsár Balázs főiskolai docens Debreceni Egyetem Műszaki Kar Műszaki Alaptárgyi Tanszék TÁJÉKOZTATÁS TANTÁRGYI TEMATIKA 1 Előadás 1. GPS műszerek és kapcsolódó szoftvereik bemutatása
FATERMÉSI FOK MEGHATÁROZÁSA AZ EGÉSZÁLLOMÁNY ÁTLAGNÖVEDÉKE ALAPJÁN
 4. évfolyam 2. szám 2 0 1 4 101 107. oldal FATERMÉSI FOK MEGHATÁROZÁSA AZ EGÉSZÁLLOMÁNY ÁTLAGNÖVEDÉKE ALAPJÁN Veperdi Gábor Nyugat-magyarországi Egyetem, Erdômérnöki Kar Kivonat A fatermési fok meghatározása
4. évfolyam 2. szám 2 0 1 4 101 107. oldal FATERMÉSI FOK MEGHATÁROZÁSA AZ EGÉSZÁLLOMÁNY ÁTLAGNÖVEDÉKE ALAPJÁN Veperdi Gábor Nyugat-magyarországi Egyetem, Erdômérnöki Kar Kivonat A fatermési fok meghatározása
Ferdetengelyű szögtartó hengervetületek a térképészetben
 EÖTVÖS LORÁND TUDOMÁNYEGYETEM TERMÉSZETTUDOMÁNYI KAR Ferdetengelyű szögtartó hengervetületek a térképészetben SZAKDOLGOZAT FÖLDTUDOMÁNYI ALAPSZAK Készítette: Fülöp Dávid térképész és geoinformatikus szakirányú
EÖTVÖS LORÁND TUDOMÁNYEGYETEM TERMÉSZETTUDOMÁNYI KAR Ferdetengelyű szögtartó hengervetületek a térképészetben SZAKDOLGOZAT FÖLDTUDOMÁNYI ALAPSZAK Készítette: Fülöp Dávid térképész és geoinformatikus szakirányú
Mély és magasépítési feladatok geodéziai munkái
 Mély és magasépítési feladatok geodéziai munkái Ágfalvi: Mérnökgeodézia 7. modul M2 tervezési segédlet: 6. Kitűzések (5. modul), 7. Kivitelezett állapotot ellenőrző mérések Detrekői-Ódor: Ipari geodézia
Mély és magasépítési feladatok geodéziai munkái Ágfalvi: Mérnökgeodézia 7. modul M2 tervezési segédlet: 6. Kitűzések (5. modul), 7. Kivitelezett állapotot ellenőrző mérések Detrekői-Ódor: Ipari geodézia
ÁLLÁSPONTOM 34TDT4105419743 VETÜLETTANI FOGALMAK
 ÁLLÁSPONTOM 34TDT4105419743 Hazánk NATO csatlakozása jelentős változásokat eredményezett a katonai feladatok térképészeti biztosításában. A változások egyrészt a katonai térképek tartalmának megváltozásában
ÁLLÁSPONTOM 34TDT4105419743 Hazánk NATO csatlakozása jelentős változásokat eredményezett a katonai feladatok térképészeti biztosításában. A változások egyrészt a katonai térképek tartalmának megváltozásában
Ausztria és Magyarország közötti vetületi transzformációk
 Vetületi átszámítások Ausztria és Magyarország között Dr. Völgyesi Lajos egyetemi docens BME Általános- és Felsőgeodézia Tanszék, MTA-BME Fizikai Geodéziai és Geodinamikai Kutató csoport Ausztria és Magyarország
Vetületi átszámítások Ausztria és Magyarország között Dr. Völgyesi Lajos egyetemi docens BME Általános- és Felsőgeodézia Tanszék, MTA-BME Fizikai Geodéziai és Geodinamikai Kutató csoport Ausztria és Magyarország
FELHASZNÁLÓI KÉZIKÖNYV
 FELHASZNÁLÓI KÉZIKÖNYV 1 BEVEZETÉS A Közlekedési Környezeti Centrum (KKC) projekt keretében létrejött ELZA (Elektronikus Levegő- és Zajvédelmi Adattár) egy online felületen elérhető alkalmazás, ahol a
FELHASZNÁLÓI KÉZIKÖNYV 1 BEVEZETÉS A Közlekedési Környezeti Centrum (KKC) projekt keretében létrejött ELZA (Elektronikus Levegő- és Zajvédelmi Adattár) egy online felületen elérhető alkalmazás, ahol a
A magyar katonai térképészet 99 éve
 A magyar katonai térképészet 99 éve Szalay László alezredes MH Geoinformációs Szolgálat szolgálatfőnök Magyar katonai térképészet Az Önálló Magyar Katonai Térképészet megalakulása: 1919. február 4. Lázár
A magyar katonai térképészet 99 éve Szalay László alezredes MH Geoinformációs Szolgálat szolgálatfőnök Magyar katonai térképészet Az Önálló Magyar Katonai Térképészet megalakulása: 1919. február 4. Lázár
Vonatkoztatási rendszerek
 2. előadás: Vonatkoztatási rendszerek 2.1. A nemzetközi földi vonatkoztatási rendszer (ITRS) A geodézia az 1900-as évek elejétől a földi pontok helyzetének meghatározásához a földtesthez (minél jobban)
2. előadás: Vonatkoztatási rendszerek 2.1. A nemzetközi földi vonatkoztatási rendszer (ITRS) A geodézia az 1900-as évek elejétől a földi pontok helyzetének meghatározásához a földtesthez (minél jobban)
RTCM alapú VITEL transzformáció felhasználó oldali beállítása Trimble Survey Controller szoftver használata esetén
 RTCM alapú VITEL transzformáció felhasználó oldali beállítása Trimble Survey Controller szoftver használata esetén A http://www.gnssnet.hu/valos_trafo.php weboldalról letöltött RTCM VITEL.dc nevű Trimble
RTCM alapú VITEL transzformáció felhasználó oldali beállítása Trimble Survey Controller szoftver használata esetén A http://www.gnssnet.hu/valos_trafo.php weboldalról letöltött RTCM VITEL.dc nevű Trimble
Volt-e Ivanicsi (Ivaniè) Sztereografikus Vetületi Rendszer?
 Volt-e Ivanicsi (Ivaniè) Sztereografikus Vetületi Rendszer? Dr. Varga József egyetemi adjunktus BME Általános- és Felsõgeodézia Tanszék Bevezetés Vetülettani tanulmányainkból mindannyian emlékszünk arra,
Volt-e Ivanicsi (Ivaniè) Sztereografikus Vetületi Rendszer? Dr. Varga József egyetemi adjunktus BME Általános- és Felsõgeodézia Tanszék Bevezetés Vetülettani tanulmányainkból mindannyian emlékszünk arra,
Kis magasságban végzett légi térképészeti munkák tapasztalatai. LÉGIFOTÓ NAP Székesfehérvár GeoSite Kft Horváth Zsolt
 Kis magasságban végzett légi térképészeti munkák tapasztalatai LÉGIFOTÓ NAP 2018 - Székesfehérvár GeoSite Kft Horváth Zsolt Az UAV technológiák térképészeti célú alkalmazásának lehetőségei, célterületei:
Kis magasságban végzett légi térképészeti munkák tapasztalatai LÉGIFOTÓ NAP 2018 - Székesfehérvár GeoSite Kft Horváth Zsolt Az UAV technológiák térképészeti célú alkalmazásának lehetőségei, célterületei:
Térképészeti alapismeretek. Mit jelent egy térkép léptéke?
 Térképészeti alapismeretek Mi a térkép? A föld felszínén illetve azzal kapcsolatban álló anyagi vagy elvont dolgoknak általában kicsinyített, generalizált, síkbeli megjelenítése. Térképészeti absztrakció
Térképészeti alapismeretek Mi a térkép? A föld felszínén illetve azzal kapcsolatban álló anyagi vagy elvont dolgoknak általában kicsinyített, generalizált, síkbeli megjelenítése. Térképészeti absztrakció
