A mátrix faktorizáció csapdája
|
|
|
- Lóránd Barta
- 5 évvel ezelőtt
- Látták:
Átírás
1 A mátrix faktorizáció csapdája Buza Antal, B. Kis Piroska Összefoglalás Az utóbbi időben egyre több cikk, előadás sugallja, hogy az ajánlórendszerekben általánosságban is milyen jól használható a mátrix faktorizáció. Ez azonban csak bizonyos, nehezen ellenőrizhető feltételek teljesülése esetén van így és erre a szerzők sajnos többnyire nem szoktak kitérni. E cikkben példákat mutatunk be arra, hogy a szükséges feltételek vizsgálata nélkül, általánosságban a mátrix faktorizáció alkalmazása az ajánló rendszerekben igen súlyos tévedéshez, hibás következtetések levonásához vezethet. Abstract Recently, more and more papers and presentations suggest that the matrix factorization is a very usable tool for recommender systems. However, the usage of matrix factorization has a lot of hardly verifiable and controllable criteria which are unfortunately not mentioned by the authors in the most of the cases. The paper presents a few matrix factorizations in order to serve as examples for that the general application of the matrix factorization may led to false conclusions. Not knowing the conditions or without checking the strict conditions, the application of the matrix factorization for recommender systems may result unpredictable haphazard solutions. Bevezetés Az ajánlórendszerek olyan rendszerek, amelyek a korábban gyűjtött tapasztalatok felhasználásával igyekeznek megítélni, hogy a még nem tapasztalt esetekre vonatkozóan mekkora lehet az igény / a hatás. film1 film2 film3 film4 néző1 16 néző néző néző4 18 néző ábra: Pontszámok, ahogy a nézők a filmeket értékelték Ajánló rendszerekkel kapcsolatban az egyik leggyakrabban említett példa a filmekkel kapcsolatos ajánlattevő rendszer. A korábban gyűjtött tapasztalat ilyenkor azt jelenti, hogy aki már látott egy filmet az közli/rögzíti, hogy hány pontra értékeli az adott filmet. Ezek az értékelések táblázatba foglalhatók, így az 1. ábrán láthatóhoz hasonló táblázatot kapunk. A feladat pedig az, hogy derítsük ki nyilván minél nagyobb biztonsággal, hogy egy-egy néző az 1
2 általa még nem látott filmeket hogyan értékelné, mert eszerint célzottan és várhatóan eredményesen tudjuk felhívni rá a figyelmét. Más megfogalmazásban tehát a pontszámok alkotta mátrixban ki nem töltött helyekre jutó értékeket kellene minél nagyobb biztonsággal megállapítanunk. Az ajánlat megkeresésének módszerei A hiányzó értékek megállapítására többféle meggondolást is használhatunk. Az egyik például a legközelebbi szomszéd módszer(ek) alkalmazása. Ennek az az alapgondolata, hogy ha két egyed tulajdonságai példánkban a két néző filmekre vonatkozó véleménye sok ponton megegyező, vagy egymáshoz közeli, akkor feltételezhető, hogy a nem ismert értékek is egyezőek, vagy legalábbis hasonlóak. Ezt a módszert többen kritizálják és hivatkoznak olyan tapasztalati példákra, melyek szerint e módszer a gyakorlatban nem mindig szolgáltat megfelelő értéket. Több szerző (Koren at al., 2009; Forbes és Zhu, 2011; Takács et al., 2008) ajánlja a mátrix faktorizáció módszerét, és néhány gyakorlati tapasztalattal támasztja alá ennek használhatóságát. A mátrix faktorizáció módszerek lényege abban áll, hogy keressünk olyan mátrixokat, amelyek szorzata az ismert helyeken éppen az ismert vagy azokhoz eléggé közeli értékeket adja. Ha találtunk ilyen mátrixokat, akkor a kiindulási mátrixunk hiányzó értékeinek tekintsük a mátrix faktorizációval kapott mátrixok szorzataként előálló mátrixban az adott helyeken szereplő értékeket. A meggondolás azon alapul, hogy a kiindulási mátrixunk elemei között van valamilyen összefüggés, amit lehet, hogy éppen a mátrix felbontása ír le helyesen. Ha nem tételeznénk fel semmilyen összefüggést, akkor semmilyen alapunk nem lenne a hiányzó értékek megjósolására. Mátrix faktorizáció Esetünkben a mátrix faktorizáció azt jelenti, hogy egy adott R, n m méretű mátrixhoz keressük olyan P, n r méretű és Q, r m méretű mátrixokat, amelyekre P Q = R teljesül. Az r értékére nincs speciális kikötés. Lehetségesség Ismeretlenek tehát a P és Q mátrixok. Jelöljük a P, Q és R mátrixok elemeit rendre p i,j, q i,j, r i,j -vel. Eldöntendő még az r érték, ezt tekintsük rögzítettnek. Megoldandó tehát az p i,1 q 1,j + p i,2 q 2,j p i,k q k,j = r i,j i = 1,..., n és j = 1,...,m 2
3 egyenletrendszer. Az ismeretlenek száma (n+m) r. Az egyenletek száma anynyi ahány értékét az R mátrixnak ismerjük, maximum n m. A szóban forgó ajánlórendszerek szempontjából nem feltétlenül szükséges a mátrix faktorizációs egyenletrendszer pontos megoldása, hanem közelítő megoldás is használható lehet. A közelítő megoldás keresése azt jelenti, hogy az R mátrix helyett egy olyan, szorzatként előálló R mátrixot keresünk meg, amely elemeinek az R mátrix összes ismert elemeitől való eltérés négyzetöszszege minimális. Tehát a négyzetes hibafüggvényt minimalizáljuk. Ennek megfelelő mátrix felbontást mutatnak be például Koren (Koren at al., 2009), Lee (Lee at al., 2001) és Yeung (Yeung, 2010) cikkeikben. A négyzetes hibafüggvény módosított változatait illetve más hibafüggvényeket is használnak. A négyzetes hibafüggvényre vonatkozó kritikai megjegyzések olvashatók például Bodon (Bodon, 2010) anyagában. Bármilyen hibafüggvényt alkalmazunk is, az olyan felbontást hibátlannak kell tekinteni, amely az ismert értékeket pontosan visszaadja. Különböző felbontások előfordulásának lehetősége Előfordulnak olyan esetek, amikor egy mátrixnak több felbontása, faktorizációja is létezik. Az 1. ábrán látható mátrixnak több különböző felbontása létezik. Ezen felbontásokból képzett szorzatmátrixok: Mindkét felbontás a faktorizálandó mátrix ismert elemeit pontosan állítja elő, így mindkettő hibája 0, ami jobb nem is lehet. Ugyanakkor látható, hogy az R mátrix első sorának negyedik elemére az első felbontásból 11-et, a másodikból 27-et kapunk eredményül. Ezek bizony lényegesen eltérő következtetésekre is vezethetnek, az első felbontásban 11 például az R mátrix első sorában a legkisebb érték, ugyanakkor a második felbontásban a 27 az R mátrix első sorában a legnagyobb érték. Ha tehát valaki egy faktorizációs eljárással megtalálja az első mátrixhoz vezető (hibátlan) felbontást, akkor egy ajánlattevő alkalmazásban arra a következtetésre jut, hogy a néző1 néző a film4 filmet a legkevesebb pontszámmal értékelné, tehát számára ezt a filmet nem érdemes javasolnunk, ugyanakkor más faktorizációs módszer a második mátrixot eredményezi, amiből pontosan ellentétes következtetés vonunk le. Mivel a különböző felbontások ellentétes következtetésekhez vezethetnek, így nem tekinthetjük mindkét felbontást jónak. A valóságos helyzetet legfeljebb az egyik felbontás tükrözheti. 3
4 Miután mindkét felbontás matematikai értelemben tökéletes, így semmilyen elméleti meggondolás alapján nem tudjuk eldönteni, hogy (amint láttuk ellentétes következtetésekre vezető) felbontások közül melyik a helyesebb, melyiket szabad a gyakorlati feladat megoldásához inkább felhasználni. A problémát az okozza, hogy a felbontáshoz nem rendeltünk valamilyen gyakorlati szempontból értelmezhető jelentést. Azt gondoljuk, hogy a feladat gyakorlati jelentésétől elvonatkoztatva, pusztán a felbontandó mátrixra alapozott matematikai meggondolásokkal ez általánosságban nem is lehetséges. Egyes mátrix felbontásokra helyes, használható értelmezést találnunk, csak az adott mátrix gyakorlati jelentésével együtt van esélyünk. Kísérlet a felbontás megértésére Láttuk, hogy előfordulhat többféle, akár ellentmondásos következtetésekre vezető mátrix felbontás. Matematikai értelemben mindegyik jó, de a valóságot nem mindegyik írja le helyesen. Fontos tehát a felbontások közül megtalálni azt, amelyik az adott valóságos alkalmazási környezetben magyarázható, értelmezhető. Értelmezhetőnek kell lennie: az r darab rejtett attribútumnak, a P és Q mátrixoknak, és annak is, hogy miért éppen ezek szorzataként áll elő a kiindulási R mátrix, hiszen nyilvánvaló, hogy a P és Q mátrixok értékeiből sokféle módon is származtatható valamilyen eredmény. A példánkban bemutatott filmeket pontozó mátrix egy értelmezhető felbontása lehet például egy olyan felbontás, amelyben a rejtett attribútumok a film írója, rendezője, és színésze(i). Ekkor a P mátrix jelentése lehet az, hogy egy-egy néző melyik írót, rendezőt, színészt mennyire kedveli, a Q mátrix jelentése lehet az, hogy az író, a rendező, a színész mennyire hat a film sikerességére. Ha még az is értelmezhető, hogy egy néző véleménye, az általa adott pontszám, az összhatás vagyis az R mátrix éppen úgy alakítható ki, hogy összegezzük a kedvel és a hatás pontszámok szorzatait, akkor a felbontást értelmezni tudtuk. Természetesen többféle értelmezés is lehetséges. Azt, hogy egy felbontás értelmezése helyes-e, részben a szakterület szakértőjével konzultálva tudjuk eldönteni, de nagyon sokat segít a döntés megalapozásában, ha akár más felmérésből legalább a P és Q mátrixok egyikére vonatkozóan vannak adataink. Ha példánkban ismerjük, hogy nézők mennyire kedvelik az írókat, rendezőket, színészeket, akkor ezzel alátámaszthatjuk, vagy éppen elvethetjük egyik vagy másik felbontásunkat. Ha a felbontással keletkezett mátrixok nem 4
5 hordoznak jelentést, sőt bizonyos jelentéssel bíró felbontások esetén is az eredeti mátrixra vonatkozó bármilyen következtetés levonása például a hiányzó értékekre vonatkozó következtetés megkérdőjelezhető, nagyon vitatható, akár kóklerkedésnek is tekinthető. Természetesen vannak olyan esetek, amikor a felbontás mátrixai biztonsággal értelmezhetők. Egy táplálkozással kapcsolatos felmérésben például előfordulhat, hogy egy mátrixban adjuk meg azt, hogy melyik megfigyelt személy milyen ételből adott napon mennyit fogyasztott, egy másik mátrix tartalma lehet az, hogy melyik étel milyen összetevőkből áll. Ekkor az egyes emberek által fogyasztott összetevők összmennyisége a két mátrix szorzataként áll elő. E utóbbi mátrix tehát felbontható legalább annak a két mátrixnak a szorzatára, amelyek szorzataként keletkezett. E példában a felbontással keletkezett mátrixok is és a szorzatmátrixuk is valamilyen, gyakorlatban értelmezett jelentéssel bírnak. Látszik az is, hogy a szorzatmátrixból az már sehogyan nem következtethető ki, hogy a felbontással keletkezett mátrixokban megjelenő rejtett attribútum micsoda és mi lehet a jelentése. Példánkban ezek a különböző ételféleségek voltak. Következtetések, nyitott kérdések A különböző mátrix felbontások az ismeretlen elemekre vonatkozóan különböző értékeket adhatnak, tehát lényegesen különböző következtetésekre vezethetik az elemzőt. Láttuk, hogy különböző felbontások is pontosan előállíthatják az ismert értékeket, matematikai szempontokkal a különböző felbontások között minőségi különbség nem állapítható meg, ugyanakkor, mint láttuk teljesen ellentétes következtetések objektív alátámasztását adják. Kijelenthető tehát, hogy pusztán a négyzetes hiba, de bármilyen más, a mátrixokat pusztán matematikai konstrukcióként tekintő hibafüggvény alkalmazása sem elegendő a felbontások minősítésére. Bármilyen hibafüggvényt alkalmaznak is, elvárható, hogy a hibafüggvénynek ott legyen minimuma, ahol nincs hiba. Önmagában mátrixelméleti meggondolásokkal nem állapítható meg, hogy a felbontások használatával a hiányzó értékekre vonatkozóan melyik jóslatunk adja meg a helyes vagy legalábbis ahhoz közeli értékeket és melyek a teljesen helytelen, tehát félrevezető, hibás következtetést okozó értékeket. Ezért fontos, hogy csak értelmezhető felbontásokat használjunk. Természetesen előfordulhat olyan eset is, amikor jó felbontást tehát olyat, amely segítségével a hiányzó elemeket, a gyakorlat által is igazoltan, eléggé pontosan tudjuk megjósolni találunk, de a komponenseket nem tudjuk értelmezni, még a szakértő bevonásával sem. Ilyenkor a felbontás értelmének, jelentésének a megkeresése önálló, komoly szakmai feladat lehet, amely eb- 5
6 ből a szempontból új ismeretekre vezethet, ebben az értelemben tehát ez is adatbányászati eredmény, hiszen az adatok elemzéséből kiindulva kapott valamilyen szakmai ismeret megtalálásához ad segítséget. A mátrix faktorizáció általánosabb értelmezése Két mátrixból nemcsak szorzással származtatható egy harmadik. Ha más származtatásnak is van gyakorlati értelmezése, akkor az is tekinthető faktorizációs alapnak, azaz annak, hogy az így faktorizált mátrixokat keressük és azokat használjuk fel a hiányzó értékek megbecsülésére Nyitott kérdések Az a meglátásunk, hogy a mátrix faktorizációnak az ajánló rendszerekben való megbízható alkalmazásához minden egyes gyakorlati esetben különkülön valamilyen szakértői ismeretekre támaszkodva meg kell találni az értelmezhető felbontásokat. Ehhez szükség van a megfelelő rejtett attribútumok használatára. Az értelmezhetőséghez tartozik az is, hogy éppen a talált mátrixok szorzása produkálja a kiinduló mátrixunk elemeit. Hivatkozott források Bodon Ferenc: Adatbányászati algoritmusok, (2010). Peter Forbes, Mu Zhu: Content-boosted Matrix Factorization for Recommender Systems: Experiments with Recipe Recommendation. RecSys'11, (2011). Yehuda Koren, Robert Bell, Chris Volinsky: Matrix factorization techniques for recommender systems. IEEE, Computer, August 2009, pp (2009). Daniel D. Lee, H. Sebastian Seung: Algorithms for Non-negative Matrix Factorization. Advances in Neural Information Processing Systems 13: Proceedings of the 2000 Conference. MIT Press. pp (2000). Gábor Takács, István Pilászy, Bottyán Németh, Domonkos Tikk: Investigation of Various Matrix Factorization Methods for Large Recommender Systems. KDD netfix workshop. (2008). Albert Au Yeung: Matrix Factorization: A Simple Tutorial and Implementation in Python, (2010). Szerzők Buza Antal, Phd, főiskolai tanár Dunaújvárosi Főiskola buza.antal@yahoo.com B. Kis Piroska, Phd, főiskolai tanár Dunaújvárosi Főiskola buzanekispiroska@yahoo.com 6
9. gyakorlat Lineáris egyenletrendszerek megoldási módszerei folyt. Néhány kiegészítés a Gauss- és a Gauss Jordan-eliminációhoz
 9. gyakorlat Lineáris egyenletrendszerek megoldási módszerei folyt. Néhány kiegészítés a Gauss- és a Gauss Jordan-eliminációhoz. Mindkét eliminációs módszer műveletigénye sokkal kisebb, mint a Cramer-szabályé:
9. gyakorlat Lineáris egyenletrendszerek megoldási módszerei folyt. Néhány kiegészítés a Gauss- és a Gauss Jordan-eliminációhoz. Mindkét eliminációs módszer műveletigénye sokkal kisebb, mint a Cramer-szabályé:
Konjugált gradiens módszer
 Közelítő és szimbolikus számítások 12. gyakorlat Konjugált gradiens módszer Készítette: Gelle Kitti Csendes Tibor Vinkó Tamás Faragó István Horváth Róbert jegyzetei alapján 1 LINEÁRIS EGYENLETRENDSZEREK
Közelítő és szimbolikus számítások 12. gyakorlat Konjugált gradiens módszer Készítette: Gelle Kitti Csendes Tibor Vinkó Tamás Faragó István Horváth Róbert jegyzetei alapján 1 LINEÁRIS EGYENLETRENDSZEREK
Egy gazdasa gmatematikai modell An economical mathematics model
 Egy gazdasa gmatematikai modell An economical mathematics model KÉZI CS. University of Debrecen, kezicsaba@science.unideb.hu Absztrakt. Az NTP-NFTÖ-17-C-159 azonosítószámú pályázat keretében az egyik fő
Egy gazdasa gmatematikai modell An economical mathematics model KÉZI CS. University of Debrecen, kezicsaba@science.unideb.hu Absztrakt. Az NTP-NFTÖ-17-C-159 azonosítószámú pályázat keretében az egyik fő
BitTorrent felhasználók értékeléseinek következtetése a viselkedésük alapján. Hegedűs István
 BitTorrent felhasználók értékeléseinek következtetése a viselkedésük alapján Hegedűs István Ajánló rendszerek Napjainkban egyre népszerűbb az ajánló rendszerek alkalmazása A cégeket is hasznos információval
BitTorrent felhasználók értékeléseinek következtetése a viselkedésük alapján Hegedűs István Ajánló rendszerek Napjainkban egyre népszerűbb az ajánló rendszerek alkalmazása A cégeket is hasznos információval
Adatbányászati feladatgyűjtemény tehetséges hallgatók számára
 Adatbányászati feladatgyűjtemény tehetséges hallgatók számára Buza Krisztián Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem Tartalomjegyék Modellek kiértékelése...
Adatbányászati feladatgyűjtemény tehetséges hallgatók számára Buza Krisztián Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem Tartalomjegyék Modellek kiértékelése...
6. gyakorlat. Gelle Kitti. Csendes Tibor Somogyi Viktor. London András. jegyzetei alapján
 Közelítő és szimbolikus számítások 6. gyakorlat Sajátérték, Gersgorin körök Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján . Mátrixok sajátértékei
Közelítő és szimbolikus számítások 6. gyakorlat Sajátérték, Gersgorin körök Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján . Mátrixok sajátértékei
Gauss-Jordan módszer Legkisebb négyzetek módszere, egyenes LNM, polinom LNM, függvény. Lineáris algebra numerikus módszerei
 A Gauss-Jordan elimináció, mátrixinvertálás Gauss-Jordan módszer Ugyanazzal a technikával, mint ahogy a k-adik oszlopban az a kk alatti elemeket kinulláztuk, a fölötte lévő elemeket is zérussá lehet tenni.
A Gauss-Jordan elimináció, mátrixinvertálás Gauss-Jordan módszer Ugyanazzal a technikával, mint ahogy a k-adik oszlopban az a kk alatti elemeket kinulláztuk, a fölötte lévő elemeket is zérussá lehet tenni.
Mátrixok, mátrixműveletek
 Mátrixok, mátrixműveletek 1 előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Mátrixok, mátrixműveletek p 1/1 Mátrixok definíciója Definíció Helyezzünk el n m elemet egy olyan téglalap
Mátrixok, mátrixműveletek 1 előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Mátrixok, mátrixműveletek p 1/1 Mátrixok definíciója Definíció Helyezzünk el n m elemet egy olyan téglalap
Mátrixok 2017 Mátrixok
 2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
Ismerd meg a vászonkép készíttetés legnagyobb buktatóit! (9 perc alatt)
 Ismerd meg a vászonkép készíttetés legnagyobb buktatóit! (9 perc alatt) És tudd meg, hogyan kerülheted el mindet! vaszonkepszalon.hu Ebben a kis doksiban igyekeztünk összegyűjteni neked azokat a buktatókat,
Ismerd meg a vászonkép készíttetés legnagyobb buktatóit! (9 perc alatt) És tudd meg, hogyan kerülheted el mindet! vaszonkepszalon.hu Ebben a kis doksiban igyekeztünk összegyűjteni neked azokat a buktatókat,
Gauss-Seidel iteráció
 Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Irodalom. (a) A T, B T, (b) A + B, C + D, D C, (c) 3A, (d) AD, DA, B T A, 1 2 B = 1 C = A = 1 0 D = (a) 1 1 3, B T = = ( ) ; A T = 1 0
 Irodalom ezek egyrészt el- A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: hangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László: Bevezetés a lineáris algebrába, Polygon
Irodalom ezek egyrészt el- A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: hangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László: Bevezetés a lineáris algebrába, Polygon
Arany Dániel Matematikai Tanulóverseny 2015/2016-os tanév 1. forduló Haladók III. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 2015/2016-os tanév 1. forduló Haladók III. kategória Megoldások és javítási útmutató 1. Az a és b befogójú derékszögű háromszögnek
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 2015/2016-os tanév 1. forduló Haladók III. kategória Megoldások és javítási útmutató 1. Az a és b befogójú derékszögű háromszögnek
A -Y és a Y- átalakítás bemutatása. Kiss László április havában
 A -Y és a Y- átalakítás bemutatása Kiss László 2011. április havában -Y átalakítás ohmos ellenállásokra Mint ismeretes, az elektrotechnikai gyakorlatban többször előfordul olyan kapcsolási kép, ami a megszokott
A -Y és a Y- átalakítás bemutatása Kiss László 2011. április havában -Y átalakítás ohmos ellenállásokra Mint ismeretes, az elektrotechnikai gyakorlatban többször előfordul olyan kapcsolási kép, ami a megszokott
Lineáris egyenletrendszerek
 Lineáris egyenletrendszerek Lineáris egyenletrendszernek nevezzük az a 11 x 1 + a 12 x 2 +... +a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... +a 2n x n = b 2.. a k1 x 1 + a k2 x 2 +... +a kn x n = b k n ismeretlenes,
Lineáris egyenletrendszerek Lineáris egyenletrendszernek nevezzük az a 11 x 1 + a 12 x 2 +... +a 1n x n = b 1 a 21 x 1 + a 22 x 2 +... +a 2n x n = b 2.. a k1 x 1 + a k2 x 2 +... +a kn x n = b k n ismeretlenes,
Lineáris algebra (10A103)
 Lineáris algebra (10A103 Kátai-Urbán Kamilla Tudnivalók Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli (beugróval, feltétele a Lineáris algebra gyakorlat
Lineáris algebra (10A103 Kátai-Urbán Kamilla Tudnivalók Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli (beugróval, feltétele a Lineáris algebra gyakorlat
Problémás regressziók
 Universitas Eotvos Nominata 74 203-4 - II Problémás regressziók A közönséges (OLS) és a súlyozott (WLS) legkisebb négyzetes lineáris regresszió egy p- változós lineáris egyenletrendszer megoldása. Az egyenletrendszer
Universitas Eotvos Nominata 74 203-4 - II Problémás regressziók A közönséges (OLS) és a súlyozott (WLS) legkisebb négyzetes lineáris regresszió egy p- változós lineáris egyenletrendszer megoldása. Az egyenletrendszer
Gauss elimináció, LU felbontás
 Közelítő és szimbolikus számítások 3. gyakorlat Gauss elimináció, LU felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 EGYENLETRENDSZEREK 1. Egyenletrendszerek
Közelítő és szimbolikus számítások 3. gyakorlat Gauss elimináció, LU felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 EGYENLETRENDSZEREK 1. Egyenletrendszerek
Normák, kondíciószám
 Normák, kondíciószám A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris egyenletrendszerek Nagyon sok probléma közvetlenül lineáris egyenletrendszer megoldásával kezelhetı Sok numerikus
Normák, kondíciószám A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Lineáris egyenletrendszerek Nagyon sok probléma közvetlenül lineáris egyenletrendszer megoldásával kezelhetı Sok numerikus
1. előadás. Lineáris algebra numerikus módszerei. Hibaszámítás Számábrázolás Kerekítés, levágás Klasszikus hibaanalízis Abszolút hiba Relatív hiba
 Hibaforrások Hiba A feladatok megoldása során különféle hibaforrásokkal találkozunk: Modellhiba, amikor a valóságnak egy közelítését használjuk a feladat matematikai alakjának felírásához. (Pl. egy fizikai
Hibaforrások Hiba A feladatok megoldása során különféle hibaforrásokkal találkozunk: Modellhiba, amikor a valóságnak egy közelítését használjuk a feladat matematikai alakjának felírásához. (Pl. egy fizikai
Regresszió. Csorba János. Nagyméretű adathalmazok kezelése március 31.
 Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Nagyméretű adathalmazok kezelése (BMEVISZM144) Reinhardt Gábor április 5.
 Asszociációs szabályok Budapesti Műszaki- és Gazdaságtudományi Egyetem 2012. április 5. Tartalom 1 2 3 4 5 6 7 ismétlés A feladat Gyakran együtt vásárolt termékek meghatározása Tanultunk rá hatékony algoritmusokat
Asszociációs szabályok Budapesti Műszaki- és Gazdaságtudományi Egyetem 2012. április 5. Tartalom 1 2 3 4 5 6 7 ismétlés A feladat Gyakran együtt vásárolt termékek meghatározása Tanultunk rá hatékony algoritmusokat
PRÓBAÉRETTSÉGI MATEMATIKA. 2003. május-június KÖZÉPSZINT JAVÍTÁSI ÚTMUTATÓ. Vizsgafejlesztő Központ
 PRÓBAÉRETTSÉGI 00. május-június MATEMATIKA KÖZÉPSZINT JAVÍTÁSI ÚTMUTATÓ Vizsgafejlesztő Központ Kedves Kolléga! Kérjük, hogy a dolgozatok javítását a javítási útmutató alapján végezze, a következők figyelembevételével.
PRÓBAÉRETTSÉGI 00. május-június MATEMATIKA KÖZÉPSZINT JAVÍTÁSI ÚTMUTATÓ Vizsgafejlesztő Központ Kedves Kolléga! Kérjük, hogy a dolgozatok javítását a javítási útmutató alapján végezze, a következők figyelembevételével.
GPK M1 (BME) Interpoláció / 16
 Interpoláció Matematika M1 gépészmérnököknek 2017. március 13. GPK M1 (BME) Interpoláció 2017 1 / 16 Az interpoláció alapfeladata - Példa Tegyük fel, hogy egy ipari termék - pl. autó - előzetes konstrukciójának
Interpoláció Matematika M1 gépészmérnököknek 2017. március 13. GPK M1 (BME) Interpoláció 2017 1 / 16 Az interpoláció alapfeladata - Példa Tegyük fel, hogy egy ipari termék - pl. autó - előzetes konstrukciójának
Gauss-eliminációval, Cholesky felbontás, QR felbontás
 Közelítő és szimbolikus számítások 4. gyakorlat Mátrix invertálás Gauss-eliminációval, Cholesky felbontás, QR felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei
Közelítő és szimbolikus számítások 4. gyakorlat Mátrix invertálás Gauss-eliminációval, Cholesky felbontás, QR felbontás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei
First Prev Next Last Go Back Full Screen Close Quit
 Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás)
 Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén
 Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén Dombi József Szegedi Tudományegyetem Bevezetés - ID3 (Iterative Dichotomiser 3) Az ID algoritmusok egy elemhalmaz felhasználásával
Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén Dombi József Szegedi Tudományegyetem Bevezetés - ID3 (Iterative Dichotomiser 3) Az ID algoritmusok egy elemhalmaz felhasználásával
M. 33. Határozza meg az összes olyan kétjegyű szám összegét, amelyek 4-gyel osztva maradékul 3-at adnak!
 Magyar Ifjúság 6 V SOROZATOK a) Három szám összege 76 E három számot tekinthetjük egy mértani sorozat három egymás után következő elemének vagy pedig egy számtani sorozat első, negyedik és hatodik elemének
Magyar Ifjúság 6 V SOROZATOK a) Három szám összege 76 E három számot tekinthetjük egy mértani sorozat három egymás után következő elemének vagy pedig egy számtani sorozat első, negyedik és hatodik elemének
A lineáris programozás alapfeladata Standard alak Az LP feladat megoldása Az LP megoldása: a szimplex algoritmus 2018/
 Operációkutatás I. 2018/2019-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Operációkutatás I. 2018/2019-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Arany Dániel Matematikai Tanulóverseny 2008/2009-es tanév első (iskolai) forduló haladók II. kategória
 Bolyai János Matematikai Társulat Oktatási és Kulturális Minisztérium Támogatáskezelő Igazgatósága támogatásával Arany Dániel Matematikai Tanulóverseny 00/009-es tanév első (iskolai) forduló haladók II.
Bolyai János Matematikai Társulat Oktatási és Kulturális Minisztérium Támogatáskezelő Igazgatósága támogatásával Arany Dániel Matematikai Tanulóverseny 00/009-es tanév első (iskolai) forduló haladók II.
(Diszkrét idejű Markov-láncok állapotainak
 (Diszkrét idejű Markov-láncok állapotainak osztályozása) March 21, 2019 Markov-láncok A Markov-láncok anaĺızise főként a folyamat lehetséges realizációi valószínűségeinek kiszámolásával foglalkozik. Ezekben
(Diszkrét idejű Markov-láncok állapotainak osztályozása) March 21, 2019 Markov-láncok A Markov-láncok anaĺızise főként a folyamat lehetséges realizációi valószínűségeinek kiszámolásával foglalkozik. Ezekben
A lineáris programozás alapfeladata Standard alak Az LP feladat megoldása Az LP megoldása: a szimplex algoritmus 2017/
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
1. Gauss-eloszlás, természetes szórás
 1. Gauss-eloszlás, természetes szórás A Gauss-eloszlásnak megfelelő függvény: amely egy σ szélességű, µ középpontú, 1-re normált (azaz a teljes görbe alatti terület 1) görbét ír le. A természetben a centrális
1. Gauss-eloszlás, természetes szórás A Gauss-eloszlásnak megfelelő függvény: amely egy σ szélességű, µ középpontú, 1-re normált (azaz a teljes görbe alatti terület 1) görbét ír le. A természetben a centrális
Osztott algoritmusok
 Osztott algoritmusok A benzinkutas példa szimulációja Müller Csaba 2010. december 4. 1. Bevezetés Első lépésben talán kezdjük a probléma ismertetésével. Adott két n hosszúságú bináris sorozat (s 1, s 2
Osztott algoritmusok A benzinkutas példa szimulációja Müller Csaba 2010. december 4. 1. Bevezetés Első lépésben talán kezdjük a probléma ismertetésével. Adott két n hosszúságú bináris sorozat (s 1, s 2
Lineáris algebra 2. Filip Ferdinánd december 7. siva.banki.hu/jegyzetek
 Lineáris algebra 2 Filip Ferdinánd filipferdinand@bgkuni-obudahu sivabankihu/jegyzetek 2015 december 7 Filip Ferdinánd 2016 februar 9 Lineáris algebra 2 1 / 37 Az el adás vázlata Determináns Determináns
Lineáris algebra 2 Filip Ferdinánd filipferdinand@bgkuni-obudahu sivabankihu/jegyzetek 2015 december 7 Filip Ferdinánd 2016 februar 9 Lineáris algebra 2 1 / 37 Az el adás vázlata Determináns Determináns
Perszonalizált tartalomajánló szolgáltatás IPTV és OTT rendszerek számára
 MEDIANET 2015 Perszonalizált tartalomajánló szolgáltatás IPTV és OTT rendszerek számára ZIBRICZKY DÁVID ImpressTV david.zibriczky@impresstv.com Kulcsszavak: ajánlórendszer, IPTV, OTT, adatbányászat, gépi
MEDIANET 2015 Perszonalizált tartalomajánló szolgáltatás IPTV és OTT rendszerek számára ZIBRICZKY DÁVID ImpressTV david.zibriczky@impresstv.com Kulcsszavak: ajánlórendszer, IPTV, OTT, adatbányászat, gépi
Algoritmusok bonyolultsága
 Algoritmusok bonyolultsága 5. előadás http://www.ms.sapientia.ro/~kasa/komplex.htm 1 / 27 Gazdaságos faváz Kruskal-algoritmus Joseph Kruskal (1928 2010) Legyen V = {v 1, v 2,..., v n }, E = {e 1, e 2,...,
Algoritmusok bonyolultsága 5. előadás http://www.ms.sapientia.ro/~kasa/komplex.htm 1 / 27 Gazdaságos faváz Kruskal-algoritmus Joseph Kruskal (1928 2010) Legyen V = {v 1, v 2,..., v n }, E = {e 1, e 2,...,
Az Nkt. 65. változásai
 Az Nkt. 65. változásai 2017.09.01. 1.2* Szakál Ferenc Pál köznevelési szakértő *A korábbi változatokban ma már nem aktuális, nem érvényes tartalmak lehetnek, így azok tartalmáért e változat közzétételétől
Az Nkt. 65. változásai 2017.09.01. 1.2* Szakál Ferenc Pál köznevelési szakértő *A korábbi változatokban ma már nem aktuális, nem érvényes tartalmak lehetnek, így azok tartalmáért e változat közzétételétől
Mátrixok február Feladat: Legyen A = ( ( B =
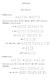 Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
A számítástudomány alapjai
 A számítástudomány alapjai Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem Legszélesebb utak Katona Gyula Y. (BME SZIT) A számítástudomány
A számítástudomány alapjai Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem Legszélesebb utak Katona Gyula Y. (BME SZIT) A számítástudomány
Vízügyeink az elmúlt évszázadoktól napjainkig
 Földrajzi Értesítő 2007. LVI. évf. 1 2. füzet, pp. 105 110. Vízügyeink az elmúlt évszázadoktól napjainkig Vágás István 1 Bevezető Egyes időszakokban szerettük magunkat hidrológiai nagyhatalomnak nevezni.
Földrajzi Értesítő 2007. LVI. évf. 1 2. füzet, pp. 105 110. Vízügyeink az elmúlt évszázadoktól napjainkig Vágás István 1 Bevezető Egyes időszakokban szerettük magunkat hidrológiai nagyhatalomnak nevezni.
Kétdimenziós mesterséges festési eljárások. Hatások és alkalmazások
 Pannon Egyetem Informatikai Tudományok Doktori Iskola Tézisfüzet Kétdimenziós mesterséges festési eljárások. Hatások és alkalmazások Kovács Levente Képfeldolgozás és Neuroszámítógépek Tanszék Témavezet
Pannon Egyetem Informatikai Tudományok Doktori Iskola Tézisfüzet Kétdimenziós mesterséges festési eljárások. Hatások és alkalmazások Kovács Levente Képfeldolgozás és Neuroszámítógépek Tanszék Témavezet
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
15. LINEÁRIS EGYENLETRENDSZEREK
 15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 3. MÉRÉSFELDOLGOZÁS
 ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 3. MÉRÉSFELDOLGOZÁS Dr. Soumelidis Alexandros 2018.10.04. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mérés-feldolgozás
ÉRZÉKELŐK ÉS BEAVATKOZÓK I. 3. MÉRÉSFELDOLGOZÁS Dr. Soumelidis Alexandros 2018.10.04. BME KÖZLEKEDÉSMÉRNÖKI ÉS JÁRMŰMÉRNÖKI KAR 32708-2/2017/INTFIN SZÁMÚ EMMI ÁLTAL TÁMOGATOTT TANANYAG Mérés-feldolgozás
Programozási módszertan. Dinamikus programozás: szerelőszalag ütemezése Mátrixok véges sorozatainak szorzása
 PM-06 p. 1/28 Programozási módszertan Dinamikus programozás: szerelőszalag ütemezése Mátrixok véges sorozatainak szorzása Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu
PM-06 p. 1/28 Programozási módszertan Dinamikus programozás: szerelőszalag ütemezése Mátrixok véges sorozatainak szorzása Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu
5. Előadás. (5. előadás) Mátrixegyenlet, Mátrix inverze március 6. 1 / 39
 5. Előadás (5. előadás) Mátrixegyenlet, Mátrix inverze 2019. március 6. 1 / 39 AX = B (5. előadás) Mátrixegyenlet, Mátrix inverze 2019. március 6. 2 / 39 AX = B Probléma. Legyen A (m n)-es és B (m l)-es
5. Előadás (5. előadás) Mátrixegyenlet, Mátrix inverze 2019. március 6. 1 / 39 AX = B (5. előadás) Mátrixegyenlet, Mátrix inverze 2019. március 6. 2 / 39 AX = B Probléma. Legyen A (m n)-es és B (m l)-es
bujdoso@inf.unideb.hu, http:www.inf.unideb.hu/~bujdoso 2 Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma, 4029 Debrecen, Csengı u. 4.
 Problémák a szövegszerkesztés verseny- és ECDL vizsgafeladataival kapcsolatban Problems in tests papers on word processing of ECDL exams and competitions BUJDOSÓ Gyöngyi 1, Ph.D., egyetemi adjunktus CSERNOCH
Problémák a szövegszerkesztés verseny- és ECDL vizsgafeladataival kapcsolatban Problems in tests papers on word processing of ECDL exams and competitions BUJDOSÓ Gyöngyi 1, Ph.D., egyetemi adjunktus CSERNOCH
2017, Diszkrét matematika
 Diszkrét matematika 10. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2017, őszi félév Miről volt szó az elmúlt előadáson? a prímszámtétel prímszámok,
Diszkrét matematika 10. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2017, őszi félév Miről volt szó az elmúlt előadáson? a prímszámtétel prímszámok,
Beton-nyomószilárdság értékelésének alulmaradási tényezője
 Beton-nyomószilárdság értékelésének alulmaradási tényezője Acceptance constant of concrete compressive strength evaluation Dr. KAUSAY Tibor okl. vasbetonépítési szakmérnök, címzetes egyetemi tanár Budapesti
Beton-nyomószilárdság értékelésének alulmaradási tényezője Acceptance constant of concrete compressive strength evaluation Dr. KAUSAY Tibor okl. vasbetonépítési szakmérnök, címzetes egyetemi tanár Budapesti
AKTUÁTOR MODELLEK KIVÁLASZTÁSA ÉS OBJEKTÍV ÖSSZEHASONLÍTÁSA
 AKTUÁTOR MODELLEK KIVÁLASZTÁSA ÉS OBJEKTÍV ÖSSZEHASONLÍTÁSA Kovács Ernő 1, Füvesi Viktor 2 1 Egyetemi docens, PhD; 2 tudományos segédmunkatárs 1 Eletrotechnikai és Elektronikai Tanszék, Miskolci Egyetem
AKTUÁTOR MODELLEK KIVÁLASZTÁSA ÉS OBJEKTÍV ÖSSZEHASONLÍTÁSA Kovács Ernő 1, Füvesi Viktor 2 1 Egyetemi docens, PhD; 2 tudományos segédmunkatárs 1 Eletrotechnikai és Elektronikai Tanszék, Miskolci Egyetem
INFORMATIKAI ALAPISMERETEK
 Informatikai alapismeretek középszint 0631 ÉRETTSÉGI VIZSGA 2006. október 24. INFORMATIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM
Informatikai alapismeretek középszint 0631 ÉRETTSÉGI VIZSGA 2006. október 24. INFORMATIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM
1. megold s: A keresett háromjegyű szám egyik számjegye a 3-as, a két ismeretlen számjegyet jelölje a és b. A feltétel szerint
 A 004{005. tan vi matematika OKTV I. kateg ria els (iskolai) fordul ja feladatainak megold sai 1. feladat Melyek azok a 10-es számrendszerbeli háromjegyű pozitív egész számok, amelyeknek számjegyei közül
A 004{005. tan vi matematika OKTV I. kateg ria els (iskolai) fordul ja feladatainak megold sai 1. feladat Melyek azok a 10-es számrendszerbeli háromjegyű pozitív egész számok, amelyeknek számjegyei közül
1. Determinánsok. Oldjuk meg az alábbi kétismeretlenes, két egyenletet tartalmaz lineáris egyenletrendszert:
 1 Determinánsok 1 Bevezet definíció Oldjuk meg az alábbi kétismeretlenes, két egyenletet tartalmaz lineáris egyenletrendszert: a 11 x 1 +a 12 x 2 = b 1 a 21 x 1 +a 22 x 2 = b 2 Szorozzuk meg az első egyenletet
1 Determinánsok 1 Bevezet definíció Oldjuk meg az alábbi kétismeretlenes, két egyenletet tartalmaz lineáris egyenletrendszert: a 11 x 1 +a 12 x 2 = b 1 a 21 x 1 +a 22 x 2 = b 2 Szorozzuk meg az első egyenletet
Módszertani megjegyzés: A kikötés az osztás műveletéhez kötődik. A jobb megértés miatt célszerű egy-két példát mu-
 . modul: ELSŐFOKÚ TÖRTES EGYENLETEK A következő órákon olyan egyenletekkel foglalkozunk, amelyek nevezőjében ismeretlen található. Ha a tört nevezőjében ismeretlen van, akkor kikötést kell tennünk: az
. modul: ELSŐFOKÚ TÖRTES EGYENLETEK A következő órákon olyan egyenletekkel foglalkozunk, amelyek nevezőjében ismeretlen található. Ha a tört nevezőjében ismeretlen van, akkor kikötést kell tennünk: az
43. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ HATODIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ
 43. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ HATODIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ 1. Ismerkedj a 100 tulajdonságaival! I.) Állítsd elő a 100-at a,, b, 3, c, 4, d, 5 négyzetszám összegeként!
43. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ HATODIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ 1. Ismerkedj a 100 tulajdonságaival! I.) Állítsd elő a 100-at a,, b, 3, c, 4, d, 5 négyzetszám összegeként!
LINEÁRIS ALGEBRA PÉLDATÁR MÉRNÖK INFORMATIKUSOKNAK
 Írta: LEITOLD ADRIEN LINEÁRIS ALGEBRA PÉLDATÁR MÉRNÖK INFORMATIKUSOKNAK Egyetemi tananyag COPYRIGHT: Dr. Leitold Adrien Pannon Egyetem Műszaki Informatika Kar Matematika Tanszék LEKTORÁLTA: Dr. Buzáné
Írta: LEITOLD ADRIEN LINEÁRIS ALGEBRA PÉLDATÁR MÉRNÖK INFORMATIKUSOKNAK Egyetemi tananyag COPYRIGHT: Dr. Leitold Adrien Pannon Egyetem Műszaki Informatika Kar Matematika Tanszék LEKTORÁLTA: Dr. Buzáné
Felvételi tematika INFORMATIKA
 Felvételi tematika INFORMATIKA 2016 FEJEZETEK 1. Természetes számok feldolgozása számjegyenként. 2. Számsorozatok feldolgozása elemenként. Egydimenziós tömbök. 3. Mátrixok feldolgozása elemenként/soronként/oszloponként.
Felvételi tematika INFORMATIKA 2016 FEJEZETEK 1. Természetes számok feldolgozása számjegyenként. 2. Számsorozatok feldolgozása elemenként. Egydimenziós tömbök. 3. Mátrixok feldolgozása elemenként/soronként/oszloponként.
3. Előadás. Megyesi László: Lineáris algebra, oldal. 3. előadás Lineáris egyenletrendszerek
 3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
Bozóki Sándor. MTA SZTAKI, Budapesti Corvinus Egyetem. Vitaliy Tsyganok
 A feszítőfákból számolt súlyvektorok mértani közepének optimalitása a logaritmikus legkisebb négyzetes célfüggvényre nézve Bozóki Sándor MTA SZTAKI, Budapesti Corvinus Egyetem Vitaliy Tsyganok Laboratory
A feszítőfákból számolt súlyvektorok mértani közepének optimalitása a logaritmikus legkisebb négyzetes célfüggvényre nézve Bozóki Sándor MTA SZTAKI, Budapesti Corvinus Egyetem Vitaliy Tsyganok Laboratory
2. előadás. Lineáris algebra numerikus módszerei. Mátrixok Mátrixműveletek Speciális mátrixok, vektorok Norma
 Mátrixok Definíció Az m n típusú (méretű) valós A mátrixon valós a ij számok alábbi táblázatát értjük: a 11 a 12... a 1j... a 1n.......... A = a i1 a i2... a ij... a in........... a m1 a m2... a mj...
Mátrixok Definíció Az m n típusú (méretű) valós A mátrixon valós a ij számok alábbi táblázatát értjük: a 11 a 12... a 1j... a 1n.......... A = a i1 a i2... a ij... a in........... a m1 a m2... a mj...
4. Fuzzy relációk. Gépi intelligencia I. Fodor János NIMGI1MIEM BMF NIK IMRI
 4. Fuzzy relációk Gépi intelligencia I. Fodor János BMF NIK IMRI NIMGI1MIEM Tartalomjegyzék I 1 Klasszikus relációk Halmazok Descartes-szorzata Relációk 2 Fuzzy relációk Fuzzy relációk véges alaphalmazok
4. Fuzzy relációk Gépi intelligencia I. Fodor János BMF NIK IMRI NIMGI1MIEM Tartalomjegyzék I 1 Klasszikus relációk Halmazok Descartes-szorzata Relációk 2 Fuzzy relációk Fuzzy relációk véges alaphalmazok
TECHNIKAI RENDSZEREK ÁLLAPOTLEÍRÁSÁNAK KÉRDÉSEI QUESTIONS REGARDING THE DESCRIPTION OF THE STATE OF TECHNICAL SYSTEMS
 űszaki tudományos közlemények 2. XV. űszaki Tudományos Ülésszak, 2014. Kolozsvár, 235 241. http://hdl.handle.net/10598/28544 TCHNIKAI RNDSZRK ÁLLAPOTLÍRÁSÁNAK KÉRDÉSI QUSTIONS RGARDING TH DSCRIPTION OF
űszaki tudományos közlemények 2. XV. űszaki Tudományos Ülésszak, 2014. Kolozsvár, 235 241. http://hdl.handle.net/10598/28544 TCHNIKAI RNDSZRK ÁLLAPOTLÍRÁSÁNAK KÉRDÉSI QUSTIONS RGARDING TH DSCRIPTION OF
6. Függvények. 1. Az alábbi függvények közül melyik szigorúan monoton növekvő a 0;1 intervallumban?
 6. Függvények I. Nulladik ZH-ban láttuk: 1. Az alábbi függvények közül melyik szigorúan monoton növekvő a 0;1 intervallumban? f x g x cos x h x x ( ) sin x (A) Az f és a h. (B) Mindhárom. (C) Csak az f.
6. Függvények I. Nulladik ZH-ban láttuk: 1. Az alábbi függvények közül melyik szigorúan monoton növekvő a 0;1 intervallumban? f x g x cos x h x x ( ) sin x (A) Az f és a h. (B) Mindhárom. (C) Csak az f.
Csima Judit november 15.
 Adatbáziskezelés Normalizálás Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2017. november 15. Csima Judit Adatbáziskezelés Normalizálás 1 / 26 Normalizálás Tétel Tetszõleges (R,
Adatbáziskezelés Normalizálás Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2017. november 15. Csima Judit Adatbáziskezelés Normalizálás 1 / 26 Normalizálás Tétel Tetszõleges (R,
Diszkrét matematika I., 12. előadás Dr. Takách Géza NyME FMK Informatikai Intézet takach november 30.
 1 Diszkrét matematika I, 12 előadás Dr Takách Géza NyME FMK Informatikai Intézet takach@infnymehu http://infnymehu/ takach 2005 november 30 Vektorok Definíció Egy tetszőleges n pozitív egész számra n-komponensű
1 Diszkrét matematika I, 12 előadás Dr Takách Géza NyME FMK Informatikai Intézet takach@infnymehu http://infnymehu/ takach 2005 november 30 Vektorok Definíció Egy tetszőleges n pozitív egész számra n-komponensű
Feladat: megoldani az alábbi egyenletrendszert: A x = b,
 Gauss Jordan-elimináció Feladat: megoldani az alábbi egyenletrendszert: ahol A négyzetes mátrix. A x = b, A Gauss Jordan-elimináció tulajdonképpen az általános iskolában tanult módszer lineáris egyenletrendszerek
Gauss Jordan-elimináció Feladat: megoldani az alábbi egyenletrendszert: ahol A négyzetes mátrix. A x = b, A Gauss Jordan-elimináció tulajdonképpen az általános iskolában tanult módszer lineáris egyenletrendszerek
VI. Magyar Földrajzi Konferencia 524-529
 Van Leeuwen Boudewijn Tobak Zalán Szatmári József 1 BELVÍZ OSZTÁLYOZÁS HAGYOMÁNYOS MÓDSZERREL ÉS MESTERSÉGES NEURÁLIS HÁLÓVAL BEVEZETÉS Magyarország, különösen pedig az Alföld váltakozva szenved aszályos
Van Leeuwen Boudewijn Tobak Zalán Szatmári József 1 BELVÍZ OSZTÁLYOZÁS HAGYOMÁNYOS MÓDSZERREL ÉS MESTERSÉGES NEURÁLIS HÁLÓVAL BEVEZETÉS Magyarország, különösen pedig az Alföld váltakozva szenved aszályos
Arany Dániel Matematikai Tanulóverseny 2014/2015-ös tanév első (iskolai) forduló Haladók II. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 01/01-ös tanév első iskolai) forduló Haladók II. kategória Megoldások és javítási útmutató 1. Adott az alábbi két egyenletrendszer:
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 01/01-ös tanév első iskolai) forduló Haladók II. kategória Megoldások és javítási útmutató 1. Adott az alábbi két egyenletrendszer:
Lineáris algebra (10A103)
 Lineáris algebra (10A103) Dr. Hartmann Miklós Tudnivalók Honlap: http://www.math.u-szeged.hu/~hartm Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli, feltétele a Lineáris algebra gyakorlat teljesítése.
Lineáris algebra (10A103) Dr. Hartmann Miklós Tudnivalók Honlap: http://www.math.u-szeged.hu/~hartm Jegyzet: Megyesi László: Lineáris algebra. Vizsga: írásbeli, feltétele a Lineáris algebra gyakorlat teljesítése.
7. gyakorlat. Lineáris algebrai egyenletrendszerek megoldhatósága
 7. gyakorlat Lineáris algebrai egyenletrendszerek megoldhatósága Egy lineáris algebrai egyenletrendszerrel kapcsolatban a következ kérdések merülnek fel: 1. Létezik-e megoldása? 2. Ha igen, hány megoldása
7. gyakorlat Lineáris algebrai egyenletrendszerek megoldhatósága Egy lineáris algebrai egyenletrendszerrel kapcsolatban a következ kérdések merülnek fel: 1. Létezik-e megoldása? 2. Ha igen, hány megoldása
Determinánsok. A determináns fogalma olyan algebrai segédeszköz, amellyel. szolgáltat az előbbi kérdésekre, bár ez nem mindig hatékony.
 Determinánsok A determináns fogalma olyan algebrai segédeszköz, amellyel jól jellemezhető a mátrixok invertálhatósága, a mátrix rangja. Segítségével lineáris egyenletrendszerek megoldhatósága dönthető
Determinánsok A determináns fogalma olyan algebrai segédeszköz, amellyel jól jellemezhető a mátrixok invertálhatósága, a mátrix rangja. Segítségével lineáris egyenletrendszerek megoldhatósága dönthető
1. Ábrázolja az f(x)= x-4 függvényt a [ 2;10 ] intervallumon! (2 pont) 2. Írja fel az alábbi lineáris függvény grafikonjának egyenletét!
![1. Ábrázolja az f(x)= x-4 függvényt a [ 2;10 ] intervallumon! (2 pont) 2. Írja fel az alábbi lineáris függvény grafikonjának egyenletét! 1. Ábrázolja az f(x)= x-4 függvényt a [ 2;10 ] intervallumon! (2 pont) 2. Írja fel az alábbi lineáris függvény grafikonjának egyenletét!](/thumbs/54/33263341.jpg) Függvények 1 1. Ábrázolja az f()= -4 függvényt a [ ;10 ] intervallumon!. Írja fel az alábbi lineáris függvény grafikonjának egyenletét! 3. Ábrázolja + 1 - függvényt a [ ;] -on! 4. Az f függvényt a valós
Függvények 1 1. Ábrázolja az f()= -4 függvényt a [ ;10 ] intervallumon!. Írja fel az alábbi lineáris függvény grafikonjának egyenletét! 3. Ábrázolja + 1 - függvényt a [ ;] -on! 4. Az f függvényt a valós
Egy forgáskúp metszéséről. Egy forgáskúpot az 1. ábra szerint helyeztünk el egy ( OXYZ ) derékszögű koordináta - rendszerben.
 Egy forgáskúp metszéséről Egy forgáskúpot az 1. ábra szerint helyeztünk el egy ( OXYZ ) derékszögű koordináta - rendszerben. Az O csúcsú, O tengelyű, γ félnyílásszögű kúpot az ( XY ) sík itt két alkotóban
Egy forgáskúp metszéséről Egy forgáskúpot az 1. ábra szerint helyeztünk el egy ( OXYZ ) derékszögű koordináta - rendszerben. Az O csúcsú, O tengelyű, γ félnyílásszögű kúpot az ( XY ) sík itt két alkotóban
Gépi tanulás. Hány tanítómintára van szükség? VKH. Pataki Béla (Bolgár Bence)
 Gépi tanulás Hány tanítómintára van szükség? VKH Pataki Béla (Bolgár Bence) BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Induktív tanulás A tanítás folyamata: Kiinduló
Gépi tanulás Hány tanítómintára van szükség? VKH Pataki Béla (Bolgár Bence) BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Induktív tanulás A tanítás folyamata: Kiinduló
11. Előadás. 11. előadás Bevezetés a lineáris programozásba
 11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
VENDÉGLÁTÓIPARI ISMERETEK ÁGAZATI SZAKMAI ÉRETTSÉGI VIZSGA II. A VIZSGA LEÍRÁSA
 VENDÉGLÁTÓIPARI ISMERETEK ÁGAZATI SZAKMAI ÉRETTSÉGI VIZSGA II. A VIZSGA LEÍRÁSA A vizsga részei Középszint Emelt szint 120 perc 15 perc 180 perc 20 perc 100 pont 50 pont 100 pont 50 pont A vizsgán használható
VENDÉGLÁTÓIPARI ISMERETEK ÁGAZATI SZAKMAI ÉRETTSÉGI VIZSGA II. A VIZSGA LEÍRÁSA A vizsga részei Középszint Emelt szint 120 perc 15 perc 180 perc 20 perc 100 pont 50 pont 100 pont 50 pont A vizsgán használható
Numerikus matematika vizsga
 1. Az a = 2, t = 4, k = 3, k + = 2 számábrázolási jellemzők mellett hány pozitív, normalizált lebegőpontos szám ábrázolható? Adja meg a legnagyobb ábrázolható számot! Mi lesz a 0.8-hoz rendelt lebegőpontos
1. Az a = 2, t = 4, k = 3, k + = 2 számábrázolási jellemzők mellett hány pozitív, normalizált lebegőpontos szám ábrázolható? Adja meg a legnagyobb ábrázolható számot! Mi lesz a 0.8-hoz rendelt lebegőpontos
Matematikai geodéziai számítások 8.
 Matematikai geodéziai számítások 8 Szintezési hálózat kiegyenlítése Dr Bácsatyai, László Matematikai geodéziai számítások 8: Szintezési hálózat kiegyenlítése Dr Bácsatyai, László Lektor: Dr Benedek, Judit
Matematikai geodéziai számítások 8 Szintezési hálózat kiegyenlítése Dr Bácsatyai, László Matematikai geodéziai számítások 8: Szintezési hálózat kiegyenlítése Dr Bácsatyai, László Lektor: Dr Benedek, Judit
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 4 IV. MINTA, ALAPsTATIsZTIKÁK 1. MATEMATIKAI statisztika A matematikai statisztika alapfeladatát nagy általánosságban a következőképpen
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x
Egy geometriai szélsőérték - feladat
 1 Egy geometriai szélsőérték - feladat A feladat: Szerkesztendő egy olyan legnagyobb területű háromszög, melynek egyik csúcsa az a és b féltengelyeivel adott ellipszis tetszőlegesen felvett pontja. Keresendő
1 Egy geometriai szélsőérték - feladat A feladat: Szerkesztendő egy olyan legnagyobb területű háromszög, melynek egyik csúcsa az a és b féltengelyeivel adott ellipszis tetszőlegesen felvett pontja. Keresendő
Az éghajlati modellek eredményeinek alkalmazhatósága hatásvizsgálatokban
 Az éghajlati modellek eredményeinek alkalmazhatósága hatásvizsgálatokban Szépszó Gabriella Országos Meteorológiai Szolgálat, szepszo.g@met.hu RCMTéR hatásvizsgálói konzultációs workshop 2015. június 23.
Az éghajlati modellek eredményeinek alkalmazhatósága hatásvizsgálatokban Szépszó Gabriella Országos Meteorológiai Szolgálat, szepszo.g@met.hu RCMTéR hatásvizsgálói konzultációs workshop 2015. június 23.
 1 2 3 4 5 Meta adat: bármilyen adat, ami a tartalomhoz kapcsolódik. Pl. filmek esetén a rendező, a főszereplő, a műfaj. Tranzakciós adat: felhasználó és az elemek közötti interakció során keletkező adat.
1 2 3 4 5 Meta adat: bármilyen adat, ami a tartalomhoz kapcsolódik. Pl. filmek esetén a rendező, a főszereplő, a műfaj. Tranzakciós adat: felhasználó és az elemek közötti interakció során keletkező adat.
Nemzetközi számvitel. 12. Előadás. IAS 8 Számviteli politika, a számviteli becslések változásai és hibák. Dr. Pál Tibor
 Dr. Pál Tibor Nemzetközi számvitel 12. Előadás IAS 8 Számviteli politika, a számviteli becslések változásai és hibák 2014.05.13. IAS 8 Bevételek 2 Az IAS 8 célja A fejezet célja, hogy bemutassa Hogyan
Dr. Pál Tibor Nemzetközi számvitel 12. Előadás IAS 8 Számviteli politika, a számviteli becslések változásai és hibák 2014.05.13. IAS 8 Bevételek 2 Az IAS 8 célja A fejezet célja, hogy bemutassa Hogyan
MATE-INFO UBB verseny, március 25. MATEMATIKA írásbeli vizsga
 BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR MATE-INFO UBB verseny, 218. március 25. MATEMATIKA írásbeli vizsga FONTOS TUDNIVALÓK: 1 A feleletválasztós feladatok,,a rész esetén
BABEŞ-BOLYAI TUDOMÁNYEGYETEM, KOLOZSVÁR MATEMATIKA ÉS INFORMATIKA KAR MATE-INFO UBB verseny, 218. március 25. MATEMATIKA írásbeli vizsga FONTOS TUDNIVALÓK: 1 A feleletválasztós feladatok,,a rész esetén
Lineáris algebra (10A103)
 Lineáris algebra (10A103) Kátai-Urbán Kamilla (1. előadás) Mátrixok 2019. február 6. 1 / 35 Bevezetés Előadás Tudnivalók (I.) Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Az előadáson készített
Lineáris algebra (10A103) Kátai-Urbán Kamilla (1. előadás) Mátrixok 2019. február 6. 1 / 35 Bevezetés Előadás Tudnivalók (I.) Honlap: http://www.math.u-szeged.hu/~katai Jegyzet: Az előadáson készített
FPI matek szakkör 8. évf. 4. szakkör órai feladatok megoldásokkal. 4. szakkör, október. 20. Az órai feladatok megoldása
 4. szakkör, 2004. október. 20. Az órai feladatok megoldása Most csak három önmagában nem nehéz feladatot kapsz, és a feladatot magadnak kell általánosítani, szisztematikusan adatot gyűjteni, általános
4. szakkör, 2004. október. 20. Az órai feladatok megoldása Most csak három önmagában nem nehéz feladatot kapsz, és a feladatot magadnak kell általánosítani, szisztematikusan adatot gyűjteni, általános
3. Fuzzy aritmetika. Gépi intelligencia I. Fodor János NIMGI1MIEM BMF NIK IMRI
 3. Fuzzy aritmetika Gépi intelligencia I. Fodor János BMF NIK IMRI NIMGI1MIEM Tartalomjegyzék I 1 Intervallum-aritmetika 2 Fuzzy intervallumok és fuzzy számok Fuzzy intervallumok LR fuzzy intervallumok
3. Fuzzy aritmetika Gépi intelligencia I. Fodor János BMF NIK IMRI NIMGI1MIEM Tartalomjegyzék I 1 Intervallum-aritmetika 2 Fuzzy intervallumok és fuzzy számok Fuzzy intervallumok LR fuzzy intervallumok
KÖZGAZDASÁGI ALAPISMERETEK (ELMÉLETI GAZDASÁGTAN)
 Közgazdasági alapismeretek (elméleti gazdaságtan) emelt szint 1421 ÉRETTSÉGI VIZSGA 2015. október 12. KÖZGAZDASÁGI ALAPISMERETEK (ELMÉLETI GAZDASÁGTAN) EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI
Közgazdasági alapismeretek (elméleti gazdaságtan) emelt szint 1421 ÉRETTSÉGI VIZSGA 2015. október 12. KÖZGAZDASÁGI ALAPISMERETEK (ELMÉLETI GAZDASÁGTAN) EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI
Varga Tamás Matematikaverseny Javítási útmutató Iskolai forduló 2016/ osztály
 1. Az erdészet dolgozói pályázaton nyert facsemetékkel ültetnek be egy adott területet. Ha 450-et ültetnének hektáronként, akkor 380 facsemete kimaradna. Ha 640 facsemetével többet nyertek volna, akkor
1. Az erdészet dolgozói pályázaton nyert facsemetékkel ültetnek be egy adott területet. Ha 450-et ültetnének hektáronként, akkor 380 facsemete kimaradna. Ha 640 facsemetével többet nyertek volna, akkor
Megoldások IV. osztály
 Bolyai Farkas Elméleti Líceum Marosvásárhely, 2015. március 20-22. Megoldások IV. osztály 1. Számkeresztrejtvény: Az alábbi keresztrejtvény ábra abban különbözik a hagyományos keresztrejtvényektől, hogy
Bolyai Farkas Elméleti Líceum Marosvásárhely, 2015. március 20-22. Megoldások IV. osztály 1. Számkeresztrejtvény: Az alábbi keresztrejtvény ábra abban különbözik a hagyományos keresztrejtvényektől, hogy
A VDA6.3 tervezett változásai 2016
 A VDA6.3 tervezett változásai 2016 Bevezetés A VDA6.3 kézikönyv, mint a VDA6-os kötetcsoport egyik tagja, a folyamatauditok végrehajtását szabályozza. A VDA6.3-at először 1998-ban adták ki, első módosítása
A VDA6.3 tervezett változásai 2016 Bevezetés A VDA6.3 kézikönyv, mint a VDA6-os kötetcsoport egyik tagja, a folyamatauditok végrehajtását szabályozza. A VDA6.3-at először 1998-ban adták ki, első módosítása
Gráfok 2. Legrövidebb utak, feszítőfák. Szoftvertervezés és -fejlesztés II. előadás. Szénási Sándor
 Gráfok 2. Legrövidebb utak, feszítőfák előadás http://nik.uni-obuda.hu/sztf2 Szénási Sándor Óbudai Egyetem,Neumann János Informatikai Kar Legrövidebb utak keresése Minimális feszítőfa keresése Gráfok 2
Gráfok 2. Legrövidebb utak, feszítőfák előadás http://nik.uni-obuda.hu/sztf2 Szénási Sándor Óbudai Egyetem,Neumann János Informatikai Kar Legrövidebb utak keresése Minimális feszítőfa keresése Gráfok 2
VÉKONYLEMEZEK ELLENÁLLÁS-PONTKÖTÉSEINEK MINŐSÉGCENTRIKUS OPTIMALIZÁLÁSA
 MISKOLCI EGYETEM GÉPÉSZMÉRNÖKI KAR VÉKONYLEMEZEK ELLENÁLLÁS-PONTKÖTÉSEINEK MINŐSÉGCENTRIKUS OPTIMALIZÁLÁSA PhD ÉRTEKEZÉS TÉZISEI KÉSZÍTETTE: SZABÓ PÉTER OKLEVELES GÉPÉSZMÉRNÖK, EWE GÉPÉSZMÉRNÖKI TUDOMÁNYOK
MISKOLCI EGYETEM GÉPÉSZMÉRNÖKI KAR VÉKONYLEMEZEK ELLENÁLLÁS-PONTKÖTÉSEINEK MINŐSÉGCENTRIKUS OPTIMALIZÁLÁSA PhD ÉRTEKEZÉS TÉZISEI KÉSZÍTETTE: SZABÓ PÉTER OKLEVELES GÉPÉSZMÉRNÖK, EWE GÉPÉSZMÉRNÖKI TUDOMÁNYOK
1. Jelölje meg az összes igaz állítást a következők közül!
 1. Jelölje meg az összes igaz állítást a következők közül! a) A while ciklusban a feltétel teljesülése esetén végrehajtódik a ciklusmag. b) A do while ciklusban a ciklusmag után egy kilépési feltétel van.
1. Jelölje meg az összes igaz állítást a következők közül! a) A while ciklusban a feltétel teljesülése esetén végrehajtódik a ciklusmag. b) A do while ciklusban a ciklusmag után egy kilépési feltétel van.
A SZEMCSEALAK ALAPJÁN TÖRTÉNŐ SZÉTVÁLASZTÁS JELENTŐSÉGE FÉMTARTALMÚ HULLADÉKOK FELDOLGOZÁSA SORÁN
 Műszaki Földtudományi Közlemények, 83. kötet, 1. szám (2012), pp. 61 70. A SZEMCSEALAK ALAPJÁN TÖRTÉNŐ SZÉTVÁLASZTÁS JELENTŐSÉGE FÉMTARTALMÚ HULLADÉKOK FELDOLGOZÁSA SORÁN SIGNIFICANCE OF SHAPE SEPARATION
Műszaki Földtudományi Közlemények, 83. kötet, 1. szám (2012), pp. 61 70. A SZEMCSEALAK ALAPJÁN TÖRTÉNŐ SZÉTVÁLASZTÁS JELENTŐSÉGE FÉMTARTALMÚ HULLADÉKOK FELDOLGOZÁSA SORÁN SIGNIFICANCE OF SHAPE SEPARATION
A feladatok részletezése az egyidejűleg megküldött ajánlattételi dokumentációban található. IV. szakasz: Eljárás IV.
 14. melléklet a 44/2015. (XI. 2.) MvM rendelethez KÖZBESZERZÉSI ADATBÁZIS I. szakasz: Ajánlatkérő I.1) Név és címek 1 (jelölje meg az eljárásért felelős összes ajánlatkérőt) Hivatalos név: Óbudai Parkolási
14. melléklet a 44/2015. (XI. 2.) MvM rendelethez KÖZBESZERZÉSI ADATBÁZIS I. szakasz: Ajánlatkérő I.1) Név és címek 1 (jelölje meg az eljárásért felelős összes ajánlatkérőt) Hivatalos név: Óbudai Parkolási
Ahol a kvantum mechanika és az Internet találkozik
 Ahol a kvantum mechanika és az Internet találkozik Imre Sándor BME Híradástechnikai Tanszék Imre Sándor "The fastest algorithm can frequently be replaced by one that is almost as fast and much easier to
Ahol a kvantum mechanika és az Internet találkozik Imre Sándor BME Híradástechnikai Tanszék Imre Sándor "The fastest algorithm can frequently be replaced by one that is almost as fast and much easier to
