PISA2003. Nyilvánosságra hozott feladatok természettudományból
|
|
|
- Marika Dobos
- 6 évvel ezelőtt
- Látták:
Átírás
1 PISA2003 Nyilvánosságra hozott feladatok természettudományból
2 Tartalom 3 A nappalok hossza 8 Klónozás
3 A nappalok hossza S129 A NAPPALOK HOSSZA Olvasd el a szöveget, majd válaszolj az azt követő kérdésekre! A NAPPAL HOSSZA JÚNIUS 22-N Míg az északi félteke lakói ma a leghosszabb napjukat ünneplik, addig Ausztráliában ma lesz az év legrövidebb nappala. Melbourne*-ben 7 óra 36-kor kel és 17 óra 08-kor nyugszik le a Nap, tehát kilenc óra 32 percen át nyújt világosságot. Hasonlítsuk össze a mai napot az év leghosszabb napjával a déli féltekén, mely december 22-én esedékes. Ekkor a Nap 5 óra 55-kor kel és 20 óra 42- kor nyugszik le, tehát 14 óra 47 percen át lesz világos. A Csillagász Társaság elnöke, Perry Vlahos elmagyarázta, hogy az északi és a déli félteke évszakainak váltakozása a Föld 23 fokos dőlésszögével van összefüggésben. * Melbourne Ausztrália egyik városa az től délre, megközelítőleg a 38. szélességi fokon. 1. kérdés: A nappalok hossza S129Q01 Melyik állítás magyarázza meg azt, hogy miért van nappal és sötétség a Földön? A B C A Föld a saját e körül forog. A Nap a saját e körül forog. A Föld e dőlt. A Föld a Nap körül kering. Kódolás Teljes értékű válasz 1-es kód: A Rossz válasz 0-s kód: Más válaszok. 9-es kód: Nincs válasz. A nappalok hossza 3
4 2. kérdés: A nappalok hossza S129Q02 Az ábrán látható, hogyan világítják meg a Napból kiinduló sugarak a Földet. Föld Napból érkező fény Ábra: A Napból jövő fénysugarak Tegyük fel, hogy ma van Melbourne-ben az év legrövidebb napja. Rajzold meg az ábrán a Föld ét, az északi és a déli féltekéket, valamint az t! Mindegyik mellé írd oda a nevét is! 4 A nappalok hossza
5 Kódolás Megjegyzés: a feladat kódolásánál a következőket kell figyelembe venni: 1. A Föld ének a rajza a Nap felé dől a függőlegeshez képest os szögtartományban, az alábbi ábra szerint. 10 O 23 O TENGELYNEK ELFOGAHATÓ 45 O A függőlegeshez képest os szögtartományon kívül eső megoldás rossz válasznak minősül. 2. Az északi és déli félteke egyértelmű felcímkézésének megléte vagy hiánya, vagy az egyik félteke felcímkézett, a másik pedig egyértelműen adódik. 3. Az rajza a vízszinteshez képest os szögben dől a Nap felé a következő ábra szerint: Az rajza lehet ellipszis vagy egy egyenes. EGYENLÍTŐNEK ELFOGAHATÓ 23 O 45 O 10 O A vízszinteshez képest os szögtartományon kívül eső megoldás rossz válasznak minősül. A nappalok hossza 5
6 Teljes értékű válasz 21-es kód: Az vonalának a rajza a vízszinteshez képest os szögben dől a Nap felé, a Föld e a függőlegeshez képest os szögben dől a Nap felé, az északi és a déli félteke megfelelő címkékkel van ellátva (vagy az egyik félteke fel van címkézve, a másik egyértelműen adódik). T Részlegesen jó válasz 11-es kód: A dőlésszöge 10 és 45 között van, az északi és/vagy a déli félteke megfelelő címkékkel van ellátva (vagy az egyik félteke fel van címkézve, a másik egyértelműen adódik), de az dőlésszöge nem 10 és 45 közé esik, vagy hiányzik. 12-es kód: Az dőlésszöge 10 és 45 között van, az északi és/vagy a déli félteke megfelelően jelölt (vagy az egyik félteke jelölt, a másik egyértelműen adódik), de a dőlésszöge nem 10 és 45 közé esik, vagy hiányzik. 6 A nappalok hossza
7 04-es kód: Egyik szempontnak sem felel meg vagy más válaszok. 99-es kód: Nincs válasz. Vissza a Tartalomhoz A nappalok hossza 7
8 Klónozás S128 KLÓNOZÁS Olvasd el az alábbi újságcikket, és válaszolj az azt követő kérdésekre! Semmi kétség: ha az 1997-es évben megrendezték volna Az év állata választást, olly lett volna a győztes! olly az a skót juh, akit a fotón láttok. Ám 5 olly nem egy hétköznapi birka. Ő egy másik birka klónja. A klón azt jelenti: másolat. A klónozás pedig nem más, mint másolatokat készíteni az egyetlen, eredeti példányból. A kutatóknak sikerült egy 10 olyan juhot (ollyt) létrehozniuk, amelyik mindenben hasonló az eredeti példány - ul szolgáló birkához. Egy skót kutató, Ian Wilmut volt az, aki megtervezte a juhokat másoló 15 berendezést. Egy felnőtt birka (birka 1) emlőjéből kivett egy parányi részt. Ebből a lőlényeket másoló gép? darabkából kivont egy sejtmagot, amit azután átültetett egy másik (nőstény) birka (birka 2) petesejtjébe. Ebből a petéből 20 előzetesen már eltávolított minden olyan alkotóelemet, amely a birka 2 leendő jellemvonásait hordozta volna abban a bárányban. Végül Wilmut ezt a manipulált petesejtet beültette egy harmadik (nőstény) 25 birkába (birka 3), amely így vemhes lett, majd világra hozott egy kisbárányt: ollyt. Egyes tudósok úgy gondolják, hogy néhány év múlva lehetőség lesz majd arra is, hogy emberi lényeket klónozzanak. 30 ppen ezért számos kormány úgy döntött, hogy törvényben tiltja meg emberek klónozását. 8 Klónozás
9 1. kérdés: Klónozás S128Q01 olly melyik birkával azonos? A Az 1-es birkával. B A 2-es birkával. C A 3-as birkával. olly apjával. Kódolás Teljes értékű válasz 1-es kód: A Rossz válasz 0-s kód: Más válaszok. 9-es kód: Nincs válasz. 2. kérdés: Klónozás S128Q02 A 16. sor a felhasznált emlőrészt parányi rész -nek nevezi. A cikk tartalmából kiderül, hogy valójában mit is jelent ez. A parányi rész A egy sejt. B egy gén. C egy sejt magja. egy kromoszóma. Kódolás Teljes értékű válasz 1-es kód: A Rossz válasz 0-s kód: Más válaszok. 9-es kód: Nincs válasz. Klónozás 9
10 3. kérdés: Klónozás S128Q03 A cikk utolsó mondatából megtudjuk, hogy számos kormány úgy döntött, hogy törvényben tiltja meg emberek klónozását. Az alábbi táblázat ennek két lehetséges indokát említi. Van tudományos alapjuk ezeknek az érveknek? Az Igen, illetve a Nem bekarikázásával válaszolhatsz. Okok A klónozott személyek bizonyos betegségekre érzékenyebbek lennének, mint a normális emberek. Az embernek nem lenne szabad átvenie a Teremtő szerepét. Tudományos? Igen / nem Igen / nem Kódolás Teljes értékű válasz 1-es kód: Két helyes válasz: Igen, Nem, ebben a sorrendben. Rossz válasz 0-s kód: Más válaszok. 9-es kód: Nincs válasz. Vissza a Tartalomhoz 10 Klónozás
A NAPPALOK HOSSZA A NAPPAL HOSSZA JÚNIUS 22-ÉN. Olvasd el a szöveget, majd válaszolj az azt követ kérdésekre!
 A NAPPALOK HOSSZA Olvasd el a szöveget, majd válaszolj az azt követ kérdésekre! A NAPPAL HOSSZA 2002. JÚNIUS 22-N Míg az északi félteke lakói ma a leghosszabb napjukat ünneplik, addig Ausztráliában ma
A NAPPALOK HOSSZA Olvasd el a szöveget, majd válaszolj az azt követ kérdésekre! A NAPPAL HOSSZA 2002. JÚNIUS 22-N Míg az északi félteke lakói ma a leghosszabb napjukat ünneplik, addig Ausztráliában ma
PISA2000. Nyilvánosságra hozott feladatok matematikából
 PISA2000 Nyilvánosságra hozott feladatok matematikából Tartalom Tartalom 3 Almafák 8 Földrész területe 12 Háromszögek 14 Házak 16 Versenyautó sebessége Almafák M136 ALMAFÁK Egy gazda kertjében négyzetrács
PISA2000 Nyilvánosságra hozott feladatok matematikából Tartalom Tartalom 3 Almafák 8 Földrész területe 12 Háromszögek 14 Házak 16 Versenyautó sebessége Almafák M136 ALMAFÁK Egy gazda kertjében négyzetrács
Tamás Ferenc: Nevezetes szögek szögfüggvényei
 Tamás Ferenc: Nevezetes szögek szögfüggvényei A derékszögű háromszögekben könnyedén fel lehet írni a nevezetes szögek szögfüggvényeit. Megjegyezni viszont nem feltétlenül könnyű! Erre van egy könnyen megjegyezhető
Tamás Ferenc: Nevezetes szögek szögfüggvényei A derékszögű háromszögekben könnyedén fel lehet írni a nevezetes szögek szögfüggvényeit. Megjegyezni viszont nem feltétlenül könnyű! Erre van egy könnyen megjegyezhető
Nyári napfordulón csillagászati mérések KDG labor
 Nyári napfordulón csillagászati mérések KDG labor Nyári napforduló az a pillanat, amikor a Föld forgástengelye a legkisebb szögben hajlik el a Nap sugaraitól. Az északi féltekén a nyári napfordulóig a
Nyári napfordulón csillagászati mérések KDG labor Nyári napforduló az a pillanat, amikor a Föld forgástengelye a legkisebb szögben hajlik el a Nap sugaraitól. Az északi féltekén a nyári napfordulóig a
Természetismereti- és környezetvédelmi vetélkedő
 Miskolc - Szirmai Református Általános Iskola, Alapfokú Művészeti Iskola és Óvoda OM 201802 e-mail: refiskola.szirma@gmail.com 3521 Miskolc, Miskolci u. 38/a. Telefon: 46/405-124; Fax: 46/525-232 Versenyző
Miskolc - Szirmai Református Általános Iskola, Alapfokú Művészeti Iskola és Óvoda OM 201802 e-mail: refiskola.szirma@gmail.com 3521 Miskolc, Miskolci u. 38/a. Telefon: 46/405-124; Fax: 46/525-232 Versenyző
ELEKTROMOSSÁG ÉS MÁGNESESSÉG
 ELEKTROMOSSÁG ÉS MÁGNESESSÉG A) változat Név:... osztály:... 1. Milyen töltésű a proton? 2. Egészítsd ki a következő mondatot! Az azonos elektromos töltések... egymást. 3. A PVC-rudat megdörzsöltük egy
ELEKTROMOSSÁG ÉS MÁGNESESSÉG A) változat Név:... osztály:... 1. Milyen töltésű a proton? 2. Egészítsd ki a következő mondatot! Az azonos elektromos töltések... egymást. 3. A PVC-rudat megdörzsöltük egy
SZKA_106_21. Utazás a világ körül Tudósítások a világból
 SZKA_106_21 Utazás a világ körül Tudósítások a világból szka106_01_d.indd 127 2007.10.16. 21:51:19 szka106_01_d.indd 128 2007.10.16. 21:51:19 tanulói utazás a világ körül 6. évfolyam 129 21/1 A kontinensek
SZKA_106_21 Utazás a világ körül Tudósítások a világból szka106_01_d.indd 127 2007.10.16. 21:51:19 szka106_01_d.indd 128 2007.10.16. 21:51:19 tanulói utazás a világ körül 6. évfolyam 129 21/1 A kontinensek
Természetismereti- és környezetvédelmi vetélkedő
 Miskolc - Szirmai Református Általános Iskola, Alapfokú Művészeti Iskola és Óvoda OM 201802 e-mail: refiskola.szirma@gmail.com 3521 Miskolc, Miskolci u. 38/a. Telefon: 46/405-124; Fax: 46/525-232 Versenyző
Miskolc - Szirmai Református Általános Iskola, Alapfokú Művészeti Iskola és Óvoda OM 201802 e-mail: refiskola.szirma@gmail.com 3521 Miskolc, Miskolci u. 38/a. Telefon: 46/405-124; Fax: 46/525-232 Versenyző
PISA2006. Nyilvánosságra hozott feladatok matematikából
 PISA2006 Nyilvánosságra hozott feladatok matematikából Tartalom Tartalom 3 Autózás 5 Füzetkészítés 7 Kerékpárok 10 Nézd a tornyot 12 Testmagasság Autózás M302 AUTÓZÁS Kati autózni ment. Útközben egy macska
PISA2006 Nyilvánosságra hozott feladatok matematikából Tartalom Tartalom 3 Autózás 5 Füzetkészítés 7 Kerékpárok 10 Nézd a tornyot 12 Testmagasság Autózás M302 AUTÓZÁS Kati autózni ment. Útközben egy macska
1.Háromszög szerkesztése három oldalból
 1 Szerkessz háromszöget, ha három oldala: a=3 cm b=4 cm c=5 cm 1.Háromszög szerkesztése három oldalból (Ugye tudod, hogy az a oldallal szemben A csúcs, b oldallal szemben B stb. van!) (homorú, hegyes,
1 Szerkessz háromszöget, ha három oldala: a=3 cm b=4 cm c=5 cm 1.Háromszög szerkesztése három oldalból (Ugye tudod, hogy az a oldallal szemben A csúcs, b oldallal szemben B stb. van!) (homorú, hegyes,
MATEMATIKAI KOMPETENCIATERÜLET A
 MATEMATIKAI KOMPETENCIATERÜLET A Matematika 6. évfolyam TANULÓI MUNKAFÜZET 2. FÉLÉV A kiadvány KHF/4356-14/2008. engedélyszámon 2008.11.25. időponttól tankönyvi engedélyt kapott Educatio Kht. Kompetenciafejlesztő
MATEMATIKAI KOMPETENCIATERÜLET A Matematika 6. évfolyam TANULÓI MUNKAFÜZET 2. FÉLÉV A kiadvány KHF/4356-14/2008. engedélyszámon 2008.11.25. időponttól tankönyvi engedélyt kapott Educatio Kht. Kompetenciafejlesztő
Harmadikos vizsga Név: osztály:
 . a) b) c) Számítsd ki az alábbi kifejezések pontos értékét! log 6 log log 49 4 7 d) log log 6 log 8 feladat pontszáma: p. Döntsd el az alábbi öt állítás mindegyikéről, hogy igaz vagy hamis! A pontozott
. a) b) c) Számítsd ki az alábbi kifejezések pontos értékét! log 6 log log 49 4 7 d) log log 6 log 8 feladat pontszáma: p. Döntsd el az alábbi öt állítás mindegyikéről, hogy igaz vagy hamis! A pontozott
1. csoport. Hónap I. II. III. IV. V. VI. VII. VIII. IX. X. XI. XII. Havi középhőmérséklet ( C) Havi csapadékmennyiség (mm)
 1. csoport 2. Vizsgáld meg a táblázatban lévő hőmérsékleti és csapadékértékeket! Végezd el a számításokat és válaszolj a kérdésekre! Hónap I. II. III. IV. V. VI. VII. VIII. IX. X. XI. XII. Havi középhőmérséklet
1. csoport 2. Vizsgáld meg a táblázatban lévő hőmérsékleti és csapadékértékeket! Végezd el a számításokat és válaszolj a kérdésekre! Hónap I. II. III. IV. V. VI. VII. VIII. IX. X. XI. XII. Havi középhőmérséklet
1. ábra Tükrös visszaverődés 2. ábra Szórt visszaverődés 3. ábra Gombostű kísérlet
 A kísérlet célkitűzései: A fény visszaverődésének kísérleti vizsgálata, a fényvisszaverődés törvényének megismerése, síktükrök képalkotásának vizsgálata. Eszközszükséglet: szivacslap A/4 írólap vonalzó,
A kísérlet célkitűzései: A fény visszaverődésének kísérleti vizsgálata, a fényvisszaverődés törvényének megismerése, síktükrök képalkotásának vizsgálata. Eszközszükséglet: szivacslap A/4 írólap vonalzó,
Csivitelő (2. osztály)
 Olvasórally 2-3. oldalhoz Csivitelő (2. osztály) 2-3. oldalhoz 1. Olvasd el az újság 2. és 3. oldalán található szövegeket, verseket! Keresd meg, mely dátumhoz mi tartozik, kösd össze! Kisboldogasszony
Olvasórally 2-3. oldalhoz Csivitelő (2. osztály) 2-3. oldalhoz 1. Olvasd el az újság 2. és 3. oldalán található szövegeket, verseket! Keresd meg, mely dátumhoz mi tartozik, kösd össze! Kisboldogasszony
NULLADIK MATEMATIKA szeptember 13.
 A NULLADIK MATEMATIKA ZÁRTHELYI 0. szeptember. Terem: Munkaidő: 0 perc. A dolgozat megírásához íróeszközön kívül semmilyen segédeszköz nem használható nálható. Válaszait csak az üres mezőkbe írja! A javítók
A NULLADIK MATEMATIKA ZÁRTHELYI 0. szeptember. Terem: Munkaidő: 0 perc. A dolgozat megírásához íróeszközön kívül semmilyen segédeszköz nem használható nálható. Válaszait csak az üres mezőkbe írja! A javítók
Koordináta-geometria. Fogalom. Jelölés. Tulajdonságok, definíciók
 Koordináta-geometria Fogalom Ezen a helyen találkozik össze a számtan és a mértan. Körök, egyenesek, háromszögek és más egyéb alakzatok, de nem szerkesztenünk kell, vagy méricskélni, hanem számolni, viszont
Koordináta-geometria Fogalom Ezen a helyen találkozik össze a számtan és a mértan. Körök, egyenesek, háromszögek és más egyéb alakzatok, de nem szerkesztenünk kell, vagy méricskélni, hanem számolni, viszont
5. Egy 21 méter magas épület emelkedési szögben látszik. A teodolit magassága 1,6 m. Milyen messze van tőlünk az épület?
 Gyakorlás 1. Az út emelkedésének nevezzük annak a szögnek a tangensét, amelyet az út a vízszintessel bezár. Ezt általában %-ban adják meg. (100 %-os emelkedésű a vízszintessel 1 tangensű szöget bezáró
Gyakorlás 1. Az út emelkedésének nevezzük annak a szögnek a tangensét, amelyet az út a vízszintessel bezár. Ezt általában %-ban adják meg. (100 %-os emelkedésű a vízszintessel 1 tangensű szöget bezáró
Gyakorlati tudnivalók a jelzőlámpás forgalomirányítás tervezésével kapcsolatban. 2013. szeptember. Dr. Kálmán László
 Gyakorlati tudnivalók a jelzőlámpás forgalomirányítás tervezésével kapcsolatban 2013. szeptember Dr. Kálmán László 4. A fázisidő terv készítésének lépései A fázissorrendek felvétele valamint a jármű
Gyakorlati tudnivalók a jelzőlámpás forgalomirányítás tervezésével kapcsolatban 2013. szeptember Dr. Kálmán László 4. A fázisidő terv készítésének lépései A fázissorrendek felvétele valamint a jármű
ÚJ LAKÁSBAN. Kedves Csilla!
 ÚJ LAKÁSBAN Kedves Csilla! Képzeld el! Új lakásban lakom! Ez a legszebb ház a környéken! Egy mesés társasházban, gyönyörű lakásban élek! Képzeld el! Van benne egy csendes hálószoba, világos nappali szoba,
ÚJ LAKÁSBAN Kedves Csilla! Képzeld el! Új lakásban lakom! Ez a legszebb ház a környéken! Egy mesés társasházban, gyönyörű lakásban élek! Képzeld el! Van benne egy csendes hálószoba, világos nappali szoba,
+ 3 5 2 3 : 1 4 : 1 1 A ) B ) C ) D ) 93
 . Mennyi az alábbi művelet eredménye? 4 + 4 : 5 : 5 + 8 07 9 A ) B ) C ) D ) E ) 9 9 9 9 9. Egy digitális órát (amely 4 órás üzemmódban működik) pontosan beállítottunk. Kiderült azonban, hogy egy nap átlagosan
. Mennyi az alábbi művelet eredménye? 4 + 4 : 5 : 5 + 8 07 9 A ) B ) C ) D ) E ) 9 9 9 9 9. Egy digitális órát (amely 4 órás üzemmódban működik) pontosan beállítottunk. Kiderült azonban, hogy egy nap átlagosan
1. Mennyi a dobókockák nem látható lapjain levő pontok ( számok ) összege? A ) 14 B ) 20 C ) 21 D ) 24
 . Mennyi a dobókockák nem látható lapjain levő pontok ( számok ) összege? A ) 4 B ) 20 C ) 2 D ) 24 2. Mennyi az alábbi művelet eredménye? 2 + 2 =? 5 6 A ) B ) C ) D ) 0. Egy könyvszekrénynek három polca
. Mennyi a dobókockák nem látható lapjain levő pontok ( számok ) összege? A ) 4 B ) 20 C ) 2 D ) 24 2. Mennyi az alábbi művelet eredménye? 2 + 2 =? 5 6 A ) B ) C ) D ) 0. Egy könyvszekrénynek három polca
pont százalék % érdemjegy (jeles) (jó) (közepes) (elégséges) alatt 1 (elégtelen
 A dolgozat feladatai az órán megoldott feladatok valamelyike, vagy ahhoz nagyon hasonló. A dolgozat 8 feladatból áll. 1. feladat 13 pont. feladat 8 pont 3. feladat 4. feladat 5. feladat 5 pont 6. feladat
A dolgozat feladatai az órán megoldott feladatok valamelyike, vagy ahhoz nagyon hasonló. A dolgozat 8 feladatból áll. 1. feladat 13 pont. feladat 8 pont 3. feladat 4. feladat 5. feladat 5 pont 6. feladat
Feladatok a MATEMATIKA. standardleírás 2. szintjéhez
 Feladatok a MATEMATIKA standardleírás 2. szintjéhez A feladat sorszáma: 1. Standardszint: 2. Gondolkodási és megismerési módszerek Halmazok Képes különböző elemek közös tulajdonságainak felismerésére.
Feladatok a MATEMATIKA standardleírás 2. szintjéhez A feladat sorszáma: 1. Standardszint: 2. Gondolkodási és megismerési módszerek Halmazok Képes különböző elemek közös tulajdonságainak felismerésére.
3. tétel Térelemek távolsága és szöge. Nevezetes ponthalmazok a síkon és a térben.
 3. tétel Térelemek távolsága és szöge. Nevezetes ponthalmazok a síkon és a térben. TÁVOLSÁG Általános definíció: két alakzat távolsága a két alakzat pontjai között húzható legrövidebb szakasz hosszaa távolság
3. tétel Térelemek távolsága és szöge. Nevezetes ponthalmazok a síkon és a térben. TÁVOLSÁG Általános definíció: két alakzat távolsága a két alakzat pontjai között húzható legrövidebb szakasz hosszaa távolság
Az elforgatott ellipszisbe írható legnagyobb területű téglalapról
 1 Az elforgatott ellipszisbe írható legnagyobb területű téglalapról Előző dolgozatunkban melynek címe: Az ellipszisbe írható legnagyobb területű négyszögről már beharangoztuk, hogy találtunk valami érdekeset
1 Az elforgatott ellipszisbe írható legnagyobb területű téglalapról Előző dolgozatunkban melynek címe: Az ellipszisbe írható legnagyobb területű négyszögről már beharangoztuk, hogy találtunk valami érdekeset
XLII. Országos Komplex Tanulmányi Verseny Megyei forduló. Matematika
 7. Matematika Az emberek csak azért gondolják, hogy a matematika nehéz, mert még nem döbbentek rá, hogy az élet maga milyen bonyolult. (Neumann János) 2017. április 04. Készítette: Szafiánné Csécsei Tímea,
7. Matematika Az emberek csak azért gondolják, hogy a matematika nehéz, mert még nem döbbentek rá, hogy az élet maga milyen bonyolult. (Neumann János) 2017. április 04. Készítette: Szafiánné Csécsei Tímea,
Tavasz van, kikelet. Olvasószint: A. Megoldások:
 Az Olvass magyarul! kiskönyvsorozat azoknak a tengeren túl élő magyar gyerekeknek készül, akik az angol mellett magyarul is tanulnak írni és olvasni. Természetesen a világ bármely részén élő magyar gyermekeknek
Az Olvass magyarul! kiskönyvsorozat azoknak a tengeren túl élő magyar gyerekeknek készül, akik az angol mellett magyarul is tanulnak írni és olvasni. Természetesen a világ bármely részén élő magyar gyermekeknek
ÉLÔ ÉS ÉLETTELEN KÖRNYEZETEM
 Tompáné Balogh Mária ÉLÔ ÉS ÉLETTELEN KÖRNYEZETEM A fák birodalma Környezetismeret TÉMAZÁRÓ FELADATLAPOK éves tanulók részére 0. kiadás Évfolyam 0... A tanuló neve pauz westermann kiadó ÔSZ A PARKBAN A.
Tompáné Balogh Mária ÉLÔ ÉS ÉLETTELEN KÖRNYEZETEM A fák birodalma Környezetismeret TÉMAZÁRÓ FELADATLAPOK éves tanulók részére 0. kiadás Évfolyam 0... A tanuló neve pauz westermann kiadó ÔSZ A PARKBAN A.
FAIPARI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2006. május 18. FAIPARI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2006. május 18. 14:00 I. Időtartam: 120 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI MINISZTÉRIUM Faipari alapismeretek
ÉRETTSÉGI VIZSGA 2006. május 18. FAIPARI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2006. május 18. 14:00 I. Időtartam: 120 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI MINISZTÉRIUM Faipari alapismeretek
Borbély Sándor Országos Tanulmányi Verseny. Vác Matematika. 5. osztály. Név: Iskola:
 Borbély Sándor Országos Tanulmányi Verseny Vác 201 Matematika 5. osztály Név: Iskola: 1. Pótold a hiányzó számokat! A Fővárosi Állat- és Növénykert története: 1. -ban nyílt meg. 2. -ban érkezett az első
Borbély Sándor Országos Tanulmányi Verseny Vác 201 Matematika 5. osztály Név: Iskola: 1. Pótold a hiányzó számokat! A Fővárosi Állat- és Növénykert története: 1. -ban nyílt meg. 2. -ban érkezett az első
A loxodrómáról. Előző írásunkban melynek címe: A Gudermann - függvényről szó esett a Mercator - vetületről,illetve az ezen alapuló térképről 1. ábra.
 1 A loxodrómáról Előző írásunkban melynek címe: A Gudermann - függvényről szó esett a Mercator - vetületről,illetve az ezen alapuló térképről 1. ábra. 1. ábra forrása: [ 1 ] Ezen a térképen a szélességi
1 A loxodrómáról Előző írásunkban melynek címe: A Gudermann - függvényről szó esett a Mercator - vetületről,illetve az ezen alapuló térképről 1. ábra. 1. ábra forrása: [ 1 ] Ezen a térképen a szélességi
1. TÁJÉKOZÓDÁS A SAKKTÁBLÁN 1
 TÁJÉKOZÓDÁS A SAKKTÁBLÁN Egy híres sakkozó nevét kapod, ha jó úton jársz. Írd át színessel a név betûit! P O V G P O L G J Á R D U J T U T D I I T 2. Moziba mentek a bábok. Nézz körül a nézôtéren, és válaszolj
TÁJÉKOZÓDÁS A SAKKTÁBLÁN Egy híres sakkozó nevét kapod, ha jó úton jársz. Írd át színessel a név betûit! P O V G P O L G J Á R D U J T U T D I I T 2. Moziba mentek a bábok. Nézz körül a nézôtéren, és válaszolj
Érettségi feladatok: Síkgeometria 1/6
 Érettségi feladatok: Síkgeometria 1/6 2005. május 10. 4. Döntse el, hogy a következő állítások közül melyik igaz és melyik hamis! A: A háromszög köré írható kör középpontja mindig valamelyik súlyvonalra
Érettségi feladatok: Síkgeometria 1/6 2005. május 10. 4. Döntse el, hogy a következő állítások közül melyik igaz és melyik hamis! A: A háromszög köré írható kör középpontja mindig valamelyik súlyvonalra
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2007. május 25. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI
ÉRETTSÉGI VIZSGA 2007. május 25. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI
MATEMATIKA HETI 5 ÓRA
 EURÓPAI ÉRETTSÉGI 2008 MATEMATIKA HETI 5 ÓRA IDŐPONT : 2008. június 5 (reggel) A VIZSGA IDŐTARTAMA: 4 óra (240 perc) MEGENGEDETT ESZKÖZÖK: Európai képletgyűjtemény Nem programozható, nem grafikus számológép
EURÓPAI ÉRETTSÉGI 2008 MATEMATIKA HETI 5 ÓRA IDŐPONT : 2008. június 5 (reggel) A VIZSGA IDŐTARTAMA: 4 óra (240 perc) MEGENGEDETT ESZKÖZÖK: Európai képletgyűjtemény Nem programozható, nem grafikus számológép
OPTIKA. Gömbtükrök képalkotása, leképezési hibák. Dr. Seres István
 OPTIKA Gömbtükrök képalkotása, Dr. Seres István Tükrök http://www.mozaik.info.hu/mozaweb/feny/fy_ft11.htm Seres István 2 http://fft.szie.hu Gömbtükrök Domború tükör képalkotása Jellegzetes sugármenetek
OPTIKA Gömbtükrök képalkotása, Dr. Seres István Tükrök http://www.mozaik.info.hu/mozaweb/feny/fy_ft11.htm Seres István 2 http://fft.szie.hu Gömbtükrök Domború tükör képalkotása Jellegzetes sugármenetek
Egybevágósági transzformációk
 Egybevágósági transzformációk Párhuzamos eltolás Geometriai transzformációk Egybevágósági transzformációk (9. osztály) Helybenhagyás Tengelyes tükrözés Középpontos tükrözés Pont körüli forgatás Párhuzamos
Egybevágósági transzformációk Párhuzamos eltolás Geometriai transzformációk Egybevágósági transzformációk (9. osztály) Helybenhagyás Tengelyes tükrözés Középpontos tükrözés Pont körüli forgatás Párhuzamos
58. ročník Fyzikálnej olympiády v školskom roku 2016/2017 Okresné kolo kategórie E Texty úloh v maďarskom jazyku
 58. ročník Fyzikálnej olympiády v školskom roku 2016/2017 Okresné kolo kategórie E Texty úloh v maďarskom jazyku Megjegyzés a feladatok megoldásához: A feladatok szövegezésében használjuk a vektor kifejezést,
58. ročník Fyzikálnej olympiády v školskom roku 2016/2017 Okresné kolo kategórie E Texty úloh v maďarskom jazyku Megjegyzés a feladatok megoldásához: A feladatok szövegezésében használjuk a vektor kifejezést,
VOLT EGYSZER, LESZ EGYSZER (Was Albert nyomán)
 VOLT EGYSZER, LESZ EGYSZER (Was Albert nyomán)... Minden esztendőnek a vége felé az Úristen emlékeztetni akarja az embereket arra, hogy a gonoszság útja hova vezet, s ezért ősszel a napok rövidülni kezdenek,
VOLT EGYSZER, LESZ EGYSZER (Was Albert nyomán)... Minden esztendőnek a vége felé az Úristen emlékeztetni akarja az embereket arra, hogy a gonoszság útja hova vezet, s ezért ősszel a napok rövidülni kezdenek,
Az idő története múzeumpedagógiai foglalkozás
 Az idő története múzeumpedagógiai foglalkozás 2. Ismerkedés a napórával FELADATLAP A az egyik legősibb időmérő eszköz, amelynek elve azon a megfigyelésen alapszik, hogy az egyes testek árnyékának hossza
Az idő története múzeumpedagógiai foglalkozás 2. Ismerkedés a napórával FELADATLAP A az egyik legősibb időmérő eszköz, amelynek elve azon a megfigyelésen alapszik, hogy az egyes testek árnyékának hossza
Lencse típusok Sík domború 2x Homorúan domború Síkhomorú 2x homorú domb. Homorú
 Jegyzeteim 1. lap Fotó elmélet 2015. október 9. 14:42 Lencse típusok Sík domború 2x Homorúan domború Síkhomorú 2x homorú domb. Homorú Kardinális elemek A lencse képalkotását meghatározó geometriai elemek,
Jegyzeteim 1. lap Fotó elmélet 2015. október 9. 14:42 Lencse típusok Sík domború 2x Homorúan domború Síkhomorú 2x homorú domb. Homorú Kardinális elemek A lencse képalkotását meghatározó geometriai elemek,
Csuklós szerkezetek reakciói és igénybevételi ábrái. Frissítve: példa: A 12. gyakorlat 1. feladata.
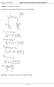 1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
Arany Dániel Matematikai Tanulóverseny 2016/2017-es tanév Kezdők III. kategória I. forduló
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 016/017-es tanév Kezdők I II. kategória II. forduló Kezdők III. kategória I. forduló Megoldások és javítási útmutató 1. Egy kört
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 016/017-es tanév Kezdők I II. kategória II. forduló Kezdők III. kategória I. forduló Megoldások és javítási útmutató 1. Egy kört
9. Jelzőlámpás csomópontok forgalomszabályozása
 9. JELZŐLÁMPÁS CSOMÓPONTOK FORGALOMSZABÁLYOZÁSA...1 9.1. ALAPFOGALMAK...1 9.1.1. Elnevezések...1 9.1.2. A forgalomirányítással összefüggő alapfogalmak...2 9.1.3. Működtetési módok...3 9.2. JELZŐLÁMPÁS
9. JELZŐLÁMPÁS CSOMÓPONTOK FORGALOMSZABÁLYOZÁSA...1 9.1. ALAPFOGALMAK...1 9.1.1. Elnevezések...1 9.1.2. A forgalomirányítással összefüggő alapfogalmak...2 9.1.3. Működtetési módok...3 9.2. JELZŐLÁMPÁS
2004_02/10 Egy derékszögű trapéz alapjainak hossza a, illetve 2a. A rövidebb szára szintén a, a hosszabb b hosszúságú.
 Geometria háromszögek, négyszögek 2004_01/10 Az ABC háromszög C csúcsánál derékszög van. A derékszöget a CT és CD szakaszok három egyenlő részre osztják. A CT szakasz a háromszög egyik magassága is egyben.
Geometria háromszögek, négyszögek 2004_01/10 Az ABC háromszög C csúcsánál derékszög van. A derékszöget a CT és CD szakaszok három egyenlő részre osztják. A CT szakasz a háromszög egyik magassága is egyben.
Aszimmetrikus nyeregtető ~ feladat 2.
 1 Aszimmetrikus nyeregtető ~ feladat 2. Ehhez tekintsük az 1. ábrát is! Itt az A és B pontok egy nyeregtető oromfali ereszpontjai, a P pont pedig a taréj pontja. Az ereszek egymástól való távolságának
1 Aszimmetrikus nyeregtető ~ feladat 2. Ehhez tekintsük az 1. ábrát is! Itt az A és B pontok egy nyeregtető oromfali ereszpontjai, a P pont pedig a taréj pontja. Az ereszek egymástól való távolságának
3. Vertikális napóra szerkesztése (2009. September 11., Friday) - Szerzõ: Ponori Thewrewk Aurél
 3. Vertikális napóra szerkesztése (2009. September 11., Friday) - Szerzõ: Ponori Thewrewk Aurél A cikk két olyan eljárást mutat be, amely a függõleges napórák elkészítésében nyújt segítséget. A fal tájolásának
3. Vertikális napóra szerkesztése (2009. September 11., Friday) - Szerzõ: Ponori Thewrewk Aurél A cikk két olyan eljárást mutat be, amely a függõleges napórák elkészítésében nyújt segítséget. A fal tájolásának
Egy tételr½ol, melyet Dürer majdnem megtalált
 Haladvány Kiadvány 2017.03.26 Egy tételr½ol, melyet Dürer majdnem megtalált Hujter Mihály hujter.misi@gmail.com A német reneszánsz legfontosabb alakjaként ismert Albrecht Dürer. Mivel apja (id½osebb Albrecht
Haladvány Kiadvány 2017.03.26 Egy tételr½ol, melyet Dürer majdnem megtalált Hujter Mihály hujter.misi@gmail.com A német reneszánsz legfontosabb alakjaként ismert Albrecht Dürer. Mivel apja (id½osebb Albrecht
Matematikai geodéziai számítások 2.
 Matematikai geodéziai számítások 2. Geodéziai vonal és ábrázolása gömbön és vetületben Dr. Bácsatyai, László Matematikai geodéziai számítások 2.: Geodéziai vonal és ábrázolása Dr. Bácsatyai, László Lektor:
Matematikai geodéziai számítások 2. Geodéziai vonal és ábrázolása gömbön és vetületben Dr. Bácsatyai, László Matematikai geodéziai számítások 2.: Geodéziai vonal és ábrázolása Dr. Bácsatyai, László Lektor:
VI. Földi János országos természettudományi verseny III. FORDULÓ - beküldési határidő: február 28.
 VI. Földi János országos természettudományi verseny III. FORDULÓ - beküldési határidő: 2019. február 28. Az I. korcsoport (3. és 4. évfolyam) feladatai: 1.9. feladat Készítsd el az ábrán látható mérleget
VI. Földi János országos természettudományi verseny III. FORDULÓ - beküldési határidő: 2019. február 28. Az I. korcsoport (3. és 4. évfolyam) feladatai: 1.9. feladat Készítsd el az ábrán látható mérleget
Koordinátageometria. M veletek vektorokkal grakusan. Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1
 Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1 Koordinátageometria M veletek vektorokkal grakusan 1. Az ABCD négyzet oldalvektorai közül a = AB és b = BC. Adja meg az AC és BD vektorokat a
Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1 Koordinátageometria M veletek vektorokkal grakusan 1. Az ABCD négyzet oldalvektorai közül a = AB és b = BC. Adja meg az AC és BD vektorokat a
Lehet hogy igaz, de nem biztos. Biztosan igaz. Lehetetlen. A paralelogrammának van szimmetria-középpontja. b) A trapéznak két szimmetriatengelye van.
 Geometria, sokszögek, szögek, -, 2004_01/5 Lili rajzolt néhány síkidomot: egy háromszöget, egy deltoidot, egy paralelogrammát és egy trapézt. A következő állítások ezekre vonatkoznak. Tegyél * jelet a
Geometria, sokszögek, szögek, -, 2004_01/5 Lili rajzolt néhány síkidomot: egy háromszöget, egy deltoidot, egy paralelogrammát és egy trapézt. A következő állítások ezekre vonatkoznak. Tegyél * jelet a
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Síkgeometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Síkgeometria 1) Döntse el, hogy a következő állítások közül melyik igaz és melyik hamis! a) A háromszög köré írható kör középpontja mindig valamelyik súlyvonalra
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Síkgeometria 1) Döntse el, hogy a következő állítások közül melyik igaz és melyik hamis! a) A háromszög köré írható kör középpontja mindig valamelyik súlyvonalra
NAPÓRA ÉS IRÁNYTŰ - KÉSZLET Winkler - Nr
 NPÓR ÉS IRÁNYTŰ - KÉSZLET Winkler - Nr. 102099 Bevezetés: föld minden helyéről nézve a nap mozog kelettől (napfelkelte) nyugatig (naplemente). Tulajdonképpen a föld 365 nap alatt fordul meg a nap körül.
NPÓR ÉS IRÁNYTŰ - KÉSZLET Winkler - Nr. 102099 Bevezetés: föld minden helyéről nézve a nap mozog kelettől (napfelkelte) nyugatig (naplemente). Tulajdonképpen a föld 365 nap alatt fordul meg a nap körül.
Fedélszerkezet kivitelezése
 Fedélszerkezet kivitelezése Összeállította: Kreinbacher Imre Nemes András - 1 - Fedélszerkezeti elemek gyártás előkészítése Fedélszerkezet kivitelezésének feltétele, hogy a fed élszerkezet alkotó elemeit
Fedélszerkezet kivitelezése Összeállította: Kreinbacher Imre Nemes András - 1 - Fedélszerkezeti elemek gyártás előkészítése Fedélszerkezet kivitelezésének feltétele, hogy a fed élszerkezet alkotó elemeit
Matematikai geodéziai számítások 10.
 Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Szög. A Wikipédiából, a szabad enciklopédiából:
 Szög A Wikipédiából, a szabad enciklopédiából: http://hu.wikipedia.org/wiki/szög A sík egy pontjából kiinduló két félegyenes a síkot két tartományra osztja. Az egyik tartomány és a két félegyenes szöget
Szög A Wikipédiából, a szabad enciklopédiából: http://hu.wikipedia.org/wiki/szög A sík egy pontjából kiinduló két félegyenes a síkot két tartományra osztja. Az egyik tartomány és a két félegyenes szöget
A kromoszómák kialakulása előtt a DNS állomány megkettőződik. A két azonos információ tartalmú DNS egymás mellé rendeződik és egy kromoszómát alkot.
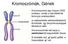 Kromoszómák, Gének A kromoszóma egy hosszú DNS szakasz, amely a sejt életének bizonyos szakaszában (a sejtosztódás előkészítéseként) tömörödik, így fénymikroszkóppal láthatóvá válik. A kromoszómák két
Kromoszómák, Gének A kromoszóma egy hosszú DNS szakasz, amely a sejt életének bizonyos szakaszában (a sejtosztódás előkészítéseként) tömörödik, így fénymikroszkóppal láthatóvá válik. A kromoszómák két
Feladatgyűjtemény matematikából
 Feladatgyűjtemény matematikából 1. Pótold a számok között a hiányzó jelet: 123: 6 a 45:9.10 2. Melyik az a kifejezés, amelyik 2c-7 tel nagyobb, mint a 3c+7 kifejezés? 3. Határozd meg azt a legnagyobb természetes
Feladatgyűjtemény matematikából 1. Pótold a számok között a hiányzó jelet: 123: 6 a 45:9.10 2. Melyik az a kifejezés, amelyik 2c-7 tel nagyobb, mint a 3c+7 kifejezés? 3. Határozd meg azt a legnagyobb természetes
Mechatronika segédlet 3. gyakorlat
 Mechatronika segédlet 3. gyakorlat 2017. február 20. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 2 Fogaskerék... 2 Nézetváltás 3D modellezéshez... 2 Könnyítés megvalósítása... 2 A fogaskerék
Mechatronika segédlet 3. gyakorlat 2017. február 20. Tartalom Vadai Gergely, Faragó Dénes Feladatleírás... 2 Fogaskerék... 2 Nézetváltás 3D modellezéshez... 2 Könnyítés megvalósítása... 2 A fogaskerék
x 2 3 y 5 6 x + y 7 9
 Táblázat készítése Táblázat: tabular a tabular első paraméterében meghatározzuk, hogy a táblázat oszlopai hogyan helyezkednek el a cellájukon belül. c: középen; l: balra zárva; r: jobbra zárva stb. Közéjük
Táblázat készítése Táblázat: tabular a tabular első paraméterében meghatározzuk, hogy a táblázat oszlopai hogyan helyezkednek el a cellájukon belül. c: középen; l: balra zárva; r: jobbra zárva stb. Közéjük
FOGALOMTÁR 9. évfolyam I. témakör A Föld és kozmikus környezete
 FOGALOMTÁR 9. évfolyam I. témakör A Föld és kozmikus környezete csillag: csillagrendszer: Nap: Naprendszer: a Naprendszer égitestei: plazmaállapot: forgás: keringés: ellipszis alakú pálya: termonukleáris
FOGALOMTÁR 9. évfolyam I. témakör A Föld és kozmikus környezete csillag: csillagrendszer: Nap: Naprendszer: a Naprendszer égitestei: plazmaállapot: forgás: keringés: ellipszis alakú pálya: termonukleáris
file://c:\coeditor\data\local\course410\tmp.xml
 1. oldal, összesen: 7 Tanulási célok: A lecke feldolgozása után Ön képes lesz: saját szavaival meghatározni a grafikus fordatervezés módszerét támogató körülményeket; saját szavaival meghatározni a grafikus
1. oldal, összesen: 7 Tanulási célok: A lecke feldolgozása után Ön képes lesz: saját szavaival meghatározni a grafikus fordatervezés módszerét támogató körülményeket; saját szavaival meghatározni a grafikus
Benapozás vizsgálat dr. Szalay Zsuzsa és a Naplopó anyagainak felhasználásával
 Benapozás vizsgálat dr. Szalay Zsuzsa és a Naplopó anyagainak felhasználásával 1. A Föld pályája a Nap körül 2. A szoláris idő 3. Nappályadiagramok 4. Árnyékszögek élleképző görbék 5. Napóra vetületek
Benapozás vizsgálat dr. Szalay Zsuzsa és a Naplopó anyagainak felhasználásával 1. A Föld pályája a Nap körül 2. A szoláris idő 3. Nappályadiagramok 4. Árnyékszögek élleképző görbék 5. Napóra vetületek
Arany Dániel Matematikai Tanulóverseny 2012/2013-as tanév 1. forduló haladók III. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 0/03-as tanév. forduló haladók III. kategória Megoldások és javítási útmutató. Egy kör kerületére felírjuk -től 3-ig az egészeket
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 0/03-as tanév. forduló haladók III. kategória Megoldások és javítási útmutató. Egy kör kerületére felírjuk -től 3-ig az egészeket
C Í M K E É V F O L Y A M ORSZÁGOS KOMPETENCIAMÉRÉS 2007 JAVÍTÓKULCS MATEMATIKA. Oktatási Hivatal Országos Közoktatási Értékelési és Vizsgaközpont
 8. Í M K E É V F O L Y A M TANULÓI AZONOSÍTÓ: ORSZÁGOS KOMPETENIAMÉRÉS 2007 JAVÍTÓKULS MATEMATIKA Oktatási Hivatal Országos Közoktatási Értékelési és Vizsgaközpont ÁLTALÁNOS TUDNIVALÓK Ön a 2007-es Országos
8. Í M K E É V F O L Y A M TANULÓI AZONOSÍTÓ: ORSZÁGOS KOMPETENIAMÉRÉS 2007 JAVÍTÓKULS MATEMATIKA Oktatási Hivatal Országos Közoktatási Értékelési és Vizsgaközpont ÁLTALÁNOS TUDNIVALÓK Ön a 2007-es Országos
1. feladat. CAD alapjai c. tárgyból nappali tagozatú ipari formatervező szakos mérnök hallgatóknak
 1. feladat CAD alapjai c. tárgyból nappali tagozatú ipari formatervező szakos mérnök hallgatóknak Vetületek képzése, alkatrészrajz készítése (formátum: A4) Készítse el a gyakorlatvezető által kiadott,
1. feladat CAD alapjai c. tárgyból nappali tagozatú ipari formatervező szakos mérnök hallgatóknak Vetületek képzése, alkatrészrajz készítése (formátum: A4) Készítse el a gyakorlatvezető által kiadott,
Borbély Sándor Országos Tanulmányi Verseny. Vác Matematika. 5. osztály. Megoldókulcs. Név: Iskola:
 Borbély Sándor Országos Tanulmányi Verseny Vác 201 Matematika 5. osztály Megoldókulcs Név: Iskola: 1. Pótold a hiányzó számokat! A Fővárosi Állat- és Növénykert története: 1. -ban nyílt meg. 1866 2. -ban
Borbély Sándor Országos Tanulmányi Verseny Vác 201 Matematika 5. osztály Megoldókulcs Név: Iskola: 1. Pótold a hiányzó számokat! A Fővárosi Állat- és Növénykert története: 1. -ban nyílt meg. 1866 2. -ban
VONALVEZETÉS TERVEZÉSE
 VONALVEZETÉS TERVEZÉSE A vonalvezetés tervezésének általános követelményei A tervezési sebesség Látótávolságok Vízszintes vonalvezetés Magassági vonalvezetés Burkolatszélek vonalvezetése Térbeli tervezés
VONALVEZETÉS TERVEZÉSE A vonalvezetés tervezésének általános követelményei A tervezési sebesség Látótávolságok Vízszintes vonalvezetés Magassági vonalvezetés Burkolatszélek vonalvezetése Térbeli tervezés
IV. Felkészítő feladatsor
 IV. Felkészítő feladatsor 1. Az A halmaz elemei a (-7)-nél nagyobb, de 4-nél kisebb egész számok. B a nemnegatív egész számok halmaza. Elemeinek felsorolásával adja meg az A \ B halmazt! I. 2. Adott a
IV. Felkészítő feladatsor 1. Az A halmaz elemei a (-7)-nél nagyobb, de 4-nél kisebb egész számok. B a nemnegatív egész számok halmaza. Elemeinek felsorolásával adja meg az A \ B halmazt! I. 2. Adott a
Trigonometria. Szögfüggvények alkalmazása derékszög háromszögekben. Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1
 Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1 Trigonometria Szögfüggvények alkalmazása derékszög háromszögekben 1. Az ABC hegyesszög háromszögben BC = 14 cm, AC = 1 cm, a BCA szög nagysága
Szent István Egyetem Gépészmérnöki Kar Matematika Tanszék 1 Trigonometria Szögfüggvények alkalmazása derékszög háromszögekben 1. Az ABC hegyesszög háromszögben BC = 14 cm, AC = 1 cm, a BCA szög nagysága
Koordináta geometria III.
 Koordináta geometria III. TÉTEL: A P (x; y) pont akkor és csak akkor illeszkedik a K (u; v) középpontú r sugarú körre (körvonalra), ha (x u) 2 + (y v) 2 = r 2. Ez az összefüggés a K (u; v) középpontú r
Koordináta geometria III. TÉTEL: A P (x; y) pont akkor és csak akkor illeszkedik a K (u; v) középpontú r sugarú körre (körvonalra), ha (x u) 2 + (y v) 2 = r 2. Ez az összefüggés a K (u; v) középpontú r
Matematikai geodéziai számítások 1.
 Matematikai geodéziai számítások 1 Ellipszoidi számítások, ellipszoid, geoid és terep metszete Dr Bácsatyai, László Created by XMLmind XSL-FO Converter Matematikai geodéziai számítások 1: Ellipszoidi számítások,
Matematikai geodéziai számítások 1 Ellipszoidi számítások, ellipszoid, geoid és terep metszete Dr Bácsatyai, László Created by XMLmind XSL-FO Converter Matematikai geodéziai számítások 1: Ellipszoidi számítások,
Általános gépészeti technológiai feladatok. Géprajzi alapismeretek Gépészeti szakszámítások
 Általános gépészeti technológiai feladatok Géprajzi alapismeretek Gépészeti szakszámítások A géprajzi feladata A gépalkatrészek gyártását és szerelését műszaki rajzok alapján végzik. A műszaki rajz valamely
Általános gépészeti technológiai feladatok Géprajzi alapismeretek Gépészeti szakszámítások A géprajzi feladata A gépalkatrészek gyártását és szerelését műszaki rajzok alapján végzik. A műszaki rajz valamely
Egy kérdés: merre folyik le az esővíz az úttestről? Ezt a kérdést az után tettük fel magunknak, hogy megláttuk az 1. ábrát.
 1 Egy kérdés: merre folyik le az esővíz az úttestről? Ezt a kérdést az után tettük fel magunknak, hogy megláttuk az 1. ábrát. 1. ábra forrása: [ 1 ] Ezen egy út tengelyvonalának egy pontjában tüntették
1 Egy kérdés: merre folyik le az esővíz az úttestről? Ezt a kérdést az után tettük fel magunknak, hogy megláttuk az 1. ábrát. 1. ábra forrása: [ 1 ] Ezen egy út tengelyvonalának egy pontjában tüntették
Diagramok elemzése. egy kozmetikai termékcsalád hatóanyagösszetételét
 Diagramok elemzése 1. Egy cég közös grafikonban ábrázolja a teljesítményét és az alkalmazottak létszámát. Le tudná-e olvasni, mekkora volt a cég teljesítménye és a dolgozók létszáma 2000-ben, ha csak az
Diagramok elemzése 1. Egy cég közös grafikonban ábrázolja a teljesítményét és az alkalmazottak létszámát. Le tudná-e olvasni, mekkora volt a cég teljesítménye és a dolgozók létszáma 2000-ben, ha csak az
Arany Dániel Matematikai Tanulóverseny 2009/2010-es tanév első (iskolai) forduló haladók II. kategória
 Bolyai János Matematikai Társulat Oktatási és Kulturális Minisztérium Támogatáskezelő Igazgatósága támogatásával Arany Dániel Matematikai Tanulóverseny 009/00-es tanév első (iskolai) forduló haladók II.
Bolyai János Matematikai Társulat Oktatási és Kulturális Minisztérium Támogatáskezelő Igazgatósága támogatásával Arany Dániel Matematikai Tanulóverseny 009/00-es tanév első (iskolai) forduló haladók II.
Versenyző kódja: 43 15/2008. (VIII. 13.) SZMM rendelet 54 521 01 0000 00 00-2013 MAGYAR KERESKEDELMI ÉS IPARKAMARA
 54 521 01 0000 00 00-2013 MAGYAR KERESKEDELMI ÉS IPARKAMARA Országos Szakmai Tanulmányi Verseny Elődöntő ÍRÁSBELI FELADAT Szakképesítés: 54 521 01 0000 00 00 SZVK rendelet száma: 15/2008. (VIII. 13.) SZMM
54 521 01 0000 00 00-2013 MAGYAR KERESKEDELMI ÉS IPARKAMARA Országos Szakmai Tanulmányi Verseny Elődöntő ÍRÁSBELI FELADAT Szakképesítés: 54 521 01 0000 00 00 SZVK rendelet száma: 15/2008. (VIII. 13.) SZMM
PRÓBAÉRETTSÉGI 2004.május MATEMATIKA. KÖZÉPSZINT I. 45 perc
 PRÓBAÉRETTSÉGI 2004.május MATEMATIKA KÖZÉPSZINT I. 45 perc A feladatok megoldására 45 perc fordítható, az idő leteltével a munkát be kell fejeznie. A feladatok megoldási sorrendje tetszőleges. A feladatok
PRÓBAÉRETTSÉGI 2004.május MATEMATIKA KÖZÉPSZINT I. 45 perc A feladatok megoldására 45 perc fordítható, az idő leteltével a munkát be kell fejeznie. A feladatok megoldási sorrendje tetszőleges. A feladatok
Az orvosi biotechnológiai mesterképzés megfeleltetése az Európai Unió új társadalmi kihívásainak a Pécsi Tudományegyetemen és a Debreceni Egyetemen
 Az orvosi biotechnológiai mesterképzés megfeleltetése az Európai Unió új társadalmi kihívásainak a Pécsi Tudományegyetemen és a Debreceni Egyetemen Azonosító szám: TÁMOP-4.1.2-08/1/A-2009-0011 Az orvosi
Az orvosi biotechnológiai mesterképzés megfeleltetése az Európai Unió új társadalmi kihívásainak a Pécsi Tudományegyetemen és a Debreceni Egyetemen Azonosító szám: TÁMOP-4.1.2-08/1/A-2009-0011 Az orvosi
I. Internetes keresési feladatok (ajánlott idő: 20 perc)
 I. Internetes keresési feladatok (ajánlott idő: 20 perc) A talált oldalak internet címét (URL) másold ki egy szöveges dokumentumba és mentsd Csapatnev_internet néven! A konkrét válaszokat ide a papírra
I. Internetes keresési feladatok (ajánlott idő: 20 perc) A talált oldalak internet címét (URL) másold ki egy szöveges dokumentumba és mentsd Csapatnev_internet néven! A konkrét válaszokat ide a papírra
XLII. Országos Komplex Tanulmányi Verseny Megyei forduló. Matematika
 6. Matematika Az emberek csak azért gondolják, hogy a matematika nehéz, mert még nem döbbentek rá, hogy az élet maga milyen bonyolult. (Neumann János) 2017. április 04. Készítette: Szafiánné Csécsei Tímea,
6. Matematika Az emberek csak azért gondolják, hogy a matematika nehéz, mert még nem döbbentek rá, hogy az élet maga milyen bonyolult. (Neumann János) 2017. április 04. Készítette: Szafiánné Csécsei Tímea,
Villamos gépek tantárgy tételei
 10. tétel Milyen mérési feladatokat kell elvégeznie a kördiagram megszerkesztéséhez? Rajzolja meg a kördiagram felhasználásával a teljes nyomatéki függvényt! Az aszinkron gép egyszerűsített kördiagramja
10. tétel Milyen mérési feladatokat kell elvégeznie a kördiagram megszerkesztéséhez? Rajzolja meg a kördiagram felhasználásával a teljes nyomatéki függvényt! Az aszinkron gép egyszerűsített kördiagramja
Grafikonok automatikus elemzése
 Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
FELADATOK ÉS MEGOLDÁSOK
 Milyen számot írnátok az üres háromszögbe? Miért? 3. osztály 5-öt (1 pont). Az alakzat oldalainak száma és a beírt szám összege mindig 8 (1 pont). Más válasz, amelyre logikus magyarázatot tudnak adni,
Milyen számot írnátok az üres háromszögbe? Miért? 3. osztály 5-öt (1 pont). Az alakzat oldalainak száma és a beírt szám összege mindig 8 (1 pont). Más válasz, amelyre logikus magyarázatot tudnak adni,
Forgásfelületek származtatása és ábrázolása
 Forgásfelületek származtatása és ábrázolása Ha egy rögzített egyenes körül egy tetszőleges görbét forgatunk, akkor a görbe úgynevezett forgásfelületet ír le; a rögzített egyenes, amely körül a görbe forog,
Forgásfelületek származtatása és ábrázolása Ha egy rögzített egyenes körül egy tetszőleges görbét forgatunk, akkor a görbe úgynevezett forgásfelületet ír le; a rögzített egyenes, amely körül a görbe forog,
ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK
 Név:... osztály:... ÉRETTSÉGI VIZSGA 2006. május 18. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2006. május 18. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati
Név:... osztály:... ÉRETTSÉGI VIZSGA 2006. május 18. ÉPÍTÉSZETI ÉS ÉPÍTÉSI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2006. május 18. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati
AZ ÓZON. 1. kérdés: AZ ÓZON. Olvasd el az ózonrétegrl szóló cikk alábbi részletét!
 AZ ÓZON Olvasd el az ózonrétegrl szóló cikk alábbi részletét! 5 10 15 20 Az atmoszféra, a leveg hatalmas óceánja a földi életet tápláló természetes források közül az egyik legértékesebb. Sajnálatos, hogy
AZ ÓZON Olvasd el az ózonrétegrl szóló cikk alábbi részletét! 5 10 15 20 Az atmoszféra, a leveg hatalmas óceánja a földi életet tápláló természetes források közül az egyik legértékesebb. Sajnálatos, hogy
VIII. Robotprogramozó Országos Csapatverseny Regionális versenyfeladatok évfolyam
 A robot portjainak kiosztása VIII. Robotprogramozó Országos Csapatverseny Regionális versenyfeladatok Motorok: B és C Szenzorok: Ütközésérzékelő: Fény/szín szenzor: Fény/szín szenzor: Ultrahang szenzor:
A robot portjainak kiosztása VIII. Robotprogramozó Országos Csapatverseny Regionális versenyfeladatok Motorok: B és C Szenzorok: Ütközésérzékelő: Fény/szín szenzor: Fény/szín szenzor: Ultrahang szenzor:
Készítsünk napórát. Marton Géza (idomester@mcse.hu)
 Készítsünk napórát Napórák a különböző történelmi kultúrákban A legrégibb időmérő a napóra, ez a minden történelmi kultúrában megtalálható lenyűgözően egyszerű eszköz. Az egyiptomi obeliszkek a szakrális
Készítsünk napórát Napórák a különböző történelmi kultúrákban A legrégibb időmérő a napóra, ez a minden történelmi kultúrában megtalálható lenyűgözően egyszerű eszköz. Az egyiptomi obeliszkek a szakrális
Assignment problem Hozzárendelési feladat (Szállítási feladat speciális esete)
 Assignment problem Hozzárendelési feladat (Szállítási feladat speciális esete) C költség mátrix költség Munkákat hozzá kell rendelni gépekhez: egy munka-egy gép c(i,j) mennyi be kerül i-dik munka j-dik
Assignment problem Hozzárendelési feladat (Szállítási feladat speciális esete) C költség mátrix költség Munkákat hozzá kell rendelni gépekhez: egy munka-egy gép c(i,j) mennyi be kerül i-dik munka j-dik
Pálya : Az a vonal, amelyen a mozgó test végighalad. Út: A pályának az a része, amelyet adott idő alatt a mozgó tárgy megtesz.
 Haladó mozgások A hely és a mozgás viszonylagos. A testek helyét, mozgását valamilyen vonatkoztatási ponthoz, vonatkoztatási rendszerhez képest adjuk meg, ahhoz viszonyítjuk. pl. A vonatban utazó ember
Haladó mozgások A hely és a mozgás viszonylagos. A testek helyét, mozgását valamilyen vonatkoztatási ponthoz, vonatkoztatási rendszerhez képest adjuk meg, ahhoz viszonyítjuk. pl. A vonatban utazó ember
Számítógépes Grafika mintafeladatok
 Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
Számítógépes Grafika mintafeladatok Feladat: Forgassunk a 3D-s pontokat 45 fokkal a X tengely körül, majd nyújtsuk az eredményt minden koordinátájában kétszeresére az origóhoz képest, utána forgassunk
A kakas. Francia népmese
 A kakas Francia népmese De nem mondtam még el, hogy amikor a legidősebb fiú világgá ment, hamarosan utána a középső is odaállt az apja elé. Ő sem akart a család terhére lenni. Apám, nem tudhatjuk, hogy
A kakas Francia népmese De nem mondtam még el, hogy amikor a legidősebb fiú világgá ment, hamarosan utána a középső is odaállt az apja elé. Ő sem akart a család terhére lenni. Apám, nem tudhatjuk, hogy
Csorba György természettudományos feladatmegoldó verseny
 Biológia 2. forduló 1. Melyik térképvázlat ábrázolja a sivatagokat, melyik a szavannákat, és melyik a trópusi esőerdőket? Írd a nevüket a megfelelő térkép alá! (3 p.) a) Húzd alá azokat az állításokat,
Biológia 2. forduló 1. Melyik térképvázlat ábrázolja a sivatagokat, melyik a szavannákat, és melyik a trópusi esőerdőket? Írd a nevüket a megfelelő térkép alá! (3 p.) a) Húzd alá azokat az állításokat,
Csillagászati földrajzzal. Megoldási útmutatókkal
 Csillagászati földrajzzal kapcsolatos feladatok Megoldási útmutatókkal A Nap delelési magasságának kiszámítása Feladat: Hány fokos szögben látják delelni a Napot június 22-én a következő szélességi körökön?
Csillagászati földrajzzal kapcsolatos feladatok Megoldási útmutatókkal A Nap delelési magasságának kiszámítása Feladat: Hány fokos szögben látják delelni a Napot június 22-én a következő szélességi körökön?
BOLYAI MATEMATIKA CSAPATVERSENY ORSZÁGOS DÖNTŐ SZÓBELI (2017. NOVEMBER 18.) 3. osztály
 3. osztály Két polcon összesen 72 könyv található. Miután az első polcról a másodikra áttettünk 14 könyvet, mindkét polcon ugyanannyi könyv lett. Hány könyv volt eredetileg az első polcon? Helyezzetek
3. osztály Két polcon összesen 72 könyv található. Miután az első polcról a másodikra áttettünk 14 könyvet, mindkét polcon ugyanannyi könyv lett. Hány könyv volt eredetileg az első polcon? Helyezzetek
EÖTVÖS LORÁND SZAKKÖZÉP- ÉS SZAKISKOLA TANÍTÁST SEGÍTŐ OKTATÁSI ANYAGOK MÉRÉS TANTÁRGY
 EÖTVÖS LORÁND SZAKKÖZÉP- ÉS SZAKISKOLA TANÍTÁST SEGÍTŐ OKTATÁSI ANYAGOK MÉRÉS TANTÁRGY SÍKIDOMOK Síkidom 1 síkidom az a térelem, amelynek valamennyi pontja ugyan abban a síkban helyezkedik el. A síkidomokat
EÖTVÖS LORÁND SZAKKÖZÉP- ÉS SZAKISKOLA TANÍTÁST SEGÍTŐ OKTATÁSI ANYAGOK MÉRÉS TANTÁRGY SÍKIDOMOK Síkidom 1 síkidom az a térelem, amelynek valamennyi pontja ugyan abban a síkban helyezkedik el. A síkidomokat
