Kerényi István VISZONTBIZTOSÍTÁS
|
|
|
- Natália Fülöp
- 8 évvel ezelőtt
- Látták:
Átírás
1 AKTUÁRIUS JEGYZETEK 5. Kerényi István VISZONTBIZTOSÍTÁS Javított kiadás Budapesti Corvinus Egyetem Operációkutatás és Aktuáriustudományok Tanszék Budapest 2011
2 2 Elő szó Ennek a tanulmánynak a célja az, hogy bemutassa a viszontbiztosítás alapjait, mind gyakorlati, mind elméleti oldalról. Az első fejezet a viszontbiztosítás fogalmát; általános matematikai modelljét mutatja be, választ ad arra a kérdésre, hogy miért van szükség viszontbiztosításra. A második és harmadik fejezet a különböző viszontbiztosítási (arányos illetve nem arányos) módszerekrő l, azok elő nyeirő l és hátrányairól szól és mindkét fejezetet egy-egy tétel bizonyítása zárja. A negyedik fejezetbő l látni fogjuk, hogy " az ÉLET egészen más", vagyis hogy az életbiztosítás viszontbiztosítása általában eltér a nem-élet (non-life) biztosításokétól. Az ötödik fejezet a viszontbiztosító társaságok speciális finanszírozó szerepét ismerteti. Végezetül szeretnék köszönetet mondani kollégáimnak a tanulmány megírásához nyújtott értékes segítségért. Budapest,
3 3 1. A viszontbiztosítás fogalma, avagy miért van szükség viszontbiztosításra A viszontbiztosítás (reinsurance, Rückversicherung, peresztrvahovanyije) tulajdonképpen a biztosítók biztosítása. Egy viszontbiztosítási szerző dés keretében egy biztosító a hozzá beérkezett biztosítási díj egy részét átengedi egy másik biztosítónak, aminek fejében a második biztosító arra vállal kötelezettséget, hogy az első nek az általa kifizetett szolgáltatások egy részét megtéríti. A biztosított (szerző d ő ) és az első biztosító között kötött szerző dést szokták direkt biztosításnak is nevezni, míg a két társaság közötti szerző dést cedálásnak vagy viszontbiztosításnak hívják. Az első társaság az ügyféllel szemben közvetlen aláíró vagy direkt biztosító (direct underwriter), míg a második társasággal szemben cedens (ceding company, Zedent) vagy viszontbiztosított. A második társaságot viszontbiztosítónak (reinsurer, Rückversicherer) nevezik. A nemzetközi gyakorlatában általában profi, csak erre a célra szakosodott, viszontbiztosítók végzik a viszontbiztosítást. Elképzelhető ugyanakkor az is, hogy ugyanaz a társaság egyik üzletben direkt biztosító a másik üzletben viszontbiztosító legyen (pl. az egyik magyar biztosító részvénytársaság viszontbiztosítja néhány kis biztosító egyesület kockázatát, de saját maga is kínálja termékeit, aminek egy részét viszont az egyik nyugat-európai viszontbiztosítónál viszontbiztosítja). Az is gyakran elő fordul, hogy a viszontbiztosító az általa átvállalt kockázatot is továbbadja és így tovább. Ezt retrocedálásnak hívják.
4 4 Vizsgáljuk most meg, hogy matematikailag hogyan modellezhető egy viszontbiztosítás: Egy direkt biztosításban a kifizetendő kárösszeg egy X valószínű ségi változó. A direkt biztosítási szerző dést jellemzi a biztosítás P díja és az F (x) eloszlás. A viszontbiztosítási szerző dést a viszontbiztosítónak átadandó P 1 díj mellett egy T mérhető függvény jellemzi: Ha a kifizetendő kárigény x, akkor a direkt biztosító a kifizetendő kárból Tx összeget fizet, míg a viszontbiztosító részesedése x-tx. Tx-et saját megtartásnak vagy önrésznek (Retention, Selbstbehalt) is szokták nevezni. Legyen F 0 (x):=p(tx<x) P 0 := P - P 1 F 1 (x):=p(x-tx<x) A direkt biztosító kockázatát ezután a (P 0,F 0 (x)), míg a viszontbiztosító kockázatát a (P 1,F 1 (x)) pár jellemzi. Amennyiben a díjszámításhoz a várható érték elvet használjuk (pótdíj nélkül) nyílván igazak a következő összefüggések:
5 5 xdf(x) =P (1.1.) ) xdf ( x 0 ) = TxdF (x =P 0 (1.2.) xdf ( x ) = ( x Tx) df ( x) =P 1 (1.3.) 1 (T mérhető, ezért a második és a harmadik integrál is létezik és véges) Ésszerű feltételezés, hogy fennálljon a 0 <= Tx <= x (1.4.) összefüggés. Tx negatívitása ugyanis a direkt biztosítót, míg x < Tx a viszontbiztosítót tenné érdekelté a kárösszeg növekedésében. Tx x azt jelenti, hogy a direkt biztosító nem köt viszontbiztosítást. Tx = 0 esetében frontingról beszélünk. Ez azt jelenti, hogy a direkt biztosító nem vállal kockázatot és a kockázati díjból sem tart meg semmit. Ezt üzletpolitikai ok vagy más jogszabályi háttér indokolhatja. (1.4.) kiintegrálásából adódik, hogy 0 <= P 0 <= P (1.5.) vagyis P 0, P 1 és P egyaránt nemnegatív.
6 6 A gyakorlat a fenti képleteknél némileg bonyolultabb, mert mind a direkt biztosító, mind viszontbiztosító költségpótlékkal dolgozik, de a direkt biztosító relatív költségigénye magasabb, mert ott merül fel az adminisztrációs költségek nagy része (pl.: kötvényesítés, kárrendezés stb.). Miért is van szükség viszontbiztosításra? Egy kézenfekvő magyarázat adódik, ha belegondolunk abba, hogy miért kötnek az emberek például CASCObiztosítást. Kovács úr, a magyar kispolgár például, tudja azt, hogy ha az autóját ellopják, nem lesz képes arra, hogy még egyszer összegyű jtsön 2 millió forintot, viszont szívesen áldoz havi néhány ezer forintot arra, hogy autóját biztonságban tudhassa. De ugyanígy gondolkodik az a vállalkozó, aki gépeit és áruit biztosítja vagy az a menedzser, aki havi néhány ezer forintért több milliós balesetbiztosítást köt. Mindegyiknek a célja egy és ugyanaz: lemondanak a jövedelmük egy részérő l, hogy ezért "biztonságot" vegyenek. A biztosító viszontbiztosításért felelő s vezető je ugyanígy gondolkodik. Mekkora az a kár, amelyet a biztosító cég ki tud fizetni, anélkül hogy pénzügyi egyensúlya felborulna? Mennyit érdemes kockáztatni? A következő kérdés persze az, hogy mivel lehet mérni a kockázat mértékét? A tönkremenés valószínű ségének minimalizálásával? A maradó állomány szórásnégyzetével? Ezek olyan kérdések, amire fel lehet
7 7 állítani matematikai modelleket, de a szubjektum szerepe jelentő s. Klasszikus formájában a viszontbiztosítás védelem a kifizetendő kárösszeg nem várt növekedése ellen. Ennek jellemző okai lehetnek például: 1. A károk gyakorisága megnő 2. Az átlagkár mértéke a vártnál jobban emelkedik 3. Nagy a károk ingadozása Ezeket a tényező ket a díjban biztonsági pótlékkal figyelembe venni túl drága lenne. De még kockázatosabb a kis valószínű ségű nagy károk esetén a biztosító helyzete, ha nem tud megfelelő kockázatközösséget kialakítani. Ha egy iparvállalat egyik telepének értéke 10 milliárd forint és a tű z keletkezésének valószínű sége a kiváló biztonsági intézkedéseknek köszönhető en évi 1 ezrelék, akkor a várható érték elve alapján a fizetendő éves díj 10 millió forint, és ez felső becslés, mert minden eseménynél totál kárt tételeztünk fel. Ugyanakkor, ha mégis bekövetkezik a kár, a tulajdonos nem fogja elfogadni a menedzsment azon érvelését, hogy ezeréves távlatban jó üzletet kötöttünk A fenti probléma fokozottan jelentkezik, ha egy eseménybő l sok kumulálódó kár következik be Ilyen példák jellemző en (bár nem kizárólag) a felelő sségbiztosítás területén fordulnak elő :1993-ban egy buszvezető nem vette figyelembe a fénysorompó piros jelzését. A következmény: 11 gyerek halt meg, többen pedig egész életükre nyomorékok lettek. Az
8 8 autóbusz-társaság felelő sségbiztosítása alapján a baleset sérültjeinek fizetett élethossziglani járadék, az áldozatok hozzátartozóinak fizetendő kártérítés és a vasúttársaságot ért közvetlen anyagi károk kompenzálása együttvéve mai értéken milliárdos összeget tesz ki. A viszontbiztosítás fenti biztosításszakmai indokán kívül a modern üzleti életben sok más olyan tényező is van, ami szükségessé teheti ilyen szerző dés megkötését. Egy ilyen ok az első höz nagyon hasonló és tulajdonképpen a kockázatvállalás mértékének szab törvényes korlátot. Az Európai Unió egyik irányelve alapján a tagállamokban mű ködő biztosítótársaságoknak eleget kell tenniük az úgynevezett fizető képességi sávra (solvency margin) vonatkozó kritériumoknak, mely szerint a nem-életbiztosítási üzletágban a biztosító szabad eszközei el kell, hogy érjék a saját megtartású üzletek éves díjbevételének 16%-át.Ha a biztosító eszközei ennél kisebbek, köteles a szavatoló t ő két feltölteni. Ez elkerülhető az állomány egy részének viszontbiztosításba adásával. De még törvényes korlát nélkül sem lenne célszerű vagy lehetséges a saját tartalékot biztonságos mértékre növelni. Az adómentesen félretehető pénz nagyságát mindenütt korlátozzák a solvency margintól függetlenül. A viszontbiztosítás lehető séget adhat arra is, hogy az egy tulajdonosi csoporthoz tartozó társaságok között a
9 9 f ő tulajdonos a profitot úgy mozgassa, hogy az számára (pl.:adózási szempontból) a legkedvező bb legyen. A viszontbiztosításnak vannak egyéb, nem mindig számszerű síthető elő nyei is. Ilyen lehet például a viszontbiztosító segítsége egy új termék fejlesztésében. Egy, az országban még nem mű velt termék bevezetésénél a nagy nemzetközi tapasztalatokkal rendelkező viszontbiztosító segítséget nyújthat a feltételek megfogalmazásához, a díjtételek megállapításához. A viszontbiztosítás legmodernebb formáiban az újonnan alakuló életbiztosítók finanszírozását szolgálja, illetve a biztosítási iparágon kívüli tő két is bevonhat a kockázatok fedezetére A viszontbiztosítás megjelente lényegében egyidő s a szervezett biztosítótársaságok létrejöttével. A világ első viszontbiztosító társasága 1846-ban Kölnben a nagy tű zvész után alakult meg. Kezdetben a viszontbiztosítási szerző dések úgynevezett arányos alapon létesültek. A nem arányos viszontbiztosítási szerző dések régen ismertek, de csak a második világháború után terjedtek el. A következő két fejezetben ezekrő l a viszontbiztosítási formákról lesz szó.
10 10 2. Arányos viszontbiztosítási formák A viszontbiztosítási szerző dés legkézenfekvő bb formája az, hogy amilyen arányban részesül a viszontbiztosító a díjakból, olyan arányban vállal részt a károk fedezésébő l. Ez azt jelenti, hogy a direkt biztosító és a viszontbiztosító egy olyan szerző dést köt, miszerint a direkt biztosító az üzletág (vagy valamilyen módozat) éves bevételének q (0 <= q <= 1) részét megtartja, míg (1 - q) részét átadja a viszontbiztosítónak, aminek fejében a viszontbiztosító a bekövetkezett károk (1 - q) részét kifizeti. Ezt a viszontbiztosítási formát kvóta (Quota-share, Quoten) viszontbiztosításnak hívják. Matematikailag ez azt jelenti, hogy az 1.fejezet végén használt jelölésekkel Tx = qx (2.1.) Vizsgáljuk most meg, hogy a várható érték elv alapján (nulla pótdíj mellett) igazságos-e a viszontbiztosítónak fizetendő díj: A viszontbiztosító kifizetésének várható értéke ) P 1 = XdF ( x 1 ) = ( X TX ) df( x = ( 1 q ) XdF ( x) =(1-q) XdF (x) =(1-q)P (2.2.) tehát ahogyan vártuk arányos kockázatviselésért, arányos díj illeti meg a viszontbiztosítót.
11 11 Azonban, amint arra már az 1. fejezetben utaltunk a gyakorlat nem ilyen szép. Mind a közvetlen aláíró, mind a viszontbiztosító költségekkel, profitért dolgozik. Ugyanakkor a viszontbiztosító azt is elismeri, hogy a direkt biztosító relatív költségei magasabbak (szerzési, kötvényesítési, kárrendezési költségek), ezért az arányos díjból jutalékot (Comission, Provision) ad. Legyen a direkt biztosító költségigénye C 1, a viszontbiztosítóé C 2. Ekkor a szerző d ő által a direkt biztosítónak fizetendő díj: Π =E(X)/(1-C 1) =P/(1-C 1 ) (2.3.) A viszontbiztosítónak fizetendő díj: Π 1 =(1-q)P/(1-C 1 )=P 1/ (1-C 1 ) (2.4.) A viszontbiztosítási jutalékkal csökkentett viszontbiztosítási díj: Π ' 1 =(1-q)P/(1-C 2 )=P 1/ (1-C 2 ) (2.5.) A viszontbiztosítási jutalék (2.4.)-bő l és (2.5.)-bő l: C 3 =1- Π ' 1 / Π 1 =1-(1-C 1 )/(1-C 2 ) (2.6.) A magyar non-life gyakorlatban C 1 40% körül van, míg a viszontbiztosítók 25% körüli jutalékot adnak. A fenti
12 12 értékeket használva 20%-os megtartásnál (q = 0,2) a kockázat és a díj megosztását az alábbi ábrákon kísérhetjük figyelemmel: Díj = 100 Kockázati díj = 60 Költség = 40 Viszontbiztosító kockázati díja=48 Direkt biztosító kockázati díja=12 illetve Díj = 100 Viszontbiztosító díja = 80 Direkt biztosító díja=20 Viszontbiztosítási jutalék=20 Viszontbiztosítónak átadott díj=60 A direkt biztosítónál maradó díj=40
13 13 Ebben a példában a viszontbiztosító tehát (60-48)/60 azaz 20%-os költséghányaddal dolgozik. Itt térünk vissza a határesetekre, tehát amikor q=0, vagy q=1. Ha q=1 az azt jelenti, hogy a két társaság megállapodik, hogy nem köt egymással szerző dést. A q=0 eset már érdekesebb kérdés. Ebben az esetben a közvetlen aláíró, mintegy üzletkötő ként, brókerként kockázatmentesen jut profithoz. Ez két okból nem gyakori: egyrészt a közvetlen aláírónak éppen az a profilja, hogy kockázatot vállaljon, másrészt a viszontbiztosító kockázat-elbírálási szempontból nem szívesen vállal olyan kockázatot, amiben a közvetlen aláíró nem érdekelt. Miért fordul elő ez mégis a gyakorlatban? Erre nézzük az alábbi tipikus példát: Egy az Európai Unióban dolgozó multinacionális vállalat minden országban igazgatóira balesetbiztosítást köt ugyanannál a biztosítónál, ezt a szabad szolgáltatásnyújtás elve alapján megteheti. Késő bb ez a vállalat leányvállalatot nyit egy EU-n kívüli országban, ahol a helyi jog szerint csak az országban bejegyzett biztosító köthet üzletet. Ekkor a vállalat megkeres egy helyi biztosítót, aki megfelelő viszontbiztosítási jutalék ellenében 100%-ban (q = 0) viszontbiztosítja a kockázatot az eredeti biztosítónál.q=0 esetén a viszontbiztosítást frontingnak a viszontbiztosítási díjat fronting fee-nek nevezik.
14 14 A kvóta - viszontbiztosítás legnagyobb elő nye, hogy rendkívül egyszerű : Nincs szükség a díjak és a károk egyedi elszámolására, bizonyos idő szakonként az eredmény-elszámolásban amúgy is szereplő összegek arányos részének különbségét utalja az egyik biztosító a másiknak. A viszontbiztosítónak nincs szüksége kockázatelbírálókra, mert a direkt biztosító minden kockázatot automatikusan cedál, míg a viszontbiztosító minden kockázatot automatikusan elfogad. A közvetlen aláíró sokkal bátrabban vállalhat, míg a viszontbiztosító biztos lehet abban, hogy a jó kockázatokból is részesedik. A kvóta - viszontbiztosítás a legegyszerű bb lehető ség arra, hogy hogyan mozgatja a fő tulajdonos társaságai között a profitot. A kvóta - szerző déseknek azonban megvannak a hátrányai: a direkt biztosító olyan kockázatokat is viszont-biztosításba ad, amelyeket pénzügyi kapacitása alapján elbírna, és nem szelektálhat a jó és rossz kockázatok között. Ezért a kvóta viszontbiztosítást csak ritkán, induló új biztosítóknál vagy induló új üzletágaknál alkalmazzák. A kvóta - viszontbiztosítás hátrányainak kiküszöbölésére vezették be a surplus viszontbiztosítási formát: Ez matematikai leírásában nagyon hasonlít a kvóta - viszontbiztosításhoz, de abban különbözik tő le, hogy q nem egységes, abban az értelemben, hogy a direkt biztosító kockázatonként egyesével dönti el, hogy milyen megtartási arányt alkalmaz.
15 15 A megtartást két korlát befolyásolja. Egyrészt adott egy felső határ, aminél többet a biztosító nem akar megtartani, másrészt adott egy alsó határ is: A szerző désben kikötik ugyanis a viszontbiztosító maximális részesedését is, ezt sávokban (line) határozzák meg. Ha a szerző dés szerint a viszontbiztosító legfeljebb c sávot vállal, az azt jelenti, hogy a viszontbiztosító legfeljebb a direkt biztosító kockázatának c-szeresét vállalja át, vagyis a saját megtartás alsó korlátja q>= 1/( 1+ c) (2.7.) A felső korlát nyilván q<= R/S (2.8.) ahol R a maximális saját megtartást, S a biztosítási összeget (maximális kárigényt) jelöli. (2.7.)-bő l és a (2.8.)-ból adódik, hogy a direkt biztosító legfeljebb, olyan kockázatot vállalhat el, melyre R/S>=1/(1+c), azaz S<=(1+c)R (2.9.) A következő oldalon levő ábra mutatja a direkt biztosító mozgásterét. Feltételezzük, hogy a szerző dés 9 sávos. A direkt biztosító maximális megtartása 100 egység. Az alsó vonal alatti részt a direkt biztosító biztosan saját megtartásában tartja, a két vonal közötti
16 16 A saját megtartás mozgástere surplus viszontbiztositás esetén megtartás maximális kockázat
17 17 területen szabadon választhat, míg a felső vonal feletti kockázat biztosan a viszontbiztosítóhoz kerül egység feletti biztosítási összeget pedig nem szabad elvállalni. A surplus viszontbiztosítás legnagyobb elő nye a direkt biztosító szempontjából, hogy megtarthatja az általa jó üzletnek vélt szerző dések kockázatát. Ez szükségképpen hátrány a viszontbiztosító számára, amely így sokkal rosszabb kárhányadú portfolióhoz fog hozzájutni. Mindkét fél számára hátrány továbbá, hogy a szerző déseket, azok q kvótáját egyedileg nyilván kell tartani. Költségcsökkentő lehet ugyanakkor, hogy a jellemző en az állomány nagy részét kitevő kiskockázatú üzletek nem kerülnek viszontbiztosításba. Ez hátrány a viszontbiztosító szempontjából, mert nem tudja közvetlenül követni a teljes állomány káralakulását. A viszontbiztosítók az antiszelekció ellen úgy védekeznek, hogy a jutalékot alacsonyabb szinten húzzák meg, viszont egy nyereséges portfolió esetén a kockázati nyereség egy részét jutalék formájában visszaadják a közvetlen aláírónak. A fejezetet egy olyan tétel bizonyításával zárjuk, mely azt mondja ki, hogy az arányos viszontbiztosítás mind a direkt, mind a viszontbiztosító számára a legkisebb kockázatot jelenti.
18 TÉTEL Tegyük fel, hogy adott az X kockázat és egy olyan D 1 2 érték, melyre 0<=D 1 2<= D 2 (X). Tegyük fel továbbá, hogy a viszontbiztosításba kerülő állomány szórásnégyzete a D 1 2 értékben rögzített, azaz D 2 (X-TX) = D 1 2 (2.10.) Ekkor van olyan 0<=q<=1, melyre (2.1.)-ben definiált transzformáció optimális abban az értelemben, hogy D 2 (TX), azaz a közvetlen aláírónál maradó állomány szórásnégyzete minimális. Bizonyítás: Legyen q = 1 - (D 1 2 /D 2 (X)) 1/2, ekkor nyílván D 2 (X-TX) = D 1 2 = (1-q) 2 D 2 (X) (2.11.) Vezessük be most a T 1 X = TX - qx (2.12.) transzformációt! D 1 2 = D 2 (X) esetén q=1 választásával az állítás triviális, feltehetjük tehát, hogy D 1 2 <D 2 (X). Nyilvánvalóan
19 19 X-TX = X - qx - T 1 X (2.13.) Innen adódik, hogy D 2 (X-TX)=D 2 (X-qX-T 1 X)= = ((x-qx-t 1 x)-e(x-qx-t 1 X))2 df(x)= = ((x-e(x))(1-q)-(t 1 x-e(t 1 X)))2 df(x)= = (1-q)2 (x-e(x)) 2-2(1-q)(x-E(X))(T 1 x-e(t 1 X))+ +(T 1 x-e(t 1 X)) 2 df(x)= = (1-q) 2 D 2 (X)-2(1-q) (x-e(x))(t 1 x-e(t 1 X))dF(x)+ +D 2 (T 1 X) (2.14.) Az átalakítás közben használtuk a szórásnégyzet definícióját, a binomiális tételt, és azt, hogy az integrálás lineáris transzformáció. (2.11.)-bő l és (2.14.)-bő l adódik, hogy (1-q) 2 D 2 (X)= =(1-q) 2 D 2 (X)-2(1-q) (x-e(x))(t 1 x-e(t 1 X))dF(x) +D 2 (T 1 X) (2.15.) átalakítás után pedig
20 20 (x-e(x)(t 1 x-e(t 1 X))dF(x)=1/(2(1-q))D2 (T 1 X) (2.16.) A megtartott rész szórásnégyzete (2.12.) felhasználásával D 2 (TX)= (Tx-E(TX)) 2 df(x)= = ((qx+t 1 x)-e(qx+t 1 X)) 2 df(x)= = (q(x-e(x))+(t 1 x-e(t 1 X)))2 df(x)= = q 2 (x-e(x)) 2 +2q(x-E(X))(T 1 x-e(t 1 X))+ +(T 1 X-E(T 1 X)) 2 df(x)= =q 2 D 2 (X)+2q (x-e(x))(t 1 x-e(t 1 X))dF(x)+ +D 2( T 1 X) (2.17.) ugyanúgy mint a (2.14.)-ben. (2.17.) elejét és végét összevetve és (2.16.)-ot felhasználva D 2( TX)=q 2 D 2 (X)+1/(1-q) D 2( T 1 X) (2.18.) Mivel 0<=q<1 és D 2( T 1 X)>0, ezért
21 21 D 2( TX)>=q 2 D 2 (X) TX qx esetén (2.18.)-ban egyenlő ség lép fel, ezzel a tételt bebizonyítottuk.
22 22 3. Nem arányos viszontbiztosítási formák A direkt biztosító számára nem mindig elő nyös, hogy arányos viszontbiztosításokat kössön. Olyan kockázatok egy részét is át kell adnia, melyeket pénzügyi kapacitása elbírna, mert annyira alacsony a maximális kár volumene, és amelyek "jó" kockázatok. Ezért a direkt biztosító arra törekszik, hogy ne az egész kárból részesedjen valamilyen arányban a viszontbiztosító, hanem egy bizonyos kárösszeg felett minden kifizetést megtérítsen a közvetlen aláírónak. A legegyszerű bb ilyen típusú szerző dés a kockázati alapú kártöbblet (Excess of Loss, XL) viszontbiztosítás, melynek definíciója a következő : TX=min(X,M), azaz TX= - X ha X<=M - M ha X>M (3.1.) ahol M konstans. Ez azt jelenti, hogy a direkt biztosító egy általa választott M összegnél vágja el felelő sségét, azaz egy kockázatra egy eseménybő l legfeljebb M-et fizet, az ezt meghaladó összeget a viszontbiztosító téríti. M-et megtartásnak szokták nevezni. Könnyű látni, hogy ha a várható érték elvet alkalmazzuk, akkor a viszontbiztosítási díj
23 23 P 1 = M 0 (x-tx)df(x)= (x-tx)df(x)+ (x-tx)df(x)= M M = 0 = M M (x-x)df(x)+ (x-m)df(x)= M M xdf(x)-m df(x) (3.2.) Amennyiben az F(x) eloszlásfüggvény abszolút folytonos, úgy létezik az f(x) sű r ű ségfüggvény is, ezért (3.2.) a következő formában írható: P 1 = M M xf(x)dx-m f(x)dx (3.3.) Az XL-viszontbiztosítás kisebb díjért, nyújt ugyanolyan biztonságot mint egy arányos viszontbiztosítás, ha most "biztonság" alatt a maximális kifizetendő kárösszeget értjük. A következő oldalon található ábrán szemléletesen látszik, hogy alakul egy surplus és egy XLviszontbiztosítás díja.
24 24 Az átadott kockázat díja surplus illetve XL viszontbiztosításnál gyakoriság 0,2 0,15 0,1 0, kárnagyság
25 25 A várható érték elv alapján a teljes kockázat díja az OSBA területtel egyezik meg. Amennyiben a közvetlen aláíró surplus viszontbiztosítást köt M megtartással a viszontbiztosítónak fizetendő díj az MSBA területtel jellemezhető, míg XL esetén a viszontbiztosítás díját az MSB terület szimbolizálja. Szemléletesen is látszik, hogy az XL-viszontbiztosítás díja sokkal kisebb. Annak, hogy kevesebb díjat kell átadni, természetesen megvan a következménye, hiszen a direkt biztosítónak nagyobb részt kell vállalnia a maximálisnál kisebb károkban. Vizsgáljuk meg most a két viszontbiztosítás díjának különbségét egy példán: Legyen az X kockázat eloszlása a (0,100) intervallumon egyenletes és tegyük fel, hogy az idő szak alatt pontosan egy kár következik be. A két biztosító költségeitő l az egyszerű ség kedvéért eltekintünk. A direkt biztosítás díja E(X)=(0+100)/2=50. Ha a direkt biztosító legfeljebb 80 egységnyi kárt kíván megtartani, akkor a kvóta-viszontbiztosítás díja P = (1-q)* E(X)= 0,2*50=10 egység, 1 míg az XL-viszontbiztosítás díja 1 M M P = xf(x)dx-m f(x)dx = x/100dx-80 1/100dx= = [ 1/100 x /2) ] ] [ 1/100*x 80 = 18-16=2 egység
26 26 Különösen hatékony az XL-viszontbiztosítás, ha kártérítés felső határa sokszorosa a szokásos mértéknek, vagy a biztosítók felelő ssége korlátlan, ami a felelő sségbiztosítás esetén elő fordulhat. Nézzünk most egy ilyen példát. Tételezzük fel, hogy az X kockázat exponenciális eloszlású a paraméterrel. Ekkor a biztosított által a közvetlen aláírónak fizetendő nettó díj E(X) = 1/a (3.4.) a kockázat sű r ű ségfüggvénye f(x)=a exp(-ax) (x0) (3.5.) Tételezzük fel, hogy a direkt biztosító által vállalt megtartás a várható érték k-szorosa azaz k/a. Ekkor az átadandó díj (3.3.)-ból k / a k / a P 1 = ax exp(-ax)-k/a a exp(-ax)= =[ 1/a exp(-ax)(-ax-1) ] k / a -k/a [ - exp(-ax) ] k / a = -1/a exp(-k)(-k-1)-(- k/a (-exp(-k)))= =(1/a (k+1)-k/a)exp(-k)=1/a exp(-k) (3.6.)
27 27 vagyis, ha a direkt biztosító csak a várható érték kétszeresét tartja meg, akkor is csak a nettó díj kb. 14%-át kell átadnia. Az XL-viszontbiztosítás további elő nye, hogy kisebbek az adminisztrációs terhek, nem kell a kockázatokat egyedileg osztályozni, mint a surplus viszontbiztosításnál. A viszontbiztosító adminisztrációs költsége is kisebb, mert míg az arányos viszontbiztosításoknál minden kárból részt kell vállalnia, addig kártöbblet szerző déseknél csak viszonylag ritkán elő forduló károknál lép be. Az XL-szerző dések ugyanakkor veszélyesek a viszontbiztosítóra nézve, mert a direkt biztosító a viszontbiztosítási védelem tudatában bátrabban vállalja a kockázatokat, mint egyébként tenné. Ez ellen többféleképpen szoktak védekezni. A szerző désben vannak kizárások, kikötések, de ilyen lehet egy kombinált XL és kvóta viszontbiztosítás, ahol az XLmegtartás feletti károkból valamilyen q részesedést vállal a közvetlen aláíró is, tehát Tx= X ha X<M M+ q (X-M) ha X>=M Másfelő l a viszontbiztosítás megtartása (melyet kapacitásnak nevezünk) a legtöbb esetben véges, ezért a viszontbiztosító kapacitásán felüli károkat a direkt biztosítónak kell fizetnie, esetleg újabb viszontbiztosító után kell néznie. Ha a viszontbiztosító
28 28 kapacitását M 1 -gyel jelöljük, az elő z ő definíciót kiegészítve ezt kapjuk: X ha X<M TX= M + q (X-M) ha M <=X<M 1 (X-M 1 )+q (M 1 -M)+M, ha M 1> X (3.8.) Ebben az esetben a viszontbiztosítónak átadandó díj. P 1 = (x-tx)df(x)= M 0 M 1 M = 0dF(x)+ (1-q)(x-M)dF(x)+ +(1-q)(M 1 -M)dF(x)= M1 M 1 M 1 M M =(1-q) xdf(x)-(1-q) MdF(x)+ (1-q) M 1 df(x) (3.9.) M 1 Ha q=0-at és M 1 = -t helyettesítjük a képletbe, visszakapjuk a (3.3.) formulát. Az XL-viszontbiztosítás legnagyobb hátránya, hogy rendkívül nehéz díjazni. Az arányos viszontbiztosítás esetén kiindulási alapnak lehet tekinteni az eredeti díjat, nincs szükség a kockázat eloszlásának ismeretére. A kártöbblet viszontbiztosítást elvben a (3.9.) képlet alapján kellene díjazni, de gyakorlatban két probléma merül fel:
29 29 Az egyik, hogy nem állnak rendelkezésre egzakt, Lebesgue-null mértékű halmaz kivételével folytonos függvények a kárnagyság eloszlására, legfeljebb ha korábbi kártapasztalatokból származó diszkrét értékekbő l tud a viszontbiztosító számolni. Gyakran azonban ez a statisztika is hiányos, mert a viszontbiztosító nem biztos, hogy be tudja szerezni a megfelelő információkat a kis összegű kifizetésekrő l. A másik probléma, hogy az átadott állomány relatív szórása az adott nettó díjhoz képest nagy, ezért a viszontbiztosító a szórás elve alapján további pótdíjat kérhet. További hátrány, hogy az XL-viszontbiztosítás nem nyújt védelmet a károk gyakoriságában bekövetkező növekedés ellen, csak a károk súlyossága ellen véd. Ezért a nem-arányos viszontbiztosítások nem megfelelő ek egy induló társaság vagy egy induló új üzletág számára. Az XL-viszontbiztosítás kockázatonkénti limittel sem mindig a legszerencsésebb a cedens számára. Egy eseménybő l eredő en sok olyan kár kumulálódhat, amelyeket a direkt biztosító egyenként meg tudna tartani saját kockázatban, de a kumulált kárösszeg megrengetné a direkt biztosító pénzügyi egyensúlyát, gondoljunk például a jégverés, vagy a földrengés károkra. A fedezet matematikai leírásához a T transzformációt a (3.7.) definícióban az X helyett a X i kockázatokra kell alkalmazni, ahol az összegzés az egy
30 30 káreseménybő l bekövetkező károkra vonatkozik. Ezt a formát esemény alapú kártöbblet (Catastrophy XL, CatXL) viszontbiztosításnak nevezik. A CatXL viszontbiztosítás általában egy üzletágra vonatkozik, de néha több üzletágat átfogó "umbrella" fedezet is: Képzeljük el, hogy egy város felett két repülő gép összeütközik. A biztosítónak fizetnie kell a légi CASCO alapján a repülő gépek testében keletkezett károkért, ipari és lakossági vagyonbiztosítások alapján a gyárakban, lakásokban keletkezett kárért, a gépjármű CASCO alapján a megrongálódott autókért, az élet- és balesetbiztosítás alapján a repülő gépen illetve a földön elpusztult emberek hozzátartozóinak, és minden egyéb vagyoni és nem-vagyoni kárért a vétkes légitársaság, forgalomirányító, vagy a hibás navigációs eszközt gyártó cég felelő sségbiztosítása alapján. Az esemény alapú kártöbblet viszontbiztosítás komoly jogi és díjazási problémákat vet fel. Rendkívül nehéz azt meghatározni, hogy mit kell "egy eseménybő l bekövetkező nek" tekinteni. Például egy több órán át tartó szélvihar első és utolsó perceiben keletkező károk, vagy egy földrengés elő - és utórengései egy eseménynek minő sülnek-e. A gyakorlatban ezt általában idő korláttal oldják meg, pl. 168 egymás követő óra. A díjazási probléma pedig még a kockázat alapú XLnél is nagyobb. A direkt biztosító különböző kockázatainak korreláltságát, kumulálódását egzakt módon kiszámítani gyakorlatilag lehetetlen.
31 31 A közelmúlt egyik szomorú eseménye rávilágított arra, hogy a megfogalmazási kérdések egyáltalán nem lényegtelenek: A szeptember 11-i terrortámadásban két repülő gép csapódott be a World Trade Centerbe. Az épület üzemeltető je és a biztosítók, viszontbiztosítók hosszasan vitatkoztak azon, hogy ez egy vagy két eseménynek minő sül-e. A bíróság végül egy eseménynek minő sítette, így a dollárban 10 jegyű limitösszeget csak egyszer kellett kifizetni Az XL-fedezet bizonyos hátrányainak kiküszöbölésére alakult ki a stop-loss viszontbiztosítási forma. Ez a forma azt jelenti, hogy ha direkt biztosító viszontbiztosított üzletága egy idő szakra eső kárainak összege meghalad egy elő re meghatározott összeget vagy a díjbevétel bizonyos százalékát, az e feletti károkat a viszontbiztosító fedezi. A matematikai definícióhoz definiáljuk az X i 1<=i<=N valószínű ségi változókat úgy, mint az i-ik kockázatból az idő szak során kifizetett károk összegét ekkor a stoploss fedezet a következő transzformációval írható le:
32 32 N 1 N X i ha X i< M 1 T( N X i )= 1 N M, h a X i>= M 1 (3.10.) A stop-loss fedezet esetén a megszövegezés egyszerű, viszonylag kicsi a viszontbiztosított állomány szórása a nettó díjhoz képest, ezért biztonságosan kalkulálható. Ez a forma fedezetet nyújt a direkt biztosító számára a kárgyakoriság növekedésébő l származó veszteségek ellen és így nevének megfelelő en "stops the loss", "megállítja a veszteséget", azaz elvben abszolút garanciát nyújt a cedensnek a tönkremenés ellen. A gyakorlat azonban nem teljesen azonos az elmélettel, mert egyrészt ha a direkt biztosító alacsonyan húzza meg a megtartási limitet, a fedezet ára elviselhetetlenül nagy lesz, másrészt a viszontbiztosító a (3.7.) definícióhoz hasonlóan elvár egy bizonyos önrészt az M feletti kárösszegbő l is. Stop-loss fedezetet érdemes kötni a nagy szórással dolgozó üzletágaknál, pl.: mező gazdaság. A fejezetet egy a kockázat alapú XL-viszontbiztosításra vonatkozó tétellel zárjuk, mely könnyen általánosítható a stop-loss formára is.
33 TÉTEL Rögzített viszontbiztosítási díj esetén van olyan M 0 melyre a T 0 = X ha XM 0 M 0 ha X>M 0 (3.1.) transzformáció optimális abban az értelemben, hogy minden más T transzformáció esetén D 2 (TX)>=D 2 (T 0 X) (3.11.) (Ez más szavakkal azt jelenti, hogy a károk változékonysága elleni biztonságot legolcsóbban a kártöbblet viszontbiztosítással vásároljuk meg.) Bizonyítás: A (3.2.) formula alapján P 1 = M (x-m)df(x) (3.12.) Könnyű látni, hogy elég általános feltételek mellett P 1 M-ben folytonos és szigorúan monoton csökkenő. Nyilván M=0 esetén P 1 =P, míg ha M a végtelenhez tart,
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT.
 CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2014. MÁSODIK NEGYEDÉV 2014. augusztus 12. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2014. MÁSODIK NEGYEDÉV 2014. augusztus 12. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
Viszontbiztosítások és az ART. Kovács Norbert SZE, Gazdálkodástudományi Tanszék
 11. Elõadás Viszontbiztosítások és az ART Kovács Norbert SZE, Gazdálkodástudományi Tanszék VISZONTBIZTOSÍTÁS Nem biztosító 1. PASSZÍV VB. (NOSTRO ÜZLET) CEDENS BIZTOSÍTÓ CEDÁLÁS.... Nem biztosító n BIZTOSÍTÓ
11. Elõadás Viszontbiztosítások és az ART Kovács Norbert SZE, Gazdálkodástudományi Tanszék VISZONTBIZTOSÍTÁS Nem biztosító 1. PASSZÍV VB. (NOSTRO ÜZLET) CEDENS BIZTOSÍTÓ CEDÁLÁS.... Nem biztosító n BIZTOSÍTÓ
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT.
 CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2016. HARMADIK NEGYEDÉV 2016. november 22. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2016. HARMADIK NEGYEDÉV 2016. november 22. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
kockázatai A befektetési egységekhez kötött életbiztosítások
 A befektetési egységekhez kötött életbiztosítások kockázatai Mennyiben jelenthet megoldást befektetési/megtakarítási céljai elérésére, nyugdíjas évei, illetve gyermekei anyagi biztonságára nézve a befektetési
A befektetési egységekhez kötött életbiztosítások kockázatai Mennyiben jelenthet megoldást befektetési/megtakarítási céljai elérésére, nyugdíjas évei, illetve gyermekei anyagi biztonságára nézve a befektetési
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT.
 CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2016. MÁSODIK NEGYEDÉV 2016. augusztus 23. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2016. MÁSODIK NEGYEDÉV 2016. augusztus 23. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
Az ajánlás célja és hatálya
 A Pénzügyi Szervezetek Állami Felügyelete elnökének 3/2012. (IV.13.) számú ajánlása a biztosítók üzleti tervének minimális tartalmi és formai elemeiről I. Az ajánlás célja és hatálya A Pénzügyi Szervezetek
A Pénzügyi Szervezetek Állami Felügyelete elnökének 3/2012. (IV.13.) számú ajánlása a biztosítók üzleti tervének minimális tartalmi és formai elemeiről I. Az ajánlás célja és hatálya A Pénzügyi Szervezetek
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT.
 CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2016. ELSŐ NEGYEDÉV 2016. május 24. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2016. ELSŐ NEGYEDÉV 2016. május 24. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
Mérleg. Szolvencia II. szerinti érték Eszközök
 Mérleg Szolvencia II. szerinti érték Eszközök C0010 Immateriális javak R0030 - Halasztott adókövetelések R0040 - Nyugdíjszolgáltatások többlete R0050 - Saját használatú ingatlanok, gépek és berendezések
Mérleg Szolvencia II. szerinti érték Eszközök C0010 Immateriális javak R0030 - Halasztott adókövetelések R0040 - Nyugdíjszolgáltatások többlete R0050 - Saját használatú ingatlanok, gépek és berendezések
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT.
 CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2014. HARMADIK NEGYEDÉV 2014. november 13. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2014. HARMADIK NEGYEDÉV 2014. november 13. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
GB117 JELÛ GRÁNIT VEGYES ÉLETBIZTOSÍTÁS KÜLÖNÖS FELTÉTELEI
 GB117 JELÛ GRÁNIT VEGYES ÉLETBIZTOSÍTÁS KÜLÖNÖS FELTÉTELEI 1. Általános rendelkezések (1) A Gránit Vegyes Életbiztosítási szerzôdés (továbbiakban: biztosítás) a jelen Különös Feltételek valamint az OTP
GB117 JELÛ GRÁNIT VEGYES ÉLETBIZTOSÍTÁS KÜLÖNÖS FELTÉTELEI 1. Általános rendelkezések (1) A Gránit Vegyes Életbiztosítási szerzôdés (továbbiakban: biztosítás) a jelen Különös Feltételek valamint az OTP
ERSTE Vienna Insurance Group Biztosító Zrt. Az ERSTE CLASSIC egyszeri Díjas, teljes életre szóló kockázati életbiztosítás (HUR3U) különös feltételei
 ERSTE Vienna Insurance Group Biztosító Zrt. Az ERSTE CLASSIC egyszeri Díjas, teljes életre szóló kockázati életbiztosítás (HUR3U) különös feltételei Jelzőszám: SV/01/2011/1 Hatályos: 2017. január 01-től
ERSTE Vienna Insurance Group Biztosító Zrt. Az ERSTE CLASSIC egyszeri Díjas, teljes életre szóló kockázati életbiztosítás (HUR3U) különös feltételei Jelzőszám: SV/01/2011/1 Hatályos: 2017. január 01-től
ERSTE Vienna Insurance Group Biztosító Zrt. Az ERSTE CLASSIC egyszeri Díjas, teljes életre szóló kockázati életbiztosítás (HUR3U) különös feltételei
 ERSTE Vienna Insurance Group Biztosító Zrt. Az ERSTE CLASSIC egyszeri Díjas, teljes életre szóló kockázati életbiztosítás (HUR3U) különös feltételei Jelzőszám: SV/01/2011/1 Hatályos: 2015. február 16-tól
ERSTE Vienna Insurance Group Biztosító Zrt. Az ERSTE CLASSIC egyszeri Díjas, teljes életre szóló kockázati életbiztosítás (HUR3U) különös feltételei Jelzőszám: SV/01/2011/1 Hatályos: 2015. február 16-tól
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT.
 CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2014. ELSŐ NEGYEDÉV 2014. május 15. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2014. ELSŐ NEGYEDÉV 2014. május 15. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
Szolvencia II. Biztosítástechnikai tartalékok 2005.04.27
 Szolvencia II. Biztosítástechnikai tartalékok 2005.04.27 Biztosítástechnikai tartalékok A. Nem-életbiztosítási tartalékok B. Életbiztosítási tartalékok C. Próbaszámolások 2005.04.27 2 A. Nem-életbiztosítási
Szolvencia II. Biztosítástechnikai tartalékok 2005.04.27 Biztosítástechnikai tartalékok A. Nem-életbiztosítási tartalékok B. Életbiztosítási tartalékok C. Próbaszámolások 2005.04.27 2 A. Nem-életbiztosítási
ERGO Unit Linked REGNUM és NOVUM életbiztosítás különös feltételeinek (alapbiztosítás) 2. sz. Függeléke (euróban)
 ERGO Unit Linked REGNUM és NOVUM életbiztosítás különös feltételeinek (alapbiztosítás) 2. sz. Függeléke (euróban) 1. Minimális díjak: - Folyamatos díjas szerzıdések esetén: Minimális éves díj: 360 Euró
ERGO Unit Linked REGNUM és NOVUM életbiztosítás különös feltételeinek (alapbiztosítás) 2. sz. Függeléke (euróban) 1. Minimális díjak: - Folyamatos díjas szerzıdések esetén: Minimális éves díj: 360 Euró
2. számú melléklet: Ajánlattevő végleges ajánlata- Tanuló baleset-biztosítás
 2. számú melléklet: Ajánlattevő végleges ajánlata- Tanuló baleset-biztosítás I. ÁLTALÁNOS ADATOK 1. A Szerződés alanyai A Biztosítási Szerződés Szerződője a Volánbusz Közlekedési Zrt. (1091 Budapest, Üllői
2. számú melléklet: Ajánlattevő végleges ajánlata- Tanuló baleset-biztosítás I. ÁLTALÁNOS ADATOK 1. A Szerződés alanyai A Biztosítási Szerződés Szerződője a Volánbusz Közlekedési Zrt. (1091 Budapest, Üllői
MÜBSE. Szolvencia és pénzügyi állapotjelentés. Közzétételek. december 31. (Monetáris összegek ezer Ft-ban)
 MÜBSE Szolvencia és pénzügyi állapotjelentés Közzétételek 217 december 31. (Monetáris összegek ezer Ft-ban) Vállalkozás neve MÜBSE A vállalkozás azonosító kódja 529973SWRVST25IQ23 A vállalkozás azonosító
MÜBSE Szolvencia és pénzügyi állapotjelentés Közzétételek 217 december 31. (Monetáris összegek ezer Ft-ban) Vállalkozás neve MÜBSE A vállalkozás azonosító kódja 529973SWRVST25IQ23 A vállalkozás azonosító
C0010 Eszközök Üzleti vagy cégérték
 S.02.01.02 Mérleg Szolvencia II. szerinti érték C0010 Eszközök Üzleti vagy cégérték R0010 Halasztott szerzési költség R0020 Immateriális javak R0030 0 Halasztott adókövetelések R0040 66.672 Nyugdíjszolgáltatások
S.02.01.02 Mérleg Szolvencia II. szerinti érték C0010 Eszközök Üzleti vagy cégérték R0010 Halasztott szerzési költség R0020 Immateriális javak R0030 0 Halasztott adókövetelések R0040 66.672 Nyugdíjszolgáltatások
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT.
 CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2016. NEGYEDIK NEGYEDÉV 2017. február 21. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2016. NEGYEDIK NEGYEDÉV 2017. február 21. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
Gépjárműfelelősségbiztosítás. Üzemi balesetbiztosítás
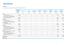 Melléklet S.05.01.02 Biztosítási díjak, kárigények és ráfordítások üzletáganként (1/3) Gyógyászati költségek térítésére vonatkozó biztosítás Jövedelembiztosítás Üzemi balesetbiztosítás Gépjárműfelelősségbiztosítás
Melléklet S.05.01.02 Biztosítási díjak, kárigények és ráfordítások üzletáganként (1/3) Gyógyászati költségek térítésére vonatkozó biztosítás Jövedelembiztosítás Üzemi balesetbiztosítás Gépjárműfelelősségbiztosítás
Közgazdaságtan alapjai. Dr. Karajz Sándor Gazdaságelméleti Intézet
 Közgazdaságtan alapjai Dr. Karajz Sándor Gazdaságelméleti 4. Előadás Az árupiac és az IS görbe IS-LM rendszer A rövidtávú gazdasági ingadozások modellezésére használt legismertebb modell az úgynevezett
Közgazdaságtan alapjai Dr. Karajz Sándor Gazdaságelméleti 4. Előadás Az árupiac és az IS görbe IS-LM rendszer A rövidtávú gazdasági ingadozások modellezésére használt legismertebb modell az úgynevezett
Jövõkép (GP71, GP71E) rendszeres és egyszeri díjas elérési életbiztosítás különös feltételei
 Feltételek Jövõkép (GP71, GP71E) rendszeres és egyszeri díjas elérési életbiztosítás különös feltételei NY. SZ.: 1-01305/01 Tartalom 1. Biztosítási események...4 2. A biztosító szolgáltatásai...4 3. Díjtartalék,
Feltételek Jövõkép (GP71, GP71E) rendszeres és egyszeri díjas elérési életbiztosítás különös feltételei NY. SZ.: 1-01305/01 Tartalom 1. Biztosítási események...4 2. A biztosító szolgáltatásai...4 3. Díjtartalék,
Lízing Üzleti tanácsok, üzleti tanácsadás: www.kisado.hu
 Lízing Lízing A lízingbevevő a lízingszerződésben rögzített lízingdíj megfizetésére vállal kötelezettséget. A lízingszerződés fedezete maga a lízing tárgya, amelynek tulajdonjogát a lízingbevevő csak a
Lízing Lízing A lízingbevevő a lízingszerződésben rögzített lízingdíj megfizetésére vállal kötelezettséget. A lízingszerződés fedezete maga a lízing tárgya, amelynek tulajdonjogát a lízingbevevő csak a
Gyermekem támogatása. Novum Életbiztosítás
 Gyermekem támogatása Novum Életbiztosítás Ma egy biztosítás, holnap gyermeke jövőjének záloga Minden szülő arra vágyik, hogy megadhassa gyerme - kének mindazt a támogatást, amellyel hozzásegítheti céljai
Gyermekem támogatása Novum Életbiztosítás Ma egy biztosítás, holnap gyermeke jövőjének záloga Minden szülő arra vágyik, hogy megadhassa gyerme - kének mindazt a támogatást, amellyel hozzásegítheti céljai
Immateriális javak Halasztott adókövetelések 0 Nyugdíjszolgáltatások többlete Saját használatú ingatlanok, gépek és berendezések
 MELLÉKLET S.02.01.02 Mérleg Eszközök Eszközök Szolvencia II. szerinti érték C0010 Immateriális javak Halasztott adókövetelések 0 Nyugdíjszolgáltatások többlete Saját használatú ingatlanok, gépek és berendezések
MELLÉKLET S.02.01.02 Mérleg Eszközök Eszközök Szolvencia II. szerinti érték C0010 Immateriális javak Halasztott adókövetelések 0 Nyugdíjszolgáltatások többlete Saját használatú ingatlanok, gépek és berendezések
Rokkantsági kockázatot tartalmazó részlet-kifizetésű életbiztosítás különös feltételei
 Rokkantsági kockázatot tartalmazó részlet-kifizetésű életbiztosítás különös feltételei 1. Általános rendelkezések A jelen alapbiztosítás feltételeiben nem rendezett kérdésekben az ÁB-AEGON Általános Biztosító
Rokkantsági kockázatot tartalmazó részlet-kifizetésű életbiztosítás különös feltételei 1. Általános rendelkezések A jelen alapbiztosítás feltételeiben nem rendezett kérdésekben az ÁB-AEGON Általános Biztosító
Gyermekem támogatása. Novum Életbiztosítás
 Gyermekem támogatása Novum Életbiztosítás Ma egy biztosítás, holnap gyermeke jövőjének záloga Minden szülő arra vágyik, hogy megadhassa gyerme - kének mindazt a támogatást, amellyel hozzásegítheti céljai
Gyermekem támogatása Novum Életbiztosítás Ma egy biztosítás, holnap gyermeke jövőjének záloga Minden szülő arra vágyik, hogy megadhassa gyerme - kének mindazt a támogatást, amellyel hozzásegítheti céljai
CIG PANNÓNIA ÉLETBIZTOSÍTÓ NYRT.
 CIG PANNÓNIA ÉLETBIZTOSÍTÓ NYRT. NEGYEDÉVES TÁJÉKOZTATÓ 2011. ELSŐ NEGYEDÉV 2011. május 18. 1. Összefoglaló A CIG Pannónia Életbiztosító Nyrt. (a továbbiakban: Kibocsátó) a mai napon nyilvánosságra hozza
CIG PANNÓNIA ÉLETBIZTOSÍTÓ NYRT. NEGYEDÉVES TÁJÉKOZTATÓ 2011. ELSŐ NEGYEDÉV 2011. május 18. 1. Összefoglaló A CIG Pannónia Életbiztosító Nyrt. (a továbbiakban: Kibocsátó) a mai napon nyilvánosságra hozza
Megtakarítási program az Ön által választott célra. Regnum Életbiztosítás
 Megtakarítási program az Ön által választott célra Regnum Életbiztosítás Akár évi 130 000 Ft értékű adókedvezménnyel! Rendszeres megtakarítással a biztos jövőért Céljaink megvalósítása jelentős kiadással
Megtakarítási program az Ön által választott célra Regnum Életbiztosítás Akár évi 130 000 Ft értékű adókedvezménnyel! Rendszeres megtakarítással a biztos jövőért Céljaink megvalósítása jelentős kiadással
A Markowitz modell: kvadratikus programozás
 A Markowitz modell: kvadratikus programozás Harry Markowitz 1990-ben kapott Közgazdasági Nobel díjat a portfolió optimalizálási modelljéért. Ld. http://en.wikipedia.org/wiki/harry_markowitz Ennek a legegyszer
A Markowitz modell: kvadratikus programozás Harry Markowitz 1990-ben kapott Közgazdasági Nobel díjat a portfolió optimalizálási modelljéért. Ld. http://en.wikipedia.org/wiki/harry_markowitz Ennek a legegyszer
CIG Pannónia Életbiztosító Zrt. Eredménykimutatás
 Sorszám PSZÁF kód CIG Pannónia Életbiztosító Zrt. Eredménykimutatás 21.6.3. Megnevezés 1 41B1 1. Megszolgált díjak, viszontbiztosítás nélkül 2 41B11 a bruttó díj 3 41B12 b viszontbiztosítónak átadott díj
Sorszám PSZÁF kód CIG Pannónia Életbiztosító Zrt. Eredménykimutatás 21.6.3. Megnevezés 1 41B1 1. Megszolgált díjak, viszontbiztosítás nélkül 2 41B11 a bruttó díj 3 41B12 b viszontbiztosítónak átadott díj
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT.
 CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2015. MÁSODIK NEGYEDÉV 2015. augusztus 18. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2015. MÁSODIK NEGYEDÉV 2015. augusztus 18. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
2007. május 19. Altenburger
 Dr. Banyár József Jelenleg a magánnyugdíjpénztári járadék (egyszer en: magánpénztári járadék) opcionális - szerencsére senki sem választja A szabályozás ugyanis hiányos és ellentmondásos A problémakör
Dr. Banyár József Jelenleg a magánnyugdíjpénztári járadék (egyszer en: magánpénztári járadék) opcionális - szerencsére senki sem választja A szabályozás ugyanis hiányos és ellentmondásos A problémakör
Kockázatkezelés és biztosítás
 Kockázatkezelés és biztosítás Dr. habil. Farkas Szilveszter PhD egyetemi docens, tanszékvezető Pénzügy Intézeti Tanszék Fő témakörök 1. Biztosítás fogalma 2. A biztosítási rendszer alapintézményei és a
Kockázatkezelés és biztosítás Dr. habil. Farkas Szilveszter PhD egyetemi docens, tanszékvezető Pénzügy Intézeti Tanszék Fő témakörök 1. Biztosítás fogalma 2. A biztosítási rendszer alapintézményei és a
Hirdetmény. 1. A biztosítási díj fizetésére vonatkozó kötelezettség teljesítése
 Hirdetmény A SIGNAL Biztosító Zrt. az alább meghatározott biztosítási szerződés típusok adott szerződési pontjai kapcsán az alábbi kiegészítéseket, pontosításokat teszi az ügyfelek mind teljeskörűbb tájékoztatása
Hirdetmény A SIGNAL Biztosító Zrt. az alább meghatározott biztosítási szerződés típusok adott szerződési pontjai kapcsán az alábbi kiegészítéseket, pontosításokat teszi az ügyfelek mind teljeskörűbb tájékoztatása
Allianz Hungária Zrt.
 Allianz Hungária Zrt. Éves jelentés 28 Éves jelentés 28 A fõbb mutatószámok alakulása Allianz Hungária Zrt. 26 26 millió Változás % 27 27 millió Változás % 28 28 millió Bruttó díjbevétel Bruttó kárkifizetés
Allianz Hungária Zrt. Éves jelentés 28 Éves jelentés 28 A fõbb mutatószámok alakulása Allianz Hungária Zrt. 26 26 millió Változás % 27 27 millió Változás % 28 28 millió Bruttó díjbevétel Bruttó kárkifizetés
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT.
 CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2014. NEGYEDIK NEGYEDÉV 2015. február 17. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2014. NEGYEDIK NEGYEDÉV 2015. február 17. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
A QIS5 mennyiségi eredményei QIS5 QIS5 QIS5 QIS. Gaálné Kodila Diána Somlóiné Tusnády Paula Varga Gábor február 28.
 A mennyiségi eredményei 2011. február 28. Gaálné Kodila Diána Somlóiné Tusnády Paula Varga Gábor 1 Tartalom Lebonyolítás, részvétel Adatminőség Általános pénzügyi hatás Tartalékok értékelése Illikviditási
A mennyiségi eredményei 2011. február 28. Gaálné Kodila Diána Somlóiné Tusnády Paula Varga Gábor 1 Tartalom Lebonyolítás, részvétel Adatminőség Általános pénzügyi hatás Tartalékok értékelése Illikviditási
Tartalom. Speciális pénzáramlások. Feladatmegoldás, jelenértékszámítások 2010.10.19. 8. hét. Speciális pénzáramlások. Örökjáradék:
 Feladatmegoldás, jelenértékszámítások 8. hét 2010.10.26. 1 Tartalom Speciális pénzáramlások Örökjáradék: Olyan végtelen számú tagból álló pénzáramlás, amelynek minden eleme megegyezik. Növekvő örökjáradék:
Feladatmegoldás, jelenértékszámítások 8. hét 2010.10.26. 1 Tartalom Speciális pénzáramlások Örökjáradék: Olyan végtelen számú tagból álló pénzáramlás, amelynek minden eleme megegyezik. Növekvő örökjáradék:
Kihirdetve: 2014. június 13. Érvényes: 2014. július 01. napjától visszavonásig
 H I R D E T M É N Y a Santander Consumer Finance Zrt. által, 2010. március 01. napját megelőzően megkötött, magánszemélyek részére nyújtott ingatlanfedezettel biztosított személyi kölcsönök költségeiről
H I R D E T M É N Y a Santander Consumer Finance Zrt. által, 2010. március 01. napját megelőzően megkötött, magánszemélyek részére nyújtott ingatlanfedezettel biztosított személyi kölcsönök költségeiről
Megtakarítás és biztonság
 Megtakarítás és biztonság kompromisszumok nélkül Aqua Életbiztosítás Rendszeres megtakarítás és többszörös gondoskodás A befektetéssel kombinált életbiztosításokról sokan azt állítják, hogy indokolatlan
Megtakarítás és biztonság kompromisszumok nélkül Aqua Életbiztosítás Rendszeres megtakarítás és többszörös gondoskodás A befektetéssel kombinált életbiztosításokról sokan azt állítják, hogy indokolatlan
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT.
 CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2015. ELSŐ NEGYEDÉV 2015. május 14. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2015. ELSŐ NEGYEDÉV 2015. május 14. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
AEGON CSOPORTOS BIZTOSÍTÁSOK FELHÍVÁS AJÁNLATTÉTELRE
 AEGON CSOPORTOS BIZTOSÍTÁSOK FELHÍVÁS AJÁNLATTÉTELRE 2013 AEGON Magyarország Általános Biztosító Zrt. Csoportos Biztosítások 1091 Budapest, Üllői út 1. 1. oldal Aegon csoportos biztosítási díjkalkuláció
AEGON CSOPORTOS BIZTOSÍTÁSOK FELHÍVÁS AJÁNLATTÉTELRE 2013 AEGON Magyarország Általános Biztosító Zrt. Csoportos Biztosítások 1091 Budapest, Üllői út 1. 1. oldal Aegon csoportos biztosítási díjkalkuláció
Allianz Hungária Biztosító Zrt.
 Allianz Hungária Biztosító Zrt. Éves jelentés 27 Éves jelentés 27 A fõbb mutatószámok alakulása Allianz Hungária Biztosító Zrt. 25 25 millió Változás % 26 26 millió Változás % 27 27 millió Bruttó díjbevétel
Allianz Hungária Biztosító Zrt. Éves jelentés 27 Éves jelentés 27 A fõbb mutatószámok alakulása Allianz Hungária Biztosító Zrt. 25 25 millió Változás % 26 26 millió Változás % 27 27 millió Bruttó díjbevétel
A QIS3 tapasztalatai. a Posta Biztosítónál. Góg Enikő 2008.03.20.
 A QIS3 tapasztalatai a Posta Biztosítónál Góg Enikő 2008.03.20. 1 Tartalom A Posta Biztosító bemutatása A projekt a munkaszervezés és a munkaterhelés tekintetében A számítások tapasztalatai Eredmények
A QIS3 tapasztalatai a Posta Biztosítónál Góg Enikő 2008.03.20. 1 Tartalom A Posta Biztosító bemutatása A projekt a munkaszervezés és a munkaterhelés tekintetében A számítások tapasztalatai Eredmények
A NEMZETGAZDASÁGI MINISZTÉRIUM FELTÉTELES ADÓMEGÁLLAPÍTÁSI HATÁROZATÁNAK ÖSSZEFOGLALÓJA
 A NEMZETGAZDASÁGI MINISZTÉRIUM FELTÉTELES ADÓMEGÁLLAPÍTÁSI HATÁROZATÁNAK ÖSSZEFOGLALÓJA Frissített verzió, 2011. július A Nemzetgazdasági Minisztérium feltételes adómegállapítási határozatának összefoglalója
A NEMZETGAZDASÁGI MINISZTÉRIUM FELTÉTELES ADÓMEGÁLLAPÍTÁSI HATÁROZATÁNAK ÖSSZEFOGLALÓJA Frissített verzió, 2011. július A Nemzetgazdasági Minisztérium feltételes adómegállapítási határozatának összefoglalója
Valószínűségi változók. Várható érték és szórás
 Matematikai statisztika gyakorlat Valószínűségi változók. Várható érték és szórás Valószínűségi változók 2016. március 7-11. 1 / 13 Valószínűségi változók Legyen a (Ω, A, P) valószínűségi mező. Egy X :
Matematikai statisztika gyakorlat Valószínűségi változók. Várható érték és szórás Valószínűségi változók 2016. március 7-11. 1 / 13 Valószínűségi változók Legyen a (Ω, A, P) valószínűségi mező. Egy X :
I. sz. melléklet S Mérleg
 S.02.01.02 Mérleg Szolvencia II. szerinti érték Eszközök C0010 Immateriális javak R0030 0 Halasztott adókövetelések R0040 0 Nyugdíjszolgáltatások többlete R0050 0 Saját használatú ingatlanok, gépek és
S.02.01.02 Mérleg Szolvencia II. szerinti érték Eszközök C0010 Immateriális javak R0030 0 Halasztott adókövetelések R0040 0 Nyugdíjszolgáltatások többlete R0050 0 Saját használatú ingatlanok, gépek és
BIZTOSÍTÁSI AJÁNLAT JÁRADÉKBIZTOSÍTÁSI SZERZŐDÉS MEGKÖTÉSÉHEZ
 2016/07/01 BIZTOSÍTÁSI AJÁNLAT JÁRADÉKBIZTOSÍTÁSI SZERZŐDÉS MEGKÖTÉSÉHEZ Partnerkód: Ellenőrizte: Kötvényesítés dátuma: Kötvény kiküldési dátuma Ajánlatszám: Kötvényszám: Beérkezés dátuma a GRAWE-hoz:
2016/07/01 BIZTOSÍTÁSI AJÁNLAT JÁRADÉKBIZTOSÍTÁSI SZERZŐDÉS MEGKÖTÉSÉHEZ Partnerkód: Ellenőrizte: Kötvényesítés dátuma: Kötvény kiküldési dátuma Ajánlatszám: Kötvényszám: Beérkezés dátuma a GRAWE-hoz:
Véletlen jelenség: okok rendszere hozza létre - nem ismerhetjük mind, ezért sztochasztikus.
 Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
Volatilitási tőkepuffer a szolvencia IIes tőkekövetelmények megsértésének kivédésére
 Volatilitási tőkepuffer a szolvencia IIes tőkekövetelmények megsértésének kivédésére Zubor Zoltán MNB - Biztosításfelügyeleti főosztály MAT Tavaszi Szimpózium 2016. május 7. 1 Háttér Bit. 99. : folyamatos
Volatilitási tőkepuffer a szolvencia IIes tőkekövetelmények megsértésének kivédésére Zubor Zoltán MNB - Biztosításfelügyeleti főosztály MAT Tavaszi Szimpózium 2016. május 7. 1 Háttér Bit. 99. : folyamatos
Határozatlan integrál (2) First Prev Next Last Go Back Full Screen Close Quit
 Határozatlan integrál () First Prev Next Last Go Back Full Screen Close Quit 1. Az összetett függvények integrálására szolgáló egyik módszer a helyettesítéssel való integrálás. Az idevonatkozó tétel pontos
Határozatlan integrál () First Prev Next Last Go Back Full Screen Close Quit 1. Az összetett függvények integrálására szolgáló egyik módszer a helyettesítéssel való integrálás. Az idevonatkozó tétel pontos
III. Döntési szintek. IV. Döntési hatáskörök. 10. Kockázatvállalási döntési hatáskörök
 10. Kockázatvállalási döntési hatáskörök III. Döntési szintek A Takarékszövetkezet üzleti tevékenysége során keletkező kockázati elemek minimalizálása érdekében a döntéseket a takarékszövetkezeti hierarchia
10. Kockázatvállalási döntési hatáskörök III. Döntési szintek A Takarékszövetkezet üzleti tevékenysége során keletkező kockázati elemek minimalizálása érdekében a döntéseket a takarékszövetkezeti hierarchia
A BEFEKTETŐ-VÉDELMI ALAP IGAZGATÓSÁGÁNAK
 Nyilvános A BEFEKTETŐ-VÉDELMI ALAP IGAZGATÓSÁGÁNAK 24/2010. (XI. 4.) számú határozata A Beva igazgatósága megvitatta a kockázatarányos díjrendszer bevezetésére vonatkozó döntés nyomán elkészített előterjesztést,
Nyilvános A BEFEKTETŐ-VÉDELMI ALAP IGAZGATÓSÁGÁNAK 24/2010. (XI. 4.) számú határozata A Beva igazgatósága megvitatta a kockázatarányos díjrendszer bevezetésére vonatkozó döntés nyomán elkészített előterjesztést,
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT.
 CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2013. ELSŐ NEGYEDÉV 2013. május 16. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2013. ELSŐ NEGYEDÉV 2013. május 16. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
GYAKORLÓ FELADATOK 1. A pénz időértéke I. rész (megoldott) Fizetés egy év múlva
 . Jelenérték (PV, NPV), jövő érték (FV) Számítsa ki az alábbi pénzáramok jelen és jövőértékét. Az A,B,C ajánlatok három külön esetet jelentenek. 0% kamatlábat használjon minden lejáratra. Jövőértéket a.
. Jelenérték (PV, NPV), jövő érték (FV) Számítsa ki az alábbi pénzáramok jelen és jövőértékét. Az A,B,C ajánlatok három külön esetet jelentenek. 0% kamatlábat használjon minden lejáratra. Jövőértéket a.
Taylor-polinomok. 1. Alapfeladatok. 2015. április 11. 1. Feladat: Írjuk fel az f(x) = e 2x függvény másodfokú Maclaurinpolinomját!
 Taylor-polinomok 205. április.. Alapfeladatok. Feladat: Írjuk fel az fx) = e 2x függvény másodfokú Maclaurinpolinomját! Megoldás: A feladatot kétféle úton is megoldjuk. Az els megoldásban induljunk el
Taylor-polinomok 205. április.. Alapfeladatok. Feladat: Írjuk fel az fx) = e 2x függvény másodfokú Maclaurinpolinomját! Megoldás: A feladatot kétféle úton is megoldjuk. Az els megoldásban induljunk el
Webinárium Jövőkulcs Classic
 Webinárium Jövőkulcs Classic 2017.01.09. Chart 1 Néhány ijesztő adat. 2 Jövőkulcs Classic Klasszikus nyugdíjbiztosítás 2017.01.01 Chart 3 Klasszikus nyugdíjbiztosítás Jövőkulcs Classic Előre rögzített
Webinárium Jövőkulcs Classic 2017.01.09. Chart 1 Néhány ijesztő adat. 2 Jövőkulcs Classic Klasszikus nyugdíjbiztosítás 2017.01.01 Chart 3 Klasszikus nyugdíjbiztosítás Jövőkulcs Classic Előre rögzített
nyugdíjbiztosítás Hosszú távú nyugdíjcélok,
 Hosszú távú nyugdíjcélok, nyugdíjbiztosítás Alapozza meg nyugdíjas éveit! Kezdjen megtakarítani mielőbb, hogy a gondtalan évek alatt az anyagi kérdések se okozhassanak problémát! ÖNGONDOSKODÁS 22 Milyen
Hosszú távú nyugdíjcélok, nyugdíjbiztosítás Alapozza meg nyugdíjas éveit! Kezdjen megtakarítani mielőbb, hogy a gondtalan évek alatt az anyagi kérdések se okozhassanak problémát! ÖNGONDOSKODÁS 22 Milyen
nyugdíjbiztosítás Hosszú távú nyugdíjcélok, Szeretné megalapozni jövője anyagi biztonságát?
 Hosszú távú nyugdíjcélok, nyugdíjbiztosítás Szeretné megalapozni jövője anyagi biztonságát? Kezdjen megtakarítani mielőbb, hogy a nyugdíjas évek alatt a pénzügyi kérdések ne okozhassanak problémát! ÖNGONDOSKODÁS
Hosszú távú nyugdíjcélok, nyugdíjbiztosítás Szeretné megalapozni jövője anyagi biztonságát? Kezdjen megtakarítani mielőbb, hogy a nyugdíjas évek alatt a pénzügyi kérdések ne okozhassanak problémát! ÖNGONDOSKODÁS
Aranyszárny. rendszeres díjas, befektetési egységekhez kötött életbiztosítás különös feltételei (G60/2012) Hatályos: 2012.
 Aranyszárny rendszeres díjas, befektetési egységekhez kötött életbiztosítás különös feltételei (G60/2012) Hatályos: 2012. november 1-jétől Nysz.: 15287 Tartalomjegyzék Aranyszárny rendszeres díjas, befektetési
Aranyszárny rendszeres díjas, befektetési egységekhez kötött életbiztosítás különös feltételei (G60/2012) Hatályos: 2012. november 1-jétől Nysz.: 15287 Tartalomjegyzék Aranyszárny rendszeres díjas, befektetési
Az NN Biztosító Zrt. 945 jelű Baleseti halál kiegészítő biztosításának különös feltételei
 Az NN Biztosító Zrt. 945 jelű Baleseti halál kiegészítő biztosításának különös feltételei 1. Általános rendelkezések a) Az NN Biztosító Zrt. (székhelye: 1068 Budapest, Dózsa György út 84/B, a továbbiakban:
Az NN Biztosító Zrt. 945 jelű Baleseti halál kiegészítő biztosításának különös feltételei 1. Általános rendelkezések a) Az NN Biztosító Zrt. (székhelye: 1068 Budapest, Dózsa György út 84/B, a továbbiakban:
Könyvelői Klub 2013..február 06. Miskolc
 Könyvelői Klub 2013..február 06. Miskolc Konzultáns: Horváth Józsefné okl. könyvvizsgáló, okl. nemzetközi áfa- és adóigazgatósági adószakértő, jogi szakokleveles közgazdász; költségvetési minősítésű könyvvizsgáló
Könyvelői Klub 2013..február 06. Miskolc Konzultáns: Horváth Józsefné okl. könyvvizsgáló, okl. nemzetközi áfa- és adóigazgatósági adószakértő, jogi szakokleveles közgazdász; költségvetési minősítésű könyvvizsgáló
Aranyszárny. rendszeres díjas, befektetési egységekhez kötött életbiztosítás különös feltételei (G60/2009) Hatályos: 2009.
 Aranyszárny rendszeres díjas, befektetési egységekhez kötött életbiztosítás különös feltételei (G60/2009) Hatályos: 2009. április 1-jétől Módosítás időpontja: 2011. július 1. Nysz.: 14755 Tartalomjegyzék
Aranyszárny rendszeres díjas, befektetési egységekhez kötött életbiztosítás különös feltételei (G60/2009) Hatályos: 2009. április 1-jétől Módosítás időpontja: 2011. július 1. Nysz.: 14755 Tartalomjegyzék
MARKETPROG Asset Management Befektetési Alapkezelő Zártkörűen Működő Részvénytársaság. Díjszabályzata. Jóváhagyta: Verzió:
 MARKETPROG Asset Management Befektetési Alapkezelő Zártkörűen Működő Részvénytársaság Díjszabályzata Jóváhagyta: Verzió: 2018.11.23. A MARKETPROG Asset Management Befektetési Alapkezelő Zártkörűen Működő
MARKETPROG Asset Management Befektetési Alapkezelő Zártkörűen Működő Részvénytársaság Díjszabályzata Jóváhagyta: Verzió: 2018.11.23. A MARKETPROG Asset Management Befektetési Alapkezelő Zártkörűen Működő
Rövid távú modell Pénzkereslet, LM görbe
 Rövid távú modell Pénzkereslet, Kuncz Izabella Makroökonómia Tanszék Budapesti Corvinus Egyetem Makroökonómia Kuncz Izabella Rövid távú modell Pénzkereslet, Mit tudunk eddig? Elkezdtük levezetni a rövid
Rövid távú modell Pénzkereslet, Kuncz Izabella Makroökonómia Tanszék Budapesti Corvinus Egyetem Makroökonómia Kuncz Izabella Rövid távú modell Pénzkereslet, Mit tudunk eddig? Elkezdtük levezetni a rövid
Függvények határértéke, folytonossága
 Függvények határértéke, folytonossága 25. február 22.. Alapfeladatok. Feladat: Határozzuk meg az f() = 23 4 5 3 + 9 a végtelenben és a mínusz végtelenben! függvény határértékét Megoldás: Vizsgáljuk el
Függvények határértéke, folytonossága 25. február 22.. Alapfeladatok. Feladat: Határozzuk meg az f() = 23 4 5 3 + 9 a végtelenben és a mínusz végtelenben! függvény határértékét Megoldás: Vizsgáljuk el
A 118 jelű rendszeres díjas befektetési egységekhez kötött életbiztosítás Különös Feltételeinek Melléklete
 NN Biztosító Zrt. A 118 jelű rendszeres díjas befektetési egységekhez kötött életbiztosítás Különös Feltételeinek Melléklete Jelen Melléklet a 118 jelű rendszeres díjas befektetési egységekhez kötött életbiztosítás
NN Biztosító Zrt. A 118 jelű rendszeres díjas befektetési egységekhez kötött életbiztosítás Különös Feltételeinek Melléklete Jelen Melléklet a 118 jelű rendszeres díjas befektetési egységekhez kötött életbiztosítás
TERMÉKTÁJÉKOZTATÓ ÉRTÉKPAPÍR ADÁS-VÉTEL MEGÁLLAPODÁSOKHOZ
 TERMÉKTÁJÉKOZTATÓ ÉRTÉKPAPÍR ADÁS-VÉTEL MEGÁLLAPODÁSOKHOZ Termék definíció Az Értékpapír adásvételi megállapodás keretében a Bank és az Ügyfél értékpapírra vonatkozó azonnali adásvételi megállapodást kötnek.
TERMÉKTÁJÉKOZTATÓ ÉRTÉKPAPÍR ADÁS-VÉTEL MEGÁLLAPODÁSOKHOZ Termék definíció Az Értékpapír adásvételi megállapodás keretében a Bank és az Ügyfél értékpapírra vonatkozó azonnali adásvételi megállapodást kötnek.
Az NN Biztosító Zrt. 303 jelű Talizmán biztosításának különös feltételei
 Az NN Biztosító Zrt. 303 jelű Talizmán biztosításának különös feltételei 1. Általános rendelkezések a) Az NN Biztosító Zrt. (székhelye: 1068 Budapest, Dózsa György út 84/B, a továbbiakban Biztosító) jelen
Az NN Biztosító Zrt. 303 jelű Talizmán biztosításának különös feltételei 1. Általános rendelkezések a) Az NN Biztosító Zrt. (székhelye: 1068 Budapest, Dózsa György út 84/B, a továbbiakban Biztosító) jelen
RÉSZEGES HATÁRIDŐS MEGÁLLAPODÁS (PARTICIPATING FORWARD)
 RÉSZEGES HATÁRIDŐS MEGÁLLAPODÁS (PARTICIPATING FORWARD) Tisztelt Ügyfelünk! Kérjük hogy az ügylet megkötése előtt jelen Ügyféltájékoztatót valamint a Befektetési szolgáltatási és a kiegészítő szolgáltatási
RÉSZEGES HATÁRIDŐS MEGÁLLAPODÁS (PARTICIPATING FORWARD) Tisztelt Ügyfelünk! Kérjük hogy az ügylet megkötése előtt jelen Ügyféltájékoztatót valamint a Befektetési szolgáltatási és a kiegészítő szolgáltatási
A GB174 JELÛ GENERÁCIÓ TÕKEMEGTAKARÍTÁSI ÉLETBIZTOSÍTÁS KÜLÖNÖS FELTÉTELEI
 A GB174 JELÛ GENERÁCIÓ TÕKEMEGTAKARÍTÁSI ÉLETBIZTOSÍTÁS KÜLÖNÖS FELTÉTELEI 1. Általános rendelkezések A Generáció Tõkemegtakarítási Életbiztosítási szerzõdés (a továbbiakban: biztosítás) a jelen Különös
A GB174 JELÛ GENERÁCIÓ TÕKEMEGTAKARÍTÁSI ÉLETBIZTOSÍTÁS KÜLÖNÖS FELTÉTELEI 1. Általános rendelkezések A Generáció Tõkemegtakarítási Életbiztosítási szerzõdés (a továbbiakban: biztosítás) a jelen Különös
. melléklet a 3 /2013. (XII. 29.) MNB rendelethez
 . melléklet a 3 /2013. (XII. 29.) MNB rendelethez 8. melléklet a 38/2013. (XII. ) MNB rendelethez Az összevont alapú felügyelet alá tartozó biztosító negyedéves és éves felügyeleti jelentése ÖSSZEFOGLALÓ
. melléklet a 3 /2013. (XII. 29.) MNB rendelethez 8. melléklet a 38/2013. (XII. ) MNB rendelethez Az összevont alapú felügyelet alá tartozó biztosító negyedéves és éves felügyeleti jelentése ÖSSZEFOGLALÓ
Mikroökonómia II. B. ELTE TáTK Közgazdaságtudományi Tanszék. 6. hét AZ IDŽ KÖZGAZDASÁGTANA, 1. rész
 MIKROÖKONÓMIA II. B ELTE TáTK Közgazdaságtudományi Tanszék Mikroökonómia II. B AZ IDŽ KÖZGAZDASÁGTANA, 1. rész Készítette: Szakmai felel s: 2011. február A tananyagot készítette: Jack Hirshleifer, Amihai
MIKROÖKONÓMIA II. B ELTE TáTK Közgazdaságtudományi Tanszék Mikroökonómia II. B AZ IDŽ KÖZGAZDASÁGTANA, 1. rész Készítette: Szakmai felel s: 2011. február A tananyagot készítette: Jack Hirshleifer, Amihai
Kockázatalapú díjfizetés az EU-s betétbiztosítóknál - az OBA-nál várható változások
 Kockázatalapú díjfizetés az EU-s betétbiztosítóknál - az OBA-nál várható változások Vajai Balázs 2018. november 16. db Az OBA tagintézetek számának alakulása 1993-2017 350 297 288 300 285 238 250 295 288
Kockázatalapú díjfizetés az EU-s betétbiztosítóknál - az OBA-nál várható változások Vajai Balázs 2018. november 16. db Az OBA tagintézetek számának alakulása 1993-2017 350 297 288 300 285 238 250 295 288
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT.
 CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2013. NEGYEDIK NEGYEDÉV 2014. február 18. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2013. NEGYEDIK NEGYEDÉV 2014. február 18. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
Rövid távú modell III. Pénzkereslet, LM görbe
 Rövid távú modell III. Pénzkereslet, Makroökonómia Tanszék Budapesti Corvinus Egyetem Makroökonómia Rövid távú modell III. Pénzkereslet, Félév végi dolgozat 40 pontos vizsga május 23. hétf 10 óra május
Rövid távú modell III. Pénzkereslet, Makroökonómia Tanszék Budapesti Corvinus Egyetem Makroökonómia Rövid távú modell III. Pénzkereslet, Félév végi dolgozat 40 pontos vizsga május 23. hétf 10 óra május
Az ERGO Életbiztosító Zrt. üzleti jelentése április december 31.
 Az ERGO Életbiztosító Zrt. üzleti jelentése 2008. április 16. 2008. december 31. Tartalom AZ ERGO BIZTOSÍTÓ PIACRA LÉPÉSE... 3 AZ ERGO BIZTOSÍTÓ FEJLŐDÉSE... 3 DÍJBEVÉTEL, BIZTOSÍTÁSI SZOLGÁLTATÁSOK, MŰKÖDÉSI
Az ERGO Életbiztosító Zrt. üzleti jelentése 2008. április 16. 2008. december 31. Tartalom AZ ERGO BIZTOSÍTÓ PIACRA LÉPÉSE... 3 AZ ERGO BIZTOSÍTÓ FEJLŐDÉSE... 3 DÍJBEVÉTEL, BIZTOSÍTÁSI SZOLGÁLTATÁSOK, MŰKÖDÉSI
Matematika A3 Valószínűségszámítás, 6. gyakorlat 2013/14. tavaszi félév
 Matematika A3 Valószínűségszámítás, 6. gyakorlat 2013/14. tavaszi félév 1. A várható érték és a szórás transzformációja 1. Ha egy valószínűségi változóhoz hozzáadunk ötöt, mínusz ötöt, egy b konstanst,
Matematika A3 Valószínűségszámítás, 6. gyakorlat 2013/14. tavaszi félév 1. A várható érték és a szórás transzformációja 1. Ha egy valószínűségi változóhoz hozzáadunk ötöt, mínusz ötöt, egy b konstanst,
Kamat Hozam - Árfolyam
 Pénzügyi számítások kamat, hozam Váltó és értékelése 7. hét 2010.10.19. 1 Kamat Hozam - Árfolyam Kamat nem egyenlő a hozammal!! Kamat-Hozam-Árfolyam összefüggés A jelenlegi gyakorlat alatt a pénz időértékének
Pénzügyi számítások kamat, hozam Váltó és értékelése 7. hét 2010.10.19. 1 Kamat Hozam - Árfolyam Kamat nem egyenlő a hozammal!! Kamat-Hozam-Árfolyam összefüggés A jelenlegi gyakorlat alatt a pénz időértékének
Vállalkozási finanszírozás kollokvium
 Harsányi János Főiskola Gazdálkodási és Menedzsment Intézet Vállalkozási finanszírozás kollokvium G Név: soport: Tagozat: Elért pont: Érdemjegy: Javította: 43 50 pont jeles 35 42 pont jó 27 34 pont közepes
Harsányi János Főiskola Gazdálkodási és Menedzsment Intézet Vállalkozási finanszírozás kollokvium G Név: soport: Tagozat: Elért pont: Érdemjegy: Javította: 43 50 pont jeles 35 42 pont jó 27 34 pont közepes
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Sorozatok II.
 Sorozatok II. DEFINÍCIÓ: (Mértani sorozat) Az (a n ) valós számsorozatot mértani sorozatnak nevezzük, ha van olyan valós szám, amellyel a sorozat bármely tagját megszorozva a következő tagot kapjuk. Jelöléssel:
Sorozatok II. DEFINÍCIÓ: (Mértani sorozat) Az (a n ) valós számsorozatot mértani sorozatnak nevezzük, ha van olyan valós szám, amellyel a sorozat bármely tagját megszorozva a következő tagot kapjuk. Jelöléssel:
Kamatjövedelmet terhelő adóról és egészségügyi hozzájárulásról szóló tájékoztató (magánszemélyek részére)
 NN Biztosító Zrt. Kamatjövedelmet terhelő adóról és egészségügyi hozzájárulásról szóló tájékoztató (magánszemélyek részére) Tájékoztatónk részletes információkkal szolgál az életbiztosításokhoz kapcsolódó
NN Biztosító Zrt. Kamatjövedelmet terhelő adóról és egészségügyi hozzájárulásról szóló tájékoztató (magánszemélyek részére) Tájékoztatónk részletes információkkal szolgál az életbiztosításokhoz kapcsolódó
Kedves Partnereink, Kedves Ügyfeleink!
 Éves jelentés 2015 Kedves Partnereink, Kedves Ügyfeleink! A hazai biztosítási piac fejlődése 2015-ben immár harmadik éve tovább folytatódott, a bruttó díjbevétel elérte a 869 milliárd forintot. A 2,2%-os
Éves jelentés 2015 Kedves Partnereink, Kedves Ügyfeleink! A hazai biztosítási piac fejlődése 2015-ben immár harmadik éve tovább folytatódott, a bruttó díjbevétel elérte a 869 milliárd forintot. A 2,2%-os
a) 16% b) 17% c) 18% d) 19%
 1. Mekkora az euró féléves paritásos határidős árfolyama, ha az azonnali árfolyam 240 HUF/EUR, a kockázatmentes forint kamatláb minden lejáratra évi 8%, a kockázatmentes euró márka kamatláb minden lejáratra
1. Mekkora az euró féléves paritásos határidős árfolyama, ha az azonnali árfolyam 240 HUF/EUR, a kockázatmentes forint kamatláb minden lejáratra évi 8%, a kockázatmentes euró márka kamatláb minden lejáratra
Mérleg Eszköz Forrás
 Az Országos Takarékpénztár és Kereskedelmi Bank Rt. elkészítette 2001. június 30-ával zárult félévre vonatkozó Nemzetközi Számviteli Standardok szerinti konszolidált, nem auditált beszámolóját. A következõkben
Az Országos Takarékpénztár és Kereskedelmi Bank Rt. elkészítette 2001. június 30-ával zárult félévre vonatkozó Nemzetközi Számviteli Standardok szerinti konszolidált, nem auditált beszámolóját. A következõkben
Vállalkozási finanszírozás kollokvium
 Harsányi János Főiskola Gazdaságtudományok tanszék Vállalkozási finanszírozás kollokvium E Név: soport: Tagozat: Elért pont: Érdemjegy: Javította: 43 50 pont jeles 35 42 pont jó 27 34 pont közepes 19 26
Harsányi János Főiskola Gazdaságtudományok tanszék Vállalkozási finanszírozás kollokvium E Név: soport: Tagozat: Elért pont: Érdemjegy: Javította: 43 50 pont jeles 35 42 pont jó 27 34 pont közepes 19 26
1000 forintos adósságunkat, de csak 600 forintunk van. Egyetlen lehetőségünk, hogy a
 A merész játékok stratégiája A következő problémával foglalkozunk: Tegyük fel, hogy feltétlenül ki kell fizetnünk 000 forintos adósságunkat, de csak 600 forintunk van. Egyetlen lehetőségünk, hogy a még
A merész játékok stratégiája A következő problémával foglalkozunk: Tegyük fel, hogy feltétlenül ki kell fizetnünk 000 forintos adósságunkat, de csak 600 forintunk van. Egyetlen lehetőségünk, hogy a még
MAMS Csoportos személybiztosítási értesítő 2009. január 01.- 2009. december 31. időszakra
 MAMS Csoportos személybiztosítási értesítő 2009. január 01.- 2009. december 31. időszakra I. Szerződő: Magyar Motorsport Szövetség (MAMS) 1143 Budapest Istvánmezei út 1-3. Biztosítottak: Díjfizetők: Kedvezményezettek:
MAMS Csoportos személybiztosítási értesítő 2009. január 01.- 2009. december 31. időszakra I. Szerződő: Magyar Motorsport Szövetség (MAMS) 1143 Budapest Istvánmezei út 1-3. Biztosítottak: Díjfizetők: Kedvezményezettek:
CIG PANNÓNIA ÉLETBIZTOSÍTÓ NYRT.
 CIG PANNÓNIA ÉLETBIZTOSÍTÓ NYRT. NEGYEDÉVES TÁJÉKOZTATÓ 2013. HARMADIK NEGYEDÉV 2013. november 13. 1. Összefoglaló A CIG Pannónia Életbiztosító Nyrt. (a továbbiakban: Biztosító) a mai napon nyilvánosságra
CIG PANNÓNIA ÉLETBIZTOSÍTÓ NYRT. NEGYEDÉVES TÁJÉKOZTATÓ 2013. HARMADIK NEGYEDÉV 2013. november 13. 1. Összefoglaló A CIG Pannónia Életbiztosító Nyrt. (a továbbiakban: Biztosító) a mai napon nyilvánosságra
1. melléklet a (./.) PSZÁF rendelethez ÖSSZEFOGLALÓ TÁBLÁZAT
 ÖSSZEFOGLALÓ TÁBLÁZAT Táblakód Megnevezés Adatszolgáltató Gyakoriság Beküldési határidő 42A1A A biztosító nem-élet üzletág állományának bemutatása a tárgyidőszak végén (darab) RT, NAGYEGY É tárgyévet követő
ÖSSZEFOGLALÓ TÁBLÁZAT Táblakód Megnevezés Adatszolgáltató Gyakoriság Beküldési határidő 42A1A A biztosító nem-élet üzletág állományának bemutatása a tárgyidőszak végén (darab) RT, NAGYEGY É tárgyévet követő
Definíciószerűen az átlagidő a kötvény hátralévő pénzáramlásainak, a pénzáramlás jelenértékével súlyozott átlagos futamideje. A duration képlete:
 meg tudjuk mondani, hogy mennyit ér ez a futamidő elején. Az évi 1% különbségeket jelenértékre átszámolva ez kb. 7.4% veszteség, a kötvényünk ára 92,64 lesz. Látható, hogy a hosszabb futamidejű kötvényre
meg tudjuk mondani, hogy mennyit ér ez a futamidő elején. Az évi 1% különbségeket jelenértékre átszámolva ez kb. 7.4% veszteség, a kötvényünk ára 92,64 lesz. Látható, hogy a hosszabb futamidejű kötvényre
Alkuszi Tevékenységet Végző Természetes Személyek Szakmai Felelősségbiztosítása
 Alkuszi Tevékenységet Végző Természetes Személyek Szakmai Felelősségbiztosítása Ügyfél-tájékoztató és biztosítási szerződési feltételek Nyomtatványszám: NF3143 Hatályos: 2018. szeptember 01- Tartalom 1.
Alkuszi Tevékenységet Végző Természetes Személyek Szakmai Felelősségbiztosítása Ügyfél-tájékoztató és biztosítási szerződési feltételek Nyomtatványszám: NF3143 Hatályos: 2018. szeptember 01- Tartalom 1.
Szabályozási szint: Információs eszköz Érvényes (-ig)**: visszavonásig
 Szám:* C-II-00-04-34 Első kiadás dátuma*: 2017. 01.31. Szabályozási szint: Információs eszköz Érvényes (-ig)**: visszavonásig Felelős oszt.: Életbiztosítás Verzió: 1.0 Szerző: Giber-Fekete Marianna Pozíció:
Szám:* C-II-00-04-34 Első kiadás dátuma*: 2017. 01.31. Szabályozási szint: Információs eszköz Érvényes (-ig)**: visszavonásig Felelős oszt.: Életbiztosítás Verzió: 1.0 Szerző: Giber-Fekete Marianna Pozíció:
Az OTP Bank Rt I. félévi összefoglaló nem konszolidált, nem auditált IAS pénzügyi adatai A Bank I. félévi fejlõdése
 Az OTP Bank Rt. 2001. I. félévi összefoglaló nem konszolidált, nem auditált IAS pénzügyi adatai Az Országos Takarékpénztár és Kereskedelmi Bank Rt. elkészítette 2001. június 30-ával zárult félévre vonatkozó
Az OTP Bank Rt. 2001. I. félévi összefoglaló nem konszolidált, nem auditált IAS pénzügyi adatai Az Országos Takarékpénztár és Kereskedelmi Bank Rt. elkészítette 2001. június 30-ával zárult félévre vonatkozó
Befektetés és biztonság
 Befektetés és biztonság kompromisszumok nélkül Terra Életbiztosítás Befektetés és többszörös gondoskodás A befektetéssel kombinált életbiztosításokról sokan azt állítják, hogy indokolatlan költségekkel
Befektetés és biztonság kompromisszumok nélkül Terra Életbiztosítás Befektetés és többszörös gondoskodás A befektetéssel kombinált életbiztosításokról sokan azt állítják, hogy indokolatlan költségekkel
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT.
 CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2013. MÁSODIK NEGYEDÉV 2013. augusztus 15. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
CIG PANNÓNIA ELSŐ MAGYAR ÁLTALÁNOS BIZTOSÍTÓ ZRT. NEGYEDÉVES TÁJÉKOZTATÓ 2013. MÁSODIK NEGYEDÉV 2013. augusztus 15. 1. Összefoglaló Jelen tájékoztató célja, hogy a CIG Pannónia Első Magyar Általános Biztosító
Megfelelési és alkalmassági teszt
 Megfelelési és alkalmassági teszt Ajánlatszám: Tanácsadó neve, kódja: Szerződő neve: Anyja neve: Születési hely, idő: Tisztelt Ügyfelünk! Jogszabályi előírás alapján a biztosítási alapú befektetési termékek
Megfelelési és alkalmassági teszt Ajánlatszám: Tanácsadó neve, kódja: Szerződő neve: Anyja neve: Születési hely, idő: Tisztelt Ügyfelünk! Jogszabályi előírás alapján a biztosítási alapú befektetési termékek
. melléklet a 3 /2013. (XII. 29.) MNB rendelethez
 . melléklet a 3 /2013. (XII. 29.) MNB rendelethez 4. melléklet a 38/2013. (XII. ) MNB rendelethez A biztosító aktuáriusi jelentése ÖSSZEFOGLALÓ TÁBLA Táblakód Megnevezés Adatszolgáltató Gyakoriság Beküldési
. melléklet a 3 /2013. (XII. 29.) MNB rendelethez 4. melléklet a 38/2013. (XII. ) MNB rendelethez A biztosító aktuáriusi jelentése ÖSSZEFOGLALÓ TÁBLA Táblakód Megnevezés Adatszolgáltató Gyakoriság Beküldési
