Stabilitás és komplexitás a közösségekben
|
|
|
- Hunor Nemes
- 6 évvel ezelőtt
- Látták:
Átírás
1 Stabilitás és komplexitás a közösségekben Def.: stabilisnak azt a közösséget nevezhetjük, amely hosszú ideig áll fenn (perzisztens) A stabilitás a zavarásra mutatott érzékenységet méri. Megvizsgálandó kérdések: 1. Mihez képest stabil (perzisztens)? 2. Mi az, ami a stabilitását (perzisztenciáját) befolyásolja, esetleg megszünteti? 3. Mitől stabil (perzisztens)? Milyen tényezők járulnak hozzá a stabilitáshoz? 4. A közösségek általában komplexek. Összefügg-e a komplexitás és a stabilitás? A komplexitás kapcsolódik a diverzitás mértékéhez, ergo a diverzitás-stabilitás összefüggés is felvethető. 1
2 1. Mihez képest stabil (perzisztens)? - más közösségek -időskálánk mérete -a hatóerők nagysága 2. Mi az, ami a stabilitását (perzisztenciáját) befolyásolja esetleg megszünteti? - zavarás (perturbáció) 3. Mitől stabil (perzisztens)? Milyen tényezők járulnak hozzá a stabilitáshoz? A stabilitás komponensei útján vizsgálható - reziliencia (rugalmasság) - rezisztencia (ellenálló képesség) - lokális és globális stabilitás - dinamikus fragilitás és robusztusság Reziliencia azt a sebességet méri, amivel az egyensúlyi helyzetéből kimozdított rendszer visszatér eredeti állapotába 2
3 Rezisztencia (ellenálló képesség) - azt az erőt méri, ami ahhoz szükséges, hogy a rendszert kimozdítsa eredeti állapotából Lokális és globális stabilitás kisebb ill. nagyobb perturbációkra mutatott válasz 3
4 Fragilitás és robusztusság azt a környezeti paraméter szélességet méri, amelyeken belül a rendszer stabil marad: ha ez szűk fragilis, ha széles robusztus 4. Hogyan függ össze a komplexitás és stabilitás? - józan ész logikája Elton (1958) a bonyolultabb rendszerek stabilabbak (egy sor tapasztalat mutatja) MacArthur (1955) a bonyolultabb rendszerben több útvonalon juthat el az energia a megfelelő helyekre - a valóság nagyon bonyolult, egyszerűbb modelleken kell vizsgálni Robert May May (1973) modellje: random összeállítású táplálkozási hálózatok β a kölcsönhatási erő i és j fajok, melyek hatnak egymásra: β ij ill. β ji mindenféle kölcsönhatás: -,- +,- +,+ 0 stb. saját fajra vonatkozók (β ii vagy β jj ): -1, minden más véletlenszerű C = konnektancia (azaz, a közvetlen kapcsolatban lévő fajpárok az összes lehetségeshez képest) S = fajszám 4
5 May azt találta, hogy a modell-hálózatai csak akkor voltak stabilak (mihez képest? az általa alkalmazott perturbációk mértékéhez képest, amelyektől még vissza tudtak térni eredeti állapotukba ezt nevezzük LJAPUNOV v. szomszédsági EGYENSÚLYnak) (milyen perturbációk? fajhozzáadás, fajtörlés, populációk méretének csökkentése, növelése stb.) ha a következő egyenlőtlenségi feltétel fennállt: Problémák: táplálkozási hurkok donor kontrolláltság melyik szintet perturbáljuk súlyosan (fajdeléció) reziliencia β ( SC) 1/ 2 < 1 C B A támogatja-e a valóság a modellt? Részben igen! Problémák: nincs elegendő adatunk a kölcsönhatási erőről May modellje a determinisztikus L-V rendszereket követi, ezért eleve erős kölcsönhatásokat tételez fel Ha csak az SC változását figyeljük (β-ról való adat hiányában): Rejmanek és Stary (1979) kísérlete levéltetvekkel. 5
6 Miért van 3 vonal az ábrán? A vonalak olyan hiperbolák, amelyek SC=2, SC=4 és SC=6 esetén adnak a lefutásuk során konstans értékeket Rejmanek és Stary a C min -t (ez 2-nek felel meg) és C max -ot (ez 4-6- nak felel meg) vizsgálta. [C min az összes kapcsolat a lehetségeshez képest, a C max az összes kapcsolat, ha kompetíció is van, pl. közös gazda parazitoidok esetén] Fajszám (S) és konnektancia (C) összefüggése különböző (szárazföldi, édesvízi és tengeri) táplálkozási hálózatok esetében. Fontos, hogy a konnektancia független lehet a fajszámtól (c ábra), vagy akár emelkedhet a fajszám függvényében (d ábra). AZ ELTELT HÚSZ ÉV ALATT! Folytonos viták a racionalitásnak ellentmondó May-modellről Új modellek McCann et al. (1998) eltérései a May-modelltől nem-egyensúlyi dinamikát tételeznek fel (attraktorok) a fogyasztás módja nem lineáris (Holling-2) gyenge interakciókat tételeznek fel (nem okoznak oszcillációt) Ezekkel a feltételekkel perzisztens TH-kat tudtak modellezni, amelyekben a komplexitás és stabilitás pozitívan függött össze! 6
7 Stabilitási modellek (összefoglalás) Klasszikus felfogás: megfigyelések alapján a komplexitás növeli a stabilitást (Lindeman, Elton, MacArthur) 1950-es évek 1. May modellje: - egyensúlyi rendszerek (L-V kikötések), - rendszer-szintű un. dinamikus egyensúly (Ljapunov), - véletlenszerűen összeállított táplálkozási hálózat, -erős kölcsönhatások, - interakciós erők nem ismertek, - donor kontrolláltságot, rezilienciát nem veszi figyelembe. Eredmény: a komplexitás csökkenti a stabilitást (1973) 2. McCann és társai modellje: - nem-egyensúlyi rendszerek, - a stabilitás általános-szintű, ha a populációk mérete nullától pozitívan eltérő értékkel növekedik, és komponens-stabilitás, ha a rezilienciával és rezisztenciával kapcsolatos, - a kölcsönhatások gyengék (nincs oszcilláció), - a predátorok csak egyfajta zsákmányt fogyasztanak egyszerre (menedék), - a predátor fogyasztása a II. típusú Holling-görbe szerint, - a kölcsönhatási erők ismertek, - a populációk kihalását attraktorok akadályozzák. Eredmény: a komplexitás növeli a stabilitást (1998) 7
8 A táplálkozási hálózatok sajátosságai és stabilitási problémái 1. Alapfogalmak R H PP R2 R1 H PP Táplálkozási lánc (3 szint) Táplálkozási hálózat (4 szint) Hány szint van? Szárazföldi (terresztris) hálózatokban átlagosan 3, vízi (akvatikus) közösségekben 4. 8
9 Hatások a táplálkozási hálózatban: A = trofodinamika (a felfelé haladó energia szerepe) B = felülről lefelé (top-down) hatás vagy kaszkádolás C = alulról felfelé (bottom-up) irányuló hatás 2. A stabilitást befolyásoló további tényezők Kompartmentalizáció (habitatokon átnyúló táplálkozási hálózat részei) 9
10 Trofikus szintek számát meghatározó tényezők maximális táplálkozási lánchosszból (= a bazális fajtól a csúcsfogyasztóig terjedő fogyasztók sora) számolható átlagos lánchossz az előző oldalon látható tápl. hálózat egyetlen bazális tagjára nézve ez: 20a a a a a a a /7= 4 szint átlagosan - energetikai korlátok Egy adott szintre, az előző szintről, az energiatartalom kb. 10 %-a jut át! - a láncok belső instabilitása (Pimm & Lawton 1977, modell): az 5-nél nagyobb szintszámú láncok instabilak a-c: horizontális, d-e: vertikális hálózatok és láncok. A felsők stabilabbak, mint az alsók. 10
11 A ragadozók sajátosságai és a stabilitás - a ragadozók általában generalisták - a ragadozók testmérete, mozgáskörzete - a ragadozók stabilitást eredményeznek (l. predációs fejezet) - a forrás és nyelő fajok aránya általában 1 : 2,5 : 1,5 DE: pl. a darázsölyv (Pernis apivorus) specialista Nyelő Forrás Forrás Nyelő Nyelő Forrás Egy táplálkozási hálózatban minden szint egyszerre forrás és nyelő alhálózat is egyben 11
12 A Laburnum anagyroides (aranyeső) trofikus hálózatának főbb résztvevői Bruchidius villosus (Bruchidae) Fitofág poloskák Triaspis thoracicus (Braconidae) Levélaknázó moly Dinarmus acutus (Chalcidoidea) (Coccinellidae) Aphidius sp. (Braconidae) Syrphidae Levéltetű (Aphis cytisorum) Kabócák Chrysopa carnea Kinolizidin alkaloid virág (beporzók) Ragadozó atkák, Aspergillus faj(ok) Lasius sp. (Formicidae) termés (egyéb termés fogyasztók) 12
13 McCann et al Nature 395, modellje 13
Predáció szerepe a közösségszerkezet alakításában
 Predáció szerepe a közösségszerkezet alakításában Def.: A populáció méretet és/vagy a fajgazdagságot befolyásoló hatást zavarásnak (diszturbancia) nevezzük A zavarás lehet: predáció/herbivoria/parazitizmus
Predáció szerepe a közösségszerkezet alakításában Def.: A populáció méretet és/vagy a fajgazdagságot befolyásoló hatást zavarásnak (diszturbancia) nevezzük A zavarás lehet: predáció/herbivoria/parazitizmus
Predáció populációdinamikai hatása
 Predáció populációdinamikai hatása Def.: olyan szervezet, amely a zsákmányát, annak elfogása után, megöli és elfogyasztja. (Ellentétben: herbivor, parazitoid, ahol késleltetett a hatás, de ezekre is a
Predáció populációdinamikai hatása Def.: olyan szervezet, amely a zsákmányát, annak elfogása után, megöli és elfogyasztja. (Ellentétben: herbivor, parazitoid, ahol késleltetett a hatás, de ezekre is a
Szigetbiogeográfia. A tapasztalat szerint:
 Szigetbiogeográfia A tapasztalat szerint: Aritmetikus tengelyen Logaritmikus tengelyen Általános összefüggése:, ahol C taxonra, abundanciára és lokalitásra jellemző állandó, A a terület mérete és z (linearizált
Szigetbiogeográfia A tapasztalat szerint: Aritmetikus tengelyen Logaritmikus tengelyen Általános összefüggése:, ahol C taxonra, abundanciára és lokalitásra jellemző állandó, A a terület mérete és z (linearizált
Az ökológia alapjai. Diverzitás és stabilitás
 Az ökológia alapjai Diverzitás és stabilitás Diverzitás = sokféleség, változatosság a sokféleség kvantitatív megjelenítése biodiverzitás: a biológiai változatosság matematikai (kvantitatív) megjelenítése
Az ökológia alapjai Diverzitás és stabilitás Diverzitás = sokféleség, változatosság a sokféleség kvantitatív megjelenítése biodiverzitás: a biológiai változatosság matematikai (kvantitatív) megjelenítése
Trofikus hálózatok sajátosságai és szabályzása
 Trofikus hálózatok sajátosságai és szabályzása Fogalmak: Táplálkozási (trofikus) hálózat: a populációk közötti fogyasztóforrás kapcsolatok összessége. Folyamat: a mintázatokat keltő akciók sorozata. Mintázat:
Trofikus hálózatok sajátosságai és szabályzása Fogalmak: Táplálkozási (trofikus) hálózat: a populációk közötti fogyasztóforrás kapcsolatok összessége. Folyamat: a mintázatokat keltő akciók sorozata. Mintázat:
Tápanyagok vízi közösségekben
 Tápanyagok vízi közösségekben eltérések a szárazföldiekhez képest: BE: KI: a legtöbb anyag kívülről mosódik be patak, folyó, kifolyásos tó kimosódás nagy tavak és óceánok ülepedés Folyóvizek Hubbard Brook:
Tápanyagok vízi közösségekben eltérések a szárazföldiekhez képest: BE: KI: a legtöbb anyag kívülről mosódik be patak, folyó, kifolyásos tó kimosódás nagy tavak és óceánok ülepedés Folyóvizek Hubbard Brook:
3. előadás Stabilitás
 Stabilitás 3. előadás 2011. 09. 19. Alapfogalmak Tekintsük dx dt = f (t, x), x(t 0) = x 0 t (, ), (1) Jelölje t x(t; t 0, x 0 ) vagy x(.; t 0, x 0 ) a KÉF megoldását. Kívánalom: kezdeti állapot kis megváltozása
Stabilitás 3. előadás 2011. 09. 19. Alapfogalmak Tekintsük dx dt = f (t, x), x(t 0) = x 0 t (, ), (1) Jelölje t x(t; t 0, x 0 ) vagy x(.; t 0, x 0 ) a KÉF megoldását. Kívánalom: kezdeti állapot kis megváltozása
Dekomponálás, detritivoria
 Dekomponálás, detritivoria Def.: azon szervezetek tevékenysége, amelyek elhalt szerves anyag feldarabolását, bontását és a mineralizáció útjára irányítását végzik. Forrásfüggvényük: dr = dt F( R), amelyből
Dekomponálás, detritivoria Def.: azon szervezetek tevékenysége, amelyek elhalt szerves anyag feldarabolását, bontását és a mineralizáció útjára irányítását végzik. Forrásfüggvényük: dr = dt F( R), amelyből
Szokol Patricia szeptember 19.
 a Haladó módszertani ismeretek című tárgyhoz 2017. szeptember 19. Legyen f : N R R adott függvény, ekkor a x n = f (n, x n 1 ), n = 1, 2,... egyenletet elsőrendű differenciaegyenletnek nevezzük. Ha még
a Haladó módszertani ismeretek című tárgyhoz 2017. szeptember 19. Legyen f : N R R adott függvény, ekkor a x n = f (n, x n 1 ), n = 1, 2,... egyenletet elsőrendű differenciaegyenletnek nevezzük. Ha még
3. Fékezett ingamozgás
 3. Fékezett ingamozgás A valóságban mindig jelen van valamilyen csillapítás. A gázban vagy folyadékban való mozgásnál, kis sebesség esetén a csillapítás arányos a sebességgel. Ha az vagy az ''+k sin =0,
3. Fékezett ingamozgás A valóságban mindig jelen van valamilyen csillapítás. A gázban vagy folyadékban való mozgásnál, kis sebesség esetén a csillapítás arányos a sebességgel. Ha az vagy az ''+k sin =0,
Ragadozás (predáció)
 Ragadozás (predáció) a predáció egyike a leglátványosabb mortalitási tényezőknek ragadozó: az a lény, amely élő zsákmányát rögtön elfogása után megöli, vagy röviddel utána Eciton burchelli - harcoshangya
Ragadozás (predáció) a predáció egyike a leglátványosabb mortalitási tényezőknek ragadozó: az a lény, amely élő zsákmányát rögtön elfogása után megöli, vagy röviddel utána Eciton burchelli - harcoshangya
ÁLTALÁNOS ÖKOLÓGIA (bb2n1101, aa2n1020) 2014/2015 I. félév
 ÁLTALÁNOS ÖKOLÓGIA (bb2n1101, aa2n1020) 2014/2015 I. félév Oktatók Herczeg Gábor ÁRT (egy. adjunktus, D-7. em. 729. szoba, t:8760) Hegyi Gergely ÁRT (egy. adjunktus, D-7. em. 712. szoba, t:8756) Kalapos
ÁLTALÁNOS ÖKOLÓGIA (bb2n1101, aa2n1020) 2014/2015 I. félév Oktatók Herczeg Gábor ÁRT (egy. adjunktus, D-7. em. 729. szoba, t:8760) Hegyi Gergely ÁRT (egy. adjunktus, D-7. em. 712. szoba, t:8756) Kalapos
Niche. Tárgya a fajok koegzisztenciájának problémája A fogalom fejlődése: Toleranciahatárok! A hutchinsoni niche fogalom definíciója:
 Niche Tárgya a fajok koegzisztenciájának problémája A fogalom fejlődése: Grinnell térbeli Elton funkcionális Hutchinson hipertérfogat modell Juhász-Nagy niche értelmezése A hutchinsoni niche fogalom definíciója:
Niche Tárgya a fajok koegzisztenciájának problémája A fogalom fejlődése: Grinnell térbeli Elton funkcionális Hutchinson hipertérfogat modell Juhász-Nagy niche értelmezése A hutchinsoni niche fogalom definíciója:
REGIONÁLIS GAZDASÁGTAN B
 REGIONÁLIS GAZDASÁGTAN B Készült a TÁMOP-4.1.2-08/2/a/KMR-2009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA
REGIONÁLIS GAZDASÁGTAN B Készült a TÁMOP-4.1.2-08/2/a/KMR-2009-0041 pályázati projekt keretében Tartalomfejlesztés az ELTE TáTK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék az MTA
Diverzitás és stabilitás. Mi a biodiverzitás?
 Diverzitás és stabilitás Szemethy László, Phd egyetemi docens SZIE VMI Szemethy.Laszlo@MKK.SZIE.hu Mi a biodiverzitás? a sokféleség sokfélesége (JNP) tudományos paradigma (tudományterület is) a diverzitás
Diverzitás és stabilitás Szemethy László, Phd egyetemi docens SZIE VMI Szemethy.Laszlo@MKK.SZIE.hu Mi a biodiverzitás? a sokféleség sokfélesége (JNP) tudományos paradigma (tudományterület is) a diverzitás
Tartalom. Robusztus stabilitás Additív hibastruktúra Multiplikatív hibastruktúra
 Tartalom Robusztus stabilitás Additív hibastruktúra Multiplikatív hibastruktúra 2015 1 Robusztus stabilitás Szabályozási rendszer tervezésének gyakorlati problémája az, hogy az aktuális rendszer G(s) átviteli
Tartalom Robusztus stabilitás Additív hibastruktúra Multiplikatív hibastruktúra 2015 1 Robusztus stabilitás Szabályozási rendszer tervezésének gyakorlati problémája az, hogy az aktuális rendszer G(s) átviteli
Az Állatökológia tárgya
 Információk Szentesi Árpád, egyetemi docens 1. Állatrendszertani és Ökológiai Tanszék 7.727. sz. szoba 8758. sz. tel. mellék e-mail: szentesi@elte.hu 2. MTA Növényvédelmi Kutatóintézete Állattani Osztály
Információk Szentesi Árpád, egyetemi docens 1. Állatrendszertani és Ökológiai Tanszék 7.727. sz. szoba 8758. sz. tel. mellék e-mail: szentesi@elte.hu 2. MTA Növényvédelmi Kutatóintézete Állattani Osztály
Software project management Áttekintés
 Software project management Áttekintés Miskolci Egyetem Általános Informatikai Tanszék PMAN / 1 Miért szükséges? A software fejlesztési tevékenység Csoportmunkát igényel Jelentős erőforrásokat használ
Software project management Áttekintés Miskolci Egyetem Általános Informatikai Tanszék PMAN / 1 Miért szükséges? A software fejlesztési tevékenység Csoportmunkát igényel Jelentős erőforrásokat használ
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
Explicit hibabecslés Maxwell-egyenletek numerikus megoldásához
 Explicit hibabecslés Maxwell-egyenletek numerikus megoldásához Izsák Ferenc 2007. szeptember 17. Explicit hibabecslés Maxwell-egyenletek numerikus megoldásához 1 Vázlat Bevezetés: a vizsgált egyenlet,
Explicit hibabecslés Maxwell-egyenletek numerikus megoldásához Izsák Ferenc 2007. szeptember 17. Explicit hibabecslés Maxwell-egyenletek numerikus megoldásához 1 Vázlat Bevezetés: a vizsgált egyenlet,
1. ábra Modell tér I.
 1 Veres György Átbocsátó képesség vizsgálata számítógépes modell segítségével A kiürítés szimuláló számítógépes modellek egyes apró, de igen fontos részletek vizsgálatára is felhasználhatóak. Az átbocsátóképesség
1 Veres György Átbocsátó képesség vizsgálata számítógépes modell segítségével A kiürítés szimuláló számítógépes modellek egyes apró, de igen fontos részletek vizsgálatára is felhasználhatóak. Az átbocsátóképesség
Sorozatok határértéke SOROZAT FOGALMA, MEGADÁSA, ÁBRÁZOLÁSA; KORLÁTOS ÉS MONOTON SOROZATOK
 Sorozatok határértéke SOROZAT FOGALMA, MEGADÁSA, ÁBRÁZOLÁSA; KORLÁTOS ÉS MONOTON SOROZATOK Sorozat fogalma Definíció: Számsorozaton olyan függvényt értünk, amelynek értelmezési tartománya a pozitív egész
Sorozatok határértéke SOROZAT FOGALMA, MEGADÁSA, ÁBRÁZOLÁSA; KORLÁTOS ÉS MONOTON SOROZATOK Sorozat fogalma Definíció: Számsorozaton olyan függvényt értünk, amelynek értelmezési tartománya a pozitív egész
Rovarökológia. Haszon: megporzás. Bevezetés: rovarok és az ember. Haszon: méhészet
 Haszon: megporzás Táplálékaink 1/3-a a megporzáshoz kötődik Virágos növények evolúciója Bevezetés: rovarok és az ember Terméstöbblet (megtermelt és fogyasztott mennyiség különbsége) pollinátorokkal és
Haszon: megporzás Táplálékaink 1/3-a a megporzáshoz kötődik Virágos növények evolúciója Bevezetés: rovarok és az ember Terméstöbblet (megtermelt és fogyasztott mennyiség különbsége) pollinátorokkal és
Közösségek jellemzése
 Közösségek jellemzése Egyensúlyi (determinisztikus) Nem-egyensúlyi (sztochasztikus) modellek, rendszerek: Szoros/erős biotikus kapcsolatok Kompetíció A habitatok homogének és telítettek Forráslimitáltság
Közösségek jellemzése Egyensúlyi (determinisztikus) Nem-egyensúlyi (sztochasztikus) modellek, rendszerek: Szoros/erős biotikus kapcsolatok Kompetíció A habitatok homogének és telítettek Forráslimitáltság
Migráció és diszperzió
 Migráció és diszperzió Migráció alapvetően magatartási fogalom, amelyben a megtett távolság és irányultság mellékes Fontos jellemzői: - aktívan kezdeményezett és fenntartott mozgás specifikus magatartás
Migráció és diszperzió Migráció alapvetően magatartási fogalom, amelyben a megtett távolság és irányultság mellékes Fontos jellemzői: - aktívan kezdeményezett és fenntartott mozgás specifikus magatartás
Software project management Áttekintés
 Software project management Áttekintés Miskolci Egyetem Általános Informatikai Tanszék PMAN /1 Miért szükséges? A software fejlesztési tevékenység Csoportmunkát igényel Jelentÿserÿforrásokat használ fel
Software project management Áttekintés Miskolci Egyetem Általános Informatikai Tanszék PMAN /1 Miért szükséges? A software fejlesztési tevékenység Csoportmunkát igényel Jelentÿserÿforrásokat használ fel
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
Populációbecslések és monitoring
 Populációbecslések és monitoring A becslés szerepe az ökológiában és a vadgazdálkodásban. A becslési módszerek csoportosítása. Teljes számlálás. Statisztikai alapfogalmak. Fontos lehet tudnunk, hogy hány
Populációbecslések és monitoring A becslés szerepe az ökológiában és a vadgazdálkodásban. A becslési módszerek csoportosítása. Teljes számlálás. Statisztikai alapfogalmak. Fontos lehet tudnunk, hogy hány
Hidraulikus hálózatok robusztusságának növelése
 Dr. Dulovics Dezső Junior Szimpózium 2018. Hidraulikus hálózatok robusztusságának növelése Előadó: Huzsvár Tamás MSc. Képzés, II. évfolyam Témavezető: Wéber Richárd, Dr. Hős Csaba www.hds.bme.hu Az előadás
Dr. Dulovics Dezső Junior Szimpózium 2018. Hidraulikus hálózatok robusztusságának növelése Előadó: Huzsvár Tamás MSc. Képzés, II. évfolyam Témavezető: Wéber Richárd, Dr. Hős Csaba www.hds.bme.hu Az előadás
Tisztán kivehetı tendencia: kommunikációs hálózatok egyre bonyolultabbakká válnak Hálózat bonyolultsága
 @ Budapest University of Technology and Economics Nagy hálózatok evolúciója Gulyás András, Heszberger Zalán High Speed Networks Laboratory Internet trendek Tisztán kivehetı tendencia: kommunikációs hálózatok
@ Budapest University of Technology and Economics Nagy hálózatok evolúciója Gulyás András, Heszberger Zalán High Speed Networks Laboratory Internet trendek Tisztán kivehetı tendencia: kommunikációs hálózatok
Fajok közötti kapcsolatok
 Egyedek közötti kölcsönkapcsolatok Környezete = a környék ható tényezôi Fajok közötti kapcsolatok Vadbiológia és ökológia h Az egymásra ható egyedek lehetnek g Fajtársak - interspecifikus kapcsolatok #
Egyedek közötti kölcsönkapcsolatok Környezete = a környék ható tényezôi Fajok közötti kapcsolatok Vadbiológia és ökológia h Az egymásra ható egyedek lehetnek g Fajtársak - interspecifikus kapcsolatok #
A lineáris programozás alapfeladata Standard alak Az LP feladat megoldása Az LP megoldása: a szimplex algoritmus 2018/
 Operációkutatás I. 2018/2019-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Operációkutatás I. 2018/2019-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Populációbecslések és monitoring
 Populációbecslések és monitoring A becslés szerepe az ökológiában és a vadgazdálkodásban. A becslési módszerek csoportosítása. Teljes számlálás. Statisztikai alapfogalmak. Fontos lehet tudnunk, hogy hány
Populációbecslések és monitoring A becslés szerepe az ökológiában és a vadgazdálkodásban. A becslési módszerek csoportosítása. Teljes számlálás. Statisztikai alapfogalmak. Fontos lehet tudnunk, hogy hány
Populációdinamika. Számítógépes szimulációk szamszimf17la
 Populációdinamika Számítógépes szimulációk szamszimf17la Csabai István, Stéger József ELTE Komplex Rendszerek Fizikája Tanszék Email: csabai@complex.elte.hu, steger@complex.elte.hu Bevezetés Dierenciálegyenletek
Populációdinamika Számítógépes szimulációk szamszimf17la Csabai István, Stéger József ELTE Komplex Rendszerek Fizikája Tanszék Email: csabai@complex.elte.hu, steger@complex.elte.hu Bevezetés Dierenciálegyenletek
MUNKAGAZDASÁGTAN. Készítette: Köllő János. Szakmai felelős: Köllő János. 2011. január
 MUNKAGAZDASÁGTAN Készült a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázati projekt keretében Tartalomfejlesztés az ELTE TátK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék, az MTA Közgazdaságtudományi
MUNKAGAZDASÁGTAN Készült a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázati projekt keretében Tartalomfejlesztés az ELTE TátK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék, az MTA Közgazdaságtudományi
Algoritmusok bonyolultsága
 Algoritmusok bonyolultsága 5. előadás http://www.ms.sapientia.ro/~kasa/komplex.htm 1 / 27 Gazdaságos faváz Kruskal-algoritmus Joseph Kruskal (1928 2010) Legyen V = {v 1, v 2,..., v n }, E = {e 1, e 2,...,
Algoritmusok bonyolultsága 5. előadás http://www.ms.sapientia.ro/~kasa/komplex.htm 1 / 27 Gazdaságos faváz Kruskal-algoritmus Joseph Kruskal (1928 2010) Legyen V = {v 1, v 2,..., v n }, E = {e 1, e 2,...,
A lineáris programozás alapfeladata Standard alak Az LP feladat megoldása Az LP megoldása: a szimplex algoritmus 2017/
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatika Intézet Számítógépes Optimalizálás Tanszék 2. Előadás LP alapfeladat A lineáris programozás (LP) alapfeladata standard formában Max c
Általános Pszichológia. Érzékelés Észlelés
 Általános Pszichológia Érzékelés Észlelés Érzékelés Észlelés Klasszikus modell Elemitől a bonyolultabbig Külvilág elemi (Fizikai) ingerei: Érzékszervek (Speciális receptorok) Észlelés -fény -hanghullám
Általános Pszichológia Érzékelés Észlelés Érzékelés Észlelés Klasszikus modell Elemitől a bonyolultabbig Külvilág elemi (Fizikai) ingerei: Érzékszervek (Speciális receptorok) Észlelés -fény -hanghullám
A fák növekedésének egy modelljéről
 1 A fák növekedésének egy modelljéről Az interneten nézelődve találtunk rá az [ 1 ] munkára, ahol a fák növekedésének azt a modelljét ismertették, melyet először [ 2 ] - ben írtak le. Úgy tűnik, ez az
1 A fák növekedésének egy modelljéről Az interneten nézelődve találtunk rá az [ 1 ] munkára, ahol a fák növekedésének azt a modelljét ismertették, melyet először [ 2 ] - ben írtak le. Úgy tűnik, ez az
Korrelációs kapcsolatok elemzése
 Korrelációs kapcsolatok elemzése 1. előadás Kvantitatív statisztikai módszerek Két változó közötti kapcsolat Független: Az X ismérv szerinti hovatartozás ismerete nem ad semmilyen többletinformációt az
Korrelációs kapcsolatok elemzése 1. előadás Kvantitatív statisztikai módszerek Két változó közötti kapcsolat Független: Az X ismérv szerinti hovatartozás ismerete nem ad semmilyen többletinformációt az
Környezet és fejlődés 2017 Ellenőrző kérdések
 Környezet és fejlődés 2017 Ellenőrző kérdések A növekedés határai 1. Mit értünk azon, hogy a Föld összetett anyagforgalmi rendszer? 2. Mely kérdésekre keresték a választ a Római Klub által megbízott kutatók,
Környezet és fejlődés 2017 Ellenőrző kérdések A növekedés határai 1. Mit értünk azon, hogy a Föld összetett anyagforgalmi rendszer? 2. Mely kérdésekre keresték a választ a Római Klub által megbízott kutatók,
A Termelésmenedzsment alapjai tárgy gyakorló feladatainak megoldása
 azdaság- és Társadalomtudományi Kar Ipari Menedzsment és Vállakozásgazdaságtan Tanszék A Termelésmenedzsment alapjai tárgy gyakorló feladatainak megoldása Készítette: dr. Koltai Tamás egyetemi tanár Budapest,.
azdaság- és Társadalomtudományi Kar Ipari Menedzsment és Vállakozásgazdaságtan Tanszék A Termelésmenedzsment alapjai tárgy gyakorló feladatainak megoldása Készítette: dr. Koltai Tamás egyetemi tanár Budapest,.
Közgazdaságtan 1. ELTE TáTK Közgazdaságtudományi Tanszék. 4. hét A KERESLETELMÉLET ALKALMAZÁSAI
 KÖZGAZDASÁGTAN I. ELTE TáTK Közgazdaságtudományi Tanszék Közgazdaságtan 1. A KERESLETELMÉLET ALKALMAZÁSAI Bíró Anikó, K hegyi Gergely, Major Klára Szakmai felel s: K hegyi Gergely 2010. június Vázlat
KÖZGAZDASÁGTAN I. ELTE TáTK Közgazdaságtudományi Tanszék Közgazdaságtan 1. A KERESLETELMÉLET ALKALMAZÁSAI Bíró Anikó, K hegyi Gergely, Major Klára Szakmai felel s: K hegyi Gergely 2010. június Vázlat
Demográfia. Def.: A születés, mortalitás, ki- és bevándorlás kvantifikálása. N jelenleg. = N korábban. + Sz M + Be Ki. A szervezetek típusai: UNITER
 Demográfia Def.: A születés, mortalitás, ki- és bevándorlás kvantifikálása N jelenleg = N korábban + Sz M + Be Ki A szervezetek típusai: UNITER MODULÁRIS Ramet Genet 1 Élőlények egyedszámának meghatározása:
Demográfia Def.: A születés, mortalitás, ki- és bevándorlás kvantifikálása N jelenleg = N korábban + Sz M + Be Ki A szervezetek típusai: UNITER MODULÁRIS Ramet Genet 1 Élőlények egyedszámának meghatározása:
TÁRSULÁSOK ÉS DIVERZITÁS
 TÁRSULÁSOK ÉS DIVERZITÁS Vadbiológia és ökológia h Jellemezôi g Törvényszerûen ismétlôdô, g Állandó megjelenésû, g Meghatározott környezeti igényû élôlényegyüttes h Biocönózis = fitocönózis + zoocönózis
TÁRSULÁSOK ÉS DIVERZITÁS Vadbiológia és ökológia h Jellemezôi g Törvényszerûen ismétlôdô, g Állandó megjelenésû, g Meghatározott környezeti igényû élôlényegyüttes h Biocönózis = fitocönózis + zoocönózis
4. Kartell két vállalat esetén
 4. Kartell két vállalat esetén 34 4. Kartell két vállalat esetén Ebben a fejezetben azzal az esettel foglalkozunk, amikor a piacot két vállalat uralja és ezek összejátszanak. A vállalatok együttműködését
4. Kartell két vállalat esetén 34 4. Kartell két vállalat esetén Ebben a fejezetben azzal az esettel foglalkozunk, amikor a piacot két vállalat uralja és ezek összejátszanak. A vállalatok együttműködését
Közgazdaságtan alapjai. Dr. Karajz Sándor Gazdaságelméleti Intézet
 Közgazdaságtan alapjai Dr. Karajz Sándor Gazdaságelméleti 9. Előadás Makrogazdasági kereslet Makrogazdasági kereslet Aggregált, vagy makrogazdasági keresletnek (AD) a kibocsátás iránti kereslet és az árszínvonal
Közgazdaságtan alapjai Dr. Karajz Sándor Gazdaságelméleti 9. Előadás Makrogazdasági kereslet Makrogazdasági kereslet Aggregált, vagy makrogazdasági keresletnek (AD) a kibocsátás iránti kereslet és az árszínvonal
Az ökológia alapjai NICHE
 Az ökológia alapjai NICHE Niche Meghatározás funkció ill. alkalmazkodás szerint a növény- és állatfajok élő és élettelen környezetükbe eltérő módon illeszkednek be ott a többi élőlénytől többé-kevésbé
Az ökológia alapjai NICHE Niche Meghatározás funkció ill. alkalmazkodás szerint a növény- és állatfajok élő és élettelen környezetükbe eltérő módon illeszkednek be ott a többi élőlénytől többé-kevésbé
Statisztika I. 12. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 1. előadás Előadó: Dr. Ertsey Imre Regresszió analízis A korrelációs együttható megmutatja a kapcsolat irányát és szorosságát. A kapcsolat vizsgálata során a gyakorlatban ennél messzebb
Statisztika I. 1. előadás Előadó: Dr. Ertsey Imre Regresszió analízis A korrelációs együttható megmutatja a kapcsolat irányát és szorosságát. A kapcsolat vizsgálata során a gyakorlatban ennél messzebb
Segítség az outputok értelmezéséhez
 Tanulni: 10.1-10.3, 10.5, 11.10. Hf: A honlapra feltett falco_exp.zip-ben lévő exploratív elemzések áttanulmányozása, érdekességek, észrevételek kigyűjtése. Segítség az outputok értelmezéséhez Leiro: Leíró
Tanulni: 10.1-10.3, 10.5, 11.10. Hf: A honlapra feltett falco_exp.zip-ben lévő exploratív elemzések áttanulmányozása, érdekességek, észrevételek kigyűjtése. Segítség az outputok értelmezéséhez Leiro: Leíró
Vállalati modellek. Előadásvázlat. dr. Kovács László
 Vállalati modellek Előadásvázlat dr. Kovács László Vállalati modell fogalom értelmezés Strukturált szervezet gazdasági tevékenység elvégzésére, nyereség optimalizálási céllal Jellemzői: gazdasági egység
Vállalati modellek Előadásvázlat dr. Kovács László Vállalati modell fogalom értelmezés Strukturált szervezet gazdasági tevékenység elvégzésére, nyereség optimalizálási céllal Jellemzői: gazdasági egység
2. Alapfeltevések és a logisztikus egyenlet
 Populáció dinamika Szőke Kálmán Benjamin - SZKRADT.ELTE 22. május 2.. Bevezetés A populációdinamika az élőlények egyedszámának és népességviszonyainak térbeli és időbeli változásának menetét adja meg.
Populáció dinamika Szőke Kálmán Benjamin - SZKRADT.ELTE 22. május 2.. Bevezetés A populációdinamika az élőlények egyedszámának és népességviszonyainak térbeli és időbeli változásának menetét adja meg.
Adatok statisztikai értékelésének főbb lehetőségei
 Adatok statisztikai értékelésének főbb lehetőségei 1. a. Egy- vagy kétváltozós eset b. Többváltozós eset 2. a. Becslési problémák, hipotézis vizsgálat b. Mintázatelemzés 3. Szint: a. Egyedi b. Populáció
Adatok statisztikai értékelésének főbb lehetőségei 1. a. Egy- vagy kétváltozós eset b. Többváltozós eset 2. a. Becslési problémák, hipotézis vizsgálat b. Mintázatelemzés 3. Szint: a. Egyedi b. Populáció
Hálózati Folyamok Alkalmazásai. Mályusz Levente BME Építéskivitelezési és Szervezési Tanszék
 Hálózati Folyamok Alkalmazásai Mályusz Levente BME Építéskivitelezési és Szervezési Tanszék Maximális folyam 7 7 9 3 2 7 source 8 4 7 sink 7 2 9 7 5 7 6 Maximális folyam feladat Adott [N, A] digráf (irányított
Hálózati Folyamok Alkalmazásai Mályusz Levente BME Építéskivitelezési és Szervezési Tanszék Maximális folyam 7 7 9 3 2 7 source 8 4 7 sink 7 2 9 7 5 7 6 Maximális folyam feladat Adott [N, A] digráf (irányított
9. AGGREGÁLT KERESLET II.
 9. AGGREGÁLT KERESLET II. Ingadozások magyaázata az LM-modellel Az és az LM göbe metszéspontja meghatáozza a nemzeti jövedelem szintjét. A nemzeti jövedelem a gazdaság övid távú egyensúlyi állapotát megváltoztatva
9. AGGREGÁLT KERESLET II. Ingadozások magyaázata az LM-modellel Az és az LM göbe metszéspontja meghatáozza a nemzeti jövedelem szintjét. A nemzeti jövedelem a gazdaság övid távú egyensúlyi állapotát megváltoztatva
Statisztika I. 8. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 8. előadás Előadó: Dr. Ertsey Imre Minták alapján történő értékelések A statisztika foglalkozik. a tömegjelenségek vizsgálatával Bizonyos esetekben lehetetlen illetve célszerűtlen a teljes
Statisztika I. 8. előadás Előadó: Dr. Ertsey Imre Minták alapján történő értékelések A statisztika foglalkozik. a tömegjelenségek vizsgálatával Bizonyos esetekben lehetetlen illetve célszerűtlen a teljes
Az egyensúly. Általános Kémia: Az egyensúly Slide 1 of 27
 Az egyensúly 6'-1 6'-2 6'-3 6'-4 6'-5 Dinamikus egyensúly Az egyensúlyi állandó Az egyensúlyi állandókkal kapcsolatos összefüggések Az egyensúlyi állandó számértékének jelentősége A reakció hányados, Q:
Az egyensúly 6'-1 6'-2 6'-3 6'-4 6'-5 Dinamikus egyensúly Az egyensúlyi állandó Az egyensúlyi állandókkal kapcsolatos összefüggések Az egyensúlyi állandó számértékének jelentősége A reakció hányados, Q:
Számítógépvezérelt irányítás és szabályozás elmélete (Bevezetés a rendszer- és irányításelméletbe, Computer Controlled Systems) 7.
 Számítógépvezérelt irányítás és szabályozás elmélete (Bevezetés a rendszer- és irányításelméletbe, Computer Controlled Systems) 7. előadás Szederkényi Gábor Pázmány Péter Katolikus Egyetem Információs
Számítógépvezérelt irányítás és szabályozás elmélete (Bevezetés a rendszer- és irányításelméletbe, Computer Controlled Systems) 7. előadás Szederkényi Gábor Pázmány Péter Katolikus Egyetem Információs
Az állatok szociális szerveződése, csoport vagy magány?
 Az állatok szociális szerveződése, csoport vagy magány? Csoport sok egyed együtt, fontosak az egyedek közötti kapcsolatok a csoport szervezettségében fokozatok vannak Az önző egyedeket csoportba kényszerítő
Az állatok szociális szerveződése, csoport vagy magány? Csoport sok egyed együtt, fontosak az egyedek közötti kapcsolatok a csoport szervezettségében fokozatok vannak Az önző egyedeket csoportba kényszerítő
[Biomatematika 2] Orvosi biometria
![[Biomatematika 2] Orvosi biometria [Biomatematika 2] Orvosi biometria](/thumbs/54/33134304.jpg) [Biomatematika 2] Orvosi biometria 2016.02.29. A statisztika típusai Leíró jellegű statisztika: összegzi egy adathalmaz jellemzőit. A középértéket jelemzi (medián, módus, átlag) Az adatok változékonyságát
[Biomatematika 2] Orvosi biometria 2016.02.29. A statisztika típusai Leíró jellegű statisztika: összegzi egy adathalmaz jellemzőit. A középértéket jelemzi (medián, módus, átlag) Az adatok változékonyságát
Populáció A populációk szerkezete
 Populáció A populációk szerkezete Az azonos fajhoz tartozó élőlények egyedei, amelyek adott helyen és időben együtt élnek és egymás között szaporodnak, a faj folytonosságát fenntartó szaporodásközösséget,
Populáció A populációk szerkezete Az azonos fajhoz tartozó élőlények egyedei, amelyek adott helyen és időben együtt élnek és egymás között szaporodnak, a faj folytonosságát fenntartó szaporodásközösséget,
Közgazdaságtan I. avagy: mikroökonómia. Dr. Nagy Benedek
 Közgazdaságtan I. avagy: mikroökonómia r. Nagy Benedek Email: Nagy.Benedek@eco.u-szeged.hu, Tel: (62) 544-676, fogadó óra: Hétfő 14-15:30, KO 311 (szorgalmi időszakban) zemélyes találkozás 4 alkalommal:
Közgazdaságtan I. avagy: mikroökonómia r. Nagy Benedek Email: Nagy.Benedek@eco.u-szeged.hu, Tel: (62) 544-676, fogadó óra: Hétfő 14-15:30, KO 311 (szorgalmi időszakban) zemélyes találkozás 4 alkalommal:
Anyag és energia az ökoszitémában -produkcióbiológia
 Prudukcióbiológia Anyag és energia az ökoszitémában -produkcióbiológia Vadbiológia és ökológia #09 h Tárgya # A bioszférában lejátszódó biológia termelés folyamatai # Az élô szervezetek anyag- és energiaforgalma
Prudukcióbiológia Anyag és energia az ökoszitémában -produkcióbiológia Vadbiológia és ökológia #09 h Tárgya # A bioszférában lejátszódó biológia termelés folyamatai # Az élô szervezetek anyag- és energiaforgalma
Dinamikai rendszerek, populációdinamika
 Dinamikai rendszerek, populációdinamika Számítógépes szimulációk 1n4i11/1 Csabai István ELTE Komplex Rendszerek Fizikája Tanszék 5.102 Email: csabaiθcomplex.elte.hu 2009 tavasz Dierenciálegyenletek a zikán
Dinamikai rendszerek, populációdinamika Számítógépes szimulációk 1n4i11/1 Csabai István ELTE Komplex Rendszerek Fizikája Tanszék 5.102 Email: csabaiθcomplex.elte.hu 2009 tavasz Dierenciálegyenletek a zikán
 A ország B ország A ország B ország A ország B ország Rövid távon a kamatparitás: két gazdaságban realizálható átlagos hozamnak azonos devizában kifejezett értéke meg kell, hogy egyezzen egymással. Hosszú
A ország B ország A ország B ország A ország B ország Rövid távon a kamatparitás: két gazdaságban realizálható átlagos hozamnak azonos devizában kifejezett értéke meg kell, hogy egyezzen egymással. Hosszú
Szimulációk egyszerősített fehérjemodellekkel. Szilágyi András
 Szimulációk egyszerősített fehérjemodellekkel Szilágyi András Szimulációs módszerek alkalmazhatósági tartományai Egyszerősített modellek Három típusát mutatjuk be: Játék rácsmodellek Realisztikusabb rácsmodellek
Szimulációk egyszerősített fehérjemodellekkel Szilágyi András Szimulációs módszerek alkalmazhatósági tartományai Egyszerősített modellek Három típusát mutatjuk be: Játék rácsmodellek Realisztikusabb rácsmodellek
A.2. Acélszerkezetek határállapotai
 A.. Acélszerkezetek határállapotai A... A teherbírási határállapotok első osztálya: a szilárdsági határállapotok A szilárdsági határállapotok (melyek között a fáradt és rideg törést e helyütt nem tárgyaljuk)
A.. Acélszerkezetek határállapotai A... A teherbírási határállapotok első osztálya: a szilárdsági határállapotok A szilárdsági határállapotok (melyek között a fáradt és rideg törést e helyütt nem tárgyaljuk)
4/24/12. Regresszióanalízis. Legkisebb négyzetek elve. Regresszióanalízis
 1. feladat Regresszióanalízis. Legkisebb négyzetek elve 2. feladat Az iskola egy évfolyamába tartozó diákok átlagéletkora 15,8 év, standard deviációja 0,6 év. A 625 fős évfolyamból hány diák fiatalabb
1. feladat Regresszióanalízis. Legkisebb négyzetek elve 2. feladat Az iskola egy évfolyamába tartozó diákok átlagéletkora 15,8 év, standard deviációja 0,6 év. A 625 fős évfolyamból hány diák fiatalabb
ELTE TáTK Közgazdaságtudományi Tanszék MAKROÖKONÓMIA. Készítette: Horváth Áron, Pete Péter. Szakmai felelős: Pete Péter
 MAKROÖKONÓMIA MAKROÖKONÓMIA Készült a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázati projekt keretében Tartalomfejlesztés az ELTE TátK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék, az
MAKROÖKONÓMIA MAKROÖKONÓMIA Készült a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázati projekt keretében Tartalomfejlesztés az ELTE TátK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék, az
Dr. Kalló Noémi. Termelés- és szolgáltatásmenedzsment. egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék. Dr.
 Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Ismertesse a legfontosabb előrejelzési módszereket és azok gyakorlati
Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Ismertesse a legfontosabb előrejelzési módszereket és azok gyakorlati
A L Hospital-szabály, elaszticitás, monotonitás, konvexitás
 A L Hospital-szabály, elaszticitás, monotonitás, konvexitás 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék A L Hospital-szabály, elaszticitás, monotonitás, konvexitás p. / A L
A L Hospital-szabály, elaszticitás, monotonitás, konvexitás 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék A L Hospital-szabály, elaszticitás, monotonitás, konvexitás p. / A L
A felhőzet hatása a Föld felszíni sugárzási egyenlegére*
 A felhőzet hatása a Föld felszíni sugárzási egyenlegére* Ács Ferenc ELTE, Földrajz- és Földtudományi Intézet, Meteorológiai Tanszék *Meghívott előadás az Apáczai Nyári Akadémián, Újvidék, 2017 július 10-14
A felhőzet hatása a Föld felszíni sugárzási egyenlegére* Ács Ferenc ELTE, Földrajz- és Földtudományi Intézet, Meteorológiai Tanszék *Meghívott előadás az Apáczai Nyári Akadémián, Újvidék, 2017 július 10-14
A vegetatív működés modelljei
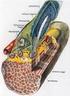 Tartalom 1 Motiváció 2 Decentralizált irányítási modellek 3 Működőképesség és stabilitás 4 Összehasonlítás 5 Következtetések Az Anti-Equilibriumtól a Hiányig Az Anti-Equilibriumban ígért konstruktív kritika:
Tartalom 1 Motiváció 2 Decentralizált irányítási modellek 3 Működőképesség és stabilitás 4 Összehasonlítás 5 Következtetések Az Anti-Equilibriumtól a Hiányig Az Anti-Equilibriumban ígért konstruktív kritika:
Hosszú távú vizsgálat jobban kimutatja a társulási szabályok változásait a másodlagos szukcesszió során, mint a tér-idő helyettesítés módszere
 Hosszú távú vizsgálat jobban kimutatja a társulási szabályok változásait a másodlagos szukcesszió során, mint a tér-idő helyettesítés módszere Anikó Csecserits, Melinda Halassy, Barbara Lhotsky, Tamás
Hosszú távú vizsgálat jobban kimutatja a társulási szabályok változásait a másodlagos szukcesszió során, mint a tér-idő helyettesítés módszere Anikó Csecserits, Melinda Halassy, Barbara Lhotsky, Tamás
17. előadás: Vektorok a térben
 17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 6. Differenciálegyenletekről röviden Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés 2 Elsőrendű differenciálegyenletek Definíciók Kezdetiérték-probléma
BIOMATEMATIKA ELŐADÁS 6. Differenciálegyenletekről röviden Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés 2 Elsőrendű differenciálegyenletek Definíciók Kezdetiérték-probléma
Folyadékszcintillációs spektroszkópia jegyz könyv
 Folyadékszcintillációs spektroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc I. Mérés vezet je: Horváth Ákos Mérés dátuma: 2010. október 21. Leadás dátuma: 2010. november 8. 1 1. Bevezetés A mérés
Folyadékszcintillációs spektroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc I. Mérés vezet je: Horváth Ákos Mérés dátuma: 2010. október 21. Leadás dátuma: 2010. november 8. 1 1. Bevezetés A mérés
3571,4=100L 0,5, L=1275,5 a munkakeresleti függvénybe helyettesítve (L(W/p) a profitmaximum feladatból) adódik.
 Jegyzet oldalszámok: IS-LM modell (69-79 oldal) Feladat megoldás: Mekkora a nominálbér? IS-LM-ből y; IS: y=0,8y+1000-10r LM: 7143/10=y-100r megoldva: y=3571,4 termelési függvényből foglalkoztatás L; 3571,4=100L
Jegyzet oldalszámok: IS-LM modell (69-79 oldal) Feladat megoldás: Mekkora a nominálbér? IS-LM-ből y; IS: y=0,8y+1000-10r LM: 7143/10=y-100r megoldva: y=3571,4 termelési függvényből foglalkoztatás L; 3571,4=100L
3. Előadás. Megyesi László: Lineáris algebra, oldal. 3. előadás Lineáris egyenletrendszerek
 3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
Lineáris algebra. (közgazdászoknak)
 Lineáris algebra (közgazdászoknak) 10A103 FELADATOK A GYAKORLATRA (3.) 2018/2019. tavaszi félév Lineáris egyenletrendszerek 3.1. Feladat. Oldjuk meg az alábbi lineáris egyenletrendszereket Gauss-eliminációval
Lineáris algebra (közgazdászoknak) 10A103 FELADATOK A GYAKORLATRA (3.) 2018/2019. tavaszi félév Lineáris egyenletrendszerek 3.1. Feladat. Oldjuk meg az alábbi lineáris egyenletrendszereket Gauss-eliminációval
Termelés- és szolgáltatásmenedzsment
 Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Előrejelzési módszerek 14. Az előrejelzési modellek felépítése
Termelés- és szolgáltatásmenedzsment egyetemi adjunktus Menedzsment és Vállalatgazdaságtan Tanszék Termelés- és szolgáltatásmenedzsment 13. Előrejelzési módszerek 14. Az előrejelzési modellek felépítése
Ez a paraméter arra szolgál, hogy kompenzáljuk a nem megfelelõ orsózási sebesség beállítást a rádión. Pl, ha a rádióban maximumon van az AILERON
 Ez a paraméter arra szolgál, hogy kompenzáljuk a nem megfelelõ orsózási sebesség beállítást a rádión. Pl, ha a rádióban maximumon van az AILERON SWASH AFR, de az orsózási sebesség nem megfelelõen nagy,
Ez a paraméter arra szolgál, hogy kompenzáljuk a nem megfelelõ orsózási sebesség beállítást a rádión. Pl, ha a rádióban maximumon van az AILERON SWASH AFR, de az orsózási sebesség nem megfelelõen nagy,
Számelméleti alapfogalmak
 1 Számelméleti alapfogalmak 1 Definíció Az a IN szám osztója a b IN számnak ha létezik c IN melyre a c = b Jelölése: a b 2 Példa a 0 bármely a számra teljesül, mivel c = 0 univerzálisan megfelel: a 0 =
1 Számelméleti alapfogalmak 1 Definíció Az a IN szám osztója a b IN számnak ha létezik c IN melyre a c = b Jelölése: a b 2 Példa a 0 bármely a számra teljesül, mivel c = 0 univerzálisan megfelel: a 0 =
Logisztikai szimulációs módszerek
 Üzemszervezés Logisztikai szimulációs módszerek Dr. Juhász János Integrált, rugalmas gyártórendszerek tervezésénél használatos szimulációs módszerek A sztochasztikus külső-belső tényezőknek kitett folyamatok
Üzemszervezés Logisztikai szimulációs módszerek Dr. Juhász János Integrált, rugalmas gyártórendszerek tervezésénél használatos szimulációs módszerek A sztochasztikus külső-belső tényezőknek kitett folyamatok
A nagy termés nyomában. Mezőhegyes, szeptember 11.
 A nagy termés nyomában Mezőhegyes, 2014. szeptember 11. Időjárás Trágyázás, növénytáplálás, talaj- és növénykondícionálás Levegőből támadó rovarok Levegőből támadó gombák Herbicid-használat Vetésidő Talajlakó
A nagy termés nyomában Mezőhegyes, 2014. szeptember 11. Időjárás Trágyázás, növénytáplálás, talaj- és növénykondícionálás Levegőből támadó rovarok Levegőből támadó gombák Herbicid-használat Vetésidő Talajlakó
 Kibernetika korábbi vizsga zárthelyi dolgozatokból válogatott tesztkérdések Figyelem! Az alábbi tesztek csak mintául szolgálnak a tesztkérdések megoldásához, azaz a bemagolásuk nem jelenti a tananyag elsajátítását
Kibernetika korábbi vizsga zárthelyi dolgozatokból válogatott tesztkérdések Figyelem! Az alábbi tesztek csak mintául szolgálnak a tesztkérdések megoldásához, azaz a bemagolásuk nem jelenti a tananyag elsajátítását
A stratégiai célok közül egy tetszőlegesen kiválasztottnak a feldolgozása!
 Biodiverzitás stratégia 2020 CÉLOK és ESZKÖZÖK Források: http://www.biodiv.hu/convention/f1117799202; http://ec.europa.eu/environment/nature/biodiversity/comm2006/2020.htm; FELADAT A stratégiai célok közül
Biodiverzitás stratégia 2020 CÉLOK és ESZKÖZÖK Források: http://www.biodiv.hu/convention/f1117799202; http://ec.europa.eu/environment/nature/biodiversity/comm2006/2020.htm; FELADAT A stratégiai célok közül
Olvassa el figyelmesen az alábbi állításokat és karikázza be a helyes válasz előtt álló betűjelet.
 Feleletválasztós kérdések 03 Hossz távú termelés, termelési tényezők Olvassa el figyelmesen az alábbi állításokat és karikázza be a helyes válasz előtt álló betűjelet. 1. érdés A termelési függvény minden
Feleletválasztós kérdések 03 Hossz távú termelés, termelési tényezők Olvassa el figyelmesen az alábbi állításokat és karikázza be a helyes válasz előtt álló betűjelet. 1. érdés A termelési függvény minden
Közgazdaságtan 1. ELTE TáTK Közgazdaságtudományi Tanszék. 2. hét KERESLET, KÍNÁLAT, EGYENSÚLY
 KÖZGAZDASÁGTAN I. ELTE TáTK Közgazdaságtudományi Tanszék Közgazdaságtan 1. KERESLET, KÍNÁLAT, EGYENSÚLY Bíró Anikó, K hegyi Gergely, Major Klára Szakmai felel s: K hegyi Gergely 2010. június Vázlat 1
KÖZGAZDASÁGTAN I. ELTE TáTK Közgazdaságtudományi Tanszék Közgazdaságtan 1. KERESLET, KÍNÁLAT, EGYENSÚLY Bíró Anikó, K hegyi Gergely, Major Klára Szakmai felel s: K hegyi Gergely 2010. június Vázlat 1
Analízis előadás és gyakorlat vázlat
 Analízis előadás és gyakorlat vázlat Készült a PTE TTK GI szakos hallgatóinak Király Balázs 2010-11. I. Félév 2 1. fejezet Számhalmazok és tulajdonságaik 1.1. Nevezetes számhalmazok ➀ a) jelölése: N b)
Analízis előadás és gyakorlat vázlat Készült a PTE TTK GI szakos hallgatóinak Király Balázs 2010-11. I. Félév 2 1. fejezet Számhalmazok és tulajdonságaik 1.1. Nevezetes számhalmazok ➀ a) jelölése: N b)
Bevezetés a kaotikus rendszerekbe
 Bevezetés a kaotikus rendszerekbe. előadás Könyvészet: Steven H. Strogatz, Nonlinear Dynamics and Chaos Káosz, fraktálok és dinamika ` Fraktálok: szépség matematikai leírás Fraktálzene: Phil Thompson Me
Bevezetés a kaotikus rendszerekbe. előadás Könyvészet: Steven H. Strogatz, Nonlinear Dynamics and Chaos Káosz, fraktálok és dinamika ` Fraktálok: szépség matematikai leírás Fraktálzene: Phil Thompson Me
Fogyasztás, beruházás és rövid távú árupiaci egyensúly kétszektoros makromodellekben
 Fogyasztás, beruházás és rövid távú árupiaci egyensúly kétszektoros makromodellekben Fogyasztáselméletek 64.) Bock Gyula [2001]: Makroökonómia ok. TRI-MESTER, Tatabánya. 33. o. 1. 65.) Keynesi abszolút
Fogyasztás, beruházás és rövid távú árupiaci egyensúly kétszektoros makromodellekben Fogyasztáselméletek 64.) Bock Gyula [2001]: Makroökonómia ok. TRI-MESTER, Tatabánya. 33. o. 1. 65.) Keynesi abszolút
ELTE TáTK Közgazdaságtudományi Tanszék OKTATÁSGAZDASÁGTAN. Készítette: Varga Júlia. Szakmai felelős: Varga Júlia június
 OKTATÁSGAZDASÁGTAN OKTATÁSGAZDASÁGTAN Készült a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázati projekt keretében Tartalomfejlesztés az ELTE TátK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék,
OKTATÁSGAZDASÁGTAN OKTATÁSGAZDASÁGTAN Készült a TÁMOP-4.1.2-08/2/A/KMR-2009-0041pályázati projekt keretében Tartalomfejlesztés az ELTE TátK Közgazdaságtudományi Tanszékén az ELTE Közgazdaságtudományi Tanszék,
Közgazdaságtan I. Tökéletes verseny - kidolgozott feladatok
 Közgazdaságtan I. Tökéletes verseny - kidolgozott feladatok Kiss Olivér 01. november 11. Ebben a dokumentumban Berde Éva: Mikroökonómiai és piacelméleti feladatgy jtemény c. feladatgy jteményéb l találtok
Közgazdaságtan I. Tökéletes verseny - kidolgozott feladatok Kiss Olivér 01. november 11. Ebben a dokumentumban Berde Éva: Mikroökonómiai és piacelméleti feladatgy jtemény c. feladatgy jteményéb l találtok
Megoldott feladatok november 30. n+3 szigorúan monoton csökken, 5. n+3. lim a n = lim. n+3 = 2n+3 n+4 2n+1
 Megoldott feladatok 00. november 0.. Feladat: Vizsgáljuk az a n = n+ n+ sorozat monotonitását, korlátosságát és konvergenciáját. Konvergencia esetén számítsuk ki a határértéket! : a n = n+ n+ = n+ n+ =
Megoldott feladatok 00. november 0.. Feladat: Vizsgáljuk az a n = n+ n+ sorozat monotonitását, korlátosságát és konvergenciáját. Konvergencia esetén számítsuk ki a határértéket! : a n = n+ n+ = n+ n+ =
Gazdálkodási modul. Gazdaságtudományi ismeretek I. Közgazdaságtan. KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI MSc
 Gazdálkodási modul Gazdaságtudományi ismeretek I. Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI MSc Az árupiaci kereslet és az egyensúlyi jövedelem 14. lecke Az árupiac Az árupiac
Gazdálkodási modul Gazdaságtudományi ismeretek I. Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI MSc Az árupiaci kereslet és az egyensúlyi jövedelem 14. lecke Az árupiac Az árupiac
Munkanélküliség és infláció I.
 GYAKORÓ FEADATOK IV. Munkanélküliség és infláció I. Munkanélküliség és infláció I.. Egy nemzetgazdaságban a munkaképes korú lakosság 7 millió fő. Ebből inaktív, millió fő. A foglalkoztatottak száma 5,4
GYAKORÓ FEADATOK IV. Munkanélküliség és infláció I. Munkanélküliség és infláció I.. Egy nemzetgazdaságban a munkaképes korú lakosság 7 millió fő. Ebből inaktív, millió fő. A foglalkoztatottak száma 5,4
A vám gazdasági hatásai NEMZETKZÖI GAZDASÁGTAN
 A vám gazdasági hatásai NEMZETKZÖI GAZDASÁGTAN Forrás: Krugman-Obstfeld-Melitz: International Economics Theory & Policy, 9th ed., Addison-Wesley, 2012 A vám típusai A vám az importált termékre kivetett
A vám gazdasági hatásai NEMZETKZÖI GAZDASÁGTAN Forrás: Krugman-Obstfeld-Melitz: International Economics Theory & Policy, 9th ed., Addison-Wesley, 2012 A vám típusai A vám az importált termékre kivetett
időpont? ütemterv számonkérés segédanyagok
 időpont? ütemterv számonkérés segédanyagok 1. Bevezetés Végeselem-módszer Számítógépek alkalmazása a szerkezettervezésben: 1. a geometria megadása, tervkészítés, 2. műszaki számítások: - analitikus számítások
időpont? ütemterv számonkérés segédanyagok 1. Bevezetés Végeselem-módszer Számítógépek alkalmazása a szerkezettervezésben: 1. a geometria megadása, tervkészítés, 2. műszaki számítások: - analitikus számítások
Közgazdaságtan alapjai. Dr. Karajz Sándor Gazdaságelméleti Intézet
 Közgazdaságtan alapjai Dr. Karajz Sándor Gazdaságelméleti 4. Előadás Az árupiac és az IS görbe IS-LM rendszer A rövidtávú gazdasági ingadozások modellezésére használt legismertebb modell az úgynevezett
Közgazdaságtan alapjai Dr. Karajz Sándor Gazdaságelméleti 4. Előadás Az árupiac és az IS görbe IS-LM rendszer A rövidtávú gazdasági ingadozások modellezésére használt legismertebb modell az úgynevezett
