Czirók András, Hegedűs Balázs, Haiman Ottó, Csahók Zoltán, Vicsek Tamás

Átírás

1 1 of :25 Czirók András, Hegedűs Balázs, Haiman Ottó, Csahók Zoltán, Vicsek Tamás A gyakorlat során bepillantás nyerhető a sejttenyésztés módszerébe, az élő sejtek megfigyelését lehetővé tevő fáziskontraszt-mikroszkópiába, a számítógépes mérésirányítás lehetőségeibe és a statisztikai módszerek biológiai felhasználásába. 1. Sejttenyésztés A szövetes testszerveződésű élőlények bizonyos szöveteinek vagy sejtjeinek élő, működő állapotban történő megfigyelése nehézségekbe ütközik. Ezért gyakran különböző modellrendszereket is tanulmányoznak, amelyekben az élőlényekből származó sejteket, szöveteket megpróbálják in vitro a fiziológiás állapotokat minél jobban megközelítő körülmények között tartani, illetve amennyiben osztódni is képesek, akkor tenyészteni. A sejttenyészetekkel nyert adatok elemzésénél azonban mindig figyelembe kell venni, hogy a sejtek közötti intercelluláris illetve a sejtközti térben található extracelluláris hálózatok molekuláris kapcsolatai a tenyésztés során nem vagy csak részben alakulnak ki. Ez okozza az in vitro és az in vivo vizsgálatok közötti egyik legfontosabb különbséget. A sejttenyésztés olyan termosztált tápoldatban történik, amely a megfelelő mennyiségben tartalmaz szervetlen ionokat (Ca 2+, Mg 2+, Na +, K + 2-, SO 4, Cl -, és - H2 PO 4, 2- HPO4 ), aminosavakat (legnagyobb mennyiségben L-glutamint, ami a sejtek legfontosabb nitrogénforrása), B-vitaminokat és szénhidrátokat (glükóz). A fentieken kívül gyakran különböző oldott gázokat (CO 2,O 2 ) is biztosítanak a szövetnedv összetételének megfelelően: a sejteket 5% CO 2 és 95% levegő keverékében tartják. A megfelelő ph kialakításában szerepet játszik egyrészt a foszforsav savmaradékionjai által alkotott pufferrendszer (NaH 2 PO 4 -por oldása), másrészt a karbonátionok alkotta pufferrendszer (NaHCO 3 hozzáadása). Ezek segítségével 7,6 körüli ph értéket állítanak be, amely a megfelelő parciális nyomású CO 2 oldódása után éri el a kívánt ph-t (7,3). Újabban a szén-dioxidot nem igénylő tápfolyadékokkal is kísérleteznek. Mivel a ph a sejttenyészet életképességének egyik legfontosabb tényezője, ennek könnyű ellenőrzése végett a tápoldat fenolvörös indikátort tartalmaz. A szövetnedvben a sejtek által kibocsájtott, nagy fontosságú, részben még ma sem ismert felépítésű vegyületek (növekedési és differenciációs faktorok, citokinek, stb.) is vannak. Emiatt gyakran valamilyen élő szervezetből származó oldat - általában csirke, borjú vagy ló véréből kivont szérum- hozzáadására is szükség van. A tenyésztés során a tápoldatot rendszeresen cserélni kell, hiszen egyes vegyületeket a sejtek felhasználnak, ugyanakkor anyagcseréjük vég- és melléktermékei felhalmozódnak. Fontos továbbá a termosztált tér 100%-os páratartalma is, mert a tápfolyadék párolgása révén annak töménysége változhat. A tápoldat összeállításakor figyelembe kell venni, hogy az ozmolalitása kb. 300 mosm/kg H 2 O legyen. Ez sajnos a pufferkapacitás korlátozottságát jelenti, hiszen az az oldott pufferek abszolút koncentrációjával arányos.

2 2 of :25 2. Automatizált videomikroszkópos rendszer (1. ábra) Ha a sejttenyészetek fejlődését folyamatosan szeretnénk mikroszkóp alatt vizsgálni, akkor kénytelenek vagyunk a szükséges feltételeket egy kisméretű inkubátorban megteremteni. A számítógép egy termisztor (elektronikus hőmérő) és néhány fűtőszál segítségével képes negatív visszacsatolással egy adott hőmérsékleten tartani a kamrát. A CO 2 parciális nyomásával változik a tápoldat ph-ja, így a megfelelő gázutánpótlás szabályozását a számítógép elvégezheti egy ph-mérővel és a gázáramot kapcsoló mágneses szeleppel. 1.ábra A készülék vázlata Az inkubátor, a megfelelő sejttenyészettel a belsejében, a mikroszkóp tárgyasztalán helyezkedik el. A tárgyasztal mozgatható függőleges irányban, hogy kiválaszthassuk, illetve a számítógép kiválaszthassa a megfelelő élességű képsíkot. A számítógép által vezérelt vízszintes irányú mozgatás lehetővé teszi, hogy egyszerre több látóteret is megfigyeljünk. A mérés során a számítógép meghatározott időközönként felvételeket készít a tenyészetről és a kamerából kiolvasott képet digitális formában rögzíti. Ezt több képsíkban elvégzi, majd az egyes képek meghatározott részletein kiszámítja az átlagszürkeséget, illetve az átlagtól való eltérést. Minél nagyobb egy képen az így jellemezhető kontraszt, feltehetően maga a kép annál élesebb (fokozottan igaz ez a fáziskontrasztos képek esetén). Az így kiválasztott felvételekből a számítógép mozgófilmet készíthet. Sok esetben ezek a filmek már önmagukban is új jelenségekre világítanak rá. 3. A fáziskontraszt eljárás

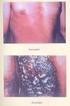
3 3 of :25 A fáziskontraszt eljárás lehetővé teszi egyformán átlátszó tárgyak olyan részleteinek a láthatóvá tételét, amelyek csak törésmutatójukban és/vagy vastagságukban különböznek egymástól.ez számunkra azért fontos, mert sejtek átlátszósága nagyjából azonos, és legtöbbször csak festési eljárásokkal lehet az egyes részletek között különbséget tenni. A fáziskontraszt eljárás nem igényel festést, így a sejtek festetlen, nem fixált, élő állapotukban vizsgálhatóak. Ezért van ennek és a hasonló optikai eljárásoknak (DIC, Nomarsky) rendkívüli jelentősége a biológiai vizsgálatokban. A hagyományos mikroszkóp képalkotásának elvét a 2. ábra mutatja be. 2.ábra A mikroszkóp pontszerű fényforrásának a kondenzor által párhuzamosított fénynyalábja érkezik a tárgyra. A tárgyon a nyaláb egy része elhajlás nélkül halad át, míg a másik részét a tárgy inhomogenitásai elhajlítják. Mind az elhajlított, mind az el nem hajlított fényhullámok az objektívbe, a tárgylencsébe jutnak. Az objektív az el nem hajlított fényhullámokból a képoldali gyújtópontjában létrehozza a pontszerű fényforrás képét, míg az elhajlított fényhullámok a képoldali gyújtósík más pontjaiban gyűlnek össze. Mindezen képek, mint másodlagos fényforrások, egymással interferálva a tubus felső részében létrehozzák a szemlencsében látható képet. Az eddig elmondottakhoz képest a fáziskontraszt-mikroszkóp különlegessége, hogy az objektív foglalatában, a gyújtósíkban egy speciális lemez található. Ennek a közepén ( a gyújtópontban) egy nagy törésmutatójú, meghatározott vastagságú réteg van, amely a rajta áthaladó hullámokat lelassítja. Így az el nem hajlított fényhullámok 90 fok fáziskésést szenvednek az elhajlítottakhoz képest. Ennek következtében a különböző vastagságú és/vagy törésmutatójú részleteknek megfelelő képpontok immár nem fáziskésés, hanem amplitudó tekintetében különböznek, ami szemmel látható fényintenzitás különbségét is eredményez. A pontszerű fényforrás fényszegény képet ad, ezért a gyakorlatban kiterjedt fényforrásokat használnak. Legmegfelelőbbnek a gyűrű alakú mutatkozott. Így a lámpa fényét egy diszperzoron vezetik át, majd ezt a közel egyenletes fény egy olyan lemezen halad át, amely közepéből egy gyűrűt kivágtak. Természetesen így az el nem hajlított fényhullámokból a képoldali gyújtósíkban alkotott kép is gyűrű alakú lesz, ezért a fáziseltoló rétegnek is gyűrű alakúnak kell lennie, hogy tökéletesen fedje ezt a képet. Az eljárás hátránya, hogy az azonos nagyítású fénymikroszkóphoz képest némileg csökken a felbontása. A sejtek felszíne körül egy világos udvar alakul ki, amely bizonyos esetekben zavaró (habár digitális képfeldolgozás során esetleg előny is) lehet. Egy fáziskontraszt eljárással keszült felvétel látható az alábbi fényképen. (A második sejtmozi egy kockája.)

4 4 of :25 A felvételekből a számítógép által összeállított filmek közül letölthetö néhány. (Ha a jobb oldali egér gombbal kattintasz rá.) Mindhárom film a legrosszindulatúbb gliaeredetű agydaganatban szenvedő három különböző páciensből származó sejttenyészetekről készült. 1. sejtmozi Az első filmen a sejtek inkább hámjellegűen növekednek, kevés nyúlvánnyal rendelkeznek és viszonylag lassan mozognak. 2. sejtmozi Ezek a sejtek már több nyúlványt növesztenek, alakjuk a migráló sejtekre jellemző. A sejtek sebessége is nagyobb az elöző sejttenyészet sejtjeiénél. 3. sejtmozi Ebben a tenyészetben a sejtek jellegzetes vándorló sejtalakot mutatnak, igen nagy sebességgel mozognak, és egy bizonyos sejtsűrűség felett a sejtek szinte áramlanak. A filmek feldolgozásának első lépése, hogy meghatározzuk az egyes sejtek koordinátáit, illetve azt, hogy mikor jelentek meg vagy tüntek el a látótérből. Ennek automatizálása még csak gömbölyded, nem letapadt, úszó sejtek esetén megoldott, így a legtöbb tenyészetről egy embernek kell ezeket az adatokat felvennie. Az így létrehozott adatbázis a statisztikai feldolgozás nyersanyaga. I. Trajektória A nyers adatbázis felhasználásával kirajzoltatható az egyes sejtek, vagy akár a látótér összes sejtjének pályája (3. ábra). Ennek alapján egy szemléletes kép alakulhat ki a tenyészet mozgásáról.

5 5 of :25

6 6 of :25 3.ábra Két azonos diagnózisú agydaganatból izolált sejtek in vitro mozgása. Mindkét ábra azonos méretű látóteret (760 x 540 mikron) azonos ideig (24 óra) mutat. A baloldali ábrán a sejtek bolyongó mozgása megfigyelhető. A jobboldali ábra sejtjei nemcsak gyorsabban mozognak (hosszabb utat járnak be azonos idő alatt), de a mozgásuk iránya is rendeződni látszik. Más vizsgálatok is azt sugallják, hogy a daganatok lefolyásában a sejtmozgásnak meghatározó szerepe lehet. II. Sejtcsaládfák Ennek segítségével ábrázolhatjuk az idő függvényében, mely sejtek tartózkodtak illetve osztódtak a látótérben (4. ábra). Elegendően nagy családfa esetén az osztódási ciklus hossza nagy pontossággal becsülhető, illetve a sejttenyészet osztódási aktivitásának homogenitása is vizsgálható. Ez utóbbi például daganatok vizsgálatakor lehet fontos kérdés. III. Sejtmigráció 4.ábra Egy 70 órás mérés családfája A digitalizálás során létrehozott adatokból ki lehet számítani az egyes sejtek adott idő alatti elmozdulását, azaz a sebességét. Ennek időbeli változásait demonstrálja a 5. ábra. A nagyszámú adat birtokában a tenyészet statisztikus jellemzésére meghatározható: (1) az egyes sejtek különböző nagyságú elmozdulásainak eloszlása

7 7 of :25 (6. ábra), (2) a látótér összes sejtjének átlagsebessége vagy (3) ezeknek az átlagsebességeknek az eloszlása. 5.ábra Három tumoreredetű sejtvonal 3-3 sejtjének sebességváltozásai a mérés ideje alatt. Jól megfigyelhető a sebesség időbeni állandó változása, fluktuációja. 6.ábra Három azonos diagnózisú tumorból származó sejtvonalak 2-2 tenyészetének sebességeloszlása:

8 8 of :25 G(v) megadja annak a valószínűségét, hogy egy véletlenszerűen kiválasztott sejt sebessége nagyobb lesz, mint v. Mint megfigyelhető, a sebességeloszlás reprodukálható és szignifikáns különbséget mutatott ki a három sejtvonal között. IV. A kemotaxis vizsgálata Az embrionális fejlődés során bizonyos sejtek hosszú vándorlás után más sejtekkel összekapcsolódva a későbbi szervek felépüléséhez szükséges sejtcsoportosulásokat alakítanak ki. Fontos feladat ezen folyamatok mechanizmusának megértése. Embrionális neuroektodermából származó tenyészeteken vizsgálható, vajon a sejtcsoportok kialakulásában szerepe lehet-e a kemotaxisnak. A mérési eredmények feldolgozásakor minden egyes sejt minden egyes elmozdulásakor kiszámítható az, hogy a többi sejt milyen távolságban és az elmozduláshoz képest milyen irányban található. Az összes sejtre vonatkozó eredményt egy koordinátarendszerben (,azaz minden egyes elmozdulást az x -tengely irányába forgatva,) ábrázolva egy felhő kapható (7. ábra). 7.ábra A kemotaxis vizsgálatához készült ábra Ennek egyenletes sűrűsége bizonyítja, hogy az egyes sejtek elmozdulásának irányára nincs hatással a többi sejt helyzete (természetesen addig, amíg a közvetlen kapcsolat ki nem alakul a sejtek között). 5. A felhasználás lehetőségei A sejttenyészetek in vitro számítógépes videomikroszkópiája és az így nyert adatok statisztikus elemzése

9 9 of :25 lehetőséget nyújt például (i) a sejtmozgás modelljeinek kísérletes vizsgálatára, (ii) a sejtek helyváltoztatásával szoros összefüggésben álló folyamatok modellrendszereinek kutatására (a fehérvérsejtek mozgása az immunreakciókban, a sérülések utáni regenerációs folyamatok, a már említett embrionális fejlődés során lezajló vándorlások), (iii) különböző természetes és szintetikus vegyületek sejtmozgásra gyakorolt hatásának vizsgálatára (gyógyszerkutatás), (iv) a dagantos betegségek kialakulásának és az áttételképzés mechanizmusának a megértésére.