A ferde szabadforgácsolásról, ill. a csúszóforgácsolásról ismét
|
|
|
- Csenge Halászné
- 8 évvel ezelőtt
- Látták:
Átírás
1 A ferde szabadforgácsolásról, ill. a csúszóforgácsolásról ismét A szabadforgácsolást [ 1 ] az alábbiak szerint definiálja, ill. jellemzi. Ha a forgácsolószerszám élének minden pontjában a forgácsolási folyamat azonos feltételek mellett játszódik le, szabadforgácsolásról beszélhetünk. Jellemzője a szabadforgácsolásnak, hogy a szerszámnak csak egy éle, a főél vesz részt a forgácsolásban.a szabadforgácsolásnak két változata van, mindkettő gyakorlati jelentősége nagy: ~ ortogonális szabadforgácsolás: jellemzője, hogy a forgácsolóél merőleges a forgácsoló főmozgás irányára 1. / a ábra; ~ ferde vagy diagonális szabadforgácsolás: jellemzője, hogy a forgácsolóél nem merőleges a főmozgás irányára, hanem azzal ( 90 λ ) szöget zár be 1. / b ábra. 1. ábra Forrása: [ 1 ] A λ szög megnevezése [ 1 ] - nél: terelőszög. A forgácsoláselméleti vizsgálatok egyik legfőbb célja annak tisztázása, hogy a keletkezett forgács milyen síkban fut le. A különböző síkok és irányok egymáshoz viszonyított helyzete szemlélhető a 2. ábrán. Itt a ferde élű szerszámot egy ( Oxyz ) térbeli derékszögű koordináta - rendszerben helyeztük el, a geometriai viszonyok könnyebb átláthatósága végett. A koordináta - rendszer x tengelyét a forgácsolási sebesség v vektorával párhuzamosan vettük fel. A síklapok által határolt szerszámtest homloklapja tartalmazza az ABC nyomhárom - szöget, melynek AB oldala a szerszám éle, ill. annak része. A szerszám élére annak D pontjában állított merőleges OCD síkban mérjük a δ metszőszöget, az itt vízszintes OAB forgácsolási síkhoz képest. A 2. ábrán még másik két δ - szög is szerepel: ~ δ : elnevezzük látszólagos metszőszögnek, [ 2 ] szerint; ~ δ t : elnevezzük tényleges metszőszögnek, [ 1 ] szerint. Jelen dolgozat célja éppen az utóbbiak közti hasonlóság, ill. különbség tanulmányozása. Első kitűzött geometriai / trigonometriai feladatunk így fogalmazható meg:
2 2 Adott: λ, δ. Keresett: δ t, ν. 2. ábra A δ szög értelmezése: az OAB síkra merőleges és az OAC síkkal párhuzamos DLN sík és az ABC sík DL metszésvonalának és annak OAB síkra vett merőleges vetületének közbezárt szöge, azaz DL hajlásszöge. A ν szög értelmezése: a DLN és a DMN síkok közbezárt szöge; ezt azért hoztuk be, mert a CD egyenessel a homloklap síkjában λ szöget bezáró DM egyenest úgy is meghatározhatjuk, mint a DMN és az ABC síkok metszésvonalát. A δ t szög értelmezése: a DMN ferde háromszög D csúcsnál lévő szöge.
3 3 Az alkalmazott szögek indoklása az alábbi. [ 1 ] szerint megfigyelés, hogy diagonális szabadforgácsolásnál a forgács képződése egy, a feltételezett főmozgás irányára merőleges síkra az alapsíkra merőleges olyan síkban megy végbe, melynek metszésvonala a homlokfelületen az élnormálsíkkal λ szöget zár be. Ennek alapján a geometriai alaphelyzet a 2. ábra szerinti, ahol a δ t tényleges metszőszöget a forgácslefutás DMN síkjában kell értelmezni. Úgy is mondhatjuk, hogy a tényleges metszőszög a forgácsolási sebesség és a forgácslefutási sebesség vektora által bezárt szög. Az idézett mű úgy fogalmaz, hogy ennek a megfigyelésnek elméleti magyarázata nincs, de gyakorlati jelentősége felbecsülhetetlen. Ez azt jelenti, hogy az adott szakma forgá - csoláselméleti tudnivalói között feltétlenül meg kell jelennie ezeknek az ismereteknek is. Először: állítsuk fel a δ t = f 1 ( δ, λ ) összefüggést! Legyen CD 1! A DLN derékszögű háromszögből: DN cos t ; ( 1 ) DM az OCD és ODN derékszögű háromszögekkel: DN ODcos 1coscos ; ( 2 ) a CDM háromszögből, szinusztétellel: CD ( 3 ) DM DM 1 Most vegyük figyelembe, hogy , majd kifejtve a két szög összegének szinuszát, kapjuk ( 3 ) - ból: 1 cos. ( 4 ) DM tg1 Ezután ( 1 ), ( 2 ), és ( 4 ) - gyel: cost cos cos cos. tg ( 5 ) 1 A BCD derékszögű háromszögből: DB tg 1 ; ( 6 ) 1 majd a BDN derékszögű háromszögből: DN DB ; ( 7 ) ( 2 ) és ( 7 ) - tel: DN cos cos cos DB ; ( 8 ) tg
4 4 most ( 6 ) és ( 8 ) - cal: cos tg 1. ( 9 ) tg Innen: cos 1 arctg. tg ( 10 ) ( 5 ) és ( 9 ) - cel: cost cos cos cos cos tg 2 coscos cos coscos, cos cos vagyis cost coscos, ( 11 ) innen: t arccos cos cos. ( 12 ) Másodszor: állítsuk fel a ν = f 2 ( δ, λ ) összefüggést! A DLM háromszögből: LM 2 ; DM 1 2 az LMN háromszögből: ( 13 ) LM. MN 90 cos ( 14 ) Most képezzük ( 13 ) és ( 14 ) hányadosát! LM DM MN t, LM DM ( 15 ) MN ahogyan az a DMN derékszögű háromszögből adódik. Másfelől ( 13 ) és ( 14 ) - gyel:
5 5 LM 2 cos DM 1 2, LM MN ( 16 ) majd ( 15 ) és ( 16 ) - ból: t, cos ahonnan 2 cos. 1 2 t ( 17 ) ( 18 ) Innen : 2 cos arc. 1 2 ( 19 ) t Meghatározandók ehhez még a φ 2 és ψ szög - adatok. Az ADC derékszögű háromszögből: AD tg 2. ( 20 ) 1 Majd: AD ODtg 1costg. ( 21 ) ( 20 ) és ( 21 ) szerint: tg2 cos tg. ( 22 ) Innen: 2 arctg(cos tg ). ( 23 ) Most az OBC derékszögű háromszögből: OC tg ; ( 24 ) OB de az OCD derékszögű háromszögből: OC 1 ; ( 25 ) továbbá az OBD derékszögű háromszögből: OD 1cos OB ; ( 26 ) majd ( 24 ), ( 25 ), ( 26 ) - tal:
6 6 1 tg tg, 1cos azaz tg tg. ( 27 ) Végül arctg tg. ( 28 ) Részeredményeinket összegyűjtve: a ( 19 ), ( 10 ), ( 23 ), ( 28 ) és a ( 12 ) képletekkel kapjuk, hogy 2 cos arc 1 2 t, ahol cos 1 arctg tg, 2 arctg costg, arctg tg, t arccos cos cos. ( 29 ) Ezzel az első geometriai / trigonometriai feladatot megoldottuk. Második kitűzött geometriai / trigonometriai feladatunk így fogalmazható meg: Adott: λ, δ. Keresett: δ. Ismét a 2. ábra alapján: OC tg ; ( 30 ) OA de OC 1 ; ( 31 ) továbbá OD 1cos OA, ( 32 ) cos cos így ( 30 ), ( 31 ), ( 32 ) - vel:
7 7 tg tgcos, cos cos vagyis tg cos tg, ( 33 ) ahonnan arctgcos tg. ( 34 ) Ezzel a második geometriai / trigonometriai feladatot is megoldottuk. A ( 29 ) és a ( 34 ) képletek szerint általában fennáll, hogy ( 35 ) t, kivéve a λ = 0 esetet. Kövessük végig a 2. ábra segítségével a λ 0 elfajulást! Most pedig térjünk rá, hogy miért foglalkoztunk ennyit e témával! Ennek oka az, hogy egy vélt vagy valós ellentmondásra bukkantunk, a szakirodalom tanulmányozása során. Ugyanis [ 2 ] - ben a csúszóforgácsolás kapcsán a ( 34 ) szerinti, míg [ 1 ] - ben a ferde szabadforgácsolás kapcsán a ( 29 ) szerinti metszőszög képletét adják meg, melyek a fentiek alapján általában eltérnek egymástól. A fentebb mondottakból kiviláglik, hogy a forgácsoláselmélet nem csak geometriai, hanem fizikai ismeretekre is támaszkodik. Ha csak a geometriát tekintjük, akkor kézenfekvő a feltevés, hogy a forgácslefutás a 2. ábra DLN síkjában mehet végbe. Ha azonban a geometriai feltevés eredményét a fizikai tapasztalatokkal szembesítjük, akkor az adódik, hogy a ν 0 esetet kell tekintenünk. Meglehet, hogy egyes szakmák forgácsoláselméleti igényeit a ν 0 feltevéssel adódó eredmények is kielégítik, ezért nem bonyolítják feleslegesen a helyzetet. Bárhogyan is legyen, az itteni eset egy újabb adalék a magyar szakmai ismeretek és a szakirodalom sajátos helyzetéhez. Felhasznált irodalom: [ 1 ] Dr. Bali János: Forgácsolás Tankönyvkiadó, Budapest, 1988 [ 2 ] Dr. Sitkei György ( szerk. ): A faipari műveletek elmélete Mezőgazdasági Szaktudás Kiadó Kft., Budapest, 1994 Sződliget, Összeállította: Galgóczi Gyula mérnöktanár
A csúszóvágásról, ill. - forgácsolásról
 A csúszóvágásról, ill. - forgácsolásról A vágás, ill. a forgácsolás célja: anyagi részek egymástól való elválasztása. A vágás, ill. a forgácsolás hagyományos eszköze: a kés. A kés a v haladási irányhoz
A csúszóvágásról, ill. - forgácsolásról A vágás, ill. a forgácsolás célja: anyagi részek egymástól való elválasztása. A vágás, ill. a forgácsolás hagyományos eszköze: a kés. A kés a v haladási irányhoz
Egy forgáskúp metszéséről. Egy forgáskúpot az 1. ábra szerint helyeztünk el egy ( OXYZ ) derékszögű koordináta - rendszerben.
 Egy forgáskúp metszéséről Egy forgáskúpot az 1. ábra szerint helyeztünk el egy ( OXYZ ) derékszögű koordináta - rendszerben. Az O csúcsú, O tengelyű, γ félnyílásszögű kúpot az ( XY ) sík itt két alkotóban
Egy forgáskúp metszéséről Egy forgáskúpot az 1. ábra szerint helyeztünk el egy ( OXYZ ) derékszögű koordináta - rendszerben. Az O csúcsú, O tengelyű, γ félnyílásszögű kúpot az ( XY ) sík itt két alkotóban
Egy érdekes nyeregtetőről
 Egy érdekes nyeregtetőről Adott egy nyeregtető, az 1 ábra szerinti adatokkal 1 ábra Végezzük el vetületi ábrázolását, az alábbi számszerű adatokkal: a = 10,00 m; b = 6,00 m; c = 3,00 m; α = 45 ; M 1:100!
Egy érdekes nyeregtetőről Adott egy nyeregtető, az 1 ábra szerinti adatokkal 1 ábra Végezzük el vetületi ábrázolását, az alábbi számszerű adatokkal: a = 10,00 m; b = 6,00 m; c = 3,00 m; α = 45 ; M 1:100!
Egy sík és a koordinátasíkok metszésvonalainak meghatározása
 1 Egy sík és a koordinátasíkok metszésvonalainak meghatározása Ehhez tekintsük az 1. ábrát! 1. ábra Itt az ( u, v, w ) tengelymetszeteivel adott S síkot látjuk, az Oxyz térbeli derékszögű koordináta -
1 Egy sík és a koordinátasíkok metszésvonalainak meghatározása Ehhez tekintsük az 1. ábrát! 1. ábra Itt az ( u, v, w ) tengelymetszeteivel adott S síkot látjuk, az Oxyz térbeli derékszögű koordináta -
Aszimmetrikus nyeregtető ~ feladat 2.
 1 Aszimmetrikus nyeregtető ~ feladat 2. Ehhez tekintsük az 1. ábrát is! Itt az A és B pontok egy nyeregtető oromfali ereszpontjai, a P pont pedig a taréj pontja. Az ereszek egymástól való távolságának
1 Aszimmetrikus nyeregtető ~ feladat 2. Ehhez tekintsük az 1. ábrát is! Itt az A és B pontok egy nyeregtető oromfali ereszpontjai, a P pont pedig a taréj pontja. Az ereszek egymástól való távolságának
Érdekes geometriai számítások Téma: A kardáncsukló kinematikai alapegyenletének levezetése gömbháromszögtani alapon
 Érdekes geometriai számítások 7. Folytatjuk a sorozatot. 7. Téma: A kardáncsukló kinematikai alapegyenletének levezetése gömbháromszögtani alapon Korábbi dolgozatainkban már többféle módon is bemutattuk
Érdekes geometriai számítások 7. Folytatjuk a sorozatot. 7. Téma: A kardáncsukló kinematikai alapegyenletének levezetése gömbháromszögtani alapon Korábbi dolgozatainkban már többféle módon is bemutattuk
További adalékok a merőleges axonometriához
 1 További adalékok a merőleges axonometriához Egy szép összefoglaló munkát [ 1 ] találtunk az interneten, melynek előző dolgoza - tunkhoz csatlakozó részeit itt dolgozzuk fel. Előző dolgozatunk címe: Kiegészítés
1 További adalékok a merőleges axonometriához Egy szép összefoglaló munkát [ 1 ] találtunk az interneten, melynek előző dolgoza - tunkhoz csatlakozó részeit itt dolgozzuk fel. Előző dolgozatunk címe: Kiegészítés
Egy másik érdekes feladat. A feladat
 Egy másik érdekes feladat Az előző dolgozatban melynek címe: Egy érdekes feladat az itteninek egy speciális esetét vizsgáltuk. Az általánosabb feladat az alábbi [ 1 ]. A feladat Adott: az ABCD zárt négyszög
Egy másik érdekes feladat Az előző dolgozatban melynek címe: Egy érdekes feladat az itteninek egy speciális esetét vizsgáltuk. Az általánosabb feladat az alábbi [ 1 ]. A feladat Adott: az ABCD zárt négyszög
t, u v. u v t A kúpra írt csavarvonalról I. rész
 A kúpra írt csavarvonalról I. rész Sokféle kúpra írt csavarvonal létezik. Ezek közül először a legegyszerűbbel foglalko - zunk. Ezt azért tesszük mert meglepő az a tény hogy eddig még szinte sehol nem
A kúpra írt csavarvonalról I. rész Sokféle kúpra írt csavarvonal létezik. Ezek közül először a legegyszerűbbel foglalko - zunk. Ezt azért tesszük mert meglepő az a tény hogy eddig még szinte sehol nem
Egy sajátos ábrázolási feladatról
 1 Egy sajátos ábrázolási feladatról Régen volt, ha volt egyáltalán. Én bizony nem emlékszem a ferde gerincvonalú túleme - lés ~ átmeneti megoldásra 1. ábra az ( erdészeti ) útépítésben. 1. ábra forrása:
1 Egy sajátos ábrázolási feladatról Régen volt, ha volt egyáltalán. Én bizony nem emlékszem a ferde gerincvonalú túleme - lés ~ átmeneti megoldásra 1. ábra az ( erdészeti ) útépítésben. 1. ábra forrása:
A közönséges csavarvonal érintőjének képeiről
 A közönséges csavarvonal érintőjének képeiről Már régóta rajzoljuk a táblára a közönséges csavarvonal vetületeinek és síkba teríté - sének ábráit, a Gépészeti alapismeretek tantárgy óráin. Úgy tűnik, itt
A közönséges csavarvonal érintőjének képeiről Már régóta rajzoljuk a táblára a közönséges csavarvonal vetületeinek és síkba teríté - sének ábráit, a Gépészeti alapismeretek tantárgy óráin. Úgy tűnik, itt
Síkbeli csuklós rúdnégyszög egyensúlya
 Síkbeli csuklós rúdnégyszög egyensúlya Két korábbi dolgozatunkban melyek címe és azonosítója: [KD ]: Egy érdekes feladat, [KD ]: Egy másik érdekes feladat azt vizsgáltuk, hogy egy csuklós rúdnégyszög milyen
Síkbeli csuklós rúdnégyszög egyensúlya Két korábbi dolgozatunkban melyek címe és azonosítója: [KD ]: Egy érdekes feladat, [KD ]: Egy másik érdekes feladat azt vizsgáltuk, hogy egy csuklós rúdnégyszög milyen
Ellipszis átszelése. 1. ábra
 1 Ellipszis átszelése Adott egy a és b féltengely - adatokkal bíró ellipszis, melyet a befoglaló téglalapjának bal alsó sarkában csuklósan rögzítettnek képzelünk. Az ellipszist e C csukló körül forgatva
1 Ellipszis átszelése Adott egy a és b féltengely - adatokkal bíró ellipszis, melyet a befoglaló téglalapjának bal alsó sarkában csuklósan rögzítettnek képzelünk. Az ellipszist e C csukló körül forgatva
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Vektorok II.
 Vektorok II. DEFINÍCIÓ: (Vektorok hajlásszöge) Két vektor hajlásszögének azt a φ (0 φ 180 ) szöget nevezzük, amelyet a vektorok egy közös pontból felmért reprezentánsai által meghatározott félegyenesek
Vektorok II. DEFINÍCIÓ: (Vektorok hajlásszöge) Két vektor hajlásszögének azt a φ (0 φ 180 ) szöget nevezzük, amelyet a vektorok egy közös pontból felmért reprezentánsai által meghatározott félegyenesek
Fa rudak forgatása II.
 Fa rudak forgatása II. Dolgozatunk I. részében egy speciális esetre oldottuk meg a kitűzött feladatokat. Most egy általánosabb elrendezés vizsgálatát végezzük el. A számítás a korábbi úton halad, ügyelve
Fa rudak forgatása II. Dolgozatunk I. részében egy speciális esetre oldottuk meg a kitűzött feladatokat. Most egy általánosabb elrendezés vizsgálatát végezzük el. A számítás a korábbi úton halad, ügyelve
Az egyenes ellipszishenger ferde síkmetszeteiről
 1 Az egyenes ellipszishenger ferde síkmetszeteiről Vegyünk egy a és b féltengelyekkel bíró ellipszist a vezérgörbét, majd az ellipszis O centrumában állítsunk merőlegest az ellipszis síkjára. Ez a merőleges
1 Az egyenes ellipszishenger ferde síkmetszeteiről Vegyünk egy a és b féltengelyekkel bíró ellipszist a vezérgörbét, majd az ellipszis O centrumában állítsunk merőlegest az ellipszis síkjára. Ez a merőleges
Egy általánosabb súrlódásos alapfeladat
 Egy általánosabb súrlódásos alapfeladat Az előző dolgozatunkban címe: Egy súrlódásos alapfeladat, jele: ( E D ) tárgyalt probléma általánosítása az alábbi, melynek forrása [ 1 ]. Tekintsük az 1. ábrát!
Egy általánosabb súrlódásos alapfeladat Az előző dolgozatunkban címe: Egy súrlódásos alapfeladat, jele: ( E D ) tárgyalt probléma általánosítása az alábbi, melynek forrása [ 1 ]. Tekintsük az 1. ábrát!
A kardáncsukló kinematikája I. A szögelfordulások közti kapcsolat skaláris levezetése
 A kardáncsukló kinematikája I. A szögelfordulások közti kapcsolat skaláris levezetése Bevezetés A Hooke -, vagy Kardán - csukló a gyakorlatban széles körben elterjedt gépelem. Feladata a forgó mozgás átszármaztatása
A kardáncsukló kinematikája I. A szögelfordulások közti kapcsolat skaláris levezetése Bevezetés A Hooke -, vagy Kardán - csukló a gyakorlatban széles körben elterjedt gépelem. Feladata a forgó mozgás átszármaztatása
Kosárra dobás I. Egy érdekes feladattal találkoztunk [ 1 ] - ben, ahol ezt szerkesztéssel oldották meg. Most itt számítással oldjuk meg ugyanezt.
![Kosárra dobás I. Egy érdekes feladattal találkoztunk [ 1 ] - ben, ahol ezt szerkesztéssel oldották meg. Most itt számítással oldjuk meg ugyanezt. Kosárra dobás I. Egy érdekes feladattal találkoztunk [ 1 ] - ben, ahol ezt szerkesztéssel oldották meg. Most itt számítással oldjuk meg ugyanezt.](/thumbs/27/11117124.jpg) osárra dobás I. Egy érdekes feladattal találkoztunk [ 1 ] - ben, ahol ezt szerkesztéssel oldották meg. Most itt számítással oldjuk meg ugyanezt. A feladat Az 1. ábrán [ 1 ] egy tornaterem hosszmetszetét
osárra dobás I. Egy érdekes feladattal találkoztunk [ 1 ] - ben, ahol ezt szerkesztéssel oldották meg. Most itt számítással oldjuk meg ugyanezt. A feladat Az 1. ábrán [ 1 ] egy tornaterem hosszmetszetét
Megoldások. Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma)
 Megoldások 1. Határozd meg az a és b vektor skaláris szorzatát, ha a = 5, b = 4 és a közbezárt szög φ = 55! Alkalmazzuk a megfelelő képletet: a b = a b cos φ = 5 4 cos 55 11,47. 2. Határozd meg a következő
Megoldások 1. Határozd meg az a és b vektor skaláris szorzatát, ha a = 5, b = 4 és a közbezárt szög φ = 55! Alkalmazzuk a megfelelő képletet: a b = a b cos φ = 5 4 cos 55 11,47. 2. Határozd meg a következő
Vonatablakon át. A szabadvezeték alakjának leírása. 1. ábra
 1 Vonatablakon át Sokat utazom vonaton, és gyakran elnézem a vonatablakon át a légvezeték(ek) táncát. Már régóta gondolom, hogy le kellene írni ezt a látszólagos mozgást. Most erről lesz szó. Ehhez tekintsük
1 Vonatablakon át Sokat utazom vonaton, és gyakran elnézem a vonatablakon át a légvezeték(ek) táncát. Már régóta gondolom, hogy le kellene írni ezt a látszólagos mozgást. Most erről lesz szó. Ehhez tekintsük
A magától becsukódó ajtó működéséről
 1 A magától becsukódó ajtó működéséről Az [ 1 ] műben találtunk egy érdekes feladatot, amit most mi is feldolgozunk. Az 1. ábrán látható az eredeti feladat másolata. A feladat kitűzése 1. ábra forrása:
1 A magától becsukódó ajtó működéséről Az [ 1 ] műben találtunk egy érdekes feladatot, amit most mi is feldolgozunk. Az 1. ábrán látható az eredeti feladat másolata. A feladat kitűzése 1. ábra forrása:
Fiók ferde betolása. A hűtőszekrényünk ajtajának és kihúzott fiókjának érintkezése ihlette az alábbi feladatot. Ehhez tekintsük az 1. ábrát!
 1 Fiók ferde betolása A hűtőszekrényünk ajtajának és kihúzott fiókjának érintkezése ihlette az alábbi feladatot. Ehhez tekintsük az 1. ábrát! 1. ábra Itt azt látjuk, hogy egy a x b méretű kis kék téglalapot
1 Fiók ferde betolása A hűtőszekrényünk ajtajának és kihúzott fiókjának érintkezése ihlette az alábbi feladatot. Ehhez tekintsük az 1. ábrát! 1. ábra Itt azt látjuk, hogy egy a x b méretű kis kék téglalapot
A csavarvonal axonometrikus képéről
 A avarvonal axonometrikus képéről Miután egyre jobban megy a Graph ingyenes függvény - ábrázoló szoftver használata, kipróbáltuk, hogy tudunk - e vele avarvonalat ábrázolni, axonometrikusan. A válasz:
A avarvonal axonometrikus képéről Miután egyre jobban megy a Graph ingyenes függvény - ábrázoló szoftver használata, kipróbáltuk, hogy tudunk - e vele avarvonalat ábrázolni, axonometrikusan. A válasz:
A tűzfalakkal lezárt nyeregtető feladatához
 1 A tűzfalakkal lezárt nyeregtető feladatához Bevezetés Ehhez először tekintsük az 1. ábrát! 1 Itt azt szemlélhetjük, hogy hogyan lehet el - kerülni egy épület tűzfalának eláztatását. A felső ábrarészen
1 A tűzfalakkal lezárt nyeregtető feladatához Bevezetés Ehhez először tekintsük az 1. ábrát! 1 Itt azt szemlélhetjük, hogy hogyan lehet el - kerülni egy épület tűzfalának eláztatását. A felső ábrarészen
Vontatás III. A feladat
 Vontatás III Ebben a részben ázoljuk a ontatási feladat egy lehetséges numerikus megoldási módját Ezt az I részben ismertetett alapegyenletre építjük fel Itt az egy ontatott kerékpár esetét izsgáljuk feladat
Vontatás III Ebben a részben ázoljuk a ontatási feladat egy lehetséges numerikus megoldási módját Ezt az I részben ismertetett alapegyenletre építjük fel Itt az egy ontatott kerékpár esetét izsgáljuk feladat
A Cassini - görbékről
 A Cassini - görbékről Giovanni Domenico Cassini, a 17-18 században élt olasz származású francia csillagász neve egyebek mellett a róla elnevezett görbékről is ismert lehet; ilyeneket mutat az 1 ábra is
A Cassini - görbékről Giovanni Domenico Cassini, a 17-18 században élt olasz származású francia csillagász neve egyebek mellett a róla elnevezett görbékről is ismert lehet; ilyeneket mutat az 1 ábra is
Két körhenger általánosabban ( Alkalmazzuk a vektoralgebrát! ) 1. ábra
 Két körhenger általánosabban ( Alkalmazzuk a vektoralgebrát! ) Egy korábbi dolgozatunkban címe: Két egyenes körhenger a merőlegesen metsződő tengelyű körhengerek áthatási feladatával foglalkoztunk. Most
Két körhenger általánosabban ( Alkalmazzuk a vektoralgebrát! ) Egy korábbi dolgozatunkban címe: Két egyenes körhenger a merőlegesen metsződő tengelyű körhengerek áthatási feladatával foglalkoztunk. Most
Egy érdekes statikai - geometriai feladat
 1 Egy érdekes statikai - geometriai feladat Előző dolgozatunkban melynek címe: Egy érdekes geometriai feladat egy olyan feladatot oldottunk meg, ami az itteni előtanulmányának is tekinthető. Az ottani
1 Egy érdekes statikai - geometriai feladat Előző dolgozatunkban melynek címe: Egy érdekes geometriai feladat egy olyan feladatot oldottunk meg, ami az itteni előtanulmányának is tekinthető. Az ottani
Járműszerkezeti anyagok és megmunkálások II / II. félév ÉLGEOMETRIA. Dr. Szmejkál Attila Ozsváth Péter
 2007-2008 / II. félév ÉLGEOMETRIA Dr. Szmejkál Attila Ozsváth Péter Budapesti Műszaki és Gazdaságtudományi Egyetem Közlekedésmérnöki Kar Járműgyártás és javítás Tanszék H-1111, Budapest Bertalan L. u.
2007-2008 / II. félév ÉLGEOMETRIA Dr. Szmejkál Attila Ozsváth Péter Budapesti Műszaki és Gazdaságtudományi Egyetem Közlekedésmérnöki Kar Járműgyártás és javítás Tanszék H-1111, Budapest Bertalan L. u.
A gúla ~ projekthez 2. rész
 1 A gúla ~ projekthez 2. rész Dolgozatunk 1. részében egy speciális esetre a négyzet alapú egyenes gúla esetére írtuk fel és alkalmaztuk képleteinket. Most a tetszőleges oldalszámú szabályos sokszög alakú
1 A gúla ~ projekthez 2. rész Dolgozatunk 1. részében egy speciális esetre a négyzet alapú egyenes gúla esetére írtuk fel és alkalmaztuk képleteinket. Most a tetszőleges oldalszámú szabályos sokszög alakú
Egy újabb térmértani feladat. Az [ 1 ] könyvben az interneten találtuk az alábbi érdekes feladatot is 1. ábra.
![Egy újabb térmértani feladat. Az [ 1 ] könyvben az interneten találtuk az alábbi érdekes feladatot is 1. ábra. Egy újabb térmértani feladat. Az [ 1 ] könyvben az interneten találtuk az alábbi érdekes feladatot is 1. ábra.](/thumbs/98/136939744.jpg) 1 Egy újabb térmértani feladat Az [ 1 ] könyvben az interneten találtuk az alábbi érdekes feladatot is 1. ábra. Úgy látjuk, érdekes és tanulságos lesz végigvenni. 2 A feladat Egy szabályos n - szög alapú
1 Egy újabb térmértani feladat Az [ 1 ] könyvben az interneten találtuk az alábbi érdekes feladatot is 1. ábra. Úgy látjuk, érdekes és tanulságos lesz végigvenni. 2 A feladat Egy szabályos n - szög alapú
Érdekes geometriai számítások Téma: Szimmetrikus kontytető tetősíkjai lapszögének meghatározásáról
 1 Folytatjuk a sorozatot. Érdekes geometriai számítások 9. 9. Téma: Szimmetrikus kontytető tetősíkjai lapszögének meghatározásáról Már több dolgozatunk témája volt két metsződő tetősík közbezárt szögének
1 Folytatjuk a sorozatot. Érdekes geometriai számítások 9. 9. Téma: Szimmetrikus kontytető tetősíkjai lapszögének meghatározásáról Már több dolgozatunk témája volt két metsződő tetősík közbezárt szögének
2011. tavaszi félév. Élgeometria. Dr. Ozsváth Péter Dr. Szmejkál Attila
 2011. tavaszi félév Élgeometria Dr. Ozsváth Péter Dr. Szmejkál Attila Budapesti Műszaki és Gazdaságtudományi Egyetem, Járműgyártás és javítás Tanszék, 1111, Budapest, Bertalan L. u. 2. Z 608., tel./fax:
2011. tavaszi félév Élgeometria Dr. Ozsváth Péter Dr. Szmejkál Attila Budapesti Műszaki és Gazdaságtudományi Egyetem, Járműgyártás és javítás Tanszék, 1111, Budapest, Bertalan L. u. 2. Z 608., tel./fax:
Néhány véges trigonometriai összegről. Határozzuk meg az alábbi véges összegek értékét!, ( 1 ) ( 2 )
 1 Néhány véges trigonometriai összegről A Fizika számos területén találkozhatunk véges számú tagból álló trigonometriai össze - gekkel, melyek a számítások során állnak elő. Ezek értékét kinézhetjük matematikai
1 Néhány véges trigonometriai összegről A Fizika számos területén találkozhatunk véges számú tagból álló trigonometriai össze - gekkel, melyek a számítások során állnak elő. Ezek értékét kinézhetjük matematikai
Henger és kúp metsződő tengelyekkel
 Henger és kúp metsződő tengelyekkel Ebben a dolgozatban egy forgáshenger és egy forgáskúp áthatását tanulmányozzuk abban az egyszerűbb esetben, amikor a két test tengelye egyazon síkban fekszik, vagyis
Henger és kúp metsződő tengelyekkel Ebben a dolgozatban egy forgáshenger és egy forgáskúp áthatását tanulmányozzuk abban az egyszerűbb esetben, amikor a két test tengelye egyazon síkban fekszik, vagyis
Érdekes geometriai számítások 9.
 1 Érdekes geometriai számítások 9. Folytatjuk a sorozatot. 9. Téma: Szimmetrikus kontytető tetősíkjai lapszögének maghatározásáról Már több dolgozatunk témája volt két metsződő tetősík közbezárt szögének
1 Érdekes geometriai számítások 9. Folytatjuk a sorozatot. 9. Téma: Szimmetrikus kontytető tetősíkjai lapszögének maghatározásáról Már több dolgozatunk témája volt két metsződő tetősík közbezárt szögének
A gúla ~ projekthez 1. rész
 1 A gúla ~ projekthez 1. rész Megint találtunk az interneten valami érdekeset: az [ 1 ], [ 2 ], [ 3 ] anyagokat. Úgy véljük, hogy az alábbi téma / témakör kiválóan alkalmas lehet projekt - módszerrel történő
1 A gúla ~ projekthez 1. rész Megint találtunk az interneten valami érdekeset: az [ 1 ], [ 2 ], [ 3 ] anyagokat. Úgy véljük, hogy az alábbi téma / témakör kiválóan alkalmas lehet projekt - módszerrel történő
Érdekes geometriai számítások 10.
 1 Érdekes geometriai számítások 10. Találtunk az interneten egy könyvrészletet [ 1 ], ahol egy a triéder - geometriában fontos összefüggést egyszerű módon vezetnek le. Ennek eredményét összevetjük más
1 Érdekes geometriai számítások 10. Találtunk az interneten egy könyvrészletet [ 1 ], ahol egy a triéder - geometriában fontos összefüggést egyszerű módon vezetnek le. Ennek eredményét összevetjük más
Egy kérdés: merre folyik le az esővíz az úttestről? Ezt a kérdést az után tettük fel magunknak, hogy megláttuk az 1. ábrát.
 1 Egy kérdés: merre folyik le az esővíz az úttestről? Ezt a kérdést az után tettük fel magunknak, hogy megláttuk az 1. ábrát. 1. ábra forrása: [ 1 ] Ezen egy út tengelyvonalának egy pontjában tüntették
1 Egy kérdés: merre folyik le az esővíz az úttestről? Ezt a kérdést az után tettük fel magunknak, hogy megláttuk az 1. ábrát. 1. ábra forrása: [ 1 ] Ezen egy út tengelyvonalának egy pontjában tüntették
Lépcső beemelése. Az interneten találkoztunk az [ 1 ] művel, benne az 1. ábrával.
![Lépcső beemelése. Az interneten találkoztunk az [ 1 ] művel, benne az 1. ábrával. Lépcső beemelése. Az interneten találkoztunk az [ 1 ] művel, benne az 1. ábrával.](/thumbs/104/162084051.jpg) 1 Lépcső beemelése Az interneten találkoztunk az [ 1 ] művel, benne az 1. ábrával. 1. ábra forrása: [ 1 ] Itt példákat látunk előregyártott vasbeton szerkezeti elemek kötéllel / lánccal történő emelésére,
1 Lépcső beemelése Az interneten találkoztunk az [ 1 ] művel, benne az 1. ábrával. 1. ábra forrása: [ 1 ] Itt példákat látunk előregyártott vasbeton szerkezeti elemek kötéllel / lánccal történő emelésére,
Egy mozgástani feladat
 1 Egy mozgástani feladat Előző dolgozatunk melynek jele és címe: ED ~ Ismét az ellipszis egyenleteiről folytatásának tekinthető ez az írás. Leválasztottuk róla, mert bár szorosan kapcsolódnak, más a céljuk.
1 Egy mozgástani feladat Előző dolgozatunk melynek jele és címe: ED ~ Ismét az ellipszis egyenleteiről folytatásának tekinthető ez az írás. Leválasztottuk róla, mert bár szorosan kapcsolódnak, más a céljuk.
A loxodrómáról. Előző írásunkban melynek címe: A Gudermann - függvényről szó esett a Mercator - vetületről,illetve az ezen alapuló térképről 1. ábra.
 1 A loxodrómáról Előző írásunkban melynek címe: A Gudermann - függvényről szó esett a Mercator - vetületről,illetve az ezen alapuló térképről 1. ábra. 1. ábra forrása: [ 1 ] Ezen a térképen a szélességi
1 A loxodrómáról Előző írásunkban melynek címe: A Gudermann - függvényről szó esett a Mercator - vetületről,illetve az ezen alapuló térképről 1. ábra. 1. ábra forrása: [ 1 ] Ezen a térképen a szélességi
Országos Középiskolai Tanulmányi Verseny 2011/2012 Matematika I. kategória (SZAKKÖZÉPISKOLA) 2. forduló - megoldások. 1 pont Ekkor
 Okta tási Hivatal Országos Középiskolai Tanulmányi Verseny 0/0 Matematika I. kategória (SZAKKÖZÉPISKOLA). forduló - megoldások. Az valós számra teljesül a 3 sin sin cos sin egyenlőség. Milyen értékeket
Okta tási Hivatal Országos Középiskolai Tanulmányi Verseny 0/0 Matematika I. kategória (SZAKKÖZÉPISKOLA). forduló - megoldások. Az valós számra teljesül a 3 sin sin cos sin egyenlőség. Milyen értékeket
A véges forgatás vektoráról
 A véges forgatás vektoráról Az idők során sokszor olvastuk azt a mondatot a mechanika - könyvekben hogy a végtelen kis szögelfordulások az elemi forgások vektornak tekinthetők [ ] Természetesen adódik
A véges forgatás vektoráról Az idők során sokszor olvastuk azt a mondatot a mechanika - könyvekben hogy a végtelen kis szögelfordulások az elemi forgások vektornak tekinthetők [ ] Természetesen adódik
Országos Középiskolai Tanulmányi Verseny 2009/2010 Matematika I. kategória (SZAKKÖZÉPISKOLA) 2. forduló feladatainak megoldása
 Oktatási Hivatal Országos Középiskolai Tanulmányi Verseny / Matematika I. kategória (SZAKKÖZÉPISKOLA) 2. forduló feladatainak megoldása. Oldja meg a valós számok legbővebb részhalmazán a egyenlőtlenséget!
Oktatási Hivatal Országos Középiskolai Tanulmányi Verseny / Matematika I. kategória (SZAKKÖZÉPISKOLA) 2. forduló feladatainak megoldása. Oldja meg a valós számok legbővebb részhalmazán a egyenlőtlenséget!
9. Írjuk fel annak a síknak az egyenletét, amely átmegy az M 0(1, 2, 3) ponton és. egyenessel;
 Síkok és egyenesek FELADATLAP Írjuk fel annak az egyenesnek az egyenletét, amely átmegy az M 0(,, ) ponton és a) az M(,, 0) ponton; b) párhuzamos a d(,, 5) vektorral; c) merőleges a x y + z 0 = 0 síkra;
Síkok és egyenesek FELADATLAP Írjuk fel annak az egyenesnek az egyenletét, amely átmegy az M 0(,, ) ponton és a) az M(,, 0) ponton; b) párhuzamos a d(,, 5) vektorral; c) merőleges a x y + z 0 = 0 síkra;
A merőleges axonometria néhány régi - új összefüggéséről
 1 A merőleges axonometria néhány régi - új összefüggéséről Most néhány régebben már megbeszélt összefüggés újabb igazolását adjuk meg, illetve más, eddig még nem látott képlet - alakokat állítunk elő.
1 A merőleges axonometria néhány régi - új összefüggéséről Most néhány régebben már megbeszélt összefüggés újabb igazolását adjuk meg, illetve más, eddig még nem látott képlet - alakokat állítunk elő.
Szökőkút - feladat. 1. ábra. A fotók forrása:
 Szökőkút - feladat Nemrégen Gyulán jártunk, ahol sok szép szökőkutat láttunk. Az egyik különösen megtetszett, ezért elhatároztam, hogy megpróbálom elemi módon leírni a ízsugarak, illete az általuk leírt
Szökőkút - feladat Nemrégen Gyulán jártunk, ahol sok szép szökőkutat láttunk. Az egyik különösen megtetszett, ezért elhatároztam, hogy megpróbálom elemi módon leírni a ízsugarak, illete az általuk leírt
Egy érdekes statikai feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladattal.
![Egy érdekes statikai feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladattal. Egy érdekes statikai feladat. Az interneten találtuk az [ 1 ] művet, benne az alábbi feladattal.](/thumbs/92/110379255.jpg) 1 Egy érdekes statikai feladat Az interneten találtuk az [ 1 ] művet, benne az alábbi feladattal. A feladat A szabályos n - szög alakú, A, B, C, csúcsú lap az A csúcsán egy sima függőleges fal - hoz támaszkodik,
1 Egy érdekes statikai feladat Az interneten találtuk az [ 1 ] művet, benne az alábbi feladattal. A feladat A szabályos n - szög alakú, A, B, C, csúcsú lap az A csúcsán egy sima függőleges fal - hoz támaszkodik,
A főtengelyproblémához
 1 A főtengelyproblémához Korábbi, az ellipszis perspektivikus ábrázolásával foglalkozó dolgozatainkban előkerült a másodrendű görbék kanonikus alakra hozása, majd ebben a főtengelyrendszert előállító elforgatási
1 A főtengelyproblémához Korábbi, az ellipszis perspektivikus ábrázolásával foglalkozó dolgozatainkban előkerült a másodrendű görbék kanonikus alakra hozása, majd ebben a főtengelyrendszert előállító elforgatási
Egy geometriai szélsőérték - feladat
 1 Egy geometriai szélsőérték - feladat A feladat: Szerkesztendő egy olyan legnagyobb területű háromszög, melynek egyik csúcsa az a és b féltengelyeivel adott ellipszis tetszőlegesen felvett pontja. Keresendő
1 Egy geometriai szélsőérték - feladat A feladat: Szerkesztendő egy olyan legnagyobb területű háromszög, melynek egyik csúcsa az a és b féltengelyeivel adott ellipszis tetszőlegesen felvett pontja. Keresendő
Az éjszakai rovarok repüléséről
 Erről ezt olvashatjuk [ ] - ben: Az éjszakai rovarok repüléséről Az a kijelentés, miszerint a repülés pályája logaritmikus spirális, a következőképpen igazolható [ 2 ].. ábra Az állandó v nagyságú sebességgel
Erről ezt olvashatjuk [ ] - ben: Az éjszakai rovarok repüléséről Az a kijelentés, miszerint a repülés pályája logaritmikus spirális, a következőképpen igazolható [ 2 ].. ábra Az állandó v nagyságú sebességgel
Ellipszis vezérgörbéjű ferde kúp felszínének meghatározásához
 1 Ellipszis vezérgörbéjű ferde kúp felszínének meghatározásához Előző dolgozatunkkal melynek címe: A ferde körkúp palástfelszínének meghatározásához már mintegy megágyaztunk a jelen írásnak. Több mindent
1 Ellipszis vezérgörbéjű ferde kúp felszínének meghatározásához Előző dolgozatunkkal melynek címe: A ferde körkúp palástfelszínének meghatározásához már mintegy megágyaztunk a jelen írásnak. Több mindent
A ferde tartó megoszló terheléseiről
 A ferde tartó megoszló terheléseiről Úgy vettem észre az idők során, hogy nem nagyon magyarázták agyon azt a kérdést, amivel itt fogunk foglalkozni. Biztos azt mondják majd megint, hogy De hisz ezt mindenki
A ferde tartó megoszló terheléseiről Úgy vettem észre az idők során, hogy nem nagyon magyarázták agyon azt a kérdést, amivel itt fogunk foglalkozni. Biztos azt mondják majd megint, hogy De hisz ezt mindenki
Kocka perspektivikus ábrázolása. Bevezetés
 1 Kocka perspektivikus ábrázolása Bevezetés Előző három dolgozatunkban ~ melyek címe: 1. Sínpár perspektivikus ábrázolása, 2. Sínpár perspektivikus ábrázolása másként, 3. Sínpár perspektivikus ábrázolása
1 Kocka perspektivikus ábrázolása Bevezetés Előző három dolgozatunkban ~ melyek címe: 1. Sínpár perspektivikus ábrázolása, 2. Sínpár perspektivikus ábrázolása másként, 3. Sínpár perspektivikus ábrázolása
Kiegészítés a merőleges axonometriához
 1 Kiegészítés a merőleges axonometriához Időnként találunk egy szép és könnyebben érthető levezetést, magyarázó ábrát, amit érdemesnek gondolunk a megosztásra. Most is ez történt, az [ 1 ] és [ 3 ] művek
1 Kiegészítés a merőleges axonometriához Időnként találunk egy szép és könnyebben érthető levezetést, magyarázó ábrát, amit érdemesnek gondolunk a megosztásra. Most is ez történt, az [ 1 ] és [ 3 ] művek
A csavart oszlop előállításáról
 1 A csavart oszlop előállításáról Egy korábbi dolgozatunkban melynek címe: A kör és ellipszis csavarmozgása során keletkező felületekről felírtuk a szakirodalom - ban ld. pl.: [ 1 ]! csavart oszlop néven
1 A csavart oszlop előállításáról Egy korábbi dolgozatunkban melynek címe: A kör és ellipszis csavarmozgása során keletkező felületekről felírtuk a szakirodalom - ban ld. pl.: [ 1 ]! csavart oszlop néven
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások
 Megoldások 1. Egy háromszög egyik oldala 10 cm hosszú, s a rajta fekvő két szög 50 és 70. Számítsd ki a hiányzó szöget és oldalakat! Legyen a = 10 cm; β = 50 és γ = 70. A két szög ismeretében a harmadik
Megoldások 1. Egy háromszög egyik oldala 10 cm hosszú, s a rajta fekvő két szög 50 és 70. Számítsd ki a hiányzó szöget és oldalakat! Legyen a = 10 cm; β = 50 és γ = 70. A két szög ismeretében a harmadik
Koordináta-geometria feladatok (emelt szint)
 Koordináta-geometria feladatok (emelt szint) 1. (ESZÉV Minta (2) 2004.05/7) Egy ABC háromszögben CAB = 30, az ACB = 45. A háromszög két csúcsának koordinátái: A(2; 2) és C(4; 2). Határozza meg a harmadik
Koordináta-geometria feladatok (emelt szint) 1. (ESZÉV Minta (2) 2004.05/7) Egy ABC háromszögben CAB = 30, az ACB = 45. A háromszög két csúcsának koordinátái: A(2; 2) és C(4; 2). Határozza meg a harmadik
Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1.
![Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1. Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1.](/thumbs/27/12197964.jpg) 1 Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1. Feladat Egy G gépkocsi állandó v 0 nagyságú sebességgel egyenes úton
1 Forogj! Az [ 1 ] munkában találtunk egy feladatot, ami beindította a HD - készítési folyamatokat. Eredményei alább olvashatók. 1. Feladat Egy G gépkocsi állandó v 0 nagyságú sebességgel egyenes úton
Rugalmas láncgörbe alapvető összefüggések és tudnivalók I. rész
 Rugalmas láncgörbe alapvető összefüggések és tudnivalók I rész evezetés rugalmas láncgörbe magyar nyelvű szakirodalma nem túl gazdag Egy viszonylag rövid ismertetés található [ 1 ] - ben közönséges ( azaz
Rugalmas láncgörbe alapvető összefüggések és tudnivalók I rész evezetés rugalmas láncgörbe magyar nyelvű szakirodalma nem túl gazdag Egy viszonylag rövid ismertetés található [ 1 ] - ben közönséges ( azaz
Az elliptikus hengerre írt csavarvonalról
 1 Az elliptikus hengerre írt csavarvonalról Erről viszonylag ritkán olvashatunk, ezért most erről lesz szó. Az [ 1 ] munkában találtuk az alábbi részt 1. ábra. 1. ábra Itt a ( c ) feladat és annak megoldása
1 Az elliptikus hengerre írt csavarvonalról Erről viszonylag ritkán olvashatunk, ezért most erről lesz szó. Az [ 1 ] munkában találtuk az alábbi részt 1. ábra. 1. ábra Itt a ( c ) feladat és annak megoldása
Feladatok Házi feladat. Keszeg Attila
 2016.01.29. 1 2 3 4 Adott egy O pont és egy λ 0 valós szám. a tér minden egyes P pontjához rendeljünk hozzá egy P pontot, a következő módon: 1 ha P = O, akkor P = P 2 ha P O, akkor P az OP egyenes azon
2016.01.29. 1 2 3 4 Adott egy O pont és egy λ 0 valós szám. a tér minden egyes P pontjához rendeljünk hozzá egy P pontot, a következő módon: 1 ha P = O, akkor P = P 2 ha P O, akkor P az OP egyenes azon
Vektorok összeadása, kivonása, szorzás számmal, koordináták
 Vektorok összeadása, kivonása, szorzás számmal, koordináták 1. Mik lesznek a P (3, 4, 8) pont C (3, 7, 2) pontra vonatkozó tükörképének a koordinátái? 2. Egy szabályos hatszög középpontja K (4, 1, 4),
Vektorok összeadása, kivonása, szorzás számmal, koordináták 1. Mik lesznek a P (3, 4, 8) pont C (3, 7, 2) pontra vonatkozó tükörképének a koordinátái? 2. Egy szabályos hatszög középpontja K (4, 1, 4),
Fénypont a falon Feladat
 Fénypont a falon 3. Dolgozat - sorozatunk. és. részében két speiális eset vizsgálatát részleteztük. Itt az általánosabb síkbeli esettel foglalkozunk, főbb vonalaiban. Ehhez tekintsük az. ábrát is! 3. Feladat.
Fénypont a falon 3. Dolgozat - sorozatunk. és. részében két speiális eset vizsgálatát részleteztük. Itt az általánosabb síkbeli esettel foglalkozunk, főbb vonalaiban. Ehhez tekintsük az. ábrát is! 3. Feladat.
w u R. x 2 x w w u 2 u y y l ; x d y r ; x 2 x d d y r ; l 2 r 2 2 x w 2 x d w 2 u 2 d 2 2 u y ; x w u y l ; l r 2 x w 2 x d R d 2 u y ;
 A négysuklós mehanizmus alapfeladata másképpen Előző dolgozatunkban melynek íme: A négysuklós mehanizmus alapfeladatáról egy általunk legegyszerűbbnek gondolt megoldási módot ismertettünk. Ott megemlítet
A négysuklós mehanizmus alapfeladata másképpen Előző dolgozatunkban melynek íme: A négysuklós mehanizmus alapfeladatáról egy általunk legegyszerűbbnek gondolt megoldási módot ismertettünk. Ott megemlítet
Lin.Alg.Zh.1 feladatok
 LinAlgZh1 feladatok 01 3d vektorok Adott három vektor ā = (0 2 4) b = (1 1 4) c = (0 2 4) az R 3 Euklideszi vektortérben egy ortonormált bázisban 1 Mennyi az ā b skalárszorzat? 2 Mennyi az n = ā b vektoriális
LinAlgZh1 feladatok 01 3d vektorok Adott három vektor ā = (0 2 4) b = (1 1 4) c = (0 2 4) az R 3 Euklideszi vektortérben egy ortonormált bázisban 1 Mennyi az ā b skalárszorzat? 2 Mennyi az n = ā b vektoriális
Ismét a fahengeres keresztmetszetű gerenda témájáról. 1. ábra forrása: [ 1 ]
![Ismét a fahengeres keresztmetszetű gerenda témájáról. 1. ábra forrása: [ 1 ] Ismét a fahengeres keresztmetszetű gerenda témájáról. 1. ábra forrása: [ 1 ]](/thumbs/50/26108823.jpg) 1 Ismét a fahengeres keresztmetszetű gerenda témájáról Az 1. ábrával már korábban is találkozhatott az Olvasó. 1. ábra forrása: [ 1 ] Ezen azt láthatjuk, hogy bizonyos esetekben a fűrészelt fagerenda a
1 Ismét a fahengeres keresztmetszetű gerenda témájáról Az 1. ábrával már korábban is találkozhatott az Olvasó. 1. ábra forrása: [ 1 ] Ezen azt láthatjuk, hogy bizonyos esetekben a fűrészelt fagerenda a
1. feladat Bizonyítsuk be, hogy egy ABCD húrnégyszögben AC BD
 1. feladat Bizonyítsuk be, hogy egy ABCD húrnégyszögben AC BD = DA AB + BC CD AB BC + CD DA. Első megoldás: A húrnégyszögnek az A, B, C, ill. D csúcsoknál levő szögét jelölje rendre α, β, γ, ill. δ, azab,
1. feladat Bizonyítsuk be, hogy egy ABCD húrnégyszögben AC BD = DA AB + BC CD AB BC + CD DA. Első megoldás: A húrnégyszögnek az A, B, C, ill. D csúcsoknál levő szögét jelölje rendre α, β, γ, ill. δ, azab,
A repülési háromszögekről. Egy repülőgép sebessége megmérhető az alábbi módon is ld. 1. ábra.
 A repülési háromszögekről I Sebességmérés repülőgépen, stopperórával Egy repülőgép sebessége megmérhető az alábbi módon is ld 1 ábra Az ábra forrása: [ 1 ] 1 ábra Sík terepen kijelölünk egy ABC háromszöget,
A repülési háromszögekről I Sebességmérés repülőgépen, stopperórával Egy repülőgép sebessége megmérhető az alábbi módon is ld 1 ábra Az ábra forrása: [ 1 ] 1 ábra Sík terepen kijelölünk egy ABC háromszöget,
Az arkhimédészi csőfelületről
 Az arkhimédészi csőfelületről Az előző dolgozatban melynek címe: Csaarokról és rokon témákról elkezdtük a csaaros témakör körüljárását. Most folytatjuk a címbeli témáal. A felület definíciója [ 1 ] szerint:
Az arkhimédészi csőfelületről Az előző dolgozatban melynek címe: Csaarokról és rokon témákról elkezdtük a csaaros témakör körüljárását. Most folytatjuk a címbeli témáal. A felület definíciója [ 1 ] szerint:
= 7, a 3. = 7; x - 4y =-8; x + 2y = 10; x + y = 7. C-bôl induló szögfelezô: (-2; 3). PA + PB = PA 1. (8; -7), n(7; 8), 7x + 8y = 10, x = 0 & P 0;
 98 Az egyenes egyenletei. a) A( 0) B(0 6) AB_ - 6i& n( ) x + y = b) x - y =- c) 6x - y = 0 d) 6x + y = e) x + y = f) x + y = a g) x - y = a.. A(a 0) B(0 b) AB_ -a bi n (b a) bx + ay = ab osszuk el a $
98 Az egyenes egyenletei. a) A( 0) B(0 6) AB_ - 6i& n( ) x + y = b) x - y =- c) 6x - y = 0 d) 6x + y = e) x + y = f) x + y = a g) x - y = a.. A(a 0) B(0 b) AB_ -a bi n (b a) bx + ay = ab osszuk el a $
Kúp és kúp metsződő tengelyekkel
 Kúp és kúp metsződő tengelyekkel Előző dolgozatainkban [ ED ], [ ED ], [ ED 3 ], [ED 4 ] már láttuk, hogyan lehet meghatározni a két legegyszerűbb forgástest a henger és a kúp áthatási görbéinek egyenleteit.
Kúp és kúp metsződő tengelyekkel Előző dolgozatainkban [ ED ], [ ED ], [ ED 3 ], [ED 4 ] már láttuk, hogyan lehet meghatározni a két legegyszerűbb forgástest a henger és a kúp áthatási görbéinek egyenleteit.
Trigonometria Megoldások. 1) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( )
 Trigonometria Megoldások Trigonometria - megoldások ) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( ) akkor a háromszög egyenlő szárú vagy derékszögű!
Trigonometria Megoldások Trigonometria - megoldások ) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( ) akkor a háromszög egyenlő szárú vagy derékszögű!
Szabályos fahengeres keresztmetszet geometriai jellemzőinek meghatározása számítással
 Szabályos fahengeres keresztmetszet geometriai jellemzőinek meghatározása számítással Előző dolgozatunkban jele: ( E ), címe: Szimmetrikusan szélezett körkeresztmetszet geometriai jellemzőinek meghatározása
Szabályos fahengeres keresztmetszet geometriai jellemzőinek meghatározása számítással Előző dolgozatunkban jele: ( E ), címe: Szimmetrikusan szélezett körkeresztmetszet geometriai jellemzőinek meghatározása
Az eltérő hajlású szarufák és a taréjszelemen kapcsolatáról 1. rész. Eltérő keresztmetszet - magasságú szarufák esete
 1 Az eltérő hajlású szarufák és a taréjszelemen kapcsolatáról 1. rész Eltérő keresztmetszet - magasságú szarufák esete Az alábbi ábrát találtuk az interneten 1. ábra 1. ábra forrás( ok ): http://www.sema-soft.com/de/forum/files/firstpfettenverschiebung_432.jpg
1 Az eltérő hajlású szarufák és a taréjszelemen kapcsolatáról 1. rész Eltérő keresztmetszet - magasságú szarufák esete Az alábbi ábrát találtuk az interneten 1. ábra 1. ábra forrás( ok ): http://www.sema-soft.com/de/forum/files/firstpfettenverschiebung_432.jpg
Összeállította: dr. Leitold Adrien egyetemi docens
 Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
Az R 3 tér geometriája Összeállította: dr. Leitold Adrien egyetemi docens 2008.09.08. 1 Vektorok Vektor: irányított szakasz Jel.: a, a, a, AB, Jellemzői: irány, hosszúság, (abszolút érték) jel.: a Speciális
A lengőfűrészelésről
 A lengőfűrészelésről Az [ 1 ] tankönyvben ezt írják a lengőfűrészről, működéséről, használatáról: A lengőfűrész árkolásra, csaprések készítésére alkalmazott, 150 00 mm átmérőjű, 3 4 mm vastag, sűrű fogazású
A lengőfűrészelésről Az [ 1 ] tankönyvben ezt írják a lengőfűrészről, működéséről, használatáról: A lengőfűrész árkolásra, csaprések készítésére alkalmazott, 150 00 mm átmérőjű, 3 4 mm vastag, sűrű fogazású
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások
 Megoldások 1. Tekintsük az alábbi szabályos hatszögben a következő vektorokat: a = AB és b = AF. Add meg az FO, DC, AO, AC, BE, FB, CE, DF vektorok koordinátáit az (a ; b ) koordinátarendszerben! Alkalmazzuk
Megoldások 1. Tekintsük az alábbi szabályos hatszögben a következő vektorokat: a = AB és b = AF. Add meg az FO, DC, AO, AC, BE, FB, CE, DF vektorok koordinátáit az (a ; b ) koordinátarendszerben! Alkalmazzuk
Tető nem állandó hajlású szarufákkal
 1 Tető nem állandó hajlású szarufákkal Már korábbi dolgozatainkban is szó volt a címbeli témáról. Most azért vettük újra elő, mert szép és érdekes ábrákat találtunk az interneten, ezzel kapcsolatban, és
1 Tető nem állandó hajlású szarufákkal Már korábbi dolgozatainkban is szó volt a címbeli témáról. Most azért vettük újra elő, mert szép és érdekes ábrákat találtunk az interneten, ezzel kapcsolatban, és
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
Végein függesztett rúd egyensúlyi helyzete. Az interneten találtuk az [ 1 ] munkát, benne az alábbi érdekes feladatot 1. ábra. Most erről lesz szó.
![Végein függesztett rúd egyensúlyi helyzete. Az interneten találtuk az [ 1 ] munkát, benne az alábbi érdekes feladatot 1. ábra. Most erről lesz szó. Végein függesztett rúd egyensúlyi helyzete. Az interneten találtuk az [ 1 ] munkát, benne az alábbi érdekes feladatot 1. ábra. Most erről lesz szó.](/thumbs/92/108783591.jpg) 1 Végein függesztett rúd egyensúlyi helyzete Az interneten találtuk az [ 1 ] munkát, benne az alábbi érdekes feladatot 1. ábra. Most erről lesz szó. A feladat Ehhez tekintsük a 2. ábrát is! 1. ábra forrása:
1 Végein függesztett rúd egyensúlyi helyzete Az interneten találtuk az [ 1 ] munkát, benne az alábbi érdekes feladatot 1. ábra. Most erről lesz szó. A feladat Ehhez tekintsük a 2. ábrát is! 1. ábra forrása:
Az élszarufa és a szelemenek kapcsolódásáról
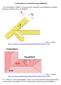 Az élszarufa és a szelemenek kapcsolódásáról A következőkben a címbeli viszonylag nehéz anyagrész megvilágítását szeretnénk elősegíteni főként szép és jó ábrákkal.. ábra forrása: http://www.dikraus.at/ingenieurbau/baustatik/baustatikflyer/s6_0.pdf.
Az élszarufa és a szelemenek kapcsolódásáról A következőkben a címbeli viszonylag nehéz anyagrész megvilágítását szeretnénk elősegíteni főként szép és jó ábrákkal.. ábra forrása: http://www.dikraus.at/ingenieurbau/baustatik/baustatikflyer/s6_0.pdf.
A térbeli mozgás leírásához
 A térbeli mozgás leírásához Az idők során már többször foglalkoztunk a címbeli témával; az előzmények vagyis a korábbi dolgozatok: ~ KD : Az R forgató mátrix I Az R forgató mátrix II ~ KD : A véges forgatás
A térbeli mozgás leírásához Az idők során már többször foglalkoztunk a címbeli témával; az előzmények vagyis a korábbi dolgozatok: ~ KD : Az R forgató mátrix I Az R forgató mátrix II ~ KD : A véges forgatás
Egy kinematikai feladathoz
 1 Egy kinematikai feladathoz Az [ 1 ] példatárból való az alábbi feladat. Egy bütyök v 0 állandó nagyságú sebességgel halad jobbról balra. Kontúrjának egyenlete a hozzá kötött, vele együtt haladó O 1 xy
1 Egy kinematikai feladathoz Az [ 1 ] példatárból való az alábbi feladat. Egy bütyök v 0 állandó nagyságú sebességgel halad jobbról balra. Kontúrjának egyenlete a hozzá kötött, vele együtt haladó O 1 xy
Kiegészítés a három erő egyensúlyához
 1 Kiegészítés a három erő egyensúlyához Egy régebbi dolgozatunkban melynek jele és címe : RD: Három erő egyensúlya ~ kéttámaszú tartó már sok mindent elmondtunk a címbeli témáról. Ez ugyanis egy megkerülhetetlen
1 Kiegészítés a három erő egyensúlyához Egy régebbi dolgozatunkban melynek jele és címe : RD: Három erő egyensúlya ~ kéttámaszú tartó már sok mindent elmondtunk a címbeli témáról. Ez ugyanis egy megkerülhetetlen
Egymásra támaszkodó rudak
 1 Egymásra támaszkodó rudak Úgy látszik, ez is egy visszatérő téma. Egy korábbi írásunkban melynek címe: A mandala - tetőről már találkoztunk az 1. ábrán vázolthoz hasonló felülnézetű szerkezettel, foglalkoztunk
1 Egymásra támaszkodó rudak Úgy látszik, ez is egy visszatérő téma. Egy korábbi írásunkban melynek címe: A mandala - tetőről már találkoztunk az 1. ábrán vázolthoz hasonló felülnézetű szerkezettel, foglalkoztunk
Matematika 11. osztály
 ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Humán tagozat Matematika 11. osztály II. rész: Trigonometria Készítette: Balázs Ádám Budapest, 018 . Tartalomjegyzék Tartalomjegyzék II. rész: Trigonometria...........................
ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Humán tagozat Matematika 11. osztály II. rész: Trigonometria Készítette: Balázs Ádám Budapest, 018 . Tartalomjegyzék Tartalomjegyzék II. rész: Trigonometria...........................
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások
 Megoldások 1. Határozd meg a szakasz hosszát, ha a végpontok koordinátái: A ( 1; ) és B (5; )! A szakasz hosszához számítsuk ki a két pont távolságát: d AB = AB = (5 ( 1)) + ( ) = 6 + 1 = 7 6,08.. Határozd
Megoldások 1. Határozd meg a szakasz hosszát, ha a végpontok koordinátái: A ( 1; ) és B (5; )! A szakasz hosszához számítsuk ki a két pont távolságát: d AB = AB = (5 ( 1)) + ( ) = 6 + 1 = 7 6,08.. Határozd
A fő - másodrendű nyomatékok meghatározása feltételes szélsőérték - feladatként
 A fő - másodrendű nomatékok meghatározása feltételes szélsőérték - feladatként A Keresztmetszeti jellemzők című mappa első lakója eg ritkábban látható levezetést mutat be amel talán segít helesen elrendezni
A fő - másodrendű nomatékok meghatározása feltételes szélsőérték - feladatként A Keresztmetszeti jellemzők című mappa első lakója eg ritkábban látható levezetést mutat be amel talán segít helesen elrendezni
A felsőmarószerszám jellemző adatai közti összefüggésekről. Az 1. ábrán feltüntettük a szerszámél egy P pontja v élsebesség - vektorát is.
 A felsőmarószerszám jellemző adatai közti összefüggésekről Bevezetés A faipari szakiskolás, valamint a szakközépiskolás a későbbi technikus tanulóknak tanított forgácsoláselméleti ismeretek átadása során
A felsőmarószerszám jellemző adatai közti összefüggésekről Bevezetés A faipari szakiskolás, valamint a szakközépiskolás a későbbi technikus tanulóknak tanított forgácsoláselméleti ismeretek átadása során
Az axonometrikus ábrázolás analitikus geometriai egyenleteinek másfajta levezetése. Bevezetés
 1 Az axonometrikus ábrázolás analitikus geometriai egyenleteinek másfajta levezetése Bevezetés Több korábbi dolgozatunkban is foglalkoztunk hasonló dolgokkal, vagyis az axonometri - kus ábrázolás alapfeladatának
1 Az axonometrikus ábrázolás analitikus geometriai egyenleteinek másfajta levezetése Bevezetés Több korábbi dolgozatunkban is foglalkoztunk hasonló dolgokkal, vagyis az axonometri - kus ábrázolás alapfeladatának
Megoldás A számtani sorozat első három eleme kifejezhető a második elemmel és a differenciával. Összegük így a 2. d =33, azaz 3a 2. a 2.
 1. Egy 33-as létszámú zenetagozatos osztályban hegedülni és zongorázni tanulnak a diákok. Minden diák játszik legalább egy hangszeren. Azok száma, akik mindkét hangszeren játszanak, akik csak hegedülnek,
1. Egy 33-as létszámú zenetagozatos osztályban hegedülni és zongorázni tanulnak a diákok. Minden diák játszik legalább egy hangszeren. Azok száma, akik mindkét hangszeren játszanak, akik csak hegedülnek,
Egy kinematikai feladat
 1 Egy kinematikai feladat Valami geometriai dologról ötlött eszembe az alábbi feladat 1. ábra. 1. ábra Adott az a és b egyenes, melyek α szöget zárnak be egymással. A b egyenesre ráfektetünk egy d hosszúságú
1 Egy kinematikai feladat Valami geometriai dologról ötlött eszembe az alábbi feladat 1. ábra. 1. ábra Adott az a és b egyenes, melyek α szöget zárnak be egymással. A b egyenesre ráfektetünk egy d hosszúságú
Koordinátageometria. , azaz ( ) a B halmazt pontosan azok a pontok alkotják, amelynek koordinátáira:
 005-0XX Emelt szint Koordinátageometria 1) a) Egy derékszögű háromszög egyik oldalegyenese valamelyik koordinátatengely, egy másik oldalegyenesének egyenlete x + y = 10, egyik csúcsa az origó. Hány ilyen
005-0XX Emelt szint Koordinátageometria 1) a) Egy derékszögű háromszög egyik oldalegyenese valamelyik koordinátatengely, egy másik oldalegyenesének egyenlete x + y = 10, egyik csúcsa az origó. Hány ilyen
A középponti és a kerületi szögek összefüggéséről szaktanároknak
 A középponti és a kerületi szögek összefüggéséről szaktanároknak Középiskolai tanulmányaink fontos része volt az elemi síkgeometriai tananyag. Ennek egyik nevezetes tétele így szól [ 1 ] : Az ugyanazon
A középponti és a kerületi szögek összefüggéséről szaktanároknak Középiskolai tanulmányaink fontos része volt az elemi síkgeometriai tananyag. Ennek egyik nevezetes tétele így szól [ 1 ] : Az ugyanazon
M/D/13. Szorozzuk meg az egyenlet mindkét oldalát a közös nevezővel, 12-vel; így a következő egyenlethez jutunk: = 24
 OKTATÁSI MINISZTÉRIUM M/D/13 Dolgozók gimnáziuma Dolgozók szakközépiskolája Szakmunkások szakközépiskolája intenzív tagozat) 003. május ) Határozza meg a következő egyenlet racionális gyökét! 1 3 4 + 5
OKTATÁSI MINISZTÉRIUM M/D/13 Dolgozók gimnáziuma Dolgozók szakközépiskolája Szakmunkások szakközépiskolája intenzív tagozat) 003. május ) Határozza meg a következő egyenlet racionális gyökét! 1 3 4 + 5
Élesmenetű csavar egyensúlya másként
 Élesmenetű csavar egyensúlya másként A szakirodalom ld pl: [ 1 ], [ 2 ], [ 3 ], [ 4 ], [ 5 ] tanulmányozása során feltűnt, hogy ~ leginkább a laposmenetű csavar erőjátékának vizsgálatát közlik, annak egyensúlyi
Élesmenetű csavar egyensúlya másként A szakirodalom ld pl: [ 1 ], [ 2 ], [ 3 ], [ 4 ], [ 5 ] tanulmányozása során feltűnt, hogy ~ leginkább a laposmenetű csavar erőjátékának vizsgálatát közlik, annak egyensúlyi
5. házi feladat. AB, CD kitér élpárra történ tükrözések: Az ered transzformáció: mivel az origó xpont, így nincs szükség homogénkoordinátás
 5. házi feladat 1.feladat A csúcsok: A = (0, 1, 1) T, B = (0, 1, 1) T, C = (1, 0, 0) T, D = ( 1, 0, 0) T AB, CD kitér élpárra történ tükrözések: 1 0 0 T AB = 0 1 0, elotlási rész:(i T AB )A = (0, 0, )
5. házi feladat 1.feladat A csúcsok: A = (0, 1, 1) T, B = (0, 1, 1) T, C = (1, 0, 0) T, D = ( 1, 0, 0) T AB, CD kitér élpárra történ tükrözések: 1 0 0 T AB = 0 1 0, elotlási rész:(i T AB )A = (0, 0, )
