A PÁROS ÖSSZEHASONLÍTÁS THURSTONE-FÉLE MÓDSZERÉNEK ALKALMAZÁSA A PSZICHOLÓGIÁBAN II. 1
|
|
|
- Gréta Székelyné
- 9 évvel ezelőtt
- Látták:
Átírás
1 ALKALMAZOTT PSZICHOLÓGIA 2012/2, A PÁROS ÖSSZEHASONLÍTÁS THURSTONE-FÉLE MÓDSZERÉNEK ALKALMAZÁSA A PSZICHOLÓGIÁBAN II. 1 BALÁZS Katalin Debreceni Egyetem Pszichológiai Intézet balazs.katalin@arts.unideb.hu CSÍZIK Tímea Debreceni Egyetem Pszichológiai Intézet csizik.timea@arts.unideb.hu HŐGYE-NAGY Ágnes Debreceni Egyetem Pszichológiai Intézet hogye-nagy.agnes@arts.unideb.hu MÜNNICH Ákos Debreceni Egyetem Pszichológiai Intézet munnich.akos@arts.unideb.hu ÖSSZEFOGLALÓ A páros összehasonlítás a pszichológiai kutatási gyakorlatban jó alternatívája lehet a nála általánosabban elterjedt skálázási eljárásoknak. A páros összehasonlítással megragadható pszichológiai problémák adatait elemezhetjük a Thurstone-féle egydimenziós modell, illetve a többdimenziós skálázás egydimenziós, illetve többdimenziós modelljének alkalmazásával. Jelen tanulmány négy gyakorlati példán keresztül demonstrálja, hogy a páros összehasonlításból nyert adatok esetén a Thurstone-féle skálázás és a többdimenziós skálázás egymás alternatívái, és adott adatbázison is érdemes mindkét módszert alkalmazni, majd a modellek illeszkedését a stresszmutató segítségével összevetni. 1 A publikáció elkészítését a TÁMOP-4.2.2/B-10/ számú projekt támogatta. A projekt az Európai Unió támogatásával, az Európai Szociális Alap társfinanszírozásával valósult meg.
2 46 BALÁZS Katalin CSÍZIK Tímea HŐGYE-NAGY Ágnes MÜNNICH Ákos BEVEZETÉS Számos olyan pszichológiai probléma létezik, ahol a vizsgálat során a vizsgált elemek viszonylagos megítélésére vagyunk kíváncsiak. Így például érdekelhet bennünket, hogy mely tulajdonságok a legfontosabbak a barátságok kialakulásánál; mely jellemzők a legmeghatározóbbak munkahelyválasztásnál; vagy egymáshoz képest hogyan értékelik az emberek a politikai pártokat. Ha adott témakörön belüli alternatívák viszonylagos megítélésre vagyunk kíváncsiak, az általában alkalmazott Likert típusú skálázáson túl (Likert, 1932) a páros összehasonlítás egy értékes, releváns módszert jelent. Megkérdezhetjük az embereket az egyes alternatívák értékeléséről például egy hétfokú skálán, azonban gyakran hasonló értékeket jelölnek meg a különböző alternatívák esetén. Sokkal differenciáltabb képet kapunk, ha az egyes elemek páros összehasonlítását kérjük a válaszadóktól, hiszen ez esetben az alternatívák viszonylagos értékéről döntenek. A páros összehasonlítás egyetlen hátránya, hogy az összehasonlítások száma exponenciálisan nő a vizsgált alternatívák számának növekedésével. Ha az alternatívák száma n, akkor a páros összehasonlítások száma n(n-1)/2. Kisebb elemszám (n) esetben azonban a módszer jól használható. Az alternatívák páros összehasonlításán keresztül az alternatívák egy vagy több dimenzión elfoglalt értékére (értékeire) szeretnénk következtetni. Az eredeti Thurstone-féle skálázás (ld. pl. Mérő, 1986, 1992; Thurstone, 1927, 1929, 1959; Thurstone és Jones, 1957) alkalmazásakor a vizsgált elemek egyetlen skálán elfoglalt helyét becsülhetjük meg, de az eljárás megfelelő többdimenziós modell illesztésére is. Fontos kitétel a Thurstone modellben a vizsgálandó ingerek, alternatívák megítélésére vonatkozó adatok normális eloszlása, ami pszichológiai problémák esetén valószínű. Egy másik módszer a páros összehasonlításból származó adatok feldolgozására a többdimenziós skálázás (TDS) alkalmazása. A módszer alapgondolata, hogy megítéléseink, akár tudattalanul is, több dimenzió mentén történnek, és a módszer lehetőséget ad arra, hogy a döntéseink alapját képező, mélyben rejlő dimenziókat feltárjuk. A módszer eredetileg a térképészetből származik, ahol először meghatározták a városok közötti távolságokat, majd a távolságok alapján megrajzolták a térképeket. Ugyanezt az elvet lehet használni a többdimenziós skálázás esetében is, amikor a vizsgált objektumokról készítünk térképeket. Az eljárás kivitelezéséhez szükségünk van egy távolságmátrixra, ami megadja, hogy az egyes alternatívák mennyire hasonlóak egymáshoz. A távolságmátrixból kiindulva, a többdimenziós skálázás meghatározza az alternatívák rendjét az egyes dimenziókon. A cél egy olyan reprezentáció kialakítása, mely az adatok legkisebb torzulásával jár. A kapott térkép (geo metriai reprezentáció) lehet egydimenziós (amikor az adatok egy egyenesre illeszkednek), kétdimenziós (ekkor ez elemek egy síkban helyezkednek el), háromdimenziós (ekkor az adatokat térben reprezentáljuk), vagy akár magasabb dimenziószámú (ebben az esetben a közvetlen geometriai reprezentáció nem lehetséges). A többdimenziós skálázásról további információ fellelhető magyarul például a Münnich, Nagy és Abari (2006) által írott elektronikus statisztika-könyvben, illetve más összefoglaló munkákban (ld. pl.: Borg és Groenen, 1997; Cox és Cox, 1994; Everitt és Rabe-Hesketh, 1997, Kruskal és Wish, 1978; Mérő, 1992).
3 A páros összehasonlítás Thurstone-féle módszerének alkalmazása A továbbiakban a Thurstone-féle skálázást, illetve a többdimenziós skálázás kivitelezését mutatjuk be a páros összehasonlításokból származó nyers adatokon. Többdimenziós skálázás alkalmazása páros összehasonlításból nyert adatokon nem egy megszokott módszer, de mindenképp megfelelő eljárás. Számos gyakorlati példán keresztül világos lesz, hogy a két módszer vezethet hasonló, vagy akár nagyon különböző eredményekhez is. Fontos a modellek illeszkedésének vizsgálata, hiszen a stresszérték mutatja, hogy melyik eljárás eredményeit vegyük figyelembe, illetve azt, hogy az eredmények érdemesek-e további felhasználásra. Ha az egydimenziós modellek nem vezetnek eredményre, érdemes többdimenziós modellt illeszteni. A páros összehasonlítás Thurstone-féle módszeréről szóló cikk első része (Balázs, Csízik, Hőgye-Nagy és Münnich, 2009) a Thurstone-féle skálázás egydimenziós alkalmazásának módját részletezte, jelen tanulmány a páros összehasonlítások többdimenziós modellezésére is kitér. Adatelemzéshez az R statisztikai programot használjuk (R-Development Core Team, 2005), amit az ingyenes szoftver gyorsan növekvő népszerűsége indokol. A páros összehasonlítás alkalmazása Az alternatívák választási valószínűsége empirikusan meghatározható, és a belőlük becsült skálaértékre vagyunk kíváncsiak: arra, hogy az alternatívák a vizsgálati szempont dimenziója mentén hogyan helyezkednek el. Ilyenkor alapesetben egy dimenzióban gondolkodunk. Az alternatívák választási valószínűségeit a páros összehasonlítás módszerével kétféleképpen kaphatjuk meg. Ha a vizsgálati mintánk nagy, dolgozhatunk dichotóm választási lehetőségekkel az egyes alternatíva-párok összehasonlításakor (A-ra vagy B-re jellemzőbb). Abban az esetben azonban, amikor egyetlen személy preferenciáira vagyunk kíváncsiak, vagy a mintánk kicsi, a dichotóm választási lehetőség helyett többfokú skálát használhatunk, pl. nullától egyig terjedő kódolással, ebben az esetben rendre a skála megjelölt értéke, illetve több vizsgálati személy esetén az értékek átlaga fejezi majd ki a választás valószínűségét. Az összehasonlíthatóság kedvéért korábbi cikkünk (Balázs, Csízik, Hőgye-Nagy és Münnich, 2009) bevezető példáját használjuk az R-ben történő alkalmazás demonstrálására. Tegyük fel, hogy öt választási alternatívánk van: A, B, C, D, E, melyeket páronként összehasonlítva a következő eredményeket, tapasztalati valószínűségeket kapjuk. 1. táblázat. Tapasztalati valószínűségek Alternatívák A B C D E A * 0,59 0,47 0,63 0,70 B 0,41 * 0,45 0,58 0,70 C 0,53 0,55 * 0,61 0,65 D 0,37 0,42 0,39 * 0,52 E 0,30 0,30 0,35 0,48 * A táblázat egy-egy cellájában annak a valószínűsége szerepel, hogy a páros összehasonlítás során a sorokban található alternatívákra a vizsgálati szempontot jellemzőbbnek ítéljük, mint az oszlopokban szereplő alternatívákat, azaz P(sorok>oszlopok), például: P(A>B) = 0,59, míg P(B>A) = 0,41. Hogy ne legyenek hiányzó elemek a mátrixban, adatbevitelkor az átlóban 0,5-öt tüntetünk fel.
4 48 BALÁZS Katalin CSÍZIK Tímea HŐGYE-NAGY Ágnes MÜNNICH Ákos A Thurstone-féle modell alkalmazása Az adatbevitel kivitelezése után, a valószínűségi értékekből kiszámoljuk a megfelelő z-értékeket a qnorm parancs segítségével, majd soronként a z-értékek átlagát véve megkapjuk az alternatíváknak megfelelő skálaértékeket (1. R parancs). p=data.frame(a=c(0.5,0.41,0.53,0.37,0.30),b=c(0.59,0.5,0.55,0.42,0.30),c=c(0.47,0.45,0.5,0.39,0.35), D=c(0.63,0.58,0.61,0.5,0.48),E=c(0.70,0.70,0.65,0.52,0.5)) m<-as.matrix(p) rownames(m)=c( A, B, C, D, E ) z=qnorm(m,0,1) skala=matrix(ncol=1, nrow=5) for(i in 1:5) skala[i]=mean(z[i,]) rownames(skala)=c( A, B, C, D, E ) print(skala) 1. R parancs par( cex=1.5, bg= white, pch=19:25 ) x=rep(1,5) plot(skala, x, type= b, xlab= Skálaértékek, ylab= ) text(skala,x+0.1,labels=rownames(m),cex=0.8) 2. R parancs A skálaértékeket grafikusan ábrázolhatjuk, pl. a 2. R parancs segítségével. 1. ábra. A Thurstone-féle modell segítségével kapott skálaértékek Szülők skálaérték Partner, kedves Barát(ok)/Barátnő(k) Kortárs segítők Szakemberek
5 A páros összehasonlítás Thurstone-féle módszerének alkalmazása A többdimenziós skálázás alkalmazása A valószínűség értékeket a többdimenziós skálázás inputjaként közvetlenül nem tudjuk felhasználni, mert a nagyobb valószínűségek nem jelentenek feltétlenül nagyobb távolságot. Például, ha A alternatívát 0,2-es valószínűséggel választják, akkor a B alternatívát 0,8-as valószínűséggel fogják választani, így a két valószínűség (0,2 és 0,8) tulajdonképpen ugyanazt a távolságot jelöli. Számos lehetőség adódik, a valószínűségmátrix transzformálására távolságmátrixszá. Alkalmazhatjuk a Bradley-Terry modellből (1952) ismert logit transzformációt, ahol i és j alternatívák távolságát (t ij ) a következő módon határozzuk meg: ahol p ij annak a valószínűsége, hogy i alternatívát választják j alternatívával szemben. Másik lehetőség, hogy a valószínűségi értékeket a standard normális eloszlás megfelelő értékeinek feleltetjük meg, ebben az esetben feltételezzük, hogy a távolságok normál eloszlást követnek. Akár a logit transzformációt (3. R parancs), akár a z eloszlásfüggvényt használjuk (4. R parancs), a távolságok abszolút értékét kell vennünk, mivel a TDS input R-ben csak pozitív számokat tartalmazhat. A távolságmátrixra lefuttathatjuk a többdimenziós skálázást oly módon, hogy egydimenziós megoldást kérünk. d1=abs(log(m/(1-m))) dist1<-as.dist(d1) tds1<-cmdscale(dist1, k=1) print(tds1,digits=3) 3. R parancs p ( ) log ij t = ij =logit i,j 1 p ij, d2=abs(qnorm(m,0,1)) dist2<-as.dist(d2) tds2<-cmdscale(dist2, k=1) print(tds2,digits=3) 4. R parancs A különböző inputokkal (logit vagy z-traszformáció) használt TDS eredményei nem különböznek jelentősen egymástól (lásd a 2. táblázatot). Azonban a Thurstone-modell eredményeként kapott skálaértékek nem egyszerűen fordított sorrendet mutatnak (ami egyszerűen a skála fordított reprezentációját jelentené), hanem az A, B és C alternatívák sorrendje másként alakul a Thurstone-modell és a TDS esetén. Ezek preferenciájáról csak a modellek illeszkedésének ellenőrzése után dönthetünk.
6 50 BALÁZS Katalin CSÍZIK Tímea HŐGYE-NAGY Ágnes MÜNNICH Ákos 2. táblázat. Skálaértékek Alternatívák Logit z-transzform. Thurstone A -0,32-0,20 0,20 B -0,27-0,17 0,07 C -0,15-0,10 0,17 D 0,21 0,13-0,15 E 0,53 0,33-0,29 A modellek illeszkedésének ellenőrzése Az illeszkedés vizsgálatához a skálaértékek alapján becsülhetjük a valószínűségeket és a becslést az empirikus értékekkel összehasonlíthatjuk. A stresszmutató szolgál a modell illeszkedésének vizsgálatára, az empirikus ( ) és a becsült valószínűségek ( p ) összehasonlítása által. stressz = ( pij pˆ ij ) i, j i, j p p ij Útmutató az értelmezéshez: 0: az illeszkedés tökéletes 0 0,05: az illeszkedés kiváló 0,05 0,10: az illeszkedés jó 0,10 0,20: az illeszkedés elfogadható 0,20 felett: a modell nem illeszkedik az adatokra 2 ij 2 Ha a stresszmutató értéke magasabb, mint 0,20, akkor a modell nem illeszkedik, nincs értelme a skálaértékeket felhasználnunk, az eredmények értelmezéséhez más módszert, vagy több dimenziós modell alkalmazását érdemes kipróbálnunk. 0,20-os stresszérték alatt azonban a modell megalapozott következtetések levonásához használható, az eredmények értelmezhetők. A stresszértékek kiszámításával az alkalmazott modellek illeszkedése összehasonlíthatóvá válik. A Thurstone-modell illeszkedése a 5. R parancs segítségével számolható és az eredményül kapott 0,053-es érték jónak mondható. Ez az érték kissé eltér a korábbi cikkünk (Balázs, Csízik, Hőgye-Nagy és Münnich, 2009) 0,06-os értékétől. A kismértékű eltérés a kerekítési pontatlanságból fakad, minthogy a fenti R parancs több tizedes jegyet figyelembe vesz, mint az általunk korábban használt Excel program. A TDS alapján kapott skálaértékek segítségével is kiszámolhatjuk a stresszmutatót. Fontos, hogy ne egyszerűen az inputban szereplő távolságokat vessük össze a modell alapján becsült távolságokkal, hanem a tapasztalati és a becsült valószínűségeket hasonlítsuk össze. Ehhez először a skálaértékekből ki kell számítanunk a távolságokat, majd a távolságokból a becsült valószínűségeket. (1) ˆij
7 A páros összehasonlítás Thurstone-féle módszerének alkalmazása Ha a logit transzformációt használtuk az input távolságok kiszámításához, akkor a becsült távolságok esetén a p ij exp( tij ) = 1 + exp( t ) transzformációt kell alkalmaznunk a valószínűség-számításhoz. A z-transzformáció esetén a becsült távolságokból a z-eloszlás segítségével kiszámítjuk a valószínűségeket. Mindezek kivitelezése R-ben az 5. R parancsnak megfelelően történik. Figyelembe kell vennünk, hogy a TDS végeredményeképpen kapott skála megfordulhat, mint ahogyan ez jelen példánál is történt. Ekkor a becsült valószínűségek transzponált mátrixa (a főátlóra tükrözött mátrix) vethető össze a tapasztalati valószínűségekkel. Mivel nem minden esetben egyértelmű, hogy a skála megfordult, érdemes a stresszértéket kiszámítani a becsült valószínűségek mátrixára és annak transzponáltjára is. A stresszérték meg fogja mutatni, hogy melyik modell illeszkedik jobban az eredeti adatokra. A logit transzformáció, illetve a z-transzformáció segítségével kapott távolságértékeken végzett TDS-sal kapott skálaértékek illeszkedése jó, közöttük elhanyagolható különbség van, a stresszértékek rendre 0,084, és 0,083. Ezek a transzponált becsült valószínűségi mátrix segítségével kapott stresszértékek, transzponálás nélkül a stresszértékek mindkét esetben 0,419. A továbbiakban minden esetben csak a kisebb stresszértéket tüntetjük fel. A Thurstone-modell segítségével kapott skálaértékek illeszkedése ennél valamivel jobb, a stresszérték 0,053, tehát ezt a modellt érdemes használnunk a továbbiakban. (Thurstone-modell) a=skala b=cbind(a,a,a,a,a) c=matrix(rbind(a,a,a,a,a), ncol=5, byrow=t) d=b-c e=pnorm(d) szam=sum((p-e)^2) nev=sum(p^2) stressz=sqrt(szam/nev) print(stressz) ij (TDS logit) a=tds1 b=cbind(a,a,a,a,a) c=matrix(rbind(a,a,a,a,a), ncol=5, byrow=t) d=b-c e=exp(d)/(1+exp(d)) e=t(e) /transzponálás, ha szükséges szam=sum((p-e)^2) nev=sum(p^2) stressz=sqrt(szam/nev) print(stressz) (TDS z-transzformáció) a=tds2 b=cbind(a,a,a,a,a) c=matrix(rbind(a,a,a,a,a), ncol=5, byrow=t) d=b-c e=pnorm(d) e=t(e) / transzponálás, ha szükséges szam=sum((p-e)^2) nev=sum(p^2) stressz=sqrt(szam/nev) print(stressz) 5. R parancs
8 52 BALÁZS Katalin CSÍZIK Tímea HŐGYE-NAGY Ágnes MÜNNICH Ákos A THURSTONE-FÉLE MODELL ÉS A TÖBBDIMENZIÓS SKÁLÁZÁS GYAKORLATI ALKALMAZÁSA A továbbiakban a két módszer működését az alkalmazott pszichológia különböző területeihez kapcsolódva, néhány konkrét problémahelyzetben mutatjuk be. A következőkben négy gyakorlati probléma demonstrálja, hogy a Thurstone-módszer és a többdimenziós skálázás egymás alternatívái, és az adatok sajátosságaitól függően az általuk kínált modell illeszkedése különbözhet. Ennélfogva, egy adott adatbázis elemzésekor mindkét módszert érdemes kipróbálni. Gyakorlati alkalmazás (1): a társas támasz keresésének vizsgálatára Egy korábbi, Thurstone-féle modellel foglalkozó cikkben (Balázs, Csízik, Hőgye-Nagy és Münnich, 2009) is bemutatott vizsgálat célja annak feltárása volt, hogy a fiatalok problémáikkal kikhez fordulnak leginkább. A vizsgált alternatívák a következők voltak: kortárssegítők; szakemberek (orvos, pszichológus, ügyvéd); partner/kedves; barát(ok)/barátnő(k); szülők. A páros összehasonlításokat 151 fiatal végezte el, aminek eredményeképpen az alternatívák választási valószínűsége a 3. táblázatban látható. A cellákban szereplő valószínűségek azt fejezik ki, hogy empirikus adatok alapján milyen valószínűséggel ítélik a sorban feltüntetett alternatívát preferáltabbnak. A táblázatban 10 adat származik a páros összehasonlításokból, a fennmaradó 10 cella tartalma a P( x) = 1 P(x) számításból ered. 3. táblázat. Tapasztalati valószínűségek Alternatívák Kortárs segít k Szakemberek Partner, kedves Barát(ok)/ Barátn (k) Szül k Kortárs segít k * 0,58 0,24 0,27 0,23 Szakemberek 0,42 * 0,20 0,18 0,14 Partner, kedves 0,76 0,80 * 0,55 0,40 Barát(ok)/Barátn (k) 0,73 0,82 0,45 * 0,26 Szül k 0,77 0,86 0,60 0,74 * A Thurstone-modell alkalmazása A fentebb bemutatott módon a skálaértékek a Thurstone-modell segítségével kiszámíthatók (ld. a 4. táblázatot), az ehhez tartozó stresszérték 0,061, ami kiváló illeszkedést jelez. A skálaértékeket megjeleníthetjük grafikus formában a 6. R parancs segítségével. b<-c(0,0,0,0,0) plot(b, skala, xlab=, ylab= skálaérték, main= Thurstone modell ) text(b, skala, rownames(skala), cex=1.2) 6. R-paracs
9 A páros összehasonlítás Thurstone-féle módszerének alkalmazása ábra E D B C A Skálaértékek A többdimenziós skálázás alkalmazása A korábbiakhoz hasonló módon alkalmazzuk a TDS-t, a kapott eredmények a 4. táblázatban láthatóak. A végeredmény nem igazán függ a transzformációtól, hiszen a skálaértékek nagyjából egymásba alakíthatók (a bal oldali skálaértékek kb. 1,6-szeresei a jobb oldali skálaértékeknek), a sorrend nem változik. Ha a Thurstone-modell skálaértékeit összevethetjük a TDS skálaértékeivel (4. táblázat), azt tapasztaljuk, hogy az alternatívák pozícióinak sorrendje megegyezik, a távolságokban azonban arányosan van különbség. 4. táblázat. Skálaértékek Alternatívák logit z-transzform. Thurstone Kortárs segít k -0,54-0,33-0,37 Szakemberek -1,02-0,61-0,61 Partner, kedves 0,47 0,29 0,28 Barát(ok)/Barátn (k) 0,36 0,22 0,15 Szül k 0,73 0,43 0,54 A kapott skálaértékeket megjeleníthetjük egyetlen ábrán (3. ábra), a 7. R-paranccsal. Az ábrán az egyes skálaértékeket sztenderdizálva jelenítettük meg, hogy a látható értékek összemérhetőek legyenek.
10 54 BALÁZS Katalin CSÍZIK Tímea HŐGYE-NAGY Ágnes MÜNNICH Ákos b<-c(0,0,0,0,0) c<-c(2,2,2,2,2) e<-c(4,4,4,4,4) adatok<-cbind(cmd1,cmd2,skala) matrix<-cbind(b,c,e) matplot(matrix, scale(adatok),pch=19,xlim=c(-2,6), ylab= Skálaértékek,xlab=expression(paste( TDS_logit, TDS_z, thurstone ))) text(matrix,scale(adatok),rownames(skala),cex=0.9) 7. R parancs Mivel a többdimenziós skálázás eredményeként kapott skála pozitív és negatív végpontjai véletlenszerűen alakulnak, fontos a tapasztalati valószínűségeket megvizsgálni ahhoz, hogy a helyes sorrendet felállítsuk. Jelen esetben a 3. táblázat alapján látjuk, hogy annak a valószínűsége, hogy a szülőhöz fordulnak inkább, minden összehasonlításban nagyobb, mint 0,5, így ez az alternatíva a leginkább preferált, nem pedig az a lehetőség, hogy szakemberekhez fordulnak. 3. ábra. 1.5 Szülők Szülők 1.0 Szülők Partner, kedves 0.5 Skálaértékek 0.0 Barát(ok)/Barátnő(k) Barát(ok)/Barátnő(k) Barát(ok)/Barátnő(k) Partner, kedves Partner, kedves -0.5 Szakemberek Szakemberek -1.0 Kortárs segítők Kortárs segítők Kortárs segítők Szakemberek TDS_logit TDS_z thurstone
11 A páros összehasonlítás Thurstone-féle módszerének alkalmazása A logit és a z-transzformációt használva a TDS stresszértéke rendre 0,086 és 0,091, ami jó illeszkedést jelez. A Thurstone-féle módszer alapján kiszámított stressz-érték 0,061, ami szintén jó illeszkedést mutat, minimálisan jobbat, mint a TDS. Azaz, ebben az esetben a két eljárás gyakorlatilag egyformán jól alkalmazható. Gyakorlati alkalmazás (2): a vásárlói döntés tényezői A páros összehasonlítás módszerét jól alkalmazhatjuk a fogyasztói magatartás vizsgálata esetében is, például, ha arra vagyunk kíváncsiak, hogy a vásárlói döntésnél mely tényezők és mekkora jelentőséggel játszanak szerepet. Természetesen ebben az esetben is szükség van elővizsgálatra, az alternatívák felmérése és kiválasztása miatt. Jól használhatóak erre a célra is a leggyakrabban alkalmazott feltáró jellegű eljárások, mint például az interjú, a fókusz csoport, a kérdőív stb. Ha például a mosószerekre vonatkozó vásárlói döntésről kívánunk általános következtetéseket levonni, fontos, hogy olyan termékjellemzőkkel dolgozzunk, melyek valóban fontosak a fogyasztók számára döntési helyzetben. Érdekes módon, annak megítélése például, hogy egy mosópor a vevő szerint mennyire jól viszi ki a foltokat, gyakran indirekt módon játszik szerepet a döntésben: az ismertebb márkákban jobban bíznak a vásárlók. Korábbi kutatások (pl. Lakner, 2002) eredményeit felhasználva, a középosztály számára az alábbi termékjellemzők tűnnek a leglényegesebbnek: márkanév, ár, csomagolás (ne legyen papír), halmazállapot (legyen folyékony), illat. Ezekből a tényezőkből 10 párt tudunk képezni. Tegyük fel, hogy 200 válaszadóval kitöltetjük a páros összehasonlításokat tartalmazó kérdőívet, és az 5. táblázatban feltüntetett tapasztalati valószínűségeket kapjuk eredményül. 5. táblázat. Tapasztalati valószínűségek A Thurstone-modell alkalmazása A Thurstone-féle modell segítségével kapott skálaértékek a 6. táblázatban vannak feltüntetve, ezek alapján a válaszadók számára a legfontosabb szempont az ár, és a legkevésbé fontos a mosószer halmazállapota. A modellhez tartozó stressz-érték: 0,131, azaz a modell illeszkedése elfogadható. A többdimenziós skálázás alkalmazása A többdimenziós skálázás egy dimenziós modelljének alkalmazásakor a 6. táblázatban található skálaértékeket kapjuk.
12 56 BALÁZS Katalin CSÍZIK Tímea HŐGYE-NAGY Ágnes MÜNNICH Ákos 6. táblázat. Skálaértékek Alternatívák logit z-transzform. Thurstone Ár 1,51-0,83 1,18 Márkanév -2,46-1,26 1,10 Csomagolás 0,48 0,29-0,30 Halmazállapot 2,12 1,10-1,16 Illat 1,28 0,70-0,69 Ha a TDS-t a logit transzformáció által nyert távolságokra alkalmazzuk, a modell illeszkedése kiváló, a stresszérték 0,047. Ha a TDS-t a z-transzformáció eredményeképpen kapott távolságokra alkalmazzuk, a modell jól illeszkedik, a stresszérték 0,056. Azaz, a vásárlói döntésekre vonatkozó adatbázis esetében a logit transzformáción keresztül nyert távolságokra alkalmazott TDS eredményeit érdemes felhasználnunk. Ennél az adatbázisnál tehát a többdimenziós skálázás vezetett jobban illeszkedő egydimenziós modellhez. Az eredmények értelmezésénél figyelembe kell venni az eredeti valószínűségi értékeket (5. táblázat): negatív értékekkel a vevők számára fontos tényezők rendelkeznek. Valós adatok esetén azt a következtetést vonnánk le, hogy a mosószerek kiválasztásánál az elvárások sorrendje a következő: ismert márkanév, műanyag csomagolás, kellemes illat, és kedvező ár, valamint folyékony halmazállapot. Gyakorlati alkalmazás (3): Közlekedési szabálysértések megítélésének vizsgálata Napjaink közlekedés-pszichológiájában egyre inkább előtérbe kerül a közlekedési szabályok megsértésének főként a szabályok tudatos megsértésének vizsgálata. A szabálysértések egyik oka, hogy a gépjárművezetők úgy vélik, ha megszegnek szabályokat, annak nem lesz következménye. Egy vizsgálatban a résztvevőknek szabálysértéseket kellett megítélniük páronként öszszehasonlítva, hogy melyiket büntetnék szigorúbban. Az elrendezésben a következő alternatívák szerepeltek: követési távolság be nem tartása (követés), piros lámpa jelzés figyelmen kívül hagyása (piros), vezetés alkoholfogyasztást követően (alkohol), előzés szembejövő forgalomnál (előzés), STOP jelzésnél a megállás elmulasztása (stop), megengedett sebesség túllépése (sebesség). A tapasztalati valószínűségeket a 7. táblázat tartalmazza. A táblázatból kiolvasható, hogy például annak a valószínűsége, hogy a helytelen követési távolságot szigorúbban büntetnék, mint az ittas vezetést, 0,21.
13 A páros összehasonlítás Thurstone-féle módszerének alkalmazása táblázat. Tapasztalati valószínűségek Alternatívák Követés Piros Alkohol El zés Stop Sebesség Követés * 0,18 0,21 0,38 0,39 0,41 Piros 0,82 * 0,39 0,58 0,59 0,61 Alkohol 0,79 0,61 * 0,69 0,69 0,72 El zés 0,62 0,42 0,31 * 0,51 0,53 Stop 0,61 0,41 0,31 0,49 * 0,52 Sebesség 0,59 0,39 0,28 0,47 0,48 * A Thurstone-modell alkalmazása A Thurstone-modell segítségével kapott skálaértékek a 8. táblázatban találhatók. Legszigorúbban az alkoholfogyasztást követő vezetést, legkevésbé szigorúan pedig a helytelen követési távolságot büntetnék a megkérdezettek. A kapott stresszérték 0,048, vagyis a modell illeszkedése kiváló. A többdimenziós skálázás alkalmazása A problémának az egydimenziós reprezentációját többdimenziós skálázás segítségével is kiszámíthatjuk, az eredmények a 8. táblázatban láthatóak. 8. táblázat. Skálaértékek Alternatívák logit z-transzform. Thurstone Követés 0,83 0,50-0,42 Piros -0,64-0,38 0,22 Alkohol -0,55-0,34 0,44 El zés 0,08 0,05-0,05 Stop 0,10 0,06-0,07 Sebesség 0,18 0,11-0,13 A többdimenziós skálázással kapott modell csak elfogadhatóan illeszkedik az adatokra, vagyis rosszabbul, mint a Thurstone-modell, a stresszérték rendre 0,108 és 0,103. Ebből következően a Thurstone-modell segítségével kapott eredmények elemzése vezet érvényes következetésekre. Gyakorlati alkalmazás (4): képzési igényfelmérés A páros összehasonlítás módszere jól használható a humán erőforrás menedzsment egyik kiemelkedő területén, a munkahelyi készség- és képességfejlesztésben is. A munkahelyi képzéseket rendszerint alapos képzési igényfelmérés előzi meg, mely eredményeként egy-egy érintett
14 58 BALÁZS Katalin CSÍZIK Tímea HŐGYE-NAGY Ágnes MÜNNICH Ákos dolgozói csoport esetében számos fejlesztendő terület merülhet fel. Az igényfelmérés során a szervezeti elvárások, és a munkatevékenységből adódó területek feltárása mellett a képzésben érintett dolgozókat is érdemes megkérdezni arról, hogy szerintük mely területeken lenne fontos fejlődniük. Egy vizsgálatban egy termelő cég tizenegy fős középvezetői csoportjának fejlesztéséhez kérdőíves módszerrel történt az egyéni igények feltárása. A felmerült fejlesztendő területek szakmai szempontok szerinti csoportosítása, összevonása és csökkentése után a csoportos, társas, tapasztalati tanulás segítségével fejleszthető területek kerültek a vizsgálat középpontjába. A következő készségek bizonyultak fontosnak: csapatépítés készsége; csapatmunka, együttműködés másokkal; emberismeret; empátia; kommunikáció; konfliktuskezelés; munkatársak motiválása; tudatos önismeret; visszajelzés adása a munkatársaknak. Ez a kilenc terület azonban még mindig túl szerteágazó ahhoz, hogy egy csoportos tréning egységes tartalmául szolgáljon, és az sem biztos, hogy ezek minden leendő résztvevő számára ugyanolyan fontossággal bírnak. Ezért a középvezetők a kilenc kiválasztott fejlesztendő területet páronként hasonlították össze (36 összehasonlítás), abból a szempontból, hogy melyik területen érzik gyengébbnek saját képességeiket. 9. táblázat. Tapasztalati valószínűségek Területek Motiválás Ember-ismeret Ön-fegyelem Empátia Visszajelzés Kommunikáció Konfliktuskezelés Együttm ködés Csapatépítés Motiválás * 0,64 0,45 0,64 0,36 0,45 0,55 0,45 0,73 Emberismeret 0,36 * 0,64 0,55 0,45 0,73 0,45 0,45 0,45 Önfegyelem 0,55 0,36 * 0,73 0,45 0,64 0,36 0,55 0,64 Empátia 0,36 0,45 0,27 * 0,18 0,27 0,55 0,45 0,55 Visszajelzés 0,64 0,55 0,55 0,82 * 0,91 0,55 0,64 0,55 Kommunikáció 0,55 0,27 0,36 0,73 0,09 * 0,55 0,64 0,55 Konfliktuskezelés 0,45 0,55 0,64 0,45 0,45 0,45 * 0,55 0,55 Együttm ködés 0,55 0,55 0,45 0,55 0,36 0,36 0,45 * 0,82 Csapatépítés 0,27 0,55 0,36 0,45 0,45 0,45 0,45 0,18 * A kérdőív eredményei alapján kiszámítható annak a valószínűssége, hogy az érintett csoport tagjai egy adott területen gyengébb képességűnek ítélik meg magukat, mint egy másikon (9. táblázat). Annak a valószínűsége például, hogy a megkérdezett vezetők gyengébbnek ítélik magukat a másoknak adott visszajelzés területén, mint a kommunikáció területén, 0,91. A Thurstone-modell alkalmazása A korábban bemutatott módon kiszámíthatóak az egyes fejlesztendő területek skálaértékei (ld. a 10. táblázatot). Jelen esetben minél nagyobb az érték, annál inkább gyengébbnek gon-
15 A páros összehasonlítás Thurstone-féle módszerének alkalmazása dolják magukat az adott területen a megkérdezett vezetők, azaz annál inkább szükséges a terület fejlesztése. Ahhoz, hogy ez az eredmény a képzési program kiindulási pontját jelenthesse, ellenőriznünk kell az alkalmazott modell illeszkedését. A stresszmutató értéke 0,204, azaz a modell nem használható az adatainkra. Így a páros összehasonlítás eredményeképpen nyert adatokat nem érdemes felhasználnunk a további lépések tervezésekor. A többdimenziós skálázás egydimenziós alkalmazása Ugyanennek a gyakorlati problémának az egydimenziós reprezentációját többdimenziós skálázás segítségével is kiszámíthatjuk a 9. táblázat tapasztalati valószínűségeit felhasználva. Ha az előzőekben tárgyalt módon járunk el, akkor eredményként a 10. táblázatban feltüntetett skálaértékeket kapjuk. 10. táblázat. Skálaértékek Alternatívák logit z-transzform. Thurstone Motiválás -0,06-0,04 0,08 Emberismeret 0,19 0,12 0,03 Önfegyelem 0,10 0,07 0,08 Empátia -0,31-0,19-0,28 Visszajelzés 1,19 0,70 0,39 Kommunikáció -1,12-0,64-0,11 Konfliktuskezelés -0,004-0,01 0,03 Együttm ködés -0,01-0,01 0,04 Csapatépítés 0,01 0,01-0,25 Azonban a logit-, illetve a z-transzformáció utáni inputokkal kapott skálaértékek segítségével számolt stresszmutató rendre 0,329-es és 0,319-es értékét is figyelembe véve, láthatjuk, hogy a TDS egydimenziós modelljei sem illeszkednek az adatokra, azaz egyik eljárás eredményét sincs értelme a továbbiakban felhasználni. Ilyen esetben érdemes többdimenziós modellt illeszteni. A többdimenziós skálázás többdimenziós alkalmazása A többdimenziós skálázás természetesen lehetőséget biztosít az adatok több dimenzióban történő reprezentációjára is. Az R program segítségével ez a korábbiakhoz hasonló módon kivitelezhető, a 3. és 4. R parancs segítségével a k paraméter módosításával a kívánt dimenziószámra. A különböző dimenziószámú modellek illeszkedésének összehasonlítása azonban egyszerűbben történhet, ha a klasszikus többdimenziós skálázást a 8. R parancs segítségével végezzük. Ehhez a parancshoz kapcsolódóan a 9. R parancs számít egy stresszértéket, amely stresszérték a 2. egyenlet alapján kerül kiszámításra és az információveszteség mértékét nézi, azaz a kisebb szám jobb illeszkedést jelez. 0,05 alatti stresszérték esetén nagyon jó az illeszkedés (Münnich, Nagy és Abari, 2006).
16 60 BALÁZS Katalin CSÍZIK Tímea HŐGYE-NAGY Ágnes MÜNNICH Ákos mds<-isomds(dist1, k=2, maxit=0) print(mds$points, digits=3) 8. R parancs print(mds$stress,digits=3) 9. R parancs stressz = i, j ( d d ) ij i, j d 2 ij ij 2 (2) 11. táblázat. Stresszértékek Dimenziószám logit z-transzform. 1 55,3 54,8 2 33,8 32,6 3 23,9 22,1 4 21,8 20,1 5 21,8 20,1 A 11. táblázat alapján a valószínűségi értékek t-transzformációja által kapott távolságadatok négy-dimenziós reprezentációja illeszkedik a legjobban, valamivel jobban, mint a háromdimenziós megoldás, ehhez képest az ötdimenziós modell már nem eredményez javulást. Azonban bármely modell messze áll attól, hogy kiváló illeszkedést eredményezzen. Ilyen esetekben érdemes lehet a TDS nem-metrikus modelljét illeszteni. A nem-metrikus TDS, ahogyan neve is mutatja, az inputokat, nem távolságokként, hanem távolság-szerű értékekként kezeli. Konkrétabban, a távolságok rangsorát próbálja a lehető legjobban modellezni. R-ben a nemmetrikus TDS a 8. R parancs segítségével kivitelezhető, az iterációs szám fixálása nélkül, azaz a, maxit=0 nélkül. Stresszértéket, továbbra is a 9. R parancs segítségével számíthatunk. A nem-metrikus TDS eredményei a 12. táblázatban találhatóak.
17 A páros összehasonlítás Thurstone-féle módszerének alkalmazása táblázat. Stresszértékek Dimenziószám logit z-transzform. 1 40,0 44,6 2 16,4 16,3 3 7,1 6,8 4 0,1 0,4 5 0,1 0,4 Az iteráció-számot az automatikus 50-es értékről tovább emelve (,maxit=100 a 8. R parancsba első sorába illesztve) az illeszkedés tovább javítható. Az iteráció-szám emelésével a z- transzformációval kapott távolságokat használva a nem-metrikus TDS négy-dimenziós modelljéhez tartozó stresszérték a 0,0846-os (0,1 kerekítve a 12. táblázatban) értékről 0,008-as értékre csökken, azaz kiváló illeszkedést eredményez. A modell által eredményezett skálaértékeket a 13. táblázat tartalmazza. 13. táblázat. Skálaértékek Alternatívák 1. dim 2.dim 3.dim. 4.dim Motiválás Emberismeret Önfegyelem Empátia Visszajelzés Kommunikáció Konfliktuskezelés Együttm ködés Csapatépítés Az eredmények alapján a négy dimenziót sorban elnevezhetnénk visszajelzés, csapatépítés, mentalizáció (mások szándékainak érzelmeinek értése) és vezetés dimenzióknak. A kommunikáció nevű alternatíva kisé kilóg a sorból, mert azt várhatnánk, hogy a visszajelzés, vezetés dimenziókban nagy szerepe lesz, de az adatok alapján nincs. Lehet, hogy annak van ebben szerepe, hogy a válaszadók azt tartották szem előtt, hogy mely készségeik fejlesztendőek, így lehet például, hogy a kommunikáció alternatíva számukra a kommunikáció azon területeit jelenti, amelyek problémát jelentenek számukra. Az eredmények mélyebb megértéséhez szükség lenne arra, hogy a válaszadók definiálják a használt alternatívákat, azon a módon, ahogy a kitöltéskor értelmezték őket.
18 62 BALÁZS Katalin CSÍZIK Tímea HŐGYE-NAGY Ágnes MÜNNICH Ákos ÖSSZEGZÉS Jelen cikkben bemutatott, az alkalmazott pszichológia területéről merített példák demonstrálták, hogy a páros összehasonlítás módszere jól alkalmazható lehetőség a Likert-féle skálázással szemben. Előnye, hogy választásra ösztönöz, ezáltal differenciált képet nyújt a nézetekről, alternatívák rendjéről, sorrendjéről. Hátránya, hogy kevés számú alternatíva esetén alkalmazható, így a vizsgálat előzetes felmérést, alternatíva szelekciót kíván meg. A fenti példák ismeretében elmondható továbbá, hogy alternatívák egy skálán való elhelyezkedéséről képet kapunk mind a Thurstone-féle skálázás, mind a többdimenziós skálázás egydimenziós modellje segítségével, a cikkben ismertetett módon az adatok logit vagy a z- transzformációja után. A páros összehasonlítások modelljei jól alkalmazhatóak, a kapott eredmények könnyen értelmezhetőek. Azonban az adatok sajátosságaitól függően a modellek illeszkedése eltérő lehet, ezért érdemes minden esetben mindkét eljárást alkalmazni és a stresszértékeket összevetni. A képzési igényfelméréshez kapcsolódó példa elemzése pedig demonstrálta, hogy a páros összehasonlításokból kiindulva többdimenziós reprezentáció is képezhető a TDS segítségével. Sok esetben fontos lehet, a jelen cikkben tárgyalt példákon túlmutat a többdimenziós páros összehasonlítások modellezése (ld. pl. Chernyshenko, Stark, Prewett, Gray, Stilson és Tuttle, 2009, Scher, 2010). SUMMARY THURSTONE S METHOD OF PAIRED COMPARISONS APPLIED IN PSYCHOLOGY II. The method of paired comparisons provides a valuable alternative to popular scaling methods. Psychological research data obtained by paired comparisons can be analyzed with Thurstone s one dimensional model, and also with multidimensional scaling choosing for one or more dimensional solution. Present study demonstrates through four practical examples that Thurstone s model and multidimensional scaling are comparable alternatives; and there is utility of following both approaches for the same data set, finishing with model fit comparison by the stress index.
19 A páros összehasonlítás Thurstone-féle módszerének alkalmazása IRODALOM BALÁZS K., CSÍZIK T., HŐGYE-NAGY Á., MÜNNICH Á. (2009): A páros összehasonlítás Thurstone-féle módszerének alkalmazása a pszichológiában I. Alkalmazott pszichológia, BORG, I., & GROENEN, P. (1997): Modern multidimensional scaling. Theory and applications. Springer, New York. BRADLEY, R.A., TERRY,M.A., (1952): Rank analysis of incomplete block designs. Biometrika, CHERNYSHENKO, O. S., STARK, S., PREWETT,M. S., GRAY, A. A., STILSON, F. R., TUTTLE, M. D. (2009): Normative scoring of multidimensional pairwise preference personality scales using IRT: empirical comparisons with other formats. Human Performance, COX, T. F., COX, M. A. A. (1994): Multidimensional scaling. Chapman & Hall, London. EVERITT, B. S., RABE-HESKETH, S. (1997): The analysis of proximity data. London: Arnold. Green, P. E., Tull, D.S. (1978): Research for Marketing Decisions, Prentice Hall, New Jersey. KRUSKAL, J. B., & WISH, M. (1978): Multidimensional Scaling, Sage University Paper series on Quantitative Application in the Social Sciences. Sage Publications, London, LAKNER Z. (2002): Adalékok a kozmetikai termékek piaci viszonyainak megismeréséhez A kozmetikai és háztartás-vegyipari termékek vásárlását befolyásoló tényezők vizsgálatára. Olaj, szappan, kozmetika, LIKERT,R. (1932): A Technique for the Measurement of Attitudes. Archives of Psychology, MÉRŐ L. (1986): A többdimenziós skálázás alapelvei. Pszichológia, MÉRŐ L. (1992): A pszichológiai skálázás matematikai alapjai. Tankönyvkiadó, Budapest. MÜNNICH Á., NAGY Á., ABARI K. (2006): Többváltozós statisztika pszichológus hallgatók számára. Debrecen: Bölcsész Konzorcium. (letölthető: (Letöltés ideje: ) R-Development Core Team (2005): R: A language and environment for statistical computing. R-Foundation for Statistical Computing, Vienna, Austria. (letölthető: (Letöltés ideje: ) SCHER,J. M. (2010): A generalized thurstonian paired comparison multicriteria heuristic model for peer evaluation of individual performance on IS team projects. Information Systems Education Journal, THURSTONE, L. L. (1927): A law of comparative judgement. Psychological Review, THURSTONE, L. L. (1929): The Measurement of Psychological Value. In SMITH, T. V., WRIGHT, W. K. (eds): Essays in Philosophy by Seventeen Doctors of Philosophy of the University of Chicago. Open Court, Chicago. THURSTONE, L.L. (1959): The Measurement of Values. Chicago: The University of Chicago Press. THURSTONE, L.L., & Jones, L.V. (1957): The rational origin for measuring subjective values, Journal of the American Statistical Association,
Conjoint-analízis példa (egyszerűsített)
 Conjoint-analízis példa (egyszerűsített) Az eljárás meghatározza, hogy a fogyasztók a vásárlás szempontjából lényeges terméktulajdonságoknak mekkora relatív fontosságot tulajdonítanak és megadja a tulajdonságok
Conjoint-analízis példa (egyszerűsített) Az eljárás meghatározza, hogy a fogyasztók a vásárlás szempontjából lényeges terméktulajdonságoknak mekkora relatív fontosságot tulajdonítanak és megadja a tulajdonságok
Jelek tanulmányozása
 Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
2011. március 9. Dr. Vincze Szilvia
 . márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
. márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
A Hozzárendelési feladat megoldása Magyar-módszerrel
 A Hozzárendelési feladat megoldása Magyar-módszerrel Virtuális vállalat 2013-2014/1. félév 3. gyakorlat Dr. Kulcsár Gyula A Hozzárendelési feladat Adott meghatározott számú gép és ugyanannyi független
A Hozzárendelési feladat megoldása Magyar-módszerrel Virtuális vállalat 2013-2014/1. félév 3. gyakorlat Dr. Kulcsár Gyula A Hozzárendelési feladat Adott meghatározott számú gép és ugyanannyi független
Párhuzamos programozás
 Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
http://www.olcsoweboldal.hu ingyenes tanulmány GOOGLE INSIGHTS FOR SEARCH
 2008. augusztus 5-én elindult a Google Insights for Search, ami betekintést nyújt a keresőt használók tömegeinek lelkivilágába, és időben-térben szemlélteti is, amit tud róluk. Az alapja a Google Trends,
2008. augusztus 5-én elindult a Google Insights for Search, ami betekintést nyújt a keresőt használók tömegeinek lelkivilágába, és időben-térben szemlélteti is, amit tud róluk. Az alapja a Google Trends,
AZ ÖNÉRTÉKELÉS SZEREPE ÉS FOLYAMATA AZ INTÉZMÉNYFEJLESZTÉSBEN M&S Consulting Kft.
 AZ ÖNÉRTÉKELÉS SZEREPE ÉS FOLYAMATA AZ INTÉZMÉNYFEJLESZTÉSBEN INNOVATÍV MINŐSÉGFEJLESZTÉSI ESZKÖZÖK A MAGYAR SZAKKÉPZÉSBEN (1.) EFQM Szakképzési Modell adaptáció 1995-1999 COMENIUS 2000 közoktatási minőségfejlesztési
AZ ÖNÉRTÉKELÉS SZEREPE ÉS FOLYAMATA AZ INTÉZMÉNYFEJLESZTÉSBEN INNOVATÍV MINŐSÉGFEJLESZTÉSI ESZKÖZÖK A MAGYAR SZAKKÉPZÉSBEN (1.) EFQM Szakképzési Modell adaptáció 1995-1999 COMENIUS 2000 közoktatási minőségfejlesztési
A fiatalok pénzügyi kultúrája Számít-e a gazdasági oktatás?
 A fiatalok pénzügyi kultúrája Számít-e a gazdasági oktatás? XXXII. OTDK Konferencia 2015. április 9-11. Készítette: Pintye Alexandra Konzulens: Dr. Kiss Marietta A kultúrától a pénzügyi kultúráig vezető
A fiatalok pénzügyi kultúrája Számít-e a gazdasági oktatás? XXXII. OTDK Konferencia 2015. április 9-11. Készítette: Pintye Alexandra Konzulens: Dr. Kiss Marietta A kultúrától a pénzügyi kultúráig vezető
A döntő feladatai. valós számok!
 OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
PONTSZÁMÍTÁSI KÉRELEM felsőfokú végzettség alapján (alap- és osztatlan képzésre jelentkezőknek)
 PONTSZÁMÍTÁSI KÉRELEM felsőfokú végzettség alapján (alap- és osztatlan képzésre jelentkezőknek) PÉCSI TUDOMÁNYEGYETEM Jelentkezői adatok Jelentkező neve: Felvételi azonosító: Születési dátum: Anyja neve:
PONTSZÁMÍTÁSI KÉRELEM felsőfokú végzettség alapján (alap- és osztatlan képzésre jelentkezőknek) PÉCSI TUDOMÁNYEGYETEM Jelentkezői adatok Jelentkező neve: Felvételi azonosító: Születési dátum: Anyja neve:
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
1. forduló. MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév
 MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév 1. forduló 1. feladat: Jancsi és Juliska Matematikai Memory-t játszik. A játék lényege, hogy négyzet alakú kártyákra vagy műveletsorokat írnak
MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév 1. forduló 1. feladat: Jancsi és Juliska Matematikai Memory-t játszik. A játék lényege, hogy négyzet alakú kártyákra vagy műveletsorokat írnak
Útmutató a vízumkérő lap kitöltéséhez
 Útmutató a vízumkérő lap kitöltéséhez A vízumkérő lap ( Visa application form of the People s Republic of China, Form V. 2013 ) az egyik legfontosabb dokumentum, amit a kínai vízumra való jelentkezésnél
Útmutató a vízumkérő lap kitöltéséhez A vízumkérő lap ( Visa application form of the People s Republic of China, Form V. 2013 ) az egyik legfontosabb dokumentum, amit a kínai vízumra való jelentkezésnél
Shared IMAP beállítása magyar nyelvű webmailes felületen
 Shared IMAP beállítása magyar nyelvű webmailes felületen A következő ismertető segítséget nyújt a szervezeti cím küldőként való beállításában a caesar Webmailes felületén. Ahhoz, hogy a Shared Imaphoz
Shared IMAP beállítása magyar nyelvű webmailes felületen A következő ismertető segítséget nyújt a szervezeti cím küldőként való beállításában a caesar Webmailes felületén. Ahhoz, hogy a Shared Imaphoz
Oktatói munka hallgatói véleményezése. Oktatók
 Oktatói munka hallgatói véleményezése Oktatók Eredmények 1. A diákok órákon való részvételi hajlandósága eltérő attitűdöket mutat. A hallgatók négyötöde (80%) gyakori látogatója az előadásoknak, szemináriumoknak.
Oktatói munka hallgatói véleményezése Oktatók Eredmények 1. A diákok órákon való részvételi hajlandósága eltérő attitűdöket mutat. A hallgatók négyötöde (80%) gyakori látogatója az előadásoknak, szemináriumoknak.
Jelentéskészítő TEK-IK () Válaszadók száma = 610
 Jelentéskészítő TEK-IK () Válaszadók száma = 0 Általános mutatók Szak értékelése - + átl.=. Felmérés eredmények Jelmagyarázat Kérdésszöveg Válaszok relatív gyakorisága Bal pólus Skála Átl. elt. Átlag Medián
Jelentéskészítő TEK-IK () Válaszadók száma = 0 Általános mutatók Szak értékelése - + átl.=. Felmérés eredmények Jelmagyarázat Kérdésszöveg Válaszok relatív gyakorisága Bal pólus Skála Átl. elt. Átlag Medián
EQ-Skill Humán Tanácsadó és Vezetőfejlesztő Kft. www.eqskill.hu 1022 Budapest, Bimbó út 5.
 JELENTKEZÉSI LAP LÓ MEDIÁLTA ÖNISMERETI TRÉNINGPROGRAM 2016. SZEPTEMBER 9-10. PORVA-SZÉPALMAPUSZTA, HOTEL SZÉPALMA ÉS MÉNESBIRTOK Kérjük, gondosan olvassa el az alábbi Jelentkezési lapot, töltse ki, és
JELENTKEZÉSI LAP LÓ MEDIÁLTA ÖNISMERETI TRÉNINGPROGRAM 2016. SZEPTEMBER 9-10. PORVA-SZÉPALMAPUSZTA, HOTEL SZÉPALMA ÉS MÉNESBIRTOK Kérjük, gondosan olvassa el az alábbi Jelentkezési lapot, töltse ki, és
Radon, Toron és Aeroszol koncentráció viszonyok a Tapolcai Tavas-barlangban
 Radon, Toron és Aeroszol koncentráció viszonyok a Tapolcai Tavas-barlangban Kutatási jelentés Veszprém 29. november 16. Dr. Kávási Norbert ügyvezetı elnök Mérési módszerek, eszközök Légtéri radon és toron
Radon, Toron és Aeroszol koncentráció viszonyok a Tapolcai Tavas-barlangban Kutatási jelentés Veszprém 29. november 16. Dr. Kávási Norbert ügyvezetı elnök Mérési módszerek, eszközök Légtéri radon és toron
Lineáris algebra gyakorlat
 Lineáris algebra gyakorlat 3 gyakorlat Gyakorlatvezet : Bogya Norbert 2012 február 27 Bogya Norbert Lineáris algebra gyakorlat (3 gyakorlat) Tartalom Egyenletrendszerek Cramer-szabály 1 Egyenletrendszerek
Lineáris algebra gyakorlat 3 gyakorlat Gyakorlatvezet : Bogya Norbert 2012 február 27 Bogya Norbert Lineáris algebra gyakorlat (3 gyakorlat) Tartalom Egyenletrendszerek Cramer-szabály 1 Egyenletrendszerek
Beszámoló: a kompetenciamérés eredményének javítását célzó intézkedési tervben foglaltak megvalósításáról. Őcsény, 2015. november 20.
 Őcsényi Perczel Mór Általános Iskola székhelye: 7143 Őcsény, Perczel Mór utca 1. Tel: 74/496-782 e-mail: amk.ocseny@altisk-ocseny.sulinet.hu Ikt.sz.: /2015. OM: 036345 Ügyintéző: Ősze Józsefné Ügyintézés
Őcsényi Perczel Mór Általános Iskola székhelye: 7143 Őcsény, Perczel Mór utca 1. Tel: 74/496-782 e-mail: amk.ocseny@altisk-ocseny.sulinet.hu Ikt.sz.: /2015. OM: 036345 Ügyintéző: Ősze Józsefné Ügyintézés
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 12 XII. STATIsZTIKA ellenőrző feladatsorok 1. FELADATsOR Megoldások: láthatók nem láthatók 1. minta: 6.10, 0.01, 6.97, 6.03, 3.85, 1.11,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 12 XII. STATIsZTIKA ellenőrző feladatsorok 1. FELADATsOR Megoldások: láthatók nem láthatók 1. minta: 6.10, 0.01, 6.97, 6.03, 3.85, 1.11,
Épületvillamosság laboratórium. Villámvédelemi felfogó-rendszer hatásosságának vizsgálata
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
A környezettan tantárgy intelligencia fejlesztő lehetőségei
 A környezettan tantárgy intelligencia fejlesztő lehetőségei Készítette: Pék Krisztina biológia környezettan szak Belső konzulens: Dr. Schróth Ágnes Külső konzulens: Dr. Széphalmi Ágnes A szakdolgozatom
A környezettan tantárgy intelligencia fejlesztő lehetőségei Készítette: Pék Krisztina biológia környezettan szak Belső konzulens: Dr. Schróth Ágnes Külső konzulens: Dr. Széphalmi Ágnes A szakdolgozatom
Mutatószám alapú értékelés
 Mutatószám alapú értékelés 2016. április 19. 17:30 A webinárium hamarosan kezdődik. Kérjük, ellenőrizze, hogy számítógépe hangszórója be van-e kapcsolva. További technikai információk: https://www.kbcequitas.hu/menu/tamogatas/tudastar/oktatas
Mutatószám alapú értékelés 2016. április 19. 17:30 A webinárium hamarosan kezdődik. Kérjük, ellenőrizze, hogy számítógépe hangszórója be van-e kapcsolva. További technikai információk: https://www.kbcequitas.hu/menu/tamogatas/tudastar/oktatas
Azonosító jel: Matematika emelt szint
 I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
Kiskunmajsa Város Önkormányzatának partnertérképe
 Kiskunmajsa Város Önkormányzatának partnertérképe Kiskunmajsa Város Önkormányzatának potenciális partnerei Helyi vállalkozások Kiskunmajsa Város Önkormányzata számára a lehetséges vállalati partnerek feltérképezéséhez
Kiskunmajsa Város Önkormányzatának partnertérképe Kiskunmajsa Város Önkormányzatának potenciális partnerei Helyi vállalkozások Kiskunmajsa Város Önkormányzata számára a lehetséges vállalati partnerek feltérképezéséhez
Arany Dániel Matematikai Tanulóverseny 2011/2012-es tanév első (iskolai) forduló haladók I. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 011/01-es tanév első (iskolai) forduló haladók I. kategória Megoldások és javítási útmutató 1. Az ábrán látható ABC derékszögű háromszög
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 011/01-es tanév első (iskolai) forduló haladók I. kategória Megoldások és javítási útmutató 1. Az ábrán látható ABC derékszögű háromszög
Amit a Hőátbocsátási tényezőről tudni kell
 Amit a Hőátbocsátási tényezőről tudni kell Úton-útfélen mindenki róla beszél, már amikor épületekről van szó. A tervezéskor találkozunk vele először, majd az építkezéstől az épület lakhatási engedélyének
Amit a Hőátbocsátási tényezőről tudni kell Úton-útfélen mindenki róla beszél, már amikor épületekről van szó. A tervezéskor találkozunk vele először, majd az építkezéstől az épület lakhatási engedélyének
Csecsemő- és gyermeknevelőgondozó. 55 761 01 0000 00 00 Csecsemő- és gyermeknevelőgondozó
 A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
Laborgyakorlat Logikai áramkörök számítógéppel segített tervezése (CAD)
 Laborgyakorlat Logikai áramkörök számítógéppel segített tervezése (CAD) Kombinációs LABOR feladatok Laborfeladat: egyszerű logikai kapuk vizsgálata Logikai műveletek Tervezz egy egyszerű logikai kapukat
Laborgyakorlat Logikai áramkörök számítógéppel segített tervezése (CAD) Kombinációs LABOR feladatok Laborfeladat: egyszerű logikai kapuk vizsgálata Logikai műveletek Tervezz egy egyszerű logikai kapukat
Analízis elo adások. Vajda István. 2012. október 3. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
M A G Y A R K O N G R E S S Z U S I I R O D A
 Magyar Turizmus Zártkörűen Működő Részvénytársaság Magyar Kongresszusi Iroda 1115 Budapest, Bartók Béla út 105-113. Tel.: (06-1) 488-8640 Fax: (06-1) 488-8641 E-mail: hcb@hungarytourism.hu www.hcb.hu A
Magyar Turizmus Zártkörűen Működő Részvénytársaság Magyar Kongresszusi Iroda 1115 Budapest, Bartók Béla út 105-113. Tel.: (06-1) 488-8640 Fax: (06-1) 488-8641 E-mail: hcb@hungarytourism.hu www.hcb.hu A
118. Szerencsi Többcélú Kistérségi Társulás
 BAZ MTrT TERVEZŐI VÁLASZ 118. Szerencsi Többcélú Kistérségi Társulás 1. Szakmai szempontból elhibázott döntésnek tartjuk a Tokaji Borvidék Világörökségi terület közvetlen környezetében erőmű létesítését.
BAZ MTrT TERVEZŐI VÁLASZ 118. Szerencsi Többcélú Kistérségi Társulás 1. Szakmai szempontból elhibázott döntésnek tartjuk a Tokaji Borvidék Világörökségi terület közvetlen környezetében erőmű létesítését.
Dinamikus geometriai programok
 2011 október 22. Eszköz és médium (fotó: http://sliderulemuseum.com) Enter MTM1007L információ: zeus.nyf.hu/ kovacsz feladatok: moodle.nyf.hu Reform mozgalmak A formális matematikát az életkori sajátosságoknak
2011 október 22. Eszköz és médium (fotó: http://sliderulemuseum.com) Enter MTM1007L információ: zeus.nyf.hu/ kovacsz feladatok: moodle.nyf.hu Reform mozgalmak A formális matematikát az életkori sajátosságoknak
Illeszkedésvizsgálat
 Slide 1 Illeszkedésvizsgálat (kategória értékű változóra) Freedman: 28. fejezet 1-3. Egy képzeletbeli országban 10M ember lakik: 30% szőke, 10% barna, 60% fekete. Slide 2 N = 200 fős mintát vettünk, a
Slide 1 Illeszkedésvizsgálat (kategória értékű változóra) Freedman: 28. fejezet 1-3. Egy képzeletbeli országban 10M ember lakik: 30% szőke, 10% barna, 60% fekete. Slide 2 N = 200 fős mintát vettünk, a
Agrárgazdasági Kutató Intézet Piac-árinformációs Szolgálat. Borpiaci információk. III. évfolyam / 7. szám 2005. április 28. 14-15.
 A K I Borpiaci információk III. évfolyam / 7. szám 25. április 28. 14- Bor piaci jelentés Borpiaci információk 1-4. táblázat, 1-8. ábra: Belföldi értékesítési-árak és mennyiségi adatok 2. oldal 3-7. oldal
A K I Borpiaci információk III. évfolyam / 7. szám 25. április 28. 14- Bor piaci jelentés Borpiaci információk 1-4. táblázat, 1-8. ábra: Belföldi értékesítési-árak és mennyiségi adatok 2. oldal 3-7. oldal
Játékok (domináns stratégia, alkalmazása. 2016.03.30.
 Játékok (domináns stratégia, Nash-egyensúly). A Nashegyensúly koncepciójának alkalmazása. 2016.03.30. Játékelmélet és közgazdaságtan 1914: Zermelo (sakk) 1944. Neumann-Morgenstern: Game Theory and Economic
Játékok (domináns stratégia, Nash-egyensúly). A Nashegyensúly koncepciójának alkalmazása. 2016.03.30. Játékelmélet és közgazdaságtan 1914: Zermelo (sakk) 1944. Neumann-Morgenstern: Game Theory and Economic
BOLYAI MATEMATIKA CSAPATVERSENY ORSZÁGOS DÖNTŐ SZÓBELI (2012. NOVEMBER 24.) 3. osztály
 3. osztály Két szám összege 33. Mennyi ennek a két számnak a különbsége, ha az egyik kétszerese a másiknak? Hány olyan háromjegyű szám van, amelyben a számjegyek összege legalább 25? 4. osztály A Zimrili
3. osztály Két szám összege 33. Mennyi ennek a két számnak a különbsége, ha az egyik kétszerese a másiknak? Hány olyan háromjegyű szám van, amelyben a számjegyek összege legalább 25? 4. osztály A Zimrili
ÉVKÖZI MINTA AZ EGÉSZSÉGÜGYI BÉR- ÉS LÉTSZÁMSTATISZTIKÁBÓL. (2004. IV. negyedév) Budapest, 2005. április
 ÉVKÖZI MINTA AZ EGÉSZSÉGÜGYI BÉR- ÉS LÉTSZÁMSTATISZTIKÁBÓL (2004. IV. negyedév) Budapest, 2005. április Évközi minta az egészségügyi bér- és létszámstatisztikából Vezet i összefoglaló Módszertan Táblázatok:
ÉVKÖZI MINTA AZ EGÉSZSÉGÜGYI BÉR- ÉS LÉTSZÁMSTATISZTIKÁBÓL (2004. IV. negyedév) Budapest, 2005. április Évközi minta az egészségügyi bér- és létszámstatisztikából Vezet i összefoglaló Módszertan Táblázatok:
IV/3. sz. melléklet: HR funkcionális specifikáció
 IV/3. sz. melléklet: HR funkcionális specifikáció 1. A követelménylista céljáról Jelen követelménylista (mint a GOP 2.2. 1 / KMOP 1.2.5 pályázati útmutató melléklete) meghatározza azokat a minimális képességeket
IV/3. sz. melléklet: HR funkcionális specifikáció 1. A követelménylista céljáról Jelen követelménylista (mint a GOP 2.2. 1 / KMOP 1.2.5 pályázati útmutató melléklete) meghatározza azokat a minimális képességeket
[MECHANIKA- HAJLÍTÁS]
![[MECHANIKA- HAJLÍTÁS] [MECHANIKA- HAJLÍTÁS]](/thumbs/39/20428431.jpg) 2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
EPER E-KATA integráció
 EPER E-KATA integráció 1. Összhang a Hivatalban A hivatalban használt szoftverek összekapcsolása, integrálása révén az egyes osztályok, nyilvántartások között egyezőség jön létre. Mit is jelent az integráció?
EPER E-KATA integráció 1. Összhang a Hivatalban A hivatalban használt szoftverek összekapcsolása, integrálása révén az egyes osztályok, nyilvántartások között egyezőség jön létre. Mit is jelent az integráció?
Fordítóprogramok Készítette: Nagy Krisztián
 Fordítóprogramok Készítette: Nagy Krisztián Reguláris kifejezések (FLEX) Alapelemek kiválasztása az x karakter. tetszőleges karakter (kivéve újsor) [xyz] karakterhalmaz; vagy egy x, vagy egy y vagy egy
Fordítóprogramok Készítette: Nagy Krisztián Reguláris kifejezések (FLEX) Alapelemek kiválasztása az x karakter. tetszőleges karakter (kivéve újsor) [xyz] karakterhalmaz; vagy egy x, vagy egy y vagy egy
Korszerű geodéziai adatfeldolgozás Kulcsár Attila
 Korszerű geodéziai adatfeldolgozás Kulcsár Attila Nyugat-Magyarországi Egyetem Geoinformatikai Főiskolai Kar Térinformatika Tanszék 8000 Székesfehérvár, Pirosalma -3 Tel/fax: (22) 348 27 E-mail: a.kulcsar@geo.info.hu.
Korszerű geodéziai adatfeldolgozás Kulcsár Attila Nyugat-Magyarországi Egyetem Geoinformatikai Főiskolai Kar Térinformatika Tanszék 8000 Székesfehérvár, Pirosalma -3 Tel/fax: (22) 348 27 E-mail: a.kulcsar@geo.info.hu.
Az MSZ EN ISO 19011:2012 szabvány változásai. Támpontok az auditorok értékeléséhez Előadó: Turi Tibor, az MSZT/MCS 901 szakértője
 Az MSZ EN ISO 19011:2012 szabvány változásai. Támpontok az auditorok értékeléséhez Előadó: Turi Tibor, az MSZT/MCS 901 szakértője 1 Bemutatkozás 1992 - irányítási rendszerek bevezetése 1994 - auditorképző
Az MSZ EN ISO 19011:2012 szabvány változásai. Támpontok az auditorok értékeléséhez Előadó: Turi Tibor, az MSZT/MCS 901 szakértője 1 Bemutatkozás 1992 - irányítási rendszerek bevezetése 1994 - auditorképző
Középiskolai felvételi eljárás. 2015-2016. tanév
 Középiskolai felvételi eljárás 2015-2016. tanév 1. Középiskolai felvételi eljárás legfontosabb dátumai 2015.11.13. Az Oktatási Hivatal közzéteszi a nyolcadik évfolyamosok számára központi írásbeli vizsgát
Középiskolai felvételi eljárás 2015-2016. tanév 1. Középiskolai felvételi eljárás legfontosabb dátumai 2015.11.13. Az Oktatási Hivatal közzéteszi a nyolcadik évfolyamosok számára központi írásbeli vizsgát
[GVMGS11MNC] Gazdaságstatisztika
![[GVMGS11MNC] Gazdaságstatisztika [GVMGS11MNC] Gazdaságstatisztika](/thumbs/40/21500887.jpg) [GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
[GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
Jelentés a kiértékelésről az előadóknak
 Debreceni Egyetem 00 Debrecen Egyetem tér. Debreceni Egyetem Tisztelt NK Úr! (személyes és bizalmas) Jelentés a kiértékelésről az előadóknak Tisztelt NK Úr! Ez az email tartalmazza a Népegészségügyi ellenõr
Debreceni Egyetem 00 Debrecen Egyetem tér. Debreceni Egyetem Tisztelt NK Úr! (személyes és bizalmas) Jelentés a kiértékelésről az előadóknak Tisztelt NK Úr! Ez az email tartalmazza a Népegészségügyi ellenõr
FIT-jelentés :: 2012. Intézményi jelentés. Összefoglalás
 FIT-jelentés :: 2012 Összefoglalás Német Nemzetiségi Gimnázium és Kollégium, Deutsches Nationalitätengymnasium und Schülerwohnheim 1203 Budapest, Serény u. 1. Összefoglalás Az intézmény létszámadatai Tanulók
FIT-jelentés :: 2012 Összefoglalás Német Nemzetiségi Gimnázium és Kollégium, Deutsches Nationalitätengymnasium und Schülerwohnheim 1203 Budapest, Serény u. 1. Összefoglalás Az intézmény létszámadatai Tanulók
KÍNAI NYELV JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Kínai nyelv emelt szint 1513 ÉRETTSÉGI VIZSGA 2016. május 24. KÍNAI NYELV EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA I. OLVASOTT SZÖVEG ÉRTÉSE
Kínai nyelv emelt szint 1513 ÉRETTSÉGI VIZSGA 2016. május 24. KÍNAI NYELV EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA I. OLVASOTT SZÖVEG ÉRTÉSE
Programozás I. - 9. gyakorlat
 Programozás I. - 9. gyakorlat Mutatók, dinamikus memóriakezelés Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 9, 2009 1 tar@dcs.vein.hu
Programozás I. - 9. gyakorlat Mutatók, dinamikus memóriakezelés Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 9, 2009 1 tar@dcs.vein.hu
Intézményi jelentés. Összefoglalás. Medgyessy Ferenc Gimnázium és Művészeti Szakközépiskola 4031 Debrecen, Holló László sétány 6 OM azonosító: 031202
 FIT-jelentés :: 2010 Medgyessy Ferenc Gimnázium és Művészeti Szakközépiskola 4031 Debrecen, Holló László sétány 6 Figyelem! A 2010. évi Országos kompetenciaméréstől kezdődően a szövegértés, illetve a matematika
FIT-jelentés :: 2010 Medgyessy Ferenc Gimnázium és Művészeti Szakközépiskola 4031 Debrecen, Holló László sétány 6 Figyelem! A 2010. évi Országos kompetenciaméréstől kezdődően a szövegértés, illetve a matematika
Az abortusz a magyar közvéleményben
 Az abortusz a magyar közvéleményben Országos felmérés a egyesület számára Módszer: országos reprezentatív felmérés a 18 éves és idősebb lakosság 1200 fős mintájának személyes megkérdezésével a Medián-Omnibusz
Az abortusz a magyar közvéleményben Országos felmérés a egyesület számára Módszer: országos reprezentatív felmérés a 18 éves és idősebb lakosság 1200 fős mintájának személyes megkérdezésével a Medián-Omnibusz
FENNTARTHATÓ FEJLŐDÉS
 FENNTARTHATÓ FEJLŐDÉS Kump Edina ÖKO-Pack Nonprofit Kft. E-mail: edina@okopack.hu Web: www.okopack.hu Dunaújváros, 2014. november 07. A FENNTARTHATÓ FEJLŐDÉS FOGALMA A fenntartható fejlődés a fejlődés
FENNTARTHATÓ FEJLŐDÉS Kump Edina ÖKO-Pack Nonprofit Kft. E-mail: edina@okopack.hu Web: www.okopack.hu Dunaújváros, 2014. november 07. A FENNTARTHATÓ FEJLŐDÉS FOGALMA A fenntartható fejlődés a fejlődés
FIT-jelentés :: 2013. Zoltánfy István Általános Iskola 6772 Deszk, Móra F. u. 2. OM azonosító: 200909 Telephely kódja: 005. Telephelyi jelentés
 FIT-jelentés :: 2013 6. évfolyam :: Általános iskola Zoltánfy István Általános Iskola 6772 Deszk, Móra F. u. 2. Létszámadatok A telephely létszámadatai az általános iskolai képzéstípusban a 6. évfolyamon
FIT-jelentés :: 2013 6. évfolyam :: Általános iskola Zoltánfy István Általános Iskola 6772 Deszk, Móra F. u. 2. Létszámadatok A telephely létszámadatai az általános iskolai képzéstípusban a 6. évfolyamon
A Közbeszerzések Tanácsa (Szerkesztőbizottsága) tölti ki A hirdetmény kézhezvételének dátuma KÉ nyilvántartási szám
 KÖZBESZERZÉSI ÉRTESÍTŐ A Közbeszerzések Tanácsának Hivatalos Lapja 1024 Budapest, Margit krt. 85. Fax: 06 1 336 7751, 06 1 336 7757 E-mail: hirdetmeny@kozbeszerzesek-tanacsa.hu On-line értesítés: http://www.kozbeszerzes.hu
KÖZBESZERZÉSI ÉRTESÍTŐ A Közbeszerzések Tanácsának Hivatalos Lapja 1024 Budapest, Margit krt. 85. Fax: 06 1 336 7751, 06 1 336 7757 E-mail: hirdetmeny@kozbeszerzesek-tanacsa.hu On-line értesítés: http://www.kozbeszerzes.hu
DPR Szakmai nap. 2011. október 17. PTE Felnőttképzési és Emberi Erőforrás Fejlesztési Kar
 PTE Felnőttképzési és Emberi Erőforrás Fejlesztési Kar A diplomás pályakövetés eredményei és a lehetséges fejlesztési irányok DPR Szakmai nap 2011. október 17. Horváth Judit A vizsgálat reprezentativitása
PTE Felnőttképzési és Emberi Erőforrás Fejlesztési Kar A diplomás pályakövetés eredményei és a lehetséges fejlesztési irányok DPR Szakmai nap 2011. október 17. Horváth Judit A vizsgálat reprezentativitása
3. Térvezérlésű tranzisztorok
 1 3. Térvezérlésű tranzisztorok A térvezérlésű tranzisztorok (Field Effect Transistor = FET) működési elve alapjaiban eltér a bipoláris tranzisztoroktól. Az áramvezetés mértéke statikus feszültséggel befolyásolható.
1 3. Térvezérlésű tranzisztorok A térvezérlésű tranzisztorok (Field Effect Transistor = FET) működési elve alapjaiban eltér a bipoláris tranzisztoroktól. Az áramvezetés mértéke statikus feszültséggel befolyásolható.
ÉVKÖZI MINTA AZ EGÉSZSÉGÜGYI BÉR- ÉS LÉTSZÁMSTATISZTIKÁBÓL. (2004. III. negyedév) Budapest, 2004. december
 ÉVKÖZI MINTA AZ EGÉSZSÉGÜGYI BÉR- ÉS LÉTSZÁMSTATISZTIKÁBÓL (2004. III. negyedév) Budapest, 2004. december Évközi minta az egészségügyi bér- és létszámstatisztikából Vezet i összefoglaló Módszertan Táblázatok:
ÉVKÖZI MINTA AZ EGÉSZSÉGÜGYI BÉR- ÉS LÉTSZÁMSTATISZTIKÁBÓL (2004. III. negyedév) Budapest, 2004. december Évközi minta az egészségügyi bér- és létszámstatisztikából Vezet i összefoglaló Módszertan Táblázatok:
Sz ekelyhidi L aszl o Val osz ın us egsz am ıt as es matematikai statisztika *************** Budapest, 1998
 Székelyhidi László Valószínűségszámítás és matematikai statisztika *************** Budapest, 1998 Előszó Ez a jegyzet a valószínűségszámításnak és a matematikai statisztikának azokat a fejezeteit tárgyalja,
Székelyhidi László Valószínűségszámítás és matematikai statisztika *************** Budapest, 1998 Előszó Ez a jegyzet a valószínűségszámításnak és a matematikai statisztikának azokat a fejezeteit tárgyalja,
Előgyergyártott konzolos és konzolos támfalas közlekedési vasbeton elemcsaládok a kerékpáros és gyalogos közlekedési területek növelésére
 Előgyergyártott konzolos és konzolos támfalas közlekedési vasbeton elemcsaládok a kerékpáros és gyalogos közlekedési területek növelésére Adott esetben hegy- és dombvidéken, vízparton, hídfőknél az egyetlen
Előgyergyártott konzolos és konzolos támfalas közlekedési vasbeton elemcsaládok a kerékpáros és gyalogos közlekedési területek növelésére Adott esetben hegy- és dombvidéken, vízparton, hídfőknél az egyetlen
Mágneses szuszceptibilitás vizsgálata
 Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
Házi dolgozat. Minta a házi dolgozat formai és tartalmi követelményeihez. Készítette: (név+osztály) Iskola: (az iskola teljes neve)
 Házi dolgozat Minta a házi dolgozat formai és tartalmi követelményeihez Készítette: (név+osztály) Iskola: (az iskola teljes neve) Dátum: (aktuális dátum) Tartalom Itt kezdődik a címbeli anyag érdemi kifejtése...
Házi dolgozat Minta a házi dolgozat formai és tartalmi követelményeihez Készítette: (név+osztály) Iskola: (az iskola teljes neve) Dátum: (aktuális dátum) Tartalom Itt kezdődik a címbeli anyag érdemi kifejtése...
Javítóvizsga témakörei matematika tantárgyból
 9.osztály Halmazok: - ismerje és használja a halmazok megadásának különböző módjait, a halmaz elemének fogalmát - halmazműveletek : ismerje és alkalmazza gyakorlati és matematikai feladatokban a következő
9.osztály Halmazok: - ismerje és használja a halmazok megadásának különböző módjait, a halmaz elemének fogalmát - halmazműveletek : ismerje és alkalmazza gyakorlati és matematikai feladatokban a következő
Bevezetés a lágy számítás módszereibe
 BLSZM-07 p. 1/10 Bevezetés a lágy számítás módszereibe Nem fuzzy halmaz kimenetű fuzzy irányítási rendszerek Egy víztisztító berendezés szabályozását megvalósító modell Viselkedésijósló tervezési példa
BLSZM-07 p. 1/10 Bevezetés a lágy számítás módszereibe Nem fuzzy halmaz kimenetű fuzzy irányítási rendszerek Egy víztisztító berendezés szabályozását megvalósító modell Viselkedésijósló tervezési példa
JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ. Egészségügyi kártevőirtó szakmunkás szakképesítés. 2454-06 Kártevőirtás modul. 1. vizsgafeladat. 2013. december 10.
 Emberi Erőforrások Minisztériuma Korlátozott terjesztésű! Érvényességi idő: az írásbeli vizsgatevékenység befejezésének időpontjáig A minősítő neve: Rauh Edit A minősítő beosztása: mb. főigazgató-helyettes
Emberi Erőforrások Minisztériuma Korlátozott terjesztésű! Érvényességi idő: az írásbeli vizsgatevékenység befejezésének időpontjáig A minősítő neve: Rauh Edit A minősítő beosztása: mb. főigazgató-helyettes
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
Oláh Attila. ESRI FlexAPI alapú bevetés irányítási rendszer
 Oláh Attila ESRI FlexAPI alapú bevetés irányítási rendszer A bonyolult helyzetek megkövetelik a modern bevetés irányítást! Ez, pedig ma már szinte elképzelhetetlen az együttműködő szervezetek és azok egységeinek
Oláh Attila ESRI FlexAPI alapú bevetés irányítási rendszer A bonyolult helyzetek megkövetelik a modern bevetés irányítást! Ez, pedig ma már szinte elképzelhetetlen az együttműködő szervezetek és azok egységeinek
Óravázlat. A szakmai karrierépítés feltételei és lehetőségei. Milyen vagyok én? Én és te. heterogén csoportmunka
 Óravázlat Tantárgy: Téma: Résztémák: osztályfőnöki A szakmai karrierépítés feltételei és lehetőségei Önismeret Milyen vagyok én? Én és te Időigény: Munkaforma: 1 óra frontális osztálymunka heterogén csoportmunka
Óravázlat Tantárgy: Téma: Résztémák: osztályfőnöki A szakmai karrierépítés feltételei és lehetőségei Önismeret Milyen vagyok én? Én és te Időigény: Munkaforma: 1 óra frontális osztálymunka heterogén csoportmunka
Gazdálkodási modul. Gazdaságtudományi ismeretek II.
 Gazdálkodási modul Gazdaságtudományi ismeretek II. Vezetés és kommunikációs ismeretek KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI MSc Vezetési módszerek, vezetési stílus 77. lecke A VEZETÉS
Gazdálkodási modul Gazdaságtudományi ismeretek II. Vezetés és kommunikációs ismeretek KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI MSc Vezetési módszerek, vezetési stílus 77. lecke A VEZETÉS
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (13. fejezet)
 Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Szerb nyelv emelt szint 0511 ÉRETTSÉGI VIZSGA 2005. november 4. SZERB NYELV EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI MINISZTÉRIUM ÁLTALÁNOS ÚTMUTATÓ 1. Jó megoldásként
Szerb nyelv emelt szint 0511 ÉRETTSÉGI VIZSGA 2005. november 4. SZERB NYELV EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI MINISZTÉRIUM ÁLTALÁNOS ÚTMUTATÓ 1. Jó megoldásként
ció különös s tekintettel az iskolás korosztályra
 Családon belüli li kommunikáci ció különös s tekintettel az iskolás korosztályra Örkényi Ágota, Dr. Aszmann Anna Országos Gyermekegészs szségügyigyi Intézet Esztergom, 2008.03.07 A családon belüli li kommunikáci
Családon belüli li kommunikáci ció különös s tekintettel az iskolás korosztályra Örkényi Ágota, Dr. Aszmann Anna Országos Gyermekegészs szségügyigyi Intézet Esztergom, 2008.03.07 A családon belüli li kommunikáci
H A T Á S V I Z S G Á L A T I
 H A T Á S V I Z S G Á L A T I L A P Iktatószám: A hatásvizsgálat elkészítésére fordított id : Hatásvizsgálatba bevont személyek, szervezetek: Dátum: Kapcsolódó hatásvizsgálati lapok: Vizsgált id táv: El
H A T Á S V I Z S G Á L A T I L A P Iktatószám: A hatásvizsgálat elkészítésére fordított id : Hatásvizsgálatba bevont személyek, szervezetek: Dátum: Kapcsolódó hatásvizsgálati lapok: Vizsgált id táv: El
ÉVKÖZI MINTA AZ EGÉSZSÉGÜGYI BÉR- ÉS LÉTSZÁMSTATISZTIKÁBÓL. (2004. I. negyedév) Budapest, 2004. július
 ÉVKÖZI MINTA AZ EGÉSZSÉGÜGYI BÉR- ÉS LÉTSZÁMSTATISZTIKÁBÓL (2004. I. negyedév) Budapest, 2004. július Évközi minta az egészségügyi bér- és létszámstatisztikából Vezet i összefoglaló Módszertan Táblázatok:
ÉVKÖZI MINTA AZ EGÉSZSÉGÜGYI BÉR- ÉS LÉTSZÁMSTATISZTIKÁBÓL (2004. I. negyedév) Budapest, 2004. július Évközi minta az egészségügyi bér- és létszámstatisztikából Vezet i összefoglaló Módszertan Táblázatok:
3. Napirendi pont ELŐTERJESZTÉS. Csabdi Község Önkormányzata Képviselő-testületének. 2014. november 27. napjára összehívott ülésére
 3. Napirendi pont ELŐTERJESZTÉS Csabdi Község Önkormányzata Képviselő-testületének 2014. november 27. napjára összehívott ülésére Előterjesztés tárgya: A helyi adókról szóló rendeletek módosítása Tárgykört
3. Napirendi pont ELŐTERJESZTÉS Csabdi Község Önkormányzata Képviselő-testületének 2014. november 27. napjára összehívott ülésére Előterjesztés tárgya: A helyi adókról szóló rendeletek módosítása Tárgykört
Érettségi feladatok Algoritmusok egydimenziós tömbökkel (vektorokkal) 1/6. Alapműveletek
 Érettségi feladatok Algoritmusok egydimenziós tömbökkel (vektorokkal) 1/6 A tömbök deklarálásakor Pascal és C/C++ nyelvekben minden esetben meg kell adni az indexelést (Pascal) vagy az elemszámot (C/C++).
Érettségi feladatok Algoritmusok egydimenziós tömbökkel (vektorokkal) 1/6 A tömbök deklarálásakor Pascal és C/C++ nyelvekben minden esetben meg kell adni az indexelést (Pascal) vagy az elemszámot (C/C++).
Határozat száma: 49/2014. (X.13.) Tárgy: Roma települési nemzetiségi képviselő választás eredményének megállapítása HATÁROZAT
 Határozat száma: 49/2014. (X.13.) Tárgy: Roma települési nemzetiségi képviselő választás eredményének megállapítása HATÁROZAT Nádudvar Város Helyi Választási Bizottsága a választási eljárásról szóló 2013.
Határozat száma: 49/2014. (X.13.) Tárgy: Roma települési nemzetiségi képviselő választás eredményének megállapítása HATÁROZAT Nádudvar Város Helyi Választási Bizottsága a választási eljárásról szóló 2013.
Füzesabony Város Polgármesteri Hivatalának szervezetfejlesztése (ÁROP-1.A.2/A - 2008-0154)
 Füzesabony Város Polgármesteri Hivatalának szervezetfejlesztése (ÁROP-1.A.2/A - 2008-0154) 2010.12.08. Erdész János Témák Projekttel szembeni elvárások Projektszakaszok, elvégzett feladatok, eredménytermékek
Füzesabony Város Polgármesteri Hivatalának szervezetfejlesztése (ÁROP-1.A.2/A - 2008-0154) 2010.12.08. Erdész János Témák Projekttel szembeni elvárások Projektszakaszok, elvégzett feladatok, eredménytermékek
A személyiség teszttől a bónuszig Oracle HR Summit 2014.02.26 Budapest Music Center
 A személyiség teszttől a bónuszig Oracle HR Summit 2014.02.26 Budapest Music Center Magyarosi Dóra Fehér Csaba 45 nap Átlagosan 45 nap szükséges egy új munkatárs megtalálásához és beléptetéséhez 3 M Ft
A személyiség teszttől a bónuszig Oracle HR Summit 2014.02.26 Budapest Music Center Magyarosi Dóra Fehér Csaba 45 nap Átlagosan 45 nap szükséges egy új munkatárs megtalálásához és beléptetéséhez 3 M Ft
Átalakuló HR szervezet, változó Business Partneri szerepek
 Átalakuló HR szervezet, változó Business Partneri szerepek dr. Jagicza Ágnes, HR és szervezetfejlesztési vezérigazgató-helyettes, Invitel Zrt. 2014. március 20. Tartalom 2 A HR szerepe a 21. században
Átalakuló HR szervezet, változó Business Partneri szerepek dr. Jagicza Ágnes, HR és szervezetfejlesztési vezérigazgató-helyettes, Invitel Zrt. 2014. március 20. Tartalom 2 A HR szerepe a 21. században
2015. ÉVI ÉVES BELSŐ ELLENŐRZÉSI TERV
 2015. ÉVI ÉVES BELSŐ ELLENŐRZÉSI TERV...../2015. Kgy.sz. határozat 1.számú melléklete Ellenőrzési tervet megalapozó elemzések címei: - 2015. évi belső ellenőri munkaterv (2. számú melléklet) - Kockázatelemzés
2015. ÉVI ÉVES BELSŐ ELLENŐRZÉSI TERV...../2015. Kgy.sz. határozat 1.számú melléklete Ellenőrzési tervet megalapozó elemzések címei: - 2015. évi belső ellenőri munkaterv (2. számú melléklet) - Kockázatelemzés
Fazekas Mihály Fővárosi Gyakorló Általános Iskola és Gimnázium
 26 Fazekas Mihály Fővárosi Gyakorló Általános Iskola és Gimnázium Az Önök telephelyére vonatkozó egyedi adatok táblázatokban és grafikonokon 1. évfolyam gimnázium szövegértés Előállítás ideje: 27.3.. 12:28:21
26 Fazekas Mihály Fővárosi Gyakorló Általános Iskola és Gimnázium Az Önök telephelyére vonatkozó egyedi adatok táblázatokban és grafikonokon 1. évfolyam gimnázium szövegértés Előállítás ideje: 27.3.. 12:28:21
Egyéb előterjesztés Békés Város Képviselő-testülete 2015. december 2-i ülésére
 Tárgy: Körösök Völgye Vidékfejlesztési Közhasznú Egyesület előfinanszírozási kérelme Előkészítette: Gál András osztályvezető Véleményező Pénzügyi Bizottság bizottság: Sorszám: IV/14 Döntéshozatal módja:
Tárgy: Körösök Völgye Vidékfejlesztési Közhasznú Egyesület előfinanszírozási kérelme Előkészítette: Gál András osztályvezető Véleményező Pénzügyi Bizottság bizottság: Sorszám: IV/14 Döntéshozatal módja:
FIT-jelentés :: 2014. Intézményi jelentés. 8. évfolyam
 FIT-jelentés :: 2014 Hőgyészi Hegyhát Általános Iskola, Gimnázium, Alapfokú Művészeti Iskola és Kollégium 7191 Hőgyész, Fő utca 1-3. Létszámadatok A telephelyek kódtáblázata A 002 - Hőgyészi Hegyhát Általános
FIT-jelentés :: 2014 Hőgyészi Hegyhát Általános Iskola, Gimnázium, Alapfokú Művészeti Iskola és Kollégium 7191 Hőgyész, Fő utca 1-3. Létszámadatok A telephelyek kódtáblázata A 002 - Hőgyészi Hegyhát Általános
Fejlesztı neve: LÉNÁRT ANETT. Tanóra / modul címe: CÉGES REKLÁMBANNER KÉSZÍTÉSE PROJEKTMÓDSZERREL
 Fejlesztı neve: LÉNÁRT ANETT Tanóra / modul címe: CÉGES REKLÁMBANNER KÉSZÍTÉSE PROJEKTMÓDSZERREL 1. Az óra tartalma A tanulási téma bemutatása; A téma és a módszer összekapcsolásának indoklása: Az órán
Fejlesztı neve: LÉNÁRT ANETT Tanóra / modul címe: CÉGES REKLÁMBANNER KÉSZÍTÉSE PROJEKTMÓDSZERREL 1. Az óra tartalma A tanulási téma bemutatása; A téma és a módszer összekapcsolásának indoklása: Az órán
Vezetőtárs értékelő kérdőív
 Vezetőtárs értékelő kérdőív Kérdőív megnevezése Jele, kódja Vezetőtárs értékelő kérdőív 11_Ovodavezetőtárs_Ért Önértékelés Értékelés Kérjük a megfelelőt aláhúzni! sorsz Megnevezés Adat 1. Óvodavezető neve
Vezetőtárs értékelő kérdőív Kérdőív megnevezése Jele, kódja Vezetőtárs értékelő kérdőív 11_Ovodavezetőtárs_Ért Önértékelés Értékelés Kérjük a megfelelőt aláhúzni! sorsz Megnevezés Adat 1. Óvodavezető neve
PÁLYÁZATI FELHÍVÁS - JELENTKEZÉSI LAP
 PÁLYÁZATI FELHÍVÁS - JELENTKEZÉSI LAP 1) A program címe: V e z e t ő i t o v á b b k é p z é s - Kategória: V e z e t ő k é p z é s 2) A program szervezője és jogtulajdonosa: Európai Vezetőképző Akadémia
PÁLYÁZATI FELHÍVÁS - JELENTKEZÉSI LAP 1) A program címe: V e z e t ő i t o v á b b k é p z é s - Kategória: V e z e t ő k é p z é s 2) A program szervezője és jogtulajdonosa: Európai Vezetőképző Akadémia
A bölcsészkari intézkedési terv sarokpontjai. DPR intézményi szakmai fórum 2011. október 17. Szalai Mónika kari alumni koordinátor (BTK PIKO)
 A bölcsészkari intézkedési terv sarokpontjai DPR intézményi szakmai fórum 2011. október 17. Szalai Mónika kari alumni koordinátor (BTK PIKO) célok 1. Képzés-, és tananyagfejlesztés 2. Karrier tanácsadás
A bölcsészkari intézkedési terv sarokpontjai DPR intézményi szakmai fórum 2011. október 17. Szalai Mónika kari alumni koordinátor (BTK PIKO) célok 1. Képzés-, és tananyagfejlesztés 2. Karrier tanácsadás
Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata. Az r-time és a TNS Hoffmann által végzett kutatás
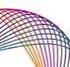 Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata Az r-time és a TNS Hoffmann által végzett kutatás 2002-2010: stabil szponzorációs részarány Televíziós reklámbevételek
Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata Az r-time és a TNS Hoffmann által végzett kutatás 2002-2010: stabil szponzorációs részarány Televíziós reklámbevételek
54 862 01 0000 00 00 Munkavédelmi technikus Munkavédelmi technikus
 161-06 A munkaeszközök, munkafolyamatok és az egyéni védőeszközök egészséget nem veszélyeztető és biztonságos alkalmazásával kapcsolatos A /2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM
161-06 A munkaeszközök, munkafolyamatok és az egyéni védőeszközök egészséget nem veszélyeztető és biztonságos alkalmazásával kapcsolatos A /2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM
31 521 09 1000 00 00 Gépi forgácsoló Gépi forgácsoló
 Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
ÚTMUTATÓ A KONTROLL ADATSZOLGÁLTATÁS ELKÉSZÍTÉSÉHEZ (2012-TŐL)
 ÚTMUTATÓ A KONTROLL ADATSZOLGÁLTATÁS ELKÉSZÍTÉSÉHEZ (2012-TŐL) A 2006-2010. évre vonatkozó, régebbi adatszolgáltatások esetében az adatszolgáltatás menete a mostanitól eltérő, a benyújtáshoz különböző
ÚTMUTATÓ A KONTROLL ADATSZOLGÁLTATÁS ELKÉSZÍTÉSÉHEZ (2012-TŐL) A 2006-2010. évre vonatkozó, régebbi adatszolgáltatások esetében az adatszolgáltatás menete a mostanitól eltérő, a benyújtáshoz különböző
Hallgatói Elégedettségi Kérdőív
 Hallgatói Elégedettségi Kérdőív Kérjük, töltse ki az elméleti képzésre vonatkozó kérdőívünket és küldje vissza nekünk a facetofacejogsi@gmail.com e-mail címre. Köszönjük, hogy véleményével hozzájárul magasabb
Hallgatói Elégedettségi Kérdőív Kérjük, töltse ki az elméleti képzésre vonatkozó kérdőívünket és küldje vissza nekünk a facetofacejogsi@gmail.com e-mail címre. Köszönjük, hogy véleményével hozzájárul magasabb
Egyszerű áramkörök vizsgálata
 A kísérlet célkitűzései: Egyszerű áramkörök összeállításának gyakorlása, a mérőműszerek helyes használatának elsajátítása. Eszközszükséglet: Elektromos áramkör készlet (kapcsolótábla, áramköri elemek)
A kísérlet célkitűzései: Egyszerű áramkörök összeállításának gyakorlása, a mérőműszerek helyes használatának elsajátítása. Eszközszükséglet: Elektromos áramkör készlet (kapcsolótábla, áramköri elemek)
- mit, hogyan, miért?
 - mit, hogyan, miért? Dr. Bélavári Csilla VITUKI Nonprofit Kft., Minőségbiztosítási és Ellenőrzési Csoport c.belavari@vituki.hu 2011.02.10. 2010. évi záróértekezlet - VITUKI, MECS 1 I. Elfogadott érték
- mit, hogyan, miért? Dr. Bélavári Csilla VITUKI Nonprofit Kft., Minőségbiztosítási és Ellenőrzési Csoport c.belavari@vituki.hu 2011.02.10. 2010. évi záróértekezlet - VITUKI, MECS 1 I. Elfogadott érték
Festetics Kristóf ÁMK Pókaszepetk Óvoda iskola átmenet segítő mikro-csoport
 Festetics Kristóf ÁMK Pókaszepetk Óvoda iskola átmenet segítő mikro-csoport Tagjai: Célok: Szocializációs különbségek csökkentése Óvoda és iskola nevelési stratégiájának, módszertanának egymáshoz való
Festetics Kristóf ÁMK Pókaszepetk Óvoda iskola átmenet segítő mikro-csoport Tagjai: Célok: Szocializációs különbségek csökkentése Óvoda és iskola nevelési stratégiájának, módszertanának egymáshoz való
VÁLTOZÁSOK ÉS EREDMÉNYESSÉG: A DÉLUTÁNIG TARTÓ ISKOLA BEVEZETÉSÉNEK INTÉZMÉNYI TAPASZTALATAI
 XXI. Századi Közoktatás (fejlesztés, koordináció) II. szakasz TÁMOP-3.1.1-11/1-2012-0001 EREDMÉNYESSÉG ÉS TÁRSADALMI BEÁGYAZOTTSÁG (TÁMOP 3.1.1. / 4.2.1.) VÁLTOZÁSOK ÉS EREDMÉNYESSÉG: A DÉLUTÁNIG TARTÓ
XXI. Századi Közoktatás (fejlesztés, koordináció) II. szakasz TÁMOP-3.1.1-11/1-2012-0001 EREDMÉNYESSÉG ÉS TÁRSADALMI BEÁGYAZOTTSÁG (TÁMOP 3.1.1. / 4.2.1.) VÁLTOZÁSOK ÉS EREDMÉNYESSÉG: A DÉLUTÁNIG TARTÓ
Struktúra Átalakítás és Fejlesztési Stratégia. Holló Imre Hollo@eib.org
 Struktúra Átalakítás és Fejlesztési Stratégia Holló Imre Hollo@eib.org A következő előadás nem az EIB hivatalos álláspontja Idézet a Zöld Könyvből 1. A Magyar Köztársaság kormánya ezért a kormányprogramban
Struktúra Átalakítás és Fejlesztési Stratégia Holló Imre Hollo@eib.org A következő előadás nem az EIB hivatalos álláspontja Idézet a Zöld Könyvből 1. A Magyar Köztársaság kormánya ezért a kormányprogramban
