Algoritmikus játékelmélet jegyzet
|
|
|
- Csaba Rácz
- 9 évvel ezelőtt
- Látták:
Átírás
1 Algoritmikus játékelmélet jegyzet Végh László szeptember Bevezetés A játékelmélet a XX. század első felében kialakult tudományterület; leginkább a matematikai közgazdaságtan részeként szokás rá tekinteni, azonban alkalmazási területei közé tartozik a szociológia, pszichológia, biológia, politikatudomány, filozófia, és a minket most leginkább érdeklő számítástudomány is. Megszületését hagyományosan Neumann János és Oskar Morgenstern Játékelmélet és gazdasági viselkedés című könyvének 1944-es megjelenéséhez kötik. Fő kérdésfeltevése olyan szituációk elemzése, amelyekben egymással érdekellentétben álló, racionálisan cselekvő egyének hoznak döntéseket. Ilyenre a legkülönbözőbb kontextusokban láthatunk példákat. Az algoritmikus játékelmélet viszonylag friss terület (minthogy maga a számítástudomány is elég fiatal); a számítástudomány és a játékelmélet kétirányú kölcsönhatásán alapul. Az algoritmikus gondolkodás itt is, ahogy a matematika számos más területén is új szemléletet adott: hogyan tudják például az egyes játékosok hatékony algoritmus segítségével megtalálni a legjobb stratégiájukat? Az internet megjelenése ugyanakkor egészen új, játékelméleti szempontból érdekes szituációkat eredményezett. Ilyen jelenség önmagában az is, hogy az internet központi irányítás nélkül, számtalan, egymástól független cselekvésből alkult egy jól működő nagy rendszerré. A minden eddiginél gyorsabb kommunikáció pedig újfajta piaci mechanizmusok megjelenését hozta magával. A jegyzetben klasszikus játékelméleti eredményeket ismertetünk algoritmikus nézőpontból, valamint újabb számítástudományi eredményeket. A jegyzetben tárgyalt témák túlnyomó része megtalálható Nisan, Roughgarden, Tardos és Vazirani Algorithmic Game Theory című könyvében (Cambridge University Press, New York, 2007). A könyv teljes egészében letölthető a Non-printable.pdf címről. A jegyzetben nem adunk hivatkozásokat, ezek a könyvben megtalálhatóak. A tárgyhoz analízis alapismeretek mellett a számítási bonyolultság alapfogalmai szükségesek (P, NP proglémaosztályok, NP-teljesség). A 2.3 és 2.4. fejezetekhez némi lineáris programozási ismeretre van szükséges: poliéder, politóp, kúp, lap, csúcs fogalmaira, és a dualitás tételre. Ezek Frank András Operációkutatás jegyzetéből ismételhetőek át/tanulhatóak meg A játék fogalma és tulajdonságai A játékelmélet központi fogalmára, a játékra bajosan lehetne az összes jelentését lefedő meghatározást adni. A 2. fejezetben adunk egy, a jegyzetben szereplő szituációk nagyrészére illő formális definíciót; előtte azonban néhány példán keresztül illusztráljuk, miféle játékokkal foglalkozik a játékelmélet. Kezdjük a közismert kő-papír-olló játékkal. Kő Papír Olló Kő (0,0) (-1,1) (1,-1) Papír (1,-1) (0,0) (-1.1) Olló (-1,1) (1,-1) (0,0) A győztes egy, a vesztes mínusz egy pontot kap, a döntetlen nulla pontot ér mindkettejüknek. A táblázat sorai az első, oszlopai a második játékos egyes döntési lehetőségeit jelentik; az egyes pozíciókban levő számpárok elemei az első, illetve a második játékos pontszámát adják meg az adott kimenetelnél. Ezt a táblázatos ábrázolási formát a játék normál formájának fogjuk nevezni. Ez egy véges, determinisztikus, kétszemélyes, nulla-összegű, szimmetrikus, teljes információs, egylépéses, szinkron játék. 1
2 Kétszemélyes mellett több (akár végtelen sok) személyes játékokkal is fogunk találkozni; egyszemélyes játékok (pl. a pasziánsz) viszont nem igazán tartoznak a játékelmélet vizsgálati körébe. Az egyes játékosok döntési lehetőségeit stratégiáknak nevezzük. A végesség ezek számára vonatkozik: véges sok játékos van, mindegyik véges sok stratégiával. Stratégia alatt mindig egy, az egész játék kimenetelét egyértelműen meghatározó döntést fogunk érteni. A sakk esetén például stratégia alatt nem a soron következő lehetséges lépésekre gondolunk, hanem a teljes játék lejátszását meghatározó szabályt. Kicsit formálisabban: mind a világos, mind a sötét játékos egy stratégiája egy olyan függvény, amely a tábla minden lehetséges állásához (és az ahhoz vezető korábbi lépések sorozatához) hozzárendel egy követekező lépést az adott színnel. Ennek megfelelően a sakkban roppant nagyméretű a stratégiák száma, ám még mindig véges; ellentétben a végtelen kockásfüzeten játszott amőbával. 1 Ezzel a szemlélettel a játék konkrét lefolyása érdektelen: a játékosok a játék legelején odaadhatnák írásban a stratégiájukat egy játékvezetőnek, amely az összes lehetséges játékhelyzethez megadja a válaszlépést (már amennyiben a világegyetemben lenne elegendő anyag ennyi papír gyártásához). Ennek birtokában a játékvezető (vagy egy számítógép) automatikusan le tudja játszani a meccset és eredményt hirdethet. Feltételezzük, hogy a játékosok az egyes kimeneteleket össze tudják hasonlítani, és el tudják dönteni, melyik kedvezőbb számukra. Sőt, általában azt az erősebb feltételezést is megtesszük, hogy minden kimenetelhez egy valós számot, a nyereségüket tudják rendelni. A veszteség negatív értékű nyereség, a nulla kimenetel pedig semlegesnek számít. Nulla-összegű a játék, ha a játékosok össznyeresége nulla, tehát egymás kárára tudnak nyerni. Egy kétszemélyes játék szimmetriája alatt azt értjük, hogy a két játékos stratégiáinak a halmaza egy-az-egyben megfeleltethető úgy, hogy felcserélve őket a másik játékos kifizetését kapjuk. Teljes információs alatt azt értjük, hogy minden játékosnak rendelkezésére áll minden olyan információ, ami a játék kimenetelét befolyásolja, és ami alapján a többiek meghozzák a döntésüket. A sakk úgyszintén teljes információs, a póker azonban nem az. Determinisztikus alatt azt értjük, hogy a játék szabályai közt semmilyen véletlen tényező nem szerepel (ellentétben a kártyajátékokkal); azt viszont általában megengedjük, hogy az egyes játékosok a saját döntésük meghozatalához a véletlent (pl. pénzfeldobás) hívják segítségül. A játékelmélet fontos feltételezése a játékosok racionalitása. Ebbe beleértjük egyrészt, hogy a játékosok tisztában vannak a saját preferenciáikkal illetve célfüggvényükkel; tisztában vannak saját lehetséges döntéseikkel; arra törekszenek, hogy a célfüggvényüket maximalizálják, és az ehhez vezető lehetséges legjobb döntéseket hozzák a rendelkezésre álló információk alapján. Az, hogy képesnek tekintjük őket egy ilyen döntés meghozatalára, valójában egy nagyon erős és egyáltalán nem természetes feltevés. A köznyelvben a racionális játék szinonimájaként használt sakkra például egyáltalán nem teljesülnek: a játékosok a borzasztó mennyiségű lehetséges döntésüknek valójában csak egy elhanyagolható szeletét tudják (ráadásul erősen korlátozottan) mérlegelni. Az első számítógépek megjelenésétől kezdve fontos törekvés volt, hogy az ember megverésére képes programot írjanak; a győzelem időpontjának 1997-et szokták hirdetni, amikor az IBM Deep Blue gépe legyőzte Kaszparovot. Mégis, a játékelmélet a sakkal kapcsolatban nem sok érdekeset tud mondani; ez a győzelem leginkább a technológiának, a hatalmasra növelt számítási kapacitásnak köszönhető. A korlátozott racionalitás azonban éppúgy igaz a számítógépekre is, valójában ők is csak egy apró szeletét látják át a lehetőségeknek. A racionalitáshoz szorosan kapcsolódó, itt éppen csak érintett fogalom a racionalitás köztudása: amellett, hogy a játékosok racionálisak, tudják egymásról is, hogy racionálisak, tudják azt, hogy mindenki más tudja hogy a többiek racionálisak, és így tovább a végtelenségig. Visszatérve a kő-papír-olló tulajdonságainak jellemzéséhez: ez egy egylépéses szinkron játék, mivel egyetlen lépésben ér véget, és a két játékosnak egyszerre, a másik döntésétől függetlenül kell megválasztani stratégiáját. Ezek egyike sem igaz a sakkra; ezt szekvenciális játéknak nevezzük. Az ilyen játékokban minden lépésben pontosan az egyik játékos lép (nem feltétlenül felváltva, de valamilyen meghatározott szabály szerint.) Mint fentebb említettük, hogy a sakkot - és általában a szekvenciális játékokat - is tekinthetjük egylépéses szinkron játéknak, ahol a játékosoknak csupán egyetlen döntést kell meghozniuk: azt, hogy milyen stratégiával játszanak Kombinatorikus játékok Egy játék szekvenciális szerkezete mégis hasznos lehet az elemzés szempontjából. Ezekkel a félév során nem foglalkozunk, viszont most mutatunk egy rájuk vonatkozó egyszerű tételt. Kombinatorikus játék alatt értsünk olyan véges, determinisztikus, kétszemélyes, teljes információs szekvenciális játékokat, amelyekben három lehetséges kimenetel van: győzelem, vereség és döntetlen. Éles kombinatorikus játékban nem engedjük meg a döntetlent. Nyerő stratégia alatt egy olyan stratégiát értünk, hogy a másik játékos tetszőleges stragégiája ellen garantáltan nyerni tudunk; nem vesztő stratégia esetén pedig nem veszthetünk. 1 A végességhez figyelembe kell vennünk azt a szabályt is, hogy ha ugyanaz az állás háromszor ismétlődik, a játék döntetlennel végetér. 2
3 1.1. Tétel. Minden éles kombinatorikus játékban pontosan az egyik játékosnak van nyerő stratégiája. Minden kombinatorikus játékban vagy az egyik játékosnak van nyerő stratégiája, vagy mindkettőnek van nem vesztő stratégiája. Bizonyítás. A bizonyítás kulcsa, hogy egy kombinatorikus játékban a lehetséges lépéseket egy (véges) fával tudjuk szemléltetni. Tegyük fel először azt, hogy a játék éles; az egyszerűség kedvéért azt is tegyük fel, hogy a két játékos felváltva lép. A fa páratlan szinten levő csúcsai az első, a páros szinten levők pedig a második játékos lépéseinek felelnek meg. A fa gyökere a legelső lépést jelképező csúcs. A levelek a játék végső kimenetei, ezeket pirosra vagy (a) (b) 1. ábra. Az (a) ábrán csak a levelek vannak jelölve, vízszintes vonalazással a kékek, függőlegessel a pirosak. A (b) ábrán a teljes fa ki lett színezve; az első játékosnak van nyerő stratégiája. kékre színezzük annak megfelelően, hogy az első vagy a második játékos nyer. A bizonyítást a 1. ábra illusztrálja. Vegyünk egy olyan z csúcsot, akinek az összes gyereke levél. Ha z páratlan szinten van (azaz az első játékos lép), és minden gyereke kék, az azt jelenti, hogy akármit is lépjen itt az első játékos, veszteni fog. Ezért z-t is kiszínezhetjük kékre. Ha viszont csak egy piros gyereke is van, akkor tud úgy lépni, hogy ő nyerjen; ennek megfelelően z-t pirosra színezzük. Ha z páros szinten van, és van egyetlen kék gyerek is, akkor a második tud nyerni, ezért őt is kékre színezzük. Pirosra akkor színezzük, ha minden gyereke piros. Alulról fölfelé haladva ezzel a módszerrel egyértelműen ki tudjuk színezni az összes csúcsot. Ha végül a gyökér piros lesz, akkor az első játékosnak van nyerő stratégiája: az aktuális csúcsból mindig egy piros gyereket választ. Ha pedig a gyökér kék, akkor a másodiknak van nyerő stratégiája. Erre vezethetjük vissza az általánosabb esetet, amikor döntetlen is lehetséges: definiáljunk úgy egy másik játékot, hogy az eredeti döntetlen is az első játékos győzelmének számít. Erre a játékra az előbbi eredményt alkalmazva azt láthatjuk, hogy az eredetiben vagy az első játékosnak van nem vesztő stratégiája, vagy a másodiknak van nyerő. Hasonlóan láthatjuk azt is, hogy vagy az első játékosnak van nyerő stratégiája, vagy a másodiknak van nem vesztő. Ebből már következik az állítás: ha egyiküknek sincs nyerő stratégiája, akkor mindkettőnek kell legyen nem vesztő Feladat. Hogyan lehetne a fenti tétel gondolatmenetét olyan szituációkra általánosítani, amikor a győzelem és vereség helyett tetszőleges valós számot megengedünk kimenetelnek, csak azt követelve meg, hogy a játék nullaösszegű legyen? 1.3. Fogolydilemma A talán legjobban ismert klasszikus játékelméleti problémában a rendőrség letartóztat két bűnözőt, akiket egy súlyos bűntény elkövetésével gyanúsítanak. Tárgyi bizonyíték azonban, nincs, beismerő vallomásra lenne szükség. A gyanúsítottakat éjszakára külön cellákba zárják, hogy ne tudjanak összebeszélni. Reggelre kell eldönteniük, hogy vallomást tesznek-e. Ha mindketten tagadnak, akkor gyorshajtásért és visszaeső közterületi alkoholfogyasztásért két évre ítélik őket. Ha mindketten vallomást tesznek, mindketten négy évet kapnak. Ha viszont az egyikük tesz vallomást, a másik tagad, akkor aki tagad, az öt évet kap, hiszen eredeti bűnén felül még hamisan is vallott. A másik is kap azért egy évet, csak a miheztartás végett. A játék kifizetési mátrixa tehát az alábbi: Vall Tagad Vall (-4,-4) (-1,-5) Tagad (-5,-1) (-2,-2) 3
4 Érdemes-e valamelyik rabnak tagadnia? Ha a másik vallomást tesz, akkor ő is jobban járna a vallomással: öt helyett csupán négy évet kapna. Szintén jobban járna a vallomással, ha a másik tagad: ekkor kettő helyett csak egy év börtönre ítélnék. Arra juthatunk tehát, hogy mindkét játékosnak inkább vallani érdemes, amivel mindketten négy évet kapnak, vagyis sokkal rosszabbul járnak, mintha egyhangúan tagadtak volna. A fogolydilemmával a legkülönbözőbb területeken találkozhatunk: valójában a kooperáló és önző magatartásformák viszonyát írja le. Lássunk néhány példát. Tegyük fel, hogy egy kisvárosi piac szabályzata szerint a kofáknak reggel pontban hatkor kell kiírni az árakat, és onnantól nem változtathatnak. Két zöldséges árul krumplit; mindketten 100 forintért szerzik be kilóját. Sokáig mindketten 150 forintért árulják, a vevők fele-fele jár hozzájuk, és mindketten haszonra tesznek szert. Egy ravasz vevő elmagyarázza azonban mindkettőnek, hogy ha másnap 130 forintra vinné le az árat, akkor kevesebb haszna lenne egy kiló krumpliból, de átcsábíthatná a másik összes vevőjét, és így összességében jobban járna. Másnap reggel háromnegyed hatkor mindketten gondterhelten leskelődnek a másik árus felé. Ha ugyanis egyikük megmarad a 150 forintnál, a másik pedig leviszi 130-ra, akkor a 150-es nyakán marad a sok zsák krumpli. Ha végül mindketten a 130 forintot választják, akkor 40%-kal csökken mindkettejük profitja (a vásárlók nagy örömére). Klasszikus fogolydilemma szituációként szokták leírni a hidegháborús fegyverkezési versenyt. A két játékos Amerika és a Szovjetúnió. Mindketten választhatnak, hogy mekkora összeget fordítanak a fegyverkezésre. Ha csak az egyikük fegyverkezik, a másik pedig nem, vagy alig, akkor az előbbi fegyverrel vagy fenyegetéssel leigázhatja az utóbbit. Ugyanaz marad a politikai helyzet, ha mindketten fegyverkeznek, vagy egyikük sem; viszont az előbbi esetben hatalmas összegeket fognak kifizetni. s 1 S C = t 1 = t 2 s 2 2. ábra. Egy informatikai példát szemléltet a 2. ábra. Két szolgáltató van, akik a C és S pontokban tudják a forgalmat a másik hálózatára átküldeni. A szolgáltatók költsége a saját hálózatukban használt élek száma. Az első szolgáltatónak s 1 -ből t 1 -be, a másiknak pedig s 2 -ből t 2 -be kell bizonyos adatmennyiséget továbbítania. Mindketten kétféleutatválaszthatnak:2vagy4egységhosszút.a2hosszúútteljesenasajáthálózatukonbelül megy,a4egység hosszúból azonban csak egy él megy a sajátban, három pedig a másikén belül. Az első felel meg az együttműködő, a második az önző magatartásnak. Ha mindketten a rövidebb utat használják, mindkettejük költsége 2; ha mindketten a hosszabbat, akkor a költségük 4. Ha viszont csak az egyik választja a rövidebb utat, a másik a hosszabbat, akkor az együttműködő költsége 5, az önzőé 1. A kifizetési mátrix tehát azonos lesz a fogolydilemmában szereplővel. Következő példaként tegyük fel, hogy egy gyanús külvárosi piacon próbálok aranyékszert venni. Az árus eladhat igazi ékszert vagy hamisat, én pedig fizethetek érte igazi vagy hamis pénzzel. Többet nem látjuk egymást: mire kiderül, hogy bóvli az ékszer, már bottal üthetem a nyomát. Érthető okokból ő sem fog a hamis pénz miatt feljelentést tenni. Ha igazi ékszert kapnék igazi pénzért, azzal mindketten jól járnánk; ha viszont a hamisítványért fizetem ki az igazi pénzt, ugyanúgy bosszankodhatok, mint ő, hogyha hamis pénzt adok valódi aranyért. Végül tehát a valószínű kimenet az, amikor mindketten becsapjuk a másikat. Az előző példa valójában tetszőleges szerződéses viszonyra alkalmazható: ha az egyik szerződő fél felrúgja a megállapodást, a másik pedig tisztességes és teljesíti a kötelességét, az előbbi nagyobb haszonra tesz szert, mint ha mindketten tartották volna a megállapodást. Mind a gazdaság, mind a jogrendszer működéséhez szükség van valamiféle olyan nyomásra, ami kikényszeríti a szerződések betartását. Ilyen kényszert jelenthet az állam, aki a hatóságokkal megtoroltatja a törvények és szerződések megszegését. Egy másik kényszerítő tényező a közvélemény ereje: hogyha tisztességtelen az üzleti magatartásom, többet senki nem fog velem üzletelni; hogyha a társadalmi korlátokat hágom át, kiközösítenek. 4
5 Ez utóbbi hatást játékelméleti szempontból a iterált fogolydilemma írja le: tegyük fel, hogy ugyanaz a két játékos egymás után sokszor játsza le a fogolydilemmát. Mint láttuk, egyetlen játék esetén mindenképp a vallomás a kifizetődőbb. Ha azonban ezt további játékok követik, azokban a másik játékos bosszút tud állni az árulásért. A tagadás jutalma tehát - a pillanatnyi alacsonyabb nyereséggel szemben - a hosszútávú együttműködésből származó haszon. Egy, a gyakorlatban legjobbnak bizonyuló stratégia a tit-for-tat: az első játékban tagadok, és minden további játékban azt cselekszem, amit ellenfelem az előző játékban. Vagyis ha a másik vall, akkor a következő körben büntetésből én is vallok; ha azonban legközelebb tagad, akkor megbocsátok neki, és utána én is tagadni fogok. Ha mindketten ezt a stratégiát játsszák, akkor végig mindketten tagadni fognak. 2 Az iterált fogolydilemma gyakorlati alkalmazására példa a peer-to-peer fájlcserélő rendszerek működése. Itt az egyes felhasználók szeretnének valamilyen tartalomhoz hozzájutni, amit a többiek osztanak meg velük. A kényelmes potyautas stratégia, ha a felhasználók csak letöltenek, és letiltják vagy erősen korlátozzák a feltöltést: hiszen részükről ennek költsége van (sávszélesség, processzorhasználat.) Természetesen ha túl sok a potyautas, a rendszer nem tud működni; ez több korábbi fájlcserélőnél is komoly problémát jelentett. A Bittorrent megoldása az, hogy a felhasználókat egy iterált fogolydilemmába kényszeríti bele. Ha le szeretnék tölteni egy fájlt, összesorsolnak néhány tucat másik felhasználóval (peer-ek), akik szintén ugyanezt szeretnék tölteni (és már rendelkeznek valamekkora részével). Közülök néhánnyal kapcsolatot hozok létre. Kezdetben ingyen engednek tölteni; ha azonban már valamekkora résszel rendelkezek, ők is adatot várnak el cserébe. Az együttműködő magatartás az, hogyha viszonzásként én is engedem őket tölteni, de potyautasként ezt meg tudom tiltani. Erre viszont ők reagálhatnak azzal, hogy nem adnak további adatokat, illetve megszüntetik a kapcsolatot. 3 Lényeges, hogy kisszámú peer-rel tudok csak kapcsolatot létesíteni; ez tudja kivédeni azt, hogy csupa különböző felhasználótól szerezzek valamennyi adatot, majd amikor cserébe ők is várnának tőlem, tovább tudjak állni egy másikhoz Szennyezési és közlegelő játék A következő két játék a fogolydilemma sokszereplős általánosításának tekinthető. A szennyezési játékban n > 3 ország szerepel. Mindegyik kétféle környezetpolitikát alkalmazhat: ha nem korlátozza a szennyezést, az 1 pénzegység kárt okoz - számára, és minden másik ország számára is. A szennyezés visszafogása 3 egységnyi befektetést igényel: ezt csak neki kell kifizetnie. Ha mindegyik ország visszafogja a szennyezést, mindegyiknek 3 lesz tehát a költsége - ha viszont mindenki szennyez, akkor mindenkinek n költséget okoz a szennyezés. Mégis, ez utóbbi forgatókönyv a természetes: ha ugyanis egy ország környezetvédelemről áttér szennyezésre, a többiek pedig nem változtatnak a politikájukon, akkor ez az ország 2-vel csökkenteni tudja a költségét(és közben az összes többiét 1-gyel megemeli). Az egyetlen stabilnak tekinthető megoldás (ezt később precízen definiáljuk, mit is jelent) az, amikor mindenki szennyez. A közlegelők tragédiájában egy falu legelője tíz tehenet tud eltartani. Tíz gazda legelteti egy-egy tehenét, mindegyik jóllakik és 10 liter tejet ad. Jól mennek a gazdaságok, úgyhogy mindegyik gazdának összegyűlik elég pénze egy második tehén vásárlására. Egy nap egyikük vesz is mégegyet: már tizenegyen legelnek. Mostmár kevesebb fű jut minden tehénnek, ezért csak 9 liter tejet adnak. A két tehenet legeltető gazda viszont 18 liter tejhez jut. Általában, ha k tehén van, akkor 20 k liter tejet adnak. Ezért mindaddig érdemes egy gazdának új tehenet kihajtani a legelőre, amíg a tehenek száma el nem éri a 18-at. Vagyis a stabil megoldás az lesz, amikor nyolc gazdának van két tehene, két gazdának pedig egy-egy, és minden tehén 2 liter tejet ad. Ekkor összesen 36 liter tejet fejnek sovány, beteg tehenekből, szemben a kiindulási 100 literrel. Míg a szennyezési játékban az egyes játékosok döntéseiből következő költségek egyszerűen összeadódtak, itt ezek a döntések erősen befolyásolják egymást: ha már 8 gazda vett második tehenet, akkor a maradék kettőnek nem érdemes. 2. Nash-egyensúly Megadunk egy formális modellt, amit a következőkben játék alatt fogunk érteni. Véges sok, n játékos van; az i. játékoshoz adott egy S i stratégiahalmaz. A játék egy lehetséges kimenetele az, hogy minden játékos választ egyszerre egy-egy stratégiát. A kimenetelek halmaza tehát S = S 1 S 2... S n. Az i. játékos nyereségét az u i : S R n függvény írja le. A játék akkor véges, ha n véges, illetve mindegyik S i halmaz véges. Az s = (s 1,...,s n ) S stratégiaválasztás Pareto-optimális, ha nincsen olyan másik s stratégiaválasztás, amivel mindenki legalább annyira jól jár, mint s-sel, és legalább egyvalaki szigorúan jobban jár, azaz u i (s ) u i (s) 2 Valójában további finomításokra van szükség. Ha pl. mindketten ezt játszák, de az egyikük egyetlen alkalommal véletlen - vagy kommunikációs hiba miatt - vall, akkor utána egy ő ütött előbb ördögi körbe kerülnek, ahol felváltva fog mindig az egyik vallani, a másik tagadni. 3 Természetesen ezeket a döntéseket helyettem a számítógépemen futó kliensek hozzák; többnyire a tit-for-tat stratégiát alkalmaza. A kliensben beállíthatom a sávszélességi korlátokat, illetve egyes programokban a stratégiát is változtathatom. 5
6 és legalább egy helyen szigorú egyenlőtlenségáll. Ha van ilyen s, akkor s-et Pareto-szuboptimálisnakhívjuk. Véges játékban könnyen látható, hogy mindig létezik Pareto-optimális stratégiaválasztás. Ha z,z S i az i. játékos két stratégiája, akkor azt mondjuk, hogy z (gyengén) dominálja z -t, ha z-vel mindig legalább olyan jól jár, mint z -vel, vagyis u(s 1,...,s i 1,z,s i+1,...,s n ) u(s 1,...,s i 1,z,s i+1,...,s n ) a többi játékos összes lehetséges s j stratégia választása esetén. Dominált stratégiát racionális játékosnak nem érdemes választani. Egy stratégia domináns, ha a játékos összes többi stratégiáját dominálja. A fogolydilemmában a vallomástétel dominálja a tagadást, tehát egyértelműen az a legjobb stratégiaválasztás, ha mindketten vallanak. Ez azonban egy Pareto-szuboptimális stratégia, hiszen mindketten jobban járnának, ha mindketten tagadnánank. (Ez azért van, mert most a játékot csak egyetlen egyszer játszuk le; a k iterációban ismételt fogolydilemma esetén egy stratégia az, ami minden i = 1,...,k-ra megmondja, hogy az előző i 1 játék kimenetelét figyelembe véve hogyan döntünk az i. körben.) Legyen s = (s 1,...,s n ) S egy stratégiaválasztás. Valamely 1 i n-re S i = j i S j az S i -től különböző stratégiahalmazok szorzata. s i S i az (s 1,...,s i 1,s i+1,...,s n ) vektort jelöli, (z,s i ) pedig (s 1,...,s i 1,z, s i+1,...,s n )-t rövidíti. Egy s = (s 1,...,s n ) stratégiaválasztás Nash-egyensúly, hogyha egyik játékos sem járhat jobban, ha megváltoztatja a stratégiáját, feltéve, hogy a többiek nem változtatnak. Formálisan, u(s i,s i ) u(z,s i ) tetszőleges z S i -re. Ha minden játékosnak van domináns stratégiája (mint a fogolydilemmában), akkor azok Nash-egyensúlyt alkotnak. Nézzünk olyan példát, amikor ez nem teljesül. A nemek harca játékban egy fiú és egy lány szeretné eldönteni, hogy Kispál vagy Tankcsapda koncertre menjen. A lány inkább a Kispált 4, a fiú inkább a Tankcsapdát szeretné, viszont mindkettejüknek az a legfontosabb, hogy együtt menjenek valahova. Fiú\Lány Kispál Tankcsapda Kispál (1,2) (0,0) Tankcsapda (0,0) (2,1) Itt két Nash-egyensúly is van, ha mindketten a Kispált vagy mindketten a Tankcsapdát választják. Tegyük most fel, hogy valójában a Kispált szeretik mindketten jobban, ez 2-2, a Tankcsapda pedig 1-1 egység örömöt szerez. Ekkor is mindkét azonos választás Nash-egyensúlyban van, annak ellenére, hogy a Tankcsapda egyértelműen rosszabb (Pareto-szuboptimális). A fogolydilemához hasonló héja-galamb játék konfliktushelyzetek modellezését célozza (kocsmai verekedések, háborúk, biológiában különböző fajok vetélkedése stb.). Mindkét félnek két stratégiája van, a provokáló (héja) és a kompromisszumkereső (galamb). A hasznossági mátrix a következő. Héja Galamb Héja (0,0) (4,1) Galamb (1,4) (3,3) Itt két Nash-egyensúly van, azok, amikor ellentétes szerepeket játszanak: az egyik héja, a másik pedig galamb. A játék másik elnevezése a gyáva nyúl : helyi vagányok azon játéka, amikor egy keskeny egyenes úton egymással szembe indul két autós. Amelyik előbb félrerántja a kormányt, az gyáva nyúl, gúny és megvetés tárgya. Ha viszont egyik sem rántja félre, akkor két bátor halottal lesz gazdagabb a helyi legendárium Vickrey-árverések Egy értékes tárgyat szeretnénk elárverezni. n érdeklődő van, ezek közül pontosan az egyik kaphatja meg. Mindenki egyidejűleg, lezárt borítékban tehet árajánlatot, ezek alapján döntjük el, kinek és mennyiért adjuk oda. Az i. játékosszámáraw i R forintot ér; ha ő kapja meg t forintért, akkorahaszna w i t (ami negatív is lehet); ha valaki más kapja, akkor nulla a haszna. A w i értéket csak az i. játékos ismeri; tehát a játék nem is teljes információs. Vegyük észre, hogy ez a játék ráadásul nem is véges, hiszen S i = R mindegyik játékosnál. Két árverési mechanizmust vizsgálunk; mindkettőben a legtöbbet ígérő játékos kapja meg a tárgyat. (Ha több ilyen van, akkor az ABC-ben utolsó nyer.) A legmagasabb áras változatban annyit kell fizetnie, amennyit licitált; a második áras árverésben pedig a második legnagyobb licit értékét kell kifizetnie. 4 A félév elején még létezett... 6
7 Minden játékos stratégiája a licit értékével jellemezhető, azaz S i = R (vagy Z, ha csak egész értéket lehet mondani). Ha t > w i, akkor a w i licit mindkét esetben dominálja a t licitet. A legmagasabb áras változatban érdemeslehet w i -nélkisebb számotmondani,hiszen ha mi nyerünk,akkorazacél,hogyminélkevesebbelmondjunk többet, mint a második legjobb licit. Mivel azonban nem ismerjük a többi licitet, csak tippelgetni tudunk, és lehet, hogy véletlen alámegyünk a másodiknak, így mégsem mi nyerünk. A következő állítás azt mutatja, hogy a második áras változatban a valós w i értéket érdemes licitálni, függetlenül a többiek értékeiről alkotott elképzeléseinktől Állítás. A második áras játékban w i az i. játékos egyértelmű domináns stratégiája. Bizonyítás. Azt már láttuk, hogy w i dominál tetszőleges t > w i licitet. Tekintsünk most egy t < w i licitet. Tegyük fel, hogy a többi játékos licitjei közül z a legnagyobb érték. Ha z > w i, akkor úgysem lett volna esélyünk nyerni, hiszen van, akinek w i -nél többet ér a tárgy. Ha w i z t, akkor w i -t licitálva megszerezhettük volna w i z nyereséggel, így pedig nem kaptuk meg. Ha t > z, akkor ugyanúgy w i z lesz a nyereségünk, mintha w i -t licitáltunk volna. Összefoglalva: z értékétől függetlenül mindig legalább annyi lenne a nyereségünk w i-t licitálva, mint t-t, és van olyan szituáció, amikor kifejezetten jobban járunk. Vagyis w i valóban domináns stratégia. Erre a példára a 5.2. fejezetben a mechanizmustervezés kapcsán fogunk részletesebben viszszatérni Kevert stratégiák Vegyük észre, hogy a 1.1. Tétel egy Nash-egyensúly létezését bizonyította kombinatorikus játékokra. Azonban általában ez nem garantált: már egy olyan egyszerű játékban sem létezik, mint első példának, a kő-papírolló. Valóban érezhető, hogy a mindig követ játszok típusú stratégiák nem igazán sikeresek; ezzel szemben jó módszernek tűnik a véletlenre bízni a választást. Ebben a fejezetben a Nash-egyensúly fogalmát terjesztjük ki oly módon, hogy véletlen stratégiaválasztást is megengedünk. Az i. játékos egy kevert stratégiája alatt valószínűségi eloszlást értünk az S i stratégiahalmazon. Ha S i véges, akkor ez egy olyan σ : S i R + vektorral jellemezhető, amelyre z S i σ(z) = 1. Tiszta stratégia alatt az értjük, hogy valamely z S i -re σ(z) = 1 és σ(z ) = 0 ha z z. Ezt χ z -vel fogjuk jelölni. Legyen i az i. játékos kevert stratégiáinak halmaza. Ha S i véges és S i = m i, akkor i az m i dimenziós szimplex, vagyis m i i = {σ R mi : σ j 0, σ j = 1}. Legyen = 1... n a kevert stratégiaválasztások halmaza. Ha a játékosok kevert stratégiái σ = (σ 1,...,σ n ), akkor az s = (s 1,...,s n ) S stratégiaválasztás valószínűsége j=1 p σ (s) = σ i (s i ). Az u i (σ) hasznosság alatt az i. játékos hasznosságának a várható értékét értjük: u i (σ) = s Sp σ (s)u i (s). Az σ = (σ 1,...,σ n ) kevert stratégiák kevert Nash-egyensúlyban vannak, ha u i (σ i,σ i ) u i (γ,σ i ) i = 1,...,n, γ i. Ettől megkülönböztetendő, a korábban definiált Nash-egyensúlyt tisztának nevezzük. (Természetesen a tiszta Nash-egyensúly kevert is egyben.) Rögzítsünk egy σ i i kevert stratégiát. γ i -t legjobb válasznak nevezzük σ i -re, ha u i (γ,σ i ) értéke a lehetséges legnagyobb. A σ kevert stratégia pontosan akkor van Nash-egyensúlyban, ha minden i-re σ i legjobb válasz σ i -re. Mindenz S i tisztastratégiárahatározzukmegu i (χ z,σ i )-t,atisztaz stratégiahasznosságátσ i -velszemben. Jelölje Z σ i S i azon z S i tiszta stratégiák halmazát, amelyekre u i (χ z,σ i ) maximális, ezeket az σ i -re adható legjobb tiszta válaszoknak nevezzük. supp(γ)-val jelöljük egy γ i stratégia tartóját, azon z S i stratégiák halmazát, melyekre γ(z) > Lemma. Egy γ i stratégia akkor és csak akkor a legjobb válasz σ i -re, ha supp(γ) Z σ i. 7
8 Bizonyítás. Legyen a legjobb tiszta stratégiáknál a várható nyereség α. Az γ stratégia várható nyereségét így írhatjuk fel: u i (γ,σ i ) = z S i γ(z)u i (χ z,σ i ). Mivel mindegyik u i (χ z,σ i ) α, ebből következik, hogy u i (γ,σ i ) α, vagyis egy kevert stratégiával elérhető nyereség legfeljebb annyi, mint a tiszta stratégiákkal elérhető legjobb nyereség. Továbbá egyenlőség pontosan akkor áll fenn, hogyha γ(z) > 0 esetén u i (χ z,σ i ) = α, ami épp az állítással ekvivalens Állítás. A kő-papír-olló játék egyetlen Nash-egyensúlya az, amikor σ 1 = σ 2 = ( 1 3, 1 3, 1 3 ). Bizonyítás. Tegyük fel indirekten, hogy van másik Nash-egyensúly is; a szimmetria miatt feltehető, hogy σ 1 (kő) σ 1 (papír) σ 1 (olló), és az első vagy második egyenlőtlenségszigorúan teljesül. Azt állítjuk, hogy a második játékos részéről papírt játszani nem tartozik a σ 1 -re adható legjobb tiszta válaszok közé. Valóban, ezzel szemben u 2 (σ 1,χ papír ) = σ 1 (kő) σ 1 (olló) < 0, u 2 (σ 1,χ olló ) = σ 1 (kő)+σ 1 (papír) 0. Az előző lemma szerint tehát σ 2 (papír) = 0. Ugyanezzelaz okoskodássalazt kaphatjuk, hogy az első játékosrészéről az olló nem egy legjobb tiszta válasz, vagyis σ 1 (olló) = 0, ami ellentmondás Gyakorlat. Határozzuk meg a nemek harca és héja-galamb játékok összes kevert Nash-egyensúlyát! Kulcsfontosságú Nash alábbi tétele: 2.5. Tétel (Nash, 1951). Ha mindegyik S i halmaz véges, akkor létezik kevert Nash-egyensúly. A bizonyításhoz használni fogjuk Brouwer analízisből ismert fixpont tételét Tétel (Brouwer, 1912). Ha C R m egy konvex és kompakt halmaz, f : C C egy folytonos függvény, akkor létezik olyan x C, amelyre f(x) = x. A 2.5. Tétel bizonyítása. A kevert stratégiaválasztások halmaza, az m = i m i dimenziós tér egy konvex kompakt részhalmaza. Ezen szeretnénk egy folytonos f függvényt definiálni, melynek fixpontjai éppen a kevert Nash-egyensúlyoknak felelnek meg. Legyen σ = (σ 1,...,σ n ) egy kevert stratégiaválasztás. Az i. játékos egy z S i stratégiájára legyen c i (z,σ) = u i (χ z,σ i ) u i (σ). Ez éppen azt jelöli, hogy mennyivel járna jobban az i. játékos, ha az σ i stratégiát a tiszta z-vel helyettesítené. Vegyük észre, hogy z S i σ i (z)c i (z,σ) = 0. (1) Legyen c + i (z,σ) = max(0,c i(z,σ)), és ˆσ i (z) = σ i(z)+c + i (z,σ) 1+ u S i c + i (u,σ). Könnyen láthatóan ˆσ i i, és f(σ) = (ˆσ 1,ˆσ 2,...,ˆσ n ) egy folytonos függvény. A 2.6. Tétel szerint létezik egy σ, amelyre f(σ) = σ. Azt állítjuk, hogy ez egy kevert Nash-egyensúly. Tegyük fel, hogy nem az, és valamelyik i-re γ i stratégia jobb lenne σ i helyett σ i ellen. Mivel 0 < u i (γ,σ i ) u i (σ) = z S i γ(z)c i (z,σ), ezért kell legyen olyan z S i, amelyre c i (z,σ) > 0; ebből következik ˆσ i (z) > 0 is. σ i (z) = ˆσ i (z) minthogy σ fixpont, tehát σ i (z)c i (z,σ) > 0. Ebből (1) alapján tudjuk, hogy létezik olyan z S i, amelyre c i (z,σ) < 0. Ekkor σ i (z) = ˆσ i (z ) = σ i (z ) 1+ u S i c + i (u,σ), ellentmondás, hiszen a nevező nagyobb mint egy. 8
9 A feltételek közül a végesség nem hagyható el, ahogy az alábbi példa is mutatja. Tegyük fel, hogy ketten (X és Y) árulnak egy adott terméket, amire három potenciális vevő van (A,B és C). Mindhárman egy egységet szeretnének venni, és legfeljebb egy egységnyi pénzt fizetnek érte. X és Y stratégiái a termék lehetséges árai, vagyis a [0, 1] intervallum egy-egy eleme (tetszőleges valós szám lehet). Az árat egyszerre kell kihirdetniük, később már nem változtathatnak. A mindenképpen X-től vásárol, C mindenképpen Y-tól, B pedig attól, aki olcsóbban adja; egyenlőség esetén azonban A-t preferálja. X és Y célja is bevételének maximalizálása Állítás. A fenti játékban nincsen tiszta Nash-egyensúly. Bizonyítás. Legyen x és y a kettejük által megszabott ár. Ha x y, akkor X bevétele 2x és Y bevétele y. Ha x > y, akkor x illetve 2y a bevételük. Az x < 1 2 választás egyértelműen dominálja x = 1, és ugyanígy y < 1 2 -et y = 1. Nash-egyensúly esetén tehát x,y 1 2. Ha x y, akkor Y-nak jobban megérné egy kicsit aláígérnie X-nek. Ha viszont x > y, akkor Y-nak megérné egy kicsit növelnie. Kicsit bonyolultabb érveléssel megmutatható az is, hogy kevert Nash-egyensúly sincsen Kétszemélyes 0-összegű játékok A 2.5. Tétel garantálja a kevert Nash-egyensúly létezését. A bizonyítás azonban nem ad semmiféle algoritmust arra, hogyan lehet egy egyensúlyt megtalálni. A következő alfejezetekben az egyensúly megtalálásának algoritmikus kérdéseit vizsgáljuk. Az első, fontos eredmény Neumann Jánostól származik 1928-ból, amelyben 0 összegű véges kétszemélyes játékok egyensúlyát írta le, sok évvel a Nash-egyensúly általános fogalmának megszületése valamint a lineáris programozás elméletének kidolgozása előtt. A tételt most a lineáris programozás dualitás tételének következményeként mutatjuk be. Tekintsünk egy olyan véges kétszemélyes játékot, ahol a két játékos kifizetésének az összege 0. Legyen S 1 = {1,...,n}, S 2 = {1,...,m}; u 1 (i,j) = u 2 (i,j). Az első játékos kifizetéseit az n m-es A mátrixszal ábrázolhatjuk, ahol az i. sor j. eleme u 1 (i,j). Legyenxilletve y az első illetve második játékosegy-egystratégiája(vagyisx,y 0, n i=1 x i = 1, m i=1 y i = 1). Az y-ra adható legjobb tiszta válasz azon i stratégiák halmaza, melyekre (Ay) i értéke maximális. Legyen ennek értéke α; ekkor a második játékos az y-t játszva garantálni tudja, hogy a várható vesztesége maximum α legyen. Hasonlóképpen, az x-re adható legjobb tiszta válaszok azon j-k, melyekre (x T A) j minimális. Ha az első játékos x-et játszik, ezzel azt tudja garantálni, hogy a várható nyeresége legalább β legyen. A tétel azt mondja ki, hogy a második játékos által elérhető minimális α ugyanaz, mint az első által elérhető maximális β Tétel (Neumann, 1928). Egy véges kétszemélyes 0-összegű játékban az egyik játékos által garantálható maximális várható nyereség egyenlő a másik játékos által garantálható minimális várható vesztességgel. Bizonyítás. A következő lineáris program optimális megoldásai azon y stratégiák, melyekre az első játékos által adható legjobb tiszta válasz a lehető legrosszabb. min α Ay 1α 1y = 1 y 0 (P) Az első játékos stratégiáira hasonlóan: min β x T A 1β 1x = 1 x 0 (Q) Ez a két lineáris program éppen egymás duálisa (miért?). A dualitás tétel alapján következik, hogy az optimum értékek megegyeznek. A lineáris komplementaritási feltételek éppen azt mutatják, hogy az optimális megoldásokhoz tartozó x és y Nash-egyensúlyt alkotnak. Mivel a lineáris programozási feladat megoldására ismertek hatékony (polinomiális) algoritmusok, ez a tétel - ellentétben a Nash-tétellel - valóban algoritmust is szolgáltat az optimum megtalálására. 9
10 2.4. Kétszemélyes szimmetrikus játékok Vegyünk most egy tetszőleges véges kétszemélyes játékot, amelyikben az első játékosnak n, a másodiknak m különböző stratégiája van. A kifizetéseiket az A 1 illetve A 2 n m-es mátrixokkal írhatjuk le. (0-összegű játéknál A 2 = A 1.) Szimmetrikusnak nevezzük a játékot, ha n = m és A 2 = A T 1. Ilyenek voltak például: kő-papír-olló, fogolydilemma, héja-galamb. Egy szimmetrikus játékban egy (σ 1,σ 2 ) kevert Nash-egyensúlyt szimmetrikusnak nevezünk, ha σ 1 = σ 2. Az következő lemma azt mutatja, hogy ha egy szimmetrikus kétszemélyes játékban tudunk szimmetrikus Nashegyensúlyt találni, akkor tetszőleges kétszemélyes játékban is tudunk. Vegyük észre, hogy ha ugyanazt az M számot hozzáadjuk A 1 és A 2 minden eleméhez, akkor a stratégiákat illetően semmi nem változik: pontosan ugyanazok lesznek a két játékban a Nash-egyensúlyok. Éppen ezért a továbbiakban feltehetjük, hogy (egy kellően nagy szám hozzáadása után) mind A 1, mind A 2 minden eleme szigorúan pozitív. Tekintsük a következő (n+m) (n+m)-es mátrixot: C = ( 0 A1 A T Lemma. Vegyük azt a kétszemélyes szimmetrikus játékot, melyben a kifizetési mátrixok C illetve C T. Legyen ebben (τ,τ) egy szimmetrikus Nash-egyensúly, ahol τ = (τ 1,τ 2 ) felbontásban τ 1 az első n, τ 2 pedig az utolsó m komponenst jelöli. Legyen a τ 1 -beli komponensek összege c, a τ 2 -belieké 1 c. Ekkor az eredeti játékban (σ 1,σ 2 ) = ( τ1 c, τ 2 1 c ) egy kevert Nash-egyensúly. Bizonyítás. Először be kell lássuk, hogy 0 < c < 1. Jelölje a stratégiákat a 1,...,a n,b 1,...,b m. Tegyük fel először, hogy c = 0, vagyis τ 1 0. Ekkor az első játékosnak tetszőleges a i tiszta stratégiára a kifizetése pozitív (mivel A 1 minden eleme pozitív), egy tetszőleges b j -re viszont 0. Vagyis τ tartójában nem a legjobb tiszta válaszok szerepelnek, ellentmondásban a 2.2. Lemmával. A játékosok szerepének felcserélésével következik c < 1 is. Ha τ 1 (a i ) > 0, akkor a i -nek legjobb tiszta válasznak kell lennie τ-ra, tehát A 1 τ 2 -t az i. sornak maximalizálnia kell. Ebből következik,hogyaz eredeti játékbanis a i legjobb tiszta válaszσ 2 -re. Ugyanígylátható, hogy ha τ 2 (b j ) > 0 akkor b j is legjobb tiszta válasz σ 1 -re, amiből ismét a 2.2. Lemma alapján készen vagyunk. A következőkben bemutatott Lemke-Howson algoritmus tetszőleges szimmetrikus kétszemélyes játékban keres szimmetrikus Nash-egyensúlyt. Az algoritmus véges lesz ugyan, de sajnos nem polinomiális futásidejű. Legyen A az első játékos kifizetési mátrixa (n n-es). Ismét feltehetjük, hogy A minden eleme szigorúan pozitív. Vegyünk egy x kevert stratégiát (azaz x i = 1, x 0.) Legyen α az Ax vektor maximális értéke. Ha a második játékos x stratégiát választja, akkor az első játékos legjobb tiszta válaszai azon i indexekhez tartoznak, melyekre (Ax) i = α. Ennek megfelelően x pontosan akkor szimmetrikus Nash-egyensúly, ha az alábbi feltétel teljesül: ). x i = 0 vagy Ax i = α teljesül minden i = 1,...n-re. (2) Legyen P = {x R n : Ax 1,x 0}. Ez egy korlátos poliéder (politóp) lesz, melynek 0 egy csúcsa. Minden csúcsában legalább n egyenlőség kell teljesüljön; egy z csúcshoz mondjuk azt, hogy az i index reprezentálva van, ha z i = 0 és (Az) i = 1 közül legalább az egyik fennáll. Ha mindkettő teljesül, akkor i duplán reprezentálva van Állítás. Ha z olyan csúcs, amelynél minden 1 i n reprezentálva van, és z 0, akkor x = P z i zi szimmetrikus Nash-egyensúly. Az állítás rögtön következik abból, hogy (2) teljesül x-re. Célunk tehát egyetlen, a 0-tól különböző olyan csúcsot találni, amelynél minden stratégia reprezentálva van. Az egyszerűség kedvéért feltesszük, hogy P nem degenerált. Ez azt jelenti, hogy minden csúcs pontosan n feltételt teljesít egyenlőséggel.(pl. az oktéder degenerált, a dodekaéder nem az.) A feltételeket egy nagyon kicsit módosítva, pl. a mátrix minden eleméhez egy kicsi véletlen számot adva tetszőleges poliédert ilyenné tehetünk úgy, hogy a módosított probléma egy Nash-egyensúlya az eredetiben is Nashegyensúly legyen. P élei ekkor azok a halmazok, melyek n 1 feltételt teljesítenek egyenlőséggel. Minden élre két csúcs illeszkedik, ezeket szomszédosaknak nevezzük. Legyen F z a z csúcsnál egyenlőséggel teljesülő feltételek halmaza. A z csúcsnak az f F z feltétel szerinti szomszédja a z csúcs, ha F z F z = F z f. Legyen most Z 0 azon csúcsok halmaza, melyeknél minden index reprezentálva van, Z pedig azoké, melyekre az első n 1 index reprezentálva van. Világos, hogy 0 Z 0 Z. Mivel a poliéder nem degenerált, a Z Z 0 -beli csúcsoknál pontosan egy index van duplán reprezentálva. 10
11 Legyen z 0 = 0, és vegyük z 0 -nak az x n 0 feltétel szerinti z 1 szomszédját. Ha z 1 Z 0, akkor készen vagyunk; egyébként van egy egyértelmű duplán reprezentált i index. Az (Ax) i 1 feltétel szerinti szomszédja z 0 ; az x i 0 feltétel szerinti szomszédja viszont egy ettől különböző z 2. Így tovább, ha az általános lépésben z t Z 0, akkor befejezzük az eljárást. Ha z t Z Z 0, akkor van egy egyértelmű duplán reprezentált i index. Ekkor az x i 0 és (Ax) i 1 feltételek szerinti egyik szomszédja z t 1, a másik pedig egy ettől különböző z t+1. Azt állítjuk, hogy z t+1 különbözik az eddigi z 0,...,z t csúcsoktól. Ebből következik, hogy ez az eljárás véges sok lépésben véget kell érjen, ami azt jelenti, hogy találunk egy 0-tól különböző Z 0 -beli csúcsot. Tegyük fel indirekten, hogy z t+1 = z j, h < t az első ismétlődés. Ekkor z t+1 a z h -ban duplán reprezentált indexhez tartozó egyik feltétel szerinti szomszédja volna. Azonban z h 1 és z h+1 már két ilyen szomszéd volt (illetve ha h = 0, akkor z 1 volt az egyetlen ilyen szomszéd). A 3. ábra szemlélteti az algoritmus menetét az alábbi mátrixszal: A = x x x 1 3. ábra Megjegyzések a bonyolultsággal kapcsolatban A fenti algoritmus véges, azonban a futásideje nem polinomiális: a poliédernek exponenciálisan sok csúcsa is lehet, és elképzelhető, hogy egy nagyon hosszú úton kell végigmennünk. Mit mondhatunk a Nash-egyensúly megtalálásának bonyolultságáról? Könnyen belátható, hogy a probléma NP-beli. A kevert Nash-egyensúly ugyanis a P poliéder egy csúcsának felel meg, amiről tudjuk, hogy csupa racionális koordinátából áll. Ha az A mátrix elemei racionális számok, akkor ráadásul a Nash-egyensúlyt leíró vektor a bemenet méretének polinomjában leírható. Vajon a Nash-egyensúly megtalálása vajon polinomiálisan megoldható egy ügyesebb algoritmussal, vagy pedig N P-teljes? A kérdés nyitott, azonban érdekes módon egyik válasz sem tűnik valószínűnek. Ez a kérdés eléggé különbözik a hagyományos N P-teljes kérdésektől (pl. egy adott gráfban létezik-e Hamiltonút?). Arra a kérdésre, hogy Létezik-e Nash-egyensúly? mindig igen a válasz. Az NP-teljesség bizonyítása a következőképpen nézhetne ki. Tegyük fel, hogy pl. a Hamilton-út létezését szeretnénk visszavezetni erre. Ehhez lenne gráfokról játékokra egy f(g) (polinomiálisan reprezentálható) leképezésünk, úgy, hogy G akkor és csak akkor tartalmaz Hamilton utat, ha az f(g) játék (tetszőleges) Nash-egyensúlya valamilyen hatékonyan ellenőrízhető Q tulajdonságot kielégít. 11
12 Ekkor azonban vegyünk egy olyan gráfot, amelyben nincsen Hamilton-út. Ennek nem létezésére polinomiális méretű bizonyíték lenne az, hogy az f(g) játékban megadunk egy Nash-egyensúlyt, ami nem elégíti ki Q-t. Ebből az következne, hogy N P = con P. Erről szintén nem bizonyított, hogy nem igaz, azonban elég valószínűtlennek tartjuk. A Nash-egyensúly létezésének egy saját bonyolultsági osztály felel meg. A Lemke-Howson algoritmusban a Z halmazon egy olyan irányított gráfot definiálunk, amelyben minden csúcs befoka és kifoka is legfeljebb egy (mindenkinek két szomszédja van irányítatlan értelemben; az irányítás kisebb technikai nehézségek árán elvégezhető). A gráf tehát irányított utak és körök dijszunkt uniója. Ebben a 0 egy nulla befokú csúcs; célunk egy nulla kifokú csúcs megtalálása. A P P AD (Polynomial Parity Arguments on Directed graphs) bonyolultsági osztály ezeket a tulajdonságokat absztrahálja. Adott egy irányított gráfunk egy esetlegesen exponenciális méretű csúcshalmazon. Minden csúcs ki- és befoka is legfeljebb egy. Ha adott egy csúcs, hatékonyan meg tudjuk találni egy kiszomszédját. Ismerünk egy forrást (nulla befokú csúcsot). Célunk egy nyelő (nulla kifokú csúcs) megtalálása. Ebbe az osztályba tartozik például egy közelítő Brouwer-fixpont megtalálása (amit most nem definiálunk pontosan), vagy a sonkásszendvics probléma: adott az R n térben n darab 2n elemű halmaz, keressünk egy olyan hipersíkot, amelynek mindegyik halmazból n pont esik mindkét oldalára. Összesen annyit tudunk, hogy P P P AD N P. Egyik helyen sem tűnik valószínűnek, hogy egyenlőség állna. Az N P-teljességhez hasonlóan definiálható a P P AD-teljesség: egy probléma akkor rendelkezik ezzel a tulajdonsággal, hogyha tetszőleges másik P P AD-beli problémát polinomiálisan vissza tudunk rá vezetni. A szimmetrikus kétszemélyes játék Nash-egyensúlyának megtalálása P P AD-teljes, éppen ezért nem valószínű, hogy polinomiálisan megoldható lenne. Megjegyzendő, hogy a Nash-egyensúly megtalálásának kérdése további, ártatlannak tetsző feltételek hozzáadásával könnyen NP-teljessé válik. Például: Létezik-e egy adott játékban két különböző Nash-egyensúly? Létezik-e olyan, amiben az első játékos haszna legalább t? Létezik-e olyan Nash-egyensúly, amelynek a tartója tartalmazza az s stratégiát? 2.6. Az anarchia ára A Nash-egyensúllyal kapcsolatban felmerülő természetes kérdés, hogy mennyire tekinthető hatékonynak. A fogolydilemma esetén például igen kevéssé: a Nash-egyensúly nem is Pareto-optimális: lenne olyan állapot, amikor mindketten jobban járnának. A játék kimeneteleit különböző célfüggvények szerint hasonlíthatjuk össze. Természetesen különböző Nash-egyensúlyokhoz különböző értékek tartozhatnak. Egy célfüggvényt tekintve az anarchia ára a legrosszabb Nash-egyensúly értékének és az optimális értéknek az aránya, a stabilitás ára pedig a legjobb Nash-egyensúly és az optimális érték aránya. (Ezek minimalizálási feladatnál egynél nagyobb, maximalizálás esetén pedig egynél kisebb számok). Ha az anarchia ára egyhez közeli érték, azt úgy értelmezhetjük, hogy a köz érdeke megközelítőleg azonos az egyéni érdekek eredőjével. A továbbiakban olyan szituációkat fogunk vizsgálni, amikor a célfüggvény költségként értelmezhető: egy s kimenetelhez egy C(s) nemnegatív értéket rendelünk, és ezt szeretnénk minimalizálni. Vagyis a stabilitás ára legalább 1, az anarchia ára pedig legalább annyi, mint a stabilitás ára. 3. Hálózati forgalmi játékok Egy városban számos autós szeretne eljutni lakásából a munkahelyére. Mindannyian olyan útvonalat szeretnének választani, ahol a lehető leggyorsabban célbaérnek. Azonban ha túl sokan mennek egy adott útszakaszon, dugók alakulhatnak ki, és emiatt jelentősen megnőhet az áthaladás ideje. A Nash-egyensúly egy ilyen szituációban egy olyan útválasztásnak felel meg, amikor senki nem tudna egy olyan alternatív útvonalat találni, ahol gyorsabban célbaérne. Tekintsük a 4. ábrán látható Pigou-tól származó példát. Egy egységnyi forgalom szeretne az s pontból a t-be eljutni; úgy tekintjük, hogy az egyes autósok ennek a forgalomnak egy nagyon kicsi töredékét alkotják. Kétféle útvonalat választhatnak: e-n egy időegység alatt lehet átérni a forgalomtól függetlenül, h-n azonban x forgalom esetén x időegység az áthaladási idő. Könnyen látható, hogy az egyetlen Nash-egyensúly az, amikor mindenki h-t. Ha ugyanis α forgalom menne e-n, 1 α pedig h-n, akkor az e-n haladó autósok jobban járnának, ha h-ra 12
13 s c e (x) = 1 t c h (x) = x 4. ábra. A Pigou-példa. módosítanának. A rendszer működésének egy természetes mérőszáma az, hogy mennyi az átlagos áthaladási idő. A Nash-egyensúlyban ez 1, azonban ha a forgalom fele-fele arányban haladna a két élen, akkor csak 3 4 lenne; könnyen látható, hogy ez a legjobb választás. Fő kérdésünk az lesz, hogy mennyi az anarchia ára: mennyivel lehet rosszabb Nash-egyensúlyban az átlagos áthaladási idő az optimálisnál. Kétféle változatban vizsgáljuk ezt a játékot: a folytonos játékban végtelen sok játékos van, akik egyenként a forgalom infinitezimális részei fölött rendelkeznek, a diszkrét változatban véges sok játék van, mindegyik pozitív igénnyel. Definiáljuk először a folytonos változatot Folytonos hálózati forgalmi játék Adott egy G = (V,E) irányított gráf, benne az (s 1,t 1 ),...,(s k,t k ) forrás-nyelő párok, ezeket igénypároknak nevezzük. Az i. igénypárra adott egy r i igény: összesen ekkora mennyiségű forgalom szeretne eljutni s i -ből t i -be. Jelölje P i az s i -ből t i -be menő összes út halmazát. Feltesszük, hogy ez minden igénypárra nemüres, azaz t i -t el lehet érni s i -ből. Legyen P = k i=1 P i. A hálózati forgalmat egy f multifolyammal reprezentáljuk, mely egy f : P R + függvény. Ennek az s i - ből t i -be menő része egy r i értékű, köröket nem tartalmazó folyam. Ezt útfelbontással reprezentáljuk: valamely P P i útra f P az ezen az úton szállított folyamérték (az a forgalommennyiség, amelyik a P utat választja). f megengedett multifolyam, ha minden 1 i k-re P P i f P = r i. Adott továbbá minden e E élre egy c e : R + R + költségfüggvény.azt tételezzük fel, hogy ezek nemnegatív, folytonos és monoton növő függvények. Ezek mind természetes feltevések, ha c e (x)-re úgy gondolunk, mint az x forgalom esetén az e élen való áthaladás ideje. A folytonos hálózati forgalmi játékot a (G, r, c) hármassal írjuk le. Játékosokról eddig egyáltalán nem esett szó; ez a modell nem illeszkedik a 2. fejezetben bevezetett játékfogalmunkhoz. Az intuitív elképzelés az, hogy végtelen sok játékosunk van, mindegyik infinitezimálisan kicsi forgalmat bonyolít le valamelyik forrás és nyelő között. Ezt igen nehézkes lenne formalizálni, így nem is tesszük meg. A (Nash)-egyensúlyt anélkül definiáljuk, hogy expliciten játékosokról beszélnénk; ez az f megengedett multifolyam egy tulajdonsága lesz. (Ami azonban azt a képet igyekszik megragadni, hogy az infinitezimális játékosok egyikének sem áll érdekében változtatni.) A játék diszkrét változata ezzel szemben egy klasszikus értelemben vett véges játék lesz. Az f multifolyamra f e = e P:P P f P az e E élen folyó mennyiség. Ennek az élnek a költsége c e (f e ), egy P P úté pedig c P (f) = c e (f e ). (3) e P A költséget áthaladási időnek képzelve, ez azt fejezi ki, mennyi idő eljutni s i -ből t i -be a P úton Definíció. A (G, r, c) hármassal adott játékban az f multifolyam akkor egyensúlyi folyam, hogyha minden i = 1,...,k igénypárra és minden P,P P i útra hogyha f P > 0, akkor c P (f) c P (f). Ez éppen azt fejezi ki, hogy minden igénypár esetén forgalom csak azokon az utakon halad, amelyek a lehető legolcsóbbak s i -ből t i -be. Az f folyam költségét így definiáljuk: C(f) = P P c P (f)f P = e Ec e (f e )f e. (4) A két alak azonossága könnyen belátható, ha c P (f) helyére behelyettesítjük (3)-et. Ezt k i=1 r i-vel leosztva éppen az átlagos útköltséget kapjuk meg. f-et akkor nevezzük optimálisnak, ha minimalizálja ezt a költséget. Meg fogjuk mutatni, hogy mindig létezik optimális folyam is és egyensúlyi folyam is. Az anarchia ára a legnagyobb költségű egyensúlyi folyam költségének és az optimális költségének az aránya, a stabilitás ára pedig a legkisebb költségű 13
14 egyensúlyi folyam költségének és az optimális költségnek az aránya. Ki fog derülni, hogy minden egyensúlyi folyam költsége ugyanaz, vagyis ebben az esetben az anarchia és a stabilitás ára megegyezik. v v x 1 x 1 s t s t 0 1 x 1 x w (a) w (b) 5. ábra. A Braess-paradoxon: az új út megépítése előtt (a), és után (b). Érdekes jelenségre hívja fel a figyelmet a 5. ábrán látható példa a Braess-paradoxon. Egy város vezetése a forgalmi dugók enyhítésére egy új, nagy kapacitású alagutat épít egy domb két oldalán levő terek között. A hatalmas költségű vállalkozás befejezésével azonban - minden várakozással ellentétesen - a helyezet nemhogy javulna, de jelentősen romlik. Hogyan lehetséges ez? Az eredeti hálózatban 1 egységnyi folyamnak kell eljutnia s-ből t-be. Az egyetlen Nash-egyensúly az az f, amikor a forgalom fele az alsó, fele a fölső úton halad, mindkettőnek a költsége 3 2 ; ekkor C(f) = 3 2. A v és w közt épített 0 költségű új él azonban felborítja ezt az egyensúlyt: az svwt út vonzóbbá válik mindkét úttal szemben. Olyannyira, hogy az egyetlen Nash-egyensúly mostmár az lesz, amikor mindenki ezt az utat választja. Ekkor C(f) = 2 lesz, az eredeti 4 3-szorosa. A 6. ábra mechanikai analógiát mutat egy hasonló jelenségre: a rugókat tartó feszes madzag elvágásával a várakozásokkal ellentétben a rendszer súlypontja nem süllyedni, hanem emelkedni fog ábra. Megmutatjuk, hogy ha tetszőleges költségfüggvényeket megengedünk az éleken, akkor az anarchia ára tetszőlegesen nagy lehet. Módosítsuk Pigou példáját (4. ábra), úgy, hogy c h (x) = x k valamilyen k > 1 egészre. Ahogy k = 1-re, általában is látható, hogy az egyetlen egyensúlyi helyzet, amikor minden forgalom a h élen halad. Az optimális megoldásban viszont kicsit kevesebbet érdemes h-ra helyezni: hogyha e-n ε mennyiség folyik, akkor 14
15 C(f) = (1 ε) k+1 + ε. Ennek a minimuma ε = 1 ( 1 k+1 )1/k -ra vétetik fel. k -re az optimális folyamérték 0-hoz fog tartani, míg a legjobb Nash egyensúly mindig 1 lesz Diszkrét hálózati forgalmi játék A diszkrét változatban az egyes játékosok egy pozitív nagyságú folyamot szeretnének célba juttatni. Mind a k igénypárt egy-egy játékosnak vesszük (különböző igénypárok forrás- és nyelőpontjai egybe is eshetnek). Az i játékos r i mennyiségetszeretne s i -ből t i -be eljuttatni. A játékotugyanúgy a (G,r,c) hármassaljellemezhetjük; az i. játékos egy f i folyamot ad meg, aminek az összege az f multifolyam. Egy tiszta stratégiája az, hogy az egyik P i -beli utat választja. Ennek a stratégiának a költsége(azaz a kifizetés 1-szerese) a választott út költsége ugyanúgy definiálva, mint a folytonos változatban. Ez egy véges játék, alkalmazható a 2.5. Tétel, tehát létezik kevert Nash-egyensúly. Kérdés, hogy létezik-e mindig tiszta Nash-egyensúly is. Ezt az alábbi módon jellemezhetjük. Az f multifolyam akkor van tiszta Nash egyensúlyban a (G,r,c)-vel adott diszkrét hálózati forgalmi játékban, ha minden i-re f pontosan egy P P i úton pozitív, ahol r i az értéke, és minden P P i útra c P (f) c P (f ) teljesül, ahol f ugyanaz, mint f, kivéve hogy P-n 0-ra csökkentjük, P -n pedig r i -re növeljük az értékét. w x+33 13x 6x 2 3x 2 v x s 47x 7. ábra. t A 7. ábra egy olyan példát mutat, amikor nincsen tiszta Nash-egyensúly. Két játékosunk van, az első r 1 = 1, a második r 2 = 2 egységet akar eljuttatni s-ből t-be. Négy lehetséges útjuk van, jelölje P 1, P 2, P 3 és P 4 rendre az s t, s v t, s w t és s v w t utakat. A következő négy állítás egyszerűen bizonyítható, és következik belőlük, hogy nem létezhet tiszta Nash-egyensúly. (i) Ha a 2. játékos a P 1 vagy P 2 utat választja, arra az 1. játékos egyetlen legjobb tiszta válasza P 4. (ii) Ha az 1. játékos P 4 -et választja, arra a 2. egyetlen legjobb tiszta válasza P 3. (iii) Ha a 2. játékos a P 3 vagy P 4 utat választja, arra az 1. játékos egyetlen legjobb tiszta válasza P 1. (iv) Ha az 1. játékos P 1 -et választja, arra a 2. egyetlen legjobb tiszta válasza P 2. A 3.4. Tételben igazolni fogjuk, hogy ha mindegyik r i azonos, akkor mindig létezik tiszta Nash-egyensúly. Ez szintén igaz akkor, ha az r i -k különbözőek is lehetnek, de minden költségfüggvény lineáris (ezt nem bizonyítjuk.) Egy másik fontos különbség a folytonos esettel szemben, hogy különböző Nash-egyensúlyoknak különböző lehet a költsége, tehát az anarchia és a stabilitás ára különböző lehet. A 8. ábrán négy játékos van, mindegyik 1 egységet szeretne szállítani az ábrán feltüntetett s i t i pontok között. Mindegyiküknek két út áll rendelkezésre: egy, illetve két él hosszúságúak. Nash-egyensúlyt kapunk, ha mindannyian a rövidebb utat választják; ekkor mindegyiküknek egy egység az áthaladási idő, tehát C(f) = 4. Ez egyben az optimális megoldás is. Ugyanakkor az is Nash-egyensúly, ha mindannyian a hosszabbik úton mennek. Ekkor az első két játékosnak 3, a 3. és 4. játékosnak pedig 2 az áthaladási idő, vagyis C(f) = 10 lesz. 15
16 s 1 = s 2 0 x 0 x t 2 = t 3 = s 4 x x 8. ábra. t 1 = s 3 = t Folytonos egyensúly A következő tételt fogjuk bizonyítani Tétel. Tetszőleges (G, r, c)-vel adott folytonos hálózati forgalmi játékban létezik egyensúlyi folyam. Ha ráadásul f és g két egyensúlyi folyam, akkor minden e élre c e (f e ) = c e (g e ). Az optimális multifolyamokat a következő rendszerrel írhatjuk le. min e Ef e c e (f e ) f e = e P f P e E f P = r i i = 1,...,k P P i f P 0 (5) A célfüggvény ugyan nem lineáris, a feltételek azonban egy korlátos poliédert (politópot) írnak le. Mivel ez egy kompakt halmaz, a Weierstrass-tétel alapján tudjuk, hogy a folytonos célfüggvény felveszi a minimumát, tehát optimális multifolyam mindig létezik. Bizonyos feltételek mellett ennél erősebb állításokat is tehetünk. Tegyük fel, hogy minden e élre az xc e (x) függvény folytonosan differenciálható és konvex. Ekkor egy konvex programozási feladatot kapunk: egy kompakt konvex tartományon minimalizálunk egy folytonos konvex függvényt. Erre könnyen látható hogy (a) két optimális megoldás tetszőleges konvex kombinációja is optimális, tehát (b) a minimum értéke egyértelmű és (c) egy megoldás pontosan akkor optimális, ha lokálisan optimális. Legyen most c e (x) = (xc e(x)) = c e (x)+xc e (x) a marginális költségfüggvény. Ez azt fejezi ki, hogy ha az e élen egy kicsi ε-nal megváltoztatnánk a folyamértéket, akkor a célfüggvényhez való hozzájárulása c e (x)ε-nal változna. Könnyen látható, hogy egy f megoldás pontosan akkor lokálisan optimális (tehát globálisan is), hogyha minden P,P P i utakra hogyha f P > 0, akkor c P (f ) c P (f ). Ebből következik az alábbi állítás: 3.3. Állítás. f akkor és csak akkor optimális megoldása a (G,r,c) feladatnak, hogyha egyensúlyi folyam az (G,r,c ) feladatra nézve. A 3.2. Tétel bizonyításához lényegében ezt az állítást fordítjuk meg: keresünk olyan h e költségfüggvényeket, amelyre h e = c e teljesül (h e (x) az xc e (x) szerepét fogja játszani). Ekkor a c-re vett egyensúlyi folyamok épp azonosak lesznek a h-ra vett optimális folyamokkal. Ezt elégíti ki a h e (x) = x 0 16 c e (t)dt
17 választás. Ha c e folytonos monoton növő függvény volt, akkor h e (x) folytonosan differenciálható és konvex lesz. A célfüggvény értéke ekkor Ψ(f) = e E h e (f e ) = e E fe 0 c e (t)dt ezt fogjuk a probléma potenciálfüggvényének nevezni. Tekinthetjük tehát a következő konvex optimalizálási feladatot: min e Eh e (f e ) f e = e P f P e E f P = r i i = 1,...,k P P i f P 0 (6) Ennek optimális megoldásai a lokálisan optimális f megoldások, amelyekre az teljesül, hogy tetszőleges P,P P i utakra hogyha f P > 0, akkor (h P) (f ) (h P ) (f ). Ez ekvivalens azzal, hogy c P (f ) c P (f ), vagyis f egyensúlyi folyam. Az állítás második feléhez legyen f és g két egyensúlyi folyam. A konvexitás miatt tudjuk, Ψ(f) = Ψ(g), és tetszőleges 0 λ 1-re λf +(1 λ)g is egyensúlyi folyam. Minden e E élre h e (λf e +(1 λ)g e ) λh e (f e )+(1 λ)h e (g e ) Mivel f és g optimális megoldások, minden élre és minden λ-ra itt egyenlőségnek kell teljesülnie. Tegyük fel indirekten, hogy valamelyik élre c e (f e ) c e (g e ); a szimmetria miatt feltehető hogy f e < g e. Legyen β = λf e +(1 λ)g e. Az előző kifejezés így alakítható: β fe ge c e (t)dt = λ c e (t)dt+(1 λ) c e (t)dt, 0 tovább írva: 0 β 0 f e c e (t)dt = (1 λ) ge f e c e (t)d t. Mivel c e monoton növő, könnyen látható, hogy ez csak a konstans függvényre teljesülhet; ekkor c e (f e ) = c e (g e ), ellentmodás Diszkrét egyensúly 3.4. Tétel. Ha mindegyik r i igény azonos, akkor létezik tiszta egyensúlyi folyam a diszkrét játékban. Bizonyítás. Tegyük fel, az egyszerűség kedvéért, hogy mindegyik r i = 1. Ismét definiálni fogunk egy potenciálfüggvényt: Ψ(f) = f e c e (i). e E i=1 Vegyük észre, hogy ez tulajdonképpen a 3.2. Tétel bizonyításában szereplő potenciálfüggvény diszkrét változata. A következő lemmából kiderül, milyen szoros kapcsolatban van ez a függvény a Nash-egyensúllyal Lemma. Legyen f egy tetszőleges megengedett multifolyam, 1 i k, és tegyük fel, hogy az i. játékos a P P i utat választotta, vagyis f P = 1. Legyen P P i egy másik lehetséges út; és f az a multifolyam, ami mindenhol megegyezik f-fel, kivéve hogy f P = 0 és f P = 1. Ekkor Ψ(f) Ψ(f ) = c P (f) c P (f ). Bizonyítás. Vegyük észre, hogy mindkét oldalon valójában ez a mennyiség szerepel: c e (f e +1) c e (f e ). e P P e P P 17
18 Mivel véges sok lehetséges f-ünk van (hiszen véges sok játékos választ véges sok út közül egyet-egyet), ezért van egy olyan f, ahol Ψ(f) minimuma felvétetik. A lemmából azonnal következik, hogy ez Nash-egyensúly. A baloldal ugyanis nempozitív, mivel f minimalizál; a jobboldalon pedig éppen az áll, hogy mennyivel változik meg az i. játékos költsége, ha P-ről P -re változtatja a stratégiáját, miközben a többi játékos választása nem változik Az anarchia ára A 3.2. Tétel következménye, hogy a folytonos hálózati forgalmi játékban ugyanaz az anarchia és a stabilitás ára Először megadunk egy egyszerű korlátot, ami azonban nem lesz éles Tétel. Tegyük fel, hogy xc e (x) γ x 0 c e (t)dt teljesül minden élre és x 0-ra. Ekkor a folytonos hálózati forgalmi játékban az anarchia ára legfeljebb γ. Bizonyítás. Legyen ismét h e (x) = x 0 c e(t)dt. Vegyük észre, hogy h e (x) xc e (x), mivel c e monoton növő. Legyen f egy egyensúlyi, g pedig egy tetszőleges multifolyam. Ekkor C(f) γψ(f) γψ(g) γc(g). Az első egyenlőtlenség a feltételből, a második h e (x) xc e (x)-ből következett. Ha például c e egy legfeljebb p-edfokú polinom, akkor γ = p + 1-gyel teljesül a feltétel. Lineáris függvényekre ez γ = 2. Be fogjuk látni, hogy ennél valójában jobb becslés is adható, sőt, szinte tetszőleges függvényosztályra meghatározható pontosan az anarchia ára Definíció. Legyen C nemnegatív, monoton növő és folytonos függvényekből álló költségfüggvény-osztály, ami tartalmazza az összes konstans függvényt. Ekkor az α(c) = sup c C sup y,r 0 mennyiséget a C-hez tartozó Pigou-korlátnak nevezzük. rc(r) yc(y)+(r y)c(r) A következőkben feltesszük C-ről, hogy nemnegatív, monoton növő és folytonos függvényekből áll Lemma. Ha C tartalmazza az összes konstans-függvényt, és a (G, r, c) folytonos hálózati forgalmi játékban minden költségfüggvény C-beli, akkor az anarchia ára tetszőlegesen közel lehet α(c)-hez. Bizonyítás. Tetszőleges ε > 0-ra válasszunk olyan c C-t, valamint y,r 0-t, amelyekre a tört értéke legalább α(c) ε. Feltehető, hogy y < r, hiszen c monoton növő, így y > r esetén a hányados értéke 1-nél kisebb. Tekintsük ismét a 4. ábrán látható Pigou-példát; legyen c e (x) = c(r), c h (x) = c(x), a forgalom mennyisége pedig r. Az egyetlen Nash-egyensúly az lesz, amikor a teljes forgalom h-n halad; ennek költsége rc(r) Ha viszont y forgalmat küldenénk e-n, akkor a költség yc(y) +(r y)c(r) lenne, ami felső becslés az optimum értékére. Tehát az anarchia ára itt legalább α(c) ε 3.9. Tétel. Egy tetszőleges C függvényosztályra, ha a (G, r, c) folytonos hálózati forgalmi játékban minden költségfüggvény C-beli, akkor az anarchia ára legfeljebb α(c). Ennek bizonyításához szükségünk lesz a Nash-egyensúly egy új jellemzésére Lemma (Variációs egyenlőtlenség). Az f megengedett multifolyam akkor és csak akkor egyensúlyi, ha minden megengedett g multifolyamra e (f e )f e e Ec c e (f e )g e. (7) e E 18
19 Bizonyítás. Rögzítsük f-et, és legyen H f (g) = k c P (f)g P = c e (f e )g e. P P i i=1 Ez tehát azt jelenti, hogy az f-hez tartozó költségeket rögzítjük, és erre nézzük a g multifolyam költségét. A két mennyiség egyenlősége ugyanúgy látható, ahogy (4)-nél. (7)-ban épp az szerepel, hogy f minimalizálja H f (g) második definícióját. Az első definícióban rögzítsünk egy i indexet. Mivel g multifolyam, ezért P P i g P = r i. Legyen a c P (f) költségek minimuma b i. Ekkor P P i c P (f)g P b i r i, tehát H f (g) k b i r i Az, hogy f Nash-egyensúlyban van, épp azt jelenti, hogy minden i-re kizárólag b i költségű utakat használ. Vagyis g = f-re itt egyenlőség áll, tehát f pontosan akkor Nash-egyensúly, ha f = g minimalizálja H f (g)-t, és ezt kellett bizonyítanunk. A 3.9. Tétel bizonyítása. Ezt felhasználva a tétel bizonyítása egyszerűen befejezhető. Legyen g egy tetszőleges multifolyam, f pedig Nash-egyensúly. A Pigou-korlát definíciója szerint minden e E élre Ezt felhasználva i=1 e E c e (g e )g e +(f e g e )c e (f e ) 1 α(c) c e(f e )f e. C(g) = e Ec e (g e )g e 1 e (f e )f e + α(c) e Ec (g e f e )c e (f e ) C(f) α(c). e E Ebből már egyszerűen levezethető az anarchia ára lineáris költségfüggvényekre Állítás. Ha minden élen lineáris a költségfüggvény, akkor az anarchia ára legfeljebb 4 3. Bizonyítás. Azt kell belátnunk, hogy a Pigou-korlát értéke 4 3. Legyen c(x) = ax+b egy költségfüggvény. a,b 0, hiszen feltettük, hogy minden költségfüggvény nemnegatív és monoton növő. Feltehető az is, hogy y r, különben a hányados értéke egynél kisebb. A bizonyítást a 9. ábra szemlélteti: a nagy téglalap a számláló, a satírozott terület pedig a nevező. ar+b ay +b b y r 9. ábra. A hányados értéke kis átalakítás után: (ar +b)r (ar+b)r a(r y)y. Látható,hogyhab-tcsökkentjük,ahányadosértékenő,tehát feltehető, hogyb = 0.(r y)y amaximumáty = r 2 -nél veszi fel. Ezeket behelyettesítve éppen 4 3 lesz az érték. 19
20 A diszkrét játékban láttuk, hogy nem mindig létezik Nash-egyensúly. A 8. ábra példája mutatja, hogy még ha létezik is, lineáris költségfüggvényekre az anarchia ára legalább 2.5. A következő tételt nem bizonyítjuk Tétel. Legyen (G,r,c) egy diszkrét forgalmi játék, amelyben minden c e költségfüggvény lineáris. Ekkor létezik egyensúlyi folyam, és az anarchia ára legfeljebb Az anarchia árának csökkentése Mit tehet egy város vezetése, vagy egy központi hálózati forgalomirányító, ha egy meglévő hálózatot szeretne hatékonyabbá tenni? Feltesszük, hogy az egyes közlekedőknek nem írhatja elő, merre menjenek, hanem ők mindig egy Nash-egyensúly szerint fognak haladni. A Braess-paradoxon kapcsán már láttunk egyféle lehetséges megközelítést, amikor új éleket adunk hozzá(ami akár rosszul is elsülhet). A következőkben két más típusú módszert mutatunk, mindkettőt a folytonos játékra Dugódíj Tegyükfel, hogyminden e élenkiszabhatunkegyegyediτ e árat,amennyitazáthaladóknakfizetnikell.ezapénz időegységre van átváltva, vagyis valójában az történik, hogy a c e költségfüggvényt c τ e = c e +τ e -vel helyettesítjük. Megmutatjuk, hogy be lehet úgy állítani a τ e díjakat, hogy c τ -ra egy egyensúlyi folyam c-szerinti költsége optimális legyen. Az eredeti (G, r, c) folytonos forgalmi játékban legyen g egy optimális multifolyam. Definiáljuk az e élen a díjat τ e = g e c e (g e)-nek. A 3.3. Állítás szerint (a c-re tett feltevések mellett) g Nash-egyensúlyban van a c költségekre nézve, ahol c e (x) = c e(x) +xc e (x), vagyis minden olyan s i t i közötti P útra, amelyre g P > 0, a c P (g) költség minimális az s i t i utak között. A c τ e (x) = c e(x) + τ e költségfüggvény épp ugyanezt a feltételt teljesíti, hiszen minden útra c P (g) = cτ P (g). A következő tételt bizonyítottuk tehát Tétel. Legyen (G,r,c) egy olyan folytonos forgalmi játék, amiben minden c e (x) függvényre xc e (x) konvex és folytonosan differenciálható. Legyen g egy optimális multifolyam, és legyen τ e = g e c e(g e ). Ekkor g egyensúlyi folyam a (G,r,c+τ) problémára Kapacitás-növelés A következő tétel tetszőleges költségfüggvényekre teljesülni fog. Legérdekesebb olyan költségfüggvények esetén lesz, amik lényegében egy élkapacitást modelleznek; ekkor a tétel következménye az lesz, hogy a közlekedők önző viselkedéséből adódó hátrányt a kapacitás kicsi növelésével ellensúlyozni lehet Tétel. Ha f egyensúlyi multifolyam a (G, r, c) folytonos forgalmi játékban, g pedig egy tetszőleges megengedett multifolyam a megduplázott kapacitásokra nézve, vagyis a (G, 2r, c) problémára, akkor C(f) C(g). Bizonyítás. Minden s i t i párra jelölje d i a minimális c P (f) útköltséget P P i -re. Az, hogy f egyensúlyi, éppen azzal ekvivalens, hogy C(f) = k i=1 r id i. Definiálunk most egy másik költségfüggvényt. Legyen c e (x) = max{c e (f e ),c e (x)}. Becsüljük c-re nézve a g multifolyam C(g) költségét! A definíció miatt c e (g e ) c e (f e ), emiatt minden P P i út c P (g) költsége legalább d i. Vagyis C(g) = k i=1 P P i c P (g)g P k d i (2r i ) = 2C(f). Becsüljük most meg C(g) C(g)-t! Azt állítjuk, hogy minden e élre és minden x 0-ra ( c e (x) c e (x))x c e (f e )f e. Valóban, ha c e (x) = c e (x) teljesül, akkor a baloldal nulla. Ha pedig c e (x) = c e (f e ), azaz c e (x) c e (f e ), akkor c e monotonitása miatt x f e, amikből szintén következik a becslés. Ezt felhasználva C(g) C(g) = e E i=1 ( c e (g e ) c e (g e ))g e e Ec e (f e )f e = C(f). Ezt az előbbi becsléssel összevetve következik, hogy C(f) C(g). 20
Játékok (domináns stratégia, alkalmazása. 2016.03.30.
 Játékok (domináns stratégia, Nash-egyensúly). A Nashegyensúly koncepciójának alkalmazása. 2016.03.30. Játékelmélet és közgazdaságtan 1914: Zermelo (sakk) 1944. Neumann-Morgenstern: Game Theory and Economic
Játékok (domináns stratégia, Nash-egyensúly). A Nashegyensúly koncepciójának alkalmazása. 2016.03.30. Játékelmélet és közgazdaságtan 1914: Zermelo (sakk) 1944. Neumann-Morgenstern: Game Theory and Economic
Párhuzamos programozás
 Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla
 MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla Jelölje Z az egész számok halmazát, N a pozitív egészek halmazát, N 0 a nem negatív egészek halmazát, Q a racionális
MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla Jelölje Z az egész számok halmazát, N a pozitív egészek halmazát, N 0 a nem negatív egészek halmazát, Q a racionális
A döntő feladatai. valós számok!
 OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
1. forduló. MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév
 MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév 1. forduló 1. feladat: Jancsi és Juliska Matematikai Memory-t játszik. A játék lényege, hogy négyzet alakú kártyákra vagy műveletsorokat írnak
MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév 1. forduló 1. feladat: Jancsi és Juliska Matematikai Memory-t játszik. A játék lényege, hogy négyzet alakú kártyákra vagy műveletsorokat írnak
Analízis elo adások. Vajda István. 2012. szeptember 24. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem 1/8 A halmaz alapfogalom, tehát nem definiáljuk. Jelölés: A halmazokat általában nyomtatott nagybetu vel jelöljük Egy H halmazt akkor tekintünk
Vajda István Neumann János Informatika Kar Óbudai Egyetem 1/8 A halmaz alapfogalom, tehát nem definiáljuk. Jelölés: A halmazokat általában nyomtatott nagybetu vel jelöljük Egy H halmazt akkor tekintünk
V. Kétszemélyes játékok
 Teljes információjú, véges, zéró összegű kétszemélyes játékok V. Kétszemélyes játékok Két játékos lép felváltva adott szabályok szerint. Mindkét játékos ismeri a maga és az ellenfele összes választási
Teljes információjú, véges, zéró összegű kétszemélyes játékok V. Kétszemélyes játékok Két játékos lép felváltva adott szabályok szerint. Mindkét játékos ismeri a maga és az ellenfele összes választási
Jelek tanulmányozása
 Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
Conjoint-analízis példa (egyszerűsített)
 Conjoint-analízis példa (egyszerűsített) Az eljárás meghatározza, hogy a fogyasztók a vásárlás szempontjából lényeges terméktulajdonságoknak mekkora relatív fontosságot tulajdonítanak és megadja a tulajdonságok
Conjoint-analízis példa (egyszerűsített) Az eljárás meghatározza, hogy a fogyasztók a vásárlás szempontjából lényeges terméktulajdonságoknak mekkora relatív fontosságot tulajdonítanak és megadja a tulajdonságok
A Hozzárendelési feladat megoldása Magyar-módszerrel
 A Hozzárendelési feladat megoldása Magyar-módszerrel Virtuális vállalat 2013-2014/1. félév 3. gyakorlat Dr. Kulcsár Gyula A Hozzárendelési feladat Adott meghatározott számú gép és ugyanannyi független
A Hozzárendelési feladat megoldása Magyar-módszerrel Virtuális vállalat 2013-2014/1. félév 3. gyakorlat Dr. Kulcsár Gyula A Hozzárendelési feladat Adott meghatározott számú gép és ugyanannyi független
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria
 005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
Operációkutatás. 2. konzultáció: Lineáris programozás (2. rész) Feladattípusok
 Operációkutatás NYME KTK, gazdálkodás szak, levelező alapképzés 00/003 tanév, II évf félév Előadó: Dr Takách Géza NyME FMK Információ Technológia Tanszék 9400 Sopron, Bajcsy Zs u 9 GT fszt 3 (99) 58 640
Operációkutatás NYME KTK, gazdálkodás szak, levelező alapképzés 00/003 tanév, II évf félév Előadó: Dr Takách Géza NyME FMK Információ Technológia Tanszék 9400 Sopron, Bajcsy Zs u 9 GT fszt 3 (99) 58 640
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
Algebra es sz amelm elet 3 el oad as Rel aci ok Waldhauser Tam as 2014 oszi f el ev
 Algebra és számelmélet 3 előadás Relációk Waldhauser Tamás 2014 őszi félév Relációk reláció lat. 1. kapcsolat, viszony; összefüggés vmivel 2. viszonylat, vonatkozás reláció lat. 3. mat halmazok elemei
Algebra és számelmélet 3 előadás Relációk Waldhauser Tamás 2014 őszi félév Relációk reláció lat. 1. kapcsolat, viszony; összefüggés vmivel 2. viszonylat, vonatkozás reláció lat. 3. mat halmazok elemei
2011. március 9. Dr. Vincze Szilvia
 . márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
. márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
Analízis elo adások. Vajda István. 2012. október 3. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
Arany Dániel Matematikai Tanulóverseny 2011/2012-es tanév első (iskolai) forduló haladók I. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 011/01-es tanév első (iskolai) forduló haladók I. kategória Megoldások és javítási útmutató 1. Az ábrán látható ABC derékszögű háromszög
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 011/01-es tanév első (iskolai) forduló haladók I. kategória Megoldások és javítási útmutató 1. Az ábrán látható ABC derékszögű háromszög
BOLYAI MATEMATIKA CSAPATVERSENY FŐVÁROSI DÖNTŐ SZÓBELI (2005. NOVEMBER 26.) 5. osztály
 5. osztály Írd be az ábrán látható hat üres körbe a 10, 30, 40, 60, 70 és 90 számokat úgy, hogy a háromszög mindhárom oldala mentén a számok összege 200 legyen! 50 20 80 Egy dobozban háromféle színű: piros,
5. osztály Írd be az ábrán látható hat üres körbe a 10, 30, 40, 60, 70 és 90 számokat úgy, hogy a háromszög mindhárom oldala mentén a számok összege 200 legyen! 50 20 80 Egy dobozban háromféle színű: piros,
Lineáris algebra gyakorlat
 Lineáris algebra gyakorlat 3 gyakorlat Gyakorlatvezet : Bogya Norbert 2012 február 27 Bogya Norbert Lineáris algebra gyakorlat (3 gyakorlat) Tartalom Egyenletrendszerek Cramer-szabály 1 Egyenletrendszerek
Lineáris algebra gyakorlat 3 gyakorlat Gyakorlatvezet : Bogya Norbert 2012 február 27 Bogya Norbert Lineáris algebra gyakorlat (3 gyakorlat) Tartalom Egyenletrendszerek Cramer-szabály 1 Egyenletrendszerek
Azonosító jel: Matematika emelt szint
 I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
Shared IMAP beállítása magyar nyelvű webmailes felületen
 Shared IMAP beállítása magyar nyelvű webmailes felületen A következő ismertető segítséget nyújt a szervezeti cím küldőként való beállításában a caesar Webmailes felületén. Ahhoz, hogy a Shared Imaphoz
Shared IMAP beállítása magyar nyelvű webmailes felületen A következő ismertető segítséget nyújt a szervezeti cím küldőként való beállításában a caesar Webmailes felületén. Ahhoz, hogy a Shared Imaphoz
Az aktiválódásoknak azonban itt még nincs vége, ugyanis az aktiválódások 30 évenként ismétlődnek!
 1 Mindannyiunk életében előfordulnak jelentős évek, amikor is egy-egy esemény hatására a sorsunk új irányt vesz. Bár ezen események többségének ott és akkor kevésbé tulajdonítunk jelentőséget, csak idővel,
1 Mindannyiunk életében előfordulnak jelentős évek, amikor is egy-egy esemény hatására a sorsunk új irányt vesz. Bár ezen események többségének ott és akkor kevésbé tulajdonítunk jelentőséget, csak idővel,
Árverés kezelés ECP WEBSHOP BEÉPÜLŐ MODUL ÁRVERÉS KEZELŐ KIEGÉSZÍTÉS. v2.9.28 ECP WEBSHOP V1.8 WEBÁRUHÁZ MODULHOZ
 v2.9.28 Árverés kezelés ECP WEBSHOP BEÉPÜLŐ MODUL ÁRVERÉS KEZELŐ KIEGÉSZÍTÉS ECP WEBSHOP V1.8 WEBÁRUHÁZ MODULHOZ AW STUDIO Nyíregyháza, Luther utca 5. 1/5, info@awstudio.hu Árverés létrehozása Az árverésre
v2.9.28 Árverés kezelés ECP WEBSHOP BEÉPÜLŐ MODUL ÁRVERÉS KEZELŐ KIEGÉSZÍTÉS ECP WEBSHOP V1.8 WEBÁRUHÁZ MODULHOZ AW STUDIO Nyíregyháza, Luther utca 5. 1/5, info@awstudio.hu Árverés létrehozása Az árverésre
Egyre nagyobb profitot generálnak a mobiltelefonnal végzett vásárlások, és egyre többet hezitálunk vásárlás előtt
 Egyre nagyobb profitot generálnak a mobiltelefonnal végzett vásárlások, és egyre többet hezitálunk vásárlás előtt 2016 ban még nagyobb hangsúlyt kapnak az e kereskedelmeben az okostelefonok. 2015 ben még
Egyre nagyobb profitot generálnak a mobiltelefonnal végzett vásárlások, és egyre többet hezitálunk vásárlás előtt 2016 ban még nagyobb hangsúlyt kapnak az e kereskedelmeben az okostelefonok. 2015 ben még
A fiatalok pénzügyi kultúrája Számít-e a gazdasági oktatás?
 A fiatalok pénzügyi kultúrája Számít-e a gazdasági oktatás? XXXII. OTDK Konferencia 2015. április 9-11. Készítette: Pintye Alexandra Konzulens: Dr. Kiss Marietta A kultúrától a pénzügyi kultúráig vezető
A fiatalok pénzügyi kultúrája Számít-e a gazdasági oktatás? XXXII. OTDK Konferencia 2015. április 9-11. Készítette: Pintye Alexandra Konzulens: Dr. Kiss Marietta A kultúrától a pénzügyi kultúráig vezető
Érettségi feladatok Algoritmusok egydimenziós tömbökkel (vektorokkal) 1/6. Alapműveletek
 Érettségi feladatok Algoritmusok egydimenziós tömbökkel (vektorokkal) 1/6 A tömbök deklarálásakor Pascal és C/C++ nyelvekben minden esetben meg kell adni az indexelést (Pascal) vagy az elemszámot (C/C++).
Érettségi feladatok Algoritmusok egydimenziós tömbökkel (vektorokkal) 1/6 A tömbök deklarálásakor Pascal és C/C++ nyelvekben minden esetben meg kell adni az indexelést (Pascal) vagy az elemszámot (C/C++).
V. Játékok. Kétszemélyes, teljes információjú, véges és determinisztikus, zéró összegű, játékok. Állapottér-reprezentáció. Grundy mama játéka
 Kétszemélyes, teljes információjú, véges és determinisztikus, zéró összegű, játékok V. Játékok Két játékos lép felváltva adott szabályok szerint, amíg a játszma véget nem ér. Mindkét játékos ismeri a maga
Kétszemélyes, teljes információjú, véges és determinisztikus, zéró összegű, játékok V. Játékok Két játékos lép felváltva adott szabályok szerint, amíg a játszma véget nem ér. Mindkét játékos ismeri a maga
[MECHANIKA- HAJLÍTÁS]
![[MECHANIKA- HAJLÍTÁS] [MECHANIKA- HAJLÍTÁS]](/thumbs/39/20428431.jpg) 2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
Spiel der Türme TORNYOK JÁTÉKA
 Spiel der Türme TORNYOK JÁTÉKA A történet a középkori Tornyok Városával kezdődik. A négy hataloméhes nemesi család mindegyike arra törekszik, hogy megszerezzék a befolyást a legerősebb torony vagy még
Spiel der Türme TORNYOK JÁTÉKA A történet a középkori Tornyok Városával kezdődik. A négy hataloméhes nemesi család mindegyike arra törekszik, hogy megszerezzék a befolyást a legerősebb torony vagy még
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
Részvénykereskedés a gyakorlatban
 Részvénykereskedés a gyakorlatban 2015. Június 2. 17:30 A webinárium hamarosan kezdődik. Kérjük, ellenőrizze, hogy számítógépe hangszórója be van-e kapcsolva. További technikai információk: https://www.kbcequitas.hu/menu/tamogatas/tudastar/oktatas
Részvénykereskedés a gyakorlatban 2015. Június 2. 17:30 A webinárium hamarosan kezdődik. Kérjük, ellenőrizze, hogy számítógépe hangszórója be van-e kapcsolva. További technikai információk: https://www.kbcequitas.hu/menu/tamogatas/tudastar/oktatas
Számítógépes vírusok
 A vírus fogalma A számítógépes vírus olyan szoftver, mely képes önmaga megsokszorozására és terjesztésére. A vírus célja általában a számítógép rendeltetésszerű működésének megzavarása, esetleg a gép tönkretétele,
A vírus fogalma A számítógépes vírus olyan szoftver, mely képes önmaga megsokszorozására és terjesztésére. A vírus célja általában a számítógép rendeltetésszerű működésének megzavarása, esetleg a gép tönkretétele,
http://www.olcsoweboldal.hu ingyenes tanulmány GOOGLE INSIGHTS FOR SEARCH
 2008. augusztus 5-én elindult a Google Insights for Search, ami betekintést nyújt a keresőt használók tömegeinek lelkivilágába, és időben-térben szemlélteti is, amit tud róluk. Az alapja a Google Trends,
2008. augusztus 5-én elindult a Google Insights for Search, ami betekintést nyújt a keresőt használók tömegeinek lelkivilágába, és időben-térben szemlélteti is, amit tud róluk. Az alapja a Google Trends,
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (13. fejezet)
 Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
Az Európai Szabadalmi Egyezmény végrehajtási szabályainak 2010. április 1-étől hatályba lépő lényeges változásai
 DANUBIA Szabadalmi és Védjegy Iroda Kft. Az Európai Szabadalmi Egyezmény végrehajtási szabályainak 2010. április 1-étől hatályba lépő lényeges változásai A Magyar Iparjogvédelmi és Szerzői Jogi Egyesület
DANUBIA Szabadalmi és Védjegy Iroda Kft. Az Európai Szabadalmi Egyezmény végrehajtási szabályainak 2010. április 1-étől hatályba lépő lényeges változásai A Magyar Iparjogvédelmi és Szerzői Jogi Egyesület
BOLYAI MATEMATIKA CSAPATVERSENY DÖNTŐ 2004. 5. osztály
 5. osztály Ha egy négyzetet az ábrán látható módon feldarabolunk, akkor a tangram nevű ősi kínai játékot kapjuk. Mekkora a nagy négyzet területe, ha a kicsié 8 cm 2? (A kis négyzet egyik csúcsa a nagy
5. osztály Ha egy négyzetet az ábrán látható módon feldarabolunk, akkor a tangram nevű ősi kínai játékot kapjuk. Mekkora a nagy négyzet területe, ha a kicsié 8 cm 2? (A kis négyzet egyik csúcsa a nagy
EPER E-KATA integráció
 EPER E-KATA integráció 1. Összhang a Hivatalban A hivatalban használt szoftverek összekapcsolása, integrálása révén az egyes osztályok, nyilvántartások között egyezőség jön létre. Mit is jelent az integráció?
EPER E-KATA integráció 1. Összhang a Hivatalban A hivatalban használt szoftverek összekapcsolása, integrálása révén az egyes osztályok, nyilvántartások között egyezőség jön létre. Mit is jelent az integráció?
BOLYAI MATEMATIKA CSAPATVERSENY ORSZÁGOS DÖNTŐ SZÓBELI (2012. NOVEMBER 24.) 3. osztály
 3. osztály Két szám összege 33. Mennyi ennek a két számnak a különbsége, ha az egyik kétszerese a másiknak? Hány olyan háromjegyű szám van, amelyben a számjegyek összege legalább 25? 4. osztály A Zimrili
3. osztály Két szám összege 33. Mennyi ennek a két számnak a különbsége, ha az egyik kétszerese a másiknak? Hány olyan háromjegyű szám van, amelyben a számjegyek összege legalább 25? 4. osztály A Zimrili
118. Szerencsi Többcélú Kistérségi Társulás
 BAZ MTrT TERVEZŐI VÁLASZ 118. Szerencsi Többcélú Kistérségi Társulás 1. Szakmai szempontból elhibázott döntésnek tartjuk a Tokaji Borvidék Világörökségi terület közvetlen környezetében erőmű létesítését.
BAZ MTrT TERVEZŐI VÁLASZ 118. Szerencsi Többcélú Kistérségi Társulás 1. Szakmai szempontból elhibázott döntésnek tartjuk a Tokaji Borvidék Világörökségi terület közvetlen környezetében erőmű létesítését.
GAZDASÁGI MATEMATIKA 1. 1. Gyakorlat
 GAZDASÁGI MATEMATIKA 1. 1. Gyakorlat Bemutatkozás Chmelik Gábor óraadó BGF-KKK Módszertani Intézeti Tanszéki Osztály chmelik.gabor@kkk.bgf.hu http://www.cs.elte.hu/ chmelik Fogadóóra: e-mailben egyeztetett
GAZDASÁGI MATEMATIKA 1. 1. Gyakorlat Bemutatkozás Chmelik Gábor óraadó BGF-KKK Módszertani Intézeti Tanszéki Osztály chmelik.gabor@kkk.bgf.hu http://www.cs.elte.hu/ chmelik Fogadóóra: e-mailben egyeztetett
Tájékoztató a szerződés módosításáról_munkaruházati termékek szállítása (5. rész)
 Tájékoztató a szerződés módosításáról_munkaruházati termékek szállítása (5. rész) Közbeszerzési Értesítő száma: 2016/61 Beszerzés tárgya: Árubeszerzés Hirdetmény típusa: Tájékoztató a szerződés módosításáról/2015
Tájékoztató a szerződés módosításáról_munkaruházati termékek szállítása (5. rész) Közbeszerzési Értesítő száma: 2016/61 Beszerzés tárgya: Árubeszerzés Hirdetmény típusa: Tájékoztató a szerződés módosításáról/2015
HÁLÓZATSEMLEGESSÉG - EGYSÉGES INTERNET SZOLGÁLTATÁS-LEÍRÓ TÁBLÁZAT
 HÁLÓZATSEMLEGESSÉG - EGYSÉGES INTERNET SZOLGÁLTATÁS-LEÍRÓ TÁBLÁZAT - 2016.04.01 után kötött szerződésekre Díjcsomag neve Go Go+ Go EU Go EU+ Kínált letöltési sebesség - 3G 42 Mbit/s 42 Mbit/s 42 Mbit/s
HÁLÓZATSEMLEGESSÉG - EGYSÉGES INTERNET SZOLGÁLTATÁS-LEÍRÓ TÁBLÁZAT - 2016.04.01 után kötött szerződésekre Díjcsomag neve Go Go+ Go EU Go EU+ Kínált letöltési sebesség - 3G 42 Mbit/s 42 Mbit/s 42 Mbit/s
Mágneses szuszceptibilitás vizsgálata
 Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 2005. november. I. rész
 Szászné Simon Judit, 005. november Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 005. november. feladat I. rész Oldjuk meg a valós számok halmazán a x 5x
Szászné Simon Judit, 005. november Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 005. november. feladat I. rész Oldjuk meg a valós számok halmazán a x 5x
Esettanulmányok és modellek 1 Termelésprogramozás az iparban
 Esettanulmányok és modellek Termelésprogramozás az iparban Készítette: Dr. Ábrahám István Egyszerű termelésprogramozási feladatok.) gép felhasználásával kétféle terméket állítanak elő. Az egyes termékekhez
Esettanulmányok és modellek Termelésprogramozás az iparban Készítette: Dr. Ábrahám István Egyszerű termelésprogramozási feladatok.) gép felhasználásával kétféle terméket állítanak elő. Az egyes termékekhez
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN
 GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten RACIONÁLIS TÖRTFÜGGVÉNYEK INTEGRÁLJA Készítette: Gábor Szakmai felel s: Gábor Vázlat
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten RACIONÁLIS TÖRTFÜGGVÉNYEK INTEGRÁLJA Készítette: Gábor Szakmai felel s: Gábor Vázlat
A skatulya-elv alkalmazásai
 1 A skatulya-elv alkalmazásai Számelmélet 1. Az első 4n darab pozitív egész számot beosztjuk n számú halmazba. Igazoljuk, hogy mindig lesz három olyan szám, amelyek ugyanabban a halmazban vannak és valamely
1 A skatulya-elv alkalmazásai Számelmélet 1. Az első 4n darab pozitív egész számot beosztjuk n számú halmazba. Igazoljuk, hogy mindig lesz három olyan szám, amelyek ugyanabban a halmazban vannak és valamely
2004. december 1. Irodalom
 LINEÁRIS LEKÉPEZÉSEK I. 2004. december 1. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László:
LINEÁRIS LEKÉPEZÉSEK I. 2004. december 1. Irodalom A fogalmakat, definíciókat illetően két forrásra támaszkodhatnak: ezek egyrészt elhangzanak az előadáson, másrészt megtalálják a jegyzetben: Szabó László:
Fordítóprogramok Készítette: Nagy Krisztián
 Fordítóprogramok Készítette: Nagy Krisztián Reguláris kifejezések (FLEX) Alapelemek kiválasztása az x karakter. tetszőleges karakter (kivéve újsor) [xyz] karakterhalmaz; vagy egy x, vagy egy y vagy egy
Fordítóprogramok Készítette: Nagy Krisztián Reguláris kifejezések (FLEX) Alapelemek kiválasztása az x karakter. tetszőleges karakter (kivéve újsor) [xyz] karakterhalmaz; vagy egy x, vagy egy y vagy egy
Boldva és Vidéke Taka r ékszövetkezet
 A Takarékszövetkezet jelen ben szereplő, változó kamatozású i termékei esetében i kamatváltozást tesz közzé, az állandó (fix) kamatozású i termékek esetében pedig a 2014.06.15-től lekötésre kerülő ekre
A Takarékszövetkezet jelen ben szereplő, változó kamatozású i termékei esetében i kamatváltozást tesz közzé, az állandó (fix) kamatozású i termékek esetében pedig a 2014.06.15-től lekötésre kerülő ekre
Boldva és Vidéke Taka r ékszövetkezet
 A Takarékszövetkezet jelen ben szereplő, változó kamatozású i termékei esetében i kamatváltozást tesz közzé, az állandó (fix) kamatozású i termékek esetében pedig a 2014.08.13-tól lekötésre kerülő ekre
A Takarékszövetkezet jelen ben szereplő, változó kamatozású i termékei esetében i kamatváltozást tesz közzé, az állandó (fix) kamatozású i termékek esetében pedig a 2014.08.13-tól lekötésre kerülő ekre
Előre is köszönjük munkádat és izgatottan várjuk válaszaidat! A Helleresek
 A Heller Farkas Szakkollégium 2016-os felvételi kérdőívét tartod a kezedben, amely által megteheted az első lépést a Helleres úton. Az írásbeli kérdőív kitöltése után a felvételi következő lépése egy szóbeli
A Heller Farkas Szakkollégium 2016-os felvételi kérdőívét tartod a kezedben, amely által megteheted az első lépést a Helleres úton. Az írásbeli kérdőív kitöltése után a felvételi következő lépése egy szóbeli
Útmutató a vízumkérő lap kitöltéséhez
 Útmutató a vízumkérő lap kitöltéséhez A vízumkérő lap ( Visa application form of the People s Republic of China, Form V. 2013 ) az egyik legfontosabb dokumentum, amit a kínai vízumra való jelentkezésnél
Útmutató a vízumkérő lap kitöltéséhez A vízumkérő lap ( Visa application form of the People s Republic of China, Form V. 2013 ) az egyik legfontosabb dokumentum, amit a kínai vízumra való jelentkezésnél
Szervezeti formák bemutatása
 Szervezeti formák bemutatása Szakgyógyszerész-jelöltek képzése Király Gyula Szervezet fogalma Csoportot egyének tulajdonságai és a köztük zajló interakciók hoznak létre. Szervezet: egymással összefüggő
Szervezeti formák bemutatása Szakgyógyszerész-jelöltek képzése Király Gyula Szervezet fogalma Csoportot egyének tulajdonságai és a köztük zajló interakciók hoznak létre. Szervezet: egymással összefüggő
Az informatika oktatás téveszméi
 Az informatika oktatás Az informatika definíciója Definíció-1: az informatika az információ keletkezésével, továbbításával, tárolásával, feldolgozásával foglalkozó tudomány. Definíció-2: informatika =
Az informatika oktatás Az informatika definíciója Definíció-1: az informatika az információ keletkezésével, továbbításával, tárolásával, feldolgozásával foglalkozó tudomány. Definíció-2: informatika =
avagy, hogyan lehetünk hatékonyabbak (nemcsak) a hivatásunkban
 avagy, hogyan lehetünk hatékonyabbak (nemcsak) a hivatásunkban Rendszerek, amelyekben élünk: Család Munkahely Baráti kör Iskolai közösség stb. - meghatározott rend szerint működnek rend, törv rvények
avagy, hogyan lehetünk hatékonyabbak (nemcsak) a hivatásunkban Rendszerek, amelyekben élünk: Család Munkahely Baráti kör Iskolai közösség stb. - meghatározott rend szerint működnek rend, törv rvények
A SZÁMFOGALOM KIALAKÍTÁSA
 A SZÁMFOGALOM KIALAKÍTÁSA TERMÉSZETES SZÁMOK ÉRTELMEZÉSE 1-5. OSZTÁLY Számok értelmezése 0-tól 10-ig: Véges halmazok számosságaként Mérőszámként Sorszámként Jelzőszámként A számok fogalmának kiterjesztése
A SZÁMFOGALOM KIALAKÍTÁSA TERMÉSZETES SZÁMOK ÉRTELMEZÉSE 1-5. OSZTÁLY Számok értelmezése 0-tól 10-ig: Véges halmazok számosságaként Mérőszámként Sorszámként Jelzőszámként A számok fogalmának kiterjesztése
HWDEV-02A GSM TERMOSZTÁT
 HWDEV-02A GSM TERMOSZTÁT 2010 HASZNÁLATI ÚTMUTATÓ A termosztát egy beépített mobiltelefonnal rendelkezik. Ez fogadja az Ön hívását ha felhívja a termosztát telefonszámát. Érdemes ezt a telefonszámot felírni
HWDEV-02A GSM TERMOSZTÁT 2010 HASZNÁLATI ÚTMUTATÓ A termosztát egy beépített mobiltelefonnal rendelkezik. Ez fogadja az Ön hívását ha felhívja a termosztát telefonszámát. Érdemes ezt a telefonszámot felírni
Dr. Schuster György. 2014. február 21. Real-time operációs rendszerek RTOS
 Real-time operációs rendszerek RTOS 2014. február 21. Az ütemező (Scheduler) Az operációs rendszer azon része (kódszelete), mely valamilyen konkurens hozzáférés-elosztási problémát próbál implementálni.
Real-time operációs rendszerek RTOS 2014. február 21. Az ütemező (Scheduler) Az operációs rendszer azon része (kódszelete), mely valamilyen konkurens hozzáférés-elosztási problémát próbál implementálni.
Épületvillamosság laboratórium. Villámvédelemi felfogó-rendszer hatásosságának vizsgálata
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
Minta. A középszintű szóbeli vizsga értékelési útmutatója
 A középszintű szóbeli vizsga értékelési útmutatója A szóbeli feladatok értékelése központilag kidolgozott analitikus skálák segítségével történik. Ez az értékelési eljárás meghatározott értékelési szempontokon,
A középszintű szóbeli vizsga értékelési útmutatója A szóbeli feladatok értékelése központilag kidolgozott analitikus skálák segítségével történik. Ez az értékelési eljárás meghatározott értékelési szempontokon,
TERMÉK AJÁNLÁSA GO GUIDE KÉSZÜLJ FEL
 TERMÉK AJÁNLÁSA GO GUIDE BEVEZETÉS TERMÉK AJÁNLÁSA MIRŐL VAN SZÓ, ÉS EZ MIÉRT FONTOS? Ahogy Bowerman is a győzelemhez szükséges előnyt kívánta megadni sportolóinak, a te feladatod sem más, mint hogy olyan
TERMÉK AJÁNLÁSA GO GUIDE BEVEZETÉS TERMÉK AJÁNLÁSA MIRŐL VAN SZÓ, ÉS EZ MIÉRT FONTOS? Ahogy Bowerman is a győzelemhez szükséges előnyt kívánta megadni sportolóinak, a te feladatod sem más, mint hogy olyan
Diszkrét matematika I. gyakorlat
 Diszkrét matematika I. gyakorlat 1. Gyakorlat Bogya Norbert Bolyai Intézet 2012. szeptember 4-5. Bogya Norbert (Bolyai Intézet) Diszkrét matematika I. gyakorlat 2012. szeptember 4-5. 1 / 21 Információk
Diszkrét matematika I. gyakorlat 1. Gyakorlat Bogya Norbert Bolyai Intézet 2012. szeptember 4-5. Bogya Norbert (Bolyai Intézet) Diszkrét matematika I. gyakorlat 2012. szeptember 4-5. 1 / 21 Információk
MATEMATIKA HETI 3 ÓRA
 EURÓPAI ÉRETTSÉGI 010 MATEMATIKA HETI 3 ÓRA IDŐPONT : 010. június 4. A VIZSGA IDŐTARTAMA : 3 óra (180 perc) MEGENGEDETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
EURÓPAI ÉRETTSÉGI 010 MATEMATIKA HETI 3 ÓRA IDŐPONT : 010. június 4. A VIZSGA IDŐTARTAMA : 3 óra (180 perc) MEGENGEDETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
Kiskunmajsa Város Önkormányzatának partnertérképe
 Kiskunmajsa Város Önkormányzatának partnertérképe Kiskunmajsa Város Önkormányzatának potenciális partnerei Helyi vállalkozások Kiskunmajsa Város Önkormányzata számára a lehetséges vállalati partnerek feltérképezéséhez
Kiskunmajsa Város Önkormányzatának partnertérképe Kiskunmajsa Város Önkormányzatának potenciális partnerei Helyi vállalkozások Kiskunmajsa Város Önkormányzata számára a lehetséges vállalati partnerek feltérképezéséhez
ORSZÁGOS KÖRNYEZETEGÉSZSÉGÜGYI INTÉZET
 ORSZÁGOS KÖRNYEZETEGÉSZSÉGÜGYI INTÉZET 197 Budapest, Gyáli út 2-6. Levélcím: 1437 Budapest Pf.: 839 Telefon: (6-1) 476-11 Fax: (6-1) 21-148 http://efrirk.antsz.hu/oki/ A PARLAGFŰ POLLENSZÓRÁSÁNAK ALAKULÁSA
ORSZÁGOS KÖRNYEZETEGÉSZSÉGÜGYI INTÉZET 197 Budapest, Gyáli út 2-6. Levélcím: 1437 Budapest Pf.: 839 Telefon: (6-1) 476-11 Fax: (6-1) 21-148 http://efrirk.antsz.hu/oki/ A PARLAGFŰ POLLENSZÓRÁSÁNAK ALAKULÁSA
Mesterséges Intelligencia. Csató Lehel. Csató Lehel. Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2006/2007
 Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2006/2007 Az Előadások Témái Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció Gráfkeresési stratégiák Szemantikus hálók
Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2006/2007 Az Előadások Témái Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció Gráfkeresési stratégiák Szemantikus hálók
Jarabin Kinga LÁBNYOMOK
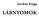 Jarabin Kinga LÁBNYOMOK Álmokkal indulunk Már egész kis korban, óvodásként is van arról elképzelésünk, mivel szeretnénk foglalkozni, ha egyszer felnövünk. Álmokkal indulunk az iskolapadba, az iskolapadból
Jarabin Kinga LÁBNYOMOK Álmokkal indulunk Már egész kis korban, óvodásként is van arról elképzelésünk, mivel szeretnénk foglalkozni, ha egyszer felnövünk. Álmokkal indulunk az iskolapadba, az iskolapadból
1. Metrótörténet. A feladat folytatása a következő oldalon található. Informatika emelt szint. m2_blaha.jpg, m3_nagyvaradter.jpg és m4_furopajzs.jpg.
 1. Metrótörténet A fővárosi metróhálózat a tömegközlekedés gerincét adja. A vonalak építésének története egészen a XIX. század végéig nyúlik vissza. Feladata, hogy készítse el a négy metróvonal történetét
1. Metrótörténet A fővárosi metróhálózat a tömegközlekedés gerincét adja. A vonalak építésének története egészen a XIX. század végéig nyúlik vissza. Feladata, hogy készítse el a négy metróvonal történetét
Vállalkozásfinanszírozás
 Vállalkozásfinanszírozás Területei Pénzügyi tervezés Beruházás finanszírozás Hitelintézeti eljárás Pénzügyi tervezés a vállalkozásnál tervezés célja: bizonytalanság kockázat csökkentése jövőbeli események,
Vállalkozásfinanszírozás Területei Pénzügyi tervezés Beruházás finanszírozás Hitelintézeti eljárás Pénzügyi tervezés a vállalkozásnál tervezés célja: bizonytalanság kockázat csökkentése jövőbeli események,
[GVMGS11MNC] Gazdaságstatisztika
![[GVMGS11MNC] Gazdaságstatisztika [GVMGS11MNC] Gazdaságstatisztika](/thumbs/40/21500887.jpg) [GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
[GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
Technikai daytrade és befektetési hitel
 Technikai daytrade és befektetési hitel 2015. október 13. 17:30 A webinárium hamarosan kezdődik. Kérjük, ellenőrizze, hogy számítógépe hangszórója be van-e kapcsolva. További technikai információk: https://www.kbcequitas.hu/menu/tamogatas/tudastar/oktatas
Technikai daytrade és befektetési hitel 2015. október 13. 17:30 A webinárium hamarosan kezdődik. Kérjük, ellenőrizze, hogy számítógépe hangszórója be van-e kapcsolva. További technikai információk: https://www.kbcequitas.hu/menu/tamogatas/tudastar/oktatas
Koordináta - geometria I.
 Koordináta - geometria I. DEFINÍCIÓ: (Helyvektor) A derékszögű koordináta - rendszerben a pont helyvektora az origóból a pontba mutató vektor. TÉTEL: Ha i az (1; 0) és j a (0; 1) pont helyvektora, akkor
Koordináta - geometria I. DEFINÍCIÓ: (Helyvektor) A derékszögű koordináta - rendszerben a pont helyvektora az origóból a pontba mutató vektor. TÉTEL: Ha i az (1; 0) és j a (0; 1) pont helyvektora, akkor
Kerékpárlabda kvalifikációs szabályzat
 Kerékpárlabda kvalifikációs szabályzat Érvényesség kezdete: Junior kategória 2016 június 1 Felnőtt kategória 2016 január 1 Tartalom I. Célja... 3 II. Szabályozás... 3 1) A versenyek meghatározása... 3
Kerékpárlabda kvalifikációs szabályzat Érvényesség kezdete: Junior kategória 2016 június 1 Felnőtt kategória 2016 január 1 Tartalom I. Célja... 3 II. Szabályozás... 3 1) A versenyek meghatározása... 3
Kombinatorika. 9. előadás. Farkas István. DE ATC Gazdaságelemzési és Statisztikai Tanszék. Kombinatorika p. 1/
 Kombinatorika 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Kombinatorika p. 1/ Permutáció Definíció. Adott n különböző elem. Az elemek egy meghatározott sorrendjét az adott
Kombinatorika 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Kombinatorika p. 1/ Permutáció Definíció. Adott n különböző elem. Az elemek egy meghatározott sorrendjét az adott
Analízis előadások. Vajda István. 2013. február 10. Neumann János Informatika Kar Óbudai Egyetem
 Analízis előadások Vajda István Neumann János Informatika Kar Óbudai Egyetem 013. február 10. Vajda István (Óbudai Egyetem) Analízis előadások 013. február 10. 1 / 3 Az elemi függvények csoportosítása
Analízis előadások Vajda István Neumann János Informatika Kar Óbudai Egyetem 013. február 10. Vajda István (Óbudai Egyetem) Analízis előadások 013. február 10. 1 / 3 Az elemi függvények csoportosítása
Kérdések és feladatok
 Kérdések és feladatok 1. A mesében több szám is szerepel. Próbáld meg felidézni ezeket, majd töltsd ki a táblázatot! Ügyelj, hogy a páros és a páratlan számok külön oszlopba kerüljenek! Hány napos volt
Kérdések és feladatok 1. A mesében több szám is szerepel. Próbáld meg felidézni ezeket, majd töltsd ki a táblázatot! Ügyelj, hogy a páros és a páratlan számok külön oszlopba kerüljenek! Hány napos volt
Halmazok és függvények
 Halmazok és függvények Óraszám: 2+2 Kreditszám: 6 Meghirdető tanszék: Analízis Debrecen, 2005. A tárgy neve: Halmazok és függvények (előadás) A tárgy oktatója: Dr. Gilányi Attila Óraszám/hét: 2 Kreditszám:
Halmazok és függvények Óraszám: 2+2 Kreditszám: 6 Meghirdető tanszék: Analízis Debrecen, 2005. A tárgy neve: Halmazok és függvények (előadás) A tárgy oktatója: Dr. Gilányi Attila Óraszám/hét: 2 Kreditszám:
Dr. Kulcsár Gyula. Virtuális vállalat 2013-2014 1. félév. Projektütemezés. Virtuális vállalat 2013-2014 1. félév 5. gyakorlat Dr.
 Projektütemezés Virtuális vállalat 03-04. félév 5. gyakorlat Dr. Kulcsár Gyula Projektütemezési feladat megoldása Projekt: Projektütemezés Egy nagy, összetett, általában egyedi igény alapján előállítandó
Projektütemezés Virtuális vállalat 03-04. félév 5. gyakorlat Dr. Kulcsár Gyula Projektütemezési feladat megoldása Projekt: Projektütemezés Egy nagy, összetett, általában egyedi igény alapján előállítandó
ÚTMUTATÓ A KONTROLL ADATSZOLGÁLTATÁS ELKÉSZÍTÉSÉHEZ (2012-TŐL)
 ÚTMUTATÓ A KONTROLL ADATSZOLGÁLTATÁS ELKÉSZÍTÉSÉHEZ (2012-TŐL) A 2006-2010. évre vonatkozó, régebbi adatszolgáltatások esetében az adatszolgáltatás menete a mostanitól eltérő, a benyújtáshoz különböző
ÚTMUTATÓ A KONTROLL ADATSZOLGÁLTATÁS ELKÉSZÍTÉSÉHEZ (2012-TŐL) A 2006-2010. évre vonatkozó, régebbi adatszolgáltatások esetében az adatszolgáltatás menete a mostanitól eltérő, a benyújtáshoz különböző
Előgyergyártott konzolos és konzolos támfalas közlekedési vasbeton elemcsaládok a kerékpáros és gyalogos közlekedési területek növelésére
 Előgyergyártott konzolos és konzolos támfalas közlekedési vasbeton elemcsaládok a kerékpáros és gyalogos közlekedési területek növelésére Adott esetben hegy- és dombvidéken, vízparton, hídfőknél az egyetlen
Előgyergyártott konzolos és konzolos támfalas közlekedési vasbeton elemcsaládok a kerékpáros és gyalogos közlekedési területek növelésére Adott esetben hegy- és dombvidéken, vízparton, hídfőknél az egyetlen
A táblázatkezelő felépítése
 A táblázatkezelés A táblázatkezelő felépítése A táblázatkezelő felépítése Címsor: A munkafüzet címét mutatja, és a program nevét, amivel megnyitottam. Menüszalag: A menüsor segítségével használhatjuk az
A táblázatkezelés A táblázatkezelő felépítése A táblázatkezelő felépítése Címsor: A munkafüzet címét mutatja, és a program nevét, amivel megnyitottam. Menüszalag: A menüsor segítségével használhatjuk az
Kooperáció és intelligencia
 Kooperáció és intelligencia Tanulás többágenses szervezetekben/2 Tanulás több ágensből álló környezetben -a mozgó cél tanulás problémája (alapvetően megerősítéses tanulás) Legyen az ágens közösség formalizált
Kooperáció és intelligencia Tanulás többágenses szervezetekben/2 Tanulás több ágensből álló környezetben -a mozgó cél tanulás problémája (alapvetően megerősítéses tanulás) Legyen az ágens közösség formalizált
Sikeres E-DETAILING KAMPÁNY receptje. GYÓGYKOMM 2016. KONFERENCIA Budapest, 2016. február 25. BALOGH JUDIT, PharmaPromo Kft.
 Sikeres E-DETAILING KAMPÁNY receptje GYÓGYKOMM 2016. KONFERENCIA Budapest, 2016. február 25. BALOGH JUDIT, PharmaPromo Kft. AZ ORVOSOK SZÍVESEN FOGADJÁK Szinapszis, 2016. 01., Online (CAWI) kérdőíves kutatás,
Sikeres E-DETAILING KAMPÁNY receptje GYÓGYKOMM 2016. KONFERENCIA Budapest, 2016. február 25. BALOGH JUDIT, PharmaPromo Kft. AZ ORVOSOK SZÍVESEN FOGADJÁK Szinapszis, 2016. 01., Online (CAWI) kérdőíves kutatás,
31 521 09 1000 00 00 Gépi forgácsoló Gépi forgácsoló
 Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Szerb középszintű szóbeli vizsga értékelési útmutató
 Szerb középszintű szóbeli vizsga értékelési útmutató Ez az értékelési eljárás meghatározott értékelési szempontokon, valamint az egyes szempontokhoz tartozó szintleírásokon alapul. Minden feleletet ezen
Szerb középszintű szóbeli vizsga értékelési útmutató Ez az értékelési eljárás meghatározott értékelési szempontokon, valamint az egyes szempontokhoz tartozó szintleírásokon alapul. Minden feleletet ezen
Adatok ábrázolása, adattípusok. Összefoglalás
 Adatok ábrázolása, adattípusok Összefoglalás Adatok ábrázolása, adattípusok Számítógépes rendszerek működés: információfeldolgozás IPO: input-process-output modell információ tárolása adatok formájában
Adatok ábrázolása, adattípusok Összefoglalás Adatok ábrázolása, adattípusok Számítógépes rendszerek működés: információfeldolgozás IPO: input-process-output modell információ tárolása adatok formájában
Programozás I. - 9. gyakorlat
 Programozás I. - 9. gyakorlat Mutatók, dinamikus memóriakezelés Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 9, 2009 1 tar@dcs.vein.hu
Programozás I. - 9. gyakorlat Mutatók, dinamikus memóriakezelés Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 9, 2009 1 tar@dcs.vein.hu
Hankiss Elemér: Társadalmi csapdák (részletek)
 Hankiss Elemér: Társadalmi csapdák (részletek) 1. A fogoly dilemmája A társadalmi dilemmák (s a belőlük gyakran kifejlődő társadalmi csapdák) olyan helyzetekben alakulnak ki, amelyeket a játékelmélet a
Hankiss Elemér: Társadalmi csapdák (részletek) 1. A fogoly dilemmája A társadalmi dilemmák (s a belőlük gyakran kifejlődő társadalmi csapdák) olyan helyzetekben alakulnak ki, amelyeket a játékelmélet a
KÖZGAZDASÁGI- MARKETING ALAPISMERETEK
 Közgazdasági-marketing alapismeretek emelt szint 0631 ÉRETTSÉGI VIZSGA 2006. október 24. KÖZGAZDASÁGI- MARKETING ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI
Közgazdasági-marketing alapismeretek emelt szint 0631 ÉRETTSÉGI VIZSGA 2006. október 24. KÖZGAZDASÁGI- MARKETING ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI
észbontó ördöglakat Megoldófüzet a szétszedéshez Egyszemélyes játék 8 éves kortól
 észbontó ördöglakat Megoldófüzet a szétszedéshez Egyszemélyes játék 8 éves kortól Importálja: Gém Klub Kft. 1092 Budapest, Ráday u. 30./B www.gemklub.hu 3 éven aluli gyerme keknek nem adható, mert az apró
észbontó ördöglakat Megoldófüzet a szétszedéshez Egyszemélyes játék 8 éves kortól Importálja: Gém Klub Kft. 1092 Budapest, Ráday u. 30./B www.gemklub.hu 3 éven aluli gyerme keknek nem adható, mert az apró
Egyéb előterjesztés Békés Város Képviselő-testülete 2015. december 2-i ülésére
 Tárgy: Körösök Völgye Vidékfejlesztési Közhasznú Egyesület előfinanszírozási kérelme Előkészítette: Gál András osztályvezető Véleményező Pénzügyi Bizottság bizottság: Sorszám: IV/14 Döntéshozatal módja:
Tárgy: Körösök Völgye Vidékfejlesztési Közhasznú Egyesület előfinanszírozási kérelme Előkészítette: Gál András osztályvezető Véleményező Pénzügyi Bizottság bizottság: Sorszám: IV/14 Döntéshozatal módja:
Lineáris programozás. Modellalkotás Grafikus megoldás Feladattípusok Szimplex módszer
 Lineáris programozás Modellalkotás Grafikus megoldás Feladattípusok Szimplex módszer Feladat: Egy gyár kétféle terméket gyárt (A, B): /db Eladási ár 1000 800 Technológiai önköltség 400 300 Normaóraigény
Lineáris programozás Modellalkotás Grafikus megoldás Feladattípusok Szimplex módszer Feladat: Egy gyár kétféle terméket gyárt (A, B): /db Eladási ár 1000 800 Technológiai önköltség 400 300 Normaóraigény
Dinamikus geometriai programok
 2011 október 22. Eszköz és médium (fotó: http://sliderulemuseum.com) Enter MTM1007L információ: zeus.nyf.hu/ kovacsz feladatok: moodle.nyf.hu Reform mozgalmak A formális matematikát az életkori sajátosságoknak
2011 október 22. Eszköz és médium (fotó: http://sliderulemuseum.com) Enter MTM1007L információ: zeus.nyf.hu/ kovacsz feladatok: moodle.nyf.hu Reform mozgalmak A formális matematikát az életkori sajátosságoknak
Elemi adatszerkezetek
 2015/10/14 13:54 1/16 Elemi adatszerkezetek < Programozás Elemi adatszerkezetek Szerző: Sallai András Copyright Sallai András, 2011, 2014 Licenc: GNU Free Documentation License 1.3 Web: http://szit.hu
2015/10/14 13:54 1/16 Elemi adatszerkezetek < Programozás Elemi adatszerkezetek Szerző: Sallai András Copyright Sallai András, 2011, 2014 Licenc: GNU Free Documentation License 1.3 Web: http://szit.hu
3. Térvezérlésű tranzisztorok
 1 3. Térvezérlésű tranzisztorok A térvezérlésű tranzisztorok (Field Effect Transistor = FET) működési elve alapjaiban eltér a bipoláris tranzisztoroktól. Az áramvezetés mértéke statikus feszültséggel befolyásolható.
1 3. Térvezérlésű tranzisztorok A térvezérlésű tranzisztorok (Field Effect Transistor = FET) működési elve alapjaiban eltér a bipoláris tranzisztoroktól. Az áramvezetés mértéke statikus feszültséggel befolyásolható.
8. Feladat Egy bútorgyár asztalosműhelyében évek óta gyártják a Badacsony elnevezésű konyhaasztalt. Az asztal gyártási anyagjegyzéke a következő:
 MRP számítások 1 8. Feladat Egy bútorgyár asztalosműhelyében évek óta gyártják a Badacsony elnevezésű konyhaasztalt. Az asztal gyártási anyagjegyzéke a következő: asztal lábszerkezet asztallap Csavar (
MRP számítások 1 8. Feladat Egy bútorgyár asztalosműhelyében évek óta gyártják a Badacsony elnevezésű konyhaasztalt. Az asztal gyártási anyagjegyzéke a következő: asztal lábszerkezet asztallap Csavar (
Lineáris algebra jegyzet
 Lineáris algebra jegyzet Készítette: Jezsoviczki Ádám Forrás: Az előadások és a gyakorlatok anyaga Legutóbbi módosítás dátuma: 2011-12-04 A jegyzet nyomokban hibát tartalmazhat, így fentartásokkal olvasandó!
Lineáris algebra jegyzet Készítette: Jezsoviczki Ádám Forrás: Az előadások és a gyakorlatok anyaga Legutóbbi módosítás dátuma: 2011-12-04 A jegyzet nyomokban hibát tartalmazhat, így fentartásokkal olvasandó!
G Szabályfelismerés 2.2. 2. feladatcsomag
 ÖSSZEFÜÉSEK Szabályfelismerés 2.2 Alapfeladat Szabályfelismerés 2. feladatcsomag összefüggés-felismerő képesség fejlesztése szabályfelismeréssel megkezdett sorozat folytatása a felismert szabály alapján
ÖSSZEFÜÉSEK Szabályfelismerés 2.2 Alapfeladat Szabályfelismerés 2. feladatcsomag összefüggés-felismerő képesség fejlesztése szabályfelismeréssel megkezdett sorozat folytatása a felismert szabály alapján
