DOKTORANDUSZ FÓRUM, 1999 Miskolc, november. Megerősítő tanulási módszerek alkalmazása az informatikában
|
|
|
- Alíz Mezeiné
- 10 évvel ezelőtt
- Látták:
Átírás
1 DOKTORANDUSZ FÓRUM, 1999 Miskolc, november Megerősítő tanulási módszerek alkalmazása az informatikában STEFÁN PÉTER Miskolci Egyetem, Alkalmazott Informatikai Tanszék 3515 Miskolc-Egyetemváros 1. BEVEZETÉS Napjainkban a gépipari, informatikai rendszereink komplexitása állandó ütemben nő. Ez a növekedés több különböző tényezőnek is betudható, többek között a számítógépes szoftver, illetve hardver erőforrások fejlődésének. A bonyolultság növekedése, és ezáltal a rendszerek átláthatóságának csökkenése arra ösztönzött számos kutatót, hogy a klasszikus mérnöki problémákhoz, a zárt matematikai formulákon túl, újabb, az emberi agy probléma-leegyszerűsítő megközelítéséhez hasonló módszereket dolgozzon ki. Ezeket az emberi információ-feldolgozó módszerek modelljeit a mesterséges intelligencia, mint tudományág foglalja össze. 2. MESTERSÉGES INTELLIGENCIA MÓDSZEREK A mesterséges intelligencia több, egymástól elkülönülő területből áll. E területek egy része megpróbálja az emberi agy működését előbb modellezni, majd megpróbál olyan szerkezetet létrehozni, amely mind jobban megközelíti az agy működését. A másik, talán szerényebb megközelítés, az, amikor megpróbáljuk az emberi gondolkodásmódot, az emberi intelligencia adaptív jellemvonását gépi környezetben megvalósítani. Ebbe a kategóriába tartoznak a tanuló, osztályozó módszerek, melyeket mind műszaki, mind gazdasági területeken is sikerrel hasznának. A tanulórendszerek osztályába számos eltérő irányvonal tartozik. Megkülönböztethetünk felügyel tanuló, illetve felügyelet nélkül tanuló rendszereket. Előbbi kategóriába például
2 az egyszerűbb neuron-hálók, vagy az osztályozó algoritmusok, míg utóbbiba az önszervező hálók tartoznak. Egy másik szempont szerint megkülönböztethetünk olyan tanulóeljárásokat, melyekre az ún. kétfázisú tanulás (betanítás előbb, majd használat) a jellemző, illetve olyanokat, amelyek egyszerre képesek tanulni illetve tudásukat kamatoztatni. Ezen utóbbi eljárások egyike a megerősítő tanulás. 3. A MEGERŐSÍTŐ TANULÁS A megerősítő tanulás egyfajta átmenetet képez a felügyelt és felügyelet-nélküli módszerek között. A felügyelt rendszerek esetén a környezet instruktív visszajelzésekkel korrigálja a tanulórendszer belső struktúráját, illetve paramétereit. Ez azt jelenti, hogy a módosítás iránya a rendszeren kívülről befelé haladó; azaz a környezet megmondja, a belső állapottól kvázi függetlenül, hogy melyek a rendszer helyes, megkívánt kimeneti jellemzői. A rendszer módosítása pedig éppen az előbbi állapotok elérése felé irányul. Koncepciójában különbözik ettől az a megoldás, amikor a tanulás belülről jövő. Ez azt jelenti, hogy a rendszer maga úgy van felépítve, hogy felfedezi, feltérképezi környezetét. Más kifejezéssel élve cselekvéseket, akciókat hajt végre, amelyek hatással vannak a környezetre, és aminek következtében a környezet visszajelzést ad, hogy a választott akciókat a környezet hogyan jutalmazta. A visszacsatolt érték, a megerősítő-jel, egy skaláris szám, melynek értéktartománya rendszerint problémafüggő. Általában egy nagy pozitív szám a környezet akcióra adott jutalmát, míg a nagy negatív szám büntetését szimbolizálja. A megerősítő tanulás sematikus rajza az 1. ábrán látható. Az ábrán két objektum található: az ágens, illetve annak környezete. Az ágens feladata egy célállapot elérése, mégpedig oly módon, hogy maximalizálja a környezetétől kapott megerősítő-jelek összegét. Ezt az egyes szituációkban, megfelelően megválasztott akciókkal éri el. A cél minden szituációban olyan akciókat választani, amelyek hosszútávon biztosítják a megerősítőjelek maximumát. Az ágens számára minden lehetséges akció előtt nyitva áll a kérdés: a
3 következő lépésben választott akcióval a már eddig elért tudását kívánja hasznosítani, vagy esetleg új megoldások reményében megpróbálja azokat az akciókat választani, amelyek nem közvetlenül a legjobb válaszreakciót adják, de lehetőséget nyújtanak más (esetleg kedvezőbb visszacsatolású) állapotok kiértékelésére is. 1. ábra: Az ágens-probléma A környezet feladata egyrészt ellátni a tanuló ágenst visszacsatolási információkkal, másrészt új állapotokat biztosítani a rendszer részére. Ez utóbbi gyakran a rendszeren belül, automatikusan is végbemehet, nem szükségszerű, hogy a környezet indukálja. A környezet gyakran helyettesíthető egy metrikával, ami automatikusan szolgáltatja a megerősítő jelet az ágens számára. A metrika, az ágens számára a környezeti modellt, a környezet viselkedését jelenti. Gyakran a tanulórendszer megalkotójának kell a metrikát definiálni, és az esetek többségében ez nem egy metrika kidolgozását jelenti, hanem egy metrika-halmazét. Érdemes megemlíteni, hogy a metrika rokon fogalom az operációkutatásban használt optimum kritériummal. 4. AZ ÁGENS-RENDSZER ÉPÍTŐKÖVEI Az ágens leírására formális nyelvi eszközöket használnak. Hogy az ágens összetevőiről beszélni lehessen, először szükséges definiálni a további tárgyalás alapját képző attribútumokat. Ezek az attribútumok a tanuló-rendszer állapotai, illetve az egyes
4 állapotok felvétele után választható akciók. A lehetséges állapotokat az állapot-halmaz, az akciókat pedig, az előbbitől függő, akcióhalmazok foglalják össze. Minden egyes állapothoz rendelhető egy akció-halmaz. Az állapotokon, illetve az akciókon kívül az ágens tartalmaz még három további függvényt. Az első a politika-függvény (policy function). Ez a függvény egyszerűbb esetben a rendszer aktuális állapotát képzi le a végrehajtandó akciók halmazára: azaz minden állapothoz hozzárendeli az ott eddig legjobbnak vélt akciót. Összetettebb esetben e függvény minden állapot-akció párhoz egy kiválasztási valószínűséget rendel. Ez a valószínűség akkor játszik szerepet, amikor nem a legkedvezőbb akciót választjuk (felderítési üzemmód esetén), és egy rossz alternatíva véletlenszerű kiválasztása nagy negatív tetszést váltana ki a környezettől. Az összetettebb politika-függvénnyel tehát súlyozzuk a lehetséges választásokat. Amikor minden állapotban a lehető legkedvezőbb akciót választjuk, azaz nem végzünk egyáltalán felderítést, mohó (greedy) algoritmusról beszélünk. A politika-függvény lehet determinisztikus, sztochasztikus, de lehet egy komplett kereső eljárás is. A második, az ágens számára szükséges elem az érték-függvény (value function). Az érték-függvény szoros kapcsolatban áll a környezet által visszaadott megerősítő-jel értékekkel. Az ágens számára minden állapotban elérhető kell, hogy legyen egy várható érték, hogy az egyes állapotokban meg tudja jósolni azt, hogy a környezet miként fogja jutalmazni egy új állapot felvételét. Illetve azt is meg kell mondani, hogy az egyes állapotokban az egyes akciók, milyen lesz a várható érték hozama. Ennek tükrében, megkülönböztethető állapot-értek (state-value) és akció-érték (action-value) függvény. Az érték függvény nemcsak azt jelöli, hogy az egyes állapotok, illetve akciók milyen várható megerősítő-jel értéket képviselnek, hanem azt is, hogy mely állapotok lesznek hosszú-távon akár sokkal jobban jutalmazva, mint bármely jelen állapotban választható akció által elért állapot. Tehát az érték-függvények funkciója az is, hogy a jól jövedelmező, de távoli, esetleg kevésbé jutalmazott állapotokat is kihangsúlyozza a jelen állapotbeli döntés számára.
5 A politika és az érték függvények céljukban is és számítási módjukban is különböznek egymástól. Míg az előbbi célja az, hogy a felfedező-ciklus esetén a véletlenszerű választást súlyozzák, utóbbi hosszabb távon befolyásolja az ágens felfedezés-felhasználás döntését. A harmadik függvény, amellyel a tanuló-rendszernek rendelkeznie kell a honoráriumfüggvény (reward function), amely állapot-akció párokat képez le a megerősítő jel lehetséges értékeinek halmazára. A metrika fogalmával analóg. A politika, illetve az érték függvények iterációs lépéseken keresztül határozhatók meg. 5. A MEGOLDHATÓ PROBLÉMÁK KÖRE A megerősítő tanulás, illetve az ágens-modell egymás segítségével definiálhatók. Megerősítő tanulási eljárásnak minden olyan eljárást nevezünk, ami az előzőekben ismertetett ágens-rendszer célja elérésének megoldásával foglalkozik. Az ágens-feladat megoldásai az alábbi csoportokba sorolhatók: dinamikus programozási eljárások (amelyek a teljes környezet ismeretét feltételezik), hőmérséklet kiegyenlítést modellező eljárások (Q-tanulás), illetve az ún. Monte Carlo eljárások (amelyek számára nem szükséges a teljes környezet ismerete). A megoldások túlnyomó többsége matematikai úton bizonyított, stabil eljárás. A megerősítő tanulás elsősorban a dinamikus feladatok megoldásában alkalmazható. Olyan környezetben, ahol például egy optimum-feladat feltételi rendszere állandó, a zárt matematikai modellek egyértelműen a leghatékonyabbak. Ellenben, ha a feltételrendszer időben változik, esetleg sztochasztikus jellegű, úgy a megerősítő tanulási módszerek, különösen nagyobb rendszer esetében, a matematikai modelleknél megvalósíthatóbbak, és jobb teljesítményt nyújtanak. 6. PÉLDA EGY MEGERŐSÍTŐ TANULÁSI ELJÁRÁSRA Jelölje S a tanuló-rendszer által felvehető állapotok halmazát, A(s) az s S állapotban választható akciókat. Legyen Q:S A [0,1] R az akció-érték függvény, π:s A a
6 politika függvény. A megerősítő tanulás egyik lehetséges algoritmusa az alábbi C-formájú algoritmus lehet: while (true) { p = véletlen szám; if (p < 0.8) {akció kiválasztása az adott politika szerint, a A} else {ennek alapján egy véletlenszeruen választott akció, a A} s új = az újonnan választott állapot felvétele (s new S); r = a környezettol kapott visszajelzett érték; hiba = r + γ*u(s new ) - Q(s,a); Q(s,a) = Q(s,a) + α*hiba; π(s) = max b A (Q(s,b)); U(s) = Q(s,π(s)); S = s új ; } 7. ÖSSZEFOGLALÁS A megerősítő tanulás egy iteratív módszer, amely a környezetével állandó kölcsönhatásban lévő, dinamikusan változó környezetbe helyezett ágens célkereső eljárását definiálja, illetve oldja meg. Az létrehozott modell keretei közé számos probléma helyezhető, mint például az Internet routing probléma, adaptív robot vezérlés, változó környezetben történő optimum-keresés, illetve logisztikai disztribúciós feladatok megoldása. 8. FELHASZNÁLT IRODALOM [1] P.STEFÁN, L.MONOSTORI, F.ERDÉLYI: Using symbolic and sub-symbolic methods for solving problems difficult to analyze, MicroCAD 99 University of Miskolc [2] Szimbolikus és szub-szimbolikus módszerek az analitikailag kezelhető problémák megoldásában, FMTÜ Kolozsvár [3] R.SUTTON, A.BARTO: Reinforcement learning
7 DOKTORANDUSZ FÓRUM, 1999 Miskolc, november Megerősítő tanulási módszerek alkalmazása az informatikában STEFÁN PÉTER Miskolci Egyetem, Alkalmazott Informatikai Tanszék 3515 Miskolc-Egyetemváros ABSTRACT Napjainkban a gépipari, informatikai rendszereink komplexitása állandó ütemben nő. A bonyolultság növekedése, és, éppen emiatt, a rendszerek átláthatóságának csökkenése arra ösztönzött számos kutatót, hogy újabb mesterséges intelligencia módszereket fejlesszen ki, illetve alkalmazzon informatikai, gazdasági, illetve műszaki problémák megoldásában. Egyik ilyen MI módszer a megerősítő tanulás, mely előnyös tulajdonságaira, illetve alkalmazási területeire a cikkben rámutatunk. FELHASZNÁLT IRODALOM [1] P.STEFÁN, L.MONOSTORI, F.ERDÉLYI: Using symbolic and sub-symbolic methods for solving problems difficult to analyze, MicroCAD 99 University of Miskolc [2] Szimbolikus és szub-szimbolikus módszerek az analitikailag kezelhető problémák megoldásában, FMTÜ Kolozsvár [3] R.SUTTON, A.BARTO: Reinforcement learning
8
Megerősítéses tanulási módszerek és alkalmazásaik
 MISKOLCI EGYETEM GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR Megerősítéses tanulási módszerek és alkalmazásaik Tompa Tamás tanársegéd Általános Informatikai Intézeti Tanszék Miskolc, 2017. szeptember 15. Tartalom
MISKOLCI EGYETEM GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR Megerősítéses tanulási módszerek és alkalmazásaik Tompa Tamás tanársegéd Általános Informatikai Intézeti Tanszék Miskolc, 2017. szeptember 15. Tartalom
FELÜGYELT ÉS MEGERŐSÍTÉSES TANULÓ RENDSZEREK FEJLESZTÉSE
 FELÜGYELT ÉS MEGERŐSÍTÉSES TANULÓ RENDSZEREK FEJLESZTÉSE Dr. Aradi Szilárd, Fehér Árpád Mesterséges intelligencia kialakulása 1956 Dartmouth-i konferencián egy maroknyi tudós megalapította a MI területét
FELÜGYELT ÉS MEGERŐSÍTÉSES TANULÓ RENDSZEREK FEJLESZTÉSE Dr. Aradi Szilárd, Fehér Árpád Mesterséges intelligencia kialakulása 1956 Dartmouth-i konferencián egy maroknyi tudós megalapította a MI területét
A megerosítéses tanulás és a szimulált hutés kombinált használata: algoritmusok és alkalmazások
 MISKOLCI EGYETEM DOKTORI (PH.D.) TÉZISFÜZETEI HATVANY JÓZSEF INFORMATIKAI TUDOMÁNYOK DOKTORI ISKOLA A megerosítéses tanulás és a szimulált hutés kombinált használata: algoritmusok és alkalmazások Készítette:
MISKOLCI EGYETEM DOKTORI (PH.D.) TÉZISFÜZETEI HATVANY JÓZSEF INFORMATIKAI TUDOMÁNYOK DOKTORI ISKOLA A megerosítéses tanulás és a szimulált hutés kombinált használata: algoritmusok és alkalmazások Készítette:
OOP. Alapelvek Elek Tibor
 OOP Alapelvek Elek Tibor OOP szemlélet Az OOP szemlélete szerint: a valóságot objektumok halmazaként tekintjük. Ezen objektumok egymással kapcsolatban vannak és együttműködnek. Program készítés: Absztrakciós
OOP Alapelvek Elek Tibor OOP szemlélet Az OOP szemlélete szerint: a valóságot objektumok halmazaként tekintjük. Ezen objektumok egymással kapcsolatban vannak és együttműködnek. Program készítés: Absztrakciós
Döntéselőkészítés. I. előadás. Döntéselőkészítés. Előadó: Dr. Égertné dr. Molnár Éva. Informatika Tanszék A 602 szoba
 I. előadás Előadó: Dr. Égertné dr. Molnár Éva Informatika Tanszék A 602 szoba Tárggyal kapcsolatos anyagok megtalálhatók: http://www.sze.hu/~egertne Konzultációs idő: (páros tan. hét) csütörtök 10-11 30
I. előadás Előadó: Dr. Égertné dr. Molnár Éva Informatika Tanszék A 602 szoba Tárggyal kapcsolatos anyagok megtalálhatók: http://www.sze.hu/~egertne Konzultációs idő: (páros tan. hét) csütörtök 10-11 30
Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017.
 Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017. Vizuális feldolgozórendszerek feladatai Mesterséges intelligencia és idegtudomány Mesterséges intelligencia és idegtudomány Párhuzamos problémák
Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017. Vizuális feldolgozórendszerek feladatai Mesterséges intelligencia és idegtudomány Mesterséges intelligencia és idegtudomány Párhuzamos problémák
Programozási módszertan. Mohó algoritmusok
 PM-08 p. 1/17 Programozási módszertan Mohó algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu PM-08 p. 2/17 Bevezetés Dinamikus programozás
PM-08 p. 1/17 Programozási módszertan Mohó algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu PM-08 p. 2/17 Bevezetés Dinamikus programozás
I. LABOR -Mesterséges neuron
 I. LABOR -Mesterséges neuron A GYAKORLAT CÉLJA: A mesterséges neuron struktúrájának az ismertetése, neuronhálókkal kapcsolatos elemek, alapfogalmak bemutatása, aktivációs függvénytípusok szemléltetése,
I. LABOR -Mesterséges neuron A GYAKORLAT CÉLJA: A mesterséges neuron struktúrájának az ismertetése, neuronhálókkal kapcsolatos elemek, alapfogalmak bemutatása, aktivációs függvénytípusok szemléltetése,
Objektumorientált paradigma és a programfejlesztés
 Objektumorientált paradigma és a programfejlesztés Vámossy Zoltán vamossy.zoltan@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Ficsor Lajos (Miskolci Egyetem) prezentációja alapján Objektumorientált
Objektumorientált paradigma és a programfejlesztés Vámossy Zoltán vamossy.zoltan@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Ficsor Lajos (Miskolci Egyetem) prezentációja alapján Objektumorientált
Bevezetés a kvantum informatikába és kommunikációba Féléves házi feladat (2013/2014. tavasz)
 Bevezetés a kvantum informatikába és kommunikációba Féléves házi feladat (2013/2014. tavasz) A házi feladatokkal kapcsolatos követelményekről Kapcsolódó határidők: választás: 6. oktatási hét csütörtöki
Bevezetés a kvantum informatikába és kommunikációba Féléves házi feladat (2013/2014. tavasz) A házi feladatokkal kapcsolatos követelményekről Kapcsolódó határidők: választás: 6. oktatási hét csütörtöki
Objektumorientált paradigma és programfejlesztés Bevezető
 Objektumorientált paradigma és programfejlesztés Bevezető Vámossy Zoltán vamossy.zoltan@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Ficsor Lajos (Miskolci Egyetem) prezentációja alapján
Objektumorientált paradigma és programfejlesztés Bevezető Vámossy Zoltán vamossy.zoltan@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Ficsor Lajos (Miskolci Egyetem) prezentációja alapján
Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén
 Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén Dombi József Szegedi Tudományegyetem Bevezetés - ID3 (Iterative Dichotomiser 3) Az ID algoritmusok egy elemhalmaz felhasználásával
Új típusú döntési fa építés és annak alkalmazása többtényezős döntés területén Dombi József Szegedi Tudományegyetem Bevezetés - ID3 (Iterative Dichotomiser 3) Az ID algoritmusok egy elemhalmaz felhasználásával
Objektum orientált programozás Bevezetés
 Objektum orientált programozás Bevezetés Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2008. 03. 04. OOPALAP / 1 A program készítés Absztrakciós folyamat, amelyben a valós világban
Objektum orientált programozás Bevezetés Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2008. 03. 04. OOPALAP / 1 A program készítés Absztrakciós folyamat, amelyben a valós világban
Optimalizálás alapfeladata Legmeredekebb lejtő Lagrange függvény Log-barrier módszer Büntetőfüggvény módszer 2017/
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 9. Előadás Az optimalizálás alapfeladata Keressük f függvény maximumát ahol f : R n R és
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 9. Előadás Az optimalizálás alapfeladata Keressük f függvény maximumát ahol f : R n R és
Absztrakció. Objektum orientált programozás Bevezetés. Általános Informatikai Tanszék Utolsó módosítás:
 Objektum orientált programozás Bevezetés Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2008. 03. 04. OOPALAP / 1 A program készítés Absztrakciós folyamat, amelyben a valós világban
Objektum orientált programozás Bevezetés Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2008. 03. 04. OOPALAP / 1 A program készítés Absztrakciós folyamat, amelyben a valós világban
TERMÉK FEJLESZTÉS PANDUR BÉLA TERMÉK TERVEZÉSE
 TERMÉK TERVEZÉSE A termék fogalma: Tevékenységek, vagy folyamatok eredménye /folyamat szemlélet /. (Minden terméknek értelmezhető, amely gazdasági potenciált közvetít /közgazdász szemlélet /.) Az ISO 8402
TERMÉK TERVEZÉSE A termék fogalma: Tevékenységek, vagy folyamatok eredménye /folyamat szemlélet /. (Minden terméknek értelmezhető, amely gazdasági potenciált közvetít /közgazdász szemlélet /.) Az ISO 8402
Megerősítéses tanulás 7. előadás
 Megerősítéses tanulás 7. előadás 1 Ismétlés: TD becslés s t -ben stratégia szerint lépek! a t, r t, s t+1 TD becslés: tulajdonképpen ezt mintavételezzük: 2 Akcióértékelő függvény számolása TD-vel még mindig
Megerősítéses tanulás 7. előadás 1 Ismétlés: TD becslés s t -ben stratégia szerint lépek! a t, r t, s t+1 TD becslés: tulajdonképpen ezt mintavételezzük: 2 Akcióértékelő függvény számolása TD-vel még mindig
Neurális hálózatok bemutató
 Neurális hálózatok bemutató Füvesi Viktor Miskolci Egyetem Alkalmazott Földtudományi Kutatóintézet Miért? Vannak feladatok amelyeket az agy gyorsabban hajt végre mint a konvencionális számítógépek. Pl.:
Neurális hálózatok bemutató Füvesi Viktor Miskolci Egyetem Alkalmazott Földtudományi Kutatóintézet Miért? Vannak feladatok amelyeket az agy gyorsabban hajt végre mint a konvencionális számítógépek. Pl.:
Adaptív menetrendezés ADP algoritmus alkalmazásával
 Adaptív menetrendezés ADP algoritmus alkalmazásával Alcím III. Mechwart András Ifjúsági Találkozó Mátraháza, 2013. szeptember 10. Divényi Dániel Villamos Energetika Tanszék Villamos Művek és Környezet
Adaptív menetrendezés ADP algoritmus alkalmazásával Alcím III. Mechwart András Ifjúsági Találkozó Mátraháza, 2013. szeptember 10. Divényi Dániel Villamos Energetika Tanszék Villamos Művek és Környezet
Matematikai modellezés
 Matematikai modellezés Bevezető A diasorozat a Döntési modellek című könyvhöz készült. Készítette: Dr. Ábrahám István Döntési folyamatok matematikai modellezése Az emberi tevékenységben meghatározó szerepe
Matematikai modellezés Bevezető A diasorozat a Döntési modellek című könyvhöz készült. Készítette: Dr. Ábrahám István Döntési folyamatok matematikai modellezése Az emberi tevékenységben meghatározó szerepe
Minőségérték. A modellezés céljának meghat. Rendszer elemzés. Módszer kiválasztása. Modell megfelelőség elemzés. Működés szimuláció
 Minőségérték. Műszaki minőségérték növelésére alkalmas módszerek: Cél: a termék teljes életciklusa során az előre látható, vagy feltételezett követelmények, teljes körű és kiegyensúlyozott kielégítése.
Minőségérték. Műszaki minőségérték növelésére alkalmas módszerek: Cél: a termék teljes életciklusa során az előre látható, vagy feltételezett követelmények, teljes körű és kiegyensúlyozott kielégítése.
OPERÁCIÓKUTATÁS, AZ ELFELEDETT TUDOMÁNY A LOGISZTIKÁBAN (A LOGISZTIKAI CÉL ELÉRÉSÉNEK ÉRDEKÉBEN)
 OPERÁCIÓKUTATÁS, AZ ELFELEDETT TUDOMÁNY A LOGISZTIKÁBAN (A LOGISZTIKAI CÉL ELÉRÉSÉNEK ÉRDEKÉBEN) Fábos Róbert 1 Alapvető elvárás a logisztika területeinek szereplői (termelő, szolgáltató, megrendelő, stb.)
OPERÁCIÓKUTATÁS, AZ ELFELEDETT TUDOMÁNY A LOGISZTIKÁBAN (A LOGISZTIKAI CÉL ELÉRÉSÉNEK ÉRDEKÉBEN) Fábos Róbert 1 Alapvető elvárás a logisztika területeinek szereplői (termelő, szolgáltató, megrendelő, stb.)
Megerősítéses tanulás 2. előadás
 Megerősítéses tanulás 2. előadás 1 Technikai dolgok Email szityu@eotvoscollegium.hu Annai levlista http://nipglab04.inf.elte.hu/cgi-bin/mailman/listinfo/annai/ Olvasnivaló: Sutton, Barto: Reinforcement
Megerősítéses tanulás 2. előadás 1 Technikai dolgok Email szityu@eotvoscollegium.hu Annai levlista http://nipglab04.inf.elte.hu/cgi-bin/mailman/listinfo/annai/ Olvasnivaló: Sutton, Barto: Reinforcement
Gépi tanulás a gyakorlatban. Kiértékelés és Klaszterezés
 Gépi tanulás a gyakorlatban Kiértékelés és Klaszterezés Hogyan alkalmazzuk sikeresen a gépi tanuló módszereket? Hogyan válasszuk az algoritmusokat? Hogyan hangoljuk a paramétereiket? Precízebben: Tegyük
Gépi tanulás a gyakorlatban Kiértékelés és Klaszterezés Hogyan alkalmazzuk sikeresen a gépi tanuló módszereket? Hogyan válasszuk az algoritmusokat? Hogyan hangoljuk a paramétereiket? Precízebben: Tegyük
Stratégiák tanulása az agyban
 Statisztikai tanulás az idegrendszerben, 2019. Stratégiák tanulása az agyban Bányai Mihály banyai.mihaly@wigner.mta.hu http://golab.wigner.mta.hu/people/mihaly-banyai/ Kortárs MI thispersondoesnotexist.com
Statisztikai tanulás az idegrendszerben, 2019. Stratégiák tanulása az agyban Bányai Mihály banyai.mihaly@wigner.mta.hu http://golab.wigner.mta.hu/people/mihaly-banyai/ Kortárs MI thispersondoesnotexist.com
Óbudai Egyetem Neumann János Informatikai Kar. Intelligens Mérnöki Rendszerek Intézet
 Óbudai Egyetem Neumann János Informatikai Kar Intelligens Mérnöki Rendszerek Intézet 1034 Budapest, Bécsi út 96/B Tel., Fax:1/666-5544,1/666-5545 http://nik.uni-obuda.hu/imri Az 2004-ben alakult IMRI (BMF)
Óbudai Egyetem Neumann János Informatikai Kar Intelligens Mérnöki Rendszerek Intézet 1034 Budapest, Bécsi út 96/B Tel., Fax:1/666-5544,1/666-5545 http://nik.uni-obuda.hu/imri Az 2004-ben alakult IMRI (BMF)
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék
 Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék 2016/17 2. félév 1-2. Előadás Dr. Kulcsár Gyula egyetemi docens A tantárgy tematikája 1.
Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék 2016/17 2. félév 1-2. Előadás Dr. Kulcsár Gyula egyetemi docens A tantárgy tematikája 1.
TARTALOMJEGYZÉK. TARTALOMJEGYZÉK...vii ELŐSZÓ... xiii BEVEZETÉS A lágy számításról A könyv célkitűzése és felépítése...
 TARTALOMJEGYZÉK TARTALOMJEGYZÉK...vii ELŐSZÓ... xiii BEVEZETÉS...1 1. A lágy számításról...2 2. A könyv célkitűzése és felépítése...6 AZ ÖSSZETEVŐ LÁGY RENDSZEREK...9 I. BEVEZETÉS...10 3. Az összetevő
TARTALOMJEGYZÉK TARTALOMJEGYZÉK...vii ELŐSZÓ... xiii BEVEZETÉS...1 1. A lágy számításról...2 2. A könyv célkitűzése és felépítése...6 AZ ÖSSZETEVŐ LÁGY RENDSZEREK...9 I. BEVEZETÉS...10 3. Az összetevő
Áttekintés LP és geometria Többcélú LP LP és egy dinamikus modell 2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 6. Előadás Áttekintés Kezdjük újra a klasszikus erőforrás allokációs problémával (katonák,
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 6. Előadás Áttekintés Kezdjük újra a klasszikus erőforrás allokációs problémával (katonák,
Keresés képi jellemzők alapján. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Válogatott fejezetek a közlekedésgazdaságtanból
 Válogatott fejezetek a közlekedésgazdaságtanból 2. Választási modellek Levelező tagozat 2015 ősz Készítette: Prileszky István http://www.sze.hu/~prile Fogalmak Választási modellek célja: annak megjósolása,
Válogatott fejezetek a közlekedésgazdaságtanból 2. Választási modellek Levelező tagozat 2015 ősz Készítette: Prileszky István http://www.sze.hu/~prile Fogalmak Választási modellek célja: annak megjósolása,
Algoritmusok helyességének bizonyítása. A Floyd-módszer
 Algoritmusok helyességének bizonyítása A Floyd-módszer Algoritmusok végrehajtása Egy A algoritmus esetében a változókat három változótípusról beszélhetünk, melyeket az X, Y és Z vektorokba csoportosítjuk
Algoritmusok helyességének bizonyítása A Floyd-módszer Algoritmusok végrehajtása Egy A algoritmus esetében a változókat három változótípusról beszélhetünk, melyeket az X, Y és Z vektorokba csoportosítjuk
C++ programozási nyelv
 C++ programozási nyelv Gyakorlat - 13. hét Nyugat-Magyarországi Egyetem Faipari Mérnöki Kar Informatikai Intézet Soós Sándor 2004. december A C++ programozási nyelv Soós Sándor 1/10 Tartalomjegyzék Objektumok
C++ programozási nyelv Gyakorlat - 13. hét Nyugat-Magyarországi Egyetem Faipari Mérnöki Kar Informatikai Intézet Soós Sándor 2004. december A C++ programozási nyelv Soós Sándor 1/10 Tartalomjegyzék Objektumok
Számítógépes döntéstámogatás. Döntések fuzzy környezetben Közelítő következtetések
 BLSZM-09 p. 1/17 Számítógépes döntéstámogatás Döntések fuzzy környezetben Közelítő következtetések Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu
BLSZM-09 p. 1/17 Számítógépes döntéstámogatás Döntések fuzzy környezetben Közelítő következtetések Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu
Számítógépes döntéstámogatás. Genetikus algoritmusok
 BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
Kvantitatív módszerek
 Kvantitatív módszerek szimuláció Kovács Zoltán Szervezési és Vezetési Tanszék E-mail: kovacsz@gtk.uni-pannon.hu URL: http://almos/~kovacsz Mennyiségi problémák megoldása analitikus numerikus szimuláció
Kvantitatív módszerek szimuláció Kovács Zoltán Szervezési és Vezetési Tanszék E-mail: kovacsz@gtk.uni-pannon.hu URL: http://almos/~kovacsz Mennyiségi problémák megoldása analitikus numerikus szimuláció
Az ISO 9001:2015 szabványban szereplő új fogalmak a tanúsító szemszögéből. Szabó T. Árpád
 Az ISO 9001:2015 szabványban szereplő új fogalmak a tanúsító szemszögéből. Szabó T. Árpád Bevezetés Az új fogalmak a TQM ből ismerősek? ISO 9001:2015 új fogalmainak az érdekelt felek általi értelmezése
Az ISO 9001:2015 szabványban szereplő új fogalmak a tanúsító szemszögéből. Szabó T. Árpád Bevezetés Az új fogalmak a TQM ből ismerősek? ISO 9001:2015 új fogalmainak az érdekelt felek általi értelmezése
Korszerű információs technológiák
 MISKOLCI EGYETEM GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR Korszerű információs technológiák Megerősítéses tanulási módszerek és alkalmazásaik Tompa Tamás tanársegéd Általános Informatikai Intézeti Tanszék Miskolc,
MISKOLCI EGYETEM GÉPÉSZMÉRNÖKI ÉS INFORMATIKAI KAR Korszerű információs technológiák Megerősítéses tanulási módszerek és alkalmazásaik Tompa Tamás tanársegéd Általános Informatikai Intézeti Tanszék Miskolc,
Bevezetés az informatikába
 Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Mérési struktúrák
 Mérési struktúrák 2007.02.19. 1 Mérési struktúrák A mérés művelete: a mérendő jellemző és a szimbólum halmaz közötti leképezés megvalósítása jel- és rendszerelméleti aspektus mérési folyamat: a leképezést
Mérési struktúrák 2007.02.19. 1 Mérési struktúrák A mérés művelete: a mérendő jellemző és a szimbólum halmaz közötti leképezés megvalósítása jel- és rendszerelméleti aspektus mérési folyamat: a leképezést
1. Informatikai trendek, ágensek, többágenses rendszerek. Intelligens Elosztott Rendszerek BME-MIT, 2018
 1. Informatikai trendek, ágensek, többágenses rendszerek A számítástechnika történetének 5 nagy trendje mindenütt jelenlévő (ubiquity) összekapcsolt (interconnection) intelligens delegált (delegation)
1. Informatikai trendek, ágensek, többágenses rendszerek A számítástechnika történetének 5 nagy trendje mindenütt jelenlévő (ubiquity) összekapcsolt (interconnection) intelligens delegált (delegation)
Gépi tanulás és Mintafelismerés
 Gépi tanulás és Mintafelismerés jegyzet Csató Lehel Matematika-Informatika Tanszék BabesBolyai Tudományegyetem, Kolozsvár 2007 Aug. 20 2 1. fejezet Bevezet A mesterséges intelligencia azon módszereit,
Gépi tanulás és Mintafelismerés jegyzet Csató Lehel Matematika-Informatika Tanszék BabesBolyai Tudományegyetem, Kolozsvár 2007 Aug. 20 2 1. fejezet Bevezet A mesterséges intelligencia azon módszereit,
1. Az informatika alapjai (vezetője: Dr. Dömösi Pál, DSc, egyetemi tanár) Kredit
 2. MELLÉKLET Az oktatási koncepciója 1. Az informatika alapjai (vezetője: Dr. Dömösi Pál, DSc, egyetemi tanár) Az informatika alapjai Tud. Min. 1 Automata hálózatok 2 V Dr. Dömösi Pál DSc 2 Automaták és
2. MELLÉKLET Az oktatási koncepciója 1. Az informatika alapjai (vezetője: Dr. Dömösi Pál, DSc, egyetemi tanár) Az informatika alapjai Tud. Min. 1 Automata hálózatok 2 V Dr. Dömösi Pál DSc 2 Automaták és
Rekurzió. Dr. Iványi Péter
 Rekurzió Dr. Iványi Péter 1 Függvényhívás void f3(int a3) { printf( %d,a3); } void f2(int a2) { f3(a2); a2 = (a2+1); } void f1() { int a1 = 1; int b1; b1 = f2(a1); } 2 Függvényhívás void f3(int a3) { printf(
Rekurzió Dr. Iványi Péter 1 Függvényhívás void f3(int a3) { printf( %d,a3); } void f2(int a2) { f3(a2); a2 = (a2+1); } void f1() { int a1 = 1; int b1; b1 = f2(a1); } 2 Függvényhívás void f3(int a3) { printf(
Közösség detektálás gráfokban
 Közösség detektálás gráfokban Önszervező rendszerek Hegedűs István Célkitűzés: valamilyen objektumok halmaza felett minták, csoportok detektálása csakis az egyedek közötti kapcsolatok struktúrájának a
Közösség detektálás gráfokban Önszervező rendszerek Hegedűs István Célkitűzés: valamilyen objektumok halmaza felett minták, csoportok detektálása csakis az egyedek közötti kapcsolatok struktúrájának a
Alapszintű formalizmusok
 Alapszintű formalizmusok dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális tervek Informális követelmények Formális modell Formalizált követelmények
Alapszintű formalizmusok dr. Majzik István BME Méréstechnika és Információs Rendszerek Tanszék 1 Mit szeretnénk elérni? Informális tervek Informális követelmények Formális modell Formalizált követelmények
Számítási intelligencia
 Botzheim János Számítási intelligencia Budapesti Műszaki és Gazdaságtudományi Egyetem, Mechatronika, Optika és Gépészeti Informatika Tanszék Graduate School of System Design, Tokyo Metropolitan University
Botzheim János Számítási intelligencia Budapesti Műszaki és Gazdaságtudományi Egyetem, Mechatronika, Optika és Gépészeti Informatika Tanszék Graduate School of System Design, Tokyo Metropolitan University
Dualitás Dualitási tételek Általános LP feladat Komplementáris lazaság 2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 7. Előadás Árazási interpretáció Tekintsük újra az erőforrás allokációs problémát (vonat
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 7. Előadás Árazási interpretáció Tekintsük újra az erőforrás allokációs problémát (vonat
Szakmai zárójelentés
 Szakmai zárójelentés A csoporttechnológia (Group Technology = GT) elvi és módszertani alapjaihoz, valamint a kapcsolódó módszerek informatikai alkalmazásaihoz kötődő kutatómunkával a Miskolci Egyetem Alkalmazott
Szakmai zárójelentés A csoporttechnológia (Group Technology = GT) elvi és módszertani alapjaihoz, valamint a kapcsolódó módszerek informatikai alkalmazásaihoz kötődő kutatómunkával a Miskolci Egyetem Alkalmazott
Integrált gyártórendszerek. Ágens technológia - ágens rendszer létrehozása Gyakorlat
 IGYR p. 1/17 Integrált gyártórendszerek Ágens technológia - ágens rendszer létrehozása Gyakorlat Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu IGYR
IGYR p. 1/17 Integrált gyártórendszerek Ágens technológia - ágens rendszer létrehozása Gyakorlat Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu IGYR
Mesterséges Intelligencia MI
 Mesterséges Intelligencia MI Racionalitás: a hasznosság és a döntés Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade
Mesterséges Intelligencia MI Racionalitás: a hasznosság és a döntés Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade
A félév során előkerülő témakörök
 A félév során előkerülő témakörök rekurzív algoritmusok rendező algoritmusok alapvető adattípusok, adatszerkezetek, és kapcsolódó algoritmusok dinamikus programozás mohó algoritmusok gráf algoritmusok
A félév során előkerülő témakörök rekurzív algoritmusok rendező algoritmusok alapvető adattípusok, adatszerkezetek, és kapcsolódó algoritmusok dinamikus programozás mohó algoritmusok gráf algoritmusok
"A tízezer mérföldes utazás is egyetlen lépéssel kezdődik."
 "A tízezert mérföldes utazás is egyetlen lépéssel kezdődik dik." A BINB INSYS Előadók: Kornafeld Ádám SYS PROJEKT Ádám MTA SZTAKI kadam@sztaki.hu Kovács Attila ELTE IK attila@compalg.inf.elte.hu Társszerzők:
"A tízezert mérföldes utazás is egyetlen lépéssel kezdődik dik." A BINB INSYS Előadók: Kornafeld Ádám SYS PROJEKT Ádám MTA SZTAKI kadam@sztaki.hu Kovács Attila ELTE IK attila@compalg.inf.elte.hu Társszerzők:
Antreter Ferenc. Termelési-logisztikai rendszerek tervezése és teljesítményének mérése
 Antreter Ferenc Termelési-logisztikai rendszerek tervezése és teljesítményének mérése Doktori értekezés Témavezetők: Dr. Várlaki Péter egyetemi tanár Széchenyi István Egyetem, Műszaki Tudományi Kar, Logisztikai
Antreter Ferenc Termelési-logisztikai rendszerek tervezése és teljesítményének mérése Doktori értekezés Témavezetők: Dr. Várlaki Péter egyetemi tanár Széchenyi István Egyetem, Műszaki Tudományi Kar, Logisztikai
Mesterséges Intelligencia MI
 Mesterséges Intelligencia MI Problémamegoldás kereséssel ha sötétben tapogatózunk Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade
Mesterséges Intelligencia MI Problémamegoldás kereséssel ha sötétben tapogatózunk Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade
NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő
 SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatika Tanszék BSC FOKOZATÚ MÉRNÖK INFORMATIKUS SZAK NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő Fejlesztői dokumentáció GROUP#6
SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatika Tanszék BSC FOKOZATÚ MÉRNÖK INFORMATIKUS SZAK NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő Fejlesztői dokumentáció GROUP#6
A C programozási nyelv II. Utasítások. A függvény.
 A C programozási nyelv II. Utasítások. A függvény. Miskolci Egyetem Általános Informatikai Tanszék A C programozási nyelv II (Utasítások, fuggvények) CBEV2 / 1 Kifejezés utasítás Kifejezés utasítás, blokk
A C programozási nyelv II. Utasítások. A függvény. Miskolci Egyetem Általános Informatikai Tanszék A C programozási nyelv II (Utasítások, fuggvények) CBEV2 / 1 Kifejezés utasítás Kifejezés utasítás, blokk
Sztöchiometriai egyenletrendszerek minimális számú aktív változót tartalmazó megoldásainak meghatározása a P-gráf módszertan alkalmazásával
 Sztöchiometriai egyenletrendszerek minimális számú aktív változót tartalmazó megoldásainak meghatározása a P-gráf módszertan alkalmazásával * Pannon Egyetem, M szaki Informatikai Kar, Számítástudomány
Sztöchiometriai egyenletrendszerek minimális számú aktív változót tartalmazó megoldásainak meghatározása a P-gráf módszertan alkalmazásával * Pannon Egyetem, M szaki Informatikai Kar, Számítástudomány
Gépi tanulás. Hány tanítómintára van szükség? VKH. Pataki Béla (Bolgár Bence)
 Gépi tanulás Hány tanítómintára van szükség? VKH Pataki Béla (Bolgár Bence) BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Induktív tanulás A tanítás folyamata: Kiinduló
Gépi tanulás Hány tanítómintára van szükség? VKH Pataki Béla (Bolgár Bence) BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Induktív tanulás A tanítás folyamata: Kiinduló
Előrenéző és paraméter tanuló algoritmusok on-line klaszterezési problémákra
 Szegedi Tudományegyetem Számítógépes Algoritmusok és Mesterséges Intelligencia Tanszék Dr. Németh Tamás Előrenéző és paraméter tanuló algoritmusok on-line klaszterezési problémákra SZTE TTIK, Móra Kollégium,
Szegedi Tudományegyetem Számítógépes Algoritmusok és Mesterséges Intelligencia Tanszék Dr. Németh Tamás Előrenéző és paraméter tanuló algoritmusok on-line klaszterezési problémákra SZTE TTIK, Móra Kollégium,
A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel
 A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel Majzik István Micskei Zoltán BME Méréstechnika és Információs Rendszerek Tanszék 1 Modell alapú fejlesztési folyamat (részlet)
A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel Majzik István Micskei Zoltán BME Méréstechnika és Információs Rendszerek Tanszék 1 Modell alapú fejlesztési folyamat (részlet)
Dunaújvárosi Főiskola Informatikai Intézet. Intelligens ágensek. Dr. Seebauer Márta. főiskolai tanár
 Dunaújvárosi Főiskola Informatikai Intézet Intelligens ágensek Dr. Seebauer Márta főiskolai tanár seebauer.marta@szgti.bmf.hu Ágens Ágens (agent) bármi lehet, amit úgy tekinthetünk, hogy érzékelők (sensors)
Dunaújvárosi Főiskola Informatikai Intézet Intelligens ágensek Dr. Seebauer Márta főiskolai tanár seebauer.marta@szgti.bmf.hu Ágens Ágens (agent) bármi lehet, amit úgy tekinthetünk, hogy érzékelők (sensors)
Modell alapú tesztelés mobil környezetben
 Modell alapú tesztelés mobil környezetben Micskei Zoltán Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék A terület behatárolása Testing is an activity performed
Modell alapú tesztelés mobil környezetben Micskei Zoltán Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék A terület behatárolása Testing is an activity performed
Bevezetés, a C++ osztályok. Pere László
 Programozás módszertan II. p. Programozás módszertan II. Bevezetés, a C++ osztályok Pere László (pipas@linux.pte.hu) PÉCSI TUDOMÁNYEGYETEM TERMÉSZETTUDOMÁNYI KAR INFORMATIKA ÉS ÁLTALÁNOS TECHNIKA TANSZÉK
Programozás módszertan II. p. Programozás módszertan II. Bevezetés, a C++ osztályok Pere László (pipas@linux.pte.hu) PÉCSI TUDOMÁNYEGYETEM TERMÉSZETTUDOMÁNYI KAR INFORMATIKA ÉS ÁLTALÁNOS TECHNIKA TANSZÉK
ÁRAMKÖRÖK SZIMULÁCIÓJA
 ÁRAMKÖRÖK SZIMULÁCIÓJA Az áramkörök szimulációja révén betekintést nyerünk azok működésébe. Meg tudjuk határozni az áramkörök válaszát különböző gerjesztésekre, különböző üzemmódokra. Végezhetők analóg
ÁRAMKÖRÖK SZIMULÁCIÓJA Az áramkörök szimulációja révén betekintést nyerünk azok működésébe. Meg tudjuk határozni az áramkörök válaszát különböző gerjesztésekre, különböző üzemmódokra. Végezhetők analóg
Gépi tanulás a gyakorlatban. Bevezetés
 Gépi tanulás a gyakorlatban Bevezetés Motiváció Nagyon gyakran találkozunk gépi tanuló alkalmazásokkal Spam detekció Karakter felismerés Fotó címkézés Szociális háló elemzés Piaci szegmentáció analízis
Gépi tanulás a gyakorlatban Bevezetés Motiváció Nagyon gyakran találkozunk gépi tanuló alkalmazásokkal Spam detekció Karakter felismerés Fotó címkézés Szociális háló elemzés Piaci szegmentáció analízis
Diverzifikáció Markowitz-modell MAD modell CAPM modell 2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 11. Előadás Portfólió probléma Portfólió probléma Portfólió probléma Adott részvények (kötvények,tevékenységek,
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 11. Előadás Portfólió probléma Portfólió probléma Portfólió probléma Adott részvények (kötvények,tevékenységek,
Matematikai programok
 Matematikai programok Mátrixalapú nyelvek MatLab Wettl Ferenc diái alapján Budapesti M szaki Egyetem Algebra Tanszék 2017.11.07 Borbély Gábor (BME Algebra Tanszék) Matematikai programok 2017.11.07 1 /
Matematikai programok Mátrixalapú nyelvek MatLab Wettl Ferenc diái alapján Budapesti M szaki Egyetem Algebra Tanszék 2017.11.07 Borbély Gábor (BME Algebra Tanszék) Matematikai programok 2017.11.07 1 /
Mesterséges Intelligencia Elektronikus Almanach. MI Almanach projektismertetı rendezvény április 29., BME, I. ép., IB.017., 9h-12h.
 Mesterséges Intelligencia Elektronikus Almanach Neurális hálózatokh 1 BME 1990: Miért neurális hálók? - az érdeklıdésünk terébe kerül a neurális hálózatok témakör - fıbb okok: - adaptív rendszerek - felismerési
Mesterséges Intelligencia Elektronikus Almanach Neurális hálózatokh 1 BME 1990: Miért neurális hálók? - az érdeklıdésünk terébe kerül a neurális hálózatok témakör - fıbb okok: - adaptív rendszerek - felismerési
Intelligens ágensek. Mesterséges intelligencia február 28.
 Intelligens ágensek Mesterséges intelligencia 2014. február 28. Ágens = cselekvő Bevezetés Érzékelői segítségével érzékeli a környezetet Beavatkozói/akciói segítségével megváltoztatja azt Érzékelési sorozat:
Intelligens ágensek Mesterséges intelligencia 2014. február 28. Ágens = cselekvő Bevezetés Érzékelői segítségével érzékeli a környezetet Beavatkozói/akciói segítségével megváltoztatja azt Érzékelési sorozat:
A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel
 A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel Majzik István Micskei Zoltán BME Méréstechnika és Információs Rendszerek Tanszék 1 Modell alapú fejlesztési folyamat (részlet)
A modellellenőrzés érdekes alkalmazása: Tesztgenerálás modellellenőrzővel Majzik István Micskei Zoltán BME Méréstechnika és Információs Rendszerek Tanszék 1 Modell alapú fejlesztési folyamat (részlet)
Kutatás-fejlesztési eredmények a Számítógépes Algoritmusok és Mesterséges Intelligencia Tanszéken. Dombi József
 Kutatás-fejlesztési eredmények a Számítógépes Algoritmusok és Mesterséges Intelligencia Tanszéken Dombi József Mesterséges intelligencia Klasszikus megközelítés (A*, kétszemélyes játékok, automatikus tételbizonyítás,
Kutatás-fejlesztési eredmények a Számítógépes Algoritmusok és Mesterséges Intelligencia Tanszéken Dombi József Mesterséges intelligencia Klasszikus megközelítés (A*, kétszemélyes játékok, automatikus tételbizonyítás,
Gyakorlatias tanácsok PLA fejlesztőknek
 Gyakorlatias tanácsok PLA fejlesztőknek Beszédes Nimród Attiláné Békéscsabai Regionális Képző Központ Képzési igazgatóhelyettes 2007. november 28-30. A jogszabályi háttérről 2001. évi CI. törvény 24/2004.
Gyakorlatias tanácsok PLA fejlesztőknek Beszédes Nimród Attiláné Békéscsabai Regionális Képző Központ Képzési igazgatóhelyettes 2007. november 28-30. A jogszabályi háttérről 2001. évi CI. törvény 24/2004.
Objektum orientált kiterjesztés A+ programozási nyelvhez
 Szegedi Tudományegyetem Informatikai Tanszékcsoport Objektum orientált kiterjesztés A+ programozási nyelvhez Diplomamunka terve Készítette: Bátori Csaba programtervező matematikus hallgató Témavezető:
Szegedi Tudományegyetem Informatikai Tanszékcsoport Objektum orientált kiterjesztés A+ programozási nyelvhez Diplomamunka terve Készítette: Bátori Csaba programtervező matematikus hallgató Témavezető:
Egyes logisztikai feladatok megoldása lineáris programozás segítségével. - bútorgyári termelési probléma - szállítási probléma
 Egyes logisztikai feladatok megoldása lineáris programozás segítségével - bútorgyári termelési probléma - szállítási probléma Egy bútorgyár polcot, asztalt és szekrényt gyárt faforgácslapból. A kereskedelemben
Egyes logisztikai feladatok megoldása lineáris programozás segítségével - bútorgyári termelési probléma - szállítási probléma Egy bútorgyár polcot, asztalt és szekrényt gyárt faforgácslapból. A kereskedelemben
Mérés és modellezés Méréstechnika VM, GM, MM 1
 Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
Méréselmélet MI BSc 1
 Mérés és s modellezés 2008.02.15. 1 Méréselmélet - bevezetés a mérnöki problémamegoldás menete 1. A probléma kitűzése 2. A hipotézis felállítása 3. Kísérlettervezés 4. Megfigyelések elvégzése 5. Adatok
Mérés és s modellezés 2008.02.15. 1 Méréselmélet - bevezetés a mérnöki problémamegoldás menete 1. A probléma kitűzése 2. A hipotézis felállítása 3. Kísérlettervezés 4. Megfigyelések elvégzése 5. Adatok
Mesterséges intelligencia alapú regressziós tesztelés
 Mesterséges intelligencia alapú regressziós tesztelés Gujgiczer Anna, Elekes Márton* * AZ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA ÚNKP-16-1-I. KÓDSZÁMÚ ÚJ NEMZETI KIVÁLÓSÁG PROGRAMJÁNAK TÁMOGATÁSÁVAL KÉSZÜLT
Mesterséges intelligencia alapú regressziós tesztelés Gujgiczer Anna, Elekes Márton* * AZ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA ÚNKP-16-1-I. KÓDSZÁMÚ ÚJ NEMZETI KIVÁLÓSÁG PROGRAMJÁNAK TÁMOGATÁSÁVAL KÉSZÜLT
2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 8. Előadás Bevezetés Egy olyan LP-t, amelyben mindegyik változó egészértékű, tiszta egészértékű
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 8. Előadás Bevezetés Egy olyan LP-t, amelyben mindegyik változó egészértékű, tiszta egészértékű
Tisztán kivehetı tendencia: kommunikációs hálózatok egyre bonyolultabbakká válnak Hálózat bonyolultsága
 @ Budapest University of Technology and Economics Nagy hálózatok evolúciója Gulyás András, Heszberger Zalán High Speed Networks Laboratory Internet trendek Tisztán kivehetı tendencia: kommunikációs hálózatok
@ Budapest University of Technology and Economics Nagy hálózatok evolúciója Gulyás András, Heszberger Zalán High Speed Networks Laboratory Internet trendek Tisztán kivehetı tendencia: kommunikációs hálózatok
Branch-and-Bound. 1. Az egészértéketű programozás. a korlátozás és szétválasztás módszere Bevezető Definíció. 11.
 11. gyakorlat Branch-and-Bound a korlátozás és szétválasztás módszere 1. Az egészértéketű programozás 1.1. Bevezető Bizonyos feladatok modellezése kapcsán előfordulhat olyan eset, hogy a megoldás során
11. gyakorlat Branch-and-Bound a korlátozás és szétválasztás módszere 1. Az egészértéketű programozás 1.1. Bevezető Bizonyos feladatok modellezése kapcsán előfordulhat olyan eset, hogy a megoldás során
VÁLLALATGAZDASÁGTAN II. Döntési Alapfogalmak
 Vállalkozási VÁLLALATGAZDASÁGTAN II. Tantárgyfelelős: Prof. Dr. Illés B. Csaba Előadó: Dr. Gyenge Balázs Az ökonómiai döntés fogalma Vállalat Környezet Döntések sorozata Jövő jövőre vonatkozik törekszik
Vállalkozási VÁLLALATGAZDASÁGTAN II. Tantárgyfelelős: Prof. Dr. Illés B. Csaba Előadó: Dr. Gyenge Balázs Az ökonómiai döntés fogalma Vállalat Környezet Döntések sorozata Jövő jövőre vonatkozik törekszik
Számítógépes képelemzés 7. előadás. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
ködös határ (félreértés, hiba)
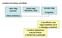 probléma formálisan specifikált: valós világ (domain) (hibás eredmény) ködös határ (félreértés, hiba) formális világ (megoldás) A szoftver fejlesztőnek meg kell értenie a felhasználó problémáját. A specifikáció
probléma formálisan specifikált: valós világ (domain) (hibás eredmény) ködös határ (félreértés, hiba) formális világ (megoldás) A szoftver fejlesztőnek meg kell értenie a felhasználó problémáját. A specifikáció
Számítógépes döntéstámogatás. Bevezetés és tematika
 SZDT-01 p. 1/18 Számítógépes döntéstámogatás Bevezetés és tematika Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Előadás SZDT-01 p. 2/18 SZDT-01
SZDT-01 p. 1/18 Számítógépes döntéstámogatás Bevezetés és tematika Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Előadás SZDT-01 p. 2/18 SZDT-01
Követelmények Motiváció Matematikai modellezés: példák A lineáris programozás alapfeladata 2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 1. Előadás Követelmények, teljesítés feltételei Vizsga anyaga Előadásokhoz tartozó diasor
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 1. Előadás Követelmények, teljesítés feltételei Vizsga anyaga Előadásokhoz tartozó diasor
Követelmények Motiváció Matematikai modellezés: példák A lineáris programozás alapfeladata 2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 1. Előadás Követelmények, teljesítés feltételei Vizsga anyaga Előadásokhoz tartozó diasor
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 1. Előadás Követelmények, teljesítés feltételei Vizsga anyaga Előadásokhoz tartozó diasor
1/ gyakorlat. Hiperbolikus programozási feladat megoldása. Pécsi Tudományegyetem PTI
 1/12 Operációkutatás 5. gyakorlat Hiperbolikus programozási feladat megoldása Pécsi Tudományegyetem PTI 2/12 Ha az Hiperbolikus programozási feladat feltételek teljesülése mellett a A x b x 0 z(x) = c
1/12 Operációkutatás 5. gyakorlat Hiperbolikus programozási feladat megoldása Pécsi Tudományegyetem PTI 2/12 Ha az Hiperbolikus programozási feladat feltételek teljesülése mellett a A x b x 0 z(x) = c
A digitális témahét program-tervezete
 A digitális témahét program-tervezete 1. LEGO Mindstorms robotikai bemutató Helyszín: 113. tanterem Vezeti: Deák Csaba 2. Elektronikai bemutató Helyszín: V3 tanterem Vezeti: Sándor Péter 3. Kiterjesztett
A digitális témahét program-tervezete 1. LEGO Mindstorms robotikai bemutató Helyszín: 113. tanterem Vezeti: Deák Csaba 2. Elektronikai bemutató Helyszín: V3 tanterem Vezeti: Sándor Péter 3. Kiterjesztett
1/12. 3. gyakorlat. Lineáris Programozási feladatok megoldása szimplex módszerrel. Pécsi Tudományegyetem PTI
 / Operációkutatás. gyakorlat Lineáris Programozási feladatok megoldása szimplex módszerrel Pécsi Tudományegyetem PTI Normál feladatok megoldása szimplex módszerrel / / Normál feladatok megoldása szimplex
/ Operációkutatás. gyakorlat Lineáris Programozási feladatok megoldása szimplex módszerrel Pécsi Tudományegyetem PTI Normál feladatok megoldása szimplex módszerrel / / Normál feladatok megoldása szimplex
Szkriptnyelvek. 1. UNIX shell
 Szkriptnyelvek 1. UNIX shell Szkriptek futtatása Parancsértelmez ő shell script neve paraméterek shell script neve paraméterek Ebben az esetben a szkript tartalmazza a parancsértelmezőt: #!/bin/bash Szkriptek
Szkriptnyelvek 1. UNIX shell Szkriptek futtatása Parancsértelmez ő shell script neve paraméterek shell script neve paraméterek Ebben az esetben a szkript tartalmazza a parancsértelmezőt: #!/bin/bash Szkriptek
Gépi tanulás Gregorics Tibor Mesterséges intelligencia
 Gépi tanulás Tanulás fogalma Egy algoritmus akkor tanul, ha egy feladat megoldása során olyan változások következnek be a működésében, hogy később ugyanazt a feladatot vagy ahhoz hasonló más feladatokat
Gépi tanulás Tanulás fogalma Egy algoritmus akkor tanul, ha egy feladat megoldása során olyan változások következnek be a működésében, hogy később ugyanazt a feladatot vagy ahhoz hasonló más feladatokat
BASH script programozás II. Vezérlési szerkezetek
 06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
angolul: greedy algorithms, románul: algoritmi greedy
 Mohó algoritmusok angolul: greedy algorithms, románul: algoritmi greedy 1. feladat. Gazdaságos telefonhálózat építése Bizonyos városok között lehet direkt telefonkapcsolatot kiépíteni, pl. x és y város
Mohó algoritmusok angolul: greedy algorithms, románul: algoritmi greedy 1. feladat. Gazdaságos telefonhálózat építése Bizonyos városok között lehet direkt telefonkapcsolatot kiépíteni, pl. x és y város
1. gyakorlat. Mesterséges Intelligencia 2.
 1. gyakorlat Mesterséges Intelligencia. Elérhetőségek web: www.inf.u-szeged.hu/~gulyasg mail: gulyasg@inf.u-szeged.hu Követelmények (nem teljes) gyakorlat látogatása kötelező ZH írása a gyakorlaton elhangzott
1. gyakorlat Mesterséges Intelligencia. Elérhetőségek web: www.inf.u-szeged.hu/~gulyasg mail: gulyasg@inf.u-szeged.hu Követelmények (nem teljes) gyakorlat látogatása kötelező ZH írása a gyakorlaton elhangzott
KÖZELÍTŐ INFERENCIA II.
 STATISZTIKAI TANULÁS AZ IDEGRENDSZERBEN KÖZELÍTŐ INFERENCIA II. MONTE CARLO MÓDSZEREK ISMÉTLÉS Egy valószínűségi modellben a következtetéseinket a látensek vagy a paraméterek fölötti poszterior írja le.
STATISZTIKAI TANULÁS AZ IDEGRENDSZERBEN KÖZELÍTŐ INFERENCIA II. MONTE CARLO MÓDSZEREK ISMÉTLÉS Egy valószínűségi modellben a következtetéseinket a látensek vagy a paraméterek fölötti poszterior írja le.
Változók. Mennyiség, érték (v. objektum) szimbolikus jelölése, jelentése Tulajdonságai (attribútumai):
 Python Változók Mennyiség, érték (v. objektum) szimbolikus jelölése, jelentése Tulajdonságai (attribútumai): Név Érték Típus Memóriacím A változó értéke (esetleg más attribútuma is) a program futása alatt
Python Változók Mennyiség, érték (v. objektum) szimbolikus jelölése, jelentése Tulajdonságai (attribútumai): Név Érték Típus Memóriacím A változó értéke (esetleg más attribútuma is) a program futása alatt
Algoritmusok Tervezése. 6. Előadás Algoritmusok 101 Dr. Bécsi Tamás
 Algoritmusok Tervezése 6. Előadás Algoritmusok 101 Dr. Bécsi Tamás Mi az algoritmus? Lépések sorozata egy feladat elvégzéséhez (legáltalánosabban) Informálisan algoritmusnak nevezünk bármilyen jól definiált
Algoritmusok Tervezése 6. Előadás Algoritmusok 101 Dr. Bécsi Tamás Mi az algoritmus? Lépések sorozata egy feladat elvégzéséhez (legáltalánosabban) Informálisan algoritmusnak nevezünk bármilyen jól definiált
Matematikai programok
 Matematikai programok Mátrixalapú nyelvek octave Wettl Ferenc Algebra Tanszék B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Wettl
Matematikai programok Mátrixalapú nyelvek octave Wettl Ferenc Algebra Tanszék B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Wettl
Döntéselméleti modellek
 Döntéselméleti modellek gyakorlat Berta Árpád Követelmények A félév során 40 pont szerezhető 0-19 pont : elégtelen (1) 20-24 pont : elégséges (2) 25-29 pont : közepes (3) 30-34 pont : jó (4) 35-40 pont
Döntéselméleti modellek gyakorlat Berta Árpád Követelmények A félév során 40 pont szerezhető 0-19 pont : elégtelen (1) 20-24 pont : elégséges (2) 25-29 pont : közepes (3) 30-34 pont : jó (4) 35-40 pont
