3) Mit fejez ki az B T DBdV kifejezés, és mi a fizikai tartalma a benne szereplő mennyiségeknek?
|
|
|
- Róbert Ernő Bakos
- 8 évvel ezelőtt
- Látták:
Átírás
1 1) Értelmezze az u=nd kifejezést! Hogyan lehet felírni egy elem tetszőleges belső pontjának elmozdulásait az elem csomóponti elmozdulásainak ismeretében? 3) Mit fejez ki az B T DBdV kifejezés, és mi a fizikai tartalma a benne szereplő mennyiségeknek?
2 4) Értelmezze az ε=dnd=bd kifejezést! Milyen mennyiségeket tartalmaz és mi azok fizikai tartalma? A nyúlást leíró egyenletrendszer 5) Értelmezze a σ=d(ε-ε 0)+σ 0 kifejezést! Milyen mennyiségeket tartalmaz és mi azok fizikai tartalma? 6) Mit fejez ki a δ(u+w)=0 variációs egyenlet? Értelmezze a benne szerepelő mennyiségeket! 7) Mit fejez ki Kd-F=0 egyenlet és hogyan oldható meg?
3 8) Ábrával magyarázza meg egy-egy húzott és hajlított szelvény feszültségeinek alakulását a rugalmas feszültségektől a képlékeny határállapotig. Húzott: Hajlított: 9) Ábrával magyarázza meg a helyi képlékeny zóna terjedését egy diszkontinuitás környezetében. 10) Rajzolja fel egy húzott próbatest rugalmas-képlékeny szakítódiagramját és értelmezze a jellegzetes pontokat.
4 11) Milyen idealizált anyagtörvényeket ismer? Válaszát ábrákkal is illusztrálja. lineárisan rugalmas merev-ideálisan képlékeny, merev-felkeményedő rugalmas- ideálisan képlékeny, rugalmas-felkeményedő
5 12) Miben különbözik a rugalmas-ideálisan képlékeny és a rugalmas-felkeményedő anyagtörvény? Válaszát ábrákkal is illusztrálja. A K-keményedési tényező értékében rugalmas- ideálisan képlékeny, rugalmas-felkeményedő 13) Értelmezze a maradó nyúlást és a maradó feszültséget rugalmas-ideálisan képlékeny anyagtörvény esetén. Válaszát ábrával is illusztrálja Maradó nyúlások és feszültségek rugalmas-ideálisan képlékeny anyagtörvény esetén 14) A mutassa be és magyarázza a folyási felület viselke dését ideálisan képlékeny esetben, valamint izotróp és kinematikai felkeményedés esetén. A folyási felület viselkedése ideálisan képlékeny esetben, valamint izotróp és kinematikai felkeményedés esetén
6 15) Mi a különbség az izotróp és a kinematikai felkeményedés között? Válaszát ábrákkal is illusztrálja. 16) Egy kéttámaszú tartó példáján keresztül mutassa be a képlékeny csukló kialakulásának folyamatát egy hajlított tartóban. Mi a teherbíró képesség határa? A hajlított tartó szelvényében M<M r feszültségen csak rugalmas feszültségek vannak. Elérve a rugalmassági határt (M=M r ) a szélső szál megfolyik, de a szelvény még rugalmas marad. Rugalmas viselkedést mutat a φ=φ(m) szögelfordulás-nyomaték függvény is. A rugalmassági határ felett (M r <M<M t ) egyre kiterjedtebb képlékeny zóna alakul ki a szelvény húzott és nyomott zónájában, a- melynek következtében a φ=φ(m) függvény is elveszti a linearitását. Az M=M t képlékeny teherbírási határon a képlékeny zónák összeérnek, a szelvény elveszti a hajlítással szembeni ellenállását, a további szögelfordulás- hoz nem szükséges többlet-nyomaték, tehát a szelvény a nyomaték szempontjából csuklóssá válik és kialakul az un. képlékeny csukló. 17) Egy bemetszett tartó példáján keresztül mutassa be a kisciklusú kifáradás jelenségét egy hajlított tartóban. Mi a kisciklusú kifáradás oka? A gép egy ingás ütőmű, amely bemetszett próbatestet tör el. Az ingát, amely jól csapágyazott tengely körül elfordítható rúdból és annak végén elhelyezett nagy tömegű (15 vagy 30 kg) ütőfejből áll, meghatározott magasságról indítják. Amikor az ingát elengedik, lefelé indul, felgyorsul, és a legnagyobb sebességét a pálya alsó pontján éri el, ahol a kezdeti helyzeti energia mozgási energiává alakul. Ide helyezik a bemetszett próbadarabot, amelyre az ütőfej ütést mér és eltöri. A töréshez szükséges munka csökkenti a mozgási energiát, így amikor az inga felfelé mozdul, felső holtpontjának magassága nem éri el az indítási magasságot. A két véghelyzet magasságának (h és h) különbségéből kiszámítható az ütőfej helyzeti energiáinak különbsége K=mg(h -h), amely a próbatest eltöréséhez szükséges munka Jouleban.
7 Elsőként tekintsük a feszültség ábrát, amely a bemetszés csúcspontjának σ feszültségét ábrázolja a terhelés függvényében! A vizsgált pont σf terhelésig (A-B szakasz) rugalmasan viselkedik, majd a teljes F t =1875N terhelés ráadásáig (B-B ) képlékeny alakváltozást mutat. Ez, az előzetes számítások tükrében egyáltalán nem meglepő. A szokatlan jelenség a leterheléskor tapasztalható, ugyanis a tehermentesítés csak a B -A szakaszon lineáris, utána ismét képlékeny alakváltozást tapasztalunk (A -A ), tehát a vizsgált pontban a leterhelés során, ellentétes előjellel, ismét jelentkezik a folyás. A megismételt felterheléskor az A -B szakasz lineáris, utána egy rövidebb képlékeny alakváltozás következik (B -B ), majd a leterhelés a korábbi B -A egyenes mentén ismét lineáris, a végén egy a B -B szakasszal azonos mértékű megfolyással (A -A ). Látható, hogy a megismételt terhelés során a feszültséggörbe hiszterézist mutat (A -B -B -A -A ), amely többszöri újraterhelés esetén már kis ciklusszám mellett is tönkremenetelt eredményez. A jelenség az un. kisciklusú kifáradás. Hasonló jelenség megy végbe egy drótdarab hajlítgatásakor, amely néhány tucat terhelési ciklus után eltörik. A hajlítgatás közben tapasztalt melegedés forrása a hiszterézis. A kisciklusú kifáradás szempontjából kitűntetett jelentősége van a B pontnak, amelyhez a 2σ F feszültséget létrehozó F t =1428 N terhelés tartozik. Ha a terhelést csak F t-ig működtetnénk (B pont), akkor a leterhelés, hiszterézis nélkül, a B -A egyenes mentén történne. Ebből következik, hogy a kisciklusú kifáradás határterhelése a 2σ F feszültséget létrehozó terhelés. 18) Mutassa be egy belső nyomással terhelt vastag falú cső rugalmas-képlékeny viselkedését. Mi a teherbíró képesség határa? 19) Magyarázza meg az autofrettázs jelenséget.
8 Rugalmas-képlékeny feladatok 20) Mutassa be és magyarázza ábrán a Newton-Raphson iterációt. Melyek a Newton-Raphson iteráció előnyei és hátrányai? Nem a kiinduló állapotból, hanem egy más terhelési szintről indítjuk az új iterálást érintővel. Előny: Nagyon gyors konvergencia Hátrány: K mx-t minden lépésnél újra kell építeni 21) Mutassa be és magyarázza ábrán a módosított Newton -Raphson iterációt. Melyek a módosított Newton-Raphson iteráció el őnyei és hátrányai? A módosított Newton-Raphson iteráció Nem érintővel, hanem párhuzamos egyenessel készítik az új iterálást. Előny: K mx-t csak egyszer kell számítani Hátrány: Lasabban konvergál K bizonyos értékénél divergencia lehet
9 22) Mutassa be és magyarázza ábrán a direkt (Line Search) iterációt. Folyamatos iteráció pontonként K=K(E)=K(E(epszilon)) Az un. direkt (Line Search) iteráció 23) Mi a különbség a Newton-Raphson és a módosított Newton-Raphson iteráció között? Mi a gyakorlaticélja a módosított Newton-Raphson iteráció használatának? A sima N-R esetén minden lépésben új K mx (K1,K2,K3) ot kell kiszámolni. A módosított N-R-nél csak egyet K1 kell az elején, és ezzel számol tovább minden lépésben. A módosított N-R nek kisebb a számítási kapacitás igénye. 24) Milyen célt szolgál a rugalmas-képlékeny végeselemes feladatokban az időlépés (Time Step)? 25) Milyen adatokat kell megadni a rugalmas-képlékeny feladatok mérnöki célú megoldása során? 26) Milyen adatok szükségesek egy rugalmas -felkeményedő anyagtörvény megadásához? F(Szigma,K)=0 folyási feltétel -Szigma: Feszültség -K: Keményedési tényező 28) Foglalja össze a geometriailag nemlineáris megoldást igénylő feladattípusokat. -nagy elmozdulás -nagy alakváltozás - stabilitás vizsgálat -érintkezési problémák
10 31) Foglalja össze az érintkezési (kontakt) feladatok típusait. - Lineáris (gap-elem) - Nem lineáris ű o kontakt elem o geometriai feltétel, egyensúlyi feltétel (erő) 32) Mi a lineáris érintkezési feladatok megoldásának alapelve? Az eljárás egy olyan iterációs algoritmusra épül, ahol az egyensúlyi feltétel az érintkező testek közti hézagmentes érintkezés 33) Mi a nemlineáris érintkezési feladatok megoldásának alapelve? A súrlódás is figyelembe vehető. A geometriai nem linearitás algoritmusokat használja fel. DINAMIKA 36) Írja fel a dinamikai feladatok megoldására szolgáló differenciálegyenletet egytömegű lengő rendszerre. 37) Milyen alapvet ő anyag- és geometriai jellemzők vannak hatással a dinamikai feladatok eredményeire? 38) Írja fel a dinamikai feladatok végeselemes tárgyalásának alapegyenletét és magyarázza az egyenletben szerepl ő mennyiségeket! 39) A vé geselemes dinamikai feladatokban hogyan definiáljuk a tömeg - és a csillapítási mátrixot? Tömeg mátrix: Csillapítási mátrix: 40) Mi a koncentrált tömegmátrix és milyen el őnyökkel jár a használata? 41) Mutassa be ábrán, hogy a csillapításnak hol van jelentősége a dinamikai feladatokban. 42) Mutassa be az Mu +Cu +Ku=F (t) egyensúlyi egyenlet időbeli megoldására szolgáló növekményes technikát. 43) Ismertesse a dinamikai vizsgálat ok kezdeti feltételeit és a számítás elindításának teendőit. 44) Ismertesse dinamikai vizsgálatok direkt integrálási lépéseit. 50) Milyen célt szolgál a nemlineáris, hőtani és dinamikai végeselemes feladatokban az id őlépés (Time Step)? 51) Milyen típusú végeselemes feladatok esetén van szükség un. kezdeti, vagy kiinduló feltételre?
Tartószerkezetek I. (Vasbeton szilárdságtan)
 Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.10.11. Vasbeton külpontos nyomása Az eső ágú σ-ε diagram miatt elvileg minden egyes esethez külön kell meghatározni a szélső szál összenyomódását.
Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.10.11. Vasbeton külpontos nyomása Az eső ágú σ-ε diagram miatt elvileg minden egyes esethez külön kell meghatározni a szélső szál összenyomódását.
Energiatételek - Példák
 9. Előadás Húzott rúd potenciális energiája: Hooke-modell: σ = Eε Geom. hetséges Geometriai egyenlet: + geom. peremfeltételek: u εx = ε = x u(0) = 0 ul () = 0 du dx Energiatételek Példák = k l 0 pudx l
9. Előadás Húzott rúd potenciális energiája: Hooke-modell: σ = Eε Geom. hetséges Geometriai egyenlet: + geom. peremfeltételek: u εx = ε = x u(0) = 0 ul () = 0 du dx Energiatételek Példák = k l 0 pudx l
Előadó: Dr. Bukovics Ádám 11. ELŐADÁS
 SZÉCHNYI ISTVÁN GYTM TARTÓSZRKZTK III. lőadó: Dr. Bukovics Ádám Az ábrák forrása:. LŐADÁS [1] Dr. Németh György: Tartószerkezetek III., Acélszerkezetek méretezésének alapjai [2] Halász Ottó Platthy Pál:
SZÉCHNYI ISTVÁN GYTM TARTÓSZRKZTK III. lőadó: Dr. Bukovics Ádám Az ábrák forrása:. LŐADÁS [1] Dr. Németh György: Tartószerkezetek III., Acélszerkezetek méretezésének alapjai [2] Halász Ottó Platthy Pál:
Végeselemes analízisen alapuló méretezési elvek az Eurocode 3 alapján. Dr. Dunai László egyetemi tanár BME, Hidak és Szerkezetek Tanszéke
 Végeselemes analízisen alapuló méretezési elvek az Eurocode 3 alapján Dr. Dunai László egyetemi tanár BME, Hidak és Szerkezetek Tanszéke 1 Tartalom Méretezési alapelvek Numerikus modellezés Analízis és
Végeselemes analízisen alapuló méretezési elvek az Eurocode 3 alapján Dr. Dunai László egyetemi tanár BME, Hidak és Szerkezetek Tanszéke 1 Tartalom Méretezési alapelvek Numerikus modellezés Analízis és
Anyagvizsgálatok. Mechanikai vizsgálatok
 Anyagvizsgálatok Mechanikai vizsgálatok Szakítóvizsgálat EN 10002-1:2002 Célja: az anyagok egytengelyű húzó igénybevétellel szembeni ellenállásának meghatározása egy szabványosan kialakított próbatestet
Anyagvizsgálatok Mechanikai vizsgálatok Szakítóvizsgálat EN 10002-1:2002 Célja: az anyagok egytengelyű húzó igénybevétellel szembeni ellenállásának meghatározása egy szabványosan kialakított próbatestet
A szerkezeti anyagok tulajdonságai és azok vizsgálata
 A szerkezeti anyagok tulajdonságai és azok vizsgálata 1 Az anyagok tulajdonságai fizikai tulajdonságok, mechanikai, termikus, elektromos, mágneses akusztikai, optikai 2 Minıség, élettartam A termék minısége
A szerkezeti anyagok tulajdonságai és azok vizsgálata 1 Az anyagok tulajdonságai fizikai tulajdonságok, mechanikai, termikus, elektromos, mágneses akusztikai, optikai 2 Minıség, élettartam A termék minısége
Gyakorlat 04 Keresztmetszetek III.
 Gyakorlat 04 Keresztmetszetek III. 1. Feladat Hajlítás és nyírás Végezzük el az alábbi gerenda keresztmetszeti vizsgálatait (tiszta esetek és lehetséges kölcsönhatások) kétféle anyaggal: S235; S355! (1)
Gyakorlat 04 Keresztmetszetek III. 1. Feladat Hajlítás és nyírás Végezzük el az alábbi gerenda keresztmetszeti vizsgálatait (tiszta esetek és lehetséges kölcsönhatások) kétféle anyaggal: S235; S355! (1)
Pere Balázs október 20.
 Végeselem anaĺızis 1. előadás Széchenyi István Egyetem, Alkalmazott Mechanika Tanszék 2014. október 20. Mi az a VégesElem Anaĺızis (VEA)? Mi az a VégesElem Anaĺızis (VEA)? Mi az a VégesElem Anaĺızis (VEA)?
Végeselem anaĺızis 1. előadás Széchenyi István Egyetem, Alkalmazott Mechanika Tanszék 2014. október 20. Mi az a VégesElem Anaĺızis (VEA)? Mi az a VégesElem Anaĺızis (VEA)? Mi az a VégesElem Anaĺızis (VEA)?
II. Gyakorlat: Hajlított vasbeton keresztmetszet ellenőrzése (Négyszög és T-alakú keresztmetszetek hajlítási teherbírása III. feszültségi állapotban)
 II. Gyakorlat: Hajlított vasbeton keresztmetszet ellenőrzése (Négyszög és T-alakú keresztmetszetek hajlítási teherbírása III. feszültségi állapotban) Készítették: Dr. Kiss Rita és Klinka Katalin -1- A
II. Gyakorlat: Hajlított vasbeton keresztmetszet ellenőrzése (Négyszög és T-alakú keresztmetszetek hajlítási teherbírása III. feszültségi állapotban) Készítették: Dr. Kiss Rita és Klinka Katalin -1- A
Végeselem analízis. 1. el adás
 Végeselem analízis 1. el adás Pere Balázs Széchenyi István Egyetem, Alkalmazott Mechanika Tanszék 2016. szeptember 7. Mi az a VégesElem Analízis (VEA)? Parciális dierenciálegyenletek (egyenletrendszerek)
Végeselem analízis 1. el adás Pere Balázs Széchenyi István Egyetem, Alkalmazott Mechanika Tanszék 2016. szeptember 7. Mi az a VégesElem Analízis (VEA)? Parciális dierenciálegyenletek (egyenletrendszerek)
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
MUNKAGÖDÖR TERVEZÉSE
 MUNKAGÖDÖR TERVEZÉSE Munkagödör tervezése Munkatérhatárolás szerkezetei Munkagödör méretezés Plaxis programmal Munkagödör méretezés Geo 5 programmal Tartalom Bevezetés VEM - geotechnikai alkalmazási területek
MUNKAGÖDÖR TERVEZÉSE Munkagödör tervezése Munkatérhatárolás szerkezetei Munkagödör méretezés Plaxis programmal Munkagödör méretezés Geo 5 programmal Tartalom Bevezetés VEM - geotechnikai alkalmazási területek
Külpontosan nyomott keresztmetszet számítása
 Külpontosan nyomott keresztmetszet számítása A TELJES TEHERBÍRÁSI VONAL SZÁMÍTÁSA Az alábbi példa egy asszimmetrikus vasalású keresztmetszet teherbírási görbéjének 9 pontját mutatja be. Az első részben
Külpontosan nyomott keresztmetszet számítása A TELJES TEHERBÍRÁSI VONAL SZÁMÍTÁSA Az alábbi példa egy asszimmetrikus vasalású keresztmetszet teherbírási görbéjének 9 pontját mutatja be. Az első részben
MECHANIKA I. rész: Szilárd testek mechanikája
 Egészségügyi mérnökképzés MECHNIK I. rész: Szilárd testek mechanikája készítette: Németh Róbert Igénybevételek térben I. z alapelv ugyanaz, mint síkban: a keresztmetszet egyik oldalán levő szerkezetrészre
Egészségügyi mérnökképzés MECHNIK I. rész: Szilárd testek mechanikája készítette: Németh Róbert Igénybevételek térben I. z alapelv ugyanaz, mint síkban: a keresztmetszet egyik oldalán levő szerkezetrészre
6. MECHANIKA-STATIKA GYAKORLAT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya, Culmann-szerkesztés, Ritter-számítás
 ZÉHENYI ITVÁN EGYETE GÉPZERKEZETTN É EHNIK TNZÉK 6. EHNIK-TTIK GYKORLT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa Egy létrát egy verembe letámasztunk
ZÉHENYI ITVÁN EGYETE GÉPZERKEZETTN É EHNIK TNZÉK 6. EHNIK-TTIK GYKORLT Kidolgozta: Triesz Péter egy. ts. Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa Egy létrát egy verembe letámasztunk
A.2. Acélszerkezetek határállapotai
 A.. Acélszerkezetek határállapotai A... A teherbírási határállapotok első osztálya: a szilárdsági határállapotok A szilárdsági határállapotok (melyek között a fáradt és rideg törést e helyütt nem tárgyaljuk)
A.. Acélszerkezetek határállapotai A... A teherbírási határállapotok első osztálya: a szilárdsági határállapotok A szilárdsági határállapotok (melyek között a fáradt és rideg törést e helyütt nem tárgyaljuk)
Gyakorlat 03 Keresztmetszetek II.
 Gyakorlat 03 Keresztmetszetek II. 1. Feladat Keresztmetszetek osztályzása Végezzük el a keresztmetszet osztályzását tiszta nyomás és hajlítás esetére! Monoszimmetrikus, hegesztett I szelvény (GY02 1. példája)
Gyakorlat 03 Keresztmetszetek II. 1. Feladat Keresztmetszetek osztályzása Végezzük el a keresztmetszet osztályzását tiszta nyomás és hajlítás esetére! Monoszimmetrikus, hegesztett I szelvény (GY02 1. példája)
6. MECHANIKA-STATIKA GYAKORLAT (kidolgozta: Triesz Péter, egy. ts.; Tarnai Gábor, mérnöktanár)
 SZÉHNYI ISTVÁN GYT LKLZOTT HNIK TNSZÉK 6. HNIK-STTIK GYKORLT (kidolgozta: Triesz Péter egy. ts.; Tarnai Gábor mérnöktanár) Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa gy létrát egy
SZÉHNYI ISTVÁN GYT LKLZOTT HNIK TNSZÉK 6. HNIK-STTIK GYKORLT (kidolgozta: Triesz Péter egy. ts.; Tarnai Gábor mérnöktanár) Négy erő egyensúlya ulmann-szerkesztés Ritter-számítás 6.. Példa gy létrát egy
Lemez- és gerendaalapok méretezése
 Lemez- és gerendaalapok méretezése Az alapmerevség hatása az alap hajlékony merev a talpfeszültség egyenletes széleken nagyobb a süllyedés teknıszerő egyenletes Terhelés hatása hajlékony alapok esetén
Lemez- és gerendaalapok méretezése Az alapmerevség hatása az alap hajlékony merev a talpfeszültség egyenletes széleken nagyobb a süllyedés teknıszerő egyenletes Terhelés hatása hajlékony alapok esetén
1. Ütvehajlító vizsgálat
 1. Ütvehajlító vizsgálat Ütvehajlító vizsgálat segítségével megvizsgálhatjuk, hogy az adott körülmények között dinamikus igénybevétel hatására hogyan viselkedik az agyagunk. A körülményektől függően egy
1. Ütvehajlító vizsgálat Ütvehajlító vizsgálat segítségével megvizsgálhatjuk, hogy az adott körülmények között dinamikus igénybevétel hatására hogyan viselkedik az agyagunk. A körülményektől függően egy
HELYI TANTERV. Mechanika
 HELYI TANTERV Mechanika Bevezető A mechanika tantárgy tanításának célja, hogy fejlessze a tanulók logikai készségét, alapozza meg a szakmai tantárgyak feldolgozását. A tanulók tanulási folyamata fejlessze
HELYI TANTERV Mechanika Bevezető A mechanika tantárgy tanításának célja, hogy fejlessze a tanulók logikai készségét, alapozza meg a szakmai tantárgyak feldolgozását. A tanulók tanulási folyamata fejlessze
A szerkezeti anyagok tulajdonságai és azok vizsgálata
 A szerkezeti anyagok tulajdonságai és azok vizsgálata 1 Az anyagok tulajdonságai fizikai tulajdonságok, mechanikai, termikus, elektromos, mágneses akusztikai, optikai 2 Minőség, élettartam A termék minősége
A szerkezeti anyagok tulajdonságai és azok vizsgálata 1 Az anyagok tulajdonságai fizikai tulajdonságok, mechanikai, termikus, elektromos, mágneses akusztikai, optikai 2 Minőség, élettartam A termék minősége
Navier-formula. Frissítve: Egyenes hajlítás
 Navier-formula Akkor beszélünk egyenes hajlításról, ha a nyomatékvektor egybeesik valamelyik fő-másodrendű nyomatéki tengellyel. A hajlítást mindig súlyponti koordinátarendszerben értelmezzük. Ez még a
Navier-formula Akkor beszélünk egyenes hajlításról, ha a nyomatékvektor egybeesik valamelyik fő-másodrendű nyomatéki tengellyel. A hajlítást mindig súlyponti koordinátarendszerben értelmezzük. Ez még a
Frissítve: Csavarás. 1. példa: Az 5 gyakorlat 1. példájához hasonló feladat.
 1. példa: Az 5 gyakorlat 1. példájához hasonló feladat. Mekkora a nyomatékok hatására ébredő legnagyobb csúsztatófeszültség? Mekkora és milyen irányú az A, B és C keresztmetszet elfordulása? Számítsuk
1. példa: Az 5 gyakorlat 1. példájához hasonló feladat. Mekkora a nyomatékok hatására ébredő legnagyobb csúsztatófeszültség? Mekkora és milyen irányú az A, B és C keresztmetszet elfordulása? Számítsuk
KIFÁRADÁSI ÉLETTARTAM MINTAFELADAT (MSc.)
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM KIFÁRADÁSI ÉLETTARTAM MINTAFELADAT (MSc.) Járműelemek és Járműszerkezetanalízis Tanszék FELADAT: Határozza meg a megadott rendszertelen terhelési folyamat
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM KIFÁRADÁSI ÉLETTARTAM MINTAFELADAT (MSc.) Járműelemek és Járműszerkezetanalízis Tanszék FELADAT: Határozza meg a megadott rendszertelen terhelési folyamat
Újdonságok 2013 Budapest
 Újdonságok 2013 Budapest Tartalom 1. Általános 3 2. Szerkesztés 7 3. Elemek 9 4. Terhek 10 5. Számítás 12 6. Eredmények 13 7. Méretezés 14 8. Dokumentáció 15 2. oldal 1. Általános A 64 bites változat lehetőséget
Újdonságok 2013 Budapest Tartalom 1. Általános 3 2. Szerkesztés 7 3. Elemek 9 4. Terhek 10 5. Számítás 12 6. Eredmények 13 7. Méretezés 14 8. Dokumentáció 15 2. oldal 1. Általános A 64 bites változat lehetőséget
Vasbeton tartók méretezése hajlításra
 Vasbeton tartók méretezése hajlításra Képlékenység-tani méretezés: A vasbeton keresztmetszet teherbírásának számításánál a III. feszültségi állapotot vesszük alapul, amelyre az jellemző, hogy a hajlításból
Vasbeton tartók méretezése hajlításra Képlékenység-tani méretezés: A vasbeton keresztmetszet teherbírásának számításánál a III. feszültségi állapotot vesszük alapul, amelyre az jellemző, hogy a hajlításból
Tevékenység: Tanulmányozza a ábrát és a levezetést! Tanulja meg a fajlagos nyúlás mértékének meghatározásának módját hajlításnál!
 Tanulmányozza a.3.6. ábrát és a levezetést! Tanulja meg a fajlagos nyúlás mértékének meghatározásának módját hajlításnál! Az alakváltozás mértéke hajlításnál Hajlításnál az alakváltozást mérnöki alakváltozási
Tanulmányozza a.3.6. ábrát és a levezetést! Tanulja meg a fajlagos nyúlás mértékének meghatározásának módját hajlításnál! Az alakváltozás mértéke hajlításnál Hajlításnál az alakváltozást mérnöki alakváltozási
2. fejezet: Vasbeton keresztmetszet ellenõrzése hajlításra
 . ejezet: Vasbeton keresztmetszet ellenõrzése hajlításra.1. Ellenõrizze az alábbi keresztmetszetet M S =105 knm hajlítónyomatékra! Beton: C16/0 Betonaél: B60.50 φ0 1.15!! = 10.667 N y = 3.783 N φ π A s
. ejezet: Vasbeton keresztmetszet ellenõrzése hajlításra.1. Ellenõrizze az alábbi keresztmetszetet M S =105 knm hajlítónyomatékra! Beton: C16/0 Betonaél: B60.50 φ0 1.15!! = 10.667 N y = 3.783 N φ π A s
Toronymerevítık mechanikai szempontból
 Andó Mátyás: Toronymerevítık méretezése, 9 Gépész Tuning Kft. Toronymerevítık mechanikai szempontból Mint a neve is mutatja a toronymerevítık használatának célja az, hogy merevebbé tegye az autó karosszériáját
Andó Mátyás: Toronymerevítık méretezése, 9 Gépész Tuning Kft. Toronymerevítık mechanikai szempontból Mint a neve is mutatja a toronymerevítık használatának célja az, hogy merevebbé tegye az autó karosszériáját
Gépészeti rendszertechnika (NGB_KV002_1)
 Gépészeti rendszertechnika (NGB_KV002_1) 2. Óra Kőrös Péter Közúti és Vasúti Járművek Tanszék Tanszéki mérnök (IS201 vagy a tanszéken) E-mail: korosp@ga.sze.hu Web: http://www.sze.hu/~korosp http://www.sze.hu/~korosp/gepeszeti_rendszertechnika/
Gépészeti rendszertechnika (NGB_KV002_1) 2. Óra Kőrös Péter Közúti és Vasúti Járművek Tanszék Tanszéki mérnök (IS201 vagy a tanszéken) E-mail: korosp@ga.sze.hu Web: http://www.sze.hu/~korosp http://www.sze.hu/~korosp/gepeszeti_rendszertechnika/
Denavit-Hartenberg konvenció alkalmazása térbeli 3DoF nyílt kinematikai láncú hengerkoordinátás és gömbi koordinátás robotra
 Budapesti M szaki És Gazdaságtudományi Egyetem Gépészmérnöki Kar M szaki Mechanikai Tanszék Denavit-Hartenberg konvenció alkalmazása térbeli 3DoF nyílt kinematikai láncú hengerkoordinátás és gömbi koordinátás
Budapesti M szaki És Gazdaságtudományi Egyetem Gépészmérnöki Kar M szaki Mechanikai Tanszék Denavit-Hartenberg konvenció alkalmazása térbeli 3DoF nyílt kinematikai láncú hengerkoordinátás és gömbi koordinátás
Dr. Márialigeti János egyetemi tanár Járműelemek és Jármű-szerkezet -analízis Tanszék BME Közlekedésmérnöki és Járműmérnöki Kar
 Dr. Márialigeti János egyetemi tanár Járműelemek és Jármű-szerkezet -analízis Tanszék BME Közlekedésmérnöki és Járműmérnöki Kar Élettartam számítás a helyi feszültségnyúlás viszonyok modellezése alapján
Dr. Márialigeti János egyetemi tanár Járműelemek és Jármű-szerkezet -analízis Tanszék BME Közlekedésmérnöki és Járműmérnöki Kar Élettartam számítás a helyi feszültségnyúlás viszonyok modellezése alapján
Az igénybevételi ábrák témakörhöz az alábbi előjelszabályokat használjuk valamennyi feladat esetén.
 Alkalmazott előjelszabályok Az igénybevételi ábrák témakörhöz az alábbi előjelszabályokat használjuk valamennyi feladat esetén. A kényszererők számításánál a következő a szabály: Az erők iránya a pozitív
Alkalmazott előjelszabályok Az igénybevételi ábrák témakörhöz az alábbi előjelszabályokat használjuk valamennyi feladat esetén. A kényszererők számításánál a következő a szabály: Az erők iránya a pozitív
Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások
 Miskolci Egyetem Műszaki Anyagtudományi Kar Anyagtudományi Intézet Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások Dr.Krállics György krallics@eik.bme.hu
Miskolci Egyetem Műszaki Anyagtudományi Kar Anyagtudományi Intézet Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások Dr.Krállics György krallics@eik.bme.hu
FERNEZELYI SÁNDOR EGYETEMI TANÁR
 MAGASÉPÍTÉSI ACÉLSZERKEZETEK 1. AZ ACÉLÉPÍTÉS FERNEZELYI SÁNDOR EGYETEMI TANÁR A vas felhasználásának felfedezése kultúrtörténeti korszakváltást jelentett. - - Kőkorszak - Bronzkorszak - Vaskorszak - A
MAGASÉPÍTÉSI ACÉLSZERKEZETEK 1. AZ ACÉLÉPÍTÉS FERNEZELYI SÁNDOR EGYETEMI TANÁR A vas felhasználásának felfedezése kultúrtörténeti korszakváltást jelentett. - - Kőkorszak - Bronzkorszak - Vaskorszak - A
A talajok összenyomódásának vizsgálata
 A talajok összenyomódásának vizsgálata Amit már tudni kellene Összenyomódás Konszolidáció Normálisan konszolidált talaj Túlkonszolidált talaj Túlkonszolidáltsági arányszám,ocr Konszolidáció az az időben
A talajok összenyomódásának vizsgálata Amit már tudni kellene Összenyomódás Konszolidáció Normálisan konszolidált talaj Túlkonszolidált talaj Túlkonszolidáltsági arányszám,ocr Konszolidáció az az időben
Fa- és Acélszerkezetek I. 1. Előadás Bevezetés. Dr. Szalai József Főiskolai adjunktus
 Fa- és Acélszerkezetek I. 1. Előadás Bevezetés Dr. Szalai József Főiskolai adjunktus Okt. Hét 1. Téma Bevezetés acélszerkezetek méretezésébe, elhelyezés a tananyagban Acélszerkezetek használati területei
Fa- és Acélszerkezetek I. 1. Előadás Bevezetés Dr. Szalai József Főiskolai adjunktus Okt. Hét 1. Téma Bevezetés acélszerkezetek méretezésébe, elhelyezés a tananyagban Acélszerkezetek használati területei
A= a keresztmetszeti felület cm 2 ɣ = biztonsági tényező
 Statika méretezés Húzás nyomás: Amennyiben a keresztmetszetre húzó-, vagy nyomóerő hat, akkor normálfeszültség (húzó-, vagy nyomó feszültség) keletkezik. Jele: σ. A feszültség: = ɣ Fajlagos alakváltozás:
Statika méretezés Húzás nyomás: Amennyiben a keresztmetszetre húzó-, vagy nyomóerő hat, akkor normálfeszültség (húzó-, vagy nyomó feszültség) keletkezik. Jele: σ. A feszültség: = ɣ Fajlagos alakváltozás:
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 1_5. Bevezetés Végeselem-módszer Végeselem-módszer 1. A geometriai tartomány (szerkezet) felosztása (véges)elemekre.. Lokális koordináta-rendszer felvétele, kapcsolat a lokális és globális koordinátarendszerek
1_5. Bevezetés Végeselem-módszer Végeselem-módszer 1. A geometriai tartomány (szerkezet) felosztása (véges)elemekre.. Lokális koordináta-rendszer felvétele, kapcsolat a lokális és globális koordinátarendszerek
Elméleti kérdések 11. osztály érettségire el ı készít ı csoport
 Elméleti kérdések 11. osztály érettségire el ı készít ı csoport MECHANIKA I. 1. Definiálja a helyvektort! 2. Mondja meg mit értünk vonatkoztatási rendszeren! 3. Fogalmazza meg kinematikailag, hogy mikor
Elméleti kérdések 11. osztály érettségire el ı készít ı csoport MECHANIKA I. 1. Definiálja a helyvektort! 2. Mondja meg mit értünk vonatkoztatási rendszeren! 3. Fogalmazza meg kinematikailag, hogy mikor
Ejtési teszt modellezése a tervezés fázisában
 Antal Dániel, doktorandusz, Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szabó Tamás, egyetemi docens, Ph.D., Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szilágyi Attila, egyetemi adjunktus,
Antal Dániel, doktorandusz, Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szabó Tamás, egyetemi docens, Ph.D., Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szilágyi Attila, egyetemi adjunktus,
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK. Acélszerkezetek II. IV. Előadás
 DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II IV. Előadás Rácsos tartók szerkezeti formái, kialakítása, tönkremeneteli módjai. - Rácsos tartók jellemzói - Méretezési kérdések
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II IV. Előadás Rácsos tartók szerkezeti formái, kialakítása, tönkremeneteli módjai. - Rácsos tartók jellemzói - Méretezési kérdések
Polimerek vizsgálatai
 SZÉCHENYI ISTVÁN EGYETEM ANYAGTUDOMÁNYI ÉS TECHNOLÓGIAI TANSZÉK Polimerek vizsgálatai DR Hargitai Hajnalka Rövid idejű mechanikai vizsgálat Szakítóvizsgálat Cél: elsősorban a gyártási körülmények megfelelőségének
SZÉCHENYI ISTVÁN EGYETEM ANYAGTUDOMÁNYI ÉS TECHNOLÓGIAI TANSZÉK Polimerek vizsgálatai DR Hargitai Hajnalka Rövid idejű mechanikai vizsgálat Szakítóvizsgálat Cél: elsősorban a gyártási körülmények megfelelőségének
Korrodált acélszerkezetek vizsgálata
 Korrodált acélszerkezetek vizsgálata 1. Szerkezeti példák és laboratóriumi alapkutatás Oszvald Katalin Témavezető : Dr. Dunai László Budapest, 2009.12.08. 1 Általános célkitűzések Korrózió miatt károsodott
Korrodált acélszerkezetek vizsgálata 1. Szerkezeti példák és laboratóriumi alapkutatás Oszvald Katalin Témavezető : Dr. Dunai László Budapest, 2009.12.08. 1 Általános célkitűzések Korrózió miatt károsodott
Polimerek vizsgálatai 1.
 SZÉCHENYI ISTVÁN EGYETEM ANYAGISMERETI ÉS JÁRMŰGYÁRTÁSI TANSZÉK POLIMERTECHNIKA NGB_AJ050_1 Polimerek vizsgálatai 1. DR Hargitai Hajnalka Szakítóvizsgálat Rövid idejű mechanikai vizsgálat Cél: elsősorban
SZÉCHENYI ISTVÁN EGYETEM ANYAGISMERETI ÉS JÁRMŰGYÁRTÁSI TANSZÉK POLIMERTECHNIKA NGB_AJ050_1 Polimerek vizsgálatai 1. DR Hargitai Hajnalka Szakítóvizsgálat Rövid idejű mechanikai vizsgálat Cél: elsősorban
Ütőmunka meghatározása acél próbatesten, Charpy-kalapáccsal, amely ingás ütő-hajlítómű (Charpyinga) Dr. Kausay Tibor
 Ütőmunka meghatározása acél próbatesten, Charpy-kalapáccsal, amely ingás ütő-hajlítómű (Charpyinga) Dr. Kausay Tibor Dr. Kausay Tibor 1 Charpy-kalapács, 10 m kp = 100 J legnagyobb ütőenergiával A vizsgálatot
Ütőmunka meghatározása acél próbatesten, Charpy-kalapáccsal, amely ingás ütő-hajlítómű (Charpyinga) Dr. Kausay Tibor Dr. Kausay Tibor 1 Charpy-kalapács, 10 m kp = 100 J legnagyobb ütőenergiával A vizsgálatot
A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS-
 A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS- Forgatónyomaték meghatározása G Á L A T A Egy erő forgatónyomatékkal hat egy pontra, ha az az erővel össze van kötve. Például
A K É T V É G É N A L Á T Á M A S Z T O T T T A R T Ó S T A T I K A I V IZS- Forgatónyomaték meghatározása G Á L A T A Egy erő forgatónyomatékkal hat egy pontra, ha az az erővel össze van kötve. Például
GEOTECHNIKA I. LGB-SE TALAJOK SZILÁRDSÁGI JELLEMZŐI
 GEOTECHNIKA I. LGB-SE005-01 TALAJOK SZILÁRDSÁGI JELLEMZŐI Wolf Ákos Mechanikai állapotjellemzők és egyenletek 2 X A X 3 normál- és 3 nyírófeszültség a hasáb oldalain Y A x y z xy yz zx Z A Y Z ZX YZ A
GEOTECHNIKA I. LGB-SE005-01 TALAJOK SZILÁRDSÁGI JELLEMZŐI Wolf Ákos Mechanikai állapotjellemzők és egyenletek 2 X A X 3 normál- és 3 nyírófeszültség a hasáb oldalain Y A x y z xy yz zx Z A Y Z ZX YZ A
5. Az acélszerkezetek méretezésének különleges kérdései: rideg törés, fáradás.
 MAGASÉPÍTÉSI ACÉLSZERKEZETEK 5. Az acélszerkezetek méretezésének különleges kérdései: rideg törés, fáradás. KÉSZÜLT FERNEZELYI SÁNDOR EGYETEMI TANÁR ELŐADÁSI JEGYZETEI ÉS AZ INTERNETEN ELÉRHETŐ MÁS ANYAGOK
MAGASÉPÍTÉSI ACÉLSZERKEZETEK 5. Az acélszerkezetek méretezésének különleges kérdései: rideg törés, fáradás. KÉSZÜLT FERNEZELYI SÁNDOR EGYETEMI TANÁR ELŐADÁSI JEGYZETEI ÉS AZ INTERNETEN ELÉRHETŐ MÁS ANYAGOK
A végeselem módszer alapjai. 2. Alapvető elemtípusok
 A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
Egy érdekes mechanikai feladat
 1 Egy érdekes mechanikai feladat 1. ábra forrása: [ 1 ] A feladat Az 1. ábra szerinti rudazat A csomópontján átvezettek egy kötelet, melynek alsó végén egy m tömegű golyó lóg. A rudak egyező nyúlási merevsége
1 Egy érdekes mechanikai feladat 1. ábra forrása: [ 1 ] A feladat Az 1. ábra szerinti rudazat A csomópontján átvezettek egy kötelet, melynek alsó végén egy m tömegű golyó lóg. A rudak egyező nyúlási merevsége
Acélszerkezetek. 3. előadás 2012.02.24.
 Acélszerkezetek 3. előadás 2012.02.24. Kapcsolatok méretezése Kapcsolatok típusai Mechanikus kapcsolatok: Szegecsek Csavarok Csapok Hegesztett kapcsolatok Tompavarrat Sarokvarrat Coalbrookdale, 1781 Eiffel
Acélszerkezetek 3. előadás 2012.02.24. Kapcsolatok méretezése Kapcsolatok típusai Mechanikus kapcsolatok: Szegecsek Csavarok Csapok Hegesztett kapcsolatok Tompavarrat Sarokvarrat Coalbrookdale, 1781 Eiffel
TERMÉKSZIMULÁCIÓ I. 9. elıadás
 TERMÉKSZIMULÁCIÓ I. 9. elıadás Dr. Kovács Zsolt egyetemi tanár Végeselem típusok Elemtípusok a COSMOSWorks Designer-ben: Lineáris térfogatelem (tetraéder) Kvadratikus térfogatelem (tetraéder) Lineáris
TERMÉKSZIMULÁCIÓ I. 9. elıadás Dr. Kovács Zsolt egyetemi tanár Végeselem típusok Elemtípusok a COSMOSWorks Designer-ben: Lineáris térfogatelem (tetraéder) Kvadratikus térfogatelem (tetraéder) Lineáris
KÉPLÉKENYALAKÍTÁS ELMÉLET
 KÉPLÉKENYALAKÍTÁS ELMÉLET KOHÓMÉRNÖK MESTERKÉPZÉS KÉPLÉKENYALAKÍTÁSI SZAKIRÁNY TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR ANYAGTUDOMÁNYI INTÉZET Miskolc, 2008. 1. TANTÁRGYLEÍRÁS
KÉPLÉKENYALAKÍTÁS ELMÉLET KOHÓMÉRNÖK MESTERKÉPZÉS KÉPLÉKENYALAKÍTÁSI SZAKIRÁNY TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR ANYAGTUDOMÁNYI INTÉZET Miskolc, 2008. 1. TANTÁRGYLEÍRÁS
Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel
 Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel Segédlet az A végeselem módszer alapjai tárgy 4. laborgyakorlatához http://www.mm.bme.hu/~kossa/vemalap4.pdf Kossa Attila (kossa@mm.bme.hu)
Hajlított tartó elmozdulásmez jének meghatározása Ritz-módszerrel Segédlet az A végeselem módszer alapjai tárgy 4. laborgyakorlatához http://www.mm.bme.hu/~kossa/vemalap4.pdf Kossa Attila (kossa@mm.bme.hu)
EC4 számítási alapok,
 Öszvérszerkezetek 2. előadás EC4 számítási alapok, beton berepedésének hatása, együttdolgozó szélesség, rövid idejű és tartós terhek, km. osztályozás, képlékeny km. ellenállás készítette: 2016.10.07. EC4
Öszvérszerkezetek 2. előadás EC4 számítási alapok, beton berepedésének hatása, együttdolgozó szélesség, rövid idejű és tartós terhek, km. osztályozás, képlékeny km. ellenállás készítette: 2016.10.07. EC4
GÉPEK DINAMIKÁJA 9.gyak.hét 1. és 2. Feladat
 Széchenyi István Egyetem Alkalmazott Mechanika Műszaki Tudományi Kar Tanszék GÉPEK DINAMIKÁJA 9.gyak.hét 1. és 2. Feladat (kidolgozta: Dr. Nagy Zoltán egyetemi adjunktus) y k c S x x m x Adatok m kg c
Széchenyi István Egyetem Alkalmazott Mechanika Műszaki Tudományi Kar Tanszék GÉPEK DINAMIKÁJA 9.gyak.hét 1. és 2. Feladat (kidolgozta: Dr. Nagy Zoltán egyetemi adjunktus) y k c S x x m x Adatok m kg c
KIFÁRADÁSI ÉLETTARTAM KISFELADAT (MSc.)
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM KIFÁRADÁSI ÉLETTARTAM KISFELADAT (MSc.) Járműelemek és Járműszerkezetanalízis Tanszék Ssz.:...... Név:......................................... Neptun kód.:.........
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM KIFÁRADÁSI ÉLETTARTAM KISFELADAT (MSc.) Járműelemek és Járműszerkezetanalízis Tanszék Ssz.:...... Név:......................................... Neptun kód.:.........
Komplex természettudomány 3.
 Komplex természettudomány 3. 1 A lendület és megmaradása Lendület (impulzus): A test tömegének és sebességének a szorzata. Jele: I. Képlete: II = mm vv mértékegysége: kkkk mm ss A lendület származtatott
Komplex természettudomány 3. 1 A lendület és megmaradása Lendület (impulzus): A test tömegének és sebességének a szorzata. Jele: I. Képlete: II = mm vv mértékegysége: kkkk mm ss A lendület származtatott
Fa- és Acélszerkezetek I. 11. Előadás Faszerkezetek II. Dr. Szalai József Főiskolai adjunktus
 Fa- és Acélszerkezetek I. 11. Előadás Faszerkezetek II. Dr. Szalai József Főiskolai adjunktus Tartalom Méretezés az Eurocode szabványrendszer szerint áttekintés Teherbírási határállapotok Húzás Nyomás
Fa- és Acélszerkezetek I. 11. Előadás Faszerkezetek II. Dr. Szalai József Főiskolai adjunktus Tartalom Méretezés az Eurocode szabványrendszer szerint áttekintés Teherbírási határállapotok Húzás Nyomás
5. Az acélszerkezetek méretezésének különleges kérdései: rideg törés, fáradás. BME Szilárdságtani és Tartószerkezeti Tanszék
 MAGASÉPÍTÉSI ACÉLSZERKEZETEK 5. Az acélszerkezetek méretezésének különleges kérdései: rideg törés, fáradás. FERNEZELYI SÁNDOR EGYETEMI TANÁR Az acél szakító diagrammja Lineáris szakasz Arányossági határnak
MAGASÉPÍTÉSI ACÉLSZERKEZETEK 5. Az acélszerkezetek méretezésének különleges kérdései: rideg törés, fáradás. FERNEZELYI SÁNDOR EGYETEMI TANÁR Az acél szakító diagrammja Lineáris szakasz Arányossági határnak
Szilárd testek rugalmassága
 Fizika villamosmérnököknek Szilárd testek rugalmassága Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1 Deformálható testek (A merev test idealizált határeset.)
Fizika villamosmérnököknek Szilárd testek rugalmassága Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1 Deformálható testek (A merev test idealizált határeset.)
Felvételi, 2018 szeptember - Alapképzés, fizika vizsga -
 Sapientia Erdélyi Magyar Tudományegyetem Marosvásárhelyi Kar Felvételi, 2018 szeptember - Alapképzés, fizika vizsga - Minden tétel kötelező Hivatalból 10 pont jár Munkaidő 3 óra I Az alábbi kérdésekre
Sapientia Erdélyi Magyar Tudományegyetem Marosvásárhelyi Kar Felvételi, 2018 szeptember - Alapképzés, fizika vizsga - Minden tétel kötelező Hivatalból 10 pont jár Munkaidő 3 óra I Az alábbi kérdésekre
Kisciklusú fárasztóvizsgálatok eredményei és energetikai értékelése
 Kisciklusú fárasztóvizsgálatok eredményei és energetikai értékelése Tóth László, Rózsahegyi Péter Bay Zoltán Alkalmazott Kutatási Közalapítvány Logisztikai és Gyártástechnikai Intézet Bevezetés A mérnöki
Kisciklusú fárasztóvizsgálatok eredményei és energetikai értékelése Tóth László, Rózsahegyi Péter Bay Zoltán Alkalmazott Kutatási Közalapítvány Logisztikai és Gyártástechnikai Intézet Bevezetés A mérnöki
Magasépítési öszvérfödémek numerikus szimuláció alapú méretezése
 BME Hidak és Szerkezetek Tanszéke Magasépítési öszvérfödémek numerikus szimuláció alapú méretezése Seres Noémi DEVSOG Témavezetı: Dr. Dunai László Bevezetés Az elıadás témája öszvérfödémek együttdolgoztató
BME Hidak és Szerkezetek Tanszéke Magasépítési öszvérfödémek numerikus szimuláció alapú méretezése Seres Noémi DEVSOG Témavezetı: Dr. Dunai László Bevezetés Az elıadás témája öszvérfödémek együttdolgoztató
DR. DEMÉNY ANDRÁS-I)R. EROSTYÁK JÁNOS- DR. SZABÓ GÁBOR-DR. TRÓCSÁNYI ZOLTÁN FIZIKA I. Klasszikus mechanika NEMZETI TANKÖNYVKIADÓ, BUDAPEST
 DR. DEMÉNY ANDRÁS-I)R. EROSTYÁK JÁNOS- DR. SZABÓ GÁBOR-DR. TRÓCSÁNYI ZOLTÁN FIZIKA I Klasszikus mechanika NEMZETI TANKÖNYVKIADÓ, BUDAPEST Előszó a Fizika című tankönyvsorozathoz Előszó a Fizika I. (Klasszikus
DR. DEMÉNY ANDRÁS-I)R. EROSTYÁK JÁNOS- DR. SZABÓ GÁBOR-DR. TRÓCSÁNYI ZOLTÁN FIZIKA I Klasszikus mechanika NEMZETI TANKÖNYVKIADÓ, BUDAPEST Előszó a Fizika című tankönyvsorozathoz Előszó a Fizika I. (Klasszikus
2. E L Ő A D Á S D R. H U S I G É Z A
 Mechatronika alapjai 2. E L Ő A D Á S D R. H U S I G É Z A elmozdulás erő nyomaték elmozdulás erő nyomaték Mechanizmusok Mechanizmus: általánosságban: A gép mechanikus elven működő részei Definíció: A
Mechatronika alapjai 2. E L Ő A D Á S D R. H U S I G É Z A elmozdulás erő nyomaték elmozdulás erő nyomaték Mechanizmusok Mechanizmus: általánosságban: A gép mechanikus elven működő részei Definíció: A
Égés és oltáselmélet I. (zárójelben a helyes válaszra adott pont)
 Égés és oltáselmélet I. (zárójelben a helyes válaszra adott pont) 1. "Az olyan rendszereket, amelyek határfelülete a tömegáramokat megakadályozza,... rendszernek nevezzük" (1) 2. "Az olyan rendszereket,
Égés és oltáselmélet I. (zárójelben a helyes válaszra adott pont) 1. "Az olyan rendszereket, amelyek határfelülete a tömegáramokat megakadályozza,... rendszernek nevezzük" (1) 2. "Az olyan rendszereket,
TERMÉKSZIMULÁCIÓ. Dr. Kovács Zsolt. Végeselem módszer. Elıadó: egyetemi tanár. Termékszimuláció tantárgy 6. elıadás március 22.
 TERMÉKZIMULÁCIÓ Végeselem módszer Termékszimuláció tantárgy 6. elıadás 211. március 22. Elıadó: Dr. Kovács Zsolt egyetemi tanár A végeselem módszer lényege A vizsgált, tetszıleges geometriai kialakítású
TERMÉKZIMULÁCIÓ Végeselem módszer Termékszimuláció tantárgy 6. elıadás 211. március 22. Elıadó: Dr. Kovács Zsolt egyetemi tanár A végeselem módszer lényege A vizsgált, tetszıleges geometriai kialakítású
Gépészmérnöki alapszak, Mérnöki fizika 2. ZH, december 05. Feladatok (maximum 3x6 pont=18 pont)
 1. 2. 3. Mondat E1 E2 NÉV: Gépészmérnöki alapszak, Mérnöki fizika 2. ZH, 2017. december 05. Neptun kód: Aláírás: g=10 m/s 2 ; ε 0 = 8.85 10 12 F/m; μ 0 = 4π 10 7 Vs/Am; c = 3 10 8 m/s Előadó: Márkus /
1. 2. 3. Mondat E1 E2 NÉV: Gépészmérnöki alapszak, Mérnöki fizika 2. ZH, 2017. december 05. Neptun kód: Aláírás: g=10 m/s 2 ; ε 0 = 8.85 10 12 F/m; μ 0 = 4π 10 7 Vs/Am; c = 3 10 8 m/s Előadó: Márkus /
Hidak Darupályatartók Tornyok, kémények (szélhatás) Tengeri építmények (hullámzás)
 Dr. Németh György Szerkezetépítés II. 1 A fáradt törés ismétlődő terhek hatására a statikus törőszilárdság feszültségszintje alatt feszültségcsúcsoknál lokális képlékeny alakváltozásból indul ki általában
Dr. Németh György Szerkezetépítés II. 1 A fáradt törés ismétlődő terhek hatására a statikus törőszilárdság feszültségszintje alatt feszültségcsúcsoknál lokális képlékeny alakváltozásból indul ki általában
2. Rugalmas állandók mérése jegyzőkönyv javított. Zsigmond Anna Fizika Bsc II. Mérés dátuma: Leadás dátuma:
 2. Rugalmas állandók mérése jegyzőkönyv javított Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 17. Leadás dátuma: 2008. 10. 08. 1 1. Mérések ismertetése Az első részben egy téglalap keresztmetszetű
2. Rugalmas állandók mérése jegyzőkönyv javított Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 17. Leadás dátuma: 2008. 10. 08. 1 1. Mérések ismertetése Az első részben egy téglalap keresztmetszetű
BME Gépészmérnöki Kar 3. vizsga (112A) Név: 1 Műszaki Mechanikai Tanszék január 11. Neptun: 2 Szilárdságtan Aláírás: 3
 BME Gépészmérnöki Kar 3. vizsga (2A) Név: Műszaki Mechanikai Tanszék 2. január. Neptun: 2 Szilárdságtan Aláírás: 3. feladat (2 pont) A vázolt befogott tartót a p intenzitású megoszló erőrendszer, az F
BME Gépészmérnöki Kar 3. vizsga (2A) Név: Műszaki Mechanikai Tanszék 2. január. Neptun: 2 Szilárdságtan Aláírás: 3. feladat (2 pont) A vázolt befogott tartót a p intenzitású megoszló erőrendszer, az F
Numerikus módszerek 1.
 Numerikus módszerek 1. 11. előadás: A Newton-módszer és társai Lócsi Levente ELTE IK 2013. november 25. Tartalomjegyzék 1 A Newton-módszer és konvergenciatételei 2 Húrmódszer és szelőmódszer 3 Általánosítás
Numerikus módszerek 1. 11. előadás: A Newton-módszer és társai Lócsi Levente ELTE IK 2013. november 25. Tartalomjegyzék 1 A Newton-módszer és konvergenciatételei 2 Húrmódszer és szelőmódszer 3 Általánosítás
KRITIKUS KÉRDÉS: ACÉL ELEMEK
 KRITIKUS KÉRDÉS: ACÉL ELEMEK KRITIKUS HŐMÉRSÉKLETE Dr. Horváth László egyetem docens Acélszerkezetek tűzvédelmi tervezése workshop, 2018. 11.09 TARTALOM Acél elemek tönkremeneteli folyamata tűzhatás alatt
KRITIKUS KÉRDÉS: ACÉL ELEMEK KRITIKUS HŐMÉRSÉKLETE Dr. Horváth László egyetem docens Acélszerkezetek tűzvédelmi tervezése workshop, 2018. 11.09 TARTALOM Acél elemek tönkremeneteli folyamata tűzhatás alatt
Trapézlemez gerincő tartók beroppanásvizsgálata
 Trapézlemez gerincő tartók beroppanásvizsgálata Témavezetı: Dr. Dunai László Készítette: Kövesdi Balázs Bevezetés Korábbi eredmények rövid áttekintése Kísérletek bemutatása és értékelése Új kutatási irányok
Trapézlemez gerincő tartók beroppanásvizsgálata Témavezetı: Dr. Dunai László Készítette: Kövesdi Balázs Bevezetés Korábbi eredmények rövid áttekintése Kísérletek bemutatása és értékelése Új kutatási irányok
W = F s A munka származtatott, előjeles skalármennyiség.
 Ha az erő és az elmozdulás egymásra merőleges, akkor fizikai értelemben nem történik munkavégzés. Pl.: ha egy táskát függőlegesen tartunk, és úgy sétálunk, akkor sem a tartóerő, sem a nehézségi erő nem
Ha az erő és az elmozdulás egymásra merőleges, akkor fizikai értelemben nem történik munkavégzés. Pl.: ha egy táskát függőlegesen tartunk, és úgy sétálunk, akkor sem a tartóerő, sem a nehézségi erő nem
Tartalom. 1. Állapotegyenletek megoldása 2. Állapot visszacsatolás (pólusallokáció)
 Tartalom 1. Állapotegyenletek megoldása 2. Állapot visszacsatolás (pólusallokáció) 2015 1 Állapotgyenletek megoldása Tekintsük az ẋ(t) = ax(t), x(0) = 1 differenciálegyenletet. Ismert, hogy a megoldás
Tartalom 1. Állapotegyenletek megoldása 2. Állapot visszacsatolás (pólusallokáció) 2015 1 Állapotgyenletek megoldása Tekintsük az ẋ(t) = ax(t), x(0) = 1 differenciálegyenletet. Ismert, hogy a megoldás
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 Tartószerkezet rekonstrukciós szakmérnök képzés Feszített és előregyártott vasbeton szerkezetek 1. előadás Előregyártott vasbeton szerkezetek kapcsolatai Dr. Sipos András Árpád 2012. november 17. Vázlat
Tartószerkezet rekonstrukciós szakmérnök képzés Feszített és előregyártott vasbeton szerkezetek 1. előadás Előregyártott vasbeton szerkezetek kapcsolatai Dr. Sipos András Árpád 2012. november 17. Vázlat
Dr. Szabó Bertalan. Hajlított, nyírt öszvértartók tervezése az Eurocode-dal összhangban
 Dr. Szabó Bertalan Hajlított, nyírt öszvértartók tervezése az Eurocode-dal összhangban Dr. Szabó Bertalan, 2017 Hungarian edition TERC Kft., 2017 ISBN 978 615 5445 49 1 Kiadja a TERC Kereskedelmi és Szolgáltató
Dr. Szabó Bertalan Hajlított, nyírt öszvértartók tervezése az Eurocode-dal összhangban Dr. Szabó Bertalan, 2017 Hungarian edition TERC Kft., 2017 ISBN 978 615 5445 49 1 Kiadja a TERC Kereskedelmi és Szolgáltató
Kizárólag oktatási célra használható fel!
 DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II III. Előadás Vékonyfalú keresztmetszetek nyírófeszültségei - Nyírófolyam - Nyírási középpont - Shear lag hatás - Csavarás Összeállította:
DEBRECENI EGYETEM, MŰSZAKI KAR, ÉPÍTŐMÉRNÖKI TANSZÉK Acélszerkezetek II III. Előadás Vékonyfalú keresztmetszetek nyírófeszültségei - Nyírófolyam - Nyírási középpont - Shear lag hatás - Csavarás Összeállította:
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
Példa: Tartó lehajlásfüggvényének meghatározása a Rayleigh Ritz-féle módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2013. szeptember 23. Javítva: 2013.10.09.
TENGELY TERHELHETŐSÉGI VIZSGÁLATA
 MISKOLCI EGYETEM GÉP- ÉS TERMÉKTERVEZÉSI TANSZÉK OKTATÁSI SEGÉDLET a GÉPSZERKEZETTAN - TERVEZÉS c. tantárgyhoz TENGELY TERHELHETŐSÉGI VIZSGÁLATA Összeállította: Dr. Szente József egyetemi docens Miskolc,
MISKOLCI EGYETEM GÉP- ÉS TERMÉKTERVEZÉSI TANSZÉK OKTATÁSI SEGÉDLET a GÉPSZERKEZETTAN - TERVEZÉS c. tantárgyhoz TENGELY TERHELHETŐSÉGI VIZSGÁLATA Összeállította: Dr. Szente József egyetemi docens Miskolc,
Vizsgatémakörök fizikából A vizsga minden esetben két részből áll: Írásbeli feladatsor (70%) Szóbeli felelet (30%)
 Vizsgatémakörök fizikából A vizsga minden esetben két részből áll: Írásbeli feladatsor (70%) Szóbeli felelet (30%) A vizsga értékelése: Elégtelen: ha az írásbeli és a szóbeli rész összesen nem éri el a
Vizsgatémakörök fizikából A vizsga minden esetben két részből áll: Írásbeli feladatsor (70%) Szóbeli felelet (30%) A vizsga értékelése: Elégtelen: ha az írásbeli és a szóbeli rész összesen nem éri el a
Tájékoztató. Értékelés Összesen: 60 pont
 A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
2.4. Coulomb-súrlódással (száraz súrlódással) csillapított szabad rezgések
 58. FEJEZET. EGY SZABADSÁGI FOKÚ LENGŐRENDSZEREK.4. Coulomb-súrlódással (száraz súrlódással) csillapított szabad rezgések.4.1. Súrlódási modell A Coulomb-féle súrlódási modellben a súrlódási erő a felületeket
58. FEJEZET. EGY SZABADSÁGI FOKÚ LENGŐRENDSZEREK.4. Coulomb-súrlódással (száraz súrlódással) csillapított szabad rezgések.4.1. Súrlódási modell A Coulomb-féle súrlódási modellben a súrlódási erő a felületeket
- Elemezze a mellékelt szerkezetet, készítse el a háromcsuklós fa fedélszék igénybevételi ábráit, ismertesse a rácsostartó rúdelemeinek szilárdsági
 1. - Elemezze a mellékelt szerkezetet, készítse el a háromcsuklós fa fedélszék igénybevételi ábráit, ismertesse a rácsostartó rúdelemeinek szilárdsági vizsgálatát. - Jellemezze a vasbeton három feszültségi
1. - Elemezze a mellékelt szerkezetet, készítse el a háromcsuklós fa fedélszék igénybevételi ábráit, ismertesse a rácsostartó rúdelemeinek szilárdsági vizsgálatát. - Jellemezze a vasbeton három feszültségi
Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet
 Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet 2. előadás A rugalmas lemezelmélet alapfeltevései A lemez anyaga homogén, izotróp, lineárisan rugalmas (Hooke törvény); A terheletlen állapotban
Vasbetonszerkezetek II. Vasbeton lemezek Rugalmas lemezelmélet 2. előadás A rugalmas lemezelmélet alapfeltevései A lemez anyaga homogén, izotróp, lineárisan rugalmas (Hooke törvény); A terheletlen állapotban
Használhatósági határállapotok. Alakváltozások ellenőrzése
 1.GYAKORLAT Használhatósági határállapotok A használhatósági határállapotokhoz tartozó teherkombinációk: Karakterisztikus (repedésmentesség igazolása) Gyakori (feszített szerkezetek repedés korlátozása)
1.GYAKORLAT Használhatósági határállapotok A használhatósági határállapotokhoz tartozó teherkombinációk: Karakterisztikus (repedésmentesség igazolása) Gyakori (feszített szerkezetek repedés korlátozása)
Vasbeton szerkezetek kifáradási vizsgálatai
 AZ ÜZEMFENNTARTÁS ÁLTALÁNOS KÉRDÉSEI 1.04 3.10 5.02 Vasbeton szerkezetek kifáradási vizsgálatai Tárgyszavak: vasbeton szerkezetek; fárasztóvizsgálatok; akusztikus emissziós vizsgálat; károsodási indikátorok.
AZ ÜZEMFENNTARTÁS ÁLTALÁNOS KÉRDÉSEI 1.04 3.10 5.02 Vasbeton szerkezetek kifáradási vizsgálatai Tárgyszavak: vasbeton szerkezetek; fárasztóvizsgálatok; akusztikus emissziós vizsgálat; károsodási indikátorok.
Hegesztett gerinclemezes tartók
 Hegesztett gerinclemezes tartók Lemezhorpadások kezelése EC szerint dr. Horváth László BME Hidak és Szerkezetek Tanszéke Bevezetés Gerinclemezes tartók vékony lemezekből: Bevezetés Összetett szelvények,
Hegesztett gerinclemezes tartók Lemezhorpadások kezelése EC szerint dr. Horváth László BME Hidak és Szerkezetek Tanszéke Bevezetés Gerinclemezes tartók vékony lemezekből: Bevezetés Összetett szelvények,
Molekuláris dinamika I. 10. előadás
 Molekuláris dinamika I. 10. előadás Miről is szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten minden részecske mozgását szimuláljuk? Hogyan tudjuk megérteni a folyadékok,
Molekuláris dinamika I. 10. előadás Miről is szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten minden részecske mozgását szimuláljuk? Hogyan tudjuk megérteni a folyadékok,
- Elemezze a mellékelt szerkezetet, készítse el a háromcsuklós fa fedélszék igénybevételi ábráit, ismertesse a rácsostartó rúdelemeinek szilárdsági
 1. - Elemezze a mellékelt szerkezetet, készítse el a háromcsuklós fa fedélszék igénybevételi ábráit, ismertesse a rácsostartó rúdelemeinek szilárdsági vizsgálatát. - Jellemezze a vasbeton három feszültségi
1. - Elemezze a mellékelt szerkezetet, készítse el a háromcsuklós fa fedélszék igénybevételi ábráit, ismertesse a rácsostartó rúdelemeinek szilárdsági vizsgálatát. - Jellemezze a vasbeton három feszültségi
Dr. Égert János Dr. Molnár Zoltán Dr. Nagy Zoltán ALKALMAZOTT MECHANIKA
 Dr. Égert János Dr. Molnár Zoltán Dr. Nagy Zoltán ALKALMAZOTT MECHANIKA UNIVERSITAS-GYŐR Nonprofit Kft. Győr, 2010 SZÉCHENYI ISTVÁN EGYETEM MŰSZAKI TUDOMÁNYI KAR ALKALMAZOTT MECHANIKA TANSZÉK ALKALMAZOTT
Dr. Égert János Dr. Molnár Zoltán Dr. Nagy Zoltán ALKALMAZOTT MECHANIKA UNIVERSITAS-GYŐR Nonprofit Kft. Győr, 2010 SZÉCHENYI ISTVÁN EGYETEM MŰSZAKI TUDOMÁNYI KAR ALKALMAZOTT MECHANIKA TANSZÉK ALKALMAZOTT
Csuklós szerkezetek reakciói és igénybevételi ábrái. Frissítve: példa: A 12. gyakorlat 1. feladata.
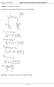 1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
1. példa: A 12. gyakorlat 1. feladata. Számítsuk ki a reakcióerőket! Rajzoljuk meg a nyomatéki ábrát! Megjegyzés: A támaszok vízszintesen egy vonalban vannak. 1 / 20 2. példa: Számítsuk ki a reakcióerőket!
Mechanika I-II. Példatár
 Budapesti Műszaki és Gazdaságtudományi Egyetem Műszaki Mechanika Tanszék Mechanika I-II. Példatár 2012. május 24. Előszó A példatár célja, hogy támogassa a mechanika I. és mechanika II. tárgy oktatását
Budapesti Műszaki és Gazdaságtudományi Egyetem Műszaki Mechanika Tanszék Mechanika I-II. Példatár 2012. május 24. Előszó A példatár célja, hogy támogassa a mechanika I. és mechanika II. tárgy oktatását
FIZIKA SZÓBELI VIZSGA TÉMAKÖREI ÉS MÉRÉSEI
 FIZIKA SZÓBELI VIZSGA TÉMAKÖREI ÉS MÉRÉSEI 1. Egyenes vonalú mozgások 2012 Mérje meg Mikola-csőben a buborék sebességét! Mutassa meg az út, és az idő közötti kapcsolatot! Három mérést végezzen, adatait
FIZIKA SZÓBELI VIZSGA TÉMAKÖREI ÉS MÉRÉSEI 1. Egyenes vonalú mozgások 2012 Mérje meg Mikola-csőben a buborék sebességét! Mutassa meg az út, és az idő közötti kapcsolatot! Három mérést végezzen, adatait
Gyakorlati útmutató a Tartók statikája I. tárgyhoz. Fekete Ferenc. 5. gyakorlat. Széchenyi István Egyetem, 2015.
 Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 Vasalt falak: 4. Vasalt falazott szerkezetek méretezési mószerei Vasalt falak 1. Vasalás fekvőhézagban vagy falazott üregben horonyban, falazóelem lyukban. 1 2 1 Vasalt falak: Vasalás fekvőhézagban vagy
Vasalt falak: 4. Vasalt falazott szerkezetek méretezési mószerei Vasalt falak 1. Vasalás fekvőhézagban vagy falazott üregben horonyban, falazóelem lyukban. 1 2 1 Vasalt falak: Vasalás fekvőhézagban vagy
