Anizotrop falazóelem numerikus és kísérleti vizsgálata
|
|
|
- Tamás Tamás
- 5 évvel ezelőtt
- Látták:
Átírás
1 2019/2020 őszi félév Hidak és Szerkezetek Tanszék TDK Dolgozat Anizotrop falazóelem numerikus és kísérleti vizsgálata Konzulensek: Dr. Haris István Hortobágyi Tamás IR7SMS Roszevák Zsolt
2 Tartalomjegyzék 1. Bevezetés Az anyagra vonatkozó információk... 6 a) Kerámia... 6 b) Mechanikai anyagmodellek... 8 c) Rideg és rugalmas-képlékeny-fellazuló anyagok komplex modelljei Az általam elvégzett laboratóriumi kísérletsorozat... 9 a) A vizsgált falazóelem... 9 b) A kísérletsorozat bemutatása c) A kísérleti eredmények Előzetes numerikus vizsgálat a) A modell b) Az eredmények Az általam elvégzett kísérlethez készített numerikus modell a) A modell b) Az eredmények c) A laborkísérleti és a numerikus eredmények összehasonlítása d) A numerikus modell kritikája A mások által végzett laboratóriumi kísérletsorozat a) A vizsgált falazóelem b) A kísérletsorozat bemutatása c) A kísérleti eredmények i. 3-as jelű próbatest ii. 4-es jelű próbatest iii. 5-ös jelű próbatest... 39
3 iv. A két laborkísérlet eredményeinek összehasonlítása A pályázati kísérlethez készített numerikus modell a) A modell i. A 1. számítás ismertetése és az eredményei ii. A 2. számítás ismertetése és az eredményei iii. A 3. számítás ismertetése és az eredményei iv. A 4. számítás ismertetése és az eredményei v. Az 5. számítás ismertetése és az eredményei Továbblépési lehetőségek... 56
4 1. Bevezetés A mai világban minden iparág törekszik a minél hatékonyabb anyagfelhasználásra, a lehető legjobb költséghatékonyság megteremtésére. Ennek eléréséhez az optimalizálás és a numerikus modellépítés igen nagy fontossággal bír, hiszen utóbbival a viszonylag drága laborkísérletek akár kiválthatók. Nincs ez máshogy az építőmérnöki gyakorlatban sem, ahol ezek a szempontok kritikus fontosságúak. A modern számítástechnikai módszerek segítségével az előbb említett kritériumok könnyebben vizsgálhatók. A számítógéppel való modellezéskor arra kell törekednünk, hogy a numerikus modell minél inkább tükrözze a szerkezet, vagy szerkezeti elem valóságos viselkedését. A szerkezeti elemeink számítógéppel való modellezése során tehát nem mindegy, hogy milyen anyagmodellt választunk, vagy milyen közelítésekkel élünk a geometria definiálásakor. Különös fontossággal bír, hogy a megalkotott numerikus modellezési eljárás milyen pontossággal adja vissza a valóságos szerkezeti elem tényleges viselkedését. Egy ilyen numerikus modell kellően pontos felépítése után van lehetőség az adott elem méretbeli, formai, illetve anyaghasználati, gyártási optimalizációjára. Ilyen, a korszerű ortotrop falazóelemekre vonatkozó elemszintű numerikus modellalkotási vizsgálat a kutatásaim alapján még nem is készült. A numerikus vizsgálathoz korábbi konzulensi tapasztalatokon kívül [3] más szakirodalomra nem tudtam támaszkodni. A modellalkotás eredményeként lehetőségünk nyílhat különböző elemek egymásra ható viselkedését is numerikusan vizsgálni, így a további kutatások a falazóelemekből épített falazat modellezésének alapjait teremthetik meg. Jelen munka keretein belül anizotrop (ortotrop) kerámia falazóelemek laboratóriumi vizsgálatával és numerikus modellezési lehetőségeivel foglalkozom. A laboratóriumi kísérletek során hat próbatestből álló kísérletsorozatot terveztem és hajtottam végre, melyeket az ún. bordákkal párhuzamos, monoton növekvő erővel tönkremenetelig terheltem (lásd 1. ábrán). Ez felel meg alapvetően a gyakorlati felhasználás terhelésének. A laboratóriumi vizsgálatoknál mértem az egyes próbatestek függőleges - a bordákkal párhuzamos - és a vízszintes - bordákra merőleges - alakváltozásait, valamint a terhelő erőt és a relatív elmozdulás értékét is a kijelölt mérési pontokban. Ezen kívül külső forrásból származó, hasonló elrendezésű, ugyanakkor másfajta elgondolással készült kísérletet is felhasználtam a munkám során. Ebben a modellezésben három darab próbatest állt rendelkezésre, ezeket szintén bordákkal 4
5 párhuzamosan, monoton növekvő erővel terhelték tönkremenetelig. A vizsgálatoknál a terhelőfej elmozdulását mérték mérésenként négy helyen. Elsőként a falazóelemek bordáinak numerikus modellezési lehetőségeit vizsgáltam, ezen belül a végeselem háló sűrűségének (lásd 2. ábrán) és a lekerekítéseknek a hatásait tanulmányoztam. A modelleket a konzulensek által korábban kifejlesztett numerikus modellezési eljárásra alapozva dolgoztam ki [3]. A modellalkotás első lépéseként egy közbenső bordaelem modellezését végeztem el. Erre azért volt szükség, mert a meglehetősen bonyolult felépítésű elem vizsgálata túl összetett feladat lett volna az alapvető modellezési hibák kiszűrésére. Erről a kutatási szakaszról egy korábbi TDK dolgozatban számoltam be [1]. Ezt követte a jelen munkában bemutatott, teljes falazóelem numerikus modelljeinek megalkotása, melyeken a kapott laboratóriumi kísérletekkel megegyező terheléses vizsgálatot hajtottam végre. A laboratóriumi és a numerikus kísérletek során elvégzett vizsgálatok eredményeit összehasonlítottam, így az erő-eltolódás diagramok, valamint az erő-függőleges alakváltozások és az erő-vízszintes alakváltozások kapcsolatai is kiértékelésre kerültek. 1. ábra: Laboratóriumi kísérlet (tönkrement falazóelem) 2. ábra: Végeselemes háló a falazóelem bordáján (felül 3 mm, alul 2 mm) [1] 5
6 2. Az anyagra vonatkozó információk a) Kerámia Az anyagkutatók meghatározása szerint kerámia minden olyan anyag, amely nem fém és nem polimer. Az agyag mellett számos más (például mesterséges) anyagból is készíthető kerámia, bár a legtöbb területen a kerámiák hő- és vegyszerállóssága jelenti a legfőbb értéket. Ezek az előnyös tulajdonságok a kerámiákon belüli atomok közötti erős (ionos, kovalens) kötésekből származnak, de sajnos ezek az erős kötéseknek a tulajdonságai okozzák a kerámiák legnagyobb hátrányát, törékenységüket is (szívósságuk csupán néhány százaléka a fémekének). A kerámiák különösen érzékenyek belső szerkezetük legparányibb megváltoztatására is. Az egyik legintenzívebben kutatott terület a kerámiák szívósságának növelése. E kutatási területbe a saját kísérleti és numerikus megoldásaim is segítséget nyújthatnak. Nagyon fontos különbség a fémekhez képest, hogy a kerámiáknál a diszlokációk szerepe jóval kisebb a hibák között, szerepüket a pont- és 3D-hibák (pórusok, üregek, zárványok) veszik át. Az erős és merev belső kötés miatt a mikroszerkezet jóval kevésbé hajlamos átrendeződésre, már egészen kicsi (a fémekéhez képest jó két nagyságrenddel kisebb) hiba esetén megindulhat az egész kötésrendszer robbanásszerű tönkremenetele (Ejtsünk betonpadlóra egy fém és egy porceláncsészét! Az eredmény jól érzékelteti a különböző típusú hibák terjedésének veszélyessége közötti különbséget). Makroszinten ez a hatás vezet a kerámiák rideg anyagi viselkedéséhez. A kerámiák többsége, valamint a ridegebb fémek (pl. öntöttvas) és a ridegebb polimerek teljesen másféleképpen törnek a fémes anyagokhoz képest. Ilyenkor közvetlenül az atomi kötések hasadnak, az első szakadás után megállíthatatlanul terjed tovább a teherbíró képesség elvesztése, nincs semmilyen helyi képlékeny zóna. Elegendő a legkisebb hiba (például egy lokális mikrorepedés az atomi lánc néhány tagjában), és a merev rendszer nem képes ennek olyan jellegű szétosztására, a belső struktúra összeomlik. Ezt a fajta törési módot rideg (angol szóval brittle ) törésnek hívják, és gyors terjedése miatt különösen veszélyes. A törési felületek ilyenkor élesek, hasadó metszetekből állnak. A mikroszerkezet sajátosságainak köszönhetően a kerámiák egy részénél az elméleti és valóságos határszilárdságban több nagyságrendi eltérés mutatkozhat. Minél több belső hiba 6
7 gyengíti a polikristályos szerkezetet, annál nagyobb a tényleges érték eltérése a határszilárdság elméletileg lehetséges értékétől. Megjegyzésként felhívnám a figyelmet a kerámiák mindenkori tönkremenetelét okozó repedés terhelési mód szerinti különbözőségére (lásd 3. ábra): 3. ábra Különböző típusú repedésterjedések kerámiákban [2] Húzás esetén a mikrorepedések csúcsainál levő feszültségkoncentrációk a szívóssági határ elérésekor dinamikus makrorepedés-terjedést indítanak, a szívóssági határhoz közeledve az anyagi stabilitást veszítjük el. Nyomott elemeknél a repedésterjedés valamivel stabilabb, a mikrorepedések (amelyekből ilyenkor rendszerint jóval több van) összefűződése kvázistatikus terhek esetén az anyag blokkokra történő szétesésével, morzsolódásával jár együtt. A kísérleteim során a falazóelemeket csak egytengelyű nyomásnak vetettem alá. [2] 7
8 b) Mechanikai anyagmodellek Az anyag viselkedésének modellezése a természettudományok legösszetettebb feladatai közé tartozik. A rendkívül változatos belső összetétel a különböző fizikai tulajdonságok olyan széles skálájával ruházza fel az anyagokat, hogy viselkedésük átfogó megértése és modellezése a tudósok és mérnökök minden erőfeszítése ellenére még nem mondható teljesnek és befejezettnek. Ma már a százezret közelíti a mérnöki gyakorlatban használt különféle anyagfajták száma. Maga az anyagmodell általános kifejezésként választ jelent, az anyag válaszát az őt ért külső hatásokra. Mivel a külső hatások mérnöki értelmezés szerint is nagyon sokfélék lehetnek, éppen ezért anyagmodell is többféle lehet. Az anyagmodell fogalma mást jelent a különböző iparágak, a különböző mérnökök számára. Nagyon fontos állításként kell tehát rögzíteni, hogy ebben a dolgozatban csak olyan feladatokat tárgyalok, amikor az anyagnak a külső hatásokra (erők, hőmérsékletváltozások, idő) adott mechanikai válaszát (belső deformációk és feszültségek) keresem. Éppen ezért a saját modelljeimet mechanikai anyagmodelleknek fogom hívni. Mivel a továbbiakban kizárólag mechanikai anyagmodellekkel foglalkozom, ezért az egyszerűség kedvéért elhagyom a mechanikai jelzőt, csupán az anyagmodell fogalmat használom, azonban mindig a fenti meghatározás adta korlátok közé szorítva annak értelmezését. [2][3] Ezek a mechanikai anyagmodellek soha nem öncélú elemei a mechanika tudományának, hanem fontos gyakorlati célokat szolgálnak. Segítségükkel képesek a mérnökök szerkezeteket tervezni vagy ellenőrizni. Nélkülük a szó szoros értelmében lehetetlenné válna a kicsit is komolyabb mérnöki munka. c) Rideg és rugalmas-képlékeny-fellazuló anyagok komplex modelljei Szerkezeteinkben használt anyagjaink viselkedése igen eltérő lehet attól függően, hogy milyen anyagszerkezeti tulajdonságokkal rendelkeznek. A betonok, rideg fémek és talajok nemlineáris viselkedése a képlékeny tulajdonságok mellett az anyagban keletkező mikro- és makroszintű repedések kialakulásától és szilárdságcsökkentő hatásától is függ. Ez a hatás akkor jelent számottevő problémát, ha az anyag mikrostruktúrájában a kristályos belső szerkezet csak lokálisan van jelen vagy a kristályrács alapvetően hibás. A mechanikában a repedések hatása két szempont alapján vizsgálható: 8
9 - Előállítható olyan anyagmodell, mely a makrorepedés-rendszer globális hatását vizsgálja, amelyben a modell a terhelt kontinuum viselkedését modellezi. - Továbbá léteznek olyan modellek, melyek a makrorepedések hatását vizsgálják az anyagban keletkező feszültség-alakváltozás koncentrációk által, valamint ezzel együtt az anyag stabilitását is képesek leírni. Az ilyen modellekkel a törésmechanika tudománya foglalkozik. [2][3] 3. Az általam elvégzett laboratóriumi kísérletsorozat a) A vizsgált falazóelem A laborkísérletben anizotrop falazóelemként a korszerű Leiertherm 30 N+F gyártmányú terméket vizsgáltam. A kísérletsorozat hat darab próbatest vizsgálatából állt. Egy elem hosszúsága 250 mm, szélessége 300 mm, magassága pedig 238 mm. A falazóelemre megadott gyártói nyomószilárdság karakterisztikus értéke: 11 N/mm 2. A falazóelem gyártási helye Mátraderecske. A téglaelemek kialakítását a 4. ábra mutatja. [4] 4. ábra: Leiertherm 30 N+F falazóelem 9
10 b) A kísérletsorozat bemutatása A kísérletsorozatot a BME Szerkezet és Anyagvizsgáló Laboratóriumában hajtottam végre. A terhelést egy Z600 típusú, telepített terhelő berendezéssel végeztam. A gép hidraulikával ellátott, manuálisan működtetett és maximálisan 600 kn terhet tud közvetíteni. Előzetesen egy elem teherbírását kb. 350 kn nagyságúra becsültem. A terhelendő próbatestet teherelosztó farostlemezek közé tettük, így terhelte meg az elemet egytengelyű nyomással a berendezés. A farostlemezek az esetleges egyenetlenségeket kívánták kiküszöbölni, hogy a nyomás a keresztmetszet minden egyes pontjában közel azonos legyen. Mindemellett a terhelőberendezés felső nyomólapja gömbcsuklós kialakítású volt (lásd 5. ábrán). 5. ábra: A kísérleti elrendezés Minden egyes próbatest két-két szemközti, a kísérleti elrendezés szempontjából az elülső, illetve a hátulsó oldalára egy-egy Hottinger Baldwin WA/20 típusú induktív elmozdulásmérő 10
11 lett felszerelve, melyek a terhelés irányában mérték a bekövetkezett összenyomódást átlagosan 12,5 cm hosszú referenciaszakaszon (lásd 6. ábrán). Az előzőekben ismertetetteken túl, két próbatest kivételével, nyúlásmérő bélyegeket is elhelyeztem. Két próbatest egy-egy oldalára függőlegesen, és két további próbatest egy-egy oldalára vízszintesen kerültek elhelyezésre a nyúlásmérő bélyegek. A kísérlethez KMT-LIAS /350-5 típusú, 84 mm hosszú nyúlásmérő ellenállásokat használtunk (lásd 7. ábrán). A mérőegységekből kapott adatokat Catman Easy szoftver segítségével detektáltam. 6. ábra: Induktív elmozdulásmérő 11
12 c) A kísérleti eredmények 7. ábra: Függőlegesen elhelyezett nyúlásmérő bélyeg A hat mérés során a maximális teherbírás szempontjából igen eltérő eredmények születtek. A becsült 350 kn körüli teherbíráshoz képest az 1. jelű próbatest esetében sokkal kisebb, mintegy 250 kn nagyságú maximális erőt mértünk. Három mérés esetében (3., 4. és 6. jelű) 300 kn és 350 kn közötti értéket, míg két mérés esetében (2. és 5. jelű) nagyobb közel 450 kn teherbírást mértem. A hat téglatest ugyanazon gyártásból és raklapról származott, így különösen meglepő az ilyen mértékű eltérés a mérési eredmények között. Az eltérő eredmények a terhelőberendezés pontatlansága, a gömbcsukló hibája miatt alakulhattak ki. Az egyes eredményeket a 8. ábra mutatja. 12
13 8. ábra: Maximális teherbírás Az induktív elmozdulásmérők is egymástól jelentősen eltérő adatokat detektáltak, amit leginkább a téglaelemek függőleges irányú erő-elmozdulás grafikonjain láthatunk (9. ábra). A 6. jelű próbatest mérési eredményei a mérőberendezés hibája miatt nem kerültek közlésre. 9. ábra: Az elemek erő-elmozdulás diagramja A próbatestek kezdeti merevsége (kb. 120 kn-os terhelésig) szinte megegyezik. Az 1. jelű próbatest esetében kezdetben megnyúlást mért az elmozdulásmérő berendezés. A nem várt mérési eredmény minden bizonnyal a próbatest terhelés alatti kezdeti helyezkedéséből 13
14 adódott, a nem tökéletesen párhuzamos felfekvési síkok miatt következhetett be. A mérési eredményekből megállapítható, hogy a terhelési sebesség megválasztása jelentősen befolyásolta a detektált viselkedést. A kisebb terhelési sebesség mellett végrehajtott kísérletek (1. és 5. jelű) esetén a kezdeti merevség után képlékenyedő fázis figyelhető meg, míg a nagyobb sebességgel terhelt (2., 3. és 4. jelű) elemek esetében ridegebb viselkedés mutatkozott. Ez arra enged következtetni, hogy a lassabb terhelési sebesség mellett van ideje a képlékeny alakváltozásoknak, esetleg kisebb lokális töréseknek kialakulni. Megfigyelhető, hogy bár a kerámia alapanyag a ridegségéről hírhedt, de a teljes falazóelem lyukacsos kialakítása számottevő képlékeny alakváltozás kialakulását teszi lehetővé. A próbatestek terhelő berendezésből való kiszedésekor egyértelmű magyarázatot látunk a jelenségre. Az alapanyag ugyan jelentős képlékeny viselkedéssel nem bír, de a belső bordaszerkezetben megjelenő repedések mentén történő apró átrendeződések a teljes elem képlékeny viselkedését mutatják. A terhelési erő és a bordairányra merőleges keresztirányú nyúlás mérési eredményeit a 3. és 6. jelű próbatest esetén a 10. és 11. ábra tartalmazza. Kizárólag ezeken az elemeken volt vízszintes nyúlásmérő bélyeg. 10. ábra: 3. jelű próbatest erő-alakváltozás diagramja 11. ábra: 6. jelű próbatest erő-alakváltozás diagramja A pozitív értékek a függőleges induktív elmozdulásmérők esetén összenyomódást, a vízszintes nyúlásmérő bélyegek esetén pedig nyúlást jelentenek. 14
15 Látható, hogy a keresztirányú elmozdulások közelíthetők lineárisan, azaz mindkét esetben kb. 200 kn nagyságú erőnél 100 µm/m-es alakváltozást mértem. Ugyanakkor észrevehető, hogy a korábban bemutatott maximális teherbírástól jelentősen eltérnek az eredmények. Ez azzal magyarázható, hogy a teljes tönkremenetel kezdetén függőleges irányú repedések jelentek meg minden esetben a próbatesteken, melyek a vízszintes ellenállásmérőkön is áthaladtak (lásd 12. ábra), így ezek után a bélyegek rossz értékeket mutattak, azokat a mérési eredményekből ki kellett zárnom. 12. ábra: Függőleges repedés A tönkremenetel hangos pattogással kezdődött, melynek következtében kisebb darabok is lerepültek a falazóelemekről. Tönkremenetelkor a terhelőgépből kiszedve a téglatest belseje teljesen összetöredezett. (lásd 13. ábra) 15
16 13. ábra: Tönkrement falazóelem A kapott mérési eredmények nagy szórást mutatnak, mely egyrészről a gyenge minőségű próbatestekkel (falazóelemek), másrészről a kezdeti kutatási fázis miatt még pontosítandó mérési eljárással magyarázható. 16
17 4. Előzetes numerikus vizsgálat a) A modell Első lépésként a minél pontosabb geometria felépítéséhez szükséges végeselemek nagyságának a vizsgálata volt a cél, annak meghatározása, hogy mekkora elemnagyságot használjak a numerikus kísérleteimhez. Ehhez a virtuális kísérlethez csupán a téglaelem egy általános belső részletét modelleztem szimmetriafeltételek kiegészítésével. (14. ábra) A numerikus vizsgálatokat a GID nevű szoftver 12-es verziójával, majd azt követően az Atena Studio V5, 3D-s, nemlineáris végeselemes programmal végeztem. 14. ábra: A modellezett részlet Az elem hossza 61,56 mm, maximális szélessége 18,84 mm, illetve magassága 125 mm, hiszen az elmozdulásmérők is ilyen hosszon mérték az értékeket. A modellezéshez szükség volt egy téglatestre, azon egy téglalap alapú acél gúla elhelyezésére a vizsgált elem tetején, melynek csúcsában definiáltam az elmozdulás értékét. (lásd 15. ábra) Így a teljes keresztmetszetre el lehet osztani az eltolódást, míg a definiált elmozdulás csupán pontszerű. Más előnye is van az acél elemnek, ugyanis a program a testben keletkező erőket és feszültségeket is jobban tudja mérni az előbb részletezett módon. 17
18 15. ábra: ATENA 3D modell A modellhez szükséges volt anyagmodelleket is definiálni. Mivel rákerült egy acél test a téglaelemre, így azt az anyagfajtát is definiálnom kellett. Az acéllemezre egy egészen egyszerű lineárisan rugalmas izotrop anyagmodell került. Megadtam az acél rugalmassági modulusát és Poisson-tényezőjét, ahogyan az alábbi, 16. ábrán látható: 16. ábra: Az acél anyagmodellje 18
19 A téglatest elemére már bonyolultabb a meghatározás, az anyagmodellt a kerámiákra, illetve rideg anyagokra parametrizálható 3D Nonlinear Cementitious 2 nevű modell segítségével vettem fel. A programban megadhatók egy teljesen egyenértékű egyirányú feszültségalakváltozás görbe pontjai, pl.: a nyomó- és húzószilárdság értéke. (lásd 17. ábra) 17. ábra: Egyirányú feszültség-alakváltozás rideg anyagokra A görbe többi pontját a program automatikusan felveszi, így azokat változtatni nem lehet. A 17. ábrán az 1-es szakasz a húzófeszültség kimerüléséig tart, itt a rugalmassági modulus lineárisnak tekinthető. A második szakaszon a repedésmegnyílás modellezése egy exponenciális függvénnyel írható le, mely a speciális törési energia és a húzószilárdság függvényéből számítható. (lásd 18. ábra) 18. ábra: Exponenciális repedésmegnyílás függvénye A 3. szakasz a nyomófeszültség maximális értékének eléréséig tart. Ez a függvény az anyag kezdeti és a maximális nyomófeszültséget metsző rugalmassági modulusok arányától, valamint a nyomószilárdság értékétől függ. A bemutatott görbe ezen a szakaszon parabolikus görbének tekinthető. Az említett 3D Nonlinear Cementitious 2 modellben tehát a következő adatok adhatók meg: 19
20 a) b) c) d) e) 19. ábra: Az anyagmodell definiálása a programban A 19./a) ábrán az általános tulajdonságok állíthatók be, mint a rugalmassági modulus, Poisson-tényező, húzó- és nyomószilárdság. A b) ábrán a húzáshoz tartozó, a c) ábrán a nyomáshoz tartozó, a d) ábrán a nyírási és az e) ábrán a vegyes tulajdonságok adhatók meg. A programnak csupán a nyomószilárdság értéket adtam meg, majd az összes többit automatikusan felvette. A modell tulajdonságain természetesen lehet változtatni, azonban a folyási függvény, a degradáció, a repedésmegnyílás, a nyírási faktor függvényeinek csak egy vagy két pontját változtathatjuk, mivel a függvények előre definiáltak. A most beállított értékek közelítő értékek, melyeket további kísérletsorozattal lehetne pontosítani. 20
21 A modell alsó síkja függőleges értelemben megtámasztott. Ahogyan korábban említettem, a terhet egy elmozdulás segítségével helyeztem el az acél gúla csúcspontjában. A maximális elmozdulás -z irányba, függőlegesen lefelé mutat és összesen 0,6 mm nagyságú volt, mely elmozdulás 20 lépcsőben került rá. Az elhelyezett végeselemes háló kétféle volt, melyet vizsgálat alá vetettem. Az egyik esetben az elem szélességében három, míg a másikban két darab végeselem helyezkedett el. Ez azt jelenti, hogy az előbbi esetben kb. 3, míg a másikban kb. 4 mm volt egy végeselem szélessége. A numerikus modellben egységesen kvadratikus bázisfüggvényeket, valamint a kerámia elemekre 10 csomópontos tetraéder végeselemeket alkalmaztam. Célszerű lett volna a téglatest alakú végeselemek kialakítása, hiszen ekkor nagyobb pontosság érhető el, viszont a sarkok lekerekítése miatt nem lehetett ezzel a módszerrel behálózni a modellt. A végeselemhálóval kapcsolatos illusztrációk a ábrán láthatók. 20. ábra: Tetraéderes végeselem geometriája 21. ábra: Ritkább háló 21
22 22. ábra: Sűrűbb háló Az eredményekhez monitorpontokat vettem fel a modell tetején, közepén, illetve a két végén, a modell hossza mentén. Az először említett két ponttal a test függőleges összenyomódásait lehet vizsgálni, míg az utána említett szélső pontokkal a harántirányú megnyúlást lehet figyelemmel követni. [3][5] b) Az eredmények A kezdeti, egy bordaelemen végzett vizsgálat eredményeit az alábbi, 23. ábra mutatja: 23. ábra: A numerikus számítás erő-elmozdulás diagramja 22
23 Megfigyelhető, hogy a kétféle végeselemes hálóval kapott numerikus eredmények között érdemi különbség nincs. Az erő-eltolódás görbék alakja megegyezik egymással. A maximális teherbírás is közel azonos, a sűrű hálóval vett számítás csupán 3%-kal mutat nagyobb teherbírást, mint a ritkább hálóval számolt verzió. A legnagyobb eltérés a számítási időben mutatkozott. Míg a sűrű hálóval felépített modell 30 percig, úgy a ritkább hálóval készített modell csupán 5 percig futott. Ez nagyon jelentős különbség, éppen ezért a továbbiakban a nagyobb, 4 mm-es hálózás alkalmazása mellett döntöttem azokban az esetekben, amikor a futási idő nagysága miatt nem tudtam alkalmazni a sűrűbb hálózást. A kialakult függőleges feszültségek szabályos képet mutatnak. Jól látszik, hogy ott, ahol a borda található, illetve az erőbevezetés helyén feszültség-csúcspontok alakulnak ki, ami a várakozásnak megfelelő. (lásd 24. ábra) 24. ábra: Függőleges feszültségábra 23
24 A harántirányú elmozdulásokat az erő függvényében a 25. ábra tartalmazza. 600 Erő - keresztirányú elmozdulás Erő (kn) , , , , , , , , ,00008 Elmozdulás (m) 25. ábra: Erő - keresztirányú elmozdulás Jól látszik, hogy a grafikon ugyanolyan lefutást mutat, mint a függőleges elmozdulás, csak egy nagységrenddel kisebbek az elmozdulások. Végül a kialakult repedések helyzetét mutatom be a 26. ábrán. 26. ábra: Repedések az elemben 24
25 5. Az általam elvégzett kísérlethez készített numerikus modell a) A modell A részletes vizsgálat során már nemcsak egy belső borda modellezésével foglalkoztam, hanem a teljes keresztmetszetet vizsgáltam, kihasználva a téglaelem egyszeresen szimmetrikus mivoltát. A felépített modell egy fél tégla, melynél a szimmetriatengelyben szimmetriafeltételeket írtam elő. A test alján mindhárom (x, y, z) irányú eltolódást meggátló támaszt állítottam be, míg a felső síkra x és y irányban - a terhelésre merőleges irányokban - került támasz. Így tudtam elérni, hogy a numerikus modell a lehető legjobban írja le az egytengelyű nyomókísérletet. A felépített modellt 11 MPa nagyságú nyomóerővel terheltem a felső síkján, függőleges irányban. A terhet 11 lépésben működtettem az elemre. Ennél a modellnél a kisebb, 3 mm-es elemnagysággal készült a végeselemes modell a számítási idő értékelhető hossza miatt, illetve a nagyobb pontosság érdekében, melynek egy részlete az x-y síkban a 27. ábrán látható: 27. ábra: Alkalmazott végeselemes háló 25
26 A modell kialakítása a 28. ábrán található: Felső megtámasztás és terhelés Monitorpontok Szimmetriabeállítások Alsó megtámasztás 28. ábra: A modell kialakítása Ahogyan korábban is, így most is tetraéder alakú végeselemeket alkalmaztam a modell megalkotásánál. Az alkalmazott anyagmodell a téglára ismét az ún. 3D Nonlinear Cementitious 2, melyet az előzetes numerikus modell fejezetében részletesen ki is fejtettem. Eltérés ahhoz képest, hogy az anyagjellemzők esetében megváltoztattam a nyomásra vonatkozó maximális feszültséget a Leiertherm katalógusában [4] található deklarált nyomószilárdság értékére, 11 MPa-ra. A többi jellemző változatlan maradt, ahogyan az látható a 29. ábrán. 26
27 b) Az eredmények 29. ábra: Az alkalmazott anyagmodell alapbeállításai A részletesebb numerikus modellen elvégzett vizsgálat eredményeként többek közt feszültség alakváltozás (erő-eltolódás) ábrákat, deformációs ábrákat és repedésképeket kaptam, melyeket össze tudtam vetni a laborkísérletben kapott eredményekkel. A numerikus modell felső középső pontjának feszültség eltolódás diagramja (lásd a 30. ábrán), jellegét tekintve megegyezik a laborkísérletekben mértekkel. Megfigyelhető, hogy a numerikus modell nagy kezdeti merevséggel rendelkezik, mely megegyezik a laborkísérlet szintén kezdeti, repedésmentes szakaszával. Ezt követően lineáris lágyulás kezdődik a 4,75 MPa 0,021 mm pontban, melyet egy felkeményedő viselkedési szakasz követ. A numerikus eredményekben is megmutatható a laborkísérletekben már megfigyelt képlékeny, repedések mentén átrendeződő viselkedési fázis. A tönkremenetelhez tartozó, szinte tökéletesen képlékeny, de kissé felkeményedő viselkedési szakasz kezdete a 9,4 MPa 0,116 mm pontnál kezdődik meg. A numerikus eredmények lágyuló görbéje 0,5-0,6 mm-es elmozdulás tartományban ér véget, amely megegyezik Van Mier (1986) betonokra végzett kísérleteiben tapasztaltakkal [6]. 27
28 30. ábra: Feszültség-eltolódás diagram A deformációs ábrák alapján (lásd 31. ábra) először a belső szerkezet repedezik és rendeződik át, (deformálódik többet), majd a külső rész károsodásával merül ki a teljes szerkezeti elem teherbírása. 31. ábra: Deformációs ábra 28
29 A 32. és 33. ábrákon látható, jellemző repedésképek azt mutatják, hogy a téglaelem felső és alsó lapjához közel az alapanyag morzsolódik, illetve a bordák mentén függőleges repedezettség jelenik meg. Ez jellegét tekintve jó egyezést mutat a laborkísérletekben megfigyelt tényleges tönkremenetelekkel. 32. ábra: Repedezettség x-z síkban 33. ábra: Repedezettség y-z síkban c) A laborkísérleti és a numerikus eredmények összehasonlítása A laborkísérletben tapasztalható nagy szórású eredmények miatt, mely a laborkísérlet pontatlanságainak és hibáinak köszönhető, a numerikus modellt egyetlen laborkísérlettel hasonlítom össze. (lásd 34. ábra). A numerikus eredményeket a legkisebb sebességgel terhelt 5. jelű próbatest mérési eredményeivel vetem össze ebben a fejezetben. A kapott erőelmozdulás diagramok (lásd 35. ábra) összehasonlításából (lásd 1. táblázat) jól látszik, hogy kezdetben szinte azonos lefutást mutatnak az ábrák, az eltérés mindösszesen 1,3% a 0,021 mmes összenyomódásnál. A lineáris lágyulással jellemezhető második viselkedési szakasz szintén jó egyezést mutat, az eltérés 0,053 mm nagyságú összenyomódásnál csupán 2,63 %. Ezt követően, a jelentős belső átrendeződésekkel járó harmadik görbeszakaszon a numerikus és laboreredmények eltávolodnak egymástól, az eltérés több, mint 28% a legkedvezőtlenebb pontban (0,116 mm összenyomódásnál). A tönkremeneteli szakasz ismét viszonylag pontosan követhető le a megmutatott modellezési eljárással. A tönkremeneteli erőben mindösszesen 5%- os eltérés mutatkozik. Összességében elmondható, hogy a vélhetően nagy gyártásminőségi és alapanyag hibákkal terhelt próbatestek közül kiválasztott mérési eredmények az általam ismertetett numerikus modellezési eljárással jellegében jól követhetők. A jelentős belső repedezettség mentén, az 29
30 amiatt átrendeződő viselkedési szakasz kivételével a valós viselkedés jól modellezhető numerikusan. Ez egyúttal azt is jelenti, hogy a modellalkotási folyamat továbbfejlesztése mindenképpen szükséges még. 34. ábra: Az 5. próbatest és a numerikus számítás erő-elmozdulás ábrája 35. ábra: A falazóelemek és a numerikus számítás erő-elmozdulás ábrája 30
31 A terhelés értékei és azok eltérései adott elmozdulások függvényében 0,021 mm 0,053 mm 0,116 mm 0,289 mm Numerikus vizsgálat 157 kn 185 kn 310 kn 330 kn Laborkísérlet - 5. elem 155 kn 190 kn 241 kn 316 kn Eltérés a laborkísérlethez képest +1,30% -2,63% +28,63% +4,43% 1. táblázat: A numerikus vizsgálat és az 5. elem erő elmozdulás ábrájának az összehasonlítása A numerikus modellből kapott törésképet (36. ábra) is összehasonlítottam a kísérleti tapasztalatokkal (37. ábra). Mindkét esetben jól látszik, hogy a próbatest alsó és felső síkjának környékén, illetve a keresztmetszet szélső függőleges bordái mentén koncentrálódnak a repedések kezdetben, melyek végig hasadása okozza a tönkremenetelt. 36. ábra: Repedezettség a laboratóriumi kísérletben 37. ábra: Repedezettség x-z síkban d) A numerikus modell kritikája A laboratóriumi kísérletek során egymástól annyira eltérő eredmények születtek, hogy nehéz megítélni, melyik viselkedés a valós, melyikre lehetne validálni a modellt. Az általam elkészített numerikus számításban feszültség-vezérelt módon definiáltam a terhelést, ami nem feltétlen fedi a valóságot, hiszen a terhelés során valószínűleg nem egyenletes feszültségek alakulnak ki a falazótéglán. Továbbá a laboratóriumban a próbatestek alá és felé egy-egy farostlemez került elhelyezésre. Ez a megoldás nem biztosít befogást egyik síkon sem, sőt, még harántirányú kontrakciót elősegítő mechanizmussal is rendelkezik, hiszen a farostlemez 31
32 rugalmas anyagú. Ezt a farostlemezt, illetve annak a viselkedését nem tudtam megfelelően modellezni, arra nem történt külön vizsgálat, hogy ezek milyen tulajdonsággal rendelkeztek. A jelenség pontos modellezéséhez másfajta megoldásra van szükség. Olyan kutatásokat kerestem tehát, amelyek más megoldásokkal dolgoznak, mint amit én használtam a kísérleteim során. Így találtam rá egy eddig nem publikált kísérletsorozatra, amely farostlemez helyett habarcsborítást alkalmazott. A továbbiakban ezt a kísérletsorozatot mutatom be, és használom fel egy új, várakozásaim szerint pontosabb numerikus modell felépítéséhez. 6. A mások által végzett laboratóriumi kísérletsorozat a) A vizsgált falazóelem A laborkísérletben anizotrop falazóelemként a korszerű Porotherm 30 N+F gyártmányú terméket vizsgálták. A kísérletsorozat három darab próbatest vizsgálatából állt. Egy elem hosszúsága 250 mm, szélessége 300 mm, magassága pedig 238 mm. A falazóelemre megadott gyártói nyomószilárdság karakterisztikus értéke: 11 N/mm 2. A téglaelemek kialakítását a 38. ábra mutatja. [7] 38. ábra: Leiertherm 30 N+F falazóelem 32
33 b) A kísérletsorozat bemutatása A kísérletsorozat az Országos Tudományos Kutatási Alapprogramok (OTKA) pályázata segítségével jöhetett létre. Az NKFI-K sorszámon futó projekten dolgozó szakemberek a falazott, húzószilárdság nélküli szerkezetek mechanikáját vizsgálják. A kutatás igen sokrétű, többek közt boltozatok és egyedi téglaelemek viselkedését is vizsgálják. A kísérletsorozat jelenleg nagyon kezdeti fázisban van, az adatok kiértékelése, publikálása sem történt még meg. A kísérletek közül a saját témámat érintőbe, a lyukacsos falazóelemek vizsgálatába tekinthettem bele. A laborkísérletsorozat részeként három darab Porotherm 30 N+F típusú terméket terheltek egyirányú nyomással (a bordairánnyal párhuzamosan, ahogyan a saját kísérletemben is) tönkremenetelig. A próbatestek alá és fölé kb cm vastag habarcsréteg került. A terhelőberendezés vége egy kb. 60 cm x 60 cm oldalhosszúságú, négyzet alakú acélelem volt, melynek négy sarkába helyezték el az elmozdulásmérőket. A kísérleti elrendezést a 39. ábrán lehet megtekinteni. Ezeknek a nyers adatait kaptam meg, és végeztem el azok kiértékelését, majd azt követően a numerikus modellezését is. A habarcs anyagjellemzőit sajnos nem mérték meg a kísérlet elvégzésekor, így a szükséges adatokat mérnöki becsléssel vettem fel. 39. ábra: Kísérleti elrendezés 33
34 c) A kísérleti eredmények A három rendelkezésre álló mérési eredményben jóval kisebb szórás mutatkozott, mint az általam elvégzett próbatestek esetében. A 3-as jelű próbatestnél közel 600 kn-os maximális teherbírás adódott, az 5-ös esetében 450 kn nagyságú erőt mért a berendezés, míg a 4-es esetében a két előbbi érték közötti 515 kn erő következtében ment tönkre a téglaelem. Az eltérő eredmények a próbatestek különféle tönkremeneteli módjából adódtak, ugyanis volt olyan eset, ahol a terhelőberendezés felső nyomólapja elferdült, így kisebb lett az adott tégla teherbírása. Ez később az elmozdulási értékekből alátámasztást is fog nyerni. A maximális teherbírási értékeket a 40. ábra mutatja. 40. ábra: Maximális teherbírás értékei Ahogyan korábban említésre került, a terhelőberendezésre négy-négy darab elmozdulásmérő került a próbatest négy sarkára. Ezek minden esetben nagy mértékben tértek el egymáshoz képest, így a kiértékelésüket részletesen mutatom be az alábbiakban. i. 3-as jelű próbatest A nyers eredményeket a 41. ábra mutatja. Megfigyelhető, hogy két-két (U_1 és U_2, illetve U_3 és U_4) mérés nagyon hasonló eredményeket mutat, csupán kismértékben térnek el egymástól, a meredekségük és a lefutásuk ugyanaz, de valamelyest eltolódtak egymástól. 34
35 41. ábra: 3-as számú próbatest nyers eredményei Feltételezhető, hogy az előbb említett méréspárok (U_1 és U_2, illetve U_3 és U_4) egymással szemben lévő mérőberendezésekből származnak, így külön kell őket kezelni, kiértékelni. Az U_1 és U_2 grafikonja között minimális az eltérés, így ott nem játszhatott közre a mérőberendezések hibája, hanem a terhelőberendezés kezdeti állása dőlt meg a tönkremenetel miatt. A maximális teherbírás elérésekor az értékek ellentétes irányba csökkennek. Mivel nem tapasztalható a közel 600 kn-os teherbírás után többletteherbírás, így a leszálló agákat nem vettem figyelembe. (42. ábra) 42. ábra: 3-as számú próbatest U_1 és U_2 mérései 35
36 A másik páros, az U_3 és U_4 grafikonja között komoly eltérés figyelhető meg, nemcsak abban, hogy a grafikonok egymáshoz képest eltolódtak, hanem egy ponton látványosan megváltozik a meredeksége a két görbének, utána pedig újra megegyezik. A tégla anyaghibái miatt feltételezhető, hogy az elem aszimmetrikus viselkedést mutatott a terhelés közben. Ha átlagoljuk a két értéket, megkaphatjuk a középső elmozdulás reális értékét. A tönkremenetel rideg, így annak ábrázolásától ismét eltekintettem. A nyers adatok az U_3, U_4 esetében és azok átlagát a 43. ábra mutatja. 43. ábra: 3-as számú próbatest U_3 és U_4 mérései, illetve azok átlaga Ha az átlagot ábrázolom az U_1 és U_2 mérésekkel, látható, hogy a gondolatmenet helytálló, illeszkedik az átlag az előbb részletezett eredményekhez. (lásd a 44. ábrán) 44. ábra: 3-as számú próbatest U_1 és U_2 mérései, illetve az U_3 és U_4 átlaga 36
37 ii. 4-es jelű próbatest A 4. számú próbatesten mért eredmények teljesen eltérnek egymástól. Meredekségük ugyanakkor szinte megegyezik minden esetben. Megfigyelhető, hogy az U_3-as eredményeknél negatív tartományban indul a grafikon. Ez a mérőberendezés nem megfelelő adatérzékeléséből származott. A mérés elrendezésekor valószínűleg ugyanazt a mintát követték, amit a 3-as jelűnél feltételeztem, így az eredmények elemzésénél ugyanúgy teszek. A nyers eredmények a 45. ábrán találhatók. 45. ábra: 4-es számú próbatest nyers eredményei Az U_1 és U_2 mérések meredeksége megegyezik, ahogy korábban is, csak egymáshoz képest eltolt lefutást mutatnak. Ez azt feltételezi, hogy a terhelésekor a téglaelem aszimmetrikus viselkedést mutatott a terhelés közben, melyet a távol lévő mérési pontok felnagyítottak. A numerikus modell szimmetriája miatt nem várható ilyen megdőlés az elemen. Mindezek miatt a két érték átlaga várható a numerikus számításban. Az átlagolással megbecsülhető a mérési pontok által kijelölt síkon az átlagos elmozdulás értéke, mely összehasonlítható a számítógéppel kiszámított adatokkal. Az átlagolás és az U_1, U_2 mérési eredmények a 46. ábrán találhatók. 37
38 46. ábra: 4-es számú próbatest U_1 és U_2 mérései, illetve azok átlaga Az U_3 és U_4 mérések grafikonjának meredeksége szintén megegyezik, és ismételten egymáshoz képest eltolva helyezkednek el. Az előbbi adatpárostól eltérően nem használható az átlagolás módszere, hiszen az U_3-as esetén negatív irányba indul el a görbe, mely egyértelműen a mérőberendezés pontatlanságát mutatja. Ha a kezdeti negatív irányba történő elindulást a helyes irányra módosítjuk, akkor az U_4-es méréshez tartó eredményt kapunk. E két görbét a 47. ábrán jelenítem meg. 47. ábra: 4-es számú próbatest U_4 és korrigált U_3 mérései 38
39 iii. 5-ös jelű próbatest Az 5-ös próbatesten két különböző típusú görbe-karakterisztika jelenik meg. Az előzőkkel megegyezve az U_1 és az U_2 mérési eredmények, illetve az U_3 és U_4 esetek hasonlítanak egymásra. Az egyik esetben (U_1-U_2) szinte megegyeznek a meredekségek, csupán egymáshoz képest eltolódtak, míg a másiknál (U_3-U_4) a görbe alaki tulajdonságai hasonlóak, ugyanakkor nagy különbség figyelhető meg a meredekségben. Utóbbi eltérést eredményezheti az egyik mérőberendezésben keletkező ismeretlen hiba, melyet nem lehet a mérés közben kiszűrni. A hibát az eredmények értékelésekor kell kiküszöbölni. A kapott nyers mérési eredményeket a 48. ábra mutatja. 48. ábra: 5-ös számú próbatest nyers eredményei Az U_1 és U_2 mérési eredmények közti különbséget a téglatest nem egyenlő tönkremenetele okozta, hiszen a grafikonok alakja, végső, a helyezkedés utáni meredekségük azonos. Átlaguk megadja, hogy mennyi lehetett átlagosan egy abba a sík eső elem elmozdulása adott terhelésnél. Az átlagot felrajzolva az eredeti értékekkel együtt a 49. ábrán láthatjuk. Az U_3 és U_4 esetében kapott értékek - ahogy korábban említettem - igen hasonló lefutást mutatnak. Az U_3-as mérés esetében a viselkedés és az értékek nagyon hasonlítanak az eddig tapasztalt görbékkel, így az U_4-es számú mérést kell felülvizsgálni. Jól látszik az 50. ábrán, hogy a korrigált mérési eredmények jobban hasonlítanak egymáshoz az alsó, kezdeti szakaszon, illetve a végső, tönkremenetelhez közeli oldalán. A közbenső szakaszon viszont nagy eltérés mutatkozik, ami az elmozdulásmérő nem megfelelően közölte az adatokat. Előfordulhat, hogy 39
40 a ragasztás csúszott meg, de az is, hogy a mérőberendezés megszorult, így hibás adatokat továbbított az eredményfeldolgozó szoftvernek. Mindezek miatt az U_4-es mérést ki kell zárni az eredmények értékeléséből, csak az U_3-as mérést lehet figyelembe venni. Az U_3-as, illetve az U_1-es és U_2-es mérés átlagából kapott grafikont egyesítve az 51. ábrán találhatjuk. 49. ábra: 5-ös számú próbatest U_1 és U_2 mérései, illetve azok átlaga 50. ábra: 5-ös számú próbatest U_3-as mérése, illetve U_4 korrigált verziója 40
41 51. ábra: 5-ös számú próbatest U_1 és U_2 mérések átlaga, illetve az U_3-as mérés Az eddig részletezett diagramokat az alábbi, 52. ábrán összesítettem. Megfigyelhető, hogy kezdetben lágy viselkedést mutat az elrendezés, majd kb. 1 mm-es elmozdulásnál felkeményedik a rendszer. Ez a kezdeti viselkedés az elrendezés helyezkedéséből adódik, a nyomólap téglára való érkezését, a gömbcsukló habarcsolt felületre fordulását mutatja. Szükséges lett volna egy tehermentesítés kb. 100 kn nagyságú erőnél, és az újraterhelés görbéje lehetett volna a kiindulási pont. Így az összesítő diagramot is korrigálni kell. 52. ábra: Összesítő diagram a kapott laboratóriumi mérésekből 41
42 Ha a felkeményedett szakaszra egy átlagot számolok és ezt a görbét a grafikon origójába eltolom (az 53. ábrán zöld szaggatott vonal jelzi), azzal az elmaradt tehermentesítést kiküszöbölhetem. Így később a numerikus modell esetében az abban kapott eredményt sokkal pontosabban fogja tükrözni, hiszen abban nem lép fel ilyen probléma, mint a kísérletkor. Az összehasonlításhoz használt diagram tehát az alábbi, 53. ábrán látható. 53. ábra: Összesítő diagram a kapott laboratóriumi mérésekből és az átlag ábrázolása, betolása origóba Összességében elmondható, hogy a kapott kísérletek konzisztensebbnek mondhatók, mint az általam végzett kísérletsorozat, illetve már három próbatest esetén is nagyobb részletességű adatok állnak rendelkezésemre. Mindezek miatt a numerikus vizsgálatot a kapott kísérleti elrendezésben is végrehajtottam és azok eredményeivel hasonlítom össze. A tönkremenetel, ahogy a saját kísérletem során is, hangos pattogással jelentkezett. Itt is megfigyelhető volt, hogy kívülről függőleges repedések jelentek meg. A függőleges repedések a minta külső felén az 54. ábrán láthatók. Amint a külső felület nem bírta a rá terhelő erőt, a tégla teljesen tönkrement, nem bírt el nagyobb terhet. Amint megtörtént a tehermentesítés, azonnal szembetűnő volt, hogy amíg a próbatest látszólag kívülről ép volt (a függőleges repedésektől eltekintve), addig a belső szerkezet darabokra tört. A tönkremeneteli jelenség is egyezik a saját tapasztalataimmal. Az összetöredezett belső szerkezet az 55. ábrán látható. 42
43 54. ábra: A külső függőleges repedés az egyik falazóelemen 55. ábra: A belső szerkezet tönkremenetele 43
44 iv. A két laborkísérlet eredményeinek összehasonlítása Ha összevetem a kapott mérés nyers, korrigált és átlagolt eredményeit a saját laborkísérletben kapott erő-elmozdulás diagramokkal, akkor szembetűnő különbségek fedezhetők fel. Először is észrevehető, hogy a mások által végzett kísérlet görbéjének meredeksége kisebb, mint az általam mért adatok esetében. Ezt az eltérést okozhatja a kísérleti elrendezések közötti különbség, ugyanis a habarcsrétegben nagyobb a felső és az alsó sík befogása, kevésbé képes alakváltozásra, ami a téglatestek teherbírására és viselkedésére is kihatással van. Ugyancsak látványos, hogy nem alakult ki képlékenyedő szakasz, mely azt támasztja alá, hogy a pályázat keretében történt mérésnél a gömbcsukló jól működött, illetve a teher ráengedése is egyenletesebb módon történt. A maximális teherbírás értéke is jóval nagyobb, mint a saját mérésnél tapasztalt erők nagy részénél. Érdekes különbség azonban, hogy az általam elvégzett kísérletben azonnal kimutatható a teherbírás, míg a projekténél kezdetben nagy alakváltozások voltak megfigyelhetőek. Ez a jelenség szintén a kísérleti elrendezésnek köszönhető, hiszen a farostlemezek jóval kisebb merevsége a habarcshoz képest kevesebb elrendezésből származtatható helyezkedést okozott a csukló esetében, az hamarabb ráfordult a falazóelem felső síkjára. Az összehasonlító grafikon az 56. ábrán látható. 56. ábra: A két kísérletsorozat összehasonlítása 44
45 7. A pályázati kísérlethez készített numerikus modell a) A modell Az előbbi részletes kísérlethez hasonlóan a mostani esetben is egy fél téglát modelleztem, hiszen az eredeti falazóelem szimmetria adottságait kihasználtam. A modell felépítése a laborkísérletet mintázza: a próbatest alá és fölé egy-egy 1 cm vastag habarcsréteg került definiálásra. A felső rétegre egy acél elem került, melynek alsó része téglatest alakú, a felső pedig egy téglalap alakú gúla. Az elrendezés az 57. ábrán látható. Ez az acélelem azért került elhelyezésre, hogy a modell elmozdulásvezérelt lehessen. Így tehát a modellre függőlegesen lefelé (azaz -z irányba) összesen 2,5 mm elmozdulást helyeztem 25 lépésben, tehát lépésenként 0,1 mm került működtetésre. A modell megfelelő oldalán a szimmetria feltételek definiálva lettek, az alsó habarcs alsó síkjára pedig felületi, minden irányban (x, y, z) megtámasztott támasz került. A különböző anyagrétegek (két esetben habarcs-tégla és egy esetben habarcs-acél) közé kontaktelemek kerültek definiálásra. A végeselemháló a korábbiakhoz hasonlóan tetraéderekből épült fel, melyek 4 mm nagyságú oldalélekkel rendelkeznek. Azért volt szükség ebben az esetben a nagyobb elemmérettel elvégezni a számítást, mert így is minimum 24 órás futtatási idővel kellett számolni. Elmozdulást figyelő monitorpontokat is elhelyeztem, a laborkísérletnek megfelelően az acél elem sarkaiba, valamint az oldalak felezőpontjaiba is egyet-egyet. Az acél elem esetében a program által lineárisan rugalmas anyagokra definiálható SOLID Elastic nevű anyagmodellt használtam. A kezdeti rugalmassági modulus értékét megnöveltem 2E+8 MPa értékűre, hogy annak az alakváltozása ne befolyásolhassa tégla, illetve a habarcsrétegek tönkremenetelét, így modellezve minél jobban a valódi laboratóriumi kísérleteket. A beállítások az 58. ábrán tekinthetők meg. 45
46 Terhelés és reakcióerőmérés Monitorpontok Szimmetriabeállítások Kontaktelemek Alsó megtámasztás 57. ábra: A numerikus kísérlet kialakítása 58. ábra: Acél anyagmodell 46
47 A kerámia, illetve a habarcs anyagmodelljeként is a korábban használt 3D Nonlinear Cementitious 2 betonokra kifejlesztett, kerámiákra ajánlott modelljét használtam kiindulásul. Az anyagok kezdőértékeihez (rugalmassági modulus, nyomószilárdság, illetve Poissontényező) Fódi Anita PhD disszertációjában mért adatokat vettem fel, hiszen ahogyan korábban említettem, semmilyen adat nem áll rendelkezésre a habarccsal kapcsolatban. [8] Kerámiák esetében a gyártók nagyon hiányos műszaki adatlapot rendelnek a falazótermékeikhez. [4][5] Mindezek fényében egy kezdeti értékekkel ellátott modell után további anyagjellemzőkkel is elvégeztem a számításokat, melyből lehet következtetni egyes változtatások milyen befolyással vannak a numerikus eredményekre. A pontos összefüggéseket és az érzékenységvizsgálatot jelen dolgozat nem tartalmazza, jövőbeni kutatások témája lesz. i. A 1. számítás ismertetése és az eredményei Minden egyes számításnál a modell kialakítása, terhelése, hálózása, a monitorpontok helye és az acél terhelőelem változatlan kialakítású, utóbbinál az anyagmodell is ugyanaz. Mindegyik érték feljebb, a numerikus modell általános ismertétesénél olvasható. Az egyes változatoknál csak a tégla, illetve a habarcs anyagmodelljének nyomó- és húzószilárdságának, illetve rugalmassági modulusuk beállításait változtattam. A kerámiához és a habarcshoz használt anyagmodell mindkét esetben a korábbi fejezetekben említett és részletezett 3D Nonlinear Cementitious 2 anyagmodell, ez sem változik a különböző modellek tekintetében. A [8]-as forrás értékei nagyon nagy eltérést mutatnak egymáshoz képest, illetve különböző módszerekkel végzik a kerámiák vizsgálatát. Ezért kezdetben a tömör téglákra vonatkozó vizsgálatuk C típusának A5 nevű mérést vettem fel. A kerámiához használt anyagmodell beállításait az alábbi, 59. ábra mutatja: 59. ábra: Kerámia anyagmodell beállításai az első számítás esetében 47
48 A habarcs esetében kezdetben nem használtam fel a disszertáció értékeit, azt a kapott kísérlet vezetője által javasolt értékekkel láttam el. A habarcshoz alkalmazott paramétereket a 60. ábra szemlélteti: 60. ábra: Habarcs anyagmodell beállításai az első számításban A kapott elmozdulásokat három pontban ismertetem, két sarokpontban és a nem szimmetrikus oldal felezőpontjában. Az eredményeket a 61. ábrán mutatom be: 61. ábra: Az első futtatás eredményei Az első szembetűnő különbség a mért és számított grafikon között, hogy a numerikus modellnek a maximális teherbírási értéke jóval kisebb, mint a kísérleteknél, illetve a merevsége is csupán a töredéke. Ez az jelenti, hogy a falazóelem merevségét jóval meg kell emelni, hiszen ez biztosítja a teherbírás legnagyobb részét. Meglepő, hogy ennyivel növelni kell azt, hiszen ahogyan azt már korábban is kiemeltem, a gyártók által biztosított deklarált nyomószilárdsági 48
49 érték 11 MPa, jóval kevesebb, mint az általam most beállított 18,58. Nemcsak az anyagjellemzőkben lehet megfigyelni érdekességet, hanem a három monitorpontban mért érték is széttart. Ez a jelenség a tönkremenetelt mutatja be remekül, hiszen a tégla elem egyik oldala nagyobb alakváltozást szenved el, mint a másik, az acél elem pedig el tud csúszni rajta, így modellezve tökéletesen a laborkísérletben tapasztalt viselkedést. Ha a repedéséket is megvizsgáljuk, jól látszik, hogy hosszirányúak és éppen ott jelennek meg nagyon intenzíven, ahol azt a laborkísérletek esetében láthattuk. Felfedezhető, hogy a habarcsrétegekben is repedések jelentek meg, különösen a jobban összenyomódott sarok felett és alatt. Ez szintén megfigyelhető volt a kísérletek során, ahol a habarcs lepattogzását lehetett látni. Az elrendezés végső elmozdulásait és a repedések képeit az alábbi, 62. ábra szemlélteti: 62. ábra: Az 1. modell végső elmozdulásai, repedésképe Jól látszik, hogy a modell változtatása során mindenképp szükség van a kerámia anyagmodell változtatására, meg kell emelni mind a rugalmassági modulus, mind a szilárdsági értékeket. Kíváncsiságképpen a habarcs érétkeit pedig lecsökkentettem, egy másik, a PhD disszertációban mért értékkel futtattam a számítást. 49
50 ii. A 2. számítás ismertetése és az eredményei Tehát a kerámia anyagjellemzőit megemeltem a disszertációban a 2. módszer 3a próbatestből kapott, az alábbi, 63. ábrán jelzett értékekre: [8] 63. ábra: Kerámia anyagmodell beállításai a második számítás esetében A habarcs anyagmodell értékeit nagyon lecsökkentettem, megnéztem milyen változás következik be ekkor a kísérleti elrendezésben. Fódi Anitáék a hibrid habarcsra kimért rugalmassági modulusát és egy fiktív, általam felvett szilárdsági értéket használtam együttesen, ahogyan az a 64. ábrán látható. 64. ábra: Habarcs anyagmodell beállításai a második számításban A kapott erő-elmozdulás értékeket a 65. ábrán tekinthetjük meg. Jól látszik rajta, hogy nőtt a maximális teherbírás, sőt, az anyag tönkre sem ment a ráhelyezett elmozdulás következtében. Ez azt jelenti, hogy a feltételezett kerámia szilárdság túl magas volt, csökkenteni szükséges azt a továbbiakban. Szintén remekül megfigyelhető, hogy az előző számításhoz képest nem nőtt 50
51 számottevően a rendszer merevsége. Utóbbi jelenség azzal magyarázható, hogy amíg a tégla modelljében növeltem a rugalmasságot, a habarcs esetében csökkentettem. A számítás további lépéseiben mindkét értéket növelnem kellett, hogy közelebb kerüljek a valósághoz. Újra megfigyelhető a három mérés során keletkező különböző érték, melyek ismét az aszimmetrikus tönkremenetelt mutatják. A jelenség mindegyik ezt követő mérésben megfigyelhető volt. A későbbiekben csak az oldalközepén mért (átlag)elmozdulást fogom ábrázolni, hiszen ez is megfelelő információértékkel bír. 65. ábra: A második futtatás eredményei A számítás befejezése után látható, hogy a habarcsrétegek teljesen tönkrementek, repedezettek és a tégla síkjai belefúródtak abba. A tégla külső felén nem tapasztalható nagy tönkremenetel, a belső bordákon azonban már megjelentek a függőleges irányú repedések, ahogyan ezt a 66. ábra mutatja. 66. ábra: A 2. modell végső deformációja, repedésképe a belső oldalon 51
Függőleges és vízszintes vasalás hatása a téglafalazat nyírási ellenállására
 Függőleges és vízszintes vasalás hatása a téglafalazat nyírási ellenállására FÓDI ANITA Témavezető: Dr. Bódi István Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki kar Hidak és Szerkezetek
Függőleges és vízszintes vasalás hatása a téglafalazat nyírási ellenállására FÓDI ANITA Témavezető: Dr. Bódi István Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki kar Hidak és Szerkezetek
Ejtési teszt modellezése a tervezés fázisában
 Antal Dániel, doktorandusz, Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szabó Tamás, egyetemi docens, Ph.D., Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szilágyi Attila, egyetemi adjunktus,
Antal Dániel, doktorandusz, Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szabó Tamás, egyetemi docens, Ph.D., Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szilágyi Attila, egyetemi adjunktus,
Magasépítési öszvérfödémek numerikus szimuláció alapú méretezése
 BME Hidak és Szerkezetek Tanszéke Magasépítési öszvérfödémek numerikus szimuláció alapú méretezése Seres Noémi DEVSOG Témavezetı: Dr. Dunai László Bevezetés Az elıadás témája öszvérfödémek együttdolgoztató
BME Hidak és Szerkezetek Tanszéke Magasépítési öszvérfödémek numerikus szimuláció alapú méretezése Seres Noémi DEVSOG Témavezetı: Dr. Dunai László Bevezetés Az elıadás témája öszvérfödémek együttdolgoztató
TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI. 1. Bevezetés
 TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI Dr. Goda Tibor egyetemi docens Gép- és Terméktervezés Tanszék 1. Bevezetés 1.1. A végeselem módszer alapjai - diszkretizáció, - szerkezet felbontása kicsi szabályos elemekre
TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI Dr. Goda Tibor egyetemi docens Gép- és Terméktervezés Tanszék 1. Bevezetés 1.1. A végeselem módszer alapjai - diszkretizáció, - szerkezet felbontása kicsi szabályos elemekre
Fogorvosi anyagtan fizikai alapjai 6.
 Fogorvosi anyagtan fizikai alapjai 6. Mechanikai tulajdonságok 1. Kiemelt témák: Rugalmas alakváltozás Merevség és összefüggése a kötési energiával A geometriai tényezők szerepe egy test merevségében Tankönyv
Fogorvosi anyagtan fizikai alapjai 6. Mechanikai tulajdonságok 1. Kiemelt témák: Rugalmas alakváltozás Merevség és összefüggése a kötési energiával A geometriai tényezők szerepe egy test merevségében Tankönyv
FÉLMEREV KAPCSOLATOK NUMERIKUS SZIMULÁCIÓJA
 FÉLMEREV KAPCSOLATOK NUMERIKUS SZIMULÁCIÓJA Vértes Katalin * - Iványi Miklós ** RÖVID KIVONAT Acélszerkezeti kapcsolatok jellemzőinek (szilárdság, merevség, elfordulási képesség) meghatározása lehetséges
FÉLMEREV KAPCSOLATOK NUMERIKUS SZIMULÁCIÓJA Vértes Katalin * - Iványi Miklós ** RÖVID KIVONAT Acélszerkezeti kapcsolatok jellemzőinek (szilárdság, merevség, elfordulási képesség) meghatározása lehetséges
Kiöntött síncsatornás felépítmény kialakításának egyes elméleti kérdései
 Kiöntött síncsatornás felépítmény kialakításának egyes elméleti kérdései VII. Városi Villamos Vasúti Pálya Napra Budapest, 2014. április 17. Major Zoltán egyetemi tanársegéd Széchenyi István Egyetem, Győr
Kiöntött síncsatornás felépítmény kialakításának egyes elméleti kérdései VII. Városi Villamos Vasúti Pálya Napra Budapest, 2014. április 17. Major Zoltán egyetemi tanársegéd Széchenyi István Egyetem, Győr
A végeselem módszer alapjai. 2. Alapvető elemtípusok
 A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
A.2. Acélszerkezetek határállapotai
 A.. Acélszerkezetek határállapotai A... A teherbírási határállapotok első osztálya: a szilárdsági határállapotok A szilárdsági határállapotok (melyek között a fáradt és rideg törést e helyütt nem tárgyaljuk)
A.. Acélszerkezetek határállapotai A... A teherbírási határállapotok első osztálya: a szilárdsági határállapotok A szilárdsági határállapotok (melyek között a fáradt és rideg törést e helyütt nem tárgyaljuk)
2011.11.08. 7. előadás Falszerkezetek
 2011.11.08. 7. előadás Falszerkezetek Falazott szerkezetek: MSZ EN 1996 (Eurocode 6) 1-1. rész: Az épületekre vonatkozó általános szabályok. Falazott szerkezetek vasalással és vasalás nélkül 1-2. rész:
2011.11.08. 7. előadás Falszerkezetek Falazott szerkezetek: MSZ EN 1996 (Eurocode 6) 1-1. rész: Az épületekre vonatkozó általános szabályok. Falazott szerkezetek vasalással és vasalás nélkül 1-2. rész:
Korrodált acélszerkezetek vizsgálata
 Korrodált acélszerkezetek vizsgálata 1. Szerkezeti példák és laboratóriumi alapkutatás Oszvald Katalin Témavezető : Dr. Dunai László Budapest, 2009.12.08. 1 Általános célkitűzések Korrózió miatt károsodott
Korrodált acélszerkezetek vizsgálata 1. Szerkezeti példák és laboratóriumi alapkutatás Oszvald Katalin Témavezető : Dr. Dunai László Budapest, 2009.12.08. 1 Általános célkitűzések Korrózió miatt károsodott
A= a keresztmetszeti felület cm 2 ɣ = biztonsági tényező
 Statika méretezés Húzás nyomás: Amennyiben a keresztmetszetre húzó-, vagy nyomóerő hat, akkor normálfeszültség (húzó-, vagy nyomó feszültség) keletkezik. Jele: σ. A feszültség: = ɣ Fajlagos alakváltozás:
Statika méretezés Húzás nyomás: Amennyiben a keresztmetszetre húzó-, vagy nyomóerő hat, akkor normálfeszültség (húzó-, vagy nyomó feszültség) keletkezik. Jele: σ. A feszültség: = ɣ Fajlagos alakváltozás:
Anyagvizsgálatok. Mechanikai vizsgálatok
 Anyagvizsgálatok Mechanikai vizsgálatok Szakítóvizsgálat EN 10002-1:2002 Célja: az anyagok egytengelyű húzó igénybevétellel szembeni ellenállásának meghatározása egy szabványosan kialakított próbatestet
Anyagvizsgálatok Mechanikai vizsgálatok Szakítóvizsgálat EN 10002-1:2002 Célja: az anyagok egytengelyű húzó igénybevétellel szembeni ellenállásának meghatározása egy szabványosan kialakított próbatestet
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
A szerkezeti anyagok tulajdonságai és azok vizsgálata
 A szerkezeti anyagok tulajdonságai és azok vizsgálata 1 Az anyagok tulajdonságai fizikai tulajdonságok, mechanikai, termikus, elektromos, mágneses akusztikai, optikai 2 Minőség, élettartam A termék minősége
A szerkezeti anyagok tulajdonságai és azok vizsgálata 1 Az anyagok tulajdonságai fizikai tulajdonságok, mechanikai, termikus, elektromos, mágneses akusztikai, optikai 2 Minőség, élettartam A termék minősége
Kisciklusú fárasztóvizsgálatok eredményei és energetikai értékelése
 Kisciklusú fárasztóvizsgálatok eredményei és energetikai értékelése Tóth László, Rózsahegyi Péter Bay Zoltán Alkalmazott Kutatási Közalapítvány Logisztikai és Gyártástechnikai Intézet Bevezetés A mérnöki
Kisciklusú fárasztóvizsgálatok eredményei és energetikai értékelése Tóth László, Rózsahegyi Péter Bay Zoltán Alkalmazott Kutatási Közalapítvány Logisztikai és Gyártástechnikai Intézet Bevezetés A mérnöki
A töréssel szembeni ellenállás vizsgálata
 A töréssel szembeni ellenállás vizsgálata 1 Az anyag viselkedése terhelés hatására Az anyagok lehetnek: szívósak, képlékenyek és ridegek. 2 Szívós vagy képlékeny anyag Az anyag törését a csúsztatófeszültségek
A töréssel szembeni ellenállás vizsgálata 1 Az anyag viselkedése terhelés hatására Az anyagok lehetnek: szívósak, képlékenyek és ridegek. 2 Szívós vagy képlékeny anyag Az anyag törését a csúsztatófeszültségek
A szerkezeti anyagok tulajdonságai és azok vizsgálata
 A szerkezeti anyagok tulajdonságai és azok vizsgálata 1 Az anyagok tulajdonságai fizikai tulajdonságok, mechanikai, termikus, elektromos, mágneses akusztikai, optikai 2 Minıség, élettartam A termék minısége
A szerkezeti anyagok tulajdonságai és azok vizsgálata 1 Az anyagok tulajdonságai fizikai tulajdonságok, mechanikai, termikus, elektromos, mágneses akusztikai, optikai 2 Minıség, élettartam A termék minısége
Dr. Fenyvesi Olivér Dr. Görög Péter Megyeri Tamás. Budapest, 2015.
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM ÉPÍTŐMÉRNÖKI KAR ÉPÍTŐANYAGOK ÉS MAGASÉPÍTÉS TANSZÉK GEOTECHNIKA ÉS MÉRNÖKGEOLÓGIA TANSZÉK Készítette: Konzulensek: Csanády Dániel Dr. Lublóy Éva Dr. Fenyvesi
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM ÉPÍTŐMÉRNÖKI KAR ÉPÍTŐANYAGOK ÉS MAGASÉPÍTÉS TANSZÉK GEOTECHNIKA ÉS MÉRNÖKGEOLÓGIA TANSZÉK Készítette: Konzulensek: Csanády Dániel Dr. Lublóy Éva Dr. Fenyvesi
Cölöpcsoport elmozdulásai és méretezése
 18. számú mérnöki kézikönyv Frissítve: 2016. április Cölöpcsoport elmozdulásai és méretezése Program: Fájl: Cölöpcsoport Demo_manual_18.gsp A fejezet célja egy cölöpcsoport fejtömbjének elfordulásának,
18. számú mérnöki kézikönyv Frissítve: 2016. április Cölöpcsoport elmozdulásai és méretezése Program: Fájl: Cölöpcsoport Demo_manual_18.gsp A fejezet célja egy cölöpcsoport fejtömbjének elfordulásának,
Végeselemes analízisen alapuló méretezési elvek az Eurocode 3 alapján. Dr. Dunai László egyetemi tanár BME, Hidak és Szerkezetek Tanszéke
 Végeselemes analízisen alapuló méretezési elvek az Eurocode 3 alapján Dr. Dunai László egyetemi tanár BME, Hidak és Szerkezetek Tanszéke 1 Tartalom Méretezési alapelvek Numerikus modellezés Analízis és
Végeselemes analízisen alapuló méretezési elvek az Eurocode 3 alapján Dr. Dunai László egyetemi tanár BME, Hidak és Szerkezetek Tanszéke 1 Tartalom Méretezési alapelvek Numerikus modellezés Analízis és
MUNKAGÖDÖR TERVEZÉSE
 MUNKAGÖDÖR TERVEZÉSE Munkagödör tervezése Munkatérhatárolás szerkezetei Munkagödör méretezés Plaxis programmal Munkagödör méretezés Geo 5 programmal Tartalom Bevezetés VEM - geotechnikai alkalmazási területek
MUNKAGÖDÖR TERVEZÉSE Munkagödör tervezése Munkatérhatárolás szerkezetei Munkagödör méretezés Plaxis programmal Munkagödör méretezés Geo 5 programmal Tartalom Bevezetés VEM - geotechnikai alkalmazási területek
FOK Fogorvosi anyagtan fizikai alapjai tárgy kolokviumi kérdései 2012/13-es tanév I. félév
 FOK Fogorvosi anyagtan fizikai alapjai tárgy kolokviumi kérdései 2012/13-es tanév I. félév A kollokviumon egy-egy tételt kell húzni az 1-10. és a 11-20. kérdések közül. 1. Atomi kölcsönhatások, kötéstípusok.
FOK Fogorvosi anyagtan fizikai alapjai tárgy kolokviumi kérdései 2012/13-es tanév I. félév A kollokviumon egy-egy tételt kell húzni az 1-10. és a 11-20. kérdések közül. 1. Atomi kölcsönhatások, kötéstípusok.
XVII. econ Konferencia és ANSYS Felhasználói Találkozó
 XVII. econ Konferencia és ANSYS Felhasználói Találkozó Hazay Máté, Bakos Bernadett, Bojtár Imre hazay.mate@epito.bme.hu PhD hallgató Budapesti Műszaki és Gazdaságtudományi Egyetem Tartószerkezetek Mechanikája
XVII. econ Konferencia és ANSYS Felhasználói Találkozó Hazay Máté, Bakos Bernadett, Bojtár Imre hazay.mate@epito.bme.hu PhD hallgató Budapesti Műszaki és Gazdaságtudományi Egyetem Tartószerkezetek Mechanikája
Mikrocölöp alapozás ellenőrzése
 36. számú mérnöki kézikönyv Frissítve: 2017. június Mikrocölöp alapozás ellenőrzése Program: Fájl: Cölöpcsoport Demo_manual_en_36.gsp Ennek a mérnöki kézikönyvnek a célja, egy mikrocölöp alapozás ellenőrzésének
36. számú mérnöki kézikönyv Frissítve: 2017. június Mikrocölöp alapozás ellenőrzése Program: Fájl: Cölöpcsoport Demo_manual_en_36.gsp Ennek a mérnöki kézikönyvnek a célja, egy mikrocölöp alapozás ellenőrzésének
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 Vasalt falak: 4. Vasalt falazott szerkezetek méretezési mószerei Vasalt falak 1. Vasalás fekvőhézagban vagy falazott üregben horonyban, falazóelem lyukban. 1 2 1 Vasalt falak: Vasalás fekvőhézagban vagy
Vasalt falak: 4. Vasalt falazott szerkezetek méretezési mószerei Vasalt falak 1. Vasalás fekvőhézagban vagy falazott üregben horonyban, falazóelem lyukban. 1 2 1 Vasalt falak: Vasalás fekvőhézagban vagy
Ebben a mérnöki kézikönyvben azt mutatjuk be, hogyan számoljuk egy síkalap süllyedését és elfordulását.
 10. számú mérnöki kézikönyv Frissítve: 2016. Február Síkalap süllyedése Program: Fájl: Síkalap Demo_manual_10.gpa Ebben a mérnöki kézikönyvben azt mutatjuk be, hogyan számoljuk egy síkalap süllyedését
10. számú mérnöki kézikönyv Frissítve: 2016. Február Síkalap süllyedése Program: Fájl: Síkalap Demo_manual_10.gpa Ebben a mérnöki kézikönyvben azt mutatjuk be, hogyan számoljuk egy síkalap süllyedését
Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások
 Miskolci Egyetem Műszaki Anyagtudományi Kar Anyagtudományi Intézet Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások Dr.Krállics György krallics@eik.bme.hu
Miskolci Egyetem Műszaki Anyagtudományi Kar Anyagtudományi Intézet Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások Dr.Krállics György krallics@eik.bme.hu
CAD-CAM-CAE Példatár
 CAD-CAM-CAE Példatár A példa megnevezése: A példa száma: A példa szintje: CAx rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: VEM Rúdszerkezet sajátfrekvenciája ÓE-A05 alap közepes haladó
CAD-CAM-CAE Példatár A példa megnevezése: A példa száma: A példa szintje: CAx rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: VEM Rúdszerkezet sajátfrekvenciája ÓE-A05 alap közepes haladó
MŰANYAGOK TULAJDONSÁGAI
 MŰANYAGOK TULAJDONSÁGAI A műszaki adatlapok csapdái A műanyagok vizsgálatával számos szabvány foglalkozik. Ezek egy része csak az adott országon belül érvényes, de vannak nemzetközi érvényű előírások is.
MŰANYAGOK TULAJDONSÁGAI A műszaki adatlapok csapdái A műanyagok vizsgálatával számos szabvány foglalkozik. Ezek egy része csak az adott országon belül érvényes, de vannak nemzetközi érvényű előírások is.
Fa- és Acélszerkezetek I. 1. Előadás Bevezetés. Dr. Szalai József Főiskolai adjunktus
 Fa- és Acélszerkezetek I. 1. Előadás Bevezetés Dr. Szalai József Főiskolai adjunktus Okt. Hét 1. Téma Bevezetés acélszerkezetek méretezésébe, elhelyezés a tananyagban Acélszerkezetek használati területei
Fa- és Acélszerkezetek I. 1. Előadás Bevezetés Dr. Szalai József Főiskolai adjunktus Okt. Hét 1. Téma Bevezetés acélszerkezetek méretezésébe, elhelyezés a tananyagban Acélszerkezetek használati területei
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 1. Bevezetés Falazott szerkezetek Tartalom Megnevezések, fal típusok Anyagok Mechanikai jellemzők 1 Falazott szerkezetek alkalmazási területei: 20. század: alacsony és középmagas épületek kb. 100 évvel
1. Bevezetés Falazott szerkezetek Tartalom Megnevezések, fal típusok Anyagok Mechanikai jellemzők 1 Falazott szerkezetek alkalmazási területei: 20. század: alacsony és középmagas épületek kb. 100 évvel
Kiválósági ösztöndíjjal támogatott kutatások az Építőmérnöki Karon c. előadóülés
 Kiválósági ösztöndíjjal támogatott kutatások az Építőmérnöki Karon c. előadóülés Hazay Máté hazay.mate@epito.bme.hu PhD hallgató Budapesti Műszaki és Gazdaságtudományi Egyetem Tartószerkezetek Mechanikája
Kiválósági ösztöndíjjal támogatott kutatások az Építőmérnöki Karon c. előadóülés Hazay Máté hazay.mate@epito.bme.hu PhD hallgató Budapesti Műszaki és Gazdaságtudományi Egyetem Tartószerkezetek Mechanikája
A talajok összenyomódásának vizsgálata
 A talajok összenyomódásának vizsgálata Amit már tudni kellene Összenyomódás Konszolidáció Normálisan konszolidált talaj Túlkonszolidált talaj Túlkonszolidáltsági arányszám,ocr Konszolidáció az az időben
A talajok összenyomódásának vizsgálata Amit már tudni kellene Összenyomódás Konszolidáció Normálisan konszolidált talaj Túlkonszolidált talaj Túlkonszolidáltsági arányszám,ocr Konszolidáció az az időben
Pattex CF 850. Műszaki tájékoztató
 BETON / TÖMÖR KŐ HASZNÁLAT FELHASZNÁLÁSI ÚTMUTATÓ 1. ALKALMAZÁSI TERÜLETEK ALAP ANYAGA: beton, tömör kő Nehéz terhet hordozó elemek rögzítése tömör kőben, betonban, porózus betonban és könnyű betonban.
BETON / TÖMÖR KŐ HASZNÁLAT FELHASZNÁLÁSI ÚTMUTATÓ 1. ALKALMAZÁSI TERÜLETEK ALAP ANYAGA: beton, tömör kő Nehéz terhet hordozó elemek rögzítése tömör kőben, betonban, porózus betonban és könnyű betonban.
Egy érdekes mechanikai feladat
 1 Egy érdekes mechanikai feladat 1. ábra forrása: [ 1 ] A feladat Az 1. ábra szerinti rudazat A csomópontján átvezettek egy kötelet, melynek alsó végén egy m tömegű golyó lóg. A rudak egyező nyúlási merevsége
1 Egy érdekes mechanikai feladat 1. ábra forrása: [ 1 ] A feladat Az 1. ábra szerinti rudazat A csomópontján átvezettek egy kötelet, melynek alsó végén egy m tömegű golyó lóg. A rudak egyező nyúlási merevsége
Szilárd testek rugalmassága
 Fizika villamosmérnököknek Szilárd testek rugalmassága Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1 Deformálható testek (A merev test idealizált határeset.)
Fizika villamosmérnököknek Szilárd testek rugalmassága Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1 Deformálható testek (A merev test idealizált határeset.)
II. Gyakorlat: Hajlított vasbeton keresztmetszet ellenőrzése (Négyszög és T-alakú keresztmetszetek hajlítási teherbírása III. feszültségi állapotban)
 II. Gyakorlat: Hajlított vasbeton keresztmetszet ellenőrzése (Négyszög és T-alakú keresztmetszetek hajlítási teherbírása III. feszültségi állapotban) Készítették: Dr. Kiss Rita és Klinka Katalin -1- A
II. Gyakorlat: Hajlított vasbeton keresztmetszet ellenőrzése (Négyszög és T-alakú keresztmetszetek hajlítási teherbírása III. feszültségi állapotban) Készítették: Dr. Kiss Rita és Klinka Katalin -1- A
ÉPÍTŐANYAGOK REOLÓGIAI TULAJDONSÁGAINAK VIZSGÁLATA A DE-ATC-MFK MÉLY- ÉS SZERKEZETÉPÍTÉSI TANSZÉKÉN
 ÉPÍTŐANYAGOK REOLÓGIAI TULAJDONSÁGAINAK VIZSGÁLATA A DE-ATC-MK MÉLY- ÉS SZERKEZETÉPÍTÉSI TANSZÉKÉN Dr. Kovács Imre PhD. tanszékvezető főiskolai docens 1 Vizsgálataink szintjei Numerikus szimuláció lineáris,
ÉPÍTŐANYAGOK REOLÓGIAI TULAJDONSÁGAINAK VIZSGÁLATA A DE-ATC-MK MÉLY- ÉS SZERKEZETÉPÍTÉSI TANSZÉKÉN Dr. Kovács Imre PhD. tanszékvezető főiskolai docens 1 Vizsgálataink szintjei Numerikus szimuláció lineáris,
BME Szilárdságtani és Tartószerkezeti Tanszék. Tartószerkezet-rekonstrukciós Szakmérnöki Képzés. Dr. Móczár Balázs
 Dr. Móczár Balázs 1 Az előadás célja MSZ EN 1997 1 szabvány 6. fejezetében és egyes mellékleteiben leírt síkalapozással kapcsolatos előírások lényegesebb elemeinek, a szabvány elveinek bemutatása Az eddig
Dr. Móczár Balázs 1 Az előadás célja MSZ EN 1997 1 szabvány 6. fejezetében és egyes mellékleteiben leírt síkalapozással kapcsolatos előírások lényegesebb elemeinek, a szabvány elveinek bemutatása Az eddig
Vasalttalaj hídfők. Tóth Gergő. Gradex Mérnöki és Szolgáltató Kft Budapest, Bécsi út 120. Telefon: +36-1/
 Vasalttalaj hídfők Tóth Gergő Gradex Mérnöki és Szolgáltató Kft. 1034 Budapest, Bécsi út 120. Telefon: +36-1/436-0990 www.gradex.hu Az előadás 1. Hagyományos hídfő kialakítások régen és most 2. Első hazai
Vasalttalaj hídfők Tóth Gergő Gradex Mérnöki és Szolgáltató Kft. 1034 Budapest, Bécsi út 120. Telefon: +36-1/436-0990 www.gradex.hu Az előadás 1. Hagyományos hídfő kialakítások régen és most 2. Első hazai
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 1_5. Bevezetés Végeselem-módszer Végeselem-módszer 1. A geometriai tartomány (szerkezet) felosztása (véges)elemekre.. Lokális koordináta-rendszer felvétele, kapcsolat a lokális és globális koordinátarendszerek
1_5. Bevezetés Végeselem-módszer Végeselem-módszer 1. A geometriai tartomány (szerkezet) felosztása (véges)elemekre.. Lokális koordináta-rendszer felvétele, kapcsolat a lokális és globális koordinátarendszerek
Rugalmas állandók mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
A vizsgált anyag ellenállása az adott geometriájú szúrószerszám behatolásával szemben, Mérnöki alapismeretek és biztonságtechnika
 Dunaújvárosi Főiskola Anyagtudományi és Gépészeti Intézet Mérnöki alapismeretek és biztonságtechnika Mechanikai anyagvizsgálat 2. Dr. Palotás Béla palotasb@mail.duf.hu Készült: Dr. Krállics György (BME,
Dunaújvárosi Főiskola Anyagtudományi és Gépészeti Intézet Mérnöki alapismeretek és biztonságtechnika Mechanikai anyagvizsgálat 2. Dr. Palotás Béla palotasb@mail.duf.hu Készült: Dr. Krállics György (BME,
Hangfrekvenciás mechanikai rezgések vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
Földstatikai feladatok megoldási módszerei
 Földstatikai feladatok megoldási módszerei Földstatikai alapfeladatok Földnyomások számítása Általános állékonyság vizsgálata Alaptörés parciális terhelés alatt Süllyedésszámítások Komplex terhelési esetek
Földstatikai feladatok megoldási módszerei Földstatikai alapfeladatok Földnyomások számítása Általános állékonyság vizsgálata Alaptörés parciális terhelés alatt Süllyedésszámítások Komplex terhelési esetek
Fogorvosi anyagtan fizikai alapjai 8. Képlékeny viselkedés. Terhelési diagram. Mechanikai tulajdonságok 2. s sz (Pa) Tankönyv fejezetei: 16-17
 rugalmas B mn 1. A rá ható erő következtében megváltozott alakját a hatás megszűntével visszanyerő. Vmihez hozzáütődve róla visszapattanó. merev B mn 1. Nem rugalmas, nem hajlékony . Rugalmasságát,
rugalmas B mn 1. A rá ható erő következtében megváltozott alakját a hatás megszűntével visszanyerő. Vmihez hozzáütődve róla visszapattanó. merev B mn 1. Nem rugalmas, nem hajlékony . Rugalmasságát,
CONSTEEL 8 ÚJDONSÁGOK
 CONSTEEL 8 ÚJDONSÁGOK Verzió 8.0 2013.11.20 www.consteelsoftware.com Tartalomjegyzék 1. Szerkezet modellezés... 2 1.1 Új szelvénykatalógusok... 2 1.2 Diafragma elem... 2 1.3 Merev test... 2 1.4 Rúdelemek
CONSTEEL 8 ÚJDONSÁGOK Verzió 8.0 2013.11.20 www.consteelsoftware.com Tartalomjegyzék 1. Szerkezet modellezés... 2 1.1 Új szelvénykatalógusok... 2 1.2 Diafragma elem... 2 1.3 Merev test... 2 1.4 Rúdelemek
Fogorvosi anyagtan fizikai alapjai 7. Képlékeny viselkedés. Terhelési diagram. Mechanikai tulajdonságok 2. s sz (Pa) Tankönyv fejezetei: 16-17
 rugalmas B mn 1. A rá ható erő következtében megváltozott alakját a hatás megszűntével visszanyerő. Vmihez hozzáütődve róla visszapattanó. merev B mn 1. Nem rugalmas, nem hajlékony . Rugalmasságát,
rugalmas B mn 1. A rá ható erő következtében megváltozott alakját a hatás megszűntével visszanyerő. Vmihez hozzáütődve róla visszapattanó. merev B mn 1. Nem rugalmas, nem hajlékony . Rugalmasságát,
Fogorvosi anyagtan fizikai alapjai 7.
 Fogorvosi anyagtan fizikai alapjai 7. Mechanikai tulajdonságok 2. Kiemelt témák: Szilárdság, rugalmasság, képlékenység és szívósság összefüggései A képlékeny alakváltozás mechanizmusa kristályokban és
Fogorvosi anyagtan fizikai alapjai 7. Mechanikai tulajdonságok 2. Kiemelt témák: Szilárdság, rugalmasság, képlékenység és szívósság összefüggései A képlékeny alakváltozás mechanizmusa kristályokban és
Fogorvosi anyagtan fizikai alapjai 7. Képlékeny viselkedés. Terhelési diagram. Mechanikai tulajdonságok 2. s sz (Pa) Tankönyv fejezetei: 16-17
 rugalmas B mn 1. A rá ható erő következtében megváltozott alakját a hatás megszűntével visszanyerő. Vmihez hozzáütődve róla visszapattanó. merev B mn 1. Nem rugalmas, nem hajlékony . Rugalmasságát,
rugalmas B mn 1. A rá ható erő következtében megváltozott alakját a hatás megszűntével visszanyerő. Vmihez hozzáütődve róla visszapattanó. merev B mn 1. Nem rugalmas, nem hajlékony . Rugalmasságát,
Polimerek vizsgálatai
 SZÉCHENYI ISTVÁN EGYETEM ANYAGTUDOMÁNYI ÉS TECHNOLÓGIAI TANSZÉK Polimerek vizsgálatai DR Hargitai Hajnalka Rövid idejű mechanikai vizsgálat Szakítóvizsgálat Cél: elsősorban a gyártási körülmények megfelelőségének
SZÉCHENYI ISTVÁN EGYETEM ANYAGTUDOMÁNYI ÉS TECHNOLÓGIAI TANSZÉK Polimerek vizsgálatai DR Hargitai Hajnalka Rövid idejű mechanikai vizsgálat Szakítóvizsgálat Cél: elsősorban a gyártási körülmények megfelelőségének
ACÉLÍVES (TH) ÜREGBIZTOSÍTÁS
 Miskolci Egyetem Bányászati és Geotechnikai Intézet Bányászati és Geotechnikai Intézeti Tanszék ACÉLÍVES (TH) ÜREGBIZTOSÍTÁS Oktatási segédlet Szerző: Dr. Somosvári Zsolt DSc professzor emeritus Szerkesztette:
Miskolci Egyetem Bányászati és Geotechnikai Intézet Bányászati és Geotechnikai Intézeti Tanszék ACÉLÍVES (TH) ÜREGBIZTOSÍTÁS Oktatási segédlet Szerző: Dr. Somosvári Zsolt DSc professzor emeritus Szerkesztette:
ahol m-schmid vagy geometriai tényező. A terhelőerő növekedésével a csúszó síkban fellép az un. kritikus csúsztató feszültség τ
 Egykristály és polikristály képlékeny alakváltozása A Frenkel féle modell, hibátlan anyagot feltételezve, nagyon nagy folyáshatárt eredményez. A rácshibák, különösen a diszlokációk jelenléte miatt a tényleges
Egykristály és polikristály képlékeny alakváltozása A Frenkel féle modell, hibátlan anyagot feltételezve, nagyon nagy folyáshatárt eredményez. A rácshibák, különösen a diszlokációk jelenléte miatt a tényleges
Toronymerevítık mechanikai szempontból
 Andó Mátyás: Toronymerevítık méretezése, 9 Gépész Tuning Kft. Toronymerevítık mechanikai szempontból Mint a neve is mutatja a toronymerevítık használatának célja az, hogy merevebbé tegye az autó karosszériáját
Andó Mátyás: Toronymerevítık méretezése, 9 Gépész Tuning Kft. Toronymerevítık mechanikai szempontból Mint a neve is mutatja a toronymerevítık használatának célja az, hogy merevebbé tegye az autó karosszériáját
Cölöpalapozások - bemutató
 12. számú mérnöki kézikönyv Frissítve: 2016. április Cölöpalapozások - bemutató Ennek a mérnöki kézikönyvnek célja, hogy bemutassa a GEO 5 cölöpalapozás számításra használható programjainak gyakorlati
12. számú mérnöki kézikönyv Frissítve: 2016. április Cölöpalapozások - bemutató Ennek a mérnöki kézikönyvnek célja, hogy bemutassa a GEO 5 cölöpalapozás számításra használható programjainak gyakorlati
5. Az acélszerkezetek méretezésének különleges kérdései: rideg törés, fáradás. BME Szilárdságtani és Tartószerkezeti Tanszék
 MAGASÉPÍTÉSI ACÉLSZERKEZETEK 5. Az acélszerkezetek méretezésének különleges kérdései: rideg törés, fáradás. FERNEZELYI SÁNDOR EGYETEMI TANÁR Az acél szakító diagrammja Lineáris szakasz Arányossági határnak
MAGASÉPÍTÉSI ACÉLSZERKEZETEK 5. Az acélszerkezetek méretezésének különleges kérdései: rideg törés, fáradás. FERNEZELYI SÁNDOR EGYETEMI TANÁR Az acél szakító diagrammja Lineáris szakasz Arányossági határnak
Síklapokból álló üvegoszlopok laboratóriumi. vizsgálata. Jakab András, doktorandusz. BME, Építőanyagok és Magasépítés Tanszék
 Síklapokból álló üvegoszlopok laboratóriumi vizsgálata Előadó: Jakab András, doktorandusz BME, Építőanyagok és Magasépítés Tanszék Nehme Kinga, Nehme Salem Georges Szilikátipari Tudományos Egyesület Üvegipari
Síklapokból álló üvegoszlopok laboratóriumi vizsgálata Előadó: Jakab András, doktorandusz BME, Építőanyagok és Magasépítés Tanszék Nehme Kinga, Nehme Salem Georges Szilikátipari Tudományos Egyesület Üvegipari
TERMÉKSZIMULÁCIÓ I. 9. elıadás
 TERMÉKSZIMULÁCIÓ I. 9. elıadás Dr. Kovács Zsolt egyetemi tanár Végeselem típusok Elemtípusok a COSMOSWorks Designer-ben: Lineáris térfogatelem (tetraéder) Kvadratikus térfogatelem (tetraéder) Lineáris
TERMÉKSZIMULÁCIÓ I. 9. elıadás Dr. Kovács Zsolt egyetemi tanár Végeselem típusok Elemtípusok a COSMOSWorks Designer-ben: Lineáris térfogatelem (tetraéder) Kvadratikus térfogatelem (tetraéder) Lineáris
Acél tartószerkezetek
 Acél tartószerkezetek laborvizsgálatok összefoglalója 217 szept 28 Az Acél tartószerkezetek tárg keretében laborvizsgálatokat végeztünk melek során a hallgatók tapasztalatokat szerezhettek az acélszerkezetek
Acél tartószerkezetek laborvizsgálatok összefoglalója 217 szept 28 Az Acél tartószerkezetek tárg keretében laborvizsgálatokat végeztünk melek során a hallgatók tapasztalatokat szerezhettek az acélszerkezetek
Akusztikus aktivitás AE vizsgálatoknál
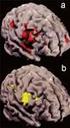 Akusztikus aktivitás AE vizsgálatoknál Kindlein Melinda, Fodor Olivér ÁEF Anyagvizsgáló Laboratórium Kft. 1112. Bp. Budaörsi út 45. Az akusztikus emissziós vizsgálat a roncsolásmentes vizsgálati módszerek
Akusztikus aktivitás AE vizsgálatoknál Kindlein Melinda, Fodor Olivér ÁEF Anyagvizsgáló Laboratórium Kft. 1112. Bp. Budaörsi út 45. Az akusztikus emissziós vizsgálat a roncsolásmentes vizsgálati módszerek
I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE
 I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE Komplex termékek gyártására jellemző, hogy egy-egy termékbe akár több ezer alkatrész is beépül. Ilyenkor az alkatrészek általában sok különböző beszállítótól érkeznek,
I. BESZÁLLÍTÓI TELJESÍTMÉNYEK ÉRTÉKELÉSE Komplex termékek gyártására jellemző, hogy egy-egy termékbe akár több ezer alkatrész is beépül. Ilyenkor az alkatrészek általában sok különböző beszállítótól érkeznek,
Hangfrekvenciás mechanikai rezgések vizsgálata
 Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Hangfrekvenciás mechanikai rezgések vizsgálata (Mérési jegyzőkönyv) Hagymási Imre 2007. május 7. (hétfő délelőtti csoport) 1. Bevezetés Ebben a mérésben a szilárdtestek rugalmas tulajdonságait vizsgáljuk
Ebben a fejezetben egy szögtámfal tervezését, és annak teljes számítását mutatjuk be.
 2. számú mérnöki kézikönyv Frissítve: 2016. Február Szögtámfal tervezése Program: Szögtámfal File: Demo_manual_02.guz Feladat: Ebben a fejezetben egy szögtámfal tervezését, és annak teljes számítását mutatjuk
2. számú mérnöki kézikönyv Frissítve: 2016. Február Szögtámfal tervezése Program: Szögtámfal File: Demo_manual_02.guz Feladat: Ebben a fejezetben egy szögtámfal tervezését, és annak teljes számítását mutatjuk
IGAZI, GEORÁCCSAL ERŐSÍTETT HÍDFŐ ELSŐ MAGYARORSZÁGI ALKALMAZÁSA. Tóth Gergő
 IGAZI, GEORÁCCSAL ERŐSÍTETT HÍDFŐ ELSŐ MAGYARORSZÁGI ALKALMAZÁSA Tóth Gergő Gradex Mérnöki és Szolgáltató Kft. 1034 Budapest, Bécsi út 120. Telefon: +36-1/436-0990 www.gradex.hu Pálossy, Scharle, Szalatkay:Tervezési
IGAZI, GEORÁCCSAL ERŐSÍTETT HÍDFŐ ELSŐ MAGYARORSZÁGI ALKALMAZÁSA Tóth Gergő Gradex Mérnöki és Szolgáltató Kft. 1034 Budapest, Bécsi út 120. Telefon: +36-1/436-0990 www.gradex.hu Pálossy, Scharle, Szalatkay:Tervezési
Hidak Darupályatartók Tornyok, kémények (szélhatás) Tengeri építmények (hullámzás)
 Dr. Németh György Szerkezetépítés II. 1 A fáradt törés ismétlődő terhek hatására a statikus törőszilárdság feszültségszintje alatt feszültségcsúcsoknál lokális képlékeny alakváltozásból indul ki általában
Dr. Németh György Szerkezetépítés II. 1 A fáradt törés ismétlődő terhek hatására a statikus törőszilárdság feszültségszintje alatt feszültségcsúcsoknál lokális képlékeny alakváltozásból indul ki általában
Tartószerkezetek I. (Vasbeton szilárdságtan)
 Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.10.11. Vasbeton külpontos nyomása Az eső ágú σ-ε diagram miatt elvileg minden egyes esethez külön kell meghatározni a szélső szál összenyomódását.
Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.10.11. Vasbeton külpontos nyomása Az eső ágú σ-ε diagram miatt elvileg minden egyes esethez külön kell meghatározni a szélső szál összenyomódását.
Akusztikai tervezés a geometriai akusztika módszereivel
 Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Polimerek vizsgálatai 1.
 SZÉCHENYI ISTVÁN EGYETEM ANYAGISMERETI ÉS JÁRMŰGYÁRTÁSI TANSZÉK POLIMERTECHNIKA NGB_AJ050_1 Polimerek vizsgálatai 1. DR Hargitai Hajnalka Szakítóvizsgálat Rövid idejű mechanikai vizsgálat Cél: elsősorban
SZÉCHENYI ISTVÁN EGYETEM ANYAGISMERETI ÉS JÁRMŰGYÁRTÁSI TANSZÉK POLIMERTECHNIKA NGB_AJ050_1 Polimerek vizsgálatai 1. DR Hargitai Hajnalka Szakítóvizsgálat Rövid idejű mechanikai vizsgálat Cél: elsősorban
PhD DISSZERTÁCIÓ TÉZISEI
 Budapesti Muszaki és Gazdaságtudományi Egyetem Fizikai Kémia Tanszék MTA-BME Lágy Anyagok Laboratóriuma PhD DISSZERTÁCIÓ TÉZISEI Mágneses tér hatása kompozit gélek és elasztomerek rugalmasságára Készítette:
Budapesti Muszaki és Gazdaságtudományi Egyetem Fizikai Kémia Tanszék MTA-BME Lágy Anyagok Laboratóriuma PhD DISSZERTÁCIÓ TÉZISEI Mágneses tér hatása kompozit gélek és elasztomerek rugalmasságára Készítette:
Segédlet: Kihajlás. Készítette: Dr. Kossa Attila BME, Műszaki Mechanikai Tanszék május 15.
 Segédlet: Kihajlás Készítette: Dr. Kossa ttila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2012. május 15. Jelen segédlet célja tömören összefoglalni a hosszú nyomott rudak kihajlásra történő ellenőrzését.
Segédlet: Kihajlás Készítette: Dr. Kossa ttila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2012. május 15. Jelen segédlet célja tömören összefoglalni a hosszú nyomott rudak kihajlásra történő ellenőrzését.
Járműelemek. Rugók. 1 / 27 Fólia
 Rugók 1 / 27 Fólia 1. Rugók funkciója A rugók a gépeknek és szerkezeteknek olyan különleges elemei, amelyek nagy (ill. korlátozott) alakváltozás létrehozására alkalmasak. Az alakváltozás, szemben más szerkezeti
Rugók 1 / 27 Fólia 1. Rugók funkciója A rugók a gépeknek és szerkezeteknek olyan különleges elemei, amelyek nagy (ill. korlátozott) alakváltozás létrehozására alkalmasak. Az alakváltozás, szemben más szerkezeti
5. Az acélszerkezetek méretezésének különleges kérdései: rideg törés, fáradás.
 MAGASÉPÍTÉSI ACÉLSZERKEZETEK 5. Az acélszerkezetek méretezésének különleges kérdései: rideg törés, fáradás. KÉSZÜLT FERNEZELYI SÁNDOR EGYETEMI TANÁR ELŐADÁSI JEGYZETEI ÉS AZ INTERNETEN ELÉRHETŐ MÁS ANYAGOK
MAGASÉPÍTÉSI ACÉLSZERKEZETEK 5. Az acélszerkezetek méretezésének különleges kérdései: rideg törés, fáradás. KÉSZÜLT FERNEZELYI SÁNDOR EGYETEMI TANÁR ELŐADÁSI JEGYZETEI ÉS AZ INTERNETEN ELÉRHETŐ MÁS ANYAGOK
Polimerek fizikai, mechanikai, termikus tulajdonságai
 SZÉCHENYI ISTVÁN EGYETEM ANYAGISMERETI ÉS JÁRMŰGYÁRTÁSI TANSZÉK POLIMERTECHNIKA NGB_AJ050_1 Polimerek fizikai, mechanikai, termikus tulajdonságai DR Hargitai Hajnalka 2011.10.05. BURGERS FÉLE NÉGYPARAMÉTERES
SZÉCHENYI ISTVÁN EGYETEM ANYAGISMERETI ÉS JÁRMŰGYÁRTÁSI TANSZÉK POLIMERTECHNIKA NGB_AJ050_1 Polimerek fizikai, mechanikai, termikus tulajdonságai DR Hargitai Hajnalka 2011.10.05. BURGERS FÉLE NÉGYPARAMÉTERES
HÍDKONFERENCIA 2019 GERENDA VÁLASZTÁS FA-BETON ÖSZVÉRTARTÓKHOZ
 HÍDKONFERENCIA 2019 GERENDA VÁLASZTÁS FA-BETON ÖSZVÉRTARTÓKHOZ Kedvcsináló 2018. évi előadás summája a nyugattól való 20-30 éves a lemaradás után, a felzárkózás szükségszerűsége; az előnyök és hátrányok
HÍDKONFERENCIA 2019 GERENDA VÁLASZTÁS FA-BETON ÖSZVÉRTARTÓKHOZ Kedvcsináló 2018. évi előadás summája a nyugattól való 20-30 éves a lemaradás után, a felzárkózás szükségszerűsége; az előnyök és hátrányok
SÍKALAPOK TERVEZÉSE. BME Szilárdságtani és Tartószerkezeti Tanszék. Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 SÍKALAPOK TERVEZÉSE SÍKALAPOK TERVEZÉSE síkalap mélyalap mélyített síkalap Síkalap, ha: - megfelelő teherbírású és vastagságú talajréteg van a felszín közelében; - a térszín közeli talajréteg teherbírása
SÍKALAPOK TERVEZÉSE SÍKALAPOK TERVEZÉSE síkalap mélyalap mélyített síkalap Síkalap, ha: - megfelelő teherbírású és vastagságú talajréteg van a felszín közelében; - a térszín közeli talajréteg teherbírása
SZIMULÁCIÓ ÉS MODELLEZÉS AZ ANSYS ALKALMAZÁSÁVAL
 SZIMULÁCIÓ ÉS MODELLEZÉS AZ ANSYS ALKALMAZÁSÁVAL MAGYAR TUDOMÁNY NAPJA KONFERENCIA 2010 GÁBOR DÉNES FŐISKOLA CSUKA ANTAL TARTALOM A KÍSÉRLET ÉS MÉRÉS JELENTŐSÉGE A MÉRNÖKI GYAKORLATBAN, MECHANIKAI FESZÜLTSÉG
SZIMULÁCIÓ ÉS MODELLEZÉS AZ ANSYS ALKALMAZÁSÁVAL MAGYAR TUDOMÁNY NAPJA KONFERENCIA 2010 GÁBOR DÉNES FŐISKOLA CSUKA ANTAL TARTALOM A KÍSÉRLET ÉS MÉRÉS JELENTŐSÉGE A MÉRNÖKI GYAKORLATBAN, MECHANIKAI FESZÜLTSÉG
LINDAB Floor könnyűszerkezetes födém-rendszer Tervezési útmutató teherbírási táblázatok
 LINDAB Floor könnyűszerkezetes födém-rendszer Tervezési útmutató teherbírási táblázatok Budapest, 2004. 1 Tartalom 1. BEVEZETÉS... 4 1.1. A tervezési útmutató tárgya... 4 1.2. Az alkalmazott szabványok...
LINDAB Floor könnyűszerkezetes födém-rendszer Tervezési útmutató teherbírási táblázatok Budapest, 2004. 1 Tartalom 1. BEVEZETÉS... 4 1.1. A tervezési útmutató tárgya... 4 1.2. Az alkalmazott szabványok...
41. ábra A NaCl rács elemi cellája
 41. ábra A NaCl rács elemi cellája Mindkét rácsra jellemző, hogy egy tetszés szerint kiválasztott pozitív vagy negatív töltésű iont ellentétes töltésű ionok vesznek körül. Különbség a közvetlen szomszédok
41. ábra A NaCl rács elemi cellája Mindkét rácsra jellemző, hogy egy tetszés szerint kiválasztott pozitív vagy negatív töltésű iont ellentétes töltésű ionok vesznek körül. Különbség a közvetlen szomszédok
Anyagvizsgálati módszerek
 Anyagvizsgáló és Állapotellenőrző Laboratórium Atomerőművi anyagvizsgálatok Az akusztikus emisszió vizsgálata a műszaki diagnosztikában Anyagvizsgálati módszerek Roncsolásos metallográfia, kémia, szakító,
Anyagvizsgáló és Állapotellenőrző Laboratórium Atomerőművi anyagvizsgálatok Az akusztikus emisszió vizsgálata a műszaki diagnosztikában Anyagvizsgálati módszerek Roncsolásos metallográfia, kémia, szakító,
Anyagismeret I. A töréssel szembeni ellenállás vizsgálata. Összeállította: Csizmazia Ferencné dr.
 Anyagismeret I. A töréssel szembeni ellenállás vizsgálata Összeállította: Csizmazia Ferencné dr. Az anyag viselkedése terhelés hatására Az anyagok lehetnek: szívósak, képlékenyek és ridegek. Szívós vagy
Anyagismeret I. A töréssel szembeni ellenállás vizsgálata Összeállította: Csizmazia Ferencné dr. Az anyag viselkedése terhelés hatására Az anyagok lehetnek: szívósak, képlékenyek és ridegek. Szívós vagy
tervezési szempontok (igénybevétel, feszültségeloszlás,
 Elhasználódási és korróziós folyamatok Bagi István BME MTAT Biofunkcionalitás Az élő emberi szervezettel való kölcsönhatás biokompatibilitás (gyulladás, csontfelszívódás, metallózis) aktív biológiai környezet
Elhasználódási és korróziós folyamatok Bagi István BME MTAT Biofunkcionalitás Az élő emberi szervezettel való kölcsönhatás biokompatibilitás (gyulladás, csontfelszívódás, metallózis) aktív biológiai környezet
Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János
 Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János VASBETON SZERKEZETEK TERVEZÉSE 2 Szabvány A tartószerkezetek tervezése jelenleg Magyarországon és az EU államaiban az Euronorm szabványsorozat alapján
Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János VASBETON SZERKEZETEK TERVEZÉSE 2 Szabvány A tartószerkezetek tervezése jelenleg Magyarországon és az EU államaiban az Euronorm szabványsorozat alapján
ÜVEG FIZIKAI TULAJDONSÁGAI,
 ÜVEG FIZIKAI TULAJDONSÁGAI, ÜVEGTERMÉKEK Erdélyi Tamás egyetemi tanársegéd BME Építészmérnöki é kar Szilárdságtani és Tartószerkezeti Tanszék 2013. február 28. Tematika alkal om 1. 2. 3. 4. 5. nap 02.28.
ÜVEG FIZIKAI TULAJDONSÁGAI, ÜVEGTERMÉKEK Erdélyi Tamás egyetemi tanársegéd BME Építészmérnöki é kar Szilárdságtani és Tartószerkezeti Tanszék 2013. február 28. Tematika alkal om 1. 2. 3. 4. 5. nap 02.28.
időpont? ütemterv számonkérés segédanyagok
 időpont? ütemterv számonkérés segédanyagok 1. Bevezetés Végeselem-módszer Számítógépek alkalmazása a szerkezettervezésben: 1. a geometria megadása, tervkészítés, 2. műszaki számítások: - analitikus számítások
időpont? ütemterv számonkérés segédanyagok 1. Bevezetés Végeselem-módszer Számítógépek alkalmazása a szerkezettervezésben: 1. a geometria megadása, tervkészítés, 2. műszaki számítások: - analitikus számítások
FÉMGYURUS FAKAPCSOLATOK PALÁSTNYOMÁSI TEHERBÍRÁSÁNAK VIZSGÁLATA PONTOSÍTOTT FELÜLETI NYOMÁSELOSZLÁS ALAPJÁN
 FÉMGYURUS FAKAPCSOLATOK PALÁSTNYOMÁSI TEHERBÍRÁSÁNAK VIZSGÁLATA PONTOSÍTOTT FELÜLETI NYOMÁSELOSZLÁS ALAPJÁN Erdodi László * - Bódi István ** RÖVID KIVONAT A BME Hidak és Szerkezetek Tanszéke Szerkezetvizsgáló
FÉMGYURUS FAKAPCSOLATOK PALÁSTNYOMÁSI TEHERBÍRÁSÁNAK VIZSGÁLATA PONTOSÍTOTT FELÜLETI NYOMÁSELOSZLÁS ALAPJÁN Erdodi László * - Bódi István ** RÖVID KIVONAT A BME Hidak és Szerkezetek Tanszéke Szerkezetvizsgáló
Navier-formula. Frissítve: Egyenes hajlítás
 Navier-formula Akkor beszélünk egyenes hajlításról, ha a nyomatékvektor egybeesik valamelyik fő-másodrendű nyomatéki tengellyel. A hajlítást mindig súlyponti koordinátarendszerben értelmezzük. Ez még a
Navier-formula Akkor beszélünk egyenes hajlításról, ha a nyomatékvektor egybeesik valamelyik fő-másodrendű nyomatéki tengellyel. A hajlítást mindig súlyponti koordinátarendszerben értelmezzük. Ez még a
Csővezetékekben lévő korróziós hibák veszélyességének értékelési rendszere
 1 Csővezetékekben lévő korróziós hibák veszélyességének értékelési rendszere Lenkeyné Biró Gyöngyv ngyvér, Balogh Zsolt, Tóth LászlL szló A kutatómunka célja 2 a végeselemes módszer alkalmazhatóságának
1 Csővezetékekben lévő korróziós hibák veszélyességének értékelési rendszere Lenkeyné Biró Gyöngyv ngyvér, Balogh Zsolt, Tóth LászlL szló A kutatómunka célja 2 a végeselemes módszer alkalmazhatóságának
Hajlított elemek kifordulása. Stabilitásvesztési módok
 Hajlított elemek kifordulása Stabilitásvesztési módok Stabilitásvesztés (3.3.fejezet) Globális: Nyomott rudak kihajlása Hajlított tartók kifordulása Lemezhorpadás (lokális stabilitásvesztés): Nyomott és/vagy
Hajlított elemek kifordulása Stabilitásvesztési módok Stabilitásvesztés (3.3.fejezet) Globális: Nyomott rudak kihajlása Hajlított tartók kifordulása Lemezhorpadás (lokális stabilitásvesztés): Nyomott és/vagy
Rugalmasan ágyazott gerenda. Szép János
 Rugalmasan ágyazott gerenda vizsgálata AXIS VM programmal Szép János 2013.10.14. LEMEZALAP TERVEZÉS 1. Bevezetés 2. Lemezalap tervezés 3. AXIS Program ismertetés 4. Példa LEMEZALAPOZÁS Alkalmazás módjai
Rugalmasan ágyazott gerenda vizsgálata AXIS VM programmal Szép János 2013.10.14. LEMEZALAP TERVEZÉS 1. Bevezetés 2. Lemezalap tervezés 3. AXIS Program ismertetés 4. Példa LEMEZALAPOZÁS Alkalmazás módjai
Rugalmas állandók mérése
 Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
A töréssel szembeni ellenállás vizsgálata
 A töréssel szembeni ellenállás vizsgálata 1 Az anyag viselkedése terhelés hatására Az anyagok lehetnek: szívósak, képlékenyek és ridegek. 2 Szívós vagy képlékeny anyag Az anyag törését a csúsztatófeszültségek
A töréssel szembeni ellenállás vizsgálata 1 Az anyag viselkedése terhelés hatására Az anyagok lehetnek: szívósak, képlékenyek és ridegek. 2 Szívós vagy képlékeny anyag Az anyag törését a csúsztatófeszültségek
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
Cölöp függőleges teherbírásának és süllyedésének CPT alapú számítása
 15. számú mérnöki kézikönyv Frissítve: 2017. március Cölöp függőleges teherbírásának és süllyedésének CPT alapú számítása Program: Cölöp CPT Fájl: Demo_manual_15.gpn Ennek a mérnöki kézikönyvnek célja,
15. számú mérnöki kézikönyv Frissítve: 2017. március Cölöp függőleges teherbírásának és süllyedésének CPT alapú számítása Program: Cölöp CPT Fájl: Demo_manual_15.gpn Ennek a mérnöki kézikönyvnek célja,
Modern Fizika Labor. 5. ESR (Elektronspin rezonancia) Fizika BSc. A mérés dátuma: okt. 25. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 25. A mérés száma és címe: 5. ESR (Elektronspin rezonancia) Értékelés: A beadás dátuma: 2011. nov. 16. A mérést végezte: Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. okt. 25. A mérés száma és címe: 5. ESR (Elektronspin rezonancia) Értékelés: A beadás dátuma: 2011. nov. 16. A mérést végezte: Szőke Kálmán Benjamin
Korszerű technológiák: zsugorodás-kompenzált és magasraktári ipari padlók
 Budapesti Műszaki és Gazdaságtudományi Egyetem Korszerű technológiák: zsugorodás-kompenzált és magasraktári ipari padlók Dr. Zsigovics István adjunktus, Építőanyagok és Mérnökgeológia Tanszék, BME Epo-Trend,
Budapesti Műszaki és Gazdaságtudományi Egyetem Korszerű technológiák: zsugorodás-kompenzált és magasraktári ipari padlók Dr. Zsigovics István adjunktus, Építőanyagok és Mérnökgeológia Tanszék, BME Epo-Trend,
CAD-CAM-CAE Példatár
 CAD-CAM-CAE Példatár A példa megnevezése: A példa száma: A példa szintje: CAx rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: VEM befogott tartó ÓE-A15 alap közepes haladó CATIA V5 CAD,
CAD-CAM-CAE Példatár A példa megnevezése: A példa száma: A példa szintje: CAx rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: VEM befogott tartó ÓE-A15 alap közepes haladó CATIA V5 CAD,
Alagútfalazat véges elemes vizsgálata
 Magyar Alagútépítő Egyesület BME Geotechnikai Tanszéke Alagútfalazat véges elemes vizsgálata Czap Zoltán mestertanár BME Geotechnikai Tanszék Programok alagutak méretezéséhez 1 UDEC 2D program, diszkrét
Magyar Alagútépítő Egyesület BME Geotechnikai Tanszéke Alagútfalazat véges elemes vizsgálata Czap Zoltán mestertanár BME Geotechnikai Tanszék Programok alagutak méretezéséhez 1 UDEC 2D program, diszkrét
EGYIRÁNYBAN ER SÍTETT KOMPOZIT RUDAK HAJLÍTÓ KARAKTERISZTIKÁJÁNAK ÉS TÖNKREMENETELI FOLYAMATÁNAK ELEMZÉSE
 Budapest M szaki és Gazdaságtudományi Egyetem Polimertecnika Tanszék EGYIRÁNYBAN ER SÍTETT KOMPOZIT RUDAK HAJLÍTÓ KARAKTERISZTIKÁJÁNAK ÉS TÖNKREMENETELI OLYAMATÁNAK ELEMZÉSE Tézisek Rácz Zsolt Témavezet
Budapest M szaki és Gazdaságtudományi Egyetem Polimertecnika Tanszék EGYIRÁNYBAN ER SÍTETT KOMPOZIT RUDAK HAJLÍTÓ KARAKTERISZTIKÁJÁNAK ÉS TÖNKREMENETELI OLYAMATÁNAK ELEMZÉSE Tézisek Rácz Zsolt Témavezet
Mérnöki faszerkezetek korszerű statikai méretezése
 Mérnöki faszerkezetek korszerű statikai méretezése okl. faip. mérnök - szerkezettervező Előadásvázlat Bevezetés, a statikai tervezés alapjai, eszközei Az EuroCode szabványok rendszere Bemutató számítás
Mérnöki faszerkezetek korszerű statikai méretezése okl. faip. mérnök - szerkezettervező Előadásvázlat Bevezetés, a statikai tervezés alapjai, eszközei Az EuroCode szabványok rendszere Bemutató számítás
