Segédlet az Informatika alapjai I. című tárgy számrendszerek fejezetéhez
|
|
|
- Csilla Barnané
- 9 évvel ezelőtt
- Látták:
Átírás
1 Segédlet az Informatika alapjai I. című tárgy számrendszerek fejezetéhez Sándor Tamás, Takács Gergely, Lektorálta: dr. Schuster György PhD, Jelen segédlet az Informatika alapjai I. tárgyhoz a Számrendszerek tématerület minél jobb megértéséhez kíván segítséget nyújtani. Számrendszerek témakörön belül az alábbi témákkal kívánunk foglalkozni: - előjel nélküli számábrázolás a 2-es, 8-as, 10-es és 16 számrendszerekben, - előjeles (kettes komplemens) számábrázolás a 2-es, 8-as, 10-es és 16 számrendszerekben, - aritmetikai műveletek a 2-es, 8-as, 10-es és 16 számrendszerekben. Előjel nélküli számábrázolás a 2-es, 8-as, 10-es és 16 számrendszerekben A következő táblázat a tanult számrendszereket, illetve azok felépítését ábrázolja: Rövidítés Számrendszer neve Szr.: Számrendszer felépítése BIN Bináris OKT Oktális DEC Decimális HEX Hexadecimális Példák a számrendszerek közötti átváltásra Mintapélda: váltsuk át adott a b számot 8-as 10-es és 16-os számrendszerbe! Legkézenfekvőbb megoldás (de nem a leggyorsabb), ha a bináris számot átváltjuk tízes számrendszerbe, majd onnan nyolcasba, illetve tizenhatosba Szám bin Szám dec 1*128 0*64 1*32 0*16 1*8 1*4 0*2 0*1 Az alsó sor értékeit összeadva: = 172 decimális értéket kapjuk. Számoljunk tovább a decimális eredménnyel, és váltsuk át nyolcas számrendszerbe:
2 Szám okt Szám dec 0*512 2*64 5*8 4*1 Első lépésként szorítsuk határok közé a számunkat: 8 0 = 1, 8 1 = 8, 8 2 = 64, 8 3 = 512 Azt láthatjuk, hogy a 172 a 64 és az 512 közé esik, tehát a számunk biztos, hogy háromjegyű szám lesz. Most bontsuk fel a 172 őt nyolc hatványaira a 64-től kezdve: 64*2+ 8*5+ 1*4=172 Rakjuk össze a nyolcas számrendszer béli számunkat: 254o! A hexadecimális számrendszerbe való átváltás ugyanígy történik: 16 0 = 1, 16 1 = 16, 16 2 = = 16*10 +1*12 = 16*Ah+1*Ch A számunk tehát ACh. A számrendszerek között közvetlenül is lehet átváltani a számokat (a tízes beiktatása nélkül). Sőt, mint látni fogjuk néha ez a megoldás gyorsabb és egyszerűbb, mint az előző. Tudjuk, hogy a nyolc és a tizenhat kettő hatványai, ebből kiindulva pedig összefüggést találhatunk ezen számrendszerek között. 2 0 = 1, 8 0 = 1, 16 0 = = 8, 8 1 = = 16, 16 1 = = 64, 8 2 = = 256, 16 2 = 256 A továbblépéshez tekintsük az alábbi táblázatot: m *2 n*4 2 3 * * * *2 4 8*16 4*16 2* d A*16 C*1 172d 8*16 0 2* Tekintsük a 16 0 oszlopot, és vegyük észre, hogy egy négyjegyű bináris szám 0-15 ig tejed decimális számrendszerben, azaz pontosan egy egyjegyű hexadecimális számnak felel meg. Ha a példát (5.-6. sor) nézzük 8d+4d = 12d = Ch, most már biztosak lehetünk abban, hogy a hexadecimális alak utolsó számjegye Ch! Vegyük a következő oszlopot (16 1 ): a második számjegy a tizenhatos számrendszerben n*16-ot jelöl, ahol 0 < n <15. A lényeg a 3. és a 4. sor, ha ezek közül összevonjuk az
3 egyiket (4), akkor a következőt kapjuk: ( ) * 16. A példában (5.-6. sor) ez így néz ki: (8+2)*16 azaz 10*16 hexadecimálisan A0h. Adjuk össze a két kapott számot, és máris megkapjuk az ACh t, azaz a végeredményt. Összefoglalva: egy bináris szám minden négy számjegye egy hexadecimális számjegyet kódol. Ha nyolcas és a kettes számrendszer között végzünk átváltásokat, akkor csak annyiban kell eltérnünk a fent vázolt módszertől, hogy a három számjegyenként képezünk a bináris számból egy oktális számjegyet. Lássunk néhány példát ehhez! (44441d) A D (59379d) E 7 F (43962d) A B B A Elég nehéz lett volna átváltani a bináris alakot decimálisba, majd 43962d őt újra átváltani hexadecimálisba, a módszerrel viszont néhány másodperc alatt elvégezhető a kívánt művelet.
4 Feladatok: 1 Váltsa át az alábbi bináris számokat a 10-es, 8-as és a 16-os számrendszerbe! a) b b) b c) b d) b 2 Váltsa át az alábbi oktális számokat a 2-es, 10-es és 16-os számrendszerbe! e) 10 o f) 125 o g) 144 o h) 33 o 3 Váltsa át az alábbi decimális számokat a 2-es, 8-as és 16-os számrendszerbe! i) 100 d j) 125 d k) 9 d l) 127 d 4 Váltsa át az alábbi hexadecimális számokat a 2-es, 8-as és 10-es számrendszerbe! m) E h n) 99 h o) FA h p) FF h 5 Váltsa át az alábbi számokat a 2-es, 8-as és 16-os számrendszerbe (tízesbe ne)! q) FED h r) b s) o t) 100 h u) o v) ABC h w) b
5 A fenti példák megoldásai: Bin Okt Dec Hex A FF B C1 C D E2 E F G H B I J D K L F M E N O FA P FF Q FED R ABBA S E5 T U FFF V ABC W AABF
6 Előjeles (kettes komplemens) számábrázolás a 2-es, 8-as, 10-es és 16 számrendszerekben Az előjeles számokat leggyakrabban előjeles (kettes komplemens) számábrázolásban használják a számítógépek. A példákban 8 biten ábrázolt előjeles számokon mutatjuk be a képzés szabályait. 8 biten előjeles számábrázolásban a értékeket adhatunk meg. Példa: Írjuk fel a decimális -118 binárisan kettes komplemens ábrázolásban! A kettes komplemes képzés szabálya: 1. Vegyük a szám abszolút értékét: -118d =118d. 2. Írjuk binárisan előjel nélküli formában: b. 3. Vegyük a szám egyes komplemensét (minden bit helyi értéken negáljuk az értéket (változtassuk ellenkezőjére az adott értéket: 1->0, 0->1)) b 4. Az eredményhez adjunk hozzá egyet: b b Az eredmény hexadecimálisan megadható: 8 Ah. A szabály alkalmazásával a következő táblázat egyes értékeit könnyen bizonyíthatjuk: Decimális érték Bináris érték Hexadecimális Oktális érték érték FE FF F 177
7 Aritmetikai műveletek a 2-es, 8-as, 10-es és 16 számrendszerekben A bemutatásra kerülő különféle számrendszerekben az aritmetikai műveletek ugyanúgy elvégezhetők, természetesen az eredményképzéskor figyelembe kell venni az adott számrendszer egyes helyi értékein ábrázolható mennyiségeket. Aritmetikai műveletek esetén két fontos fogalmat előzetesen rögzíteni kell. A két fogalom az átvitel és a túlcsordulás. Az átvitel (carry) akkor keletkezik, amikor előjel nélküli számábrázolás esetén a műveletvégzés után az eredmény az adott számtartományban nem ábrázolható, az ábrázoláshoz számtartomány határait túl kell lépni. A túllépést az átvitel tárolóban jelezzük. A túlcsordulás (overflow) akkor keletkezik, amikor előjeles számábrázolás esetén a műveletvégzés után az eredmény az adott számtartományban nem ábrázolható, az ábrázoláshoz számtartomány határait túl kell lépni. A túllépést a túlcsordulás tárolóban jelezzük. Aritmetikai műveletek előjel nélküli számábrázolásban Mintapéldák összeadásra: 1. feladat: Végezze el a kijelölt műveletet a következő bináris számokkal: b b! b 55 d b 30 d b 85 d A megoldás lépésein látható, hogy az összeadás módszere semmiben sem különbözik az általános iskolában tanultaktól. Természetesen átvitel akkor van, ha az adott helyi értéken az eredmény nem fér el az ábrázolási tartományban. Lássuk részletesen az oszlopokat jobbról balra haladva: 1+0 = 1, átvitel = 10, átvitel = 11 átvitel = 10 átvitel = 11 átvitel = 10 átvitel = 1 átvitel = 0 átvitel 0 Ellenőrzés: váltsuk át tízes számrendszerbe és végezzük el az összeadást!
8 Az egyszerűség kedvéért a következő példa is ezekkel a számokkal dolgozik! 2. feladat: Végezze el a kijelölt műveletet a következő oktális számokkal: 67o + 36o! 67 o +36 o 125 o részletesen: 7+6 = 15o (13d) átvitel = 12o (10d) átvitel 1 1 = 1o (1d) átvitel 1 3. feladat : Végezze el a kijelölt műveletet a következő hexadecimális számokkal: 37h + 1Eh! 37h +1Eh 55h részletesen: 7+E = 15h (21d) átvitel = 5h (10d) átvitel 0 Mintapéldák kivonásra: A módszer ugyanaz lesz, amit a tízes számrendszernél megszokhattunk: 4 feladat: Végezze el a kijelölt műveletet b b bináris számokkal! b 55 d b 30 d b 15 d Mint látható a kivonás módszere sem különbözik a tízes számrendszerben tanultaktól. Az átvitel szabályai megegyeznek az összeadásnál ismertetekkel. Lássuk részletesen az oszlopokat jobbról balra haladva: 1-0 = 1, átvitel = 0, átvitel = 0 átvitel = 1 átvitel 1 (a kivonás valójában így néz ki: 10-1=1, és az átvitel ezért keletkezik) = 1 átvitel 1 1-1= 0 átvitel = 0, átvitel = 0, átvitel 0 Az egyszerűség kedvéért a következő példa is ezekkel a számokkal dolgozik!
9 5. feladat: Végezze el a kijelölt műveletet a következő oktális számokkal 67o - 36o! 67 o - 36 o 31 o részletesen: 7-6 = 1o átvitel = 3o átvitel 0 6. feladat : Végezze el a kijelölt műveletet a következő hexadecimális számokkal 37h - 1Eh! 37h -1Eh 19h részletesen: 7-E = 9h átvitel 1 (a kivonás valójában így néz ki: 17h-Eh=9h, és az átvitel ezért keletkezik) = 1h átvitel 0. Mintapéldák szorzásra: Az osztást és a szorzást csak bináris számokkal tárgyaljuk! Látható lesz, hogy a kettes számrendszerben elvégzett szorzás a legegyszerűbb műveletek egyike, hiszen vagy egyel vagy nullával kell szoroznunk. 7. feladat: Végezze el a kijelölt műveletet b * b bináris számokkal! A műveletvégzésnél a számok elején található vezető nullákat elhagytuk, hiszen a műveletvégzést nem befolyásolják, csak a részművelet végrehajtási számot növelik * d *10 d d Miután elvégeztük a szorzást, a részeredményeket összeadjuk, figyelve a nullaértékű tagok helyi érték eltolására. Mindenki tudja, hogy milyen egyszerű tízes számrendszerben egy számot tízzel, vagy annak valamelyik hatványával megszorozni. Ezeknél a szorzásoknál csak a hatvány értéknek megfelelő számú nullát kell a szám után írni ahhoz, hogy megkapjuk a végeredményt. Ha folytatjuk a gondolatmenetet, észrevehetjük, hogy ebben az esetben a szorzást a tízestől eltérő számrendszerben nem a tízzel, mint értékkel való szorzást értjük, hanem egy olyan számmal való szorzást, amelynek az alakja, az adott számrendszerben egy, nulla (1 0).
10 Osztás: Az előzőekből az következik, hogy az 1 0 számrendszerenként más értéket jelöl. Nézzük erre egy példát: *10 55* Ha néggyel szorzunk meg egy számot (1 0 0 b), akkor két nullát kell odaírnunk a végére, de fogalmazhatunk úgy is, hogy a számot kettővel eltoljuk balra. Attól függően, hogy a kettőnek hányadik hatványával szorzunk, annyival kell a számot balra eltolnunk. Mi történik akkor, ha kettő negatív hatványával szorozzuk (ezt tulajdonképpen azt jelenti, hogy kettő pozitív hatványával osztunk) a számot? Ez esetben nem kell mást tenni, mint jobbra eltolni a számot, ami a következő műveletet ismertetésekor bemutatásra is kerül. A jobbra történő eltolás a kettes számrendszerben a kettő negatív hatványával való szorzás, de ha jobban belegondolunk, ez nem jelent mást, mint osztás egy ( 1 0 ) alakú számmal. Osztásnál alapvetően két esetet különböztetünk meg, a maradék nélküli és a maradékos osztást, lássunk most mindkettőre példát: 8. feladat: Végezze el a kijelölt műveletet b : b! ell: b : b = b maradék: 0 54 d : 2d = 27d 9. feladat: Végezze el a kijelölt műveletet b * b! b : b = b maradék 11b (3d) ell: 55 d : 4 d = 52d (maradék 3d)
11 Aritmetikai műveletek előjeles számábrázolásban Mintapéldák összeadásra: 1. feladat: Végezze el a kijelölt műveletet a következő bináris számokkal: b b! b -73 d b +30 d b -43 d A megoldás lépésein látható, hogy az összeadás módszere semmiben sem különbözik az előjel nélküli számábrázolásban tanultaktól. Az előjeles számábrázolásban az adott helyi értéken keletkező többletet NEM átvitelnek, hanem túlcsordulásnak (overflow) hívjuk. Lássuk részletesen az oszlopokat jobbról balra haladva: 1+0 = 1, túlcsordulás = 10, túlcsordulás = 11 túlcsordulás = 10 túlcsordulás = 11 túlcsordulás = 10 túlcsordulás = 1 túlcsordulás = 0 túlcsordulás 0 Ellenőrzés: váltsuk át tízes számrendszerbe és végezzük el az összeadást! Az egyszerűség kedvéért a következő példa is ezekkel a számokkal dolgozik! Mintapéldák kivonásra: A módszer ugyanaz lesz, amit a tízes számrendszernél megszokhattunk: 2. feladat: Végezze el a kijelölt műveletet b b bináris számokkal! b -73 d b +30 d b -103 d Mint látható a kivonás módszere sem különbözik a tízes számrendszerben tanultaktól. A túlcsordulás szabályai megegyeznek az összeadásnál ismertetekkel. Lássuk részletesen az oszlopokat jobbról balra haladva: 1-0 = 1, túlcsordulás = 0, túlcsordulás 0
12 1-1 = 0 túlcsordulás = 1 túlcsordulás 1 (a kivonás valójában így néz ki: 10-1=1, és a túlcsordulás ezért keletkezik) = 1 túlcsordulás 1 1-1= 0 túlcsordulás = 0, túlcsordulás = 1, túlcsordulás 0 Az egyszerűség kedvéért a következő példa is ezekkel a számokkal dolgozik! Mintapéldák szorzásra: Az osztást és a szorzást csak bináris számokkal tárgyaljuk! Látható lesz, hogy a kettes számrendszerben elvégzett szorzás a legegyszerűbb műveletek egyike, hiszen vagy egyel vagy nullával kell szoroznunk. 3. feladat: Végezze el a kijelölt műveletet b * b bináris számokkal! A műveletvégzésnél a számok elején található vezető nullákat elhagytuk, hiszen a műveletvégzést nem befolyásolják, csak a részművelet végrehajtási számot növelik * d *10 d d Osztás: Miután elvégeztük a szorzást, a részeredményeket összeadjuk, figyelve a nullaértékű tagok helyi érték eltolására. Az előjel nélküli számábrázolásnál elmondottak ugyan úgy igazak a kettő hatványaival történő szorzásra is előjeles esetben is. Az előzőekből az következik, hogy az 1 0 számrendszerenként más értéket jelöl. Nézzük erre egy példát: *10-73* A jobbra történő eltolás a kettes számrendszerben a kettő negatív hatványával való szorzás, de ha jobban belegondolunk, ez nem jelent mást, mint osztás egy ( 1 0 ) alakú számmal. Osztásnál alapvetően két esetet különböztetünk meg, a maradék nélküli és a maradékos osztást, lássunk most mindkettőre példát:
13 4. feladat: Végezze el a kijelölt műveletet b : b! ell: b : b = b maradék: 0 54 d : 2d = 27d 5. feladat: Végezze el a kijelölt műveletet b * b! b : b = b maradék 11b (3d) ell: 55 d : 4 d = 52d (maradék 3d)
14 Példák összeadásra Adja össze a következő bináris számokat: Adja össze a következő oktális számokat: Adja össze a következő hexadecimális számokat: Megoldások: 11 ABCD B 13 15B2 + C4F DDD 15 1A2B3C + 68F = = = = = = = = = = ABCD = BCDE B = 11B 13 15B2 + C4F = DDD = A2B3C + 68F = 1A31CB
15 Példák kivonásra Határozza meg a következő bináris számok különbségét: Határozza meg a következő oktális számok különbségét: Határozza meg a következő hexadecimális számok különbségét: 11 ABC FFDD - AAAA 13 4E5D EE Megoldások: = = = = = = = = = = ABC = FFDD - AAAA = E5D = 4D19 14 EE9-94 = E = FF
16 Példák szorzásra: Végezze el a kijelölt szorzásokat: Végezze el a kijelölt osztásokat: * * * * * : : : : : 1 Megoldások: * 10 = * = * 101 = * 110 = * 11 = : 100 = : 10 = : 101 = : 111 = 1100 maradék : 1 =
Harmadik gyakorlat. Számrendszerek
 Harmadik gyakorlat Számrendszerek Ismétlés Tízes (decimális) számrendszer: 2 372 =3 2 +7 +2 alakiérték valódi érték = aé hé helyiérték helyiértékek a tízes szám hatványai, a számjegyek így,,2,,8,9 Kettes
Harmadik gyakorlat Számrendszerek Ismétlés Tízes (decimális) számrendszer: 2 372 =3 2 +7 +2 alakiérték valódi érték = aé hé helyiérték helyiértékek a tízes szám hatványai, a számjegyek így,,2,,8,9 Kettes
SZÁMRENDSZEREK KÉSZÍTETTE: JURÁNYINÉ BESENYEI GABRIELLA
 SZÁMRENDSZEREK KÉSZÍTETTE: JURÁNYINÉ BESENYEI GABRIELLA BINÁRIS (kettes) ÉS HEXADECIMÁLIS (tizenhatos) SZÁMRENDSZEREK (HELYIÉRTÉK, ÁTVÁLTÁSOK, MŰVELETEK) A KETTES SZÁMRENDSZER A computerek világában a
SZÁMRENDSZEREK KÉSZÍTETTE: JURÁNYINÉ BESENYEI GABRIELLA BINÁRIS (kettes) ÉS HEXADECIMÁLIS (tizenhatos) SZÁMRENDSZEREK (HELYIÉRTÉK, ÁTVÁLTÁSOK, MŰVELETEK) A KETTES SZÁMRENDSZER A computerek világában a
ÁTVÁLTÁSOK SZÁMRENDSZEREK KÖZÖTT, SZÁMÁBRÁZOLÁS, BOOLE-ALGEBRA
 1. Tízes (decimális) számrendszerből: a. Kettes (bináris) számrendszerbe: Vegyük a 2634 10 -es számot, és váltsuk át bináris (kettes) számrendszerbe! A legegyszerűbb módszer: írjuk fel a számot, és húzzunk
1. Tízes (decimális) számrendszerből: a. Kettes (bináris) számrendszerbe: Vegyük a 2634 10 -es számot, és váltsuk át bináris (kettes) számrendszerbe! A legegyszerűbb módszer: írjuk fel a számot, és húzzunk
Assembly programozás: 2. gyakorlat
 Assembly programozás: 2. gyakorlat Számrendszerek: Kettes (bináris) számrendszer: {0, 1} Nyolcas (oktális) számrendszer: {0,..., 7} Tízes (decimális) számrendszer: {0, 1, 2,..., 9} 16-os (hexadecimális
Assembly programozás: 2. gyakorlat Számrendszerek: Kettes (bináris) számrendszer: {0, 1} Nyolcas (oktális) számrendszer: {0,..., 7} Tízes (decimális) számrendszer: {0, 1, 2,..., 9} 16-os (hexadecimális
Bevezetés az informatikába gyakorló feladatok Utoljára módosítva:
 Tartalom 1. Számrendszerek közti átváltás... 2 1.1. Megoldások... 4 2. Műveletek (+, -, bitműveletek)... 7 2.1. Megoldások... 8 3. Számítógépes adatábrázolás... 12 3.1. Megoldások... 14 A gyakorlósor lektorálatlan,
Tartalom 1. Számrendszerek közti átváltás... 2 1.1. Megoldások... 4 2. Műveletek (+, -, bitműveletek)... 7 2.1. Megoldások... 8 3. Számítógépes adatábrázolás... 12 3.1. Megoldások... 14 A gyakorlósor lektorálatlan,
Bevezetés az informatikába gyakorló feladatok Utoljára módosítva:
 Tartalom 1. Számrendszerek közti átváltás... 2 1.1. Megoldások... 4 2. Műveletek (+, -, bitműveletek)... 7 2.1. Megoldások... 8 3. Számítógépes adatábrázolás... 10 3.1. Megoldások... 12 A gyakorlósor lektorálatlan,
Tartalom 1. Számrendszerek közti átváltás... 2 1.1. Megoldások... 4 2. Műveletek (+, -, bitműveletek)... 7 2.1. Megoldások... 8 3. Számítógépes adatábrázolás... 10 3.1. Megoldások... 12 A gyakorlósor lektorálatlan,
Kedves Diákok! A feladatok legtöbbször egy pontot érnek. Ahol ettől eltérés van, azt külön jelöljük.
 Kedves Diákok! Szeretettel köszöntünk Benneteket abból az alkalomból, hogy a Ceglédi Közgazdasági és Informatikai Szakközépiskola informatika tehetséggondozásának első levelét olvassátok! A tehetséggondozással
Kedves Diákok! Szeretettel köszöntünk Benneteket abból az alkalomból, hogy a Ceglédi Közgazdasági és Informatikai Szakközépiskola informatika tehetséggondozásának első levelét olvassátok! A tehetséggondozással
4. Fejezet : Az egész számok (integer) ábrázolása
 4. Fejezet : Az egész számok (integer) ábrázolása The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson
4. Fejezet : Az egész számok (integer) ábrázolása The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson
SZÁMÉRTÉKEK (ÁT)KÓDOLÁSA
 1 ELSŐ GYAKORLAT SZÁMÉRTÉKEK (ÁT)KÓDOLÁSA A feladat elvégzése során a következőket fogjuk gyakorolni: Számrendszerek közti átváltás előjelesen és előjel nélkül. Bináris, decimális, hexadexcimális számrendszer.
1 ELSŐ GYAKORLAT SZÁMÉRTÉKEK (ÁT)KÓDOLÁSA A feladat elvégzése során a következőket fogjuk gyakorolni: Számrendszerek közti átváltás előjelesen és előjel nélkül. Bináris, decimális, hexadexcimális számrendszer.
Aritmetikai utasítások I.
 Aritmetikai utasítások I. Az értékadó és aritmetikai utasítások során a címzési módok különböző típusaira látunk példákat. A 8086/8088-as mikroprocesszor memóriája és regiszterei a little endian tárolást
Aritmetikai utasítások I. Az értékadó és aritmetikai utasítások során a címzési módok különböző típusaira látunk példákat. A 8086/8088-as mikroprocesszor memóriája és regiszterei a little endian tárolást
Dr. Oniga István DIGITÁLIS TECHNIKA 2
 Dr. Oniga István DIGITÁLIS TECHNIKA 2 Számrendszerek A leggyakrabban használt számrendszerek: alapszám számjegyek Tízes (decimális) B = 10 0, 1, 8, 9 Kettes (bináris) B = 2 0, 1 Nyolcas (oktális) B = 8
Dr. Oniga István DIGITÁLIS TECHNIKA 2 Számrendszerek A leggyakrabban használt számrendszerek: alapszám számjegyek Tízes (decimális) B = 10 0, 1, 8, 9 Kettes (bináris) B = 2 0, 1 Nyolcas (oktális) B = 8
Fixpontos és lebegőpontos DSP Számrendszerek
 Fixpontos és lebegőpontos DSP Számrendszerek Ha megnézünk egy DSP kinálatot, akkor észrevehetjük, hogy két nagy család van az ajánlatban, az ismert adattipus függvényében. Van fixpontos és lebegőpontos
Fixpontos és lebegőpontos DSP Számrendszerek Ha megnézünk egy DSP kinálatot, akkor észrevehetjük, hogy két nagy család van az ajánlatban, az ismert adattipus függvényében. Van fixpontos és lebegőpontos
Programozás II. Segédlet az első dolgozathoz
 Programozás II. Segédlet az első dolgozathoz 1 Tartalomjegyzék 1. Bevezető 4 2. Számrendszerek közötti átváltások 5 2.1 Tízes számrendszerből tetszőleges számrendszerbe................. 5 2.1.1 Példa.....................................
Programozás II. Segédlet az első dolgozathoz 1 Tartalomjegyzék 1. Bevezető 4 2. Számrendszerek közötti átváltások 5 2.1 Tízes számrendszerből tetszőleges számrendszerbe................. 5 2.1.1 Példa.....................................
2. Fejezet : Számrendszerek
 2. Fejezet : Számrendszerek The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson Wong, Bentley College
2. Fejezet : Számrendszerek The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson Wong, Bentley College
3. gyakorlat. Kettes számrendszer: {0, 1} Tízes számrendszer: {0, 1, 2,..., 9} 16-os (hexadecimális számrendszer): {0, 1, 2,..., 9, A, B, C, D, E, F}
 3. gyakorlat Számrendszerek: Kettes számrendszer: {0, 1} Tízes számrendszer: {0, 1, 2,..., 9} 16-os (hexadecimális számrendszer): {0, 1, 2,..., 9, A, B, C, D, E, F} Alaki érték: 0, 1, 2,..., 9,... Helyi
3. gyakorlat Számrendszerek: Kettes számrendszer: {0, 1} Tízes számrendszer: {0, 1, 2,..., 9} 16-os (hexadecimális számrendszer): {0, 1, 2,..., 9, A, B, C, D, E, F} Alaki érték: 0, 1, 2,..., 9,... Helyi
The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003
 . Fejezet : Számrendszerek The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach. kiadás, Irv Englander John Wiley and Sons Wilson Wong, Bentley College Linda Senne,
. Fejezet : Számrendszerek The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach. kiadás, Irv Englander John Wiley and Sons Wilson Wong, Bentley College Linda Senne,
LEBEGŐPONTOS SZÁMÁBRÁZOLÁS
 LEBEGŐPONTOS SZÁMÁBRÁZOLÁS A fixpontos operandusoknak azt a hátrányát, hogy az ábrázolás adott hossza miatt csak korlátozott nagyságú és csak egész számok ábrázolhatók, a lebegőpontos számábrázolás küszöböli
LEBEGŐPONTOS SZÁMÁBRÁZOLÁS A fixpontos operandusoknak azt a hátrányát, hogy az ábrázolás adott hossza miatt csak korlátozott nagyságú és csak egész számok ábrázolhatók, a lebegőpontos számábrázolás küszöböli
Informatikai Rendszerek Alapjai
 Informatikai Rendszerek Alapjai Egész és törtszámok bináris ábrázolása http://uni-obuda.hu/users/kutor/ IRA 5/1 A mintavételezett (egész) számok bináris ábrázolása 2 n-1 2 0 1 1 0 1 0 n Most Significant
Informatikai Rendszerek Alapjai Egész és törtszámok bináris ábrázolása http://uni-obuda.hu/users/kutor/ IRA 5/1 A mintavételezett (egész) számok bináris ábrázolása 2 n-1 2 0 1 1 0 1 0 n Most Significant
(jegyzet) Bérci Norbert szeptember 10-i óra anyaga. 1. Számrendszerek A számrendszer alapja és a számjegyek
 Egész számok ábrázolása (jegyzet) Bérci Norbert 2015. szeptember 10-i óra anyaga Tartalomjegyzék 1. Számrendszerek 1 1.1. A számrendszer alapja és a számjegyek........................ 1 1.2. Alaki- és
Egész számok ábrázolása (jegyzet) Bérci Norbert 2015. szeptember 10-i óra anyaga Tartalomjegyzék 1. Számrendszerek 1 1.1. A számrendszer alapja és a számjegyek........................ 1 1.2. Alaki- és
A feladatok legtöbbször egy pontot érnek. Ahol ettől eltérés van, azt külön jelöljük.
 Szeretettel üdvözlünk Benneteket abból az alkalomból, hogy a Ceglédi Közgazdasági és Informatikai Szakközépiskola informatika tehetséggondozásának első levelét olvassátok! A tehetséggondozással az a célunk,
Szeretettel üdvözlünk Benneteket abból az alkalomból, hogy a Ceglédi Közgazdasági és Informatikai Szakközépiskola informatika tehetséggondozásának első levelét olvassátok! A tehetséggondozással az a célunk,
Számrendszerek. Bináris, hexadecimális
 Számrendszerek Bináris, hexadecimális Mindennapokban használt számrendszerek Decimális 60-as számrendszer az időmérésre DNS-ek vizsgálata négyes számrendszerben Tetszőleges természetes számot megadhatunk
Számrendszerek Bináris, hexadecimális Mindennapokban használt számrendszerek Decimális 60-as számrendszer az időmérésre DNS-ek vizsgálata négyes számrendszerben Tetszőleges természetes számot megadhatunk
1. előadás. Lineáris algebra numerikus módszerei. Hibaszámítás Számábrázolás Kerekítés, levágás Klasszikus hibaanalízis Abszolút hiba Relatív hiba
 Hibaforrások Hiba A feladatok megoldása során különféle hibaforrásokkal találkozunk: Modellhiba, amikor a valóságnak egy közelítését használjuk a feladat matematikai alakjának felírásához. (Pl. egy fizikai
Hibaforrások Hiba A feladatok megoldása során különféle hibaforrásokkal találkozunk: Modellhiba, amikor a valóságnak egy közelítését használjuk a feladat matematikai alakjának felírásához. (Pl. egy fizikai
I+K technológiák. Számrendszerek, kódolás
 I+K technológiák Számrendszerek, kódolás A tárgyak egymásra épülése Magas szintű programozás ( számítástechnika) Alacsony szintű programozás (jelfeldolgozás) I+K technológiák Gépi aritmetika Számítógép
I+K technológiák Számrendszerek, kódolás A tárgyak egymásra épülése Magas szintű programozás ( számítástechnika) Alacsony szintű programozás (jelfeldolgozás) I+K technológiák Gépi aritmetika Számítógép
10-es számrendszer, 2-es számrendszer, 8-as számrendszer, 16-os számr. Számjegyek, alapműveletek.
 Számrendszerek: 10-es számrendszer, 2-es számrendszer, 8-as számrendszer, 16-os számr. Számjegyek, alapműveletek. ritmetikai műveletek egész számokkal 1. Összeadás, kivonás (egész számokkal) 2. Negatív
Számrendszerek: 10-es számrendszer, 2-es számrendszer, 8-as számrendszer, 16-os számr. Számjegyek, alapműveletek. ritmetikai műveletek egész számokkal 1. Összeadás, kivonás (egész számokkal) 2. Negatív
5. Fejezet : Lebegőpontos számok. Lebegőpontos számok
 5. Fejezet : Lebegőpontos The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson Wong, Bentley College Linda
5. Fejezet : Lebegőpontos The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson Wong, Bentley College Linda
5.1.4 Laborgyakorlat: A Windows számológép használata hálózati címeknél
 5.1.4 Laborgyakorlat: A Windows számológép használata hálózati címeknél Célok Átkapcsolás a Windows Számológép két működési módja között. A Windows Számológép használata a decimális (tízes), a bináris
5.1.4 Laborgyakorlat: A Windows számológép használata hálózati címeknél Célok Átkapcsolás a Windows Számológép két működési módja között. A Windows Számológép használata a decimális (tízes), a bináris
DIGITÁLIS TECHNIKA I BINÁRIS SZÁMRENDSZER BEVEZETŐ ÁTTEKINTÉS BINÁRIS SZÁMRENDSZER HELYÉRTÉK. Dr. Lovassy Rita Dr.
 26..5. DIGITÁLIS TEHNIK I Dr. Lovassy Rita Dr. Pődör álint Óbudai Egyetem KVK Mikroelektronikai és Technológia Intézet INÁRIS SZÁMRENDSZER 5. ELŐDÁS 2 EVEZETŐ ÁTTEKINTÉS 6. előadás témája a digitális rendszerekben
26..5. DIGITÁLIS TEHNIK I Dr. Lovassy Rita Dr. Pődör álint Óbudai Egyetem KVK Mikroelektronikai és Technológia Intézet INÁRIS SZÁMRENDSZER 5. ELŐDÁS 2 EVEZETŐ ÁTTEKINTÉS 6. előadás témája a digitális rendszerekben
Máté: Számítógép architektúrák
 Fixpontos számok Pl.: előjeles kétjegyű decimális számok : Ábrázolási tartomány: [-99, +99]. Pontosság (két szomszédos szám különbsége): 1. Maximális hiba: (az ábrázolási tartományba eső) tetszőleges valós
Fixpontos számok Pl.: előjeles kétjegyű decimális számok : Ábrázolási tartomány: [-99, +99]. Pontosság (két szomszédos szám különbsége): 1. Maximális hiba: (az ábrázolási tartományba eső) tetszőleges valós
Számokkal kapcsolatos feladatok.
 Számokkal kapcsolatos feladatok. 1. Egy tört számlálója -tel kisebb, mint a nevezője. Ha a tört számlálójához 17-et, a nevezőjéhez -t adunk, akkor a tört reciprokát kapjuk. Melyik ez a tört? A szám: 17
Számokkal kapcsolatos feladatok. 1. Egy tört számlálója -tel kisebb, mint a nevezője. Ha a tört számlálójához 17-et, a nevezőjéhez -t adunk, akkor a tört reciprokát kapjuk. Melyik ez a tört? A szám: 17
A számrendszerekrl általában
 A számrendszerekrl általában Készítette: Dávid András A számrendszerekrl általában Miért foglalkozunk vele? (Emlékeztet) A mai számítógépek többsége Neumann-elv. Neumann János a következ elveket fektette
A számrendszerekrl általában Készítette: Dávid András A számrendszerekrl általában Miért foglalkozunk vele? (Emlékeztet) A mai számítógépek többsége Neumann-elv. Neumann János a következ elveket fektette
5. Fejezet : Lebegőpontos számok
 5. Fejezet : Lebegőpontos The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson Wong, Bentley College Linda
5. Fejezet : Lebegőpontos The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson Wong, Bentley College Linda
Bevezetés az informatikába Tételsor és minta zárthelyi dolgozat 2014/2015 I. félév
 Bevezetés az informatikába Tételsor és minta zárthelyi dolgozat 2014/2015 I. félév Az informatika története (ebből a fejezetből csak a félkövér betűstílussal szedett részek kellenek) 1. Számítástechnika
Bevezetés az informatikába Tételsor és minta zárthelyi dolgozat 2014/2015 I. félév Az informatika története (ebből a fejezetből csak a félkövér betűstílussal szedett részek kellenek) 1. Számítástechnika
Digitális technika VIMIAA hét
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK VIMIAA02 14. hét Fehér Béla BME MIT Rövid visszatekintés, összefoglaló
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK VIMIAA02 14. hét Fehér Béla BME MIT Rövid visszatekintés, összefoglaló
3. óra Számrendszerek-Szg. történet
 3. óra Számrendszerek-Szg. történet 1byte=8 bit 2 8 =256 256-féle bináris szám állítható elő 1byte segítségével. 1 Kibibyte = 1024 byte mert 2 10 = 1024 1 Mebibyte = 1024 Kibibyte = 1024 * 1024 byte 1
3. óra Számrendszerek-Szg. történet 1byte=8 bit 2 8 =256 256-féle bináris szám állítható elő 1byte segítségével. 1 Kibibyte = 1024 byte mert 2 10 = 1024 1 Mebibyte = 1024 Kibibyte = 1024 * 1024 byte 1
Laborgyakorlat Logikai áramkörök számítógéppel segített tervezése (CAD)
 Laborgyakorlat Logikai áramkörök számítógéppel segített tervezése (CAD) Bevezetés A laborgyakorlatok alapvető célja a tárgy későbbi laborgyakorlataihoz szükséges ismeretek átadása, az azokban szereplő
Laborgyakorlat Logikai áramkörök számítógéppel segített tervezése (CAD) Bevezetés A laborgyakorlatok alapvető célja a tárgy későbbi laborgyakorlataihoz szükséges ismeretek átadása, az azokban szereplő
Máté: Számítógép architektúrák
 Bit: egy bináris számjegy, vagy olyan áramkör, amely egy bináris számjegy ábrázolására alkalmas. Bájt (Byte): 8 bites egység, 8 bites szám. Előjeles fixpontok számok: 2 8 = 256 különböző 8 bites szám lehetséges.
Bit: egy bináris számjegy, vagy olyan áramkör, amely egy bináris számjegy ábrázolására alkalmas. Bájt (Byte): 8 bites egység, 8 bites szám. Előjeles fixpontok számok: 2 8 = 256 különböző 8 bites szám lehetséges.
Digitális technika VIMIAA hét
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika VIMIAA02 14. hét Fehér Béla BME MIT Digitális technika
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika VIMIAA02 14. hét Fehér Béla BME MIT Digitális technika
3. óra Számrendszerek-Szg. történet
 3. óra Számrendszerek-Szg. történet 1byte=8 bit 2 8 =256 256-féle bináris szám állítható elő 1byte segítségével. 1 Kibibyte = 1024 byte mert 2 10 = 1024 1 Mebibyte = 1024 Kibibyte = 1024 * 1024 byte 1
3. óra Számrendszerek-Szg. történet 1byte=8 bit 2 8 =256 256-féle bináris szám állítható elő 1byte segítségével. 1 Kibibyte = 1024 byte mert 2 10 = 1024 1 Mebibyte = 1024 Kibibyte = 1024 * 1024 byte 1
Digitális technika VIMIAA02 1. EA Fehér Béla BME MIT
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK VIMIAA02 1. EA Fehér Béla BME MIT Digitális Rendszerek Számítógépek Számítógép
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK VIMIAA02 1. EA Fehér Béla BME MIT Digitális Rendszerek Számítógépek Számítógép
Digitális technika VIMIAA02 1. EA
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika VIMIAA02 1. EA Fehér Béla BME MIT Digitális Rendszerek
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika VIMIAA02 1. EA Fehér Béla BME MIT Digitális Rendszerek
Digitális technika VIMIAA01
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika VIMIAA01 Fehér Béla BME MIT Digitális Rendszerek Számítógépek
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika VIMIAA01 Fehér Béla BME MIT Digitális Rendszerek Számítógépek
A programozás alapjai előadás. A C nyelv típusai. Egész típusok. C típusok. Előjeles egészek kettes komplemens kódú ábrázolása
 A programozás alapjai 1 A C nyelv típusai 4. előadás Híradástechnikai Tanszék C típusok -void - skalár: - aritmetikai: - egész: - eger - karakter - felsorolás - lebegőpontos - mutató - függvény - union
A programozás alapjai 1 A C nyelv típusai 4. előadás Híradástechnikai Tanszék C típusok -void - skalár: - aritmetikai: - egész: - eger - karakter - felsorolás - lebegőpontos - mutató - függvény - union
Digitális technika VIMIAA01
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK VIMIAA01 Fehér Béla BME MIT Digitális Rendszerek Számítógépek Számítógép
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK VIMIAA01 Fehér Béla BME MIT Digitális Rendszerek Számítógépek Számítógép
OSZTHATÓSÁG. Osztók és többszörösök : a 3 többszörösei : a 4 többszörösei Ahol mindkét jel megtalálható a 12 többszöröseit találjuk.
 Osztók és többszörösök 1783. A megadott számok elsõ tíz többszöröse: 3: 3 6 9 12 15 18 21 24 27 30 4: 4 8 12 16 20 24 28 32 36 40 5: 5 10 15 20 25 30 35 40 45 50 6: 6 12 18 24 30 36 42 48 54 60 1784. :
Osztók és többszörösök 1783. A megadott számok elsõ tíz többszöröse: 3: 3 6 9 12 15 18 21 24 27 30 4: 4 8 12 16 20 24 28 32 36 40 5: 5 10 15 20 25 30 35 40 45 50 6: 6 12 18 24 30 36 42 48 54 60 1784. :
Számrendszerek. A római számok írására csak hét jelt használtak. Ezek segítségével, jól meghatározott szabályok szerint képezték a különböz számokat.
 Számrendszerek A római számok írására csak hét jelt használtak Ezek segítségével, jól meghatározott szabályok szerint képezték a különböz számokat Római számjegyek I V X L C D M E számok értéke 1 5 10
Számrendszerek A római számok írására csak hét jelt használtak Ezek segítségével, jól meghatározott szabályok szerint képezték a különböz számokat Római számjegyek I V X L C D M E számok értéke 1 5 10
Gyakorló feladatok. /2 Maradék /16 Maradék /8 Maradék
 Gyakorló feladatok Számrendszerek: Feladat: Ábrázold kettes számrendszerbe a 639 10, 16-os számrendszerbe a 311 10, 8-as számrendszerbe a 483 10 számot! /2 Maradék /16 Maradék /8 Maradék 639 1 311 7 483
Gyakorló feladatok Számrendszerek: Feladat: Ábrázold kettes számrendszerbe a 639 10, 16-os számrendszerbe a 311 10, 8-as számrendszerbe a 483 10 számot! /2 Maradék /16 Maradék /8 Maradék 639 1 311 7 483
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Számelmélet I.
 Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
1. fogalom. Add meg az összeadásban szereplő számok elnevezéseit! Milyen tulajdonságai vannak az összeadásnak? Hogyan ellenőrizzük az összeadást?
 1. fogalom Add meg az összeadásban szereplő számok 73 + 19 = 92 összeadandók (tagok) összeg Összeadandók (tagok): amiket összeadunk. Összeg: az összeadás eredménye. Milyen tulajdonságai vannak az összeadásnak?
1. fogalom Add meg az összeadásban szereplő számok 73 + 19 = 92 összeadandók (tagok) összeg Összeadandók (tagok): amiket összeadunk. Összeg: az összeadás eredménye. Milyen tulajdonságai vannak az összeadásnak?
1. forduló. 1.1. Az adat, az információ és a hír jelentése és tartalma. A kommunikáció
 1. Az információ 1.1. Az adat, az információ és a hír jelentése és tartalma. A kommunikáció A tárgyaknak mérhető és nem mérhető, számunkra fontos tulajdonságait adatnak nevezzük. Egy tárgynak sok tulajdonsága
1. Az információ 1.1. Az adat, az információ és a hír jelentése és tartalma. A kommunikáció A tárgyaknak mérhető és nem mérhető, számunkra fontos tulajdonságait adatnak nevezzük. Egy tárgynak sok tulajdonsága
Laborgyakorlat Logikai áramkörök számítógéppel segített tervezése (CAD)
 Laborgyakorlat Logikai áramkörök számítógéppel segített tervezése (CAD) Összeadó áramkör A legegyszerűbb összeadó két bitet ad össze, és az egy bites eredményt és az átvitelt adja ki a kimenetén, ez a
Laborgyakorlat Logikai áramkörök számítógéppel segített tervezése (CAD) Összeadó áramkör A legegyszerűbb összeadó két bitet ad össze, és az egy bites eredményt és az átvitelt adja ki a kimenetén, ez a
Oszthatósági problémák
 Oszthatósági problémák Érdekes kérdés, hogy egy adott számot el lehet-e osztani egy másik számmal (maradék nélkül). Ezek eldöntésére a matematika tanulmányok során néhány speciális esetre látunk is példát,
Oszthatósági problémák Érdekes kérdés, hogy egy adott számot el lehet-e osztani egy másik számmal (maradék nélkül). Ezek eldöntésére a matematika tanulmányok során néhány speciális esetre látunk is példát,
Negatív alapú számrendszerek
 2015. március 4. Negatív számok Legyen b > 1 egy adott egész szám. Ekkor bármely N 0 egész szám egyértelműen felírható N = m a k b k k=1 alakban, ahol 0 a k < b egész szám. Negatív számok Legyen b > 1
2015. március 4. Negatív számok Legyen b > 1 egy adott egész szám. Ekkor bármely N 0 egész szám egyértelműen felírható N = m a k b k k=1 alakban, ahol 0 a k < b egész szám. Negatív számok Legyen b > 1
Informatika érettségi vizsga
 Informatika 11/L/BJ Informatika érettségi vizsga ÍRÁSBELI GYAKORLATI VIZSGA (180 PERC - 120 PONT) SZÓBELI SZÓBELI VIZSGA (30 PERC FELKÉSZÜLÉS 10 PERC FELELET - 30 PONT) Szövegszerkesztés (40 pont) Prezentáció-készítés
Informatika 11/L/BJ Informatika érettségi vizsga ÍRÁSBELI GYAKORLATI VIZSGA (180 PERC - 120 PONT) SZÓBELI SZÓBELI VIZSGA (30 PERC FELKÉSZÜLÉS 10 PERC FELELET - 30 PONT) Szövegszerkesztés (40 pont) Prezentáció-készítés
Számelmélet. 4. Igazolja, hogy ha hat egész szám összege páratlan, akkor e számok szorzata páros!
 Számelmélet - oszthatóság definíciója - oszthatósági szabályok - maradékos osztás - prímek definíciója - összetett szám definíciója - legnagyobb közös osztó definíciója - legnagyobb közös osztó meghatározása
Számelmélet - oszthatóság definíciója - oszthatósági szabályok - maradékos osztás - prímek definíciója - összetett szám definíciója - legnagyobb közös osztó definíciója - legnagyobb közös osztó meghatározása
Műveletek mátrixokkal. Kalkulus. 2018/2019 ősz
 2018/2019 ősz Elérhetőségek Előadó: (safaro@math.bme.hu) Fogadóóra: hétfő 9-10 (H épület 3. emelet 310-es ajtó) A pontos tárgykövetelmények a www.math.bme.hu/~safaro/kalkulus oldalon találhatóak. A mátrix
2018/2019 ősz Elérhetőségek Előadó: (safaro@math.bme.hu) Fogadóóra: hétfő 9-10 (H épület 3. emelet 310-es ajtó) A pontos tárgykövetelmények a www.math.bme.hu/~safaro/kalkulus oldalon találhatóak. A mátrix
Digitális technika VIMIAA01
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika VIMIAA01 Fehér Béla BME MIT Digitális Rendszerek Számítógépek
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika VIMIAA01 Fehér Béla BME MIT Digitális Rendszerek Számítógépek
DIGITÁLIS TECHNIKA I SZÁMRENDSZEREK HELYÉRTÉK SZÁMRENDSZEREK RÓMAI SZÁMOK ÉS RENDSZERÜK. Dr. Lovassy Rita Dr.
 6..6. DIGITÁLIS TECHNIK I Dr. Lovassy Rita Dr. Pődör álint Óbudai Egyetem KVK Mikroelektronikai és Technológia Intézet SZÁMRENDSZEREK 8. ELŐDÁS 8. előadás témája a digitális rendszerekben központi szerepet
6..6. DIGITÁLIS TECHNIK I Dr. Lovassy Rita Dr. Pődör álint Óbudai Egyetem KVK Mikroelektronikai és Technológia Intézet SZÁMRENDSZEREK 8. ELŐDÁS 8. előadás témája a digitális rendszerekben központi szerepet
I. el adás, A számítógép belseje
 2008. október 8. Követelmények Félévközi jegy feltétele két ZH teljesítése. Ha egy ZH nem sikerült, akkor lehetséges a pótlása. Mindkét ZH-hoz van pótlás. A pótzh körülbelül egy héttel az eredeti után
2008. október 8. Követelmények Félévközi jegy feltétele két ZH teljesítése. Ha egy ZH nem sikerült, akkor lehetséges a pótlása. Mindkét ZH-hoz van pótlás. A pótzh körülbelül egy héttel az eredeti után
S z á m í t á s t e c h n i k a i a l a p i s m e r e t e k
 S z á m í t á s t e c h n i k a i a l a p i s m e r e t e k T a r t a l o m Mintafeladatok... 4 Számrendszerek, logikai mőveletek... 4 Gyakorló feladatok... 19 Számrendszerek, logikai mőveletek... 19 Megoldások...
S z á m í t á s t e c h n i k a i a l a p i s m e r e t e k T a r t a l o m Mintafeladatok... 4 Számrendszerek, logikai mőveletek... 4 Gyakorló feladatok... 19 Számrendszerek, logikai mőveletek... 19 Megoldások...
Bevezetés az informatikába
 Bevezetés az informatikába Az összeadás, kivonás, szorzás algoritmusai. Prefixumok az informatikában Előjel nélküli egész számok ábrázolása a digitális számítógépeknél. Szorzás, összeadás, kivonás. Előjeles
Bevezetés az informatikába Az összeadás, kivonás, szorzás algoritmusai. Prefixumok az informatikában Előjel nélküli egész számok ábrázolása a digitális számítógépeknél. Szorzás, összeadás, kivonás. Előjeles
(jegyzet) Bérci Norbert szeptember i óra anyaga A számrendszer alapja és a számjegyek Alaki- és helyiérték...
 Számábrázolás és karakterkódolás (jegyzet) Bérci Norbert 2014. szeptember 15-16-i óra anyaga Tartalomjegyzék 1. Számrendszerek 1 1.1. A számrendszer alapja és a számjegyek........................ 2 1.2.
Számábrázolás és karakterkódolás (jegyzet) Bérci Norbert 2014. szeptember 15-16-i óra anyaga Tartalomjegyzék 1. Számrendszerek 1 1.1. A számrendszer alapja és a számjegyek........................ 2 1.2.
Pótvizsga anyaga 5. osztály (Iskola honlapján is megtalálható!) Pótvizsga: beadandó feladatok 45 perces írásbeli szóbeli a megadott témakörökből
 Pótvizsga anyaga 5. osztály (Iskola honlapján is megtalálható!) Természetes számok: 0123 (TK 4-49.oldal) - tízes számrendszer helyi értékei alaki érték valódi érték - becslés kerekítés - alapműveletek:
Pótvizsga anyaga 5. osztály (Iskola honlapján is megtalálható!) Természetes számok: 0123 (TK 4-49.oldal) - tízes számrendszer helyi értékei alaki érték valódi érték - becslés kerekítés - alapműveletek:
Bevezetés az informatikába
 Bevezetés az informatikába 4. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Bevezetés az informatikába 4. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
A Gray-kód Bináris-kóddá alakításának leírása
 A Gray-kód Bináris-kóddá alakításának leírása /Mechatronikai Projekt II. házi feladat/ Bodogán János 2005. április 1. Néhány szó a kódoló átalakítókról Ezek az eszközök kiegészítő számlálók nélkül közvetlenül
A Gray-kód Bináris-kóddá alakításának leírása /Mechatronikai Projekt II. házi feladat/ Bodogán János 2005. április 1. Néhány szó a kódoló átalakítókról Ezek az eszközök kiegészítő számlálók nélkül közvetlenül
Számrendszerek. 1. ábra: C soportosítás 2-es számrendszerben. Helyiértékek: A szám leírva:
 . Elméleti alapok Számrendszerek.. A kettes számrendszerről Számlálás közben mi tízesével csoportosítunk (valószínűleg azért, mert ujjunk van). Ezt a számírásunk is követi. A helyiértékek: egy, tíz, száz
. Elméleti alapok Számrendszerek.. A kettes számrendszerről Számlálás közben mi tízesével csoportosítunk (valószínűleg azért, mert ujjunk van). Ezt a számírásunk is követi. A helyiértékek: egy, tíz, száz
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
Programozott soros szinkron adatátvitel
 Programozott soros szinkron adatátvitel 1. Feladat Név:... Irjon programot, mely a P1.0 kimenet egy lefutó élének időpontjában a P1.1 kimeneten egy adatbitet ad ki. A bájt legalacsonyabb helyiértéke 1.
Programozott soros szinkron adatátvitel 1. Feladat Név:... Irjon programot, mely a P1.0 kimenet egy lefutó élének időpontjában a P1.1 kimeneten egy adatbitet ad ki. A bájt legalacsonyabb helyiértéke 1.
Mátrixok február Feladat: Legyen A = ( ( B =
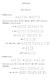 Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
DIGITÁLIS TECHNIKA BINÁRIS SZÁMRENDSZER BEVEZETŐ ÁTTEKINTÉS BINÁRIS SZÁMRENDSZER HELYÉRTÉK. Dr. Lovassy Rita Dr.
 7.4.. DIGITÁLIS TECHNIK Dr. Lovassy Rita Dr. Pődör álint Óbudai Egyetem KVK Mikroelektronikai és Technológia Intézet INÁRIS SZÁMRENDSZER 3. ELŐDÁS EVEZETŐ ÁTTEKINTÉS 6. előadás témája a digitális rendszerekben
7.4.. DIGITÁLIS TECHNIK Dr. Lovassy Rita Dr. Pődör álint Óbudai Egyetem KVK Mikroelektronikai és Technológia Intézet INÁRIS SZÁMRENDSZER 3. ELŐDÁS EVEZETŐ ÁTTEKINTÉS 6. előadás témája a digitális rendszerekben
Gyakorló feladatok. Bipoláris tranzisztor
 Gyakorló feladatok Bipoláris tranzisztor A tranzisztor három kivezetéses félvezető eszköz, mellyel elektromos jelek erősíthető vagy kapcsolhatók. Manapság a tranzisztorokat általában szilíciumból készítik
Gyakorló feladatok Bipoláris tranzisztor A tranzisztor három kivezetéses félvezető eszköz, mellyel elektromos jelek erősíthető vagy kapcsolhatók. Manapság a tranzisztorokat általában szilíciumból készítik
TANMENETJAVASLAT. Dr. Korányi Erzsébet MATEMATIKA. tankönyv ötödikeseknek. címû tankönyvéhez
 TANMENETJAVASLAT Dr. Korányi Erzsébet MATEMATIKA tankönyv ötödikeseknek címû tankönyvéhez A heti 3 óra, évi 111 óra B heti 4 óra, évi 148 óra Javaslat témazáró dolgozatra: Dr. Korányi Erzsébet: Matematika
TANMENETJAVASLAT Dr. Korányi Erzsébet MATEMATIKA tankönyv ötödikeseknek címû tankönyvéhez A heti 3 óra, évi 111 óra B heti 4 óra, évi 148 óra Javaslat témazáró dolgozatra: Dr. Korányi Erzsébet: Matematika
Assembly Utasítások, programok. Iványi Péter
 Assembly Utasítások, programok Iványi Péter Assembly programozás Egyszerű logikán alapul Egy utasítás CSAK egy dolgot csinál Magas szintű nyelven: x = 5 * z + y; /* 3 darab művelet */ Assembly: Szorozzuk
Assembly Utasítások, programok Iványi Péter Assembly programozás Egyszerű logikán alapul Egy utasítás CSAK egy dolgot csinál Magas szintű nyelven: x = 5 * z + y; /* 3 darab művelet */ Assembly: Szorozzuk
IT - Alapismeretek. Feladatgyűjtemény
 IT - Alapismeretek Feladatgyűjtemény Feladatok PowerPoint 2000 1. FELADAT TÖRTÉNETI ÁTTEKINTÉS Pótolja a hiányzó neveket, kifejezéseket! Az első négyműveletes számológépet... készítette. A tárolt program
IT - Alapismeretek Feladatgyűjtemény Feladatok PowerPoint 2000 1. FELADAT TÖRTÉNETI ÁTTEKINTÉS Pótolja a hiányzó neveket, kifejezéseket! Az első négyműveletes számológépet... készítette. A tárolt program
Hardverközeli programozás 1 1. gyakorlat. Kocsis Gergely 2015.02.17.
 Hardverközeli programozás 1 1. gyakorlat Kocsis Gergely 2015.02.17. Információk Kocsis Gergely http://irh.inf.unideb.hu/user/kocsisg 2 zh + 1 javító (a gyengébbikre) A zh sikeres, ha az elért eredmény
Hardverközeli programozás 1 1. gyakorlat Kocsis Gergely 2015.02.17. Információk Kocsis Gergely http://irh.inf.unideb.hu/user/kocsisg 2 zh + 1 javító (a gyengébbikre) A zh sikeres, ha az elért eredmény
Egész számok. pozitív egész számok: 1; 2; 3; 4;... negatív egész számok: 1; 2; 3; 4;...
 Egész számok természetes számok ( ) pozitív egész számok: 1; 2; 3; 4;... 0 negatív egész számok: 1; 2; 3; 4;... egész számok ( ) 1. Írd a következõ számokat a halmazábra megfelelõ helyére! 3; 7; +6 ; (
Egész számok természetes számok ( ) pozitív egész számok: 1; 2; 3; 4;... 0 negatív egész számok: 1; 2; 3; 4;... egész számok ( ) 1. Írd a következõ számokat a halmazábra megfelelõ helyére! 3; 7; +6 ; (
Törtek. Rendelhetőek nagyon jó szemléltethető eszközök könyvesboltokban és internetek is, pl:
 Törtek A törteknek kétféle értelmezése van: - Egy egészet valamennyi részre (nevező) osztunk, és abból kiválasztunk valahány darabot (számláló) - Valamennyi egészet (számláló), valahány részre osztunk
Törtek A törteknek kétféle értelmezése van: - Egy egészet valamennyi részre (nevező) osztunk, és abból kiválasztunk valahány darabot (számláló) - Valamennyi egészet (számláló), valahány részre osztunk
Informatika elméleti alapjai. January 17, 2014
 Szám- és kódrendszerek Informatika elméleti alapjai Horváth Árpád January 17, 2014 Contents 1 Számok és ábrázolásuk Számrendszerek Helyiérték nélküliek, pl római számok (MMVIIII) Helyiértékesek a nulla
Szám- és kódrendszerek Informatika elméleti alapjai Horváth Árpád January 17, 2014 Contents 1 Számok és ábrázolásuk Számrendszerek Helyiérték nélküliek, pl római számok (MMVIIII) Helyiértékesek a nulla
Mechatronika Modul 1: Alapismeretek
 Mechatronika Modul : Alapismeretek Oktatói segédlet (Elképzelés) Készítették: Matthias Römer Chemnitz-i Műszaki Egyetem, Szerszámgépek és Gyártási Folyamatok Intézete, Németország Cser Adrienn Corvinus
Mechatronika Modul : Alapismeretek Oktatói segédlet (Elképzelés) Készítették: Matthias Römer Chemnitz-i Műszaki Egyetem, Szerszámgépek és Gyártási Folyamatok Intézete, Németország Cser Adrienn Corvinus
INFO1 Számok és karakterek
 INFO1 Számok és karakterek Wettl Ferenc 2015. szeptember 29. Wettl Ferenc INFO1 Számok és karakterek 2015. szeptember 29. 1 / 22 Tartalom 1 Bináris számok, kettes komplemens számábrázolás Kettes számrendszer
INFO1 Számok és karakterek Wettl Ferenc 2015. szeptember 29. Wettl Ferenc INFO1 Számok és karakterek 2015. szeptember 29. 1 / 22 Tartalom 1 Bináris számok, kettes komplemens számábrázolás Kettes számrendszer
Műveletek lebegőpontos adatokkal
 Budapesti Műszaki Főiskola Regionális Oktatási és Innovációs Központ Székesfehérvár Műveletek lebegőpontos adatokkal Dr. Seebauer Márta főiskolai tanár seebauer.marta@roik.bmf.hu Műveletek az IEEE 754
Budapesti Műszaki Főiskola Regionális Oktatási és Innovációs Központ Székesfehérvár Műveletek lebegőpontos adatokkal Dr. Seebauer Márta főiskolai tanár seebauer.marta@roik.bmf.hu Műveletek az IEEE 754
DIGITÁLIS TECHNIKA I 6. ELİADÁS SZÁMRENDSZEREK BEVEZETİ ÁTTEKINTÉS. Római számok és rendszerük. Helyérték
 DIGITÁLIS TECHNIK I Dr. Pıdör Bálint BMF KVK Mikroelektronikai és Technológia Intézet. ELİDÁS: BINÁRIS SZÁMRENDSZER. ELİDÁS. elıadás témája a digitális rendszerekben központi szerepet játszó számrendszerek
DIGITÁLIS TECHNIK I Dr. Pıdör Bálint BMF KVK Mikroelektronikai és Technológia Intézet. ELİDÁS: BINÁRIS SZÁMRENDSZER. ELİDÁS. elıadás témája a digitális rendszerekben központi szerepet játszó számrendszerek
Adattípusok. Dr. Seebauer Márta. Budapesti Műszaki Főiskola Regionális Oktatási és Innovációs Központ Székesfehérvár
 Budapesti Műszaki Főiskola Regionális Oktatási és Innovációs Központ Székesfehérvár Adattípusok Dr. Seebauer Márta főiskolai tanár seebauer.marta@roik.bmf.hu Az adatmanipulációs fa z adatmanipulációs fa
Budapesti Műszaki Főiskola Regionális Oktatási és Innovációs Központ Székesfehérvár Adattípusok Dr. Seebauer Márta főiskolai tanár seebauer.marta@roik.bmf.hu Az adatmanipulációs fa z adatmanipulációs fa
BÖLCS BAGOLY LEVELEZŐS MATEMATIKAVERSENY IV. forduló MEGOLDÁSOK
 IV. forduló 1. Hány olyan legfeljebb 5 jegyű, 5-tel nem osztható természetes szám van, amelynek minden jegye prím? Mivel a feladatban számjegyekről van szó, akkor az egyjegyű prímszámokról lehet szó: 2;
IV. forduló 1. Hány olyan legfeljebb 5 jegyű, 5-tel nem osztható természetes szám van, amelynek minden jegye prím? Mivel a feladatban számjegyekről van szó, akkor az egyjegyű prímszámokról lehet szó: 2;
Bevezetés az informatikába
 Bevezetés az informatikába 2. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Bevezetés az informatikába 2. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
A racionális számok és a fixpontos processzorok numerikus felületének a kapcsolata
 7.2.1. A racionális számok és a fixpontos processzorok numerikus felületének a kapcsolata A valósidejű jel- és képfeldolgozás területére eső alkalmazások esetében legtöbbször igény mutatkozik arra, hogy
7.2.1. A racionális számok és a fixpontos processzorok numerikus felületének a kapcsolata A valósidejű jel- és képfeldolgozás területére eső alkalmazások esetében legtöbbször igény mutatkozik arra, hogy
1. Halmazok, számhalmazok, alapműveletek
 1. Halmazok, számhalmazok, alapműveletek I. Nulladik ZH-ban láttuk: 1. Határozza meg az (A B)\C halmaz elemszámát, ha A tartalmazza az összes 19-nél kisebb természetes számot, továbbá B a prímszámok halmaza
1. Halmazok, számhalmazok, alapműveletek I. Nulladik ZH-ban láttuk: 1. Határozza meg az (A B)\C halmaz elemszámát, ha A tartalmazza az összes 19-nél kisebb természetes számot, továbbá B a prímszámok halmaza
A fejlesztés várt eredményei a 1. évfolyam végén
 A tanuló legyen képes: A fejlesztés várt eredményei a 1. évfolyam végén - Halmazalkotásra, összehasonlításra az elemek száma szerint; - Állítások igazságtartalmának eldöntésére, állítások megfogalmazására;
A tanuló legyen képes: A fejlesztés várt eredményei a 1. évfolyam végén - Halmazalkotásra, összehasonlításra az elemek száma szerint; - Állítások igazságtartalmának eldöntésére, állítások megfogalmazására;
Számítógép architektúrák
 Számítógép architektúrák Számítógépek felépítése Digitális adatábrázolás Digitális logikai szint Mikroarchitektúra szint Gépi utasítás szint Operációs rendszer szint Assembly nyelvi szint Probléma orientált
Számítógép architektúrák Számítógépek felépítése Digitális adatábrázolás Digitális logikai szint Mikroarchitektúra szint Gépi utasítás szint Operációs rendszer szint Assembly nyelvi szint Probléma orientált
4,5 1,5 cm. Ezek alapján 8 és 1,5 cm lesz.
 1. Tekintse az oldalsó ábrát! a. Mekkora lesz a 4. sor téglalap mérete? b. Számítsa ki az ábrán látható három téglalap területösszegét! c. Mekkora lesz a 018. sorban a téglalap oldalai? d. Hány téglalapot
1. Tekintse az oldalsó ábrát! a. Mekkora lesz a 4. sor téglalap mérete? b. Számítsa ki az ábrán látható három téglalap területösszegét! c. Mekkora lesz a 018. sorban a téglalap oldalai? d. Hány téglalapot
Nagypontosságú aritmetika I.
 Nagypontosságú aritmetika I. Nagypontosságú aritmetika Problémák: sokjegyű (100 vagy 1000 vagy...) egész számok kellenek több alkalmazásban; jó lenne, ha 1/3*3 értéke 1 lenne, azaz kellenének racionális
Nagypontosságú aritmetika I. Nagypontosságú aritmetika Problémák: sokjegyű (100 vagy 1000 vagy...) egész számok kellenek több alkalmazásban; jó lenne, ha 1/3*3 értéke 1 lenne, azaz kellenének racionális
A számolás története
 A számolás története Tulajdonképpen az ember azóta tud számolni, hogy ember lett. Igaz, a kezdet kezdetén, az ősember még nem úgy számolt, mint ahogyan ma számolunk. De összeadni, és kivonni bizonyos határok
A számolás története Tulajdonképpen az ember azóta tud számolni, hogy ember lett. Igaz, a kezdet kezdetén, az ősember még nem úgy számolt, mint ahogyan ma számolunk. De összeadni, és kivonni bizonyos határok
Miről lesz ma szó? A PROGAMOZÁS ALAPJAI 1. Programtervezési stratégiák. Top-down tervezés. Top-down tervezés. Bottom-up tervezés. 4.
 212. február 28. A PROGAMOZÁS ALAPJAI 1 Vitéz András egyetemi adjunktus BME Híradástechnikai Tanszék vitez@hit.bme.hu Miről lesz ma szó? Programtervezési stratégiák Top-down Bottom-up Függvények Szintaxis
212. február 28. A PROGAMOZÁS ALAPJAI 1 Vitéz András egyetemi adjunktus BME Híradástechnikai Tanszék vitez@hit.bme.hu Miről lesz ma szó? Programtervezési stratégiák Top-down Bottom-up Függvények Szintaxis
Elemi matematika szakkör
 Elemi matematika szakkör Kolozsvár, 2015. október 5. 1.1. Feladat. Egy pozitív egész számot K tulajdonságúnak nevezünk, ha számjegyei nullától különböznek és nincs két azonos számjegye. Határozd meg az
Elemi matematika szakkör Kolozsvár, 2015. október 5. 1.1. Feladat. Egy pozitív egész számot K tulajdonságúnak nevezünk, ha számjegyei nullától különböznek és nincs két azonos számjegye. Határozd meg az
XX. Nemzetközi Magyar Matematika Verseny
 XX. Nemzetközi Magyar Matematika Verseny Bonyhád, 011. március 11 15. 10. osztály 1. feladat: Legyen egy háromszög három oldalának a hossza a, b és c. Bizonyítsuk be, hogy 3 (a+b+c) ab+bc+ca 4 Mikor állhat
XX. Nemzetközi Magyar Matematika Verseny Bonyhád, 011. március 11 15. 10. osztály 1. feladat: Legyen egy háromszög három oldalának a hossza a, b és c. Bizonyítsuk be, hogy 3 (a+b+c) ab+bc+ca 4 Mikor állhat
DIGITÁLIS TECHNIKA I KÓD IRODALOM SZIMBÓLUMKÉSZLET KÓDOLÁS ÉS DEKÓDOLÁS
 DIGITÁLIS TECHNIKA I Dr. Pıdör Bálint BMF KVK Mikroelektronikai és Technológia Intézet 7. ELİADÁS 7. ELİADÁS 1. Kódok és kódolás alapfogalmai 2. Numerikus kódok. Tiszta bináris kódok (egyenes kód, 1-es
DIGITÁLIS TECHNIKA I Dr. Pıdör Bálint BMF KVK Mikroelektronikai és Technológia Intézet 7. ELİADÁS 7. ELİADÁS 1. Kódok és kódolás alapfogalmai 2. Numerikus kódok. Tiszta bináris kódok (egyenes kód, 1-es
Matematika. 1. osztály. 2. osztály
 Matematika 1. osztály - képes halmazokat összehasonlítani az elemek száma szerint, halmazt alkotni; - képes állítások igazságtartalmának eldöntésére, állításokat megfogalmazni; - halmazok elemeit összehasonlítja,
Matematika 1. osztály - képes halmazokat összehasonlítani az elemek száma szerint, halmazt alkotni; - képes állítások igazságtartalmának eldöntésére, állításokat megfogalmazni; - halmazok elemeit összehasonlítja,
4. hét: Ideális és valódi építőelemek. Steiner Henriette Egészségügyi mérnök
 4. hét: Ideális és valódi építőelemek Steiner Henriette Egészségügyi mérnök Digitális technika 2015/2016 Digitális technika 2015/2016 Bevezetés Az ideális és valódi építőelemek Digitális technika 2015/2016
4. hét: Ideális és valódi építőelemek Steiner Henriette Egészségügyi mérnök Digitális technika 2015/2016 Digitális technika 2015/2016 Bevezetés Az ideális és valódi építőelemek Digitális technika 2015/2016
Kombinációs hálózatok Számok és kódok
 Számok és kódok A történelem folyamán kétféle számábrázolási mód alakult ki: helyiértékes számrendszerek nem helyiértékes számrendszerek n N = b i B i=0 i n b i B i B = (természetes) szám = számjegy az
Számok és kódok A történelem folyamán kétféle számábrázolási mód alakult ki: helyiértékes számrendszerek nem helyiértékes számrendszerek n N = b i B i=0 i n b i B i B = (természetes) szám = számjegy az
;3 ; 0; 1 7; ;7 5; 3. pozitív: ; pozitív is, negatív is: ;
 . A racion lis sz mok A tanult sz mok halmaza A) Ábrázold számegyenesen az alábbi számokat! 8 + + 0 + 7 0 7 7 0 0. 0 Válogasd szét a számokat aszerint, hogy pozitív: pozitív is, negatív is: negatív: sem
. A racion lis sz mok A tanult sz mok halmaza A) Ábrázold számegyenesen az alábbi számokat! 8 + + 0 + 7 0 7 7 0 0. 0 Válogasd szét a számokat aszerint, hogy pozitív: pozitív is, negatív is: negatív: sem
Gyors fejszámolási tippek, trükkök és ötletek (II. rész)
 Gyors fejszámolási tippek, trükkök és ötletek (II. rész) Tuzson Zoltán, Székelyudvarhely Az előző részben bemutatott trükkök után, most következzenek sajátos alakú kétjegyű számok szorzása, és hatványozása:
Gyors fejszámolási tippek, trükkök és ötletek (II. rész) Tuzson Zoltán, Székelyudvarhely Az előző részben bemutatott trükkök után, most következzenek sajátos alakú kétjegyű számok szorzása, és hatványozása:
