Forgó áramlástechnikai berendezések numerikus szimulációja
|
|
|
- Amanda Boros
- 9 évvel ezelőtt
- Látták:
Átírás
1 MISKOLCI EGYETEM Gépészmérnöki és Informatikai Kar Áramlás- és Hőtechnikai Gépek Tanszéke Forgó áramlástechnikai berendezések numerikus szimulációja Oktatási segédlet műszakiaknak Készítette: Fodor Béla tanársegéd Miskolci Egyetem Áramlás- és Hőtechnikai Gépek Tanszéke Miskolc
2 I. Előszó A Forgó áramlástechnikai berendezések numerikus szimulációja c. oktatási segédlet segítséget nyújt forgógépek szimulációjának háromdimenziós térben történő felépítésében. A segédlet a számítógéppel segített numerikus vizsgálatok fontosabb állomásait és megfontolásait részletezi, mely bevezetést nyújt a CFD (Computation Fluid Dynamics) területére. Ezt követően konkrét alkalmazási példákon keresztül részletezzük a forgó áramlástechnikai berendezések numerikus szimulációjának megfontolásait és konkrét beállításait. Az oktatási segédlet a Kaplan turbina numerikus szimulációja c. kutató munka keretén belül a TÁMOP B-10/2/KONV jelű projekt részeként az Új Magyarország Fejlesztési Terv keretében az Európai Unió támogatásával, az Európai Szociális Alap társfinanszírozásával valósul meg. ii
3 Tartalomjegyzék Tartalomjegyzék 2 1. Numerikus vizsgálat alapjai 2 2. A vizsgálat során alkalmazott numerikus szimuláció lépései Előfeldolgozás (Pre-Processing) Megoldó futtatása (Solver) Utófeldolgozás (Post-Processing) 5 3. Forgó berendezések a numerikus áramlástanban és az alkalmazott egyenletek Az áramlás alapegyenletei Keverőtartály Geometriai előkészítés Numerikus háló Numerikus szimuláció Forgó lapátozású keverőtartályok összehasonlító vizsgálata A vizsgálat célja A vizsgálat eredményei Alkalmazási példák forgó gépek numerikus szimulációjára Egyszerűsített forgó vonatkoztatási rendszerben Egyszerűsített forgó vonatkoztatási rendszer Feladat ismertetése Beállítások és megoldás Irodalom NUMERIKUS VIZSGÁLAT ALAPJAI A folyadékok numerikus vizsgálatának egy gyűjtőneve a CFD (Computation Fluid Dynamics), mely a fluidumok áramlási jellemzőinek, hő- és tömegtranszportjának valamint kémiai reakciók és sok más fizikai jelenség vizsgálatára alkalmas eszköz. A CFD analízis alkalmazási területei: Ipar és kutatás: A technikai fejlődés és a megkívánt gazdasági szempontok valamint az energiafelhasználás mind a gyártás mind az üzemeltetés szempontjából a berendezések fejlesztését követeli meg, ezért az ipar számára elengedhetetlen a felsorolt szempontok figyelembe vétele. A numerikus szimuláció a termelési és üzemeltetési folyamat bármely szakaszába beilleszthető. 2
4 Meglévő tervek koncepcionális tanulmányozása és kiértékelése: Még gyártásba nem került azonban tervezőasztalon elkészített berendezések esetén alkalmazható. A megkonstruált berendezésekről (alkatrészekről) CAD (Computer Aided Design Számítógéppel segített tervezés) rendszer segítségével modell készíthetünk melyet numerikus módszereken alapuló CFD rendszerek segítségével működtethetünk. A szimulációk eredményeit feldolgozva képet kaphatunk a prototípusgyártást követő várható eredményekről, így a prototípusmérések módja is feltárható. Termékek részének vagy egészének fejlesztése: A gyártást követően a forgalomba került berendezések folyamatos fejlesztést igényelnek, mely a berendezésekkel szemben támasztott elvárásokat követelnek meg. A berendezések üzemi jellemzőinek javítása CFD rendszer segítségével hatékonyan elvégezhető. Hibafeltárás: Különböző rendszerek és folyamatok hibái és feltárásuk jelentős beruházásokkal járhatnak. A hibák érinthetnek gazdasági szempontokat melyek üzemkiesésből esetleges hatásfokromlásból eredhetek, lehetnek környezetvédelmi szempontok melyek hibásan működő berendezésekből kiáramló vagy kémiai reakciók révén keletkező szennyezőanyagokat eredményezhet. Egy működő folyamatban számtalan hibatípus alakulhat ki, melyre a numerikus szimulációk hatékony támogatás nyújtanak. Újratervezés: Új korszerűbb alkatrészek és anyagok alkalmazása már üzemelő berendezések és folyatok esetén. Tesztelés: Az prototípusgyártás elengedhetetlen korszerű eszköze a számítógépes numerikus szimuláció mely az elsődleges lépés egy új berendezés üzemi jellemzőinek feltérképezésére. Meglévő szimulációk kiértékelése és adatainak feldolgozása: Projektben működő más-más részfeladatokon dolgozó fejlesztési csoportok számára biztosítani kell az eredmények újbóli kiértékelését vagy a szimulációk összekapcsolását. Egy jól megkonstruált numerikus szimuláció lehetőséget ad az részfeladatok között átjárhatóságra és a folyamatos kiértékelésre. A CFD vizsgálatok alkalmazása a mindennapi élet bármely területén alkalmazható. Csővezeték rendszerek Alakítási eljárások Motordiagnosztika Motorfejlesztés Autókarosszéria deformációja Légtechnikai jellemzők vizsgálat A típusok abból a szempontból különböztethetünk meg, hogy a vizsgálati tartományon milyen jelenséget vizsgálunk, például egy hálózott tér esetén csak a diszkretizáció során döntjük el, hogy szilárd vagy folyadéktérről beszélünk valamint azt, hogy abban áramlási vagy hővezetési jellemzőket vizsgálunk, ezen kívül számos más kombinációban is felépíthetjük a szimulációt. 2. A VIZSGÁLAT SORÁN ALKALMAZOTT NUMERIKUS SZIMULÁCIÓ LÉPÉSEI Az 1. ábra a numerikus vizsgálat fontosabb lépéseit mutatja. A numerikus vizsgálat topológikus felépítését követően kerül sor az előfeldolgozásra, amely során meghatározzuk a 3
5 geometria kétdimenziós (2D) vagy háromdimenziós (3D) modelljét. Majd a geometria függvényében felépítjük a vizsgálati tér numerikus hálóját. A numerikus vizsgálat tekintetében a hálózás a legfontosabb, mivel a matematikai egyenletek diszkretizációja ezen a hálózott térben történik. (3. fejezet) 1. ábra CFD szimuláció folyamata 2.1 Előfeldolgozás (Pre-Processing) A modellezés céljának meghatározása A modellezési tartomány meghatározása Import/Export különböző CAD rendszerekből A geometria és a háló elkészítése Az előfeldolgozást követi a peremfeltételek és kezdeti értékek bevitele. Majd a számítás melynek ideje a háló sűrűségének és felhasznált egyenleteknek függvénye, így a futásidő percek, akár hetek vagy hónapok is lehetnek. A megoldást folyamatosan ellenőrizni kell, mely eredményezheti az előfeldolgozás fázisában történő módosításokat. A futtatás előtt szem előtt kell tartani mely információkat szeretnénk megkapni a szimuláció végeredményeként. 2.2 Megoldó futtatása (Solver) Fizikai modell meghatározása, beállítása A numerikus modell meghatározása, paramétereinek beállítása A számítás és a megoldás monitorozása, követése A fizikai terek és numerikus matematikai kapcsolatok meghatározása Leállási kritériumok A szimuláció ellenőrző lépéseit és a végeredményének feldolgozását az utófeldolgozó fázisban végezzük el, mely szintén eredményezheti a korábbi fázisok módosítását, esetleg újbóli elkezdését. 4
6 2.3 Utófeldolgozás (Post-Processing) Eredmények vizsgálata, kiértékelése A modell esetleges módosítása (például hálófinomítás) 3. FORGÓ BERENDEZÉSEK A NUMERIKUS ÁRAMLÁSTANBAN ÉS AZ ALKALMAZOTT EGYENLETEK A mindennapi életben különbféle technológiai és folyadékszállítási feladatok esetén alkalmazunk forgó áramlástechnikai berendezéseket. A technológiai folyamatok kémiai technológiai rendszerekben keverési műveleteknél, ahol tartályokban elhelyezett különböző anyagok homogenizálását vagy szétválasztását végzik. A technológiai rendszerekben az anyagokat szállítóberendezések segítségével mozgatják egyik technológiai pontból a másikba, ebbe a csoportba tartoznak a szivattyúk. Mindkét felsorolt csoportba tengelyen bevitt mechanikai teljesítmény adódik át a rendszerben lévő közegnek, ezáltal a közeg mozgási energiája megváltozik vagy hő formájában elnyelődik. 3.1 Az áramlás alapegyenletei Az összenyomhatatlannak tekinthető folyékony közeg turbulens áramlása esetére az áramlás terében az alábbi alapegyenletek írhatók fel: Tömegmegmaradás tétele: v 0 Reynolds féle mozgásegyenlet: v p 1 ( ) v v U v Div FR t ahol: U az erőtér potenciál függvénye, FR v v látszólagos turbulens feszültségtenzor. (0.1) (0.2) Izotermikus turbulens áramlás esetében a fenti négy skalár egyenlet áll rendelkezésre a p r, t nyomás-eloszlás meghatározására, azonban a fenti vr,t egyenletekben az sebesség- és F R látszólagos turbulens feszültségtenzor és az turbulens disszipáció számítása során további ismeretlen függvények is fellépnek. Így az ismeretlen függvények száma több mint a rendelkezésre álló skalár differenciál egyenletek száma: vagyis a megoldandó differenciálegyenlet-rendszer alulhatározott. Ebből az következik, hogy a fenti egyenletrendszert ki kell még egészíteni további egyenletekkel. E cél teljesítésének érdekében felírhatjuk a 2 energia alábbi mérlegegyenletet k v v összefüggéssel definiált fajlagos turbulens kinetikus 5
7 ahol: dk v v p v v : v div v k Div v v 0 dt 2 v : v v turbulens disszipáció 3.2 Keverőtartály Geometriai előkészítés A szimuláció első lépése az áramlás terének geometriai kialakítása, amelynek főméretei a mellékelt műhelyrajzon láthatóak ( 2. ábra). A vázolt tartály egy zárt keverőteret határol, amely egy szigetelt fedéllel van ellátva. A fedélen lévő nyílások különféle mérő és kiegészítő berendezések felszerelésére, valamint a keverő tartály feltöltésére szolgálnak. A tartály fedőlapjának közepén látható a keverőszár kivezetése, amelyhez közvetlenül egy hajtómotor csatlakozik. A szimulációhoz a műhelyrajz adatai alapján GAMBIT modellező szoftverrel az alábbi geometria készült (3. ábra). A keverőtartályban a hajtó tengely alsó részén három darab, a vízszinteshez képest kb. 15 fokos szöget bezáró enyhén ívelt ellipszis profilú és ívelt keverőlapát helyezkedik el. A lapátok a hajtó tengelyhez való csatlakozásánál a kis hajlásszögű bonyolult háromdimenziós görbék menti felületek csatlakozását eredményezi, amely a hálózás során nem elhanyagolható jelentőségű lesz. 2. ábra Keverőtartály 6
8 A számítások végrehajtása érdekében a vizsgálati áramlási tartomány három egy a lapátot tartalmazó keverő, egy ívelt fenéklappal határolt hengeres, valamint egy hengerpalásttal határolt térre lett felosztva, amelyet a 3. ábra szemléltet. A modellező szoftver segítségével választottuk meg a térfogati tartományok anyagjellemzőit, illetve a határoló felületek szerepét a későbbi szimuláció során Numerikus háló 3. ábra Keverőtartály A numerikus szimulációjához a vizsgálandó áramlási teret fel kell osztani egy háromdimenziós elemekből álló hálózott térre. A matematikai megoldót és a perem, valamit a kezdeti feltételeket ezekre az elemi terekre inicializáljuk. A számítás gyorsasága és pontossága lényegesesen függ a létrehozott hálóelemek összetételétől és kialakításától. A hálózás során a bonyolult geometria és a korábban említett kis hajlásszögű felületcsatlakozások sűrű és nem jól kezelhető hálót eredményeztek. Ezért a cellaméretet - ennek megfelelően - nem lehetett egy bizonyos érték felé emelni, mert ezen érték felett a térfogati hálózás nem volt eredményes, vagy nem szolgáltatott elfogadható eredményeket a futtatás végeztével. 4. ábra Cellatípusok 7
9 Az áramlási térben lévő bonyolult csatlakozások miatt a kézi hálózás adta előnyök sem voltak kihasználhatók, mert a hálózás nem eredményezett térfogati cellákat. A számítógép ilyen próbálkozásaink esetében mindig hibaüzenettel állt le. Így végül a felsorolt nehézségek miatt automatikus TGrid típusú hálózási eljárás került alkalmazásra, amely során a Tet/Hybrid hálóelemek 0.2-es hálóosztással bizonyultak megfelelőnek (megjegyzés: 1.8 m tartálymagasság a geometria létrehozása során 18 egységet jelentett, ennek megfelelően pedig egy hálóosztás 0.2 egységet!). A TGrid típusú hálózással elsősorban négylapú ún. tetrahedral, másodsorban pedig hatlapú (hexahedral), gúla (pyramidal) és ék (wedge) alakú térfogati elemek kombinációja került alkalmazásra. 5. ábra TGrid típusú hálózott tér A felület hálózás hatása TGrid hálózásal követhető nyomon a 2. ábra különböző képein. Az (a) kép a négylapú hálóelemek általános alakját mutatja, amikor felület hálózás nem előzte meg a TGrid hálózási típus alkalmazását, vagy ha az összes előhálózott felület Tri-Pave séma használatával került behálózásra. Ha egy Quad-Map hálót hoz létre a test valamelyik felületén a TGrid hálózást megelőzően, akkor a (b) ábrának megfelelő elrendezést kapja. Majd a GAMBIT gúla hálóelemeket hoz létre ennek a felületnek a közelében (3. ábra c) és négylapú elemeket az áramlási tér további részein. A szimulációhoz elkészített térfogati háló darab cellát tartalmazott, amely hálózatot a 4. ábra szemlélteti. Az ábrán jól látható a három térfogati tartomány és a Tet/Hybrid hálózat elrendeződése Numerikus szimuláció A numerikus szimuláció során a 4. bekezdésben megadott alapegyenletek megoldását a FLUENT szimulációs szoftver által felkínált un. renormalizált (RNG) k- turbulencia modell alkalmazásával végeztük el. Ahol a fajlagos kinetikai energia mérlegegyenlete az alábbi egyenlet formájában kerül alkalmazásra. 8
10 k k ku G G Y S t x x x i k eff k b M k i j j A fenti kifejezésben is szereplő turbulens disszipáció meghatározására pedig a 2 u C G C G C R S t x x x k k i eff 1 k 3 b 2 i j j traszport egyenletet alkalmazzuk. Az renormalizált (RNG) modell az általános amely magában foglalja a következőket: k k modell egy finomított változata, Az RNG modell az egyenlet hozzáadásával lényegesen javítja az áramlás számítási pontosságát a gyorsan változó tartományokban. Magában foglalja a turbulencia örvénylő hatását, így fokozza az örvényes áramlás számítási pontosságát. Az RNG modell el van látva egy analitikus formulával a turbulens Prandtl szám kiszámításához, mert az általános k modell egy alkalmazásfüggő konstans értéket használ. Míg az általános k modell nagy Reynolds számoknál alkalmazható, addig az RNG modell a viszkozitás hatásához analitikusan származtatott differenciál formulájával alkalmazható az áramlás alacsony Reynolds számoknál is. Ez azonban függ a fal közeli régiók megfelelő használatától. Az RNG modell az áramlás pontosabb és valóságosabb közelítését teszi lehetővé és szélesebb körben alkalmazható mint az általános k modell. A modell által használt viszkozitás hatását az alábbi egyenlettel vehetjük figyelembe. k 2 k d 1.72 ˆ 3 ˆ 1 Ahol az egyenletekben szereplő tagok értékei a következő formában adódnak: ˆ= eff C R 100 C 0,0845 C 1 1 k V dˆ Sk ; 4,38; 0,012 C 1, 42; C 1, A mozgó felületek és pontok esetén a numerikus hálón a csomópontok egymáshoz képest elmozdulnak, amely illesztési, valamint fizikai és numerikus hibát eredményezhet. Azonban ez csökkenthető a háló finomításával, esetleg újabb felosztással. 9
11 6. ábra Mozgó határok 2D-ben 7. ábra Illeszkedő hálók Az 6. ábra elrendezése alapján láthatók a csatlakozási pontokban egymáshoz illeszkedő hálók. Ezt az illesztést a FLUENT peremfeltételek beállításainál kell elvégezni, hogy a számítások a határon át tudjanak jutni és ezáltal az egész áramlási térre számítani tudják a megoldandó differenciálegyenleteket. Az illesztés újabb számítókapacitást igényel, mert a kapcsolódási felületen lévő csomópontok többnyire nem esnek egybe így azok egymáshoz való viszonyát is figyelme kell venni. A mozgásokat a szimuláció futtatása során úgyszintén inicializálni kell a numerikus hálóra. Mivel a numerikus vizsgálat egyik célja a lapát forgatásához szükséges nyomaték meghatározása, ezért a keverőtér és tengely fordulatszámát a szimuláció során 60 [ ]-re állítottam és számítandó nyomaték helyét a lapát középpontjától 1 méter magasságban határoztam meg. Teret kitöltő folyadék víz volt. A futtatás a 25 órás futtatási ciklus alatt elfogadható eredményt hozott, mert a iterációtól a szimuláció konstans értéket mutatott a nyomaték tekintetében (8. ábra). A kialakult sebességteret a 9. ábra mutatja, melyen látható hogy a keverőlapáttól felfelé távolodva a keveredési intenzitás egyre csökken. min ábra Nyomaték számított értékének alakulása az iteráció során 10
12 9. ábra Sebességeloszlás z0.3, z1.5 axiális síkban Mindamellett a hiba alakulása is csökkenő tendenciát mutatott azonban az iterációs lépés során sem érte el minden iterációs érték az előre megadott es hibahatárt (10. ábra). 10. ábra Reziduális hiba alakulása Az elvégzett számítási feladat és az alkalmazott matematikai modell egy következő lépése, hogy a már meglévő eredményekre támaszkodva alkalmazhassunk további turbulencia modelleket is [2]. Ennek implementálása folyamatban van a FLUENT szoftverbe és ezeknek a modelleknek a validálásához a már meglévő eredményeket szeretnék felhasználni. 11
13 3.3 Forgó lapátozású keverőtartályok összehasonlító vizsgálata A 3.2 bekezdés megfontolásai alapján, a numerikus szimulációt használhatjuk összehasonlító vizsgálatokra ahol különböző keverővel ellátott tartályok áramlástechnikai viszonyait vizsgálhatjuk A vizsgálat célja Két 11cm magas és 5,9cm átmérőjű henger alakú főzőedényben egyenként mágneses és lapátos keverőlapáttal felszerelt berendezések keverési hatásának összehasonlítása. Alkalmazott anyagok: SNF FO4440SH típusú polimer (régi nevén SNF528+) kationos polielektrolit 0,05 g/l-es hígításban. Szuszpenzió: mádi kaolin szuszpenzió. 10 perc ultrahangos kezelés után a 24 óra alatt nem ülepedő frakció leválasztása melett, majd annak szárazanyagtartalma mérve: 0,1 g/l-es töménységű. A numerikus szimulációt megelőzően méréseket végeztek mindkét berendezésen ugyanazon feltételek mellett. A két berendezés használata során kapott eredmények összehasonlíthatók volta. Az két keverési mód összehasonlítása az 1. táblázat alapján az átmérő és fordulatszám függvényében történt. Fordulatszám D=4 cm keverőlapát [1/min] 1. táblázat Fordulatszám D=3 cm mágneses keverő [1/min] A mérési eredmények a fentebb vázolt összehasonlíthás esetén a Reynolds szám segítségével végezhetjük ahol: Re 2 D Re, a számított Reynolds szám D, a keverőlapát legnagyobb átmérője ω, szögsebesség, a víz kinematikai viszkozitás értéke 1,004 mm2/sec A vizsgálat eredményei Alkalmazott modell a szakirodalomban használt VOF modell. A felhasznált numerikus háló db elemet tartalmazott. Az eredmények egyszerűsített grafikus kiértékelését az 11. ábra ábra tartalmazza 500 [1/min] fordulatszám esetén. 12
14 Mágneses keverő használtatával kialakult eloszlások 11. ábra Numerikus háló 12. ábra Sebességeloszlás a sebességmaximumok szemléltetéséhez [m/s] 13. ábra Sebességeloszlás y=0 síkban [m/s] 13
15 14. ábra Turbulencia intenzitás az y=0 síkben [Pa] 15. ábra Statikus nyomáseloszlás az y=0 síkban [Pa] Lapátos keverő használtatával kialakult eloszlások 16. ábra Lapátozott keverő szemből és oldalnézeti képei 14
16 17. ábra Sebességeloszlás a sebességmaximumok szemléltetéséhez [m/s] 18. ábra Sebességeloszlás y=0 síkban [m/s] 19. ábra Turbulencia intenzitás az y=0 síkben [Pa] 20. ábra Statikus nyomáseloszlás az y=0 síkban [Pa] 4. ALKALMAZÁSI PÉLDÁK FORGÓ GÉPEK NUMERIKUS SZIMULÁCIÓJÁRA EGYSZERŰSÍTETT FORGÓ VONATKOZTATÁSI RENDSZERBEN [2] A oktatási segédlet célja konkrét alkalmazási példákon keresztül bemutatni forgó berendezések numerikus szimulációját. A fejezet három alkalmazási példán keresztül vezeti be az olvasót a numerikus szimulációnál alkalmazott technikákba. 15
17 4.1 Egyszerűsített forgó vonatkoztatási rendszer Feladat ismertetése 1 Adott egy szimmetriatengelyével adott elő- és hátlapjával behatárolt forgó hengeres meridián csatorna (továbbiakban járókerék). A járókerék kilépő (külső) átmérője 88,6cm. A közeg a belépő 8,86cm étmérőjű hengeres keresztmetszeten lép be 1,146m/s sebességgel. A meridiáncsatorna szélessége 6,2cm. A járókerék fordulatszáma 71,08 [ford/min]. A geometriát a 21. ábra szemlélteti. 21. ábra Járókerék kétdimenziós nézete Alkalmazott szoftver a ANSYS Fluent numerikus megoldó! A numerikus vizsgálatot kétdimenziós térben végezzük Beállítások és megoldás 1. Olvassa be a hálót File Read Case 2. Ellenőrizze a hálót Grid Check 3. Jelenítse meg a numerikus hálót Display Grid I. Lépés: Háló 1 A feladathoz előkészített numerikus hálót a single_rotating.zip elnevezésű csatolt állományban mellékeljük. 16
18 Mindent hagyjon alapbeállításon Kattintson a Display parancsra Zárja be a Grid Display panelt 22. ábra 2D meridiánmetszet elkészített hálója II. lépés: Mértékegységek 1. Állítsa be a fordulatszám (angular velocity) és a hosszúság (length) egységeit. Define Unit 17
19 Válassza ki az kerületi sebességet (angular-velocity) a mértékegységek (quantities) közül, és állítsa az értékét (unit) rpm-re. Válassza ki az hosszúságot (lenght) a mértékegységek (quantities) közül, és állítsa az értékét cm-re. Zárja be a Set Units panelt. 1. III. lépés: Számítási modell Állítsa be a számítás során alkalmazandó megoldót (solver) és engedélyezze a forgó axisszimmetrikus megoldót (Axisymmetric Swirl). Define Models Solver Tartsa meg az alapértelmezett nyomás alapú (pressure based) megoldót Válassza a forgó axisszimmetrikus kapcsolót a dimenzió (Space) listából Tarsa meg az abszolút (Absolute) kapcsolót a sebességformula (Velocity Formulation) listából Tartsa meg az alapértelmezett cella alapu Green-Gauss (Green-Gauss Cell Based) opciót a gradiens (Gradient Lis) listából Tartsa meg az alapértelmezett felületi sebesség (Superfical Velocity) beállítást a porozus formulák (Porosus Formulation) listában Zárja be a megoldó panelt. 2. Engedélyezze az általános k - turbulencia modellt a fokozott fal közeli módszerrel Define Models Viscous 18
20 Válassza a k epsilon -t a modell (Model) listából. Itt kinyílik a viszkózus (Viscous Modell) panel. Tarsa meg az alapértelmezett általános (Standard) beállítást a k-epsilon listában. Válassza a fokozott fal közeli módszert (Enhanced Wall Treatment) a fal közeli módszerek (Near-Wall Treatment) listából. Válassza az elfogadás (OK) nyomógombot az ablak bezárásához. IV. lépés: Anyagjellemzők 1. Használja a levegő (air) alapértelmezett beállításait Define Material Define Boundary onditions V. lépés: Peremfeltételek 19
21 1. Határozza meg a forgó vonatkoztatási rendszert a fluid-7 folyadéktérre. Válassza a mozgó vonatkoztatási rendszert (Moving Reference Frame) a mozgás típusok (Motion Type) listából Írja be a 71,08 ford/min sebesség értéket a kerületi sebesség szövegdobozba. Válassza az elfogadás (OK) nyomógombot az ablak bezárásához. 2. Állítsa be a belépésnél előírandó peremfeltételeket (velocity-inlet-2) 20
22 Válassza a sebesség beállításoknál (Velocity Specification Method) a legördülő listából a komponensenként (Components) lehetőséget Axiális sebesség 1,146 m/s Válassza a turbulencia (Turbulence) csoporton belül a legördülő menüben az intenzitás és hidraulikai átmérők (Intensity and Hydraulic Diameter) paramétereket. Turbulencia intenzitás 2,6% Hidraulikai átmérő 8,86cm Válassza az elfogadás (OK) nyomógombot az ablak bezárásához. 3. Állítsa be a kilépésnél előírandó peremfeltételeket (pressure-outlet-3) Hagyja a visszaáramlás irányának módszerét (Backflow Direction Specification Method) alapértelmezetten. (Normal to Boundary) Válassza a turbulencia (Turbulence) csoporton belül a legördülő menüben az intenzitás és viszkozitás (Intensity and Viskosity Ratio) paramétereket. Visszaáramlás turbulencia intenzitása 5% Visszaáramlás turbulens viszkozitásána aránya 10 Válassza az elfogadás (OK) nyomógombot az ablak bezárásához. 4. Fogadja el az előlap és hátlap falának alapértelmezett beállításait (wall-6) 21
23 5. Zárja be a peremfeltételek panelt VI. Lépés: Általános k - modell használata 1. A megoldó paramétereinek beállítása Solve Controls Solution Válassza a diszkretizáció csoport legördülő menüi közül a nyomás (Pressure) esetén PRESTO!-t. Válassza a másodrendű hátralépő numerikus közelítést (Second Order Upwind) közelítést a Momentum, Swirl Velocity, Turbulent Kinetik Energy, és Turbulens Dissipation Rate esetén. Hagyja alapértelmezetten az Under-Relaxation Factor értékeit. Válassza az elfogadás (OK) nyomógombot az ablak bezárásához. 2. Engedélyezze a reziduálosk monitorra nyomtatást (plotting) a számítás folyamán. Solve Monitors Residual 22
24 Engedélyezze az opciók (Options) csoportban a monitorra nyomtatás (Plot) parancsot Kattintson az OK-ra 3. Engedélyezze a tömegáram monitorra nyomtatását a kimeneti keresztmetszeten Solve Monitors Surface Válasza a felületi monitorok (Surface Monitors) számát 1-re Enegedélyezze a monitor-1 esetén a monitorra nyomtatást (Plot) és file-be való iratást (Write). Kattintson a monitor beállításaira nyomógombra (Define ), és nyissa mega felületi monitor panelt (Define Surface Monitor), a monitor speciális beállításaihoz. 23
25 4. Vállassza a monitorozni kívánt típusok (Report Type) legördülő menüből a tömegáramot (Mass Flow Rate) Válassza a pressure-outlet-3 nevű felületet a felületek listájából Válassza az OK gombot a monitorbeállítások elfogadásához Válassza az elfogadás (OK) nyomógombot az ablak bezárásához. Inicializálja az áramlási teret a velocity-inlet-2 elnevezésű peremfeltétel beállításai alapján Solve Initialize Initialize Válassza a számolás..-tól (Compute From) legördülő listából a velocityinlet-2 elemet Kattintson az Init nyomógombr, és zárja be a megoldó inicializálása (Solution Initialization) panelt. 5. Mentse el a case filet (disk-ke.cas.gz) File Write Case 6. Inditsa el a számítás 500db iterációval. Solve Iterate Irjon be 500-at az iterációk száma (Number of Iterations) mezőbe Kattintson az iteráció (Iterate) nyomógombra Zárja be az iteráció panelt. Az eredményt a 23. ábra mutatja. 24
26 7. Ellenőrizze a tömegmérleget Report Fluxes 23. ábra Tömegáram lefutási görbe Válassza a pressure-outlet-3 és velocity-inlet-2 felületelt a peremek (Boundaries) közül Hagyja alapértelmezetten a tömegáram kapcsolót (Mass Flow Rate) Kattintson a számítás (Compute) nyomógombra a fluxus meghatározásához. 8. Mentse el az adatfile-t (dsik-ke.dat.gz) File Write Data 25
27 VII. lépés: Az általános k - modell utófeldolgozása (kiértékelése) 1. Jelenítse meg a sebességeloszlást Display Vektors Állítsa a skálázás (Scale) értékét 50-re Állítsa a kihagyandó csomópontok számát (Skip) 1-re Kattintson a vektorbeállítások nyomógombra (Vektor Options..) hogy a vektorok beállítása panel megnyíljon Kapcsolja ki a Z komponens választógombját (Z component) Kattintson az elfogadás (Apply) nyomógombra, és zárja be a panelt (Close) Kattintson a Vektor panelen a Display nyomógombra és jelenítse meg a vektoros ábrát. (24. ábra) Zárja be a vektor panelt. 26
28 24. ábra Abszolút sebességeloszlás 2 Statikus nyomás ábrázolása színekkel kitöltött szintvonalakkal Display Contours Hagyja a Contours of legördülő menüben a Nyomás.. (Pressure ) és a Statikus nyomás (Static Pressure) választható értékekekt. Engedélyezze a kitöltést (Filled) opciót Kattintson a Display (25. ábra) nyomógombra és zárja be a Contours panelt. 27
29 25. ábra Statikus nyomáseloszlás 3. Készítsen egy y=állandó felületet a kiértékeléshez Surface Iso-Surface Válassza a konstans felületek legördülő menüből (Surface of Constans) a háló (Grid ) és Y-Koordináta (Y_Coordinate) értékeket. Kattintson a számolás (Compute) nyomógomra, a minimum és maximum értékek meghatározásához Írjon be az konstas Iso-Values ablakába 37cm-t. Nevezze el az új felületet y=37cm -nek az új felület név (New Surface Name) bekérő ablakban Kattitson a Készít nyomógombra (Create) a felület elkészítéséhez. Zárja be a panelt 28
30 4 Rajzoltassa ki a radiális sebesség értékeét az y=37cm felületen Plot XY Plot Válassza az Y tengely (Y Axis Function) esetén a sebesség (Velocity..) és ezen belül a radiális sebességet (Radial Velocity). Válassza ki a felületek közül (Surface) az y=37cm elnevezésű felületet. Kattintson a Plot (megjelenítás) nyomógombra. (26. ábra) Enegedélyezze az opciók menüben a irás file-ba (Write to File) aradiális sebesség profiljának elmentéséhez Kattintson az írás (Write ) nyomógombra, amire megjelenik a file választás (Select File) panel. Írja be a ke-date.xy file elnevezést a bekérőablakba és zárja be az ablakot. Zárja be a XY Plot panelt. 29
31 26. ábra Radiális irányú sebesség az y=37cm felületen VIII. Lépés: RNG k - turbulencia modell alkalmazása 1. Kapcsolja be az RNG k - modelt a fokozott fal közeli módszer opcióval Define Models Viscous 30
32 Válassza a k-epszilon listából az RNG modellt. Engedélyezze az RNG opciók között a más viszkozitási modell használata (Differential Viscosity Model) és jelentősen örvénylő áramlás (Swirl Dominated Flow) modellt. Tartsa meg a a fal közeli módszernél (Near-Wall Treatment) a fokozott fal menti módszer opciót. Kattintson az OK-ra a panel bezásáráshoz. 2. Folytassa a számolást 200 iteráción keresztül Solve Iterate 3. Mentse el a case és dat file-t (disk-rng.cas.gz és disk-rng.dat.gz) File Write Case & Data 1. IX. Lépés: Az RNG k - modell utófeldolgozása Jelenítse mega rradiális sebesség eloszlását az RNG megoldással, és hasonlítsa össze az általános k - megoldással. Plot XY Plot Kattintson a File betöltése (Load File..) nyomógombrak - adatok betöltéséhez Válassza ki a ke-data.xy file-t a választó böngésző ablakból. Kattintson az OK-ra Bizonyosodjon meg róla hogy az Y tengelyen a sebesség (Velocity..) és radiális sebesség (Radial Velocity) van kiválasztva a legördülő menüben. Bizonyosodjon meg róla hogy az y=37cm felület van e kiválasztva a felület listában. Kapcsolja ki a file-be írás opciót (Write to File) Kattintson a görbék nyomógombra (Curves..) és nyissa meg a görbék az XY megjelítése panelt (Curves Solution XY Plot), ahol megadhatunk az RNG k - 31
33 modellhát más jelölőket. Válassza a 0. számú görbét a Curve # ablakban Válassza a (x) jelölőt a szimbólumok közül Kattintson az elfogadás (Apply) nyomógombra és zárja be a panelt Kattintson a megjelenítés parancsra (Plot) a Solution XY Plot panelon. (27. ábra) 27. ábra összehasonlító diagram Válassza a tengelyek (Axes ) nyomógombot, és nyissa meg az Axes Solution XY plot panelt, ahol állítsa be az x tengelyet a következőképpen. 32
34 Kapcsolja ki az automatikus skálázást (Auto Range) az opciók között Állítsa a minimum értéket 0-ra a maximum értéket 1-re. Fogadja el a beállításokat (Apply) és zárja be a panelt. Kattinson a megjelenítés nyomógombra a Solution XY Plot panelon 28. ábra Sebességprofil az x=0..1cm között 33
35 5. IRODALOM [1] Galántai, A., Jeney, A. Numerikus módszerek Miskolci Egyetem, 2006, MET [2] ANSYS Inc. Fluent és Gambit szoftverek dokumentációi [3] Fodor, B. CFD alapjai oktatási segédlet Miskolci Egyetem, 2012 [4] Czibere, T. Calculating Turbulent Flows Based on a Stochastic Model Journal of Computational and Applied Mechanics, Vol. 7. No. 1., (2006), pp [5] Czibere, T. Kalmár, L. Janiga, G. Fully-developed Isothermal and Incompressible Turbulent Flows in Passages, CMFF 06, The International Conference on Fluid Flow Technologies, 2006, Budapest [6] Czibere, T Folyékony kontinuumok turbulens mozgása Előadásvázlat,
HÍDTARTÓK ELLENÁLLÁSTÉNYEZŐJE
 HÍDTARTÓK ELLENÁLLÁSTÉNYEZŐJE Csécs Ákos * - Dr. Lajos Tamás ** RÖVID KIVONAT A Budapesti Műszaki és Gazdaságtudományi Egyetem Hidak és Szerkezetek Tanszéke megbízta a BME Áramlástan Tanszékét az M8-as
HÍDTARTÓK ELLENÁLLÁSTÉNYEZŐJE Csécs Ákos * - Dr. Lajos Tamás ** RÖVID KIVONAT A Budapesti Műszaki és Gazdaságtudományi Egyetem Hidak és Szerkezetek Tanszéke megbízta a BME Áramlástan Tanszékét az M8-as
Szívókönyökök veszteségeinek és sebességprofiljainak vizsgálata CFD szimuláció segítségével
 GANZ ENGINEERING ÉS ENERGETIKAI GÉPGYÁRTÓ KFT. Szívókönyökök veszteségeinek és sebességprofiljainak vizsgálata CFD szimuláció segítségével Készítette: Bogár Péter Háznagy Gergely Egyed Csaba Zombor Csaba
GANZ ENGINEERING ÉS ENERGETIKAI GÉPGYÁRTÓ KFT. Szívókönyökök veszteségeinek és sebességprofiljainak vizsgálata CFD szimuláció segítségével Készítette: Bogár Péter Háznagy Gergely Egyed Csaba Zombor Csaba
HŐÁTADÁS MODELLEZÉSE
 HŐÁTADÁS MODELLEZÉSE KOHÓMÉRNÖKI MESTERKÉPZÉSI SZAK HŐENERGIAGAZDÁLKODÁSI SZAKIRÁNY TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR TÜZELÉSTANI ÉS HŐENERGIA INTÉZETI TANSZÉK
HŐÁTADÁS MODELLEZÉSE KOHÓMÉRNÖKI MESTERKÉPZÉSI SZAK HŐENERGIAGAZDÁLKODÁSI SZAKIRÁNY TANTÁRGYI KOMMUNIKÁCIÓS DOSSZIÉ MISKOLCI EGYETEM MŰSZAKI ANYAGTUDOMÁNYI KAR TÜZELÉSTANI ÉS HŐENERGIA INTÉZETI TANSZÉK
SZAKDOLGOZAT VIRÁG DÁVID
 SZAKDOLGOZAT VIRÁG DÁVID 2010 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Áramlástan Tanszék SZÁRNY KÖRÜLI TURBULENS ÁRAMLÁS NUMERIKUS SZIMULÁCIÓJA NYÍLT FORRÁSKÓDÚ SZOFTVERREL VIRÁG
SZAKDOLGOZAT VIRÁG DÁVID 2010 Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Áramlástan Tanszék SZÁRNY KÖRÜLI TURBULENS ÁRAMLÁS NUMERIKUS SZIMULÁCIÓJA NYÍLT FORRÁSKÓDÚ SZOFTVERREL VIRÁG
Írja fel az általános transzportegyenlet integrál alakban! Definiálja a konvektív és konduktív fluxus fogalmát!
 Írja fel az általános transzportegyenlet integrál alakban! Definiálja a konvektív és konduktív fluxus fogalmát! Írja fel az általános transzportegyenletet differenciál alakban! Milyen mennyiségeket képviselhet
Írja fel az általános transzportegyenlet integrál alakban! Definiálja a konvektív és konduktív fluxus fogalmát! Írja fel az általános transzportegyenletet differenciál alakban! Milyen mennyiségeket képviselhet
Gázturbina égő szimulációja CFD segítségével
 TEHETSÉGES HALLGATÓK AZ ENERGETIKÁBAN AZ ESZK ELŐADÁS-ESTJE Gázturbina égő szimulációja CFD segítségével Kurucz Boglárka Gépészmérnök MSc. hallgató kurucz.boglarka@eszk.org 2015. ÁPRILIS 23. Tartalom Bevezetés
TEHETSÉGES HALLGATÓK AZ ENERGETIKÁBAN AZ ESZK ELŐADÁS-ESTJE Gázturbina égő szimulációja CFD segítségével Kurucz Boglárka Gépészmérnök MSc. hallgató kurucz.boglarka@eszk.org 2015. ÁPRILIS 23. Tartalom Bevezetés
Overset mesh módszer alkalmazása ANSYS Fluent-ben
 Overset mesh módszer alkalmazása ANSYS Fluent-ben Darázs Bence & Laki Dániel 2018.05.03. www.econengineering.com1 Overset / Chimaera / Overlapping / Composite 2018.05.03. www.econengineering.com 2 Khimaira
Overset mesh módszer alkalmazása ANSYS Fluent-ben Darázs Bence & Laki Dániel 2018.05.03. www.econengineering.com1 Overset / Chimaera / Overlapping / Composite 2018.05.03. www.econengineering.com 2 Khimaira
Négycsuklós mechanizmus modelljének. Adams. elkészítése, kinematikai vizsgálata,
 A példa megnevezése: A példa száma: A példa szintje: Modellezõ rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: Négycsuklós mechanizmus modellezése SZIE-K2 alap közepes - haladó Adams
A példa megnevezése: A példa száma: A példa szintje: Modellezõ rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: Négycsuklós mechanizmus modellezése SZIE-K2 alap közepes - haladó Adams
SZIMULÁCIÓ ÉS MODELLEZÉS AZ ANSYS ALKALMAZÁSÁVAL
 SZIMULÁCIÓ ÉS MODELLEZÉS AZ ANSYS ALKALMAZÁSÁVAL MAGYAR TUDOMÁNY NAPJA KONFERENCIA 2010 GÁBOR DÉNES FŐISKOLA CSUKA ANTAL TARTALOM A KÍSÉRLET ÉS MÉRÉS JELENTŐSÉGE A MÉRNÖKI GYAKORLATBAN, MECHANIKAI FESZÜLTSÉG
SZIMULÁCIÓ ÉS MODELLEZÉS AZ ANSYS ALKALMAZÁSÁVAL MAGYAR TUDOMÁNY NAPJA KONFERENCIA 2010 GÁBOR DÉNES FŐISKOLA CSUKA ANTAL TARTALOM A KÍSÉRLET ÉS MÉRÉS JELENTŐSÉGE A MÉRNÖKI GYAKORLATBAN, MECHANIKAI FESZÜLTSÉG
Szennyezőanyagok terjedésének numerikus szimulációja, MISKAM célszoftver
 Szennyezőanyagok terjedésének numerikus szimulációja, MISKAM célszoftver 1. A numerikus szimulációról általában A szennyeződés-terjedési modellek numerikus megoldása A szennyeződés-terjedési modellek transzportegyenletei
Szennyezőanyagok terjedésének numerikus szimulációja, MISKAM célszoftver 1. A numerikus szimulációról általában A szennyeződés-terjedési modellek numerikus megoldása A szennyeződés-terjedési modellek transzportegyenletei
Biomechanika előadás: Háromdimenziós véráramlástani szimulációk
 Biomechanika előadás: Háromdimenziós véráramlástani szimulációk Benjamin Csippa 1111, Budapest, Műegyetem rkp. 3. D ép. 3. em www.hds.bme.hu Tartalom Mire jó a CFD? 3D szimuláció előállítása Orvosi képtől
Biomechanika előadás: Háromdimenziós véráramlástani szimulációk Benjamin Csippa 1111, Budapest, Műegyetem rkp. 3. D ép. 3. em www.hds.bme.hu Tartalom Mire jó a CFD? 3D szimuláció előállítása Orvosi képtől
PONTSZÁM:S50p / p = 0. Név:. NEPTUN kód: ÜLŐHELY sorszám
 Kérem, þ jellel jelölje be képzését! AKM1 VBK Környezetmérnök BSc AT01 Ipari termék- és formatervező BSc AM01 Mechatronikus BSc AM11 Mechatronikus BSc ÁRAMLÁSTAN 2. FAK.ZH - 2013.0.16. 18:1-19:4 KF81 Név:.
Kérem, þ jellel jelölje be képzését! AKM1 VBK Környezetmérnök BSc AT01 Ipari termék- és formatervező BSc AM01 Mechatronikus BSc AM11 Mechatronikus BSc ÁRAMLÁSTAN 2. FAK.ZH - 2013.0.16. 18:1-19:4 KF81 Név:.
0,00 0,01 0,02 0,03 0,04 0,05 0,06 Q
 1. Az ábrában látható kapcsolási vázlat szerinti berendezés két üzemállapotban működhet. A maximális vízszint esetében a T jelű tolózár nyitott helyzetben van, míg a minimális vízszint esetén az automatikus
1. Az ábrában látható kapcsolási vázlat szerinti berendezés két üzemállapotban működhet. A maximális vízszint esetében a T jelű tolózár nyitott helyzetben van, míg a minimális vízszint esetén az automatikus
Forgattyús mechanizmus modelljének. Adams. elkészítése, kinematikai vizsgálata,
 A példa megnevezése: A példa száma: A példa szintje: Modellezõ rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: Forgattyús mechanizmus modellezése SZIE-K1 alap közepes - haladó Adams
A példa megnevezése: A példa száma: A példa szintje: Modellezõ rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: Forgattyús mechanizmus modellezése SZIE-K1 alap közepes - haladó Adams
Végeselem módszer 8. gyakorlat
 SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK Végeselem módszer 8. gyakorlat Feladat: tengelycsonk szilárdsági vizsgálata 30 40 35 25 3 5 60 15 1. ábra: Tengely meridián metszete A tengely mint
SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK Végeselem módszer 8. gyakorlat Feladat: tengelycsonk szilárdsági vizsgálata 30 40 35 25 3 5 60 15 1. ábra: Tengely meridián metszete A tengely mint
munkafüzet open eseményéhez
 Makrók használata az Excelben - munkafüzet open eseményéhez VBA-eljárás létrehozása Az Auto_Open makróval kapcsolatos fenti korlátozások megkerülhetők az Open eseményhez rendelt VBA-eljárással. Példa Auto_open
Makrók használata az Excelben - munkafüzet open eseményéhez VBA-eljárás létrehozása Az Auto_Open makróval kapcsolatos fenti korlátozások megkerülhetők az Open eseményhez rendelt VBA-eljárással. Példa Auto_open
TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI. 1. Bevezetés
 TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI Dr. Goda Tibor egyetemi docens Gép- és Terméktervezés Tanszék 1. Bevezetés 1.1. A végeselem módszer alapjai - diszkretizáció, - szerkezet felbontása kicsi szabályos elemekre
TERMÉKTERVEZÉS NUMERIKUS MÓDSZEREI Dr. Goda Tibor egyetemi docens Gép- és Terméktervezés Tanszék 1. Bevezetés 1.1. A végeselem módszer alapjai - diszkretizáció, - szerkezet felbontása kicsi szabályos elemekre
Technikai áttekintés SimDay 2013. H. Tóth Zsolt FEA üzletág igazgató
 Technikai áttekintés SimDay 2013 H. Tóth Zsolt FEA üzletág igazgató Next Limit Technologies Alapítva 1998, Madrid Számítógépes grafika Tudományos- és mérnöki szimulációk Mottó: Innováció 2 Kihívás Technikai
Technikai áttekintés SimDay 2013 H. Tóth Zsolt FEA üzletág igazgató Next Limit Technologies Alapítva 1998, Madrid Számítógépes grafika Tudományos- és mérnöki szimulációk Mottó: Innováció 2 Kihívás Technikai
1.1 Hasonlítsa össze a valós ill. ideális folyadékokat legfontosabb sajátosságaik alapján!
 Kérem, þ jellel jelölje be képzését! AKM VBK Környezetmérnök BSc AT0 Ipari termék- és formatervező BSc AM0 Mechatronikus BSc AM Mechatronikus BSc ÁRAMLÁSTAN. FAKULTATÍV ZH 203.04.04. KF8 Név:. NEPTUN kód:
Kérem, þ jellel jelölje be képzését! AKM VBK Környezetmérnök BSc AT0 Ipari termék- és formatervező BSc AM0 Mechatronikus BSc AM Mechatronikus BSc ÁRAMLÁSTAN. FAKULTATÍV ZH 203.04.04. KF8 Név:. NEPTUN kód:
FELADAT LEÍRÁSA MEGOLDÁS ANSYS-BAN
 FELADAT LEÍRÁSA Határozzuk meg az alábbi ábrán látható tartó reakcióit, súlypontvonalának eltolódását ANSYS végeselemes szoftver használatával 2, illetve 3 gerendaelem alkalmazásával. Hasonlítsuk össze
FELADAT LEÍRÁSA Határozzuk meg az alábbi ábrán látható tartó reakcióit, súlypontvonalának eltolódását ANSYS végeselemes szoftver használatával 2, illetve 3 gerendaelem alkalmazásával. Hasonlítsuk össze
A mikroskálájú modellek turbulencia peremfeltételeiről
 A mikroskálájú modellek turbulencia peremfeltételeiről Adjunktus Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Áramlástan Tanszék 27..23. 27..23. / 7 Általános célú CFD megoldók alkalmazása
A mikroskálájú modellek turbulencia peremfeltételeiről Adjunktus Budapesti Műszaki és Gazdaságtudományi Egyetem Gépészmérnöki Kar Áramlástan Tanszék 27..23. 27..23. / 7 Általános célú CFD megoldók alkalmazása
Projektfeladatok 2014, tavaszi félév
 Projektfeladatok 2014, tavaszi félév Gyakorlatok Félév menete: 1. gyakorlat: feladat kiválasztása 2-12. gyakorlat: konzultációs rendszeres beszámoló a munka aktuális állásáról (kötelező) 13-14. gyakorlat:
Projektfeladatok 2014, tavaszi félév Gyakorlatok Félév menete: 1. gyakorlat: feladat kiválasztása 2-12. gyakorlat: konzultációs rendszeres beszámoló a munka aktuális állásáról (kötelező) 13-14. gyakorlat:
Bonded és No Separation
 Bonded és No Separation Kun Péter Z82ADC Bonded A bonded contact magyarul kötöttséget, kötött érintkezést jelent. Két olyan alkatrészről van szó, amelyek érintkezési felületeiken nem tudnak elválni egymástól,
Bonded és No Separation Kun Péter Z82ADC Bonded A bonded contact magyarul kötöttséget, kötött érintkezést jelent. Két olyan alkatrészről van szó, amelyek érintkezési felületeiken nem tudnak elválni egymástól,
Végeselem módszer 7. gyakorlat
 SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK Végeselem módszer 7. gyakorlat (kidolgozta: Szüle Veronika egyetemi ts.) Feladat: harang sajátrezgéseinek meghatározása 500 100 500 1000 250 250 1.
SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK Végeselem módszer 7. gyakorlat (kidolgozta: Szüle Veronika egyetemi ts.) Feladat: harang sajátrezgéseinek meghatározása 500 100 500 1000 250 250 1.
CFX számítások a BME NTI-ben
 CFX számítások a BME NTI-ben Dr. Aszódi Attila igazgató, egyetemi docens BME Nukleáris Technikai Intézet CFD Workshop, 2005. április 18. Dr. Aszódi Attila, BME NTI CFD Workshop, 2005. április 18. 1 Hűtőközeg-keveredés
CFX számítások a BME NTI-ben Dr. Aszódi Attila igazgató, egyetemi docens BME Nukleáris Technikai Intézet CFD Workshop, 2005. április 18. Dr. Aszódi Attila, BME NTI CFD Workshop, 2005. április 18. 1 Hűtőközeg-keveredés
Az úszás biomechanikája
 Az úszás biomechanikája Alapvető összetevők Izomerő Kondíció állóképesség Mozgáskoordináció kivitelezés + Nem levegő, mint közeg + Izmok nem gravitációval szembeni mozgása + Levegővétel Az úszóra ható
Az úszás biomechanikája Alapvető összetevők Izomerő Kondíció állóképesség Mozgáskoordináció kivitelezés + Nem levegő, mint közeg + Izmok nem gravitációval szembeni mozgása + Levegővétel Az úszóra ható
Akusztikai tervezés a geometriai akusztika módszereivel
 Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
FELADAT LEÍRÁSA. A váz egyszerűsített geometria modelljét az alábbi ábra szemlélteti.
 FELADAT LEÍRÁSA Határozzuk meg az alábbi szorító vázában keletkező feszültségeloszlást, ha a csavaros szorítással biztosított szorító erő nagysága 1500 N. A váz anyaga alumínium, rugalmassági modulusza
FELADAT LEÍRÁSA Határozzuk meg az alábbi szorító vázában keletkező feszültségeloszlást, ha a csavaros szorítással biztosított szorító erő nagysága 1500 N. A váz anyaga alumínium, rugalmassági modulusza
PÉLDATÁR 10. 10. BEGYAKORLÓ FELADAT TÉRBELI FELADAT MEGOLDÁSA VÉGESELEM- MÓDSZERREL
 PÉLDATÁR 10. 10. BEGYAKORLÓ FELADAT TÉRBELI FELADAT MEGOLDÁSA VÉGESELEM- MÓDSZERREL Szerző: Dr. Oldal István 2 Végeselem-módszer 10. TÉRBELI FELADAT MEGOLDÁSA 10.1. Lépcsős tengely vizsgálata Tömör testként,
PÉLDATÁR 10. 10. BEGYAKORLÓ FELADAT TÉRBELI FELADAT MEGOLDÁSA VÉGESELEM- MÓDSZERREL Szerző: Dr. Oldal István 2 Végeselem-módszer 10. TÉRBELI FELADAT MEGOLDÁSA 10.1. Lépcsős tengely vizsgálata Tömör testként,
GÉPÉSZETI ALKALMAZOTT SZÁMÍTÁSTECHNIKA f iskolai mérnökhallgatók számára. A 4. gyakorlat anyaga. Adott: Geometriai méretek:
 SZÉCHENYI ISTVÁN EGYETEM KÖZLEKEDÉSI ÉS GÉPÉSZMÉRNÖKI INTÉZET ÁLTALÁNOS GÉPÉSZETI TANSZÉK GÉPÉSZETI ALKALMAZOTT SZÁMÍTÁSTECHNIKA f iskolai mérnökhallgatók számára A 4. gyakorlat anyaga Feladat: Saját síkjában
SZÉCHENYI ISTVÁN EGYETEM KÖZLEKEDÉSI ÉS GÉPÉSZMÉRNÖKI INTÉZET ÁLTALÁNOS GÉPÉSZETI TANSZÉK GÉPÉSZETI ALKALMAZOTT SZÁMÍTÁSTECHNIKA f iskolai mérnökhallgatók számára A 4. gyakorlat anyaga Feladat: Saját síkjában
A gradiens törésmutatójú közeg I.
 10. Előadás A gradiens törésmutatójú közeg I. Az ugrásszerű törésmutató változással szemben a TracePro-ban lehetőség van folytonosan változó törésmutatójú közeg definiálására. Ilyen érdekes típusú közegek
10. Előadás A gradiens törésmutatójú közeg I. Az ugrásszerű törésmutató változással szemben a TracePro-ban lehetőség van folytonosan változó törésmutatójú közeg definiálására. Ilyen érdekes típusú közegek
Numerical Modeling of Fluid Flows (BMEGEÁTAM5) 2014. 04. 01.
 Numerical Modeling of Fluid Flows (BMEGEÁTAM5) 2014. 04. 01. Balázs Farkas farkas [at] ara.bme.hu www.ara.bme.hu/~benedek/cfd/workbench Rule #1: Whatever you do, do NOT use space and accents in file names!
Numerical Modeling of Fluid Flows (BMEGEÁTAM5) 2014. 04. 01. Balázs Farkas farkas [at] ara.bme.hu www.ara.bme.hu/~benedek/cfd/workbench Rule #1: Whatever you do, do NOT use space and accents in file names!
Numerikus szimuláció a városklíma vizsgálatokban
 Numerikus szimuláció a városklíma vizsgálatokban BME Áramlástan Tanszék 2004. 1 Tartalom 1. Miért használunk numerikus szimulációt? 2. A numerikus szimuláció alapjai a MISKAM példáján 3. Egy konkrét MISKAM
Numerikus szimuláció a városklíma vizsgálatokban BME Áramlástan Tanszék 2004. 1 Tartalom 1. Miért használunk numerikus szimulációt? 2. A numerikus szimuláció alapjai a MISKAM példáján 3. Egy konkrét MISKAM
A diplomaterv keretében megvalósítandó feladatok összefoglalása
 A diplomaterv keretében megvalósítandó feladatok összefoglalása Diplomaterv céljai: 1 Sclieren résoptikai módszer numerikus szimulációk validálására való felhasználhatóságának vizsgálata 2 Lamináris előkevert
A diplomaterv keretében megvalósítandó feladatok összefoglalása Diplomaterv céljai: 1 Sclieren résoptikai módszer numerikus szimulációk validálására való felhasználhatóságának vizsgálata 2 Lamináris előkevert
A végeselem módszer alapjai. 2. Alapvető elemtípusok
 A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
(Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja.
 Testmodellezés Testmodellezés (Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja. A tervezés (modellezés) során megadjuk a objektum geometria
Testmodellezés Testmodellezés (Solid modeling, Geometric modeling) Testmodell: egy létező vagy elképzelt objektum digitális reprezentációja. A tervezés (modellezés) során megadjuk a objektum geometria
A keverés fogalma és csoportosítása
 A keverés A keverés fogalma és csoportosítása olyan vegyipari művelet, melynek célja a homogenizálás (koncentráció-, hőmérséklet-, sűrűség-, viszkozitás kiegyenlítése) vagy a részecskék közvetlenebb érintkezésének
A keverés A keverés fogalma és csoportosítása olyan vegyipari művelet, melynek célja a homogenizálás (koncentráció-, hőmérséklet-, sűrűség-, viszkozitás kiegyenlítése) vagy a részecskék közvetlenebb érintkezésének
XXI. NEMZETKÖZI GÉPÉSZETI TALÁLKOZÓ
 XXI. NEMZETKÖZI GÉPÉSZETI TALÁLKOZÓ Szaszák Norbert II. éves doktoranduszhallgató, Dr. Szabó Szilárd Miskolci Egyetem, Áramlás- és Hőtechnikai Gépek Tanszéke 2013. Összefoglaló Doktori téma: turbulenciagenerátorok
XXI. NEMZETKÖZI GÉPÉSZETI TALÁLKOZÓ Szaszák Norbert II. éves doktoranduszhallgató, Dr. Szabó Szilárd Miskolci Egyetem, Áramlás- és Hőtechnikai Gépek Tanszéke 2013. Összefoglaló Doktori téma: turbulenciagenerátorok
Artériás véráramlások modellezése
 Artériás véráramlások modellezése Csippa Benjamin 1111, Budapest, Műegyetem rkp. 3. D ép. 3. em www.hds.bme.hu Előadás tartalma Bevezetés Aneurizmák Modellezési lehetőségek Orvosi képfeldolgozás Numerikus
Artériás véráramlások modellezése Csippa Benjamin 1111, Budapest, Műegyetem rkp. 3. D ép. 3. em www.hds.bme.hu Előadás tartalma Bevezetés Aneurizmák Modellezési lehetőségek Orvosi képfeldolgozás Numerikus
Első lépések. File/New. A mentés helyét érdemes módosítani! Pl. Dokumentumok. Fájlnév: pl. Proba
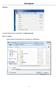 Első lépések File/New A mentés helyét érdemes módosítani! Pl. Dokumentumok Fájlnév: pl. Proba (megj. ékezetes karaktereket nem használhatunk a fájlnévben) 1 Konvejor pálya elkészítése System/New Rendszer
Első lépések File/New A mentés helyét érdemes módosítani! Pl. Dokumentumok Fájlnév: pl. Proba (megj. ékezetes karaktereket nem használhatunk a fájlnévben) 1 Konvejor pálya elkészítése System/New Rendszer
Csatlakozás a végeselem modulhoz SolidWorks-ben
 Csatlakozás a végeselem modulhoz SolidWorks-ben Meglévő alkatrész vagy összeállítás modellt ellenőrizhetünk különböző terhelési esetekben a CAD rendszer végeselem moduljával ( SolidWorks Simulation ).
Csatlakozás a végeselem modulhoz SolidWorks-ben Meglévő alkatrész vagy összeállítás modellt ellenőrizhetünk különböző terhelési esetekben a CAD rendszer végeselem moduljával ( SolidWorks Simulation ).
Nyomtató telepítése. 1. ábra Nyomtatók és faxok Nyomtató hozzáadása
 Ha ki szeretnénk nyomtatni az elkészített dokumentumainkat, akkor a nyomtató vezérlőprogramját a számítógépre kell telepítenünk. Ezáltal a számítógép irányítani tudja a nyomtatót, érzékeli üzeneteit. A
Ha ki szeretnénk nyomtatni az elkészített dokumentumainkat, akkor a nyomtató vezérlőprogramját a számítógépre kell telepítenünk. Ezáltal a számítógép irányítani tudja a nyomtatót, érzékeli üzeneteit. A
QGIS gyakorló. --tulajdonságok--stílus fül--széthúzás a terjedelemre).
 QGIS gyakorló Cím: A Contour-, a Point sampling tool és a Terrain profile pluginek használata. DEM letöltése: http://www.box.net/shared/1v7zq33leymq1ye64yro A következő gyakorlatban szintvonalakat fogunk
QGIS gyakorló Cím: A Contour-, a Point sampling tool és a Terrain profile pluginek használata. DEM letöltése: http://www.box.net/shared/1v7zq33leymq1ye64yro A következő gyakorlatban szintvonalakat fogunk
ANSYS indítása, majd válasszunk munkakönyvtárat és jobname-t. A munkakönyvtár legyen pl C:\Temp. Utility Menu -> File -> Change Directory...
 ANSYS indítása, majd válasszunk munkakönyvtárat és jobname-t. A munkakönyvtár legyen pl C:\Temp. Utility Menu -> File -> Change Directory... Utility Menu -> File -> Change Jobname... Utility Menu -> File
ANSYS indítása, majd válasszunk munkakönyvtárat és jobname-t. A munkakönyvtár legyen pl C:\Temp. Utility Menu -> File -> Change Directory... Utility Menu -> File -> Change Jobname... Utility Menu -> File
Hidraulika. 1.előadás A hidraulika alapjai. Szilágyi Attila, NYE, 2018.
 Hidraulika 1.előadás A hidraulika alapjai Szilágyi Attila, NYE, 018. Folyadékok mechanikája Ideális folyadék: homogén, súrlódásmentes, kitölti a rendelkezésre álló teret, nincs nyírófeszültség. Folyadékok
Hidraulika 1.előadás A hidraulika alapjai Szilágyi Attila, NYE, 018. Folyadékok mechanikája Ideális folyadék: homogén, súrlódásmentes, kitölti a rendelkezésre álló teret, nincs nyírófeszültség. Folyadékok
TURBÓFÚVÓ AGGREGÁT ÁRAMLÁS- ÉS HŐTECHNIKAI NUMERIKUS ANALÍZISE
 Multidiszciplináris tudományok, Z. kötet. (2013) 1. sz. pp. 133-140. TURBÓFÚVÓ AGGREGÁT ÁRAMLÁS- ÉS HŐTECHNIKAI NUMERIKUS ANALÍZISE Fodor Béla 1, Kalmár László 2 1 tanársegéd, 2 ny. egyetemi docens Miskolci
Multidiszciplináris tudományok, Z. kötet. (2013) 1. sz. pp. 133-140. TURBÓFÚVÓ AGGREGÁT ÁRAMLÁS- ÉS HŐTECHNIKAI NUMERIKUS ANALÍZISE Fodor Béla 1, Kalmár László 2 1 tanársegéd, 2 ny. egyetemi docens Miskolci
Előszó.. Bevezetés. 1. A fizikai megismerés alapjai Tér is idő. Hosszúság- és időmérés.
 SZABÓ JÁNOS: Fizika (Mechanika, hőtan) I. TARTALOMJEGYZÉK Előszó.. Bevezetés. 1. A fizikai megismerés alapjai... 2. Tér is idő. Hosszúság- és időmérés. MECHANIKA I. Az anyagi pont mechanikája 1. Az anyagi
SZABÓ JÁNOS: Fizika (Mechanika, hőtan) I. TARTALOMJEGYZÉK Előszó.. Bevezetés. 1. A fizikai megismerés alapjai... 2. Tér is idő. Hosszúság- és időmérés. MECHANIKA I. Az anyagi pont mechanikája 1. Az anyagi
Fluid-structure interaction (FSI)
 Fluid-structure interaction (FSI) Készítette: Bárdossy Gergely tanársegéd 1111, Budapest, Műegyetem rkp. 3. D ép. 3. em Tel: 463 16 80 Fax: 463 30 91 www.hds.bme.hu Tartalom Bevezetés, alapfogalmak Áramlás
Fluid-structure interaction (FSI) Készítette: Bárdossy Gergely tanársegéd 1111, Budapest, Műegyetem rkp. 3. D ép. 3. em Tel: 463 16 80 Fax: 463 30 91 www.hds.bme.hu Tartalom Bevezetés, alapfogalmak Áramlás
Artériás véráramlások modellezése
 Artériás véráramlások modellezése Csippa Benjamin 1111, Budapest, Műegyetem rkp. 3. D ép. 3. em www.hds.bme.hu Előadás tartalma Bevezetés Aneurizmák Modellezési lehetőségek Orvosi képfeldolgozás Numerikus
Artériás véráramlások modellezése Csippa Benjamin 1111, Budapest, Műegyetem rkp. 3. D ép. 3. em www.hds.bme.hu Előadás tartalma Bevezetés Aneurizmák Modellezési lehetőségek Orvosi képfeldolgozás Numerikus
Lemezalkatrész modellezés. SolidEdge. alkatrészen
 A példa megnevezése: A példa száma: A példa szintje: Modellezõ rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: Lemezalkatrész modellezés SZIE-A5 alap közepes - haladó SolidEdge CAD 3D
A példa megnevezése: A példa száma: A példa szintje: Modellezõ rendszer: Kapcsolódó TÁMOP tananyag rész: A feladat rövid leírása: Lemezalkatrész modellezés SZIE-A5 alap közepes - haladó SolidEdge CAD 3D
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Épületgépészeti és Gépészeti Eljárástechnika Tanszék HALLGATÓI SEGÉDLET
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Épületgépészeti és Gépészeti Eljárástechnika Tanszék HALLGATÓI SEGÉDLET Keverő ellenállás tényezőjének meghatározása Készítette: Hégely László, átdolgozta
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM Épületgépészeti és Gépészeti Eljárástechnika Tanszék HALLGATÓI SEGÉDLET Keverő ellenállás tényezőjének meghatározása Készítette: Hégely László, átdolgozta
LabVIEW példák és bemutatók KÉSZÍTETTE: DR. FÜVESI VIKTOR
 LabVIEW példák és bemutatók KÉSZÍTETTE: DR. FÜVESI VIKTOR LabVIEW-ról National Instruments (NI) által fejlesztett Grafikus programfejlesztő környezet, méréstechnikai, vezérlési, jelfeldolgozási feladatok
LabVIEW példák és bemutatók KÉSZÍTETTE: DR. FÜVESI VIKTOR LabVIEW-ról National Instruments (NI) által fejlesztett Grafikus programfejlesztő környezet, méréstechnikai, vezérlési, jelfeldolgozási feladatok
Hidrosztatika. Folyadékok fizikai tulajdonságai
 Hidrosztatika A Hidrosztatika a nyugalomban lévő folyadékoknak a szilárd testekre, felületekre gyakorolt hatásával foglalkozik. Tárgyalja a nyugalomban lévő folyadékok nyomásviszonyait, vizsgálja a folyadékba
Hidrosztatika A Hidrosztatika a nyugalomban lévő folyadékoknak a szilárd testekre, felületekre gyakorolt hatásával foglalkozik. Tárgyalja a nyugalomban lévő folyadékok nyomásviszonyait, vizsgálja a folyadékba
Végeselem módszer 5. gyakorlat
 SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK Végeselem módszer 5. gyakorlat Feladat: szakító próbatest szilárdsági vizsgálata A szakító próbatest, lévén forgásszimmetrikus geometriával rendelkező
SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK Végeselem módszer 5. gyakorlat Feladat: szakító próbatest szilárdsági vizsgálata A szakító próbatest, lévén forgásszimmetrikus geometriával rendelkező
KÖSZÖNTJÜK HALLGATÓINKAT!
 2010. november 10. KÖSZÖNTJÜK HALLGATÓINKAT! Önök Dr. Horváth Zoltán Módszerek, amelyek megváltoztatják a világot A számítógépes szimuláció és optimalizáció jelentősége c. előadását hallhatják! 1 Módszerek,
2010. november 10. KÖSZÖNTJÜK HALLGATÓINKAT! Önök Dr. Horváth Zoltán Módszerek, amelyek megváltoztatják a világot A számítógépes szimuláció és optimalizáció jelentősége c. előadását hallhatják! 1 Módszerek,
NYOMÁS ÉS NYOMÁSKÜLÖNBSÉG MÉRÉS. Mérési feladatok
 Hidrodinamikai Rendszerek Tanszék Készítette:... kurzus Elfogadva: Dátum:...év...hó...nap NYOMÁS ÉS NYOMÁSKÜLÖNBSÉG MÉRÉS Mérési feladatok 1. Csővezetékben áramló levegő nyomásveszteségének mérése U-csöves
Hidrodinamikai Rendszerek Tanszék Készítette:... kurzus Elfogadva: Dátum:...év...hó...nap NYOMÁS ÉS NYOMÁSKÜLÖNBSÉG MÉRÉS Mérési feladatok 1. Csővezetékben áramló levegő nyomásveszteségének mérése U-csöves
Autodesk Inventor Professional New Default Standard.ipt
 Adaptív modellezési technika használata Feladat: Készítse el az alábbi ábrán látható munkahenger összeállítási modelljét adaptív technikával! 1. Indítson egy új feladatot! New Default Standard.ipt 2. A
Adaptív modellezési technika használata Feladat: Készítse el az alábbi ábrán látható munkahenger összeállítási modelljét adaptív technikával! 1. Indítson egy új feladatot! New Default Standard.ipt 2. A
Végeselem módszer 5. gyakorlat (kidolgozta: Dr. Pere Balázs) Feladat: Forgásszimmetrikus test elmozdulás- és feszültség állapotának vizsgálata
 SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK Végeselem módszer 5. gyakorlat (kidolgozta: Dr. Pere Balázs) Feladat: Forgásszimmetrikus test elmozdulás- és feszültség állapotának vizsgálata Adottak
SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK Végeselem módszer 5. gyakorlat (kidolgozta: Dr. Pere Balázs) Feladat: Forgásszimmetrikus test elmozdulás- és feszültség állapotának vizsgálata Adottak
Rajz 06 gyakorló feladat
 Rajz 06 gyakorló feladat Attribútumos szövegmező A feladat megoldásához szükséges fájlok: Rjz06k_Szelepház.ipt Feladat: Készítsen attribútumos szövegmezőt, ahol is a szövegmező rovatai a modell iproperties
Rajz 06 gyakorló feladat Attribútumos szövegmező A feladat megoldásához szükséges fájlok: Rjz06k_Szelepház.ipt Feladat: Készítsen attribútumos szövegmezőt, ahol is a szövegmező rovatai a modell iproperties
MATLAB alapismeretek X. Egy összetettebb példa grafikus felhasználói felület (GUI) létrehozására
 Alkalmazott Informatikai Intézeti Tanszék MŰSZAKI INFORMATIKA Dr.Dudás László 0. MATLAB alapismeretek X. Alkalmazott Informatikai Intézeti Tanszék MŰSZAKI INFORMATIKA Dr.Dudás László 1. Készítsük el az
Alkalmazott Informatikai Intézeti Tanszék MŰSZAKI INFORMATIKA Dr.Dudás László 0. MATLAB alapismeretek X. Alkalmazott Informatikai Intézeti Tanszék MŰSZAKI INFORMATIKA Dr.Dudás László 1. Készítsük el az
GIRO GSM MODEM/VPN KAPCSOLAT TELEPÍTÉSI ÚTMUTATÓ
 GIRO GSM MODEM/VPN KAPCSOLAT TELEPÍTÉSI ÚTMUTATÓ Készítette A jelen dokumentum tartalma szerzői jogi védelem alatt áll, a mű felhasználói jogai a -t illetik. A dokumentumot az Ügyfél korlátlan számban
GIRO GSM MODEM/VPN KAPCSOLAT TELEPÍTÉSI ÚTMUTATÓ Készítette A jelen dokumentum tartalma szerzői jogi védelem alatt áll, a mű felhasználói jogai a -t illetik. A dokumentumot az Ügyfél korlátlan számban
Oktatás. WiFi hálózati kapcsolat beállítása Windows XP és Windows 7-es számítógépeken. SZTE Egyetemi Számítóközpont
 Oktatás WiFi hálózati kapcsolat beállítása Windows XP és Windows 7-es számítógépeken SZTE Egyetemi Számítóközpont WLAN kapcsolat beállítása 1 Tartalom Windows XP... 2 Tanúsítvány telepítése... 2 WPA2 védett
Oktatás WiFi hálózati kapcsolat beállítása Windows XP és Windows 7-es számítógépeken SZTE Egyetemi Számítóközpont WLAN kapcsolat beállítása 1 Tartalom Windows XP... 2 Tanúsítvány telepítése... 2 WPA2 védett
Rácsvonalak parancsot. Válasszuk az Elsődleges függőleges rácsvonalak parancs Segédrácsok parancsát!
 Konduktometriás titrálás kiértékelése Excel program segítségével (Office 2007) Alapszint 1. A mérési adatokat írjuk be a táblázat egymás melletti oszlopaiba. Az első oszlopba kerül a fogyás, a másodikba
Konduktometriás titrálás kiértékelése Excel program segítségével (Office 2007) Alapszint 1. A mérési adatokat írjuk be a táblázat egymás melletti oszlopaiba. Az első oszlopba kerül a fogyás, a másodikba
Bevezető. Mi is az a GeoGebra? Tények
 Bevezető Mi is az a GeoGebra? dinamikus matematikai szoftver könnyen használható csomagolásban az oktatás minden szintjén alkalmazható tanításhoz és tanuláshoz egyaránt egyesíti az interaktív geometriát,
Bevezető Mi is az a GeoGebra? dinamikus matematikai szoftver könnyen használható csomagolásban az oktatás minden szintjén alkalmazható tanításhoz és tanuláshoz egyaránt egyesíti az interaktív geometriát,
A hatékony mérnöki tervezés eszközei és módszerei a gyakorlatban
 A hatékony mérnöki tervezés eszközei és módszerei a gyakorlatban Korszerű mérnöki technológiák (CAD, szimuláció, stb.) alkalmazásának bemutatása a készülékfejlesztés kapcsán Előadó: Szarka Zsolt H-TEC
A hatékony mérnöki tervezés eszközei és módszerei a gyakorlatban Korszerű mérnöki technológiák (CAD, szimuláció, stb.) alkalmazásának bemutatása a készülékfejlesztés kapcsán Előadó: Szarka Zsolt H-TEC
Folyami hidrodinamikai modellezés
 Folyami hidrodinamikai modellezés Dr. Krámer Tamás egyetemi docens BME Vízépítési és Vízgazdálkodási Tanszék Numerikus modellezés 0D 1D 2D 3D Alacsony Kézi számítások Részletesség és pontosság Bonyolultság
Folyami hidrodinamikai modellezés Dr. Krámer Tamás egyetemi docens BME Vízépítési és Vízgazdálkodási Tanszék Numerikus modellezés 0D 1D 2D 3D Alacsony Kézi számítások Részletesség és pontosság Bonyolultság
PÉLDATÁR 7. 7. BEGYAKORLÓ FELADAT SÍKFESZÜLTSÉGI PÉLDA MEGOLDÁSA VÉGESELEM-MÓDSZERREL
 PÉLDATÁR 7. 7. BEGYAKORLÓ FELADAT SÍKFESZÜLTSÉGI PÉLDA MEGOLDÁSA VÉGESELEM-MÓDSZERREL Szerző: Dr. Oldal István 2 Végeselem-módszer 7. PÉLDA SÍKFESZÜLTSÉGI ÁLLAPOTRA 7.1. Saroklemez vizsgálata Határozzuk
PÉLDATÁR 7. 7. BEGYAKORLÓ FELADAT SÍKFESZÜLTSÉGI PÉLDA MEGOLDÁSA VÉGESELEM-MÓDSZERREL Szerző: Dr. Oldal István 2 Végeselem-módszer 7. PÉLDA SÍKFESZÜLTSÉGI ÁLLAPOTRA 7.1. Saroklemez vizsgálata Határozzuk
1. feladat Összesen 25 pont
 1. feladat Összesen 25 pont Centrifugál szivattyúval folyadékot szállítunk az 1 jelű, légköri nyomású tartályból a 2 jelű, ugyancsak légköri nyomású tartályba. A folyadék sűrűsége 1000 kg/m 3. A nehézségi
1. feladat Összesen 25 pont Centrifugál szivattyúval folyadékot szállítunk az 1 jelű, légköri nyomású tartályból a 2 jelű, ugyancsak légköri nyomású tartályba. A folyadék sűrűsége 1000 kg/m 3. A nehézségi
Segédlet a gördülőcsapágyak számításához
 Segédlet a gördülőcsapágyak számításához Összeállította: Dr. Nguyen Huy Hoang Budapest 25 Feladat: Az SKF gyártmányú, SNH 28 jelű osztott csapágyházba szerelt 28 jelű egysorú mélyhornyú golyóscsapágy üzemi
Segédlet a gördülőcsapágyak számításához Összeállította: Dr. Nguyen Huy Hoang Budapest 25 Feladat: Az SKF gyártmányú, SNH 28 jelű osztott csapágyházba szerelt 28 jelű egysorú mélyhornyú golyóscsapágy üzemi
New Default Standard.ipt
 Adaptív modellezési technika használata Feladat: Készítse el az alábbi ábrán látható fejes szeg parametrikus modelljét! A kidolgozáshoz használja az MSZ EN 22341-es szabványban megadott értékeket! 1 1.
Adaptív modellezési technika használata Feladat: Készítse el az alábbi ábrán látható fejes szeg parametrikus modelljét! A kidolgozáshoz használja az MSZ EN 22341-es szabványban megadott értékeket! 1 1.
Pontfelhő létrehozás és használat Regard3D és CloudCompare nyílt forráskódú szoftverekkel. dr. Siki Zoltán
 Pontfelhő létrehozás és használat Regard3D és CloudCompare nyílt forráskódú szoftverekkel dr. Siki Zoltán siki.zoltan@epito.bme.hu Regard3D Nyílt forráskódú SfM (Structure from Motion) Fényképekből 3D
Pontfelhő létrehozás és használat Regard3D és CloudCompare nyílt forráskódú szoftverekkel dr. Siki Zoltán siki.zoltan@epito.bme.hu Regard3D Nyílt forráskódú SfM (Structure from Motion) Fényképekből 3D
Molekuláris dinamika I. 10. előadás
 Molekuláris dinamika I. 10. előadás Miről is szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten minden részecske mozgását szimuláljuk? Hogyan tudjuk megérteni a folyadékok,
Molekuláris dinamika I. 10. előadás Miről is szól a MD? nagy részecskeszámú rendszerek ismerjük a törvényeket mikroszkópikus szinten minden részecske mozgását szimuláljuk? Hogyan tudjuk megérteni a folyadékok,
Területi elemzések. Budapest, 2015. április
 TeIR Területi elemzések Felhasználói útmutató Budapest, 2015. április Tartalomjegyzék 1. BEVEZETŐ... 3 2. AZ ELEMZÉSBEN SZEREPLŐ MUTATÓ KIVÁLASZTÁSA... 4 3. AZ ELEMZÉSI FELTÉTELEK DEFINIÁLÁSA... 5 3.1.
TeIR Területi elemzések Felhasználói útmutató Budapest, 2015. április Tartalomjegyzék 1. BEVEZETŐ... 3 2. AZ ELEMZÉSBEN SZEREPLŐ MUTATÓ KIVÁLASZTÁSA... 4 3. AZ ELEMZÉSI FELTÉTELEK DEFINIÁLÁSA... 5 3.1.
Numerikus Áramlástan, Áramlások Numerikus Szimulációja
 Numerikus Áramlástan, Áramlások Numerikus Szimulációja (BMEGEÁTAG03, BMEGEÁTAG26) 2016. tavasz, 4. hét Dr. Kristóf Gergely tananyaga alapján (link) összeállította: Benedek Tamás E-mail: benedek [at] ara.bme.hu
Numerikus Áramlástan, Áramlások Numerikus Szimulációja (BMEGEÁTAG03, BMEGEÁTAG26) 2016. tavasz, 4. hét Dr. Kristóf Gergely tananyaga alapján (link) összeállította: Benedek Tamás E-mail: benedek [at] ara.bme.hu
Netis Vezetékes ADSL2+, N Modem Router Gyors Telepítési Útmutató
 Netis Vezetékes ADSL2+, N Modem Router Gyors Telepítési Útmutató Modell szám: DL4201 Tartalomjegyzék 1. A csomag tartalma... 1 2. Hardware csatlakoztatása... 1 3. A modem webes felületen történő beüzemelése...
Netis Vezetékes ADSL2+, N Modem Router Gyors Telepítési Útmutató Modell szám: DL4201 Tartalomjegyzék 1. A csomag tartalma... 1 2. Hardware csatlakoztatása... 1 3. A modem webes felületen történő beüzemelése...
Végeselem módszer 1. gyakorlat
 SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK Végeselem módszer 1. gyakorlat (kidolgozta: Dr. Pere Balázs egyetemi docens, Szüle Veronika, egyetemi tanársegéd) Feladat: síkbeli rácsos tartó y
SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK Végeselem módszer 1. gyakorlat (kidolgozta: Dr. Pere Balázs egyetemi docens, Szüle Veronika, egyetemi tanársegéd) Feladat: síkbeli rácsos tartó y
Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea
 Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea Geometrikus deformálható modellek Görbe evolúció Level set módszer A görbe evolúció parametrizálástól független mindössze geometriai
Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea Geometrikus deformálható modellek Görbe evolúció Level set módszer A görbe evolúció parametrizálástól független mindössze geometriai
Netis vezeték nélküli, N típusú Router Gyors Telepítési Útmutató
 Netis vezeték nélküli, N típusú Router Gyors Telepítési Útmutató Tartalomjegyzék 1. A csomag tartalma... 1 2. Hardware csatlakoztatása... 1 3. A router webes felületen történő beüzemelése... 2 4. Hibaelhárítás...
Netis vezeték nélküli, N típusú Router Gyors Telepítési Útmutató Tartalomjegyzék 1. A csomag tartalma... 1 2. Hardware csatlakoztatása... 1 3. A router webes felületen történő beüzemelése... 2 4. Hibaelhárítás...
Számítógéppel segített folyamatmodellezés p. 1/20
 Számítógéppel segített folyamatmodellezés Piglerné Lakner Rozália Számítástudomány Alkalmazása Tanszék Pannon Egyetem Számítógéppel segített folyamatmodellezés p. 1/20 Tartalom Modellező rendszerektől
Számítógéppel segített folyamatmodellezés Piglerné Lakner Rozália Számítástudomány Alkalmazása Tanszék Pannon Egyetem Számítógéppel segített folyamatmodellezés p. 1/20 Tartalom Modellező rendszerektől
Dinamikus modellek felállítása mérnöki alapelvek segítségével
 IgyR - 3/1 p. 1/20 Integrált Gyártórendszerek - MSc Dinamikus modellek felállítása mérnöki alapelvek segítségével Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék IgyR - 3/1 p. 2/20
IgyR - 3/1 p. 1/20 Integrált Gyártórendszerek - MSc Dinamikus modellek felállítása mérnöki alapelvek segítségével Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék IgyR - 3/1 p. 2/20
ReszlAd fájl, kitöltési útmutató:
 1 ReszlAd fájl, kitöltési útmutató: A ReszlAd táblázat egy adott látogatás részletes adatait tartalmazza. A szaktanácsadó által hiánytalanul kitöltött, és elnevezett fájlt e-mail üzenetben kérjük elküldeni
1 ReszlAd fájl, kitöltési útmutató: A ReszlAd táblázat egy adott látogatás részletes adatait tartalmazza. A szaktanácsadó által hiánytalanul kitöltött, és elnevezett fájlt e-mail üzenetben kérjük elküldeni
Hálózat hidraulikai modell integrálása a Soproni Vízmű Zrt. térinformatikai rendszerébe
 Hálózat hidraulikai modell integrálása a térinformatikai rendszerébe Hálózathidraulikai modellezés - Szakmai nap MHT Vízellátási Szakosztály 2015. április 9. Térinformatikai rendszer bemutatása Működési
Hálózat hidraulikai modell integrálása a térinformatikai rendszerébe Hálózathidraulikai modellezés - Szakmai nap MHT Vízellátási Szakosztály 2015. április 9. Térinformatikai rendszer bemutatása Működési
VIDÉKFEJLESZTÉSI MINISZTÉRIUM. Petrik Lajos Két Tanítási Nyelvű Vegyipari, Környezetvédelmi és Informatikai Szakközépiskola
 A versenyző kódja:... VIDÉKFEJLESZTÉSI MINISZTÉRIUM Petrik Lajos Két Tanítási Nyelvű Vegyipari, Környezetvédelmi és Informatikai Szakközépiskola Budapest, Thököly út 48-54. XV. KÖRNYEZETVÉDELMI ÉS VÍZÜGYI
A versenyző kódja:... VIDÉKFEJLESZTÉSI MINISZTÉRIUM Petrik Lajos Két Tanítási Nyelvű Vegyipari, Környezetvédelmi és Informatikai Szakközépiskola Budapest, Thököly út 48-54. XV. KÖRNYEZETVÉDELMI ÉS VÍZÜGYI
CAD-CAM-CAE Példatár
 CAD-CAM-CAE Példatár A példa megnevezése: A példa száma: A példa szintje: CAx rendszer: Kapcsolódó TÁMOP tananyag: A feladat rövid leírása: Mőanyag alkatrész fröccsöntésének szimulációja ÓE-B09 alap közepes
CAD-CAM-CAE Példatár A példa megnevezése: A példa száma: A példa szintje: CAx rendszer: Kapcsolódó TÁMOP tananyag: A feladat rövid leírása: Mőanyag alkatrész fröccsöntésének szimulációja ÓE-B09 alap közepes
Új Magyarország Fejlesztési Terv Tájékoztató A ZMNE-n bevezetett wifi szolgáltatásról KMOP-4.2.1/B-2008-0016
 Új Magyarország Fejlesztési Terv Tájékoztató A ZMNE-n bevezetett wifi szolgáltatásról KMOP-4.2.1/B-2008-0016 Tájékoztató A ZMNE Egyetemi Informatikai Szolgáltató Központ (EISZK) a 2010/2011-es tanévtől
Új Magyarország Fejlesztési Terv Tájékoztató A ZMNE-n bevezetett wifi szolgáltatásról KMOP-4.2.1/B-2008-0016 Tájékoztató A ZMNE Egyetemi Informatikai Szolgáltató Központ (EISZK) a 2010/2011-es tanévtől
Simított részecskedinamika Smoothed Particle Hydrodynamics (SPH)
 Smoothed Particle Hydrodynamics (SPH) Áramlások numerikus modellezése II. Tóth Balázs BME-ÉMK Vízépítési és Vízgazdálkodási Tanszék Numerikus módszerek Osztályozás A numerikus sémák két csoportosítási
Smoothed Particle Hydrodynamics (SPH) Áramlások numerikus modellezése II. Tóth Balázs BME-ÉMK Vízépítési és Vízgazdálkodási Tanszék Numerikus módszerek Osztályozás A numerikus sémák két csoportosítási
Robotok inverz geometriája
 Robotok inverz geometriája. A gyakorlat célja Inverz geometriai feladatot megvalósító függvények implementálása. A megvalósított függvénycsomag tesztelése egy kétszabadságfokú kar előírt végberendezés
Robotok inverz geometriája. A gyakorlat célja Inverz geometriai feladatot megvalósító függvények implementálása. A megvalósított függvénycsomag tesztelése egy kétszabadságfokú kar előírt végberendezés
feszültségek ábrázolása a cső vastagsága mentén sugár irányban.
 SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK Végeselem analízis 4. gyakorlat (kidolgozta: Aczél Ákos egyetemi tanársegéd, Bojtár Gergely egyetemi tanársegéd) Feladat: Sík-alakváltozás (vastag
SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK Végeselem analízis 4. gyakorlat (kidolgozta: Aczél Ákos egyetemi tanársegéd, Bojtár Gergely egyetemi tanársegéd) Feladat: Sík-alakváltozás (vastag
Mérnöki Optimálás Példatár
 Mérnöki Optimálás Példatár A példa megnevezése: A példa száma: A példa szintje: A feladat rövid leírása: Autó tetőbokszának optimálása több célfüggvény alkalmazásával OPT-BME-3 alap A mérnöki optimálás
Mérnöki Optimálás Példatár A példa megnevezése: A példa száma: A példa szintje: A feladat rövid leírása: Autó tetőbokszának optimálása több célfüggvény alkalmazásával OPT-BME-3 alap A mérnöki optimálás
Útmutató EDC kézivezérlőhöz
 Útmutató EDC kézivezérlőhöz ALAPFUNKCIÓK A kézivezérlő használata során állítsa az EDC vezérlő előlapján található forgó kapcsolót 0 állásba. Ezáltal a felhasználó a kézivezérlő segítségével férhet hozzá,
Útmutató EDC kézivezérlőhöz ALAPFUNKCIÓK A kézivezérlő használata során állítsa az EDC vezérlő előlapján található forgó kapcsolót 0 állásba. Ezáltal a felhasználó a kézivezérlő segítségével férhet hozzá,
TÉRFOGATÁRAM MÉRÉSE. Mérési feladatok
 Készítette:....kurzus Dátum:...év...hó...nap TÉRFOGATÁRAM MÉRÉSE Mérési feladatok 1. Csővezetékben áramló levegő térfogatáramának mérése mérőperemmel 2. Csővezetékben áramló levegő térfogatáramának mérése
Készítette:....kurzus Dátum:...év...hó...nap TÉRFOGATÁRAM MÉRÉSE Mérési feladatok 1. Csővezetékben áramló levegő térfogatáramának mérése mérőperemmel 2. Csővezetékben áramló levegő térfogatáramának mérése
Végeselem módszer 4. gyakorlat Gát (SA feladat)
 5000 10000 10000 15000 SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK Feladat: sík alakváltozási feladat Végeselem módszer 4. gyakorlat Gát (SA feladat) Az 1. ábra egy folyó hosszú egyenes szakaszának
5000 10000 10000 15000 SZÉCHENYI ISTVÁN EGYETEM ALKALMAZOTT MECHANIKA TANSZÉK Feladat: sík alakváltozási feladat Végeselem módszer 4. gyakorlat Gát (SA feladat) Az 1. ábra egy folyó hosszú egyenes szakaszának
Modern Fizika Labor. 2. Elemi töltés meghatározása
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Égés és oltáselmélet I. (zárójelben a helyes válaszra adott pont)
 Égés és oltáselmélet I. (zárójelben a helyes válaszra adott pont) 1. "Az olyan rendszereket, amelyek határfelülete a tömegáramokat megakadályozza,... rendszernek nevezzük" (1) 2. "Az olyan rendszereket,
Égés és oltáselmélet I. (zárójelben a helyes válaszra adott pont) 1. "Az olyan rendszereket, amelyek határfelülete a tömegáramokat megakadályozza,... rendszernek nevezzük" (1) 2. "Az olyan rendszereket,
Új Magyarország Fejlesztési Terv Tájékoztató A ZMNE-n bevezetett wifi szolgáltatásról KMOP-4.2.1/B-2008-0016
 Új Magyarország Fejlesztési Terv Tájékoztató A ZMNE-n bevezetett wifi szolgáltatásról KMOP-4.2.1/B-2008-0016 Tájékoztató A ZMNE Egyetemi Informatikai Szolgáltató Központ (EISZK) 2010. június 21-étől kísérleti
Új Magyarország Fejlesztési Terv Tájékoztató A ZMNE-n bevezetett wifi szolgáltatásról KMOP-4.2.1/B-2008-0016 Tájékoztató A ZMNE Egyetemi Informatikai Szolgáltató Központ (EISZK) 2010. június 21-étől kísérleti
Ventilátor (Ve) [ ] 4 ahol Q: a térfogatáram [ m3. Nyomásszám:
![Ventilátor (Ve) [ ] 4 ahol Q: a térfogatáram [ m3. Nyomásszám: Ventilátor (Ve) [ ] 4 ahol Q: a térfogatáram [ m3. Nyomásszám:](/thumbs/60/44642901.jpg) Ventilátor (Ve) 1. Definiálja a következő dimenziótlan számokat és írja fel a képletekben szereplő mennyiségeket: φ (mennyiségi szám), Ψ (nyomásszám), σ (fordulatszám tényező), δ (átmérő tényező)! Mennyiségi
Ventilátor (Ve) 1. Definiálja a következő dimenziótlan számokat és írja fel a képletekben szereplő mennyiségeket: φ (mennyiségi szám), Ψ (nyomásszám), σ (fordulatszám tényező), δ (átmérő tényező)! Mennyiségi
Közegek és felületek megadása
 3. Előadás Közegek és felületek megadása A gyakorlatban nem közömbös, hogy az adott közeg milyen anyagi tulajdonságokkal bír. (Törésmutató, felület típusa, érdessége ) Lehetőség van az anyagok közegének,
3. Előadás Közegek és felületek megadása A gyakorlatban nem közömbös, hogy az adott közeg milyen anyagi tulajdonságokkal bír. (Törésmutató, felület típusa, érdessége ) Lehetőség van az anyagok közegének,
Matlab Fuzzy Logic Toolbox
 Matlab Fuzzy Logic Toolbox The Future looks Fuzzy Newsweek, May, 28, 1990. A fuzzy irányítási rendszerek vizsgálatára Windows alatt futó Matlab programcsomag szimulációs eszközeit és a Matlab-ra ráépülő
Matlab Fuzzy Logic Toolbox The Future looks Fuzzy Newsweek, May, 28, 1990. A fuzzy irányítási rendszerek vizsgálatára Windows alatt futó Matlab programcsomag szimulációs eszközeit és a Matlab-ra ráépülő
3.1.5 Laborgyakorlat: Egyszerű egyenrangú hálózat építése
 Otthoni és kisvállalati hálózatok kezelése 3.1.5 Laborgyakorlat: Egyszerű egyenrangú hálózat építése Célkitűzések Egyszerű egyenrangú hálózat tervezése és kiépítése az oktató által biztosított keresztkötésű
Otthoni és kisvállalati hálózatok kezelése 3.1.5 Laborgyakorlat: Egyszerű egyenrangú hálózat építése Célkitűzések Egyszerű egyenrangú hálózat tervezése és kiépítése az oktató által biztosított keresztkötésű
IMI INTERNATIONAL KFT
 Épületgépész Szakosztály IMI INTERNATIONAL KFT www.imi-international.hu IMI International, Department, Name Vörös Szilárd okl. épületgépész-mérnök 0//00 Mihez kezdesz egy kazánházban a Bernoulli-egyenlettel?.
Épületgépész Szakosztály IMI INTERNATIONAL KFT www.imi-international.hu IMI International, Department, Name Vörös Szilárd okl. épületgépész-mérnök 0//00 Mihez kezdesz egy kazánházban a Bernoulli-egyenlettel?.
