Sage alapok. A Sage program használható egyszerő számolási feladatok elvégzésére: #Összeadás #Kivonás
|
|
|
- Krisztina Szőkené
- 8 évvel ezelőtt
- Látták:
Átírás
1 1 / :48 To print higher-resolution math symbols, click the Hi-Res Fonts for Printing button on the jsmath control panel. If the math symbols print as black boxes, turn off image alpha channels using the Options pane of the jsmath control panel. Sage alapok A Sage program használható egyszerő számolási feladatok elvégzésére: #Összeadás #Kivonás #A szorzás jele a * 3*6 18 #Az osztás jele a /. Nem használható a :, ami papíron szokásos 32/5 32/5 #Az elızı eredményt közönséges tört formájában kaptuk meg. #Ha tizedestört alakban szeretném megkapni, akkor kasználhatjuk az n() függvényt, n(32/5) #Vagy az N() függvényt, N(32/5) #Vagy az.n() metódust: 32/5.n() #Az értékes jegyek számát megváltoztathatjuk. n(32/5,digits=5) /5.n(digits=4) N(32/5,digits=4) n(pi) n(pi,digits=3) 3.14 n(pi,digits=100) \ #Elıírhatjuk azt is, hogy hány bitet használjon fel a program az
2 2 / :48 eredmény ábrázolására n(pi,prec=20) #Ha az eredménynek csak az egészrésze érdekel bennünket, használhatjuk az egészosztást. 32//5 6 #Az osztás maradékát is megkaphatjuk a % (maradék) mővelettel. 32%5 2 #A hatványozás jele a ^, illetve a ** 3^ ** #A négyzetgyökvonás az sqrt() függvény, vagy az.sqrt() metódus segítségével végezhetı el. sqrt(25) 5 25.sqrt() 5 #Ha a gyökvonás eredménye nem egész, a Sage a pontos értéket adja meg algebrai formában. 30.sqrt() sqrt(30) sqrt(48) 4*sqrt(3) #Ha a közelítı értékre vagyunk kíváncsiak, a szokásos n() függvényt (és társait) használhatjuk. n(sqrt(48)) #Egy cellában több parancsot is kiadhatunk. Visszatérési értéket azonban csak az utolsó parancs esetén kapunk. sqrt(30).n() sqrt(48).n() #Ha több számolás eredményét is szeretnénk látni ugyanannak a cellának a kimenetében, akkor használhatjuk a print parancsot. print sqrt(30).n() print sqrt(48).n() #A print paranccsal szövegeket is ki tudunk iratni. A szöveg (string) két idézıjel vagy két aposztrofjel között kell legyen. print "Hello vilag" print 'Romeo es Julia' Hello vilag Romeo es Julia
3 3 / :48 #Az egyes print parancsok eredménye alapértelmezésben külön sorba kerül, de ezt megváltoztathatjuk, ha a parancs végére egy vesszıt teszünk print "Hello vilag", print 'Romeo es Julia' Hello vilag Romeo es Julia #Ugyanezt egy print paranccsal is megkaphatjuk print "Hello vilag", 'Romeo es Julia' Hello vilag Romeo es Julia #Stringek alkalmazásával az outputok olvashatóbbá tehetık print 'A 30 négyzetgyöke közelítıleg',sqrt(30).n() A 30 négyzetgyöke közelítıleg #Az.nth_root() metódus lehetıvé teszi a gyökvonást nagyobb gyökkitevı esetén is. print "A 81 negyedik gyöke =",81.nth_root(4) A 81 negyedik gyöke = 3 #Faktoriálisok kiszámítása a.factorial() metódus segítségével print "5!=",5.factorial() 5!= 120 Szimbolikus számítások #Ha a Sage programban értéket adunk egy változónak, amit itt nemcsak egyetlen bető jelölhet, akkor a Sage ezt a változót ezzel az értékkel azonosítja, mindaddig, míg az értékadás érvényét nem veszti. a=8 b=5 a 8 b a+b 5 13 #Ha újra értéket adunk a változónak, akkor korábbi értékét elveszti a=12 a 12 #A matematikában gyakran számolunk szimbólumokkal (pl. betők), amelyek egy változót, paramétert vagy ismeretlent jelölnek. Ha ilyen szimbólumként akarjuk, használni valamelyik változót, akkor ezt a var() függvénnyel jelezhetjük a Sage programnak. (a,b)=var('a,b') a a #Látható, hogy a var() függvény hatására a változó elveszítette a korábbi értékét. (a+b)^2 (a + b)^2
4 4 / :48 #A szimbolikus kifejezés matematikai formáját a show() függvénnyel vagy.show() metódussal kapjuk meg. show((a+b)^2) (a +b) 2 ((a+b)^2).show() (a +b) 2 #Az algebrai kifejezéseket összeggé alakíthatjuk az expand() függvénnyel vagy.expand() metódussal ((a+b)^2).expand() a^2 + 2*a*b + b^2 ((a+b)^3).expand() a^3 + 3*a^2*b + 3*a*b^2 + b^3 ((a+b)^10).expand() a^ *a^9*b + 45*a^8*b^ *a^7*b^ *a^6*b^ *a^5*b^ *a^4*b^ *a^3*b^7 + 45*a^2*b^8 + 10*a*b^9 + b^10 #Az összeggé alakítás megfordítása algebrai kifejezések esetén a szorzattá alakítás. Ezt a factor() függvénnyel vagy.factor() metódussal lehet elérni akár számok, akár szimbolikus kifejezések esetén factor(187) 11 * factor() 11 * 17 (x,y)=var('x,y') (3*x*y^2+12*x*y+6*x^2*y^2).factor() 3*(2*x*y + y + 4)*x*y show(_) 3 (2x y +y + 4) xy tort=(2*x^2+4*x)/(x+2) show(tort) 2 (x 2 + 2x) (x + 2) #A felírt törtet egyszerősíteni szeretném, de ez a.simplify() metódussal nem most sikerül. tort.simplify() #!!! 2*(x^2 + 2*x)/(x + 2) #Megtörténik azonban az egyszerősítés a.simplify_full(), illetve a.simplify_rational() metódusok alkalmazása esetén. tort.simplify_full() 2*x
5 5 / :48 tort.simplify_rational() 2*x #Ugyancsak végbemegy az egyszerősítés, ha a.factor() metódust alkalmazzuk, mert a számláló és a nevezı szorzattá bontása után a Sage azonnal felismeri azok azonos tényezıit és automatikusan egyszerősít. tort.factor() 2*x #ÍMég egy példa a szorzattá alakításra: (a,b)=var('a,b') (a^2-b^2).factor() (a - b)*(a + b) Relációk #Konkrét számok vagy azok kifejezései között a szokásos egyenlıség vagy #egyenlıtlenségrelációkat felírva a Sage azt kiértékeli és igaz értéket (True) vagy hamisat #(False) ad vissza. 3==2+1 True 2*2==5 False 12>9 True 12>15 False 5>=5 True #Ugyanez a helyzet, ha a reláció szimbólumokat is tartalmaz, ha azok értéke adott. a=2 a<5 True b=2 a==b True 2*a>3*b False #Ha a szimbólumnak nem adtunk konkrét értéket, akkor a Sage a relációt adja vissza outputként. x^2>=0 x^2 >= 0 #Ebben az esetben is kikényszeríthetı azonban a reláció kiértékelése a bool() függvénnyel. bool(x^2>=0) True Függvények ábrázolása
6 6 / :48 #A plot() függvény a grafikus objektumot ad vissza, amely megjeleníthetı. #A plot() függvény elsı paramétere maga az ábrázolandó függvény, második paramétere az az intervallum, amelyen ábrázolni akarjuk. plot(x^2,(-3,3)) #Ha azt szeretnénk, hogy a két tengelyen az egységek ugyanakkorák legyenek, akkor szükség van #egy harmadik (opcionális) paraméterre is: be kell állítanunk az aspect_ratio értékét 1-re plot(x^2,(-3,3),aspect_ratio=1)
7 7 / :48 #Két ismert trigonometrikus függvény: plot(sin,(-pi,2*pi))
8 8 / :48 #Itt most a grafikon színét pirosnak választjuk plot(sin,(-pi,2*pi),rgbcolor='red') #A két függvény egy koordinátarendszerben is ábrázolható, ha egy-egy változónév alatt elmentjük a két grafikos objektumot és a show() függvény segítségével jelenítjük meg ıket g1=plot(sin,(-2*pi,2*pi)) g2=plot(cos,(-2*pi,2*pi),rgbcolor='red') show(g1+g2) #Megjeleníthetjük az egyes függvények nevét is. g1=plot(sin,(-2*pi,2*pi))+text('sin',(6.6,-0.2),rgbcolor='blue') g2=plot(cos,(-2*pi,2*pi),rgbcolor='red')+text('cos', (6.6,0.8),rgbcolor='red') show(g1+g2)
9 9 / :48 #A tangens és kotangens függvények ábrázolása itt nem sikeres, mert a szakadási helyek #környékén felvett nagy abszolútértékő számok miatt az y-tengelyen nagyon kicsi lett az egység g3=plot(tan,(x,-2*pi,2*pi))+text('tg',(5,10),rgbcolor='blue') g4=plot(cot,(x,-2*pi,2*pi),rgbcolor='red')+text('ctg', (6.6,-3.5),rgbcolor='red') show(g3+g4) #Ha a show() függvény ymin, ymax paramétereivel megakadályozzuk a túl nagy értékek ábrázolását, #akkor használhatóbb ábrát kapunk. #Ennek az ábrának már csak az a szépséghibája, hogy a függıleges aszimptotákat is mutatja. g3=plot(tan,(x,-2*pi,2*pi))+text('tg',(5,10),rgbcolor='blue')
10 10 / :48 g4=plot(cot,(x,-2*pi,2*pi),rgbcolor='red')+text('ctg', (6.6,-3.5),rgbcolor='red') show(g3+g4,ymin=-10,ymax=10) #Az aszimptoták ábrázolását kikapcsolhatjuk a plot() függvényben, ha a detect_poles paraméter #értékét igazra állítjuk. g3=plot(tan,(x,-2*pi,2*pi),detect_poles=true)+text('tg', (5,10),rgbcolor='blue') g4=plot(cot, (x,-2*pi,2*pi),detect_poles=true,rgbcolor='red')+text('ctg', (6.6,-3.5),rgbcolor='red') show(g3+g4,ymin=-10,ymax=10) Trigonometrikus kifejezések
11 11 / :48 (sin(x))^2+(cos(x))^2 #A Sage a matematikai jelöléstıl eltérı jelölést használ! sin(x)^2 + cos(x)^2 #Brrr!!!!! ((sin(x))^2+(cos(x))^2).show() sin x 2 + cos x 2 #Konkrét értékek esetén a Sage esetleg kiszámítja a kifejezés értékét. (sin(pi/3))^2+(cos(pi/3))^2 1 #De nem mindig! (sin(2))^2+(cos(2))^2 sin(2)^2 + cos(2)^2 #Ha az argumentum lebegıpontos, akkor az eredményt is ilyen alakban kapjuk vissza. (sin(2.1))^2+(cos(2.1))^ (sin(2.))^2+(cos(2.))^ #Ha a kifejezés szimbólumot tartalmaz, ugyancsak elmaradhat a kiértékelés #Ezen még a.simplify() metódus sem tud segíteni. ((sin(x))^2+(cos(x))^2).simplify() sin(x)^2 + cos(x)^2 #Segít viszon a.simplify_trig() metódus! ((sin(x))^2+(cos(x))^2).simplify_trig() 1 #Megtörténik az egyszerőbb alakra hozás a.simplify_full() metódussal is. ((sin(x))^2+(cos(x))^2).simplify_full() 1 #Hasonló a helyzet az összefüggés átrendezett alakjával is: 1-(sin(x))^2 -sin(x)^2 + 1 (1-(sin(x))^2).simplify() -sin(x)^2 + 1 (1-(sin(x))^2).simplify_trig() cos(x)^2 (1-(sin(x))^2).simplify_full() cos(x)^2 #Használhatjuk a görög betőket is szimbólumként (alpha,beta)=var('alpha,beta') sin(alpha+beta) sin(alpha + beta) #A show() függvénnyel vagy a.show() metódussal megjeleníthetjük ıket a szokásos alakban
12 12 / :48 sin(alpha+beta).show() sin + #Az.expand() metódus a trigonometrikus függvényeket nem tudja összeggé alakítani. (sin(alpha+beta)).expand().show() sin + #Az expand_trig() azonban már igen. (sin(alpha+beta)).expand_trig().show() sin cos + sin cos Paraméteres függvény a=var('a') g(x)=(x^2-a*x)/(x+2) g(3) -3/5*a + 9/5 #A sub() metódus segítségével kiszámíthatjuk a helyettesítési értéket a paraméter egy konkrét #értéke esetén g(3).subs(a=1) 6/5 g(3).subs(a=2) 3/5 #Nem ábrázolhatjuk a függvényt, ha a paraméter nincs megadva plot(g,(-4,4)) Traceback (click to the left for traceback)... ValueError: free variable: a #A paraméter egy adott értéke esetén a függvény már ábrázolható show(plot(g.subs(a=5),(-20,10),detect_poles=true),ymin=-30,ymax=30)
13 13 / :48
Komputeralgebra Rendszerek
 Komputeralgebra Rendszerek Normálformák, algebrai reprezentáció Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2014. április 8. TARTALOMJEGYZÉK 1 of 113 TARTALOMJEGYZÉK I 1 TARTALOMJEGYZÉK 2 Az absztrakció
Komputeralgebra Rendszerek Normálformák, algebrai reprezentáció Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2014. április 8. TARTALOMJEGYZÉK 1 of 113 TARTALOMJEGYZÉK I 1 TARTALOMJEGYZÉK 2 Az absztrakció
A MATLAB alapjai. Kezdő lépések. Változók. Aktuális mappa Parancs ablak. Előzmények. Részei. Atomerőművek üzemtana
 A MATLAB alapjai Kezdő lépések - Matlab Promt: >> - Help: >> help sqrt >> doc sqrt - Kilépés: >> quit >> exit >> Futó script leállítása: >> ctrl+c - Változók listásása >> who >> whos - Változók törlése
A MATLAB alapjai Kezdő lépések - Matlab Promt: >> - Help: >> help sqrt >> doc sqrt - Kilépés: >> quit >> exit >> Futó script leállítása: >> ctrl+c - Változók listásása >> who >> whos - Változók törlése
ALGEBRAI KIFEJEZÉSEK, EGYENLETEK
 ALGEBRAI KIFEJEZÉSEK, EGYENLETEK AZ ALGEBRAI KIFEJEZÉS FOGALMÁNAK KIALAKÍTÁSA (7-9. OSZTÁLY) Racionális algebrai kifejezés (betűs kifejezés): betűket és számokat a négy alapművelet véges sokszori alkalmazásával
ALGEBRAI KIFEJEZÉSEK, EGYENLETEK AZ ALGEBRAI KIFEJEZÉS FOGALMÁNAK KIALAKÍTÁSA (7-9. OSZTÁLY) Racionális algebrai kifejezés (betűs kifejezés): betűket és számokat a négy alapművelet véges sokszori alkalmazásával
Alapok. tisztán funkcionális nyelv, minden függvény (a konstansok is) nincsenek hagyományos változók, az első értékadás után nem módosíthatók
 Haskell 1. Alapok tisztán funkcionális nyelv, minden függvény (a konstansok is) nincsenek hagyományos változók, az első értékadás után nem módosíthatók elég jól elkerülhetők így a mellékhatások könnyebben
Haskell 1. Alapok tisztán funkcionális nyelv, minden függvény (a konstansok is) nincsenek hagyományos változók, az első értékadás után nem módosíthatók elég jól elkerülhetők így a mellékhatások könnyebben
2018/2019. Matematika 10.K
 Egész éves dolgozat szükséges felszerelés: toll, ceruza, radír, vonalzó, körző, számológép, függvénytáblázat 2 órás, 4 jegyet ér 2019. május 27-31. héten Aki hiányzik, a következő héten írja meg, e nélkül
Egész éves dolgozat szükséges felszerelés: toll, ceruza, radír, vonalzó, körző, számológép, függvénytáblázat 2 órás, 4 jegyet ér 2019. május 27-31. héten Aki hiányzik, a következő héten írja meg, e nélkül
Másodfokú egyenletek, egyenlőtlenségek
 Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x + 1x + 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x + 1x + 16 = 0.
Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x + 1x + 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x + 1x + 16 = 0.
Programozás C- és Matlab nyelven C programozás kurzus BMEKOKAM603 Előfeldolgozó rendszer Tömbök. Dr. Bécsi Tamás 4. Előadás
 Programozás C- és Matlab nyelven C programozás kurzus BMEKOKAM603 Előfeldolgozó rendszer Tömbök Dr. Bécsi Tamás 4. Előadás A?: operátor Nézzük meg a következő kifejezést: if (a>b) z=a; else z=b; Ez felírható
Programozás C- és Matlab nyelven C programozás kurzus BMEKOKAM603 Előfeldolgozó rendszer Tömbök Dr. Bécsi Tamás 4. Előadás A?: operátor Nézzük meg a következő kifejezést: if (a>b) z=a; else z=b; Ez felírható
Excel Hivatkozások, függvények használata
 Excel Hivatkozások, függvények használata 1. Fejezet Adatok, képletek, függvények Adatok táblázat celláiba írjuk, egy cellába egy adat kerül lehet szám, vagy szöveg * szám esetén a tizedes jegyek elválasztásához
Excel Hivatkozások, függvények használata 1. Fejezet Adatok, képletek, függvények Adatok táblázat celláiba írjuk, egy cellába egy adat kerül lehet szám, vagy szöveg * szám esetén a tizedes jegyek elválasztásához
Komplex számok. Wettl Ferenc előadása alapján Wettl Ferenc előadása alapján Komplex számok / 18
 Komplex számok Wettl Ferenc előadása alapján 2015.09.23. Wettl Ferenc előadása alapján Komplex számok 2015.09.23. 1 / 18 Tartalom 1 Számok A számfogalom bővülése 2 Algebrai alak Trigonometrikus alak Egységgyökök
Komplex számok Wettl Ferenc előadása alapján 2015.09.23. Wettl Ferenc előadása alapján Komplex számok 2015.09.23. 1 / 18 Tartalom 1 Számok A számfogalom bővülése 2 Algebrai alak Trigonometrikus alak Egységgyökök
Másodfokú egyenletek, egyenlőtlenségek
 Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x 1x 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x 1x 16 =. 1. lépés:
Másodfokú egyenletek, egyenlőtlenségek A másodfokú egyenlet grafikus megoldása Példa1. Ábrázold az f(x) = x 1x 16 függvényt, majd olvasd le az ábráról az alábbi egyenlet megoldását: x 1x 16 =. 1. lépés:
Excel Hivatkozások, függvények használata
 Excel Hivatkozások, függvények használata 1. Fejezet Adatok, képletek, függvények Adatok táblázat celláiba írjuk, egy cellába egy adat kerül lehet szám, vagy szöveg * szám esetén a tizedes jegyek elválasztásához
Excel Hivatkozások, függvények használata 1. Fejezet Adatok, képletek, függvények Adatok táblázat celláiba írjuk, egy cellába egy adat kerül lehet szám, vagy szöveg * szám esetén a tizedes jegyek elválasztásához
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 016. ősz 1. Diszkrét matematika 1. középszint 1. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 016. ősz 1. Diszkrét matematika 1. középszint 1. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Abszolútértékes és gyökös kifejezések Megoldások
 Abszolútértékes és gyökös kifejezések Megoldások ) Igazolja, hogy az alábbi négy egyenlet közül az a) és b) jelű egyenletnek pontosan egy megoldása van, a c) és d) jelű egyenletnek viszont nincs megoldása
Abszolútértékes és gyökös kifejezések Megoldások ) Igazolja, hogy az alábbi négy egyenlet közül az a) és b) jelű egyenletnek pontosan egy megoldása van, a c) és d) jelű egyenletnek viszont nincs megoldása
Komplex számok trigonometrikus alakja
 Komplex számok trigonometrikus alakja 015. február 15. 1. Alapfeladatok 1. Feladat: Határozzuk meg az alábbi algebrai alakban adott komplex számok trigonometrikus alakját! z 1 = 4 + 4i, z = 4 + i, z =
Komplex számok trigonometrikus alakja 015. február 15. 1. Alapfeladatok 1. Feladat: Határozzuk meg az alábbi algebrai alakban adott komplex számok trigonometrikus alakját! z 1 = 4 + 4i, z = 4 + i, z =
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
Baran Ágnes. Gyakorlat Függvények, Matlab alapok
 Matematika Mérnököknek 1. Baran Ágnes Gyakorlat Függvények, Matlab alapok Matematika Mérnököknek 1. A gyakorlatok fóliái: https://arato.inf.unideb.hu/baran.agnes/oktatas.html Feladatsorok: https://arato.inf.unideb.hu/baran.agnes/oktatas.html
Matematika Mérnököknek 1. Baran Ágnes Gyakorlat Függvények, Matlab alapok Matematika Mérnököknek 1. A gyakorlatok fóliái: https://arato.inf.unideb.hu/baran.agnes/oktatas.html Feladatsorok: https://arato.inf.unideb.hu/baran.agnes/oktatas.html
Megoldások. Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) 1. Számítsd ki a következő kifejezések pontos értékét!
 Megoldások. Számítsd ki a következő kifejezések pontos értékét! 8 8 ( ) ( ) ( ) Használjuk a gyökvonás azonosságait. 0 8 8 8 8 8 8 ( ) ( ) ( ) 0 8 . Határozd meg a következő kifejezések értelmezési tartományát!
Megoldások. Számítsd ki a következő kifejezések pontos értékét! 8 8 ( ) ( ) ( ) Használjuk a gyökvonás azonosságait. 0 8 8 8 8 8 8 ( ) ( ) ( ) 0 8 . Határozd meg a következő kifejezések értelmezési tartományát!
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 2. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 2. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
HÁZI FELADATOK. 2. félév. 1. konferencia Komplex számok
 Figyelem! A feladatok megoldása legyen áttekinthet és részletes, de férjen el az arra szánt helyen! Ha valamelyik HÁZI FELADATOK. félév. konferencia Komple számok Értékelés:. egység: önálló feladatmegoldás
Figyelem! A feladatok megoldása legyen áttekinthet és részletes, de férjen el az arra szánt helyen! Ha valamelyik HÁZI FELADATOK. félév. konferencia Komple számok Értékelés:. egység: önálló feladatmegoldás
Algoritmusok Tervezése. 1. Előadás MATLAB 1. Dr. Bécsi Tamás
 Algoritmusok Tervezése 1. Előadás MATLAB 1. Dr. Bécsi Tamás Tárgy adatok Előadó: Bécsi Tamás, St 106, becsi.tamas@mail.bme.hu Előadás:2, Labor:2 Kredit:5 Félévközi jegy 2 db Zh 1 hallgatói feladat A félév
Algoritmusok Tervezése 1. Előadás MATLAB 1. Dr. Bécsi Tamás Tárgy adatok Előadó: Bécsi Tamás, St 106, becsi.tamas@mail.bme.hu Előadás:2, Labor:2 Kredit:5 Félévközi jegy 2 db Zh 1 hallgatói feladat A félév
Programozás BMEKOKAA146. Dr. Bécsi Tamás 2. előadás
 Programozás BMEKOKAA146 Dr. Bécsi Tamás 2. előadás Szintaktikai alapok Alapvető típusok, ismétlés C# típus.net típus Méret (byte) Leírás byte System.Byte 1Előjel nélküli 8 bites egész szám (0..255) char
Programozás BMEKOKAA146 Dr. Bécsi Tamás 2. előadás Szintaktikai alapok Alapvető típusok, ismétlés C# típus.net típus Méret (byte) Leírás byte System.Byte 1Előjel nélküli 8 bites egész szám (0..255) char
a) A logaritmus értelmezése alapján: x 8 0 ( x 2 2 vagy x 2 2) (1 pont) Egy szorzat értéke pontosan akkor 0, ha valamelyik szorzótényező 0.
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
Maple: Deriváltak és a függvény nevezetes pontjai
 Maple: Deriváltak és a függvény nevezetes pontjai Bevezető Tudjuk, hogy a Maple könnyűszerrel képes végrehajtani a szimbólikus matematikai számításokat, ezért a Maple egy ideális program differenciál-
Maple: Deriváltak és a függvény nevezetes pontjai Bevezető Tudjuk, hogy a Maple könnyűszerrel képes végrehajtani a szimbólikus matematikai számításokat, ezért a Maple egy ideális program differenciál-
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Abszolútértékes és Gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
A MATLAB alapjai. Kezdő lépések. Változók. Aktuális mappa Parancs ablak. Előzmények. Részei
 A MATLAB alapjai Atomerőművek üzemtanának fizikai alapjai - 2016. 03. 04. Papp Ildikó Kezdő lépések - Matlab Promt: >> - Help: >> help sqrt >> doc sqrt - Kilépés: >> quit >> exit - Változók listásása >>
A MATLAB alapjai Atomerőművek üzemtanának fizikai alapjai - 2016. 03. 04. Papp Ildikó Kezdő lépések - Matlab Promt: >> - Help: >> help sqrt >> doc sqrt - Kilépés: >> quit >> exit - Változók listásása >>
LEGO robotok. XII. rész
 LEGO robotok XII. rész III.1.22. Változók és konstansok A változó fogalma a matematikában egy értelmezési tartománnyal rendelkező, ebből bármilyen értéket felvehető objektum, melynek értéke logikailag
LEGO robotok XII. rész III.1.22. Változók és konstansok A változó fogalma a matematikában egy értelmezési tartománnyal rendelkező, ebből bármilyen értéket felvehető objektum, melynek értéke logikailag
Számítástechnika I. BMEKOKAA152 BMEKOKAA119 Infokommunikáció I. BMEKOKAA606. Dr. Bécsi Tamás 2. előadás
 Számítástechnika I. BMEKOKAA152 BMEKOKAA119 Infokommunikáció I. BMEKOKAA606 Dr. Bécsi Tamás 2. előadás Console I/O bővebben Lásd mintaprogram 2015.09.21. Számítástechnika I. 2. Előadás 2 Számábrázolásról
Számítástechnika I. BMEKOKAA152 BMEKOKAA119 Infokommunikáció I. BMEKOKAA606 Dr. Bécsi Tamás 2. előadás Console I/O bővebben Lásd mintaprogram 2015.09.21. Számítástechnika I. 2. Előadás 2 Számábrázolásról
Baran Ágnes, Burai Pál, Noszály Csaba. Gyakorlat Differenciálegyenletek numerikus megoldása
 Matematika Mérnököknek 2. Baran Ágnes, Burai Pál, Noszály Csaba Gyakorlat Differenciálegyenletek numerikus megoldása Baran Ágnes, Burai Pál, Noszály Csaba Matematika Mérnököknek 2. Gyakorlat 1 / 18 Fokozatos
Matematika Mérnököknek 2. Baran Ágnes, Burai Pál, Noszály Csaba Gyakorlat Differenciálegyenletek numerikus megoldása Baran Ágnes, Burai Pál, Noszály Csaba Matematika Mérnököknek 2. Gyakorlat 1 / 18 Fokozatos
Függvények Megoldások
 Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Baran Ágnes. Gyakorlat Halmazok, függvények, Matlab alapok. Baran Ágnes Matematika Mérnököknek Gyakorlat 1 / 34
 Matematika Mérnököknek 1. Baran Ágnes Gyakorlat Halmazok, függvények, Matlab alapok Baran Ágnes Matematika Mérnököknek 1. 1.-2. Gyakorlat 1 / 34 Matematika Mérnököknek 1. A gyakorlatok fóliái: https://arato.inf.unideb.hu/baran.agnes/oktatas.html
Matematika Mérnököknek 1. Baran Ágnes Gyakorlat Halmazok, függvények, Matlab alapok Baran Ágnes Matematika Mérnököknek 1. 1.-2. Gyakorlat 1 / 34 Matematika Mérnököknek 1. A gyakorlatok fóliái: https://arato.inf.unideb.hu/baran.agnes/oktatas.html
SCILAB programcsomag segítségével
 Felhasználói függvények de niálása és függvények 3D ábrázolása SCILAB programcsomag segítségével 1. Felhasználói függvények de niálása A Scilab programcsomag rengeteg matematikai függvényt biztosít a számítások
Felhasználói függvények de niálása és függvények 3D ábrázolása SCILAB programcsomag segítségével 1. Felhasználói függvények de niálása A Scilab programcsomag rengeteg matematikai függvényt biztosít a számítások
Közönséges differenciálegyenletek megoldása Mapleben
 Közönséges differenciálegyenletek megoldása Mapleben Differenciálegyenlet alatt egy olyan egyenletet értünk, amelyben a meghatározandó ismeretlen egy függvény, és az egyenlet tartalmazza az ismeretlen
Közönséges differenciálegyenletek megoldása Mapleben Differenciálegyenlet alatt egy olyan egyenletet értünk, amelyben a meghatározandó ismeretlen egy függvény, és az egyenlet tartalmazza az ismeretlen
Matlab alapok. Baran Ágnes. Grafika. Baran Ágnes Matlab alapok Grafika 1 / 21
 Matlab alapok Baran Ágnes Grafika Baran Ágnes Matlab alapok Grafika / 2 Vonalak, pontok síkon figure nyit egy új grafikus ablakot plot(x,y) ahol x és y ugyanolyan méretű vektorok, ábrázolja az (x i,y i
Matlab alapok Baran Ágnes Grafika Baran Ágnes Matlab alapok Grafika / 2 Vonalak, pontok síkon figure nyit egy új grafikus ablakot plot(x,y) ahol x és y ugyanolyan méretű vektorok, ábrázolja az (x i,y i
Vektorok. Octave: alapok. A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István
 Vektorok A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Octave: alapok Az octave mint számológép: octave:##> 2+2 ans = 4 Válasz elrejtése octave:##> 2+2; octave:##> + - / * () Hatványozás:
Vektorok A fizika numerikus módszerei I. mf1n1a06- mf1n2a06 Csabai István Octave: alapok Az octave mint számológép: octave:##> 2+2 ans = 4 Válasz elrejtése octave:##> 2+2; octave:##> + - / * () Hatványozás:
Numerikus matematika
 Numerikus matematika Baran Ágnes Gyakorlat Numerikus integrálás Matlab-bal Baran Ágnes Numerikus matematika 8. Gyakorlat 1 / 20 Anoním függvények, function handle Függvényeket definiálhatunk parancssorban
Numerikus matematika Baran Ágnes Gyakorlat Numerikus integrálás Matlab-bal Baran Ágnes Numerikus matematika 8. Gyakorlat 1 / 20 Anoním függvények, function handle Függvényeket definiálhatunk parancssorban
Matematika tanmenet 10. osztály (heti 3 óra) A gyökvonás 14 óra
 Matematika tanmenet 10. osztály (heti 3 óra) Tankönyv: Ábrahám Gábor Dr. Kosztolányiné Nagy Erzsébet Tóth Julianna: Matematika 10. Példatárak: Fuksz Éva Riener Ferenc: É rettségi feladatgyűjtemény matematikából
Matematika tanmenet 10. osztály (heti 3 óra) Tankönyv: Ábrahám Gábor Dr. Kosztolányiné Nagy Erzsébet Tóth Julianna: Matematika 10. Példatárak: Fuksz Éva Riener Ferenc: É rettségi feladatgyűjtemény matematikából
Közönséges differenciál egyenletek megoldása numerikus módszerekkel: egylépéses numerikus eljárások
 Közönséges differenciál egyenletek megoldása numerikus módszerekkel: egylépéses numerikus eljárások Bevezetés Ebben a cikkben megmutatjuk, hogyan használhatóak a Mathematica egylépéses numerikus eljárásai,
Közönséges differenciál egyenletek megoldása numerikus módszerekkel: egylépéses numerikus eljárások Bevezetés Ebben a cikkben megmutatjuk, hogyan használhatóak a Mathematica egylépéses numerikus eljárásai,
Excel 2010 függvények
 Molnár Mátyás Excel 2010 függvények Csak a lényeg érthetően! Tartalomjegyzék FÜGGVÉNYHASZNÁLAT ALAPJAI 1 FÜGGVÉNYEK BEVITELE 1 HIBAÉRTÉKEK KEZELÉSE 4 A VARÁZSLATOS AUTOSZUM GOMB 6 SZÁMÍTÁSOK A REJTETT
Molnár Mátyás Excel 2010 függvények Csak a lényeg érthetően! Tartalomjegyzék FÜGGVÉNYHASZNÁLAT ALAPJAI 1 FÜGGVÉNYEK BEVITELE 1 HIBAÉRTÉKEK KEZELÉSE 4 A VARÁZSLATOS AUTOSZUM GOMB 6 SZÁMÍTÁSOK A REJTETT
Függvények határértéke és folytonosság
 Függvények határértéke és folytonosság ) Bizonyítsa be a határérték definíciója alapján, hogy teljesül! + 5 + = Megoldás Heine definíciója alapján): Igazolandó, hogy a függvény értelmezve van a egy környezetében,
Függvények határértéke és folytonosság ) Bizonyítsa be a határérték definíciója alapján, hogy teljesül! + 5 + = Megoldás Heine definíciója alapján): Igazolandó, hogy a függvény értelmezve van a egy környezetében,
1. Alapok. #!/bin/bash
 1. oldal 1.1. A programfájlok szerkezete 1. Alapok A bash programok tulajnképpen egyszerű szöveges fájlok, amelyeket bármely szövegszerkesztő programmal megírhatunk. Alapvetően ugyanazokat a at használhatjuk
1. oldal 1.1. A programfájlok szerkezete 1. Alapok A bash programok tulajnképpen egyszerű szöveges fájlok, amelyeket bármely szövegszerkesztő programmal megírhatunk. Alapvetően ugyanazokat a at használhatjuk
9. Trigonometria. I. Nulladik ZH-ban láttuk: 1. Tegye nagyság szerint növekvő sorrendbe az alábbi értékeket! Megoldás:
 9. Trigonometria I. Nulladik ZH-ban láttuk: 1. Tegye nagyság szerint növekvő sorrendbe az alábbi értékeket! x = cos 150 ; y = sin 5 ; z = tg ( 60 ) (A) z < x < y (B) x < y < z (C) y < x < z (D) z < y
9. Trigonometria I. Nulladik ZH-ban láttuk: 1. Tegye nagyság szerint növekvő sorrendbe az alábbi értékeket! x = cos 150 ; y = sin 5 ; z = tg ( 60 ) (A) z < x < y (B) x < y < z (C) y < x < z (D) z < y
Maple. Maple. Dr. Tóth László egyetemi docens Pécsi Tudományegyetem, 2007
 Maple Dr. Tóth László egyetemi docens Pécsi Tudományegyetem, 2007 A Maple egy matematikai formula-manipulációs (vagy számítógép-algebrai) rendszer, amelyben nem csak numerikusan, hanem formális változókkal
Maple Dr. Tóth László egyetemi docens Pécsi Tudományegyetem, 2007 A Maple egy matematikai formula-manipulációs (vagy számítógép-algebrai) rendszer, amelyben nem csak numerikusan, hanem formális változókkal
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 1. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2017. ősz 1. Diszkrét matematika 1. középszint 1. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Komputeralgebra Rendszerek
 Komputeralgebra Rendszerek Számkezelés Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2015. február 24. TARTALOMJEGYZÉK 1 of 53 TARTALOMJEGYZÉK 1 TARTALOMJEGYZÉK 2 Az egzakt aritmetika Bignum aritmetika
Komputeralgebra Rendszerek Számkezelés Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2015. február 24. TARTALOMJEGYZÉK 1 of 53 TARTALOMJEGYZÉK 1 TARTALOMJEGYZÉK 2 Az egzakt aritmetika Bignum aritmetika
Osztályozó- és javítóvizsga. Matematika tantárgyból
 Osztályozó- és javítóvizsga Matematika tantárgyból 2018-2019 A vizsga 60 perces írásbeli vizsga (feladatlap) a megadott témakörökből. A megjelölt százalék (50%) nem teljesítése esetén szóbeli vizsga is,
Osztályozó- és javítóvizsga Matematika tantárgyból 2018-2019 A vizsga 60 perces írásbeli vizsga (feladatlap) a megadott témakörökből. A megjelölt százalék (50%) nem teljesítése esetén szóbeli vizsga is,
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
1. Komplex számok. x 2 = 1 és x 2 + x + 1 = 0. egyenletek megoldását számnak tekinthessük:
 . Komplex számok A valós számok és a számegyenes pontjai között kölcsönösen egyértelmű megfeleltetés létesíthető. A számfogalom a számegyenes pontjainak körében nem bővíthető tovább. A számfogalom bővítését
. Komplex számok A valós számok és a számegyenes pontjai között kölcsönösen egyértelmű megfeleltetés létesíthető. A számfogalom a számegyenes pontjainak körében nem bővíthető tovább. A számfogalom bővítését
Matematikai programok
 Matematikai programok Mátrixalapú nyelvek octave Wettl Ferenc Algebra Tanszék B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Wettl
Matematikai programok Mátrixalapú nyelvek octave Wettl Ferenc Algebra Tanszék B U D A P E S T I M Ű S Z A K I M A T E M A T I K A É S G A Z D A S Á G T U D O M Á N Y I I N T É Z E T E G Y E T E M Wettl
x = 1 = ı (imaginárius egység), illetve x 12 = 1 ± 1 4 2
 Komplex számok A valós számok és a számegyenes pontjai között kölcsönösen egyértelmű megfeleltetés létesíthető. A számfogalom a számegyenes pontjainak körében nem bővíthető tovább. A számfogalom bővítését
Komplex számok A valós számok és a számegyenes pontjai között kölcsönösen egyértelmű megfeleltetés létesíthető. A számfogalom a számegyenes pontjainak körében nem bővíthető tovább. A számfogalom bővítését
Tanmenet a Matematika 10. tankönyvhöz
 Tanmenet a Matematika 10. tankönyvhöz (111 óra, 148 óra, 185 óra) A tanmenetben olyan órafelosztást adunk, amely alkalmazható mind a középszintû képzés (heti 3 vagy heti 4 óra), mind az emelt szintû képzés
Tanmenet a Matematika 10. tankönyvhöz (111 óra, 148 óra, 185 óra) A tanmenetben olyan órafelosztást adunk, amely alkalmazható mind a középszintû képzés (heti 3 vagy heti 4 óra), mind az emelt szintû képzés
2. Algebrai átalakítások
 I. Nulladik ZH-ban láttuk: 2. Algebrai átalakítások 1. Mi az alábbi kifejezés legegyszerűbb alakja a változó lehetséges értékei esetén? (A) x + 1 x 1 (x 1)(x 2 + 3x + 2) (1 x 2 )(x + 2) (B) 1 (C) 2 (D)
I. Nulladik ZH-ban láttuk: 2. Algebrai átalakítások 1. Mi az alábbi kifejezés legegyszerűbb alakja a változó lehetséges értékei esetén? (A) x + 1 x 1 (x 1)(x 2 + 3x + 2) (1 x 2 )(x + 2) (B) 1 (C) 2 (D)
Követelmény a 7. évfolyamon félévkor matematikából
 Követelmény a 7. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Elemek halmazba rendezése több szempont alapján. Halmazok ábrázolása. A nyelv logikai elemeinek helyes használata.
Követelmény a 7. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Elemek halmazba rendezése több szempont alapján. Halmazok ábrázolása. A nyelv logikai elemeinek helyes használata.
BASH script programozás II. Vezérlési szerkezetek
 06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
Diszkrét matematika 1.
 Diszkrét matematika 1. Nagy Gábor nagy@compalg.inf.elte.hu nagygabr@gmail.com ELTE IK Komputeralgebra Tanszék 014. ősz 014-15 őszi félév Gyakorlat: 1. ZH tervezett időpontja: október 1.,. ZH tervezett
Diszkrét matematika 1. Nagy Gábor nagy@compalg.inf.elte.hu nagygabr@gmail.com ELTE IK Komputeralgebra Tanszék 014. ősz 014-15 őszi félév Gyakorlat: 1. ZH tervezett időpontja: október 1.,. ZH tervezett
Matematika 8. osztály
 ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Hat évfolyamos Matematika 8. osztály I. rész: Algebra Készítette: Balázs Ádám Budapest, 2018 2. Tartalomjegyzék Tartalomjegyzék I. rész: Algebra................................
ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Hat évfolyamos Matematika 8. osztály I. rész: Algebra Készítette: Balázs Ádám Budapest, 2018 2. Tartalomjegyzék Tartalomjegyzék I. rész: Algebra................................
Komputeralgebra Rendszerek
 Komputeralgebra Rendszerek Konstansok, változók, típusok Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2015. február 24. TARTALOMJEGYZÉK 1 of 110 TARTALOMJEGYZÉK I 1 TARTALOMJEGYZÉK 2 Nevek kezelése
Komputeralgebra Rendszerek Konstansok, változók, típusok Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék 2015. február 24. TARTALOMJEGYZÉK 1 of 110 TARTALOMJEGYZÉK I 1 TARTALOMJEGYZÉK 2 Nevek kezelése
TANMENET 2015/16. Készítette: KOVÁCS ILONA, Felhasználja: Juhász Orsolya
 Tantárgy: Matematika Osztály: 10. B Készítette: KOVÁCS ILONA, Felhasználja: Juhász Orsolya Vetési Albert Gimnázium, Veszprém Heti óraszám: 3 Éves óraszám: 108 Tankönyv: Hajdu Sándor Czeglédy István Hajdu
Tantárgy: Matematika Osztály: 10. B Készítette: KOVÁCS ILONA, Felhasználja: Juhász Orsolya Vetési Albert Gimnázium, Veszprém Heti óraszám: 3 Éves óraszám: 108 Tankönyv: Hajdu Sándor Czeglédy István Hajdu
SZÁMÍTÁSOK A TÁBLÁZATBAN
 SZÁMÍTÁSOK A TÁBLÁZATBAN Az Excelben az egyszerű adatok bevitelén kívül számításokat is végezhetünk. Ezeket a cellákba beírt képletek segítségével oldjuk meg. A képlet: olyan egyenlet, amely a munkalapon
SZÁMÍTÁSOK A TÁBLÁZATBAN Az Excelben az egyszerű adatok bevitelén kívül számításokat is végezhetünk. Ezeket a cellákba beírt képletek segítségével oldjuk meg. A képlet: olyan egyenlet, amely a munkalapon
Matematikai programok
 Matematikai programok Mátrixalapú nyelvek MatLab Wettl Ferenc diái alapján Budapesti M szaki Egyetem Algebra Tanszék 2017.11.07 Borbély Gábor (BME Algebra Tanszék) Matematikai programok 2017.11.07 1 /
Matematikai programok Mátrixalapú nyelvek MatLab Wettl Ferenc diái alapján Budapesti M szaki Egyetem Algebra Tanszék 2017.11.07 Borbély Gábor (BME Algebra Tanszék) Matematikai programok 2017.11.07 1 /
Differenciálegyenletek. Vajda István március 4.
 Analízis előadások Vajda István 2009. március 4. Függvényegyenletek Definíció: Az olyan egyenleteket, amelyekben a meghatározandó ismeretlen függvény, függvényegyenletnek nevezzük. Függvényegyenletek Definíció:
Analízis előadások Vajda István 2009. március 4. Függvényegyenletek Definíció: Az olyan egyenleteket, amelyekben a meghatározandó ismeretlen függvény, függvényegyenletnek nevezzük. Függvényegyenletek Definíció:
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATLAB OKTATÁS 1. ELŐADÁS ALAPOK. Dr. Bécsi Tamás Hegedüs Ferenc
 MATLAB OKTATÁS 1. ELŐADÁS ALAPOK Dr. Bécsi Tamás Hegedüs Ferenc BEVEZETŐ A Matlab egy sokoldalú matematikai programcsomag, amely a mérnöki számításokat egyszerusíti le. (A Matlab neve a MATrix és a LABoratory
MATLAB OKTATÁS 1. ELŐADÁS ALAPOK Dr. Bécsi Tamás Hegedüs Ferenc BEVEZETŐ A Matlab egy sokoldalú matematikai programcsomag, amely a mérnöki számításokat egyszerusíti le. (A Matlab neve a MATrix és a LABoratory
Java II. I A Java programozási nyelv alapelemei
 Java2 / 1 Java II. I A Java programozási nyelv alapelemei Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2009. 02. 09. Java II.: Alapelemek JAVA2 / 1 A Java formalizmusa A C, illetve
Java2 / 1 Java II. I A Java programozási nyelv alapelemei Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2009. 02. 09. Java II.: Alapelemek JAVA2 / 1 A Java formalizmusa A C, illetve
Egyenletek, egyenletrendszerek, egyenlőtlenségek Megoldások
 ) Egyenletek, egyenletrendszerek, egyenlőtlenségek - megoldások Egyenletek, egyenletrendszerek, egyenlőtlenségek Megoldások a) Oldja meg a valós számok halmazán az alábbi egyenletet! = 6 (5 pont) b) Oldja
) Egyenletek, egyenletrendszerek, egyenlőtlenségek - megoldások Egyenletek, egyenletrendszerek, egyenlőtlenségek Megoldások a) Oldja meg a valós számok halmazán az alábbi egyenletet! = 6 (5 pont) b) Oldja
9.fejezet: Függvények és külső eljárások
 9.fejezet: Függvények és külső eljárások Úgy érzem, éppen itt az ideje, hogy összeszedjünk mindent, amit az eljárásokról, illetve a függvényekről tudni kell és rendszerezzük!nos, az alapvető eljárás ugye
9.fejezet: Függvények és külső eljárások Úgy érzem, éppen itt az ideje, hogy összeszedjünk mindent, amit az eljárásokról, illetve a függvényekről tudni kell és rendszerezzük!nos, az alapvető eljárás ugye
Kalkulus. Komplex számok
 Komplex számok Komplex számsík A komplex számok a valós számok természetes kiterjesztése, annak érdekében, hogy a gyökvonás művelete elvégezhető legyen a negatív számok körében is. Vegyük tehát hozzá az
Komplex számok Komplex számsík A komplex számok a valós számok természetes kiterjesztése, annak érdekében, hogy a gyökvonás művelete elvégezhető legyen a negatív számok körében is. Vegyük tehát hozzá az
2018, Funkcionális programozás
 Funkcionális programozás 3. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018, tavaszi félév Miről volt szó? A Haskell programozási nyelv főbb
Funkcionális programozás 3. előadás Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2018, tavaszi félév Miről volt szó? A Haskell programozási nyelv főbb
Számítástechnika I. BMEKOKAA152 BMEKOKAA119 Infokommunikáció I. BMEKOKAA606. Dr. Bécsi Tamás 3. előadás
 Számítástechnika I. BMEKOKAA152 BMEKOKAA119 Infokommunikáció I. BMEKOKAA606 Dr. Bécsi Tamás 3. előadás A Math osztály (System.Math) Metódus Művelet Math.Sin(x) sin(x), ahol az x szög értékét radiánban
Számítástechnika I. BMEKOKAA152 BMEKOKAA119 Infokommunikáció I. BMEKOKAA606 Dr. Bécsi Tamás 3. előadás A Math osztály (System.Math) Metódus Művelet Math.Sin(x) sin(x), ahol az x szög értékét radiánban
PHP. Telepítése: Indítás/újraindítás/leállítás: Beállítások: A PHP nyelv
 PHP A PHP rövidítés jelentése hivatalosan: PHP Hypertext Preprocessor. Ez egy kiszolgáló-oldali parancsnyelv, amit jellemzően HTML oldalakon használnak. A különbség a két nyelv között az, hogy a kiszolgáló
PHP A PHP rövidítés jelentése hivatalosan: PHP Hypertext Preprocessor. Ez egy kiszolgáló-oldali parancsnyelv, amit jellemzően HTML oldalakon használnak. A különbség a két nyelv között az, hogy a kiszolgáló
2012. október 9 és 11. Dr. Vincze Szilvia
 2012. október 9 és 11. Dr. Vincze Szilvia Egyváltozós valós függvények nevezetes osztályai I. Algebrai függvények Racionális egész függvények (polinomok) Racionális törtfüggvények Irracionális függvények
2012. október 9 és 11. Dr. Vincze Szilvia Egyváltozós valós függvények nevezetes osztályai I. Algebrai függvények Racionális egész függvények (polinomok) Racionális törtfüggvények Irracionális függvények
Függvények ábrázolása
 Függvények ábrázolása Matematikai függvényeket analitikusan nem tudunk a matlabban megadni (tudunk, de ilyet még nem tanulunk). Ahhoz, hogy egy függvényt ábrázoljuk, hasonlóan kell eljárni, mint a házi
Függvények ábrázolása Matematikai függvényeket analitikusan nem tudunk a matlabban megadni (tudunk, de ilyet még nem tanulunk). Ahhoz, hogy egy függvényt ábrázoljuk, hasonlóan kell eljárni, mint a házi
Osztályozó- és javítóvizsga témakörei MATEMATIKA tantárgyból 2016 / tanév
 9. évfolyam I. Halmazok Osztályozó- és javítóvizsga témakörei MATEMATIKA tantárgyból 2016 / 2017. tanév 1. Halmaz, részhalmaz fogalma, részhalmazok száma, jelölések 2. Intervallumok 3. Halmazműveletek
9. évfolyam I. Halmazok Osztályozó- és javítóvizsga témakörei MATEMATIKA tantárgyból 2016 / 2017. tanév 1. Halmaz, részhalmaz fogalma, részhalmazok száma, jelölések 2. Intervallumok 3. Halmazműveletek
TANMENET. a matematika tantárgy tanításához 10. E.osztályok számára
 Az iskola fejbélyegzője TANMENET a matematika tantárgy tanításához 10. E.osztályok számára Készítette: Természettudományi Munkaközösség matematikát tanító tanárai Készült: a gimnáziumi tanterv alapján
Az iskola fejbélyegzője TANMENET a matematika tantárgy tanításához 10. E.osztályok számára Készítette: Természettudományi Munkaközösség matematikát tanító tanárai Készült: a gimnáziumi tanterv alapján
Karakterkészlet. A kis- és nagybetűk nem különböznek, a sztringliterálok belsejét leszámítva!
 A PL/SQL alapelemei Karakterkészlet Az angol ABC kis- és nagybetűi: a-z, A-Z Számjegyek: 0-9 Egyéb karakterek: ( ) + - * / < > =! ~ ^ ; :. ' @ %, " # $ & _ { }? [ ] Szóköz, tabulátor, kocsivissza A kis-
A PL/SQL alapelemei Karakterkészlet Az angol ABC kis- és nagybetűi: a-z, A-Z Számjegyek: 0-9 Egyéb karakterek: ( ) + - * / < > =! ~ ^ ; :. ' @ %, " # $ & _ { }? [ ] Szóköz, tabulátor, kocsivissza A kis-
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Abszolútértékes és gyökös kifejezések
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Abszolútértékes és gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Abszolútértékes és gyökös kifejezések A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval
Függvények csoportosítása, függvénytranszformációk
 Függvények csoportosítása, függvénytranszformációk 4. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Függvények csoportosítása p. 1/2 Függvények nevezetes osztályai Algebrai függvények
Függvények csoportosítása, függvénytranszformációk 4. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Függvények csoportosítása p. 1/2 Függvények nevezetes osztályai Algebrai függvények
Komputeralgebra rendszerek
 Komputeralgebra rendszerek III. Változók Czirbusz Sándor czirbusz@gmail.com Komputeralgebra Tanszék ELTE Informatika Kar 2009-2010 ősz Index I 1 Szimbolikus konstansok kezelés A konstansok Nevek levédése
Komputeralgebra rendszerek III. Változók Czirbusz Sándor czirbusz@gmail.com Komputeralgebra Tanszék ELTE Informatika Kar 2009-2010 ősz Index I 1 Szimbolikus konstansok kezelés A konstansok Nevek levédése
Limesz, Derivált, Integrál
 Modellezés Limesz, Derivált, Integrál Direkt (normál) értékadás (=) p legyen a 6. Chebysev polinom. p ChebyshevT6, x 8 x 48 x 4 3 x 6 (Formális) derivált Dp, x 36 x9 x 3 9 x DSinx, x Cosx DSinx, x, Sinx
Modellezés Limesz, Derivált, Integrál Direkt (normál) értékadás (=) p legyen a 6. Chebysev polinom. p ChebyshevT6, x 8 x 48 x 4 3 x 6 (Formális) derivált Dp, x 36 x9 x 3 9 x DSinx, x Cosx DSinx, x, Sinx
2018, Diszkrét matematika
 Diszkrét matematika 5. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? Python alapfogalmak:
Diszkrét matematika 5. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? Python alapfogalmak:
Komputeralgebra rendszerek
 Komputeralgebra rendszerek III. Változók Czirbusz Sándor czirbusz@gmail.com Komputeralgebra Tanszék ELTE Informatika Kar 2009-2010 ősz Index I 1 Szimbolikus konstansok kezelés A konstansok Nevek levédése
Komputeralgebra rendszerek III. Változók Czirbusz Sándor czirbusz@gmail.com Komputeralgebra Tanszék ELTE Informatika Kar 2009-2010 ősz Index I 1 Szimbolikus konstansok kezelés A konstansok Nevek levédése
Matematika 11. osztály
 ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Humán tagozat Matematika 11. osztály I. rész: Hatvány, gyök, logaritmus Készítette: Balázs Ádám Budapest, 018 . Tartalomjegyzék Tartalomjegyzék
ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Humán tagozat Matematika 11. osztály I. rész: Hatvány, gyök, logaritmus Készítette: Balázs Ádám Budapest, 018 . Tartalomjegyzék Tartalomjegyzék
Komputeralgebrai Algoritmusok
 Komputeralgebrai Algoritmusok Adatábrázolás Czirbusz Sándor, Komputeralgebra Tanszék 2015-2016 Ősz Többszörös pontosságú egészek Helyiértékes tárolás: l 1 s d i B i i=0 ahol B a számrendszer alapszáma,
Komputeralgebrai Algoritmusok Adatábrázolás Czirbusz Sándor, Komputeralgebra Tanszék 2015-2016 Ősz Többszörös pontosságú egészek Helyiértékes tárolás: l 1 s d i B i i=0 ahol B a számrendszer alapszáma,
Függvények július 13. f(x) = 1 x+x 2 f() = 1 ()+() 2 f(f(x)) = 1 (1 x+x 2 )+(1 x+x 2 ) 2 Rendezés után kapjuk, hogy:
 Függvények 015. július 1. 1. Feladat: Határozza meg a következ összetett függvényeket! f(x) = cos x + x g(x) = x f(g(x)) =? g(f(x)) =? Megoldás: Összetett függvény el állításához a küls függvényben a független
Függvények 015. július 1. 1. Feladat: Határozza meg a következ összetett függvényeket! f(x) = cos x + x g(x) = x f(g(x)) =? g(f(x)) =? Megoldás: Összetett függvény el állításához a küls függvényben a független
A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a
 a Matematika mérnököknek I. című tárgyhoz Függvények. Függvények A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a szabadon eső test sebessége az idő függvénye. Konstans hőmérsékleten
a Matematika mérnököknek I. című tárgyhoz Függvények. Függvények A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a szabadon eső test sebessége az idő függvénye. Konstans hőmérsékleten
>> x1 = linspace( ); plot(x1,sin(x1),'linewidth',1,'color',[1 0 0]);
![>> x1 = linspace( ); plot(x1,sin(x1),'linewidth',1,'color',[1 0 0]); >> x1 = linspace( ); plot(x1,sin(x1),'linewidth',1,'color',[1 0 0]);](/thumbs/33/15888313.jpg) 1 5. GYAKORLAT SAJÁT FÜGGVÉNYEK, GRAFIKA, FÜGGVÉNYVIZSGÁLAT A PLOT UTASÍTÁS A plot utasítás a legegyszerűbb esetben (x, y) pontpárok összekötött megjelenítésére szolgál (a pontok koordinátáit vektorok
1 5. GYAKORLAT SAJÁT FÜGGVÉNYEK, GRAFIKA, FÜGGVÉNYVIZSGÁLAT A PLOT UTASÍTÁS A plot utasítás a legegyszerűbb esetben (x, y) pontpárok összekötött megjelenítésére szolgál (a pontok koordinátáit vektorok
Mathematica automatikusan dolgozik nagy pontossággal, például 3 a 100-dik hatványon egy szám 48 tizedes jeggyel:
 Mathematica mint egy számológép Használhatja a Mathematica-t, mint egy közönséges számológépet, begépelve egy kifejezést, és a SHIFT + ENTER gombok egyidejű lenyomása után a Mathematica kiszámítja és megadja
Mathematica mint egy számológép Használhatja a Mathematica-t, mint egy közönséges számológépet, begépelve egy kifejezést, és a SHIFT + ENTER gombok egyidejű lenyomása után a Mathematica kiszámítja és megadja
M. 33. Határozza meg az összes olyan kétjegyű szám összegét, amelyek 4-gyel osztva maradékul 3-at adnak!
 Magyar Ifjúság 6 V SOROZATOK a) Három szám összege 76 E három számot tekinthetjük egy mértani sorozat három egymás után következő elemének vagy pedig egy számtani sorozat első, negyedik és hatodik elemének
Magyar Ifjúság 6 V SOROZATOK a) Három szám összege 76 E három számot tekinthetjük egy mértani sorozat három egymás után következő elemének vagy pedig egy számtani sorozat első, negyedik és hatodik elemének
ködös határ (félreértés, hiba)
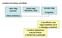 probléma formálisan specifikált: valós világ (domain) (hibás eredmény) ködös határ (félreértés, hiba) formális világ (megoldás) A szoftver fejlesztőnek meg kell értenie a felhasználó problémáját. A specifikáció
probléma formálisan specifikált: valós világ (domain) (hibás eredmény) ködös határ (félreértés, hiba) formális világ (megoldás) A szoftver fejlesztőnek meg kell értenie a felhasználó problémáját. A specifikáció
First Prev Next Last Go Back Full Screen Close Quit. Komplex számok (2)
 2. előadás Komplex számok (2) 1. A a + bi (a, b) kölcsönösen egyértelmű megfeleltetés lehetővé teszi, hogy a komplex számokat a sík pontjaival, illetve helyvektoraival ábrázoljuk. A derékszögű koordináta
2. előadás Komplex számok (2) 1. A a + bi (a, b) kölcsönösen egyértelmű megfeleltetés lehetővé teszi, hogy a komplex számokat a sík pontjaival, illetve helyvektoraival ábrázoljuk. A derékszögű koordináta
MATEMATIKA TANMENET SZAKKÖZÉPISKOLA 11B OSZTÁLY HETI 4 ÓRA 37 HÉT/ ÖSSZ 148 ÓRA
 MINŐSÉGIRÁNYÍTÁSI ELJÁRÁS MELLÉKLET Tanmenetborító Azonosító: ME-III.1./1 Változatszám: 2 Érvényesség 2013. 09. 01. kezdete: Oldal/összes: 1/5 Fájlnév: ME- III.1.1.Tanmenetborító SZK- DC-2013 MATEMATIKA
MINŐSÉGIRÁNYÍTÁSI ELJÁRÁS MELLÉKLET Tanmenetborító Azonosító: ME-III.1./1 Változatszám: 2 Érvényesség 2013. 09. 01. kezdete: Oldal/összes: 1/5 Fájlnév: ME- III.1.1.Tanmenetborító SZK- DC-2013 MATEMATIKA
Analízis elo adások. Vajda István. 2012. szeptember 10. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem 1 / 36 Bevezetés A komplex számok értelmezése Definíció: Tekintsük a valós számpárok R2 halmazát és értelmezzük ezen a halmazon a következo két
Vajda István Neumann János Informatika Kar Óbudai Egyetem 1 / 36 Bevezetés A komplex számok értelmezése Definíció: Tekintsük a valós számpárok R2 halmazát és értelmezzük ezen a halmazon a következo két
Bevezetés a MATLAB programba
 Bevezetés a MATLAB programba 1. Mi az a MATLAB? A MATLAB egy olyan matematikai programcsomag, amely mátrix átalakításokat használ a komplex numerikus számítások elvégzésére. A Mathematica és Maple programokkal
Bevezetés a MATLAB programba 1. Mi az a MATLAB? A MATLAB egy olyan matematikai programcsomag, amely mátrix átalakításokat használ a komplex numerikus számítások elvégzésére. A Mathematica és Maple programokkal
Csima Judit március 9. és 16.
 Grafika Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2017. március 9. és 16. Csima Judit Grafika 1 / 18 Grafika általában Grafika az R-ben Van néhány alapvető package az ábrázolásra:
Grafika Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2017. március 9. és 16. Csima Judit Grafika 1 / 18 Grafika általában Grafika az R-ben Van néhány alapvető package az ábrázolásra:
A lineáris algebrában központi szerepet betöltı vektortér fogalmát értelmezzük most, s megvizsgáljuk e struktúra legfontosabb egyszerő tulajdonságait.
 2. VEKTORTÉR A lineáris algebrában központi szerepet betöltı vektortér fogalmát értelmezzük most, s megvizsgáljuk e struktúra legfontosabb egyszerő tulajdonságait. Legyen K egy test és V egy nem üres halmaz,
2. VEKTORTÉR A lineáris algebrában központi szerepet betöltı vektortér fogalmát értelmezzük most, s megvizsgáljuk e struktúra legfontosabb egyszerő tulajdonságait. Legyen K egy test és V egy nem üres halmaz,
Diszkrét matematika 1. estis képzés
 Diszkrét matematika 1. estis képzés 2019. tavasz 1. Diszkrét matematika 1. estis képzés 5. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
Diszkrét matematika 1. estis képzés 2019. tavasz 1. Diszkrét matematika 1. estis képzés 5. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján
A C# PROGRAMOZÁSI NYELV
 A C# PROGRAMOZÁSI NYELV 2010.02.23. Bevezetés C# nyelv jellemzői 2 Kis és NAGY betű érzékeny Minden utasítást pontos vessző zár. Utasítás zárójel a:,. .NET Framework keretrendszerek 3 Microsoft.NET Framework
A C# PROGRAMOZÁSI NYELV 2010.02.23. Bevezetés C# nyelv jellemzői 2 Kis és NAGY betű érzékeny Minden utasítást pontos vessző zár. Utasítás zárójel a:,. .NET Framework keretrendszerek 3 Microsoft.NET Framework
Beregszászi István Programozási példatár
 Beregszászi István Programozási példatár 2 1. fejezet 1. laboratóriumi munka 1.1. Matematikai kifejezések Írja fel algoritmikus nyelven a megadott kifejezést megfelelő típusú változók segítségével! Figyeljen
Beregszászi István Programozási példatár 2 1. fejezet 1. laboratóriumi munka 1.1. Matematikai kifejezések Írja fel algoritmikus nyelven a megadott kifejezést megfelelő típusú változók segítségével! Figyeljen
Egyenletek, egyenlőtlenségek V.
 Egyenletek, egyenlőtlenségek V. DEFINÍCIÓ: (Másodfokú egyenlet) Az ax + bx + c = 0 alakban felírható egyenletet (a, b, c R; a 0), ahol x a változó, másodfokú egyenletnek nevezzük. TÉTEL: Az ax + bx + c
Egyenletek, egyenlőtlenségek V. DEFINÍCIÓ: (Másodfokú egyenlet) Az ax + bx + c = 0 alakban felírható egyenletet (a, b, c R; a 0), ahol x a változó, másodfokú egyenletnek nevezzük. TÉTEL: Az ax + bx + c
Az osztályozóvizsgák követelményrendszere 9. évfolyam
 Az osztályozóvizsgák követelményrendszere 9. évfolyam Kombinatorika, halmazok Összeszámlálási feladatok Halmazok, halmazműveletek, halmazok elemszáma Logikai szita Számegyenesek intervallumok Algebra és
Az osztályozóvizsgák követelményrendszere 9. évfolyam Kombinatorika, halmazok Összeszámlálási feladatok Halmazok, halmazműveletek, halmazok elemszáma Logikai szita Számegyenesek intervallumok Algebra és
1. A komplex számok definíciója
 1. A komplex számok definíciója A számkör bővítése Tétel Nincs olyan n természetes szám, melyre n + 3 = 1. Bizonyítás Ha n természetes szám, akkor n+3 3. Ezért bevezettük a negatív számokat, közöttük van
1. A komplex számok definíciója A számkör bővítése Tétel Nincs olyan n természetes szám, melyre n + 3 = 1. Bizonyítás Ha n természetes szám, akkor n+3 3. Ezért bevezettük a negatív számokat, közöttük van
