3. Fejezet Csonka Gábor István MTA Doktori Értekezés
|
|
|
- Andrea Biróné
- 6 évvel ezelőtt
- Látták:
Átírás
1 3. Az elektronkorreláció és a bázis függvények hatása a disziloxán hajlítási potenciális energiagörbéjére I. Csonka, G. I., Erdõsy, M. and Réffy, J., Structure of Disiloxane: Semiempirical and post-artree-fock study, J. Comp. Chem. 15 (1994) 925. II. Csonka, G. I and Réffy, J., Density-functional study of the equilibrium geometry and Si-O-Si potential energy curve of disiloxane, Chem. Phys. Lett. 229 (1994) 191. V. Csonka, G. I. and Réffy, J., The failure of the MO-based theoretical explanations for bending of disiloxane, J. Mol. Struct. (Theochem), 332 (1995) Bevezetés A disziloxán szerkezetének meghatározása kísérletileg és elméletileg egyaránt nehéznek bizonyult. A kísérleti nehézségek fõ forrása két nagy amplitúdójú mozgás, a Si 3 csoportok forgása és az Si-O-Si kötés behajlása. A 3.1. táblázatban foglaltam össze a rendelkezésre álló, egymásnak ellentmondó adatokat. Kutatásunk célja annak eldöntése volt, hogy mennyi a valóságos eredmény és milyen számítási módszerrel lehet azt reprodukálni táblázat. A hajlítási energiagát (kcal/mol), az Si-O-Si kötésszög ( ) és az Si-O kötéstávolság (Å) disziloxánban az irodalmi adatok szerint. Módszer/bázis Gátmagasság <(Si-O-Si) r(si - O) ivatkozás Kísérlet (IR+Raman) Kísérlet (ED) Kísérlet (Raman) Kísérlet (Raman) ± 2 4 Kísérlet (Raman) Kísérlet (X-Ray) ± RF/STO-3G RF/4-31G RF/6-31G(d) MP2/6-31G(d)//RF/6-31G(d) MP3/6-31G(d)//RF/6-31G(d) CPFa RF/TZ(2d) CISD/TZ(2d) MP2/6-31G(d) MP2/6-311G(d,p) MP2/6-311G(2d,p) RF/CEP-31G RF/CEP-31G(d) a részben optimalizált geometria, nem standard bázissal számítva. A 3.1. táblázat adataiból az a következtetés vonható le, hogy a korábbi számítások alapján nem lehet dönteni a háromféle kísérleti eredmény között. A disziloxán molekulára vonatkozóan megállapítható, hogy az Si-O-Si kötés lineárissá alakításához szükséges számított energia érzékeny az alkalmazott bázis polarizációs függvényeire. A jó minõségû, 6-311G(d) vagy TZ(d) 15
2 tripla-zéta bázist egyetlen d pálya készlettel (amely 6 egyedi pályából áll) kiegészí tve nagyon alacsony, vagy nulla gátat kapunk. a 6-311G(2d) bázissal végezzük a számításokat, a gátmagasság jelentõsen megnõ Eredmények Az általunk végzett nagyon pontosnak tekinthetõ CCSD(T)/6-311G(d) számítások szerint a gátmagasság 0,23 kcal/mol (0,96 kj/mol), a CCSD(T)/6-311G(2d) számítások szerint a gátmagasság 1,36 kcal/mol (5,69 kj/mol) (3.2. táblázat, az I. és II. közlemény alapján). A gátmagasság-növekedés módszer és bázis független, ami arra utal, hogy kizárólag a polarizációs függvények a felelõsek a jelenségért. Számításaimhoz a 3.1. Ábrán látható Cs szimmetriájú konformációt használtam. t O t Si Si 3.1. ábra. A számításokhoz használt C s szimmetriájú disziloxán konformáció. t jelöli a szimmetriasíkban lévõ hidrogénatomokat. Az Si 3 csoport forgatásakor ennek a konformernek a legalacsonyabb az energiája. Megjegyzendõ, hogy a lineáris szerkezet esetén az Si 3 csoportok forgásának energia gátja gyakorlatilag nulla, míg az Si-O-Si kötés behajlításakor a 3.1. Ábrán látható konformáció válik a legstabilabbá. Minél kisebb az Si-O-Si kötésszög, annál nagyobb lesz a forgás gátja táblázat. A disziloxán legalacsonyabb energiájú és lineáris alakjának különbözõ módszerekkel számított teljes energiája (artree), az energiagát magassága (kcal/mol) és a számításhoz használt geometria fõbb jellemzõi ( és Å). Módszer/bázis Teljes energia Energiagát <(Si-O-Si) r(si - O) r(si - t) r(si - ) F/6-311G(d) B3-P86/6-311G(d) B3-P86/6-311G(d) B-P86/6-311G(d) B-P86/6-311G(d) MP2/6-311G(d) MP2/6-311G(d) CCSD(T)/6-311G(d) a CCSD(T)/6-311G(d) a F/6-311G(2d) F/6-311G(2d) B3-P86/6-311G(2d) B3-P86/6-311G(2d) B-P86/6-311G(2d) b B-P86/6-311G(2d) b
3 3.2. táblázat folytatása. Módszer/bázis Teljes energia Energiagát <(Si-O-Si) r(si - O) r(si - t) r(si - ) MP2/6-311G(2d) a MP2/6-311G(2d) a CCSD(T)/6-311G(2d) a CCSD(T)/6-311G(2d) a F/6-311+G(3d) F/6-311+G(3d) B-P86/6-311+G(3d) B-P86/6-311+G(3d) MP2/6-311+G(3d) a MP2/6-311+G(3d) a F/6-311+G(3df) F/6-311+G(3df) B3-P86/6-311+G(3df) B3-P86/6-311+G(3df) B-LYP/6-311+G(3df) B-LYP/6-311+G(3df) B-P86/6-311+G(3df) B-P86/6-311+G(3df) MP2/6-311+G(3df) a MP2/6-311+G(3df) a a Az MP2/6-311G(d) módszerrel optimalizált geometriát használva. b A geometriát finom ráccsal újra optimalizáltam (Int=FineGrid), hogy meggyõzõdhessünk az eredmény stabilitásáról. A 3.2. táblázat adatai alapján látható, hogy további d, valamint diffúz pályák hozzáadása nem változtatja meg lényegesen a gátmagasságot, viszont az f pályák hozzáadása lényegesen csökkenti azt. A polarizációs függvények hatását az Si-O-Si kötésszög behajlításának potenciális energia görbéjére a 3.2., 3.3. és 3.4. Ábrán mutatom be (az ábrák a I és II közleményekben jelentek meg). A 3.2. táblázatban és a 3.2., 3.3. és 3.4. Ábrán bemutatott módszerek mellett még vizsgáltam a CCD, CCSD és CISD módszereket is [I]. Megállapí tható hogy az MP2 módszerrel számí tott potenciális energiagörbe az elõbbi 3 módszerrel számított energiagörbénél közelebb esik a legpontosabb CCSD(T) módszerrel számított potenciális energiagörbéhez (ezek az ábrák a I. publikációban találhatók). Ezért a nagyon nagy bázissal végzett számí tások esetében, amikor a CCSD(T) számítások rendkívül költségesek lennének, az MP2 eredményeket használtam referenciaként. 17
4 Relative Energy (kcal/mol) G(d) F MP2 B3-P86 B-P86 CCSD(T) Si-O-Si bond angle 3.2. ábra. Az Si-O-Si kötés behajlításának potenciális energiagörbéje a 6-311G(d) bázissal számítva. A F, a B-P86, a B3-P86 geometriákat rögzített Si-O-Si kötésszögek mellett teljesen optimalizáltam. A CCSD(T) energiákat a megfelelõ MP2/6-311G(d) optimalizált geometriák alapján számítottam. A F görbét -0,27 kcal/mol-lal elcsúsztattam. 18
5 Relative Energy (kcal/mol) G(2d) F MP2 B3-P86 B-P86 CCSD(T) Si-O-Si bond angle 3.3 ábra. Az Si-O-Si kötés behajlí tásának potenciális energiagörbéje a 6-311G(2d) bázissal számítva. A F, a B-P86, a B3-P86 geometriákat rögzített Si-O-Si kötésszögek mellett teljesen optimalizáltam. A CCSD(T) energiákat a megfelelõ MP2/6-311G(d) optimalizált geometriák alapján számítottam. A B-P86 görbét 0,05 kcal/mol-lal elcsúsztattam. A 3.3. és 3.4. Ábrákon látható, hogy több polarizációs függvény használata esetén az MP2 és a B-P86 görbék közel esnek egymáshoz, és a 3.3. Ábrán látható, hogy a B-P86 görbe közelíti jobban a CCSD(T) potenciális energiagörbét. Legjobb minõségû számításaim alapján megállapítható, hogy az Si-O-Si kötés behajlításának helyes leírásához szükség van az f polarizációs függvények használatára és az elektron korreláció figyelembe vételére. Eredményeim alapján az Si-O-Si kötésszög nem lineáris és a 0,30 kcal/mol kísérleti érték megerõsíthetõ [II]. A 3.2., 3.3., és 3.4. ábra alapján megállapítható, hogy az egyensúlyi Si-O-Si kötésszög hasonló módon függ a bázistól mint a gátmagasság. Magas gát esetén kisebb, alacsony gát esetén nagyobb kötésszöget kapunk. 19
6 1.40 Relative Energy (kcal/mol) F/+G(3d) MP2/+G(3d) B-P86/+G(3d) F/+G(3df) MP2/+G(3df) B-P86/+G(3df) Si-O-Si bond angle 3.4. ábra. Az Si-O-Si kötés behajlításának potenciális energiagörbéje a G(3d) és G(3df) bázissal számítva. A F és a B-P86 geometriákat rögzített Si- O-Si kötésszögek mellett teljesen optimalizáltam. A CCSD(T) energiákat a megfelelõ MP2/6-311G(d) optimalizált geometriák alapján számítottam. A F/+G(3d) görbét 0,10 kcal/mol-lal, a B-P86/+G(3d) görbét 0,05 kcal/mol-lal, a B3-P86/+G(3d) görbét -0,05 kcal/mol-lal, a F/+G(3df) görbét -0,32 kcal/mollal elcsúsztattam. Az, hogy a disziloxánban erõsen függ az egyensúlyi kötésszög az alkalmazott bázistól, lehetõséget nyújtott egy korábbi feltételezés alkalmazhatóságának ellenõrzésére. Shambayati és mtsai 8 azzal magyarázták a disziloxán dimetil-éterhez viszonyított nagyobb oxigén centrumú kötésszögét, hogy a legfelsõ betöltött molekulapályák hajlításkor fellépõ stabilizáló hatása a disziloxán esetében jóval kisebb, és ezt sikeresen kompenzálja a b 2 szimmetriájú OMO-2 pálya destabilizáló hatása. Eredményeim alapján megállapítható, hogy Az Si-O-Si hajlí tási gátmagasság a disziloxánban érzékenyen függ az alkalmazott polarizációs függvények számától. Tripla-zéta, 6-311G bázis egy d polarizációs függvénykészlettel nagyon alacsony (CCSD(T) módszerrel számítva 0,23 kcal/mol), vagy nulla (F módszerrel számítva), két d polarizációs függvénykészlettel magas (CCSD(T) módszerrel számítva 1,36 kcal/mol), három d és egy f polarizációs függvénykészlettel ismét alacsony hajlítási gátat ad (0,3-0,4 20
7 kcal/mol ACM, GGA-DFT és MP2 módszerekkel számítva). Számításaim a 0,32 kcal/mol kísérleti hajlítási gátmagasságot támasztják alá. A DFT és az MP2 eredmények jól egyeznek a CCSD(T) eredményekkel, ezért megbízhatóak. A CEP bázis valamennyi módszerrel és egy d polarizációs függvénykészlettel is magas gátat ad, így nem ajánlható Si-O-Si hajlítás tanulmányozására [I,II]. Az Si-O-Si egyensúlyi kötésszög a gátmagassághoz hasonlóan függ a bázistól. Tripla zéta, 6-311G bázis egy d polarizációs függvénykészlettel 155 fölötti, két d polarizációs függvénykészlettel 140 alatti szöget eredményez. árom d és egy f polarizációs függvénykészlettel a kísérleti kal jól egyezõ eredményt kapunk. Általában megállapítható, hogy magasabb gátmagasság kisebb egyensúlyi kötésszöggel jár együtt [I,II]. Az Si-O kötéstávolság és az Si-O-Si kötésszög közötti szilikát kristályok alapján felállított összefüggés nem egyezik a számítások által gáz fázisban megjósolt összefüggéssel [I]. Az ab iníció elektrosztatikus pontenciál alapján származtatott töltések konvergenciát mutattak. Az ú.n. CELPG algoritmus szerint számított töltések az Si-O-Si kötésszög csökkenésével nõnek. A Mulliken töltések nem mutattak konvergenciát, használatuk az eredmények alapján nem ajánlatos [I]. A hexametil-disziloxánra végzett számí tásaim szerint ebben a molekulában az Si-O távolság 1 pm-rel hosszabb, az Si-O-Si kötésszög nagyobb és az Si-O-Si hajlí tási gátmagasság kisebb, mint a disziloxánban. A CELPG, BMK és NPA (természetes populációs analízis) eredmények szerint az Si-O kötés hexametil-disziloxánban erõsebben ionos jellegû mint a disziloxánban [I]. Az az elmélet, amely szerint disziloxánban a legfelsõ molekulapályák energiájának az Si-O-Si kötésszög behajlításakor bekövetkezõ megváltozása ad az alacsony energiagátra és nagy kötésszögére magyarázatot, nem bizonyult érvényesnek. Számításaink szerint a hajlítási energiagát magassága és az Si-O-Si kötésszög nagyon erõsen függ a bázistól, de ezzel szemben a pályaenergiák Si-O-Si kötésszög behajlításakor bekövetkezõ megváltozása az alkalmazott bázistól független [V]. Irodalomjegyzék Lord, R. C.; Robinson, D. W.; Schumb, W. C. J. Am. Chem. Soc. 78, 1327 (1957). Almenningen, A.; Bastiansen, O.; Ewing, V.; edberg, K.; Tretteberg, M. Acta. Shem. Scand. 17, 2455 (1963). Aronson, J. R.; Lord, R. C.; Robinson, D. W. J. Chem. Phys. 33, 1004 (1960). J. R. Durig M. J. Flanagan, V. F. Kalasinsky, J. Chem. Phys. 66, 2775 (1977). Koput, J.; Wierzbicki, A. J. Mol. Specrosc. 99, 116 (1983). M. J Barrow, E. A. Ebsworth, M. M. arding, Acta Crytallogr. B35, 2093 (1979). Sauer, J.; Zurawski, B. Chem. Phys. Lett. 65, 587 (1979). S. Shambayati, J. F. Blake, Wierschke, S. G. Jorgensen, W. L.; Schreiber, S. L., J. Am. Chem Soc. 112, 697 (1990). J. Koput, Chem. Phys. 148, 299 (1990). Nicholas, J. B.; Winans, R. E.;arrison, R. J.; Iton, L. E.; Curtiss, L. A.; opfinger, A. J., J. Phys. Chem. 96, 7958 (1992). B. T. Luke, J. Phys. Chem. 97, 7505 (1993). C. W. Earley, J. Comp. Chem. 14, 216 (1993). 21
4. Fejezet Csonka Gábor István MTA Doktori Értekezés
 4. A -()- molekula ab iníció egyensúlyi geometriája és egy disszociációs csatornája. A CT2 módszer. A DFT módszerek teljesítõképessége kéntartalmú molekulák esetében III. IV. Csonka, G. I., Loos, M., Kucsman,
4. A -()- molekula ab iníció egyensúlyi geometriája és egy disszociációs csatornája. A CT2 módszer. A DFT módszerek teljesítõképessége kéntartalmú molekulák esetében III. IV. Csonka, G. I., Loos, M., Kucsman,
5. Az elektronkorreláció szerepe a metil-amin nagy amplitúdójú mozgásainak leírásában. DFT és poszt Hartree- Fock számítások
 5. Az elektronkorreláció szerepe a metil-amin nagy amplitúdójú mozgásainak leírásában. DFT és poszt artree- Fock számítások VI. XIX. Csonka, G. I. and Sztraka L., Density functional and post artree-fock
5. Az elektronkorreláció szerepe a metil-amin nagy amplitúdójú mozgásainak leírásában. DFT és poszt artree- Fock számítások VI. XIX. Csonka, G. I. and Sztraka L., Density functional and post artree-fock
8. Egyszerû tesztek sûrûség funkcionál módszerek minõsítésére
 8. Egyszerû tesztek sûrûség funkcionál módszerek minõsítésére XX. Csonka, G. I., Nguyen, N. A., Kolossváry, I., Simple tests for density functionals, J. Comput. Chem. 18 (1997) 1534. XXII. Csonka, G. I.,
8. Egyszerû tesztek sûrûség funkcionál módszerek minõsítésére XX. Csonka, G. I., Nguyen, N. A., Kolossváry, I., Simple tests for density functionals, J. Comput. Chem. 18 (1997) 1534. XXII. Csonka, G. I.,
Kémiai kötés. Általános Kémia, szerkezet Dia 1 /39
 Kémiai kötés 4-1 Lewis elmélet 4-2 Kovalens kötés: bevezetés 4-3 Poláros kovalens kötés 4-4 Lewis szerkezetek 4-5 A molekulák alakja 4-6 Kötésrend, kötéstávolság 4-7 Kötésenergiák Általános Kémia, szerkezet
Kémiai kötés 4-1 Lewis elmélet 4-2 Kovalens kötés: bevezetés 4-3 Poláros kovalens kötés 4-4 Lewis szerkezetek 4-5 A molekulák alakja 4-6 Kötésrend, kötéstávolság 4-7 Kötésenergiák Általános Kémia, szerkezet
Modern Fizika Labor. Fizika BSc. Értékelés: A mérés dátuma: A mérés száma és címe: 13. mérés: Molekulamodellezés PC-n. 2008. április 29.
 Modern Fizika Labor Fizika BSc A mérés dátuma: A mérés száma és címe: 13. mérés: Molekulamodellezés PC-n Értékelés: A beadás dátuma: 2008. május 6. A mérést végezte: 1/5 A mérés célja A mérés célja az
Modern Fizika Labor Fizika BSc A mérés dátuma: A mérés száma és címe: 13. mérés: Molekulamodellezés PC-n Értékelés: A beadás dátuma: 2008. május 6. A mérést végezte: 1/5 A mérés célja A mérés célja az
Kémiai kötés. Általános Kémia, szerkezet Dia 1 /39
 Kémiai kötés 4-1 Lewis-elmélet 4-2 Kovalens kötés: bevezetés 4-3 Poláros kovalens kötés 4-4 Lewis szerkezetek 4-5 A molekulák alakja 4-6 Kötésrend, kötéstávolság 4-7 Kötésenergiák Általános Kémia, szerkezet
Kémiai kötés 4-1 Lewis-elmélet 4-2 Kovalens kötés: bevezetés 4-3 Poláros kovalens kötés 4-4 Lewis szerkezetek 4-5 A molekulák alakja 4-6 Kötésrend, kötéstávolság 4-7 Kötésenergiák Általános Kémia, szerkezet
Kémiai kötés. Általános Kémia, szerkezet Slide 1 /39
 Kémiai kötés 12-1 Lewis elmélet 12-2 Kovalens kötés: bevezetés 12-3 Poláros kovalens kötés 12-4 Lewis szerkezetek 12-5 A molekulák alakja 12-6 Kötésrend, kötéstávolság 12-7 Kötésenergiák Általános Kémia,
Kémiai kötés 12-1 Lewis elmélet 12-2 Kovalens kötés: bevezetés 12-3 Poláros kovalens kötés 12-4 Lewis szerkezetek 12-5 A molekulák alakja 12-6 Kötésrend, kötéstávolság 12-7 Kötésenergiák Általános Kémia,
A kémiai kötés magasabb szinten
 A kémiai kötés magasabb szinten 11-1 Mit kell tudnia a kötéselméletnek? 11- Vegyérték kötés elmélet 11-3 Atompályák hibridizációja 11-4 Többszörös kovalens kötések 11-5 Molekulapálya elmélet 11-6 Delokalizált
A kémiai kötés magasabb szinten 11-1 Mit kell tudnia a kötéselméletnek? 11- Vegyérték kötés elmélet 11-3 Atompályák hibridizációja 11-4 Többszörös kovalens kötések 11-5 Molekulapálya elmélet 11-6 Delokalizált
Kémiai kötés. Általános Kémia, szerkezet Slide 1 /39
 Kémiai kötés 4-1 Lewis elmélet 4-2 Kovalens kötés: bevezetés 4-3 Poláros kovalens kötés 4-4 Lewis szerkezetek 4-5 A molekulák alakja 4-6 Kötésrend, kötéstávolság 4-7 Kötésenergiák Általános Kémia, szerkezet
Kémiai kötés 4-1 Lewis elmélet 4-2 Kovalens kötés: bevezetés 4-3 Poláros kovalens kötés 4-4 Lewis szerkezetek 4-5 A molekulák alakja 4-6 Kötésrend, kötéstávolság 4-7 Kötésenergiák Általános Kémia, szerkezet
A SZILÁRDTEST FOGALMA. Szilárdtest: makroszkópikus, szilárd, rendezett anyagdarab. molekula klaszter szilárdtest > σ λ : rel.
 A SZILÁRDTEST FOGALMA Szilárdtest: makroszkópikus, szilárd, rendezett anyagdarab. a) Méret: b) Szilárdság: molekula klaszter szilárdtest > ~ 100 Å ideálisan rugalmas test: λ = 1 E σ λ : rel. megnyúlás
A SZILÁRDTEST FOGALMA Szilárdtest: makroszkópikus, szilárd, rendezett anyagdarab. a) Méret: b) Szilárdság: molekula klaszter szilárdtest > ~ 100 Å ideálisan rugalmas test: λ = 1 E σ λ : rel. megnyúlás
A kémiai kötés magasabb szinten
 A kémiai kötés magasabb szinten 13-1 Mit kell tudnia a kötéselméletnek? 13- Vegyérték kötés elmélet 13-3 Atompályák hibridizációja 13-4 Többszörös kovalens kötések 13-5 Molekulapálya elmélet 13-6 Delokalizált
A kémiai kötés magasabb szinten 13-1 Mit kell tudnia a kötéselméletnek? 13- Vegyérték kötés elmélet 13-3 Atompályák hibridizációja 13-4 Többszörös kovalens kötések 13-5 Molekulapálya elmélet 13-6 Delokalizált
A kovalens kötés elmélete. Kovalens kötésű molekulák geometriája. Molekula geometria. Vegyértékelektronpár taszítási elmélet (VSEPR)
 4. előadás A kovalens kötés elmélete Vegyértékelektronpár taszítási elmélet (VSEPR) az atomok kötő és nemkötő elektronpárjai úgy helyezkednek el a térben, hogy egymástól minél távolabb legyenek A központi
4. előadás A kovalens kötés elmélete Vegyértékelektronpár taszítási elmélet (VSEPR) az atomok kötő és nemkötő elektronpárjai úgy helyezkednek el a térben, hogy egymástól minél távolabb legyenek A központi
Kémiai kötés Lewis elmélet
 Kémiai kötés 10-1 Lewis elmélet 10-2 Kovalens kötés: bevezetés 10-3 Poláros kovalens kötés 10-4 Lewis szerkezetek 10-5 A molekulák alakja 10-6 Kötésrend, kötéstávolság 10-7 Kötésenergiák Általános Kémia,
Kémiai kötés 10-1 Lewis elmélet 10-2 Kovalens kötés: bevezetés 10-3 Poláros kovalens kötés 10-4 Lewis szerkezetek 10-5 A molekulák alakja 10-6 Kötésrend, kötéstávolság 10-7 Kötésenergiák Általános Kémia,
? ligandum kötés konformációs változás aktiválási energia számítás pka számítás kötési energiák
 Szabadenergia Definíció:? ligandum kötés konformációs változás aktiválási energia számítás pka számítás kötési energiák Fázistér teljes térfogatára kell számítani! Mennyiség átlagértéke: Sokaság-átlag
Szabadenergia Definíció:? ligandum kötés konformációs változás aktiválási energia számítás pka számítás kötési energiák Fázistér teljes térfogatára kell számítani! Mennyiség átlagértéke: Sokaság-átlag
A kovalens kötés polaritása
 Általános és szervetlen kémia 4. hét Kovalens kötés A kovalens kötés kialakulásakor szabad atomokból molekulák jönnek létre. A molekulák létrejötte mindig energia csökkenéssel jár. A kovalens kötés polaritása
Általános és szervetlen kémia 4. hét Kovalens kötés A kovalens kötés kialakulásakor szabad atomokból molekulák jönnek létre. A molekulák létrejötte mindig energia csökkenéssel jár. A kovalens kötés polaritása
FELADATMEGOLDÁS. Tesztfeladat: Válaszd ki a helyes megoldást!
 FELADATMEGOLDÁS Tesztfeladat: Válaszd ki a helyes megoldást! 1. Melyik sorozatban található jelölések fejeznek ki 4-4 g anyagot? a) 2 H 2 ; 0,25 C b) O; 4 H; 4 H 2 c) 0,25 O; 4 H; 2 H 2 ; 1/3 C d) 2 H;
FELADATMEGOLDÁS Tesztfeladat: Válaszd ki a helyes megoldást! 1. Melyik sorozatban található jelölések fejeznek ki 4-4 g anyagot? a) 2 H 2 ; 0,25 C b) O; 4 H; 4 H 2 c) 0,25 O; 4 H; 2 H 2 ; 1/3 C d) 2 H;
Elektronegativitás. Elektronegativitás
 Általános és szervetlen kémia 3. hét Elektronaffinitás Az az energiaváltozás, ami akkor következik be, ha 1 mól gáz halmazállapotú atomból 1 mól egyszeresen negatív töltésű anion keletkezik. Mértékegysége:
Általános és szervetlen kémia 3. hét Elektronaffinitás Az az energiaváltozás, ami akkor következik be, ha 1 mól gáz halmazállapotú atomból 1 mól egyszeresen negatív töltésű anion keletkezik. Mértékegysége:
Fizikai kémia 2. Előzmények. A Lewis-féle kötéselmélet A VB- és az MO-elmélet, a H 2+ molekulaion
 06.07.5. Fizikai kémia. 4. A VB- és az -elmélet, a H + molekulaion Dr. Berkesi ttó ZTE Fizikai Kémiai és Anyagtudományi Tanszéke 05 Előzmények Az atomok szerkezetének kvantummehanikai leírása 90-30-as
06.07.5. Fizikai kémia. 4. A VB- és az -elmélet, a H + molekulaion Dr. Berkesi ttó ZTE Fizikai Kémiai és Anyagtudományi Tanszéke 05 Előzmények Az atomok szerkezetének kvantummehanikai leírása 90-30-as
Adatgyőjtés, mérési alapok, a környezetgazdálkodás fontosabb mőszerei
 GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
Kutatási terület. Szervetlen és szerves molekulák szerkezetének ab initio tanulmányozása
 Kutatási terület zervetlen és szerves molekulák szerkezetének ab initio tanulmányozása Cél: a molekulák disszociatív ionizációja során keletkező semleges és ionizált fragmentumok energetikai paramétereinek
Kutatási terület zervetlen és szerves molekulák szerkezetének ab initio tanulmányozása Cél: a molekulák disszociatív ionizációja során keletkező semleges és ionizált fragmentumok energetikai paramétereinek
Kötések kialakítása - oktett elmélet
 Kémiai kötések Az elemek és vegyületek halmazai az atomok kapcsolódásával - kémiai kötések kialakításával - jönnek létre szabad atomként csak a nemesgázatomok léteznek elsődleges kémiai kötések Kötések
Kémiai kötések Az elemek és vegyületek halmazai az atomok kapcsolódásával - kémiai kötések kialakításával - jönnek létre szabad atomként csak a nemesgázatomok léteznek elsődleges kémiai kötések Kötések
Általános és szervetlen kémia 3. hét Kémiai kötések. Kötések kialakítása - oktett elmélet. Lewis-képlet és Lewis szerkezet
 Általános és szervetlen kémia 3. hét Kémiai kötések Az elemek és vegyületek halmazai az atomok kapcsolódásával - kémiai kötések kialakításával - jönnek létre szabad atomként csak a nemesgázatomok léteznek
Általános és szervetlen kémia 3. hét Kémiai kötések Az elemek és vegyületek halmazai az atomok kapcsolódásával - kémiai kötések kialakításával - jönnek létre szabad atomként csak a nemesgázatomok léteznek
Savak bázisok. Csonka Gábor Általános Kémia: 7. Savak és bázisok Dia 1 /43
 Savak bázisok 121 Az Arrhenius elmélet röviden 122 BrønstedLowry elmélet 123 A víz ionizációja és a p skála 124 Erős savak és bázisok 125 Gyenge savak és bázisok 126 Több bázisú savak 127 Ionok mint savak
Savak bázisok 121 Az Arrhenius elmélet röviden 122 BrønstedLowry elmélet 123 A víz ionizációja és a p skála 124 Erős savak és bázisok 125 Gyenge savak és bázisok 126 Több bázisú savak 127 Ionok mint savak
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
Kémiai reakciók mechanizmusa számítógépes szimulációval
 Kémiai reakciók mechanizmusa számítógépes szimulációval Stirling András stirling@chemres.hu Elméleti Kémiai Osztály Budapest Stirling A. (MTA Kémiai Kutatóközpont) Reakciómechanizmus szimulációból 2007.
Kémiai reakciók mechanizmusa számítógépes szimulációval Stirling András stirling@chemres.hu Elméleti Kémiai Osztály Budapest Stirling A. (MTA Kémiai Kutatóközpont) Reakciómechanizmus szimulációból 2007.
Compton-effektus. Zsigmond Anna. jegyzıkönyv. Fizika BSc III.
 Compton-effektus jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Csanád Máté Mérés dátuma: 010. április. Leadás dátuma: 010. május 5. Mérés célja A kvantumelmélet egyik bizonyítékának a Compton-effektusnak
Compton-effektus jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Csanád Máté Mérés dátuma: 010. április. Leadás dátuma: 010. május 5. Mérés célja A kvantumelmélet egyik bizonyítékának a Compton-effektusnak
Elektrosztatikus számítások. Elektrosztatikus számítások. Elektrosztatikus számítások. Elektrosztatikus számítások Definíciók
 Jelentősége szubsztrát kötődés szolvatáció ionizációs állapotok (pka) mechanizmus katalízis ioncsatornák szimulációk (szerkezet) all-atom dipolar fluid dipolar lattice continuum Definíciók töltéseloszlás
Jelentősége szubsztrát kötődés szolvatáció ionizációs állapotok (pka) mechanizmus katalízis ioncsatornák szimulációk (szerkezet) all-atom dipolar fluid dipolar lattice continuum Definíciók töltéseloszlás
Periódusos rendszer (Mengyelejev, 1869) nemesgáz csoport: zárt héj, extra stabil
 s-mezı (fémek) Periódusos rendszer (Mengyelejev, 1869) http://www.ptable.com/ nemesgáz csoport: zárt héj, extra stabil p-mezı (nemfém, félfém, fém) d-mezı (fémek) Rendezés elve: növekvı rendszám (elektronszám,
s-mezı (fémek) Periódusos rendszer (Mengyelejev, 1869) http://www.ptable.com/ nemesgáz csoport: zárt héj, extra stabil p-mezı (nemfém, félfém, fém) d-mezı (fémek) Rendezés elve: növekvı rendszám (elektronszám,
Lendület. Lendület (impulzus): A test tömegének és sebességének szorzata. vektormennyiség: iránya a sebesség vektor iránya.
 Lendület Lendület (impulzus): A test tömegének és sebességének szorzata. vektormennyiség: iránya a sebesség vektor iránya. Lendülettétel: Az lendület erő hatására változik meg. Az eredő erő határozza meg
Lendület Lendület (impulzus): A test tömegének és sebességének szorzata. vektormennyiség: iránya a sebesség vektor iránya. Lendülettétel: Az lendület erő hatására változik meg. Az eredő erő határozza meg
Szá molá si feládáttí pusok á Ko zgázdásá gtán I. (BMEGT30A003) tá rgy zá rthelyi dolgozátá hoz á 3. oktátá si he t tánányágá hoz kápcsolo do án
 Szá molá si feládáttí pusok á Ko zgázdásá gtán I. (BMEGT30A003) tá rgy zá rthelyi dolgozátá hoz á 3. oktátá si he t tánányágá hoz kápcsolo do án 1. feladattípus Egyváltozós keresleti, vagy kínálati függvények
Szá molá si feládáttí pusok á Ko zgázdásá gtán I. (BMEGT30A003) tá rgy zá rthelyi dolgozátá hoz á 3. oktátá si he t tánányágá hoz kápcsolo do án 1. feladattípus Egyváltozós keresleti, vagy kínálati függvények
Erőterek. Erőterek. Erőterek. Erőterek. Erőterek. Erőterek. Probléma: fehérjéknél nagy dimenziók értelmetlen QM eredmények.
 fehérjéknél nagy dimenziók értelmetlen QM eredmények Megoldás: egyszerűsítés dimenzió-csökkentés Közelítések Born-Oppenheimer közelítés (Ψ mol = Ψ el Ψ mag ; E tot =E el +E mag ) az energia párkölcsönhatások
fehérjéknél nagy dimenziók értelmetlen QM eredmények Megoldás: egyszerűsítés dimenzió-csökkentés Közelítések Born-Oppenheimer közelítés (Ψ mol = Ψ el Ψ mag ; E tot =E el +E mag ) az energia párkölcsönhatások
A periódusos rendszer, periodikus tulajdonságok
 A periódusos rendszer, periodikus tulajdonságok Szalai István ELTE Kémiai Intézet 1/45 Az előadás vázlata ˆ Ismétlés ˆ Történeti áttekintés ˆ Mengyelejev periódusos rendszere ˆ Atomsugár, ionsugár ˆ Ionizációs
A periódusos rendszer, periodikus tulajdonságok Szalai István ELTE Kémiai Intézet 1/45 Az előadás vázlata ˆ Ismétlés ˆ Történeti áttekintés ˆ Mengyelejev periódusos rendszere ˆ Atomsugár, ionsugár ˆ Ionizációs
Cikloalkánok és származékaik konformációja
 1 ikloalkánok és származékaik konformációja telített gyűrűs szénhidrogének legegyszerűbb képviselője a ciklopropán. Gyűrűje szabályos háromszög alakú, ennek megfelelően szénatomjai egy síkban helyezkednek
1 ikloalkánok és származékaik konformációja telített gyűrűs szénhidrogének legegyszerűbb képviselője a ciklopropán. Gyűrűje szabályos háromszög alakú, ennek megfelelően szénatomjai egy síkban helyezkednek
Az egyensúly. Általános Kémia: Az egyensúly Slide 1 of 27
 Az egyensúly 6'-1 6'-2 6'-3 6'-4 6'-5 Dinamikus egyensúly Az egyensúlyi állandó Az egyensúlyi állandókkal kapcsolatos összefüggések Az egyensúlyi állandó számértékének jelentősége A reakció hányados, Q:
Az egyensúly 6'-1 6'-2 6'-3 6'-4 6'-5 Dinamikus egyensúly Az egyensúlyi állandó Az egyensúlyi állandókkal kapcsolatos összefüggések Az egyensúlyi állandó számértékének jelentősége A reakció hányados, Q:
A II. kategória Fizika OKTV mérési feladatainak megoldása
 Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Savak bázisok. Csonka Gábor Általános Kémia: 7. Savak és bázisok Dia 1 /43
 Savak bázisok 12-1 Az Arrhenius elmélet röviden 12-2 Brønsted-Lowry elmélet 12-3 A víz ionizációja és a p skála 12-4 Erős savak és bázisok 12-5 Gyenge savak és bázisok 12-6 Több bázisú savak 12-7 Ionok
Savak bázisok 12-1 Az Arrhenius elmélet röviden 12-2 Brønsted-Lowry elmélet 12-3 A víz ionizációja és a p skála 12-4 Erős savak és bázisok 12-5 Gyenge savak és bázisok 12-6 Több bázisú savak 12-7 Ionok
Súlytámfal ellenőrzése
 3. számú mérnöki kézikönyv Frissítve: 2016. Február Súlytámfal ellenőrzése Program: Súlytámfal Fájl: Demo_manual_03.gtz Ebben a fejezetben egy meglévő súlytámfal számítását mutatjuk be állandó és rendkívüli
3. számú mérnöki kézikönyv Frissítve: 2016. Február Súlytámfal ellenőrzése Program: Súlytámfal Fájl: Demo_manual_03.gtz Ebben a fejezetben egy meglévő súlytámfal számítását mutatjuk be állandó és rendkívüli
Alapvető bimolekuláris kémiai reakciók dinamikája
 Alapvető bimolekuláris kémiai reakciók dinamikája Czakó Gábor Emory University (008 011) és ELTE (011. december ) Szedres, 01. október 13. A Polanyi szabályok Haladó mozgás (ütközési energia) vs. rezgő
Alapvető bimolekuláris kémiai reakciók dinamikája Czakó Gábor Emory University (008 011) és ELTE (011. december ) Szedres, 01. október 13. A Polanyi szabályok Haladó mozgás (ütközési energia) vs. rezgő
A kémiai kötés eredete; viriál tétel 1
 A kémiai kötés ereete; viriál tétel 1 Probléma felvetés Ha egy molekula atommagjai közötti távolság csökken, akkor a közöttük fellép elektrosztatikus taszításhoz tartozó energia n. Ugyanez igaz az elektronokra
A kémiai kötés ereete; viriál tétel 1 Probléma felvetés Ha egy molekula atommagjai közötti távolság csökken, akkor a közöttük fellép elektrosztatikus taszításhoz tartozó energia n. Ugyanez igaz az elektronokra
Akusztikai tervezés a geometriai akusztika módszereivel
 Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
3. A kémiai kötés. Kémiai kölcsönhatás
 3. A kémiai kötés Kémiai kölcsönhatás ELSŐDLEGES MÁSODLAGOS OVALENS IONOS FÉMES HIDROGÉN- KÖTÉS DIPÓL- DIPÓL, ION- DIPÓL, VAN DER WAALS v. DISZPERZIÓS Kémiai kötések Na Ionos kötés Kovalens kötés Fémes
3. A kémiai kötés Kémiai kölcsönhatás ELSŐDLEGES MÁSODLAGOS OVALENS IONOS FÉMES HIDROGÉN- KÖTÉS DIPÓL- DIPÓL, ION- DIPÓL, VAN DER WAALS v. DISZPERZIÓS Kémiai kötések Na Ionos kötés Kovalens kötés Fémes
1.7. Felületek és katalizátorok
 Mobilitás és Környezet Konferencia Magyar Tudományos Akadémia Budapest, 2012. január 23. 1.7. Felületek és katalizátorok Polimer töltőanyagként alkalmazható agyagásvány nanostruktúrák előállítása Horváth
Mobilitás és Környezet Konferencia Magyar Tudományos Akadémia Budapest, 2012. január 23. 1.7. Felületek és katalizátorok Polimer töltőanyagként alkalmazható agyagásvány nanostruktúrák előállítása Horváth
Nehézségi gyorsulás mérése megfordítható ingával
 Nehézségi gyorsulás mérése megfordítható ingával (Mérési jegyzőkönyv) Hagymási Imre 2007. április 21. (hétfő délelőtti csoport) 1. A mérés elmélete A nehézségi gyorsulás mérésének egy klasszikus módja
Nehézségi gyorsulás mérése megfordítható ingával (Mérési jegyzőkönyv) Hagymási Imre 2007. április 21. (hétfő délelőtti csoport) 1. A mérés elmélete A nehézségi gyorsulás mérésének egy klasszikus módja
Kémiai alapismeretek 3. hét
 Kémiai alapismeretek 3. hét Horváth Attila Pécsi Tudományegyetem, Természettudományi Kar, Kémia Intézet, Szervetlen Kémiai Tanszék 2013. szeptember 17.-20. 1/15 2013/2014 I. félév, Horváth Attila c : Molekulákon
Kémiai alapismeretek 3. hét Horváth Attila Pécsi Tudományegyetem, Természettudományi Kar, Kémia Intézet, Szervetlen Kémiai Tanszék 2013. szeptember 17.-20. 1/15 2013/2014 I. félév, Horváth Attila c : Molekulákon
Hemoglobin - myoglobin. Konzultációs e-tananyag Szikla Károly
 Hemoglobin - myoglobin Konzultációs e-tananyag Szikla Károly Myoglobin A váz- és szívizom oxigén tároló fehérjéje Mt.: 17.800 153 aminosavból épül fel A lánc kb 75 % a hélix 8 db hélix, köztük nem helikális
Hemoglobin - myoglobin Konzultációs e-tananyag Szikla Károly Myoglobin A váz- és szívizom oxigén tároló fehérjéje Mt.: 17.800 153 aminosavból épül fel A lánc kb 75 % a hélix 8 db hélix, köztük nem helikális
Atomszerkezet. Atommag protonok, neutronok + elektronok. atompályák, alhéjak, héjak, atomtörzs ---- vegyérték elektronok
 Atomszerkezet Atommag protonok, neutronok + elektronok izotópok atompályák, alhéjak, héjak, atomtörzs ---- vegyérték elektronok periódusos rendszer csoportjai Periódusos rendszer A kémiai kötés Kémiai
Atomszerkezet Atommag protonok, neutronok + elektronok izotópok atompályák, alhéjak, héjak, atomtörzs ---- vegyérték elektronok periódusos rendszer csoportjai Periódusos rendszer A kémiai kötés Kémiai
A racionális gyógyszertervezés lehetőségei. A racionális gyógyszertervezés lehetőségei. A racionális gyógyszertervezés lehetőségei
 Cél: kis koncentrációban kötődő célvegyület tervezése Agonista: segíti az enzim működését, hatékonyabb, mint a természetes szubsztrát Antagonista: gátolja az enzim működését, ellentétes hatású, mint a
Cél: kis koncentrációban kötődő célvegyület tervezése Agonista: segíti az enzim működését, hatékonyabb, mint a természetes szubsztrát Antagonista: gátolja az enzim működését, ellentétes hatású, mint a
Magspektroszkópiai gyakorlatok
 Magspektroszkópiai gyakorlatok jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Deák Ferenc Mérés dátuma: 010. április 8. Leadás dátuma: 010. április 13. I. γ-spekroszkópiai mérések A γ-spekroszkópiai
Magspektroszkópiai gyakorlatok jegyzıkönyv Zsigmond Anna Fizika BSc III. Mérés vezetıje: Deák Ferenc Mérés dátuma: 010. április 8. Leadás dátuma: 010. április 13. I. γ-spekroszkópiai mérések A γ-spekroszkópiai
A kémiai kötés. Kémiai kölcsönhatás
 A kémiai kötés Kémiai kölcsönhatás ELSŐDLEGES MÁSODLAGOS KOVALENS IONOS FÉMES HIDROGÉN- KÖTÉS DIPÓL- DIPÓL, ION- DIPÓL, VAN DER WAALS v. DISZPERZIÓS Ionos kötés Na Cl Ionpár képződése e - Na + Cl - Na:
A kémiai kötés Kémiai kölcsönhatás ELSŐDLEGES MÁSODLAGOS KOVALENS IONOS FÉMES HIDROGÉN- KÖTÉS DIPÓL- DIPÓL, ION- DIPÓL, VAN DER WAALS v. DISZPERZIÓS Ionos kötés Na Cl Ionpár képződése e - Na + Cl - Na:
Axiomatikus felépítés az axiómák megalapozottságát a felépített elmélet teljesítképessége igazolja majd!
 Hol vagyunk most? Definiáltuk az alapvet fogalmakat! - TD-i rendszer, fajtái - Környezet, fal - TD-i rendszer jellemzi - TD-i rendszer leírásához szükséges változók, állapotjelzk, azok csoportosítása -
Hol vagyunk most? Definiáltuk az alapvet fogalmakat! - TD-i rendszer, fajtái - Környezet, fal - TD-i rendszer jellemzi - TD-i rendszer leírásához szükséges változók, állapotjelzk, azok csoportosítása -
Sugárzások kölcsönhatása az anyaggal
 Radioaktivitás Biofizika előadások 2013 december Sugárzások kölcsönhatása az anyaggal PTE ÁOK Biofizikai Intézet, Orbán József Összefoglaló radioaktivitás alapok Nukleononkénti kötési energia (MeV) Egy
Radioaktivitás Biofizika előadások 2013 december Sugárzások kölcsönhatása az anyaggal PTE ÁOK Biofizikai Intézet, Orbán József Összefoglaló radioaktivitás alapok Nukleononkénti kötési energia (MeV) Egy
A évi TOP20 kukorica hibridek terméseinek stabilitásvizsgálata
 A 2017. évi TOP20 kukorica hibridek terméseinek stabilitásvizsgálata Árendás Tamás MTA ATK Mezőgazdasági Intézet, Martonvásár A 2017. évi kisparcellás kísérletek eredményei alapján az egymástól eltérő,
A 2017. évi TOP20 kukorica hibridek terméseinek stabilitásvizsgálata Árendás Tamás MTA ATK Mezőgazdasági Intézet, Martonvásár A 2017. évi kisparcellás kísérletek eredményei alapján az egymástól eltérő,
Coming soon. Pénzkereslet
 Coming soon Akkor és most Makroökonómia 11. hét 40 pontos vizsga Május 23. hétfő, 10 óra Május 27. péntek, 14 óra Június 2. csütörtök, 12 óra Csak egyszer lehet megírni! Minimumkövetelmény: 40% (16 pont)
Coming soon Akkor és most Makroökonómia 11. hét 40 pontos vizsga Május 23. hétfő, 10 óra Május 27. péntek, 14 óra Június 2. csütörtök, 12 óra Csak egyszer lehet megírni! Minimumkövetelmény: 40% (16 pont)
A behajlási teknő geometriája
 A behajlási teknő geometriája Geometry of Deflection Bowl Forrás: http://www.ctre.iastate.edu/research/ PRIMUSZ Péter Erdőmérnök, (NYME) TÓTH Csaba Építőmérnök, (H-TPA) 1. Teherbírás vagy Merevség? A teherbírást
A behajlási teknő geometriája Geometry of Deflection Bowl Forrás: http://www.ctre.iastate.edu/research/ PRIMUSZ Péter Erdőmérnök, (NYME) TÓTH Csaba Építőmérnök, (H-TPA) 1. Teherbírás vagy Merevség? A teherbírást
Az egyensúly. Általános Kémia: Az egyensúly Slide 1 of 27
 Az egyensúly 10-1 Dinamikus egyensúly 10-2 Az egyensúlyi állandó 10-3 Az egyensúlyi állandókkal kapcsolatos összefüggések 10-4 Az egyensúlyi állandó számértékének jelentősége 10-5 A reakció hányados, Q:
Az egyensúly 10-1 Dinamikus egyensúly 10-2 Az egyensúlyi állandó 10-3 Az egyensúlyi állandókkal kapcsolatos összefüggések 10-4 Az egyensúlyi állandó számértékének jelentősége 10-5 A reakció hányados, Q:
Katalízis. Tungler Antal Emeritus professzor 2017
 Katalízis Tungler Antal Emeritus professzor 2017 Fontosabb időpontok: sósav oxidáció, Deacon process 1860 kéndioxid oxidáció 1875 ammónia oxidáció 1902 ammónia szintézis 1905-1912 metanol szintézis 1923
Katalízis Tungler Antal Emeritus professzor 2017 Fontosabb időpontok: sósav oxidáció, Deacon process 1860 kéndioxid oxidáció 1875 ammónia oxidáció 1902 ammónia szintézis 1905-1912 metanol szintézis 1923
Periódusosság. Általános Kémia, Periódikus tulajdonságok. Slide 1 of 35
 Periódusosság 11-1 Az elemek csoportosítása: a periódusos táblázat 11-2 Fémek, nemfémek és ionjaik 11-3 Az atomok és ionok mérete 11-4 Ionizációs energia 11-5 Elektron affinitás 11-6 Mágneses 11-7 Az elemek
Periódusosság 11-1 Az elemek csoportosítása: a periódusos táblázat 11-2 Fémek, nemfémek és ionjaik 11-3 Az atomok és ionok mérete 11-4 Ionizációs energia 11-5 Elektron affinitás 11-6 Mágneses 11-7 Az elemek
Periódusosság. Általános Kémia, Periódikus tulajdonságok. Slide 1 of 35
 Periódusosság 3-1 Az elemek csoportosítása: a periódusos táblázat 3-2 Fémek, nemfémek és ionjaik 3-3 Az atomok és ionok mérete 3-4 Ionizációs energia 3-5 Elektron affinitás 3-6 Mágneses 3-7 Az elemek periodikus
Periódusosság 3-1 Az elemek csoportosítása: a periódusos táblázat 3-2 Fémek, nemfémek és ionjaik 3-3 Az atomok és ionok mérete 3-4 Ionizációs energia 3-5 Elektron affinitás 3-6 Mágneses 3-7 Az elemek periodikus
Hajlított elemek kifordulása. Stabilitásvesztési módok
 Hajlított elemek kifordulása Stabilitásvesztési módok Stabilitásvesztés (3.3.fejezet) Globális: Nyomott rudak kihajlása Hajlított tartók kifordulása Lemezhorpadás (lokális stabilitásvesztés): Nyomott és/vagy
Hajlított elemek kifordulása Stabilitásvesztési módok Stabilitásvesztés (3.3.fejezet) Globális: Nyomott rudak kihajlása Hajlított tartók kifordulása Lemezhorpadás (lokális stabilitásvesztés): Nyomott és/vagy
A mérés célkitűzései: A matematikai inga lengésidejének kísérleti vizsgálata, a nehézségi gyorsulás meghatározása.
 A mérés célkitűzései: A matematikai inga lengésidejének kísérleti vizsgálata, a nehézségi gyorsulás meghatározása. Eszközszükséglet: Bunsen állvány lombik fogóval 50 g-os vasból készült súlyok fonál mérőszalag,
A mérés célkitűzései: A matematikai inga lengésidejének kísérleti vizsgálata, a nehézségi gyorsulás meghatározása. Eszközszükséglet: Bunsen állvány lombik fogóval 50 g-os vasból készült súlyok fonál mérőszalag,
Makroökonómia. 11. hét
 Makroökonómia 11. hét Coming soon 40 pontos vizsga Május 23. hétfő, 10 óra Május 27. péntek, 14 óra Június 2. csütörtök, 12 óra Csak egyszer lehet megírni! Minimumkövetelmény: 40% (16 pont) Akkor és most
Makroökonómia 11. hét Coming soon 40 pontos vizsga Május 23. hétfő, 10 óra Május 27. péntek, 14 óra Június 2. csütörtök, 12 óra Csak egyszer lehet megírni! Minimumkövetelmény: 40% (16 pont) Akkor és most
9. Laboratóriumi gyakorlat NYOMÁSÉRZÉKELŐK
 9. Laboratóriumi gyakorlat NYOMÁSÉRZÉKELŐK 1.A gyakorlat célja Az MPX12DP piezorezisztiv differenciális nyomásérzékelő tanulmányozása. A nyomás feszültség p=f(u) karakterisztika megrajzolása. 2. Elméleti
9. Laboratóriumi gyakorlat NYOMÁSÉRZÉKELŐK 1.A gyakorlat célja Az MPX12DP piezorezisztiv differenciális nyomásérzékelő tanulmányozása. A nyomás feszültség p=f(u) karakterisztika megrajzolása. 2. Elméleti
Idegen atomok hatása a grafén vezet képességére
 hatása a grafén vezet képességére Eötvös Loránd Tudományegyetem, Komplex Rendszerek Fizikája Tanszék Mahe Tisk'11 Vázlat 1 Kisérleti eredmények Kémiai szennyez k hatása a Fermi-energiára A vezet képesség
hatása a grafén vezet képességére Eötvös Loránd Tudományegyetem, Komplex Rendszerek Fizikája Tanszék Mahe Tisk'11 Vázlat 1 Kisérleti eredmények Kémiai szennyez k hatása a Fermi-energiára A vezet képesség
A fogyasztási kereslet elméletei
 6. lecke A fogyasztási kereslet elméletei A GDP, a rendelkezésre álló jövedelem, a fogyasztás és a megtakarítás kapcsolata. Az abszolút jövedelem hipotézis és a keynesi fogyasztáselmélet. A permanens jövedelem
6. lecke A fogyasztási kereslet elméletei A GDP, a rendelkezésre álló jövedelem, a fogyasztás és a megtakarítás kapcsolata. Az abszolút jövedelem hipotézis és a keynesi fogyasztáselmélet. A permanens jövedelem
Toluol (Bruckner II/1 476) µ= 0.33 Debye
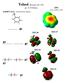 E(RHF/3-21G= -268.24021020 Hartree Toluol (Bruckner II/1 476) µ= 0.33 Debye -0.04 töltés. 0.04 φ6 MO 26 MO 27 φ4 φ5 MO 24 MO 25 φ2 MO 21 φ1 TD ρ= 0.0004 a.u. Anilin (Bruckner II/1 476) µ= 1.44 Debye E(RHF/6-311++G(d,p))=
E(RHF/3-21G= -268.24021020 Hartree Toluol (Bruckner II/1 476) µ= 0.33 Debye -0.04 töltés. 0.04 φ6 MO 26 MO 27 φ4 φ5 MO 24 MO 25 φ2 MO 21 φ1 TD ρ= 0.0004 a.u. Anilin (Bruckner II/1 476) µ= 1.44 Debye E(RHF/6-311++G(d,p))=
Ponthibák azonosítása félvezető szerkezetekben hiperfinom tenzor számításával
 Ponthibák azonosítása félvezető szerkezetekben hiperfinom tenzor számításával (munkabeszámoló) Szász Krisztián MTA Wigner SZFI, PhD hallgató 2013.05.07. Szász Krisztián Ponthibák azonosítása 1/ 13 Vázlat
Ponthibák azonosítása félvezető szerkezetekben hiperfinom tenzor számításával (munkabeszámoló) Szász Krisztián MTA Wigner SZFI, PhD hallgató 2013.05.07. Szász Krisztián Ponthibák azonosítása 1/ 13 Vázlat
Modern Fizika Labor Fizika BSC
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. május 4. A mérés száma és címe: 9. Röntgen-fluoreszencia analízis Értékelés: A beadás dátuma: 2009. május 13. A mérést végezte: Márton Krisztina Zsigmond
Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. május 4. A mérés száma és címe: 9. Röntgen-fluoreszencia analízis Értékelés: A beadás dátuma: 2009. május 13. A mérést végezte: Márton Krisztina Zsigmond
Kémiai reakciók sebessége
 Kémiai reakciók sebessége reakciósebesség (v) = koncentrációváltozás változáshoz szükséges idő A változás nem egyenletes!!!!!!!!!!!!!!!!!! v= ± dc dt a A + b B cc + dd. Melyik reagens koncentrációváltozását
Kémiai reakciók sebessége reakciósebesség (v) = koncentrációváltozás változáshoz szükséges idő A változás nem egyenletes!!!!!!!!!!!!!!!!!! v= ± dc dt a A + b B cc + dd. Melyik reagens koncentrációváltozását
Atomfizika. A hidrogén lámpa színképei. Elektronok H atom. Fényképlemez. emisszió H 2. gáz
 Atomfizika A hidrogén lámpa színképei - Elektronok H atom emisszió Fényképlemez V + H 2 gáz Az atom és kvantumfizika fejlődésének fontos szakasza volt a hidrogén lámpa színképeinek leírása, és a vonalas
Atomfizika A hidrogén lámpa színképei - Elektronok H atom emisszió Fényképlemez V + H 2 gáz Az atom és kvantumfizika fejlődésének fontos szakasza volt a hidrogén lámpa színképeinek leírása, és a vonalas
Kémiai kötések. Kémiai kötések. A bemutatót összeállította: Fogarasi József, Petrik Lajos SZKI, 2011
 Kémiai kötések A bemutatót összeállította: Fogarasi József, Petrik Lajos SZKI, 2011 1 Cl + Na Az ionos kötés 1. Cl + - + Na Klór: 1s 2 2s 2 2p 6 3s 2 3p 5 Kloridion: 1s2 2s2 2p6 3s2 3p6 Nátrium: 1s 2 2s
Kémiai kötések A bemutatót összeállította: Fogarasi József, Petrik Lajos SZKI, 2011 1 Cl + Na Az ionos kötés 1. Cl + - + Na Klór: 1s 2 2s 2 2p 6 3s 2 3p 5 Kloridion: 1s2 2s2 2p6 3s2 3p6 Nátrium: 1s 2 2s
Átmenetifém-komplexek mágneses momentuma
 Átmenetifém-komplexek mágneses momentuma Csakspin-momentum μ g e S(S 1) μ B μ n(n 2) μ B A komplexek mágneses momentuma többnyire közel van ahhoz a csakspin-momentum értékhez, ami az adott elektronkonfigurációjú
Átmenetifém-komplexek mágneses momentuma Csakspin-momentum μ g e S(S 1) μ B μ n(n 2) μ B A komplexek mágneses momentuma többnyire közel van ahhoz a csakspin-momentum értékhez, ami az adott elektronkonfigurációjú
A gravitáció hatása a hőmérsékleti sugárzásra
 A gravitáció hatása a hőmérsékleti sugárzásra Lendvai József A sugárnyomás a teljes elektromágneses spektrumban ismert jelenség. A kutatás során olyan kísérlet készült, mellyel az alacsony hőmérsékleti
A gravitáció hatása a hőmérsékleti sugárzásra Lendvai József A sugárnyomás a teljes elektromágneses spektrumban ismert jelenség. A kutatás során olyan kísérlet készült, mellyel az alacsony hőmérsékleti
GAZDASÁGI ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Gazdasági ismeretek emelt szint 1712 ÉRETTSÉGI VIZSGA 2017. május 25. GAZDASÁGI ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA I. TESZTFELADATOK 18
Gazdasági ismeretek emelt szint 1712 ÉRETTSÉGI VIZSGA 2017. május 25. GAZDASÁGI ISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA I. TESZTFELADATOK 18
Reakciókinetika. Általános Kémia, kinetika Dia: 1 /53
 Reakciókinetika 9-1 A reakciók sebessége 9-2 A reakciósebesség mérése 9-3 A koncentráció hatása: a sebességtörvény 9-4 Nulladrendű reakció 9-5 Elsőrendű reakció 9-6 Másodrendű reakció 9-7 A reakciókinetika
Reakciókinetika 9-1 A reakciók sebessége 9-2 A reakciósebesség mérése 9-3 A koncentráció hatása: a sebességtörvény 9-4 Nulladrendű reakció 9-5 Elsőrendű reakció 9-6 Másodrendű reakció 9-7 A reakciókinetika
Módszer az ASEA-ban található reaktív molekulák ellenőrzésére
 Módszer az ASEA-ban található reaktív molekulák ellenőrzésére Az ASEA-ban található reaktív molekulák egy komplex szabadalmaztatott elektrokémiai folyamat, mely csökkenti és oxidálja az alap sóoldatot,
Módszer az ASEA-ban található reaktív molekulák ellenőrzésére Az ASEA-ban található reaktív molekulák egy komplex szabadalmaztatott elektrokémiai folyamat, mely csökkenti és oxidálja az alap sóoldatot,
Makroökonómia. 12. hét
 Makroökonómia 12. hét A félév végi zárthelyi dolgozatról Nincs összevont vizsga! Javító és utóvizsga van csak, amelyen az a hallgató vehet részt, aki a szemináriumi dolgozat + 40 pontos dolgozat kombinációból
Makroökonómia 12. hét A félév végi zárthelyi dolgozatról Nincs összevont vizsga! Javító és utóvizsga van csak, amelyen az a hallgató vehet részt, aki a szemináriumi dolgozat + 40 pontos dolgozat kombinációból
Kémiai kötések. Kémiai kötések kj / mol 0,8 40 kj / mol
 Kémiai kötések A természetben az anyagokat felépítő atomok nem önmagukban, hanem gyakran egymáshoz kapcsolódva léteznek. Ezeket a kötéseket összefoglaló néven kémiai kötéseknek nevezzük. Kémiai kötések
Kémiai kötések A természetben az anyagokat felépítő atomok nem önmagukban, hanem gyakran egymáshoz kapcsolódva léteznek. Ezeket a kötéseket összefoglaló néven kémiai kötéseknek nevezzük. Kémiai kötések
TÖBBKOMPONENS RENDSZEREK FÁZISEGYENSÚLYAI IV.
 TÖBBKOMPONENS RENDSZEREK FÁZISEGYENSÚLYAI IV. TÖBBFÁZISÚ, TÖBBKOMPONENS RENDSZEREK Kétkomponens szilárd-folyadék egyensúlyok Néhány fogalom: - olvadék - ötvözetek - amorf anyagok Állapotok feltüntetése:
TÖBBKOMPONENS RENDSZEREK FÁZISEGYENSÚLYAI IV. TÖBBFÁZISÚ, TÖBBKOMPONENS RENDSZEREK Kétkomponens szilárd-folyadék egyensúlyok Néhány fogalom: - olvadék - ötvözetek - amorf anyagok Állapotok feltüntetése:
Makroökonómia. 9. szeminárium
 Makroökonómia 9. szeminárium Ezen a héten Árupiac Kiadási multiplikátor, adómultiplikátor IS görbe (Investment-saving) Árupiac Y = C + I + G Ikea-gazdaságot feltételezünk, extrém rövid táv A vállalati
Makroökonómia 9. szeminárium Ezen a héten Árupiac Kiadási multiplikátor, adómultiplikátor IS görbe (Investment-saving) Árupiac Y = C + I + G Ikea-gazdaságot feltételezünk, extrém rövid táv A vállalati
Spontaneitás, entrópia
 Spontaneitás, entrópia 11-1 Spontán és nem spontán folyamat 11-2 Entrópia 11-3 Az entrópia kiszámítása 11-4 Spontán folyamat: a termodinamika második főtétele 11-5 Standard szabadentalpia változás, ΔG
Spontaneitás, entrópia 11-1 Spontán és nem spontán folyamat 11-2 Entrópia 11-3 Az entrópia kiszámítása 11-4 Spontán folyamat: a termodinamika második főtétele 11-5 Standard szabadentalpia változás, ΔG
Modern fizika laboratórium
 Modern fizika laboratórium Röntgen-fluoreszcencia analízis Készítette: Básti József és Hagymási Imre 1. Bevezetés A röntgen-fluoreszcencia analízis (RFA) egy roncsolásmentes anyagvizsgálati módszer. Rövid
Modern fizika laboratórium Röntgen-fluoreszcencia analízis Készítette: Básti József és Hagymási Imre 1. Bevezetés A röntgen-fluoreszcencia analízis (RFA) egy roncsolásmentes anyagvizsgálati módszer. Rövid
W = F s A munka származtatott, előjeles skalármennyiség.
 Ha az erő és az elmozdulás egymásra merőleges, akkor fizikai értelemben nem történik munkavégzés. Pl.: ha egy táskát függőlegesen tartunk, és úgy sétálunk, akkor sem a tartóerő, sem a nehézségi erő nem
Ha az erő és az elmozdulás egymásra merőleges, akkor fizikai értelemben nem történik munkavégzés. Pl.: ha egy táskát függőlegesen tartunk, és úgy sétálunk, akkor sem a tartóerő, sem a nehézségi erő nem
Orvosi Biofizika I. 12. vizsgatétel. IsmétlésI. -Fény
 Orvosi iofizika I. Fénysugárzásanyaggalvalókölcsönhatásai. Fényszóródás, fényabszorpció. Az abszorpciós spektrometria alapelvei. (Segítséga 12. tételmegértéséhezésmegtanulásához, továbbá a Fényabszorpció
Orvosi iofizika I. Fénysugárzásanyaggalvalókölcsönhatásai. Fényszóródás, fényabszorpció. Az abszorpciós spektrometria alapelvei. (Segítséga 12. tételmegértéséhezésmegtanulásához, továbbá a Fényabszorpció
Grafikonok automatikus elemzése
 Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Grafikonok automatikus elemzése MIT BSc önálló laboratórium konzulens: Orosz György 2016.05.18. A feladat elsődleges célkitűzései o eszközök adatlapján található grafikonok feldolgozása, digitalizálása
Szabó-bakoseszter. Makroökonómia. Árupiacrövidtávon,kiadásimultiplikátor, adómultiplikátor,isgörbe
 Szabó-bakoseszter Makroökonómia Árupiacrövidtávon,kiadásimultiplikátor, adómultiplikátor,isgörbe Számítási és geometriai feladatok 1. feladat Tételezzük fel, hogy az általunk vizsgált gazdaságban a gazdasági
Szabó-bakoseszter Makroökonómia Árupiacrövidtávon,kiadásimultiplikátor, adómultiplikátor,isgörbe Számítási és geometriai feladatok 1. feladat Tételezzük fel, hogy az általunk vizsgált gazdaságban a gazdasági
Közgazdaságtan alapjai. Dr. Karajz Sándor Gazdaságelméleti Intézet
 Közgazdaságtan alapjai Dr. Karajz Sándor Gazdaságelméleti 10. Előadás Makrogazdasági kínálat és egyensúly Az előadás célja A makrogazdasági kínálat levezetése a következő feladatunk. Ezt a munkapiaci összefüggések
Közgazdaságtan alapjai Dr. Karajz Sándor Gazdaságelméleti 10. Előadás Makrogazdasági kínálat és egyensúly Az előadás célja A makrogazdasági kínálat levezetése a következő feladatunk. Ezt a munkapiaci összefüggések
Szalai István. ELTE Kémiai Intézet 1/74
 Elsőrendű kötések Szalai István ELTE Kémiai Intézet 1/74 Az előadás vázlata ˆ Ismétlés ˆ Ionos vegyületek képződése ˆ Ionok típusai ˆ Kovalens kötés ˆ Fémes kötés ˆ VSEPR elmélet ˆ VB elmélet 2/74 Periodikus
Elsőrendű kötések Szalai István ELTE Kémiai Intézet 1/74 Az előadás vázlata ˆ Ismétlés ˆ Ionos vegyületek képződése ˆ Ionok típusai ˆ Kovalens kötés ˆ Fémes kötés ˆ VSEPR elmélet ˆ VB elmélet 2/74 Periodikus
Gázok. 5-7 Kinetikus gázelmélet 5-8 Reális gázok (korlátok) Fókusz: a légzsák (Air-Bag Systems) kémiája
 Gázok 5-1 Gáznyomás 5-2 Egyszerű gáztörvények 5-3 Gáztörvények egyesítése: Tökéletes gázegyenlet és általánosított gázegyenlet 5-4 A tökéletes gázegyenlet alkalmazása 5-5 Gáz reakciók 5-6 Gázkeverékek
Gázok 5-1 Gáznyomás 5-2 Egyszerű gáztörvények 5-3 Gáztörvények egyesítése: Tökéletes gázegyenlet és általánosított gázegyenlet 5-4 A tökéletes gázegyenlet alkalmazása 5-5 Gáz reakciók 5-6 Gázkeverékek
Mivel foglalkozik a hőtan?
 Hőtan Gáztörvények Mivel foglalkozik a hőtan? A hőtan a rendszerek hőmérsékletével, munkavégzésével, és energiájával foglalkozik. A rendszerek stabilitása áll a fókuszpontjában. Képes megválaszolni a kérdést:
Hőtan Gáztörvények Mivel foglalkozik a hőtan? A hőtan a rendszerek hőmérsékletével, munkavégzésével, és energiájával foglalkozik. A rendszerek stabilitása áll a fókuszpontjában. Képes megválaszolni a kérdést:
A 2017/2018. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA JAVÍTÁSI ÚTMUTATÓ. Pohár rezonanciája
 Oktatási Hivatal A 017/018. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA JAVÍTÁSI ÚTMUTATÓ Pohár rezonanciája A mérőberendezés leírása: A mérőberendezés egy változtatható
Oktatási Hivatal A 017/018. tanévi Országos Középiskolai Tanulmányi Verseny döntő forduló FIZIKA II. KATEGÓRIA JAVÍTÁSI ÚTMUTATÓ Pohár rezonanciája A mérőberendezés leírása: A mérőberendezés egy változtatható
Modern Fizika Labor. Fizika BSc. Értékelés: A mérés dátuma: A mérés száma és címe: 12. mérés: Infravörös spektroszkópia. 2008. május 6.
 Modern Fizika Labor Fizika BSc A mérés dátuma: A mérés száma és címe: 12. mérés: Infravörös spektroszkópia Értékelés: A beadás dátuma: 28. május 13. A mérést végezte: 1/5 A mérés célja A mérés célja az
Modern Fizika Labor Fizika BSc A mérés dátuma: A mérés száma és címe: 12. mérés: Infravörös spektroszkópia Értékelés: A beadás dátuma: 28. május 13. A mérést végezte: 1/5 A mérés célja A mérés célja az
A bifiláris felfüggesztésű rúd mozgásáról
 1 A bifiláris felfüggesztésű rúd mozgásáról A végein fonállal felfüggesztett egyenes rúd részleges erőtani vizsgálatát mutattuk be egy korábbi dolgozatunkban, melynek címe: Forgatónyomaték mérése - I.
1 A bifiláris felfüggesztésű rúd mozgásáról A végein fonállal felfüggesztett egyenes rúd részleges erőtani vizsgálatát mutattuk be egy korábbi dolgozatunkban, melynek címe: Forgatónyomaték mérése - I.
Jegyzet. Kémia, BMEVEAAAMM1 Műszaki menedzser hallgatók számára Dr Csonka Gábor, egyetemi tanár Dr Madarász János, egyetemi docens.
 Kémia, BMEVEAAAMM Műszaki menedzser hallgatók számára Dr Csonka Gábor, egyetemi tanár Dr Madarász János, egyetemi docens Jegyzet dr. Horváth Viola, KÉMIA I. http://oktatas.ch.bme.hu/oktatas/konyvek/anal/
Kémia, BMEVEAAAMM Műszaki menedzser hallgatók számára Dr Csonka Gábor, egyetemi tanár Dr Madarász János, egyetemi docens Jegyzet dr. Horváth Viola, KÉMIA I. http://oktatas.ch.bme.hu/oktatas/konyvek/anal/
Tömegmérés stopperrel és mérőszalaggal
 Tömegmérés stopperrel és mérőszalaggal 1. Általános tudnivalók Mérőhelyén egy játékpisztolyt, négy lövedéket, valamint egy jól csapágyazott, fatalpra erősített fémlemezt talál. A lentebb közölt utasítások
Tömegmérés stopperrel és mérőszalaggal 1. Általános tudnivalók Mérőhelyén egy játékpisztolyt, négy lövedéket, valamint egy jól csapágyazott, fatalpra erősített fémlemezt talál. A lentebb közölt utasítások
Szemináriumi feladatok (alap) I. félév
 Szemináriumi feladatok (alap) I. félév I. Szeminárium 1. Az alábbi szerkezet-párok közül melyek reprezentálják valamely molekula, vagy ion rezonancia-szerkezetét? Indokolja válaszát! A/ ( ) 2 ( ) 2 F/
Szemináriumi feladatok (alap) I. félév I. Szeminárium 1. Az alábbi szerkezet-párok közül melyek reprezentálják valamely molekula, vagy ion rezonancia-szerkezetét? Indokolja válaszát! A/ ( ) 2 ( ) 2 F/
Gyakorlati útmutató a Tartók statikája I. tárgyhoz. Fekete Ferenc. 5. gyakorlat. Széchenyi István Egyetem, 2015.
 Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
Gyakorlati útmutató a tárgyhoz Fekete Ferenc 5. gyakorlat Széchenyi István Egyetem, 015. 1. ásodrendű hatások közelítő számítása A következőkben egy, a statikai vizsgálatoknál másodrendű hatások közelítő
NA61/SHINE: Az erősen kölcsönható anyag fázisdiagramja
 NA61/SHINE: Az erősen kölcsönható anyag fázisdiagramja László András Wigner Fizikai Kutatóintézet, Részecske- és Magfizikai Intézet 1 Kivonat Az erősen kölcsönható anyag és fázisai Megfigyelések a fázisszerkezettel
NA61/SHINE: Az erősen kölcsönható anyag fázisdiagramja László András Wigner Fizikai Kutatóintézet, Részecske- és Magfizikai Intézet 1 Kivonat Az erősen kölcsönható anyag és fázisai Megfigyelések a fázisszerkezettel
Termodinamika (Hőtan)
 Termodinamika (Hőtan) Termodinamika A hőtan nagyszámú részecskéből (pl. gázmolekulából) álló makroszkópikus rendszerekkel foglalkozik. A nagy számok miatt érdemes a mólt bevezetni, ami egy Avogadro-számnyi
Termodinamika (Hőtan) Termodinamika A hőtan nagyszámú részecskéből (pl. gázmolekulából) álló makroszkópikus rendszerekkel foglalkozik. A nagy számok miatt érdemes a mólt bevezetni, ami egy Avogadro-számnyi
Fermi Dirac statisztika elemei
 Fermi Dirac statisztika elemei A Fermi Dirac statisztika alapjai Nagy részecskeszámú rendszerek fizikai jellemzéséhez statisztikai leírást kell alkalmazni. (Pl. gázokra érvényes klasszikus statisztika
Fermi Dirac statisztika elemei A Fermi Dirac statisztika alapjai Nagy részecskeszámú rendszerek fizikai jellemzéséhez statisztikai leírást kell alkalmazni. (Pl. gázokra érvényes klasszikus statisztika
Víz. Az élő anyag szerkezeti egységei. A vízmolekula szerkezete. Olyan mindennapi, hogy fel sem tűnik, milyen különleges
 Az élő anyag szerkezeti egységei víz nukleinsavak fehérjék membránok Olyan mindennapi, hogy fel sem tűnik, milyen különleges A Föld felszínének 2/3-át borítja Előfordulása az emberi szövetek felépítésében
Az élő anyag szerkezeti egységei víz nukleinsavak fehérjék membránok Olyan mindennapi, hogy fel sem tűnik, milyen különleges A Föld felszínének 2/3-át borítja Előfordulása az emberi szövetek felépítésében
