matematikus-informatikus szemével

A Szemantikus világháló alapjai

A Szemantikus világháló alapjai Szeredi Péter Lukácsy Gergely Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi és Információelméleti Tanszék ➀ A szemantikus világhálóról általában ➁ Matematikai

Leíró Logikai Programozás

DLP I.-1 Leíró Logikai Programozás Szeredi Péter szeredi@cs.bme.hu Lukácsy Gergely lukacsy@cs.bme.hu BME Számítástudományi és Információelméleti Tanszék 2006. október 17. Leíró Logika+ Logikai Programozás

Ismeretalapú modellezés XI. Leíró logikák

XI. Leíró logikák 1 eddig volt nyílt internetes rendszerekben miért van szükség ismeretalapú re ontológia készítés kérdései ontológiák jellemzői milyen ontológiák vannak most jön mai internetes ontológiák

Szemantikus világháló a BME-n

Szemantikus világháló a BME-n Lukácsy Gergely Szeredi Péter Budapesti Mûszaki és Gazdaságtudományi Egyetem ßÐÙ Ý Þ Ö Ð º Ñ º Ù Számítástudományi és Információelméleti Tanszék ➀ Szemantikus technológiák

A szemantikus világháló oktatása

A szemantikus világháló oktatása Szeredi Péter Lukácsy Gergely Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi és Információelméleti Tanszék ➀ A szemantikus világháló... c. tárgy ➁ A tananyag

Hatékony keresés a szemantikus világhálón

Hatékony keresés a szemantikus világhálón Lukácsy Gergely Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem Magyarországi Web Konferencia 2008 W3C szekció Lukácsy

Ontológiák, 2. Leíró logikák. Kooperáció és intelligencia, DT-MT, BME-MIT

Ontológiák, 2. Leíró logikák Célkitűzés egy jó logikai apparátus kategóriák, nem az a lényeges, hogy objektumokból állnak, amiket változókkal kellene követni (kvantor nem kell) lényeges a hierarchia, öröklődés,

Contents. 1 Bevezetés 11

2 Contents I Fogalmi háttér 9 1 Bevezetés 11 2 Mesterséges Intelligencia háttér 15 2.1 Intelligencia és intelligens viselkedés............ 15 2.2 Turing teszt......................... 16 2.3 Az emberi

Legyen Ön is milliomos, kedves Számítógép!

MI-1 Szeredi Péter szeredi@cs.bme.hu BME Számítástudományi és Információelméleti Tanszék NJSZT Mesterséges Intelligencia Szakosztály 2011. május 27. A gép és az ember vetélkedője MI-2 A vetélkedő: Jeopardy

Ontológiák és adatbázisok következtetés nyílt és zárt világokban

DL/Ontosz-1 Ontológiák és adatbázisok következtetés nyílt és zárt világokban Szeredi Péter szeredi@cs.bme.hu BME VIK Számítástudományi és Információelméleti Tanszék 2008. március 26. Bevezető példa: adatbázis

Szemantikus Web Semantic Web A szemantikus web alkalmas megközelítés, illetve megfelel nyelvekkel, eszközökkel támogatja az intelligens információs

Szemantikus Web Semantic Web A szemantikus web alkalmas megközelítés, illetve megfelel nyelvekkel, eszközökkel támogatja az intelligens információs rendszerek fejlesztését az elosztott információs környezetben.

Név: Neptun kód: április

Név: Neptun kód:.. 2019. április 2. 8.15-9.15 Integrációs és ellenőrzési technikák zárthelyi Rendelkezésre álló idő: 60 perc ZH maximális pontszám: 40 + 8 IMSC pont Megfelelt szint: 16 pont Teszt kérdések

Ontológia nyelvek (Szemantikus Világhálótól...)

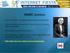Ontológia nyelvek (Szemantikus Világhálótól...) XML XML, DTD RDF Tudásreprezentáció Univerzális kifejező erő Szintaktikai interoperabilitás Szemantikai interoperabilitás RDFS DAML+OIL OWL OWL-Lite OWL-DL

Bevezetés a szemantikus technológiákba

Bevezetés a szemantikus technológiákba Szeredi Péter szeredi@cs.bme.hu BME Számítástudományi és Információelméleti Tanszék Korábbi társelőadók: Lukácsy Gergely, Zombori Zsolt, Csorba János 2014 tavaszi

Bevezetés s a szemantikus technológi

Bevezetés s a szemantikus technológi giákba Szemantikus technológi giák Rendszerelemek jelentés logikai formula Elvárások logikai formula Az elvárások megvalósítása sa a rendszerelemek segíts tségével

Adatbázisok MSc. 12. téma. Ontológia és SPARQL

Adatbázisok MSc 12. téma Ontológia és SPARQL Igény az automatikus tudáskezelése Az adat és tudáskezelés szintjei adatok összesítő adatok domain leírása következtetések tudás kontexus ismerete RDBMS OLAP

Szemantikus Web Semantic Web A szemantikus web alkalmas megközelítés, illetve megfelel nyelvekkel, eszközökkel támogatja az intelligens információs

Szemantikus Web Semantic Web A szemantikus web alkalmas megközelítés, illetve megfelel nyelvekkel, eszközökkel támogatja az intelligens információs rendszerek fejlesztését az elosztott információs környezetben.

Fülöp Csaba, Kovács László, Micsik András

Rendszerek Osztály Metaadatsémák nyilvántartása szemantikus web alapon Fülöp Csaba, Kovács László, Micsik András MTA SZTAKI Bemutatás A CORES az európai közösség projektje a Szemantikus Web témakörben

I. rész Bevezetés. Bevezetés a szemantikus technológiákba. Szemantikus technológiák. A kurzus felépítése. Szeredi Péter tavaszi félév

Bevezetés a szemantikus technológiákba Szeredi Péter I. rész Bevezetés szeredi@cs.bme.hu BME Számítástudományi és Információelméleti Tanszék 1 Bevezetés Korábbi társelőadók: Lukácsy Gergely, Zombori Zsolt,

Szemantikus Technológia

Szemantikus Technológia Kornai András BME MOKK és MetaCarta Inc., Cambridge, MA HLT-PLATFORM 2008. december 2. Az előadás terve Mitől szemantikus egy technológia? A szemantikus web Eleve mi az a szemantika?

Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) Egy halmaz akkor adott, ha minden objektumról eldönthető, hogy

1. előadás: Halmazelmélet Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető, hogy hozzátartozik-e,

1. Történeti vonatkozások - Tudásalapú eszközök piaca. 1. Történeti vonatkozások - MI kutatási területek ter. (folyt) Tudásalapú eszközök piaca

MI kutatási területek ter. Tematika ELTE TTK (visszaidézés) ÁSZT, 2002/2003 tanév 1. Történeti vonatkozások mesterséges élet 2. Elméleti alapok (tudásrepr., bizonytalanságkez.) 3. Ismeretalapú szakértő

Csima Judit október 24.

Adatbáziskezelés Funkcionális függőségek Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2018. október 24. Csima Judit Adatbáziskezelés Funkcionális függőségek 1 / 1 Relációs sémák

Elsőrendű logika. Mesterséges intelligencia március 28.

Elsőrendű logika Mesterséges intelligencia 2014. március 28. Bevezetés Ítéletkalkulus: deklaratív nyelv (mondatok és lehetséges világok közti igazságrelációk) Részinformációkat is kezel (diszjunkció, negáció)

Képek használata az oktatás hétköznapjaiban

Képek használata az oktatás hétköznapjaiban 2008. március 18. Forczek Erzsébet Szanyi Ágnes SZTE, ÁOK Orvosi Informatikai Intézet PTE, Kommunikáció Doktori Iskola Hagyományos oktatás: egy téma klasszikus

Óbudai Egyetem Neumann János Informatikai Kar. Intelligens Mérnöki Rendszerek Intézet

Óbudai Egyetem Neumann János Informatikai Kar Intelligens Mérnöki Rendszerek Intézet 1034 Budapest, Bécsi út 96/B Tel., Fax:1/666-5544,1/666-5545 http://nik.uni-obuda.hu/imri Az 2004-ben alakult IMRI (BMF)

Ontológiák, 1. Kooperáció és intelligencia, BME-MIT

Ontológiák, 1. Elmélet Mechanizmusfeltáró elmélet prediktív (jósló) modell Tartalomelmélet deskriptív (leíró) modell - ontológia objektumok, objektumok tulajdonságai objektumok közötti relációk Arisztotelész

Mesterséges Intelligencia MI

Mesterséges Intelligencia MI Tudásbázis építése Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade A tudásbázis építése

Emerald: Integrált jogi modellező keretrendszer

Emerald: Integrált jogi modellező keretrendszer Förhécz András Szőke Ákos Kőrösi Gábor Strausz György Budapesti Műszaki és Gazdaságtudományi Egyetem Multilogic Kft, Budapest Networkshop 2011 2011. április

Ontológiák és alkalmazásuk orvosi területen

Ontológiák és alkalmazásuk orvosi területen Lukácsy Gergely, IQSYS Rt., BME Szeredi Péter, IQSYS Rt., BME A cikk áttekinti az ontológiák témakörét, és bemutat egy kísérleti ontológiakezelô rendszert, hangsúlyt

1. előadás: Halmazelmélet, számfogalom, teljes

1. előadás: Halmazelmélet, számfogalom, teljes indukció Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető,

ONTOLÓGIA és TUDÁSREPREZENTÁCIÓ

ONTOLÓGIA és TUDÁSREPREZENTÁCIÓ Szıts Miklós Alkalmazott Logikai Laboratórium szots@all.hu ONTOLÓGIA mi az? a formal specification of a shared conceptualization a logical theory which gives an explicit,

Célkitűzés Megoldandó feladatok A tesztkörnyezet komponensei V&V folyamatok Eszközintegrációs szintek. Megfelelőség tanúsítása modell alapon

Megfelelőség tanúsítása modell alapon Dr. Polgár Balázs polgar@mit.bme.hu Miről lesz szó? 2 Tartalom Célkitűzés Megoldandó feladatok A tesztkörnyezet komponensei folyamatok Eszközintegrációs szintek Megfelelőségtanúsítás

Steps Towards an Ontology Based Learning Environment. Anita Pintér Corvinno Technologia Transzfer Kft apinter@corvinno.hu

Steps Towards an Ontology Based Learning Environment Anita Pintér Corvinno Technologia Transzfer Kft apinter@corvinno.hu Ontológia alapú elektronikus tanulási környezet megteremtése Anita Pintér Corvinno

Pozícióinformáció. Sikeres helyfüggő szolgáltatások mobilra

Distributed Systems A hely nem elég MTA SZTAKI Elosztott Rendszerek Osztály - Mátételki Péter matetelki@sztaki.hu Mihez nem elég a hely? Sikeres helyfüggő szolgáltatások mobilra Navigáció (hely + térkép

Szolgáltatásintegráció (VIMIM234) tárgy bevezető

Szolgáltatásintegráció Szolgáltatásintegráció (VIMIM234) tárgy bevezető Gönczy László gonczy@mit.bme.hu A tárgyról A tantárgy célja a hallgatók megismertetése a komplex informatikai rendszerek integrációs

Logika es sz am ıt aselm elet I. r esz Logika 1/36

1/36 Logika és számításelmélet I. rész Logika 2/36 Elérhetőségek Tejfel Máté Déli épület, 2.606 matej@inf.elte.hu http://matej.web.elte.hu Tankönyv 3/36 Tartalom 4/36 Bevezető fogalmak Ítéletlogika Ítéletlogika

A SINTAGMA szemantikus integrációs rendszer áttekintés

A SINTAGMA szemantikus integrációs rendszer áttekintés Lukácsy Gergely Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi és Információelméleti Tanszék ➀ Motiváció, információintegráció ➁

Adatbázisok elmélete 12. előadás

Adatbázisok elmélete 12. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu http://www.cs.bme.hu/ kiskat 2005 ADATBÁZISOK ELMÉLETE

DECOS Nemzeti Nap október 15. Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék

Megfelelőség tanúsítása modell alapon Dr. Polgár Balázs polgar@mit.bme.hu Miről lesz szó? 2 Tartalom Célkitűzés Megoldandó feladatok A tesztkörnyezet komponensei folyamatok Eszközintegrációs szintek Megfelelőségtanúsítás

Bizonyossági tényező az M1-ben bizonyossági faktor cf [0,100] cf=100 teljes bizonyosság cf=20 a hihetőség alsó küszöbe cf=0 teljesen elvetve

1. HOGYAN ALKALMAZHATÓ SZABÁLY ALAPÚ RENDSZEREKBEN A BIZONYTALANSÁGKEZELÉS HEURISZTIKUS MODELLJE? Szabályalapú rendszerekben az ismeretek HA feltétel AKKOR következmény alakúak Bizonytalanság kezelése

8. J ELENTÉSALAPÚ TECHNOLÓGIÁK

8. J ELENTÉSALAPÚ TECHNOLÓGIÁK Krauth Péter A legkülönbözőbb formákban és helyeken tárolt információk egymáshoz, valamint az emberi tudáshoz való viszonyát leíró METAADATok hatékony és sokoldalú kezelése

Szemantikus Web: egy rövid bevezetés

Szemantikus Web: egy rövid bevezetés Herman Iván World Wide Web Consortium email: ivan@w3.org 1. Bevezetés A Weben lévő információk típusa igen nagy változatosságot mutat. A klasszikus szöveges információk

Számítási intelligencia

Botzheim János Számítási intelligencia Budapesti Műszaki és Gazdaságtudományi Egyetem, Mechatronika, Optika és Gépészeti Informatika Tanszék Graduate School of System Design, Tokyo Metropolitan University

Magas szintű adatmodellek Egyed/kapcsolat modell I.

Magas szintű adatmodellek Egyed/kapcsolat modell I. Ullman-Widom: Adatbázisrendszerek. Alapvetés. 4.fejezet Magas szintű adatmodellek (4.1-4.3.fej.) (köv.héten folyt.köv. 4.4-4.6.fej.) Az adatbázis modellezés

Hely- és kontextusfüggő alkalmazások fejlesztését támogató keretrendszer mobil környezetben

Department of Distributed Systems Hely- és kontextusfüggő alkalmazások fejlesztését támogató keretrendszer mobil környezetben MTA SZTAKI Elosztott Rendszerek Osztály - Mátételki Péter matetelki@sztaki.hu

Adatbázis rendszerek 6.. 6. 1.1. Definíciók:

Adatbázis Rendszerek Budapesti Műszaki és Gazdaságtudományi Egyetem Fotogrammetria és Térinformatika 6.1. Egyed relációs modell lényegi jellemzői 6.2. Egyed relációs ábrázolás 6.3. Az egyedtípus 6.4. A

Bánki Zsolt István Csáki Zoltán Petőfi Irodalmi Múzeum Könyvtár és Informatika. Networkshop 2014 Pécs

Bánki Zsolt István Csáki Zoltán Petőfi Irodalmi Múzeum Könyvtár és Informatika Networkshop 2014 Pécs A szemantikus web építőelemeinek számító terminológiákat (Linked Open Data ajánlásoknak) megfelelő formátumban

Szakterületi modell A fogalmak megjelenítése. 9. fejezet Applying UML and Patterns Craig Larman

Szakterületi modell A fogalmak megjelenítése 9. fejezet Applying UML and Patterns Craig Larman 1 Néhány megjegyzés a diagramokhoz Ez a tárgy a rendszer elemzésről és modellezésről szól. Noha például egy

ADATBÁZISOK ELMÉLETE 5. ELŐADÁS 3/22. Az F formula: ahol A, B attribútumok, c érték (konstans), θ {<, >, =,,, } Példa:

Adatbázisok elmélete 5. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu http://www.cs.bme.hu/ kiskat 2005 ADATBÁZISOK ELMÉLETE

Diszkrét matematika I.

Diszkrét matematika I. középszint 2014. ősz 1. Diszkrét matematika I. középszint 2. előadás Mérai László diái alapján Komputeralgebra Tanszék 2014. ősz Matematikai logika Diszkrét matematika I. középszint

Alkalmazásokban. Dezsényi Csaba Ovitas Magyarország kft.

Tudásmodellezés Kereskedelmi Alkalmazásokban Dezsényi Csaba Ovitas Magyarország kft. Tudásmenedzsment Adat -> Információ -> Tudás Intézményi tudásvagyon hatékony kezelése az üzleti célok megvalósításának

Mi is volt ez? és hogy is volt ez?

Mi is volt ez? és hogy is volt ez? El zmények: 60-as évek kutatási iránya: matematikai logika a programfejlesztésben 70-es évek, francia és angol kutatók: logikai programozás, Prolog nyelv 1975: Szeredi

Diszkrét matematika I.

Diszkrét matematika I. középszint 2013 ősz 1. Diszkrét matematika I. középszint 8. előadás Mérai László merai@compalg.inf.elte.hu compalg.inf.elte.hu/ merai Komputeralgebra Tanszék 2013 ősz Kombinatorika

SZÁMÍTÁSELMÉLETI SZAKIRÁNY A BME MÉRNÖK-INFORMATIKUS MSC KÉPZÉSÉBEN

SZÁMÍTÁSELMÉLETI SZAKIRÁNY A BME MÉRNÖK-INFORMATIKUS MSC KÉPZÉSÉBEN COMPUTER SCIENCE SPECIALISATION IN THE BUTE SOFTWARE ENGINEERING MSC PROGRAMME Friedl Katalin, Szeredi Péter Budapesti Műszaki és Gazdaságtudományi

Kaposi Ambrus. University of Nottingham Functional Programming Lab. Hackerspace Budapest 2015. január 6.

Bizonyítás és programozás Kaposi Ambrus University of Nottingham Functional Programming Lab Hackerspace Budapest 2015. január 6. Bizonyítás, érvelés Példa: sáros a csizmám ha vizes a föld, esett az eső

Sor és oszlopkalkulus

Adatbáziskezelés Sor és oszlopkalkulus Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2017. szeptember 29. Csima Judit Adatbáziskezelés Sor és oszlopkalkulus 1 / 1 Sorkalkulus Formális

TUDÁSREPREZENTÁCIÓ 1.0-3.0 víziók, szemantikai modellek, eszközök

TUDÁRPRZNTÁCIÓ 1.0-3.0 víziók, szemantikai modellek, eszközök Dr. BNDK András - igazgató MÁRKU Zsolt projektvezető I Informatikai Oktatóközpont Alapítvány TUDÁRPRZNTÁCIÓ 1.0 1956 A Dartmouth Konferenciától

Többnyelvű tezaurusz építése és szolgáltatása webes környezetben

Többnyelvű tezaurusz építése és szolgáltatása webes környezetben Förhécz András, fand_lev@freemail.hu Mészáros Tamás, meszaros@mit.bme.hu BME Méréstechnika és Információs Rendszerek Tanszék Áttekintés

Kiss Gergő, Kovács László, Micsik András, Moldován István

Rendszerek Osztály HEKTÁR: Hazai elektronikus könyvtári rendszerek összekapcsolása Kiss Gergő, Kovács László, Micsik András, Moldován István MTA SZTAKI A HEKTÁR projektről HEKTÁR: Nyílt archívumi ajánlások

Szolgáltatásintegráció (VIMIM234) tárgy bevezető

Szolgáltatásintegráció Szolgáltatásintegráció (VIMIM234) tárgy bevezető Gönczy László gonczy@mit.bme.hu A tárgyról A tantárgy célja a hallgatók megismertetése a komplex informatikai rendszerek integrációs

SZÁMÍTÁSTUDOMÁNY ALAPJAI

SZÁMÍTÁSTUDOMÁNY ALAPJAI INBGM0101-17 Előadó: Dr. Mihálydeák Tamás Sándor Gyakorlatvezető: Kovács Zita 2017/2018. I. félév 2. gyakorlat Az alábbi összefüggések közül melyek érvényesek minden A, B halmaz

Nyílt hozzáférésű informatikai rendszerek BME VIMM 5294

Nyílt hozzáférésű informatikai rendszerek BME VIMM 5294 Übelhart István ubelhart@mit.bme.hu Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszéke Nyílt rendszerek

Kogníció, koncepciók, modellek

Kogníció, koncepciók, modellek A szoftver-technológia koncepcionális alapjai Irodalom Pléh Csaba: Bevezetés a megismeréstudományba, Typotex, 1998 Kognitív tudomány, Szerk.: Pléh Csaba, Osiris, 1996 M.

Összeállította Horváth László egyetemi tanár

Óbudai Egyetem Neumann János Informatikai Kar Intelligens Mérnöki Rendszerek Intézet Intelligens Mérnöki Rendszerek Szakirány a Mérnök informatikus alapszakon Összeállította Horváth László Budapest, 2011

2014. szeptember 24. és 26. Dr. Vincze Szilvia

2014. szeptember 24. és 26. Dr. Vincze Szilvia Mind a hétköznapi, mind a tudományos életben gyakran előfordul, hogy bizonyos halmazok elemei között kapcsolat figyelhető meg. A kapcsolat fogalmának matematikai

Diszkrét matematika 1. középszint

Diszkrét matematika 1. középszint 2017. sz 1. Diszkrét matematika 1. középszint 3. el adás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra

Logika es sz am ıt aselm elet I. r esz Logika Harmadik el oad as 1/33

1/33 Logika és számításelmélet I. rész Logika Harmadik előadás Tartalom 2/33 Elsőrendű logika bevezetés Az elsőrendű logika szintaxisa 3/33 Nulladrendű állítás Az ítéletlogikában nem foglalkoztunk az álĺıtások

1. Logikailag ekvivalens

Informatikai logikai alapjai Mérnök informatikus 4. gyakorlat 1. Logikailag ekvivalens 1. Az alábbi formulák közül melyek logikailag ekvivalensek a ( p p) formulával? A. ((q p) q) B. (q q) C. ( p q) D.

Algoritmuselmélet. 2-3 fák. Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem. 8.

Algoritmuselmélet 2-3 fák Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 8. előadás Katona Gyula Y. (BME SZIT) Algoritmuselmélet 8. előadás

Adatbázisok I 2012.05.11. Adatmodellek komponensei. Adatbázis modellek típusai. Adatbázisrendszer-specifikus tervezés

Adatbázisok I Szemantikai adatmodellek Szendrői Etelka PTE-PMMK Rendszer és Szoftvertechnológiai Tanszék szendroi@pmmk.pte.hu Adatmodellek komponensei Adatmodell: matematikai formalizmus, mely a valóság

SZEMANTIKUS WEB. Méréstechnika és Információs Rendszerek Tanszék

SZEMANTIKUS WEB Méréstechnika és Információs Rendszerek Tanszék https://www.mit.bme.hu/oktatas/targyak/vimiac04 1 Szolgáltatások Forrás leírás Web lapok Strukturált adatok Forrás fúzionálás/ Lekérdezés

Á Á Ó É ö ó ó É í ó ü ó ö ö í ó ö ó í ó í ú Í í ó í ö í ó ű ű ü ó ó ú í ö í ö ü ú í í ü ü ó ó ó ó ó ú í ü í ű ó í í ö ü ü í ű ó í ó ü ö ü í í ü ó ű ó í ü ü ó í ó ó í ó í ú í ó ó í ö ó ö Á óö ö í í ó ó

ó ü ú ü ú ó ó ú ü ú ü ú ö ö ű ü ö ö ö ú ó ü ö ö ö ü ö ö ö óó ü ö ö ó ó ö ó ö ú ó ó ó ó ű ö ö ó ö ó ó ú ű ü ö ö óó ú ó ö ö ü ó ó ó ó ó ó ó ü ó ú ű ü ó ö ú ű ó ü ö ö ó ó ü Á ó ű ó ü ó ó ú ó ú ó ó ö ö ü ú

ö ö ö ó ö ö ú ö ö ö ö ö ú ő ő ö ő ö ó ó ő ű ó ö őö ő ü ő ő ú ó Á Á Á Á ó ü ó ó ú Á Á Á ő ő ö ő ö ü É Á Á ú ö Á Á É É ö ü ö ö ő Í Á Ő É Ő ú Á É É ö ű ü ő ő ö ü ó ö Á É É ő ó ó ö ő ó Ö ő ó Ő ő ü ö ö ó ö

Ö Í Ő Ó ó ö ó ó ő ö ú ö ú ö ö ú Í ó ö őö ő ü É É ő ő ö ö ó ó ö ő ő ő Ü É ü ú Ö Ö É É ő Ü Ö Í É Ó Ö Ó Ü É Ö ú Ó É Ő É É ö ö ü ö Ü ö ö ő ö ő ő Ö Ú Ő É Ő Ú É É ö ű ő ő ö ó ö Ú É É Ő Ó Ó ö Ó ö ó ő ó ő ó ű

Ó Ó ö ő ő Ü ö Ü ő ö ö Ü Ó ö Ó Ó Ü ö Ó Ó Ü Ó Ü ö ö ő Ü ő ö Ü ő Ó Ü ő ö Ó Ó Ü ö ő Ü Ü Ü Ó ö ö ő Ü Ó Ö ö Ó Ü Ó Ü Ó ő ö ö Ü Ü ő ö Ó Ü Ó ö Ó Ó ö Ü ö ő ö Ó ö ö ö ö ö ö ö ö ö Ü ő ű ű ö Ó ű ő Ó Ó Ü Ó Ü ő Ü Ó

Í ú Ó Á Á ö ö ő ö ő ö Á ö ő Í Í Í ö ö ő Í ö ö ű ö ü ö ú ü ő ü ő ö ő ö ő ú ő ö ő ö ő ö É ő ü ő ő ö ő ő Í ő ö ő ő ő ö ö ö ö ü ő Í ő ö ő Ó ü ő ő ü ü ő ő ő ő ü ő ö ű ő ő ő ő ő ő ű ő ő ő Í ű ő ö ö ő ő ő ű ő

É É ő ü ó ü ú ü ó Ö ű ő ú ű ő ü ó ó Ö Ü ó ó ő ü ú ü ű ó ő ő ő ő ő ó ő ő ü ó ő ó ő ő Ö ó ő ő Ö ő ü ó ü Ö ő ü ó ő ő Á Á ő ó ó ó ő ő Á ű ő ó ó ő ü ő ü ő ő Á ú ü ü ó ő ű ő ő ő ó ü ó ő ő ü ó ó ó Á ő Á ő ó ő

ü ö ú ü ü ö ú ő ö ő ő ű ö ú ő ű ö ü ü ő ú ö ü ü ö ö ő ö ú ű ü ö ő ű ö őö ő ü ő ö ő ö ö ü ü ő ű ö ö ü ü ő ü ü ő ü ú ö ö ü ö ü ö ö ő ú ő ő ú ü ő ő ü ö ú ő ö ü ő ú ő ő ö ö ö ő ő Á ő ö ő ü ő ö ő ú ü ü ő ő

Ó ú ö ő Á ö ő ő ő Á ú ú ő ő ö ú ő ő ü ö ö ü ő ö ő ö ő Ó ö ö Ó ö ö ú ö ö ő ö ö ö ü ú ő ú ö ú ő ő ő ő ö ő ő ú ő ő ö ú ú ő ő ú ő ö ö ü ő ö ö ö ö ő ü ő ö ö ő ö ö ü ő ő ö ő ö ő ö ő ö ö ö ö ő ö ö ő ő ű ű ű ö

ö Ö ő Í Ó ö ö Ö ő ő ű ö ő ö ö ö ö ő ő ö ő ő ő ő Ö ő ö ö Ö ö Ö ö ő ö Ö ő ö ő ö Ú ő ő ö ö Ö ő ö Ó ő ő ő Ö ö ő ö ö ú ö ő ö ö ö ö ű ö Ö ö Ó ö ú ú ö ő ö ú ö ö ö ö ö Ó ő ő öő ő Á ű ő ö Ö ő Á Ó ö Ó Ó ö ű ú ú

ö ú Ú ö ö Ú Á É Á ő ú Ú Ú É É ő É É ö ú Ú ö É Á Á Á ö ö ö É ö ö ö Ú É ö Ú É ö ő ú Ú É ö Ü ö ö Ü ö Á Á ö ő ű ú ö ú Ú É É ö ű ú É ú ö ő ű ö ü É ú ú ö É ö ű É ú ö ú Ü ü É Á ö ő ű ö ö ú É ú ü ú É ö ű ú Á ü

LOGIKA ÉS ÉRVELÉSTECHNIKA

LOGIKA ÉS ÉRVELÉSTECHNIKA ELTE TáTK Közgazdaságtudományi Tanszék Logika és érveléstechnika NULLADREND LOGIKA 1. Készítette: Szakmai felel s: 2011. február Készült a következ m felhasználásával: Ruzsa

SZEMANTIKUS WEB. Integrációs és ellenőrzési technikák VIMIAC04, tavasz

Integrációs és ellenőrzési technikák VIMIAC04, 2019. tavasz SZEMANTIKUS WEB Méréstechnika és Információs Rendszerek Tanszék https://www.mit.bme.hu/oktatas/targyak/vimiac04 1 Szolgáltatások Forrás leírás

2. Logika gyakorlat Függvények és a teljes indukció

2. Logika gyakorlat Függvények és a teljes indukció Folláth János Debreceni Egyetem - Informatika Kar 2012/13. I. félév Áttekintés 1 Függvények Relációk Halmazok 2 Természetes számok Formulák Definíció

1. Mondjon legalább három példát predikátumra. 4. Mikor van egy változó egy kvantor hatáskörében?

Definíciók, tételkimondások 1. Mondjon legalább három példát predikátumra. 2. Sorolja fel a logikai jeleket. 3. Milyen kvantorokat ismer? Mi a jelük? 4. Mikor van egy változó egy kvantor hatáskörében?

Formális szemantika. Kifejezések szemantikája. Horpácsi Dániel ELTE Informatikai Kar

Formális szemantika Kifejezések szemantikája Horpácsi Dániel ELTE Informatikai Kar 2016-2017-2 Az előadás témája Egyszerű kifejezések formális szemantikája Az első lépés a programozási nyelvek szemantikájának

Nagy Gábor compalg.inf.elte.hu/ nagy

Diszkrét matematika 1. estis képzés 2017. ősz 1. Diszkrét matematika 1. estis képzés 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján

Logika és informatikai alkalmazásai

Logika és informatikai alkalmazásai 4. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás

A logikai következmény

Logika 3 A logikai következmény A logika egyik feladata: helyes következtetési sémák kialakítása. Példa következtetésekre : Minden veréb madár. Minden madár gerinces. Minden veréb gerinces 1.Feltétel 2.Feltétel

Az e-learning-től az u-learning-ig

Az e-learning-től az u-learning-ig Tananyagfejlesztés, tanulás több (web, mobil és digitális televíziós) csatornán keresztül. MÁRKUS Zsolt László Antenna Hungária Zrt. TARTALOMJEGYZÉK BEVEZETŐ CÉLOK, EREDMÉNYEK

Logika es sz am ıt aselm elet I. r esz Logika Negyedik el oad as 1/26

1/26 Logika és számításelmélet I. rész Logika Negyedik előadás Tartalom 2/26 Az elsőrendű logika szemantikája Formulák és formulahalmazok szemantikus tulajdonságai Elsőrendű logikai nyelv interpretációja

Logika és informatikai alkalmazásai

Logika és informatikai alkalmazásai 4. gyakorlat Németh L. Zoltán http://www.inf.u-szeged.hu/~zlnemeth SZTE, Informatikai Tanszékcsoport 2011 tavasz Irodalom Szükséges elmélet a mai gyakorlathoz Előadás

MUNKAERŐPIACI IGÉNYEKNEK A FOLYAMATOS ÖSSZEHANGOLÁSA A WEB 2.0 KORSZAKÁBAN

A FELSŐOKTATÁS TARTALMÁNAK ÉS A MUNKAERŐPIACI IGÉNYEKNEK A FOLYAMATOS ÖSSZEHANGOLÁSA A WEB 2.0 KORSZAKÁBAN Határterületek tanterve Milyen közgazdasági ismeretekre van szüksége egy jogásznak, mérnöknek,

LOGIKA ÉS ÉRVELÉSTECHNIKA

LOGIKA ÉS ÉRVELÉSTECHNIKA ELTE TáTK Közgazdaságtudományi Tanszék Logika és érveléstechnika NULLADREND LOGIKA 3. Készítette: Szakmai felel s: 2011. február Készült a következ m felhasználásával: Ruzsa

Algoritmuselmélet. Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem. 12.

Algoritmuselmélet NP-teljes problémák Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 12. előadás Katona Gyula Y. (BME SZIT) Algoritmuselmélet

Operációs rendszerek. 10. gyakorlat. AWK - bevezetés UNIVERSITAS SCIENTIARUM SZEGEDIENSIS UNIVERSITY OF SZEGED

UNIVERSITAS SCIENTIARUM SZEGEDIENSIS UNIVERSITY OF SZEGED AWK - bevezetés Operációs rendszerek 10. gyakorlat Szegedi Tudományegyetem Természettudományi és Informatikai Kar Csuvik Viktor 1 / 15 Reguláris

6. ELŐADÁS DIFFERENCIÁLSZÁMÍTÁS II. DIFFERENCIÁLÁSI SZABÁLYOK. BSc Matematika I. BGRMA1HNND, BGRMA1HNNC

6. ELŐADÁS DIFFERENCIÁLSZÁMÍTÁS II. DIFFERENCIÁLÁSI SZABÁLYOK BSc Matematika I. BGRMAHNND, BGRMAHNNC A következő diákon szereplő állítások mindegyikét az előadáson fogjuk igazolni, és példákkal bőségesen

KÉPI INFORMÁCIÓK KEZELHETŐSÉGE. Forczek Erzsébet SZTE ÁOK Orvosi Informatikai Intézet. Összefoglaló

KÉPI INFORMÁCIÓK KEZELHETŐSÉGE Forczek Erzsébet SZTE ÁOK Orvosi Informatikai Intézet Összefoglaló Tanórákon és az önálló tanulás részeként is, az informatika világában a rendelkezésünkre álló óriási mennyiségű