Az adatkapcsolati réteg
|
|
|
- Tivadar Kelemen
- 8 évvel ezelőtt
- Látták:
Átírás
1 Az adatkapcsolati réteg Programtervező informatikus BSc Számítógép hálózatok és architektúrák előadás Az adatkapcsolati réteg A fizikai átviteli hibáinak elfedése a hálózati réteg elől Keretezés Adatfolyam tördelése Küldés sorrendben Nyugtázás (megbízható szolgáltatás) Kerethatárok felismerése Forgalomszabályozás Elárasztás elleni védelem (felsőbb rétegekben is) Adó tájékoztatása a vevő szabad puffereiről Összeköttetés iránya (szimplex, fél duplex, duplex) Osztott csatornához való hozzáférés szabályozása Az adatkapcsolati réteg Tervezési szempontok Jól definiált interfész biztosítása a hálózati rétegnek Az átviteli hibák kezelése Az adatforgalom szabályozása Megvalósítás: Keretezés A hálózati réteg csomagjainak keretbe foglalása keret fejrész adatmező keret farokrész
2 Szolgáltatások típusai a hálózati réteg felé I. Nyugtázatlan összeköttetés mentes szolgálat Egymástól független keretek küldése a forrástól a célig Nincs előzetes kapcsolatépítés és bontás Az elveszett kereteket nem állítja helyre a réteg Alkalmazhatóság Alacsony hibaarány esetén (javítás a felsőbb rétegekben) Valós idejű adatforgalom esetén (hangátvitel) Nyugtázott összeköttetés mentes szolgálat Szintén nincs előzetes kapcsolatépítés és bontás Minden egyes keret megérkezését nyugtázza a cél állomás Alkalmazhatóság Pl.: vezeték nélküli kapcsolatoknál Szolgáltatások típusai a hálózati réteg felé II. Nyugtázott összeköttetés alapú szolgálat Összeköttetés felépítése az adatátvitel előtt Sorszámozott keretek minden keret garantáltan megérkezik minden keret garantáltan egyszer érkezik meg minden keret a megfelelő sorrendben érkezik meg Az átvitel folyamata összeköttetés felépítése (számlálók, változók inicializálása) keret(ek) továbbítása összeköttetés bontása (számlálók, változók felszabadítása) Keretezés A fizikai réteg nem garantál hibamentes átvitelt A réteg feladata ezen hibák jelzése, javítása Keretezés Az adatfolyam feldarabolása kisebb részekre (keret) Ellenőrző összegek számítása minden kerethez Az átvitel ellenőrzése A fogadott adatok alapján az ellenőrző összeg kiszámítása A fogadott és az újraszámolt összeg összehasonlítása A kerethatárok jelölésének problémái Szünetek beszúrása az egyes keretek közé?
3 A kerethatárok jelölése - Karakterszámlálás Minden keret fejrészében megadásra kerül a keret karaktereinek száma A vevő a fejrészből tudja, hány karakter tartozik a kerethez Illetve, hogy hol lesz a keret vége (a következő eleje) Problémák: A karakterszám mezőt is érheti átviteli hiba A vevő kiesik a szinkronból, nem találja a következő keretet Hibás ellenőrző összeg hibás keret de hol kezdődik a következő keret? Az újraküldés sem megoldás Kezdő- és végkarakterek karakterbeszúrással A kerethatárok jelzése egy különleges karakterrel Régebben eltérő protokollok eltérő bájtot használtak Manapság egységes "jelző bájt" (flag byte) jellemző Ha a vevő kiesik a szinkronból csak megvárja a következő flag byte-ot Az első flag byte az adott keret vége A második flag byte a következő keret eleje Mi történik ha a flag byte-nak megfelelő karaktert akarunk átvinni? (bináris átvitel) Kivétel bájt (escape byte) beszúrása És ha escape byte-ot kell átvinni? Kezdő- és végjelek bitbeszúrással A karakterkódok hossza ne legyen része a keretezésnek Tetszőleges számú bit legyen átvihető egy keretben Flag byte: Az adó minden ötödik -es után beszúr egy -t A vevő minden ötödik -es után törli a követő -t A jelző bájt is probléma nélkül átvihető Adási oldal: Vételi oldal: Transzparens átvitel mindkét irányban Adatfolyam az adó oldalán: Átviteli vonal: Adatfolyam a vevő oldalán:
4 Fizikai rétegbeli kódolássértés Alkalmazható ha a fizikai réteg kódolása redundáns Például ahol egy bit kódolása is jelváltással történik Előnyös: a vevő könnyen felismeri a bithatárokat Nincsenek szinkronizációs problémák Logikai magas szint: magas alacsony jelváltás Logikai alacsony szint: alacsony magas jelváltás Nincs magas magas vagy alacsony alacsony átmenet Ezek használhatók a kerethatárok jelzésére A gyakorlatban több megoldás kombinációja használt Forgalomszabályozás A lassabb (terhelt) gép védelme elárasztás ellen A túlterhelés keretek elvesztéséhez vezet Visszacsatolás alapú forgalomszabályozás A vevő tájékoztatja az adót a pillanatnyi állapotáról A vevő engedélyezi az adónak a további küldést Az adatkapcsolati réteg jellemző megoldása Sebesség alapú forgalomszabályozás A protokoll tartalmazza a sebességkorlátozást Ez minden adóra nézve kötelező érvényű Hibakezelés Lehetséges problémák Megérkezett-e minden keret? Minden keret csak egyszer érkezett-e meg? A keretek megfelelő sorrendben érkeztek-e meg? Visszacsatolás szükséges a vevő felől Pozitív és negatív nyugták Ha nem érkezik meg a keret? Időzítők alkalmazása Keretek újraküldése Többször megérkezhet ugyanaz a keret Kimenő keretek sorszámozása
5 Egybites és csoportos hibák Egybites hibák Csoportos hibák Bizonyos közegek esetén sokkal gyakoribb Azonos hibaarány mellett kevesebb hibás keret Jelzése és javítása lényegesen nehezebb Példa: adatblokk legyen bit, a hibaarány =,% Független hibák esetén átlagban minden keret hibás lesz bites csoportos hibáknál -ból - keret lesz hibás Hibajelző és hibajavító kódok Hibajelző kódok Csak a hibás átvitel tényét jelzi újraküldés Alacsony hibaarány mellett lehet praktikus Hibajavító kódok A hibás adatokból helyreállítható a helyes üzenet Alkalmas lehet bizonytalan átviteli közegek esetén Redundancia m - adatbitek r - redundáns bitek n = m + r (teljes keret - n bites kódszó) Hamming-távolság Azonos helyen előforduló különböző bitek (XOR) Teljes kód Hamming-távolsága d számú hiba jelzéséhez d+ Hamming-távolságú kód szükséges d számú hiba javításához d+ Hamming-távolságú kód szükséges Paritásbit alkalmazása Hamming-távolság: Alkalmas bites hibák jelzésére
6 Hibajavító Hamming-kód Az üzenet bitjeit balról jobbra -től számozzuk egész számú hatványai lesznek az ellenőrző bitek Az egyéb bitek az adatbitek 9,,,,,,,,, Minden paritás számításában azok a bitek vesznek részt amelyekben kettő adott hatványa szerepel Például -es paritásbit:,,, 9, bitek -es paritásbit:,, bitek Hamming-kód példa 9,,,,,,,,, Kódolandó bitek: 9 Hiba az átvitel során a -os számú biten 9 Történt-e átviteli hiba? Hányadik bit a hibás? Csoportos hibák javítása Hamming-kóddal Alapesetben egy bit javítható, csoportos hiba nem Rendezzünk k darab kódszót egymás alá Az átvitel ne kódszavanként és azon belül bitenként Hanem oszloponként, azon belül bitenként végezzük k bitnyi csoportos hiba esetén Minden kódszóban csak egy bitnyi hiba lesz Minden kódszó javítható Ellenőrző bitek száma = kr Adatblokk mérete = km k hosszúságú csoportos hiba javítható!
7 CRC hibaellenőrzés CRC - Cyclic Redundancy Code Polinom kód A leggyakrabban alkalmazott megoldás hibajelzésre A bitsorozatokat polinomoknak tekintjük pl.: x +x +x + hetedfokú polinom Műveletek Összeadásnál, kivonásnál nincs átvitel XOR Osztás: mint a bináris osztás A kivonásnál nincs átvitel Az osztó megvan az osztandóban ha az osztandó ugyanannyi bitet tartalmaz mint az osztó CRC hibaellenőrzés Továbbítandó keret: M(x) Generátor polinom G(x) Az adónak és a vevőnek is ismerni kell A legfelső és legalsó bitnek -nek kell lennie Rövidebbnek kell lennie mint a továbbítandó keretnek Feladat: fűzzünk ellenőrző összeget a kerethez, hogy az így kapott keret (polinom) osztható legyen G(x)-el Átvitel ellenőrzése: a vevő elosztja a vett keretet a generátorral, ha van maradék akkor hibás az átvitel CRC ellenőrző összeg számítása Legyen r G(x) foka. Fűzzünk r darab értékű bitet a keret alacsony helyi értékű végéhez x r M(x) amely m + r bitből áll. Osszuk el a az így kapott keretünket [x r M(x)] a generátor G(x) bitsorozatával. Vonjuk ki a maradékot a bővített keretből így megkapjuk az ellenőrző összeggel ellátott továbbítandó keretet T(x)
8 A CRC erőssége Minden egybites hibát képes jelezni Két izolált egybites hiba is jelezhető G(x) nem oszthatja x k + -et, ahol k<kerethossz Alacsony fokszámú polinomok, hosszú keretek védelmére Pl.: x + x + nem osztja x k + -et ha k< Minden páratlan számú hibás bitet tartalmazó hiba felismerhető ha G(x) osztható x + -gyel Minden r ellenőrző bittel ellátott polinomkód minden maximum r hosszúságú csoportos hibát tud jelezni Néhány klasszikus CRC polinom CRC = x + x + x + x + bites karakterek kódolására CRC = x + x + x + bites karakterek kódolására Képes felismerni: bites hibák, bites hibák Páratlan hibás bitet tartalmazó hibák vagy kevesebb bitet tartalmazó csoportos hibát bites csoportos hibák 99,99%-át vagy nagyobb bitszámú csoportos hibák 99,99%-át CRC-CCITT = x + x + x + bites karakterek kódolására (CCITT ajánlás) CRC problémák? Bonyolult algoritmus az ellenőrző összeg számításához? Áramkörileg egyszerűen megvalósítható léptető regiszteres áramkör - Peterson és Brown Gyakorlatilag szinte minden LAN használja Véletlenszerű-e a keretek tartalma? Eredeti feltételezés: igen Partridge és társai (99) Valós adatok elemzése Alaptalan az eredeti feltevés, nem teljesen véletlenszerű Gyakoribbak lehetnek a felderítetlen hibák
7. Adatkapcsolati réteg
 7. Adatkapcsolati réteg A fejezet tárgya a megbízható, hatékony kommunikáció megvalósítása két szomszédos gép között. Az alapvető követelmény az, hogy a továbbított bitek helyesen, s a küldés sorrendjében
7. Adatkapcsolati réteg A fejezet tárgya a megbízható, hatékony kommunikáció megvalósítása két szomszédos gép között. Az alapvető követelmény az, hogy a továbbított bitek helyesen, s a küldés sorrendjében
Számítógépes Hálózatok
 Számítógépes Hálózatok 4. Előadás: Adatkapcsolati réteg Based on slides from Zoltán Ács ELTE and D. Choffnes Northeastern U., Philippa Gill from StonyBrook University, Revised Spring 2016 by S. Laki Adatkapcsolati
Számítógépes Hálózatok 4. Előadás: Adatkapcsolati réteg Based on slides from Zoltán Ács ELTE and D. Choffnes Northeastern U., Philippa Gill from StonyBrook University, Revised Spring 2016 by S. Laki Adatkapcsolati
Számítógépes Hálózatok 2012
 Számítógépes Hálózatok 22 4. Adatkapcsolati réteg CRC, utólagos hibajavítás Hálózatok, 22 Hibafelismerés: CRC Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Számítógépes Hálózatok 22 4. Adatkapcsolati réteg CRC, utólagos hibajavítás Hálózatok, 22 Hibafelismerés: CRC Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Számítógépes Hálózatok
 Számítógépes Hálózatok 4. Előadás: Adatkapcsolati réteg II. Based on slides from Zoltán Ács ELTE and D. Choffnes Northeastern U., Philippa Gill from StonyBrook University, Revised Spring 2016 by S. Laki
Számítógépes Hálózatok 4. Előadás: Adatkapcsolati réteg II. Based on slides from Zoltán Ács ELTE and D. Choffnes Northeastern U., Philippa Gill from StonyBrook University, Revised Spring 2016 by S. Laki
AST_v3\ 3.1.3. 3.2.1.
 AST_v3\ 3.1.3. 3.2.1. Hibakezelés Az adatfolyam eddig megismert keretekre bontása hasznos és szükséges, de nem elégséges feltétele az adatok hibamentes és megfelelő sorrendű átvitelének. Az adatfolyam
AST_v3\ 3.1.3. 3.2.1. Hibakezelés Az adatfolyam eddig megismert keretekre bontása hasznos és szükséges, de nem elégséges feltétele az adatok hibamentes és megfelelő sorrendű átvitelének. Az adatfolyam
Számítógépes Hálózatok. 4. gyakorlat
 Számítógépes Hálózatok 4. gyakorlat Feladat 0 Számolja ki a CRC kontrollösszeget az 11011011001101000111 üzenetre, ha a generátor polinom x 4 +x 3 +x+1! Mi lesz a 4 bites kontrollösszeg? A fenti üzenet
Számítógépes Hálózatok 4. gyakorlat Feladat 0 Számolja ki a CRC kontrollösszeget az 11011011001101000111 üzenetre, ha a generátor polinom x 4 +x 3 +x+1! Mi lesz a 4 bites kontrollösszeg? A fenti üzenet
12. fejezet Hibajelző kódok és Adatkapcsolati protokollok
 12. fejezet Hibajelző kódok és Adatkapcsolati protokollok Hibajelző kódok Az előzőekben tárgyalt hibajavító kódokat jellemzően olyan átviteli közegekben célszerű használni, ahol a kapcsolat kevésbé megbízható,
12. fejezet Hibajelző kódok és Adatkapcsolati protokollok Hibajelző kódok Az előzőekben tárgyalt hibajavító kódokat jellemzően olyan átviteli közegekben célszerű használni, ahol a kapcsolat kevésbé megbízható,
3. Az adatkapcsolati réteg
 3. Az adatkapcsolati réteg Ebben a fejezetben a 2. - adatkapcsolati - réteg tervezését fogjuk tanulmányozni. A vizsgálódás tárgya az lesz, hogy hogyan lehet megbízható, hatékony kommunikációt megvalósítani
3. Az adatkapcsolati réteg Ebben a fejezetben a 2. - adatkapcsolati - réteg tervezését fogjuk tanulmányozni. A vizsgálódás tárgya az lesz, hogy hogyan lehet megbízható, hatékony kommunikációt megvalósítani
Hibadetektáló és javító kódolások
 Hibadetektáló és javító kódolások Számítógépes adatbiztonság Hibadetektálás és javítás Zajos csatornák ARQ adatblokk meghibásodási valószínségének csökkentése blokk bvítése redundáns információval Hálózati
Hibadetektáló és javító kódolások Számítógépes adatbiztonság Hibadetektálás és javítás Zajos csatornák ARQ adatblokk meghibásodási valószínségének csökkentése blokk bvítése redundáns információval Hálózati
10. fejezet Az adatkapcsolati réteg
 10. fejezet Az adatkapcsolati réteg Az adatkapcsolati réteg (Data Link Layer) Előzetesen összefoglalva, az adatkapcsolati réteg feladata abban áll, hogy biztosítsa azt, hogy az adó oldali adatok a vevő
10. fejezet Az adatkapcsolati réteg Az adatkapcsolati réteg (Data Link Layer) Előzetesen összefoglalva, az adatkapcsolati réteg feladata abban áll, hogy biztosítsa azt, hogy az adó oldali adatok a vevő
Hibafelismerés: CRC. Számítógépes Hálózatok Polinóm aritmetika modulo 2. Számolás Z 2 -ben
 Hibafelismerés: CRC Számítógépes Hálózatok 27 6. Adatkapcsolati réteg CRC, utólagos hibajavítás, csúszó ablakok Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Hibafelismerés: CRC Számítógépes Hálózatok 27 6. Adatkapcsolati réteg CRC, utólagos hibajavítás, csúszó ablakok Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Adatkapcsolati réteg (Data Link Layer) Számítógépes Hálózatok Az adatkapcsolati réteg lehetséges szolgáltatásai
 (Data Link Layer) Számítógépes Hálózatok 2013 3. Hibafelismerés és javítás, Hamming távolság, blokk kódok Az adatkapcsolati réteg feladatai: Szolgáltatásokat rendelkezésre bocsátani a hálózati rétegnek
(Data Link Layer) Számítógépes Hálózatok 2013 3. Hibafelismerés és javítás, Hamming távolság, blokk kódok Az adatkapcsolati réteg feladatai: Szolgáltatásokat rendelkezésre bocsátani a hálózati rétegnek
Számítógépes Hálózatok. 5. gyakorlat
 Számítógépes Hálózatok 5. gyakorlat Feladat 0 Számolja ki a CRC kontrollösszeget az 11011011001101000111 üzenetre, ha a generátor polinom x 4 +x 3 +x+1! Mi lesz a 4 bites kontrollösszeg? A fenti üzenet
Számítógépes Hálózatok 5. gyakorlat Feladat 0 Számolja ki a CRC kontrollösszeget az 11011011001101000111 üzenetre, ha a generátor polinom x 4 +x 3 +x+1! Mi lesz a 4 bites kontrollösszeg? A fenti üzenet
Számítógépes Hálózatok 2008
 Számítógépes Hálózatok 28 5. Adatkapcsolati réteg CRC, utólagos hibajavítás, csúszó ablakok Hibafelismerés: CRC Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Számítógépes Hálózatok 28 5. Adatkapcsolati réteg CRC, utólagos hibajavítás, csúszó ablakok Hibafelismerés: CRC Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Számítógépes Hálózatok. 7. gyakorlat
 Számítógépes Hálózatok 7. gyakorlat Gyakorlat tematika Hibajelző kód: CRC számítás Órai / házi feladat Számítógépes Hálózatok Gyakorlat 7. 2 CRC hibajelző kód emlékeztető Forrás: Dr. Lukovszki Tamás fóliái
Számítógépes Hálózatok 7. gyakorlat Gyakorlat tematika Hibajelző kód: CRC számítás Órai / házi feladat Számítógépes Hálózatok Gyakorlat 7. 2 CRC hibajelző kód emlékeztető Forrás: Dr. Lukovszki Tamás fóliái
Számítógépes Hálózatok 2013
 Számítógépes Hálózatok 2013 3. Adatkapcsolati réteg Hibafelismerés és javítás, Hamming távolság, blokk kódok 1 Adatkapcsolati réteg (Data Link Layer) Az adatkapcsolati réteg feladatai: Szolgáltatásokat
Számítógépes Hálózatok 2013 3. Adatkapcsolati réteg Hibafelismerés és javítás, Hamming távolság, blokk kódok 1 Adatkapcsolati réteg (Data Link Layer) Az adatkapcsolati réteg feladatai: Szolgáltatásokat
Számítógépes Hálózatok
 Számítógépes Hálózatok 6. Előadás: Fizikai réteg + Adatkapcsolati réteg Based on slides from Zoltán Ács ELTE and D. Choffnes Northeastern U., Philippa Gill from StonyBrook University, Revised Spring 2016
Számítógépes Hálózatok 6. Előadás: Fizikai réteg + Adatkapcsolati réteg Based on slides from Zoltán Ács ELTE and D. Choffnes Northeastern U., Philippa Gill from StonyBrook University, Revised Spring 2016
Hibajavítás, -jelzés. Informatikai rendszerek alapjai. Horváth Árpád november 24.
 Hibajavítás és hibajelzés Informatikai rendszerek alapjai Óbudai Egyetem Alba Regia M szaki Kar (AMK) Székesfehérvár 2016. november 24. Vázlat 1 Hibákról 2 Információátvitel diagrammja forrás csatorna
Hibajavítás és hibajelzés Informatikai rendszerek alapjai Óbudai Egyetem Alba Regia M szaki Kar (AMK) Székesfehérvár 2016. november 24. Vázlat 1 Hibákról 2 Információátvitel diagrammja forrás csatorna
Számítógépes Hálózatok ősz Adatkapcsolati réteg Hibafelismerés és javítás, Hamming távolság, blokk kódok
 Számítógépes Hálózatok ősz 2006 5. Adatkapcsolati réteg Hibafelismerés és javítás, Hamming távolság, blokk kódok 1 Adatkapcsolati réteg (Data Link Layer) Az adatkapcsolati réteg feladatai: Szolgáltatásokat
Számítógépes Hálózatok ősz 2006 5. Adatkapcsolati réteg Hibafelismerés és javítás, Hamming távolság, blokk kódok 1 Adatkapcsolati réteg (Data Link Layer) Az adatkapcsolati réteg feladatai: Szolgáltatásokat
Hibafelismerés: CRC. Számítógépes Hálózatok Polinóm aritmetika modulo 2. Számolás Z 2 -ben
 Hibafelismerés: CRC Számítógépes Hálózatok 2 4. Adatkapcsolati réteg CRC, utólagos hibajavítás, csúszó ablakok Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Hibafelismerés: CRC Számítógépes Hálózatok 2 4. Adatkapcsolati réteg CRC, utólagos hibajavítás, csúszó ablakok Hatékony hibafelismerés: Cyclic Redundancy Check (CRC) A gyakorlatban gyakran használt kód
Bevezet. Keretképzés. Adatkapcsolati réteg és protokolljai. Webprogramozó + ISGT
 Bevezet Adatkapcsolati réteg és protokolljai Webprogramozó + ISGT a fizikai rétegre épül az adatkapcsolati réteg feladata, hogy szolgáltatást nyújtson a hálózati rétegnek. legfontosabb szolgáltatás az
Bevezet Adatkapcsolati réteg és protokolljai Webprogramozó + ISGT a fizikai rétegre épül az adatkapcsolati réteg feladata, hogy szolgáltatást nyújtson a hálózati rétegnek. legfontosabb szolgáltatás az
Adatkapcsolati réteg 1
 Adatkapcsolati réteg 1 Főbb feladatok Jól definiált szolgáltatási interfész biztosítása a hálózati rétegnek Az átviteli hibák kezelése Az adatforgalom szabályozása, hogy a lassú vevőket ne árasszák el
Adatkapcsolati réteg 1 Főbb feladatok Jól definiált szolgáltatási interfész biztosítása a hálózati rétegnek Az átviteli hibák kezelése Az adatforgalom szabályozása, hogy a lassú vevőket ne árasszák el
Számítógépes Hálózatok
 Számítógépes Hálózatok 3. Előadás: Fizikai réteg II.rész Adatkapcsolati réteg Based on slides from Zoltán Ács ELTE and D. Choffnes Northeastern U., Philippa Gill from StonyBrook University, Revised Spring
Számítógépes Hálózatok 3. Előadás: Fizikai réteg II.rész Adatkapcsolati réteg Based on slides from Zoltán Ács ELTE and D. Choffnes Northeastern U., Philippa Gill from StonyBrook University, Revised Spring
ADATKAPCSOLATI PROTOKOLLOK
 ADATKAPCSOLATI PROTOKOLLOK Hálózati alapismeretek OSI 1 Adatkapcsolati réteg működése Az adatkapcsolati protokollok feladata egy összeállított keret átvitele két csomópont között. Az adatokat a hálózati
ADATKAPCSOLATI PROTOKOLLOK Hálózati alapismeretek OSI 1 Adatkapcsolati réteg működése Az adatkapcsolati protokollok feladata egy összeállított keret átvitele két csomópont között. Az adatokat a hálózati
Számítógép-hálózatok Az adatkapcsolati réteg
 Számítógép-hálózatok Az adatkapcsolati réteg 2016/2017. tanév, I. félév Dr. Kovács Szilveszter E-mail: szkovacs@iit.uni-miskolc.hu Informatikai Intézet 106/a. Tel: (46) 565-111 / 21-07 Dr. Kovács Szilveszter
Számítógép-hálózatok Az adatkapcsolati réteg 2016/2017. tanév, I. félév Dr. Kovács Szilveszter E-mail: szkovacs@iit.uni-miskolc.hu Informatikai Intézet 106/a. Tel: (46) 565-111 / 21-07 Dr. Kovács Szilveszter
ADATKAPCSOLATI RÉTEG
 ADATKAPCSOLATI RÉTEG Az adatkapcsolati réteg az OSI hivatkozási modell második rétege. Itt a csatorna adategységei a keretek. A réteg alapvető feladata a hibamentes átvitel biztosítása a szomszéd gépek
ADATKAPCSOLATI RÉTEG Az adatkapcsolati réteg az OSI hivatkozási modell második rétege. Itt a csatorna adategységei a keretek. A réteg alapvető feladata a hibamentes átvitel biztosítása a szomszéd gépek
Számítógépes Hálózatok
 Számítógépes Hálózatok 3. Előadás: Fizikai réteg II.rész Adatkapcsolati réteg Based on slides from Zoltán Ács ELTE and D. Choffnes Northeastern U., Philippa Gill from StonyBrook University, Revised Spring
Számítógépes Hálózatok 3. Előadás: Fizikai réteg II.rész Adatkapcsolati réteg Based on slides from Zoltán Ács ELTE and D. Choffnes Northeastern U., Philippa Gill from StonyBrook University, Revised Spring
Programozható vezérlő rendszerek KOMMUNIKÁCIÓS HÁLÓZATOK 2.
 KOMMUNIKÁCIÓS HÁLÓZATOK 2. CAN busz - Autóipari alkalmazásokhoz fejlesztették a 80-as években - Elsőként a BOSCH vállalat fejlesztette - 1993-ban szabvány (ISO 11898: 1993) - Később fokozatosan az iparban
KOMMUNIKÁCIÓS HÁLÓZATOK 2. CAN busz - Autóipari alkalmazásokhoz fejlesztették a 80-as években - Elsőként a BOSCH vállalat fejlesztette - 1993-ban szabvány (ISO 11898: 1993) - Később fokozatosan az iparban
13. Egy x és egy y hosszúságú sorozat konvolúciójának hossza a. x-y-1 b. x-y c. x+y d. x+y+1 e. egyik sem
 1. A Huffman-kód prefix és forráskiterjesztéssel optimálissá tehető, ezért nem szükséges hozzá a forrás valószínűség-eloszlásának ismerete. 2. Lehet-e tökéletes kriptorendszert készíteni? Miért? a. Lehet,
1. A Huffman-kód prefix és forráskiterjesztéssel optimálissá tehető, ezért nem szükséges hozzá a forrás valószínűség-eloszlásának ismerete. 2. Lehet-e tökéletes kriptorendszert készíteni? Miért? a. Lehet,
Hibajavító kódolás (előadásvázlat, 2012. november 14.) Maróti Miklós
 Hibajavító kódolás (előadásvázlat, 2012 november 14) Maróti Miklós Ennek az előadásnak a megértéséhez a következő fogalmakat kell tudni: test, monoid, vektortér, dimenzió, mátrixok Az előadáshoz ajánlott
Hibajavító kódolás (előadásvázlat, 2012 november 14) Maróti Miklós Ennek az előadásnak a megértéséhez a következő fogalmakat kell tudni: test, monoid, vektortér, dimenzió, mátrixok Az előadáshoz ajánlott
Diszkrét matematika II. feladatok
 Diszkrét matematika II. feladatok 1. Gráfelmélet 1.1. Könnyebb 1. Rajzold le az összes, páronként nem izomorf 3, 4, illetve 5 csúcsú egyszerű gráfot! 2. Van-e olyan (legalább kétpontú) gráf, melyben minden
Diszkrét matematika II. feladatok 1. Gráfelmélet 1.1. Könnyebb 1. Rajzold le az összes, páronként nem izomorf 3, 4, illetve 5 csúcsú egyszerű gráfot! 2. Van-e olyan (legalább kétpontú) gráf, melyben minden
I+K technológiák. Számrendszerek, kódolás
 I+K technológiák Számrendszerek, kódolás A tárgyak egymásra épülése Magas szintű programozás ( számítástechnika) Alacsony szintű programozás (jelfeldolgozás) I+K technológiák Gépi aritmetika Számítógép
I+K technológiák Számrendszerek, kódolás A tárgyak egymásra épülése Magas szintű programozás ( számítástechnika) Alacsony szintű programozás (jelfeldolgozás) I+K technológiák Gépi aritmetika Számítógép
A továbbiakban Y = {0, 1}, azaz minden szóhoz egy bináris sorozatot rendelünk
 1. Kódelmélet Legyen X = {x 1,..., x n } egy véges, nemüres halmaz. X-et ábécének, elemeit betűknek hívjuk. Az X elemeiből képzett v = y 1... y m sorozatokat X feletti szavaknak nevezzük; egy szó hosszán
1. Kódelmélet Legyen X = {x 1,..., x n } egy véges, nemüres halmaz. X-et ábécének, elemeit betűknek hívjuk. Az X elemeiből képzett v = y 1... y m sorozatokat X feletti szavaknak nevezzük; egy szó hosszán
Véges állapotú gépek (FSM) tervezése
 Véges állapotú gépek (FSM) tervezése F1. A 2. gyakorlaton foglalkoztunk a 3-mal vagy 5-tel osztható 4 bites számok felismerésével. Abban a feladatban a bemenet bitpárhuzamosan, azaz egy időben minden adatbit
Véges állapotú gépek (FSM) tervezése F1. A 2. gyakorlaton foglalkoztunk a 3-mal vagy 5-tel osztható 4 bites számok felismerésével. Abban a feladatban a bemenet bitpárhuzamosan, azaz egy időben minden adatbit
* Rendelje a PPP protokollt az TCP/IP rétegmodell megfelelő rétegéhez. Kapcsolati réteg
 ét * Rendelje a PPP protokollt az TCP/IP rétegmodell megfelelő Kapcsolati réteg A Pont-pont protokoll (általánosan használt rövidítéssel: PPP az angol Point-to-Point Protocol kifejezésből) egy magas szintű
ét * Rendelje a PPP protokollt az TCP/IP rétegmodell megfelelő Kapcsolati réteg A Pont-pont protokoll (általánosan használt rövidítéssel: PPP az angol Point-to-Point Protocol kifejezésből) egy magas szintű
3. gyakorlat. Kettes számrendszer: {0, 1} Tízes számrendszer: {0, 1, 2,..., 9} 16-os (hexadecimális számrendszer): {0, 1, 2,..., 9, A, B, C, D, E, F}
 3. gyakorlat Számrendszerek: Kettes számrendszer: {0, 1} Tízes számrendszer: {0, 1, 2,..., 9} 16-os (hexadecimális számrendszer): {0, 1, 2,..., 9, A, B, C, D, E, F} Alaki érték: 0, 1, 2,..., 9,... Helyi
3. gyakorlat Számrendszerek: Kettes számrendszer: {0, 1} Tízes számrendszer: {0, 1, 2,..., 9} 16-os (hexadecimális számrendszer): {0, 1, 2,..., 9, A, B, C, D, E, F} Alaki érték: 0, 1, 2,..., 9,... Helyi
Az Informatika Elméleti Alapjai
 Az Informatika Elméleti Alapjai dr. Kutor László Minimális redundanciájú kódok Statisztika alapú tömörítő algoritmusok http://mobil.nik.bmf.hu/tantargyak/iea.html Felhasználónév: iea Jelszó: IEA07 BMF
Az Informatika Elméleti Alapjai dr. Kutor László Minimális redundanciájú kódok Statisztika alapú tömörítő algoritmusok http://mobil.nik.bmf.hu/tantargyak/iea.html Felhasználónév: iea Jelszó: IEA07 BMF
Az Internet működésének alapjai
 Az Internet működésének alapjai Második, javított kiadás ( Dr. Nagy Rezső) A TCP/IP protokollcsalád áttekintése Az Internet néven ismert világméretű hálózat működése a TCP/IP protokollcsaládon alapul.
Az Internet működésének alapjai Második, javított kiadás ( Dr. Nagy Rezső) A TCP/IP protokollcsalád áttekintése Az Internet néven ismert világméretű hálózat működése a TCP/IP protokollcsaládon alapul.
A CAN hálózat alapjai
 A CAN hálózat alapjai 2009.10.24 1 Bevezető A CAN (Controller Area Network) egy nagybiztonságú soros kommunikációs protokoll, adatok valósidejű átvitelének hatékony támogatására. A protokoll kifejlesztésekor
A CAN hálózat alapjai 2009.10.24 1 Bevezető A CAN (Controller Area Network) egy nagybiztonságú soros kommunikációs protokoll, adatok valósidejű átvitelének hatékony támogatására. A protokoll kifejlesztésekor
Hálózatok. Alapismeretek. A hálózatok célja, építőelemei, alapfogalmak
 Hálózatok Alapismeretek A hálózatok célja, építőelemei, alapfogalmak A hálózatok célja A korai időkben terminálokat akartak használni a szabad gépidők lekötésére, erre jó lehetőség volt a megbízható és
Hálózatok Alapismeretek A hálózatok célja, építőelemei, alapfogalmak A hálózatok célja A korai időkben terminálokat akartak használni a szabad gépidők lekötésére, erre jó lehetőség volt a megbízható és
OSI-ISO modell. Az OSI rétegek feladatai: Adatkapcsolati réteg (data link layer) Hálózati réteg (network layer)
 OSI-ISO modell Több világcég megalkotta a saját elképzelései alapján a saját hálózati architektúráját, de az eltérések miatt egységesíteni kellett, amit csak nemzetközi szinten lehetett megoldani. Ez a
OSI-ISO modell Több világcég megalkotta a saját elképzelései alapján a saját hálózati architektúráját, de az eltérések miatt egységesíteni kellett, amit csak nemzetközi szinten lehetett megoldani. Ez a
Hatványozás. A hatványozás azonosságai
 Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
Számítógép Architektúrák
 Perifériakezelés a PCI-ban és a PCI Express-ben Horváth Gábor 2017. február 14. Budapest docens BME Hálózati Rendszerek és Szolgáltatások Tanszék ghorvath@hit.bme.hu A PCI PCI = Peripheral Component Interfész,
Perifériakezelés a PCI-ban és a PCI Express-ben Horváth Gábor 2017. február 14. Budapest docens BME Hálózati Rendszerek és Szolgáltatások Tanszék ghorvath@hit.bme.hu A PCI PCI = Peripheral Component Interfész,
Hamming-kód. Definíció. Az 1-hibajavító, perfekt lineáris kódot Hamming-kódnak nevezzük. F 2 fölötti vektorokkal foglalkozunk.
 Definíció. Hamming-kód Az -hibajavító, perfekt lineáris kódot Hamming-kódnak nevezzük. F fölötti vektorokkal foglalkozunk. Hamming-kód készítése: r egész szám (ellenırzı jegyek száma) n r a kódszavak hossza
Definíció. Hamming-kód Az -hibajavító, perfekt lineáris kódot Hamming-kódnak nevezzük. F fölötti vektorokkal foglalkozunk. Hamming-kód készítése: r egész szám (ellenırzı jegyek száma) n r a kódszavak hossza
Ennek két lépéssel balra történõ ciklikus eltolása az alábbi.
 CIKLIKUS KÓDOK (Az alábbiak feltételezik a "Hiradástechnika" c. könyv "7. Hibakorlátozó kódolás" fejezetének és a modulo-2 algebra alapjainak ismeretét.) 1. Alapfogalmak Definíció: egy lineáris kód ciklikus,
CIKLIKUS KÓDOK (Az alábbiak feltételezik a "Hiradástechnika" c. könyv "7. Hibakorlátozó kódolás" fejezetének és a modulo-2 algebra alapjainak ismeretét.) 1. Alapfogalmak Definíció: egy lineáris kód ciklikus,
Diszkrét matematika alapfogalmak
 2014 tavaszi félév Diszkrét matematika alapfogalmak 1 GRÁFOK 1.1 GRÁFÁBRÁZOLÁSOK 1.1.1 Adjacenciamátrix (szomszédsági mátrix) Szomszédok felsorolása, csak egyszerű gráfok esetén használható 1.1.2 Incidenciamátrix
2014 tavaszi félév Diszkrét matematika alapfogalmak 1 GRÁFOK 1.1 GRÁFÁBRÁZOLÁSOK 1.1.1 Adjacenciamátrix (szomszédsági mátrix) Szomszédok felsorolása, csak egyszerű gráfok esetén használható 1.1.2 Incidenciamátrix
Hibajavító kódok május 31. Hibajavító kódok 1. 1
 Hibajavító kódok 2007. május 31. Hibajavító kódok 1. 1 Témavázlat Hibajavító kódolás Blokk-kódok o Hamming-távolság, Hamming-súly o csoportkód o S n -beli u középpontú t sugarú gömb o hibajelzı képesség
Hibajavító kódok 2007. május 31. Hibajavító kódok 1. 1 Témavázlat Hibajavító kódolás Blokk-kódok o Hamming-távolság, Hamming-súly o csoportkód o S n -beli u középpontú t sugarú gömb o hibajelzı képesség
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 207. tavasz. Diszkrét matematika 2.C szakirány 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 207.
Diszkrét matematika 2.C szakirány 207. tavasz. Diszkrét matematika 2.C szakirány 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 207.
Informatikai Rendszerek Alapjai
 Informatikai Rendszerek Alapjai Dr. Kutor László A redundancia fogalma és mérése Minimális redundanciájú kódok 1. http://uni-obuda.hu/users/kutor/ IRA 2014 könyvtár Óbudai Egyetem, NIK Dr. Kutor László
Informatikai Rendszerek Alapjai Dr. Kutor László A redundancia fogalma és mérése Minimális redundanciájú kódok 1. http://uni-obuda.hu/users/kutor/ IRA 2014 könyvtár Óbudai Egyetem, NIK Dr. Kutor László
4. Fejezet : Az egész számok (integer) ábrázolása
 4. Fejezet : Az egész számok (integer) ábrázolása The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson
4. Fejezet : Az egész számok (integer) ábrázolása The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson
Digitális technika VIMIAA02 1. EA Fehér Béla BME MIT
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK VIMIAA02 1. EA Fehér Béla BME MIT Digitális Rendszerek Számítógépek Számítógép
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK VIMIAA02 1. EA Fehér Béla BME MIT Digitális Rendszerek Számítógépek Számítógép
A kódok típusai Kódolás: adatok megváltoztatása. Dekódolás: a megváltoztatott adatból az eredeti visszanyerése.
 1. Hibajavító kódok A kódok típusai Kódolás: adatok megváltoztatása. Dekódolás: a megváltoztatott adatból az eredeti visszanyerése. Célok Titkosírás (kriptográfia). A megváltoztatott adat illetéktelenek
1. Hibajavító kódok A kódok típusai Kódolás: adatok megváltoztatása. Dekódolás: a megváltoztatott adatból az eredeti visszanyerése. Célok Titkosírás (kriptográfia). A megváltoztatott adat illetéktelenek
Számítógép hálózatok gyakorlat
 Számítógép hálózatok gyakorlat 5. Gyakorlat Ethernet alapok Ethernet Helyi hálózatokat leíró de facto szabvány A hálózati szabványokat az IEEE bizottságok kezelik Ezekről nevezik el őket Az Ethernet így
Számítógép hálózatok gyakorlat 5. Gyakorlat Ethernet alapok Ethernet Helyi hálózatokat leíró de facto szabvány A hálózati szabványokat az IEEE bizottságok kezelik Ezekről nevezik el őket Az Ethernet így
Digitális technika VIMIAA02 1. EA
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika VIMIAA02 1. EA Fehér Béla BME MIT Digitális Rendszerek
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika VIMIAA02 1. EA Fehér Béla BME MIT Digitális Rendszerek
Véges állapotú gépek (FSM) tervezése
 Véges állapotú gépek (FSM) tervezése F1. Tervezzünk egy soros mintafelismerőt, ami a bemenetére ciklikusan, sorosan érkező 4 bites számok közül felismeri azokat, amelyek 3-mal vagy 5-tel oszthatók. A fenti
Véges állapotú gépek (FSM) tervezése F1. Tervezzünk egy soros mintafelismerőt, ami a bemenetére ciklikusan, sorosan érkező 4 bites számok közül felismeri azokat, amelyek 3-mal vagy 5-tel oszthatók. A fenti
x 3 - x 3 +x x = R(x) x 3 + x x 3 + x ; rendben, nincs maradék.
 Péla CRC számításra Legyen az üzenet: 0 0 M(x) x 5 + x 4 + x 2 + (m 5) Legyen a gen. olinóm: 0 G(x) x 3 +x 2 + (r 3) Aáshoz R(x) kézése M(x)*x r x 8 + x 7 + x 5 +x 3 (M(x)*x r )/G(x) (x 8 + x 7 + x 5 +x
Péla CRC számításra Legyen az üzenet: 0 0 M(x) x 5 + x 4 + x 2 + (m 5) Legyen a gen. olinóm: 0 G(x) x 3 +x 2 + (r 3) Aáshoz R(x) kézése M(x)*x r x 8 + x 7 + x 5 +x 3 (M(x)*x r )/G(x) (x 8 + x 7 + x 5 +x
Digitális technika VIMIAA01
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika VIMIAA01 Fehér Béla BME MIT Digitális Rendszerek Számítógépek
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika VIMIAA01 Fehér Béla BME MIT Digitális Rendszerek Számítógépek
Digitális technika VIMIAA01
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK VIMIAA01 Fehér Béla BME MIT Digitális Rendszerek Számítógépek Számítógép
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK VIMIAA01 Fehér Béla BME MIT Digitális Rendszerek Számítógépek Számítógép
MACAW. MAC protokoll vezetéknélküli LAN hálózatokhoz. Vaduvur Bharghavan Alan Demers, Scott Shenker, Lixia Zhang
 MACAW MAC protokoll vezetéknélküli LAN hálózatokhoz Vaduvur Bharghavan Alan Demers, Scott Shenker, Lixia Zhang készítette a fenti cikk alapján: Bánsághi Anna programtervező matematikus V. 2009. tavaszi
MACAW MAC protokoll vezetéknélküli LAN hálózatokhoz Vaduvur Bharghavan Alan Demers, Scott Shenker, Lixia Zhang készítette a fenti cikk alapján: Bánsághi Anna programtervező matematikus V. 2009. tavaszi
A vezérlő alkalmas 1x16, 2x16, 2x20, 4x20 karakteres kijelzők meghajtására. Az 1. ábrán látható a modul bekötése.
 Soros LCD vezérlő A vezérlő modul lehetővé teszi, hogy az LCD-t soros vonalon illeszthessük alkalmazásunkhoz. A modul több soros protokollt is támogat, úgy, mint az RS232, I 2 C, SPI. Továbbá az LCD alapfunkcióit
Soros LCD vezérlő A vezérlő modul lehetővé teszi, hogy az LCD-t soros vonalon illeszthessük alkalmazásunkhoz. A modul több soros protokollt is támogat, úgy, mint az RS232, I 2 C, SPI. Továbbá az LCD alapfunkcióit
Bevezetés az informatikába gyakorló feladatok Utoljára módosítva:
 Tartalom 1. Számrendszerek közti átváltás... 2 1.1. Megoldások... 4 2. Műveletek (+, -, bitműveletek)... 7 2.1. Megoldások... 8 3. Számítógépes adatábrázolás... 10 3.1. Megoldások... 12 A gyakorlósor lektorálatlan,
Tartalom 1. Számrendszerek közti átváltás... 2 1.1. Megoldások... 4 2. Műveletek (+, -, bitműveletek)... 7 2.1. Megoldások... 8 3. Számítógépes adatábrázolás... 10 3.1. Megoldások... 12 A gyakorlósor lektorálatlan,
2. Fejezet : Számrendszerek
 2. Fejezet : Számrendszerek The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson Wong, Bentley College
2. Fejezet : Számrendszerek The Architecture of Computer Hardware and Systems Software: An Information Technology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003 Wilson Wong, Bentley College
A digitális átviteltechnika második generációja. Szinkron Digitális Hierarchia
 A digitális átviteltechnika második generációja Közcélú hálózatok 2003 1 zinkron igitális ierarchia A 80-as években: Legyen lehetőség közvetlen hozzáférésre Legyenek szinkronban az összetevő jelek Legyen
A digitális átviteltechnika második generációja Közcélú hálózatok 2003 1 zinkron igitális ierarchia A 80-as években: Legyen lehetőség közvetlen hozzáférésre Legyenek szinkronban az összetevő jelek Legyen
Kódolás, hibajavítás. Tervezte és készítette Géczy LászlL. szló 2002
 Kódolás, hibajavítás Tervezte és készítette Géczy LászlL szló 2002 Jelkapcsolat A jelkapcsolatban van a jelforrás, amely az üzenő, és a jelérzékelő (vevő, fogadó), amely az értesített. Jelforrás üzenet
Kódolás, hibajavítás Tervezte és készítette Géczy LászlL szló 2002 Jelkapcsolat A jelkapcsolatban van a jelforrás, amely az üzenő, és a jelérzékelő (vevő, fogadó), amely az értesített. Jelforrás üzenet
Mobil kommunikáció /A mobil hálózat/ /elektronikus oktatási segédlet/ v3.0
 Mobil kommunikáció /A mobil hálózat/ /elektronikus oktatási segédlet/ v3.0 Dr. Berke József berke@georgikon.hu 2006-2008 A MOBIL HÁLÓZAT - Tartalom RENDSZERTECHNIKAI FELÉPÍTÉS CELLULÁRIS FELÉPÍTÉS KAPCSOLATFELVÉTEL
Mobil kommunikáció /A mobil hálózat/ /elektronikus oktatási segédlet/ v3.0 Dr. Berke József berke@georgikon.hu 2006-2008 A MOBIL HÁLÓZAT - Tartalom RENDSZERTECHNIKAI FELÉPÍTÉS CELLULÁRIS FELÉPÍTÉS KAPCSOLATFELVÉTEL
Jel, adat, információ
 Kommunikáció Jel, adat, információ Jel: érzékszerveinkkel, műszerekkel felfogható fizikai állapotváltozás (hang, fény, feszültség, stb.) Adat: jelekből (számítástechnikában: számokból) képzett sorozat.
Kommunikáció Jel, adat, információ Jel: érzékszerveinkkel, műszerekkel felfogható fizikai állapotváltozás (hang, fény, feszültség, stb.) Adat: jelekből (számítástechnikában: számokból) képzett sorozat.
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2016. ősz 1. Diszkrét matematika 2.C szakirány 10. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2016.
Diszkrét matematika 2.C szakirány 2016. ősz 1. Diszkrét matematika 2.C szakirány 10. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2016.
EuroOffice Professzionális Vonalkód és QR kód generátor
 1. oldal EuroOffice Professzionális Vonalkód és QR kód generátor Az EuroOffice Professzionális Vonalkód és QR kód generátor segítségével könnyen elkészítheti az EuroOffice (vagy egyéb OpenOffice.org alkalmazás)
1. oldal EuroOffice Professzionális Vonalkód és QR kód generátor Az EuroOffice Professzionális Vonalkód és QR kód generátor segítségével könnyen elkészítheti az EuroOffice (vagy egyéb OpenOffice.org alkalmazás)
Számítógépes Hálózatok. 5. gyakorlat
 Számítógépes Hálózatok 5. gyakorlat Óra eleji kiszh Elérés: https://oktnb6.inf.elte.hu Számítógépes Hálózatok Gyakorlat 2 Gyakorlat tematika Szinkron CDMA Órai / házi feladat Számítógépes Hálózatok Gyakorlat
Számítógépes Hálózatok 5. gyakorlat Óra eleji kiszh Elérés: https://oktnb6.inf.elte.hu Számítógépes Hálózatok Gyakorlat 2 Gyakorlat tematika Szinkron CDMA Órai / házi feladat Számítógépes Hálózatok Gyakorlat
Hálózati protokoll tervezése
 Hálózati protokoll tervezése A gyakorlat célja: Hálózati protokoll tervezésének a megvalósítása Elméleti bevezető: Ahhoz, hogy a hálózatba kötött gépek kommunikálni tudjanak egymással, szükség van egy
Hálózati protokoll tervezése A gyakorlat célja: Hálózati protokoll tervezésének a megvalósítása Elméleti bevezető: Ahhoz, hogy a hálózatba kötött gépek kommunikálni tudjanak egymással, szükség van egy
Dr. Oniga István DIGITÁLIS TECHNIKA 2
 Dr. Oniga István DIGITÁLIS TECHNIKA 2 Számrendszerek A leggyakrabban használt számrendszerek: alapszám számjegyek Tízes (decimális) B = 10 0, 1, 8, 9 Kettes (bináris) B = 2 0, 1 Nyolcas (oktális) B = 8
Dr. Oniga István DIGITÁLIS TECHNIKA 2 Számrendszerek A leggyakrabban használt számrendszerek: alapszám számjegyek Tízes (decimális) B = 10 0, 1, 8, 9 Kettes (bináris) B = 2 0, 1 Nyolcas (oktális) B = 8
4. Hivatkozási modellek
 4. Hivatkozási modellek Az előző fejezetben megismerkedtünk a rétegekbe szervezett számítógépes hálózatokkal, s itt az ideje, hogy megemlítsünk néhány példát is. A következő részben két fontos hálózati
4. Hivatkozási modellek Az előző fejezetben megismerkedtünk a rétegekbe szervezett számítógépes hálózatokkal, s itt az ideje, hogy megemlítsünk néhány példát is. A következő részben két fontos hálózati
Hálózati Architektúrák és Protokollok GI BSc. 3. laborgyakorlat
 Hálózati Architektúrák és Protokollok GI BSc. 3. laborgyakorlat Erdős András (demonstrátor) Debreceni Egyetem - Informatikai Kar Informatikai Rendszerek és Hálózatok Tanszék 2016 9/20/2016 9:41 PM 1 Adatkapcsolati
Hálózati Architektúrák és Protokollok GI BSc. 3. laborgyakorlat Erdős András (demonstrátor) Debreceni Egyetem - Informatikai Kar Informatikai Rendszerek és Hálózatok Tanszék 2016 9/20/2016 9:41 PM 1 Adatkapcsolati
Hálózati réteg. Feladata: a csomag eljusson a célig Több útválasztó Ez a legalacsonyabb rétek, mely a két végpont
 Hálózati réteg Hálózati réteg Feladata: a csomag eljusson a célig Több útválasztó Ez a legalacsonyabb rétek, mely a két végpont közötti átvitellel foglalkozik. Ismernie kell a topológiát Útvonalválasztás,
Hálózati réteg Hálózati réteg Feladata: a csomag eljusson a célig Több útválasztó Ez a legalacsonyabb rétek, mely a két végpont közötti átvitellel foglalkozik. Ismernie kell a topológiát Útvonalválasztás,
1. fogalom. Add meg az összeadásban szereplő számok elnevezéseit! Milyen tulajdonságai vannak az összeadásnak? Hogyan ellenőrizzük az összeadást?
 1. fogalom Add meg az összeadásban szereplő számok 73 + 19 = 92 összeadandók (tagok) összeg Összeadandók (tagok): amiket összeadunk. Összeg: az összeadás eredménye. Milyen tulajdonságai vannak az összeadásnak?
1. fogalom Add meg az összeadásban szereplő számok 73 + 19 = 92 összeadandók (tagok) összeg Összeadandók (tagok): amiket összeadunk. Összeg: az összeadás eredménye. Milyen tulajdonságai vannak az összeadásnak?
Alapfogalmak a Diszkrét matematika II. tárgyból
 Alapfogalmak a Diszkrét matematika II. tárgyból (A szakirány, 2015-2016 tavaszi félév) A számonkérés során ezeknek a definícióknak, tételkimondásoknak az alapos megértését is számon kérjük. A példakérdések
Alapfogalmak a Diszkrét matematika II. tárgyból (A szakirány, 2015-2016 tavaszi félév) A számonkérés során ezeknek a definícióknak, tételkimondásoknak az alapos megértését is számon kérjük. A példakérdések
Megoldás. Feladat 1. Statikus teszt Specifikáció felülvizsgálat
 Megoldás Feladat 1. Statikus teszt Specifikáció felülvizsgálat A feladatban szereplő specifikáció eredeti, angol nyelvű változata egy létező eszköz leírása. Nem állítjuk, hogy az eredeti dokumentum jól
Megoldás Feladat 1. Statikus teszt Specifikáció felülvizsgálat A feladatban szereplő specifikáció eredeti, angol nyelvű változata egy létező eszköz leírása. Nem állítjuk, hogy az eredeti dokumentum jól
loop() Referencia: https://www.arduino.cc/en/reference/homepage
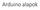 Arduino alapok Sketch ~ Solution Forrás:.ino (1.0 előtt.pde).c,.cpp,.h Külső könyvtárak (legacy / 3rd party) Mintakódok (example) setup() Induláskor fut le, kezdeti értékeket állít be, inicializálja a
Arduino alapok Sketch ~ Solution Forrás:.ino (1.0 előtt.pde).c,.cpp,.h Külső könyvtárak (legacy / 3rd party) Mintakódok (example) setup() Induláskor fut le, kezdeti értékeket állít be, inicializálja a
DIGITÁLIS TECHNIKA I BINÁRIS SZÁMRENDSZER BEVEZETŐ ÁTTEKINTÉS BINÁRIS SZÁMRENDSZER HELYÉRTÉK. Dr. Lovassy Rita Dr.
 26..5. DIGITÁLIS TEHNIK I Dr. Lovassy Rita Dr. Pődör álint Óbudai Egyetem KVK Mikroelektronikai és Technológia Intézet INÁRIS SZÁMRENDSZER 5. ELŐDÁS 2 EVEZETŐ ÁTTEKINTÉS 6. előadás témája a digitális rendszerekben
26..5. DIGITÁLIS TEHNIK I Dr. Lovassy Rita Dr. Pődör álint Óbudai Egyetem KVK Mikroelektronikai és Technológia Intézet INÁRIS SZÁMRENDSZER 5. ELŐDÁS 2 EVEZETŐ ÁTTEKINTÉS 6. előadás témája a digitális rendszerekben
Frekvencia tartományok. Számítógépes Hálózatok és Internet Eszközök. Frekvencia tartományok rádió kommunikációhoz
 Frekvencia tartományok Számítógépes Hálózatok és Internet Eszközök 2007 5. Fizikai réteg Médium közös használata, példa: ADSL LF (Low Frequency) = LW (Langwelle) = hosszúhullám MF (Medium Frequency) =
Frekvencia tartományok Számítógépes Hálózatok és Internet Eszközök 2007 5. Fizikai réteg Médium közös használata, példa: ADSL LF (Low Frequency) = LW (Langwelle) = hosszúhullám MF (Medium Frequency) =
;3 ; 0; 1 7; ;7 5; 3. pozitív: ; pozitív is, negatív is: ;
 . A racion lis sz mok A tanult sz mok halmaza A) Ábrázold számegyenesen az alábbi számokat! 8 + + 0 + 7 0 7 7 0 0. 0 Válogasd szét a számokat aszerint, hogy pozitív: pozitív is, negatív is: negatív: sem
. A racion lis sz mok A tanult sz mok halmaza A) Ábrázold számegyenesen az alábbi számokat! 8 + + 0 + 7 0 7 7 0 0. 0 Válogasd szét a számokat aszerint, hogy pozitív: pozitív is, negatív is: negatív: sem
Hálózati architektúrák laborgyakorlat
 Hálózati architektúrák laborgyakorlat 4. hét Dr. Orosz Péter, Skopkó Tamás 2012. szeptember Hálózati réteg (L3) Kettős címrendszer Interfész konfigurációja IP címzés: címosztályok, alhálózatok, szuperhálózatok,
Hálózati architektúrák laborgyakorlat 4. hét Dr. Orosz Péter, Skopkó Tamás 2012. szeptember Hálózati réteg (L3) Kettős címrendszer Interfész konfigurációja IP címzés: címosztályok, alhálózatok, szuperhálózatok,
2. fejezet Hálózati szoftver
 2. fejezet Hálózati szoftver Hálózati szoftver és hardver viszonya Az első gépek összekötésekor (azaz a hálózat első megjelenésekor) a legfontosabb lépésnek az számított, hogy elkészüljön az a hardver,
2. fejezet Hálózati szoftver Hálózati szoftver és hardver viszonya Az első gépek összekötésekor (azaz a hálózat első megjelenésekor) a legfontosabb lépésnek az számított, hogy elkészüljön az a hardver,
1. A maradékos osztás
 1. A maradékos osztás Egész számok osztása Példa 223 = 7 31+6. Visszaszorzunk Kivonunk 223 : 7 = 31 21 13 7 6 Állítás (számelméletből) Minden a,b Z esetén, ahol b 0, létezik olyan q,r Z, hogy a = bq +
1. A maradékos osztás Egész számok osztása Példa 223 = 7 31+6. Visszaszorzunk Kivonunk 223 : 7 = 31 21 13 7 6 Állítás (számelméletből) Minden a,b Z esetén, ahol b 0, létezik olyan q,r Z, hogy a = bq +
Járműfedélzeti hálózatok. Digitális adatátviteli alapfogalmak Aradi Szilárd
 Járműfedélzeti hálózatok Digitális adatátviteli alapfogalmak Aradi Szilárd Hálózati struktúrák A számítógép-hálózat egy olyan speciális rendszer, amely a számítógépek egymás közötti kommunikációját biztosítja.
Járműfedélzeti hálózatok Digitális adatátviteli alapfogalmak Aradi Szilárd Hálózati struktúrák A számítógép-hálózat egy olyan speciális rendszer, amely a számítógépek egymás közötti kommunikációját biztosítja.
A CAN mint ipari kommunikációs protokoll CAN as industrial communication protocol
 A CAN mint ipari kommunikációs protokoll CAN as industrial communication protocol Attila FODOR 1), Dénes FODOR Dr. 1), Károly Bíró Dr. 2), Loránd Szabó Dr. 2) 1) Pannon Egyetem, H-8200 Veszprém Egyetem
A CAN mint ipari kommunikációs protokoll CAN as industrial communication protocol Attila FODOR 1), Dénes FODOR Dr. 1), Károly Bíró Dr. 2), Loránd Szabó Dr. 2) 1) Pannon Egyetem, H-8200 Veszprém Egyetem
A számítógép-hálózatok tervezését struktúrális módszerrel végzik, azaz a hálózat egyes részeit réteg-ekbe (layer) vagy más néven szint-ekbe (level)
 A számítógép-hálózatok tervezését struktúrális módszerrel végzik, azaz a hálózat egyes részeit réteg-ekbe (layer) vagy más néven szint-ekbe (level) szervezik, melyek mindegyike az előzőre épül. 2 A gép
A számítógép-hálózatok tervezését struktúrális módszerrel végzik, azaz a hálózat egyes részeit réteg-ekbe (layer) vagy más néven szint-ekbe (level) szervezik, melyek mindegyike az előzőre épül. 2 A gép
Nagy Gábor compalg.inf.elte.hu/ nagy
 Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 3. estis képzés 2018. ősz 1. Diszkrét matematika 3. estis képzés 11. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
2.5 Soros adatkommunikációs rendszerek CAN (Ötödik rész)
 2.5 Soros adatkommunikációs rendszerek CAN (Ötödik rész) 3.4. A CAN adatbusz rendszerek üzenetformátuma Az információt a soros adatátviteli rendszereknél szabványosított keretformátumba foglalják. A teljes
2.5 Soros adatkommunikációs rendszerek CAN (Ötödik rész) 3.4. A CAN adatbusz rendszerek üzenetformátuma Az információt a soros adatátviteli rendszereknél szabványosított keretformátumba foglalják. A teljes
The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach 3. kiadás, Irv Englander John Wiley and Sons 2003
 . Fejezet : Számrendszerek The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach. kiadás, Irv Englander John Wiley and Sons Wilson Wong, Bentley College Linda Senne,
. Fejezet : Számrendszerek The Architecture of Computer Hardware and Systems Software: An InformationTechnology Approach. kiadás, Irv Englander John Wiley and Sons Wilson Wong, Bentley College Linda Senne,
Diszkrét matematika 2.
 Diszkrét matematika 2. 2019. május 3. 1. Diszkrét matematika 2. 10. előadás Fancsali Szabolcs Levente nudniq@cs.elte.hu www.cs.elte.hu/ nudniq Mérai László diái alapján Komputeralgebra Tanszék 2019. május
Diszkrét matematika 2. 2019. május 3. 1. Diszkrét matematika 2. 10. előadás Fancsali Szabolcs Levente nudniq@cs.elte.hu www.cs.elte.hu/ nudniq Mérai László diái alapján Komputeralgebra Tanszék 2019. május
A TCP/IP modell szállítási rétege
 A TCP/IP modell szállítási rétege Ismerkedés a szállítási réteggel A szállítási réteg elsődleges feladatai a forrás és a cél közötti információáramlás pontos szabályozása, valamint az adatok megbízható
A TCP/IP modell szállítási rétege Ismerkedés a szállítási réteggel A szállítási réteg elsődleges feladatai a forrás és a cél közötti információáramlás pontos szabályozása, valamint az adatok megbízható
SZÁMRENDSZEREK KÉSZÍTETTE: JURÁNYINÉ BESENYEI GABRIELLA
 SZÁMRENDSZEREK KÉSZÍTETTE: JURÁNYINÉ BESENYEI GABRIELLA BINÁRIS (kettes) ÉS HEXADECIMÁLIS (tizenhatos) SZÁMRENDSZEREK (HELYIÉRTÉK, ÁTVÁLTÁSOK, MŰVELETEK) A KETTES SZÁMRENDSZER A computerek világában a
SZÁMRENDSZEREK KÉSZÍTETTE: JURÁNYINÉ BESENYEI GABRIELLA BINÁRIS (kettes) ÉS HEXADECIMÁLIS (tizenhatos) SZÁMRENDSZEREK (HELYIÉRTÉK, ÁTVÁLTÁSOK, MŰVELETEK) A KETTES SZÁMRENDSZER A computerek világában a
INVERSE E1 MULTIPLEXER LAN BRIDGE
 INVERSE E1 MULTIPLEXER LAN BRIDGE SP 7403 és SP 7405 INVERSE E1 MULTIPLEXER LAN BRIDGE 1/11 Tartalomjegyzék Általános ismertetés...3 Funkció...3 WAN interfész...3 LAN interfész...3 Felügyelet...3 Tápfeszültség...3
INVERSE E1 MULTIPLEXER LAN BRIDGE SP 7403 és SP 7405 INVERSE E1 MULTIPLEXER LAN BRIDGE 1/11 Tartalomjegyzék Általános ismertetés...3 Funkció...3 WAN interfész...3 LAN interfész...3 Felügyelet...3 Tápfeszültség...3
Bevezetés az informatikába gyakorló feladatok Utoljára módosítva:
 Tartalom 1. Számrendszerek közti átváltás... 2 1.1. Megoldások... 4 2. Műveletek (+, -, bitműveletek)... 7 2.1. Megoldások... 8 3. Számítógépes adatábrázolás... 12 3.1. Megoldások... 14 A gyakorlósor lektorálatlan,
Tartalom 1. Számrendszerek közti átváltás... 2 1.1. Megoldások... 4 2. Műveletek (+, -, bitműveletek)... 7 2.1. Megoldások... 8 3. Számítógépes adatábrázolás... 12 3.1. Megoldások... 14 A gyakorlósor lektorálatlan,
Számítógépes hálózatok
 Számítógépes hálózatok 3.gyakorlat Fizikai réteg Kódolások, moduláció, CDMA Laki Sándor lakis@inf.elte.hu http://lakis.web.elte.hu 1 Második házi feladat 2 AM és FM analóg jel modulációja esetén Forrás:
Számítógépes hálózatok 3.gyakorlat Fizikai réteg Kódolások, moduláció, CDMA Laki Sándor lakis@inf.elte.hu http://lakis.web.elte.hu 1 Második házi feladat 2 AM és FM analóg jel modulációja esetén Forrás:
Bevezetés. Számítógép-hálózatok. Dr. Lencse Gábor. egyetemi docens Széchenyi István Egyetem, Távközlési Tanszék
 Bevezetés Számítógép-hálózatok Dr. Lencse Gábor egyetemi docens Széchenyi István Egyetem, Távközlési Tanszék lencse@sze.hu Tartalom Alapfogalmak, definíciók Az OSI és a TCP/IP referenciamodell Hálózati
Bevezetés Számítógép-hálózatok Dr. Lencse Gábor egyetemi docens Széchenyi István Egyetem, Távközlési Tanszék lencse@sze.hu Tartalom Alapfogalmak, definíciók Az OSI és a TCP/IP referenciamodell Hálózati
SZÁMÉRTÉKEK (ÁT)KÓDOLÁSA
 1 ELSŐ GYAKORLAT SZÁMÉRTÉKEK (ÁT)KÓDOLÁSA A feladat elvégzése során a következőket fogjuk gyakorolni: Számrendszerek közti átváltás előjelesen és előjel nélkül. Bináris, decimális, hexadexcimális számrendszer.
1 ELSŐ GYAKORLAT SZÁMÉRTÉKEK (ÁT)KÓDOLÁSA A feladat elvégzése során a következőket fogjuk gyakorolni: Számrendszerek közti átváltás előjelesen és előjel nélkül. Bináris, decimális, hexadexcimális számrendszer.
Digitális technika VIMIAA hét
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK VIMIAA02 14. hét Fehér Béla BME MIT Rövid visszatekintés, összefoglaló
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK VIMIAA02 14. hét Fehér Béla BME MIT Rövid visszatekintés, összefoglaló
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Számelmélet I.
 Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
