Modellezés Gregorics Tibor Mesterséges intelligencia
|
|
|
- Donát Hegedüs
- 6 évvel ezelőtt
- Látták:
Átírás
1 Modellezés
2 1. Állapottér-reprezentáció Állapottér: a probléma leírásához szükséges adatok által felvett érték-együttesek (azaz állapotok) halmaza az állapot többnyire egy összetett szerkezetű érték gyakran egy bővebb alaphalmazzal és egy azon értelmezett invariáns állítással definiáljuk Műveletek: állapotból állapotba vezetnek megadásukhoz: előfeltétel és hatás leírása invariáns tulajdonságot tartó leképezés Kezdőállapot(ok) vagy azokat leíró kezdeti feltétel Végállapot(ok) vagy célfeltétel
3 Állapottér-reprezentáció állapot-gráfja Állapottér modell Állapot-gráf o állapot ~ csúcs o művelet hatása egy állapotra ~ irányított él o művelet költsége ~ él költsége o kezdő állapot ~ startcsúcs o célállapot ~ célcsúcs Gráf-reprezentáció: állapot-gráf, startcsúcs, célcsúcsok o egy műveletsorozat hatása ~ irányított út o megoldás ~ irányított út a startcsúcsból egy célcsúcsba
4 Hanoi tornyai probléma Állapottér: Kezdőállapot Végállapot [3,3,3] [1,1,1] AT ={1,2,3} n megjegyzés : a tömb i-dik eleme mutatja az i-dik korong rúdjának számát; a korongok a rudakon méretük szerint fentről lefelé növekvő sorban vannak. Művelet: Rak(honnan, hova):at AT HA a honnan és hova létezik és nem azonos, és van korong a honnan rúdon, és a hova rúd üres vagy a mozgatandó korong (honnan rúd felső korongja) kisebb, mint a hova rúd felső korongja, AKKOR this[honnan legfelső korongja] := hova this:at az aktuális állapot 1..n intervallummal indexelt egydimenziós tömb, amely elemei az {1,2,3} halmazból származnak.
5 Implementáció template <int n = 3> class Hanoi { int _a[n]; // its elements are between 1 and 3 public : bool move (int from, int to) { if ((from<1 from>3 to<1 to>3) (from==to)) return false; bool l1; int i; // l1 ~ from is not empty, i ~ upper disc on from for(l1=false, i=0;!l1 && i<n; ++i) l1 = (_a[i]==from); if (! l1) return false; bool l2; int j; // l2 ~ to is not empty, j ~ upper disc on to for(l2=false, j=0;!l2 && j<n; ++j) l2 = (_a[j]==to) ; if ( l2 i<j ){ _a[i] = to; return true; } else return false; } bool final() const { bool l=true; for(int i=0; l && i<n;++i) l = (_a[i]==1); return l; } void init() { for(int i=0;i<n;++i) _a[i] = 3; } };
6 Hanoi tornyai [3,3,3] start állapot-gráfja csúcsok száma : 3 n csúcs ki-foka: 2, 3 körök hosszai: 2, 3, 6, 7, 9, [1,1,2] [1,1,3] [2,1,3] [2,3,3] [3,1,3] [3,2,3] [1,3,3] [1,2,3] [2,2,3] [2,2,1] [3,1,2] [2,1,2] [1,2,1] [3,2,1] [3,2,2] [2,3,2] [1,3,1] [3,1,1] [2,2,2] [1,2,2] [1,3,2] [3,3,2] [3,3,1] [2,3,1] [2,1,1] [1,1,1] cél
7 általános állapot n-királynő probléma 1. utófeltételnek megfelelő állapot Állapottér: AT = {, _ } n n invariáns: egy állapot (tábla) pontosan n darab királynőt tartalmaz Művelet: Áthelyez(x,y,u,v):AT AT (this:at) HA AKKOR 1 x,y,u,v n és this[x,y]= és this[u,v]=_ this[x,y] this[u,v] csere kétdimenziós tömb (n n-es mátrix), mely elemei {, _ } halmazbeliek
8 Állapot-gráf részlet csúcsok száma: csúcsok ki-foka: n*(n 2 n) n 2 n adott csúcsból induló k hosszú utak száma az oda-vissza lépések nélkül: (n*(n 2 n)) k
9 Állapottér vs. problématér A problématér elemeit (lehetséges megoldásokat) a startcsúcsból induló különböző hosszúságú irányított utak szimbolizálják. Egy feladat állapottér-reprezentációja és problématere között szoros kapcsolat áll fenn, de az állapottér nem azonos a problématérrel. A Hanoi tornyai problémánál a megoldások a startcsúcsból célcsúcsba vezető irányított utak. Az n-királynő problémánál egy állapotot (célcsúcsot) keresünk, de ebben az esetben is egy alkalmas operátor-sorozat (azaz irányított út) vezet el ahhoz, azaz végsősoron ilyenkor is utat keresünk.
10 Állapot-gráf bonyolultsága Állapot-gráf bonyolultsága Problématér mérete Keresés számításigénye A bonyolultság a start csúcsból kivezető utak számától függ, amely nyilván függvénye a csúcsok és élek számának csúcsok ki-fokának körök gyakoriságának, és hosszuk sokféleségének
11 Csökkentsük a problématér méretét Ugyanannak a feladatnak több modellje lehet : érdemes olyat keresni, amely kisebb problémateret jelöl ki. o o o Az n-királynő probléma reprezentációjánál a problématér mérete, a lehetséges utak száma, óriási. Adjunk jobb modellt! Bővítsük az állapotteret az n-nél kevesebb királynőt tartalmazó állásokkal, és használjunk új műveletet : királynő-felhelyezést (kezdő állás az üres tábla). Műveletek előfeltételének szigorításával csökken az állapotgráf átlagos ki-foka: - Sorról sorra haladva csak egy-egy királynőt helyezzünk fel a táblára! - Ütést tartalmazó állásra ne tegyünk királynőt!
12 n-királynő probléma 2. kezdőállapot végállapot Állapottér: AT = {, _ } n n nincs már üres sor és nincs ütés invariáns: az első néhány sor egy-egy királynőt tartalmaz Művelet: Helyez(oszlop): AT AT (this:at) HA közbülső állapot 1 oszlop n és a this-beli soron következő üres sor n és nincs ütés a this-ben AKKOR this[a this-beli soron következő üres sor,oszlop] :=
13 csúcsok száma < (n n+1 1)/(n 1) csúcs ki-foka: n Állapot-gráf start ágak száma < n n cél
14 Művelet végrehajtásának hatékonysága A művelet kiszámítási bonyolultsága csökkenthető, ha az állapotokat extra információval egészítjük ki, vagy az invariáns szigorításával szűkítjük az állapotteret. Például o o Egy állapotban a tábla soron következő üres sorának sorszámát eltárolhatjuk a tábla mellett, így új királynő elhelyezésekor ezt nem kell kiszámolni, ugyanakkor egy művelet végrehajtásakor könnyen aktualizálhatjuk (eggyel növeljük). Ne engedjünk meg ütést létrehozni a táblán, hogy ne kelljen ezt a tulajdonságot külön ellenőrizni. Ennek céljából megjelöljük az ütés alatt álló üres (tehát már nem szabad) mezőket, amelyekre nem helyezhetünk fel királynőt. Egy mező státusza három féle lesz: szabad, ütés alatt álló vagy foglalt, amelyeket a művelet végrehajtásakor kell karbantartani.
15 n-királynő probléma 3. kezdőállapot: kövsor = 1 közbülső állapot: kövsor = 3 végállapot : kövsor = 5 Állapottér: AT = rec(t :{,, _ } n n, kövsor : N) invariáns: kövsor n+1, az első kövsor 1 darab sor egy-egy királynőt tartalmaz, királynők nem ütik egymást, jelölés : egy királynő által ütött üres mezőt jelöli, _ az ütésben nem álló (szabad) üres mezőt jelöli.
16 n-királynő probléma 3. folytatás Művelet: új királynő elhelyezése a soron következő sorba Helyez(oszlop): AT AT HA (this:at) 1 oszlop n és this.kövsor n és this.t[this.kövsor,oszlop]=_ AKKOR this.t[this.kövsor,oszlop] := i [this.kövsor+1.. n] : this.t[i, oszlop]:= ha (i n+this.kövsor oszlop) this.t[i, i this.kövsor+oszlop]:= ha (i this.kövsor+oszlop 1) this.t[i, this.kövsor+oszlop i]:= this.kövsor := this.kövsor+1 Kezdőállapot: this.t egy üres mátrix, this.kövsor:=1 Végállapot: this.kövsor>n előfeltétel számításigénye: konstans hatás számításigénye: lineáris célfeltétel nagyon egyszerű lett
17 start Állapot-gráf cél
18 Kezdőállapot: tetszőleges Tologató játék (8-as, 15-ös) Állapottér: AT = rec(mátrix :{0..8} 3 3, üres :{1..3} {1..3}) invariáns: egy állapot mátrixának sorfolytonos kiterítése a számok egy permutációja, az üres hely a 0 elem mátrixbeli sor és oszlopindexe. Művelet: HA AKKOR Tol(irány): AT AT koordinátánként értendő irány {(0,-1),(-1,0),(0,1),(1,0)} és (1,1) this.üres+irány (3,3) (this: AT) this.mátrix[this.üres] this.mátrix[this.üres +irány] this.üres := this.üres +irány Végállapot: szokásos
19 start Állapot-gráf cél
20 2. Probléma dekompozíció Egy probléma dekomponálása során a problémát részproblémákra bontjuk, majd azokat tovább részletezzük, amíg nyilvánvalóan megoldható problémákat nem kapunk. Sokszor egy probléma megoldását akár többféleképpen is fel lehet bontani részproblémák megoldásaira. probléma részprobl 11 részprobl 12 részprobl 21 részprobl 22 részprobl23 rész 1 rész 2 rész 3 rész 4
21 Integrálszámítás (5 x 2 +x e x )dx + 5 x 2 dx x e x dx x 2 dx x e x e x dx ⅓ x 3 e x Probléma általános leírása: szintaktikusan helyes kifejezés Kiinduló probléma: adott integrál-kifejezés Egyszerű probléma: integráljel nélküli kifejezés Dekomponáló operátorok: integrálási szabályok ½ x 2 e x ½ x 2 e x dx * ½ x 2 e x dx Megoldás gráf: alternatívákat nem tartalmazó levezetés egy olyan részfa, amelynek belső csúcsaiból egyetlen élköteg indul ki, levelei egyszerű megoldható problémák Megoldás: a megoldó részfa leveleit balról jobbra haladva kötjük össze a dekomponálások algebrai műveleteivel
22 Hanoi tornyai probléma megoldása H(3, 3 1, 2) dekompozícióval H(2,3 2,1) H(2,2 1,3) H(1,3 1,2) H(1,3 1,2) H(1,3 2,1) H(1,1 2,3) H(1,2 3,1) H(1,2 1,3) H(1,3 1,2) Probléma általános leírása: H(n, i j, k) n korongot vigyünk át az i. rúdról a j. rúdra a k. rúd segítségével Kiinduló probléma: H(3, 3 1, 2) Egyszerű probléma: H(1, i j, k) eldönthető, hogy megoldható-e Dekomponálás: H(n, i j, k) <H(n 1,i k, j), H(1, i j, k), H(n 1, k j, i)> Megoldás gráf: kiinduló problémát egyszerű problémákra visszavezető fa Megoldás: a részfa leveleit kell balról jobbra haladva összeolvasni
23 Dekompozíciós reprezentáció fogalma A reprezentációhoz meg kell adnunk: a feladat részproblémáinak általános leírását, a kiinduló problémát, az egyszerű problémákat, amelyekről könnyen eldönthető, hogy megoldhatók-e vagy sem, és a dekomponáló műveleteket: D: probléma probléma + és D(p)=<p 1,, p n >
24 A dekompozíció modellezése ÉS/VAGY gráffal Dekompozíciós modell ÉS/VAGY gráf o részprobléma ~ csúcs o dekomponáló művelet hatása ~ irányított hiper-él o művelet költsége ~ hiper-él költsége o kiinduló probléma ~ startcsúcs o megoldható probléma ~ célcsúcs Gráf-reprezentáció: ÉS/VAGY gráf, startcsúcs, célcsúcsok o egy dekompozíciós folyamat ~ hiper-út o megoldás ~ megoldás-gráf: hiper-út startcsúcsból célcsúcsok sorozatába
25 Hiper-él Egy csúcsból kivezető éleknek egy kötege, a hiperél jeleníti meg egy dekomponáló művelet hatását: a dekomponált probléma csúcsából a dekomponálással előállított részproblémák csúcsaiba vezet. a hiperél élei között ÉS kapcsolat van: egy dekomponált problémának minden részproblémáját meg kell oldani; egy csúcsból több hiperél is indulhat, ha egy probléma többféleképpen dekomponálható. Két ilyen hiperél egyegy éle között VAGY kapcsolat áll fenn: választhatunk, hogy melyik dekomponálást alkalmazzuk a problémára.
26 ÉS/VAGY gráfok 1. Az R=(N,A) élsúlyozott irányított hiper-gráf, ahol az N a csúcsok halmaza, A (n,m) N N + 0 M < } a hiper-élek halmaza, M a hiper-él rendje a (c(n,m) az (n,m) költsége) 2. Egy csúcsból véges sok hiper-él indulhat 3. (0< c(n,m)) c b f g d e i j h
27 Megoldás-gráf Az eredeti problémát egyszerű problémákra visszavezető dekomponálási folyamatot az ÉS/VAGY gráf speciális részgráfja, az ún. megoldás-gráf jeleníti meg, amelynek része a startcsúcs minden csúcsába vezet közönséges út a startcsúcsból, és minden csúcsából vezet közönséges út egy olyan célcsúcsba, amely a megoldás-gráf része egy éllel együtt az összes azzal ÉS kapcsolatban álló él is (azaz a teljes élköteg) része a megoldás-gráfnak nem tartalmaz VAGY kapcsolatban álló él párokat A megoldás ebből a megoldás-gráfból olvasható ki.
28 Az n csúcsból az M csúcs-sorozatba vezető irányított hiper-út fogalma Az n M hiper-út (n N, M N + ) egy olyan véges részgráf, amelyben M csúcsaiból nem indul hiper-él, M-en kívüli csúcsokból csak egy hiper-él indul, minden csúcs elérhető az n csúcsból egy közönséges irányított úton. A megoldás-gráf egy olyan hiper-út, amely a startcsúcsból csupa célcsúcsba vezet. c b f g d e i j a h a <d,e>
29 Az n M hiper-út egy bejárásán a hiper-út csúcsaiból képzett sorozatoknak a felsorolását értjük: első sorozat: <n> Hiper-út bejárása a C sorozatot a C k K sorozat követi (ahol a k C, és k minden C-beli előfordulása helyén a K sorozat szerepel) feltéve, hogy a hiper-útnak van olyan (k,k) hiper-éle, ahol k M. c d Így egy hiper-utat közönséges irányított útnak foghatunk fel, igaz többféleképpen, mert több bejárása is lehet: <n> <a,b> <n> <a,b> <a,a> < c,d,c,d > <c,d,b > <c,d,a> < c,d,c,d > n b
30 Útkeresés ÉS/VAGY gráfban ÉS/VAGY gráfbeli megoldás-gráf keresése visszavezethető egy közönséges irányított gráfban történő útkeresésre. A startcsúcsból induló hiper-utakat (köztük a megoldásgráfokat is) a bejárásukkal ábrázolhatjuk, és ezek a bejárások egy közönséges irányított gráfot határoznak meg. Ebben a csúcsok az eredeti ÉS/VAGY gráf csúcsainak sorozatai, a startcsúcs az ÉS/VAGY gráf startcsúcsából álló egy elemű sorozat, a célcsúcsok az ÉS/VAGY gráf célcsúcsainak egy részét tartalmazó sorozatok. A megfeleltetett közönséges irányított gráf megoldási újai az eredeti ÉS/VAGY gráf megoldás-gráfja.
II. Állapottér-reprezentáció
 Állapottér-reprezentáció elemei II. Állapottér-reprezentáció Állapottér: a feladat homlokterében álló adat (objektum) lehetséges értékeinek (állapotainak) halmaza lényegében egyetlen típusérték-halmaz
Állapottér-reprezentáció elemei II. Állapottér-reprezentáció Állapottér: a feladat homlokterében álló adat (objektum) lehetséges értékeinek (állapotainak) halmaza lényegében egyetlen típusérték-halmaz
II. Állapottér-reprezentáció
 II. Állapottér-reprezentáció 1 Állapottér-reprezentáció elemei Állapottér: a feladat homlokterében álló adategyüttes (objektum) lehetséges értékeinek (állapotainak) halmaza lényegében egyetlen típusérték-halmaz
II. Állapottér-reprezentáció 1 Állapottér-reprezentáció elemei Állapottér: a feladat homlokterében álló adategyüttes (objektum) lehetséges értékeinek (állapotainak) halmaza lényegében egyetlen típusérték-halmaz
Mesterséges Intelligencia. Csató Lehel. Csató Lehel. Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2007/2008
 Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 007/008 Az Előadások Témái Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció i stratégiák Szemantikus hálók / Keretrendszerek
Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 007/008 Az Előadások Témái Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció i stratégiák Szemantikus hálók / Keretrendszerek
Mesterséges Intelligencia. Csató Lehel. Csató Lehel. Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2007/2008
 Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2007/2008 Az Előadások Témái Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció Gráfkeresési stratégiák Szemantikus hálók
Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2007/2008 Az Előadások Témái Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció Gráfkeresési stratégiák Szemantikus hálók
Mesterséges intelligencia. Gregorics Tibor people.inf.elte.hu/gt/mi
 people.inf.elte.hu/gt/mi Szakirodalom Könyvek Fekete István - - Nagy Sára: Bevezetés a mesterséges intelligenciába, LSI Kiadó, Budapest, 1990, 1999. ELTE-Eötvös Kiadó, Budapest, 2006. Russel, J. S., Norvig,
people.inf.elte.hu/gt/mi Szakirodalom Könyvek Fekete István - - Nagy Sára: Bevezetés a mesterséges intelligenciába, LSI Kiadó, Budapest, 1990, 1999. ELTE-Eötvös Kiadó, Budapest, 2006. Russel, J. S., Norvig,
2. Visszalépéses stratégia
 2. Visszalépéses stratégia A visszalépéses keres rendszer olyan KR, amely globális munkaterülete: út a startcsúcsból az aktuális csúcsba (ezen kívül a még ki nem próbált élek nyilvántartása) keresés szabályai:
2. Visszalépéses stratégia A visszalépéses keres rendszer olyan KR, amely globális munkaterülete: út a startcsúcsból az aktuális csúcsba (ezen kívül a még ki nem próbált élek nyilvántartása) keresés szabályai:
Struktúra nélküli adatszerkezetek
 Struktúra nélküli adatszerkezetek Homogén adatszerkezetek (minden adatelem azonos típusú) osztályozása Struktúra nélküli (Nincs kapcsolat az adatelemek között.) Halmaz Multihalmaz Asszociatív 20:24 1 A
Struktúra nélküli adatszerkezetek Homogén adatszerkezetek (minden adatelem azonos típusú) osztályozása Struktúra nélküli (Nincs kapcsolat az adatelemek között.) Halmaz Multihalmaz Asszociatív 20:24 1 A
Programozási Módszertan definíciók, stb.
 Programozási Módszertan definíciók, stb. 1. Bevezetés Egy adat típusát az adat által felvehető lehetséges értékek halmaza (típusérték halmaz, TÉH), és az ezen értelmezett műveletek (típusműveletek) együttesen
Programozási Módszertan definíciók, stb. 1. Bevezetés Egy adat típusát az adat által felvehető lehetséges értékek halmaza (típusérték halmaz, TÉH), és az ezen értelmezett műveletek (típusműveletek) együttesen
Mesterséges Intelligencia. Csató Lehel. Csató Lehel. Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2010/2011 1/363
 1/6 Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2010/2011 Az Előadások Témái 46/6 Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció stratégiák Szemantikus hálók
1/6 Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2010/2011 Az Előadások Témái 46/6 Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció stratégiák Szemantikus hálók
Bevezetés az informatikába
 Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Amortizációs költségelemzés
 Amortizációs költségelemzés Amennyiben műveleteknek egy M 1,...,M m sorozatának a futási idejét akarjuk meghatározni, akkor egy lehetőség, hogy külön-külön minden egyes művelet futási idejét kifejezzük
Amortizációs költségelemzés Amennyiben műveleteknek egy M 1,...,M m sorozatának a futási idejét akarjuk meghatározni, akkor egy lehetőség, hogy külön-külön minden egyes művelet futási idejét kifejezzük
1. Milyen hatással van a heurisztika általában a keresõ rendszerek mûködésére?
 2012. 06. 20. 1. Milyen hatással van a heurisztika általában a keresõ rendszerek mûködésére? A heurisztika olyan, a feladathoz kapcsolódó ötlet, amelyet közvetlenül építünk be egy algoritmusba, azért,
2012. 06. 20. 1. Milyen hatással van a heurisztika általában a keresõ rendszerek mûködésére? A heurisztika olyan, a feladathoz kapcsolódó ötlet, amelyet közvetlenül építünk be egy algoritmusba, azért,
INFORMATIKA javítókulcs 2016
 INFORMATIKA javítókulcs 2016 ELMÉLETI TÉTEL: Járd körbe a tömb fogalmát (Pascal vagy C/C++): definíció, egy-, két-, több-dimenziós tömbök, kezdőértékadás definíciókor, tömb típusú paraméterek átadása alprogramoknak.
INFORMATIKA javítókulcs 2016 ELMÉLETI TÉTEL: Járd körbe a tömb fogalmát (Pascal vagy C/C++): definíció, egy-, két-, több-dimenziós tömbök, kezdőértékadás definíciókor, tömb típusú paraméterek átadása alprogramoknak.
2. Visszalépéses keresés
 2. Visszalépéses keresés Visszalépéses keresés A visszalépéses keresés egy olyan KR, amely globális munkaterülete: egy út a startcsúcsból az aktuális csúcsba (az útról leágazó még ki nem próbált élekkel
2. Visszalépéses keresés Visszalépéses keresés A visszalépéses keresés egy olyan KR, amely globális munkaterülete: egy út a startcsúcsból az aktuális csúcsba (az útról leágazó még ki nem próbált élekkel
A félév során előkerülő témakörök
 A félév során előkerülő témakörök rekurzív algoritmusok rendező algoritmusok alapvető adattípusok, adatszerkezetek, és kapcsolódó algoritmusok dinamikus programozás mohó algoritmusok gráf algoritmusok
A félév során előkerülő témakörök rekurzív algoritmusok rendező algoritmusok alapvető adattípusok, adatszerkezetek, és kapcsolódó algoritmusok dinamikus programozás mohó algoritmusok gráf algoritmusok
1. AZ MI FOGALMA. I. Bevezetés. Ers mesterséges intelligencia (EMI) Gyenge mesterséges intelligencia. MI története. Els szakasz (60-as évek)
 1. AZ MI FOGALMA I. Bevezetés 1. A mesterséges intelligencia (MI) fogalma 2. Probléma modellezés 3. Keres rendszerek az MI-ben 1956 nyár. Darthmouth College-i konferencia Kezdeti cél: Az emberi gondolkodás
1. AZ MI FOGALMA I. Bevezetés 1. A mesterséges intelligencia (MI) fogalma 2. Probléma modellezés 3. Keres rendszerek az MI-ben 1956 nyár. Darthmouth College-i konferencia Kezdeti cél: Az emberi gondolkodás
Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 1
 Halmazok 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 2 A fejezet legfontosabb elemei Halmaz megadási módjai Halmazok közti műveletek (metszet,
Halmazok 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 2 A fejezet legfontosabb elemei Halmaz megadási módjai Halmazok közti műveletek (metszet,
Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé.
 HA 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) HA 2 Halmazok HA 3 Megjegyzések A halmaz, az elem és az eleme fogalmakat nem definiáljuk, hanem alapfogalmaknak
HA 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) HA 2 Halmazok HA 3 Megjegyzések A halmaz, az elem és az eleme fogalmakat nem definiáljuk, hanem alapfogalmaknak
Keresések Gregorics Tibor Mesterséges intelligencia
 Keresések ADAT := kezdeti érték while terminálási feltétel(adat) loop SELECT SZ FROM alkalmazható szabályok ADAT := SZ(ADAT) endloop KR vezérlési szintjei vezérlési stratégia általános modellfüggő heurisztikus
Keresések ADAT := kezdeti érték while terminálási feltétel(adat) loop SELECT SZ FROM alkalmazható szabályok ADAT := SZ(ADAT) endloop KR vezérlési szintjei vezérlési stratégia általános modellfüggő heurisztikus
Gráfelmélet. I. Előadás jegyzet (2010.szeptember 9.) 1.A gráf fogalma
 Készítette: Laczik Sándor János Gráfelmélet I. Előadás jegyzet (2010.szeptember 9.) 1.A gráf fogalma Definíció: a G=(V,E) párt egyszerű gráfnak nevezzük, (V elemeit a gráf csúcsainak/pontjainak,e elemeit
Készítette: Laczik Sándor János Gráfelmélet I. Előadás jegyzet (2010.szeptember 9.) 1.A gráf fogalma Definíció: a G=(V,E) párt egyszerű gráfnak nevezzük, (V elemeit a gráf csúcsainak/pontjainak,e elemeit
Felvételi vizsga mintatételsor Informatika írásbeli vizsga
 BABEȘ BOLYAI TUDOMÁNYEGYETEM MATEMATIKA ÉS INFORMATIKA KAR A. tételsor (30 pont) Felvételi vizsga mintatételsor Informatika írásbeli vizsga 1. (5p) Egy x biten tárolt egész adattípus (x szigorúan pozitív
BABEȘ BOLYAI TUDOMÁNYEGYETEM MATEMATIKA ÉS INFORMATIKA KAR A. tételsor (30 pont) Felvételi vizsga mintatételsor Informatika írásbeli vizsga 1. (5p) Egy x biten tárolt egész adattípus (x szigorúan pozitív
22. GRÁFOK ÁBRÁZOLÁSA
 22. GRÁFOK ÁBRÁZOLÁSA A megoldandó feladatok, problémák modellezése során sokszor gráfokat alkalmazunk. A gráf fogalmát a matematikából ismertnek vehetjük. A modellezés során a gráfok több változata is
22. GRÁFOK ÁBRÁZOLÁSA A megoldandó feladatok, problémák modellezése során sokszor gráfokat alkalmazunk. A gráf fogalmát a matematikából ismertnek vehetjük. A modellezés során a gráfok több változata is
Ellenőrző kérdések. 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t
 Ellenőrző kérdések 2. Kis dolgozat kérdései 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t 37. Ha t szintű indexet használunk,
Ellenőrző kérdések 2. Kis dolgozat kérdései 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t 37. Ha t szintű indexet használunk,
1. Alapfogalmak Algoritmus Számítási probléma Specifikáció Algoritmusok futási ideje
 1. Alapfogalmak 1.1. Algoritmus Az algoritmus olyan elemi műveletekből kompozíciós szabályok szerint felépített összetett művelet, amelyet megadott feltételt teljesítő bemeneti adatra végrehajtva, a megkívánt
1. Alapfogalmak 1.1. Algoritmus Az algoritmus olyan elemi műveletekből kompozíciós szabályok szerint felépített összetett művelet, amelyet megadott feltételt teljesítő bemeneti adatra végrehajtva, a megkívánt
Kiterjesztések sek szemantikája
 Kiterjesztések sek szemantikája Példa D Integer = {..., -1,0,1,... }; D Boolean = { true, false } D T1... T n T = D T 1... D Tn D T Az összes függvf ggvény halmaza, amelyek a D T1,..., D Tn halmazokból
Kiterjesztések sek szemantikája Példa D Integer = {..., -1,0,1,... }; D Boolean = { true, false } D T1... T n T = D T 1... D Tn D T Az összes függvf ggvény halmaza, amelyek a D T1,..., D Tn halmazokból
2. Rekurzió. = 2P2(n,n) 2 < 2P2(n,n) 1
 2. Rekurzió Egy objektum definícióját rekurzívnak nevezünk, ha a definíció tartalmazza a definiálandó objektumot. Egy P eljárást (vagy függvényt) rekurzívnak nevezünk, ha P utasításrészében előfordul magának
2. Rekurzió Egy objektum definícióját rekurzívnak nevezünk, ha a definíció tartalmazza a definiálandó objektumot. Egy P eljárást (vagy függvényt) rekurzívnak nevezünk, ha P utasításrészében előfordul magának
Diszkrét matematika 2. estis képzés
 Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 10. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 10. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
9. előadás. Programozás-elmélet. Programozási tételek Elemi prog. Sorozatszámítás Eldöntés Kiválasztás Lin. keresés Megszámolás Maximum.
 Programozási tételek Programozási feladatok megoldásakor a top-down (strukturált) programtervezés esetén három vezérlési szerkezetet használunk: - szekvencia - elágazás - ciklus Eddig megismertük az alábbi
Programozási tételek Programozási feladatok megoldásakor a top-down (strukturált) programtervezés esetén három vezérlési szerkezetet használunk: - szekvencia - elágazás - ciklus Eddig megismertük az alábbi
Algoritmusok és adatszerkezetek II.
 Algoritmusok és adatszerkezetek II. Horváth Gyula Szegedi Tudományegyetem Természettudományi és Informatikai Kar horvath@inf.u-szeged.hu 3. Kiegyensúlyozott keresőfák A T tulajdonság magasság-egyensúlyozó
Algoritmusok és adatszerkezetek II. Horváth Gyula Szegedi Tudományegyetem Természettudományi és Informatikai Kar horvath@inf.u-szeged.hu 3. Kiegyensúlyozott keresőfák A T tulajdonság magasság-egyensúlyozó
Dinamikus modellek szerkezete, SDG modellek
 Diagnosztika - 3. p. 1/2 Modell Alapú Diagnosztika Diszkrét Módszerekkel Dinamikus modellek szerkezete, SDG modellek Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék Diagnosztika - 3.
Diagnosztika - 3. p. 1/2 Modell Alapú Diagnosztika Diszkrét Módszerekkel Dinamikus modellek szerkezete, SDG modellek Hangos Katalin PE Villamosmérnöki és Információs Rendszerek Tanszék Diagnosztika - 3.
Előfeltétel: legalább elégséges jegy Diszkrét matematika II. (GEMAK122B) tárgyból
 ÜTEMTERV Programozás-elmélet c. tárgyhoz (GEMAK233B, GEMAK233-B) BSc gazdaságinformatikus, programtervező informatikus alapszakok számára Óraszám: heti 2+0, (aláírás+kollokvium, 3 kredit) 2019/20-es tanév
ÜTEMTERV Programozás-elmélet c. tárgyhoz (GEMAK233B, GEMAK233-B) BSc gazdaságinformatikus, programtervező informatikus alapszakok számára Óraszám: heti 2+0, (aláírás+kollokvium, 3 kredit) 2019/20-es tanév
ELEMI PROGRAMOZÁSI TÉTELEK
 ELEMI PROGRAMOZÁSI TÉTELEK 1. FELADATMEGOLDÁS PROGRAMOZÁSI TÉTELEKKEL 1.1 A programozási tétel fogalma A programozási tételek típusalgoritmusok, amelyek alkalmazásával garantáltan helyes megoldást adhatunk
ELEMI PROGRAMOZÁSI TÉTELEK 1. FELADATMEGOLDÁS PROGRAMOZÁSI TÉTELEKKEL 1.1 A programozási tétel fogalma A programozási tételek típusalgoritmusok, amelyek alkalmazásával garantáltan helyes megoldást adhatunk
V. Kétszemélyes játékok
 Teljes információjú, véges, zéró összegű kétszemélyes játékok V. Kétszemélyes játékok Két játékos lép felváltva adott szabályok szerint. Mindkét játékos ismeri a maga és az ellenfele összes választási
Teljes információjú, véges, zéró összegű kétszemélyes játékok V. Kétszemélyes játékok Két játékos lép felváltva adott szabályok szerint. Mindkét játékos ismeri a maga és az ellenfele összes választási
ALAPFOGALMAK 1. A reláció az program programfüggvénye, ha. Azt mondjuk, hogy az feladat szigorúbb, mint az feladat, ha
 ALAPFOGALMAK 1 Á l l a p o t t é r Legyen I egy véges halmaz és legyenek A i, i I tetszőleges véges vagy megszámlálható, nem üres halmazok Ekkor az A= A i halmazt állapottérnek, az A i halmazokat pedig
ALAPFOGALMAK 1 Á l l a p o t t é r Legyen I egy véges halmaz és legyenek A i, i I tetszőleges véges vagy megszámlálható, nem üres halmazok Ekkor az A= A i halmazt állapottérnek, az A i halmazokat pedig
3. Előadás. Megyesi László: Lineáris algebra, oldal. 3. előadás Lineáris egyenletrendszerek
 3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
A továbbiakban Y = {0, 1}, azaz minden szóhoz egy bináris sorozatot rendelünk
 1. Kódelmélet Legyen X = {x 1,..., x n } egy véges, nemüres halmaz. X-et ábécének, elemeit betűknek hívjuk. Az X elemeiből képzett v = y 1... y m sorozatokat X feletti szavaknak nevezzük; egy szó hosszán
1. Kódelmélet Legyen X = {x 1,..., x n } egy véges, nemüres halmaz. X-et ábécének, elemeit betűknek hívjuk. Az X elemeiből képzett v = y 1... y m sorozatokat X feletti szavaknak nevezzük; egy szó hosszán
26. MINIMÁLIS KÖLTSÉGŰ UTAK MINDEN CSÚCSPÁRRA
 26. MINIMÁLIS KÖLTSÉGŰ UTAK MINDEN CSÚCSPÁRRA Az előző két fejezetben tárgyalt feladat általánosításaként a gráfban található összes csúcspárra szeretnénk meghatározni a legkisebb költségű utat. A probléma
26. MINIMÁLIS KÖLTSÉGŰ UTAK MINDEN CSÚCSPÁRRA Az előző két fejezetben tárgyalt feladat általánosításaként a gráfban található összes csúcspárra szeretnénk meghatározni a legkisebb költségű utat. A probléma
Bánsághi Anna 2014 Bánsághi Anna 1 of 33
 IMPERATÍV PROGRAMOZÁS Bánsághi Anna anna.bansaghi@mamikon.net 7. ELŐADÁS - ABSZTRAKT ADATTÍPUS 2014 Bánsághi Anna 1 of 33 TEMATIKA I. ALAPFOGALMAK, TUDOMÁNYTÖRTÉNET II. IMPERATÍV PROGRAMOZÁS Imperatív
IMPERATÍV PROGRAMOZÁS Bánsághi Anna anna.bansaghi@mamikon.net 7. ELŐADÁS - ABSZTRAKT ADATTÍPUS 2014 Bánsághi Anna 1 of 33 TEMATIKA I. ALAPFOGALMAK, TUDOMÁNYTÖRTÉNET II. IMPERATÍV PROGRAMOZÁS Imperatív
Kupac adatszerkezet. A[i] bal fia A[2i] A[i] jobb fia A[2i + 1]
![Kupac adatszerkezet. A[i] bal fia A[2i] A[i] jobb fia A[2i + 1] Kupac adatszerkezet. A[i] bal fia A[2i] A[i] jobb fia A[2i + 1]](/thumbs/27/11691656.jpg) Kupac adatszerkezet A bináris kupac egy majdnem teljes bináris fa, amely minden szintjén teljesen kitöltött kivéve a legalacsonyabb szintet, ahol balról jobbra haladva egy adott csúcsig vannak elemek.
Kupac adatszerkezet A bináris kupac egy majdnem teljes bináris fa, amely minden szintjén teljesen kitöltött kivéve a legalacsonyabb szintet, ahol balról jobbra haladva egy adott csúcsig vannak elemek.
Műveletek mátrixokkal. Kalkulus. 2018/2019 ősz
 2018/2019 ősz Elérhetőségek Előadó: (safaro@math.bme.hu) Fogadóóra: hétfő 9-10 (H épület 3. emelet 310-es ajtó) A pontos tárgykövetelmények a www.math.bme.hu/~safaro/kalkulus oldalon találhatóak. A mátrix
2018/2019 ősz Elérhetőségek Előadó: (safaro@math.bme.hu) Fogadóóra: hétfő 9-10 (H épület 3. emelet 310-es ajtó) A pontos tárgykövetelmények a www.math.bme.hu/~safaro/kalkulus oldalon találhatóak. A mátrix
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 3. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2017.
Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 3. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2017.
Elérhetőségi analízis Petri hálók dinamikus tulajdonságai
 Elérhetőségi analízis Petri hálók dinamikus tulajdonságai dr. Bartha Tamás Dr. Pataricza András BME Méréstechnika és Információs Rendszerek Tanszék Petri hálók vizsgálata Az elemzés mélysége szerint: Vizsgálati
Elérhetőségi analízis Petri hálók dinamikus tulajdonságai dr. Bartha Tamás Dr. Pataricza András BME Méréstechnika és Információs Rendszerek Tanszék Petri hálók vizsgálata Az elemzés mélysége szerint: Vizsgálati
GROVER-algoritmus. Sinkovicz Péter. ELTE, MSc II dec.15.
 ELTE, MSc II. 2011.dec.15. Áttekintés Feladat Algoritmus Kvantum keresési algoritmus áttekintése Input: N = 2 n elemű tömb, Ψ 1 = 0 1 kezdőállapot, f x0 (x) orákulum függvény. Output: x 0 keresett elem
ELTE, MSc II. 2011.dec.15. Áttekintés Feladat Algoritmus Kvantum keresési algoritmus áttekintése Input: N = 2 n elemű tömb, Ψ 1 = 0 1 kezdőállapot, f x0 (x) orákulum függvény. Output: x 0 keresett elem
5. előadás. Programozás-elmélet. Programozás-elmélet 5. előadás
 Elemi programok Definíció Az S A A program elemi, ha a A : S(a) { a, a, a, a,..., a, b b a}. A definíció alapján könnyen látható, hogy egy elemi program tényleg program. Speciális elemi programok a kövekezők:
Elemi programok Definíció Az S A A program elemi, ha a A : S(a) { a, a, a, a,..., a, b b a}. A definíció alapján könnyen látható, hogy egy elemi program tényleg program. Speciális elemi programok a kövekezők:
Programozási alapismeretek 3. előadás
 Programozási alapismeretek 3. előadás Tartalom Ciklusok specifikáció+ algoritmika +kódolás Egy bevezető példa a tömbhöz A tömb Elágazás helyett tömb Konstans tömbök 2/42 Ciklusok Feladat: Határozzuk meg
Programozási alapismeretek 3. előadás Tartalom Ciklusok specifikáció+ algoritmika +kódolás Egy bevezető példa a tömbhöz A tömb Elágazás helyett tömb Konstans tömbök 2/42 Ciklusok Feladat: Határozzuk meg
Bánsághi Anna 2014 Bánsághi Anna 1 of 68
 IMPERATÍV PROGRAMOZÁS Bánsághi Anna anna.bansaghi@mamikon.net 3. ELŐADÁS - PROGRAMOZÁSI TÉTELEK 2014 Bánsághi Anna 1 of 68 TEMATIKA I. ALAPFOGALMAK, TUDOMÁNYTÖRTÉNET II. IMPERATÍV PROGRAMOZÁS Imperatív
IMPERATÍV PROGRAMOZÁS Bánsághi Anna anna.bansaghi@mamikon.net 3. ELŐADÁS - PROGRAMOZÁSI TÉTELEK 2014 Bánsághi Anna 1 of 68 TEMATIKA I. ALAPFOGALMAK, TUDOMÁNYTÖRTÉNET II. IMPERATÍV PROGRAMOZÁS Imperatív
Adatszerkezetek I. 7. előadás. (Horváth Gyula anyagai felhasználásával)
 Adatszerkezetek I. 7. előadás (Horváth Gyula anyagai felhasználásával) Bináris fa A fa (bináris fa) rekurzív adatszerkezet: BinFa:= Fa := ÜresFa Rekord(Elem,BinFa,BinFa) ÜresFa Rekord(Elem,Fák) 2/37 Bináris
Adatszerkezetek I. 7. előadás (Horváth Gyula anyagai felhasználásával) Bináris fa A fa (bináris fa) rekurzív adatszerkezet: BinFa:= Fa := ÜresFa Rekord(Elem,BinFa,BinFa) ÜresFa Rekord(Elem,Fák) 2/37 Bináris
MestInt gyakorlat visszalépéses keresés
 MestInt gyakorlat visszalépéses keresés Probléma leírása N királynő probléma Az n királynő probléma, azt a kérdést veti fel, hányféleképpen lehet lerakni n darab királynőt egy n n-es táblán úgy, hogy a
MestInt gyakorlat visszalépéses keresés Probléma leírása N királynő probléma Az n királynő probléma, azt a kérdést veti fel, hányféleképpen lehet lerakni n darab királynőt egy n n-es táblán úgy, hogy a
ködös határ (félreértés, hiba)
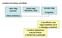 probléma formálisan specifikált: valós világ (domain) (hibás eredmény) ködös határ (félreértés, hiba) formális világ (megoldás) A szoftver fejlesztőnek meg kell értenie a felhasználó problémáját. A specifikáció
probléma formálisan specifikált: valós világ (domain) (hibás eredmény) ködös határ (félreértés, hiba) formális világ (megoldás) A szoftver fejlesztőnek meg kell értenie a felhasználó problémáját. A specifikáció
Algoritmusok helyességének bizonyítása. A Floyd-módszer
 Algoritmusok helyességének bizonyítása A Floyd-módszer Algoritmusok végrehajtása Egy A algoritmus esetében a változókat három változótípusról beszélhetünk, melyeket az X, Y és Z vektorokba csoportosítjuk
Algoritmusok helyességének bizonyítása A Floyd-módszer Algoritmusok végrehajtása Egy A algoritmus esetében a változókat három változótípusról beszélhetünk, melyeket az X, Y és Z vektorokba csoportosítjuk
tétel: különböző típusú adatokat csoportosít, ezeket egyetlen adatként kezeli, de hozzáférhetünk az elemeihez is
 A tétel (record) tétel: különböző típusú adatokat csoportosít, ezeket egyetlen adatként kezeli, de hozzáférhetünk az elemeihez is A tétel elemei mezők. Például tétel: személy elemei: név, lakcím, születési
A tétel (record) tétel: különböző típusú adatokat csoportosít, ezeket egyetlen adatként kezeli, de hozzáférhetünk az elemeihez is A tétel elemei mezők. Például tétel: személy elemei: név, lakcím, születési
Formális nyelvek és automaták vizsgához statisztikailag igazolt várható vizsgakérdések
 1. Feladat Az első feladatban szereplő - kérdések 1 Minden környezet független nyelv felismerhető veremautomatával. Minden környezet független nyelv felismerhető 1 veremmel. Minden 3. típusú nyelv felismerhető
1. Feladat Az első feladatban szereplő - kérdések 1 Minden környezet független nyelv felismerhető veremautomatával. Minden környezet független nyelv felismerhető 1 veremmel. Minden 3. típusú nyelv felismerhető
Hatékonyság 1. előadás
 Hatékonyság 1. előadás Mi a hatékonyság Bevezetés A hatékonyság helye a programkészítés folyamatában: csak HELYES programra Erőforrásigény: a felhasználó és a fejlesztő szempontjából A hatékonyság mérése
Hatékonyság 1. előadás Mi a hatékonyság Bevezetés A hatékonyság helye a programkészítés folyamatában: csak HELYES programra Erőforrásigény: a felhasználó és a fejlesztő szempontjából A hatékonyság mérése
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 4. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2017.
Diszkrét matematika 2.C szakirány 2017. tavasz 1. Diszkrét matematika 2.C szakirány 4. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2017.
ÖSSZEFOGLALÁS a Bsc záróvizsga mesterséges intelligenciáról szóló témaköréhez
 ÖSSZEFOGLALÁS a Bsc záróvizsga mesterséges intelligenciáról szóló témaköréhez Az MI az informatikának az a területe, amelyik az intelligens gondolkodás számítógépes reprodukálása szempontjából hasznos
ÖSSZEFOGLALÁS a Bsc záróvizsga mesterséges intelligenciáról szóló témaköréhez Az MI az informatikának az a területe, amelyik az intelligens gondolkodás számítógépes reprodukálása szempontjából hasznos
Diszkrét matematika 2.C szakirány
 Diszkrét matematika 2.C szakirány 2015. ősz 1. Diszkrét matematika 2.C szakirány 3. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2015.
Diszkrét matematika 2.C szakirány 2015. ősz 1. Diszkrét matematika 2.C szakirány 3. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék 2015.
Kiegészítő részelőadás 1. Az algoritmusok hatékonyságának mérése
 Kiegészítő részelőadás 1. Az algoritmusok hatékonyságának mérése Dr. Kallós Gábor 2014 2015 1 Az Ordó jelölés Azt mondjuk, hogy az f(n) függvény eleme az Ordó(g(n)) halmaznak, ha van olyan c konstans (c
Kiegészítő részelőadás 1. Az algoritmusok hatékonyságának mérése Dr. Kallós Gábor 2014 2015 1 Az Ordó jelölés Azt mondjuk, hogy az f(n) függvény eleme az Ordó(g(n)) halmaznak, ha van olyan c konstans (c
Feladat. Ternáris fa. Típusspecikáció. Reprezentáció. Absztrakt implementáció. Érdi Gerg EAF II. 4/3.
 Feladat djuk meg, hogy egy ternáris fa INORDER bejárás szerint sorozatba f zött értékei között mekkora a leghosszabb csupa pozitív számot tartalmazó részsorozat. Ternáris fa Típusspecikáció z alaphalmaz
Feladat djuk meg, hogy egy ternáris fa INORDER bejárás szerint sorozatba f zött értékei között mekkora a leghosszabb csupa pozitív számot tartalmazó részsorozat. Ternáris fa Típusspecikáció z alaphalmaz
2018, Diszkrét matematika
 Diszkrét matematika 12. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, ománia 2018, őszi félév Miről volt szó az elmúlt előadáson? a diszkrét logaritmus,
Diszkrét matematika 12. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, ománia 2018, őszi félév Miről volt szó az elmúlt előadáson? a diszkrét logaritmus,
21. Adatszerkezetek Az adattípus absztrakciós szintjei Absztrakt adattípus (ADT) Absztrakt adatszerkezet (ADS) Egyszerű adattípusok Tömbök
 2. Adatszerkezetek Az adattípus absztrakciós szintjei http://people.inf.elte.hu/fekete/docs_/adt_ads.pdf Absztrakt adattípus (ADT) Az adattípust úgy specifikáljuk, hogy szerkezetére, reprezentálására,
2. Adatszerkezetek Az adattípus absztrakciós szintjei http://people.inf.elte.hu/fekete/docs_/adt_ads.pdf Absztrakt adattípus (ADT) Az adattípust úgy specifikáljuk, hogy szerkezetére, reprezentálására,
Fraktálok. Kontrakciók Affin leképezések. Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék. TARTALOMJEGYZÉK Kontrakciók Affin transzformációk
 Fraktálok Kontrakciók Affin leképezések Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék TARTALOMJEGYZÉK 1 of 71 A Lipschitz tulajdonság ÁTMÉRŐ, PONT ÉS HALMAZ TÁVOLSÁGA Definíció Az (S, ρ) metrikus tér
Fraktálok Kontrakciók Affin leképezések Czirbusz Sándor ELTE IK, Komputeralgebra Tanszék TARTALOMJEGYZÉK 1 of 71 A Lipschitz tulajdonság ÁTMÉRŐ, PONT ÉS HALMAZ TÁVOLSÁGA Definíció Az (S, ρ) metrikus tér
Diszkrét matematika 2. estis képzés
 Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 7. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 7. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Tuesday, March 6, 12. Hasító táblázatok
 Hasító táblázatok Halmaz adattípus U (kulcsuniverzum) K (aktuális kulcsok) Függvény adattípus U (univerzum) ÉT (értelmezési tartomány) ÉK (érték készlet) Milyen az univerzum? Közvetlen címzésű táblázatok
Hasító táblázatok Halmaz adattípus U (kulcsuniverzum) K (aktuális kulcsok) Függvény adattípus U (univerzum) ÉT (értelmezési tartomány) ÉK (érték készlet) Milyen az univerzum? Közvetlen címzésű táblázatok
Kétszemélyes játékok Gregorics Tibor Mesterséges intelligencia
 Kétszemélyes játékok Kétszemélyes, teljes információjú, véges, determinisztikus,zéró összegű játékok Két játékos lép felváltva adott szabályok szerint, amíg a játszma véget nem ér. Mindkét játékos ismeri
Kétszemélyes játékok Kétszemélyes, teljes információjú, véges, determinisztikus,zéró összegű játékok Két játékos lép felváltva adott szabályok szerint, amíg a játszma véget nem ér. Mindkét játékos ismeri
Visszalépéses felsoroló
 Visszalépéses felsoroló Gregorics Tibor gt@inf.elte.hu ELTE IK Absztrakt. A visszalépéses keresésnek több változata is ismert. Ebben a cikkben azon feladatokat megoldó visszalépéses algoritmusokra fókuszálunk,
Visszalépéses felsoroló Gregorics Tibor gt@inf.elte.hu ELTE IK Absztrakt. A visszalépéses keresésnek több változata is ismert. Ebben a cikkben azon feladatokat megoldó visszalépéses algoritmusokra fókuszálunk,
S0-02 Típusmodellek (Programozás elmélet)
 S0-02 Típusmodellek (Programozás elmélet) Tartalom 1. Absztrakt adattípus 2. Adattípus specifikációja 3. Adattípus osztály 4. Paraméterátadás 5. Reprezentációs függvény 6. Öröklődés és polimorfizmus 7.
S0-02 Típusmodellek (Programozás elmélet) Tartalom 1. Absztrakt adattípus 2. Adattípus specifikációja 3. Adattípus osztály 4. Paraméterátadás 5. Reprezentációs függvény 6. Öröklődés és polimorfizmus 7.
Véges automaták, reguláris nyelvek
 Véges automaták, reguláris nyelvek Kiegészítő anyag az lgoritmuselmélet tárgyhoz (a Rónyai Ivanyos Szabó: lgoritmusok könyv mellé) Friedl Katalin BME SZIT friedl@cs.bme.hu 27. augusztus 3. véges automata
Véges automaták, reguláris nyelvek Kiegészítő anyag az lgoritmuselmélet tárgyhoz (a Rónyai Ivanyos Szabó: lgoritmusok könyv mellé) Friedl Katalin BME SZIT friedl@cs.bme.hu 27. augusztus 3. véges automata
Programozás I. Matematikai lehetőségek Műveletek tömbökkel Egyszerű programozási tételek & gyakorlás V 1.0 OE-NIK,
 Programozás I. Matematikai lehetőségek Műveletek tömbökkel Egyszerű programozási tételek & gyakorlás OE-NIK, 2013 1 Hallgatói Tájékoztató A jelen bemutatóban található adatok, tudnivalók és információk
Programozás I. Matematikai lehetőségek Műveletek tömbökkel Egyszerű programozási tételek & gyakorlás OE-NIK, 2013 1 Hallgatói Tájékoztató A jelen bemutatóban található adatok, tudnivalók és információk
Adatszerkezetek II. 1. előadás
 Adatszerkezetek II. 1. előadás Gráfok A gráf fogalma: Gráf(P,E): P pontok (csúcsok) és E P P élek halmaza Fogalmak: Irányított gráf : (p 1,p 2 ) E-ből nem következik, hogy (p 2,p 1 ) E Irányítatlan gráf
Adatszerkezetek II. 1. előadás Gráfok A gráf fogalma: Gráf(P,E): P pontok (csúcsok) és E P P élek halmaza Fogalmak: Irányított gráf : (p 1,p 2 ) E-ből nem következik, hogy (p 2,p 1 ) E Irányítatlan gráf
Evolúciós algoritmusok
 Evolúciós algoritmusok Evolúció, mint kereső rendszer A problémára adható néhány lehetséges választ, azaz a problématér több egyedét tároljuk egyszerre. Ez a populáció. Kezdetben egy többnyire véletlen
Evolúciós algoritmusok Evolúció, mint kereső rendszer A problémára adható néhány lehetséges választ, azaz a problématér több egyedét tároljuk egyszerre. Ez a populáció. Kezdetben egy többnyire véletlen
Java II. I A Java programozási nyelv alapelemei
 Java II. I A Java programozási nyelv alapelemei Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2008. 02. 19. Java II.: Alapelemek JAVA2 / 1 A Java formalizmusa A C, illetve az annak
Java II. I A Java programozási nyelv alapelemei Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2008. 02. 19. Java II.: Alapelemek JAVA2 / 1 A Java formalizmusa A C, illetve az annak
Algoritmuselmélet. Bonyolultságelmélet. Katona Gyula Y.
 Algoritmuselmélet Bonyolultságelmélet Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 12. előadás Katona Gyula Y. (BME SZIT) Algoritmuselmélet
Algoritmuselmélet Bonyolultságelmélet Katona Gyula Y. Számítástudományi és Információelméleti Tanszék Budapesti Műszaki és Gazdaságtudományi Egyetem 12. előadás Katona Gyula Y. (BME SZIT) Algoritmuselmélet
Adatszerkezetek. Nevezetes algoritmusok (Keresések, rendezések)
 Adatszerkezetek Nevezetes algoritmusok (Keresések, rendezések) Keresések A probléma általános megfogalmazása: Adott egy N elemű sorozat, keressük meg azt az elemet (határozzuk meg a helyét a sorozatban),
Adatszerkezetek Nevezetes algoritmusok (Keresések, rendezések) Keresések A probléma általános megfogalmazása: Adott egy N elemű sorozat, keressük meg azt az elemet (határozzuk meg a helyét a sorozatban),
1. ábra. Egy rekurzív preorder bejárás. Egy másik rekurzív preorder bejárás
 Preorder ejárás Fa bejárásán olyan algoritmust értünk, amelynek bemenete egy F fa és egy M művelet, és az algoritmus adott sorrendben pontosan egyszer végrehajtja az M műveletet a fa pontjaiban lévő adatokra.
Preorder ejárás Fa bejárásán olyan algoritmust értünk, amelynek bemenete egy F fa és egy M művelet, és az algoritmus adott sorrendben pontosan egyszer végrehajtja az M műveletet a fa pontjaiban lévő adatokra.
Algoritmizálás, adatmodellezés tanítása 7. előadás
 Algoritmizálás, adatmodellezés tanítása 7. előadás Oszd meg és uralkodj! Több részfeladatra bontás, amelyek hasonlóan oldhatók meg, lépései: a triviális eset (amikor nincs rekurzív hívás) felosztás (megadjuk
Algoritmizálás, adatmodellezés tanítása 7. előadás Oszd meg és uralkodj! Több részfeladatra bontás, amelyek hasonlóan oldhatók meg, lépései: a triviális eset (amikor nincs rekurzív hívás) felosztás (megadjuk
Kupac adatszerkezet. 1. ábra.
 Kupac adatszerkezet A bináris kupac egy majdnem teljes bináris fa, amely minden szintjén teljesen kitöltött kivéve a legalacsonyabb szintet, ahol balról jobbra haladva egy adott csúcsig vannak elemek.
Kupac adatszerkezet A bináris kupac egy majdnem teljes bináris fa, amely minden szintjén teljesen kitöltött kivéve a legalacsonyabb szintet, ahol balról jobbra haladva egy adott csúcsig vannak elemek.
Mátrixok 2017 Mátrixok
 2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
2017 számtáblázatok" : számok rendezett halmaza, melyben a számok helye két paraméterrel van meghatározva. Például lineáris egyenletrendszer együtthatómátrixa 2 x 1 + 4 x 2 = 8 1 x 1 + 3 x 2 = 1 ( 2 4
Logika es sz am ıt aselm elet I. r esz Logika 1/36
 1/36 Logika és számításelmélet I. rész Logika 2/36 Elérhetőségek Tejfel Máté Déli épület, 2.606 matej@inf.elte.hu http://matej.web.elte.hu Tankönyv 3/36 Tartalom 4/36 Bevezető fogalmak Ítéletlogika Ítéletlogika
1/36 Logika és számításelmélet I. rész Logika 2/36 Elérhetőségek Tejfel Máté Déli épület, 2.606 matej@inf.elte.hu http://matej.web.elte.hu Tankönyv 3/36 Tartalom 4/36 Bevezető fogalmak Ítéletlogika Ítéletlogika
Mesterséges intelligencia
 Mesterséges intelligencia Problémák és az útkeresések kapcsolata Az MI problémái, hogy a megoldandó feladatai nehezek, hatalmas a lehetséges válaszok tere (problématér), a helyes válaszok megtalálása intuíciót,
Mesterséges intelligencia Problémák és az útkeresések kapcsolata Az MI problémái, hogy a megoldandó feladatai nehezek, hatalmas a lehetséges válaszok tere (problématér), a helyes válaszok megtalálása intuíciót,
Multihalmaz, intervallumhalmaz
 Multihalmaz, intervallumhalmaz Halmaz féleségek 1. Halmaz Gyümölcsök: {alma,körte,szilva,barack} 2. Multihalmaz Állatok: {(macska,4),(rigó,2),(galamb,3)} 3. Intervallumhalmaz diszjunkt Óráim: {[8-10],[13-14],[16-20)}
Multihalmaz, intervallumhalmaz Halmaz féleségek 1. Halmaz Gyümölcsök: {alma,körte,szilva,barack} 2. Multihalmaz Állatok: {(macska,4),(rigó,2),(galamb,3)} 3. Intervallumhalmaz diszjunkt Óráim: {[8-10],[13-14],[16-20)}
Adatszerkezetek és algoritmusok
 Adatszerkezetek és algoritmusok 1 Bevezetés Adatszerkezet egyszerű vagy összetett alapadatok rendszerének matematikai, logikai modellje elég jó ahhoz, hogy tükrözze a valós kapcsolatokat elég egyszerű
Adatszerkezetek és algoritmusok 1 Bevezetés Adatszerkezet egyszerű vagy összetett alapadatok rendszerének matematikai, logikai modellje elég jó ahhoz, hogy tükrözze a valós kapcsolatokat elég egyszerű
Diszkrét matematika 2.
 Diszkrét matematika 2. Mérai László előadása alapján Készítette: Nagy Krisztián 1. előadás Gráfok halmaza, gráf, ahol a csúcsok halmaza, az élek illesztkedés reláció: illesztkedik az élre, ha ( -él illesztkedik
Diszkrét matematika 2. Mérai László előadása alapján Készítette: Nagy Krisztián 1. előadás Gráfok halmaza, gráf, ahol a csúcsok halmaza, az élek illesztkedés reláció: illesztkedik az élre, ha ( -él illesztkedik
Kronecker-modulusok kombinatorikája és alkalmazások
 Kronecker-modulusok kombinatorikája és alkalmazások BBTE, Magyar Matematika es Informatika Intézet Tegezek Meghatározás Egy Q tegez egy irányított multigráf (két csomópont között több irányított él is
Kronecker-modulusok kombinatorikája és alkalmazások BBTE, Magyar Matematika es Informatika Intézet Tegezek Meghatározás Egy Q tegez egy irányított multigráf (két csomópont között több irányított él is
Diszkrét matematika 2. estis képzés
 Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 4-6. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 4-6. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Algoritmizálás, adatmodellezés 1. előadás
 Algoritmizálás, adatmodellezés 1. előadás Algoritmus-leíró eszközök Folyamatábra Irányított gráf, amely csomópontokból és őket összekötő élekből áll, egyetlen induló és befejező éle van, az induló élből
Algoritmizálás, adatmodellezés 1. előadás Algoritmus-leíró eszközök Folyamatábra Irányított gráf, amely csomópontokból és őket összekötő élekből áll, egyetlen induló és befejező éle van, az induló élből
Rendezések. A rendezési probléma: Bemenet: Kimenet: n számot tartalmazó (a 1,a 2,,a n ) sorozat
 9. Előadás Rendezések A rendezési probléma: Bemenet: n számot tartalmazó (a 1,a 2,,a n ) sorozat Kimenet: a bemenő sorozat olyan (a 1, a 2,,a n ) permutációja, hogy a 1 a 2 a n 2 Rendezések Általánosabban:
9. Előadás Rendezések A rendezési probléma: Bemenet: n számot tartalmazó (a 1,a 2,,a n ) sorozat Kimenet: a bemenő sorozat olyan (a 1, a 2,,a n ) permutációja, hogy a 1 a 2 a n 2 Rendezések Általánosabban:
Matematika pótvizsga témakörök 9. V
 Matematika pótvizsga témakörök 9. V 1. Halmazok, műveletek halmazokkal halmaz, halmaz eleme halmazok egyenlősége véges, végtelen halmaz halmazok jelölése, megadása természetes számok egész számok racionális
Matematika pótvizsga témakörök 9. V 1. Halmazok, műveletek halmazokkal halmaz, halmaz eleme halmazok egyenlősége véges, végtelen halmaz halmazok jelölése, megadása természetes számok egész számok racionális
Visszalépéses keresés
 Visszalépéses keresés Backtracking előadás http://nik.uni-obuda.hu/prog2 Szénási Sándor szenasi.sandor@nik.uni-obuda.hu Óbudai Egyetem,Neumann János Informatikai Kar Alapvető működése Továbbfejlesztési
Visszalépéses keresés Backtracking előadás http://nik.uni-obuda.hu/prog2 Szénási Sándor szenasi.sandor@nik.uni-obuda.hu Óbudai Egyetem,Neumann János Informatikai Kar Alapvető működése Továbbfejlesztési
38. A gráfalgoritmusok alkalmazása
 38. A gráfalgoritmusok alkalmazása Állapotok és átmenetek A gráf adattípus nagyon sokféle feladat megoldásánál alkalmazható. Rejtvények, játékok, közlekedési és szállítási problémák, stratégiai feladatok
38. A gráfalgoritmusok alkalmazása Állapotok és átmenetek A gráf adattípus nagyon sokféle feladat megoldásánál alkalmazható. Rejtvények, játékok, közlekedési és szállítási problémák, stratégiai feladatok
Algoritmizálás és adatmodellezés tanítása 1. előadás
 Algoritmizálás és adatmodellezés tanítása 1. előadás Algoritmus-leíró eszközök Folyamatábra Irányított gráf, amely csomópontokból és őket összekötő élekből áll, egyetlen induló és befejező éle van, az
Algoritmizálás és adatmodellezés tanítása 1. előadás Algoritmus-leíró eszközök Folyamatábra Irányított gráf, amely csomópontokból és őket összekötő élekből áll, egyetlen induló és befejező éle van, az
INFORMATIKAI ALAPISMERETEK
 Informatikai alapismeretek középszint 1021 ÉRETTSÉGI VIZSGA 2011. május 13. INFORMATIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐFORRÁS MINISZTÉRIUM
Informatikai alapismeretek középszint 1021 ÉRETTSÉGI VIZSGA 2011. május 13. INFORMATIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ NEMZETI ERŐFORRÁS MINISZTÉRIUM
Matematika alapjai; Feladatok
 Matematika alapjai; Feladatok 1. Hét 1. Tekintsük a,, \ műveleteket. Melyek lesznek a.) kommutativok b.) asszociativak c.) disztributívak-e a, műveletek? Melyik melyikre? 2. Fejezzük ki a műveletet a \
Matematika alapjai; Feladatok 1. Hét 1. Tekintsük a,, \ műveleteket. Melyek lesznek a.) kommutativok b.) asszociativak c.) disztributívak-e a, műveletek? Melyik melyikre? 2. Fejezzük ki a műveletet a \
Diszkrét matematika 2. estis képzés
 Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Diszkrét matematika 2. estis képzés 2018. tavasz 1. Diszkrét matematika 2. estis képzés 9. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Komputeralgebra Tanszék
Gráfkeresések A globális munkaterületén a startcsúcsból kiinduló már feltárt utak találhatók (ez az ún. kereső gráf), külön megjelölve az utak azon
 ÖSSZEFOGLALÁS Az MI az intelligens gondolkodás számítógépes reprodukálása szempontjából hasznos elveket, módszereket, technikákat kutatja, fejleszti, rendszerezi. Miről ismerhető fel az MI? Megoldandó
ÖSSZEFOGLALÁS Az MI az intelligens gondolkodás számítógépes reprodukálása szempontjából hasznos elveket, módszereket, technikákat kutatja, fejleszti, rendszerezi. Miről ismerhető fel az MI? Megoldandó
Algoritmusok bonyolultsága
 Algoritmusok bonyolultsága 11. előadás http://www.ms.sapientia.ro/~kasa/komplex.htm () 1 / 1 NP-telesség Egy L nyelv NP-teles, ha L NP és minden L NP-re L L. Egy Π döntési feladat NP-teles, ha Π NP és
Algoritmusok bonyolultsága 11. előadás http://www.ms.sapientia.ro/~kasa/komplex.htm () 1 / 1 NP-telesség Egy L nyelv NP-teles, ha L NP és minden L NP-re L L. Egy Π döntési feladat NP-teles, ha Π NP és
SZAKDOLGOZAT. Szatmári László
 SZAKDOLGOZAT Szatmári László Debrecen 2010 Debreceni Egyetem Informatika Kar Kereső algoritmusok hatékonyságának összehasonlítása a Hanoi problémán keresztül Témavezető: Dr. Várterész Magda egyetemi docens
SZAKDOLGOZAT Szatmári László Debrecen 2010 Debreceni Egyetem Informatika Kar Kereső algoritmusok hatékonyságának összehasonlítása a Hanoi problémán keresztül Témavezető: Dr. Várterész Magda egyetemi docens
Objektumelvű programozás
 Objektum, osztály Objektumelvű programozás Az elemzés együttműködő objektumok rendszereként fogalmazza meg a feladatot. Objektum-központú elemzés A tervezés a feladat tárgyköreit egy-egy objektum felelősségévé
Objektum, osztály Objektumelvű programozás Az elemzés együttműködő objektumok rendszereként fogalmazza meg a feladatot. Objektum-központú elemzés A tervezés a feladat tárgyköreit egy-egy objektum felelősségévé
INFORMATIKA tétel 2019
 INFORMATIKA tétel 2019 ELIGAZÍTÁS: 1 pont hivatalból; Az 1-4 feladatokban (a pszeudokód programrészletekben): (1) a kiír \n utasítás újsorba ugratja a képernyőn a kurzort; (2) a / operátor osztási hányadost
INFORMATIKA tétel 2019 ELIGAZÍTÁS: 1 pont hivatalból; Az 1-4 feladatokban (a pszeudokód programrészletekben): (1) a kiír \n utasítás újsorba ugratja a képernyőn a kurzort; (2) a / operátor osztási hányadost
Alkalmazott modul: Programozás
 Eötvös Loránd Tudományegyetem Informatikai Kar Alkalmazott modul: Programozás Feladatgyűjtemény Összeállította: Giachetta Roberto groberto@inf.elte.hu http://people.inf.elte.hu/groberto Frissítve: 2015.
Eötvös Loránd Tudományegyetem Informatikai Kar Alkalmazott modul: Programozás Feladatgyűjtemény Összeállította: Giachetta Roberto groberto@inf.elte.hu http://people.inf.elte.hu/groberto Frissítve: 2015.
HORVÁTH ZSÓFIA 1. Beadandó feladat (HOZSAAI.ELTE) ápr 7. 8-as csoport
 10-es Keressünk egy egész számokat tartalmazó négyzetes mátrixban olyan oszlopot, ahol a főátló alatti elemek mind nullák! Megolda si terv: Specifika cio : A = (mat: Z n m,ind: N, l: L) Ef =(mat = mat`)
10-es Keressünk egy egész számokat tartalmazó négyzetes mátrixban olyan oszlopot, ahol a főátló alatti elemek mind nullák! Megolda si terv: Specifika cio : A = (mat: Z n m,ind: N, l: L) Ef =(mat = mat`)
