2. Az anyagok szerkezete
|
|
|
- Teréz Biróné
- 9 évvel ezelőtt
- Látták:
Átírás
1 2. Az anyagok szerkezete 2.1. Anyagszerkezeti alapismeretek Az előző fejezetben számos oldalról megvizsgáltuk az anyag mibenlétét, és a jellemzésükre szolgáló szempontok néhány típusát. Külön fejezetben kell tárgyalni azt a két fontos szempontrendszert, amely az anyagok sajátosságait a műszaki, a fizikai és a kémiai ismeretek együttes alkalmazásával írja le: ez a két nagy fogalomkör az anyagszerkezet és a mechanikai tulajdonságok. Az atomokból felépülő anyag szerkezetének milyensége ugyanolyan jelentőségű körülmény, mint az, hogy a szóban forgó szerkezetet milyen kémiai elemek alkotják. Az anyagszerkezet amelyet a továbbiakban mikroszerkezetnek fogunk nevezni abból az egyszerű megfontolásból, hogy az e fogalomkörben vizsgált objektumok jellemzően mikrométer körüli (a nanométertől a milliméterig) nagyságrendű sík- vagy térbeli objektumok a legáltalánosabb értelemben voltaképpen az atomok rendezettségének mértékével írható le. Ezt a rendezettséget döntően befolyásolja a hőmérséklet és a nyomás, bár ez utóbbi állapottényezőnek a gyakorlatban ritkán van érzékelhető szerepe. A 4. táblázat azt szemlélteti, hogy a hőmérséklet, valamint az atomok rendezettségének kiterjedtsége függvényében miként különíthetők el a gáz, a folyadék és a szilárd fázisok (lásd a 2. ábrát), és azoknak milyen főbb csoportjait különböztetjük meg. A szilárd anyagokat a mikroszerkezetük (10. ábr és az ezzel szorosan összefüggő fizikai és kémiai tulajdonságaik alapján 3 nagy osztályba soroljuk: fémek és ötvözetek, szerves polimerek kerámiák. Rendezettségi hatótávolság, r 0 = atomsugár Hőmérséklet Gáz Folyadék Szilárd r 0 > 100 r 0 Tökéletes gáz Tökéletes rendezetlenség Reális gáz Folyadék Amorf szilárdtest Rövid hatótávú rend Üveg Polimer 4. táblázat Reális kristály Hosszú hatótávú rend Fém 8 Tökéletes kristály Tökéletes rend 10. ábra Fémek (fent), polimerek (középen) és kerámiák (lent) mikroszerkezete töretfelületi képeken Szobahőmérsékleten a fémek nagy többsége szilárd halmazállapotú atomos szilárdtest. A legelterjedtebben alkalmazott fémek a vas, az alumínium és a réz. A fémötvözetek két vagy több fém atomjainak egyenletes eloszlású kombinációi (példa erre a réz és a horgany ötvözete, a sárgaréz), olykor pedig fémes és nemfémes komponensek alkotják az ötvözetet (a vas és a szén ötvözete az acél és az öntöttvas). A fémek általában jó hő- és villamos vezetők, a látható fény hullámhossztartományában nem átlátszók. A mechanikai tulajdonságaik, pl. a keménység vagy az alakíthatóság széles tartományban változnak, de a színfémek általában jóval lágyabbak, mint az ötvözeteik. 8. oldal
2 A szerves polimerek általában szénatomok hosszú molekulaláncaiból felépülő anyagok, amelyekben a szénlánchoz atomok (H, Cl) vagy atomcsoportok (CH 3 ) kapcsolódnak, és további elemek (S, N, Si stb.) is beépülhetnek a molekulaláncokba, amelyeket egymáshoz rendszerint gyenge kötések kapcsolnak. Majdnem mindegyik szerves polimer villamosan páratlanul jó szigetelő, elterjedésüket a kis sűrűség, a kiváló formázhatóság és a sokoldalú alkalmazhatóság magyarázza. A kerámiák szervetlen vegyületek, amelyeket valamely fém (Mg, Al, Si, Fe stb.) alkot egy nemfémes anyaggal leggyakrabban az oxigénnel. Eredeileg a kerámia szó csak az oxidokra vonatkozott (Al 2 O 3, SiO 2 ), de számos karbid, nitrid, borid stb. került be az iparilag alkalmazott kerámiák közé. A kerámiák alapvető jellemzője a nagy mechanikai szilárdság és a hőállóság. Legtöbbjük kiváló villamos szigetelő, ugyanakkor közülük kerülnek ki a legjobb hővezetők is (pl. gyémánt, grafit). Számos kerámia, pl. az üvegek amorf szerkezetű. A kompozitok (más néven társított anyagok) az anyagok imént ismertetett három nagy osztályának keverékei, amint a 11. ábra szemlélteti. A kompozitokat alkotó mátrix is és az erősítő anyag is lehet fém, kerámia, ill. polimer A szilárd anyagok szerkezete A hőmérséklet kellő mértékű csökkenésekor az anyagok megszilárdulnak. Az anyagot felépítő atomok, ill. molekulaláncok rendezettségének mértékétől függően a szilárd fázisú anyag lehet: kristályos (a fémek és számos kerámia, ill. a kristályosodó polimerek, pl. a PE) vagy amorf (a kerámiák közt az ásványi üvegek, az üvegesedő polimerek között, pl. a gumi). A kristályos megszilárdulásnál az atomok egy szabályos térrács a kristályrács rácspontjaira illeszkednek. A kristályos anyag minden atomja rácspontban ül, és minden rácspontban van atom, s végül a kristály alakja szabályos. Ha e feltételek egyike nem teljesül, a kristály nem tökéletes, pontosabban fogalmazva: nem hibamentes. A térbeli kristályrácsot képzeletben elemi darabokra lehet bontani, amelyek közül a legkisebbet elemi cellának nevezzük. A szorosan egymáshoz illeszkedő elemi cellák tehát a kristályos anyag geometriai egységei. Amennyiben a kristályrács a vizsgált anyag minden pontján azonosan irányított elemi cellákból épül fel, egykristályról beszélünk: a 12.a. ábra egy egyszerű síkrácsot ábrázol, amelynek elemi cellái a rácsot alkotó négyzetek. Ám ha az anyag belsejében elhatárolhatók olyan tartományok, amelyek irányítottsága (orientációj eltérő, polikristályról beszélünk (12.b. ábr. A szabálytalan alakú kristályt általában szemcsének vagy krisztallitnak nevezzük, és a szemcsehatár választja el őket egymástól: a 13. ábra tiszta vas metszeti felületén mutat néhány szemcsét és a köztük lévő szemcsehatárokat (szövetszerkezeti képen). 11. ábra Az anyagok 3 nagy osztálya és néhány példa a belőlük felépülő kompozitokra A polimerek szerkezetét és tulajdonságait az Anyagismeret c. tantárgy második fele Czvikovszky professzor előadásában kiemelten és külön tárgyalja, ezért e jegyzetben a polimerekkel nem foglalkozunk. 12. ábra Egykristály ( és polikristály ( síkmetszetének vázlata 9. oldal
3 13. ábra Polikristályos vas optikai mikroszkópos képe: a sötét vonalak a szemcsehatárok A polikristályos anyag lehet egyfázisú vagy többfázisú. A 13. ábrán bemutatott polikristályos vas nem tartalmaz más fázisokat (ha eltekintünk az apró foltoktól, amelyek nemfémes zárványok), ugyanakkor a 14. ábrán látható szövetképen többféle (színben, méretben, alakban eltérő) fázis is megfigyelhető (a fázis fogalmát lásd az szakaszban). c) d) 15. ábra Kiválások vázlata: a fázishatár lehet koherens (a és, szemikoherens (c), inkoherens (d) 14. ábra Duplex acél optikai mikroszkópos képe A fázishatár mint felület mentén tehát egymástól gyakran jelentős mértékben eltérő tulajdonságú anyagok érintkeznek. Attól függően, hogy e határfelület mentén a kristályrácsok mennyire illeszkednek, 3 féle fázishatártípust különböztetjük meg ( ábr: koherens (összefüggő), inkoherens (nem összefüggő), szemikoherens (félig összefüggő). A fázishatároknak, illetve azok koherenciájának a szerepe a fémes anyagok nem kis részénél nagyon jelentős. Azokról az anyagokról van szó, amelyekben az eredeti alapanyagtól (a mátrixtól) eltérő fázisok, ún. kiválások jönnek létre 16. ábr. Tudatosan gyártanak így, pl. alumíniumötvözeteket, turbinalapátokat stb.), ill. a hegesztés közben is képződhetnek kiválások és okozhatnak nemkívánatos hatást számos anyagban. A kiválások szerepére külön is kitér a 3.4. fejezet. Koherens kiválások (Guinier Preston-zónák) (Fotó: Toyohiko J. Konno, Tohoku University) Inkoherens Fe-kiválások (Fe,Mg)2SiO4 olivinban (Fotó: Hugues Leroux, Univ. Sci. et Tech. Lille) 16. ábra Kiválások transzmissziós elektronmikroszkópi (TEM-) képe. A képeken látható a léptékvonal. 10. oldal
4 A polimerek és a kerámiák jelentős részénél, ill. a rendkívül gyorsan hűtött fémolvadékoknál (fémüvegek) figyelhető meg az a jelenség, hogy az atomok nem alkotnak kristályrácsot: ezek az amorf anyagok, amelyek szerkezetének síkbeli vázlatát a 17. ábra mutatja. 17. ábra Az amorf anyagok mikroszerkezetének vázlata 2.3. A kristályos anyagok mikroszerkezete Kristályrendszerek A kristályos anyagok atomjai tehát térbeli kristályrácsot alkotnak: ennek legkisebb egysége az elemi cella, amelyet vázlatosan a 18. ábra szemléltet. Az elemi cella az a legkisebb térelem, amely a kristályrács 3, egymástól független irányában folyamatosan ismétlődik. A szóban forgó irányok és a térelemek távolsága adja a 3 transzlációs egységvektort, és ezek hossza (a, b, c), valamint az egymással bezárt szögük (α, β, γ) egyértelműen meghatározza a kristályrendszert. A természetben előforduló összes kristályos anyag besorolható 7 kristályrendszerbe, melyeknek összesen 14 alaptípusa létezik a szerint, hogy az elemi cella csúcsain kívül hol található még atom: a cella, a lapok vagy az alaplapok középpontjában. Mindezeket August Bravais határozta meg 1849-ben. A kristályrendszerek és a Bravais-féle térrácsok a következők: köbös vagy kockarács (Al, Cu, Fe, W), tetragonális (Cl, α-sn, TiO 2, martenzit), ortorombos (α-s, Ga, Fe 3 C, α-u), hexagonális (Be, Mg, Ti, Zn, grafit), romboéderes vagy trigonális (Sb, Bi, Hg), monoklin vagy egyhajlású (F, α-s, Se), triklin vagy háromhajlású (K 2 CrO 7 ). Az egyes kristályrendszerek elemi celláit és az azt kifeszítő transzlációs egységvektorok jellemzőit a 19. ábra szemlélteti. 18. ábra A térrács és az elemi cella 19. ábra A térrács és az elemi cella. A színjelölések jelentése: kék = primitív, zöld = térközepes, piros = lapközepes, lila = alaplapközepes 11. oldal
5 PK TKK LKK A térrácsban tehát a gömb alakúnak tekintett atomok olyan elrendeződést vesznek fel, amely számukra a legszorosabb illeszkedést biztosítja. Minden rácstípusban megtalálhatók azok az irányok, ill. síkok, amelyek mentén, ill. amelyeken az atomok érintkeznek a legközelebbi szomszédaikkal. Ezek az ún. legsűrűbb síkok és legsűrűbb irányok kitüntetett szerepet játszanak az anyagok képlékeny alakváltozásának folyamatában. A primitív köbös rácsban a legsűrűbb irányok az elemi cellának amely egy kocka az élei, a legsűrűbb síkok pedig a kocka lapjai. Ugyanilyen módon belátható, hogy a TKK rácsban a legsűrűbb irányok a kocka térátlói, az LKK rácsban pedig a kocka lapátlói. Ez utóbbi kristályrács 3 féle elrendezésű legsűrűbb síkjának A B C A B C típusú rétegződését mutatja a 21.a. ábra vázlata. A grafit egymáson könnyen elcsúszni képes legsűrűbb síkjainak A B A B típusú rétegződése a 21.b. ábrán látható. gyémánt 20. ábra A köbös rácsok 3 alaptípusának, valamint a gyémántrácsnak a golyómodellje A 19. ábrán bemutatott 14 féle térrács közül a a legjelentősebb a köbös rácsrendszer, ugyanis a gyakorlati életben használt legfontosabb fémek és ötvözetek legnagyobb részét valamelyik köbös térrács jellemzi. A 19. ábrával ellentétben, amelyen a gömbök nem atomokat jelentenek, hanem csak rácspontokat, a valóságot sokkal inkább érzékelteti a 20. ábra, amely azt mutatja, hogy a térrácsban az atomok a lehetséges legszorosabb elrendeződést veszik fel, tehát a geometriai adottságok szerint egymással érintkező gömböknek tekinthetők. A köbös térrács alapváltozatai és jellemző példái a következők: Primitív (egyszerű) köbös; rövid jele: PK, amelyre az egyetlen példa a polónium (Po). Térközepes köbös; rövid jele: TKK, pl. Li, K, Na, Mo, α-fe, Nb, Ra, Ta, V, W stb. Lapközepes köbös; rövid jele: LKK, pl. Ag, Al, Au, Ce, Cu, Ir, Ni, Pb, Pt, Rh, γ-fe. Gyémántrács; rövid jele: DIA, pl. gyémánt, Si, Ge, α-sn ( szürkeón ) 13 C alatti hőmérsékleten. 21. ábra Az LKK rácsok legsűrűbb síkjainak ABCABC (, és a hexagonális grafit ABABAB rétegződése ( Fontos kristálytani jellegzetessége egy kristályrácsnak a térkitöltési tényező, amely az atomok által elfoglalt, az elemi cella belsejébe eső térfogat, valamint teljes elemicella-térfogat hányadosa: a térkitöltés az LKK rácsban a legnagyobb, értéke 74%. 12. oldal
6 A kristályhibák áttekintése A kristályrács definíciójából következik, hogy ha akár csak egyetlen rácspontra vagy atomra nem teljesül az egyértelmű feltétel, ott rácshiba alakul ki. Szigorúan véve nem is létezhet tökéletes kristály, hiszen annak végtelennek kellene lennie, viszont még a kivételesen nagy egykristályok mint pl. a nagy ásványi kristályok vagy az egykristályként növesztett turbinalapátok is legfeljebb néhány kg tömegűek. Az összetettség szerint haladva a kristályhibákat az alábbi csoportokba sorolhatjuk: rácsrezgések vagy fononok, pontszerű rácshibák, vonalszerű rácshibák és felületszerű rácshibák. A ponthibák Amikor a kristályrács egyetlen pontban nem tökéletes, az adott helyen ponthiba alakult ki. A ponthibák legjellemzőbb típusai: üres rácshely v. vakancia (22.a. ábr, saját fajtájú intersztíciós atom (22.b. ábr, idegen fajtájú intersztíciós (22.c. ábr, szubsztitúciós atom (22.d. ábr, intersztíciós atompár (22.e. ábr. Többalkotós ionrácsokban (22.f. ábr: Schottky-féle hiba (22.g. ábr, Frenkel-féle hiba (22.h. ábr Csoportos hibák, klaszterek (22.i. ábr. A ponthibák keletkezésére nézve többféle elméletet megfogalmaztak, de ezek ismertetése nélkül csak arra utalunk, hogy a ponthibákat a legjelentősebb mennyiségben a neutronokkal való besugárzás, valamint a hőmérséklet erőteljes növelése termeli. A hőmérséklet növekedésével nem csak a ponthibák sűrűsége növekszik, de a mozgékonyságuk is: mind a vakanciák (23. ábr, mind pedig az atomok képesek a kristályrácsban való mozgásra, és ezt a jelenséget nevezzük diffúziónak. Amikor a fém vagy más szilárd fázisú anyag többféle atomot tartalmaz (többkomponensű), ill. több szilárd fázis van benne egyidejűleg jelen (többfázisú), a diffúzió révén számottevően módosulhat az egyes fázisok kémiai összetétele, ha egyes alkotóelemek gyorsabban, mások pedig lassabban tudnak diffundálni. A diffúzió fontos szerepet tölt be az ötvözetek tulajdonságainak kialakulásában, valamint a hőmérséklettel gyorsuló, ún. termikusan aktivált folyamatokban. c) d) e) Kation Anion f) g) h) i) 22. ábra Pontszerű rácshibák sematikus képe 23. ábra Vakanciák Ge felületi rétegben; pásztázó alagútmikroszkópos (STM-) felvétel (fotó: Bernard Aufray, CRMC2 Univ. Marseille) 13. oldal
7 A vonalszerű rácshibák, a diszlokációk Diszlokációnak az olyan kristályrácshibát nevezzük, amelyre az jellemző, hogy a rács szabályos rendje egy vonal mentén sérül. A 24. ábra ezt egy olyan metszetben szemlélteti, amelynek a síkja merőleges a diszlokáció vonalára. A diszlokáció merőleges a síkra (tehát a papírra is), és egyben egy olyan extrafélsík végződése is, amelynek metszésvonalát a 3 jelű vonal jelzi. Attól függően, hogy a diszlokáció vonala milyen helyzetű a helyi rácstorzultság irányát mutató vektorral (Burgers-vektor), 3 féle diszlokációalaptípusról beszélhetünk: éldiszlokáció (24. és 27. ábr, csavardiszlokáció (25. ábr, vegyes diszlokáció, pl. hurok. A diszlokációk környezetében a rács torzul, feszültségek ébrednek: a 24.b. ábrán a vízszintes egyenes jelöli az éldiszlokáció csúszósíkját, amely felett a kristályrácsot nyomófeszültség, alatta pedig húzófeszültség terheli. A csavardiszlokáció vonala mentén a kristályrácsra csak nyomófeszültség hat. 25. ábra Csavardiszlokáció környezetének térbeli vázlata A ponthibák kapcsán láttuk, hogy azok a diffúzió révén mozgásra képesek. A diszlokációk esetében talán még nagyobb hangsúlyt kap a mozgásra való képesség, azonban a jelen tananyagban csak a legfontosabb mozgásformát említjük meg: a csúszást. A csúszás, amely a kristályrács maradó (képlékeny) alakváltozását eredményezi, a diszlokációk legalapvetőbb mozgástípusa, amelyet a csúszósíkban ható csúsztatófeszültség indít meg, ha annak nagysága meghalad egy kritikus értéket. Ha a feszültség csúszósíkba eső komponense ezt a kritikus értéket nem éri el, a kristályrács csak rugalmasan torzul, és a terhelés megszűnte után visszanyeri eredeti alakját. A diszlokáció csúszásának elemi lépéseit a 26. ábra szemlélteti. Nyomott zóna Húzott zóna 24. ábra Éldiszlokáció környezetének keresztmetszete. A világos zónát húzó-, a sötétet nyomófeszültség terheli ábra Éldiszlokáció elektronmikroszkópi képe 26. ábra Éldiszlokáció csúszásának elemi lépései 14. oldal
8 A diszlokáció csúszásának szemléltetésére bizonyosan szemléletes példa egy hosszú szőnyeg elmozdítása, illetve a giliszta vagy a hernyó tovahaladásának mechanizmusa (28. ábr. Valóban, a három példa és az éldiszlokáció csúszása is olyan mozgásmechanizmust jelent, amelynél egyszerre nem az egész anyagmennyiség, hanem annak csak egy egészen kis része van mozgásban (a T vagy a jel utal a diszlokáció pillanatnyi helyére). 28. ábra Az éldiszlokáció mozgásának analógiája (Barrett, Nix, Tetelman, The principles of engineering materials) A példaként mutatott adatokból szembe ötlik, hogy az erősen alakított fémekben a diszlokációsűrűség nagyságrendekkel megnő (T alakítási < ½T olvadáspont hőmérsékleten). Azt, hogy a képlékenyalakítás (pl. hengerlés, kovácsolás, hajlítás stb.) hatására a szemcsék alakja megváltozik, a szövetszerkezet optikai mikroszkópos vizsgálatakor észlelni lehet (29. ábr. Ez a deformáció minden egyes krisztallitot érint, bár koránt sem biztos, hogy azonos mértékben. Ha egyetlen szemcsét választanánk ki a sokkristályos anyagból, annak az egyetlen krisztallitnak a képlékeny alakváltozása a 30. ábrán látható módon menne végbe: a csúszósíkokon végighaladó diszlokációk mindegyike egy-egy elemi elmozdulással járul hozzá a makroszkopikusan is észlelhető alakváltozáshoz. Mivel a makroszkopikus képlékeny deformáció sok esetben többtíz százalék is lehet, a lágyított anyagok mégoly nagy (10 7 cm 2 ) diszlokációsűrűsége sem lenne elegendő ennek teljesítéséhez. Ezt a problémát az anyag oly módon oldja meg, hogy az alakváltozás közben, az azt létrehozó feszültség hatására diszlokációk termelődnek a krisztallitokban, az ún. Frank Read-források aktiválódása eredményeként. Ily módon az anyag makroszkopikus képlékeny alakváltozásának magyarázata is egyszerűvé válik, és az a 100 éve még megoldatlan probléma is feloldható, hogy a tiszta fémek gyakorlati szilárdsága több nagyságrenddel elmarad az ún. elméleti szilárdságtól, a G csúsztató rugalmassági modulustól. A diszlokációelmélet megalapozása Sir Geoffrey Ingram Taylor nevéhez fűződik, és a kidolgozásában igen jelentős szerepet játszott a magyar Orowan Egon ( ) is. 29. ábra Szövetszerkezeti kép hengerlés előtt és után Az gyakorlatban használt anyagok szinte elképesztően nagy számban tartalmaznak diszlokációkat. A diszlokációsűrűséget röntgendiffrakciós mérésekkel lehet meghatározni, és vagy az egységnyi térfogatra jutó diszlokációk összes hosszúságával, vagy pedig az egységnyi keresztmetszetet döfő diszlokációk számával adjuk meg az utóbbi az elterjedt dimenzió. Álljon itt néhány példa a diszlokációsűrűség értékére: Kristályos félvezetők cm 2 Kerámiák cm 2 Nagytisztaságú fémek 10 5 cm 2 Lágyított fémek cm 2 Erősen alakított fémek cm ábra Az alakváltozásnál lezajló elcsúszások vázlata és egy húzással alakított Zn-egykristály képe A Frank Read-források működését, és a kristályrácshibák egészét részletesen tárgyalja: Prohászka János, A fémek és ötvözetek mechanikai tulajdonságai, Műegyetemi Kiadó oldal
9 A diszlokációk valamely külső hatásra sajátos alakzatokat tudnak a kristályrácsban létrehozni: hurkokat (31.a. ábr felhalmozódásokat valamely akadály pl. kiválás, zárvány körül (31.b. ábr, diszlokációfalakat (31.c. ábr vagy spirálokat (31.d. ábr. A felületszerű kristályrácshibák Amennyiben a kristályrács hibát tartalmazó részének mérete kétdimenziós, síkhibáról, általánosabb esetben felületszerű vagy kétméretű hibáról beszélünk. A felületszerű hibák fő típusai a következők: szabad felület, fázishatár, szemcsehatár és szubszemcsehatár, ikerhatár, rétegződési hiba. A szilárdtesteket az őket körbevevő fázistól (többnyire gáz) a szabad felület választja el, amely csak ritkán sima, de atomi méretekben még ilyenkor is lépcsőket, gödröket, dudorokat tartalmaz. Jól mutatja az atomi dimenziókban uralkodó helyzetet egy tükrösre munkált Cupróbatest felületén a 32. ábra. Minden felület mivel rajta a termodinamikai egyensúlytól nagyon távoli energiaviszonyok uralkodnak egy felületi energia jellemez, amely függ egyebek mellett a kristályorientációtól is: a legkisebb energia az atomokkal legsűrűbben pakolt síkokat jellemzi, mivel e síkok atomjainak kötései vannak a legkevésbé elszakítva. A szabad felület fontos szerepet játszik számos folyamatban, mint pl. a súrlódás, a katalízis, a hegesztés, az oxidáció vagy a vékonyrétegek növesztése. c) d) 31. ábra Diszlokációkból felépülő különféle alakzatok transzmissziós elektronmikroszkópi képe 32. ábra Réz felületének atomierő-mikroszkópos ( és pásztázó alagútmikroszkópos képe ( 16. oldal
10 A fázishatárokat a 15. ábra kapcsán már bemutattuk. A szemcsehatárokról is már elmondtuk, hogy elválasztják a különböző orientációjú térfogatelemeit a kristályos anyagnak (33. ábr. A szemcsehatárok között kialakulásuk és az elválasztott tartományok orientációjának különbsége alapján megkülönböztetjük a következő típusokat: Kisszögű határ: az orientációkülönbség < 10 (nem ritkán: < 15 ). Gyakran nevezik őket szubszemcsehatároknak is, az általuk elválasztott tartományokat pedig szubszemcséknek. Nagyszögű határ: az orientációkülönbség > 10 (nem ritkán: > 15 ). A szemcsehatárokhoz is jelentős szabadenergia-többlet társul, ezért a kristályos anyag metastabilis részeinek számítanak, ami azt is jelenti, hogy megfelelő viszonyok között (pl. izzításkor) képesek elmozdulni, amelynek eredménye többnyire az összes szemcsehatár-felület csökkenése. Az idegen atomok, pl. a szennyezők előszeretettel dúsulnak a szemcsehatárokon, általában gyorsabb itt a diffúzió, a korrózió, ugyanakkor az éldiszlokációk fennakadnak rajtuk. Mindebből érzékelhető, hogy a szemcsehatárok kitüntetett szerepet játszanak a mechanikai tulajdonságok alakulásában. Az ikerhatárok az ikresedés következtében alakulnak ki, amely utóbbi jelenség egy további lehetőség (a csúszáson kívül; lásd a 26. ábrát) a kristályos anyagokban a képlékeny alakváltozásra. Az ikresedés a kristálysíkok átrendeződése a kristálynak egy többnyire szűk tartományában. Ebben a tartományban az ikerben az elmozdult atomok új helyzete tükörszimmetrikus az eredetivel, és az a két (esetleg töb sík, amely határolja az ikret, maga a szimmetriatengely, ezt mutatja a 34. ábra. 34. ábra Az ikresedés síkbeli és térbeli vázlata Szemcsehatárok elrendeződésének vázlata: B C = kisszögű határ, A B = nagyszögű határ Nagy hőmérsékletű szupravezető kerámia szemcsehatárának nagyfeloldású TEM-képe (fotó: G. Hammerl, University of Augsburg) 33. ábra Szemcsehatárok 35. ábra Ikerhatárok képe mikroszkópi csiszolaton: ausztenitben (fotó: Verő Balázs, 1980.) Vörösréz próbatest maratott felületén 17. oldal
11 A rétegződési hibák annak a szabályos sorrendnek a lokális zavara esetén jönnek létre, amelyet a 21.a. ábra szemléltetett az LKK kristályrács atomokkal legsűrűbben rakott síkjainak példáján, ill. itt is látható a 36. ábrán. Felületi hibák lévén, a rétegződési hibák növelik a kristályrács szabadenergiáját, ezzel közrejátszanak a nagy hőmérsékleten lejátszódó, valamint az ismétlődő terhelés miatt bekövetkező károsodási folyamatokban. Transzmissziós elektronmikroszkóppal jól megfigyelhetők, amint a ábra mutatja. 38. ábra Nagyméretű rétegződési hibák TEM-képe 36. ábra Az legsűrűbb illeszkedésű síkok ABCABCABC rétegződése a hibamentes LKK rácsban (fent), és az alsó képen, valamint a rétegződési hibában: ABCABABC 37. ábra Kisméretű rétegződési hibák TEM-képe A nanoszerkezetű anyagok Az utóbbi 2 évtizedben kialakult nanoszerkezet szó is abba a csoportba tartozik, amelyben a kifejezések a kis méretre utalnak. A szóban forgó csoporton belül a ma már klasszikus kifejezések a mikro előtaggal kezdődnek, mint pl. a mikroelektronika. A nano elõtag a nm hosszegységbõl származtatható, és arra utal, hogy ez a tudományterület de ma már talán inkább: ez az iparág a nanométeres dimenziókban kívánja befolyásolni az anyag szerveződését. A nanoszerkezet kifejezést a szabványosítás a következő értelmezésben említi: az anyag pontos, különleges alakzatban való atomos elrendezését jelenti, amely magában foglal legalább egy nélkülözhetetlen alkotóelemet. Ez az alkotóelem kizárólag egy atomból, egy molekulából vagy az atomok és molekulák módfelett korlátozott csoportjából áll, amely mennyiség optikai mikroszkóppal nem ismerhető fel, és amelyeket atomjaiknak vagy molekuláiknak mint különálló egységeknek az egyedi manipulálásával formáltak. A nanoanyagok, illetőleg a nanokristályos anyagok említésekor olyan anyagokra kell gondolni, amelyekben a gyártáskor kialakuló szemcseméret az nm mérettartományba esik. Ide sorolják azokat az anyagokat is, amelyeknél ez a feltétel legalább a tér egyik irányában mérve teljesül. Mindez akkor igazán figyelemkeltő, ha meggondoljuk, hogy a hagyományos kristályos anyagok átlagos szemcsemérete a µm (1 µm = 1000 nm) tartományba esik, ill. azt, hogy az atomok átlagos mérete 1 2 angström (1 nm = 10 Å). Tehát a nanokristályos anyagokban alig néhány tucat atom alkot 1 kristályt. A nanoszerkezetű anyagokat különleges mechanikai tulajdonságaik emelték a figyelem középpontjába: rendkívül nagy a szilárdságuk, kemények, de egyben szívósak még nagy hőmérsékleteken is, jól ellenállnak a legkülönfélébb 18. oldal
12 koptató és korróziós hatásoknak, más típusaik viszont kémiailag nagyon aktívak lehetnek. A harmadik évezredbe lépve, világszerte óriási lendületet kapott a nanoszerkezetű anyagok kutatása, széles értelemben a nanotechnológia. Jól példázza ezt a 39. ábra, amely a nanotechnológia államilag finanszírozott kutatási költségvetésének változását mutatja a legfejlettebb ipari régiókban: A nanokristályos anyagok számos kutatási és mindennapi területen jelen vannak. Az űrkutatásban SiC nanocsöveket használnak a sugárzásés hőálló szenzorokhoz (40.a. ábr. Az energiatárolást forradalmasíthatják a szén nanocsövek. Olyan közismert területen is megjelentek, mint az adattárolás: a nanokristályos szilícium alapú elektronikus gyorsmemóriák (40.b c. ábr ma már széles körben elterjedt informatikai eszközök. Jelképének a Buckminster-fullerént, azaz a C 60 molekulát tekinti a nanotechnológia (40.d. ábr. A szénatomoknak ezt a különleges szerveződési formáját H. Kroto, J. Heath, S. O'Brien, R. Curl és R. Smalley publikálta először 1985-ben, a Nature c. folyóiratban. Költségvetési ráfordítás, [ millió USD ] Ny-Európa Japán USA Egyéb Összes ábra A nanotechnológia állami ráfordításainak trendje A 39. ábra azt jelzi, hogy szinte páratlan forráskoncentráció valósul meg a nanotechnológiai területre, s ebben egymással versengenek a nagy ipari központok. Az ábra külön nem is tünteti fel, de pl. a Koreai Köztársaság 2002-re 1,56 Mrd USD forrást rendelt a nanotechnológiai kutatásokra (EE Times, ), Kína pedig 2005-re 3 Mrd USD-t tervez (Taipei Times, ). Magyarországon is államilag dotált kutatási prioritás a nanotechnológia, és a BME doktori témái között szerepel, pl. a hegesztés során kialakuló nanoszerkezet és a makroszkopikus tulajdonságok közötti kapcsolat meghatározása. c) d) 40. ábra Nanokristályos anyagok szerkezete: szén nanocsövek ( és fullerén makromolekula (d), valamint alkalmazási példák (b c) 19. oldal
13 A fázisátalakulások A fémes szerkezeti anyagok tulajdonságainak megismerése, és az ezeket a tulajdonságokat nagymértékben determináló gyártási és feldolgozási technológiai folyamatoknak a megértése érdekében kiemelkedő jelentőséggel bír a fázisátalakulások ismerete. A fázis fogalmát már definiáltuk az szakaszban; a definícióból következően leszögezhetjük, hogy amennyiben a tömegére nézve állandónak tekintett anyag pillanatnyi fázisviszonyaiban valamilyen akár mennyiségi, akár minőségi változás következik be, az csak fázisátalakulás révén következhet be. A fázisátalakulás(ok) eredménye tehát jelentheti a fázisok számának és mennyiségének a változást, ill. a kettőt egyszerre. A fázisviszonyok egyensúlyával és megváltozásával kapcsolatos folyamatokat egy komoly tudományág, a termodinamika vizsgálja és értelmezi. A jelen tananyag keretében ennek mindössze egyetlen és leegyszerűsített törvényére, a Gibbs-féle fázisszabályra hivatkozunk: e szerint egy termodinamikai rendszert alkotó komponensek (K), az azokból létrehozható fázisok (F) és a szabadon változható állapothatározók (SZ = szabadsági fok, jellemzően a hőmérséklet és a koncentráció) száma között az alábbi öszszefüggés áll fenn: F + SZ = K + 1. A fázisátalakulások általános esetben a halmazállapot-változásokat jelentik, megnevezésük a 41. ábrán látható. A szublimáció jelenségéről akkor beszélünk, amikor a szilárd fázisú anyag közvetlenül elpárolog. Ily módon is fogynak a gleccserek, és az élelmiszerek kiszárításának egyik módszere, a liofilizálás is a szublimáció jelenségén alapul. A szublimáció inverz fázisátalakulása az alapja a korszerű bevonatolási és vékonyréteg-technológiáknak (PVD és CVD ), amelyek arra szolgálnak, hogy a gőz fázisból a céltárgy felületére jussanak az előzőleg elporlasztott anyag atomjai. A fémes anyagok esetében a fagyás kifejezés helyett a dermedés, kristályosodás, illetve megszilárdulás kifejezéseket illik használni. A fémolvadékok kristályosodásának számos típusa ismert, amelyek közül átfogó rendszerezés és termodinamikai leírás nélkül megemlítjük a dendrites kristályosodást, amely a 42.a. ábrán látható, jellegzetes szerkezetet eredményez. 41. ábra A halmazállapot-változások rendszerezése A halmazállapot-változások 42. ábra korrózióálló acél dendrites kristálya (fotó: L. A. Boatner, J. Gardner, D. Corrigan, Oak Ridge National Laboratory), hókristályok, c) Ho-Mg-Zn kvázikristály (fotó: I.R. Fisher, 1999) CVD = chemical vapor deposition, kémiai gőzfázisú leválasztás, PVD = physical vapor deposition, fizikai gőzfázisú leválasztás (gyakran vákuumporlasztásként, vákuumgőzölésként is emlegetik) 20. oldal
14 Az allotrop átalakulás Egyes fémek és sok ötvözet hűtésekor vagy hevítésekor olyan fázisátalakulások figyelhetők meg, amelyeknél mind az eredeti, mind az új fázis szilárd. Az ilyen fázisátalakulások neve: allotrop átalakulás. Egy anyagnak ama tulajdonságát, hogy atomjai a hőmérséklet függvényében többféle kristályrácsot alkotnak, polimorfizmusnak nevezik; pl. a szénnek allotrop módosulata a grafit, a gyémánt és a C 60 makromolekula (43. ábr, ill. az ónnak a fehér- és szürkeón. A gyakorlati fontosság miatt a vas, ill. a szenet tartalmazó változata, az acél allotrop átalakulásai mondhatók a legjelentősebbnek: a δ-vas (TKK) γ-vas (LKK) α-vas (TKK) átalakulás hűtéskor, ellenkezője hevítéskor játszódik le. 43. ábra A szén allotrop módosulatai A diffúzió szerepe a fázisátalakulásokban A diffúzió (lásd a szakaszt) a fémek és ötvözetek tulajdonságainak egyik meghatározója lehet. A fázisátalakulások egyik lehetséges csoportosítása szerint megkülönböztetünk: diffúziós átalakulásokat és diffúzió nélküli átalakulásokat. A diffúziós átalakulások közé a hevítéskor és hűtéskor, avagy izotermikusan lezajló olyan allotrop átalakulásokat soroljuk, amelyekben a diffúzió az atomok koncentráció-, hőmérséklet- és időfüggő mozgása a meghatározó. Ugyancsak diffúziós átalakulások az ún. termikusan aktivált folyamatok, pl. a kiválások képződése. Az izotermikus diffúziós átalakulások időbeli lefolyását szigmoid görbe alakú függvények (44.a. ábr írják le, pl. a Johnson Mehl Avrami-egyenlet, amelyben y az átalakult tömeghányad, t az idő, k és n konstansok: n ( k t ) y = 1 exp. A 44.a. ábra alapján a valamely hőmérsékleten már nem stabil fázisok diffúziós átalakulásának fontosabb jellemzői a következők: Nem azonnal kezdődik meg, hanem egy bizonyos t i inkubációs idő után. Az átalakulás időbeli lefolyását szigmoid görbe jellegű függvény írja le. Állandó hőmérsékleten is teljes, tehát az eredeti fázis teljes mennyisége átalakul. Első lépésként az eredeti fázis valamely kitüntetett pontján (főleg a szemcsehatárokon) kialakul az új fázis egy csírája, és ha ez eléri a kritikus méretet, a magképződést növekedés követi. A diffúzió nélküli v. martenzites átalakulásokról akkor beszélünk, amikor a kristályrács átalakulása nem az atomok diffúziós mozgásával, hanem komplex nyíró-alakváltozás okozta átrendeződésével megy végbe, jellemzően a gyors hűtés alkalmával. Az acélok példáját véve, az eredeti fázis az ausztenit, az új fázis a martenzit, és az átalakult tömeghányadot az alábbi egyenlet írja le, amelyben y az átalakult tömeghányad, T a hőmérséklet, M S az anyagtól függő határhőmérséklet ( martenzit start ), k és n konstansok: Átalakult tömeghányad Hőmérséklet 1,0 0,8 0,6 0,4 0,2 0,0 M S M 50 M 98 M F y = 1 exp[ k( M S T ) )]. t i T 75% 50% 25% Ausztenit Martenzit T = állandó m M t 25 t 50 t 75 t át n Idő, lg(t) 0,0 0,5 1,0 Átalakult tömeghányad 44. ábra A diffúziós és a martenzites átalakulás menete 0,5 ma A 44.b. ábra alapján a martenzites átalakulás néhány lényeges jellemzője a következő: Amint a hőmérséklet az M S alá csökken, azonnal, inkubációs idő nélkül elkezdődik. Ha a hőmérséklet nem csökken az M F ( martenzit finis ) érték alá, az átalakulás nem megy végbe teljes mértékben: a 44.b. ábra szerint T hőmérsékleten m A mennyiségű maradék ausztenit marad az anyagban. Az átalakulás kvázi-pillanatszerű. Az acélokban csak hűtéskor játszódhat le, de több ötvözetben (pl. Ni-Ti) hevítéskor is, vagy mechanikai feszültség hatására. 21. oldal
ANYAGTUDOMÁNY ÉS TECHNOLÓGIA TANSZÉK. Anyagismeret 2009/10. Rácshibák. Dr. Mészáros István Dr. Reé András. Az előadás fő pontjai
 ANYAGTUDOMÁNY ÉS TECHNOLÓGIA TANSZÉK Anyagismeret 2009/10 Rácshibák Dr. Mészáros István Dr. Reé András 1 Az előadás fő pontjai A rácshibák jelentősége Pontszerű (0 méretű) hibák Vonalszerű hibák (1 méretű),
ANYAGTUDOMÁNY ÉS TECHNOLÓGIA TANSZÉK Anyagismeret 2009/10 Rácshibák Dr. Mészáros István Dr. Reé András 1 Az előadás fő pontjai A rácshibák jelentősége Pontszerű (0 méretű) hibák Vonalszerű hibák (1 méretű),
Anyagszerkezet és vizsgálat. 3. Előadás
 SZÉCHENYI ISTVÁN EGYETEM Anyagtudományi és Technológiai Tanszék Anyagszerkezet és vizsgálat NGB_AJ021_1 3. Előadás Dr. Hargitai Hajnalka (Csizmazia Ferencné dr. előadásanyagai alapján) 1 Tematika Színfémek
SZÉCHENYI ISTVÁN EGYETEM Anyagtudományi és Technológiai Tanszék Anyagszerkezet és vizsgálat NGB_AJ021_1 3. Előadás Dr. Hargitai Hajnalka (Csizmazia Ferencné dr. előadásanyagai alapján) 1 Tematika Színfémek
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI
 SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 12 KRISTÁLYkÉMIA XII. KÖTÉsTÍPUsOK A KRIsTÁLYOKBAN 1. KÉMIAI KÖTÉsEK Valamennyi kötéstípus az atommag és az elektronok, illetve az elektronok egymás közötti
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 12 KRISTÁLYkÉMIA XII. KÖTÉsTÍPUsOK A KRIsTÁLYOKBAN 1. KÉMIAI KÖTÉsEK Valamennyi kötéstípus az atommag és az elektronok, illetve az elektronok egymás közötti
A kristályrendszerek leírása
 Néhány fogalom Térrács: Kiterjedés nélküli pontok szabályos rendje a térben. A térelem a térrácsot adja (pontokkal), az elemi cella az anyagot adja (atomokkal). Kristálytani adatok: olyan adatok, amely
Néhány fogalom Térrács: Kiterjedés nélküli pontok szabályos rendje a térben. A térelem a térrácsot adja (pontokkal), az elemi cella az anyagot adja (atomokkal). Kristálytani adatok: olyan adatok, amely
3. alkalom, gyakorlat
 Vegyület-félvezető struktúrák technológiája és alkalmazásaik: III-V és II-VI típusú vegyület-félvezetők; direkt és indirekt sávszerkezet; optikai tulajdonságok és alkalmazásuk 3. alkalom, gyakorlat A GYAKORLAT
Vegyület-félvezető struktúrák technológiája és alkalmazásaik: III-V és II-VI típusú vegyület-félvezetők; direkt és indirekt sávszerkezet; optikai tulajdonságok és alkalmazásuk 3. alkalom, gyakorlat A GYAKORLAT
Mágneses szuszceptibilitás vizsgálata
 Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
Anyagismeret. 1. Metallográfiai alapfogalmak
 Anyagismeret 1. Metallográfiai alapfogalmak Az anyagok szerkezete Halmazállapotok A rendszereknek három alapvető halmazállapotuk van, amelyek az állapotjelzők függvényében külön-külön, vagy egyidőben is
Anyagismeret 1. Metallográfiai alapfogalmak Az anyagok szerkezete Halmazállapotok A rendszereknek három alapvető halmazállapotuk van, amelyek az állapotjelzők függvényében külön-külön, vagy egyidőben is
Az aktiválódásoknak azonban itt még nincs vége, ugyanis az aktiválódások 30 évenként ismétlődnek!
 1 Mindannyiunk életében előfordulnak jelentős évek, amikor is egy-egy esemény hatására a sorsunk új irányt vesz. Bár ezen események többségének ott és akkor kevésbé tulajdonítunk jelentőséget, csak idővel,
1 Mindannyiunk életében előfordulnak jelentős évek, amikor is egy-egy esemény hatására a sorsunk új irányt vesz. Bár ezen események többségének ott és akkor kevésbé tulajdonítunk jelentőséget, csak idővel,
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI
 SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 11 KRISTÁLYkÉMIA XI. ATOMOK És IONOK 1. AZ ATOM Az atom az anyag legkisebb olyan része, amely még hordozza a kémiai elem jellegzetességeit. Ezért az ásványtanban
SZAKÁLL SÁNDOR, ÁsVÁNY- És kőzettan ALAPJAI 11 KRISTÁLYkÉMIA XI. ATOMOK És IONOK 1. AZ ATOM Az atom az anyag legkisebb olyan része, amely még hordozza a kémiai elem jellegzetességeit. Ezért az ásványtanban
Fogorvosi anyagtan fizikai alapjai 5. Általános anyagszerkezeti ismeretek Anyagcsaládok (fémek, kerámiák, polimerek, kompozitok)
 Fogászati anyagok fajtái FÉMEK KERÁMIÁK Fémes és nemfémes elemek vegyületei. POLIMEREK KOMPOZITOK Fogorvosi anyagtan fizikai alapjai 5. Általános anyagszerkezeti ismeretek Anyagcsaládok (fémek, kerámiák,
Fogászati anyagok fajtái FÉMEK KERÁMIÁK Fémes és nemfémes elemek vegyületei. POLIMEREK KOMPOZITOK Fogorvosi anyagtan fizikai alapjai 5. Általános anyagszerkezeti ismeretek Anyagcsaládok (fémek, kerámiák,
Anyagszerkezettan vizsgajegyzet
 - 1 - Anyagszerkezettan vizsgajegyzet Előadástémák: 1. Atomszerkezet 1.1. Atommag 1.2. Atomszám 1.3. Atomtömeg 1.4. Bohr-féle atommodell 1.5. Schrödinger-egyenlet 1.6. Kvantumszámok 1.7. Elektron orbitál
- 1 - Anyagszerkezettan vizsgajegyzet Előadástémák: 1. Atomszerkezet 1.1. Atommag 1.2. Atomszám 1.3. Atomtömeg 1.4. Bohr-féle atommodell 1.5. Schrödinger-egyenlet 1.6. Kvantumszámok 1.7. Elektron orbitál
Hőhidak meghatározásának bizonytalansága. Sólyomi Péter ÉMI Nonprofit Kft.
 Hőhidak meghatározásának bizonytalansága Sólyomi Péter ÉMI Nonprofit Kft. 7./2006. (V. 24.) TNM r e n d e l e t Épülethatároló szerkezet A hőátbocsátási tényező követelményértéke U W/m 2 K Külső fal 0,45
Hőhidak meghatározásának bizonytalansága Sólyomi Péter ÉMI Nonprofit Kft. 7./2006. (V. 24.) TNM r e n d e l e t Épülethatároló szerkezet A hőátbocsátási tényező követelményértéke U W/m 2 K Külső fal 0,45
Fa- és Acélszerkezetek I. 5. Előadás Stabilitás I. Dr. Szalai József Főiskolai adjunktus
 Fa- és Acélszerkezetek I. 5. Előadás Stabilitás I. Dr. Szalai József Főiskolai adjunktus Tartalom Egyensúly elágazási határállapot Rugalmas nyomott oszlop kritikus ereje (Euler erő) Valódi nyomott oszlopok
Fa- és Acélszerkezetek I. 5. Előadás Stabilitás I. Dr. Szalai József Főiskolai adjunktus Tartalom Egyensúly elágazási határállapot Rugalmas nyomott oszlop kritikus ereje (Euler erő) Valódi nyomott oszlopok
Amit a Hőátbocsátási tényezőről tudni kell
 Amit a Hőátbocsátási tényezőről tudni kell Úton-útfélen mindenki róla beszél, már amikor épületekről van szó. A tervezéskor találkozunk vele először, majd az építkezéstől az épület lakhatási engedélyének
Amit a Hőátbocsátási tényezőről tudni kell Úton-útfélen mindenki róla beszél, már amikor épületekről van szó. A tervezéskor találkozunk vele először, majd az építkezéstől az épület lakhatási engedélyének
Épületvillamosság laboratórium. Villámvédelemi felfogó-rendszer hatásosságának vizsgálata
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
A döntő feladatai. valós számok!
 OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
[MECHANIKA- HAJLÍTÁS]
![[MECHANIKA- HAJLÍTÁS] [MECHANIKA- HAJLÍTÁS]](/thumbs/39/20428431.jpg) 2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
4. elıadás KRISTÁLYTANI ALAPOK
 4. elıadás KRISTÁLYTANI ALAPOK SZTEREOGRAFIKUS VETÜLET Cél: a térbeli kristályt síkban tudjuk ábrázolni. Más szóval: a háromdimenziós poliédert két dimenzióban ábrázoljuk. Lépések: 1. A kristályt egy gömb
4. elıadás KRISTÁLYTANI ALAPOK SZTEREOGRAFIKUS VETÜLET Cél: a térbeli kristályt síkban tudjuk ábrázolni. Más szóval: a háromdimenziós poliédert két dimenzióban ábrázoljuk. Lépések: 1. A kristályt egy gömb
Az elektromágneses anyagvizsgálat alapjai
 BME, Anyagtudomány és Technológia Tanszék Az elektromágneses anyagvizsgálat alapjai Dr. Mészáros István Habilitációs előadás BME 216. március 3. 1 B = µ H Mágneses tér anyag kölcsönhatás B = µ µ r H =
BME, Anyagtudomány és Technológia Tanszék Az elektromágneses anyagvizsgálat alapjai Dr. Mészáros István Habilitációs előadás BME 216. március 3. 1 B = µ H Mágneses tér anyag kölcsönhatás B = µ µ r H =
Előgyergyártott konzolos és konzolos támfalas közlekedési vasbeton elemcsaládok a kerékpáros és gyalogos közlekedési területek növelésére
 Előgyergyártott konzolos és konzolos támfalas közlekedési vasbeton elemcsaládok a kerékpáros és gyalogos közlekedési területek növelésére Adott esetben hegy- és dombvidéken, vízparton, hídfőknél az egyetlen
Előgyergyártott konzolos és konzolos támfalas közlekedési vasbeton elemcsaládok a kerékpáros és gyalogos közlekedési területek növelésére Adott esetben hegy- és dombvidéken, vízparton, hídfőknél az egyetlen
Analízis elo adások. Vajda István. 2012. október 3. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
Szilárd anyagok. Műszaki kémia, Anyagtan I. 7. előadás. Dolgosné dr. Kovács Anita egy.doc. PTE MIK Környezetmérnöki Tanszék
 Szilárd anyagok Műszaki kémia, Anyagtan I. 7. előadás Dolgosné dr. Kovács Anita egy.doc. PTE MIK Környezetmérnöki Tanszék Szilárd anyagok felosztása Szilárd anyagok Kristályos szerkezetűek Üvegszerű anyagok
Szilárd anyagok Műszaki kémia, Anyagtan I. 7. előadás Dolgosné dr. Kovács Anita egy.doc. PTE MIK Környezetmérnöki Tanszék Szilárd anyagok felosztása Szilárd anyagok Kristályos szerkezetűek Üvegszerű anyagok
Kristályszerkezetek és vizsgálatuk
 Kristályszerkezetek és vizsgálatuk Az anyagk tulajdnságait atmjaik fajtája, kémiai kötésük jellege és kristályszerkezete együttesen határzza meg. A fentiekre a szén egy tipikus példa. A tiszta szén gyémánt
Kristályszerkezetek és vizsgálatuk Az anyagk tulajdnságait atmjaik fajtája, kémiai kötésük jellege és kristályszerkezete együttesen határzza meg. A fentiekre a szén egy tipikus példa. A tiszta szén gyémánt
Adatgyőjtés, mérési alapok, a környezetgazdálkodás fontosabb mőszerei
 GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
1. Metrótörténet. A feladat folytatása a következő oldalon található. Informatika emelt szint. m2_blaha.jpg, m3_nagyvaradter.jpg és m4_furopajzs.jpg.
 1. Metrótörténet A fővárosi metróhálózat a tömegközlekedés gerincét adja. A vonalak építésének története egészen a XIX. század végéig nyúlik vissza. Feladata, hogy készítse el a négy metróvonal történetét
1. Metrótörténet A fővárosi metróhálózat a tömegközlekedés gerincét adja. A vonalak építésének története egészen a XIX. század végéig nyúlik vissza. Feladata, hogy készítse el a négy metróvonal történetét
Házi dolgozat. Minta a házi dolgozat formai és tartalmi követelményeihez. Készítette: (név+osztály) Iskola: (az iskola teljes neve)
 Házi dolgozat Minta a házi dolgozat formai és tartalmi követelményeihez Készítette: (név+osztály) Iskola: (az iskola teljes neve) Dátum: (aktuális dátum) Tartalom Itt kezdődik a címbeli anyag érdemi kifejtése...
Házi dolgozat Minta a házi dolgozat formai és tartalmi követelményeihez Készítette: (név+osztály) Iskola: (az iskola teljes neve) Dátum: (aktuális dátum) Tartalom Itt kezdődik a címbeli anyag érdemi kifejtése...
Ha a síkot egyenes vagy görbe vonalakkal feldaraboljuk, akkor síkidomokat kapunk.
 Síkidomok Ha a síkot egyenes vagy görbe vonalakkal feldaraboljuk, akkor síkidomokat kapunk. A határoló vonalak által bezárt síkrész a síkidom területe. A síkidomok határoló vonalak szerint lehetnek szabályos
Síkidomok Ha a síkot egyenes vagy görbe vonalakkal feldaraboljuk, akkor síkidomokat kapunk. A határoló vonalak által bezárt síkrész a síkidom területe. A síkidomok határoló vonalak szerint lehetnek szabályos
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria
 005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
BOLYAI MATEMATIKA CSAPATVERSENY FŐVÁROSI DÖNTŐ SZÓBELI (2005. NOVEMBER 26.) 5. osztály
 5. osztály Írd be az ábrán látható hat üres körbe a 10, 30, 40, 60, 70 és 90 számokat úgy, hogy a háromszög mindhárom oldala mentén a számok összege 200 legyen! 50 20 80 Egy dobozban háromféle színű: piros,
5. osztály Írd be az ábrán látható hat üres körbe a 10, 30, 40, 60, 70 és 90 számokat úgy, hogy a háromszög mindhárom oldala mentén a számok összege 200 legyen! 50 20 80 Egy dobozban háromféle színű: piros,
Agrárgazdasági Kutató Intézet Piac-árinformációs Szolgálat. Borpiaci információk. III. évfolyam / 7. szám 2005. április 28. 14-15.
 A K I Borpiaci információk III. évfolyam / 7. szám 25. április 28. 14- Bor piaci jelentés Borpiaci információk 1-4. táblázat, 1-8. ábra: Belföldi értékesítési-árak és mennyiségi adatok 2. oldal 3-7. oldal
A K I Borpiaci információk III. évfolyam / 7. szám 25. április 28. 14- Bor piaci jelentés Borpiaci információk 1-4. táblázat, 1-8. ábra: Belföldi értékesítési-árak és mennyiségi adatok 2. oldal 3-7. oldal
Azonosító jel: Matematika emelt szint
 I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
A Tömegspektrométer elve AZ ATOMMAG FIZIKÁJA. Az atommag szerkezete (40-44 oldal) A tömegspektrométer elve. Az atommag komponensei:
 AZ ATOMMAG FIZIKÁJA Az atommag szerkezete (40-44 oldal) A tömegspektrométer elve Az atommag komponensei izotópok Tömeghiány, kötési energia, stabilitás Magerők Magmodellek Az atommag stabilitásának tényezői
AZ ATOMMAG FIZIKÁJA Az atommag szerkezete (40-44 oldal) A tömegspektrométer elve Az atommag komponensei izotópok Tömeghiány, kötési energia, stabilitás Magerők Magmodellek Az atommag stabilitásának tényezői
A jelenség magyarázata. Fényszórás mérése. A dipólus keletkezése. Oszcilláló dipólusok. A megfigyelhető jelenségek. A fény elektromágneses hullám.
 Fényszórás mérése A jelenség magyarázata A megfigyelhető jelenségek A fény elektromágneses hullám. Az elektromos tér töltésekre erőhatást fejt ki. A dipólus keletkezése Dipólusok: a pozitív és a negatív
Fényszórás mérése A jelenség magyarázata A megfigyelhető jelenségek A fény elektromágneses hullám. Az elektromos tér töltésekre erőhatást fejt ki. A dipólus keletkezése Dipólusok: a pozitív és a negatív
BETONACÉLOK HAJLÍTÁSÁHOZ SZÜKSÉGES l\4"yomaték MEGHATÁROZÁSÁNAK EGYSZERŰ MÓDSZERE
 BETONACÉLOK HAJLÍTÁSÁHOZ SZÜKSÉGES l\4"yomaték MEGHATÁROZÁSÁNAK EGYSZERŰ MÓDSZERE BACZY"SKI Gábor Budape?ti 1Iűszaki Egyetem, Közlekedésmérnöki Kar Epítő- és Anyagmozgató Gépek Tanszék Körkeresztmetszet{Í
BETONACÉLOK HAJLÍTÁSÁHOZ SZÜKSÉGES l\4"yomaték MEGHATÁROZÁSÁNAK EGYSZERŰ MÓDSZERE BACZY"SKI Gábor Budape?ti 1Iűszaki Egyetem, Közlekedésmérnöki Kar Epítő- és Anyagmozgató Gépek Tanszék Körkeresztmetszet{Í
MATEMATIKA HETI 3 ÓRA
 EURÓPAI ÉRETTSÉGI 010 MATEMATIKA HETI 3 ÓRA IDŐPONT : 010. június 4. A VIZSGA IDŐTARTAMA : 3 óra (180 perc) MEGENGEDETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
EURÓPAI ÉRETTSÉGI 010 MATEMATIKA HETI 3 ÓRA IDŐPONT : 010. június 4. A VIZSGA IDŐTARTAMA : 3 óra (180 perc) MEGENGEDETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
A forgácsolás alapjai
 NGB_AJ012_1 Forgácsoló megmunkálás (Forgácsolás és szerszámai) A forgácsolás alapjai Dr. Pintér József 2015. FONTOS! KÉREM, NE FELEDJÉK, HOGY A PowerPoint ELŐADÁS VÁZLAT NEM HELYETTESÍTI, CSAK ÖSSZEFOGLALJA,
NGB_AJ012_1 Forgácsoló megmunkálás (Forgácsolás és szerszámai) A forgácsolás alapjai Dr. Pintér József 2015. FONTOS! KÉREM, NE FELEDJÉK, HOGY A PowerPoint ELŐADÁS VÁZLAT NEM HELYETTESÍTI, CSAK ÖSSZEFOGLALJA,
A környezettan tantárgy intelligencia fejlesztő lehetőségei
 A környezettan tantárgy intelligencia fejlesztő lehetőségei Készítette: Pék Krisztina biológia környezettan szak Belső konzulens: Dr. Schróth Ágnes Külső konzulens: Dr. Széphalmi Ágnes A szakdolgozatom
A környezettan tantárgy intelligencia fejlesztő lehetőségei Készítette: Pék Krisztina biológia környezettan szak Belső konzulens: Dr. Schróth Ágnes Külső konzulens: Dr. Széphalmi Ágnes A szakdolgozatom
Ipari és vasúti szénkefék
 www.schunk-group.com Ipari és vasúti szénkefék A legjelentősebb anyagminőségek fizikai tulajdonságai A legjelentősebb anyagminőségek fizikai tulajdonságai A szénkefetestként használt szén és grafit anyagminőségek
www.schunk-group.com Ipari és vasúti szénkefék A legjelentősebb anyagminőségek fizikai tulajdonságai A legjelentősebb anyagminőségek fizikai tulajdonságai A szénkefetestként használt szén és grafit anyagminőségek
VASÚTI PÁLYA DINAMIKÁJA
 VASÚTI PÁLYA DINAMIKÁJA Dynamics of the railway track Liegner Nándor BME Út és Vasútépítési Tanszék A vasúti felépítmény szerkezeti elemeiben ébredő igénybevételek A Zimmermann Eisenmann elmélet alapján
VASÚTI PÁLYA DINAMIKÁJA Dynamics of the railway track Liegner Nándor BME Út és Vasútépítési Tanszék A vasúti felépítmény szerkezeti elemeiben ébredő igénybevételek A Zimmermann Eisenmann elmélet alapján
Analízis elo adások. Vajda István. 2012. szeptember 24. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem 1/8 A halmaz alapfogalom, tehát nem definiáljuk. Jelölés: A halmazokat általában nyomtatott nagybetu vel jelöljük Egy H halmazt akkor tekintünk
Vajda István Neumann János Informatika Kar Óbudai Egyetem 1/8 A halmaz alapfogalom, tehát nem definiáljuk. Jelölés: A halmazokat általában nyomtatott nagybetu vel jelöljük Egy H halmazt akkor tekintünk
Atomerőművi anyagvizsgálatok 4. előadás: Fémtan
 Budapesti Műszaki- és Gazdaságtudományi Egyetem (BME) Nukleáris Technikai Intézet (NTI) Atomerőművi anyagvizsgálatok 4. előadás: Fémtan Tárgyfelelős: Dr. Aszódi Attila Előadó: Kiss Attila 2012-2013. ősz
Budapesti Műszaki- és Gazdaságtudományi Egyetem (BME) Nukleáris Technikai Intézet (NTI) Atomerőművi anyagvizsgálatok 4. előadás: Fémtan Tárgyfelelős: Dr. Aszódi Attila Előadó: Kiss Attila 2012-2013. ősz
1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi
 1 Mélyhúzott edény teríték méretének meghatározása 1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi A mélyhúzott edény kiindulási teríték átmérőjének meghatározása a térfogat-állandóság alapján
1 Mélyhúzott edény teríték méretének meghatározása 1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi A mélyhúzott edény kiindulási teríték átmérőjének meghatározása a térfogat-állandóság alapján
Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között
 Dr. Nyári Tibor Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között tökéletes színeket visszaadni. A digitális
Dr. Nyári Tibor Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között tökéletes színeket visszaadni. A digitális
Homlokzati tűzterjedés vizsgálati módszere
 Homlokzati tűzterjedés vizsgálati módszere Siófok 2008. április 17. Dr. Bánky Tamás Nyílásos homlokzatok esetén a tűzterjedési gát kritériumait nem kielégítő homlokzati megoldásoknál továbbá nyílásos homlokzatokon
Homlokzati tűzterjedés vizsgálati módszere Siófok 2008. április 17. Dr. Bánky Tamás Nyílásos homlokzatok esetén a tűzterjedési gát kritériumait nem kielégítő homlokzati megoldásoknál továbbá nyílásos homlokzatokon
Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata. Az r-time és a TNS Hoffmann által végzett kutatás
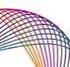 Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata Az r-time és a TNS Hoffmann által végzett kutatás 2002-2010: stabil szponzorációs részarány Televíziós reklámbevételek
Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata Az r-time és a TNS Hoffmann által végzett kutatás 2002-2010: stabil szponzorációs részarány Televíziós reklámbevételek
Párhuzamos programozás
 Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
Conjoint-analízis példa (egyszerűsített)
 Conjoint-analízis példa (egyszerűsített) Az eljárás meghatározza, hogy a fogyasztók a vásárlás szempontjából lényeges terméktulajdonságoknak mekkora relatív fontosságot tulajdonítanak és megadja a tulajdonságok
Conjoint-analízis példa (egyszerűsített) Az eljárás meghatározza, hogy a fogyasztók a vásárlás szempontjából lényeges terméktulajdonságoknak mekkora relatív fontosságot tulajdonítanak és megadja a tulajdonságok
IKU WORLD KOCKA Játékszabály. IKU WORLD Gondolkodásfejlesztő Vállalkozás
 NN IKU WORLD KOCKA Játékszabály MAGYAR OLASZ IKU WORLD Gondolkodásfejlesztő Vállalkozás IKU WORLD KOCKA Logikai társasjáték Egy új játék, melyet sokféleképpen lehet használni: kirakójáték, társasjáték,
NN IKU WORLD KOCKA Játékszabály MAGYAR OLASZ IKU WORLD Gondolkodásfejlesztő Vállalkozás IKU WORLD KOCKA Logikai társasjáték Egy új játék, melyet sokféleképpen lehet használni: kirakójáték, társasjáték,
A nyugalomban levő levegő fizikai jellemzői. Dr. Lakotár Katalin
 A nyugalomban levő levegő fizikai jellemzői Dr. Lakotár Katalin Száraz, nyugalomban levő levegő légköri jellemzői egyszerűsített légkör modell állapotjelzői: sűrűség vagy fajlagos térfogat térfogategységben
A nyugalomban levő levegő fizikai jellemzői Dr. Lakotár Katalin Száraz, nyugalomban levő levegő légköri jellemzői egyszerűsített légkör modell állapotjelzői: sűrűség vagy fajlagos térfogat térfogategységben
2011. március 9. Dr. Vincze Szilvia
 . márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
. márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
Szigetelők Félvezetők Vezetők
 Dr. Báder Imre: AZ ELEKTROMOS VEZETŐK Az anyagokat elektromos erőtérben tapasztalt viselkedésük alapján két alapvető csoportba soroljuk: szigetelők (vagy dielektrikumok) és vezetők (vagy konduktorok).
Dr. Báder Imre: AZ ELEKTROMOS VEZETŐK Az anyagokat elektromos erőtérben tapasztalt viselkedésük alapján két alapvető csoportba soroljuk: szigetelők (vagy dielektrikumok) és vezetők (vagy konduktorok).
[GVMGS11MNC] Gazdaságstatisztika
![[GVMGS11MNC] Gazdaságstatisztika [GVMGS11MNC] Gazdaságstatisztika](/thumbs/40/21500887.jpg) [GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
[GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (13. fejezet)
 Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
Természettudomány. 1-2. témakör: Atomok, atommodellek Anyagok, gázok
 Természettudomány 1-2. témakör: Atomok, atommodellek Anyagok, gázok Atommodellek viták, elképzelések, tények I. i.e. 600. körül: Thálész: a víz az ősanyag i.e. IV-V. század: Démokritosz: az anyagot parányi
Természettudomány 1-2. témakör: Atomok, atommodellek Anyagok, gázok Atommodellek viták, elképzelések, tények I. i.e. 600. körül: Thálész: a víz az ősanyag i.e. IV-V. század: Démokritosz: az anyagot parányi
Folyadék-gáz, szilárd-gáz folyadék-folyadék és folyadék-szilárd határfelületek. Adszorpció és orientáció a határfelületen. Adszorpció oldatból és
 Folyadék-gáz, szilárd-gáz folyadék-folyadék és folyadék-szilárd határfelületek. Adszorpció és orientáció a határfelületen. Adszorpció oldatból és elegyből. Görbült felületek, Laplace nyomás levegő p 1
Folyadék-gáz, szilárd-gáz folyadék-folyadék és folyadék-szilárd határfelületek. Adszorpció és orientáció a határfelületen. Adszorpció oldatból és elegyből. Görbült felületek, Laplace nyomás levegő p 1
A szilárd testek szerkezete
 Reális kristályok A szilárd testek szerkezete Reális kristályok, kristályhib lyhibák Aszimmetrikus erők, Anharmonikus rezgés, Kvantummechanikai rendszer Kvantált rezgési állapotok U o nem a potenciálgödör
Reális kristályok A szilárd testek szerkezete Reális kristályok, kristályhib lyhibák Aszimmetrikus erők, Anharmonikus rezgés, Kvantummechanikai rendszer Kvantált rezgési állapotok U o nem a potenciálgödör
(C) Dr. Bagyinszki Gyula: ANYAGTECHNOLÓGIA II.
 HŐKEZELÉS Hőkezelés az anyagok ill. a belőlük készült fél- és készgyártmányok meghatározott program szerinti felhevítése hőntartása lehűtése a mikroszerkezet ill. a feszültségállapot megváltoztatása és
HŐKEZELÉS Hőkezelés az anyagok ill. a belőlük készült fél- és készgyártmányok meghatározott program szerinti felhevítése hőntartása lehűtése a mikroszerkezet ill. a feszültségállapot megváltoztatása és
Programozható irányítóberendezések és szenzorrendszerek ZH. Távadók. Érdemjegy
 Név Neptun-kód Hallgató aláírása 0-15 pont: elégtelen (1) 16-21 pont: elégséges (2) 22-27 pont: közepes (3) 28-33 pont: jó (4) 34-40 pont: jeles (5) Érzékelők jellemzése Hőmérsékletérzékelés Erő- és nyomásmérés
Név Neptun-kód Hallgató aláírása 0-15 pont: elégtelen (1) 16-21 pont: elégséges (2) 22-27 pont: közepes (3) 28-33 pont: jó (4) 34-40 pont: jeles (5) Érzékelők jellemzése Hőmérsékletérzékelés Erő- és nyomásmérés
Kiskunmajsa Város Önkormányzatának partnertérképe
 Kiskunmajsa Város Önkormányzatának partnertérképe Kiskunmajsa Város Önkormányzatának potenciális partnerei Helyi vállalkozások Kiskunmajsa Város Önkormányzata számára a lehetséges vállalati partnerek feltérképezéséhez
Kiskunmajsa Város Önkormányzatának partnertérképe Kiskunmajsa Város Önkormányzatának potenciális partnerei Helyi vállalkozások Kiskunmajsa Város Önkormányzata számára a lehetséges vállalati partnerek feltérképezéséhez
INFORMÁCIÓS MEMORANDUM
 INFORMÁCIÓS MEMORANDUM Kőkút út 7., Hrsz.: 2939/1 3200 GYÖNGYÖS MAGYARORSZÁG INGATLAN SZ.: 008 2011. július Rev.01 Page 1 of 6 Megye Régió Heves Mátra / Gyöngyös Lakosság száma Kb. 35.000 Autópálya csatlakozás
INFORMÁCIÓS MEMORANDUM Kőkút út 7., Hrsz.: 2939/1 3200 GYÖNGYÖS MAGYARORSZÁG INGATLAN SZ.: 008 2011. július Rev.01 Page 1 of 6 Megye Régió Heves Mátra / Gyöngyös Lakosság száma Kb. 35.000 Autópálya csatlakozás
Jelek tanulmányozása
 Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
Reológia 2. Bányai István DE Kolloid- és Környezetkémiai Tanszék
 Reológia 2 Bányai István DE Kolloid- és Környezetkémiai Tanszék Mérése nyomásesés áramlásra p 1 p 2 v=0 folyás csőben z r p 1 p 2 v max I V 1 p p t 8 l 1 2 r 2 x Höppler-típusú viszkoziméter v 2g 9 2 testgömb
Reológia 2 Bányai István DE Kolloid- és Környezetkémiai Tanszék Mérése nyomásesés áramlásra p 1 p 2 v=0 folyás csőben z r p 1 p 2 v max I V 1 p p t 8 l 1 2 r 2 x Höppler-típusú viszkoziméter v 2g 9 2 testgömb
BOLYAI MATEMATIKA CSAPATVERSENY ORSZÁGOS DÖNTŐ SZÓBELI (2012. NOVEMBER 24.) 3. osztály
 3. osztály Két szám összege 33. Mennyi ennek a két számnak a különbsége, ha az egyik kétszerese a másiknak? Hány olyan háromjegyű szám van, amelyben a számjegyek összege legalább 25? 4. osztály A Zimrili
3. osztály Két szám összege 33. Mennyi ennek a két számnak a különbsége, ha az egyik kétszerese a másiknak? Hány olyan háromjegyű szám van, amelyben a számjegyek összege legalább 25? 4. osztály A Zimrili
V. Furatszerelt alkatrészek szerelése újraömlesztéses forrasztási technológiával
 V. Furatszerelt alkatrészek szerelése újraömlesztéses forrasztási technológiával A mérés célja: az úgynevezett pin in paste (továbbiakban PIP) forrasztási technológia megismerése. A mérési feladat: furatszerelt
V. Furatszerelt alkatrészek szerelése újraömlesztéses forrasztási technológiával A mérés célja: az úgynevezett pin in paste (továbbiakban PIP) forrasztási technológia megismerése. A mérési feladat: furatszerelt
3. KÖRGEOMETRIA. 3.1. Körrel kapcsolatos alapismeretek
 3. KÖRGEOMETRIA Hajós György: Bevezetés a geometriába, Tankönyvkiadó, Budapest, 89 109. és 121. oldal. Pelle Béla: Geometria, Tankönyvkiadó, Budapest, 86 97. és 117 121. oldal. Kovács Zoltán: Geometria,
3. KÖRGEOMETRIA Hajós György: Bevezetés a geometriába, Tankönyvkiadó, Budapest, 89 109. és 121. oldal. Pelle Béla: Geometria, Tankönyvkiadó, Budapest, 86 97. és 117 121. oldal. Kovács Zoltán: Geometria,
Az abortusz a magyar közvéleményben
 Az abortusz a magyar közvéleményben Országos felmérés a egyesület számára Módszer: országos reprezentatív felmérés a 18 éves és idősebb lakosság 1200 fős mintájának személyes megkérdezésével a Medián-Omnibusz
Az abortusz a magyar közvéleményben Országos felmérés a egyesület számára Módszer: országos reprezentatív felmérés a 18 éves és idősebb lakosság 1200 fős mintájának személyes megkérdezésével a Medián-Omnibusz
2010.05.12. 1300 Infó Rádió. Hírek
 2010.05.12. 1300 Infó Rádió Hírek 100512 1303 [1127h GAZ MKIK - pozitív index MTI km 100512] Jelentősen javultak a magyar vállalatok várakozásai a következő félévre a Magyar Kereskedelmi és Iparkamara
2010.05.12. 1300 Infó Rádió Hírek 100512 1303 [1127h GAZ MKIK - pozitív index MTI km 100512] Jelentősen javultak a magyar vállalatok várakozásai a következő félévre a Magyar Kereskedelmi és Iparkamara
Osztályozó vizsga kérdések. Mechanika. I.félév. 2. Az erőhatás jellege, jelölések, mértékegységek
 Osztályozó vizsga kérdések Mechanika I.félév 1. Az erő fogalma, jellemzői, mértékegysége 2. Az erőhatás jellege, jelölések, mértékegységek 4 A 4. 4 3. A statika I., II. alaptörvénye 4. A statika III. IV.
Osztályozó vizsga kérdések Mechanika I.félév 1. Az erő fogalma, jellemzői, mértékegysége 2. Az erőhatás jellege, jelölések, mértékegységek 4 A 4. 4 3. A statika I., II. alaptörvénye 4. A statika III. IV.
A mérés célkitűzései: Kaloriméter segítségével az étolaj fajhőjének kísérleti meghatározása a Joule-féle hő segítségével.
 A mérés célkitűzései: Kaloriméter segítségével az étolaj fajhőjének kísérleti meghatározása a Joule-féle hő segítségével. Eszközszükséglet: kaloriméter fűtőszállal digitális mérleg tanulói tápegység vezetékek
A mérés célkitűzései: Kaloriméter segítségével az étolaj fajhőjének kísérleti meghatározása a Joule-féle hő segítségével. Eszközszükséglet: kaloriméter fűtőszállal digitális mérleg tanulói tápegység vezetékek
1. forduló. MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév
 MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév 1. forduló 1. feladat: Jancsi és Juliska Matematikai Memory-t játszik. A játék lényege, hogy négyzet alakú kártyákra vagy műveletsorokat írnak
MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév 1. forduló 1. feladat: Jancsi és Juliska Matematikai Memory-t játszik. A játék lényege, hogy négyzet alakú kártyákra vagy műveletsorokat írnak
Árverés kezelés ECP WEBSHOP BEÉPÜLŐ MODUL ÁRVERÉS KEZELŐ KIEGÉSZÍTÉS. v2.9.28 ECP WEBSHOP V1.8 WEBÁRUHÁZ MODULHOZ
 v2.9.28 Árverés kezelés ECP WEBSHOP BEÉPÜLŐ MODUL ÁRVERÉS KEZELŐ KIEGÉSZÍTÉS ECP WEBSHOP V1.8 WEBÁRUHÁZ MODULHOZ AW STUDIO Nyíregyháza, Luther utca 5. 1/5, info@awstudio.hu Árverés létrehozása Az árverésre
v2.9.28 Árverés kezelés ECP WEBSHOP BEÉPÜLŐ MODUL ÁRVERÉS KEZELŐ KIEGÉSZÍTÉS ECP WEBSHOP V1.8 WEBÁRUHÁZ MODULHOZ AW STUDIO Nyíregyháza, Luther utca 5. 1/5, info@awstudio.hu Árverés létrehozása Az árverésre
Mit lehet kiolvasni a japán gyertyákból?
 Mit lehet kiolvasni a japán gyertyákból? X-Trade Brokers Magyarországi Fióktelepe Szűcs Tímea Mit árulnak nekünk el a gyertyák? A Japán gyertyákra nem csak úgy tekinthetünk, mint egy téglalapra, ami megmutatja
Mit lehet kiolvasni a japán gyertyákból? X-Trade Brokers Magyarországi Fióktelepe Szűcs Tímea Mit árulnak nekünk el a gyertyák? A Japán gyertyákra nem csak úgy tekinthetünk, mint egy téglalapra, ami megmutatja
A táblázatkezelő felépítése
 A táblázatkezelés A táblázatkezelő felépítése A táblázatkezelő felépítése Címsor: A munkafüzet címét mutatja, és a program nevét, amivel megnyitottam. Menüszalag: A menüsor segítségével használhatjuk az
A táblázatkezelés A táblázatkezelő felépítése A táblázatkezelő felépítése Címsor: A munkafüzet címét mutatja, és a program nevét, amivel megnyitottam. Menüszalag: A menüsor segítségével használhatjuk az
Sillabusz az Orvosi kémia szemináriumokhoz. Pécsi Tudományegyetem Általános Orvostudományi Kar 2010/2011. 1
 Sillabusz az Orvosi kémia szemináriumokhoz 1. Az anyag Pécsi Tudományegyetem Általános Orvostudományi Kar 2010/2011. 1 Kémia: az anyag tudománya Kémia: az anyagok összetételével, szerkezetével, tulajdonságaival
Sillabusz az Orvosi kémia szemináriumokhoz 1. Az anyag Pécsi Tudományegyetem Általános Orvostudományi Kar 2010/2011. 1 Kémia: az anyag tudománya Kémia: az anyagok összetételével, szerkezetével, tulajdonságaival
B1: a tej pufferkapacitását B2: a tej fehérjéinek enzimatikus lebontását B3: a tej kalciumtartalmának meghatározását. B.Q1.A a víz ph-ja = [0,25 pont]
![B1: a tej pufferkapacitását B2: a tej fehérjéinek enzimatikus lebontását B3: a tej kalciumtartalmának meghatározását. B.Q1.A a víz ph-ja = [0,25 pont] B1: a tej pufferkapacitását B2: a tej fehérjéinek enzimatikus lebontását B3: a tej kalciumtartalmának meghatározását. B.Q1.A a víz ph-ja = [0,25 pont]](/thumbs/41/22606346.jpg) B feladat : Ebben a kísérleti részben vizsgáljuk, Összpontszám: 20 B1: a tej pufferkapacitását B2: a tej fehérjéinek enzimatikus lebontását B3: a tej kalciumtartalmának meghatározását B1 A tej pufferkapacitása
B feladat : Ebben a kísérleti részben vizsgáljuk, Összpontszám: 20 B1: a tej pufferkapacitását B2: a tej fehérjéinek enzimatikus lebontását B3: a tej kalciumtartalmának meghatározását B1 A tej pufferkapacitása
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
GENERÁTOR FORGÓRÉSZ ELLENŐRZÉS A FLUXUS SZONDA FELÉPÍTÉSE, MŰKÖDÉSE
 GENERÁTOR FORGÓRÉSZ ELLENŐRZÉS A FLUXUS SZONDA FELÉPÍTÉSE, MŰKÖDÉSE Készítette: Ács György RTO FORRÁS: FLUXUS SZONDA ÉS ALKALMAZÁSA KTT MÉRNÖKI IRODA 11SP mérési eredményei A forgórész menetzárlat okozta
GENERÁTOR FORGÓRÉSZ ELLENŐRZÉS A FLUXUS SZONDA FELÉPÍTÉSE, MŰKÖDÉSE Készítette: Ács György RTO FORRÁS: FLUXUS SZONDA ÉS ALKALMAZÁSA KTT MÉRNÖKI IRODA 11SP mérési eredményei A forgórész menetzárlat okozta
Földrajzi helymeghatározás
 A mérés megnevezése, célkitűzései: Földrajzi fokhálózat jelentősége és használata a gyakorlatban Eszközszükséglet: Szükséges anyagok: narancs Szükséges eszközök: GPS készülék, földgömb, földrajz atlasz,
A mérés megnevezése, célkitűzései: Földrajzi fokhálózat jelentősége és használata a gyakorlatban Eszközszükséglet: Szükséges anyagok: narancs Szükséges eszközök: GPS készülék, földgömb, földrajz atlasz,
BOLYAI MATEMATIKA CSAPATVERSENY DÖNTŐ 2004. 5. osztály
 5. osztály Ha egy négyzetet az ábrán látható módon feldarabolunk, akkor a tangram nevű ősi kínai játékot kapjuk. Mekkora a nagy négyzet területe, ha a kicsié 8 cm 2? (A kis négyzet egyik csúcsa a nagy
5. osztály Ha egy négyzetet az ábrán látható módon feldarabolunk, akkor a tangram nevű ősi kínai játékot kapjuk. Mekkora a nagy négyzet területe, ha a kicsié 8 cm 2? (A kis négyzet egyik csúcsa a nagy
MŰTRÁGYA ÉRTÉKESÍTÉS 2009. I-III. negyedév
 Agrárgazdasági Kutató Intézet Statisztikai Osztály MŰTRÁGYA ÉRTÉKESÍTÉS 2009. I-III. negyedév A K I BUDAPEST 2009. december Készült: Agrárgazdasági Kutató Intézet Gazdaságelemzési Igazgatóság Statisztikai
Agrárgazdasági Kutató Intézet Statisztikai Osztály MŰTRÁGYA ÉRTÉKESÍTÉS 2009. I-III. negyedév A K I BUDAPEST 2009. december Készült: Agrárgazdasági Kutató Intézet Gazdaságelemzési Igazgatóság Statisztikai
EPER E-KATA integráció
 EPER E-KATA integráció 1. Összhang a Hivatalban A hivatalban használt szoftverek összekapcsolása, integrálása révén az egyes osztályok, nyilvántartások között egyezőség jön létre. Mit is jelent az integráció?
EPER E-KATA integráció 1. Összhang a Hivatalban A hivatalban használt szoftverek összekapcsolása, integrálása révén az egyes osztályok, nyilvántartások között egyezőség jön létre. Mit is jelent az integráció?
FENNTARTHATÓ FEJLŐDÉS
 FENNTARTHATÓ FEJLŐDÉS Kump Edina ÖKO-Pack Nonprofit Kft. E-mail: edina@okopack.hu Web: www.okopack.hu Dunaújváros, 2014. november 07. A FENNTARTHATÓ FEJLŐDÉS FOGALMA A fenntartható fejlődés a fejlődés
FENNTARTHATÓ FEJLŐDÉS Kump Edina ÖKO-Pack Nonprofit Kft. E-mail: edina@okopack.hu Web: www.okopack.hu Dunaújváros, 2014. november 07. A FENNTARTHATÓ FEJLŐDÉS FOGALMA A fenntartható fejlődés a fejlődés
Tartószerkezetek I. (Vasbeton szilárdságtan)
 Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.09.27. Hajlított vasbeton keresztmetszetek vizsgálata 2 3 Jelölések, elnevezések b : a keresztmetszet szélessége h : a keresztmetszet magassága
Tartószerkezetek I. (Vasbeton szilárdságtan) Szép János 2012.09.27. Hajlított vasbeton keresztmetszetek vizsgálata 2 3 Jelölések, elnevezések b : a keresztmetszet szélessége h : a keresztmetszet magassága
31 525 03 1000 00 00 Karosszérialakatos Karosszérialakatos
 A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
Az éves statisztikai összegezés STATISZTIKAI ÖSSZEGEZÉS AZ ÉVES KÖZBESZERZÉSEKRŐL A KLASSZIKUS AJÁNLATKÉRŐK VONATKOZÁSÁBAN
 11. melléklet a 92/2011. (XII.30.) NFM rendelethez Az éves statisztikai összegezés STATISZTIKAI ÖSSZEGEZÉS AZ ÉVES KÖZBESZERZÉSEKRŐL A KLASSZIKUS AJÁNLATKÉRŐK VONATKOZÁSÁBAN I. SZAKASZ: AJÁNLATKÉRŐ I.1)
11. melléklet a 92/2011. (XII.30.) NFM rendelethez Az éves statisztikai összegezés STATISZTIKAI ÖSSZEGEZÉS AZ ÉVES KÖZBESZERZÉSEKRŐL A KLASSZIKUS AJÁNLATKÉRŐK VONATKOZÁSÁBAN I. SZAKASZ: AJÁNLATKÉRŐ I.1)
G Szabályfelismerés 2.2. 2. feladatcsomag
 ÖSSZEFÜÉSEK Szabályfelismerés 2.2 Alapfeladat Szabályfelismerés 2. feladatcsomag összefüggés-felismerő képesség fejlesztése szabályfelismeréssel megkezdett sorozat folytatása a felismert szabály alapján
ÖSSZEFÜÉSEK Szabályfelismerés 2.2 Alapfeladat Szabályfelismerés 2. feladatcsomag összefüggés-felismerő képesség fejlesztése szabályfelismeréssel megkezdett sorozat folytatása a felismert szabály alapján
SZOLGÁLATI TITOK! KORLÁTOZOTT TERJESZTÉSŰ!
 A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
A 10/2007 (II. 27.) SzMM rendelettel módosított 1/2006 (II. 17.) OM rendelet Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről alapján. Szakképesítés,
#instagramads Az első tapasztalatok. Contact: Eva Drienyovszki Senior Search Specialist eva.drienyovszki@mecglobal.com
 #instagramads Az első tapasztalatok Contact: Eva Drienyovszki Senior Search Specialist eva.drienyovszki@mecglobal.com 2010. július 16. Az első fotó az Instagramon 2011. január 27. Az első hashtaggel ellátott
#instagramads Az első tapasztalatok Contact: Eva Drienyovszki Senior Search Specialist eva.drienyovszki@mecglobal.com 2010. július 16. Az első fotó az Instagramon 2011. január 27. Az első hashtaggel ellátott
Térgeometria feladatok. 2. Egy négyzetes oszlop magassága háromszor akkora, mint az alapéle, felszíne 504 cm 2. Mekkora a testátlója és a térfogata?
 Térgeometria feladatok Téglatest 1. Egy téglatest éleinek aránya 2 : 3 : 5, felszíne 992 cm 2. Mekkora a testátlója és a 2. Egy négyzetes oszlop magassága háromszor akkora, mint az alapéle, felszíne 504
Térgeometria feladatok Téglatest 1. Egy téglatest éleinek aránya 2 : 3 : 5, felszíne 992 cm 2. Mekkora a testátlója és a 2. Egy négyzetes oszlop magassága háromszor akkora, mint az alapéle, felszíne 504
Budapest, 2015. április A beutazó turizmus jellemzői és alakulása 2015-ben A KSH keresletfelmérésének adatai alapján
 Budapest, 2015. április A beutazó jellemzői és alakulása 2015-ben A KSH keresletfelmérésének adatai alapján 2015-ben 20,2 millió külföldi turista látogatott Magyarországra, számuk 17,0%-kal nőtt 2014-hez
Budapest, 2015. április A beutazó jellemzői és alakulása 2015-ben A KSH keresletfelmérésének adatai alapján 2015-ben 20,2 millió külföldi turista látogatott Magyarországra, számuk 17,0%-kal nőtt 2014-hez
Fúvókás sugárbefúvó cső DSA-RR
 Fúvókás sugárbefúvó cső DSA-RR Ferdinand Schad KG Steigstraße 25-27 D-78600 Kolbingen Telefon +49 (0) 74 63-980 - 0 Telefax +49 (0) 74 63-980 - 200 info@schako.de www.schako.de Tartalom Leírás... 3 Kialakítás...
Fúvókás sugárbefúvó cső DSA-RR Ferdinand Schad KG Steigstraße 25-27 D-78600 Kolbingen Telefon +49 (0) 74 63-980 - 0 Telefax +49 (0) 74 63-980 - 200 info@schako.de www.schako.de Tartalom Leírás... 3 Kialakítás...
Az anyagok mágneses tulajdonságai
 BME, Anyagtudomány és Technológia Tanszék Dr. Mészáros István Mágneses tulajdonságok, mágneses anyagok Előadásvázlat 2013. 1 Az anyagok mágneses tulajdonságai Alkalmazási területek Jelentőségük (lágy:
BME, Anyagtudomány és Technológia Tanszék Dr. Mészáros István Mágneses tulajdonságok, mágneses anyagok Előadásvázlat 2013. 1 Az anyagok mágneses tulajdonságai Alkalmazási területek Jelentőségük (lágy:
Bevezetés a lágy számítás módszereibe
 BLSZM-07 p. 1/10 Bevezetés a lágy számítás módszereibe Nem fuzzy halmaz kimenetű fuzzy irányítási rendszerek Egy víztisztító berendezés szabályozását megvalósító modell Viselkedésijósló tervezési példa
BLSZM-07 p. 1/10 Bevezetés a lágy számítás módszereibe Nem fuzzy halmaz kimenetű fuzzy irányítási rendszerek Egy víztisztító berendezés szabályozását megvalósító modell Viselkedésijósló tervezési példa
Statisztika 2016. március 11. A csoport Neptun kód
 Statisztika 2016. március 11. A csoport Név Neptun kód 1. Egy közösségben az élelmiszerre fordított kiadások az alábbiak szerint alakultak: osszeg (ezer Ft) csalad(db) 20 7 20:1 30 12 30:1 40 20 40:1 50
Statisztika 2016. március 11. A csoport Név Neptun kód 1. Egy közösségben az élelmiszerre fordított kiadások az alábbiak szerint alakultak: osszeg (ezer Ft) csalad(db) 20 7 20:1 30 12 30:1 40 20 40:1 50
MATEMATIKA ÍRÁSBELI VIZSGA 2012. május 8.
 MATEMATIKA ÍRÁSBELI VIZSGA 2012. május 8. I. rész Fontos tudnivalók A feladatok megoldásához szöveges adatok tárolására és megjelenítésére nem alkalmas zsebszámológépet és bármelyik négyjegyű függvénytáblázatot
MATEMATIKA ÍRÁSBELI VIZSGA 2012. május 8. I. rész Fontos tudnivalók A feladatok megoldásához szöveges adatok tárolására és megjelenítésére nem alkalmas zsebszámológépet és bármelyik négyjegyű függvénytáblázatot
Hegységképződési folyamat: A hegységek keletkezése két lépcsőben zajlik, egyik lépcső a tektogenezis, másik az orogenezis.
 Hegységképződés Hegységrendszernek nevezzük az egy hegységképződési időszak során keletkezett hegységek együttesét. Egy-egy hegységképződési időszak több millió éves folyamat. Hegységképződési folyamat:
Hegységképződés Hegységrendszernek nevezzük az egy hegységképződési időszak során keletkezett hegységek együttesét. Egy-egy hegységképződési időszak több millió éves folyamat. Hegységképződési folyamat:
Fókuszban a formahibák. Konzultációs nap Minőségfejlesztési Iroda 2013. szeptember 18. Fekete Krisztina
 Fókuszban a formahibák Konzultációs nap Minőségfejlesztési Iroda 2013. szeptember 18. Fekete Krisztina Néhány számadat 2 Benyújtott kérelmek száma: 127 Formai okokból hiánypótlásra felszólított kérelmezők
Fókuszban a formahibák Konzultációs nap Minőségfejlesztési Iroda 2013. szeptember 18. Fekete Krisztina Néhány számadat 2 Benyújtott kérelmek száma: 127 Formai okokból hiánypótlásra felszólított kérelmezők
Miskolci Egyetem. Műszaki Anyagtudományi Kar. Kerpely Antal Anyagtudományok és Technológiák Doktori Iskola VISELKEDÉSE ZÖMÍTÉS SORÁN.
 Miskolci Egyetem Műszaki Anyagtudományi Kar Kerpely Antal Anyagtudományok és Technológiák Doktori Iskola ALUMÍNIUM-MAGNÉZIUM ÖTVÖZETEK FOLYÁSI VISELKEDÉSE ZÖMÍTÉS SORÁN DOKTORI (PH.D.) ÉRTEKEZÉS Mikó Tamás
Miskolci Egyetem Műszaki Anyagtudományi Kar Kerpely Antal Anyagtudományok és Technológiák Doktori Iskola ALUMÍNIUM-MAGNÉZIUM ÖTVÖZETEK FOLYÁSI VISELKEDÉSE ZÖMÍTÉS SORÁN DOKTORI (PH.D.) ÉRTEKEZÉS Mikó Tamás
Anyagismeret fémes anyagok
 Anyagismeret fémes anyagok 1. FEJEZET: AZ ANYAGOK SOKFÉLESÉGE 1.1. Az anyagok csoportosítása az eredet és az emberi szükségletek szerint Eredet szerint: - természetes anyagok (állati, növényi, ásványi)
Anyagismeret fémes anyagok 1. FEJEZET: AZ ANYAGOK SOKFÉLESÉGE 1.1. Az anyagok csoportosítása az eredet és az emberi szükségletek szerint Eredet szerint: - természetes anyagok (állati, növényi, ásványi)
