A mérőszám az egységtől függ, egység-váltással megváltozik ugyan a (mérő)szám, mégis ugyanazt a mért értéket jelenti.
|
|
|
- Diána Szekeres
- 9 évvel ezelőtt
- Látták:
Átírás
1 Mérőszám, mértékegység, mérési bizonytalanság Mérés: ahol a (természet)filozófia és a matematika összeér. Műszer: ahol találkozik a valóság és a tudás. A mérés nem gondolatkísérlet. A mérés gyakorlati, kalibrált eszközt használó, objektív művelet, amely megadja egy jól definiált (mérendő) mennyiség ismeretlen nagyságának relatív (ismert egységhez viszonyított) értékét (ún. egység-alapú paradigma). A mérés: arány felfedezése összehasonlítással. Csakis egynemű mennyiségek hasonlíthatók össze. Skalár (nagyság) Vektor (nagyság és irány) Az anyagmennyiség (amount of stuff, QoM: quantity of matter) pl. megadható mint tömeg (vas), térfogat (víz), terület (szőnyeg), hossz (kötél), számosság (molekulák) fontos tehát tudni, hogy mit is mérünk (milyen anyagról van szó)! A mérés-szó eltérő jelentésű [lehet] a különböző tudományágakban; a szubjektív ítéletalkotások (felmérések: szavazás, teszt-válasz, véleményalkotás) a mérés elnevezéssel annak igazoló / jósló erejét kívánják eljárásuknak tulajdonítani. A mérőeszköz nem varázsdoboz, amely csak úgy kidob egy számot. A mérőszám a mérendő mennyiség relatív nagyságának matematikai tükörképe. A (mérő)számot az egység értelmezi szimbolikus szorzat formájában. (Ez az ártatlan formula jó néhány körmönfont feltételezést rejt, aminek feltárásával [ méréselmélet] indokolható, hogy vannak dolgok, amik nem mérhetők, pl. szépség.) A reprezentáló szám lehetővé teszi, hogy számítással helyettesítsünk gyakorlati manipulációt (pl. mekkora polc kell adott számú, megmért [ismert] vastagságú könyvhöz? ). Ez nem szám-misztika és nem hasonlítható a régi kultúráknak a nevek mágikus erejébe vetett hitéhez. A mértékegységet nem mérjük. A mértékegység definiált érték, nincs igazság kritériuma, csak használhatósága és validitása. Az egység a mérendő mennyiséggel egynemű, célszerűen kiválasztott, fix érték. Az egység-használat történelmileg jóval megelőzte a mennyiségek formális fogalmának, majd a méréselméletnek a kialakulását. ( Nem tudták, de tették. ) Előfordul, hogy különnemű mennyiségeknek azonos elnevezésű (de persze eltérő jelentésű!) az egysége, pl. fok [º] (síkszög ill. hőmérséklet). A mérőszám az egységtől függ, egység-váltással megváltozik ugyan a (mérő)szám, mégis ugyanazt a mért értéket jelenti. Csakis egynemű mennyiségek azonos egységű mérőszámai adhatók össze. A mérési bizonytalanság (régebben: hiba) nem azt jelenti, hogy érvénytelen / rossz / elvetendő a mért érték. Az elkerülhetetlen mérési bizonytalanság egy szűk (jól becsülhető) intervallum: az a mért érték körüli tartomány, amelyen belül van ( szinte biztosan, nagy valószínűséggel) a mérendő értéke. Ez az adat nélkülözhetetlen része a mérési eredménynek, és ismeretünk korlátozott (becsülhető pontosságú) voltát jelenti. 1
2 A mérőeszköz nem varázsdoboz, ami csak úgy kidob egy számot. A mérőszám a (mérendő)mennyiség relatív nagyságának numerikus tükörképe. Mennyiség nagyságának reprezentálása számmal Mennyiségek nagyságának és a (reprezentáló) számoknak a struktúra-azonossága (az empirikus [konkrét] és numerikus [absztrakt] tartományok között relációk/műveletek összekapcsolása) a közvetlen mérés elvi alapja. Illusztratív példa: (a) Összehasonlítva a tömegeket, az eltérő nagyságúakat eltérő számokkal jelöljük, de magától értetődően ha két tömeg azonos nagyságú (pl. az összehasonlításhoz használt kétkarú mérleg egyensúlyban van), akkor ugyanazt a számot rendeljük hozzá: Az nem tűnik megfelelő választásnak, hogy a legnagyobb szám nem a legnagyobb tömeget jelöli, viszont van információ arról, hogy vannak azonos nagyságú tömegek. A számok itt csak elkülönítik, megjelölik a különböző tömegeket (mint pl. a futball játékosokat a mez-számok, ahol persze egy csapaton belül nincsenek azonos számok). (b) Rendezzük nagyság szerint (az összehasonlítás alapján) a tömegeket, és a nagyobb tömeghez nagyobb számot rendeljünk: Itt a számok már jól tükrözik a nagyság szerinti azonosságot (egyenlő) és az eltérést (nagyobb/ kisebb), de a számok még nem adják meg a tömegek helyes arányát tehát még nem használtunk ki minden lehetőséget, ami a számokban rejlik : hányszor nagyobb az egyik tömeg a másiknál (pl. láthatóan az első két tömeg fele a harmadiknak). (c) Kombináljuk a tömegeket, és ha a rendezett sorban egyik tömeg két másik (fizikai) egyesítése 1 /együttese (pl. azokat kétkarú mérleg azonos serpenyőjébe tesszük), akkor logikusan olyan számot rendeljünk hozzá, amely a két összetevőhöz rendelt szám (matematikai) összege (itt a harmadiktól kezdve az előző kettő összege): vagy Így már helyesen reprezentálják a számok a nagyságok egyenlőségét, eltérését és arányát is. A jobboldali ábrán, ahol pl. a legkisebb tömeg nagyságának értékét egységnek választottuk, a számok mérőszámok, vagyis a (mérő)szám és (mérték)egység szorzata a tömeg mért értéke. (A baloldali ábrán az egység értéke az előbbi negyede.) A relációk itt közvetlenül felfedezhetők (pl. kétkarú mérleg egyensúlyban van, ha az első két tömeget az egyik, a harmadikat pedig a másik serpenyőbe tesszük). A nagyságok arányai függetlenek a választott egységtől, ez a relatív mennyiségek állandóságának törvénye. A mérés adja meg az ismeretlen nagyság értékét (ismert egységhez viszonyított arányát). [Ábrák: T. Sider, Properties (2011)] 1 Csak óvatosan az anyag-választással (nehogy robbanás vagy tűz lépjen fel) 2
3 A matematikában, logikában van IGEN/NEM, a méréstechnikában csak: TALÁN. Ezért jellemezni kell a mérés minőségét is (korrekt-e az eredmény). Mérési bizonytalanság A mért érték és a mérendő aktuális értékének eltérése (különbsége) a (mérési) hiba 1, és kis hiba nagy pontosságot jelent: azt minősítik, hogy a két adat mennyire van közel egymáshoz, mennyire megbízható a mérés. A hiba megadásához persze tudni kell(ene) az aktuális értéket de ha azt ismernénk, miért is mérnénk?! Az aktuális értéket a mért érték közelíti, ennek a korlátozott ismeretnek a mértékére becslés a mérési bizonytalanság (ami tehát nem teljes bizonyosságú, de nagy megbízhatóságú adat) és megadásához nem kell ismerni az aktuális értéket! A mérési bizonytalanság meghatározásának nemzetközileg elfogadott, szabványos technikája van (GUM: Guide to the expression of Uncertainty in Measurement), amelynek az a filozófiája, hogy először azonosítja és modellezi az összes fontos összetevőt, elvégzi a lehetséges korrekciót, majd statisztikai vagy más tapasztalati módszerrel becsli az eredő mérési bizonytalanságot: azt a mért érték körüli tartományt (intervallumot) 2, amelyen belül van ( majdnem biztosan, nagy valószínűséggel) a mérendő aktuális (de persze ismeretlen, exakt) értéke. Ez a specifikáció ad bizalmat az eredmény iránt: minél kisebb (szűkebb tartományú) a bizonytalanság, annál nagyobb (több, pontosabb) a tudásunk a mérendőről. Csakis annak a mérésnek van bizonytalansága, amelyikét meghatározták. Két példa (miért is fontos a mért értékhez társított mérési bizonytalanság): (1) Különböző mérőeszközökkel mért adatok összevetésénél, csak a bizonytalansági intervallum ( hiba-sáv ) megadásával tehát (b) és (c) esetben dönthető el, hogy a mért értékek közötti eltérés szignifikáns-e (c), avagy az átlapolódás miatt, ekvivalensnek tekinthető-e a két adat (b). mért érték: (1) (2) határérték (2) Határérték komparálásnál (Go/NOgo): az (a) és (d) eset teljesen egyértelmű, míg a (b) és (c) eset elfogadható (accept) vagy elutasítható (reject) függően a döntés egyéb feltételeitől (pl. életvédelem, gazdaságosság, ár ) 2. 1 Vigyázat: mérési hiba (error), és nem meghibásodás (mistake), a (mérési) bizonytalanság szakkifejezés, és nem a köznapi/naiv értelemben vett jelentésű 2 ±1 hibakorlát, biscuit1, biscuit2 3
4 Megjegyzés: A miért is mérnénk, ha a mérendő aktuális értékét ismernénk kérdésre speciális válasz: ha hitelesítjük 3 / kalibráljuk 4 a mérőeszközt, akkor ismerjük a mérendőt. Ez a minősítési, mérési bizonytalanságot feltérképező (vagy csak néhány paramétert beállító) folyamat történhet közvetlenül a mérés előtt, vagy stabil eszköz esetén korábban szabályos időközönként is, esetleg külső szakértő / akkreditált 5 labor igénybevételével. Szemléletes hasonlattal élve: ugyanaz a helyzet, mint amikor koncert előtt a zenekar tagjai referencia hanghoz igazítva behangolják (zenei)eszközeiket, kivéve pl. a zongorát (amit korábban, ha szükséges, egy szakértő hangol). [Ábra: A. Majcen, Accred Qual Assur (2009)] 3 Az eszköz hitelesítése során a mérésügyi hatóság műszaki vizsgálattal ellenőrzi és tanúsító jellel és/vagy hitelesítési bizonyítvánnyal igazolja, hogy az eszköz megfelel a hitelesítési engedélyében foglalt követelményeknek. A joghatással járó mérés csak a mérési feladat elvégzésére alkalmas hiteles mérőeszközzel (hiteles anyagmintával), vagy használati etalonnal ellenőrzött mérőeszközzel lehet végezni. (Joghatással jár a mérés, ha annak eredménye az állampolgárok és/vagy jogi személyek jogát vagy jogi érdekeit érinti, különösen, ha a mérési eredményt mennyiség és/vagy minőség tanúsítására - a szolgáltatás és ellenszolgáltatás mértékének megállapítására - vagy hatósági ellenőrzésre és bizonyításra használják fel; továbbá az élet- és egészségvédelem, a környezetvédelem és a vagyonvédelem területén.) 4 A kalibrálás (nem hatósági tevékenység) azoknak a műveleteknek az összessége, amelyekkel (meghatározott feltételek mellett) megállapítható az összefüggés a mérőeszköz vagy a mérőrendszer értékmutatása, illetve a mérendő mennyiségnek mértékkel vagy anyagminta által megtestesített, vagy használati etalonnal megvalósított (aktuális) értéke között. 5 minőség-hitelesített 4
5 A mérés célja a bizonyosság, de legalább is a bizonytalanság csökkentése. Alapegyenlet: additív modell (három ekvivalens alak) Abszolút hiba: H x + H = N Δx x: ismeretlen mérendő, Analóg (folytonos) jel H: abszolút hiba, csak tartománya becsülhető, aktuális értéke ismeretlen N: (meg)ismert mérőszám, EGÉSZ szám, Digitális (diszkrét) adat Δx: ismert (választott) mértékegység A mért érték: m = N Δx, és a szorzás ( ) formális, ha a mért érték megjelenítés (digitális kijelzés = display) a cél, azt tizedespont és dimenzió megadása helyettesíti; valóságos, ha pl. beavatkozó jelként kell a mért érték, azt fizikai eszköz: D/A átalakító valósítja meg; x, H, Δx egynemű (és azonos dimenziójú) mennyiségek. Példák (mért érték megjelenítés): f = 92.1 MHz (vagyis a mérőszám N = 921, Δf = 0.1 MHz = 100 khz a legkisebb helyérték értéke [a mértékegység] és M = 10 6, k = 10 3 ún. prefixum); u = 0.05 V (N = 5, a vezető nullákat nem mértük, Δu = 10 mv és m =10-3 ). Kérdés: N = 25 és Δt = 10 ns (n = 10-9 ) esetén t =? (display) Hibaterjedés: összeadás és kivonás műveletnél az abszolút hibák összegződnek. (Elvileg a hibák kiejthetik egymást, de ezt nem tudjuk!) 1 Csakis egynemű, azonos mértékegységű mennyiségek adhatók össze. Példa: x 1 = 23 ± 0.3 cm és x 2 = 17 ± 0.3 cm, ezzel x 1 + x 2 = 40 ± 0.6 cm Relatív hiba: h H H x ( 1+ h) = m, ahol h =, mert h << 1 (azaz x m) x m Szokásosan a relatív hibát %-ban adjuk meg (h 100); az egyenletben h nem % értékben szerepel! Hibaterjedés: szorzás és osztás műveletnél a relatív (%-os) hibák összegződnek. (Eltekintünk a másodrendű kicsiny tagtól, vagyis a hiba hibájától.) 1 Példa: s = 15 m, 2% és t = 5 s, 1% ezekkel az adatokkal v = s/t = 3 m/s, 3%. (Megjegyzés: 3% esetén h = = 0.03 << 1.) Szám hiba: c x H + c = N, ahol c = és min c < 1/2 Δx Δx A mérés arány felfedezése (pontosabban: az EGÉSZ rész, a mérőszám megadása az egységgel történő összehasonlítással), az ezt megvalósító fizikai eszköz: A/D átalakító, ami tehát osztást realizál. Jellegzetes a ±1 hibakorlát ( c < 1), amely pl. kapuzott esemény-számlálás (időtartam ill. frekvencia mérés) esetén lép fel. 1 Csak hibakorlát becsléseket tekintünk. 5
6 Az alapegyenlet jól szemlélteti, hogy egy folytonos mennyiség nagyságát megadó valós arány csak diszkrét számként: mérőszámként ismerhető meg, amit az előzetesen kiválasztott, mesterséges nagyság: a mértékegység, és a becsült hiba-sáv értelmez! A szám egyedül nem mérési eredmény és van mérési bizonytalanság. Különösen digitális kijelzésnél, pontosnak hihetjük a mért értéket, valójában ennek környezetében van (mégpedig a hiba-sávnak megfelelően) a mérendő aktuális értéke. A mérésnek (az egységgel történő összehasonlításnak) egyik de csak egyik! részművelete lehet a számlálás, mint pl. kapuzott esemény-számlálás (időtartam ill. frekvencia mérésnél). A mérés referenciája egynemű (és azonos dimenziójú) a mérendő mennyiséggel. Egység-váltás lehetséges, az új mérőszám ugyanazt az értéket jelenti (pl. 72 km/h = 20 m/s). Ezzel szemben, a diszkrét entitások (elemi részek, részecskék /pl. levegő szennyezettség/, objektumok, események, ) darabszáma közvetlen (le)számlálással adódik (tehát nincs elméleti, csak esetleg gyakorlati probléma), vagyis a számosság értéke pontos 2 és megvan a maga sajátos, természetes egysége: az 1 szám (1 entitás 3, ami nem osztható). A közvetlen számlálás tehát nem ekvivalens a méréssel. A (le)számlálás (vagyis a számosság) bizonyossága 4 és a mérés bizonytalansága a diszkrét entitás és a folytonos mennyiség különbözőségét tükrözi. 2 Feltéve, hogy nem extrém nagy számosságról van szó. Például a kémia használja a (makro- és mikro-világot összekötő) N AVO ~ egység-csomagot. 3 Tekinthető tehát akár dimenziós mennyiségként is (a makroszkópikus minta számossága), a dimenzió: ent (az entitás egysége, konkrét esetben: pcl = number of particles, mcl = number of molecules, cnt = counts, cyl = cycles, ). Ebben az értelmezésben: 1 mol = N AVO ent. (Valójában N AVO konverziós faktor.) Megjegyzés (az extrém nagy számú diszkrét entitás folytonos mennyiségként való értelmezéséhez / észleléséhez): ha van érzékelhető különbség egyetlen (vagy néhány) entitás hozzáadásával, akkor az számosság, ha nincs, akkor nagyság. Mint például a homokdomb-paradoxon esetén: egyetlen vagy néhány (sőt több) homokszem még biztosan nem domb, de egy ponton túl (extrém sok homokszemnél) már igen. Kérdés persze: hol van ez a pont? 4 Igen nagy értékű számosság esetén már valós a hiba lehetősége (pl. stadion beléptetésnél kettős számlálás vagy kihagyás), és így akár adható (többnyire szubjektív becsléssel) bizonytalanság hozzárendelés. 6
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
Mágneses szuszceptibilitás vizsgálata
 Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
[MECHANIKA- HAJLÍTÁS]
![[MECHANIKA- HAJLÍTÁS] [MECHANIKA- HAJLÍTÁS]](/thumbs/39/20428431.jpg) 2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
Mértékegységrendszerek 2006.09.28. 1
 Mértékegységrendszerek 2006.09.28. 1 Mértékegységrendszerek első mértékegységek C. Huygens XVII sz. természeti állandók Párizsi akadémia 1791 hosszúság méter tömeg kilogramm idő másodperc C. F. Gauss 1832
Mértékegységrendszerek 2006.09.28. 1 Mértékegységrendszerek első mértékegységek C. Huygens XVII sz. természeti állandók Párizsi akadémia 1791 hosszúság méter tömeg kilogramm idő másodperc C. F. Gauss 1832
Jelek tanulmányozása
 Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria
 005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
A döntő feladatai. valós számok!
 OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (13. fejezet)
 Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
- mit, hogyan, miért?
 - mit, hogyan, miért? Dr. Bélavári Csilla VITUKI Nonprofit Kft., Minőségbiztosítási és Ellenőrzési Csoport c.belavari@vituki.hu 2011.02.10. 2010. évi záróértekezlet - VITUKI, MECS 1 I. Elfogadott érték
- mit, hogyan, miért? Dr. Bélavári Csilla VITUKI Nonprofit Kft., Minőségbiztosítási és Ellenőrzési Csoport c.belavari@vituki.hu 2011.02.10. 2010. évi záróértekezlet - VITUKI, MECS 1 I. Elfogadott érték
tetszőleges időpillanatban értelmezhető végtelen sok időpont értéke egy véges tartományban bármilyen értéket felvehet végtelen sok érték
 Elektronika 2 tetszőleges időpillanatban értelmezhető végtelen sok időpont értéke egy véges tartományban bármilyen értéket felvehet végtelen sok érték Diszkrét időpillanatokban értelmezhető (időszakaszos)
Elektronika 2 tetszőleges időpillanatban értelmezhető végtelen sok időpont értéke egy véges tartományban bármilyen értéket felvehet végtelen sok érték Diszkrét időpillanatokban értelmezhető (időszakaszos)
HATÁROZAT. A Győr-Moson-Sopron Megyei Kormányhivatal, mint fogyasztóvédelmi hatóság
 Iktatószám: Tárgy: GY/001/00619-0004/2016 Elsőfokú kötelezést kiszabó határozat Határozatszám: 1607K-00117 HATÁROZAT I. A Győr-Moson-Sopron Megyei Kormányhivatal, mint fogyasztóvédelmi hatóság (továbbiakban:
Iktatószám: Tárgy: GY/001/00619-0004/2016 Elsőfokú kötelezést kiszabó határozat Határozatszám: 1607K-00117 HATÁROZAT I. A Győr-Moson-Sopron Megyei Kormányhivatal, mint fogyasztóvédelmi hatóság (továbbiakban:
1. forduló. MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév
 MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév 1. forduló 1. feladat: Jancsi és Juliska Matematikai Memory-t játszik. A játék lényege, hogy négyzet alakú kártyákra vagy műveletsorokat írnak
MEGOLDÁSOK Pontszerző Matematikaverseny 2015/2016-os tanév 1. forduló 1. feladat: Jancsi és Juliska Matematikai Memory-t játszik. A játék lényege, hogy négyzet alakú kártyákra vagy műveletsorokat írnak
Kockázatelméleti alapfogalmak: bizonytalanság. Kovács Norbert SZE, Gazdálkodástudományi Tanszék
 2. Elõadás Kockázatelméleti alapfogalmak: bizonytalanság és kockázat. A kockázatok csoportosítása Kovács Norbert SZE, Gazdálkodástudományi Tanszék A folyamatokat kísérõ bizonytalanság p 1 Várt eredményhez
2. Elõadás Kockázatelméleti alapfogalmak: bizonytalanság és kockázat. A kockázatok csoportosítása Kovács Norbert SZE, Gazdálkodástudományi Tanszék A folyamatokat kísérõ bizonytalanság p 1 Várt eredményhez
Analízis elo adások. Vajda István. 2012. október 3. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
Kiskunmajsa Város Önkormányzatának partnertérképe
 Kiskunmajsa Város Önkormányzatának partnertérképe Kiskunmajsa Város Önkormányzatának potenciális partnerei Helyi vállalkozások Kiskunmajsa Város Önkormányzata számára a lehetséges vállalati partnerek feltérképezéséhez
Kiskunmajsa Város Önkormányzatának partnertérképe Kiskunmajsa Város Önkormányzatának potenciális partnerei Helyi vállalkozások Kiskunmajsa Város Önkormányzata számára a lehetséges vállalati partnerek feltérképezéséhez
Mérési hibák 2007.02.22. 1
 Mérési hibák 007.0.. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák/ Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség általánosított
Mérési hibák 007.0.. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák/ Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség általánosított
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
A Közbeszerzések Tanácsa (Szerkesztőbizottsága) tölti ki A hirdetmény kézhezvételének dátuma KÉ nyilvántartási szám
 KÖZBESZERZÉSI ÉRTESÍTŐ A Közbeszerzések Tanácsának Hivatalos Lapja 1024 Budapest, Margit krt. 85. Fax: 06 1 336 7751, 06 1 336 7757 E-mail: hirdetmeny@kozbeszerzesek-tanacsa.hu On-line értesítés: http://www.kozbeszerzes.hu
KÖZBESZERZÉSI ÉRTESÍTŐ A Közbeszerzések Tanácsának Hivatalos Lapja 1024 Budapest, Margit krt. 85. Fax: 06 1 336 7751, 06 1 336 7757 E-mail: hirdetmeny@kozbeszerzesek-tanacsa.hu On-line értesítés: http://www.kozbeszerzes.hu
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 12 XII. STATIsZTIKA ellenőrző feladatsorok 1. FELADATsOR Megoldások: láthatók nem láthatók 1. minta: 6.10, 0.01, 6.97, 6.03, 3.85, 1.11,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 12 XII. STATIsZTIKA ellenőrző feladatsorok 1. FELADATsOR Megoldások: láthatók nem láthatók 1. minta: 6.10, 0.01, 6.97, 6.03, 3.85, 1.11,
Az aktiválódásoknak azonban itt még nincs vége, ugyanis az aktiválódások 30 évenként ismétlődnek!
 1 Mindannyiunk életében előfordulnak jelentős évek, amikor is egy-egy esemény hatására a sorsunk új irányt vesz. Bár ezen események többségének ott és akkor kevésbé tulajdonítunk jelentőséget, csak idővel,
1 Mindannyiunk életében előfordulnak jelentős évek, amikor is egy-egy esemény hatására a sorsunk új irányt vesz. Bár ezen események többségének ott és akkor kevésbé tulajdonítunk jelentőséget, csak idővel,
http://www.olcsoweboldal.hu ingyenes tanulmány GOOGLE INSIGHTS FOR SEARCH
 2008. augusztus 5-én elindult a Google Insights for Search, ami betekintést nyújt a keresőt használók tömegeinek lelkivilágába, és időben-térben szemlélteti is, amit tud róluk. Az alapja a Google Trends,
2008. augusztus 5-én elindult a Google Insights for Search, ami betekintést nyújt a keresőt használók tömegeinek lelkivilágába, és időben-térben szemlélteti is, amit tud róluk. Az alapja a Google Trends,
FENNTARTHATÓ FEJLŐDÉS
 FENNTARTHATÓ FEJLŐDÉS Kump Edina ÖKO-Pack Nonprofit Kft. E-mail: edina@okopack.hu Web: www.okopack.hu Dunaújváros, 2014. november 07. A FENNTARTHATÓ FEJLŐDÉS FOGALMA A fenntartható fejlődés a fejlődés
FENNTARTHATÓ FEJLŐDÉS Kump Edina ÖKO-Pack Nonprofit Kft. E-mail: edina@okopack.hu Web: www.okopack.hu Dunaújváros, 2014. november 07. A FENNTARTHATÓ FEJLŐDÉS FOGALMA A fenntartható fejlődés a fejlődés
Egyszerű áramkörök vizsgálata
 A kísérlet célkitűzései: Egyszerű áramkörök összeállításának gyakorlása, a mérőműszerek helyes használatának elsajátítása. Eszközszükséglet: Elektromos áramkör készlet (kapcsolótábla, áramköri elemek)
A kísérlet célkitűzései: Egyszerű áramkörök összeállításának gyakorlása, a mérőműszerek helyes használatának elsajátítása. Eszközszükséglet: Elektromos áramkör készlet (kapcsolótábla, áramköri elemek)
[GVMGS11MNC] Gazdaságstatisztika
![[GVMGS11MNC] Gazdaságstatisztika [GVMGS11MNC] Gazdaságstatisztika](/thumbs/40/21500887.jpg) [GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
[GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
Jelentéskészítő TEK-IK () Válaszadók száma = 610
 Jelentéskészítő TEK-IK () Válaszadók száma = 0 Általános mutatók Szak értékelése - + átl.=. Felmérés eredmények Jelmagyarázat Kérdésszöveg Válaszok relatív gyakorisága Bal pólus Skála Átl. elt. Átlag Medián
Jelentéskészítő TEK-IK () Válaszadók száma = 0 Általános mutatók Szak értékelése - + átl.=. Felmérés eredmények Jelmagyarázat Kérdésszöveg Válaszok relatív gyakorisága Bal pólus Skála Átl. elt. Átlag Medián
Conjoint-analízis példa (egyszerűsített)
 Conjoint-analízis példa (egyszerűsített) Az eljárás meghatározza, hogy a fogyasztók a vásárlás szempontjából lényeges terméktulajdonságoknak mekkora relatív fontosságot tulajdonítanak és megadja a tulajdonságok
Conjoint-analízis példa (egyszerűsített) Az eljárás meghatározza, hogy a fogyasztók a vásárlás szempontjából lényeges terméktulajdonságoknak mekkora relatív fontosságot tulajdonítanak és megadja a tulajdonságok
TÖMEGMÉRÉSEK ÉS MÉRLEGVIZSGÁLAT
 TÖMEGMÉRÉSEK ÉS MÉRLEGVIZSGÁLAT Az Magyar Kereskedelmi és Engedélyezési Hivatal Metrológiai Hatósága a tömegmérések területén egyaránt ellát jogilag szabályozott (hatósági), illetve jogilag nem szabályozott
TÖMEGMÉRÉSEK ÉS MÉRLEGVIZSGÁLAT Az Magyar Kereskedelmi és Engedélyezési Hivatal Metrológiai Hatósága a tömegmérések területén egyaránt ellát jogilag szabályozott (hatósági), illetve jogilag nem szabályozott
Az Európai Szabadalmi Egyezmény végrehajtási szabályainak 2010. április 1-étől hatályba lépő lényeges változásai
 DANUBIA Szabadalmi és Védjegy Iroda Kft. Az Európai Szabadalmi Egyezmény végrehajtási szabályainak 2010. április 1-étől hatályba lépő lényeges változásai A Magyar Iparjogvédelmi és Szerzői Jogi Egyesület
DANUBIA Szabadalmi és Védjegy Iroda Kft. Az Európai Szabadalmi Egyezmény végrehajtási szabályainak 2010. április 1-étől hatályba lépő lényeges változásai A Magyar Iparjogvédelmi és Szerzői Jogi Egyesület
EPER E-KATA integráció
 EPER E-KATA integráció 1. Összhang a Hivatalban A hivatalban használt szoftverek összekapcsolása, integrálása révén az egyes osztályok, nyilvántartások között egyezőség jön létre. Mit is jelent az integráció?
EPER E-KATA integráció 1. Összhang a Hivatalban A hivatalban használt szoftverek összekapcsolása, integrálása révén az egyes osztályok, nyilvántartások között egyezőség jön létre. Mit is jelent az integráció?
Beszámoló: a kompetenciamérés eredményének javítását célzó intézkedési tervben foglaltak megvalósításáról. Őcsény, 2015. november 20.
 Őcsényi Perczel Mór Általános Iskola székhelye: 7143 Őcsény, Perczel Mór utca 1. Tel: 74/496-782 e-mail: amk.ocseny@altisk-ocseny.sulinet.hu Ikt.sz.: /2015. OM: 036345 Ügyintéző: Ősze Józsefné Ügyintézés
Őcsényi Perczel Mór Általános Iskola székhelye: 7143 Őcsény, Perczel Mór utca 1. Tel: 74/496-782 e-mail: amk.ocseny@altisk-ocseny.sulinet.hu Ikt.sz.: /2015. OM: 036345 Ügyintéző: Ősze Józsefné Ügyintézés
A mérés célkitűzései: Kaloriméter segítségével az étolaj fajhőjének kísérleti meghatározása a Joule-féle hő segítségével.
 A mérés célkitűzései: Kaloriméter segítségével az étolaj fajhőjének kísérleti meghatározása a Joule-féle hő segítségével. Eszközszükséglet: kaloriméter fűtőszállal digitális mérleg tanulói tápegység vezetékek
A mérés célkitűzései: Kaloriméter segítségével az étolaj fajhőjének kísérleti meghatározása a Joule-féle hő segítségével. Eszközszükséglet: kaloriméter fűtőszállal digitális mérleg tanulói tápegység vezetékek
Dinamikus geometriai programok
 2011 október 22. Eszköz és médium (fotó: http://sliderulemuseum.com) Enter MTM1007L információ: zeus.nyf.hu/ kovacsz feladatok: moodle.nyf.hu Reform mozgalmak A formális matematikát az életkori sajátosságoknak
2011 október 22. Eszköz és médium (fotó: http://sliderulemuseum.com) Enter MTM1007L információ: zeus.nyf.hu/ kovacsz feladatok: moodle.nyf.hu Reform mozgalmak A formális matematikát az életkori sajátosságoknak
Az informatika oktatás téveszméi
 Az informatika oktatás Az informatika definíciója Definíció-1: az informatika az információ keletkezésével, továbbításával, tárolásával, feldolgozásával foglalkozó tudomány. Definíció-2: informatika =
Az informatika oktatás Az informatika definíciója Definíció-1: az informatika az információ keletkezésével, továbbításával, tárolásával, feldolgozásával foglalkozó tudomány. Definíció-2: informatika =
Homlokzati tűzterjedés vizsgálati módszere
 Homlokzati tűzterjedés vizsgálati módszere Siófok 2008. április 17. Dr. Bánky Tamás Nyílásos homlokzatok esetén a tűzterjedési gát kritériumait nem kielégítő homlokzati megoldásoknál továbbá nyílásos homlokzatokon
Homlokzati tűzterjedés vizsgálati módszere Siófok 2008. április 17. Dr. Bánky Tamás Nyílásos homlokzatok esetén a tűzterjedési gát kritériumait nem kielégítő homlokzati megoldásoknál továbbá nyílásos homlokzatokon
Vállalkozásfinanszírozás
 Vállalkozásfinanszírozás Területei Pénzügyi tervezés Beruházás finanszírozás Hitelintézeti eljárás Pénzügyi tervezés a vállalkozásnál tervezés célja: bizonytalanság kockázat csökkentése jövőbeli események,
Vállalkozásfinanszírozás Területei Pénzügyi tervezés Beruházás finanszírozás Hitelintézeti eljárás Pénzügyi tervezés a vállalkozásnál tervezés célja: bizonytalanság kockázat csökkentése jövőbeli események,
HITELESÍTÉSI ELŐÍRÁS ADATTÁROLÓS VITELDÍJJELZŐK ELLENÖRZŐ KÉSZÜLÉKEI HE 110-2001
 HITELESÍTÉSI ELŐÍRÁS HE 110-2001 Az adatbázisban lévő elektronikus változat az érvényes! A nyomtatott forma kizárólag tájékoztató anyag! TARTALOMJEGYZÉK 1. AZ ELŐÍRÁS HATÁLYA...3 2. MÉRTÉKEGYSÉGEK, JELÖLÉSEK...3
HITELESÍTÉSI ELŐÍRÁS HE 110-2001 Az adatbázisban lévő elektronikus változat az érvényes! A nyomtatott forma kizárólag tájékoztató anyag! TARTALOMJEGYZÉK 1. AZ ELŐÍRÁS HATÁLYA...3 2. MÉRTÉKEGYSÉGEK, JELÖLÉSEK...3
Egységes jelátalakítók
 6. Laboratóriumi gyakorlat Egységes jelátalakítók 1. A gyakorlat célja Egységes feszültség és egységes áram jelformáló áramkörök tanulmányozása, átviteli karakterisztikák felvétele, terhelésfüggőségük
6. Laboratóriumi gyakorlat Egységes jelátalakítók 1. A gyakorlat célja Egységes feszültség és egységes áram jelformáló áramkörök tanulmányozása, átviteli karakterisztikák felvétele, terhelésfüggőségük
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
MATEMATIKA HETI 3 ÓRA
 EURÓPAI ÉRETTSÉGI 010 MATEMATIKA HETI 3 ÓRA IDŐPONT : 010. június 4. A VIZSGA IDŐTARTAMA : 3 óra (180 perc) MEGENGEDETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
EURÓPAI ÉRETTSÉGI 010 MATEMATIKA HETI 3 ÓRA IDŐPONT : 010. június 4. A VIZSGA IDŐTARTAMA : 3 óra (180 perc) MEGENGEDETT SEGÉDESZKÖZÖK : Európai képletgyűjtemény Nem programozható, nem grafikus kalkulátor
Épületvillamosság laboratórium. Villámvédelemi felfogó-rendszer hatásosságának vizsgálata
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
Árverés kezelés ECP WEBSHOP BEÉPÜLŐ MODUL ÁRVERÉS KEZELŐ KIEGÉSZÍTÉS. v2.9.28 ECP WEBSHOP V1.8 WEBÁRUHÁZ MODULHOZ
 v2.9.28 Árverés kezelés ECP WEBSHOP BEÉPÜLŐ MODUL ÁRVERÉS KEZELŐ KIEGÉSZÍTÉS ECP WEBSHOP V1.8 WEBÁRUHÁZ MODULHOZ AW STUDIO Nyíregyháza, Luther utca 5. 1/5, info@awstudio.hu Árverés létrehozása Az árverésre
v2.9.28 Árverés kezelés ECP WEBSHOP BEÉPÜLŐ MODUL ÁRVERÉS KEZELŐ KIEGÉSZÍTÉS ECP WEBSHOP V1.8 WEBÁRUHÁZ MODULHOZ AW STUDIO Nyíregyháza, Luther utca 5. 1/5, info@awstudio.hu Árverés létrehozása Az árverésre
A környezettan tantárgy intelligencia fejlesztő lehetőségei
 A környezettan tantárgy intelligencia fejlesztő lehetőségei Készítette: Pék Krisztina biológia környezettan szak Belső konzulens: Dr. Schróth Ágnes Külső konzulens: Dr. Széphalmi Ágnes A szakdolgozatom
A környezettan tantárgy intelligencia fejlesztő lehetőségei Készítette: Pék Krisztina biológia környezettan szak Belső konzulens: Dr. Schróth Ágnes Külső konzulens: Dr. Széphalmi Ágnes A szakdolgozatom
1. Nyomásmérővel mérjük egy gőzvezeték nyomását. A hőmérő méréstartománya 0,00 250,00 kpa,
 1. Nyomásmérővel mérjük egy gőzvezeték nyomását. A hőmérő méréstartománya 0,0 250,0 kpa, pontossága 3% 2 osztás. Mekkora a relatív hibája a 50,0 kpa, illetve a 210,0 kpa értékek mérésének? rel. hiba_tt
1. Nyomásmérővel mérjük egy gőzvezeték nyomását. A hőmérő méréstartománya 0,0 250,0 kpa, pontossága 3% 2 osztás. Mekkora a relatív hibája a 50,0 kpa, illetve a 210,0 kpa értékek mérésének? rel. hiba_tt
Arany Dániel Matematikai Tanulóverseny 2011/2012-es tanév első (iskolai) forduló haladók I. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 011/01-es tanév első (iskolai) forduló haladók I. kategória Megoldások és javítási útmutató 1. Az ábrán látható ABC derékszögű háromszög
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 011/01-es tanév első (iskolai) forduló haladók I. kategória Megoldások és javítási útmutató 1. Az ábrán látható ABC derékszögű háromszög
A Hozzárendelési feladat megoldása Magyar-módszerrel
 A Hozzárendelési feladat megoldása Magyar-módszerrel Virtuális vállalat 2013-2014/1. félév 3. gyakorlat Dr. Kulcsár Gyula A Hozzárendelési feladat Adott meghatározott számú gép és ugyanannyi független
A Hozzárendelési feladat megoldása Magyar-módszerrel Virtuális vállalat 2013-2014/1. félév 3. gyakorlat Dr. Kulcsár Gyula A Hozzárendelési feladat Adott meghatározott számú gép és ugyanannyi független
Jelentés a kiértékelésről az előadóknak
 Debreceni Egyetem 00 Debrecen Egyetem tér. Debreceni Egyetem Tisztelt NK Úr! (személyes és bizalmas) Jelentés a kiértékelésről az előadóknak Tisztelt NK Úr! Ez az email tartalmazza a Népegészségügyi ellenõr
Debreceni Egyetem 00 Debrecen Egyetem tér. Debreceni Egyetem Tisztelt NK Úr! (személyes és bizalmas) Jelentés a kiértékelésről az előadóknak Tisztelt NK Úr! Ez az email tartalmazza a Népegészségügyi ellenõr
Fókuszban a formahibák. Konzultációs nap Minőségfejlesztési Iroda 2013. szeptember 18. Fekete Krisztina
 Fókuszban a formahibák Konzultációs nap Minőségfejlesztési Iroda 2013. szeptember 18. Fekete Krisztina Néhány számadat 2 Benyújtott kérelmek száma: 127 Formai okokból hiánypótlásra felszólított kérelmezők
Fókuszban a formahibák Konzultációs nap Minőségfejlesztési Iroda 2013. szeptember 18. Fekete Krisztina Néhány számadat 2 Benyújtott kérelmek száma: 127 Formai okokból hiánypótlásra felszólított kérelmezők
eredete: Vilfredo Pareto, 80/20 szabály tételek viszonylag kis hányada meghatározó jelentőségű az összességében túlsúlyban lévő sok kis tétellel
 eredete: Vilfredo Pareto, 80/20 szabály tételek viszonylag kis hányada meghatározó jelentőségű az összességében túlsúlyban lévő sok kis tétellel szemben számos területen alkalmazott Minőségmenedzsment:
eredete: Vilfredo Pareto, 80/20 szabály tételek viszonylag kis hányada meghatározó jelentőségű az összességében túlsúlyban lévő sok kis tétellel szemben számos területen alkalmazott Minőségmenedzsment:
Kapcsolt vállalkozások évzáráshoz kapcsolódó egyéb feladatai. Transzferár dokumentálás Szokásos piaci ár levezetés
 Kapcsolt vállalkozások évzáráshoz kapcsolódó egyéb feladatai Transzferár dokumentálás Szokásos piaci ár levezetés Feladatok I. Kapcsoltság vizsgálat II. Cégcsoport méret feltérképezés III. Transzferár
Kapcsolt vállalkozások évzáráshoz kapcsolódó egyéb feladatai Transzferár dokumentálás Szokásos piaci ár levezetés Feladatok I. Kapcsoltság vizsgálat II. Cégcsoport méret feltérképezés III. Transzferár
A 27/2012 (VIII. 27.) NGM rendelet szakmai és vizsgakövetelménye alapján.
 A 27/2012 (VIII. 27.) NGM rendelet szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 34 582 08 Kőműves és hidegburkoló Tájékoztató A vizsgázó az első lapra írja fel a
A 27/2012 (VIII. 27.) NGM rendelet szakmai és vizsgakövetelménye alapján. Szakképesítés, azonosító száma és megnevezése 34 582 08 Kőműves és hidegburkoló Tájékoztató A vizsgázó az első lapra írja fel a
Azonosító jel: Matematika emelt szint
 I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
STANDARDOK ÉS ÉRETTSÉGI ÚJ-ZÉLANDON
 XXI. Századi Közoktatás (fejlesztés, koordináció) II. szakasz TÁMOP-3.1.1-11/1-2012-0001 STANDARDOK ÉS ÉRETTSÉGI ÚJ-ZÉLANDON Új-Zéland geográfia és demográfia Terület: 269.057 km 2 Lakosság: 4,5 millió
XXI. Századi Közoktatás (fejlesztés, koordináció) II. szakasz TÁMOP-3.1.1-11/1-2012-0001 STANDARDOK ÉS ÉRETTSÉGI ÚJ-ZÉLANDON Új-Zéland geográfia és demográfia Terület: 269.057 km 2 Lakosság: 4,5 millió
Dr. Schuster György. 2014. február 21. Real-time operációs rendszerek RTOS
 Real-time operációs rendszerek RTOS 2014. február 21. Az ütemező (Scheduler) Az operációs rendszer azon része (kódszelete), mely valamilyen konkurens hozzáférés-elosztási problémát próbál implementálni.
Real-time operációs rendszerek RTOS 2014. február 21. Az ütemező (Scheduler) Az operációs rendszer azon része (kódszelete), mely valamilyen konkurens hozzáférés-elosztási problémát próbál implementálni.
Házi dolgozat. Minta a házi dolgozat formai és tartalmi követelményeihez. Készítette: (név+osztály) Iskola: (az iskola teljes neve)
 Házi dolgozat Minta a házi dolgozat formai és tartalmi követelményeihez Készítette: (név+osztály) Iskola: (az iskola teljes neve) Dátum: (aktuális dátum) Tartalom Itt kezdődik a címbeli anyag érdemi kifejtése...
Házi dolgozat Minta a házi dolgozat formai és tartalmi követelményeihez Készítette: (név+osztály) Iskola: (az iskola teljes neve) Dátum: (aktuális dátum) Tartalom Itt kezdődik a címbeli anyag érdemi kifejtése...
Beszerzések, közbeszerzési eljárások; Összeférhetetlenség, szabálytalanság. Előadó: dr. Keszler Gábor NFFKÜ Zrt.
 Beszerzések, közbeszerzési eljárások; Összeférhetetlenség, szabálytalanság Előadó: dr. Keszler Gábor NFFKÜ Zrt. Irányadó jogszabályok - az EGT Finanszírozási Mechanizmus és a Norvég Finanszírozási Mechanizmus
Beszerzések, közbeszerzési eljárások; Összeférhetetlenség, szabálytalanság Előadó: dr. Keszler Gábor NFFKÜ Zrt. Irányadó jogszabályok - az EGT Finanszírozási Mechanizmus és a Norvég Finanszírozási Mechanizmus
Analízis elo adások. Vajda István. 2012. szeptember 24. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem 1/8 A halmaz alapfogalom, tehát nem definiáljuk. Jelölés: A halmazokat általában nyomtatott nagybetu vel jelöljük Egy H halmazt akkor tekintünk
Vajda István Neumann János Informatika Kar Óbudai Egyetem 1/8 A halmaz alapfogalom, tehát nem definiáljuk. Jelölés: A halmazokat általában nyomtatott nagybetu vel jelöljük Egy H halmazt akkor tekintünk
Amit a Hőátbocsátási tényezőről tudni kell
 Amit a Hőátbocsátási tényezőről tudni kell Úton-útfélen mindenki róla beszél, már amikor épületekről van szó. A tervezéskor találkozunk vele először, majd az építkezéstől az épület lakhatási engedélyének
Amit a Hőátbocsátási tényezőről tudni kell Úton-útfélen mindenki róla beszél, már amikor épületekről van szó. A tervezéskor találkozunk vele először, majd az építkezéstől az épület lakhatási engedélyének
MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla
 MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla Jelölje Z az egész számok halmazát, N a pozitív egészek halmazát, N 0 a nem negatív egészek halmazát, Q a racionális
MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla Jelölje Z az egész számok halmazát, N a pozitív egészek halmazát, N 0 a nem negatív egészek halmazát, Q a racionális
Sz ekelyhidi L aszl o Val osz ın us egsz am ıt as es matematikai statisztika *************** Budapest, 1998
 Székelyhidi László Valószínűségszámítás és matematikai statisztika *************** Budapest, 1998 Előszó Ez a jegyzet a valószínűségszámításnak és a matematikai statisztikának azokat a fejezeteit tárgyalja,
Székelyhidi László Valószínűségszámítás és matematikai statisztika *************** Budapest, 1998 Előszó Ez a jegyzet a valószínűségszámításnak és a matematikai statisztikának azokat a fejezeteit tárgyalja,
Bevezetés a lágy számítás módszereibe
 BLSZM-07 p. 1/10 Bevezetés a lágy számítás módszereibe Nem fuzzy halmaz kimenetű fuzzy irányítási rendszerek Egy víztisztító berendezés szabályozását megvalósító modell Viselkedésijósló tervezési példa
BLSZM-07 p. 1/10 Bevezetés a lágy számítás módszereibe Nem fuzzy halmaz kimenetű fuzzy irányítási rendszerek Egy víztisztító berendezés szabályozását megvalósító modell Viselkedésijósló tervezési példa
Programozás I. - 9. gyakorlat
 Programozás I. - 9. gyakorlat Mutatók, dinamikus memóriakezelés Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 9, 2009 1 tar@dcs.vein.hu
Programozás I. - 9. gyakorlat Mutatók, dinamikus memóriakezelés Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 9, 2009 1 tar@dcs.vein.hu
Kiterjesztett csomagolás Hiteles fogyasztói tájékoztatás
 Kiterjesztett csomagolás Hiteles fogyasztói tájékoztatás By David Twice Global Comics 2013 All rights reserved Egy reggelem a SafeBrand-del reggel 8.00 Jaj! Feleségecském nincs szabin reggeli reggeli??
Kiterjesztett csomagolás Hiteles fogyasztói tájékoztatás By David Twice Global Comics 2013 All rights reserved Egy reggelem a SafeBrand-del reggel 8.00 Jaj! Feleségecském nincs szabin reggeli reggeli??
2012.03.01. Méréselmélet PE MIK MI, VI BSc 1
 Mérési hibák 2012.03.01. Méréselmélet PE MIK MI, VI BSc 1 Mérés jel- és rendszerelméleti modellje Mérési hibák/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális
Mérési hibák 2012.03.01. Méréselmélet PE MIK MI, VI BSc 1 Mérés jel- és rendszerelméleti modellje Mérési hibák/2 Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális
KÖZLEKEDÉSI ALAPISMERETEK (KÖZLEKEDÉS - ÜZEMVITEL, KÖZLEKEDÉS-TECHNIKA) KÖZLEKEDÉSI ALAPISMERETEK ÉRETTSÉGI VIZSGA II.
 A vizsga részei KÖZLEKEDÉSI ALAPISMERETEK (KÖZLEKEDÉS - ÜZEMVITEL, KÖZLEKEDÉS-TECHNIKA) KÖZLEKEDÉSI ALAPISMERETEK ÉRETTSÉGI VIZSGA II. A VIZSGA LEÍRÁSA Emelt szint Írásbeli vizsga Szóbeli vizsga Írásbeli
A vizsga részei KÖZLEKEDÉSI ALAPISMERETEK (KÖZLEKEDÉS - ÜZEMVITEL, KÖZLEKEDÉS-TECHNIKA) KÖZLEKEDÉSI ALAPISMERETEK ÉRETTSÉGI VIZSGA II. A VIZSGA LEÍRÁSA Emelt szint Írásbeli vizsga Szóbeli vizsga Írásbeli
Radon, Toron és Aeroszol koncentráció viszonyok a Tapolcai Tavas-barlangban
 Radon, Toron és Aeroszol koncentráció viszonyok a Tapolcai Tavas-barlangban Kutatási jelentés Veszprém 29. november 16. Dr. Kávási Norbert ügyvezetı elnök Mérési módszerek, eszközök Légtéri radon és toron
Radon, Toron és Aeroszol koncentráció viszonyok a Tapolcai Tavas-barlangban Kutatási jelentés Veszprém 29. november 16. Dr. Kávási Norbert ügyvezetı elnök Mérési módszerek, eszközök Légtéri radon és toron
Egy heti edzés leírása (5. sz. melléklet)
 Egy heti edzés leírása (5. sz. melléklet) PÉCSI TUDOMÁNYEGYETEM Név:. EHA kód: Szak/Munkarend:.. Sportág:. Kiválasztott csapat/csoport/egyén:. A kiválasztott csoport/csapat/egyén minősítése:. Az edzés
Egy heti edzés leírása (5. sz. melléklet) PÉCSI TUDOMÁNYEGYETEM Név:. EHA kód: Szak/Munkarend:.. Sportág:. Kiválasztott csapat/csoport/egyén:. A kiválasztott csoport/csapat/egyén minősítése:. Az edzés
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN
 GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten RACIONÁLIS TÖRTFÜGGVÉNYEK INTEGRÁLJA Készítette: Gábor Szakmai felel s: Gábor Vázlat
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten RACIONÁLIS TÖRTFÜGGVÉNYEK INTEGRÁLJA Készítette: Gábor Szakmai felel s: Gábor Vázlat
1. Írja fel prímszámok szorzataként a 420-at! 2. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen!
 1. Írja fel prímszámok szorzataként a 40-at! 40 =. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen! A részek: 3. Egy sejttenyészetben naponta kétszereződik meg a sejtek száma.
1. Írja fel prímszámok szorzataként a 40-at! 40 =. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen! A részek: 3. Egy sejttenyészetben naponta kétszereződik meg a sejtek száma.
A SZÁMFOGALOM KIALAKÍTÁSA
 A SZÁMFOGALOM KIALAKÍTÁSA TERMÉSZETES SZÁMOK ÉRTELMEZÉSE 1-5. OSZTÁLY Számok értelmezése 0-tól 10-ig: Véges halmazok számosságaként Mérőszámként Sorszámként Jelzőszámként A számok fogalmának kiterjesztése
A SZÁMFOGALOM KIALAKÍTÁSA TERMÉSZETES SZÁMOK ÉRTELMEZÉSE 1-5. OSZTÁLY Számok értelmezése 0-tól 10-ig: Véges halmazok számosságaként Mérőszámként Sorszámként Jelzőszámként A számok fogalmának kiterjesztése
Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 2005. november. I. rész
 Szászné Simon Judit, 005. november Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 005. november. feladat I. rész Oldjuk meg a valós számok halmazán a x 5x
Szászné Simon Judit, 005. november Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 005. november. feladat I. rész Oldjuk meg a valós számok halmazán a x 5x
Párhuzamos programozás
 Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
Vezetékes gyorsjelentés. 2012. március
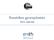 Vezetékes gyorsjelentés 212. március Vezetékes gyorsjelentés, 212. március Adatszolgáltatók: Magyar Telekom Nyrt., Invitel Zrt., GTS Hungary Kft., UPC Magyarország Kft., DIGI Kft., PR- TELEKOM Zrt, Tarr
Vezetékes gyorsjelentés 212. március Vezetékes gyorsjelentés, 212. március Adatszolgáltatók: Magyar Telekom Nyrt., Invitel Zrt., GTS Hungary Kft., UPC Magyarország Kft., DIGI Kft., PR- TELEKOM Zrt, Tarr
BETONACÉLOK HAJLÍTÁSÁHOZ SZÜKSÉGES l\4"yomaték MEGHATÁROZÁSÁNAK EGYSZERŰ MÓDSZERE
 BETONACÉLOK HAJLÍTÁSÁHOZ SZÜKSÉGES l\4"yomaték MEGHATÁROZÁSÁNAK EGYSZERŰ MÓDSZERE BACZY"SKI Gábor Budape?ti 1Iűszaki Egyetem, Közlekedésmérnöki Kar Epítő- és Anyagmozgató Gépek Tanszék Körkeresztmetszet{Í
BETONACÉLOK HAJLÍTÁSÁHOZ SZÜKSÉGES l\4"yomaték MEGHATÁROZÁSÁNAK EGYSZERŰ MÓDSZERE BACZY"SKI Gábor Budape?ti 1Iűszaki Egyetem, Közlekedésmérnöki Kar Epítő- és Anyagmozgató Gépek Tanszék Körkeresztmetszet{Í
BOLYAI MATEMATIKA CSAPATVERSENY FŐVÁROSI DÖNTŐ SZÓBELI (2005. NOVEMBER 26.) 5. osztály
 5. osztály Írd be az ábrán látható hat üres körbe a 10, 30, 40, 60, 70 és 90 számokat úgy, hogy a háromszög mindhárom oldala mentén a számok összege 200 legyen! 50 20 80 Egy dobozban háromféle színű: piros,
5. osztály Írd be az ábrán látható hat üres körbe a 10, 30, 40, 60, 70 és 90 számokat úgy, hogy a háromszög mindhárom oldala mentén a számok összege 200 legyen! 50 20 80 Egy dobozban háromféle színű: piros,
Javítóvizsga témakörei matematika tantárgyból
 9.osztály Halmazok: - ismerje és használja a halmazok megadásának különböző módjait, a halmaz elemének fogalmát - halmazműveletek : ismerje és alkalmazza gyakorlati és matematikai feladatokban a következő
9.osztály Halmazok: - ismerje és használja a halmazok megadásának különböző módjait, a halmaz elemének fogalmát - halmazműveletek : ismerje és alkalmazza gyakorlati és matematikai feladatokban a következő
Algebra es sz amelm elet 3 el oad as Rel aci ok Waldhauser Tam as 2014 oszi f el ev
 Algebra és számelmélet 3 előadás Relációk Waldhauser Tamás 2014 őszi félév Relációk reláció lat. 1. kapcsolat, viszony; összefüggés vmivel 2. viszonylat, vonatkozás reláció lat. 3. mat halmazok elemei
Algebra és számelmélet 3 előadás Relációk Waldhauser Tamás 2014 őszi félév Relációk reláció lat. 1. kapcsolat, viszony; összefüggés vmivel 2. viszonylat, vonatkozás reláció lat. 3. mat halmazok elemei
Kerékpárlabda kvalifikációs szabályzat
 Kerékpárlabda kvalifikációs szabályzat Érvényesség kezdete: Junior kategória 2016 június 1 Felnőtt kategória 2016 január 1 Tartalom I. Célja... 3 II. Szabályozás... 3 1) A versenyek meghatározása... 3
Kerékpárlabda kvalifikációs szabályzat Érvényesség kezdete: Junior kategória 2016 június 1 Felnőtt kategória 2016 január 1 Tartalom I. Célja... 3 II. Szabályozás... 3 1) A versenyek meghatározása... 3
xdsl Optika Kábelnet Mért érték (2012. II. félév): SL24: 79,12% SL72: 98,78%
 Minőségi mutatók Kiskereskedelmi mutatók (Internet) Megnevezés: Új hozzáférés létesítési idő Meghatározás: A szolgáltatáshoz létesített új hozzáféréseknek, az esetek 80%ban teljesített határideje. Mérési
Minőségi mutatók Kiskereskedelmi mutatók (Internet) Megnevezés: Új hozzáférés létesítési idő Meghatározás: A szolgáltatáshoz létesített új hozzáféréseknek, az esetek 80%ban teljesített határideje. Mérési
AZ EOMA SZINTEZÉSI HÁLÓZAT KIEGYENLÍTÉSE
 AZ EOMA SZINTEZÉSI HÁLÓZAT KIEGYENLÍTÉSE Virág Gábor Földmérési és Távérzékelési Intézet Kozmikus Geodéziai Obszervatórium PENC, 2010. 11. 16. ELŐZMÉNYEK ELŐZMÉNYEK Nadap Magassági ősjegy Terebesfejérpatak
AZ EOMA SZINTEZÉSI HÁLÓZAT KIEGYENLÍTÉSE Virág Gábor Földmérési és Távérzékelési Intézet Kozmikus Geodéziai Obszervatórium PENC, 2010. 11. 16. ELŐZMÉNYEK ELŐZMÉNYEK Nadap Magassági ősjegy Terebesfejérpatak
Kockázatkezelés és biztosítás
 Kockázatkezelés és biztosítás Dr. habil. Farkas Szilveszter PhD egyetemi docens, tanszékvezető Pénzügy Intézeti Tanszék Témák 1. Kockáztatott eszközök 2. Károkozó tényezők (vállalati kockázatok) 3. Holisztikus
Kockázatkezelés és biztosítás Dr. habil. Farkas Szilveszter PhD egyetemi docens, tanszékvezető Pénzügy Intézeti Tanszék Témák 1. Kockáztatott eszközök 2. Károkozó tényezők (vállalati kockázatok) 3. Holisztikus
1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi
 1 Mélyhúzott edény teríték méretének meghatározása 1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi A mélyhúzott edény kiindulási teríték átmérőjének meghatározása a térfogat-állandóság alapján
1 Mélyhúzott edény teríték méretének meghatározása 1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi A mélyhúzott edény kiindulási teríték átmérőjének meghatározása a térfogat-állandóság alapján
VASÚTI PÁLYA DINAMIKÁJA
 VASÚTI PÁLYA DINAMIKÁJA Dynamics of the railway track Liegner Nándor BME Út és Vasútépítési Tanszék A vasúti felépítmény szerkezeti elemeiben ébredő igénybevételek A Zimmermann Eisenmann elmélet alapján
VASÚTI PÁLYA DINAMIKÁJA Dynamics of the railway track Liegner Nándor BME Út és Vasútépítési Tanszék A vasúti felépítmény szerkezeti elemeiben ébredő igénybevételek A Zimmermann Eisenmann elmélet alapján
Intézményi jelentés. Összefoglalás. Medgyessy Ferenc Gimnázium és Művészeti Szakközépiskola 4031 Debrecen, Holló László sétány 6 OM azonosító: 031202
 FIT-jelentés :: 2010 Medgyessy Ferenc Gimnázium és Művészeti Szakközépiskola 4031 Debrecen, Holló László sétány 6 Figyelem! A 2010. évi Országos kompetenciaméréstől kezdődően a szövegértés, illetve a matematika
FIT-jelentés :: 2010 Medgyessy Ferenc Gimnázium és Művészeti Szakközépiskola 4031 Debrecen, Holló László sétány 6 Figyelem! A 2010. évi Országos kompetenciaméréstől kezdődően a szövegértés, illetve a matematika
Vektorok összeadása, kivonása, szorzás számmal, koordináták, lineáris függetlenség
 Vektoralgebra Vektorok összeadása, kivonása, szorzás számmal, koordináták, lineáris függetlenség Feladatok: 1) A koordinátarendszerben úgy helyezzük el az egységkockát, hogy az origó az egyik csúcsba essék,
Vektoralgebra Vektorok összeadása, kivonása, szorzás számmal, koordináták, lineáris függetlenség Feladatok: 1) A koordinátarendszerben úgy helyezzük el az egységkockát, hogy az origó az egyik csúcsba essék,
Ö S S Z E G E Z É S A Z A J Á N L A T O K E L B Í R Á L Á S Á R Ó L
 Ö S S Z E G E Z É S A Z A J Á N L A T O K E L B Í R Á L Á S Á R Ó L 1. Az ajánlatkérő neve és címe: Szociális és Gyermekvédelmi Főigazgatóság (székhely: 1132 Budapest, Visegrádi utca 49.) 2. A közbeszerzés
Ö S S Z E G E Z É S A Z A J Á N L A T O K E L B Í R Á L Á S Á R Ó L 1. Az ajánlatkérő neve és címe: Szociális és Gyermekvédelmi Főigazgatóság (székhely: 1132 Budapest, Visegrádi utca 49.) 2. A közbeszerzés
Fazekas Mihály Fővárosi Gyakorló Általános Iskola és Gimnázium
 26 Fazekas Mihály Fővárosi Gyakorló Általános Iskola és Gimnázium Az Önök telephelyére vonatkozó egyedi adatok táblázatokban és grafikonokon 1. évfolyam gimnázium szövegértés Előállítás ideje: 27.3.. 12:28:21
26 Fazekas Mihály Fővárosi Gyakorló Általános Iskola és Gimnázium Az Önök telephelyére vonatkozó egyedi adatok táblázatokban és grafikonokon 1. évfolyam gimnázium szövegértés Előállítás ideje: 27.3.. 12:28:21
Puskás Tivadar Távközlési Technikum
 27 Puskás Tivadar Távközlési Technikum Az Önök telephelyére vonatkozó egyedi adatok táblázatokban és grafikonokon 1. évfolyam szakközépiskola matematika Előállítás ideje: 28.3.6. 6:48:31 197 Budapest,
27 Puskás Tivadar Távközlési Technikum Az Önök telephelyére vonatkozó egyedi adatok táblázatokban és grafikonokon 1. évfolyam szakközépiskola matematika Előállítás ideje: 28.3.6. 6:48:31 197 Budapest,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 5 V. BECsLÉsELMÉLET 1. STATIsZTIKAI becslés A becsléselméletben gyakran feltesszük, hogy a megfigyelt mennyiségek független valószínűségi
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 5 V. BECsLÉsELMÉLET 1. STATIsZTIKAI becslés A becsléselméletben gyakran feltesszük, hogy a megfigyelt mennyiségek független valószínűségi
Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata. Az r-time és a TNS Hoffmann által végzett kutatás
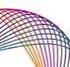 Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata Az r-time és a TNS Hoffmann által végzett kutatás 2002-2010: stabil szponzorációs részarány Televíziós reklámbevételek
Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata Az r-time és a TNS Hoffmann által végzett kutatás 2002-2010: stabil szponzorációs részarány Televíziós reklámbevételek
Digitális technika (VIMIAA01) Laboratórium 1
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika (VIMIAA01) Laboratórium 1 Fehér Béla Raikovich Tamás,
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika (VIMIAA01) Laboratórium 1 Fehér Béla Raikovich Tamás,
Számviteli elemzéshez mutatók
 Számviteli elemzéshez mutatók 1 Cégek helyzetének elemzése Információforrás: E-cégjegyzék (tevékenység, tulajdonosok, telephely, könyvvizsgálat, FB) Cégközlöny (felszámolás, végelszámolás, csődeljárás)
Számviteli elemzéshez mutatók 1 Cégek helyzetének elemzése Információforrás: E-cégjegyzék (tevékenység, tulajdonosok, telephely, könyvvizsgálat, FB) Cégközlöny (felszámolás, végelszámolás, csődeljárás)
Mesterséges Intelligencia. Csató Lehel. Csató Lehel. Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2006/2007
 Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2006/2007 Az Előadások Témái Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció Gráfkeresési stratégiák Szemantikus hálók
Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2006/2007 Az Előadások Témái Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció Gráfkeresési stratégiák Szemantikus hálók
TART TECH KFT. 9611 Csénye, Sport u. 26. Tel.: 95/310-221 Fax: 95/310-222 Mobil: 30/9973-852 E-mail: tarttech@mail.globonet.hu www.tart-tech.
 TART TECH KFT. 9611 Csénye, Sport u. 26. Tel.: 95/310-221 Fax: 95/310-222 Mobil: 30/9973-852 E-mail: tarttech@mail.globonet.hu www.tart-tech.hu HASZNÁLATI UTASÍTÁS S3000/L típusú silómérleg vezérlőegységhez
TART TECH KFT. 9611 Csénye, Sport u. 26. Tel.: 95/310-221 Fax: 95/310-222 Mobil: 30/9973-852 E-mail: tarttech@mail.globonet.hu www.tart-tech.hu HASZNÁLATI UTASÍTÁS S3000/L típusú silómérleg vezérlőegységhez
Pozitron-emissziós tomográf (PET) mire való és hogyan működik?
 Pozitron-emissziós tomográf (PET) mire való és hogyan működik? Major Péter Atomoktól csillagokig, 2011. nov. 10. Vázlat Mi az hogy Tomográf? (fajták, képek) Milyen tomográfok vannak, miért van ennyi? Milyen
Pozitron-emissziós tomográf (PET) mire való és hogyan működik? Major Péter Atomoktól csillagokig, 2011. nov. 10. Vázlat Mi az hogy Tomográf? (fajták, képek) Milyen tomográfok vannak, miért van ennyi? Milyen
A fiatalok pénzügyi kultúrája Számít-e a gazdasági oktatás?
 A fiatalok pénzügyi kultúrája Számít-e a gazdasági oktatás? XXXII. OTDK Konferencia 2015. április 9-11. Készítette: Pintye Alexandra Konzulens: Dr. Kiss Marietta A kultúrától a pénzügyi kultúráig vezető
A fiatalok pénzügyi kultúrája Számít-e a gazdasági oktatás? XXXII. OTDK Konferencia 2015. április 9-11. Készítette: Pintye Alexandra Konzulens: Dr. Kiss Marietta A kultúrától a pénzügyi kultúráig vezető
Sikeres E-DETAILING KAMPÁNY receptje. GYÓGYKOMM 2016. KONFERENCIA Budapest, 2016. február 25. BALOGH JUDIT, PharmaPromo Kft.
 Sikeres E-DETAILING KAMPÁNY receptje GYÓGYKOMM 2016. KONFERENCIA Budapest, 2016. február 25. BALOGH JUDIT, PharmaPromo Kft. AZ ORVOSOK SZÍVESEN FOGADJÁK Szinapszis, 2016. 01., Online (CAWI) kérdőíves kutatás,
Sikeres E-DETAILING KAMPÁNY receptje GYÓGYKOMM 2016. KONFERENCIA Budapest, 2016. február 25. BALOGH JUDIT, PharmaPromo Kft. AZ ORVOSOK SZÍVESEN FOGADJÁK Szinapszis, 2016. 01., Online (CAWI) kérdőíves kutatás,
Felhasználás. Készülék jellemzők. Kalibra59
 RISH Multi 20 Digitális multiméter 5 ¾ digites kijelzés Felhasználás RISH Multi 20 5 ¾ digites multiméter felbontása és alacsony mérési bizonytalansága miatt kiválóan alkalmas mind oktatási, folyamatmérési,
RISH Multi 20 Digitális multiméter 5 ¾ digites kijelzés Felhasználás RISH Multi 20 5 ¾ digites multiméter felbontása és alacsony mérési bizonytalansága miatt kiválóan alkalmas mind oktatási, folyamatmérési,
Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között
 Dr. Nyári Tibor Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között tökéletes színeket visszaadni. A digitális
Dr. Nyári Tibor Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között tökéletes színeket visszaadni. A digitális
2000 db speciális komposztláda, 0,3 m3 térfogatú
 2000 db speciális komposztláda, 0,3 m3 térfogatú Közbeszerzési Értesítő száma: 2005/13 Beszerzés tárgya: Árubeszerzés; Árubeszerzés Hirdetmény típusa: Tájékoztató az eljárás eredményéről (14-es minta)
2000 db speciális komposztláda, 0,3 m3 térfogatú Közbeszerzési Értesítő száma: 2005/13 Beszerzés tárgya: Árubeszerzés; Árubeszerzés Hirdetmény típusa: Tájékoztató az eljárás eredményéről (14-es minta)
Útmutató a vízumkérő lap kitöltéséhez
 Útmutató a vízumkérő lap kitöltéséhez A vízumkérő lap ( Visa application form of the People s Republic of China, Form V. 2013 ) az egyik legfontosabb dokumentum, amit a kínai vízumra való jelentkezésnél
Útmutató a vízumkérő lap kitöltéséhez A vízumkérő lap ( Visa application form of the People s Republic of China, Form V. 2013 ) az egyik legfontosabb dokumentum, amit a kínai vízumra való jelentkezésnél
