A talaj szorpcióval kötött foszfortartalmának tanulmányozása adszorpciós és többlépéses deszorpciós vizsgálatokkal
|
|
|
- Gusztáv Varga
- 9 évvel ezelőtt
- Látták:
Átírás
1 A talaj szorpcióval kötött foszfortartalmának tanulmányozása adszorpciós és többlépéses deszorpciós vizsgálatokkal Tolner László, Füleky György Összefoglaló A talajba juttatott vízben jól oldható formájú foszfátok jelentős része megkötődik a talaj szilárd fázisán. A kötés különböző mértékben reverzibilis. A reverzibilitás időben is változik. A talaj folyékony és szilárd fázisa közötti megoszlás reverzibilis része egyszerű adszorpciós folyamatként kezelhető, a folyamat adszorpciós izoterma modellekkel leírható. Az irreverzibilis folyamatok miatt az adszorpció során megismerhető egyensúlyokból számítható adszorpció modell csak korlátozottan használható a deszorpciós folyamat leírására is. Vizsgálataink során a többlépéses deszorpciós vizsgálatokkal kapott deszorbeálható Q 0 értékek a kezelés mértékétől függően egyre nagyobb mértékben meghaladják az adszorpciós összefüggések 0 egyensúlyi oldatra extrapolált értékeiként kapott Q 0 értékeket. Az eltérés oka a két vizsgálati metodika közötti eltérésből fakad. A többlépéses deszorpció során olyan foszfor mennyiségek is oldatfázisba jutnak, amelyek eredetileg kötöttebb fázisban voltak. Az eltérések ellenére mindkét adat értékes. Az adszorpcióval meghatározott érték a pillanatnyi foszforszolgáltatás lehetőségéről informál, míg a többlépéses deszorpcióval kapott érték a hosszútávon felszabaduló tartós tápanyag-szolgáltató képességet közelíti. Ez utóbbi fontos akkor is, amikor a talaj foszfortartalmát, mint környezet számára potenciális veszélyforrást vizsgáljuk (eutrofizáció). Bevezetés A talajba juttatott vízben jól oldható formájú foszfátok jelentős része megkötődik a talaj szilárd fázisán. Ennek egy része reverzibilis adszorpciót jelent, más része viszont nehezen mobilizálható formában a beépül a talaj szilárd fázisába (Potarski et al., 1999). Mindkét megkötődés függ az oldatban hozzáadott foszfátok koncentrációjától. Az adszorpciós megkötődés leírására adszorpciós izoterma modelleket használnak. Leggyakrabban a Langmuír és a Freundlich izotermát használják. Különböző talajok, illetve azok különbözőképpen kezelt formáin tapasztalható adszorpciós jelenségek összehasonlítására célszerű a lehető legkevesebb paraméterű összefüggést használni. Tolner és Füleky (1995) foszfátok talajon való megkötődésére legalkalmasabbnak találták olyan 1/3 kitevőjű adszorpciós izoterma alkalmazását, amely az eredetileg adszorpciósan kötött állapotú foszfor mennyiségét (Q) is tartalmazza. P adsz. = k * c 1/3 + Q A Q értékét ioncserélő műgyanta segítségével (Fitter and Sutton, 1975, Tolner and Füleky, 1987, Duffera and Robarge, 1999), az izotóposan kicserélhető foszfortartalommal E érték (Olsen and 190
2 A TALAJ SZORPCIÓVAL KÖTÖTT FOSZFORTARTALMÁNAK TANULMÁNYOZÁSA ADSZORPCIÓS ÉS TÖBBLÉPÉSES DESZORPCIÓS VIZSGÁLATOKKAL FÜLEKY70 Watanabe 1957, Bache and Williams 1971) - esetleg az Olsen módszer segítségével (Nychas 1982) lehet - az adszorpciós izotermától független mérés vagy mérések során meghatározni. A Q értékét az adszorpciós görbe 0 egyensúlyi koncentrációra való extrapolációjával is ki lehet számolni (Fitter and Sutton 1975, Rheinheimer et al., 2003, Füleky et al., 2006, Gustafsson et al., 2012). Az így meghatározott Q értékét erősen befolyásolja az, hogy milyen modellt alkalmazunk (Barrow 1978). Mivel a talajon megkötődött mennyiségét az oldatkoncentráció változásából számítjuk ezért mind a független, mind a függő változó ugyanazzal a hibával terhelt. Ez jelentősen befolyásolja a modellillesztés megbízhatóságát (Tellinghausen and Bloster, 2010). Hartikainen (1991) alacsony koncentrációjú foszfátoldatokkal végzett adszorpció esetén lineáris összefüggést kapott. Így a Q számítását lineáris extrapolációval oldotta meg. A több lépéses deszorpciót szemléltethetjük kumulatív görbe segítségével. Ekkor az adott lépésben és a korábbi lépések során oldatba jutó foszfor mennyiségének összegét ábrázoljuk az egyes lépésekben kialakuló egyensúlyi oldat foszforkoncentrációjának függvényében. Az így nyert pontokra formálisan Langmuir izoterma összefüggés illeszthető (Fried & Shapiro, 1956). Valódi deszorpciós izotermát úgy kaphatunk, ha az oldatba jutó mennyiséggel csökkentett talajfoszformennyiséget ábrázoljuk az egyensúlyi oldat foszfor koncentrációjának függvényében (Tolner et al., 1996, Füleky et al., 2006). Q n i= 1 S c i = k c 1 3 n Ha előzőleg adszorpciót végeztünk, és az adszorbeálódott mennyiség visszanyerésére többlépéses deszorpciót végzünk, akkor a deszorpció egyes lépéseit jellemző pontok rendre az adszorpciós izoterma felett helyezkednek el. Ennek Kafkafi és munkatársai (1967) szerint az az oka, hogy az adszorpció során a talajra kerülő foszformennyiség egy része erősebben kötött állapotba kerül, így nem vesz részt az egyensúlyi állapot kialakításában. Ez a távolság az adszorpciós és deszorpciós görbék között elhanyagolhatóvá válik, ha a két folyamat között csak 12 óra telik el, illetve, ha ez az időtartam nem haladja meg az öt napot (Muljadi et al, 1966). Barrow és Shaw (1975) vitatják azt, hogy a deszorpciós lépések során nem kerülhet további számottevő mennyiségű foszfor erősebben kötött állapotba. A megkötődés mértéke függ a folyamat időtartamától, és már akkor is jelentős lehet, ha az adszorpció és a deszorpció között két nap telik el. A több lépéses deszorpció modellezésére Freundlich izoterma összefüggések olyan kombinációját használták, amely figyelembe veszi a szorpciónál lassabban lejátszódó megkötődés folyamatát is. Okajima és munkatársai (1983) a deszorpció reverzibilitását, az adszorpció és deszorpció folyamatok hiszterzisét vizsgálták. A talaj foszfortartalmának csökkenését az egyensúlyi koncentráció logaritmusának függvényében ábrázolták. Közelítőleg egyeneseket kaptak, amelyek meredeksége jellemző volt a folyamat reverzibilitására. Anyag és módszer A modell kipróbálásához szükséges foszforszorpciós kísérletet Orosházáról származó Mélyben szolonyeces csernozjom talaj szántott rétegéből vett mintával végeztük. A talaj vizes ph-ja 7.1, kalcium- 191
3 karbonát-tartalma 1,7%, humusztartalma 3,7%. Fizikai félesége vályog. Foszfortartalma Olsen szerint 8,2 mg.kg -1, izotópos E értéke 17,2 mg.kg -1. A talajmintát különböző (0, 40, 80, 160, és 320 µg.g -1 P) foszforkezelést követően szobahőmérsékleten hét hónapig nedvesen (szántóföldi vízkapacitáson) érleltük. Az érlelt talajmintákat különböző mennyiségű kálium-dihidrogén-foszfáttal készített oldatokkal (0, 40, 80, 160 és 320 µg g -1 P) 1:10 arányú vizes szuszpenzióban 24 órás rázatással egyensúlyba hoztuk. A talajt a vizes fázistól centrifugálással választottuk el. Az oldatkoncentrációk alapján értékeltük az adszorpciót. A centrifugálással elválasztott talajmintákon többlépéses deszorpciós vizsgálatokat végeztünk. A deszorpciós vizsgálat során a talajmintához 1:10 arányban desztillált vizet adtunk, majd 24 órás rázatással egyensúlyba hoztuk. A talajt a vizes fázistól szintén centrifugálással választottuk el. A folyamatot a talajmintákkal 19-szer megismételtük. A kísérlet felépítése az 1. táblázatban látható. 1. táblázat. Az adszorpciós, majd az azt követő deszorpciós kísérlet felépítése Előzetes P kezelés, 7 hónap érlelés 0 µg/g 40 µg/g 80 µg/g 160 µg/g 320 µg/g Friss P adszorpció 0 µg/g 0 µg/g 0 µg/g 0 µg/g 0 µg/g 40 µg/g 40 µg/g 40 µg/g 40 µg/g 40 µg/g 80 µg/g 80 µg/g 80 µg/g 80 µg/g 80 µg/g 160 µg/g 160 µg/g 160 µg/g 160 µg/g 160 µg/g 320 µg/g 320 µg/g 320 µg/g 320 µg/g 320 µg/g Az egyensúlyi oldatok foszfortartalmát Murphy and Riley (1962) módszerrel határoztuk meg. Az eredmények és értékelésük Munkánk során kétféleképpen közelítjük meg méréssel számítással a talajon a korábbi kezelés hatására kialakult szorpciós kötésben levő foszfor mennyiségét. Az egyik a friss kezelésekkel felvett adszorpciós összefüggések 0 egyensúlyi oldatra extrapolált értékei (adsz.q 0 ) ), a másik a többlépéses deszorpciós vizsgálatok során kapott deszorbeálható Q 0 (desz.q 0 ) értékek. Adszorpciós vizsgálatok Az adszorpciós vizsgálat során a különböző korábbi P kezelések (0, 40, 80,160, 320 µg/g) hatására létrejött eltérő mennyiségű kötött foszfort tartalmazó talajokon különböző koncentrációjú kiindulási oldatok segítségével adszorpciós izotermákat veszünk fel. Az adszorpciós izotermák a korábbi kezeléstől függően különböző egyensúlyi koncentráció értékeknél metszik az x tengelyt (1. ábra, bal oldal). 192
4 A TALAJ SZORPCIÓVAL KÖTÖTT FOSZFORTARTALMÁNAK TANULMÁNYOZÁSA ADSZORPCIÓS ÉS TÖBBLÉPÉSES DESZORPCIÓS VIZSGÁLATOKKAL FÜLEKY70 1. ábra. Adszorpciós izotermák (bal oldal). Az adszorpciós izotermák kezdeti szakasza (jobb oldal) és extrapolálása (szaggatott vonal.) 0 egyensúlyi koncentrációra extrapolálva megkapjuk az adszorbeált állapotban levő foszfor mennyiségét (1. ábra, jobb oldal). Az extrapolációval kapott y tengelymetszetek (adsz.q 0 ) értékek jelentősen függnek az extrapoláláskor alkalmazott modellfüggvénytől. Korábbi munkánk során nagyszámú különböző talaj vizsgálatával az 1/3 kitevőjű Freundlich izotermát találtuk a legkedvezőbbnek (Tolner and Füleky 1995). y = k * c 1/3 + Q 0 A függvény illesztésekor megkapott Q 0 érték az c=0 értékhez tartozó extrapolált y tengelymetszet (adsz.q 0 ) (Füleky and Tolner 2006). Mind az 5 méréssorra elvégezve a regresszió-számítást nagyon hasonló k értékeket kaptunk (47, 49, 57, 52, 62). A Q 0 értékek összehasonlíthatósága érdekében célszerűnek látszott korábbi kezeléstől független közös k értéket használni a modellekben, hogy az eltérések csak a Q 0 értékekben jelentkezzenek. Ez nem okozott jelentős hibát, mivel a közös illesztés összesített szórása 1,7-nek adódott illetve a mért és számított értékek közötti összefüggés meredeksége 0,9983, valamint a determinációs koefficiens R 2 =0,9967. A közös k érték 53,98-nak adódott. Az adszorpcióval meghatározott adsz.q 0 értékek az 2. táblázatban találhatók. 2. táblázat. Az adszorpcióval meghatározott adsz.q 0 értékek (µg/g P) Korábbi kezelés P Adsz.Q 0 47,3 67,1 82,3 123,7 193,8 Az adszorpcióval meghatározott Q 0 értékek (adsz.q 0 ) szoros lineáris összefüggést mutattak a korábbi foszforkezelésék értékeivel (2. ábra). 193
5 200,00 180,00 160,00 140,00 120,00 100,00 80,00 60,00 40,00 20,00 0,00 y = 0,459x + 47,738 R² = 0, ábra. Az adszorpcióval meghatározott Q 0 értékek ((adsz.q 0 ) (y tengely) összefüggése a korábbi foszforkezelésekkel (x tengely) (µg/g P) Deszorpciós vizsgálatok A különböző korábbi P kezelések (0, 40, 80, 160, 320 µg/g) hatására létrejött eltérő mennyiségű kötött foszfort tartalmazó talajokat újabb (0, 40, 80,160, 320 µg/g adagú) kezelésnek megfelelő koncentrációjú oldatokkal hoztuk egyensúlyba. Ez a korábbi kezelések függvényében eltérő friss foszforkezeléseket eredményezett. Az így kialakult 25-féle eltérő korábbi és friss foszforkezelést kapott minták szorpciós állapotban levő foszfortartalmát többlépéses egyensúlyi deszorpcióval vizsgáltuk (Tolner et al., 1996). A deszorpciós vizsgálatok eredményeképpen csökkenő egyensúlyi koncentrációjú oldatsorozatokat kaptunk (3. ábra) ábra. A deszorpció lépéseinek függvényében csökkenő egyensúlyi koncentrációjú oldatsorozatok a korábban 80 µg/g kezelést kapott talajmintákon. A görbék felülről lefelé a 320, 160, 80, 40, 0 µg/g friss kezelést kaptak. A pontokat az összetartozás szemléltetése érdekében kötöttük össze. 194
6 A TALAJ SZORPCIÓVAL KÖTÖTT FOSZFORTARTALMÁNAK TANULMÁNYOZÁSA ADSZORPCIÓS ÉS TÖBBLÉPÉSES DESZORPCIÓS VIZSGÁLATOKKAL FÜLEKY70 Korábbi munkánk (Tolner et al., 1996) során bemutattuk, hogy az eredetileg adszorbeált állapotban levő Q mennyiségből levonjuk az adott lépést megelőző korábbi lépésekben eltávolított foszfor mennyiségek összegét, akkor ez a mennyiség ugyanúgy függ az adott egyensúlyi koncentrációtól, mint az adszorpció leírásánál. S értéke a hígítás. Értéke megfelelően megválasztott mértékegységek esetén 1. átrendezve: Ismert k esetén az aktuális és a korábbi lépések koncentrációiból Q kiszámítható. A modell szerint megfelelően megválasztott k esetén az egymást követő deszorpciós lépések mindegyikében ugyanazt a Q értéket kell kapnunk. Ha jó a modell és a Q értékek mégis eltérnek, akkor eltéréseknek két oka lehet. Az egyik a nem megfelelő k érték megválasztása a másik a mérési hibák. Megfelelő k értéknek azt választjuk, ahol a 19 lépésben kiszámított Q értékek szórása a legkisebb. Ugyanúgy, mint az adszorpciós extrapoláció számításakor úgy tekintjük, hogy k azonos az azonos korábbi kezelést, de különböző friss kezelést kapott minták esetében. Ezért az azonos korábbi kezelést kapott és 5 féle friss kezelést kapott mintákra kapott 5*19 Q értékre kapott közös értékének minimumát határoztuk meg a k értékének függvényében. Az így számított szórás a k függvényében egy minimumot mutató görbével ábrázolható (4. ábra). 4. ábra. A korábban 80 µg/g kezelést kapott minta Q i értékeinek együttes szórása a k függvényében. Az ábráról leolvasható, hogy ebben az estben az optimális k érték 44,3. A többi kezelésre is a számításokat elvégezve az eredmények 3. táblázatban láthatók. 195
7 3. táblázat. A k értékek a korábbi kezelések függvényében és a Q értékek a korábbi és a friss kezelések függvényében (µg/g). Korábbi P kezelés k , Friss P 0 53,19 69,69 90,09 126,02 172, ,42 96,20 129,40 137,31 217, ,45 105,00 141,96 146,37 217, ,54 166,97 187,46 206,24 274, ,68 279,72 323,60 346,80 403,95 Ahhoz, hogy megvizsgálhassuk, hogy ezek a Q értékek hogyan függnek a friss kezelések értékétől, pontosítanunk kell ez utóbbiak értékét. A friss kezelések úgy keletkeztek, hogy a különböző korábban kezelést kapott mintákra a friss kezeléseknek megfelelő kiindulási koncentrációjú (0, 40, 80, 160, 320 µg/g talajra számolva) oldatot töltöttünk. Az egyensúly beálltával az egyensúlyi oldatot eltávolítottuk a belekerült, illetve benne maradt foszfortartalommal együtt. Ezek képezték az adszorpciós vizsgálatok egyensúlyi oldatait. Az egyensúlyi oldattal eltávolított foszfortartalmat figyelembe véve kiszámítottuk a friss kezelések értékeit (4. táblázat). 4. táblázat. A korrigált friss kezelések értékei. Korábi P kezelés Hozzáadott friss P ,53 36,10 69,42 102,10 211, ,70 33,35 64,20 122,27 197, ,52 30,10 61,39 112,91 194, ,97 21,96 48,34 95,89 161, ,29-1,09 20,58 55,26 138,33 A többlépéses deszorpcióval mért, számított Q értékek korrigált friss kezelések értékeitől való függését mutatja az 5. ábra ábra. A korrigált friss kezelések és többlépéses deszorpcióval mért, számított Q értékek összefüggése.
8 A TALAJ SZORPCIÓVAL KÖTÖTT FOSZFORTARTALMÁNAK TANULMÁNYOZÁSA ADSZORPCIÓS ÉS TÖBBLÉPÉSES DESZORPCIÓS VIZSGÁLATOKKAL FÜLEKY70 Az egyenesek és a mellettük feltüntetett egyenletek felülről lefelé 320, 160, 80, 40, 0 µg/g kezelésekre vonatkoznak. Az egyenletek alatt feltüntetett determinációs koefficiensek (R 2 ) mutatják a szoros illeszkedést. Az egyenesek meredeksége a növekvő korábbi kezelések függvényében növekvő értékű. Ez azt mutatja, hogy a foszforral jobban telített talajon a frissen adott foszfor nagyobb aránya marad szorbeált (reverzibilis) fázisban. Az egyenesek y tengelyt metsző pontjai a 0 korrigált friss kezelésre számított Q 0 értékek. Ezek jellemzők az adott korábbi kezelésű mintában a deszorbeálható állapotú foszfor mennyiségére (µg/g). A Q 0 értékek a 5. ábrán levő egyenesek egyenleteinek konstans értékei. Ugyanezek láthatók a 5. táblázatban is. A deszorbeálható Q 0 értékeket (5. táblázat) a korábbi P kezelés függvényében ábrázolva másodfokú polinommal leírható összefüggést kapunk (6. ábra). 6. ábra. A deszorbeálható Q 0 értékek a korábbi P kezelés függvényében (µg/g). Kétféleképpen vizsgáltuk azt, hogy a korábbi kezelés során adott mennyiségekhez (P.kez.) képest milyen arányban sikerült visszanyerni (desz.q 0 ) foszfort. Az egyik esetben a kezelés hatására létrejött deszorbeálható Q 0 többletet viszonyítottuk a kezelés értékéhez. Például a 320 µg/g korábbi kezelés esetén (294,0-53,6)/320 = 75%. Ezek a visszanyerési % értékek (5. táblázat, visszanyerési % oszlop) a 320 µg/g korábbi kezelésre kapott 75% értéken kívül a kisebb értékű kezelések esetén % között ingadoztak. 5. táblázat. A deszorbeálható Q 0 értékek és a korábbi P kezelés összefüggései (µg/g). P.kez. desz.q 0 visszanyerés % dq/dp ,0 75 1, ,2 59 0, ,0 46 0, ,6 58 0, ,6 0,41 197
9 A másik esetben a kezelés növekmény hatására létrejövő deszorbeálható Q 0 növekmény értékét vizsgáltuk. Ez a 6. ábrán látható trendfüggvény deriváltja (dq/dp). dq/dp = 0,00107*x + 0,40527 Az egyes kezelés értékekre a deriváltat kiszámolva azt kapjuk, hogy a visszanyerési százalék % között a kezelés szintjével növekvő értéket mutat (5. táblázat dq/dp oszlop) Munkánk során kétféleképpen közelítettük meg méréssel számítással a talajon a korábbi kezelés hatására kialakult szorpciós kötésben levő foszfor mennyiségét. Az egyik a friss kezelésekkel felvett adszorpciós összefüggések 0 egyensúlyi oldatra extrapolált értékei (adsz.q 0 ), a másik a többlépéses deszorpciós vizsgálatok során kapott deszorbeálható Q 0 (desz.q 0 ) értékek (6. táblázat). 6. táblázat. Az adszorpciós és többlépéses deszorpciós vizsgálatokkal kapott Q 0 értékek (µg/g). P.kez. adsz.q 0 desz.q ,3 53, ,1 76, ,3 90, ,7 148, ,8 294,0 Látható, hogy a többlépéses deszorpciós vizsgálatok során kapott deszorbeálható Q 0 értékek a kezelés mértékétől függően egyre nagyobb mértékben meghaladják az adszorpciós összefüggések 0 egyensúlyi oldatra extrapolált értékeiként kapott Q 0 értékeket. Konklúzió Vizsgálataink során a többlépéses deszorpciós vizsgálatokkal kapott deszorbeálható Q 0 értékek a kezelés mértékétől függően egyre nagyobb mértékben meghaladják az adszorpciós összefüggések 0 egyensúlyi oldatra extrapolált értékeiként kapott Q 0 értékeket. Az eltérés oka a két vizsgálati metodika közötti eltérésből fakad. A többlépéses deszorpció során olyan foszfor mennyiségek is oldatfázisba jutnak, amelyek eredetileg kötöttebb fázisban voltak. Az eltérések ellenére mindkét adat értékes. Az adszorpcióval meghatározott érték a pillanatnyi foszforszolgáltatás lehetőségéről informál, míg a többlépéses deszorpcióval kapott érték a hosszútávon felszabaduló tartós tápanyag-szolgáltató képességet közelíti. Ez utóbbi fontos akkor is, amikor a talaj foszfortartalmát, mint környezet számára potenciális veszélyforrást vizsgáljuk (eutrofizáció). Irodalom Bache, B. W., and E. G. Williams A phosphate sorption index for soils. J. Soil Sci. 22: Barrow, N.J The description of phosphate adsorption curves. J. Soil Sci. 29: Barrow, N. J. & Shaw, T. C., The slow reactions between soil and anions: 5. Effect of period of prior contact on the desorption of phosphate from soils. Soil Sci Duffera M - Robarge WP. (1999): Soil characteristics and management effects on phosphorus sorption by highland plateau soils of Ethiopia. SOIL SCI SOC AM J 63 (5):
10 A TALAJ SZORPCIÓVAL KÖTÖTT FOSZFORTARTALMÁNAK TANULMÁNYOZÁSA ADSZORPCIÓS ÉS TÖBBLÉPÉSES DESZORPCIÓS VIZSGÁLATOKKAL FÜLEKY70 Fitter, A.H., and C.D. Sutton The use of the Freundlich isotherm for soil phosphate sorption data. J. Soil Sci. 26: Fried, M. & Shapiro, R. E Phosphate supply pattern of various soils. Soil Sci. Soc. Proc Füleky Gy. - Tolner L. (2006): Determination of the phosphate content originally adsorbed on the soil by fitting an adsorption isotherm model. Applied Ecology and Environmental Research, 4 (2): Füleky Gy. - Tolner L. - Wahdan A. (2006): Effect of acidification on recovery of fertilizer phosphorus with three water extraction methods. Cereal Research Communications, Gustafsson J.P. - Mwamila L.B. - Kergoat K. (2012): The ph dependence of phosphate sorption and desorption in Swedish agricultural soils. Geoderma : Hartikainen, H. (1991): Potential mobility of accumlated phosphorus in soil as estimated by the indices of Q/I plots and by extractant. Soil Sci. 152: Kafkafi, U., Posner, A. M. és Quirk, J. P., Desorption of phosphate from kaolinite. Soil Sci. Soc. Amer. Proc Muljadi, D., Posner, A. M. & Quirk, J. P., The mechanism of phosphate adsorption by kaolinite, gibbsite and pseudoboehmite: I. The isotherms and the effect of ph on adsorption. J. Soil Sci Murphy, J. & Riley, J. P. 1962: A modified single solution method for the determination of phosphate in natural waters. Anal. Chim. Acta Nychas, A.E Phosphate sorption by Greek alkaline soils evaluated with a modified Freundlich equation. Z. Pflanzenernahr. Bodenk. 145: Okajima, H., Kubota, H. & Sakuma. T Hysteresis in the phosphorus sorption and desorption processes of soils. Soil Sci. Plant Nutr Olsen, S.R., and F.S. Watanabe A method to determine a phosphorus adsorption maximum of soils as measured by the Langmuir isotherm. Soil Sci. Soc. Amer. Proc. 21: Potarzycki J. - Gaj R. - Schung E. (2004): Phosphorous adsorption in soils after 20 years (cattle slurry) and mineral (NPK) fertilization. Landbauforschung Völkenrode 54: Rheinheimer DS. - Anghinoni I. - Conte E.(2003): Phosphorus sorption in soil in relation to the initial content and soil management. Revista Brasileira de Ciencia Solo 27 (1): Tellinghuisen J. - Bolster C.H. (2010): Least-Squares Analysis of Phosphorus Soil Sorption Data with Weighting from Variance Function Estimation: A Statistical Case for the Freundlich Isotherm. Environmental Science & Technology 44 (13): Tolner L. & Fuleky Gy Availability of soil phosphorus by anion exchange resin. Bull. Univ. Agric. Sci. Gödöllő Tolner L. - Füleky Gy. (1995): Determination of the Originally Adsorbed Soil Phosphorus by Modified Freundlich Isotherm. Commun. Soil Sci. Plant Anal Tolner L. - Wahdan A. - Füleky Gy. (1996): A talajban adszorbeálódott foszfáttartalom többlépéses deszorpciójának modellezése. Modelling of the Multistep Desorption of the Phosphate Content Adsorbed by the Soil. Agrokémia s Talajtan
A talajban adszorbeálódott foszfáttartalom több lépéses deszorpciójának modellezése
 295 A talajban adszorbeálódott foszfáttartalom több lépéses deszorpciójának modellezése TOLNER LÁZLÓ, ANA A. WAHDAN, FÜLEKY GYÖRGY Agrártudományi Egyetem, Talajtani és Agrokémiai Tanszék, Gödöllı A talajon
295 A talajban adszorbeálódott foszfáttartalom több lépéses deszorpciójának modellezése TOLNER LÁZLÓ, ANA A. WAHDAN, FÜLEKY GYÖRGY Agrártudományi Egyetem, Talajtani és Agrokémiai Tanszék, Gödöllı A talajon
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
Mágneses szuszceptibilitás vizsgálata
 Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
Mágneses szuszceptibilitás vizsgálata Mérést végezte: Gál Veronika I. A mérés elmélete Az anyagok külső mágnesen tér hatására polarizálódnak. Általában az anyagok mágnesezhetőségét az M mágnesezettség
Radon, Toron és Aeroszol koncentráció viszonyok a Tapolcai Tavas-barlangban
 Radon, Toron és Aeroszol koncentráció viszonyok a Tapolcai Tavas-barlangban Kutatási jelentés Veszprém 29. november 16. Dr. Kávási Norbert ügyvezetı elnök Mérési módszerek, eszközök Légtéri radon és toron
Radon, Toron és Aeroszol koncentráció viszonyok a Tapolcai Tavas-barlangban Kutatási jelentés Veszprém 29. november 16. Dr. Kávási Norbert ügyvezetı elnök Mérési módszerek, eszközök Légtéri radon és toron
B1: a tej pufferkapacitását B2: a tej fehérjéinek enzimatikus lebontását B3: a tej kalciumtartalmának meghatározását. B.Q1.A a víz ph-ja = [0,25 pont]
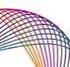
![B1: a tej pufferkapacitását B2: a tej fehérjéinek enzimatikus lebontását B3: a tej kalciumtartalmának meghatározását. B.Q1.A a víz ph-ja = [0,25 pont] B1: a tej pufferkapacitását B2: a tej fehérjéinek enzimatikus lebontását B3: a tej kalciumtartalmának meghatározását. B.Q1.A a víz ph-ja = [0,25 pont]](/thumbs/41/22606346.jpg) B feladat : Ebben a kísérleti részben vizsgáljuk, Összpontszám: 20 B1: a tej pufferkapacitását B2: a tej fehérjéinek enzimatikus lebontását B3: a tej kalciumtartalmának meghatározását B1 A tej pufferkapacitása
B feladat : Ebben a kísérleti részben vizsgáljuk, Összpontszám: 20 B1: a tej pufferkapacitását B2: a tej fehérjéinek enzimatikus lebontását B3: a tej kalciumtartalmának meghatározását B1 A tej pufferkapacitása
1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi
 1 Mélyhúzott edény teríték méretének meghatározása 1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi A mélyhúzott edény kiindulási teríték átmérőjének meghatározása a térfogat-állandóság alapján
1 Mélyhúzott edény teríték méretének meghatározása 1. Mintapélda, amikor a fenék lekerekítési sugár (Rb) kicsi A mélyhúzott edény kiindulási teríték átmérőjének meghatározása a térfogat-állandóság alapján
Épületvillamosság laboratórium. Villámvédelemi felfogó-rendszer hatásosságának vizsgálata
 Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
Budapesti Műszaki és Gazdaságtudományi Egyetem Villamos Energetika Tanszék Nagyfeszültségű Technika és Berendezések Csoport Épületvillamosság laboratórium Villámvédelemi felfogó-rendszer hatásosságának
Egységes jelátalakítók
 6. Laboratóriumi gyakorlat Egységes jelátalakítók 1. A gyakorlat célja Egységes feszültség és egységes áram jelformáló áramkörök tanulmányozása, átviteli karakterisztikák felvétele, terhelésfüggőségük
6. Laboratóriumi gyakorlat Egységes jelátalakítók 1. A gyakorlat célja Egységes feszültség és egységes áram jelformáló áramkörök tanulmányozása, átviteli karakterisztikák felvétele, terhelésfüggőségük
PARABOLIKUS HATÁSFÜGGVÉNY ÉRTELMEZÉSE
 PARABOLIKUS HATÁSFÜGGVÉNY ÉRTELMEZÉSE Tolner László 1 Kiss Szendille 2 Czinkota Imre 1 1 Szent István Egyetem, MKK, Talajtani és Agrokémiai Tanszék 2100 Gödöllő, Páter K. u. 1. E-mail: Tolner.Laszlo@mkk.szie.hu
PARABOLIKUS HATÁSFÜGGVÉNY ÉRTELMEZÉSE Tolner László 1 Kiss Szendille 2 Czinkota Imre 1 1 Szent István Egyetem, MKK, Talajtani és Agrokémiai Tanszék 2100 Gödöllő, Páter K. u. 1. E-mail: Tolner.Laszlo@mkk.szie.hu
Bevezetés a lágy számítás módszereibe
 BLSZM-07 p. 1/10 Bevezetés a lágy számítás módszereibe Nem fuzzy halmaz kimenetű fuzzy irányítási rendszerek Egy víztisztító berendezés szabályozását megvalósító modell Viselkedésijósló tervezési példa
BLSZM-07 p. 1/10 Bevezetés a lágy számítás módszereibe Nem fuzzy halmaz kimenetű fuzzy irányítási rendszerek Egy víztisztító berendezés szabályozását megvalósító modell Viselkedésijósló tervezési példa
Párhuzamos programozás
 Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
A mérések eredményeit az 1. számú táblázatban tüntettük fel.
 Oktatási Hivatal A Mérések függőleges, vastag falú alumínium csőben eső mágnesekkel 2011/2012. tanévi Fizika Országos Középiskolai Tanulmányi Verseny döntő feladatának M E G O L D Á S A I. kategória. A
Oktatási Hivatal A Mérések függőleges, vastag falú alumínium csőben eső mágnesekkel 2011/2012. tanévi Fizika Országos Középiskolai Tanulmányi Verseny döntő feladatának M E G O L D Á S A I. kategória. A
A fiatalok pénzügyi kultúrája Számít-e a gazdasági oktatás?
 A fiatalok pénzügyi kultúrája Számít-e a gazdasági oktatás? XXXII. OTDK Konferencia 2015. április 9-11. Készítette: Pintye Alexandra Konzulens: Dr. Kiss Marietta A kultúrától a pénzügyi kultúráig vezető
A fiatalok pénzügyi kultúrája Számít-e a gazdasági oktatás? XXXII. OTDK Konferencia 2015. április 9-11. Készítette: Pintye Alexandra Konzulens: Dr. Kiss Marietta A kultúrától a pénzügyi kultúráig vezető
[GVMGS11MNC] Gazdaságstatisztika
![[GVMGS11MNC] Gazdaságstatisztika [GVMGS11MNC] Gazdaságstatisztika](/thumbs/40/21500887.jpg) [GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
[GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
Összefoglalás. Summary. Bevezetés
 A talaj kálium ellátottságának vizsgálata módosított Baker-Amacher és,1 M CaCl egyensúlyi kivonószerek alkalmazásával Berényi Sándor Szabó Emese Kremper Rita Loch Jakab Debreceni Egyetem Agrár és Műszaki
A talaj kálium ellátottságának vizsgálata módosított Baker-Amacher és,1 M CaCl egyensúlyi kivonószerek alkalmazásával Berényi Sándor Szabó Emese Kremper Rita Loch Jakab Debreceni Egyetem Agrár és Műszaki
A környezettan tantárgy intelligencia fejlesztő lehetőségei
 A környezettan tantárgy intelligencia fejlesztő lehetőségei Készítette: Pék Krisztina biológia környezettan szak Belső konzulens: Dr. Schróth Ágnes Külső konzulens: Dr. Széphalmi Ágnes A szakdolgozatom
A környezettan tantárgy intelligencia fejlesztő lehetőségei Készítette: Pék Krisztina biológia környezettan szak Belső konzulens: Dr. Schróth Ágnes Külső konzulens: Dr. Széphalmi Ágnes A szakdolgozatom
A követelés-elengedés eredményeként az Ön tartozása <tartozás csökkenésének mértéke> forinttal csökken.
 KITÖLTÉSI ÚTMUTATÓ AZ MNB 14/2015. (X. 27.) AJÁNLÁSÁNAK MELLÉKLETEIHEZ 1. Az ajánlás 1. számú mellékletben szereplő táblázat adattartalma Tájékoztatjuk, hogy a szerződés módosítása esetén a fent megjelölt
KITÖLTÉSI ÚTMUTATÓ AZ MNB 14/2015. (X. 27.) AJÁNLÁSÁNAK MELLÉKLETEIHEZ 1. Az ajánlás 1. számú mellékletben szereplő táblázat adattartalma Tájékoztatjuk, hogy a szerződés módosítása esetén a fent megjelölt
Környezettechnológiai laboratóriumi gyakorlatok M É R É S I J E G Y Z Ő K Ö N Y V. Enzimtechnológia. című gyakorlathoz
 Környezettechnológiai laboratóriumi gyakorlatok M É R É S I J E G Y Z Ő K Ö N Y V az Enzimtechnológia című gyakorlathoz nevek: beugró zárthelyi gyakorlati munka jegyzőkönyv Mérés helye: Mérés ideje: Gyakorlatvezető:
Környezettechnológiai laboratóriumi gyakorlatok M É R É S I J E G Y Z Ő K Ö N Y V az Enzimtechnológia című gyakorlathoz nevek: beugró zárthelyi gyakorlati munka jegyzőkönyv Mérés helye: Mérés ideje: Gyakorlatvezető:
A Hozzárendelési feladat megoldása Magyar-módszerrel
 A Hozzárendelési feladat megoldása Magyar-módszerrel Virtuális vállalat 2013-2014/1. félév 3. gyakorlat Dr. Kulcsár Gyula A Hozzárendelési feladat Adott meghatározott számú gép és ugyanannyi független
A Hozzárendelési feladat megoldása Magyar-módszerrel Virtuális vállalat 2013-2014/1. félév 3. gyakorlat Dr. Kulcsár Gyula A Hozzárendelési feladat Adott meghatározott számú gép és ugyanannyi független
A táblázatkezelő felépítése
 A táblázatkezelés A táblázatkezelő felépítése A táblázatkezelő felépítése Címsor: A munkafüzet címét mutatja, és a program nevét, amivel megnyitottam. Menüszalag: A menüsor segítségével használhatjuk az
A táblázatkezelés A táblázatkezelő felépítése A táblázatkezelő felépítése Címsor: A munkafüzet címét mutatja, és a program nevét, amivel megnyitottam. Menüszalag: A menüsor segítségével használhatjuk az
Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata. Az r-time és a TNS Hoffmann által végzett kutatás
 Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata Az r-time és a TNS Hoffmann által végzett kutatás 2002-2010: stabil szponzorációs részarány Televíziós reklámbevételek
Mehet!...És működik! Non-szpot televíziós hirdetési megjelenések hatékonysági vizsgálata Az r-time és a TNS Hoffmann által végzett kutatás 2002-2010: stabil szponzorációs részarány Televíziós reklámbevételek
BETONACÉLOK HAJLÍTÁSÁHOZ SZÜKSÉGES l\4"yomaték MEGHATÁROZÁSÁNAK EGYSZERŰ MÓDSZERE
 BETONACÉLOK HAJLÍTÁSÁHOZ SZÜKSÉGES l\4"yomaték MEGHATÁROZÁSÁNAK EGYSZERŰ MÓDSZERE BACZY"SKI Gábor Budape?ti 1Iűszaki Egyetem, Közlekedésmérnöki Kar Epítő- és Anyagmozgató Gépek Tanszék Körkeresztmetszet{Í
BETONACÉLOK HAJLÍTÁSÁHOZ SZÜKSÉGES l\4"yomaték MEGHATÁROZÁSÁNAK EGYSZERŰ MÓDSZERE BACZY"SKI Gábor Budape?ti 1Iűszaki Egyetem, Közlekedésmérnöki Kar Epítő- és Anyagmozgató Gépek Tanszék Körkeresztmetszet{Í
2014. évi kukoricakísérlet
 214. évi kukoricakísérlet A Polgári Agrokémiai Kft több, mint egy évtizede végez közös kutatásokat a Debreceni Egyetem Mezőgazdaság-, Élelmiszertudományi és Környezetgazdálkodási Kar Növénytudományi Intézetével
214. évi kukoricakísérlet A Polgári Agrokémiai Kft több, mint egy évtizede végez közös kutatásokat a Debreceni Egyetem Mezőgazdaság-, Élelmiszertudományi és Környezetgazdálkodási Kar Növénytudományi Intézetével
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
Egyszerű áramkörök vizsgálata
 A kísérlet célkitűzései: Egyszerű áramkörök összeállításának gyakorlása, a mérőműszerek helyes használatának elsajátítása. Eszközszükséglet: Elektromos áramkör készlet (kapcsolótábla, áramköri elemek)
A kísérlet célkitűzései: Egyszerű áramkörök összeállításának gyakorlása, a mérőműszerek helyes használatának elsajátítása. Eszközszükséglet: Elektromos áramkör készlet (kapcsolótábla, áramköri elemek)
Programozás I. - 9. gyakorlat
 Programozás I. - 9. gyakorlat Mutatók, dinamikus memóriakezelés Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 9, 2009 1 tar@dcs.vein.hu
Programozás I. - 9. gyakorlat Mutatók, dinamikus memóriakezelés Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 9, 2009 1 tar@dcs.vein.hu
A döntő feladatai. valós számok!
 OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
Semmelweis Egyetem Orvosi Biokémia Intézet Orvosi Biokémia és Molekuláris Biológia gyakorlati jegyzet: Transzaminázok TRANSZAMINÁZOK
 TRANSZAMINÁZOK Az aminosavak α-aminocsoportjainak α-ketosavakra történő transzferét az aminotranszferázok (transzaminázok) katalizálják. A transzamináz enzimek prosztetikus csoportja a piridoxál- foszfát.
TRANSZAMINÁZOK Az aminosavak α-aminocsoportjainak α-ketosavakra történő transzferét az aminotranszferázok (transzaminázok) katalizálják. A transzamináz enzimek prosztetikus csoportja a piridoxál- foszfát.
A biológiai anyagok vízkötési potenciálja meghatározásának elméleti és kísérleti háttere
 A biológiai anyagok vízkötési potenciálja meghatározásának elméleti és kísérleti háttere Kovács Attila József Neményi Miklós Nyugat-Magyarországi Egyetem, Mezőgazdaság- és Élelmiszertudományi Kar, Mosonmagyaróvár
A biológiai anyagok vízkötési potenciálja meghatározásának elméleti és kísérleti háttere Kovács Attila József Neményi Miklós Nyugat-Magyarországi Egyetem, Mezőgazdaság- és Élelmiszertudományi Kar, Mosonmagyaróvár
Fa- és Acélszerkezetek I. 5. Előadás Stabilitás I. Dr. Szalai József Főiskolai adjunktus
 Fa- és Acélszerkezetek I. 5. Előadás Stabilitás I. Dr. Szalai József Főiskolai adjunktus Tartalom Egyensúly elágazási határállapot Rugalmas nyomott oszlop kritikus ereje (Euler erő) Valódi nyomott oszlopok
Fa- és Acélszerkezetek I. 5. Előadás Stabilitás I. Dr. Szalai József Főiskolai adjunktus Tartalom Egyensúly elágazási határállapot Rugalmas nyomott oszlop kritikus ereje (Euler erő) Valódi nyomott oszlopok
Folyadék-gáz, szilárd-gáz folyadék-folyadék és folyadék-szilárd határfelületek. Adszorpció és orientáció a határfelületen. Adszorpció oldatból és
 Folyadék-gáz, szilárd-gáz folyadék-folyadék és folyadék-szilárd határfelületek. Adszorpció és orientáció a határfelületen. Adszorpció oldatból és elegyből. Görbült felületek, Laplace nyomás levegő p 1
Folyadék-gáz, szilárd-gáz folyadék-folyadék és folyadék-szilárd határfelületek. Adszorpció és orientáció a határfelületen. Adszorpció oldatból és elegyből. Görbült felületek, Laplace nyomás levegő p 1
Polikondenzációs termékek
 Polikondenzációs termékek 4. hét Kötı és ragasztó anyagok aminoplasztok (UF, MF, UMF) fenoplasztok (PF) poliamidok (PA) szilikonok (SI) Felületkezelı anyagok poliészterek (alkidgyanták) poliamidok (PA)
Polikondenzációs termékek 4. hét Kötı és ragasztó anyagok aminoplasztok (UF, MF, UMF) fenoplasztok (PF) poliamidok (PA) szilikonok (SI) Felületkezelı anyagok poliészterek (alkidgyanták) poliamidok (PA)
[MECHANIKA- HAJLÍTÁS]
![[MECHANIKA- HAJLÍTÁS] [MECHANIKA- HAJLÍTÁS]](/thumbs/39/20428431.jpg) 2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
2010. Eötvös Loránd Szakközép és Szakiskola Molnár István [MECHANIKA- HAJLÍTÁS] 1 A hajlításra való méretezést sok helyen lehet használni, sok mechanikai probléma modelljét vissza lehet vezetni a hajlítás
ELLENÁLLÁSOK PÁRHUZAMOS KAPCSOLÁSA, KIRCHHOFF I. TÖRVÉNYE, A CSOMÓPONTI TÖRVÉNY ELLENÁLLÁSOK PÁRHUZAMOS KAPCSOLÁSA. 1. ábra
 ELLENÁLLÁSOK PÁRHUZAMOS KAPCSOLÁSA Három háztartási fogyasztót kapcsoltunk egy feszültségforrásra (hálózati feszültségre: 230V), vagyis közös kapocspárra, tehát párhuzamosan. A PÁRHUZAMOS KAPCSOLÁS ISMÉRVE:
ELLENÁLLÁSOK PÁRHUZAMOS KAPCSOLÁSA Három háztartási fogyasztót kapcsoltunk egy feszültségforrásra (hálózati feszültségre: 230V), vagyis közös kapocspárra, tehát párhuzamosan. A PÁRHUZAMOS KAPCSOLÁS ISMÉRVE:
TÁMOP-4.1.1.F-14/1/KONV-2015-0006. Anyagátadási ADSZORPC IÓ
 TÁMOP-4.1.1.F-14/1/KONV-2015-0006 Anyagátadási ADSZORPC IÓ Előkezelés Downstream műveletek Elsődleges szeparálás Tisztítás Végsőformátumú termék Szilárd test külső és belső felületein történő anyagmegkötődés
TÁMOP-4.1.1.F-14/1/KONV-2015-0006 Anyagátadási ADSZORPC IÓ Előkezelés Downstream műveletek Elsődleges szeparálás Tisztítás Végsőformátumú termék Szilárd test külső és belső felületein történő anyagmegkötődés
Repceolaj-alapú félig szintetikus olajok kenési tulajdonságai
 ÜZEMFENNTARTÁSI TEVÉKENYSÉGEK 3.3 Repceolaj-alapú félig szintetikus olajok kenési tulajdonságai Tárgyszavak: észterezett repceolaj; kenési jellemzők; kopási tulajdonság; adalékanyagok hatása. A félig szintetikus
ÜZEMFENNTARTÁSI TEVÉKENYSÉGEK 3.3 Repceolaj-alapú félig szintetikus olajok kenési tulajdonságai Tárgyszavak: észterezett repceolaj; kenési jellemzők; kopási tulajdonság; adalékanyagok hatása. A félig szintetikus
- mit, hogyan, miért?
 - mit, hogyan, miért? Dr. Bélavári Csilla VITUKI Nonprofit Kft., Minőségbiztosítási és Ellenőrzési Csoport c.belavari@vituki.hu 2011.02.10. 2010. évi záróértekezlet - VITUKI, MECS 1 I. Elfogadott érték
- mit, hogyan, miért? Dr. Bélavári Csilla VITUKI Nonprofit Kft., Minőségbiztosítási és Ellenőrzési Csoport c.belavari@vituki.hu 2011.02.10. 2010. évi záróértekezlet - VITUKI, MECS 1 I. Elfogadott érték
Transzformátor vizsgálata
 A kísérlet, mérés célkitűzései: A transzformátor működési elvének megértése, gyakorlati alkalmazás lehetőségeinek megismerése kísérletek útján. Eszközszükséglet: Tanulói transzformátor készlet digitális
A kísérlet, mérés célkitűzései: A transzformátor működési elvének megértése, gyakorlati alkalmazás lehetőségeinek megismerése kísérletek útján. Eszközszükséglet: Tanulói transzformátor készlet digitális
Fazekas Mihály Fővárosi Gyakorló Általános Iskola és Gimnázium
 26 Fazekas Mihály Fővárosi Gyakorló Általános Iskola és Gimnázium Az Önök telephelyére vonatkozó egyedi adatok táblázatokban és grafikonokon 1. évfolyam gimnázium szövegértés Előállítás ideje: 27.3.. 12:28:21
26 Fazekas Mihály Fővárosi Gyakorló Általános Iskola és Gimnázium Az Önök telephelyére vonatkozó egyedi adatok táblázatokban és grafikonokon 1. évfolyam gimnázium szövegértés Előállítás ideje: 27.3.. 12:28:21
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (13. fejezet)
 Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
Áramlástechnikai gépek soros és párhuzamos üzeme, grafikus és numerikus megoldási módszerek (3. fejezet). Egy H I = 70 m - 50000 s /m 5 Q jelleggörbéjű szivattyú a H c = 0 m + 0000 s /m 5 Q jelleggörbéjű
Hibridspecifikus tápanyag-és vízhasznosítás kukoricánál csernozjom talajon
 Hibridspecifikus tápanyag-és vízhasznosítás kukoricánál csernozjom talajon Karancsi Lajos Gábor Debreceni Egyetem Agrár és Gazdálkodástudományok Centruma Mezőgazdaság-, Élelmiszertudományi és Környezetgazdálkodási
Hibridspecifikus tápanyag-és vízhasznosítás kukoricánál csernozjom talajon Karancsi Lajos Gábor Debreceni Egyetem Agrár és Gazdálkodástudományok Centruma Mezőgazdaság-, Élelmiszertudományi és Környezetgazdálkodási
Teherbíró-képesség meghatározásának lehetőségei
 Teherbíró-képesség meghatározásának lehetőségei H-TPA Kft. technológus, BME PhD hallgató 11. Útépítési Akadémia A dinamikus teherbírás adatainak felhasználása az útpályaszerkezetek korszerűsítésében 1
Teherbíró-képesség meghatározásának lehetőségei H-TPA Kft. technológus, BME PhD hallgató 11. Útépítési Akadémia A dinamikus teherbírás adatainak felhasználása az útpályaszerkezetek korszerűsítésében 1
Reológia 2. Bányai István DE Kolloid- és Környezetkémiai Tanszék
 Reológia 2 Bányai István DE Kolloid- és Környezetkémiai Tanszék Mérése nyomásesés áramlásra p 1 p 2 v=0 folyás csőben z r p 1 p 2 v max I V 1 p p t 8 l 1 2 r 2 x Höppler-típusú viszkoziméter v 2g 9 2 testgömb
Reológia 2 Bányai István DE Kolloid- és Környezetkémiai Tanszék Mérése nyomásesés áramlásra p 1 p 2 v=0 folyás csőben z r p 1 p 2 v max I V 1 p p t 8 l 1 2 r 2 x Höppler-típusú viszkoziméter v 2g 9 2 testgömb
Jelek tanulmányozása
 Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
Lineáris algebra gyakorlat
 Lineáris algebra gyakorlat 3 gyakorlat Gyakorlatvezet : Bogya Norbert 2012 február 27 Bogya Norbert Lineáris algebra gyakorlat (3 gyakorlat) Tartalom Egyenletrendszerek Cramer-szabály 1 Egyenletrendszerek
Lineáris algebra gyakorlat 3 gyakorlat Gyakorlatvezet : Bogya Norbert 2012 február 27 Bogya Norbert Lineáris algebra gyakorlat (3 gyakorlat) Tartalom Egyenletrendszerek Cramer-szabály 1 Egyenletrendszerek
A mérés célja: Példák a műveleti erősítők lineáris üzemben történő felhasználására, az előadásokon elhangzottak alkalmazása a gyakorlatban.
 E II. 6. mérés Műveleti erősítők alkalmazása A mérés célja: Példák a műveleti erősítők lineáris üzemben történő felhasználására, az előadásokon elhangzottak alkalmazása a gyakorlatban. A mérésre való felkészülés
E II. 6. mérés Műveleti erősítők alkalmazása A mérés célja: Példák a műveleti erősítők lineáris üzemben történő felhasználására, az előadásokon elhangzottak alkalmazása a gyakorlatban. A mérésre való felkészülés
Országos Középiskolai Tanulmányi Verseny 2011/2012. tanév. Kémia II. kategória 2. forduló. Megoldások
 ktatási Hivatal rszágos Középiskolai Tanulmányi Verseny 011/01. tanév Kémia II. kategória. forduló Megoldások I. feladatsor 1. D 5. A 9. B 1. D. B 6. C 10. B 14. A. C 7. A 11. E 4. A 8. A 1. D 14 pont
ktatási Hivatal rszágos Középiskolai Tanulmányi Verseny 011/01. tanév Kémia II. kategória. forduló Megoldások I. feladatsor 1. D 5. A 9. B 1. D. B 6. C 10. B 14. A. C 7. A 11. E 4. A 8. A 1. D 14 pont
Feladatlap. I. forduló
 Feladatlap a Ki Mit Tud a statisztika világáról szakmai versenyhez I. forduló 2010. szeptember 14. 1. feladat (12 pont) A vállalkozás beszerzéseinek adatai Mennyiség Egységár (Ft/db) (db) megoszlása (%)
Feladatlap a Ki Mit Tud a statisztika világáról szakmai versenyhez I. forduló 2010. szeptember 14. 1. feladat (12 pont) A vállalkozás beszerzéseinek adatai Mennyiség Egységár (Ft/db) (db) megoszlása (%)
Arany Dániel Matematikai Tanulóverseny 2011/2012-es tanév első (iskolai) forduló haladók I. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 011/01-es tanév első (iskolai) forduló haladók I. kategória Megoldások és javítási útmutató 1. Az ábrán látható ABC derékszögű háromszög
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 011/01-es tanév első (iskolai) forduló haladók I. kategória Megoldások és javítási útmutató 1. Az ábrán látható ABC derékszögű háromszög
OTKA Nyilvántartási szám: T 043410 ZÁRÓJELENTÉS
 OTKA Nyilvántartási szám: T 043410 ZÁRÓJELENTÉS Témavezető neve: Dr. Vágó Imre A téma címe: Talajok könnyen felvehető bórkészletének meghatározására alkalmas kivonószer kidolgozása, az egyes talajtulajdonságok
OTKA Nyilvántartási szám: T 043410 ZÁRÓJELENTÉS Témavezető neve: Dr. Vágó Imre A téma címe: Talajok könnyen felvehető bórkészletének meghatározására alkalmas kivonószer kidolgozása, az egyes talajtulajdonságok
Conjoint-analízis példa (egyszerűsített)
 Conjoint-analízis példa (egyszerűsített) Az eljárás meghatározza, hogy a fogyasztók a vásárlás szempontjából lényeges terméktulajdonságoknak mekkora relatív fontosságot tulajdonítanak és megadja a tulajdonságok
Conjoint-analízis példa (egyszerűsített) Az eljárás meghatározza, hogy a fogyasztók a vásárlás szempontjából lényeges terméktulajdonságoknak mekkora relatív fontosságot tulajdonítanak és megadja a tulajdonságok
Agrárgazdasági Kutató Intézet Piac-árinformációs Szolgálat. Borpiaci információk. III. évfolyam / 7. szám 2005. április 28. 14-15.
 A K I Borpiaci információk III. évfolyam / 7. szám 25. április 28. 14- Bor piaci jelentés Borpiaci információk 1-4. táblázat, 1-8. ábra: Belföldi értékesítési-árak és mennyiségi adatok 2. oldal 3-7. oldal
A K I Borpiaci információk III. évfolyam / 7. szám 25. április 28. 14- Bor piaci jelentés Borpiaci információk 1-4. táblázat, 1-8. ábra: Belföldi értékesítési-árak és mennyiségi adatok 2. oldal 3-7. oldal
Adatgyőjtés, mérési alapok, a környezetgazdálkodás fontosabb mőszerei
 GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
GazdálkodásimodulGazdaságtudományismeretekI.Közgazdaságtan KÖRNYEZETGAZDÁLKODÁSIMÉRNÖKIMScTERMÉSZETVÉDELMIMÉRNÖKIMSc Tudományos kutatásmódszertani, elemzési és közlési ismeretek modul Adatgyőjtés, mérési
Puskás Tivadar Távközlési Technikum
 27 Puskás Tivadar Távközlési Technikum Az Önök telephelyére vonatkozó egyedi adatok táblázatokban és grafikonokon 1. évfolyam szakközépiskola matematika Előállítás ideje: 28.3.6. 6:48:31 197 Budapest,
27 Puskás Tivadar Távközlési Technikum Az Önök telephelyére vonatkozó egyedi adatok táblázatokban és grafikonokon 1. évfolyam szakközépiskola matematika Előállítás ideje: 28.3.6. 6:48:31 197 Budapest,
Statisztika 2016. március 11. A csoport Neptun kód
 Statisztika 2016. március 11. A csoport Név Neptun kód 1. Egy közösségben az élelmiszerre fordított kiadások az alábbiak szerint alakultak: osszeg (ezer Ft) csalad(db) 20 7 20:1 30 12 30:1 40 20 40:1 50
Statisztika 2016. március 11. A csoport Név Neptun kód 1. Egy közösségben az élelmiszerre fordított kiadások az alábbiak szerint alakultak: osszeg (ezer Ft) csalad(db) 20 7 20:1 30 12 30:1 40 20 40:1 50
MINTA. Fizetendô összeg: 62 136,00 HUF. Telefonon: 06 40 / 20 99 20 ben: Interneten:
 Részszámla Számla. eredeti példány / oldal Elszámolási idôszak: 00.0. - 00.09.. Partnerszám: 000009 Fizetési határidô: 00.09.0. Vevô neve, címe: Minta út. Fizetendô összeg:, Minta út. Szerzôdéses folyószámla
Részszámla Számla. eredeti példány / oldal Elszámolási idôszak: 00.0. - 00.09.. Partnerszám: 000009 Fizetési határidô: 00.09.0. Vevô neve, címe: Minta út. Fizetendô összeg:, Minta út. Szerzôdéses folyószámla
Kombinatorika. 9. előadás. Farkas István. DE ATC Gazdaságelemzési és Statisztikai Tanszék. Kombinatorika p. 1/
 Kombinatorika 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Kombinatorika p. 1/ Permutáció Definíció. Adott n különböző elem. Az elemek egy meghatározott sorrendjét az adott
Kombinatorika 9. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Kombinatorika p. 1/ Permutáció Definíció. Adott n különböző elem. Az elemek egy meghatározott sorrendjét az adott
Illeszkedésvizsgálat
 Slide 1 Illeszkedésvizsgálat (kategória értékű változóra) Freedman: 28. fejezet 1-3. Egy képzeletbeli országban 10M ember lakik: 30% szőke, 10% barna, 60% fekete. Slide 2 N = 200 fős mintát vettünk, a
Slide 1 Illeszkedésvizsgálat (kategória értékű változóra) Freedman: 28. fejezet 1-3. Egy képzeletbeli országban 10M ember lakik: 30% szőke, 10% barna, 60% fekete. Slide 2 N = 200 fős mintát vettünk, a
VITAFORT ZRT SZAKMAI NAP 2016 06 02
 VITAFORT ZRT SZAKMAI NAP 2016 06 02 Az ellés körüli időszak néhány kritikus tényezője 2 Energiahiány (NEB) Akut kalciumhiány ellési bénulás Alacsonyabb takarmányfelvétel Oltógyomor áthelyeződés Egyéb anyagforgalmi
VITAFORT ZRT SZAKMAI NAP 2016 06 02 Az ellés körüli időszak néhány kritikus tényezője 2 Energiahiány (NEB) Akut kalciumhiány ellési bénulás Alacsonyabb takarmányfelvétel Oltógyomor áthelyeződés Egyéb anyagforgalmi
WALTER-LIETH LIETH DIAGRAM
 TBGL0702 Meteorológia és klimatológia II. Bíróné Kircsi Andrea Egyetemi tanársegéd DE Meteorológiai Tanszék [ C] A diagram fejlécében fel kell tüntetni: - az állomás nevét, - tengerszint feletti magasságát,
TBGL0702 Meteorológia és klimatológia II. Bíróné Kircsi Andrea Egyetemi tanársegéd DE Meteorológiai Tanszék [ C] A diagram fejlécében fel kell tüntetni: - az állomás nevét, - tengerszint feletti magasságát,
A mérés célkitűzései: Kaloriméter segítségével az étolaj fajhőjének kísérleti meghatározása a Joule-féle hő segítségével.
 A mérés célkitűzései: Kaloriméter segítségével az étolaj fajhőjének kísérleti meghatározása a Joule-féle hő segítségével. Eszközszükséglet: kaloriméter fűtőszállal digitális mérleg tanulói tápegység vezetékek
A mérés célkitűzései: Kaloriméter segítségével az étolaj fajhőjének kísérleti meghatározása a Joule-féle hő segítségével. Eszközszükséglet: kaloriméter fűtőszállal digitális mérleg tanulói tápegység vezetékek
http://www.olcsoweboldal.hu ingyenes tanulmány GOOGLE INSIGHTS FOR SEARCH
 2008. augusztus 5-én elindult a Google Insights for Search, ami betekintést nyújt a keresőt használók tömegeinek lelkivilágába, és időben-térben szemlélteti is, amit tud róluk. Az alapja a Google Trends,
2008. augusztus 5-én elindult a Google Insights for Search, ami betekintést nyújt a keresőt használók tömegeinek lelkivilágába, és időben-térben szemlélteti is, amit tud róluk. Az alapja a Google Trends,
Cu, Zn, Pb és Cd megkötődési formáinak vizsgálata
 Cu, Zn, Pb és Cd megkötődési formáinak vizsgálata Sz. Molnár Katalin Debreceni Egyetem Agrártudományi Centrum, Mezőgazdaságtudományi Kar, Talajtani és Mikrobiológiai Tanszék, Debrecen ÖSSZEFOGLALÁS Réz,
Cu, Zn, Pb és Cd megkötődési formáinak vizsgálata Sz. Molnár Katalin Debreceni Egyetem Agrártudományi Centrum, Mezőgazdaságtudományi Kar, Talajtani és Mikrobiológiai Tanszék, Debrecen ÖSSZEFOGLALÁS Réz,
xdsl Optika Kábelnet Mért érték (2012. II. félév): SL24: 79,12% SL72: 98,78%
 Minőségi mutatók Kiskereskedelmi mutatók (Internet) Megnevezés: Új hozzáférés létesítési idő Meghatározás: A szolgáltatáshoz létesített új hozzáféréseknek, az esetek 80%ban teljesített határideje. Mérési
Minőségi mutatók Kiskereskedelmi mutatók (Internet) Megnevezés: Új hozzáférés létesítési idő Meghatározás: A szolgáltatáshoz létesített új hozzáféréseknek, az esetek 80%ban teljesített határideje. Mérési
VASÚTI PÁLYA DINAMIKÁJA
 VASÚTI PÁLYA DINAMIKÁJA Dynamics of the railway track Liegner Nándor BME Út és Vasútépítési Tanszék A vasúti felépítmény szerkezeti elemeiben ébredő igénybevételek A Zimmermann Eisenmann elmélet alapján
VASÚTI PÁLYA DINAMIKÁJA Dynamics of the railway track Liegner Nándor BME Út és Vasútépítési Tanszék A vasúti felépítmény szerkezeti elemeiben ébredő igénybevételek A Zimmermann Eisenmann elmélet alapján
ORSZÁGOS KÖRNYEZETEGÉSZSÉGÜGYI INTÉZET
 ORSZÁGOS KÖRNYEZETEGÉSZSÉGÜGYI INTÉZET 197 Budapest, Gyáli út 2-6. Levélcím: 1437 Budapest Pf.: 839 Telefon: (6-1) 476-11 Fax: (6-1) 21-148 http://efrirk.antsz.hu/oki/ A PARLAGFŰ POLLENSZÓRÁSÁNAK ALAKULÁSA
ORSZÁGOS KÖRNYEZETEGÉSZSÉGÜGYI INTÉZET 197 Budapest, Gyáli út 2-6. Levélcím: 1437 Budapest Pf.: 839 Telefon: (6-1) 476-11 Fax: (6-1) 21-148 http://efrirk.antsz.hu/oki/ A PARLAGFŰ POLLENSZÓRÁSÁNAK ALAKULÁSA
Borpiaci információk. V. évfolyam / 11. szám 2007. június 20. 22-23. hét. Borpiaci jelentés. Hazai borpiaci tendenciák
 A K I Borpiaci információk V. évfolyam / 11. szám 2007. június 20. 22-23. hét Borpiaci jelentés Hazai borpiaci tendenciák 2. old. 1-2. táblázat, 1-8. ábra: Belföldön termelt fehérborok értékesített mennyisége
A K I Borpiaci információk V. évfolyam / 11. szám 2007. június 20. 22-23. hét Borpiaci jelentés Hazai borpiaci tendenciák 2. old. 1-2. táblázat, 1-8. ábra: Belföldön termelt fehérborok értékesített mennyisége
Kapcsolt vállalkozások évzáráshoz kapcsolódó egyéb feladatai. Transzferár dokumentálás Szokásos piaci ár levezetés
 Kapcsolt vállalkozások évzáráshoz kapcsolódó egyéb feladatai Transzferár dokumentálás Szokásos piaci ár levezetés Feladatok I. Kapcsoltság vizsgálat II. Cégcsoport méret feltérképezés III. Transzferár
Kapcsolt vállalkozások évzáráshoz kapcsolódó egyéb feladatai Transzferár dokumentálás Szokásos piaci ár levezetés Feladatok I. Kapcsoltság vizsgálat II. Cégcsoport méret feltérképezés III. Transzferár
Házi dolgozat. Minta a házi dolgozat formai és tartalmi követelményeihez. Készítette: (név+osztály) Iskola: (az iskola teljes neve)
 Házi dolgozat Minta a házi dolgozat formai és tartalmi követelményeihez Készítette: (név+osztály) Iskola: (az iskola teljes neve) Dátum: (aktuális dátum) Tartalom Itt kezdődik a címbeli anyag érdemi kifejtése...
Házi dolgozat Minta a házi dolgozat formai és tartalmi követelményeihez Készítette: (név+osztály) Iskola: (az iskola teljes neve) Dátum: (aktuális dátum) Tartalom Itt kezdődik a címbeli anyag érdemi kifejtése...
dr.majoros Mária Kinpán Dániel: Költői művek zeneiségének vizsgálata a hangtan alapján
 dr.majoros Mária Kinpán Dániel: Költői művek zeneiségének vizsgálata a hangtan alapján A kutatásunk arra irányult, hogy megpróbáljunk állítást megfogalmazni azzal kapcsolatban, hogy a hangzás milyen mértékben
dr.majoros Mária Kinpán Dániel: Költői művek zeneiségének vizsgálata a hangtan alapján A kutatásunk arra irányult, hogy megpróbáljunk állítást megfogalmazni azzal kapcsolatban, hogy a hangzás milyen mértékben
Analízis előadások. Vajda István. 2013. február 10. Neumann János Informatika Kar Óbudai Egyetem
 Analízis előadások Vajda István Neumann János Informatika Kar Óbudai Egyetem 013. február 10. Vajda István (Óbudai Egyetem) Analízis előadások 013. február 10. 1 / 3 Az elemi függvények csoportosítása
Analízis előadások Vajda István Neumann János Informatika Kar Óbudai Egyetem 013. február 10. Vajda István (Óbudai Egyetem) Analízis előadások 013. február 10. 1 / 3 Az elemi függvények csoportosítása
A nyugalomban levő levegő fizikai jellemzői. Dr. Lakotár Katalin
 A nyugalomban levő levegő fizikai jellemzői Dr. Lakotár Katalin Száraz, nyugalomban levő levegő légköri jellemzői egyszerűsített légkör modell állapotjelzői: sűrűség vagy fajlagos térfogat térfogategységben
A nyugalomban levő levegő fizikai jellemzői Dr. Lakotár Katalin Száraz, nyugalomban levő levegő légköri jellemzői egyszerűsített légkör modell állapotjelzői: sűrűség vagy fajlagos térfogat térfogategységben
Programozható irányítóberendezések és szenzorrendszerek ZH. Távadók. Érdemjegy
 Név Neptun-kód Hallgató aláírása 0-15 pont: elégtelen (1) 16-21 pont: elégséges (2) 22-27 pont: közepes (3) 28-33 pont: jó (4) 34-40 pont: jeles (5) Érzékelők jellemzése Hőmérsékletérzékelés Erő- és nyomásmérés
Név Neptun-kód Hallgató aláírása 0-15 pont: elégtelen (1) 16-21 pont: elégséges (2) 22-27 pont: közepes (3) 28-33 pont: jó (4) 34-40 pont: jeles (5) Érzékelők jellemzése Hőmérsékletérzékelés Erő- és nyomásmérés
Kerékpárlabda kvalifikációs szabályzat
 Kerékpárlabda kvalifikációs szabályzat Érvényesség kezdete: Junior kategória 2016 június 1 Felnőtt kategória 2016 január 1 Tartalom I. Célja... 3 II. Szabályozás... 3 1) A versenyek meghatározása... 3
Kerékpárlabda kvalifikációs szabályzat Érvényesség kezdete: Junior kategória 2016 június 1 Felnőtt kategória 2016 január 1 Tartalom I. Célja... 3 II. Szabályozás... 3 1) A versenyek meghatározása... 3
Agrár-környezetvédelmi Modul Agrár-környezetvédelem, agrotechnológia. KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI MSc
 Agrár-környezetvédelmi Modul Agrár-környezetvédelem, agrotechnológia KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI MSc Terméstérképezés, betakarítás I. 149.lecke A betakarítás és terméstérképezés
Agrár-környezetvédelmi Modul Agrár-környezetvédelem, agrotechnológia KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI MSc Terméstérképezés, betakarítás I. 149.lecke A betakarítás és terméstérképezés
Beszámoló: a kompetenciamérés eredményének javítását célzó intézkedési tervben foglaltak megvalósításáról. Őcsény, 2015. november 20.
 Őcsényi Perczel Mór Általános Iskola székhelye: 7143 Őcsény, Perczel Mór utca 1. Tel: 74/496-782 e-mail: amk.ocseny@altisk-ocseny.sulinet.hu Ikt.sz.: /2015. OM: 036345 Ügyintéző: Ősze Józsefné Ügyintézés
Őcsényi Perczel Mór Általános Iskola székhelye: 7143 Őcsény, Perczel Mór utca 1. Tel: 74/496-782 e-mail: amk.ocseny@altisk-ocseny.sulinet.hu Ikt.sz.: /2015. OM: 036345 Ügyintéző: Ősze Józsefné Ügyintézés
Az Európai Szabadalmi Egyezmény végrehajtási szabályainak 2010. április 1-étől hatályba lépő lényeges változásai
 DANUBIA Szabadalmi és Védjegy Iroda Kft. Az Európai Szabadalmi Egyezmény végrehajtási szabályainak 2010. április 1-étől hatályba lépő lényeges változásai A Magyar Iparjogvédelmi és Szerzői Jogi Egyesület
DANUBIA Szabadalmi és Védjegy Iroda Kft. Az Európai Szabadalmi Egyezmény végrehajtási szabályainak 2010. április 1-étől hatályba lépő lényeges változásai A Magyar Iparjogvédelmi és Szerzői Jogi Egyesület
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
VII. Gyermekszív Központ
 VII. Gyermekszív Központ Dr. Szatmári András Magyarországon évente kb. 75-8 gyermek születik szívhibával, mely adat teljesen megegyezik az európai országok statisztikáival, nevezetesen, hogy 1 millió lakosra
VII. Gyermekszív Központ Dr. Szatmári András Magyarországon évente kb. 75-8 gyermek születik szívhibával, mely adat teljesen megegyezik az európai országok statisztikáival, nevezetesen, hogy 1 millió lakosra
Azonosító jel: Matematika emelt szint
 I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
A TALAJOK KÖNNYEN KIOLDHATÓ ELEMTARTALMÁNAK VÁLTOZÁSA BIOGÁZ GYÁRTÁS MELLÉKTERMÉKÉNEK HATÁSÁRA
 A TALAJOK KÖNNYEN KIOLDHATÓ ELEMTARTALMÁNAK VÁLTOZÁSA BIOGÁZ GYÁRTÁS MELLÉKTERMÉKÉNEK HATÁSÁRA CHANGES OF ELEMENT CONTENT OF SOIL ON APPLICATION OF BIOGAS FERMENTATION SLUDGE Vágó Imre 1 Makádi Marianna
A TALAJOK KÖNNYEN KIOLDHATÓ ELEMTARTALMÁNAK VÁLTOZÁSA BIOGÁZ GYÁRTÁS MELLÉKTERMÉKÉNEK HATÁSÁRA CHANGES OF ELEMENT CONTENT OF SOIL ON APPLICATION OF BIOGAS FERMENTATION SLUDGE Vágó Imre 1 Makádi Marianna
1. Eset-kontroll vizsgálatok nem megfelelően kivitelezett kontroll szelektálása
 LEGGYAKORIBB TÍPUSHIBÁK: 1. Eset-kontroll vizsgálatok nem megfelelően kivitelezett kontroll szelektálása Vizsgálati kérdés: posztmenopauzális ösztrogén szubsztitúció szívinfarktus Eset: kórházban kezelt
LEGGYAKORIBB TÍPUSHIBÁK: 1. Eset-kontroll vizsgálatok nem megfelelően kivitelezett kontroll szelektálása Vizsgálati kérdés: posztmenopauzális ösztrogén szubsztitúció szívinfarktus Eset: kórházban kezelt
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria
 005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
Sz ekelyhidi L aszl o Val osz ın us egsz am ıt as es matematikai statisztika *************** Budapest, 1998
 Székelyhidi László Valószínűségszámítás és matematikai statisztika *************** Budapest, 1998 Előszó Ez a jegyzet a valószínűségszámításnak és a matematikai statisztikának azokat a fejezeteit tárgyalja,
Székelyhidi László Valószínűségszámítás és matematikai statisztika *************** Budapest, 1998 Előszó Ez a jegyzet a valószínűségszámításnak és a matematikai statisztikának azokat a fejezeteit tárgyalja,
A közbeszerzési eljárások egyszerősítése - a lengyel tapasztalatok
 - a lengyel tapasztalatok Dariusz Piasta Nemzetközi Konferencia a Közbeszerzések Tanácsa szervezésében Budapest, 2011. november 17. Az elıadás vázlata: 1. Egyszerősítés - jelentése és korlátai 2. A kiindulási
- a lengyel tapasztalatok Dariusz Piasta Nemzetközi Konferencia a Közbeszerzések Tanácsa szervezésében Budapest, 2011. november 17. Az elıadás vázlata: 1. Egyszerősítés - jelentése és korlátai 2. A kiindulási
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 12 XII. STATIsZTIKA ellenőrző feladatsorok 1. FELADATsOR Megoldások: láthatók nem láthatók 1. minta: 6.10, 0.01, 6.97, 6.03, 3.85, 1.11,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 12 XII. STATIsZTIKA ellenőrző feladatsorok 1. FELADATsOR Megoldások: láthatók nem láthatók 1. minta: 6.10, 0.01, 6.97, 6.03, 3.85, 1.11,
IKT FEJLESZTŐ MŰHELY KONTAKTUS Dél-dunántúli Regionális Közoktatási Hálózat Koordinációs Központ
 Óratervezet: Kémia 7. osztály Témakör: Kémiai kötések Óra anyaga: Molekulák építése, térbeli modellezése Eszközök:, aktív tábla, projektor, számítógépek A tanóra részei Tanári tevékenység Tanulói tevékenység
Óratervezet: Kémia 7. osztály Témakör: Kémiai kötések Óra anyaga: Molekulák építése, térbeli modellezése Eszközök:, aktív tábla, projektor, számítógépek A tanóra részei Tanári tevékenység Tanulói tevékenység
Ablakok használata. 1. ábra Programablak
 Ha elindítunk egy programot, az egy Ablakban jelenik meg. A program az üzeneteit szintén egy újabb ablakban írja ki számunkra. Mindig ablakokban dolgozunk. Az ismertetett operációs rendszer is az Ablakok
Ha elindítunk egy programot, az egy Ablakban jelenik meg. A program az üzeneteit szintén egy újabb ablakban írja ki számunkra. Mindig ablakokban dolgozunk. Az ismertetett operációs rendszer is az Ablakok
FENNTARTHATÓ FEJLŐDÉS
 FENNTARTHATÓ FEJLŐDÉS Kump Edina ÖKO-Pack Nonprofit Kft. E-mail: edina@okopack.hu Web: www.okopack.hu Dunaújváros, 2014. november 07. A FENNTARTHATÓ FEJLŐDÉS FOGALMA A fenntartható fejlődés a fejlődés
FENNTARTHATÓ FEJLŐDÉS Kump Edina ÖKO-Pack Nonprofit Kft. E-mail: edina@okopack.hu Web: www.okopack.hu Dunaújváros, 2014. november 07. A FENNTARTHATÓ FEJLŐDÉS FOGALMA A fenntartható fejlődés a fejlődés
Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között
 Dr. Nyári Tibor Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között tökéletes színeket visszaadni. A digitális
Dr. Nyári Tibor Bár a digitális technológia nagyon sokat fejlődött, van még olyan dolog, amit a digitális fényképezőgépek nem tudnak: minden körülmények között tökéletes színeket visszaadni. A digitális
Intézményi jelentés. Összefoglalás. Medgyessy Ferenc Gimnázium és Művészeti Szakközépiskola 4031 Debrecen, Holló László sétány 6 OM azonosító: 031202
 FIT-jelentés :: 2010 Medgyessy Ferenc Gimnázium és Művészeti Szakközépiskola 4031 Debrecen, Holló László sétány 6 Figyelem! A 2010. évi Országos kompetenciaméréstől kezdődően a szövegértés, illetve a matematika
FIT-jelentés :: 2010 Medgyessy Ferenc Gimnázium és Művészeti Szakközépiskola 4031 Debrecen, Holló László sétány 6 Figyelem! A 2010. évi Országos kompetenciaméréstől kezdődően a szövegértés, illetve a matematika
31 521 09 1000 00 00 Gépi forgácsoló Gépi forgácsoló
 Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Az Országos Képzési Jegyzékről és az Országos Képzési Jegyzékbe történő felvétel és törlés eljárási rendjéről szóló 133/2010. (IV. 22.) Korm. rendelet alapján. Szakképesítés, szakképesítés-elágazás, rész-szakképesítés,
Borpiaci információk. IV. évfolyam / 24. szám 2006. december 14. 47-48. hét. Bor piaci jelentés
 A K I Borpiaci információk IV. évfolyam / 24. szám 26. 14. 47-48. hét Bor piaci jelentés Hazai borpiaci információk Magyar borászati termékek exportja 1-2. táblázat, 1-8. ábra: Belföldi értékesítési árak
A K I Borpiaci információk IV. évfolyam / 24. szám 26. 14. 47-48. hét Bor piaci jelentés Hazai borpiaci információk Magyar borászati termékek exportja 1-2. táblázat, 1-8. ábra: Belföldi értékesítési árak
A KÖZOP-3.5.0-09-11-2012-0018 projekt rövid bemutatása
 A KÖZOP-3.5.0-09-11-2012-0018 projekt rövid bemutatása Rétháti András Célkitűzés: az utóbbi évtizedben számos országban alkalmazott 2+1 / 1+2 sávos keresztmetszetű utak hazai bevezetési lehetőségeinek,
A KÖZOP-3.5.0-09-11-2012-0018 projekt rövid bemutatása Rétháti András Célkitűzés: az utóbbi évtizedben számos országban alkalmazott 2+1 / 1+2 sávos keresztmetszetű utak hazai bevezetési lehetőségeinek,
Termékkatalógus 2016.
 Hasítókúp kínálatunk 70, 90, valamint 120 mm átmérőjű hasítókúpokból áll. Átmérő (mm) Hossz (mm) 70 220 90 250 120 300 Az összes kúp edzett, cserélhető véggel szerelt. A kúp anyaga: 20MnCr5 Póthegyek anyaga:
Hasítókúp kínálatunk 70, 90, valamint 120 mm átmérőjű hasítókúpokból áll. Átmérő (mm) Hossz (mm) 70 220 90 250 120 300 Az összes kúp edzett, cserélhető véggel szerelt. A kúp anyaga: 20MnCr5 Póthegyek anyaga:
1. Írja fel prímszámok szorzataként a 420-at! 2. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen!
 1. Írja fel prímszámok szorzataként a 40-at! 40 =. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen! A részek: 3. Egy sejttenyészetben naponta kétszereződik meg a sejtek száma.
1. Írja fel prímszámok szorzataként a 40-at! 40 =. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen! A részek: 3. Egy sejttenyészetben naponta kétszereződik meg a sejtek száma.
Lécgerenda. 1. ábra. 2. ábra
 Lécgerenda Egy korábbi dolgozatunkban melynek címe: Karimás csőillesztés már szóltunk arról, hogy a szeezetek számításaiban néha célszerű lehet a diszkrét mennyiségeket folyto - nosan megoszló mennyiségekkel
Lécgerenda Egy korábbi dolgozatunkban melynek címe: Karimás csőillesztés már szóltunk arról, hogy a szeezetek számításaiban néha célszerű lehet a diszkrét mennyiségeket folyto - nosan megoszló mennyiségekkel
G Szabályfelismerés 2.2. 2. feladatcsomag
 ÖSSZEFÜÉSEK Szabályfelismerés 2.2 Alapfeladat Szabályfelismerés 2. feladatcsomag összefüggés-felismerő képesség fejlesztése szabályfelismeréssel megkezdett sorozat folytatása a felismert szabály alapján
ÖSSZEFÜÉSEK Szabályfelismerés 2.2 Alapfeladat Szabályfelismerés 2. feladatcsomag összefüggés-felismerő képesség fejlesztése szabályfelismeréssel megkezdett sorozat folytatása a felismert szabály alapján
AGROTECHNIKAI TÉNYEZŐK HATÁSA A KULTÚRNÖVÉNYEKRE ÉS A GYOMOSODÁSRA
 PANNON EGYETEM GEORGIKON KAR NÖVÉNYVÉDELMI INTÉZET NÖVÉNYTERMESZTÉSI ÉS KERTÉSZETI TUDOMÁNYOK DOKTORI ISKOLA ISKOLA VEZETŐ DR. GÁBORJÁNYI RICHARD MTA DOKTORA AGROTECHNIKAI TÉNYEZŐK HATÁSA A KULTÚRNÖVÉNYEKRE
PANNON EGYETEM GEORGIKON KAR NÖVÉNYVÉDELMI INTÉZET NÖVÉNYTERMESZTÉSI ÉS KERTÉSZETI TUDOMÁNYOK DOKTORI ISKOLA ISKOLA VEZETŐ DR. GÁBORJÁNYI RICHARD MTA DOKTORA AGROTECHNIKAI TÉNYEZŐK HATÁSA A KULTÚRNÖVÉNYEKRE
Mérési hibák 2007.02.22. 1
 Mérési hibák 007.0.. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák/ Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség általánosított
Mérési hibák 007.0.. 1 Mérés jel- és rendszerelméleti modellje Mérési hibák/ Mérési hibák mérési hiba: a meghatározandó értékre a mérés során kapott eredmény és ideális értéke közötti különbség általánosított
