TITOKMEGOSZTÁS ÉS TÖBBRÉSZTVEVŐS SZÁMÍTÁSOK. Szakdolgozat. Írta: Zentai Dániel Matematika bsc szak Alkalmazott matematikus szakirány.
|
|
|
- György Hegedüs
- 9 évvel ezelőtt
- Látták:
Átírás
1 TITOKMEGOSZTÁS ÉS TÖBBRÉSZTVEVŐS SZÁMÍTÁSOK Szakdolgozat Írta: Zentai Dániel Matematika bsc szak Alkalmazott matematikus szakirány Témavezető: Dr. Csirmaz László Konzulens: Dr. Sziklai Péter Eötvös Loránd Tudományegyetem Természettudományi Kar
2
3 Tartalomjegyzék 1. Bevezetés 2 2. Alapfogalmak ismertetése A támadás modellezése A kommunikáció modellezése Titokmegosztás Példák Algebrai titokmegosztás Geometriai titokmegosztás Optikai titokmegosztás Biztonság passzív támadás ellen Biztonság aktív támadás ellen Az előző tételek hiányossága Többrésztvevős számítások Példák Milliomosok problémája Ebédlő kriptográfusok Általános tételek A szükséges műveletek Üzenetszórás A bizánci generálisok problémája Szimulált üzenetszórás
4 1. fejezet Bevezetés Egy kalózkapitány zsákmányolt kincseit elássa, és a rejtekhelyről készít egy térképet. A vagyonát három fiára szeretné hagyni hagyni, ezért három részre vágja a térképet és minden gyerekének ad egy-egy darabot, hogy csak közösen tudják megtalálni a kincset. Egy bankban minden széfhez két kulcs tartozik. Az egyik kulcs a széf bérlőjénél van, a másik egy banki alkalmazottnál. Csak ezen két személy együttes jelenlétében lehetséges a széf kinyitása. Számtalan ehhez hasonló szituációt el tudunk képzelni, a lényege azonban mindegyiknek ugyanaz: van egy titkunk, amihez csak több ember együttműködése révén juthatunk hozzá. Erre a problémára kínál megoldást a titokmegosztás, és a hozzá szorosan kapcsolódó többrésztvevős számítások. A titokmegosztás fogalmát egymástól függetlenül Shamir [10] és Blakley [3] vezette be 1979-ben. A többrésztvevős számítások fogalma Yao [11] nevéhez fűződik. Dolgozatom célja ezen két témakör bemutatása. A dolgozat írása során főként Maurer [8] cikkére támaszkodtam. A 2. fejezetben ismertetem a dolgozatban előforduló alapfogalmakat, definíciókat. A 3. fejezetben szerepelnek egyszerű példák titokmegosztásra, illetve a [8]-ban szereplő titokmegosztással kapcsolatos tételek, eljárások. A 4. fejezetben az előző fejezet tételeinek, eljárásainak egy hibájára mutatok rá, és javítom ezt hibát. Az 5. fejezetben többrésztvevős számítással kapcsolatos példákat, általános tételeket, számolási módszereket mutatok. A 6. fejezetben az üzenetszórás szimulálásáról, és ennek helyességéről lesz szó. 2
5 2. fejezet Alapfogalmak ismertetése 2.1. A támadás modellezése Titokmegosztásnál és többrésztvevős számításnál úgy modellezzük a támadást, hogy külső fenyegetést tételezünk fel, egy támadót, aki a résztvevők bizonyos részhalmazait tudja támadni. Tekinthetünk erre a támadóra például úgy, mint egy hackerre, aki a résztvevők számítógépébe képes betörni. Két fajtáját különböztethetjük meg a támadásnak. A passzív támadás azt jelenti, hogy a támadó betekintést nyerhet a résztvevők által birtokolt információkba, de ettől eltekintve a résztvevők továbbra is szabályszerűen vesznek részt a protokollban. A továbbiakban a passzív támadás alatt álló résztvevőket tisztességes, de kíváncsi résztvevőknek hívjuk. Az aktív támadás azt jelenti, hogy a támadó teljesen átveszi az irányítást a résztvevők fölött. Ekkor az is megtörténhet, hogy a résztvevők nem követik a protokoll szabályait, és a számítás során téves információkat közölnek a többi résztvevővel. Az aktív támadás alatt álló résztvevőket a továbbiakban tisztességtelen résztvevőknek hívjuk. Azokat a résztvevőket, akik sem aktív, sem passzív támadás alatt nem állnak tisztességes résztvevőknek hívjuk. Természetes feltevés, hogy a résztvevők egy támadható halmazának bármely részhalmaza is támadható Definíció. Legyen P véges halmaz. Azt mondjuk, hogy Π 2 P egy struktúra, ha Π zárt a részhalmazképzésre, azaz S Π, és S S esetén S Π. 3
6 Definíció. Legyen P véges halmaz. Azt mondjuk, hogy Π 2 P egy anti-struktúra, ha Π zárt a tartalmazásra, azaz S Π, és S S esetén S Π Definíció. Legyen Π 1 és Π 2 struktúra. Ekkor Π 1 Π 2 jelöli a Π 1 és Π 2 struktúra elemenkénti unióját, azaz Π 1 Π 2 = {S 1 S 2 : S 1 Π 1, S 2 Π 2 } Megjegyzés. Egy struktúra megadásánál elegendő csak a legbővebb halmazokat felsorolni, hiszen ha Π egy struktúra, és S Π, akkor minden S S-re automatikusan teljesül S Π Definíció. Legyen P véges halmaz, Σ 2 P, Σ struktúra. Egy (Σ, )-támadó egy olyan támadó, aki a Σ-beli halmazokat csak passzívan, a -beli halmazokat aktívan is támadhatja. Mind a passzív, mind az aktív támadó lehet statikus, illetve adaptív. A statikus támadó csak a számítási protokoll kezdete előtt választhatja ki, hogy mely részhalmazokat támadja passzívan, és melyeket aktívan. Az adaptív támadó a protokoll futása közben is újra választhat a támadható részhalmazok közül A kommunikáció modellezése Biztonság szempontjából a kommunikáció kétféle lehet. Kriptográfiai biztonságról akkor beszélünk, ha a támadó számítási kapacitására megszabunk egy korlátot, vagy bizonyos feladatokról feltesszük, hogy a támadó nem ismer a megoldásukra hatékony algoritmust (például ezzel a feltevésssel élünk az RSA titkosítás esetén a prímfaktorizációval kapcsolatban.) Információ-elméleti, vagy tökéletes biztonságról akkor beszélünk, ha a támadónak korlátlan számítási kapacitás áll rendelkezésre, mégsem tudhat meg semmit a kommunikációról. A kommunikációs csatorna is kétféle lehet. Szinkronizált a csatorna, ha az üzenetek küldése összehangolt, és minden üzenet megérkezik egy adott időkorláton belül. Ekkor a kommunikáció körökre van osztva, egy körön belül minden résztvevő küldhet üzenetet az összes többi résztvevőnek, és az üzenetek megérkeznek a következő kör kezdete előtt. 4
7 Aszinkronizált a csatorna, ha az üzenetküldés nincs összehangolva, és az üzenetek érkezése sincs időkorlátok közé szorítva. Üzenetszórásról beszélünk, ha az üzenetet úgy küldjük el, hogy azt az összes résztvevő megkapja egyszerre. Az üzenetszórás nem mindig valósítható meg. Ilyenkor az üzenetszórást szimulálni szokás. Az üzenetszórás szimulálását később részletesen tárgyaljuk. 5
8 3. fejezet Titokmegosztás Arra, hogy egy többrésztvevős számításban a biztonságot garantálni tudjuk, titokmegosztást használunk. A résztvevők véges P = {p 1,..., p n } halmazának elemei között szeretnénk egy titkot szétosztani úgy, hogy bármely k résztvevő együtt vissza tudja állítani a titkot, de semelyik k 1 résztvevő se tudjon meg többet a titokról, mint amit az inputjából, és a végeredményből megtudhat. A titok tipikusan valamely F véges test elemei közül kerül ki. A titokrészeket szétosztó résztvevőt osztónak nevezzük Definíció. Legyenek S 1,..., S n véges halmazok, ahol S i a p i résztvevőnek kiosztható titkok halmaza, és legyen S = S 1 S n. S elemeit titokmegosztásnak hívjuk Definíció. Az olyan titokmegosztási sémát, melyben bármely k résztvevő vissza tudja állítani a titkot, de semelyik k 1 résztvevőnek sincs semmilyen plusz információja a titokról, k-küszöb sémának nevezzük Definíció. Egy P P halmaz kvalifikált, ha a benne szereplő résztvevők vissza tudják állítani a titkot. P P ignorált, ha nem kvalifikált Definíció. Legyen Γ a kvalifikált részhalmazokból, Σ az ignorált részhalmazokból álló struktúta. Γ-t elérési struktúrának, Σ-t biztonsági struktúrának hívjuk Megjegyzés. Itt az elérési struktúra csak egy elnevezés. Γ valójában egy anti-struktúra, hiszen ha a résztvevőknek egy részhalmaza vissza tudja állítani a titkot, akkor minden ennél bővebb részhalmaz is vissza tudja állítani. 6
9 3.1. Példák Algebrai titokmegosztás Titokmegosztásra először Shamir dolgozott ki algoritmust 1979-ben [10]. Shamir titokmegosztásának bemutatása előtt áttekintjük a Lagrangeinterpoláció algoritmusát: Legyen F egy véges test, F k + 1, C F, C = k + 1 f(x) F[x] egy k-adfokú egyváltozós polinom. Ha ennek a polinomnak ismerjük k + 1 helyen a helyettesítési értékét, akkor Lagrange-interpolációval meg tudjuk határozni magát a polinomot, mégpedig f(x) = f(i)l i (x) i C, ahol l i (x) egy k-adfokú polinom, melyre l i (j) = 0, ha i j, és l i (j) = 1, ha i = j. Formálisan. l i (x) = j C,j i Ezek után Shamir algoritmusa a következő: x j i j Tekintsünk egy F véges testet, és egy f(x) F[x] polinomot. Legyen f(x) = a k x k +... a 1 x+a 0, ahol f(0) = a 0 a titok, a 1,..., a n -et pedig azonos (tipikusan egyenletes) eloszlás szerint, egymástól függetlenül választjuk F-ből. Mivel az f polinom k-adfokú, bármely k + 1 résztvevő Lagrange-interpolációval rekonstruálni tudja f-et, és ezáltal a polinom konstans tagját, azaz titkot is, de semelyik k résztvevő sem tudhat meg semmit a titokról, azaz ez az algoritmus egy (k + 1)-küszöb sémát ad Geometriai titokmegosztás Shamirtól függetlenül szintén 1979-ben Blakley is kidolgozott egy módszert titokmegosztásra [3]. Legyen most a titok egy tetszőleges Q pont az n-dimenziós euklideszi térben. A titokrészek legyenek a Q pont koordinátái, azaz kapja minden résztvevő a Q pont egy koordinátáját. Ekkor n résztvevő együtt meg tudja határozni a Q 7
10 pont összes koordinátáját, de bármely n 1 résztvevő csak az n-dimenziós tér egy olyan n 1-dimenziós alterét ismeri, amin a Q pont található, így magát a Q pontot nem tudja visszaállítani semelyik n 1 résztvevő. Ez az eljárás egy n-küszöb séma Optikai titokmegosztás Következő példánk egy 2-küszöb séma. Felosztunk két átlátszó fóliát kis téglalapokra, majd az egyik fólián minden kis téglalapot kiszínezünk úgy, hogy az egyik oldala fekete legyen, a másik pedig átlátszó maradjon. Mindig 1/2 valószínűséggel színezzük a bal oldalát, 1/2 valószínűséggel pedig a jobb oldalát feketére. A másik fóliát úgy színezzük ki, hogy a két fóliát egymással fedésbe hozva a titok (egy kép, vagy egy szöveg) rajzolódjon ki. Azaz azokat a téglalapokat, ahol a titoknak ki kell rajzolódnia, ellentétesen színezzük, mint az első fólián, a többi téglalapot pedig ugyanúgy, mint az első fólián. Mindkét fólia színezése csak a másik fóliától függ, önmagában minden kis téglalapot egymástól függetlenül, azonos eloszlás szerint színeztünk ki. A következő két ábra egy egyszerű példát mutat optikai titokmegosztásra ábra. A két fólia külön 8
11 ábra. A két fólia egymással fedésbe hozva 3.2. Biztonság passzív támadás ellen Ebben a fejezetben olyan protokollokat tekintünk át, amelyek passzív támadás ellen biztonságosak. Mivel csak passzív támadást feltételezünk, ebben a fejezetben =. A titokrészek szétosztásához egy építőelem a k-ból k titokmegosztás. Legyen a szétosztandó titok s F, ahol F egy véges test. K-ból k titokmegosztás (1) Válasszunk k elemet, s 1,..., s n -et egymástól függetlenül, azonos (tipikusan egyenletes) eloszlás szerint F-ből. (2) Legyen s = k i=1 s i. Amennyiben s s, újra választjuk s 1,..., s n -et. Ha s = s, akkor az i. titokrészt s i -nek választjuk. Ekkor k résztvevő együtt vissza tudja állítani a titkot, hiszen a titok épp az általuk birtokolt titokrészek összege. Azonban bármely legfeljebb k 1 résztvevő csak egymástól és a titoktól statisztikailag független valószínűségi változókat ismer, melyek összege szintén független a titoktól. 9
12 Titokmegosztás Σ = {T 1,..., T k } biztonsági struktúrában (1) Részekre osztjuk a titkot k-ból k titokmegosztással. (2) Szétosztjuk a titkot a résztvevők között úgy, hogy p j akkor kapja meg az s i titokrészt, ha p j T i. Ezzel a titokmegosztási sémával titokrészek lineáris függvényeit biztonságosan ki lehet számolni, hiszen a linearitás miatt ezeket a függvényeket a résztvevők lokálisan ki tudják számítani, így nincs szükség kommunikációra. A biztonság garantált, hiszen minden T i Σ halmazra teljesül s i / T i, így egyetlen Σ- beli halmaz sem tudja visszaállítani a titkot. Ugyanakkor ha Γ elérési struktúra, akkor minden S Γ minden i-re tartalmaz p / T i résztvevőt. Ez a p résztvevő ismeri az s i titokrészt, így az S-beli résztvevők ismerik az összes titokrészt Definíció. Legyenek s = k i=1 s i és t = k j=1 t j titkok. Ekkor s és t szorzatát a következőképp definiálhatjuk: k k st = ( s i )( t i ) = i=1 j=1 k k s i t j. i=1 j=1 Szorzás protokoll (1) Osszuk fel az {(i, j) : 1 i, j n} halmazt az U 1,..., U n halmazokra úgy, hogy (i, j) U m p m T i T j. (2) Osszuk szét az s = k i=1 s i és a t = k j=1 t j titkokat. (3) Minden 1 m n-re p m kiszámolja a v m = (i,j) U m s i t j értéket, és ezt megosztja az összes többi résztvevővel. (4) Az összes résztvevő kiszámolja a v = n m=1 v m értéket Biztonság aktív támadás ellen A passzív támadáshoz képest ebben az esetben két fontos változtatást kell eszközölnünk. A résztvevők továbbra is a titokrészek lineáris függvényeit és szorzatát számolják ki, de az alkalmazott protokollokat ellenállóvá kell tennünk egy aktív támadóval szemben is, ezen kívül azt a problémát is orvosolnunk kell, ha esetleg az osztó is tisztességtelen. Az eddigi titokmegosztási sémák használhatatlanok aktív támadók jelenlétében, mert nincs semmi jele annak, ha egy résztvevő nem a valós eredményt közli a többiekkel számítás közben, és ezáltal a végeredmény sem lesz helyes. Ezt a 10
13 problémát oldja meg az ellenőrizhető titokmegosztás Definíció. Az ellenőrizhető titokmegosztási séma egy (Megoszt, Visszaállít) protokoll pár, ahol a következők teljesülnek egy (Σ, )-támadó jelenlétében: 1. Ha a Megoszt protokoll sikeresen lefut, akkor a Visszaállít protokoll a támadó minden lehetséges stratégiája esetén ugyanazt a fix értéket fogja visszaadni. 2. Ha az osztó megbízható a Megoszt protokoll futása alatt, akkor a Visszaállít protokoll mindig az osztó inputját adja vissza. 3. Ha az osztó megbízható, akkor a támadó semmilyen plusz információt nem tudhat meg a titokról Tétel. [8] Pontosan akkor lehet tökéletesen biztonságos egy ellenőrizhető titokmegosztás egy (Σ, )-támadó ellen, ha P / Σ, azaz ha a résztvevők teljes halmazát nem lehet lefedni semelyik kettő tisztességtelen, illetve egy tisztességes, de kíváncsi halmaz uniójával Tétel. [8] Pontosan akkor szimulálható üzenetszórás biztonságosan egy (Σ, )-támadó ellen, ha P /, azaz ha a résztvevők teljes halmazát nem lehet lefedni semelyik három tisztességtelen halmaz uniójával. Megoszt protokoll (1) Osszuk szét a titkot passzív támadás ellen biztonságos titokmegosztással. (2) Minden s i titokrészre a T i -beli résztvevők páronként ellenőrzik, hogy mindegyikük ugyanazt az s i értéket kapta -e. Ha eltérést találnak, azt üzenetszórással jelzik. (3) Az osztó üzenetszórással elküldi az összes résztvevőnek az összes olyan s i titokrészt, amelyre a résztvevők hibát jeleztek. Amennyiben az osztó megtagadja az üzenetszórást, a protokoll leáll. 11
14 Itt (2)-re azért van szükség, hogy az osztót is tudjuk ellenőrizni. Ugyanis a passzív támadással ellentétben, aktív támadásnál előfordulhat, hogy az osztó tisztességtelen, és nem ugyanazt az s i titokrészt küldi az összes T i -beli résztvevőnek. Visszaállít protokoll (1) Minden résztvevő elküldi az általa ismert titokrészeket az összes többi résztvevőnek. (2) Minden résztvevő lokálisan kiszámolja az s = k i=1 s i értéket. (3) Legyen v j az az érték, amit a p j T i résztvevő küld el a többi résztvevőnek. A titok az a v értek lesz, amire létezik olyan A, hogy v j = v minden p j T i A-ra. A titokrészek lineáris függvényeinek számolásakor ebben az esetben sincs probléma, hiszen a linearitás miatt ezeket a függvényeket a résztvevők lokálisan ki tudják számítani, így nincs szükség kommunikációra. A Szorzás protokollt azonban meg kell változtatnunk úgy, hogy tisztességtelen résztvevők jelenlétében is biztonságos maradjon. Azaz kezelnünk kell azt a problémát, amikor egy, vagy több résztvevő nem valós információkat közöl a többi résztvevővel. Az aktív támadás ellen is biztonságos Szorzás protokoll a következő: 12
15 Szorzás protokoll (1) Ellenőrizhető titokmegosztással megosztjuk az s = k j=1 s i és a t = k j=1 t j titkokat. (2) Minden p m résztvevő kiszámolja azon s i t j titokrészeket, melyekre p m T i T j, majd megosztja ezeket ellenőrizhető titokmegosztással. (3) Minden (i, j) párra legyen {p m1,..., p mr } azon résztvevők halmaza, akik a s i t j titokrészt számolták ki. (4) A résztvevők kiszámolják a p m1 és p mi,(i = 2,..., r) által küldött s i t j titokrészek különbségét. Ha minden esetben 0 az eredmény, elfogadják s i t j - t, különben rekonstruálják s i -t és t j -t, p 1 megkapja s i t j -t, a többi résztvevő pedig 0-t. (5) Minden résztvevő kiszámolja st = ( k i=1 s i)( k j=1 t i) = k j=1 s it j -t. k i=1 13
16 4. fejezet Az előző tételek hiányossága A [8]-ban közölt tételek, illetve protokollok némelyikének van egy hiányossága, ugyanis sérülhet a titokmegosztás biztonsága bizonyos értelemben. Ugyan a támadó továbbra sem juthat hozzá illetéktelenül semmilyen információhoz, de azt elérheti, hogy tisztességes résztvevők egy halmaza olyan információhoz jusson, amire a résztvevők lennének jogosultak. Az s i titokrész páronkénti ellenőrzésekor egy tisztességtelen résztvevő mondhatja azt, hogy ő egy s i s i titokrészt kapott, még ha az osztó valóban tisztességes is volt, és minden T i -beli résztvevőnek ugyanazt a titokrészt adta. Ekkor a résztvevők jelzik az eltérést az osztónak, aki üzenetszórással elküldi mindenkinek s i -t. Ekkor pedig a T i -beli résztvevők is megtudják s i -t. Ha a T i - beli résztvevők egyike sem tisztességes, akkor nem sérül a biztonság, ugyanis vagy azért volt szükség üzenetszórásra, mert az osztó volt tisztességtelen, vagy azért, mert legalább egy tisztességtelen résztvevő már megtudta s i -t, és mindkét esetben az összes tisztességtelen, illetve tisztességes, de kíváncsi résztvevő megtudhatja s i -t, hiszen ezek a résztvevők együttműködhetnek. Ha viszont T i -ben voltak tisztességes résztvevők, akkor ezen résztvevők plusz információhoz jutottak az üzenetszórás miatt. Ahhoz, hogy ne sérülhessen ilyen módon a biztonság, az előbbi tételekben, illetve protokollokban némi változást kell eszközölnünk. Egyrészt az Tételt kell módosítanunk úgy, hogy az s i titokrész szétosztásából kihagyott T i halmazon kívül is biztonságosan működhessen a titokmegosztás, azaz azt szeretnénk, hogy a T i halmazra is teljesüljenek a tétel feltételei. Ehhez az kell, hogy T i -t ne lehessen lefedni semelyik kettő tisztességtelen és egy tisztességes, de kíváncsi halmaz uniójával. 14
17 Mivel T i Σ, az Tételben szereplő feltételt a következőképp kell módosítanunk a Megoszt protokoll esetében: Tétel. Pontosan akkor lehet tökéletesen biztonságos egy ellenőrizhető titokmegosztás egy (Σ, )-támadó ellen, ha P / Σ Σ, azaz ha a résztvevők teljes halmazát nem lehet lefedni semelyik kettő tisztességtelen, illetve semelyik kettő tisztességes, de kíváncsi halmaz uniójával. Ezenkívül módosítanunk kell a Megoszt protokollt, hogy ha a résztvevők hibát jeleznek (akár valós, akár valótlan hibát), az osztó üzenetszórása által az s i titokrész ne juthasson el a T i halmaz résztvevőihez. Ez a következő módosítással érhetjük el. A Megoszt protokoll (1) Osszuk szét a titkot passzív támadás ellen biztonságos titokmegosztással. (2) Minden s i titokrészre a T i -beli résztvevők páronként ellenőrzik, hogy mindegyikük ugyanazt az s i értéket kapta -e. Ha eltérést találnak, azt üzenetszórással jelzik. (3) Az osztó szimulált üzenetszórással elküldi az összes T i -beli résztvevőnek az s i titokrészt, amennyiben a résztvevők hibát jeleztek s i szétosztásakor. Amennyiben az osztó megtagadja az üzenetszórást, a protokoll leáll. Mivel ebben a módosított Megoszt protokollban olyan szimulált üzenetszórásra van szükségünk, amely minden Σ = {T 1,..., T k }-beli halmazon kívül biztonságosan működik, módosítanunk kell a Tételt is Tétel. Pontosan akkor szimulálható üzenetszórás biztonságosan egy (Σ, )-támadó ellen, ha P / Σ, azaz ha a résztvevők teljes halmazát nem lehet lefedni semelyik három tisztességtelen, illetve egy tisztességes, de kíváncsi halmaz uniójával. Maga a Szorzás protokoll nem szorul módosításra, a módosítást már megtettük a protokoll (1) lépésében szereplő Megoszt protokollban. Azonban szintén a protokoll (1) lépésében csak az olyan p m résztvevők tudják kiszámítani az s i t j szorzatot, melyekre p m / T i T j. Tehát az ellenőrizhető titokmegosztásnak a T i T j halmazon is biztonságosnak kell lennie, azaz az Tétel feltételeinek 15
18 teljesülnie kell a T i T j = T i T j halmazra. Mivel T i T j Σ Σ, az 5. Tételben szereplő feltételt a következőképp kell módosítanunk a Szorzás protokoll esetében: Tétel. Pontosan akkor lehet tökéletesen biztonságos egy ellenőrizhető titokmegosztás egy (Σ, )-támadó ellen, ha P / Σ Σ Σ, azaz ha a résztvevők teljes halmazát nem lehet lefedni semelyik kettő tisztességtelen, illetve semelyik három tisztességes, de kíváncsi halmaz uniójával. 16
19 5. fejezet Többrésztvevős számítások Többrésztvevős számítás alatt azt értjük, hogy n résztvevő egy f : F F függvény értékét kiszámítja biztonságosan, ahol F egy véges test. Konkrétabban, ha a résztvevők véges halmaza P = {p 1,..., p n } az inputok x 1,..., x n F, ahol p i ismeri az x i inputot, akkor a résztvevők kiszámítják egy adott f : F F függvényre f(x 1,..., x n ) = (y 1,..., y n )-t. A biztonság itt azt jelenti, hogy garantáljuk a végeredmény helyességét, illetve azt, hogy egyik résztvevő sem tudhat meg semmilyen plusz információt a kommunikációból. Azaz minden résztvevő csak azt tudhatja, amit az általa ismert inputból és a végeredményből ki tud találni, és ennél többet még akkor sem tudhat, ha a résztvevők között nem mindenki tisztességes. Mivel a számolásokat a résztvevők egy F véges test fölött végzik, elegendő, ha csak a következő műveleteket használják. Egyrészt szükség van valamilyen titokmegosztási sémára, mellyel minden résztvevő szétosztja a birtokában lévő inputot. Ezenkívül szükség van a szétosztott titokrészek összeadására, összeszorzására, illetve konstanssal való szorzására. Ezekkel a műveletekkel minden F-beli polinom előallítható. Arra, hogy miért elég csak polinomokkal számolni, a következő tétel ad magyarázatot Tétel. Véges test fölött minden függvény polinom. 17
20 5.1. Példák Milliomosok problémája Egy példa többrésztvevős számításra a Yao-féle milliomosok problémája [11]: Két milliomos rá szeretne jönni, hogy melyikük a gazdagabb, mindezt anélkül, hogy bármelyikük megtudná, hogy a másiknak mennyi pénze van. Ebben az esetben mindkét résztvevő csak a saját vagyonát ismerheti, illetve azt, hogy melyikük a gazdagabb. Ez egy kétrésztvevős számítás, ahol az input két egész szám, a végeredmény pedig annak az igazságértéke, hogy az első szám volt -e a nagyobb. A következőt tehetik a milliomosok: Legyen a két milliomos A és B. A-nak van i millió forintja, B-nek j milliója. Tegyük fel, hogy 0 < i, j < 100, i és j egészek. Jelölje egy x üzenet A nyilvános kulcsával való titkosítását y = E A (x), ennek visszafejtését x = D A (y). 1. B generál egy N jegyű véletlen egész számot, ahol N páros pozitív egész. Legyen ez a szám x. B elküldi A-nak a k j + 1 értéket, ahol k = E A (x). 2. A kiszámolja y u = D A (k j + u)-t, u = 1,..., A generál egy N/2 jegyű p prímszámot, és kiszámolja z u = y u (mod p)-t minden u-ra. Ezt ismétli, amíg olyan z u -kat nem kap, melyeknek páronkénti különbsége legalább A elküldi B-nek a p, z 1,..., z i, z i + 1,..., z (mod p) számokat. 5. B megnézi p-t nem számítva a j. számot. Ha ez egyenlő x-szel (mod p), akkor i j, különben i < j Ebédlő kriptográfusok Egy másik példa többrésztvevős számításra a Chaum-féle ebédlő kriptográfusok problémája [4]: Három kriptográfus elmegy ebédelni egy étterembe, majd amikor fizetni szeretnének, a pincér közli velük, hogy a számla már ki van egyenlítve. Két lehetőség van. Vagy az NSA (az Amerikai Nemzetbiztonsági Hivatal) fizette ki az ebédjüket, vagy hármuk közül valaki. Ki szeretnék deríteni, hogy mi is történt, de úgy, hogy ha hármuk közül rendezte valaki a számlát, akkor ne derüljön ki, hogy melyikük. Ez egy háromrésztvevős számítás, ahol a számítás előtt minden résztvevő csak azt tudja, hogy ő maga fizetett -e, a 18
21 számítás után pedig mindhárman tudják, hogy az NSA fizetett -e, vagy hármuk közül valaki. A következőt kell tenniük: Leülnek körben egy asztalhoz, és feldobnak egy-egy pénzérmét. Mindegyikük úgy helyezi el az érmét, hogy csak ő és a tőle jobbra ülő kollégája láthassa azt. A fejnek megfeleltetik a 0, az írásnak az 1 értéket. Összeadják az általuk látott érméknek megfelelő értéket modulo 2, és az, aki fizetett, még 1-et hozzáad az eredményhez modulo 2. Mindhárman megmondják a kapott eredményt, majd ezeket is összeadják modulo 2. Mivel minden 1-est és minden 0-t pontosan két ember lát, ezért ha ezeket összeadják modulo 2 a végeredmény 0 lesz, kivéve ha egyikük még hozzáadott az eredményhez 1-et modulo 2. Így ha a végeredmény 0, akkor az NSA fizetett, ha pedig 1, akkor hármuk közül valaki Általános tételek Ahhoz, hogy egy többrésztvevős számítás biztonságos lehessen, korlátoznunk kell a támadható résztvevők számát. A következő tételek felső korlátot adnak a passzívan, illetve az aktívan támadható résztvevők számára Tétel. [6] Legyen t a az aktívan, t p a passzívan támadható résztvevők száma. Egy n résztvevős számítás pontosan akkor lehet kriptográfiailag biztonságos, ha t p < n, és t a < n/ Tétel. [2],[5] Legyen t a az aktívan, t p a passzívan támadható résztvevők száma. Egy n résztvevős számítás pontosan akkor lehet tökéletesen biztonságos, ha t p < n/2, és t a < n/ Tétel. [9],[1] Legyen t a az aktívan támadható résztvevők száma. Egy n résztvevős számítás üzenetszórásos csatornával pontosan akkor lehet tökéletesen biztonságos, ha t a < n/ Tétel. [8] Pontosan akkor lehet tökéletesen biztonságos egy többrésztvevős számítás egy (Σ, )-támadó ellen, ha P / Σ Σ, azaz ha a résztvevők teljes halmazát nem lehet lefedni semelyik kettő tisztességes, de kíváncsi, illetve egy tisztességtelen halmaz uniójával. 19
22 5.3. A szükséges műveletek Ebben a fejezetben áttekintjük, hogy hogyan végezhetjük el biztonságosan a többrésztvevős számításhoz szükséges műveleteket. Mint már említettük a szükséges műveletek a titokrészek összeadása, a konstanssal való szorzás, illetve a titokrészek szorzása. Tökéletes biztonságot szeretnénk elérni, így az Tétel alapján fel kell tennünk, hogy t p < n/2, valamint t a < n/3, ahol n az összes résztvevő száma, t p a tisztességes, de kíváncsi résztvevők száma, t a pedig a tisztességtelen résztvevők száma. Az inputok szétosztása. Az összes p i résztvevő titokmegosztással szétosztja a birtokában lévő x i F inputot. Összeadás. Legyen a és b két szétosztandó input, a 1,..., a n és b 1,..., b n rendre a hozzájuk tartozó titokrészek. Ekkor mindegyik p i résztvevő lokálisan kiszámolja a i + b i -t. Az a 1 + b 1,..., a n + b n titokrészek pedig egyértelműen meghatározzák az a + b titkot. Konstanssal való szorzás. Legyen a egy szétosztandó input, a 1,..., a n a hozzá tartozó titokrészek, d F egy konstans. Ekkor mindegyik p i résztvevő lokálisan kiszámolja da i -t. A da 1,..., da n titokrészek pedig egyértelműen meghatározzák az a + b titkot. Szorzás. Legyen a és b két szétosztandó input, a 1,..., a n és b 1,..., b n rendre a hozzájuk tartozó titokrészek. Ekkor mindegyik p i résztvevő lokálisan kiszámolja c i = a i b i -t, majd p i szétosztja c i -t. Legyenek a c i -hez tartozó titokrészek c i1,..., c in, ahol a p j résztvevő megkapja a c ij titokrészt. Ezután a c i1,..., c in titokrészek egyértelműen meghatározzák c j -t, a c 1,..., c n titokrészek pedig egyértelműen meghatározzák a c = ab titkot. 20
23 6. fejezet Üzenetszórás 6.1. A bizánci generálisok problémája A bizánci generálisok problémája [7] a következő. A bizánci hadsereg két hadnagya parancsot vár a parancsnoktól. A parancsnok kétféle utasítást adhat: támadás, vagy visszavonulás. Miután a parancsnok kiadta az utasítást, a két hadnagy megbeszéli egymással, hogy mi a teendő. Probléma akkor van, ha a parancsnok, illetve a két hadnagy közül valaki nem tisztességes. A problémát a következő két ábra szemlélteti. 21
24 ábra. Az egyik hadnagy tisztességtelen ábra. A parancsnok tisztességtelen 22
25 Tegyük fel, hogy Hadnagy 1 tisztességes. Ekkor ha Hadnagy 2 tisztességtelen, és a Parancsnok mindkét hadnagynak a "támadás" utasítást adta, akkor Hadnagy 2 a "visszavonulás" utasítást fogja továbbadni Hadnagy 1-nek. Ha a Parancsnok a tisztességtelen, és Hadnagy 1-nek a "támadás", Hadnagy 2-nek pedig a "visszavonulás utasítást adta", Hadnagy 2 ebben az esetben is a "visszavonulás" utasítást fogja továbbadni Hadnagy 1-nek. Hadnagy 1 mindkét esetben ugyanazt fogja tapasztalni, mégpedig hogy a Parancsnok azt mondta, hogy "támadás", Hadnagy 2 pedig azt, hogy "visszavonulás". Így Hadnagy 1 nem fogja tudni, hogy melyikük hazudott, azaz nem tudja kiszűrni a tisztességtelen résztvevőt. Ezt a problémát hivatott megoldani a szimulált üzenetszórás Szimulált üzenetszórás Szimulált üzenetszórásnál [7] az üzenetszóráshoz hasonlóan az a célunk, hogy minden résztvevőnek eljuttassuk ugyanazt az üzenetet úgy, hogy a bizánci generálisok problémáját elkerüljük. Ez csak abban az esetben lehetséges, ha a kommunikációs csatorna szinkronizált. Az üzenetszórás szimulálását a következő algoritmussal valósíthatjuk meg. Minden résztvevő konstruál egy fát, melynek éleit megcímkézi a résztvevők P = {p 1,..., p n } halmazának elemeivel úgy, hogy a gyökértől a levelekig a p 1,..., p n elemek mindegyike pontosan egyszer forduljon elő az összes lehetséges sorrendben, azaz a fa első szintjén az élek p 1,..., p n címkét kapnak, a második szinten a p i él alatt már csak a p 1,..., p i 1, p i+1,..., p n címkék szerepelnek, és így tovább. Ezután a fának törlik néhány csúcsát és élét, mégpedig úgy, hogy a fa gyökerétől indulva haladnak lefelé az éleken addig, amíg egy olyan élt nem találnak, amit az eddigiekhez hozzávéve a kapott {p i1,..., p il } élhalmaz már nem lehet tisztességtelen, azaz teljesül rá {p i1,..., p il } /. Az első ilyen él alatt lévő összes többi élt a hozzájuk tartozó csúcsokkal együtt törlik. Ezt megismétlik az összes lehetséges úttal. A következő ábrán egy egyszerű példával szemléltetjük a fa konstrukcióját. 23
26 ábra. A fa konstrukciója P = {A, B, C} és = {{A, B}, {C}} esetén A fa konsrukciója után a résztvevők kitöltik a fa csúcsait. A fa gyökeréhez mindegyikük hozzárendeli azt az értéket, amit ő kapott az osztótól. Ha az osztó tisztességes, ez az érték minden résztvevő esetében ugyanaz lesz. Első lépésben minden résztvevő elküldi ezt az értéket az összes többi résztvevőnek, majd kitölti a második szintet. Hasonlóan a k. lépésben minden résztvevő elküldi az összes többi résztvevőnek a k. szinthez tartozó értékeket, majd kitölti a k + 1. szintet. A kitöltés úgy történik, hogy minden résztvevő azt az értéket rendeli a v csúcshoz, ami tudomása szerint a p i résztvevő fájában az u csúcshoz rendelt érték, ahol u és v a p i -vel címkézett él két végpontja, és u a v csúcs szülője. A csúcsok kitöltése után az összes csúcsokhoz rendelt értéket kitörlik a leveleken kívül. Ezután rekonstruálják a fát. Ha egy v csúcsnak az összes gyereke ki van már töltve, a v csúcsot is ki tudjuk tölteni. Legyenek a v csúcs és a gyerekei között futó élek a p i1,..., p il résztvevőkkel megcímkézve. Felosztjuk a {p i1,..., p il } halmazt az A 1,..., A k halmazokra úgy, hogy azok a résztvevők kerülnek egy halmazba, akik ugyanazt az értéket mondták a v csúcs alatti szint kitöltésekor. Ha pontosan egy olyan j van, melyre A j /, akkor azt az értéket rendeljük a v csúcshoz, amit az A j -beli résztvevők mondtak. Ha nincs ilyen j, vagy több is van, akkor a v csúcshoz a karaktert rendeljük. Ezt az eljárást ismételjük a gyökérig. 24
27 Azt, hogy ez az eljárás valóban szimulálja az üzenetszórást, az alábbi tételben fogalmazzuk meg Tétel. Minden tisztességes résztvevő a saját maga által konstruált fának a gyökerében ugyanazt az értéket kapja. A tétel bizonyítása előtt bebizonyítunk két lemmát Lemma. Ha A egy tisztességes résztvevő, akkor minden résztvevő fájában az A-val címkézett él v végpontjában ugyanaz az érték szerepel, mint A fájában ugyanezen él egy szinttel feljebb lévő végpontjában, azaz a v csúcs szülőjében. Bizonyítás. Ha A a legalsó szinten van, akkor tisztességes volta miatt A mindenkinek ugyanazt az értéket mondja, így a fa konstrukciója miatt valóban igaz az állítás. Ha A nem a legalsó szinten van, tegyük fel hogy A egy x értéket rendelt a v csúcshoz. Ekkor a fa konstrukciója miatt az összes tisztességes résztvevő ugyanezt az x értéket rendelte a v csúcs A-val címkézett élén lévő gyerekéhez. Azok a résztvevők, akik a fa rekonstruálásánál nem az x értéket küldték a többi résztvevőnek, tisztességtelenek, azaz -beli résztvevők. Akik nincsenek az A- val címkézett él alatti részfában, szintén -beli résztvevők, így azon résztvevők, akik az x értéket küldték a többi résztvevőnek, nem lehetnek -beli résztvevők a Tételben szereplő feltétel miatt, miszerint P /, azaz ezek a résztvevők nem lehetnek tisztességtelenek. Így a fa rekonstrukciós szabályai miatt valóban igaz a lemma Lemma. Ha egy v csúcsból kiindulva minden ágon van tisztességes résztvevő, akkor a v csúcshoz minden résztvevő ugyanazt az értéket rendeli. Bizonyítás. Ha v minden gyereke tisztességes, a lemma triviálisan igaz. Ha v-nek van egy w tisztességtelen gyereke, akkor ez alatt a csúcs alatt minden ágon kell lennie tisztességes résztvevőnek. Ekkor a w csúcshoz minden résztvevő ugyanazt az értéket rendeli. Emiatt a v csúcs összes gyerekéhez minden résztvevő ugyanazt az értéket rendeli, így ez a Lemma miatt a v csúcsra is teljesül. A Tétel bizonyítása. Azt szeretnénk megmutatni, hogy minden tisztességes résztvevő a saját maga által konstruált fának a gyökerében ugyanazt az értéket kapja. Valóban, a fa konstruálásakor addig tartottuk meg az éleket, 25
28 amíg találtunk egy olyat, amivel együtt a fa gyökerétől idáig vezető út már nem lehet -ban. Emiatt a fa gyökeréből kiindulva minden ágon van tisztességes résztvevő, így a Lemma miatt a fa gyökeréhez minden résztvevő ugyanazt az értéket rendeli. 26
29 Köszönetnyilvánítás Szeretnék köszönetet mondani témavezetőmnek, Csirmaz Lászlónak a dolgozat írása során nyújtott segítségéért, türelméért, és hasznos tanácsaiért. 27
30 Irodalomjegyzék [1] D. Beaver. Secure multi-party protocols and zero-knowledge proof systems tolerating a faulty minority. Journal of Cryprology vol.4, no. 2, 1991 [2] M. Ben-Or, S. Goldwasser, A. Wigderson. Completeness theorems for noncryptographic fault-tolerant distributed computation. 20th ACM Symposium on the Theory of Computing, 1988 [3] G. R. Blakley. Safeguarding cryptographic keys. Proceedings of the National Computer Conference, 1979 [4] D. Chaum. The Dining Cryptographers Problem: Unconditional Sender and Recipient Untraceability. Journal of Cryptology, 1988 [5] D. Chaum, C. Crépeau, I. Damgård. Multi-party unconditionally secure protocols (extended abstract). 20th ACM Symposium on the Theory of Computing, 1988 [6] O. Goldreich, S. Micali, A. Wigderson. How to play any mental game - a completeness theorem for protocols with honest majority. 19th ACM Symposium on the Theory of Computing, 1987 [7] L. Lamport, R. Shostak, M. Pease. The Byzantine generals problem. ACM Transactions on Programming Languages and Systems, 1982 [8] U. Maurer. Secure Multi-Party Computation Made Simple. Security in Communication Networks (SCN 02), 2003 [9] T. Rabin, M. Ben-Or. Verifiable secret-sharing and multiparty protocols with honest majority. 21st ACM Symposium on the Theory of Computing, 1989 [10] A. Shamir. How to share a secret. Communications of the ACM, 1979 [11] A. C. Yao. Protocols for secure computations. 23rd IEEE Symposium on the Foundations of Computer Science,
6. AZ EREDMÉNYEK ÉRTELMEZÉSE
 6. AZ EREDMÉNYEK ÉRTELMEZÉSE A kurzus anyagát felhasználva összeállíthatunk egy kitűnő feladatlapot, de még nem dőlhetünk nyugodtan hátra. Diákjaink teljesítményét még osztályzatokra kell átváltanunk,
6. AZ EREDMÉNYEK ÉRTELMEZÉSE A kurzus anyagát felhasználva összeállíthatunk egy kitűnő feladatlapot, de még nem dőlhetünk nyugodtan hátra. Diákjaink teljesítményét még osztályzatokra kell átváltanunk,
Matematikai alapismeretek. Huszti Andrea
 Tartalom 1 Matematikai alapismeretek Algebrai struktúrák Oszthatóság Kongruenciák Algebrai struktúrák Az S = {x, y, z,... } halmazban definiálva van egy művelet, ha az S-nek minden x, y elempárjához hozzá
Tartalom 1 Matematikai alapismeretek Algebrai struktúrák Oszthatóság Kongruenciák Algebrai struktúrák Az S = {x, y, z,... } halmazban definiálva van egy művelet, ha az S-nek minden x, y elempárjához hozzá
Jogosultságkezelés felhasználói leírás
 Jogosultságkezelés felhasználói leírás 1149 Budapest, Egressy út 17-21. Telefon: +36 1 469 4021; fax: +36 1 469 4029 1/14 Tartalomjegyzék 1. Jogosultságkezelés a DOAS rendszerben... 3 1.1. Bevezetés...
Jogosultságkezelés felhasználói leírás 1149 Budapest, Egressy út 17-21. Telefon: +36 1 469 4021; fax: +36 1 469 4029 1/14 Tartalomjegyzék 1. Jogosultságkezelés a DOAS rendszerben... 3 1.1. Bevezetés...
22. szakkör (Csoportelméleti alapfogalmak 1.)
 22. szakkör (Csoportelméleti alapfogalmak 1.) A) A PERMUTÁCIÓK CIKLIKUS SZERKEZETE 1. feladat: Egy húsztagú társaság ül az asztal körül. Néhányat közülük (esetleg az összeset) párba állítunk, és a párok
22. szakkör (Csoportelméleti alapfogalmak 1.) A) A PERMUTÁCIÓK CIKLIKUS SZERKEZETE 1. feladat: Egy húsztagú társaság ül az asztal körül. Néhányat közülük (esetleg az összeset) párba állítunk, és a párok
FELADATOK ÉS MEGOLDÁSOK
 3. osztály Egy asztal körül 24-en ülnek, mindannyian mindig igazat mondanak. Minden lány azt mondja, hogy a közvetlen szomszédjaim közül pontosan az egyik fiú, és minden fiú azt mondja, hogy mindkét közvetlen
3. osztály Egy asztal körül 24-en ülnek, mindannyian mindig igazat mondanak. Minden lány azt mondja, hogy a közvetlen szomszédjaim közül pontosan az egyik fiú, és minden fiú azt mondja, hogy mindkét közvetlen
Gráfelmélet/Diszkrét Matematika MSc hallgatók számára. Párosítások
 Gráfelmélet/Diszkrét Matematika MSc hallgatók számára Párosítások 2012. november 19. Előadó: Hajnal Péter 1. Alapfogalmak Emlékeztető. Legyen G egy gráf, E(G) a G élhalmaza, V (G) gráfunk csúcshalmaza.
Gráfelmélet/Diszkrét Matematika MSc hallgatók számára Párosítások 2012. november 19. Előadó: Hajnal Péter 1. Alapfogalmak Emlékeztető. Legyen G egy gráf, E(G) a G élhalmaza, V (G) gráfunk csúcshalmaza.
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Számelmélet I.
 Számelmélet I. DEFINÍCIÓ: (Ellentett) Egy szám ellentettjén azt a számot értjük, amelyet a számhoz hozzáadva az 0 lesz. Egy szám ellentettje megegyezik a szám ( 1) szeresével. Számfogalmak kialakítása:
Számelmélet I. DEFINÍCIÓ: (Ellentett) Egy szám ellentettjén azt a számot értjük, amelyet a számhoz hozzáadva az 0 lesz. Egy szám ellentettje megegyezik a szám ( 1) szeresével. Számfogalmak kialakítása:
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 7 VII. Gyűrűk 1. Gyűrű Definíció Egy a következő axiómákat: gyűrű alatt olyan halmazt értünk, amelyben definiálva van egy összeadás és egy szorzás, amelyek teljesítik (1) egy
KOVÁCS BÉLA, MATEmATIkA I. 7 VII. Gyűrűk 1. Gyűrű Definíció Egy a következő axiómákat: gyűrű alatt olyan halmazt értünk, amelyben definiálva van egy összeadás és egy szorzás, amelyek teljesítik (1) egy
BEVEZETÉS AZ ÁBRÁZOLÓ GEOMETRIÁBA
 Pék Johanna BEVEZETÉS AZ ÁBRÁZOLÓ GEOMETRIÁBA (Matematika tanárszakos hallgatók számára) Tartalomjegyzék Előszó ii 0. Alapismeretek 1 0.1. Térgeometriai alapok............................. 1 0.2. Az ábrázoló
Pék Johanna BEVEZETÉS AZ ÁBRÁZOLÓ GEOMETRIÁBA (Matematika tanárszakos hallgatók számára) Tartalomjegyzék Előszó ii 0. Alapismeretek 1 0.1. Térgeometriai alapok............................. 1 0.2. Az ábrázoló
BUDAPESTI KÖZGAZDASÁGTUDOMÁNYI EGYETEM. Puskás Csaba, Szabó Imre, Tallos Péter LINEÁRIS ALGEBRA JEGYZET
 BUDAPESTI KÖZGAZDASÁGTUDOMÁNYI EGYETEM Puskás Csaba, Szabó Imre, Tallos Péter LINEÁRIS ALGEBRA JEGYZET BUDAPEST, 1997 A szerzők Lineáris Algebra, illetve Lineáris Algebra II c jegyzeteinek átdolgozott
BUDAPESTI KÖZGAZDASÁGTUDOMÁNYI EGYETEM Puskás Csaba, Szabó Imre, Tallos Péter LINEÁRIS ALGEBRA JEGYZET BUDAPEST, 1997 A szerzők Lineáris Algebra, illetve Lineáris Algebra II c jegyzeteinek átdolgozott
Megoldókulcs. Matematika D kategória (11-12. osztályosok) 2015. február 6.
 Megoldókulcs Matematika D kategória (11-12. osztályosok) 2015. február 6. 1. Az ABC háromszög mindhárom csúcsából merőlegeseket állítunk a többi csúcs külső és belső szögfelezőire. Igazoljuk, hogy az így
Megoldókulcs Matematika D kategória (11-12. osztályosok) 2015. február 6. 1. Az ABC háromszög mindhárom csúcsából merőlegeseket állítunk a többi csúcs külső és belső szögfelezőire. Igazoljuk, hogy az így
Feladatok és megoldások a 4. hétre
 Feladatok és megoldások a. hétre Építőkari Matematika A3. Pisti nem tanult semmit a vizsgára, ahol 0 darab eldöntendő kérdésre kell válaszolnia. Az anyagból valami kicsi dereng, ezért kicsit több, mint
Feladatok és megoldások a. hétre Építőkari Matematika A3. Pisti nem tanult semmit a vizsgára, ahol 0 darab eldöntendő kérdésre kell válaszolnia. Az anyagból valami kicsi dereng, ezért kicsit több, mint
Szeminárium-Rekurziók
 1 Szeminárium-Rekurziók 1.1. A sorozat fogalma Számsorozatot kapunk, ha pozitív egész számok mindegyikéhez egyértelműen hozzárendelünk egy valós számot. Tehát a számsorozat olyan függvény, amelynek az
1 Szeminárium-Rekurziók 1.1. A sorozat fogalma Számsorozatot kapunk, ha pozitív egész számok mindegyikéhez egyértelműen hozzárendelünk egy valós számot. Tehát a számsorozat olyan függvény, amelynek az
Analízisfeladat-gyűjtemény IV.
 Oktatási segédanyag a Programtervező matematikus szak Analízis. című tantárgyához (003 004. tanév tavaszi félév) Analízisfeladat-gyűjtemény IV. (Függvények határértéke és folytonossága) Összeállította
Oktatási segédanyag a Programtervező matematikus szak Analízis. című tantárgyához (003 004. tanév tavaszi félév) Analízisfeladat-gyűjtemény IV. (Függvények határértéke és folytonossága) Összeállította
Véletlenített algoritmusok. 4. előadás
 Véletlenített algoritmusok 4. előadás Tartalomjegyzék: elfoglalási probléma, születésnap probléma, kupongyűjtő probléma, stabil házassági feladat, Chernoff korlát (példák), forgalomirányítási probléma.
Véletlenített algoritmusok 4. előadás Tartalomjegyzék: elfoglalási probléma, születésnap probléma, kupongyűjtő probléma, stabil házassági feladat, Chernoff korlát (példák), forgalomirányítási probléma.
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 5 V ELEmI ALGEbRA 1 BINÁRIS műveletek Definíció Az halmazon definiált bináris művelet egy olyan függvény, amely -ből képez -be Ha akkor az elempár képét jelöljük -vel, a művelet
KOVÁCS BÉLA, MATEmATIkA I 5 V ELEmI ALGEbRA 1 BINÁRIS műveletek Definíció Az halmazon definiált bináris művelet egy olyan függvény, amely -ből képez -be Ha akkor az elempár képét jelöljük -vel, a művelet
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Gráfelmélet II. Gráfok végigjárása
 Gráfelmélet II. Gráfok végigjárása DEFINÍCIÓ: (Séta) A G gráf egy olyan élsorozatát, amelyben a csúcsok és élek többször is szerepelhetnek, sétának nevezzük. Egy lehetséges séta: A; 1; B; 2; C; 3; D; 4;
Gráfelmélet II. Gráfok végigjárása DEFINÍCIÓ: (Séta) A G gráf egy olyan élsorozatát, amelyben a csúcsok és élek többször is szerepelhetnek, sétának nevezzük. Egy lehetséges séta: A; 1; B; 2; C; 3; D; 4;
MATEMATIKA ÉRETTSÉGI 2006. május 9. EMELT SZINT
 ) A PQRS négyszög csúcsai: MATEMATIKA ÉRETTSÉGI 006. május 9. EMELT SZINT P 3; I., Q ;3, R 6; és S 5; 5 Döntse el, hogy az alábbi három állítás közül melyik igaz és melyik hamis! Tegyen * jelet a táblázat
) A PQRS négyszög csúcsai: MATEMATIKA ÉRETTSÉGI 006. május 9. EMELT SZINT P 3; I., Q ;3, R 6; és S 5; 5 Döntse el, hogy az alábbi három állítás közül melyik igaz és melyik hamis! Tegyen * jelet a táblázat
mobil rádióhálózatokban
 Magyar Tudomány 2007/7 Az interferencia elnyomása mobil rádióhálózatokban Pap László az MTA rendes tagja, egyetemi tanár BME Híradástechnikai Tanszék pap@hit.bme.hu Imre Sándor az MTA doktora, egyetemi
Magyar Tudomány 2007/7 Az interferencia elnyomása mobil rádióhálózatokban Pap László az MTA rendes tagja, egyetemi tanár BME Híradástechnikai Tanszék pap@hit.bme.hu Imre Sándor az MTA doktora, egyetemi
Valószínűségszámítás
 Eszterházy Károly Főiskola Matematikai és Informatikai Intézet Tómács Tibor Valószínűségszámítás programtervező informatikusok részére Eger, 010. szeptember 0. Tartalomjegyzék 1. Véletlen események...............................
Eszterházy Károly Főiskola Matematikai és Informatikai Intézet Tómács Tibor Valószínűségszámítás programtervező informatikusok részére Eger, 010. szeptember 0. Tartalomjegyzék 1. Véletlen események...............................
ALGORITMUSOK ÉS BONYOLULTSÁGELMÉLET Matematika MSc hallgatók számára. 3. Előadás
 ALGORITMUSOK ÉS BONYOLULTSÁGELMÉLET Matematika MSc hallgatók számára 3. Előadás Előadó: Hajnal Péter Jegyzetelő: Sallai Gyöngyi 2011. február 15. 1. Eldöntő Turing-gépek Emlékeztető. L Σ nyelv pontosan
ALGORITMUSOK ÉS BONYOLULTSÁGELMÉLET Matematika MSc hallgatók számára 3. Előadás Előadó: Hajnal Péter Jegyzetelő: Sallai Gyöngyi 2011. február 15. 1. Eldöntő Turing-gépek Emlékeztető. L Σ nyelv pontosan
2) = 0 ahol x 1 és x 2 az ax 2 + bx + c = 0 ( a,b, c R és a 0 )
 Fogalom gyűjtemény Abszcissza: az x tengely Abszolút értékes egyenletek: azok az egyenletek, amelyekben abszolút érték jel szerepel. Abszolútérték-függvény: egy elemi egyváltozós valós függvény, mely minden
Fogalom gyűjtemény Abszcissza: az x tengely Abszolút értékes egyenletek: azok az egyenletek, amelyekben abszolút érték jel szerepel. Abszolútérték-függvény: egy elemi egyváltozós valós függvény, mely minden
1992. évi verseny, 2. nap. legkisebb d szám, amelyre igaz, hogy bárhogyan veszünk fel öt pontot
 1991. évi verseny, 1. nap 1. Bizonyítsd be, hogy 1 101 + 1 102 + 1 103 +... + 1 200 < 1 2. 2. Egy bálon 42-en vettek részt. Az első lány elmondta, hogy 7 fiúval táncolt, a második lány 8-cal, a harmadik
1991. évi verseny, 1. nap 1. Bizonyítsd be, hogy 1 101 + 1 102 + 1 103 +... + 1 200 < 1 2. 2. Egy bálon 42-en vettek részt. Az első lány elmondta, hogy 7 fiúval táncolt, a második lány 8-cal, a harmadik
Gráfokkal megoldható hétköznapi problémák
 Eötvös Loránd Tudományegyetem Természettudományi Kar Gráfokkal megoldható hétköznapi problémák Szakdolgozat Készítette Vincze Ágnes Melitta Konzulens Héger Tamás Budapest, 2015 Tartalomjegyzék Bevezetés
Eötvös Loránd Tudományegyetem Természettudományi Kar Gráfokkal megoldható hétköznapi problémák Szakdolgozat Készítette Vincze Ágnes Melitta Konzulens Héger Tamás Budapest, 2015 Tartalomjegyzék Bevezetés
2. Hatványozás, gyökvonás
 2. Hatványozás, gyökvonás I. Elméleti összefoglaló Egész kitevőjű hatvány értelmezése: a 1, ha a R; a 0; a a, ha a R. Ha a R és n N; n > 1, akkor a olyan n tényezős szorzatot jelöl, aminek minden tényezője
2. Hatványozás, gyökvonás I. Elméleti összefoglaló Egész kitevőjű hatvány értelmezése: a 1, ha a R; a 0; a a, ha a R. Ha a R és n N; n > 1, akkor a olyan n tényezős szorzatot jelöl, aminek minden tényezője
Miskolci Egyetem. Diszkrét matek I. Vizsga-jegyzet. Hegedűs Ádám Imre 2010.12.28.
 Miskolci Egyetem Diszkrét matek I. Vizsga-jegyzet Hegedűs Ádám Imre 2010.12.28. KOMBINATORIKA Permutáció Ismétlés nélküli permutáció alatt néhány különböző dolognak a sorba rendezését értjük. Az "ismétlés
Miskolci Egyetem Diszkrét matek I. Vizsga-jegyzet Hegedűs Ádám Imre 2010.12.28. KOMBINATORIKA Permutáció Ismétlés nélküli permutáció alatt néhány különböző dolognak a sorba rendezését értjük. Az "ismétlés
Legrövidebb utat kereső algoritmusok. BFS (szélességi keresés)
 Legrövidebb utat kereső algoritmusok Adott gráfban szeretnénk egkeresni két pont között a legrövidebb utat (a két pont távolsága érdekel). Ezt úgy fogjuk tudni megtenni, hogy közben megkapjuk az összes
Legrövidebb utat kereső algoritmusok Adott gráfban szeretnénk egkeresni két pont között a legrövidebb utat (a két pont távolsága érdekel). Ezt úgy fogjuk tudni megtenni, hogy közben megkapjuk az összes
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika emelt szint 05 ÉRETTSÉGI VIZSGA 006. május 9. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI MINISZTÉRIUM Formai előírások: Fontos tudnivalók A dolgozatot
Matematika emelt szint 05 ÉRETTSÉGI VIZSGA 006. május 9. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI MINISZTÉRIUM Formai előírások: Fontos tudnivalók A dolgozatot
FRAKTÁLOK ÉS A KÁOSZ
 FRAKTÁLOK ÉS A KÁOSZ Meszéna Tamás Ciszterci Rend Nagy Lajos Gimnáziuma és Kollégiuma, Pécs, meszena.tamas@gmail.com, az ELTE Fizika Tanítása doktori program hallgatója ÖSSZEFOGLALÁS A fraktálok olyan
FRAKTÁLOK ÉS A KÁOSZ Meszéna Tamás Ciszterci Rend Nagy Lajos Gimnáziuma és Kollégiuma, Pécs, meszena.tamas@gmail.com, az ELTE Fizika Tanítása doktori program hallgatója ÖSSZEFOGLALÁS A fraktálok olyan
noannb Számítógépek automatizált tervezése
 noannb * HlR A DA SItCMHIK Al TUDOMÁNYOS totislítei LÁMA DRASNY JÓZSEF Számítástechnikai Koordinációs Intézet Számítógépek automatizált tervezése BTO: 6S1.3.001.2;6S1.3.06 Napjainkban a számítógépek a
noannb * HlR A DA SItCMHIK Al TUDOMÁNYOS totislítei LÁMA DRASNY JÓZSEF Számítástechnikai Koordinációs Intézet Számítógépek automatizált tervezése BTO: 6S1.3.001.2;6S1.3.06 Napjainkban a számítógépek a
Csődvalószínűségek becslése a biztosításban
 Csődvalószínűségek becslése a biztosításban Diplomamunka Írta: Deák Barbara Matematikus szak Témavezető: Arató Miklós, egyetemi docens Valószínűségelméleti és Statisztika Tanszék Eötvös Loránd Tudományegyetem,
Csődvalószínűségek becslése a biztosításban Diplomamunka Írta: Deák Barbara Matematikus szak Témavezető: Arató Miklós, egyetemi docens Valószínűségelméleti és Statisztika Tanszék Eötvös Loránd Tudományegyetem,
Átrendezések és leszámlálások ÚTMUTATÓ Hegedüs Pál 1-2015.június 30.
 Átrendezések és leszámlálások ÚTMUTATÓ Hegedüs Pál 1-2015.június 30. 1. Határozzuk meg, hány egybevágósága van egy négyzetnek! Melyek azonos jellegűek ezek között? Ez egy általános bevezető feladat tud
Átrendezések és leszámlálások ÚTMUTATÓ Hegedüs Pál 1-2015.június 30. 1. Határozzuk meg, hány egybevágósága van egy négyzetnek! Melyek azonos jellegűek ezek között? Ez egy általános bevezető feladat tud
Diplomaterv Portál. Elektronikus szakdolgozat és diplomaterv nyilvántartó és archiváló rendszer. Felhasználói útmutató v11
 Elektronikus szakdolgozat és diplomaterv nyilvántartó és archiváló rendszer v11 Tevesz Gábor 2013. február 8. Bevezetés A 2010/11 tanév kezdetétől a Villamosmérnöki és Informatikai Kar a Szakdolgozat készítés
Elektronikus szakdolgozat és diplomaterv nyilvántartó és archiváló rendszer v11 Tevesz Gábor 2013. február 8. Bevezetés A 2010/11 tanév kezdetétől a Villamosmérnöki és Informatikai Kar a Szakdolgozat készítés
Általános statisztika II. Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László
 Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Publication
Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Általános statisztika II Kriszt, Éva Varga, Edit Kenyeres, Erika Korpás, Attiláné Csernyák, László Publication
Biztosítási ügynökök teljesítményének modellezése
 Eötvös Loránd Tudományegyetem Természettudományi Kar Budapest Corvinus Egyetem Közgazdaságtudományi Kar Biztosítási ügynökök teljesítményének modellezése Szakdolgozat Írta: Balogh Teréz Biztosítási és
Eötvös Loránd Tudományegyetem Természettudományi Kar Budapest Corvinus Egyetem Közgazdaságtudományi Kar Biztosítási ügynökök teljesítményének modellezése Szakdolgozat Írta: Balogh Teréz Biztosítási és
A titkosító vírusok működéséről
 A titkosító vírusok működéséről A fájlokat titkosító és a számítógépeket a felhasználók előtt lezáró kártevők a legveszélyesebbek közé tartoznak, mivel a kódolás feltörésére a legtöbbször nincs mód, és
A titkosító vírusok működéséről A fájlokat titkosító és a számítógépeket a felhasználók előtt lezáró kártevők a legveszélyesebbek közé tartoznak, mivel a kódolás feltörésére a legtöbbször nincs mód, és
Nyitott mondatok Bennfoglalás maradékkal
 Matematika A 2. évfolyam Nyitott mondatok Bennfoglalás maradékkal 35. modul Készítette: Szitányi Judit 2 modulleírás A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A képességfejlesztés
Matematika A 2. évfolyam Nyitott mondatok Bennfoglalás maradékkal 35. modul Készítette: Szitányi Judit 2 modulleírás A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A képességfejlesztés
MATEMATIKA C 9. évfolyam
 MATEMATIKA C 9. évfolyam 6. modul GONDOLKODOM, TEHÁT VAGYOK Készítette: Kovács Károlyné MATEMATIKA C 9. ÉVFOLYAM 6. MODUL: GONDOLKODOM, TEHÁT VAGYOK TANÁRI ÚTMUTATÓ 2 MODULLEÍRÁS A modul célja Időkeret
MATEMATIKA C 9. évfolyam 6. modul GONDOLKODOM, TEHÁT VAGYOK Készítette: Kovács Károlyné MATEMATIKA C 9. ÉVFOLYAM 6. MODUL: GONDOLKODOM, TEHÁT VAGYOK TANÁRI ÚTMUTATÓ 2 MODULLEÍRÁS A modul célja Időkeret
Felvételi vizsga Mesterképzés, gazdaságinformatikus szak BME Villamosmérnöki és Informatikai Kar. 2010. június 2.
 GI pont(45) : Felvételi vizsga Mesterképzés, gazdaságinformatikus szak BME Villamosmérnöki és Informatikai Kar 2010. június 2. A dolgozat minden lapjára, a kerettel jelölt részre írja fel nevét, valamint
GI pont(45) : Felvételi vizsga Mesterképzés, gazdaságinformatikus szak BME Villamosmérnöki és Informatikai Kar 2010. június 2. A dolgozat minden lapjára, a kerettel jelölt részre írja fel nevét, valamint
Lineáris Algebra gyakorlatok
 A V 2 és V 3 vektortér áttekintése Lineáris Algebra gyakorlatok Írta: Simon Ilona Lektorálta: DrBereczky Áron Áttekintjük néhány témakör legfontosabb definícióit és a feladatokban használt tételeket kimondjuk
A V 2 és V 3 vektortér áttekintése Lineáris Algebra gyakorlatok Írta: Simon Ilona Lektorálta: DrBereczky Áron Áttekintjük néhány témakör legfontosabb definícióit és a feladatokban használt tételeket kimondjuk
FELADATOK ÉS MEGOLDÁSOK
 3. osztály Az első oldalon 1-gyel kezdve egyesével beszámozták egy könyv összes oldalát. Hány oldalas ez a könyv, ha ehhez 55 számjegyet használtak fel? Az első 9 oldalhoz 9 számjegyet használtak, a további
3. osztály Az első oldalon 1-gyel kezdve egyesével beszámozták egy könyv összes oldalát. Hány oldalas ez a könyv, ha ehhez 55 számjegyet használtak fel? Az első 9 oldalhoz 9 számjegyet használtak, a további
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Geometria I.
 Geometria I. Alapfogalmak: Az olyan fogalmakat, amelyeket nem tudunk egyszerűbb fogalmakra visszavezetni, alapfogalmaknak nevezzük, s ezeket nem definiáljuk. Pl.: pont, egyenes, sík, tér, illeszkedés.
Geometria I. Alapfogalmak: Az olyan fogalmakat, amelyeket nem tudunk egyszerűbb fogalmakra visszavezetni, alapfogalmaknak nevezzük, s ezeket nem definiáljuk. Pl.: pont, egyenes, sík, tér, illeszkedés.
23. Kombinatorika, gráfok
 I Elméleti összefoglaló Leszámlálási alapfeladatok 23 Kombinatorika, gráfok A kombinatorikai alapfeladatok esetek, lehetőségek összeszámlálásával foglalkoznak Általában n jelöli a rendelkezésre álló különbözőfajta
I Elméleti összefoglaló Leszámlálási alapfeladatok 23 Kombinatorika, gráfok A kombinatorikai alapfeladatok esetek, lehetőségek összeszámlálásával foglalkoznak Általában n jelöli a rendelkezésre álló különbözőfajta
Fejezetek az abszolút geometriából 6. Merőleges és párhuzamos egyenesek
 Fejezetek az abszolút geometriából 6. Merőleges és párhuzamos egyenesek Ebben a fejezetben megadottnak feltételezzük az abszolút tér egy síkját és tételeink mindig ebben a síkban értendők. T1 (merőleges
Fejezetek az abszolút geometriából 6. Merőleges és párhuzamos egyenesek Ebben a fejezetben megadottnak feltételezzük az abszolút tér egy síkját és tételeink mindig ebben a síkban értendők. T1 (merőleges
Az analízis néhány közgazdaságtani alkalmazása
 Az analízis néhány közgazdaságtani alkalmazása Szakdolgozat Írta: Simon Anita Matematika Bsc szak Matematikai elemző szakirány Témavezető: Sikolya Eszter, adjunktus Alkalmazott Analízis és Számításmatematikai
Az analízis néhány közgazdaságtani alkalmazása Szakdolgozat Írta: Simon Anita Matematika Bsc szak Matematikai elemző szakirány Témavezető: Sikolya Eszter, adjunktus Alkalmazott Analízis és Számításmatematikai
Juhász Tibor. Lineáris algebra
 Juhász Tibor Lineáris algebra Eszterházy Károly Főiskola Matematikai és Informatikai Intézet Juhász Tibor Lineáris algebra Eger, 2013 Készült a TÁMOP-425B-11/1-2011-0001 támogatásával Tartalomjegyzék
Juhász Tibor Lineáris algebra Eszterházy Károly Főiskola Matematikai és Informatikai Intézet Juhász Tibor Lineáris algebra Eger, 2013 Készült a TÁMOP-425B-11/1-2011-0001 támogatásával Tartalomjegyzék
Dungeon Twister - Paladinok és Sárkányok
 Dungeon Twister - Paladinok és Sárkányok Figyelem: Ahhoz, hogy ezt a kiegészítőt használni tudd, szükséged lesz egy Dungeon Twister alapcsomagra. Tartalom: 8 négyzet alakú szoba 2 szett token (mindkét
Dungeon Twister - Paladinok és Sárkányok Figyelem: Ahhoz, hogy ezt a kiegészítőt használni tudd, szükséged lesz egy Dungeon Twister alapcsomagra. Tartalom: 8 négyzet alakú szoba 2 szett token (mindkét
Könyvelői Klub 2012. október 11. Debrecen. Ruszin Zsolt ADÓELLENŐZÉS, EURÓPAI BÍRÓSÁGI JOGGYAKORLAT,
 Könyvelői Klub 2012. október 11. Debrecen Ruszin Zsolt ADÓELLENŐZÉS, EURÓPAI BÍRÓSÁGI JOGGYAKORLAT, ÚJ ADÓFORMÁK (KATA, KIVA), PDF-BEN VALÓ SZÁMLÁZÁS, ÁFAVÁLTOZÁSOK, TÉTELES ÁFA 2013. évi adóellenőrzés
Könyvelői Klub 2012. október 11. Debrecen Ruszin Zsolt ADÓELLENŐZÉS, EURÓPAI BÍRÓSÁGI JOGGYAKORLAT, ÚJ ADÓFORMÁK (KATA, KIVA), PDF-BEN VALÓ SZÁMLÁZÁS, ÁFAVÁLTOZÁSOK, TÉTELES ÁFA 2013. évi adóellenőrzés
Lineáris programozás. Modellalkotás Grafikus megoldás Feladattípusok Szimplex módszer
 Lineáris programozás Modellalkotás Grafikus megoldás Feladattípusok Szimplex módszer Feladat: Egy gyár kétféle terméket gyárt (A, B): /db Eladási ár 1000 800 Technológiai önköltség 400 300 Normaóraigény
Lineáris programozás Modellalkotás Grafikus megoldás Feladattípusok Szimplex módszer Feladat: Egy gyár kétféle terméket gyárt (A, B): /db Eladási ár 1000 800 Technológiai önköltség 400 300 Normaóraigény
Tudományos publikációs pályázat. Az érvénytelen szerződés jogkövetkezményeinek dogmatikai szemlélete a 2013. évi V. törvényben
 Miskolci Egyetem Állam és Jogtudományi Kar Civilisztikai Tudományok Intézete Polgári jogi Tanszék Novotni Alapítvány a Magánjog Fejlesztéséért Tudományos publikációs pályázat Az érvénytelen szerződés jogkövetkezményeinek
Miskolci Egyetem Állam és Jogtudományi Kar Civilisztikai Tudományok Intézete Polgári jogi Tanszék Novotni Alapítvány a Magánjog Fejlesztéséért Tudományos publikációs pályázat Az érvénytelen szerződés jogkövetkezményeinek
Geometriai axiómarendszerek és modellek
 Verhóczki László Geometriai axiómarendszerek és modellek ELTE TTK Matematikai Intézet Geometriai Tanszék Budapest, 2011 1) Az axiómákra vonatkozó alapvető ismeretek Egy matematikai elmélet felépítésének
Verhóczki László Geometriai axiómarendszerek és modellek ELTE TTK Matematikai Intézet Geometriai Tanszék Budapest, 2011 1) Az axiómákra vonatkozó alapvető ismeretek Egy matematikai elmélet felépítésének
Valószínűségszámítás és statisztika. István Fazekas
 Valószínűségszámítás és statisztika István Fazekas Tartalomjegyzék 1. fejezet. A valószínűségszámítás alapfogalmai 5 1.1. A valószínűség 5 1.2. Halmazalgebrák és σ-algebrák 11 1.3. A feltételes valószínűség
Valószínűségszámítás és statisztika István Fazekas Tartalomjegyzék 1. fejezet. A valószínűségszámítás alapfogalmai 5 1.1. A valószínűség 5 1.2. Halmazalgebrák és σ-algebrák 11 1.3. A feltételes valószínűség
Korszerű raktározási rendszerek. Szakdolgozat
 Gépészmérnöki és Informatikai Kar Mérnök Informatikus szak Logisztikai Rendszerek szakirány Korszerű raktározási rendszerek Szakdolgozat Készítette: Buczkó Balázs KOKIOC 3770 Sajószentpéter, Ady Endre
Gépészmérnöki és Informatikai Kar Mérnök Informatikus szak Logisztikai Rendszerek szakirány Korszerű raktározási rendszerek Szakdolgozat Készítette: Buczkó Balázs KOKIOC 3770 Sajószentpéter, Ady Endre
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika emelt szint 0613 ÉRETTSÉGI VIZSGA 007. május 8. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Formai előírások: Fontos tudnivalók
Matematika emelt szint 0613 ÉRETTSÉGI VIZSGA 007. május 8. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Formai előírások: Fontos tudnivalók
MATEMATIKA tankönyvcsaládunkat
 Bemutatjuk a NAT 01 és a hozzá kapcsolódó új kerettantervek alapján készült MATEMATIKA tankönyvcsaládunkat 9 10 1 MATEMATIKA A KÖTETEKBEN FELLELHETŐ DIDAKTIKAI ESZKÖZTÁR A SOROZAT KÖTETEI A KÖVETKEZŐ KERETTANTERVEK
Bemutatjuk a NAT 01 és a hozzá kapcsolódó új kerettantervek alapján készült MATEMATIKA tankönyvcsaládunkat 9 10 1 MATEMATIKA A KÖTETEKBEN FELLELHETŐ DIDAKTIKAI ESZKÖZTÁR A SOROZAT KÖTETEI A KÖVETKEZŐ KERETTANTERVEK
MATEMATIKA FELADATGYŰJTEMÉNY
 Pék Johanna MATEMATIKA FELADATGYŰJTEMÉNY Nem matematika alapszakos hallgatók számára Tartalomjegyzék Előszó iii. Lineáris algebra.. Mátrixok...................................... Lineáris egyenletrendszerek..........................
Pék Johanna MATEMATIKA FELADATGYŰJTEMÉNY Nem matematika alapszakos hallgatók számára Tartalomjegyzék Előszó iii. Lineáris algebra.. Mátrixok...................................... Lineáris egyenletrendszerek..........................
2. ALPROJEKT FELHASZNÁLÓI KÉZIKÖNYV
 2. ALPROJEKT FELHASZNÁLÓI KÉZIKÖNYV 2. OKJ összehangolása a hatósági képesítésekkel Hatósági képesítések modul Publikus funkciók, konverziós adatbázis, lekérdezések modul a TÁMOP 2.2.1-12/1-2012-0001 A
2. ALPROJEKT FELHASZNÁLÓI KÉZIKÖNYV 2. OKJ összehangolása a hatósági képesítésekkel Hatósági képesítések modul Publikus funkciók, konverziós adatbázis, lekérdezések modul a TÁMOP 2.2.1-12/1-2012-0001 A
JANUS PANNONIUS TUDOMÁNYEGYETEM. Schipp Ferenc ANALÍZIS I. Sorozatok és sorok
 JANUS PANNONIUS TUDOMÁNYEGYETEM Schipp Ferenc ANALÍZIS I. Sorozatok és sorok Pécs, 1994 Lektorok: Dr. FEHÉR JÁNOS egyetemi docens, kandidtus. Dr. SIMON PÉTER egyetemi docens, kandidtus 1 Előszó Ez a jegyzet
JANUS PANNONIUS TUDOMÁNYEGYETEM Schipp Ferenc ANALÍZIS I. Sorozatok és sorok Pécs, 1994 Lektorok: Dr. FEHÉR JÁNOS egyetemi docens, kandidtus. Dr. SIMON PÉTER egyetemi docens, kandidtus 1 Előszó Ez a jegyzet
BAUSFT. Pécsvárad Kft. 7720 Pécsvárad, Pécsi út 49. Tel/Fax: 72/465-266 http://www.bausoft.hu. ISO-bau. Szigetelés kiválasztó. 1.02 verzió.
 BAUSFT Pécsvárad Kft. 7720 Pécsvárad, Pécsi út 49. Tel/Fax: 72/465-266 http://www.bausoft.hu ISO-bau Szigetelés kiválasztó 1.02 verzió Szerzők: dr. Baumann József okl. villamosmérnök 1188 Budapest, Fenyőfa
BAUSFT Pécsvárad Kft. 7720 Pécsvárad, Pécsi út 49. Tel/Fax: 72/465-266 http://www.bausoft.hu ISO-bau Szigetelés kiválasztó 1.02 verzió Szerzők: dr. Baumann József okl. villamosmérnök 1188 Budapest, Fenyőfa
Azonosító jel: MATEMATIKA EMELT SZINTŰ ÍRÁSBELI VIZSGA. 2008. október 21. 8:00. Az írásbeli vizsga időtartama: 240 perc
 É RETTSÉGI VIZSGA 2008. október 21. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI VIZSGA 2008. október 21. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM
É RETTSÉGI VIZSGA 2008. október 21. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI VIZSGA 2008. október 21. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM
Bankó Az OTP Bank ügyfélmagazinja
 Lakásügyeink különszám Bankó Az OTP Bank ügyfélmagazinja XiX. Évfolyam, 4. szám, 2011. augusztus www.otpbank.hu Mentôöv az adósoknak Mi az az Otthonvédelmi Akcióterv? Futamidô hosszabbítás, törlesztéscsökkentés
Lakásügyeink különszám Bankó Az OTP Bank ügyfélmagazinja XiX. Évfolyam, 4. szám, 2011. augusztus www.otpbank.hu Mentôöv az adósoknak Mi az az Otthonvédelmi Akcióterv? Futamidô hosszabbítás, törlesztéscsökkentés
Hibatűrő TDMA ütemezés tervezése ciklikus vezeték nélküli hálózatokban. Orosz Ákos, Róth Gergő, Simon Gyula. Pannon Egyetem
 Hibatűrő TDMA ütemezés tervezése ciklikus vezeték nélküli hálózatokban Orosz Ákos, Róth Gergő, Simon Gyula Pannon Egyetem Rendszer- és Számítástudományi Tanszék Email: {orosz, roth, simon}@dcs.uni-pannon.hu
Hibatűrő TDMA ütemezés tervezése ciklikus vezeték nélküli hálózatokban Orosz Ákos, Róth Gergő, Simon Gyula Pannon Egyetem Rendszer- és Számítástudományi Tanszék Email: {orosz, roth, simon}@dcs.uni-pannon.hu
Hraskó András, Surányi László: 11-12. spec.mat szakkör Tartotta: Surányi László. Feladatok
 Feladatok 1. Színezzük meg a koordinátarendszer rácspontjait két színnel, kékkel és pirossal úgy, hogy minden vízszintes egyenesen csak véges sok kék rácspont legyen és minden függőleges egyenesen csak
Feladatok 1. Színezzük meg a koordinátarendszer rácspontjait két színnel, kékkel és pirossal úgy, hogy minden vízszintes egyenesen csak véges sok kék rácspont legyen és minden függőleges egyenesen csak
1. Melyek azok a kétjegyű számok, amelyek oszthatók számjegyeik
 1991. évi verseny, 1. nap 1. Számold össze, hány pozitív osztója van 16 200-nak! 2. Bontsd fel a 60-at két szám összegére úgy, hogy az egyik szám hetede egyenlő legyen a másik szám nyolcadával! 3. Van
1991. évi verseny, 1. nap 1. Számold össze, hány pozitív osztója van 16 200-nak! 2. Bontsd fel a 60-at két szám összegére úgy, hogy az egyik szám hetede egyenlő legyen a másik szám nyolcadával! 3. Van
Soukup Dániel, Matematikus Bsc III. év Email cím: dsoukup123@gmail.com Témavezető: Szentmiklóssy Zoltán, egyetemi adjunktus
 Síktopológiák a Sorgenfrey-egyenes ötletével Soukup Dániel, Matematikus Bsc III. év Email cím: dsoukup123@gmail.com Témavezető: Szentmiklóssy Zoltán, egyetemi adjunktus 1. Bevezetés A Sorgenfrey-egyenes
Síktopológiák a Sorgenfrey-egyenes ötletével Soukup Dániel, Matematikus Bsc III. év Email cím: dsoukup123@gmail.com Témavezető: Szentmiklóssy Zoltán, egyetemi adjunktus 1. Bevezetés A Sorgenfrey-egyenes
Lineáris algebra és mátrixok alkalmazása a numerikus analízisben
 Eötvös Loránd Tudományegyetem Természettudományi kar Lineáris algebra és mátrixok alkalmazása a numerikus analízisben Szakdolgozat Készítette: Borostyán Dóra Matematika BSc matematikai elemző Témavezető:
Eötvös Loránd Tudományegyetem Természettudományi kar Lineáris algebra és mátrixok alkalmazása a numerikus analízisben Szakdolgozat Készítette: Borostyán Dóra Matematika BSc matematikai elemző Témavezető:
5 HOZZÁFÉRÉS-VÉDELEM. A fejezet VIDEOTON fejlesztési dokumentációk felhasználásával készült
 5 HOZZÁFÉRÉS-VÉDELEM A rejtjelezésben az adatvédelem hatékony és az adathálózat védelmében nélkülözhetetlen eszközét ismertük meg. Természetesen annak sincs semmilyen elvi akadálya, hogy a rejtjelezést
5 HOZZÁFÉRÉS-VÉDELEM A rejtjelezésben az adatvédelem hatékony és az adathálózat védelmében nélkülözhetetlen eszközét ismertük meg. Természetesen annak sincs semmilyen elvi akadálya, hogy a rejtjelezést
Matematika POKLICNA MATURA
 Szakmai érettségi tantárgyi vizsgakatalógus Matematika POKLICNA MATURA A tantárgyi vizsgakatalógus a 0-es tavaszi vizsgaidőszaktól kezdve alkalmazható mindaddig, amíg új nem készül. A katalógus érvényességét
Szakmai érettségi tantárgyi vizsgakatalógus Matematika POKLICNA MATURA A tantárgyi vizsgakatalógus a 0-es tavaszi vizsgaidőszaktól kezdve alkalmazható mindaddig, amíg új nem készül. A katalógus érvényességét
LÁNG CSABÁNÉ SZÁMELMÉLET. Példák és feladatok. ELTE IK Budapest 2010-10-24 2. javított kiadás
 LÁNG CSABÁNÉ SZÁMELMÉLET Példák és feladatok ELTE IK Budapest 2010-10-24 2. javított kiadás Fels oktatási tankönyv Lektorálták: Kátai Imre Bui Minh Phong Burcsi Péter Farkas Gábor Fülöp Ágnes Germán László
LÁNG CSABÁNÉ SZÁMELMÉLET Példák és feladatok ELTE IK Budapest 2010-10-24 2. javított kiadás Fels oktatási tankönyv Lektorálták: Kátai Imre Bui Minh Phong Burcsi Péter Farkas Gábor Fülöp Ágnes Germán László
Széchenyi István Egyetem, 2005
 Gáspár Csaba, Molnárka Győző Lineáris algebra és többváltozós függvények Széchenyi István Egyetem, 25 Vektorterek Ebben a fejezetben a geometriai vektorfogalom ( irányított szakasz ) erős általánosítását
Gáspár Csaba, Molnárka Győző Lineáris algebra és többváltozós függvények Széchenyi István Egyetem, 25 Vektorterek Ebben a fejezetben a geometriai vektorfogalom ( irányított szakasz ) erős általánosítását
Kombinatorika. 9 10. évfolyam. Szerkesztette: Surányi László Ábrák: Hraskó András. 2015. december 6.
 Kombinatorika 9 10. évfolyam Szerkesztette: Surányi László Ábrák: Hraskó András 2015. december 6. A kötet létrehozását 2008-tól 2010-ig a Fővárosi Közoktatásfejlesztési Közalapítvány támogatta Technikai
Kombinatorika 9 10. évfolyam Szerkesztette: Surányi László Ábrák: Hraskó András 2015. december 6. A kötet létrehozását 2008-tól 2010-ig a Fővárosi Közoktatásfejlesztési Közalapítvány támogatta Technikai
Analízis lépésről - lépésre
 Analízis lépésről - lépésre interaktív tananyag Dr. Stettner Eleonóra Klingné Takács Anna Analízis lépésről - lépésre: interaktív tananyag írta Dr. Stettner Eleonóra és Klingné Takács Anna Tartalom Előszó...
Analízis lépésről - lépésre interaktív tananyag Dr. Stettner Eleonóra Klingné Takács Anna Analízis lépésről - lépésre: interaktív tananyag írta Dr. Stettner Eleonóra és Klingné Takács Anna Tartalom Előszó...
LINEÁRIS ALGEBRA PÉLDATÁR MÉRNÖK INFORMATIKUSOKNAK
 Írta: LEITOLD ADRIEN LINEÁRIS ALGEBRA PÉLDATÁR MÉRNÖK INFORMATIKUSOKNAK Egyetemi tananyag COPYRIGHT: Dr. Leitold Adrien Pannon Egyetem Műszaki Informatika Kar Matematika Tanszék LEKTORÁLTA: Dr. Buzáné
Írta: LEITOLD ADRIEN LINEÁRIS ALGEBRA PÉLDATÁR MÉRNÖK INFORMATIKUSOKNAK Egyetemi tananyag COPYRIGHT: Dr. Leitold Adrien Pannon Egyetem Műszaki Informatika Kar Matematika Tanszék LEKTORÁLTA: Dr. Buzáné
ÍRÁSBELI KIVONÁS. 31. modul. Készítette: KONRÁD ÁGNES
 Matematika A 3. évfolyam ÍRÁSBELI KIVONÁS 31. modul Készítette: KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 31. modul ÍRÁSBELI KIVONÁS MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
Matematika A 3. évfolyam ÍRÁSBELI KIVONÁS 31. modul Készítette: KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 31. modul ÍRÁSBELI KIVONÁS MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
Nemetz O.H. Tibor emlékére. 2011 május 9.
 Adatbiztonság és valószínűségszámítás 1 / 22 Adatbiztonság és valószínűségszámítás Nemetz O.H. Tibor emlékére Csirmaz László Közép Európai Egyetem Rényi Intézet 2011 május 9. Adatbiztonság és valószínűségszámítás
Adatbiztonság és valószínűségszámítás 1 / 22 Adatbiztonság és valószínűségszámítás Nemetz O.H. Tibor emlékére Csirmaz László Közép Európai Egyetem Rényi Intézet 2011 május 9. Adatbiztonság és valószínűségszámítás
6. Bizonyítási módszerek
 6. Bizonyítási módszere I. Feladato. Egy 00 00 -as táblázat minden mezőjébe beírju az,, 3 számo valamelyiét és iszámítju soronént is, oszloponént is, és a ét átlóban is az ott lévő 00-00 szám öszszegét.
6. Bizonyítási módszere I. Feladato. Egy 00 00 -as táblázat minden mezőjébe beírju az,, 3 számo valamelyiét és iszámítju soronént is, oszloponént is, és a ét átlóban is az ott lévő 00-00 szám öszszegét.
MATEMATIKA 9. osztály Segédanyag 4 óra/hét
 MATEMATIKA 9. osztály Segédanyag 4 óra/hét - 1 - Az óraszámok az AROMOBAN követhetőek nyomon! A tananyag feldolgozása a SOKSZÍNŰ MATEMATIKA (Mozaik, 013) tankönyv és a SOKSZÍNŰ MATEMATIKA FELADATGYŰJTEMÉNY
MATEMATIKA 9. osztály Segédanyag 4 óra/hét - 1 - Az óraszámok az AROMOBAN követhetőek nyomon! A tananyag feldolgozása a SOKSZÍNŰ MATEMATIKA (Mozaik, 013) tankönyv és a SOKSZÍNŰ MATEMATIKA FELADATGYŰJTEMÉNY
Bináris keres fák kiegyensúlyozásai. Egyed Boglárka
 Eötvös Loránd Tudományegyetem Természettudományi Kar Bináris keres fák kiegyensúlyozásai BSc szakdolgozat Egyed Boglárka Matematika BSc, Alkalmazott matematikus szakirány Témavezet : Fekete István, egyetemi
Eötvös Loránd Tudományegyetem Természettudományi Kar Bináris keres fák kiegyensúlyozásai BSc szakdolgozat Egyed Boglárka Matematika BSc, Alkalmazott matematikus szakirány Témavezet : Fekete István, egyetemi
EMELT SZINTŰ ÍRÁSBELI VIZSGA
 ÉRETTSÉGI VIZSGA 2006. május 9. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI VIZSGA 2006. május 9. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI MINISZTÉRIUM Matematika
ÉRETTSÉGI VIZSGA 2006. május 9. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI VIZSGA 2006. május 9. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI MINISZTÉRIUM Matematika
MEOSZ Oktatási, Továbbképző és Távmunka Intézet SAJTÓFIGYELÉS. Költözés
 2006. november 21. Békés Megyei Hírlap MEOSZ Oktatási, Továbbképző és Távmunka Intézet SAJTÓFIGYELÉS Költözés November 20-tól új helyen, a Vajda Péter Művelődési Központban várja tagjait a Mozgáskorlátozottak
2006. november 21. Békés Megyei Hírlap MEOSZ Oktatási, Továbbképző és Távmunka Intézet SAJTÓFIGYELÉS Költözés November 20-tól új helyen, a Vajda Péter Művelődési Központban várja tagjait a Mozgáskorlátozottak
KETTŐS KÖNYVELÉS PROGRAM
 KETTŐS KÖNYVELÉS PROGRAM Kezelési leírás 1993-2015 Program azonosító: UJEGYKE Fejlesztő: B a l o g h y S z o f t v e r K f t. Keszthely, Vak Bottyán utca 41. 8360 Tel: 83/515-080 Fax: 83/515-082 E-mail:
KETTŐS KÖNYVELÉS PROGRAM Kezelési leírás 1993-2015 Program azonosító: UJEGYKE Fejlesztő: B a l o g h y S z o f t v e r K f t. Keszthely, Vak Bottyán utca 41. 8360 Tel: 83/515-080 Fax: 83/515-082 E-mail:
Az adatfeldolgozás és adatátvitel biztonsága. Az adatfeldolgozás biztonsága. Adatbiztonság. Automatikus adatazonosítás, adattovábbítás, adatbiztonság
 Az adatfeldolgozás és adatátvitel biztonsága Automatikus adatazonosítás, adattovábbítás, adatbiztonság Az adatfeldolgozás biztonsága A védekezés célja Védelem a hamisítás és megszemélyesítés ellen Biztosított
Az adatfeldolgozás és adatátvitel biztonsága Automatikus adatazonosítás, adattovábbítás, adatbiztonság Az adatfeldolgozás biztonsága A védekezés célja Védelem a hamisítás és megszemélyesítés ellen Biztosított
Bevezetés a Gröbner-bázisok elméletébe
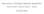 Bevezetés a Gröbner-bázisok elméletébe Oktatási segédlet a Komputer algebra c. tárgyhoz Felszeghy Bálint Tartalomjegyzék 1. Bevezetés 3 2. Alapfogalmak és a Gröbner-bázisok elemi tulajdonságai 5 2.1. Jelölések..............................
Bevezetés a Gröbner-bázisok elméletébe Oktatási segédlet a Komputer algebra c. tárgyhoz Felszeghy Bálint Tartalomjegyzék 1. Bevezetés 3 2. Alapfogalmak és a Gröbner-bázisok elemi tulajdonságai 5 2.1. Jelölések..............................
EMTP, EGY ÚJ LEVELEZÕ PROTOKOLL ÉS IMPLEMENTÁCIÓJA
 EMTP, EGY ÚJ LEVELEZÕ PROTOKOLL ÉS IMPLEMENTÁCIÓJA Iványi Tibor, ivanyit@tigris.klte.hu Csukás Levente, csukasl@fox.klte.hu Kossuth Lajos Tudományegyetem Informatikai és Számító Központ Abstract The well
EMTP, EGY ÚJ LEVELEZÕ PROTOKOLL ÉS IMPLEMENTÁCIÓJA Iványi Tibor, ivanyit@tigris.klte.hu Csukás Levente, csukasl@fox.klte.hu Kossuth Lajos Tudományegyetem Informatikai és Számító Központ Abstract The well
MATEMATIKA C 5. évfolyam 1. modul DOMINÓ
 MATEMATIKA C 5. évfolyam 1. modul DOMINÓ Készítette: Köves Gabriella MATEMATIKA C 5. ÉVFOLYAM 1. MODUL: DOMINÓ TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A tudatos
MATEMATIKA C 5. évfolyam 1. modul DOMINÓ Készítette: Köves Gabriella MATEMATIKA C 5. ÉVFOLYAM 1. MODUL: DOMINÓ TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A tudatos
3 Hogyan határozzuk meg az innováció szükségszerűségét egy üzleti probléma esetén
 3 Hogyan határozzuk meg az innováció szükségszerűségét egy üzleti probléma esetén 3.1 A Black Box eljárás Kulcsszavak: Black Box, Kísérleti stratégia, Elosztás, Határérték, A döntéshozatali tábla tesztje
3 Hogyan határozzuk meg az innováció szükségszerűségét egy üzleti probléma esetén 3.1 A Black Box eljárás Kulcsszavak: Black Box, Kísérleti stratégia, Elosztás, Határérték, A döntéshozatali tábla tesztje
Az álláspályázat szóbeli része
 Az álláspályázat szóbeli része Az állásinterjú Az állásinterjúra való meghívással döntő ponthoz érkezett a jövőbeli munkahely megszerzésének útján. Fontos mérföldkövet ért el. Ekkor már tudhatja, hogy
Az álláspályázat szóbeli része Az állásinterjú Az állásinterjúra való meghívással döntő ponthoz érkezett a jövőbeli munkahely megszerzésének útján. Fontos mérföldkövet ért el. Ekkor már tudhatja, hogy
ProAnt Felhasználói Útmutató
 ProAnt Felhasználói Útmutató http://www.proant.hu/ 2014. október 17. Adminisztrátor 6722 Szeged, Gogol u. 3. 1 TARTALOMJEGYZÉK 1 Tartalomjegyzék... 2 2 A ProAnt szoftverről... 4 3 Jelszó módosítása...
ProAnt Felhasználói Útmutató http://www.proant.hu/ 2014. október 17. Adminisztrátor 6722 Szeged, Gogol u. 3. 1 TARTALOMJEGYZÉK 1 Tartalomjegyzék... 2 2 A ProAnt szoftverről... 4 3 Jelszó módosítása...
44. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY. Országos döntő, 1. nap - 2015. május 29.
 44. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY Országos döntő, 1. nap - 015. május 9. ÖTÖDIK OSZTÁLY - ok 1. Egy háromjegyű szám középső számjegyét elhagyva egy kétjegyű számot kaptunk. A két szám összege
44. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY Országos döntő, 1. nap - 015. május 9. ÖTÖDIK OSZTÁLY - ok 1. Egy háromjegyű szám középső számjegyét elhagyva egy kétjegyű számot kaptunk. A két szám összege
Hálózati protokoll tervezése
 Hálózati protokoll tervezése A gyakorlat célja: Hálózati protokoll tervezésének a megvalósítása Elméleti bevezető: Ahhoz, hogy a hálózatba kötött gépek kommunikálni tudjanak egymással, szükség van egy
Hálózati protokoll tervezése A gyakorlat célja: Hálózati protokoll tervezésének a megvalósítása Elméleti bevezető: Ahhoz, hogy a hálózatba kötött gépek kommunikálni tudjanak egymással, szükség van egy
19. Hasításos technikák (hash-elés)
 19. Hasításos technikák (hash-elés) Példák: 1. Ha egy telefon előfizetőket a telefonszámaikkal azonosítjuk, mint kulcsokkal, akkor egy ritkán kitöltött kulcstartományhoz jutunk. A telefonszám tehát nem
19. Hasításos technikák (hash-elés) Példák: 1. Ha egy telefon előfizetőket a telefonszámaikkal azonosítjuk, mint kulcsokkal, akkor egy ritkán kitöltött kulcstartományhoz jutunk. A telefonszám tehát nem
Sztojka Miroszláv LINEÁRIS ALGEBRA Egyetemi jegyzet Ungvár 2013
 UKRAJNA OKTATÁSI ÉS TUDOMÁNYÜGYI MINISZTÉRIUMA ÁLLAMI FELSŐOKTATÁSI INTÉZMÉNY UNGVÁRI NEMZETI EGYETEM MAGYAR TANNYELVŰ HUMÁN- ÉS TERMÉSZETTUDOMÁNYI KAR FIZIKA ÉS MATEMATIKA TANSZÉK Sztojka Miroszláv LINEÁRIS
UKRAJNA OKTATÁSI ÉS TUDOMÁNYÜGYI MINISZTÉRIUMA ÁLLAMI FELSŐOKTATÁSI INTÉZMÉNY UNGVÁRI NEMZETI EGYETEM MAGYAR TANNYELVŰ HUMÁN- ÉS TERMÉSZETTUDOMÁNYI KAR FIZIKA ÉS MATEMATIKA TANSZÉK Sztojka Miroszláv LINEÁRIS
KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA
 ÉRETTSÉGI VIZSGA 2007. október 25. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2007. október 25. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Matematika
ÉRETTSÉGI VIZSGA 2007. október 25. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2007. október 25. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Matematika
Elsôfokú egyenletek, egyenletrendszerek, egyenlôtlenségek
 Elsôfokú egyváltozós egyenletek 6 Elsôfokú egyenletek, egyenletrendszerek, egyenlôtlenségek. Elsôfokú egyváltozós egyenletek 000. Érdemes egyes tagokat, illetve tényezôket alkalmasan csoportosítani, valamint
Elsôfokú egyváltozós egyenletek 6 Elsôfokú egyenletek, egyenletrendszerek, egyenlôtlenségek. Elsôfokú egyváltozós egyenletek 000. Érdemes egyes tagokat, illetve tényezôket alkalmasan csoportosítani, valamint
XIII. Bolyai Konferencia Bodnár József Eötvös József Collegium, ELTE TTK, III. matematikus. A véletlen nyomában
 XIII. Bolyai Konferencia Bodnár József Eötvös József Collegium, ELTE TTK, III. matematikus A véletlen nyomában Mi is az a véletlen? 1111111111, 1010101010, 1100010111 valószínűsége egyaránt 1/1024 Melyiket
XIII. Bolyai Konferencia Bodnár József Eötvös József Collegium, ELTE TTK, III. matematikus A véletlen nyomában Mi is az a véletlen? 1111111111, 1010101010, 1100010111 valószínűsége egyaránt 1/1024 Melyiket
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika emelt szint 051 ÉRETTSÉGI VIZSGA 007. május 8. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Formai előírások: Fontos tudnivalók
Matematika emelt szint 051 ÉRETTSÉGI VIZSGA 007. május 8. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Formai előírások: Fontos tudnivalók
Dualitás Dualitási tételek Általános LP feladat Komplementáris lazaság 2015/2016-2. Szegedi Tudományegyetem Informatikai Tanszékcsoport
 Operációkutatás I. 2015/2016-2. Szegedi Tudományegyetem Informatikai Tanszékcsoport Számítógépes Optimalizálás Tanszék 6. Előadás Árazási interpretáció Tekintsük újra az erőforrás allokációs problémát
Operációkutatás I. 2015/2016-2. Szegedi Tudományegyetem Informatikai Tanszékcsoport Számítógépes Optimalizálás Tanszék 6. Előadás Árazási interpretáció Tekintsük újra az erőforrás allokációs problémát
Az anyagdefiníciók szerepe és használata az Architectural Desktop programban
 Az anyagdefiníciók szerepe és használata az Architectural Desktop programban Az Architectural Desktop program 2004-es változatáig kellett várni arra, hogy az AutoCAD alapú építész programban is megjelenjenek
Az anyagdefiníciók szerepe és használata az Architectural Desktop programban Az Architectural Desktop program 2004-es változatáig kellett várni arra, hogy az AutoCAD alapú építész programban is megjelenjenek
Analízis előadás és gyakorlat vázlat
 Analízis előadás és gyakorlat vázlat Készült a PTE TTK GI szakos hallgatóinak Király Balázs 00-. I. Félév . fejezet Számhalmazok és tulajdonságaik.. Nevezetes számhalmazok ➀ a) jelölése: N b) elemei:
Analízis előadás és gyakorlat vázlat Készült a PTE TTK GI szakos hallgatóinak Király Balázs 00-. I. Félév . fejezet Számhalmazok és tulajdonságaik.. Nevezetes számhalmazok ➀ a) jelölése: N b) elemei:
9. előadás Környezetfüggetlen nyelvek
 9. előadás Környezetfüggetlen nyelvek Dr. Kallós Gábor 2015 2016 1 Tartalom Bevezetés CF nyelv példák Nyelvek és nyelvtanok egy- és többértelműsége Bal- és jobboldali levezetések A fák magassága és határa
9. előadás Környezetfüggetlen nyelvek Dr. Kallós Gábor 2015 2016 1 Tartalom Bevezetés CF nyelv példák Nyelvek és nyelvtanok egy- és többértelműsége Bal- és jobboldali levezetések A fák magassága és határa
