ZsakmanySzim Szlávi Péter
|
|
|
- Géza Juhász
- 6 évvel ezelőtt
- Látták:
Átírás
1 ZsakmanySzim ZSÁKMÁNYSZERZÉSI MODELL Szlávi Péter TARTALOM 1. Elvárások A problémák Szimulációs keret Szimulációs lépés a lényeg A szimulációhoz tartozó reprezentáció A szimulációhoz tartozó implementáció A keretprogram Feladatok Alapfeladat Modellezési feladatok Intelligencia Memória egyed-paraméterezés Csoportszellem Szorgalmi feladat A teljes anyag Függelék Néhány futáseredmény Függelék További megfontolások... 16
2 1. Elvárások Az elvárásokat legjobban az alábbi, futás során keletkezett ábrasor fejezi ki. 1. ábra. Egy futási kép Tájékoztató 2. ábra. Egy futási kép Paraméterezés 2
3 3. ábra. Egy futási kép Szimuláció közben (T=110) Amint a futási képekből kitűnik: egy üres, XY-diagram nevű ablak is a felszínre került. Ez egy fejlesztési lehetőség, amely később szóba fog kerülni, mint megoldandó feladat. Lássunk egy in live próbát: ZsakmanyMo.exe. 2. A problémák Induljunk ki a Gáz-modellből a zsákmány-szerzési modell, és programja megalkotásához! Így számos reprezentációs és implementációs kérdést megoldottnak vehetünk. (L. Gáz-modell!) Algoritmikusan csak maga a szimuláció tisztázandó Szimulációs keret A modellezés alapadatai: T idő N,M territórium-méretek Ra0,Zs0 a kezdetben elhelyezendő kétféle állat száma RaDb,ZsDb a pillanatnyi darabszámok RaSz,ZsSz a szül(et)ési ráták, ennyi eséllyel szül pontosan egy utódot a kiválasztott egyed RaH,ZsH a halálozási ráták, ennyi eséllyel múlik a kiválasztott egyed 3
4 A nagyvonalú algoritmusa (alig változik a korábbihoz képest): üzemmod:=lépesenkénti Tájékoztató Inicializálás; T:=0 KezdőKépernyő EredményMegjelenités Ciklus amíg nem VégeE T:+1 SzimulációsLépés EredményMegjelenítés Ciklus vége Zárás ÖsszefoglalóMegjelenítés A Zárás az Inicializálás párja. Feladata a futás felhasználóbarát lezárása. Ellenőrzi, hogy a felhasználó óhaja vagy valami automatizmus miatt ért-e véget a szimuláció. Ha az utóbbi miatt, akkor nyilván a felhasználónak fe kell hívni a figyelmét erre. Mivel ennél a modellnél az esetleges későbbi feldolgozás kedvéért naplózzuk a történéseket, ezért a zárás másik teendője a naplófájlba a végállapotot rögzíteni Szimulációs lépés a lényeg A véletlenszerűen kiválasztott egyeddel lezajlik egy teljes élet ciklus, amelybe beletartozik a kimúlás, vagy továbbélés; ez utóbbi esetében az esetleges szülés A szimulációhoz tartozó reprezentáció Változó [Ablakok:] TérAblak: TAblak [Territórium] KarAblak: TKarAblak [Karakteres információk] Graf1, Graf2 : THisztAblak [Hisztogramok] XYDiag : TXYAblak [XY-diagram] [Szimulációs adatok: paraméterek:] T : Egész [Kellően nagy, mert hosszú futásra kell számítani] N,M, Ra0,Zs0, RaDb,ZsDb: Egész ReaTér : TReaTér [ideillőbb lenne persze a Territórium kifejezés] RaSz,ZsSz, RaH,ZsH : Valós A szimulációhoz tartozó implementáció Eljáros SzimulációsLépés: Változó i,j: Egész [az aktív állat: (i,j)] Ciklus i:=random(n)+1; j:=random(m)+1 amíg nem ReaTér(i,j) [Ragadozó,Zsákmány] Ciklus vége 4
5 Elágazás ReaTér(i,j)=Ragadozó esetén RagadozóVáltozás(i,j) ReaTér(i,j)=Zsákmány esetén ZsákmányVáltozás(i,j) Elágazás vége Mozgás(i,j) Eljárás vége. A későbbikben többféle helykeresésre is szükség lesz. Ehhez be kell vezetnünk a helykeresés eredményét tároló adat típusát (l. keresés tétel): Típus TVanHol=Rekord(vanE:Logikai, si,sj:egész [szomszéd i-, j-koordinátája]) Eljárás RagadozóVáltozás(Konstans i,j:egész): Változó ker:tvanhol [a keresés tétel kimenete] ker:=szomszédkereses(zsákmány,i,j) Elágazás nem ker.vane vagy Random<RaH esetén [meghal] ReaTér(i,j):=Üres RaDb:-1 [ker.vane és] Random<RaSz esetén [zsákmányt eszik + szül] ReaTér(ker.si,ker.sj):=Ragadozó RaDb:+1 ZsDb:-1 egyéb esetben [zsákmányt eszik] ReaTér(ker.si,ker.sj):=Üres ZsDb:-1 Elágazás vége Eljárás vége. Eljárás ZsákmányVáltozás(Konstans i,j:egész): Változó ker:tvanhol [a keresés tétel kimenete] Ha Random<ZsH akkor [meghal] ReaTér(i,j):=Üres ZsDb:-1 különben [túlél] ker:=szomszédkeresés(üres,i,j) Ha ker.vane és Random<ZsSz akkor [szül] ReaTér(ker.si,ker.sj):=Zsákmány ZsDb:+1 Elágazás vége Elágazás vége Eljárás vége. Függvény SzomszédKeresés(Konstans mit:tcella; i,j:egész):tvanhol Konstans MaxIsm:Egész(18) [a véletlen keresés maximális ismétlés-száma] Változó k,l,ism: Egész vane: Logikai 5
6 vane:=hamis; ism:=1 Ciklus amíg ism MaxIsm és nem vane k:=i+random(3)-1; l:=j+random(3)-1 vane:=(i k vagy j l) és ReaTér(k,l)=mit ism:+1 Ciklus vége SzomszédKeresés:=TVanHol(vanE,k,l) Függvény vége. Eljárás Mozgás(Konstans i,j:egész): Változó k,l: Egész Ciklus k:=i+random(3)-1; l:=j+random(3)-1 amíg ReaTér(k,l)=Fal Ciklus vége Csere(ReaTér(i,j),ReaTér(k,l)) Eljárás vége. 3. A keretprogram Az ablak-kezelés rutinjai ugyan nem változnak meg, de a szimulációs tér megjelenítése miatt van változás. Ezért új az Ablakok unit. L. ZsakmanyKe.pas. AblakokBio.pas. 4. Feladatok 4.1. Alapfeladat A keretprogram hiányzó részeit pótolni, azaz (*ide kell a kód*) megjegyzéssel megjelölt részek kitöltése: SzimulaciosLepes-ben OsszefoglaloMegjelenites bővítése a KonkluzioFajl-lal összefüggésben 4.2. Modellezési feladatok Intelligencia Hogyan vihető némi intelligencia a modellbe, pontosabban az élőlények mozgási stratégiájába? Ötlet: a ragadozó már könyörtelenül elpusztít egy környezetében leledző zsákmányállatot, de a zsákmány oktalanul akár a közelben lévő ragadozó karmába szalad, illetve nem törekszik a távolság növelésére. Ezt alighanem a SzomszédKeresés függvény bonyolításával lehetne megoldani Memória egyed-paraméterezés Az életszerűség növelése céljából értelmezzük át a egyes eseményeket. Például a ragadozó ne feltétlenül pusztuljon bele abba, ha nem talál maga körül élelmet. Egy paraméter írja le azt, hogy hány sikertelen koplalás után legyen vége. Ehhez azonban tudnunk kell a próbálkozások számát. Az ötlet: a) egy a territóriummal (ReaTér-rel) párhuzamos sík létrehozása (paramétertér: ParTér(i,j) a ReaTér(i,j)-beli egyed paraméterei); b) a territórium minden egyede egy 6
7 összetett típussal legyen leírható, amelyben helyet kapnak az egyed fajtája mellett a paraméterei: TCella=Rekord(fajta:TFajta, éhség:egész, )). A szimuláció során, ha a ragadozó sikerrel járt a zsákmányolásban, akkor az éhség-paramétere (ParTér(i,j) vagy ReaTér(i,j).éhség) a beolvasott kiinduló értéket veszi föl. Amint kudarcos volt a zsákmányolás, e paramétere eggyel csökken. Ha a paramétere 0-ra csökken, akkor éhen hal. Mindkét esetben az Ablakok unithoz is nyúlni kell Csoportszellem Hogyan vehető bele a modellbe az a fajta társas viselkedés, hogy ha sok azonos zsákmány egyed egymáshoz közel tartózkodik, akkor a ragadozókkal szemben némileg védve vannak? 4.3. Szorgalmi feladat Az XY-diagram jól ismert a táblázatkezelők révén. Ebben két azonos hosszúságú számsorozatot egyetlen ábrában újszerűen vonnak össze. A két sorozat azonos indexű elemei egy síkbeli pont koordinátáiként kerül ki a képre. Nagy előnye ennek a diagramtípusnak, hogy ha a két sorozat véges értékhalmaz rendelkezik (ez a mi modellünkben igaz, hiszen a tér befogadóképessége határt szab az egyes fajtájú egyedeknek), akkor előre meghatározott síktartományban ábrázolható egy tetszőleges hosszúságú sorozat-pár. 4. ábra. A sin(x) és a sin(x+ /3) (x=0..6,5; 0,1 lépésközzel) két függvény által leírt egyetlen síkgörbe az XY-térben. Mint látható nagyon látványosan és helytakarékosan mutat be egy ciklikus sorozatpárt. A vizsgálatok szerint a ragadozó-zsákmány modellek rendelkeznek (kvázi) ciklikussággal, ezért lehet hasznos egy ilyen ablakfajta. Valósítsa meg az XY-diagram fajtájú ablakot, azaz bővítse a unitot ilyen típussal, és hangolja ehhez a fő programot is! 7
8 5. ábra. Egy futási kép XY-diagrammal: amikor a ragadozók fogyatkozni kezdenek. 5. A teljes anyag 6. ábra. Egy futási kép XY-diagrammal: a ciklus majdnem bezárul. Ez a kézirat, források, lefordított kódok, súgófájl...: ZsakmanyKe.zip. 8
9 1. Függelék Néhány futáseredmény Az alábbi ábrák alapján milyen következtetésekre lehet jutni? Illetve milyen paraméterezés mellett futtatná újra, hogy további következtetéseket vonhasson le? A reprodukálhatóság kedvért megjegyzem: Randomize nélküli futások eredményeit láthatjuk alább. Tudjuk, hogy a kezdő állapotot egy véletlenszerűen generált állapot jelent. (Ez a következtetések egyike-másika szempontjából fontos. 1 ) F1.1. ábra. Optimális életesélyű ragadozók és zsákmányok, extra kicsi méretű térben, T=67700 (4 futás!). 1 A később az XY-diagramon megjelenő szabályosnak minősített görbe azt az állapotváltozást írja le, amely során a véletlenszerű feltöltöttségből egy csapatokba rendezett állapotba vezet. Ekkor a darabszámok nagy változásokat mutatnak! 9
10 F1.2. ábra. Optimális életesélyű ragadozók és zsákmányok, kisméretű térben, T=64150 (4 futás!). F1.3. ábra. Optimális életesélyű ragadozók és zsákmányok, közel maximális méretű térben, T= (110 futás). 10
11 F1.4. ábra. Optimális életesélyű ragadozók és zsákmányok, nagyméretű térben, T= (felül); és a folytatása; T= (alul, 76 futás). 11
12 F1.5. ábra. Optimális életesélyű ragadozók és zsákmányok, közepes méretű térben, T= (12 futás). Mire lehet következtetni: hogyan függ a szimuláció a tér méretparamétereitől? Miért bomlik az XY-diagram jól érzékelhetően egy szabályosan változó és egy szabálytalanul kunkorodó szakaszra? Annyit tudni kell és lehet, hogy a szabályossal kezdődik. 12
13 F1.6. ábra. A valóságoshoz jobban hasonlító paraméterekkel, közepes méretű térben, T= (felső kép); egy T= kori állapot (alsó kép; 37 ). Már a korábbiaknál is megfogalmazódhatott az a vágy, hogy jó lenne az XY-diagram egyes részleteit finomabban megvizsgálni. Ne feledjük, hogy 1) a naplófájl relatíve kis időegységenként (most éppen 200) minden fontos állapot-paramétert megőrzött; 2) mégpedig a táblázatkezelők körében általánosan ismert fájl-formátumban (csv), ami bármikor újra felhasználható! Ha tehát egy táblázatkezelőbe beolvassuk, akkor abban további vizsgálatokat végezhetünk. Például az 13
14 XY-diagramnak egy-egy érdekesebbnek vélt, vagy nem kellően kivehető részletét kiragadhatjuk, újrarajzoltathatjuk. Ciklusokat kereshetünk F1.7. ábra. Az F6. ábrán látható futás eredményét Excelbe bevíve, alkalmas beállításokkal a részletek jobban kivehetőkké tehetők. (felül) A középső kép az utolsó , az alsó az utolsó időegységet emeli ki. A ritkítás a lehető legmechanikusabb módja a trend előállításának. Ezt mutatja az alábbi ábra. 14
15 F1.8. ábra. Ritkítással drasztikusan egyszerűsödnek a fenti ábrák: balra az eredeti, jobbra a 100-adára ritkított. A hagyományos vonal-diagrammal a létszámok alakulás látható a következő ábrán. Ebből (is) látszik, hogy az idő múlásával csillapodik mind a ragadozók, mind a zsákmányok száma. Némi fázis eltolódás végig látható. 15
16 F1.9. ábra. A teljes szimuláció létszámának alakulása az idő függvényében. Ritkított adatok alapján. Piros a ragadozókhoz, zöld a zsákmányokhoz tartozik. Alkosson további lényegkiemelő módszereket a táblázatkezelő képességeire építve! 2. Függelék További megfontolások Figyelmünket összpontosítsuk az elméletre! Az általunk vizsgált probléma legegyszerűbb és legkorábbi matematikai modelljére, a jól ismert Lotka-Volterra modellre. Ez az alábbi differenciál-egyenletrendszerre épül: dh/dt = rh aph (1) dp/dt = bph mp (2) Átvettük most Alexei Sharov On Line Lectures c. anyagának fejezetének jelöléseit. Az egyenletből a következők látszanak: H és P a zsákmány, ill. a ragadozók száma; r és b a zsákmány, ill. ragadozók születési hajlandósága ; a és m pedig a zsákmány, ill. a ragadozók halálozási esélye. Az egyenlet működése így interpretálható: A zsákmányok számának változása csak saját létszámukból adódó (halálozáson felüli) születéstől függ pozitíve (r születési ráta és halálozási ráta különbsége), valamint a saját és a ragadozók számának szorzatától negatíve. A pozitív rész nyilvánvaló, a negatív azzal magyarázható, hogy nyilván annál nagyobb az esélye (így a várható értéke is) annak, hogy zsákmány áldozatul esik a ragadozónak, minél több van
17 belőle és a ragadozóból. A ragadozók növekedése annál nagyobb, minél nagyobb az esélye annak, hogy egy ragadozó zsákmányra bukkan, azaz ezek számának szorzatával arányos, a fogyást kizárólag a halálozás okozza, ami annál nagyobb, minél többen vannak. A modellel játszva a számalakulásra jellegzetes görbéket kapunk. F2.1. ábra. A Lotka-Volterra modell megoldása, és a megoldásgörbék kirajzolása. A balra a szokásos XY-diagram, a jobbra az idődiagram. Az egyenlet paramétereit változtatgatva gyakorta jutunk a fenti ábra által mutatott periodikus eredményhez. Összevetve az eddigi eredményeinkkel elgondolkodtató különbséget fedezhetünk föl: a mi modelljeink kivétel nélkül kisebb-nagyobb szabálytalansággal egy egyensúlyi állapot felé konvergálnak. Mi lehet a magyarázat? A kérdés annál is meglepőbb, mert a szimulációs részt megvizsgálva azt találjuk, hogy ugyanúgy kellene függnie a változásnak a pillanatnyi létszámtól, mint ahogy azt fentebb leírtuk. Az a megfigyelés vezet el a magyarázathoz, hogy a szimuláció legelején még egészen úgy változik az XY-diagram, ahogy az elméleti modellben látszik, csak később válik a görbe szűkülővé és egyre beljebb konvergálóbbá. Kérdés tehát, mi változik a számokon túl az idővel a szimulációs modellben? Még egyszer elemezve a szimulációs lépést, rájövünk, hogy minden esemény, ami növekedést hoz, az annak az elemnek a közelében született egyedek által következik be, vagyis lokálisan érinti a következő generációt. Ugyanez a lokalitás a territórium mintázatán is kiválóan érzékelhető. Az a gondolat vetődhet föl bennünk, hogy az egyedek kezdetben még megvolt egyenletességének drasztikus elromlása áll a jelenség hátterében. Az egyenletekre tekintve az érvelés jogosnak tűnik. A matematikai elemzés helyett most empirikusan ellenőrizzük sejtésünket! Ha igaz a sejtésünk, akkor csak a kiinduláskori egyenletességet kell fenntartanunk a szimuláció során. Erre több mód is kínálkozik: 1) gyakorta keverjük össze az egyedeket; 2) a keveredés esetleg nem ilyen mesterkélten is, valószerűbben is elérhető, ha az egyedek intelligensen a számukra kellemetlen szomszédtól elfelé menekülnek, illetve a fennmaradás szempontjából fontos szomszédság felé mozdulnak, emellett kicsit megengedőbbek leszünk a ragadozókhoz azzal, hogy több sikertelen zsákmányolási kísérletet is megengedünk (újabb paraméter). Az 1) elképzelés egy lehetséges megvalósításának eredményeit mutatja a következő ábra. 17
18 F2.2. ábra. Egy közepes méretű territórium, többé-kevésbé reális paraméterek melletti futás végállapoti képe (fent); a teljes szimuláció létszámváltozása (középen), ugyanez XY-diagrammal (alul). Megnyugtató a látvány, mely szerint a kezdeti bizonytalankodás után a szimuláció eredménye is közel periodikussá válik. 18
GazSzim Szlávi Péter
 GazSzim 2015.12.02. GÁZ-MODELL Szlávi Péter 2000-2012 TARTALOM GÁZ-MODELL... 1 1. Elvárások... 2 2. A problémák... 4 2.1. A reprezentációs lényeg Ablakok unit... 4 2.2. Az implementált műveletek fejsorai
GazSzim 2015.12.02. GÁZ-MODELL Szlávi Péter 2000-2012 TARTALOM GÁZ-MODELL... 1 1. Elvárások... 2 2. A problémák... 4 2.1. A reprezentációs lényeg Ablakok unit... 4 2.2. Az implementált műveletek fejsorai
Utolsó módosítás: Feladat egy kétváltozós valós függvény kirajzolása különféle megjelenítési módszerekkel.
 Utolsó módosítás: 2008.09.04. Kétváltozós függvények ábrázolása 1 Bevezetés Feladat egy kétváltozós valós függvény kirajzolása különféle megjelenítési módszerekkel. Például: szintvonalakkal, pontfelhővel,
Utolsó módosítás: 2008.09.04. Kétváltozós függvények ábrázolása 1 Bevezetés Feladat egy kétváltozós valós függvény kirajzolása különféle megjelenítési módszerekkel. Például: szintvonalakkal, pontfelhővel,
Demográfiai modellek (folytatás)
 Demográfiai modellek (folytatás) 4. A teljesebb anyag 4.1. A megoldás egy változata Alábbiakban az előző gyakorlaton szereplő keretprogramból kapható egy lehetséges megoldást részletezzük. (Ha már a sajátja
Demográfiai modellek (folytatás) 4. A teljesebb anyag 4.1. A megoldás egy változata Alábbiakban az előző gyakorlaton szereplő keretprogramból kapható egy lehetséges megoldást részletezzük. (Ha már a sajátja
Programozási nyelvek 1. előadás
 Programozási nyelvek 1. előadás I. A nyelv története Logo Seymour Papert, 1968,1969 - szövegkezelés, M.I.T. Később: grafika, mikroszámítógépekre átdolgozva Cél: minél kisebb gyerekeknek is, természetes
Programozási nyelvek 1. előadás I. A nyelv története Logo Seymour Papert, 1968,1969 - szövegkezelés, M.I.T. Később: grafika, mikroszámítógépekre átdolgozva Cél: minél kisebb gyerekeknek is, természetes
EGY ABLAK - GEOMETRIAI PROBLÉMA
 EGY ABLAK - GEOMETRIAI PROBLÉMA Írta: Hajdu Endre A számítógépemhez tartozó két hangfal egy-egy négyzet keresztmetszetű hasáb hely - szűke miatt az ablakpárkányon van elhelyezve (. ábra).. ábra Hogy az
EGY ABLAK - GEOMETRIAI PROBLÉMA Írta: Hajdu Endre A számítógépemhez tartozó két hangfal egy-egy négyzet keresztmetszetű hasáb hely - szűke miatt az ablakpárkányon van elhelyezve (. ábra).. ábra Hogy az
Hatékonyság 1. előadás
 Hatékonyság 1. előadás Mi a hatékonyság Bevezetés A hatékonyság helye a programkészítés folyamatában: csak HELYES programra Erőforrásigény: a felhasználó és a fejlesztő szempontjából A hatékonyság mérése
Hatékonyság 1. előadás Mi a hatékonyság Bevezetés A hatékonyság helye a programkészítés folyamatában: csak HELYES programra Erőforrásigény: a felhasználó és a fejlesztő szempontjából A hatékonyság mérése
BIOMATEMATIKA ELŐADÁS
 BIOMATEMATIKA ELŐADÁS 6. Differenciálegyenletekről röviden Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés 2 Elsőrendű differenciálegyenletek Definíciók Kezdetiérték-probléma
BIOMATEMATIKA ELŐADÁS 6. Differenciálegyenletekről röviden Debreceni Egyetem, 2015 Dr. Bérczes Attila, Bertók Csanád A diasor tartalma 1 Bevezetés 2 Elsőrendű differenciálegyenletek Definíciók Kezdetiérték-probléma
Szélsőérték-számítás
 Szélsőérték-számítás Jelölések A következő jelölések mind az f függvény x szerinti parciális deriváltját jelentik: Ugyanígy az f függvény y szerinti parciális deriváltja: f x = xf = f x f y = yf = f y
Szélsőérték-számítás Jelölések A következő jelölések mind az f függvény x szerinti parciális deriváltját jelentik: Ugyanígy az f függvény y szerinti parciális deriváltja: f x = xf = f x f y = yf = f y
10. Koordinátageometria
 I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
I. Nulladik ZH-ban láttuk: 0. Koordinátageometria. Melyek azok a P x; y pontok, amelyek koordinátái kielégítik az Ábrázolja a megoldáshalmazt a koordináta-síkon! x y x 0 egyenlőtlenséget? ELTE 00. szeptember
A brachistochron probléma megoldása
 A brachistochron probléma megoldása Adott a függőleges síkban két nem egy függőleges egyenesen fekvő P 0 és P 1 pont, amelyek közül a P 1 fekszik alacsonyabban. Azt a kérdést fogjuk vizsgálni. hogy van-e
A brachistochron probléma megoldása Adott a függőleges síkban két nem egy függőleges egyenesen fekvő P 0 és P 1 pont, amelyek közül a P 1 fekszik alacsonyabban. Azt a kérdést fogjuk vizsgálni. hogy van-e
Sorozatok I. Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma)
 Sorozatok I. DEFINÍCIÓ: (Számsorozat) A számsorozat olyan függvény, amelynek értelmezési tartománya a pozitív egész számok halmaza, értékkészlete a valós számok egy részhalmaza. Jelölés: (a n ), {a n }.
Sorozatok I. DEFINÍCIÓ: (Számsorozat) A számsorozat olyan függvény, amelynek értelmezési tartománya a pozitív egész számok halmaza, értékkészlete a valós számok egy részhalmaza. Jelölés: (a n ), {a n }.
Felvételi tematika INFORMATIKA
 Felvételi tematika INFORMATIKA 2016 FEJEZETEK 1. Természetes számok feldolgozása számjegyenként. 2. Számsorozatok feldolgozása elemenként. Egydimenziós tömbök. 3. Mátrixok feldolgozása elemenként/soronként/oszloponként.
Felvételi tematika INFORMATIKA 2016 FEJEZETEK 1. Természetes számok feldolgozása számjegyenként. 2. Számsorozatok feldolgozása elemenként. Egydimenziós tömbök. 3. Mátrixok feldolgozása elemenként/soronként/oszloponként.
Demográfiai modellek
 Demográfiai modellek 0. A modell rövid ismertetése A modellünkkel megvizsgáljuk, hogy hogyan függ egy populáció egyedszáma és korcsoporteloszlása a korcsoportokhoz rendelt numerikus jellemzőktől. A jellemzők
Demográfiai modellek 0. A modell rövid ismertetése A modellünkkel megvizsgáljuk, hogy hogyan függ egy populáció egyedszáma és korcsoporteloszlása a korcsoportokhoz rendelt numerikus jellemzőktől. A jellemzők
Osztott algoritmusok
 Osztott algoritmusok A benzinkutas példa szimulációja Müller Csaba 2010. december 4. 1. Bevezetés Első lépésben talán kezdjük a probléma ismertetésével. Adott két n hosszúságú bináris sorozat (s 1, s 2
Osztott algoritmusok A benzinkutas példa szimulációja Müller Csaba 2010. december 4. 1. Bevezetés Első lépésben talán kezdjük a probléma ismertetésével. Adott két n hosszúságú bináris sorozat (s 1, s 2
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
Hódmezővásárhelyi Városi Matematikaverseny április 14. A osztályosok feladatainak javítókulcsa
 Hódmezővásárhelyi Városi Matematikaverseny 2003. április 14. A 11-12. osztályosok feladatainak javítókulcsa 1. feladat Egy számtani sorozatot az első eleme és különbsége egyértelműen meghatározza, azt
Hódmezővásárhelyi Városi Matematikaverseny 2003. április 14. A 11-12. osztályosok feladatainak javítókulcsa 1. feladat Egy számtani sorozatot az első eleme és különbsége egyértelműen meghatározza, azt
Szimuláció RICHARD M. KARP és AVI WIGDERSON. (Készítette: Domoszlai László)
 Szimuláció RICHARD M. KARP és AVI WIGDERSON A Fast Parallel Algorithm for the Maximal Independent Set Problem című cikke alapján (Készítette: Domoszlai László) 1. Bevezetés A következőkben megadott algoritmus
Szimuláció RICHARD M. KARP és AVI WIGDERSON A Fast Parallel Algorithm for the Maximal Independent Set Problem című cikke alapján (Készítette: Domoszlai László) 1. Bevezetés A következőkben megadott algoritmus
Programozási nyelvek a közoktatásban alapfogalmak I. előadás
 Programozási nyelvek a közoktatásban alapfogalmak I. előadás Szempontok Programozási nyelvek osztályozása Felhasználói kör (amatőr, professzionális) Emberközelség (gépi nyelvektől a természetes nyelvekig)
Programozási nyelvek a közoktatásban alapfogalmak I. előadás Szempontok Programozási nyelvek osztályozása Felhasználói kör (amatőr, professzionális) Emberközelség (gépi nyelvektől a természetes nyelvekig)
Algoritmizálás és adatmodellezés tanítása 2. előadás
 Algoritmizálás és adatmodellezés tanítása 2. előadás Tartalom Összegzés vektorra, mátrixra Megszámolás vektorra, mátrixra Maximum-kiválasztás vektorra, mátrixra Eldöntés vektorra, mátrixra Kiválasztás
Algoritmizálás és adatmodellezés tanítása 2. előadás Tartalom Összegzés vektorra, mátrixra Megszámolás vektorra, mátrixra Maximum-kiválasztás vektorra, mátrixra Eldöntés vektorra, mátrixra Kiválasztás
1. megold s: A keresett háromjegyű szám egyik számjegye a 3-as, a két ismeretlen számjegyet jelölje a és b. A feltétel szerint
 A 004{005. tan vi matematika OKTV I. kateg ria els (iskolai) fordul ja feladatainak megold sai 1. feladat Melyek azok a 10-es számrendszerbeli háromjegyű pozitív egész számok, amelyeknek számjegyei közül
A 004{005. tan vi matematika OKTV I. kateg ria els (iskolai) fordul ja feladatainak megold sai 1. feladat Melyek azok a 10-es számrendszerbeli háromjegyű pozitív egész számok, amelyeknek számjegyei közül
DIFFERENCIAEGYENLETEK, MINT A MODELLEZÉS ESZKÖZEI AZ ISKOLAI MATEMATIKÁBAN
 DIFFERENCIAEGYENLETEK, MINT A MODELLEZÉS ESZKÖZEI AZ ISKOLAI MATEMATIKÁBAN KOVÁCS ZOLTÁN 1. Bevezetés A természeti jelenségeket sokszor differenciálegyenletekkel lehet leírni: a vizsgált mennyiség például
DIFFERENCIAEGYENLETEK, MINT A MODELLEZÉS ESZKÖZEI AZ ISKOLAI MATEMATIKÁBAN KOVÁCS ZOLTÁN 1. Bevezetés A természeti jelenségeket sokszor differenciálegyenletekkel lehet leírni: a vizsgált mennyiség például
Algoritmizálás, adatmodellezés tanítása 1. előadás
 Algoritmizálás, adatmodellezés 1. előadás Az algoritmus fogalma végrehajtható (van hozzá végre-hajtó) lépésenként hajtható végre a lépések maguk is algoritmusok pontosan definiált, adott végre-hajtási
Algoritmizálás, adatmodellezés 1. előadás Az algoritmus fogalma végrehajtható (van hozzá végre-hajtó) lépésenként hajtható végre a lépések maguk is algoritmusok pontosan definiált, adott végre-hajtási
Forgalmi modellezés BMEKOKUM209
 BME Közlekedésüzemi és Közlekedésgazdasági Tanszék Forgalmi modellezés BMEKOKUM209 Szimulációs modellezés Dr. Juhász János A forgalmi modellezés célja A közlekedési igények bővülése és a motorizáció növekedése
BME Közlekedésüzemi és Közlekedésgazdasági Tanszék Forgalmi modellezés BMEKOKUM209 Szimulációs modellezés Dr. Juhász János A forgalmi modellezés célja A közlekedési igények bővülése és a motorizáció növekedése
Infobionika ROBOTIKA. X. Előadás. Robot manipulátorok II. Direkt és inverz kinematika. Készült a HEFOP P /1.0 projekt keretében
 Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Regresszió. Csorba János. Nagyméretű adathalmazok kezelése március 31.
 Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Rekurzív algoritmusok
 Rekurzív algoritmusok 11. előadás Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2011. november 14. Sergyán (OE NIK) AAO 11 2011. november 14. 1 / 32 Rekurzív
Rekurzív algoritmusok 11. előadás Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2011. november 14. Sergyán (OE NIK) AAO 11 2011. november 14. 1 / 32 Rekurzív
Egyenes és sík. Wettl Ferenc szeptember 29. Wettl Ferenc () Egyenes és sík szeptember / 15
 Egyenes és sík Wettl Ferenc 2006. szeptember 29. Wettl Ferenc () Egyenes és sík 2006. szeptember 29. 1 / 15 Tartalom 1 Egyenes és szakasz Egyenes Szakasz Egyenesvonalú egyenletes mozgás Egyenes és pont
Egyenes és sík Wettl Ferenc 2006. szeptember 29. Wettl Ferenc () Egyenes és sík 2006. szeptember 29. 1 / 15 Tartalom 1 Egyenes és szakasz Egyenes Szakasz Egyenesvonalú egyenletes mozgás Egyenes és pont
Méréselmélet MI BSc 1
 Mérés és s modellezés 2008.02.15. 1 Méréselmélet - bevezetés a mérnöki problémamegoldás menete 1. A probléma kitűzése 2. A hipotézis felállítása 3. Kísérlettervezés 4. Megfigyelések elvégzése 5. Adatok
Mérés és s modellezés 2008.02.15. 1 Méréselmélet - bevezetés a mérnöki problémamegoldás menete 1. A probléma kitűzése 2. A hipotézis felállítása 3. Kísérlettervezés 4. Megfigyelések elvégzése 5. Adatok
V. Kétszemélyes játékok
 Teljes információjú, véges, zéró összegű kétszemélyes játékok V. Kétszemélyes játékok Két játékos lép felváltva adott szabályok szerint. Mindkét játékos ismeri a maga és az ellenfele összes választási
Teljes információjú, véges, zéró összegű kétszemélyes játékok V. Kétszemélyes játékok Két játékos lép felváltva adott szabályok szerint. Mindkét játékos ismeri a maga és az ellenfele összes választási
Nagy Péter: Fortuna szekerén...
 Nagy Péter: Fortuna szekerén... tudni: az ész rövid, az akarat gyenge, hogy rá vagyok bízva a vak véletlenre. És makacs reménnyel mégis, mégis hinni, hogy amit csinálok, az nem lehet semmi. (Teller Ede)
Nagy Péter: Fortuna szekerén... tudni: az ész rövid, az akarat gyenge, hogy rá vagyok bízva a vak véletlenre. És makacs reménnyel mégis, mégis hinni, hogy amit csinálok, az nem lehet semmi. (Teller Ede)
First Prev Next Last Go Back Full Screen Close Quit
 Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Egyenletek, egyenlőtlenségek VII.
 Egyenletek, egyenlőtlenségek VII. Magasabbfokú egyenletek: A 3, vagy annál nagyobb fokú egyenleteket magasabb fokú egyenleteknek nevezzük. Megjegyzés: Egy n - ed fokú egyenletnek legfeljebb n darab valós
Egyenletek, egyenlőtlenségek VII. Magasabbfokú egyenletek: A 3, vagy annál nagyobb fokú egyenleteket magasabb fokú egyenleteknek nevezzük. Megjegyzés: Egy n - ed fokú egyenletnek legfeljebb n darab valós
NULLADIK MATEMATIKA ZÁRTHELYI
 NULLADIK MATEMATIKA ZÁRTHELYI 08-09-07 Terem: Munkaidő: 0 perc. A dolgozat megírásához íróeszközön kívül semmilyen segédeszköz nem használható! A feladatlap kizárólag kék vagy fekete tollal tölthető ki.
NULLADIK MATEMATIKA ZÁRTHELYI 08-09-07 Terem: Munkaidő: 0 perc. A dolgozat megírásához íróeszközön kívül semmilyen segédeszköz nem használható! A feladatlap kizárólag kék vagy fekete tollal tölthető ki.
GRÁFELMÉLET. 7. előadás. Javító utak, javító utak keresése, Edmonds-algoritmus
 GRÁFELMÉLET 7. előadás Javító utak, javító utak keresése, Edmonds-algoritmus Definíció: egy P utat javító útnak nevezünk egy M párosításra nézve, ha az út páratlan hosszú, kezdő- és végpontjai nem párosítottak,
GRÁFELMÉLET 7. előadás Javító utak, javító utak keresése, Edmonds-algoritmus Definíció: egy P utat javító útnak nevezünk egy M párosításra nézve, ha az út páratlan hosszú, kezdő- és végpontjai nem párosítottak,
Ensemble előrejelzések: elméleti és gyakorlati háttér HÁGEL Edit Országos Meteorológiai Szolgálat Numerikus Modellező és Éghajlat-dinamikai Osztály 34
 Ensemble előrejelzések: elméleti és gyakorlati háttér HÁGEL Edit Országos Meteorológiai Szolgálat Numerikus Modellező és Éghajlat-dinamikai Osztály 34. Meteorológiai Tudományos Napok Az előadás vázlata
Ensemble előrejelzések: elméleti és gyakorlati háttér HÁGEL Edit Országos Meteorológiai Szolgálat Numerikus Modellező és Éghajlat-dinamikai Osztály 34. Meteorológiai Tudományos Napok Az előadás vázlata
Webes vizsgakezelés folyamata Oktatói felületek
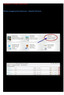 Vizsgakezelés az ETR megújult webes felületén Webes vizsgakezelés folyamata Oktatói felületek A vizsgák kezelésével kapcsolatban számos paraméterezési lehetőség áll rendelkezésre az ETR rendszerében. Jelen
Vizsgakezelés az ETR megújult webes felületén Webes vizsgakezelés folyamata Oktatói felületek A vizsgák kezelésével kapcsolatban számos paraméterezési lehetőség áll rendelkezésre az ETR rendszerében. Jelen
8. gyakorlat Pointerek, dinamikus memóriakezelés
 8. gyakorlat Pointerek, dinamikus memóriakezelés Házi ellenőrzés Egy számtani sorozat első két tagja A1 és A2. Számítsa ki a sorozat N- dik tagját! (f0051) Egy mértani sorozat első két tagja A1 és A2.
8. gyakorlat Pointerek, dinamikus memóriakezelés Házi ellenőrzés Egy számtani sorozat első két tagja A1 és A2. Számítsa ki a sorozat N- dik tagját! (f0051) Egy mértani sorozat első két tagja A1 és A2.
Számítógépes döntéstámogatás. Genetikus algoritmusok
 BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
BLSZM-10 p. 1/18 Számítógépes döntéstámogatás Genetikus algoritmusok Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu BLSZM-10 p. 2/18 Bevezetés 1950-60-as
Kísérlettervezés alapfogalmak
 Kísérlettervezés alapfogalmak Rendszermodellezés Budapest University of Technology and Economics Fault Tolerant Systems Research Group Budapest University of Technology and Economics Department of Measurement
Kísérlettervezés alapfogalmak Rendszermodellezés Budapest University of Technology and Economics Fault Tolerant Systems Research Group Budapest University of Technology and Economics Department of Measurement
Trigonometria Megoldások. 1) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( )
 Trigonometria Megoldások Trigonometria - megoldások ) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( ) akkor a háromszög egyenlő szárú vagy derékszögű!
Trigonometria Megoldások Trigonometria - megoldások ) Igazolja, hogy ha egy háromszög szögeire érvényes az alábbi összefüggés: sin : sin = cos + : cos +, ( ) ( ) akkor a háromszög egyenlő szárú vagy derékszögű!
Mesterséges Intelligencia MI
 Mesterséges Intelligencia MI Problémamegoldás kereséssel - csak lokális információra alapozva Pataki Béla BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Lokálisan
Mesterséges Intelligencia MI Problémamegoldás kereséssel - csak lokális információra alapozva Pataki Béla BME I.E. 414, 463-26-79 pataki@mit.bme.hu, http://www.mit.bme.hu/general/staff/pataki Lokálisan
A Cournot-féle duopólium
 A Cournot-féle duopólium. Kínálati duopólium: két termelő állít elő termékeket. Verseny a termékmennyiségekkel 3. A piaci kereslet inverz függvénye: p a. Valamely ár mellett kialakuló keresletet két vállalat
A Cournot-féle duopólium. Kínálati duopólium: két termelő állít elő termékeket. Verseny a termékmennyiségekkel 3. A piaci kereslet inverz függvénye: p a. Valamely ár mellett kialakuló keresletet két vállalat
Véletlenszám generátorok és tesztelésük. Tossenberger Tamás
 Véletlenszám generátorok és tesztelésük Tossenberger Tamás Érdekességek Pénzérme feldobó gép: $0,25-os érme 1/6000 valószínűséggel esik az élére 51% eséllyel érkezik a felfelé mutató oldalára Pörgetésnél
Véletlenszám generátorok és tesztelésük Tossenberger Tamás Érdekességek Pénzérme feldobó gép: $0,25-os érme 1/6000 valószínűséggel esik az élére 51% eséllyel érkezik a felfelé mutató oldalára Pörgetésnél
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével
 Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Példa: Tartó lehajlásfüggvényének meghatározása végeselemes módszer segítségével Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 213. október 8. Javítva: 213.1.13. Határozzuk
Kétszemélyes játékok Gregorics Tibor Mesterséges intelligencia
 Kétszemélyes játékok Kétszemélyes, teljes információjú, véges, determinisztikus,zéró összegű játékok Két játékos lép felváltva adott szabályok szerint, amíg a játszma véget nem ér. Mindkét játékos ismeri
Kétszemélyes játékok Kétszemélyes, teljes információjú, véges, determinisztikus,zéró összegű játékok Két játékos lép felváltva adott szabályok szerint, amíg a játszma véget nem ér. Mindkét játékos ismeri
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
Visszalépéses kiválogatás
 elépő a tudás közösségébe Informatika szakköri segédanyag Heizlerné akonyi iktória, Horváth Győző, Menyhárt László, Szlávi Péter, Törley Gábor, Zsakó László Szerkesztő: Abonyi-Tóth Andor, Zsakó László
elépő a tudás közösségébe Informatika szakköri segédanyag Heizlerné akonyi iktória, Horváth Győző, Menyhárt László, Szlávi Péter, Törley Gábor, Zsakó László Szerkesztő: Abonyi-Tóth Andor, Zsakó László
A PiFast program használata. Nagy Lajos
 A PiFast program használata Nagy Lajos Tartalomjegyzék 1. Bevezetés 3 2. Bináris kimenet létrehozása. 3 2.1. Beépített konstans esete.............................. 3 2.2. Felhasználói konstans esete............................
A PiFast program használata Nagy Lajos Tartalomjegyzék 1. Bevezetés 3 2. Bináris kimenet létrehozása. 3 2.1. Beépített konstans esete.............................. 3 2.2. Felhasználói konstans esete............................
Súlytámfal ellenőrzése
 3. számú mérnöki kézikönyv Frissítve: 2016. Február Súlytámfal ellenőrzése Program: Súlytámfal Fájl: Demo_manual_03.gtz Ebben a fejezetben egy meglévő súlytámfal számítását mutatjuk be állandó és rendkívüli
3. számú mérnöki kézikönyv Frissítve: 2016. Február Súlytámfal ellenőrzése Program: Súlytámfal Fájl: Demo_manual_03.gtz Ebben a fejezetben egy meglévő súlytámfal számítását mutatjuk be állandó és rendkívüli
Kvantitatív módszerek
 Kvantitatív módszerek szimuláció Kovács Zoltán Szervezési és Vezetési Tanszék E-mail: kovacsz@gtk.uni-pannon.hu URL: http://almos/~kovacsz Mennyiségi problémák megoldása analitikus numerikus szimuláció
Kvantitatív módszerek szimuláció Kovács Zoltán Szervezési és Vezetési Tanszék E-mail: kovacsz@gtk.uni-pannon.hu URL: http://almos/~kovacsz Mennyiségi problémák megoldása analitikus numerikus szimuláció
Bevezetés az informatikába
 Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Programozási nyelvek 6. előadás
 Programozási nyelvek 6. előadás Szempontok Programozási nyelvek osztályozása Felhasználói kör (amatőr, professzionális) Emberközelség (gépi nyelvektől a természetes nyelvekig) Számítási modell (hogyan
Programozási nyelvek 6. előadás Szempontok Programozási nyelvek osztályozása Felhasználói kör (amatőr, professzionális) Emberközelség (gépi nyelvektől a természetes nyelvekig) Számítási modell (hogyan
HÁZI DOLGOZAT. Érmefeldobások eredményei és statisztikája. ELTE-TTK Kémia BSc Tantárgy: Kémia felzárkóztató (A kémia alapjai)
 ELTE-TTK Kémia BSc Tantárgy: Kémia felzárkóztató (A kémia alapjai) HÁZI DOLGOZAT Érmefeldobások eredményei és statisztikája Készítette: Babinszki Bence EHA-kód: BABSAET.ELTE E-mail cím: Törölve A jelentés
ELTE-TTK Kémia BSc Tantárgy: Kémia felzárkóztató (A kémia alapjai) HÁZI DOLGOZAT Érmefeldobások eredményei és statisztikája Készítette: Babinszki Bence EHA-kód: BABSAET.ELTE E-mail cím: Törölve A jelentés
11. Előadás. 11. előadás Bevezetés a lineáris programozásba
 11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
11. Előadás Gondolkodnivalók Sajátérték, Kvadratikus alak 1. Gondolkodnivaló Adjuk meg, hogy az alábbi A mátrixnak mely α értékekre lesz sajátértéke a 5. Ezen α-ák esetén határozzuk meg a 5 sajátértékhez
Algoritmizálás és adatmodellezés tanítása beadandó feladat: Algtan1 tanári beadandó /99 1
 Algoritmizálás és adatmodellezés tanítása beadandó feladat: Algtan1 tanári beadandó /99 1 Készítette: Gipsz Jakab Neptun-azonosító: ABC123 E-mail: gipszjakab@seholse.hu Kurzuskód: IT-13AAT1EG 1 A fenti
Algoritmizálás és adatmodellezés tanítása beadandó feladat: Algtan1 tanári beadandó /99 1 Készítette: Gipsz Jakab Neptun-azonosító: ABC123 E-mail: gipszjakab@seholse.hu Kurzuskód: IT-13AAT1EG 1 A fenti
20. tétel A kör és a parabola a koordinátasíkon, egyenessel való kölcsönös helyzetük. Másodfokú egyenlőtlenségek.
 . tétel A kör és a parabola a koordinátasíkon, egyenessel való kölcsönös helyzetük. Másodfokú egyenlőtlenségek. Először megadom a síkbeli definíciójukat, mert ez alapján vezetjük le az egyenletüket. Alakzat
. tétel A kör és a parabola a koordinátasíkon, egyenessel való kölcsönös helyzetük. Másodfokú egyenlőtlenségek. Először megadom a síkbeli definíciójukat, mert ez alapján vezetjük le az egyenletüket. Alakzat
I. Internetes keresési feladatok (ajánlott idő: 20 perc)
 I. Internetes keresési feladatok (ajánlott idő: 20 perc) A talált oldalak internet címét (URL) másold ki egy szöveges dokumentumba és mentsd Csapatnev_internet néven! A konkrét válaszokat ide a papírra
I. Internetes keresési feladatok (ajánlott idő: 20 perc) A talált oldalak internet címét (URL) másold ki egy szöveges dokumentumba és mentsd Csapatnev_internet néven! A konkrét válaszokat ide a papírra
Modern Fizika Labor. Fizika BSc. Értékelés: A mérés dátuma: A mérés száma és címe: 12. mérés: Infravörös spektroszkópia. 2008. május 6.
 Modern Fizika Labor Fizika BSc A mérés dátuma: A mérés száma és címe: 12. mérés: Infravörös spektroszkópia Értékelés: A beadás dátuma: 28. május 13. A mérést végezte: 1/5 A mérés célja A mérés célja az
Modern Fizika Labor Fizika BSc A mérés dátuma: A mérés száma és címe: 12. mérés: Infravörös spektroszkópia Értékelés: A beadás dátuma: 28. május 13. A mérést végezte: 1/5 A mérés célja A mérés célja az
7. gyakorlat Sorozatok, Fájlkezelés
 7. gyakorlat Sorozatok, Fájlkezelés Házi ellenőrzés - f0124 Írj programot, amelyben a felhasználónak egy, a program által meghatározott számot kell kitalálnia! A felhasználó tippjét a program vagy elfogadja,
7. gyakorlat Sorozatok, Fájlkezelés Házi ellenőrzés - f0124 Írj programot, amelyben a felhasználónak egy, a program által meghatározott számot kell kitalálnia! A felhasználó tippjét a program vagy elfogadja,
Gyalogos elütések szimulációs vizsgálata
 Gyalogos elütések szimulációs vizsgálata A Virtual Crash program validációja Dr. Melegh Gábor BME Gépjárművek tanszék Budapest, Magyarország Vida Gábor BME Gépjárművek tanszék Budapest, Magyarország Ing.
Gyalogos elütések szimulációs vizsgálata A Virtual Crash program validációja Dr. Melegh Gábor BME Gépjárművek tanszék Budapest, Magyarország Vida Gábor BME Gépjárművek tanszék Budapest, Magyarország Ing.
konvergensek-e. Amennyiben igen, számítsa ki határértéküket!
 1. Határértékek 1. Állapítsa meg az alábbi sorozatokról, hogy van-e határértékük, konvergensek-e. Amennyiben igen, számítsa ki határértéküket! 2 2...2 2 (n db gyökjel), lim a) lim n b) lim n (sin(1)) n,
1. Határértékek 1. Állapítsa meg az alábbi sorozatokról, hogy van-e határértékük, konvergensek-e. Amennyiben igen, számítsa ki határértéküket! 2 2...2 2 (n db gyökjel), lim a) lim n b) lim n (sin(1)) n,
Kísérlettervezés alapfogalmak
 Kísérlettervezés alapfogalmak Rendszermodellezés Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Kísérlettervezés Cél: a modell paraméterezése a valóság alapján
Kísérlettervezés alapfogalmak Rendszermodellezés Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika és Információs Rendszerek Tanszék Kísérlettervezés Cél: a modell paraméterezése a valóság alapján
Adatszerkezetek I. 7. előadás. (Horváth Gyula anyagai felhasználásával)
 Adatszerkezetek I. 7. előadás (Horváth Gyula anyagai felhasználásával) Bináris fa A fa (bináris fa) rekurzív adatszerkezet: BinFa:= Fa := ÜresFa Rekord(Elem,BinFa,BinFa) ÜresFa Rekord(Elem,Fák) 2/37 Bináris
Adatszerkezetek I. 7. előadás (Horváth Gyula anyagai felhasználásával) Bináris fa A fa (bináris fa) rekurzív adatszerkezet: BinFa:= Fa := ÜresFa Rekord(Elem,BinFa,BinFa) ÜresFa Rekord(Elem,Fák) 2/37 Bináris
Matematikai alapok és valószínőségszámítás. Valószínőségi eloszlások Binomiális eloszlás
 Matematikai alapok és valószínőségszámítás Valószínőségi eloszlások Binomiális eloszlás Bevezetés A tudományos életben megfigyeléseket teszünk, kísérleteket végzünk. Ezek többféle különbözı eredményre
Matematikai alapok és valószínőségszámítás Valószínőségi eloszlások Binomiális eloszlás Bevezetés A tudományos életben megfigyeléseket teszünk, kísérleteket végzünk. Ezek többféle különbözı eredményre
Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Pataki János; dátum: november. I. rész
 Pataki János, november Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Pataki János; dátum: november I rész feladat Oldja meg az alábbi egyenleteket: a) log 7 log log log 7 ; b) ( )
Pataki János, november Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Pataki János; dátum: november I rész feladat Oldja meg az alábbi egyenleteket: a) log 7 log log log 7 ; b) ( )
Abszolútértékes és gyökös kifejezések Megoldások
 Abszolútértékes és gyökös kifejezések Megoldások ) Igazolja, hogy az alábbi négy egyenlet közül az a) és b) jelű egyenletnek pontosan egy megoldása van, a c) és d) jelű egyenletnek viszont nincs megoldása
Abszolútértékes és gyökös kifejezések Megoldások ) Igazolja, hogy az alábbi négy egyenlet közül az a) és b) jelű egyenletnek pontosan egy megoldása van, a c) és d) jelű egyenletnek viszont nincs megoldása
Kupacrendezés. Az s sorban lévő elemeket rendezzük a k kupac segítségével! k.empty. not s.isempty. e:=s.out k.insert(e) not k.
 10. Előadás Beszúró rendezés Használjuk a kupacokat rendezésre! Szúrd be az elemeket egy kupacba! Amíg a sor ki nem ürül, vedd ki a kupacból a maximális elemet, és tedd az eredmény (rendezett) sorba! 2
10. Előadás Beszúró rendezés Használjuk a kupacokat rendezésre! Szúrd be az elemeket egy kupacba! Amíg a sor ki nem ürül, vedd ki a kupacból a maximális elemet, és tedd az eredmény (rendezett) sorba! 2
Mérés és modellezés Méréstechnika VM, GM, MM 1
 Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
Informatikai tehetséggondozás:
 Ég és Föld vonzásában a természet titkai Informatikai tehetséggondozás: isszalépéses kiválogatás TÁMOP-4.2.3.-12/1/KON isszalépéses kiválogatás 1. Az összes lehetséges sorrend Sokszor előfordul feladatként,
Ég és Föld vonzásában a természet titkai Informatikai tehetséggondozás: isszalépéses kiválogatás TÁMOP-4.2.3.-12/1/KON isszalépéses kiválogatás 1. Az összes lehetséges sorrend Sokszor előfordul feladatként,
Gráfok bejárása. Szlávi Péter, Zsakó László: Gráfok II :17
 Gráfok 2. előadás Gráfok bejárása A gráf bejárása = minden elem feldolgozása Probléma: Lineáris elrendezésű sokaság (sorozat) bejárása könnyű, egyetlen ciklussal elvégezhető. Hálós struktúra bejárása nem
Gráfok 2. előadás Gráfok bejárása A gráf bejárása = minden elem feldolgozása Probléma: Lineáris elrendezésű sokaság (sorozat) bejárása könnyű, egyetlen ciklussal elvégezhető. Hálós struktúra bejárása nem
Keresés képi jellemzők alapján. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Függvények ábrázolása
 Függvények ábrázolása Matematikai függvényeket analitikusan nem tudunk a matlabban megadni (tudunk, de ilyet még nem tanulunk). Ahhoz, hogy egy függvényt ábrázoljuk, hasonlóan kell eljárni, mint a házi
Függvények ábrázolása Matematikai függvényeket analitikusan nem tudunk a matlabban megadni (tudunk, de ilyet még nem tanulunk). Ahhoz, hogy egy függvényt ábrázoljuk, hasonlóan kell eljárni, mint a házi
Mérés és modellezés 1
 Mérés és modellezés 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni kell
Mérés és modellezés 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni kell
ÁRAMKÖRÖK SZIMULÁCIÓJA
 ÁRAMKÖRÖK SZIMULÁCIÓJA Az áramkörök szimulációja révén betekintést nyerünk azok működésébe. Meg tudjuk határozni az áramkörök válaszát különböző gerjesztésekre, különböző üzemmódokra. Végezhetők analóg
ÁRAMKÖRÖK SZIMULÁCIÓJA Az áramkörök szimulációja révén betekintést nyerünk azok működésébe. Meg tudjuk határozni az áramkörök válaszát különböző gerjesztésekre, különböző üzemmódokra. Végezhetők analóg
1. Alapfogalmak Algoritmus Számítási probléma Specifikáció Algoritmusok futási ideje
 1. Alapfogalmak 1.1. Algoritmus Az algoritmus olyan elemi műveletekből kompozíciós szabályok szerint felépített összetett művelet, amelyet megadott feltételt teljesítő bemeneti adatra végrehajtva, a megkívánt
1. Alapfogalmak 1.1. Algoritmus Az algoritmus olyan elemi műveletekből kompozíciós szabályok szerint felépített összetett művelet, amelyet megadott feltételt teljesítő bemeneti adatra végrehajtva, a megkívánt
3. Előadás. Megyesi László: Lineáris algebra, oldal. 3. előadás Lineáris egyenletrendszerek
 3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
3. Előadás Megyesi László: Lineáris algebra, 47. 50. oldal. Gondolkodnivalók Determinánsok 1. Gondolkodnivaló Determinánselméleti tételek segítségével határozzuk meg a következő n n-es determinánst: 1
Rekurzió. Dr. Iványi Péter
 Rekurzió Dr. Iványi Péter 1 Függvényhívás void f3(int a3) { printf( %d,a3); } void f2(int a2) { f3(a2); a2 = (a2+1); } void f1() { int a1 = 1; int b1; b1 = f2(a1); } 2 Függvényhívás void f3(int a3) { printf(
Rekurzió Dr. Iványi Péter 1 Függvényhívás void f3(int a3) { printf( %d,a3); } void f2(int a2) { f3(a2); a2 = (a2+1); } void f1() { int a1 = 1; int b1; b1 = f2(a1); } 2 Függvényhívás void f3(int a3) { printf(
Programozás I. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar szeptember 10.
 Programozás I. 1. előadás Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. szeptember 10. Sergyán (OE NIK) Programozás I. 2012. szeptember 10. 1 /
Programozás I. 1. előadás Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. szeptember 10. Sergyán (OE NIK) Programozás I. 2012. szeptember 10. 1 /
VALÓSZÍNŰSÉG, STATISZTIKA TANÍTÁSA
 VALÓSZÍNŰSÉG, STATISZTIKA TANÍTÁSA A VALÓSZÍNŰSÉGI SZEMLÉLET ALAPOZÁSA 1-6. OSZTÁLY A biztos, a lehetetlen és a lehet, de nem biztos események megkülünböztetése Valószínűségi játékok, kísérletek események
VALÓSZÍNŰSÉG, STATISZTIKA TANÍTÁSA A VALÓSZÍNŰSÉGI SZEMLÉLET ALAPOZÁSA 1-6. OSZTÁLY A biztos, a lehetetlen és a lehet, de nem biztos események megkülünböztetése Valószínűségi játékok, kísérletek események
Algoritmusok és adatszerkezetek 2.
 Algoritmusok és adatszerkezetek 2. Varga Balázs gyakorlata alapján Készítette: Nagy Krisztián 1. gyakorlat Nyílt címzéses hash-elés A nyílt címzésű hash táblákban a láncolással ellentétben egy indexen
Algoritmusok és adatszerkezetek 2. Varga Balázs gyakorlata alapján Készítette: Nagy Krisztián 1. gyakorlat Nyílt címzéses hash-elés A nyílt címzésű hash táblákban a láncolással ellentétben egy indexen
Adatszerkezetek II. 1. előadás
 Adatszerkezetek II. 1. előadás Gráfok A gráf fogalma: Gráf(P,E): P pontok (csúcsok) és E P P élek halmaza Fogalmak: Irányított gráf : (p 1,p 2 ) E-ből nem következik, hogy (p 2,p 1 ) E Irányítatlan gráf
Adatszerkezetek II. 1. előadás Gráfok A gráf fogalma: Gráf(P,E): P pontok (csúcsok) és E P P élek halmaza Fogalmak: Irányított gráf : (p 1,p 2 ) E-ből nem következik, hogy (p 2,p 1 ) E Irányítatlan gráf
Kép mátrix. Feladat: Pap Gáborné-Zsakó László: Algoritmizálás, adatmodellezés 2/35
 Grafika I. Kép mátrix Feladat: Egy N*M-es raszterképet nagyítsunk a két-szeresére pontsokszorozással: minden régi pont helyébe 2*2 azonos színű pontot rajzolunk a nagyított képen. Pap Gáborné-Zsakó László:
Grafika I. Kép mátrix Feladat: Egy N*M-es raszterképet nagyítsunk a két-szeresére pontsokszorozással: minden régi pont helyébe 2*2 azonos színű pontot rajzolunk a nagyított képen. Pap Gáborné-Zsakó László:
Makroökonómia. 6. szeminárium
 Makroökonómia 6. szeminárium Ismétlés: egy főre jutó makromutatók Népességnövekedés L Y t = ak t α L t 1 α Konstans, (1+n) ütemben növekszik Egy főre jutó értékek Egyensúlyi növekedési pálya Összes változó
Makroökonómia 6. szeminárium Ismétlés: egy főre jutó makromutatók Népességnövekedés L Y t = ak t α L t 1 α Konstans, (1+n) ütemben növekszik Egy főre jutó értékek Egyensúlyi növekedési pálya Összes változó
Fiók ferde betolása. A hűtőszekrényünk ajtajának és kihúzott fiókjának érintkezése ihlette az alábbi feladatot. Ehhez tekintsük az 1. ábrát!
 1 Fiók ferde betolása A hűtőszekrényünk ajtajának és kihúzott fiókjának érintkezése ihlette az alábbi feladatot. Ehhez tekintsük az 1. ábrát! 1. ábra Itt azt látjuk, hogy egy a x b méretű kis kék téglalapot
1 Fiók ferde betolása A hűtőszekrényünk ajtajának és kihúzott fiókjának érintkezése ihlette az alábbi feladatot. Ehhez tekintsük az 1. ábrát! 1. ábra Itt azt látjuk, hogy egy a x b méretű kis kék téglalapot
Programozási alapismeretek 1. előadás
 Programozási alapismeretek 1. előadás Tartalom A problémamegoldás lépései programkészítés folyamata A specifikáció Az algoritmus Algoritmikus nyelvek struktogram A kódolás a fejlesztői környezet 2/33 A
Programozási alapismeretek 1. előadás Tartalom A problémamegoldás lépései programkészítés folyamata A specifikáció Az algoritmus Algoritmikus nyelvek struktogram A kódolás a fejlesztői környezet 2/33 A
Bevezető feldatok. Elágazás és összegzés tétele
 Bevezető feldatok 1. Szövegértés és algoritmikus gondolkodás Kátai Zoltán https://people.inf.elte.hu/szlavi/infodidact15/manuscripts/kz.pdf Elágazás és összegzés tétele Táblázatkezelési feladatok Feladatok
Bevezető feldatok 1. Szövegértés és algoritmikus gondolkodás Kátai Zoltán https://people.inf.elte.hu/szlavi/infodidact15/manuscripts/kz.pdf Elágazás és összegzés tétele Táblázatkezelési feladatok Feladatok
Adatelemzés SAS Enterprise Guide használatával. Soltész Gábor solteszgabee[at]gmail.com
![Adatelemzés SAS Enterprise Guide használatával. Soltész Gábor solteszgabee[at]gmail.com Adatelemzés SAS Enterprise Guide használatával. Soltész Gábor solteszgabee[at]gmail.com](/thumbs/62/48167704.jpg) Adatelemzés SAS Enterprise Guide használatával Soltész Gábor solteszgabee[at]gmail.com Tartalom SAS Enterprise Guide bemutatása Kezelőfelület Adatbeolvasás Szűrés, rendezés Új változó létrehozása Elemzések
Adatelemzés SAS Enterprise Guide használatával Soltész Gábor solteszgabee[at]gmail.com Tartalom SAS Enterprise Guide bemutatása Kezelőfelület Adatbeolvasás Szűrés, rendezés Új változó létrehozása Elemzések
Egészrészes feladatok
 Kitűzött feladatok Egészrészes feladatok Győry Ákos Miskolc, Földes Ferenc Gimnázium 1. feladat. Oldjuk meg a valós számok halmazán a { } 3x 1 x+1 7 egyenletet!. feladat. Bizonyítsuk be, hogy tetszőleges
Kitűzött feladatok Egészrészes feladatok Győry Ákos Miskolc, Földes Ferenc Gimnázium 1. feladat. Oldjuk meg a valós számok halmazán a { } 3x 1 x+1 7 egyenletet!. feladat. Bizonyítsuk be, hogy tetszőleges
A fűrészmozgás kinetikai vizsgálata
 A fűrészmozgás kinetikai vizsgálata Az alábbi dolgozat az 1988 - ban Sopronban, a kandidátusi fokozat elnyerése céljából írt értekezésem alapján készült, melynek címe: Balesetvédelmi és környezetkímélő
A fűrészmozgás kinetikai vizsgálata Az alábbi dolgozat az 1988 - ban Sopronban, a kandidátusi fokozat elnyerése céljából írt értekezésem alapján készült, melynek címe: Balesetvédelmi és környezetkímélő
Ellenőrző kérdések. 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t
 Ellenőrző kérdések 2. Kis dolgozat kérdései 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t 37. Ha t szintű indexet használunk,
Ellenőrző kérdések 2. Kis dolgozat kérdései 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t 37. Ha t szintű indexet használunk,
HÁZI FELADAT PROGRAMOZÁS I. évf. Fizikus BSc. 2009/2010. I. félév
 1. feladat (nehézsége:*****). Készíts C programot, mely a felhasználó által megadott függvényt integrálja (numerikusan). Gondosan tervezd meg az adatstruktúrát! Tervezz egy megfelelő bemeneti nyelvet.
1. feladat (nehézsége:*****). Készíts C programot, mely a felhasználó által megadott függvényt integrálja (numerikusan). Gondosan tervezd meg az adatstruktúrát! Tervezz egy megfelelő bemeneti nyelvet.
Programozás I. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar szeptember 10.
 Programozás I. 1. előadás Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. szeptember 10. Sergyán (OE NIK) Programozás I. 2012. szeptember 10. 1 /
Programozás I. 1. előadás Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. szeptember 10. Sergyán (OE NIK) Programozás I. 2012. szeptember 10. 1 /
Információk. Ismétlés II. Ismétlés. Ismétlés III. A PROGRAMOZÁS ALAPJAI 2. Készítette: Vénné Meskó Katalin. Algoritmus. Algoritmus ábrázolása
 1 Információk 2 A PROGRAMOZÁS ALAPJAI 2. Készítette: Vénné Meskó Katalin Elérhetőség mesko.katalin@tfk.kefo.hu Fogadóóra: szerda 9:50-10:35 Számonkérés időpontok Április 25. 9 00 Május 17. 9 00 Június
1 Információk 2 A PROGRAMOZÁS ALAPJAI 2. Készítette: Vénné Meskó Katalin Elérhetőség mesko.katalin@tfk.kefo.hu Fogadóóra: szerda 9:50-10:35 Számonkérés időpontok Április 25. 9 00 Május 17. 9 00 Június
Bevezetés a programozásba I 3. gyakorlat. PLanG: Programozási tételek. Programozási tételek Algoritmusok
 Pázmány Péter Katolikus Egyetem Információs Technológiai Kar Bevezetés a programozásba I 3. gyakorlat PLanG: 2011.09.27. Giachetta Roberto groberto@inf.elte.hu http://people.inf.elte.hu/groberto Algoritmusok
Pázmány Péter Katolikus Egyetem Információs Technológiai Kar Bevezetés a programozásba I 3. gyakorlat PLanG: 2011.09.27. Giachetta Roberto groberto@inf.elte.hu http://people.inf.elte.hu/groberto Algoritmusok
Demografia / Demográfiai modell
 Demográfiai modell 0. A modell rövid ismertetése A modellünkkel megvizsgáljuk, hogy hogyan függ egy populáció egyedszáma és korcsoporteloszlása a korcsoportokhoz rendelt numerikus jellemzőktől. A jellemzők
Demográfiai modell 0. A modell rövid ismertetése A modellünkkel megvizsgáljuk, hogy hogyan függ egy populáció egyedszáma és korcsoporteloszlása a korcsoportokhoz rendelt numerikus jellemzőktől. A jellemzők
A PC Connect számlázó program kezelése.
 A PC Connect számlázó program kezelése. A PC Connect számlázó program egy kifejezetten kis vállalatok számára kifejlesztett számlázó program. A számlázót az asztalon található PC Connect számlázó ikonnal
A PC Connect számlázó program kezelése. A PC Connect számlázó program egy kifejezetten kis vállalatok számára kifejlesztett számlázó program. A számlázót az asztalon található PC Connect számlázó ikonnal
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
AZ EGÉSZSÉGESEN ÉS A FOGYATÉKOSSÁG NÉLKÜL LEÉLT ÉVEK VÁRHATÓ SZÁMA MAGYARORSZÁGON
 AZ EGÉSZSÉGESEN ÉS A FOGYATÉKOSSÁG NÉLKÜL LEÉLT ÉVEK VÁRHATÓ SZÁMA MAGYARORSZÁGON DR. PAKSY ANDRÁS A lakosság egészségi állapotát jellemző morbiditási és mortalitási mutatók közül a halandósági tábla alapján
AZ EGÉSZSÉGESEN ÉS A FOGYATÉKOSSÁG NÉLKÜL LEÉLT ÉVEK VÁRHATÓ SZÁMA MAGYARORSZÁGON DR. PAKSY ANDRÁS A lakosság egészségi állapotát jellemző morbiditási és mortalitási mutatók közül a halandósági tábla alapján
Számítógépes képelemzés 7. előadás. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Programozás alapjai gyakorlat. 2. gyakorlat C alapok
 Programozás alapjai gyakorlat 2. gyakorlat C alapok 2016-2017 Bordé Sándor 2 Forráskód, fordító, futtatható állomány Először megírjuk a programunk kódját (forráskód) Egyszerű szövegszerkesztőben vagy fejlesztőkörnyezettel
Programozás alapjai gyakorlat 2. gyakorlat C alapok 2016-2017 Bordé Sándor 2 Forráskód, fordító, futtatható állomány Először megírjuk a programunk kódját (forráskód) Egyszerű szövegszerkesztőben vagy fejlesztőkörnyezettel
