Programozás. A programkészítés lépései. Program = egy feladat megoldására szolgáló, a számítógép számára értelmezhető utasítássorozat.
|
|
|
- Ödön Balla
- 9 évvel ezelőtt
- Látták:
Átírás
1 Programozás Programozás # 1 Program = egy feladat megoldására szolgáló, a számítógép számára értelmezhető utasítássorozat. ADATOK A programkészítés lépései 1. A feladat meghatározása PROGRAM EREDMÉNY A cél kitűzése A kimenetek (jelentések, kimutatások, ) elemzése A bemenetek (űrlapok, számlák, ).meghatározása 2. Programtervezés (SPECFKÁCÓ) Menüszerkezet Képernyőtervek Adatszerkezetek Algoritmusok elkészítése 3. Kódolás (PROGRAMOZÁS) Programnyelv generációk (GENERATON LANGUAGE) 1GL: gépi kód 2GL: assembly (MNEMONC) 3GL: magasszintű procedurális utasítás-orientált (BASC, PASCAL) kifejezés-orientált (C) 4GL: probléma-orientált nyelvek funkcionális (LSP) logikai (PROLOG) adatbázis-kezelő (SQL) objektum-orientált (C++, JAVA) 5GL: természetes nyelvek Fordítás: A fordítóprogram (COMPLER) a forrásprogramot gépi kódra fordítja. Utána a program futtatásához se a forráskód, se a fordító nem kell. Értelmezés: Az értelmező program (NTERPRETER) a forrásprogramot utasításonként értelmezi és hajtja végre minden futáskor, így a program végrehajtása lassabb lesz. 4. Tesztelés Forrásprogram FORDÍTÓ ÉRTELMEZŐ Gépi kódú program Végrehajtás Futtatás 5. Dokumentálás (FELASZNÁLÓ ÉS FEJLESZTŐ KÉZKÖNYV)
2 Algoritmusok Programozás # 2 Algoritmus = egy feladat megoldására szolgáló lépéssorozat Az algoritmus jellemzői 1. elvégezhető (elemi, végrehajtható lépésekből áll) 2. meghatározott (minden lépés pontosan definiált) 3. véges (véges számú lépés után véget ér) 4. meghatározott input halmazra érvényes 5. adekvát output halmazt eredményez (az adatok meghatározzák az eredményt) 6. egy feladatosztály megoldására szolgál Algoritmusok tervezése Modularitás - Önálló részfeladatokra bontás, egymástól független elkészítés, kapcsolódás, adatelrejtés Top-down tervezés - Lépésenkénti finomítás Bottom-up tervezés - Alulról felfelé építkezés kész modulokból Strukturált programozás - Egy algoritmus a következő elemekből építhető fel: Szekvencia: Egymás után végrehajtandó ek sorozata. Szelekció: Adott ek közötti választás. teráció: Adott ek többszöri ismételt végrehajtása. Feltétel nélküli ugrás: A vezérlés átadása a program egy másik pontjára. Áttekinthetőbb program, Dijkstra, Böhm és Jacopini tétele Algoritmus leíró eszközök 1. Pszeudokód Mondatszerű leírás. 2. Folyamatábra Blokkdiagram. 3. Struktogram Egyetlen téglalap tagolása, amely a teljes feladat részekre bontását jelenti. Felülről lefelé történő tervezés, strukturált programozási stílus. 4. Jackson-ábra Szerkezeti ábra. A vezérlőszerkezeteteket ábrázoló téglalapok kifejtése külön téglalapokban történik.
3 Folyamatábra Programozás # 3 Program eleje Bevitel Be: változó(k) Kivitel Ki: változó(k) Tevékenység Elágazás Címke C C Program vége
4 Programszerkezetek Programozás # 4 Szekvencia 1 2 Szelekció Egyágú szelekció Kétágú szelekció tev2 felt tev1 teráció Elöltesztelő ciklus átultesztelő ciklus Növekményes ciklus i := 1 vált := tól.. ig i < n i := i + 1
5 Programozás # 5 Példa folyamatábrára FELADAT: Két természetes szám osztási maradéka Be: a, b a N b N m := b mod a a > b m := a mod b Ki: m
6 Programozás # 6 Struktogram Program eleje Modulnév Bevitel Be: változó(k) Kivitel Ki: változó(k) Tevékenység Elágazás 1 2 Ciklus
7 Programszerkezetek Programozás # 7 Szekvencia 1 2 Szelekció Egyágú szelekció Kétágú szelekció: Többágú szelekció: _1 _2... egyébként teráció Elöltesztelő ciklus átultesztelő ciklus Növekményes ciklus vált := tól.. ig
8 Programozás # 8 Példa a struktogramra FELADAT: Két természetes szám osztási maradéka Maradék Be: a, b (a N b N) m := a mod b a > b Ki: m m := b mod a
9 Példák a programszerkezetekre Programozás # 9 PÉLDA A SZEKVENCÁRA: Egy téglalap kerületének és területének kiszámítása Változók: a: Valós a téglalap egyik oldala b: Valós a téglalap másik oldala k: Valós a téglalap kerülete T: Valós a téglalap területe Be: a, b TÉGLA k := 2 * ( a + b ) Be: a, b k := 2 * ( a + b ) T := a * b Ki: k, T T := a * b Ki: k, T PÉLDA A SZELEKCÓRA: Egy számelőjele az előjel függvény szerint Változók: x: Valós szám sign: Valós a szám előjele 1, ha x > 0 sign( x) : = 0, ha x = 0 1, ha x < 0 Be: x x = 0 sign:=0 sign := -1 x > 0 sign := 1 Ki: sign
10 PÉLDA AZ TERÁCÓRA: Két természetes szám legnagyobb közös osztója Programozás # megoldás Be: a, b x := b a < b x := a a&b mod x = 0 Ki: x x := x megoldás: Euklides algoritmusa 3. megoldás: Javított Euklides a b LNKO a b LNKO Be: a,b a b a>b Be: a,b a*b 0 a>b a:=a-b Ki: a b:=b-a a:=a mod b b:=b mod a Ki: a+b
11 Programozás # 11 PÉLDA: Egy természetes számról el kell dönteni, hogy prímszám e FOLYAMATÁBRA Be: x x Ν i := 2 Ki: nem x osztója i i := i+1 i i = x Ki: prim STRUKTOGRAM PRM Be: x x Ν i := 2 i nem osztója x-nek i := i + 1 i = x Ki: prim Ki: nem prim
Algoritmusok. Dr. Iványi Péter
 Algoritmusok Dr. Iványi Péter Egyik legrégebbi algoritmus i.e. IV század, Alexandria, Euklidész két természetes szám legnagyobb közös osztójának meghatározása Tegyük fel, hogy a és bpozitív egész számok
Algoritmusok Dr. Iványi Péter Egyik legrégebbi algoritmus i.e. IV század, Alexandria, Euklidész két természetes szám legnagyobb közös osztójának meghatározása Tegyük fel, hogy a és bpozitív egész számok
Magas szintű programozási nyelvek 1. Előadás. Bevezetés. Espák Miklós. Juhász István jegyzete alapján
 Magas szintű programozási nyelvek 1 Előadás Bevezetés Espák Miklós espakm@unideb.hu Juhász István jegyzete alapján Valós világ leírása Egyedek Modellezés Tulajdonságok Kapcsolatok Viselkedés Egyedek osztályozhatók:
Magas szintű programozási nyelvek 1 Előadás Bevezetés Espák Miklós espakm@unideb.hu Juhász István jegyzete alapján Valós világ leírása Egyedek Modellezés Tulajdonságok Kapcsolatok Viselkedés Egyedek osztályozhatók:
Adatok ábrázolása, adattípusok. Összefoglalás
 Adatok ábrázolása, adattípusok Összefoglalás Adatok ábrázolása, adattípusok Számítógépes rendszerek működés: információfeldolgozás IPO: input-process-output modell információ tárolása adatok formájában
Adatok ábrázolása, adattípusok Összefoglalás Adatok ábrázolása, adattípusok Számítógépes rendszerek működés: információfeldolgozás IPO: input-process-output modell információ tárolása adatok formájában
MATEMATIKA ÍRÁSBELI VIZSGA 2011. május 3.
 MATEMATIKA ÍRÁSBELI VIZSGA I. rész Fontos tudnivalók A megoldások sorrendje tetszőleges. A feladatok megoldásához szöveges adatok tárolására és megjelenítésére nem alkalmas zsebszámológépet és bármelyik
MATEMATIKA ÍRÁSBELI VIZSGA I. rész Fontos tudnivalók A megoldások sorrendje tetszőleges. A feladatok megoldásához szöveges adatok tárolására és megjelenítésére nem alkalmas zsebszámológépet és bármelyik
Analízis elo adások. Vajda István. 2012. szeptember 24. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem 1/8 A halmaz alapfogalom, tehát nem definiáljuk. Jelölés: A halmazokat általában nyomtatott nagybetu vel jelöljük Egy H halmazt akkor tekintünk
Vajda István Neumann János Informatika Kar Óbudai Egyetem 1/8 A halmaz alapfogalom, tehát nem definiáljuk. Jelölés: A halmazokat általában nyomtatott nagybetu vel jelöljük Egy H halmazt akkor tekintünk
Minta programterv a 1. házi feladathoz
 Programozás Minta programterv a 1. házi feladathoz Gregorics Tibor EHACODE.ELTE gt@inf.elte.hu 0.csoport 1. beadandó/0.feladat 1. 2011. december 28. Feladat Egy osztályba n diák jár, akik m darab tantárgyat
Programozás Minta programterv a 1. házi feladathoz Gregorics Tibor EHACODE.ELTE gt@inf.elte.hu 0.csoport 1. beadandó/0.feladat 1. 2011. december 28. Feladat Egy osztályba n diák jár, akik m darab tantárgyat
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
KOVÁCS BÉLA, MATEmATIkA I 10 X DETERmINÁNSOk 1 DETERmINÁNS ÉRTELmEZÉSE, TULAJdONSÁGAI A másodrendű determináns értelmezése: A harmadrendű determináns értelmezése és annak első sor szerinti kifejtése: A
Mesterséges Intelligencia. Csató Lehel. Csató Lehel. Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2006/2007
 Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2006/2007 Az Előadások Témái Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció Gráfkeresési stratégiák Szemantikus hálók
Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2006/2007 Az Előadások Témái Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció Gráfkeresési stratégiák Szemantikus hálók
Jelek tanulmányozása
 Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
Jelek tanulmányozása A gyakorlat célja A gyakorlat célja a jelekkel való műveletek megismerése, a MATLAB környezet használata a jelek vizsgálatára. Elméleti bevezető Alapműveletek jelekkel Amplitudó módosítás
Párhuzamos programozás
 Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
Párhuzamos programozás Rendezések Készítette: Györkő Péter EHA: GYPMABT.ELTE Nappali tagozat Programtervező matematikus szak Budapest, 2009 május 9. Bevezetés A számítástechnikában felmerülő problémák
Fejlesztı neve: LÉNÁRT ANETT. Tanóra / modul címe: CÉGES REKLÁMBANNER KÉSZÍTÉSE PROJEKTMÓDSZERREL
 Fejlesztı neve: LÉNÁRT ANETT Tanóra / modul címe: CÉGES REKLÁMBANNER KÉSZÍTÉSE PROJEKTMÓDSZERREL 1. Az óra tartalma A tanulási téma bemutatása; A téma és a módszer összekapcsolásának indoklása: Az órán
Fejlesztı neve: LÉNÁRT ANETT Tanóra / modul címe: CÉGES REKLÁMBANNER KÉSZÍTÉSE PROJEKTMÓDSZERREL 1. Az óra tartalma A tanulási téma bemutatása; A téma és a módszer összekapcsolásának indoklása: Az órán
Függvényvizsgálat. Végezzük el az alábbi függvények teljes függvényvizsgálatát:
 Végezzük el az alábbi függvények teljes függvényvizsgálatát: Függvényvizsgálat. f HL := 4-4. f HL := - 4 + 8. f HL := 5 + 5 4 4. f HL := 5. f HL := 6. f HL := - 9. f HL := + + 0. f HL := - 7. f HL :=.
Végezzük el az alábbi függvények teljes függvényvizsgálatát: Függvényvizsgálat. f HL := 4-4. f HL := - 4 + 8. f HL := 5 + 5 4 4. f HL := 5. f HL := 6. f HL := - 9. f HL := + + 0. f HL := - 7. f HL :=.
SZAKDOLGOZAT. Kiss Albert
 SZAKDOLGOZAT Kiss Albert Debrecen 2009 Debreceni Egyetem Informatikai Kar A VIZUÁLIS PROGRAMOZÁS TANÍTÁSA A DEBRECENI MECHWART ANDRÁS GÉPIPARI ÉS INFORMATIKAI SZAKKÖZÉPISKOLÁBAN Témavezető: Nyakóné dr.
SZAKDOLGOZAT Kiss Albert Debrecen 2009 Debreceni Egyetem Informatikai Kar A VIZUÁLIS PROGRAMOZÁS TANÍTÁSA A DEBRECENI MECHWART ANDRÁS GÉPIPARI ÉS INFORMATIKAI SZAKKÖZÉPISKOLÁBAN Témavezető: Nyakóné dr.
Analízis elo adások. Vajda István. 2012. október 3. Neumann János Informatika Kar Óbudai Egyetem. Vajda István (Óbudai Egyetem)
 Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
Vajda István Neumann János Informatika Kar Óbudai Egyetem / 40 Fogalmak A függvények értelmezése Definíció: Az (A, B ; R ) bináris relációt függvénynek nevezzük, ha bármely a A -hoz pontosan egy olyan
Mikrokontrollerek. Tihanyi Attila 2007. május 8
 Mikrokontrollerek Tihanyi Attila 2007. május 8 !!! ZH!!! Pótlási lehetőség külön egyeztetve Feladatok: 2007. május 15. Megoldási idő 45 perc! Feladatok: Első ZH is itt pótolható Munkapont számítás Munkapont
Mikrokontrollerek Tihanyi Attila 2007. május 8 !!! ZH!!! Pótlási lehetőség külön egyeztetve Feladatok: 2007. május 15. Megoldási idő 45 perc! Feladatok: Első ZH is itt pótolható Munkapont számítás Munkapont
Javítóvizsga témakörei matematika tantárgyból
 9.osztály Halmazok: - ismerje és használja a halmazok megadásának különböző módjait, a halmaz elemének fogalmát - halmazműveletek : ismerje és alkalmazza gyakorlati és matematikai feladatokban a következő
9.osztály Halmazok: - ismerje és használja a halmazok megadásának különböző módjait, a halmaz elemének fogalmát - halmazműveletek : ismerje és alkalmazza gyakorlati és matematikai feladatokban a következő
A döntő feladatai. valós számok!
 OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
OKTV 006/007. A döntő feladatai. Legyenek az x ( a + d ) x + ad bc 0 egyenlet gyökei az x és x valós számok! Bizonyítsa be, hogy ekkor az y ( a + d + abc + bcd ) y + ( ad bc) 0 egyenlet gyökei az y x és
Algoritmusok. Hogyan csináljam?
 Algoritmusok Hogyan csináljam? 1 Az algoritmus fogalma Algoritmusnak olyan pontos előírást nevezünk, amely megmondja, hogy bizonyos feladat megoldásakor milyen műveleteket milyen meghatározott sorrendben
Algoritmusok Hogyan csináljam? 1 Az algoritmus fogalma Algoritmusnak olyan pontos előírást nevezünk, amely megmondja, hogy bizonyos feladat megoldásakor milyen műveleteket milyen meghatározott sorrendben
Vektoros elemzés végrehajtása QGIS GRASS moduljával 1.7 dr. Siki Zoltán
 Vektoros elemzés végrehajtása QGIS GRASS moduljával 1.7 dr. Siki Zoltán Egy mintapéldán keresztül mutatjuk be a GRASS vektoros elemzési műveleteit. Az elemzési mintafeladat során gumipitypang termesztésére
Vektoros elemzés végrehajtása QGIS GRASS moduljával 1.7 dr. Siki Zoltán Egy mintapéldán keresztül mutatjuk be a GRASS vektoros elemzési műveleteit. Az elemzési mintafeladat során gumipitypang termesztésére
Feladatok megoldásokkal a negyedik gyakorlathoz (Függvényvizsgálat) f(x) = 2x 2 x 4. 2x 2 x 4 = 0, x 2 (2 x 2 ) = 0.
 Feladatok megoldásokkal a negyedik gyakorlathoz (Függvényvizsgálat). Feladat. Végezzük el az f(x) = x x 4 ) Értelmezési tartomány: x R. ) A zérushelyet az f(x) = 0 egyenlet megoldásával kapjuk: amiből
Feladatok megoldásokkal a negyedik gyakorlathoz (Függvényvizsgálat). Feladat. Végezzük el az f(x) = x x 4 ) Értelmezési tartomány: x R. ) A zérushelyet az f(x) = 0 egyenlet megoldásával kapjuk: amiből
Adatstruktúrák Algoritmusok Objektumok
 Adatstruktúrák Algoritmusok Objektumok A számítógépes problémamegoldás modellezésének módszerei. Programozási elvek és módszerek: imperatív, strukturált, moduláris, objektumorientált programozás. Programozási
Adatstruktúrák Algoritmusok Objektumok A számítógépes problémamegoldás modellezésének módszerei. Programozási elvek és módszerek: imperatív, strukturált, moduláris, objektumorientált programozás. Programozási
Fordítóprogramok Készítette: Nagy Krisztián
 Fordítóprogramok Készítette: Nagy Krisztián Reguláris kifejezések (FLEX) Alapelemek kiválasztása az x karakter. tetszőleges karakter (kivéve újsor) [xyz] karakterhalmaz; vagy egy x, vagy egy y vagy egy
Fordítóprogramok Készítette: Nagy Krisztián Reguláris kifejezések (FLEX) Alapelemek kiválasztása az x karakter. tetszőleges karakter (kivéve újsor) [xyz] karakterhalmaz; vagy egy x, vagy egy y vagy egy
A készülék használata elõtt kérjük olvassa el figyelmesen a használati utasítást.
 7LC048A 7LC048A E B D C C DD E E g e P 112 D 0 e B A B B A e D B26 B B E B D C C DD E E g e P 112 D 0 e B A B B A e D B26 B B K H K K H K A B P C D E 123 456 789 *0# g B A P D C E : 0 9* # # A B P C
7LC048A 7LC048A E B D C C DD E E g e P 112 D 0 e B A B B A e D B26 B B E B D C C DD E E g e P 112 D 0 e B A B B A e D B26 B B K H K K H K A B P C D E 123 456 789 *0# g B A P D C E : 0 9* # # A B P C
Programozás alapjai Bevezetés
 Programozás alapjai Bevezetés Miskolci Egyetem Általános Informatikai Tanszék Programozás alapjai Bevezetés SWF1 / 1 Tartalom A gépi kódú programozás és hátrányai Amagasszintÿ programozási nyelv fogalma
Programozás alapjai Bevezetés Miskolci Egyetem Általános Informatikai Tanszék Programozás alapjai Bevezetés SWF1 / 1 Tartalom A gépi kódú programozás és hátrányai Amagasszintÿ programozási nyelv fogalma
Lineáris algebra gyakorlat
 Lineáris algebra gyakorlat 3 gyakorlat Gyakorlatvezet : Bogya Norbert 2012 február 27 Bogya Norbert Lineáris algebra gyakorlat (3 gyakorlat) Tartalom Egyenletrendszerek Cramer-szabály 1 Egyenletrendszerek
Lineáris algebra gyakorlat 3 gyakorlat Gyakorlatvezet : Bogya Norbert 2012 február 27 Bogya Norbert Lineáris algebra gyakorlat (3 gyakorlat) Tartalom Egyenletrendszerek Cramer-szabály 1 Egyenletrendszerek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria
 005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
005-05 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Trigonometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett
A Hozzárendelési feladat megoldása Magyar-módszerrel
 A Hozzárendelési feladat megoldása Magyar-módszerrel Virtuális vállalat 2013-2014/1. félév 3. gyakorlat Dr. Kulcsár Gyula A Hozzárendelési feladat Adott meghatározott számú gép és ugyanannyi független
A Hozzárendelési feladat megoldása Magyar-módszerrel Virtuális vállalat 2013-2014/1. félév 3. gyakorlat Dr. Kulcsár Gyula A Hozzárendelési feladat Adott meghatározott számú gép és ugyanannyi független
A SZÁMFOGALOM KIALAKÍTÁSA
 A SZÁMFOGALOM KIALAKÍTÁSA TERMÉSZETES SZÁMOK ÉRTELMEZÉSE 1-5. OSZTÁLY Számok értelmezése 0-tól 10-ig: Véges halmazok számosságaként Mérőszámként Sorszámként Jelzőszámként A számok fogalmának kiterjesztése
A SZÁMFOGALOM KIALAKÍTÁSA TERMÉSZETES SZÁMOK ÉRTELMEZÉSE 1-5. OSZTÁLY Számok értelmezése 0-tól 10-ig: Véges halmazok számosságaként Mérőszámként Sorszámként Jelzőszámként A számok fogalmának kiterjesztése
Széchenyi István Szakképző Iskola
 A SZAKKÖZÉPISKOLAI SZAKMACSOPORTOS ALAPOZÓ OKTATÁS EMELT SZINTŰ ISKOLAI PROGRAMJA 11-12. évolyam Érvényes a 2003-2004-es tanévtől felmenő rendszerben Átdolgozva, utolsó módosítás: 2004. április 26. Az
A SZAKKÖZÉPISKOLAI SZAKMACSOPORTOS ALAPOZÓ OKTATÁS EMELT SZINTŰ ISKOLAI PROGRAMJA 11-12. évolyam Érvényes a 2003-2004-es tanévtől felmenő rendszerben Átdolgozva, utolsó módosítás: 2004. április 26. Az
Dr. Schuster György. 2014. február 21. Real-time operációs rendszerek RTOS
 Real-time operációs rendszerek RTOS 2014. február 21. Az ütemező (Scheduler) Az operációs rendszer azon része (kódszelete), mely valamilyen konkurens hozzáférés-elosztási problémát próbál implementálni.
Real-time operációs rendszerek RTOS 2014. február 21. Az ütemező (Scheduler) Az operációs rendszer azon része (kódszelete), mely valamilyen konkurens hozzáférés-elosztási problémát próbál implementálni.
2011. március 9. Dr. Vincze Szilvia
 . márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
. márius 9. Dr. Vinze Szilvia Tartalomjegyzék.) Elemi bázistranszformáió.) Elemi bázistranszformáió alkalmazásai.) Lineáris függőség/függetlenség meghatározása.) Kompatibilitás vizsgálata.) Mátri/vektorrendszer
Vektorok összeadása, kivonása, szorzás számmal, koordináták, lineáris függetlenség
 Vektoralgebra Vektorok összeadása, kivonása, szorzás számmal, koordináták, lineáris függetlenség Feladatok: 1) A koordinátarendszerben úgy helyezzük el az egységkockát, hogy az origó az egyik csúcsba essék,
Vektoralgebra Vektorok összeadása, kivonása, szorzás számmal, koordináták, lineáris függetlenség Feladatok: 1) A koordinátarendszerben úgy helyezzük el az egységkockát, hogy az origó az egyik csúcsba essék,
Digitális technika (VIMIAA01) Laboratórium 1
 BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika (VIMIAA01) Laboratórium 1 Fehér Béla Raikovich Tamás,
BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM VILLAMOSMÉRNÖKI ÉS INFORMATIKAI KAR MÉRÉSTECHNIKA ÉS INFORMÁCIÓS RENDSZEREK TANSZÉK Digitális technika (VIMIAA01) Laboratórium 1 Fehér Béla Raikovich Tamás,
A tételek. Szóbeli tételsor. Minden hallgató egy A és egy B tételt húz.
 Szóbeli tételsor Minden hallgató egy A és egy B tételt húz. A tételek 1. A pénzügyi beszámolás egységesítésének indokai. A globális számviteli rendszerek azonosítása és konvergenciája. Az IFRS-ek és IFRIC-ek
Szóbeli tételsor Minden hallgató egy A és egy B tételt húz. A tételek 1. A pénzügyi beszámolás egységesítésének indokai. A globális számviteli rendszerek azonosítása és konvergenciája. Az IFRS-ek és IFRIC-ek
A skatulya-elv alkalmazásai
 1 A skatulya-elv alkalmazásai Számelmélet 1. Az első 4n darab pozitív egész számot beosztjuk n számú halmazba. Igazoljuk, hogy mindig lesz három olyan szám, amelyek ugyanabban a halmazban vannak és valamely
1 A skatulya-elv alkalmazásai Számelmélet 1. Az első 4n darab pozitív egész számot beosztjuk n számú halmazba. Igazoljuk, hogy mindig lesz három olyan szám, amelyek ugyanabban a halmazban vannak és valamely
Diszkrét matematika I. gyakorlat
 Diszkrét matematika I. gyakorlat 1. Gyakorlat Bogya Norbert Bolyai Intézet 2012. szeptember 4-5. Bogya Norbert (Bolyai Intézet) Diszkrét matematika I. gyakorlat 2012. szeptember 4-5. 1 / 21 Információk
Diszkrét matematika I. gyakorlat 1. Gyakorlat Bogya Norbert Bolyai Intézet 2012. szeptember 4-5. Bogya Norbert (Bolyai Intézet) Diszkrét matematika I. gyakorlat 2012. szeptember 4-5. 1 / 21 Információk
[GVMGS11MNC] Gazdaságstatisztika
![[GVMGS11MNC] Gazdaságstatisztika [GVMGS11MNC] Gazdaságstatisztika](/thumbs/40/21500887.jpg) [GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
[GVMGS11MNC] Gazdaságstatisztika 4 előadás Főátlagok összehasonlítása http://uni-obudahu/users/koczyl/gazdasagstatisztikahtm Kóczy Á László KGK-VMI Viszonyszámok (emlékeztető) Jelenség színvonalának vizsgálata
Junior Szoftvertesztelő mérnök
 Kutatási-fejlesztési területen tevékenykedő nemzetközi cég számára keresek Junior Szoftvertesztelő mérnök munkatársat, budapesti vagy veszprém megyei munkavégzésre. Szoftvertesztek tervezése Automatizált
Kutatási-fejlesztési területen tevékenykedő nemzetközi cég számára keresek Junior Szoftvertesztelő mérnök munkatársat, budapesti vagy veszprém megyei munkavégzésre. Szoftvertesztek tervezése Automatizált
Alkalmazott modul: Programozás 1. fejezet. Szoftverfejlesztés, programozási paradigmák. Giachetta Roberto
 Eötvös Loránd Tudományegyetem Informatikai Kar Alkalmazott modul: Programozás 1. fejezet Szoftverfejlesztés, programozási paradigmák Giachetta Roberto A jegyzet az ELTE Informatikai Karának 2015. évi Jegyzetpályázatának
Eötvös Loránd Tudományegyetem Informatikai Kar Alkalmazott modul: Programozás 1. fejezet Szoftverfejlesztés, programozási paradigmák Giachetta Roberto A jegyzet az ELTE Informatikai Karának 2015. évi Jegyzetpályázatának
Laborgyakorlat Logikai áramkörök számítógéppel segített tervezése (CAD)
 Laborgyakorlat Logikai áramkörök számítógéppel segített tervezése (CAD) Kombinációs LABOR feladatok Laborfeladat: egyszerű logikai kapuk vizsgálata Logikai műveletek Tervezz egy egyszerű logikai kapukat
Laborgyakorlat Logikai áramkörök számítógéppel segített tervezése (CAD) Kombinációs LABOR feladatok Laborfeladat: egyszerű logikai kapuk vizsgálata Logikai műveletek Tervezz egy egyszerű logikai kapukat
Programozás elmélet tananyag
 2016/04/01 01:25 1/41 Programozás elmélet tananyag < Programozás elmélet Programozás elmélet tananyag Szerző: Sallai András Copyright Sallai András, 2011, 2013, 2014 Licenc: GNU Free Documentation License
2016/04/01 01:25 1/41 Programozás elmélet tananyag < Programozás elmélet Programozás elmélet tananyag Szerző: Sallai András Copyright Sallai András, 2011, 2013, 2014 Licenc: GNU Free Documentation License
4. Programozási nyelvek osztályozása. Amatőr és professzionális
 4. Programozási nyelvek osztályozása. Amatőr és professzionális programozási nyelvek. Számítási modellek (Neumann-elvű, automataelvű, funkcionális, logikai). Programozási nyelvekkel kapcsolatos fogalmak
4. Programozási nyelvek osztályozása. Amatőr és professzionális programozási nyelvek. Számítási modellek (Neumann-elvű, automataelvű, funkcionális, logikai). Programozási nyelvekkel kapcsolatos fogalmak
Minőségbiztosítás a Méliusz Könyvtárban. 2016. május 9. Dr. Csontosné Skara Ilona skara.ilona@meliusz.hu
 Minőségbiztosítás a Méliusz Könyvtárban 2016. május 9. Dr. Csontosné Skara Ilona skara.ilona@meliusz.hu Előzmények 12/2010. (III.11.) OKM rendelet : Minősített Könyvtári cím és a Könyvtári Minőségi Díj
Minőségbiztosítás a Méliusz Könyvtárban 2016. május 9. Dr. Csontosné Skara Ilona skara.ilona@meliusz.hu Előzmények 12/2010. (III.11.) OKM rendelet : Minősített Könyvtári cím és a Könyvtári Minőségi Díj
Tájékoztató az önkéntes nyugdíjpénztárak számára a 2012-től érvényes felügyeleti adatszolgáltatási változásokról
 Tájékoztató az önkéntes nyugdíjpénztárak számára a 2012-től érvényes felügyeleti adatszolgáltatási változásokról Szeles Angelika Monitoring szakreferens Adatszolgáltatási és monitoring főosztály Budapest,
Tájékoztató az önkéntes nyugdíjpénztárak számára a 2012-től érvényes felügyeleti adatszolgáltatási változásokról Szeles Angelika Monitoring szakreferens Adatszolgáltatási és monitoring főosztály Budapest,
Az informatika oktatás téveszméi
 Az informatika oktatás Az informatika definíciója Definíció-1: az informatika az információ keletkezésével, továbbításával, tárolásával, feldolgozásával foglalkozó tudomány. Definíció-2: informatika =
Az informatika oktatás Az informatika definíciója Definíció-1: az informatika az információ keletkezésével, továbbításával, tárolásával, feldolgozásával foglalkozó tudomány. Definíció-2: informatika =
Koordináta - geometria I.
 Koordináta - geometria I. DEFINÍCIÓ: (Helyvektor) A derékszögű koordináta - rendszerben a pont helyvektora az origóból a pontba mutató vektor. TÉTEL: Ha i az (1; 0) és j a (0; 1) pont helyvektora, akkor
Koordináta - geometria I. DEFINÍCIÓ: (Helyvektor) A derékszögű koordináta - rendszerben a pont helyvektora az origóból a pontba mutató vektor. TÉTEL: Ha i az (1; 0) és j a (0; 1) pont helyvektora, akkor
Tanácsok egyszerű programok készítéséhez
 Tanácsok egyszerű programok készítéséhez Egyszerű programon azt a konzolos (a felhasználóval egy konzol-ablakon keresztül kommunikáló) alkalmazást értjük, amely utasításai egyetlen forrásállományban, egy
Tanácsok egyszerű programok készítéséhez Egyszerű programon azt a konzolos (a felhasználóval egy konzol-ablakon keresztül kommunikáló) alkalmazást értjük, amely utasításai egyetlen forrásállományban, egy
MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla
 MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla Jelölje Z az egész számok halmazát, N a pozitív egészek halmazát, N 0 a nem negatív egészek halmazát, Q a racionális
MBLK12: Relációk és műveletek (levelező) (előadásvázlat) Maróti Miklós, Kátai-Urbán Kamilla Jelölje Z az egész számok halmazát, N a pozitív egészek halmazát, N 0 a nem negatív egészek halmazát, Q a racionális
Információs technológiák 4. Ea: A lélek. A csak szidható kézzelfoghatatlan
 Információs technológiák 4. Ea: A lélek A csak szidható kézzelfoghatatlan 226/1 B ITv: MAN 2015.09.08 Témakörök Szoftver alapok Operációs rendszerek Felhasználói programok Segédprogramok Programfejlesztő
Információs technológiák 4. Ea: A lélek A csak szidható kézzelfoghatatlan 226/1 B ITv: MAN 2015.09.08 Témakörök Szoftver alapok Operációs rendszerek Felhasználói programok Segédprogramok Programfejlesztő
Érettségi feladatok Algoritmusok egydimenziós tömbökkel (vektorokkal) 1/6. Alapműveletek
 Érettségi feladatok Algoritmusok egydimenziós tömbökkel (vektorokkal) 1/6 A tömbök deklarálásakor Pascal és C/C++ nyelvekben minden esetben meg kell adni az indexelést (Pascal) vagy az elemszámot (C/C++).
Érettségi feladatok Algoritmusok egydimenziós tömbökkel (vektorokkal) 1/6 A tömbök deklarálásakor Pascal és C/C++ nyelvekben minden esetben meg kell adni az indexelést (Pascal) vagy az elemszámot (C/C++).
A FOGLAKOZÁS ADATAI: SZERZŐ. Vindics Dóra A FOGLALKOZÁS CÍME. Zenélő robotok
 A FOGLAKOZÁS ADATAI: SZERZŐ Vindics Dóra A FOGLALKOZÁS CÍME Zenélő robotok A FOGLALKOZÁS RÖVID LEÍRÁSA A foglalkozás kapcsolatot teremt a zene és a programozás között. Egy dallamot ABC-s hangokkal leírunk,
A FOGLAKOZÁS ADATAI: SZERZŐ Vindics Dóra A FOGLALKOZÁS CÍME Zenélő robotok A FOGLALKOZÁS RÖVID LEÍRÁSA A foglalkozás kapcsolatot teremt a zene és a programozás között. Egy dallamot ABC-s hangokkal leírunk,
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
KOVÁCS BÉLA, MATEmATIkA I 15 XV DIFFERENCIÁLSZÁmÍTÁS 1 DERIVÁLT, deriválás Az f függvény deriváltján az (1) határértéket értjük (feltéve, hogy az létezik és véges) Az függvény deriváltjának jelölései:,,,,,
Beszámoló: a kompetenciamérés eredményének javítását célzó intézkedési tervben foglaltak megvalósításáról. Őcsény, 2015. november 20.
 Őcsényi Perczel Mór Általános Iskola székhelye: 7143 Őcsény, Perczel Mór utca 1. Tel: 74/496-782 e-mail: amk.ocseny@altisk-ocseny.sulinet.hu Ikt.sz.: /2015. OM: 036345 Ügyintéző: Ősze Józsefné Ügyintézés
Őcsényi Perczel Mór Általános Iskola székhelye: 7143 Őcsény, Perczel Mór utca 1. Tel: 74/496-782 e-mail: amk.ocseny@altisk-ocseny.sulinet.hu Ikt.sz.: /2015. OM: 036345 Ügyintéző: Ősze Józsefné Ügyintézés
Számrendszerek közötti átváltások
 Számrendszerek közötti átváltások 10-es számrendszerből tetszőleges számrendszerbe Legyen az átváltani kívánt szám: 723, 10-es számrendszerben. Ha 10-esből bármilyen számrendszerbe kívánunk átváltani,
Számrendszerek közötti átváltások 10-es számrendszerből tetszőleges számrendszerbe Legyen az átváltani kívánt szám: 723, 10-es számrendszerben. Ha 10-esből bármilyen számrendszerbe kívánunk átváltani,
BOLYAI MATEMATIKA CSAPATVERSENY FŐVÁROSI DÖNTŐ SZÓBELI (2005. NOVEMBER 26.) 5. osztály
 5. osztály Írd be az ábrán látható hat üres körbe a 10, 30, 40, 60, 70 és 90 számokat úgy, hogy a háromszög mindhárom oldala mentén a számok összege 200 legyen! 50 20 80 Egy dobozban háromféle színű: piros,
5. osztály Írd be az ábrán látható hat üres körbe a 10, 30, 40, 60, 70 és 90 számokat úgy, hogy a háromszög mindhárom oldala mentén a számok összege 200 legyen! 50 20 80 Egy dobozban háromféle színű: piros,
IKT FEJLESZTŐ MŰHELY KONTAKTUS Dél-dunántúli Regionális Közoktatási Hálózat Koordinációs Központ
 Óratervezet: Kémia 7. osztály Témakör: Kémiai kötések Óra anyaga: Molekulák építése, térbeli modellezése Eszközök:, aktív tábla, projektor, számítógépek A tanóra részei Tanári tevékenység Tanulói tevékenység
Óratervezet: Kémia 7. osztály Témakör: Kémiai kötések Óra anyaga: Molekulák építése, térbeli modellezése Eszközök:, aktív tábla, projektor, számítógépek A tanóra részei Tanári tevékenység Tanulói tevékenység
Spiel der Türme TORNYOK JÁTÉKA
 Spiel der Türme TORNYOK JÁTÉKA A történet a középkori Tornyok Városával kezdődik. A négy hataloméhes nemesi család mindegyike arra törekszik, hogy megszerezzék a befolyást a legerősebb torony vagy még
Spiel der Türme TORNYOK JÁTÉKA A történet a középkori Tornyok Városával kezdődik. A négy hataloméhes nemesi család mindegyike arra törekszik, hogy megszerezzék a befolyást a legerősebb torony vagy még
V. Kétszemélyes játékok
 Teljes információjú, véges, zéró összegű kétszemélyes játékok V. Kétszemélyes játékok Két játékos lép felváltva adott szabályok szerint. Mindkét játékos ismeri a maga és az ellenfele összes választási
Teljes információjú, véges, zéró összegű kétszemélyes játékok V. Kétszemélyes játékok Két játékos lép felváltva adott szabályok szerint. Mindkét játékos ismeri a maga és az ellenfele összes választási
Kerékpárlabda kvalifikációs szabályzat
 Kerékpárlabda kvalifikációs szabályzat Érvényesség kezdete: Junior kategória 2016 június 1 Felnőtt kategória 2016 január 1 Tartalom I. Célja... 3 II. Szabályozás... 3 1) A versenyek meghatározása... 3
Kerékpárlabda kvalifikációs szabályzat Érvényesség kezdete: Junior kategória 2016 június 1 Felnőtt kategória 2016 január 1 Tartalom I. Célja... 3 II. Szabályozás... 3 1) A versenyek meghatározása... 3
Algebra es sz amelm elet 3 el oad as Rel aci ok Waldhauser Tam as 2014 oszi f el ev
 Algebra és számelmélet 3 előadás Relációk Waldhauser Tamás 2014 őszi félév Relációk reláció lat. 1. kapcsolat, viszony; összefüggés vmivel 2. viszonylat, vonatkozás reláció lat. 3. mat halmazok elemei
Algebra és számelmélet 3 előadás Relációk Waldhauser Tamás 2014 őszi félév Relációk reláció lat. 1. kapcsolat, viszony; összefüggés vmivel 2. viszonylat, vonatkozás reláció lat. 3. mat halmazok elemei
Felvételi előkészítő tájékoztató 2012.
 Felvételi előkészítő tájékoztató 2012. Néhány gondolat a központi felvételiről! A központi Matematika felvételi az elmúlt években sok 8. osztályos diák számára igen csak komoly megmérettetésnek bizonyult.
Felvételi előkészítő tájékoztató 2012. Néhány gondolat a központi felvételiről! A központi Matematika felvételi az elmúlt években sok 8. osztályos diák számára igen csak komoly megmérettetésnek bizonyult.
Programozás I. - 9. gyakorlat
 Programozás I. - 9. gyakorlat Mutatók, dinamikus memóriakezelés Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 9, 2009 1 tar@dcs.vein.hu
Programozás I. - 9. gyakorlat Mutatók, dinamikus memóriakezelés Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Rendszer- és Számítástudományi Tanszék Utolsó frissítés: November 9, 2009 1 tar@dcs.vein.hu
EPER E-KATA integráció
 EPER E-KATA integráció 1. Összhang a Hivatalban A hivatalban használt szoftverek összekapcsolása, integrálása révén az egyes osztályok, nyilvántartások között egyezőség jön létre. Mit is jelent az integráció?
EPER E-KATA integráció 1. Összhang a Hivatalban A hivatalban használt szoftverek összekapcsolása, integrálása révén az egyes osztályok, nyilvántartások között egyezőség jön létre. Mit is jelent az integráció?
MATEMATIKA ÍRÁSBELI VIZSGA 2012. május 8.
 MATEMATIKA ÍRÁSBELI VIZSGA 2012. május 8. I. rész Fontos tudnivalók A feladatok megoldásához szöveges adatok tárolására és megjelenítésére nem alkalmas zsebszámológépet és bármelyik négyjegyű függvénytáblázatot
MATEMATIKA ÍRÁSBELI VIZSGA 2012. május 8. I. rész Fontos tudnivalók A feladatok megoldásához szöveges adatok tárolására és megjelenítésére nem alkalmas zsebszámológépet és bármelyik négyjegyű függvénytáblázatot
... ahol l 0. Minden tranzakcióhoz létezik. = f(σ i. A sorozat nem bővíthető. Ha véges, akkor az utolsó konfigurációnak nincs rákövetkezője.
 Szekvenciális tranzakciós s diagram A program vezérlési szerkezete egy címkékkel ellátott irányított gráf. Tranzakciós diagram T = ( L, T, s, t ) Gráf csúcsok a program állapotai entry kitüntetett csúcs:
Szekvenciális tranzakciós s diagram A program vezérlési szerkezete egy címkékkel ellátott irányított gráf. Tranzakciós diagram T = ( L, T, s, t ) Gráf csúcsok a program állapotai entry kitüntetett csúcs:
1. Írja fel prímszámok szorzataként a 420-at! 2. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen!
 1. Írja fel prímszámok szorzataként a 40-at! 40 =. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen! A részek: 3. Egy sejttenyészetben naponta kétszereződik meg a sejtek száma.
1. Írja fel prímszámok szorzataként a 40-at! 40 =. Bontsa fel a 36 000-et két részre úgy, hogy a részek aránya 5 : 4 legyen! A részek: 3. Egy sejttenyészetben naponta kétszereződik meg a sejtek száma.
Játékok (domináns stratégia, alkalmazása. 2016.03.30.
 Játékok (domináns stratégia, Nash-egyensúly). A Nashegyensúly koncepciójának alkalmazása. 2016.03.30. Játékelmélet és közgazdaságtan 1914: Zermelo (sakk) 1944. Neumann-Morgenstern: Game Theory and Economic
Játékok (domináns stratégia, Nash-egyensúly). A Nashegyensúly koncepciójának alkalmazása. 2016.03.30. Játékelmélet és közgazdaságtan 1914: Zermelo (sakk) 1944. Neumann-Morgenstern: Game Theory and Economic
Java programozási nyelv
 Java programozási nyelv 2. rész Vezérlő szerkezetek Nyugat-Magyarországi Egyetem Faipari Mérnöki Kar Informatikai Intézet Soós Sándor 2005. szeptember A Java programozási nyelv Soós Sándor 1/23 Tartalomjegyzék
Java programozási nyelv 2. rész Vezérlő szerkezetek Nyugat-Magyarországi Egyetem Faipari Mérnöki Kar Informatikai Intézet Soós Sándor 2005. szeptember A Java programozási nyelv Soós Sándor 1/23 Tartalomjegyzék
SW process Feladatok. SW process Feladatok
 SW process Feladatok 2009.06.11 3. Feladat Adja meg a szoftver fejlesztési folyamat ICOM modelljét! 2009.06.11 6. Feladat Nevezze meg sorrendben a CMM (Capability Maturity Model) szintjeit! 2009.06.18
SW process Feladatok 2009.06.11 3. Feladat Adja meg a szoftver fejlesztési folyamat ICOM modelljét! 2009.06.11 6. Feladat Nevezze meg sorrendben a CMM (Capability Maturity Model) szintjeit! 2009.06.18
Azonosító jel: Matematika emelt szint
 I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
I. 1. Hatjegyű pozitív egész számokat képezünk úgy, hogy a képzett számban szereplő számjegy annyiszor fordul elő, amekkora a számjegy. Hány ilyen hatjegyű szám képezhető? 11 pont írásbeli vizsga 1012
A FOGLAKOZÁS ADATAI: SZERZŐ. Kiss Róbert A FOGLALKOZÁS CÍME. Rajzolás robotképernyőn A FOGLALKOZÁS RÖVID
 A FOGLAKOZÁS ADATAI: SZERZŐ Kiss Róbert A FOGLALKOZÁS CÍME Rajzolás robotképernyőn A FOGLALKOZÁS RÖVID LEÍRÁSA A LOGO MindStorms NXT/EV3 robot grafikus képernyőjét használva különböző ábrákat tudunk rajzolni.
A FOGLAKOZÁS ADATAI: SZERZŐ Kiss Róbert A FOGLALKOZÁS CÍME Rajzolás robotképernyőn A FOGLALKOZÁS RÖVID LEÍRÁSA A LOGO MindStorms NXT/EV3 robot grafikus képernyőjét használva különböző ábrákat tudunk rajzolni.
Műszaki ábrázolás II. 3. Házi feladat. Hegesztett szerkezet
 Hegesztett szerkezet Feladat: Hegesztett szerkezet rajzának elkészítése. Szükséges eszközök: A3-as fehér rajzlap az összeállítási és alkatrészrajzokhoz szerkesztési táblázat az anyagminőségek és a szabványos
Hegesztett szerkezet Feladat: Hegesztett szerkezet rajzának elkészítése. Szükséges eszközök: A3-as fehér rajzlap az összeállítási és alkatrészrajzokhoz szerkesztési táblázat az anyagminőségek és a szabványos
Arany Dániel Matematikai Tanulóverseny 2011/2012-es tanév első (iskolai) forduló haladók I. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 011/01-es tanév első (iskolai) forduló haladók I. kategória Megoldások és javítási útmutató 1. Az ábrán látható ABC derékszögű háromszög
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 011/01-es tanév első (iskolai) forduló haladók I. kategória Megoldások és javítási útmutató 1. Az ábrán látható ABC derékszögű háromszög
Vezérlőegység. Dr. Seebauer Márta. Budapesti Műszaki Főiskola Regionális Oktatási és Innovációs Központ Székesfehérvár
 Budapesti Műszaki Főiskola Regionális Oktatási és Innovációs Központ Székesfehérvár Vezérlőegység Dr. Seebauer Márta főiskolai tanár seebauer.marta@roik.bmf.hu Vezérlés A vezérlés célja az utasítás-végrehajtás
Budapesti Műszaki Főiskola Regionális Oktatási és Innovációs Központ Székesfehérvár Vezérlőegység Dr. Seebauer Márta főiskolai tanár seebauer.marta@roik.bmf.hu Vezérlés A vezérlés célja az utasítás-végrehajtás
Többfelhasználós adatbázis környezetek, tranzakciók, internetes megoldások
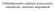 Többfelhasználós adatbázis környezetek, tranzakciók, internetes megoldások Alkalmazás modellek Egy felhasználós környezet Több felhasználós környezet adatbázis Központi adatbázis adatbázis Osztott adatbázis
Többfelhasználós adatbázis környezetek, tranzakciók, internetes megoldások Alkalmazás modellek Egy felhasználós környezet Több felhasználós környezet adatbázis Központi adatbázis adatbázis Osztott adatbázis
Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 2005. november. I. rész
 Szászné Simon Judit, 005. november Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 005. november. feladat I. rész Oldjuk meg a valós számok halmazán a x 5x
Szászné Simon Judit, 005. november Emelt szintű érettségi feladatsorok és megoldásaik Összeállította: Szászné Simon Judit; dátum: 005. november. feladat I. rész Oldjuk meg a valós számok halmazán a x 5x
MEZŐGAZDASÁGI ALAPISMERETEK ÉRETTSÉGI VIZSGA II. A VIZSGA LEÍRÁSA
 A vizsga részei MEZŐGAZDASÁGI ALAPISMERETEK ÉRETTSÉGI VIZSGA II. A VIZSGA LEÍRÁSA Középszint Emelt szint 180 perc 15 perc 240 perc 20 perc 100 pont 50 pont 100 pont 50 pont A vizsgán használható segédeszközök
A vizsga részei MEZŐGAZDASÁGI ALAPISMERETEK ÉRETTSÉGI VIZSGA II. A VIZSGA LEÍRÁSA Középszint Emelt szint 180 perc 15 perc 240 perc 20 perc 100 pont 50 pont 100 pont 50 pont A vizsgán használható segédeszközök
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN
 GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten RACIONÁLIS TÖRTFÜGGVÉNYEK INTEGRÁLJA Készítette: Gábor Szakmai felel s: Gábor Vázlat
GAZDASÁGMATEMATIKA KÖZÉPHALADÓ SZINTEN ELTE TáTK Közgazdaságtudományi Tanszék Gazdaságmatematika középhaladó szinten RACIONÁLIS TÖRTFÜGGVÉNYEK INTEGRÁLJA Készítette: Gábor Szakmai felel s: Gábor Vázlat
Egyszerű programozási tételek
 Egyszerű programozási tételek Sorozatszámítás tétele Például az X tömbben kövek súlyát tároljuk. Ha ki kellene számolni az összsúlyt, akkor az S = f(s, X(i)) helyére S = S + X(i) kell írni. Az f0 tartalmazza
Egyszerű programozási tételek Sorozatszámítás tétele Például az X tömbben kövek súlyát tároljuk. Ha ki kellene számolni az összsúlyt, akkor az S = f(s, X(i)) helyére S = S + X(i) kell írni. Az f0 tartalmazza
Közhasznúsági beszámoló
 Közhasznúsági beszámoló Hangadók Közhasznú Alapítvány 2440 Százhalombatta, Liszt Ferenc sétány 29. 2009. évről A Közhasznúsági Jelentést a Kuratórium 2010. május 31-i ülésén fogadta el. Tartalom 1. Számviteli
Közhasznúsági beszámoló Hangadók Közhasznú Alapítvány 2440 Százhalombatta, Liszt Ferenc sétány 29. 2009. évről A Közhasznúsági Jelentést a Kuratórium 2010. május 31-i ülésén fogadta el. Tartalom 1. Számviteli
tetszőleges időpillanatban értelmezhető végtelen sok időpont értéke egy véges tartományban bármilyen értéket felvehet végtelen sok érték
 Elektronika 2 tetszőleges időpillanatban értelmezhető végtelen sok időpont értéke egy véges tartományban bármilyen értéket felvehet végtelen sok érték Diszkrét időpillanatokban értelmezhető (időszakaszos)
Elektronika 2 tetszőleges időpillanatban értelmezhető végtelen sok időpont értéke egy véges tartományban bármilyen értéket felvehet végtelen sok érték Diszkrét időpillanatokban értelmezhető (időszakaszos)
Számítógép-használati szokások az általános iskolások körében
 Generációk az információs társadalomban Infokommunikációs kultúra, értékrend, biztonságkeresési stratégiák Projekt záró workshop TÁMOP-4.2.1/B-09/1/KONV-2010-0005 Program Számítógép-használati szokások
Generációk az információs társadalomban Infokommunikációs kultúra, értékrend, biztonságkeresési stratégiák Projekt záró workshop TÁMOP-4.2.1/B-09/1/KONV-2010-0005 Program Számítógép-használati szokások
BOLYAI MATEMATIKA CSAPATVERSENY ORSZÁGOS DÖNTŐ SZÓBELI (2012. NOVEMBER 24.) 3. osztály
 3. osztály Két szám összege 33. Mennyi ennek a két számnak a különbsége, ha az egyik kétszerese a másiknak? Hány olyan háromjegyű szám van, amelyben a számjegyek összege legalább 25? 4. osztály A Zimrili
3. osztály Két szám összege 33. Mennyi ennek a két számnak a különbsége, ha az egyik kétszerese a másiknak? Hány olyan háromjegyű szám van, amelyben a számjegyek összege legalább 25? 4. osztály A Zimrili
Házi dolgozat. Minta a házi dolgozat formai és tartalmi követelményeihez. Készítette: (név+osztály) Iskola: (az iskola teljes neve)
 Házi dolgozat Minta a házi dolgozat formai és tartalmi követelményeihez Készítette: (név+osztály) Iskola: (az iskola teljes neve) Dátum: (aktuális dátum) Tartalom Itt kezdődik a címbeli anyag érdemi kifejtése...
Házi dolgozat Minta a házi dolgozat formai és tartalmi követelményeihez Készítette: (név+osztály) Iskola: (az iskola teljes neve) Dátum: (aktuális dátum) Tartalom Itt kezdődik a címbeli anyag érdemi kifejtése...
Időzített rendszerek és az UPPAAL
 Időzített rendszerek és az UPPAAL Dr. Németh L. Zoltán (zlnemeth@inf.u-szeged.hu) SZTE, Informatikai Tanszékcsoport 2008/2009 I. félév 2008.11.14 MODELL 10 1 Időzített rendszerek Real Time Systems = valós
Időzített rendszerek és az UPPAAL Dr. Németh L. Zoltán (zlnemeth@inf.u-szeged.hu) SZTE, Informatikai Tanszékcsoport 2008/2009 I. félév 2008.11.14 MODELL 10 1 Időzített rendszerek Real Time Systems = valós
MINTA. Fizetendô összeg: 62 136,00 HUF. Telefonon: 06 40 / 20 99 20 ben: Interneten:
 Részszámla Számla. eredeti példány / oldal Elszámolási idôszak: 00.0. - 00.09.. Partnerszám: 000009 Fizetési határidô: 00.09.0. Vevô neve, címe: Minta út. Fizetendô összeg:, Minta út. Szerzôdéses folyószámla
Részszámla Számla. eredeti példány / oldal Elszámolási idôszak: 00.0. - 00.09.. Partnerszám: 000009 Fizetési határidô: 00.09.0. Vevô neve, címe: Minta út. Fizetendô összeg:, Minta út. Szerzôdéses folyószámla
DLookup függvény 1. (5)
 DLookup függvény 1. (5) Hatókör: Microsoft Office Access 2000, 2003, 2007 A DLookup függvénnyel megkaphatja egy adott mező értékét egy adott rekordkészletből egy tartományból (tartomány: Tábla, lekérdezés
DLookup függvény 1. (5) Hatókör: Microsoft Office Access 2000, 2003, 2007 A DLookup függvénnyel megkaphatja egy adott mező értékét egy adott rekordkészletből egy tartományból (tartomány: Tábla, lekérdezés
3. Térvezérlésű tranzisztorok
 1 3. Térvezérlésű tranzisztorok A térvezérlésű tranzisztorok (Field Effect Transistor = FET) működési elve alapjaiban eltér a bipoláris tranzisztoroktól. Az áramvezetés mértéke statikus feszültséggel befolyásolható.
1 3. Térvezérlésű tranzisztorok A térvezérlésű tranzisztorok (Field Effect Transistor = FET) működési elve alapjaiban eltér a bipoláris tranzisztoroktól. Az áramvezetés mértéke statikus feszültséggel befolyásolható.
Néprajzi Múzeum. Új hely Új épület(ek) Új elképzelések. Museum 2.0 2016.04.26
 Néprajzi Múzeum Új hely Új épület(ek) Új elképzelések A Néprajzi Múzeum nyitott kulturális tér, ahol összeér a múlt a mával, a tudomány a tanítással, ahol kultúrák és generációk találkoznak és beszélnek
Néprajzi Múzeum Új hely Új épület(ek) Új elképzelések A Néprajzi Múzeum nyitott kulturális tér, ahol összeér a múlt a mával, a tudomány a tanítással, ahol kultúrák és generációk találkoznak és beszélnek
Ha a síkot egyenes vagy görbe vonalakkal feldaraboljuk, akkor síkidomokat kapunk.
 Síkidomok Ha a síkot egyenes vagy görbe vonalakkal feldaraboljuk, akkor síkidomokat kapunk. A határoló vonalak által bezárt síkrész a síkidom területe. A síkidomok határoló vonalak szerint lehetnek szabályos
Síkidomok Ha a síkot egyenes vagy görbe vonalakkal feldaraboljuk, akkor síkidomokat kapunk. A határoló vonalak által bezárt síkrész a síkidom területe. A síkidomok határoló vonalak szerint lehetnek szabályos
Programozás alapjai C nyelv 3. gyakorlat. Előző óra összefoglalása. Karakter típus (char) Algoritmus leírása. C nyelv tulajdonságai
 Programozás alapja C yelv 3. gyakorlat Szeberéy Imre BME IIT Programozás alapja I. (C yelv, gyakorlat) BME-IIT Sz.I. 25..3.. -- Előző óra összefoglalása Algortmus leírása Sztaxs leírása
Programozás alapja C yelv 3. gyakorlat Szeberéy Imre BME IIT Programozás alapja I. (C yelv, gyakorlat) BME-IIT Sz.I. 25..3.. -- Előző óra összefoglalása Algortmus leírása Sztaxs leírása
Engedélyszám: 18211-2/2011-EAHUF Verziószám: 1. 2385-09 Rögzített fogpótlás készítése követelménymodul szóbeli vizsgafeladatai
 1. feladat Rögzített fogpótláshoz a munka sikeressége érdekében tájékoztatja új kollégáját, a jó fogszín maghatározás és a színvétel feltételeiről. Tartsa meg a tájékoztatást! a színmeghatározás feltételei
1. feladat Rögzített fogpótláshoz a munka sikeressége érdekében tájékoztatja új kollégáját, a jó fogszín maghatározás és a színvétel feltételeiről. Tartsa meg a tájékoztatást! a színmeghatározás feltételei
Számítógépes vírusok
 A vírus fogalma A számítógépes vírus olyan szoftver, mely képes önmaga megsokszorozására és terjesztésére. A vírus célja általában a számítógép rendeltetésszerű működésének megzavarása, esetleg a gép tönkretétele,
A vírus fogalma A számítógépes vírus olyan szoftver, mely képes önmaga megsokszorozására és terjesztésére. A vírus célja általában a számítógép rendeltetésszerű működésének megzavarása, esetleg a gép tönkretétele,
TANTÁRGYI ÚTMUTATÓ. Prezentáció és íráskészségfejlesztés. tanulmányokhoz
 I. évfolyam GM és PSZ szak BA TANTÁRGYI ÚTMUTATÓ Prezentáció és íráskészségfejlesztés tanulmányokhoz TÁVOKTATÁS Tanév (2014/2015) I. félév A KURZUS ALAPADATAI Tárgy megnevezése: Prezentáció és íráskészség
I. évfolyam GM és PSZ szak BA TANTÁRGYI ÚTMUTATÓ Prezentáció és íráskészségfejlesztés tanulmányokhoz TÁVOKTATÁS Tanév (2014/2015) I. félév A KURZUS ALAPADATAI Tárgy megnevezése: Prezentáció és íráskészség
Közhasznúsági jelentés 2007
 Közhasznúsági jelentés 2007 I. Számviteli beszámoló (mérleg, eredmény levezetés) II. Kimutatás a vagyon felhasználásáról III. Kimutatás a kapott támogatásokról IV. Beszámolás a közhasznú tevékenységről
Közhasznúsági jelentés 2007 I. Számviteli beszámoló (mérleg, eredmény levezetés) II. Kimutatás a vagyon felhasználásáról III. Kimutatás a kapott támogatásokról IV. Beszámolás a közhasznú tevékenységről
Ö S S Z E G E Z É S A Z A J Á N L A T O K E L B Í R Á L Á S Á R Ó L
 Ö S S Z E G E Z É S A Z A J Á N L A T O K E L B Í R Á L Á S Á R Ó L 1. Az ajánlatkérő neve és címe: Szociális és Gyermekvédelmi Főigazgatóság (székhely: 1132 Budapest, Visegrádi utca 49.) 2. A közbeszerzés
Ö S S Z E G E Z É S A Z A J Á N L A T O K E L B Í R Á L Á S Á R Ó L 1. Az ajánlatkérő neve és címe: Szociális és Gyermekvédelmi Főigazgatóság (székhely: 1132 Budapest, Visegrádi utca 49.) 2. A közbeszerzés
ÁFA felhasználói dokumentum Lezárva: 2015.11.10.
 ÁFA felhasználói dokumentum Lezárva: 2015.11.10. Griffsoft Informatikai Zrt. 6723 Szeged, Felső-Tisza part 31-34 M lph. fszt.2. Telefon: (62) 549-100 Telefax: (62) 401-417 TARTALOM 1 ÁFA... 2 1.1 HALASZTOTT
ÁFA felhasználói dokumentum Lezárva: 2015.11.10. Griffsoft Informatikai Zrt. 6723 Szeged, Felső-Tisza part 31-34 M lph. fszt.2. Telefon: (62) 549-100 Telefax: (62) 401-417 TARTALOM 1 ÁFA... 2 1.1 HALASZTOTT
Kiphard-féle szenzomotoros és pszichoszociális fejlődési táblázat
 Kiphard-féle szenzomotoros és pszichoszociális fejlődési táblázat Kondákor Ágnes kondakor.agnes@peto.hu 2016. április 26. A mérés célja Meghatározott korosztály mérésére szolgál A fejlődési táblázat, képet
Kiphard-féle szenzomotoros és pszichoszociális fejlődési táblázat Kondákor Ágnes kondakor.agnes@peto.hu 2016. április 26. A mérés célja Meghatározott korosztály mérésére szolgál A fejlődési táblázat, képet
Az aktiválódásoknak azonban itt még nincs vége, ugyanis az aktiválódások 30 évenként ismétlődnek!
 1 Mindannyiunk életében előfordulnak jelentős évek, amikor is egy-egy esemény hatására a sorsunk új irányt vesz. Bár ezen események többségének ott és akkor kevésbé tulajdonítunk jelentőséget, csak idővel,
1 Mindannyiunk életében előfordulnak jelentős évek, amikor is egy-egy esemény hatására a sorsunk új irányt vesz. Bár ezen események többségének ott és akkor kevésbé tulajdonítunk jelentőséget, csak idővel,
