Fejmozgás alapú gesztusok felismerése
|
|
|
- Magda Borbély
- 6 évvel ezelőtt
- Látták:
Átírás
1 Fejmozgás alapú gesztusok felismerése Bertók Kornél, Fazekas Attila Debreceni Egyetem Informatikai Kar Debreceni Képfeldolgozó Csoport H-4010 Debrecen, Pf.:12. Absztrakt. Jelen cikk témája egy fejmozgás alapú gesztusfelismerő rendszer, mely segítségével lehetőségünk nyílik mozdulatsorok valósidejű felismerésére, megértésére, azok rögzítésére és később adatbányászati eszközökkel történő elemzésére. Mindezek mellett a rendszernek részét képezi egy fejmozgás alapú gesztusokat tartalmazó adatbázis is, melyet az egyes gesztusok felismerése során bizonyos feltételek mentén online bővítünk, így lehetőségünk nyílik a felismerés futási idejű javítására. Jelen tanulmány egy módszert definiál a kamera képeken, mint képszekvenciákon megjelenő fejmozgás alapú gesztusok reprezentációjára, tér-, és időbeli behatárolására, gesztus-osztályok kialakítására, továbbá bevezet egy metrikát az osztályokkal történő összehasonlítására. Meg kell jegyeznünk azt is, hogy az elkészült rendszer jól illeszkedhet egy multimodális ember-gép kommunikációt leíró modellbe is, mert használata új fejezetet nyit a metakommunikációhoz tartozó csatornák vizsgálatában. Kulcsszavak: fejmozgás, gesztus felismerés, gesztus reprezentáció, gesztus adatbázis. 1 Bevezetés Az ember-számítógép interakció kutatási feladatai közé tartozik, hogy olyan új, esetlegesen alternatív kommunikációs eszközöket és módszereket fejlesszen, amelyek segítik az ember-gép kapcsolatot az ember számára minél természetesebbé, magától értetődővé tenni. A különböző eszközök és programok vezérlésére sokféle megoldás létezik. Csakhogy az eszközök és programok számának növekedésével a különböző vezérlő megoldások száma is növekszik. Tehát mindenképpen szükséges egy természetesebb, eszköz-független módot találni az irányítására. A kommunikáció egyszerűsítésével kapcsolatos ötleteket célszerű a mindennapi életünkben keresni. A szóbeliség (verbális jelek halmaza) az emberi kommunikáció legtipikusabb módja, jelentős információhordozó. Ugyanakkor gyakran lehet félreértések forrása is, mivel azzal a feltételezéssel élünk, hogy egy-egy szó azonos jelentéssel bír mindenki számára. Pedig azt, hogy egy-egy szónak az adott pillanatban milyen jelentést tulajdonítunk, aktuális szükségleteink is jelentős mértékben befolyásolják. Ezért az egyes kommunikációs szituációkat kontrollálni kell. 736
2 A verbális jelek mellett a szóbeli információk kiegészítésére, ellenőrzésére vagy éppen hangsúlyozására a nem szóbeli, úgynevezett non-verbális jelrendszert alkalmazzuk. A non-verbális jelek tipikus megnyilvánulásai a mimika, a tekintet szemkontaktus szemmozgás, az úgynevezett vokális jelek, mint hangnem, hanghordozás, hangerő, hangszín; a gesztusok, a testtartás és a távolságtartástérközszabályozás. Jelen tanulmány a gesztusok, mint non-verbális jelek felismerésére korlátozódik. Gesztusok alatt értjük a fej-, a kéz-, és a karok mozgását. A fejmozgások gyakoribb jelentései: az igenlés, a tagadás, a helytelenítés, a megszégyenülés, elszomorodás. A kéz-, és karmozgások jelentése: a hívás, elutasítás, tiltakozás, kérés, könyörgés, fenyegetés, köszöntés. A gesztusokat a partner beszédének szabályozására (magyarázás, gyorsítás-lassítás stb.) is használjuk. E mozgásoknak jelentésük van, egy részük tudatos, másik felük öntudatlan. Jelen cikk témája egy gesztusfelismerő rendszer ismertetése, mely segítségével felismerhetőek és megérthetőek a tudatos fejmozgások. Továbbá egy eszközrendszert biztosít a gesztusok rögzítésére és később adatbányászati eszközökkel történő elemzésére, valamint a már rögzített mozdulatsorok segítségével a felismerés futási idejű javítására. 1.1 Irodalmi áttekintés A meglévő gesztusfelismerő rendszerekkel kapcsolatban egy áttekintő összefoglalót ismertet a [1] tanulmány. Ebben az alfejezetben csak néhány olyan munkát foglalunk össze, melyeket az előző összefoglalón kívül alaposabban tanulmányoztunk. A fejmozgás alapú vagy általánosságban csak a mozgás alapú gesztusfelismerő eljárások két csoportba oszthatóak: modell alapú és mintaillesztéses módszerekre. A modell alapú eljárások csoportjába tartoznak a különböző rejtett Markov modellek (továbbiakban: HMM) és azok variánsai. Példának okán, Marcel és munkatársai [2] egy input-output HMM-et készítettek az úgynevezett várható értéket maximalizáló algoritmus (EM algoritmus) segítségével. A kapott modellt később arra alkalmazták, hogy a kézfej körvonalából ismerjenek fel gesztusokat. A szakirodalomban megtalálható a hagyományos HMM-ek néhány javított változata is, ezek között akadnak olyanok, melyek működését szemantikus hálók használatával tökéletesítették [3], sok hivatkozást találunk a nem-paraméteres HMM-ek [4] használatára, illetve a feltételes valószínűségi mezők (Hidden Conditional Random Field) [5] alkalmazására is találunk példát. Ezen variánsok bizonyos esetekben egyrészt csökkentik a tanítás költségét, másrészt növelik az osztályozás pontosságát. Népszerű modell alapú eljárások a véges állapotú gépek [6], valamint a dinamikus Bayes hálók [7] is. Ezek az eljárások feltételezik, hogy a fej mozgásának trajektóriája vagyis az artikuláció ismert. Ezekkel az eljárásokkal bíztató eredményeket lehet elérni, de meg kell jegyezni, hogy a robusztusságuk nagyban függ az arc detektálásának és a mozgás követésének sikerétől. Az sem elhanyagolható tény, hogy használatukat megelőzően sok adatra és számításigényes eljárások alkalmazására van szükség. Ezzel szemben a mintaillesztéses módszerekkel elkerülhető a modell alapú eljárásokban rejlő nehézségek egy része. Ez az egyes gesztusok invariáns 737
3 reprezentálásával és azok közvetlen egymáshoz illesztésével érhető el. A meglévő módszerekben leggyakrabban tértől és időtől függő leírókat használnak [8,9,10,11]. A mintaillesztéses módszerek referencia eljárását Laptov és munkatársai [12] alkották meg. Az általuk megalkotott módszer irányított gradiensek (HOG) és az optikai áramlás hisztogramjai (HOF) mint leírók alkalmazásán alapul. Mindezeken kívül egyéb módszerek is léteznek a szakirodalomban, melyek a mozgás pályájának; tér-, és időbeli gradienseknek; illetve az optikai áramláshoz tartozó globális hisztogramok [10] felhasználásán alapulnak. Ezeknek az eljárások az a legnagyobb hátránya, hogy a futás során közvetlenül illesztik az egyes gesztusokat egy már meglévő adatbázisra, mely rontja az eljárások skálázhatóságát. 2 Fejmozgás reprezentálása A legfontosabb kérdés, amit a munkálatok elkezdése előtt meg kell válaszolni, hogy milyen jellegű mozgásokat szeretnénk felismerni? A felismerni kívánt mozdulatsorozatok várhatóan 3-5 másodperc hosszúak lesznek elegendő elképzelni egy fejrázás mozdulatsorát. Ugyanakkor az emberek két mozdulatsort, ha nincsenek tudatában annak, hogy hogyan végzik, igen kis valószínűséggel fogják ugyan abban az ütemben elvégezni, tehát a probléma egy nemlineáris illesztést igényel. Lévén itt egy valósidejű felismerést szeretnénk megvalósítani, ezért már egy 10 másodperces intervallumon kívül nincs is értelme mintákat keresni, továbbá a gesztusok viszonylag rövid időtartama miatt már kisszámú adat alapján is jól meg kell tudni különböztetni a gesztusokat. Ebben a fejezetben részletesen ismertetjük a gesztusfelismerő rendszerünket. Megadunk egy új és hatékony vizuális reprezentációt a fejmozgást leíró jellemzők kinyeréséhez, amely elengedhetetlen a felismerő rendszer nagyméretű gesztusadatbázison történő használatához. Az általunk bevezetett reprezentáció lényegében a mozgás menetét ábrázoló képsorozat tagjain alapul. A sorozat minden tagján egy egyszerű FAST (Features from Accelerated Segment Test) detektorral meghatározzuk azokat a régiókat, melyek a legmeghatározóbbak a mozgás szempontjából. Következő lépésben a képsorozat minden szomszédos tagjára kiszámoljuk azokat az optikai áramlás vektorokat, melyek a FAST által meghatározott régiókhoz tartoznak. A régiók mozgása alapján meghatározzuk a fejmozgás globális mozgásvektorát, így lényegében egy irányvektort kapunk a gesztus sorozat minden szomszédos tagjára. Következő lépésben szegmentáljuk a képsorozatot, vagyis kijelöljük azokat a tagokat, melyek a gesztust határolják. Végezetül a gesztushoz tartozó irányvektorok sorozatát a dinamikus idővetemítés segítségével egy előre definiált gesztus-adatbázis elemeihez hasonlítjuk. 2.1 Mozgás ábrázolása A mozgás megjelenítésére az úgynevezett MHI (Motion History Image) reprezentációt választottuk, mely egy képszekvencia mozgó objektumainak változásait írja le [13]. Az MHI reprezentáció egy időalapú sablonozó eljárás eredménye, mely ugyan egyszerű, de robusztus a mozgó objektumokra nézve. A 738
4 metódus leírásához legyen adva egy képszekvencia és egy bináris maszk, mely a képszekvencia azon régióit jelöli ki, ahol mozgás történt a t-edik időpillanatban. A MHI reprezentáció egy az időtől is függő sablonként értelmezhető, ahol minden egyes pixel értéke a mozgás egy függvényeként értelmezhető. Az eljárás az alábbi képlettel számolható: - - (1) ahol a képszekvencia aktuális időbélyege, mely egyfajta korlátként működik, ugyanis általa nem jelennek meg az MHI reprezentációban azok a mozgások, melyek -nál régebben történtek. Vagyis az MHI-val jelölt kép összes olyan pixele, ahol mozgás volt értéket fog felvenni, még azok a részek ahol nem volt mozgás, fokozatosan elhalványulnak, majd törlődnek. Az eljárás grafikus reprezentációját az 1. ábra mutatja. Az MHI eljárást a mozgás szegmentálásában is felhasználtuk. A gesztus a képszekvencia részsorozataként tekinthető, vagy máshogy fogalmazva a képszekvencia szegmensei alatt jelenik meg. A szegmensre teljesülnie kell a következő feltételnek: olyan nyitó és záró tagok határolják, hogy a hozzájuk számított MHI képek átlagintenzitás értéke alacsonyabb, mint egy előre definiált küszöbérték. Vagyis olyan képkockák határolják a szegmenst, ahol a mozgás intenzitása alacsony volt. 1. ábra. A bal oldali ábrán egy mozdulatsorhoz tartozó D(x, y, t) maszk látható, a jobb oldalin pedig a MHI reprezentáció. 2.2 A mozgást meghatározó régiók Következő lépésben megkeressük azokat a régiókat az MHI reprezentáción, melyek meghatározzák a fejmozgást. Erre a FAST (Features from Accelerated Segment Test) algoritmust [14] használtuk. Ez lényegében egy egyszerű sarokdetektor, melynek hatékonysága az alacsony számításigényében rejlik. Működése során veszi a kép egyes pixelét, melyeknek egy adott sugarú környezetében vizsgálja a többi pixel értékét (lásd 2. ábra). Ha a környezetben szerepelő intenzitás értékek jelentősen nagyobbak, vagy kisebbek, mint a középpont, akkor azt sarokként osztályozza. Általában sarkok egy halmazát találja meg, ezért szokás mérni valahogy a sarkok erősségét is. 739
5 2. ábra. A FAST detektor által vizsgált tartomány egy potenciális sarokpont esetén. A detektor egy vizsgált pont körüli kör mentén vizsgálódik. Ha ebből valahány eltér a pixelnél legalább egy küszöbbel magasabb értékkel, akkor az adott középpont egy jellemző pont. Ebben az esetben a kör sugara 3 és 9 darab pixel tér el a küszöbtől. 2.3 Optikai áramlás A következő lépésben a FAST által visszaadott jellemzőpontokra (lásd 3. ábra) számítjuk ki az optikai áramláshoz tartozó vektorokat az aktuális és a megelőző képkockára. Az optikai áramlás (Optical Flow) meghatározása lényegében nem más, mint több képen azonos képrészletek megfeleltetése. Az eredmény egy vektormező, amely az elmozdulásokat, vagyis a sebességvektorokat tartalmazza. Optikai folyamon tehát azt értjük, ahogy a képintenzitások mozgása megjelenik egymás utáni képeken. 3. ábra. A baloldali ábrán az MHI képről kinyert FAST jellemzőpontok láthatók. A jobboldalin ábrán, ugyanezen pontok az arc régióra szűkítve szegmensek képpárjain ezekre számítjuk az optikai áramláshoz tartozó vektorokat. Az optikai folyam algoritmusok az összetartozó képpontok megtalálásához feltételezik, hogy ezek intenzitása közel megegyezik. Szinte az összes módszer alapját ez a feltételezés adja, amit optikai folyam korlátozásként ismerünk. Jelölje egy adott pillanatban a képintenzitást, amely egy időben változó képsorozatból származik. A továbbiakhoz a következő feltételezéssel élünk: a mozgó vagy álló objektumok pontjainak intenzitása (lényegében) nem változik az idő múlásával. Legyen néhány objektum a képen, ami idő alatt (a gyakorlatban egymás utáni képvétel alatt) elmozdul távolságra. Az intenzitásértékek Taylorsorba fejtésével és az előbb feltételezett állítások felhasználásával kapjuk: - (2) 740
6 Ezt a kifejezést rendszerint az optikai folyam feltételi egyenletének (vagy csak optikai folyamkorlátozásnak) nevezik, ahol és az optikai folyammező és koordináta irányú összetevői. Az egyenlet két ismeretlent tartalmaz. A megoldásra, a Lucas Kanade módszert [15] választottuk, mely úgy tekint egy pont sebességére, hogy az csak a pont helyi környezetétől függ. A szakirodalomban gyakran használják ennek a módszernek a piramisos változatát is. 2.4 Fejmozgás iránya A gesztusok felismeréséhez le kell tudni írni azokat az optikai folyam vektorok függvényében. Ismeretes, hogy annyi optikai folyam vektor fog keletkezni a képszekvencia két szomszédos tagja között, amennyi sarokponttal a FAST eljárás tért vissza. A gesztusok könnyebb definiálása és felismerése érdekében definiálunk egy átlagvektort, az darab optikai folyam vektor számtani közepeként. Majd ennek meghatározzuk az tengely pozitív oldalával bezárt szögét az alábbi egyenlet segítségével: - -, (3) ahol függvény az és által meghatározott érték arkusz tangensét adja vissza radiánban. Ez hasonló az arkusz tangenséhez, attól eltekintve, hogy a paraméterek előjele meghatározza, hogy az eredmény melyik körnegyedbe esik. Az egységesség miatt gondoskodunk arról, hogy a koordinátarendszerünk jobbsodrású legyen (lásd (4)-es egyenlet). (4) 4. ábra. Adott szegmens egy képpárja közötti fejmozdulás értéke szögben. Így a vizsgált szegmens minden egyes képpárjára kapunk egy szöget, amelyet szögosztályok valamelyikébe soroljuk be az alábbi formulában definiált függvény segítségével:. (5) Az (5)-ös formula segítségével tulajdonképpen annyit csinálunk, hogy minden egyes szöget a teljes szög azon tizenhatodába soroljuk be, amelyikbe esik. Így a képszekvencia. szegmense alatt megjelenő gesztus leírható az sorozattal, ahol az. képpárhoz számított átlagvektornak az tengely pozitív oldalával bezárt szöge. A modul kimenetét a 4. ábra mutatja. 741
7 3 Gesztusfelismerés Ebben a fejezetben egy eljárást ismertetünk az előző fejezetben definiált szögsorozatok egymáshoz történő illesztésére. Az illesztéshez szükség lesz egy előre definiált gesztus-adatbázisra. Az adatbázisban elempárokat tárolunk, melyekben benne van a gesztus neve és ahhoz egy előzetesen meghatározott szögsorozat. Erre látható egy példa a (6)-os formulában, melyben idézőjelek között szerepel az adott gesztus neve és mellette szögletes zárójelek között soroljuk fel a gesztus egyik szögsorozatát (az egyszerűség kedvéért fokokban):. (6) A gesztusfelismerés során a képszekvencia minden egyes szegmensére meghatározzuk a hozzá tartozó szögsorozatot. Ezt követően a kapott szögsorozatot az úgynevezett dinamikus idővetemítés (DTW) [16] segítségével illesztjük az előre definiált gesztus-adatbázis elemeihez. Az adatbázisban egy gesztushoz több szögsorozat is létezhet, így az adatbázison belül a gesztusok csoportokat alkotnak. Az aktuális szögsorozatnak képezzük a gesztus-adatbázis összes elemével a DTW távolságát, majd ahhoz a gesztus-csoporthoz soroljuk be, melyhez a DTW átlagosan a legkisebb távolságot adta. 3.1 Dinamikus idővetemítés Az eljárás során tehát a felismerendő szögsorozatot az összes gesztus-csoport összes referenciamintájával össze kell hasonlítani, és az átlagosan legkisebb távolságú csoport neve lesz a felismerés eredménye. A DTW eljárás ismertetéséhez két szögsorozatnak, mint vektornak az egymáshoz való illesztésére redukáljuk a feladatot. A DTW feladata, hogy azonos időtengelyre vetítsen egy aktuálisan detektált-, és egy tárolt fejmozgást, azaz hogy egy szögsorozatot összevethessünk a tárolt referenciákkal (a gesztus-csoportok elemeivel). Az összehasonlításhoz definiálni kell egy távolságot. A DTW algoritmusa lényegében egy dimenziós vektort illeszt egy dimenziós felismerendő vektorhoz. Az illesztés során a kezdőpontból a végpontba kell eljutni. Közben az útvonalkereső algoritmus lépésenként haladva a mintákat egymással összehasonlítja, és a távolság minimalizálására törekszik. A két vektor távolságát többféleképpen számíthatjuk ki, tapasztalataink azonban azt mutatták, hogy a leggyakrabban használt módszerek közül az euklideszi távolság biztosítja a leghatékonyabb összehasonlítást, ezért a programunk is ezzel a távolsággal dolgozik. Az 5. ábra pontjából induló, pontjában végződő szakasza vagyis a téglalap átlója jelenti azt az utat, amely mentén haladva egyenletesen nyújtjuk, illetve zsugorítjuk a bemenő vektort az összehasonlításhoz. Ez a lineáris idővetemítés. A vetemítő-görbe (az ábrán kék törött vonallal jelezve) tulajdonságai közé tartozik, hogy mindig monoton növekvő, lokális korlátok jellemzik és hogy lokális optimumokon keresztül elért teljes optimum. A vetemítés útvonala tehát nem lehet tetszés szerinti. Nem haladhat visszafelé. Ezen kívül az előre haladást is 742
8 sokféleképpen korlátozhatjuk, attól függően, hogy mekkora ingadozást engedünk meg az illesztés vonalán. 5. ábra. Egy futás alatti fejrázás gesztus illesztése az adatbázis egy fejrázás csoportjába tartozó elmére. A lineáris illesztést a koordinátarendszer pontjából induló és pontjában végződő szakasz jelentené. Az optimális nem lineáris illesztést a kék törött vonal jelzi. A DTW által adott távolság a két sorozatra: 5, Gesztus adatbázis bővítése Az előző fejezetben már tárgyaltuk, hogy a képszekvencia egyes szegmenseihez számított szögsorozatokat egy előre definiált adatbázis elemeihez illesztjük. Az illesztés jósága függ az adatbázisban tárolt rekordok darabszámától, illetve azok eloszlásától. kézenfekvőnek tűnt a rendszer működését úgy beállítani, hogy ha futás során a. szegmenst fejrázásnak osztályoztuk, akkor új elemként felvesszük az adatbázis fejrázás osztályába a. szegmenshez tartozó szögsorozatot. Ezzel a módszerrel a következő szegmens osztályozása során már egy bővebb információ halmaz áll a rendelkezésünkre az adott gesztus megjelenési formájáról. 4 Kísérletek és eredmények A tesztelés célja lényegében az volt, hogy megtaláljuk azokat a paramétereket, melyekkel a DTW algoritmus, a gesztus-adatbázis alapján kellő pontossággal képes diszkriminálni a különböző gesztusokat. Tehát tesztelés mellett lehetőségünk nyílik az optimális rendszer paraméterek beállítására is. Az alábbiakban felsoroljuk a fontosabb rendszerparamétereket: 1. Minimális és maximális gesztus hossz, 2. Maximális hiba, 3. Gesztus-adatbázis felépítése. 743
9 Átlagos DTW távolság A minimális gesztushossz meghatározása azért fontos, mert a DTW könnyen ráillesztené a túl rövid gesztusokat a már egy kicsit is hasonló adatsorokra. Ez persze a maximális meredekség kritériumát állítva korlátozható. Ezért a minimális gesztushossz kezdetben nagyobb, mint egy másodperc. A DTW algoritmus futási ideje nagyban függ a gesztusok számától és azok hosszától. Célszerű tehát egy maximális gesztushosszt is meghatározni. Ha egy-egy gesztus maximális hossza 3-4 másodperc, és a rendszer 30FPS-sel halad végig a képszekvencián, akkor szükség van egy olyan pufferre, melyben közel 150 darab szöget el lehet menteni. Azonban a mintavételezés sebességét lecsökkentjük a harmadára, akkor a főbb mozdulatkomponensek, de az illesztést gyorsítandó a gesztusok maximális hossza lecsökken 50-re. A maximális DTW hibát (ami valójában a gesztusok távolsága az aktuális szögsorozattól) legegyszerűbben empirikus módon lehet meghatározni. Mivel a DTW algoritmussal átlaghibát számoltatunk, ezért ennek maximális értéke könnyen becsülhető pár megfigyelés alapján is. Elvégeztük a rendszer betanítását három gesztusra, majd teljesen véletlenszerű mozgás közben figyeltük az átlaghiba változását. A mérések azt mutatták, hogy között változott a hiba. Amikor valamelyik gesztushoz hasonló mozdulatsort végeztünk, akkor 15 alá csökkent. Ezek alapján a maximális távolságot (hibát) 15-re állítottuk. Másik alapvető fontosságú jellemzője a rendszernek az előre definiált gesztusadatbázis. Egyelőre nem minden részletében tisztázott az, hogy a gesztus csoportok számosságát hogyan célszerű megválasztani. Azonban az alábbi grafikonból (lásd 6. ábra) jól látszik, hogy bizonyos határok között érdemes az adatbázist online bővíteni a felismerés során. Erre vonatkozóan elvégeztünk egy tesztet. Az egyszerűség kedvéért három különböző gesztus osztály számosságát vizsgáltuk: a fejrázásét, a bólintásét és a körkörös fejmozgásét. A futás során körkörös fejmozgáshoz hasonló gesztusokat illesztettünk az előbbi három osztály elemeihez Fejrázás Bólintás Körkörös mozgás db 10 db 15 db 6. ábra. Az osztályonkénti átlagos DTW távolság 20 darab körkörös fejmozgásra. Látható, hogy javul a DTW szeparáló teljesítménye, ha bizonyos határok között növeljük az egyes osztályok számosságát. 744
10 A 6. ábra, 20 darab körkörös fejmozgásnak az előbbi három darab gesztus osztálytól vett átlagos DTW távolságát szemlélteti különböző méretű 5, 10 és 15 gesztus osztályonként gesztus-adatbázisok esetén. Az ábrán jól látszik, hogy minél nagyobb az adatbázis mérete, annál kisebb az illesztett gesztusnak az átlagos távolsága a saját osztályától. A másik két osztálynál is megfigyelhető egy ellentétes irányú tendencia, habár ez nem minden esetben szembetűnő. Általánosságban elmondható, hogy egy bővebb gesztus-adatbázis jó hatással lehet az osztályozás pontosságának növelésére és, hogy a gesztus-adatbázis online bővítésével is jobban illeszkedhet a gesztus-adatbázis az aktuális felhasználó gesztikulálásához. Azonban a gesztus-adatbázis mérete valós idejű feldolgozás követelménye miatt nem nőhet tetszőlegesen nagyra. Még abban az esetben sem, ha a DTW által illesztett szögsorozatok hossza nem lehet nagyobb 50-nél. A jelenlegi rendszerben nyolc különböző gesztust szerepeltetünk, a négy alapirányt (fel, le, jobbra, balra), a körkörös-, és cikkcakk alakú fejmozgást, valamint a fejrázást és a bólintást. Ezekhez az osztályokhoz előzetesen harminc darab gesztust definiáltunk osztályonként a gesztus-adatbázisban. A futási idejű felismerés, azaz az osztályok szeparálása közel 100%-os, az egyes gesztusok és gesztusosztályok között hasonló DTW távolságok adódnak, mint amit a 6. ábra is mutat. 4.1 Összefoglalás A jelenlegi rendszer kétségkívül bebizonyította, hogy alkalmas valós idejű, fejmozgás alapú gesztusok felismerésére. Mindemellett pár nyitott kérdést is megfogalmazott. Ilyen például a gesztus-adatbázisbeli osztályok méretének ésszerű meghatározása. További érdekes feladat lehet egy olyan összetettebb metrika készítése, mely a futás során a mozgás szegmensekből kinyert gesztusokat nem csak azoknak a gesztusosztályoktól vett távolsága alapján ismeri fel, hanem egyéb az adatbázisból kinyert információt is alkalmaz. Használható javítás lehet az is, ha valahogy csökkentjük a gesztus-adatbázisbeli elemekkel való illesztések számát, vagy ha ajánlást adunk arra vonatkozóan, hogy mely elemekhez célszerű illeszteni a vizsgált sorozatot. Véleményünk szerint további érdekes törvényszerűségeket lehet felfedezni az emberi gesztikulációra vonatkozóan, ha adatbányászati eszközökkel alaposabban megvizsgáljuk a gesztus-adatbázist. Mindenféleképpen szükséges az adatbázisba új gesztus-osztályokat felvenni, ezáltal némi ráfordítással elkészíthető egy olyan rendszer, mellyel fejmozgás segítségével lehet például szavakat táplálni a számítógépbe. Végül, de nem utolsó sorban az elért eredményeket meg lehet próbálni felhasználni a szándékos és a nem-szándékos fejmozgások vizsgálatára is. Köszönetnyilvánítás A publikáció elkészítését a TÁMOP C-11/1/KONV számú projekt támogatta. A projekt az Európai Unió támogatásával, az Európai Szociális Alap társfinanszírozásával valósul meg. 745
11 Irodalomjegyzék [1] T. Acharya S. Mitra, "Gesture recognition: a survey," IEEE Trans. on Systems, Man and Cybernetics, pp , [2] O. Bernier, D. Collobert S. Marcel, "Hand gesture recognition using input output hidden Markov models," Proceedings Fourth IEEE International Conference on Automatic Face and Gesture Recognition, pp , [3] G. Qian, T. Ingalls, J. James S. Rajko, "Real-time gesture recognition with minimal training requirements and on-line learning," CVPR '07. IEEE Conference on Computer Vision and Pattern Recognition, pp. 1-8, [4] V. Shet, Y. Yacoob, L.S. Davis A. Elgammal, "Learning dynamics for exemplar-based gesture recognition," IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2003), pp , [5] A. Quattoni, L.P. Morency, D. Demirdjian, T. Darrell S. Wang, "Hidden conditional random fields for gesture recognition," IEEE Computer Society Conference on Computer Vision and Pattern Recognition, [6] M. Turk, T.S. Huang P. Hong, "Gesture modeling and recognition using finite state machines," FG, pp , [7] B. Sin, S. Lee H. Suk, "Recognizing hand gestures using dynamic bayesian network," 8th IEEE International Conference on Automatic Face & Gesture Recognition, pp. 1-6, [8] V. Rabaud, G. Cottrell, S. Belongie P. Dollár, "Behavior recognition via sparse spatiotemporal features," 2nd Joint IEEE International Workshop on Visual Surveillance and Performance Evaluation of Tracking and Surveillance, pp , [9] T. Tuytelaars, L.J.V. Gool G. Willems, "An efficient dense and scale-invariant spatiotemporal interest point detector," ECCV '08 Proceedings of the 10th European Conference on Computer Vision, pp , [10] A. Ravichandran, G. Hager, R. Vidal R. Chaudhry, "Histograms of oriented optical flow and binet-cauchy kernels on nonlinear dynamical systems for the recognition of human actions," IEEE Conference on Computer Vision and Pattern Recognition, pp , [11] J. Ahmed, M. Shah M.D. Rodriguez, "Action MACH a spatio-temporal Maximum Average Correlation Height filter for action recognition," IEEE Conference on Computer Vision and Pattern Recognition, pp. 1-8, [12] T. Lindeberg I. Laptev, "Space-time interest points," International Journal of Computer Vision, vol. 64, no. 2, pp , [13] G. Bradski J. Davis, "Motion segmentation and pose recognition with motion history gradients," IEEE Workshop on Applications of Computer Vision, pp , [14] T. Drummond E. Rosten, "Machine learning for high-speed corner detection," Proceedings of the 9th European conference on Computer Vision, pp , [15] T. Kanade B. Lucas, "An Iterative Image Registration Technique with an Application to Stereo Vision," 7th International Joint Conference on Artificial Intelligence, pp , [16] M. Müller, Information Retrieval for Music and Motion, 1st ed.: Springer,
Fejmozgás Alapú Gesztusok Felismerése
 Fejmozgás Alapú Gesztusok Felismerése Bertók Kornél, Fazekas Attila Debreceni Egyetem Informatikai Kar Debreceni Képfeldolgozó Csoport H-4010 Debrecen, Pf.:12. bertok.kornel@inf.unideb.hu, attila.fazekas@inf.unideb.hu
Fejmozgás Alapú Gesztusok Felismerése Bertók Kornél, Fazekas Attila Debreceni Egyetem Informatikai Kar Debreceni Képfeldolgozó Csoport H-4010 Debrecen, Pf.:12. bertok.kornel@inf.unideb.hu, attila.fazekas@inf.unideb.hu
8. Pontmegfeleltetések
 8. Pontmegfeleltetések Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Példa: panoráma kép készítés 1. Jellemzőpontok detektálása mindkét
8. Pontmegfeleltetések Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Példa: panoráma kép készítés 1. Jellemzőpontok detektálása mindkét
Regresszió. Csorba János. Nagyméretű adathalmazok kezelése március 31.
 Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Virtuális Egér. Horváth Zsolt, Schnádenberger Gábor, Varjas Viktor. 2011. március 20.
 Számítógépes Látás Projekt Virtuális Egér Horváth Zsolt, Schnádenberger Gábor, Varjas Viktor 011. március 0. Feladat kiírás: Egy olyan rendszer megvalósítása, melyben kamera értelmezi a kéz és az ujjak
Számítógépes Látás Projekt Virtuális Egér Horváth Zsolt, Schnádenberger Gábor, Varjas Viktor 011. március 0. Feladat kiírás: Egy olyan rendszer megvalósítása, melyben kamera értelmezi a kéz és az ujjak
Infobionika ROBOTIKA. X. Előadás. Robot manipulátorok II. Direkt és inverz kinematika. Készült a HEFOP P /1.0 projekt keretében
 Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Infobionika ROBOTIKA X. Előadás Robot manipulátorok II. Direkt és inverz kinematika Készült a HEFOP-3.3.1-P.-2004-06-0018/1.0 projekt keretében Tartalom Direkt kinematikai probléma Denavit-Hartenberg konvenció
Képfeldolgozás Szegmentálás Osztályozás Képfelismerés Térbeli rekonstrukció
 Mesterséges látás Miről lesz szó? objektumok Bevezetés objektumok A mesterséges látás jelenlegi, technikai eszközökön alapuló világunkban gyakorlatilag azonos a számítógépes képfeldolgozással. Számítógépes
Mesterséges látás Miről lesz szó? objektumok Bevezetés objektumok A mesterséges látás jelenlegi, technikai eszközökön alapuló világunkban gyakorlatilag azonos a számítógépes képfeldolgozással. Számítógépes
17. előadás: Vektorok a térben
 17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
17. előadás: Vektorok a térben Szabó Szilárd A vektor fogalma A mai előadásban n 1 tetszőleges egész szám lehet, de az egyszerűség kedvéért a képletek az n = 2 esetben szerepelnek. Vektorok: rendezett
Miről lesz szó? Videó tartalom elemzés (VCA) leegyszerűsített működése Kültéri védelem Közúthálózat megfigyelés Emberszámlálás
 Videóanalitikát mindenhova! Princz Adorján Miről lesz szó? Videó tartalom elemzés (VCA) leegyszerűsített működése Kültéri védelem Közúthálózat megfigyelés Emberszámlálás VCA alapú detektorok Videótartalom
Videóanalitikát mindenhova! Princz Adorján Miről lesz szó? Videó tartalom elemzés (VCA) leegyszerűsített működése Kültéri védelem Közúthálózat megfigyelés Emberszámlálás VCA alapú detektorok Videótartalom
A KLT (Kanade Lucas Tomasi) Feature Tracker Működése (jellegzetes pontok választása és követése)
 A KL (Kanade Lucas omasi) Feature racker Működése (jellegzetes pontok választása és követése) Készítette: Hajder Levente 008.11.18. 1. Feladat A rendelkezésre álló videó egy adott képkockájából minél több
A KL (Kanade Lucas omasi) Feature racker Működése (jellegzetes pontok választása és követése) Készítette: Hajder Levente 008.11.18. 1. Feladat A rendelkezésre álló videó egy adott képkockájából minél több
Kontrollcsoport-generálási lehetőségek retrospektív egészségügyi vizsgálatokhoz
 Kontrollcsoport-generálási lehetőségek retrospektív egészségügyi vizsgálatokhoz Szekér Szabolcs 1, Dr. Fogarassyné dr. Vathy Ágnes 2 1 Pannon Egyetem Rendszer- és Számítástudományi Tanszék, szekersz@gmail.com
Kontrollcsoport-generálási lehetőségek retrospektív egészségügyi vizsgálatokhoz Szekér Szabolcs 1, Dr. Fogarassyné dr. Vathy Ágnes 2 1 Pannon Egyetem Rendszer- és Számítástudományi Tanszék, szekersz@gmail.com
Keresés képi jellemzők alapján. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Keresés képi jellemzők alapján Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Lusta gépi tanulási algoritmusok Osztályozás: k=1: piros k=5: kék k-legközelebbi szomszéd (k=1,3,5,7)
Függvények Megoldások
 Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
BitTorrent felhasználók értékeléseinek következtetése a viselkedésük alapján. Hegedűs István
 BitTorrent felhasználók értékeléseinek következtetése a viselkedésük alapján Hegedűs István Ajánló rendszerek Napjainkban egyre népszerűbb az ajánló rendszerek alkalmazása A cégeket is hasznos információval
BitTorrent felhasználók értékeléseinek következtetése a viselkedésük alapján Hegedűs István Ajánló rendszerek Napjainkban egyre népszerűbb az ajánló rendszerek alkalmazása A cégeket is hasznos információval
A mérési eredmény megadása
 A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
A mérési eredmény megadása A mérés során kapott értékek eltérnek a mérendő fizikai mennyiség valódi értékétől. Alapvetően kétféle mérési hibát különböztetünk meg: a determinisztikus és a véletlenszerű
AKTUÁTOR MODELLEK KIVÁLASZTÁSA ÉS OBJEKTÍV ÖSSZEHASONLÍTÁSA
 AKTUÁTOR MODELLEK KIVÁLASZTÁSA ÉS OBJEKTÍV ÖSSZEHASONLÍTÁSA Kovács Ernő 1, Füvesi Viktor 2 1 Egyetemi docens, PhD; 2 tudományos segédmunkatárs 1 Eletrotechnikai és Elektronikai Tanszék, Miskolci Egyetem
AKTUÁTOR MODELLEK KIVÁLASZTÁSA ÉS OBJEKTÍV ÖSSZEHASONLÍTÁSA Kovács Ernő 1, Füvesi Viktor 2 1 Egyetemi docens, PhD; 2 tudományos segédmunkatárs 1 Eletrotechnikai és Elektronikai Tanszék, Miskolci Egyetem
AUTOMATIKUS KÉPFELDOLGOZÁS A HADITECHNIKÁBAN A CELLULÁRIS NEURÁLIS HÁLÓZAT
 Buzási Tibor AUTOMATIKUS KÉPFELDOLGOZÁS A HADITECHNIKÁBAN A CELLULÁRIS NEURÁLIS HÁLÓZAT A következő bemutató témája a Celluláris Neurális Hálózat (CNN) technológiára épülő, a hagyományos képfeldolgozási
Buzási Tibor AUTOMATIKUS KÉPFELDOLGOZÁS A HADITECHNIKÁBAN A CELLULÁRIS NEURÁLIS HÁLÓZAT A következő bemutató témája a Celluláris Neurális Hálózat (CNN) technológiára épülő, a hagyományos képfeldolgozási
A matematikai feladatok és megoldások konvenciói
 A matematikai feladatok és megoldások konvenciói Kozárné Fazekas Anna Kántor Sándor Matematika és Informatika Didaktikai Konferencia - Szatmárnémeti 2011. január 28-30. Konvenciók Mindenki által elfogadott
A matematikai feladatok és megoldások konvenciói Kozárné Fazekas Anna Kántor Sándor Matematika és Informatika Didaktikai Konferencia - Szatmárnémeti 2011. január 28-30. Konvenciók Mindenki által elfogadott
Panorámakép készítése
 Panorámakép készítése Képregisztráció, 2009. Hantos Norbert Blaskovics Viktor Összefoglalás Panoráma (image stitching, planar mosaicing): átfedő képek összeillesztése Lépések: Előfeldolgozás (pl. intenzitáskorrekciók)
Panorámakép készítése Képregisztráció, 2009. Hantos Norbert Blaskovics Viktor Összefoglalás Panoráma (image stitching, planar mosaicing): átfedő képek összeillesztése Lépések: Előfeldolgozás (pl. intenzitáskorrekciók)
1. tétel. 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója 7 cm. Mekkora a háromszög átfogója? (4 pont)
 1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
Sergyán Szabolcs szeptember 21.
 Éldetektálás Sergyán Szabolcs Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2009. szeptember 21. Sergyán Sz. (BMF NIK) Éldetektálás 2009. szeptember 21. 1 / 28 Mit nevezünk élnek? Intuitív
Éldetektálás Sergyán Szabolcs Budapesti Műszaki Főiskola Neumann János Informatikai Kar 2009. szeptember 21. Sergyán Sz. (BMF NIK) Éldetektálás 2009. szeptember 21. 1 / 28 Mit nevezünk élnek? Intuitív
Kinematika szeptember Vonatkoztatási rendszerek, koordinátarendszerek
 Kinematika 2014. szeptember 28. 1. Vonatkoztatási rendszerek, koordinátarendszerek 1.1. Vonatkoztatási rendszerek A test mozgásának leírása kezdetén ki kell választani azt a viszonyítási rendszert, amelyből
Kinematika 2014. szeptember 28. 1. Vonatkoztatási rendszerek, koordinátarendszerek 1.1. Vonatkoztatási rendszerek A test mozgásának leírása kezdetén ki kell választani azt a viszonyítási rendszert, amelyből
Tömegpontok mozgása egyenes mentén, hajítások
 2. gyakorlat 1. Feladatok a kinematika tárgyköréből Tömegpontok mozgása egyenes mentén, hajítások 1.1. Feladat: Mekkora az átlagsebessége annak pontnak, amely mozgásának első szakaszában v 1 sebességgel
2. gyakorlat 1. Feladatok a kinematika tárgyköréből Tömegpontok mozgása egyenes mentén, hajítások 1.1. Feladat: Mekkora az átlagsebessége annak pontnak, amely mozgásának első szakaszában v 1 sebességgel
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
4. Jellemző pontok kinyerése és megfeleltetése
 4. Jellemző pontok kinyerése és megfeleltetése Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Jellemzők és megfeleltetésük A képfeldolgozás,
4. Jellemző pontok kinyerése és megfeleltetése Kató Zoltán Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/) 2 Jellemzők és megfeleltetésük A képfeldolgozás,
Adaptív dinamikus szegmentálás idősorok indexeléséhez
 Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
Adaptív dinamikus szegmentálás idősorok indexeléséhez IPM-08irAREAE kurzus cikkfeldolgozás Balassi Márton 1 Englert Péter 1 Tömösy Péter 1 1 Eötvös Loránd Tudományegyetem Informatikai Kar 2013. november
A távérzékelt felvételek tematikus kiértékelésének lépései
 A távérzékelt felvételek tematikus kiértékelésének lépései Csornai Gábor László István Földmérési és Távérzékelési Intézet Mezőgazdasági és Vidékfejlesztési Igazgatóság Az előadás 2011-es átdolgozott változata
A távérzékelt felvételek tematikus kiértékelésének lépései Csornai Gábor László István Földmérési és Távérzékelési Intézet Mezőgazdasági és Vidékfejlesztési Igazgatóság Az előadás 2011-es átdolgozott változata
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 14. Digitális Alakzatrekonstrukció - Bevezetés http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr.
3D számítógépes geometria és alakzatrekonstrukció 14. Digitális Alakzatrekonstrukció - Bevezetés http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01 Dr. Várady Tamás, Dr.
Modern Fizika Labor Fizika BSC
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. április 20. A mérés száma és címe: 20. Folyadékáramlások 2D-ban Értékelés: A beadás dátuma: 2009. április 28. A mérést végezte: Márton Krisztina Zsigmond
Modern Fizika Labor Fizika BSC A mérés dátuma: 2009. április 20. A mérés száma és címe: 20. Folyadékáramlások 2D-ban Értékelés: A beadás dátuma: 2009. április 28. A mérést végezte: Márton Krisztina Zsigmond
Quadkopter szimulációja LabVIEW környezetben Simulation of a Quadcopter with LabVIEW
 Quadkopter szimulációja LabVIEW környezetben Simulation of a Quadcopter with LabVIEW T. KISS 1 P. T. SZEMES 2 1University of Debrecen, kiss.tamas93@gmail.com 2University of Debrecen, szemespeter@eng.unideb.hu
Quadkopter szimulációja LabVIEW környezetben Simulation of a Quadcopter with LabVIEW T. KISS 1 P. T. SZEMES 2 1University of Debrecen, kiss.tamas93@gmail.com 2University of Debrecen, szemespeter@eng.unideb.hu
NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő
 SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatika Tanszék BSC FOKOZATÚ MÉRNÖK INFORMATIKUS SZAK NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő Fejlesztői dokumentáció GROUP#6
SZÉCHENYI ISTVÁN EGYETEM Műszaki Tudományi Kar Informatika Tanszék BSC FOKOZATÚ MÉRNÖK INFORMATIKUS SZAK NGB_IN040_1 SZIMULÁCIÓS TECHNIKÁK dr. Pozna Claudio Radu, Horváth Ernő Fejlesztői dokumentáció GROUP#6
Akusztikai tervezés a geometriai akusztika módszereivel
 Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Akusztikai tervezés a geometriai akusztika módszereivel Fürjes Andor Tamás BME Híradástechnikai Tanszék Kép- és Hangtechnikai Laborcsoport, Rezgésakusztika Laboratórium 1 Tartalom A geometriai akusztika
Osztott algoritmusok
 Osztott algoritmusok A benzinkutas példa szimulációja Müller Csaba 2010. december 4. 1. Bevezetés Első lépésben talán kezdjük a probléma ismertetésével. Adott két n hosszúságú bináris sorozat (s 1, s 2
Osztott algoritmusok A benzinkutas példa szimulációja Müller Csaba 2010. december 4. 1. Bevezetés Első lépésben talán kezdjük a probléma ismertetésével. Adott két n hosszúságú bináris sorozat (s 1, s 2
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
b) Ábrázolja ugyanabban a koordinátarendszerben a g függvényt! (2 pont) c) Oldja meg az ( x ) 2
 1) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) b) c) ( ) ) Határozza meg az 1. feladatban megadott, ; intervallumon
1) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) b) c) ( ) ) Határozza meg az 1. feladatban megadott, ; intervallumon
Az egyenes egyenlete: 2 pont. Az összevont alak: 1 pont. Melyik ábrán látható e függvény grafikonjának egy részlete?
 1. Írja fel annak az egyenesnek az egyenletét, amely áthalad az (1; 3) ponton, és egyik normálvektora a (8; 1) vektor! Az egyenes egyenlete: 2. Végezze el a következő műveleteket, és vonja össze az egynemű
1. Írja fel annak az egyenesnek az egyenletét, amely áthalad az (1; 3) ponton, és egyik normálvektora a (8; 1) vektor! Az egyenes egyenlete: 2. Végezze el a következő műveleteket, és vonja össze az egynemű
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Kétdimenziós mesterséges festési eljárások. Hatások és alkalmazások
 Pannon Egyetem Informatikai Tudományok Doktori Iskola Tézisfüzet Kétdimenziós mesterséges festési eljárások. Hatások és alkalmazások Kovács Levente Képfeldolgozás és Neuroszámítógépek Tanszék Témavezet
Pannon Egyetem Informatikai Tudományok Doktori Iskola Tézisfüzet Kétdimenziós mesterséges festési eljárások. Hatások és alkalmazások Kovács Levente Képfeldolgozás és Neuroszámítógépek Tanszék Témavezet
A gradiens törésmutatójú közeg I.
 10. Előadás A gradiens törésmutatójú közeg I. Az ugrásszerű törésmutató változással szemben a TracePro-ban lehetőség van folytonosan változó törésmutatójú közeg definiálására. Ilyen érdekes típusú közegek
10. Előadás A gradiens törésmutatójú közeg I. Az ugrásszerű törésmutató változással szemben a TracePro-ban lehetőség van folytonosan változó törésmutatójú közeg definiálására. Ilyen érdekes típusú közegek
Számítógépes képelemzés 7. előadás. Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék
 Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Számítógépes képelemzés 7. előadás Dr. Balázs Péter SZTE, Képfeldolgozás és Számítógépes Grafika Tanszék Momentumok Momentum-alapú jellemzők Tömegközéppont Irányultáság 1 2 tan 2 1 2,0 1,1 0, 2 Befoglaló
Statisztikai eljárások a mintafelismerésben és a gépi tanulásban
 Statisztikai eljárások a mintafelismerésben és a gépi tanulásban Varga Domonkos (I.évf. PhD hallgató) 2014 május A prezentáció felépítése 1) Alapfogalmak 2) A gépi tanulás, mintafelismerés alkalmazási
Statisztikai eljárások a mintafelismerésben és a gépi tanulásban Varga Domonkos (I.évf. PhD hallgató) 2014 május A prezentáció felépítése 1) Alapfogalmak 2) A gépi tanulás, mintafelismerés alkalmazási
First Prev Next Last Go Back Full Screen Close Quit
 Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
Többváltozós függvények (2) First Prev Next Last Go Back Full Screen Close Quit 1. Egyváltozós függvények esetén a differenciálhatóságból következett a folytonosság. Fontos tudni, hogy abból, hogy egy
3D számítógépes geometria és alakzatrekonstrukció
 3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
3D számítógépes geometria és alakzatrekonstrukció 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiima01
Visszacsatolt (mély) neurális hálózatok
 Visszacsatolt (mély) neurális hálózatok Visszacsatolt hálózatok kimenet rejtett rétegek bemenet Sima előrecsatolt neurális hálózat Visszacsatolt hálózatok kimenet rejtett rétegek bemenet Pl.: kép feliratozás,
Visszacsatolt (mély) neurális hálózatok Visszacsatolt hálózatok kimenet rejtett rétegek bemenet Sima előrecsatolt neurális hálózat Visszacsatolt hálózatok kimenet rejtett rétegek bemenet Pl.: kép feliratozás,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 9 IX. ROBUsZTUs statisztika 1. ROBUsZTUssÁG Az eddig kidolgozott módszerek főleg olyanok voltak, amelyek valamilyen értelemben optimálisak,
Autonóm jármű forgalomszimulátorba illesztése
 Autonóm jármű forgalomszimulátorba illesztése Szalai Mátyás 2018 Konzulens: Dr. Tettamanti Tamás A szimulációs feladat Miért hasznos? Biztonságos környezetben nyújt lehetőséget az autonóm járművek forgalmi
Autonóm jármű forgalomszimulátorba illesztése Szalai Mátyás 2018 Konzulens: Dr. Tettamanti Tamás A szimulációs feladat Miért hasznos? Biztonságos környezetben nyújt lehetőséget az autonóm járművek forgalmi
Kódverifikáció gépi tanulással
 Kódverifikáció gépi tanulással Szoftver verifikáció és validáció kiselőadás Hidasi Balázs 2013. 12. 12. Áttekintés Gépi tanuló módszerek áttekintése Kódverifikáció Motiváció Néhány megközelítés Fault Invariant
Kódverifikáció gépi tanulással Szoftver verifikáció és validáció kiselőadás Hidasi Balázs 2013. 12. 12. Áttekintés Gépi tanuló módszerek áttekintése Kódverifikáció Motiváció Néhány megközelítés Fault Invariant
Mechanika Kinematika. - Kinematikára: a testek mozgását tanulmányozza anélkül, hogy figyelembe venné a kiváltó
 Mechanika Kinematika A mechanika a fizika része mely a testek mozgásával és egyensúlyával foglalkozik. A klasszikus mechanika, mely a fénysebességnél sokkal kisebb sebességű testekre vonatkozik, feloszlik:
Mechanika Kinematika A mechanika a fizika része mely a testek mozgásával és egyensúlyával foglalkozik. A klasszikus mechanika, mely a fénysebességnél sokkal kisebb sebességű testekre vonatkozik, feloszlik:
ICT ÉS BP RENDSZEREK HATÉKONY TELJESÍTMÉNY SZIMULÁCIÓJA DR. MUKA LÁSZLÓ
 ICT ÉS BP RENDSZEREK HATÉKONY TELJESÍTMÉNY SZIMULÁCIÓJA DR. MUKA LÁSZLÓ 1 TARTALOM 1.1 A MODELLEZÉS ÉS SZIMULÁCIÓ META-SZINTŰ HATÉKONYSÁGÁNAK JAVÍTÁSA A. Az SMM definiálása, a Jackson Keys módszer kiterjesztése
ICT ÉS BP RENDSZEREK HATÉKONY TELJESÍTMÉNY SZIMULÁCIÓJA DR. MUKA LÁSZLÓ 1 TARTALOM 1.1 A MODELLEZÉS ÉS SZIMULÁCIÓ META-SZINTŰ HATÉKONYSÁGÁNAK JAVÍTÁSA A. Az SMM definiálása, a Jackson Keys módszer kiterjesztése
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
A maximum likelihood becslésről
 A maximum likelihood becslésről Definíció Parametrikus becsléssel foglalkozunk. Adott egy modell, mellyel elképzeléseink szerint jól leírható a meghatározni kívánt rendszer. (A modell típusának és rendszámának
A maximum likelihood becslésről Definíció Parametrikus becsléssel foglalkozunk. Adott egy modell, mellyel elképzeléseink szerint jól leírható a meghatározni kívánt rendszer. (A modell típusának és rendszámának
Csima Judit március 9. és 16.
 Grafika Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2017. március 9. és 16. Csima Judit Grafika 1 / 18 Grafika általában Grafika az R-ben Van néhány alapvető package az ábrázolásra:
Grafika Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2017. március 9. és 16. Csima Judit Grafika 1 / 18 Grafika általában Grafika az R-ben Van néhány alapvető package az ábrázolásra:
EEE Kutatólaboratórium MTA-SZTAKI Magyar Tudományos Akadémia
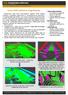 DElosztott I S T R I B U T EEsemények D EV E N T S A NElemzé A L Y S I S se R E SKutatólaboratór E A R C H L A B O R A T Oium R Y L I D A R B a s e d S u r v e i l l a n c e Városi LIDAR adathalmaz szegmentációja
DElosztott I S T R I B U T EEsemények D EV E N T S A NElemzé A L Y S I S se R E SKutatólaboratór E A R C H L A B O R A T Oium R Y L I D A R B a s e d S u r v e i l l a n c e Városi LIDAR adathalmaz szegmentációja
Élpont osztályozáson alapuló robusztus tekintetkövetés
 KÉPFELDOLGOZÁS Élpont osztályozáson alapuló robusztus tekintetkövetés HELFENBEIN TAMÁS Ipari Kommunikációs Technológiai Intézet, Bay Zoltán Alkalmazott Kutatási Közalapítvány helfenbein@ikti.hu Lektorált
KÉPFELDOLGOZÁS Élpont osztályozáson alapuló robusztus tekintetkövetés HELFENBEIN TAMÁS Ipari Kommunikációs Technológiai Intézet, Bay Zoltán Alkalmazott Kutatási Közalapítvány helfenbein@ikti.hu Lektorált
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
Sorozatok határértéke SOROZAT FOGALMA, MEGADÁSA, ÁBRÁZOLÁSA; KORLÁTOS ÉS MONOTON SOROZATOK
 Sorozatok határértéke SOROZAT FOGALMA, MEGADÁSA, ÁBRÁZOLÁSA; KORLÁTOS ÉS MONOTON SOROZATOK Sorozat fogalma Definíció: Számsorozaton olyan függvényt értünk, amelynek értelmezési tartománya a pozitív egész
Sorozatok határértéke SOROZAT FOGALMA, MEGADÁSA, ÁBRÁZOLÁSA; KORLÁTOS ÉS MONOTON SOROZATOK Sorozat fogalma Definíció: Számsorozaton olyan függvényt értünk, amelynek értelmezési tartománya a pozitív egész
A dinamikus geometriai rendszerek használatának egy lehetséges területe
 Fejezetek a matematika tanításából A dinamikus geometriai rendszerek használatának egy lehetséges területe Készítette: Harsányi Sándor V. matematika-informatika szakos hallgató Porcsalma, 2004. december
Fejezetek a matematika tanításából A dinamikus geometriai rendszerek használatának egy lehetséges területe Készítette: Harsányi Sándor V. matematika-informatika szakos hallgató Porcsalma, 2004. december
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
Hibadetektáló rendszer légtechnikai berendezések számára
 Hibadetektáló rendszer légtechnikai berendezések számára Tudományos Diákköri Konferencia A feladatunk Légtechnikai berendezések Monitorozás Hibadetektálás Újrataníthatóság A megvalósítás Mozgásérzékelő
Hibadetektáló rendszer légtechnikai berendezések számára Tudományos Diákköri Konferencia A feladatunk Légtechnikai berendezések Monitorozás Hibadetektálás Újrataníthatóság A megvalósítás Mozgásérzékelő
Újfajta, automatikus, döntési fa alapú adatbányászati módszer idősorok osztályozására
 VÉGZŐS KONFERENCIA 2009 2009. május 20, Budapest Újfajta, automatikus, döntési fa alapú adatbányászati módszer idősorok osztályozására Hidasi Balázs hidasi@tmit.bme.hu Konzulens: Gáspár-Papanek Csaba Budapesti
VÉGZŐS KONFERENCIA 2009 2009. május 20, Budapest Újfajta, automatikus, döntési fa alapú adatbányászati módszer idősorok osztályozására Hidasi Balázs hidasi@tmit.bme.hu Konzulens: Gáspár-Papanek Csaba Budapesti
Pontműveletek. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar február 20.
 Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
(Independence, dependence, random variables)
 Két valószínűségi változó együttes vizsgálata Feltételes eloszlások Két diszkrét változó együttes eloszlása a lehetséges értékpárok és a hozzájuk tartozó valószínűségek (táblázat) Példa: Egy urna 3 fehér,
Két valószínűségi változó együttes vizsgálata Feltételes eloszlások Két diszkrét változó együttes eloszlása a lehetséges értékpárok és a hozzájuk tartozó valószínűségek (táblázat) Példa: Egy urna 3 fehér,
Nehézségi gyorsulás mérése megfordítható ingával
 Nehézségi gyorsulás mérése megfordítható ingával (Mérési jegyzőkönyv) Hagymási Imre 2007. április 21. (hétfő délelőtti csoport) 1. A mérés elmélete A nehézségi gyorsulás mérésének egy klasszikus módja
Nehézségi gyorsulás mérése megfordítható ingával (Mérési jegyzőkönyv) Hagymási Imre 2007. április 21. (hétfő délelőtti csoport) 1. A mérés elmélete A nehézségi gyorsulás mérésének egy klasszikus módja
6. Éldetektálás. Kató Zoltán. Képfeldolgozás és Számítógépes Grafika tanszék SZTE (http://www.inf.u-szeged.hu/~kato/teaching/)
 6. Éldetektálás Kató Zoltán Képeldolgozás és Számítógépes Graika tanszék SZTE (http://www.in.u-szeged.hu/~kato/teaching/) 2 Élek A képen ott található él, ahol a kép-üggvény hirtelen változik. A kép egy
6. Éldetektálás Kató Zoltán Képeldolgozás és Számítógépes Graika tanszék SZTE (http://www.in.u-szeged.hu/~kato/teaching/) 2 Élek A képen ott található él, ahol a kép-üggvény hirtelen változik. A kép egy
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás
 3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
3D - geometriai modellezés, alakzatrekonstrukció, nyomtatás 15. Digitális Alakzatrekonstrukció Méréstechnológia, Ponthalmazok regisztrációja http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav54
NULLADIK MATEMATIKA ZÁRTHELYI
 A NULLADIK MATEMATIKA ZÁRTHELYI 20-09-2 Terem: Munkaidő: 0 perc. A dolgozat megírásához íróeszközön kívül semmilyen segédeszköz nem használható! Csak és kizárólag tollal tölthető ki a feladatlap, a ceruzával
A NULLADIK MATEMATIKA ZÁRTHELYI 20-09-2 Terem: Munkaidő: 0 perc. A dolgozat megírásához íróeszközön kívül semmilyen segédeszköz nem használható! Csak és kizárólag tollal tölthető ki a feladatlap, a ceruzával
Struktúra nélküli adatszerkezetek
 Struktúra nélküli adatszerkezetek Homogén adatszerkezetek (minden adatelem azonos típusú) osztályozása Struktúra nélküli (Nincs kapcsolat az adatelemek között.) Halmaz Multihalmaz Asszociatív 20:24 1 A
Struktúra nélküli adatszerkezetek Homogén adatszerkezetek (minden adatelem azonos típusú) osztályozása Struktúra nélküli (Nincs kapcsolat az adatelemek között.) Halmaz Multihalmaz Asszociatív 20:24 1 A
ismertetem, hogy milyen probléma vizsgálatában jelent meg ez az eredmény. A kérdés a következő: Mikor mondhatjuk azt, hogy bizonyos események közül
 A Borel Cantelli lemma és annak általánosítása. A valószínűségszámítás egyik fontos eredménye a Borel Cantelli lemma. Először informálisan ismertetem, hogy milyen probléma vizsgálatában jelent meg ez az
A Borel Cantelli lemma és annak általánosítása. A valószínűségszámítás egyik fontos eredménye a Borel Cantelli lemma. Először informálisan ismertetem, hogy milyen probléma vizsgálatában jelent meg ez az
3D-s számítógépes geometria és alakzatrekonstrukció
 3D-s számítógépes geometria és alakzatrekonstrukció 14. Digitális Alakzatrekonstrukció - Bevezetés http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav08 Dr. Várady Tamás,
3D-s számítógépes geometria és alakzatrekonstrukció 14. Digitális Alakzatrekonstrukció - Bevezetés http://cg.iit.bme.hu/portal/node/312 https://www.vik.bme.hu/kepzes/targyak/viiiav08 Dr. Várady Tamás,
Funkcionálanalízis. n=1. n=1. x n y n. n=1
 Funkcionálanalízis 2011/12 tavaszi félév - 2. előadás 1.4. Lényeges alap-terek, példák Sorozat terek (Folytatás.) C: konvergens sorozatok tere. A tér pontjai sorozatok: x = (x n ). Ezen belül C 0 a nullsorozatok
Funkcionálanalízis 2011/12 tavaszi félév - 2. előadás 1.4. Lényeges alap-terek, példák Sorozat terek (Folytatás.) C: konvergens sorozatok tere. A tér pontjai sorozatok: x = (x n ). Ezen belül C 0 a nullsorozatok
Érettségi feladatok: Trigonometria 1 /6
 Érettségi feladatok: Trigonometria 1 /6 2003. Próba 14. Egy hajó a Csendes-óceán egy szigetéről elindulva 40 perc alatt 24 km-t haladt észak felé, majd az eredeti haladási irányhoz képest 65 -ot nyugat
Érettségi feladatok: Trigonometria 1 /6 2003. Próba 14. Egy hajó a Csendes-óceán egy szigetéről elindulva 40 perc alatt 24 km-t haladt észak felé, majd az eredeti haladási irányhoz képest 65 -ot nyugat
A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a
 a Matematika mérnököknek I. című tárgyhoz Függvények. Függvények A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a szabadon eső test sebessége az idő függvénye. Konstans hőmérsékleten
a Matematika mérnököknek I. című tárgyhoz Függvények. Függvények A Föld középpontja felé szabadon eső test sebessége növekszik, azaz, a szabadon eső test sebessége az idő függvénye. Konstans hőmérsékleten
OPTIKAI KÖVETK VETÉS. Steiner Henriette április 29.
 OPTIKAI KÖVETK VETÉS Lehetőségek és limitáci ciók Steiner Henriette 2009. április 29. MEGISMERÉS = Érzékelés + Fogalomalkotás MEGISMERÉS = Érzékelés + Fogalomalkotás LÁTÁS = SZEM + AGY MEGISMERÉS = Érzékelés
OPTIKAI KÖVETK VETÉS Lehetőségek és limitáci ciók Steiner Henriette 2009. április 29. MEGISMERÉS = Érzékelés + Fogalomalkotás MEGISMERÉS = Érzékelés + Fogalomalkotás LÁTÁS = SZEM + AGY MEGISMERÉS = Érzékelés
A KUTATÁS EREDMÉNYEI ZÁRÓJELENTÉS 2004-2006.
 ÖNELLENŐRZÉS ÉS FUTÁSIDEJŰ VERIFIKÁCIÓ SZÁMÍTÓGÉPES PROGRAMOKBAN OTKA T-046527 A KUTATÁS EREDMÉNYEI ZÁRÓJELENTÉS 2004-2006. Témavezető: dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem
ÖNELLENŐRZÉS ÉS FUTÁSIDEJŰ VERIFIKÁCIÓ SZÁMÍTÓGÉPES PROGRAMOKBAN OTKA T-046527 A KUTATÁS EREDMÉNYEI ZÁRÓJELENTÉS 2004-2006. Témavezető: dr. Majzik István Budapesti Műszaki és Gazdaságtudományi Egyetem
Hipotézis STATISZTIKA. Kétmintás hipotézisek. Munkahipotézis (H a ) Tematika. Tudományos hipotézis. 1. Előadás. Hipotézisvizsgálatok
 STATISZTIKA 1. Előadás Hipotézisvizsgálatok Tematika 1. Hipotézis vizsgálatok 2. t-próbák 3. Variancia-analízis 4. A variancia-analízis validálása, erőfüggvény 5. Korreláció számítás 6. Kétváltozós lineáris
STATISZTIKA 1. Előadás Hipotézisvizsgálatok Tematika 1. Hipotézis vizsgálatok 2. t-próbák 3. Variancia-analízis 4. A variancia-analízis validálása, erőfüggvény 5. Korreláció számítás 6. Kétváltozós lineáris
} számtani sorozat első tagja és differenciája is 4. Adja meg a sorozat 26. tagját! A = { } 1 pont. B = { } 1 pont. x =
 . Az { a n } számtani sorozat első tagja és differenciája is 4. Adja meg a sorozat 26. tagját! a = 26 2. Az A és B halmazokról tudjuk, hogy A B = {;2;3;4;5;6}, A \ B = {;4} és A B = {2;5}. Sorolja fel
. Az { a n } számtani sorozat első tagja és differenciája is 4. Adja meg a sorozat 26. tagját! a = 26 2. Az A és B halmazokról tudjuk, hogy A B = {;2;3;4;5;6}, A \ B = {;4} és A B = {2;5}. Sorolja fel
MATEMATIKA PRÓBAÉRETTSÉGI 2013 I. rész
 MATEMATIKA PRÓBAÉRETTSÉGI 203 I. rész. Oldja meg a következő egyenletet: x 2 25. Az egyenlet megoldása: 2. Egy vállalat 280 000 Ft-ért vásárol egy számítógépet. A számítógép évente 5%-ot veszít az értékéből.
MATEMATIKA PRÓBAÉRETTSÉGI 203 I. rész. Oldja meg a következő egyenletet: x 2 25. Az egyenlet megoldása: 2. Egy vállalat 280 000 Ft-ért vásárol egy számítógépet. A számítógép évente 5%-ot veszít az értékéből.
Elengedhetetlen a játékokban, mozi produkciós eszközökben Nélküle kvantum hatás lép fel. Az objektumok áthaladnak a többi objektumon
 Bevezetés Ütközés detektálás Elengedhetetlen a játékokban, mozi produkciós eszközökben Nélküle kvantum hatás lép fel Az objektumok áthaladnak a többi objektumon A valósághű megjelenítés része Nem tisztán
Bevezetés Ütközés detektálás Elengedhetetlen a játékokban, mozi produkciós eszközökben Nélküle kvantum hatás lép fel Az objektumok áthaladnak a többi objektumon A valósághű megjelenítés része Nem tisztán
Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea
 Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea Geometrikus deformálható modellek Görbe evolúció Level set módszer A görbe evolúció parametrizálástól független mindössze geometriai
Éldetektálás, szegmentálás (folytatás) Orvosi képdiagnosztika 11_2 ea Geometrikus deformálható modellek Görbe evolúció Level set módszer A görbe evolúció parametrizálástól független mindössze geometriai
Gépi tanulás a gyakorlatban. Lineáris regresszió
 Gépi tanulás a gyakorlatban Lineáris regresszió Lineáris Regresszió Legyen adott egy tanuló adatbázis: Rendelkezésünkre áll egy olyan előfeldolgozott adathalmaz, aminek sorai az egyes ingatlanokat írják
Gépi tanulás a gyakorlatban Lineáris regresszió Lineáris Regresszió Legyen adott egy tanuló adatbázis: Rendelkezésünkre áll egy olyan előfeldolgozott adathalmaz, aminek sorai az egyes ingatlanokat írják
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Függvények ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x
EGYSZERŰ, NEM IRÁNYÍTOTT (IRÁNYÍTATLAN) GRÁF
 Összefoglaló Gráfok / EGYSZERŰ, NEM IRÁNYÍTOTT (IRÁNYÍTATLAN) GRÁF Adott a G = (V, E) gráf ahol a V a csomópontok, E az élek halmaza E = {(x, y) x, y V, x y (nincs hurokél) és (x, y) = (y, x)) Jelölések:
Összefoglaló Gráfok / EGYSZERŰ, NEM IRÁNYÍTOTT (IRÁNYÍTATLAN) GRÁF Adott a G = (V, E) gráf ahol a V a csomópontok, E az élek halmaza E = {(x, y) x, y V, x y (nincs hurokél) és (x, y) = (y, x)) Jelölések:
Segédlet: Főfeszültségek meghatározása Mohr-féle feszültségi körök alkalmazásával
 Segédlet: Főfeszültségek meghatározása Mohr-féle feszültségi körök alkalmazásával Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 212. október 16. Frissítve: 215. január
Segédlet: Főfeszültségek meghatározása Mohr-féle feszültségi körök alkalmazásával Készítette: Dr. Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 212. október 16. Frissítve: 215. január
PONTFELHŐ REGISZTRÁCIÓ
 PONTFELHŐ REGISZTRÁCIÓ ITERATIVE CLOSEST POINT Cserteg Tamás, URLGNI, 2018.11.22. TARTALOM Röviden Alakzatrekonstrukció áttekintés ICP algoritmusok Projektfeladat Demó FORRÁSOK Cikkek Efficient Variants
PONTFELHŐ REGISZTRÁCIÓ ITERATIVE CLOSEST POINT Cserteg Tamás, URLGNI, 2018.11.22. TARTALOM Röviden Alakzatrekonstrukció áttekintés ICP algoritmusok Projektfeladat Demó FORRÁSOK Cikkek Efficient Variants
Radioaktív anyag felezési idejének mérése
 A pályázótársam által ismertetett mérési módszer alkalmazásához Labview szoftverrel készítettem egy mérőműszert, ami lehetőséget nyújt radioaktív anyag felezési idejének meghatározására. 1. ábra: Felhasználói
A pályázótársam által ismertetett mérési módszer alkalmazásához Labview szoftverrel készítettem egy mérőműszert, ami lehetőséget nyújt radioaktív anyag felezési idejének meghatározására. 1. ábra: Felhasználói
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
Q 1 D Q 2 (D x) 2 (1.1)
 . Gyakorlat 4B-9 Két pontszerű töltés az x tengelyen a következőképpen helyezkedik el: egy 3 µc töltés az origóban, és egy + µc töltés az x =, 5 m koordinátájú pontban van. Keressük meg azt a helyet, ahol
. Gyakorlat 4B-9 Két pontszerű töltés az x tengelyen a következőképpen helyezkedik el: egy 3 µc töltés az origóban, és egy + µc töltés az x =, 5 m koordinátájú pontban van. Keressük meg azt a helyet, ahol
Függvények növekedési korlátainak jellemzése
 17 Függvények növekedési korlátainak jellemzése A jellemzés jól bevált eszközei az Ω, O, Θ, o és ω jelölések. Mivel az igények általában nemnegatívak, ezért az alábbi meghatározásokban mindenütt feltesszük,
17 Függvények növekedési korlátainak jellemzése A jellemzés jól bevált eszközei az Ω, O, Θ, o és ω jelölések. Mivel az igények általában nemnegatívak, ezért az alábbi meghatározásokban mindenütt feltesszük,
Térbeli transzformációk, a tér leképezése síkra
 Térbeli transzformációk, a tér leképezése síkra Homogén koordináták bevezetése térben A tér minden P pontjához kölcsönösen egyértelműen egy valós (x, y, z) számhármast rendeltünk hozzá. (Descartes-féle
Térbeli transzformációk, a tér leképezése síkra Homogén koordináták bevezetése térben A tér minden P pontjához kölcsönösen egyértelműen egy valós (x, y, z) számhármast rendeltünk hozzá. (Descartes-féle
Anatómiai régiók automatikus felismerése
 Anatómiai régiók automatikus felismerése Kutatási beszámoló 2015. június Készítette: Tóth Márton József Bevezetés A mai klinikai gyakorlatban a háromdimenziós orvosi képalkotó rendszerek használata igen
Anatómiai régiók automatikus felismerése Kutatási beszámoló 2015. június Készítette: Tóth Márton József Bevezetés A mai klinikai gyakorlatban a háromdimenziós orvosi képalkotó rendszerek használata igen
Algoritmizálás, adatmodellezés tanítása 6. előadás
 Algoritmizálás, adatmodellezés tanítása 6. előadás Tesztelési módszerek statikus tesztelés kódellenőrzés szintaktikus ellenőrzés szemantikus ellenőrzés dinamikus tesztelés fekete doboz módszerek fehér
Algoritmizálás, adatmodellezés tanítása 6. előadás Tesztelési módszerek statikus tesztelés kódellenőrzés szintaktikus ellenőrzés szemantikus ellenőrzés dinamikus tesztelés fekete doboz módszerek fehér
Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017.
 Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017. Vizuális feldolgozórendszerek feladatai Mesterséges intelligencia és idegtudomány Mesterséges intelligencia és idegtudomány Párhuzamos problémák
Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017. Vizuális feldolgozórendszerek feladatai Mesterséges intelligencia és idegtudomány Mesterséges intelligencia és idegtudomány Párhuzamos problémák
6. Függvények. Legyen függvény és nem üreshalmaz. A függvényt az f K-ra való kiterjesztésének
 6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
1. Adatok kiértékelése. 2. A feltételek megvizsgálása. 3. A hipotézis megfogalmazása
 HIPOTÉZIS VIZSGÁLAT A hipotézis feltételezés egy vagy több populációról. (pl. egy gyógyszer az esetek 90%-ában hatásos; egy kezelés jelentősen megnöveli a rákos betegek túlélését). A hipotézis vizsgálat
HIPOTÉZIS VIZSGÁLAT A hipotézis feltételezés egy vagy több populációról. (pl. egy gyógyszer az esetek 90%-ában hatásos; egy kezelés jelentősen megnöveli a rákos betegek túlélését). A hipotézis vizsgálat
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén
 Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
Példa: Normálfeszültség eloszlása síkgörbe rúd esetén Készítette: Kossa Attila (kossa@mm.bme.hu) BME, Műszaki Mechanikai Tanszék 2011. március 20. Az 1. ábrán vázolt síkgörbe rúd méretei és terhelése ismert.
Információ megjelenítés Számítógépes ábrázolás. Dr. Iványi Péter
 Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter Raszterizáció OpenGL Mely pixelek vannak a primitíven belül fragment generálása minden ilyen pixelre Attribútumok (pl., szín) hozzárendelése
Információ megjelenítés Számítógépes ábrázolás Dr. Iványi Péter Raszterizáció OpenGL Mely pixelek vannak a primitíven belül fragment generálása minden ilyen pixelre Attribútumok (pl., szín) hozzárendelése
Numerikus integrálás
 Közelítő és szimbolikus számítások 11. gyakorlat Numerikus integrálás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján 1. Határozatlan integrál
Közelítő és szimbolikus számítások 11. gyakorlat Numerikus integrálás Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor Vinkó Tamás London András Deák Gábor jegyzetei alapján 1. Határozatlan integrál
Mérési adatok illesztése, korreláció, regresszió
 Mérési adatok illesztése, korreláció, regresszió Korreláció, regresszió Két változó mennyiség közötti kapcsolatot vizsgálunk. Kérdés: van-e kapcsolat két, ugyanabban az egyénben, állatban, kísérleti mintában,
Mérési adatok illesztése, korreláció, regresszió Korreláció, regresszió Két változó mennyiség közötti kapcsolatot vizsgálunk. Kérdés: van-e kapcsolat két, ugyanabban az egyénben, állatban, kísérleti mintában,
ACM Snake. Orvosi képdiagnosztika 11. előadás első fele
 ACM Snake Orvosi képdiagnosztika 11. előadás első fele ACM Snake (ismétlés) A szegmentáló kontúr egy paraméteres görbe: x Zs s X s, Y s,, s A szegmentáció energia funkcionál minimalizálása: E x Eint x
ACM Snake Orvosi képdiagnosztika 11. előadás első fele ACM Snake (ismétlés) A szegmentáló kontúr egy paraméteres görbe: x Zs s X s, Y s,, s A szegmentáció energia funkcionál minimalizálása: E x Eint x
STATISZTIKA. A maradék független a kezelés és blokk hatástól. Maradékok leíró statisztikája. 4. A modell érvényességének ellenőrzése
 4. A modell érvényességének ellenőrzése STATISZTIKA 4. Előadás Variancia-analízis Lineáris modellek 1. Függetlenség 2. Normális eloszlás 3. Azonos varianciák A maradék független a kezelés és blokk hatástól
4. A modell érvényességének ellenőrzése STATISZTIKA 4. Előadás Variancia-analízis Lineáris modellek 1. Függetlenség 2. Normális eloszlás 3. Azonos varianciák A maradék független a kezelés és blokk hatástól
