1-A 1-B. francia. francia - 3 -
|
|
|
- Ádám Fazekas
- 8 évvel ezelőtt
- Látták:
Átírás
1 1-A A 11-B osztályban háromféle nyelvet lehet tanulni (,, ). Az osztály minden tanulója legalább egy idegen nyelvet tanul. Mindhárom nyelvet 14 gyerek tanulja. Angolt és franciát is 17, t és et is 1, et és franciát is 21 gyerek tanul. Angol nyelvet 33, et 34, franciát pedig 33 gyerek tanul. Töltsd ki a halmazábrát! Hány tanulója van az osztálynak? 1-B A 11-B osztályban háromféle nyelvet lehet tanulni (,, ). Az osztály minden tanulója legalább egy idegen nyelvet tanul. Mindhárom nyelvet gyerek tanulja. Angolt és franciát is 13, t és et is 12, et és franciát is 11 gyerek tanul. Angol nyelvet 26, et 21, franciát pedig 24 gyerek tanul. Töltsd ki a halmazábrát! Hány tanulója van az osztálynak? - 3 -
2 1-C A 11-B osztályban háromféle nyelvet lehet tanulni (,, ). Az osztály minden tanulója legalább egy idegen nyelvet tanul. Mindhárom nyelvet 5 gyerek tanulja. Angolt és franciát is 11, t és et is 13, et és franciát is 6 gyerek tanul. Angol nyelvet 34, et 23, franciát pedig 24 gyerek tanul. Töltsd ki a halmazábrát! Hány tanulója van az osztálynak? 1-D A 11-B osztályban háromféle nyelvet lehet tanulni (,, ). Az osztály minden tanulója legalább egy idegen nyelvet tanul. Mindhárom nyelvet 7 gyerek tanulja. Angolt és franciát is 10, t és et is 12, et és franciát is 16 gyerek tanul. Angol nyelvet 23, et 31, franciát pedig 32 gyerek tanul. Töltsd ki a halmazábrát! Hány tanulója van az osztálynak? - 4 -
3 1-E A -C osztályban kétféle nyelvet lehet tanulni (, ). 1-an járnak az osztályba, és mindenki tanul legalább egy idegen nyelvet. Angolt 12, et pedig 11 gyerek tanul. Töltsd ki a halmazábrát! Hány tanulják mindkét nyelvet? 1-F A -C osztályban kétféle nyelvet lehet tanulni (, ). 2-en járnak az osztályba, és mindenki tanul legalább egy idegen nyelvet. Angolt 17, et pedig 21 gyerek tanul. Töltsd ki a halmazábrát! Hány tanulják mindkét nyelvet? 1-G A -C osztályban kétféle nyelvet lehet tanulni (, ). 2-en járnak az osztályba, és mindenki tanul legalább egy idegen nyelvet. Angolt 16, et pedig 1 gyerek tanul. Töltsd ki a halmazábrát! Hány tanulják mindkét nyelvet? - 5 -
4 1-H, és az iskolaújság szerkesztıi. A legújabb számban összesen 47 nyomdahibát találtak. 23, 22, pedig 23 hibát talált meg. 10 olyan hiba volt, amit és is, olyan, amit és is, és 6 olyan, amit és is megtalált. Töltsd ki a halmazábrát! Hány hibát talált meg mindhárom lány? 1-I, és az iskolaújság szerkesztıi. A legújabb számban összesen 51 nyomdahibát találtak. 27, 25, pedig 27 hibát talált meg. olyan hiba volt, amit és is, 12 olyan, amit és is, és 12 olyan, amit és is megtalált. Töltsd ki a halmazábrát! Hány hibát talált meg mindhárom lány? - 6 -
5 1-J, és az iskolaújság szerkesztıi. A legújabb számban összesen 57 nyomdahibát találtak. 26, 30, pedig 31 hibát talált meg. 14 olyan hiba volt, amit és is, 12 olyan, amit és is, és 13 olyan, amit és is megtalált. Töltsd ki a halmazábrát! Hány hibát talált meg mindhárom lány? 1-K, és az iskolaújság szerkesztıi. A legújabb számban összesen 61 nyomdahibát találtak. 33, 36, pedig 31 hibát talált meg. 17 olyan hiba volt, amit és is, 14 olyan, amit és is, és 1 olyan, amit és is megtalált. Töltsd ki a halmazábrát! Hány hibát talált meg mindhárom lány? - 7 -
6 1-L és az iskolaújság szerkesztıi. A legújabb számban összesen 30 nyomdahibát találtak. 1, pedig 1 hibát talált meg. Töltsd ki a halmazábrát! Hány hibát talált meg mindkét lány? 1-M és az iskolaújság szerkesztıi. A legújabb számban összesen 32 nyomdahibát találtak. 21, pedig 20 hibát talált meg. Töltsd ki a halmazábrát! Hány hibát talált meg mindkét lány? 1-N és az iskolaújság szerkesztıi. A legújabb számban összesen 2 nyomdahibát találtak. 16, pedig 21 hibát talált meg. Töltsd ki a halmazábrát! Hány hibát talált meg mindkét lány? - -
7 1-O Egy matematikaversenyen három feladatot tőztek ki. Az 55 résztvevı mindegyike megoldott legalább egy feladatot. Mindhárom feladatot, csak a 2. feladatot 12, csak a 3. feladatot 10 tanuló oldotta meg. Az 1. és 2. feladatot is 16, a 2. és 3. feladatot is 11, az 1. és 3. feladatot is 13 tanuló oldotta meg. Töltsd ki a halmazábrát! Hány tanuló volt, aki csak az 1. feladatot oldotta meg? 1-P Egy matematikaversenyen három feladatot tőztek ki. Az 50 résztvevı mindegyike megoldott legalább egy feladatot. Mindhárom feladatot 4, csak az 1. feladatot 7, csak a 3. feladatot tanuló oldotta meg. Az 1. és 2. feladatot is 13, a 2. és 3. feladatot is 10, az 1. és 3. feladatot is 11 tanuló oldotta meg. Töltsd ki a halmazábrát! Hány tanuló volt, aki csak a 2. feladatot oldotta meg? - -
8 1-Q Egy matematikaversenyen három feladatot tőztek ki. Az 52 résztvevı mindegyike megoldott legalább egy feladatot. Mindhárom feladatot 6, csak az 1. feladatot 13, csak a 2. feladatot 12 tanuló oldotta meg. Az 1. és 2. feladatot is, a 2. és 3. feladatot is 10, az 1. és 3. feladatot is 11 tanuló oldotta meg. Töltsd ki a halmazábrát! Hány tanuló volt, aki csak a 3. feladatot oldotta meg? 1-R Egy matematikaversenyen három feladatot tőztek ki. Az 5 résztvevı mindegyike megoldott legalább egy feladatot. Mindhárom feladatot 3, csak az 1. feladatot 14, csak a 3. feladatot 12 tanuló oldotta meg. Az 1. és 2. feladatot is 10, a 2. és 3. feladatot is, az 1. és 3. feladatot is tanuló oldotta meg. Töltsd ki a halmazábrát! Hány tanuló volt, aki csak a 2. feladatot oldotta meg?
9 1-S Egy matematikaversenyen két feladatot tőztek ki. Minden résztvevı megoldott legalább egy feladatot. Az 1. feladatot 12, a 2. feladatot 13, mindkét feladatot 5 tanuló oldotta meg. Töltsd ki a halmazábrát! Hány tanuló vett részt a versenyen? 1-T Egy matematikaversenyen két feladatot tőztek ki. Minden résztvevı megoldott legalább egy feladatot. Az 1. feladatot 16, a 2. feladatot 1, mindkét feladatot 7 tanuló oldotta meg. Töltsd ki a halmazábrát! Hány tanuló vett részt a versenyen? 1-U Egy matematikaversenyen két feladatot tőztek ki. Minden résztvevı megoldott legalább egy feladatot. Az 1. feladatot 1, a 2. feladatot 24, mindkét feladatot 11 tanuló oldotta meg. Töltsd ki a halmazábrát! Hány tanuló vett részt a versenyen?
10 Megoldások 1-A 1-B C 1-D E 1-F G
11 1-H 1-I J 1-K L 1-M N
12 1-O 1-P Q 1-R S 1-T U
HALMAZOK TULAJDONSÁGAI,
Halmazok definíciója, megadása HALMAZOK TULAJDONSÁGAI, 1. A következő definíciók közül melyek határoznak meg egyértelműen egy-egy halmazt? a) A: a csoport tanulói b) B: Magyarország városai ma c) C: Pilinszky
Alapfeladatok halmazábra készítésére, egyszerű halmazműveletekre: különbség, metszet, unió.
HLMZOK 9. évfolyam lapfeladatok halmazábra készítésére, egyszerű halmazműveletekre: különbség, metszet, unió. 1.1. dott az = {1; 2; 3; 4; 5} és = {3; 4; 5; 6; 7} halmaz. Készíts halmazábrát, majd sorold
az Energetikai Szakközépiskola és Kollégium kisérettségiző diákjai számára ; halmaz összes részhalmazát!
1. témakör: HALMAZELMÉLET A feladatok megoldásához használjuk a Négyjegyű függvénytáblázatot! Halmazok: 8-9. oldal 1. Sorold fel az a b x y halmaz összes részhalmazát!. AdottU alaphalmaz, és annak két
3.Példa. Megoldás 4. Példa: Megoldás
Megoldott feladatok 3.Példa. Egy osztályban 30 tanuló van. Ezek háromféle sportkörre járnak: futballozni, kosarazni és úszni. 20 tanuló futballozik, 6 tanuló kosarazik, 0 tanuló úszik, -en futballoznak
Halmazok. A és B különbsége: A \ B. A és B metszete: A. A és B uniója: A
Halmazok Érdekes feladat lehet, amikor bizonyos mennyiségű adatok között keressük az adott tulajdonsággal rendelkezők számát. A következőekben azt szeretném megmutatni, hogy a halmazábrák segítségével,
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Halmazok
MTEMTIK ÉRETTSÉGI TÍPUSFELDTOK KÖZÉP SZINT Halmazok szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
Halmazműveletek feladatok
Halmazműveletek feladatok Soroljuk fel a {a; b; c} halmaz összes részhalmazát! Határozza meg az A és B halmazokat, ha tudja, hogy A B ={1;2;3;4;5}; A B ={3;5}; A\B={1}; B\A={2;4 A={-1; 0; 1; 2; 5; 7; 8}
HALMAZOK 2. Feladat Év Kész Nem ment. 1) Egy osztály tanulói valamennyien vettek. 2) Egy 10 tagú csoportban mindenki beszéli az
HALMAZOK 2 Feladat Év Kész Nem ment 1) Egy osztály tanulói valamennyien vettek színházjegyet. Kétféle előadásra rendeltek jegyeket: az elsőre 18-at, a másodikra 24-et. 16 tanuló csak a második előadásra
Halmazelméleti feladatok (középszint)
Halmazelméleti feladatok (középszint) (KSZÉV Minta (1) 2004.05/I/9) Adott két intervallum: ] 1; 3[ és [0; 4]. a) Ábrázolja számegyenesen a két intervallum metszetét! b) Adja meg a metszetintervallumot!
1.1. Halmazok. 2. Minta - 5. feladat (2 pont) Adott két halmaz:
1.1. Halmazok 2009. május id. - 11. feladat (3 pont) A H halmaz elemei legyenek a KATALINKA szó betűi, a G halmaz elemei pedig a BICEBÓCA szó betűi. Írja fel a H U G halmaz elemeit! 2010. október - 1.
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Halmazok
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Halmazok 1) Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Halmazok
MTEMTIK ÉRETTSÉGI TÍPUSFELDTOK MEGOLDÁSI KÖZÉP SZINT Halmazok szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Halmazok
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Halmazok 1) Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat.
Érettségi feladatok: Halmazok, logika
Érettségi feladatok: Halmazok, logika 2005. május 10 18. Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először Ádám
45. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY HARMADIK OSZTÁLY
45. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY Megyei forduló Javítási útmutató HARMADIK OSZTÁLY 1. Marci tolltartójában fekete, piros és kék ceruzák vannak, összesen 20 darab. Hány fekete ceruza van
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Halmazok
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Halmazok A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Halmazelméleti feladatok (középszint)
Halmazelméleti feladatok (középszint) 1. (KSZÉV Minta (1) 2004.05/I/9) Adott két intervallum: ] 1; 3[ és [0; 4]. a) Ábrázolja számegyenesen a két intervallum metszetét! b) Adja meg a metszetintervallumot!
Megyei matematikaverseny évfolyam 2. forduló
Megyei matematikaverseny 0. 9. évfolyam. forduló. különbözı pozitív egész szám átlaga. Legfeljebb mekkora lehet ezen számok közül a legnagyobb? (A) (B) 8 (C) 9 (D) 78 (E) 44. 00 009 + 008 007 +... + 4
46. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY HARMADIK OSZTÁLY
46. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY Megyei forduló Javítási útmutató HARMADIK OSZTÁLY. Írd be a körökbe a 2, 3, 4 és 5 számokat úgy, hogy a szomszédos számok különbsége -nél nagyobb legyen!
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK EMELT SZINT Statisztika
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK EMELT SZINT Statisztika A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Halmazok Megoldások. c) Fogalmazza meg a következő állítás tagadását! Enikő minden eltérést
2005-20XX Középszint Halmazok Megoldások 1) Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először Ádám és Tamás
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Halmazok
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Halmazok A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
A III. forduló megoldásai
A III. forduló megoldásai 1. Egy dobozban pénzérmék és golyók vannak, amelyek vagy ezüstből, vagy aranyból készültek. A dobozban lévő tárgyak 20%-a golyó, a pénzérmék 40%-a ezüst. A dobozban levő tárgyak
HALMAZOK TULAJDONSÁGAI,
Halmazok definíciója, megadása HALMAZOK TULAJDONSÁGAI,. A következő definíciók közül melyek határoznak meg egyértelműen egy-egy halmazt? a) A:= { a csoport tanulói b) B:= { Magyarország városai ma c) C:=
ISKOLÁD NEVE:... Az első három feladat feleletválasztós. Egyenként 5-5 pontot érnek. Egy feladatnak több jó megoldása is lehet. A) 6 B) 8 C) 10 D) 12
2. OSZTÁLY 1. Mennyi az alábbi kifejezés értéke: 0 2 + 4 6 + 8 10 + 12 14 + 16 18 + 20 A) 6 B) 8 C) 10 D) 12 2. Egy szabályos dobókockával kétszer dobok. Mennyi nem lehet a dobott számok összege? A) 1
MATEMATIKA VERSENY --------------------
Eötvös Károly Közös Fenntartású Általános Iskola 2013. és Alapfokú Művészetoktatási Intézmény 831 Vonyarcvashegy, Fő u. 8/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen,
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Halmazok
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Halmazok A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Gyakorló feladatok 9.évf. halmaznak, írd fel az öt elemű részhalmazokat!. Add meg a következő halmazokat és ábrázold Venn-diagrammal:
Gyakorló feladatok 9.évf.. Mennyi az összes részhalmaza az A a c; d; e; f halmaznak, írd fel az öt elemű részhalmazokat!. Legyen U ;;;;;6;7;8;9, A ;;6;7; és B ;;8. Add meg a következő halmazokat és ábrázold
Halmazok Megoldások. Az osztály tanulóinak átlagmagassága 168,0 cm
005-0XX Emelt szint Halmazok Megoldások 1) Egy gimnázium egyik érettségiző osztályába 30 tanuló jár, közülük 1 lány. A lányok testmagassága centiméterben mérve az osztályozó naplóbeli sorrend szerint:
Érettségi feladatok: Halmazok, logika
Érettségi feladatok: Halmazok, logika 2005. május 10 18. Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először Ádám
Érettségi feladatok: Szöveges feladatok
Érettségi feladatok: Szöveges feladatok 2005. május 10. 17. Anna és Zsuzsi is szeretné megvenni az újságosnál az egyik magazint, de egyik lánynak sincs elegendő pénze. Anna pénzéből hiányzik a magazin
Halmazok. d) Mennyi annak a valószínűsége, hogy egy eltérést véletlenszerűen kiválasztva, azt legalább ketten megtalálták?
Halmazok Halmazok 1) Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először Ádám és Tamás nézték meg figyelmesen
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Halmazok
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Halmazok A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások. A: József Attila hosszú versei D: az osztály legokosabb tanulója
Megoldások 1. Melyik határoz meg halmazt az alábbiak közül? A: József Attila hosszú versei D: az osztály legokosabb tanulója B: az első tíz prímszám E: Debrecen általános iskolái C: néhány darab páros
MATEMATIKA ÉRETTSÉGI május 10. KÖZÉP SZINT I.
1) Adott két pont: A ; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. MATEMATIKA ÉRETTSÉGI 005. május 10. KÖZÉP SZINT I. és B 1; Írja fel az AB szakasz 1 1 F ; F ;1 ) Az ábrán egy ; intervallumon
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK EMELT SZINT Statisztika
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK EMELT SZINT Statisztika A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Az elektronikus információszabadságról szóló 2005. évi XC. törvény 6. (3) bekezdése alapján a közfeladatot ellátó intézmény fenntartója a
Az elektronikus információszabadságról szóló 2005. évi XC. törvény 6. (3) bekezdése alapján a közfeladatot ellátó intézmény fenntartója a közfeladatot ellátó intézményre a törvényben meghatározott közzéteendő
MATEMATIKAI KOMPETENCIATERÜLET A
MATEMATIKAI KOMPETENCIATERÜLET A Matematika. évfolyam FÓLIÁk tánítók részére. félév 9. modul. melléklet. évfolyam tanítói fólia 9. modul 4. melléklet. évfolyam tanítói fólia 1-szer -szer 3-szer 4-szer
Halmazelmélet. 1. Jelenítsük meg Venn-diagrammon az alábbi halmazokat: a) b) c) 2. Milyen halmazokat határoznak meg az alábbi Venn-diagrammok?
Halmazelmélet Alapfogalmak Unió: ; metszet: ; különbség: ; komplementer: (itt U egy univerzum halmaz). Egyenlőség: két halmaz egyenlő, ha ugyanazok az elemeik. Ezzel ekvivalens, hogy. Tartalmazás: ; valódi
3. Venn-diagrammok használata nélkül bizonyítsuk be az alábbi összefüggéseket!
Halmazelmélet Alapfogalmak Unió: A B = {x x A vagy x B}; metszet: A B = {x x A és x B}; különbség: A\B = A B = {x x A és x B}; komplementer: A = {x x A és x U} (itt U egy univerzum halmaz). Egyenlőség:
A pályaválasztási napon válaszoló tanulók nemenkénti megoszlása
A Pályaválasztási Napok rendezvényén 302 tanuló válaszolt kérdéseinkre. A kérdezett neme: A pályaválasztási napon válaszoló tanulók nemenkénti megoszlása fiú 42% lány 58% Hányadik osztályba jársz? A pályaválasztási
MATEMATIKA VERSENY
Vonyarcvashegyi Eötvös Károly Általános Iskola 2016. 8314 Vonyarcvashegy, Fő u. 84/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen, majd oldd meg a feladatokat! A részeredményeket
PRÓBAÉRETTSÉGI MATEMATIKA május-június EMELT SZINT JAVÍTÁSI ÚTMUTATÓ. Vizsgafejlesztő Központ
PRÓBAÉRETTSÉGI 003. május-június MATEMATIKA EMELT SZINT JAVÍTÁSI ÚTMUTATÓ Vizsgafejlesztő Központ PRÓBAÉRETTSÉGI 003 MATEMATIKA Kedves Kolléga! Kérjük, hogy a dolgozatok javítását a javítási útmutató alapján
Képzési rend 2016-2017. tanév. Iskolánk képzési rendje és pontszámítás az egyes képzési formákban
Képzési rend 2016-2017. tanév Iskolánk képzési rendje és pontszámítás az egyes képzési formákban 9. A humán tantervű osztály magyar nyelv és irodalom csoport (17 fő) Tagozatkód: 001 1. : angol nyelv, német
Ezek a mai fiatalok?
Ezek a mai fiatalok? A magyarországi 18-29 éves fiatalok szocioökonómiai sajátosságai a Magyar Ifjúság 2012 kutatás eredményei tükrében Hámori Ádám Szociológus, főiskolai tanársegéd, KRE TFK hamori.adam@kre.hu
Íme a 2010-es matematika érettségi megoldásai
1. oldal, összesen: 25 Délmagyarország, www.delmagyar.hu Minden jog fenntartva. Íme a 2010-es matematika érettségi megoldásai DELMAGYAR.HU 2010.05.04. 13:15 Rendben lezajlottak a matematika írásbelik kedden
2700 Cegléd, Rákóczi út 46. tel: (53)-310-934, (53)-500-525 fax:(53)-500-625 E-mail: cklg@cklg.hu www.cklg.hu
Beiskolázási tájékoztató a 2015/2016-os tanévre Ceglédi Kossuth Lajos Gimnázium OM azonosító: 032549 2700 Cegléd, Rákóczi út 46. tel: (53)-310-934, (53)-500-525 fax:(53)-500-625 E-mail: cklg@cklg.hu www.cklg.hu
Jó munkát! 8. OSZTÁLY 2 = C = A B =
BEM JÓZSEF Jelszó:... MEGYEI MATEMATIKAVERSENY Terem: I. FORDULÓ 2019. január 1. Hely:.... Tiszta versenyidő: 4 perc. Minden feladatot indoklással együtt oldj meg! A részműveletek is pontot érnek. Számológép
Halmazok. Gyakorló feladatsor a 9-es évfolyamdolgozathoz
Halmazok 1. Feladat. Adott négy halmaz: az alaphalmaz, melynek részhalmazai az A, a B és a C halmaz: U {1, 2,,..., 20}, az A elemei a páros számok, a B elemei a hárommal oszthatók, a C halmaz elemei pedig
A 4. 5. kérdést csak akkor töltse ki, ha az Ön házastársa nem magyar anyanyelvű. Ellenkező esetben kérem folytassa a 6. kérdéstől!
A kérdőív kitöltője: az anya az apa A kitöltés helye (tartomány, város): A kitöltés dátuma: 1. Hol született (ország)? 2. Mióta él Németországban (évszám)? 3. Mi az anyanyelve? A 4. 5. kérdést csak akkor
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Logika-Gráfok
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Logika-Gráfok A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Gráfok
MTEMTIK ÉRETTSÉGI TÍPUSFELDTOK MEGOLDÁSI KÖZÉP SZINT Gráfok 1) Egy gráfban 4 csúcs van. z egyes csúcsokból 3; 2; 2; 1 él indul. Hány éle van a gráfnak? Egy lehetséges ábrázolás: gráfnak 4 éle van. (ábra
A Pályaválasztási Napok rendezvényén 324 tanuló válaszolt kérdéseinkre. A pályaválasztási napon válaszoló tanulók nemenkénti megoszlása
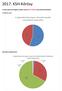2017. KSH-Kőrösy A Pályaválasztási Napok rendezvényén 324 tanuló válaszolt kérdéseinkre. A kérdezett neme: A pályaválasztási napon válaszoló tanulók nemenkénti megoszlása fiú 45% lány 55% Hányadik osztályba
1. Pál kertje téglalap alakú, 15 méter hosszú és 7 méter széles. Hány métert tesz meg Pál, ha körbesétálja a kertjét?
1. Pál kertje téglalap alakú, 15 méter hosszú és 7 méter széles. Hány métert tesz meg Pál, ha körbesétálja a kertjét? A) 37 m B) 22 m C) 30 m D) 44 m E) 105 m 2. Ádám három barátjával közösen a kis kockákból
ZRÍNYI MIKLÓS GIMNÁZIUM
ZRÍNYI MIKLÓS GIMNÁZIUM OM azonosító: 037 632 Címe: 8900 Zalaegerszeg, Rákóczi út 30. Igazgató: Horváth Attila Beiskolázási felelıs: Horváth Attila Telefon/fax: 92/313-490 Honlap: www.zmgzeg.sulinet.hu
Továbbtanulásról szóló kérdőív középiskolások részére
Iskola azonosító sorszáma osztály sorszáma (A kérdező tölti ki a kérdőív kitöltetése előtt) Továbbtanulásról szóló kérdőív középiskolások részére Szia! Végzős középiskolások érettségi utáni terveivel kapcsolatos
VI. Vályi Gyula Emlékverseny november
VI. Vályi Gyula Emlékverseny 1999. november 19-1. VI. osztály 1. Ki a legidősebb, ha Attila 10 000 órás, Balázs 8 000 napos, Csanád 16 éves, Dániel 8000000 perces, Ede 00 hónapos. (A) Attila (B) Balázs
Írd le, a megoldások gondolatmenetét, indoklását is!
088 Budapest VIII., Bródy Sándor u. 6. Postacím: 4 Budapest, Pf. 76 Telefon: 7-8900 Fa: 7-890 44. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ 05. április. NEGYEDIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ
KOMPETENCIA ALAPÚ LEVELEZŐ MATEMATIKA VERSENY
Név:.Iskola: KOMPETENCIA ALAPÚ LEVELEZŐ MATEMATIKA VERSENY 2012. november 12. 9. évfolyam I. forduló Pótlapok száma db Matematika 9. évfolyam 1. forduló 1. Írja be a megrajzolt halmazábrába az A és B halmazok
Logika, gráfok. megtalált.
1) Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először Ádám és Tamás nézték meg figyelmesen az ábrákat: Ádám 11,
MATEMATIKA VERSENY
Vonyarcvashegyi Eötvös Károly Általános Iskola 2015. 8314 Vonyarcvashegy, Fő u. 84/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen, majd oldd meg a feladatokat! A részeredményeket
Bodó Beáta - MATEMATIKA II 1
Bodó Beáta - MATEMATIKA II 1 FELTÉTELES VALÓSZÍNŰSÉG, FÜGGETLENSÉG 1. Legyen P (A) = 0, 7; P (B) = 0, 6 és P (A B) = 0, 5. Határozza meg a következő valószínűségeket! (a) B,V P (A B) 0, 8333 (b) B,V P
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
Matematika emelt szint 0801 ÉRETTSÉGI VIZSGA 009. május 5. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Formai előírások: Fontos tudnivalók
2700 Cegléd, Rákóczi út 46. tel: (53)-310-934, (53)-500-525 fax:(53)-500-625 E-mail: cklg@cklg.hu www.cklg.hu
Beiskolázási tájékoztató a 2016/2017-es tanévre Ceglédi Kossuth Lajos Gimnázium OM azonosító: 032549 Telephely kódja: 001 2700 Cegléd, Rákóczi út 46. tel: (53)-310-934, (53)-500-525 fax:(53)-500-625 E-mail:
1. Célnyelvi kompetenciamérés a két tanítási nyelvű osztályokban
Célnyelvi kompetenciamérés a két tanítási nyelvű osztályokban 6. c 3. Maximá lisan összpont sz. Összponts zám Nyelvi szint (megfelelt/n em felelt meg) T495-F995 15 19 18 60 52 A2 Megfelelt 86% S493-E330
Halmazelmélet. 1 Halmazelmélet
Halmazelmélet 1. feladat 2006. május 1. (2 pont) idegennyelvi Az A halmaz elemei a 10-nél nem kisebb és a 20-nál nem nagyobb páros számok, a B halmaz elemei a néggyel osztható pozitív számok. Adja meg
IX. PANGEA Matematika Verseny I. forduló 5. évfolyam. 1. Öt gyerek összesen 50 éves. Hány év múlva lesznek együttvéve 65 évesek?
1. Öt gyerek összesen 50 éves. Hány év múlva lesznek együttvéve 65 évesek? A) 3 B) 5 C) 10 D) 15 2. Egy 8-tagú család minden tagja vesz 1-1 ajándékot a többieknek, de mindenki csak a nála idősebbeknek.
JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MATEMATIKA EMELT SZINTŰ ÍRÁSBELI 1. FELADATSORHOZ
JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MATEMATIKA EMELT SZINTŰ ÍRÁSBELI 1. FELADATSORHOZ Formai előírások: A dolgozatot a vizsgázó által használt színűtől eltérő színű tollal kell javítani, és a tanári gyakorlatnak
ANYABANK PAPABANK. Készítette:
ANYABANK PAPABANK Készítette: A Magánpénzügyi Akadémia - vagyonteremtés önerőből - A Magánpénzügyi Akadémia küldetése: közérthetővé tenni a pénzügyeket, ezzel az évtized végére 10 ezer ember előtt megnyitva
Arany Dániel Matematikai Tanulóverseny 2012/2013-as tanév kezdők III. kategória I. forduló
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 01/013-as tanév kezdők I II. kategória II. forduló kezdők III. kategória I. forduló Megoldások és javítási útmutató 1. Egy osztályban
MATEMATIKA KISÉRETTSÉGI Ponthatárok: (5) (4) (3) (2) (1) Pontszám
MATEMATIKA KISÉRETTSÉGI 011. Ponthatárok: (5) 83-100 (4) 65-8 (3) 47-64 () 30-46 (1) 0-9 Név, osztály Pontszám I. rész - A rendelkezésre álló idő: 45 perc I. rész 30 pont Érdemjegy II. rész 70 pont Összesen
JELENTÉS. Középiskolát végzett diákok helyzete - 2012-2013 -
- 0 - HMTJ 25 /2015 Ikt. szám:1855/27.01.2015 JELENTÉS Középiskolát végzett diákok helyzete - 2012-2013 - Előterjesztő: Elemző Csoport www.judetulharghita.ro www.hargitamegye.ro www.harghitacounty.ro HU
Tanulói elégedettség mérés 2011/2012. tanév
1 Tanulói elégedettség mérés 2011/2012. tanév Kiküldött kérdőívek száma: Visszaküldött kérdőívek száma (): Visszaküldött kérdőívek száma (): Visszaküldött kérdőívek száma (): Visszaküldött kérdőívek száma
1. Hány király él a mesében? egy... Hány lánya van neki? három... Hány országa van? három...
A SÓ (népmese) Hol volt, hol nem volt, élt egyszer egy öreg király s volt három szép lánya. Volt néki három dúsgazdag országa, mindhárom lányának jutott egy-egy ország. Hanem ahogy mondják: nincs három
Azonosító jel: MATEMATIKA EMELT SZINTŰ ÍRÁSBELI VIZSGA május 5. 8:00. Az írásbeli vizsga időtartama: 240 perc
ÉRETTSÉGI VIZSGA 2009. május 5. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI VIZSGA 2009. május 5. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM
Fiatalok helyzete a Szobi Járás területén
Fiatalok helyzete a Szobi Járás területén A Börzsöny Duna Ipoly Vidékfejlesztési Egyesület felmérést végez a 16 35 éves Szobi Járásban lakó fiatalok körében. A felmérés eredményeit a Helyi Fejlesztési
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Statisztika
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Statisztika A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Az új Tanulási stílus kérdőív. A kérdőív skálái, használati javaslatok, kutatási eredmények
Az új Tanulási stílus kérdőív A kérdőív skálái, használati javaslatok, kutatási eredmények Miről lesz szó? Az új tanulási stílus kérdőív kialakítása A kérdőív és az alskálák bemutatása A kérdőív használata
ANGOL MUNKAKÖZÖSSÉG KÉPZÉSI FORMÁK. Hat évfolyamos képzés. Munkaközösségünkhöz 11 kolléga tartozik. Hegedűsné Lellei Andrea. Vinczéné Farkas Györgyi
ANGOL MUNKAKÖZÖSSÉG Munkaközösségünkhöz 11 kolléga tartozik. Bajczi Tünde Drubina Éva Hegedűsné Lellei Andrea Kiss Gergely Ladinszki István Palicz Éva Pesti Pálma Price Andrew Szányelné Ősz Andrea Vasváry
Hányan vannak ilyenek, ha? Halmazelmélet 2. feladatcsomag
Halmazelmélet 3.2 Hányan vannak ilyenek, ha? Halmazelmélet 2. feladatcsomag Életkor: Fogalmak, eljárások: 13 16 halmazok halmazműveletek halmazok számossága Venn-diagram logikai szita 2 halmazra alkalmazva
A Bornemisza Péter Gimnázium, Általános Iskola, Alapfokú Művészeti Iskola, Óvoda és Sportiskola tájékoztatója a 2017/2018. tanévben induló tanulmányi
A Bornemisza Péter Gimnázium, Általános Iskola, Alapfokú Művészeti Iskola, Óvoda és Sportiskola tájékoztatója a 2017/2018. tanévben induló tanulmányi területek képzési struktúrájáról Tájékoztató a tagozatokról
Curie Matematika Emlékverseny 6. évfolyam Országos döntő Megoldása 2017/2018.
Feladatokat írta: Tóth Jánosné Szolnok Kódszám: Lektorálta: Kis Olga Szolnok 018.04.07. Curie Matematika Emlékverseny 6. évfolyam Országos döntő Megoldása 017/018. Feladat 1... 4.. 6. Összesen Elérhető
Logika, gráfok Megoldások
Logika, gráfok Megoldások 1) Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először Ádám és Tamás nézték meg figyelmesen
Diósgyőri Gimnázium. A 2013/2014-es tanévben induló képzések
Diósgyőri Gimnázium OM azonosító: 029262 Cím: 3534 Miskolc Kiss tábornok 42. Tel/Fax: 46/370-701 E-mail: suli@dig-misk.sulinet.hu Honlap: www.dig-misk.sulinet.hu A 2013/2014-es tanévben induló képzések
Varga Tamás Matematikaverseny Javítási útmutató Iskolai forduló 2018/ osztály
1. Dóri a könyveit két polcon tartotta úgy, hogy a felső polcon volt könyveinek egyharmada. Egyszer átrendezte a könyveket: az alsó polcon lévő könyvek egyharmadát feltette a felső polcra, majd az eredetileg
Curie Matematika Emlékverseny 5. évfolyam Országos döntő Megoldása 2017/2018.
Feladatokat írta: Tóth Jánosné Szolnok Kódszám: Lektorálta: Kis Olga Szolnok 08.04.07. Curie Matematika Emlékverseny. évfolyam Országos döntő Megoldása 07/08... Feladat.. 3. 4... összesen Elérhető 4 7
Gimnáziumi (4,5,6,8 évf.), szakközépiskolai, szakiskolai Adatlap
Gimnáziumi (4,5,6,8 évf.), szakközépiskolai, szakiskolai Adatlap Intézmény neve: Kossuth Lajos Evangélikus Általános Iskola, Gimnázium és Pedagógiai Szakközépiskola 1. Általános felvételi eljárásban felvételi
ZA4986. Flash Eurobarometer 260 (Students and Higher Education Reform) Country Specific Questionnaire Hungary
ZA4986 Flash Eurobarometer 260 (Students and Higher Education Reform) Country Specific Questionnaire Hungary FLASH 260 STUDENTS AND HIGHER EDUCATION REFORM Kérdező azonosító Település neve Válaszadó azonosító
50. modul 1. melléklet 2. évfolyam tanítói fólia
50. modul 1. melléklet 2. évfolyam tanítói fólia 50. modul 2. melléklet 2. évfolyam tanítói fólia 50. modul 3. melléklet 2. évfolyam tanítói fólia 50. modul 4. melléklet 2. évfolyam tanítói fólia és csoport
Írd le, a megoldások gondolatmenetét, indoklását is!
0 Budapest VIII., Bródy Sándor u.. Postacím: Budapest, Pf. 7 Telefon: 7-900 Fax: 7-90. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ 0. április. HARMADIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ Írd le,
A GENERÁCIÓK MEGKÖZELÍTÉSE ÉS ÖNREFLEXIÓJA
A GENERÁCIÓK MEGKÖZELÍTÉSE ÉS ÖNREFLEXIÓJA Amikor tizennégy éves voltam, apámat annyira tudatlannak találtam, hogy alig bírtam elviselni jelenlétét. Amikor huszonegy lettem, megdöbbentett, milyen sokat
III. 1. feladat. forduló
1. feladat Teki egy négyjegyű számot írt fel egy számkártyára. Erről a számról a következőket árulta el: Négy szomszédos számjegy szerepel benne összekeverve. Van benne 9-es számjegy. Az egyesek helyén
33. modul 1. melléklet 3. évfolyam Mérőlap/1. Név:. 1. Becsüld meg az összegeket! A tagok százasokra kerekített értékeivel végezd a becslést! Majd végezd is el az összeadásokat. Számításaidat kivonással
A B.Sc. képzésben résztvevı hallgatók számára a diploma megszerzésének feltétele
szöveg: Hajdók Ibolya TÁJÉKOZTATÓ (1) (2010 szeptemberében beiratkozó elsıéves hallgatóknak) A DIPLOMA MEGSZERZÉSÉNEK NYELVI FELTÉTELEI 1. AKKREDITÁLT NYELVVIZSGA A B.Sc. képzésben résztvevı hallgatók
AVASI GIMNÁZIUM FELVÉTELI TÁJÉKOZTATÓ 2014/2015-ÖS TANÉV. Általános kerettantervű képzés, emelt szintű nyelvoktatással (Tagozatkód: 13)
AVASI GIMNÁZIUM FELVÉTELI TÁJÉKOZTATÓ 2014/2015-ÖS TANÉV Cím: 3524 Miskolc, Klapka Gy. u. 2. OM kód: 029264 Telefon: 46/562-289; 46/366-620 E-mail: titkarsag@avasi.hu Honlap: www.avasi.hu I. A 2014/2015.
Gyakorló feladatsor matematika javítóvizsgára évfolyam.docx
1) Öt barát, András, Bea, Cili, Dani, Endre versenyt fut egymással. Hányféle beérkezési sorrend lehetséges, ha nincs holtverseny? 2) Hat barát, András, Bea, Cili, Dani, Endre, Fruzsina versenyt úsznak
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Statisztika
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI EMELT SZINT Statisztika A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Hetedikesek levelező matematikaversenye IV. forduló
Hetedikesek levelező matematikaversenye IV. forduló 1. Tudjuk, hogy A = 3 + és B =. Számítsd ki a következő értékeket: a) A + B b) A B c) d) A B Számítsuk ki A és B értékét, végezzük el a műveleteket:
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Számelmélet
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Számelmélet A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek