Programrendszer LC szűrők tervezésére
|
|
|
- János Somogyi
- 9 évvel ezelőtt
- Látták:
Átírás
1 DR. H E R E N D I MIKLÓS Műszeripari Kutató Intézet Programrendszer LC szűrők tervezésére BTO 519.6S Z A Műszeripari Kutató Intézetben több, mint 10 év óta folynak a számítógépes tervezés egyes problémáinak megoldására irányuló munkák. Egyik hosszú idő óta művelt témakör az LC és az aktív RC szűrők tervezése. Az LC szűrők tervezése különösen számításigényes feladat. Ez az oka annak, hogy az üzemi paraméteres tervezés elvének szélesebb körű felhasználására csak a számítógépek elterjedése után került sor. Az újabb, kedvezőbb számítási módszerek kutatása azóta is folyik. A fejlődés fontos lépése volt a transzformált frekvenciaváltozó bevezetése. Az első transzformált frekvenciát használó programot Szentirmai [1] készítette, Magyarországon pedig Radványi Jenő írta [2]. A szerző is hosszabb ideje foglalkozik ilyen programok megvalósításával [3, 4]. Az a munka, melyről ez a cikk beszámol a KGM CF 22. Számítógépes áramkör tervező, gyártó és ellenőrző rendszerek" célfeladatán belül folyt és eredménye része a TKI, SZTAKI, KFKI, MIKI és HIKI együttműködésével megvalósuló AUTER rendszernek. 1. Kiinduló meggondolások Ebben a fejezetben megkíséreljük megfogalmazni egy LC szűrőket tervező programmal szemben támasztandó legfontosabb elvárásokat és megvizsgáljuk, hogyan lehet ezeket teljesíteni Alapkövetelmények Vizsgáljuk meg először is, hogy milyen követelményeket kell kielégítenie egy olyan programnak, amely a szűrőtervezési feladatok jelentős részének megoldására használható. Aluláteresztő és sávszűrő tervezése Az aluláteresztő és a sávszűrő az a két legtöbbször előforduló szűrőfajta, melyeknek közvetlen terve- Beérkezett: IV. 23. zéséről nem mondhatunk le. Már más a helyzet a felüláteresztővel. Amíg veszteségmentes szűrőről van szó, aluláteresztő tartományba transzformált követelmények alapján aluláteresztőt tervezhetünk, melyből reaktancia-transzformációval kapható a felüláteresztő. A veszteséges felüláteresztővel azonban az irodalom nagyon mostohán bánik. Még az(l) helyett aluláteresztő, felüláteresztő és sávszűrő esetére egyaránt használható 2 2 =(1 eo;f 2 co 2 )/(co- 2 co a ) transzformációt sem javasolták. Egyelőre mondjunk le róla. A sávzáró esetét könnyen elintézhetjük. 0 és =» frekvenciás tolóelemek hiányában a lefejtés a szokásos módon nem oldható meg, tervezésre tulajdonképpen csak az aluláteresztő sávszűrő reaktanciatranszformáció használható. Maximális laposságú és egyenletes közelítésű áteresztőrész i Mindkét típus tervezhetősége alapvető szükséglet. Bonyolultabb áteresztőrészbeli csillapításkövetelmények kielégítése hasonló módszerrel volna lehetséges, mint amit a zárórész közelítésére használunk [5], de ez ritkán elkerülhetetlen. Lépcsős toleranciasémát kielégítő zárórész A max. lapos és egyenletes közelítésű szűrők -zárórészében a csillapítást nagyon könnyen lehet számítani asztali programozható kalkulátoron a 3.4 pontban bemutatott képletekkel. A csillapításpólusokat felvéve és módosítva, próbálgatással is használható eredményt lehet elérni, ha az előírások elég enyhék. Szigorúbb követelmények, illetve magasabb fokszámú szűrő esetén feltétlenül a precíz eredményeket adó számítás látszik célszerűnek. Veszteséges szűrő tervezése előtorzítással A veszteségek figyelembevétele el nem kerülhető. Nagyon szigorú előírású vagy nagyon széles sávú szűrőktől eltekintve az egyszerű előtorzítás legtöbbször elfogadható eredményt ad még akkor is, ha a szűrő veszteségeloszlása nem felel meg a számításnál feltételezett egyenletes eloszlásnak. Ez utóbbi nehézségen segítene a Darlington [6] vagy a Zdunek [7] által javasolt bonyolult tervezési módszer, nagypontosságú szűrőknél azonban az alkatrészek veszteségi tényezőinek frekvenciafüggése miatt úgyis további 225
2 HÍRADÁSTECHNIKA XXX. ÉVF SZ. hibák lépnek fél. Ezek korrigálásakor a veszteségeloszlás okozta eltérés is javítható. Szimmetrikus és antimetrikus konvencionális szűrők A szűrési feladatok nagy része megoldható a Skwirzynski-féle osztályozás [8] szerinti 2 és 4 osztályú ahtimetrikus, 3 és 5 osztályú szimmetrikus aluláteresztőkkel, valamint a 10 és 20 osztályú antimetrikus, 12 és 18 osztályú szimmetrikus sávszűrőkkel (1. 5. fejezet). Ezek az ún. konvencionális max. lapos és csebisevi áteresztőrészű szűrők csillapítás tekintetében optimálisak, minthogy karakterisztikus függvényeik zérushelyei a képzetes tengelyén helyezkednek el, vagy veszteséges esetben legalábbis a jellegük ilyen. A valós <Z>-zérus(oka)t tartalmazó paraméteres szűrők tervezése bonyolult és az alapkövetelmények közül elhagyható. Tervezés transzformált frekvencián A szűrők tervezésének bizonyos lépései során az adatok fokozatosan veszítenek pontosságukból. Ezt a hatást sokjegyű számok, használatával [9], a függvények zérus- és pólushelyeit széthúzó frekvenciatranszformációval [1] és a polinomok együtthatói helyett gyökeik tárolásával [10], sőt e módszerek kombinálásával [11] szokták csökkenteni. A transzformált frekvencia alkalmazása több approximációs feladatnál is egyszerűsítést jelent. Programozási tekintetben előnyei és hátrányai is vannak. Végeredményben az approximációs és realizációs számításokban egyaránt célszerű használni. FORTRAN programozási nyelv, DOUBLE PRECISION változók Az IBM System 360/370 és az ESzR gépek térhódításával párhuzamosan az ALGOL programozási nyelv háttérbe szorult és a FORTRAN nyelv használata a műszaki számításoknál általános lett. Elterjedtsége és szabványosítási helyzete [12] alapján használata előnyös, a programok könnyen honosíthatók más gépeken is. Az említett gépek REAL változói céljainkra nem adnak elég pontosságot. Mantisszájuk effektív hoszsza számítás közben a hexadecimális normalizálás miatt 21 bitre csökkenhet, ami csak kb. 6,3 decimális jegynek felel meg. A nehézségeket még növeli a műveletek eredményeinek csonkítása. így a DOUBLE PRECISION típusú változók használata elkerülhetetlen. Analízis A tervezés során a kívánt szűrő többé-kevésbé ideális modellje jön létre. Fontos, hogy rendelkezésre álljon egy analízis program, mellyel a számítás eredményét realisztikusabb körülmények között vizsgálhatjuk, vagy a tervezéskor figyelembe nem vett hatásokat (futási idő, tűrések) ellenőrzizhetjük. Sokoldalúság bővíthetőség Egy tekintélyes szellemi és anyagi ráfordítással létrehozott nagy program merevségének gyors elavulás (vagy az állandó módosítgatás) a következménye. Arra kell törekedni, hogy a program a feladatok széles körének megoldására legyen használható, ideértve esetleg ma még ismeretlerí feladatokat is. Az a tapasztalat, hogy sok tervezési feladatnál merülnek fel különleges kívánalmak. Ezeknek teljesítése során a sokoldalúság nagy előny. Bonyolultabb feladatok sokszor csak bővítéssel oldhatók ^meg. Ilyen esetekben nagy előny, ha a bővítés könnyen csatlakoztatható az eredeti programhoz. A sokoldalúság megkövetelése mellett is célszerű arra törekedni, hogy egy feladat adatainak összeállítása ne legyen bonyolult. Előnyös emellett, ha egy tervezés a specifikációtól a realizálás.egy minél későbbi fázisáig egy szervesen összefüggő adatsorral előírható Megvalósítási lehetőségek Ilyen méretű feladat megvalósítását legegyszerűbb nagy számitógépen elképzelni. A program nagyságát géptől, fordítóprogramtól függően kbytera becsülhetjük. A GILDA program [4] kb. 300, a FILSYN program kb. 200 kbyte [11] egy modernebb gépen. A megoldás előnyei: a nagygép sokoldalú szolgáltatásai rendelkezésre állnak; időosztásos üzemmódban a központi egység által fogyasztott idő kicsi. Hátrányok: az egy felhasználó által igénybe vehető tárterület rendszerint korlátozott, ezért a programot overlay stukturájúra kell készíteni; drága a program fejlesztése, mert a nagy program szerkesztése idő- és tárigényes; minden javítás, módosítás sokba kerül és minden bővítés bonyolítja az overlay struktúrát; a felhasználó testben és lélekben távol van a géptől, nem befolyásolhatja a feladat futását. A kitűzött cél megvalósítására felhasználható másik lehetőség: kisszámítógépen futtatott-kis programok rendszere. A rendszer szó külön hangsúlyozandó, mert nem szervesen összekapcsolódó programok sorozata ilyen nagyságú feladat megoldására nem használható. A kisszámítógép helyett viszont egyre inkább elképzelhető egy korszerű programozható kalkulátor. A megoldás előnyei: a rendszer egyes programjai külön-külön írhatók, szerkeszthetők, tesztelhetők, javíthatók; a rendszer könnyen bővíthető új programokkal. Hátrányok: kicsi a rendelkezésre álló tárterület; a tárterület jelentős részét teszik ki az adatok; kevés hely marad a program számára; a program egy részét a program felosztottsága miatt ismétlődő feladatokra vagyunk kénytelenek elhasználni; meg kell oldani két feladatot, a programok egymás közti adatforgalmát és a programok egymás utáni betöltését és indítását. A DPLC programrendszer.kidolgozásakor a második lehetőséget tartottuk szem előtt. Ügy véljük azonban, hogy a választott megoldások nem zárják 226
3 DB. HERENDI M.: PROGRAMRENDSZER LC SZŰRŐK TERVEZÉSÉRE ki a rendszer egy nagygépes megvalósítását, sőt úgy tekintjük, hogy az overlay ágakra való felbontását és az ágak tesztelését jórészt elvégeztük. 2. A DPLC programrendszer jellemzése A DPLC programrendszer kidolgozása a Műszeripari Kutató Intézet R12 számítógépén történt. A gép operatív memóriája 64 kbyte. Az operátori konzol alfanumerikus display, amit mátrixnyomtató egészít ki. A rendszerlemez kb. 800 kbyte kapacitású fix lemezegység. Lyukszalagolvasó és -lyukasztó, kártyaolvasó, sornyomtató és két ESz5052 lemezegység képezik a perifériákat. A rendszer az OS12 operációs rendszert használja az MPBMDR monitorral. A programok a BG zónában futnak, betöltési hosszuk 30 kbyte alatt lehet. A programok egy ESz 5052 lemez file-jaiból binárisan tölthetők a tárba BATCH vezérlés alatt. A betölthető különböző programok számát ekkor csak a lemez kapacitása korlátozza (jóval 100 felett). Ez a módszer azonban lassú és nehézkes. Sokkal kedvezőbb a programokat a rendszerlemeznek a futtatható programok (EP) könyvtárából az operátori konzolról vagy a futó programokból kezdeményezett parancscsal betölteni és elindítani. így a futtatható különböző programok számát a könyvtár kapacitása esetleg korlátozza. A programok betöltési és indítási módjai egy feladaton belül is kombinálhatók. Az adatok átadása a futó programban kijelölt közös adatmezőknek a rendszerlemez GIGO zónájába írásával, ill. onnan visszaolvasásával történik. A felhasználó adataival közvetlen kapcsolatban álló minden program a FORTRAN 6 byte hosszúságú DOUBLE PRECISION típusúként specifikált változóit használja. / A felhasználó adatainak hordozója páros paritású ISO 7 (ASCII) kódú lyukszalag, lyukkártya, vagy ESz 5052 lemez file lehet. Az adathordozók váltására is lehetőség van. Később sok helyen egyszerűen az adatszalagra fogunk hivatkozni akkor is, ha ez esetleg más adathordozót is jelenthet. A DPLC programrendszer megfelel az 1.1. pontban felállított követelményeknek. E cikk további fejezeteivel az Olvasót is igyekszünk erről meggyőzni. 3. Számítási módszerek A DPCL programrendszer kidolgozása során sok hálózatelméleti és matematikai feladat merült fel. Ezek közül itt csak néhánnyal foglalkozhatunk. A fontosabb jelölések a következők: a csillapítás [db], a p megengedett csillapításingadozás az áteresztőrészben [db], b forgatás, k =yio»/ío-i m a véges nemzérus csillapításpólusok száma, n =2m + n 0 + n a, a szűrő fokszáma, n 0 a zérusfrekvencián lévő csillapításpólusok száma, n a végtelén frekvencián lévő csillapításpólusok száma, P t z a fi r 0 eoi / 0 I < IHG65-WM 1 0) ábra. A z 2 = - - függvény cui 0) = o + ja> komplex frekvencia változó, transzformált frekvenciaváltozó, -eofz 2 átviteli függvény, karakterisztikus függvény, alsó hatáfrekvencia, felső határfrekvencia A transzformált frekvenciaváltozó Szentirmai javaslata [1], valamint Orchard és Temes munkássága nyomán [13] alakult ki a transzformált frekvenciaváltozó használatának módszere. Definiáljuk sávszűrőre a Z" = eo?+p 2 Re z>0 (1) transzformációt. Az aluláteresztő mint az co^o speciális eset értelmezhető. A p-sík képzetes tengelye co 2 függvényében az 1. ábra szerint képeződik le a z 2 változóra. A ± és + ja> 2 közötti áteresztőrésznek a z-síkon a teljes képzetes tengely felel meg. A F átviteli és a 0 karakterisztikus függvény zérusai és pólusai melyek a p-síkon az u> t és co 2 határfrekvenciák környezetében tömörülnek az síkon széthúzódnak, hiszen a határfrekvenciák transzformáltjai 0 és. Az így adódó kedvezőbb numerikus viszonyok a számítások pontosságát kedvezően befolyásolják. Az (1) transzformáció megfordítása cofz 2 z 2 -l l a (2) 227
4 228 HÍRADÁSTKCHNrKA XXX. ÉVF SZ Egyenletes közelítésű áteresztőrész [ ] approximációj'á Legyen célunk olyan karakterisztikus függvény felírása, amely 0 és a p között ingadozó csillapítást eredményez az áteresztőrészben és a zárórészbeh előírt csillapításpólusai vannak, ez az általános paraméterű szűrő approximációs feladata. Evégből képezzük a P(z) =(t+z)"i 1 +2)"- JJ( Zi + zf = E + zf (3) Hurwitz-polinomot, ahol az au, előírt pólusfrekvenciához (1) szerint Zr- 0)2 mjj ml Oili tartozik. A kívánt karakterisztikus függvény abszolút értékének négyzete (4) k 2 E 2 \0(z)\ 2 = (5) Ennek a z 2 <0 tartományban (az 1. ábrából tudjuk, hogy z 2 <0 az áteresztőrésznek felel meg) minimuma E zérushelyeinél 0, maximuma zf zérushelyeinél k 2 és az ingadozások száma a lehető legnagyobb a Hurwitz jelleg előírása következtében. A csillapításpólusokat a nevező, azaz E 2 -z 2 F 2 =(E+zF)(E-zF) = P(z)P( -z) = m = ( í 2-2$#»'(1 - z 2 )"~ JJ (z? - z 2 ) 2 ( 6) 1=1 zérushelyei adják úgy, amint előírtuk. alakban lehet felírni egyenletes közelítés esetén, míg c + z 2 \" ( c + z 2 \ n - SL ( c + z 2^2 a(z)^10 log k 2 t 2 -z* 1- n =i z: (11) maximális laposságú áteresztőrész esetén. Amikor a csillapítás toleranciasémája van a zárórészben előírva, akkor n a, n x ismertnek tekinthető, meghatározandó m értéke és az m darab z t - csillapításpólus. Erre a célra a Smith és Temes által javasolt módszert [14] használjuk. A csillapítás és a toleranciaséma közötti különbségnek, a csillapítástártaléknak minimuma lépcsős toleránciaséma esetén csak ennek szakadási pontjaiban, vagy a belógások legalsó pontjaiban lehet [15]. Ezeknek a lokális minimumoknak az abszcisszáit meghatározva egy nemlineáris egyenletrendszer írható fel a minimumok zárórészenkénti kiegyenlítésére. Az egyenletrendszert linearizálva, iterációsán oldjuk meg. A minimumkereséshez és az egyenletrendszer linearizálásához a deriváltak egyszerűen felírhatok. Egyenletes közelítés esetén da(z) 1z~' = n 0 t + - W^z 2 ' 1-z 2 3a{z) -2z dzj -z]-z 2 míg max. lapos közelítéshez da(z) dz 3 r U [c + z 2 + m 0,2 itízf-z 2 f "* 2MU 2 - (12) (13) (14) 3.3. Maximális laposságú áteresztőrész approximációja da(z) ^ -2zj dz, ~-z)-z 2 ' (15) Möst a maximális laposságú áteresztőrész mellett ugyancsak előírt csillapításpólusokat kívánunk megvalósítani. A karakterisztikus függvény abszolút értékének négyzete ekkor k 2 (z 2 + c) n \0(Z)\ 2 = (7) E 2 -z 2 F 2 ahol a nevező polinomjait ugyancsak (3) definiálja, míg á c állandó z 2 -nek azt az értékét jelenti, amelynél a deriváltak zérusok. A határfrekvenciákra előírt egyenlő csillapításokból 3.4. A zárórészek közelítése A db-ben kifejezett a(z)= 10 lcg[l+ <Z>(z) 2 ] (9) csillapítást a záróreszben közelítőleg az Figyelemre méltó, hogy ezek a képletek [15,16] az irodalomban közöltekkel [13,14] szemben nem tartalmaznak hiperbolikus függvényeket, ezért nagyobb sebességgel számíthatók A láncmátrix elemeinek előállítása A karakterisztikus függvény abszolút értéke négyzetének ismeretében a következő lépés 0 és r előállítása. Eltekitnve most az egyszerűsítéseket megengedő esetektől, tekintsük át a számítás folyamatát az általános veszteséges esetben. A 2. árjrán a számítás felülről lefelé halad és az egyes oszlopok a 0,\0\ 2, \r\ 2 és r reprezentációjának felelnek meg. A beírt nevek a megfelelő funkciót végző szubrutinok nevei. Vegyük röviden sorra a műveleteket. 0. A kiinduló függvény legyen (5) vagy (7). írjuk ezt (5ö) ^'HSf alakban, ahol az index helyén lévő csillag a változó előjelváltását jelenti.
5 DR. HERENDI M.: PROGRAMRENDSZER LC SZŰRŐK TERVEZÉSÉRE \SECT0R T IC0MP0S Át, e* lepi* I0I 2 \FACT0R] 1 irf- \FACWR 1 1 KMjN \SECTOR\ COUPOS Ar, Sr fh 665-HM ábra. A lefejtéshez szükséges polinomok előállítása 9. Az előtorzított karakterisztikus függvény- ar> szolút értékének számlálóját állítjuk elő, azután a höz hasonló gyöktényezőkre * bontás következik. 11. Az egyszerűség kedvéért 0 bal félsíkra eső zérusait tartalmazó gyöktényezőket választjuk ki. 12. A gyöktényezők szorzataként a COMPOS szubrutin előállítja a karakterisztikus függvény számlálóját. A 0 {z 2 ) + B^)f^ (20) alakban. 13. A szűrőt megvalósító reaktáns négypólus láncmátrixa elemeinek előállításához a z 2 -től függő polinomok szükségesek. 7t = A r +A i> \ g=b r +B 0 y=b r -B 9 A r A 0 a = - oc/9 (21) 1. A Feldtkeller-összefüggés [17, 5.5 fej.] felhasználásával FF 4-PP \r\ 2 =i+\ \ 2 =^j pt. 2. Az FF% + PP% polinomot (i6) z l + Mz 2 + N, illetve z 2 -L (17) tényezőkre bontjuk. Ezek egy konjugált komplex zéruspárt, ill. egy valós zérust és a képzetes tengelyre vett tükörképét tartalmazzák. 3. A 2 szerinti gyöktényezőkből a SECTOR szubrutin előállítja azokat a Pz 2 + Q + RY^P (18a) alakú másodfokú, ill. (aluláteresztőnél) Q + Y* (186) alakú elsőfokú gyöktényezőket, melyeknek a p-sík bal félsíkjára eső zérus felel meg. Itt látszik már, hogy a transzformált változó használata nehézségekkel is jár, hiszen a gyökös kifejezéseket is kezelni kell a számítás folyamán. 4. 7\3-beli gyöktényezőinek együtthatóit kell úgy megváltoztatni, hogy a p-síkon megkívánt előtorzítás létrejöjjön. 5. A gyöktényezőkből a COMPOS szubrutin állítja elő az átviteli függvény számlálóját l AAz^ + BA* 2 )^ (19) alakban. (19) két része a p-síkon a páros, ill. páratlan résznek felel meg.. 6. (19)-ből visszafelé ismét elő kell állítanunk a K-\r\ 2 függvényt, ahol a K állandót nem ismerjük; ebből 7. A KMIN szubrutin megkeresi a minimum értékét. 8. A minimum értékével való osztás után \r\ 2 a realizálási feltételeket kielégíti A lefejtendő immittanciák e's a lefejtés A kapcsolási elemek meghatározására használható immittanciák reaktánsak, a p változóban páratlan függvények, a z változóban tehát mindig tartalmaznak egy gyökös kifejezést, a-t vagy fi-t. Szentirmai javasolta [1] a Z/p vagy Y/p alak alkalmazását, ezek csak z 2 függvényei. Az 1. táblázat a lefejtéshez felhasználható primer és szekunder üresjárási és rövidzárási impedanciákat foglalja össze. Aluláteresztő esetén definíciószerűen /3=1. A vastag keretű impedanciákból a szűrő öszszes kapcsolási elemei meghatározhatók, a többieknél a lezárások miatt a fokszám kisebb. 2 osztályú aluláteresztő primer oldali üresjárási impedanciájában például az utolsó soros tekercs nem szerepel, (1. 6. ábra), ezért Z JÜ /p-ből nem lehet meghatározni. A DPLC programrendszer automatikus realizálás esetén mindig a teljes fokszámú primer oldali impedanciát választja a lefejtés kiindulásául. A kapcsolási elemek értékeit meghatározó eljárás tárgyalásába itt nem bocsátkozhatunk. Lefejthető impedanciák 1. táblázat Osztály %2ü LP BP v v. ~v~ P 2 10 txer cty 71 V Q 71 '> Q 71 y Pv PQ n e O.Q 4 20 Pv (la a.y (X.0 OCQ a.a 71 Q 71 V 229
6 HÍRADÁSTECHNIKA XXX. ÉVF SZ. 3.7, R 2 meghatározása Az R 2 szekunder oldali lezáró ellenállás meghatározásának szokásos módszere a szűrő kétoldali (részleges) lefejtése és az azonos kapcsolási elemek kétoldali értékeinek összehasonlítása. Ez két lefejtést jelent, valamint a kapcsolás megfordítását, ami egyébként nem is mindig lehetséges [1]. Az alább ismertetett módszer lehetővé teszi a szekunder oldali lezáró ellenállás meghatározását egy oldalról való lefejtés és bármilyen transzformáció után. 3. ábra. Ka meghatározása H 665-MM3 Tekintsük a 3. ábrát. Az N szűrő kapcsolási elemeit a lefejtés során meghatároztuk, primer oldala R ± ellenállással van lezárva, keressük a helyes R 2 lezáró ellenállást. Kiindulópontunk az, hogy a reflexiós mátrix,s 22 eleme (a szekunder oldali reflexiós tényező) zérus, ha Z 2 =R 2. ^~Z 2 +R, Megfordítva íí 2 =Z 2 s aa =o reaktáns hálózatra pedig igaz az, hogy (22) (23) S*A-Pi) = 0. ha 0( Pi ) = O, i=l n, (24) úgyhogy R 2 =Z 2 (- Pj ), ;c{l,2,...,n}. (25) Tehát a szekunder oldali lezáró ellenállás egyenlő a szekunder oldali bemenő impedanciával a karakterisztikus függvény zérushelyeinek ellentétes előjellel vett értékeinél. A módszer veszteséges szűrő előtorzítással való tervezésére is igaz, hiszen ennek lényege éppen az, hogy a veszteséges szűrő tervezését reaktáns szűrő számítására vezeti vissza. A számítási hibák miatt a (25) szerint nyert R 2 értékek nem lesznek egyformák és nem lesznek tiszta valósak. Az eltérésekből a pontosság becsülhető Az analízis A szűrő csillapításának számítási módszere a korábbiakban [19] már alkalmazott kontinuáns-módszer. A szűrő tárolt leírásában hatféle ág szerepel. Az első négy megfelel az Saal-Ulbrich-féle szekciónak (1. 6. ábra, [18]), az ötödik féle egy antirezonáns, a hatodik féle pedig egy rezonáns ág, mint azt a 4. ábra mutatja. így a páratlan számmal jelzett ágak sorosak, a páros számmal jelzettek sönt ágak. A program ezt felhasználja arra, hogy az ág jelzését a sorszámával összehasonlítsa és egy üres ellentétes jellegű ágat vegyen figyelembe olyankor, amikor két egyforma párosságú ág következik egymás után. A futási idő számítása különösen egyszerű közelítő módszerrel történik. A F átviteli függvény logaritmusát a p komplex változó függvényeként valós és képzetes részekre bontva és a futási idő g \n r(a + ]'ta) = a( a, co) + jb( a, co) (26) 3b_ r(ft)): ~'dco (27) alakban fejezhető ki. Most gondoljuk meg, hogy a p-síkon a szűrő áteresztőrésze környezetében P-nak és In -T-nak nincs szingularitása, tehát g e tartományban reguláris és így érvényesek a da da'' Cauchy Riemann lyett tehát db_ dm da dco ÉL da differenciálegyenletek, _da T ~da _ n (28) (26) he- (29) írható, amit a programban véges Av veszteségitényező-növelés hatására bekövetkező Aa [db] csillapításváltozásból a In Aa (30) kifejezéssel közelítünk. Egy futási idő érték tehát még egy csillapításérték számítását igényli minden logikai vizsgálat nélkül. A (30) képlét hibájának vizsgálata azt mutatja, hogy a valós részű, a képzetes tengelyhez közel álló konjugált komplex.t-zéruspárra vonatkozó (relatív) hiba-rész abszolút értéke minden frekvencián kisebb, mint \ Av/2o\. A programban Aif=10~ i, mivel ilyen mérvű bizonytalanság a valóságos LC elemek veszteségi tényezőiben is előfordul. Ih o r * -o Q o o~ 4. ábra. Az analízisprogramban használható szűrőágak [H 6G5" MM
7 DR. HERENDI M.: PROGRAMRENDSZER LC SZŰRÖK TERVEZÉSÉRE -\. Szervezési és programozási kérdések Tériünk át a számítások lebonyolításának kérdéseire. Először bemutatjuk az adatstruktúrát, utána egyéb általános jellegű problémákat tárgyalunk meg Az adatkezelés A közös adatterület A rendszer programjai 6 közös adatmezőt tartal- máznak. Ezek tárolják mindazt az információt, amit a helyes működés biztosítására meg kell őrizni és át kell adni. Az egyes adatmezőket nevükkel azonosítjuk (címkézett COMMON blokkok). CM80 Az utoljára beolvasott input rekordot tartalmazza. Nyilvántartja az utoljára vizsgált karakter sorszámát és annak az adathalmaznak a számát, amelyből a következő rekordot olvasni kell. PRI CPP T1M TIN Tartalma az eredménylap megkezdett oldalán írt sorok száma, a sorok maximális száma, az oldalszám, a hibaszám, valamint a prefixek és dimenziók táblázata. Tartalma a paramétertömb (pl. az analízis frekvenciáit tárolja) és két eredménytömb (pl. a csillapításokat és futási időket tárolják) Tartalmazza az időfeljegyzéseket és az azok azonosítására szolgáló címkéket. A program nevét, a dátumot és a feladat címét tartalmazza. COM A rendszer fő adatterületét, a DAR tömböt tartalmazza. Az ismertetett adatterület teljes hossza 8078 byte. A közös adatterület kezelése Az előzőkben röviden ismertetett közös adatterületen keresztül adják át az egyes programok a számításaik és egyáltalán működésük eredményeit. Az átadás ennek az adatterületnek a rendszerlemez GIGO zónájába való kiírásával, ill. beolvasásával történik. A COMIO szubrutin végzi az ezzel kapcsolatos műveleteket: kivitelnél katalogizálja a tételt, beolvasásnál ellenőrzi a tétel nevét, hosszát, típusát. Természetesen ellenőrzi az átvitelek helyességét. A katalogizálás következtében az adatmező a futtatható programok könyvtárába (EP) felvehető, vagy valamilyen adathordozóra kivihető és így viszszaolvasva akárhányszor felhasználható. Az ar tömb kezelése A COM nevű COMMON mező DAR tömbjét úgy kezeljük, hogy a felhasználó egy real array ar [0:31, 0:29j; Algol deklaráciával előírt tömböt használ. Az ar tömb ar[i, j] elemére az áttekinthetőség érdekében az input adatokból looi + j alakban hivatkozunk. Az ar tömb sorait vektoroknak neveztük el. Minden vektor 0 indexű eleme a vektor elemeinek számát mutatja. Ezzel a számmal is lehet műveleteket végezni. Azok az eljárások, amelyek a vektorokban tárolt mennyiségeket kezelik, a 0 idexű elemet is mindig leolvassák, illetve beállítják. Egy vektor tartalmazhat egy egyszerű adatsorozatot, pl. a csillapításpólusok frekvenciáit, vagy egy polinom együtthatóit a növekvő hatványok sorrendjében. Több vektor együttesen tárolhat egy összetett adatcsoportot. Pl. egymást követő sorszámú két vektor tárolja egy átviteli függvény zérushelyeinek valós, ill. képzetes részeit, vagy egymást követő három vektor tárolja egy polinom gyöktényezőinek együtthatóit. A 0 sorszámú vektor egy ~x polinomot tartalmaz, valamint általánosan használt értékeket, mint pl. a határfrekvenciák, a zérus és a végtelen frekvencián előírt csillapításpólusok száma, a veszteségi tényező, stb. A 30 és 31 sorszámú vektorok területét a rendszer egyes programjai munkaterületként is használják. Az ar tömb elemeibe, vektoraiba, vektorpárjaiba, vagy vektorhármasaiba a READ vezérszó (1. alább) segítségével lehet adatokat beolvasni. Az olvasás terminátorig.folyik, így nem kell előre megadni az adatok mennyiségét. Az említett elemek és vektorok eredménylapra, egységes formában való kinyomtatása a PRINT vezérszóvei indítható. Ezt a funkciót a READ vezérszóval végzett beolvasás önműködően is aktivizálja. Más eljárások is kiírják az eredménylapra a beolvasott adatókat. A DPLC programrendszer sokoldalúságához nagyban hozzájárul az ar tömb univerzális felhasználása. Néhány példa a következő: A számított vagy beolvasott létrakapcsolás tárolása az ar tömb 3 egymást követő vektorában történik. (Ezekhez további vektorok csatlakoznak, amelyek az egyes kapcsolási elemek veszteségi tényezőit tárolják.) így a kapcsolási elemek, sőt a kapcsolás megváltoztatása (pl. felüláteresztőbe transzformálása, parazita elemekkel való kiegészítése) is igen egyszerű. Az ar tömb tartalmaz néhány előre beállított (default) értéket is, melyeket az inputból felül lehet írni, valamilyen kívánt hatás előidézése érdekében, így például az ar tömb egyik elemének egyre nagyobb értékét adva bizonyos eljárások egyre részletesebb eredménykiírásokat produkálnak. A túlságosan nagy előtorzítást is egy default érték korlátozza, amit a felhasználó felülírhat, enyhítve ezzel a korlátot. Az adatmegadás rendszere A FORTRAN igen nehézkes, merev beolvasását csak az egyes input rekordoknak a CH80 COMMON mezőbe való beolvasására használjuk. Minden további input és konverziós funkciót a programrendszer szubrutinjai végeznek. Ezek megírásakor a fő szempont a felhasználó kényelme volt (ami a hibamentes adatok készítését is elősegíti.) Az olvasó eljárások az olvasást az előző olvasás utolsó (terminátor) karakterével kezdik és az illető olvasó eljárásra jellemző első terminátor karakterig olvasnak, vagy ilyen hiányában addig, amíg az olvasásnak értelme van; hibajelzést nenij adnak. A számok betűkhöz karakterekkel tagolhatok, valós számoknak nem kötelező tizedespontot vagy 10 hatványát tartalmazni és a jegyek száma sincs korlátozva. 231
8 \ HfRADÁSTECHNIKA XXX. ÉVF SZ. Az input rekordban levő ; karakter a következő rekord beolvasását eredményezi, mögötte megjegyzések lehetnek. Az adatok felépítése nagyon jellemző: az adatok ún. vezérszavakból állnak, melyek legalábbis a rendszer számára értelmes betűsorozatok nembetű terminátorral lezárva. A vezérszavakat egy WORD nevű eljárás olvassa és legfeljebb első 6 karakterét összahasonlítja egy szótár-tömb elemeivel. A vezérszavakat sok esetben a számparaméterek vagy számadatok követik. A programrendszer egyes programjai részfeladatok sorozatát hajtják végre. A feladatot az input rekordból kiolvasott vezérszó szabja meg. A szükséges számparamétereket legtöbbször ugyancsak az input rekordok szolgáltatják. A feladat végrehajtása után a program a következő vezérszó olvasására tér át. Ennek a rendszernek az előnyei abban vannak, hogy a vezérszavak az input adatokat könnyen olvashatóvá és ellenőrizhetővé teszik, a vezérszavak és számok váltakozása erős kontrollt jelent: egy többlet, egy hiányzó vagy helytelenül beírt adat általában hibajelzésre vezet, az adatmegadás sorrendje kötetlen, pontosabban csak az az előírás, hogy egy funkció aktivizálásakor a szükséges adatok rendelkezésre' álljanak, v ha csak az adatok egy része változik ismétlődő számításoknál, csak az új adatokat kell"beolvasni, a számításokat könnyen lehet változtatni, eredményüket korrigálni, kiíratni, átmásolva megőrizni stb. Egy sávszűrő tervezéséhez szükséges adatszalag részleteit mutatja be az 5. ábra. Az első sor a feladat címe, a második a határfrekvenciákat, az áteresztőrészben megengedett csillapításingadozást és n 0, n értékét adja meg. Utána a toleranciaséma előírása következik az alsó és a felső zárórészre, majd a csebisevi áteresztőrész előírása és megállás. A második részlet a (21) polinomok kiírásától kezdve látható. A REAL programban a 18 osztályú realizálást írjuk elő, amit a SYLF program hajt végre, utána 1500 O primer oldali lezáró ellenállással DPLC 110 KHZ BANDPASS FILTER* CUTOFFOOO 000, ) AP=1 DB NZNÍO, 1) TOLLOW( , 50, , 60) TOLUPP( , 40) CHEB STOP TITLE Pl AND RHO POLYNOMIALS-c PRINT2(1) TITLE GAMMA AND SIGMA POLYN0MIALS< PRINT2(3) CALL REAL CLASS(18) CALL SYLF SYNTH DENORM(1500) CALL LFAN PAGE ' FREF= LPRINT FREQ LINU1, , 500) LOSS VC(0) VLÍ ) LOSS FREQ LOG(61, , ) LOSS STOP H 665-HM "] 5. ábra. Sávszürőtervezés adatszalagjának ké}< részlete denormalizál. Ezután az LFAN programban végzett analízis adatai következnek Egyéb szervezési kérdések A programok elindítása és megállítása A DPLC programrendszer programjai elindíthatok" egyedileg (pl. tesztelési célokra), vagy rendszerben. Egy feladat első programját operátori vagy BATCH parancs tölti be és indítja el. A program a 4.1 pontban említett COMIO szubrutin segítségével megvizsgálja a rendszerlemez GIGO zónájának tartalmát. Ha ott nem talál névre, hosszra, típusra megfelelő tételt, beolvassa az első input rekordot. Ha az első vezérszó DPLC, törli a COM mezőt, inicializálja a PRI, TIM és TIN COMMON mezőket, majd folytatja a vezérszavak olvasását. Ha a program a GIGO zónában megfelelő tételt talál, beolvassa és a következő vezérszó olvasásával folytatja a megkezdett input rekord feldolgozását. A STOP vezérszó hatására a program először az a közös adatmezőket menti, majd a FORTRAN STOP parancsát hajtja végre. Minden programnak egyéni STOP-száma van, melyet a FORTRAN rendszer az eredménylapra is kiír. A CALL vezérszó felismerésekor a program beolvassa a következő (vezér) szót is, ez lesz a következőként indítandó program neve. A NEXTPR szubrutin a nevet megkeresi az EP könyvtár katalógusában és a betöltéshez szükséges adatokat átadja az operációs rendszer task-kezelő moduljainak az adott program késleltetett (ls) indítására vonatkozó előírással, majd a STOP vezérszónál ismertetett módon megáll. A kijelölt program betöltődik és az e pontban leírt módon elindul. így a programfutások sorozata az adatokból tetszés szerinti sorrendben előírható. Előfordult már, hogy egy-egy bonyolult feladat futtatása 15 programindítást is megkívánt. Időfeljegyzések A DPLC programrendszer egyes programjai induláskor és megálláskor, valamint az egyes fontosabb funkciókat végrehajtó programrészek kezdetén és végén a CLOCK szubrutin paraméterében megadott 6 karakteres azonosító címkét és az operációs rendszerből kiolvasott időpontot beírják a 4.1 pontban említett TIM COMMON mező következő szabad helyére. Hely takarékosság miatt csal a rendszer egyik programja tartalmazza a CLREC szubrutint, amely az időfeljegyzéseket (max. 64) kinyomtatja. Az eredménylapok felépítése A rendszer programjai az eredménylapra kiírt sorokat számlálják. Kiírás előtt ellenőrzik, hogy az előírt kiíratás elfér-e az adott lapon. Ha nem, a lapváltás a PAGE szubrutin segítségével történik, ami a program nevét, a dátumot, a lapszámot és a feladat címét is felírja az új lap tetejére. A PRINT vezérszó (4.1 pont) hatására végzett kiíratás elé a TITLE vezérszó segítségével lehet feliratot előírni, de a kiírt elem vagy vektor(ok) azonosítása enélkül is megtörténik. A megtervezett létrakapcsolású szűrőt az LFAN program vázlatosan ábrázolja. Itt is és az analízis 232
9 DR. HERENDI M.: PROGRAMRENDSZER LG SZŰRÖK TERVEZÉSÉRE eredményeinél is a dimenziós számértékek prefixekkel és a megfelelő dimenziókkal szerepelnek. Az analízis eredményei a sornyomtatón készült ábrán jelennek meg, amely a pontos számértékeket is tartalmazza; A hibajelzések '.. Az egyes programok által felfedezett hibák. az ERREND szubrutint aktivizálják, amely kiírjá á hiba számát és az utolsóként beolvasott input rekordot. Ezalatt egy nyíl mutat az utoljára vizsgált karakterre. A program ezután a közös adatmezők kivitele nélkül áll meg, tehát nem írja felül a korábban kiírt adatmezőt. így egy hosszú számítás hibátlan eredményei nem vesznek el. Nem FORTRAN nyelvű alprogramok A rendszer működése szempontjából alapvető fontosságú NEXTPR és COMIO szubrutinok assembler nyelvűek. Ezenkívül két kis alprogram az input rekordok feldolgozásához, továbbá a dátum és időpont kiolvasására szolgáló alprogramok készültek assembler nyelven. 5. A DPLC programrendszer felépítése Ebben a fejezetben röviden összefoglaljuk a jelenlegi 11 program funkcióját. STAP program A STAP program standard T2 és C típusú aluláteresztők és az ezekből közönséges frekvenciatranszformációval származó sávszűrők csillapításpólusainak frekvenciáit számítja, beállítja továbbá a 0 és frekvencián lévő csillapításpólusok számát is. Minthogy létrakapcsolással kívánjuk a szűrőt megvalósítani, a páros fokszámú aluláteresztők utolsó csillapításpólusát egy fokszámtartó transzformációval oo frekvenciára kell áttenni [18]. Ezt a transzformációt a program elvégzi és a páros fokszámú szűrőknek frekvenián 2 (sávszűrőknek zérus frekvencián is 2) csillapításpólusuk lesz. GEST, GESAPP, POLES programok E három program lépcsős toleranciasémával megadott csillapításelőíráshoz a szükséges csillapításpólusok számát és frekvenciáit határozza meg. n 0 és /? értékét előre meg kell adni, mert ez a tervezendő szűrő kapcsolását erősen befolyásolja. A programok egymás között más csatlakozási felületet használnak, mint a rendszer többi programjával kapcsolódó GEST program és transzformált frekvencián REAL változókkal számolnak. Realizálható LC szűrők tervezésekor ugyan nem követelmény, de aktív RC szűrők zárórészének approximálása során előfordul, hogy n 0 és/vagy n zérus. E programok ilyenkor is helyesen működnek. GEPAA, GEPAB, GROOT programok E három program együttes feladata, hogy a határfrekvenciákból, az áteresztőrészben megengedett leg-^ nagyobb csillapításból, az n 0 és n számokból, valamint a csillapításpólusok frekvenciáiból előállítsák a kapcsolás lefejtéséhez szükséges láncparamétereket a 3.5 pont szerint és ha a szekunder oldali lezáró ellenállást is meg kell határozni, akkor még a karakt terisztikus függvény gyökeit is elő kell álítaniuk. Veszteséges szűrő esetén a számítást előtorzítással kell végezni. Ennek a bonyolult feladatnak a megoldása érdekében a három program egy sor műveletet képes elvégezni, melyeket az input rekordokban írunk elő. Ilyen műveletek: az ar tömb elemeivel végzett számítások, - polinomok és tömbelemek közötti műveletek, polinomok összeadása, kivonása, szorzása, törlése, mozgatása, polinom páros és páratlan részének szétválasztása, polinom gyökereinek és/vagy gyöktényezőinek megkeresése, a P(z) polinom felépítése (3) szerint, transzformációk a p és z tartományok között, a bal félsíkra eső gyökök kiválasztása, polinom osztása elsőfokú gyöktényezővel, két z 2 változójú polinom hányadosa minimumának megkeresése, és hasonlóak. Az approximáció tehát ezeknek a műveleteknek a kombinálásával végezhető el. A szokásos aluláteresztő és sávszűrő esetekre max. lapos és csebisevi áteresztőrész mellett (előtorzítással vagy anélkül), valamint előírt.t-zérusok esetére kidolgozott és kipróbált procedúrák vannak. Ezek lyukkártyán vagy lyukszalagon hozzáférhetők. Szükség esetén további approximációk is kidolgozhatók. A három program szoros összefüggése miatt a programok egymás vezérszavait is felismerik és az elvégzendő feladatot is át tudják adni. REAL program. A REAL program lefejtésnek, azaz a kapcsolási elemek meghatározásának előkészítését végzi. Ha a felhasználónak nincsenek különleges kívánságai, CLASS vezérszóval megadható az a szűrőosztály (6. ábra, [8]), amelynek megfelelően a szűrőt realizálni kívánjuk. A REAL program ekkor ellenőrzi n 0 és n«, kompatibilitását egymással és a megadott osztállyal, majd meghatározza a szűrő kapcsolását. Sávszűrők esetén általános n Q, n és m számok mellett ez a feladat eléggé határozatlan. Legtöbbször azonban n 0 +n = 4 és ekkor a program cikcakk szűrő realizálását írja elő. n mellett a 0 és frekvenciás csillapításpólusokat realizáló szekciók a cikcakk kapcsolású szűrőrész után következnek. Az T I 0 + n < 4 eset alárendelt jelentőségű. A CLASS funkció végrehajtása végén a program standard helyükre viszi át a lefejtendő impedancia számlálóját és nevezőjét képező polinomokat, melyeket az 1. táblázatban foglaltuk össze. A felhasználónak nem kell ragaszkodnia a standard lefejtéshez. Skwirzynski cikkének 2. ábrájából meghatározható a létraszűrő összes lehetséges kapcsolása és ezek közül a REAL programban a 9 és 10 szekciót nem tartalmazó bármelyik előírható egyszerűen a 7. ábrán feltüntetett szekciók sorrendjének megadásával. Ilyenkor azonban nem lehetséges és ezért elmarad n 0 és n ellenőrzése (hiszen paraméteres szűrőt is lefejthetünk) és a felhasználónak kell előírnia a 233
10 HÍRADÁSTECHNIKA XXX. ÉVF SZ. *Ci U. N <o Uj j SÁVSZŰRŐK ' 2. osztóig "7 "1 f ' ' OW n páros \ ' * -W^ - -r fjtf^-l-. 3. osztály ' oj j /7 páration _^ j 4. osztály ^ poros Sf ' '.+ í. osztály! ^ -J T * * *. párolton r to. osztály --X.-VÍ i!; «\ -i» :T_..... r W ' m tt. osztály ^ - TI * *. M -ipáratlan T. _». OSZÍ*^ *~3"P ' " *; r^tr - ' n 0,n páration 0(^5 ' oí T= 3 n, SÍ 3 1 =t i \>, i...i.. o«/d/ y, *; j.. r -- rt"^ n,,n páros J \ j oj [fí 665-TTFT61 6. ííi>ra. Konvencionális szűrők jellegzetes kapcsolásai Jel Kapcsolás Pólusfrekv. M O ^» 0 QfÜ^ «é 0 6 Kapcsolás > 1. frekv. 7 >G> >CÜ 2. IHS66-HM7I 7. ábra. A SYLF programmal lefejthető szekciók fh"665-hm8 8..ábra. Csíllapításpólust realizáló 8. szekció tolóeleme DECOMP vezérszóval azt az impedanciát is, amelyből a realizálás történik. Ha több olyan csillapításpólus van, amelyik ugyanabba a zárótartományba esik, ezek realizálási sorrendje is előírható a POLORD vezérszó után. Ilyen előírás hiányában a SYLF program ezt a sorrendet automatikusan határozza meg. SYLF program A REAL program előkészítése után a SYLF program határozza meg a szűrő tényleges kapcsolási elemértékeit azáltal, hogy az előkészített impedanciát a szekciók előírt sorrendben való lefejtésével realizálja. Ez a művelet ugyanígy, mint az approximáció a DPLC programban transzformált frekvencián történik a pontosság megőrzése érdekében, hiszen ez az egyik legkevésbé pontosságtartó művelet. Ha a csillapításpólusok realizálási sorrendje többféle lehet és a sorrend nincs előírva, a SYLF program a Szentirmai által javasolt módszerrel a lehetségesek közül azt a csillapításpólust választja ki, amelyikhez kisebb tolóelem-immittancia tartozik. Egy 8. szekció megvalósításakor például a C t kapacitás (8. ábra) képezi azt a tolóelemet [17], amellyel az antirezonáns kör lefejtése előkészíthető. Ilyenkor a SYLF program mindegyik számbajöhető co y csillapításpólus-frekvenciára kiszámítja C tj értékét és azt a / sorszámú pólust realizálja, melynél C tj a többi C tk, k^j értéknél kisebb.. Bár ez az eljárás elméletileg nincsen megalapozva és csak arra a feltevésre épül, hogy ha a tolóelemből minden lépésnél a legkevesebbet használjuk el, nagyobb valószínűséséggel marad belőle az utolsó eltolódáshoz is, a gyakorlatban bevált. A SYLF program következő feladata a szekunder oldali lezáró ellenállás meghatározása. A program ezt a számítást önműködően elvégzi, ha a helyükön találja a szükséges komplex frekvenciákat ( pont), egyébként LOARD vezérszó indítja a számítást A lefejtés végén a kapcsolási elemek még normalizáltak. Ha a megadott határfrekvenciák nem normalizált értékek, akkor DENORM vezérszó paramétereként előírt ellenállással denormalizálható a kapcsolás. LFAN program A LFAN program általánosan használható analízisprogram létrakapcsolási szűrők csillapításának és futási idejének számítására. Az LREAD vezérszó hatására egy szűrő leírását, kapcsolási elemeit és lezáró ellenállásait olvassa be. A kapcsolás egyes ágai a 4. ábrán látható ágakkal adhatók meg. A LPRINT vezérszó hatására a program a tárolt kapcsolást kinyomtatja az eredménylapra. Az FREF vezérszóval lehet megadni azt a frekvenciát, amelyre a VL és VC vezérszóval beolvasható veszteségi tényezők vonatkoznak (a jósági tényezőket a program a frekvenciával arányosnak veszi.) A veszteségi tényezők külön sorozatként adhatók meg a tekercsekre és külön a kapacitásokra. Az olvasás) terminátorig folyik és az utolsó érték érvényes lesz azokra az elemekre is, amelyek közvetlenül nem kaptak értéket, így egyetlen értéket elég megadni zárójelben, ha a veszteségi tényezők egyenlők. 234
11 r T)R. HERENDI M.: PROGRAMRENDSZER I.C SZŰRŐK TERVEZÉSÉRE A FREQ vezérszóval az analízis frekvenciáinak generálását lehet indítani. Egyszerre legfeljebb 64 frekvencia írható elő számtani, mértani haladványokból és egyedi frekvenciaértékekből összeállítva. A LOSS ill. DELAY vezérszó a csillapítás, ill. a csillapítás és a futási idő számítását eredményezi. Az eredmények sornyomtatón készült ábrákon jelennek meg, melyek a frekvencia és a számított jellemző számértékét is tartalmazzák. A felhasznált sornyomtató csak 80 karakter széles, az ábrázolás feloldóképességének megtartása érdekében a pontot ábrázoló csillag és a számszerű adatok az ábra ellentétes oldalán helyezkednek el. TESTB program A TESTB program az elkészült szűrő ellenőrzését van hivatva elősegíteni azáltal, hogy mérőautomata vezérléséhez szükséges lyukszalagot készít. A programban előírható egy frekvenciasorozat, vagy átvehető az LFAN programban használt utolsó frekvenciasor. E frekvenciák mindegyikén előírható egy alsó és egy felső csillapításhatár. A TESTB program az adatok alapján elkészíti a mérőautomatát vezérlő ISO 7 (ASCII) kódú lyukszalagot. ytíograu (KI 2) 116 KHZ BANDPASS FILTER LQWER STOPBAKD LOSS CliARACTEfllSTICS FREQUENCr LOSS ( EQUAL ÍUPPLE PASSBAND ) " KHZ ff) KHZ t DB * KHZ DB! KHZ DB I * KHZ DB I KHZ D3!» KHZ DB t KH DB KHZ D3 1 * KHZ DB I KHZ KHZ DB KHZ D3 * KHZ DB 9.?646 KHZ D3 a\.3622 KHZ DB KHZ D3 > Í KHZ D KHZ DB 66.Í.221 KHZ DB í^.2849 KHZ DB KHZ DB DB KHZ " KHZ DB * " KHZ 62.9' DP, T KHZ DB 7^.^094 KHZ D5 "''.4H?7 KHZ DE! KHZ DB "4.9''30 Y.-.YÍ, 0 KHZ 6?.0C DB "fi.2 8'í DB.! ">>.9I 9; KHZ DB 1» KHZ fez.31 U» 1» 73.1??h DB n 9 K'F, DP.» ~?.:4 3ÍJ K.T.: t3.?4 DP - -. > 7 % R KHZ DB * 80.2^04 64.í9 DP 65.6ü DB KHZ b6.99 DB?. 1.7': 7 0 rjíz 5 0.7^ DP. 3i K!!~ DB * KHZ DB 0 = DB b' : «B0.4 7 DB * 60 K;:Z 7?.?? DB 1.!!/ DV. fi. Példák Az elmondottakat egy sávszűrő példájával illusztráljuk. Ezután röviden megemlítünk néhány érdekesebb feladatot. 110 khz sávszűrő Egy sávszűrő csillapításelőírását a 9. ábra mutatja. Az áteresztőrészben írjunk elő csebisevi közelítést és legyen n 0 = 3, n = \, hogy 18 osztályú cikcakk kapcsolású szűrővel lehessen a feladatot megoldani. A csillapításpólusok számának és frekvenciájának megállapításához a GEST programot kell indítani az 5. ábrán látható adatszalag első részletével. A számítás eredményét a 10a és 106 ábrák mutatják: a két zárórészben a toleranciasémát és a számított csillapítást tüntetik fel egy nemlineáris frekvenciaskála felett. Az adatszalag következő mintegy 25 sora a n, Q, y, a polinomok előállítását írja elő a 2. ábra szerint. a [db] 60 (T7 50'- T77? F 10/a ábra. A 110 khz-es sávszűrő alsó zárórésze UPPER STOFBAND LOSS ÍESQUENCX LOSS KHZ DB KHZ DB KHZ D KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ 45.7* DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ 41.1? DB KHZ DB KHZ DB KHZ DB KHZ D KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KH DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB KHZ DB FINITE LOSS POLES C;IAIUCTERI5TICS , Ess -flh36i 10 jb ábra. A 110 khz-es sávszűrő felső zárórésze f[kt1z] ábra. 110 khz-es sávszűrő csülapitáselőírása ÍHT65-'HM"g] Ezt a részletet az 5. ábrából elhagytuk. Látható viszont a befejező rész, melynek vezérszavai az 5. fejezet alapján könnyen értelmezhetők. A kapcsolást a 11. ábra, az áteresztőrész számított csillapítását veszteségmentes kondenzátorok és Q L 300 tekercsjóságok mellett, a 12. ábra mutatja. A hasonló jósági tényezőjű tekercsekkel megépített szűrő mérőautomatával mért csillapításkarakterisztikája az alkatré- 235
12 HÍRADÁSTECHNIKA XXX. ÉVF SZ. szek értékbeállítása után, finomhangolás nélkül a }3. ábrán látható. KARAKTERISZTIKA LETAPOGATÁSA ÁBRÁZOLT CSILL.TARTOMAt:*: (DB) Antimetrikus ülesztőszürő MERES SZAM: 41 VIZS3ALT FREKV. TAÍÍTOtlAr.T: (KHZ) Szentirmai javasolta antimetrikus P vagy 7\ típusú aluláteresztő alkalmazását sávszűrő helyett két különböző ellenállás közötti illesztő hálózat céljára [20]. A DPLC programrendszerrel ilyen szűrőt sávszűrőként tervezhetünk, melynek azonban 0 frekvencián nincs csillapításpólusa. Adott lezáró ellenállások, sávhatárok és fokszám mellett előírandó a p számítását az adatszalagról vezérelve lehet elvégezni a GEPAA programban. Üresen járó vagy feszültségforrásról táplált szűrő A GEPAA és G'EPAB programok által végzett számítások módosításával extrém lezárású szűrők is tervezhetők. Az analízist í? 2 =400 kü vagy f? 2 = 2,5 IxQ lezárással végezve a csillapítások 50 db-lel megnövelt értékeit kapjuk. Bal és jobb félsíkon elosztott 0-zérusok A 3.5. pontban említettük, hogy standard számításoknál a karakterisztikus függvény bal félsíkra eső zérusait használjuk. A felhasználó az adatszalagról LÉPÉSKÖZ 0.? (KKZ) ETALON FREKVENCIA; 1ŰŰ.625 (KHZ) ALAPCSILLAPITAS: 1, (DB) Q ! ' E Ű0OOOE-0I?.?0O000E-O1 6.10O00OE-O E E E+00 Ö E E E DQQE E E E O0OÖE ŰQOOE OOOO0E-01 ; QE E E J90000E+ŰO E QOOOE E O0O00S E O00OE E Q0000E E OO00E O00OE ŰOOOOE-01 I E OQ00E+0-O 1.29OOO0E+0O E E O00E-O E E+00 / ' KARAKTERISZTIKA LETAPOGATÁS VEGE ' jh 665--HM*13l FREFl KHZ CIRCUIT OF THE FILTER J-C-Ii-1 I I 1 C--1 I--L--I I I O B KO UH NF 355.I27459H UH NF NF 12.4M59J94 NF PF MIH KO NF UH KHZ KHZ 11. ábra. A 110 khz-es sávszűrő kapcsolása LOSS CHARACTERISTICS KHZ KHZ KHZ KHZ KHZ KHZ KHZ KUK J KH KHZ KHZ KHZ KHZ KHZ KHZ KHZ KHZ ZBZ B E KHZ KHZ KHZ KHZ KH KHZ KH KHZ KHZ KHZ KHZ KHZ KH KHZ 1U.500 KHZ 115.Ú00 KHZ KHZ D KH Kf KHZ KHZ KHZ DB EB DB DB ábra. A 110 khz-es sávszűrő számított csillapítása az áteresztőrészben s 13. ábra. A 110 khz-es sávszűrő mérőautomatával mért csillapítása az áteresztőrészben 0 K--0 t!!--l--1 I! Í--C- I bármelyik konjugált komplex vagy valós 0-zérmt a jobb félsikra helyezheti át és a szintézist folytathatja, sőt akár az összes lehetőséget is kipróbálhatja anélkül, hogy a megelőző számításokat ismételten el kellene végezni. Csatolt-rezonátoros keskenysávú sávszűrő tervezése Felső kapacitív csatolású rezgőkörökből álló (18 osztályú) keskenysávú sávszűrők lefejtésekor két nehézség lép fel: egyrészt az impedanciaszint nagyon megnő a lefejtés előrehaladása folyamán, másrészt csak egy sor transzformációval lehet a szűrőt arra a kedvező alakra átszámítani, amelyre az egyenlő önindukciók jellemzők. Felhasználva egy korábban kidolgozott módszert [21], minden önindukció lefejtése előtt megállapítható az előírt önindukcióérték beállításához szükséges transzformátor áttétele. Ezt kondenzátorokból megvalósítva jól realizálható szűrőt kapunk. A számítás elvégezhető a GEPAA programban adatszalagról vezérelve is, de kedvezőbbnek látszott erre a célra kidolgozni a SYLF pogram SYCRF nevű változatát, mely az említett számításokat a lefejtés közben elvégzi. 7. Összefoqialás Az LG szűrők tervezésére készült DPLC programrendszert mutattuk be nagy vonalaiban. A kidolgozáshoz felhasználva a szerző korábbi ilyen irányú munkáit kb. 3 ember-évre volt szükség. A lefuttatott tervezési feladatok igazolták a programrendszer sokoldalúságát. Eddig csak néhány kisebb, könnyen javítható hiba merült fel. 236
13 DR. HERENDI M.: PROGRAMRENDSZER LC SZŰRŐK TERVEZÉSÉRE Örömmel említem meg a nevét munkatársaimnak, akik a munkában résztvettek. Dr. Horváth Judit írta a GEST, GESAPP POLES program-hármast és a TESTB programot. A 110 khz-es sávszűrőt Egri Tamás építette meg. A MIKI mérőautomata mérőprogramját Szilárdi Tibor írta. Dr. Scultéty László hasznos tanácsaival járult hozzá a munka sikeréhez. IRODALOM [1] G. Szentirmai: Theoretical basis of a digital computer program package for filter synthesis. First Allerton Gonf. on Circuit and System Theory, Nov , [2] Radvány Jenő: Számítógép-program aluláteresztő és sávszűrő üzemi paraméteres méretezésére. Híradástechnika, XXI. évf., 3. sz., 1970 március, pp [3] Herendi Miklós: Általános paraméterű LG szűrőket tervező program. Híradástechnika, XXIII. évf., 11. sz., 1972 november, pp [4] Herendi Miklós: Alkalmazási utasítás a G I L D A programrendszerhez. Műszeripari Kutató Intézet, 1975 december. [5] G. Gordos: Ghebyshev appróximation of a constant with prescribed nonuniform error. Proc. Int. Symp. NetWork Theory, Belgrádé, Yugoslavia, Sept. 1968, pp [6] S. Darlington: Synthesis of reactance 4-poles which produce prescribed insertion loss characteristics. Journal of Mathematics and Physics, XVIII. évf. (1939), pp [7] J. Zdunek : General design of ladder networks with arbitrarily distributed uniform losess between coils and capacitors. Proc. IEE, 110, Feb. 1963, pp [8] J. K. Skwirzynski: On synthesis of filters. IEEE Trans., GT-18, Jan. 1971, pp [9] L. Marék, H. Müller, M. Tuero: Designing filters by the insertion loss method. Brown Boverl Rev., 52, May/June 1965, pp [10] C. Norek: Product method for the calculation of the effective loss LG filters. Proc. Int. Symp. Network Theory, Belgrádé, Yugoslavia, Sept. 1968, pp [11] G. Szentirmai: FILSIN A generál purpose filter synthesis program. Proc. IEEE, 65, Oct. 1977, pp [12] American National Standard Programming Language FORTRAN, X Programming Language FORTRAN, ISO/R MSZ 7785/1-74 FORTRAN programnyelv. [13] H. J. Orchard, G. C. Temes: Filter design using transformed variables. IEEE Trans., CT 15, Dec. 1968, pp [14] B. R. Smith, G. C. Temes: An iterative appróximation procedure for automatlc filter synthesis. IEEE Trans., CT 12, March 1965, pp [15] Herendi Miklós: Általános paraméterű szűrők zárórészének közelítése. Műszeripari Kutató Intézet Közleményei, 16. sz., 1973 október, pp [16] Miklós Herendi, Judit Horváth: Computer aided design of LC filters. Proc. Summer School on Circuit Theory 1974, Prague, 2 6 Sept. 1974, Vol. 2., pp [17] Géher Károly: Lineáris hálózatok. Műszaki Könyvkiadó, Budapest, 1975, [18] R. Saal, E. Ulbrich: On the design of filters by synthesis. IRE Trans., CT 5, Dec. 1958, pp ]19] Herendi Miklós: A kontinuánsok és alkalmazásuk lánckapcsolású hálózatok gépi számítására. Híradástechnika, XIX. évf., 1. sz., 1968 január, pp [20] G. Szentirmai: Barid-pass matching filter in the form of polynomial low-pass filter. IEEE Trans., GT-11, March 1964, pp [21] Herendi Miklós: Keskenysávú LG szűrők tervezése. Kutatási jelentés, Műszeripari Kutató Intézet, 1975 december. Pályázati felhívás! A Híradástechnikai Judományos Egyesület diplomaterv- és szakdolgozat-pályázatot hirdet a Budapesti Műszaki Egyetem Villamosmérnöki Karán a Kandó Kálmán Villamosipari Műszaki Főiskola Gyengeáramú Karának Híradásipari Alkatrészgyártó és Számítástechnika Szakán a Zrínyi Miklós Katonai Akadémián, valamint a Győri Közlekedési és Távközlési Műszaki Főiskolán A pályázaton mindazon hallgató részt vehet, aki államvizsgáját legkésőbb^ október 31-ig feles, jó eredménnyel leteszi, és diplomatervét, illetve szakdolgozatát az Állami Vizsgáztató Bizottság a pályázatra alkalmasnak tartja. A pályázat célja a jó tanulmányi eredményt elért és a legjobb diplomatervet, illetve szakdolgozatot kidolgozó végzős szakemberek megbecsülése és munkájuk külön jutalmazása. A pályázatra az Állami Vizsgáztató Bizottság közvetítésével lehet jelentkezni. Pályadíjak: a diplomaterv-pályázaton: I. díj 1500,- Ft II. díj 1200,- Ft III. díj 1000,- Ft a szakdolgozat-pályázaton: I. díj 1200,- Ft II. díj 1000,- Ft III. díj 800,- Ft A díjak odaítéléséről bíráló bizottság dönt, amelynek elnökét és két tagját a HTE, további két tagját az iskola jelöli ki. A díjakat az Egyesület ünnepélyes ülésén nyújtják át a nyerteseknek. A díjnyertesek a HTE rendezvényei keretében munkájukról előadást tarthatnak és tanulmányt jelentethetnek meg az Egyesület tudományos folyóiratában, a HÍRADÁSTECHNIKÁ-bah. Dr. Házmán István a HTE Oktatási Bizottságának vezetője A műszaki és gazdasági irányítás alapján szélesíteni kívánjuk háttéripari tevékenységünket. Ezen belül kistranszformátorok, mágnes- és egyéb tekercsek gyártására szakosodunk. TIPIZÁLT KISTR ANSZFORMÁTOR AINK felhasználásával kapcsolatban készséggel állunk információval és tanácsadással rendelkezésükre. Felvilágosítással szolgálunk mind a hagyományos M, El és MAM típusú, mind pedig a nyakba ültetett és a tekercselt vasmagos transzformátorok területén. PUSKÁS TIVADAR Műszer és Gépipari Szövetkezet 1388 Bp., Pf. 62. Tel.:
KANDÓ KÁLMÁN VILLAMOSMÉRNÖKI FŐISKOLAI KAR. Mikroelektronikai és Technológiai Intézet. Aktív Szűrők. Analóg és Hírközlési Áramkörök
 KANDÓ KÁLMÁN VILLAMOSMÉRNÖKI FŐISKOLAI KAR Mikroelektronikai és Technológiai Intézet Analóg és Hírközlési Áramkörök Laboratóriumi Gyakorlatok Készítette: Joó Gábor és Pintér Tamás OE-MTI 2011 1.Szűrők
KANDÓ KÁLMÁN VILLAMOSMÉRNÖKI FŐISKOLAI KAR Mikroelektronikai és Technológiai Intézet Analóg és Hírközlési Áramkörök Laboratóriumi Gyakorlatok Készítette: Joó Gábor és Pintér Tamás OE-MTI 2011 1.Szűrők
2. A számítási módszer
 D R. H E R E N D MKLÓS a műszaki tudományok kandidátusa Műszeripari Kutató ntézet r Általános paraméterű LC szűrőket tervező program ETO: 627.,372.54.001.2: 681.3.06 Napjainkban a hullámparaméteres szűrőtervezési
D R. H E R E N D MKLÓS a műszaki tudományok kandidátusa Műszeripari Kutató ntézet r Általános paraméterű LC szűrőket tervező program ETO: 627.,372.54.001.2: 681.3.06 Napjainkban a hullámparaméteres szűrőtervezési
1. előadás. Lineáris algebra numerikus módszerei. Hibaszámítás Számábrázolás Kerekítés, levágás Klasszikus hibaanalízis Abszolút hiba Relatív hiba
 Hibaforrások Hiba A feladatok megoldása során különféle hibaforrásokkal találkozunk: Modellhiba, amikor a valóságnak egy közelítését használjuk a feladat matematikai alakjának felírásához. (Pl. egy fizikai
Hibaforrások Hiba A feladatok megoldása során különféle hibaforrásokkal találkozunk: Modellhiba, amikor a valóságnak egy közelítését használjuk a feladat matematikai alakjának felírásához. (Pl. egy fizikai
Dr. Gyurcsek István. Példafeladatok. Helygörbék Bode-diagramok HELYGÖRBÉK, BODE-DIAGRAMOK DR. GYURCSEK ISTVÁN
 Dr. Gyurcsek István Példafeladatok Helygörbék Bode-diagramok 1 2016.11.11.. Helygörbe szerkesztése VIZSGÁLAT: Mi a következménye annak, ha az áramkör valamelyik jellemző paramétere változik? Helygörbe
Dr. Gyurcsek István Példafeladatok Helygörbék Bode-diagramok 1 2016.11.11.. Helygörbe szerkesztése VIZSGÁLAT: Mi a következménye annak, ha az áramkör valamelyik jellemző paramétere változik? Helygörbe
10.1. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ
 101 ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ Ma az analóg jelek feldolgozása (is) mindinkább digitális eszközökkel történik A feldolgozás előtt az analóg jeleket digitalizálni kell Rendszerint az
101 ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ Ma az analóg jelek feldolgozása (is) mindinkább digitális eszközökkel történik A feldolgozás előtt az analóg jeleket digitalizálni kell Rendszerint az
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2008. május 26. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2008. május 26. 8:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
ÉRETTSÉGI VIZSGA 2008. május 26. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2008. május 26. 8:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2015. október 12. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2015. október 12. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2015. október 12. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2015. október 12. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2009. május 22. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2009. május 22. 8:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KLTRÁLIS
ÉRETTSÉGI VIZSGA 2009. május 22. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2009. május 22. 8:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KLTRÁLIS
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2011. október 17. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2011. október 17. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
ÉRETTSÉGI VIZSGA 2011. október 17. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2011. október 17. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
ELEKTRONIKAI ALAPISMERETEK
 Elektronikai alapismeretek középszint 4 ÉETTSÉGI VIZSG 06. május 8. ELEKTONIKI LPISMEETEK KÖZÉPSZINTŰ ÍÁSBELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMTTÓ EMBEI EŐFOÁSOK MINISZTÉIM Egyszerű, rövid feladatok
Elektronikai alapismeretek középszint 4 ÉETTSÉGI VIZSG 06. május 8. ELEKTONIKI LPISMEETEK KÖZÉPSZINTŰ ÍÁSBELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMTTÓ EMBEI EŐFOÁSOK MINISZTÉIM Egyszerű, rövid feladatok
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2014. október 13. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2014. október 13. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2014. október 13. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2014. október 13. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÁGAZATI SZAKMAI ÉRETTSÉGI VIZSGA VILLAMOSIPAR ÉS ELEKTRONIKA ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ
 VILLAMOSIPAR ÉS ELEKTRONIKA ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ I. feladatlap Egyszerű, rövid feladatok megoldása Maximális pontszám: 40. feladat 4 pont
VILLAMOSIPAR ÉS ELEKTRONIKA ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ I. feladatlap Egyszerű, rövid feladatok megoldása Maximális pontszám: 40. feladat 4 pont
6. Függvények. Legyen függvény és nem üreshalmaz. A függvényt az f K-ra való kiterjesztésének
 6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
6. Függvények I. Elméleti összefoglaló A függvény fogalma, értelmezési tartomány, képhalmaz, értékkészlet Legyen az A és B halmaz egyike sem üreshalmaz. Ha az A halmaz minden egyes eleméhez hozzárendeljük
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Számelmélet I.
 Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2014. október 13. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2014. október 13. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2014. október 13. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2014. október 13. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
AUTOMATIKAI ÉS ELEKTRONIKAI ISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ A MINTAFELADATOKHOZ
 ATOMATKA ÉS ELEKTONKA SMEETEK KÖZÉPSZNTŰ ÍÁSBEL VZSGA JAVÍTÁS-ÉTÉKELÉS ÚTMTATÓ A MNTAFELADATOKHOZ Egyszerű, rövid feladatok Maximális pontszám: 40. Egy A=,5 mm keresztmetszetű alumínium (ρ= 0,08 Ω mm /m)
ATOMATKA ÉS ELEKTONKA SMEETEK KÖZÉPSZNTŰ ÍÁSBEL VZSGA JAVÍTÁS-ÉTÉKELÉS ÚTMTATÓ A MNTAFELADATOKHOZ Egyszerű, rövid feladatok Maximális pontszám: 40. Egy A=,5 mm keresztmetszetű alumínium (ρ= 0,08 Ω mm /m)
Függvények december 6. Határozza meg a következő határértékeket! 1. Feladat: x 0 7x 15 x ) = lim. Megoldás: lim. 2. Feladat: lim.
 Függvények 05. december 6. Határozza meg a következő határértékeket!. Feladat: ( + 7 5 ) ( + 7 5 ) ( + 0 ). Feladat: ( + 7 5 ) ( + 7 5 ) ( + 0) 3. Feladat: ( + 0 7 5 ) 4. Feladat: ( + 0 7 5 ) ( + 7 0 5
Függvények 05. december 6. Határozza meg a következő határértékeket!. Feladat: ( + 7 5 ) ( + 7 5 ) ( + 0 ). Feladat: ( + 7 5 ) ( + 7 5 ) ( + 0) 3. Feladat: ( + 0 7 5 ) 4. Feladat: ( + 0 7 5 ) ( + 7 0 5
X. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ
 X. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ Ma az analóg jelek feldolgozása (is) mindinkább digitális eszközökkel és módszerekkel történik. A feldolgozás előtt az analóg jeleket digitalizálni kell.
X. ANALÓG JELEK ILLESZTÉSE DIGITÁLIS ESZKÖZÖKHÖZ Ma az analóg jelek feldolgozása (is) mindinkább digitális eszközökkel és módszerekkel történik. A feldolgozás előtt az analóg jeleket digitalizálni kell.
Passzív és aktív aluláteresztő szűrők
 7. Laboratóriumi gyakorlat Passzív és aktív aluláteresztő szűrők. A gyakorlat célja: A Micro-Cap és Filterlab programok segítségével tanulmányozzuk a passzív és aktív aluláteresztő szűrők elépítését, jelátvitelét.
7. Laboratóriumi gyakorlat Passzív és aktív aluláteresztő szűrők. A gyakorlat célja: A Micro-Cap és Filterlab programok segítségével tanulmányozzuk a passzív és aktív aluláteresztő szűrők elépítését, jelátvitelét.
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2007. május 25. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
ÉRETTSÉGI VIZSGA 2007. május 25. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2007. május 25. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
Felvételi tematika INFORMATIKA
 Felvételi tematika INFORMATIKA 2016 FEJEZETEK 1. Természetes számok feldolgozása számjegyenként. 2. Számsorozatok feldolgozása elemenként. Egydimenziós tömbök. 3. Mátrixok feldolgozása elemenként/soronként/oszloponként.
Felvételi tematika INFORMATIKA 2016 FEJEZETEK 1. Természetes számok feldolgozása számjegyenként. 2. Számsorozatok feldolgozása elemenként. Egydimenziós tömbök. 3. Mátrixok feldolgozása elemenként/soronként/oszloponként.
15. LINEÁRIS EGYENLETRENDSZEREK
 15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
15 LINEÁRIS EGYENLETRENDSZEREK 151 Lineáris egyenletrendszer, Gauss elimináció 1 Definíció Lineáris egyenletrendszernek nevezzük az (1) a 11 x 1 + a 12 x 2 + + a 1n x n = b 1 a 21 x 1 + a 22 x 2 + + a
Elektronika Előadás. Analóg és kapcsolt kapacitású szűrők
 Elektronika 2 8. Előadás Analóg és kapcsolt kapacitású szűrők Irodalom - Megyeri János: Analóg elektronika, Tankönyvkiadó, 1990 - Ron Mancini (szerk): Op Amps for Everyone, Texas Instruments, 2002 16.
Elektronika 2 8. Előadás Analóg és kapcsolt kapacitású szűrők Irodalom - Megyeri János: Analóg elektronika, Tankönyvkiadó, 1990 - Ron Mancini (szerk): Op Amps for Everyone, Texas Instruments, 2002 16.
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2016. május 18. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2016. május 18. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2016. május 18. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2016. május 18. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ELEKTRONIKAI ALAPISMERETEK
 Azonosító jel NSZI 0 6 0 6 OKTATÁSI MINISZTÉRIUM Szakmai előkészítő érettségi tantárgyi verseny 2006. február 23. ELEKTRONIKAI ALAPISMERETEK ELŐDÖNTŐ ÍRÁSBELI FELADATOK Az írásbeli időtartama: 180 perc
Azonosító jel NSZI 0 6 0 6 OKTATÁSI MINISZTÉRIUM Szakmai előkészítő érettségi tantárgyi verseny 2006. február 23. ELEKTRONIKAI ALAPISMERETEK ELŐDÖNTŐ ÍRÁSBELI FELADATOK Az írásbeli időtartama: 180 perc
First Prev Next Last Go Back Full Screen Close Quit. Matematika I
 Matematika I (Analízis) Készítette: Horváth Gábor Kötelező irodalom: Ács László, Gáspár Csaba: Analízis 1 Oktatási segédanyagok és a tantárgyi követelményrendszer megtalálható a http://rs1.szif.hu/ horvathg/horvathg.html
Matematika I (Analízis) Készítette: Horváth Gábor Kötelező irodalom: Ács László, Gáspár Csaba: Analízis 1 Oktatási segédanyagok és a tantárgyi követelményrendszer megtalálható a http://rs1.szif.hu/ horvathg/horvathg.html
Operációs rendszerek. 11. gyakorlat. AWK - szintaxis, vezérlési szerkezetek UNIVERSITAS SCIENTIARUM SZEGEDIENSIS UNIVERSITY OF SZEGED
 UNIVERSITAS SCIENTIARUM SZEGEDIENSIS UNIVERSITY OF SZEGED AWK - szintaxis, vezérlési szerkezetek Operációs rendszerek 11. gyakorlat Szegedi Tudományegyetem Természettudományi és Informatikai Kar Csuvik
UNIVERSITAS SCIENTIARUM SZEGEDIENSIS UNIVERSITY OF SZEGED AWK - szintaxis, vezérlési szerkezetek Operációs rendszerek 11. gyakorlat Szegedi Tudományegyetem Természettudományi és Informatikai Kar Csuvik
ELEKTRONIKAI ALAPISMERETEK
 Elektronikai alapismeretek emelt szint 06 ÉETTSÉGI VIZSG 007. május 5. EEKTONIKI PISMEETEK EMET SZINTŰ ÍÁSBEI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKEÉSI ÚTMTTÓ OKTTÁSI ÉS KTÁIS MINISZTÉIM Teszt jellegű kérdéssor
Elektronikai alapismeretek emelt szint 06 ÉETTSÉGI VIZSG 007. május 5. EEKTONIKI PISMEETEK EMET SZINTŰ ÍÁSBEI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKEÉSI ÚTMTTÓ OKTTÁSI ÉS KTÁIS MINISZTÉIM Teszt jellegű kérdéssor
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2014. május 20. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2014. május 20. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2014. május 20. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2014. május 20. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ELEKTRONIKAI ALAPISMERETEK
 Elektronikai alapismeretek középszint 06 ÉRETTSÉGI VIZSG 007. május 5. ELEKTRONIKI LPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSG JVÍTÁSI-ÉRTÉKELÉSI ÚTMTTÓ OKTTÁSI ÉS KLTRÁLIS MINISZTÉRIM Teszt jellegű
Elektronikai alapismeretek középszint 06 ÉRETTSÉGI VIZSG 007. május 5. ELEKTRONIKI LPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSG JVÍTÁSI-ÉRTÉKELÉSI ÚTMTTÓ OKTTÁSI ÉS KLTRÁLIS MINISZTÉRIM Teszt jellegű
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2010. október 18. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2010. október 18. 1:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
ÉRETTSÉGI VIZSGA 2010. október 18. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2010. október 18. 1:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
Analóg elektronika - laboratóriumi gyakorlatok
 Analóg elektronika - laboratóriumi gyakorlatok. Mûveleti erõsítõk váltakozó-áramú alkalmazásai. Elmélet Az integrált mûveleti erõsítõk váltakozó áramú viselkedését a. fejezetben (jegyzet és prezentáció)
Analóg elektronika - laboratóriumi gyakorlatok. Mûveleti erõsítõk váltakozó-áramú alkalmazásai. Elmélet Az integrált mûveleti erõsítõk váltakozó áramú viselkedését a. fejezetben (jegyzet és prezentáció)
HORVÁTH ZSÓFIA 1. Beadandó feladat (HOZSAAI.ELTE) ápr 7. 8-as csoport
 10-es Keressünk egy egész számokat tartalmazó négyzetes mátrixban olyan oszlopot, ahol a főátló alatti elemek mind nullák! Megolda si terv: Specifika cio : A = (mat: Z n m,ind: N, l: L) Ef =(mat = mat`)
10-es Keressünk egy egész számokat tartalmazó négyzetes mátrixban olyan oszlopot, ahol a főátló alatti elemek mind nullák! Megolda si terv: Specifika cio : A = (mat: Z n m,ind: N, l: L) Ef =(mat = mat`)
További programozási esetek Hiperbolikus, kvadratikus, integer, bináris, többcélú programozás
 További programozási esetek Hiperbolikus, kvadratikus, integer, bináris, többcélú programozás Készítette: Dr. Ábrahám István Hiperbolikus programozás Gazdasági problémák optimalizálásakor gyakori, hogy
További programozási esetek Hiperbolikus, kvadratikus, integer, bináris, többcélú programozás Készítette: Dr. Ábrahám István Hiperbolikus programozás Gazdasági problémák optimalizálásakor gyakori, hogy
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2015. május 19. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2015. május 19. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2015. május 19. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2015. május 19. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ELEKTRONIKAI ALAPISMERETEK
 Elektronikai alapismeretek emelt szint ÉETTSÉG VZSGA 0. október 5. ELEKTONKA ALAPSMEETEK EMELT SZNTŰ ÍÁSBEL ÉETTSÉG VZSGA JAVÍTÁS-ÉTÉKELÉS ÚTMTATÓ EMBE EŐFOÁSOK MNSZTÉMA Egyszerű, rövid feladatok Maximális
Elektronikai alapismeretek emelt szint ÉETTSÉG VZSGA 0. október 5. ELEKTONKA ALAPSMEETEK EMELT SZNTŰ ÍÁSBEL ÉETTSÉG VZSGA JAVÍTÁS-ÉTÉKELÉS ÚTMTATÓ EMBE EŐFOÁSOK MNSZTÉMA Egyszerű, rövid feladatok Maximális
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
LINEÁRIS PROGRAMOZÁSI FELADATOK MEGOLDÁSA SZIMPLEX MÓDSZERREL
 LINEÁRIS PROGRAMOZÁSI FELADATOK MEGOLDÁSA SZIMPLEX MÓDSZERREL x 1-2x 2 6 -x 1-3x 3 = -7 x 1 - x 2-3x 3-2 3x 1-2x 2-2x 3 4 4x 1-2x 2 + x 3 max Alapfogalmak: feltételrendszer (narancs színnel jelölve), célfüggvény
LINEÁRIS PROGRAMOZÁSI FELADATOK MEGOLDÁSA SZIMPLEX MÓDSZERREL x 1-2x 2 6 -x 1-3x 3 = -7 x 1 - x 2-3x 3-2 3x 1-2x 2-2x 3 4 4x 1-2x 2 + x 3 max Alapfogalmak: feltételrendszer (narancs színnel jelölve), célfüggvény
Négypólusok helyettesítő kapcsolásai
 Transzformátorok Magyar találmány: Bláthy Ottó Titusz (1860-1939), Déry Miksa (1854-1938), Zipernovszky Károly (1853-1942), Ganz Villamossági Gyár, 1885. Felépítés, működés Transzformátor: négypólus. Működési
Transzformátorok Magyar találmány: Bláthy Ottó Titusz (1860-1939), Déry Miksa (1854-1938), Zipernovszky Károly (1853-1942), Ganz Villamossági Gyár, 1885. Felépítés, működés Transzformátor: négypólus. Működési
Tömbök kezelése. Példa: Vonalkód ellenőrzőjegyének kiszámítása
 Tömbök kezelése Példa: Vonalkód ellenőrzőjegyének kiszámítása A számokkal jellemzett adatok, pl. személyi szám, adószám, taj-szám, vonalkód, bankszámlaszám esetében az elírásból származó hibát ún. ellenőrző
Tömbök kezelése Példa: Vonalkód ellenőrzőjegyének kiszámítása A számokkal jellemzett adatok, pl. személyi szám, adószám, taj-szám, vonalkód, bankszámlaszám esetében az elírásból származó hibát ún. ellenőrző
Konjugált gradiens módszer
 Közelítő és szimbolikus számítások 12. gyakorlat Konjugált gradiens módszer Készítette: Gelle Kitti Csendes Tibor Vinkó Tamás Faragó István Horváth Róbert jegyzetei alapján 1 LINEÁRIS EGYENLETRENDSZEREK
Közelítő és szimbolikus számítások 12. gyakorlat Konjugált gradiens módszer Készítette: Gelle Kitti Csendes Tibor Vinkó Tamás Faragó István Horváth Róbert jegyzetei alapján 1 LINEÁRIS EGYENLETRENDSZEREK
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2013. október 14. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2013. október 14. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2013. október 14. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2013. október 14. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
Írjon olyan programot a standard könyvtár alkalmazásával, amely konzolról megadott valós adatokból meghatározza és kiírja a minimális értékűt!
 Írjon olyan programot a standard könyvtár alkalmazásával, amely konzolról megadott valós adatokból meghatározza és kiírja a minimális értékűt! valós adatokat növekvő sorrendbe rendezi és egy sorba kiírja
Írjon olyan programot a standard könyvtár alkalmazásával, amely konzolról megadott valós adatokból meghatározza és kiírja a minimális értékűt! valós adatokat növekvő sorrendbe rendezi és egy sorba kiírja
Struktúra nélküli adatszerkezetek
 Struktúra nélküli adatszerkezetek Homogén adatszerkezetek (minden adatelem azonos típusú) osztályozása Struktúra nélküli (Nincs kapcsolat az adatelemek között.) Halmaz Multihalmaz Asszociatív 20:24 1 A
Struktúra nélküli adatszerkezetek Homogén adatszerkezetek (minden adatelem azonos típusú) osztályozása Struktúra nélküli (Nincs kapcsolat az adatelemek között.) Halmaz Multihalmaz Asszociatív 20:24 1 A
AWK programozás, minták, vezérlési szerkezetek
 10 AWK programozás, minták, vezérlési szerkezetek AWK adatvezérelt szkriptnyelv text processing, adat kiterjesztés, tagolt adatok automatizált soronkénti feldolgozása a forrásállományt soronként beolvassa
10 AWK programozás, minták, vezérlési szerkezetek AWK adatvezérelt szkriptnyelv text processing, adat kiterjesztés, tagolt adatok automatizált soronkénti feldolgozása a forrásállományt soronként beolvassa
ELEKTRONIKAI ALAPISMERETEK
 Elektronikai alapismeretek középszint 4 ÉETTSÉGI VIZSGA 04. október. ELEKTONIKAI ALAPISMEETEK KÖZÉPSZINTŰ ÍÁSELI ÉETTSÉGI VIZSGA JAVÍTÁSI-ÉTÉKELÉSI ÚTMTATÓ EMEI EŐFOÁSOK MINISZTÉIMA Egyszerű, rövid feladatok
Elektronikai alapismeretek középszint 4 ÉETTSÉGI VIZSGA 04. október. ELEKTONIKAI ALAPISMEETEK KÖZÉPSZINTŰ ÍÁSELI ÉETTSÉGI VIZSGA JAVÍTÁSI-ÉTÉKELÉSI ÚTMTATÓ EMEI EŐFOÁSOK MINISZTÉIMA Egyszerű, rövid feladatok
Hatványozás. A hatványozás azonosságai
 Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
2005_01/1 Leírtunk egymás mellé hét racionális számot úgy, hogy a két szélső kivételével mindegyik eggyel nagyobb a két szomszédja szorzatánál.
 Számolásos feladatok, műveletek 2004_1/1 Töltsd ki az alábbi bűvös négyzet hiányzó mezőit úgy, hogy a négyzetben szereplő minden szám különböző legyen, és minden sorban, oszlopban és a két átlóban is ugyanannyi
Számolásos feladatok, műveletek 2004_1/1 Töltsd ki az alábbi bűvös négyzet hiányzó mezőit úgy, hogy a négyzetben szereplő minden szám különböző legyen, és minden sorban, oszlopban és a két átlóban is ugyanannyi
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2015. május 19. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2015. május 19. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2015. május 19. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2015. május 19. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
AWK programozás Bevezetés
 09 AWK programozás Bevezetés AWK adatvezérelt szkriptnyelv text processing, adat kiterjesztés, tagolt adatok automatizált soronkénti feldolgozása a forrásállományt soronként beolvassa és feldolgozhatóvá
09 AWK programozás Bevezetés AWK adatvezérelt szkriptnyelv text processing, adat kiterjesztés, tagolt adatok automatizált soronkénti feldolgozása a forrásállományt soronként beolvassa és feldolgozhatóvá
Fourier-sorfejtés vizsgálata Négyszögjel sorfejtése, átviteli vizsgálata
 Fourier-sorfejtés vizsgálata Négyszögjel sorfejtése, átviteli vizsgálata Reichardt, András 27. szeptember 2. 2 / 5 NDSM Komplex alak U C k = T (T ) ahol ω = 2π T, k módusindex. Időfüggvény előállítása
Fourier-sorfejtés vizsgálata Négyszögjel sorfejtése, átviteli vizsgálata Reichardt, András 27. szeptember 2. 2 / 5 NDSM Komplex alak U C k = T (T ) ahol ω = 2π T, k módusindex. Időfüggvény előállítása
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2008. október 20. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2008. október 20. 1:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS
ÉRETTSÉGI VIZSGA 2008. október 20. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2008. október 20. 1:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS
Matematikai geodéziai számítások 10.
 Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Matematikai geodéziai számítások 10. Hibaellipszis, talpponti görbe és közepes ponthiba Dr. Bácsatyai, László Matematikai geodéziai számítások 10.: Hibaellipszis, talpponti görbe és Dr. Bácsatyai, László
Számítási feladatok megoldással a 6. fejezethez
 Számítási feladatok megoldással a 6. fejezethez. Egy szinuszosan változó áram a polaritás váltás után μs múlva éri el első maximumát. Mekkora az áram frekvenciája? T = 4 t = 4 = 4ms 6 f = = =,5 Hz = 5
Számítási feladatok megoldással a 6. fejezethez. Egy szinuszosan változó áram a polaritás váltás után μs múlva éri el első maximumát. Mekkora az áram frekvenciája? T = 4 t = 4 = 4ms 6 f = = =,5 Hz = 5
ELEKTRONIKAI ALAPISMERETEK
 Elektronikai alapismeretek emelt szint ÉETTSÉGI VIZSG 0. októr. ELEKTONIKI LPISMEETEK EMELT SZINTŰ ÍÁSELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMTTÓ EMEI EŐFOÁSOK MINISZTÉIM Egyszerű, rövid feladatok Maximális
Elektronikai alapismeretek emelt szint ÉETTSÉGI VIZSG 0. októr. ELEKTONIKI LPISMEETEK EMELT SZINTŰ ÍÁSELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMTTÓ EMEI EŐFOÁSOK MINISZTÉIM Egyszerű, rövid feladatok Maximális
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
ANALÓG ÉS DIGITÁLIS TECHNIKA I
 ANALÓG ÉS DIGITÁLIS TECHNIKA I Dr. Lovassy Rita lovassy.rita@kvk.uni-obuda.hu Óbudai Egyetem KVK Mikroelektronikai és Technológia Intézet 2. ELŐADÁS 2010/2011 tanév 2. félév 1 Aktív szűrőkapcsolások A
ANALÓG ÉS DIGITÁLIS TECHNIKA I Dr. Lovassy Rita lovassy.rita@kvk.uni-obuda.hu Óbudai Egyetem KVK Mikroelektronikai és Technológia Intézet 2. ELŐADÁS 2010/2011 tanév 2. félév 1 Aktív szűrőkapcsolások A
ELEKTRONIKAI ALAPISMERETEK
 Elektronikai alapismeretek emelt szint ÉETTSÉG VZSG 0. május. ELEKTONK LPSMEETEK EMELT SZNTŰ ÍÁSEL ÉETTSÉG VZSG JVÍTÁS-ÉTÉKELÉS ÚTMTTÓ EME EŐFOÁSOK MNSZTÉM Egyszerű, rövid feladatok Maximális pontszám:
Elektronikai alapismeretek emelt szint ÉETTSÉG VZSG 0. május. ELEKTONK LPSMEETEK EMELT SZNTŰ ÍÁSEL ÉETTSÉG VZSG JVÍTÁS-ÉTÉKELÉS ÚTMTTÓ EME EŐFOÁSOK MNSZTÉM Egyszerű, rövid feladatok Maximális pontszám:
Jelkondicionálás. Elvezetés. a bioelektromos jelek kis amplitúdójúak. extracelluláris spike: néhányszor 10 uv. EEG hajas fejbőrről: max 50 uv
 Jelkondicionálás Elvezetés 2/12 a bioelektromos jelek kis amplitúdójúak extracelluláris spike: néhányszor 10 uv EEG hajas fejbőrről: max 50 uv EKG: 1 mv membránpotenciál: max. 100 mv az amplitúdó növelésére,
Jelkondicionálás Elvezetés 2/12 a bioelektromos jelek kis amplitúdójúak extracelluláris spike: néhányszor 10 uv EEG hajas fejbőrről: max 50 uv EKG: 1 mv membránpotenciál: max. 100 mv az amplitúdó növelésére,
7. Laboratóriumi gyakorlat: Vezérlési szerkezetek II.
 7. Laboratóriumi gyakorlat: Vezérlési szerkezetek II. A gyakorlat célja: 1. A shell vezérlő szerkezetei használatának gyakorlása. A használt vezérlő szerkezetek: if/else/fi, for, while while, select, case,
7. Laboratóriumi gyakorlat: Vezérlési szerkezetek II. A gyakorlat célja: 1. A shell vezérlő szerkezetei használatának gyakorlása. A használt vezérlő szerkezetek: if/else/fi, for, while while, select, case,
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2012. október 15. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2012. október 15. 1:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2012. október 15. ELEKTRONIKAI ALAPISMERETEK EMELT SZINTŰ ÍRÁSBELI VIZSGA 2012. október 15. 1:00 Az írásbeli vizsga időtartama: 20 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
Az együttfutásról általában, és konkrétan 2.
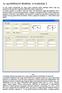 Az együttfutásról általában, és konkrétan 2. Az első részben áttekintettük azt, hogy milyen számítási eljárás szükséges ahhoz, hogy egy szuperheterodin készülék rezgőköreit optimálisan tudjuk megméretezni.
Az együttfutásról általában, és konkrétan 2. Az első részben áttekintettük azt, hogy milyen számítási eljárás szükséges ahhoz, hogy egy szuperheterodin készülék rezgőköreit optimálisan tudjuk megméretezni.
Megjegyzés: A programnak tartalmaznia kell legalább egy felhasználói alprogramot. Példa:
 1. Tétel Az állomány két sort tartalmaz. Az első sorában egy nem nulla természetes szám van, n-el jelöljük (5
1. Tétel Az állomány két sort tartalmaz. Az első sorában egy nem nulla természetes szám van, n-el jelöljük (5
ÁRAMKÖRÖK SZIMULÁCIÓJA
 ÁRAMKÖRÖK SZIMULÁCIÓJA Az áramkörök szimulációja révén betekintést nyerünk azok működésébe. Meg tudjuk határozni az áramkörök válaszát különböző gerjesztésekre, különböző üzemmódokra. Végezhetők analóg
ÁRAMKÖRÖK SZIMULÁCIÓJA Az áramkörök szimulációja révén betekintést nyerünk azok működésébe. Meg tudjuk határozni az áramkörök válaszát különböző gerjesztésekre, különböző üzemmódokra. Végezhetők analóg
Függvények Megoldások
 Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
SZÁMÍTÁSOK A TÁBLÁZATBAN
 SZÁMÍTÁSOK A TÁBLÁZATBAN Az Excelben az egyszerű adatok bevitelén kívül számításokat is végezhetünk. Ezeket a cellákba beírt képletek segítségével oldjuk meg. A képlet: olyan egyenlet, amely a munkalapon
SZÁMÍTÁSOK A TÁBLÁZATBAN Az Excelben az egyszerű adatok bevitelén kívül számításokat is végezhetünk. Ezeket a cellákba beírt képletek segítségével oldjuk meg. A képlet: olyan egyenlet, amely a munkalapon
Határozatlan integrál (2) First Prev Next Last Go Back Full Screen Close Quit
 Határozatlan integrál () First Prev Next Last Go Back Full Screen Close Quit 1. Az összetett függvények integrálására szolgáló egyik módszer a helyettesítéssel való integrálás. Az idevonatkozó tétel pontos
Határozatlan integrál () First Prev Next Last Go Back Full Screen Close Quit 1. Az összetett függvények integrálására szolgáló egyik módszer a helyettesítéssel való integrálás. Az idevonatkozó tétel pontos
MINTA Írásbeli Záróvizsga Mechatronikai mérnök MSc. Debrecen,
 MINTA Írásbeli Záróvizsga Mechatronikai mérnök MSc Debrecen, 2017. 01. 03. Név: Neptun kód: Megjegyzések: A feladatok megoldásánál használja a géprajz szabályait, valamint a szabványos áramköri elemeket.
MINTA Írásbeli Záróvizsga Mechatronikai mérnök MSc Debrecen, 2017. 01. 03. Név: Neptun kód: Megjegyzések: A feladatok megoldásánál használja a géprajz szabályait, valamint a szabványos áramköri elemeket.
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2015. október 12. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2015. október 12. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2015. október 12. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2015. október 12. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ELEKTRONIKAI ALAPISMERETEK
 Elektronikai alapismeretek emelt szint 08 ÉETTSÉGI VIZSG 00. október 8. ELEKTONIKI LPISMEETEK EMELT SZINTŰ ÍÁSELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMUTTÓ NEMZETI EŐFOÁS MINISZTÉIUM Egyszerű, rövid feladatok
Elektronikai alapismeretek emelt szint 08 ÉETTSÉGI VIZSG 00. október 8. ELEKTONIKI LPISMEETEK EMELT SZINTŰ ÍÁSELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMUTTÓ NEMZETI EŐFOÁS MINISZTÉIUM Egyszerű, rövid feladatok
Segédlet az Informatika alapjai I. című tárgy számrendszerek fejezetéhez
 Segédlet az Informatika alapjai I. című tárgy számrendszerek fejezetéhez Sándor Tamás, sandor.tamas@kvk.bmf.hu Takács Gergely, takacs.gergo@kvk.bmf.hu Lektorálta: dr. Schuster György PhD, hal@k2.jozsef.kando.hu
Segédlet az Informatika alapjai I. című tárgy számrendszerek fejezetéhez Sándor Tamás, sandor.tamas@kvk.bmf.hu Takács Gergely, takacs.gergo@kvk.bmf.hu Lektorálta: dr. Schuster György PhD, hal@k2.jozsef.kando.hu
Gyakorlat 34A-25. kapcsolunk. Mekkora a fűtőtest teljesítménye? I o = U o R = 156 V = 1, 56 A (3.1) ezekkel a pillanatnyi értékek:
 3. Gyakorlat 34-5 Egy Ω ellenállású elektromos fűtőtestre 56 V amplitúdójú váltakozó feszültséget kapcsolunk. Mekkora a fűtőtest teljesítménye? Jelölések: R = Ω, U o = 56 V fűtőtestben folyó áram amplitudója
3. Gyakorlat 34-5 Egy Ω ellenállású elektromos fűtőtestre 56 V amplitúdójú váltakozó feszültséget kapcsolunk. Mekkora a fűtőtest teljesítménye? Jelölések: R = Ω, U o = 56 V fűtőtestben folyó áram amplitudója
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2008. május 26. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2008. május 26. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
ÉRETTSÉGI VIZSGA 2008. május 26. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2008. május 26. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS
1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás)
 Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
Matematika A2c gyakorlat Vegyészmérnöki, Biomérnöki, Környezetmérnöki szakok, 2017/18 ősz 1. feladatsor: Vektorterek, lineáris kombináció, mátrixok, determináns (megoldás) 1. Valós vektorterek-e a következő
ALGEBRAI KIFEJEZÉSEK, EGYENLETEK
 ALGEBRAI KIFEJEZÉSEK, EGYENLETEK AZ ALGEBRAI KIFEJEZÉS FOGALMÁNAK KIALAKÍTÁSA (7-9. OSZTÁLY) Racionális algebrai kifejezés (betűs kifejezés): betűket és számokat a négy alapművelet véges sokszori alkalmazásával
ALGEBRAI KIFEJEZÉSEK, EGYENLETEK AZ ALGEBRAI KIFEJEZÉS FOGALMÁNAK KIALAKÍTÁSA (7-9. OSZTÁLY) Racionális algebrai kifejezés (betűs kifejezés): betűket és számokat a négy alapművelet véges sokszori alkalmazásával
A matematikai feladatok és megoldások konvenciói
 A matematikai feladatok és megoldások konvenciói Kozárné Fazekas Anna Kántor Sándor Matematika és Informatika Didaktikai Konferencia - Szatmárnémeti 2011. január 28-30. Konvenciók Mindenki által elfogadott
A matematikai feladatok és megoldások konvenciói Kozárné Fazekas Anna Kántor Sándor Matematika és Informatika Didaktikai Konferencia - Szatmárnémeti 2011. január 28-30. Konvenciók Mindenki által elfogadott
Matematikai geodéziai számítások 6.
 Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Matematikai geodéziai számítások 6. Lineáris regresszió számítás elektronikus távmérőkre Dr. Bácsatyai, László Matematikai geodéziai számítások 6.: Lineáris regresszió számítás elektronikus távmérőkre
Számítási feladatok a 6. fejezethez
 Számítási feladatok a 6. fejezethez 1. Egy szinuszosan változó áram a polaritás váltás után 1 μs múlva éri el első maximumát. Mekkora az áram frekvenciája? 2. Egy áramkörben I = 0,5 A erősségű és 200 Hz
Számítási feladatok a 6. fejezethez 1. Egy szinuszosan változó áram a polaritás váltás után 1 μs múlva éri el első maximumát. Mekkora az áram frekvenciája? 2. Egy áramkörben I = 0,5 A erősségű és 200 Hz
Gauss-Seidel iteráció
 Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
Közelítő és szimbolikus számítások 5. gyakorlat Iterációs módszerek: Jacobi és Gauss-Seidel iteráció Készítette: Gelle Kitti Csendes Tibor Somogyi Viktor London András Deák Gábor jegyzetei alapján 1 ITERÁCIÓS
I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI
 I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI 1 A digitális áramkörökre is érvényesek a villamosságtanból ismert Ohm törvény és a Kirchhoff törvények, de az elemzés és a tervezés rendszerint nem ezekre épül.
I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI 1 A digitális áramkörökre is érvényesek a villamosságtanból ismert Ohm törvény és a Kirchhoff törvények, de az elemzés és a tervezés rendszerint nem ezekre épül.
Megoldott feladatok november 30. n+3 szigorúan monoton csökken, 5. n+3. lim a n = lim. n+3 = 2n+3 n+4 2n+1
 Megoldott feladatok 00. november 0.. Feladat: Vizsgáljuk az a n = n+ n+ sorozat monotonitását, korlátosságát és konvergenciáját. Konvergencia esetén számítsuk ki a határértéket! : a n = n+ n+ = n+ n+ =
Megoldott feladatok 00. november 0.. Feladat: Vizsgáljuk az a n = n+ n+ sorozat monotonitását, korlátosságát és konvergenciáját. Konvergencia esetén számítsuk ki a határértéket! : a n = n+ n+ = n+ n+ =
Komplex számok trigonometrikus alakja
 Komplex számok trigonometrikus alakja 015. február 15. 1. Alapfeladatok 1. Feladat: Határozzuk meg az alábbi algebrai alakban adott komplex számok trigonometrikus alakját! z 1 = 4 + 4i, z = 4 + i, z =
Komplex számok trigonometrikus alakja 015. február 15. 1. Alapfeladatok 1. Feladat: Határozzuk meg az alábbi algebrai alakban adott komplex számok trigonometrikus alakját! z 1 = 4 + 4i, z = 4 + i, z =
Pontműveletek. Sergyán Szabolcs Óbudai Egyetem Neumann János Informatikai Kar február 20.
 Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
Pontműveletek Sergyán Szabolcs sergyan.szabolcs@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar 2012. február 20. Sergyán (OE NIK) Pontműveletek 2012. február 20. 1 / 40 Felhasznált irodalom
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2007. október 24. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2007. október 24. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS
ÉRETTSÉGI VIZSGA 2007. október 24. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2007. október 24. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS
P ÓTVIZSGA F ELKÉSZÍTŐ FÜZETEK UNIÓS RENDSZERŰ PÓTVIZSGÁHOZ. 9. osztályosoknak SZAKKÖZÉP
 J UHÁSZ I STVÁN P ÓTVIZSGA F ELKÉSZÍTŐ FÜZETEK UNIÓS RENDSZERŰ PÓTVIZSGÁHOZ T é m a k ö r ö k é s p r ó b a f e l a d a t s o r 9. osztályosoknak SZAKKÖZÉP 1. oldal 9. OSZTÁLYOS PÓTVIZSGA TÉMAKÖRÖK: I.
J UHÁSZ I STVÁN P ÓTVIZSGA F ELKÉSZÍTŐ FÜZETEK UNIÓS RENDSZERŰ PÓTVIZSGÁHOZ T é m a k ö r ö k é s p r ó b a f e l a d a t s o r 9. osztályosoknak SZAKKÖZÉP 1. oldal 9. OSZTÁLYOS PÓTVIZSGA TÉMAKÖRÖK: I.
Algebra es sz amelm elet 3 el oad as Nevezetes sz amelm eleti probl em ak Waldhauser Tam as 2014 oszi f el ev
 Algebra és számelmélet 3 előadás Nevezetes számelméleti problémák Waldhauser Tamás 2014 őszi félév Tartalom 1. Számok felbontása hatványok összegére 2. Prímszámok 3. Algebrai és transzcendens számok Tartalom
Algebra és számelmélet 3 előadás Nevezetes számelméleti problémák Waldhauser Tamás 2014 őszi félév Tartalom 1. Számok felbontása hatványok összegére 2. Prímszámok 3. Algebrai és transzcendens számok Tartalom
Általános algoritmustervezési módszerek
 Általános algoritmustervezési módszerek Ebben a részben arra mutatunk példát, hogy miként használhatóak olyan általános algoritmustervezési módszerek mint a dinamikus programozás és a korlátozás és szétválasztás
Általános algoritmustervezési módszerek Ebben a részben arra mutatunk példát, hogy miként használhatóak olyan általános algoritmustervezési módszerek mint a dinamikus programozás és a korlátozás és szétválasztás
Kutatási beszámoló. 2015. február. Tangens delta mérésére alkalmas mérési összeállítás elkészítése
 Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
Kutatási beszámoló 2015. február Gyüre Balázs BME Fizika tanszék Dr. Simon Ferenc csoportja Tangens delta mérésére alkalmas mérési összeállítás elkészítése A TKI-Ferrit Fejlsztő és Gyártó Kft.-nek munkája
ELEKTRONIKAI ALAPISMERETEK
 Név:... osztály:... ÉRETTSÉGI VIZSGA 2006. május 18. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2006. május 18. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati
Név:... osztály:... ÉRETTSÉGI VIZSGA 2006. május 18. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2006. május 18. 14:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati
Matematikai geodéziai számítások 6.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Bácsatyai László Matematikai geodéziai számítások 6. MGS6 modul Lineáris regresszió számítás elektronikus távmérőkre SZÉKESFEHÉRVÁR 2010 Jelen szellemi
Taylor-polinomok. 1. Alapfeladatok. 2015. április 11. 1. Feladat: Írjuk fel az f(x) = e 2x függvény másodfokú Maclaurinpolinomját!
 Taylor-polinomok 205. április.. Alapfeladatok. Feladat: Írjuk fel az fx) = e 2x függvény másodfokú Maclaurinpolinomját! Megoldás: A feladatot kétféle úton is megoldjuk. Az els megoldásban induljunk el
Taylor-polinomok 205. április.. Alapfeladatok. Feladat: Írjuk fel az fx) = e 2x függvény másodfokú Maclaurinpolinomját! Megoldás: A feladatot kétféle úton is megoldjuk. Az els megoldásban induljunk el
ALAPFOGALMIKÉRDÉSEK VILLAMOSSÁGTANBÓL 1. EGYENÁRAM
 ALAPFOGALMIKÉRDÉSEK VILLAMOSSÁGTANBÓL INFORMATIKUS HALLGATÓK RÉSZÉRE 1. EGYENÁRAM 1. Vezesse le a feszültségosztó képletet két ellenállás (R 1 és R 2 ) esetén! Az összefüggésben szerepl mennyiségek jelölését
ALAPFOGALMIKÉRDÉSEK VILLAMOSSÁGTANBÓL INFORMATIKUS HALLGATÓK RÉSZÉRE 1. EGYENÁRAM 1. Vezesse le a feszültségosztó képletet két ellenállás (R 1 és R 2 ) esetén! Az összefüggésben szerepl mennyiségek jelölését
ELEKTRONIKAI ALAPISMERETEK
 Elektronikai alapismeretek középszint 5 ÉETTSÉGI VIZSG 05. május 9. ELEKTONIKI LPISMEETEK KÖZÉPSZINTŰ ÍÁSBELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMUTTÓ EMBEI EŐFOÁSOK MINISZTÉIUM Egyszerű, rövid feladatok
Elektronikai alapismeretek középszint 5 ÉETTSÉGI VIZSG 05. május 9. ELEKTONIKI LPISMEETEK KÖZÉPSZINTŰ ÍÁSBELI ÉETTSÉGI VIZSG JVÍTÁSI-ÉTÉKELÉSI ÚTMUTTÓ EMBEI EŐFOÁSOK MINISZTÉIUM Egyszerű, rövid feladatok
Bevezetés a méréstechnikába és jelfeldolgozásba 7. mérés RC tag Bartha András, Dobránszky Márk
 Bevezetés a méréstechnikába és jelfeldolgozásba 7. mérés 2015.05.13. RC tag Bartha András, Dobránszky Márk 1. Tanulmányozza át az ELVIS rendszer rövid leírását! Áttanulmányoztuk. 2. Húzzon a tartóból két
Bevezetés a méréstechnikába és jelfeldolgozásba 7. mérés 2015.05.13. RC tag Bartha András, Dobránszky Márk 1. Tanulmányozza át az ELVIS rendszer rövid leírását! Áttanulmányoztuk. 2. Húzzon a tartóból két
Görbe- és felületmodellezés. Szplájnok Felületmodellezés
 Görbe- és felületmodellezés Szplájnok Felületmodellezés Spline (szplájn) Spline: Szakaszosan, parametrikus polinomokkal leírt görbe A spline nevét arról a rugalmasan hajlítható vonalzóról kapta, melyet
Görbe- és felületmodellezés Szplájnok Felületmodellezés Spline (szplájn) Spline: Szakaszosan, parametrikus polinomokkal leírt görbe A spline nevét arról a rugalmasan hajlítható vonalzóról kapta, melyet
Határozott integrál és alkalmazásai
 Határozott integrál és alkalmazásai 5. május 5.. Alapfeladatok. Feladat: + d = Megoldás: Egy határozott integrál kiszámolása a feladat. Ilyenkor a Newton-Leibniz-tételt használhatjuk, mely azt mondja ki,
Határozott integrál és alkalmazásai 5. május 5.. Alapfeladatok. Feladat: + d = Megoldás: Egy határozott integrál kiszámolása a feladat. Ilyenkor a Newton-Leibniz-tételt használhatjuk, mely azt mondja ki,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
ELEKTRONIKAI ALAPISMERETEK
 ÉRETTSÉGI VIZSGA 2012. május 25. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2012. május 25. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
ÉRETTSÉGI VIZSGA 2012. május 25. ELEKTRONIKAI ALAPISMERETEK KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2012. május 25. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
7. fejezet: Mutatók és tömbök
 7. fejezet: Mutatók és tömbök Minden komolyabb programozási nyelvben vannak tömbök, amelyek gondos kezekben komoly fegyvert jelenthetnek. Először is tanuljunk meg tömböt deklarálni! //Tömbök használata
7. fejezet: Mutatók és tömbök Minden komolyabb programozási nyelvben vannak tömbök, amelyek gondos kezekben komoly fegyvert jelenthetnek. Először is tanuljunk meg tömböt deklarálni! //Tömbök használata
