Wolf Ákos. Cölöpalapok viselkedése szeizmikus terhelés hatására szemcsés talajkörnyezetben
|
|
|
- Boglárka Halászné
- 4 évvel ezelőtt
- Látták:
Átírás
1 Wolf Ákos Cölöpalapok viselkedése szeizmikus terhelés hatására szemcsés talajkörnyezetben doktori értekezés Témavezető: Dr. Richard P. Ray egyetemi tanár Széchenyi István Egyetem Építész-, Építő- és Közlekedésmérnöki Kar Szerkezetépítési és Geotechnikai Tanszék Infrastrukturális Rendszerek Modellezése és Fejlesztése Multidiszciplináris Műszaki Tudományi Doktori Iskola Győr, 2018
2 Köszönetnyilvánítás Elsőként köszönetemet és hálámat szeretném kifejezni témavezetőmnek, Dr. Richard P. Ray professzornak, aki a dinamika, talajdinamika témakörébe bevezetett. Mindig bizalommal fordulhattam hozzá kérdéseimmel, nehézségeimmel, s irányt mutató válaszai, gondolatai mellett biztatása és pozitív szemlélete is nagyban segítette az előrehaladást. Hálával mondok köszönetet Dr. Szepesházi Róbertnek, aki felkeltette a geotechnika iránti érdeklődésemet, pályám kezdetétől nagyban támogatta szakmai fejlődésemet, lehetőséget adott, hogy a győri geotechnikai műhely tagja legyek, s a doktori kutatásomat is építő gondolataival táplálta. Köszönöm a Szerkezetépítési és Geotechnikai Tanszéken dolgozó kollégáimnak, különösen Dr. Szilvágyi Zsoltnak, Hudacsek Péternek, Dr. Koch Edinának és Dr. Kegyes-Brassai Orsolyának, segítségüket, támogatásukat. Végül hálásan köszönöm szeretett feleségemnek és két kislányomnak, hogy biztos hátteret teremtve, türelemmel, s odaadással támogattak utamon. ii
3 Összefoglaló Disszertációmban a cölöpalapozások földrengés alatti viselkedését tárgyalom. Az Eurocode 8 bevezetése a korábbi gyakorlattal szemben előtérbe helyezte a földrengési teherre való méretezést, mely a tervező mérnökök számára új kihívást jelentett. Az elmúlt évben hazánkban egyre elterjedtebben alkalmazott cölöpalapozások földrengés alatti viselkedésének nemzetközi szakirodalma nagyon széles körű, de hazánkban ez idáig nem került a kutatások előterébe. A cölöpöket a földrengések során egyrészről a környező talaj deformációjából eredő kinematikai, másrészről a felszerkezet kilengéséből keletkező tehetetlenségi hatás terheli. A kétféle hatás időben kissé eltoltan jelentkezik, s a talaj-cölöp-felszerkezet kölcsönhatástól függ melyik vezérli az alapozás szerkezeti tervezését. A kinematikai vizsgálatot, melyet számos tényező befolyásol és máig nincsen egzakt eljárás rá, a szabvány feltételhez köti, s ennek megítéléséhez a felszín közeli talajok dinamikai értékelése is szükséges. Megvizsgálom, hogy a hazai tervezői gyakorlatban alapeszközként használt nyomószondázási (CPT Cone Penetration Test) eredményekből milyen módon becsülhető a talajok nyíróhullám terjedési sebessége. A szakirodalom áttekintése után a rendelkezésemre álló adatbázison keresztül elemzem a szakirodalmi becslések pontosságát, illetve új javaslatokat fogalmazok meg a hazai talajviszonyokra. Részletes szakirodalom kutatáson keresztül áttekintem a cölöpök földrengés alatti viselkedésének vizsgálati lehetőségeit, rávilágítok a cölöpviselkedés főbb jellemzőire, ismertetem a befolyásoló tényezőket és azok hatását, valamint a kinematikai és tehetetlenségi hatás viszonyát. Saját vizsgálataimhoz 3D geotechnikai végeselemes szoftvert (Plaxis 3D) használtam, melyben a talajok modellezésére azok nemlineáris a feszültség- és alakváltozási szinttől függő viselkedését leíró anyagmodellt alkalmaztam, a cölöpöt térfogati elemmel és a beágyazott gerenda elemmel is modelleztem. Az általam verifikált, az alsó síkján gyorsulás-idő függvénnyel gerjesztett modellen vizsgáltam a kétféle cölöpmodellezési technika előnyeit, hátrányait, korlátait. Elemeztem, hogy a földrengés jellemzői, illetve a rétegződés miként befolyásolja a cölöpben ébredő kinematikai igénybevételeket. A két hatás kapcsolatát a felszerkzetet súlyának cölöpfejbe való koncentrálásával és azt egyszabadságfokú rendszerként modellezve vizsgálom. Kutatásaim eredményeit 4 téziscsoportban, összesen 9 tézisben fogalmaztam meg, melyet az értekezés záró fejezetében foglalok össze, s ugyanitt adok javaslatot a kutatási téma továbbvitelére. iii
4 Summary In the PhD dissertation the behaviour of pile foundation under seismic loading is analysed and discussed. With the introduction of Eurocode 8 a need for structural analysis for seismic loads was emerged. The previously omitted questions therefore raised new challenges for the design engineers. Apparently the seismic behaviour of piled foundations was an important field of international geotechnical research recently. In Hungary this field has been largely neglected despite the increasing popularity of piled foundations in the last years. During earthquakes piles are subject to kinematic loads resulting from the deformation of the subsoil their embedded in and inertial loads due to the dynamic response of the superstructure. The two effects are lagged relative to each other and the nature of the soil- foundation-superstructure interaction determines which mechanism will provide the loads to be considered in the structural design of the piles. For the analysis of the kinematic effects the involvement of numerous factors seems to be essential and no universal solution for the problem has been proposed to date. The standard requires the detailed analysis of the kinematic effects on the piles to be carried out if certain conditions are met. The dynamic performance of the soil environment is one of the factors that needs to be considered when assessing whether or not the analysis for kinematic loads should be carried out. As in Hungary CPT sounding is a fundamental tool in geotechnical design, CPT based methods available for the estimations of the shear wave velocity were analysed. Following the revision of the literature the accuracies of the available methods were assessed by analysing the correlations between the predicted and measured values of shear wave velocities for cases where direct field measurement results were available. New CPT based shear wave velocity correlations for local soils have also been proposed from the further analysis of the measurement data. Key features of piles subject to earthquake loads and the effects of the influencing factors were presented in a detailed literature review. Analysis methods for problem and the interaction between the kinematic and inertial effect are reviewed and discussed as well. A detailed numerical parametric study has been carried out using a 3D geotechnical FEM package (Plaxis 3D). For modelling the soil environment, a nonlinear constitutive model with stress and strain level dependent stiffness has been used. The piles were modelled using both the volume pile and the embedded beam modelling techniques. The advantages, disadvantages and limitations of both techniques were assessed by running a matrix of tests using a box model, iv
5 which was verified prior to running the test series. The models were subject to irregular acceleration time history excitation prescribed at the base plane of the modelled domain. Test variables included in the investigation matrix for the analysis of the kinematic effects of the earthquake on the piles were the properties of the earthquake and the stratification of the soil profile. For the assessment of the interaction between the two loading mechanisms two different sets of models were analysed. In the first set the mass of the superstructure was concentrated in the pile cap while in the other group single degree of freedom models were tested. The results of the research were summarised in the closing chapter of the dissertation in 9 thesis statements presented in 4 statement groups. In this chapter suggestions for future research are also included. v
6 Tartalomjegyzék: 1. Bevezetés A téma aktualitása, gyakorlati jelentősége PhD kutatásaim célkitűzései, várt eredményei, a disszertáció tartalma Talajbesorolás javítása a hazai talajviszonyokra Szeizmikus terhelésű cölöpök modellezésének fejlesztése Kinematikailag terhelt cölöpök viselkedésének vizsgálata Tehetetlenségi és kinematikai igénybevétel kapcsolata Talajosztály meghatározásának fejlesztése Szakirodalom feldolgozás Talajosztályozás az Eurocode 8-1 szerint Talajok nyíróhullám terjedési sebességének becslése CPT alapján Összefoglalás Adatbázis Helyszín, geológiai és geotechnikai adottságok Adatkiválasztás Szakirodalmi ajánlások értékelése a hazai talajviszonyokra vs és CPT mintatávolságok különbözőségének kezelése Szakirodalmi ajánlások összehasonlítása Új ajánlások kidolgozása Áttekintés Korrelációk a kor és keletkezés szerint elkülönített négy talajcsoportra Korrelációk geológiailag hiányosan ismert helyekre Összefoglalás Cölöpviselkedés végeselemes modellezése földrengés teherre Szakirodalom feldolgozás Cölöpalapozás tervezése az Eurocode 8 szerint Cölöpök földrengések alatti viselkedésének vizsgálati lehetőségei Modellezés célja Modellalkotás Talajmodell Cölöpparaméterek Gyorsulásdiagramok Modellméret, véges elemes hálósűrűség Modell-verifikálás Talajválasz elemzés HSS anyagmodellel Más számítási modell reprodukálása Cölöp igénybevételek kinyerése a fejtömb környezetében VP esetén Cölöpmodellezési technikák összevetése
7 Gerjesztés jellemzőinek szerepe a modellezési technikák alkalmazhatóságában Cölöpátmérő szerepe a cölöpmodellezési technikák alkalmazhatóságában Összefoglalás Kinematikai igénybevétel vizsgálata Szakirodalom feldolgozás Cölöpök földrengés alatti viselkedése Réteghatáron ébredő kinematikai igénybevétel Cölöpfejnél ébredő kinematikai igénybevétel Összefoglalás Vizsgálat célja Gerjesztés jellemzőinek hatása a cölöp igénybevételeire Réteghatáron fellépő igénybevétel vizsgálata Cölöpfejnél ébredő nyomatékok elemzése Rétegződés hatása az igénybevételekre Összefoglalás Tehetetlenségi és kinematikai igénybevétel kapcsolata Szakirodalom feldolgozás Támaszmerevség hatása a felszerkezet válaszára Kinematikai és tehetetlenségi hatás időbeli viszonya Alkalmazható cölöpátmérő tartomány Modellezés célja és eszköze Fejtömb súlyának hatása az igénybevételekre Felszerkezet egyszabadságfokú szerkezetként vizsgálva Komplex modellezés hatása a felszerkezet viselkedésére Kinematikai és tehetetlenségi nyomaték viszonya Összefoglalás Tézisek és javaslat a további kutatási témákra Doktori értekezés tudományos eredményeinek összefoglalása téziscsoport: talajok nyíróhullám terjedési sebességének becslése téziscsoport: cölöpmodellezési lehetőségek vizsgálata téziscsoport: a gerjesztés hatása a cölöpök kinematikai igénybevételére téziscsoport: kinematikai és tehetetlenségi hatás kapcsolata Kutatás által felvetett tovább vizsgálandó kérdések Irodalomjegyzék Alkalmazott jelölések
8 1. Bevezetés 1.1. A téma aktualitása, gyakorlati jelentősége A nagyobb építmények, épületek, műtárgyak többsége hazánkban az utóbbi negyedszázadban mélyalapozással, elsősorban cölöpalapozással készül. Ennek oka egyrészről, hogy az új létesítmények jelentős részét a korábban éppen a kedvezőtlen geotechnikai adottságok miatt be nem épített területekre tervezik. Másrészről a szerkezetek méretének növekedése a terhelések emelkedésével jár, s harmadrészt a különleges szerkezetek (pl. acél-üveg konstrukciók) a süllyedések, illetve süllyedéskülönbségek minimalizálását igénylik. A cölöpök geometriai méreteinek meghatározását elsősorban a függőleges terhelésre való megfeleltetés vezérli, mellyel számos hazai kutató foglalkozott az elmúlt évtizedekben (Mahler, 2007) (Szepesházi, 2011). Az ő munkásságuknak, illetve a nagyszámú cölöp-próbaterhelési eredményeknek köszönhetően a nyomószondázás (Cone Penetration Test, továbbiakban CPT) alapú méretezési eljárások a geotechnikai tervezési gyakorlatban megszokott megbízhatósági követelményeknek alapvetően megfelelnek. A cölöpök szerkezeti méretezését az előírt minimális vasmennyiség betartásán túl a vízszintes teherre való megfeleltetés határozza meg. Ekkor a cölöpöket általában Winkler elvén, rugalmasan ágyazott gerendaként vizsgálják a felső pontban működtetett vízszintes teherre. A méretezéshez a talaj és a szerkezet kölcsönhatását (Soil-Structure Interaction, továbbiakban SSI) szimuláló rugók merevségét általában tapasztalati alapokon választják meg a talaj típusától, állapotától függően, de sajnos sok esetben a geotechnikai adottságoktól függetlenül végzik az analízist. Az utóbbi években egyre gyakrabban lineárisan rugalmas-tökéletesen képlékeny megtámasztást vesznek figyelembe a rugókhoz csúszkát kapcsolva vagy végeselemes analízissel a talajt ilyen viselkedést leíró közegként kezelve. Ennek elterjedésében a győri Szerkezetépítési és Geotechnikai Tanszéken végzett korábbi kutatások is szerepet játszottak (Szepesházi, et al., 2008) (Szép, 2014). Az Eurocode bevezetésével, s különösen az Eurocode 8 (MSZ EN 1998, továbbiakban EC 8) hatályba lépésével a geotechnikai és a tartószerkezeti tervezőknek új kihívásokkal kellett szembe nézniük, valamennyi szerkezetet, szerkezeti elemet a földrengési hatásokra is méretezni kell. A korábbi tervezői gyakorlatban e hatást általában elhanyagolták, a jelenleginél alacsonyabb gyorsulási értékekkel számolva ugyanis vízszintes értelemben a szélteher volt a mértékadó, csak speciális esetekben ellenőrizték a szeizmikus terhekre való megfelelést. 3
9 A mélyalapozást a földrengés során kétféle hatás éri (1-1. ábra). Egyrészről a cölöp körüli talaj hullámterjedésből keletkező deformációja a merevebb szerkezetre kinematikai hatást fejt ki, másrészről a felszerkezet kilengéséből a cölöp felső pontján tehetetlenségi igénybevétel ébred ábra: Kinematikus és tehetetlenségi hatás a cölöpalapozáson (Mylonakis, et al., 2014) A felszerkezetről átadódó teherre minden mélyalapozást ellenőrizni kell, s azt az előzőekben ismertetett módon, pszeudostatikus terhelésként szokás végrehajtani. A felszerkezetről az alapozásra jutó teher nagyságát befolyásolja a felszerkezet tömege, szerkezeti rendszere, a területre jellemző a szabványban megadott alapkőzetre vonatkozó maximális talajgyorsulás és a felszín közeli talajrétegződés. Utóbbi szerepe egyrészt a földrengési teher felnagyításában, másrészt az SSI-ben egyaránt megjelenik. A kinematikai hatást az EC 8-5 előírásai szerint akkor kell részletesen vizsgálni, ha az alábbi feltételek együttesen fennállnak: a talajosztály D, S1 vagy S2, a megtámasztott szerkezet fontossági osztálya III vagy IV, a felszíni talajgyorsulás nagyobb, mint 0,1g. Az utolsó hazánkban szinte mindenhol teljesül, így valójában egy III vagy IV fontossági osztályú épület (például irodaház, színház, völgyhíd, Duna hidak stb.) esetén a talajosztály besorolás határozza meg a kinematikai vizsgálat szükségességét. A szabvány a talajrétegződés hatásának számításba vételéhez talajosztályokat vezet be, melyekbe a felső 30 m vastag talajzóna alapján lehet a besorolást megtenni. A besorolás alapja a nyíróhullám átlagos terjedési sebessége (vs,30) vagy a talaj drénezetlen nyírószilárdsága (cu) vagy pedig az SPT szondázás (Standard Penetration Test, standard penetrációs vizsgálat) ütésszáma (N30), esetleg egy jellemző rétegleírás. A hazai gyakorlatban a nyíróhullám terjedési sebesség mérésére irányuló helyszíni vagy laboratóriumi mérést azok magas költségvonzata miatt 4
10 csak nagy projektekhez végeznek. Az SPT szondázás helyett a magyarországi geotechnikai tervezési gyakorlat elsősorban a CPT szondázásra támaszkodik. Ennek oka, hogy a hazánkban jellemző, főként negyedidőszaki képződményekben a CPT szondázás hatékonyan alkalmazható. Ennél fogva leggyakrabban a besorolás csak a rétegleírás alapján, illetve esetenként valamilyen módon becsült drénezetlen nyírószilárdság alapján valósul meg. A győri Szerkezetépítési és Geotechnikai Tanaszéken az elmúlt időszakban folytatott kutatások rávilágítottak arra, hogy a talajrétegződésnek a felszíni válaszra nagyon jelentős hatása van ( (Kegyes-Brassai & Ray, 2015), (Szilvágyi, et al., 2017), (Kegyes-Brassai, et al., 2017)), így a pontosabb talajbesorolás nagyban csökkentheti a méretezési kockázatot. Hazánk geológiai adottságaiból fakadóan, amennyiben a fontossági osztály szükségessé teszi, sok esetben a kinematikai hatást is értékelni kell. Ezt érzékelteti Budapest talajbesorolás térképe is (1-2. ábra), melyen sok folt jelez D talajosztályt, illetve Magyarország talajfolyósodási veszélyeztetettségét mutató térkép is (1-3. ábra) ábra: Budapest talajkategória térképe (Győri, et al., 2010) 1-3. ábra: Magyarország talajfolyósodási veszélyeztetettségi térképe (Győri, et al., 2004) A kinematikai hatást számos tényező befolyásolja, mint a talajrétegződés, talajok dinamikai jellemzői, a talaj-szerkezet merevségi aránya, a gerjesztés jellemzői, a cölöp-cölöpfej kapcsolata. Ebből adódik, hogy a cölöpök földrengés alatti viselkedésének vizsgálata komplex feladat, nemzetközi szinten is csak az elmúlt évben került a kutatás középpontjába, hazai kutatás pedig e területen eddig még nem volt. Néhány ajánlás található az irodalomban az igénybevételek becslésére, ugyanakkor egységesen elfogadott eljárás nem ismert. Vélhetően ez az oka, hogy a kinematikai vizsgálatra az EC 8-5 szabvány sem ad iránymutatást. Ezek alapján indokolt az eddig hazánkban nem vizsgált téma kutatása, s olyan vizsgálati eszköz választása, amely a geotechnikai tervezési gyakorlatban ma már elérhető. 5
11 Magam építőmérnöki diplomám megszerzése óta az oktatás mellett geotechnikai tervezőként tevékenykedek, s volt alkalmam részt venni számos mélyalapozási projekt előkészítésében, tervezésében, valamint cölöp-próbaterhelések végrehajtásában, értékelésében. E körülmények irányították a figyelmemet a cölöpök földrengés alatti viselkedésére, melyben szerepet játszott az is, hogy néhány évvel ezelőtt Richard P. Ray professzor vezetésével a győri Széchenyi István Egyetem Szerkezetépítési és Geotechnikai Tanszékén földrengéssel, talajdinamikával foglalkozó kutatócsoport alakult. A csoport kutatási témái között szerepel többek között a talajok dinamikai paramétereinek meghatározása (Szilvágyi, 2018), a városi építmények földrengés veszélyeztetettsége (Kegyes-Brassai, 2014), illetve a hídhoz csatlakozó töltés dinamikus vasúti terhelés alatti viselkedésének modellezése (Koch & Hudacsek, 2017) PhD kutatásaim célkitűzései, várt eredményei, a disszertáció tartalma Talajbesorolás javítása a hazai talajviszonyokra Amint arra rámutattam, a szerkezetek (köztük a cölöpalapozások) földrengésre való tervezésének fontos eleme az EC 8-1 szabvány által előírt talajosztály besorolás, melyet a geotechnikus mérnökök a talajvizsgálati jelentésben adnak meg. A besorolás általában a költséges, a talajok dinamikai paramétereinek meghatározására irányuló helyszíni és laboratóriumi vizsgálatok hiányában a rétegződés leírásán alapul. Nagy volumenű projektek költségkerete teszi csak lehetővé szeizmikus vizsgálatok elkészítését, például helyszíni felszíni szeizmikus refrakciós, furatbeli crosshole, downhole és a szondázáshoz kapcsolódó SCPT vizsgálatokat vagy laboratóriumban a torziós nyíró-, rezonanciás talajhenger és a Bender-elemes vizsgálatokat (Ray, et al., 2014). Ugyanakkor mára a geotechnikai feltárási programok alapvető részévé vált a CPT. CPT adatokból a nyíróhullám terjedési sebesség becslését számos kutató vizsgálta, valamennyi elemzés általában konkrét helyszínre vonatkozóan ad ajánlást (pl. (Andrus, et al., 2007) (Hegazy & Mayne, 1995)). A hazai talajviszonyokra vonatkozóan ezidáig ilyen elemzés nem áll rendelkezésre. Ezért a kutatásom egyik célja az volt, hogy megvizsgáljam a nemzetközi szakirodalomban fellelhető összefüggések hazai talajviszonyokra való alkalmazhatóságát, illetve eljárást adjak, miként becsülhető a CPT szondázás eredményeiből a nyíróhullám terjedési sebessége hazai talajviszonyok esetében. Célom olyan korrelációk felállítása volt, melyek a talajleírásnál megbízhatóbb alapot szolgáltatnak a besoroláshoz, illetve egy építési terület változékonyságának feltérképezéséhez a földrengésveszélyesség szempontjából, továbbá segíthetik a szeizmikus mérések helyének kijelölését és azok eredményeinek kiterjesztését. 6
12 E témát tárgyalja a 2. fejezet. Ennek elején a témával foglalkozó szakirodalom feldolgozását ismertetem, melynek keretében kigyűjtöttem a hazai talajokra alkalmazhatónak ítélt korrelációs összefüggéseket. Ezt követően előbb a hazai geotechnikai tervező cégektől kapott információkból összeállított adatbázist mutatom be, majd ennek alapján értékelem a kiválasztott ajánlások alkalmazhatóságát. A fejezet utolsó részében a hazai talajviszonyokra új javaslatokat adok, melyek figyelembe veszik a talaj típusát, geológiai korát és eredetét Szeizmikus terhelésű cölöpök modellezésének fejlesztése A cölöpökön álló szerkezetek földrengés alatt rendkívül komplex módon viselkednek. Válaszukat befolyásolja a felszerkezet kialakítása (magasság, merevség, tömeg, stb.), az alapozás tulajdonságai (módszer, geometria, merevség, anyagjellemzők, stb.), a talajrétegződés (rétegződés, állapot, mechanikai jellemzők, nemlinearitás, stb.) és a szeizmikus hatás jellemzői (csúcsgyorsulás, időtörténet, frekvenciatartalom) valamint mindezek kölcsönhatásai. Az EC 8 bevezetésével a földrengésre való méretezés előtérbe került hazánkban, az e témát taglaló kutatások és azzal kapcsolatos gyakorlati problémák, nehézségek száma jelentősen megnőtt. A cölöpalapozás tekintetében a talajdeformációból származó kinematikai és a felszerkezet kilengése okozta tehetetlenségi hatást is számos tényező befolyásolja. Ezen tényezők hatását különféle modelleken vizsgálták, legelterjedtebb a Winkler szerint rugalmasan ágyazott gerenda modell dinamikai kérdésekre fejlesztett (BDWF beam on dynamic Winkler foundation) változata, illetve a véges elemes módszer alkalmazása. A vizsgálatok rendre lineárisan rugalmas viszkózus, a mélységgel konstans paraméterekkel rendelkező talajprofilba ágyazott cölöpökre fókuszálnak. A véges elemes módszerben a cölöpöket térfogati elemmel modellezték. Kutatásomhoz véges elemes módszert alkalmaztam, s munkámhoz a Plaxis 3D geotechnikai szoftvert használtam. Ennek alkalmazási lehetőségeit sokfelé kutatják, dinamikai moduljának földrengési hatásokra való elemzési potenciálját is elemzik már, mint például: (Sedighi, et al., 2017). A cölöpök dinamikai viselkedésének analizálásáról szóló publikációt viszont nem találtam. A Plaxis 2D szoftver ilyen célú felhasználási potenciálját (van der Kwaak, 2015) elemezte. A szoftverben a talajok nemlineáris viselkedésének leírására számos anyagmodell áll rendelkezésre, melyek közül kutatásomban a felkeményedő talajmodell kis alakváltozási tartományban mutatkozó merevebb viselkedést is magában foglaló változatát alkalmaztam (Hardening Soil Small Stiffness modell HSS). Az anyagmodell számításba veszi a kis alakváltozási tartomány- 7
13 ban jellemző nagyobb merevséget, illetve annak az alakváltozás növekedésével való csökkenését (leromlását), s a mélységgel növekvő merevséggel kalkulál. Ezen jellemzők a valóságot jobban lekövető vizsgálódást tesznek lehetővé a korábbi elemzésekkel szemben. A cölöpök modellezésére a térfogati elemen túl egy speciális, úgynevezett beágyazott gerenda elemet ( embedded beam EP) is felkínál a szoftver, mely hatékonyabb számítást tesz lehetővé. Ez a térfogati elemekkel modellezett cölöpökkel szemben a számítási idő csökkenését és az igénybevételek könnyebb kinyerhetőségét is szolgálhatja. Az előzőken túl a szoftverválasztást indokolta az is, hogy a hazai geotechnikai tervezői társadalom komplex feladatok vizsgálatára leginkább a Plaxis 2D szoftvert hívja segítségül, s egyes tervezőirodákban már a Plaxis 3D is elérhető. E szoftver a számítástechnika további fejlődése révén várhatóan a közeljövőben a geotechnikai tervezői gyakorlat alapeszközeként fog funkcionálni. Kutatásaim második célja az volt, hogy vizsgálja a Plaxis 3D szoftver alkalmazhatóságát a földrengés okozta kinematikai terhelésnek és a cölöpök válaszának modellezésére. A 3. fejezet elején ismertetem a nemzetközi gyakorlatban alkalmazott vizsgálati eljárásokat, s összefoglalom a szoftver ilyen modellezéssel kapcsolatos főbb lehetőségeit. Ezt követően bemutatom az alkalmazandó modellt és annak verifikációját. A fejezet végén két modellezéstechnikai kérdést elemzek, a térfogati elemmel modellezett cölöpből az igénybevételek kinyerési lehetőségeit más szerkezethez való csatlakozásnál, illetve a cölöpmodellezési lehetőségeket vizsgálva azok alkalmazhatóságát, előnyeit, hátrányait Kinematikailag terhelt cölöpök viselkedésének vizsgálata A cölöpöket a kinematikai és tehetetlenségi hatásra a gyakorlatban rendre elkülönülten vizsgálják. A kinematikai igénybevételek nagyságát egyedi, a cölöpfejnél esetleg elfordulás ellen megfogott, terheletlen cölöp modellen analizálják, s itt a nyíróhullám terjedéséből keletkező talajdeformáció jelenti a hatást. A kinematikai igénybevétel a cölöpökben két eltérő merevségű réteg határának környezetében, illetve a cölöpfejhez való kapcsolódásnál számottevő. Az igénybevételek nagyságát elsősorban a talaj-cölöp merevségi viszonya, a talajrétegződés beleértve a rétegek merevségi arányát és a nyíróhullám terjedési sebességének változékonyságát, illetve a gerjesztés jellemző frekvenciatartománya befolyásolja. Ezek hatását számos kutató vizsgálta már paraméteranalízissel az előző fejezetben említett vizsgálati módszerekkel. Kutatásom keretében célom a többféle befolyásoló tényező közül a gerjesztésként alkalmazott földrengések jellemzőinek és a felső laza réteg vastagságának hatását elemezni a korábbiaknál komplexebb modellen. 8
14 A 4. fejezet elején a szakirodalom feldolgozásán keresztül áttekintést adok a cölöpök földrengés alatti viselkedéséről, a főbb befolyásoló tényezőkről és azok hatásairól, valamint ismertetem a nyomatéki igénybevételek becslési eljárásait. A fejezet második részében saját vizsgálataimat foglalom össze továbbá értékelem azok eredményeit Tehetetlenségi és kinematikai igénybevétel kapcsolata A cölöpalapozások komplex, a felszerkezetet is magában foglaló modellezése nagy számítási igényt támaszt, ezért általában a méretezéséhez a kinematikai és a tehetetlenségi hatást elkülönülten vizsgálják, melyeket a szuperpozíció elvét alkalmazva egyesítenek (Gazetas, 1984): 1) talaj és alapozás kölcsönhatásának vizsgálata a felszerkezetet nélkül (kinematikai hatás) 2) alapozás dinamikus impedancia paramétereinek meghatározása (rugómerevség, csillapítás) 3) felszerkezet vizsgálata az 1)-ben meghatározott hatásra a 2) szerinti támaszjellemzőkkel. A cölöpök méretezése ezt követően az 1) pontban meghatározott kinematikai és a 3) pontban meghatározott tehetetlenségi igénybevételek összegére (szuperpozíciójára) történhet. Azonban a talajban terjedő földrengési hullám elsőként a cölöpre fejt ki kinematikai hatást, s az hozza mozgásba a felszerkezetet, így a két komponens időben kissé eltolódva jelentkezik. Ennél fogva a két komponens maximális értékének szuperponálása esetleg túlméretezéshez vezethet. Másrészről a kinematikai hatást, mint láttuk, nem minden esetben kell elemezni, s annak elhanyagolása a cölöpök alultervezését eredményezheti. A két hatás kapcsolatát a komplex viselkedést egyszerűsített modellen elemzem. Egyik esetben a tehetetlenségi hatás a fejtömbbe koncentrált felszerkezeti súlyból származik. Másik modellen az egyedi cölöp felett a felszerkezetet egyszabadságfokú szerkezetként, egy oszlop tetején levő tömeggel reprezentálom. Vizsgálom, hogy a földrengés alatti viselkedést miként befolyásolja a szerkezet merevsége (keresztmetszeti méretei) és tömege, azaz annak periódusideje. Az eredményeken keresztül arra keresem a választ, hogy egyrészről miként befolyásolja a felszerkezet viselkedését az alapozás komplex modellezése, másrészről milyen kapcsolatban van a cölöpben ébredő kinematikai és tehetetlenségi, illetve teljes igénybevétel. Az 5. fejezet első részében a két komponens kapcsolatát foglalom össze a szakirodalom feldolgozása alapján, majd saját számítások eredményei révén elemzem a kinematikai és tehetetlenségi hatás kapcsolatát. 9
15 mélység [m] 2. Talajosztály meghatározásának fejlesztése 2.1. Szakirodalom feldolgozás E fejezetben az első kutatási célhoz kapcsolódóan a talajosztályozást segítendő, a nyíróhullám talajban való terjedési sebességének CPT adatokból való becslési lehetőségeit taglaló szakirodalmakat tekintem át. Bevezetésként a kutatási téma ötletét is adó EC 8 ide vonatkozó részeit foglalom össze Talajosztályozás az Eurocode 8-1 szerint A földrengés felszíni hatását egyéb tényezők, mint például a földrengés erőssége, az epicentrum mélysége mellett alapvetően befolyásolják a felszín közeli talajrétegek. Merev, kemény rétegekben a nyíróhullám magas frekvencián terjed, puha, laza talajokban az alacsonyabb frekvenciával egyidejűleg azok amplitúdója megnövekszik, így a szerkezetek szempontjából kedvezőtlenebb hatás éri el azokat. A felszín közeli talaj felnagyító hatásának számításba vételére az EC 8-1 hét talajosztályt definiál (ld táblázat). Ezek közül öt (A-E) v s [m/s] A általános adottságú talajösszlet, míg kettő (S1 és S2) speciális talajokat foglal magában. Egy 5 B konkrét helyszín besorolását elsősorban a nyíróhullám terjedési sebességének felső 30 m-re jellemző átlaga (vs,30) szerint kell elvégezni, melynek számítása C E v s, hi v i1,n si (2-1) 20 D képlettel történhet, ahol hi és vsi az egyes rétegek vastagsága és nyíróhullám terjedési sebességének értéke. Jellemző vs-profilokat mutat a 2-1. ábra. A talajosztály megállapítható a talajleírás, a 2-1. ábra: Talajosztályok jellemző nyíróhullám terjedési sebessége (Faccioli, 2007) drénezetlen nyírószilárdság (cu) és az SPT-vizsgálat eredménye (NSPT) alapján is, s ahogy azt korábban már említettem a gyakorlat sokszor csak az elsőt alkalmazza
16 Ez a talajosztályozás valószínűleg egyszerűsége révén terjedt el, ugyanakkor meg kell említeni azt a hátrányát, hogy nem veszi számításba a 30 m alatti talajzónák hatását. Kifogásolható, hogy az egyes talajosztályok tág tartományt fednek le, miközben azokon belül is jelentősen eltérhet ugyanazon földrengés felszíni hatása (Kegyes-Brassai, 2014) táblázat: Talajosztályok az MSZ EN szerint Altalajosztály A rétegszelvény leírása v s,30 (m/s) Paraméterek N SPT (ütés/30cm) c u (kpa) A B Szilárd kőzet vagy kőzetszerűen viselkedő geológiai képződmény, amely felett legfeljebb gyengébb fedőréteg van Nagyon tömör homok-, kavics- vagy kemény agyagrétegek, legalább több tíz m vastagságban, a mechanikai jellemzők a mélységgel fokozatosan növekednek C Tömör vagy közepesen tömör homok-, kavics- vagy merev agyagrétegek, több tíz vagy akár több száz m vastagságban D E Laza vagy közepesen tömör kohézió nélküli talaj (némi puha kötött réteggel vagy anélkül), vagy túlnyomóan puha gyúrható kötött talaj Felszíni üledékréteg, amely a v s érték szerint C vagy D osztályú, 5 és 20 m közötti vastagságú, alatta 800 m/snál nagyobb nyíróhullám-sebességű, merevebb anyag S 1 Puha agyagból/iszapból álló vagy legalább egy vastag agyagot/iszapot tartalmazó, nagy plaszticitású (PI 40) és nagy víztartalmú rétegek < S 2 Folyósodásra hajlamos talajok, érzékeny agyagok vagy más olyan talajrétegek, amelyek nem sorolhatók az A E vagy S 1 osztályba Ahogy a bevezetőben említettem a cölöpök kinematikai ellenőrzésének szükségességét a szabvány által támasztott feltételek közül alapvetően a talajosztály határozza meg. Meg kell említeni, hogy a szabvány az E talajosztályt nem támasztja feltételnek, holott éppen annál jellemző a réteghatáron markáns merevségi változás. Az ilyen a hazánkban is előforduló talajkörnyezetben nagy terhelésű építmény esetén kézenfekvő olyan cölöpalapozás alkalmazása, mely beköt az alaprétegbe, s a terheit talpfelületén annak adja át. Az ilyen cölöpöket viszont a réteghatáron egy esetleges földrengés esetén jelentős igénybevétel érheti, melyre a cölöpöt méretezni szükséges. 11
17 Talajok nyíróhullám terjedési sebességének becslése CPT alapján Az előzőekben ismertetettek szerint a szeizmikus tervezés első lépése a terület geotechnikai adottságainak, a talajrétegződés dinamikai jellemzőinek értékelése, melyhez elsősorban a nyíróhullám terjedési sebesség (vs) meghatározása szükséges. Ez és a nyírási modulus (G) tekinthető a talaj alapvető dinamikus paramétereinek. A nyíróhullám terjedési sebességének sokféle mérési lehetőségei közül praktikus okok miatt a szeizmikus CPT (SCPT) és szeizmikus dilatométer vizsgálatoknak különös jelentősége van. Ezekben a hagyományos szondázást kombinálják a down-hole jellegű szeizmikus méréssel. A disszertációban feldolgozott nyíróhullám terjedési sebesség adatokat (ld fejezet) SCPT műszerrel mérték, melyhez a CPT mérőfejet két, egymástól jellemzően 50 cm-re elhelyezkedő geofonnal szerelik fel. A vs méréshez egy adott mélységben a mérőfejet megállítják, majd a felszínen a talajnak nyomott gerenda ütésével nyíróhullámot gerjesztenek, melyek keresztülhaladva a talajrétegeken érik el a geofonokat (ld ábra). Az érzékelőkhöz való beérkezési idők közötti különbség a rögzített jelekből számítható, amiből l v s (2-2) t Geofon 1 Nyíróhullám gerjesztés ahol l a két geofon közötti távolság (általában 50 cm) és t a hullám két érzékelő közötti terjedési ideje. Ezen mérési elv szerint a mért vs értékek cm vastag rétegeket jellemeznek. Geofon ábra: Szeizmikus CPT működési elve Az elmúlt egy-két évtizedben több publikáció jelent meg, mely összefüggést ad a talajok dinamikai paramétereinek, elsősorban nyíróhullám terjedési sebességének becslésére CPT szondázási eredményekből (pl.: (Andrus, et al., 2007), (Robertson, 2009), (Tonni & Simonini, 2013)) A nyíróhullám terjedési sebesség (és a nyírási modulus is) a talajok kis és rugalmas alakváltozási tartományára vonatkozó paraméterek. A CPT szonda behatolása viszont nagy alakváltozási tartományban kialakuló törési állapotot eredményez, a mért qc csúcsellenállás és fs palástsúrlódás ezt jellemezi. Így a két paraméter az alakváltozási tartomány két ellentétes végére érvényes (ld ábra). 12
18 Normalizált nyírási modulus, G/G 0 [-] 1 Használhatósági határállapot Teherbírási határállapot Támszerkezetek Alapozások Alagutak 0 Nagyon DMT kis PMT alakváltozás Kis alakváltozás Nagy alakváltozás SCPT Geofizikai vizsgálatok Hagyományos talajvizsgálatok CPT Nyírási alakváltozás, g s [-] 2-3. ábra: Nyírási modulus változása a nyírási alakváltozás szerint (Obrzud, 2010) nyomán (Schneider, et al., 2004) bemutatták, hogy ugyan a vs, illetve qc+fs paramétereket nagyon eltérő jelenség szabályozza, de értéküket hasonló paraméterek befolyásolják. Meghatározóak a hatékony feszültségek, a relatív tömörség és a szemcseméret, kisebb hatása van a geológiai kornak és a cementáltságnak. Ezekből adódik, hogy fel lehet lelni korrelációt a vs, illetve qc+fs paraméterek között, különösen fiatal, normálisan konszolidált üledékek esetében. A szakirodalomban az 1980-as évek közepétől lehet találni a témával foglalkozó publikációkat, (Baldi, et al., 1989), (Robertson, et al., 1992), (Mayne & Rix, 1995), (Hegazy & Mayne, 1995). A szeizmikus CPT elterjedésével a publikációk száma markánsan megnövekedett, melyekben az aktuális feszültségállapot (mélység), a talajtípus és a geológiai kor hatását is kimutatták (Madiai & Simoni, 2004), (Andrus, et al., 2007), (Karl, et al., 2006), (Robertson, 2009). A szakirodalomban fellelhető korrelációs képletek többsége helyspecifikus adathalmazból, statisztikai értékeléssel nyert összefüggés, így elsősorban az adott helyre vonatkozóan tekinthető pontosnak, általános érvényű, széles adatbázison alapuló ajánlás kevés található. (Baldi, et al., 1989) a Pó folyó homokos üledékeiben crosshole vizsgálattal mért vs értékek és a hatékony feszültséggel (v0 ) normalizált qc csúcsellenállás kapcsolatát felírva publikált elsőként a témáról. (Mayne & Rix, 1995) 31 helyszínről származó adathalmaz többváltozós regressziós analízise alapján kimutatta, hogy agyag talajokban a hézagtényező (e) ismerete nagymértékben javítja vs becslésének megbízhatóságát, ugyanakkor a függőleges feszültség figyelembevétele szerintük nem hoz számottevő javulást. (Mayne & Rix, 1995) saját vizsgálataik alapján rávilágított arra 13
19 is, hogy a plaszticitási index (Ipl) és a vs között fordított arányosság áll fenn, de a plaszticitási index hatásával kapcsolatosan a szakmában nincsen egyetértés. A két paraméter között egyes kutatások egyenes, mások fordított arányosságot mutattak ki, s vannak olyanok is, melyek semlegességet jeleznek, ugyanakkor jobb korreláció kapható, ha a plaszticitási indexet és a túlkonszolidáltsági fokot együtt veszik számításba (Carlton, 2014). (Hegazy & Mayne, 1995) agyagtalajokra az előző ajánlást javította nagyobb adatbázis értékelése alapján, s bemutatta, hogy a becslés két legfontosabb paramétere a kezdeti hézagtényező (eo) és a CPT csúcsellenállás (qc). E képletek hátránya, hogy a hézagtényező mélység szerinti változása a legritkább esetben áll csak rendelkezésre. Homoktalajok esetén a legjobb becslésre a qc és kezdeti hatékony feszültség (v0 ) számításba vételével jutottak, s úgy találták, hogy az fs-nek számottevő hatása nincs a pontosságra. (Hegazy & Mayne, 1995) elsők között voltak, akik általános érvényű talajtípustól független képletet is adtak. Az alábbi összefüggést 323 adatpárral végzett regressziós analízis alapján állították elő, determinisztikus együtthatója R 2 = 0,695: v s f s 10. 1log qc q (2-3) c Az eddig ismertetett, és más itt részletesen nem tárgyalt kutatások negyedidőszaki képződményekre fókuszáltak a geológiai kor további bontása nélkül. (Madiai & Simoni, 2004) vizsgálta, hogy a korreláció pontossága javítható-e a holocén és pleisztocén rétegek különválasztásával. Részletes analízisükben a kor mellett a talajtípust is szétválasztották durva és finomszemcséjű rétegekre, így csoportonként adatpárt elemeztek. A közvetlenül mért értékek (qc és vs, illetve qc+fs és vs) közötti korreláción túl vizsgálták a normalizált értékek közötti kapcsolatot is. Ehhez a normalizált nyíróhullám terjedési sebességet (vs1) (Robertson, et al., 1992) nyomán a v s1 v s pa v0' 0, 25 (2-4) képlettel számították, ahol a már értelmezett jelölések mellett pa az atmoszférikus nyomás. A normalizált csúcsellenállást (Robertson & Wride, 1998) ajánlását követve vették fel: q c1n q p c a p a v0' 0, 5 (2-5) Vizsgálati eredményeik szerint pontosabb becslés adható a mért értékek alkalmazásával, továbbá a geológiai kor számításba vétele nem javította érdemben a becslés pontosságát. Elképzelhető, hogy ez a rendelkezésükre álló kevés adattal magyarázható, hiszen ezzel ellentétben 14
20 (Andrus, et al., 2007) kutatásai éppen a geológiai kor fontos hatására hívták fel a figyelmet. A 2-4. ábra a nyíróhullám mért terjedési sebességének és a CPT csúcsellenállás pórusvíznyomással korrigált értékének (qt) kapcsolatát mutatja a geológiai kor bontásában. Eszerint azonos csúcsellenállás mellett a pleisztocén korú rétegek terjedési sebessége 22 %-kal, míg a harmadidőszaki (tercier) képződményeké 130 %-kal nagyobb, mint a holocén korú talajoké. Nyíróhullám terjedési sebesség, v s [m/s] Holocén Pleisztocén Harmadidőszak CPT csúcsellenállás, q t [MPa] 2-4. ábra: A mért v s és CPT csúcsellenállás kapcsolata geológiai kor szerint (Andrus, et al., 2007) A korábban említett kutatók eredményei szerint a talaj típusa befolyásolja a korreláció alakját, s ennek számításba vételére (Andrus, et al., 2007) az úgynevezett talaj viselkedési tényezőt (soil behaviour type index, Ic) vezették be, mely (Robertson & Wride, 1998) nyomán a I 2 2 0, 3, 47 log Q log F (2-6) c, képlettel számítható, ahol Q és F a normalizált CPT csúcsellenállást illetve normalizált súrlódási arányt jelöli: qt v0 Q (2-7) ' v0 F q t f s v0 100 (2-8) ahol a már ismert jelölések mellett v0 a teljes függőleges feszültség. A talajviselkedési tényező bevezetését az is indokolta, hogy nem mindig áll rendelkezésre talajmechanikai fúrással vett talajminta laboratóriumi vizsgálati eredménye a CPT szondázás közvetlen környezetéből. A talajviselkedési tényező a nevéből adódóan a talaj viselkedéséről ad tájékoztatást, ahogy azt a 2-2. táblázat és ahhoz kapcsolódóan a 2-5. ábra összefoglalja. 15
21 Talajviselkedési tényező I c [-] I c < 1,31 Talajviselkedési csoport kavicsos homok (7 zóna) 1,31 < I c < 2,05 homok talajok (6 zóna) 2,05 < I c < 2,60 homokos talajkeverékek (5 zóna) 2,60 < I c < 2,95 iszapos talajok (4 zóna) Normalizált csúcsellenállás, Q 2,95 < I c < 3,60 agyag talajok (3 zóna) 3,60 < I c szerves talajok (2 zóna) 2-2. táblázat: Talajviselkedési tényező jellemző határai (Lunne, et al., 2002) Normalizált súrlódási arány, F 2-5. ábra: I c kontúrok a talajosztályozási diagramon (Robertson, 2009) (Andrus, et al., 2007) a negyedidőszaki képződményekre (pleisztocén és holocén talajokra együttesen) végül a következő hatványfüggvényt adta: v s 0,395 t 0,912 c 0,124 2,62 q I z SF (2-9) ahol a korábbiakban ismertetett jelöléseken túl z a felszíntől mért mélység méterben kifejezve, mely valójában a feszültségszinttel van kapcsolatban. Az SF (scale factor) a geológiai korok közötti különbséget reprezentálja, értéke holocén esetén 0,92, amivel a 72 adatból álló adatbázisra R 2 = 0,709 adódott. Az idősebb üledékekre az ajánlott érték SF = 1,12, vagyis visszaadódik a korábban említett 22%-os különbség. Megemlítem, hogy pleisztocén rétegekben, köszönhetően a csúcsellenállás tág tartományának (ld ábra) nagyobb a bizonytalanság, ezt igazolja, hogy a (2-9) képlettel a determinisztikus együttható R 2 = 0,430. (Robertson, 2009) a normalizált csúcsellenállást (Qtn) az alábbiak szerint pontosította: Q tn qt p a v0 p a v0' n (2-10) ahol a korábban definiált változókon túl az n kitevő a talajviselkedési tényező függvényében: n 0,381 I c v 0,05 p 0 a ' 0,15 1,0 (2-11) A képletből adódik, hogy amennyiben Ic > 2,6, akkor a (2-10) egyenlet azonos (2-7) képlettel, ám ha Ic < 2,6, akkor iterációra van szükség a normalizált csúcsellenállás meghatározásához. 16
22 A 2-6. ábra a normalizált talajviselkedési diagramon (Normalized Soil Behavior Type Chart, SBTN) több mint 1000 negyedidőszaki (holocén és pleisztocén) adatpont alapján szerkesztett normalizált nyíróhullám terjedési sebességet (vs1) mutat (Robertson, 2009). Az ábra alapján az alábbi képletek adódtak: 0, 55I 1, 68 0, Q 5 c vs 1 10 tn (2-12) v s 10 0, 55Ic 1, 68 q t p a v0 0, 5 (2-13) melyek pleisztocén rétegek esetén kissé alábecsülhetik vs értékét. A (2-13) képlettel becsült nyíróhullám terjedési sebesség Győr térségében végzett összehasonlító számítás szerint jó egyezést mutat a mért értékekkel (Kegyes-Brassai, et al., 2017). Olaszországi kutatások rávilágítottak arra, hogy hasonló ásványtani eredetű és súrlódási jellemzőjű, de különböző szemcseösszetételű talajok eltérő viselkedési trendet mutatnak (Tonni & Simonini, 2013) (ld ábra). A vizsgálódás eredményeként a (2-13) egyenletben szereplő konstansokat optimalizálták, s az alábbi összefüggésre jutottak R 2 = 0,76 determinisztikus együttható mellett: v s 10 0, 31 Ic 0, 77 q t p a v0 0, 5 (2-14) Normalizált csúcsellenállás, Q tn Mért nyíróhullám terjedési sebesség, v s [m/s] Homok- hom. talajkev. Iszap- iszapos talajkev. Normalizált súrlódási arány, F r 2-6. ábra: SBTN diagram v s1 kontúrokkal (Robertson, 2009) Korrigált csúcsellenállás, q t [MPa] 2-7. ábra: Szeizmikus CPT-vel mért v s és korrigált q c közötti kapcsolat (Tonni & Simonini, 2013) 17
23 A nyíróhullám terjedési sebesség a mélységgel növekszik, gyakorlatban rendre alkalmazzák a vs ' v0 (2-15) közelítést is a vs becslésére, melyben az és konstansokat az adott helyen végzett mérési eredmények alapján veszik fel. A bemutatott ajánlások csak a CPT mért eredményeire támaszkodnak, nem kellenek hozzájuk laboratóriumi vizsgálati eredmények. Láttuk ugyanakkor, hogy kötött talaj esetén a hézagtényező (Hegazy & Mayne, 1995), míg szemcsés talajok esetén a szemcseösszetétel (Karray, et al., 2011) javíthatja a becslés pontosságát. Többen rámutattak arra is, hogy elengedhetetlen a geológiai kor, a cementáltság mérlegelése is (Amoroso, 2014) Összefoglalás A felszín közeli rétegek befolyásolják a földrengések felszíni hatását. Ennek számításba vételére az EC 8 a felső 30 m vastag réteg jellemzése alapján talajosztályokat vezetett be. Az osztályba sorolást legpontosabban a nyíróhullám terjedési sebességének e rétegtartományra vett átlaga alapján tehetjük meg. A talajok dinamikai paramétereinek célirányos mérésére a hazai gyakorlatban csak nagy projektek esetében van mód, így felmerül az igény annak a gyakorlatban széles körben alkalmazott feltárási eredményekből való becslésére. A magyarországi geológiai adottságokhoz igazodóan leggyakrabban a CPT szondázást alkalmazzuk közvetett talajfeltárásként. A két paraméter közötti kapcsolatot leíró összefüggések általában konkrét helyszínre geológiai kor, eredet, geotechnikai adottság vonatkozóan statisztikai értékelésen alapulnak. Széles körű adatbázisra támaszkodó korreláció csupán néhány lelhető fel. Ezért ezen képletek hazai talajviszonyokra való alkalmazhatóságának feltétele, hogy azokat konkrét mérési eredmények alapján ellenőrizzük. Továbbá cél olyan korrelációk előállítása, melyek a hazai geológiai és geotechnikai adottságokhoz igazodnak Adatbázis Helyszín, geológiai és geotechnikai adottságok A korrelációk elemzéséhez hazai geotechnikai tervezői cégektől hat városból, de hét különböző helyszínről származó CPT eredményeket és hozzájuk tartozó nyíróhullám terjedési sebesség adatokat szereztem be. A helyszíneket a 2-8. ábra mutatja, Pakson belül két különböző geológiai adottságú helyről is származtak adatok. Minden helyszínről az in situ vizsgálati eredményeken túl a fúrási naplókban leírt talajprofil és a talajvíz helyzete is rendelkezésemre állt, a 18
24 talajok laboratóriumi vizsgálati eredményei viszont nem, így az összehasonlításhoz csak a helyszíni mérési eredményeket használtam fel. Egyéb adat hiányában, a függőleges feszültségeket minden esetben egységesen gn = 19,5 kn/m 3 térfogatsúllyal számítottam. Tivadar Komárom Budapest Szolnok Paks Kaposvár 2-8. ábra: Vizsgálati helyszínek A korábbi vizsgálatok rámutattak arra, hogy a geológiai eredetnek jelentős hatása lehet a becslés megbízhatóságára (Andrus, et al., 2007), ezért a vizsgálati helyszíneket a geológiai adottságok alapján négy fő csoportba soroltam: holocén fluviális (folyami) üledék (HF), pleisztocén fluviális (folyami) üledék (PF), pleisztocén eolikus (szél hordta) üledék (PE), harmadidőszaki rétegek (TR). A HF talajcsoportba tartozik a Tisza fiatal, holocén korú, alapvetően puha-gyúrható állapotú finomszemcsés (homokos iszap-agyag, iszap, agyag) üledéke, mely a vizsgált helyszínek közül Szolnok és Tivadar környékén fordul elő. A CPT szondázás rendre alacsony csúcsellenállás (qc = 1,0 MPa) mellett haladt, a talajviselkedési tényező Ic 3,0 volt. A felszíntől számított 6-8 m mélységig a magasabb homoktartalom kissé kedvezőbb adottságot eredményez. A Duna, jellemzően durvaszemcsés üledékeit foglalja magában a PF talajcsoport, mely a pleisztocén végén rakódott le, de képződését egyes geológusok a holocén kor elejére teszik. A tömör-nagyon tömör rétegek talajosztályozás szerint homok, homokos kavics, kavicsos homok talajnak nevezhetők, ennek megfelelően a viselkedési tényező Ic = 1-2. A változatos szemcse- 19
25 összetétel következtében a CPT csúcsellenállás tág határok között változott, de mindvégig kedvező állapotot tükrözött (qc = MPa). E csoportba Komárom, Budapest és az egyik paksi (Paks-1) helyszín tartozik. A kaposvári és a másik paksi helyszínen (Paks-2) végzett mérési eredmények kerültek a PE talajcsoportba. A pleisztocénben az előbbi fluviális üledék mellett a szélhordta homok és lösz volt a jellegzetes hazai formáció. Ez jellemzően iszap méretű szemcsékből áll, s gyakran meszes kötésű üledék, melyet alacsony plaszticitási index (Ipl = 10-13%) és magas iszap+agyag tartalom (S0,063 = 30-50%) jellemez. A talajviselkedési tényező tipikusan Ic = 2,7-3,0, s a mért csúcsellenállás qc = 1-5 MPa között változott. Harmadidőszaki képződményekre vonatkozó adat kevés állt rendelkezésre, de amennyi volt, azokat külön a TR talajcsoportba gyűjtve vizsgáltam. A budapesti helyszínen a Duna hordaléka miocén korú agyagokra rakódott le, míg a Paks-1 helyszínen az alapréteget pannon homokos agyag képezi. A CPT szondázási eredmények a két helyszínen közel azonosak voltak, a csúcsellenállás qc = 7-13 MPa között változott, míg a talajviselkedési tényező Ic = 2,3-2,7. A bemutatott CPT csúcsellenállási értékek és talajviselkedési tényező értékek az adott talajcsoportokra jellemzőnek tekinthetők, más, azonos geológiai adottságú helyen végzett mérésekkel jó egyezést mutatnak Adatkiválasztás Valamennyi, a témában végzett kutatás a nyíróhullám helyszínen mért terjedési sebességét tekinti valósnak, így magam is eszerint jártam el. Nyilvánvaló persze, hogy ennek mérésében is van bizonytalanság, melynek minimalizálására a talajfelszínhez nyomott gerenda ellentétes oldalának ütésével két mérést végeznek, s a két vs eredmény átlagértékét adják meg. Egyes helyszínek esetében a két mérési sorozat eredményei is rendelkezésemre álltak, ezeknél a vs mérésből származó hiba hatásának csökkentése végett kivettem az adatbázisból azokat, amelyeknél nagy volt a különbség (±15 m/s). A felszínhez közeli mérések esetében a gerjesztés helyének és a mérőfejnek a távolságát nagyobb mértékben befolyásolja azok vízszintes távolsága, ami aránytalanul megnövelheti a hullám terjedési idejét. E zónában gyakran feltöltés, szerves rétegek vannak, azaz nem az egyébként megnevezett domináns talajfajták. Ezeket is szem előtt tartva csak a 3-4 m-nél nagyobb mélységből származó adatokat vettem be az adatbázisba, hasonlóan más kutatókhoz (Madiai & Simoni, 2004) (Andrus, et al., 2007). 20
26 Nem vettem továbbá számításba az elemzéskor közvetlenül a réteg- illetve geológiai kor határokról származó adatokat sem, azok bizonytalan besorolhatósága miatt. A szakirodalomból megismert kutatások során az egy-egy vs értékkel jellemzett mélységtartomány azon adatpárjait, amelyek qc és fs értékeiben jelentős volt a változás, nem vették figyelembe, a változékonyság mérőszámát viszont nem definiálták. Magam e jelenségnek a becslések pontosságára gyakorolt hatását a fejezetben ismertetett következő négy ajánláson keresztül vizsgáltam: 10 1,67 f s 100 c q c (Hegazy & Mayne, 1995) (2-3) egy.: v,1 log q 11,4 s 0,3 (Andrus, et al., 2007) (2-9) egy.: v s 2,62 q 0,395 t I 0,912 c z 0,124 SF (Robertson, 2009) (2-13) egy.: v s 10 0, 55Ic 1, 68 qt p a v0 0, 5 (Tonni & Simonini, 2013) (2-14) egy.: v s 10 0, 31 Ic 0, 77 qt p a v0 0, 5 A csúcsellenállás változékonyságát az adott tartományra vonatkozó relatív szórással (dr,qc) jellemeztem, s a dr,qc > 0,5 értékűeket eleve kiszűrtem, mely azonban csak néhány adatpárt érintett. Az egyes becslések pontosságát a következőképpen értelmezett relatív hiba (er) alapján vetettem össze: e r vse vsm / vsm (2-16) ahol vse a nyíróhullám becsült, vsm pedig a mért terjedési sebessége. er előjele arról tájékoztat, hogy egy korreláció alul- vagy felülbecsüli vs értékét, abszolút értéke a hiba mértékét fejezi ki. A relatív hiba eloszlása szemrevételezés alapján valamennyi esetben normáleloszlású, ahogy azt példaként mutatja a 2-9. ábra a teljes adathalmazra vonatkozóan (Andrus, et al., 2007) ajánlása esetén. A ábra a CPT csúcsellenállás relatív szórásának a becslés pontosságára való hatását szemlélteti a relatív hibával (bal oldal) és annak szórásával (jobb oldal). Az ábrán piros szín jelöli az adott CPT csúcsellenállás relatív szórásához tartozó adatpár számát, lila jelöli (Hegazy & Mayne, 1995) ajánlását (H&M), barna (Andrus, et al., 2007) által javasolt összefüggéssel kapott eredményeket értékeli (A), fekete (Robertson, 2009) munkásságát jelöli (R) és végül zöld (Tonni & Simonini, 2013) eredményeit (T&S). A diagrammokról megállapítható, hogy H&M a többi háromtól kissé eltérő tendenciát mutat a dr,qc változásának függvényében: átlagosan a 21
27 legjobb becslést adja, ugyanakkor ennek a legnagyobb a relatív szórása, s a dr,qc növekedésével a megbízhatósága kissé romlik. A többi három ajánlás pontossága az adatbázis növekedésével javul mind az átlagos relatív hiba, mind pedig annak szórása csökken. 3,0 100 gyakoriság [%] 2,4 1,8 1,2 0, összegzett gyakoriság [%] 0,0 0-0,5-0,25 0 0,25 0,5 relatív hiba, e r [-] 2-9. ábra: Relatív hiba gyakorisága és összegzett gyakorisága (Andrus, et al., 2007) ajánlása esetén Összességében az állapítható meg, hogy a CPT csúcsellenállás változékonyságának a becslés pontosságára érdemi hatása nincsen, így a további értékelésbe a teljes adatbázist bevontam. Összesen 281 mért és számított vs adatot dolgoztam fel, melyek a geológiai csoportok között az alábbi szerint oszlottak meg: holocén fluviális üledék (HF): pleisztocén fluviális üledék (PF): pleisztocén eolikus üledék (PE): harmadidőszaki rétegek (TR): 32 adatpár 154 adatpár 64 adatpár 31 adatpár. a) q c maximális relatív szórása, d r,qc b) q c maximális relatív szórása, d r,qc 0,0 0,1 0,2 0,3 0,4 0,5 0,0 0,1 0,2 0,3 0,4 0, relatív hiba, e r [%] adat szám H&M A R T&S 50 adatok száma 0 0 adat szám H&M A R T&S ábra: Relatív hiba (a) és szórása (b) a q c relatív szórásának függvényében relatív hiba szórása [%] adatok száma 22
28 2.3. Szakirodalmi ajánlások értékelése a hazai talajviszonyokra vs és CPT mintatávolságok különbözőségének kezelése Az összehasonlítandó mért adatok különböző intervallumokra vonatkoznak. A szeizmikus méréssel a nyíróhullám geofonok közötti, jellemzően Hi = 50 cm vastag tartományra érvényes terjedési sebessége határozható meg. A CPT szondázás során hi = 1 vagy hi = 2 cm távolságközökben van mérés, így egy Hi = 50 cm tartományra 25 vagy 50 CPT adategyüttes esik. A szakirodalomban nem találtam utalást arra, hogy a mintatávolságok közötti különbséget mások miként hidalták át. A legkézenfekvőbb megoldás, hogy a CPT adatokat a Hi = 50 cm-es tartományok átlagértékével jellemezzük, s ekkor a talajviselkedési tényező (Ic) kétféleképpen számítható: az átlagos CPT adatokból (avgic): I c hi f qci ; f si H i a mérési adatokból egyenként számított talajviselkedési tényező átlagaként (Ic-avgCPT): I c hi H i f q ci ; f si (2-17) (2-18) Amennyiben valamennyi CPT mérési adatsorból meghatározzuk a nyíróhullám terjedési sebességet, akkor annak Hi = 50 cm-re vonatkozó értéke is kétféle módon számítható a mért CPT adatokból egyenként számított vsi értékek átlagaként (avgvs) v s hi H i v si q ci ; f si (2-19) a mért CPT adatokból egyenként számított vsi értékekből a hi mérésközökre számított ti terjedési idők összegéből (vs50) v s v si H i h q ; f v q ; f ci i si si H i hi 1 ci si (2-20) A teljes adathalmazra vonatkozóan a négy számítási mód által adott átlagos nyíróhullám terjedési sebességet a négy ajánlásra mutatja a ábra együtt a mért sebesség átlagával. Értelemszerűen a talajviselkedési tényezővel nem számoló H&M ajánlás az első két esetre azonos eredményt hoz. A diagram alapján megállapítható, hogy a négy számítási mód érdemi különbséget 23
29 nem ad, az egyes ajánlásokon belül a maximális eltérés legfeljebb 5 m/s, de a valós értékhez legközelebbi eredményt mindegyik ajánlás esetében az avgic számítási mód hozza átlagos v s [m/s] mért H&M A R T&S avgic Ic-avgCPT avgvs vs ábra: Átlagos nyíróhullám terjedési sebesség a négy eljárásra és a mért értékkel A 2-3. táblázat tartalmazza az átlagos hiba értékeket és szórásukat. H&M esetén az utolsó kettő számítási mód ad kisebb hibát, s az ezekhez tartozó szórás közel azonos az első számítási móddal, valamint nagyobb, mint a többi három ajánlás esetén kiadódó. A másik három ajánlásra a legkedvezőbb eredményt az első, azaz a CPT átlagértékéből (avgic) való számítás hozza táblázat: Átlagos hiba értékek és szórásuk avgic Ic-avgCPT avgvs vs50 átlag szórás átlag szórás átlag szórás átlag szórás H&M 1,7% 21,5% 1,7% 21,5% 1,2% 21,5% 0,8% 21,4% A -6,5% 18,8% -7,7% 18,4% -7,2% 18,5% -7,3% 18,5% R -4,7% 19,0% -6,3% 18,6% -5,4% 18,8% -5,6% 18,8% T&S -3,1% 18,4% -5,0% 17,9% -3,9% 18,2% -4,1% 18,1% Ezen eredmények alapján megállapítható, hogy a CPT adatok átlagából való számítás (avgic) elfogadható, jellemzően ez eredményezi a legkisebb hibát, s emellett számítástechnikai szempontból is legkönnyebben kezelhető. (Wolf & Ray, 2017a) (Wolf & Ray, 2017b) Szakirodalmi ajánlások összehasonlítása A négy ajánlás hazai talajviszonyokra vonatkoztatható megbízhatósági értékelésének célja elsősorban a képletek hazai talajviszonyokra való alkalmazhatóságának megítélése, s másodsorban a befolyásoló tényezők tisztázása. 24
30 Az egyes becslési eljárások megbízhatóságának értékelését a relatív hiba és annak szórása mellett a CPT adatokból számolt és mért adatokra illesztett trendvonal meredeksége és determinisztikus együtthatója adja. mért nyíróhullám terjedési seb., vsm [m/s] mért nyíróhullám terjedési seb., vsm [m/s] y = 1,001x R² = 0,251 HM trendvonal becsült nyíróhullám terjedési seb., v se [m/s] y = 1,064x R² = 0, becsült nyíróhullám terjedési seb., v se [m/s] R trendvonal mért nyíróhullám terjedési seb., vsm [m/s] mért nyíróhullám terjedési seb., vsm [m/s] y = 1,079x R² = 0, becsült nyíróhullám terjedési seb., v se [m/s] y = 1,049x R² = 0,395 A trendvonal T&S trendvonal becsült nyíróhullám terjedési seb., v se [m/s] ábra: Teljes adatbázisra vonatkozóan a mért és becsült v s értékek kapcsolata ajánlásonként A teljes adatbázist tekintve a becsült és mért nyíróhullám terjedési sebességek kapcsolatát, az ezekre felrajzolható lineáris trendvonalat és azok paramétereit a négy vizsgált ajánlásra a ábra szemlélteti. A diagramok illetve a relatív hiba adatok alapján megállapítható, hogy az átlagot tekintve H&M ajánlása a legpontosabb, annak trendvonala gyakorlatilag egybe esik a diagramon szaggatott fekete vonallal jelölt vse = vsm egyenessel. Az is érzékelhető, s ezt a determinációs együttható is kifejezi, hogy ennek a legnagyobb a szórása, a pontok itt alkotják a 25
31 legnagyobb felhőt. Ez feltételezhetően abból ered, hogy a (2-3) egyenletben a talaj típusát csak (fs/qc) arányszám reprezentálja. A másik három korreláció (A, R, T&S) hasonló trendet követ: átlagosan alábecsüli a talajok dinamikai jellemzőit, mely mint a későbbiekben látható lesz a PE talajcsoportra kiadódott nagymértékű hibából ered. Ezen ajánlásoknak a szórása már kissé kisebb, az R 2 érték alapján már a negyediknél jobb, de még mindig nem túl erős korreláció jellemző. A geológiai csoportokat külön-külön elemezve a következőkre jutunk: A holocén folyóvízi üledékekre adható a legpontosabb becslés a vizsgált képletekkel. Ezek közül (Robertson, 2009) ajánlása javasolható, a csoportra jellemző vs = m/s nyíróhullám terjedési sebességet mindössze átlagosan 2,4%-os hibával becsüli, s ehhez magas (R 2 = 0,87) determinisztikus együttható tartozik. Az A és T&S becslés is hasonlóan jó korrelációt mutat (R 2 = 0,87), de ott a becsült és mért eredményekre fektetett trendvonal meredeksége jobban eltér az egységnyitől, értékük 0,94-0,96. A H&M ajánlás ugyanakkor jóval nagyobb hibával dolgozik, átlagosan 15%-kal nagyobb dinamikai paramétert eredményez a valósnál. A pleisztocén folyóvízi üledékek esetén szintén jó becslés adható, a trendvonalak meredeksége 1,014-1,036, de nagyobb a szórás mértéke, ahogy ezt a ábra is érzékelteti. Ez a HF talajcsoporténál nagyobb bizonytalanság származhat abból, hogy a durvaszemcsés rétegekben a CPT mérési eredmények ingadozása nagyobb, mint a finomszemcsésekben, viszont a nyíróhullám terjedési sebessége nem változik ilyen érzékenyen. Megemlítem, hogy az összehasonlító elemzés készítésekor a (2-9) egyenletben levő szorzótényezőt (SF) elsőkörben egységnyinek választottam, s láthattuk, hogy így e képlettel közelítően pontos eredményt kaptam. (Andrus, et al., 2007) által a holocén rétegre javasolt 0,92 és pleisztocén rétegre javasolt 1,12 értékek bevezetése a becslés pontosságában romlást, kb % hibát eredményezett, így ezeket a hazai talajviszonyokra nem indokolt alkalmazni. A pleisztocén folyóvízi üledékekre is a legjobb becslés (Robertson, 2009) képletével (2-13) kapható, de a holocén üledékekre tapasztaltakkal összhangban (Andrus, et al., 2007) és (Tonni & Simonini, 2013) javaslata is jó egyezést eredményez. A pleisztocén eolikus képződmények esetében a nyíróhullám terjedési sebességek azonos CPT szondázási ellenállás mellett nagyobbak, mint a folyóvízi üledékeké. Mind a négy vizsgált ajánlás alábecsüli a vs értékét (ld ábra). H&M képlete átlagosan 14%-kal, a többi három eljárás 18-24%-kal ad kisebbet a mért értéknél. Meg kell említeni, hogy (Andrus, et al., 2007) ha- 26
32 sonló megállapításra jutott, 22%-kal nagyobb vs értéket kaptak azonos CPT szondaeredményekre, mint holocén talajkörnyezetben (ld ábra). Ezért javasolták az SF szorzótényező bevezetését, amivel ugyan a HF és PF talajcsoportra rosszabb egyezést kaptam, de e talajcsoportra azzal jobb becslésre jutnánk. (Robertson, 2009) szintén említi, hogy az általa javasolt (2-13) képlet pleisztocén rétegekre alábecsülheti a nyíróhullám terjedési sebességet, de annak mértékéről nem ad tájékoztatást. mért nyíróhullám terjedési seb., v sm [m/s] ábra: Becsült és mért nyíróhullám terjedési sebesség kapcsolata a PF csoportra HM A R T&S becsült nyíróhullám terjedési seb., v se [m/s] mért nyíróhullám terjedési seb., v sm [m/s] ábra: Becsült és mért nyíróhullám terjedési sebesség kapcsolata a PE csoportra H&M A R T&S becsült nyíróhullám terjedési seb., v se [m/s] Az elemzések nyomán látható volt, hogy e talajok esetében nem a geológiai kor a mérvadó, hanem a keletkezési mód. Feltételezhető, hogy a nagyobb vs értékeket a löszre jellemző enyhe cementáltság eredményezheti. Összességében e rétegcsoportra a meglévő ajánlások az elfogadhatónál nagyobb mértékű hibával képesek csak a vs-t becsülni, így azok pontosítása, javítása feltétlenül szükséges. A harmadidőszaki képződményekről kevesebb adat van, s ezek két helyszínén a keletkezés is kissé eltérő. A vizsgálat azt mutatta, hogy a (2-9) képlet (A) és a (2-13) képlet (R) is jó eredményt hoz, mindkettő átlagos hibája közel nulla, s szórása kisebb, mint 15%. H&M ajánlása viszont nagyon túlbecsüli a vs értékét. 27
33 2.4. Új ajánlások kidolgozása Áttekintés E fejezetben a meglévő képletek javítását mutatom be valamennyi talajcsoportra és együtt a teljes adathalmazra. Kiindulásul (Andrus, et al., 2007) és (Robertson, 2009) képletét használtam. Mint láttuk (Tonni & Simonini, 2013) képlete formailag azonos (Robertson, 2009) képletével. (Hegazy & Mayne, 1995) ajánlását figyelmen kívül hagytam, mivel az nem veszi figyelembe a talaj típusát. Az összeállított adatbázis alapján tehát a következő képletek javítását céloztam meg: v s a q b t I c c z d (2-21) v s 10 1Ic 1 qt p a v0 0, 5 (2-22) v s 10 q p 2Ic 2 t v0 a g 2 (2-23) A képletekben szereplő konstansokat ((2-21) a, b, c, d; (2-22) 1, 1; (2-23) 2, 2, g2) az Excel szoftver Solver bővítményével határoztam meg úgy, hogy a mért és becsült nyíróhullám terjedési sebesség különbségének négyzetösszege minimum legyen. Az előző fejezetekben leírtak szerint a geológiai kornak a CPT mérési adatok és a talaj nyíróhullám terjedési sebessége közötti korrelációjában jelentős szerepe van, melyet érzékeltet a ábra is, ahol a mért nyíróhullám terjedési sebességet a CPT csúcsellenállás függvényében ábrázoltam a geológiai csoportok szerint. A legnagyobb változékonyság a PF csoportra figyelhető meg (kék háromszög), melyet már az előző fejezetben tapasztalt jelentős szórás is jelzett, míg például a PE csoport pontjai (fekete rombusz) egy sávban tömörülnek. A fluviális üledékekre vonatkozóan mind a holocén, mind pedig a pleisztocén csoportra a várttal összhangban csekély javulást lehet csak elérni a konstansok optimalizálásával. A HF csoportra vonatkozóan a vizsgált szakirodalmi ajánlások is nagyon jó korrelációt eredményeztek, míg a PF talajcsoportra vonatkozóan a nagyobb szórás oka nem a becslési formula hibájából, hanem a kiindulási adatok változékonyságából eredt, ahogy ezt a ábra is mutatja. 28
34 600 nyíróhullám terj. seb., v s [m/s] HF PE PF TR CPT csúcsellenállás, q c [MPa] ábra: Mért v s és q c kapcsolata a geológiai kor szerint Korrelációk a kor és keletkezés szerint elkülönített négy talajcsoportra A holocén folyami üledékek esetén a (2-21) képletből kiindulva adódott a legpontosabb eredmény, melyhez a determinációs együttható R 2 = 0,91, ami nagyon szoros korrelációt jelent, az ehhez tartozó képlet: v s 0,201 t 0,321 c 17,66 q I z 0,249 (2-24) A másik két összefüggésből is hasonlóan jó (R 2 = 0,88) eredményre juthatunk. A pleisztocén folyami üledékekre vonatkozóan a (2-22) alakú képletből kiindulva a konstansok változtatásával érdemben jobb becslés nem volt elérhető, a trendvonal meredekségének eggyé válása mellett (az eredeti vsm = 1,014 vse) a determinisztikus együttható csupán egy századdal nőtt. Ugyan a (2-21) képlet pontosítása az eredeti azonos alakú egyenlethez képest jelentősebb javulást eredményezett, de (Robertson, 2009) ajánlásánál így sem adódott sokkal jobb összefüggés, a determinisztikus együttható R 2 = 0,39-re növekedett az alábbi képlettel: v s 3, 25 q 0, 412 t I 0, 819 c (2-25) A képletből kitűnik, hogy a pleisztocén folyami üledékek esetén a becslés pontosságára a mélységnek közvetlenül nincs hatása. Az eredeti képletben is alacsony kitevő tartozott a mélységhez, jelezve annak csekély szerepét. Ebből nem következik, hogy a nyíróhullám terjedési sebesség értéke e talajzónában a mélységtől független. Hiszen egyrészről a CPT csúcsellenállás értékét befolyásolja a mélység, illetve a geosztatikai nyomás, másrészről a talajviselkedési tényező meghatározásánál a függőleges feszültséggel normalizált mérési eredményekből indulunk ki. 29
35 A ábra a fluviális üledékre vonatkozóan mutatja az új képletekkel számított és mért vsértékek viszonyát. A diagramon narancssárga körök jelölik a holocén talajokat, melyekhez a (2-24) összefüggést alkalmaztam, míg kék háromszögek a (2-25) képlettel a pleisztocén talajokra nyert pontokat szemléltetik. Ez az ábra is érzékelteti, hogy a HF talajcsoportba eső talajok esetén nagy pontossággal becsülhető vs, míg a PF talajcsoportban nagyobb a bizonytalanság. 500 mért nyíróhullám terjedési seb., v sm [m/s] HF v sm = 1.0 v se R 2 = 0.91 PF v sm = 1.0 v se R 2 = 0.39 HF PF becsült nyíróhullám terjedési seb., v se [m/s] ábra: Becsült és mért v s kapcsolata a kétféle fluviális talajra A pleisztocén eolikus üledékekre vonatkozóan a szakirodalmi ajánlások rendre komoly hibát eredményeztek, %-kal alábecsülték a nyíróhullám terjedési sebességét, tehát leginkább ezekre vonatkozóan indokolt a képletek javítása. A legjobb becslés a (2-21) egyenletben szereplő konstansok helyes megválasztásával érhető el, mely esetben a determinisztikus együttható már R 2 = 0,57, ami érzékelhető-szoros kapcsolatot jelent (2-17. ábra). Az ehhez tartozó egyenlet v s 0,176 t 0,713 c 25,69 q I z 0,13 (2-26) A harmadidőszaki képződmények esetében a két helyszínen különböző vs volt jellemző, miközben nagyon hasonló qc értékeket mértek. A budapesti helyszínen a felszín alatt m-es tartományra vs = m/s volt jellemző, a Paks-1 helyszínen a felszín alatt m mélységben vs = m/s értéket mértek. A szoftveres analízis ezzel összhangban a v s 91,03 z 0,456 (2-27) 30
36 képletet hozta legjobb közelítésként, vagyis e talajokban e helyszíneken csak a mélységtől függ vs értéke, a CPT ellenállásokkal való korreláció nem mutatható ki. Ezt a harmadidőszaki talajokra azonban általánosítani helytelen volna. A (2-27) képlettel számított és mért értékek viszonyát a ábra mutatja, ahol a teli négyzet jelöli a budapesti miocén korú talajokban végzett méréseket, míg az üres négyzet a paksi helyszínen a pannon alaprétegbeli eredményeket mért nyíróhullám terjedési seb., v sm [m/s] v sm = 1.0 v se R 2 = becsült nyíróhullám terjedési seb., v se [m/s] mért nyíróhullám terjedési seb., v sm [m/s] v sm = 1.0 v se R 2 = 0.63 TR-Bp TR-Paks becsült nyíróhullám terjedési seb., v se [m/s] ábra: Becsült és mért v s kapcsolata a pleisztocén eolikus (PE) üledékekre ábra: Becsült és mért v s kapcsolata a harmadidőszaki (TR) képződményekre Korrelációk geológiailag hiányosan ismert helyekre Gyakran előfordul, hogy egy adott helyszín geológiai jellemzőit illetően korlátos az ismeretünk, esetleg vegyes, kor és keletkezés szerint nehezen elkülöníthető összletekkel van dolgunk. Gyakori volt pl. a pleisztocénban az eolikus és a fluviális üledékek keveredése, illetve mint már utaltunk rá egyes fluviális üledékek korbesorolása vitatott. Ezért érdemes volt az adathalmazt összevontan is elemezni, s a hazai talajokra általánosabb érvényű korrelációkat is keresni. Előre bocsátható azonban, hogy az ilyenek megbízhatósága értelemszerűen kisebb, s csak óvatosan szabad használni azokat. A kétféle fluviális üledék (HF és PF talajcsoportok) együttes elemzéséből mindhárom alapegyenletből kiindulva közel azonos eredményre jutottam, a determinációs együttható minden esetben R 2 = 0,52-ra adódott: v s 0,388 t 0,802 c 4,0 q I z 0,017 (2-28) 31
37 mért nyíróhullám terjedési seb., v sm [m/s] v s 10 0, 538Ic 1, 713 qt p a v0 0, 5 (2-29) v s 10 0, 522Ic 2, 341 qt p a v0 0, 446 (2-30) A negyedidőszaki (holocén és pleisztocén) képződményekre vonatkozóan, (HF+PF+PE) együtt vizsgálva a (2-23) egyenletből kiindulva jutottam a legjobb becsléshez, azonban ennek is elég jelentős a szórása, amint azt a ábra is bemutatja. A v s 10 0, 672Ic 2, 393 qt p a v0 0, 423 (2-31) képlettel a pontok 80%-a esik ±25%-os hibahatáron belülre v sm = 1.0 v se R 2 = becsült nyíróhullám terjedési seb., v se [m/s] ábra: Becsült és mért v s viszonya negyedidőszaki (HF+PF+PE) talajokra Megvizsgálva a teljes adathalmazt (négy csoport együttesét) a vs értéke a kortól és a keletkezés módjától függetlenül az alábbi képlettel becsülhető legpontosabban: v s 0,262 t 0,709 c 11,97 q I z 0,107 (2-32) Ezen képlet esetén a vse = vsm trendvonalhoz R 2 = 0,43 determinációs együttható tartozik, mely érezhető, de nem erős korrelációt jelent. 32
38 2.5. Összefoglalás A földrengés okozta felszíni válasz elemzéséhez az EC 8-1 szerint a legfelső 30 m-es talajösszletet talajosztályba kell besorolni. Ez elméletileg legpontosabban a nyíróhullám terjedési sebességén alapulhat, amire sokféle helyszíni és laboratóriumi vizsgálat ad lehetőséget. Ezek készítésére azonban a költségvonzatuk okán csak nagyobb projektek esetében van mód. A CPT szondázás a mai főként cölöpalapozási tervezési gyakorlatban a talajvizsgálatok alapvető eszközévé vált. Ezért célszerű volt annak lehetőségét vizsgálni, hogy miként lehet a nyíróhullám terjedési sebességét CPT adatokból a jellegzetes hazai talajokra vonatkozóan becsülni, kiindulva a szakirodalomban felkutatott ajánlásokból. Hét helyszínről származó több mint 280 adategyüttes elemzését végeztem el négy szakirodalmi ajánlás összevetésére és új korrelációs összefüggések felállítására. Az adatbázist geológiai jellemzők szerint négy talajcsoportra osztottam: holocén fluviális üledék (HF), pleisztocén fluviális üledék (PF), pleisztocén eolikus üledékek (PE), harmadidőszaki képződmények (TR). A szakirodalomban fellelt képletek közül az alábbiakat vettem az elemzés tárgyává: (Hegazy & Mayne, 1995) (2-3) egy.: v 101, log q 114, s c 1, 67 f 100 q s c 0, 3 (Andrus, et al., 2007) (2-9) egy.: v s 2,62 q 0,395 t I 0,912 c z 0,124 SF (Robertson, 2009) (2-13) egy.: v s 10 0, 55Ic 1, 68 qt p a v0 0, 5 (Tonni & Simonini, 2013) (2-14) egy.: v s 10 0, 31 Ic 0, 77 qt p a v0 0, 5 Ezek összehasonlítása alapján az alábbi megállapításokra jutottam: az ajánlások mindegyike átlagosan alábecsüli vs értékét, főként a PE talajcsoportra kiadódott 15-25%-os hiba következtében. a teljes adathalmazra a legjobb becslést (Tonni & Simonini, 2013) ajánlása adta, (Robertson, 2009) és (Andrus, et al., 2007) ajánlásai ennél kissé pontatlanabbak, míg 33
39 (Hegazy & Mayne, 1995) ajánlását a nagy szórás miatt a legpontatlanabbnak kellett minősíteni, jóllehet az átlagos hibája a legkisebbnek bizonyult; a negyediszaki fluviális képződményekre mindegyik ajánlás jó becslést ad, legpontosabb becslésre (Robertson, 2009) képletével juthatunk, de (Andrus, et al., 2007) ajánlása sem sokkal gyengébb, a geológiai kor növekedésével viszont a becslés egyre bizonytalanabb; a pleisztocén eolikus képződményekre az ajánlások durván alábecsülik vs értékét, a hiba mértéke 15-25% közötti; a vizsgálati eredmények szerint ugyanazon CPT szondázási értékek mellett az eolikus talajok dinamikai paraméterei kb %-kal nagyobbak, mint a fluviális üledékeké; a harmadidőszaki képződmények esetében (Andrus, et al., 2007) és (Robertson, 2009) ajánlásai alkalmazhatók, de átlagos hibájuk 10-11% lehet. Ezen megállapítások nyomán a hazai talajviszonyokra (Andrus, et al., 2007) és (Robertson, 2009) ajánlásaiban szereplő konstansokat az Excel szoftver Solver bővítményével a hibanégyzet összegét minimalizálva optimalizáltam. Ennek alapján az alábbi megállapítások tehetők: ha ismert a geológiai kor és a keletkezés módja, akkor a legjobb becslést a holocén fluviális üledékekre (pl. Tisza folyó fiatal hordalékai) a v s 0,201 0,321 0,249 17,66 qt Ic z képlet (2-24), a pleisztocén fluviális üledékekre a v s 0, 412 t 0, 819 c 3, 25 q I képlet (2-25), míg a pleisztocén eolikus üledékekre a v s 0,176 0,713 0,13 25,69 qt Ic z képlet (2-26) adja; ha bizonyosan negyedidőszaki képződményről van szó, de a keletkezés módjáról nincs pontosabb információ, akkor a v s 10 0, 672Ic 2, 393 qt p a v0 0, 423 egyenlet (2-31) használható, ha nincs információnk a talajösszlet geológiai jellemzőiről, vagy vegyes összletről van szó, akkor a v 0,262 0,709 0,107 s 11,97 qt Ic z képlettel (2-32) dolgozhatunk. 34
40 3. Cölöpviselkedés végeselemes modellezése földrengés teherre 3.1. Szakirodalom feldolgozás E fejezet célja a cölöpök földrengés alatti viselkedés vizsgálati módszereinek áttekintése, értékelése, mely bevezetőjeként az EC szerinti cölöptervezés részeit foglalom össze Cölöpalapozás tervezése az Eurocode 8 szerint A cölöpözési technológia kiválasztása után a cölöpök geometriai méreteit elsősorban a függőleges irányú terhelésre való megfelelőség határozza meg. A teljes ellenállás meghatározható statikus próbaterheléssel, talajszelvény alapján való számítással vagy dinamikus próbaterheléssel (MSZ EN (P)). Az építmények többségében ez a nyomási ellenállásra való megfeleltetést jelenti, melyre a hazai tervezési gyakorlat elterjedten a CPT statikus szondázási eredményeken alapuló számítási eljárást alkalmazza, elsősorban (Szepesházi, 2011) munkásságán alapulva. Az állami infrastrukturális beruházásokon a számított teherbírások ellenőrzésére rendre készül statikus cölöp-próbaterhelés, melyek eredményei az elmúlt néhány évben rávilágítottak speciális esetekre, mint például a nagyon kövér meszes agyagokban visszaeső palástellenállásra. Így időszerű lehet az új tapasztalatok beépítése a számítási eljárásokba. Az EC 7 (MSZ EN 1997) a cölöpök függőleges teherbírás tervezési értékének számításához a biztonságot két lépcsőben rendeli hozzá. A vizsgálatok számától és módjától függő korrelációs tényezők segítségével a teljes ellenállásból annak karakterisztikus értéke származtatható, melyből a tervezési érték a technológiától függő parciális tényezővel való osztással áll elő. Az EC 7 szerint a cölöpök ellenőrzendők keresztirányú terhelésre is, mely hatás származhat a felszerkezetről átadódó vízszintes terhelésből, a cölöpök különböző oldalain fellépő eltérő terhelésből és földrengésből is (MSZ EN (2)). A tartószerkezeti méretezést elsősorban a keresztirányú terhelésből fellépő igénybevételek határozzák meg. A szabvány a keresztirányú terhelés tekintetében kétféle törési mechanizmust említ: rövid cölöpök esetén merev testként való elfordulást, eltolódást, mely a felső talajzónában lokális talajtörést okozhat, hosszú, karcsú cölöpök esetén a szerkezetek hajlítási törését. Utóbbi vizsgálatára az EC 7-1 a felső végén terhelt, vízszintes tényezővel jellemzett, deformálódó közeg által megtámasztott gerenda modelljét javasolja, míg előbbire konkrét irányelvet 35
41 nem ad. A hazai gyakorlatban az ágyazási tényezőt a Winkler-féle elvet követve a terhelési szinttől függetlenül állandónak tekintik, sőt gyakran a rétegződéstől függetlenül valamilyen ökölszabály szerint veszik fel. Vannak azonban hazai iránymutatások a talaj viselkedését pontosabban leíró, a teherbírást is számításba vevő paraméterek felvételére is (Szép, 2014). Az alapozások szeizmikus teherre való méretezésével az EC 8-5 (MSZ EN :2009) foglalkozik, ez kiegészíti az EC 7 szabályait, amely nem tartalmazza a szeizmikus tervezés speciális követelményeit (MSZ EN : (P)). Meg kell említeni, hogy a két szabvány közötti kapcsolat bizonyos szempontokból kifogásolható (Fardis, et al., 2005): Az EC 7-1 által bevezetett geotechnikai kategóriákat az EC 8-5 nem említi. Az EC 7-1 szerint az erősen földrengésveszélyes térségbe kerülő szerkezetek a 3. geotechnikai kategóriába sorolandók, s ezekre alternatív óvintézkedések és szabályok betartását írja elő. Ilyeneket azonban nem fogalmaz meg, talán az EC 8-5 előírásait tekinthetjük azoknak. Az EC 8-5 nem használja az EC 7-1 és más EC kötetek által részletesen taglalt karakterisztikus érték fogalmát, a paraméterek felvétele kapcsán viszont kiolvasható belőle az EC 7-1 és EC 0 szellemisége. Az EC 8-5 nem említi az EC 7-1 által bevezetett, a biztonság hozzárendelését szabályozó tervezési módszereket, s a nemzeti melléklet sem ad erre iránymutatást. Az EC 8-5 a talajfizikai paraméterekre vonatkozóan definiál parciális tényezőket, mely alapvetően a 3. tervezési módszernek (DA-3) felel meg. Hazánkban ugyanakkor az EC 7-1 nemzeti melléklete szerint az alapozásokat a 2. tervezési módszer szerint kell méretezni, mely a parciális tényezőket a hatásokhoz (igénybevételekhez) és az ellenállásokhoz rendeli. Mindezek a tervezői körbe helyezik a szeizmikus tervezés biztonságának értelmezését (Ray, 2014). A probléma feloldásán jelenleg nemzetközi munkacsoport dolgozik, s a 2020-ra előirányzott második generációs EC-k e téren bizonyosan egyértelmű iránymutatást fognak adni. Az EC 8-5 szerint a szeizmikus tervezési állapotot illetően a cölöpöket kétféle igénybevételre kell méretezni: tehetetlenségi erőkre, melyek a felszerkezet kilengéséből keletkeznek, kinematikai erőkre, melyek a környező talaj szeizmikus hullámok okozta deformációjából erednek. Az előbbit a statikus terhekkel kombinálva az EC 8-1 és az EC 0 vonatkozó előírásai szerint kell számításba venni. A tehetetlenségi erő nagyságát a földrengés mértéke, a felszerkezet súlya 36
42 és merevsége (periódusideje), beleértve annak csillapítási jellemzőit is, a felszín közeli talajok felnagyító hatása és a talaj-szerkezet kölcsönhatás határozza meg. Meg kell még említeni az EC 8-5 azon előírását, mely szerint a szerkezetek méretezésekor figyelembe kell venni az alakváltozási szinttől való nyíróhullám terjedési sebesség és nyírási modulus csökkenését. Ehhez a szabvány a 3-1. táblázatban szereplő mértékeket ajánlja 20 m- es mélységig érvényes talajjellemzőkre táblázat: EC 8-5 szerint ajánlott csillapítási és csökkentő tényezők Talajgyorsulási viszony, S Csillapítási tényező v s/v s,max G/G max 0,10 0,03 0,90 (±0,07) 0,80 (±0,10) 0,20 0,06 0,70 (±0,15) 0,50 (±0,20) 0,30 0,10 0,60 (±0,15) 0,36 (±0,20) A kinematikai igénybevétel a fejtömbhöz való csatlakozásnál, jelentősen eltérő merevségű talajrétegek határán, illetve egy esetlegesen megfolyósodott talajzóna okozta tartományban számottevő. A szabvány nem ad semmilyen iránymutatást a kinematikai vizsgálathoz. Ennek hiányában a tervező feladata azon számítási metódus kiválasztása is, mely összhangban van az általános elvekkel, kellően pontosan írja le a cölöpök földrengés alatti viselkedését, így alapja lehet a méretezésnek. Mint a későbbiekben látni fogjuk, a cölöpök viselkedését földrengéskor nagyon sok tényező befolyásolja, s bár az elmúlt évben a téma a kutatások kereszttűzébe került, nincs mindenre kiterjedő, elfogadott méretezési eljárás. Vélhetően ennek tudható be, hogy a szabvány ilyet nem tartalmaz, s e tekintetben homályosan fogalmaz Cölöpök földrengések alatti viselkedésének vizsgálati lehetőségei Cölöpöket érő hatások A cölöpök és a környező talaj vízszintes terheléskor jelentkező kölcsönhatását a 3-1. ábra érzékelteti. Nyugalmi állapotban (bal ábrarészlet) a cölöpre ható nyugalmi földnyomás tengelyszimmetrikus, az eredő egy vízszintes metszetben zérus. Ha a cölöp egy V erő hatására kimozdul (jobb ábrarészlet) a cölöpre ható vízszintes feszültség a nyugalmi állapothoz képest egyik oldalon a passzív, az ellentétes oldalán az aktív állapot irányába módosul, melyek eredője egy adott keresztmetszetben, y eltolódás esetén p vonalmenti erő. 37
43 A felszerkezet kilengéséből ébredő tehetetlenségi erőre való méretezés során melyet valamennyi szerkezetnél elvégeznek általában a cölöpöt rugalmasan ágyazott gerendaként vizsgálják pszeudostatikus teherre. Ha a cölöp be van fogva egy cölöpösszefogó szerkezetbe, akkor a maximális nyomaték itt, a fejtömbhöz való csatlakozásnál ébred, s a mélységgel gyorsan csökken. Azt a mélységet, amely alatt a cölöp felső pontján működő vízszintes erőnek már nincsen hatása aktív cölöp hossznak (La) hívjuk, s statikus esetre (Randolph, 1981) az alábbi képletet ajánlotta: L a E 1, 5 E p s 1 / 4 d (3-1) ahol Ep és Es a cölöp és a talaj rugalmassági modulusa, d a cölöp átmérője. V y cölöp elhajlás cölöp p egyenletes talajfeszültség egyenletlen talajfeszültség a vízszintes terhelés hatására 3-1. ábra: Cölöp-talaj kölcsönhatás (Wolf, 2012) A szakirodalomban több ajánlás létezik statikus (pl.: (Velez, et al., 1983)) és dinamikus (pl. (Velez, et al., 1983) és (Gazetas & Dobry, 1984a)) esetre egyaránt, melyek formailag megegyeznek a (3-1) képlettel. E képletekbe a talaj várható alakváltozási szintjéhez tartozó rugalmassági modulust kell megadni, s ebből adódik, hogy valójában az aktív cölöphossz nem egy konstans érték, hanem az a terhelés szintjétől és a talaj leromlási jellemzőjétől függően változik. A (3-1) képlet eredetileg lineárisan rugalmas megtámasztású gerenda modell esetén érvényes. A képletek eredményeként kiadódó, a cölöp átmérőjéhez viszonyított aktív cölöphossz csak kismértékben tér el. Laboratóriumi vizsgálatokkal (Goit, et al., 2014) igazolták, hogy az aktív cölöphosszt a gerjesztés frekvenciája nem befolyásolja. 38
44 A hazai mélyépítési gyakorlatban elsősorban vasbeton cölöpöket alkalmaznak, melyek rugalmassági modulusa a beton minőségétől és a cölöp korától függően Ep = GPa. Azon talajzónák rugalmassági modulusa, melyekben a kinematikai igénybevétel vizsgálandó, Es = MPa-ra tehető, s ezekből az aktív cölöphosszra az alábbi arány adódik: 4, 7 7, 4 d (3-2) L a A kinematikai hatás a talaj és a cölöp eltérő merevségéből ered, a talajban terjedő hullámok okozta alakváltozást a cölöp nem követi le, abban igénybevétel ébred. Számottevő kinematikai nyomaték egyrészt két, eltérő merevségű (nyírási modulusú) réteg határán, másrészt a cölöpfejnél alakul ki. A két igénybevételnek egymásra nincs hatása, ha a réteghatár az aktív cölöphossznál nagyobb mélységben van (Nikolaou, et al., 2001). A témával az 1980-as évektől foglalkoznak a kutatók, amikor egyre több földrengés utáni felmérés (pl. (Mizuno, 1987)) dokumentált tönkremenetelt a cölöpök mélyebb részében, például Mexico City-ben az 1985-ben kirobban földrengés után, a Kobe (Japán) földrengés után ben vagy Chi Chi (Taivan) városában 1999-ben (Maiorano, et al., 2009). Ezek egyértelműen nem a cölöp tetején működő tehetetlenségi igénybevétellel voltak összefüggésbe hozhatók. A két hatás időben elkülönülten jelentkezik. A kinematikai hatás érvényesül először, hiszen a földrengés hullámok a mélyből felfelé terjedve először a cölöpöket érik el, majd annak kimozdításával hozzák rezgésbe a felszerkezetet, s ennek kilengése kelti a tehetetlenségi erőt Cölöpigénybevétel analitikus számítása a rengés okozta talajgörbületből A legegyszerűbb számítás, melyet alapvetően homogén talajkörnyezetben végtelen hosszú cölöpre alkottak, azon alapszik, hogy a cölöp követi a talaj deformációját, s a gerjesztésből például egydimenziós hullámterjedés elmélettel a deformált alak, a görbület meghatározható, s ebből a cölöpben ébredő nyomaték adódik (Margason & Holloway, 1977). A tetszőleges z mélységben t időpillanatban a cölöpben ébredő nyomaték (M(z,t)) ekkor: M z,t 1 E p I p (3-3) R z,t ahol Ep Ip a cölöp hajlítási merevsége, és 1/(R(z,t)) a cölöp görbülete. Mivel e képlet elhanyagolja a talaj-szerkezet kölcsönhatást, nem veszi figyelembe a talaj-szerkezet merevségi arányát, a cölöp karcsúsági arányát (hossz/átmérő) és a csillapítást, ezért durva közelítésnek tekinthető. A görbület a maximális felszíni gyorsulás (as,max) és a talaj nyíróhullám terjedési sebességének (vs) függvényeként adható meg (Margason & Holloway, 1977): 39
45 1 R a s,max (3-4) 2 z, t v s Homogén talajkörnyezetre a cölöpben ébredő igénybevétel javítható, ha a talaj-szerkezet kölcsönhatását számításba vesszük. Ekkor a cölöp deformált alakja és a talaj elmozdulása között, illetve e kapcsolat kétszeri mélység szerinti deriválásával előálló görbületek között végtelen hosszú cölöpöt feltételezve az alábbi összefüggést alkalmazhatjuk (Nikolaou, et al., 2001), (Mylonakis, 2001) (Di Laora, et al., 2013): Y U z z ff 1/ R 1/ R p s (3-5) ahol az eddig ismeretlen Uff (z) a talaj elmozdulása, s dimenzió nélküli választényező (response factor) 4 mp 4 Ep I p (3-6) q A képletben a fentebb rögzítetteken túl mp a cölöp folyóméterre vonatkozó tömege, a ciklikus gerjesztés frekvenciája, és s és p a talaj és a cölöp hullámszáma: s (3-7) v * s 1/ 4 k i D 4 p (3-8) E p I p ahol v * v 1 i 2 D a nyíróhullám csillapított terjedési sebessége a talajban, melynél Ds s s s a frekvencia független csillapítási tényező, k a Winkler féle rugó merevség (ágyazási tényező), D a csillapítási tényező. A (3-8) képletben k értékét a talaj rugalmassági modulusával arányosan szokás felvenni, annak 1-3-szorosára függően a cölöp karcsúságától, a talaj-cölöp merevségi viszonyától és a cölöpfejnél levő befogási viszonytól, amire a későbbiekben még kitérek. Ezen összefüggések jól érzékeltetik, hogy az első ajánlásokkal ellentétben a talaj és cölöp görbülete nem azonos. A (3-6) illetve (Mylonakis, 1995) és (Nikolaou, et al., 2001) merev réteg feletti, h vastagságú talajzónába készített, a fejtömbnél elfordulás ellen megtámasztott, talpon álló cölöpre adott összefüggés dimenzió nélküli frekvenciától függő változását a 3-2. ábra mutatja. A két ábra 0,7-es talaj és cölöp sűrűségi arány (s/p = 0,7), s = 0,4 talaj Poisson tényező és Ds = 0,05 értékekre vonatkozik. A végtelen hosszú cölöpre vonatkozó bal oldali diagramon 40
46 érzékelhető, hogy alacsony frekvencia esetén a két görbület megegyezik. A frekvencia növekedésével a görbületi arány csökken, s e tendencia erősödik a cölöp-talaj merevségi arányának növekedésével. A h vastagságú rétegre Ep/Es = 1000 merevségi arányra érvényes jobb oldali ábra reprezentálja, hogy alacsony frekvencia esetén szemben a végtelen féltérrel a görbületi arány eltérhet az egységnyi értéktől, valamint mindenkori értékét a réteg relatív vastagsága is befolyásolja. görbületi arány, (1/R) p /(1/R) s talajréteg sajátfrekvenciája dimenzió nélküli frekvencia, d/v s 3-2. ábra: Talaj-cölöp görbületi arány a frekvencia függvényében (a) végtelen hosszú cölöpre és (b) h vastagságú rétegre vonatkozóan (Di Laora, et al., 2013) Dinamikus rugókkal megtámasztott gerenda modell Cölöpalapozást csak nagyon ritka esetben alkalmazunk homogén talajkörnyezetben, ugyanis a kinematikai szempontból kedvezőtlen felső gyenge réteg esetén a cölöpök bizonyosan mélyebbre, egy teherbíróbb rétegig hatolnak. Eltérő merevségű talajrétegek határán a nyírási alakváltozásban diszkontinuitás, s ebből adódóan végtelen görbület alakul ki, így az eddigiekben ismertetett eljárás nem alkalmazható. Ilyen esetekben a talaj-szerkezet kölcsönhatás negligálása nem engedhető meg (Kavvadas & Gazetas, 1993) A rétegek közötti merevségi különbség okozta kinematikai nyomaték kialakulását a 3-3. ábra érzékelteti, mely a modell alján konstans gyorsulást feltételezve készült. Homogén talajkörnyezetben a cölöp szinte követi a talaj mozgását, s ennél fogva a cölöpfej befogási viszonyaitól függően alakul a nyomatéki eloszlás a cölöp mentén. Ettől eltérő viselkedés tapasztalható két különböző merevségű (G2/G1) réteg határán, ahol az alsó réteg a merevségkülönbség növekedésével egyre erősödő megtámasztó hatást fejt ki, ennél fogva a réteghatáron ellentétes irányú nyomaték keletkezik. Kis merevségi aránynál (G2/G1 < 1,5) ez a nyomaték a homogén 41
47 talajkörnyezetben keletkezőhez képest csökkenést eredményez, míg nagyobb különbségnél jelentős igénybevétel ébredhet. befogott cölöpfej szabad cölöpfej inflexiós pont (M = 0) szabad talaj elmozdulás réteghatár szabad talaj elm. cölöp elm. inflexiós pont (M = 0) cölöp elmozdulás 3-3. ábra: Kinematikai nyomaték kialakulása a rétegek merevségi viszonyának következtében (Di Laora, et al., 2012) Az első kutatásokban a cölöpök viselkedését, a réteghatáron fellépő nyomaték mértékét rugalmasan ágyazott gerendaként vizsgálták. (Dobry & O'Rourke, 1983) a talaj-szerkezet kölcsönhatását modellező Winkler rugók merevségét a talaj nyírási modulusának háromszorosára választotta, s az alábbi közelítéssekkel élt: a cölöpöt hosszúnak, s a két réteget kellően vastagnak tekintette, hogy azok peremfeltételei ne befolyásolják a réteghatáron fellépő igénybevételt, számításaiban egységnyi feszültségmező hatását elemezte, mely konstans nyírási alakváltozást indukált. A rugalmasan ágyazott gerenda modellt, melyben a talaj-szerkezet közötti kölcsönhatást párhuzamosan kapcsolt rugók és csúszkák együttesen modellezik (BDWF beam on dynamic Winkler foundation) eleinte a cölöpfejnél működtetett rezgések vizsgálatára használták. A cölöpök kinematikai igénybevételeinek meghatározásához e modellt fejlesztették tovább úgy, hogy a cölöp körüli talaj egyrészt, mint szabad közeg jelenik meg, melyben a nyíróhullám vertikálisan terjed, s azt a cölöp jelenléte nem befolyásolja. Másrészt a talaj-szerkezet kölcsönhatását modellező csúszkák és rugók sorozataként van jelen, mely viselkedésére már a cölöpnek is hatása van (Kavvadas & Gazetas, 1993). Ezt szemlélteti a 3-4. ábra. 42
48 szabad közeg elmozdulása U ff (z) cölöp elmozdulása U p (z) cölöp E p, I p, p függőleges nyíróhullám 3-4. ábra: BDWF modell (Kavvadas & Gazetas, 1993) A számítás két lépcsőben történik: először a talaj általában harmonikusan gerjesztett hullám terjedés okozta elmozdulását számították egydimenziós analízissel (Uff(z,t)), majd ezen alakváltozást, mint támasz-elmozdulást működtették a modellen, s vizsgálták a cölöp reakcióját a rugók és csúszkák által közvetített hatásra. A számításokban elsősorban harmonikus gerjesztést vizsgáltak különböző frekvencia tartományokban, majd ezen eredményekből diszkrét Fourier transzformációval állították elő az időfüggő igénybevételeket. A modellt egyedi cölöpök vizsgálatára dolgozták ki. Analitikus vizsgálatokra támaszkodva kimutatták, hogy a kinematikai igénybevétel esetén a cölöpcsoport hatásnak, a cölöpök közötti kölcsönhatásnak másodlagos a szerepe, szemben a cölöp tetején megjelenő tehetetlenségi hatással (Kaynia & Kausel, 1982) (Gazetas & Mylonakis, 1998). (Maiorano, et al., 2009) háromdimenziós véges elemes analízissel, a modellt valós idő-gyorsulás függvényekkel gerjesztve a cölöpfejnél elfordulás ellen befogott cölöpökön szintén ezen eredményre jutott. Egy cölöpcsoportban levő cölöp kinematikai igénybevételei függetlenül a cölöpök tengelytávolságától egyedi cölöpként is vizsgálhatók. Megemlítem, hogy a cölöp fejtömbhöz való kapcsolódása a valóságban nem tekinthető teljesen befogottnak, s a fejtömb elfordulási merevsége sem végtelen. Így a cölöp darabszám kismértékben befolyásolhatja a cölöp felső pontján ébredő igénybevételeket. Ugyanakkor a kapcsolat és a fejtömb elfordulás merevségének meghatározása nehéz, 43
49 s számos körülmény befolyásolja, ezért a kutatási és tervezési gyakorlatban a kapcsolatot vagy csuklósnak vagy végtelen merevnek szokás közelíteni. A számítás pontossága a talaj és a cölöpök közötti kölcsönhatást leíró rugók és csúszkák paramétereinek meghatározásától függ. A rugó merevségét (k) közelítőleg a frekvenciától függetlenül (pl. minden rétegre azonos és a mélységtől függetlenül) szokás figyelembe venni, s a talaj rugalmassági modulusának (Es) függvényében megadni: k E s Az első analíziseket (Roesset, 1980) nyomán = 1,2 értékkel végezték. Ezen arányszám a felső pontban gerjesztett cölöp viselkedésének vizsgálatán alapult, ennél fogva kinematikai vizsgálathoz csak kezdetleges értéknek tekinthető. A vizsgálatok szerint a cölöpfej elmozdulása néhány frekvenciától eltekintve nem érzékeny a rugómerevség értékére, azt alapvetően a talaj elmozdulása befolyásolja. Ugyanakkor a cölöpben ébredő igénybevételekre (nyomaték, nyíróerő) a értékének számottevő hatása van, a két érték között egyenes arányosság áll fenn (Kavvadas & Gazetas, 1993) (Sica, et al., 2011). (Kavvadas & Gazetas, 1993) a szorzót (opt) véges elemes modellezéssel kalibrálta, a talajösszlet sajátfrekvenciájával megegyező gerjesztés esetén kiadódó maximális nyomaték értékére, s részletes regresszió analízis alapján a következő összefüggést javasolta: 1/ 8 4 1/ 8 1/ 12 1/ 15 2 Es 1 d L h1 vs 1 opt 2 1 v E s p I p d h 2 v (3-10) s2 (3-9) A képletben Es1 a felső réteg rugalmassági modulusa, d és L a cölöp átmérője és hossza, h1 és h2 a felső és alsó rétegek vastagsága, míg vs1 és vs2 a nyíróhullám jellemző terjedési sebessége a két rétegben. A cx csillapítási paraméter a radiális és hiszterézises csillapítást is magában foglalja, értékét korábbi kutatásokra támaszkodva (pl.: (Gazetas & Dobry, 1984a) (Gazetas & Dobry, 1984b)) az alábbi képlettel lehet felvenni: 5 / 4 v c 1 / 4 c x 2 d s vs 1 a0 2 k vs ahol x (3-11) 44
50 a 0 d v s (3-12) dimenzió nélküli frekvencia és vc a longitudinális hullám látszólagos terjedési sebessége. Mylonakis (2001) relatíve hosszú cölöpökre (L/d 40) és azonos vastagságú rétegekre vonatkozóan az alábbiak szerint egyszerűsítette a (3-10) egyenletet: E 6 E p s1 1/ 8 (3-13) Meg kell említeni, hogy egyes szoftverek a rugók és csúszkák paramétereit nem külön-külön veszik fel, hanem a reakcióerő-elmozdulás (p-y) kapcsolatát függvénnyel írják le. Egyik legismertebb az (American Petroleum Institute, 2000) által ajánlott hiperbolikus függvény p Es z A p y u tanh (3-14) A pu ahol A a terhelés típusától függő szorzó, Es a talaj rugalmassági modulusa, pu a talaj teherbírása (maximális talajreakció) s z a felszíntől számított mélység. Számos szoftver használja a rugalmasan ágyazott gerenda elvet cölöpök vízszintes terhelés alatti vizsgálatára (pl. LPILE), az okból kifolyólag, mert ezzel gyorsan juthatunk eredményre. Az eljárással kapcsolatosan különösen dinamikai vizsgálat esetén kifogásolható viszont, hogy a talaj viselkedését, a talaj-szerkezet közötti kölcsönhatást csak közelítő módon, rugókkal és csúszkákkal írja le, s ezzel a talaj nemlineáris viselkedése csak nagyon nehezen reprezentálható Végeselemes analízis (VEM) Egyre gyakrabban használják a véges elemes módszert a cölöpök szeizmikus terhelés alatti viselkedésének vizsgálatára is, mert ezzel a talaj-szerkezet kölcsönhatás pontosabban leírható. Általában 3D modellekkel dolgoznak, csak kevés síkbeli modellről szóló publikáció lelhető fel (pl. (Di Laora & Rovithis, 2014) és (Durante, et al., 2015)). Az alkalmazott szoftver köre széles: ANSYS: (Di Laora & Rovithis, 2014), (Di Laora, et al., 2012)), ABAQUS: (Durante, et al., 2015), (Dezi, et al., 2011), FLAC (Durante, et al., 2015), VERSAT 3D (pl. (Maiorano, et al., 2009) és (de Sanctis, et al., 2010). 45
51 Az általam alkalmazott Plaxis 3D szoftver ilyen irányú használatára publikációt nem találtam, a Plaxis 2D szoftverére is csupán egyet (van der Kwaak, 2015). A felsorolt kutatások eredményeivel a 4.1. fejezetben foglalkozom részletesen, itt a modellek mechanikai jellemzőire, az alkalmazott anyagmodellekre, elemtípusokra és a vizsgálati módszerre fókuszálok. E kutatásokban a talajt hasonlóan a BDWF modellezéshez elsősorban lineáris, viszkózusan rugalmas anyagmodellel írják le, s a paraméterek a mélységgel nem változnak. A csillapítási tényezőt jellemzően D = 10%-ban határozzák meg. Ez a valóság jelentős egyszerűsítését jelenti, hiszen a talaj nyírási modulusa (nyíróhullám terjedési sebessége) és csillapítása a mélységgel általában növekszik (Kramer, 1996), ahogy ezt a 2. fejezet kapcsán is már láthattuk. További közelítés, hogy a talajok merevsége és csillapítása az alakváltozás szintjétől is függ, melyet e modellek nem vesznek számításba, konstans paraméterekkel számolnak. A csillapítás értéke befolyásolja a cölöpben ébredő igénybevételeket is (Mucciacciaro & Sica, 2015), a két paraméter között fordított arányosság áll fenn. A 3-5. ábra érzékelteti, a szokásosan számításba vett csillapítás felezése az igénybevétel másfélszerezését eredményezheti (Sica, et al., 2011). A fentiek közül a mélységgel folyamatosan, különböző függvények szerint változó merevség hatását csak (Di Laora & Rovithis, 2014) vizsgálta. A talaj alakváltozási szinttől függő merevségét (Durante, et al., 2015) a Ramberg-Osgood anyagmodellel írta le, melynek dunai szemcsés talajokra való alkalmazhatóságát (Szilvágyi, 2018) is igazolta ábra: Csillapítás és réteghatáron fellépő nyomaték viszonya (Sica, et al., 2011) A cölöpöket rendre lineárisan rugalmas, esetleg rugalmas-képlékeny anyagmodellel írják le, s jellemzően térfogati elemmel modellezik. (Grassi & Massimino, 2009) konkrét földrengési hatásra végzett összehasonlító elemzése rávilágított arra, hogy a cölöpök gerendaelemként való 46
52 modellezése a talaj-szerkezet kölcsönhatást illetően okozhat bizonytalanságokat, a térfogati elemmel való modellezéssel a rétegek merevségi viszonyától függően 15-30%-kal nagyobb nyomatéki igénybevételt kaptak a gerendamodellezéshez képest. Az analízisekben az utóbbi időben túlnyomórészt több konkrét, azonos maximális gyorsulásra skálázott gyorsulás-idő függvényt (accelerogrammokat) működtetnek a modell alsó síkján a frekvencia térben történő vizsgálat helyett. A modell függőleges méretét rendre 30 m-re választották, melynek oka vélhetően az EC 8 által a talajosztályozásnál számításba vett talajréteg vastagsággal magyarázható. Megemlítem, hogy a talaj-cölöp kölcsönhatás tekintetében a modell függőleges mérete nem releváns, viszont a talajválasz tekintetében meghatározó. Összességében elmondható, hogy e kutatások a talaj leírására használt anyagmodell tekintetében egyszerűsítéseket tartalmaznak, azok nem írják le a talajok valós viselkedését kellően pontosan. Saját kutatásomban alkalmazott szoftver (Plaxis 3D) a talaj leírására fejlettebb anyagmodell alkalmazását kínálja, s a cölöp modellezésére is speciális elem áll rendelkezésre, melyeket a következő alfejezetben ismertetek részletesebben Plaxis 3D VEM szoftver Azt, hogy a cölöp szeizmikus terhelés alatti viselkedésének vizsgálatára a Plaxis 3D szoftvert alkalmaztam több tényező is indokolta. Egyrészt, hogy az a talaj nemlineáris viselkedésének lekövetésére olyan anyagmodellt kínál, amely az alakváltozási szinttől függő merevséget is számításba tudja venni (Benz, 2006). Másrészt a cölöp modellezésére a térfogati cölöpmodell mellett egy speciális elem alkalmazására (beágyazott gerenda elem embedded beam) is lehetőség van, s célul tűztem ki annak e témakörben való alkalmazhatóságának ellenőrzését. Harmadrészt, hogy e szoftvert a hazai geotechnikai tervezői gyakorlat is előszeretettel használja. Meg kell említeni, hogy a szoftver tudja kezelni a gyorsulásdiagramokat, s így a modell alsó síkján a földrengésteher is számításba vehető. Az elmúlt időszakban a győri Szerkezetépítési és Geotechnikai Tanszéken kedvező tapasztalatok mellett vonatok dinamikus hatását már vizsgáltuk a Plaxis 3D alkalmazásával (pl.: (Hudacsek, et al., 2017) (Koch & Hudacsek, 2017)). Ezek révén a szoftver lehetőséget kínál a korábbiaknál magasabb rendű analízis végrehajtására a cölöpök viselkedése tekintetében. A következőkben rövid áttekintést adok az alkalmazott anyagmodellről és a cölöpmodellezési lehetőségekről. 47
53 Talajmodell Számításaimban a felkeményedő talaj modelljének a kis alakváltozási tartományban mutatkozó merevebb viselkedést is magában foglaló változatát alkalmaztam (Hardening Soil Small Stiffness modell HSS). Az anyagmodell a kompressziós és a nyírási felkeményedést is hatványfüggvénnyel írja le. Előbbi az ödométeres vizsgálattal nyert összenyomódási modulus feszültségszint emelkedésével való növekedését, míg utóbbi az elsődleges deviatorikus terhelés lágyabb viselkedéséhez képest a rugalmas-merevebb alakváltozási tulajdonságú tartomány növekedését jelenti. A törési (helyesebben a képlékeny) határállapot bekövetkeztét a Mohr-Coulomb törési feltétel szerint számítja, azaz a talaj szilárdságát a belső súrlódási szög (), kohézió (c), dilatációs szög () és húzószilárdság (t) értékével jellemezhetjük. A deviátorfeszültség (q) változásának hatására bekövetkező alakváltozásokat a szoftver hiperbolával közelíti (3-6. ábra). A görbe kezdeti meredekségét a törést előidéző deviátorfeszültség feléhez tartozó húrmodulussal (E50) kell megadni, s a modell az m ref c cos sin E E (3-15) c cos pref sin egyenlettel figyelembe veszi ennek a 3 hatékony főfeszültséggel való javulását, ahol E50 ref a referencia feszültséghez (p ref ) tartozó modulus, m a felkeményedés mértékét kifejező kitevő. A tehermentesítési és újraterhelési folyamatokban amint a 3-6. ábra mutatja a modell kizárólag rugalmas alakváltozással számol, s az ezt jellemző modulus (Eur) az E50-hez hasonló módon a feszültségszinttől függ. Az ödometrikus felkeményedést a modell az összenyomódási modulus (Eoed) 1 hatékony főfeszültséggel való növekedésével írja le (3-7. ábra): E oed E ref oed m c ctg 1 (3-16) c ctg p ref ahol Eoed ref az Eoed pref referenciafeszültségre vonatkozó értéke. A modell valamennyi alakváltozási paramétere ödométeres és triaxiális vizsgálatokkal meghatározható, ehhez az alakváltozások nagyon pontos mérése, illetve tehermentesítési és újraterhelési ciklusok beiktatása szükséges. Az m hatványkitevő a kompressziós görbe adataira, vagy a 48
54 különböző 3 feszültségekkel elvégzett triaxiális kísérletek eredményeire illeszthető egyenletből határozható meg. A szakirodalomban számos ajánlás található: a szemcsés talajok esetében általában m = 0,5, kötött talajok esetében m = 0,7 1,0 értékek vehetők fel ábra: Konszolidált, drénezett (CD) triaxiális vizsgálat q-ε 1 görbéjének közelítése hiperbolával (Plaxis, 2016a) 3-7. ábra: Kompressziós görbe leírása (Plaxis, 2016a) Ha a triaxiális vizsgálatban az 1 alakváltozást nem lehet kellő pontossággal mérni, akkor az E50 ref Eoed ref összefüggés használható, illetve ha nem vizsgálják a tehermentesítés-újraterhelés 3 4 E értékkel. folyamatát, akkor számolhatunk ur oed E A dilatációs szög pontos meghatározásához olyan triaxiális vizsgálat szükséges, melyben a minta keresztirányú alakváltozását vagy a térfogatváltozását is mérjük. A legtöbbször azonban a = -30 közelítéssel élünk. A húzószilárdságot csak kőzetszerű talajok esetén vehetjük zérusnál nagyobbra. A talajok a valóságban a kis (g 10-5 ) alakváltozási tartományban sokkal merevebben viselkednek, mint a hagyományos laborvizsgálatokkal mért alakváltozások szintjén (g 10-2 ), amit a 2-3. ábra kapcsán már bemutattam. Megfordítva a talajmerevség az alakváltozások növekedésével csökken, amit a HSS anyagmodell a következő hiperbolikus függvénnyel ír le: G s G a g g 0,7 (3-17) A képletben Gs a g alakváltozási szinthez tartozó szelő nyírási modulus, G0 a nyírási modulus maximális értéke, és g0,7 a nyírási alakváltozás azon értéke, melynél a nyírási modulus a maximális érték 72,2%-ra csökken (G = 0,722 G0). Az a konstans értéke a legjobb illeszkedéshez 0,385 (Santos & Correia, 2001). A leromlási görbe alakja s a modell szempontjából azt leíró 49
55 g0,7 laboratóriumi körülmények között meghatározható (ld. pl. (Szilvágyi, 2018)), illetve szakirodalmi ajánlások alapján vehető fel. A (3-17) függvénnyel leírt görbe alsó szakaszát már nem tekintjük érvényesnek, mert az már a nagy alakváltozási tartományba esik, s a nyírási modulus nem csökkenhet a tehermentesítésiújraterhelési folyamatokat leíró nyírási modulus (Gur) alá (ld ábra). szelő nyírási modulus, G s [kpa] érintő nyírási modulus, G t [kpa] nyírási alakváltozás, g s [-] nyírási alakváltozás, g s [-] 3-8. ábra: A szelő és érintő modulus levágott leromlási görbéje a HSS anyagmodellben (Benz, 2006) Az anyagmodell a hiszterézis viselkedés leírására (Masing, 1926) szabályát követi (3-9. ábra), mely szerint a feszültség-alakváltozás görbe kezdeti érintője megegyezik a kezdeti terhelésével, illetve a tehermentesítés-újraterhelés görbéjének alakja megegyezik a kezdeti görbéjével, de mérete kétszerese. E hiszterézises viselkedés alapján egy terhelési ciklus alatt az alakváltozás -gc től +gc-ig növekszik majd vissza -gc-ig az elnyelt energia a hiszterézis hurok területével egyenlő, azaz a 3-9. ábra alapján az az alakváltozási szint emelkedésével növekszik. Ezt, illetve a korlátozási szint kezdeti és újraterhelési modulus arányától függő értékét szemlélteti a ábra. A modell szerint a csillapítás az érintő modulus Gur értékének elérése után már nem növekszik tovább, de a talajban a nagy alakváltozások mellett bekövetkező felkeményedés (plasztikus alakváltozás) további energia elnyelést foglal magában ábra: A nyírási modulusok értelmezése (Brinkgreve, et al., (Brinkgreve, et al., 2007) 2007) 50
56 30% 25% 20% g 0,7 =1E-4 g 0,7 =2E-4 g 0,7 =3E-4 G 0 =10 G ur csillapítás 15% 10% 5% G 0 =5 G ur G 0 =2,5 G ur 0% 0, ,0001 0,001 0,01 nyírási alakváltozás ábra: Csillapítás és annak korlátozása a nyírási alakváltozás valamint a nyírási modulus függvényében (Brinkgreve, et al., 2007) nyomán A kezdeti, maximális nyírási modulus laboratóriumban közvetlenül mérhető, vagy helyszíni és laboratóriumi vizsgálatokkal (pl. (Szilvágyi, 2012) (Szilvágyi, et al., 2016) (Ray, et al., 2014)) mért nyíróhullámi terjedési sebességből az alábbi képlettel meghatározható: G v 2 0 s (3-18) A G0 paraméter csakúgy mint a HSS modell főbb alakváltozási paraméterei a feszültségszinttel (mélységgel) változik a (3-16) képlet formájában Szerkezeti anyagmodell A Plaxis 3D szoftverben a cölöpök modellezésének lehetőségeit és azok főbb jellemzőit az alábbiakban foglalom össze (Brinkgreve, 2014) nyomán: térfogati elem (solid, volume - VP): a valós geometriával bevitt cölöp és talaj közötti kölcsönhatást határfelületi elemmel (interface) modellezhetjük. A határfelületi elem szilárdságát a talaj szilárdságának arányában (Rinter) adhatjuk meg. A számításához szükséges lokálisan sűrűbb háló nagy számítási igényt támaszt. Közvetlenül a szerkezeti igénybevételek nem nyerhetők ki, ehhez a cölöp közepébe egy, a valóságnál jóval kisebb (pl értékkel osztott) merevségű gerenda elemet helyezhetünk, s az a cölöppel azonos alakváltozást szenved, így az igénybevételek abból kivehetők (Dao, 2011); gerenda elem (beam): nincs térfogati kiterjedése, a talaj-szerkezet kölcsönhatást nem realisztikusan közelíti; 51
57 beágyazott gerenda elem (embedded beam EP, (Sadek & Shahrour, 2004)) (3-11. ábra): a cölöpöt a talajközegbe tetszőleges irányban beágyazott gerenda elem reprezentálja. A 3 csomópontú gerendaelem és a 10 csomópontú talajelem csatlakozási pontjainál virtuális csomópontok vannak, mely a talaj diszkretizálását nem befolyásolja. A cölöp tengelye körül a feltételezett szerkezeti térfogatot talaj tölti ki, melyben ugyanakkor képlékeny alakváltozást nem vesz számításba a program. A cölöp viselkedése tehát gerenda elemként modellezett, de a talaj-szerkezet kölcsönhatást a csomópontokban kapcsolódó rugók képviselik, amik paramétereit a talajfizikai paraméterekből és a kiindulási adatként beadandó palást- és talpellenállás határértékéből származtat a szoftver. Ebből adódik, hogy a talaj-szerkezet kölcsönhatás a csomópontokban, s nem pedig a cölöp köpenyfelülete mentén alakul ki. virtuális talaj csomópont EP rugalmas tartomány (palást) EP talaj elem rugalmas tartomány (talp) ábra: Beágyazott gerenda elem modellje (Marjanovic, et al., 2016) A cölöpöt a vizsgálatokban lineárisan rugalmas anyagmodellel szokás leírni, annak nemlineáris viselkedését általában elhanyagolják. Meg kell említeni, hogy ez tervezés során még közelítőleg elfogadhatónak ítélhető, de meglévő létesítmények vizsgálata során természetesen a cölöp nemlineáris (berepedés) viselkedésének számításba vétele indokolt lehet. Az EP és VP modellezési technikákat különböző geotechnikai problémákra számos kutató hasonlította össze, így például nyomott cölöpök modellezését (Engin, et al., 2007) és (Sheil & McCabe, 2012) vizsgálta, valamint cölöpcsoportok függőleges teher alatti viselkedését (Engin, et al., 2008) és (Tschuchnigg & Schweiger, 2015) elemezte. Rézsű lábvonalában álló, s így a talaj vízszintes deformációja által terhelt cölöpön végzett összehasonlítás szerint a két modell közel azonos eredményt ad (Dao, 2011). Felső pontjában vízszintesen terhelt egyedi cölöp esetében a két modellezési technikával nyert eredmények jól egyeznek, amennyiben az Rinter = 1. Az Rinter csökkenése a két modell közötti különbség növekedésével jár, a VP modell azonos teher hatására nagyobb deformációt szenved (Marjanovic, et al., 2016). Ezzel összhangban levő 52
58 eredményeket kapott (Szép, 2014) is, aki a határfelületi elem arányszámát Rinter = 0,7-re választotta. Cölöpcsoportok vizsgálatánál a két modell nagyobb eltérést mutatott, de e kutatásban a hálósűrűség hatását egyelőre nem vizsgálták (Marjanovic, et al., 2016). Kutatásomban a térfogati elemként (VP) és a beágyazott gerendaelemként (EP) való modellezést alkalmaztam, s ezekre elsőként összehasonlító számításokat végeztem Kísérleti vizsgálatok A mélyalapozások, illetve a talaj, az alapozás és a felszerkezet kölcsönhatás szeizmikus és dinamikus terhelés alatti elemzési eljárásainak fejlődése, az egyre szofisztikáltabb elméletek alkalmazása szükségessé teszi azok verifikálását próbavizsgálatokkal. A cölöp méretéből és a terhelés típusából adódóan az alábbi vizsgálati módok jöhetnek szóba: valós méretű cölöpön helyszíni vizsgálat, laboratóriumi vizsgálat kisméretű modellcölöpön valamint centrifugában. Mélyalapozások tekintetében valós cölöpön csak a gépalapok és a felszerkezet kilengéséből keletkező hatások elemzése lehetséges. (Dezi, et al., 2011) és (Roia, 2011) Olaszországban 15,5 m hosszúságú vibrált acél cölöp felső pontján kifejtett hatását vizsgálta a próba- és mellette lehajtott két cölöpön, s a mérések alapján kalibrálta az ABAQUS számításokat. Laboratóriumi körülmények között homokba telepített modellcölöp viselkedését a cölöpfejnél működtetett ciklikus terhelésre (Kikuchi, 2008) vizsgálta, míg (Rosquoet, et al., 2007) centrifugában. Vizsgálataikban ciklikusan változó erőt működtettek, s azt tapasztalták, hogy a cölöp vízszintes elmozdulása a ciklusszám logaritmusával lineárisan nőtt. A győri Széchenyi István Egyetem Geotechnikai laboratóriumában TDK és szakdolgozat keretében készült vizsgálat homokba ágyazott epoxi anyagú modellcölöp válaszának elemzésére lökésszerű vízszintes teher hatására különféle felszíni terhelés mellett (Nepusz, 2017). A földrengés alatti viselkedést csak laboratóriumi körülmények között van mód vizsgálni rázóasztal vagy centrifuga segítségével. A 1990-es évek második felében a University of California, Berkeley laboratóriumában rázóasztalon puha agyag talajba helyezett cölöpök és cölöp-felszerkezet viselkedését elemezték. A főbb eredményeket röviden a következőkben lehet összefoglalni (Meymand, 1998): a felszerkezeti teher növekedésével a tehetetlenségi igénybevétel válik dominánssá a cölöpfej környezetében; felszerkezeti teher nélkül a cölöp válasza szinte azonos a talaj válaszával; 53
59 a felszerkezeti súly cölöpfej feletti magasságával arányosan nő a cölöpfejnél ébredő tehetetlenségi igénybevétel, az aktív cölöphossz alatt a mérések hasonló eredményeket hoztak; a cölöpfej talajba ágyazásának nincsen jelentős hatása a cölöpben ébredő igénybevételre. Megemlítem, hogy az első megállapítással azonos eredményre jutott (Chen & UENG, 2011) is telített laza homok talajba helyezett cölöp rázóasztalon való vizsgálatával. A RELUIS (Rete dei Laboratory univertari di Iiggengrie Seismica) program keretében szemcsés talajba helyezett cölöp-felszerkezet viselkedését vizsgálták nagy méretű nyíródobozban az alsó síkon való gerjesztés hatására. Kísérleteik eredményeként kimutatták, hogy két réteg határán kialakuló nyomaték különösen függ a két réteg merevségi arányától. Az igénybevétel értékét a gerjesztés frekvencia tartománya és energiatartama is befolyásolja, valamint a cölöpfej fixálása és a felszerkezet jelenléte a nyomatéki maximum felfelé való eltolódását eredményezi (Dihoru, et al., 2009). Eredményeiket, a talajt és a szerkezetet lineáris, illetve a talaj nem-lineáris (ekvivalent lineáris) anyagmodellel leírva, BDWF modellel vetették össze. Eredményül a réteghatáron a mértnél kisebb, míg a felső talajrétegben a mértnél nagyobb igénybevételt kaptak (Bhattacharya, et al., 2010). A kísérleteket a SERIES (Seismic Engineering Research Infrastructures for European Synergies) program keretében folytatták. Itt cölöpcsoportok viselkedésére fókuszáltak, s elemezték egy cölöp felső pontján levő súly, illetve néhány cölöp összekötésének hatását (Simonelli, et al., 2012). A kutatási eredmények alapján többek között megállapították, hogy a felszerkezet jelenléte esetén a cölöp a gerjesztés végeztével tovább deformálódik, s reziduális nyomaték mérhető a talaj nem rugalmas alakváltozása miatt. E maradó igénybevétel nagysága a gerjesztés alatti igénybevétellel arányos (Simonelli, et al., 2014). A kísérleti eredmények numerikus modellezéssel való összevetését később FLAC szoftverrel végezték el (Durante, et al., 2015) Modellezés célja Kutatásomban a Plaxis 3D véges elemes geotechnikai szoftver dinamikai modulját használom. A kutatás céljaként az alábbiakat fogalmaztam meg a szoftver által felkínált fejlett anyagmodell és speciális cölöpmodell alkalmazási lehetőségeinek feltárása, értékelése, a kinematikai igénybevételeket befolyásoló paraméterek hatásának elemzése, tehetetlenségi és kinematikai igénybevételek kapcsolatának vizsgálata. 54
60 E fejezet elején a modellalkotás folyamatát, a paraméterek megválasztási módját ismertetem, azt követően bemutatom a modell verifikációját és a cölöpmodellezési technikákat vetem össze Modellalkotás Talajmodell Kutatásaim során a Plaxis 3D szoftver által felkínált HSS anyagmodellt alkalmaztam, mely elvi alapjait a fejezetben ismertettem. E modell előnye, hogy számításba veszi a talaj azon sajátosságát, hogy merevsége az alakváltozások mértékétől és a feszültségszinttől függ. Ennél fogva a szokásosan alkalmazott, a mélységtől független, konstans merevség helyett automatikusan a valóságot jobban közelítve a mélységgel növekvő merevséget vesz figyelembe. (Di Laora & Rovithis, 2014) is hasonló talajmodellt alkalmazott, de homogén talajt vizsgált, míg én saját modellezésemmel egy kétrétegű talajkörnyezet viselkedését elemeztem. A modell magasságát 30 m-re választottam egyrészről azért, mert az EC 8 ilyen vastagságú réteg számításba vételét várja el a szeizmikus hatás számításához, másrészről az előző fejezetben ismertetett kutatások is hasonló modellmérettel dolgoztak. A felső réteget 8 m vastagságúra vettem, és laza iszapos homokként definiáltam, alá közepesen tömör - tömör homokot feltételeztem. A két szemcsés réteg alatt merev alapréteget vettem figyelembe. A szemcsés rétegek paramétereit szakirodalmi adatok és saját tapasztalataim alapján választottam meg, azok változását figyelembe véve, hogy azt számos kutatás már vizsgálta nem elemeztem, egyéb befolyásoló tényezők hatására fókuszáltam. Az ödométeres (Eoed) és a húrmodulust (E50) mindig azonosra vettem, míg a tehermentesítési-újraterhelési modulust (Eur) ezek háromszorosára. A nyírási modulusnak az alakváltozás növekedésével való leromlását (Vucetic & Dobry, 1991) plaszticitás nélküli talajra (PI = 0) adott ajánlása alapján vettem fel. Az így kiadódott leromlási és csillapítási görbéket a ábra mutatja. Az ábrán a pontvonal (Vucetic & Dobry, 1991) eredeti ajánlását reprezentálja, a szaggatott vonalak a fejezetben ismertetett függvényekkel előálló görbéket mutatják, a folytonos vonal a szoftver által alkalmazott levágást jeleníti meg. A Plaxis csak az érintő modulust (Gt) használja a számításban, szemben a majd alkalmazandó Strata szoftverrel, mely ekvilineáris számításában a szelő modulussal (Gs) számol. 55
61 mélység, z [m] G/G max [-] csillapítás, D [%] ,8 16 0,6 12 G V&D 0,4 V&D-G Gs s 8 Gs-cut s,cut 0,2 Gt t 4 Gt-cut t,cut 0 0 0,0001 0,001 0,01 0,1 1 0,0001 0,001 0,01 0,1 1 nyírási alakváltozás, g [%] nyírási alakváltozás, g [%] ábra: Közepesen tömör-tömör homokra alkalmazott leromlási és csillapítási görbe (Vucetic & Dobry, 1991) nyomán A hiszterézises csillapítás a g= % nyírási alakváltozásnál nagyobb tartományra jellemző, nagyon alacsony alakváltozási szinten azonban a talaj viselkedése szintén nem tökéletesen rugalmas. Ezért ajánlott a Rayleigh csillapítás alkalmazása alacsony csillapítási tényezővel (Laera & Brinkgreve, 2015). A Rayleigh csillapítási formula a csillapítási mátrixot a tömegmátrix és a merevségi mátrix részeinek összegeként határozza meg: C M K (3-19) ahol és jelöli a Rayleigh-tényezőket, melyek kalibrálásához célfrekvenciák és az azokra jellemző csillapítási tényezők ismerete szükséges. A csillapítási tényezőt a két célfrekvenciára ajánlatos azonosra venni. Értékét 0,5-2,0 %-ra javasolják (Laera & Brinkgreve, 2015), saját számításaimban 1,5 % csillapítást vettem figyelembe. (Hashash & Park, 2002) ajánlása szerint az első célfrekvenciát (f1) a talajréteg sajátfrekvenciájára, a másodikat (f2) a gerjesztés domináns frekvenciájának (fi) és a talaj sajátfrekvenciájának (f1) hányadosánál (fi/f1) nagyobb páratlan számra kell megválasztani (Plaxis, 2016b). Egy h vastagságú réteg sajátfrekvenciája vs f1 (3-20) 4 h ahol vs a rétegen a nyíróhullám átlagos terjedési sebessége. A fejezetben látni fogjuk, hogy az alkalmazott gyorsulásdiagramok domináns frekvenciája fi = D V&D V&D-D D DD-cut nyírási modulus, G [MPa] GG 5 vsv s nyíróhullám terj.seb., v s [m/s] ábra: v s és G mélység szerinti változása 56
62 1,6-5,6 Hz közötti, így jellemzőnek fi,átl = 2,5 Hz értéket választottam. A talajparaméterekhez, s így a hiszterézises csillapításhoz hasonlóan a Rayleigh csillapítás változásának hatását nem vizsgáltam, végig e paraméterekkel dolgoztam. A felvett talajprofil nyírási modulusának és a nyíróhullám terjedési sebességének mélység szerinti változását szemlélteti a ábra. A réteghatáron kb. háromszoros merevségi ugrás adódott a felvett talajprofillal, de a két réteg átlagértékét tekintve a hányados már közel hétszeres. A talajparamétereket a 3-2. táblázat tartalmazza táblázat: Alkalmazott talajparaméterek laza iszapos homok közepesen tömör tömör homok térfogatsúly, g [kn/m 3 ] összenyomódási modulus, E oed [MPa] 8 20 újraterhelési modulus, E ur (MPa) kohézió, c [kpa] 1 1 belső súrlódási szög, [ ] kezdeti nyírási modulus referenciaértéke, G 0,ref [MPa] nyírási alakváltozás ahol G=0,722 G 0, g 0,7 [%] 0,009 0,009 átlagos nyíróhullám terjedési sebesség, v s,átl [m/s] 107,5 282,0 Rayleigh 1. célfrekvencia, f 1 [Hz] 3,4 3,2 Rayleigh 2. célfrekvencia, f 2 [Hz] 1,0 1,0 Rayleigh csillapítási tényező, [%] 1,5 1,5 A talajösszlet saját periódus idejét (Sawada, 2004) ajánlása alapján határoztam meg, mely eljárás a szokásosan alkalmazott számításokkal szemben figyelembe veszi a réteghatáron való iránytörést is. Az ajánlás szerint egy kőzet feletti rétegsor saját periódus ideje T g N 1 N Si ti 9 Si ti i1 i1 N 1 4 i1 8 i 2 i S t N 1 i1 i 2 i S t N 1 i1 i 4 i S t (3-21) ahol t i i k1 4 H v sk k (3-22) S i v v s,i 1 s,i 1 v v s,i s,i (3-23) 57
63 melyben vs,k (vs,i) a nyíróhullám terjedési sebessége a k-dik (i-dik) rétegben, Hk a k-dik réteg vastagsága. A vs érték ábra bemutatott, vagy más hasonló mélység szerinti változása esetén az egyes rétegek további részrétegekre tagolásával lehet célt érni. Így számítva a modellezett összlet saját periódus ideje Tg = 0,56 s, azaz sajátfrekvenciája fg = 1,78 Hz lett. Az EC 8 szerinti, a felső 30 m-re vonatkozó átlagos nyíróhullám terjedési sebesség e rétegződés esetén vs,30 = 194 m/s-ra adódott, mely éppen már a C talajosztálynak felel meg, de alig haladja meg az átalagos sebesség a D talajosztályhoz tartozó felső értéket Cölöpparaméterek A modellezés keretében a hazánkban jellemzően alkalmazott cölöpök vizsgálatára törekedtem. Az újonnan épülő műtárgyak, épületek terheit a mai gyakorlatban jellemzően d = cm átmérőjű és L = m hosszú cölöpök továbbítják az altalajra. A Plaxis szoftver a cölöpözési technológia hatását közvetlenül nem tudja számításba venni, így elsősorban talajhelyettesítéses cölöpök elemzésére alkalmas. Ezek alapján a hazánkban leggyakrabban alkalmazott CFA technológiájú cölöpökre vizsgálódásaim érvényesek lehetnek. Kutatásaimban alapvetően d = 60 cm átmérőjű és L = 12 m hosszú vasbeton cölöp viselkedését elemeztem, de egyes esetekre a cölöpátmérő és a cölöphossz változásának hatását is analizáltam. A cölöpöt lineárisan rugalmas anyagmodellel jellemeztem a fejezetben megfogalmazottak alapján, a rugalmassági modulusát Ep = 20 GPa értékre vettem fel. Testelemmel történő cölöpmodellezés esetén az igénybevételek kinyerésére a cölöp tengelyébe egy hajlékony gerenda elemet (beam) illesztettem, melynek geometriai méreteit a cölöpével azonosra vettem, rugalmassági modulusát pedig Epb = 20 kpa-ban határoztam meg. E modellelem a testelemmel modellezett cölöp komplex viselkedését nem befolyásolja, ugyanakkor a valós és a számításba vett rugalmassági modulusok arányával (10 6 -nal) felszorozva az igénybevételek kiolvashatók. Amikor a cölöpöt beágyazott gerenda elemmel (EP) modelleztem, szintén az előbbi geometriai és anyagjellemzőket használtam. A cölöp és a talaj közötti függőleges irányú ellenállás meghatározásakor az egyszerűsítés végett a fajlagos palástellenállást egységesen qs = 40 kpa-ra vettem, a két réteg közötti különbségtől eltekintettem, mivel vizsgálódásom alapvetően a földrengési hatásra, azaz a vízszintes irányú erőkre és ellenállásokra fókuszál. A talpellenállást óvatosan qb = 2000 kpa értékre vettem fel, így a megadott geometriájú cölöp teljes ellenállása Rc = 1470 kn, amelyből az EC 7 szerinti tervezési ellenállás Rc,d 900 kn. 58
64 Mindkét modellezés esetén a cölöp tetejére egy 2 m x 2 m alapterületű, 50 cm vastag fejtömböt helyeztem, a cölöpével azonos rugalmassági modulussal jellemezve azt. Az EP modell esetében a fejtömböt lemez (plate) elemmel modelleztem, mely a terepszinten közvetlenül kapcsolódik az EP felső pontjához, s ott a két szerkezet között merev kapcsolat van. VP esetében a fejtömböt is testelemmel vittem be a modellbe annak valós méreteivel. A cölöp tengelyébe illesztett hajlékony gerenda felső szabad pontjában nyomatéki igénybevétel nem alakulhatna ki, ami nem felel meg a valóságnak. Ezért a fejtömb közepébe egy hajlékony lemezt vettem fel a gerenda elemmel azonos rugalmassági modulussal, s a cölöpbeli gerenda elemet eddig felnyújtottam. E közelítés esetén sem használható ugyanakkor a cölöpbeli gerenda elem az igénybevételek kinyerésére a cölöp felső, fejtömbhöz csatlakozó szakaszán, amivel részletesen a 3.5. fejezetben foglalkozom. A két cölöpmodell lényegét a ábra mutatja. fejtömb (lemez) fejtömb (térfogati elem) térfogati cölöp (VP) beágyazott cölöp (EP) ábra: Cölöpmodellek A cölöpfejnél elfordulás ellen fix megtámasztást, azaz a cölöp cölöpfejbe való teljes befogását feltételeztem. Ezt úgy értem el, hogy a cölöp tetején levő cölöpfej felső síkján a függőleges irányú elmozdulását megakadályoztam, így az csak vízszintesen tudott mozogni. Vizsgálataim a cölöpben ébredő igénybevételek alakulására fókuszáltak, ez valamennyi vizsgálat összehasonlításának alapja. Külön elemzem viszont a réteghatáron és a cölöpfejnél fellépő nyomatékokat. 59
65 Gyorsulásdiagramok A modell alsó síkján, a hosszabbik oldallal párhuzamosan valós, a magyarországi jellemző csúcsgyorsulásértékre (ag = 0,15g) átskálázott gyorsulás-idő függvényeket működtettem, s annak hatására vizsgáltam a cölöp és a talajkörnyezet viselkedését. A gyorsulás-idő adatsorokat általában a kőzetek felszíni kibukkanásainál, gyorsulásmérőkkel rögzítik. A kutatói-tervezői gyakorlatban az elemzésekhez az így nyert adatsorokkal veszik figyelembe a talajrétegek alatti alapkőzeten a gerjesztést. Az adatsorokat azonban a műszer dinamikai jellemzőit figyelembe vevő korrekció ellenére hibák terhelik. Ha feltételezzük, hogy a mérési időközökben a gyorsulásváltozás lineáris (3-15. ábra bal oldali diagramja), akkor e függvény integrálásával előálló sebesség-idő függvény a végén zérustól eltérő értéket eredményez, és a sebesség-idő függvény integrálásával előálló elmozdulás végén sem zérus adódik, ami fizikailag nem lehetséges. A hivatalos gyorsulásadatsorok időtartama jellemzően s, a szerkezetek szempontjából releváns, nagy amplitúdójú rezgések azonban csak 5-10 s hosszúak, a kezdeti és végső szakaszokon magas frekvencia és alacsony amplitúdó a jellemző, mely a szerkezetekben számottevő igénybevételt nem ébreszt. A számítási (idő és kapacitás) igények csökkentése végett a teljes hosszú adatsorok alkalmazása nemlineáris, idő-függő számítás esetén nem ajánlatos, elegendő a gyorsulásdiagramok nagy amplitúdójú szakaszait alkalmazni (Wilson, 2002). Ennek megfelelően a kiválasztott gyorsulás-idő soroknak csak a nagy amplitúdójú szakaszát működtettem a modellen. A levágott idősorok korrekciójával biztosítottam az alapvető fizikai törvények teljesülését, azaz az idősor végén mind az elmozdulás, mind pedig a sebesség zérus voltát. A korrekciót (Wilson, 2002) ajánlása alapján végeztem el, mely azon alapul, hogy minden gyorsulás diagram valójában gyorsulási impulzusok (ld ábra jobb oldala) összessége. A korrekciót két lépésben hajtottam végre, elsőként az adatsor első L számú, jellemzően 1 vagy 2 s-on belüli gyorsulási értékeket módosítottam úgy, hogy a végén kialakuló elmozdulás zérus legyen. A diszkontinuitás elkerülése végett a korrekciót lineárisan súlyozva alkalmaztam, azaz az első elemen teljes mértékben, míg az L-dik elemen a súlyozás 0 (Wilson, 2002). A levágott s így korrigált adatsor végén az elmozdulás zérus lesz, ugyanakkor a sebesség értéke nem feltétlenül. Ennek javítására (Wilson, 2002) az utolsó néhány gyorsulási érték módosítását javasolja, a saját korrekciómban az utolsó N = 20 érték azonos léptékű súlyozatlan módosításával jártam el. A két korrekciós eljárást addig kell folytatni, míg mind a sebesség, mind pedig az elmozdulás zérus nem lesz. 60
66 Ennek automatizálására az MS Excel szoftver VBA programnyelvében célprogramot írtam, mely a beadott eredeti gyorsulás idő függvényből a definiált időtartamot kivágja, majd az elmozdulási és sebességi feltételek teljesüléséhez szükséges iterációs korrekciót elvégezve állítja elő a szerkezetek analíziséhez használható gyorsulás-idő adatsort. idő idő ábra: Földrengés gyorsulás-idő diagramja és annak impulzusának értelmezése (Wilson, 2002) Az alkalmazott gyorsulásdiagram csoportot (7 db) a győri Szerkezetépítési és Geotechnikai Tanszéken futó más kutatásokhoz, elsősorban kockázatértékeléshez (Kegyes-Brassai, 2014), és talajválasz elemzéshez ( (Szilvágyi, et al., 2017), (Kegyes-Brassai, et al., 2017)) már használtuk. A gyorsulásdiagramok az Európai Földrengés Adatbázisból (European Strong-Motion Database - (Ambraseys, et al., 2000)) REXEL (Iervolino, et al., 2010) szoftver segítségével kerültek kiválasztásra, mely a magnitúdó-skálázás technikáját alkalmazza. A gyorsulásdiagramok A talajosztályra, az EC 8 szerinti 1. típusú válaszspektrumra és 0-50 km közötti epicentrum távolságra vonatkoznak (Kegyes-Brassai & Ray, 2015). A kiválasztott földrengések jellemzőit a 3-3. táblázat foglalja össze, a korrigált idősorokból meghatározott spektrumokat a ábra mutatja be táblázat: Alkalmazott földrengések jellemzői jel név dátum magnitúdó epicentrum mélység [km] adatsor hossz [s] amplitúdó [g] levágott adatsor hossza [s] domináns frekvencia [Hz] A1 Friuli , ,05 1, ,00 A2 Valnerina , ,96 0, ,22 A3 Chenoua , ,01 0, ,27 A4 Umbria Marche , ,08 0, ,60 A5 Umbria Marche , ,98 0, ,78 A6 Sicilia-Orientale , ,35 1, ,58 A7 Mt. Vatnafjoll , ,98 0, ,61 61
67 spektrális gyorsulás, S e [g] elmozdulás [mm] magnitúdó 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0 A1 A2 A3 A4 A5 A6 A periódusidő, T [s] 0, ábra: Alkalmazott gyorsulás-idő sorok spektrumai eredeti gyorsulásdiagram 0,2 gyorsulás [g] 0,0-0,2-0, A3 vágás eleje vágás vége idő [s] levágott korrigált idő [s] ábra: A3 gyorsulásdiagram a levágott tartománnyal, a korrigált elmozdulás-idő függvény és a 0,05 0,04 0,03 0,02 0,01 0,00 frekvencia összetétel a simítással A3 A3 simított frekvencia [Hz] 62
68 A levágott, korrigált gyorsulásdiagramok jellemzésére a domináns frekvenciát használtam. Minden adatsor felírható eltérő amplitúdójú és frekvenciájú harmonikus rezgések összegeként. Az egyes idősorok ilyen módú összetételét a Strata szoftver segítségével végzett FFT (Fast Fourier Transform) adja meg. Ebből a domináns a legnagyobb magnitúdójú frekvencia, amihez az FFT eredményeként kiadódó függvényt annak mozgó átlagával simítottam. A ábra példaként mutatja az A3 jelű gyorsulásdiagram eredeti és korrigált eredményeinek egy részét. A dinamikai számításokban az alkalmazott számítási lépcső (dinamikus időlépcső - dynamic time step) fontos szerepet játszik a pontosság és stabilitás tekintetében (Sedighi, et al., 2017). A Plaxis automatikusan képes az alkalmazandó időlépcsők maximális számának optimális meghatározására, de ajánlott azt a gerjesztés időlépcsőinek számával azonosra választani (Laera & Brinkgreve, 2015). Az alkalmazott gyorsulásdiagramok 0,01 s-onként tartalmaznak értékeket, így a s hosszú adatsorok adatpárt foglaltak magukban, ezért ezt alkalmaztam az időlépcsők maximális számának Modellméret, véges elemes hálósűrűség A mozgás irányával párhuzamos peremfelületen nem vettem figyelembe csillapítást, ott görgős megtámasztást modelleztem. Tekintettel arra, hogy a gerjesztés a teljes alsó síkon működik, a modell szélessége, amennyiben a cölöp okozta feszültségek szét tudnak terjedni, nem befolyásolja a cölöp válaszát. Érzékenység vizsgálat alapján a modell szélességét 12 m-re vettem fel. A mozgásra merőleges végen a szoftver által felkínált viszkózus csillapítást alkalmaztam. Az ilyen alapbeállításokkal figyelembe vett peremfeltétel a csak nyomóhullámokat teljes egészében elnyeli, de nyíróhullámok esetén van visszaverődés. Figyelembe véve, hogy több eltérő frekvenciatartományú gyorsulás-idő diagramot alkalmaztam, így a peremet elérő hullámok különbözők lehetnek, ez okból valamennyi esetre a viszkózus perem paramétereit kalibrálni kellett volna. Ezért a modell hosszát, melyben az egyedi cölöp a modell közepén helyezkedik el, azzal a céllal határoztam meg, hogy a cölöptől mindkét irányban m-es távolságon belül a földrengésre adott talajválasz azonos legyen, s így a peremfeltételek ne befolyásolják a cölöp viselkedését. E beállításokkal a modell hosszabbik oldala 140 m-re adódott, ami az általánosan alkalmazott d = 60 cm esetén az átmérő ~235-szerese, míg a legnagyobb vizsgált átmérőnek (d = 120 cm) a ~115-szerese. 63
69 A véges elemes háló sűrűségét abból a két feltételből választottam meg, hogy a modell a kontinuumban való hullámterjedést lekövesse, s a cölöpben ébredő igénybevételeket kellő pontossággal megállapíthassa. Az előbbire (Kuhlmeyer & Lysmer, 1973) azt javasolta, hogy az elemméret egyenlő vagy kisebb legyen a hullámhossz nyolcadánál-tizedénél, amit (Bathe, 1996) pontosított aszerint, hogy a távolság a csomópontok között érvényes. A Plaxis 3D szoftverben alkalmazott 10-pontú tetraéder elemre vonatkozóan így az átlagos elemméret: L átl 4 5 v s,min 4 5 f max (3-24) ahol vs,min a nyíróhullám legkisebb terjedési sebessége a talajban, míg fmax a gerjesztés legnagyobb, még észlelhető energiával rendelkező frekvenciája. Az alkalmazott gyorsulásdiagramokra és talajmodellekre ez az érték 2,0-3,8 m. A cölöp környezetében az igénybevételek minél pontosabb kinyerése végett a véges elemes háló további sűrítése vált indokolttá. Ennek megfelelően az alkalmazott véges elemes háló a cölöp környezetében jellemzően ~0,80 m oldalhoszszúságú, míg a modell széle felé fokozatosan növekszik átlagosan 3,0 m-re (ld ábra). A túlzottan nagy méretű elemek a rövid hullámhosszú hullámokat kiszűrik (Kontoe, 2006). E jelenség a modell széle felé kismértékben érvényesülhetett, de az ottani elemméret is megfelel az irányelvnek. Az egyes modellekben jellemzően elem és csomópont volt ábra: Geotechnikai modell 64
70 3.4. Modell-verifikálás Az alkalmazott modell teljes körű verifikálása nem lehetséges. Egyrészt, mert a cölöpök földrengés alatti viselkedése valós méretben nem, csak laboratóriumi körülmények között, modellcölöpön vizsgálhatók, így valós méretű mérési adat nem áll rendelkezésre. Másrészt az alkalmazott anyagmodellt számos paraméter írja le, melyek felvétele igényes laboratóriumi vizsgálatokat követelnek. Ezek alapján a modell megfelelőségének igazolása érdekében egyrészt a talajmodell talajválasz elemzésre való alkalmazhatóságának igazolását, másrészt az igénybevételek más eredményekkel való összevetését tűztem ki. Előbbihez a HSS anyagmodellel végzett talajválasz elemzés eredményét hasonlítottam össze az összes alkalmazott gyorsulásdiagrammal való gerjesztés esetére a Strata szoftverrel végzett hasonló számítással. Az igénybevételek ellenőrzését két lépésben végeztem, egyrészt egy meglévő más, igazolt modellel, lineárisan rugalmas viszkózusan képlékeny anyagmodellel végzett számítás eredményeivel vetettem össze ugyanazon paraméterekkel végzett saját számításom eredményeit. Másrészt vizsgáltam, hogy a szakirodalomban fellelt becslési képletek által kapott igénybevételek és a számított értékek hogyan viszonyulnak egymáshoz Talajválasz elemzés HSS anyagmodellel A Plaxis szoftver kiadott lineárisan rugalmas talajmodellre vonatkozóan verifikációt egydimenziós hullámterjedésre (Plaxis, 2016d) és talajválasz elemzésre (Plaxis, 2016c) vonatkozóan egyaránt. Az általam alkalmazott HSS anyagmodell ilyen célú felhasználhatóságának igazolásához a bemutatott modellel számított felszíni választ összehasonlítottam egydimenziós, egyenértékű lineáris talajválasz elemzés eredményével. Az egyenértékű-lineáris talajválasz elemzéshez a Strata (Kottke, et al., 2013) szoftvert használtam. Az egydimenziós vizsgálat a talaj nemlineáris viselkedését úgy közelíti, hogy a lineárisan rugalmas paramétereket a kialakult nyírási alakváltozás szintjéhez igazítja, és iteratív módon keresi az alakváltozás és paraméterek kompatibilitását. A ábra jól mutatta, hogy bár a kis alakváltozási tartományban a leromlási görbe a szakirodalmi ajánlás (Vucetic & Dobry, 1991) és a Plaxisban megadott talajmodellben az illesztésnek köszönhetően közel azonos, azonban a nagy alakváltozási tartományban a Plaxis által alkalmazott levágás révén különbség adódik. Megfigyelhető a különbség a csillapítási görbén is. Ahogy korábban említettem, a nagy alakváltozási tartományban a véges elemes modellezés a 65
71 hiszterézises csillapításon túl anyagi csillapítást is számításba vesz a képlékeny alakváltozásokból eredően, melynek lekövetésére a Strata nem képes. A két szoftver által adott eredmény összehasonlíthatósága végett a Strata szoftverbe bevittem a Plaxis által leírt leromlási és csillapítási görbéket úgy, hogy a csillapítást a gcut-nál nagyobb alakváltozási tartományban a (Vucetic & Dobry, 1991) görbéhez igazítottam vissza. Példaként a ábra mutatja az alkalmazott görbéket a laza iszapos homokra, ahol folytonos vonal a Strataba bevitt, szaggatott a Plaxis által számításba vett és folytonos (Vucetic & Dobry, 1991) által javasolt görbéket jeleníti meg. G/G max [-] 1 0,8 0,6 0,4 V&D-G G V&D G s,strata csillapítás, D [%] 0,2 Gs-Strata GGt-cut t,cut ,0001 0,001 0,01 0,1 1 0,0001 0,001 0,01 0,1 1 nyírási alakváltozás, g [%] nyírási alakváltozás, g [%] ábra: Leromlási és csillapítási görbe a Strata szoftverhez laza homok esetén Az összevetést a fejezetben ismertetett gyorsulásdiagramokkal elvégeztem homogén (teljes vastagságában laza iszapos homok) talajra, valamint a kétrétegű talajprofilra is mind cölöp nélkül, mind pedig mindkét cölöpmodellezési technikával (EP és VP) bevitt cölöppel együtt. Ezen összehasonlításokban a cölöp átmérője d = 60 cm, hossza L = 12,0 m. Az összehasonlításban valamennyi gyorsulásdiagramra közel azonos tendenciák adódtak. Példaként a ábra mutatja a felszíni válaszspektrumokat az A1 gyorsulásdiagramra. A diagramon zöld szín jelöli a cölöp nélkül (NP), fekete a beágyazott gerendával (EP), piros a térfogati cölöppel (VP) kiadódó eredményeket. A folytonos vonal a modell közepén, a szaggatott vonal attól 10 m távolságra, a pontvonal a középpontól 20 m-re kialakuló felszíni választ szemlélteti. Sárgával jelöltem a Strata által adott választ, s érdekességként szürke vonal jelöli az EC 8 szerinti C talajosztályra vonatkozó rugalmas válaszspektrumot. A bemutatott, illetve a többi, itt nem közölt ábráról a következő általános évrényű megállapítások tehetők: a két számítási eljárás nagyságrendileg azonos választ eredményez, a T < 0,25 s periódusidő esetén a Strata rendre kisebb választ ad a Plaxisnál, a kirajzolódó platók egyes szakaszain a Strata ~15%-kal alacsonyabb eredményt hoz, V&D-D D V&D Strata-D D Plaxis-cut D Pl,cut 66
72 gyorsulás, a [m/s 2 ] a Plaxis számítások közel azonos görbéket adtak a teljes periódusidő spektrumra, kivéve a cölöpös modellek középpontját, ott a cölöp jelenléte az alacsony periódusidők tartományában csökkenti a választ. A kis periódusidők tartományában a Strata kisebb gyorsulásokat hozott, mely azzal magyarázható, hogy míg a Strata a teljes vizsgálat során egy, a nyírási alakváltozás alapján meghatározott csökkentett modulussal számol, addig a Plaxis időfüggő analízise alatt a merevség minden időlépcsőben változik igazodva az aktuális nyírási alakváltozáshoz (Wolf & Ray, 2018). spektrális gyorsulás [g] 1,4 1,2 1,0 0,8 0,6 0,4 0,2 NP-0 NP-10 NP-20 EP-0 EP-10 EP-20 VP-0 VP-10 VP-20 Strata EC-8 C-T1 0,0 0,01 0,1 periódusidő, T [s] ábra: Talajválasz összevetés A1 gyorsulásdiagram esetén 3,0 2,5 2,0 1,5 1,0 0,5 0,0-0,5-1,0-1,5-2,0-2,5-3,0 NP-0 NP-10 NP-20 EP-0 EP-10 EP-20 VP-0 VP-10 VP-20 strata idő [s] ábra: Felszíni gyorsulás időbeli alakulása A3 gyorsulásdiagram esetén A talajfelszín gyorsulásának időbeli változását az A3 jelű gerjesztésre mutatja az ábra az előzőekben ismertetett jelölésrendszerrel. A három Plaxis modell gyakorlatilag azonos eredményeket mutat, és ezekkel a Strata eredményvonala is lényegileg azonos. Az egyenértékű lineáris 67
73 számítási eljárás lényegéből eredően a Strata görbéje simább lefutású, mint a komplexebb számítási eljárást alkalmazó Plaxissal végzett futtatásé. A 7 gyorsulásdiagrammal végzett számítások eredményeit összehasonlító diagramokról azt is megállapíthattam, hogy a kiválasztott 3 felszíni pont eredményei nagyon hasonlóak, a modell közbenső ~40 m-es szakasza gyakorlatilag teljesen azonos gerjesztést közvetít Más számítási modell reprodukálása A cölöp, illetve a talaj-szerkezet kölcsönhatás modellezésének ellenőrzésére egy más kutatók által, verifikált modellen végzett számítást reprodukáltam, és vetettem össze a cölöpökben ébredő igénybevételeket. Ehhez (Maiorano, et al., 2009) munkásságát vettem alapul, akik VERSAT-P3D véges elemes szoftverrel végezték kutatásaikat, s az alkalmazott eljárás pontosságát egyedi cölöp centrifuga vizsgálatával való összevetése alapján (Finn, 2005) igazolta. (Maiorano, et al., 2009) az általam is alkalmazni kívánt modellezési esethez hasonlót vizsgált, egy 30 m magas, kétrétegű modell közepébe helyezett egyedi cölöp illetve 3x3 db-os cölöpcsoport viselkedését elemezte. Ehhez a talajt lineárisan rugalmas anyagmodellel írta le, a felső réteghez vs1 = 50 és 100 m/s nyíróhullám terjedési sebességet rendelve, illetve a két réteg merevségi arányát 2-re illetve 4-re választva. A talaj térfogatsűrűsége s = 1,94 g/cm 3, Poisson tényezője s = 0,4. A talaj csillapításának számításához Rayleigh elvét alkalmazta, melyhez az első célfrekvenciát (f1) a cölöp-talaj szerkezet sajátfrekvenciájára vette, a második célfrekvenciát (f2) annak négyszeresére. Mindkét frekvencián D = 10 %-os csillapítási tényezőt vett számításba. A cölöp átmérője d = 60 cm, hossza L = 20 m, rugalmassági modulusa Ep = 25 GPa. Az összehasonlításhoz kiválasztott esetben a felső h1 = 15 m vastag réteg nyíróhullám terjedési sebessége vs1 = 100 m/s, a rétegek merevségi aránya, vs2/vs1 = 4 volt. Saját modellemben a talajra lineárisan rugalmas anyagmodellt alkalmaztam a megadott paraméterekkel. A talaj-cölöp rendszer sajátfrekvenciáját (Maiorano, et al., 2009) publikációja nem tartalmazta, így az abban rejlő bizonytalanság kiküszöbölésére három számítást végeztem. Egyik esetben f1 értékét a talajoszlop sajátfrekvenciájával vettem azonosra, s ehhez azt a fejezetben említett (Sawada, 2004) ajánlása alapján számítottam, értéke f1 = 0,7 Hz. Tekintettel arra, hogy a cölöp a rendszer sajátfrekvenciáját befolyásolja, így két másik esetet is elemeztem, egy kisebb (f1 = 0,5Hz) és egy nagyobb (f1 = 1,0 Hz) értékből indultam ki. A cölöpöt beágyazott gerenda elemmel vizsgáltam. 68
74 A modell alján működtetett idő-gyorsulás adatsor (3-22. ábra) az 1976-os Friuli földrengés során rögzített A-TMZ000 jelű adatok ag,max = 0,35 g-re átskálázott értékei. gyorsulás, a [g] 0,4 0,3 0,2 0,1 0-0,1-0,2-0,3-0, idő, t [s] ábra: Gyorsulás-idő függvény A cölöpigénybevétel mélység szerinti alakulását a ábra mutatja, ahol a fekete négyzetek az etalonnak tekintett (Maiorano, et al., 2009) eredmények, a másik három adatsor saját számításból származik. A piros kör esetén a Rayleigh célfrekvencia a talajoszlop sajátfrekvenciájával azonos, a zöld reprezentálja a kisebb és kék a nagyobb célfrekvenciával nyert eredményeket. Az eredménysor alapján elmondható, hogy az igénybevételek lefutása a két modellel a cölöp hosszának nagy részén nagyon jól egyezik, a réteghatáron kialakuló csúcsértékben az eltérés mindössze maximum 3%. Az is megállapítható, hogy a Rayleigh csillapítás célfrekvenciájának megválasztása érdemi különbséget az igénybevételekben nem eredményezett. mélység, z [m] nyomaték, M [knm] M (Maiorano et al, et 2009 al, 2009) Mverifikáció (f 1 =0,5Hz) (f1=0,5hz) 4 6 Mverifikáció (f 1 =0,7Hz) (f1=0,7hz) Mverifikáció (f 1 =1,0Hz) (f1=1,0hz) ábra: Cölöpigénybevételek mélység szerinti alakulása Ezen eredmények mellett a saját analízisek során kapott cölöp igénybevételeket összevetettem a becslési képletekkel, s azok azonos nagyságrendet mutattak, melyekről még a későbbiekben lesz szó. Az itt bemutatott eredmények, valamint az előző alfejezetben ismertetettek alapján a modellt a vizsgált probléma elemzésére alkalmasnak ítéltem. 69
75 3.5. Cölöp igénybevételek kinyerése a fejtömb környezetében VP esetén A fejezetben említettem, hogy a cölöp testelemmel való modellezésekor az igénybevételek könnyebb kinyerését szolgáló hajlékony gerenda elem alkalmazása más szerkezethez való csatlakozás környezetében bizonytalan. Az EP-fejtömb kapcsolat modellezéstechnikai tekintetben és az igénybevételek kinyerhetősége szempontjából is problémamentesnek tekinthető. E fejezetben a VP modell ezen részleteit kívánom áttekinteni. A VP esetében a cölöpben ébredő igénybevételek tekintetében a tapasztalatok az eljárás (hajlékony gerenda elem) megfelelőségét már igazolták, ugyanakkor a cölöp-fejtömb kapcsolatban van bizonytalanság. A hajlékony gerenda- és lemez-elemek kapcsolatánál a nyomatéki igénybevétel lényegesen kisebb, mint ami a cölöp felső 1-2 m-es tartományában jellemző, s ez közvetlenül a fejtömbhöz való csatlakozásnál befolyásolja a hajlékony gerenda elemből kinyerhető igénybevételt. Ezt érzékelteti a ábra, amelyen két átmérő és két különböző súlyú fejtömb esetében fellépő maximális igénybevételeket tűntettem fel. A felső ábrasoron piros vonal jelzi a hajlékony gerenda elemmel (HG) kiolvasható igénybevételeket, melyek mindegyike a felszín alatt kb. 0,25-0,50 m mélységtől felfelé gyorsan csökken. A következő ábrasor a felszín alatt 30 cm-rel mutatja a cölöp normálfeszültség eloszlását és azok szélsőértékeit. Ezek jól érzékeltetik, hogy szinte tisztán hajlított keresztmetszetről van szó. A keresztmetszetek feszültségeloszlásából visszaszámított nyomatéki értékeket a felső ábrán kék vonal jelzi (keresztmetszet - KM). A két nyomatéki ábra cm-től lefelé közel azonos, igazolva a vékony gerenda elem alkalmazhatóságát, ugyanakkor e szint felett a térfogati elemben ébredő feszültségből visszaszámított nyomaték jóval nagyobb, s alakja olyan, amelyet egy befogott kapcsolatra várhatunk. A két szerkezeti elem csatlakozásának modellezése kapcsán meg kell még említeni, hogy míg az EP modell esetében a lemez elemnek nincs kiterjedése, így annak tehetetlensége nem jelenik meg a modellben, addig a VP esetében az 50 cm magas fejtömb többlet tehetetlenséget jelent. A függőleges irányú elmozdulást s ezáltal az elfordulást a fejtömb felső síkján gátoltam, de ettől még a VP esetében a fejtömb deformációja nincs kizárva. Egyfelől ez úgy jelenik meg, hogy a cölöp felső síkján fellépő nyomaték a fejtömböt modellező testelemekben deformációt okoz, melyet a ábra érzékeltet, ahol a fejtömb alsó (a cölöp felső) síkjának függőleges 70
76 irányú elmozdulásai láthatók d = 120 cm átmérőjű cölöp esetére. Jól érzékelhető hogy az kismértékben elfordul, s ennek következtében ugyan alig, de csökkenti a kapcsolat merevségét. Ez lehet az oka a ábra felső diagramsorán a kék vonalak felső visszafordulásának. gyorsulásdiagram A1 A1 A1 cölöpátmérő d = 60 cm d = 120 cm d = 60 cm cölöpfej súlya W = 0 kn W = 0 kn W = 900 kn igénybevételi ábra normálfeszültség eloszlás ábra (z = -0,30 m) mélység [m] 0,25 0,00-0,25-0,50-0,75-1,00-1,25-1,50-1,75 nyomaték [knm] HG KM mélység [m] 0,25 0,00-0,25-0,50-0,75-1,00-1,25-1,50-1,75 nyomaték [knm] HG KM mélység [m] 0,25 0,00-0,25-0,50-0,75-1,00-1,25-1,50-1,75 nyomaték[knm] HG KM max [kpa] min [kpa] ábra: Nyomatéki ábra és normálfeszültség eloszlás térfogati cölöp esetén három esetre Másfelől a vízszintes gyorsulás a fejtömbben nyírási alakváltozást okoz. A ábra azt mutatom be, hogy miként változik időben a cölöp felső pontjának (z = 0 m) elmozdulása (piros vonal), illetve az e pont és a fejtömb középpontja közötti elmozdulás különbség (kék vonal). Kivehető, hogy ugyan csekély mértékű, de van eltérés, ami befolyással lehet a hajlékony gerenda elemben ébredő nyomatékokra ábra: Fejtömb alsó, cölöp felső síkjának függőleges irányú elmozdulása a maximális nyomaték időpillanatában d = 1,20 m átmérőjű cölöp esetén 71
77 elmozdulás, u x [cm] 2,0 0,02 1,5 1,0 0,01 0,5 0,0 0,00-0,5-1,0-0,01-1,5-2,0 VP-0-0,02-2,5 VP ft -3,0-0, idő, t [s] ábra: Cölöp felső pont elmozdulás és a fejtömb alsó felének elmozdulás különbsége az idő változásával d = 1,2 m átmérő esetén Vizsgáltam van-e hatása annak, hogy az igénybevételek kinyerését szolgáló hajlékony lemezt a fejtömb felső síkjába helyezem, s a cölöpbeli hajlékony gerenda elemet addig felnyújtom. Az derült ki, hogy az utóbbiban ébredő nyomaték a releváns tartományban nem változik, így ezzel a fogással a modell nem javítható. A bemutatott eredmények rávilágítottak a cölöp-fejtömb kapcsolat kritikus kérdéseire, s az eredmények kinyerésének nehézségeire, ami a szerkezetek térfogati elemmel való modellezésének általános érvényű problémája. Megállapítható tehát, hogy a VP modell esetében a cölöp felső, a fejtömbhöz mereven kapcsolódó szakaszában ébredő igénybevételek kiolvasására a hajlékony gerenda elem nem használható, nem adja vissza a valós igénybevételeket. Ezért az itteni cölöp-igénybevételeket a térfogati elemben fellépő és kiolvasható feszültségek eloszlásából kell származtatni. Meg kell említeni, hogy a cölöp-fejtömb kapcsolat merevsége önmagában is a tervezés egy bizonytalan eleme, ugyanis a kivitelezésből adódóan a két szerkezet között itt munkahézag van. A kapcsolatot a fejtömbbe bevezetett betonacél armatúra testesíti meg, melynek elvárt lehorgonyzása azonban nem minden esetben valósul meg. A tervezési gyakorlatban a felszerkezeti modellekben gyakran eltekintenek a befogástól és csak csuklós kapcsolatot alkalmaznak, amit a biztonság javára való közelítéssel indokolnak. Ugyanakkor mint látni fogjuk, éppen földrengés okozta terhelés esetén a részleges befogás is képes nyomatékot átadni, ami lokális repedéseket okozhat, s ennélfogva a betonacélok korrózióját eredményezheti. elmozdulás különbség, u x [mm] 72
78 Mindezek miatt úgy határoztam, hogy a két modellezési technika (EP-VP) összehasonlításához a felszín alatt 1,0 m mélységben ébredő nyomatékokat használom, mert ott a felsorolt zavarok már nem érvényesülnek. Megemlítem, hogy az összehasonlítás során vizsgált esetekben a nyomaték a felső 1-2 m-es tartományban alig változik Cölöpmodellezési technikák összevetése A cölöpmodellezési (EP és VP) technikákat a modellezett cölöpben ébredő igénybevételeinek és a cölöp elmozdulásainak összevetésével értékeltem. Ehhez a cölöp jellegzetes pontjaiban, a cölöpfejnél, a két, eltérő merevségű talajréteg határán és általában méterenként vizsgáltam a kialakuló igénybevételek és elmozdulások időbeli alakulását, s kigyűjtöttem azok szélső értékeit. A cölöp görbült alakját e szélső értékekhez tartozó időpontokra vonatkozóan elemeztem. A bevezetőben leírtak szerint a cölöpben a tervezés szempontjából meghatározó kinematikai igénybevétel a cölöpfejnél és az eltérő merevségű rétegek határának környezetében ébred. A könnyebb kezelhetőség végett pontosan a réteghatáron fellépő nyomatékot vizsgáltam, s nem elemeztem, hogy annak környezetében van-e és hol van nagyobb érték, ugyanis e különbség mint majd néhány eredményen bemutatom nem számottevő. Elsőként azt vizsgálom, hogy a kétféle cölöpmodellezési technika alkalmasságát befolyásoljae, hogy milyen gerjesztésről van szó, s hogy az milyen talajkörnyezetben és milyen hosszú cölöp körül terjed szét. Tekintettel arra, hogy a cölöpátmérő hatás fontosabbnak gondolható, hiszen korábban bemutattam, hogy a gerjesztett nyomatékok az átmérő harmadik, illetve negyedik hatványával arányosan változnak, ezért annak szerepét külön alfejezetben taglalom Gerjesztés jellemzőinek szerepe a modellezési technikák alkalmazhatóságában E fejezetben bemutatott eredmények mindegyike d = 60 cm átmérőjű cölöp vizsgálódásából ered. A ábra az A1 gyorsulásfüggvény hatására L = 12 m hosszú cölöpben a cölöpfejnél és a réteghatáron fellépő maximális nyomatékok kialakulásának időpillanatára mutatja az elmozdulás és a nyomaték mélység szerinti változását. A diagramon a korábbi jelölésekkel egyezően fekete vonal mutatja az EP, míg piros vonal a VP modellel adódó a hajlékony gerenda elemből kinyert eredményeket, s a folytonos vonalak a nyomaték, a szaggatottak az elmozdulást érzékeltetik. Az ábra jól szemlélteti, hogy a két modellezési technika az alkalmazott peremfeltételekkel gyakorlatilag azonos eredményt hoz, mind az elmozdulás, mind pedig a nyomaték tekintetében az eltérés minimális. 73
79 mélység, z [m] mélység, z [m] a) elmozdulás, u [cm] -1,5-1,0-0,5 0,0 0,5 1,0 1,5 0-1 MEP EP M MVP VP M -2 u EP ux -3 u VP ux -4 b) elmozdulás, u [cm] -1,5-1,0-0,5 0,0 0,5 1,0 1, MEP-M MVP-M uep-ux VP-ux u VP nyomaték, M [knm] nyomaték, M [knm] ábra: Nyomaték és elmozdulás mélység szerinti változása d = 60 cm és L = 12 m méretű cölöp, kétrétegű talajmodell és A1 gyorsulás esetén a cölöpfejnél (a) és a réteghatáron (b) ébredő maximális nyomaték fellépésének időpillanatában A ábra a két módszerrel, 7 különböző gyorsulásdiagrammal számított nyomatéki szélsőértékek abszolútértékének viszonyát mutatja d = 60 cm átmérőjű cölöpre. A diagramon MH a homogén talajkörnyezetre utal, melyre vonatkozóan a felszíntől számított 1,0 m illetve 4,0 m mélységben levő nyomatéki értékek vannak ábrázolva. Az MCAP jelölés a cölöp tetején (pontosabban a -1,0 m-es szinten), az MIF jelölés a réteghatáron fellépő nyomatékokat reprezentálja. A fekete és sárga jelölők a bemutatott talajrétegződés és L = 12 m cölöphossz esetén adódó eredmények, a kék és piros jelölők 10 m vastag laza üledékbe mélyített L = 20 m hosszú cölöpben ébredő igénybevételeket ábrázolják. A szaggatott vonal a 10%-os hibahatárt mutatja. Az ábrán minden adatpár az MEP = MVP vonal mentén sorakozik, a nyomatékok közötti különbség szinte mindig kisebb 10 %-nál, az eltérések véletlenszerűnek látszanak. Nem érzékelhető eltérés a tekintetben sem, hogy a réteghatáron vagy a cölöpfejnél ébredő nyomatékokról van-e szó, illetve, hogy melyik gerjesztés váltotta ki azokat. Az a tény, hogy 7 különböző gerjesztésre kiadódott nyomatékokra tapasztalhattuk ezeket annak megfogalmazására bátoríthat, hogy a 74
80 vizsgálatokhoz hasonló intenzitású gerjesztésekre a két modellezési technika alternatíva lehet egymás számára d = 60 cm átmérőjű cölöpökre vonatkozóan nyomaték, M EP [knm] ±10% Mtop-8m CAP (8m) MIF-8m (8m) Mtop-10m CAP (10m) MIF-10m (10m) MH H nyomaték, M VP [knm] ábra: EP és VP modellezéssel különböző esetekre számított nyomatékok szélsőértékeinek összehasonlítása (d = 60 cm) A kétféle modellezés általánosabb megfelelőségét egyébként igazolja az a tény is, hogy a réteghatárra kapott nyomatékok hasonlók a majd a 4.1 fejezetben bemutatandó becslési eljárásokkal számíthatókhoz, amire részletesebben az 4.3. fejezetben térek ki (Wolf & Ray, 2018) Cölöpátmérő szerepe a cölöpmodellezési technikák alkalmazhatóságában Az EP cölöpmodellezési technika alkalmazhatóságának kiterjesztése végett az átmérő szerepének feltárására d = cm átmérőtartományban is végeztem összehasonlító vizsgálatot a kétrétegű talajprofilra és A1 gyorsulásdiagramra. A kétféle technikával nyert nyomatéki igénybevételek átmérő szerinti változását a ábra mutatja. A bal oldali diagram a cölöpfejnél ébredő nyomaték, a jobb oldali a réteghatáron keletkező nyomaték átmérő szerinti változását szemlélteti. A ábra a nyomaték hatására a cölöpkeresztmetszet szélső pontjában keletkező alakváltozás szerepel az átmérő függvényében. A diagramokon a min és max jelek az ellentétes irányba forgató nyomatékok szélsőértékeit jelentik. A réteghatáron fellépő nyomaték-értékekben nincs jelentős különbség, az eltérést jobban érzékelteti a fajlagos alakváltozást szemléltető diagram, ez a viselkedés tendenciáját is mutatja. Valamennyi esetben az átmérő növekedésével a nyomatéki alakváltozás csökken, kivéve a VP cölöpökre adódott minimális nyomaték értékét. Ezen eredmények összhangban vannak 75
81 (Mylonakis, 2001) eredményeivel, aki kimutatta, hogy ugyan az átmérőnek nincsen hatása a nyomatéki alakváltozására, de a felső réteg relatív vastagsága (h1/d) kismértékben befolyásolja azt. A 4-2. ábra szerint adott rétegek közötti merevségi arány és cölöp-talaj merevségi viszonyszám esetén az átmérő növekedésével (h1/d csökkenésével) az alakváltozás átviteli tényező csökken. A pozitív maximum értékek nagyon jó egyezést mutatnak, míg a negatív maximumokat (min) kissé nagyobb szórás jellemzi, de összességében a két cölöpmodellezési technikával nyert igénybevételek jól egybeesnek. a) nyomaték, M CAP [knm] nyomatéki alakváltozás, p,cap [%] nyomatéki alakváltozás, p,if [%] EP min VP min EP max VP max 600 b) EP min VP min 500 EP max VP max 400 nyomaték, M IF [knm] átmérő [cm] átmérő [cm] ábra: Nyomaték alakulása cölöpfejnél (a) és réteghatáron (b) az átmérő függvényében a) 0,025 b) 0,025 0,020 0,020 0,015 0,015 0,010 0,005 0,000 EP min VP min EP max VP max átmérő [cm] 0,010 0,005 0,000 EP min VP min EP max VP max átmérő [cm] ábra: Nyomatéki alakváltozás alakulása cölöpfejnél (a) és réteghatáron (b) az átmérő függvényében A réteghatárra adódott jó egyezéssel szemben markáns különbség rajzolódik ki a cölöp-fejtömb kapcsolatánál ébredő nyomatékokban (ld ábra és ábra). A nyomaték d 70 cm 76
82 mélység, z [m] mélység, z [m] esetén még közel azonos, az igénybevételek (MEP/MVP) aránya az 1-től legfeljebb 10%-kal tér el. A d = cm átmérőtartományban az EP modell ad nagyobb nyomatékot, majd ez fokozatosan megváltozik, s d > 80 cm esetén a különbség már nagyobb mint 10 %, s a vizsgált legnagyobb átmérőre az EP modell által adott nyomaték már csak 60%-a a VP modellel kapotténak. A különbség érzékeltetésére a ábra d = 110 cm és d = 120 cm átmérőjű cölöpök nyomatéknak és elmozdulásának mélység szerinti változását mutatom be. Az értékek a cölöpfejnél maximális nyomaték fellépésekor jelentkeztek. (A 3.5. fejezetben ismertetettek szerint a piros folytonos vonalak a felső tartományban nem görbülnek vissza). Az elmozdulási görbék a VP modell esetében a felső, laza talajrétegre, de különösen a cölöpfej környezetére kisebb értékeket mutatnak e zónában így itt a cölöp görbülete és ezáltal a nyomatéka is nagyobb. a) elmozdulás, u [cm] -1,5-1,0-0,5 0,0 0,5 1,0 1, MEP EP M MVP VP M uep EP ux VP ux u VP b) elmozdulás, u [cm] -1,5-1,0-0,5 0,0 0,5 1,0 1,5 0 EP M -1 EP M VP M VP M -2 u EP ux u VP ux nyomaték, M [knm] nyomaték, M [knm] ábra: Nyomaték és elmozdulás mélység szerinti eloszlása d = 1,10 m (a) és d = 1,20 m (b) átmérő a cölöpfejnél ébredő maximális nyomaték pillanatában A különbség okának megtalálásához szükséges alaposabban megvizsgálni a két modellezési technika közötti különbséget, amit vízszintes teherre sematikusan a ábra mutat. A VP modellben a cölöpöt egy térfogati elem reprezentálja, melynek súlya és kiterjedése van, ugyanakkor az EP modell esetében a cölöp geometriai és merevségi paraméterei egy vonalelembe 77
83 vannak koncentrálva. Utóbbi esetben a cölöp valós térfogatán belül a szoftver a környező talaj paramétereivel számol, de csak rugalmas alakváltozásokat engedélyez. E többlet talajtérfogat egyrészt a cölöp komplex viselkedése szempontjából egy bizonyos többlet-tömeget jelent, másrészt e többlet a hajlítási merevséget is növeli, bár mindkettő hatása vélhetően csekély. terhelt talajzóna terhelt talajzóna rugalmas tartomány térfogati cölöp (VP) erő beágyazott gerenda (EP) erő ábra: Erőátadási mechanizmus VP (bal) és EP (jobb) esetén A két modelltípus erőátadási formája is különbözik. A térfogati cölöp keresztmetszete a vízszintes erő hatására nem torzul, csak eltolódik és elfordulhat, valamint annak erővel ellentétes oldalán nagy feszültség keletkezhet. Az EP a terhet a talajra csomópontokban adja át, s az a valós cölöptestnek megfelelő talajzónában (nevezzük ezt feszültség átviteli zónának) már szétterül, miközben e zónát deformálja is. Ez egyrészről a feszültségek eloszlásában okoz különbséget, másrészről egy többlet alakváltozást eredményez a valós cölöptérfogaton belül. Kitekintésképpen a statikus esetre vonatkozóan e körülmények hatásának érzékeltetésére számítást végeztem d = 60 cm és d = 120 cm átmérőjű, a cölöpfejnél vízszintesen statikus erővel terhelt cölöpökre. Az eredmények jó egyezést mutattak (Szép, 2014) munkájával, vagyis a VP modellek rendre nagyobb alakváltozást hoztak. Ezt érzékelteti a ábra, mely a felszín alatt 0,5 m-rel mutatja a vízszintes elmozdulásokat a kétféle cölöpmodellre. A VP cölöp merevtest-szerű elmozdulása az erővel ellentétes oldalon, a cölöp szélén nagy többletfeszültséget okoz, mely akár a talaj képlékenyedését is eredményezheti. Az EP esetén a feszültség átviteli zóna deformációja révén a cölöp felülete hozzásimul a talajhoz, s ezáltal a feszültségeket nagyobb felületen osztja szét. Ezt érzékelteti a ábra a 0,5 méter mélységben keletkező vízszintes feszültségeket szemléltetve. feszültség átviteli zóna A többféle cölöpátmérővel elvégzett dinamikai számítások eredményei szerint az alkalmazotthoz hasonló, mérsékelten szeizmikus területre jellemző gerjesztésekre, e modellezéstechnikai eltérések nem okoznak számottevő különbséget a talaj és a szerkezet közötti kölcsönhatásban. Ezt igazolja a réteghatárra kiadódott jó egyezés, s támasztja alá továbbá annak a számításnak 78
84 az eredménye is, melyben fejtömb nélküli (szabad fej) d = 60 cm és d = 120 cm átmérőjű cölöpök viselkedését elemeztem a bemutatott kétrétegű talajmodellel és A1 gerjesztéssel. A ábra tanulsága szerint a két modellezési technika közötti különbség mindössze 10% ábra: Statikus teherrel terhelt VP (bal) valamint EP (jobb) cölöp és környezetének elmozdulás ábrája a cölöpfej alatt 0,5 m-rel (d = 60 cm) ábra: Statikus teherrel terhelt VP (bal) és EP (jobb) cölöp és környezetének vízszintes feszültség ábrája a cölöpfej alatt 0,5 m-rel (d = 60 cm) A talaj-cölöp-cölöpfej kölcsönhatásának vizsgálatakor azonban az átmérő növekedésével az e fejezetben felsorolt hatások, illetve a cölöp-cölöpfej körüli talaj képlékeny alakváltozása együttesen egyre markánsabb különbséget eredményez. Megállapítható, hogy a két modell (EP és VP) d 0,70 m esetén jó egyezést mutat, nagyobb átmérőjű cölöpök fejtömbhöz (vagy más szerkezetekhez) mereven kapcsolódó szakaszának szeizmikus viselkedésének vizsgálatára viszont az EP modell használata nem javasolható. Számításaimban valamennyi átmérőhöz azonos, 2,0 m x 2,0 m x 0,5 m méretű fejtömböt alkalmaztam. A nagyátmérőjű cölöpök esetében ebből adódóan a cölöp és a fejtömb széle közötti 79
85 mélység, z [m] mélység, z [m] távolság csökken, ezért megvizsgáltam, hogy nagyobb fejtömb s ezáltal annak nagyobb merevsége gyakorol-e hatást az eredményekre. A d = 120 cm átmérőjű cölöphöz kapcsolódó 3,0 m x 3,0 m x 1,0 m méretű fejtömbbel mind az elmozdulás, mind pedig a nyomaték közel azonos volt, mint amit a kisebb fejtömbbel kaptam, mindössze 4% lett a többlet. a) elmozdulás, u [cm] -2,0-1,5-1,0-0,5 0,0 0,5 1,0 1,5 2,0 0 MEP EP M -1 MVP VP M -2 u EP ux u VP ux b) elmozdulás, u [cm] -2,0-1,5-1,0-0,5 0,0 0,5 1,0 1,5 2,0 0 MEP -1 EP M MVP VP M -2 uep EP ux u VP ux nyomaték, M [knm] nyomaték, M [knm] ábra: Nyomaték és elmozdulás mélység szerinti változása szabad cölöpfej esetén d = 60 cm (a) és d = 120 cm (b) átmérőjű cölöpre Fontos, hogy a fenti gondolatok, számítási eredmények rávilágítanak a cölöp-fejtömb kapcsolatának modellezési nehézségeire, s annak az igénybevételek mértékét befolyásoló hatására. E problémakör további vizsgálódást igényel, ami túlmutat a jelen doktori kutatásaimon, Összefoglalás E fejezetben a cölöpök földrengés alatti viselkedésének modellezését taglaltam. Elsőként a szakirodalom feldolgozásán keresztül bemutattam a vizsgálati lehetőségeket, rávilágítva az eddig alkalmazott modellek korlátaira, kritikus elemeire. 80
86 Ezt követően ismertettem a vizsgálataimhoz alkalmazott modell felépítését, kiindulási paramétereit, valamint a modell verifikációját. A számításhoz kétrétegű, szemcsés talajmodellt alkalmaztam, a talaj viselkedésének leírására a HSS anyagmodellt használtam. Az időtérben való elemzéshez a hazánkhoz hasonlóan mérsékelten szeizmikus területekre jellemző valós gyorsulás-idő függvényeket működtettem a modell alján. Az alkalmazandó modell verifikálása, a vizsgálat tárgya és az alkalmazott fejlett anyagmodell miatt nehézkes. A modell megfelelőségének igazolásához ezért az alábbiakat végeztem el: A Plaxis által lineárisan rugalmas anyagmodellre verifikált talajválasz elemzést kiterjesztettem az általam alkalmazandó HSS anyagmodellre kétféle rétegződés, 7 eltérő gerjesztés vizsgálata alapján. A cölöpre a beágyazott gerenda elem alkalmazhatóságát (Maiorano, et al., 2009) által alkalmazottal azonos modellen, az eredményeket azzal összevetve analizáltam, és jó egyezést tapasztalva azt igazoltnak találtam. Mindezeken felül a cölöpben ébredő igénybevételeket összevetettem a becslési képletekkel, s azok azonos nagyságrendet mutattak. Ezeket együttesen értékelve a modellt verifikáltnak tekintettem. A fejezet végén két modellezéstechnikai részletet vizsgáltam. Rávilágítottam arra, hogy testelemmel való cölöpmodellezéskor (VP) az igénybevételek kinyerését segítő hajlékony gerenda elem más szerkezeti elemhez való csatlakozásnál nem adja vissza a valós igénybevételeket, a térfogati elem feszültségeloszlásából kell azokat meghatározni. A cölöpöt mind térfogati elemmel (VP), mind pedig beágyazott gerenda elemmel (EP) modelleztem és vizsgáltam a két modellezési technika közötti különbségeket. Az összehasonlító vizsgálat alapján megállapítottam, hogy a talaj-szerkezet kölcsönhatást a mérsékelten szeizmikus területen mindkét cölöpmodellezési technikával lehet végezni, a réteghatáron fellépő igénybevétel a két esetre közel azonosra adódott. Különbség van azonban a talaj-cölöp-cölöpfej kapcsolatának modellezésében. Az eltérő modellezési technika a cölöp felső szakaszának alakváltozására, s ezáltal igénybevételére az átmérő növekedésével egyre jelentősebb eltérést eredményez. Vizsgálataim szerint d 70 cm esetén a két számítás közel azonos, így ekkor mindkét modellezési technika alkalmazható, nagyobb átmérő esetén az EP modell nem javasolható. 81
87 4. Kinematikai igénybevétel vizsgálata 4.1. Szakirodalom feldolgozás Cölöpök földrengés alatti viselkedése A cölöp-talaj-felszerkezet kölcsönhatását egy egyedi cölöp esetében a 4-1. ábra érzékelteti. A teljes modellt a felszerkezet, a cölöpfej, a cölöp és a talaj alkotja. Utóbbin belül megkülönböztetünk közeli (near field) és távoli (free field - szabad) közeget a már a BDWF modellnél említett elven. A komplex viselkedést a kinematikai, a tehetetlenségi és a fizikai kölcsönhatás, valamint a radiális csillapítás határozza meg (Meymand, 1998): kinematikai kölcsönhatás: a cölöpalapozásra átadódó földrengés okozta talajdeformáció, mely a talaj szabad válaszától eltérő gerjesztést eredményez a felszerkezeten; tehetetlenségi kölcsönhatás: a felszerkezet kilengéséből a cölöpre jutó hatás, mely vízszintes és nyomatéki igénybevételt ébreszt; talaj-cölöp közötti fizikai kölcsönhatás: a cölöp és talaj közötti kapcsolat, melybe soroljuk a cölöpkészítés és a cölöpterhelés okozta feszültség átrendeződéseket, a talajkörnyezet elmozdulásainak hatását, valamint a földrengés során a hézagképződést a felszín közelében a talaj és a cölöp között; radiális csillapítás: a talajban a cölöpről átadódó hullámok távolterjedése révén kialakuló csillapítás, mely a cölöp-talaj érintkezési felületén alapvetően a cölöpről átadódó magas frekvenciájú rezgéseket nyeli el. Az előzőekben láthattuk, hogy a földrengések alatt a cölöpöket kinematikai és tehetetlenségi hatás éri, s az új szabályozás definiált esetekre mindkettő számításba vételét elvárja. Ehhez cölöp-talaj-felszerkezet együttesét az alábbi lépésekkel vizsgálhatjuk (Gazetas & Mylonakis, 1998) (Wolf, 1985): cölöp-talaj kinematikai kölcsönhatásának vizsgálata a felszerkezet nélkül (i) a cölöpben ébredő igénybevételek és (ii) a cölöpfej mozgásának (FIM foundation input motion) meghatározása céljából, a felszerkezet tehetetlenségi kölcsönhatásának vizsgálata az előző pontban meghatározott mozgásra, ami a cölöpben többlet igénybevételt és elmozdulást indukál, cölöp méretezése a rá jutó igénybevételekre. 82
88 FELSZERKEZET nemlináris válasz CÖLÖPFEJ CÖLÖP merevség anyagi csillapítás statikus tengelyirányú teher dinamikus tengelyirányú teher cölöpfej merevség cölöpkészítés hatása negatív köpenysúrlódás rés/kimosódás vízszintes válasz függőleges válasz radiális csillapítás TALAJ (KÖZELI) hiszterézis csillapítás cölöpfej beágyazási ellenállás KÖLCSÖNHATÁS MÓDJA: kinematikai tehetetlenségi radiális cölöp-talaj nyíróhullám TALAJ (TÁVOLI) hiszterézis csillapítás felszíni hullám SZEIZMIKUS FORRÁS 4-1. ábra: Egyedi cölöp szeizmikus válaszát befolyásoló tényezők (Meymand, 1998) Réteghatáron ébredő kinematikai igénybevétel A réteghatáron ébredő kinematikai igénybevételt számos paraméter befolyásolja, a legfontosabbak: a két réteg merevségének aránya, a cölöp és a talaj merevségi viszonya, a réteghatár és cölöpfej távolsága, melynek kis értéke esetén a cölöp-cölöpfej kapcsolata, a gerjesztés jellemzői (frekvenciatartomány, ciklusszám). Ezek hatását számos kutató vizsgálta, s néhányan ajánlást fogalmaztak meg az igénybevételek becslésére. Először a becslési képleteket mutatom be, majd az egyes befolyásoló tényezők hatását ismertetem a szakirodalom alapján Réteghatáron ébredő kinematikai igénybevétel becslése (Dobry & O'Rourke, 1983) két réteg határán földrengés hatására fellépő igénybevétel becslésére rugalmas ágyazású gerenda modellel végzett vizsgálatok alapján az alábbi explicit formulát adta: M 3/ 4 1/ 4 E p I p G1 FM 1,86 g 1 (4-1) 83
89 ahol a korábban értelmezett paramétereken túl, G1 a felső talajréteg nyírási modulusa, g1 a maximális nyírási alakváltozás a réteghatáron a felső talajban szabad felszínű rezgés esetén, melyet szabad felszínű válasz analízis alapján vagy a felszíni gyorsulásból közelítő képlettel (Seed & Idriss, 1982) lehet számítani: rd s 1 h1 a g1 G 1 s,max (4-2) ahol r d 1 0, 015 z mélységi tényező, as,max a talajfelszín csúcsgyorsulása, s1 és h1 felső réteg sűrűsége és vastagsága. A (4-1) képletben FM dimenzió nélküli, a rétegek nyírási modulusának hányadosát figyelembe vevő tényező: F M amelyben cg 1 cg c c 1 c c G 1/ 4 G G G G 2 c G (4-4) G 1 (Mylonakis, 2001) a kinematikai hatás értékeléséhez a nyomatéki igénybevétel helyett a nyomatéki alakváltozást (p, bending strain) alkalmazta, (4-3) p M E I p p d 2 (4-5) mivel az dimenzió nélküli, könnyebben mérhető illetve közvetlenül értelmezhető a tönkremenetel, s anyagtól függetlenül közel azonos érték jellemző. Bevezetve a (3-8) képlethez hasonló, de frekvenciától független Winkler paramétert: W k1 4 Ep I p 1/ 4 (4-6) a (4-1) egyenlet átalakításával a cölöpben kialakuló nyomatéki alakváltozás és a talaj nyírási alakváltozásának hányadosa, az úgynevezett alakváltozás-átviteli tényező (strain transmissibility function): p g1 W1 d F M (4-7) E képlet jobb oldala az SSI-t fejezi ki, mely kör keresztmetszetű cölöpökre: 84
90 p k 1,5 g1 E 1 p 1/ 4 F M (4-8) (Mylonakis, 2001) BDWF modellel végzett számításai alapján fejlesztette tovább (Dobry & O'Rourke, 1983) ajánlását az aktív cölöphossznál nagyobb vastagságú felső rétegbe ágyazott cölöpökre, így a réteghatáron fellépő igénybevételt nem befolyásolja a cölöp-cölöpfej kapcsolat. A harmonikus gerjesztéssel végzett számításokban a talaj radiális és anyagi csillapítását is figyelembe vette. Ez alapján a cölöpben ébredő nyomatékot az M 2 E p p I p g 1 g 1 d (4-9) formában definiálta, melyben a korábbiakon túl a gerjesztés frekvenciájának hatását számításba vevő tényező. A statikus esetre ( = 0) az alakváltozás-átviteli tényező jellemző paraméterekre való függvényeit a 4-2. ábra mutatja, melyet tervezési diagramként is lehet alkalmazni. A 4-3. ábra azt mutatja, miként alakul a frekvencia változásával a tényező, mellyel a (4-9) képlet szerint az alakváltozás-átviteli tényező is arányosan nő. A gyakorlatban előforduló alacsony frekvenciatartományban és jellemző merevségi viszonyok mellett 1,25. tervezési diagram alakváltozás-átviteli tényező, p /g 1 alsó limit tervezéshez rétegek merevségi aránya, G 2 /G ábra: Az alakváltozás átviteli tényező és a réteg merevségi arányának összefüggése különböző cölöp-talaj merevségi arányok és felső réteg vastagság esetén (Mylonakis & Nikolaou, 2002) 85
91 dimenzió nélküli frekvencia, a 0 = d/v s1 dimenzió nélküli frekvencia, a 0 = d/v s ábra: Az alakváltozás-átviteli tényező változása a dimenziónélküli frekvencia függvényében (Mylonakis, 2001) (Nikolaou, et al., 2001) frekvenciától függő rugó merevséggel és csúszka jellemzőkkel működő BDWF modellen végrehajtott részletes paraméteranalízis eredményei alapján a következő öszszefüggést vezette le az állandósult rezgés esetére: 0,30 0,65 0,50 3 L Ep v s2 M 0,042 c d E (4-10) d s1 vs 1 amelyben az úgynevezett karakterisztikus nyírófeszültség (c) arányos a réteghatáron fellépő feszültséggel, s a szabad felszín gyorsulásából (as,max) számítható: a c s, max s 1 h1 (4-11) Az eddigiekben bemutatott becslések kidolgozásakor állandósult rezgésekből indultak ki, a földrengések viszont rövidebb ideig, eltérő frekvenciájú rezgések együtteseként hatnak, amelyek kisebb igénybevételt ébresztenek a cölöpben (Nikolaou, et al., 2001). Ez nem jelenti a képletek alkalmazhatóságának korlátait, hiszen az azokban a földrengés hatását reprezentáló nyírófeszültség, nyírási alakváltozás, felszíni gyorsulás a földrengés jellemzőit figyelembe veszi. (Di Laora, et al., 2012) ANSYS szoftverrel, valós gyorsulás-idő adatokkal gerjesztett modell paraméteranalízise alapján az olyan réteghatáron fellépő nyomatékra, amely a cölöpfejtől legalább az aktív cölöphosszal azonos mélységben van, az alábbi összefüggést adta: 2 E p I p p M max g 1 2 g, dyn (4-12) d 1 st melyben a statikus esetre vonatkozó átviteli tényező 86
92 p g 1 st h1 0, 74 0, 5 d 1 E E p 1 0, 25 c 1 0, 5 (4-13) illetve a maximális nyírási alakváltozást (g1,dyn) talajválaszelemzésből, például EERA vagy Strata szoftverrel lehet számítani, 2 pedig a gerjesztés frekvenciájának hatását számításba vevő tényező hasonlóan -hez, s értéke 1,0-1,5. Talajválasz elemzés hiányában alkalmazva a (4-2) képletet a felszíni gyorsulásból is becsülhető a maximális nyomatéki igénybevétel: 2 E I a h p p p s s1 1 M max 1, s d g1 G st 1 (4-14) ahol 1,s jellemzően egynél kisebb (4-4. ábra), köszönhetően a réteghatáron fellépő nyírási alakváltozás képletéből hiányzó feszültség-csökkentő rd tényezőnek ábra: 1,s a gerjesztés frekvenciájának függvényében (Di Laora, et al., 2012) Réteghatáron ébredő kinematikai igénybevételt befolyásoló tényezők hatása A fejezet elején bemutattam, hogy a cölöpben ébredő igénybevételt alapvetően négy tényező befolyásolja. Ezek közül a talajrétegek merevségi viszonyának (G2/G1), illetve a talaj és szerkezet merevségi arányának (Ep/Es1) alapvető szerepét a (4-7) és (4-8) képletek is mutatják. Ezeket érzékelteti a 4-5. ábra, ahol a jelölésben K&G (Kavvadas & Gazetas, 1993) a (3-10) képlettel számított rugóállandót jelöli, míg D&O a (Dobry & O'Rourke, 1983) ajánlását ismerteti, amelyet = 0,4 értékkel számítottam. A jelölésben szereplő számok az Ep/Es1 arányra utalnak. Ezek alapján az átviteli tényező értéke 0,05-0,40 között változik, s hajlékonyabb cölöpöknél, illetve markáns rétegváltás esetén nagyobb az p azonos g1 esetén. (Mylonakis, 2001) A rétegek merevségi arányának (G2/G1, vagy a nyíróhullám terjedési sebességben értelmezve vs2/vs1) jelentős befolyásoló szerepét számos más kutató is kimutatta (pl.: (Di Laora, et al., 2012), (Sica, et al., 2011), (Maiorano, et al., 2009)). Az előbbi megállapítások azonban csak a gyakorlatban leginkább előforduló cölöp-talaj merevségi arányra érvényesek (Ep/Es ), ugyanis annak további növekedésével a nyomatéki alakváltozás egy határértékhez tart. Nagyon merev cölöp esetén (Ep/Es ) a rétegek merevségi arányának növekedésével a nyomatéki alakváltozás kezdetben csökken, majd egy határértéket elérve nem változik (Di Laora, et al., 2012) (Gazetas, 1984). 87
93 alakváltozás átviteli tényező, p /g 1 0,50 0,45 0,40 0,35 0,30 0,25 0,20 0,15 0,10 0,05 0,00 K&G K&G K&G K&G D&O D&O D&O D&O rétegek merevségi aránya, G 2 /G ábra: Alakváltozás-átviteli tényező a rétegek, valamint a cölöp és a felső talajréteg merevségi arányának függvényében (Sica, et al., 2007), (Sica, et al., 2011) BDWF modellel, 18 valós gyorsulás-idő függvényt alkalmazva végzett paraméteranalízis alapján ugyanolyan vs2/vs1 arány mellett jóval nagyobb igénybevételeket kaptak D talajosztályra, mint C talajosztályba sorolható rétegződésre, ami a talaj-cölöp merevség változásának tudható be. Eszerint C talajosztály és a rétegek nyíróhullám terjedési sebességének 2-nél nagyobb aránya (vs2/vs1 > 2) esetén a réteghatáron ébredő nyomatéki igénybevételt már figyelembe kell venni. E megállapítás az EC 8 előírásainál szigorúbb, ugyanis az csak a D talajosztályra írja elő a kinematikai hatás vizsgálatát. A merevségi arányok mellett a felső réteg vastagsága cölöpfej és a réteghatár távolsága is befolyásolja az igénybevételt, s ahogy azt a 4-2. ábra mutatja, annak relatív vastagságától (h1/d) csak kismértékben függ. Ebből adódóan azonos rétegződés esetén az átmérő növekedésével az átviteli tényező csökken, illetve ugyanazon átmérő esetén a felső réteg vastagságának növekedése a nyomaték növekedését eredményezi (Mylonakis, 2001). (Maiorano, et al., 2009) eredményei szerint ugyanakkor a felső réteg vastagságának növekedésével nem minden esetben nőtt az igénybevétel, a talajrétegződéstől és a gerjesztéstől függően esetenként ingadozott. Látható, hogy ha a felső réteg vékonyabb az aktív cölöphossznál, akkor a réteghatáron és a cölöpfejnél kialakuló nyomaték egymásra hatása jelentős, s mindinkább a cölöpfejnél kialakuló nyomaték lesz a mértékadó, mellyel a következő fejezetben részletesebben foglalkozom. A gerjesztés jellemzői, annak domináns frekvenciája és időtartama is befolyásolja az ébredő igénybevételt. A gerjesztés domináns frekvenciája és a talajrétegződés saját frekvenciájának kapcsolata meghatározó (Nikolaou, et al., 2001) (Sica, et al., 2011). A 4-6. ábra jól szemlélteti, 88
94 hogy a talaj sajátfrekvenciájával azonos gerjesztés esetén adódik a legnagyobb nyomaték, viszont attól kismértékben eltérve is már jelentős a csökkenés. Ez harmonikus gerjesztés esetén összhangban van a felnagyítási tényezővel, mely szerint az első rezgésalaknak van számottevő hatása. Mindemellett hosszabban tartó erős mozgás (strong motion) a nyomatéki igénybevétel növekedését okozza, még ha az adott gerjesztés domináns frekvenciája a rezonancia frekvenciától távolabb is esik, aminek oka a ciklusszám növekedésében keresendő (Sica, et al., 2007). Meg kell említeni, hogy a (4-7) képlet rávilágít arra is, hogy a réteghatáron fellépő nyomatéki alakváltozás független a cölöp átmérőjétől. A (4-1) egyenlet szerint a nyomaték abszolút értéke az átmérő növekedésével nő, éspedig annak harmadik hatványával arányosan. Ezt (Dezi, et al., 2010) saját analitikus modelljükkel végzett részletes paraméteranalízisük alapján szintén kimutatták. A cölöpök nyomatéki teherbírásában is meghatározó szerepe van az átmérőnek, lényegileg az is annak harmadik hatványával arányos, de természetesen a teherbírásban szerepe van a vasbeton cölöpök esetében a vasalásnak, s az acélcölöpök falvastagságának. Mindezek alapján felül kell vizsgálni azt a korábbi megállapítást, miszerint a földrengésállóság szempontjából a kisebb cölöpátmérő egyértelműen kedvezőbb, a réteghatáron fellépő nyomatékkal szemben az átmérő csökkenésével nem lehet javítani a tervezési biztonságot (Di Laora, et al., 2013). cölöp nyom. alakvált., p 10-4 cölöpfej réteghatár: befogott cölöpfej réteghatár: szabad cölöpfej gerjesztés normalizált periódusideje, T/T ábra: Réteghatáron kialakuló nyomatéki alakváltozás (a) (Nikolaou, et al., 2001) és nyomaték (b) (Sica, et al., 2011) konkrét példák időfüggő analízisének eredményeként (Dezi, et al., 2010) azt is kimutatta, hogy a réteghatáron fellépő nyomatékot az alsó rétegbe való befogás mértéke nem befolyásolja, ha az nagyobb, mint az átmérő háromszorosa. A bemutatott becslési képletek és az igénybevételt befolyásoló tényezők hatása rendre a mélységgel nem változó talajmerevség és lineáris számításon alapul. Célszerűnek látszik azt vizsgálni, hogy a valóságot jobban leíró, mélységgel növekvő talajmerevség és a talaj nemlineáris viselkedését számításba vevő anyagmodellel kapott eredmények hogyan viszonyulnak az eddigi tapasztalatokhoz. 89
95 Cölöpfejnél ébredő kinematikai igénybevétel Gyakran a cölöpöket mereven kapcsolják a cölöpösszefogó szerkezetekhez. Az ilyenkor a cölöp felső pontjában a kinematikai hatásból ébredő igénybevétel korábban nem kapott kellő hangsúlyt, holott itt a kinematikai és tehetetlenségi igénybevétel szuperponálódhat, amiről a következő fejezetben lesz szó. A cölöpfejnél ébredő kinematikai nyomaték figyelmen kívül hagyása a szerkezet alultervezését eredményezheti (Di Laora, et al., 2013). Mint már említettem a cölöpfej és cölöp kapcsolatának merevsége meglehetősen bizonytalan kérdés. A kutatásokban a két szélső esetet, csuklós és befogott kapcsolatot szoktak vizsgálni, utóbbi releváns a fejtömbnél ébredő nyomaték szempontjából. Homogén talajkörnyezetre vonatkozóan a cölöpben ébredő igénybevételt a cölöp és talaj görbülete közti viszony alapján lehet meghatározni, amiről már a fejezetben volt szó. (Nikolaou, et al., 1995) BDWF modellel végzett széles körű paraméteranalízis alapján kimutatta, hogy a cölöpfejnél ébredő nyomaték (MCAP) az eltérő merevségű rétegek határán ébredő nyomatéknál (MIF) általában kisebb, illetve közel azonos, de egyes esetekben MCAP kifejezetten nagyobb lehet. A két nyomaték aránya (MCAP/MIF) növekszik a felső réteg vastagságának csökkenésével és a két réteg merevségi arányának (G2/G1) csökkenésével. A közelmúltban a cölöpfejnél kialakuló igénybevételt is több kutató különböző módszerekkel első sorban véges elemes analízissel vizsgálta: (de Sanctis, et al., 2010), (Dezi, et al., 2010), (Di Laora, et al., 2013) és (Di Laora, et al., 2011). E vizsgálatok szerint a felső réteg merevsége és vastagsága, a cölöp-talaj merevségi arány és a cölöpátmérő a meghatározó. A felső réteg vastagságának a hatása a rétegek vs értékének arányától függően változik, növekedésével valamelyest csökken az igénybevétel, de egy határértéken túl már alig befolyásolja azt. Ezt valamennyi idézett kutatás igazolta, s ezt érzékelteti a 4-7. ábra is. A réteghatáron fellépő és cölöpfejnél kialakuló nyomatékok viszonyát a 4-8. ábra által bemutatott egyszerű modellel lehet elemezni (Di Laora, et al., 2013), (Di Laora, et al., 2011). A gerenda a cölöp felső rétegbe eső szakaszát reprezentálja, M a réteghatáron fellépő kinematikai hatásból keletkező nyomatékot, mint hatást jelenti, R a cölöpfejnél ébredő reakciónyomaték. Az arányukat szemlélteti a diagram a dimenzió nélküli gerenda hosszra (L/pr), ahol 4 E I 4 E I p p p p 4 4 pr (4-15) k Es a karakterisztikus hullámhossz, a (4-6) szerinti Winkler-paraméter reciproka. 90
96 4-7. ábra: Cölöpfejnél ébredő nyomaték a felső réteg vastagságának függvényében konkrét földrengésekre v s1 = 100 m/s, L = 20 m, d = 0,6 m paraméterek esetén (a) (Maiorano, et al., 2009) és (b) (de Sanctis, et al., 2010) szerint nyomatéki arány, R/M cölöpfej réteghatár dimenzió nélküli gerenda hossz, h/ pr 4-8. ábra: Befogási reakció (R) függése egy Winkler ágyazású gerenda dimenzió nélküli hosszától a másik végén terhelő M nyomatékra (Di Laora, et al., 2013) Érzékelhető, hogy h p 3 értékig a reakció nyomaték azonos irányú a hatással, majd előjelet 4 vált, s a cölöphossz, azaz a rétegvastagság növekedésével a két nyomaték aránya zérushoz közelít. A (4-15) egyenletből, = 2,5 értéket feltételezve az előjelváltás a E hc 1 1, 25 d E p 1 0, 25 (4-16) mélységbe esik, míg a hatást (hc2) kb. ennek kétszeres hosszáig tekinthetjük számottevőnek (Di Laora, et al., 2013). A cölöp és talaj rugalmassági modulusának a hazai viszonyokra jellemző, a fejezetben említett értékeiből a hatás határértéke: h c d (4-17) 91
97 4-9. ábra: Cölöpfejnél ébredő nyomaték (M CAP) és a felszíni csúcsgyorsulás (a maxs) viszonya v s1 = 100 m/s jellemzőjű talaj esetén Amennyiben a rétegvastagság a hatásmélységnél (hc2) nagyobb, akkor a talaj és a cölöp görbülete a cölöpfej környezetében azonosnak tekinthető, azaz a talaj-cölöp kölcsönhatását nem kell vizsgálni, s az igénybevétel a talajfelszín gyorsulásából becsülhető (Di Laora, et al., 2013) összhangban a (3-3) és (3-4) képletekkel: M CAP E p I p a v s 2 s1 (4-18) (de Sanctis, et al., 2010) analíziseik nyomán hasonló megállapításra jutottak, a számítási eredményeik regresszió analízise alapján az igénybevétel becslésére az alábbi formulát javasolták: M CAP 64 E p I p CAP as,max s (4-19) E melyben CAP korrelációs tényező értéke kiindulásként CAP = 0,129-re vehető nagy frekvenciájú rezgésekre (ld ábra). E képletben is megjelenik a cölöp-talaj merevségi arány, ez reprezentálja a két elem közötti kölcsönhatást. Ha a felső réteg vastagsága a hc1 és hc2 értékek közé esik, akkor a réteghatáron fellépő nyomaték kismértékben növeli a cölöpfej s1 görbületi arány, (1/R) p /(1/R) s ábra: Görbületi arány a cölöpfejnél G 2/G 1 arány függvényében (Di Laora, et al., 2013) 92
98 nyomatékát a homogén talajkörnyezetre kiadódóhoz képest, de e többlet 10%-nál nem nagyobb. Ilyen esetben ezért a tervezésben óvatosan eljárva 1,1 szorzót alkalmazhatunk. (Di Laora, et al., 2013). Ha a felső réteg vastagsága a hc1 értéknél kisebb, akkor az MCAP kisebb a homogén talajkörnyezetre kiadódónál. Ezt érzékelteti a ábra is Ep/Es1 = 300 arányra, amiből a két határérték hc1 = 5,2 d és hc2 = 10,4 d, s ennek megfelelően a 2 és 4 h1/d arányra a görbületi arány kisebb egynél, majd a 6 és 8 arányra egynél nagyobb értékek adódnak, míg a h1/d = 10 esetén közel a görbületek aránya függetlenül a rétegek merevségi arányától. Ezzel összhangban vannak (Dezi, et al., 2010) eredményei is, melyet a ábra mutat ábra: Normalizált (M(d=400mm)) nyomaték a cölöpfejnél (Dezi, et al., 2010) Ezzel összhangban vannak még (Di Laora, 2009) eredményei is, melyek arra is rávilágítottak, hogy ha a felső réteg vastagsága nagyobb az aktív cölöphossznál (h1 > La ), a réteghatárnak nincsen közvetlen hatása a nyomaték értékére, de a talajfelszín gyorsulásának módosításával a felső réteg vastagsága közvetetten mégis befolyásolja azt. Összességében megállapítható, hogy általános esetben a felső réteg vastagsága csekély mértékben befolyásolja a cölöpfejnél ébredő nyomatékot. Vékony felső réteg esetén ez a hatás a biztonság javára el is hanyagolható. A réteghatáron fellépő igénybevételhez hasonlóan a cölöpfejnél ébredő nyomatékot a gerjesztés frekvenciája is befolyásolja, amit a ábra bal oldali diagramja szemléltet. A gerjesztés frekvenciájának növekedésével a cölöp egyre kevésbé képes a talaj mozgását, a rövid hullámokat lekövetni, s ebből következően a görbületi arány is csökken. A frekvencia növekedésével a rétegek közötti merevségi aránynak (G2/G1) is egyre kisebb a befolyásoló hatása függetlenül a felső réteg vastagságától. (Di Laora, et al., 2013) 93
99 A felső réteg dinamikai jellemzőinek, illetve a talaj-cölöp merevségi aránynak a hatása evidens, az a (4-18) képletben is megjelenik a talajfelszín gyorsulása és a cölöp hajlítási merevsége révén. A ábra jobb oldali diagramja a cölöp-talaj merevségi arány (Ep/Es1) hatását is érzékelteti. Látható, hogy a merevségi arány növekedésével a görbületi arány csökken, azaz minél merevebb anyagú cölöpöt építünk, annál kevésbé tudja az a talaj mozgását követni, s ennélfogva a nyomatéki igénybevétel ugyanolyan peremfeltételek mellett kisebb lesz. görbületi arány, (1/R) p /(1/R) s a) b) gerjesztés dimenzió nélküli frekvenciája, d/v s ábra: Görbületi arány a cölöpfejnél a dimenzió nélküli frekvencia függvényében (a) különböző h 1/d arányokra, E p/e 1 = 1000 és G 2/G 1 = 10 esetén, illetve (b) különböző E p/e 1 arányokra h 1/d = 10 és és G 2/G 1 = 10 esetén (Di Laora, et al., 2013) A cölöpátmérő nyomatékra gyakorolt hatása a (4-8) képlet szerint az inerciával, azaz az átmérő negyedik hatványával (d 4 ) arányos. A kör keresztmetszetű cölöpök teherbírása az átmérő köbével (d 3 ) arányos, ezért létezik a teherbírás szempontjából maximális átmérő (dmax) (Di Laora, et al., 2013) (Mylonakis, et al., 2014), mellyel az 5.1. fejezetben még foglalkozom. (Dezi, et al., 2010) a cölöpfejnél és a réteghatáron fellépő nyomaték becsléséhez valamennyi számítási eredményét a vs1 = 400 m/s jellemzőjű talajra nyert számítási eredménnyel normalizálta (ld ábra). Kutatásaikban merev alapréteg (vsb = 800 m/s) feletti homogén talajkörnyezetet vizsgáltak, s a nyomatékot az alábbi formában keresték: PGA f d, h1 s1 400 M 400, 1 v CAP M d h e (4-20) 0,25 g 94
100 melyben a PGA/0,25g hányados a szeizmikus intenzitást veszi számításba lineáris tendenciát feltételezve. Az adott geometriai viszonyokra vonatkozó M400(d,h1) nyomatékot és az f(d,h1) tényezőt a számítási eredményeik alapján kalibrálták. Mint ahogy az előző fejezetekben láttuk, a talaj merevsége a mélységgel általában növekszik, s legfeljebb erős közelítésként tekinthető konstansnak. Amennyiben a nyírási modulus a mélységgel lineárisan vagy akár parabolikusan is változik, akkor az előbbi megállapítások nem érvényesek, a megadott számítási eljárások nem alkalmazhatók, ugyanis ekkor a felszínen a talaj görbülete akár végtelen nagy is lehet. (Di Laora & Rovithis, 2014) Feltételezhető, hogy a cölöpfejnél kialakuló görbületet nem csak a talaj felszínén jellemző görbülete, hanem a cölöp mentén kialakuló talajgörbület is szabályozza, ezért ilyen esetekre vezették be az úgynevezett effektív talaj görbületet (4-13. ábra) (Di Laora & Rovithis, 2014): 1 R s, eff g s z z eff eff (4-21) cölöp szabad közeg ábra: A talaj és cölöp görbületének mélység szerinti változása és az effektív talaj görbület definiálása (Di Laora & Rovithis, 2014) A képletben zeff az effektív mélység, míg gs(zeff) az ehhez a mélységhez tartozó talajgörbület. Az effektív mélység tekinthető úgy, hogy e talajzóna határozza meg a cölöpfejnél a nyomaték mértékét, és ez arányos a talaj-cölöp karakterisztikus hullámhosszával (, (Mylonakis, 1995): 1 L a La 0 W z dz (4-22) amelyben az aktív cölöphossz első közelítésben (La) az átmérő 10-szeresére vehető, s a (4-6) szerinti Winkler tényező. Ezekből az effektív mélység közelítőleg a 95
101 z eff 1,25 (4-23) A mélységgel különböző függvények szerint növekvő merevségek esetén az aktív cölöphossz a ábra alapján (Di Laora & Rovithis, 2014): közelítő egyenlet: 0,3 ( L) 3 konstans lineáris (z) parabolikus lineáris (0,5z) 2,50 L a (4-24) Ha a cölöp hossza ennél nagyobb, akkor a görbülete megegyezik a talaj effektív görbületével, amennyiben a cölöp hossza rövidebb, akkor a ábra számított görbéire illesztett egyenletből lehet meghatározni a cölöp-talaj görbületi arányt, azaz: 1 1/ R / R p s,eff L 2 0, 3 (4-25) aktív cölöphossz javasolt értéke ábra: A cölöp és a talaj effektív görbületének aránya a dimenzió nélküli cölöphossz függvényében (Di Laora & Rovithis, 2014) Összefoglalás A szakirodalom feldolgozásán keresztül láthattuk, hogy a cölöpökben ébredő kinematikai hatást a következők befolyásolják: a gerjesztés jellemzői: időtartam, frekvencia, amplitúdó; a talajadottságok: a cölöpökkel harántolt rétegek vastagsága, talajok dinamikai jellemzői (nyíróhullám terjedési sebessége, nyírási modulus, csillapítás), a rétegek merevségének aránya; a cölöp jellemzői: átmérő, hossz, merevség; cölöp-fejtömb kapcsolata. Az előző alfejezetekben az egyes tényezők hatását is bemutattam, s összefoglaltam az igénybevételek becslési képleteit. Ezen eredmények rendre lineárisan rugalmas, viszkózus anyagmodellel végzett vizsgálatokon alapulnak, így célszerű azt vizsgálni, hogy a talaj nemlineáris viselkedését számításba vevő anyagmodell esetén az egyes tényezők miként befolyásolják az igénybevételeket. 96
102 4.2. Vizsgálat célja Kutatásomban a 3.3. fejezetben bemutatott modellel az alábbi kérdésekre keresem a választ: 1. A felszerkezet viselkedését és a cölöpben ébredő igénybevétel alakulását általában a felszíni gyorsulás alapján határozzuk meg, melyet az alapkőzetre jellemző csúcsgyorsulásból és a felszín közeli rétegződés felnagyító hatásából származtatunk. A földrengési hatás jellemzésére a leggyakrabban a maximális vízszintes gyorsulást (peak horizontal acceleration PHA) alkalmazzák, ugyanakkor ez nem ad információt a rengés tartósságáról és frekvenciatartományáról. Ismert ugyanakkor, hogy például magas frekvencián rövid ideig tartó nagy PHA nem okoz jelentős kárt (Kramer, 1996). Ezért itt megvizsgálom, hogy az alkalmazott 7 gyorsulásdiagram frekvenciatartománya és a belőlük keletkező igénybevételek milyen kapcsolatban vannak, van-e jelentősége a talajrétegződés és a gyorsulásdiagram viszonyának az igénybevételekre. 2. A szakirodalom szerint a réteghatáron fellépő igénybevétel független a cölöpfej befogási viszonyaitól, amennyiben a réteghatár az aktív cölöphossznál mélyebben van. Ezt az állítást az általam alkalmazott modellezési eljárásokkal indokolt felülvizsgálni, ezért elemzem a réteghatár helyzetének és a keletkező igénybevételek viszonyát, s ebbe a következő fejezetben majd részletesebben tárgyalt cölöpfejbe koncentrált felszerkezeti teher hatását is bevezetem. A vizsgálatokat egységesen d = 60 cm átmérőjű és L = 12 m hosszúságú, EP modellel leírt cölöpökkel végeztem, s hozzájuk lemezelemmel (plate) modellezett fejtömböt kapcsolatam, miután az előző fejezetben e modellezési technika és a méret hatását már tisztáztam Gerjesztés jellemzőinek hatása a cölöp igénybevételeire A 4.1. fejezetben bemutattam, hogy a talaj válaszához hasonlóan a gerjesztés jellemzői, frekvenciája és időtartama befolyásolja a cölöpben ébredő igénybevételeket is. A fejezetben leírtak szerint a modellezett talaj sajátfrekvenciája fg = 1,78 Hz, az alkalmazott gyorsulások domináns frekvenciái pedig fi = 1,58-5,60 Hz között változtak (ld táblázat). Az A5 jelű gyorsulásdiagram domináns frekvenciája éppen azonos a talaj sajátfrekvenciájával Réteghatáron fellépő igénybevétel vizsgálata A ábra mutatja, hogy miként alakulnak a cölöpökben a réteghatáron és a cölöpfejnél fellépő, a Plaxis szoftverrel számított nyomatékok abszolút értékeinek maximumai a működtetett rengéseknek a talaj sajátfrekvenciájával normalizált domináns frekvenciájától (fi /fg) függően. 97
103 gyorsulás, a [m/s 2 ] A diagramon a korábbi jelöléssel összhangban az MCAP a cölöpfejnél, MIF a réteghatáron ébredő nyomatékot reprezentálja nyomaték, M [knm] M IF M CAP MIF MCAP 0 0,0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 normalizált frekvencia f i / f g [-] ábra: Nyomaték értéke a normalizált frekvencia függvényében A réteghatáron fellépő nyomaték jellemzően MIF = knm, ami alól kivételt éppen az fi / fg = 1 hányadoshoz tartozó érték jelent, amelyik MIF = 135 knm. Nagyobb igénybevételt kaptam az A4 gyorsulás diagrammal való gerjesztésre is, arra amelyiknek domináns frekvenciája a legtávolabb van a talaj sajátfrekvenciájától, ám a nagy amplitúdójú gerjesztés a legtartósabb a ciklusszám itt a legnagyobb ahogy azt a ábra a jellemzőnek tekinthető A1 jelűvel való összevetéssel érzékelteti. 1,5 1,0 0,5 0,0-0,5-1,0-1,5 A1 A idő,t [s] ábra: Az A1 és A4 jelű gyorsulásdiagramok 98
104 A ábra jól mutatja azt is, hogy a gerjesztésben a talaj sajátfrekvenciájától való kis eltérés is a nyomatékok nagyfokú csökkenését eredményezi. Ezek az eredmények összhangban vannak más kutatókéval ( (Nikolaou, et al., 2001) és (Sica, et al., 2011). A kapott igénybevételeket a szakirodalomban ismertetett alábbi négy ajánlással vetettem össze (a képletekben szereplő jelöléseket részletesen a fejezet tartalmazza): 1,86 E I G g F (Dobry & O'Rourke, 1983) (4-1) egy. (DO): p p 1 M M 3 / 4 1/ 4 1 (Mylonakis, 2001) (4-9) egy. (M): M E p I p p g 1 g 1 r (Nikolaou, et al., 2001) (4-10) egy. (N): M 0, 042 d c 3 L d 0, 30 E E p 1 0, 65 v v s2 s1 0, 50 2 E p I p p (Di Laora, et al., 2012) (4-12) egy. (DL): M max g 1 2 g, dyn d 1 Valamennyi képletben szerepel a két réteg merevségi (nyíróhullám terjedési sebességben kifejezett) aránya, s az igénybevétel a merevségi aránnyal nő. A képletek megalkotásakor rendre a mélységgel konstans talajmerevségeket vettek számításba, és a talaj merevségének alakváltozási szinttől való függését figyelmen kívül hagyták. Modellemben a mélységgel hatványfüggvény szerint növekvő merevséget alkalmaztam, s a választott anyagmodell merevsége a nyírási alakváltozás növekedésével csökken. A következőkben a képletekkel való becslés során azt is vizsgálom, hogy a kis alakváltozási paraméterek (vs,max, Gmax) vagy az alakváltozási szintnek megfelelő leromlott értékek számításba vételével kapok e jobb becslést a számított értékekhez viszonyítva. Az idézett képletek többsége a réteghatáron a felső gyenge rétegben kialakuló nyírási alakváltozásból (g1) származtatja a cölöpben ébredő nyomatékot. Ez meghatározható közvetlenül talajválasz elemzésből, és/vagy a talajfelszín gyorsulásából a (4-2) képlettel, az abban szereplő nyírási modulust a réteg átlagaként értelmezve. A ábra a Plaxis és Strata szoftverekkel közvetlenül számított (Plaxis piros négyzet (Pl), Strata fekete négyzet (St)) és a felszínen meghatározott maximális gyorsulásból a (4-2) képlettel becsülhető (Plaxis piros kör (PL-a), Strata fekete kör (St-a)) nyírási alakváltozásokat mutatja. Utóbbihoz elsőként a nyírási modulus maximumaiból indultam ki. Az ábrán feltüntettem az EC 8 szerint 1. típusú válaszspektrumhoz tartozó talajgyorsulásból származtatható nyírási alakváltozást is mind C, mind pedig D st 99
105 nyírási alakváltozás, g 1 [%] talajosztály esetére. Ehhez a felszíni maximális gyorsulást a rugalmas válaszspektrumból a zérus periódusidőhöz olvashatjuk le, azaz a EC a g S (4-26) ahol S az EC 8 szerinti talajtényező. A diagram alapján az alábbi megállapítások tehetők: a talajválasz elemzésből kinyert nyírási alakváltozások (Pl és St) a gerjesztés domináns és a talajoszlop sajátfrekvenciájának kapcsolatát jól reprezentálják, az fi /fg = 1 környezetében rendre nagyobb értékek jellemzők, a felszíni gyorsulásból származtatott nyírási alakváltozások (St-a és Pl-a) gyakorlatilag egy tartományban vannak (g1 = 0,13-0,19 %), s az fi /fg hányadostól való függés mindkét számítási mód esetében megfigyelhető, de a Strata eredménye az fi /fg = 1 esetben jobban kiugrik, a Plaxis eredményeiben e téren kisebb az eltérés, a felszíni gyorsulásból származtatott (Pl-a és St-a) és közvetlenül számított (Pl és St) nyírási alakváltozások mindkét szoftver esetében véletlenszerűen térnek el egymáshoz képest, a számított és származtatott értékek többsége nagyobb, mint az EC szabvány szerint meghatározott értékek. 0,25 0,20 Pl St EC-T1-C Pl-a St-a EC-T1-D 0,15 0,10 0,05 0,00 0,0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 normalizált frekvencia, f i /f g [-] ábra: A réteghatáron fellépő nyírási alakváltozások Plaxis és Strata szoftverrel közvetlenül számított és a felszíni gyorsulásértékekből becsült értékei A diagramm kapcsán meg kell jegyezni azt is, hogy bár az értékek egy tartományba esnek, az egymáshoz viszonyított arányokat tekintve nagyobb különbségek is előfordulnak. Ez az arány 100
106 a nyomatéki értékekben közvetlenül jelentkezik, hiszen a vizsgálandó képletek többsége szerint a nyomaték értéke a nyírási alakváltozással lineárisan változik. A bemutatott nyírási alakváltozási értékek azt is jelzik, hogy a felső talajzónában jelentős a leromlás mértéke. A nyírási alakváltozás mélység szerinti lefutását néhány gerjesztésre mutatja a ábra mind a Plaxis, mind pedig a Strata szoftver esetén. A Plaxis értéke (folytonos vonal) a maximális igénybevétel pillanatában a cölöptől kb. 5 m távolságban felvett függélyben kivett adatsor, a Strata eredmények (szaggatott vonal) a maximális nyírási alakváltozást mutatják. A felső rétegben a nyírási alakváltozás kb. egy nagyságrenddel nagyobb, mint a mélyebb, közepesen tömör-tömör rétegben, s annak mértékét a gerjesztés számottevően nem befolyásolja. Az átlagos g1 = (1-2) 10-3 a felszínhez közeledve, a felső 1-2 m tartományban visszaesik. Az alsó rétegben a Strata szoftverrel rendre nagyobb alakváltozást kaptam, s itt az értékekben is nagyobb a szórás. A Plaxis eredmények kb. g2 = (1-2) 10-4 értéket hoztak. nyírási alakváltozás, g [-] 1,E-05 1,E-04 1,E-03 1,E mélység, z [m] A2 20 A2-St A4 25 A4-St A6 A6-St ábra: Nyírási alakváltozás mélység szerinti alakulása Ezen nyírási alakváltozási szintek az alkalmazott leromlási görbékkel (3-12. ábra) a felső rétegben G/Gmax 0,30, az alsó rétegben G/Gmax 0,55 merevség csökkenést jelentenek. Megemlítem, hogy az EC 8-5 által ajánlott leromlási érték (3-1. táblázat) az adott talajosztály és csúcsgyorsulás esetén G/Gmax 0,58. A felső rétegben a nyírási alakváltozás számításánál a csökkenés figyelembe vétele a (4-2) képletből adódóan kb. háromszoros értéket eredményez, mely jelentős túlbecslést jelent. Ezek alapján, a réteghatáron fellépő nyomaték becsléséhez a 101
107 nyírási alakváltozás értékét célszerűen konkrét talajválasz elemzésből ajánlott venni, ennek hiányában viszont annak becsléséhez a nyírási modulus kezdeti értékéből lehet kiindulni. A réteghatárnál a cölöpben ébredő nyomaték értékét a képletekből kiindulva a nyírási alakváltozás értékének befolyásoló hatásán túl két körülmény határozza meg. Egyrészről a mélységgel változó talajmerevség miatt vizsgálandó, hogy a réteghatár körül milyen vastag talajtartomány meghatározó a talaj-szerkezet kölcsönhatása szempontjából az ott ébredő nyomatékot illetően. Másrészről azt is vizsgálni szükséges, hogy a kiadódó leromlások alapján milyen talajmerevség veendő számításba a nyomatéki igénybevétel becsléséhez. A fejezetben leírtak szerint, a két réteg merevségi arányának növekedésével valamennyi képlet szerint nő a nyomatéki igénybevétel a réteghatáron. A 4-1. táblázatban bemutatom a figyelembe vett rétegvastagság függvényében kiadódó jellemző vs értékeket és azok arányát. Ebből látszik az, hogy a réteghatártól mért távolságok alacsony, az átmérő 3-5-szörös értékére felvett rétegvastagságok esetén érdemi különbség nincs. A felső rétegben nagyobb vastagság számításba vétele a felszín közeli alacsony értékek folytán csökkentik az arra jellemző nyíróhullám terjedési sebességet, így az arány jelentősebben megnő. A továbbiakban csak a táblázat jobb oldali két esetét elemzem táblázat: Rétegek jellemző v s értéke és aránya a figyelembe vett vastagság függvényében v s2/v s1 arány réteghatártól mért távolság átlaga 2 m 3 m a cölöp hoszsza mentén felső réteg nyíróhullám terj. seb., v s1 [m/s] alsó réteg nyíróhullám terj. seb., v s2 [m/s] rétegek merevségi aránya, v s2/v s1 [-] 1,80 1,85 2,27 Szintén a fejezetben rávilágítottam arra, hogy a felső réteg nyírási modulusának csökkenése a nyomaték csökkenését eredményezi azonos nyírási alakváltozás esetén, mivel a cölöptalaj merevségarányának növekedésével a cölöp egyre kevésbé tudja a talaj deformációját lekövetni. Természetesen azonos gerjesztés esetén kisebb merevségű felső rétegben a nyírási alakváltozás növekszik, így eredően a nyomatéki igénybevétel is növekszik. (Nikolaou, et al., 2001) ajánlása független a nyírási alakváltozástól, abban a nyírási modulus és a nyomaték között fordított arányosság van. A leromlás mértékét tekintve négy esetet vizsgáltam: kezdeti paraméterek; teljes szelvényben azonos leromlás; a Plaxis nyírási alakváltozási szintből visszaszámítható rétegenkénti érték és az utóbbiból egy átlagos érték a teljes viselkedés alatt (LR-1 LR4, ld táblázat). 102
108 nyomaték, M [knm] 4-2. táblázat: Figyelembe vett leromlás mérték (G/G max) az egyes esetekben felső réteg alsó réteg LR1 100% 100% LR2 55% 55% LR3 30% 55% LR4 60% 80% Ezek és a figyelembe vett rétegvastagság hatását az A1 gyorsulásdiagramon keresztül mutatja a ábra. A jelölésben a leromlás a 4-2. táblázat szerinti, P jelöli a teljes cölöp mentén és IF a réteghatártól mért 3 m-es tartományra vett talajmerevség átlagokat. A piros vonal a Plaxis által adott nyomatéki igénybevételt jeleníti meg. Ez alapján megállapítható, hogy DO, M és DL képletei nem nagyon érzékenyek a merevségi arányokra, leromlási viszonyokra, a nyomatéki értékek az átlaghoz képest ±10%-on belül vannak, a rétegvastagságbeli eltérést is figyelembe véve ez a küszöbérték már ±15(20)%. A legnagyobb nyomatéki értéket minden esetben az LR1 eset hozta, s az LR1 és LR4 közel azonosat adott. N képlet ezzel szemben nagy érzékenységet mutat, a különböző esetekre a nyomaték MN = knm között változott. Ebben az esetben a legnagyobb nyomaték az LR3 esethez tartozott, s az jóval nagyobb, mint a valósnak tekintett Plaxis eredmény LR1-P LR1-IF 100 LR2-P 80 LR2-IF 60 LR3-P LR3-IF 40 LR4-P 20 LR4-IF Plaxis 0 DO N M DL ábra: Nyomaték értéke a becslési képletekkel a Plaxis által adott nyírási alakváltozásból különböző leromlást és számításba vett rétegvastagság esetén Globálisan elmondható, hogy a képletek alapvetően alábecsülik a nyomaték értékét a réteghatáron. Ebből adódik, hogy a teljes cölöpre vonatkozó talajparaméterekből való kiindulás adja e tekintetben a kedvezőbb értéket, hiszen akkor nagyobb a merevségi arány a két réteg között. Átlagosan a legjobb becslést az LR4 jelű merevség csökkenésből kiindulva a cölöp mentén 103
109 felvett átlagos talajparaméterekből kaptam. Az idézett 4 képlettel számított nyomatékokat a ábra mutatja a Plaxis által meghatározott felszíni gyorsulásból (jelölésben a), illetve a réteghatáron fellépő nyírási alakváltozásból kiindulva. Erről megállapítható, hogy átlagát tekintve a becslési képletekkel meghatározott nyomaték alulról közelíti a Plaxis eredményét, de az éppen a talaj sajátfrekvenciájával azonos gerjesztésből kiadódó kiugró nyomatékot egyik sem tükrözi. A legjobb becslést (Nikolaou, et al., 2001) ajánlása (barna kereszt) adja nyomaték, M [knm] ,0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 normalizált frekvencia, f i /f g [-] M (Pl) N DO-a DO M-a M DL-a DL ábra: Szakirodalmi ajánlások szerint, Plaxis-modellből nyert talajválaszok alapján számított nyomatékok az LR4 esetre Az eddig bemutatott nyomatékokhoz a nyírási alakváltozást a talaj kezdeti nyírási merevségéből származtattam. A ábra esetében a nyírási alakváltozást a felső rétegben azonos leromlást feltételezve kalkuláltam, mint a talaj-szerkezet kölcsönhatásánál. Érzékelhető, hogy így jelentős túlbecslés adódik a nyomatékokat tekintve. Ez az eljárás a biztonság javára jelentős közelítésként tekinthető. A 4-3. táblázatban megadtam az EC 8 szerinti felszíni gyorsulásból az idézett ajánlások szerint számítható nyomatékokat a talaj-szerkezet kölcsönhatásában az LR4 jelű redukciókkal kalkulálva. Feltűntettem a nyírási alakváltozás maximális és csökkentett merevségből való becslését is. Jól érzékelhető, hogy mindkét talajosztály esetén az értékek jelentősen elmaradnak a Plaxis eredményeitől. Összefoglalóan elmondható, hogy a becslési képletek közül (Nikolaou, et al., 2001) ajánlása javasolható úgy, hogy a nyírási modulust átlagos leromlással vesszük számításba. A többi képlettel végzett számítások esetében szintén ezen leromlás figyelembe vétele ajánlható, de ezek rendre kissé alábecsülik a nyomaték értékét. 104
110 nyomaték, M [knm] ,0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 normalizált frekvencia, f i /f g [-] M (Pl) N DO-a M-a DL-a ábra: Szakirodalmi ajánlások szerint, Plaxis-modellből nyert felszíni gyorsulásból a talaj leromlását figyelembe véve számított nyomatékok az LR4 esetre 4-3. táblázat: Szakirodalmi ajánlásokkal számított nyomaték EC szerinti talajgyorsulásból ajánlás DO N M DL g 1 szám G max G red G max G red G max G red G max G red EC-T1-C 25,2 42,0 38,3 38,3 27,9 46,6 27,9 46,5 EC-T1-D 29,6 49,3 45,0 45,0 32,8 54,7 32,7 54, Cölöpfejnél ébredő nyomatékok elemzése Megvizsgáltam, hogy a fejezetben ismertetett alábbi ajánlásokkal adódó igénybevételek hogyan viszonyulnak az általam számítottakhoz: (de Sanctis, et al., 2010) (4-19) egy. (ds): M CAP PGA M 0, 25 g 64 a max S E p I E f d,h1 vs1 400 (Dezi, et al., 2010) (4-20) egy. (D): as (Di Laora, et al., 2013) (4-18) egy. (DL): M CAP E p I p 2 v M CAP 400 d,h 1 e 1 s1 p (Di Laora & Rovithis, 2014) (4-21) egy. (DLR): M CAP E p I p a s G z s eff Láttuk, hogy a cölöpfejnél ébredő nyomaték érdemben nem változik, ha a réteg vastagsága, illetve a cölöp hossza nagyobb, mint az aktív cölöphossz. A képletek közül egyedül (Di Laora & Rovithis, 2014) által ajánlott vonatkozik a mélységgel változó talajmerevségre, s kimutatták, hogy a cölöpfejnél ébredő nyomatékot a felső effektív vastagságú (zeff) réteg viselkedése hatá- 105
111 rozza meg. Ebből következik, hogy a többi esetben is helytelen a teljes rétegre vonatkozó átlagos nyíróhullám terjedési sebességgel számolni. Az aktív cölöphossz meghatározását (Di Laora & Rovithis, 2014) ajánlása alapján végeztem, melyhez a talaj mélységgel növekvő merevségét a Plaxis szoftver által a feszültségszinttől függően, (3-16) képlettel azonos formában vettem fel, a rugómerevséghez (k) a szorzótényezőt (Mylonakis, 2001) (3-13) képlete adta. Ahogy arról a fejezetben már volt szó, a talaj merevségének csökkenésével az aktív cölöphossz növekszik. A vizsgált modellre vonatkozóan a leromlás mértékének függvényében kiadódó aktív cölöphosszt a ábra szemlélteti. Kivehető, hogy a kezdeti paraméterekkel a lehatás nem éri el a 4 m-t, de az észlelt G/Gmax 0,30 leromlás esetén már az 5 m-t is meghaladja. Amennyiben az aktív cölöphosszra a figyelembe veendő nyírási modulust, illetve nyíróhullám terjedési se ,2 0,4 0,6 0,8 1 leromlás mértéke, G/G max [-] ábra: Aktív cölöphossz a leromlás függvényében bességet a merevségváltozást figyelembe véve számítjuk, akkor DL és DLR képletek azonos eredményre vezetnek, így a továbbiakban már csak DL-lel számolt eredményeket tűntetem fel. A ábra szerint a leromlás mértéke a felszínhez közel kisebb, s a mélységgel nő, kb. 2 m mélységben már a felső rétegre jellemző nyírási alakváltozási szint figyelhető meg. Ezek alapján a kezdeti paraméterek mellett három leromlást vizsgáltam: G/Gmax = 0,6; 0,4; 0,3. Az első az időben átlagként tekinthető érték, a második az aktív cölöphosszon vehető átlagosnak, míg az utolsó a maximális, ami kb. 2 m mélységtől jellemző. A számításhoz a Plaxis szoftver által meghatározott talajfelszín gyorsulást vettem alapul, a belőlük számított igénybevételeket a ábra érzékelteti, ahol a jelölésben a képlet jele után található szám a leromlás mértékét reprezentálja. Látható, hogy a cölöpfejnél fellépő igénybevételek hasonlóan alakulnak a réteghatáron fellépőhöz. A nyomatékok nagysága is hasonló, holott a megválasztott réteghatár az aktív cölöphossznál mélyebben van. A maximális igénybevétel itt is az A5 accelerogram esetében lép fel (fi /fg = 1). Kitűnik, hogy a kezdeti talajmerevséggel számolva ds és DL képletek jócskán alábecsülik a számított értékeket, viszont D értéke ekkor is már a jellemzőnek tekinthető nyomatéki értékek körüli eredményt hoz. A felső réteg merevségének csökkentésével a nyomatéki igénybevétel aktív cölöphossz, L a [m] 106
112 növekszik, ezért érzékelteti, hogy egyre feljebb toldónak a becslési képletekkel kiadódó igénybevételi pontok. Amennyiben a leromlás mértékét az aktív cölöphosszon kiadódó átlagaként vesszük fel (G/Gmax = 0,40), akkor a becsült és Plaxissal számított nyomatékok jól egyeznek. nyomaték, M [knm] ,0 0,5 1,0 1,5 2,0 2,5 3,0 3,5 normalizált frekvencia, f i /f g [-] M (Pl) ds-1 D-1 DL-1 ds-0,6 D-0,6 DL-0,6 ds-0,4 D-0,4 DL-0,4 ds-0,3 D-0,3 DL-0, ábra: Szakirodalmi ajánlások szerint a Plaxis modellel megállapított felszíni gyorsulásból kiindulva számított nyomatékok Összességében az állapítható meg, hogy (Dezi, et al., 2010) ajánlása a leromlás elhanyagolása esetén is jól becsüli a nyomaték értékét, s mivel kevésbé érzékeny a leromlás mértékére, ezért annak számításba vétele esetén sem ad nagy túlbecslést. A többi három képlet ugyanakkor csak akkor ad közelítően jó becslést, ha számításba vesszük a talajrétegek leromlását a nagy nyírási deformációk miatt Rétegződés hatása az igénybevételekre Megvizsgáltam azt is, hogy a felső réteg vastagsága, miként befolyásolja a cölöpben ébredő igénybevételeket. Ehhez a fejezetben ismertetett kétrétegű modellt módosítottam úgy, hogy a felső réteg vastagságát (h1) csökkentettem 2,0, 4,0 és 6,0 m-re. A laza réteg vastagságának csökkentése a teljes 30 m vastag összlet sajátfrekvenciáját növeli, s a rétegződés változása módosítja a felszíni gyorsulás számításakor alkalmazandó nagyítás mértékét is. Ennek érzékeltetésére a 4-4. táblázatban kigyűjtöttem a négyféle rétegvastagságra előálló maximális felszíni gyorsulásokat és a nagyítási tényezőket. Érzékelhető, hogy a legnagyobb felszíni hatást a vártnak megfelelően a legvastagabb gyenge réteg esetén kapjuk, ugyanakkor a nagyítási tényező változása a felső réteg nagyobb vastagsága esetén kisebb. 107
113 A réteghatáron a két réteg merevségi aránya (G2/G1) a vastagsággal nem változik, 2,8 körül van, a rétegek átlagos nyíróhullám terjedési sebességének aránya viszont a felső réteg vastagságának csökkenésével egyre nagyobb (4-4. táblázat). rétegvastagság h 1 [m] 4-4. táblázat: Felszíni gyorsulás és nagyítási tényező a rétegvastagság függvényében felszíni csúcsgyorsulás a g,max [g] nagyítási tényező a gmax/a i [-] felső réteg átlagos nyíróhullám seb. v s1 [m/s] alsó réteg átlagos nyíróhullám seb. v s2 [m/s] nyíróhullám terj. sebességek aránya v s2/v s1 [-] 2,0 0,188 1,25 80,7 260,4 3,23 4,0 0,259 1,73 92,6 269,2 2,91 6,0 0,276 1,84 100,9 276,1 2,74 8,0 0,278 1,86 107,5 282,0 2,62 Mindezekkel összhangban van a ábra, amely a cölöpnek a fejtömbnél ébredő maximális nyomaték időpillanatában érvényes nyomatéki ábráját mutatja. Az egyes diagramok nem azonos időpillanatban mutatják a cölöp mentén ébredő igénybevételeket, mivel a rétegződés markánsan befolyásolja a cölöp válaszának időbeli alakulását. A 4 m-es vagy annál vastagabb felső rétegekre hasonló változások érzékelhetők, továbbá a rétegvastagság növekedésével a negatív szélsőértékek egyre mélyebbre tolódnak, s a réteghatár közelében jelentkeznek. A felső réteg legkisebb (2,0 m) vastagságára kiadódott értékek vonala viszont ezektől lényegesen különbözik. Ez adta a legkisebb felső nyomatékot, a többi esetben jóval nagyobbat kaptam. A 2,0 m-es (legkisebb) rétegvastagság hatása tehát csekély, aminek oka valószínűleg az, hogy az ilyen vékony felső réteg felnagyító hatása már elhanyagolható, s így érdemi hatást már nem tud kifejteni a d = 60 cm átmérőjű és a réteg tetején befogott cölöpökre. Megemlítem, hogy ezekkel összhangban van az egyes számítások eredményeként kapott, a réteghatáron és a cölöpfejnél ébredő nyomatékok időbeli alakulása is. A legvékonyabb felső rétegre kapott idősorok nem hasonlítanak a többi rétegvastagságra kapottakéhoz, az alig változik az idő függvényében. A 4 m-es vagy annál vastagabb felső réteg esetében az igénybevételek időbeli változása már hasonló, s a vastagság növekedésével a szélsőértékek egyre hangsúlyosabban rajzolódnak ki. Láttuk az előző fejezetben, hogy az aktív cölöphossz is ekörül adódik a leromlás mértékének függvényében. A következő fejezetben részletesen vizsgálni fogom, hogy a felszerkezet súlyának a fejtömbbe való koncentrálása milyen mértékben befolyásolja a cölöpben ébredő igénybevételeket. Itt azt elemzem, hogy a rétegvastagság hatását miként befolyásolja a fejtömb súlya. A ábra bal 108
114 nyomaték, M CAP [knm] nyomaték, M IF [knm] oldali diagramja a cölöpfejnél, míg a jobb oldali ábra a réteghatáron ébredő igénybevételt mutatja a felső réteg vastagságától és a fejtömb súlyától függően. (A fekete vonal jelzi a terheletlen cölöpöt.) nyomaték [knm] mélység [m] m 4m 6m 8m ábra: Cölöp nyomatéki ábrája különböző felső rétegvastagság esetén a fejtömbnél ébredő maximum időpillanatában felső réteg vastagsága, h 1 [m] felső réteg vastagsága, h 1 [m] ábra: Fejtömbnél és réteghatáron fellépő nyomaték a felső réteg vastagságának függvényében különböző fejtömbsúlyok esetén A cölöp felső pontján ébredő nyomaték a réteg vastagságával növekszik, s a növekedés jellegét a fejtömb szeszélyesen befolyásolja, a nyomatékok nagyságában a fejtömb súlyának hatása 109
115 sokkal nagyobb. A kisebb súlyok mellett a rétegvastagság szerepe viszonylag csekély, a két nagyobbnál már jelentős. Ez szintén az aktív cölöphosszal hozható összefüggésbe, a nagyobb fejtömbsúlyok nagyobb igénybevételt és deformációt okoznak, melyek a talajban nagyobb merevségi csökkenést, s ezáltal megnövekedett aktív cölöphosszt váltanak ki. A fejtömb súlya megsokszorozza a nyomatékokat, a 800 kn nagyságú fejtömbsúlyhoz kiadódott legnagyobb 550 knm nyomatékok nagyon erős vasalást kívánnak. E növekedés a fejtömb okozta tehetetlenségi hatással magyarázható, melyet részletesebben még a következő fejezetben elemzek. A réteghatáron fellépő nyomaték tekintetében a réteg vastagság növekedésével a fejtömb súlyának hatása egyre kisebb. A fejtömb súlyának a réteghatáron fellépő nyomatéknövelő szerepe a kisebb vastagságoknál tetemes, aztán egyre kisebb. A vizsgált legnagyobb rétegvastagság esetén a nyomatékok értéke már szinte független a fejtömb súlyától (MIF = knm), ez esetben a réteg vastagsága már nagyobb az aktív cölöphossznál, így a kettő között nincsen kölcsönhatás. A h1 = 4 m esetén adódnak majdnem minden esetben a legnagyobb igénybevételek, s ezek értéke közel kétszerese is lehet a más rétegvastagságokénál számítottnak Összefoglalás E fejezetben a földrengés alatt a cölöpben ébredő kinematikai igénybevételeket vizsgáltam. A talajdeformációból származó nyomaték a fejtömbhöz való csatlakozásnál, illetve két, eltérő merevségű réteg határán számottevő. Bemutattam, hogy az igénybevétel értékét számos tényező befolyásolja, s összefoglaltam azok becslési képleteit a szakirodalomból. Saját vizsgálataim keretében arra kerestem választ, hogy a gerjesztés jellemzői és a rétegvastagság miként befolyásolja a cölöpben ébredő igénybevételeket. Az EP cölöpmodellel végzett Plaxis futtatásokkal nyert eredményeket összevetettem a szakirodalomban fellelt becslési eljárásokkal is. Az elvégzett paraméteranalízis alapján összefoglalóan az alábbi megállapítások tehetőek: a talaj sajátfrekvenciájával azonos domináns frekvenciájú gerjesztés esetén a nyomatékok jóval nagyobbak, mint minden más gerjesztés esetében, a réteghatáron fellépő nyírási alakváltozás felszíni gyorsulásból való becsléséhez a talajok kezdeti nyírási modulusa ajánlott, a valós leromlás számításba vétele a talajválasz elemzésből kapott értéknek többszörösét eredményezi, az aktív cölöphossz mértékét a talaj leromlása jelentősen befolyásolja, 110
116 réteghatáron ébredő nyomatékot (Nikolaou, et al., 2001) képletével lehet legpontosabban becsülni a nyírási modulus időben vett átlagos leromlását figyelembe véve az egyes rétegekre jellemző talajparamétereket a teljes cölöphossz átlagaként megválasztva, a többi vizsgált képlet e peremfeltételekkel kb %-kal alábecsüli a nyomaték értékét, a cölöpfejnél ébredő nyomatékot valamennyi vizsgált képlet jól becsüli, ha a talaj merevségét az aktív cölöphosszra jellemző maximális leromlás átlagaként vesszük fel, az EC 8 szerint felvehető felszíni csúcsgyorsulásból végzett számítás alábecsüli a nyomaték értékét. a rétegvastagság növekedése a réteghatáron ébredő igénybevételek növekedésével jár, a fejtömb súlyának növekedése a réteghatáron fellépő nyomatékot is jelentősen befolyásolhatja. 111
117 5. Tehetetlenségi és kinematikai igénybevétel kapcsolata 5.1. Szakirodalom feldolgozás Támaszmerevség hatása a felszerkezet válaszára A talaj és a cölöp közötti kinematikai kölcsönhatás a cölöp felső pontjának szeizmikus válaszát, s ezáltal a felszerkezetet érő hatást is befolyásolja. Alacsony frekvenciájú gerjesztés esetén a nagy hullámhossz révén a cölöp követi a talaj válaszát, a frekvencia növekedésével viszont a cölöp válasza a talajfelszínéhez képest csökken. A közepes frekvenciák tartományában a csökkenés drasztikus, a magas frekvenciájú térben pedig a két elmozdulási válasz hányadosa csekély (0,2-0,4) lesz (Di Laora, 2009). Ezt mutatja be az 5-1. ábra, melynek függőleges tengelyén az elmozdulások kinematikai kölcsönhatási tényezője (displacement kinematic interaction factor), azaz a cölöp és a szabad felszínű talaj elmozdulásának aránya (Iu) (Gazetas, 1984) szerepel. Az egyes tartományokat elválasztó határértékeket (a01 és a02) a talajrétegződés, a cölöp-talaj merevség aránya, a cölöpfej elfordulási merevsége és a cölöpcsoport kialakítása befolyásolja, például rétegzett talajkörnyezetben jellemzően a01 = 0,05, míg homogén talajra a01 = 0,2 0,3. (Di Laora, 2009) A felszerkezetet érő hatáson túl annak válasza szempontjából is fontos a talaj-szerkezet közötti u Iu u 0,5 0 a 01 a 02 a ábra: Elmozdulások kölcsönhatási tényezője és dimenzió nélküli frekvencia kapcsolata (Fan, et al., 1991) kölcsönhatás, s ennél fogva az a vizsgálódásom tárgyát képező cölöpigénybevételt is befolyásolja. Egy építmény földrengésre adott válaszát több tényező együttesen határozza meg: alaprajzi és függőleges elrendezés, tömegeloszlás, merevségi viszonyok, felhasznált anyagok jellemzői és azok duktilitása, illetve a megtámasztási viszonyok. A tervezői gyakorlatban a felszerkezet földrengési teherre való méretezésekor s gyakran statikus teher esetén is a talaj-szerkezet kölcsönhatást elhanyagolják a modellezés egyszerűsítése végett. A valóságosnál nagyobb támaszmerevség számításba vétele teherbírási szempontból a biztonság javára elkövetett közelítés (Dulácska, et al., 2008), (Mylonakis & Gazetas, 2000), ugyanakkor nagyobb alakváltozásokat eredményezhet. 1 p ff 112
118 szeizmikus válasz tényező Az alapmerevség figyelembe vétele többféle módon hat a felszerkezet válaszára (ld ábra): a rugalmas megtámasztás növeli a szerkezet saját periódus idejét (Di Laora, 2009) (Mylonakis & Gazetas, 2000); az energia egy része a talaj radiális és hiszterézises csillapítása révén elnyelődik. E hatásokon keresztül a szerkezetre jutó igénybevételek akár sokkal kisebbek lehetnek, mint amilyen merev alátámasztást feltételezve kiadódik, ahogy ezt a válaszspektrumon keresztül az 5-3. ábra érzékelteti. periódusidő T < at ~ H K, D csillapítás D < D ~ K x K R D 0 3 befogott szerkezet 3 rugalmasan megtámasztott szerkezet 3 2 T ~ 2 D ~ ,5 T D 1 1 K x H 2 /K R =0 D 0 /D= ,0 1,5 2,0 ~ K/K x T /T 5-2. ábra: Az SSI hatása a szerkezet periódus idejére és a csillapításra (Mylonakis & Gazetas, 2000) D V D ~ T T ~ szerkezet periódusideje, T str [s] 5-3. ábra: Tervezési alapnyíróerő csökkenése az SSI számításba vételével (Mylonakis & Gazetas, 2000) 113
119 Egy 8 szintes vasbeton vázas épületre végzett vizsgálat igazolta az eddig kifejtetteket (Ray & Wolf, 2013). A szerkezet periódusideje SAP2000 szoftverrel végzett modálanalízis szerint merev megtámasztás esetén TFB = 0,69 s, míg C talajosztályt feltételezve (Dai & Roesset, 2010a) ajánlásai szerint meghatározott támaszmerevséggel TSB = 0,79 s. Az EC 8-1 közelítő képletével pedig TEC = 0,85 s adódik. A periódusidőkhöz tartozó választ és a válaszspektrumokat az 5-4. ábra mutatja be. Érzékelhető, hogy a legnagyobb terhelés a merev támaszra adódik, s ez a valóságot jobban leíró rugalmas megtámasztáshoz képest a biztonság javára téved. Az EC 8 közelítő képlete ugyanakkor épp ellenkező irányba vét hibát. (Ray & Wolf, 2013) 6 5 I. típus - terv. II. típus - terv. I. típus - A II. típus - A I. típus - B II. típus - B I. típus - C II. típus - C I. típus - D II. típus - D 4 S D /a g [-] ,0 0,4 0,8 1,2 1,6 2,0 periódusidő, T [sec] 5-4. ábra: Rugalmas válaszspektrumok az EC8 szerint a példabeli periódusidőkkel (Ray & Wolf, 2013) Az ábráról az is leolvasható, hogy az I. típusú válaszspektrum esetén jóval nagyobb teher adódik, s ez hazánkban igaz az épületek jelentős részére, ugyanis azok periódusideje rendre a példából is kiadódott tartományba esik. Hazánk területén előfordulhatnak mérsékelt földrengések, mint ahogy arra (Ray, 2014) is rávilágít, melyekre a 2. típusú válaszspektrum a jellemző, ezek rezgésideje ugyanis kisebb, mint a nagyobb, távoli földrengéseké Kinematikai és tehetetlenségi hatás időbeli viszonya A felszerkezet kilengéséből az alapozásra tehetetlenségi igénybevétel jut, s az a kinematikai igénybevétellel együtt terheli a cölöpöt. A 4.1. fejezet bevezetőjében bemutattam, hogy általában e két hatást külön-külön vizsgáljuk, s a cölöpöket ezekből kiadódó igénybevételek összegére ellenőrizzük. 114
120 A tehetetlenségi hatást általában két lépésben analizálják (Gazetas, 1984): talaj és alapozás kölcsönhatásának vizsgálata a felszerkezetet súlytalannak tekintve (kinematikai hatás) az alapozás dinamikus impedancia paraméterei (rugómerevség, csillapítási jellemzők) és a felszerkezetet érő hatás meghatározására, felszerkezet vizsgálata a meghatározott támaszmerevségekkel és szeizmikus hatásokra. Homogén féltérre és a mélységgel függvény szerint változó merevségre mind síkalapozásra, mind pedig cölöpalapozásra vonatkozó merevségi és csillapítási jellemzőket (Gazetas, 1991) tanulmánya tartalmazza. A kinematikai igénybevétel számításba vételét, ahogy azt korábban már láttuk, az EC 8 csak speciális esetekre követeli meg, ugyanakkor e feltételek között a szerkezet tömege és annak eloszlása nem szerepel. Belátható, hogy amennyiben a kinematikai igénybevétel a tehetetlenségihez képest csekély, akkor az valóban elhanyagolható. Természetesen e megállapítás csak a cölöpfejnél ébredő igénybevételre lehet érvényes, két eltérő merevségű réteg határán fellépő kinematikai igénybevételeket ez nem befolyásolja. (Di Laora, 2009) analitikus eszközzel vizsgálta 3x3 db-os cölöpcsoportra a kétféle hatás viszonyát, s a befolyásoló paraméterek hatását. A teljesség igénye nélkül az 5-5. ábra két diagramjával, melyen sematikusan a cölöpcsoport egynegyede jelenik meg, néhány fontos megállapításukat emelem ki (a diagramok konkrét paraméterekre vonatkoznak, így azok tendenciáit szabad csak alapul venni): a cölöp átmérő növekedésével a kinematikai hatás válik dominánssá, a kinematikai igénybevétel független a csoporthatástól, a tehetetlenségi igénybevétel viszont a szélső cölöpökben nagyobb, mint a közbensőkben, a felszerkezet periódus ideje értelemszerűen (a válaszspektrum szerint) befolyásolja a tehetetlenségi hatást, s ennél fogva a kinematikai és tehetetlenségi igénybevétel arányát is. A kinematikai igénybevétel a talaj merevségének növekedésével hirtelen csökken (ld. előző fejezet), így a tehetetlenségi igénybevétel aránya egyre markánsabbá válik. A földrengés hullámai elsőként a cölöpöket érik el, abban kinematikai igénybevételt ébresztenek, majd a felszerkezet kilengése kelti a tehetetlenségi hatást, amiből az adódik, hogy a két hatás között fáziseltolódás van. A két hatás szuperpozíciójának elve egyszerűségéből adódóan jól használható, egyes esetekben azonban ez az igénybevételek jelentős túlbecslését eredményezheti, hiszen a tehetetlenségi hatás időbeli változása akár épp az ellenkezője is lehet, mint a kinematikai igénybevételé. 115
121 tehetetlenségi/kinematikai nyomaték [-] kinematikai A cölöp B cölöp C cölöp D cölöp cölöpfejnél ébredő kinematikai nyomaték [MNm] tehetetlenségi/kinematikai nyomaték [-] kinematikai A cölöp B cölöp C cölöp D cölöp cölöpfejnél ébredő kinematikai nyomaték [MNm] cölöp átmérő, d [m] nyomaték/vízszintes erő [m] 5-5. ábra: A cölöp átmérő és a nyomaték/vízszintes erő hányados hatása a tehetetlenségi és kinematikai igénybevételek arányára (Di Laora & Mandolini, 2011) 5-6. ábra: Cölöp elmozdulási képe a cölöpfej elfordulása és eltolódása révén (Di Laora, 2010) A felszerkezet kilengése az alapozáson vízszintes erőt és nyomatékot ébreszt, egyszabadságfokú rendszer esetén az utóbbi az erő és a magasság szorzata. E hatások a cölöpfej eltolódását és elfordulását okozzák, s nyomatékot ébresztenek, ám ellentétes előjellel, ahogy az az elmozdulási képből (ld ábra) is kivehető. Frekvencia térben való vizsgálódás esetén a cölöpfejnél ébredő kinematikai igénybevétel a gerjesztésből egy átviteli függvénnyel számítható, s ehhez hasonlóan a felszíni gyorsulás is meghatározható. Igazolható, hogy e két mennyiség azonos fázisban van. A magas frekvenciák figyelmen kívül hagyása esetén a cölöp felső pontjának gyorsulása a talajéval azonosnak tekinthető, s ebből adódóan a kinematikai és tehetetlenségi igénybevétel fáziseltolódását a tehetetlenségi igénybevételt meghatározó átviteli függvény adja. Amennyiben a tehetetlenségi kölcsönhatáson belül a cölöpfejnél ébredő nyomaték uralkodóan a cölöpfej elmozdulásából adódik, akkor a fáziseltolódás (()) az egyszabadságfokú rendszeren keletkező erő és annak 116
122 cölöp feszültség [kpa] cölöp feszültség [kpa] elmozdulása közötti fáziseltolódással azonos (ld ábra) (Di Laora, 2010) (Di Laora & Mandolini, 2011). Csillapítás nélküli esetben a fázisszög a szerkezet a talaj-szerkezet kölcsönhatását is figyelembe vevő saját frekvenciájánál kisebb frekvencia esetén 0. A diagram azt is érzékelteti, hogy a csillapítás hogyan befolyásolja a fáziseltolódást. fázis szög [-] D = 10% D = 5% D = ábra: Egyszabadságfokú rendszer erő és elmozdulás közötti fáziseltolódás (Di Laora & Mandolini, 2011) Értelemszerűen, amennyiben a cölöpfejnél ébredő nyomaték a fejtömb elfordulásából ered uralkodóan, akkor az előzőek ellenkezője igaz. Ezt reprezentálja az 5-8. ábra, ahol ugyanazon fölrengés hatása figyelhető meg, de a felső ábrán a nyomaték a fejtömb elfordulásából domináns, míg az alsó ábrán a fejtömb eltolódásából. teljes kinematikai tehetetlenségi idő [s] 5-8. ábra: Kinematikai, tehetetlenségi és teljes nyomaték az idő függvényében konkrét példára (Di Laora & Mandolini, 2011) 117
123 A fáziseltolódás előzetesen prognosztizálható úgy, hogy a talajválasz elemzéssel meghatározott felszíni idő-gyorsulás függvény domináns frekvenciáját összevetjük a felszerkezet talaj-szerkezet kölcsönhatást is számításba vevő saját frekvenciájával. (Di Laora, 2010) (Di Laora & Mandolini, 2011). E megközelítés helyénvaló, mert a cölöpalapozás szűrő hatása (filtering effects) csak a magas frekvenciákat érinti (Gazetas, 1984), a domináns frekvencia nem változik. Abban az esetben, ha a cölöpben ébredő tehetetlenségi igénybevételt alapvetően a cölöpfej elfordulása okozza, akkor a fáziseltolódás csökkenthető (Di Laora & Mandolini, 2011) a szerkezet saját frekvenciájának csökkentésével, a talaj sajátfrekvenciájának növelésével, a gerjesztés frekvencia tartományának a magasabb frekvenciák felé történő eltolásával. Mindezek alapján tervezéskor a cölöpöt zérus fáziseltolódás esetén a két hatás összegére méretezhetjük, míg 180 fázisszög esetén a kettő közül a nagyobb igénybevételre. Ha a fáziseltolódás kb. 90, akkor javasolható szintén a tehetetlenségi és kinematikai nyomaték összegét alapul venni, ami a biztonság javára való közelítést jelent (Di Laora & Mandolini, 2011). Meg kell említeni, hogy a fáziseltolódás a földrengés teljes időtartama alatt nem feltétlenül azonos. A cölöp felső pontjában keletkező kinematikai igénybevétel és a tehetetlenségi hatás okozta igénybevétel fázisösszetétele eltérhet a felszerkezet dinamikai jellemzőitől függően. Az igénybevételek viszonyát a nagy amplitúdójú tartományban kell értékelni, s azt kell vizsgálni, hogy abban az időintervallumban a két igénybevétel komponens hogyan viszonyul egymáshoz Alkalmazható cölöpátmérő tartomány Az előző fejezetben rávilágítottam arra, hogy a kinematikai hatás az átmérő negyedik hatványával, míg a cölöp teherbírása a harmadik hatványával lineárisan változik, így e tekintetben a cölöpátmérőnek van egy maximális értéke, amelyre még a cölöp teherbírása igazolható. A tehetetlenségi igénybevétel a felszerkezet súlyával arányos, s ha azt a cölöp teherbírásával (Wp) vesszük azonosra, akkor a nyomaték értéke Winkler elméletből levezethetően kör keresztmetszetű cölöpökre (Di Laora, et al., 2013), (Mylonakis, et al., 2014): M in 1 4 0, 25 as g E E p s 0, 25 S a W p d (5-1) ahol a korábban már definiált jelöléseken túl Sa a dimenzió nélküli spektrális nagyítási tényező. Ezt összevetve a cölöp nyomatéki teherbírásával megkapjuk azt a legkisebb cölöpátmérőt, amellyel a tehetetlenségi hatás még felvehető. 118
124 cölöpátmérő, d [m] A két korlát együttes számításba vétele megadja a cölöpátmérő alkalmazható tartományát. Ennek határai acél csőcölöpökre levezethetők (ld. (Mylonakis, et al., 2014)), ugyanakkor a hazánkban elterjedten alkalmazott vasbeton cölöpökre, amelynek inerciája jóval nagyobb, viszont a beton elhanyagolható húzószilárdsága révén a nyomatéki teherbírást a vasalás adja, nehéz megadni. Az 5-9. ábra konkrét numerikus számítási eredményeket mutat mélységgel lineárisan növekvő talajmerevségre. A diagramok szerint a maximális cölöpátmérő nem jelent korlátot, a görbék bal oldala rendre közel függőleges. Konstans talajmerevség esetén a kinematikai igénybevétel eltérő fontosságából adódóan a bal oldali szakaszok kissé befordulnak. A kinematikai hatásnak közvetetten van szerepe a minimum átmérőre is, ahogy ezt az ábra is érzékelteti: a talajfelszín gyorsulása érzékenyen befolyásolja az alkalmazható átmérők tartományát. Ehhez hasonló hatása van a vashányadnak (cölöp keresztmetszet teherbírásának), a szilárdsági paraméterek ugyanakkor valamelyest kisebb mértékben befolyásolják az átmérő tartományát. talaj Young modulus növekedés, E s [MPa/m] 5-9. ábra: Alkalmazható cölöpátmérő vasbeton cölöp és mélységgel lineárisan növekvő talajmerevség esetén (Mylonakis, et al., 2014) Hangsúlyozni kell, hogy a maximális átmérő valójában csak puha talajkörnyezetre releváns, amelyben a kinematikai hatás jelentős, minden más esetben csak a tehetetlenségi hatás által meghatározott minimális átmérőt kell számításba venni. Meg kell még egyszer említeni, hogy mindezek a cölöpfejnél ébredő igénybevételekre érvényesek, a két eltérő merevségű réteg határán fellépő hatást e körülményektől függetlenül kell vizsgálni. 119
125 5.2. Modellezés célja és eszköze A 4. fejezetben a kinematikai hatást befolyásoló körülményeket vizsgáltam, de tudvalevő, hogy a cölöpméretezést ez és a tehetetlenségi hatás együttesen vezérli a cölöpfejhez való kapcsolódásnál (mélyebben, két eltérő merevségű réteg határán a kinematikai hatás a mérvadó). E fejezetben egyszerű modelleken keresztül vizsgálom, hogy miként befolyásolja a cölöp földrengésre adott válaszát a felszerkezet jelenléte, hogyan alakul a kinematikai és tehetetlenségi hatás viszonya, mikor lehet eltekinteni a kinematikai igénybevétel figyelembe vételétől. Első közelítésként vizsgálatokat végeztem arra vonatkozóan, hogy miként alakulnak az igénybevételek, ha a felszerkezet súlyát a cölöpfejbe koncentrálva figyelembe vesszük, hogyan befolyásolja ez a cölöp földrengés alatti viselkedését. Ennek során a fejtömb súlyát a zérustól (amivel az előző fejezethez készített számítások is készültek) kezdve 100 kn-onként növeltem a cölöp fejezetben megadott nyomási ellenállásáig (~900 kn). Második körben az előző fejezetben alkalmazott modellt bővítettem egy egyszabadságfokú szerkezettel. A fejtömb középpontjába egy 3 m magas gerenda elemet állítottam, amely tetején lemezelemként helyeztem el a szerkezetet reprezentáló tömeget. A tömegpont magasságát a vizsgálat során nem változtattam, csak az oszlop keresztmetszetét (hajlítási merevségét), illetve a tömeg mértékét. A négyzet keresztmetszetű oszlop oldalhosszát ao = cmre vettem, rugalmassági modulusát a cölöp és fejtömb paraméterével azonosra (Eo = 20 GPa). A felszerkezet súlya kn, de az ao = 30 cm oldalhosszúságú oszloppal végzett vizsgálatokat kiterjesztettem a 100 és 900 kn közötti tartományra 100 kn-onként változtatva a súlyt. Az alkalmazott modell sematikus vázlatát az ábra mutatja. A modellezéshez mindkét esetben az eredetileg ismertetett kétrétegű talajprofilt, d = 60 cm átmérőjű és L = 12 m hosszú cölöpöt használtam. A fejtömbsúly vizsgálata során elemeztem továbbá a gerjesztés jellemzőinek hatását is. Mivel e fejezetben alapvetően az előbbiek szerint kezelt felszerkezet hatásának vizsgálata volt a célom, a többi tényező, mint a talajrétegződés, talajparaméterek, cölöpgeometria a vizsgálatok során állandó maradt. szerkezeti tömeg (lemez) ábra: Geometriai modell oszlop fejtömb (lemez) 120
Geotechnikai szondázások eszközök
 Geotechnikai szondázások eszközök Dr. Horváth Tibor GEOVIL Kft. Canterbury Enginnering Association (UK) 2013. november 26. GEOVIL KFT. GEOVIL Kft. GEOTECHNIKAI IRODA 2000 Szentendre, Pf. 121. www.geovil.hu;
Geotechnikai szondázások eszközök Dr. Horváth Tibor GEOVIL Kft. Canterbury Enginnering Association (UK) 2013. november 26. GEOVIL KFT. GEOVIL Kft. GEOTECHNIKAI IRODA 2000 Szentendre, Pf. 121. www.geovil.hu;
M0 autópálya szélesítése az Anna-hegyi csúszás WOLF ÁKOS
 1 M0 autópálya szélesítése az Anna-hegyi csúszás térségében WOLF ÁKOS 2 HELYSZÍN HELYSZÍN 3 TÖRÖKBÁLINT ANNA-HEGYI PIHENŐ ÉRD DIÓSD ELŐZMÉNY, KORÁBBI CSÚSZÁS 4 1993. október 5. ELŐZMÉNY, KORÁBBI CSÚSZÁS
1 M0 autópálya szélesítése az Anna-hegyi csúszás térségében WOLF ÁKOS 2 HELYSZÍN HELYSZÍN 3 TÖRÖKBÁLINT ANNA-HEGYI PIHENŐ ÉRD DIÓSD ELŐZMÉNY, KORÁBBI CSÚSZÁS 4 1993. október 5. ELŐZMÉNY, KORÁBBI CSÚSZÁS
Cölöpalapozások - bemutató
 12. számú mérnöki kézikönyv Frissítve: 2016. április Cölöpalapozások - bemutató Ennek a mérnöki kézikönyvnek célja, hogy bemutassa a GEO 5 cölöpalapozás számításra használható programjainak gyakorlati
12. számú mérnöki kézikönyv Frissítve: 2016. április Cölöpalapozások - bemutató Ennek a mérnöki kézikönyvnek célja, hogy bemutassa a GEO 5 cölöpalapozás számításra használható programjainak gyakorlati
DETERMINATION OF SHEAR STRENGTH OF SOLID WASTES BASED ON CPT TEST RESULTS
 Műszaki Földtudományi Közlemények, 83. kötet, 1. szám (2012), pp. 271 276. HULLADÉKOK TEHERBÍRÁSÁNAK MEGHATÁROZÁSA CPT-EREDMÉNYEK ALAPJÁN DETERMINATION OF SHEAR STRENGTH OF SOLID WASTES BASED ON CPT TEST
Műszaki Földtudományi Közlemények, 83. kötet, 1. szám (2012), pp. 271 276. HULLADÉKOK TEHERBÍRÁSÁNAK MEGHATÁROZÁSA CPT-EREDMÉNYEK ALAPJÁN DETERMINATION OF SHEAR STRENGTH OF SOLID WASTES BASED ON CPT TEST
Alagútfalazat véges elemes vizsgálata
 Magyar Alagútépítő Egyesület BME Geotechnikai Tanszéke Alagútfalazat véges elemes vizsgálata Czap Zoltán mestertanár BME Geotechnikai Tanszék Programok alagutak méretezéséhez 1 UDEC 2D program, diszkrét
Magyar Alagútépítő Egyesület BME Geotechnikai Tanszéke Alagútfalazat véges elemes vizsgálata Czap Zoltán mestertanár BME Geotechnikai Tanszék Programok alagutak méretezéséhez 1 UDEC 2D program, diszkrét
Mérnökgeológia. 3. előadás. Szepesházi Róbert
 Mérnökgeológia 3. előadás Szepesházi Róbert 1 Geológia irodalomkutatás (desk study) Topográfiai térképek Geológiai térképek Geotechnikai térképek Geológiai, földrajzi leírások Felszínrendezési tervek Meglévő
Mérnökgeológia 3. előadás Szepesházi Róbert 1 Geológia irodalomkutatás (desk study) Topográfiai térképek Geológiai térképek Geotechnikai térképek Geológiai, földrajzi leírások Felszínrendezési tervek Meglévő
TALAJOK OSZTÁLYOZÁSA ÉS MEGNEVEZÉSE AZ EUROCODE
 TALAJOK OSZTÁLYOZÁSA ÉS MEGNEVEZÉSE AZ EUROCODE ALAPJÁN Dr. Móczár Balázs BME Geotechnikai Tanszék Szabványok MSz 14043/2-79 MSZ EN ISO 14688 MSZ 14043-2:2006 ISO 14689 szilárd kőzetek ISO 11259 talajtani
TALAJOK OSZTÁLYOZÁSA ÉS MEGNEVEZÉSE AZ EUROCODE ALAPJÁN Dr. Móczár Balázs BME Geotechnikai Tanszék Szabványok MSz 14043/2-79 MSZ EN ISO 14688 MSZ 14043-2:2006 ISO 14689 szilárd kőzetek ISO 11259 talajtani
Dr. Móczár Balázs 1, Dr. Mahler András 1, Polgár Zsuzsanna 2 1 BME Építőmérnöki Kar, Geotechnikai Tanszék 2 HBM Kft.
 TALAJ ÉS SZERKEZET KÖLCSÖNHATÁSÁNAK ÖSSZEHASONLÍTÓ VIZSGÁLATAI VASBETON LEMEZALAPOZÁSÚ VÁZAS ÉPÜLETEK ESETÉN COMPARITIVE TESTS OF SOIL AND STRUCTURE INTERACTION IN CASE OF FRAMED STRUCTURES WITH RAFT FOUNDATION
TALAJ ÉS SZERKEZET KÖLCSÖNHATÁSÁNAK ÖSSZEHASONLÍTÓ VIZSGÁLATAI VASBETON LEMEZALAPOZÁSÚ VÁZAS ÉPÜLETEK ESETÉN COMPARITIVE TESTS OF SOIL AND STRUCTURE INTERACTION IN CASE OF FRAMED STRUCTURES WITH RAFT FOUNDATION
BME Szilárdságtani és Tartószerkezeti Tanszék. Tartószerkezet-rekonstrukciós Szakmérnöki Képzés. Dr. Móczár Balázs
 Dr. Móczár Balázs 1 Az előadás célja MSZ EN 1997 1 szabvány 6. fejezetében és egyes mellékleteiben leírt síkalapozással kapcsolatos előírások lényegesebb elemeinek, a szabvány elveinek bemutatása Az eddig
Dr. Móczár Balázs 1 Az előadás célja MSZ EN 1997 1 szabvány 6. fejezetében és egyes mellékleteiben leírt síkalapozással kapcsolatos előírások lényegesebb elemeinek, a szabvány elveinek bemutatása Az eddig
TALAJVIZSGÁLATI JELENTÉS /2 FÉLÉV
 ÓVODA-1 TALAJVIZSGÁLATI JELENTÉS 2015-16/2 FÉLÉV 1. ELŐZMÉNYEK, KIINDULÁSI ADATOK A Szerkezetépítési Projekt tantárgy A munkacsoportja megbízta társaságunkat Győr belterületén óvoda tervezéséhez talajvizsgálati
ÓVODA-1 TALAJVIZSGÁLATI JELENTÉS 2015-16/2 FÉLÉV 1. ELŐZMÉNYEK, KIINDULÁSI ADATOK A Szerkezetépítési Projekt tantárgy A munkacsoportja megbízta társaságunkat Győr belterületén óvoda tervezéséhez talajvizsgálati
dr. Szepesházi Róbert Az Eurocode-ok végleges bevezetése elé
 www.sze.hu/~szepesr Geotechnika 2009 áckeve dr. Szepesházi óbert Széchenyi István Egyetem, Gyır Az Eurocode-ok végleges bevezetése elé A geotechnikai tevékenység változása a tervezési folyamatban Geotechnikai
www.sze.hu/~szepesr Geotechnika 2009 áckeve dr. Szepesházi óbert Széchenyi István Egyetem, Gyır Az Eurocode-ok végleges bevezetése elé A geotechnikai tevékenység változása a tervezési folyamatban Geotechnikai
Talajmechanika. Aradi László
 Talajmechanika Aradi László 1 Tartalom Szemcsealak, szemcsenagyság A talajok szemeloszlás-vizsgálata Természetes víztartalom Plasztikus vizsgálatok Konzisztencia határok Plasztikus- és konzisztenciaindex
Talajmechanika Aradi László 1 Tartalom Szemcsealak, szemcsenagyság A talajok szemeloszlás-vizsgálata Természetes víztartalom Plasztikus vizsgálatok Konzisztencia határok Plasztikus- és konzisztenciaindex
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 Épület alapozása síkalappal (1. rajz feladat) Minden építmény az önsúlyát és a rájutó terheléseket az altalajnak adja át, s állékonysága, valamint tartóssága attól függ, hogy sikerült-e az építmény és
Épület alapozása síkalappal (1. rajz feladat) Minden építmény az önsúlyát és a rájutó terheléseket az altalajnak adja át, s állékonysága, valamint tartóssága attól függ, hogy sikerült-e az építmény és
Szilvágyi László: M6 autópálya alagutak geológiai és geotechnikai adottságai
 Szilvágyi László: M6 autópálya alagutak geológiai és geotechnikai adottságai 2/23 M6/M60 autópálya (E73, V/C folyosó) tervezése 1998 2007 3/23 Geresdi dombság o ÉNY - DK-i dombhátak és völgyek o ÉK - DNY-i
Szilvágyi László: M6 autópálya alagutak geológiai és geotechnikai adottságai 2/23 M6/M60 autópálya (E73, V/C folyosó) tervezése 1998 2007 3/23 Geresdi dombság o ÉNY - DK-i dombhátak és völgyek o ÉK - DNY-i
TÖLTÉSALAPOZÁS ESETTANULMÁNY MÁV ÁGFALVA -NAGYKANIZSA
 48 Ágfalva Nagykanizsa vasútvonal, Nemesszentandrás külterülete Több évtizede tartó függőleges és vízszintes mozgások Jelentős károk, folyamatos karbantartási igény 49 Helyszín Zalai dombság É-D-i völgye,
48 Ágfalva Nagykanizsa vasútvonal, Nemesszentandrás külterülete Több évtizede tartó függőleges és vízszintes mozgások Jelentős károk, folyamatos karbantartási igény 49 Helyszín Zalai dombság É-D-i völgye,
A STATIKUS ÉS GEOTECHNIKUS MÉRNÖKÖK EGYMÁSRA UTALTSÁGA EGY SZEGEDI PÉLDÁN KERESZTÜL. Wolf Ákos
 A STATIKUS ÉS GEOTECHNIKUS MÉRNÖKÖK EGYMÁSRA UTALTSÁGA EGY SZEGEDI PÉLDÁN KERESZTÜL Wolf Ákos Bevezetés 2 Miért fontos a geotechnikus és statikus mérnök együttm ködése? Milyen esetben kap nagy hangsúlyt
A STATIKUS ÉS GEOTECHNIKUS MÉRNÖKÖK EGYMÁSRA UTALTSÁGA EGY SZEGEDI PÉLDÁN KERESZTÜL Wolf Ákos Bevezetés 2 Miért fontos a geotechnikus és statikus mérnök együttm ködése? Milyen esetben kap nagy hangsúlyt
A geotechnikai tervezés alapjai az Eurocode 7 szerint
 A geotechnikai tervezés alapjai az Eurocode 7 szerint Tartószerkezeti Eurocode-ok EN 1990 EC-0 A tartószerkezeti tervezés alapjai EN 1991 EC-1: A tartószerkezeteket érő hatások EN 1992 EC-2: Betonszerkezetek
A geotechnikai tervezés alapjai az Eurocode 7 szerint Tartószerkezeti Eurocode-ok EN 1990 EC-0 A tartószerkezeti tervezés alapjai EN 1991 EC-1: A tartószerkezeteket érő hatások EN 1992 EC-2: Betonszerkezetek
Cölöpcsoport elmozdulásai és méretezése
 18. számú mérnöki kézikönyv Frissítve: 2016. április Cölöpcsoport elmozdulásai és méretezése Program: Fájl: Cölöpcsoport Demo_manual_18.gsp A fejezet célja egy cölöpcsoport fejtömbjének elfordulásának,
18. számú mérnöki kézikönyv Frissítve: 2016. április Cölöpcsoport elmozdulásai és méretezése Program: Fájl: Cölöpcsoport Demo_manual_18.gsp A fejezet célja egy cölöpcsoport fejtömbjének elfordulásának,
TÁJÉKOZTATÓ. az MSZ EN 1998-5 (EC8-5) szerinti földrengésre történő alapozás tervezéshez. Összeállította: Dr. Dulácska Endre
 Magyar Mérnöki Kamara Tartószerkezeti Tagozat TÁJÉKOZTATÓ az MSZ EN 1998-5 (EC8-5) szerinti földrengésre történő alapozás tervezéshez Összeállította: Dr. Dulácska Endre A tájékoztatót a MMK-TT következő
Magyar Mérnöki Kamara Tartószerkezeti Tagozat TÁJÉKOZTATÓ az MSZ EN 1998-5 (EC8-5) szerinti földrengésre történő alapozás tervezéshez Összeállította: Dr. Dulácska Endre A tájékoztatót a MMK-TT következő
Munkatérhatárolás szerkezetei. programmal. Munkagödör méretezés Geo 5
 MUNKAGÖDÖR TERVEZÉSE Munkagödör tervezése 2 Munkatérhatárolás szerkezetei Munkagödör méretezés Plaxis programmal Munkagödör méretezés Geo 5 Munkagödör méretezés Geo 5 programmal Tartalom 3 Alapadatok Geometria
MUNKAGÖDÖR TERVEZÉSE Munkagödör tervezése 2 Munkatérhatárolás szerkezetei Munkagödör méretezés Plaxis programmal Munkagödör méretezés Geo 5 Munkagödör méretezés Geo 5 programmal Tartalom 3 Alapadatok Geometria
Rugalmasan ágyazott gerenda. Szép János
 Rugalmasan ágyazott gerenda vizsgálata AXIS VM programmal Szép János 2013.10.14. LEMEZALAP TERVEZÉS 1. Bevezetés 2. Lemezalap tervezés 3. AXIS Program ismertetés 4. Példa LEMEZALAPOZÁS Alkalmazás módjai
Rugalmasan ágyazott gerenda vizsgálata AXIS VM programmal Szép János 2013.10.14. LEMEZALAP TERVEZÉS 1. Bevezetés 2. Lemezalap tervezés 3. AXIS Program ismertetés 4. Példa LEMEZALAPOZÁS Alkalmazás módjai
Ebben a mérnöki kézikönyvben azt mutatjuk be, hogyan számoljuk egy síkalap süllyedését és elfordulását.
 10. számú mérnöki kézikönyv Frissítve: 2016. Február Síkalap süllyedése Program: Fájl: Síkalap Demo_manual_10.gpa Ebben a mérnöki kézikönyvben azt mutatjuk be, hogyan számoljuk egy síkalap süllyedését
10. számú mérnöki kézikönyv Frissítve: 2016. Február Síkalap süllyedése Program: Fájl: Síkalap Demo_manual_10.gpa Ebben a mérnöki kézikönyvben azt mutatjuk be, hogyan számoljuk egy síkalap süllyedését
Földtani alapismeretek
 Földtani alapismeretek A Földkérget alakító hatások és eredményük A Föld felépítése és alakító hatásai A Föld folyamatai Atmoszféra Belső geoszférák A kéreg felépítése és folyamatai A mállás típusai a
Földtani alapismeretek A Földkérget alakító hatások és eredményük A Föld felépítése és alakító hatásai A Föld folyamatai Atmoszféra Belső geoszférák A kéreg felépítése és folyamatai A mállás típusai a
Cölöp függőleges teherbírásának és süllyedésének CPT alapú számítása
 15. számú mérnöki kézikönyv Frissítve: 2017. március Cölöp függőleges teherbírásának és süllyedésének CPT alapú számítása Program: Cölöp CPT Fájl: Demo_manual_15.gpn Ennek a mérnöki kézikönyvnek célja,
15. számú mérnöki kézikönyv Frissítve: 2017. március Cölöp függőleges teherbírásának és süllyedésének CPT alapú számítása Program: Cölöp CPT Fájl: Demo_manual_15.gpn Ennek a mérnöki kézikönyvnek célja,
Jellemző szelvények alagút
 Alagútépítés Jellemző szelvények alagút 50 50 Jellemző szelvény - alagút 51 AalagútDél Nyugati járat Keleti járat 51 Alagúttervezés - geotechnika 52 Technológia - Új osztrák építési módszer (NÖT) 1356
Alagútépítés Jellemző szelvények alagút 50 50 Jellemző szelvény - alagút 51 AalagútDél Nyugati járat Keleti járat 51 Alagúttervezés - geotechnika 52 Technológia - Új osztrák építési módszer (NÖT) 1356
SÍKALAPOK TERVEZÉSE. BME Szilárdságtani és Tartószerkezeti Tanszék. Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 SÍKALAPOK TERVEZÉSE SÍKALAPOK TERVEZÉSE síkalap mélyalap mélyített síkalap Síkalap, ha: - megfelelő teherbírású és vastagságú talajréteg van a felszín közelében; - a térszín közeli talajréteg teherbírása
SÍKALAPOK TERVEZÉSE SÍKALAPOK TERVEZÉSE síkalap mélyalap mélyített síkalap Síkalap, ha: - megfelelő teherbírású és vastagságú talajréteg van a felszín közelében; - a térszín közeli talajréteg teherbírása
BME Szilárdságtani és Tartószerkezeti Tanszék. Tartószerkezet-rekonstrukciós Szakmérnöki Képzés. Dr. Móczár Balázs
 Dr. Móczár Balázs 1 Az előadás célja MSZ EN 1997 1 szabvány 6. fejezetében és egyes mellékleteiben leírt síkalapozással kapcsolatos előírások lényegesebb elemeinek, a szabvány elveinek bemutatása Az eddig
Dr. Móczár Balázs 1 Az előadás célja MSZ EN 1997 1 szabvány 6. fejezetében és egyes mellékleteiben leírt síkalapozással kapcsolatos előírások lényegesebb elemeinek, a szabvány elveinek bemutatása Az eddig
CSARNOK-4 TALAJVIZSGÁLATI JELENTÉS
 CSARNOK-4 TALAJVIZSGÁLATI JELENTÉS 1. ELŐZMÉNYEK, KIINDULÁSI ADATOK A Szerkezetépítési Projekt tatnárgy C munkacsoportja megbízta társaságunkat Szigetszentmiklós település területén létesítendő csarnok
CSARNOK-4 TALAJVIZSGÁLATI JELENTÉS 1. ELŐZMÉNYEK, KIINDULÁSI ADATOK A Szerkezetépítési Projekt tatnárgy C munkacsoportja megbízta társaságunkat Szigetszentmiklós település területén létesítendő csarnok
5. Talajdinamika. -talajparaméterek -helyettesítő lineáris modell -laboratóriumi mérések -helyszíni mérések
 82 5. Talajdinamika -talajparaméterek -helyettesítő lineáris modell -laboratóriumi mérések -helyszíni mérések Talajdinamika 83 Talaj és szerkezet kölcsönhatása Eurocode 8-5 3.2. (1) A szeizmikus hatás
82 5. Talajdinamika -talajparaméterek -helyettesítő lineáris modell -laboratóriumi mérések -helyszíni mérések Talajdinamika 83 Talaj és szerkezet kölcsönhatása Eurocode 8-5 3.2. (1) A szeizmikus hatás
TALAJVIZSGÁLATI JELENTÉS ÉS TANÁCSADÁS. Kunfehértó, Rákóczi u. 13. sz.-ú telken épülő piactér tervezéséhez 2017.
 TALAJVIZSGÁLATI JELENTÉS ÉS TANÁCSADÁS Kunfehértó, Rákóczi u. 13. sz.-ú telken épülő piactér tervezéséhez 2017. 1 I. Tervezési, kiindulási adatok A talajvizsgálati jelentés a Fehértó Non-profit Kft. megbízásából
TALAJVIZSGÁLATI JELENTÉS ÉS TANÁCSADÁS Kunfehértó, Rákóczi u. 13. sz.-ú telken épülő piactér tervezéséhez 2017. 1 I. Tervezési, kiindulási adatok A talajvizsgálati jelentés a Fehértó Non-profit Kft. megbízásából
GEOTECHNIKA I. LGB-SE TALAJOK SZILÁRDSÁGI JELLEMZŐI
 GEOTECHNIKA I. LGB-SE005-01 TALAJOK SZILÁRDSÁGI JELLEMZŐI Wolf Ákos Mechanikai állapotjellemzők és egyenletek 2 X A X 3 normál- és 3 nyírófeszültség a hasáb oldalain Y A x y z xy yz zx Z A Y Z ZX YZ A
GEOTECHNIKA I. LGB-SE005-01 TALAJOK SZILÁRDSÁGI JELLEMZŐI Wolf Ákos Mechanikai állapotjellemzők és egyenletek 2 X A X 3 normál- és 3 nyírófeszültség a hasáb oldalain Y A x y z xy yz zx Z A Y Z ZX YZ A
FÉLMEREV KAPCSOLATOK NUMERIKUS SZIMULÁCIÓJA
 FÉLMEREV KAPCSOLATOK NUMERIKUS SZIMULÁCIÓJA Vértes Katalin * - Iványi Miklós ** RÖVID KIVONAT Acélszerkezeti kapcsolatok jellemzőinek (szilárdság, merevség, elfordulási képesség) meghatározása lehetséges
FÉLMEREV KAPCSOLATOK NUMERIKUS SZIMULÁCIÓJA Vértes Katalin * - Iványi Miklós ** RÖVID KIVONAT Acélszerkezeti kapcsolatok jellemzőinek (szilárdság, merevség, elfordulási képesség) meghatározása lehetséges
Földstatikai feladatok megoldási módszerei
 Földstatikai feladatok megoldási módszerei Földstatikai alapfeladatok Földnyomások számítása Általános állékonyság vizsgálata Alaptörés parciális terhelés alatt Süllyedésszámítások Komplex terhelési esetek
Földstatikai feladatok megoldási módszerei Földstatikai alapfeladatok Földnyomások számítása Általános állékonyság vizsgálata Alaptörés parciális terhelés alatt Süllyedésszámítások Komplex terhelési esetek
A végeselem módszer alapjai. 2. Alapvető elemtípusok
 A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
A végeselem módszer alapjai Előadás jegyzet Dr. Goda Tibor 2. Alapvető elemtípusok - A 3D-s szerkezeteket vagy szerkezeti elemeket gyakran egyszerűsített formában modellezzük rúd, gerenda, 2D-s elemek,
Geometriai adatok. réteghatárok magassági helyzete földkiemelési szintek geotechnikai szerkezet méretei
 24. terepmagasság térszín hajlása vízszintek Geometriai adatok réteghatárok magassági helyzete földkiemelési szintek geotechnikai szerkezet méretei a d =a nom + a a: az egyes konkrét szerkezetekre vonatkozó
24. terepmagasság térszín hajlása vízszintek Geometriai adatok réteghatárok magassági helyzete földkiemelési szintek geotechnikai szerkezet méretei a d =a nom + a a: az egyes konkrét szerkezetekre vonatkozó
MUNKAGÖDÖR TERVEZÉSE
 MUNKAGÖDÖR TERVEZÉSE Munkagödör tervezése Bevezetés Munkagödör méretezése Plaxis programmal Munkagödör méretezése Geo 5 programmal MUNKAGÖDÖR TERVEZÉSE Bevezetés Wolf Ákos BEVEZETÉS Napjaink mélyépítési
MUNKAGÖDÖR TERVEZÉSE Munkagödör tervezése Bevezetés Munkagödör méretezése Plaxis programmal Munkagödör méretezése Geo 5 programmal MUNKAGÖDÖR TERVEZÉSE Bevezetés Wolf Ákos BEVEZETÉS Napjaink mélyépítési
Különleges alapozások Építészet, MSC. Dr. Vásárhelyi Balázs vasarhelyib@gmail.com
 Különleges alapozások Építészet, MSC Dr. Vásárhelyi Balázs vasarhelyib@gmail.com A geotechnikai elıkészítı tevékenység tartalma, rendje Mélyépítés esetén irodalmazás Térképek leírások Szóbeli közlések
Különleges alapozások Építészet, MSC Dr. Vásárhelyi Balázs vasarhelyib@gmail.com A geotechnikai elıkészítı tevékenység tartalma, rendje Mélyépítés esetén irodalmazás Térképek leírások Szóbeli közlések
Töltésalapozások tervezése II.
 Töltésalapozások tervezése II. Talajmechanikai problémák 2 alaptörés állékonyságvesztés vastag gyenge altalaj deformációk, elmozdulások nagymértékű, egyenlőtlen, időben elhúzódó süllyedés szétcsúszás vastag
Töltésalapozások tervezése II. Talajmechanikai problémák 2 alaptörés állékonyságvesztés vastag gyenge altalaj deformációk, elmozdulások nagymértékű, egyenlőtlen, időben elhúzódó süllyedés szétcsúszás vastag
EC7 ALKALMAZÁSA A GYAKORLATBAN DR. MÓCZÁR BALÁZS
 EC7 ALKALMAZÁSA A GYAKORLATBAN DR. MÓCZÁR BALÁZS Építész szakmérnöki 2016. Bevezetés 2 k é z s s é n a épz T i ik t e z k e ö k n r r új dokumentum típusok e é z s m ó ak t új szemlélet r a z S T s s é
EC7 ALKALMAZÁSA A GYAKORLATBAN DR. MÓCZÁR BALÁZS Építész szakmérnöki 2016. Bevezetés 2 k é z s s é n a épz T i ik t e z k e ö k n r r új dokumentum típusok e é z s m ó ak t új szemlélet r a z S T s s é
MÉLYVIBRÁCIÓS TÖMÖRÍTÉS- A TALAJJAVÍTÁS ELLENŐRZÉSE SZEIZMIKUS CPT SZONDÁVAL
 MÉLYVIBRÁCIÓS TÖMÖRÍTÉS- A TALAJJAVÍTÁS ELLENŐRZÉSE SZEIZMIKUS CPT SZONDÁVAL Nagy Péter 1, Dietmar Adam 1, Scheuring Ferenc 2 1 Institut für Geotechnik, Technische Universität Wien 2 Fugro Consult Kft
MÉLYVIBRÁCIÓS TÖMÖRÍTÉS- A TALAJJAVÍTÁS ELLENŐRZÉSE SZEIZMIKUS CPT SZONDÁVAL Nagy Péter 1, Dietmar Adam 1, Scheuring Ferenc 2 1 Institut für Geotechnik, Technische Universität Wien 2 Fugro Consult Kft
Ejtési teszt modellezése a tervezés fázisában
 Antal Dániel, doktorandusz, Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szabó Tamás, egyetemi docens, Ph.D., Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szilágyi Attila, egyetemi adjunktus,
Antal Dániel, doktorandusz, Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szabó Tamás, egyetemi docens, Ph.D., Miskolci Egyetem Robert Bosch Mechatronikai Tanszék Szilágyi Attila, egyetemi adjunktus,
Elérhetőségek. Dr. Varga Gabriella K.mf.20. varga_gabriella@hotmail.com gvarga@mail.bme.hu. Tanszéki honlap: www.gtt.bme.hu
 1. Elérhetőségek Dr. Varga Gabriella K.mf.20. varga_gabriella@hotmail.com gvarga@mail.bme.hu Tanszéki honlap: www.gtt.bme.hu 2. Hallgatói feladatok Zárthelyi dolgozat: 30% 1. HF: 40 % (határidő: 8. hét,
1. Elérhetőségek Dr. Varga Gabriella K.mf.20. varga_gabriella@hotmail.com gvarga@mail.bme.hu Tanszéki honlap: www.gtt.bme.hu 2. Hallgatói feladatok Zárthelyi dolgozat: 30% 1. HF: 40 % (határidő: 8. hét,
TERVEZÉS FÖLDRENGÉSRE LGM_SE_013_1
 TERVEZÉS FÖLDRENGÉSRE LGM_SE_013_1 se.sze.hu Szilvágyi Zsolt szilvagyi@sze.hu 2 www.eeri.org TÉMAKÖRÖK 3 1. FÖLDRENGÉSEK HATÁSAI 2. FÖLDRENGÉSI HULLÁMOK 3. FÖLDRENGÉSEK JELLEMZŐI 4. DINAMIKAI ALAPOK 5.
TERVEZÉS FÖLDRENGÉSRE LGM_SE_013_1 se.sze.hu Szilvágyi Zsolt szilvagyi@sze.hu 2 www.eeri.org TÉMAKÖRÖK 3 1. FÖLDRENGÉSEK HATÁSAI 2. FÖLDRENGÉSI HULLÁMOK 3. FÖLDRENGÉSEK JELLEMZŐI 4. DINAMIKAI ALAPOK 5.
Tervezés alatt az M6 autópálya déli szakasza
 Tervezés alatt az M6 autópálya déli szakasza Sánta László Schell Péter Geotechnikai 2004 Ráckeve október 26. Gyorsforgalmi úthálózat fejlesztési program Katowice Balti Helsinki V/C. jelű folyosó része
Tervezés alatt az M6 autópálya déli szakasza Sánta László Schell Péter Geotechnikai 2004 Ráckeve október 26. Gyorsforgalmi úthálózat fejlesztési program Katowice Balti Helsinki V/C. jelű folyosó része
Wolf Ákos. Királyegyháza, cementgyár - esettanulmány
 Wolf Ákos Királyegyháza, cementgyár - esettanulmány Királyegyháza, cementgyár - esettanulmányok Tartalom Bevezetés Projekt ismertetés, helyszín bemutatása bb m tárgyak, létesítmények Talajadottságok bemutatása
Wolf Ákos Királyegyháza, cementgyár - esettanulmány Királyegyháza, cementgyár - esettanulmányok Tartalom Bevezetés Projekt ismertetés, helyszín bemutatása bb m tárgyak, létesítmények Talajadottságok bemutatása
Mikrocölöp alapozás ellenőrzése
 36. számú mérnöki kézikönyv Frissítve: 2017. június Mikrocölöp alapozás ellenőrzése Program: Fájl: Cölöpcsoport Demo_manual_en_36.gsp Ennek a mérnöki kézikönyvnek a célja, egy mikrocölöp alapozás ellenőrzésének
36. számú mérnöki kézikönyv Frissítve: 2017. június Mikrocölöp alapozás ellenőrzése Program: Fájl: Cölöpcsoport Demo_manual_en_36.gsp Ennek a mérnöki kézikönyvnek a célja, egy mikrocölöp alapozás ellenőrzésének
Mérési metodika és a műszer bemutatása
 Mérési metodika és a műszer bemutatása CPT kábelnélküli rendszer felépítése A Cone Penetration Test (kúpbehatolási vizsgálat), röviden CPT, egy olyan talajvizsgálati módszer, amely segítségével pontos
Mérési metodika és a műszer bemutatása CPT kábelnélküli rendszer felépítése A Cone Penetration Test (kúpbehatolási vizsgálat), röviden CPT, egy olyan talajvizsgálati módszer, amely segítségével pontos
SZEMMEL méretezm. ldrengésre. Előadó: Tornai László tartószerkezeti vezető tervező KÉSZ Építő Zrt. 2011. december 16. 1
 A FÖLDRENGF LDRENGÉSRŐL L MÉRNM RNÖK SZEMMEL 3. rész: r méretezm retezés s földrengf ldrengésre Előadó: Tornai László tartószerkezeti vezető tervező KÉSZ Építő Zrt. 2011. december 16. 1 A FÖLDRENGF LDRENGÉS-MÉRETEZÉS
A FÖLDRENGF LDRENGÉSRŐL L MÉRNM RNÖK SZEMMEL 3. rész: r méretezm retezés s földrengf ldrengésre Előadó: Tornai László tartószerkezeti vezető tervező KÉSZ Építő Zrt. 2011. december 16. 1 A FÖLDRENGF LDRENGÉS-MÉRETEZÉS
Autópályahidak mélyalapozásának fejlődése Varsányi Tamás főmérnök. Visegrád, június 11.
 Autópályahidak mélyalapozásának fejlődése Varsányi Tamás főmérnök Az előadás tartalma Magyarország autópálya hálózata Cölöpözési technológiák az autópálya hidak alapozásának kivitelezésében: Franki cölöp
Autópályahidak mélyalapozásának fejlődése Varsányi Tamás főmérnök Az előadás tartalma Magyarország autópálya hálózata Cölöpözési technológiák az autópálya hidak alapozásának kivitelezésében: Franki cölöp
Turai Péter 1 Dr. Nagy László 2 Dr. Takács Attila 3
 ZAGYTÁROZÓGÁT ALATTI PÓRUSVÍZNYOMÁS VÉGESELEMES MODELLEZÉSE NUMERICAL MODELING FOR PORE PRESSURE PREDICTION UNDER TAILINGS DAM Turai Péter 1 Dr. Nagy László 2 Dr. Takács Attila 3 1 MSc. hallgató, BME,
ZAGYTÁROZÓGÁT ALATTI PÓRUSVÍZNYOMÁS VÉGESELEMES MODELLEZÉSE NUMERICAL MODELING FOR PORE PRESSURE PREDICTION UNDER TAILINGS DAM Turai Péter 1 Dr. Nagy László 2 Dr. Takács Attila 3 1 MSc. hallgató, BME,
TALAJVIZSGÁLATI JELENTÉS /2 FÉLÉV
 LOGISZTIKAI CSARNOK TALAJVIZSGÁLATI JELENTÉS 2013-14/2 FÉLÉV 1. ELŐZMÉNYEK, KIINDULÁSI ADATOK A Szerkezetépítési Projekt tatnárgy A munkacsoportja megbízta társaságunkat Páli település külterületén létesítendő
LOGISZTIKAI CSARNOK TALAJVIZSGÁLATI JELENTÉS 2013-14/2 FÉLÉV 1. ELŐZMÉNYEK, KIINDULÁSI ADATOK A Szerkezetépítési Projekt tatnárgy A munkacsoportja megbízta társaságunkat Páli település külterületén létesítendő
se és alkalmazása Alun Thomas RHK Kft. SDMTS
 Plate loading módszer m ismertetése se és alkalmazása Alun Thomas SDMTS RHK Kft. Témák Bevezetés San Diego Hindhead Bátaapáti Következtetések Milyen egy helyszíni mérés? Bármilyen vizsgálat, amit valós
Plate loading módszer m ismertetése se és alkalmazása Alun Thomas SDMTS RHK Kft. Témák Bevezetés San Diego Hindhead Bátaapáti Következtetések Milyen egy helyszíni mérés? Bármilyen vizsgálat, amit valós
Szilvágyi Zsolt. Dunai homokok dinamikus talajparaméterei
 PhD Tézisfüzet Konzulens: Dr. Richard P. Ray PhD egyetemi tanár Szerkezetépítési és Geotechnikai Tanszék Építész-, Építő- és Közlekedésmérnöki Kar Széchenyi István Egyetem Infrastrukturális Rendszerek
PhD Tézisfüzet Konzulens: Dr. Richard P. Ray PhD egyetemi tanár Szerkezetépítési és Geotechnikai Tanszék Építész-, Építő- és Közlekedésmérnöki Kar Széchenyi István Egyetem Infrastrukturális Rendszerek
TALAJVIZSGÁLATI JELENTÉS TALAJMECHANIKAI SZAKVÉLEMÉNY SZÚRÓPONT
 TALAJVIZSGÁLATI JELENTÉS TALAJMECHANIKAI SZAKVÉLEMÉNY Besenyszög, Jászladányi út 503/3 hrsz. SZÚRÓPONT tervezéséhez Nagykörű 2013 december 07. Horváth Ferenc okl. építőmérnök okl. geotechnikai szakmérnök
TALAJVIZSGÁLATI JELENTÉS TALAJMECHANIKAI SZAKVÉLEMÉNY Besenyszög, Jászladányi út 503/3 hrsz. SZÚRÓPONT tervezéséhez Nagykörű 2013 december 07. Horváth Ferenc okl. építőmérnök okl. geotechnikai szakmérnök
TÚLKONSZOLIDÁLTSÁG HATÁSA A GEOTECHNIKAI EREDMÉNYEKRE EFFECT OF OVERCONSOLIDATION ON THE GEOTECHNICAL RESULTS
 TÚLKONSZOLIDÁLTSÁG HATÁSA A GEOTECHNIKAI EREDMÉNYEKRE ÖSSZEFOGLALÁS EFFECT OF OVERCONSOLIDATION ON THE GEOTECHNICAL RESULTS Józsa Vendel BME Geotechnikai Tanszék, PhD hallgató Hazánkban egyre nagyobb szükség
TÚLKONSZOLIDÁLTSÁG HATÁSA A GEOTECHNIKAI EREDMÉNYEKRE ÖSSZEFOGLALÁS EFFECT OF OVERCONSOLIDATION ON THE GEOTECHNICAL RESULTS Józsa Vendel BME Geotechnikai Tanszék, PhD hallgató Hazánkban egyre nagyobb szükség
A talajok összenyomódásának vizsgálata
 A talajok összenyomódásának vizsgálata Amit már tudni kellene Összenyomódás Konszolidáció Normálisan konszolidált talaj Túlkonszolidált talaj Túlkonszolidáltsági arányszám,ocr Konszolidáció az az időben
A talajok összenyomódásának vizsgálata Amit már tudni kellene Összenyomódás Konszolidáció Normálisan konszolidált talaj Túlkonszolidált talaj Túlkonszolidáltsági arányszám,ocr Konszolidáció az az időben
RIGID INCLUSION ALAPOZÁSI RENDSZERREL KÉSZÜLT SILÓ 3D NUMERIKUS VIZSGÁLATA. Geotechnika és Mérnökgeológia Tanszék
 RIGID INCLUSION ALAPOZÁSI RENDSZERREL KÉSZÜLT SILÓ 3D NUMERIKUS VIZSGÁLATA Lődör Kristóf 1, Dr. Móczár Balázs 2, Dr. Mahler András 3 1,2,3 Budapesti Műszaki és Gazdaságtudományi Egyetem, Geotechnika és
RIGID INCLUSION ALAPOZÁSI RENDSZERREL KÉSZÜLT SILÓ 3D NUMERIKUS VIZSGÁLATA Lődör Kristóf 1, Dr. Móczár Balázs 2, Dr. Mahler András 3 1,2,3 Budapesti Műszaki és Gazdaságtudományi Egyetem, Geotechnika és
SOIL MECHANICS BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GEOTECHNIKAI TANSZÉK KONSZOLIDÁCIÓ
 2008 PJ-MA SOIL MECHANICS BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GEOTECHNIKAI TANSZÉK KONSZOLIDÁCIÓ Tanszék: K épület, mfsz. 10. & mfsz. 20. Geotechnikai laboratórium: K épület, alagsor 20. BME
2008 PJ-MA SOIL MECHANICS BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GEOTECHNIKAI TANSZÉK KONSZOLIDÁCIÓ Tanszék: K épület, mfsz. 10. & mfsz. 20. Geotechnikai laboratórium: K épület, alagsor 20. BME
SZERKEZETI MŰSZAKI LEÍRÁS + STATIKAI SZÁMÍTÁS
 454 Iváncsa, Arany János utca Hrsz: 16/8 Iváncsa Faluház felújítás 454 Iváncsa, Arany János utca Hrsz.: 16/8 Építtető: Iváncsa Község Önkormányzata Iváncsa, Fő utca 61/b. Fedélszék ellenőrző számítása
454 Iváncsa, Arany János utca Hrsz: 16/8 Iváncsa Faluház felújítás 454 Iváncsa, Arany János utca Hrsz.: 16/8 Építtető: Iváncsa Község Önkormányzata Iváncsa, Fő utca 61/b. Fedélszék ellenőrző számítása
Szép János. Hídszerkezetek modellezése a talaj és a szerkezet kölcsönhatásának figyelembevételével
 Szép János Hídszerkezetek modellezése a talaj és a szerkezet kölcsönhatásának figyelembevételével doktori tézisek Témavezető Dr. Scharle Péter CSc Széchenyi István Egyetem MTK Szerkezetépítési és Geotechnikai
Szép János Hídszerkezetek modellezése a talaj és a szerkezet kölcsönhatásának figyelembevételével doktori tézisek Témavezető Dr. Scharle Péter CSc Széchenyi István Egyetem MTK Szerkezetépítési és Geotechnikai
Gyakorlat 04 Keresztmetszetek III.
 Gyakorlat 04 Keresztmetszetek III. 1. Feladat Hajlítás és nyírás Végezzük el az alábbi gerenda keresztmetszeti vizsgálatait (tiszta esetek és lehetséges kölcsönhatások) kétféle anyaggal: S235; S355! (1)
Gyakorlat 04 Keresztmetszetek III. 1. Feladat Hajlítás és nyírás Végezzük el az alábbi gerenda keresztmetszeti vizsgálatait (tiszta esetek és lehetséges kölcsönhatások) kétféle anyaggal: S235; S355! (1)
6. Eurocode 8. általános szabályok meglévő épületek geotechnikai vonatkozások
 144 6. Eurocode 8 általános szabályok meglévő épületek geotechnikai vonatkozások Eurocode 8 145 1998 1 Általános szabályok, épületek 1998 2 Hidak 1998 3 Épületek értékelése és helyreállítása 1998 4 Tárolók,
144 6. Eurocode 8 általános szabályok meglévő épületek geotechnikai vonatkozások Eurocode 8 145 1998 1 Általános szabályok, épületek 1998 2 Hidak 1998 3 Épületek értékelése és helyreállítása 1998 4 Tárolók,
FŐMTERV ENVECON Konzorcium. Intermodális közösségi közlekedési csomópont kialakítása Győrött. Melléklet Geotechnikai szakvélemény
 FŐMTERV ENVECON Konzorcium Tsz: 12.12.125 Intermodális közösségi közlekedési csomópont kialakítása Győrött (KÖZOP-5.5.0-09-11-2011-0005) Melléklet Geotechnikai szakvélemény Megbízó: Győr Megyei Jogú Város
FŐMTERV ENVECON Konzorcium Tsz: 12.12.125 Intermodális közösségi közlekedési csomópont kialakítása Győrött (KÖZOP-5.5.0-09-11-2011-0005) Melléklet Geotechnikai szakvélemény Megbízó: Győr Megyei Jogú Város
Mechanikai vizsgáltok
 Mechanikai vizsgáltok Modellező vizsgáltok Egyszerű modellek Szűk érvényességi tartomány A vizsgálati feltételek megadása különösen fontos Általános érvényű vizsgálati eredmények A vizsgálati program célja
Mechanikai vizsgáltok Modellező vizsgáltok Egyszerű modellek Szűk érvényességi tartomány A vizsgálati feltételek megadása különösen fontos Általános érvényű vizsgálati eredmények A vizsgálati program célja
Szepesházi Róbert. Széchenyi István Egyetem, Gyır. Hídépítési esettanulmányok
 Szepesházi Róbert Széchenyi István Egyetem, Gyır Hídépítési esettanulmányok Tervek a múltból Hídalapozás síkalapozás? Típusalépítmény 2000-2010 2010 Hídalapozás = cölöpalapozás? A negatív köpenysúrlódás
Szepesházi Róbert Széchenyi István Egyetem, Gyır Hídépítési esettanulmányok Tervek a múltból Hídalapozás síkalapozás? Típusalépítmény 2000-2010 2010 Hídalapozás = cölöpalapozás? A negatív köpenysúrlódás
STATIKAI SZÁMÍTÁS (KIVONAT) A TOP Társadalmi és környezeti szempontból fenntartható turizmusfejlesztés című pályázat keretében a
 Kardos László okl. építőmérnök 4431 Nyíregyháza, Szivárvány u. 26. Tel: 20 340 8717 STATIKAI SZÁMÍTÁS (KIVONAT) A TOP-6.1.4.-15 Társadalmi és környezeti szempontból fenntartható turizmusfejlesztés című
Kardos László okl. építőmérnök 4431 Nyíregyháza, Szivárvány u. 26. Tel: 20 340 8717 STATIKAI SZÁMÍTÁS (KIVONAT) A TOP-6.1.4.-15 Társadalmi és környezeti szempontból fenntartható turizmusfejlesztés című
A.2. Acélszerkezetek határállapotai
 A.. Acélszerkezetek határállapotai A... A teherbírási határállapotok első osztálya: a szilárdsági határállapotok A szilárdsági határállapotok (melyek között a fáradt és rideg törést e helyütt nem tárgyaljuk)
A.. Acélszerkezetek határállapotai A... A teherbírási határállapotok első osztálya: a szilárdsági határállapotok A szilárdsági határállapotok (melyek között a fáradt és rideg törést e helyütt nem tárgyaljuk)
Dr. Móczár Balázs. BME Szilárdságtani és Tartószerkezeti Tanszék. Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 Dr. Móczár Balázs 1 A z e l ő a d á s c é l j a MSZ EN 1997-1 szabvány 6. fejezetében és egyes mellékleteiben leírt síkalapozással kapcsolatos előírások lényegesebb elemeinek, a szabvány elveinek bemutatása
Dr. Móczár Balázs 1 A z e l ő a d á s c é l j a MSZ EN 1997-1 szabvány 6. fejezetében és egyes mellékleteiben leírt síkalapozással kapcsolatos előírások lényegesebb elemeinek, a szabvány elveinek bemutatása
Egyedi cölöp függőleges teherbírásának számítása
 13. számú mérnöki kézikönyv Frissítve: 2013. árilis Egyedi cölö függőleges teherbírásának számítása Program: Fájl: Cölö Demo_manual_13.gi Ennek a mérnöki kézikönyvnek a célja, egy egyedi cölö függőleges
13. számú mérnöki kézikönyv Frissítve: 2013. árilis Egyedi cölö függőleges teherbírásának számítása Program: Fájl: Cölö Demo_manual_13.gi Ennek a mérnöki kézikönyvnek a célja, egy egyedi cölö függőleges
Talajok osztályozása az új szabványok szerint
 Talaj- és kőzetosztályozás Talajok osztályozása az új szabványok szerint :5 Geotechnikai vizsgálatok. 1. rész: Azonosítás és leírás. MSZ EN ISO 14688-2:5 Geotechnikai vizsgálatok. 2. rész: Osztályozási
Talaj- és kőzetosztályozás Talajok osztályozása az új szabványok szerint :5 Geotechnikai vizsgálatok. 1. rész: Azonosítás és leírás. MSZ EN ISO 14688-2:5 Geotechnikai vizsgálatok. 2. rész: Osztályozási
Mérnöki faszerkezetek korszerű statikai méretezése
 Mérnöki faszerkezetek korszerű statikai méretezése okl. faip. mérnök - szerkezettervező Előadásvázlat Bevezetés, a statikai tervezés alapjai, eszközei Az EuroCode szabványok rendszere Bemutató számítás
Mérnöki faszerkezetek korszerű statikai méretezése okl. faip. mérnök - szerkezettervező Előadásvázlat Bevezetés, a statikai tervezés alapjai, eszközei Az EuroCode szabványok rendszere Bemutató számítás
Földrengésvédelem Példák 1.
 Rezgésidő meghatározása, válaszspektrum-módszer Budapesti Műszaki és Gazdaságtudományi Egyetem Szilárdságtani és Tartószerkezeti Tanszék 017. március 16. A példák kidolgozásához felhasznált irodalom: [1]
Rezgésidő meghatározása, válaszspektrum-módszer Budapesti Műszaki és Gazdaságtudományi Egyetem Szilárdságtani és Tartószerkezeti Tanszék 017. március 16. A példák kidolgozásához felhasznált irodalom: [1]
Acélszerkezetek korszerű tűzvédelmének néhány kérdése
 Acélszerkezetek korszerű tűzvédelmének néhány kérdése A viselkedés-alapú tervezés elemei Dr. Horváth László PhD, egyetemi docens 1 Tartalom Viselkedés-alapú tervezés fogalma Alkalmazási lehetőségei Acélszerkezetek
Acélszerkezetek korszerű tűzvédelmének néhány kérdése A viselkedés-alapú tervezés elemei Dr. Horváth László PhD, egyetemi docens 1 Tartalom Viselkedés-alapú tervezés fogalma Alkalmazási lehetőségei Acélszerkezetek
FELSZÍN ALATTI VIZEK RADONTARTALMÁNAK VIZSGÁLATA ISASZEG TERÜLETÉN
 FELSZÍN ALATTI VIZEK RADONTARTALMÁNAK VIZSGÁLATA ISASZEG TERÜLETÉN Készítette: KLINCSEK KRISZTINA környezettudomány szakos hallgató Témavezető: HORVÁTH ÁKOS egyetemi docens ELTE TTK Atomfizika Tanszék
FELSZÍN ALATTI VIZEK RADONTARTALMÁNAK VIZSGÁLATA ISASZEG TERÜLETÉN Készítette: KLINCSEK KRISZTINA környezettudomány szakos hallgató Témavezető: HORVÁTH ÁKOS egyetemi docens ELTE TTK Atomfizika Tanszék
MUNKAGÖDÖR TERVEZÉSE
 MUNKAGÖDÖR TERVEZÉSE Munkagödör tervezése Munkatérhatárolás szerkezetei Munkagödör méretezés Plaxis programmal Munkagödör méretezés Geo 5 programmal Tartalom Bevezetés VEM - geotechnikai alkalmazási területek
MUNKAGÖDÖR TERVEZÉSE Munkagödör tervezése Munkatérhatárolás szerkezetei Munkagödör méretezés Plaxis programmal Munkagödör méretezés Geo 5 programmal Tartalom Bevezetés VEM - geotechnikai alkalmazási területek
RÉSZLETEZŐ OKIRAT (1) a NAH /2017 nyilvántartási számú akkreditált státuszhoz
 RÉSZLETEZŐ OKIRAT (1) a NAH-1-1736/2017 nyilvántartási számú akkreditált státuszhoz 1) Az akkreditált szervezet neve és címe: FUGRO Consult Kft Geotechnikai Vizsgálólaboratórium 1115 Budapest, Kelenföldi
RÉSZLETEZŐ OKIRAT (1) a NAH-1-1736/2017 nyilvántartási számú akkreditált státuszhoz 1) Az akkreditált szervezet neve és címe: FUGRO Consult Kft Geotechnikai Vizsgálólaboratórium 1115 Budapest, Kelenföldi
Támfal építés monitoring védelmében a Budapest körüli M0 útgyűrűn
 Támfal építés monitoring védelmében a Budapest körüli M0 útgyűrűn Construction works and monitoring of a retaining wall on the M0 motorway ring around Budapest SZILVÁGYI László, WOLF Ákos Geoplan Kft,
Támfal építés monitoring védelmében a Budapest körüli M0 útgyűrűn Construction works and monitoring of a retaining wall on the M0 motorway ring around Budapest SZILVÁGYI László, WOLF Ákos Geoplan Kft,
Lemez- és gerendaalapok méretezése
 Lemez- és gerendaalapok méretezése Az alapmerevség hatása az alap hajlékony merev a talpfeszültség egyenletes széleken nagyobb a süllyedés teknıszerő egyenletes Terhelés hatása hajlékony alapok esetén
Lemez- és gerendaalapok méretezése Az alapmerevség hatása az alap hajlékony merev a talpfeszültség egyenletes széleken nagyobb a süllyedés teknıszerő egyenletes Terhelés hatása hajlékony alapok esetén
Végeselemes analízisen alapuló méretezési elvek az Eurocode 3 alapján. Dr. Dunai László egyetemi tanár BME, Hidak és Szerkezetek Tanszéke
 Végeselemes analízisen alapuló méretezési elvek az Eurocode 3 alapján Dr. Dunai László egyetemi tanár BME, Hidak és Szerkezetek Tanszéke 1 Tartalom Méretezési alapelvek Numerikus modellezés Analízis és
Végeselemes analízisen alapuló méretezési elvek az Eurocode 3 alapján Dr. Dunai László egyetemi tanár BME, Hidak és Szerkezetek Tanszéke 1 Tartalom Méretezési alapelvek Numerikus modellezés Analízis és
Gyakorlat 03 Keresztmetszetek II.
 Gyakorlat 03 Keresztmetszetek II. 1. Feladat Keresztmetszetek osztályzása Végezzük el a keresztmetszet osztályzását tiszta nyomás és hajlítás esetére! Monoszimmetrikus, hegesztett I szelvény (GY02 1. példája)
Gyakorlat 03 Keresztmetszetek II. 1. Feladat Keresztmetszetek osztályzása Végezzük el a keresztmetszet osztályzását tiszta nyomás és hajlítás esetére! Monoszimmetrikus, hegesztett I szelvény (GY02 1. példája)
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011.
 BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
BAGME11NNF Munkavédelmi mérnökasszisztens Galla Jánosné, 2011. 1 Mérési hibák súlya és szerepe a mérési eredményben A mérési hibák csoportosítása A hiba rendűsége Mérési bizonytalanság Standard és kiterjesztett
Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki Kar
 M Ű E G Y E T E M 1 7 8 2 Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki Kar AZ ÁGYAZATRAGASZTÁSI TECHNOLÓGIÁVAL STABILIZÁLT ZÚZOTTKŐ ÁGYAZATÚ VASÚTI FELÉPÍTMÉNY STATIKUS ÉS DINAMIKUS TERHEKRE
M Ű E G Y E T E M 1 7 8 2 Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki Kar AZ ÁGYAZATRAGASZTÁSI TECHNOLÓGIÁVAL STABILIZÁLT ZÚZOTTKŐ ÁGYAZATÚ VASÚTI FELÉPÍTMÉNY STATIKUS ÉS DINAMIKUS TERHEKRE
A budapesti 4 sz. metróvonal II. szakaszának vonalvezetési és építéstechnológiai tanulmányterve. Ráckeve 2005 Schell Péter
 A budapesti 4 sz. metróvonal II. szakaszának vonalvezetési és építéstechnológiai tanulmányterve Az előadás vázlata: Bevezetés Helyszíni viszonyok Geológiai adottságok Talajviszonyok Mérnökgeológiai geotechnikai
A budapesti 4 sz. metróvonal II. szakaszának vonalvezetési és építéstechnológiai tanulmányterve Az előadás vázlata: Bevezetés Helyszíni viszonyok Geológiai adottságok Talajviszonyok Mérnökgeológiai geotechnikai
Magyar Mérnöki Kamara. Az évente kötelező szakmai továbbképzés tananyaga a geotechnikai jogosultsághoz. Talajdinamika, földrengésre való méretezés
 Magyar Mérnöki Kamara Az évente kötelező szakmai továbbképzés tananyaga a geotechnikai jogosultsághoz Talajdinamika, földrengésre való méretezés Előterjeszti: Összeállította: Magyar Mérnöki Kamara Geotechnikai
Magyar Mérnöki Kamara Az évente kötelező szakmai továbbképzés tananyaga a geotechnikai jogosultsághoz Talajdinamika, földrengésre való méretezés Előterjeszti: Összeállította: Magyar Mérnöki Kamara Geotechnikai
Korai vasbeton építmények tartószerkezeti biztonságának megítélése
 Korai vasbeton építmények tartószerkezeti biztonságának megítélése Dr. Orbán Zoltán, Dormány András, Juhász Tamás Pécsi Tudományegyetem Műszaki és Informatikai Kar Építőmérnök Tanszék A megbízhatóság értelmezése
Korai vasbeton építmények tartószerkezeti biztonságának megítélése Dr. Orbán Zoltán, Dormány András, Juhász Tamás Pécsi Tudományegyetem Műszaki és Informatikai Kar Építőmérnök Tanszék A megbízhatóság értelmezése
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 2010. szeptember X. Budapesti Műszaki és Gazdaságtudományi Egyetem Geotechnikai Tanszék Alapozás Rajzfeladatok Hallgató Bálint részére Megtervezendő egy 30 m 18 m alapterületű épület síkalapozása és a
2010. szeptember X. Budapesti Műszaki és Gazdaságtudományi Egyetem Geotechnikai Tanszék Alapozás Rajzfeladatok Hallgató Bálint részére Megtervezendő egy 30 m 18 m alapterületű épület síkalapozása és a
A talajok nyírószilárdsága
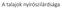 A talajok nyírószilárdsága Célok: A talajok nyírószilárdságának értelmezése. Drénezett és drénezetlen viselkedés közötti különbségek értelmezése A terepi állapotokat szimuláló vizsgálatok kiválasztása.
A talajok nyírószilárdsága Célok: A talajok nyírószilárdságának értelmezése. Drénezett és drénezetlen viselkedés közötti különbségek értelmezése A terepi állapotokat szimuláló vizsgálatok kiválasztása.
Szádfal szerkezet ellenőrzés Adatbev.
 Szádfal szerkezet ellenőrzés Adatbev. Projekt Dátum : 8.0.05 Beállítások (bevitel az aktuális feladathoz) Anyagok és szabványok Beton szerkezetek : Acél szerkezetek : Acél keresztmetszet teherbírásának
Szádfal szerkezet ellenőrzés Adatbev. Projekt Dátum : 8.0.05 Beállítások (bevitel az aktuális feladathoz) Anyagok és szabványok Beton szerkezetek : Acél szerkezetek : Acél keresztmetszet teherbírásának
Fogorvosi anyagtan fizikai alapjai 6.
 Fogorvosi anyagtan fizikai alapjai 6. Mechanikai tulajdonságok 1. Kiemelt témák: Rugalmas alakváltozás Merevség és összefüggése a kötési energiával A geometriai tényezők szerepe egy test merevségében Tankönyv
Fogorvosi anyagtan fizikai alapjai 6. Mechanikai tulajdonságok 1. Kiemelt témák: Rugalmas alakváltozás Merevség és összefüggése a kötési energiával A geometriai tényezők szerepe egy test merevségében Tankönyv
Kádár István 1 Dr. Nagy László 1 1 Budapesti Műszaki és Gazdaságtudományi Egyetem,
 TANULSÁGOK A NYÍRÓSZILÁRDSÁGI PARAMÉTEREK STATISZTIKAI ÉRTÉKELÉSÉBŐL LESSONS OF THE STATISTICAL EVALUATION OF SHEAR STRENGTH PARAMETERS Kádár István 1 Dr. Nagy László 1 1 Budapesti Műszaki és Gazdaságtudományi
TANULSÁGOK A NYÍRÓSZILÁRDSÁGI PARAMÉTEREK STATISZTIKAI ÉRTÉKELÉSÉBŐL LESSONS OF THE STATISTICAL EVALUATION OF SHEAR STRENGTH PARAMETERS Kádár István 1 Dr. Nagy László 1 1 Budapesti Műszaki és Gazdaságtudományi
Tiszai árvízvédelmi töltések károsodásainak geotechnikai tapasztalatai
 Tiszai árvízvédelmi töltések károsodásainak geotechnikai tapasztalatai Koch Edina Sánta László RÁCKEVE Tiszai árvízvédelmi töltések károsodásainak geotechnikai tapasztalatai Jelentős Tiszai árvizek 1731,
Tiszai árvízvédelmi töltések károsodásainak geotechnikai tapasztalatai Koch Edina Sánta László RÁCKEVE Tiszai árvízvédelmi töltések károsodásainak geotechnikai tapasztalatai Jelentős Tiszai árvizek 1731,
SÍKALAPOK TEHERBÍRÁSÁNAK EGYSZERûSÍTETT SZÁMÍTÁSA AZ Eurocode 7 ELVEINEK FIGYELEMBEVÉTELÉVEL
 SÍKALAPOK TEHERBÍRÁSÁNAK EGYSZERûSÍTETT SZÁMÍTÁSA AZ Eurocode 7 ELVEINEK FIGYELEMBEVÉTELÉVEL Dr. Móczár Balázs Dr. Szendefy János A korábban előtervezésre és kisebb jelentőségű épületek alapozásának megtervezésére
SÍKALAPOK TEHERBÍRÁSÁNAK EGYSZERûSÍTETT SZÁMÍTÁSA AZ Eurocode 7 ELVEINEK FIGYELEMBEVÉTELÉVEL Dr. Móczár Balázs Dr. Szendefy János A korábban előtervezésre és kisebb jelentőségű épületek alapozásának megtervezésére
Tervezés földrengés hatásra: bevezetés az Eurocode 8 alapú tervezésbe
 artószerkezetek IV. 204/205 I. félév Előadás /9 204. október 3., péntek, 9 50-30, B- terem ervezés földrengés hatásra: bevezetés az Eurocode 8 alapú tervezésbe Alapvető fogalmak Földrengés hatás ervezési
artószerkezetek IV. 204/205 I. félév Előadás /9 204. október 3., péntek, 9 50-30, B- terem ervezés földrengés hatásra: bevezetés az Eurocode 8 alapú tervezésbe Alapvető fogalmak Földrengés hatás ervezési
Előregyártott fal számítás Adatbev.
 Soil Boring co. Előregyártott fal számítás Adatbev. Projekt Dátum : 8.0.0 Beállítások (bevitel az aktuális feladathoz) Anyagok és szabványok Beton szerkezetek : CSN 0 R Fal számítás Aktív földnyomás számítás
Soil Boring co. Előregyártott fal számítás Adatbev. Projekt Dátum : 8.0.0 Beállítások (bevitel az aktuális feladathoz) Anyagok és szabványok Beton szerkezetek : CSN 0 R Fal számítás Aktív földnyomás számítás
A mélyépítési munkák elıkészítése
 A mélyépítési munkák elıkészítése A geotechnikai elıkészítı tevékenység tartalma, rendje A geotechnikai tevékenység alapelve A geotechnikában az altalaj állapotának ismerete az elvégzett geotechnikai vizsgálatok
A mélyépítési munkák elıkészítése A geotechnikai elıkészítı tevékenység tartalma, rendje A geotechnikai tevékenység alapelve A geotechnikában az altalaj állapotának ismerete az elvégzett geotechnikai vizsgálatok
KRITIKUS KÉRDÉS: ACÉL ELEMEK
 KRITIKUS KÉRDÉS: ACÉL ELEMEK KRITIKUS HŐMÉRSÉKLETE Dr. Horváth László egyetem docens Acélszerkezetek tűzvédelmi tervezése workshop, 2018. 11.09 TARTALOM Acél elemek tönkremeneteli folyamata tűzhatás alatt
KRITIKUS KÉRDÉS: ACÉL ELEMEK KRITIKUS HŐMÉRSÉKLETE Dr. Horváth László egyetem docens Acélszerkezetek tűzvédelmi tervezése workshop, 2018. 11.09 TARTALOM Acél elemek tönkremeneteli folyamata tűzhatás alatt
Kiválósági ösztöndíjjal támogatott kutatások az Építőmérnöki Karon c. előadóülés
 Kiválósági ösztöndíjjal támogatott kutatások az Építőmérnöki Karon c. előadóülés Hazay Máté hazay.mate@epito.bme.hu PhD hallgató Budapesti Műszaki és Gazdaságtudományi Egyetem Tartószerkezetek Mechanikája
Kiválósági ösztöndíjjal támogatott kutatások az Építőmérnöki Karon c. előadóülés Hazay Máté hazay.mate@epito.bme.hu PhD hallgató Budapesti Műszaki és Gazdaságtudományi Egyetem Tartószerkezetek Mechanikája
Függőleges és vízszintes vasalás hatása a téglafalazat nyírási ellenállására
 Függőleges és vízszintes vasalás hatása a téglafalazat nyírási ellenállására FÓDI ANITA Témavezető: Dr. Bódi István Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki kar Hidak és Szerkezetek
Függőleges és vízszintes vasalás hatása a téglafalazat nyírási ellenállására FÓDI ANITA Témavezető: Dr. Bódi István Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki kar Hidak és Szerkezetek
GEOTECHNIKA III. NGB-SE005-03
 GEOTECHNIKA III. NGB-SE005-03 HORGONYZOTT SZERKEZETEK Wolf Ákos 2015/16 2. félév Horgony 2 horgonyfej a szabad szakasz befogási szakasz Alkalmazási terület 3 Alkalmazási terület 4 Alkalmazási terület 5
GEOTECHNIKA III. NGB-SE005-03 HORGONYZOTT SZERKEZETEK Wolf Ákos 2015/16 2. félév Horgony 2 horgonyfej a szabad szakasz befogási szakasz Alkalmazási terület 3 Alkalmazási terület 4 Alkalmazási terület 5
Talajvizsgálati jelentés. Szentendre, Pipiske utca II. útépítés és a hozzá kapcsolódó vízelvezetés tervezése
 dr. Vásárhelyi Balázs Budapest, 1126 Geotechnikai tervező Hollósy S. u. 3 vasarhelyib@gmail.com 06-20/460-11-82 Talajvizsgálati jelentés Szentendre, Pipiske utca II. útépítés és a hozzá kapcsolódó vízelvezetés
dr. Vásárhelyi Balázs Budapest, 1126 Geotechnikai tervező Hollósy S. u. 3 vasarhelyib@gmail.com 06-20/460-11-82 Talajvizsgálati jelentés Szentendre, Pipiske utca II. útépítés és a hozzá kapcsolódó vízelvezetés
