A HOMOKOK SZEMELOSZLÁSA ÉS MÁS TALAJFIZIKAI JELLEMZŐI KÖZÖTTI KAPCSOLAT
|
|
|
- Enikő Molnár
- 8 évvel ezelőtt
- Látták:
Átírás
1 A HOMOKOK SZEMELOSZLÁSA ÉS MÁS TALAJFIZIKAI JELLEMZŐI KÖZÖTTI KAPCSOLAT Imre Emőke 1 Király Csaba 1 Rajkai Kálmán 2 Laufer Imre 3 Juhász Miklós 4 Lőrincz János 4 Szent István Egyetem 1, MTA ATK TAKI 2, Lambda Kft 3, Tengizchevroil 4 Kulcsszavak homok, tömörség, nyírószilárdság, kompresszió 1 BEVEZETÉS A szemeloszlási görbe jellemzésére kevesebb paramétert használunk, mint amennyit mérünk, és ezek sem a legmegfelelőbbek. Ezen a problémán segít az statisztikus entrópia alkalmazása, amely minden mérési adatot magában foglaló entrópia koordinátákat használ. Az entrópia koordináták és mérések összevetése alapján áttörés volt lehetséges számos területen (a vázszerkezet stabilitása, szemcsehalmazok szétosztályozódása, szűrőszabályok, a kötött talajok esetén alkalmazott mésszel való módosítás sikerességének megértése, a diszperzív jelleg, buzgárosodásra való hajlam megértése, száraz térfogatsűrűség a leglazább állapotban. ([1,2]). A folyamatban lévő kutatás a homokok szemeloszlási görbéje, térfogatsűrűsége, víztartási görbéje, nyírószilárdsága és kompressziója közötti kapcsolatot elemzi, laboratóriumi és numerikus kísérletek segítségével. Ehhez optimális (szemeloszlási entrópia elméleti szempontból átlagos) és szemcse-hiányos szemeloszlásokat alkalmaz, és bemutatja a mért adatok entrópia koordinátákkal való kapcsolatát. E munka a többszakaszos közvetlen nyíró- és kompressziós kísérletek eredményét tárgyalja a korábbi minimális száraz térfogatsűrűség vagy e max (s min ) kísérlet kísérletek alapján, valamint numerikus kísérletek lehetőségét mutatja be. 1. táblázat Az i-dik frakció saját entrópiája S 0,i i D [mm] S 0,i
2 Entropy increment, S [-] 2.8 N=7 N=6 2.4 N=5 2.0 N=4 1.6 N=3 1.2 N= Base entropy, S 0 [-] 1. ábra. A 7 frakciós szemeloszlások tere (hat dimenziós szimplex) reprezentálható a folytonos rész-szimplexek hálójával. A folytonos rész-szimplexek entrópiadiagramban vett képének maximális vonalai. 2 VÁLTOZÓK Szemeloszlási görbe tér A szemcseátmérő széles határok között változhat, így gyakorlati megfontolásból a szemeloszlási vizsgálatnál használt sziták átmérője és így a frakciók mérete duplázódik. Az i-edik frakció esetén a szemcsék átmérője (d) az alábbi i 1 i határok között van: 2 d min d 2 d min ahol d min egy önkényesen választott méret. A frakciók átmérője és i sorszáma egy értelmű kapcsolatban áll egymással. Az i-edik frakció relatív gyakorisága x i alapján (i=1..n) felírható: N x 1; x 0 (1) i= 1 i i ahol N a frakciók száma. Ez az egyenlet egyúttal egy N-1 dimenziós szimplex definiáló egyenlete, amely korlátos és zárt, és azonosítható az N frakciós, adott minimális frakciójú szemeloszlások terével. A nulla, egy, két vagy három-dimenziós szimplex ábrázolható a három dimenziós térben, a nagyobb dimenziós nem. Ábrázolható viszont pl. a folytonos rész-szimplexek szerkezete (1). Az entrópia koordináták A szemeloszlási entrópia két részből áll (az entrópia koordinátákból): S = S N 0 S, S0 xis0i i= 1 1 N, S xi ln xi ln 2 (2) i= 1
3 ahol S 0 az alap entrópia, S entrópia növekmény, S 0i a frakciók saját entrópiája (1. táblázat). A normált entrópia koordináták az A relatív alap entrópia és B a normalizált entrópia növekmény: S A = S o o max S S o min o min, S B = ln(n) (3) Az entrópia koordináták jelentése Az S 0 alap entrópia lényegében azonos az átlagos frakciómérettel (azaz átlagos absztrakt szemcseátmérő, i 0 ). Az A relatív alap entrópia ennek szemcseátmérő terjedelemmel normalizált változata (átlagos, normált absztrakt szemcseátmérő, k m ), kifejezve, hogy az átlagos érték mennyire van közel a maximálishoz. A S entrópia növekmény maximuma az azonos S 0 értékű szemeloszlások átlagát jelöli ki, az ún. optimális szemeloszlást. E szemeloszlási görbék eloszlása véges fraktál. Entrópia diagram Bármely szemeloszlási görbe egy ponttal jellemezhető az entrópia koordináták terében. Az N-1 dimenziós szimplex képe e leképezés során korlátos és zárt. Így az entrópia diagramnak (és minden rész-szimplex képének) van maximum és minimum vonala. A maximum vonalak (1 ábra) lényegében az 1 ábra szerinti szerkezetet mutatják. A maximum vonal őse a folytonos rész-szimplex optimális vagy átlagos vonala, pontjai pedig az ún. optimum pontok vagy optimális szemeloszlások, melyek fraktál eloszlások. A szimplex képének minimum vonalát általában az 1-N ik él képével helyettesítjük, ez a maximálisan szemcsehiányos keverékek képe. Mivel minden folytonos részszimplexhez csak egy optimum vonal, és egy 1-N típusú él rendelhető, ezen 1-N típusú élek szerkezete is az reprezentálható az 1 ábrán látható hálóval. E munka során ezt az ábrázolást használtuk. Geotechnikai paraméterek a tömörség leírására A munka során használt szokásos tömörségi paraméterek a hézagtényező e, a száraz térfogatsűrűség d = s s ahol a szilárd fázis térfogati aránya s= 1/(1 e), és a szemcsék sűrűsége s. A homokok minimális száraz térfogatsűrűség vagy e max kísérletének eredményét két paraméterrel jellemezzük Lőrincz [1] alapján: s s s0 = ( s s0 ) s0 (4) ahol s(=s min ) a keverék mért minimális száraz térfogatsűrűség értéke, s 0 ennek egy matematikai súlyozott átlaggal történő lineáris közelítése:
4 i max s 0 = x i s (5) i i min ahol i a frakció szám s i a mért frakció sűrűség.* i 3 A MÓDSZEREK A mérések során 5 homokfrakció (2. táblázat) és az ezekből készült olyan optimális és frakcióhiányos keverékek kerültek vizsgálatra, amelyek részszimplex optimális vonalainak és 1-N típusú éleinek pontjaival reprezentálhatók mind Lőrincz [1], mind a jelen vizsgálat esetén. A minimális száraz térfogatsűrűség vagy e max (s min ) kísérlet esetén a talajt tölcséren a Proctor edénybe töltik, ez 10 cm-es átmérő mérete miatt nem okoz átboltozódást a mintában ([4, 5]). A kompressziós kísérletek főbb adatai a következők voltak: 50, 100, 200, 400 kpa terhelés tehermentesítéssel, mindkét szakasz hossza 5 perc, d=7,5 cm; h=2 cm. A többlépcsős nyírókísérletek (a mintát visszahúzzák, nem veszik ki az egyes szakaszok után) adatai a következők voltak. A terhelések: 31,5 kpa, 62,5 kpa, 112,5 kpa; a nyíródoboz mérete 6 cm x 6 cm x4.2 cm. A homokminták lég-szárazon, a lehető legnagyobb hézagtérfogattal kerültek bekészítésre a nyírási és kompressziós kísérletek során. A kis edényméret miatt a bekészítési tömörség csak közelítően volt a leglazább. 2. táblázat Felhasznált szemcsefrakciók Frakció d mm 1 0,063-0, ,125-0,25 3 0,25-0,5 4 0,5-1,0 5 1,0-2,0 4 AZ EREDMÉNYEK Lőrincz [1] méréseit feldolgozva látható, hogy a frakció sorszámával nő a tömörség (2 ábra), az s 0 lényegében egyértelműen követi ugyanezt az aszimmetrikus trendet matematikai definíciója alapján. A keverési növekmény (s - s 0 ) jellegében ugyanúgy (szimmetrikusan) változik az S 0
5 és N szerint, mint a S (lásd 1 és 2 ábra), de kissé eltérően optimális és szemcsehiányos keverékek esetén. A 3. ábra szerint a kompressziós kísérletek eredménye nem tér el a talajok esetén ismert képtől: A terhelés-tehermentesítés görbe rugalmasképlékeny jellemzőket és előterhelési hatást látszik mutatni. A térfogati alakváltozás maximuma csökken az i frakció sorszám növekedésével. A 4 ábra szerint a többlépcsős nyírókísérletek során minden szakasz ellenkező irányú, maradó nyírási alakváltozással fejeződött be. A 4 ábra szerint a többlépcsős nyírókísérletek eredménye az első szakaszban a leglazább állapotban bekészített mintáknál is kompressziót, térfogat-csökkenést mutat a második-harmadik szakasztól minden esetben, de sok esetben már az első nyírási szakaszban is, minden szakasz maradó kompressziós alakváltozással fejeződött be. Az 5. ábra szerint a Mohr-Coulomb burkoló tipikus alakja nemlineáris, parabolával jól közelíthető. A 6. ábra szerint, a harmadik terhelési lépcsőben lineáris burkoló feltételezésével számolt súrlódási szög nő az i frakció sorszámmal. A nyírókísérletek és a kompressziós kísérletek bekészítésből, mintaméretből és falsúrlódásból [7] eredő hibái miatt numerikus DEM kísérletek tervezését kezdtük meg. Az előzetes vizsgálatok szerint bizonyos keverékek modellje gond nélkül futtatható, de vannak olyan keverékek, amelyek nagy számú gömböt igényelnek a modellben. Dry density difference s [-] 1E-1 8E-2 4E-2 N=2 N=3 N=5 N=5 gap Abstract mean diameter i0 [-] 2. ábra Lőrincz [1] eredményei [2] Frakciók. Optimális keverékek a maximális szemcsehiányos bemutatásával
6 0.00 v [mm] v [mm] [kpa] [kpa] 0.00 v [mm] v [mm] [kpa] (c) [kpa] (d) 3. ábra. Kompressziós kísérletek. - (c) Rugalmas-képlékeny viselkedés. (d) A frakció sorszám és a kompressziós görbe. 4. ábra. A nyírókísérletek Feszültség-alakváltozás. Térfogatváltozás 4. ábra. A Mohr-Coulomb burkoló (kék: mért, barna: illesztett)
7 5 TÁRGYALÁS, ÖSSZEGEZÉS A szemeloszlási entrópia elmélet A szemeloszlási koordináták hiányoznak jelenleg a talajmechanikai szakvélemények eszköztárából, jóllehet bizonyítást nyert, hogy döntő fontosságuk van a szemcsés talajok viselkedésének (pl. erózióra való hajlam megítélése, szűrőszabály) szempontjából. Homokok minimális száraz térfogatsűrűsége Lőrincz ([1], [2]) a minimális száraz térfogatsűrűségét két részre bontotta. A mért adatok újrafeldolgozása alapján látható, hogy ezek változása a frakciók sorszámával illetve azok átlagával (amit S 0 ír le) kétféle kapcsolatban van, az egyik rész szimmetrikus, a másik aszimmetrikus, ez utóbbi kapcsolata S 0 al egyértelmű. 6. ábra. A súrlódási szög, a harmadik lépcsőben lineáris burkolóval számolva. optimális keverékek frakcióhiányos keverékek
8 A fizikai magyarázat a következő. A gömb-halmaz sűrűsége növekszik, ha a gömbök átmérője nagyobb tartományban változhat. Ez a tartomány nő a frakciók sorszámának átlagával (amit S 0 ír le, aszimmetrikus rész) és szimmetrikusan változik mind a frakciók számával és az A relatív alap entrópiával (ami S függéséhez hasonló). Homokok összenyomhatósága és szilárdsága A kompressziós kísérletek eredményét a nagy falsúrlódás miatt, a a többszakaszos közvetlen nyírókísérletek eredményét a relatíve kis nyíródoboz méret miatt feltehetően jelentős hiba terheli. Annyi megállapíthatónak látszik, hogy mind a súrlódási szög, mind a maximális térfogati alakváltozás határozott kapcsolatban van a frakciók sorszámával illetve azok átlagával (amit S 0 ír le). IRODALOM 1. Lőrincz, J (1986). Grading entropy of soils Doctoral Thesis, Technical Sciences, TU of Budapest. 2. Imre E, Hazay M, Juhász M, Lőrincz J, Rajkai K, Schanz T, Lins Y, Hortobágyi Zs (2014) Sand mixture density.proceedings of UNSAT2014 Sydney, Australia, 2-4 July : Király Cs (2014) Szakdolgozat. Telítetlen talajok egyes laboratóriumi kísérletei. SZIE. 4. Imre E, Fityus S, Keszeyné E, Schanz T(2011) A Comment on the Ratio of the Maximum and Minimum Dry Density for Sands. Geotechnical Engineering 42(4) pp Imre, E & Gerendai, E & Szalkai, R &Lőrincz, J & Lins, Y & Schanz T Some notes concerning the dry density testing standards. In: Proc 18th ICSMGE. Paris Einav Breakage mechanics Part I. Theory Journal of the Mech. and Physics of Solids, 55: Kézdi Árpád Talajmechanika I., Tankönyvkiadó,Budapest, Imre, E; Lőrincz, J.; Szendefy, J.; Trang, P.Q.; Nagy, L.; Singh, V.P.; Fityus, S "Case Studies and Benchmark Examples for the Use of Grading Entropy in Geotechnics." Entropy Entropy-Switz 14, no. 6:
9
RÉSZLETEZŐ OKIRAT (1) a NAH /2017 nyilvántartási számú akkreditált státuszhoz
 RÉSZLETEZŐ OKIRAT (1) a NAH-1-1736/2017 nyilvántartási számú akkreditált státuszhoz 1) Az akkreditált szervezet neve és címe: FUGRO Consult Kft Geotechnikai Vizsgálólaboratórium 1115 Budapest, Kelenföldi
RÉSZLETEZŐ OKIRAT (1) a NAH-1-1736/2017 nyilvántartási számú akkreditált státuszhoz 1) Az akkreditált szervezet neve és címe: FUGRO Consult Kft Geotechnikai Vizsgálólaboratórium 1115 Budapest, Kelenföldi
A talajok összenyomódásának vizsgálata
 A talajok összenyomódásának vizsgálata Amit már tudni kellene Összenyomódás Konszolidáció Normálisan konszolidált talaj Túlkonszolidált talaj Túlkonszolidáltsági arányszám,ocr Konszolidáció az az időben
A talajok összenyomódásának vizsgálata Amit már tudni kellene Összenyomódás Konszolidáció Normálisan konszolidált talaj Túlkonszolidált talaj Túlkonszolidáltsági arányszám,ocr Konszolidáció az az időben
GEOTECHNIKA I. LGB-SE TALAJOK SZILÁRDSÁGI JELLEMZŐI
 GEOTECHNIKA I. LGB-SE005-01 TALAJOK SZILÁRDSÁGI JELLEMZŐI Wolf Ákos Mechanikai állapotjellemzők és egyenletek 2 X A X 3 normál- és 3 nyírófeszültség a hasáb oldalain Y A x y z xy yz zx Z A Y Z ZX YZ A
GEOTECHNIKA I. LGB-SE005-01 TALAJOK SZILÁRDSÁGI JELLEMZŐI Wolf Ákos Mechanikai állapotjellemzők és egyenletek 2 X A X 3 normál- és 3 nyírófeszültség a hasáb oldalain Y A x y z xy yz zx Z A Y Z ZX YZ A
Vizsgálati eredmények értelmezése
 Vizsgálati eredmények értelmezése Egyszerű mechanikai vizsgálatok Feladat: töltésépítésre alkalmasnak ítélt talajok mechanikai jellemzőinek vizsgálata Adottak: Proktor vizsgálat eredményei, szemeloszlás,
Vizsgálati eredmények értelmezése Egyszerű mechanikai vizsgálatok Feladat: töltésépítésre alkalmasnak ítélt talajok mechanikai jellemzőinek vizsgálata Adottak: Proktor vizsgálat eredményei, szemeloszlás,
TALAJOK OSZTÁLYOZÁSA ÉS MEGNEVEZÉSE AZ EUROCODE
 TALAJOK OSZTÁLYOZÁSA ÉS MEGNEVEZÉSE AZ EUROCODE ALAPJÁN Dr. Móczár Balázs BME Geotechnikai Tanszék Szabványok MSz 14043/2-79 MSZ EN ISO 14688 MSZ 14043-2:2006 ISO 14689 szilárd kőzetek ISO 11259 talajtani
TALAJOK OSZTÁLYOZÁSA ÉS MEGNEVEZÉSE AZ EUROCODE ALAPJÁN Dr. Móczár Balázs BME Geotechnikai Tanszék Szabványok MSz 14043/2-79 MSZ EN ISO 14688 MSZ 14043-2:2006 ISO 14689 szilárd kőzetek ISO 11259 talajtani
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 2008 PJ-MA SOIL MECHANICS Talajok tömörítése BME Geotechnikai Tanszék Tömörség értelmezése Építési terület D r T r r Tömörségi fok: e max e max r d helyszín r e d max e helyszín min 100 100 [%] [%] 2008
2008 PJ-MA SOIL MECHANICS Talajok tömörítése BME Geotechnikai Tanszék Tömörség értelmezése Építési terület D r T r r Tömörségi fok: e max e max r d helyszín r e d max e helyszín min 100 100 [%] [%] 2008
Talajmechanika. Aradi László
 Talajmechanika Aradi László 1 Tartalom Szemcsealak, szemcsenagyság A talajok szemeloszlás-vizsgálata Természetes víztartalom Plasztikus vizsgálatok Konzisztencia határok Plasztikus- és konzisztenciaindex
Talajmechanika Aradi László 1 Tartalom Szemcsealak, szemcsenagyság A talajok szemeloszlás-vizsgálata Természetes víztartalom Plasztikus vizsgálatok Konzisztencia határok Plasztikus- és konzisztenciaindex
A talajok nyírószilárdsága
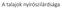 A talajok nyírószilárdsága Célok: A talajok nyírószilárdságának értelmezése. Drénezett és drénezetlen viselkedés közötti különbségek értelmezése A terepi állapotokat szimuláló vizsgálatok kiválasztása.
A talajok nyírószilárdsága Célok: A talajok nyírószilárdságának értelmezése. Drénezett és drénezetlen viselkedés közötti különbségek értelmezése A terepi állapotokat szimuláló vizsgálatok kiválasztása.
Talajmechanika II. ZH (1)
 Nev: Neptun Kod: Talajmechanika II. ZH (1) 1./ Az ábrán látható állandó víznyomású készüléken Q = 148 cm^3 mennyiségű víz folyt keresztül 5 perc alatt. A mérőeszköz adatai: átmérő [d = 15 cm]., talajminta
Nev: Neptun Kod: Talajmechanika II. ZH (1) 1./ Az ábrán látható állandó víznyomású készüléken Q = 148 cm^3 mennyiségű víz folyt keresztül 5 perc alatt. A mérőeszköz adatai: átmérő [d = 15 cm]., talajminta
SOIL MECHANICS BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GEOTECHNIKAI TANSZÉK KONSZOLIDÁCIÓ
 2008 PJ-MA SOIL MECHANICS BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GEOTECHNIKAI TANSZÉK KONSZOLIDÁCIÓ Tanszék: K épület, mfsz. 10. & mfsz. 20. Geotechnikai laboratórium: K épület, alagsor 20. BME
2008 PJ-MA SOIL MECHANICS BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GEOTECHNIKAI TANSZÉK KONSZOLIDÁCIÓ Tanszék: K épület, mfsz. 10. & mfsz. 20. Geotechnikai laboratórium: K épület, alagsor 20. BME
ÖDOMÉTERES VIZSGÁLAT LÉPCSŐZETES TERHELÉSSEL MSZE CEN ISO/TS 17892-5 BEÁLLÍTÁS ADAT. Zavartalan 4F/6,0 m Mintadarab mélysége (m)
 BEÁLLÍTÁS ADAT Minta leírás Barna iszap Előkészítési módszer magmintából Részecske-sűrűség (Mg/m³) 2.70 Feltételezett / Mért Feltételezett Betöltés sorrend információ Kezdeti mérések (gyűrű) Terhelési
BEÁLLÍTÁS ADAT Minta leírás Barna iszap Előkészítési módszer magmintából Részecske-sűrűség (Mg/m³) 2.70 Feltételezett / Mért Feltételezett Betöltés sorrend információ Kezdeti mérések (gyűrű) Terhelési
LABORATÓRIUMI SOROZATMÉRÉSEK HATÁSA TALAJOK ÁLLÉKONYSÁGI PARAMÉTEREIRE EFFECT OF LABORATORY MEASUREMENTS TO THE GEOTECHNICAL PARAMETERS OF SOILS
 Műszaki Földtudományi Közlemények, 83. kötet, 1. szám (2012), pp. 71 80. LABORATÓRIUMI SOROZATMÉRÉSEK HATÁSA TALAJOK ÁLLÉKONYSÁGI PARAMÉTEREIRE EFFECT OF LABORATORY MEASUREMENTS TO THE GEOTECHNICAL PARAMETERS
Műszaki Földtudományi Közlemények, 83. kötet, 1. szám (2012), pp. 71 80. LABORATÓRIUMI SOROZATMÉRÉSEK HATÁSA TALAJOK ÁLLÉKONYSÁGI PARAMÉTEREIRE EFFECT OF LABORATORY MEASUREMENTS TO THE GEOTECHNICAL PARAMETERS
Talajmechanika, földművek (BMEEOGT-L43) levelező kiegészítő képzés
 Talajmechanika, földművek (BMEEOGT-L43) levelező kiegészítő képzés Tanszék: Előadó: BME Geotechnikai Tanszék (K ép. magasföldszint 1.) Szendefy János (K.ép.. alagsor 3.) Ajánlott irodalom: Dr. Kabai Imre:
Talajmechanika, földművek (BMEEOGT-L43) levelező kiegészítő képzés Tanszék: Előadó: BME Geotechnikai Tanszék (K ép. magasföldszint 1.) Szendefy János (K.ép.. alagsor 3.) Ajánlott irodalom: Dr. Kabai Imre:
Alagútfalazat véges elemes vizsgálata
 Magyar Alagútépítő Egyesület BME Geotechnikai Tanszéke Alagútfalazat véges elemes vizsgálata Czap Zoltán mestertanár BME Geotechnikai Tanszék Programok alagutak méretezéséhez 1 UDEC 2D program, diszkrét
Magyar Alagútépítő Egyesület BME Geotechnikai Tanszéke Alagútfalazat véges elemes vizsgálata Czap Zoltán mestertanár BME Geotechnikai Tanszék Programok alagutak méretezéséhez 1 UDEC 2D program, diszkrét
RÉSZLETEZŐ OKIRAT (1) a NAH /2018 nyilvántartási számú akkreditált státuszhoz
 RÉSZLETEZŐ OKIRAT (1) a NAH-1-1743/2018 nyilvántartási számú akkreditált státuszhoz 1) Az akkreditált szervezet neve és címe: Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki Kar Geotechnika
RÉSZLETEZŐ OKIRAT (1) a NAH-1-1743/2018 nyilvántartási számú akkreditált státuszhoz 1) Az akkreditált szervezet neve és címe: Budapesti Műszaki és Gazdaságtudományi Egyetem Építőmérnöki Kar Geotechnika
DETERMINATION OF SHEAR STRENGTH OF SOLID WASTES BASED ON CPT TEST RESULTS
 Műszaki Földtudományi Közlemények, 83. kötet, 1. szám (2012), pp. 271 276. HULLADÉKOK TEHERBÍRÁSÁNAK MEGHATÁROZÁSA CPT-EREDMÉNYEK ALAPJÁN DETERMINATION OF SHEAR STRENGTH OF SOLID WASTES BASED ON CPT TEST
Műszaki Földtudományi Közlemények, 83. kötet, 1. szám (2012), pp. 271 276. HULLADÉKOK TEHERBÍRÁSÁNAK MEGHATÁROZÁSA CPT-EREDMÉNYEK ALAPJÁN DETERMINATION OF SHEAR STRENGTH OF SOLID WASTES BASED ON CPT TEST
Folyadékszcintillációs spektroszkópia jegyz könyv
 Folyadékszcintillációs spektroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc I. Mérés vezet je: Horváth Ákos Mérés dátuma: 2010. október 21. Leadás dátuma: 2010. november 8. 1 1. Bevezetés A mérés
Folyadékszcintillációs spektroszkópia jegyz könyv Zsigmond Anna Julia Fizika MSc I. Mérés vezet je: Horváth Ákos Mérés dátuma: 2010. október 21. Leadás dátuma: 2010. november 8. 1 1. Bevezetés A mérés
Modern Fizika Labor. 11. Spektroszkópia. Fizika BSc. A mérés dátuma: dec. 16. A mérés száma és címe: Értékelés: A beadás dátuma: dec. 21.
 Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. dec. 16. A mérés száma és címe: 11. Spektroszkópia Értékelés: A beadás dátuma: 2011. dec. 21. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 2011. dec. 16. A mérés száma és címe: 11. Spektroszkópia Értékelés: A beadás dátuma: 2011. dec. 21. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
Síklapokból álló üvegoszlopok laboratóriumi. vizsgálata. Jakab András, doktorandusz. BME, Építőanyagok és Magasépítés Tanszék
 Síklapokból álló üvegoszlopok laboratóriumi vizsgálata Előadó: Jakab András, doktorandusz BME, Építőanyagok és Magasépítés Tanszék Nehme Kinga, Nehme Salem Georges Szilikátipari Tudományos Egyesület Üvegipari
Síklapokból álló üvegoszlopok laboratóriumi vizsgálata Előadó: Jakab András, doktorandusz BME, Építőanyagok és Magasépítés Tanszék Nehme Kinga, Nehme Salem Georges Szilikátipari Tudományos Egyesület Üvegipari
Rugalmas állandók mérése
 Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
Rugalmas állandók mérése (Mérési jegyzőkönyv) Hagymási Imre 2007. április 23. (hétfő délelőtti csoport) 1. Young-modulus mérése behajlásból 1.1. A mérés menete A mérés elméleti háttere megtalálható a jegyzetben
A talajok általános tulajdonságai, osztályozásuk
 A talajok általános tulajdonságai, osztályozásuk A talajok felépítése, tulajdonságaikat meghatározó jellemzők Főalkotók A talaj alkotórészei szemcsék - szilárd fázis víz - folyékony fázis levegő - légnemű
A talajok általános tulajdonságai, osztályozásuk A talajok felépítése, tulajdonságaikat meghatározó jellemzők Főalkotók A talaj alkotórészei szemcsék - szilárd fázis víz - folyékony fázis levegő - légnemű
KOMPOZITLEMEZ ORTOTRÓP
 KOMPOZITLEMEZ ORTOTRÓP ANYAGJELLEMZŐINEK MEGHATÁROZÁSA ÉS KÍSÉRLETI IGAZOLÁSA Nagy Anna anna.nagy@econengineering.com econ Engineering econ Engineering Kft. 2019 H-1116 Budapest, Kondorosi út 3. IV. emelet
KOMPOZITLEMEZ ORTOTRÓP ANYAGJELLEMZŐINEK MEGHATÁROZÁSA ÉS KÍSÉRLETI IGAZOLÁSA Nagy Anna anna.nagy@econengineering.com econ Engineering econ Engineering Kft. 2019 H-1116 Budapest, Kondorosi út 3. IV. emelet
SZIMULÁCIÓ ÉS MODELLEZÉS AZ ANSYS ALKALMAZÁSÁVAL
 SZIMULÁCIÓ ÉS MODELLEZÉS AZ ANSYS ALKALMAZÁSÁVAL MAGYAR TUDOMÁNY NAPJA KONFERENCIA 2010 GÁBOR DÉNES FŐISKOLA CSUKA ANTAL TARTALOM A KÍSÉRLET ÉS MÉRÉS JELENTŐSÉGE A MÉRNÖKI GYAKORLATBAN, MECHANIKAI FESZÜLTSÉG
SZIMULÁCIÓ ÉS MODELLEZÉS AZ ANSYS ALKALMAZÁSÁVAL MAGYAR TUDOMÁNY NAPJA KONFERENCIA 2010 GÁBOR DÉNES FŐISKOLA CSUKA ANTAL TARTALOM A KÍSÉRLET ÉS MÉRÉS JELENTŐSÉGE A MÉRNÖKI GYAKORLATBAN, MECHANIKAI FESZÜLTSÉG
A II. kategória Fizika OKTV mérési feladatainak megoldása
 Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Nyomaték (x 0 Nm) O k t a t á si Hivatal A II. kategória Fizika OKTV mérési feladatainak megoldása./ A mágnes-gyűrűket a feladatban meghatározott sorrendbe és helyre rögzítve az alábbi táblázatban feltüntetett
Nemzeti Akkreditáló Testület. SZŰKÍTETT RÉSZLETEZŐ OKIRAT (1) a NAT /2012 nyilvántartási számú akkreditált státuszhoz
 Nemzeti Akkreditáló Testület SZŰKÍTETT RÉSZLETEZŐ OKIRAT (1) a NAT-1-1220/2012 nyilvántartási számú akkreditált státuszhoz Az EULAB Laboratóriumi és Technológiai Kft. Vizsgáló Laboratórium (2120 Dunakeszi,
Nemzeti Akkreditáló Testület SZŰKÍTETT RÉSZLETEZŐ OKIRAT (1) a NAT-1-1220/2012 nyilvántartási számú akkreditált státuszhoz Az EULAB Laboratóriumi és Technológiai Kft. Vizsgáló Laboratórium (2120 Dunakeszi,
XVII. econ Konferencia és ANSYS Felhasználói Találkozó
 XVII. econ Konferencia és ANSYS Felhasználói Találkozó Hazay Máté, Bakos Bernadett, Bojtár Imre hazay.mate@epito.bme.hu PhD hallgató Budapesti Műszaki és Gazdaságtudományi Egyetem Tartószerkezetek Mechanikája
XVII. econ Konferencia és ANSYS Felhasználói Találkozó Hazay Máté, Bakos Bernadett, Bojtár Imre hazay.mate@epito.bme.hu PhD hallgató Budapesti Műszaki és Gazdaságtudományi Egyetem Tartószerkezetek Mechanikája
Matematika osztályozó vizsga témakörei 9. évfolyam II. félév:
 Matematika osztályozó vizsga témakörei 9. évfolyam II. félév: 7. Függvények: - függvények fogalma, megadása, ábrázolás koordináta- rendszerben - az elsőfokú függvény, lineáris függvény - a másodfokú függvény
Matematika osztályozó vizsga témakörei 9. évfolyam II. félév: 7. Függvények: - függvények fogalma, megadása, ábrázolás koordináta- rendszerben - az elsőfokú függvény, lineáris függvény - a másodfokú függvény
2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv. Zsigmond Anna Fizika Bsc II. Mérés dátuma: Leadás dátuma:
 2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 24. Leadás dátuma: 2008. 10. 01. 1 1. Mérések ismertetése Az 1. ábrán látható összeállításban
2. Hangfrekvenciás mechanikai rezgések vizsgálata jegyzőkönyv Zsigmond Anna Fizika Bsc II. Mérés dátuma: 2008. 09. 24. Leadás dátuma: 2008. 10. 01. 1 1. Mérések ismertetése Az 1. ábrán látható összeállításban
Hangfrekvenciás mechanikai rezgések vizsgálata
 KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
KLASSZIKUS FIZIKA LABORATÓRIUM 3. MÉRÉS Hangfrekvenciás mechanikai rezgések vizsgálata Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 23. Szerda délelőtti csoport 1. A
Kiválósági ösztöndíjjal támogatott kutatások az Építőmérnöki Karon c. előadóülés
 Kiválósági ösztöndíjjal támogatott kutatások az Építőmérnöki Karon c. előadóülés Hazay Máté hazay.mate@epito.bme.hu PhD hallgató Budapesti Műszaki és Gazdaságtudományi Egyetem Tartószerkezetek Mechanikája
Kiválósági ösztöndíjjal támogatott kutatások az Építőmérnöki Karon c. előadóülés Hazay Máté hazay.mate@epito.bme.hu PhD hallgató Budapesti Műszaki és Gazdaságtudományi Egyetem Tartószerkezetek Mechanikája
GEOTECHNIKAI VIZSGÁLATOK 2012. 10.29.
 1 GEOTECHNIKAI VIZSGÁLATOK 2012. 10.29. Laborvizsgálatok 2 Talajazonosító vizsgálatok Víztartalom Szemeloszlás Konzisztencia határok Térfogatsűrűség Hidraulikai jellemzők vizsgálata Áteresztőképesség Összenyomódási
1 GEOTECHNIKAI VIZSGÁLATOK 2012. 10.29. Laborvizsgálatok 2 Talajazonosító vizsgálatok Víztartalom Szemeloszlás Konzisztencia határok Térfogatsűrűség Hidraulikai jellemzők vizsgálata Áteresztőképesség Összenyomódási
TALAJAZONOSÍTÁS Kötött talajok
 2008 PJ-MA SOIL MECHANICS BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GEOTECHNIKAI TANSZÉK TALAJAZONOSÍTÁS Kötött talajok Előadó: Dr. Mahler András mahler@mail.bme.hu Tanszék: K épület, mfsz. 10. &
2008 PJ-MA SOIL MECHANICS BUDAPESTI MŰSZAKI ÉS GAZDASÁGTUDOMÁNYI EGYETEM GEOTECHNIKAI TANSZÉK TALAJAZONOSÍTÁS Kötött talajok Előadó: Dr. Mahler András mahler@mail.bme.hu Tanszék: K épület, mfsz. 10. &
(Independence, dependence, random variables)
 Két valószínűségi változó együttes vizsgálata Feltételes eloszlások Két diszkrét változó együttes eloszlása a lehetséges értékpárok és a hozzájuk tartozó valószínűségek (táblázat) Példa: Egy urna 3 fehér,
Két valószínűségi változó együttes vizsgálata Feltételes eloszlások Két diszkrét változó együttes eloszlása a lehetséges értékpárok és a hozzájuk tartozó valószínűségek (táblázat) Példa: Egy urna 3 fehér,
Tartószerkezet-rekonstrukciós Szakmérnöki Képzés
 Épület alapozása síkalappal (1. rajz feladat) Minden építmény az önsúlyát és a rájutó terheléseket az altalajnak adja át, s állékonysága, valamint tartóssága attól függ, hogy sikerült-e az építmény és
Épület alapozása síkalappal (1. rajz feladat) Minden építmény az önsúlyát és a rájutó terheléseket az altalajnak adja át, s állékonysága, valamint tartóssága attól függ, hogy sikerült-e az építmény és
Regresszió. Csorba János. Nagyméretű adathalmazok kezelése március 31.
 Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
Regresszió Csorba János Nagyméretű adathalmazok kezelése 2010. március 31. A feladat X magyarázó attribútumok halmaza Y magyarázandó attribútumok) Kérdés: f : X -> Y a kapcsolat pár tanítópontban ismert
CPT PÓRUSVÍZNYOMÁS DISSZIPÁCIÓS VIZSGÁLATOK MÉLYSÉGI SZIKES KÖRNYEZETBEN. Kulcsszavak disszipációs kísérlet, CPTu, Szeged, szikes talaj, puha talaj
 CPT PÓRUSVÍZNYOMÁS DISSZIPÁCIÓS VIZSGÁLATOK MÉLYSÉGI SZIKES KÖRNYEZETBEN Imre Emőke 1 Juhász Miklós 1 Hegedűs Márton 2 Bakacsi Zsófia 3 Rajkai Kálmán 3 Pozsár László 4 Richter László 5 1 Szent István Egyetem,
CPT PÓRUSVÍZNYOMÁS DISSZIPÁCIÓS VIZSGÁLATOK MÉLYSÉGI SZIKES KÖRNYEZETBEN Imre Emőke 1 Juhász Miklós 1 Hegedűs Márton 2 Bakacsi Zsófia 3 Rajkai Kálmán 3 Pozsár László 4 Richter László 5 1 Szent István Egyetem,
Melléklet. 4. Telep fluidumok viselkedésének alapjai Olajtelepek
 Melléklet 4. Telep fluidumok viselkedésének alapjai 4.1. Olajtelepek A nyersolaj fizikai tulajdonságok és kémiai összetétel alapján igen széles tartományt fednek le, ezért célszerű őket csoportosítani,
Melléklet 4. Telep fluidumok viselkedésének alapjai 4.1. Olajtelepek A nyersolaj fizikai tulajdonságok és kémiai összetétel alapján igen széles tartományt fednek le, ezért célszerű őket csoportosítani,
Geotechika 2005 konferencia, Ráckeve A dinamikus tömörségmérés aktuális kérdései. Subert István AndreaS Kft.
 Geotechika 2005 konferencia, Ráckeve A dinamikus tömörségmérés aktuális kérdései Subert István AndreaS Kft. Hagyományos tömörség ellenőrző módszerek MSZ 15320 ÚT 2-3.103 MSZ 14043-7 Földművek tömörségének
Geotechika 2005 konferencia, Ráckeve A dinamikus tömörségmérés aktuális kérdései Subert István AndreaS Kft. Hagyományos tömörség ellenőrző módszerek MSZ 15320 ÚT 2-3.103 MSZ 14043-7 Földművek tömörségének
NYÍRÓSZILÁRDSÁG MEGHATÁROZÁSA KÖZVETLEN NYÍRÁSSAL (kis dobozos nyírókészülékben) Közvetlen nyíróvizsgálat MSZE CEN ISO/TS BEÁLLÍTÁSI ADATOK
 BEÁLLÍTÁSI ADATOK Fúrás száma 6F Minta típusa Tömörített kohéziómentes Minta száma 6F/6.0 m Minta leírása Sárgásszürke homokos agyagos iszap Részecske sűrűség (Mg/m³) 2.70 Feltételezett/Mért Feltételezett
BEÁLLÍTÁSI ADATOK Fúrás száma 6F Minta típusa Tömörített kohéziómentes Minta száma 6F/6.0 m Minta leírása Sárgásszürke homokos agyagos iszap Részecske sűrűség (Mg/m³) 2.70 Feltételezett/Mért Feltételezett
A talajok alapvető jellemzői
 A talajok alapvető jellemzői A talajok felépítése és a tulajdonságaikat meghatározó fő jellemzők Főalkotók A talaj alkotórészei szemcsék - szilárd fázis víz - folyékony fázis levegő - légnemű fázis Egyéb
A talajok alapvető jellemzői A talajok felépítése és a tulajdonságaikat meghatározó fő jellemzők Főalkotók A talaj alkotórészei szemcsék - szilárd fázis víz - folyékony fázis levegő - légnemű fázis Egyéb
Statisztika I. 12. előadás. Előadó: Dr. Ertsey Imre
 Statisztika I. 1. előadás Előadó: Dr. Ertsey Imre Regresszió analízis A korrelációs együttható megmutatja a kapcsolat irányát és szorosságát. A kapcsolat vizsgálata során a gyakorlatban ennél messzebb
Statisztika I. 1. előadás Előadó: Dr. Ertsey Imre Regresszió analízis A korrelációs együttható megmutatja a kapcsolat irányát és szorosságát. A kapcsolat vizsgálata során a gyakorlatban ennél messzebb
a NAT /2006 számú akkreditált státuszhoz
 Nemzeti Akkreditáló Testület SZÛKÍTETT RÉSZLETEZÕ OKIRAT a NAT-1-1056/2006 számú akkreditált státuszhoz A H-TPA Innovációs és Minõségvizsgáló Kft. Pécs Laboratórium (7628 Pécs, Eperfás u. 6.; 8900 Zalaegerszeg,
Nemzeti Akkreditáló Testület SZÛKÍTETT RÉSZLETEZÕ OKIRAT a NAT-1-1056/2006 számú akkreditált státuszhoz A H-TPA Innovációs és Minõségvizsgáló Kft. Pécs Laboratórium (7628 Pécs, Eperfás u. 6.; 8900 Zalaegerszeg,
Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások
 Miskolci Egyetem Műszaki Anyagtudományi Kar Anyagtudományi Intézet Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások Dr.Krállics György krallics@eik.bme.hu
Miskolci Egyetem Műszaki Anyagtudományi Kar Anyagtudományi Intézet Fémtechnológiák Fémek képlékeny alakítása 1. Mechanikai alapfogalmak, anyagszerkezeti változások Dr.Krállics György krallics@eik.bme.hu
1. Feladat. a) Mekkora radiális, tangenciális és axiális feszültségek ébrednek a csőfalban, ha a csővég zárt?
 1. Feladat Egy a = mm első és = 150 mm külső sugarú cső terhelése p = 60 MPa első ill. p k = 30 MPa külső nyomás. a) Mekkora radiális, tangenciális és axiális feszültségek érednek a csőfalan, ha a csővég
1. Feladat Egy a = mm első és = 150 mm külső sugarú cső terhelése p = 60 MPa első ill. p k = 30 MPa külső nyomás. a) Mekkora radiális, tangenciális és axiális feszültségek érednek a csőfalan, ha a csővég
7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék)
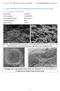 7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék) 7.1.1. SPS: 1150 C; 5 (1312 K1) Mért sűrűség: 3,795 g/cm 3 3,62 0,14 GPa Három pontos törés teszt: 105 4,2 GPa Súrlódási együttható:
7.1. Al2O3 95%+MLG 5% ; 3h; 4000rpm; Etanol; ZrO2 G1 (1312 keverék) 7.1.1. SPS: 1150 C; 5 (1312 K1) Mért sűrűség: 3,795 g/cm 3 3,62 0,14 GPa Három pontos törés teszt: 105 4,2 GPa Súrlódási együttható:
Talajok osztályozása az új szabványok szerint
 Talaj- és kőzetosztályozás Talajok osztályozása az új szabványok szerint :5 Geotechnikai vizsgálatok. 1. rész: Azonosítás és leírás. MSZ EN ISO 14688-2:5 Geotechnikai vizsgálatok. 2. rész: Osztályozási
Talaj- és kőzetosztályozás Talajok osztályozása az új szabványok szerint :5 Geotechnikai vizsgálatok. 1. rész: Azonosítás és leírás. MSZ EN ISO 14688-2:5 Geotechnikai vizsgálatok. 2. rész: Osztályozási
Nemzeti Akkreditáló Testület. SZŰKÍTETT RÉSZLETEZŐ OKIRAT (1) a NAT-1-1244/2012 nyilvántartási számú akkreditált státuszhoz
 Nemzeti Akkreditáló Testület SZŰKÍTETT RÉSZLETEZŐ OKIRAT (1) a NAT-1-1244/2012 nyilvántartási számú akkreditált státuszhoz Az INNOTESZT Minőségvizsgáló, Technológiai és Fejlesztési Kft. Mobil Nagylabor
Nemzeti Akkreditáló Testület SZŰKÍTETT RÉSZLETEZŐ OKIRAT (1) a NAT-1-1244/2012 nyilvántartási számú akkreditált státuszhoz Az INNOTESZT Minőségvizsgáló, Technológiai és Fejlesztési Kft. Mobil Nagylabor
Mechanikai vizsgáltok
 Mechanikai vizsgáltok Modellező vizsgáltok Egyszerű modellek Szűk érvényességi tartomány A vizsgálati feltételek megadása különösen fontos Általános érvényű vizsgálati eredmények A vizsgálati program célja
Mechanikai vizsgáltok Modellező vizsgáltok Egyszerű modellek Szűk érvényességi tartomány A vizsgálati feltételek megadása különösen fontos Általános érvényű vizsgálati eredmények A vizsgálati program célja
Szilárd testek rugalmassága
 Fizika villamosmérnököknek Szilárd testek rugalmassága Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1 Deformálható testek (A merev test idealizált határeset.)
Fizika villamosmérnököknek Szilárd testek rugalmassága Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1 Deformálható testek (A merev test idealizált határeset.)
Rugalmas állandók mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
KLASSZIKUS FIZIKA LABORATÓRIUM 2. MÉRÉS Rugalmas állandók mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. november 16. Szerda délelőtti csoport 1. A mérés rövid leírása Mérésem
Véletlen bolyongás. Márkus László március 17. Márkus László Véletlen bolyongás március / 31
 Márkus László Véletlen bolyongás 2015. március 17. 1 / 31 Véletlen bolyongás Márkus László 2015. március 17. Modell Deníció Márkus László Véletlen bolyongás 2015. március 17. 2 / 31 Modell: Egy egyenesen
Márkus László Véletlen bolyongás 2015. március 17. 1 / 31 Véletlen bolyongás Márkus László 2015. március 17. Modell Deníció Márkus László Véletlen bolyongás 2015. március 17. 2 / 31 Modell: Egy egyenesen
Árvízvédelmi töltésből kimosott talaj szemeloszlási entrópia vizsgálata
 Mérnökgeológia-Kőzetmechanika 2015 (Szerk: Török Á., Görög P. & Vásárhelyi B.) oldalak: 363 370 Árvízvédelmi töltésből kimosott talaj szemeloszlási entrópia vizsgálata Usage of the grading entropy to evaluate
Mérnökgeológia-Kőzetmechanika 2015 (Szerk: Török Á., Görög P. & Vásárhelyi B.) oldalak: 363 370 Árvízvédelmi töltésből kimosott talaj szemeloszlási entrópia vizsgálata Usage of the grading entropy to evaluate
Véletlen jelenség: okok rendszere hozza létre - nem ismerhetjük mind, ezért sztochasztikus.
 Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
Valószín ségelméleti és matematikai statisztikai alapfogalmak összefoglalása (Kemény Sándor - Deák András: Mérések tervezése és eredményeik értékelése, kivonat) Véletlen jelenség: okok rendszere hozza
További programozási esetek Hiperbolikus, kvadratikus, integer, bináris, többcélú programozás
 További programozási esetek Hiperbolikus, kvadratikus, integer, bináris, többcélú programozás Készítette: Dr. Ábrahám István Hiperbolikus programozás Gazdasági problémák optimalizálásakor gyakori, hogy
További programozási esetek Hiperbolikus, kvadratikus, integer, bináris, többcélú programozás Készítette: Dr. Ábrahám István Hiperbolikus programozás Gazdasági problémák optimalizálásakor gyakori, hogy
VALÓSZÍNŰSÉG, STATISZTIKA TANÍTÁSA
 VALÓSZÍNŰSÉG, STATISZTIKA TANÍTÁSA A VALÓSZÍNŰSÉGI SZEMLÉLET ALAPOZÁSA 1-6. OSZTÁLY A biztos, a lehetetlen és a lehet, de nem biztos események megkülünböztetése Valószínűségi játékok, kísérletek események
VALÓSZÍNŰSÉG, STATISZTIKA TANÍTÁSA A VALÓSZÍNŰSÉGI SZEMLÉLET ALAPOZÁSA 1-6. OSZTÁLY A biztos, a lehetetlen és a lehet, de nem biztos események megkülünböztetése Valószínűségi játékok, kísérletek események
Konzulensek: Czeglédi Ádám Dr. Bojtár Imre
 Konzulensek: Czeglédi Ádám Dr. Bojtár Imre FLAC : explicit véges differenciás program Kőzettömeg felosztása Zónákra Rácspontok Mozgásegyenlet Rácspont Zóna & u σ i ij ρ = + ρg t x j t+ t / 2) u& ( = u&
Konzulensek: Czeglédi Ádám Dr. Bojtár Imre FLAC : explicit véges differenciás program Kőzettömeg felosztása Zónákra Rácspontok Mozgásegyenlet Rácspont Zóna & u σ i ij ρ = + ρg t x j t+ t / 2) u& ( = u&
SZŰKÍTETT RÉSZLETEZŐ OKIRAT (1) a NAH /2015 nyilvántartási számú 1 akkreditált státuszhoz
 SZŰKÍTETT RÉSZLETEZŐ OKIRAT (1) a NAH-1-1220/2015 nyilvántartási számú 1 akkreditált státuszhoz Az EULAB Laboratóriumi és Technológiai Kft. Vizsgáló Laboratórium (Dunakeszi Vizsgálóhely: 2120 Dunakeszi,
SZŰKÍTETT RÉSZLETEZŐ OKIRAT (1) a NAH-1-1220/2015 nyilvántartási számú 1 akkreditált státuszhoz Az EULAB Laboratóriumi és Technológiai Kft. Vizsgáló Laboratórium (Dunakeszi Vizsgálóhely: 2120 Dunakeszi,
Nemzeti Akkreditáló Hatóság. RÉSZLETEZŐ OKIRAT a NAH /2016 nyilvántartási számú akkreditált státuszhoz
 Nemzeti Akkreditáló Hatóság RÉSZLETEZŐ OKIRAT a NAH-1-1779/2016 nyilvántartási számú akkreditált státuszhoz A MASTER WAY Építőipari Kft. Labor (Lakitelki Mobil Laboratórium: 2750 Nagykőrös, Széchenyi tér
Nemzeti Akkreditáló Hatóság RÉSZLETEZŐ OKIRAT a NAH-1-1779/2016 nyilvántartási számú akkreditált státuszhoz A MASTER WAY Építőipari Kft. Labor (Lakitelki Mobil Laboratórium: 2750 Nagykőrös, Széchenyi tér
Nagy számok törvényei Statisztikai mintavétel Várható érték becslése. Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem
 agy számok törvényei Statisztikai mintavétel Várható érték becslése Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem A mérés mint statisztikai mintavétel A méréssel az eloszlásfüggvénnyel
agy számok törvényei Statisztikai mintavétel Várható érték becslése Dr. Berta Miklós Fizika és Kémia Tanszék Széchenyi István Egyetem A mérés mint statisztikai mintavétel A méréssel az eloszlásfüggvénnyel
Modern fizika laboratórium
 Modern fizika laboratórium 11. Az I 2 molekula disszociációs energiája Készítette: Hagymási Imre A mérés dátuma: 2007. október 3. A beadás dátuma: 2007. október xx. 1. Bevezetés Ebben a mérésben egy kétatomos
Modern fizika laboratórium 11. Az I 2 molekula disszociációs energiája Készítette: Hagymási Imre A mérés dátuma: 2007. október 3. A beadás dátuma: 2007. október xx. 1. Bevezetés Ebben a mérésben egy kétatomos
Megjegyzések (észrevételek) a szabad energia és a szabad entalpia fogalmához
 Dr. Pósa Mihály Megjegyzések (észrevételek) a szabad energia és a szabad entalpia fogalmához 1. Bevezetés Shillady Don professzor az Amerikai Kémiai Szövetség egyik tanácskozásán felhívta a figyelmet a
Dr. Pósa Mihály Megjegyzések (észrevételek) a szabad energia és a szabad entalpia fogalmához 1. Bevezetés Shillady Don professzor az Amerikai Kémiai Szövetség egyik tanácskozásán felhívta a figyelmet a
Szádfal szerkezet ellenőrzés Adatbev.
 Szádfal szerkezet ellenőrzés Adatbev. Projekt Dátum : 8.0.05 Beállítások (bevitel az aktuális feladathoz) Anyagok és szabványok Beton szerkezetek : Acél szerkezetek : Acél keresztmetszet teherbírásának
Szádfal szerkezet ellenőrzés Adatbev. Projekt Dátum : 8.0.05 Beállítások (bevitel az aktuális feladathoz) Anyagok és szabványok Beton szerkezetek : Acél szerkezetek : Acél keresztmetszet teherbírásának
Nemzeti Akkreditáló Testület. MÓDOSÍTOTT RÉSZLETEZŐ OKIRAT (1) a NAT /2013 nyilvántartási számú akkreditált státuszhoz
 Nemzeti Akkreditáló Testület MÓDOSÍTOTT RÉSZLETEZŐ OKIRAT (1) a NAT-1-1691/2013 nyilvántartási számú akkreditált státuszhoz A Colas Hungária Építőipari Zrt. Technológiai Igazgatóság Keleti laboratórium
Nemzeti Akkreditáló Testület MÓDOSÍTOTT RÉSZLETEZŐ OKIRAT (1) a NAT-1-1691/2013 nyilvántartási számú akkreditált státuszhoz A Colas Hungária Építőipari Zrt. Technológiai Igazgatóság Keleti laboratórium
Matematika szóbeli érettségi témakörök 2016/2017-es tanév őszi vizsgaidőszak
 Matematika szóbeli érettségi témakörök 2016/2017-es tanév őszi vizsgaidőszak Halmazok Halmazok egyenlősége Részhalmaz, valódi részhalmaz Üres halmaz Véges és végtelen halmaz Halmazműveletek (unió, metszet,
Matematika szóbeli érettségi témakörök 2016/2017-es tanév őszi vizsgaidőszak Halmazok Halmazok egyenlősége Részhalmaz, valódi részhalmaz Üres halmaz Véges és végtelen halmaz Halmazműveletek (unió, metszet,
NSZ/NT betonok alkalmazása az M7 ap. S65 jelű aluljáró felszerkezetének építésénél
 NSZ/NT betonok alkalmazása az M7 ap. S65 jelű aluljáró felszerkezetének építésénél Betontechnológiai kísérletek Az I. kísérlet sorozatban azt vizsgáltuk, hogy azonos betonösszetétel mellett milyen hatást
NSZ/NT betonok alkalmazása az M7 ap. S65 jelű aluljáró felszerkezetének építésénél Betontechnológiai kísérletek Az I. kísérlet sorozatban azt vizsgáltuk, hogy azonos betonösszetétel mellett milyen hatást
Követelmény a 7. évfolyamon félévkor matematikából
 Követelmény a 7. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Elemek halmazba rendezése több szempont alapján. Halmazok ábrázolása. A nyelv logikai elemeinek helyes használata.
Követelmény a 7. évfolyamon félévkor matematikából Gondolkodási és megismerési módszerek Elemek halmazba rendezése több szempont alapján. Halmazok ábrázolása. A nyelv logikai elemeinek helyes használata.
Tárgyszavak: kapilláris, telítéses porometria; pórustérfogat-mérés; szűrés; átáramlásmérés.
 A TERMELÉSI FOLYAMAT MINÕSÉGKÉRDÉSEI, VIZSGÁLATOK 2.4 2.5 Porózus anyagok új, környezetkímélő mérése Tárgyszavak: kapilláris, telítéses porometria; pórustérfogat-mérés; szűrés; átáramlásmérés. A biotechnológiában,
A TERMELÉSI FOLYAMAT MINÕSÉGKÉRDÉSEI, VIZSGÁLATOK 2.4 2.5 Porózus anyagok új, környezetkímélő mérése Tárgyszavak: kapilláris, telítéses porometria; pórustérfogat-mérés; szűrés; átáramlásmérés. A biotechnológiában,
MÓDOSÍTOTT RÉSZLETEZŐ OKIRAT (1) a NAH /2016 nyilvántartási számú akkreditált státuszhoz
 MÓDOSÍTOTT RÉSZLETEZŐ OKIRAT (1) a NAH-1-1779/2016 nyilvántartási számú akkreditált státuszhoz A MASTER WAY Építőipari Kft. MASTER WAY Labor 1 (Lakiteleki Mobil Laboratórium: 4272 Sáránd külterület 105
MÓDOSÍTOTT RÉSZLETEZŐ OKIRAT (1) a NAH-1-1779/2016 nyilvántartási számú akkreditált státuszhoz A MASTER WAY Építőipari Kft. MASTER WAY Labor 1 (Lakiteleki Mobil Laboratórium: 4272 Sáránd külterület 105
A.2. Acélszerkezetek határállapotai
 A.. Acélszerkezetek határállapotai A... A teherbírási határállapotok első osztálya: a szilárdsági határállapotok A szilárdsági határállapotok (melyek között a fáradt és rideg törést e helyütt nem tárgyaljuk)
A.. Acélszerkezetek határállapotai A... A teherbírási határállapotok első osztálya: a szilárdsági határállapotok A szilárdsági határállapotok (melyek között a fáradt és rideg törést e helyütt nem tárgyaljuk)
1/ gyakorlat. Lineáris Programozási feladatok megoldása szimplex módszerrel. Pécsi Tudományegyetem PTI
 / Operációkutatás. gyakorlat Lineáris Programozási feladatok megoldása szimplex módszerrel Pécsi Tudományegyetem PTI /. Legyen adott az alábbi LP-feladat: x + 4x + x 9 x + x x + x + x 6 x, x, x x + x +
/ Operációkutatás. gyakorlat Lineáris Programozási feladatok megoldása szimplex módszerrel Pécsi Tudományegyetem PTI /. Legyen adott az alábbi LP-feladat: x + 4x + x 9 x + x x + x + x 6 x, x, x x + x +
Vasalttalaj hídfők. Tóth Gergő. Gradex Mérnöki és Szolgáltató Kft Budapest, Bécsi út 120. Telefon: +36-1/
 Vasalttalaj hídfők Tóth Gergő Gradex Mérnöki és Szolgáltató Kft. 1034 Budapest, Bécsi út 120. Telefon: +36-1/436-0990 www.gradex.hu Az előadás 1. Hagyományos hídfő kialakítások régen és most 2. Első hazai
Vasalttalaj hídfők Tóth Gergő Gradex Mérnöki és Szolgáltató Kft. 1034 Budapest, Bécsi út 120. Telefon: +36-1/436-0990 www.gradex.hu Az előadás 1. Hagyományos hídfő kialakítások régen és most 2. Első hazai
A Termelésmenedzsment alapjai tárgy gyakorló feladatainak megoldása
 azdaság- és Társadalomtudományi Kar Ipari Menedzsment és Vállakozásgazdaságtan Tanszék A Termelésmenedzsment alapjai tárgy gyakorló feladatainak megoldása Készítette: dr. Koltai Tamás egyetemi tanár Budapest,.
azdaság- és Társadalomtudományi Kar Ipari Menedzsment és Vállakozásgazdaságtan Tanszék A Termelésmenedzsment alapjai tárgy gyakorló feladatainak megoldása Készítette: dr. Koltai Tamás egyetemi tanár Budapest,.
MÓDOSÍTOTT RÉSZLETEZŐ OKIRAT (1) a NAH /2015 nyilvántartási számú (1) akkreditált státuszhoz
 MÓDOSÍTOTT RÉSZLETEZŐ OKIRAT (1) a NAH-1-1659/2015 nyilvántartási számú (1) akkreditált státuszhoz Az IQC Mérnöki Kft. Vizsgáló laboratórium (1112 Budapest, Repülőtéri u. 2.) akkreditált területe Talaj
MÓDOSÍTOTT RÉSZLETEZŐ OKIRAT (1) a NAH-1-1659/2015 nyilvántartási számú (1) akkreditált státuszhoz Az IQC Mérnöki Kft. Vizsgáló laboratórium (1112 Budapest, Repülőtéri u. 2.) akkreditált területe Talaj
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I 16 XVI A DIFFERENCIÁLSZÁmÍTÁS ALkALmAZÁSAI 1 Érintő ÉS NORmÁLIS EGYENES, L HOSPITAL-SZAbÁLY Az görbe abszcisszájú pontjához tartozó érintőjének egyenlete (1), normálisának egyenlete
KOVÁCS BÉLA, MATEmATIkA I 16 XVI A DIFFERENCIÁLSZÁmÍTÁS ALkALmAZÁSAI 1 Érintő ÉS NORmÁLIS EGYENES, L HOSPITAL-SZAbÁLY Az görbe abszcisszájú pontjához tartozó érintőjének egyenlete (1), normálisának egyenlete
Microsoft Excel 2010. Gyakoriság
 Microsoft Excel 2010 Gyakoriság Osztályközös gyakorisági tábla Nagy számú mérési adatokat csoportokba (osztályokba) rendezése -> könnyebb áttekintés Osztályokban szereplő adatok száma: osztályokhoz tartozó
Microsoft Excel 2010 Gyakoriság Osztályközös gyakorisági tábla Nagy számú mérési adatokat csoportokba (osztályokba) rendezése -> könnyebb áttekintés Osztályokban szereplő adatok száma: osztályokhoz tartozó
Nemzeti Akkreditáló Testület. RÉSZLETEZŐ OKIRAT a NAT /2014 nyilvántartási számú akkreditált státuszhoz
 Nemzeti Akkreditáló Testület RÉSZLETEZŐ OKIRAT a NAT-1-1741/2014 nyilvántartási számú akkreditált státuszhoz Az Útlabor Laboratóriumi és Technológiai Kft. (9151 Abda, Bécsi út 15.) akkreditált területe
Nemzeti Akkreditáló Testület RÉSZLETEZŐ OKIRAT a NAT-1-1741/2014 nyilvántartási számú akkreditált státuszhoz Az Útlabor Laboratóriumi és Technológiai Kft. (9151 Abda, Bécsi út 15.) akkreditált területe
Mikroszkóp vizsgálata Folyadék törésmutatójának mérése
 KLASSZIKUS FIZIKA LABORATÓRIUM 8. MÉRÉS Mikroszkóp vizsgálata Folyadék törésmutatójának mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 12. Szerda délelőtti csoport
KLASSZIKUS FIZIKA LABORATÓRIUM 8. MÉRÉS Mikroszkóp vizsgálata Folyadék törésmutatójának mérése Mérést végezte: Enyingi Vera Atala ENVSAAT.ELTE Mérés időpontja: 2011. október 12. Szerda délelőtti csoport
Nem-lineáris programozási feladatok
 Nem-lineáris programozási feladatok S - lehetséges halmaz 2008.02.04 Dr.Bajalinov Erik, NyF MII 1 Elég egyszerű példa: nemlineáris célfüggvény + lineáris feltételek Lehetséges halmaz x 1 *x 2 =6.75 Gradiens
Nem-lineáris programozási feladatok S - lehetséges halmaz 2008.02.04 Dr.Bajalinov Erik, NyF MII 1 Elég egyszerű példa: nemlineáris célfüggvény + lineáris feltételek Lehetséges halmaz x 1 *x 2 =6.75 Gradiens
Jellemző szelvények alagút
 Alagútépítés Jellemző szelvények alagút 50 50 Jellemző szelvény - alagút 51 AalagútDél Nyugati járat Keleti járat 51 Alagúttervezés - geotechnika 52 Technológia - Új osztrák építési módszer (NÖT) 1356
Alagútépítés Jellemző szelvények alagút 50 50 Jellemző szelvény - alagút 51 AalagútDél Nyugati járat Keleti járat 51 Alagúttervezés - geotechnika 52 Technológia - Új osztrák építési módszer (NÖT) 1356
Nemzeti Akkreditáló Testület. RÉSZLETEZŐ OKIRAT a NAT-1-1659/2015 nyilvántartási számú akkreditált státuszhoz
 Nemzeti Akkreditáló Testület RÉSZLETEZŐ OKIRAT a NAT-1-1659/2015 nyilvántartási számú akkreditált státuszhoz Az IQC Mérnöki Kft. Vizsgáló laboratórium (1112 Budapest, Repülőtéri u. 2.) akkreditált területe
Nemzeti Akkreditáló Testület RÉSZLETEZŐ OKIRAT a NAT-1-1659/2015 nyilvántartási számú akkreditált státuszhoz Az IQC Mérnöki Kft. Vizsgáló laboratórium (1112 Budapest, Repülőtéri u. 2.) akkreditált területe
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 8 VIII. REGREssZIÓ 1. A REGREssZIÓs EGYENEs Két valószínűségi változó kapcsolatának leírására az eddigiek alapján vagy egy numerikus
Mérési adatok illesztése, korreláció, regresszió
 Mérési adatok illesztése, korreláció, regresszió Korreláció, regresszió Két változó mennyiség közötti kapcsolatot vizsgálunk. Kérdés: van-e kapcsolat két, ugyanabban az egyénben, állatban, kísérleti mintában,
Mérési adatok illesztése, korreláció, regresszió Korreláció, regresszió Két változó mennyiség közötti kapcsolatot vizsgálunk. Kérdés: van-e kapcsolat két, ugyanabban az egyénben, állatban, kísérleti mintában,
RÉSZLETEZŐ OKIRAT a NAH /2017 nyilvántartási számú akkreditált státuszhoz
 RÉSZLETEZŐ OKIRAT a NAH-1-1728/2017 nyilvántartási számú akkreditált státuszhoz A CRH Magyarország Kft. Műszaki Szolgáltató Központ Építőanyag-vizsgáló Laboratórium (Budapesti egység: 1151 Budapest, Károlyi
RÉSZLETEZŐ OKIRAT a NAH-1-1728/2017 nyilvántartási számú akkreditált státuszhoz A CRH Magyarország Kft. Műszaki Szolgáltató Központ Építőanyag-vizsgáló Laboratórium (Budapesti egység: 1151 Budapest, Károlyi
A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9
 A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9 Név: Pitlik László Mérés dátuma: 2014.12.04. Mérőtársak neve: Menkó Orsolya Adatsorok: M24120411 Halmy Réka M14120412 Sárosi
A kálium-permanganát és az oxálsav közötti reakció vizsgálata 9a. mérés B4.9 Név: Pitlik László Mérés dátuma: 2014.12.04. Mérőtársak neve: Menkó Orsolya Adatsorok: M24120411 Halmy Réka M14120412 Sárosi
Követelmények Motiváció Matematikai modellezés: példák A lineáris programozás alapfeladata 2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 1. Előadás Követelmények, teljesítés feltételei Vizsga anyaga Előadásokhoz tartozó diasor
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 1. Előadás Követelmények, teljesítés feltételei Vizsga anyaga Előadásokhoz tartozó diasor
MUNKAGÖDÖR TERVEZÉSE
 MUNKAGÖDÖR TERVEZÉSE Munkagödör tervezése Munkatérhatárolás szerkezetei Munkagödör méretezés Plaxis programmal Munkagödör méretezés Geo 5 programmal Tartalom Bevezetés VEM - geotechnikai alkalmazási területek
MUNKAGÖDÖR TERVEZÉSE Munkagödör tervezése Munkatérhatárolás szerkezetei Munkagödör méretezés Plaxis programmal Munkagödör méretezés Geo 5 programmal Tartalom Bevezetés VEM - geotechnikai alkalmazási területek
MATEMATIKA ÉRETTSÉGI május 8. EMELT SZINT
 MATEMATIKA ÉRETTSÉGI 007. május 8. EMELT SZINT 1) Oldja meg a valós számok halmazán az alábbi egyenletet! x x 4 log 9 10 sin x x 6 I. (11 pont) sin 1 lg1 0 log 9 9 x x 4 Így az 10 10 egyenletet kell megoldani,
MATEMATIKA ÉRETTSÉGI 007. május 8. EMELT SZINT 1) Oldja meg a valós számok halmazán az alábbi egyenletet! x x 4 log 9 10 sin x x 6 I. (11 pont) sin 1 lg1 0 log 9 9 x x 4 Így az 10 10 egyenletet kell megoldani,
Elhangzott gyakorlati tananyag óránkénti bontásban. Mindkét csoport. Rövidítve.
 TTK, Matematikus alapszak Differenciálegyenletek 1 (BMETE93AM15) Elhangzott gyakorlati tananyag óránkénti bontásban Mindkét csoport Rövidítve 1 gyakorlat 017 szeptember 7 T01 csoport Elsőrendű közönséges
TTK, Matematikus alapszak Differenciálegyenletek 1 (BMETE93AM15) Elhangzott gyakorlati tananyag óránkénti bontásban Mindkét csoport Rövidítve 1 gyakorlat 017 szeptember 7 T01 csoport Elsőrendű közönséges
Descartes-féle, derékszögű koordináta-rendszer
 Descartes-féle, derékszögű koordináta-rendszer A derékszögű koordináta-rendszerben a sík minden pontjához egy rendezett valós számpár rendelhető. A számpár első tagja (abszcissza) a pont y tengelytől mért
Descartes-féle, derékszögű koordináta-rendszer A derékszögű koordináta-rendszerben a sík minden pontjához egy rendezett valós számpár rendelhető. A számpár első tagja (abszcissza) a pont y tengelytől mért
CSAPADÉK ÉS TALAJVÍZSZINT ÉRTÉKEK SPEKTRÁLIS ELEMZÉSE A MEZŐKERESZTES-I ADATOK ALAPJÁN*
 A Miskolci Egyetem Közleménye A sorozat, Bányászat, 66. kötet, (2004) p. 103-108 CSAPADÉK ÉS TALAJVÍZSZINT ÉRTÉKEK SPEKTRÁLIS ELEMZÉSE A MEZŐKERESZTES-I ADATOK ALAPJÁN* Dr.h.c.mult. Dr. Kovács Ferenc az
A Miskolci Egyetem Közleménye A sorozat, Bányászat, 66. kötet, (2004) p. 103-108 CSAPADÉK ÉS TALAJVÍZSZINT ÉRTÉKEK SPEKTRÁLIS ELEMZÉSE A MEZŐKERESZTES-I ADATOK ALAPJÁN* Dr.h.c.mult. Dr. Kovács Ferenc az
Követelmények Motiváció Matematikai modellezés: példák A lineáris programozás alapfeladata 2017/ Szegedi Tudományegyetem Informatikai Intézet
 Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 1. Előadás Követelmények, teljesítés feltételei Vizsga anyaga Előadásokhoz tartozó diasor
Operációkutatás I. 2017/2018-2. Szegedi Tudományegyetem Informatikai Intézet Számítógépes Optimalizálás Tanszék 1. Előadás Követelmények, teljesítés feltételei Vizsga anyaga Előadásokhoz tartozó diasor
Modern Fizika Labor. 12. Infravörös spektroszkópia. Fizika BSc. A mérés dátuma: okt. 04. A mérés száma és címe: Értékelés:
 Modern Fizika Labor Fizika BSc A mérés dátuma: 011. okt. 04. A mérés száma és címe: 1. Infravörös spektroszkópia Értékelés: A beadás dátuma: 011. dec. 1. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
Modern Fizika Labor Fizika BSc A mérés dátuma: 011. okt. 04. A mérés száma és címe: 1. Infravörös spektroszkópia Értékelés: A beadás dátuma: 011. dec. 1. A mérést végezte: Domokos Zoltán Szőke Kálmán Benjamin
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika emelt szint 0801 ÉRETTSÉGI VIZSGA 009. május 5. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Formai előírások: Fontos tudnivalók
Matematika emelt szint 0801 ÉRETTSÉGI VIZSGA 009. május 5. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Formai előírások: Fontos tudnivalók
x 2 e x dx c) (3x 2 2x)e 2x dx x sin x dx f) x cosxdx (1 x 2 )(sin 2x 2 cos 3x) dx e 2x cos x dx k) e x sin x cosxdx x ln x dx n) (2x + 1) ln 2 x dx
 Integrálszámítás II. Parciális integrálás. g) i) l) o) e ( + )(e e ) cos h) e sin j) (sin 3 cos) m) arctg p) arcsin e (3 )e sin f) cos ( )(sin cos 3) e cos k) e sin cos ln n) ( + ) ln. e 3 e cos 3 3 cos
Integrálszámítás II. Parciális integrálás. g) i) l) o) e ( + )(e e ) cos h) e sin j) (sin 3 cos) m) arctg p) arcsin e (3 )e sin f) cos ( )(sin cos 3) e cos k) e sin cos ln n) ( + ) ln. e 3 e cos 3 3 cos
Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ)
 Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ) KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba
Méréselmélet és mérőrendszerek 2. ELŐADÁS (1. RÉSZ) KÉSZÍTETTE: DR. FÜVESI VIKTOR 2016. 10. Mai témáink o A hiba fogalma o Méréshatár és mérési tartomány M é r é s i h i b a o A hiba megadása o A hiba
Utak földművei. Útfenntartási és útüzemeltetési szakmérnök szak 2012. I. félév 2./1. témakör. Dr. Ambrus Kálmán
 Utak földművei Útfenntartási és útüzemeltetési szakmérnök szak 2012. I. félév 2./1. témakör Dr. Ambrus Kálmán 1. Az utak földműveiről általában 2. A talajok vizsgálatánál használatos fogalmak 3. A talajok
Utak földművei Útfenntartási és útüzemeltetési szakmérnök szak 2012. I. félév 2./1. témakör Dr. Ambrus Kálmán 1. Az utak földműveiről általában 2. A talajok vizsgálatánál használatos fogalmak 3. A talajok
Modern Fizika Labor. 2. Elemi töltés meghatározása
 Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Modern Fizika Labor Fizika BSC A mérés dátuma: 2011.09.27. A mérés száma és címe: 2. Elemi töltés meghatározása Értékelés: A beadás dátuma: 2011.10.11. A mérést végezte: Kalas György Benjámin Németh Gergely
Al-Mg-Si háromalkotós egyensúlyi fázisdiagram közelítő számítása
 l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
l--si háromalkotós egyensúlyi fázisdiagram közelítő számítása evezetés Farkas János 1, Dr. Roósz ndrás 1 doktorandusz, tanszékvezető egyetemi tanár Miskolci Egyetem nyag- és Kohómérnöki Kar Fémtani Tanszék
Alumínium ötvözetek aszimmetrikus hengerlése
 A Miskolci Egyetemen működő tudományos képzési műhelyek összehangolt minőségi fejlesztése TÁMOP-4.2.2/B-10/1-2010-0008 Tehetségeket gondozunk! Alumínium ötvözetek aszimmetrikus hengerlése 2011. November
A Miskolci Egyetemen működő tudományos képzési műhelyek összehangolt minőségi fejlesztése TÁMOP-4.2.2/B-10/1-2010-0008 Tehetségeket gondozunk! Alumínium ötvözetek aszimmetrikus hengerlése 2011. November
