Dr. Bognár Katalin 2010.
|
|
|
- Regina Budai
- 6 évvel ezelőtt
- Látták:
Átírás
1 1 Tudásalapú rendszerek és technológiák Dr. Bognár Katalin 2010.
2 2
3 Contents I Fogalmi háttér 9 1 Bevezetés 11 2 Mesterséges Intelligencia háttér Intelligencia és intelligens viselkedés Turing teszt Az emberi problémamegoldó gondolkodás A szakmai fejlődés lépcsőfokai Mesterséges intelligencia Algoritmikus megközelítés Algoritmikusan megoldható problémák Nem algoritmikus megoldható problémák Az MI és a klasszikus informatika Alkalmazási területek Az adatok természete Az adatok pontossága A felmerült probléma megoldása Fogalmi rendszerezés Adat, információ, ismeret fogalma Adat Információ Tudás vagy ismeret A szakértő rendszer fogalma
4 4 CONTENTS II Tudásalapú, szakértő rendszerek 29 4 Az ismeretalapú rendszerek Az ismeretalapú rendszerek jellemzői Az emberi tudás és a szakértő rendszer összevetése A szakértő rendszer előnyei A szakértő rendszer hátrányai A szakértő rendszer tudásszintje Az ismeretalapú rendszerek felépítése Ismeretbázis Következtetőgép Magyarázó alrendszer Ismeretbázis fejlesztő alrendszer Felhasználói felület Ismeretszerzés Ismeretszerzés célja Az ismeretszerzés részterületei Szereplők Az ismeretszerzés nehézségei A tudásmegszerzés módszerei Ismeretábrázolás Szabályalapú ismeretreprezentáció Következtetési stratégiák Szabályalapú rendszerek értékelése Szemantikus (asszociatív) hálók Előnyök Keretalapú ismeretreprezentáció Öröklődés Démonok A keretalapú ismeretábrázolás előnyei A keretalapú ismeretábrázolás hátrányai Példa A hierarchikus struktúráról Példa démon alkalmazására
5 CONTENTS 5 7 Leíró logikák Bevezetés A leíró logikák kialakulásának története A leíró nyelvek szintaxisa és szemantikája A leíró nyelvek szintaxisa Példák A leíró nyelvek szemantikája Az ALCN R nyelv szemantikája Hierarchia a fogalmak és a szerepek körében Egyszerű példák alárendelésre Az SHIQ nyelvcsalád Az SHIQ Az SHIQ nyelv szemantikája A leíró ismeretbázis fogalma Példa leíró ismeretbázisra Következtetési eljárások egy leíró ismeretbázisban Példa az egyedesítésre Nyíltvilág és zárt világ szemantika A leíró logika, a klasszikus logika és az objektum alapú ismeretábrázolás Alkalmazások Az osztályozás fogalmának háló alapú bevezetése Bevezetés Hálóelméleti alapfogalmak A háló fogalma Példák A hálók tulajdonságai Moduláris hálók Disztributív hálók Boole-algebra Fogalmi hierarchia Az osztályozási eljárás Egy klasszifikációs algoritmus Példák Összegzés
6 6 CONTENTS 9 Bizonytalanságkezelés Bevezetés A bizonytalanságkezelés módszereinek, modelljeinek osztályozása Numerikus modellek, a Bayes-tételen alapuló módszer Kísérlet, esemény és ellentett esemény Műveletek eseményekkel, teljes eseményrendszer Valószínűségi mérték, feltételes valószínűség, Bayes tétele Példa a Bayes módszer alkalmazására Fuzzy logika Bevezetés Fuzzy halmazelmélet Lukasiewicz fuzzy logikája Gödel fuzzy logikája A fuzzy rendszerek értékelése A Bayes módszer, a fuzzy modell és a heurisztikus modellek Következtető rendszerek Következtetési módok Formális következtetés Procedurális következtetés Analógián alapuló következtetés Általánosításon és absztrakción alapuló következtetés Eset-alapú következtetés Közelítő következtetés Hipotetikus következtetés Alapértelmezésen alapuló Kvalitatív következtetés Hasonlóságon alapuló következtetés Eset alapú következtetés A CBR életciklusa CBR az OOKBR-ben Objektum alapú ismeretábrázolás Az esetek hierarchikus szervezése Példa Eset visszakeresés, adaptáció Eset visszakeresés
7 CONTENTS Példa eset visszakeresésre Adaptáció Példa adaptációra Gyenge osztályozás Példa gyenge osztályozásra III Tudáskezelési technológiák Ágensek Bevezetés Az ágens szó eredete Az ágens általános jelentése Ágens definíciók Az ágensek csoportos ása Kölcsönható ágensek ADAPTÍV, TANULÓ ÁGENSEK ÁGENSEK ALKALMAZÁSA INFORMÁCIÓS REND- SZEREKBEN FELHASZNÁLÓI MODELLEZÉS ÁGENS REND- SZEREKBEN INTERNET ÉS WWW-ÁGENSEK ÁGENSEK AZ ELEKTRONIKUS KERESKEDELEM- BEN INTERFÉSZ ÁGENSEK ASSZISZTENSEK OKTATÓ ÁGENSEK MOBIL ÁGENSEK A MOBIL ALKALMAZÁSOK PROBLÉMÁI TIPIKUS ALKALMAZÁSOK Struktúrák és részben-struktúrált adatok Részben-struktúrált adatok Szemantikus web A gépekhez beszélő Web Alkalmazások
8 8 CONTENTS
9 Part I Fogalmi háttér 9
10
11 Chapter 1 Bevezetés Az információ nagy mértékű elektronikus felhalmozását követően az üzleti életben egyre nagyobb szerepet kap a tudásmenedzsment, amely a vállalati szervezeti tudás előállítását, összegyűjtését, megosztását, felhasználását és megújulását valósítja meg az üzleti siker, illetve a versenyelőny megszerzése és megtartása érdekében. A vállalat információkat, tudást, tapasztalatot szerez, majd a megszerzett tudást leírhatóvá alakítjuk, és a tudásdisztribúció folyamán a közös tudást mindenki számára hozzáférhetővé tesszük. A tudásmenedzsment rendszer lehet személyorientált, ahol a szakértők teljesen egyedi problémákra adnak egyedi, kreatív választ; vagy dokumentumorientált, ahol a szakértők számára a magas szakmai színvonalon létrehozott dokumentumrendszer tartalmazza a problémák megoldásának folyamatát és részleteit. A tudásmérnökség elméleti keretét az ismeretszerzés biztosítja, ahol egy szakértő ismereteinek empirikus vagy pszichológiai modellezésének célja egy szakértő rendszer kialakítása. Gyakran a probléma nyelvi megfogalmazásából indulunk ki - szakértői interjúk, technikai leírások, különböző dokumentumok analizálásával - azzal a céllal, hogy kidolgozzuk a probléma formális reprezentációját, definiáljuk a probléma formális modelljéhez szükséges ismereteket. Klasszikus értelemben az ismeretszerzés olyan eljárásokat javasol, amelyek a következtetési módok modellezését teszik lehetővé a tárgyterület absztrakciójával. Az utóbbi években a tudásmérnökség kutatásai úgy fejlődtek, hogy minden olyan információs rendszerre vonatkoznak, amelyek valami- 11
12 12 CHAPTER 1. BEVEZETÉS képpen tudásra épülnek, anélkül hogy ez a tudás explicite modellezve lenne a rendszerben. A tudásmérnökség a tudásalapú rendszerek ismeretszerzési területéből kinőve önálló, általánosabb kutatási területté vált, amelybe beletartozik az ismeret nyelvi megfogalmazásának tanulmányozása, a fogalmi terminológiák meghatározása, a formális modellek kidolgozása, a modellek manipulálása és megvalósítása, a rendszer viselkedésének és tulajdonságainak interpretálása. Azt mondhatjuk, hogy a tudásmérnökség fogalmakat, módszereket és technikákat javasol az ismeretek modellezése, formalizálása és megszerzése érdekében a vállalati szervezettségben széles értelemben vett működtetési, strukturálási és kezelési célzattal. Ebben a könyvben az előbb felsorolt gyakorlati problémák hátterét biztosító tudásalapú rendszerek és technológiák elméleti megalapozását tűzzük ki célul, elsősorban informatikus szakemberek számára megfogalmazott formában. A tudásalapú rendszerek a mesterséges intelligencia szakterület olyan programjai, amelyekben az adott probléma megoldásához szükséges ismereteket a rendszer többi részétől elkülönített modulban, az úgynevezett tudásbázisban tároljuk szimbolikus módon, a probléma megoldása pedig szimbólum manipulációk révén történik. A tudásalapú rendszerekben egy probléma megoldása során olyan ismereteket tudunk felhasználni, amelyeket előzőleg valamilyen formalizmus szerint ábrázoltunk, reprezentáltunk. A probléma megoldásához pedig szükségünk van az ismeretábrázolásnak megfelelő következtetési mechanizmusra. Gondoljunk a klasszikus logikában a formulák megadására (szintaxis) és az interpretációra (szemantika), amelyekhez különféle kalkulusok (tábla-módszer, predikátumkalkulus, Gentzen-kalkulus) definiálhatóak mint következtetési módszerek. A könyv felépítése a következő: az első részben néhány alapfogalmat mutatunk be, köztük bevezetjük a mesterséges intelligencia fogalmát. A második rész a szakértő rendszerekkel foglalkozik, melyben a tudásalapú rendszerek felépítésének, az ismeretszerzésnek, az ismeretábrázolásnak, a bizonytalanságkezelésnek és a következtetési eljárásoknak szentelünk egy-egy fejezetet. A harmadik rész az ágensek,
13 szemistruktúrák, szemantikus web fogalmak köré épülve ad betekintést a napjainkban elterjedt tudásalapú technológiák alkalmazhatóságára. 13
14 14 CHAPTER 1. BEVEZETE S
15 Chapter 2 Mesterséges Intelligencia háttér 2.1 Intelligencia és intelligens viselkedés Mi is az intelligencia, lehetséges-e egyáltalán definiálni az intelligenciát? Intuitíve jól látjuk, hogy egy sokszorosan összetett fogalomról van szó. Olyan szellemi képességekről beszélünk mint a megfigyelés, a megértés, a tanulás, a csodálkozás, stb. Einstein intelligenciája más mint Picassoé. Valójában különböző megközelítési módok és változatok vannak az intelligencia fogalom mögött, hiszen az intelligencia nem mérhető a maga teljességében. Különösen nem szabad összekeverni az intelligencia és a tudás fogalmait, azaz nem elegendő az ismereteket tesztelni az intelligencia méréséhez. Nem szabad összetéveszteni a butaságot a tudatlansággal. Ha vizsgáljuk az intelligenciát, akkor megfigyeljük a viselkedést, a fejlődés minőségét. Bár pontosan nem definiáljuk, ez nem akadályoz meg minket abban, hogy az emberrel kapcsolatos intelligenciáról beszéljünk. Idézzük fel Ikarusz esetét a repülő szerkezettel. Ikarusz a legenda szerint, majd őt követően a XIX. század végének és a XX. század elejének úttörői mindvégig olyan szerkezetek megalkotásával probálkoztak, amelyek madarak módjára, szárnyaikkal verdesve képesek repülni. Ma vajon kinek támadna az az ötlete, hogy a modern repülők nem repülnek, csak azért mert nem verdesnek a szárnyaikkal. 15
16 16 CHAPTER 2. MESTERSÉGES INTELLIGENCIA HÁTTÉR Az emberi intelligencia az észlelésnek, az ismeretek memorizálásának, struktúrálásának és új ismeretekre való következtetésnek a képessége. Egy adottság a megértésre, a tanulásra, a csodálkozásra. A problémamegoldásra irányuló szellemi tevékenységek összessége, olyan komplex képesség, amelynek részét képezi a gondolkodás gyorsasága, az összefüggések átlátására való képesség, a memória, az általános ismeretek. Az intelligencia annak a képességnek a birtoklása, mellyel szükség esetén képesek vagyunk alkalmazkodni a környezetünkhöz vagy úgy, hogy saját magunkat, vagy a környezetet változtatjuk meg, illetve ha ez nem lehetséges, akkor egy új környezetet keresünk. Ennek a viselkedésen alapuló megközelítésnek megvan az az érdeme, hogy segítségével megalapozhatjuk a kérdést: Hogyan beszélhetünk intelligenciáról a programok és gépek kapcsán? Ezt illusztrálja a Turing által javasolt, imitációs játék néven ismert kísérlet. 2.2 Turing teszt Egy bírálónak rendelkezésére áll kérdések és problémák egy halmaza, amelyeket egymás után feltehet egy tetszőleges egyénnek. A visszakapott válaszokból (és ez a bírálat egyedüli kritériuma), kell eldöntenie, az egyén intelligenciájának a mértékét. A bíráló egy szobában ül, ahonnan folyamatosan adja ki a Q 1, Q 2,... Q n kérdéseket két entitás számára, akik egy másik szobában helyezkednek el. Egyikük ember, a másik egy számítógép. Minden egyes Q i kérdésre a bíráló névtelenül két választ kap R i és S i -t. Természetesen előzetesen nem tudja, hogy ki az R és S sorozat szerzője, pontosan ez az, amit ki kell találnia. A Turing-teszt akkor tekinthető sikeresnek, ha a kérdező nem tudja a válaszok alapján egyértelműen eldönteni, hogy melyik szobában van a számítógép. Turing szerint ebben az esetben, minden okunk meglenne rá, hogy a komputert intelligensnek tekintsük. Turing javaslatai a következőek : Ha egy bizonyos számú kérdés után a korrekt azonosítás valószínűsége mindig 1/2 körül van, akkor van jogunk azt mondani, hogy egyik entitásunk éppen olyan intelligens mint a másik. Ha az embertől kapott válaszok alapján jogunk van azt állítani,
17 2.3. AZ EMBERI PROBLÉMAMEGOLDÓ GONDOLKODÁS 17 hogy intelligens viselkedést mutat, miért ne mondhatnánk ugyanezt a számítógép által adott válaszok esetében is? A kérdés tehát az, hogyan készítsünk olyan programokat és gépeket, amelyek viselkedését habozás nélkül intelligensnek minősítenénk, ha embertől származna. 2.3 Az emberi problémamegoldó gondolkodás A tudás elve szerint a problémamegoldás képessége nem az alkalmazott formalizmustól és a következtetési módszertől függ, hanem attól, hogy mennyi és milyen magasan kvalifikált ismeretanyag áll rendelkezésre az adott tárgyterület vonatkozásában. Tudásunk az általánosság foka szerint módszertani, szakterület specifikus, az adott probléma megoldására vonatkozó. Az ember még akkor sem a formális logika segítségével következtet, ha az adott probléma leírására a formális logika eszközei tökéletesen alkalmasak. Ehelyett analógiák, típuspéldák, mentális modellek alkalmazásával jutunk eredményre. A megértés a gondolatok összerendeződése, a gondolkodási séma összeállása. Itt most nem definiáljuk a gondolkodási séma fogalmát, inább néhány szinonímával segítjük megértését: sablon, pattern, mesterfogás, trükk, kötött asszociáció. 2.4 A szakmai fejlődés lépcsőfokai A laikus fejében sok lehetőség kínálkozik, a mesterében csak kevés. (Daisetz Teitaro Suzuki) Mérő László Észjárások című könyvében a szakmai fejlődés állomásait a sakkból kölcsönzött megfogalmazás szerint kezdő, haladó, mesterjelölt és nagymester fokozatokra osztja a szakmai következtetés és tudás sémák nagyságrendjének függvényében. A kezdő kevés tényszerű ismerettel rendelkezik a szakterületről, ezért hétköznapi sémákat alkalmaz. A haladó már ismer sok szakmai tényt, tudásában néhány száz
18 18 CHAPTER 2. MESTERSÉGES INTELLIGENCIA HÁTTÉR szakmai séma keveredik hétköznapi sémákkal. Ha szakemberrel konzultál, azonnal kitűnik, hogy még nem eléggé érti a szakmát. A teljesen kívülállóval is nehezen ért szót, mert a szakmai fogalmakat még nem tudja a hétköznapi szintre visszaegyszerűsíteni. A mesterjelölt lényegében elsajátította a szakma alapjait, ismer és képes alkalmazni néhány ezer szakmai sémát és különválnak a szakmai és hétköznapi sémák. Gondolkodása analitikus, a problémákat sémái segítségével lépésről lépésre oldja meg. Vitaképes és racionális. A nagymester több tízezer szakmai sémát ismer, melyek számára annyira természetesek, hogy egy részüket nem képes verbálisan kifejezni. Gondolkodása intuitív, egzakt szakmai levezetések nélkül is képes egy-egy probléma lényegére rátapintani és megoldását megtalálni. Nem szavakat, mondanivalót fogalmaz meg. 2.5 Mesterséges intelligencia Az emberi gondolkodás tanulmányozását (megérteni mi is az intelligencia), illetve e folyamatok gépen történő ábrázolásának kutatását célzó mesterséges intelligencia (MI a továbbiakban) fogalmával kapcsolatos definíciók két csoportba sorolhatóak. Az egyik megközelítés szerint az MI célja az emberi intelligencia minél jobb megismerése, annak vizsgálata, hogyan működik az agyunk, az érzékelésünk, stb. (antropomorf MI). A pragmatikus MI célja információs modell és számítógéppel végrehajtható szoftverek létrehozása, amelyek intelligens viselkedést mutatnak összetett, az ismeretek nagy mennyiségének felhasználását igénylő problémák megoldása során. Természetesen a két terület nem ellentétes egymással, sőt egymás kiegészítői lehetnek. Az alábbiakban néhány MI definíciót mutatunk meg. Elméleti és kísérleti tanulmányok az intellektuális és érzékelési folyamatokról (MI antropomorf). A számítógépnek olyan képességet adni, amellyel nehéz problémák megoldására komplex ismeretek struktúráját használni tudja (MI pragmatikus).
19 2.5. MESTERSÉGES INTELLIGENCIA 19 Az MI a számítástudomány olyan ága, amely a szimbolikus, nemalgoritmikus problémamegoldó módszerekkel foglalkozik (MI pragmatikus). A tudás megszerzésének, ábrázolásának és felhasználásának a tanulmányozása (egy kicsit mindkettő). Más megközelítés szerint csoportosítva ezen definíciókat: Az emberhez hasonlóan gondolkodni: Az MI egy izgalmas erőfeszítés a számítógépek gondolkodóvá tételére, értelemmel bíró gépek létrehozására a szó szoros értelmében (Haugenland 1985). Az MI az emberi gondolkodáshoz asszociált tevékenységek, mint a döntéshozatal, problémamegoldás, tanulás automatizálása vizsgálata (Bellman 1978). Racionálisan gondolkodni: Az MI a mentális képességek tanulmányozása számítógépes modellek segítségével (Charniak 1985). Az MI az érzékelést, gondolkodást és cselekvést lehetővé tevő számítások tanulmányozása (Winston 1992). Az emberhez hasonlóan cselekedni: Az MI olyan funkciók megvalósítására alkalmas gépek megalkotásának tudománya, mely funkciókhoz intelligenciára van szükség, amennyiben azokat emberek valósítják meg (Kurzweil 1990). Az MI annak tanulmányozása, hogyan lehet számítógéppel olyan dolgokat tenni, melyeket jelenleg az emberek jobban tudnak (Rich 1991). Racionálisan cselekedni: Az MI olyan tudományterület, amely számítási eljárásokkal próbálja magyarázni és utánozni az intelligens viselkedést (Schalkoff 1990).
20 20 CHAPTER 2. MESTERSÉGES INTELLIGENCIA HÁTTÉR Az MI a számítástudomány azon ága, mely az intelligens viselkedés automatizálásával foglalkozik (Luger 1993). 2.6 Algoritmikus megközelítés Algoritmikusan megoldható problémák Tekintsük a következő példákat: keressük meg egy másodfokú egyenlet megoldásait, találjuk meg két egész szám legnagyobb közös osztóját, határozzuk meg egy gráfban a leghosszabb utat, szereljünk össze egy kit-ben szállított műszert. Mindegyik említett esetben cselekvések egy sorozatát hajtjuk végre, amelyekről tudjuk (kevésbé fontos hogyan), hogy a várt eredményre vezetnek. Minden egyes esetben egy algoritmust alkalmazunk. Egy algoritmust azzal jellemezhetünk alapvetően, hogy rendezett cselekvésekből tevődik össze. Az informatika nagy része abból áll, hogy olyan algoritmusokat dolgoz ki, amelyeket egy számítógép végre tud hajtani. Ez az a terület, amit a későbbiekben klasszikus informatikának nevezünk. Megjegyzendő, hogy világosan meg kell különböztetni egy algoritmus elvét és egy adott problémára vonatkoztatott végrehajtását. Az algoritmus elve bonyolult elméletek alkalmazását kívánhatja meg és egy adott terület kiváló eredménye lehet. Egy algoritmus végrehajtása ellenben tisztán mechanikus, nem szükséges az elv megértése. Pl. összeszerelhetünk egy kit-ből egy oszcillátort egy csavarhúzó és egy forrasztópáka segítségével a legelemibb elektronikai alapismeretek nélkül. A másodikos gimnazista, aki a másodfokú egyenlet megoldási algoritmusát hibátlanul végrehajtja zavarba jöhet, ha megkérdezzük az algoritmus bizonyítását. Képesek korrektül végrehajtani - ez minden; ugyanezt teszi a számítógép is egy megfelelő programmal. Akár egyik, akár másik esetben nehéz lenne intelligens viselkedésről beszélni.
21 2.6. ALGORITMIKUS MEGKÖZELÍTÉS Nem algoritmikus megoldható problémák Ha az adott területen létezik egy (vagy több) algoritmus, amely(ek) minden egyes esetben ésszerű idő alatt elvezet(nek) a megoldáshoz, azt (azokat) ki kell dolgozni, be kell programozni. Ekkor belül maradunk a klasszikus informatika tárgykörén. Ám ez a kedvező helyzet távolról sem általános. Először is, vannak problémák, amelyekre noha létezik elméleti algoritmus, az a gyakorlatban nem végrehajtható, mert kombinatorikus robbanáshoz vezet. Jó példa erre a sakkjáték. Sőt létezik számos olyan terület, amelyekre egyáltalán nincs megoldó algoritmus, mi több, nem is képzelhető el, hogy valaha lesz. A nem algoritmikus területek (vagy azok amelyekre csak gyakorlatilag nem végrehajtható algoritmusok léteznek) azok, amelyeket az MI a vizsgálódásai körébe von. Ide számít az emberi cselekvések nagy többsége, beleértve a leginkább hétköznapiakat. Az esetek nagy többségében meg tudunk csinálni bizonyos dolgokat, de képtelenek vagyunk rá, hogy elmondjuk az eredményre vezető pontos eljárást. Például : megfejteni egy kézzel írt szöveget (karakterek, szavak felismerése: Alakfelismerés), hallgatni valakit aki hozzánk beszél (felismerni a hangokat, szavakat: Beszédfelismerés), megérteni egy szövegnek az értelmét (Természetes nyelvek megértése), elkészíteni egy orvosi diagnózist, bonyolult játékokat játszani, elképzelni egy matematikai tétel bizonyítását. (A könyvekben lévő bizonyításokat ellenőrizhetjük lépésről lépésre, de általában semmilyen jelzést nem találunk arra vonatkozóan hogyan találta meg a szerző a bizonyítás módszerét. Sőt néha a szerző sincs annak tudatában.) Mondhatjuk, hogy számos terület megszökik az algoritmusok elől és nem hasznosíthatja a klasszikus programozási eszközöket. Ellenben belép az MI alkalmazási területére. Elegendő csak a fenti példákat
22 22 CHAPTER 2. MESTERSÉGES INTELLIGENCIA HÁTTÉR venni ahhoz, hogy a nem-algoritmikus területek számos közös vonását felfedezzük: még a látszólag egyszerű problémák megoldásához is az ismeretek nagy mennyisége szükséges, számos ismeret alapos vizsgálatára van szüség, a lehetséges és kizárandó esetek alapos vizsgálatára van szükség, szimbólikus ismeretekkel kell manipulálni. Azt is meg kell jegyeznünk, hogy ezek a területek, amik az algoritmikus problémákon kívül esnek, olyan hétköznapi jelenségek, amelyekkel vagy valamennyien szembesülünk nap-mint nap (egy átlagos egyén el tud olvasni egy kézzel írt szöveget és általában megérti annak jelentését), vagy egy kissé szűkebb, de jól meghatározott réteg, a terület szakértője találkozik vele (az orvos képes orvosi diagnózisra, a matematikus tételbizonyításra stb.). 2.7 Az MI és a klasszikus informatika Ebben a fejezetben megpróbáljuk összegyűjteni az alapvető különbségeket a (a 2. fejezet értelmében vett) klasszikus informatika és a (pragmatikus irányzatú) MI között Alkalmazási területek klasszikus informatika Azok a területek, ahol létezik megoldási algoritmus. rendszerek, tudományos számítások, stb. Irányítási MI Nem algoritmikus területek (vagy csak a gyakorlatban nem végrehajtható algoritmusok léteznek, vagy, s ez a gyakoribb, egyáltalán nincsenek algoritmusok). Beszédfelismerés, természetes nyelv megértése, képelemzés, hiba-diagnosztika, költség-elemzés, tervezés, termelésirányítás.
23 2.7. AZ MI ÉS A KLASSZIKUS INFORMATIKA Az adatok természete klasszikus informatika numerikus adatok MI szimbolikus adatok, közülük néhány leíró jellegű, míg mások inkább következtetések levonására szolgálnak Az adatok pontossága klasszikus informatika Az adatokat pontosnak tekintjük (adott pontossággal). Ez a pontosság általában ismert. Akár mert bevitt adat, akár mert a programot végrehajtó gép által elérhető maximális pontosságról van szó. MI A szimbolikus adatok, amelyekkel dolgozunk gyakran közelítőek. Gyakran beszélünk az MI-ben nemcsak pontatlan adatokról, de az adatok bizonytalanságáról is. Ugyanakkor az ábrázolt univerzum leírása nem teljes. Ez éppúgy vonatkozik az ismeretek természetére (amiket ábrázolni akarunk), mint a választott ábrázolási modellre. Egy olyan ismeret, hogy Péter fiatal, bár megjelenésében egyszerű, már interpretálási problémát vet fel. Ha Péter 30 éves, akkor vajon fiatal-e? Elegendő-e egy kor-léptéket felállítani? A ragyog minősítésnek ugyanaz-e az értelme, ha azt állítjuk, hogy A hold ragyog, mintha A nap ragyog? Látható, hogy ismerni kell ennek a két ismeretnek a megjelenési kontextusát ahhoz, hogy válaszolhassunk a kérdésre. A közelítő jelző nem kizárólagosan a leíró adatok sajátja, előfordul a következtetéses adatoknál is. Könnyen elképzelhetjük az adatok közelítő természetéből fakadó problémákat. Milyen bizonytalanság járul egy eredményhez, ha heurisztikus szabályt alkalmazva közelítő kiindulási adatokból nyertük?
24 24 CHAPTER 2. MESTERSÉGES INTELLIGENCIA HÁTTÉR A felmerült probléma megoldása klasszikus informatika Legyen P egy probléma és C az a problémaosztály, amelyikhez P tartozik. A P probléma megoldását a P problémát jellemző numerikus adatok bevitele után a C problémaosztály algoritmusának megfelelő számítások végrehajtásával érjük el. A számítógép a problémamegoldó algoritmusok bármelyikének ideális végrehajtója (abszolút megbízhatósággal) feltéve, hogy az algoritmust korrektül programozták. MI Egy adott P probléma megoldását a P-t jellemző szimbolikus adatok végrehajtása után szimbolikus következtetés útján nyerjük. Az ismeretek természetéből adódóan nem garantált, hogy a teljes P probléma megoldható. Az ábrázolás és a következtetés használt módszereinek biztosítaniuk kell, hogy ha egy program megoldásra vezet, akkor ez biztosan elfogadható (még akkor is, ha nem optimális).
25 2.7. AZ MI ÉS A KLASSZIKUS INFORMATIKA 25 Hagyományos rendszerek MI alapú rendszerek Numerikus dolgoznak fel információkat Szimbolikus dolgoznak ismeretekkel Algoritmikus feladatmegoldás Az adatokat és algoritmusokat viszonylag könnyű megszerezni Az adatok pontosak Feladatmegoldás következtetéssel, heurisztikák alkalmazásával A tudás megszerzése összetett feladat A felhasznált tudás nem pontos, zajos, hiányos és gyakran ellentmondásos Programtesztelés a programozási nyelv adottságai alapján a fejlesztő számára Felhasználóbarát magyarázatok, indoklások generálása a program futása közben Table 2.1: A hagyományos és az MI alapú rendszerek összehasonlítása
26 26 CHAPTER 2. MESTERSÉGES INTELLIGENCIA HÁTTÉR
27 Chapter 3 Fogalmi rendszerezés 3.1 Adat, információ, ismeret fogalma A tudás, ismeret fogalmak definiálása filozófiai jellegű kérdés, mellyel nem kívánunk itt foglalkozni. Ugyanakkor definiálni kívánjuk az adat, információ és ismeret fogalmak közötti különbséget kizárólag szakmai szempontok szerint. Ez az az ok, amiért a tudás és ismeret szavak között nem teszünk különbséget, bár talán filozófiai szempontból, érzelmi alapon lehet magyarázatot találni Adat Az adat észlelt, de nem értelmezett szimbólum, jelminta, mintázat. Az adat jelentés nélküli, szintaktikai fogalom. Egy programhoz vagy egy rendszerhez kapcsolható, annak viselkedését módosítja Információ Az információ a telekommunikáció igénye szerint megjelent technikai fogalom. A fogalom hátterében hivatkozásként kódolás, dekódolás, adatátvitel, üzenetküldés állhat. Szemantikai jellegű, hiszen az adat - mint szintaktikai egység - értelmezése révén keletkezik. 27
28 28 CHAPTER 3. FOGALMI RENDSZEREZÉS Tudás vagy ismeret Az ismeret fogalma az információ felhasználásának kontextusában jelenik meg. Ez azt jelenti, hogy az ismeretet nem izoláltan értékeljük, hanem abban a környezetben, amelyben kidolgozták és interpretálták. Az ismeret ily módon önmagában nem létezik, csak az adott probléma, tárgyterület, előfordulási környezet figyelembe vételével. 3.2 A szakértő rendszer fogalma A szakirodalomban gyakran találkozunk mind a szakértő, mind a szakértői rendszer megjelöléssel. Miután nyelvtanilag mindkettő helyes, nézzük a két fogalom jelentését. A szakértői rendszer (hasonlóan vásárlói szokás, szállítói megbízás) összetételben az első szó egy célcsoportra (szakértők, vásárlók, szállítók) utal, s így azt fejezi ki, hogy ez a célcsoport birtokosa a második szónak, azaz a szakértő számára készült rendszer (a vásárlók kialakult szokása). A szakértő rendszer (hasonlóan szállító eszköz) egy jelzős szerkezet, amelyik a második szó egy tulajdonságát írja le, azaz a rendszer képes a szakértés (a jármű a szállítás) cselekvésének megvalósítására. Ebben az értelmezésben világos, hogy mi a szakértő rendszer fogalmat használjuk, hiszen olyan rendszerek készítését tűztük ki célul, amelyek a felhasználó számára egy szakterületen döntés-támogatást, szakértést biztosítanak.
29 Part II Tudásalapú, szakértő rendszerek 29
30
31 Chapter 4 Az ismeretalapú rendszerek A mesterséges intelligencia programok olyan módon oldják meg a problémákat, amit emberek esetében intelligensnek neveznénk: bonyolult problémákat oldanak meg, általában tanulnak a korábbi tapasztalatukból, megértenek természetes nyelvű közléseket, képeket értelmeznek, stb. Az ismeretalapú rendszerek (KBS - knowledge Based Systems) a problématerületet explicit módon leíró ismereteket a rendszer többi részétől elkülönített komponensben, az ismeretbázisban tárolják. Ezek esetében a feladatmegoldás nem előre beprogramozott megoldási utakra felfűzött algoritmusok révén, hanem a következtetési módszereket realizáló következtető gép által, az ismeretbázisból kiválasztott ismeretdarabkák végrehajtásával megy végbe. Az ismeretalapú rendszerek közül azokat, amelyek szakértői ismeretek felhasználásával magas szintű teljesítményt nyújtanak egy szűk problémakör kezelésében, szakértő rendszereknek (ES - expert systems) nevezzük. 4.1 Az ismeretalapú rendszerek jellemzői Szimbolikus információkkal dolgoznak. Feladatleírásuk általában deklaratív módon történik. A feladatmegoldást elfogadható következtetéssel, heurisztikák alkalmazásával valósítják meg. Az ismeretbázisba a szakértői tudást 31
32 32 CHAPTER 4. AZ ISMERETALAPÚ RENDSZEREK építik be, az ismeretszerzés bonyolult feladat. A szaktudás jellegzetesen nem-pontos, hiányos, zajos és gyakran ellentmondásos. A tudásalapú rendszerek szükségképpen tartalmaznak felhasználóbarát magyarázatot, indoklást, azért hogy a felhasználó követni tudja a feladatmegoldás elvét és elemi lépéseit. 4.2 Az emberi tudás és a szakértő rendszer összevetése Emberi szaktudás Mulandó - ha nem használjuk, elfelejtjük Nehéz átadni, reprodukálni; oktatással terjeszthető Nehéz dokumentálni Nem mindig következetes, gyakran labilis, emocionális hatásokra érzékeny Kreatív, innovatív A körülményekhez alkalmazkodik, tanul (ismeretbővítés, képesség-fejlesztés) A gondolkodási folyamatok változatosak, nehezen követhetőek Dinamikusan, a helyzethez alkalmazkodva több aspektusból vizsgálja a problémákat Az embert hétköznapi józan esze és hatalmas háttérinformáció segíti Szakértő ismeretbázisa Állandó, tartós rendszer Könnyű átvinni, reprodukálni Könnyen dokumentálható Mindig következetes, bár érzéketlen Ötlettelen, lélektelen Csak a beépített tudást hasznosítja, gépi tanulási mechanizmusok igénye A következtetési módszerek gazdagsága. Nehezen definiálhtaó, mikor melyik a célravezető Szűk technikai látószögből, csak a beépített aspektusokból képes a problémákhoz közelíteni Az elemi hétköznapi ismeretek hiánya gátolja széleskörű alkalmazhatóságát 4.3 A szakértő rendszer előnyei Pótolja a szakértő hiányt.
33 4.4. A SZAKÉRTŐ RENDSZER HÁTRÁNYAI 33 Jól követi a tárgyterület változásait. Növeli a szakértő képességét. Fokozza a szakértő produktivitását. Megőrzi a szakértelmet. Következetes megoldási módot alkalmaz. Részleges, hiányos, részben ellentmondásos adatokkal is tud dolgozni. Magyarázatot ad, indokol. 4.4 A szakértő rendszer hátrányai Ismeretei egy adott szűk tárgyterületről származnak. Nem oldható meg teljes biztonsággal a rendszer verifikálása, validálása, és hitelesítése. Válaszai nem mindig korrektek. Nincs hétköznapi józan esze, az elemi ismereteket nehéz beépíteni. Az ismeretszerzés bonyolult folyamat. A fejlesztés hosszú. A rendszer futási paraméterei gyakran nem kedvezőek. 4.5 A szakértő rendszer tudásszintje Sikerülhet-e kielégítő színvonalú szakértő rendszert létrehozni? A területnek eléggé szűknek kell lennie ahhoz, hogy a szükséges tudást jól meg lehessen ismerni.
34 34 CHAPTER 4. AZ ISMERETALAPÚ RENDSZEREK A problémának elég bonyolultnak kell lennie, hogy a szakértelemre igény mutatkozzon. Az illető területen elegendő emberi szakértő álljon rendelkezésre, akiknek a tudásából ki lehet indulni a rendszer elkészítéséhez. Fontos, hogy az emberi szakértők között a szakterület alapkérdéseinek megítélésében nagyfokú egyetértés legyen. Szükséges, hogy az adott szakterületen számos tanpélda, alapadat rendelkezésre álljon, mert csak így lehet a szakértő rendszert megbízhatóan tesztelni, tudásának korlátait meghatározni. Általában egy területen annál jobb szakértő rendszert lehet építeni, minél jobban feltördelhető az illető terület olyan részproblémákra, amelyek csak kevéssé interferálnak egymással. 4.6 Az ismeretalapú rendszerek felépítése Ismeretbázis Az adott problémakörre, tárgykörre vonatkozó specifikus ismeretek (tények, objektumok, kapcsolatok, heurisztikák) szimbolikus leírását tartalmazza valamely ismeretreprezentációs módszer szerint szervezve. Jellemzően megtalálhatók itt az adott tárgykör szakértőjének heurisztikáit megfogalmazó szabályok Következtetőgép Az adott ismeretreprezentációs módokat kiszolgáló megoldáskereső stratégia implementációja Magyarázó alrendszer A feladat megoldása közben felhasználóbarát módon tájékoztatja a felhasználót a megoldás aktuális állapotáról és megindokolja a rendszer
35 4.6. AZ ISMERETALAPÚ RENDSZEREK FELÉPÍTÉSE 35 Tudásbázis Munkamemória Következtetőgép Speciális felületek Tudásszerzés Magyarázat Tudásmérnök Felhasználói felület Végfelhasználó Table 4.1: Az ismeretalapú rendszerek felépítése
36 36 CHAPTER 4. AZ ISMERETALAPÚ RENDSZEREK javaslatát Ismeretbázis fejlesztő alrendszer Az ismeretbázis megépítéséhez, teszteléséhez, módosításához nyújt fejlesztői szolgáltatásokat. Az ismeretszerzés a rendszerépítő tudásmérnök és a tárgyterületi szakértő közötti, a szakértői ismeretek megszerzését célzó együttműködés mind a fejlesztési mind az aktualizálási fázisokban, amelynek célja az adott feladatra vonatkozó ismeretek, valamint a szakértői feladatmegoldás során alkalmazott módszerek, szabályok, eljárások forrásainak feltárása, a megszerzett ismeretek rendszerezése és formalizálása, a feladathoz illő ismeretreprezentáció és következtetési stratégia kiválasztása Felhasználói felület Végfelhasználó A rendszerrel tanácsadó partnerként konzultál. A magyarázó alrendszer által adott indoklások figyelembevételével dönt a megoldási javaslatokról. Tudásmérnök A tárgyköri ismeretek megszerzésében, az ismeretek formalizálásában jártas számítástechnikai szakember. Feladatai közé tartozik az ismeretek elrendezése, a tudás analízise, formalizálása, dokumentálása, a megfelelő fejlesztő eszköz kiválasztása, a rendszer elkészítése. Tárgyköri szakértő A tudásmérnök szakmai konzultánsa. Ő végzi a rendszer tesztelését.
37 Chapter 5 Ismeretszerzés 5.1 Ismeretszerzés célja A tudásbeszerzés több különböző technikával is végezhető, melyek mindegyike megpróbálja orvosolni azokat a problémákat, melyek felmerülnek a folyamat során. A tudás legtöbbször a szakértők fejében van, nem pedig kézzelfogható forrásokban. A szakértők óriási mennyiségű információval rendelkeznek a szakterületükön Problémát jelent a szakértők passzív tudása, azaz a szakértő nincs tisztában azzal, hogy milyen ismereteket birtokol és használ. Az igazi szakértők nehezen érhetőek el, általában elfoglalt emberek. Nincs olyan szakértő, aki mindent tudna az adott területről. Előfordulhat, hogy két ugyanazon területen dolgozó szakértőnek más-más a véleménye egy adott problémáról. Ezek fényében olyan tudásbeszerzési technikákra van szüksége, melyek csak rövid időre rabolják el a szakértőket a munkájuktól. Lehetővé teszik, hogy egyszerűen fogalmazzuk meg a tudást. Csak a rendszer szempontjából lényeges ismeretekre fókuszálnak. Lehetővé teszik a passzív tudás megragadását. Lehetővé teszik, hogy a tudást több különböző szakértőtől is beszerezhessük. Lehetővé teszik a tudás ellenőrzését és bővítését. Az ismeretszerzés a tudásalapú rendszert építő tudásmérnök és a tárgyterületi szakértő közötti, a szakértői ismeretek megszerzését célzó együttműködés. Tevékenysége kiterjed mind a fejlesztési mind az aktualizálási fázisokra. Eredményeként megvalósul 37
38 38 CHAPTER 5. ISMERETSZERZÉS az adott feladatra vonatkozó ismeretek, valamint a szakértői feladatmegoldás során alkalmazott módszerek, szabályok, eljárások forrásainak feltárása, a megszerzett ismeretek rendszerezése és formalizálása, a feladathoz illő ismeretreprezentáció és következtetési stratégia kiválasztása. 5.2 Az ismeretszerzés részterületei A szakterület ontológiája Az alkalmazási területre jellemző fogalmakat, kifejezéseket illetve a köztük fennálló kapcsolatot írja le. Ismeretbázis A logikai ismereteket tárolja a szakterület ontológiájában előforduló fogalmakra. Problemamegoldó módszerek A vezérlési stratégiákat tartalmazza (klasszifikáció, hiba diagnosztika, tervezés). A leképezés A szakterület ontológiájában szereplő fogalmakat, valamint az ismeretbázist összerendeli a probémamegoldó módszerek igényeivel Szereplők Tudásmérnök A tárgyköri ismeretek megszerzésében, az ismeretek formalizálásában jártas számítástechnikai szakember. Feladatai az ismeretek elrendezése, a tudás analízise, formalizálása, dokumentálása, a megfelelő fejlesztő eszköz kiválasztása, a rendszer elkészítése.
39 5.3. AZ ISMERETSZERZÉS NEHÉZSÉGEI 39 Tárgyköri szakértő A tudásmérnök szakmai konzultánsa és a rendszer tesztelője. Rendszerszervező Tudásbázis adminisztrátor 5.3 Az ismeretszerzés nehézségei Az ismeretszerzés közben felmerülő problémák a megfelelő szakértő megtalálása, több szakértő bevonása (együttműküdés), ütemezési kérdések, felhasználók bekapcsolása a kezdetei szakaszoktól. Leggyakrabban nem az általános elvek tisztázásával kell kezdeni, hanem a tipikus esetek, problémák, megoldások megbeszélésével. Nem szabad kényszeríteni a szakértőt a számára szokatlan formalizmusok, tudás reprezentációs módszerek használatára 5.4 A tudásmegszerzés módszerei Közvetlen (emberi segédlettel) direkt interjú, protokoll elemzés, közvetlen megfigyelés, a fogalmak hierarchikus elrendezése. indirekt A tudásmérnök pszichológiailag átgondolt feladatok elé állítja a szakértőt abból a célból, hogy a nem tudatosult tudására, annak szerveződésére következtessen.
40 40 CHAPTER 5. ISMERETSZERZÉS Automatikus módszerek Adatbányászat, adatbázisok elemzése, ok-okozati összefüggések feltárása.
41 Chapter 6 Ismeretábrázolás Az ismeretalapú rendszerek a problématerületet leíró ismereteket a rendszer többi résztől elkülönített komponensben, a tudásbázisban tárolják különféle reprezentációs technikákat alkalmazva. Akármelyik reprezentációs technikát alkalmazzuk is, szükségünk van egy leíró eszközre, a szintaxisra, a reprezentált elemek jelentését meghatározó szemantikára, valamint olyan módszerekre, amelyek lehetővé teszik a meglévő ismeretekből újabb ismeretek előállítását, azaz következtetési módszerekre. A reprezentációban megjelenő ismeretek lehetnek tényszerű, következtető és vezérlő természetűek. A reprezentációs módszerek osztályozása több szempont szerint lehetséges. A problémamegoldási stratégia megadása szerint Procedurális (algoritmikus) hogyan Deklaratív (leíró) mit A probléma leírásában szerepet játszó struktúra szerint Egyszerű (struktúra nélküli, elemi szint objektumok és azok kapcsolatai) Struktúrált (attribútummal rendelkező objektumok) Az egyik legismertebb egyszerű reprezentáció a logika alapú reprezentáció. A logikai nyelvek sokféleségében a a megoldandó probléma természetéből adódóan válogathatunk a szakértő rendszer megvalósítása során. Ebben 41
42 42 CHAPTER 6. ISMERETÁBRÁZOLÁS a könyvben azonban nem térünk ki részleteiben a logikai nyelvekre, egyedül a nem-klasszikus leíró logikákat tárgyaljuk a 7. fejezetben. Az érdeklődők könnyen találnak irodalmat a további logikai nyelvekre. Itt most csak a logikák sokféleségére utalunk az alábbi osztályozással. az adható modell szerint: klasszikus, nem-klasszikus változók szerint : zérusrendű, elsőrendű, másod-és magasabb rendű igazságértek szerint: kétértékű, véges értékű, fuzzy a feltételrendszer természete szerint: monoton, nem-monoton (modális, temporális) 6.1 Szabályalapú ismeretreprezentáció A szabályalapú ismeretreprezentáció alapgondolatának első megfogalmazása - produkciós szabályok megnevezéssel - a 40-es évekre tehető. A produkciós rendszereket az emberi problémamegoldás modellezésére Newell és Simon alkalmazták először, és mindmáig leggyakrabban alkalmazott tudásreprezentációs módszer. Kíválóan alkalmas a köznapi gondolkodás modellezésére és a szakértő tapasztalatait kifejező heurisztikák leírására. Szabályok segítségével fogalmazhatók meg a tárgyterület tényei és a közöttük fennálló relációk, a meglevő tényekből új tényeket következtető ismeretek, a feladat megoldási stratégiájának módosítására szolgáló metaismeretek. Egy szabály HA feltétel AKKOR következmény formában egy ismeretelemet reprezentál, ahol a feltétel a szabály alkalmazásának feltételeit megadó (tény)állítás, vagy ilyenekből ÉS/VAGY kapcsolókkal képzett összetett kifejezés; a következmény a szabály alkalmazásának egy vagy több következményét írja le (akciók, műveletek, tevékenységek, érvényes állítások), a munkamemória tartalmát módosító akciókat (adatelemek beírása, törlése, módosítása),
43 6.1. SZABÁLYALAPÚ ISMERETREPREZENTÁCIÓ 43 különböző eljáráshívásokat (amelyek a belső és külső környezet közötti információcserét biztosítják), a rendszer által vezérelt folyamatba történő beavatkozást (pl. egy kapcsoló bekapcsolását), a felhasználótól való információkérést. Ha a feltétel teljesül, akkor a következményben előírt tevékenységek rendre végrehajtódnak. A vezérlő komponens háromfázisú motorként működik: 1. mintaillesztéssel megkeresi azokat a szabályokat, amelyek feltételrésze a a munkamemória pillanatnyi tartalma fölött igaz, és ezeket a végrehajtásra alkalmas, ún. tüzelőképes szabályokat belehelyezi egy konfliktus halmazba; 2. kiválaszt a konfliktushalmazból egy szabályt végrehajtásra - a kiválasztásban a (beépített) vezérlési stratégiára támaszkodik; 3. alkalmazza, végrehajtja a kiválasztott szabályt, vagyis érvényesíti a szabály következményét. Közben a vezérlő komponens figyeli a célt megfogalmazó terminális feltétel bekövetkezését, amikor is a végrehajtás leáll; ellenkező esetben újra indul az 1) fázis. A 2) fázisban felhasznált szabály-kiválasztási stratégia sokféle lehet: előnyben részesülhetnek pl. a munkamemóriába legutóbb bekerült (legfrissebben beírt) adatra hivatkozó, vagy a legbonyolultabb feltételrésszel rendelkező szabályok, történhet a választás a szabályokhoz rendelt prioritás szerint Következtetési stratégiák Kétféle következtetési módszer társulhat egy szabályalapú rendszerhez. A célvezérelt következtetés egy feltételezett célállapotból kiindulva próbálja bebizonyítani azt, hogy az csakugyan célállapot, vagyis, hogy az elérhető valamely kezdőállapotból. Az adatvezérelt következtetés fordítva érvel: egy kezdőállapotból kiindulva keres valamely megoldást jelentő célállapotot.
44 44 CHAPTER 6. ISMERETÁBRÁZOLÁS Egy célvezérelt, visszafelé haladó vagy hátraláncoló rendszer egy feltételezett célállapotból visszafelé elindulva, megpróbálja a cél igazolását visszavezetni a rendszer által ismert tényekre, vagy korábban igazolt állításokra. Eközben, ha az adott cél (ill. közbülső részcél) még igazolásra szorul, a rendszer keres egy ezzel illeszthető következményű szabályt, és az annak feltételében szereplő állítások (mint részcélok) igazolására vezeti vissza a munkát. Ha eközben zsákutcába jut, visszalépést alkalmaz, és új irányban próbálkozik. (Angol terminológia: goal-directed, backward reasoning vagy backward chaining system.) Egy adatvezérelt, előrefelé haladó vagy előreláncoló rendszer a kezdőállapotból elindulva (a kiinduló adatokat a munkamemóriába helyezve), valamely célállapot elérése érdekében halad előrefelé. Mindaddig, amíg célhoz nem ér, keres egy olyan szabályt, amelynek feltétele a munkamemória pillanatnyi tartalma fölött igazolható, és végrehajtja az annak következményében leírt akció(ka)t. Amennyiben egyszerre több szabály is alkalmazható lenne, konfliktus keletkezik, melyet valamely stratégia alkalmazásával felold. (Angol terminológia: data-directed, forward reasoning vagy forward chaining system.) Mind a cél-, mind az adatvezérelt esetben a végrehajtás során maga a rendszer állítja elő azt a műveletsorozatot vagy utat (szabály-alkalmazási láncot), amely a szóban forgó kezdő- és célállapotot összeköti. A célvezérelt következtetés ciklusa Az igazolandó célt elhelyezi a részcélok halmazában. A konfliktushalmaz és a feldolgozott részcélok halmaza legyen üres, zsákutcajelzés hamis. 1. Célkiválasztás A még igazolandó részcélok közül kiválaszt egyet. Ha a részcélok halmaza üres, akkor a feladat megoldása sikeresen véget ér. Ha a zsákutca jelzés igaz, akkor
45 6.1. SZABÁLYALAPÚ ISMERETREPREZENTÁCIÓ 45 Visszalépés a legutóbb feldolgozott részcélhoz. Ha a konfliktushalmaz üres és a kiindulási célnál járunk, akkor sikertelen vége, egyébként folytatja a visszalépést. Ha a konfliktushalmaz nem üres, akkor a 2. lépést kihagyva a 3.lépésnél folytatódik a ciklus. 2. Mintaillesztés Kikeresi azokat a szabályokat, amelyek következményrésze illeszthető a kiválasztott részcélhoz. Ezek bekerülnek az adott részcél konfliktushalmazába. Ha a konfliktushalmaz üres, akkor a következtetés zsákutcába jutott, és zsákutca jelzéssel indul a következő ciklus az 1. lépéssel. 3. Konfliktusfeloldás Amennyiben a konfliktushalmazban több végrehajtható szabály van, akkor kiválaszt egyet végrehajtásra. (szabályválasztási stratégia) 4. Végrehajtás, szabályalkalmazás A kiválasztott szabály végrehajtása. Az aktuális részcél törlődik a részcélok halmazából, és bekerül a feldolgozott részcélok közé (verem). A konfliktushalmaz legyen üres és a zsákutcajelzés hamis. 5. Indítja a következő ciklust. Az adatvezérelt következtetés ciklusa A munkamemóriába betöltjük a tényeket. 1. Mintaillesztés Azok a szabályok, amelyek feltételrésze illeszthető a munkamemóriában tárolt tények valamelyikével bekerülnek a konfliktushalmazba. 2. Konfliktusfeloldás Ha a konfliktus halmaz üres, akkor sikertelenül vége. Amennyiben a konfliktushalmazban több végrehajtható szabály van, akkor kiválaszt egyet végrehajtásra. (szabályválasztási stratégia) 3. Végrehajtás, szabályalkalmazás A kiválasztott szabály végrehajtása. Ha a célt megfogalmazó terminálási feltétel teljesül, akkor sikeresen vége.
46 46 CHAPTER 6. ISMERETÁBRÁZOLÁS A B E H G C A B E H G C A B E H G C illeszt B illeszt C illeszt A igazolandó F igazolandó D HA FB AKKOR Z HA FB AKKOR Z HA FB AKKOR Z HA CD AKKOR F HA CD AKKOR F HA CD AKKOR F HA A AKKOR D HA A AKKOR D HA A AKKOR D célállítás Z Figure 6.1: célvezŕelt 4. A konfliktushalmaz legyen üres. Indítja a következő ciklust. A következtetés iránya Nézzük, milyen szempontokat kell figyelembe vennünk, amikor az adatvezérelt és célvezérelt stratégiák között választunk. Meg kell gondolni, hogy miből van több, lehetséges kezdő állapotból vagy célállapotból. Célszerűbb a kisebb halmazból kiindulva a másik irányba haladva keresni a megoldást. Nyilvánvaló például, hogy könnyebb egy kevéssé ismert környékről autóval hazavezetni, mint fordítva, otthonról eljutni egy ismeretlen helyre. Noha fizikailag egy kiinduló állapot és egy célállapot van a feladatban, az első esetben a célállapottal (otthonunkkal) egyenértékűnek vehető minden olyan hely, ahonnan már tudjuk az utat haza. Itt célszerűbb a célvezérelt következtetést választani. Ellenben, ha a szimbolikus integrálás problémájánál egy adott formulához keressük azt
47 6.1. SZABÁLYALAPÚ ISMERETREPREZENTÁCIÓ 47 A B A B A B A B E E E H E H G H G H G G C C D C C D D F F Z illeszt illeszt illeszt HA FB AKKOR Z HA FB AKKOR Z HA FB AKKOR Z HA CD AKKOR F HA CD AKKOR F HA CD AKKOR F HA A AKKOR D HA A AKKOR D HA A AKKOR D célállítás Z Figure 6.2: adatvezérelt a formulát, amely nem tartalmaz integráljelet és ekvivalens a kiinduló formula integráljával, akkor reménytelen lenne a szóba jövő nagyszámú célformula mindegyikéből kiindulva vizsgálni, hogy differenciálási szabályokkal eljutunk-e a kiinduló formulához. Itt az előrehaladó (adatvezérelt) alkalmazás a megfelelő. Figyelembe kell venni, hogy melyik irányban nagyobb az elágazási tényező az állapottéren. Célszerűbb azt az irányt választani, amely mentén kisebb ez a szám. Ha egy matematikai tétel bizonyítása a feladat, akkor ehhez a kiindulást az adott terület néhány axiómája jelenti. Ebből a néhány axiómából általában nagy számú tétel vezethető le. Az egyes tételekből viszont általában nem lehet nagyszámú útvonalon visszajutni az axiómákhoz. Itt az elágazási tényező előre haladva jóval nagyobb, így a visszafelé haladó következtetés lehet célszerűbb. Figyelembe kell venni azt is, hogy a következtetést végző programnak meg kell-e magyaráznia egyes lépéseit. Ha igen, akkor
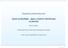
Bizonyossági tényező az M1-ben bizonyossági faktor cf [0,100] cf=100 teljes bizonyosság cf=20 a hihetőség alsó küszöbe cf=0 teljesen elvetve
![Bizonyossági tényező az M1-ben bizonyossági faktor cf [0,100] cf=100 teljes bizonyosság cf=20 a hihetőség alsó küszöbe cf=0 teljesen elvetve Bizonyossági tényező az M1-ben bizonyossági faktor cf [0,100] cf=100 teljes bizonyosság cf=20 a hihetőség alsó küszöbe cf=0 teljesen elvetve](/thumbs/52/29386275.jpg) 1. HOGYAN ALKALMAZHATÓ SZABÁLY ALAPÚ RENDSZEREKBEN A BIZONYTALANSÁGKEZELÉS HEURISZTIKUS MODELLJE? Szabályalapú rendszerekben az ismeretek HA feltétel AKKOR következmény alakúak Bizonytalanság kezelése
1. HOGYAN ALKALMAZHATÓ SZABÁLY ALAPÚ RENDSZEREKBEN A BIZONYTALANSÁGKEZELÉS HEURISZTIKUS MODELLJE? Szabályalapú rendszerekben az ismeretek HA feltétel AKKOR következmény alakúak Bizonytalanság kezelése
Szakértői rendszerek bemutatása. Haindrich Henrietta
 Szakértői rendszerek bemutatása Haindrich Henrietta Mi a szakértő rendszer? Ismeretalapú rendszer (KBS:Knowledge-Based System): a rendelkezésére álló információkból bizonyos keresési stratégia szerint
Szakértői rendszerek bemutatása Haindrich Henrietta Mi a szakértő rendszer? Ismeretalapú rendszer (KBS:Knowledge-Based System): a rendelkezésére álló információkból bizonyos keresési stratégia szerint
Mesterséges Intelligencia. Csató Lehel. Csató Lehel. Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 2007/2008
 Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 007/008 Az Előadások Témái Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció i stratégiák Szemantikus hálók / Keretrendszerek
Matematika-Informatika Tanszék Babeş Bolyai Tudományegyetem, Kolozsvár 007/008 Az Előadások Témái Bevezető: mi a mesterséges intelligencia... Tudás reprezentáció i stratégiák Szemantikus hálók / Keretrendszerek
Intelligens Rendszerek Elmélete. Tudásalapú technikák Szakértői és döntéstámogató rendszerek
 Intelligens Rendszerek Elmélete Dr. Kutor László Tudásalapú technikák Szakértői és döntéstámogató rendszerek http://mobil.nik.bmf.hu/tantargyak/ire.html Login név: ire jelszó: IRE07 IRE 6/1 A megadott
Intelligens Rendszerek Elmélete Dr. Kutor László Tudásalapú technikák Szakértői és döntéstámogató rendszerek http://mobil.nik.bmf.hu/tantargyak/ire.html Login név: ire jelszó: IRE07 IRE 6/1 A megadott
VII. Keretalapú ismeretábrázolás
 Collins és Quillian kísérlete VII. Keretalapú ismeretábrázolás Tud-e a kanári énekelni? 1.3 mp Képes-e a kanári? 1.4 mp Van-e a kanárinak bőre? 1.5 mp A kanári egy kanári? 1.0 mp A kanári egy madár? 1.2
Collins és Quillian kísérlete VII. Keretalapú ismeretábrázolás Tud-e a kanári énekelni? 1.3 mp Képes-e a kanári? 1.4 mp Van-e a kanárinak bőre? 1.5 mp A kanári egy kanári? 1.0 mp A kanári egy madár? 1.2
Intelligens partner rendszer virtuális kórházi osztály megvalósításához
 Intelligens partner rendszer virtuális kórházi osztály megvalósításához 1. Célkitűzések A pályázat célja egy virtuális immunológiai osztály kialakítása, amelynek segítségével a különböző betegségekkel
Intelligens partner rendszer virtuális kórházi osztály megvalósításához 1. Célkitűzések A pályázat célja egy virtuális immunológiai osztály kialakítása, amelynek segítségével a különböző betegségekkel
Contents. 1 Bevezetés 11
 2 Contents I Fogalmi háttér 9 1 Bevezetés 11 2 Mesterséges Intelligencia háttér 15 2.1 Intelligencia és intelligens viselkedés............ 15 2.2 Turing teszt......................... 16 2.3 Az emberi
2 Contents I Fogalmi háttér 9 1 Bevezetés 11 2 Mesterséges Intelligencia háttér 15 2.1 Intelligencia és intelligens viselkedés............ 15 2.2 Turing teszt......................... 16 2.3 Az emberi
PROGRAMTERVEZŐ INFORMATIKUS ALAPKÉPZÉSI SZAK
 PROGRAMTERVEZŐ INFORMATIKUS ALAPKÉPZÉSI SZAK 1. Az alapképzési szak megnevezése: programtervező informatikus (Computer Science) 2. Az alapképzési szakon szerezhető végzettségi szint és a szakképzettség
PROGRAMTERVEZŐ INFORMATIKUS ALAPKÉPZÉSI SZAK 1. Az alapképzési szak megnevezése: programtervező informatikus (Computer Science) 2. Az alapképzési szakon szerezhető végzettségi szint és a szakképzettség
Szakterületi modell A fogalmak megjelenítése. 9. fejezet Applying UML and Patterns Craig Larman
 Szakterületi modell A fogalmak megjelenítése 9. fejezet Applying UML and Patterns Craig Larman 1 Néhány megjegyzés a diagramokhoz Ez a tárgy a rendszer elemzésről és modellezésről szól. Noha például egy
Szakterületi modell A fogalmak megjelenítése 9. fejezet Applying UML and Patterns Craig Larman 1 Néhány megjegyzés a diagramokhoz Ez a tárgy a rendszer elemzésről és modellezésről szól. Noha például egy
Bevezetés az informatikába
 Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
S0-02 Típusmodellek (Programozás elmélet)
 S0-02 Típusmodellek (Programozás elmélet) Tartalom 1. Absztrakt adattípus 2. Adattípus specifikációja 3. Adattípus osztály 4. Paraméterátadás 5. Reprezentációs függvény 6. Öröklődés és polimorfizmus 7.
S0-02 Típusmodellek (Programozás elmélet) Tartalom 1. Absztrakt adattípus 2. Adattípus specifikációja 3. Adattípus osztály 4. Paraméterátadás 5. Reprezentációs függvény 6. Öröklődés és polimorfizmus 7.
Ismeretalapú rendszerek tervezése, ismeretszerzés, ismeretalapú rendszerek fejlesztése
 Ismeretalapú rendszerek tervezése, ismeretszerzés, ismeretalapú rendszerek fejlesztése Takács Eszter Magdolna DFSVDK Mesterséges intelligencia, szakértői rendszerek VEMISAM254M Utolsó módosítás: 2013.
Ismeretalapú rendszerek tervezése, ismeretszerzés, ismeretalapú rendszerek fejlesztése Takács Eszter Magdolna DFSVDK Mesterséges intelligencia, szakértői rendszerek VEMISAM254M Utolsó módosítás: 2013.
Méréselmélet MI BSc 1
 Mérés és s modellezés 2008.02.15. 1 Méréselmélet - bevezetés a mérnöki problémamegoldás menete 1. A probléma kitűzése 2. A hipotézis felállítása 3. Kísérlettervezés 4. Megfigyelések elvégzése 5. Adatok
Mérés és s modellezés 2008.02.15. 1 Méréselmélet - bevezetés a mérnöki problémamegoldás menete 1. A probléma kitűzése 2. A hipotézis felállítása 3. Kísérlettervezés 4. Megfigyelések elvégzése 5. Adatok
- Adat, információ, tudás definíciói, összefüggéseik reprezentációtípusok Részletesebben a téma az AI alapjai című tárgyban
 I. Intelligens tervezőrendszerek - Adat, információ, tudás definíciói, összefüggéseik reprezentációtípusok Részletesebben a téma az AI alapjai című tárgyban Adat = struktúrálatlan tények, amelyek tárolhatók,
I. Intelligens tervezőrendszerek - Adat, információ, tudás definíciói, összefüggéseik reprezentációtípusok Részletesebben a téma az AI alapjai című tárgyban Adat = struktúrálatlan tények, amelyek tárolhatók,
Ember-gép rendszerek megbízhatóságának pszichológiai vizsgálata. A Rasmussen modell.
 Ember-gép rendszerek megbízhatóságának pszichológiai vizsgálata. A Rasmussen modell. A bonyolult rendszerek működtetésének biztonsága egyre pontosabb, naprakész gondolati, beavatkozási sémákat igényel
Ember-gép rendszerek megbízhatóságának pszichológiai vizsgálata. A Rasmussen modell. A bonyolult rendszerek működtetésének biztonsága egyre pontosabb, naprakész gondolati, beavatkozási sémákat igényel
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 1 I. HALmAZOk 1. JELÖLÉSEk A halmaz fogalmát tulajdonságait gyakran használjuk a matematikában. A halmazt nem definiáljuk, ezt alapfogalomnak tekintjük. Ez nem szokatlan, hiszen
KOVÁCS BÉLA, MATEmATIkA I. 1 I. HALmAZOk 1. JELÖLÉSEk A halmaz fogalmát tulajdonságait gyakran használjuk a matematikában. A halmazt nem definiáljuk, ezt alapfogalomnak tekintjük. Ez nem szokatlan, hiszen
Struktúra nélküli adatszerkezetek
 Struktúra nélküli adatszerkezetek Homogén adatszerkezetek (minden adatelem azonos típusú) osztályozása Struktúra nélküli (Nincs kapcsolat az adatelemek között.) Halmaz Multihalmaz Asszociatív 20:24 1 A
Struktúra nélküli adatszerkezetek Homogén adatszerkezetek (minden adatelem azonos típusú) osztályozása Struktúra nélküli (Nincs kapcsolat az adatelemek között.) Halmaz Multihalmaz Asszociatív 20:24 1 A
Összeállította Horváth László egyetemi tanár
 Óbudai Egyetem Neumann János Informatikai Kar Intelligens Mérnöki Rendszerek Intézet Intelligens Mérnöki Rendszerek Szakirány a Mérnök informatikus alapszakon Összeállította Horváth László Budapest, 2011
Óbudai Egyetem Neumann János Informatikai Kar Intelligens Mérnöki Rendszerek Intézet Intelligens Mérnöki Rendszerek Szakirány a Mérnök informatikus alapszakon Összeállította Horváth László Budapest, 2011
S atisztika 2. előadás
 Statisztika 2. előadás 4. lépés Terepmunka vagy adatgyűjtés Kutatási módszerek osztályozása Kutatási módszer Feltáró kutatás Következtető kutatás Leíró kutatás Ok-okozati kutatás Keresztmetszeti kutatás
Statisztika 2. előadás 4. lépés Terepmunka vagy adatgyűjtés Kutatási módszerek osztályozása Kutatási módszer Feltáró kutatás Következtető kutatás Leíró kutatás Ok-okozati kutatás Keresztmetszeti kutatás
OOP. Alapelvek Elek Tibor
 OOP Alapelvek Elek Tibor OOP szemlélet Az OOP szemlélete szerint: a valóságot objektumok halmazaként tekintjük. Ezen objektumok egymással kapcsolatban vannak és együttműködnek. Program készítés: Absztrakciós
OOP Alapelvek Elek Tibor OOP szemlélet Az OOP szemlélete szerint: a valóságot objektumok halmazaként tekintjük. Ezen objektumok egymással kapcsolatban vannak és együttműködnek. Program készítés: Absztrakciós
Fogalmi modellezés. Ontológiák Alkalmazott modellező módszertan (UML)
 Fogalmi modellezés Ontológiák Alkalmazott modellező módszertan (UML) Fogalom képzés / kialakítás Cél: Példák: A fogalom képzés segít minket abban, hogy figyelmen kívül hagyjuk azt, ami lényegtelen idealizált
Fogalmi modellezés Ontológiák Alkalmazott modellező módszertan (UML) Fogalom képzés / kialakítás Cél: Példák: A fogalom képzés segít minket abban, hogy figyelmen kívül hagyjuk azt, ami lényegtelen idealizált
GONDOLKODÁS ÉS NYELV
 GONDOLKODÁS ÉS NYELV GONDOLKODÁS A. Propozicionális B. Képzeleti Propozicionális gondolkodás Propozíció kijelentés, amely egy tényállásra vonatkozik, meghatározott viszonyban összekombinált fogalmakból
GONDOLKODÁS ÉS NYELV GONDOLKODÁS A. Propozicionális B. Képzeleti Propozicionális gondolkodás Propozíció kijelentés, amely egy tényállásra vonatkozik, meghatározott viszonyban összekombinált fogalmakból
Mérés és modellezés 1
 Mérés és modellezés 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni kell
Mérés és modellezés 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni kell
Alkalmazásokban. Dezsényi Csaba Ovitas Magyarország kft.
 Tudásmodellezés Kereskedelmi Alkalmazásokban Dezsényi Csaba Ovitas Magyarország kft. Tudásmenedzsment Adat -> Információ -> Tudás Intézményi tudásvagyon hatékony kezelése az üzleti célok megvalósításának
Tudásmodellezés Kereskedelmi Alkalmazásokban Dezsényi Csaba Ovitas Magyarország kft. Tudásmenedzsment Adat -> Információ -> Tudás Intézményi tudásvagyon hatékony kezelése az üzleti célok megvalósításának
Nagyméretű adathalmazok kezelése (BMEVISZM144) Reinhardt Gábor április 5.
 Asszociációs szabályok Budapesti Műszaki- és Gazdaságtudományi Egyetem 2012. április 5. Tartalom 1 2 3 4 5 6 7 ismétlés A feladat Gyakran együtt vásárolt termékek meghatározása Tanultunk rá hatékony algoritmusokat
Asszociációs szabályok Budapesti Műszaki- és Gazdaságtudományi Egyetem 2012. április 5. Tartalom 1 2 3 4 5 6 7 ismétlés A feladat Gyakran együtt vásárolt termékek meghatározása Tanultunk rá hatékony algoritmusokat
Predikátumkalkulus. 1. Bevezet. 2. Predikátumkalkulus, formalizálás. Predikátumkalkulus alapfogalmai, formalizálás, tagadás, logikailag igaz formulák.
 Predikátumkalkulus Predikátumkalkulus alapfogalmai, formalizálás, tagadás, logikailag igaz formulák. 1. Bevezet Nézzük meg a következ két kijelentést: Minden almához tartozik egy fa, amir l leesett. Bármely
Predikátumkalkulus Predikátumkalkulus alapfogalmai, formalizálás, tagadás, logikailag igaz formulák. 1. Bevezet Nézzük meg a következ két kijelentést: Minden almához tartozik egy fa, amir l leesett. Bármely
Adatbázismodellek. 1. ábra Hierarchikus modell
 Eddig az adatbázisokkal általános szempontból foglalkoztunk: mire valók, milyen elemekből épülnek fel. Ennek során tisztáztuk, hogy létezik az adatbázis fogalmi modellje (adatbázisterv), amely az egyedek,
Eddig az adatbázisokkal általános szempontból foglalkoztunk: mire valók, milyen elemekből épülnek fel. Ennek során tisztáztuk, hogy létezik az adatbázis fogalmi modellje (adatbázisterv), amely az egyedek,
Mesterséges Intelligencia MI
 Mesterséges Intelligencia MI Tudásbázis építése Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade A tudásbázis építése
Mesterséges Intelligencia MI Tudásbázis építése Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade A tudásbázis építése
ÍTÉLETKALKULUS (NULLADRENDŰ LOGIKA)
 ÍTÉLETKALKULUS SZINTAXIS ÍTÉLETKALKULUS (NULLADRENDŰ LOGIKA) jelkészlet elválasztó jelek: ( ) logikai műveleti jelek: ítéletváltozók (logikai változók): p, q, r,... ítéletkonstansok: T, F szintaxis szabályai
ÍTÉLETKALKULUS SZINTAXIS ÍTÉLETKALKULUS (NULLADRENDŰ LOGIKA) jelkészlet elválasztó jelek: ( ) logikai műveleti jelek: ítéletváltozók (logikai változók): p, q, r,... ítéletkonstansok: T, F szintaxis szabályai
Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé.
 HA 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) HA 2 Halmazok HA 3 Megjegyzések A halmaz, az elem és az eleme fogalmakat nem definiáljuk, hanem alapfogalmaknak
HA 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) HA 2 Halmazok HA 3 Megjegyzések A halmaz, az elem és az eleme fogalmakat nem definiáljuk, hanem alapfogalmaknak
Átlag (standard hiba)
 Képességpont A képességpont valószínűségi modellel számított érték, amely a tanuló teszten elért eredményét egy mesterséges, a matematikai eszköztudást, illetve szövegértési képességet jelképező skálára
Képességpont A képességpont valószínűségi modellel számított érték, amely a tanuló teszten elért eredményét egy mesterséges, a matematikai eszköztudást, illetve szövegértési képességet jelképező skálára
Vezetői információs rendszerek
 Vezetői információs rendszerek Kiadott anyag: Vállalat és információk Elekes Edit, 2015. E-mail: elekes.edit@eng.unideb.hu Anyagok: eng.unideb.hu/userdir/vezetoi_inf_rd 1 A vállalat, mint információs rendszer
Vezetői információs rendszerek Kiadott anyag: Vállalat és információk Elekes Edit, 2015. E-mail: elekes.edit@eng.unideb.hu Anyagok: eng.unideb.hu/userdir/vezetoi_inf_rd 1 A vállalat, mint információs rendszer
Számítógépes döntéstámogatás. Döntések fuzzy környezetben Közelítő következtetések
 BLSZM-09 p. 1/17 Számítógépes döntéstámogatás Döntések fuzzy környezetben Közelítő következtetések Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu
BLSZM-09 p. 1/17 Számítógépes döntéstámogatás Döntések fuzzy környezetben Közelítő következtetések Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu
Logikai ágensek. Mesterséges intelligencia március 21.
 Logikai ágensek Mesterséges intelligencia 2014. március 21. Bevezetés Eddigi példák tudásra: állapotok halmaza, lehetséges operátorok, ezek költségei, heurisztikák Feltételezés: a világ (lehetséges állapotok
Logikai ágensek Mesterséges intelligencia 2014. március 21. Bevezetés Eddigi példák tudásra: állapotok halmaza, lehetséges operátorok, ezek költségei, heurisztikák Feltételezés: a világ (lehetséges állapotok
12.3. Az automatizált technológiai tervezés módszerei A variáns módszer
 12.3. Az automatizált technológiai tervezés módszerei A technológiai tudás és a tervezési feladat egymáshoz rendeltetését, a feladatok típusait, a tervezési műveleteket, a megoldások környezetfüggőségét
12.3. Az automatizált technológiai tervezés módszerei A technológiai tudás és a tervezési feladat egymáshoz rendeltetését, a feladatok típusait, a tervezési műveleteket, a megoldások környezetfüggőségét
Intelligens Rendszerek Elmélete
 Intelligens Rendszerek Elmélete 9 IRE 8/30/1 Tudásalapú technikák, szakértői és döntéstámogató rendszerek http://uni-obuda.hu/users/kutor/ IRE 8/30/2 Tudásalapú rendszerek Olyan számítógépes rendszerek,
Intelligens Rendszerek Elmélete 9 IRE 8/30/1 Tudásalapú technikák, szakértői és döntéstámogató rendszerek http://uni-obuda.hu/users/kutor/ IRE 8/30/2 Tudásalapú rendszerek Olyan számítógépes rendszerek,
Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 1
 Halmazok 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 2 A fejezet legfontosabb elemei Halmaz megadási módjai Halmazok közti műveletek (metszet,
Halmazok 1 Mindent olyan egyszerűvé kell tenni, amennyire csak lehet, de nem egyszerűbbé. (Albert Einstein) Halmazok 2 A fejezet legfontosabb elemei Halmaz megadási módjai Halmazok közti műveletek (metszet,
Intelligens Rendszerek Elmélete
 Intelligens Rendszerek Elmélete 8 Tudásalapú technikák, szakértői és döntéstámogató rendszerek http://uni-obuda.hu/users/kutor/ IRE 8/30/1 IRE 8/30/2 A TUDÁS ELVE Tudásalapú rendszerek A feladatmegoldás
Intelligens Rendszerek Elmélete 8 Tudásalapú technikák, szakértői és döntéstámogató rendszerek http://uni-obuda.hu/users/kutor/ IRE 8/30/1 IRE 8/30/2 A TUDÁS ELVE Tudásalapú rendszerek A feladatmegoldás
Adatbázis rendszerek 6.. 6. 1.1. Definíciók:
 Adatbázis Rendszerek Budapesti Műszaki és Gazdaságtudományi Egyetem Fotogrammetria és Térinformatika 6.1. Egyed relációs modell lényegi jellemzői 6.2. Egyed relációs ábrázolás 6.3. Az egyedtípus 6.4. A
Adatbázis Rendszerek Budapesti Műszaki és Gazdaságtudományi Egyetem Fotogrammetria és Térinformatika 6.1. Egyed relációs modell lényegi jellemzői 6.2. Egyed relációs ábrázolás 6.3. Az egyedtípus 6.4. A
Dunaújvárosi Főiskola Informatikai Intézet. Intelligens ágensek. Dr. Seebauer Márta. főiskolai tanár
 Dunaújvárosi Főiskola Informatikai Intézet Intelligens ágensek Dr. Seebauer Márta főiskolai tanár seebauer.marta@szgti.bmf.hu Ágens Ágens (agent) bármi lehet, amit úgy tekinthetünk, hogy érzékelők (sensors)
Dunaújvárosi Főiskola Informatikai Intézet Intelligens ágensek Dr. Seebauer Márta főiskolai tanár seebauer.marta@szgti.bmf.hu Ágens Ágens (agent) bármi lehet, amit úgy tekinthetünk, hogy érzékelők (sensors)
Az Országos kompetenciamérés (OKM) tartalmi kerete. a 20/2012. (VIII. 31.) EMMI rendelet 3. melléklete alapján
 Az Országos kompetenciamérés (OKM) tartalmi kerete a 20/2012. (VIII. 31.) EMMI rendelet 3. melléklete alapján Az OKM tartalmi keret Célja: definiálja azokat a tényezőket és szempontrendszereket, amelyek
Az Országos kompetenciamérés (OKM) tartalmi kerete a 20/2012. (VIII. 31.) EMMI rendelet 3. melléklete alapján Az OKM tartalmi keret Célja: definiálja azokat a tényezőket és szempontrendszereket, amelyek
Mesterséges Intelligencia MI
 Mesterséges Intelligencia MI Problémamegoldás kereséssel ha sötétben tapogatózunk Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade
Mesterséges Intelligencia MI Problémamegoldás kereséssel ha sötétben tapogatózunk Dobrowiecki Tadeusz Eredics Péter, és mások BME I.E. 437, 463-28-99 dobrowiecki@mit.bme.hu, http://www.mit.bme.hu/general/staff/tade
Problémamegoldás kereséssel. Mesterséges intelligencia március 7.
 Problémamegoldás kereséssel Mesterséges intelligencia 2014. március 7. Bevezetés Problémamegoldó ágens Kívánt állapotba vezető cselekvéseket keres Probléma megfogalmazása Megoldás megfogalmazása Keresési
Problémamegoldás kereséssel Mesterséges intelligencia 2014. március 7. Bevezetés Problémamegoldó ágens Kívánt állapotba vezető cselekvéseket keres Probléma megfogalmazása Megoldás megfogalmazása Keresési
Interaktív, grafikus környezet. Magasszintû alkalmazási nyelv (KAL) Integrált grafikus interface könyvtár. Intelligens kapcsolat más szoftverekkel
 Készítette: Szabó Gábor, 1996 Az Az IntelliCorp IntelliCorp stratégiája: stratégiája: Kifinomult, Kifinomult, objektum-orientált objektum-orientált környezetet környezetet biztosít biztosít tervezéséhez,
Készítette: Szabó Gábor, 1996 Az Az IntelliCorp IntelliCorp stratégiája: stratégiája: Kifinomult, Kifinomult, objektum-orientált objektum-orientált környezetet környezetet biztosít biztosít tervezéséhez,
22. GRÁFOK ÁBRÁZOLÁSA
 22. GRÁFOK ÁBRÁZOLÁSA A megoldandó feladatok, problémák modellezése során sokszor gráfokat alkalmazunk. A gráf fogalmát a matematikából ismertnek vehetjük. A modellezés során a gráfok több változata is
22. GRÁFOK ÁBRÁZOLÁSA A megoldandó feladatok, problémák modellezése során sokszor gráfokat alkalmazunk. A gráf fogalmát a matematikából ismertnek vehetjük. A modellezés során a gráfok több változata is
Matematikai modellezés
 Matematikai modellezés Bevezető A diasorozat a Döntési modellek című könyvhöz készült. Készítette: Dr. Ábrahám István Döntési folyamatok matematikai modellezése Az emberi tevékenységben meghatározó szerepe
Matematikai modellezés Bevezető A diasorozat a Döntési modellek című könyvhöz készült. Készítette: Dr. Ábrahám István Döntési folyamatok matematikai modellezése Az emberi tevékenységben meghatározó szerepe
KERESKEDELMI ÉS MARKETING ALAPISMERETEK ÉRETTSÉGI VIZSGA II. A VIZSGA LEÍRÁSA
 KERESKEDELMI ÉS MARKETING ALAPISMERETEK ÉRETTSÉGI VIZSGA A vizsga részei II. A VIZSGA LEÍRÁSA Középszint Emelt szint 180 perc 15 perc 180 perc 20 perc 100 pont 50 pont 100 pont 50 pont A vizsgán használható
KERESKEDELMI ÉS MARKETING ALAPISMERETEK ÉRETTSÉGI VIZSGA A vizsga részei II. A VIZSGA LEÍRÁSA Középszint Emelt szint 180 perc 15 perc 180 perc 20 perc 100 pont 50 pont 100 pont 50 pont A vizsgán használható
Önálló labor feladatkiírásaim tavasz
 Önálló labor feladatkiírásaim 2016. tavasz (ezekhez kapcsolódó saját témával is megkereshetnek) Mészáros Tamás http://www.mit.bme.hu/~meszaros/ Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika
Önálló labor feladatkiírásaim 2016. tavasz (ezekhez kapcsolódó saját témával is megkereshetnek) Mészáros Tamás http://www.mit.bme.hu/~meszaros/ Budapesti Műszaki és Gazdaságtudományi Egyetem Méréstechnika
Rekurzió. Dr. Iványi Péter
 Rekurzió Dr. Iványi Péter 1 Függvényhívás void f3(int a3) { printf( %d,a3); } void f2(int a2) { f3(a2); a2 = (a2+1); } void f1() { int a1 = 1; int b1; b1 = f2(a1); } 2 Függvényhívás void f3(int a3) { printf(
Rekurzió Dr. Iványi Péter 1 Függvényhívás void f3(int a3) { printf( %d,a3); } void f2(int a2) { f3(a2); a2 = (a2+1); } void f1() { int a1 = 1; int b1; b1 = f2(a1); } 2 Függvényhívás void f3(int a3) { printf(
Számítógépes döntéstámogatás. Fogalmakat is kezelni tudó számítógépes döntéstámogatás A DoctuS rendszer
 SZDT-07 p. 1/20 Számítógépes döntéstámogatás Fogalmakat is kezelni tudó számítógépes döntéstámogatás A DoctuS rendszer Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu
SZDT-07 p. 1/20 Számítógépes döntéstámogatás Fogalmakat is kezelni tudó számítógépes döntéstámogatás A DoctuS rendszer Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu
PIACKUTATÁS (MARKETINGKUTATÁS)
 PIACKUTATÁS (MARKETINGKUTATÁS). FŐBB PONTOK A kutatási terv fogalmának meghatározása, a különböző kutatási módszerek osztályozása, a feltáró és a következtető kutatási módszerek közötti különbségtétel
PIACKUTATÁS (MARKETINGKUTATÁS). FŐBB PONTOK A kutatási terv fogalmának meghatározása, a különböző kutatási módszerek osztályozása, a feltáró és a következtető kutatási módszerek közötti különbségtétel
Logika es sz am ıt aselm elet I. r esz Logika 1/36
 1/36 Logika és számításelmélet I. rész Logika 2/36 Elérhetőségek Tejfel Máté Déli épület, 2.606 matej@inf.elte.hu http://matej.web.elte.hu Tankönyv 3/36 Tartalom 4/36 Bevezető fogalmak Ítéletlogika Ítéletlogika
1/36 Logika és számításelmélet I. rész Logika 2/36 Elérhetőségek Tejfel Máté Déli épület, 2.606 matej@inf.elte.hu http://matej.web.elte.hu Tankönyv 3/36 Tartalom 4/36 Bevezető fogalmak Ítéletlogika Ítéletlogika
Számítógép architektúra
 Budapesti Műszaki Főiskola Regionális Oktatási és Innovációs Központ Székesfehérvár Számítógép architektúra Dr. Seebauer Márta főiskolai tanár seebauer.marta@roik.bmf.hu Irodalmi források Cserny L.: Számítógépek
Budapesti Műszaki Főiskola Regionális Oktatási és Innovációs Központ Székesfehérvár Számítógép architektúra Dr. Seebauer Márta főiskolai tanár seebauer.marta@roik.bmf.hu Irodalmi források Cserny L.: Számítógépek
A SIKER KOVÁCSA, VAGY A KUDARC KÓDJA?
 A SIKER KOVÁCSA, VAGY A KUDARC KÓDJA? A döntéshozatali tudatosság hiányosságai és lehetőségei a projekt menedzsmentben Török L. Gábor PhD Sikeres és sikertelen projektek arányai PMI nemzetközi felmérés
A SIKER KOVÁCSA, VAGY A KUDARC KÓDJA? A döntéshozatali tudatosság hiányosságai és lehetőségei a projekt menedzsmentben Török L. Gábor PhD Sikeres és sikertelen projektek arányai PMI nemzetközi felmérés
Mi a mesterséges intelligencia? Történeti áttekintés. Mesterséges intelligencia február 21.
 Mi a mesterséges intelligencia? Történeti áttekintés Mesterséges intelligencia 2014. február 21. Bevezetés Homo sapiens = gondolkodó ember Gondolkodás mint az emberi faj sajátja Hogyan gondolkozunk? Hogyan
Mi a mesterséges intelligencia? Történeti áttekintés Mesterséges intelligencia 2014. február 21. Bevezetés Homo sapiens = gondolkodó ember Gondolkodás mint az emberi faj sajátja Hogyan gondolkozunk? Hogyan
INFORMÁCI CIÓS ERŐFORRÁSOK ÉS RENDSZEREK
 INFORMÁCI CIÓS ERŐFORRÁSOK ÉS INFORMÁCI CIÓS RENDSZEREK Milyen ismereteket sajátítunk tunk el e téma keretében? Adat Információ Tudás Az információ mint stratégiai erőforrás A vállalat információs rendszere
INFORMÁCI CIÓS ERŐFORRÁSOK ÉS INFORMÁCI CIÓS RENDSZEREK Milyen ismereteket sajátítunk tunk el e téma keretében? Adat Információ Tudás Az információ mint stratégiai erőforrás A vállalat információs rendszere
Mérés és modellezés Méréstechnika VM, GM, MM 1
 Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
Mérés és modellezés 2008.02.04. 1 Mérés és modellezés A mérnöki tevékenység alapeleme a mérés. A mérés célja valamely jelenség megismerése, vizsgálata. A mérés tervszerűen végzett tevékenység: azaz rögzíteni
Feladataink, kötelességeink, önkéntes és szabadidős tevékenységeink elvégzése, a közösségi életformák gyakorlása döntések sorozatából tevődik össze.
 INFORMATIKA Az informatika tantárgy ismeretkörei, fejlesztési területei hozzájárulnak ahhoz, hogy a tanuló az információs társadalom aktív tagjává válhasson. Az informatikai eszközök használata olyan eszköztudást
INFORMATIKA Az informatika tantárgy ismeretkörei, fejlesztési területei hozzájárulnak ahhoz, hogy a tanuló az információs társadalom aktív tagjává válhasson. Az informatikai eszközök használata olyan eszköztudást
Bevezetés a kvantum informatikába és kommunikációba Féléves házi feladat (2013/2014. tavasz)
 Bevezetés a kvantum informatikába és kommunikációba Féléves házi feladat (2013/2014. tavasz) A házi feladatokkal kapcsolatos követelményekről Kapcsolódó határidők: választás: 6. oktatási hét csütörtöki
Bevezetés a kvantum informatikába és kommunikációba Féléves házi feladat (2013/2014. tavasz) A házi feladatokkal kapcsolatos követelményekről Kapcsolódó határidők: választás: 6. oktatási hét csütörtöki
A programozás alapjai előadás. Amiről szólesz: A tárgy címe: A programozás alapjai
 A programozás alapjai 1 1. előadás Híradástechnikai Tanszék Amiről szólesz: A tárgy címe: A programozás alapjai A számítógép részegységei, alacsony- és magasszintű programnyelvek, az imperatív programozási
A programozás alapjai 1 1. előadás Híradástechnikai Tanszék Amiről szólesz: A tárgy címe: A programozás alapjai A számítógép részegységei, alacsony- és magasszintű programnyelvek, az imperatív programozási
Előadó: Horváth Judit
 Előadó: Horváth Judit mindennapi élet életszituációk problémahelyzetek megoldása meggyőződés tanulási szokások - szövegmegértés - értelmezés - a gondolkodási műveletek használata - problémamegoldás Adott
Előadó: Horváth Judit mindennapi élet életszituációk problémahelyzetek megoldása meggyőződés tanulási szokások - szövegmegértés - értelmezés - a gondolkodási műveletek használata - problémamegoldás Adott
Tárgyszavak: vevőkapcsolatok; CRM; szoftverértékelés.
 A VÁLLALATVEZETÉS EGYES TERÜLETEI CRM-rendszerek értékelése és felépítése Bármerre tekintünk a verseny egyre élesebb. A vállalatok nagy feladat előtt állnak: régi ügyfeleiket meg kell tartaniuk, és újakat
A VÁLLALATVEZETÉS EGYES TERÜLETEI CRM-rendszerek értékelése és felépítése Bármerre tekintünk a verseny egyre élesebb. A vállalatok nagy feladat előtt állnak: régi ügyfeleiket meg kell tartaniuk, és újakat
Integrált gyártórendszerek. Ágens technológia - ágens rendszer létrehozása Gyakorlat
 IGYR p. 1/17 Integrált gyártórendszerek Ágens technológia - ágens rendszer létrehozása Gyakorlat Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu IGYR
IGYR p. 1/17 Integrált gyártórendszerek Ágens technológia - ágens rendszer létrehozása Gyakorlat Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu IGYR
A matematikai feladatok és megoldások konvenciói
 A matematikai feladatok és megoldások konvenciói Kozárné Fazekas Anna Kántor Sándor Matematika és Informatika Didaktikai Konferencia - Szatmárnémeti 2011. január 28-30. Konvenciók Mindenki által elfogadott
A matematikai feladatok és megoldások konvenciói Kozárné Fazekas Anna Kántor Sándor Matematika és Informatika Didaktikai Konferencia - Szatmárnémeti 2011. január 28-30. Konvenciók Mindenki által elfogadott
A nélkülözhetetlen tapasztalatszerzés és az elvont matematikai fogalmak kialakítása. Előadó: Horváth Judit
 A nélkülözhetetlen tapasztalatszerzés és az elvont matematikai fogalmak kialakítása Előadó: Horváth Judit A matematikatanuláshoz szükséges fogalmak kialakulása és kialakítása kisgyermekkorban Tárgyfogalom
A nélkülözhetetlen tapasztalatszerzés és az elvont matematikai fogalmak kialakítása Előadó: Horváth Judit A matematikatanuláshoz szükséges fogalmak kialakulása és kialakítása kisgyermekkorban Tárgyfogalom
Objektumorientált paradigma és a programfejlesztés
 Objektumorientált paradigma és a programfejlesztés Vámossy Zoltán vamossy.zoltan@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Ficsor Lajos (Miskolci Egyetem) prezentációja alapján Objektumorientált
Objektumorientált paradigma és a programfejlesztés Vámossy Zoltán vamossy.zoltan@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Ficsor Lajos (Miskolci Egyetem) prezentációja alapján Objektumorientált
Ismeretalapú modellezés XI. Leíró logikák
 XI. Leíró logikák 1 eddig volt nyílt internetes rendszerekben miért van szükség ismeretalapú re ontológia készítés kérdései ontológiák jellemzői milyen ontológiák vannak most jön mai internetes ontológiák
XI. Leíró logikák 1 eddig volt nyílt internetes rendszerekben miért van szükség ismeretalapú re ontológia készítés kérdései ontológiák jellemzői milyen ontológiák vannak most jön mai internetes ontológiák
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI
 FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
FEGYVERNEKI SÁNDOR, Valószínűség-sZÁMÍTÁs És MATEMATIKAI statisztika 10 X. SZIMULÁCIÓ 1. VÉLETLEN számok A véletlen számok fontos szerepet játszanak a véletlen helyzetek generálásában (pénzérme, dobókocka,
3. előadás. Programozás-elmélet. A változó fogalma Kiterjesztések A feladat kiterjesztése A program kiterjesztése Kiterjesztési tételek Példa
 A változó fogalma Definíció Legyen A = A 1 A 2... A n állapottér. A pr Ai projekciós függvényeket változóknak nevezzük: : A A i pr Ai (a) = a i ( a = (a 1, a 2,..., a n ) A). A változók jelölése: v i =
A változó fogalma Definíció Legyen A = A 1 A 2... A n állapottér. A pr Ai projekciós függvényeket változóknak nevezzük: : A A i pr Ai (a) = a i ( a = (a 1, a 2,..., a n ) A). A változók jelölése: v i =
SZOFTVERES SZEMLÉLTETÉS A MESTERSÉGES INTELLIGENCIA OKTATÁSÁBAN _ Jeszenszky Péter Debreceni Egyetem, Informatikai Kar jeszenszky.peter@inf.unideb.
 SZOFTVERES SZEMLÉLTETÉS A MESTERSÉGES INTELLIGENCIA OKTATÁSÁBAN _ Jeszenszky Péter Debreceni Egyetem, Informatikai Kar jeszenszky.peter@inf.unideb.hu Mesterséges intelligencia oktatás a DE Informatikai
SZOFTVERES SZEMLÉLTETÉS A MESTERSÉGES INTELLIGENCIA OKTATÁSÁBAN _ Jeszenszky Péter Debreceni Egyetem, Informatikai Kar jeszenszky.peter@inf.unideb.hu Mesterséges intelligencia oktatás a DE Informatikai
I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI
 I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI 1 A digitális áramkörökre is érvényesek a villamosságtanból ismert Ohm törvény és a Kirchhoff törvények, de az elemzés és a tervezés rendszerint nem ezekre épül.
I. A DIGITÁLIS ÁRAMKÖRÖK ELMÉLETI ALAPJAI 1 A digitális áramkörökre is érvényesek a villamosságtanból ismert Ohm törvény és a Kirchhoff törvények, de az elemzés és a tervezés rendszerint nem ezekre épül.
Programozási nyelvek a közoktatásban alapfogalmak I. előadás
 Programozási nyelvek a közoktatásban alapfogalmak I. előadás Szempontok Programozási nyelvek osztályozása Felhasználói kör (amatőr, professzionális) Emberközelség (gépi nyelvektől a természetes nyelvekig)
Programozási nyelvek a közoktatásban alapfogalmak I. előadás Szempontok Programozási nyelvek osztályozása Felhasználói kör (amatőr, professzionális) Emberközelség (gépi nyelvektől a természetes nyelvekig)
Általános algoritmustervezési módszerek
 Általános algoritmustervezési módszerek Ebben a részben arra mutatunk példát, hogy miként használhatóak olyan általános algoritmustervezési módszerek mint a dinamikus programozás és a korlátozás és szétválasztás
Általános algoritmustervezési módszerek Ebben a részben arra mutatunk példát, hogy miként használhatóak olyan általános algoritmustervezési módszerek mint a dinamikus programozás és a korlátozás és szétválasztás
Programfejlesztési Modellek
 Programfejlesztési Modellek Programfejlesztési fázisok: Követelmények leírása (megvalósíthatósági tanulmány, funkcionális specifikáció) Specifikáció elkészítése Tervezés (vázlatos és finom) Implementáció
Programfejlesztési Modellek Programfejlesztési fázisok: Követelmények leírása (megvalósíthatósági tanulmány, funkcionális specifikáció) Specifikáció elkészítése Tervezés (vázlatos és finom) Implementáció
Objektumorientált paradigma és programfejlesztés Bevezető
 Objektumorientált paradigma és programfejlesztés Bevezető Vámossy Zoltán vamossy.zoltan@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Ficsor Lajos (Miskolci Egyetem) prezentációja alapján
Objektumorientált paradigma és programfejlesztés Bevezető Vámossy Zoltán vamossy.zoltan@nik.uni-obuda.hu Óbudai Egyetem Neumann János Informatikai Kar Ficsor Lajos (Miskolci Egyetem) prezentációja alapján
A benchmarking fogalma
 Benchmarking Dr. Koczor Zoltán 1 A fogalma Összevetésként használt szervezet Felhasznált erőforrások ESZKÖZÖK CÉLOK Belső folyamatszabályozás Dr. Koczor Zoltán 2 1 A célja Értékelnünk kell a jelenlegi
Benchmarking Dr. Koczor Zoltán 1 A fogalma Összevetésként használt szervezet Felhasznált erőforrások ESZKÖZÖK CÉLOK Belső folyamatszabályozás Dr. Koczor Zoltán 2 1 A célja Értékelnünk kell a jelenlegi
Cselekvési tervek generálása. Máté Annamária
 Cselekvési tervek generálása Máté Annamária Tartalom Általánosan a cselekvés tervezésről Értelmezés, megközelítés Klasszikus modellek Mint keresés Mint logikai következtetés Alapvető feltevések és fogalmak
Cselekvési tervek generálása Máté Annamária Tartalom Általánosan a cselekvés tervezésről Értelmezés, megközelítés Klasszikus modellek Mint keresés Mint logikai következtetés Alapvető feltevések és fogalmak
Témaválasztás, kutatási kérdések, kutatásmódszertan
 Témaválasztás, kutatási kérdések, kutatásmódszertan Dr. Dernóczy-Polyák Adrienn PhD egyetemi adjunktus, MMT dernoczy@sze.hu A projekt címe: Széchenyi István Egyetem minőségi kutatói utánpótlás nevelésének
Témaválasztás, kutatási kérdések, kutatásmódszertan Dr. Dernóczy-Polyák Adrienn PhD egyetemi adjunktus, MMT dernoczy@sze.hu A projekt címe: Széchenyi István Egyetem minőségi kutatói utánpótlás nevelésének
Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017.
 Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017. Vizuális feldolgozórendszerek feladatai Mesterséges intelligencia és idegtudomány Mesterséges intelligencia és idegtudomány Párhuzamos problémák
Mit látnak a robotok? Bányai Mihály Matemorfózis, 2017. Vizuális feldolgozórendszerek feladatai Mesterséges intelligencia és idegtudomány Mesterséges intelligencia és idegtudomány Párhuzamos problémák
Fuzzy rendszerek és neurális hálózatok alkalmazása a diagnosztikában
 Budapesti Műszaki és Gazdaságtudományi Egyetem Fuzzy rendszerek és neurális hálózatok alkalmazása a diagnosztikában Cselkó Richárd 2009. október. 15. Az előadás fő témái Soft Computing technikák alakalmazásának
Budapesti Műszaki és Gazdaságtudományi Egyetem Fuzzy rendszerek és neurális hálózatok alkalmazása a diagnosztikában Cselkó Richárd 2009. október. 15. Az előadás fő témái Soft Computing technikák alakalmazásának
Számítógépes döntéstámogatás. Bevezetés és tematika
 SZDT-01 p. 1/18 Számítógépes döntéstámogatás Bevezetés és tematika Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Előadás SZDT-01 p. 2/18 SZDT-01
SZDT-01 p. 1/18 Számítógépes döntéstámogatás Bevezetés és tematika Werner Ágnes Villamosmérnöki és Információs Rendszerek Tanszék e-mail: werner.agnes@virt.uni-pannon.hu Előadás SZDT-01 p. 2/18 SZDT-01
Mérési struktúrák
 Mérési struktúrák 2007.02.19. 1 Mérési struktúrák A mérés művelete: a mérendő jellemző és a szimbólum halmaz közötti leképezés megvalósítása jel- és rendszerelméleti aspektus mérési folyamat: a leképezést
Mérési struktúrák 2007.02.19. 1 Mérési struktúrák A mérés művelete: a mérendő jellemző és a szimbólum halmaz közötti leképezés megvalósítása jel- és rendszerelméleti aspektus mérési folyamat: a leképezést
Dunaújvárosi Főiskola Informatikai Intézet
 Dunaújvárosi Főiskola Informatikai Intézet Tudásalapú rendszerek Dr. Seebauer Márta főiskolai tanár seebauer.marta@szgti.bmf.hu Tudás fogalma Tudás a valós világ tükröződése az emberi tudatban, amelynek
Dunaújvárosi Főiskola Informatikai Intézet Tudásalapú rendszerek Dr. Seebauer Márta főiskolai tanár seebauer.marta@szgti.bmf.hu Tudás fogalma Tudás a valós világ tükröződése az emberi tudatban, amelynek
Emerald: Integrált jogi modellező keretrendszer
 Emerald: Integrált jogi modellező keretrendszer Förhécz András Szőke Ákos Kőrösi Gábor Strausz György Budapesti Műszaki és Gazdaságtudományi Egyetem Multilogic Kft, Budapest Networkshop 2011 2011. április
Emerald: Integrált jogi modellező keretrendszer Förhécz András Szőke Ákos Kőrösi Gábor Strausz György Budapesti Műszaki és Gazdaságtudományi Egyetem Multilogic Kft, Budapest Networkshop 2011 2011. április
Az informatika kulcsfogalmai
 Az informatika kulcsfogalmai Kulcsfogalmak Melyek azok a fogalmak, amelyek nagyon sok más fogalommal kapcsolatba hozhatók? Melyek azok a fogalmak, amelyek más-más környezetben újra és újra megjelennek?
Az informatika kulcsfogalmai Kulcsfogalmak Melyek azok a fogalmak, amelyek nagyon sok más fogalommal kapcsolatba hozhatók? Melyek azok a fogalmak, amelyek más-más környezetben újra és újra megjelennek?
Szoftverminőségbiztosítás
 NGB_IN003_1 SZE 2014-15/2 (13) Szoftverminőségbiztosítás Szoftverminőség és formális módszerek Formális módszerek Formális módszer formalizált módszer(tan) Formális eljárások alkalmazása a fejlesztésben
NGB_IN003_1 SZE 2014-15/2 (13) Szoftverminőségbiztosítás Szoftverminőség és formális módszerek Formális módszerek Formális módszer formalizált módszer(tan) Formális eljárások alkalmazása a fejlesztésben
Hely- és kontextusfüggő alkalmazások fejlesztését támogató keretrendszer mobil környezetben
 Department of Distributed Systems Hely- és kontextusfüggő alkalmazások fejlesztését támogató keretrendszer mobil környezetben MTA SZTAKI Elosztott Rendszerek Osztály - Mátételki Péter matetelki@sztaki.hu
Department of Distributed Systems Hely- és kontextusfüggő alkalmazások fejlesztését támogató keretrendszer mobil környezetben MTA SZTAKI Elosztott Rendszerek Osztály - Mátételki Péter matetelki@sztaki.hu
Értékesítések (összes, geográfiai -, ügyfelenkénti-, termékenkénti megoszlás)
 Saját vállalkozás Értékesítések (összes, geográfiai -, ügyfelenkénti-, termékenkénti megoszlás) Piaci részesedés Haszonkulcs Marketing folyamatok Marketing szervezet Értékesítési/marketing kontrol adatok
Saját vállalkozás Értékesítések (összes, geográfiai -, ügyfelenkénti-, termékenkénti megoszlás) Piaci részesedés Haszonkulcs Marketing folyamatok Marketing szervezet Értékesítési/marketing kontrol adatok
A döntéstámogatás területén a 90-es évek főárama a tudásbázisú rendszerek fejlesztése. A tudásbázisú rendszer az első olyan döntéstámogató módszer, am
 Fogalmakat is kezelni tudó számítógépes döntéstámogatás Starkné Dr. Werner Ágnes A döntéstámogatás területén a 90-es évek főárama a tudásbázisú rendszerek fejlesztése. A tudásbázisú rendszer az első olyan
Fogalmakat is kezelni tudó számítógépes döntéstámogatás Starkné Dr. Werner Ágnes A döntéstámogatás területén a 90-es évek főárama a tudásbázisú rendszerek fejlesztése. A tudásbázisú rendszer az első olyan
Tudásalapú információ-kereső rendszerek elemzése és kifejlesztése
 Tudásalapú információ-kereső rendszerek elemzése és kifejlesztése 1 Tudásalapú információ-kereső rendszerek elemzése és kifejlesztése Természetes nyelv feldolgozás 2 Tudásalapú információ-kereső rendszerek
Tudásalapú információ-kereső rendszerek elemzése és kifejlesztése 1 Tudásalapú információ-kereső rendszerek elemzése és kifejlesztése Természetes nyelv feldolgozás 2 Tudásalapú információ-kereső rendszerek
Adatbázisok elmélete 12. előadás
 Adatbázisok elmélete 12. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu http://www.cs.bme.hu/ kiskat 2005 ADATBÁZISOK ELMÉLETE
Adatbázisok elmélete 12. előadás Katona Gyula Y. Budapesti Műszaki és Gazdaságtudományi Egyetem Számítástudományi Tsz. I. B. 137/b kiskat@cs.bme.hu http://www.cs.bme.hu/ kiskat 2005 ADATBÁZISOK ELMÉLETE
Térinformatika amit tudni kell Márkus Béla
 Térinformatika amit tudni kell Márkus Béla V. EURÓPAI FÖLDMÉRŐK ÉS GEOINFORMATIKUSOK NAPJA - 2016. március 17. Térinformatika amit tudni kell? Mit? Az előadás célja, támogatást adni e kérdés megválaszolásához.
Térinformatika amit tudni kell Márkus Béla V. EURÓPAI FÖLDMÉRŐK ÉS GEOINFORMATIKUSOK NAPJA - 2016. március 17. Térinformatika amit tudni kell? Mit? Az előadás célja, támogatást adni e kérdés megválaszolásához.
MATEMATIKA 5 8. ALAPELVEK, CÉLOK
 MATEMATIKA 5 8. ALAPELVEK, CÉLOK Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről.
MATEMATIKA 5 8. ALAPELVEK, CÉLOK Az iskolai matematikatanítás célja, hogy hiteles képet nyújtson a matematikáról mint tudásrendszerről és mint sajátos emberi megismerési, gondolkodási, szellemi tevékenységről.
Programozási módszertan
 1 Programozási módszertan 1. Alapfogalmak Feldhoffer Gergely 2012 Féléves tananyag terve 2 Program helyességének bizonyítása Reprezentáció Logikai-matematikai eszköztár Programozási tételek bizonyítása
1 Programozási módszertan 1. Alapfogalmak Feldhoffer Gergely 2012 Féléves tananyag terve 2 Program helyességének bizonyítása Reprezentáció Logikai-matematikai eszköztár Programozási tételek bizonyítása
Csima Judit október 24.
 Adatbáziskezelés Funkcionális függőségek Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2018. október 24. Csima Judit Adatbáziskezelés Funkcionális függőségek 1 / 1 Relációs sémák
Adatbáziskezelés Funkcionális függőségek Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2018. október 24. Csima Judit Adatbáziskezelés Funkcionális függőségek 1 / 1 Relációs sémák
A MODELLALKOTÁS ELVEI ÉS MÓDSZEREI
 SZENT ISTVÁN EGYETEM GÖDÖLLŐ MECHANIKAI ÉS GÉPTANI INTÉZET A MODELLALKOTÁS ELVEI ÉS MÓDSZEREI Dr. M. Csizmadia Béla egyetemi tanár, az MMK Gépészeti Tagozatának elnöke Budapest 2013. október. 25. BPMK
SZENT ISTVÁN EGYETEM GÖDÖLLŐ MECHANIKAI ÉS GÉPTANI INTÉZET A MODELLALKOTÁS ELVEI ÉS MÓDSZEREI Dr. M. Csizmadia Béla egyetemi tanár, az MMK Gépészeti Tagozatának elnöke Budapest 2013. október. 25. BPMK
Rendszer szekvencia diagram
 Rendszer szekvencia diagram Célkitűzések A rendszer események azonosítása. Rendszer szekvencia diagram készítése az eseményekre. 2 1.Iteráció Az első igazi fejlesztési iteráció. A projekt kezdeti szakaszában
Rendszer szekvencia diagram Célkitűzések A rendszer események azonosítása. Rendszer szekvencia diagram készítése az eseményekre. 2 1.Iteráció Az első igazi fejlesztési iteráció. A projekt kezdeti szakaszában
A logikai következmény
 Logika 3 A logikai következmény A logika egyik feladata: helyes következtetési sémák kialakítása. Példa következtetésekre : Minden veréb madár. Minden madár gerinces. Minden veréb gerinces 1.Feltétel 2.Feltétel
Logika 3 A logikai következmény A logika egyik feladata: helyes következtetési sémák kialakítása. Példa következtetésekre : Minden veréb madár. Minden madár gerinces. Minden veréb gerinces 1.Feltétel 2.Feltétel
Objektum orientált programozás Bevezetés
 Objektum orientált programozás Bevezetés Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2008. 03. 04. OOPALAP / 1 A program készítés Absztrakciós folyamat, amelyben a valós világban
Objektum orientált programozás Bevezetés Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2008. 03. 04. OOPALAP / 1 A program készítés Absztrakciós folyamat, amelyben a valós világban
A törzsszámok sorozatáról
 A törzsszámok sorozatáról 6 = 2 3. A 7 nem bontható fel hasonló módon két tényez őre, ezért a 7-et törzsszámnak nevezik. Törzsszámnak [1] nevezzük az olyan pozitív egész számot, amely nem bontható fel
A törzsszámok sorozatáról 6 = 2 3. A 7 nem bontható fel hasonló módon két tényez őre, ezért a 7-et törzsszámnak nevezik. Törzsszámnak [1] nevezzük az olyan pozitív egész számot, amely nem bontható fel
