FIGYELEM! NE NYISSA KI ADDIG, AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ UTASÍTÁST!
|
|
|
- Zsolt Boros
- 6 évvel ezelőtt
- Látták:
Átírás
1 Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA IULIE 2018 COD BROŞURĂ 6 FIGYELEM! NE NYISSA KI ADDIG, AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ UTASÍTÁST! 1. Minden feladatnak egyetlen helyes válasza van. 2. A válaszlapon jelölje be az Ön által helyesnek vélt válasznak megfelelő mezőt, a helytelen válaszoknak megfelelő mezőket NE JELÖLJE BE! 3. A Feladatlapban öt, I-V-el jelölt különböző típusú feladat van. A feladatok megoldhatóak bármilyen sorrendben. 4. A Válaszlap kitöltése során fordítson különös figyelmet adott kérdés számának a Feladatlapon és a Válaszlapon való megfelelésnek. SOK SIKERT! 1
2 I. Az alábbiakban mátrix sorozatokat láthatnak, amelyek geometriai elemeket tartalmaznak. A geometriai elemeknek a pozíciója egy bizonyos szabály szerint változik. Az Ön feladata ezt a szabályt felfedezni és kiválasztani a válaszlehetőségek közül azt, amelyik a szabálynak megfelelően folytatja a sorozatot. 1) 2) a b c d e 3) a b c d e 4) a b c d e 5) a b c d e a b c d e 2
3 6) 7) a b c d e 8) a b c d e 9) a b c d e 10) a b c d e a b c d e 3
4 II. Az alábbi feladatokban két számsort láthatnak (I-gyel és II-vel jelölve), közülük az egyik teljes (I), a másik hiányos (II). Mindkét sor azonos szabály szerint van megalkotva. Az Ön feladata megtalálni azt a szabályt, amely alapjául szolgált a teljes sor megalkotásának. Aztán a felfedezett szabálynak megfelelően jelölnie kell a válaszlapon azt a válaszlehetőséget, amelyik a legjobban kiegészíti a hiányos sort (II). 11) I. 33, 40, 47 II. 22, 29, a. 32 b. 33 c. 37 d. 27 e ) I. 7, 9, 13, 21 II. 10, 15, 25, a. 45 b. 28 c. 120 d. 115 e ) I. 63, 51, 64, 50 II. 39, 27, 40, a. 27 b. 26 c. 55 d. 53 e ) I. 2, 10, 42 II. 5, 22, a. 28 b. 24 c. 14 d. 90 e ) I. 5, 10, 3, 8 II. 9, 14, 7, a. 68 b. 16 c. 25 d. 12 e ) I. 1, 8, 9, 17 II. 5, 12, 17, a. 29 b. 22 c. 25 d. 21 e ) I. 9, 13, 18, 24 II. 18, 22, 27, a. 30 b. 33 c. 23 d. 25 e ) I. 1, 2, 6, 24 II. 3, 6, 18, a. 44 b. 68 c. 72 d. 55 e ) I. 49, 98, 196 II. 9, 18, a. 30 b. 136 c. 116 d. 16 e ) I. 3, 9, 81 II. 2, 4, a. 20 b. 21 c. 26 d. 16 e. 81 4
5 III. Tekintsünk egy-egy szópárt a // jel egyik és másik oldalán. Mindkét szópárra ugyanaz a viszony jellemző (pl. Ellentét LÁGY : KEMÉNY // HOMÁLYOS : ÁTLÁTSZÓ). Mindenik párból hiányzik legalább egy elem, amelyet az I, illetve a II jelöl. A javasolt alternatívák, amelyek az I-gyel jelölt elemet helyettesíthetik, az ABCD válaszsorban találhatók, a II-vel jelölt elemet helyettesítők pedig a PQRS sorban. Az Ön feladata kiválasztani a javasolt variánsok közül azt, amelyik a legjobban egészíti ki az adott szópárokat. 21) I : Csökken // Emelkedik : II I. (A) Fogy (B) Növekszik (C) Ár (D) Leszállít II. (P) Emel (Q) Mászik (R) Hegy (S) Ereszkedik a. BP b. AS c. BS d. DR e. BP 26) Egész : Rész // I : II I. (A) Tanuló (B) Iskola (C) Igazgató (D) Teljes II. (P) Tanár (Q) Diák(R) Egyetem (S) Osztály a. AQ b. AR c. CR d. BS e. DS 22) I : Tanuló // II : Egyetemista I. (A) Líceum (B) Érettségi (C) Serdülő (D) Félelem II. (P) Nyugdíjas (Q) Egyetem (R) Licenc vizsga (S) Profil a. DP b. BS c. CQ d. AR e. AQ 27) I : Valódi // II : Előd I. (A) Festészet (B) Eredeti (C) Művészet (D) Értelmiségi II. (P) Felmenő (Q) Leszármazott (R) Utód (S) Haladó a. DR b. BP c. CS d. AQ e. BQ 23) Modern : I // II : Régi I. (A) Kortárs (B) Újkeletű (C) Civilizáció (D) Antik II. (P) Nem használt (Q) Új (R) Fiatal (S) Iparosított a. AR b. DQ c. AQ d. CS e. BS 28) Beleegyezett : I // II : Eltitkolt I. (A) Helytelenített (B) Jóváhagyott (C) Aláírt (D) Visszautasított II. (P) Leplezett (Q) Rejtett (R) Bűn (S) Bevallott a. BR b. DP c. AP d. AS e. BS 24) I : Igazgató // Ország : II I. (A) Beosztott (B) Cég (C) Ügyvezető (D) Generális II. (P) Miniszterelnök (Q) Állampolgár (R) Enklávé (S) Megye a. DQ b. AR c. DP d. BP e. BS 29) Költő : I // Építész : II I. (A) Kritika (B) Regényíró (C) Tehetség (D) Vers II. (P) Középszerűség (Q) Értékelő (R) Tervrajz (S) Design a. DR b. DQ c. AP d. CP e. BS 25) I : Privát // Szabadság : II I. (A) Telek (B) Publikus (C) Intézmény (D) Birtok II. (P) Függetlenség (Q) Elnyomás (R) Autonómia (S) Felszabadulás a. BQ b. DP c. AQ d. BS e. CR 30) Csúcs : I // Vonzó : II I. (A) Orom (B) Látványos (C) Fokoz (D) Juhász II. (P) Visszataszító (Q) Undorító (R) Fizetés (S) Csábító a. DS b. AP c. AS d. BP e. CR 5
6 IV. Az alábbi ábrák különböző szemantikus kategóriák közötti viszonyt jelképeznek (pl. Orvos, Ember, Halandó közötti viszonyok megfelelnek az I-es ábrának; vagy az Euro, Dollár, Pénzegység közötti viszonyok megfelelnek a II-es ábrának). A továbbiakban, minden kérdés három kategóriát mutat be. Az Ön feladata, hogy a felsorolt válaszlehetőségek közül kiválassza azt, amely a legjobban jelképezi a három kategória közötti viszonyt. I. II. III. IV. V. VI. VII. VIII. 31) Melyik ábra jelképezi a következő kategóriák közötti viszonyt: Gitár, Hangszer, Furulya a. V-ös ábra. b. VII-es ábra. c. II-es ábra. d. III-as ábra. 36) Melyik ábra jelképezi a következő kategóriák közötti viszonyt: Személyautó, Jármű, Spatula a. VI-os ábra. b. IV-es ábra. c. III-as ábra. d. II-es ábra. 32) Melyik ábra jelképezi a következő kategóriák közötti viszonyt: Kézilabdás, Sportoló, Fiú a. IV-es ábra. b. III-as ábra. c. VI-os ábra. d. II-es ábra. e. VIII-as ábra. 37) Melyik ábra jelképezi a következő kategóriák közötti viszonyt: Tűzfegyver, Puska, Háziállat a. VI-os ábra. b. III-as ábra. c. IV-es ábra. d. VII-es ábra. 32) Melyik ábra jelképezi a következő kategóriák közötti viszonyt: Állat, Madár, Csóka a. IV-es ábra. b. I-es ábra. c. VI-os ábra. d. III-as ábra. e. II-es ábra. 38) Melyik ábra jelképezi a következő kategóriák közötti viszonyt: Macskaféle, Tigris, Emlős a. III-as ábra. b. I-es ábra. c. II-es ábra. d. IV-es ábra. e. VI-os ábra. 34) Melyik ábra jelképezi a következő kategóriák közötti viszonyt: Idős, Kamasz, Géniusz a. I-es ábra. b. V-ös ábra. c. VII-es ábra. d. III-as ábra. e. IV-es ábra. 39) Melyik ábra jelképezi a következő kategóriák közötti viszonyt: Bors, Fűszer, Smaragd a. VI-os ábra. b. V-ös ábra. c. III-as ábra. d. IV-es ábra. 35) Melyik ábra jelképezi a következő kategóriák közötti viszonyt: Alma, Barack, Gyümölcs a. VIII-as ábra. b. VI-os ábra. c. II-es ábra. d. I-es ábra. e. V-ös ábra. 40) Melyik ábra jelképezi a következő kategóriák közötti viszonyt: Tanár, Egyetemi tanár, Biológus a. VIII-as ábra. b. V-ös ábra. c. III-as ábra. d. VII-es ábra. 6
7 V. Olvassa el figyelmesen az alábbi szövegeket. Minden egyes szöveget több kérdés követ. Minden egyes kérdés esetében jelölje meg a válaszlapon azt a választ, amelyet a feladat helyes megoldásának tart. Figyelem, minden kérdés megválaszolható a szövegben megadott információk alapján! 1. SZÖVEG A kutatók egyes baktérium törzseket, tulajdonságaik alapján, a latin ábécé különböző betűivel jelölt osztályokba sorolnak. A rajtuk elvégzett kutatások a következő tényeket tárták fel: i) Minden Q törzs egyben I törzs is; ii) minden I törzs egyben U törzs is; iii) minden R törzs egyben U törzs is; iv) egyetlen Q törzs sem R törzs; v) egyes I törzsek egyben R törzsek is; vi) létezik olyan U törzs, amely se nem R, se nem I és se nem Q. 41) Az alábbi kijelentések közül melyik igaz I. Létezik olyan I amely nem Q, egy olyan állítás, amely, logikailag levezethető a megfogalmazott ismeretekből. II. Létezik olyan I amely nem Q, egy olyan állítás, amely, konzisztens (nem mond ellent), azonban nem vezethető le logikailag a megfogalmazott ismeretekből. III. Létezik olyan I amely nem Q, egy olyan állítás, amely, logikailag levezethető a megfogalmazott ismeretekből, azzal a feltétellel, hogy Minden U egyben R is állítás igaz. a. csak az I-es és a II-es állítások igazak. b. csak az I-es állítás igaz. c. csak a II-es állítás igaz. d. egyetlen állítás sem igaz. e. csak a III-as állítás igaz. 42) Az alábbi állítások közül, melyik nem vezethető le logikailag a fenti megszorításokból a. minden R egyben I is. b. egyetlen R sem Q. c. minden Q egyben U is. d. egyetlen Q sem R. e. létezik olyan I amely nem R. 43) Ha minden D egyben I törzs is, az alábbi állítások közül, melyik igaz a. ha létezik olyan D amely egyben Q törzs is, akkor azok egyben R törzsek is. b. minden D egyben Q is. c. minden D egyben U is. d. egyetlen D sem R törzs. e. egyetlen D sem Q törzs. 44) A kutatók felfedeztek egy új baktérium törzset (A), amely esetében igaz a következő állítás, Egyes A törzsek egyben Q törzsek is. A megadott ismeretek alapján az alábbi állítások közül, melyiknek kell igaznak lennie a. egyes A egyben R is. b. minden A egyben Q is. c. egyetlen A sem I. d. létezik olyan A, amely nem R. e. minden A egyben U is. 45) Ha tudjuk, hogy Létezik olyan T törzs, amely egyben R is, anélkül, hogy I lenne, az alábbi állítások közül, melyik igaz a. létezik olyan T, amely egyben U is. b. egyes I törzsek, amelyek egyben Q törzsek is, T törzsek is. c. minden T egyben U is. d. egyes T törzsek egyben Q törzsek is. e. minden T egyben I is. 2. SZÖVEG Nyolc diák (Florina, Georgeta, Helga, Ioana, Julian, Klaus, Leon és Marcel) a TIFF filmfesztivál jegyirodája előtt állnak sorban. Válaszoljon a következő kérdésekre tudva azt, hogy: i) a sorban a harmadik helyen Georgeta vagy Klaus áll; ii) Helga, a sorban valahol Georgeta mögött áll; iii) Helga a sorban, valahol Marcel előtt áll; iv) Ioana egy páratlan helyen áll a sorban; v) a sorban a hatodik helyen egy lány áll. 46) A megadott információk alapján, melyik állításnak kell igaznak lennie a. a fiúk egymást követő helyeket foglalnak el a sorban. b. a lányok nem egymást követő helyeket foglalnak el a sorban. c. a fiúk nem egymást követő helyeket foglalnak el a sorban. d. egyetlen állítás sem igaz. e. a lányok egymást követő helyeket foglalnak el a sorban. 47) Ha Marcel és Ioana, a sorban közvetlenül egymást követő helyeket foglalnak el (nem feltétlenül ebben a sorrendben), melyik az a hely, amelyet Florina nem foglalhat el a sorban a. az első. b. a hetedik. c. az ötödik. d. a negyedik. e. a második. 48) Az alábbi sorok közül, melyik mutathatja helyesen a diákok sorrendjét a sorban (a sorok az elsővel kezdődnek) a. Julian, Florina, Klaus, Ioana, Georgeta, Helga, Marcel, Leon. b. Julian, Georgeta, Florina, Klaus, Ioana, Helga, Marcel, Leon. c. Julian, Florina, Georgeta, Klaus, Ioana, Helga, Marcel, Leon. d. Ioana, Florina, Georgeta, Helga, Julian, Klaus, Marcel, Leon. e. Julian, Georgeta, Klaus, Leon, Marcel, Florina, Ioana, Helga. 49) Ha Florina az egyetlen személy, aki a sorban Julian és Leon között áll, az allábiak közül kik foglalhatnak el közvetlen egymás melletti helyeket a sorban a. Ioana és Marcel. b. Ioana és Leon. c. Helga és Ioana. d. Georgeta és Klaus. e. Helga és Marcel. 50) Ha a sor első két helyén Florina és Georgeta áll (nem feltétlenül ebben a sorrendben), az allábiak közül kiknek kell közvetlen egymás melletti helyett elfoglalniuk a sorban a. Julian és Leon. b. Helga és Marcel. c. Georgeta és Klaus. d. Ioana és Julian. e. Helga és Ioana. 7
8 3. SZÖVEG Az Egzakt Tudományok Karának ügyvezetői csoportját, három adminisztrátor (Andrei, Bogdana és Cristian), valamin öt titkárnő (Daniela, Elena, Felicia, Georgiana és Ioana) alkotja. A kar egy másik városba való terjeszkedésre készül, s az új részlegnek az adminisztratív csoportja öt tagból állna, akiket a kar jelenlegi alkalmazottjai közül jelölnek majd ki (három titkárnőt és két adminisztrátort). Figyelembe véve a korábbi kihelyezések alkalmával tapasztalt viszonyokat az alkalmazottak között, a kar vezetősége az áthelyezés alapjául szolgáló kritériumokat a következő képpen állapította meg: i) Mivel több projektben kiderült, hogy Andrei és Cristian nem tudnak együttműködni, ezért nem kerülhetnek együtt áthelyezésre; ii) Mind Cristian, mind Elena, egyénileg jól dolgozik, de közösen nem, ezért nem fogják mindkettőjüket áthelyezni; iii) Daniela és Georgiana civakodnak egymással, ezért nem szerepelhetnek együtt az új csoportban; iv) Daniela és Felicia, a legutóbbi előreléptetés óta ellenséges viszonyban vannak, tehát nem lehet őket együtt áthelyezni. 51) Ha Andreit adminisztrátorként áthelyezik, az alábbi csoportok közül, melyik nem teljesíti a választási kritériumokat a. Andrei, Bogdana, Daniela, Georgiana és Ioana. b. Andrei, Bogdana, Elena, Georgiana és Ioana. c. Andrei, Bogdana, Daniela, Elena és Ioana. d. Andrei, Bogdana, Elena, Felicia és Ioana. e. Andrei, Bogdana, Felicia, Georgiana és Elena. 52) Ha Cristian és Felicia szerepel az áthelyezett csapatban hány lehetséges módozata van a csapat összeállításának a. 3. b. 2. c. 4. d. 5. e ) Ha Cristiant áthelyezik, a következő alkalmazottak közül, kit nem lehet áthelyezni a megfogalmazott választási kritériumok alapján a. Daniela. b. Bogdana. c. Georgiana. d. Ioana. e. Felicia. 54) Ha Danielát áthelyezik, a következő állítások közül melyik igaz állítás I. Cristiant nem lehet áthelyezni; II. Andreit nem lehet áthelyezni; III. Ioanat át kell helyezni. a. Csak az I. állítás igaz. b. Csak az I. és a III. állítások igazak. c. Csak a III. állítás igaz. d. Csak az I. és a II. állítások igazak. e. Az összes állítás igaz. 55) A megállapított kritériumok alapján kit kell föltétlenül áthelyezni az alkalmazottak közül a. Daniela. b. Elena. c. Georgiana. d. Bogdana. e. Ioana. 4. SZÖVEG A Kolozsvári Napok fesztivál szervezőbizottsága a 2019-es esemény szervezésekor 8 napra szándékszik kiterjeszteni a fesztivál időtartamát május 15-től (szerdától) kezdődően május 22-ig bezárólag. A szervezők a különböző zenei műfajoknak (dance, folk, electro-house, steet band, rock és klasszikus zene) egy-egy napot kívánnak szentelni az alábbi módon: i) minden zenei műfajnak legyen egy saját napja; ii) A rock koncertet ne programálják az utolsó napra; iii) az electrohouse koncertet programálják a dance koncerteket megelőző napra; iv) a klasszikus zene napja nem lehet sem szerda sem szombat; v) a csütörtök és a vasárnap más eseményeknek van szentelve, ezeken a napokon nem lehetnek koncertek; vi) a street band koncertek napja hétfő kell hogy legyen; vii) a dance és a klasszikus zenének szentelt napok között pontosan két fesztivál napnak kell lennie. 56) A megállapított kritériumok alapján, melyik lesz az elsőnek programált koncert a. az electro-house. b. a rock. c. a dance. d. a street band. e. a klasszikus zene. 57) Hány fesztiválnap lesz a rock-zenének szentelt nap és a klasszikus zene napja között a. 2. b. 3. c. 4. d. 5. e ) A két szerdai napra milyen zenei műfajokat programálnak a. rock és folk zene. b. klasszikus zene és rockzene. c. rock és dance zene. d. dance és electro-house zene. e. rock és street band zene. 59) Melyik zenei műfaj előzi meg a fesztivál második zenei szünetnapját a. rockzene. b. klasszikus zene. c. electro-house zene. d. folk zene. e. dance zene. 60) Az electro-house zenének szentelt napot milyen zenei műfajnak szentelt nap előz meg a. dance. b. klasszikus zene. c. street band. d. rock. e. folk. 8
FIGYELEM! NE NYISSA KI ADDIG, AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ UTASÍTÁST!
 Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA IULIE 2018 COD BROŞURĂ 5 FIGYELEM! NE NYISSA KI ADDIG, AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA IULIE 2018 COD BROŞURĂ 5 FIGYELEM! NE NYISSA KI ADDIG, AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
FIGYELEM! NE NYISSA KI ADDIG, AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ UTASÍTÁST!
 Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA SEPTEMBRIE 2018 COD BROŞURĂ 3 FIGYELEM! NE NYISSA KI ADDIG, AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA SEPTEMBRIE 2018 COD BROŞURĂ 3 FIGYELEM! NE NYISSA KI ADDIG, AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ UTASÍTÁST!
 Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA IULIE 2015 COD BROŞURĂ 5 FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA IULIE 2015 COD BROŞURĂ 5 FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ UTASÍTÁST!
 Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA IULIE 2015 COD BROŞURĂ 6 FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA IULIE 2015 COD BROŞURĂ 6 FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
VI. Vályi Gyula Emlékverseny november
 VI. Vályi Gyula Emlékverseny 1999. november 19-1. VI. osztály 1. Ki a legidősebb, ha Attila 10 000 órás, Balázs 8 000 napos, Csanád 16 éves, Dániel 8000000 perces, Ede 00 hónapos. (A) Attila (B) Balázs
VI. Vályi Gyula Emlékverseny 1999. november 19-1. VI. osztály 1. Ki a legidősebb, ha Attila 10 000 órás, Balázs 8 000 napos, Csanád 16 éves, Dániel 8000000 perces, Ede 00 hónapos. (A) Attila (B) Balázs
FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ UTASÍTÁST!
 Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA IULIE 2015 COD BROŞURĂ 8 FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA IULIE 2015 COD BROŞURĂ 8 FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
2014. évi Bolyai János Megyei Matematikaverseny MEGOLDÁSI ÉS ÉRTÉKELÉSI ÚTMUTATÓ 9. osztály
 01. évi Bolyai János Megyei Matematikaverseny A közölt megoldási utak a feladatoknak nem az egyetlen helyes megoldási módját adják meg, több eltérő megoldás is lehetséges. Az útmutatótól eltérő megoldásokat
01. évi Bolyai János Megyei Matematikaverseny A közölt megoldási utak a feladatoknak nem az egyetlen helyes megoldási módját adják meg, több eltérő megoldás is lehetséges. Az útmutatótól eltérő megoldásokat
Érettségi feladatok: Halmazok, logika
 Érettségi feladatok: Halmazok, logika 2005. május 10 18. Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először Ádám
Érettségi feladatok: Halmazok, logika 2005. május 10 18. Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először Ádám
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Halmazok
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Halmazok 1) Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat.
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Halmazok 1) Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat.
Érettségi feladatok: Halmazok, logika
 Érettségi feladatok: Halmazok, logika 2005. május 10 18. Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először Ádám
Érettségi feladatok: Halmazok, logika 2005. május 10 18. Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először Ádám
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Halmazok
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Halmazok 1) Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Halmazok 1) Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először
BÁBUK - 4 pont Fejtsd meg az öt szám közötti kölcsönös összefüggést, amelyekbõl a bábu össze van állítva, és számítsd ki a C bábunál hiányzó számot.
 ÖSSZEFÜGGÉS - 1 pont Keresd meg a képben elrejtett összes összefüggést, és találd ki, melyik szám van elrejtve a kérdõjel alatt! ABLAKOK - pont A házon lévõ 9 ablak nem véletlenszerûen van elhelyezve.
ÖSSZEFÜGGÉS - 1 pont Keresd meg a képben elrejtett összes összefüggést, és találd ki, melyik szám van elrejtve a kérdõjel alatt! ABLAKOK - pont A házon lévõ 9 ablak nem véletlenszerûen van elhelyezve.
A Békásmegyeri Veres Péter Gimnázium felvételt hirdet négy és nyolc évfolyamos gimnáziumi osztályaiba a 2020/2021-es tanévre az alábbiak szerint
 A Békásmegyeri Veres Péter Gimnázium felvételt hirdet négy és nyolc évfolyamos gimnáziumi osztályaiba a 2020/2021-es tanévre az alábbiak szerint A.) Négy évfolyamos gimnázium (Egy osztály általános tantervű)
A Békásmegyeri Veres Péter Gimnázium felvételt hirdet négy és nyolc évfolyamos gimnáziumi osztályaiba a 2020/2021-es tanévre az alábbiak szerint A.) Négy évfolyamos gimnázium (Egy osztály általános tantervű)
A Békásmegyeri Veres Péter Gimnázium felvételt hirdet négy és nyolc évfolyamos gimnáziumi osztályaiba a 2019/2020-as tanévre az alábbiak szerint
 A Békásmegyeri Veres Péter Gimnázium felvételt hirdet négy és nyolc évfolyamos gimnáziumi osztályaiba a 2019/2020-as tanévre az alábbiak szerint A.) Négy évfolyamos gimnázium (Egy osztály általános tantervű)
A Békásmegyeri Veres Péter Gimnázium felvételt hirdet négy és nyolc évfolyamos gimnáziumi osztályaiba a 2019/2020-as tanévre az alábbiak szerint A.) Négy évfolyamos gimnázium (Egy osztály általános tantervű)
Figyelembe véve Maros Megyei Lakoság-nyilvántartási Igazgatóság /8998 sz. kérelmét,
 A másolatnak megfelelő, román nyelvről magyar nyelvre történő fordítás MAROS MEGYEI TANÁCS 164. számú HATÁROZAT 2016. október 27-i a Maros Megyei Lakoság-nyilvántartási Igazgatóság Szervezeti struktúrájának,
A másolatnak megfelelő, román nyelvről magyar nyelvre történő fordítás MAROS MEGYEI TANÁCS 164. számú HATÁROZAT 2016. október 27-i a Maros Megyei Lakoság-nyilvántartási Igazgatóság Szervezeti struktúrájának,
Feladatlap. a hatosztályos speciális matematika tantervű osztályok írásbeli vizsgájára (2006)
 Feladatlap a hatosztályos speciális matematika tantervű osztályok írásbeli vizsgájára (2006) 1) Karcsi januárban betegség miatt háromszor hiányzott az iskolából:12-én,14-én és 24-én. Milyen napra esett
Feladatlap a hatosztályos speciális matematika tantervű osztályok írásbeli vizsgájára (2006) 1) Karcsi januárban betegség miatt háromszor hiányzott az iskolából:12-én,14-én és 24-én. Milyen napra esett
SOROZATOK (SZÁMTANI SOROZAT)
 SOROZATOK (SZÁMTANI SOROZAT) Egy sorozat első tagja -1, második tagja 1. Minden további tag a közvetlenül előtte álló két tag összegével egyenlő. Számítsa ki a sorozat első hat tagjának összegét! Számítását
SOROZATOK (SZÁMTANI SOROZAT) Egy sorozat első tagja -1, második tagja 1. Minden további tag a közvetlenül előtte álló két tag összegével egyenlő. Számítsa ki a sorozat első hat tagjának összegét! Számítását
Halmazelmélet. 1 Halmazelmélet
 Halmazelmélet 1. feladat 2006. május 1. (2 pont) idegennyelvi Az A halmaz elemei a 10-nél nem kisebb és a 20-nál nem nagyobb páros számok, a B halmaz elemei a néggyel osztható pozitív számok. Adja meg
Halmazelmélet 1. feladat 2006. május 1. (2 pont) idegennyelvi Az A halmaz elemei a 10-nél nem kisebb és a 20-nál nem nagyobb páros számok, a B halmaz elemei a néggyel osztható pozitív számok. Adja meg
FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ UTASÍTÁST!
 Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA IULIE 2015 COD BROŞURĂ 5 FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA IULIE 2015 COD BROŞURĂ 5 FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ UTASÍTÁST!
 Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA IULIE 2015 COD BROŞURĂ 6 FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA IULIE 2015 COD BROŞURĂ 6 FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
Ismétlés nélküli permutáció
 Ismétlés nélküli permutáció Hányféleképpen lehet sorba rendezni n különböz elemet úgy, hogy a sorrend számít? (Ezt n elem ismétlés nélküli permutációjának nevezzük.) Például hány féleképpen lehet sorba
Ismétlés nélküli permutáció Hányféleképpen lehet sorba rendezni n különböz elemet úgy, hogy a sorrend számít? (Ezt n elem ismétlés nélküli permutációjának nevezzük.) Például hány féleképpen lehet sorba
A pillangóval jelölt feladatok mindenki számára könnyen megoldhatók. a mókussal jelölt feladatok kicsit nehezebbek, több figyelmet igényelnek.
 Kedves második osztályos tanuló! Bizonyára te is szívesen tanulod a matematikát. A 2. osztályban is sok érdekes feladattal találkozhatsz. A Számoljunk! című munkafüzetünk segítségedre lesz a gyakorlásban.
Kedves második osztályos tanuló! Bizonyára te is szívesen tanulod a matematikát. A 2. osztályban is sok érdekes feladattal találkozhatsz. A Számoljunk! című munkafüzetünk segítségedre lesz a gyakorlásban.
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Halmazok
 MTEMTIK ÉRETTSÉGI TÍPUSFELDTOK KÖZÉP SZINT Halmazok szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
MTEMTIK ÉRETTSÉGI TÍPUSFELDTOK KÖZÉP SZINT Halmazok szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek megoldásához!
Arany Dániel Matematikai Tanulóverseny 2012/2013-as tanév 1. forduló haladók III. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 0/03-as tanév. forduló haladók III. kategória Megoldások és javítási útmutató. Egy kör kerületére felírjuk -től 3-ig az egészeket
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 0/03-as tanév. forduló haladók III. kategória Megoldások és javítási útmutató. Egy kör kerületére felírjuk -től 3-ig az egészeket
KÖZZÉTÉTELI LISTA Ajkai Bródy Imre Gimnázium és Alapfokú Művészeti Iskola. Zeneművészeti ág:
 KÖZZÉTÉTELI LISTA Ajkai Bródy Imre Gimnázium és Alapfokú Művészeti Iskola Zeneművészeti ág: 1. A pedagógusok iskolai végzettsége és szakképzettsége hozzárendelve a helyi tanterv tantárgyfelosztásához Sorszám
KÖZZÉTÉTELI LISTA Ajkai Bródy Imre Gimnázium és Alapfokú Művészeti Iskola Zeneművészeti ág: 1. A pedagógusok iskolai végzettsége és szakképzettsége hozzárendelve a helyi tanterv tantárgyfelosztásához Sorszám
FELADATOK ÉS MEGOLDÁSOK
 3. osztály Apa és fia együtt fűrészelnek. Minden fahasábot 5 részre darabolnak. Megszakítás nélkül mennyi ideig dolgoznak, ha 10 hasábot vágnak fel, és egy vágás kettejüknek együtt 3 percig tart? (Egy
3. osztály Apa és fia együtt fűrészelnek. Minden fahasábot 5 részre darabolnak. Megszakítás nélkül mennyi ideig dolgoznak, ha 10 hasábot vágnak fel, és egy vágás kettejüknek együtt 3 percig tart? (Egy
( ) ( ) Bontsuk fel a zárójeleket: *1 pont Mindkét oldalon vonjunk össze, majd rendezzük az egyenletet: 34 = 2 x,
 1. Egy 31 fős osztály játékos rókavadászaton vett részt. Az erdőben elrejtett papír rókafejeket kellett összegyűjteniük. Minden lány 4 rókafejet talált, a fiúk mindegyike pedig 5 darabot. Ha minden lány
1. Egy 31 fős osztály játékos rókavadászaton vett részt. Az erdőben elrejtett papír rókafejeket kellett összegyűjteniük. Minden lány 4 rókafejet talált, a fiúk mindegyike pedig 5 darabot. Ha minden lány
1 pont Az eredmény bármilyen formában elfogadható. Pl.: 100 perc b) 640 cl 1 pont
 2012. január 28. 8. évfolyam TMat1 feladatlap Javítókulcs / 1 Javítókulcs MATEMATIKA FELADATOK 8. évfolyamosok számára, tehetséggondozó változat TMat1 A javítókulcsban feltüntetett válaszokra a megadott
2012. január 28. 8. évfolyam TMat1 feladatlap Javítókulcs / 1 Javítókulcs MATEMATIKA FELADATOK 8. évfolyamosok számára, tehetséggondozó változat TMat1 A javítókulcsban feltüntetett válaszokra a megadott
KockaKobak Országos Matematikaverseny 10. osztály
 KockaKobak Országos Matematikaverseny 10. osztály 014. november 7. A feladatsort készítette: RÓKA SÁNDOR Lektorálta: DR. KISS GÉZA Anyanyelvi lektor: ASZÓDINÉ KOVÁCS MÁRIA www.kockakobak.hu A válaszlapról
KockaKobak Országos Matematikaverseny 10. osztály 014. november 7. A feladatsort készítette: RÓKA SÁNDOR Lektorálta: DR. KISS GÉZA Anyanyelvi lektor: ASZÓDINÉ KOVÁCS MÁRIA www.kockakobak.hu A válaszlapról
Arany Dániel Matematikai Tanulóverseny 2015/2016-os tanév 1. forduló Haladók III. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 2015/2016-os tanév 1. forduló Haladók III. kategória Megoldások és javítási útmutató 1. Az a és b befogójú derékszögű háromszögnek
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 2015/2016-os tanév 1. forduló Haladók III. kategória Megoldások és javítási útmutató 1. Az a és b befogójú derékszögű háromszögnek
Próba érettségi feladatsor április I. RÉSZ
 Név: osztály: Próba érettségi feladatsor 2007 április 17-18 I RÉSZ Figyelem! A dolgozatot tollal írja; az ábrákat ceruzával is rajzolhatja A megoldást minden esetben a feladat szövege melletti keretbe
Név: osztály: Próba érettségi feladatsor 2007 április 17-18 I RÉSZ Figyelem! A dolgozatot tollal írja; az ábrákat ceruzával is rajzolhatja A megoldást minden esetben a feladat szövege melletti keretbe
FELVÉTELI VIZSGA 2014 2015. A. SZAKOK Kar Szakterület Szak Bölcsészettudományi Nyelv és irodalom szak
 FELVÉTELI VIZSGA 2014 2015 A. SZAKOK Kar Szakterület Szak 1 ROMÁN NYELV ÉS IRODALOM 2 ROMÁN NYELV ÉS IRODALOM (ROMÁN MINT IDEGENNYELV) 4 (3 év, nappali képzés, magyar tagozat) 5 ROMÁN NYELV ÉS IRODALOM
FELVÉTELI VIZSGA 2014 2015 A. SZAKOK Kar Szakterület Szak 1 ROMÁN NYELV ÉS IRODALOM 2 ROMÁN NYELV ÉS IRODALOM (ROMÁN MINT IDEGENNYELV) 4 (3 év, nappali képzés, magyar tagozat) 5 ROMÁN NYELV ÉS IRODALOM
VERSENYKIÍRÁS AZ OKTATÁSI HIVATAL ÁLTAL TÁMOGATOTT. Tiszán innen, Dunán túl - Országos Népdaléneklési Verseny az általános- és középiskolások számára
 VERSENYKIÍRÁS AZ OKTATÁSI HIVATAL ÁLTAL TÁMOGATOTT Tiszán innen, Dunán túl - Országos Népdaléneklési Verseny az általános- és középiskolások számára FŐVÁROSI FORDULÓ A verseny pedagógiai célja: a tehetséggondozás,
VERSENYKIÍRÁS AZ OKTATÁSI HIVATAL ÁLTAL TÁMOGATOTT Tiszán innen, Dunán túl - Országos Népdaléneklési Verseny az általános- és középiskolások számára FŐVÁROSI FORDULÓ A verseny pedagógiai célja: a tehetséggondozás,
BERCZIK SÁRA BUDAI TÁNCKLUB 2018/2019. TANÉV I. FÉLÉV ÓRARENDJE MŰFAJONKÉNT
 BERCZIK SÁRA BUDAI TÁNCKLUB 2018/2019. TANÉV I. FÉLÉV ÓRARENDJE MŰFAJONKÉNT MŰVÉSZI TORNA 15.15-16.00 ISKOLÁS (11-12 ÉVESEK) SZOLLÁS ERZSÉBET 16.15-17.00 ÓVODÁS (4-5 ÉVESEK) SZOLLÁS ERZSÉBET 17.00-17.45
BERCZIK SÁRA BUDAI TÁNCKLUB 2018/2019. TANÉV I. FÉLÉV ÓRARENDJE MŰFAJONKÉNT MŰVÉSZI TORNA 15.15-16.00 ISKOLÁS (11-12 ÉVESEK) SZOLLÁS ERZSÉBET 16.15-17.00 ÓVODÁS (4-5 ÉVESEK) SZOLLÁS ERZSÉBET 17.00-17.45
Kombinatorika. Permutáció
 Kombinatorika Permutáció 1. Adva van az 1, 2, 3, 4, 5, 6, 7, 8, 9 számjegy. Hány különböző 9-jegyű szám állítható elő ezekkel a számjegyekkel, ha a számjegyek nem ismétlődhetnek? Mi van akkor, ha a szám
Kombinatorika Permutáció 1. Adva van az 1, 2, 3, 4, 5, 6, 7, 8, 9 számjegy. Hány különböző 9-jegyű szám állítható elő ezekkel a számjegyekkel, ha a számjegyek nem ismétlődhetnek? Mi van akkor, ha a szám
FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ UTASÍTÁST!
 Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA SEPTEMBRIE 2015 COD BROŞURĂ 3 FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA SEPTEMBRIE 2015 COD BROŞURĂ 3 FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
1.) Csaba egy 86 oldalas könyv 50 oldalát elolvasta. Hány nap alatt fejezi be a könyvet ha egy nap 9 oldalt olvas belőle? A) 6 B) 4 C) 3 D) 5
 WWW.ORCHIDEA.HU 1 1.) Csaba egy 86 oldalas könyv 50 oldalát elolvasta. Hány nap alatt fejezi be a könyvet ha egy nap 9 oldalt olvas belőle? A) 6 B) 4 C) 3 D) 5 2.) Számítsd ki a végeredményt: 1 1 1 1 1
WWW.ORCHIDEA.HU 1 1.) Csaba egy 86 oldalas könyv 50 oldalát elolvasta. Hány nap alatt fejezi be a könyvet ha egy nap 9 oldalt olvas belőle? A) 6 B) 4 C) 3 D) 5 2.) Számítsd ki a végeredményt: 1 1 1 1 1
Írd le, a megoldások gondolatmenetét, indoklását is!
 0 Budapest VIII., Bródy Sándor u.. Postacím: Budapest, Pf. 7 Telefon: 7-900 Fax: 7-90. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ 0. április. HARMADIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ Írd le,
0 Budapest VIII., Bródy Sándor u.. Postacím: Budapest, Pf. 7 Telefon: 7-900 Fax: 7-90. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ 0. április. HARMADIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ Írd le,
BOLYAI MATEMATIKA CSAPATVERSENY ORSZÁGOS DÖNTŐ SZÓBELI (2016. NOVEMBER 19.) 3. osztály
 3. osztály Apa és fia együtt fűrészelnek. Minden fahasábot 5 részre darabolnak. Megszakítás nélkül mennyi ideig dolgoznak, ha 10 hasábot vágnak fel, és egy vágás kettejüknek együtt 3 percig tart? (Egy
3. osztály Apa és fia együtt fűrészelnek. Minden fahasábot 5 részre darabolnak. Megszakítás nélkül mennyi ideig dolgoznak, ha 10 hasábot vágnak fel, és egy vágás kettejüknek együtt 3 percig tart? (Egy
Arany Dániel Matematikai Tanulóverseny 2012/2013-as tanév kezdők III. kategória I. forduló
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 01/013-as tanév kezdők I II. kategória II. forduló kezdők III. kategória I. forduló Megoldások és javítási útmutató 1. Egy osztályban
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 01/013-as tanév kezdők I II. kategória II. forduló kezdők III. kategória I. forduló Megoldások és javítási útmutató 1. Egy osztályban
Mátrixok február Feladat: Legyen A = ( ( B =
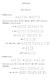 Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Különös közzétételi lista - Alapfokú művészetoktatási intézmények. [11/1994. (VI.8. )MKM rendelet,10. sz. melléklet]
![Különös közzétételi lista - Alapfokú művészetoktatási intézmények. [11/1994. (VI.8. )MKM rendelet,10. sz. melléklet] Különös közzétételi lista - Alapfokú művészetoktatási intézmények. [11/1994. (VI.8. )MKM rendelet,10. sz. melléklet]](/thumbs/56/39225215.jpg) Különös közzétételi lista - Alapfokú művészetoktatási intézmények [11/1994. (VI.8. )MKM rendelet,10. sz. melléklet] 1. A pedagógusok iskolai végzettsége és szakképzettsége hozzárendelve a helyi tanterv
Különös közzétételi lista - Alapfokú művészetoktatási intézmények [11/1994. (VI.8. )MKM rendelet,10. sz. melléklet] 1. A pedagógusok iskolai végzettsége és szakképzettsége hozzárendelve a helyi tanterv
A tankötelezettségi korhatár változásainak hatása Leíró elemzés. Hermann Zoltán 2014. november
 A tankötelezettségi korhatár változásainak hatása Leíró elemzés Hermann Zoltán 2014. november Tankötelezettségi kor a kétezres ekben - a tankötelezettség annak a tannek a végéig tart, amikor a diák eléri
A tankötelezettségi korhatár változásainak hatása Leíró elemzés Hermann Zoltán 2014. november Tankötelezettségi kor a kétezres ekben - a tankötelezettség annak a tannek a végéig tart, amikor a diák eléri
Arany Dániel Matematikai Tanulóverseny 2008/2009-es tanév első (iskolai) forduló haladók I. kategória
 Bolyai János Matematikai Társulat Oktatási és Kulturális Minisztérium Támogatáskezelő Igazgatósága támogatásával Arany Dániel Matematikai Tanulóverseny 2008/2009-es tanév első (iskolai) forduló haladók
Bolyai János Matematikai Társulat Oktatási és Kulturális Minisztérium Támogatáskezelő Igazgatósága támogatásával Arany Dániel Matematikai Tanulóverseny 2008/2009-es tanév első (iskolai) forduló haladók
VI. HAJDÚDOROGI KULTURÁLIS NAPOK rendezvénysorozat programjaira
 HAJDÚDOROG VÁROS ÖNKORMÁNYZATA és a HAJDÚDOROGI HONISMERETI ÉS VÁROSVÉDÕ EGYESÜLET nevében tisztelettel meghívjuk Önt és hozzátartozóját a VI. HAJDÚDOROGI KULTURÁLIS NAPOK rendezvénysorozat programjaira
HAJDÚDOROG VÁROS ÖNKORMÁNYZATA és a HAJDÚDOROGI HONISMERETI ÉS VÁROSVÉDÕ EGYESÜLET nevében tisztelettel meghívjuk Önt és hozzátartozóját a VI. HAJDÚDOROGI KULTURÁLIS NAPOK rendezvénysorozat programjaira
Beiskolázási tájékoztató
 Dugonics András Piarista Gimnázium, Alapfokú Művészeti Iskola és Kollégium 6724 Szeged, Bálint S. u. 14. Telefon: 62-549-091 Honlapcím: www.szepi.hu Bemutatkozó oldal Beiskolázási tájékoztató 1720-ban
Dugonics András Piarista Gimnázium, Alapfokú Művészeti Iskola és Kollégium 6724 Szeged, Bálint S. u. 14. Telefon: 62-549-091 Honlapcím: www.szepi.hu Bemutatkozó oldal Beiskolázási tájékoztató 1720-ban
JUBILEUMI VÁCI HÉT 2014. FEBRUÁR 10 MÁRCIUS 7.
 JUBILEUMI VÁCI HÉT 2014. FEBRUÁR 10 MÁRCIUS 7. KEDVES INTÉZMÉNYVEZETŐ! Egy ünnepi programfüzetet tart a kezében, amely a Váci Mihály Gimnázium fennállásának 50. évfordulója alkalmából színes, tartalmas,
JUBILEUMI VÁCI HÉT 2014. FEBRUÁR 10 MÁRCIUS 7. KEDVES INTÉZMÉNYVEZETŐ! Egy ünnepi programfüzetet tart a kezében, amely a Váci Mihály Gimnázium fennállásának 50. évfordulója alkalmából színes, tartalmas,
MATEMATIKA ÉRETTSÉGI május 10. KÖZÉP SZINT I.
 1) Adott két pont: A ; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. MATEMATIKA ÉRETTSÉGI 005. május 10. KÖZÉP SZINT I. és B 1; Írja fel az AB szakasz 1 1 F ; F ;1 ) Az ábrán egy ; intervallumon
1) Adott két pont: A ; 1 felezőpontjának koordinátáit! AB felezőpontja legyen F. MATEMATIKA ÉRETTSÉGI 005. május 10. KÖZÉP SZINT I. és B 1; Írja fel az AB szakasz 1 1 F ; F ;1 ) Az ábrán egy ; intervallumon
M. 33. Határozza meg az összes olyan kétjegyű szám összegét, amelyek 4-gyel osztva maradékul 3-at adnak!
 Magyar Ifjúság 6 V SOROZATOK a) Három szám összege 76 E három számot tekinthetjük egy mértani sorozat három egymás után következő elemének vagy pedig egy számtani sorozat első, negyedik és hatodik elemének
Magyar Ifjúság 6 V SOROZATOK a) Három szám összege 76 E három számot tekinthetjük egy mértani sorozat három egymás után következő elemének vagy pedig egy számtani sorozat első, negyedik és hatodik elemének
PRÓFÉTAPARÁDÉ A Łódź Kaliska csoport művészeti projektje
 2017 január február január 8-ig február 9-ig január 11. február 9. 19.00 január 11 15. 18.00 január 14. 20.00 január 16. 18.00 január 30. 18.00 február 9. március 17. 18.00 február 13. 18.00 február 13.
2017 január február január 8-ig február 9-ig január 11. február 9. 19.00 január 11 15. 18.00 január 14. 20.00 január 16. 18.00 január 30. 18.00 február 9. március 17. 18.00 február 13. 18.00 február 13.
Nyitott mondatok Bennfoglalás maradékkal
 Matematika A 2. évfolyam Nyitott mondatok Bennfoglalás maradékkal 35. modul Készítette: Szitányi Judit 2 modulleírás A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A képességfejlesztés
Matematika A 2. évfolyam Nyitott mondatok Bennfoglalás maradékkal 35. modul Készítette: Szitányi Judit 2 modulleírás A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A képességfejlesztés
XXIII. Vályi Gyula Emlékverseny május 13. V. osztály
 XXIII. Vályi Gyula Emlékverseny Marosvásárhely 207. május 3. V. osztály. Sári néni a piacon 00 db háromféle tojást vásárolt 00 RON értékben. Tudva azt, hogy a tyúktojás ára 50 bani, a libatojás 5 RON és
XXIII. Vályi Gyula Emlékverseny Marosvásárhely 207. május 3. V. osztály. Sári néni a piacon 00 db háromféle tojást vásárolt 00 RON értékben. Tudva azt, hogy a tyúktojás ára 50 bani, a libatojás 5 RON és
Azonosító jel: FÖLDRAJZ EMELT SZINTŰ ÍRÁSBELI VIZSGA. 2008. május 15. 14:00. Az írásbeli vizsga időtartama: 240 perc
 ÉRETTSÉGI VIZSGA 2008. május 15. FÖLDRAJZ EMELT SZINTŰ ÍRÁSBELI VIZSGA 2008. május 15. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM
ÉRETTSÉGI VIZSGA 2008. május 15. FÖLDRAJZ EMELT SZINTŰ ÍRÁSBELI VIZSGA 2008. május 15. 14:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM
III. osztály 1 Orchidea Iskola IV. Matematika verseny 2011/2012 II. forduló
 III. osztály 1 Orchidea Iskola IV. Matematika verseny 2011/2012 II. forduló 1. Mennyi az eredmény 15+17 15+17 15+17=? A) 28 B) 35 C) 36 D)96 2. Melyik szám van a piramis csúcsán? 42 82 38 A) 168 B) 138
III. osztály 1 Orchidea Iskola IV. Matematika verseny 2011/2012 II. forduló 1. Mennyi az eredmény 15+17 15+17 15+17=? A) 28 B) 35 C) 36 D)96 2. Melyik szám van a piramis csúcsán? 42 82 38 A) 168 B) 138
január :00 Lengyel táncosok a SzólóDuó 2018 Nemzetközi Tánc Fesztiválon.
 2018 JANUÁR FEBRUÁR január 11 14. 20:00 Lengyel táncosok a SzólóDuó 2018 Nemzetközi Tánc Fesztiválon. január 16. 17:00 január 17 február 28. 19:00 január 22 február 3. január 24 28. február 12 március
2018 JANUÁR FEBRUÁR január 11 14. 20:00 Lengyel táncosok a SzólóDuó 2018 Nemzetközi Tánc Fesztiválon. január 16. 17:00 január 17 február 28. 19:00 január 22 február 3. január 24 28. február 12 március
BOLYAI MATEMATIKA CSAPATVERSENY ORSZÁGOS DÖNTŐ SZÓBELI (2011. NOVEMBER 26.) 3. osztály
 3. osztály Egy fa tövétől a fára mászik fel egy csiga. Nappalonként 3 métert mászik felfelé, de éjszakánként 2 métert visszacsúszik. Az indulástól számított 10. nap délutánjáig felér a csúcsra. Milyen
3. osztály Egy fa tövétől a fára mászik fel egy csiga. Nappalonként 3 métert mászik felfelé, de éjszakánként 2 métert visszacsúszik. Az indulástól számított 10. nap délutánjáig felér a csúcsra. Milyen
VERSENYKIÍRÁS. Országos Kötélugró Csapatbajnokság Szentes, 2015. november 28.
 Magyar Ugrókötelesek Szövetsége 2836 Baj, Petőfi S. u. 137. ugrokotel@gmail.com Tel.: +3670/3650236 VERSENYKIÍRÁS Országos Kötélugró Csapatbajnokság Szentes, 2015. november 28. Időpont: 2015. november
Magyar Ugrókötelesek Szövetsége 2836 Baj, Petőfi S. u. 137. ugrokotel@gmail.com Tel.: +3670/3650236 VERSENYKIÍRÁS Országos Kötélugró Csapatbajnokság Szentes, 2015. november 28. Időpont: 2015. november
Versenykiírás MAGYARORSZÁG ÉVI EGYÉNI IDŐFUTAM BAJNOKSÁGA Debrecen-Bocskaikert, 354-es számú út, június 23. csütörtök 10:00 óra
 Versenykiírás MAGYARORSZÁG 2016. ÉVI EGYÉNI IDŐFUTAM BAJNOKSÁGA Debrecen-Bocskaikert, 354-es számú út, 2016. június 23. csütörtök 10:00 óra 1. A verseny védnökei: Tasó László, közlekedéspolitikáért felelős
Versenykiírás MAGYARORSZÁG 2016. ÉVI EGYÉNI IDŐFUTAM BAJNOKSÁGA Debrecen-Bocskaikert, 354-es számú út, 2016. június 23. csütörtök 10:00 óra 1. A verseny védnökei: Tasó László, közlekedéspolitikáért felelős
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Logika-Gráfok
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Logika-Gráfok A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉPSZINT Logika-Gráfok A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ UTASÍTÁST!
 Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA SEPTEMBRIE 2015 COD BROŞURĂ 2 FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
Universitatea Babeş-Bolyai din Cluj-Napoca Facultatea de Drept BROŞURĂ CU SUBIECTE ADMITERE - SESIUNEA SEPTEMBRIE 2015 COD BROŞURĂ 2 FIGYELEM! NE NYISSA KI ADDIG AMÍG A FELVIGYÁZÓ TANÁR NEM AD ERRE VONATKOZÓ
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Halmazok
 MTEMTIK ÉRETTSÉGI TÍPUSFELDTOK MEGOLDÁSI KÖZÉP SZINT Halmazok szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MTEMTIK ÉRETTSÉGI TÍPUSFELDTOK MEGOLDÁSI KÖZÉP SZINT Halmazok szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Megjegyzés: A programnak tartalmaznia kell legalább egy felhasználói alprogramot. Példa:
 1. Tétel Az állomány két sort tartalmaz. Az első sorában egy nem nulla természetes szám van, n-el jelöljük (5
1. Tétel Az állomány két sort tartalmaz. Az első sorában egy nem nulla természetes szám van, n-el jelöljük (5
1. tétel. Valószínűségszámítás vizsga Frissült: 2013. január 19. Valószínűségi mező, véletlen tömegjelenség.
 1. tétel Valószínűségszámítás vizsga Frissült: 2013. január 19. Valószínűségi mező, véletlen tömegjelenség. A valószínűségszámítás tárgya: véletlen tömegjelenségek vizsgálata. véletlen: a kísérlet kimenetelét
1. tétel Valószínűségszámítás vizsga Frissült: 2013. január 19. Valószínűségi mező, véletlen tömegjelenség. A valószínűségszámítás tárgya: véletlen tömegjelenségek vizsgálata. véletlen: a kísérlet kimenetelét
A 2017/2018. tanév rendje
 A 2017/2018. tanév rendje A 2017/2018. tanévben a szorgalmi idő első tanítási napja 2017. szeptember 1. (péntek) és utolsó tanítási napja 2018. június 15. (péntek). A tanítási napok száma: 180 nap. A szorgalmi
A 2017/2018. tanév rendje A 2017/2018. tanévben a szorgalmi idő első tanítási napja 2017. szeptember 1. (péntek) és utolsó tanítási napja 2018. június 15. (péntek). A tanítási napok száma: 180 nap. A szorgalmi
Andragógia BA képzés ELTE PPK
 Andragógia BA képzés ELTE PPK 2015. január 30. Dr. Kereszty Orsolya egyetemi docens Andragógia szak, 2015 Készítette: Dr. Benkei-Kovács Balázs Andragógia szak, 2015 Készítette: Stéber Andrea Andragógia
Andragógia BA képzés ELTE PPK 2015. január 30. Dr. Kereszty Orsolya egyetemi docens Andragógia szak, 2015 Készítette: Dr. Benkei-Kovács Balázs Andragógia szak, 2015 Készítette: Stéber Andrea Andragógia
2014/2015 tanév. Jelenleg a Dunaföldvári Alapfokú Művészeti Iskolában 8 pedagógus végzi a munkáját:
 Dunaföldvári Bölcskei Madocsai Általános Iskola, Gimnázium és Szakiskola Dunaföldvári Alapfokú Művészeti Iskola 7020 Dunaföldvár, Templom u. 9. 75/541-247, Tel /Fax: 75/541-013 OM 201167 2014/2015 tanév
Dunaföldvári Bölcskei Madocsai Általános Iskola, Gimnázium és Szakiskola Dunaföldvári Alapfokú Művészeti Iskola 7020 Dunaföldvár, Templom u. 9. 75/541-247, Tel /Fax: 75/541-013 OM 201167 2014/2015 tanév
1.1. Halmazok. 2. Minta - 5. feladat (2 pont) Adott két halmaz:
 1.1. Halmazok 2009. május id. - 11. feladat (3 pont) A H halmaz elemei legyenek a KATALINKA szó betűi, a G halmaz elemei pedig a BICEBÓCA szó betűi. Írja fel a H U G halmaz elemeit! 2010. október - 1.
1.1. Halmazok 2009. május id. - 11. feladat (3 pont) A H halmaz elemei legyenek a KATALINKA szó betűi, a G halmaz elemei pedig a BICEBÓCA szó betűi. Írja fel a H U G halmaz elemeit! 2010. október - 1.
I. LÉTSZÁM. Tanszakok szerinti megoszlás a tanév elején a következő volt: Kehidakustányban: 1 fő 5 fő (mind Zalaszentgróton tanul)
 1 I. LÉTSZÁM A Deák Ferenc ÁGM Erkel Ferenc Alapfokú Művészeti Iskolája a 2014/2015-ös tanévet 144 fő zeneiskolás tanulóval kezdte. A gyerekek megoszlása telephelyenként a következő volt: Központi Iskola
1 I. LÉTSZÁM A Deák Ferenc ÁGM Erkel Ferenc Alapfokú Művészeti Iskolája a 2014/2015-ös tanévet 144 fő zeneiskolás tanulóval kezdte. A gyerekek megoszlása telephelyenként a következő volt: Központi Iskola
FORMÁLIS NYELVEK ÉS FORDÍTÓPROGRAMOK. LABORGYAKORLATOK
 FORMÁLIS NYELVEK ÉS FORDÍTÓPROGRAMOK LABORGYAKORLATOK http://www.ms.sapientia.ro/~kasa/formalis.htm 0 Formális nyelvek és fordítóprogramok http://www.ms.sapientia.ro/~kasa/formalis.htm Jelenlét kötelezõ!
FORMÁLIS NYELVEK ÉS FORDÍTÓPROGRAMOK LABORGYAKORLATOK http://www.ms.sapientia.ro/~kasa/formalis.htm 0 Formális nyelvek és fordítóprogramok http://www.ms.sapientia.ro/~kasa/formalis.htm Jelenlét kötelezõ!
Egyesületünk. A Dancing Feet Akrobatikus Rock And Roll Sportegyesület ben alakult, és 1993-tól egyesületként működik Tatabányán.
 Bemutatkozunk Egyesületünk A Dancing Feet Akrobatikus Rock And Roll Sportegyesület 1992- ben alakult, és 1993-tól egyesületként működik Tatabányán. Az egyesületünk célja Célunk a rock and roll tánc műfajának
Bemutatkozunk Egyesületünk A Dancing Feet Akrobatikus Rock And Roll Sportegyesület 1992- ben alakult, és 1993-tól egyesületként működik Tatabányán. Az egyesületünk célja Célunk a rock and roll tánc műfajának
VII. Apáczai Matematika Kupa 7. osztály 2011. Pontozási útmutató
 1. feladat: VII. Apáczai Matematika Kupa 7. osztály 011. Pontozási útmutató Egy szöcske ugrál a számegyenesen. Ugrásainak hossza egység. A számegyenesen a 10-et jelölő pontból a 1-et jelölő pontba ugrással
1. feladat: VII. Apáczai Matematika Kupa 7. osztály 011. Pontozási útmutató Egy szöcske ugrál a számegyenesen. Ugrásainak hossza egység. A számegyenesen a 10-et jelölő pontból a 1-et jelölő pontba ugrással
III. Gráfok. 1. Irányítatlan gráfok:
 III. Gráfok 1. Irányítatlan gráfok: Jelölés: G=(X,U), X a csomópontok halmaza, U az élek halmaza X={1,2,3,4,5,6}, U={[1,2], [1,4], [1,6], [2,3], [2,5], [3,4], [3,5], [4,5],[5,6]} Értelmezések: 1. Fokszám:
III. Gráfok 1. Irányítatlan gráfok: Jelölés: G=(X,U), X a csomópontok halmaza, U az élek halmaza X={1,2,3,4,5,6}, U={[1,2], [1,4], [1,6], [2,3], [2,5], [3,4], [3,5], [4,5],[5,6]} Értelmezések: 1. Fokszám:
A Solti György Zenei Alapfokú Művészeti Iskola
 A Solti György Zenei Alapfokú Művészeti Iskola 2014/2015. tanév éves intézményi munkaterve Dátum Nap Óra Esemény Helyszín augusztus 25. 11.00 Tanszakvezetői alakuló Solti értekezlet augusztus 26 29. Vonószenekar
A Solti György Zenei Alapfokú Művészeti Iskola 2014/2015. tanév éves intézményi munkaterve Dátum Nap Óra Esemény Helyszín augusztus 25. 11.00 Tanszakvezetői alakuló Solti értekezlet augusztus 26 29. Vonószenekar
A marketing tevékenység megszervezése a sepsiszentgyörgyi kis- és közepes vállalatok keretében
 531 JEGYZETLAPOK Domokos Ernő Krájnik Izabella A marketing tevékenység megszervezése a sepsiszentgyörgyi kis- és közepes vállalatok keretében A kolozsvári Babeş Bolyai Tudományegyetem sepsiszentgyörgyi
531 JEGYZETLAPOK Domokos Ernő Krájnik Izabella A marketing tevékenység megszervezése a sepsiszentgyörgyi kis- és közepes vállalatok keretében A kolozsvári Babeş Bolyai Tudományegyetem sepsiszentgyörgyi
PRÓBAÉRETTSÉGI 2004.május MATEMATIKA. KÖZÉPSZINT I. 45 perc
 PRÓBAÉRETTSÉGI 2004.május MATEMATIKA KÖZÉPSZINT I. 45 perc A feladatok megoldására 45 perc fordítható, az idő leteltével a munkát be kell fejeznie. A feladatok megoldási sorrendje tetszőleges. A feladatok
PRÓBAÉRETTSÉGI 2004.május MATEMATIKA KÖZÉPSZINT I. 45 perc A feladatok megoldására 45 perc fordítható, az idő leteltével a munkát be kell fejeznie. A feladatok megoldási sorrendje tetszőleges. A feladatok
Arany Dániel Matematikai Tanulóverseny 2010/2011-es tanév 1. forduló haladók III. kategória
 Bolyai János Matematikai Társulat Oktatásért Közalapítvány támogatásával Arany Dániel Matematikai Tanulóverseny 2010/2011-es tanév 1. forduló haladók III. kategória Megoldások és javítási útmutató 1. Határozzuk
Bolyai János Matematikai Társulat Oktatásért Közalapítvány támogatásával Arany Dániel Matematikai Tanulóverseny 2010/2011-es tanév 1. forduló haladók III. kategória Megoldások és javítási útmutató 1. Határozzuk
A tanév munkarendje SZEPTEMBER
 A tanév munkarendje 2016. SZEPTEMBER 01. csütörtök munkanap 1 Első tanítási nap 02. péntek munkanap 2 03. szombat pihenőnap 04. vasárnap pihenőnap 05. hétfő munkanap 3 Jelentkezési határidő az őszi érettségire
A tanév munkarendje 2016. SZEPTEMBER 01. csütörtök munkanap 1 Első tanítási nap 02. péntek munkanap 2 03. szombat pihenőnap 04. vasárnap pihenőnap 05. hétfő munkanap 3 Jelentkezési határidő az őszi érettségire
Halmazelméleti feladatok (középszint)
 Halmazelméleti feladatok (középszint) (KSZÉV Minta (1) 2004.05/I/9) Adott két intervallum: ] 1; 3[ és [0; 4]. a) Ábrázolja számegyenesen a két intervallum metszetét! b) Adja meg a metszetintervallumot!
Halmazelméleti feladatok (középszint) (KSZÉV Minta (1) 2004.05/I/9) Adott két intervallum: ] 1; 3[ és [0; 4]. a) Ábrázolja számegyenesen a két intervallum metszetét! b) Adja meg a metszetintervallumot!
Halmazelméleti feladatok (középszint)
 Halmazelméleti feladatok (középszint) 1. (KSZÉV Minta (1) 2004.05/I/9) Adott két intervallum: ] 1; 3[ és [0; 4]. a) Ábrázolja számegyenesen a két intervallum metszetét! b) Adja meg a metszetintervallumot!
Halmazelméleti feladatok (középszint) 1. (KSZÉV Minta (1) 2004.05/I/9) Adott két intervallum: ] 1; 3[ és [0; 4]. a) Ábrázolja számegyenesen a két intervallum metszetét! b) Adja meg a metszetintervallumot!
Versenykiírás MAGYARORSZÁG ÉVI EGYÉNI IDŐFUTAM BAJNOKSÁGA Bocskaikert, 354-es számú út, június 28. csütörtök 10:00 óra
 Versenykiírás MAGYARORSZÁG 2018. ÉVI EGYÉNI IDŐFUTAM BAJNOKSÁGA Bocskaikert, 354-es számú út, 2018. június 28. csütörtök 10:00 óra 1. A verseny védnökei: Priczinger Péter, az MKSZ elnöke Szőllős Sándor,
Versenykiírás MAGYARORSZÁG 2018. ÉVI EGYÉNI IDŐFUTAM BAJNOKSÁGA Bocskaikert, 354-es számú út, 2018. június 28. csütörtök 10:00 óra 1. A verseny védnökei: Priczinger Péter, az MKSZ elnöke Szőllős Sándor,
1. Írd le kis írott betűkkel a nyomtatott betűket! 10/ a b é f ly d ó zs g j. 2. Írd le nagy írott betűkkel a nyomtatott betűket!
 Név: A csoport 1. Írd le kis írott betűkkel a nyomtatott betűket! 10/ a b é f ly d ó zs g j 2. Írd le nagy írott betűkkel a nyomtatott betűket! 10/ N R Cs D Ü T Ő Gy L E 3. Másold le a szavakat írott betűkkel!
Név: A csoport 1. Írd le kis írott betűkkel a nyomtatott betűket! 10/ a b é f ly d ó zs g j 2. Írd le nagy írott betűkkel a nyomtatott betűket! 10/ N R Cs D Ü T Ő Gy L E 3. Másold le a szavakat írott betűkkel!
Logika, gráfok. megtalált.
 1) Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először Ádám és Tamás nézték meg figyelmesen az ábrákat: Ádám 11,
1) Egy rejtvényújságban egymás mellett két, szinte azonos rajz található, amelyek között 23 apró eltérés van. Ezek megtalálása a feladat. Először Ádám és Tamás nézték meg figyelmesen az ábrákat: Ádám 11,
44. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY. Megyei forduló április mal, így a számjegyeinek összege is osztható 3-mal.
 44. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY Megyei forduló - 2015. április 11. HATODIK OSZTÁLY - Javítási útmutató 1. Melyik a legkisebb 3-mal osztható négyjegyű szám, amelynek minden számjegye különböző,
44. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY Megyei forduló - 2015. április 11. HATODIK OSZTÁLY - Javítási útmutató 1. Melyik a legkisebb 3-mal osztható négyjegyű szám, amelynek minden számjegye különböző,
Kérdéstípusok és kérdőívek
 Kérdéstípusok és kérdőívek Segítség kérdőívek készítéséhez A könyvtár-pedagógia módszertana képzés 2011. május 4. Készítette: Gaskó Krisztina Nyílt kérdések véleménykérdések; miért kérdések (indokláskérő
Kérdéstípusok és kérdőívek Segítség kérdőívek készítéséhez A könyvtár-pedagógia módszertana képzés 2011. május 4. Készítette: Gaskó Krisztina Nyílt kérdések véleménykérdések; miért kérdések (indokláskérő
MATEMATIKA VERSENY
 Eötvös Károly Közös Fenntartású Óvoda, Általános Iskola 2012. és Alapfokú Művészetoktatási Intézmény 8314 Vonyarcvashegy, Fő u. 84/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen,
Eötvös Károly Közös Fenntartású Óvoda, Általános Iskola 2012. és Alapfokú Művészetoktatási Intézmény 8314 Vonyarcvashegy, Fő u. 84/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen,
Harmadikos vizsga Név: osztály:
 . a) b) c) Számítsd ki az alábbi kifejezések pontos értékét! log 6 log log 49 4 7 d) log log 6 log 8 feladat pontszáma: p. Döntsd el az alábbi öt állítás mindegyikéről, hogy igaz vagy hamis! A pontozott
. a) b) c) Számítsd ki az alábbi kifejezések pontos értékét! log 6 log log 49 4 7 d) log log 6 log 8 feladat pontszáma: p. Döntsd el az alábbi öt állítás mindegyikéről, hogy igaz vagy hamis! A pontozott
GYERMEKMOSOLY ÓVODA INTÉZMÉNYI KÖZZÉTÉTELI LISTA 2015/2016. NEVELÉSI ÉV
 GYERMEKMOSOLY ÓVODA INTÉZMÉNYI KÖZZÉTÉTELI LISTA 2015/2016. NEVELÉSI ÉV A Nemzeti Erőforrás Miniszter 229/2012. (VIII. 28) Kormány-rendelet 10. fejezet 23. -a, (1.- 2.) bekezdés alapján az alábbi adatokat
GYERMEKMOSOLY ÓVODA INTÉZMÉNYI KÖZZÉTÉTELI LISTA 2015/2016. NEVELÉSI ÉV A Nemzeti Erőforrás Miniszter 229/2012. (VIII. 28) Kormány-rendelet 10. fejezet 23. -a, (1.- 2.) bekezdés alapján az alábbi adatokat
V. ZENEI VERSENY VERSENYKIÍRÁS
 V. PREMIER MŰVÉSZETI NAPOK 2017. MÁRCIUS 17. V. PREMIER TÁNC ÉS ZENEI VERSENY V. ZENEI VERSENY VERSENYKIÍRÁS 2017. március 17. (péntek) SZEGED Az. V. Premier Tánc- és Zenei Versenyt meghirdető intézmény
V. PREMIER MŰVÉSZETI NAPOK 2017. MÁRCIUS 17. V. PREMIER TÁNC ÉS ZENEI VERSENY V. ZENEI VERSENY VERSENYKIÍRÁS 2017. március 17. (péntek) SZEGED Az. V. Premier Tánc- és Zenei Versenyt meghirdető intézmény
Matematika kisérettségi I. rész 45 perc NÉV:...
 Matematika kisérettségi I. rész 45 perc NÉV:... 1. Az A halmaz elemei a háromnál nagyobb egyjegyű számok, a B halmaz elemei pedig a húsznál kisebb pozitív páratlan számok. Sorolja fel az halmaz elemeit!
Matematika kisérettségi I. rész 45 perc NÉV:... 1. Az A halmaz elemei a háromnál nagyobb egyjegyű számok, a B halmaz elemei pedig a húsznál kisebb pozitív páratlan számok. Sorolja fel az halmaz elemeit!
TUDOMÁNYOS ISMERETTERJESZTŐ TÁRSULAT
 Javítókulcs 4. osztály megyei 1. Titkos üzenetet kaptál, amelyben a hét minden napja le van írva egyszer, kivéve azt a napot, amelyiken találkozol az üzenet küldőjével. Minden betű helyett egy szimbólumot
Javítókulcs 4. osztály megyei 1. Titkos üzenetet kaptál, amelyben a hét minden napja le van írva egyszer, kivéve azt a napot, amelyiken találkozol az üzenet küldőjével. Minden betű helyett egy szimbólumot
A Veres Péter Gimnázium felvételt hirdet 4 és 8 osztályos gimnáziumi osztályaiba a 2012/2013-as tanévre az alábbiak szerint
 A Veres Péter Gimnázium felvételt hirdet 4 és 8 osztályos gimnáziumi osztályaiba a 2012/2013-as tanévre az alábbiak szerint 1.) Négyosztályos gimnázium (általános tantervő) Kód: 01 a) Oktatott idegen nyelvek:
A Veres Péter Gimnázium felvételt hirdet 4 és 8 osztályos gimnáziumi osztályaiba a 2012/2013-as tanévre az alábbiak szerint 1.) Négyosztályos gimnázium (általános tantervő) Kód: 01 a) Oktatott idegen nyelvek:
Pilisszentkereszti Közösségi Ház és Könyvtár MUNKATERVE 2012.
 Pilisszentkereszti Közösségi Ház és Könyvtár MUNKATERVE 2012. 1 A Közösségi Ház közművelődési és szabadidős feladatokat ellátó többcélú intézmény. Közművelődési tevékenység: A polgárok iskolán kívüli,
Pilisszentkereszti Közösségi Ház és Könyvtár MUNKATERVE 2012. 1 A Közösségi Ház közművelődési és szabadidős feladatokat ellátó többcélú intézmény. Közművelődési tevékenység: A polgárok iskolán kívüli,
Arany Dániel Matematikai Tanulóverseny 2012/2013-as tanév első (iskolai) forduló haladók II. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 2012/2013-as tanév első (iskolai) forduló haladók II. kategória Megoldások és javítási útmutató 1. A 23-as szám című misztikus filmben
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 2012/2013-as tanév első (iskolai) forduló haladók II. kategória Megoldások és javítási útmutató 1. A 23-as szám című misztikus filmben
HEXAÉDEREK. 5. Hányféleképpen lehet kiolvasni Erdős Pál nevét, ha csak jobbra és lefelé haladhatunk?
 HEXAÉDEREK 0. Két prímszám szorzata 85. Mennyi a két prímszám összege? 1. Nyolc epszilon találkozik egy születésnapi bulin, majd mindenki kézfogással üdvözli egymást. Ha eddig 11 kézfogás történt, hány
HEXAÉDEREK 0. Két prímszám szorzata 85. Mennyi a két prímszám összege? 1. Nyolc epszilon találkozik egy születésnapi bulin, majd mindenki kézfogással üdvözli egymást. Ha eddig 11 kézfogás történt, hány
Nagy Gábor compalg.inf.elte.hu/ nagy ősz
 Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 8. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
Diszkrét matematika 1. középszint 2016. ősz 1. Diszkrét matematika 1. középszint 8. előadás Nagy Gábor nagygabr@gmail.com nagy@compalg.inf.elte.hu compalg.inf.elte.hu/ nagy Mérai László diái alapján Komputeralgebra
KÖZZÉTÉTELI LISTA Ajkai Bródy Imre Gimnázium és Alapfokú Művészeti Iskola. Zeneművészeti ág:
 KÖZZÉTÉTELI LISTA Ajkai Bródy Imre Gimnázium és Alapfokú Művészeti Iskola Zeneművészeti ág: Az első minősítés évéhez viszonyítva hány előképző, alapfokú és továbbképző évfolyamot működtet 2018-2019 tanév
KÖZZÉTÉTELI LISTA Ajkai Bródy Imre Gimnázium és Alapfokú Művészeti Iskola Zeneművészeti ág: Az első minősítés évéhez viszonyítva hány előképző, alapfokú és továbbképző évfolyamot működtet 2018-2019 tanév
MATEMATIKA ÉRETTSÉGI május 8. KÖZÉPSZINT
 MATEMATIKA ÉRETTSÉGI 007. május 8. KÖZÉPSZINT ) Egyszerűsítse a következő törtet! (a; b valós szám, ab 0)! a b ab ab ab ( a ) a ab I. Összesen: pont ) Egy mértani sorozat második eleme 3, hatodik eleme.
MATEMATIKA ÉRETTSÉGI 007. május 8. KÖZÉPSZINT ) Egyszerűsítse a következő törtet! (a; b valós szám, ab 0)! a b ab ab ab ( a ) a ab I. Összesen: pont ) Egy mértani sorozat második eleme 3, hatodik eleme.
1. tétel. 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója 7 cm. Mekkora a háromszög átfogója? (4 pont)
 1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
NULLADIK MATEMATIKA szeptember 13.
 A NULLADIK MATEMATIKA ZÁRTHELYI 0. szeptember. Terem: Munkaidő: 0 perc. A dolgozat megírásához íróeszközön kívül semmilyen segédeszköz nem használható nálható. Válaszait csak az üres mezőkbe írja! A javítók
A NULLADIK MATEMATIKA ZÁRTHELYI 0. szeptember. Terem: Munkaidő: 0 perc. A dolgozat megírásához íróeszközön kívül semmilyen segédeszköz nem használható nálható. Válaszait csak az üres mezőkbe írja! A javítók
VEGYIPARI ALAPISMERETEK
 ÉRESÉGI VIZSG 010. május 14. VEGYIPRI LPISMEREEK KÖZÉPSZINŰ ÍRÁSBELI VIZSG 010. május 14. 8:00 z írásbeli vizsga időtartama: 180 perc Pótlapok száma isztázati Piszkozati OKÁSI ÉS KULURÁLIS MINISZÉRIUM
ÉRESÉGI VIZSG 010. május 14. VEGYIPRI LPISMEREEK KÖZÉPSZINŰ ÍRÁSBELI VIZSG 010. május 14. 8:00 z írásbeli vizsga időtartama: 180 perc Pótlapok száma isztázati Piszkozati OKÁSI ÉS KULURÁLIS MINISZÉRIUM
