Geodézia 5. Vízszintes mérések alapműveletei
|
|
|
- Nóra Jázmin Takács
- 9 évvel ezelőtt
- Látták:
Átírás
1 Geodézia 5. Vízszintes mérések alapműveletei Tarsoly, Péter, Nyugat-magyarországi Egyetem Geoinformatikai Kar Tóth, Zoltán, Nyugat-Magyarországi Egyetem Geoinformatikai Kar
2 Geodézia 5.: Vízszintes mérések alapműveletei írta Tarsoly, Péter és Tóth, Zoltán Lektor: Homolya, András Ez a modul a TÁMOP /1/A Tananyagfejlesztéssel a GEO-ért projekt keretében készült. A projektet az Európai Unió és a Magyar Állam Ft összegben támogatta. v 1.0 Publication date 2010 Szerzői jog 2010 Nyugat-magyarországi Egyetem Geoinformatikai Kar Kivonat Ez a modul a vízszintes mérések alapműveleteit tárgyalja. Ezen az eljárások egy része a korszerű elektrooptikai távmérők megjelenéséig alapvető fontosságú volt a terepi geodéziai méréseknél. Jelentőségük azóta csökkent, de fontosnak tartjuk tárgyalásukat. Jelen szellemi terméket a szerzői jogról szóló évi LXXVI. törvény védi. Egészének vagy részeinek másolása, felhasználás kizárólag a szerző írásos engedélyével lehetséges.
3 Tartalom 5. Vízszintes mérések alapműveletei Bevezetés A vízszintes mérések feladatai Egyenes vonalak kitűzése A kitűzőrúd Egyenes vonalak kitűzése beintéssel vagy beállással Távolságok meghatározása Állandó nagyságú szögek kitűzése Derékszögű koordinátamérés Derékszögű kitűzési méretek meghatározása A vízszintes szögmérés módszerei Az iránymérés Az egyszerű szögmérés Poláris részletmérés A magassági szögmérés módszerei A vízszintes és magassági szögmérés eredményeinek előzetes feldolgozása Mérési jegyzet, mérési vázlat, tömbrajz Mérési jegyzet Mérési vázlat Tömbrajz Összefoglalás iii
4
5 5. fejezet - Vízszintes mérések alapműveletei Bevezetés Jelen modul a Geodézia tárgy egyik modulja. Az itt következő ismeretek megértéséhez javasoljuk, hogy olvassa el a Geodézia tárgy korábbi moduljait is. Ez a modul a karunk gondozásában megjelent Csepregi Szabolcs Gyenes Róbert - Tarsoly Péter (2009): Geodézia I. jegyzet megfelelő - 7. A vízszintes mérések alapműveletei, írta: Tarsoly Péter- fejezetének átszerkesztett, átdolgozott változata. Ebből a fejezetből megismerheti: a derékszögű koordinátamérés elméleti alapjait, gyakorlati végrehajtását, egyenesek kitűzésének módszereit, a vízszintes- és magassági szögmérés módszereit. A fejezet elsajátítása után képes lesz: a derékszögű koordinátamérés, a vízszintes- és magassági szögmérés végrehajtására. 2. A vízszintes mérések feladatai A vízszintes mérés feladata, hogy a földi pontok vízszintes vetületét egymáshoz viszonyítva meghatározza, a pontokat és a pontokkal jellemzett alakzatokat ábrázolja, továbbá a tervezett létesítmények előre meghatározott helyét a terepen kijelölje. Az első feladatot felmérésnek, a másodikat térképezésnek, a harmadikat pedig kitűzésnek nevezzük. A földi pontok a terepen meglévő, illetve kijelölt idomok alakjelző pontjai. Ezeket a pontokat részletpontoknak nevezzük. A részletpontokat az alappontokra támaszkodva határozzuk meg. A vízszintes mérések tehát két nagy csoportra oszthatóak: az alappontok és a részletpontok meghatározására. A vízszintes méréseknél először a meghatározandó pontokat meg kell jelölni, majd azok relatív helyzetét mérésekkel meg kell határozni. A mérési eredményekből számítással határozzuk meg a pontok helyét jellemző koordinátákat. A vízszintes mérések a következő alapműveletekből tevődnek össze. Pontok megjelölése Egyenes vonalak kitűzése Állandó nagyságú szögek kitűzése Távolságok meghatározása Szögek mérése A pontok jelöléséről már egy korábbi modulban volt szó, így most folytassuk a leírást az egyenes vonalak kitűzésével Egyenes vonalak kitűzése A vízszintes mérések szempontjából a függőleges sík és az egyenes vonal ekvivalens fogalmak. Ha például két, függőlegesen álló kitűzőrudat tűzünk le, akkor azok egy függőleges síkot, de egyben egy egyenest is kijelölnek. Egyenesek kitűzése alatt azt a műveletet értjük, amelynek során az egyenes két végpontját összekötő egyenes vonalon vagy a végpontok között, vagy valamelyik végpont kihosszabbításán egy vagy több további pontot jelölünk meg. A műveletnek két alapesete van: a beintés és a beállás. 1
6 A kitűzőrúd A legegyszerűbb iránykitűző eszköz a kitűzőrúd, amellyel nemcsak a megirányzandó pontot jelölhetjük meg, hanem kitűzhetjük a két kitűzőrúddal már kijelölt egyenes szakasz közbülső pontjait vagy az egyenes szakasz folytatását. A kitűzőrúd 3-6 cm átmérőjű kör vagy háromszög keresztmetszetű, 2-3 m hosszú egyenes fém-, műanyag, vagy impregnált farúd. A kitűzőrúd egyik végét kemény heggyel látják el, a másik végét gyakran további kitűzőrúd csatlakoztatására, több kitűzőrúd összeillesztésére alkalmasra készítik. Általában 20 vagy 50 cm közökben váltakozva piros-fehérre, vagy fekete-fehérre festik, hogy messziről is látható legyen. A jelzőrudat kétféleképpen használjuk: vagy a földbe szúrva vagy a pont fölé helyezve. Mindkét esetben a rúdnak függőlegesnek kell lennie. A jelzőrúd függőlegesé tételét vagy függővel végezzük, vagy két egymásra merőleges irányból kell nézni, hogy a rúd függőleges-e, de megoldás lehet a karóállító libella használata is. Kemény talajon vagy betonon elterjedt a csíptetős állvány vagy a háromlábú vasállvány használata Egyenes vonalak kitűzése beintéssel vagy beállással Beintéskor a kitűzést irányító személy nem tartózkodik a kitűzendő ponton, míg beálláskor a kitűzendő ponton végrehajtott művelettel ő maga végzi el a pont kitűzését. Az egyenesek kitűzése kisebb pontossággal különféle egyszerű eszközökkel (kitűzőrúddal, zsineggel, huzallal, szögprizmával), szabatosan pedig teodolittal vagy mérőállomással végezhető el. Beintéskor, miután az egyenes két végpontját egy-egy jelzőrúddal megjelöltük, elmegyünk az egyenes valamelyik végpontja mögé mintegy 5-6 méterrel. A beintendő rudat a segédmunkás az egyenes megfelelő helyén függőlegesen lógatva tartja (5-1. ábra). A két végpont érintősíkján átnézve addig intjük, irányítjuk a beintendő rudat, amíg annak széleit fedésbe nem látjuk a két végponttal. A beintést mindig a tőlünk legtávolabbi rúddal kell kezdeni ábra A beintés művelete (Csepregi,2000) Ha a kitűzendő pont az egyenes meghosszabbításában van, és nem törekszünk szélső pontosságra, akkor a feladatot egyenesbe állással is megoldhatjuk. Ekkor a beállítandó kitűzőrudat magunk elé tartva könnyedén lógatjuk a levegőben, és addig visszük jobbra vagy balra, amíg a széleit a két végpont érintősíkjában nem látjuk (5-2. ábra). A kitűzést egyenesbe állásnál mindig a legközelebb álló rúddal kell kezdeni. 2
7 5-2. ábra Az egyenesbe állás művelete (Csepregi,2000) Egyenesek közbülső pontjainak a kitűzését végezhetjük fokozatos közelítéssel is abban az esetben, ha valamilyen ok miatt nem tudunk elmenni a két végpont mögé, vagy terepakadály miatt a beintés nem végezhető el közvetlenül. Ebben az esetben mindig két rudat kell használni. Az egyiket közelítőleg az egyenesbe állítjuk, és mögüle nézve a másik kitűzőrúd beinthető a végpont és az első rúd egyenesébe. Majd a másik végpont és az utólag beintett rúd egyenesébe az első rudat intjük be. Ezt a folyamatot addig kell ismételni, ameddig a kitűzőrudak egymás mögül szemlélve egy egyenesbe nem esnek (5-3. ábra) ábra Egyenes kitűzése fokozatos közelítéssel (Gyenes, 2005) Távolságok meghatározása Két pont távolságán a két pont összekötő egyenesén mért hosszúságot értjük. Ezt ferde távolságnak nevezzük. A vízszintes méréseknél a térszíni pontok természetes vetületét az alapfelületen összekötő legrövidebb vonal hosszúságára van szükségünk. Két alapfelületi pontot összekötő végtelen sok felületi görbe közül azt, amelyiknek a két pont közé eső ívhossza a legkisebb, geodéziai vonalnak nevezzük. Két térszíni pont természetes vetületét az alapfelületen összekötő geodéziai vonal hosszúságát a két pont alapfelületi távolságának nevezzük (5-4. ábra). 3
8 5-4. ábra alapfelületi távolság értelmezése (Gyenes, 2005) A terep felszínén végrehajtott méréseink a ferde távolságot eredményezik. A ferde távolságból számítással kell levezetnünk az alapfelületi távolságot, a mért hosszakat redukciókkal kell ellátnunk. A ferde távolságból először redukálással a vízszintes távolságot, majd az alapfelületi távolságot tudjuk számítani. A redukáláshoz ismernünk kell a mért távolság, mint térbeli irány magassági vagy zenitszögét, továbbá az átlagos tengerszint feletti magasságot. A távolságot közvetlen vagy közvetett módszerrel tudjuk meghatározni. Közvetlennek mondjuk az olyan mérést, amelynél a távolságot ismert hosszúságú mérőeszköznek a vonalon való ismételt végigfektetésével kapjuk meg. Ezt a módszert hosszmérésnek nevezzük, és napjainkban leggyakrabban használt eszköze a mérőszalag. A geodéziai gyakorlatban kézifogantyús, keretes, méter hosszúságú mérőszalagokat alkalmaznak. Szélességük mm, vastagságuk mm, anyaguk pedig műanyag, üvegszál, acél vagy inváracél. Ez utóbbit nagyobb pontosságú méréseknél használjuk, ugyanis ezek hőtágulási együtthatója kicsiny, így hőmérséklet okozta hosszváltozásuk elhanyagolható. Minden mérőszalaghoz általában tartozik egy 11 szegből és két fémkarikából álló jelzőszeg készlet. A szalagmérés a mérendő távolság két végpontját összekötő egyenes kitűzésével kezdődik. Kisebb pontosságú mérésnél kb méterenként kitűzőrudakkal, szabatos szalagmérésnél zsinórral vagy teodolittal és legalább a mérőeszköz hosszának megfelelő távolságokban jelöljük meg az egyenes közbülső pontjait. Kisebb pontosságú mérésnél az egyenes kitűzése után két mérőszemély kihúzza a szalagot. A hátsó a szalag végét közelítőleg a kezdőpontra illeszti és a szalag másik végét az egyenes vonalába beinti. Az elöl lévő a szalag végének lehelyezése előtt a szalagot egyenesre igazítja, csapatja, hogy az egész hosszában az egyenesbe illeszkedjen. Ezután a hátsó a szalagot pontosan a kezdőpontra illeszti, az elöl lévő megfeszíti és a végvonásnál egy jelzőszeget szúr a talajba. Ezután az előző lépések szerint addig haladnak előre, amíg a távolság végpontját el nem érik. Közben az elmaradó jelzőszegeket a hátul lévő ember a nála lévő üres karikára fűzi. Amikor a mérendő távolság végpontja az utoljára leszúrt mérőszeghez illesztett mérőszalag hosszán belülre került, leolvassuk a távolság végpontjának a helyét a szalagon. Ez a maradék leolvasás. A teljes szalagfekvések száma megegyezik a hátul lévő ember karikáján lévő szegek és a földben lévő szeg összegével. A mért ferde távolságot megkapjuk, ha a mérőszalag hosszát megszorozzuk a teljes szalagfekvések számával és ezt összevonjuk a maradék leolvasással. Nagyobb pontosság elérése érdekében a távolságot két irányban, oda-vissza szokás megmérni. A hosszúság közvetett megmérését távmérésnek, eszközeit távmérőknek nevezzük. A távmérést az jellemzi, hogy nem magát a keresett távolságot, hanem vele összefüggésben lévő más mennyiséget mérünk meg, és a keresett távolságott azután a megmért mennyiséggel fennálló összefüggésből számítjuk ki. Aszerint, hogy a keresett távolsággal összefüggő milyen mennyiséget mérünk meg, a távmérési eljárásokat két fő csoportra osztjuk: 1. távmérés geometriai alapon 2. távmérés fizikai alapon. A geometriai távmérés alapelve bármely mérési módszer esetén visszavezethető egy vagy két háromszög megoldására. Tételezzünk fel egy ABP háromszöget, amelynél az AP háromszögoldal hosszát, mint távolságot szeretnénk meghatározni. Ha ismerjük az AB háromszögoldal hosszát, valamint a rajta, mint alapon fekvő két 4
9 szöget, akkor a vele szemben lévő P pontnál lévő szög, majd ezt követően az AP oldal hossza számítható. Ezt a módszert korábban gyakrabban használták a mindennapi mérnöki gyakorlatban olyan pontok távolságának meghatározására, amelyekhez közvetlen hosszméréssel nem lehetett hozzáférni. A háromszög megmért oldalát alapvonalnak, vagy más néven bázisnak nevezzük, az alapvonallal szemközti szöget pedig távmérő szögnek, vagy más néven parallaktikus, diasztimométeres szögnek. Az alapvonal lehet földön kitűzött (rendszerint hosszabb) vagy műszeren lévő (viszonylag rövid), és helyzete alapján lehet vízszintes vagy függőleges. Belsőnek nevezzük, ha egyik végpontja az a pont, amelyről a távmérést végezzük (tehát ahol a távmérő műszer áll), külsőnek pedig akkor, ha az alapvonal egyik végpontja azonos a meghatározandó távolság másik végpontjával. Ezen az alapon megkülönböztetünk: 1. belső alapvonalú távmérőket és távmérési eljárásokat 2. külső alapvonalú távmérőket és távmérési eljárásokat. További osztályozási lehetőséget nyújt az a körülmény, ha valamely távmérési eljárásban a távmérőszög állandó, akkor az alapvonal hossza a meghatározandó távolságtól függően változik, ha pedig az alapvonal hosszát vesszük állandónak, akkor a távmérőszög változó. Eszerint vannak: 1. állandó távmérőszögű, változó alapvonal hosszúságú távmérők és távmérési eljárásoj, 2. változó távmérőszögű, állandó alapvonal hosszúságú távmérők és távmérési eljárások. Az első esetben a távmérési eljárás az állandó távmérőszöghöz tartozó alapvonal hosszának a meghatározásából, a második esetben pedig az állandó alapvonalhoz tartozó távmérőszög meghatározásából áll. A gyakorlati méréseknél a háromszög egyik szögét célszerűen 90 -nak választották. A fizikai alapú távolságmérésekre elektromágneses hullámokat használunk. A távolság egyik végpontján elhelyezett energiaforrás (adóberendezés) hullámokat bocsát ki, a távolság másik végpontján elhelyezett visszaverő-berendezés, pedig a hullámokat visszaveri az adó felé. Ha az adót felszerelik olyan berendezéssel is, amelyik alkalmas a hullám által oda-vissza meg tett utat meghatározó valamilyen fizikai jellemző (például az út megtételéhez szükséges időnek, vagy a kibocsátott és visszaérkezett hullám fáziseltolódásának stb.) mérésére, a berendezés távmérésre alkalmassá válik. A fizikai alapú távmérőkészülékeket a felhasznált elektromágneses hullámok hossza szerint két csoportba sorolhatjuk. Az elsőbe tartoznak a fényhullámokkal működő készülékek, vagy más néven elektrooptikai távmérők, a másodikba pedig azok, amelyek cm-es hullámhosszúságú mikrohullámokat használnak. Ez utóbbit rádiótávmérésnek nevezzük. Az elektrooptikai távmérés esetén a hullámhossz mikrométer nagyságrendű, az infravörös sugárzás tartományába esik. Két alapvető típusa alakult ki: 1. időméréses távmérés: amelynél a mérőjel kétszeres futási idejét mérjük meg 2. fázisméréses távmérés: amelynél a kibocsátott és beérkező mérőjel fázisát (rezgésállapotát) mérjük, majd ezt a ciklusszámot távolsággá alakítjuk. Az elektrooptikai távmérő berendezésekkel, valamint a különböző távmérési módszerekkel, a mért eredmények redukálásával részletesen fogunk foglalkozni a Geodézia II, és a Geodéziai hálózatok című tantárgyakban Állandó nagyságú szögek kitűzése Vízszintes szögek kitűzésére minden szögmérő műszer alkalmas, mégis szerkesztettek olyan egyszerű szerkezetű külön műszereket is, amelyekkel csak egy bizonyos, állandó nagyságú szöget lehet kitűzni. Ezekkel az egyszerű szögkitűző eszközökkel és 45 -os szögeket lehet kitűzni. A szögkitűző műszereket két nagy csoportba lehet osztani: dioptrás és tükröző műszerekre. Ezeket az eszközöket ma már csak elvétve alkalmazzák a gyakorlatban, ezért részletes ismertetésüktől eltekintünk, leírásuk megtalálható bármely régebbi szakirodalmi műben. Ebben a fejezetben egyedül a tükrös szögkitűző műszerek egy fajtájával, a szögprizmák közé tartozó kettős szögprizmákkal fogunk röviden megismerkedni. 5
10 A kettős szögprizmák olyan műszerek, amelyekkel az egyenes közbülső pontjainak a kitűzése egyenesbe állással, illetve egy az egyenesen kívül fekvő pont merőleges talppontjának a megkeresése segédrúd nélkül megvalósítható. Kettős szögprizmát úgy állíthatunk elő, hogy két prizmát megfelelő elrendezésben egymás fölé helyezünk. A két prizma nem fekszik közvetlenül egymáson, hanem köztük kb. 1.5 mm-es rés van, amelyen keresztül az egyenesre merőleges irányban nézhetünk. A kettős szögprizmák Magyarországon legjobban elterjedt fajtája a MOM-féle duplex prizma, melynek sematikus felépítését és sugármenetét mutatja az 5-5. ábra ábra A MOM-féle duplex prizma sematikus felépítése és sugármenete (Csepregi, 2000) A szögprizmákat vetítőbotra szerelve használjuk. A prizma látómezeje függőleges irányban három részre osztható. Az alsó és felső részben az egyenes két végpontján lévő kitűzőrudak láthatók kicsinyített képként, míg középen valódi nagyságban az egyenesre merőlegesen elhelyezett kitűzőrúd szemlélhető (5-6. ábra). Kettős szögprizmákkal két művelet végezhető el: az egyenesbe állás és a talppontkeresés. A derékszög kitűzése ez utóbbi műveletnek az inverze ábra Egyenesbeállás és talppontkeresés művelete (Csepregi, 2000) 5-7. ábra Egyenesbeállás és talppontkeresés művelete (Csepregi, 2000) Egyenesbe állásnál a feladatunk az, hogy a két végpontján kitűzőrúddal jelölt egyenesbe a megfelelő helyen pontosan beálljunk, pl. egy pont talppontjánál. Az egyenesbe állás műveleténél a vonalra merőlegesen előre hátra kell mozogni egészen addig, amíg a prizma alsó és felső részében látható kicsinyített kitűzőrúd képek fedésbe nem kerülnek. Talppontkeresésnél, már az egyenes mentén kell mozognunk jobbra-balra egészen addig, 6
11 amíg a szögprizma középső részében látható valódi kitűzőrúd fedésbe nem kerül a prizma alsó és felső részében látható kitűzőrúd képekkel. (5-7.ábra) Derékszögű koordinátamérés A derékszögű koordinátamérés (vagy másképpen ortogonális koordinátamérés) alapelve az, hogy a részletpontok közelében lévő két ismert alappont egyenesén, az úgynevezett mérési vonalon megkeressük a részletpont talppontját, majd a mérési vonalon megmérjük az egyik ismert ponttól a talppontig terjedő távolságot (a=abszcissza), valamint a talpponttól a részletpontig terjedő távolságot (b=ordináta) (5-8.ábra) 5-8. ábra A derékszögű koordinátamérés elve (Gyenes, 2005) A derékszögű koordinátamérés a mérési vonal kitűzésével kezdődik, amit a már ismertetett módon végezhetünk el. A mérési vonal kitűzése után ennek egyenesébe fektetünk egy mérőszalagot úgy, hogy kezdőpontja egybeessen a mérési vonal kezdőpontjával. A lefektetett szalag mellett a kettős szögprizmával a mérési iránynak megfelelően felkeressük azoknak a részletpontoknak a talppontját, amelyek az első szalagfekvésen belül esnek. Végre kell hajtanunk az egyenesbe állás és a talppontkeresés műveletét is, majd meg kell mérnünk a pont abszcissza és ordináta méretét. A mérési eredményeket mérési jegyzeten (manuálén) tüntetjük fel, majd később mérési vázlaton vagy tömbrajzon letisztázzuk. (7.23. ábra) Ha az első szalagfekvésen belül eső valamennyi részletpont talppontját megkerestük és a szükséges méreteket feljegyeztük, a mérőeszközt a szalagmérés szabályainak megfelelően visszük tovább. Amikor a szalaggal a mérési vonal végpontjához érünk, itt leolvassuk a végméretet. Szükség esetén a bemérést a mérési vonal meghosszabbításában is elvégezhetjük, de a meghosszabbítás legfeljebb a mérési vonal hosszának 1/3-a lehet. A meghosszabbításon végzett leolvasásokat is a kezdőponttól kiindulva folytatólagosan végezzük. A részletpontokat mindig a legközelebbi mérési vonalról, tehát minnél rövidebb ordinátával kell megmérni. Ugyanannak a tereptárgynak a pontjait lehetőleg ugyanarról a mérési vonalról kell lemérni. Ellenőrző mérésekre azonban szükség van. Az egyenes vonalba eső részletpontok beméréséhez csak az egyenes kezdő és végpontját szabad derékszögű koordinátaméréssel bemérni, az egyenesben lévő többi pontot pedig ezek között mérjük be folytatólagos méréssel. Ezzel biztosítjuk azt, hogy ami egyenes a valóságban, az egyenes marad a térképen is. Épületeknek mindig a hosszabbik oldalát kell megmérnünk. Épületeknél mindig csak annyi pontot szabad megmérni, amely a tárgy képének a megszerkesztéséhez okvetlenül szükséges. Ha az épületen több ki-beugrás van, akkor csak az uralkodó falsík végpontjait mérjük be, a többi pontot pedig ezen pontok között határozzuk meg. A földfelszín feletti pontokat le kell vetíteni a földfelszínre, és a levetített ponthelyeket kell bemérni. Íves vonalak esetében annyi pontot kell megmérni, hogy a szomszédos pontokat egyenes vonallal összekötve az ívet a megkívánt pontossággal ábrázolni tudjuk. A derékszögű koordinátamérés számítása lényegében síkbeli hasonlósági transzformáció. A forrás-rendszer egy helyi rendszer (a,b), a cél-rendszer pedig az országos koordináta-rendszer (Y,X). A korábbi fejezetben már ismertetett síkbeli hasonlósági transzformáció alapképleteit ismertnek véve a derékszögű koordináta mérés számítását a ábrák és a következő képletek alapján végezhetjük: 7
12 5-9. ábra A derékszögű koordinátamérés számítása (Gyenes, 2005) A 5-9. ábrán K jelöli a mérési vonal kezdőpontját, V pedig a végpontot, mely pontok az országos koordináta rendszerben Y és X koordinátával adottak. A P pont abszcissza és ordináta mérete a és b. Az YX koordinátatengelyek a geodéziai koordinátarendszert szemléltetik. A feladat az, hogy határozzuk meg a P pont Y és X koordinátáját, ha terepen mértük a-t és b-t. A síkbeli hasonlósági transzformáció paraméterei: eltolás (Y K, X K), elforgatás (α) valamint egy s méretaránytényező. Az s értelmezését a ábra mutatja. A terepen mért végméret és a koordinátákból számított végméret nem egyeznek meg egymással, mert a mérést mérési hibák, a koordinátákat pedig kerethibák terhelik. A kettő hányadosa adja a méretarány tényezőt ábra A méretaránytényező értelmezése (Gyenes, 2005) A számításhoz a már ismert mátrixos megoldást írjuk fel: A forgatómátrix elemei: A transzformáció alapképlete: 5-1. Egyenlet A transzformáció alapképlete: 5-2. Egyenlet 8
13 5-3. Egyenlet Kifejtve: 5-4. Egyenlet Összefoglalva: 5-5. Egyenlet Méretaránytényező számítása paraméterekből: 5-6. Egyenlet Derékszögű koordináta mérés végrehajtásakor nagy hangsúlyt kell fektetnünk az abszcissza és az ordináta méretek előjelére. Ha a mérési vonal kezdőpontjára képzeljük magunkat és a végpont felé nézünk, akkor a végpont felé értelmezzük az abszcissza méreteket pozitív előjellel, a hátunk mögött pedig negatív előjellel. Az ordináta méretek jobb kéz felé negatívak, bal kéz felé pedig pozitívak. (5.11. ábra) ábra Az abszcissza és ordináta előjelének értelmezése (Gyenes, 2005) A gyakorlati mérések során előfordul, hogy nem tudunk mérési vonalat létesíteni közvetlenül a K és V országos koordinátákkal adott pontok között. Ebben az esetben a mérési vonalat eltolva kell felvennünk. Ezt a vonalat nevezzük szabad vonalnak. Ebben az esetben a kezdő-és végpont kijelölése tetszőleges lehet, azonban a részletpontok abszcissza és ordináta méretein kívül a K és V pont adatait is meg kell mérnünk. A számítás hasonló az egyszerű derékszögű koordinátaméréshez, és a ábra és az alábbi képletek magyarázzák: 9
14 5-12. ábra A szabad mérési vonal értelmezése (Gyenes, 2005) 5-7. Egyenlet 5-8. Egyenlet 5-9. Egyenlet Egyenlet Az 5.9-ből kifejezve: Egyenlet 5.11-t az 5.10-es egyenletbe helyettesítve: Egyenlet 5.12-t az 5.11-es egyenletbe helyettesítve: Egyenlet A gyakorlatban számítjuk minden egyes pont kezdőpontra vonatkozó abszcissza és ordináta különbségét, majd az r és m paramétereket, valamint a mérési vonal hosszát a mérési eredményekből és a koordinátákból (5.13. ábra). 10
15 5-13. ábra A szabad mérési vonal gyakorlati számítása (Gyenes, 2005) Derékszögű kitűzési méretek meghatározása A kitűzés feladata a tervezés eredményeként kapott részletpontok terepen való kijelölése. A kitűzések sokféle megoldása közül ebben a fejezetrészben a legegyszerűbb kitűzési módszert, az ortogonális kitűzést tárgyaljuk. Korlátozott pontossága és a ma már rendelkezésünkre álló jobb mérőfelszerelés miatt jelentőségéből sokat veszített, háttérbe szorult. Egy pont kitűzése a terepen már megjelölt pontokhoz viszonyított helymeghatározók, ún. kitűzési méretek alapján történik. Az egyes pontokat a terepen megjelölt pontokhoz viszonyítva vagy derékszögű adatokkal vagy poláris adatokkal (irányszög és távolság) tűzzük ki. Egy pont derékszögű adatokkal való kitűzése lényegében egy pont derékszögű koordinátaméréssel történő bemérésének fordított művelete. Ebben az esetben a transzformáció forrás-rendszere az országos rendszer (Y,X), cél-rendszere pedig a helyi rendszer.(a,b) Minden kitűzendő pontnak adottak tehát az országos rendszerbeli koordinátái, és keressük a helyi rendszerbeli koordinátáikat. A kitűzendő pont talppontjánál (tehát az abszcissza méretnél) be kell állni az egyenesbe, majd be kell inteni a kitűzőrudat a merőlegesbe. Ezután a kitűzőrúd mellé kell fektetni egy szalagot, és azon kitűzni az ordináta méretet. Az ábra és az alábbi képletek alapján tekintsük át az ortogonális kitűzési méretek számításának menetét: mivel s=1, ezért ábra Ortogonális kitűzési méretek számítása (Gyenes, 2005) 11
16 5-14. Egyenlet Egyenlet Egyenlet Egyenlet A vízszintes szögmérés módszerei A vízszintes szögmérés feladata az álláspontból kiinduló irányok egymáshoz viszonyított helyzetének a meghatározása. A vízszintes szögmérés végrehajtására alapvetően két módszer alakult ki. Ezek az iránymérés, tulajdonképpeni szögmérés Az iránymérés Iránymérés esetén a mérendő irányokat iránysorozatba foglaljuk. A mérés előkészítéseként az irányzandó pontokat ideiglenesen megjelöljük, irányzás céljából láthatóvá tesszük. Erre a célra leggyakrabban műszerállványra helyezett prizmát, jeltáblát, vagy prizmát jeltáblával kiegészítve alkalmazunk. Ha a növényzet a jelet takarná, akkor a középrészre egy irányzó toldatot szerelünk fel, amelynek a hossza általában méter, így a jeltáblát és a prizmát a toldat végére erősítjük (5.15. ábra). Ha az iránysorozatba magaspontokat is belefoglalunk, akkor az előkészítés során a pontleírást felhasználva győződjünk meg az irányzandó központ helyéről ábra Prizma irányzó toldatra helyezve A műszer felállítása során az álláspont körül a talajt tisztítsuk meg, a fűcsomókat a fémsaruk helyén távolítsuk el. A műszer felállítását követően ellenőrizzük a pontok láthatóságát azért, hogy a keresésükkel a tényleges mérés folyamán felesleges időt ne töltsünk. A szálkereszt képét a távcső előkészítéseként állítsuk élesre (5.16. ábra). Ellenőrizzük az objektív és az okulár tisztaságát, szükség esetén a műszerdobozban található törlőkendővel tisztítsuk meg azokat. A pontok láthatósága alapján döntsük el, melyiket választjuk kezdőiránynak. Ez a mérendő pontok közül a legjobban látható, és legegyértelműbben irányozható legyen. A műszer felállítását és bekapcsolását követően adjuk meg a mérési jegyzőkönyv-állomány nevét, ahová a mérési adatokat és az egyéb kiegészítő információkat rögzítjük. A műszerekben található beépített programoktól és a felhasználói beállításoktól függően végezzük el az álláspont adatainak a rögzítését. Adjuk meg az 12
17 álláspont számát, jelölését, az észlelést végző személy nevét vagy egyéb, a későbbiekben egyértelműen az észlelőre utaló azonosítót. Egyes műszerek lehetővé teszik az időjárásra vonatkozó megjegyzések bevitelét. Ilyen például a napos, szélcsendes, vagy borult enyhén szeles időjárás, stb ábra Az okulár előkészítése: a szálkereszt beállítása az éleslátás távolságának megfelelően (Gyenes, 2005) Az adott feladat műszaki előírásaitól vagy egyéb követelményeinek megfelelően az iránymérést végezhetjük egy vagy több fordulóban vagy távcsőállásban. A két távcsőállásban, egy fordulóban történő mérést a mai gyakorlatban ritkán alkalmazzuk. Ennek fő oka, hogy a mértékadó szabályos hibák a méréssel valós időben, számítással figyelembe vehetők. Ha azonban a szabályos hibákra vonatkozóan nem rendelkezünk friss információval, akkor a méréseket két távcsőállásban, egy fordulóban végezzük. A forduló mérését első távcsőállásban kezdjük. Első távcsőállásról akkor beszélünk, ha a távcsövet az okulár felől szemlélve a magassági kör a balkéz felől helyezkedik el. Egyes műszerek a kijelzőn az adott távcsőállást római számokkal jelenítik meg, vagy esetleg más szöveges formátumban. Az első távcsőállást a kezdőirány mérésével kezdjük, majd sorban irányozzuk a többi pontot az óramutató járásával egyező értelemben. Az első távcsőállás befejezéseként a műszerállvány elcsavarodásának ellenőrzése érdekében a kezdőirányt ismételten mérjük, azaz horizontzárást végzünk. Ezután a távcsövet áthajtjuk és átforgatjuk, majd a kezdőirány ismételt mérésével elkezdjük a pontokat a második távcsőállásban az óramutató járásával ellentétes irányban irányozni. A második távcsőállást is horizontzárással fejezzük be, azaz a kezdőirányt ismételten megmérjük. Az egy fordulóban végzett iránysorozat-mérés végrehajtását az ábra szemlélteti ábra Az iránysorozat mérése egy fordulóban (Gyenes, 2005) A pontok irányzását két lépésben hajtjuk végre. Először az irányzó kollimátorral közelítő irányzást (durva irányzást) végzünk, amelynek eredményeként a távcső látómezejében megjelenik a pont képe. Ezt követően a kötőcsavarokkal rögzítjük az alhidádét és a távcsövet. Szervomotoros műszerek esetén ez a művelet természetesen elmarad. A parallaxis csavar forgatásával megszüntetjük a parallaxist, majd a paránycsavarok segítségével elvégezzük a pontos irányzást. Ha csak vízszintes értelmű helymeghatározást végzünk, akkor az állószálat a pont képével hozzuk fedésbe (7.16. ábra). A jel képének méretétől függően a pontosabb irányzás érdekében gyakran úgynevezett biszektoros irányzást végzünk a pont képének kettős szállal történő közrefogásával. 13
18 5-18. ábra A vízszintes értelmű irányzás végrehajtásának módszerei (Gyenes, 2005) A ábrán látunk példát jeltáblával kiegészített prizma, valamint magaspontok helyes irányzásának végrehajtására ábra Irányzás végrehajtása: prizma jeltáblával, valamint magaspontok vízszintes értelmű irányzása (Gyenes, 2005) ábra Kémény bal-jobb irányzása (Gyenes, 2005) Kémények esetén az irányzást a kémény két szélén végezzük, úgynevezett bal-jobb irányzást végrehajtva, majd a két leolvasást összeközepelve. (5.20. ábra). Az irányok mérésekor ügyeljünk az irányzott pont adatainak helyes bevitelére. Ha lehetőség van rá, akkor az irányzandó pontra vonatkozó kiegészítő adatokat a durva irányzás végrehajtása előtt adjuk meg. Egyes műszerek programjai azonban fordított logika alapján működnek, a kiegészítő adatokat a leolvasás végrehajtására szolgáló utasítást követően kell bevinni. Tipikusan ilyen megoldást találunk a Sokkia műszereknél. A kiegészítő adatok bevitelét és a leolvasás végrehajtását követő utasítás után ne feledkezzünk meg az adatok rögzítéséről. Egyes műszereknél a leolvasás elvégzése és rögzítése egyetlen funkciógomb megnyomásával történik (pl. Leica műszer), de ez gyakran függ a felhasználó által elvégzett beállításoktól is (pl. Topcon). Az álláspont mérésének befejezését követően ellenőrizzük az adatrögzítés helyességét. Tekintsük meg a rögzített adatokat, elsősorban a pontok azonosítóira vonatkozó adatokat. Ezt elegendő általában valamilyen listaművelettel elvégezni. Szintén a mérés befejeztével ellenőrizzük a két távcsőállásban végzett leolvasások különbségeit. Elsősorban a kollimáció hiba következtében egyes irányokra vonatkozóan a két távcsőállás leolvasásainak különbségének közel azonos értékűnek kell lennie. A mérés elfogadható, ha a leolvasások különbségének átlagtól való eltérésének abszolút értéke nem haladja meg a műszerrel elérhető és az adott feladatra vonatkozó vízszintes szögmérés pontosságának a négyszeresét. A horizontzárás ellenőrzésére vonatkozóan szintén ez a hibahatár az érvényes. 14
19 Ha a szabályos hibákat valós időben számítással vesszük figyelembe, a műszerállvány elcsavarodásának ellenőrzésére vonatkozóan horizontzárást kell végezni. A horizontzárás szükségességét a mérendő irányok száma is meghatározza. Horizontzárást általában csak négynél több irány mérése esetén végzünk. Megfelelő előkészítés esetén egy pont mérése, beleértve az irányzást, az adatbevitelt és az adatrögzítést, perc, átlagos mérési körülményeket figyelembe véve. A mérés időszükséglete egyben meghatározza az iránysorozatba foglalható irányok számát. Egy forduló mérése lehetőleg ne tartson tovább 30 percnél, ami azt jelenti, hogy 8-10 iránynál többet ne foglaljunk egyetlen iránysorozatba. Ha a mérendő irányok száma az említett értéknél több, akkor csonkasorozatot alakítunk ki. Csonkasorozat esetén az irányokat szektorokba foglaljuk, amelyeknek közös szárait minden csonkasorozatban megmérünk. A csonkasorozatok egy fordulóban történő mérésének menetét szemlélteti a ábra két szektor esetén. A mai földi alappontmeghatározási gyakorlatban csonkasorozatokban történő mérést nem alkalmazunk. Alkalmazására elsősorban speciális mérnökgeodéziai feladatok esetében kerülhet sor ábra Csonkasorozat kialakítása Egyes feladatok pontossági követelményei több fordulóban végzett iránymérés végrehajtását igénylik. Többfordulós mérés esetén a pontraállást minden forduló megkezdése előtt meg kell ismételni a pontraállás hibájának véletlen jellegűvé tétele érdekében. Ennek megfelelően akkor járnánk el helyesen, ha ugyanezt az irányzandó pontoknál elhelyezett jelekre is elvégeznénk. Ettől a gyakorlatban ennek időigényessége miatt el szoktak tekinteni, de a pontraállás helyességét minden egyes forduló megkezdése előtt ellenőrizzük. Többfordulós mérés esetén a kezdőirány leolvasására a könnyebb ellenőrizhetőség érdekében minden egyes forduló megkezdése előtt egy kerek értéket, általában 0 00' 00'' vagy attól néhány másodperccel nagyobb értéket állítanak be. Fontos, hogy minden megkezdett forduló előtt az álláspont adatait ismételten rögzítsük. Ha a már említett mértékadó szabályos hibákat valós időben számítással vesszük figyelembe, akkor egyfordulós mérés helyett csak egy távcsőállásban végezzük a mérést. A mérések végrehajtására vonatkozó szabályok egyébként ugyanazok, mint a fordulóban történő méréskor. Az irányokat a kezdőirány mérését követően szintén az óramutató járásával egyező irányban mérjük, és szintén végzünk horizontzárást is. Több fordulóban történő mérés helyett több, egy távcsőállásban végrehajtott mérést végzünk, de minden egyes sorozat megkezdése előtt az álláspontra vonatkozó adatok rögzítését el kell végezni, valamint ellenőrizni kell a pontraállás és az állótengely függőlegességének a helyességét is Az egyszerű szögmérés Ebben az esetben mindig csak két irányt vonunk be a mérésbe, függetlenül attól, hogy az állásponton a mérendő irányok száma kettőnél több is lehet. A mérés előkészítése megegyezik az iránymérésnél leírtakéval. Az egyszerű szögmérés (más néven tulajdonképpeni szögmérés) esetén az egy fordulóban történő mérést a következőképpen végezzük. Létesítünk egy új, vagy választunk egy meglévő jegyzőkönyv-állományt, és rögzítjük az álláspontra vonatkozó adatokat. Miután az előkészítés során eldöntöttük, mi legyen a mérendő szög bal szára és jobb szára, első távcsőállásban megirányozzuk a választott bal szárhoz tartozó pontot és rögzítjük a mérési eredményeket. Ezt követően első távcsőállásban mérjük a jobb szárhoz tartozó pontot, rögzítjük az adatokat, majd második távcsőállásban ismét a jobb szögszárat, végül pedig a bal szögszárhoz tartozó pontot mérjük. Szakmatörténeti okokból megemlítjük az egyszerű szögmérés alkalmazásának azt az esetét, amikor egy állásponton n számú irány mérése volt a feladat, amelyet minden kombinációban végzett szögméréssel oldottak 15
20 meg (5.22. ábra). A minden kombinációban végzett szögmérés esetén az n számú irány között n (n-1)/2 számú szög mérhető a tulajdonképpeni szögmérés módszerével úgy, hogy a kiegészítő szögeket nem mérjük. A minden kombinációban végzett szögmérést a mai földi vízszintes helymeghatározásban már nem alkalmazzuk. Korábban az úgynevezett felsőrendű háromszögelésben alkalmazták ennek a módszernek egy továbbfejlesztett változatát, amelyet Schreiber-féle minden kombinációban végzett szögmérésnek neveztek Poláris részletmérés ábra Minden kombinációban végzett szögmérés esete Ma a poláris részletmérés a részletmérés egyik leggyakoribb módszere, mivel ennek korszerű eszközei a mérőállomások széles körben elterjedtek. A mérés pontossága centiméteres kategóriába esik, a mérés hatótávolsága több száz méter, így jó kilátású helyről nagy terület felmérhető. Poláris mérés alatt azt a mérési módszert értjük, amikor az új pontokat poláris koordinátáikkal (δ, t) határozzuk meg. A mérés úgy történik, hogy egy mérőállomással felállunk egy adott koordinátájú ponton és mérünk tájékozó irányokat (adott koordinátájú pontról adott koordinátájú pontra menő irányokat) azért, hogy a limbusz kört tájékozni tudjuk. Ezzel lényegében meghatározzuk a limbuszkör nulla osztásvonásának a koordinátarendszer x tengelyével párhuzamos iránnyal bezárt szögét, vagyis a nulla osztás irányszögét, a tájékozási szöget. Ezután minden egyes részletpontra irányt, távolságot és zenitszöget mérünk. Ezekből az adatokból a pont két vízszintes koordinátája és a pont magassága számítható. A mérés során az adatokat a műszer adattárolójába rögzítjük. A rögzítendő adatokat két főbb csoportba oszthatjuk: az adminisztrációs adatok és a mérési eredmények adatai. Az adminisztrációs adatok közül legfontosabbak a munkaterület nevének megadása, műszer száma, észlelő neve, mérés időpontja. Ide tartoznak még a meteorológiai adatok, úgy mint a hőmérséklet és a légnyomás. Leíró adatnak kell még tekintenünk az álláspont számát és jellegét, azaz az állandósítás módját, a műszermagasságot, a részletpontok számát és jellegét, valamint a jelmagasságot. A rögzítendő adatok másik csoportja közvetlenül a méréshez tartozik. Minden egyes bemért pontnál rögzítjük az irányértéket, zenitszöget és ferde távolságot. Ezek az adatok lehetővé teszik majd, hogy a következő fejezetben megismert poláris koordinátamérés számításával minden egyes bemért pontnak koordinátát adjunk A magassági szögmérés módszerei A magassági szögmérést a mai gyakorlatban a vízszintes szögméréssel egyidejűleg hajtjuk végre. Ennek az oka, hogy csak magasságkülönbség-meghatározást ma elektronikus teodolitokkal és mérőállomásokkal nem végzünk, hanem azt mindig kombináljuk a vízszintes helymeghatározással. Ennek megfelelően a pont irányzását egyértelműen, a szálkereszt metszéspontjával végezzük el. Ha a méréseket egy fordulóban végezzük, akkor a pontok irányzási sorrendjére az iránysorozat mérésénél leírtak a mérvadók. Ennek a magassági szögmérésre vonatkozó hátránya az, hogy a refrakciós viszonyok egy pont két távcsőállásban történő mérése között jelentősen változhatnak. Figyelembe véve, hogy a magassági szögmérésen alapuló magasságkülönbségmeghatározást ma már elsősorban olyan pontok meghatározására alkalmazzuk, ahol az irányzási távolság néhány száz méter, így a refrakciós viszonyok megváltozása a pontosságot jelentősen nem befolyásolja. Ha az indexhiba értékét előzetesen tároltuk és számítással figyelembe vesszük, akkor a méréseket csak egy távcsőállásban végezzük. A magasságkülönbségek meghatározása érdekében magassági szögméréskor mérni kell a műszermagasságot és a jelmagasságot. Abban az esetben, ha a refrakció hatását számítással akarjuk 16
21 figyelembe venni, akkor a törésmutató és annak változásához mérnünk kell a hőmérsékletet, a légnyomást és a fizikai modelltől függően a páranyomás értékét is A vízszintes és magassági szögmérés eredményeinek előzetes feldolgozása A vízszintes és a magassági szögmérés eredményeinek előzetes feldolgozásán az irányérték és a zenitszög számítását értjük. A feldolgozás lehet valós idejű vagy utólagos. Valós idejű feldolgozásról akkor beszélünk, amikor a korábbi modulokban megismert szabályos hibákat a mérések során számítással vesszük figyelembe, így a rögzített adatok már a megfelelő javításokkal el vannak látva. Utólagos feldolgozás során a mérési eredmények számítógépre történő kiolvasását követően számoljuk az irányértéket és a zenitszöget. Fordulóban végzett méréskor az irányértéket a két távcsőállás számtani középértékeként, a zenitszöget pedig az indexhiba számításánál megismert összefüggések alapján számítjuk. A nyomtatott formátumú jegyzőkönyvnek vagy jegyzőkönyv-állománynak célszerűen tartalmaznia kell minden, a mérésre vonatkozó és a további feldolgozás alapjául szolgáló adatot. Ezek a következők: mérés helye és ideje, az észlelést végző személy neve, időjárási körülményekre vonatkozó utalások, álláspont száma, jelölése, valamint a műszermagasság értéke, irányzott pont száma, jelölése, valamint a jelmagasság értéke, vízszintes és magassági körleolvasások, szabályos hibák figyelembevételére utaló megjegyzések. Két távcsőállásban történő mérés során a két távcsőállás mérési eredményeit egymás mellett tüntetjük fel, és nem a mérés végrehajtásának megfelelően egymás alá felsorolva. Az irányérték számítása előtt kiszámoljuk a vízszintes körleolvasások első és második távcsőállásbeli különbségeit, valamint a magassági körleolvasások összegét és 360 -tól való eltérésüket és azok átlagát. Az átlagtól való eltérés abszolút értékben nem haladhatja meg a vízszintes és a magassági szögmérés adott mérésre vonatkozó pontosságának négyszeresét. Több fordulóban végzett mérés esetén kiszámoljuk a nullára forgatott irányértékeket, amelyet nullára forgatásnak is szokás nevezni. A nullára forgatás az egyes irányok kezdőiránnyal bezárt szögének a számítását jelenti, azaz a kezdőirány irányértékét levonjuk a többi mért irány irányértékéből. A nullára forgatást minden egyes fordulóra el kell végezni. Egyazon iránysorozat többszöri, egy távcsőállásban történő mérésekor szintén kiszámoljuk a nullára forgatott irányértékeket. Abban az esetben, ha a kezdőirány irányértékére az iránysorozat ismételt mérése előtt mindig egy adott és ugyanazt az értéket adjuk meg, akkor a nullára forgatás számításától el szoktak tekinteni. Többfordulós, vagy több, egy távcsőállásban történő mérés során végleges irányértéknek az egyes fordulók irányértékeinek a számtani középértékét fogadjuk el. A teljesség kedvéért megemlítjük, hogy a nullára forgatást, valamint a csonkasorozatok klasszikus összeforgatását a mai gyakorlatban elhagyják akkor, ha a méréseket a később tanulandó kiegyenlítő számítások módszereivel dolgozzák fel. Erre azonban még későbbi tanulmányaink során visszatérünk Mérési jegyzet, mérési vázlat, tömbrajz A terepi részletmérés eredményét a könnyebb szemlélhetőség érdekében rajzi munkarészeken tüntetjük fel. Kint a terepen nehéz lenne méretarány helyes rajzot készíteni, ezért a bemérés végrehajtásakor mérési jegyzetet (manuálét) készítünk. Az irodában a mérési jegyzetből egy méretarányhelyes mérési vázlatot vagy tömbrajzot szerkesztünk. Ebben a fejezetben a mérési jegyzet, mérési vázlat és a tömbrajz szerkesztésének szabályait tekintjük át Mérési jegyzet A terepi részletmérések eredményeit mérési jegyzeten, vagy másképpen manuálén ábrázoljuk. A helyzeti vagy másnéven geometriai adatok gyűjtése mellett általában leíró, attribútum adatok gyűjtésével is foglalkozunk. A 17
22 mérési jegyzetet ceruzával, szabadkézzel, alakhelyesen kell megrajzolni. Készítésénél arra kell törekedni, hogy a tereptárgyak alakhelyes ábrázolása mellett a rájuk vonatkozó mérési eredmények hovatartozását minden kétséget kizáróan meg lehessen állapítani. A következő felsorolásban röviden összefoglaljuk a mérési jegyzet legfontosabb tulajdonságait: Általában terepen végzett felmérések adataiból készül Helyzeti (geometriai) adatok meghatározása: felmérések mérőállomással felmérések GPS-vevőkkel fotogrammetriai felmérések ortogonális felmérések meglévő digitális térképek átvétele Attribútum (leíró) adatok gyűjtése: terepi adatgyűjtés meglévő leíró adatokat tartalmazó adatbázisok átvétele Tulajdonságai: Ceruzával, alakhelyesen, szabadkézzel rajzoljuk Tartalmazza a község nevét, északi irányt, mérési jegyzet azonosítóját, időpontot Felmérési egységenként össze kell fűzni Az eredeti mérési jegyzetet mindenkor meg kell őrizni! Mérési vázlat A belterületek (települések állandó lakhatás céljára szolgáló részei) és külterületek (települések mező-vagy erdőgazdasági művelés alatt álló részei) felmérésekor a manuálékról olyan egységes vázlatot készítünk, amely a felmért területet a térkép szelvénybeosztásának megfelelően ábrázolja. Ezt a rajzi munkarészt nevezzük mérési vázlatnak. A mérési vázlatok általában a térkép méretarányában készülnek (1:1000, 1:200,1:4000), azonban olyan felmérendő területeken, ahol sok mérendő részletpont van, készülhet a térkép méretarányának a többszörösében is. (1:500, 1:250) A mérési vázlat a mérés módszerétől függően poláris vagy ortogonális részletmérések eredményeit tartalmazza. Ezen mérési eredmények ábrázolásának hosszú idő óta kialakult hagyományai vannak, amelyek ismerete és betartása nagyon fontos a szakmai hitelesség és a későbbi, más szakember által történő érhetőség, feldolgozás, vagy ellenőrzés érdekében. A következő felsorolásban röviden összefoglaljuk a mérési vázlatok legfontosabb tulajdonságait, továbbá az ortogonális és poláris részletmérés ábrázolásának szabályait. Tulajdonságai: Mérési vázlatot a terepen készült mérési jegyzetből szerkeszthetjük, esetleg a mérési vázlat közvetlen a terepen is elkészülhet Legyen áttekinthető, világos, a térképezés és bemérés minden mozzanata követhető legyen Készülhet tussal vagy számítógépes térképező szoftverrel Értelemzavaró, téves térképezésre vezető elrajzolásokat nem szabad elkövetni Szelvényhatárral párhuzamosan készül, számozása is a szelvényszámhoz kötődik 18
23 Be kell jegyezni a művelési ágakat pl. kert, rét stb. Lakóházakba be kell írni a házszámot A lakóház és gazdasági épület elválasztó vonalát mérni és ábrázolni kell, meg kell írni az épületek rendeltetését Vasúti vonalaknak a középvonala ábrázolandó Vonalas létesítmények feliratait és a helyrajziszámokat a hossztengellyel párhuzamosan kell megírni Kelet-nyugati szelvényvonallal párhuzamosan kell megírni: dűlők, puszták, majorok, középületek, gyárak, romok, erdők, hegyek, völgyek nevét A vízfolyások irányát nyíllal kell megjelölni Település vagy országhatárnál meg kell írni a csatlakozó település vagy ország nevét Minden szelvényre: felül középen a méretarányt, jobboldalon a község nevét továbbá a térképszelvény számát Több csatlakozó mérési vázlatról célszerű átnézeti vázlatot készíteni, az ábrázolt területrész kerületvonalának és a csatlakozó mérési vázlat számainak feltüntetésével Részletes szabályok-ortogonális felmérésnél mérés kezdőpontját és irányát nyíllal kell megjelölni az ordinátát jelző pontozott vonal elé a részletponttal egyező oldalra a merőlegességet jelző jelet kell tenni a végméretet zárójelbe kell tenni jól olvasható számokat kell használni, értékük és hovatartozások kétséget kizáróan megállapítható legyen a méretek a mérési vázlat elfordítása nélkül olvashatóak legyenek az alappontok számát a keleti-nyugati szelvényvonallal párhuzamosan kell megírni abszcissza méretet a folytatólagos mérést jelző jellel a merőlegességet jelző jel elé kell írni a mérési vonallal párhuzamosan sok abszcissza méret esetén egymás fölött kell őket megírni ha kihosszabbításon mérünk, akkor a végméret utáni utolsó méretet szögletes zárójelbe kell tenni, kihosszabbító jel használata az ordináta méretet a mérési vonalra merőlegesen, a merőlegességi jellel azonos oldalra, lehetőleg a vonal közepére kell elhelyezni minden felirat dél-délnyugatról olvasható legyen 19
24 5-23. ábra Mérési vázlat (részlet) (Lehetne nagyobb az ábra. Így nem igen olvasható!) Általános szabályok-poláris felmérésnél az álláspont az állandósításnak megfelelő jelkulccsal legyen feltüntetve a bemért poláris részletpontokra poláris mérés irányát jelölő jelkulcs (15 mm hosszan) kerül, mindig az álláspont felé fordulva a részletpontok számát meg kell írni Tömbrajz ábra Mérési vázlat (részlet) Városi belterületek vagy városias jellegű települések belterületeinek felméréséről tömbrajzot szokás készíteni. A tömbrajz szerkesztési szabályai megegyeznek a mérési vázlat szerkesztési szabályaival, azonban míg a mérési vázlatot a térképszelvény határolja, addig a tömbrajzot az úgynevezett tömbhatár. Tömböknek nevezzük a közterületekkel határolt település részeket, tehát a legtöbb esetben a tömböket utak, utcák vagy terek határolják. (5.25. ábra) A tömbrajz méretaránya tetszőleges lehet, általában 1:200, 1:250 vagy 1:500; mindenképpen célszerű azonban olyan méretarányt választani, hogy a kész tömbrajz kezelhető méretű papírlapon helyezkedjen el. A következő felsorolásban összefoglaljuk a tömbrajz mérési vázlattól eltérő, egyedi tulajdonságait: Tulajdonságai: tömbrajz általában városias, zsúfolt belterület esetén készül 20
25 szerkesztési szabályai megegyeznek a mérési vázlat szerkesztési szabályaival vonalas létesítmények illetve a belterület határa határolja a tömbrajzot 1:200, 1:250-es vagy 1:500-as méretarányban szerkesztjük tussal a számítógépes térképező szoftverrel készített tömbrajz lényegében mérési vázlat szerepet tölt be Összefoglalás ábra Tömbrajz A fejezetben a vízszintes mérések alapműveleteit foglaltuk össze. Kitértünk az egyenesek kitűzésének gyakorlati kérdésivel. Ismertettük a derékszögű koordinátamérés elvét, valamint a derékszögű kitűzési méretek számításának módját, csakúgy, mint a vízszintes szögmérés két módszerének, az iránymérés és az egyszerű szögmérés végrehajtásának módját. Kitértünk a mérési jegyzettel, a mérési vázlattal szemben támasztott gyakorlati elvárásokra. Önellenőrző kérdések: Ismertesse az egyenes vonalak kitűzésének módszereit! /4.oldal/ Mit értünk távolság alatt? /7.oldal/ Hogyan történik az állandó nagyságú szögek kitűzése? /10.oldal/ Ismertesse a derékszögű koordinátamérés menetét és összefüggéseit! /12.oldal/ Ismertesse a derékszögű kitűzési méretek meghatározását! /18.oldal/ Mi a különbség iránymérés és szögmérés között? /19.oldal/ Ismertesse a következő fogalmakat: mérési jegyzet, mérési vázlat, tömbrajz! /30.oldal/ Melyek a szabályai a mérési jegyzet készítésének? /30.oldal/ Milyen tulajdonságai vannak a mérési vázlatnak? /31.oldal/ 21
Mérnökgeodézia 5. Mérnökgeodéziai kitűzési munkák. Dr. Ágfalvi, Mihály
 Mérnökgeodézia 5. Mérnökgeodéziai kitűzési munkák. Dr. Ágfalvi, Mihály Mérnökgeodézia 5.: Mérnökgeodéziai kitűzési munkák. Dr. Ágfalvi, Mihály Lektor: Dr. Ottófi, Rudolf Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027
Mérnökgeodézia 5. Mérnökgeodéziai kitűzési munkák. Dr. Ágfalvi, Mihály Mérnökgeodézia 5.: Mérnökgeodéziai kitűzési munkák. Dr. Ágfalvi, Mihály Lektor: Dr. Ottófi, Rudolf Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027
Geodézia 4. Vízszintes helymeghatározás Gyenes, Róbert
 Geodézia 4. Vízszintes helymeghatározás Gyenes, Róbert Geodézia 4.: Vízszintes helymeghatározás Gyenes, Róbert Lektor: Homolya, András Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027 Tananyagfejlesztéssel
Geodézia 4. Vízszintes helymeghatározás Gyenes, Róbert Geodézia 4.: Vízszintes helymeghatározás Gyenes, Róbert Lektor: Homolya, András Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027 Tananyagfejlesztéssel
Nyugat-magyarországi Egyetem Geoinformatikai Kara. Gyenes Róbert. Geodézia 4. GED4 modul. Vízszintes helymeghatározás
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Gyenes Róbert Geodézia 4. GED4 modul Vízszintes helymeghatározás SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról szóló 1999. évi LXXVI. törvény
Nyugat-magyarországi Egyetem Geoinformatikai Kara Gyenes Róbert Geodézia 4. GED4 modul Vízszintes helymeghatározás SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról szóló 1999. évi LXXVI. törvény
Geodéziai hálózatok 3.
 Geodéziai hálózatok 3. A vízszintes pontmeghatározás Dr. Busics, György Geodéziai hálózatok 3.: A vízszintes pontmeghatározás Dr. Busics, György Lektor: Dr. Németh, Gyula Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027
Geodéziai hálózatok 3. A vízszintes pontmeghatározás Dr. Busics, György Geodéziai hálózatok 3.: A vízszintes pontmeghatározás Dr. Busics, György Lektor: Dr. Németh, Gyula Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027
Topográfia 7. Topográfiai felmérési technológiák I. Mélykúti, Gábor
 Topográfia 7. Topográfiai felmérési technológiák I. Mélykúti, Gábor Topográfia 7. : Topográfiai felmérési technológiák I. Mélykúti, Gábor Lektor : Alabér, László Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027
Topográfia 7. Topográfiai felmérési technológiák I. Mélykúti, Gábor Topográfia 7. : Topográfiai felmérési technológiák I. Mélykúti, Gábor Lektor : Alabér, László Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027
I.- V. rendű vízszintes alapponthálózat I.- III. rendű magassági alapponthálózat Állandó- és ideiglenes pontjelölések Őrjelek Végleges pontjelölések
 Ismétl tlés I.- V. rendű vízszintes alapponthálózat I.- III. rendű magassági alapponthálózat Állandó- és ideiglenes pontjelölések Őrjelek Végleges pontjelölések (mérőtorony) 2 Egyszerű eszközök Egyszerű
Ismétl tlés I.- V. rendű vízszintes alapponthálózat I.- III. rendű magassági alapponthálózat Állandó- és ideiglenes pontjelölések Őrjelek Végleges pontjelölések (mérőtorony) 2 Egyszerű eszközök Egyszerű
Geodézia 9. Magasságok meghatározása Tarsoly, Péter
 Geodézia 9. Magasságok meghatározása Tarsoly, Péter Geodézia 9.: Magasságok meghatározása Tarsoly, Péter Lektor: Homolya, András Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027 Tananyagfejlesztéssel a GEO-ért
Geodézia 9. Magasságok meghatározása Tarsoly, Péter Geodézia 9.: Magasságok meghatározása Tarsoly, Péter Lektor: Homolya, András Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027 Tananyagfejlesztéssel a GEO-ért
Nyugat-magyarországi Egyetem Geoinformatikai Kara. Tarsoly Péter. Geodézia 9. GED9 modul. Magasságok meghatározása
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Tarsoly Péter Geodézia 9. GED9 modul Magasságok meghatározása SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról szóló 1999. évi LXXVI. törvény
Nyugat-magyarországi Egyetem Geoinformatikai Kara Tarsoly Péter Geodézia 9. GED9 modul Magasságok meghatározása SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról szóló 1999. évi LXXVI. törvény
BARTHA GÁbOR, HAVASI ISTVÁN, TÉRINFORMATIKAI ALAPISMERETEK
 BARTHA GÁbOR, HAVASI ISTVÁN, TÉRINFORMATIKAI ALAPISMERETEK 3 III. MÉRÉSI ELJÁRÁSOK 1. RÉSZLETES FELMÉRÉS A részletes felmérés a térképezést megelőző munkafázis, amelynek alapját az érintett területen meglévő
BARTHA GÁbOR, HAVASI ISTVÁN, TÉRINFORMATIKAI ALAPISMERETEK 3 III. MÉRÉSI ELJÁRÁSOK 1. RÉSZLETES FELMÉRÉS A részletes felmérés a térképezést megelőző munkafázis, amelynek alapját az érintett területen meglévő
Agrár-környezetvédelmi Modul Vízgazdálkodási ismeretek. KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI MSc
 Agrár-környezetvédelmi Modul Vízgazdálkodási ismeretek KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI MSc Geodéziai alapismeretek II. 25.lecke Vízszintes szögmérés Teodolit: Az egy pontból
Agrár-környezetvédelmi Modul Vízgazdálkodási ismeretek KÖRNYEZETGAZDÁLKODÁSI MÉRNÖKI MSc TERMÉSZETVÉDELMI MÉRNÖKI MSc Geodéziai alapismeretek II. 25.lecke Vízszintes szögmérés Teodolit: Az egy pontból
3. A földi helymeghatározás lényege, tengerszintfeletti magasság
 1. A geodézia tárgya és a földmûvek, mûtárgyak kitûzése A földméréstan (geodézia) a Föld fizikai felszínén illetve a felszín alatt lévõ természetes és mesterséges alakzatok méreteinek és helyének meghatározásával,
1. A geodézia tárgya és a földmûvek, mûtárgyak kitûzése A földméréstan (geodézia) a Föld fizikai felszínén illetve a felszín alatt lévõ természetes és mesterséges alakzatok méreteinek és helyének meghatározásával,
Matematikai statisztikai elemzések 6.
 Matematikai statisztikai elemzések 6. Regressziószámítás: kétváltozós lineáris és nemlineáris regresszió, többváltozós regresszió Prof. Dr. Závoti, József Matematikai statisztikai elemzések 6.: Regressziószámítás:
Matematikai statisztikai elemzések 6. Regressziószámítás: kétváltozós lineáris és nemlineáris regresszió, többváltozós regresszió Prof. Dr. Závoti, József Matematikai statisztikai elemzések 6.: Regressziószámítás:
Teodolit. Alapismeretek - leolvasások
 Teodolit Alapismeretek - leolvasások A teodolit elve Szögmérő műszer, amellyel egy adott pontból tetszőleges más pontok felé menő irányok egymással bezárt szögét tudjuk megmérni, ill. egy alapiránytól
Teodolit Alapismeretek - leolvasások A teodolit elve Szögmérő műszer, amellyel egy adott pontból tetszőleges más pontok felé menő irányok egymással bezárt szögét tudjuk megmérni, ill. egy alapiránytól
Kompenzátoros szintezőműszer horizontsík ferdeségi vizsgálata
 TDK Konferencia 2010. Kompenzátoros szintezőműszer horizontsík ferdeségi vizsgálata Készítette: Zemkó Szonja Konzulens: Kiss Albert (ÁFGT tanszék) A témaválasztás indoklása: az építőiparban széleskörűen
TDK Konferencia 2010. Kompenzátoros szintezőműszer horizontsík ferdeségi vizsgálata Készítette: Zemkó Szonja Konzulens: Kiss Albert (ÁFGT tanszék) A témaválasztás indoklása: az építőiparban széleskörűen
Navicom-Plusz Bt. E-mail: office@navicom.hu. Navicom Plusz Bt. H-1112 Budapest, Repülőtéri út 2. Tel.: +36 1 248 04 22
 2013 TOPCON ATB optiikaii sziintező csallád Navicom-Plusz Bt. Tel.: +36 1 248 04 22 E-mail: office@navicom.hu Topcon AT-B szintezőműszer család A Navicom büszkén mutatja be a japán Topcon legújabb fejlesztésű,
2013 TOPCON ATB optiikaii sziintező csallád Navicom-Plusz Bt. Tel.: +36 1 248 04 22 E-mail: office@navicom.hu Topcon AT-B szintezőműszer család A Navicom büszkén mutatja be a japán Topcon legújabb fejlesztésű,
MUNKAANYAG. Földi László. Szögmérések, külső- és belső kúpos felületek mérése. A követelménymodul megnevezése:
 Földi László Szögmérések, külső- és belső kúpos felületek mérése A követelménymodul megnevezése: Általános anyagvizsgálatok és geometriai mérések A követelménymodul száma: 0225-06 A tartalomelem azonosító
Földi László Szögmérések, külső- és belső kúpos felületek mérése A követelménymodul megnevezése: Általános anyagvizsgálatok és geometriai mérések A követelménymodul száma: 0225-06 A tartalomelem azonosító
Geometriai példatár 2.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Baboss Csaba Szabó Gábor Geometriai példatár 2 GEM2 modul Metrikus feladatok SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról szóló 1999 évi
Nyugat-magyarországi Egyetem Geoinformatikai Kara Baboss Csaba Szabó Gábor Geometriai példatár 2 GEM2 modul Metrikus feladatok SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői jogról szóló 1999 évi
Mérnökgeodézia 6. A lézertechnika, és mérnökgeodéziai alkalmazása Dr. Ágfalvi, Mihály
 Mérnökgeodézia 6. A lézertechnika, és mérnökgeodéziai Dr. Ágfalvi, Mihály Mérnökgeodézia 6.: A lézertechnika, és mérnökgeodéziai Dr. Ágfalvi, Mihály Lektor: Dr. Ottófi, Rudolf Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027
Mérnökgeodézia 6. A lézertechnika, és mérnökgeodéziai Dr. Ágfalvi, Mihály Mérnökgeodézia 6.: A lézertechnika, és mérnökgeodéziai Dr. Ágfalvi, Mihály Lektor: Dr. Ottófi, Rudolf Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027
Nagyméretarányú térképezés 7.
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Vincze László Nagyméretarányú térképezés 7. NMT7 modul Digitális fotogrammetriai módszerek és dokumentálása DAT készítéséhez SZÉKESFEHÉRVÁR 2010 Jelen
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Vincze László Nagyméretarányú térképezés 7. NMT7 modul Digitális fotogrammetriai módszerek és dokumentálása DAT készítéséhez SZÉKESFEHÉRVÁR 2010 Jelen
Nyugat-magyarországi Egyetem Geoinformatikai Kara. Dr. Engler Péter. Fotogrammetria 2. FOT2 modul. A fotogrammetria geometriai és matematikai alapjai
 Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Engler Péter Fotogrammetria 2. FOT2 modul A fotogrammetria geometriai és matematikai alapjai SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői
Nyugat-magyarországi Egyetem Geoinformatikai Kara Dr. Engler Péter Fotogrammetria 2. FOT2 modul A fotogrammetria geometriai és matematikai alapjai SZÉKESFEHÉRVÁR 2010 Jelen szellemi terméket a szerzői
MUNKAANYAG. Földi László. Méret- és alakellenőrzések idomszerekkel, speciális mérőeszközökkel. A követelménymodul megnevezése:
 Földi László Méret- és alakellenőrzések idomszerekkel, speciális mérőeszközökkel A követelménymodul megnevezése: Általános anyagvizsgálatok és geometriai mérések A követelménymodul száma: 0225-06 A tartalomelem
Földi László Méret- és alakellenőrzések idomszerekkel, speciális mérőeszközökkel A követelménymodul megnevezése: Általános anyagvizsgálatok és geometriai mérések A követelménymodul száma: 0225-06 A tartalomelem
2.3.2.2.1.2.1 Visszatérítő nyomaték és visszatérítő kar
 2.3.2.2.1.2 Keresztirányú stabilitás nagy dőlésszögeknél A keresztirányú stabilitás számszerűsítésénél, amint korábban láttuk, korlátozott a metacentrikus magasságra való támaszkodás lehetősége. Csak olyankor
2.3.2.2.1.2 Keresztirányú stabilitás nagy dőlésszögeknél A keresztirányú stabilitás számszerűsítésénél, amint korábban láttuk, korlátozott a metacentrikus magasságra való támaszkodás lehetősége. Csak olyankor
#Bevezetés Beállítások NA 3000 # 1.1.
 Bevezetés A szinthal1 program szintezéssel mért magassági hálózatok kiegyenlítésére alkalmas program. Lehetőségünk van mind beillesztett, mind önálló hálózat számítására. Önálló hálózat kiegyenlítésekor
Bevezetés A szinthal1 program szintezéssel mért magassági hálózatok kiegyenlítésére alkalmas program. Lehetőségünk van mind beillesztett, mind önálló hálózat számítására. Önálló hálózat kiegyenlítésekor
2. OPTIKA 2.1. Elmélet 2.1.1. Geometriai optika
 2. OPTIKA 2.1. Elmélet Az optika tudománya a látás élményéből fejlődött ki. A tárgyakat azért látjuk, mert fényt bocsátanak ki, vagy a rájuk eső fényt visszaverik, és ezt a fényt a szemünk érzékeli. A
2. OPTIKA 2.1. Elmélet Az optika tudománya a látás élményéből fejlődött ki. A tárgyakat azért látjuk, mert fényt bocsátanak ki, vagy a rájuk eső fényt visszaverik, és ezt a fényt a szemünk érzékeli. A
Mérnökgeodézia 8. Vonalas létesítmények építésének, gépészeti berendezések szerelésének geodéziai feladatai. Ágfalvi, Mihály
 Mérnökgeodézia 8. Vonalas létesítmények építésének, gépészeti berendezések szerelésének geodéziai feladatai Ágfalvi, Mihály Mérnökgeodézia 8.: Vonalas létesítmények építésének, gépészeti berendezések szerelésének
Mérnökgeodézia 8. Vonalas létesítmények építésének, gépészeti berendezések szerelésének geodéziai feladatai Ágfalvi, Mihály Mérnökgeodézia 8.: Vonalas létesítmények építésének, gépészeti berendezések szerelésének
FAUR KRISZTINA BEÁTA, SZAbÓ IMRE, GEOTECHNIkA
 FAUR KRISZTINA BEÁTA, SZAbÓ IMRE, GEOTECHNIkA 7 VII. A földművek, lejtők ÁLLÉkONYSÁgA 1. Földművek, lejtők ÁLLÉkONYSÁgA Valamely földművet, feltöltést vagy bevágást építve, annak határoló felületei nem
FAUR KRISZTINA BEÁTA, SZAbÓ IMRE, GEOTECHNIkA 7 VII. A földművek, lejtők ÁLLÉkONYSÁgA 1. Földművek, lejtők ÁLLÉkONYSÁgA Valamely földművet, feltöltést vagy bevágást építve, annak határoló felületei nem
Mérnöki létesítmények alapponthálózatai Vízszintes alapponthálózatok
 NYME GEO GEODÉZIA TANSZÉK MÉRNÖKGEODÉZIA TANTÁRGYI KÓD: GBNFMGEOB és GBLFMGEOB Mérnöki létesítmények alapponthálózatai Vízszintes alapponthálózatok Mérnöki létesítmények alapponthálózatai Állami alapponthálózat
NYME GEO GEODÉZIA TANSZÉK MÉRNÖKGEODÉZIA TANTÁRGYI KÓD: GBNFMGEOB és GBLFMGEOB Mérnöki létesítmények alapponthálózatai Vízszintes alapponthálózatok Mérnöki létesítmények alapponthálózatai Állami alapponthálózat
Az alap- és a képfelület fogalma, megadási módjai és tulajdonságai
 A VETÜLETEK ALAP- ÉS KÉPFELÜLETE Az alap- és a képfelület fogalma, megadási módjai és tulajdonságai A geodézia, a térinformatika és a térképészet a görbült földfelületen elhelyezkedő geometriai alakzatokat
A VETÜLETEK ALAP- ÉS KÉPFELÜLETE Az alap- és a képfelület fogalma, megadási módjai és tulajdonságai A geodézia, a térinformatika és a térképészet a görbült földfelületen elhelyezkedő geometriai alakzatokat
MUNKAANYAG. Dr. Engler Péter. A mérőfénykép. A követelménymodul megnevezése: Fotogrammetria feladatai
 Dr. Engler Péter A mérőfénykép A követelménymodul megnevezése: Fotogrammetria feladatai A követelménymodul száma: 2241-06 A tartalomelem azonosító száma és célcsoportja: SzT-009-50 A MÉRŐFÉNYKÉP ESETFELVETÉS
Dr. Engler Péter A mérőfénykép A követelménymodul megnevezése: Fotogrammetria feladatai A követelménymodul száma: 2241-06 A tartalomelem azonosító száma és célcsoportja: SzT-009-50 A MÉRŐFÉNYKÉP ESETFELVETÉS
MUNKAANYAG. Tóth György. Gyalugépek ellenőrzése, beállítása. A követelménymodul megnevezése: A biztonságos munkavégzés feladatai
 Tóth György Gyalugépek ellenőrzése, beállítása A követelménymodul megnevezése: A biztonságos munkavégzés feladatai A követelménymodul száma: 2273-06 A tartalomelem azonosító száma és célcsoportja: SzT-011-30
Tóth György Gyalugépek ellenőrzése, beállítása A követelménymodul megnevezése: A biztonságos munkavégzés feladatai A követelménymodul száma: 2273-06 A tartalomelem azonosító száma és célcsoportja: SzT-011-30
SZABADALMI LEÍRÁS SZOLGÁLATI TALÁLMÁNY
 MAGYAR NÉPKÖZTÁRSASÁG SZABADALMI LEÍRÁS SZOLGÁLATI TALÁLMÁNY Bejelentés napja 1970. IX. 22. (CE-781) Nemzetközi osztályozás: G Ot n 1/00, G 01 n 3/00, G 01 n 25/00 ORSZÁGOS TALÁLMÁNYI HIVATAL Közzététel
MAGYAR NÉPKÖZTÁRSASÁG SZABADALMI LEÍRÁS SZOLGÁLATI TALÁLMÁNY Bejelentés napja 1970. IX. 22. (CE-781) Nemzetközi osztályozás: G Ot n 1/00, G 01 n 3/00, G 01 n 25/00 ORSZÁGOS TALÁLMÁNYI HIVATAL Közzététel
Fotogrammetria 5. Az információszerzés eszközei Dr. Engler, Péter
 Fotogrammetria 5. Az információszerzés eszközei Dr. Engler, Péter Fotogrammetria 5. : Az információszerzés eszközei Dr. Engler, Péter Lektor : Dr. Barsi, Árpád Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027
Fotogrammetria 5. Az információszerzés eszközei Dr. Engler, Péter Fotogrammetria 5. : Az információszerzés eszközei Dr. Engler, Péter Lektor : Dr. Barsi, Árpád Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027
Csomópontok és üzemi létesítmények
 Csomópontok és üzemi létesítmények Az utak egyes szakaszain lévő útbecsatlakozásokat, útkereszteződéseket és útelágazásokat csomópontoknak nevezzük. A csomópontok feladata a csatlakozó, keresztező és elágazó
Csomópontok és üzemi létesítmények Az utak egyes szakaszain lévő útbecsatlakozásokat, útkereszteződéseket és útelágazásokat csomópontoknak nevezzük. A csomópontok feladata a csatlakozó, keresztező és elágazó
4. modul Poliéderek felszíne, térfogata
 Matematika A 1. évfolyam 4. modul Poliéderek felszíne, térfogata Készítette: Vidra Gábor Matematika A 1. évfolyam 4. modul: POLIÉDEREK FELSZÍNE, TÉRFOGATA Tanári útmutató A modul célja Időkeret Ajánlott
Matematika A 1. évfolyam 4. modul Poliéderek felszíne, térfogata Készítette: Vidra Gábor Matematika A 1. évfolyam 4. modul: POLIÉDEREK FELSZÍNE, TÉRFOGATA Tanári útmutató A modul célja Időkeret Ajánlott
Fogalom-meghatározások
 Egy kis kitérőt szeretnék tenni, hogy szó szerint megvilágosodjunk. Mondhatnám azt is, hogy ez a cikk azért hasznos nekünk, villamos matrózoknak, nehogy a csúnya áltengerészek zátonyra futtassák hajónkat
Egy kis kitérőt szeretnék tenni, hogy szó szerint megvilágosodjunk. Mondhatnám azt is, hogy ez a cikk azért hasznos nekünk, villamos matrózoknak, nehogy a csúnya áltengerészek zátonyra futtassák hajónkat
Tető nem állandó hajlású szarufákkal
 1 Tető nem állandó hajlású szarufákkal Már korábbi dolgozatainkban is szó volt a címbeli témáról. Most azért vettük újra elő, mert szép és érdekes ábrákat találtunk az interneten, ezzel kapcsolatban, és
1 Tető nem állandó hajlású szarufákkal Már korábbi dolgozatainkban is szó volt a címbeli témáról. Most azért vettük újra elő, mert szép és érdekes ábrákat találtunk az interneten, ezzel kapcsolatban, és
MUNKAANYAG. Fekete Éva. Marási műveletek végzése fogazó. marógéppel, másoló marógéppel, láncmarógéppel, és pánthely maró géppel
 Fekete Éva Marási műveletek végzése fogazó marógéppel, másoló marógéppel, láncmarógéppel, és pánthely maró géppel A követelménymodul megnevezése: Alapvető tömörfa megmunkálási feladatok A követelménymodul
Fekete Éva Marási műveletek végzése fogazó marógéppel, másoló marógéppel, láncmarógéppel, és pánthely maró géppel A követelménymodul megnevezése: Alapvető tömörfa megmunkálási feladatok A követelménymodul
Nagyméretarányú térképezés 19.
 Nagyméretarányú térképezés 19. A térképi változások átvezetése a Dr. Vincze, László Nagyméretarányú térképezés 19.: A térképi változások átvezetése a Dr. Vincze, László Lektor: Dr. Hankó, András Ez a modul
Nagyméretarányú térképezés 19. A térképi változások átvezetése a Dr. Vincze, László Nagyméretarányú térképezés 19.: A térképi változások átvezetése a Dr. Vincze, László Lektor: Dr. Hankó, András Ez a modul
O 1.1 A fény egyenes irányú terjedése
 O 1.1 A fény egyenes irányú terjedése 1 blende 1 és 2 rés 2 összekötő vezeték Előkészület: A kísérleti lámpát teljes egészében egy ív papírlapra helyezzük. A négyzetes fénynyílást széttartó fényként használjuk
O 1.1 A fény egyenes irányú terjedése 1 blende 1 és 2 rés 2 összekötő vezeték Előkészület: A kísérleti lámpát teljes egészében egy ív papírlapra helyezzük. A négyzetes fénynyílást széttartó fényként használjuk
ACÉLÍVES (TH) ÜREGBIZTOSÍTÁS
 Miskolci Egyetem Bányászati és Geotechnikai Intézet Bányászati és Geotechnikai Intézeti Tanszék ACÉLÍVES (TH) ÜREGBIZTOSÍTÁS Oktatási segédlet Szerző: Dr. Somosvári Zsolt DSc professzor emeritus Szerkesztette:
Miskolci Egyetem Bányászati és Geotechnikai Intézet Bányászati és Geotechnikai Intézeti Tanszék ACÉLÍVES (TH) ÜREGBIZTOSÍTÁS Oktatási segédlet Szerző: Dr. Somosvári Zsolt DSc professzor emeritus Szerkesztette:
Geodézia. Felosztása:
 Geodézia Görög eredetű szó. Geos = föld, geometria = földmérés A geodézia magyarul földméréstan, a Föld felületének, alakjána méreteinek, valamint a Föld felületén levő létesítmények és ponto helymeghatározásával,
Geodézia Görög eredetű szó. Geos = föld, geometria = földmérés A geodézia magyarul földméréstan, a Föld felületének, alakjána méreteinek, valamint a Föld felületén levő létesítmények és ponto helymeghatározásával,
4. A szükséges kötözésmennyiség számítása
 4. A szükséges kötözésmennyiség számítása Ha kötözéssel kívánjuk megakadályozni mind a rakomány csúszását, mind a felbillenését, a következőképpen járjunk el: Számítsuk ki a csúszás megakadályozásához
4. A szükséges kötözésmennyiség számítása Ha kötözéssel kívánjuk megakadályozni mind a rakomány csúszását, mind a felbillenését, a következőképpen járjunk el: Számítsuk ki a csúszás megakadályozásához
5. Az egy-, két- és háromdimenziós pontmeghatározás együttműködése
 5. Az egy-, két- és háromdimenziós pontmeghatározás együttműködése 5.1. Vízszintes alappontok magasságának meghatározása 5.1.1. Trigonometriai magasságmérés alkalmazása 5.1.1.1. A mérés technológiája Minden
5. Az egy-, két- és háromdimenziós pontmeghatározás együttműködése 5.1. Vízszintes alappontok magasságának meghatározása 5.1.1. Trigonometriai magasságmérés alkalmazása 5.1.1.1. A mérés technológiája Minden
MUNKAANYAG. Szabó László. Szilárdságtan. A követelménymodul megnevezése:
 Szabó László Szilárdságtan A követelménymodul megnevezése: Kőolaj- és vegyipari géprendszer üzemeltetője és vegyipari technikus feladatok A követelménymodul száma: 047-06 A tartalomelem azonosító száma
Szabó László Szilárdságtan A követelménymodul megnevezése: Kőolaj- és vegyipari géprendszer üzemeltetője és vegyipari technikus feladatok A követelménymodul száma: 047-06 A tartalomelem azonosító száma
III/1. Kisfeszültségű vezetékméretezés általános szempontjai (feszültségesés, teljesítményveszteség fogalma, méretezésben szokásos értékei.
 III/1. Kisfeszültségű vezetékméretezés általános szempontjai (feszültségesés, teljesítményveszteség fogalma, méretezésben szokásos értékei. A vezetékméretezés során, mint minden műszaki berendezés tervezésénél
III/1. Kisfeszültségű vezetékméretezés általános szempontjai (feszültségesés, teljesítményveszteség fogalma, méretezésben szokásos értékei. A vezetékméretezés során, mint minden műszaki berendezés tervezésénél
MUNKAANYAG. Forrai Jánosné. Előkészítő munka. A követelménymodul megnevezése: Monolit beton készítése I.
 Forrai Jánosné Előkészítő munka A követelménymodul megnevezése: Monolit beton készítése I. A követelménymodul száma: 0482-06 A tartalomelem azonosító száma és célcsoportja: SzT-002-30 ELŐKÉSZÍTŐMUNKA
Forrai Jánosné Előkészítő munka A követelménymodul megnevezése: Monolit beton készítése I. A követelménymodul száma: 0482-06 A tartalomelem azonosító száma és célcsoportja: SzT-002-30 ELŐKÉSZÍTŐMUNKA
MATEMATIKA A 10. évfolyam
 MATEMATIKA A 10. évfolyam 8. modul Hasonlóság és alkalmazásai Készítették: Vidra Gábor, Lénárt István Matematika A 10. évfolyam 8. modul: Hasonlóság és alkalmazásai A modul célja Időkeret Ajánlott korosztály
MATEMATIKA A 10. évfolyam 8. modul Hasonlóság és alkalmazásai Készítették: Vidra Gábor, Lénárt István Matematika A 10. évfolyam 8. modul: Hasonlóság és alkalmazásai A modul célja Időkeret Ajánlott korosztály
9. modul Szinusz- és koszinusztétel. Készítette: Csákvári Ágnes
 9. modul Szinusz- és koszinusztétel Készítette: Csákvári Ágnes Matematika A 11. évfolyam 9. modul: Szinusz- és koszinusztétel Tanári útmutató A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
9. modul Szinusz- és koszinusztétel Készítette: Csákvári Ágnes Matematika A 11. évfolyam 9. modul: Szinusz- és koszinusztétel Tanári útmutató A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
Tevékenység: Gyűjtse ki és tanulja meg a kötőcsavarok szilárdsági tulajdonságainak jelölési módját!
 Csavarkötés egy külső ( orsó ) és egy belső ( anya ) csavarmenet kapcsolódását jelenti. A következő képek a motor forgattyúsházában a főcsapágycsavarokat és a hajtókarcsavarokat mutatják. 1. Kötőcsavarok
Csavarkötés egy külső ( orsó ) és egy belső ( anya ) csavarmenet kapcsolódását jelenti. A következő képek a motor forgattyúsházában a főcsapágycsavarokat és a hajtókarcsavarokat mutatják. 1. Kötőcsavarok
TARTALOMJEGYZÉK ELŐSZÓ... 7 1. GONDOLKOZZ ÉS SZÁMOLJ!... 9 2. HOZZÁRENDELÉS, FÜGGVÉNY... 69
 TARTALOMJEGYZÉK ELŐSZÓ............................................................ 7 1. GONDOLKOZZ ÉS SZÁMOLJ!............................. 9 Mit tanultunk a számokról?............................................
TARTALOMJEGYZÉK ELŐSZÓ............................................................ 7 1. GONDOLKOZZ ÉS SZÁMOLJ!............................. 9 Mit tanultunk a számokról?............................................
ZAJCSILLAPÍTOTT SZÁMÍTÓGÉPHÁZ TERVEZÉSE
 ZAJCSILLAPÍTOTT SZÁMÍTÓGÉPHÁZ TERVEZÉSE Kovács Gábor 2006. április 01. TARTALOMJEGYZÉK TARTALOMJEGYZÉK... 2 1. FELADAT MEGFOGALMAZÁSA... 3 2. LÉGCSATORNA ZAJCSILLAPÍTÁSA... 3 2.1 Négyzet keresztmetszet...
ZAJCSILLAPÍTOTT SZÁMÍTÓGÉPHÁZ TERVEZÉSE Kovács Gábor 2006. április 01. TARTALOMJEGYZÉK TARTALOMJEGYZÉK... 2 1. FELADAT MEGFOGALMAZÁSA... 3 2. LÉGCSATORNA ZAJCSILLAPÍTÁSA... 3 2.1 Négyzet keresztmetszet...
Térinformatikai alkalmazások 4.
 Térinformatikai alkalmazások 4. Földinformációs rendszerek (LIS) dr. Végső, Ferenc Térinformatikai alkalmazások 4. : Földinformációs rendszerek (LIS) dr. Végső, Ferenc Lektor : Keringer, Zsolt Ez a modul
Térinformatikai alkalmazások 4. Földinformációs rendszerek (LIS) dr. Végső, Ferenc Térinformatikai alkalmazások 4. : Földinformációs rendszerek (LIS) dr. Végső, Ferenc Lektor : Keringer, Zsolt Ez a modul
PRÓBAÉRETTSÉGI MATEMATIKA. 2003. május-június SZÓBELI EMELT SZINT. Tanulói példány. Vizsgafejlesztő Központ
 PRÓBAÉRETTSÉGI 2003. május-június MATEMATIKA SZÓBELI EMELT SZINT Tanulói példány Vizsgafejlesztő Központ 1. Halmazok, halmazműveletek Alapfogalmak, halmazműveletek, számosság, számhalmazok, nevezetes ponthalmazok
PRÓBAÉRETTSÉGI 2003. május-június MATEMATIKA SZÓBELI EMELT SZINT Tanulói példány Vizsgafejlesztő Központ 1. Halmazok, halmazműveletek Alapfogalmak, halmazműveletek, számosság, számhalmazok, nevezetes ponthalmazok
Keresztmetszeti megmunkálás többfejes gyalugépekkel
 Szabó Árpád Kálmán Keresztmetszeti megmunkálás többfejes gyalugépekkel A követelménymodul megnevezése: Alapvető tömörfa megmunkálási feladatok A követelménymodul száma: 2302-06 A tartalomelem azonosító
Szabó Árpád Kálmán Keresztmetszeti megmunkálás többfejes gyalugépekkel A követelménymodul megnevezése: Alapvető tömörfa megmunkálási feladatok A követelménymodul száma: 2302-06 A tartalomelem azonosító
Jelentés a friss beton konzisztenciájának (folyósságának) mérésére vonatkozó vizsgálatokról
 - 1 - Jelentés a friss beton konzisztenciájának (folyósságának) mérésére vonatkozó vizsgálatokról Budapest, 1952. szeptember 29. Az Építéshelyi anyagvizsgálati módszerek kutatása témakörben kísérleteket
- 1 - Jelentés a friss beton konzisztenciájának (folyósságának) mérésére vonatkozó vizsgálatokról Budapest, 1952. szeptember 29. Az Építéshelyi anyagvizsgálati módszerek kutatása témakörben kísérleteket
Három dimenziós barlangtérkép elkészítésének matematikai problémái
 Szegedi Tudományegyetem Természettudományi és Informatikai Kar Bolyai Intézet Geometria Tanszék Három dimenziós barlangtérkép elkészítésének matematikai problémái Szakdolgozat Írta: Pásztor Péter Matematika
Szegedi Tudományegyetem Természettudományi és Informatikai Kar Bolyai Intézet Geometria Tanszék Három dimenziós barlangtérkép elkészítésének matematikai problémái Szakdolgozat Írta: Pásztor Péter Matematika
BALESETVÉDELMI TUDNIVALÓK ÉS MUNKASZABÁLYOK
 1./ BEVEZETÉS Amikor kísérletet hajtunk végre, valójában "párbeszédet" folytatunk a természettel. A kísérleti összeállítás a kérdés feltevése, a lejátszódó jelenség pedig a természet "válasza" a feltett
1./ BEVEZETÉS Amikor kísérletet hajtunk végre, valójában "párbeszédet" folytatunk a természettel. A kísérleti összeállítás a kérdés feltevése, a lejátszódó jelenség pedig a természet "válasza" a feltett
Kollimáció hiba hatása Távcsőállás fok perc mp perc mp fok perc mp mp 10 I 209 00 00 08 07 208 59 54-14 42 II 28 59
 KRITÉRIUM FELDTHOZ Kollimáció Vízszintes körleolvasások Irányérték hiba hatása Távcsőállás fok perc mp perc mp fok perc mp mp 10 I 09 00 00 08 07 08 59 54-14 4 II 8 59 59 41 40 Közepelés: (09-00-10 + 09-00-07)/=09-00-08
KRITÉRIUM FELDTHOZ Kollimáció Vízszintes körleolvasások Irányérték hiba hatása Távcsőállás fok perc mp perc mp fok perc mp mp 10 I 09 00 00 08 07 08 59 54-14 4 II 8 59 59 41 40 Közepelés: (09-00-10 + 09-00-07)/=09-00-08
Széchenyi István Egyetem, 2005
 Gáspár Csaba, Molnárka Győző Lineáris algebra és többváltozós függvények Széchenyi István Egyetem, 25 Vektorterek Ebben a fejezetben a geometriai vektorfogalom ( irányított szakasz ) erős általánosítását
Gáspár Csaba, Molnárka Győző Lineáris algebra és többváltozós függvények Széchenyi István Egyetem, 25 Vektorterek Ebben a fejezetben a geometriai vektorfogalom ( irányított szakasz ) erős általánosítását
MUNKAANYAG. Szám János. Síkmarás, gépalkatrész befoglaló méreteinek és alakjának kialakítása marógépen. A követelménymodul megnevezése:
 Szám János Síkmarás, gépalkatrész befoglaló méreteinek és alakjának kialakítása marógépen A követelménymodul megnevezése: Általános gépészeti technológiai feladatok II. (forgácsoló) A követelménymodul
Szám János Síkmarás, gépalkatrész befoglaló méreteinek és alakjának kialakítása marógépen A követelménymodul megnevezése: Általános gépészeti technológiai feladatok II. (forgácsoló) A követelménymodul
Magyarkúti József. Anyagvizsgálatok. A követelménymodul megnevezése: Mérőtermi feladatok
 Magyarkúti József Anyagvizsgálatok A követelménymodul megnevezése: Mérőtermi feladatok A követelménymodul száma: 0275-06 A tartalomelem azonosító száma és célcsoportja: SzT-001-50 ANYAGVIZSGÁLATOK ANYAGVIZSGÁLATOK
Magyarkúti József Anyagvizsgálatok A követelménymodul megnevezése: Mérőtermi feladatok A követelménymodul száma: 0275-06 A tartalomelem azonosító száma és célcsoportja: SzT-001-50 ANYAGVIZSGÁLATOK ANYAGVIZSGÁLATOK
A Megyeri híd terhelésvizsgálatának támogatása földi lézerszkenneléssel
 A Megyeri híd terhelésvizsgálatának támogatása földi lézerszkenneléssel Dr. Lovas Tamás 1 Berényi Attila 1,3 dr. Barsi Árpád 1 dr. Dunai László 2 1 Fotogrammetria és Térinformatika Tanszék, BME 2 Hidak
A Megyeri híd terhelésvizsgálatának támogatása földi lézerszkenneléssel Dr. Lovas Tamás 1 Berényi Attila 1,3 dr. Barsi Árpád 1 dr. Dunai László 2 1 Fotogrammetria és Térinformatika Tanszék, BME 2 Hidak
FELHASZNÁLÓI KÉZIKÖNYV Verzió 1.0 Magyar PIPER 100 / 200
 FELHASZNÁLÓI KÉZIKÖNYV Verzió 1.0 Magyar PIPER 100 / 200 PIPER 100 / 200 2 Bevezetés Gratulálunk a Leica Geosystems új Csőlézerének a megvásárlásához. Termék Termék Azonosítás A Piper 100 és 200 lézeres
FELHASZNÁLÓI KÉZIKÖNYV Verzió 1.0 Magyar PIPER 100 / 200 PIPER 100 / 200 2 Bevezetés Gratulálunk a Leica Geosystems új Csőlézerének a megvásárlásához. Termék Termék Azonosítás A Piper 100 és 200 lézeres
Verzió 2.0 Magyar. Leica NA720/724/ 728/730/730 plus Felhasználói Kézikönyv
 Verzió 2.0 Magyar Leica NA720/724/ 728/730/730 plus Felhasználói Kézikönyv NA720/724/728/730/730 plus, Bevezetés Bevezetés 2 Vásárlás Gratulálunk a Leica NA720/724/728/730/730 plus műszer megvásárlásához.
Verzió 2.0 Magyar Leica NA720/724/ 728/730/730 plus Felhasználói Kézikönyv NA720/724/728/730/730 plus, Bevezetés Bevezetés 2 Vásárlás Gratulálunk a Leica NA720/724/728/730/730 plus műszer megvásárlásához.
Geodézia 1. A helymeghatározás alapjai Gyenes, Róbert
 Geodézia 1. A helymeghatározás alapjai Gyenes, Róbert Geodézia 1.: A helymeghatározás alapjai Gyenes, Róbert Lektor: Homolya, András Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027 Tananyagfejlesztéssel a
Geodézia 1. A helymeghatározás alapjai Gyenes, Róbert Geodézia 1.: A helymeghatározás alapjai Gyenes, Róbert Lektor: Homolya, András Ez a modul a TÁMOP - 4.1.2-08/1/A-2009-0027 Tananyagfejlesztéssel a
GEODÉZIAI TEREPGYAKORLAT 2005
 GEODÉZIAI TEREPGYAKORLAT 2005 A terepgyakorlat csoport beosztása Időpont A csoport B csoport C csoport Április 25-29. Sukoró Topográfia Fehérvár Május 2-6. Fehérvár Sukoró Topográfia Május 9-13. Feldolgozás
GEODÉZIAI TEREPGYAKORLAT 2005 A terepgyakorlat csoport beosztása Időpont A csoport B csoport C csoport Április 25-29. Sukoró Topográfia Fehérvár Május 2-6. Fehérvár Sukoró Topográfia Május 9-13. Feldolgozás
MUNKAANYAG. Péntekné Simon Edina. Női szoknya alapszerkesztése, modellezése, szabásminta készítése és szériázása. A követelménymodul megnevezése:
 Péntekné Simon Edina Női szoknya alapszerkesztése, modellezése, szabásminta készítése és szériázása A követelménymodul megnevezése: Gyártmányfejlesztés és gyártáselőkészítés a ruhaiparban A követelménymodul
Péntekné Simon Edina Női szoknya alapszerkesztése, modellezése, szabásminta készítése és szériázása A követelménymodul megnevezése: Gyártmányfejlesztés és gyártáselőkészítés a ruhaiparban A követelménymodul
MUNKAANYAG. Szám János. Furatesztergálás technológiai tervezése, szerszámok, készülékek megválasztása, paraméterek meghatározása
 Szám János Furatesztergálás technológiai tervezése, szerszámok, készülékek megválasztása, paraméterek meghatározása A követelménymodul megnevezése: Általános gépészeti technológiai feladatok II. (forgácsoló)
Szám János Furatesztergálás technológiai tervezése, szerszámok, készülékek megválasztása, paraméterek meghatározása A követelménymodul megnevezése: Általános gépészeti technológiai feladatok II. (forgácsoló)
BEVEZETÉS AZ ÁBRÁZOLÓ GEOMETRIÁBA
 Pék Johanna BEVEZETÉS AZ ÁBRÁZOLÓ GEOMETRIÁBA (Matematika tanárszakos hallgatók számára) Tartalomjegyzék Előszó ii 0. Alapismeretek 1 0.1. Térgeometriai alapok............................. 1 0.2. Az ábrázoló
Pék Johanna BEVEZETÉS AZ ÁBRÁZOLÓ GEOMETRIÁBA (Matematika tanárszakos hallgatók számára) Tartalomjegyzék Előszó ii 0. Alapismeretek 1 0.1. Térgeometriai alapok............................. 1 0.2. Az ábrázoló
2) = 0 ahol x 1 és x 2 az ax 2 + bx + c = 0 ( a,b, c R és a 0 )
 Fogalom gyűjtemény Abszcissza: az x tengely Abszolút értékes egyenletek: azok az egyenletek, amelyekben abszolút érték jel szerepel. Abszolútérték-függvény: egy elemi egyváltozós valós függvény, mely minden
Fogalom gyűjtemény Abszcissza: az x tengely Abszolút értékes egyenletek: azok az egyenletek, amelyekben abszolút érték jel szerepel. Abszolútérték-függvény: egy elemi egyváltozós valós függvény, mely minden
AKKUMULÁTOROS ÜTVEFÚRÓ ÉS CSAVARBEHAJTÓ GÉP. Használati utasítás 8270D 8280D 8390D
 AKKUMULÁTOROS ÜTVEFÚRÓ ÉS CSAVARBEHAJTÓ GÉP Használati utasítás 8270D 8280D 8390D 2 Magyarázatok az ábrák számozott részleteihez 1. Nyomógomb 2. Blokkakkumulátor 3. Kioldó kapcsoló 4. Irányváltó kapcsolókar
AKKUMULÁTOROS ÜTVEFÚRÓ ÉS CSAVARBEHAJTÓ GÉP Használati utasítás 8270D 8280D 8390D 2 Magyarázatok az ábrák számozott részleteihez 1. Nyomógomb 2. Blokkakkumulátor 3. Kioldó kapcsoló 4. Irányváltó kapcsolókar
Matematikai statisztikai elemzések 2.
 Matematikai statisztikai elemzések 2. Helyzetmutatók, átlagok, kvantilisek. A szórás és szóródás Prof. Dr. Závoti, József Matematikai statisztikai elemzések 2.: Helyzetmutatók, átlagok, Prof. Dr. Závoti,
Matematikai statisztikai elemzések 2. Helyzetmutatók, átlagok, kvantilisek. A szórás és szóródás Prof. Dr. Závoti, József Matematikai statisztikai elemzések 2.: Helyzetmutatók, átlagok, Prof. Dr. Závoti,
(összevont laboratóriumi tananyag I.) Szerzők: az ELTE Természettudományi Kar oktatói. Szerkesztette: Havancsák Károly
 FIZIKAI MÉRÉSEK (összevont laboratóriumi tananyag I.) Szerzők: az ELTE Természettudományi Kar oktatói Szerkesztette: Havancsák Károly Lektorálta: Kemény Tamás ELTE 2013 Tartalomjegyzék 1. Amit már az elején
FIZIKAI MÉRÉSEK (összevont laboratóriumi tananyag I.) Szerzők: az ELTE Természettudományi Kar oktatói Szerkesztette: Havancsák Károly Lektorálta: Kemény Tamás ELTE 2013 Tartalomjegyzék 1. Amit már az elején
103. számú melléklet: 104. számú Elıírás. Hatályba lépett az Egyezmény mellékleteként 1998. január 15-én
 1998. január 22. ENSZ - EGB 104. sz. Elıírás EGYEZMÉNY A KEREKES JÁRMŐVEKRE, VALAMINT AZ ILYEN JÁRMŐVEKRE FELSZERELHETİ ÉS/VAGY ILYENEKEN ALKALMAZHATÓ SZERELVÉNYEKRE ÉS ALKATRÉSZEKRE VONATKOZÓ EGYSÉGES
1998. január 22. ENSZ - EGB 104. sz. Elıírás EGYEZMÉNY A KEREKES JÁRMŐVEKRE, VALAMINT AZ ILYEN JÁRMŐVEKRE FELSZERELHETİ ÉS/VAGY ILYENEKEN ALKALMAZHATÓ SZERELVÉNYEKRE ÉS ALKATRÉSZEKRE VONATKOZÓ EGYSÉGES
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika középszint 161 ÉRETTSÉGI VIZSGA 016. május. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos tudnivalók Formai előírások:
Matematika középszint 161 ÉRETTSÉGI VIZSGA 016. május. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos tudnivalók Formai előírások:
Vízszintes mérés egyszerű eszközök. Földméréstan
 Vízszintes mérés egyszerű eszközök Egyszerű eszközök kitűző rúd Jelölési módok: Kitűző rúd elsősorban a bemérendő és kitűzendő pontok megjelölésére, láthatóvá tételére a mérési vonalak egymásra merőleges
Vízszintes mérés egyszerű eszközök Egyszerű eszközök kitűző rúd Jelölési módok: Kitűző rúd elsősorban a bemérendő és kitűzendő pontok megjelölésére, láthatóvá tételére a mérési vonalak egymásra merőleges
FELADATOK ÉS MEGOLDÁSOK
 3. osztály Egy asztal körül 24-en ülnek, mindannyian mindig igazat mondanak. Minden lány azt mondja, hogy a közvetlen szomszédjaim közül pontosan az egyik fiú, és minden fiú azt mondja, hogy mindkét közvetlen
3. osztály Egy asztal körül 24-en ülnek, mindannyian mindig igazat mondanak. Minden lány azt mondja, hogy a közvetlen szomszédjaim közül pontosan az egyik fiú, és minden fiú azt mondja, hogy mindkét közvetlen
Ponyvagarázs. Összeszerelési útmutató. Verzió: 480 cm X 250 cm X 180(220) cm Dátum: 2009. december 10. Készítette: minimumgarazs.
 Ponyvagarázs Összeszerelési útmutató Verzió: 480 cm X 250 cm X 180(220) cm Dátum: 2009. december 10. Készítette: minimumgarazs.hu 2 Biztonsági előírások Ellenőrizze a ponyvagarázs csomagolásaiban található
Ponyvagarázs Összeszerelési útmutató Verzió: 480 cm X 250 cm X 180(220) cm Dátum: 2009. december 10. Készítette: minimumgarazs.hu 2 Biztonsági előírások Ellenőrizze a ponyvagarázs csomagolásaiban található
SZABADALMI LEÍRÁS 771H7. szám.
 Megjelent 1 í>1920. évi szeptember hó 18-án. MAGYAR KIRÁLYI SZABADALMI HIVATAL. SZABADALMI LEÍRÁS 771H7. szám. VII/a. OSZTÁLY. Eljárás és kéazülék rendszerestávlati (torzított)átvitelreoptikai vagyfényképészeti
Megjelent 1 í>1920. évi szeptember hó 18-án. MAGYAR KIRÁLYI SZABADALMI HIVATAL. SZABADALMI LEÍRÁS 771H7. szám. VII/a. OSZTÁLY. Eljárás és kéazülék rendszerestávlati (torzított)átvitelreoptikai vagyfényképészeti
S100 SOROZAT - TOLÓAJTÓK (acél rendszer)
 Peremfeltételek: S100 SOROZAT - TOLÓAJTÓK (acél rendszer) alsó futású tolóajtók - maximális nyílásméretek: magasság 200 mm, szélesség tetszőleges egyenként 000 mm-ig terjedő részegységek esetén. - az egyes
Peremfeltételek: S100 SOROZAT - TOLÓAJTÓK (acél rendszer) alsó futású tolóajtók - maximális nyílásméretek: magasság 200 mm, szélesség tetszőleges egyenként 000 mm-ig terjedő részegységek esetén. - az egyes
Világítási tartószerkezetek
 Világítási tartószerkezetek A világítási pozíciók függvényében a fényvetők pozícióban történő rögzítéséhez különböző eszközöket alkalmazunk. Három csoportra oszthatók, az első a függesztő elemek csoportja,
Világítási tartószerkezetek A világítási pozíciók függvényében a fényvetők pozícióban történő rögzítéséhez különböző eszközöket alkalmazunk. Három csoportra oszthatók, az első a függesztő elemek csoportja,
Palotai Zoltán. Előrajzolás. A követelménymodul megnevezése: Általános gépészeti technológiai feladatok I. (szerelő)
 Palotai Zoltán Előrajzolás A követelménymodul megnevezése: Általános gépészeti technológiai feladatok I. (szerelő) A követelménymodul száma: 0111-06 A tartalomelem azonosító száma és célcsoportja: SzT-016-30
Palotai Zoltán Előrajzolás A követelménymodul megnevezése: Általános gépészeti technológiai feladatok I. (szerelő) A követelménymodul száma: 0111-06 A tartalomelem azonosító száma és célcsoportja: SzT-016-30
MUNKAANYAG. Dzúró Zoltán. Tengelyszerű munkadarab készítése XY típusú. esztergagépen, a munkafolyamat, a méret-, alakpontosság
 Dzúró Zoltán Tengelyszerű munkadarab készítése XY típusú esztergagépen, a munkafolyamat, a méret-, alakpontosság és felületminőség ellenőrzése, dokumentálása A követelménymodul megnevezése: Általános gépészeti
Dzúró Zoltán Tengelyszerű munkadarab készítése XY típusú esztergagépen, a munkafolyamat, a méret-, alakpontosság és felületminőség ellenőrzése, dokumentálása A követelménymodul megnevezése: Általános gépészeti
BBBZ kódex --------------------------------------------------------------------------------------------------------- 4.3.2.5 Hajócsavar-gyártás
 4.3.2.5 Hajócsavar-gyártás A hajócsavarok gyártása erősen speciális tevékenység, amelynél olyan eszközökre is szükség van, mint a nagy méretű öntvények készítéséhez használt berendezések, azok megmunkálására
4.3.2.5 Hajócsavar-gyártás A hajócsavarok gyártása erősen speciális tevékenység, amelynél olyan eszközökre is szükség van, mint a nagy méretű öntvények készítéséhez használt berendezések, azok megmunkálására
Mozgásátalakítók, csigahajtás, csavarorsó felépítése és működése.hibalehetőségek és javításuk
 Molnár István Mozgásátalakítók, csigahajtás, csavarorsó felépítése és működése.hibalehetőségek és javításuk A követelménymodul megnevezése: Gépelemek szerelése A követelménymodul száma: 0221-06 A tartalomelem
Molnár István Mozgásátalakítók, csigahajtás, csavarorsó felépítése és működése.hibalehetőségek és javításuk A követelménymodul megnevezése: Gépelemek szerelése A követelménymodul száma: 0221-06 A tartalomelem
Készítsen elvi szabadkézi vázlatokat! Törekedjen a témával kapcsolatos lényeges jellemzők kiemelésére!
 1 6 ) M u t a s s a b e a s á r g a r é z c s ő v e z e t é k k é s z í t é s é t a z a l á b b i v á z l a t f e lh a s z n á l á s á v a l Készítsen elvi szabadkézi vázlatokat! Törekedjen a témával kapcsolatos
1 6 ) M u t a s s a b e a s á r g a r é z c s ő v e z e t é k k é s z í t é s é t a z a l á b b i v á z l a t f e lh a s z n á l á s á v a l Készítsen elvi szabadkézi vázlatokat! Törekedjen a témával kapcsolatos
23. ISMERKEDÉS A MŰVELETI ERŐSÍTŐKKEL
 23. ISMEKEDÉS A MŰVELETI EŐSÍTŐKKEL Céltűzés: A műveleti erősítők legfontosabb tlajdonságainak megismerése. I. Elméleti áttentés A műveleti erősítők (továbbiakban: ME) nagy feszültségerősítésű tranzisztorokból
23. ISMEKEDÉS A MŰVELETI EŐSÍTŐKKEL Céltűzés: A műveleti erősítők legfontosabb tlajdonságainak megismerése. I. Elméleti áttentés A műveleti erősítők (továbbiakban: ME) nagy feszültségerősítésű tranzisztorokból
SZÁMOLÁSTECHNIKAI ISMERETEK
 SZÁMOLÁSTECHNIKAI ISMERETEK Műveletek szögekkel Geodéziai számításaink során gyakran fogunk szögekkel dolgozni. Az egyszerűbb írásmód kedvéért ilyenkor a fok ( o ), perc (, ), másodperc (,, ) jelét el
SZÁMOLÁSTECHNIKAI ISMERETEK Műveletek szögekkel Geodéziai számításaink során gyakran fogunk szögekkel dolgozni. Az egyszerűbb írásmód kedvéért ilyenkor a fok ( o ), perc (, ), másodperc (,, ) jelét el
Miskolci Egyetem, Gyártástudományi Intézet, Prof. Dr. Dudás Illés
 6. MENETMEGMUNKÁLÁSOK A csavarfelületek egyrészt gépelemek összekapcsolására (kötő menetek), másrészt mechanizmusokban mozgás átadásra (kinematikai menetek) szolgálnak. 6.1. Gyártási eljárások a) Öntés
6. MENETMEGMUNKÁLÁSOK A csavarfelületek egyrészt gépelemek összekapcsolására (kötő menetek), másrészt mechanizmusokban mozgás átadásra (kinematikai menetek) szolgálnak. 6.1. Gyártási eljárások a) Öntés
A rádiólokációs információfeldolgozás folyamata
 DR. SERES GYÖRGY mérnök alezredes a hadtudományok kandidátusa A rádiólokációs információfeldolgozás folyamata A Haditechnikai Szemle 1981. évi 2. számában Néhány gondolat a rádiólokációs rendszertechnikáról"
DR. SERES GYÖRGY mérnök alezredes a hadtudományok kandidátusa A rádiólokációs információfeldolgozás folyamata A Haditechnikai Szemle 1981. évi 2. számában Néhány gondolat a rádiólokációs rendszertechnikáról"
MATEMATIKA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
 Matematika középszint 1413 ÉRETTSÉGI VIZSGA 015. május 5. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos tudnivalók Formai előírások:
Matematika középszint 1413 ÉRETTSÉGI VIZSGA 015. május 5. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Fontos tudnivalók Formai előírások:
Terra Kombi Kombinátor. Gépkönyv
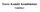 Terra Kombi Kombinátor Gépkönyv l./ ÁLTALÁNOS ISMERTETÉS 1.1 Munkagépek-felhasználási-területe Tavaszi és őszi vetésű növények magágykészítése Kelőfélben lévő gyomok szántóföldi irtása Mütrágyák, vegyszerek
Terra Kombi Kombinátor Gépkönyv l./ ÁLTALÁNOS ISMERTETÉS 1.1 Munkagépek-felhasználási-területe Tavaszi és őszi vetésű növények magágykészítése Kelőfélben lévő gyomok szántóföldi irtása Mütrágyák, vegyszerek
46/2010. (IV. 27.) FVM rendelet. az állami alapadatok felhasználásával végzett sajátos célú földmérési és térképészeti tevékenységről
 46/2010. (IV. 27.) FVM rendelet az állami alapadatok felhasználásával végzett sajátos célú földmérési és térképészeti tevékenységről A földmérési és térképészeti tevékenységről szóló 1996. évi LXXVI. törvény
46/2010. (IV. 27.) FVM rendelet az állami alapadatok felhasználásával végzett sajátos célú földmérési és térképészeti tevékenységről A földmérési és térképészeti tevékenységről szóló 1996. évi LXXVI. törvény
MUNKAANYAG. Szabó László. Oldható kötések alkalmazása, szerszámai, technológiája. A követelménymodul megnevezése: Épületgépészeti alapfeladatok
 Szabó László Oldható kötések alkalmazása, szerszámai, technológiája A követelménymodul megnevezése: Épületgépészeti alapfeladatok A követelménymodul száma: 0109-06 A tartalomelem azonosító száma és célcsoportja:
Szabó László Oldható kötések alkalmazása, szerszámai, technológiája A követelménymodul megnevezése: Épületgépészeti alapfeladatok A követelménymodul száma: 0109-06 A tartalomelem azonosító száma és célcsoportja:
Axonometria és perspektíva. Szemléltető céllal készülő ábrák
 Axonometria és perspektíva Szemléltető céllal készülő ábrák Axonometria Jelentése: tengelyek mentén való mérés (axis: tengely, metrum: mérték) Az axonometria a koordinátarendszer tengelyein mért távolságok,
Axonometria és perspektíva Szemléltető céllal készülő ábrák Axonometria Jelentése: tengelyek mentén való mérés (axis: tengely, metrum: mérték) Az axonometria a koordinátarendszer tengelyein mért távolságok,
AutoN cr. Automatikus Kihajlási Hossz számítás AxisVM-ben. elméleti háttér és szemléltető példák. 2016. február
 AutoN cr Automatikus Kihajlási Hossz számítás AxisVM-ben elméleti háttér és szemléltető példák 2016. február Tartalomjegyzék 1 Bevezető... 3 2 Célkitűzések és alkalmazási korlátok... 4 3 Módszertan...
AutoN cr Automatikus Kihajlási Hossz számítás AxisVM-ben elméleti háttér és szemléltető példák 2016. február Tartalomjegyzék 1 Bevezető... 3 2 Célkitűzések és alkalmazási korlátok... 4 3 Módszertan...
SZÉLEZŐGÉP 3708 3708F. Használati utasítás
 MAKITA SZÉLEZŐGÉP 3708 3708F Használati utasítás A jelen használati útmutatóban szereplő tartozékok nem feltétlenül leszállított tartozékok! A leszállított tartozékokról kérem érdeklődjön viszonteladóinknál!
MAKITA SZÉLEZŐGÉP 3708 3708F Használati utasítás A jelen használati útmutatóban szereplő tartozékok nem feltétlenül leszállított tartozékok! A leszállított tartozékokról kérem érdeklődjön viszonteladóinknál!
Térinformatikai alkalmazások 2.
 Térinformatikai alkalmazások 2. A térinformatikai alkalmazások dr. Végső, Ferenc Térinformatikai alkalmazások 2. : A térinformatikai alkalmazások dr. Végső, Ferenc Lektor : Keringer, Zsolt Ez a modul a
Térinformatikai alkalmazások 2. A térinformatikai alkalmazások dr. Végső, Ferenc Térinformatikai alkalmazások 2. : A térinformatikai alkalmazások dr. Végső, Ferenc Lektor : Keringer, Zsolt Ez a modul a
ÖSSZEADÁS, KIVONÁS AZ EGY 0-RA VÉGZŐDŐ SZÁMOK KÖRÉBEN
 Matematika A 3. évfolyam ÖSSZEADÁS, KIVONÁS AZ EGY 0-RA VÉGZŐDŐ SZÁMOK KÖRÉBEN 16. modul Készítette: KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 16. modul összeadás, kivonás az egy 0-ra végződő számok körében
Matematika A 3. évfolyam ÖSSZEADÁS, KIVONÁS AZ EGY 0-RA VÉGZŐDŐ SZÁMOK KÖRÉBEN 16. modul Készítette: KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 16. modul összeadás, kivonás az egy 0-ra végződő számok körében
