Aritmetikai kifejezések lengyelformára hozása
|
|
|
- Emil Mezei
- 6 évvel ezelőtt
- Látták:
Átírás
1 Aritmetikai kifejezések lengyelformára hozása Készítették: Santák Csaba és Kovács Péter, 2005 ELTE IK programtervező matematikus szak
2 Aritmetikai kifejezések kiértékelése - Gyakran felmerülő programozási feladat, hogy egy adott aritmetikai kifejezést kell kiértékelni (kiszámolni). - A probléma nehézségét az okozza, hogy a kifejezések megszokott, természetes formája (az ún. infix írásmód, amikor az egyes műveleti jelek az operandusaik között helyezkednek el) nem egyértelmű és algoritmikusan nehezen kezelhető. - Az egyik legjobb és leghatékonyabb megoldási módszer az, hogy a kifejezést első lépésben átalakítjuk ún. lengyelformává, utána pedig azt értékeljük ki.
3 A lengyelforma - Łukasiewicz lengyel matematikus kidolgozta az aritmetikai formulák egy olyan átalakítási módját, amelynek segítségével a kiértékelés rendkívül egyszerűen és gyorsan megvalósítható. Ennek egy módosított változata terjedt el az informatikában. - Ebben az alakban a műveleti jelek az operandusaik után állnak, ezért postfix formának, illetve a szerző tiszteletére lengyelformának nevezik*. (Angol szakirodalomban: reverse Polish notation, RPN) * Megjegyezzük, hogy egy kifejezés lengyelformája megegyezik a kifejezésfa postorder bejárásával.
4 Példák - a+b ab+ - a+b*c abc*+ - a*b+(c-d)/2 ab*cd-2/+ - a+b+c*d/2-e*f ab+cd*2/+ef*- - x:=a+b xab+:= - x:=a*b^2 xab2^*:= -
5 A lengyelforma tulajdonságai Foglaljuk össze a lengyelfoma legfontosabb jellemzőit: - nincs benne zárójel, - az operandusok sorrendje ugyanaz, mint az eredeti kifejezésben, - a műveleti jelek sorrendje megegyezik a kifejezés helyes kiértékeléséhez szükséges elvégzési sorrendjükkel, - a műveleti jeleket közvetlenül megelőzik az operandusai (erre utal a postfix elnevezés). Ezek biztosítják, hogy egy lengyelformára hozott kifejezés kiértékelése könnyen elvégezhető legyen.
6 Aritmetikai kifejezések Az algoritmus tárgyalása előtt foglaljuk össze a szükséges fogalmakat és szabályokat. Műveletek precedenciái: Ebben a tárgyalásban hat műveletet tekintünk megengedettnek: a négy alapműveletet, a hatványozást és az értékadást. Ezek precedencia-szintjei legalacsonyabbig): - ^ (hatványozás) - *, / (szorzás, osztás) - +, - (összeadás, kivonás) - := (értékadás, definiáló egyenlőség*) a következők (a legmagasabbtól a * Több programozási nyelvhez hasonlóan megengedettnek tekintjük a többszörös értékadásokat is (pl. a:=b:=0).
7 Aritmetikai kifejezések Kifejezések kiértékelésekor figyelembe kell vennünk az egyes műveletek asszociativitási (zárójeleződési) szabályait is. 1. A négy alapművelet megegyezés szerint balról jobbra zárójeleződik: a+b+c ((a+b)+c) 2. A hatványozás és az értékadás megegyezés szerint jobbról balra zárójeleződik*: x^2^3 (x^(2^3)) = x^8 (Ha balról jobbra zárójeleznénk, akkor x^6-t kapnánk.) * Többszörös értékadás esetén a balról jobbra zárójeleződés nem is értelmezhető. Pl. a:=b:=1 (a:=b):=1 nem értelmezhető megfelelően, csak az a:=(b:=1).
8 A lengyelformára hozás feladata - Adott egy szintaktikusan helyes infix aritmetikai kifejezést tartalmazó szekvenciális input. Alakítsuk át lengyelformára. - Tegyük fel, hogy az input elemei nem karakterek, hanem a kifejezés egységei (lexikális elemei): operandus (változó, konstans stb.), operátor vagy zárójel; és minden elemről egyértelműen el tudjuk dönteni, hogy ezek közül melyik.
9 Lengyelformára hozás Az algoritmus során az inputot szekvenciálisan dolgozzuk fel, és egy (kezdetben üres) verem segítségével állítjuk elő a lengyelformát: Ha a kifejezésben a soron következő elem operandus, akkor azt kiírjuk a kimenetre (operandus tehát sosem kerül a verembe!). Ha nyitó zárójel következik, akkor azt a verembe dobjuk. Ha csukó zárójel következik, akkor sorban kivesszük a verem tetejéről az elemeket az első (legfelső) nyitó zárójelig, és kiírjuk őket a kimenetre, majd a nyitó zárójelet is kivesszük és eldobjuk (zárójelek tehát nem fognak megjelenni a kimeneten, és csukó zárójel sem kerül soha a verembe).
10 Lengyelformára hozás Ha operátor következik, akkor az első nála alacsonyabb (illetve jobbról balra zárójeleződő művelet esetén az első nem magasabb) precedenciájú operátorig, vagy az első nyitó zárójelig kivesszük a verem tetejéről az operátorokat, és kiírjuk a kimenetre. Végül a most olvasott operátort betesszük a verembe. Amikor az input végére érünk, a veremből az összes még benne lévő operátort kivesszük és kiírjuk a kimenetre.
11 Példa a+b+c*d/2-e*f Hozzuk lengyelformára az alábbi kifejezést: a+b+c*d/2-e*f Adjuk meg lépésről lépésre a verem tartalmát és a kimenetet. A verem kezdetben üres. Az első jel operandus, tehát kiírjuk a kimenetre. a
12 Példa a+b+c*d/2-e*f Operátor következik, tehát betesszük a verembe. a
13 Példa a+b+c*d/2-e*f Operandus következik, így kiírjuk a kimenetre. a b
14 Példa a+b+c*d/2-e*f Operátor következik. Mivel vele azonos precedenciájú operátor van a veremben, így azt kiírjuk a kimenetre, az új + jelet pedig betesszük a verembe. (Az összeadás ugyanis balról jobbra zárójeleződik.) a b +
15 Példa a+b+c*d/2-e*f Operandus következik, kiírjuk a kimenetre. a b + c
16 Példa a+b+c*d/2-e*f Operátor következik, ezért mivel magasabb precedenciájú a verem tetején lévő operátornál, betesszük a verembe. a b + c
17 Példa a+b+c*d/2-e*f Operandus következik, kiírjuk a kimenetre. a b + c d
18 Példa a+b+c*d/2-e*f Operátor következik. Mivel vele azonos precedenciájú operátor van a veremben, így azt kiírjuk a kimenetre, a most olvasott / jelet pedig betesszük a verembe. a b + c d *
19 Példa a+b+c*d/2-e*f Operandus következik, kiírjuk a kimenetre. a b + c d * 2
20 Példa a+b+c*d/2-e*f Operátor következik. Mivel a veremben egy nála magasabb, majd utána egy vele azonos precedenciájú operátor van, így azokat kiírjuk a kimenetre, a most olvasott - jelet pedig betesszük a verembe. a b + c d * 2 / +
21 Példa a+b+c*d/2-e*f Operandus következik, kiírjuk a kimenetre. a b + c d * 2 / + e
22 Példa a+b+c*d/2-e*f Operátor következik. Betesszük a verembe, mivel magasabb precedenciájú, mint a verem tetején lévő operátor. a b + c d * 2 / + e
23 Példa a+b+c*d/2-e*f Operandus következik, kiírjuk a kimenetre. a b + c d * 2 / + e f
24 Példa a+b+c*d/2-e*f A kifejezés végére értünk, a veremben lévő összes operátort kivesszük és kiírjuk a kimenetre. a b + c d * 2 / + e f * -
25 Az algoritmus struktogramja A korábbiakban megfogalmazott kikötések, egyszerűsítések mellett adjuk meg az algoritmus struktogramját is. Ehhez először is vezessünk be két segédfüggvényt, amelyek megadják egy operátor precedenciáját és zárójeleződésének irányát:
26 Az algoritmus struktogramja
27 Az algoritmus struktogramja Megjegyzés: A fenti elágazás két (szerkezetileg azonos) ága összevonható, ha egy bonyolultabb ciklusfeltételt írunk fel: IsEmpty(v) Top(v) "(" ( (zárójelezés(x) = balról precednecia(x) <= precedencia(top(v))) (zárójelezés(x) = jobbról precednecia(x) < precedencia(top(v))) )
28 Az algoritmus struktogramja Ha a precedencia függvényünket a nyitó zárójelre is értelmezzük oly módon, hogy annak a precedenciája legyen a legalacsonyabb (nulla), akkor az operator(x) ágban szereplő ciklusok feltételei leegyszerűsödnek:
29 További példák 1. x:=a+b^3^2 Hozzuk lengyelformára a fenti kifejezést, és nézzük meg minden lépésnél a verem tartalmát, illetve a lengyelforma kimenetének aktuális állását. A verem kezdetben üres.
30 1. x:=a+b^3^2 Operandus jön, tehát kiírjuk a kimenetre. A verem még mindig üres. x
31 1. x:=a+b^3^2 Operátor jön, berakjuk a verembe. x
32 1. x:=a+b^3^2 Operandus jön, tehát kiírjuk a kimenetre. x a
33 1. x:=a+b^3^2 Operátor jön, berakjuk a verembe a szabályoknak megfelelően. x a
34 1. x:=a+b^3^2 Operandus jön, tehát kiírjuk a kimenetre. x a b
35 1. x:=a+b^3^2 Operátor jön, berakjuk a verembe a szabályoknak megfelelően. x a b
36 1. x:=a+b^3^2 Operandus jön, tehát kiírjuk a kimenetre. x a b 3
37 1. x:=a+b^3^2 Operátor jön, berakjuk a verembe a szabályoknak megfelelően. x a b 3
38 1. x:=a+b^3^2 Operandus jön, tehát kiírjuk a kimenetre. x a b 3 2
39 1. x:=a+b^3^2 A kifejezés elfogyott, így kiírjuk a verem tartalmát a kimenetre. x a b 3 2 ^ ^ + := A verem kiürült.
40 2. (a+b)*(c-d) Hozzuk lengyelformára a fenti kifejezést. Nyitó zárójel az első jel, tehát betesszük a verembe. A verem tartalma:
41 2. (a+b)*(c-d) Operandus következik, tehát kiírjuk a kimenetre. a
42 2. (a+b)*(c-d) Operátor következik, tehát betesszük a verembe. a
43 2. (a+b)*(c-d) Operandus következik, tehát kiírjuk a kimenetre. a b
44 2. (a+b)*(c-d) Csukó zárójel következik, tehát a nyitózárójelig mindent kiírunk a veremből, a zárójelpárt eldobjuk. A verem újra üres lesz. a b +
45 2. (a+b)*(c-d) Operátor következik, tehát betesszük a verembe. a b +
46 2. (a+b)*(c-d) Nyitó zárójel következik, tehát betesszük a verembe. a b +
47 2. (a+b)*(c-d) Operandus következik, tehát kiírjuk a kimenetre. a b + c
48 2. (a+b)*(c-d) Operátor következik, tehát betesszük a verembe. a b + c
49 2. (a+b)*(c-d) Operandus következik, tehát kiírjuk a kimenetre. a b + c d
50 2. (a+b)*(c-d) Csukó zárójel következik, tehát a nyitózárójelig mindent kiírunk a veremből, a zárójelpárt eldobjuk. a b + c d -
51 2. (a+b)*(c-d) Végül ürítsük ki a vermet, mivel a kifejezés végére értünk. a b + c d - *
52 3. x:=(a+b)*c-(a+b)^2 Hozzuk lengyelformára a fenti kifejezést. Operandus következik, így kiírjuk a kimenetre. x
53 3. x:=(a+b)*c-(a+b)^2 Operátor következik, így betesszük a verembe. x
54 3. x:=(a+b)*c-(a+b)^2 Nyitó zárójel következik, így betesszük a verembe. x
55 3. x:=(a+b)*c-(a+b)^2 Operandus következik, így kiírjuk a kimenetre. x a
56 3. x:=(a+b)*c-(a+b)^2 Operátor következik, így betesszük a verembe. x a
57 3. x:=(a+b)*c-(a+b)^2 Operandus következik, így kiírjuk a kimenetre. x a b
58 3. x:=(a+b)*c-(a+b)^2 Csukó zárójel következik, így a nyitó zárójelig mindent kiürítünk a veremből, majd a zárójelpárt eldobjuk. x a b +
59 3. x:=(a+b)*c-(a+b)^2 Operátor következik, így betesszük a verembe. x a b +
60 3. x:=(a+b)*c-(a+b)^2 Operandus következik, így kiírjuk a kimenetre. x a b + c
61 3. x:=(a+b)*c-(a+b)^2 Operátor következik, mivel nála magasabb precedenciájú operátor van a veremben, azt kiírjuk, a - -t pedig betesszük a verembe. x a b + c *
62 3. x:=(a+b)*c-(a+b)^2 Nyitó zárójel következik, így betesszük a verembe. x a b + c *
63 3. x:=(a+b)*c-(a+b)^2 Operandus következik, így kiírjuk a kimenetre. x a b + c * a
64 3. x:=(a+b)*c-(a+b)^2 Operátor következik, így betesszük a verembe. x a b + c * a
65 3. x:=(a+b)*c-(a+b)^2 Operandus következik, így kiírjuk a kimenetre. x a b + c * a b
66 3. x:=(a+b)*c-(a+b)^2 Csukó zárójel következik, így a nyitó zárójelig mindent kiürítünk a veremből, majd a zárójelpárt eldobjuk. x a b + c * a b +
67 3. x:=(a+b)*c-(a+b)^2 Operátor következik, így betesszük a verembe. x a b + c * a b +
68 3. x:=(a+b)*c-(a+b)^2 Operandus következik, így kiírjuk a kimenetre. x a b + c * a b + 2
69 3. x:=(a+b)*c-(a+b)^2 A kifejezés végére értünk, így kiürítjük a vermet. x a b + c * a b + 2 ^ - :=
70 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Hozzuk lengyelformára a fenti kifejezést. Operandus következik, így kiírjuk a kimenetre. x
71 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operátor következik, így betesszük a verembe. x
72 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Nyitó zárójel következik, így betesszük a verembe. x
73 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operandus következik, így kiírjuk a kimenetre. x a
74 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operátor következik, így betesszük a verembe. x a
75 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operandus következik, így kiírjuk a kimenetre. x a b
76 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operátor következik, a nála magasabb precedenciájú operátort kiírjuk, a + -t betesszük a verembe. x a b *
77 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operandus következik, így kiírjuk a kimenetre. x a b * 1
78 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Csukó zárójel következik, így kiírjuk a kimenetre a vermet a nyitó zárójelig, a zárójelpárt eldobjuk. x a b * 1 +
79 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operátor következik, így betesszük a verembe. x a b * 1 +
80 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) 2 db nyitó zárójel következik, így betesszük azokat a verembe. x a b * 1 +
81 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operandus következik, így kiírjuk a kimenetre. x a b * 1 + x
82 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operátor következik, így betesszük a verembe. x a b * 1 + x
83 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operandus következik, így kiírjuk a kimenetre. x a b * 1 + x y
84 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operátor következik, és mivel jobbról-balra szabály van, a vele azonos precedenciájú operátort nem írjuk ki. Az operátort betesszük a verembe. x a b * 1 + x y
85 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operandus következik, így kiírjuk a kimenetre. x a b * 1 + x y 2
86 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operátor következik, 2 db nála magasabb precedenciájú operátor van a veremben így azokat kiírjuk a kimenetre. A + operátort a verembe rakjuk. x a b * 1 + x y 2 ^ ^
87 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operandus következik, így kiírjuk a kimenetre. x a b * 1 + x y 2 ^ ^ u
88 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operátor következik, nincs vele egyenlő, illetve nála magasabb precedenciájú operátor a veremben, így betesszük a verembe. x a b * 1 + x y 2 ^ ^ u
89 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Nyitó zárójel következik, így betesszük a verembe. x a b * 1 + x y 2 ^ ^ u
90 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operandus következik, így kiírjuk a kimenetre. x a b * 1 + x y 2 ^ ^ u v
91 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operátor következik, így betesszük a verembe. x a b * 1 + x y 2 ^ ^ u v
92 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operandus következik, így kiírjuk a kimenetre. x a b * 1 + x y 2 ^ ^ u v 3
93 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Csukó zárójel következik, így kiírjuk a kimenetre a következő nyitó zárójelig az összes operátort, majd a zárójelpárt eldobjuk. x a b * 1 + x y 2 ^ ^ u v 3 -
94 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Szintén csukó zárójel következik, így kiírjuk a kimenetre a következő nyitó zárójelig az összes operátort, majd a zárójelpárt eldobjuk. x a b * 1 + x y 2 ^ ^ u v 3 - * +
95 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operátor következik, így betesszük a verembe. x a b * 1 + x y 2 ^ ^ u v 3 - * +
96 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Nyitó zárójel következik, így betesszük a verembe. x a b * 1 + x y 2 ^ ^ u v 3 - * +
97 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operandus következik, így kiírjuk a kimenetre. x a b * 1 + x y 2 ^ ^ u v 3 - * + f
98 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operátor következik, így betesszük a verembe. x a b * 1 + x y 2 ^ ^ u v 3 - * + f
99 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operandus következik, így kiírjuk a kimenetre. x a b * 1 + x y 2 ^ ^ u v 3 - * + f g
100 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operátor következik, mivel vele azonos precedenciájú operátor van a veremben, azt kiírjuk, a - -t pedig betesszük a verembe. x a b * 1 + x y 2 ^ ^ u v 3 - * + f g +
101 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) Operandus következik, így kiírjuk a kimenetre. x a b * 1 + x y 2 ^ ^ u v 3 - * + f g + 4
102 4. x:=(a*b+1)/((x^y^2+u*(v-3))*(f+g-4)) 2 db csukó zárójel következik, azután a kifejezésnek vége lesz, így lényegében mindent kiírunk a veremből, természetesen a zárójeleket eldobjuk. A végeredmény: x a b * 1 + x y 2 ^ ^ u v 3 - * + f g * / :=
4. VEREM. Üres: V Verembe: V E V Veremből: V V E Felső: V E
 4. VEREM A mindennapokban is találkozunk verem alapú tároló struktúrákkal. Legismertebb példa a névadó, a mezőgazdaságban használt verem. Az informatikában legismertebb veremalkalmazások az eljáráshívások
4. VEREM A mindennapokban is találkozunk verem alapú tároló struktúrákkal. Legismertebb példa a névadó, a mezőgazdaságban használt verem. Az informatikában legismertebb veremalkalmazások az eljáráshívások
Készítette: Nagy Tibor István
 Készítette: Nagy Tibor István Operátorok Műveletek Egy (vagy több) műveleti jellel írhatók le A műveletet operandusaikkal végzik Operátorok fajtái operandusok száma szerint: egyoperandusú operátorok (pl.:
Készítette: Nagy Tibor István Operátorok Műveletek Egy (vagy több) műveleti jellel írhatók le A műveletet operandusaikkal végzik Operátorok fajtái operandusok száma szerint: egyoperandusú operátorok (pl.:
Adatszerkezetek Adatszerkezet fogalma. Az értékhalmaz struktúrája
 Adatszerkezetek Összetett adattípus Meghatározói: A felvehető értékek halmaza Az értékhalmaz struktúrája Az ábrázolás módja Műveletei Adatszerkezet fogalma Direkt szorzat Minden eleme a T i halmazokból
Adatszerkezetek Összetett adattípus Meghatározói: A felvehető értékek halmaza Az értékhalmaz struktúrája Az ábrázolás módja Műveletei Adatszerkezet fogalma Direkt szorzat Minden eleme a T i halmazokból
Absztrakt adatstruktúrák A bináris fák
 ciós lámpa a legnagyobb élettartamú és a legjobb hatásfokú fényforrásnak tekinthető, nyugodtan mondhatjuk, hogy a jövő fényforrása. Ezt bizonyítja az a tény, hogy ezen a területen a kutatások és a bejelentett
ciós lámpa a legnagyobb élettartamú és a legjobb hatásfokú fényforrásnak tekinthető, nyugodtan mondhatjuk, hogy a jövő fényforrása. Ezt bizonyítja az a tény, hogy ezen a területen a kutatások és a bejelentett
Adatszerkezetek és algoritmusok
 2009. november 13. Ismétlés El z órai anyagok áttekintése Ismétlés Specikáció Típusok, kifejezések, m veletek, adatok ábrázolása, típusabsztakció Vezérlési szerkezetek Függvények, paraméterátadás, rekurziók
2009. november 13. Ismétlés El z órai anyagok áttekintése Ismétlés Specikáció Típusok, kifejezések, m veletek, adatok ábrázolása, típusabsztakció Vezérlési szerkezetek Függvények, paraméterátadás, rekurziók
Verem Verem mutató 01
 A számítástechnikában a verem (stack) egy speciális adatszerkezet, amiben csak kétféle művelet van. A berak (push) egy elemet a verembe rak, a kivesz (pop) egy elemet elvesz a verem tetejéről. Mindig az
A számítástechnikában a verem (stack) egy speciális adatszerkezet, amiben csak kétféle művelet van. A berak (push) egy elemet a verembe rak, a kivesz (pop) egy elemet elvesz a verem tetejéről. Mindig az
Objektum elvű alkalmazások fejlesztése Kifejezés lengyel formára hozása és kiértékelése
 Objektum elvű alkalmazások fejlesztése Kifejezés lengyel formára hozása és kiértékelése Készítette: Gregorics Tibor Szabóné Nacsa Rozália Alakítsunk át egy infix formájú aritmetikai kifejezést postfix
Objektum elvű alkalmazások fejlesztése Kifejezés lengyel formára hozása és kiértékelése Készítette: Gregorics Tibor Szabóné Nacsa Rozália Alakítsunk át egy infix formájú aritmetikai kifejezést postfix
Szoftvertervezés és -fejlesztés I.
 Szoftvertervezés és -fejlesztés I. Operátorok Vezérlési szerkezetek Gyakorlás 1 Hallgatói Tájékoztató A jelen bemutatóban található adatok, tudnivalók és információk a számonkérendő anyag vázlatát képezik.
Szoftvertervezés és -fejlesztés I. Operátorok Vezérlési szerkezetek Gyakorlás 1 Hallgatói Tájékoztató A jelen bemutatóban található adatok, tudnivalók és információk a számonkérendő anyag vázlatát képezik.
Programozás BMEKOKAA146. Dr. Bécsi Tamás 2. előadás
 Programozás BMEKOKAA146 Dr. Bécsi Tamás 2. előadás Szintaktikai alapok Alapvető típusok, ismétlés C# típus.net típus Méret (byte) Leírás byte System.Byte 1Előjel nélküli 8 bites egész szám (0..255) char
Programozás BMEKOKAA146 Dr. Bécsi Tamás 2. előadás Szintaktikai alapok Alapvető típusok, ismétlés C# típus.net típus Méret (byte) Leírás byte System.Byte 1Előjel nélküli 8 bites egész szám (0..255) char
Mit tudunk már? Programozás alapjai C nyelv 4. gyakorlat. Legnagyobb elem keresése. Feltételes operátor (?:) Legnagyobb elem keresése (3)
 Programozás alapjai C nyelv 4. gyakorlat Szeberényi Imre BME IIT Mit tudunk már? Típus fogalma char, int, float, double változók deklarációja operátorok (aritmetikai, relációs, logikai,
Programozás alapjai C nyelv 4. gyakorlat Szeberényi Imre BME IIT Mit tudunk már? Típus fogalma char, int, float, double változók deklarációja operátorok (aritmetikai, relációs, logikai,
Programozás alapjai C nyelv 4. gyakorlat. Mit tudunk már? Feltételes operátor (?:) Típus fogalma char, int, float, double
 Programozás alapjai C nyelv 4. gyakorlat Szeberényi Imre BME IIT Programozás alapjai I. (C nyelv, gyakorlat) BME-IIT Sz.I. 2005.10.10.. -1- Mit tudunk már? Típus fogalma char, int, float,
Programozás alapjai C nyelv 4. gyakorlat Szeberényi Imre BME IIT Programozás alapjai I. (C nyelv, gyakorlat) BME-IIT Sz.I. 2005.10.10.. -1- Mit tudunk már? Típus fogalma char, int, float,
Járműfedélzeti rendszerek II. 1. előadás Dr. Bécsi Tamás
 Járműfedélzeti rendszerek II. 1. előadás Dr. Bécsi Tamás A tárgy órái Előadás hetente (St101) csüt. 8:15 Bécsi Tamás C elmélet Ajánlott irodalom Dennis Ritchie: A C programozási nyelv Gyakorlat hetente
Járműfedélzeti rendszerek II. 1. előadás Dr. Bécsi Tamás A tárgy órái Előadás hetente (St101) csüt. 8:15 Bécsi Tamás C elmélet Ajánlott irodalom Dennis Ritchie: A C programozási nyelv Gyakorlat hetente
Kifejezések. Kozsik Tamás. December 11, 2016
 Kifejezések Kozsik Tamás December 11, 2016 Kifejezések Lexika Szintaktika Szemantika Lexika azonosítók (változó-, metódus-, típus- és csomagnevek) literálok operátorok, pl. + zárójelek: (), [], {},
Kifejezések Kozsik Tamás December 11, 2016 Kifejezések Lexika Szintaktika Szemantika Lexika azonosítók (változó-, metódus-, típus- és csomagnevek) literálok operátorok, pl. + zárójelek: (), [], {},
Kifejezések. A programozás alapjai előadás. Operátorok. Kifejezések. Operátorok precedenciája. Operátorok precedenciája
 A programozás alapjai 1 Kifejezések 5. előadás Híradástechnikai Tanszék Operandusok Literál Azonosító Kifejezés Kifejezések Precedencia Melyik hajtódik először végre? Asszociativitás Balról jobbra vagy
A programozás alapjai 1 Kifejezések 5. előadás Híradástechnikai Tanszék Operandusok Literál Azonosító Kifejezés Kifejezések Precedencia Melyik hajtódik először végre? Asszociativitás Balról jobbra vagy
infix kifejezés a+b ab+ +ab postfix kifejezés prefix kifejezés a+b ab+ +ab a+b ab+ +ab Készítette: Szabóné Nacsa Rozália
 infix kifejezés a+b ab+ +ab Készítette: Szabóné Nacsa Rozália nacsa@inf.elte.hu postfix kifejezés prefix kifejezés a+b ab+ +ab a+b ab+ +ab 4 Lengyelforma J. Lukasewitz lengyel matematikus használta el
infix kifejezés a+b ab+ +ab Készítette: Szabóné Nacsa Rozália nacsa@inf.elte.hu postfix kifejezés prefix kifejezés a+b ab+ +ab a+b ab+ +ab 4 Lengyelforma J. Lukasewitz lengyel matematikus használta el
Számítástechnika I. BMEKOKAA152 BMEKOKAA119 Infokommunikáció I. BMEKOKAA606. Dr. Bécsi Tamás 2. előadás
 Számítástechnika I. BMEKOKAA152 BMEKOKAA119 Infokommunikáció I. BMEKOKAA606 Dr. Bécsi Tamás 2. előadás Console I/O bővebben Lásd mintaprogram 2015.09.21. Számítástechnika I. 2. Előadás 2 Számábrázolásról
Számítástechnika I. BMEKOKAA152 BMEKOKAA119 Infokommunikáció I. BMEKOKAA606 Dr. Bécsi Tamás 2. előadás Console I/O bővebben Lásd mintaprogram 2015.09.21. Számítástechnika I. 2. Előadás 2 Számábrázolásról
Bevezetés az informatikába
 Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Bevezetés az informatikába 6. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Logikai áramkörök. Informatika alapjai-5 Logikai áramkörök 1/6
 Informatika alapjai-5 Logikai áramkörök 1/6 Logikai áramkörök Az analóg rendszerekben például hangerősítő, TV, rádió analóg áramkörök, a digitális rendszerekben digitális vagy logikai áramkörök működnek.
Informatika alapjai-5 Logikai áramkörök 1/6 Logikai áramkörök Az analóg rendszerekben például hangerősítő, TV, rádió analóg áramkörök, a digitális rendszerekben digitális vagy logikai áramkörök működnek.
Ellenőrző kérdések. 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t
 Ellenőrző kérdések 2. Kis dolgozat kérdései 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t 37. Ha t szintű indexet használunk,
Ellenőrző kérdések 2. Kis dolgozat kérdései 36. Ha t szintű indexet használunk, mennyi a keresési költség blokkműveletek számában mérve? (1 pont) log 2 (B(I (t) )) + t 37. Ha t szintű indexet használunk,
az Excel for Windows programban
 az Excel for Windows táblázatkezelőblázatkezel programban Mit nevezünk nk képletnek? A táblt blázatkezelő programok nagy előnye, hogy meggyorsítj tják és könnyebbé teszik a felhasználó számára a számítási
az Excel for Windows táblázatkezelőblázatkezel programban Mit nevezünk nk képletnek? A táblt blázatkezelő programok nagy előnye, hogy meggyorsítj tják és könnyebbé teszik a felhasználó számára a számítási
Karakterkészlet. A kis- és nagybetűk nem különböznek, a sztringliterálok belsejét leszámítva!
 A PL/SQL alapelemei Karakterkészlet Az angol ABC kis- és nagybetűi: a-z, A-Z Számjegyek: 0-9 Egyéb karakterek: ( ) + - * / < > =! ~ ^ ; :. ' @ %, " # $ & _ { }? [ ] Szóköz, tabulátor, kocsivissza A kis-
A PL/SQL alapelemei Karakterkészlet Az angol ABC kis- és nagybetűi: a-z, A-Z Számjegyek: 0-9 Egyéb karakterek: ( ) + - * / < > =! ~ ^ ; :. ' @ %, " # $ & _ { }? [ ] Szóköz, tabulátor, kocsivissza A kis-
Kifejezések. Kozsik Tamás. December 11, 2016
 Kifejezések Kozsik Tamás December 11, 2016 Kifejezés versus utasítás C/C++: kifejezés plusz pontosvessző: utasítás kiértékeli a kifejezést jellemzően: mellékhatása is van például: értékadás Ada: n = 5;
Kifejezések Kozsik Tamás December 11, 2016 Kifejezés versus utasítás C/C++: kifejezés plusz pontosvessző: utasítás kiértékeli a kifejezést jellemzően: mellékhatása is van például: értékadás Ada: n = 5;
1. előadás. Lineáris algebra numerikus módszerei. Hibaszámítás Számábrázolás Kerekítés, levágás Klasszikus hibaanalízis Abszolút hiba Relatív hiba
 Hibaforrások Hiba A feladatok megoldása során különféle hibaforrásokkal találkozunk: Modellhiba, amikor a valóságnak egy közelítését használjuk a feladat matematikai alakjának felírásához. (Pl. egy fizikai
Hibaforrások Hiba A feladatok megoldása során különféle hibaforrásokkal találkozunk: Modellhiba, amikor a valóságnak egy közelítését használjuk a feladat matematikai alakjának felírásához. (Pl. egy fizikai
DISZKRÉT MATEMATIKA: STRUKTÚRÁK Előadáson mutatott példa: Bércesné Novák Ágnes
 1. Algebrai alapok: DISZKRÉT MATEMATIKA: STRUKTÚRÁK Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz
1. Algebrai alapok: DISZKRÉT MATEMATIKA: STRUKTÚRÁK Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz
Algoritmusok és adatszerkezetek I. 2. előadás
 Algoritmusok és adatszerkezetek I. 2. előadás Verem Verem= speciális sorozattípus Műveletei: Üres, üres?, Verembe, Veremből, tető Üres: Verem üres?(verem): Logikai tető(verem): Elem {NemDef} Verembe(Verem,Elem):
Algoritmusok és adatszerkezetek I. 2. előadás Verem Verem= speciális sorozattípus Műveletei: Üres, üres?, Verembe, Veremből, tető Üres: Verem üres?(verem): Logikai tető(verem): Elem {NemDef} Verembe(Verem,Elem):
Kalkulus. Komplex számok
 Komplex számok Komplex számsík A komplex számok a valós számok természetes kiterjesztése, annak érdekében, hogy a gyökvonás művelete elvégezhető legyen a negatív számok körében is. Vegyük tehát hozzá az
Komplex számok Komplex számsík A komplex számok a valós számok természetes kiterjesztése, annak érdekében, hogy a gyökvonás művelete elvégezhető legyen a negatív számok körében is. Vegyük tehát hozzá az
Raszteres elemzés végrehajtása QGIS GRASS moduljával 1.7 dr. Siki Zoltán
 Raszteres elemzés végrehajtása QGIS GRASS moduljával 1.7 dr. Siki Zoltán Egy mintapéldán keresztül mutatjuk be a GRASS raszteres elemzési műveleteit. Az elemzési mintafeladat során gumipitypang termesztésére
Raszteres elemzés végrehajtása QGIS GRASS moduljával 1.7 dr. Siki Zoltán Egy mintapéldán keresztül mutatjuk be a GRASS raszteres elemzési műveleteit. Az elemzési mintafeladat során gumipitypang termesztésére
2005_01/1 Leírtunk egymás mellé hét racionális számot úgy, hogy a két szélső kivételével mindegyik eggyel nagyobb a két szomszédja szorzatánál.
 Számolásos feladatok, műveletek 2004_1/1 Töltsd ki az alábbi bűvös négyzet hiányzó mezőit úgy, hogy a négyzetben szereplő minden szám különböző legyen, és minden sorban, oszlopban és a két átlóban is ugyanannyi
Számolásos feladatok, műveletek 2004_1/1 Töltsd ki az alábbi bűvös négyzet hiányzó mezőit úgy, hogy a négyzetben szereplő minden szám különböző legyen, és minden sorban, oszlopban és a két átlóban is ugyanannyi
A fordítóprogramok szerkezete. Kódoptimalizálás. A kódoptimalizálás célja. A szintézis menete valójában. Kódoptimalizálási lépések osztályozása
 A fordítóprogramok szerkezete Forrásprogram Forrás-kezelő (source handler) Kódoptimalizálás Fordítóprogramok előadás (A,C,T szakirány) Lexikális elemző (scanner) Szintaktikus elemző (parser) Szemantikus
A fordítóprogramok szerkezete Forrásprogram Forrás-kezelő (source handler) Kódoptimalizálás Fordítóprogramok előadás (A,C,T szakirány) Lexikális elemző (scanner) Szintaktikus elemző (parser) Szemantikus
Halmazelmélet. 1. előadás. Farkas István. DE ATC Gazdaságelemzési és Statisztikai Tanszék. Halmazelmélet p. 1/1
 Halmazelmélet 1. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Halmazelmélet p. 1/1 A halmaz fogalma, jelölések A halmaz fogalmát a matematikában nem definiáljuk, tulajdonságaival
Halmazelmélet 1. előadás Farkas István DE ATC Gazdaságelemzési és Statisztikai Tanszék Halmazelmélet p. 1/1 A halmaz fogalma, jelölések A halmaz fogalmát a matematikában nem definiáljuk, tulajdonságaival
Lekérdezések az SQL SELECT utasítással
 Lekérdezések az SQL SELECT utasítással Az SQL SELECT utasítás lehetőségei Vetítés Kiválasztás 1. tábla 1. tábla Összekapcsolás 1. tábla 2. tábla Elemi SELECT utasítások SELECT * {[DISTINCT] column expression
Lekérdezések az SQL SELECT utasítással Az SQL SELECT utasítás lehetőségei Vetítés Kiválasztás 1. tábla 1. tábla Összekapcsolás 1. tábla 2. tábla Elemi SELECT utasítások SELECT * {[DISTINCT] column expression
Algoritmusok és adatszerkezetek I. 2. előadás
 Algoritmusok és adatszerkezetek I. 2. előadás Verem Verem= speciális sorozattípus Műveletei: Üres, üres?, Verembe, Veremből, tető Üres: Verem üres?(verem): Logikai tető(verem): Elem {NemDef} Verembe(Verem,Elem):
Algoritmusok és adatszerkezetek I. 2. előadás Verem Verem= speciális sorozattípus Műveletei: Üres, üres?, Verembe, Veremből, tető Üres: Verem üres?(verem): Logikai tető(verem): Elem {NemDef} Verembe(Verem,Elem):
FUNKCIONÁLIS PROGRAMOZÁS
 FUNKCIONÁLIS PROGRAMOZÁS A funkcionális programozás néhány jellemzője Funkcionális programozás 1-2 Funkcionális, más néven applikatív programozás Funkcionális = függvényalapú, függvényközpontú Applikatív
FUNKCIONÁLIS PROGRAMOZÁS A funkcionális programozás néhány jellemzője Funkcionális programozás 1-2 Funkcionális, más néven applikatív programozás Funkcionális = függvényalapú, függvényközpontú Applikatív
A 2016/2017 tanévi Országos Középiskolai Tanulmányi Verseny második fordulójának feladatai. INFORMATIKA II. (programozás) kategória
 Oktatási Hivatal A 2016/2017 tanévi Országos özépiskolai Tanulmányi Verseny második fordulójának feladatai INFORMATIA II. (programozás) kategória 1. feladat: Legalább 2 bolygón volt élet (33 pont) Egy
Oktatási Hivatal A 2016/2017 tanévi Országos özépiskolai Tanulmányi Verseny második fordulójának feladatai INFORMATIA II. (programozás) kategória 1. feladat: Legalább 2 bolygón volt élet (33 pont) Egy
Megoldások. Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) 1. Számítsd ki a következő kifejezések pontos értékét!
 Megoldások. Számítsd ki a következő kifejezések pontos értékét! 8 8 ( ) ( ) ( ) Használjuk a gyökvonás azonosságait. 0 8 8 8 8 8 8 ( ) ( ) ( ) 0 8 . Határozd meg a következő kifejezések értelmezési tartományát!
Megoldások. Számítsd ki a következő kifejezések pontos értékét! 8 8 ( ) ( ) ( ) Használjuk a gyökvonás azonosságait. 0 8 8 8 8 8 8 ( ) ( ) ( ) 0 8 . Határozd meg a következő kifejezések értelmezési tartományát!
A C programozási nyelv I. Bevezetés
 A C programozási nyelv I. Bevezetés Miskolci Egyetem Általános Informatikai Tanszék A C programozási nyelv I. (bevezetés) CBEV1 / 1 A C nyelv története Dennis M. Ritchie AT&T Lab., 1972 rendszerprogramozás,
A C programozási nyelv I. Bevezetés Miskolci Egyetem Általános Informatikai Tanszék A C programozási nyelv I. (bevezetés) CBEV1 / 1 A C nyelv története Dennis M. Ritchie AT&T Lab., 1972 rendszerprogramozás,
FUNKCIONÁLIS PROGRAMOZÁS GYAKORLAT JEGYZET
 FUNKCIONÁLIS PROGRAMOZÁS GYAKORLAT JEGYZET Szerkesztette: Balogh Tamás 2013. május 17. Ha hibát találsz, kérlek jelezd a info@baloghtamas.hu e-mail címen! Ez a Mű a Creative Commons Nevezd meg! - Ne add
FUNKCIONÁLIS PROGRAMOZÁS GYAKORLAT JEGYZET Szerkesztette: Balogh Tamás 2013. május 17. Ha hibát találsz, kérlek jelezd a info@baloghtamas.hu e-mail címen! Ez a Mű a Creative Commons Nevezd meg! - Ne add
A C programozási nyelv I. Bevezetés
 A C programozási nyelv I. Bevezetés Miskolci Egyetem Általános Informatikai Tanszék A C programozási nyelv I. (bevezetés) CBEV1 / 1 A C nyelv története Dennis M. Ritchie AT&T Lab., 1972 rendszerprogramozás,
A C programozási nyelv I. Bevezetés Miskolci Egyetem Általános Informatikai Tanszék A C programozási nyelv I. (bevezetés) CBEV1 / 1 A C nyelv története Dennis M. Ritchie AT&T Lab., 1972 rendszerprogramozás,
5. KOMBINÁCIÓS HÁLÓZATOK LEÍRÁSÁNAK SZABÁLYAI
 5. KOMBINÁCIÓS HÁLÓZATOK LEÍRÁSÁNAK SZABÁLYAI 1 Kombinációs hálózatok leírását végezhetjük mind adatfolyam-, mind viselkedési szinten. Az adatfolyam szintű leírásokhoz az assign kulcsszót használjuk, a
5. KOMBINÁCIÓS HÁLÓZATOK LEÍRÁSÁNAK SZABÁLYAI 1 Kombinációs hálózatok leírását végezhetjük mind adatfolyam-, mind viselkedési szinten. Az adatfolyam szintű leírásokhoz az assign kulcsszót használjuk, a
1. Algebrai alapok: Melyek műveletek az alábbiak közül?
 1. Algebrai alapok: Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz egyértelműen hozzárendel egy
1. Algebrai alapok: Művelet: Egy H nemüres halmazon értelmezett (kétváltozós) műveleten egy H H H függvényt értünk, azaz egy olyan leképezést, amely bármely a,b H elempárhoz egyértelműen hozzárendel egy
A verem (stack) A verem egy olyan struktúra, aminek a tetejéről kivehetünk egy (vagy sorban több) elemet. A verem felhasználása
 A verem (stack) A verem egy olyan struktúra, aminek a tetejére betehetünk egy új (vagy sorban több) elemet a tetejéről kivehetünk egy (vagy sorban több) elemet A verem felhasználása Függvény visszatérési
A verem (stack) A verem egy olyan struktúra, aminek a tetejére betehetünk egy új (vagy sorban több) elemet a tetejéről kivehetünk egy (vagy sorban több) elemet A verem felhasználása Függvény visszatérési
Információk. Ismétlés II. Ismétlés. Ismétlés III. A PROGRAMOZÁS ALAPJAI 2. Készítette: Vénné Meskó Katalin. Algoritmus. Algoritmus ábrázolása
 1 Információk 2 A PROGRAMOZÁS ALAPJAI 2. Készítette: Vénné Meskó Katalin Elérhetőség mesko.katalin@tfk.kefo.hu Fogadóóra: szerda 9:50-10:35 Számonkérés időpontok Április 25. 9 00 Május 17. 9 00 Június
1 Információk 2 A PROGRAMOZÁS ALAPJAI 2. Készítette: Vénné Meskó Katalin Elérhetőség mesko.katalin@tfk.kefo.hu Fogadóóra: szerda 9:50-10:35 Számonkérés időpontok Április 25. 9 00 Május 17. 9 00 Június
1. A polinom fogalma. Számolás formális kifejezésekkel. Feladat Oldjuk meg az x2 + x + 1 x + 1. = x egyenletet.
 1. A polinom fogalma Számolás formális kifejezésekkel. Feladat Oldjuk meg az x2 + x + 1 x + 1 = x egyenletet. Megoldás x + 1-gyel átszorozva x 2 + x + 1 = x 2 + x. Innen 1 = 0. Ez ellentmondás, így az
1. A polinom fogalma Számolás formális kifejezésekkel. Feladat Oldjuk meg az x2 + x + 1 x + 1 = x egyenletet. Megoldás x + 1-gyel átszorozva x 2 + x + 1 = x 2 + x. Innen 1 = 0. Ez ellentmondás, így az
NAGYPONTOSSÁGÚ EGÉSZ-ARITMETIKA TARTALOM
 NAGYPONTOSSÁGÚ EGÉSZ-ARITMETIKA TARTALOM 0. A feladat... 2 1. Az Egész számok ábrázolásai... 2 2. A műveletek szignatúrája... 3 3. A keretprogram... 4 4. Technikai tanácsok... 7 5. Elegancianövelő lehetőségek
NAGYPONTOSSÁGÚ EGÉSZ-ARITMETIKA TARTALOM 0. A feladat... 2 1. Az Egész számok ábrázolásai... 2 2. A műveletek szignatúrája... 3 3. A keretprogram... 4 4. Technikai tanácsok... 7 5. Elegancianövelő lehetőségek
2. Algebrai átalakítások
 I. Nulladik ZH-ban láttuk: 2. Algebrai átalakítások 1. Mi az alábbi kifejezés legegyszerűbb alakja a változó lehetséges értékei esetén? (A) x + 1 x 1 (x 1)(x 2 + 3x + 2) (1 x 2 )(x + 2) (B) 1 (C) 2 (D)
I. Nulladik ZH-ban láttuk: 2. Algebrai átalakítások 1. Mi az alábbi kifejezés legegyszerűbb alakja a változó lehetséges értékei esetén? (A) x + 1 x 1 (x 1)(x 2 + 3x + 2) (1 x 2 )(x + 2) (B) 1 (C) 2 (D)
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Algebra
 Algebra Műveletek tulajdonságai: kommutativitás (felcserélhetőség): a b = b a; a b = b a asszociativitás (átcsoportosíthatóság): (a b) c = a (b c); a (b c) = (a b) c disztributivitás (széttagolhatóság):
Algebra Műveletek tulajdonságai: kommutativitás (felcserélhetőség): a b = b a; a b = b a asszociativitás (átcsoportosíthatóság): (a b) c = a (b c); a (b c) = (a b) c disztributivitás (széttagolhatóság):
... fi. ... fk. 6. Fabejáró algoritmusok Rekurzív preorder bejárás (elsőfiú-testvér ábrázolásra)
 6. Fabejáró algoritmusok Fa bejárásán olyan algoritmust értünk, amelynek bemenete egy F fa és egy M művelet, és az algoritmus adott sorrendben pontosan egyszer végrehajtja az M műveletet a fa pontjaiban
6. Fabejáró algoritmusok Fa bejárásán olyan algoritmust értünk, amelynek bemenete egy F fa és egy M művelet, és az algoritmus adott sorrendben pontosan egyszer végrehajtja az M műveletet a fa pontjaiban
Egész számok. pozitív egész számok: 1; 2; 3; 4;... negatív egész számok: 1; 2; 3; 4;...
 Egész számok természetes számok ( ) pozitív egész számok: 1; 2; 3; 4;... 0 negatív egész számok: 1; 2; 3; 4;... egész számok ( ) 1. Írd a következõ számokat a halmazábra megfelelõ helyére! 3; 7; +6 ; (
Egész számok természetes számok ( ) pozitív egész számok: 1; 2; 3; 4;... 0 negatív egész számok: 1; 2; 3; 4;... egész számok ( ) 1. Írd a következõ számokat a halmazábra megfelelõ helyére! 3; 7; +6 ; (
A programozás alapjai előadás. Amiről szólesz: A tárgy címe: A programozás alapjai
 A programozás alapjai 1 1. előadás Híradástechnikai Tanszék Amiről szólesz: A tárgy címe: A programozás alapjai A számítógép részegységei, alacsony- és magasszintű programnyelvek, az imperatív programozási
A programozás alapjai 1 1. előadás Híradástechnikai Tanszék Amiről szólesz: A tárgy címe: A programozás alapjai A számítógép részegységei, alacsony- és magasszintű programnyelvek, az imperatív programozási
A 2016/2017 tanévi Országos Középiskolai Tanulmányi Verseny második forduló javítási-értékelési útmutató. INFORMATIKA II. (programozás) kategória
 Oktatási Hivatal A 2016/2017 tanévi Országos özépiskolai Tanulmányi Verseny második forduló javítási-értékelési útmutató INFORMATIA II. (programozás) kategória 1. feladat: Legalább 2 bolygón volt élet
Oktatási Hivatal A 2016/2017 tanévi Országos özépiskolai Tanulmányi Verseny második forduló javítási-értékelési útmutató INFORMATIA II. (programozás) kategória 1. feladat: Legalább 2 bolygón volt élet
3 A C programozási nyelv szintaktikai egységei
 3 A C programozási nyelv szintaktikai egységei 3.1 Azonosítók Betűk és számjegyek sorozata, betűvel vagy _ (aláhúzás) karakterrel kell kezdődnie. A nagy- és kisbetűk különbözőek. Az azonosítók tetszőleges
3 A C programozási nyelv szintaktikai egységei 3.1 Azonosítók Betűk és számjegyek sorozata, betűvel vagy _ (aláhúzás) karakterrel kell kezdődnie. A nagy- és kisbetűk különbözőek. Az azonosítók tetszőleges
Algoritmusok. Dr. Iványi Péter
 Algoritmusok Dr. Iványi Péter Egyik legrégebbi algoritmus i.e. IV század, Alexandria, Euklidész két természetes szám legnagyobb közös osztójának meghatározása Tegyük fel, hogy a és b pozitív egész számok
Algoritmusok Dr. Iványi Péter Egyik legrégebbi algoritmus i.e. IV század, Alexandria, Euklidész két természetes szám legnagyobb közös osztójának meghatározása Tegyük fel, hogy a és b pozitív egész számok
file./script.sh > Bourne-Again shell script text executable << tartalmat néz >>
 I. Alapok Interaktív shell-ben vagy shell-scriptben megadott karaktersorozat feldolgozásakor az első lépés a szavakra tördelés. A szavakra tördelés a következő metakarakterek mentén zajlik: & ; ( ) < >
I. Alapok Interaktív shell-ben vagy shell-scriptben megadott karaktersorozat feldolgozásakor az első lépés a szavakra tördelés. A szavakra tördelés a következő metakarakterek mentén zajlik: & ; ( ) < >
PHP. Telepítése: Indítás/újraindítás/leállítás: Beállítások: A PHP nyelv
 PHP A PHP rövidítés jelentése hivatalosan: PHP Hypertext Preprocessor. Ez egy kiszolgáló-oldali parancsnyelv, amit jellemzően HTML oldalakon használnak. A különbség a két nyelv között az, hogy a kiszolgáló
PHP A PHP rövidítés jelentése hivatalosan: PHP Hypertext Preprocessor. Ez egy kiszolgáló-oldali parancsnyelv, amit jellemzően HTML oldalakon használnak. A különbség a két nyelv között az, hogy a kiszolgáló
Programozás I gyakorlat
 Programozás I. - 3. gyakorlat Operátorok, típuskonverziók, matematikai függvények Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Számítástudomány Alkalmazása Tanszék Utolsó frissítés: September 24,
Programozás I. - 3. gyakorlat Operátorok, típuskonverziók, matematikai függvények Tar Péter 1 Pannon Egyetem M szaki Informatikai Kar Számítástudomány Alkalmazása Tanszék Utolsó frissítés: September 24,
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
KOVÁCS BÉLA MATEmATIkA I 6 VI KOmPLEX SZÁmOk 1 A komplex SZÁmOk HALmAZA A komplex számok olyan halmazt alkotnak amelyekben elvégezhető az összeadás és a szorzás azaz két komplex szám összege és szorzata
MATLAB alapismeretek I.
 Alkalmazott Informatikai Intézeti Tanszék MŰSZAKI INFORMATIKA Dr.Dudás László 0. MATLAB alapismeretek I. A MATLAB bemutatása MATLAB filozófia MATLAB modulok A MATLAB felhasználói felülete MATLAB tulajdonságok
Alkalmazott Informatikai Intézeti Tanszék MŰSZAKI INFORMATIKA Dr.Dudás László 0. MATLAB alapismeretek I. A MATLAB bemutatása MATLAB filozófia MATLAB modulok A MATLAB felhasználói felülete MATLAB tulajdonságok
Programozási nyelvek (ADA)
 Programozási nyelvek (ADA) Kozsik Tamás előadása alapján Készítette: Nagy Krisztián 1. előadás Hasznos weboldal http://kto.web.elte.hu Program felépítése Programegységek (program unit) eljárások (procedure)
Programozási nyelvek (ADA) Kozsik Tamás előadása alapján Készítette: Nagy Krisztián 1. előadás Hasznos weboldal http://kto.web.elte.hu Program felépítése Programegységek (program unit) eljárások (procedure)
1. előadás: Halmazelmélet, számfogalom, teljes
 1. előadás: Halmazelmélet, számfogalom, teljes indukció Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető,
1. előadás: Halmazelmélet, számfogalom, teljes indukció Szabó Szilárd Halmazok Halmaz: alapfogalom, bizonyos elemek (matematikai objektumok) összessége. Egy halmaz akkor adott, ha minden objektumról eldönthető,
Miről lesz ma szó? A PROGAMOZÁS ALAPJAI 1. Bemutatkozás. Bemutatkozás. Bemutatkozás. Bemutatkozás. 1. előadás. A tárgy címe: A programozás alapjai 1
 Miről lesz ma szó? A PROGAMOZÁS ALAPJAI 1 Ajánlott irodalom A programozás fogalma Vitéz András egyetemi adjunktus BME Híradástechnikai Tanszék vitez@hit.bme.hu 2012. február 7. A tárgy címe: A tárgy adminisztratív
Miről lesz ma szó? A PROGAMOZÁS ALAPJAI 1 Ajánlott irodalom A programozás fogalma Vitéz András egyetemi adjunktus BME Híradástechnikai Tanszék vitez@hit.bme.hu 2012. február 7. A tárgy címe: A tárgy adminisztratív
SZÁMÍTÓGÉPEK BELSŐ FELÉPÍTÉSE - 1
 INFORMATIKAI RENDSZEREK ALAPJAI (INFORMATIKA I.) 1 NEUMANN ARCHITEKTÚRÁJÚ GÉPEK MŰKÖDÉSE SZÁMÍTÓGÉPEK BELSŐ FELÉPÍTÉSE - 1 Ebben a feladatban a következőket fogjuk áttekinteni: Neumann rendszerű számítógép
INFORMATIKAI RENDSZEREK ALAPJAI (INFORMATIKA I.) 1 NEUMANN ARCHITEKTÚRÁJÚ GÉPEK MŰKÖDÉSE SZÁMÍTÓGÉPEK BELSŐ FELÉPÍTÉSE - 1 Ebben a feladatban a következőket fogjuk áttekinteni: Neumann rendszerű számítógép
Excel 2010 függvények
 Molnár Mátyás Excel 2010 függvények Csak a lényeg érthetően! Tartalomjegyzék FÜGGVÉNYHASZNÁLAT ALAPJAI 1 FÜGGVÉNYEK BEVITELE 1 HIBAÉRTÉKEK KEZELÉSE 4 A VARÁZSLATOS AUTOSZUM GOMB 6 SZÁMÍTÁSOK A REJTETT
Molnár Mátyás Excel 2010 függvények Csak a lényeg érthetően! Tartalomjegyzék FÜGGVÉNYHASZNÁLAT ALAPJAI 1 FÜGGVÉNYEK BEVITELE 1 HIBAÉRTÉKEK KEZELÉSE 4 A VARÁZSLATOS AUTOSZUM GOMB 6 SZÁMÍTÁSOK A REJTETT
2. Rekurzió. = 2P2(n,n) 2 < 2P2(n,n) 1
 2. Rekurzió Egy objektum definícióját rekurzívnak nevezünk, ha a definíció tartalmazza a definiálandó objektumot. Egy P eljárást (vagy függvényt) rekurzívnak nevezünk, ha P utasításrészében előfordul magának
2. Rekurzió Egy objektum definícióját rekurzívnak nevezünk, ha a definíció tartalmazza a definiálandó objektumot. Egy P eljárást (vagy függvényt) rekurzívnak nevezünk, ha P utasításrészében előfordul magának
Bevezetés az informatikába
 Bevezetés az informatikába 3. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
Bevezetés az informatikába 3. előadás Dr. Istenes Zoltán Eötvös Loránd Tudományegyetem Informatikai Kar Programozáselmélet és Szoftvertechnológiai Tanszék Matematikus BSc - I. félév / 2008 / Budapest Dr.
1. Alapok. #!/bin/bash
 1. oldal 1.1. A programfájlok szerkezete 1. Alapok A bash programok tulajnképpen egyszerű szöveges fájlok, amelyeket bármely szövegszerkesztő programmal megírhatunk. Alapvetően ugyanazokat a at használhatjuk
1. oldal 1.1. A programfájlok szerkezete 1. Alapok A bash programok tulajnképpen egyszerű szöveges fájlok, amelyeket bármely szövegszerkesztő programmal megírhatunk. Alapvetően ugyanazokat a at használhatjuk
Programozás alapjai. (GKxB_INTM023) Dr. Hatwágner F. Miklós augusztus 29. Széchenyi István Egyetem, Gy r
 Programozás alapjai (GKxB_INTM023) Széchenyi István Egyetem, Gy r 2019. augusztus 29. Feladat: írjuk ki az els 10 természetes szám négyzetét! #i n c l u d e i n t main ( v o i d ) { p r
Programozás alapjai (GKxB_INTM023) Széchenyi István Egyetem, Gy r 2019. augusztus 29. Feladat: írjuk ki az els 10 természetes szám négyzetét! #i n c l u d e i n t main ( v o i d ) { p r
Programozás alapjai gyakorlat. 4. gyakorlat Konstansok, tömbök, stringek
 Programozás alapjai gyakorlat 4. gyakorlat Konstansok, tömbök, stringek Házi ellenőrzés (f0069) Valósítsd meg a linuxos seq parancs egy egyszerűbb változatát, ami beolvas két egész számot, majd a kettő
Programozás alapjai gyakorlat 4. gyakorlat Konstansok, tömbök, stringek Házi ellenőrzés (f0069) Valósítsd meg a linuxos seq parancs egy egyszerűbb változatát, ami beolvas két egész számot, majd a kettő
1. fogalom. Add meg az összeadásban szereplő számok elnevezéseit! Milyen tulajdonságai vannak az összeadásnak? Hogyan ellenőrizzük az összeadást?
 1. fogalom Add meg az összeadásban szereplő számok 73 + 19 = 92 összeadandók (tagok) összeg Összeadandók (tagok): amiket összeadunk. Összeg: az összeadás eredménye. Milyen tulajdonságai vannak az összeadásnak?
1. fogalom Add meg az összeadásban szereplő számok 73 + 19 = 92 összeadandók (tagok) összeg Összeadandók (tagok): amiket összeadunk. Összeg: az összeadás eredménye. Milyen tulajdonságai vannak az összeadásnak?
Adatszerkezetek és algoritmusok
 2010. január 8. Bevezet El z órák anyagainak áttekintése Ismétlés Adatszerkezetek osztályozása Sor, Verem, Lengyelforma Statikus, tömbös reprezentáció Dinamikus, láncolt reprezentáció Láncolt lista Lassú
2010. január 8. Bevezet El z órák anyagainak áttekintése Ismétlés Adatszerkezetek osztályozása Sor, Verem, Lengyelforma Statikus, tömbös reprezentáció Dinamikus, láncolt reprezentáció Láncolt lista Lassú
Operációs rendszerek. 11. gyakorlat. AWK - szintaxis, vezérlési szerkezetek UNIVERSITAS SCIENTIARUM SZEGEDIENSIS UNIVERSITY OF SZEGED
 UNIVERSITAS SCIENTIARUM SZEGEDIENSIS UNIVERSITY OF SZEGED AWK - szintaxis, vezérlési szerkezetek Operációs rendszerek 11. gyakorlat Szegedi Tudományegyetem Természettudományi és Informatikai Kar Csuvik
UNIVERSITAS SCIENTIARUM SZEGEDIENSIS UNIVERSITY OF SZEGED AWK - szintaxis, vezérlési szerkezetek Operációs rendszerek 11. gyakorlat Szegedi Tudományegyetem Természettudományi és Informatikai Kar Csuvik
Relációs algebra 1.rész alapok
 Relációs algebra 1.rész alapok Tankönyv: Ullman-Widom: Adatbázisrendszerek Alapvetés Második, átdolgozott kiadás, Panem, 2009 Lekérdezések a relációs modellben 2.4. Egy algebrai lekérdező nyelv, relációs
Relációs algebra 1.rész alapok Tankönyv: Ullman-Widom: Adatbázisrendszerek Alapvetés Második, átdolgozott kiadás, Panem, 2009 Lekérdezések a relációs modellben 2.4. Egy algebrai lekérdező nyelv, relációs
Negatív alapú számrendszerek
 2015. március 4. Negatív számok Legyen b > 1 egy adott egész szám. Ekkor bármely N 0 egész szám egyértelműen felírható N = m a k b k k=1 alakban, ahol 0 a k < b egész szám. Negatív számok Legyen b > 1
2015. március 4. Negatív számok Legyen b > 1 egy adott egész szám. Ekkor bármely N 0 egész szám egyértelműen felírható N = m a k b k k=1 alakban, ahol 0 a k < b egész szám. Negatív számok Legyen b > 1
Amortizációs költségelemzés
 Amortizációs költségelemzés Amennyiben műveleteknek egy M 1,...,M m sorozatának a futási idejét akarjuk meghatározni, akkor egy lehetőség, hogy külön-külön minden egyes művelet futási idejét kifejezzük
Amortizációs költségelemzés Amennyiben műveleteknek egy M 1,...,M m sorozatának a futási idejét akarjuk meghatározni, akkor egy lehetőség, hogy külön-külön minden egyes művelet futási idejét kifejezzük
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Számelmélet I.
 Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
Számelmélet I. DEFINÍCIÓ: (Osztó, többszörös) Ha egy a szám felírható egy b szám és egy másik egész szám szorzataként, akkor a b számot az a osztójának, az a számot a b többszörösének nevezzük. Megjegyzés:
BASH script programozás II. Vezérlési szerkezetek
 06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
06 BASH script programozás II. Vezérlési szerkezetek Emlékeztető Jelölésbeli különbség van parancs végrehajtása és a parancs kimenetére való hivatkozás között PARANCS $(PARANCS) Jelölésbeli különbség van
Objektumorientált Programozás III.
 Objektumorientált Programozás III. Vezérlési szerkezetek ismétlés Matematikai lehetőségek Feladatok 1 Hallgatói Tájékoztató A jelen bemutatóban található adatok, tudnivalók és információk a számonkérendő
Objektumorientált Programozás III. Vezérlési szerkezetek ismétlés Matematikai lehetőségek Feladatok 1 Hallgatói Tájékoztató A jelen bemutatóban található adatok, tudnivalók és információk a számonkérendő
Fordítóprogramok. Aszalós László. 2009. szeptember 7.
 Fordítóprogramok Aszalós László 2009. szeptember 7. 1. Bemelegítés Honlap: www.inf.unideb.hu/ aszalos/diak.html (Fordítóprogramok, 2009) Jegymegajánló: utolsó hét előadásán. PótZH (csak gyakorlat) vizsgaidőszak
Fordítóprogramok Aszalós László 2009. szeptember 7. 1. Bemelegítés Honlap: www.inf.unideb.hu/ aszalos/diak.html (Fordítóprogramok, 2009) Jegymegajánló: utolsó hét előadásán. PótZH (csak gyakorlat) vizsgaidőszak
Programozás. (GKxB_INTM021) Dr. Hatwágner F. Miklós február 18. Széchenyi István Egyetem, Gy r
 Programozás (GKxB_INTM021) Széchenyi István Egyetem, Gy r 2018. február 18. Minimum és maximumkeresés u s i n g n a m e s p a c e s t d ; i n t main ( ) { c o u t
Programozás (GKxB_INTM021) Széchenyi István Egyetem, Gy r 2018. február 18. Minimum és maximumkeresés u s i n g n a m e s p a c e s t d ; i n t main ( ) { c o u t
Vezérlési szerkezetek
 Vezérlési szerkezetek Szelekciós ok: if, else, switch If Segítségével valamely ok végrehajtását valamely feltétel teljesülése esetén végezzük el. Az if segítségével valamely tevékenység () végrehajtását
Vezérlési szerkezetek Szelekciós ok: if, else, switch If Segítségével valamely ok végrehajtását valamely feltétel teljesülése esetén végezzük el. Az if segítségével valamely tevékenység () végrehajtását
A valós számok halmaza
 VA 1 A valós számok halmaza VA 2 A valós számok halmazának axiómarendszere és alapvető tulajdonságai Definíció Az R halmazt a valós számok halmazának nevezzük, ha teljesíti a következő axiómarendszerben
VA 1 A valós számok halmaza VA 2 A valós számok halmazának axiómarendszere és alapvető tulajdonságai Definíció Az R halmazt a valós számok halmazának nevezzük, ha teljesíti a következő axiómarendszerben
Adatszerkezetek I. 7. előadás. (Horváth Gyula anyagai felhasználásával)
 Adatszerkezetek I. 7. előadás (Horváth Gyula anyagai felhasználásával) Bináris fa A fa (bináris fa) rekurzív adatszerkezet: BinFa:= Fa := ÜresFa Rekord(Elem,BinFa,BinFa) ÜresFa Rekord(Elem,Fák) 2/37 Bináris
Adatszerkezetek I. 7. előadás (Horváth Gyula anyagai felhasználásával) Bináris fa A fa (bináris fa) rekurzív adatszerkezet: BinFa:= Fa := ÜresFa Rekord(Elem,BinFa,BinFa) ÜresFa Rekord(Elem,Fák) 2/37 Bináris
Hatványozás. A hatványozás azonosságai
 Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
2018, Diszkrét matematika
 Diszkrét matematika 3. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? számtartományok: természetes
Diszkrét matematika 3. előadás mgyongyi@ms.sapientia.ro Sapientia Egyetem, Matematika-Informatika Tanszék Marosvásárhely, Románia 2018, őszi félév Miről volt szó az elmúlt előadáson? számtartományok: természetes
A SZÁMFOGALOM KIALAKÍTÁSA
 A SZÁMFOGALOM KIALAKÍTÁSA TERMÉSZETES SZÁMOK ÉRTELMEZÉSE 1-5. OSZTÁLY Számok értelmezése 0-tól 10-ig: Véges halmazok számosságaként Mérőszámként Sorszámként Jelzőszámként A számok fogalmának kiterjesztése
A SZÁMFOGALOM KIALAKÍTÁSA TERMÉSZETES SZÁMOK ÉRTELMEZÉSE 1-5. OSZTÁLY Számok értelmezése 0-tól 10-ig: Véges halmazok számosságaként Mérőszámként Sorszámként Jelzőszámként A számok fogalmának kiterjesztése
GPU Lab. 4. fejezet. Fordítók felépítése. Grafikus Processzorok Tudományos Célú Programozása. Berényi Dániel Nagy-Egri Máté Ferenc
 4. fejezet Fordítók felépítése Grafikus Processzorok Tudományos Célú Programozása Fordítók Kézzel assembly kódot írni nem érdemes, mert: Egyszerűen nem skálázik nagy problémákhoz arányosan sok kódot kell
4. fejezet Fordítók felépítése Grafikus Processzorok Tudományos Célú Programozása Fordítók Kézzel assembly kódot írni nem érdemes, mert: Egyszerűen nem skálázik nagy problémákhoz arányosan sok kódot kell
SZÁMÍTÁSOK A TÁBLÁZATBAN
 SZÁMÍTÁSOK A TÁBLÁZATBAN Az Excelben az egyszerű adatok bevitelén kívül számításokat is végezhetünk. Ezeket a cellákba beírt képletek segítségével oldjuk meg. A képlet: olyan egyenlet, amely a munkalapon
SZÁMÍTÁSOK A TÁBLÁZATBAN Az Excelben az egyszerű adatok bevitelén kívül számításokat is végezhetünk. Ezeket a cellákba beírt képletek segítségével oldjuk meg. A képlet: olyan egyenlet, amely a munkalapon
Mátrixok február Feladat: Legyen A = ( ( B =
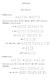 Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Mátrixok 26. február 6.. Feladat: Legyen ( 3 2 B ( 3 4 Határozzuk meg A + B, A B, 2A, 3B, 2A 3B,A T és (B T T mátrixokat. A definíciók alapján ( + 3 + 3 + A + B 2 + 4 + + ( 4 2 6 2 ( ( 3 3 2 4 A B 2 4
Rekurzió. Dr. Iványi Péter
 Rekurzió Dr. Iványi Péter 1 Függvényhívás void f3(int a3) { printf( %d,a3); } void f2(int a2) { f3(a2); a2 = (a2+1); } void f1() { int a1 = 1; int b1; b1 = f2(a1); } 2 Függvényhívás void f3(int a3) { printf(
Rekurzió Dr. Iványi Péter 1 Függvényhívás void f3(int a3) { printf( %d,a3); } void f2(int a2) { f3(a2); a2 = (a2+1); } void f1() { int a1 = 1; int b1; b1 = f2(a1); } 2 Függvényhívás void f3(int a3) { printf(
Műveletek egész számokkal
 Mit tudunk az egész számokról? 1. Döntsd el, hogy igazak-e a következő állítások az A halmaz elemeire! a) Az A halmaz elemei között 3 pozitív szám van. b) A legkisebb szám abszolút értéke a legnagyobb.
Mit tudunk az egész számokról? 1. Döntsd el, hogy igazak-e a következő állítások az A halmaz elemeire! a) Az A halmaz elemei között 3 pozitív szám van. b) A legkisebb szám abszolút értéke a legnagyobb.
Segédlet az Informatika alapjai I. című tárgy számrendszerek fejezetéhez
 Segédlet az Informatika alapjai I. című tárgy számrendszerek fejezetéhez Sándor Tamás, sandor.tamas@kvk.bmf.hu Takács Gergely, takacs.gergo@kvk.bmf.hu Lektorálta: dr. Schuster György PhD, hal@k2.jozsef.kando.hu
Segédlet az Informatika alapjai I. című tárgy számrendszerek fejezetéhez Sándor Tamás, sandor.tamas@kvk.bmf.hu Takács Gergely, takacs.gergo@kvk.bmf.hu Lektorálta: dr. Schuster György PhD, hal@k2.jozsef.kando.hu
1. Halmazok, számhalmazok, alapműveletek
 1. Halmazok, számhalmazok, alapműveletek I. Nulladik ZH-ban láttuk: 1. Határozza meg az (A B)\C halmaz elemszámát, ha A tartalmazza az összes 19-nél kisebb természetes számot, továbbá B a prímszámok halmaza
1. Halmazok, számhalmazok, alapműveletek I. Nulladik ZH-ban láttuk: 1. Határozza meg az (A B)\C halmaz elemszámát, ha A tartalmazza az összes 19-nél kisebb természetes számot, továbbá B a prímszámok halmaza
sallang avagy Fordítótervezés dióhéjban Sallai Gyula
 sallang avagy Fordítótervezés dióhéjban Sallai Gyula Az előadás egy kis példaprogramon keresztül mutatja be fordítók belső lelki világát De mit is jelent, az hogy fordítóprogram? Mit csinál egy fordító?
sallang avagy Fordítótervezés dióhéjban Sallai Gyula Az előadás egy kis példaprogramon keresztül mutatja be fordítók belső lelki világát De mit is jelent, az hogy fordítóprogram? Mit csinál egy fordító?
2016, Diszkrét matematika
 Diszkrét matematika 2. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2016, őszi félév Miről volt szó az elmúlt előadáson? Követelmények,
Diszkrét matematika 2. előadás Sapientia Egyetem, Műszaki és Humántudományok Tanszék Marosvásárhely, Románia mgyongyi@ms.sapientia.ro 2016, őszi félév Miről volt szó az elmúlt előadáson? Követelmények,
Java II. I A Java programozási nyelv alapelemei
 Java II. I A Java programozási nyelv alapelemei Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2008. 02. 19. Java II.: Alapelemek JAVA2 / 1 A Java formalizmusa A C, illetve az annak
Java II. I A Java programozási nyelv alapelemei Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2008. 02. 19. Java II.: Alapelemek JAVA2 / 1 A Java formalizmusa A C, illetve az annak
Adatok ábrázolása, adattípusok
 Adatok ábrázolása, adattípusok Összefoglalás Adatok ábrázolása, adattípusok Számítógépes rendszerek működés: információfeldolgozás IPO: input-process-output modell információ tárolása adatok formájában
Adatok ábrázolása, adattípusok Összefoglalás Adatok ábrázolása, adattípusok Számítógépes rendszerek működés: információfeldolgozás IPO: input-process-output modell információ tárolása adatok formájában
Matematika 11. osztály
 ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Humán tagozat Matematika 11. osztály I. rész: Hatvány, gyök, logaritmus Készítette: Balázs Ádám Budapest, 018 . Tartalomjegyzék Tartalomjegyzék
ELTE Apáczai Csere János Gyakorló Gimnázium és Kollégium Humán tagozat Matematika 11. osztály I. rész: Hatvány, gyök, logaritmus Készítette: Balázs Ádám Budapest, 018 . Tartalomjegyzék Tartalomjegyzék
Adatbázisok I A relációs algebra
 Adatbázisok I A relációs algebra Relációs algebra Az adatmodell műveleti része definiálja a rendelkezésre álló operátorokat. Műveletek típusai: -adat definiáló(ddl) Data DefinitionLanguage -adatkezelő(dml)
Adatbázisok I A relációs algebra Relációs algebra Az adatmodell műveleti része definiálja a rendelkezésre álló operátorokat. Műveletek típusai: -adat definiáló(ddl) Data DefinitionLanguage -adatkezelő(dml)
Algoritmusok Tervezése. 1. Előadás MATLAB 1. Dr. Bécsi Tamás
 Algoritmusok Tervezése 1. Előadás MATLAB 1. Dr. Bécsi Tamás Tárgy adatok Előadó: Bécsi Tamás, St 106, becsi.tamas@mail.bme.hu Előadás:2, Labor:2 Kredit:5 Félévközi jegy 2 db Zh 1 hallgatói feladat A félév
Algoritmusok Tervezése 1. Előadás MATLAB 1. Dr. Bécsi Tamás Tárgy adatok Előadó: Bécsi Tamás, St 106, becsi.tamas@mail.bme.hu Előadás:2, Labor:2 Kredit:5 Félévközi jegy 2 db Zh 1 hallgatói feladat A félév
Bevezetés az informatikába Tételsor és minta zárthelyi dolgozat 2014/2015 I. félév
 Bevezetés az informatikába Tételsor és minta zárthelyi dolgozat 2014/2015 I. félév Az informatika története (ebből a fejezetből csak a félkövér betűstílussal szedett részek kellenek) 1. Számítástechnika
Bevezetés az informatikába Tételsor és minta zárthelyi dolgozat 2014/2015 I. félév Az informatika története (ebből a fejezetből csak a félkövér betűstílussal szedett részek kellenek) 1. Számítástechnika
Java II. I A Java programozási nyelv alapelemei
 Java2 / 1 Java II. I A Java programozási nyelv alapelemei Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2009. 02. 09. Java II.: Alapelemek JAVA2 / 1 A Java formalizmusa A C, illetve
Java2 / 1 Java II. I A Java programozási nyelv alapelemei Miskolci Egyetem Általános Informatikai Tanszék Utolsó módosítás: 2009. 02. 09. Java II.: Alapelemek JAVA2 / 1 A Java formalizmusa A C, illetve
