MATEMATIKA C 8. évfolyam 3. modul BETŰZZÜK KI!
|
|
|
- Árpád Hegedűs
- 8 évvel ezelőtt
- Látták:
Átírás
1 MATEMATIKA C 8. évfolyam. modul BETŰZZÜK KI! Készítette: Surányi Szabolcs
2 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A képességfejlesztés fókuszai A betűs kifejezések elfogadása. A tanulói ismeretek tudatosítása, különféle játékokkal az eddigi ismeretek elmélyítése. A szövegértelmezési, szövegalkotási képesség fejlesztése. x 45 perc 1 14 évesek; 8. évfolyam Tágabb környezetben: Fizika, kémia. Szűkebb környezetben: 8. o. C. modul. Ajánlott megelőző tevékenységek: Tanórai algebrai ismeretek. Gondolkodási képességek: Problémaérzékenység, problémamegoldás, Együttműködés, eredetiség, kreativitás, asszociatív memória, szövegértés, szövegértelmezés. Kommunikációs képességek: Rendszerezés, gondolkodási sebesség. AJÁNLÁS Az algebrai kifejezések általános, értő használata a 8. osztálytól válik hangsúlyossá. Nehezen lesz a matematikai modellalkotás eszköze a betűs kifejezésekből a tanuló kezében, ha az algebrai kifejezésekkel való foglalkozás néha inkább unalmas és fárasztó programokkal történik. Az első két foglalkozás célja mindenekelőtt az, hogy a tanulókkal megkedveltesse ezen kifejezéseket, és játékos formában mutassa be használatukat. A harmadik foglalkozáson a tanulók saját szövegalkotásukkal törhetik meg az egyenletekkel kapcsolatos, sokszor fárasztónak és monotonnak tűnő munkájukat.
3 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ MODULVÁZLAT Lépések, tevékenységek Kiemelt készségek, képességek Eszközök, mellékletek I. Betűszámtan 1. Verses szöveges feladatok megoldása Betűrejtvények Szövegértés, számolási képesség, műveletvégzési sebesség, probléma-érzékenység, eredetiség, nyelvi fejlettség. Keresztrejtvény-játék Szövegértés, számolási képesség, műveletvégzési sebesség, probléma-érzékenység, eredetiség, nyelvi fejlettség. Szókereső játék Szövegértés, számolási képesség, műveletvégzési sebesség, probléma-érzékenység, eredetiség, nyelvi fejlettség Tanulói munkafüzet: A feladatlap B feladatlap Melléklet a tanároknak: Az A feladatlap és megoldása A B feladatlap és megoldása Tanulói munkafüzet: C feladatlap Melléklet a tanároknak: A C feladatlap és megoldása
4 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 4 Lépések, tevékenységek Kiemelt készségek, képességek Eszközök, mellékletek II. Kártyavár 1. Játék egynemű algebrai kifejezésekkel Probléma-érzékenység, probléma-reprezentáció, együttműködés, szövegértés, szövegértelmezés. Játék összeg és szorzat alakú algebrai kifejezésekkel Probléma-érzékenység, probléma-reprezentáció, együttműködés, szövegértés, szövegértelmezés Eszközök: 1. Kártyakészlet fénymásolata csoportonként 1 példányban (lehetőleg keményebb papírra), olló Tanulói munkafüzet: A játékok leírása Melléklet a tanároknak: A kifejezések a kártyapaklikban A játékok leírása 1. Kártyák a játékhoz 1. Eszközök:. Kártyakészlet fénymásolata csoportonként 1 példányban (lehetőleg keményebb papírra), olló Tanulói munkafüzet: D feladatlap Melléklet a tanároknak: A D feladatlap és megoldása A játékok leírása. Kártyák a játékhoz.
5 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 5 Lépések, tevékenységek Kiemelt készségek, képességek Eszközök, mellékletek III. Szövegelő 1. Szöveg befejezése, majd szöveg alapján egyenlet felírása Szövegértés, szövegértelmezés, problémaérzékenység, problémamegoldás eredetiség, kreativitás. Egyenlet alapján szöveg alkotása Szövegértés, szövegértelmezés, problémaérzékenység, problémamegoldás eredetiség, kreativitás Tanulói munkafüzet: E feladatlap F feladatlap Melléklet a tanároknak: A E feladatlap és megoldása Az F feladatlap és megoldása Tanulói munkafüzet: F feladatlap Melléklet a tanároknak: Az F feladatlap és megoldása
6 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 6 I. BETŰSZÁMTAN Ráhangolódás (10 perc) Tanulói munkafüzet: A feladatlap Melléklet a tanároknak: Az A feladatlap és megoldása A tanulói munkafüzetben találtok három verset, mindegyiknek van köze a matematikához. Igazából mindhárom vers egy-egy matematikai problémát is rejt, ami megoldható, és a megoldás minden esetben egy szám. Ki tudná közületek megmondani, melyek ezek a számok? Olvassa fel egy-egy vállalkozó szellemű diák a verseket, (ha nincs vállalkozó, akkor a tanár), ezután hagyja a tanulókat, hogy gondolkozzanak a megoldáson, majd a csoport közösen beszélje meg a megoldást! Nem kell feltétlenül egyenlettel megoldani a versekben kitűzött feladatot, lehet következtetéssel, visszafele stb. is, de ha többféle gondolatmenet jelenik meg a csoport tanulóinál, akkor érdemes mindegyikről beszélni egy kicsit. 1. Betűrejtvények (Javasolt idő: 0 perc; Munkaforma: párban) Tanulói munkafüzet: B feladatlap Melléklet a tanároknak: A B feladatlap és megoldása Rendeződjetek párokba! Nyissátok ki a munkafüzetet a. modul B feladatlapjánál! Mindegyik rejtvényben a betűk számjegyeket jelölnek, egy rejtvényen belül az azonosak azonos, a különböző betűk különböző számjegyeket jelölnek! Ki tudná megmondani a megfejtésüket? Vigyázat, van olyan, amelyiknek több megfejtése is van! Válasszon minden tanuló párt magának, majd csak ezután nyissák ki a munkafüzetüket a rejtvényeknél! Bíztassa a tanár a párosokat, hogy közösen válasszanak maguknak rejtvényt, és ha azt már megoldották, csak akkor folytassák a következővel. A rejtvények nem egyforma nehezek, ezért nem kell azokat a kitűzés sorrendjében megoldani. Csak akkor beszélje meg közösen az egész csoport valamely rejtvény megoldását, ha arra felmerül az igény. Ebben az esetben valamely csoport ismertesse a megoldást, és annak menetét. Ha az ismertetett megoldás nem teljes, pontosításra szorul, akkor egy másik csoport tagjai segítsenek! Javasolhatja a tanár a tanulóknak, hogy a meg nem oldott rejtvényeken odahaza is gondolkodhatnak, de ez semmiképpen se legyen kötelező! Végül javasolja a tanár minden tanulónak, hogy alkossanak további hasonló rejtvényeket, melyeket a következő foglalkozás elején bemutathatnak a csoport többi tagjának! (Ez történhet korábban is, ha valamely csoport tagjai hamar készen vannak.) Javasolja például nekik, hogy írjanak fel egy összeadást, és a számokat cseréljék ki betűkre, majd próbálják meg megoldani a rejtvényt.
7 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 7. Szókereső játék (Javasolt idő: 15 perc; Munkaforma: párban, majd 4 fős csoportokban) Tanulói munkafüzet: C feladatlap Melléklet a tanároknak: A C feladatlap és megoldása Cseréljetek párt! Itt van három keresztrejtvény, melyek négyzeteibe a matematikával kapcsolatos fogalmakat kell beírnotok. Ki találja meg leghamarabb a megfejtéseket? Válasszon mindenki (lehetőleg az előzőtől különböző) párt magának, majd nyissák ki a tanulók a munkafüzetet a rejtvényeknél. Ha a diákok nagy része nem találkozott valamely fogalommal a meghatározások közül, de van közöttük olyan, aki ismeri a megfejtést, akkor az a tanuló ismertesse a többiekkel azt. Ebben az esetben az osztály megbeszélheti az adott fogalom jelentését is. Ha valamely fogalmat a diákok egyike sem ismeri, akkor a tanár segítse őket, de az egész csoportot egyszerre, tehát ne csak egy-két párosnak mondja meg a megfejtést. Ilyenkor beszélje meg az osztály az adott fogalom jelentését. A megfejtéseket csak abban az esetben beszélje meg az osztály közösen, ha a diákoknak kifejezetten ez a kívánsága.
8 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 8 MELLÉKLET A TANÁROKNAK Ráhangolódás A feladatlap 1. vers: Egy gúnár döcögve kiszalad, Mert zajt hallott a bozótban, S ím arra jön épp egy libahad, Miután megfürdött a tóban. A gúnár: Köszöntelek titeket, S igazán meg vagyok lepve, Szinte betöltitek a ligetet, Vagytok vagy százan egybe. Egy okos kis liba így felel: Túlbecsülted a számunkat bőven, Száz liba itt bizony nem megy el, Számolj utána szépen. Duplázd meg kérlek a számunkat, Meg a felét vedd még hozzá És a negyedét, sőt még Te magad: Akkor lesz épp százzá.. vers Egy szép számot választottam, 107-tel még megtoldottam, Aztán 100-zal elosztottam, Végül néggyel megszoroztam. Amit kaptam ezután: Nem más, mint a 7-es szám.. vers Egy ifjú pásztor erdők felett 1008 juhot legeltetett, Míg csak a nap búcsúfénye El nem tűnt a messzi mélybe. Ekkor 1 csapatban Elindultak, s egy csoportban Kettővel több a juh éppen, Mint az előtte menőben. Mondd, hány van az első rajban, S a többiben is, mondjad, hány van? Megoldások: 1. vers: x x x =, amiből x = 6.. vers: x = 7 100, amiből x = 68.. vers: Az első csapatban x juh volt, akkor: x + ( x + ) ( x + ) = 1008, amiből 1 x + 1 = 1008, vagyis x = 7, így sorban 7, 75,, 95 juh volt a csoportokban.
9 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 9 1. Betűrejtvények B feladatlap és megoldása 1. A B C A B + C 0 0. A A + B B C C. A B B A A 4. Ö T + Ö T T Í Z 5. S O K S O K K I S + K O S O K O S 6. A B B B A B + B B A B B B 0 7. A + A = B + A A = B B B = 0 8. AA ABA = AAAA 9. AB AB = CAB 10. AA N = ANNA Megoldások:
10 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 10 Az A csak 1-et vagy -őt jelölhet. 1 nem lehet, mert akkor az összeg kisebb lenne 00-nál. Az utolsó oszlopban az összeg 10 vagy 0, mert csak így keletkezik átvitel, vagyis B legfeljebb 8, legalább Egy kétjegyű és egy egyjegyű szám összege csak úgy lehet háromjegyű, ha a kétjegyű szám nagyobb 90-nél, így A = 9. (B =1 az átvitel miatt, ugyanezért a C = 0.) Az eredmény akkor lesz egyjegyű, ha A = B T = 1 lehet csak, így Z =, Ö lehet 5, 7,8,9, így Í értéke rendre 0, 4, 6, 8. (Ö nem lehet 6, mert akkor Í = Z lenne.) Négy háromjegyű szám összege kisebb 4000-nél, így O legfeljebb. Ekkor a tizesek helyén az összeg 10 és 0 közé esik, vagyis a százasokhoz az átvitel 1. A százasok és az egyesek helyén ugyan azok a számok állnak, csak más sorrendben, így K = S + 1. Tehát az egyesek helyén az összeget vizsgálva 4S + értéke 10 + S, 0 + S vagy 0 + S lehet, ami csak abban az esetben ad egész megoldást, ha 4S + = 0 + S, ebből S = Az egyesek helyén megnézve A + B 10 vagy 0 lehet, a százasok helyén megnézve csak 10 lehet. Három háromjegyű szám összege kisebb, mint 000, így B csak 1 vagy lehet.
11 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ = 4 + = = 0 A 0 és a az a szám, mely önmagával vett összege és szorzata megegyezik, de ha A = 0, akkor B is 0, ami nem lehet = 1111 Az utolsó jegyek szorzatát vizsgálva A csak 1, 5 vagy 6 lehet, vagy egy AAAA alakú számot elosztunk egy AA alakú számmal, mindig 101-et kapunk = 65 Mivel a szám négyzete 1000-nél kisebb, így A csak 1, vagy lehet. Ha egy szám négyzetének utolsó jegye megegyezik a szám utolsó jegyével, akkor ez a jegy 0, 1, 5 vagy 6 lehet. (Ha az első jegy, akkor csak 0 vagy 1 az első feltétel miatt.) = 11 Mivel ötjegyű, így ha N =, akkor A csak 1 lehet, ha A nagyobb 1-nél, akkor N csak lehet.. Szókereső játék C feladatlap 1. Töltsd ki az üres négyzeteket úgy, hogy a sorokban az alábbi matematikai fogalmakhoz jussunk: S 1. félátmérő. számelméleti alapfogalom. mértani test 4. ilyen szám például a ilyen az összes szám S S S S
12 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 1. Írj be váltakozva öt- és hatbetűs szavakat a sorokba, melyek kezdőbetűit összeolvasva egy mértani alakzat nevét kapjuk! 1. kis prímszám. egy test alaplapját határolják. -éder 4. pl. az előző testet is ezek határolják 5. S betűvel az elején az egyik tényező neve 6. rómaiaknál az V M eredménye 7. híres német matematikus, módszert neveztek el róla. Ha az alábbi rejtvényben a meghatározásoknak megfelelő nyolcbetűs szavakat írod, akkor a megjelölt átlóban egy matematikai fogalmat kapod meg! 1. ilyen például a 11. az osztásnál keletkezhet. zárt görbe 4. szabályos test 5. ilyen sorozat is van 6. meg kell oldani 7. köbtartalom 8. így kell megoldani a feladatot (nem matematikai fogalom)
13 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 1 Megoldások: 1. S U G Á R O S Z T Ó H A S Á B E G É S Z V A L Ó S. H Á R O M A L A P É L T E T R A S I K L A P Z O R Z Ó Ö T E Z E R G A U S S. P R Í M S Z Á M H Á N Y A D O S K Ö R V O N A L O K T A É D E R S Z Á M T A N I E G Y E N L E T T É R F O G A T H E L Y E S E N
14 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 14 II. KÁRTYAVÁR Ráhangolódás (kb. 10 perc) Aki hozott magával számrejtvényt, az mutassa be a csoportnak feladványát! Rendeződjetek kisebb csoportokba, válasszatok a felkínált rejtvények közül párat, és oldjátok meg azokat! A hozott rejtvényeket írják fel a tanulók a táblára, majd kisebb csoportokba rendeződve oldjanak meg néhányat közülük! Segítséget mindig a kitűzőtől kérhetnek a csoportok. Akik feladatot hoztak, azokat bíztathatja a tanár arra, hogy szépen írják le rejtvényeiket egy papírra, a papír hátoldalára a megoldással, és ezt kitűzhetik a terem falára, hogy később is foglalkozhasson vele az, aki kedvet érez hozzá. 1. Játék egynemű algebrai kifejezésekkel (Javasolt idő: 0 perc; Eszközök: A tanári melléklet kártyáinak fénymásolata csoportonként 1 példányban (lehetőleg keményebb papírra), olló; Munkaforma: -4 fős csoportokban) Rendeződjetek 4 fős csoportokba! Csoportonként kiosztok 1-1 kártyapaklit (csak szét kell vágnotok a kapott lapokat), mindegyik pakliban 56 db lapot találtok. A kártyákon algebrai kifejezések szerepelnek. Mindegyik kifejezésből 4-4 db egynemű található, s ennek megfelelően 14 db különböző kifejezést találtok a pakliban. Játszunk ezekkel a kártyákkal! A játék leírását és annak variációit megtaláljátok a munkafüzetben is. Tanulói munkafüzet: A játékok leírása 1. Melléklet a tanároknak: A kifejezések a kártyapaklikban A játékok leírása 1. Kártyák a játékhoz 1. A tanár ismertesse a játék leírását a tanulókkal, majd felügyelje a játékot! Ha valamely csoport megunja az egyik játékot, akkor bíztassa őket a tanár, hogy próbálják ki a másikat is! A kártyapaklikat a játék végeztével szedje össze a tanár, hogy a későbbi foglalkozásokon, ha a tanulók igénylik, újra elő lehessen venni azokat a játékhoz.. Játék összeg és szorzat alakú algebrai kifejezésekkel (Javasolt idő: 0 perc; Eszközök: A tanári melléklet kártyáinak fénymásolata csoportonként 1 példányban (lehetőleg keményebb papírra); Munkaforma: -4 fős csoportokban) Tanulói munkafüzet: D feladatlap Melléklet a tanároknak: A D feladatlap és megoldása Találtok a munkafüzetben 10 ábrát, mindegyiken egy-egy téglalap látható. A téglalapok oldalait részekre osztották. Írjátok fel a téglalapok területét kétféleképpen, egyszer összeg alakú, és egyszer szorzat alakú algebrai kifejezéssel!
15 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 15 Vannak olyan ábrák, ahol a téglalap egy részét szürkére színezték, ott ennek a résznek a területét kell csak megadni. Ha valamely csoport készen van a kifejezések felírásával, akkor ellenőrizze azokat a tanár. Ha készen vagytok, akkor csoportonként kaptok egy-egy újabb kártyapaklit, amelyeken ezek az ábrák, illetve a kifejezések szerepelnek. A tanár ossza ki a kártyákat tartalmazó lapok fénymásolatát, amit a diákok vágjanak szét lapokra. A kártyákon külön-külön lapokon szerepelnek az ábrák, az összegalakok, illetve a szorzatalakok. Játszunk most az új paklikkal. Megadom két játék leírását, minden csoport válasszon kedvére valót! Tanulói munkafüzet: A játékok leírása. Melléklet a tanároknak: A játékok leírása. Kártyák a játékhoz. A játékismertetés után most is csak felügyelje a tanár a játékot. A második játék szabályát valószínűleg jól ismerik a tanulók, így csak az első ismertetésére érdemes nagyobb gondot fordítania. A szabályleírást az első játék esetében most is érdemes külön a tanári asztalra kirakni, ha azt a tanulók nem értenék, vagy vita alakulna ki közöttük. Az eső játékot tanuló játszhatja, a másodikhoz 4 tanuló kell. Ha valamely csoport megunta a játékot, akkor most is próbálja meg rávenni őket a tanár, hogy játsszanak a másik játékkal is, esetleg térjenek vissza a foglalkozás első felében megismert játékokhoz. Az elkészült kártyapaklikat a játék végeztével most is szedje össze a tanár, hogy a későbbi foglalkozásokon, ha a tanulók igénylik, újra elő lehessen venni azokat a játékhoz.
16 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 16 MELLÉKLET A TANÁROKNAK 1. Játék egynemű algebrai kifejezésekkel A kifejezések: Ezekkel egynemű kifejezések szerepelnek a kártyapaklikban 4 4 x; y; x ; xy; y ; x ; x y; xy ; y ; x ; x y; x y ; xy ; y. A játékok leírása játék: Römi-szerű játék A 4 játékos mindegyike osztáskor 1 lapot kap. A játékosok sorban húznak a pakli maradék részéből, majd mindenki minden körben dob egy lapot. A cél az, hogy a lapok elfogyjanak a játékos kezéből. Ez úgy érhető el, hogy azokat leteszi az asztalra. Letenni egyszerre minimum három lapot lehet a következő szabályok szerint: Egynemű kifejezésekhez tartalmazó lapokat tesz le a játékos. Sort rak le a játékos, ekkor az egyik ismeretlen hatványkitevője állandó, a másiké egyesével nő, például az x; xy; xy -el, vagy ezekkel a kifejezésekkel egynemű kifejezéseket tartal- mazó lapokat. Olyan kifejezéseket tesz le a játékos, melyekben az ismeretlenek kitevőjének összege állandó (azonos fokszámú kifejezések), és nincs közöttük két egynemű kifejezés, például az x y; x ; xy -el egynemű kifejezésekkel egyneműeket tartalmazó lapokat. Ha egy játékos már tett le az asztalra, akkor a maradék lapjaiból hozzátehet a mások által letett lapokhoz, de az előző szabályokat be kell tartania. Ha a maradék pakli elfogy, akkor a dobott lapokat össze kell keverni, és ebből húzhatnak újra a játékosok. Játékvariációk Rablójáték: A játékosok nem dobnak a kezükben tartott lapokból, és átrendezhetik a már letett lapokat a szabályok betartásával, tehát a már letett lapok mindegyikének az asztalon kell maradniuk. Játék dobókockával: Mielőtt a játékos letenne lapokat az asztalra, dob kettőt dobókockával. A dobott számokat behelyettesíti a leteendő kártyákon lévő kifejezésekbe (az első dobott számot az egyik, a második dobott számot a másik ismeretlen helyére mindegyik kifejezésben), és ha a kapott számok összege meghalad/nem halad meg egy előre meghatározott értéket, akkor teheti csak le a lapokat. Játék feltétellel: Csak akkor teheti le a játékos a lapokat, ha az egyszerre letenni kívánt lapokon lévő kifejezések együtthatóinak összege meghalad (nem halad meg) egy előre megbeszélt értéket. Ha több leosztást is játszik a csoport, akkor egy-egy leosztás végén dobjanak kettőt a dobókockával, és a két számot helyettesítsék be a kezekben maradt kártyákon lévő kifejezésekbe, ez az adott kártya értéke. Minden játékos adja össze a kezében maradt kártyák értékét, ennyi pontot kap a leosztás után. A játék végén az nyer, akinek a leosztások után kapott pontjainak az összege a legkisebb. Ezzel a paklival Memóriajátékot is játszhatunk lásd a leírást A játékok leírása.-ben.
17 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 17 Kártyák a játékhoz 1. x x 5 x x 4y y 7 1 y 5y 5
18 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 18 x x 1 x 7 x xy xy x 5 y 1 xy
19 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 19 1 y y y 7 y 4 x 5 x x 7 x 4
20 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 0 x y x y 1 x y 4x y xy 1 xy 4 xy xy 5
21 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 1 y 4 y 5 y 9 y 5 4 5x 4x 4 4 x 6 5 x 4
22 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ x y x y 1 x y 7 10 x y x y x y 5 x y 7 x y
23 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ xy 4 xy 5 xy 9 xy 5 4 y 4 y y 9 y 5 4
24 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 4. Játék összeg és szorzat alakú algebrai kifejezésekkel D feladatlap és megoldása A kártyák, valamint a felírt kifejezések összeg, illetve szorzat alakban: 1. ábra: y x Szorzat alak: ( x + )( y + ) Összeg alak: xy + x + y + 6. ábra: x 5 y Szorzat alak: y ( x + 5) Összeg alak: xy + 5y
25 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 5. ábra: a b Szorzat alak: a ( b ) Összeg alak: ab a 4. ábra: a b a b Szorzat alak: ( a + b) Összeg alak: a + + ab b
26 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 6 5. ábra: a a b b Szorzat alak: ( a b) Összeg alak: 6. ábra: a + ab b y 1 x Szorzat alak: x ( y +1) Összeg alak: xy + x
27 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 7 7. ábra: x x 1 1 Szorzat alak: ( x 1) Összeg alak: x x ábra: b b Szorzat alak: ( b + ) Összeg alak: b + b + 1
28 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 8 9. ábra: a b c d Szorzat alak: ( a + b)( c + d) Összeg alak: ac + ad + bc + bd 10. ábra: c a b a Szorzat alak: ( c + a)( b + a) Összeg alak: bc + ab + ac + a A játékok leírása. 1. játék: A játékmester az ábrákhoz tartozó összeg és szorzat alakú kifejezéseket tartalmazó kártyákat (Kártyák a játékhoz.) kiosztja a két játékosnak, ügyelve arra, hogy az egyik játékos az öszszegalakot tartalmazó kártyát, a másik játékos a szorzatalakú kártyát kapja meg. Ez történhet például úgy, hogy a kártyákat párosítja a játékmester, és a két kártyából felváltva húznak a játékosok, és aki nem húzott éppen, az kapja a másik kártyát. Miután a játékmester kiosztotta a paklit, felcsap egyet az ábrákat tartalmazó lapok közül (l. a fenti 10 ábra kártyáját), amire a játékosoknak ki kell választaniuk a kezükben lévő lapok közül azt, ami az adott ábrához tartozik. Amelyik játékos gyorsabb volt és jól választott, az
29 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 9 megkapja az ábrát tartalmazó lapot, az algebrai kifejezést tartalmazó saját lapját, és az ellenfélét abban az esetben, ha a kifejezés másik alakját is jól el tudja mondani. Ha a gyorsabb játékos rosszat tett, akkor az általa letett lapot elveszti, azt átadja a játékmesternek, aki ezeket a lapokat fejjel lefelé fordítva külön gyűjti. Ha a gyorsabb rosszat tett, akkor a másik játékos még próbálkozhat az előbbi szabály szerint. A játék végén az nyer, aki több kártyát gyűjtött. Ha a csoport többször játszik a játékkal, akkor a tagok felváltva legyenek játékmesterek, és a végén az győz, aki összesen a legtöbb lapot gyűjtötte.. játék: Memóriajáték Az asztal egyik részére fejjel lefelé rakják ki a játékosok az algebrai kifejezéseket tartalmazó paklit, ettől elkülönülten az ábrákat tartalmazó kártyákat, szintén fejjel lefelé. A játékosok egymás után felfordítanak két olyan kártyát, amin algebrai kifejezés van, és egy olyat, amin ábra van. A játékos megkapja az általa felfordított három lapot, ha a megfelelő ábrához mindkét algebrai kifejezést megtalálta. A játék végén az nyer, akinek a legtöbb lapja van. Kártyák a játékhoz. ( x + )( y + ) xy + x + y + 6 y( x + 5) xy + 5y
30 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 0 a ( b ) ab a ( a + b) a + + ab b ( a b) a + ab b ( y +1) x xy + x
31 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 1 ( 1) x x x + 1 ( + ) b b + b + 1 ( a + b)( c + d) ac + ad + bc + bd ( c a)( b + a) + bc + ab + ac + a
32 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ III. SZÖVEGELŐ Ráhangolódás (kb. 5 perc) Ha az előző két foglalkozáson megismert játékok között volt olyan, amelyik tetszett a tanulóknak, akkor játsszanak avval egy kicsit! 1. Szöveges feladatok gyártása (Javasolt idő: 15 perc; Munkaforma: - fős csoportban) Tanulói munkafüzet: E feladatlap Melléklet a tanároknak: Az E feladatlap és megoldása Rendeződjetek csoportokba! Minden csoport kap elkezdett feladatokat. Megadom, hogy milyen egyenlet lett felírva a szöveg alapján. Egészítsétek ki ennek megfelelően a szövegeket! A csoportokat úgy alakítsa ki a tanár, hogy lehetőleg fősek legyenek. Abban az esetben legyen kétfős csoport, ha kevés a diák, vagy ha a tanulók száma hárommal nem osztható. A csoporton belül a tanulók osszák fel a feladatokat, a csoporton belül mindenki más feladaton dolgozzon. Valószínűleg lesznek olyan tanulók, akinek nehezen megy a feladatkiegészítés, őket segítse a tanár, például: Milyen információt lehetne még megadni? Mi lehetne a kérdés? Esetleg a megadott egyenlet egy részét kiemelve fogalmaztassa meg azt szövegesen, majd mutassa meg, hogyan lehet további részekre szedni az egyenletet! Adjátok oda a csoportotok valamely tagjának az általatok alkotott szövegeket! A kapott szöveg alapján mindenki próbáljon meg egyenletet felírni. Ha készen vagytok, akkor oldjátok meg azokat az egyenleteket, amiket eredetileg kaptatok, és azokat is, amiket ti írtatok fel. Hasonlítsátok össze közösen az általatok felírt egyenletet az eredetileg megadottal, valamint a kapott megoldásokat! Ha különbözik az eredetitől, annak mi az oka? Mire következtethettek akkor, ha azonos, és mire akkor, ha különböző megoldás jött ki?. Egyenlet alapján szöveg alkotása, majd szöveg alapján egyenlet felírása (Javasolt idő: 5 perc; Munkaforma: - fős csoportban) Tanulói munkafüzet: F feladatlap Melléklet a tanároknak: Az F feladatlap és megoldása Minden csoport kap pár szöveget, ezeket kell úgy kiegészítenetek, hogy egy-egy szöveges feladat legyen belőle. Ügyeljen a tanár arra, hogy a szövegalkotás során egy csoport tagjai lehetőleg ne segítsenek egymásnak, inkább egy másik csoport olyan tagja nyújtson segítséget, aki ugyanavval a problémával foglalkozik. A nagyon tanácstalan tanulókat a foglalkozás elején ismertetett módon segítheti a tanár.
33 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ Ne minősítse semmilyen formában a tanár az elkészült szövegeket, akkor sem, ha felesleges információk is kerültek bele, vagy ha nem teljes a feladat, majd a következő lépésben a csoportok közösen kijavíthatják ezeket. Cseréljék ki a csoportok tagjai egymás között a szövegeket! Nézzétek meg, milyen feladatokat sikerült készítenie a társatoknak! Próbáljátok meg megoldani a feladatokat! Dolgozhattok közösen is! A tanulók habitusától függően hagyja őket egyénileg vagy csoportosan dolgozni a tanár, csak arra ügyeljen, hogy tényleg a problémákkal foglalkozzanak! Motiválhatja őket például avval, hogy válasszák ki azt a feladatot, amelyik a legjobban sikerült, a legjobban tetszik a csoport minden tagjának. Valószínűleg több esetben is előfordul majd, hogy úgy sikerült a feladatot valamely tanulónak befejeznie, hogy annak nincs megoldása, vagy nem közöl elég információt. Ebben az esetben a tanár bíztassa a csoport tagjait, hogy próbálják meg közösen kijavítani a feladatot úgy, hogy az megoldható legyen! A megoldások keresése során nem szükséges rávenni a tanulókat arra, hogy mindenképpen egyenlettel oldják meg a feladatokat, de erre bíztathatja őket a tanár. Ha valamely csoport tagjai hamar készen vannak, akkor játszhatnak az első foglalkozás végén ismertetett szókígyó játékkal, vagy az előző foglalkozáson megismert kártyajátékokkal.
34 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 4 MELLÉKLET A TANÁROKNAK 1. Szöveges feladatok gyártása E feladatlap és megoldása Első tanulónak: 1. Egy anya évvel idősebb a fiánál, és évvel fiatalabb a férjénél..életkora összesen év. Hány évesek külön-külön? Az egyenlet: x + x + x + 5 = 96 Megoldás: Anya 8, apa 4, a gyerek 15 éves. A szöveg egy lehetséges kiegészítése: Egy anya évvel idősebb a fiánál, és 5 évvel fiatalabb a férjénél. Hármójuk életkora összesen 96 év. Hány évesek külön-külön?. Egy osztályba 5-en járnak. A fiúk számának fele megegyezik a lányok Hány fiú, és hány lány jár az osztályba? f 5 f Az egyenlet: = Megoldás: 14 fiú és 1 lány jár az osztályba. A szöveg egy lehetséges kiegészítése: Egy osztályba 5-en járnak. A fiúk számának fele megegyezik a lányok számának harmadával. Hány fiú, és hány lány jár az osztályba?. Hány kg 6%-os kénsavat kell kénsavhoz keverni, hogy kapjunk? Az egyenlet: 0,6x + 0,68 40 = 0,(40 + x) Megoldás: 40 kg-ot. A szöveg egy lehetséges kiegészítése: Mennyi 6 tömeg %-os kénsavat kell 40 kg 68 tömeg %-os kénsavhoz keverni, hogy tömeg %-os kénsavat kapjunk?
35 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 5 Második tanulónak: 1. A két zsebemben összesen van. Az egyik zsebemben harmada Hány forint van az egyik, mennyi a másik zsebemben? x Az egyenlet: = 600 x Megoldás: 450 Ft az egyik, 150 Ft a másik zsebben. A szöveg egy lehetséges kiegészítése: A két zsebemben összesen 600 Ft van. Az egyik zsebemben lévő összeg harmada pont a másik zsebemben lévő összegnek felel meg. Hány forint van az egyik, mennyi a másik zsebemben?. Egy kötélnek levágtuk a részét és még, így a negyedénél. maradt. Milyen hosszú? 1 Az egyenlet: x 7 = x 4 4 Megoldás: 6 méter A szöveg egy lehetséges kiegészítése: Egy kötélnek levágtuk a részét és még 7 métert, így a negyedénél 4 méterrel rövidebb darab maradt. Milyen hosszú volt a kötél eredetileg?. Egy kétjegyű szám jegyeinek összege. Ha a jegyeit felcseréljük, akkor az szám háromszorosánál kisebb számot kapunk. Melyik ez a szám? Az egyenlet: 10(8 x ) + x = (10x + 8 x) 16 Megoldás: 6 A szöveg egy lehetséges kiegészítése: Egy kétjegyű szám számjegyeinek összege 8. Ha a jegyeit felcseréljük, akkor az eredeti szám háromszorosánál 16-tal kisebb számot kapunk. Melyik ez a szám?
36 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 6 Harmadik tanulónak: 1. Egy ezerforintost felváltottunk 10 és forintosokra. Összesen pénzérménk van. Hány 10 és.? Az egyenlet: 10 x + 0(90 x) = 1000 Megoldás: 80 db 10-est, és 10 db 0-ast kaptunk. A szöveg egy lehetséges kiegészítése: Egy ezerforintost felváltottunk 10 és 0 forintosokra. Összesen 90 darab pénzérmét kaptunk. Hány 10, és hány 0 forintos van az érmék között?. Egy iskolába tanuló jár. A fiúk számának 90%-a.Hány fiú és.? Az egyenlet: 0,9x = 0,7(800 x) Megoldás: 40 fiú és 450 lány. A szöveg egy lehetséges kiegészítése: Egy iskolába 800 tanuló jár. A fiúk számának 90%-a megegyezik a lányok számának 70%- ával. Hány fiú, és hány lány jár ebbe az iskolába?. Egy medence az első csapon át 10 óra alatt, a második csapon telik meg. Mennyi idő alatt telik meg az üres medence, ha? Az egyenlet: t 5 + t = Megoldás: 8 óra alatt A szöveg egy lehetséges kiegészítése: Egy medence az első csapon át 10 óra alatt, a második csapon át 15 óra alatt telik meg. Menynyi idő alatt telik meg az üres medence, ha az első csap megnyitása után 5 órával nyitjuk meg a második csapot?
37 MATEMATIKA C 8. ÉVFOLYAM. MODUL: BETŰZZÜK KI! TANÁRI ÚTMUTATÓ 7. Egyenlet alapján szöveg alkotása, majd szöveg alapján egyenlet felírása F feladatlap Első tanulónak: 1. Az apa öt évvel ezelőtt ötször annyi idős volt, mint a fia, három év múlva. Az egyik zsebemben a másik zsebemben lévő pénz kétszeresénél. Egy osztály tanulóinak része lány, a fiúk száma 5 Második tanulónak: 1. Két testvér életkorának összege 15 év. Két évvel ezelőtt. Egy kétjegyű szám egyik számjegye kétszer akkora, mint a másik. Ha a szám számjegyeit felcseréljük, 4. Mennyit kell a számlálójához és a nevezőjéhez hozzáadni, hogy 11 Harmadik tanulónak: 1. Két szomszédos páratlan szám összege. Elolvastam egy könyv részét, és még 1 oldalt, így hátra van a könyv 7. A főnök fizetése 7%-kal nagyobb a titkárnője fizetésénél. Kettőjük fizetése együtt
17. modul: EGYENLETEK, EGYENLŐTLENSÉGEK, KÉTISMERETLENES EGYENLETEK
 MATEMATIK A 9. évfolyam 17. modul: EGYENLETEK, EGYENLŐTLENSÉGEK, KÉTISMERETLENES EGYENLETEK KÉSZÍTETTE: DARABOS NOÉMI ÁGNES Készítette: Darabos Noémi Ágnes Matematika A 9. évfolyam. 17. modul: EGYENLETEK,
MATEMATIK A 9. évfolyam 17. modul: EGYENLETEK, EGYENLŐTLENSÉGEK, KÉTISMERETLENES EGYENLETEK KÉSZÍTETTE: DARABOS NOÉMI ÁGNES Készítette: Darabos Noémi Ágnes Matematika A 9. évfolyam. 17. modul: EGYENLETEK,
ISKOLÁD NEVE:... Az első három feladat feleletválasztós. Egyenként 5-5 pontot érnek. Egy feladatnak több jó megoldása is lehet. A) 6 B) 8 C) 10 D) 12
 2. OSZTÁLY 1. Mennyi az alábbi kifejezés értéke: 0 2 + 4 6 + 8 10 + 12 14 + 16 18 + 20 A) 6 B) 8 C) 10 D) 12 2. Egy szabályos dobókockával kétszer dobok. Mennyi nem lehet a dobott számok összege? A) 1
2. OSZTÁLY 1. Mennyi az alábbi kifejezés értéke: 0 2 + 4 6 + 8 10 + 12 14 + 16 18 + 20 A) 6 B) 8 C) 10 D) 12 2. Egy szabályos dobókockával kétszer dobok. Mennyi nem lehet a dobott számok összege? A) 1
0567. MODUL TÖRTEK. Törtekről tanultak összefoglalása KÉSZÍTETTE: BENCZÉDY-LACZKA KRISZTINA, MALMOS KATALIN
 07. MODUL TÖRTEK Törtekről tanultak összefoglalása KÉSZÍTETTE: BENCZÉDY-LACZKA KRISZTINA, MALMOS KATALIN 07. Törtek Törtekről tanultak összefoglalása Tanári útmutató MODULLEÍRÁS A modul célja Időkeret
07. MODUL TÖRTEK Törtekről tanultak összefoglalása KÉSZÍTETTE: BENCZÉDY-LACZKA KRISZTINA, MALMOS KATALIN 07. Törtek Törtekről tanultak összefoglalása Tanári útmutató MODULLEÍRÁS A modul célja Időkeret
Számolási eljárások 12. feladatcsomag
 Számolási eljárások 3.12 Alapfeladat Számolási eljárások 12. feladatcsomag számok bontásának gyakorlása 20-as számkörben összeadás, kivonás gyakorlása 20-as számkörben A feladatok listája 1. Mennyi van
Számolási eljárások 3.12 Alapfeladat Számolási eljárások 12. feladatcsomag számok bontásának gyakorlása 20-as számkörben összeadás, kivonás gyakorlása 20-as számkörben A feladatok listája 1. Mennyi van
IV.3. GONDOLJ, GONDOLJ... A feladatsor jellemzői
 IV.3. GONDOLJ, GONDOLJ... Tárgy, téma A feladatsor jellemzői Elsőfokú egyenletek, egyenlőtlenségek megoldása. Ezek felhasználása szöveges feladatok megoldásánál. Előzmények Egyenletek, egyszerűbb algebrai
IV.3. GONDOLJ, GONDOLJ... Tárgy, téma A feladatsor jellemzői Elsőfokú egyenletek, egyenlőtlenségek megoldása. Ezek felhasználása szöveges feladatok megoldásánál. Előzmények Egyenletek, egyszerűbb algebrai
0564. MODUL TÖRTEK. Törtek egyszerűsítése, bővítése KÉSZÍTETTE: BENCZÉDY-LACZKA KRISZTINA, MALMOS KATALIN
 0. MODUL TÖRTEK Törtek egyszerűsítése, bővítése KÉSZÍTETTE: BENCZÉDY-LACZKA KRISZTINA, MALMOS KATALIN 0. Törtek Törtek egyszerűsítése, bővítése Tanári útmutató MODULLEÍRÁS A modul célja Időkeret Ajánlott
0. MODUL TÖRTEK Törtek egyszerűsítése, bővítése KÉSZÍTETTE: BENCZÉDY-LACZKA KRISZTINA, MALMOS KATALIN 0. Törtek Törtek egyszerűsítése, bővítése Tanári útmutató MODULLEÍRÁS A modul célja Időkeret Ajánlott
MATEMATIKA C 8. évfolyam 9. modul HOL A VÉGE?
 MATEMATIKA C 8. évfolyam 9. modul HOL A VÉGE? Készítette: Surányi Szabolcs MATEMATIKA C 8. ÉVFOLYAM 9. HOL A VÉGE? TANÁRI ÚTMUTATÓ A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A
MATEMATIKA C 8. évfolyam 9. modul HOL A VÉGE? Készítette: Surányi Szabolcs MATEMATIKA C 8. ÉVFOLYAM 9. HOL A VÉGE? TANÁRI ÚTMUTATÓ A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A
4. modul EGYENES ÉS FORDÍTOTT ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS
 Matematika A 9. szakiskolai évfolyam 4. modul EGYENES ÉS FORDÍTOTT ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS MATEMATIKA A 9. szakiskolai évfolyam 4. modul: EGYENES ÉS FORDÍTOTT ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS Tanári útmutató
Matematika A 9. szakiskolai évfolyam 4. modul EGYENES ÉS FORDÍTOTT ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS MATEMATIKA A 9. szakiskolai évfolyam 4. modul: EGYENES ÉS FORDÍTOTT ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS Tanári útmutató
MATEMATIK A 9. évfolyam. 1. modul: HALMAZOK KÉSZÍTETTE: LÖVEY ÉVA
 MATEMATIK A 9. évfolyam 1. modul: HALMAZOK KÉSZÍTETTE: LÖVEY ÉVA Matematika A 9. évfolyam. 1. modul: HALMAZOK Tanári útmutató 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok Halmazokkal
MATEMATIK A 9. évfolyam 1. modul: HALMAZOK KÉSZÍTETTE: LÖVEY ÉVA Matematika A 9. évfolyam. 1. modul: HALMAZOK Tanári útmutató 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok Halmazokkal
Módszertani megjegyzés: A kikötés az osztás műveletéhez kötődik. A jobb megértés miatt célszerű egy-két példát mu-
 . modul: ELSŐFOKÚ TÖRTES EGYENLETEK A következő órákon olyan egyenletekkel foglalkozunk, amelyek nevezőjében ismeretlen található. Ha a tört nevezőjében ismeretlen van, akkor kikötést kell tennünk: az
. modul: ELSŐFOKÚ TÖRTES EGYENLETEK A következő órákon olyan egyenletekkel foglalkozunk, amelyek nevezőjében ismeretlen található. Ha a tört nevezőjében ismeretlen van, akkor kikötést kell tennünk: az
MATEMATIKA C 9. évfolyam 4. modul OSZTOZZUNK!
 MATEMATIKA C 9. évfolyam 4. modul OSZTOZZUNK! Készítette: Kovács Károlyné MATEMATIKA C 9. ÉVFOLYAM 4. MODUL: OSZTOZZUNK! TANÁRI ÚTMUTATÓ 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
MATEMATIKA C 9. évfolyam 4. modul OSZTOZZUNK! Készítette: Kovács Károlyné MATEMATIKA C 9. ÉVFOLYAM 4. MODUL: OSZTOZZUNK! TANÁRI ÚTMUTATÓ 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN. 10. modul TESTRÉSZEINK! Készítette: Schmittinger Judit
 MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 10. modul TESTRÉSZEINK! Készítette: Schmittinger Judit MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 10. modul: TESTRÉSZEINK 2 A modul célja Időkeret Ajánlott
MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 10. modul TESTRÉSZEINK! Készítette: Schmittinger Judit MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 10. modul: TESTRÉSZEINK 2 A modul célja Időkeret Ajánlott
16. modul: ALGEBRAI AZONOSSÁGOK
 MATEMATIK A 9. évfolyam 16. modul: ALGEBRAI AZONOSSÁGOK KÉSZÍTETTE: VIDRA GÁBOR, DARABOS NOÉMI ÁGNES Matematika A 9. évfolyam. 16. modul: ALGEBRAI AZONOSSÁGOK Tanári útmutató 2 A modul célja Időkeret Ajánlott
MATEMATIK A 9. évfolyam 16. modul: ALGEBRAI AZONOSSÁGOK KÉSZÍTETTE: VIDRA GÁBOR, DARABOS NOÉMI ÁGNES Matematika A 9. évfolyam. 16. modul: ALGEBRAI AZONOSSÁGOK Tanári útmutató 2 A modul célja Időkeret Ajánlott
Számokkal kapcsolatos feladatok.
 Számokkal kapcsolatos feladatok. 1. Egy tört számlálója -tel kisebb, mint a nevezője. Ha a tört számlálójához 17-et, a nevezőjéhez -t adunk, akkor a tört reciprokát kapjuk. Melyik ez a tört? A szám: 17
Számokkal kapcsolatos feladatok. 1. Egy tört számlálója -tel kisebb, mint a nevezője. Ha a tört számlálójához 17-et, a nevezőjéhez -t adunk, akkor a tört reciprokát kapjuk. Melyik ez a tört? A szám: 17
MATEMATIKA C 12. évfolyam 4. modul Még egyszer!
 MATEMATIKA C 1. évfolyam 4. modul Még egyszer! Készítette: Kovács Károlyné Matematika C 1. évfolyam 4. modul: Még eygszer! Tanári útmutató A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok
MATEMATIKA C 1. évfolyam 4. modul Még egyszer! Készítette: Kovács Károlyné Matematika C 1. évfolyam 4. modul: Még eygszer! Tanári útmutató A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok
SZÁMKERESZTREJTVÉNYEK
 Róka Sándor SZÁMKERESZTREJTVÉNYEK Bővített és átdolgozott kiadás TARTALOM Bevezetés 7 Keresztező feladatok (1 26 számkeresztrejtvény) 11 Egyszerűbb számkeresztrejtvények (27 33. számkeresztrejtvény) 83
Róka Sándor SZÁMKERESZTREJTVÉNYEK Bővített és átdolgozott kiadás TARTALOM Bevezetés 7 Keresztező feladatok (1 26 számkeresztrejtvény) 11 Egyszerűbb számkeresztrejtvények (27 33. számkeresztrejtvény) 83
DIAGNOSZTIKUS MÉRÉS. 33. modul
 Matematika A 3. évfolyam DIAGNOSZTIKUS MÉRÉS 33. modul Készítette: KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 33. modul DIAGNOSZTIKUS MÉRÉS MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
Matematika A 3. évfolyam DIAGNOSZTIKUS MÉRÉS 33. modul Készítette: KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 33. modul DIAGNOSZTIKUS MÉRÉS MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
KÉSZÍTSÜNK ÁBRÁT évfolyam
 Boronkay György Műszaki Középiskola és Gimnázium 2600 Vác, Németh László u. 4-6. : 27-317 - 077 /fax: 27-315 - 093 WEB: http://boronkay.vac.hu e-mail: boronkay@vac.hu Levelező Matematika Szakkör 2018/2019.
Boronkay György Műszaki Középiskola és Gimnázium 2600 Vác, Németh László u. 4-6. : 27-317 - 077 /fax: 27-315 - 093 WEB: http://boronkay.vac.hu e-mail: boronkay@vac.hu Levelező Matematika Szakkör 2018/2019.
Matematika A 9. szakiskolai évfolyam. 13. modul SZÖVEGES FELADATOK. Készítette: Vidra Gábor
 Matematika A 9. szakiskolai évfolyam 13. modul SZÖVEGES FELADATOK Készítette: Vidra Gábor MATEMATIKA A 9. SZAKISKOLAI ÉVFOLYAM 13. modul: SZÖVEGES FELADATOK TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott
Matematika A 9. szakiskolai évfolyam 13. modul SZÖVEGES FELADATOK Készítette: Vidra Gábor MATEMATIKA A 9. SZAKISKOLAI ÉVFOLYAM 13. modul: SZÖVEGES FELADATOK TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott
Matematika A 9. szakiskolai évfolyam. 11. modul EGYENLETEK, EGYENLŐTLENSÉGEK MEGOLDÁSA. Készítették: Vidra Gábor és Koller Lászlóné dr.
 Matematika A 9. szakiskolai évfolyam 11. modul EGYENLETEK, EGYENLŐTLENSÉGEK MEGOLDÁSA Készítették: Vidra Gábor és Koller Lászlóné dr. MATEMATIKA A 9. SZAKISKOLAI ÉVFOLYAM 11. modul: EGYENLETEK, EGYENLŐTLENSÉGEK
Matematika A 9. szakiskolai évfolyam 11. modul EGYENLETEK, EGYENLŐTLENSÉGEK MEGOLDÁSA Készítették: Vidra Gábor és Koller Lászlóné dr. MATEMATIKA A 9. SZAKISKOLAI ÉVFOLYAM 11. modul: EGYENLETEK, EGYENLŐTLENSÉGEK
Számelmélet Megoldások
 Számelmélet Megoldások 1) Egy számtani sorozat második tagja 17, harmadik tagja 1. a) Mekkora az első 150 tag összege? (5 pont) Kiszámoltuk ebben a sorozatban az első 111 tag összegét: 5 863. b) Igaz-e,
Számelmélet Megoldások 1) Egy számtani sorozat második tagja 17, harmadik tagja 1. a) Mekkora az első 150 tag összege? (5 pont) Kiszámoltuk ebben a sorozatban az első 111 tag összegét: 5 863. b) Igaz-e,
IV.3. GONDOLJ, GONDOLJ... A feladatsor jellemzői
 IV.3. GONDOLJ, GONDOLJ... Tárgy, téma A feladatsor jellemzői Elsőfokú egyenletek, egyenlőtlenségek megoldása. Ezek felhasználása szöveges feladatok megoldásánál. Előzmények Egyenletek, egyszerűbb algebrai
IV.3. GONDOLJ, GONDOLJ... Tárgy, téma A feladatsor jellemzői Elsőfokú egyenletek, egyenlőtlenségek megoldása. Ezek felhasználása szöveges feladatok megoldásánál. Előzmények Egyenletek, egyszerűbb algebrai
13. modul: MÁSODFOKÚ FÜGGVÉNYEK
 MATEMATIK A 9. évfolyam 13. modul: MÁSODFOKÚ FÜGGVÉNYEK KÉSZÍTETTE: CSÁKVÁRI ÁGNES Matematika A 9. évfolyam. 13. modul: MÁSODFOKÚ FÜGGVÉNYEK Tanári útmutató 2 A modul célja Időkeret Ajánlott korosztály
MATEMATIK A 9. évfolyam 13. modul: MÁSODFOKÚ FÜGGVÉNYEK KÉSZÍTETTE: CSÁKVÁRI ÁGNES Matematika A 9. évfolyam. 13. modul: MÁSODFOKÚ FÜGGVÉNYEK Tanári útmutató 2 A modul célja Időkeret Ajánlott korosztály
Matematika A 9. szakiskolai évfolyam. 1. modul GONDOLKODJUNK, RENDSZEREZZÜNK!
 Matematika A 9. szakiskolai évfolyam 1. modul GONDOLKODJUNK, RENDSZEREZZÜNK! MATEMATIKA A 9. szakiskolai évfolyam 1. modul:gondolkodjunk, RENDSZEREZZÜNK! Tanári útmutató 2 A modul célja Időkeret Ajánlott
Matematika A 9. szakiskolai évfolyam 1. modul GONDOLKODJUNK, RENDSZEREZZÜNK! MATEMATIKA A 9. szakiskolai évfolyam 1. modul:gondolkodjunk, RENDSZEREZZÜNK! Tanári útmutató 2 A modul célja Időkeret Ajánlott
Számelmélet, műveletek, egyenletek, algebrai kifejezések, egyéb
 Számelmélet, műveletek, egyenletek, algebrai kifejezések, egyéb 2004_02/4 Tegyél * jelet a táblázat megfelelő rovataiba! Biztosan Lehet hogy, de nem biztos Lehetetlen a) b) c) Négy egymást követő természetes
Számelmélet, műveletek, egyenletek, algebrai kifejezések, egyéb 2004_02/4 Tegyél * jelet a táblázat megfelelő rovataiba! Biztosan Lehet hogy, de nem biztos Lehetetlen a) b) c) Négy egymást követő természetes
MATEMATIKA C 6. évfolyam 2. modul TANGRAMOK
 MATEMATIKA C 6. évfolyam 2. modul TANGRAMOK Készítette: Köves Gabriella MATEMATIKA C 6. ÉVFOLYAM 2. MODUL: TANGRAMOK TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott korosztály A képességfejlesztés fókuszai
MATEMATIKA C 6. évfolyam 2. modul TANGRAMOK Készítette: Köves Gabriella MATEMATIKA C 6. ÉVFOLYAM 2. MODUL: TANGRAMOK TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott korosztály A képességfejlesztés fókuszai
Megyei matematikaverseny évfolyam 2. forduló
 Megyei matematikaverseny 0. 9. évfolyam. forduló. Mennyi a tizenkilencedik prím és a tizenkilencedik összetett szám szorzata? (A) 00 (B) 0 (C) 0 (D) 04 (E) Az előző válaszok egyike sem helyes.. Az 000
Megyei matematikaverseny 0. 9. évfolyam. forduló. Mennyi a tizenkilencedik prím és a tizenkilencedik összetett szám szorzata? (A) 00 (B) 0 (C) 0 (D) 04 (E) Az előző válaszok egyike sem helyes.. Az 000
Óravázlat Matematika. 1. osztály
 Óravázlat Matematika 1. osztály Készítette: Dr. Jandóné Bapka Katalin Az óra anyaga: Számok kapcsolatai, számpárok válogatása kapcsolataik szerint Osztály: 1. osztály Készség-és képességfejlesztés: - Megfigyelőképesség
Óravázlat Matematika 1. osztály Készítette: Dr. Jandóné Bapka Katalin Az óra anyaga: Számok kapcsolatai, számpárok válogatása kapcsolataik szerint Osztály: 1. osztály Készség-és képességfejlesztés: - Megfigyelőképesség
Boronkay György Műszaki Középiskola és Gimnázium Vác, Németh László u : /fax:
 200 Vác, Németh László u. 4-. : 27-17 - 077 /fax: 27-1 - 09. OSZTÁLY 1.) Hány olyan négyjegyű természetes szám van, melynek jegyei között az 1 és 2 számjegyek közül legalább az egyik szerepel? Négyjegyű
200 Vác, Németh László u. 4-. : 27-17 - 077 /fax: 27-1 - 09. OSZTÁLY 1.) Hány olyan négyjegyű természetes szám van, melynek jegyei között az 1 és 2 számjegyek közül legalább az egyik szerepel? Négyjegyű
2015. évi Bolyai János Megyei Matematikaverseny MEGOLDÁSI ÉS ÉRTÉKELÉSI ÚTMUTATÓ 9. osztály
 A közölt megoldási utak a feladatoknak nem az egyetlen helyes megoldási módját adják meg, több eltérő megoldás is lehetséges. Az útmutatótól eltérő megoldásokat a kialakult tanári gyakorlat alapján, az
A közölt megoldási utak a feladatoknak nem az egyetlen helyes megoldási módját adják meg, több eltérő megoldás is lehetséges. Az útmutatótól eltérő megoldásokat a kialakult tanári gyakorlat alapján, az
148 feladat 21 + + 20 20 ) + ( 1 21 + 2 200 > 1 2. 1022 + 1 51 + 1 52 + + 1 99 2 ) (1 1 100 2 ) =?
 148 feladat a Kalmár László Matematikaversenyről 1. ( 1 19 + 2 19 + + 18 19 ) + ( 1 20 + 2 20 + + 19 20 ) + ( 1 21 + 2 21 + + 20 21 ) + ( 1 22 + 2 22 + + 21 22 ) =? Kalmár László Matematikaverseny megyei
148 feladat a Kalmár László Matematikaversenyről 1. ( 1 19 + 2 19 + + 18 19 ) + ( 1 20 + 2 20 + + 19 20 ) + ( 1 21 + 2 21 + + 20 21 ) + ( 1 22 + 2 22 + + 21 22 ) =? Kalmár László Matematikaverseny megyei
A III. forduló megoldásai
 A III. forduló megoldásai 1. Egy dobozban pénzérmék és golyók vannak, amelyek vagy ezüstből, vagy aranyból készültek. A dobozban lévő tárgyak 20%-a golyó, a pénzérmék 40%-a ezüst. A dobozban levő tárgyak
A III. forduló megoldásai 1. Egy dobozban pénzérmék és golyók vannak, amelyek vagy ezüstből, vagy aranyból készültek. A dobozban lévő tárgyak 20%-a golyó, a pénzérmék 40%-a ezüst. A dobozban levő tárgyak
Feladatlap. a hatosztályos speciális matematika tantervű osztályok írásbeli vizsgájára (2006)
 Feladatlap a hatosztályos speciális matematika tantervű osztályok írásbeli vizsgájára (2006) 1) Karcsi januárban betegség miatt háromszor hiányzott az iskolából:12-én,14-én és 24-én. Milyen napra esett
Feladatlap a hatosztályos speciális matematika tantervű osztályok írásbeli vizsgájára (2006) 1) Karcsi januárban betegség miatt háromszor hiányzott az iskolából:12-én,14-én és 24-én. Milyen napra esett
7! (7 2)! = 7! 5! = 7 6 5! 5 = = ből 4 elem A lehetőségek száma megegyezik az 5 elem negyedosztályú variációjának számával:
 Kombinatorika Variáció - megoldások 1. Hány kétjegyű szám képezhető a 2, 3, 5, 6, 7, 8, 9 számjegyekből. ha minden számjegyet csak egyszer használhatunk fel? A lehetőségek száma annyi, mint amennyi 7 elem
Kombinatorika Variáció - megoldások 1. Hány kétjegyű szám képezhető a 2, 3, 5, 6, 7, 8, 9 számjegyekből. ha minden számjegyet csak egyszer használhatunk fel? A lehetőségek száma annyi, mint amennyi 7 elem
Írásbeli összeadás. Háromjegyű számok összeadása. 1. Végezd el az összeadásokat! 2. a) Számítsd ki, mennyibe kerül a következő 2-2 báb!
 Írásbeli összeadás Háromjegyű számok összeadása 1. Végezd el az összeadásokat! 254 + 200 = 162 + 310 = 235 + 240 = 351 + 124 = 2. a) Számítsd ki, mennyibe kerül a következő 2-2 báb! 213 Ft 164 Ft 222 Ft
Írásbeli összeadás Háromjegyű számok összeadása 1. Végezd el az összeadásokat! 254 + 200 = 162 + 310 = 235 + 240 = 351 + 124 = 2. a) Számítsd ki, mennyibe kerül a következő 2-2 báb! 213 Ft 164 Ft 222 Ft
MATEMATIKA C 9. évfolyam 1. modul IDŐBEN A TÉRBEN
 MATEMATIKA C 9. évfolyam 1. modul IDŐBEN A TÉRBEN Készítette: Kovács Károlyné MATEMATIKA C 9. ÉVFOLYAM 1. MODUL: IDŐBEN A TÉRBEN TANÁRI ÚTMUTATÓ 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály
MATEMATIKA C 9. évfolyam 1. modul IDŐBEN A TÉRBEN Készítette: Kovács Károlyné MATEMATIKA C 9. ÉVFOLYAM 1. MODUL: IDŐBEN A TÉRBEN TANÁRI ÚTMUTATÓ 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály
4. modul: MŰVELETEK A VALÓS SZÁMOK KÖRÉBEN
 MATEMATIK A 9. évfolyam 4. modul: MŰVELETEK A VALÓS SZÁMOK KÖRÉBEN KÉSZÍTETTE: DARABOS NOÉMI ÁGNES Matematika A 9. évfolyam. 4. modul: MŰVELETEK A VALÓS SZÁMOK KÖRÉBEN Tanári útmutató 2 A modul célja Időkeret
MATEMATIK A 9. évfolyam 4. modul: MŰVELETEK A VALÓS SZÁMOK KÖRÉBEN KÉSZÍTETTE: DARABOS NOÉMI ÁGNES Matematika A 9. évfolyam. 4. modul: MŰVELETEK A VALÓS SZÁMOK KÖRÉBEN Tanári útmutató 2 A modul célja Időkeret
;3 ; 0; 1 7; ;7 5; 3. pozitív: ; pozitív is, negatív is: ;
 . A racion lis sz mok A tanult sz mok halmaza A) Ábrázold számegyenesen az alábbi számokat! 8 + + 0 + 7 0 7 7 0 0. 0 Válogasd szét a számokat aszerint, hogy pozitív: pozitív is, negatív is: negatív: sem
. A racion lis sz mok A tanult sz mok halmaza A) Ábrázold számegyenesen az alábbi számokat! 8 + + 0 + 7 0 7 7 0 0. 0 Válogasd szét a számokat aszerint, hogy pozitív: pozitív is, negatív is: negatív: sem
Hatványozás. A hatványozás azonosságai
 Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
Hatványozás Definíció: a 0 = 1, ahol a R, azaz bármely szám nulladik hatványa mindig 1. a 1 = a, ahol a R, azaz bármely szám első hatványa önmaga a n = a a a, ahol a R, n N + n darab 3 4 = 3 3 3 3 = 84
PYTAGORIÁDA Az országos forduló feladatai 37. évfolyam, 2015/2016-os tanév
 Kategória P 6 1. Zsombornak a szekrényben csak fekete, barna és kék pár zoknija van. Ingjei csak fehérek és lilák, nadrágjai csak kékek és barnák. Hányféleképpen felöltözve tud Zsombor iskolába menni,
Kategória P 6 1. Zsombornak a szekrényben csak fekete, barna és kék pár zoknija van. Ingjei csak fehérek és lilák, nadrágjai csak kékek és barnák. Hányféleképpen felöltözve tud Zsombor iskolába menni,
MATEMATIKA VERSENY --------------------
 Eötvös Károly Közös Fenntartású Általános Iskola 2013. és Alapfokú Művészetoktatási Intézmény 831 Vonyarcvashegy, Fő u. 8/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen,
Eötvös Károly Közös Fenntartású Általános Iskola 2013. és Alapfokú Művészetoktatási Intézmény 831 Vonyarcvashegy, Fő u. 8/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen,
Gyakorló feladatok javítóvizsgára szakközépiskola matematika 9. évfolyam
 Gyakorló feladatok javítóvizsgára szakközépiskola matematika 9. évfolyam Halmazok:. Adott két halmaz: A = kétjegyű pozitív, 4-gyel osztható számok B = 0-nél nagyobb, de 0-nál nem nagyobb pozitív egész
Gyakorló feladatok javítóvizsgára szakközépiskola matematika 9. évfolyam Halmazok:. Adott két halmaz: A = kétjegyű pozitív, 4-gyel osztható számok B = 0-nél nagyobb, de 0-nál nem nagyobb pozitív egész
DIAGNOSZTIKUS MÉRÉS. 23. modul
 Matematika A 3. évfolyam DIAGNOSZTIKUS MÉRÉS 23. modul Készítette: C. NEMÉNYI ESZTER KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 23. modul DIAGNOSZTIKUS MÉRÉS MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály
Matematika A 3. évfolyam DIAGNOSZTIKUS MÉRÉS 23. modul Készítette: C. NEMÉNYI ESZTER KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 23. modul DIAGNOSZTIKUS MÉRÉS MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály
IX.2. ÁTLAGOS FELADATOK I. A feladatsor jellemzői
 IX.2. ÁTLAGOS FELADATOK I. Tárgy, téma Algebra, statisztika. Előzmények A feladatsor jellemzői Az aritmetikai átlag fogalma, oszthatósági alapismeretek, prímszám fogalma, a számtani sorozat elemeinek összegére
IX.2. ÁTLAGOS FELADATOK I. Tárgy, téma Algebra, statisztika. Előzmények A feladatsor jellemzői Az aritmetikai átlag fogalma, oszthatósági alapismeretek, prímszám fogalma, a számtani sorozat elemeinek összegére
 33. modul 1. melléklet 3. évfolyam Mérőlap/1. Név:. 1. Becsüld meg az összegeket! A tagok százasokra kerekített értékeivel végezd a becslést! Majd végezd is el az összeadásokat. Számításaidat kivonással
33. modul 1. melléklet 3. évfolyam Mérőlap/1. Név:. 1. Becsüld meg az összegeket! A tagok százasokra kerekített értékeivel végezd a becslést! Majd végezd is el az összeadásokat. Számításaidat kivonással
Varga Tamás Matematikaverseny Javítási útmutató Iskolai forduló 2016/ osztály
 1. Az erdészet dolgozói pályázaton nyert facsemetékkel ültetnek be egy adott területet. Ha 450-et ültetnének hektáronként, akkor 380 facsemete kimaradna. Ha 640 facsemetével többet nyertek volna, akkor
1. Az erdészet dolgozói pályázaton nyert facsemetékkel ültetnek be egy adott területet. Ha 450-et ültetnének hektáronként, akkor 380 facsemete kimaradna. Ha 640 facsemetével többet nyertek volna, akkor
0644. MODUL SZÁMELMÉLET. Közös osztók, közös többszörösök KÉSZÍTETTE: PINTÉR KLÁRA
 0644. MODUL SZÁMELMÉLET Közös osztók, közös többszörösök KÉSZÍTETTE: PINTÉR KLÁRA 0644. Számelmélet Közös osztók, közös többszörösök Tanári útmutató MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály
0644. MODUL SZÁMELMÉLET Közös osztók, közös többszörösök KÉSZÍTETTE: PINTÉR KLÁRA 0644. Számelmélet Közös osztók, közös többszörösök Tanári útmutató MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály
Tananyag: Számfogalom erősítése a 100-as számkörben. Játékpénzzel számolunk.
 Óravázlat 2. osztályos matematika Tananyag: Számfogalom erősítése a 100-as számkörben. Játékpénzzel számolunk. Oktatási cél: Pénzhasználat, pénzváltás. Játék a játékpénzzel párokban. Megismerési képességek
Óravázlat 2. osztályos matematika Tananyag: Számfogalom erősítése a 100-as számkörben. Játékpénzzel számolunk. Oktatási cél: Pénzhasználat, pénzváltás. Játék a játékpénzzel párokban. Megismerési képességek
MATEMATIK A 9. évfolyam. 2. modul: LOGIKA KÉSZÍTETTE: VIDRA GÁBOR
 MATEMATIK A 9. évfolyam 2. modul: LOGIKA KÉSZÍTETTE: VIDRA GÁBOR Matematika A 9. évfolyam. 2. modul: LOGIKA Tanári útmutató 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok
MATEMATIK A 9. évfolyam 2. modul: LOGIKA KÉSZÍTETTE: VIDRA GÁBOR Matematika A 9. évfolyam. 2. modul: LOGIKA Tanári útmutató 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok
1. Írd le számjegyekkel illetve betűkkel az alábbi számokat! Tízezer-hétszáztizenkettő Huszonhétmillió-hétezer-nyolc
 1. Írd le számjegyekkel illetve betűkkel az alábbi számokat! Tízezer-hétszáztizenkettő Huszonhétmillió-hétezer-nyolc 10 325 337 30 103 000 002 2. Végezd el az alábbi műveleteket, ahol jelölve van ellenőrizz!
1. Írd le számjegyekkel illetve betűkkel az alábbi számokat! Tízezer-hétszáztizenkettő Huszonhétmillió-hétezer-nyolc 10 325 337 30 103 000 002 2. Végezd el az alábbi műveleteket, ahol jelölve van ellenőrizz!
OSZTHATÓSÁG. Osztók és többszörösök : a 3 többszörösei : a 4 többszörösei Ahol mindkét jel megtalálható a 12 többszöröseit találjuk.
 Osztók és többszörösök 1783. A megadott számok elsõ tíz többszöröse: 3: 3 6 9 12 15 18 21 24 27 30 4: 4 8 12 16 20 24 28 32 36 40 5: 5 10 15 20 25 30 35 40 45 50 6: 6 12 18 24 30 36 42 48 54 60 1784. :
Osztók és többszörösök 1783. A megadott számok elsõ tíz többszöröse: 3: 3 6 9 12 15 18 21 24 27 30 4: 4 8 12 16 20 24 28 32 36 40 5: 5 10 15 20 25 30 35 40 45 50 6: 6 12 18 24 30 36 42 48 54 60 1784. :
5. modul: ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS
 MATEMATIK A 9. évfolyam 5. modul: ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS KÉSZÍTETTE: VIDRA GÁBOR Matematika A 9. évfolyam. 5. modul: ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS Tanári útmutató 2 A modul célja Időkeret Ajánlott
MATEMATIK A 9. évfolyam 5. modul: ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS KÉSZÍTETTE: VIDRA GÁBOR Matematika A 9. évfolyam. 5. modul: ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS Tanári útmutató 2 A modul célja Időkeret Ajánlott
Óravázlat. Tananyag: Műveletvégzés a 20-as számkörben tízes átlépéssel. A természetes szám fogalmának mélyítése a számtulajdonságok megfigyelésével.
 Óravázlat Tantárgy: Matematika Osztály: BONI Széchenyi István Általános Iskola 1. e Tanít: Dr. Szudi Lászlóné Tananyag: Műveletvégzés a 20-as számkörben tízes átlépéssel Kiemelt kompetenciák: Matematika
Óravázlat Tantárgy: Matematika Osztály: BONI Széchenyi István Általános Iskola 1. e Tanít: Dr. Szudi Lászlóné Tananyag: Műveletvégzés a 20-as számkörben tízes átlépéssel Kiemelt kompetenciák: Matematika
ÓRAVÁZLAT. Az óra címe: Ismeretek a kis számokról. Osztály. nyújtott 1. évfolyam első év A tanóra célja
 ÓRAVÁZLAT Az óra címe: Ismeretek a kis számokról Készítette: Nagy Istvánné Osztály nyújtott 1. évfolyam első év A tanóra célja Tudatos észlelés, megfigyelés és a figyelem fejlesztése, pontosítása. Tapasztalatszerzés
ÓRAVÁZLAT Az óra címe: Ismeretek a kis számokról Készítette: Nagy Istvánné Osztály nyújtott 1. évfolyam első év A tanóra célja Tudatos észlelés, megfigyelés és a figyelem fejlesztése, pontosítása. Tapasztalatszerzés
7. Számelmélet. 1. Lehet-e négyzetszám az a pozitív egész szám, amelynek tízes számrendszerbeli alakjában 510 darab 1-es és valahány 0 szerepel?
 7. Számelmélet I. Nulladik ZH-ban láttuk: 1. Lehet-e négyzetszám az a pozitív egész szám, amelynek tízes számrendszerbeli alakjában 510 darab 1-es és valahány 0 szerepel? ELTE 2006. október 27. (matematika
7. Számelmélet I. Nulladik ZH-ban láttuk: 1. Lehet-e négyzetszám az a pozitív egész szám, amelynek tízes számrendszerbeli alakjában 510 darab 1-es és valahány 0 szerepel? ELTE 2006. október 27. (matematika
Elemi matematika szakkör
 Elemi matematika szakkör Kolozsvár, 2015. október 5. 1.1. Feladat. Egy pozitív egész számot K tulajdonságúnak nevezünk, ha számjegyei nullától különböznek és nincs két azonos számjegye. Határozd meg az
Elemi matematika szakkör Kolozsvár, 2015. október 5. 1.1. Feladat. Egy pozitív egész számot K tulajdonságúnak nevezünk, ha számjegyei nullától különböznek és nincs két azonos számjegye. Határozd meg az
PYTAGORIÁDA Az országos forduló feladatai 35. évfolyam, 2013/2014-es tanév. Kategória P 6
 Kategória P 6 1. Írjátok le azt a számot, amely a csillag alatt rejtőzik: *. 5 = 9,55 2. Babszem Jankó 25 ször kisebb, mint Kukorica Jancsi. Írjátok le, hogy hány centiméter Babszem Jankó, ha Kukorica
Kategória P 6 1. Írjátok le azt a számot, amely a csillag alatt rejtőzik: *. 5 = 9,55 2. Babszem Jankó 25 ször kisebb, mint Kukorica Jancsi. Írjátok le, hogy hány centiméter Babszem Jankó, ha Kukorica
50. modul 1. melléklet 2. évfolyam tanítói fólia
 50. modul 1. melléklet 2. évfolyam tanítói fólia 50. modul 2. melléklet 2. évfolyam tanítói fólia 50. modul 3. melléklet 2. évfolyam tanítói fólia 50. modul 4. melléklet 2. évfolyam tanítói fólia és csoport
50. modul 1. melléklet 2. évfolyam tanítói fólia 50. modul 2. melléklet 2. évfolyam tanítói fólia 50. modul 3. melléklet 2. évfolyam tanítói fólia 50. modul 4. melléklet 2. évfolyam tanítói fólia és csoport
Sorba rendezés és válogatás
 Sorba rendezés és válogatás Keress olyan betűket és számokat, amelyeknek vízszintes tükörtengelyük van! Írd le! Keress olyan szavakat, amelyeknek minden betűje tükrös (szimmetrikus), amilyen például a
Sorba rendezés és válogatás Keress olyan betűket és számokat, amelyeknek vízszintes tükörtengelyük van! Írd le! Keress olyan szavakat, amelyeknek minden betűje tükrös (szimmetrikus), amilyen például a
OLVASÁS FEJLESZTÉSE 6.HÉT PROGRAMJA
 OLVASÁS FEJLESZTÉSE 6.HÉT PROGRAMJA OLVASÁS FEJLESZTÉSE 1.NAP PROGRAMJA Elsőként megismerkedünk azokkal a betűkkel, amelyekkel ezen a héten dolgozni fogunk. Ezek pedig: b,d,p Nem elég, hogy vizuálisan
OLVASÁS FEJLESZTÉSE 6.HÉT PROGRAMJA OLVASÁS FEJLESZTÉSE 1.NAP PROGRAMJA Elsőként megismerkedünk azokkal a betűkkel, amelyekkel ezen a héten dolgozni fogunk. Ezek pedig: b,d,p Nem elég, hogy vizuálisan
1 = 1x1 1+3 = 2x2 1+3+5 = 3x3 1+3+5+7 = 4x4
 . Orchidea Iskola VI. Matematika verseny 0/0 II. forduló = x + = x ++ = x +++ = x Ennek ismeretében mennyivel egyenlő ++++...+9+99=? A ) 0. D ) 0 000 6 C ) 0 D ) A Földközi-tengerben a só-víz aránya :
. Orchidea Iskola VI. Matematika verseny 0/0 II. forduló = x + = x ++ = x +++ = x Ennek ismeretében mennyivel egyenlő ++++...+9+99=? A ) 0. D ) 0 000 6 C ) 0 D ) A Földközi-tengerben a só-víz aránya :
OLVASÁSI KÉPESSÉGEKET FEJLESZTŐ PROGRAM
 OLVASÁSI KÉPESSÉGEKET FEJLESZTŐ PROGRAM 1. NAP PROGRAMJA Ezen a héten újabb, egymáshoz nagyon hasonló betűkkel játsszunk! Azonban ők már nem csak hárman vannak, hanem bizony nyolcan, így a dolgunk is nehezebb
OLVASÁSI KÉPESSÉGEKET FEJLESZTŐ PROGRAM 1. NAP PROGRAMJA Ezen a héten újabb, egymáshoz nagyon hasonló betűkkel játsszunk! Azonban ők már nem csak hárman vannak, hanem bizony nyolcan, így a dolgunk is nehezebb
X. PANGEA Matematika Verseny II. forduló 10. évfolyam. 1. Az b matematikai műveletet a következőképpen értelmezzük:
 1. Az a @ b matematikai műveletet a következőképpen értelmezzük: @ a a b b, feltéve, hogy a 0. a Melyik állítás igaz a P és Q mennyiségekre? P = ((2 @ 1) @ (1 @ 2)) Q = ((7 @ 8) @ (8 @ 7)) A) P > Q B)
1. Az a @ b matematikai műveletet a következőképpen értelmezzük: @ a a b b, feltéve, hogy a 0. a Melyik állítás igaz a P és Q mennyiségekre? P = ((2 @ 1) @ (1 @ 2)) Q = ((7 @ 8) @ (8 @ 7)) A) P > Q B)
MATEMATIKA C 9. évfolyam
 MATEMATIKA C 9. évfolyam 6. modul GONDOLKODOM, TEHÁT VAGYOK Készítette: Kovács Károlyné MATEMATIKA C 9. ÉVFOLYAM 6. MODUL: GONDOLKODOM, TEHÁT VAGYOK TANÁRI ÚTMUTATÓ 2 MODULLEÍRÁS A modul célja Időkeret
MATEMATIKA C 9. évfolyam 6. modul GONDOLKODOM, TEHÁT VAGYOK Készítette: Kovács Károlyné MATEMATIKA C 9. ÉVFOLYAM 6. MODUL: GONDOLKODOM, TEHÁT VAGYOK TANÁRI ÚTMUTATÓ 2 MODULLEÍRÁS A modul célja Időkeret
NULLADIK MATEMATIKA ZÁRTHELYI
 NULLADIK MATEMATIKA ZÁRTHELYI 08-09-07 Terem: Munkaidő: 0 perc. A dolgozat megírásához íróeszközön kívül semmilyen segédeszköz nem használható! A feladatlap kizárólag kék vagy fekete tollal tölthető ki.
NULLADIK MATEMATIKA ZÁRTHELYI 08-09-07 Terem: Munkaidő: 0 perc. A dolgozat megírásához íróeszközön kívül semmilyen segédeszköz nem használható! A feladatlap kizárólag kék vagy fekete tollal tölthető ki.
MATEMATIKA C 5. évfolyam 5. modul JÁTÉK A ZSEBSZÁMOLÓGÉPPEL
 MATEMATIKA C 5. évfolyam 5. modul JÁTÉK A ZSEBSZÁMOLÓGÉPPEL Készítette: Abonyi Tünde MATEMATIKA C 5. ÉVFOLYAM 5. MODUL: JÁTÉK A ZSEBSZÁMOLÓGÉPPEL TANÁRI ÚTMUTATÓ 2 A modul célja A tudatos észlelés, a megfigyelés
MATEMATIKA C 5. évfolyam 5. modul JÁTÉK A ZSEBSZÁMOLÓGÉPPEL Készítette: Abonyi Tünde MATEMATIKA C 5. ÉVFOLYAM 5. MODUL: JÁTÉK A ZSEBSZÁMOLÓGÉPPEL TANÁRI ÚTMUTATÓ 2 A modul célja A tudatos észlelés, a megfigyelés
Érdekességek az elemi matematika köréből
 Érdekességek az elemi matematika köréből Csizmadia László Bolyai Intézet, Szegedi Tudományegyetem Kutatók éjszakája Szeged, SZTE L. Csizmadia (Szeged) Kutatók éjszakája 2011. 2011.09.23. 1 / 17 Társasház
Érdekességek az elemi matematika köréből Csizmadia László Bolyai Intézet, Szegedi Tudományegyetem Kutatók éjszakája Szeged, SZTE L. Csizmadia (Szeged) Kutatók éjszakája 2011. 2011.09.23. 1 / 17 Társasház
Számelmélet. 4. Igazolja, hogy ha hat egész szám összege páratlan, akkor e számok szorzata páros!
 Számelmélet - oszthatóság definíciója - oszthatósági szabályok - maradékos osztás - prímek definíciója - összetett szám definíciója - legnagyobb közös osztó definíciója - legnagyobb közös osztó meghatározása
Számelmélet - oszthatóság definíciója - oszthatósági szabályok - maradékos osztás - prímek definíciója - összetett szám definíciója - legnagyobb közös osztó definíciója - legnagyobb közös osztó meghatározása
MATEMATIKA C 8. évfolyam 6. modul ATTÓL FÜGG?
 MATEMATIKA C 8. évfolyam 6. modul ATTÓL FÜGG? Készítette: Surányi Szabolcs MATEMATIKA C 8. ÉVFOLYAM 6. MODUL: ATTÓL FÜGG? TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
MATEMATIKA C 8. évfolyam 6. modul ATTÓL FÜGG? Készítette: Surányi Szabolcs MATEMATIKA C 8. ÉVFOLYAM 6. MODUL: ATTÓL FÜGG? TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
0645. MODUL SZÁMELMÉLET. Gyakorlás, mérés KÉSZÍTETTE: PINTÉR KLÁRA
 0645. MODUL SZÁMELMÉLET Gyakorlás, mérés KÉSZÍTETTE: PINTÉR KLÁRA 0645. Számelmélet Gyakorlás, mérés Tanári útmutató 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A
0645. MODUL SZÁMELMÉLET Gyakorlás, mérés KÉSZÍTETTE: PINTÉR KLÁRA 0645. Számelmélet Gyakorlás, mérés Tanári útmutató 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A
MATEMATIKA ÍRÁSBELI VIZSGA KÖZÉPSZINT% II. ÉRETTSÉGI VIZSGA május 3. MINISZTÉRIUM NEMZETI ERFORRÁS május 3. 8:00. Idtartam: 135 perc
 a feladat sorszáma maximális elért összesen II./A rész 13. 12 14. 12 15. 12 II./B rész 17 17 m nem választott feladat ÖSSZESEN 70 maximális elért I. rész 30 II. rész 70 Az írásbeli vizsgarész a 100 dátum
a feladat sorszáma maximális elért összesen II./A rész 13. 12 14. 12 15. 12 II./B rész 17 17 m nem választott feladat ÖSSZESEN 70 maximális elért I. rész 30 II. rész 70 Az írásbeli vizsgarész a 100 dátum
Szabolcs-Szatmár-Bereg megyei Ambrózy Géza Matematikaverseny 2012/2013 II. forduló 5. osztály
 5. osztály 1. Hány olyan téglalap van, amelynek minden oldala centiméterben kifejezve egész szám, és a területe 60 cm 2? 2. Adott a síkon egy ABC szabályos háromszög. Keresd meg a síkon az összes olyan
5. osztály 1. Hány olyan téglalap van, amelynek minden oldala centiméterben kifejezve egész szám, és a területe 60 cm 2? 2. Adott a síkon egy ABC szabályos háromszög. Keresd meg a síkon az összes olyan
} számtani sorozat első tagja és differenciája is 4. Adja meg a sorozat 26. tagját! A = { } 1 pont. B = { } 1 pont. x =
 . Az { a n } számtani sorozat első tagja és differenciája is 4. Adja meg a sorozat 26. tagját! a = 26 2. Az A és B halmazokról tudjuk, hogy A B = {;2;3;4;5;6}, A \ B = {;4} és A B = {2;5}. Sorolja fel
. Az { a n } számtani sorozat első tagja és differenciája is 4. Adja meg a sorozat 26. tagját! a = 26 2. Az A és B halmazokról tudjuk, hogy A B = {;2;3;4;5;6}, A \ B = {;4} és A B = {2;5}. Sorolja fel
3. Egyenletek, egyenletrendszerek, egyenlőtlenségek
 . Egyenletek, egyenletrendszerek, egyenlőtlenségek I. Nulladik ZH-ban láttuk: 1. Mennyi a 2x 2 8x 5 = 0 egyenlet gyökeinek a szorzata? (A) 10 (B) 2 (C) 2,5 (D) 4 (E) ezek egyike sem Megoldás I.: BME 2011.
. Egyenletek, egyenletrendszerek, egyenlőtlenségek I. Nulladik ZH-ban láttuk: 1. Mennyi a 2x 2 8x 5 = 0 egyenlet gyökeinek a szorzata? (A) 10 (B) 2 (C) 2,5 (D) 4 (E) ezek egyike sem Megoldás I.: BME 2011.
MATEMATIKA VERSENY ABASÁR, 2018
 MATEMATIKA VERSENY ABASÁR, 2018 1. osztály 2018 /55 pont 1. Folytasd a sort! 0 1 1 2 3 5 /4 pont 2. Melyik ábra illik a kérdőjel helyére? Karikázd be a betűjelét! (A) (B) (C) (D) (E) 3. Számold ki a feladatokat,
MATEMATIKA VERSENY ABASÁR, 2018 1. osztály 2018 /55 pont 1. Folytasd a sort! 0 1 1 2 3 5 /4 pont 2. Melyik ábra illik a kérdőjel helyére? Karikázd be a betűjelét! (A) (B) (C) (D) (E) 3. Számold ki a feladatokat,
1 pont Bármely formában elfogadható pl.:, avagy. 24 4
 2012. február 2. 8. évfolyam TMat2 feladatlap Javítókulcs / 1 Javítókulcs MATEMATIKA FELADATOK 8. évfolyamosok számára, tehetséggondozó változat TMat2 A javítókulcsban feltüntetett válaszokra a megadott
2012. február 2. 8. évfolyam TMat2 feladatlap Javítókulcs / 1 Javítókulcs MATEMATIKA FELADATOK 8. évfolyamosok számára, tehetséggondozó változat TMat2 A javítókulcsban feltüntetett válaszokra a megadott
kié nagyobb? 10. modul Készítette: Abonyi tünde
 kié nagyobb? 10. modul Készítette: Abonyi tünde kié nagyobb? A modul célja Időkeret Ajánlott korosztály A tudatos észlelés, a megfigyelés és a figyelem fejlesztése. Saját megfigyelések, megtapasztalások
kié nagyobb? 10. modul Készítette: Abonyi tünde kié nagyobb? A modul célja Időkeret Ajánlott korosztály A tudatos észlelés, a megfigyelés és a figyelem fejlesztése. Saját megfigyelések, megtapasztalások
Boronkay György Műszaki Középiskola és Gimnázium Vác, Németh László u : /fax:
 5. OSZTÁLY 1.) Apám 20 lépésének a hossza 18 méter, az én 10 lépésemé pedig 8 méter. Hány centiméterrel rövidebb az én lépésem az édesapáménál? 18m = 1800cm, így apám egy lépésének hossza 1800:20 = 90cm.
5. OSZTÁLY 1.) Apám 20 lépésének a hossza 18 méter, az én 10 lépésemé pedig 8 méter. Hány centiméterrel rövidebb az én lépésem az édesapáménál? 18m = 1800cm, így apám egy lépésének hossza 1800:20 = 90cm.
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Számelmélet
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Számelmélet A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Számelmélet A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
A) 0 B) 2 C) 8 D) 20 E) 32
 1. X és Y egyjegyű nemnegatív számok. Az X378Y ötjegyű szám osztható 72-vel. Mennyi X és Y szorzata? A) 0 B) 2 C) 8 D) 20 E) 32 2. Hány valós gyöke van a következő egyenletnek? (x 2 1) (x + 1) (x 2 1)
1. X és Y egyjegyű nemnegatív számok. Az X378Y ötjegyű szám osztható 72-vel. Mennyi X és Y szorzata? A) 0 B) 2 C) 8 D) 20 E) 32 2. Hány valós gyöke van a következő egyenletnek? (x 2 1) (x + 1) (x 2 1)
Az egyszerűsítés utáni alak:
 1. gyszerűsítse a következő törtet, ahol b 6. 2 b 36 b 6 Az egyszerűsítés utáni alak: 2. A 2, 4 és 5 számjegyek mindegyikének felhasználásával elkészítjük az összes, különböző számjegyekből álló háromjegyű
1. gyszerűsítse a következő törtet, ahol b 6. 2 b 36 b 6 Az egyszerűsítés utáni alak: 2. A 2, 4 és 5 számjegyek mindegyikének felhasználásával elkészítjük az összes, különböző számjegyekből álló háromjegyű
PYTAGORIÁDA. 1. Két szám összege 156. Az első összeadandó a 86 és a 34 különbsége. Mekkora a másik összeadandó?
 Az iskolai forduló feladatai 2006/2007-es tanév Kategória P 3 1. Két szám összege 156. Az első összeadandó a 86 és a 34 különbsége. Mekkora a másik összeadandó? 2. Számítsd ki: 19 18 + 17 16 + 15 14 =
Az iskolai forduló feladatai 2006/2007-es tanév Kategória P 3 1. Két szám összege 156. Az első összeadandó a 86 és a 34 különbsége. Mekkora a másik összeadandó? 2. Számítsd ki: 19 18 + 17 16 + 15 14 =
MATEMATIKA VERSENY
 Vonyarcvashegyi Eötvös Károly Általános Iskola 2016. 8314 Vonyarcvashegy, Fő u. 84/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen, majd oldd meg a feladatokat! A részeredményeket
Vonyarcvashegyi Eötvös Károly Általános Iskola 2016. 8314 Vonyarcvashegy, Fő u. 84/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen, majd oldd meg a feladatokat! A részeredményeket
2 2 = 2 p. = 2 p. 2. Végezd el a kijelölt műveleteket! 3. Végezd el a kijelölt műveleteket! 4. Alakítsad szorzattá az összeget!
 Matematika vizsga 014. 9. osztály Név: Az 1-1. feladatok megoldását a feladatlapra írd! A 1-19. feladatokat a négyzetrácsos lapon oldd meg! 1. Számítsd ki az alábbi kifejezések pontos értékét! 0, = = p
Matematika vizsga 014. 9. osztály Név: Az 1-1. feladatok megoldását a feladatlapra írd! A 1-19. feladatokat a négyzetrácsos lapon oldd meg! 1. Számítsd ki az alábbi kifejezések pontos értékét! 0, = = p
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Számelmélet
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Számelmélet A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Számelmélet A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Írd le, a megoldások gondolatmenetét, indoklását is!
 088 Budapest VIII., Bródy Sándor u. 6. Postacím: 4 Budapest, Pf. 76 Telefon: 7-8900 Fa: 7-890 44. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ 05. április. NEGYEDIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ
088 Budapest VIII., Bródy Sándor u. 6. Postacím: 4 Budapest, Pf. 76 Telefon: 7-8900 Fa: 7-890 44. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY MEGYEI FORDULÓ 05. április. NEGYEDIK OSZTÁLY JAVÍTÁSI ÚTMUTATÓ
Rejtélyes rejtvényes Koordináta-rendszer 2. feladatcsomag
 Rejtélyes rejtvényes Koordináta-rendszer 2. feladatcsomag Életkor: Fogalmak, eljárások: 11 17 év számintervallumok ábrázolása tájékozódás a derékszögű koordináta-rendszerben, helymeghatározás, adott tulajdonságú
Rejtélyes rejtvényes Koordináta-rendszer 2. feladatcsomag Életkor: Fogalmak, eljárások: 11 17 év számintervallumok ábrázolása tájékozódás a derékszögű koordináta-rendszerben, helymeghatározás, adott tulajdonságú
KOMPETENCIA ALAPÚ OKTATÁS BEVEZETÉSE FELMENŐ RENDSZERBEN A GYOMAENDRŐDI OKTATÁSI INTÉZMÉNYEKBEN AZONOSÍTÓ SZÁM: TÁMOP-3.1.
 Fejtörő fejtörők - önálló innovációs tevékenység - Készítette: Fekécs Éva Kis Bálint Általános lános Iskola és Óvoda Gyomaendrőd "A természet nagy könyvében csak az tud olvasni, aki ismeri azt a nyelvet,
Fejtörő fejtörők - önálló innovációs tevékenység - Készítette: Fekécs Éva Kis Bálint Általános lános Iskola és Óvoda Gyomaendrőd "A természet nagy könyvében csak az tud olvasni, aki ismeri azt a nyelvet,
Egész számok. pozitív egész számok: 1; 2; 3; 4;... negatív egész számok: 1; 2; 3; 4;...
 Egész számok természetes számok ( ) pozitív egész számok: 1; 2; 3; 4;... 0 negatív egész számok: 1; 2; 3; 4;... egész számok ( ) 1. Írd a következõ számokat a halmazábra megfelelõ helyére! 3; 7; +6 ; (
Egész számok természetes számok ( ) pozitív egész számok: 1; 2; 3; 4;... 0 negatív egész számok: 1; 2; 3; 4;... egész számok ( ) 1. Írd a következõ számokat a halmazábra megfelelõ helyére! 3; 7; +6 ; (
Arany Dániel Matematikai Tanulóverseny 2015/2016-os tanév 1. forduló Haladók III. kategória
 Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 2015/2016-os tanév 1. forduló Haladók III. kategória Megoldások és javítási útmutató 1. Az a és b befogójú derékszögű háromszögnek
Bolyai János Matematikai Társulat Arany Dániel Matematikai Tanulóverseny 2015/2016-os tanév 1. forduló Haladók III. kategória Megoldások és javítási útmutató 1. Az a és b befogójú derékszögű háromszögnek
Kártyajátékok. 10. modul. Készítette: Abonyi tünde
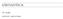 Kártyajátékok. modul Készítette: Abonyi tünde matematika c. ÉVFOLYAM. modul: Kártyajátékok Kártyajátékok A modul célja Időkeret Ajánlott korosztály A tudatos észlelés, a megfigyelés és a figyelem fejlesztése.
Kártyajátékok. modul Készítette: Abonyi tünde matematika c. ÉVFOLYAM. modul: Kártyajátékok Kártyajátékok A modul célja Időkeret Ajánlott korosztály A tudatos észlelés, a megfigyelés és a figyelem fejlesztése.
I. Egyenlet fogalma, algebrai megoldása
 11 modul: EGYENLETEK, EGYENLŐTLENSÉGEK MEGOLDÁSA 6 I Egyenlet fogalma, algebrai megoldása Módszertani megjegyzés: Az egyenletek alaphalmazát, értelmezési tartományát később vezetjük be, a törtes egyenletekkel
11 modul: EGYENLETEK, EGYENLŐTLENSÉGEK MEGOLDÁSA 6 I Egyenlet fogalma, algebrai megoldása Módszertani megjegyzés: Az egyenletek alaphalmazát, értelmezési tartományát később vezetjük be, a törtes egyenletekkel
Minta 2. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI FELADATSOR. I. rész
 2. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI FELADATSOR I. rész A feladatok megoldására 45 perc fordítható, az idő leteltével a munkát be kell fejeznie. A feladatok megoldási sorrendje tetszőleges. A feladatok megoldásához
2. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI FELADATSOR I. rész A feladatok megoldására 45 perc fordítható, az idő leteltével a munkát be kell fejeznie. A feladatok megoldási sorrendje tetszőleges. A feladatok megoldásához
EGYENLETEK. Mérleg-elv. = + x 1. = x + 12 2. 2 x + = 1 3x 10. = 1. 17. 13 3x. 5 x 11. ( ) Abszolutértékes egyenletek, egyenlőtlenségek. 28.
 EGYENLETEK Mérleg-elv..... 6. + = 7 = + = 7+ 7+ 6 + = + = = ( ) 7. = + + 6 8 6 8. = 7 7 9.. 7 = + ( ) + + =. + Abszolutértékes egyenletek, egyenlőtlenségek. = 7. =. =. 8 = 6. 7 9 = 7. = 8. 8 = 9. =. 6.
EGYENLETEK Mérleg-elv..... 6. + = 7 = + = 7+ 7+ 6 + = + = = ( ) 7. = + + 6 8 6 8. = 7 7 9.. 7 = + ( ) + + =. + Abszolutértékes egyenletek, egyenlőtlenségek. = 7. =. =. 8 = 6. 7 9 = 7. = 8. 8 = 9. =. 6.
BOLYAI MATEMATIKA CSAPATVERSENY ORSZÁGOS DÖNTŐ SZÓBELI (2018. NOVEMBER 24.) 3. osztály
 3. osztály Milyen számot írnátok az üres háromszögbe? Miért? Számpiramist kezdtünk építeni valamilyen szabály szerint (lásd az ábrán). Keressétek meg, mi lehet a szabály, és írjátok a betűk helyére a megfelelő
3. osztály Milyen számot írnátok az üres háromszögbe? Miért? Számpiramist kezdtünk építeni valamilyen szabály szerint (lásd az ábrán). Keressétek meg, mi lehet a szabály, és írjátok a betűk helyére a megfelelő
VI. Felkészítő feladatsor
 VI. Felkészítő feladatsor I. 1. Egyszerűsítse az y 3 y 2 y 1 törtet, ha y 1. 2. Milyen számjegy állhat az X helyén, ha a négyjegyű 450X szám 6-tal osztható? 3. Minden utca zajos. Válassza ki az alábbiak
VI. Felkészítő feladatsor I. 1. Egyszerűsítse az y 3 y 2 y 1 törtet, ha y 1. 2. Milyen számjegy állhat az X helyén, ha a négyjegyű 450X szám 6-tal osztható? 3. Minden utca zajos. Válassza ki az alábbiak
Másodfokú egyenletek. 2. Ábrázoljuk és jellemezzük a következő,a valós számok halmazán értelmezett függvényeket!
 Másodfokú egyenletek 1. Alakítsuk teljes négyzetté a következő kifejezéseket! a.) - 4 + 4 b.) - 6 + 8 c.) + 8 - d.) - 4 + 9 e.) - + 8 - f.) - - 4 + 3 g.) + 8-5 h.) - 4 + 3 i.) -3 + 6 + 1. Ábrázoljuk és
Másodfokú egyenletek 1. Alakítsuk teljes négyzetté a következő kifejezéseket! a.) - 4 + 4 b.) - 6 + 8 c.) + 8 - d.) - 4 + 9 e.) - + 8 - f.) - - 4 + 3 g.) + 8-5 h.) - 4 + 3 i.) -3 + 6 + 1. Ábrázoljuk és
46. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY HARMADIK OSZTÁLY
 46. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY Megyei forduló Javítási útmutató HARMADIK OSZTÁLY. Írd be a körökbe a 2, 3, 4 és 5 számokat úgy, hogy a szomszédos számok különbsége -nél nagyobb legyen!
46. ORSZÁGOS TIT KALMÁR LÁSZLÓ MATEMATIKAVERSENY Megyei forduló Javítási útmutató HARMADIK OSZTÁLY. Írd be a körökbe a 2, 3, 4 és 5 számokat úgy, hogy a szomszédos számok különbsége -nél nagyobb legyen!
9-10. évfolyam felnőttképzés Heti óraszám: 3 óra
 9-10. évfolyam felnőttképzés Heti óraszám: 3 óra Fejlesztési cél/ kompetencia lehetőségei: Gondolkodási képességek: rendszerezés, kombinativitás, deduktív következtetés, valószínűségi Tudásszerző képességek:
9-10. évfolyam felnőttképzés Heti óraszám: 3 óra Fejlesztési cél/ kompetencia lehetőségei: Gondolkodási képességek: rendszerezés, kombinativitás, deduktív következtetés, valószínűségi Tudásszerző képességek:
