Alternating Permutations
|
|
|
- Rebeka Oroszné
- 6 évvel ezelőtt
- Látták:
Átírás
1 Alternating Permutations Richard P. Stanley M.I.T.
2 Definitions A sequence a 1, a 2,..., a k of distinct integers is alternating if a 1 > a 2 < a 3 > a 4 <, and reverse alternating if a 1 < a 2 > a 3 < a 4 >.
3 Definitions A sequence a 1, a 2,..., a k of distinct integers is alternating if a 1 > a 2 < a 3 > a 4 <, and reverse alternating if a 1 < a 2 > a 3 < a 4 >. S n : symmetric group of all permutations of 1, 2,..., n
4 E n E n = #{w S n : w is alternating} = #{w S n : w is reverse alternating} via a 1 a 2 a n n + 1 a 1, n + 1 a 2,..., n + 1 a n
5 E n E n = #{w S n : w is alternating} = #{w S n : w is reverse alternating} via a 1 a 2 a n n + 1 a 1, n + 1 a 2,..., n + 1 a n E.g., E 4 = 5: 2143, 3142, 3241, 4132, 4231
6 André s theorem Theorem (Désiré André, 1879) y := n 0 E n x n n! = sec x + tan x
7 André s theorem Theorem (Désiré André, 1879) y := n 0 E n x n n! = sec x + tan x E n is an Euler number, E 2n a secant number, E 2n 1 a tangent number.
8 Naive proof }{{} alternating 1826 }{{} alternating
9 Naive proof }{{} alternating 1826 }{{} alternating Obtain w that is either alternating or reverse alternating.
10 Naive proof }{{} alternating 1826 }{{} alternating Obtain w that is either alternating or reverse alternating. 2E n+1 = n k=0 ( ) n E k E n k, n 1 k
11 Completion of proof 2E n+1 = n k=0 ( ) n E k E n k, n 1 k
12 Completion of proof 2E n+1 = n k=0 ( ) n E k E n k, n 1 k 2 n 0 E n+1 x n n! = 2y n 0 ( n k=0 ( ) n x )E n k E n k k n! = 1 + y 2
13 Completion of proof 2E n+1 = n k=0 ( ) n E k E n k, n 1 k 2 n 0 E n+1 x n n! = 2y n 0 ( n k=0 ( ) n x )E n k E n k k n! = 1 + y 2 2y = 1 + y 2, etc.
14 A generalization more sophisticated approaches. E.g., let f k (n) = #{w S n : w(r) < w(r + 1) k r} f 2 (n) = E n
15 A generalization more sophisticated approaches. E.g., let f k (n) = #{w S n : w(r) < w(r + 1) k r} f 2 (n) = E n Theorem. k 0 f k (kn) xkn (kn)! = ( n 0 ) 1 ( 1) n xkn. (kn)!
16 Combinatorial trigonometry Define sec x and tan x by sec x + tan x = n 0 E n x n n!.
17 Combinatorial trigonometry Define sec x and tan x by sec x + tan x = n 0 E n x n n!. Exercise. sec 2 x = 1 + tan 2 x
18 Combinatorial trigonometry Define sec x and tan x by sec x + tan x = n 0 E n x n n!. Exercise. sec 2 x = 1 + tan 2 x Exercise. tan(x + y) = tan x + tan y 1 (tan x)(tan y)
19 Some occurences of Euler numbers (1) E 2n 1 is the number of complete increasing binary trees on the vertex set [2n + 1] = {1, 2,..., 2n + 1}.
20 Five vertices
21 Five vertices Slightly more complicated for E 2n
22 Simsun permutations Definition. A permutation w = a 1 a n S n is simsun if for all 1 k n, the restriction b 1 b k of w to 1, 2,..., k has no double descents b i 1 > b i > b i+1.
23 Simsun permutations Definition. A permutation w = a 1 a n S n is simsun if for all 1 k n, the restriction b 1 b k of w to 1, 2,..., k has no double descents b i 1 > b i > b i+1. Example is not simsun: restriction to 1, 2, 3, 4 is 3421.
24 Simsun permutations Definition. A permutation w = a 1 a n S n is simsun if for all 1 k n, the restriction b 1 b k of w to 1, 2,..., k has no double descents b i 1 > b i > b i+1. Example is not simsun: restriction to 1, 2, 3, 4 is Theorem (R. Simion and S. Sundaram) The number of simsun permutations w S n is E n.
25 Chains of partitions (2) Start with n one-element sets {1},..., {n}.
26 Chains of partitions (2) Start with n one-element sets {1},..., {n}. Merge together two at a time until reaching {1, 2,..., n}.
27 Chains of partitions (2) Start with n one-element sets {1},..., {n}. Merge together two at a time until reaching {1, 2,..., n} , , , ,
28 Chains of partitions (2) Start with n one-element sets {1},..., {n}. Merge together two at a time until reaching {1, 2,..., n} , , , , S n acts on these chains.
29 Chains of partitions (2) Start with n one-element sets {1},..., {n}. Merge together two at a time until reaching {1, 2,..., n} , , , , S n acts on these chains. Theorem. The number of S n -orbits is E n 1.
30 Orbit representatives for n =
31 A polytope volume Let P n be the convex polytope in R n with equations x i 0, 1 i n x i + x i+1 1, 1 i n 1.
32 A polytope volume Let P n be the convex polytope in R n with equations x i 0, 1 i n x i + x i+1 1, 1 i n 1. Theorem. vol(p n ) = 1 n! E n
33 Ulam s problem Let E(n) be the expected length is(w) of the longest increasing subsequence of w.
34 Ulam s problem Let E(n) be the expected length is(w) of the longest increasing subsequence of w. w = is(w) = 3
35 Two highlights Long story...
36 Two highlights Long story... Logan-Shepp, Vershik-Kerov: E(n) 2 n
37 Two highlights Long story... Logan-Shepp, Vershik-Kerov: E(n) 2 n Write is n (w) for is(w) when w S n. Baik-Deift-Johansson: ( lim Prob isn (w) 2 n n n 1/6 the Tracy-Widom distribution. ) t = F (t),
38 Alternating subsequences? as(w) = length of longest alternating subseq. of w w = as(w) = 5
39 The main lemma MAIN LEMMA. w S n alternating subsequence of maximal length that contains n.
40 The main lemma MAIN LEMMA. w S n alternating subsequence of maximal length that contains n. a k (n) = #{w S n : as(w) = k} b k (n) = a 1 (n) + a 2 (n) + + a k (n) = #{w S n : as(w) k}.
41 Recurrence for a k (n) 2r+s=k 1 a k (n) = n j=1 ( ) n 1 j 1 (a 2r (j 1) + a 2r+1 (j 1)) a s (n j)
42 The main generating function Theorem. Define B(x, t) = B(x, t) = where ρ= 1 t 2. k,n 0 b k (n)t k xn n! 2/ρ 1 1 ρ t e ρx 1 ρ,
43 Formulas for b k (n) Corollary. b 1 (n) = 1 b 2 (n) = n b 3 (n) = 1 4 (3n 2n + 3) b 4 (n) = 1 8 (4n (2n 4)2 n ).
44 Formulas for b k (n) Corollary. b 1 (n) = 1 b 2 (n) = n b 3 (n) = 1 4 (3n 2n + 3) b 4 (n) = 1 8 (4n (2n 4)2 n ) no such formulas for longest increasing subsequences.
45 Mean (expectation) of as(w) D(n) = 1 n! w S n as(w), the expectation of as(n) for w S n
46 Mean (expectation) of as(w) D(n) = 1 n! w S n as(w), the expectation of as(n) for w S n Let A(x, t) = a k (n)t k xn = (1 t)b(x, t) n! k,n 0 ( ) 2/ρ = (1 t) 1 1 ρ t e 1. ρx ρ
47 Formula for D(n) n 0 D(n)x n = A(x, 1) t = 6x 3x2 + x 3 6(1 x) 2 = x + n 2 4n x n.
48 Formula for D(n) n 0 D(n)x n = A(x, 1) t = 6x 3x2 + x 3 6(1 x) 2 = x + n 2 4n x n. A(n) = 4n + 1 6, n 2
49 Formula for D(n) n 0 D(n)x n = A(x, 1) t = 6x 3x2 + x 3 6(1 x) 2 = x + n 2 4n x n. A(n) = 4n + 1, n 2 6 Recall E(n) 2 n.
50 Variance of as(w) V (n) = 1 n! w S n ( as(w) 4n + 1 ) 2, n 2 6 the variance of as(n) for w S n
51 Variance of as(w) V (n) = 1 n! w S n ( as(w) 4n + 1 ) 2, n 2 6 the variance of as(n) for w S n Corollary. V (n) = 8 45 n , n 4
52 Variance of as(w) V (n) = 1 n! w S n ( as(w) 4n + 1 ) 2, n 2 6 the variance of as(n) for w S n Corollary. V (n) = 8 45 n , n 4 similar results for higher moments
53 A new distribution? P (t) = lim n Prob w Sn ( as(w) 2n/3 n ) t
54 A new distribution? P (t) = lim n Prob w Sn Stanley distribution? ( as(w) 2n/3 n ) t
55 Limiting distribution Theorem (Pemantle, Widom, (Wilf)). ( as(w) 2n/3 lim Prob w S n n n ) t (Gaussian distribution) = 1 t 45/4 π e s2 ds
56 Limiting distribution Theorem (Pemantle, Widom, (Wilf)). ( as(w) 2n/3 lim Prob w S n n n ) t (Gaussian distribution) = 1 t 45/4 π e s2 ds
57 Umbral enumeration Umbral formula: involves E k, where E is an indeterminate (the umbra). Replace E k with the Euler number E k. (Technique from 19th century, modernized by Rota et al.)
58 Umbral enumeration Umbral formula: involves E k, where E is an indeterminate (the umbra). Replace E k with the Euler number E k. (Technique from 19th century, modernized by Rota et al.) Example. (1 + E 2 ) 3 = 1 + 3E 2 + 3E 4 + E 6 = 1 + 3E 2 + 3E 4 + E 6 = = 80
59 Another example (1 + t) E = 1 + Et + ( ) E t ( ) E t = 1 + Et E(E 1)t2 + = 1 + E 1 t (E 2 E 1 ))t 2 + = 1 + t (1 1)t2 + = 1 + t + O(t 3 ).
60 Alt. fixed-point free involutions fixed point free involution w S 2n : all cycles of length two
61 Alt. fixed-point free involutions fixed point free involution w S 2n : all cycles of length two Let f(n) be the number of alternating fixed-point free involutions in S 2n.
62 Alt. fixed-point free involutions fixed point free involution w S 2n : all cycles of length two Let f(n) be the number of alternating fixed-point free involutions in S 2n. n = 3 : = (1, 2)(3, 4)(5, 6) = (1, 6)(2, 4)(3, 5) f(3) = 2
63 An umbral theorem Theorem. F (x) = n 0 f(n)x n
64 An umbral theorem Theorem. F (x) = n 0 f(n)x n = ( ) (E 1 + x 2 +1)/4 1 x
65 An umbral theorem Theorem. F (x) = n 0 f(n)x n = ( ) (E 1 + x 2 +1)/4 1 x Proof. Uses representation theory of the symmetric group S n. In particular, there is a nice representation of dimension E n.
66 Ramanujan s Lost Notebook Theorem (Ramanujan, Berndt, implicitly) As x 0+, 2 n 0 ( ) n(n+1) 1 x 1 + x k 0 f(k)x k = F (x), an analytic (non-formal) identity.
67 A formal identity Corollary (via Ramanujan, Andrews). F (x) = 2 n 0 n q n j=1 (1 q2j 1 ) 2n+1 j=1 (1 + qj ), where q = ( 1 x 1+x) 2/3, a formal identity.
68 Simple result, hard proof Recall: number of n-cycles in S n is (n 1)!.
69 Simple result, hard proof Recall: number of n-cycles in S n is (n 1)!. Theorem. Let b(n) be the number of alternating n-cycles in S n. Then if n is odd, b(n) = 1 n µ(d)( 1) (d 1)/2 E n/d. d n
70 Special case Corollary. Let p be an odd prime. Then b(p) = 1 ) (E p ( 1) (p 1)/2. p
71 Special case Corollary. Let p be an odd prime. Then b(p) = 1 ) (E p ( 1) (p 1)/2. p Combinatorial proof?
72 Another such result Recall: the expected number of fixed points of w S n is 1.
73 Another such result Recall: the expected number of fixed points of w S n is 1. J(n) = expected number of fixed points of reverse alternating w S n Theorem. J(2n) = 1 E 2n (E 2n ( 1) n ). Similar (but more complicated) for n odd or for alternating permutations.
74 Another such result Recall: the expected number of fixed points of w S n is 1. J(n) = expected number of fixed points of reverse alternating w S n Theorem. J(2n) = 1 E 2n (E 2n ( 1) n ). Similar (but more complicated) for n odd or for alternating permutations. Combinatorial proof?
75 Descent sets Let w = a 1 a 2 a n S n. Descent set of w: D(w) = {i : a i > a i+1 } {1,..., n 1}
76 Descent sets Let w = a 1 a 2 a n S n. Descent set of w: D(w) = {i : a i > a i+1 } {1,..., n 1} D( ) = {1, 4, 5} D( ) = {1, 3, 5} (alternating) D( ) = {2, 4, 6} (reverse alternating)
77 β n (S) β n (S) = #{w S n : D(w) = S}
78 β n (S) β n (S) = #{w S n : D(w) = S} w D(w) {1} 312 {1} 132 {2} 231 {2} 321 {1, 2} β 3 ( ) = 1, β 3 (1) = 2 β 3 (2) = 2, β 3 (1, 2) = 1
79 u S Fix n. Let S {1,, n 1}. Let u S = t 1 t n 1, where { a, i S t i = b, i S.
80 u S Fix n. Let S {1,, n 1}. Let u S = t 1 t n 1, where { a, i S t i = b, i S. Example. n = 8, S = {2, 5, 6} {1,..., 7} u S = abaabba
81 A noncommutative gen. function Ψ n (a, b) = S {1,...,n 1} β n (S)u S.
82 A noncommutative gen. function Ψ n (a, b) = Example. Recall S {1,...,n 1} β n (S)u S. β 3 ( ) = 1, β 3 (1) = 2, β 3 (2) = 2, β 3 (1, 2) = 1 Thus Ψ 3 (a, b) = aa + 2ab + 2ba + bb
83 A noncommutative gen. function Ψ n (a, b) = Example. Recall S {1,...,n 1} β n (S)u S. β 3 ( ) = 1, β 3 (1) = 2, β 3 (2) = 2, β 3 (1, 2) = 1 Thus Ψ 3 (a, b) = aa + 2ab + 2ba + bb = (a + b) 2 + (ab + ba)
84 The cd-index Theorem. There exists a noncommutative polynomial Φ n (c, d), called the cd-index of S n, with nonnegative integer coefficients, such that Ψ n (a, b) = Φ n (a + b, ab + ba).
85 The cd-index Theorem. There exists a noncommutative polynomial Φ n (c, d), called the cd-index of S n, with nonnegative integer coefficients, such that Example. Recall Ψ n (a, b) = Φ n (a + b, ab + ba). Ψ 3 (a, b) = aa + 2ab + 2ba + b 2 = (a + b) 2 + (ab + ba). Therefore Φ 3 (c, d) = c 2 + d.
86 Small values of Φ n (c, d) Φ 1 = 1 Φ 2 = c Φ 3 = c 2 + d Φ 4 = c 3 + 2cd + 2dc Φ 5 = c 4 + 3c 2 d + 5cdc + 3dc 2 + 4d 2 Φ 6 = c 5 + 4c 3 d + 9c 2 dc + 9cdc 2 + 4dc 3 +12cd dcd + 12d 2 c.
87 The set S µ Recall: w = a 1 a n S n is simsun if for all 1 k n, the restriction b 1 b k of w to 1, 2,..., k has no double descents b i 1 > b i > b i+1.
88 The set S µ Recall: w = a 1 a n S n is simsun if for all 1 k n, the restriction b 1 b k of w to 1, 2,..., k has no double descents b i 1 > b i > b i+1. Given a cd-monomial µ, let c 0, d 10, and remove final 0. Example. µ = cd 2 c 2 d , the characteristic vector of S µ = {2, 4, 8}.
89 The coefficients of Φ n (c, d) Theorem (Simion-Sundaram) Let µ be a cd-monomial of degree n 1. The coefficient of µ in Φ n (c, d) is the number of simsun permutations w S n 1 with descent set S µ.
90 The case n = 4 w D(w) µ 123 c dc dc cd cd 01 Φ 4 (c, d) = c 3 + 2dc + 2cd
91 Expansion of cd-monomials Let m = m(c, d) be a cd-monomial, e.g., c 2 d 2 cd. Expand m(a + b, ab + ba): (a + b) 2 (ab + ba) 2 (a + b)(ab + ba) = a 9 + ba 8 +.
92 Expansion of cd-monomials Let m = m(c, d) be a cd-monomial, e.g., c 2 d 2 cd. Expand m(a + b, ab + ba): (a + b) 2 (ab + ba) 2 (a + b)(ab + ba) = a 9 + ba 8 +. Key observation: m(a + b, ab + ba) is a sum of distinct monomials, always including ababab and bababa.
93 Alternating permutations The coefficient of ababab and of bababa in Ψ n (a, b) is β n (2, 4, 6,... ) = β n (1, 3, 5,... ) = E n.
94 Alternating permutations The coefficient of ababab and of bababa in Ψ n (a, b) is Hence: β n (2, 4, 6,... ) = β n (1, 3, 5,... ) = E n. Theorem. (a) Φ n (1, 1) = E n (can interpret coefficients combinatorially). (b) For all S {1,..., n 1}, β n (S) β n (1, 3, 5,... ) = E n.
95 An example Φ 5 = 1c 4 + 3c 2 d + 5cdc + 3dc 2 + 4d = 16 = E 5
96 Comments NOTE. (b) is due originally to Niven and later de Bruijn (different proofs).
97 Comments NOTE. (b) is due originally to Niven and later de Bruijn (different proofs). NOTE. Not hard to show that β n (S) < E n unless S = {1, 3, 5,... } or S = {2, 4, 6,... }.
98
On The Number Of Slim Semimodular Lattices
 On The Number Of Slim Semimodular Lattices Gábor Czédli, Tamás Dékány, László Ozsvárt, Nóra Szakács, Balázs Udvari Bolyai Institute, University of Szeged Conference on Universal Algebra and Lattice Theory
On The Number Of Slim Semimodular Lattices Gábor Czédli, Tamás Dékány, László Ozsvárt, Nóra Szakács, Balázs Udvari Bolyai Institute, University of Szeged Conference on Universal Algebra and Lattice Theory
Véges szavak általánosított részszó-bonyolultsága
 Véges szavak általánosított részszó-bonyolultsága KÁSA Zoltán Sapientia Erdélyi Magyar Tudományegyetem Kolozsvár Marosvásárhely Csíkszereda Matematika-Informatika Tanszék, Marosvásárhely Budapest, 2010.
Véges szavak általánosított részszó-bonyolultsága KÁSA Zoltán Sapientia Erdélyi Magyar Tudományegyetem Kolozsvár Marosvásárhely Csíkszereda Matematika-Informatika Tanszék, Marosvásárhely Budapest, 2010.
Construction of a cube given with its centre and a sideline
 Transformation of a plane of projection Construction of a cube given with its centre and a sideline Exercise. Given the center O and a sideline e of a cube, where e is a vertical line. Construct the projections
Transformation of a plane of projection Construction of a cube given with its centre and a sideline Exercise. Given the center O and a sideline e of a cube, where e is a vertical line. Construct the projections
Local fluctuations of critical Mandelbrot cascades. Konrad Kolesko
 Local fluctuations of critical Mandelbrot cascades Konrad Kolesko joint with D. Buraczewski and P. Dyszewski Warwick, 18-22 May, 2015 Random measures µ µ 1 µ 2 For given random variables X 1, X 2 s.t.
Local fluctuations of critical Mandelbrot cascades Konrad Kolesko joint with D. Buraczewski and P. Dyszewski Warwick, 18-22 May, 2015 Random measures µ µ 1 µ 2 For given random variables X 1, X 2 s.t.
Mapping Sequencing Reads to a Reference Genome
 Mapping Sequencing Reads to a Reference Genome High Throughput Sequencing RN Example applications: Sequencing a genome (DN) Sequencing a transcriptome and gene expression studies (RN) ChIP (chromatin immunoprecipitation)
Mapping Sequencing Reads to a Reference Genome High Throughput Sequencing RN Example applications: Sequencing a genome (DN) Sequencing a transcriptome and gene expression studies (RN) ChIP (chromatin immunoprecipitation)
Erdős-Ko-Rado theorems on the weak Bruhat lattice
 Erdős-Ko-Rado theorems on the weak Bruhat lattice arxiv:1904.01436v1 [math.co] 2 Apr 2019 Susanna Fishel, Glenn Hurlbert, Vikram Kamat, Karen Meagher April 3, 2019 Abstract Let L = (X, ) be a lattice.
Erdős-Ko-Rado theorems on the weak Bruhat lattice arxiv:1904.01436v1 [math.co] 2 Apr 2019 Susanna Fishel, Glenn Hurlbert, Vikram Kamat, Karen Meagher April 3, 2019 Abstract Let L = (X, ) be a lattice.
Statistical Inference
 Petra Petrovics Statistical Inference 1 st lecture Descriptive Statistics Inferential - it is concerned only with collecting and describing data Population - it is used when tentative conclusions about
Petra Petrovics Statistical Inference 1 st lecture Descriptive Statistics Inferential - it is concerned only with collecting and describing data Population - it is used when tentative conclusions about
Schwarz lemma, the Carath eodory and Kobayashi metrics and applications in complex analysis
 Schwarz lemma, the Carath eodory and Kobayashi metrics and applications in complex analysis Workshop: The perturbation of the generalized inverses, geometric structures, xed point theory and applications
Schwarz lemma, the Carath eodory and Kobayashi metrics and applications in complex analysis Workshop: The perturbation of the generalized inverses, geometric structures, xed point theory and applications
Cluster Analysis. Potyó László
 Cluster Analysis Potyó László What is Cluster Analysis? Cluster: a collection of data objects Similar to one another within the same cluster Dissimilar to the objects in other clusters Cluster analysis
Cluster Analysis Potyó László What is Cluster Analysis? Cluster: a collection of data objects Similar to one another within the same cluster Dissimilar to the objects in other clusters Cluster analysis
MATEMATIKA ANGOL NYELVEN MATHEMATICS
 ÉRETTSÉGI VIZSGA 2005. május 10. MATEMATIKA ANGOL NYELVEN MATHEMATICS EMELT SZINTŰ ÍRÁSBELI VIZSGA HIGHER LEVEL WRITTEN EXAMINATION Az írásbeli vizsga időtartama: 240 perc Time allowed for the examination:
ÉRETTSÉGI VIZSGA 2005. május 10. MATEMATIKA ANGOL NYELVEN MATHEMATICS EMELT SZINTŰ ÍRÁSBELI VIZSGA HIGHER LEVEL WRITTEN EXAMINATION Az írásbeli vizsga időtartama: 240 perc Time allowed for the examination:
Performance Modeling of Intelligent Car Parking Systems
 Performance Modeling of Intelligent Car Parking Systems Károly Farkas Gábor Horváth András Mészáros Miklós Telek Technical University of Budapest, Hungary EPEW 2014, Florence, Italy Outline Intelligent
Performance Modeling of Intelligent Car Parking Systems Károly Farkas Gábor Horváth András Mészáros Miklós Telek Technical University of Budapest, Hungary EPEW 2014, Florence, Italy Outline Intelligent
Introduction. Lecture 1
 Intrductin Lecture 1 Bimathematics Bimatematika prgram. I. Függvény fgalma, A függvények tulajdnságai. Elemi és összetett függvények. Határérték. Függvények határértéke, flytnsság. Számsrzatk és végtelen
Intrductin Lecture 1 Bimathematics Bimatematika prgram. I. Függvény fgalma, A függvények tulajdnságai. Elemi és összetett függvények. Határérték. Függvények határértéke, flytnsság. Számsrzatk és végtelen
PELL EGYENLETEK MEGOLDÁSA LINEÁRIS REKURZÍV SOROZATOK SEGÍTSÉGÉVEL
 PELL EGYENLETEK MEGOLDÁSA LINEÁRIS REKURZÍV SOROZATOK SEGÍTSÉGÉVEL KISS PÉTER Legyenek A, B, G 0, G x rögzített egész számok, melyekre AB ^ 0 és G 0, G x nem mindkettője zérus. Az egész számok G 0, G 1(
PELL EGYENLETEK MEGOLDÁSA LINEÁRIS REKURZÍV SOROZATOK SEGÍTSÉGÉVEL KISS PÉTER Legyenek A, B, G 0, G x rögzített egész számok, melyekre AB ^ 0 és G 0, G x nem mindkettője zérus. Az egész számok G 0, G 1(
Eötvös Loránd Tudományegyetem Informatikai Kar. Additív számelméleti függvények eloszlása
 Eötvös Loránd Tudományegyetem Informatikai Kar Additív számelméleti függvények eloszlása Doktori értekezés tézisei Germán László Témavezető Prof. Dr. Kátai Imre akadémikus Informatika Doktori Iskola vezető:
Eötvös Loránd Tudományegyetem Informatikai Kar Additív számelméleti függvények eloszlása Doktori értekezés tézisei Germán László Témavezető Prof. Dr. Kátai Imre akadémikus Informatika Doktori Iskola vezető:
Efficient symmetric key private authentication
 Efficient symmetric key private authentication Cryptographic Protocols (EIT ICT MSc) Dr. Levente Buttyán Associate Professor BME Hálózati Rendszerek és Szolgáltatások Tanszék Lab of Cryptography and System
Efficient symmetric key private authentication Cryptographic Protocols (EIT ICT MSc) Dr. Levente Buttyán Associate Professor BME Hálózati Rendszerek és Szolgáltatások Tanszék Lab of Cryptography and System
Ensemble Kalman Filters Part 1: The basics
 Ensemble Kalman Filters Part 1: The basics Peter Jan van Leeuwen Data Assimilation Research Centre DARC University of Reading p.j.vanleeuwen@reading.ac.uk Model: 10 9 unknowns P[u(x1),u(x2),T(x3),.. Observations:
Ensemble Kalman Filters Part 1: The basics Peter Jan van Leeuwen Data Assimilation Research Centre DARC University of Reading p.j.vanleeuwen@reading.ac.uk Model: 10 9 unknowns P[u(x1),u(x2),T(x3),.. Observations:
Genome 373: Hidden Markov Models I. Doug Fowler
 Genome 373: Hidden Markov Models I Doug Fowler Review From Gene Prediction I transcriptional start site G open reading frame transcriptional termination site promoter 5 untranslated region 3 untranslated
Genome 373: Hidden Markov Models I Doug Fowler Review From Gene Prediction I transcriptional start site G open reading frame transcriptional termination site promoter 5 untranslated region 3 untranslated
Bevezetés a kvantum-informatikába és kommunikációba 2015/2016 tavasz
 Bevezetés a kvantum-informatikába és kommunikációba 2015/2016 tavasz Kvantumkapuk, áramkörök 2016. március 3. A kvantummechanika posztulátumai (1-2) 1. Állapotleírás Zárt fizikai rendszer aktuális állapota
Bevezetés a kvantum-informatikába és kommunikációba 2015/2016 tavasz Kvantumkapuk, áramkörök 2016. március 3. A kvantummechanika posztulátumai (1-2) 1. Állapotleírás Zárt fizikai rendszer aktuális állapota
Simonovits M. Elekes Gyuri és az illeszkedések p. 1
 Elekes Gyuri és az illeszkedések Simonovits M. Elekes Gyuri és az illeszkedések p. 1 On the number of high multiplicity points for 1-parameter families of curves György Elekes, Miklós Simonovits and Endre
Elekes Gyuri és az illeszkedések Simonovits M. Elekes Gyuri és az illeszkedések p. 1 On the number of high multiplicity points for 1-parameter families of curves György Elekes, Miklós Simonovits and Endre
To make long stories short from the last 24 years
 To make long stories short from the last 24 years András Sebő, CNRS, G-SCOP, Grenoble Kathie: We would like the talks to be easy to understand. Jack prefers talks on stuff he should have known years ago
To make long stories short from the last 24 years András Sebő, CNRS, G-SCOP, Grenoble Kathie: We would like the talks to be easy to understand. Jack prefers talks on stuff he should have known years ago
ACTA ACADEMIAE PAEDAGOGICAE AGRIENSIS
 Separatum ACTA ACADEMIAE PAEDAGOGICAE AGRIESIS OVA SERIES TOM. XXII. SECTIO MATEMATICAE TÓMÁCS TIBOR Egy rekurzív sorozat tagjainak átlagáról EGER, 994 Egy rekurzív sorozat tagjainak átlagáról TÓMÁCS TIBOR
Separatum ACTA ACADEMIAE PAEDAGOGICAE AGRIESIS OVA SERIES TOM. XXII. SECTIO MATEMATICAE TÓMÁCS TIBOR Egy rekurzív sorozat tagjainak átlagáról EGER, 994 Egy rekurzív sorozat tagjainak átlagáról TÓMÁCS TIBOR
Characterizations and Properties of Graphs of Baire Functions
 Characterizations and Properties of Graphs of Baire Functions BSc Szakdolgozat Szerz : Témavezet : Maga Balázs Buczolich Zoltán Matematika BSc Matematikus Egyetemi tanár Analízis Tanszék Eötvös Loránd
Characterizations and Properties of Graphs of Baire Functions BSc Szakdolgozat Szerz : Témavezet : Maga Balázs Buczolich Zoltán Matematika BSc Matematikus Egyetemi tanár Analízis Tanszék Eötvös Loránd
SQL/PSM kurzorok rész
 SQL/PSM kurzorok --- 2.rész Tankönyv: Ullman-Widom: Adatbázisrendszerek Alapvetés Második, átdolgozott kiadás, Panem, 2009 9.3. Az SQL és a befogadó nyelv közötti felület (sormutatók) 9.4. SQL/PSM Sémában
SQL/PSM kurzorok --- 2.rész Tankönyv: Ullman-Widom: Adatbázisrendszerek Alapvetés Második, átdolgozott kiadás, Panem, 2009 9.3. Az SQL és a befogadó nyelv közötti felület (sormutatók) 9.4. SQL/PSM Sémában
Correlation & Linear Regression in SPSS
 Petra Petrovics Correlation & Linear Regression in SPSS 4 th seminar Types of dependence association between two nominal data mixed between a nominal and a ratio data correlation among ratio data Correlation
Petra Petrovics Correlation & Linear Regression in SPSS 4 th seminar Types of dependence association between two nominal data mixed between a nominal and a ratio data correlation among ratio data Correlation
Többszörösen élesen tranzitív halmazok véges csoportokban
 Többszörösen élesen tranzitív halmazok véges csoportokban habilitációs tudományos előadás Nagy Gábor Péter Szegedi Tudományegyetem Bolyai Intézet, Geometria Tanszék 2013. március 12. 1 / 19 Áttekintés
Többszörösen élesen tranzitív halmazok véges csoportokban habilitációs tudományos előadás Nagy Gábor Péter Szegedi Tudományegyetem Bolyai Intézet, Geometria Tanszék 2013. március 12. 1 / 19 Áttekintés
Publikációs lista. Vásárhelyi Bálint Márk
 Publikációs lista Vásárhelyi Bálint Márk 018 A disszertáció a következ közleményeken alapul: 1. Béla Csaba, Bálint Márk Vásárhelyi, On embedding degree sequences, Informatica (SI), 018+, megjelenés alatt.
Publikációs lista Vásárhelyi Bálint Márk 018 A disszertáció a következ közleményeken alapul: 1. Béla Csaba, Bálint Márk Vásárhelyi, On embedding degree sequences, Informatica (SI), 018+, megjelenés alatt.
MATEMATIKA ANGOL NYELVEN
 ÉRETTSÉGI VIZSGA 2012. május 8. MATEMATIKA ANGOL NYELVEN EMELT SZINTŰ ÍRÁSBELI VIZSGA 2012. május 8. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
ÉRETTSÉGI VIZSGA 2012. május 8. MATEMATIKA ANGOL NYELVEN EMELT SZINTŰ ÍRÁSBELI VIZSGA 2012. május 8. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
16F628A megszakítás kezelése
 16F628A megszakítás kezelése A 'megszakítás' azt jelenti, hogy a program normális, szekvenciális futása valamilyen külső hatás miatt átmenetileg felfüggesztődik, és a vezérlést egy külön rutin, a megszakításkezelő
16F628A megszakítás kezelése A 'megszakítás' azt jelenti, hogy a program normális, szekvenciális futása valamilyen külső hatás miatt átmenetileg felfüggesztődik, és a vezérlést egy külön rutin, a megszakításkezelő
ELEKTRONIKAI ALAPISMERETEK ANGOL NYELVEN
 ÉRETTSÉGI VIZSGA 2008. május 26. ELEKTRONIKAI ALAPISMERETEK ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2008. május 26. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI
ÉRETTSÉGI VIZSGA 2008. május 26. ELEKTRONIKAI ALAPISMERETEK ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2008. május 26. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI
Adattípusok. Max. 2GByte
 Adattípusok Típus Méret Megjegyzés Konstans BIT 1 bit TRUE/FALSE SMALLINT 2 byte -123 INTEGER 4 byte -123 COUNTER 4 byte Automatikus 123 REAL 4 byte -12.34E-2 FLOAT 8 byte -12.34E-2 CURRENCY / MONEY 8
Adattípusok Típus Méret Megjegyzés Konstans BIT 1 bit TRUE/FALSE SMALLINT 2 byte -123 INTEGER 4 byte -123 COUNTER 4 byte Automatikus 123 REAL 4 byte -12.34E-2 FLOAT 8 byte -12.34E-2 CURRENCY / MONEY 8
Phenotype. Genotype. It is like any other experiment! What is a bioinformatics experiment? Remember the Goal. Infectious Disease Paradigm
 It is like any other experiment! What is a bioinformatics experiment? You need to know your data/input sources You need to understand your methods and their assumptions You need a plan to get from point
It is like any other experiment! What is a bioinformatics experiment? You need to know your data/input sources You need to understand your methods and their assumptions You need a plan to get from point
Probabilistic Analysis and Randomized Algorithms. Alexandre David B2-206
 Probabilistic Analysis and Randomized Algorithms Alexandre David B2-206 Today Counting. Basic probability. Appendix C Introduction to randomized algorithms. Chapter 5 27-10-2006 AA1 2 Counting Rule of
Probabilistic Analysis and Randomized Algorithms Alexandre David B2-206 Today Counting. Basic probability. Appendix C Introduction to randomized algorithms. Chapter 5 27-10-2006 AA1 2 Counting Rule of
Adattípusok. Max. 2GByte
 Adattípusok Típus Méret Megjegyzés Konstans BIT 1 bit TRUE/FALSE TINIINT 1 byte 12 SMALLINT 2 byte -123 INTEGER 4 byte -123 COUNTER 4 byte Automatikus 123 REAL 4 byte -12.34E-2 FLOAT 8 byte -12.34E-2 CURRENCY
Adattípusok Típus Méret Megjegyzés Konstans BIT 1 bit TRUE/FALSE TINIINT 1 byte 12 SMALLINT 2 byte -123 INTEGER 4 byte -123 COUNTER 4 byte Automatikus 123 REAL 4 byte -12.34E-2 FLOAT 8 byte -12.34E-2 CURRENCY
Figurális számok és diofantikus egyenletek
 Egyetemi doktori (PhD) értekezés tézisei Figurális számok és diofantikus egyenletek Varga Nóra Témavezető: Dr. Pintér Ákos Debreceni Egyetem Matematika- és Számítástudományok Doktori Iskola Debrecen, 2016
Egyetemi doktori (PhD) értekezés tézisei Figurális számok és diofantikus egyenletek Varga Nóra Témavezető: Dr. Pintér Ákos Debreceni Egyetem Matematika- és Számítástudományok Doktori Iskola Debrecen, 2016
MATEMATIKA ANGOL NYELVEN
 ÉRETTSÉGI VIZSGA 2014. május 6. MATEMATIKA ANGOL NYELVEN EMELT SZINTŰ ÍRÁSBELI VIZSGA 2014. május 6. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2014. május 6. MATEMATIKA ANGOL NYELVEN EMELT SZINTŰ ÍRÁSBELI VIZSGA 2014. május 6. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
Általánosan, bármilyen mérés annyit jelent, mint meghatározni, hányszor van meg
 LMeasurement.tex, March, 00 Mérés Általánosan, bármilyen mérés annyit jelent, mint meghatározni, hányszor van meg a mérendő mennyiségben egy másik, a mérendővel egynemű, önkényesen egységnek választott
LMeasurement.tex, March, 00 Mérés Általánosan, bármilyen mérés annyit jelent, mint meghatározni, hányszor van meg a mérendő mennyiségben egy másik, a mérendővel egynemű, önkényesen egységnek választott
Miskolci Egyetem Gazdaságtudományi Kar Üzleti Információgazdálkodási és Módszertani Intézet. Hypothesis Testing. Petra Petrovics.
 Hypothesis Testing Petra Petrovics PhD Student Inference from the Sample to the Population Estimation Hypothesis Testing Estimation: how can we determine the value of an unknown parameter of a population
Hypothesis Testing Petra Petrovics PhD Student Inference from the Sample to the Population Estimation Hypothesis Testing Estimation: how can we determine the value of an unknown parameter of a population
Combinatorics, Paul Erd}os is Eighty (Volume 2) Keszthely (Hungary), 1993, pp. 1{46. Dedicated to the marvelous random walk
 BOLYAI SOCIETY MATHEMATICAL STUDIES, 2 Combinatorics, Paul Erd}os is Eighty (Volume 2) Keszthely (Hungary), 1993, pp. 1{46. Random Walks on Graphs: A Survey L. LOV ASZ Dedicated to the marvelous random
BOLYAI SOCIETY MATHEMATICAL STUDIES, 2 Combinatorics, Paul Erd}os is Eighty (Volume 2) Keszthely (Hungary), 1993, pp. 1{46. Random Walks on Graphs: A Survey L. LOV ASZ Dedicated to the marvelous random
Word and Polygon List for Obtuse Triangular Billiards II
 Word and Polygon List for Obtuse Triangular Billiards II Richard Evan Schwartz August 19, 2008 Abstract This is the list of words and polygons we use for our paper. 1 Notation To compress our notation
Word and Polygon List for Obtuse Triangular Billiards II Richard Evan Schwartz August 19, 2008 Abstract This is the list of words and polygons we use for our paper. 1 Notation To compress our notation
EN United in diversity EN A8-0206/419. Amendment
 22.3.2019 A8-0206/419 419 Article 2 paragraph 4 point a point i (i) the identity of the road transport operator; (i) the identity of the road transport operator by means of its intra-community tax identification
22.3.2019 A8-0206/419 419 Article 2 paragraph 4 point a point i (i) the identity of the road transport operator; (i) the identity of the road transport operator by means of its intra-community tax identification
A rosszindulatú daganatos halálozás változása 1975 és 2001 között Magyarországon
 A rosszindulatú daganatos halálozás változása és között Eredeti közlemény Gaudi István 1,2, Kásler Miklós 2 1 MTA Számítástechnikai és Automatizálási Kutató Intézete, Budapest 2 Országos Onkológiai Intézet,
A rosszindulatú daganatos halálozás változása és között Eredeti közlemény Gaudi István 1,2, Kásler Miklós 2 1 MTA Számítástechnikai és Automatizálási Kutató Intézete, Budapest 2 Országos Onkológiai Intézet,
A logaritmikus legkisebb négyzetek módszerének karakterizációi
 A logaritmikus legkisebb négyzetek módszerének karakterizációi Csató László laszlo.csato@uni-corvinus.hu MTA Számítástechnikai és Automatizálási Kutatóintézet (MTA SZTAKI) Operációkutatás és Döntési Rendszerek
A logaritmikus legkisebb négyzetek módszerének karakterizációi Csató László laszlo.csato@uni-corvinus.hu MTA Számítástechnikai és Automatizálási Kutatóintézet (MTA SZTAKI) Operációkutatás és Döntési Rendszerek
Széchenyi István Egyetem www.sze.hu/~herno
 Oldal: 1/6 A feladat során megismerkedünk a C# és a LabVIEW összekapcsolásának egy lehetőségével, pontosabban nagyon egyszerű C#- ban írt kódból fordítunk DLL-t, amit meghívunk LabVIEW-ból. Az eljárás
Oldal: 1/6 A feladat során megismerkedünk a C# és a LabVIEW összekapcsolásának egy lehetőségével, pontosabban nagyon egyszerű C#- ban írt kódból fordítunk DLL-t, amit meghívunk LabVIEW-ból. Az eljárás
discosnp demo - Peterlongo Pierre 1 DISCOSNP++: Live demo
 discosnp demo - Peterlongo Pierre 1 DISCOSNP++: Live demo Download and install discosnp demo - Peterlongo Pierre 3 Download web page: github.com/gatb/discosnp Chose latest release (2.2.10 today) discosnp
discosnp demo - Peterlongo Pierre 1 DISCOSNP++: Live demo Download and install discosnp demo - Peterlongo Pierre 3 Download web page: github.com/gatb/discosnp Chose latest release (2.2.10 today) discosnp
INDEXSTRUKTÚRÁK III.
 2MU05_Bitmap.pdf camü_ea INDEXSTRUKTÚRÁK III. Molina-Ullman-Widom: Adatbázisrendszerek megvalósítása Panem, 2001könyv 5.4. Bittérkép indexek fejezete alapján Oracle: Indexek a gyakorlatban Oracle Database
2MU05_Bitmap.pdf camü_ea INDEXSTRUKTÚRÁK III. Molina-Ullman-Widom: Adatbázisrendszerek megvalósítása Panem, 2001könyv 5.4. Bittérkép indexek fejezete alapján Oracle: Indexek a gyakorlatban Oracle Database
ELEKTRONIKAI ALAPISMERETEK ANGOL NYELVEN
 ÉRETTSÉGI VIZSGA 200. május 4. ELEKTRONIKAI ALAPISMERETEK ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 200. május 4. 8:00 Az írásbeli vizsga időtartama: 80 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI
ÉRETTSÉGI VIZSGA 200. május 4. ELEKTRONIKAI ALAPISMERETEK ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 200. május 4. 8:00 Az írásbeli vizsga időtartama: 80 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI
Klaszterezés, 2. rész
 Klaszterezés, 2. rész Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 208. április 6. Csima Judit Klaszterezés, 2. rész / 29 Hierarchikus klaszterezés egymásba ágyazott klasztereket
Klaszterezés, 2. rész Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 208. április 6. Csima Judit Klaszterezés, 2. rész / 29 Hierarchikus klaszterezés egymásba ágyazott klasztereket
MATEMATIKA ANGOL NYELVEN
 ÉRETTSÉGI VIZSGA 2016. május 3. MATEMATIKA ANGOL NYELVEN EMELT SZINTŰ ÍRÁSBELI VIZSGA 2016. május 3. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
ÉRETTSÉGI VIZSGA 2016. május 3. MATEMATIKA ANGOL NYELVEN EMELT SZINTŰ ÍRÁSBELI VIZSGA 2016. május 3. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK
MATEMATIKA ANGOL NYELVEN
 ÉRETTSÉGI VIZSGA 2015. május 5. MATEMATIKA ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2015. május 5. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Matematika
ÉRETTSÉGI VIZSGA 2015. május 5. MATEMATIKA ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2015. május 5. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Matematika
Statistical Dependence
 Statistical Dependence Petra Petrovics Statistical Dependence Deinition: Statistical dependence exists when the value o some variable is dependent upon or aected by the value o some other variable. Independent
Statistical Dependence Petra Petrovics Statistical Dependence Deinition: Statistical dependence exists when the value o some variable is dependent upon or aected by the value o some other variable. Independent
Nonrelativistic, non-newtonian gravity
 Nonrelativistic, non-newtonian gravity Dieter Van den Bleeken Bog azic i University based on arxiv:1512.03799 and work in progress with C ag ın Yunus IPM Tehran 27th May 2016 Nonrelativistic, non-newtonian
Nonrelativistic, non-newtonian gravity Dieter Van den Bleeken Bog azic i University based on arxiv:1512.03799 and work in progress with C ag ın Yunus IPM Tehran 27th May 2016 Nonrelativistic, non-newtonian
FÖLDRAJZ ANGOL NYELVEN GEOGRAPHY
 Földrajz angol nyelven középszint 0623 ÉRETTSÉGI VIZSGA 2007. május 15. FÖLDRAJZ ANGOL NYELVEN GEOGRAPHY KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA INTERMEDIATE LEVEL WRITTEN EXAM JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
Földrajz angol nyelven középszint 0623 ÉRETTSÉGI VIZSGA 2007. május 15. FÖLDRAJZ ANGOL NYELVEN GEOGRAPHY KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA INTERMEDIATE LEVEL WRITTEN EXAM JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ
Miskolci Egyetem Gazdaságtudományi Kar Üzleti Információgazdálkodási és Módszertani Intézet Nonparametric Tests
 Nonparametric Tests Petra Petrovics Hypothesis Testing Parametric Tests Mean of a population Population proportion Population Standard Deviation Nonparametric Tests Test for Independence Analysis of Variance
Nonparametric Tests Petra Petrovics Hypothesis Testing Parametric Tests Mean of a population Population proportion Population Standard Deviation Nonparametric Tests Test for Independence Analysis of Variance
FÖLDRAJZ ANGOL NYELVEN
 Földrajz angol nyelven középszint 1311 ÉRETTSÉGI VIZSGA 2013. május 15. FÖLDRAJZ ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Paper
Földrajz angol nyelven középszint 1311 ÉRETTSÉGI VIZSGA 2013. május 15. FÖLDRAJZ ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI ÉRETTSÉGI VIZSGA JAVÍTÁSI-ÉRTÉKELÉSI ÚTMUTATÓ EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Paper
Tudományos Ismeretterjesztő Társulat
 Sample letter number 5. International Culture Festival PO Box 34467 Harrogate HG 45 67F Sonnenbergstraße 11a CH-6005 Luzern Re: Festival May 19, 2009 Dear Ms Atkinson, We are two students from Switzerland
Sample letter number 5. International Culture Festival PO Box 34467 Harrogate HG 45 67F Sonnenbergstraße 11a CH-6005 Luzern Re: Festival May 19, 2009 Dear Ms Atkinson, We are two students from Switzerland
W
 W To Gabriela, Heidi, Hanni and Peter Preface Trees are a fundamental object in graph theory and combinatorics as well as a basic object for data structures and algorithms in computer science. During
W To Gabriela, Heidi, Hanni and Peter Preface Trees are a fundamental object in graph theory and combinatorics as well as a basic object for data structures and algorithms in computer science. During
Using the CW-Net in a user defined IP network
 Using the CW-Net in a user defined IP network Data transmission and device control through IP platform CW-Net Basically, CableWorld's CW-Net operates in the 10.123.13.xxx IP address range. User Defined
Using the CW-Net in a user defined IP network Data transmission and device control through IP platform CW-Net Basically, CableWorld's CW-Net operates in the 10.123.13.xxx IP address range. User Defined
KIEGÉSZÍTŽ FELADATOK. Készlet Bud. Kap. Pápa Sopr. Veszp. Kecsk. 310 4 6 8 10 5 Pécs 260 6 4 5 6 3 Szomb. 280 9 5 4 3 5 Igény 220 200 80 180 160
 KIEGÉSZÍTŽ FELADATOK (Szállítási probléma) Árut kell elszállítani három telephelyr l (Kecskemét, Pécs, Szombathely) öt területi raktárba, melyek Budapesten, Kaposváron, Pápán, Sopronban és Veszprémben
KIEGÉSZÍTŽ FELADATOK (Szállítási probléma) Árut kell elszállítani három telephelyr l (Kecskemét, Pécs, Szombathely) öt területi raktárba, melyek Budapesten, Kaposváron, Pápán, Sopronban és Veszprémben
Supplementary materials to: Whole-mount single molecule FISH method for zebrafish embryo
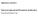 Supplementary materials to: Whole-mount single molecule FISH method for zebrafish embryo Yuma Oka and Thomas N. Sato Supplementary Figure S1. Whole-mount smfish with and without the methanol pretreatment.
Supplementary materials to: Whole-mount single molecule FISH method for zebrafish embryo Yuma Oka and Thomas N. Sato Supplementary Figure S1. Whole-mount smfish with and without the methanol pretreatment.
Számítógéppel irányított rendszerek elmélete. Gyakorlat - Mintavételezés, DT-LTI rendszermodellek
 Számítógéppel irányított rendszerek elmélete Gyakorlat - Mintavételezés, DT-LTI rendszermodellek Hangos Katalin Villamosmérnöki és Információs Rendszerek Tanszék e-mail: hangos.katalin@virt.uni-pannon.hu
Számítógéppel irányított rendszerek elmélete Gyakorlat - Mintavételezés, DT-LTI rendszermodellek Hangos Katalin Villamosmérnöki és Információs Rendszerek Tanszék e-mail: hangos.katalin@virt.uni-pannon.hu
- Bevándoroltak részére kiadott személyazonosító igazolvány
 HUNGARY - Bevándoroltak részére kiadott személyazonosító igazolvány (Blue booklet form or card format issued for permanent residents - from 1 January 2000 a new card format has been introduced and issued)
HUNGARY - Bevándoroltak részére kiadott személyazonosító igazolvány (Blue booklet form or card format issued for permanent residents - from 1 January 2000 a new card format has been introduced and issued)
MATEMATIKA ANGOL NYELVEN
 ÉRETTSÉGI VIZSGA 2010. október 19. MATEMATIKA ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2010. október 19. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS MINISZTÉRIUM
ÉRETTSÉGI VIZSGA 2010. október 19. MATEMATIKA ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2010. október 19. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS MINISZTÉRIUM
Small Dynamical Heights for Quadratic Polynomials and Rational Functions
 Experimental Mathematics, 23:433 447, 2014 Copyright C Taylor & Francis Group, LLC ISSN: 1058-6458 print / 1944-950X online DOI: 10.1080/10586458.2014.938203 Small Dynamical Heights for Quadratic Polynomials
Experimental Mathematics, 23:433 447, 2014 Copyright C Taylor & Francis Group, LLC ISSN: 1058-6458 print / 1944-950X online DOI: 10.1080/10586458.2014.938203 Small Dynamical Heights for Quadratic Polynomials
Dependency preservation
 Adatbázis-kezelés. (4 előadás: Relácó felbontásai (dekomponálás)) 1 Getting lossless decomposition is necessary. But of course, we also want to keep dependencies, since losing a dependency means, that
Adatbázis-kezelés. (4 előadás: Relácó felbontásai (dekomponálás)) 1 Getting lossless decomposition is necessary. But of course, we also want to keep dependencies, since losing a dependency means, that
A modern e-learning lehetőségei a tűzoltók oktatásának fejlesztésében. Dicse Jenő üzletfejlesztési igazgató
 A modern e-learning lehetőségei a tűzoltók oktatásának fejlesztésében Dicse Jenő üzletfejlesztési igazgató How to apply modern e-learning to improve the training of firefighters Jenő Dicse Director of
A modern e-learning lehetőségei a tűzoltók oktatásának fejlesztésében Dicse Jenő üzletfejlesztési igazgató How to apply modern e-learning to improve the training of firefighters Jenő Dicse Director of
8. Gyakorlat SQL. DDL (Data Definition Language) adatdefiníciós nyelv utasításai:
 8. Gyakorlat SQL SQL: Structured Query Language; a relációs adatbáziskezelők szabványos, strukturált lekérdező nyelve SQL szabványok: SQL86, SQL89, SQL92, SQL99, SQL3 Az SQL utasításokat mindig pontosvessző
8. Gyakorlat SQL SQL: Structured Query Language; a relációs adatbáziskezelők szabványos, strukturált lekérdező nyelve SQL szabványok: SQL86, SQL89, SQL92, SQL99, SQL3 Az SQL utasításokat mindig pontosvessző
Budapest By Vince Kiado, Klösz György
 Budapest 1900 2000 By Vince Kiado, Klösz György Download Ebook : budapest 1900 2000 in PDF Format. also available for mobile reader If you are looking for a book Budapest 1900-2000 by Vince Kiado;Klosz
Budapest 1900 2000 By Vince Kiado, Klösz György Download Ebook : budapest 1900 2000 in PDF Format. also available for mobile reader If you are looking for a book Budapest 1900-2000 by Vince Kiado;Klosz
Nemzetközi Kenguru Matematikatábor
 Nemzetközi Kenguru Matematikatábor 2011. augusztus 19-27., Werbellinsee, Németország BESZÁMOLÓ Bevezető Idén hetedik alkalommal került megrendezére a Nemzetközi Kenguru Matematikatábor (7. Internationale
Nemzetközi Kenguru Matematikatábor 2011. augusztus 19-27., Werbellinsee, Németország BESZÁMOLÓ Bevezető Idén hetedik alkalommal került megrendezére a Nemzetközi Kenguru Matematikatábor (7. Internationale
BEVEZETÉS Az objektum fogalma
 BEVEZETÉS Az objektum fogalma Program (1) Adat (2) Objektum Kiadványszerkesztés Word Táblázatkezelés Excel CAD AutoCad Adatbáziskezelés Access 1 Program (1) Adat (2) Objektum Adatmodell (2) A valós világ
BEVEZETÉS Az objektum fogalma Program (1) Adat (2) Objektum Kiadványszerkesztés Word Táblázatkezelés Excel CAD AutoCad Adatbáziskezelés Access 1 Program (1) Adat (2) Objektum Adatmodell (2) A valós világ
ELEKTRONIKAI ALAPISMERETEK ANGOL NYELVEN
 ÉRETTSÉGI VIZSGA 2011. május 13. ELEKTRONIKAI ALAPISMERETEK ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2011. május 13. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati NEMZETI
ÉRETTSÉGI VIZSGA 2011. május 13. ELEKTRONIKAI ALAPISMERETEK ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2011. május 13. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati NEMZETI
Adatbázisok* tulajdonságai
 Gazdasági folyamatok térbeli elemzése 4. előadás 2010. 10. 05. Adatbázisok* tulajdonságai Rendezett, logikailag összefüggő és meghatározott szempont szerint tárolt adatok és/vagy információk halmaza Az
Gazdasági folyamatok térbeli elemzése 4. előadás 2010. 10. 05. Adatbázisok* tulajdonságai Rendezett, logikailag összefüggő és meghatározott szempont szerint tárolt adatok és/vagy információk halmaza Az
MATEMATIKA ANGOL NYELVEN
 ÉRETTSÉGI VIZSGA 2011. május 3. MATEMATIKA ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2011. május 3. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS MINISZTÉRIUM Matematika
ÉRETTSÉGI VIZSGA 2011. május 3. MATEMATIKA ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2011. május 3. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS MINISZTÉRIUM Matematika
MATEMATIKA ANGOL NYELVEN
 ÉRETTSÉGI VIZSGA 2018. május 8. MATEMATIKA ANGOL NYELVEN EMELT SZINTŰ ÍRÁSBELI VIZSGA 2018. május 8. 8:00 Időtartam: 300 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Matematika
ÉRETTSÉGI VIZSGA 2018. május 8. MATEMATIKA ANGOL NYELVEN EMELT SZINTŰ ÍRÁSBELI VIZSGA 2018. május 8. 8:00 Időtartam: 300 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Matematika
Cashback 2015 Deposit Promotion teljes szabályzat
 Cashback 2015 Deposit Promotion teljes szabályzat 1. Definitions 1. Definíciók: a) Account Client s trading account or any other accounts and/or registers maintained for Számla Az ügyfél kereskedési számlája
Cashback 2015 Deposit Promotion teljes szabályzat 1. Definitions 1. Definíciók: a) Account Client s trading account or any other accounts and/or registers maintained for Számla Az ügyfél kereskedési számlája
New Trends in Intuitive Geometry
 Bolyai Society Mathematical Studies 27 Gergely Ambrus Imre Bárány Károly J. Böröczky Gábor Fejes Tóth János Pach Editors New Trends in Intuitive Geometry BOLYAI SOCIETY MATHEMATICAL STUDIES 27 More information
Bolyai Society Mathematical Studies 27 Gergely Ambrus Imre Bárány Károly J. Böröczky Gábor Fejes Tóth János Pach Editors New Trends in Intuitive Geometry BOLYAI SOCIETY MATHEMATICAL STUDIES 27 More information
Miskolci Egyetem Gazdaságtudományi Kar Üzleti Információgazdálkodási és Módszertani Intézet. Correlation & Regression
 Correlation & Regression Types of dependence association between nominal data mixed between a nominal and a ratio data correlation among ratio data Correlation describes the strength of a relationship,
Correlation & Regression Types of dependence association between nominal data mixed between a nominal and a ratio data correlation among ratio data Correlation describes the strength of a relationship,
First experiences with Gd fuel assemblies in. Tamás Parkó, Botond Beliczai AER Symposium 2009.09.21 25.
 First experiences with Gd fuel assemblies in the Paks NPP Tams Parkó, Botond Beliczai AER Symposium 2009.09.21 25. Introduction From 2006 we increased the heat power of our units by 8% For reaching this
First experiences with Gd fuel assemblies in the Paks NPP Tams Parkó, Botond Beliczai AER Symposium 2009.09.21 25. Introduction From 2006 we increased the heat power of our units by 8% For reaching this
Correlation & Linear Regression in SPSS
 Correlation & Linear Regression in SPSS Types of dependence association between two nominal data mixed between a nominal and a ratio data correlation among ratio data Exercise 1 - Correlation File / Open
Correlation & Linear Regression in SPSS Types of dependence association between two nominal data mixed between a nominal and a ratio data correlation among ratio data Exercise 1 - Correlation File / Open
PETER PAZMANY CATHOLIC UNIVERSITY Consortium members SEMMELWEIS UNIVERSITY, DIALOG CAMPUS PUBLISHER
 SEMMELWEIS UNIVERSITY PETER PAMANY CATLIC UNIVERSITY Development of Complex Curricula for Molecular Bionics and Infobionics Programs within a consortial* framework** Consortium leader PETER PAMANY CATLIC
SEMMELWEIS UNIVERSITY PETER PAMANY CATLIC UNIVERSITY Development of Complex Curricula for Molecular Bionics and Infobionics Programs within a consortial* framework** Consortium leader PETER PAMANY CATLIC
Supplementary Table 1. Cystometric parameters in sham-operated wild type and Trpv4 -/- rats during saline infusion and
 WT sham Trpv4 -/- sham Saline 10µM GSK1016709A P value Saline 10µM GSK1016709A P value Number 10 10 8 8 Intercontractile interval (sec) 143 (102 155) 98.4 (71.4 148) 0.01 96 (92 121) 109 (95 123) 0.3 Voided
WT sham Trpv4 -/- sham Saline 10µM GSK1016709A P value Saline 10µM GSK1016709A P value Number 10 10 8 8 Intercontractile interval (sec) 143 (102 155) 98.4 (71.4 148) 0.01 96 (92 121) 109 (95 123) 0.3 Voided
Miskolci Egyetem Gazdaságtudományi Kar Üzleti Információgazdálkodási és Módszertani Intézet. Correlation & Linear. Petra Petrovics.
 Correlation & Linear Regression in SPSS Petra Petrovics PhD Student Types of dependence association between two nominal data mixed between a nominal and a ratio data correlation among ratio data Exercise
Correlation & Linear Regression in SPSS Petra Petrovics PhD Student Types of dependence association between two nominal data mixed between a nominal and a ratio data correlation among ratio data Exercise
MATEMATIKA ANGOL NYELVEN
 ÉRETTSÉGI VIZSGA 2011. május 3. MATEMATIKA ANGOL NYELVEN EMELT SZINTŰ ÍRÁSBELI VIZSGA 2011. május 3. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
ÉRETTSÉGI VIZSGA 2011. május 3. MATEMATIKA ANGOL NYELVEN EMELT SZINTŰ ÍRÁSBELI VIZSGA 2011. május 3. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati NEMZETI ERŐFORRÁS
Választási modellek 3
 Választási modellek 3 Prileszky István Doktori Iskola 2018 http://www.sze.hu/~prile Forrás: A Self Instructing Course in Mode Choice Modeling: Multinomial and Nested Logit Models Prepared For U.S. Department
Választási modellek 3 Prileszky István Doktori Iskola 2018 http://www.sze.hu/~prile Forrás: A Self Instructing Course in Mode Choice Modeling: Multinomial and Nested Logit Models Prepared For U.S. Department
Descriptive Statistics
 Descriptive Statistics Petra Petrovics DESCRIPTIVE STATISTICS Definition: Descriptive statistics is concerned only with collecting and describing data Methods: - statistical tables and graphs - descriptive
Descriptive Statistics Petra Petrovics DESCRIPTIVE STATISTICS Definition: Descriptive statistics is concerned only with collecting and describing data Methods: - statistical tables and graphs - descriptive
Tételek a konvex geometria és
 Tételek a konvex geometria és az analízis határán Doktori értekezés Ambrus Gergely Témavezető: Dr. Fodor Ferenc Matematika és Számítástudományok Doktori Iskola Szegedi Tudományegyetem Természettudományi
Tételek a konvex geometria és az analízis határán Doktori értekezés Ambrus Gergely Témavezető: Dr. Fodor Ferenc Matematika és Számítástudományok Doktori Iskola Szegedi Tudományegyetem Természettudományi
Index. day, xxxiv, xxxix, xli, 73 75, 81, 82, calculation, xxxii, 7, 21, 27, 54, 83
 Index Āryabhaṭa, xi, xiii, xvi xix, xxi, xxvii, xxxii, xxxiii, xxxv, xxxix, xl, xlii xlviii, li, liii, 1, 2, 6, 9, 17, 18, 39, 58, 71, 86, 108, 121, 133, 137, 150, 152 altitude, xxxix, 73, 74, 118 arc,
Index Āryabhaṭa, xi, xiii, xvi xix, xxi, xxvii, xxxii, xxxiii, xxxv, xxxix, xl, xlii xlviii, li, liii, 1, 2, 6, 9, 17, 18, 39, 58, 71, 86, 108, 121, 133, 137, 150, 152 altitude, xxxix, 73, 74, 118 arc,
MAKING MODERN LIVING POSSIBLE. Danfoss Heating Solutions
 MAKING MODERN LIVING POSSIBLE Danfoss Danfoss Link Link HC Hidronikus HC Hydronic szabályozó Controller Szerelési Installation útmutató Guide Danfoss Heating Solutions Szerelési útmutató Tartalomjegyzék
MAKING MODERN LIVING POSSIBLE Danfoss Danfoss Link Link HC Hidronikus HC Hydronic szabályozó Controller Szerelési Installation útmutató Guide Danfoss Heating Solutions Szerelési útmutató Tartalomjegyzék
Lecture 11: Genetic Algorithms
 Lecture 11 1 Linear and Combinatorial Optimization Lecture 11: Genetic Algorithms Genetic Algorithms - idea Genetic Algorithms - implementation and examples Lecture 11 2 Genetic algorithms Algorithm is
Lecture 11 1 Linear and Combinatorial Optimization Lecture 11: Genetic Algorithms Genetic Algorithms - idea Genetic Algorithms - implementation and examples Lecture 11 2 Genetic algorithms Algorithm is
ANGOL NYELVI SZINTFELMÉRŐ 2013 A CSOPORT. on of for from in by with up to at
 ANGOL NYELVI SZINTFELMÉRŐ 2013 A CSOPORT A feladatok megoldására 45 perc áll rendelkezésedre, melyből körülbelül 10-15 percet érdemes a levélírási feladatra szánnod. Sok sikert! 1. Válaszd ki a helyes
ANGOL NYELVI SZINTFELMÉRŐ 2013 A CSOPORT A feladatok megoldására 45 perc áll rendelkezésedre, melyből körülbelül 10-15 percet érdemes a levélírási feladatra szánnod. Sok sikert! 1. Válaszd ki a helyes
Kvantum-informatika és kommunikáció 2015/2016 ősz. A kvantuminformatika jelölésrendszere szeptember 11.
 Kvantum-informatika és kommunikáció 2015/2016 ősz A kvantuminformatika jelölésrendszere 2015. szeptember 11. Mi lehet kvantumbit? Kvantum eszközök (1) 15=5 3 Bacsárdi Képek forrása: IBM's László, Almaden
Kvantum-informatika és kommunikáció 2015/2016 ősz A kvantuminformatika jelölésrendszere 2015. szeptember 11. Mi lehet kvantumbit? Kvantum eszközök (1) 15=5 3 Bacsárdi Képek forrása: IBM's László, Almaden
FÖLDRAJZ ANGOL NYELVEN GEOGRAPHY
 Földrajz angol nyelven középszint 0513 ÉRETTSÉGI VIZSGA 2005. május 18. FÖLDRAJZ ANGOL NYELVEN GEOGRAPHY KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA STANDARD LEVEL WRITTEN EXAMINATION Duration of written examination:
Földrajz angol nyelven középszint 0513 ÉRETTSÉGI VIZSGA 2005. május 18. FÖLDRAJZ ANGOL NYELVEN GEOGRAPHY KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA STANDARD LEVEL WRITTEN EXAMINATION Duration of written examination:
Supporting Information
 Supporting Information Cell-free GFP simulations Cell-free simulations of degfp production were consistent with experimental measurements (Fig. S1). Dual emmission GFP was produced under a P70a promoter
Supporting Information Cell-free GFP simulations Cell-free simulations of degfp production were consistent with experimental measurements (Fig. S1). Dual emmission GFP was produced under a P70a promoter
Minden az adatról. Csima Judit. 2015. február 11. BME, VIK, Csima Judit Minden az adatról 1 / 41
 Minden az adatról Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2015. február 11. Csima Judit Minden az adatról 1 / 41 Adat: alapfogalmak Adathalmaz elvileg bármi, ami információt
Minden az adatról Csima Judit BME, VIK, Számítástudományi és Információelméleti Tanszék 2015. február 11. Csima Judit Minden az adatról 1 / 41 Adat: alapfogalmak Adathalmaz elvileg bármi, ami információt
MATEMATIKA ANGOL NYELVEN
 ÉRETTSÉGI VIZSGA 2016. október 18. MATEMATIKA ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2016. október 18. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA
ÉRETTSÉGI VIZSGA 2016. október 18. MATEMATIKA ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2016. október 18. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA
Graph Coloring with Local and Global Constraints
 Graph Coloring with Local and Global Constraints Graph Coloring with Local and Global Constraints by Dániel Marx Under the supervision of Dr. Katalin Friedl Department of Computer Science and Information
Graph Coloring with Local and Global Constraints Graph Coloring with Local and Global Constraints by Dániel Marx Under the supervision of Dr. Katalin Friedl Department of Computer Science and Information
ELEKTRONIKAI ALAPISMERETEK ANGOL NYELVEN
 ÉRETTSÉGI VIZSGA 2013. május 23. ELEKTRONIKAI ALAPISMERETEK ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2013. május 23. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI
ÉRETTSÉGI VIZSGA 2013. május 23. ELEKTRONIKAI ALAPISMERETEK ANGOL NYELVEN KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2013. május 23. 8:00 Az írásbeli vizsga időtartama: 180 perc Pótlapok száma Tisztázati Piszkozati EMBERI
To Gabriela, Heidi, Hanni and Peter
 W To Gabriela, Heidi, Hanni and Peter Preface Trees are a fundamental object in graph theory and combinatorics as well as a basic object for data structures and algorithms in computer science. During
W To Gabriela, Heidi, Hanni and Peter Preface Trees are a fundamental object in graph theory and combinatorics as well as a basic object for data structures and algorithms in computer science. During
AZ ACM NEMZETKÖZI PROGRAMOZÓI VERSENYE
 AZ ACM NEMZETKÖZI PROGRAMOZÓI VERSENYE Kuki Attila, kuki@math.klte.hu Kossuth Lajos Tudományegyetem, Információ Technológia Tanszék Abstract This paper is dedicated to the Scholastic Programming Contest
AZ ACM NEMZETKÖZI PROGRAMOZÓI VERSENYE Kuki Attila, kuki@math.klte.hu Kossuth Lajos Tudományegyetem, Információ Technológia Tanszék Abstract This paper is dedicated to the Scholastic Programming Contest
USER MANUAL Guest user
 USER MANUAL Guest user 1 Welcome in Kutatótér (Researchroom) Top menu 1. Click on it and the left side menu will pop up 2. With the slider you can make left side menu visible 3. Font side: enlarging font
USER MANUAL Guest user 1 Welcome in Kutatótér (Researchroom) Top menu 1. Click on it and the left side menu will pop up 2. With the slider you can make left side menu visible 3. Font side: enlarging font
Could René Descartes Have Known This?
 Experimental Mathematics, 00:1 11, 2015 Copyright C Taylor & Francis Group, LLC ISSN: 1058-6458 print / 1944-950X online DOI: 10.1080/10586458.2015.1030051 Could René Descartes Have Known This? Jens Forsgård
Experimental Mathematics, 00:1 11, 2015 Copyright C Taylor & Francis Group, LLC ISSN: 1058-6458 print / 1944-950X online DOI: 10.1080/10586458.2015.1030051 Could René Descartes Have Known This? Jens Forsgård
