LOGO grafikák: - Bevezetés - Válogatás a szakkörösök legszebb munkáiból
|
|
|
- Sándor Szilágyi
- 9 évvel ezelőtt
- Látták:
Átírás
1 BEVEZETÉS LOGO grafikák: - Bevezetés - Válogatás a szakkörösök legszebb munkáiból Aki egy picit is megérti a LOGO programozás lényegét, néhány soros programmal nagyon szép rajzokat készíthet. Ha tudja a színezés egy-két fortélyát és az animációkészítés alapelvét is, diszkófényeket is varázsolhat a képernyőjére. Ez a kis tanulmány segítséget ad e trükkök elsajátításához. LOGO-ban a képernyő egy nagy rajzlapnak tekinthető, melyen a festő és rajzoló szerepét a Teknőc veszi át - sétál a rajzmezőn, miközben vonalakat is tud húzni ceruzájával. Tolla (ceruzája) lehet vékony, lehet vastag; lehet színes. Ecsete is van - ezzel tud színezni; s ha az ecset alakját is változtatja, szép mintásra festi az alakzatokat. Nézzük a legegyszerűbb utasításokat (bár ha figyeltél számítástechnika órákon, ezek többsége már ismerős számodra)! A színek értéke 0, 1,..., 15 lehet! tr - töröld le a rajzlapot tollszín! s1 - vedd a kezedbe az s1 színű tollat! tf - emeld fel a tollat töltőszín! s2 - vedd a kezedbe az s2 színű ecsetet! tl - tedd le a tollat tv! 3 - legyen 3-as vastagságú a ceruzád! e 20 - menj előre 20 egységet tölt! - fess a megadott tollszínnel és mintával! h 30 - menj hátrafelé 20 egységet tollradír - séta közben törölj le minden pontot! j 60 - fordulj jobbra 60 fokot várj várj 100 időegységet b 60 - fordulj balra 60 fokot vsz 16 - választ egy számot 0 és 15 között Hang - Zenélő utasítás (ld. Help!) betűzd ab - a rajzlapra írja az ab betűket ; megjegyzések a programban lenyomat - a teknőc alakja rákerül a képernyőre Egy kicsit bonyolultabb parancsok: ism 3[... ] - ismételd háromszor a zárójelben megadott utasításokat Ennyi bevezető után lássunk néhány egyszerű ábrát: ism 4[e 50 j 90] tr ism 3[e 40 b 120] tr j 90 ism 3[e 10 tf e 20 tl] Ha azt szeretnénk, hogy a Teknőc más méretű négyzetet rajzoljon, az e (előre) utáni számot kell módosítanunk! Kicsit unalmas mindig beírni a négyzetet rajzoló parancssort. A Teknőc arra is képes, hogy új parancsot tanuljon. Az új parancsot eljárásnak nevezzük, s az eljárásoknak nevet adunk. Például arra taníthatjuk a Teknőcöt, hogy négyzet szóra egy négyzetet rajzoljon! Azt is megtehetjük, hogy a négyzet méretét csak a négyzet szó begépelése után mondjuk meg - úgy, ahogy az előre sétáláskor megadjuk a lépések számát. Károlyi István 12 Évfolyamos Gimnázium LOGO grafikák/1. Évkönyvbe
2 Ha egy zárt alakzatot be akarunk festeni, akkor előtte felemelt tollal be kell mennünk az alakzat belsejébe, majd festőszínt és festőmintát választunk; töltünk, majd kisétálunk az alakzatból. Ez a módszer hasonlít ahhoz, ahogy a PAINT rajzolóprogrammal szoktunk festeni. Például 1 : tanuld négyzet :a ism 4 [e :a j 90] tanuld négyzet1 :a :sz1 négyzet :a tf j 45 e :a / 2 tl tsz! :sz1 tölt tf h :a / 2 b 45 tl négyzet 50 tsz! 2 négyzet (zölddel rajzolt, 40 egység oldalhosszúságú sárga négyzet) A tsz! parancs a tollszín! rövidítése! Figyeld meg, hogy a négyzet1 eljárás használja (azaz hívja) a négyzetet! Gyakorló feladatok Ha nem négyzetet, hanem ötszöget, hatszöget stb. szeretnénk rajzolni, akkor azt úgy rajzoljuk, hogy rajzolunk egy vonalat, fordulunk, ismét rajzolunk - fordulunk és így tovább, amíg vissza nem érünk a kiinduló helyünkre. Ezalatt éppen egy teljes kört, azaz 360 fokot fordultunk. Ha a lépések száma és a fordulatok nagysága különböző, nehéz kiszámítani, hogyan érjünk vissza a START-ra. Szabályos sokszöget viszont nagyon könnyű rajzolni - mindig egyformát kell lépnünk és ugyanannyit fordulnunk. Egy sokszög megrajzolása után rajzolhatunk mellé, alá, fölé, vagy elforgatva egy ugyanakkorát, vagy hasonlót vagy más oldalszámút is. Ha ügyes vagy, megfejted az alábbi algoritmusokat és te is tudsz hasonlókat készíteni. tanuld soksz :a :db ism :db [e :a j 360 / :db] tanuld soksz1 :a :db :sz1 soksz :a :db tf j 5 e :a / 2 tl tsz! :sz1 tölt tsz! 0 tf h :a / 2 b 5 tl tv! 2 soksz tv! 1 ism 8[soksz 30 8 j 45] b 30 ism 3[hsz 50 e 50 j 120] j 30 Ahol a hsz eljárás következő: tanuld hsz :a ism 3 [e :a b 120] ism 3[soksz 30 6 tf j 90 e 60 b 90 tl] És egy újabb eljárás: tanuld soksz2 :a :db soksz :a :db tf jobbra 5 előre :a / 2 tl tsz! vsz 16 tölt tsz! 0 tf hátra :a / 2 balra 5 tl 1 Ha kíváncsi vagy, hogyan kell használnod a Comenius LOGO programozási nyelvet, vedd elő az órákon használt informatika tankönyveidet ezekben megtalálod a részletes leírást, sok érdekes rajzzal, gyakorló feladattal. (Gál Mariann: Informatika jegyzet és munkafüzet az 5-6. osztály részére, Gál Mariann: Informatika jegyzet és munkafüzet a 7. osztály részére; SULI-SOFT kiadó). Károlyi István 12 Évfolyamos Gimnázium LOGO grafikák/2. Évkönyvbe
3 Próbáld kitalálni, mi lesz a következő parancssorok eredménye! 1. soksz soksz soksz soksz soksz ism 5[tr soksz soksz soksz soksz várj 10] 3. tr soksz soksz soksz soksz soksz soksz soksz soksz tr ism 2[soksz soksz soksz soksz soksz soksz soksz soksz balra 180] 5. ism 15[tr ism 2[soksz soksz soksz soksz soksz soksz soksz soksz balra 180] várj 5] A megfejtéseket a cikk végén olvashatod. Itt újabb feladatokat is találsz! Ismétlés: Válogatás Ruszki Bálint és Lipták Bence előző tanévi munkáiból Útjelzők, zászlók - egyesével és sorban egymás után (lu06-01.lgp) tanuld négyzet :a ismétlés 4 [e :a j 90] tanuld fel :a tollatfel előre :a tollatle tanuld tovább :a tf j 90 e :a b 90 tl tanuld zászló :a :b e :a négyzet :b h :a tanuld útjelző :a :b e :a b 45 négyzet :b j 45 h :a tanuld útsor :db :a :b :t ism :db [útjelző :a :b tovább :b + :t] tovább - :db * ( :b + :t ) tanuld váltósor :db :a :b :t ism :db [négyzet :b tovább :b + :t ~ útjelző :a :b tovább :b + :t] tovább - :db * 2 * ( :b + :t ) Feladatok: 1. Készíts olyan váltósort, amelyben a zászlók és az útjelzők váltják egymást! 2. Készíts olyan sormintát, ahol a zászlók, négyzetek és az útjelzők váltják egymást! 3. Készíts olyan sort, amelyben a zászlók után négyzet, majd útjelző és ismét négyzet váltja egymást! Károlyi István 12 Évfolyamos Gimnázium LOGO grafikák/3. Évkönyvbe
4 A LOGO szakkör tematikája A szakkör elsődleges célja a programozás megszerettetése, majd felkészítés a Neumann János Számítógéptudományi Társaság által 1997 óta szervezett Országos Logo Programozói Versenyre. Az alapok (egyszerű alakzatok rajzolása, sorminta, oszlop, mozaik) átismétlése után elsősorban a színezéssel és a rekurzióval foglalkoztunk. Ehhez kapcsolódtak a szakkörösök ötletei: zenéljen a teknőc, készítsünk animációt az ábrák váltogatásával, stb. Mi is a rekurzió? Ez a fogalom a matematika egyik fontos fogalma. Azt jelenti, hogy sosincs annak, amit csinálunk azaz amikor azt hisszük, hogy valamit befejezünk, egy kis módosítással újra kezdjük. Először ez bonyolultnak tűnhet, valójában pedig nem is az! Gondolj az egyszerű halász meséjére: A halász kifogja a tengerből az aranyhalat. Az aranyhal arra kéri, dobja vissza a tengerbe, cserébe teljesíti három kívánságát! Ha Te lennél a halász, elsőre kérsz valamit, másodszorra kérsz valami mást. A harmadik kívánsággal azonban vigyázol, mert úgy tűnik, ez az utolsó kívánságod! De a harmadik kívánság is lehet bármi! Ha furfangos vagy, a harmadik kívánságod az lesz, hogy Legyen még három kívánságom!. Így a kívánságlistát a végtelenségig folytathatod! A Legyen még három kívánságom kérés hacsak el nem rontod akár a végtelenségig is folytatható és ez a rekurzió. Érdekes LOGO programok: Válogatás a szakkörösök munkáiból 5. osztály Egy érdekes rekurzió - Egyházi Anna (ea lgp 2 ) tanuld vm :a ha :a > 2 [ism 6 [e :a j 90] vm :a - 40] Próbáld ki az alábbi paraméterekkel: (A képernyő letörlése után a betűzd i paranccsal jelöltük a Teki kiinduló helyét. Így láthatod, hogy a Teki nem ott fejezi be a rajzot, ahol elkezdte!) Rekurzió - vonalvariációk (mg lgp, lm lgp, lb lgp) Vannak olyan rajzok, amelyeket csak rekurzióval lehet elkészíteni ilyen például a csigavonal. Csigavonalat úgy rajzolunk, hogy rajzolunk egy szakaszt, majd fordulunk valamennyit, ezután ismét rajzolunk, majd fordulunk ezt a két lépést ismételjük. A csigavonalfajták száma végtelen, mert változtathatjuk a kiinduló szakasz hosszát, a fordulás szögét; a következő lépésben megint változhat a szakasz hossza és a fordulás szöge is. Erre látunk néhány példát. 2 A szakkörösök kedvéért emlékeztetőnek megadom, melyik LOGO projektben találják meg a munkájukat. Károlyi István 12 Évfolyamos Gimnázium LOGO grafikák/4. Évkönyvbe
5 A vonal olyan csigavonalat rajzol, melyben az első vonal hosszát mi adjuk meg. Ezután derékszögben jobbra fordulunk, majd ismét meghívjuk a vonal eljárást ez már rekurzió. A másodszori hívásnál 5 egységgel hosszabb vonalat rajzolunk, fordulunk, majd ismét hívjuk a vonal eljárást. A rajzolásnak csak akkor van, ha a Stop gombra kattintunk. A vonal1 eljárás a vonal módosításával készült: csak addig rajzolunk, amíg a rajzolandó vonal rövidebb kisebb 200 képpontnál. A vonal1a eljárásban már mi adjuk meg, mekkora legyen a leghosszabb vonal. tanuld vonal :a tanuld vonal1 :a előre :a jobbra 90 előre :a jobbra 90 vonal :a + 5 ha :a < 200 [vonal1 :a + 5] tanuld vonal1a :a :meddig előre :a jobbra 90 ha :a < :meddig [vonal1a :a + 5 :meddig] Megadhatjuk, hogy az előző vonalnál mennyivel legyen hosszabb a következő? Természetesen! A vonal2a eljárásban már azt is megadjuk, mennyivel változzon a következő vonal hossza! A vonal3a eljárásban a fordulás szögét is mi adjuk meg! A vonal4a eljárásban lépésenként változtatjuk a fordulás szögét is! Károlyi István 12 Évfolyamos Gimnázium LOGO grafikák/5. Évkönyvbe
6 tanuld vonal2a :a :mennyit :meddig előre :a jobbra 90 ha :a < :meddig [vonal2a :a + :mennyit :mennyit :meddig] tanuld vonal3a :a :mennyit :szög :meddig előre :a jobbra :szög ha :a < :meddig [vonal3a :a + :mennyit :mennyit :szög :meddig] tanuld vonal4a :a :mennyit :szög :szögnöv :meddig előre :a jobbra :szög ha :a < :meddig [vonal4a :a + :mennyit :mennyit :szög + :szögnöv ~ :szögnöv :meddig] Ha egy utasítássorozatot egy sorba kell írni és nem fér ki egy sorba, a sor végére a ~ jelet 3 kell írni. tr vonal4a tr vonal4a Próbáld ki az alábbi hívásokat is: vonal4a vonal4a Lipták Bence (7. oszt.) megoldásai: tanuld vonal4a_1 :a :mennyit :szög :s :meddig ha :a < :meddig [előre :a jobbra :szög ~ vonal4a_1 :a + :mennyit :mennyit :szög + :s :s :meddig] Próbáld ki mindkét eljárást! Mi a különbség köztük 4? 3 4 A ~ helye a billentyűzeten: <Alt Gr> + <1>. Megfejtés: A vonal4a eljárás 9 vonalat rajzol, felfelé kezdve; a vonal4a_1 pedig csak nyolcat, jobbra kezdve. Magyarázat: A vonal4a először előre megy, majd fordul, s csak ezután ellenőrzi, folytathatja-e a rajzolást. A vonal4a_1 először ellenőriz, s csak ezután rajzol! Ellenőrzés: tanuld vonal4a_próba tr tollszín! 0 lenyomat vonal4a tf haza tl tollszín! 12 ; lenyomat vonal4a_ Károlyi István 12 Évfolyamos Gimnázium LOGO grafikák/6. Évkönyvbe
7 6-7. osztály Karácsonyfa - Ruszki Bálint (rb lgp) Ez a feladat a 2004-es verseny 1. fordulójában szerepelt (3-4. osztály). tanuld csill balra 20 ismétlés 5 [előre 20 jobbra 144] jobbra 20 tanuld karácsonyfa tollatfel előre 100 tollatle j 150 e 50 j 120 e 12,5 b 120 e 50 j 120 e 12,5 b 120 e 50 j 120 e 50 b 90 e 50 j 180 e 50 b 90 e 50 j 120 e 50 b 120 e 12,5 j 120 e 50 b 120 e 12,5 j 120 e 50 b 30 csill Telefonálunk? Animációkkal - Lipták Bence (lb lgp) Telefoncsörgés - alap eljárás tanuld alaptef ism 4 [hang [700 50] hang [550 50]] Telefoncsörgés - két sorozat tanuld telefon ismétlés 2 [alaptef] Telefoncsörgés - ezzel könnyen megviccelhetsz bárkit (lb lgp) tanuld telefon :hossz ism :hossz [ism 6 [hang [450 50] hang [800 50]] várj 800] Egy másik telefon (lb lgp) tanuld telefon1 :h ism :h [ism 6 [ism 2 [hang [450 50] hang [800 50]]] v 1500] Megadott számú festékpöttyök váltják egymást - a fényhatás bombarobbanáshoz hasonlít Telefoncsörgés közben színes "bomba" robban A telefoncsörgésnek sosincs! Sőt, közben a bombák nyoma betölti az egész képernyőt! tanuld színbomba :szám tv! vsz 15 tsz! vsz 16 e vsz 5 ha tv < 8 [j vsz 360][b vsz 360] ha :szám = 0 [stop][színbomba :szám - 1] tanuld csörgőbomba :szám színbomba 1 alaptef ha :szám = 0 [stop][csörgőbomba :szám - 1] tanuld megcsinál :a előre :a jobbra 90 alaptef színbomba 5 megcsinál :a + 2 Károlyi István 12 Évfolyamos Gimnázium LOGO grafikák/7. Évkönyvbe
8 Bahama zászlója (lb lgp) A évi LOGO verseny 2. fordulójában zászlókat kellett rajzolni (3-5. osztály). Például: tanuld bahama ism 2 [e 60 j 90 e 100 j 90] ismétlés 3 [előre 60 jobbra 120] j 90 e 100 b 90 e 20 b 90 e 65 h 65 j 90 e 20 b 90 e 65 Gyufa és fejtörő - Ruszki Bálint (rb lgp) A 2006-os LOGO verseny 2. fordulójának egyik szép feladata volt ez a fejtörő (5-6. osztály). A gyufa eljárás egy gyufaszálat rajzol, a fejtörő pedig a gyufaszálakból készül. A gyufaszál magassága az elsőnek, szélessége pedig a másodiknak megadott szám. tanuld gyufa :a :b tégla :a :b j 45 színez :b / 10 9 b 45 e :a j 90 e :b / 2 b 180 kör :b / 2 j 45 színez :b / 4 12 b 45 e :b / 2 b 90 e :a j 180 tanuld tégla :a :b ism 2 [e :a j 90 e :b j 90] tanuld színez :be :színkód tf e :be tl töltőszín! :színkód tölt töltőszín! 0 tf h :be tl tanuld fejtörő :a :b ism 3 [gyufa :a :b ~ j 90 e :b tf e :b tl b 90] tf e :b * 2 tl j 90 gyufa :a :b b 90 tf e :b * 2 tl j 90 gyufa :a :b b 90 tf h :b * 4 j 90 e :a + :b * 2 b 90 tl gyufa :a :b j 90 e :b tf e :b tl b 90 gyufa :a :b j 90 e :b tf e :b b 90 e :b * 3 j 90 tl gyufa :a :b j 90 tf e :b * 3 b 90 e :a + :b * 2 b 90 tl gyufa :a :b tanuld kör :r ismétlés 360 [e :r * 0,0174 j 1] Dobókocka animáció - Lipták Bence (lb lgp) A évi LOGO verseny 2. fordulójában a 3-4. osztályosoknak dobókockákat kellett rajzolni. Ez a feladat egy animáció készítésére inspirálta Bencét. A dobókocka parancs begépelése után dobókockák helyett egy féldominók váltják egymást a képernyőn mindaddig, amíg a STOP-ra nem kattintunk. (A kör és a színez eljárást ld. a Gyufa-projektnél!) Károlyi István 12 Évfolyamos Gimnázium LOGO grafikák/8. Évkönyvbe
9 tanuld dobókocka let "sz véletlenszám 10 if :sz = 0 [dobókocka][kocka :sz wait 500 tr dobókocka] tanuld pötty ismétlés 8 [előre 10 jobbra 45] j 45 tf e 10 tölt h 10 b 45 tl Kis szépséghibája az eljáráscsomagnak, hogy a kocka pöttyei nyolcszögek és elhelyezkedésük sem mindig pontos! Ha ügyes vagy, e kis pontatlanságokat Te is ki tudod javítani! (A wait parancs a várj angol megfelelője!) tanuld kocka :n ha :n > 9 [kiír [Az :n paraméter nem lehet 9 - nél nagyobb!] hang [ ] stop] ism 4 [e 100 j 90] ha :n = 1 [j 90 tf e 40 b 90 e 45 tl pötty tf h 45 b 90 e 40 j 90 tl] ha :n = 2 [j 90 e 10 tf b 90 e 75 tl pötty tf h 75 j 90 e 55 ~ b 90 e 10 tl pötty tf h 10 b 90 e 65 j 90 tl] ha :n = 3 [kocka 1 kocka 2] ha :n = 4 [kocka 2 e 100 j 90 kocka 2 b 90 h 100] ha :n = 5 [kocka 1 kocka 4] ha :n = 6 [kocka 4 j 90 e 10 b 90 tf e 45 tl pötty tf h 45 ~ j 90 e 55 b 90 e 40 tl pötty tf h 40 b 90 e 65 j 90 tl] ha :n = 7 [kocka 6 j 90 tf e 40 b 90 e 75 tl pötty tf h 75 b 90 e 40 j 90 tl] ha :n = 8 [kocka 7 j 90 e 35 tf b 90 e 15 tl pötty tf h 15 b 90 e 35 j 90 tl] ha :n = 9 [kocka 8 kocka 1] Ötszögek - Ruszki Bálint (rb lgp) A évi LOGO verseny 2. fordulójában a 3-4. osztályosok feladata volt az Összerakó ennek egyik részfeladata az ötszögek. tanuld ötszög :a ism 5 [ötszögelem :a j 360 / 5] j 150 színez :a / b 150 tanuld ötszögelem :a tégla :a :a / 10 j 45 színez :a / 10 / 2 9 b 45 e :a j 90 5szög :a / 10 b 25 színez :a / j 25 e :a / 10 j 90 e :a j 180 tanuld négyszög :a ism 4 [tégla :a / 10 :a / 10 ~ j 45 színez :a / 10 / 2 12 b 45 e :a / 10 ~ tégla :a - :a / 10 :a / 10 ~ j 45 színez :a / 10 / 2 9 b 45 e :a - :a / 10 j 90] Egy kis hibája van az Ötszögelem-nek - nem mindig színez pirosra. Ki tudod javítani a színező eljárást? tanuld 5szög :a ism 5 [e :a b 360 / 5] A színez és a tégla eljárások ugyanazok, mint amik a Gyufa projektben szerepelnek! Károlyi István 12 Évfolyamos Gimnázium LOGO grafikák/9. Évkönyvbe
10 Propeller - Ruszki Bálint (rb lgp) Az Összerakó feladataiban a téglalapokon háromszögeket, négyzeteket, hatszögeket kellett elhelyezni, s ezeket a sokszögek oldalszáma szerint kellett megismételni. A háromszög inspirálta Bálintot egy propeller elkészítésére. (A színez, tégla eljárásokat ld. a Gyufa projektnél!) tanuld propeller :a ha :a > []~ [háromszög :a propeller :a + 10] tanuld háromszög :a ism 3 [tégla :a :a / 10 j 45 ~ színez :a / 10 9 ~ b 45 e :a j 90 hszög :a / 10 ~ e :a / 10 / 2 b 90 ~ színez :a / j 90 e :a / 10 / 2 j 90 e :a b 60] j 120 színez :a / b 120 tanuld hszög :a e :a b 120 e :a b 120 e :a b 120 Térhatás (lb lgp) Ha rajzolunk egy síkidomot például egy kört; néhány fokos fordulás után és ismét rajzolunk, s ezt a két lépést ismételgetjük, igen érdekes térhatárú ábrákat kapunk. tanuld térhatás :db ism :db [ism 360 [e 1 j 1] j 360 / :db] tanuld térhatás2 :fok ism 360 / :fok [ism 360 [e 1 j 1] j :fok] Próbáld ki mindkét eljárást! Feladvány: Mi a különbség köztük 5? Feladatok: 1. Kör helyett rajzolj négyzetet! 2. Próbáld ki más síkidommal is például háromszöggel, ötszöggel, hatszöggel stb. Érdemes megfigyelni a rajzolás folyamatát. A következő ábrák a térhatás 2 3 parancsra készültek. 5 Megfejtés: az elsőnél azt adod meg, hány kört rajzoljunk; a másodiknál pedig azt, hány fokkal forduljunk el két kör között. Károlyi István 12 Évfolyamos Gimnázium LOGO grafikák/10. Évkönyvbe
11 És a redmény: Országos Logo Verseny Ezen a versenyen minden szakkörös elindult, s valamennyien bejutottak a második fordulóba! Ezen Egyházi Anna kivételével mindenki részt vett, ahol Mátis Gergő 39, Zsinka Bernadett 36, Ruszki Bálint 60, Lipták Bence 98 pontot szerzett. Bálint és Bence továbbjutottak a harmadik (országos) fordulóba, ahol Bálint az 51., Bence a 3. helyet érte el. Most a versenyfeladatokból következik egy kis válogatás. Első forduló, II. kategória (5-6. osztály), 1. feladat 1. feladat: Minták (21 pont) Készítsd el azokat a Logo eljárásokat, amelyek az alábbi mintákat rajzolják ki. A minták négyzetekből épülnek fel úgy, hogy ezek néhány részletét kitöröljük vagy megvastagítjuk minta1 100 minta2 100 minta3 100 Károlyi István 12 Évfolyamos Gimnázium LOGO grafikák/11. Évkönyvbe
12 Zsinka Bernadett mintái (Rajzolás után a teknőc nem tér vissza a kiinduló helyére. A harmadik mintában a kis négyzet oldala mindig 12,4 egység!) tanuld minta1 :a e :a j 90 e :a j 90 e :a / 2 j 90 e :a / 4 h :a / 4 b 90 tf e :a / 4 tl j 90 tv! 5 e :a / 4 b 90 e :a / 4 j 90 tf e :a / 4 j 90 tl tv! 1 e :a / 4 h :a / 4 b 90 e :a / 2 j 90 tanuld minta2 :a tv! 5 h :a / 4 b 90 e :a / 2 j 90 e :a j 90 e :a j 90 e :a / 2 j 90 e :a / 4 tf e :a / 4 tl j 90 tv! 1 e :a / 4 b 90 e :a / 8 b 90 e :a / 16 tf e :a / 16 j 90 e :a / 16 tl e :a / 16 b 90 e :a / 8 b 90 e :a / 4 tanuld minta3 :a j 180 e :a / 4 kisn2 tv! 1 e :a / 2 kisn2 tv! 1 e :a kisn2 tv! 1 e :a kisn2 tv! 1 e :a / 2 kisn2 tv! 1 e :a / 4 tanuld kisn2 tv! 5 ism 3[e 12,4 b 90] e 12,4 Ruszki Bálint mintái (A rajz állapotátlátszó, azaz rajzolás után a teknőc visszatér a kiinduló helyére.) tanuld minta1 :a j 90 e :a / 2 b 90 e :a / 4 h :a / 4 j 90 tf e :a / 4 tl b 90 tv! 6 e :a / 4 j 90 e :a / 4 h :a / 4 b 90 h :a / 4 b 90 tv! 1 tf e :a / 4 tl e :a / 2 j 90 e :a j 90 e :a j 90 e :a / 2 j 90 e :a / 4 h :a / 4 j 90 e :a / 2 b 90 e :a b 90 e :a j 180 tanuld minta2 :a tv! 6 e :a j 90 e :a j 90 e :a / 2 j 90 e :a / 4 tv! 1 tf e :a / 4 tl j 90 e :a / 4 b 90 e :a / 8 b 90 e :a / 16 tf e :a / 16 j 90 e :a / 16 tl e :a / 16 b 90 e :a / 8 b 90 e :a / 4 j 90 tf e :a / 4 tl tv! 6 e :a / 4 j 90 e :a / 2 tv! 1 j 90 tanuld minta3 :a j 90 e :a / 2 b 90 e :a / 4 h :a / 4 h :a / 8 tv! 4 négyzet :a / 8 tv! 1 e :a / 8 b 90 e :a / 2 b 90 tv! 4 négyzet :a / 8 tv! 1 j 180 e :a b 90 tv! 4 négyzet :a / 8 tv! 1 j 180 e :a b 90 tv! 4 négyzet :a / 8 tv! 1 j 180 e :a / 2 b 90 tv! 4 négyzet :a / 8 tv! 1 j 180 e :a / 4 h :a / 4 j 90 e :a / 2 b 90 e :a b 90 e :a j 180 tanuld négyzet :a ism 4[előre :a jobbra 90] Károlyi István 12 Évfolyamos Gimnázium LOGO grafikák/12. Évkönyvbe
13 Első forduló, III. kategória (7-8. osztály), 1. feladat: Minták (21 pont) Készítsd el azokat a Logo eljárásokat, amelyek az alábbi mintákat rajzolják ki. A minták különböző méretű négyzetekből épülnek fel úgy, hogy ezek néhány részletét kitöröljük, összekötjük vagy megvastagítjuk. minta1 100 minta2 100 minta3 100 Lipták Bence megoldása tanuld ab :a b 45 e :a j 90 e :a j 90 e :a / 2 j 90 e :a / 4 b 45 e :a / 4 * gyök 2 b 45 e :a / 4 j 90 e :a / 2 j 135 tanuld aj :a b 45 e :a / 2 j 90 e :a / 4 b 45 e :a / 4 * gyök 2 b 45 e :a / 4 j 90 e :a / 2 j 90 e :a j 90 e :a j 135 tanuld minta1 :a tv! 5 e :a / 2 h :a / 2 b 90 e :a j 90 e :a * 2 j 90 e :a * 2 j 90 e :a j 90 e :a / 2 tv! 1 tf e :a / 2 tl e :a / 2 j 90 e :a / 4 j 90 e :a / 8 tf e :a / 8 b 90 e :a / 8 tl e :a / 8 j 90 e :a / 4 j 90 e :a / 2 tf e :a j 180 tl tanuld minta2 :a b 45 e :a j 90 e :a j 90 e :a / 2 j 45 tv! 5 e :a / 2 * gyök 2 tv! 1 j 45 e :a / 2 j 90 e :a h :a j 90 e :a / 2 tv! 5 j 90 e :a / 2 b 90 e :a / 2 b 45 e :a / 2 * gyök 2 b 45 e :a / 2 b 90 e :a / 2 h :a / 2 j 90 h :a / 2 tv! 1 j 90 e :a / 2 j 90 e :a j 90 e :a j 90 e :a / 2 tanuld minta3 :a ab :a j 45 tf e :a / 4 * 3 b 45 tl e :a / 4 * gyök 2 tv! 5 j 45 e :a / 4 j 90 e :a / 4 j 45 tv! 1 e :a / 4 * gyök 2 tv! 5 j 45 e :a / 4 j 90 e :a / 4 tv! 1 tf h :a / 4 j 90 e :a / 4 b 90 h :a / 4 * 3 tl j 45 aj :a Első forduló, III. kategória (7-8. osztály), 2. feladat: 2. feladat: Fa (24 pont) Készítsd el az ábrán látható fát rajzoló Logo eljárást (fa :h :g)! A fa törzse barna színű, alul 10-es, középen 8-as, felül 6-os vonalvastagságú legyen! Az ágak zöld színűek, a vonalvastagságuk kifelé egyesével csökken, legkívül 2-es. A gyümölcsök szára is zöld, de csak egyszeres vonalvastagságú, a gyümölcsök pedig pirosak legyenek! A törzs 6*:h magasságú legyen, az ágak felülről lefelé :h, 2*:h, illetve 4*:h hosszúságúak legyenek! Az ágakon felülről lefelé 1, 2, illetve 4 gyümölcs lógjon (balra és jobbra is), egymástól :h/2 egység távolságra! A gyümölcsök szára :g, a gyümölcsök oldalai pedig :g/2 méretűek legyenek, a szögek 60 és 120 fokosak! Készíts külön eljárást az ágak (balág :db :h :g, jobbág :db :h :g) és a gyümölcsök (gyümölcs :g) megrajzolására! Károlyi István 12 Évfolyamos Gimnázium LOGO grafikák/13. Évkönyvbe
14 Lipták Bence megoldása tanuld gyümölcs :g tv! 1 tsz! 3 e :g tsz! 12 b 30 ism 2 [e :g / 2 j 60 e :g / 2 j 120] tf j 30 h :g tsz! 0 tl tanuld balág :db :h :g ha :db = 1 [stop][tsz! 10 tv! :db + 1 e :h ~ b 90 gyümölcs :g tsz! 10 j 90 ~ balág :db - 1 :h :g] tanuld jobbág :db :h :g ha :db = 1 [stop][tsz! 10 tv! :db + 1 e :h ~ j 90 gyümölcs :g tsz! 10 b 90 ~ jobbág :db - 1 :h :g] tanuld fa :h :g tv! 10 tsz! 6 e :h * 2 b 90 balág 5 :h :g tf h :h * 4 tl j 180 jobbág 5 :h :g tf h :h * 4 tl b 90 tv! 8 tsz! 6 e :h * 2 b 90 balág 3 :h :g tf h :h * 2 tl j 180 jobbág 3 :h :g tf h :h * 2 tl b 90 tv! 6 tsz! 6 e :h * 2 b 90 balág 2 :h :g tf h :h tl j 180 jobbág 2 :h :g Természetesen sokféle fát rajzolhatunk. Figyeld meg, hogyan változnak a fák, ha híváskor más paramétereket adsz meg. Károlyi István 12 Évfolyamos Gimnázium LOGO grafikák/14. Évkönyvbe
15 Animációt is készítünk A Comenius Logo programcsomaghoz tartozik egy képsorszerkesztő, amellyel animációkat lehet készíteni. A tanév levezetéseként áprilistól ezzel foglalkoztunk. A legötletesebbeket letöltheted a SULI-SOFT honlapjáról 6 : Zsinka Bernadett: Száll a lepke virágról virágra (5zsbe01.lgw) Mátis Gergő: Jön a vonat (5mage01.lgw) Lipták Bence: A nagy bajvívás (lb lgw) Lipták Bence: Kosárdobás (lb lgw) Ruszki Bálint: Kékhalál (6ruba001.lgw) 25. fázis 28. fázis 29. fázis 33. fázis 36. fázis 50. fázis 53. fázis 57. fázis 58. fázis 63. fázis 68. fázis Ha kedvet kaptál a LOGO programozáshoz és a többi feladat is érdekel, szeretettel várlak a 2008/2009. tanév programozói szakkörén. Lugosi Márta néni Bp július Károlyi István 12 Évfolyamos Gimnázium LOGO grafikák/15. Évkönyvbe
16 Megfejtések: 1. soksz soksz soksz soksz soksz (egyre kisebb színes nyolcszögek) 2. ism 5[tr soksz soksz soksz soksz várj 10] (ez már majdnem a diszkó élménye : egyre kisebb színes hétszögek váltják egymást) 3. tr soksz soksz soksz soksz soksz soksz soksz soksz (100 oldalhosszúságú, egyre kisebb oldalszámú színes szabályos sokszögek) 4. tr ism 2[soksz soksz soksz soksz soksz soksz soksz soksz balra 180] (A 3. példabeli ábrához hasonló rajz és annak tükörképe ; csak most a sokszögek oldala 50 egység.) 5. ism 15[tr ism 2[soksz soksz soksz soksz soksz soksz soksz soksz balra 180] várj 5] ( Diszkófény a 4. példabeli alakzatokból) Módosítsunk!!! Próbáld ki, mi történik, ha a parancsokban változtatod a soksz2 eljárásban szereplő első számot! a soksz2 eljárásban szereplő második számot! az ismétlések számát! a várj parancs mögötti számot! a 4. példában az ismétlések számát és a balra fordulás szögét! Károlyi István 12 Évfolyamos Gimnázium LOGO grafikák/16. Évkönyvbe
Comenius Logo feladatok
 Comenius Logo feladatok 1. Milyen betűt rajzol az alábbi utasítássorozat, ha a teknőc kezdetben a képernyő közepén áll és felfelé néz? e 100 j 145 e 120 b 145 e 100 A) M betűt B) V betűt C) N betűt D)
Comenius Logo feladatok 1. Milyen betűt rajzol az alábbi utasítássorozat, ha a teknőc kezdetben a képernyő közepén áll és felfelé néz? e 100 j 145 e 120 b 145 e 100 A) M betűt B) V betűt C) N betűt D)
KissS. A l g o r i t m u s o k I m a g i n e L o g o b a n. Algoritmusok
 Algoritmusok Ebben a tárgykörben a ComeniusLogo-val foglalkozunk. "A teknőc számítógéppel vezérelt kibernetikus lény." A Logo-filozófia: "Hogy valamit megtanulhass, először találd meg az értelmét." Maga
Algoritmusok Ebben a tárgykörben a ComeniusLogo-val foglalkozunk. "A teknőc számítógéppel vezérelt kibernetikus lény." A Logo-filozófia: "Hogy valamit megtanulhass, először találd meg az értelmét." Maga
Tanulási segédlet 4. osztály
 Tanulási segédlet 4. osztály 1. Az informatikai eszközök használata 2. Alkalmazói ismeretek 3. Problémamegoldás informatikai eszközökkel 4. Infokommunikáció 5. Az információs társadalom 6. Könyvtári informatika
Tanulási segédlet 4. osztály 1. Az informatikai eszközök használata 2. Alkalmazói ismeretek 3. Problémamegoldás informatikai eszközökkel 4. Infokommunikáció 5. Az információs társadalom 6. Könyvtári informatika
TÁMOP 3.1.4-12/2-2012-0979
 TÁMOP 3.1.4-12/2-2012-0979 Szakkör címe: Informatika tantárgy tanításának fejlesztése: informatika szakkör (60 órás) Program anyaga: Számítógépes alapismeretek Helyszín: Izsáki Táncsics Mihály Általános
TÁMOP 3.1.4-12/2-2012-0979 Szakkör címe: Informatika tantárgy tanításának fejlesztése: informatika szakkör (60 órás) Program anyaga: Számítógépes alapismeretek Helyszín: Izsáki Táncsics Mihály Általános
Vektorgrafikus rajzeszközök
 8. nap Vektorgrafikus rajzeszközök A fejezet címe kicsit megtévesztõ lehet. Mivel a Flash alapvetõen vektorgrafikus alapú képek animálására szolgál, ezért a programon belül használható rajzeszközök mindegyikével
8. nap Vektorgrafikus rajzeszközök A fejezet címe kicsit megtévesztõ lehet. Mivel a Flash alapvetõen vektorgrafikus alapú képek animálására szolgál, ezért a programon belül használható rajzeszközök mindegyikével
Logo. tára. Logo OSzTV 1998-2002. Szerkesztette: Mészáros Tamásné Zsakó László
 Logo tára Logo OSzTV 1998-2002. Szerkesztette: Mészáros Tamásné Zsakó László Neumann János Számítógép-tudományi Társaság 2013 A verseny feladatsorait Mészáros Tamásné (Művészeti Általános Iskola) és Zsakó
Logo tára Logo OSzTV 1998-2002. Szerkesztette: Mészáros Tamásné Zsakó László Neumann János Számítógép-tudományi Társaság 2013 A verseny feladatsorait Mészáros Tamásné (Művészeti Általános Iskola) és Zsakó
4. osztály. Évi óraszám: 37 óra
 4. osztály Évi óraszám: 37 óra Órakeret 1. Az informatikai eszközök használata 4 óra 2. Alkalmazói ismeretek 14 óra 3. Problémamegoldás informatikai eszközökkel és módszerekkel 8 óra 4. Infokommunikációs
4. osztály Évi óraszám: 37 óra Órakeret 1. Az informatikai eszközök használata 4 óra 2. Alkalmazói ismeretek 14 óra 3. Problémamegoldás informatikai eszközökkel és módszerekkel 8 óra 4. Infokommunikációs
Informatika óravázlat 4. osztály oldal 15
 14. dec. 3. hét Algortimusok és adatok III. Programozzunk Imagine Logo vs. Comenius Logo Alapparancsok közti különbségek megfigyelése. Legfontosabb logo parancsok használata. Okos állat a Teki, szeret
14. dec. 3. hét Algortimusok és adatok III. Programozzunk Imagine Logo vs. Comenius Logo Alapparancsok közti különbségek megfigyelése. Legfontosabb logo parancsok használata. Okos állat a Teki, szeret
Készítette: niethammer@freemail.hu
 VLogo VRML generáló program Készítette: Niethammer Zoltán niethammer@freemail.hu 2008 Bevezetés A VLogo az általános iskolákban használt Comenius Logo logikájára épülő programozási nyelv. A végeredmény
VLogo VRML generáló program Készítette: Niethammer Zoltán niethammer@freemail.hu 2008 Bevezetés A VLogo az általános iskolákban használt Comenius Logo logikájára épülő programozási nyelv. A végeredmény
13. A Paint rajzolóprogram
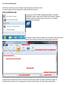 13. A Paint rajzolóprogram A Windows operációs rendszer beépített rajzolóprogramja, tartozéka a Paint. A program egyszerű ábrák rajzolására és képek kezelésére alkalmas. PAINT A WINDOWS-7-BEN A programot
13. A Paint rajzolóprogram A Windows operációs rendszer beépített rajzolóprogramja, tartozéka a Paint. A program egyszerű ábrák rajzolására és képek kezelésére alkalmas. PAINT A WINDOWS-7-BEN A programot
Imagine Logo Tanmenet évfolyam
 Imagine Logo Tanmenet 5. 6. 7. évfolyam 5. évfolyam 18. óra: Algoritmus fogalma, hétköznapi algoritmusok. Tkv. 72-73. oldal feladatai + Imagine Logo Demóválasztás (Játékok) 19. óra: Térbeli tájékozódást
Imagine Logo Tanmenet 5. 6. 7. évfolyam 5. évfolyam 18. óra: Algoritmus fogalma, hétköznapi algoritmusok. Tkv. 72-73. oldal feladatai + Imagine Logo Demóválasztás (Játékok) 19. óra: Térbeli tájékozódást
NEMZEDÉKEK TUDÁSA TANKÖNYVKIADÓ
 POLGÁR JUDIT SAKKPALOTA 1 Képességfejlesztô sakktankönyv NEMZEDÉKEK TUDÁSA TANKÖNYVKIADÓ Budapest TARTALOMJEGYZÉK 1. Ismerkedés a sakk világával... 3 2. Ismerkedés a sakkbábokkal... 7 3. Ismerkedés a sakktáblával...
POLGÁR JUDIT SAKKPALOTA 1 Képességfejlesztô sakktankönyv NEMZEDÉKEK TUDÁSA TANKÖNYVKIADÓ Budapest TARTALOMJEGYZÉK 1. Ismerkedés a sakk világával... 3 2. Ismerkedés a sakkbábokkal... 7 3. Ismerkedés a sakktáblával...
mintásfal 60 40 2 2 mintásfal :m :sz :dbjobbra :dbfel
 6.osztály 1.foglalkozás 6.osztály 2.foglalkozás kocka kockafal :db minta Készítsd el ezt a mintát! A minta hosszú oldala 60 a rövid oldala 40 egység hosszú. A hosszú oldal harmada a négyzet oldala! A háromszög
6.osztály 1.foglalkozás 6.osztály 2.foglalkozás kocka kockafal :db minta Készítsd el ezt a mintát! A minta hosszú oldala 60 a rövid oldala 40 egység hosszú. A hosszú oldal harmada a négyzet oldala! A háromszög
Tükrözés a sík átfordításával
 Matematika A 2. évfolyam Tükrözés a sík átfordításával 37. modul Készítette: Szili Judit 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A képességfejlesztés fókuszai
Matematika A 2. évfolyam Tükrözés a sík átfordításával 37. modul Készítette: Szili Judit 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A képességfejlesztés fókuszai
Az ellipszis, a henger AF 22 TORZS/ HATODIK/Tor62al98.doc
 Az ellipszis, a henger AF 22 TORZS/ HATODIK/Tor62al98.doc..\..\Tartalomjegyzék.doc - Az ellipszis Cél: Látvány utáni tanulmány. Szakkörön, rajziskolában heteken át szerkezeti rajzokat készítenénk, átlag
Az ellipszis, a henger AF 22 TORZS/ HATODIK/Tor62al98.doc..\..\Tartalomjegyzék.doc - Az ellipszis Cél: Látvány utáni tanulmány. Szakkörön, rajziskolában heteken át szerkezeti rajzokat készítenénk, átlag
Programozási nyelvek 1. előadás
 Programozási nyelvek 1. előadás I. A nyelv története Logo Seymour Papert, 1968,1969 - szövegkezelés, M.I.T. Később: grafika, mikroszámítógépekre átdolgozva Cél: minél kisebb gyerekeknek is, természetes
Programozási nyelvek 1. előadás I. A nyelv története Logo Seymour Papert, 1968,1969 - szövegkezelés, M.I.T. Később: grafika, mikroszámítógépekre átdolgozva Cél: minél kisebb gyerekeknek is, természetes
Rátz László Matematikai kvízverseny 5. osztály
 Rátz László Matematikai kvízverseny 5. osztály 2010. november 26. 1. feladat Ez a különleges óra a pontos időt mutatja. Az első sor ötórás intervallumokat számol (minden ötóránként vált szürkére), a második
Rátz László Matematikai kvízverseny 5. osztály 2010. november 26. 1. feladat Ez a különleges óra a pontos időt mutatja. Az első sor ötórás intervallumokat számol (minden ötóránként vált szürkére), a második
Alkotások síkban mozaiklapokkal, szívószállal
 Matematika A 2. évfolyam Alkotások síkban mozaiklapokkal, szívószállal 27. modul Készítette: Szili Judit Szitányi Judit 2 matematika A 2. ÉVFOLYAM 27. modul Alkotások síkban mozaiklapokkal, szívószállal
Matematika A 2. évfolyam Alkotások síkban mozaiklapokkal, szívószállal 27. modul Készítette: Szili Judit Szitányi Judit 2 matematika A 2. ÉVFOLYAM 27. modul Alkotások síkban mozaiklapokkal, szívószállal
C Í M K E É V F O L Y A M ORSZÁGOS KOMPETENCIAMÉRÉS 2007 JAVÍTÓKULCS MATEMATIKA. Oktatási Hivatal Országos Közoktatási Értékelési és Vizsgaközpont
 8. Í M K E É V F O L Y A M TANULÓI AZONOSÍTÓ: ORSZÁGOS KOMPETENIAMÉRÉS 2007 JAVÍTÓKULS MATEMATIKA Oktatási Hivatal Országos Közoktatási Értékelési és Vizsgaközpont ÁLTALÁNOS TUDNIVALÓK Ön a 2007-es Országos
8. Í M K E É V F O L Y A M TANULÓI AZONOSÍTÓ: ORSZÁGOS KOMPETENIAMÉRÉS 2007 JAVÍTÓKULS MATEMATIKA Oktatási Hivatal Országos Közoktatási Értékelési és Vizsgaközpont ÁLTALÁNOS TUDNIVALÓK Ön a 2007-es Országos
MATEMATIKA TAGOZAT 5-8. BEVEZETŐ. 5. évfolyam
 BEVEZETŐ Ez a helyi tanterv a kerettanterv Emelet matematika A változata alapján készült. Az emelt oktatás során olyan tanulóknak kívánunk magasabb szintű ismerteket nyújtani, akik matematikából átlag
BEVEZETŐ Ez a helyi tanterv a kerettanterv Emelet matematika A változata alapján készült. Az emelt oktatás során olyan tanulóknak kívánunk magasabb szintű ismerteket nyújtani, akik matematikából átlag
TARTALOMJEGYZÉK ELŐSZÓ... 7 1. GONDOLKOZZ ÉS SZÁMOLJ!... 9 2. HOZZÁRENDELÉS, FÜGGVÉNY... 69
 TARTALOMJEGYZÉK ELŐSZÓ............................................................ 7 1. GONDOLKOZZ ÉS SZÁMOLJ!............................. 9 Mit tanultunk a számokról?............................................
TARTALOMJEGYZÉK ELŐSZÓ............................................................ 7 1. GONDOLKOZZ ÉS SZÁMOLJ!............................. 9 Mit tanultunk a számokról?............................................
Feltételes formázás az Excel 2007-ben
 Az új verzió legnagyobb újdonsága Feltételes formázás az Excel 2007-ben Formázás tekintetében a feltételes formázás területén változott a legnagyobbat a program. Valljuk meg, a régebbi változatoknál a
Az új verzió legnagyobb újdonsága Feltételes formázás az Excel 2007-ben Formázás tekintetében a feltételes formázás területén változott a legnagyobbat a program. Valljuk meg, a régebbi változatoknál a
1. Melyek azok a kétjegyű számok, amelyek oszthatók számjegyeik
 1991. évi verseny, 1. nap 1. Számold össze, hány pozitív osztója van 16 200-nak! 2. Bontsd fel a 60-at két szám összegére úgy, hogy az egyik szám hetede egyenlő legyen a másik szám nyolcadával! 3. Van
1991. évi verseny, 1. nap 1. Számold össze, hány pozitív osztója van 16 200-nak! 2. Bontsd fel a 60-at két szám összegére úgy, hogy az egyik szám hetede egyenlő legyen a másik szám nyolcadával! 3. Van
Készítette: Lipták István. Szükséges eszközök, javasolt szoftverek. Idı 1., 6. Puzzle 25. Puzzle hardvereszközökbıl
 Puzzle hardvereszközökbıl A számítógép fıbb részeit, perifériáit ábrázoló puzzle-k kirakása csoportokban. (Pl.: monitor, gépház, egér, billentyőzet, nyomtató.)a puzzle online felületen is elkészíthetı:
Puzzle hardvereszközökbıl A számítógép fıbb részeit, perifériáit ábrázoló puzzle-k kirakása csoportokban. (Pl.: monitor, gépház, egér, billentyőzet, nyomtató.)a puzzle online felületen is elkészíthetı:
Prezentáció használata
 Prezentáció használata A számítógép alkalmazásának egyik lehetséges területe, amikor a számítógépet mint segédeszközt hívjuk segítségül, annak érdekében, hogy előadásunk vagy ismertetőnk során elhangzottakat
Prezentáció használata A számítógép alkalmazásának egyik lehetséges területe, amikor a számítógépet mint segédeszközt hívjuk segítségül, annak érdekében, hogy előadásunk vagy ismertetőnk során elhangzottakat
4. Lecke. Körök és szabályos sokszögek rajzolása. 4.Lecke / 1.
 4.Lecke / 1. 4. Lecke Körök és szabályos sokszögek rajzolása Az előző fejezetekkel ellentétben most nem újabb programozási utasításokról vagy elvekről fogunk tanulni. Ebben a fejezetben a sokszögekről,
4.Lecke / 1. 4. Lecke Körök és szabályos sokszögek rajzolása Az előző fejezetekkel ellentétben most nem újabb programozási utasításokról vagy elvekről fogunk tanulni. Ebben a fejezetben a sokszögekről,
MATEMATIKA A. feladatlapok. 2. évfolyam. 2. félév
 MATEMATIKA A feladatlapok. évfolyam. félév A kiadvány KHF/3993-18/008. engedélyszámon 008.08.18. időponttól tankönyvi engedélyt kapott Educatio Kht. Kompetenciafejlesztő oktatási program kerettanterv A
MATEMATIKA A feladatlapok. évfolyam. félév A kiadvány KHF/3993-18/008. engedélyszámon 008.08.18. időponttól tankönyvi engedélyt kapott Educatio Kht. Kompetenciafejlesztő oktatási program kerettanterv A
Scherlein Márta Dr. Hajdu Sándor Köves Gabriella Novák Lászlóné MATEMATIKA 1. A FELMÉRŐ FELADATSOROK ÉRTÉKELÉSE
 Scherlein Márta Dr. Hajdu Sándor Köves Gabriella Novák Lászlóné MATEMATIKA 1. A FELMÉRŐ FELADATSOROK ÉRTÉKELÉSE A felmérő feladatsorok értékelése A felmérő feladatsorokat úgy állítottuk össze, hogy azok
Scherlein Márta Dr. Hajdu Sándor Köves Gabriella Novák Lászlóné MATEMATIKA 1. A FELMÉRŐ FELADATSOROK ÉRTÉKELÉSE A felmérő feladatsorok értékelése A felmérő feladatsorokat úgy állítottuk össze, hogy azok
Programozási nyelvek 2. előadás
 Programozási nyelvek 2. előadás Logo forgatás tétel Forgatás tétel Ha az ismétlendő rész T fok fordulatot végez és a kezdőhelyére visszatér, akkor az ismétlések által rajzolt ábrák egymás T fokkal elforgatottjai
Programozási nyelvek 2. előadás Logo forgatás tétel Forgatás tétel Ha az ismétlendő rész T fok fordulatot végez és a kezdőhelyére visszatér, akkor az ismétlések által rajzolt ábrák egymás T fokkal elforgatottjai
Tananyag, tartalom, tevékenység - minimum és optimum
 Informatika /2. osztály NAT Digitális kompetencia A digitális kompetencia felöleli az információs társadalom technológiáinak (Information Society Technology, a továbbiakban: IST) magabiztos és kritikus
Informatika /2. osztály NAT Digitális kompetencia A digitális kompetencia felöleli az információs társadalom technológiáinak (Information Society Technology, a továbbiakban: IST) magabiztos és kritikus
Programozás 7.o Az algoritmus fogalma (ismétlés)
 Programozás 7.o Az algoritmus fogalma (étlés) Az algoritmus olyan leírás, felsorolás, amely az adott feladat megoldásához szükséges jól definiált utasítások s számú sorozata. Egy probléma megoldására kidolgozott
Programozás 7.o Az algoritmus fogalma (étlés) Az algoritmus olyan leírás, felsorolás, amely az adott feladat megoldásához szükséges jól definiált utasítások s számú sorozata. Egy probléma megoldására kidolgozott
ÉLETPÁLYA- ÉPÍTÉS MATEMATIKA TANÁRI ÚTMUTATÓ KOMPETENCIATERÜLET B. 6. évfolyam
 ÉLETPÁLYA- ÉPÍTÉS KOMPETENCIATERÜLET B MATEMATIKA TANÁRI ÚTMUTATÓ 6. évfolyam A kiadvány az Educatio Kht. kompetenciafejlesztő oktatási program kerettanterve alapján készült. A kiadvány a Nemzeti Fejlesztési
ÉLETPÁLYA- ÉPÍTÉS KOMPETENCIATERÜLET B MATEMATIKA TANÁRI ÚTMUTATÓ 6. évfolyam A kiadvány az Educatio Kht. kompetenciafejlesztő oktatási program kerettanterve alapján készült. A kiadvány a Nemzeti Fejlesztési
fmaozaik :n :m :h :s járóóra
 A változók 3+2 = mit írnál a helyére? 12 + 8 > mit írnál a helyére? A fióknak először is adni kell egy értéket, majd egy nevet is! Kétféleképpen nézhetjük meg, mi van a fiókunkban. mutat parancs mutat_:mit
A változók 3+2 = mit írnál a helyére? 12 + 8 > mit írnál a helyére? A fióknak először is adni kell egy értéket, majd egy nevet is! Kétféleképpen nézhetjük meg, mi van a fiókunkban. mutat parancs mutat_:mit
Több feladat megoldásához használnod kell az általunk előkészített állományokat, melyeket a tankönyvhöz tartozó, www.pedellusinfo.
 1. Informatikai eszközök használata / 4 2. Dokumentumkészítés / 15 3. Problémamegoldás / 24 4. Infokommunikáció / 35 5. Könyvtárhasználat / 37 Több feladat megoldásához használnod kell az általunk előkészített
1. Informatikai eszközök használata / 4 2. Dokumentumkészítés / 15 3. Problémamegoldás / 24 4. Infokommunikáció / 35 5. Könyvtárhasználat / 37 Több feladat megoldásához használnod kell az általunk előkészített
MATEMATIKAI KOMPETENCIATERÜLET A
 MATEMATIKAI KOMPETENCIATERÜLET A Matematika 6. évfolyam TANULÓI MUNKAFÜZET 2. FÉLÉV A kiadvány KHF/4356-14/2008. engedélyszámon 2008.11.25. időponttól tankönyvi engedélyt kapott Educatio Kht. Kompetenciafejlesztő
MATEMATIKAI KOMPETENCIATERÜLET A Matematika 6. évfolyam TANULÓI MUNKAFÜZET 2. FÉLÉV A kiadvány KHF/4356-14/2008. engedélyszámon 2008.11.25. időponttól tankönyvi engedélyt kapott Educatio Kht. Kompetenciafejlesztő
Matematika felvételi feladatok bővített levezetése 2013 (8. osztályosoknak)
 Matematika felvételi feladatok bővített levezetése 2013 (8. osztályosoknak) Erre a dokumentumra az Edemmester Gamer Blog kiadványokra vonatkozó szabályai érvényesek. 1. feladat: Határozd meg az a, b és
Matematika felvételi feladatok bővített levezetése 2013 (8. osztályosoknak) Erre a dokumentumra az Edemmester Gamer Blog kiadványokra vonatkozó szabályai érvényesek. 1. feladat: Határozd meg az a, b és
MATEMATIKA KOMPETENCIATERÜLET A
 MATEMATIKA KOMPETENCIATERÜLET A Matematika 7. évfolyam TANULÓI MUNKAFÜZET 2. félév A kiadvány KHF/4002-17/2008 engedélyszámon 2008. 08. 18. időponttól tankönyvi engedélyt kapott Educatio Kht. Kompetenciafejlesztő
MATEMATIKA KOMPETENCIATERÜLET A Matematika 7. évfolyam TANULÓI MUNKAFÜZET 2. félév A kiadvány KHF/4002-17/2008 engedélyszámon 2008. 08. 18. időponttól tankönyvi engedélyt kapott Educatio Kht. Kompetenciafejlesztő
KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA
 ÉRETTSÉGI VIZSGA 2016. május 3. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2016. május 3. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Matematika középszint
ÉRETTSÉGI VIZSGA 2016. május 3. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2016. május 3. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Matematika középszint
Tájékozódás számvonalon, számtáblázatokon
 Matematika A 2. évfolyam Tájékozódás számvonalon, számtáblázatokon 12. modul Készítette: Bóta Mária Kőkúti Ágnes matematika A 2. évfolyam 12 modul Tájékozódás számvonalon, számtáblázatokon modulleírás
Matematika A 2. évfolyam Tájékozódás számvonalon, számtáblázatokon 12. modul Készítette: Bóta Mária Kőkúti Ágnes matematika A 2. évfolyam 12 modul Tájékozódás számvonalon, számtáblázatokon modulleírás
Országos Logikai Rejtvénybajnokság 2008. szeptember 14. Instrukciós füzet
 1. feladatsor: 100 perc, 1000 pont Instrukciós füzet Kertek (15+30) Az ábrában kertek oldallal szomszédos négyzetekből álló fehér területek rejtőznek, amelyeket egy összefüggő érintkező oldalak mentén
1. feladatsor: 100 perc, 1000 pont Instrukciós füzet Kertek (15+30) Az ábrában kertek oldallal szomszédos négyzetekből álló fehér területek rejtőznek, amelyeket egy összefüggő érintkező oldalak mentén
Módszertani ajánlás tanítóknak, az informatika alsó tagozatos tanításához és alkalmazásához
 Módszertani ajánlás tanítóknak, az informatika alsó tagozatos tanításához és alkalmazásához E módszertani útmutatóban, mint egy lehetőséget, kipróbált, részletes tematikát szeretnék bemutatni. A feltüntetett
Módszertani ajánlás tanítóknak, az informatika alsó tagozatos tanításához és alkalmazásához E módszertani útmutatóban, mint egy lehetőséget, kipróbált, részletes tematikát szeretnék bemutatni. A feltüntetett
ÍRÁSBELI ÖSSZEADÁS, KIVONÁS. A MŰVELETI SORREND SZÁMÍTÁSOKBAN ÉS SZÖVEGES FELADATOK MEGOLDÁSA SORÁN. 9. modul
 Matematika A 4. évfolyam ÍRÁSBELI ÖSSZEADÁS, KIVONÁS. A MŰVELETI SORREND SZÁMÍTÁSOKBAN ÉS SZÖVEGES FELADATOK MEGOLDÁSA SORÁN 9. modul Készítette: KONRÁD ÁGNES matematika A 4. ÉVFOLYAM 9. modul ÍRÁSBELI
Matematika A 4. évfolyam ÍRÁSBELI ÖSSZEADÁS, KIVONÁS. A MŰVELETI SORREND SZÁMÍTÁSOKBAN ÉS SZÖVEGES FELADATOK MEGOLDÁSA SORÁN 9. modul Készítette: KONRÁD ÁGNES matematika A 4. ÉVFOLYAM 9. modul ÍRÁSBELI
EGÉSZ SZÁMOK. 36. modul
 Matematika A 3. évfolyam EGÉSZ SZÁMOK 36. modul Készítette: zsinkó erzsébet matematika A 3. ÉVFOLYAM 36. modul EGÉSZ számok MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok
Matematika A 3. évfolyam EGÉSZ SZÁMOK 36. modul Készítette: zsinkó erzsébet matematika A 3. ÉVFOLYAM 36. modul EGÉSZ számok MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok
A LOGO MOTION TANÍTÁSA
 A LOGO MOTION TANÍTÁSA ÍRTA: SZABÓ JÁNOS TANÍTÓ 2010, KECEL LOGO MOTION TANÍTÁSA KÉSZÍTETTE: SZABÓ JÁNOS TANÍTÓ 2010. 1 1. FOGLALKOZÁS Kattintsunk a Logo motion ikonjára. A Színes teki. Ez a program ablaka.
A LOGO MOTION TANÍTÁSA ÍRTA: SZABÓ JÁNOS TANÍTÓ 2010, KECEL LOGO MOTION TANÍTÁSA KÉSZÍTETTE: SZABÓ JÁNOS TANÍTÓ 2010. 1 1. FOGLALKOZÁS Kattintsunk a Logo motion ikonjára. A Színes teki. Ez a program ablaka.
Curie Matematika Emlékverseny 5. évfolyam Országos döntő 2011/2012. Fontos tudnivalók
 A feladatokat írta: Kódszám: Tóth Jánosné, Szolnok Lektorálta:. Kozma Lászlóné, Sajószentpéter 2012.április 14. Curie Matematika Emlékverseny 5. évfolyam Országos döntő 2011/2012. Feladat 1. 2. 3. 4. 5.
A feladatokat írta: Kódszám: Tóth Jánosné, Szolnok Lektorálta:. Kozma Lászlóné, Sajószentpéter 2012.április 14. Curie Matematika Emlékverseny 5. évfolyam Országos döntő 2011/2012. Feladat 1. 2. 3. 4. 5.
A FOGLAKOZÁS ADATAI: SZERZŐ. Vindics Dóra. Vezérelj robotot! A FOGLALKOZÁS CÍME A FOGLALKOZÁS RÖVID
 A FOGLAKOZÁS ADATAI: SZERZŐ Vindics Dóra A FOGLALKOZÁS CÍME Vezérelj robotot! A FOGLALKOZÁS RÖVID LEÍRÁSA A tanulók gyakran nem értik, hogy miért van szükség arra, amit matematika órán tanulnak. Ebben
A FOGLAKOZÁS ADATAI: SZERZŐ Vindics Dóra A FOGLALKOZÁS CÍME Vezérelj robotot! A FOGLALKOZÁS RÖVID LEÍRÁSA A tanulók gyakran nem értik, hogy miért van szükség arra, amit matematika órán tanulnak. Ebben
11. Balra zárt igazítás A bekezdés sorai a bal oldali margóhoz igazodnak. 12. Beillesztés
 1. Ablak A képernyő azon része, amelyben programok futhatnak. 2. Aláhúzott A karakter egyszeres vonallal történő aláhúzása a szövegben. 3. Algoritmus Egy feladat megoldását eredményező, véges számú lépések
1. Ablak A képernyő azon része, amelyben programok futhatnak. 2. Aláhúzott A karakter egyszeres vonallal történő aláhúzása a szövegben. 3. Algoritmus Egy feladat megoldását eredményező, véges számú lépések
MATEMATIKA ÍRÁSBELI VIZSGA EMELT SZINT% ÉRETTSÉGI VIZSGA 2013. május 7. MINISZTÉRIUMA. 2013. május 7. 8:00 EMBERI ERFORRÁSOK
 I. rész II. rész a feladat sorszáma maximális pontszám elért pontszám maximális pontszám 1. 11 2. 13 51 3. 13 4. 14 16 16 64 16 16 8 nem választott feladat Az írásbeli vizsgarész pontszáma 115 elért pontszám
I. rész II. rész a feladat sorszáma maximális pontszám elért pontszám maximális pontszám 1. 11 2. 13 51 3. 13 4. 14 16 16 64 16 16 8 nem választott feladat Az írásbeli vizsgarész pontszáma 115 elért pontszám
Beszámoló Programozási készségek fejlesztése Logo nyelven műhelymunka NTP-MTI-13 Emberi Erőforrások Minisztériuma
 Beszámoló Programozási készségek fejlesztése Logo nyelven műhelymunka A matematikai, a természettudományos és a műszaki, informatikai kompetenciák, valamint a szakmatanuláshoz szükséges kompetenciák erősítése
Beszámoló Programozási készségek fejlesztése Logo nyelven műhelymunka A matematikai, a természettudományos és a műszaki, informatikai kompetenciák, valamint a szakmatanuláshoz szükséges kompetenciák erősítése
Az anyagdefiníciók szerepe és használata az Architectural Desktop programban
 Az anyagdefiníciók szerepe és használata az Architectural Desktop programban Az Architectural Desktop program 2004-es változatáig kellett várni arra, hogy az AutoCAD alapú építész programban is megjelenjenek
Az anyagdefiníciók szerepe és használata az Architectural Desktop programban Az Architectural Desktop program 2004-es változatáig kellett várni arra, hogy az AutoCAD alapú építész programban is megjelenjenek
PYTAGORIÁDA Az iskolai forduló feladatai 35. évfolyam, 2013/2014-es tanév KATEGÓRIA P3
 KATEGÓRIA P3 1. Írjátok le, melyik alakzat nem tartozik a többi közé: négyzet, háromszög, egyenes, kör, téglalap 2. Számítsátok ki: 15 + 17= 24 + 59 = 50 + 20 = Az eredményeket adjátok össze és ezt az
KATEGÓRIA P3 1. Írjátok le, melyik alakzat nem tartozik a többi közé: négyzet, háromszög, egyenes, kör, téglalap 2. Számítsátok ki: 15 + 17= 24 + 59 = 50 + 20 = Az eredményeket adjátok össze és ezt az
PYTAGORIÁDA Súťažné úlohy okresného kola maďarský preklad 35. ročník, školský rok 2013/2014 KATEGÓRIA P 3
 KATEGÓRIA P 3 1. Misi két csomag rágógumiért 4 eurót fizetne. Írjátok le, hogy hány eurót fog Misi fizetni, ha mindhárom testvérének egy-egy csomag, saját magának pedig két csomag rágógumit vett! 2. Írjátok
KATEGÓRIA P 3 1. Misi két csomag rágógumiért 4 eurót fizetne. Írjátok le, hogy hány eurót fog Misi fizetni, ha mindhárom testvérének egy-egy csomag, saját magának pedig két csomag rágógumit vett! 2. Írjátok
Lerakó 7. modul készítette: köves GaBrIeLLa
 Lerakó 7. modul Készítette: KÖVES GABRIELLA 2 Lerakó A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A tudatos észlelés, a megfigyelés és a figyelem fejlesztése Párban, kis csoportban
Lerakó 7. modul Készítette: KÖVES GABRIELLA 2 Lerakó A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A tudatos észlelés, a megfigyelés és a figyelem fejlesztése Párban, kis csoportban
TANMENET MATEMATIKA. 1. osztály 2009-2010. (modulos rendszerű) Készítette: Tóthné Szendrődy Réka
 TANMENET 1. osztály MATEMATIKA (modulos rendszerű) Készítette: Tóthné Szendrődy Réka 2009-2010 IDŐ TANANYAG FEJLESZTENDŐ Szept. 1-7 1. modul Tájékozódj unk, tanuljunk! Megismerési képességek alapozása:
TANMENET 1. osztály MATEMATIKA (modulos rendszerű) Készítette: Tóthné Szendrődy Réka 2009-2010 IDŐ TANANYAG FEJLESZTENDŐ Szept. 1-7 1. modul Tájékozódj unk, tanuljunk! Megismerési képességek alapozása:
TÖRTSZÁMOK, MÉRÉSEK. 34. modul
 Matematika A 3. évfolyam TÖRTSZÁMOK, MÉRÉSEK 34. modul Készítette: SZITÁNYI JUDIT matematika A 3. ÉVFOLYAM 34. modul TÖRTSZÁMOK, MÉRÉSEK MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
Matematika A 3. évfolyam TÖRTSZÁMOK, MÉRÉSEK 34. modul Készítette: SZITÁNYI JUDIT matematika A 3. ÉVFOLYAM 34. modul TÖRTSZÁMOK, MÉRÉSEK MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Gráfelmélet II. Gráfok végigjárása
 Gráfelmélet II. Gráfok végigjárása DEFINÍCIÓ: (Séta) A G gráf egy olyan élsorozatát, amelyben a csúcsok és élek többször is szerepelhetnek, sétának nevezzük. Egy lehetséges séta: A; 1; B; 2; C; 3; D; 4;
Gráfelmélet II. Gráfok végigjárása DEFINÍCIÓ: (Séta) A G gráf egy olyan élsorozatát, amelyben a csúcsok és élek többször is szerepelhetnek, sétának nevezzük. Egy lehetséges séta: A; 1; B; 2; C; 3; D; 4;
TÉGLATEST, KOCKA, GÖMB TÉGLALAP, NÉGYZET, KÖR
 Matematika A 3. évfolyam TÉGLATEST, KOCKA, GÖMB TÉGLALAP, NÉGYZET, KÖR 40. modul Készítette: SZILI JUDIT (A 11., 13., 15. PONTOT: LÉNÁRT ISTVÁN) matematika A 3. ÉVFOLYAM 40. modul TÉGLATEST, KOCKA, GÖMB
Matematika A 3. évfolyam TÉGLATEST, KOCKA, GÖMB TÉGLALAP, NÉGYZET, KÖR 40. modul Készítette: SZILI JUDIT (A 11., 13., 15. PONTOT: LÉNÁRT ISTVÁN) matematika A 3. ÉVFOLYAM 40. modul TÉGLATEST, KOCKA, GÖMB
A ceruza AF 3Tor/otodik/TOR52AL98.doc
 A ceruza AF 3Tor/otodik/TOR52AL98.doc (Vissza a tartalomjegyzékhez:..\..\tartalomjegyzék.doc - A ceruza) (Vissza a Technikákhoz:..\..\TECHNIKA\Technika.doc) Cél: technikai tanulmány Előző óránkon belekóstolhattunk
A ceruza AF 3Tor/otodik/TOR52AL98.doc (Vissza a tartalomjegyzékhez:..\..\tartalomjegyzék.doc - A ceruza) (Vissza a Technikákhoz:..\..\TECHNIKA\Technika.doc) Cél: technikai tanulmány Előző óránkon belekóstolhattunk
Az 5. 14. modul. Készítette: bóta mária kőkúti ágnes
 Matematika A 1. évfolyam Az 5 14. modul Készítette: bóta mária kőkúti ágnes matematika A 1. ÉVFOLYAM 14. modul Az 5 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A képességfejlesztés
Matematika A 1. évfolyam Az 5 14. modul Készítette: bóta mária kőkúti ágnes matematika A 1. ÉVFOLYAM 14. modul Az 5 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A képességfejlesztés
Általános tudnivalók
 Általános tudnivalók A versenyen tetszőleges íróeszköz használható. (Például ceruza, toll, filctoll, színes ceruza.) Az íróeszközökről a versenyzőknek maguknak kell gondoskodniuk. Instrukciós füzetekkel
Általános tudnivalók A versenyen tetszőleges íróeszköz használható. (Például ceruza, toll, filctoll, színes ceruza.) Az íróeszközökről a versenyzőknek maguknak kell gondoskodniuk. Instrukciós füzetekkel
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Geometria I.
 Geometria I. Alapfogalmak: Az olyan fogalmakat, amelyeket nem tudunk egyszerűbb fogalmakra visszavezetni, alapfogalmaknak nevezzük, s ezeket nem definiáljuk. Pl.: pont, egyenes, sík, tér, illeszkedés.
Geometria I. Alapfogalmak: Az olyan fogalmakat, amelyeket nem tudunk egyszerűbb fogalmakra visszavezetni, alapfogalmaknak nevezzük, s ezeket nem definiáljuk. Pl.: pont, egyenes, sík, tér, illeszkedés.
1. Az ábrán a pontok a szabályos háromszögrács 10 pontját jelentik (tehát az ABC háromszög egyenlőoldalú, a BDE háromszög egyenlőoldalú, a CEF
 1. Az ábrán a pontok a szabályos háromszögrács 10 pontját jelentik (tehát az ABC háromszög egyenlőoldalú, a BDE háromszög egyenlőoldalú, a CEF háromszög egyenlőoldalú, stb ). A 10 pont közül ki kell választani
1. Az ábrán a pontok a szabályos háromszögrács 10 pontját jelentik (tehát az ABC háromszög egyenlőoldalú, a BDE háromszög egyenlőoldalú, a CEF háromszög egyenlőoldalú, stb ). A 10 pont közül ki kell választani
EMELT SZINTŰ ÍRÁSBELI VIZSGA
 ÉRETTSÉGI VIZSGA 2006. május 9. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI VIZSGA 2006. május 9. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI MINISZTÉRIUM Matematika
ÉRETTSÉGI VIZSGA 2006. május 9. MATEMATIKA EMELT SZINTŰ ÍRÁSBELI VIZSGA 2006. május 9. 8:00 Az írásbeli vizsga időtartama: 240 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI MINISZTÉRIUM Matematika
148 feladat 21 + + 20 20 ) + ( 1 21 + 2 200 > 1 2. 1022 + 1 51 + 1 52 + + 1 99 2 ) (1 1 100 2 ) =?
 148 feladat a Kalmár László Matematikaversenyről 1. ( 1 19 + 2 19 + + 18 19 ) + ( 1 20 + 2 20 + + 19 20 ) + ( 1 21 + 2 21 + + 20 21 ) + ( 1 22 + 2 22 + + 21 22 ) =? Kalmár László Matematikaverseny megyei
148 feladat a Kalmár László Matematikaversenyről 1. ( 1 19 + 2 19 + + 18 19 ) + ( 1 20 + 2 20 + + 19 20 ) + ( 1 21 + 2 21 + + 20 21 ) + ( 1 22 + 2 22 + + 21 22 ) =? Kalmár László Matematikaverseny megyei
Szeminárium-Rekurziók
 1 Szeminárium-Rekurziók 1.1. A sorozat fogalma Számsorozatot kapunk, ha pozitív egész számok mindegyikéhez egyértelműen hozzárendelünk egy valós számot. Tehát a számsorozat olyan függvény, amelynek az
1 Szeminárium-Rekurziók 1.1. A sorozat fogalma Számsorozatot kapunk, ha pozitív egész számok mindegyikéhez egyértelműen hozzárendelünk egy valós számot. Tehát a számsorozat olyan függvény, amelynek az
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Térgeometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Térgeometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Térgeometria A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Mozaikozás szabadon és másolással
 Matematika A 1. évfolyam Mozaikozás szabadon és másolással 39. modul Készítette: szili judit matematika A 1. ÉVFOLYAM 39. modul mozaikozás szabadon és másolással modulleírás A modul célja Időkeret Ajánlott
Matematika A 1. évfolyam Mozaikozás szabadon és másolással 39. modul Készítette: szili judit matematika A 1. ÉVFOLYAM 39. modul mozaikozás szabadon és másolással modulleírás A modul célja Időkeret Ajánlott
KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA
 ÉRETTSÉGI VIZSGA 2007. október 25. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2007. október 25. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Matematika
ÉRETTSÉGI VIZSGA 2007. október 25. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2007. október 25. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Matematika
INFORMATIKA KÖZÉPSZINT%
 Szövegszerkesztés 1. Ivóvíz Prezentáció, grafika és weblapkészítés 2. Italos karton Táblázatkezelés 3. Bérautó Adatbázis-kezelés 4. Felajánlás maximális A gyakorlati vizsgarész a 120 40 30 30 20 elért
Szövegszerkesztés 1. Ivóvíz Prezentáció, grafika és weblapkészítés 2. Italos karton Táblázatkezelés 3. Bérautó Adatbázis-kezelés 4. Felajánlás maximális A gyakorlati vizsgarész a 120 40 30 30 20 elért
3. lecke: Fürdőszoba tervezés - Burkolás
 3. lecke: Fürdőszoba tervezés - Burkolás ARCHLine.XP Az oktatási anyagot, melyet a kezében tart minden leendő és jelenlegi ARCHLine.XP felhasználónak ajánljuk. Segítségével bárki könnyedén, lépésről lépésre
3. lecke: Fürdőszoba tervezés - Burkolás ARCHLine.XP Az oktatási anyagot, melyet a kezében tart minden leendő és jelenlegi ARCHLine.XP felhasználónak ajánljuk. Segítségével bárki könnyedén, lépésről lépésre
Logo-pedagógia Pedagógiai informatika, tanítás a Logóval
 Iskolakultúra 2003/10 Farkas Károly Logo-pedagógia Pedagógiai informatika, tanítás a Logóval Seymour Papert, mint Piaget tanítványa, mint LEGO-professzor, beül a gyerekek közé, abba a szobába, amelyet
Iskolakultúra 2003/10 Farkas Károly Logo-pedagógia Pedagógiai informatika, tanítás a Logóval Seymour Papert, mint Piaget tanítványa, mint LEGO-professzor, beül a gyerekek közé, abba a szobába, amelyet
NIKerettanterv MATEMATIKA 1. évfolyan Éves óraszám: 180 óra, heti 5 óra
 NIKerettanterv MATEMATIKA 1. évfolyan Éves óraszám: 180 óra, heti 5 óra A matematikatanítás célja, hogy lehetővé tegye a tanulók számára a környező világ térformáinak, mennyiségi viszonyainak, összefüggéseinek
NIKerettanterv MATEMATIKA 1. évfolyan Éves óraszám: 180 óra, heti 5 óra A matematikatanítás célja, hogy lehetővé tegye a tanulók számára a környező világ térformáinak, mennyiségi viszonyainak, összefüggéseinek
Programozási nyelvek 3. előadás
 Programozási nyelvek 3. előadás Logo sokszög variációk Sokszög rekurzívan Az N oldalú sokszögvonal 1 oldalból és egy N-1 oldalú sokszögvonalból áll. eljárás reksokszög :n :hossz :szög előre :hossz balra
Programozási nyelvek 3. előadás Logo sokszög variációk Sokszög rekurzívan Az N oldalú sokszögvonal 1 oldalból és egy N-1 oldalú sokszögvonalból áll. eljárás reksokszög :n :hossz :szög előre :hossz balra
A Batthyány Általános Iskola és Sportiskola félévi/év végi beszámolója
 1.sz. Függelék: A Batthyány Általános Iskola és Sportiskola félévi/év végi beszámolója Osztályfőnökök részére..tanév.. félév..osztály 1. A szakmai munka áttekintése: Statisztika Az osztály létszáma:. fő
1.sz. Függelék: A Batthyány Általános Iskola és Sportiskola félévi/év végi beszámolója Osztályfőnökök részére..tanév.. félév..osztály 1. A szakmai munka áttekintése: Statisztika Az osztály létszáma:. fő
Máté: Számítógépes grafika alapjai
 Téglalap kitöltése Kör, ellipszis kitöltése Területi primitívek: Zárt görbék által határolt területek (pl. kör, ellipszis, poligon) Megjeleníthetők a) Csak a határvonalat reprezentáló pontok kirajzolásával
Téglalap kitöltése Kör, ellipszis kitöltése Területi primitívek: Zárt görbék által határolt területek (pl. kör, ellipszis, poligon) Megjeleníthetők a) Csak a határvonalat reprezentáló pontok kirajzolásával
Oktatáskutató és Fejlesztő Intézet TÁMOP-3.1.1-11/1-2012-0001 XXI. századi közoktatás (fejlesztés, koordináció) II. szakasz. Fejlesztőfeladatok
 Oktatáskutató és Fejlesztő Intézet TÁMOP-3.1.1-11/1-2012-0001 XXI. századi közoktatás (fejlesztés, koordináció) II. szakasz Fejlesztőfeladatok MATEMATIKA 4. szint 2015 Oktatáskutató és Fejlesztő Intézet
Oktatáskutató és Fejlesztő Intézet TÁMOP-3.1.1-11/1-2012-0001 XXI. századi közoktatás (fejlesztés, koordináció) II. szakasz Fejlesztőfeladatok MATEMATIKA 4. szint 2015 Oktatáskutató és Fejlesztő Intézet
Javítókulcs M a t e m a t i k a
 6. évfolyam Javítókulcs M a t e m a t i k a Országos kompetenciamérés 2011 Oktatási Hivatal ÁLTALÁNOS TUDNIVALÓK Ön a 2011-es Országos kompetenciamérés matematikafeladatainak Javítókulcsát tartja a kezében.
6. évfolyam Javítókulcs M a t e m a t i k a Országos kompetenciamérés 2011 Oktatási Hivatal ÁLTALÁNOS TUDNIVALÓK Ön a 2011-es Országos kompetenciamérés matematikafeladatainak Javítókulcsát tartja a kezében.
TANMENETJAVASLAT AZ ÚJ KERETTANTERVHEZ MATEMATIKA 1. ÉVFOLYAM KÉSZÍTETTÉK: KURUCZNÉ BORBÉLY MÁRTA ÉS VARGA LÍVIA TANKÖNYVSZERZŐK 2013
 TANMENETJAVASLAT AZ ÚJ KERETTANTERVHEZ MATEMATIKA 1. ÉVFOLYAM KÉSZÍTETTÉK: KURUCZNÉ BORBÉLY MÁRTA ÉS VARGA LÍVIA TANKÖNYVSZERZŐK 2013 1 Kedves Kollégák! Tanmenet javaslatunkkal segítséget kívánunk nyújtani
TANMENETJAVASLAT AZ ÚJ KERETTANTERVHEZ MATEMATIKA 1. ÉVFOLYAM KÉSZÍTETTÉK: KURUCZNÉ BORBÉLY MÁRTA ÉS VARGA LÍVIA TANKÖNYVSZERZŐK 2013 1 Kedves Kollégák! Tanmenet javaslatunkkal segítséget kívánunk nyújtani
MATEMATIKA C 6. évfolyam 3. modul LERAKÓS, TOLOGATÓS JÁTÉKOK
 MATEMATIKA C 6. évfolyam 3. modul LERAKÓS, TOLOGATÓS JÁTÉKOK Készítette: Köves Gabriella MATEMATIKA C 6. ÉVFOLYAM 3. MODUL: LERAKÓS, TOLOGATÓS JÁTÉKOK TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott
MATEMATIKA C 6. évfolyam 3. modul LERAKÓS, TOLOGATÓS JÁTÉKOK Készítette: Köves Gabriella MATEMATIKA C 6. ÉVFOLYAM 3. MODUL: LERAKÓS, TOLOGATÓS JÁTÉKOK TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Térgeometria
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Térgeometria 1) Egy gömb alakú labda belső sugara 13 cm. Hány liter levegő van benne? Válaszát indokolja! 2) Egy forgáskúp alapkörének átmérője egyenlő a
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK KÖZÉP SZINT Térgeometria 1) Egy gömb alakú labda belső sugara 13 cm. Hány liter levegő van benne? Válaszát indokolja! 2) Egy forgáskúp alapkörének átmérője egyenlő a
Fıvárosi Önkormányzat Benedek Elek Óvoda, Általános Iskola, Speciális Szakiskola és Egységes Gyógypedagógiai és Módszertani Intézmény
 Fıvárosi Önkormányzat Benedek Elek Óvoda, Általános Iskola, Speciális Szakiskola és Egységes Gyógypedagógiai és Módszertani Intézmény Egységes szerkezetben foglalt módosított Pedagógiai program V. kötet
Fıvárosi Önkormányzat Benedek Elek Óvoda, Általános Iskola, Speciális Szakiskola és Egységes Gyógypedagógiai és Módszertani Intézmény Egységes szerkezetben foglalt módosított Pedagógiai program V. kötet
10. JAVÍTÓKULCS ORSZÁGOS KOMPETENCIAMÉRÉS MATEMATIKA. példaválaszokkal. s u l i N o v a K h t. É R T É K E L É S I K Ö Z P O N T É V F O L Y A M
 10. É V F O L Y A M ORSZÁGOS KOMPETENCIAMÉRÉS JAVÍTÓKULCS MATEMATIKA s u l i N o v a K h t. É R T É K E L É S I K Ö Z P O N T 2 0 0 6 példaválaszokkal Hány órából áll egy hét? Válasz: A feleletválasztós
10. É V F O L Y A M ORSZÁGOS KOMPETENCIAMÉRÉS JAVÍTÓKULCS MATEMATIKA s u l i N o v a K h t. É R T É K E L É S I K Ö Z P O N T 2 0 0 6 példaválaszokkal Hány órából áll egy hét? Válasz: A feleletválasztós
1. A MÁSODIK OSZTÁLYBAN TANULTAK ISMÉTLÉSE
 1. A MÁSODIK OSZTÁLYBAN TANULTAK ISMÉTLÉSE 1. Írd le számokkal! Hat, tizenhat,,hatvan, hatvanhat, ötven, száz, tizenhét, húsz nyolcvankettı, nyolcvanöt. 2. Tedd ki a vagy = jelet! 38 40 2 42 50+4
1. A MÁSODIK OSZTÁLYBAN TANULTAK ISMÉTLÉSE 1. Írd le számokkal! Hat, tizenhat,,hatvan, hatvanhat, ötven, száz, tizenhét, húsz nyolcvankettı, nyolcvanöt. 2. Tedd ki a vagy = jelet! 38 40 2 42 50+4
A Adobe Flash CS4 grafikus felülete
 Bevezető Az Internet valódi sikerét a W W W (World Wide Web - Világháló) hozta, és a grafikák megjelentek a publikált oldalakon. Pontosan úgy, mint a száz évvel ezelőtti fénykép esetében, ma már nem elégszünk
Bevezető Az Internet valódi sikerét a W W W (World Wide Web - Világháló) hozta, és a grafikák megjelentek a publikált oldalakon. Pontosan úgy, mint a száz évvel ezelőtti fénykép esetében, ma már nem elégszünk
Teljes kétjegyűek összeadása és kivonása különféle eljárásokkal és a műveleti tulajdonságok felhasználásával; szöveges feladatok
 Matematika A 2. évfolyam Teljes kétjegyűek összeadása és kivonása különféle eljárásokkal és a műveleti tulajdonságok felhasználásával; szöveges feladatok 23. modul Készítette: Szili Judit Szitányi Judit
Matematika A 2. évfolyam Teljes kétjegyűek összeadása és kivonása különféle eljárásokkal és a műveleti tulajdonságok felhasználásával; szöveges feladatok 23. modul Készítette: Szili Judit Szitányi Judit
KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA
 ÉRETTSÉGI VIZSGA 2009. május 5. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2009. május 5. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Matematika középszint
ÉRETTSÉGI VIZSGA 2009. május 5. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2009. május 5. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati OKTATÁSI ÉS KULTURÁLIS MINISZTÉRIUM Matematika középszint
Szövegszerkesztő programok: Jegyzettömb, WordPad, Microsoft Word
 Szövegszerkesztő programok: Jegyzettömb, WordPad, Microsoft Word A szövegszerkesztők közül az elkészítendő szöveg jellegétől függően választunk programot, és nem feltétlenül azt, amelyiket alapértelmezésben
Szövegszerkesztő programok: Jegyzettömb, WordPad, Microsoft Word A szövegszerkesztők közül az elkészítendő szöveg jellegétől függően választunk programot, és nem feltétlenül azt, amelyiket alapértelmezésben
Osztályozóvizsga követelményei
 Osztályozóvizsga követelményei Képzés típusa: Tantárgy: Általános iskola Matematika Évfolyam: 1 Emelt óraszámú csoport Emelt szintű csoport Vizsga típusa: Írásbeli Követelmények, témakörök: Halmazok összehasonlítása
Osztályozóvizsga követelményei Képzés típusa: Tantárgy: Általános iskola Matematika Évfolyam: 1 Emelt óraszámú csoport Emelt szintű csoport Vizsga típusa: Írásbeli Követelmények, témakörök: Halmazok összehasonlítása
VISUAL BASIC ALAPISMERETEK
 11. Grafika VISUAL BASIC ALAPISMERETEK 11. Gyakorlat témaköre: Kiválasztógomb (Option Button) és a jelölőnégyzet (CheckBox) használata Kör, ellipszis (Circle) rajzolása. Circle (X, Y), Sugár, QBColor(Szín),
11. Grafika VISUAL BASIC ALAPISMERETEK 11. Gyakorlat témaköre: Kiválasztógomb (Option Button) és a jelölőnégyzet (CheckBox) használata Kör, ellipszis (Circle) rajzolása. Circle (X, Y), Sugár, QBColor(Szín),
Útmutató a Matematika 1. tankönyv használatához
 Útmutató a Matematika 1. tankönyv használatához ELŐSZÓ Kedves Tanító Kollégák! Ebben a rövid útmutatóban összefoglaljuk azokat a szerintünk alapvető tudnivalókat, amelyek az 1. évfolyam matematikaóráinak
Útmutató a Matematika 1. tankönyv használatához ELŐSZÓ Kedves Tanító Kollégák! Ebben a rövid útmutatóban összefoglaljuk azokat a szerintünk alapvető tudnivalókat, amelyek az 1. évfolyam matematikaóráinak
Üdvözöljük. Solid Edge kezdő lépések 2
 Üdvözöljük A Solid Edge 19-es verziója az innovatív megoldásokra és a vállalaton belüli kommunikációra fókuszál, ezzel célozva meg a közepes méretű vállalatok igényeit. Több száz újdonsággal a Solid Edge
Üdvözöljük A Solid Edge 19-es verziója az innovatív megoldásokra és a vállalaton belüli kommunikációra fókuszál, ezzel célozva meg a közepes méretű vállalatok igényeit. Több száz újdonsággal a Solid Edge
MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA. 2013. május 7. 8:00. Időtartam: 45 perc EMBERI ERŐFORRÁSOK MINISZTÉRIUMA
 ÉRETTSÉGI VIZSGA 2013. május 7. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2013. május 7. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Matematika középszint
ÉRETTSÉGI VIZSGA 2013. május 7. MATEMATIKA KÖZÉPSZINTŰ ÍRÁSBELI VIZSGA 2013. május 7. 8:00 I. Időtartam: 45 perc Pótlapok száma Tisztázati Piszkozati EMBERI ERŐFORRÁSOK MINISZTÉRIUMA Matematika középszint
Kombinatorika. 9 10. évfolyam. Szerkesztette: Surányi László Ábrák: Hraskó András. 2015. december 6.
 Kombinatorika 9 10. évfolyam Szerkesztette: Surányi László Ábrák: Hraskó András 2015. december 6. A kötet létrehozását 2008-tól 2010-ig a Fővárosi Közoktatásfejlesztési Közalapítvány támogatta Technikai
Kombinatorika 9 10. évfolyam Szerkesztette: Surányi László Ábrák: Hraskó András 2015. december 6. A kötet létrehozását 2008-tól 2010-ig a Fővárosi Közoktatásfejlesztési Közalapítvány támogatta Technikai
GEOMATECH TANULMÁNYI VERSENYEK 2015. JANUÁR
 GEOMATECH TANULMÁNYI VERSENYEK 2015. JANUÁR Letöltöttétek már a GeoGebra legfrissebb verzióját? Ha igen, a Nézet menüpontban nyissátok meg a 3D-s nézetet! Ha nem, töltsétek le a www.geogebra.org oldalon
GEOMATECH TANULMÁNYI VERSENYEK 2015. JANUÁR Letöltöttétek már a GeoGebra legfrissebb verzióját? Ha igen, a Nézet menüpontban nyissátok meg a 3D-s nézetet! Ha nem, töltsétek le a www.geogebra.org oldalon
Számítógépes grafika
 Számítógépes grafika XXIII. rész Grafika DOS alatt I. A DOS operációs rendszer a személyi számítógépek szöveges üzemmódú parancssoros operációs rendszere. Grafikus alkalmazásokat is lehetett DOS alatt
Számítógépes grafika XXIII. rész Grafika DOS alatt I. A DOS operációs rendszer a személyi számítógépek szöveges üzemmódú parancssoros operációs rendszere. Grafikus alkalmazásokat is lehetett DOS alatt
hatására hátra lép x egységgel a toll
 Ciklusszervező utasítások minden programozási nyelvben léteznek, így például a LOGO-ban is. LOGO nyelven, (vagy legalábbis LOGO-szerű nyelven) írt programok gyakran szerepelnek az iskola számítástechnikai
Ciklusszervező utasítások minden programozási nyelvben léteznek, így például a LOGO-ban is. LOGO nyelven, (vagy legalábbis LOGO-szerű nyelven) írt programok gyakran szerepelnek az iskola számítástechnikai
10. évfolyam, negyedik epochafüzet
 10. évfolyam, negyedik epochafüzet (Geometria) Tulajdonos: NEGYEDIK EPOCHAFÜZET TARTALOM I. Síkgeometria... 4 I.1. A háromszög... 4 I.2. Nevezetes négyszögek... 8 I.3. Sokszögek... 14 I.4. Kör és részei...
10. évfolyam, negyedik epochafüzet (Geometria) Tulajdonos: NEGYEDIK EPOCHAFÜZET TARTALOM I. Síkgeometria... 4 I.1. A háromszög... 4 I.2. Nevezetes négyszögek... 8 I.3. Sokszögek... 14 I.4. Kör és részei...
A Paint program használata
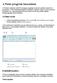 A Paint program használata A Windows rendszerbe épített Paint program segítségével képeket rajzolhat, színezhet és szerkeszthet. A Paint használható digitális rajztáblaként. Egyszerű képek és kreatív projektek
A Paint program használata A Windows rendszerbe épített Paint program segítségével képeket rajzolhat, színezhet és szerkeszthet. A Paint használható digitális rajztáblaként. Egyszerű képek és kreatív projektek
