EGYENLETEK, EGYENLŐTLENSÉGEK
|
|
|
- Karola Papp
- 8 évvel ezelőtt
- Látták:
Átírás
1 0691. MODUL EGYENLETEK, EGYENLŐTLENSÉGEK Nyitott mondat, egyenlet, egyenlőtlenség KÉSZÍTETTE: OROSHÁZI KATALIN
2 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A képességfejlesztés fókuszai Az állítás, nyitott mondat fogalmának alakítása. Egyszerű logikai állítások igazságértékének megállapítása. Az egyenlet, egyenlőtlenség, azonosság, azonos egyenlőtlenség, alaphalmaz és igazsághalmaz fogalmának megalapozása. Egyenletek és egyenlőtlenségek megoldása próbálgatással, lebontogatással. 3 óra 6. osztály Szűkebb környezetben: műveletek racionális számokkal. Inverz műveletek. Mérlegelv. Tágabb környezetben: problémamegoldás. Változó mennyiségek közötti kapcsolatok felismerése. A logikai gondolkodás fejlesztése. Rendszerező képesség. Összefüggés felismerő képesség. Ajánlás Ültessük a gyerekeket négyes asztalok köré, és használjunk kooperatív tanulási technikákat. Ügyeljünk rá, hogy a csoporton belül a különböző szerepekben mindenki kipróbálhassa magát. Minden órán elevenítsük fel az előző órán történteket, és mindig tegyük lehetővé a házi feladat ellenőrzését részletes, közös megbeszéléssel, faliújságra kitett megoldásokkal, vagy fóliáról való kivetítéssel. Az órákon feldolgozandó feladatcsoportok fokozatosan nehezedő feladatokat tartalmaznak. Az osztály és az egyes gyerekek ismeretében bátran válogassunk belőlük, akár úgy, hogy a végéről hagyunk el feladatokat, akár úgy, hogy az ügyesebbeknek megengedjük, hogy a gyakorlást az összetettebb feladatokkal kezdjék. Támogató rendszer: Számkártyák, szerepkártyák, tanulói munkafüzet, feladatgyűjtemény, fólia, faliújság. Értékelés: Megfigyelés alapján.
3 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 3 MODULVÁZLAT Lépések, tevékenységek Kiemelt készségek, képességek Eszközök, Feladatok I. Állítások, nyitott mondatok 1. Állítások Logikai gondolkodás 1. feladatlap1., Világatlasz, állathatározó, Toldi, Internet 2. Nyitott mondatok Az ismerethordozók használata. 1. feladatlap 2., Világatlasz, állathatározó, Toldi, Internet 3. Alaphalmaz, igazsághalmaz Halmaz szemlélet. Ábrázolás számegyenesen. Rendszerező képesség Számkártyák 30-tól +30-ig, dobozok, Számegyenes 4. Egyenlet, egyenlőtlenség Definiálás 5. Azonosság, azonos egyenlőtlenség Az ismeretek alkalmazása. Besorolás. 1. feladatlap A házi feladat előkészítése Az ismeretek alkalmazása. Analizálás, összehasonlítás, besorolás. 1. feladatlap 4., Feladatlapok, gyűjtemények, füzetek II. Egyenletek, egyenlőtlenségek megoldása lebontogatással 1. Ráhangolás Ismeretek összekapcsolása. Felidézés. Asszociáció. Az ismeretek alkalmazása. 2. Egyenletek és egyenlőtlenségek felépítése és Analízis, szintézis, analógia. 2. feladatlap 1. 2., Papírcsíkok lebontogatása 3. Az egyenletek, egyenlőtlenségek megoldásának gyakorlása lebontogatás Gondolkodási műveletek. 2. feladatlap 3.
4 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 4 4. A házi feladat előkészítése. (A pályázat kihirdetése.) Motiváció. 3. feladatlap 1. 2., Faliújság III. Egyenletek, egyenlőtlenségek megoldásának gyakorlása lebontogatással 1. Ráhangolás Memória. Kommunikáció. 1. tanári melléklet, faliújság 2. Csoportalakítás. A szóvivő szerep kipróbálása Több szempont egyidejű érvényesítése. Csoportnév kártyák, Szerepkártya Együttműködés. 3. Csoportos gyakorlás Önfegyelem. Kommunikáció. A gátlások 3. feladatlap 3. feloldása. Együttműködés. Megfigyelés. Közös felelősségvállalás. 4. Frontális megbeszélés Kommunikáció 2. tanári melléklet 5. A házi feladat kitűzése Az ismeretek önálló alkalmazása, ellenőrzés. 3. feladatlap 4.
5 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 5 A FELDOLGOZÁS MENETE I. Állítások, nyitott mondatok 1. Állítások a) Kérdezzük meg a gyerekeket, hogy mi jut eszükbe az állítás szóról, majd kérjünk példákat állításokra! Írjunk ezek közül néhányat a táblára, és kérdezzük meg, hogy igazak vagy hamisak! Pl.: Magyarország európai ország. A 27 kétjegyű szám. Nagypapa fiatalabb, mint az unokája. Van legnagyobb páros szám. Ezeknek a kijelentő mondatoknak az igazságértéke egyértelműen eldönthető. Vannak azonban olyan kijelentő mondatok is, amelyek igazságértéke nem dönthető el egyértelműen. Pl.: Péter a legerősebb fiú. A foltos szalamandra szép állat. A 15 nagy szám. Ezeket a kijelentő mondatokat nem tekintjük állításoknak. b) Oldassuk meg az 1. Feladatlap 1. Feladatát! Gyorsabb és hatékonyabb lehet a munka, ha az egy asztalnál ülők csoportban dolgoznak. A megbeszélésnél sorsolhatjuk, hogy melyik csoport ismertetheti a megoldást, ha a csoportokat, pl. számmal megkülönböztetjük. A többi csoport színes kartonlap felmutatásával jelezheti egyetértését (zöld), tiltakozását (piros) vagy kiegészítési szándékát (kék). Előzőleg készítsünk be néhány könyvet, vagy ha van Internet hozzáférésünk, engedjük annak a használatát, hogy vitás esetben segítsen eldönteni az állításokról, hogy melyik igaz, melyik hamis! (Pl. Világatlasz, Állathatározó, Arany: Toldi) 1. FELADATLAP 1. Állapítsd meg a következő állítások közül, melyik igaz (i), melyik hamis (h)! a) Az 5 nagyobb, mint a 2. i b) A fácán szó ige. h c) = 5 i d) Törökország -i állam.? e) i f) A Föld leghosszabb folyója a Duna. h g) 2 x 4 = 2? h) a legjobb matekos az osztályban.? Beszéljük meg, hogy a d) g) h) állítások nyitott mondatok! A kiegészítéstől függ, hogy igazak lesznek, vagy hamisak. Kérjünk olyan kiegészítéseket, amelyek igazzá teszik, és olyanokat is, amelyek hamissá teszik ezeket a nyitott mondatokat! 2. Nyitott mondatok Miután megbeszéltük az 1. Feladatot, kérdezzük meg a gyerekeket az 1. Feladatlap 2. Feladatában szereplő mondatokról is! Néhány vélemény meghallgatása után ajánljuk fel a gyereknek, hogy ha akarják, beszéljék meg a feladatok megoldását a mellettük ülővel! 2. Állapítsd meg, hogy a nyitott mondatokat a megadott halmazok mely elemei teszik igazzá! a) Arany János Toldi című elbeszélő költeményének egyik szereplője: A = {V. László, Bence, Nagy Lajos, Jóka, Toldi György}
6 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 6 b) A a Naprendszer bolygója. B = {Hold, Mars, Göncöl-szekér, Föld, Plútó} Felvethetik a gyerekek, hogy a Hold is kering, bár a Föld körül, és nem csillag, hiszen nincs saját fénye. Tisztázzuk, hogy a bolygók a csillagok körül keringő saját fény nélküli égitestek. c) 2x 1= 5 C = { 3; 3; 0; 5; 6; 1} d) z 4 > 0 D= { 1; 0; 2; 4; 6} e) 2 x 1 < 5 E = {2; 1; 0; 1; 2} f) A Magyarországon honos állat. F = {zebra, fácán, feketerigó, víziló, vízisikló} g) európai állam. G = {Ausztria, Argentína, Szlovénia, Örményország, Románia, Tunézia} h) A prímszám. H = {5; 9; 8; 11; 29; 51; 23} i) 11 I = {5; 9; 7; 2; 3; 8; 10; 4; 1} j) 5 y 15 J = { 3 ; 2; 1; 0; 1; 2; 3} k) A összetett szám K = {8; 12; 26; 6548; } l) A összetett szín. L = {sárga, kék, piros} Egyeztessük a megoldásokat! A vitás kérdésekben vegyük le a polcról a szükséges könyveket! 3. Alaphalmaz, igazsághalmaz Beszéljük meg, hogy az előző feladatban megadott halmazokat, amelyekben a megoldásokat kerestük, alaphalmaznak nevezzük, az alaphalmaznak azt a részhalmazát, amelynek elemeire az állítást igaznak találtuk, megoldáshalmaznak vagy igazsághalmaznak hívjuk! Írjuk fel a táblára kékkel a 2 x + 3 < 31 nyitott mondatot, és helyezzünk az asztalra egy ALAPHALMAZ feliratú dobozt, amelybe előzőleg számkártyákat tettünk! (Javaslom: 30-tól +30 ig az egészeket) Tegyünk mellé két másik dobozt, az egyiknek IGAZSÁGHALMAZ, a másiknak HAMISHALMAZ legyen a felirata! (A HAMISHALMAZ nem bevett kifejezés a matematikában, aki zavarónak érzi, használjon helyette más feliratot, pl. IGAZZÁ TESZIK ill. NEM TESZIK IGAZZÁ is lehet a két doboz felirata.) A táblára rajzoljunk egy számegyenest, amelyen azokat a számokat ábrázoltuk, amelyeknek kártyái az ALAPHALMAZ feliratú dobozba kerültek, vagy használjuk a műanyag számegyenest 20-tól +20-ig számozva! Kérjük a gyerekeket, hogy egyenként húzzanak egy számkártyát, mutassák fel, és helyezzék a megfelelő dobozba! A többiek ellenőrizzék, hogy jó helyre kerültek-e a kártyák! Aki olyan számot húzott, amelyre a nyitott mondat igaznak bizonyult, színezze kékre a számegyenes megfelelő pontját is! (x < 14)
7 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 7 Miután visszaraktuk a kártyákat az ALAPHALMAZ dobozba, írjuk fel a táblára zölddel a 13 2 x + 3 nyitott mondatot, és keressük meg az előbbi módon ennek az igazsághalmazát is! Most karikáztassuk be zölddel a számegyenes megfelelő pontjait! ( 8 x) Ezután írjuk fel pirossal a táblára a 13 2 x + 3 < 31 nyitott mondatot, és kérdezzük meg, vajon milyen számkártyák teszik igazzá ezt, ha ugyanaz az alaphalmaz, mint eddig! Valószínűleg többen is rájönnek, hogy az előbbi két igazsághalmaz közös része a megoldás, vagyis a kékkel és zölddel egyaránt megjelölt számok. Kereteztessük be ezeket pirossal! ( 8 x < 14) Ha tartunk az idő szorításától, a feladatot úgy is megoldhatjuk, hogy az alaphalmazban lévő számkártyákat mindkét esetben szétosztjuk a gyerekek között. Így egyszerre többen is dolgozhatnak. A számegyenes alapján a gyanús számokat feltétlenül ellenőrizzük, akkor is, ha a gyerekek közül esetleg senki nem veszi észre a hibát! Ugyanígy járjunk el az intervallumok határszámaival is! 4. Egyenlet, egyenlőtlenség Hívjuk fel a gyerekek figyelmét arra, hogy a számokra vonatkozó nyitott mondatok között volt olyan, amelyben az állítás két oldalát = jellel kapcsoltuk össze, ezeket egyenleteknek nevezzük, és volt olyan, amelyben az állítás két oldalát <, >,,, vagy jelek valamelyikével kapcsoltuk össze, az ilyeneket egyenlőtlenségeknek hívjuk! Kérjük meg a gyerekeket, hogy keressenek egyenletet és egyenlőtlenséget az órán eddig megismert nyitott mondatok között! Pl.: egyenlet: 2x 1= 5 egyenlőtlenség: 2 x + 3 < 31; 13 2 x + 3; 11 stb. 5. Azonosság, azonos egyenlőtlenség Beszéljük meg, hogy a továbbiakban az egyenletekkel és az egyenlőtlenségekkel foglalkozunk! Javaslom, hogy a négyes csoport tagjai osszák fel maguk között az 1. feladatlap 3. feladatának négy feladatát, majd mondják el tapasztalataikat egymásnak. Végül sorsoljunk beszámoló csoportokat az egyes feladatokhoz! A csoportok a színes lapok felmutatásával jelezzék véleményüket! Ha nincs egyetértés, vagy nincs jó megoldás, részletes megbeszélés után korrigáljunk! 3. A következő feladatban az alaphalmazunkat A betűvel jelöltük. Az alaphalmazban megadtuk azokat a számokat, amelyeket a nyitott mondatokba behelyettesíthetsz. Határozd meg a következő egyenletek és egyenlőtlenségek megoldását az adott alaphalmazban! a) 4 a 2 = 2 (2 a 1) A = { 1; 0; 1; 0,5} A b) 3 b 5 < 2 b + 1 A = { 1; 0; 2; 0,1} A c) 2 c + 3 = 4 c 9 A = { 2; 0; 2; 1} {2} d) 2 d + 1 d + 5 A = { 1; 0; 4; 5} {4; 5} Beszéljük meg, hogy az olyan egyenlőséget, amelynek igazsághalmaza az egész alaphalmaz, az adott halmazon azonosságnak, az olyan egyenlőtlenséget, amelynek igazsághalmaza az egész alaphalmaz, az adott alaphalmazon azonos egyenlőtlenségnek nevezzük!
8 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 8 6. Házi feladat előkészítése Az órán szereplő nyitott mondatokat csoportosítsák a gyerekek: gyűjtsenek egyenletet, egyenlőtlenséget, azonosságot, azonos egyenlőtlenséget! Az ügyesebb osztályokban, ill. bármely osztályban az ügyesebbeknek igényesebb feladatot is adhatunk: A 2. és az 5. témakörben az idén és korábbi tanulmányaik során is találkoztak már a gyerekek nyitott mondatokkal. Nézzék át a füzeteiket, feladatlapjaikat, feladatgyűjteményeiket, és gyűjtsenek egyenleteket, egyenlőtlenségeket, esetleg azonosságokat, azonos egyenlőtlenségeket is! Ezeket külön papírcsíkokra írják, és helyezzék el a faliújságon, a megfelelő feliratok alá! 4. Csoportosítsd az órán előforduló matematikai nyitott mondatokat! egyenlet egyenlőtlenség = < > azonosság nem azonosság azonos egyenlőtlenség nem azonos egyenlőtlenség II. Egyenletek, egyenlőtlenségek megoldása lebontogatással 1. Ráhangolás a) Négy egyszerű szöveges feladatot olvasunk fel egyenként a gyerekeknek, és arra kérjük őket, írják fel azokat nyitott mondattal. A helyes felírást megbeszéljük. Miután mind a négy nyitott mondat a füzetekben van, arra kérjük a gyerekeket, hogy keressék meg a nyitott mondatok megoldását, majd olvassák össze a megoldásokat az egyenletek sorrendjében. Bíztassunk páros munkára, de javasoljunk az előző óraitól eltérő párosítást! A kapott négyjegyű szám Nagy Lajos trónra kerülésének (Károly Róbert halálának) éve: Emlékeztessük a gyerekeket, hogy Nagy Lajos korában játszódik a Toldi! A felolvasandó feladatok: Írd fel nyitott mondattal: Gondoltam egy számot, hozzáadtam 3-at, és így 2-t kaptam. Melyik számra gondoltam? Pl.: x + ( 3) = 2 x =1 Melyik az a szám, amelynek a 3-szorosa 9? Pl.: 3 y = 9 y =3 Gondoltam egy számot, elosztottam 2-vel, és 2-t kaptam. Melyik számra gondoltam? Pl.: v : 2 = 2 v = 4 Melyik az a szám, amelynél 5-tel kisebb a 3 Pl. z 5 = 3 z = 2 Oldd meg a nyitott mondatokat, és a megoldásokat írd egymás mellé a feladatok elhangzásának sorrendjében! Milyen évszámhoz jutottál?
9 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 9 b) A házi feladat megbeszélése A faliújságot használjuk, az előre elkészített feliratokkal: egyenlet egyenlőtlenség = < > azonosság nem azonosság azonos egyenlőtlenség nem azonos egyenlőtlenség A feliratok alá gyűjtjük a gyerekek által összeírt nyitott mondatokat. Az előző órán előforduló nyitott mondatokat célszerű, ha a tanár előre papírcsíkokra írja. Az azonosságoknál, azonos egyenlőtlenségeknél megbeszéljük, hogy milyen alaphalmazon azok. Egy-egy egyenletet ill. egyenlőtlenséget kiválasztunk, és megbeszéljük a benne szereplő műveletek sorrendjét, és a lebontogatást. Pl.: Nagy méretben a táblára kerül: 3 x + 9 = 15 Megbeszéljük, hogy hogyan épült fel ez az egyenlet, a műveletek milyen sorrendben követték egymást. Ez után azt mondjuk, hogy a bal oldalt becsomagoljuk. Ez a táblán úgy jelenik meg, hogy egy papírcsíkkal letakarjuk. (Javaslom a rögzítő gyurma használatát) Jónak tartom, ha a gyerekeknek is van papírcsíkjuk ezt készítsük elő megfelelő szélességű csíkot vágva, hogy a papírvágás ne terelje el a figyelmet a lényegről, ne vegyen el fölöslegesen időt, és velünk együtt végzik a be és kicsomagolást. Ekkor ez látszik: =15 = 15 Most elkezdjük kibontani a csomagot, azaz az utolsó műveletről (+9) visszahajtjuk a papírcsíkot. Keressük azt a számot, amelyhez 9-et adva 15-öt kapunk = 15 A csomagban tehát 15 9 = 6 érték van. Most tovább bontjuk a csomagot, ami a táblán így jelenik meg: 3 = 6, mivel visszahajtottuk a papírt az együtthatóról. Keressük azt a számot, amelyet ( 3)-mal megszorozva 6-ot kapunk. Ebből már látszik, hogy az utolsó csomag értéke 6 : ( 3) = 2 Jó, ha a csomagolós módszert alkalmazzuk több, összetettebb egyenlettel is. Ha azonban a lebontogatás jól megy, elegendő lehet kevesebb, akár egyetlen kicsomagolás végrehajtása is.
10 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 10 5 (x 4) + 7 = 32 = = 32 Melyik az a szám, amelyhez 7-et adva32-t kapunk? = 25 5 = 25 Melyik az a szám, amelyet 5-tel megszorozva25-öt kapunk? = 5 4 = 5 Melyik az a szám, amelyből 4-et kivonva5-höz jutunk? = 9 x = 9 (y 4) = 13 = = 13 Melyik az a szám, amelyhez 3-at adva 13-at kapunk? = 10 2 = 10 Melyik az a szám, amelynek a kétszerese 10? = 5 4 = 5 Melyik az a szám, amelyből 4-et kivonva 5-öt kapunk? = 9 y = 9 2 z 3 < 9 3 < 9 Melyik az a szám, amiből 3-at kivonva 12-nél kisebb számot kapunk? < 9 < 12 2 < 12
11 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 11 Mely számok kétszerese kisebb 12-nél? < 6 z < 6 Ha az előbbi típusokhoz hasonlókat hoztak a gyerekek, akkor a csomagolást azokon végezzük el. 2. Egyenletek és egyenlőtlenségek felépítése és lebontogatása A következő feladatsor megoldásánál dolgozzanak a gyerekek négyes csoportban úgy, hogy mindenki egy feladatot old meg, és a megoldást elmondja a társainak! Végül a megoldások helyességét mindenki ellenőrzi behelyettesítéssel. Előre tisztázzuk, hogy a csoport minden tagjának értenie, tudnia kell a végére valamennyi egyenlet megoldását! 2. FELADATLAP 1. Állapítsátok meg, hogyan épültek fel a következő nyitott mondatok! Oldjátok meg ezeket lebontogatással, majd ellenőrizzétek behelyettesítéssel! Írjátok a nyilakra a műveleteket! Tegyétek ki a relációs jeleket ott, ahol hiányzik! a) 3 x + 5 = x 3 x 3 x : 3 5 Ha nem adtam volna hozzá 5-öt, 21 lenne, mert 26 5 = 21. Ha nem szoroztam volna meg 3-mal, 7 lenne, mert 21 : 3 = 7 b) 2 y 1 = y 2 y 2 y : Ha nem vontam volna ki 1-et, akkor 10 lenne, mert = 10 Ha nem szoroztam volna 2-vel, akkor 5 lenne, mert 10 : 2 = 5
12 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 12 c) 3 x 9 = 15 ( 3) 9 x 3 x 3 x : ( 3) + 9 Ha nem vontam volna ki belőle 9-et, akkor 24 lenne, mert = 24. Ha nem szoroztam volna meg ( 3)-mal, akkor 8 lenne, mert 24 : ( 3) = 8 d) 5 (x 4) + 7 = x x 4 5 (x 4) 5 (x 4) : 5 7 Ha nem adtam volna hozzá hetet, akkor 25 lenne, mert 32 7 = 25. Ha nem szoroztam volna meg 5-tel, akkor 5 lenne, mert 25 : 5 = 5. Ha nem vontam volna ki 4-et, akkor 9 lenne, mert = 9. B. A következő feladattal készítjük elő a 2. Feladatlap 2. Feladatát, ezért a táblán és a füzetben kövessük annak formáját! Minden lépésnél beszéljük meg, hogyan írható az fel a matematika nyelvén! Oldjuk meg közösen a következő szöveges feladatot: Gondoltam egy számot x Megszoroztam 3-mal 3 x A szorzatot növeltem 4-gyel 3 x + 4 Az összeget megdupláztam ( 3 x + 4) 2 A szorzatból kivontam 1 2 -et ( 3 x + 4) ,5-et kaptam. ( 3 x + 4) = 13,5 Melyik számra gondoltam? 1 ( 3) x 3 x 3 x + 4 ( 3 x + 4) 2 ( 3 x + 4) =13,5 x = [(13,5 + 1/2) : 2 4] : ( 3) x = 1 A 2. feladatnál is az első feladatnál alkalmazott csoportos munkaformát alkalmazzuk. Kérjük, hogy először írják föl valamennyi nyitott mondatot, és csak a felírások megbeszélése után oldják meg azokat! A nyitott mondatok felírásának megbeszélése után megállapodhatunk
13 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 13 abban is, hogy a négyes csoport minden tagja egy-egy nyitott mondatot old meg társa kontrollja mellett, majd a négyes csoportban meghallgatják egymás megoldását, és rögzítik azt a füzetükben. Ezután végezzék el az ellenőrzést behelyettesítéssel! Idő hiányában az első két nyitott mondat megoldásával is megelégedhetünk. Hívjuk fel a figyelmet a szorzótényezők felcserélhetőségére! Javasoljuk, hogy a zárójelre vonatkozó szorzót írják a zárójel elé, de tisztázzuk, hogy az sem hiba, ha a zárójel mögé írják azt! 2. Építsetek fel egyenleteket és egyenlőtlenségeket az útmutatások szerint, majd oldjátok meg azokat lebontogatással! Ellenőrizzétek a megoldások helyességét behelyettesítéssel! a) ( 3) a b) + 0,5 2 7 b = 3 c) : c d) 5 3 : 2 d Megoldások: 1 a) 2 3 a + 1= 3 a = b + 0, 5 7= 3 b = 1,5 b) ( ) c c) = 19 2 d) 5 d 3 > 3,5 2 c = 4 d > 2 = 3 > 3,5 Kérdezzük meg, hogy volt-e olyan gyerek vagy páros, akinek a megoldását az ellenőrzés nem igazolta! Ha igen, keressük meg a hibát közösen! Ábrázoljuk együtt a műanyag számegyenesen vagy a táblán az egyes nyitott mondatok megoldáshalmazát! Kérhetünk a gyerekektől szöveget az egyes nyitott mondatokhoz. = 19
14 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató Az egyenletek és egyenlőtlenségek megoldásának gyakorlása lebontogatás 3. Oldjátok meg lebontogatással! Ellenőrizzétek a megoldások helyességét! A megoldáshalmazt ábrázoljátok számegyenesen! Javasoljuk a gyerekeknek, hogy az összetartozó egyenletek és egyenlőtlenségek igazsághalmazát közös számegyenesen ábrázolják két különböző színnel. Nem baj, ha nem jut el mindenki a feladatsor végére. Ezt mondjuk is el a gyerekeknek. Ha úgy gondoljuk, hogy az osztálynak ezek a feladatok nagyobb nehézségeket okozhatnak, akkor azt is megtehetjük, hogy az első feladatot közösen oldjuk meg, azután pedig kettesével haladunk, kettesével beszéljük meg a feladatokat, amelyeket a gyerekek párban oldanak meg, felváltva betöltve a megoldó ill. megfigyelő szerepét. Szükség esetén eltekinthetünk az egyenlőtlenségek megoldásától. a) 5 (x : 2 + 3) = 15 x = 0 5 (x : 2 + 3) < 15 x < 0 b) (5 x + 3) : 2 = 14 x =5 (5 x + 3) : 2 14 x 5 c) 5 (x + 3) : 2 = 5 x = 1 5 (x + 3) : 2 > 5 x > 1 d) 5 x : = 13 x = 4 5 x : x 4 e) {(4 x 3) : 5 } : 5 = 0,2 x = 2 {(4 x 3) : 5 } : 5 < 0,2 x < 2 f) 4 x : 5 3 = 0,2 x = 3,5 4 x : 5 3 > 0,2 x > 3,5 g) 2 (x 3) + 5 =17 x = 9 2 (x 3) x 9 4. Házi feladat előkészítése 3. FELADATLAP 1. Vizsgáld meg a következő példákat! a) Ázsia a Föld legnagyobb kontinense. b) 19 < 17 c) A bogár. {katica, légy, szúnyog, cserebogár, szitakötő} d) 2 x < 3 x {pozitív számok} e) 2 x < 3 x {racionális számok} f) 2 x = 3 x {0} g) Dr. Bubó okos ember. h) 2 x = 3 x {racionális számok} i) Az a legkisebb természetes szám. { 2; 0; 5; 2 3 ; 1 } 2 j) Minden egész szám felírható tört alakban. k) 2 x + 3 = 3 x {az egész számok} l) 2 x + 3 = 3 x {a pozitív számok} Az előbbi példák közül melyekre igazak a következő állítások? Válaszolj a példa betűjelével! (1) Kijelentés: a, b, g, j (2) Nyitott mondat: c, d, e, f, h, i, k, l (3) Egyenlet: f, h, k, l (4) Egyenlőtlenség: d, e (5) Azonosság: f (6) Azonos egyenlőtlenség: d
15 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 15 Csak két nyitott mondat megoldását adjuk kötelező házi feladatnak, de teremtsünk olyan hangulatot, hogy minél többen próbálkozzanak a többi feladat megoldásával is, és legyenek büszkék erre! A nehezebb nyitott mondatok megoldását tegyük ki a faliújságra! 2. Oldd meg lebontogatással a következő nyitott mondatokat, majd ellenőrizd a megoldások helyességét behelyettesítéssel! Az egyenlőtlenségek megoldáshalmazát ábrázold számegyenesen! a) 4 x + 8 = 12 x = 1 b) 4 (x + 8) = 24 x = 14 c) (x 3) : 6 = 1 x = 9 d) (x + 6) 5 = 4 x = 5 e) 2 x + 5 < 2 x< 1,5 f*) 3 (5 x) > 9 x< 2 Pályázat: ufonauták landolnak az osztályteremben, nem értik, hogy miről beszélünk. Meg kellene magyarázni nekik, mit nevezünk mi a./ kijelentésnek, b./ nyitott mondatnak, c./ egyenletnek, d./ egyenlőtlenségnek, e./ azonosságnak, f./ azonos egyenlőtlenségnek, g./ alaphalmaznak, h./ igazsághalmaznak. Kérjük, hogy a magyarázatokat külön-külön, egy-egy fél írólapra írják, hogy kitehessük a faliújságra. III. Egyenletek, egyenlőtlenségek megoldásának gyakorlása lebontogatással 1. Ráhangolás a) A házi feladat ellenőrzése Érdemes a tanárnak a 3. feladatlap 2. feladatát fóliára feldolgozni az 1. tanári melléklet szerint, és az ellenőrzést ennek segítségével végezni. Javasoljuk a gyerekeknek, hogy az egymás mellett ülők cseréljenek füzetet, ugyanis a friss szemnek könnyebb észrevenni a hibát! b) A fogalommagyarázó pályázat állásának értékelése Ha vannak pályázók, akkor ismertessék a fogalommagyarázatokat, és tűzzük ki azokat a faliújságra! Mondjuk el, hogy lehet még pályázni, és a legjobb magyarázatokat írjuk majd fel a tudnivalók közé. A szerző szüleit értesítjük a jó teljesítményről. A döntésre a témakör utolsó előtti óráján kerül sor. A magyarázatokat mindig a tanár nézze meg először! Helyesírási hibával ne tegyünk ki szöveget a faliújságra! 2. Csoportalkotás, a szóvivő szerep kipróbálása Kagan nyomán: Keveredj, állj meg, csoportosulj! Egyszerű egyenleteket írunk a táblára. Az osztály feladata, hogy olyan csoportokat alkosson, amelyeknek a létszáma megegyezik az adott egyenlet megoldásával. A kimaradók a tanár
16 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 16 mellett tartalékot képeznek. Egy tanuló csak egyszer lehet tartalék. Ha másodszor is tartalék lenne, egyezkednie kell egy társával. Az egyenletek egyenként kerülnek a táblára. Az utolsó egyenlet megoldása 4, tehát az utolsó esetben az osztály négyes csoportokat alkot. Ez a csoportosulás lesz a következő néhány óra szervezeti formája. (Ha az osztálylétszám nem osztható 4-gyel, akkor a maradék létszámától függően egy hármas vagy két ötös vagy egy ötös csoport alkotása célszerű) Az egyenletek: a : 2 = d = g = 20 4 Utoljára tehát a gyerekek négyes csoportokban állnak. Megkérjük őket, hogy így üljenek le a négyfős asztalokhoz. Sorsolással adjunk nevet a csoportoknak. Készítsünk elő névkártyákat. A csoportok megnevezésére használhatjuk pl. a görög abc betűit, vagy híres matematikusok nevét, esetleg a négyszögek fajtáit, de a gyerekek által kitalált fantázianeveket is. Ettől nem kell félteni a tantárgy tekintélyét, a pozitív attitűd viszont sokat segíthet. Első közös feladatuk annak megbeszélése, hogy hogyan oldották meg az egyenleteket? Hogyan számolták ki, hogy hányas csoportokat kell éppen alkotniuk. Közben a tanár SZÓVIVŐ kártyát ad a csoportok egy egy tagjának. Javaslat: érdemes olyan gyereket választani szóvivőnek, aki visszahúzódó, ritkán szokott jelentkezni. Beszéljük meg, hogy néhány órán át a csoportok tagjai egy szoros szövetségben dolgoznak majd. Legyen a jelszavuk: Egy mindenkiért, mindenki egyért. Tudatosítsuk: Az a cél, hogy a csoport minden tagja értse, képes legyen megoldani a feladatokat. Tehát a csoporttagok hol tanárok, hol tanulók lesznek. Közös felelősségük minden csoporttag boldogulása. Értékelésnél csoportjegyet is kapnak majd, ami az egyéni teljesítmények átlagából áll elő. Ezután megkérdezzük, hogyan számoltak. Ha egy csoport szóvivője megszólalt csoportja képviseletében, adja tovább a szóvivő kártyát! Ugyanahhoz a gyerekhez csak akkor kerülhet, ha már mind a négyen képviselték a csoportot. 3. Csoportos gyakorlás A gyerekek feladatlapból dolgoznak majd. Kérjük meg őket, hogy az egyes feladatok megoldását két formában rögzítsék. Az egymás mellett ülő párok egymás között osszák fel a feladatot. Egyikük írja le egy sorban a lebontogatás során végzett műveleteket, másikuk pedig a lebontogatás egyes lépései utáni állapotokat rögzítse, minden állapotot új sorba írva. Mutassunk mintát! Adjunk lehetőséget kérdezésre! Táblán vagy fólián: Pl.: 5 (x 2) +8 = 43 Kérjünk önként vállalkozót a táblai munkához. Ha nincs önkéntes, vagy túl sok van, akkor sorsoljuk ki a csoportot, amelynek aktuális szóvivője bemutatja a megoldást a segítségünkkel. Egyik lejegyzés: x = (43 8) : x = 9 Másik lejegyzés: 5 (x 2) +8 = 43 5 (x 2) = 35 x 2 = 7 x = 9
17 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 17 Mielőtt a páros munkát elkezdenénk, adjunk lehetőséget a kérdezésre! Ha a gyerekek nem vetették fel, akkor is beszéljük meg, hogy az f) és a g) feladatot hogyan lehetett volna másképpen felírni! (2 q 7) : = 7 3 (4 r) : 2 1 = 5 E két feladat megoldását ne várjuk el mindenkitől, használjuk differenciálásra, bízzuk meg vele a legügyesebbeket! 3. Oldjátok meg a következő egyenleteket! Ellenőrizzétek a megoldások helyességét behelyettesítéssel! a) 2 x 3 =7 x = 5 b) 2 (y 3) = 8 y = 7 c) 1 (v + 2) = 9 v = 11 d) 5 (p + 4) 7 = 5 p = 1 e) 3 (9 4 z) + 2 = 1 z = 2 f) 2 q 7 + 5= 7 3 q = 6,5 g) 3 ( 4 r) 1= 5 2 r = 8 4. Frontális megbeszélés A 3. feladatot is dolgozzuk fel a 2. tanári melléklet szerint. Ezen a fólián minden feladat kétféle lejegyzése szerepeljen, ennek alapján számolnak be a csoportok. Figyelmeztessük a gyerekeket a megbeszélés előtt, hogy legyen új szóvivője a csoportnak! Sorsolással döntsük el, hogy melyik csoport számol be az adott feladatról. Egy dobozban legyen ott a tanár mellett minden csoport névtáblájának másodpéldánya, és innen húzza ki feladatonként a megoldást ismertető csoport nevét! Célszerű, ha a kihúzott névtáblát visszateszi a dobozba. Így bármelyik csoport akár újra is sorra kerülhet, de mivel a szóvivő kártyát a csoporton belül minden megszólalás után továbbadják, más-más gyerek képviseli a csoportot. Figyelmeztessük a diákokat, hogy a csoport minden szóvivő szerepléséért felelős, és fordítva! 5. Házi feladat kitűzése 3. feladatlap 4. feladat: kínáljuk fel, hogy válasszanak a feladatsorból feladatot a gyerekek! Vagy az a d feladatok mindegyikének megoldását kérjük ellenőrzéssel együtt, vagy az e g feladatokból legalább kettőt. 4. Oldd meg a nyitott mondatokat, és ellenőrizd a megoldások helyességét! a) 4 x + 5 = 17 x =3 b) 3 (x 1) 6 = 12 x = 1 c) (2 x + 3) : 2 6 = 4 x = 0,5 d) [(x 2) ] : 2 = 4 x = 1 e) {(5 3 x) : 4 3} 2 5 = 5,5 x = 2 f) 3 x 2 < 5 1 x < 2 3 g) (3 + 2 x) : > 1 x > 7,5 Kérjük a gyerekektől, hogy a házi feladatban is igyekezzenek mindkét lejegyzési módot használni. Ezen kívül gondolják át, és néhány mondatban szóban fogalmazzák meg, hogy
18 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 18 elég alaposan sikerült-e elsajátítaniuk a témakör első három órájának anyagát! Ennek megítélésében segíti őket a házi feladat megoldása. Mennyi idő alatt, az ellenőrzés tanúsága szerint mennyire jól oldották meg a feladatokat? Ami nem ment, annak pótlását egyedül vagy csoporttársaik segítségével képesek-e elvégezni, kérnek-e tanári segítséget? FELADATGYŰJTEMÉNY 1. Vizsgáld meg a következő példákat! a) 5 < 7 b) x + 8 > 3 {A 5-nél nagyobb, de +5-nél kisebb egész számok} c) 2 y 0,4 = 2 ( 0,2 y ) 1 { 1; ; 0; ; 1} d) z 5 > 2 z 7 {100; 11; 5; 0; 10} e) A 2 a legkisebb prímszám f) 3 p 6 = 5 {Az egész számok} g) 2 q + 1 = 21 {Az egész számok} Az előbbi példák közül melyekre igazak a következő állítások? Válaszolj a példa betűjelével! 1. Kijelentés: a, e 2. Nyitott mondat: b, c, d, f, g 3. Egyenlet: c, f, g 4. Egyenlőtlenség: b, d 5. Azonosság: c 6. Azonos egyenlőtlenség: d 2. Oldd meg lebontogatással a következő nyitott mondatokat, majd ellenőrizd a megoldások helyességét behelyettesítéssel! a) 3 a 8 = 1 a = 3 b) 2 (b + 6) = 18 b = 15 9 c) 5 2 c = 1 d) 2 d 7 = 3 3 d = 8 3. Oldd meg a nyitott mondatokat, és ellenőrizd a megoldások helyességét! a) 2 (k 7) = 6 k = 10 b) 5 l 2 = 2 9 l = 4 c) ( 2 m + 5) 3 = 6 2 m = 4,5 2 ( 7 n) + 1 d) 8= 7 3 n = 8 4. Alaphalmaz U = { 5; 3; 1; 0; 1; 3; 5; 8} Keresd meg az alábbi nyitott mondatok igazsághalmazát: a) x = x x 0 {0; 1; 3; 5; 8} b) x 3 = 5 x = 8
19 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 19 c) 1 = 0 x + 3 nincs megoldás d) 2 x 4 = 2 (x 2) U e) 2 x 4 = x + ( 4) x = 0 f) 3 (x 1) 1 = 3 x 4 U g) x < x x < 0 { 5; 3; 1} h) (x + 1) (x 3) = 0 x 1 = 1; x 2 = 3 i) x + 1 = x + 1 x 1 { 5; 3; 1} j) x > 0 x + 1 x > 0 vagy x < 1{ 5; 3; 1; 3; 5; 8} Állapítsd meg, hogy az előbbi nyitott mondatok közül melyik azonosság, melyik azonos egyenlőtlenség az adott alaphalmazban? azonosság: d, f 5. A következő szöveges feladatoknak megfelelő nyitott mondatokat találhatsz a 4. feladatban. Keresd meg, hogy az egyes szöveges feladatoknak melyik nyitott mondat felel meg? p) Gondoltam egy számot. A nála 3-mal nagyobb szám reciproka 0. Melyik számra gondoltam? c q) Melyik az a szám, amelyre igaz, hogy a nála 1-gyel nagyobb és a nála 3-mal kisebb szám szorzata 0? h r) Mely számokra igaz, hogy ha elosztjuk őket a náluk 1-gyel nagyobb számmal, akkor pozitív számhoz jutunk? j s) Gondoltam egy számot. Ha a nála 1-gyel kisebb szám háromszorosából kivonok 1-gyet, akkor a szám 3-szorosánál 4-gyel kisebb számot kapok. Melyik számra gondoltam? f 6. Oldd meg, és ellenőrizd! a) x + 9 = 11 x = 2 1,9 + y = 7,8 y = 5,9 2 5 v + = 3 3 v= z + = z = b) x 7 = 5 x = 12 5 y = 9 y = v = 2 4 v = z = z = c) 4 x = 12 x = 3 2,5 y = 15 y = v = 7 2 v = 0,7 5 z = 2,5 z = 0,5 d) x = 025, 4 x = 1 15 : y = 6 y = 2,5
20 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató 20 9 = 1 v v = 9 z : 7 = 3 4 z = 5,25 7. Oldd meg, és ellenőrizd! a) 2 a + 9 = 11 a = 1 b) 5 b 7 = 17 b = 2 c) 2 (c 1) + 9 = 13 c = 3 d) 3 (2 d + 1) 11 = 10 d = 4 e) e = e = 14 f) f f = 5 g) g + = g = 5 4 h) ( h 5) : ( 9) + 1,5 = 2 h = 1 2
21 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató tanári melléklet 3. feladatlap 2. feladatához Fóliára nyomva, osztályonként 1 db. a) b) c) 4 x + 8 = 12 4 x = 4 x = 1 4 (x + 8) = 24 x + 8 = 6 x = 14 x 3 = 1 6 x 3 = 6 x = 9 x = (12 8) : 4 = 1 x = 24 : 4 8 = 14 x = = 9 d) x + 6 5= 4 3 x + 6 = 1 3 x + 6 = 3 x = 3 e) 2 x + 5 < 2 2 x < 3 x < 1,5 x = ( 4 + 5) 3 6 = 3 x < (2 5) : 2 = 1,5 f) 3 ( 5 x ) > 9 5 x > 3 x > 2 x < 2 x < (9 : 3 5) ( 1) = 2
22 0691. Egyenletek, egyenlőtlenségek Nyitott mondat, egyenlet, egyenlőtlenség Tanári útmutató tanári melléklet 3. feladatlap 3. feladatához Fóliára nyomva, osztályonként 1 db. a) 2 x 3 =7 2 x = 10 x = 5 b) 2 (y 3) = 8 y 3 = 4 y = 7 c) 1 (v + 2) = 9 v + 2 = 9 v = 11 d) 5 (p + 4) 7 = 5 5 (p + 4) = 2 (p + 4) = 3 p + 4 = 3 p = 1 e) 3 ( 9 4 z ) + 2 = 1 3 (9 4 z) = 3 (9 4 z) = 1 4 z = 8 z = 2 f) 2 q 7 + 5= q 7 = q 7 = 6 2 q = 13 q = 6,5 g) 3 ( 4 r ) 1= ( 4 r) = (4 r) = 12 4 r = 4 r = 8 r = 8 x = (7 + 3) : 2 = 5 y = 8 : = 7 v = 9 : ( 1) 2 = 11 p = ( ) : ( 1) 4 = 1 z = [( 1 2) : ( 3) 9] : ( 4) = 2 q = [(7 5) 3 + 7] : 2 = 6,5 r = [(5 + 1) 2 : ( 3) 4 ] : ( 1) = 8
17. modul: EGYENLETEK, EGYENLŐTLENSÉGEK, KÉTISMERETLENES EGYENLETEK
 MATEMATIK A 9. évfolyam 17. modul: EGYENLETEK, EGYENLŐTLENSÉGEK, KÉTISMERETLENES EGYENLETEK KÉSZÍTETTE: DARABOS NOÉMI ÁGNES Készítette: Darabos Noémi Ágnes Matematika A 9. évfolyam. 17. modul: EGYENLETEK,
MATEMATIK A 9. évfolyam 17. modul: EGYENLETEK, EGYENLŐTLENSÉGEK, KÉTISMERETLENES EGYENLETEK KÉSZÍTETTE: DARABOS NOÉMI ÁGNES Készítette: Darabos Noémi Ágnes Matematika A 9. évfolyam. 17. modul: EGYENLETEK,
Módszertani megjegyzés: A kikötés az osztás műveletéhez kötődik. A jobb megértés miatt célszerű egy-két példát mu-
 . modul: ELSŐFOKÚ TÖRTES EGYENLETEK A következő órákon olyan egyenletekkel foglalkozunk, amelyek nevezőjében ismeretlen található. Ha a tört nevezőjében ismeretlen van, akkor kikötést kell tennünk: az
. modul: ELSŐFOKÚ TÖRTES EGYENLETEK A következő órákon olyan egyenletekkel foglalkozunk, amelyek nevezőjében ismeretlen található. Ha a tört nevezőjében ismeretlen van, akkor kikötést kell tennünk: az
I. Egyenlet fogalma, algebrai megoldása
 11 modul: EGYENLETEK, EGYENLŐTLENSÉGEK MEGOLDÁSA 6 I Egyenlet fogalma, algebrai megoldása Módszertani megjegyzés: Az egyenletek alaphalmazát, értelmezési tartományát később vezetjük be, a törtes egyenletekkel
11 modul: EGYENLETEK, EGYENLŐTLENSÉGEK MEGOLDÁSA 6 I Egyenlet fogalma, algebrai megoldása Módszertani megjegyzés: Az egyenletek alaphalmazát, értelmezési tartományát később vezetjük be, a törtes egyenletekkel
Óravázlat Matematika. 1. osztály
 Óravázlat Matematika 1. osztály Készítette: Dr. Jandóné Bapka Katalin Az óra anyaga: Számok kapcsolatai, számpárok válogatása kapcsolataik szerint Osztály: 1. osztály Készség-és képességfejlesztés: - Megfigyelőképesség
Óravázlat Matematika 1. osztály Készítette: Dr. Jandóné Bapka Katalin Az óra anyaga: Számok kapcsolatai, számpárok válogatása kapcsolataik szerint Osztály: 1. osztály Készség-és képességfejlesztés: - Megfigyelőképesség
MATEMATIK A 9. évfolyam. 1. modul: HALMAZOK KÉSZÍTETTE: LÖVEY ÉVA
 MATEMATIK A 9. évfolyam 1. modul: HALMAZOK KÉSZÍTETTE: LÖVEY ÉVA Matematika A 9. évfolyam. 1. modul: HALMAZOK Tanári útmutató 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok Halmazokkal
MATEMATIK A 9. évfolyam 1. modul: HALMAZOK KÉSZÍTETTE: LÖVEY ÉVA Matematika A 9. évfolyam. 1. modul: HALMAZOK Tanári útmutató 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok Halmazokkal
Matematika A 9. szakiskolai évfolyam. 11. modul EGYENLETEK, EGYENLŐTLENSÉGEK MEGOLDÁSA. Készítették: Vidra Gábor és Koller Lászlóné dr.
 Matematika A 9. szakiskolai évfolyam 11. modul EGYENLETEK, EGYENLŐTLENSÉGEK MEGOLDÁSA Készítették: Vidra Gábor és Koller Lászlóné dr. MATEMATIKA A 9. SZAKISKOLAI ÉVFOLYAM 11. modul: EGYENLETEK, EGYENLŐTLENSÉGEK
Matematika A 9. szakiskolai évfolyam 11. modul EGYENLETEK, EGYENLŐTLENSÉGEK MEGOLDÁSA Készítették: Vidra Gábor és Koller Lászlóné dr. MATEMATIKA A 9. SZAKISKOLAI ÉVFOLYAM 11. modul: EGYENLETEK, EGYENLŐTLENSÉGEK
0644. MODUL SZÁMELMÉLET. Közös osztók, közös többszörösök KÉSZÍTETTE: PINTÉR KLÁRA
 0644. MODUL SZÁMELMÉLET Közös osztók, közös többszörösök KÉSZÍTETTE: PINTÉR KLÁRA 0644. Számelmélet Közös osztók, közös többszörösök Tanári útmutató MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály
0644. MODUL SZÁMELMÉLET Közös osztók, közös többszörösök KÉSZÍTETTE: PINTÉR KLÁRA 0644. Számelmélet Közös osztók, közös többszörösök Tanári útmutató MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály
4. modul EGYENES ÉS FORDÍTOTT ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS
 Matematika A 9. szakiskolai évfolyam 4. modul EGYENES ÉS FORDÍTOTT ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS MATEMATIKA A 9. szakiskolai évfolyam 4. modul: EGYENES ÉS FORDÍTOTT ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS Tanári útmutató
Matematika A 9. szakiskolai évfolyam 4. modul EGYENES ÉS FORDÍTOTT ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS MATEMATIKA A 9. szakiskolai évfolyam 4. modul: EGYENES ÉS FORDÍTOTT ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS Tanári útmutató
Matematika A 9. szakiskolai évfolyam. 13. modul SZÖVEGES FELADATOK. Készítette: Vidra Gábor
 Matematika A 9. szakiskolai évfolyam 13. modul SZÖVEGES FELADATOK Készítette: Vidra Gábor MATEMATIKA A 9. SZAKISKOLAI ÉVFOLYAM 13. modul: SZÖVEGES FELADATOK TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott
Matematika A 9. szakiskolai évfolyam 13. modul SZÖVEGES FELADATOK Készítette: Vidra Gábor MATEMATIKA A 9. SZAKISKOLAI ÉVFOLYAM 13. modul: SZÖVEGES FELADATOK TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott
16. modul: ALGEBRAI AZONOSSÁGOK
 MATEMATIK A 9. évfolyam 16. modul: ALGEBRAI AZONOSSÁGOK KÉSZÍTETTE: VIDRA GÁBOR, DARABOS NOÉMI ÁGNES Matematika A 9. évfolyam. 16. modul: ALGEBRAI AZONOSSÁGOK Tanári útmutató 2 A modul célja Időkeret Ajánlott
MATEMATIK A 9. évfolyam 16. modul: ALGEBRAI AZONOSSÁGOK KÉSZÍTETTE: VIDRA GÁBOR, DARABOS NOÉMI ÁGNES Matematika A 9. évfolyam. 16. modul: ALGEBRAI AZONOSSÁGOK Tanári útmutató 2 A modul célja Időkeret Ajánlott
Egyenletek, egyenlőtlenségek, egyenletrendszerek I.
 Egyenletek, egyenlőtlenségek, egyenletrendszerek I. DEFINÍCIÓ: (Nyitott mondat) Az olyan állítást, amelyben az alany helyén változó szerepel, nyitott mondatnak nevezzük. A nyitott mondatba írt változót
Egyenletek, egyenlőtlenségek, egyenletrendszerek I. DEFINÍCIÓ: (Nyitott mondat) Az olyan állítást, amelyben az alany helyén változó szerepel, nyitott mondatnak nevezzük. A nyitott mondatba írt változót
Műveletek egész számokkal
 Mit tudunk az egész számokról? 1. Döntsd el, hogy igazak-e a következő állítások az A halmaz elemeire! a) Az A halmaz elemei között 3 pozitív szám van. b) A legkisebb szám abszolút értéke a legnagyobb.
Mit tudunk az egész számokról? 1. Döntsd el, hogy igazak-e a következő állítások az A halmaz elemeire! a) Az A halmaz elemei között 3 pozitív szám van. b) A legkisebb szám abszolút értéke a legnagyobb.
MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN. 10. modul TESTRÉSZEINK! Készítette: Schmittinger Judit
 MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 10. modul TESTRÉSZEINK! Készítette: Schmittinger Judit MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 10. modul: TESTRÉSZEINK 2 A modul célja Időkeret Ajánlott
MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 10. modul TESTRÉSZEINK! Készítette: Schmittinger Judit MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 10. modul: TESTRÉSZEINK 2 A modul célja Időkeret Ajánlott
IV.3. GONDOLJ, GONDOLJ... A feladatsor jellemzői
 IV.3. GONDOLJ, GONDOLJ... Tárgy, téma A feladatsor jellemzői Elsőfokú egyenletek, egyenlőtlenségek megoldása. Ezek felhasználása szöveges feladatok megoldásánál. Előzmények Egyenletek, egyszerűbb algebrai
IV.3. GONDOLJ, GONDOLJ... Tárgy, téma A feladatsor jellemzői Elsőfokú egyenletek, egyenlőtlenségek megoldása. Ezek felhasználása szöveges feladatok megoldásánál. Előzmények Egyenletek, egyszerűbb algebrai
Hasonlítsd össze! Melyik nagyobb, mennyivel? Tedd ki a jelet!
 49. modul 1. melléklet 2. évfolyam tanítói fólia és tanuló Hasonlítsd össze! Melyik nagyobb, mennyivel? Tedd ki a jelet! 26 + 33 25 + 33 12 + 35 12 + 31 62 + 15 63 + 14 43 26 53 26 35 13 35 15 62 18 72
49. modul 1. melléklet 2. évfolyam tanítói fólia és tanuló Hasonlítsd össze! Melyik nagyobb, mennyivel? Tedd ki a jelet! 26 + 33 25 + 33 12 + 35 12 + 31 62 + 15 63 + 14 43 26 53 26 35 13 35 15 62 18 72
4. modul: MŰVELETEK A VALÓS SZÁMOK KÖRÉBEN
 MATEMATIK A 9. évfolyam 4. modul: MŰVELETEK A VALÓS SZÁMOK KÖRÉBEN KÉSZÍTETTE: DARABOS NOÉMI ÁGNES Matematika A 9. évfolyam. 4. modul: MŰVELETEK A VALÓS SZÁMOK KÖRÉBEN Tanári útmutató 2 A modul célja Időkeret
MATEMATIK A 9. évfolyam 4. modul: MŰVELETEK A VALÓS SZÁMOK KÖRÉBEN KÉSZÍTETTE: DARABOS NOÉMI ÁGNES Matematika A 9. évfolyam. 4. modul: MŰVELETEK A VALÓS SZÁMOK KÖRÉBEN Tanári útmutató 2 A modul célja Időkeret
0653. MODUL TÖRTEK. Szorzás törttel, osztás törttel KÉSZÍTETTE: BENCZÉDY LACZKA KRISZTINA, MALMOS KATALIN
 06. MODUL TÖRTEK Szorzás törttel, osztás törttel KÉSZÍTETTE: BENCZÉDY LACZKA KRISZTINA, MALMOS KATALIN 06. Törtek Szorzás törttel, osztás törttel Tanári útmutató MODULLEÍRÁS A modul célja Időkeret Ajánlott
06. MODUL TÖRTEK Szorzás törttel, osztás törttel KÉSZÍTETTE: BENCZÉDY LACZKA KRISZTINA, MALMOS KATALIN 06. Törtek Szorzás törttel, osztás törttel Tanári útmutató MODULLEÍRÁS A modul célja Időkeret Ajánlott
MATEMATIK A 9. évfolyam. 2. modul: LOGIKA KÉSZÍTETTE: VIDRA GÁBOR
 MATEMATIK A 9. évfolyam 2. modul: LOGIKA KÉSZÍTETTE: VIDRA GÁBOR Matematika A 9. évfolyam. 2. modul: LOGIKA Tanári útmutató 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok
MATEMATIK A 9. évfolyam 2. modul: LOGIKA KÉSZÍTETTE: VIDRA GÁBOR Matematika A 9. évfolyam. 2. modul: LOGIKA Tanári útmutató 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok
IX.2. ÁTLAGOS FELADATOK I. A feladatsor jellemzői
 IX.2. ÁTLAGOS FELADATOK I. Tárgy, téma Algebra, statisztika. Előzmények A feladatsor jellemzői Az aritmetikai átlag fogalma, oszthatósági alapismeretek, prímszám fogalma, a számtani sorozat elemeinek összegére
IX.2. ÁTLAGOS FELADATOK I. Tárgy, téma Algebra, statisztika. Előzmények A feladatsor jellemzői Az aritmetikai átlag fogalma, oszthatósági alapismeretek, prímszám fogalma, a számtani sorozat elemeinek összegére
Számelmélet, műveletek, egyenletek, algebrai kifejezések, egyéb
 Számelmélet, műveletek, egyenletek, algebrai kifejezések, egyéb 2004_02/4 Tegyél * jelet a táblázat megfelelő rovataiba! Biztosan Lehet hogy, de nem biztos Lehetetlen a) b) c) Négy egymást követő természetes
Számelmélet, műveletek, egyenletek, algebrai kifejezések, egyéb 2004_02/4 Tegyél * jelet a táblázat megfelelő rovataiba! Biztosan Lehet hogy, de nem biztos Lehetetlen a) b) c) Négy egymást követő természetes
Segítünk egymásnak. A matematika nem játék? 2. ÉVFOLYAM É N É S A M Á S I K. Készítette: Lissai Katalin
 SZKb_102_06 Segítünk egymásnak A matematika nem játék? É N É S A M Á S I K Készítette: Lissai Katalin SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK 2. ÉVFOLYAM tanári SEGÍTÜNK EGYMÁSNAK 53 MODULVÁZLAT
SZKb_102_06 Segítünk egymásnak A matematika nem játék? É N É S A M Á S I K Készítette: Lissai Katalin SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK 2. ÉVFOLYAM tanári SEGÍTÜNK EGYMÁSNAK 53 MODULVÁZLAT
2 2 = 2 p. = 2 p. 2. Végezd el a kijelölt műveleteket! 3. Végezd el a kijelölt műveleteket! 4. Alakítsad szorzattá az összeget!
 Matematika vizsga 014. 9. osztály Név: Az 1-1. feladatok megoldását a feladatlapra írd! A 1-19. feladatokat a négyzetrácsos lapon oldd meg! 1. Számítsd ki az alábbi kifejezések pontos értékét! 0, = = p
Matematika vizsga 014. 9. osztály Név: Az 1-1. feladatok megoldását a feladatlapra írd! A 1-19. feladatokat a négyzetrácsos lapon oldd meg! 1. Számítsd ki az alábbi kifejezések pontos értékét! 0, = = p
13. modul: MÁSODFOKÚ FÜGGVÉNYEK
 MATEMATIK A 9. évfolyam 13. modul: MÁSODFOKÚ FÜGGVÉNYEK KÉSZÍTETTE: CSÁKVÁRI ÁGNES Matematika A 9. évfolyam. 13. modul: MÁSODFOKÚ FÜGGVÉNYEK Tanári útmutató 2 A modul célja Időkeret Ajánlott korosztály
MATEMATIK A 9. évfolyam 13. modul: MÁSODFOKÚ FÜGGVÉNYEK KÉSZÍTETTE: CSÁKVÁRI ÁGNES Matematika A 9. évfolyam. 13. modul: MÁSODFOKÚ FÜGGVÉNYEK Tanári útmutató 2 A modul célja Időkeret Ajánlott korosztály
2. modul MŰVELETEK RACIONÁLIS SZÁMOK KÖRÉBEN
 Matematika A 9. szakiskolai évfolyam 2. modul MŰVELETEK RACIONÁLIS SZÁMOK KÖRÉBEN MATEMATIKA A 9. szakiskolai évfolyam 2. modul: MŰVELETEK RACIONÁLIS SZÁMOK KÖRÉBEN Tanári útmutató 2 A modul célja Időkeret
Matematika A 9. szakiskolai évfolyam 2. modul MŰVELETEK RACIONÁLIS SZÁMOK KÖRÉBEN MATEMATIKA A 9. szakiskolai évfolyam 2. modul: MŰVELETEK RACIONÁLIS SZÁMOK KÖRÉBEN Tanári útmutató 2 A modul célja Időkeret
Feladatkörök a kooperatív munkában
 SZKb_102_07 A méhek Feladatkörök a kooperatív munkában É N É S A M Á S I K Készítette: Nagy Erika SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK 2. ÉVFOLYAM 62 Szociális, életviteli és környezeti kompetenciák
SZKb_102_07 A méhek Feladatkörök a kooperatív munkában É N É S A M Á S I K Készítette: Nagy Erika SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK 2. ÉVFOLYAM 62 Szociális, életviteli és környezeti kompetenciák
TÖMEGMÉRÉS ÖSSZEHASONLÍTÁSSAL KOFÁK A PIACON
 MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 5. modul TÖMEGMÉRÉS ÖSSZEHASONLÍTÁSSAL KOFÁK A PIACON Készítette: Schmittinger Judit MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 5. modul: TÖMEGMÉRÉS KOFÁK
MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 5. modul TÖMEGMÉRÉS ÖSSZEHASONLÍTÁSSAL KOFÁK A PIACON Készítette: Schmittinger Judit MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 5. modul: TÖMEGMÉRÉS KOFÁK
2017/2018. Matematika 9.K
 2017/2018. Matematika 9.K Egész éves dolgozat szükséges felszerelés: toll, ceruza, radír, vonalzó, körző, számológép 2 órás, 4 jegyet ér 2018. május 28. hétfő 1-2. óra A312 terem Aki hiányzik, a következő
2017/2018. Matematika 9.K Egész éves dolgozat szükséges felszerelés: toll, ceruza, radír, vonalzó, körző, számológép 2 órás, 4 jegyet ér 2018. május 28. hétfő 1-2. óra A312 terem Aki hiányzik, a következő
Feladatok a MATEMATIKA. standardleírás 2. szintjéhez
 Feladatok a MATEMATIKA standardleírás 2. szintjéhez A feladat sorszáma: 1. Standardszint: 2. Gondolkodási és megismerési módszerek Halmazok Képes különböző elemek közös tulajdonságainak felismerésére.
Feladatok a MATEMATIKA standardleírás 2. szintjéhez A feladat sorszáma: 1. Standardszint: 2. Gondolkodási és megismerési módszerek Halmazok Képes különböző elemek közös tulajdonságainak felismerésére.
Matematika A 9. szakiskolai évfolyam. 1. modul GONDOLKODJUNK, RENDSZEREZZÜNK!
 Matematika A 9. szakiskolai évfolyam 1. modul GONDOLKODJUNK, RENDSZEREZZÜNK! MATEMATIKA A 9. szakiskolai évfolyam 1. modul:gondolkodjunk, RENDSZEREZZÜNK! Tanári útmutató 2 A modul célja Időkeret Ajánlott
Matematika A 9. szakiskolai évfolyam 1. modul GONDOLKODJUNK, RENDSZEREZZÜNK! MATEMATIKA A 9. szakiskolai évfolyam 1. modul:gondolkodjunk, RENDSZEREZZÜNK! Tanári útmutató 2 A modul célja Időkeret Ajánlott
Egész számok. pozitív egész számok: 1; 2; 3; 4;... negatív egész számok: 1; 2; 3; 4;...
 Egész számok természetes számok ( ) pozitív egész számok: 1; 2; 3; 4;... 0 negatív egész számok: 1; 2; 3; 4;... egész számok ( ) 1. Írd a következõ számokat a halmazábra megfelelõ helyére! 3; 7; +6 ; (
Egész számok természetes számok ( ) pozitív egész számok: 1; 2; 3; 4;... 0 negatív egész számok: 1; 2; 3; 4;... egész számok ( ) 1. Írd a következõ számokat a halmazábra megfelelõ helyére! 3; 7; +6 ; (
Matematika. 1. évfolyam. I. félév
 Matematika 1. évfolyam - Biztos számfogalom a 10-es számkörben - Egyjegyű szám fogalmának ismerete - Páros, páratlan fogalma - Sorszám helyes használata szóban - Növekvő, csökkenő számsorozatok felismerése
Matematika 1. évfolyam - Biztos számfogalom a 10-es számkörben - Egyjegyű szám fogalmának ismerete - Páros, páratlan fogalma - Sorszám helyes használata szóban - Növekvő, csökkenő számsorozatok felismerése
DIAGNOSZTIKUS MÉRÉS. 33. modul
 Matematika A 3. évfolyam DIAGNOSZTIKUS MÉRÉS 33. modul Készítette: KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 33. modul DIAGNOSZTIKUS MÉRÉS MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
Matematika A 3. évfolyam DIAGNOSZTIKUS MÉRÉS 33. modul Készítette: KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 33. modul DIAGNOSZTIKUS MÉRÉS MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
11. modul: LINEÁRIS FÜGGVÉNYEK
 MATEMATIK A 9. évfolyam 11. modul: LINEÁRIS FÜGGVÉNYEK KÉSZÍTETTE: CSÁKVÁRI ÁGNES Matematika A 9. évfolyam. 11. modul: LINEÁRIS FÜGGVÉNYEK Tanári útmutató 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
MATEMATIK A 9. évfolyam 11. modul: LINEÁRIS FÜGGVÉNYEK KÉSZÍTETTE: CSÁKVÁRI ÁGNES Matematika A 9. évfolyam. 11. modul: LINEÁRIS FÜGGVÉNYEK Tanári útmutató 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
0563. MODUL TÖRTEK. Törtek összehasonlítása KÉSZÍTETTE: BENCZÉDY-LACZKA KRISZTINA, MALMOS KATALIN
 0. MODUL TÖRTEK Törtek összehasonlítása KÉSZÍTETTE: BENCZÉDY-LACZKA KRISZTINA MALMOS KATALIN 0. Törtek Törtek összehasonlítása Tanári útmutató MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
0. MODUL TÖRTEK Törtek összehasonlítása KÉSZÍTETTE: BENCZÉDY-LACZKA KRISZTINA MALMOS KATALIN 0. Törtek Törtek összehasonlítása Tanári útmutató MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
MATEMATIKA A 10. évfolyam
 MATEMATIKA A 10. évfolyam 7. modul Négyzetgyökös egyenletek Készítette: Gidófalvi Zsuzsa Matematika A 10. évfolyam 7. modul: Négyzetgyökös egyenletek Tanári útmutató A modul célja Időkeret Ajánlott korosztály
MATEMATIKA A 10. évfolyam 7. modul Négyzetgyökös egyenletek Készítette: Gidófalvi Zsuzsa Matematika A 10. évfolyam 7. modul: Négyzetgyökös egyenletek Tanári útmutató A modul célja Időkeret Ajánlott korosztály
HALMAZOK. A racionális számok halmazát olyan számok alkotják, amelyek felírhatók b. jele:. A racionális számok halmazának végtelen sok eleme van.
 HALMAZOK Tanulási cél Halmazok megadása, halmazműveletek megismerése és alkalmazása, halmazok ábrázolása Venn diagramon. Motivációs példa Egy fogyasztó 80 000 pénzegység jövedelmet fordít két termék, x
HALMAZOK Tanulási cél Halmazok megadása, halmazműveletek megismerése és alkalmazása, halmazok ábrázolása Venn diagramon. Motivációs példa Egy fogyasztó 80 000 pénzegység jövedelmet fordít két termék, x
Fejlesztı neve: Tavi Orsolya. Tanóra / modul címe: DINAMIKAI ISMERETEK RENDSZEREZÉSE, ÖSSZEFOGLALÁSA KOOPERATÍV TECHNIKÁVAL
 Fejlesztı neve: Tavi Orsolya Tanóra / modul címe: DINAMIKAI ISMERETEK RENDSZEREZÉSE, ÖSSZEFOGLALÁSA KOOPERATÍV TECHNIKÁVAL 1. Az óra tartalma A tanulási téma bemutatása; A téma és a módszer összekapcsolásának
Fejlesztı neve: Tavi Orsolya Tanóra / modul címe: DINAMIKAI ISMERETEK RENDSZEREZÉSE, ÖSSZEFOGLALÁSA KOOPERATÍV TECHNIKÁVAL 1. Az óra tartalma A tanulási téma bemutatása; A téma és a módszer összekapcsolásának
MATEMATIKA VERSENY --------------------
 Eötvös Károly Közös Fenntartású Általános Iskola 2013. és Alapfokú Művészetoktatási Intézmény 831 Vonyarcvashegy, Fő u. 8/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen,
Eötvös Károly Közös Fenntartású Általános Iskola 2013. és Alapfokú Művészetoktatási Intézmény 831 Vonyarcvashegy, Fő u. 8/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen,
MATEMATIKA C 9. évfolyam 1. modul IDŐBEN A TÉRBEN
 MATEMATIKA C 9. évfolyam 1. modul IDŐBEN A TÉRBEN Készítette: Kovács Károlyné MATEMATIKA C 9. ÉVFOLYAM 1. MODUL: IDŐBEN A TÉRBEN TANÁRI ÚTMUTATÓ 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály
MATEMATIKA C 9. évfolyam 1. modul IDŐBEN A TÉRBEN Készítette: Kovács Károlyné MATEMATIKA C 9. ÉVFOLYAM 1. MODUL: IDŐBEN A TÉRBEN TANÁRI ÚTMUTATÓ 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály
A kooperatív tanuláshoz szükséges feladatkörök megismertetése
 26 Szociális, életviteli és környezeti kompetenciák B tanári SZKb_102_03 Tóban és tóparton É N É S A M Á S I K A kooperatív tanuláshoz szükséges feladatkörök megismertetése Készítette: Nagy Erika SZOCIÁLIS,
26 Szociális, életviteli és környezeti kompetenciák B tanári SZKb_102_03 Tóban és tóparton É N É S A M Á S I K A kooperatív tanuláshoz szükséges feladatkörök megismertetése Készítette: Nagy Erika SZOCIÁLIS,
É N É S A V I L Á G. Készítette: ádám Ferencné Szabó Anna Kornélia Zágon Bertalanné SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK A 5.
 szka105_26 É N É S A V I L Á G Élet a Földön Készítette: ádám Ferencné Szabó Anna Kornélia Zágon Bertalanné SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK A 5. ÉVFOLYAM 356 Szociális, életviteli és környezeti
szka105_26 É N É S A V I L Á G Élet a Földön Készítette: ádám Ferencné Szabó Anna Kornélia Zágon Bertalanné SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK A 5. ÉVFOLYAM 356 Szociális, életviteli és környezeti
MATEMATIKA VERSENY ABASÁR, 2018
 MATEMATIKA VERSENY ABASÁR, 2018 1. osztály 2018 /55 pont 1. Folytasd a sort! 0 1 1 2 3 5 /4 pont 2. Melyik ábra illik a kérdőjel helyére? Karikázd be a betűjelét! (A) (B) (C) (D) (E) 3. Számold ki a feladatokat,
MATEMATIKA VERSENY ABASÁR, 2018 1. osztály 2018 /55 pont 1. Folytasd a sort! 0 1 1 2 3 5 /4 pont 2. Melyik ábra illik a kérdőjel helyére? Karikázd be a betűjelét! (A) (B) (C) (D) (E) 3. Számold ki a feladatokat,
Gál Józsefné. Tanmenetjavaslat. a Matematika csodái 2. osztályos tankönyvhöz és munkafüzethez
 Gál Józsefné Tanmenetjavaslat a Matematika csodái 2. osztályos tankönyvhöz és munkafüzethez Dinasztia Tankönyvkiadó Budapest, 2002 Írta: Gál Józsefné Felelôs szerkesztô: Ballér Judit ISBN 963 657 144 9
Gál Józsefné Tanmenetjavaslat a Matematika csodái 2. osztályos tankönyvhöz és munkafüzethez Dinasztia Tankönyvkiadó Budapest, 2002 Írta: Gál Józsefné Felelôs szerkesztô: Ballér Judit ISBN 963 657 144 9
0567. MODUL TÖRTEK. Törtekről tanultak összefoglalása KÉSZÍTETTE: BENCZÉDY-LACZKA KRISZTINA, MALMOS KATALIN
 07. MODUL TÖRTEK Törtekről tanultak összefoglalása KÉSZÍTETTE: BENCZÉDY-LACZKA KRISZTINA, MALMOS KATALIN 07. Törtek Törtekről tanultak összefoglalása Tanári útmutató MODULLEÍRÁS A modul célja Időkeret
07. MODUL TÖRTEK Törtekről tanultak összefoglalása KÉSZÍTETTE: BENCZÉDY-LACZKA KRISZTINA, MALMOS KATALIN 07. Törtek Törtekről tanultak összefoglalása Tanári útmutató MODULLEÍRÁS A modul célja Időkeret
Egyenletek, egyenlőtlenségek VII.
 Egyenletek, egyenlőtlenségek VII. Magasabbfokú egyenletek: A 3, vagy annál nagyobb fokú egyenleteket magasabb fokú egyenleteknek nevezzük. Megjegyzés: Egy n - ed fokú egyenletnek legfeljebb n darab valós
Egyenletek, egyenlőtlenségek VII. Magasabbfokú egyenletek: A 3, vagy annál nagyobb fokú egyenleteket magasabb fokú egyenleteknek nevezzük. Megjegyzés: Egy n - ed fokú egyenletnek legfeljebb n darab valós
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
A pillangóval jelölt feladatok mindenki számára könnyen megoldhatók. a mókussal jelölt feladatok kicsit nehezebbek, több figyelmet igényelnek.
 Kedves második osztályos tanuló! Bizonyára te is szívesen tanulod a matematikát. A 2. osztályban is sok érdekes feladattal találkozhatsz. A Számoljunk! című munkafüzetünk segítségedre lesz a gyakorlásban.
Kedves második osztályos tanuló! Bizonyára te is szívesen tanulod a matematikát. A 2. osztályban is sok érdekes feladattal találkozhatsz. A Számoljunk! című munkafüzetünk segítségedre lesz a gyakorlásban.
Előadó: Horváth Judit
 Előadó: Horváth Judit Előkészítés Tapasztalatszerzés: tevékenység eszközhasználat játék Az összeadás, kivonás típusai Változtatás Hasonlítás Egyesítés A típusok variánsai Fordított, indirekt szövegű feladatok
Előadó: Horváth Judit Előkészítés Tapasztalatszerzés: tevékenység eszközhasználat játék Az összeadás, kivonás típusai Változtatás Hasonlítás Egyesítés A típusok variánsai Fordított, indirekt szövegű feladatok
2017/2018. Matematika 9.K
 2017/2018. Matematika 9.K Matematika javítóvizsga 2018. augusztus szóbeli 3 rövidebb (feladat, definíció, tétel) és 3 hosszabb feladat megoldása a 30 perces felkészülési idő alatt a megoldás ismertetése
2017/2018. Matematika 9.K Matematika javítóvizsga 2018. augusztus szóbeli 3 rövidebb (feladat, definíció, tétel) és 3 hosszabb feladat megoldása a 30 perces felkészülési idő alatt a megoldás ismertetése
Brósch Zoltán (Debreceni Egyetem Kossuth Lajos Gyakorló Gimnáziuma) Megoldások
 Megoldások 1. Oldd meg a következő egyenleteket! (Alaphalmaz: Z) a) (x 1) (x + 1) 7x + 1 = x (4 + x) + 2 b) 1 2 [5 (x 1) (1 + 2x) 2 4x] = (7 x) x c) 2 (x + 5) (x 2) 2 + (x + 1) 2 = 6 (2x + 1) d) 6 (x 8)
Megoldások 1. Oldd meg a következő egyenleteket! (Alaphalmaz: Z) a) (x 1) (x + 1) 7x + 1 = x (4 + x) + 2 b) 1 2 [5 (x 1) (1 + 2x) 2 4x] = (7 x) x c) 2 (x + 5) (x 2) 2 + (x + 1) 2 = 6 (2x + 1) d) 6 (x 8)
5. modul: ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS
 MATEMATIK A 9. évfolyam 5. modul: ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS KÉSZÍTETTE: VIDRA GÁBOR Matematika A 9. évfolyam. 5. modul: ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS Tanári útmutató 2 A modul célja Időkeret Ajánlott
MATEMATIK A 9. évfolyam 5. modul: ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS KÉSZÍTETTE: VIDRA GÁBOR Matematika A 9. évfolyam. 5. modul: ARÁNYOSSÁG, SZÁZALÉKSZÁMÍTÁS Tanári útmutató 2 A modul célja Időkeret Ajánlott
nyitott mondatok (szóbeli) előkészítése
 Matematika A 1. évfolyam nyitott mondatok (szóbeli) előkészítése 11. modul Készítette: bóta mária kőkúti ágnes matematika A 1. ÉVFOLYAM 11. modul nyitott mondatok (szóbeli) előkészítése MODULLEÍRÁS A modul
Matematika A 1. évfolyam nyitott mondatok (szóbeli) előkészítése 11. modul Készítette: bóta mária kőkúti ágnes matematika A 1. ÉVFOLYAM 11. modul nyitott mondatok (szóbeli) előkészítése MODULLEÍRÁS A modul
Matematika A 9. szakiskolai évfolyam. 16. modul EGYBEVÁGÓSÁGOK. Készítette: Vidra Gábor
 Matematika A 9. szakiskolai évfolyam 16. modul EGYBEVÁGÓSÁGOK Készítette: Vidra Gábor MATEMATIKA A 9. SZAKISKOLAI ÉVFOLYAM 16. modul: EGYBEVÁGÓSÁGOK TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott korosztály
Matematika A 9. szakiskolai évfolyam 16. modul EGYBEVÁGÓSÁGOK Készítette: Vidra Gábor MATEMATIKA A 9. SZAKISKOLAI ÉVFOLYAM 16. modul: EGYBEVÁGÓSÁGOK TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott korosztály
Óravázlat. Tananyag: Műveletvégzés a 20-as számkörben tízes átlépéssel. A természetes szám fogalmának mélyítése a számtulajdonságok megfigyelésével.
 Óravázlat Tantárgy: Matematika Osztály: BONI Széchenyi István Általános Iskola 1. e Tanít: Dr. Szudi Lászlóné Tananyag: Műveletvégzés a 20-as számkörben tízes átlépéssel Kiemelt kompetenciák: Matematika
Óravázlat Tantárgy: Matematika Osztály: BONI Széchenyi István Általános Iskola 1. e Tanít: Dr. Szudi Lászlóné Tananyag: Műveletvégzés a 20-as számkörben tízes átlépéssel Kiemelt kompetenciák: Matematika
Függvények Megoldások
 Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
Függvények Megoldások ) Az ábrán egy ; intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát! a) x x b) x x + c) x ( x + ) b) Az x függvény
I.4. BALATONI NYARALÁS. A feladatsor jellemzői
 I.4. BALATONI NYARALÁS Tárgy, téma A feladatsor jellemzői Logikai fogalmak: logikai kijelentés; minden; van olyan; ha, akkor; és; vagy kifejezések jelentése. Egyszerű logikai kapcsolatok mondatok között.
I.4. BALATONI NYARALÁS Tárgy, téma A feladatsor jellemzői Logikai fogalmak: logikai kijelentés; minden; van olyan; ha, akkor; és; vagy kifejezések jelentése. Egyszerű logikai kapcsolatok mondatok között.
EGYENLETEK, EGYENLŐTLENSÉGEK
 069. MODUL EGYENLETEK, EGYENLŐTLENSÉGEK Egyenletek, egyenlőtlenségek megoldása mérleg elvvel KÉSZÍTETTE: OROSHÁZI KATALIN 069. Egyenletek, egyenlőtlenségek Egyenletek, egyenlőtlenségek megoldása mérleg
069. MODUL EGYENLETEK, EGYENLŐTLENSÉGEK Egyenletek, egyenlőtlenségek megoldása mérleg elvvel KÉSZÍTETTE: OROSHÁZI KATALIN 069. Egyenletek, egyenlőtlenségek Egyenletek, egyenlőtlenségek megoldása mérleg
Egy halmazt elemei megadásával tekintünk ismertnek. Az elemeket felsorolással,vagy ha lehet a rájuk jellemző közös tulajdonság megadásával adunk meg.
 Halmazelmélet A matematikai halmazelmélet megalapítója Georg Cantor (1845 1918) matematikus. Cantor Oroszországban született, de életét Németországban töltötte. Egy halmazt elemei megadásával tekintünk
Halmazelmélet A matematikai halmazelmélet megalapítója Georg Cantor (1845 1918) matematikus. Cantor Oroszországban született, de életét Németországban töltötte. Egy halmazt elemei megadásával tekintünk
A játékosok választanak különböző színű bábukat, mindenki 3 fél színből. Kettő a tényezőké, egy a szorzat bábu színe. Ezeket megjegyzik.
 SAJÁT KÉSZÍTÉSŰ FEJLESZTŐ ESZKÖZÖK 1 2 3 3 4 5 6 7 4 Szerző: Szabó Ottilia 1. SZORZÁS MÁTRIX TÁBLA Eszközök: - szorzatokat tartalmazó tábla, a tényezők fent és bal oldalon - 20-30 bábu - 1-1 vagy 2-2 db
SAJÁT KÉSZÍTÉSŰ FEJLESZTŐ ESZKÖZÖK 1 2 3 3 4 5 6 7 4 Szerző: Szabó Ottilia 1. SZORZÁS MÁTRIX TÁBLA Eszközök: - szorzatokat tartalmazó tábla, a tényezők fent és bal oldalon - 20-30 bábu - 1-1 vagy 2-2 db
ÓRAVÁZLAT. Az óra címe: Ismeretek a kis számokról. Osztály. nyújtott 1. évfolyam első év A tanóra célja
 ÓRAVÁZLAT Az óra címe: Ismeretek a kis számokról Készítette: Nagy Istvánné Osztály nyújtott 1. évfolyam első év A tanóra célja Tudatos észlelés, megfigyelés és a figyelem fejlesztése, pontosítása. Tapasztalatszerzés
ÓRAVÁZLAT Az óra címe: Ismeretek a kis számokról Készítette: Nagy Istvánné Osztály nyújtott 1. évfolyam első év A tanóra célja Tudatos észlelés, megfigyelés és a figyelem fejlesztése, pontosítása. Tapasztalatszerzés
Modul bevezetése. Matematika 5. osztály 2009-2010. A negatív számok 0541. modul
 Modul bevezetése Matematika 5. osztály 2009-2010 A negatív számok 0541. modul MODULLEÍRÁS A modul célja Időkeret Korosztály Modulkapcsolódási pontok A képességfejlesztés fókuszai Számfogalom bővítése.
Modul bevezetése Matematika 5. osztály 2009-2010 A negatív számok 0541. modul MODULLEÍRÁS A modul célja Időkeret Korosztály Modulkapcsolódási pontok A képességfejlesztés fókuszai Számfogalom bővítése.
Az egyenlőtlenség mindkét oldalát szorozzuk meg 4 16-al:
 Bevezető matematika kémikusoknak., 04. ősz. feladatlap. Ábrázoljuk számegyenesen a következő egyenlőtlenségek megoldáshalmazát! (a) x 5 < 3 5 x < 3 x 5 < (d) 5 x
Bevezető matematika kémikusoknak., 04. ősz. feladatlap. Ábrázoljuk számegyenesen a következő egyenlőtlenségek megoldáshalmazát! (a) x 5 < 3 5 x < 3 x 5 < (d) 5 x
Szorzás, osztás 1000-ig. A műveletek tulajdonságai 1. Hány pötty van Erika rajzán? Írj róla összeadást és szorzást is!
 Szorzás, osztás 1000-ig. A műveletek tulajdonságai 1. Hány pötty van Erika rajzán? Írj róla összeadást és szorzást is! Ha a zöld vonalak mentén lévő pöttyöket adod össze, akkor 5+5+5=, vagy 3 =. Ha a piros
Szorzás, osztás 1000-ig. A műveletek tulajdonságai 1. Hány pötty van Erika rajzán? Írj róla összeadást és szorzást is! Ha a zöld vonalak mentén lévő pöttyöket adod össze, akkor 5+5+5=, vagy 3 =. Ha a piros
1. Írd le számjegyekkel illetve betűkkel az alábbi számokat! Tízezer-hétszáztizenkettő Huszonhétmillió-hétezer-nyolc
 1. Írd le számjegyekkel illetve betűkkel az alábbi számokat! Tízezer-hétszáztizenkettő Huszonhétmillió-hétezer-nyolc 10 325 337 30 103 000 002 2. Végezd el az alábbi műveleteket, ahol jelölve van ellenőrizz!
1. Írd le számjegyekkel illetve betűkkel az alábbi számokat! Tízezer-hétszáztizenkettő Huszonhétmillió-hétezer-nyolc 10 325 337 30 103 000 002 2. Végezd el az alábbi műveleteket, ahol jelölve van ellenőrizz!
Matematika (alsó tagozat)
 Matematika (alsó tagozat) Az értékelés elvei és eszközei A tanév során az értékelés alapja a tanulók állandó megfigyelése. Folyamatos fejlesztő célzatú szóbeli értékelés visszajelzést ad a tanuló számára
Matematika (alsó tagozat) Az értékelés elvei és eszközei A tanév során az értékelés alapja a tanulók állandó megfigyelése. Folyamatos fejlesztő célzatú szóbeli értékelés visszajelzést ad a tanuló számára
3. Egyenletek, egyenletrendszerek, egyenlőtlenségek
 . Egyenletek, egyenletrendszerek, egyenlőtlenségek I. Nulladik ZH-ban láttuk: 1. Mennyi a 2x 2 8x 5 = 0 egyenlet gyökeinek a szorzata? (A) 10 (B) 2 (C) 2,5 (D) 4 (E) ezek egyike sem Megoldás I.: BME 2011.
. Egyenletek, egyenletrendszerek, egyenlőtlenségek I. Nulladik ZH-ban láttuk: 1. Mennyi a 2x 2 8x 5 = 0 egyenlet gyökeinek a szorzata? (A) 10 (B) 2 (C) 2,5 (D) 4 (E) ezek egyike sem Megoldás I.: BME 2011.
ARITMETIKA ÉS ALGEBRA ISMÉTLÉS
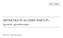 08. MODUL ARITMETIKA ÉS ALGEBRA ISMÉTLÉS Egyenletek, egyenlőtlenségek KÉSZÍTETTE: OROSHÁZI KATALIN Tanári útmutató MODULLEÍRÁS A modul célja A műveletekben szereplő mennyiségek nevének, a műveleti összefüggéseknek
08. MODUL ARITMETIKA ÉS ALGEBRA ISMÉTLÉS Egyenletek, egyenlőtlenségek KÉSZÍTETTE: OROSHÁZI KATALIN Tanári útmutató MODULLEÍRÁS A modul célja A műveletekben szereplő mennyiségek nevének, a műveleti összefüggéseknek
KOVÁCS BÉLA, MATEMATIKA I.
 KOVÁCS BÉLA, MATEmATIkA I. 1 I. HALmAZOk 1. JELÖLÉSEk A halmaz fogalmát tulajdonságait gyakran használjuk a matematikában. A halmazt nem definiáljuk, ezt alapfogalomnak tekintjük. Ez nem szokatlan, hiszen
KOVÁCS BÉLA, MATEmATIkA I. 1 I. HALmAZOk 1. JELÖLÉSEk A halmaz fogalmát tulajdonságait gyakran használjuk a matematikában. A halmazt nem definiáljuk, ezt alapfogalomnak tekintjük. Ez nem szokatlan, hiszen
IDŐMÉRÉS AZ IDŐ MÚLÁSA
 MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 11. modul IDŐMÉRÉS AZ IDŐ MÚLÁSA Készítette: Schmittinger Judit MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 11. modul: IDŐMÉRÉS AZ IDŐ MÚLÁSA 2 A modul célja
MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 11. modul IDŐMÉRÉS AZ IDŐ MÚLÁSA Készítette: Schmittinger Judit MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 11. modul: IDŐMÉRÉS AZ IDŐ MÚLÁSA 2 A modul célja
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉP SZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
1. tétel. 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója 7 cm. Mekkora a háromszög átfogója? (4 pont)
 1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
1. tétel 1. Egy derékszögű háromszög egyik szöge 50, a szög melletti befogója cm. Mekkora a háromszög átfogója? (4 pont). Adott az ábrán két vektor. Rajzolja meg a b, a b és az a b vektorokat! (6 pont)
MATEMATIKA VERSENY
 Vonyarcvashegyi Eötvös Károly Általános Iskola 2016. 8314 Vonyarcvashegy, Fő u. 84/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen, majd oldd meg a feladatokat! A részeredményeket
Vonyarcvashegyi Eötvös Károly Általános Iskola 2016. 8314 Vonyarcvashegy, Fő u. 84/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen, majd oldd meg a feladatokat! A részeredményeket
SEGÍTŐ SZOLGÁLATOK, SEGÍTŐ SZAKEMBEREK
 POLGÁR A DEMOKRÁCIÁBAN SEGÍTŐ SZOLGÁLATOK, SEGÍTŐ SZAKEMBEREK Készítette: Sallai Éva SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIA 8. ÉVFOLYAM SZKA208_48 612 SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK
POLGÁR A DEMOKRÁCIÁBAN SEGÍTŐ SZOLGÁLATOK, SEGÍTŐ SZAKEMBEREK Készítette: Sallai Éva SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIA 8. ÉVFOLYAM SZKA208_48 612 SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK
A kompetencia alapú matematika oktatás. tanmenete a 9. osztályban. Készítette Maitz Csaba
 A kompetencia alapú matematika oktatás tanmenete a 9. osztályban Készítette Maitz Csaba Szerkesztési feladatok 1. Síkgeometriai alapfogalmak 2. Egyszerűbb rajzok, szerkesztések körző, vonalzó használata
A kompetencia alapú matematika oktatás tanmenete a 9. osztályban Készítette Maitz Csaba Szerkesztési feladatok 1. Síkgeometriai alapfogalmak 2. Egyszerűbb rajzok, szerkesztések körző, vonalzó használata
MATEMATIKA VERSENY
 Eötvös Károly Közös Fenntartású Óvoda, Általános Iskola 2012. és Alapfokú Művészetoktatási Intézmény 8314 Vonyarcvashegy, Fő u. 84/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen,
Eötvös Károly Közös Fenntartású Óvoda, Általános Iskola 2012. és Alapfokú Művészetoktatási Intézmény 8314 Vonyarcvashegy, Fő u. 84/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen,
Matematika A 9. szakiskolai évfolyam. 8. modul AZ ABSZOLÚTÉRTÉK-FÜGGVÉNY ÉS MÁS NEMLINEÁRIS FÜGGVÉNYEK
 Matematika A 9. szakiskolai évfolyam 8. modul AZ ABSZOLÚTÉRTÉK-FÜGGVÉNY ÉS MÁS NEMLINEÁRIS FÜGGVÉNYEK Matematika A 9. szakiskolai évfolyam 8. modul: Az abszolútérték-függvény és más nemlineáris függvények
Matematika A 9. szakiskolai évfolyam 8. modul AZ ABSZOLÚTÉRTÉK-FÜGGVÉNY ÉS MÁS NEMLINEÁRIS FÜGGVÉNYEK Matematika A 9. szakiskolai évfolyam 8. modul: Az abszolútérték-függvény és más nemlineáris függvények
0643. MODUL SZÁMELMÉLET. Törzsszám (prímszám), összetett szám, prímtényezős felbontás KÉSZÍTETTE: PINTÉR KLÁRA
 0643. MODUL SZÁMELMÉLET Törzsszám (prímszám), összetett szám, prímtényezős felbontás KÉSZÍTETTE: PINTÉR KLÁRA 0643. Számelmélet Törzsszám (prímszám), összetett szám, prímtényezős felbontás Tanári útmutató
0643. MODUL SZÁMELMÉLET Törzsszám (prímszám), összetett szám, prímtényezős felbontás KÉSZÍTETTE: PINTÉR KLÁRA 0643. Számelmélet Törzsszám (prímszám), összetett szám, prímtényezős felbontás Tanári útmutató
nyelv: 2) Kérdezz meg 3 embert a környezetedben arról, milyen nyelven tud beszélni, írni, olvasni. Írd le a válaszaikat!
 nyelv: A nyelv arra való, hogy el tudjuk mondani másoknak, amit gondolunk, és mások gondolatait meg tudjuk érteni. Nagyon régen alakult ki, és folyamatosan változik. A nyelv részei: a hangok, a szavak,
nyelv: A nyelv arra való, hogy el tudjuk mondani másoknak, amit gondolunk, és mások gondolatait meg tudjuk érteni. Nagyon régen alakult ki, és folyamatosan változik. A nyelv részei: a hangok, a szavak,
MATEMATIKA VERSENY
 Vonyarcvashegyi Eötvös Károly Általános Iskola 2015. 8314 Vonyarcvashegy, Fő u. 84/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen, majd oldd meg a feladatokat! A részeredményeket
Vonyarcvashegyi Eötvös Károly Általános Iskola 2015. 8314 Vonyarcvashegy, Fő u. 84/1. 2. osztály MATEMATIKA VERSENY -------------------- név Olvasd el figyelmesen, majd oldd meg a feladatokat! A részeredményeket
ÍRÁSBELI ÖSSZEADÁS, KIVONÁS. A MŰVELETI SORREND SZÁMÍTÁSOKBAN ÉS SZÖVEGES FELADATOK MEGOLDÁSA SORÁN. 9. modul
 Matematika A 4. évfolyam ÍRÁSBELI ÖSSZEADÁS, KIVONÁS. A MŰVELETI SORREND SZÁMÍTÁSOKBAN ÉS SZÖVEGES FELADATOK MEGOLDÁSA SORÁN 9. modul Készítette: KONRÁD ÁGNES matematika A 4. ÉVFOLYAM 9. modul ÍRÁSBELI
Matematika A 4. évfolyam ÍRÁSBELI ÖSSZEADÁS, KIVONÁS. A MŰVELETI SORREND SZÁMÍTÁSOKBAN ÉS SZÖVEGES FELADATOK MEGOLDÁSA SORÁN 9. modul Készítette: KONRÁD ÁGNES matematika A 4. ÉVFOLYAM 9. modul ÍRÁSBELI
Oszthatósági problémák
 Oszthatósági problémák Érdekes kérdés, hogy egy adott számot el lehet-e osztani egy másik számmal (maradék nélkül). Ezek eldöntésére a matematika tanulmányok során néhány speciális esetre látunk is példát,
Oszthatósági problémák Érdekes kérdés, hogy egy adott számot el lehet-e osztani egy másik számmal (maradék nélkül). Ezek eldöntésére a matematika tanulmányok során néhány speciális esetre látunk is példát,
HALMAZOK TULAJDONSÁGAI,
 Halmazok definíciója, megadása HALMAZOK TULAJDONSÁGAI, 1. A következő definíciók közül melyek határoznak meg egyértelműen egy-egy halmazt? a) A: a csoport tanulói b) B: Magyarország városai ma c) C: Pilinszky
Halmazok definíciója, megadása HALMAZOK TULAJDONSÁGAI, 1. A következő definíciók közül melyek határoznak meg egyértelműen egy-egy halmazt? a) A: a csoport tanulói b) B: Magyarország városai ma c) C: Pilinszky
szka102_27 É N É S A V I L Á G Készítette: Özvegy Judit SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK A 2. ÉVFOLYAM
 szka102_27 É N É S A V I L Á G Séta a vízparton Készítette: Özvegy Judit SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK A 2. ÉVFOLYAM 300 Szociális, életviteli és környezeti kompetenciák Tanári MODULVÁZLAT
szka102_27 É N É S A V I L Á G Séta a vízparton Készítette: Özvegy Judit SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK A 2. ÉVFOLYAM 300 Szociális, életviteli és környezeti kompetenciák Tanári MODULVÁZLAT
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények
 MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
MATEMATIKA ÉRETTSÉGI TÍPUSFELADATOK MEGOLDÁSAI KÖZÉPSZINT Függvények A szürkített hátterű feladatrészek nem tartoznak az érintett témakörhöz, azonban szolgálhatnak fontos információval az érintett feladatrészek
Matematika A 9. szakiskolai évfolyam. 15. modul SÍKIDOMOK. Készítette: Vidra Gábor
 Matematika A 9. szakiskolai évfolyam 15. modul SÍKIDOMOK Készítette: Vidra Gábor MATEMATIKA A 9. SZAKISKOLAI ÉVFOLYAM 15. modul: SÍKIDOMOK TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
Matematika A 9. szakiskolai évfolyam 15. modul SÍKIDOMOK Készítette: Vidra Gábor MATEMATIKA A 9. SZAKISKOLAI ÉVFOLYAM 15. modul: SÍKIDOMOK TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási
Az egyenes egyenlete: 2 pont. Az összevont alak: 1 pont. Melyik ábrán látható e függvény grafikonjának egy részlete?
 1. Írja fel annak az egyenesnek az egyenletét, amely áthalad az (1; 3) ponton, és egyik normálvektora a (8; 1) vektor! Az egyenes egyenlete: 2. Végezze el a következő műveleteket, és vonja össze az egynemű
1. Írja fel annak az egyenesnek az egyenletét, amely áthalad az (1; 3) ponton, és egyik normálvektora a (8; 1) vektor! Az egyenes egyenlete: 2. Végezze el a következő műveleteket, és vonja össze az egynemű
48. modul 1. melléklet 2. évfolyam tanító
 48. modul 1. melléklet 2. évfolyam tanító 39 + 41 40 + 40 100 19 90 9 28 + 33 81 30 80 29 90 10 30 + 31 57 + 16 26 + 47 27 + 33 6 6 12 2 12 3 24 + 12 12 + 30 7 6 8 7 56 / 8 7 4 35 70 14 14 + 14 48. modul
48. modul 1. melléklet 2. évfolyam tanító 39 + 41 40 + 40 100 19 90 9 28 + 33 81 30 80 29 90 10 30 + 31 57 + 16 26 + 47 27 + 33 6 6 12 2 12 3 24 + 12 12 + 30 7 6 8 7 56 / 8 7 4 35 70 14 14 + 14 48. modul
Építések, kirakások (geometria és kombinatorika)
 Matematika A 1. évfolyam Építések, kirakások (geometria és kombinatorika) 25. modul Készítették: Szabóné Vajna Kinga Harzáné Kälbli Éva Molnár Éva matematika A 1. ÉVFOLYAM 25. modul építések, kirakások
Matematika A 1. évfolyam Építések, kirakások (geometria és kombinatorika) 25. modul Készítették: Szabóné Vajna Kinga Harzáné Kälbli Éva Molnár Éva matematika A 1. ÉVFOLYAM 25. modul építések, kirakások
Matematika A 9. szakiskolai évfolyam. 14. modul GEOMETRIAI ALAPFOGALMAK. Készítette: Vidra Gábor
 Matematika A 9. szakiskolai évfolyam 14. modul GEOMETRIAI ALAPFOGALMAK Készítette: Vidra Gábor MATEMATIKA A 9. SZAKISKOLAI ÉVFOLYAM 14. modul: GEOMETRIAI ALAPFOGALMAK TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret
Matematika A 9. szakiskolai évfolyam 14. modul GEOMETRIAI ALAPFOGALMAK Készítette: Vidra Gábor MATEMATIKA A 9. SZAKISKOLAI ÉVFOLYAM 14. modul: GEOMETRIAI ALAPFOGALMAK TANÁRI ÚTMUTATÓ 2 A modul célja Időkeret
ÖSSZEADÁS, KIVONÁS AZ EGY 0-RA VÉGZŐDŐ SZÁMOK KÖRÉBEN
 Matematika A 3. évfolyam ÖSSZEADÁS, KIVONÁS AZ EGY 0-RA VÉGZŐDŐ SZÁMOK KÖRÉBEN 16. modul Készítette: KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 16. modul összeadás, kivonás az egy 0-ra végződő számok körében
Matematika A 3. évfolyam ÖSSZEADÁS, KIVONÁS AZ EGY 0-RA VÉGZŐDŐ SZÁMOK KÖRÉBEN 16. modul Készítette: KONRÁD ÁGNES matematika A 3. ÉVFOLYAM 16. modul összeadás, kivonás az egy 0-ra végződő számok körében
HOSSZÚSÁGMÉRÉS ÖSSZEHASONLÍTÁSSAL ÁLLATI LEGEK
 MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 3. modul HOSSZÚSÁGMÉRÉS ÖSSZEHASONLÍTÁSSAL ÁLLATI LEGEK Készítette: Schmittinger Judit MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 3. modul: HOSSZÚSÁGMÉRÉS
MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 3. modul HOSSZÚSÁGMÉRÉS ÖSSZEHASONLÍTÁSSAL ÁLLATI LEGEK Készítette: Schmittinger Judit MATEMATIKA B 1. ÉVFOLYAM EMBER A TERMÉSZETBEN 3. modul: HOSSZÚSÁGMÉRÉS
1. Melyek azok a kétjegyű számok, amelyek oszthatók számjegyeik
 1991. évi verseny, 1. nap 1. Számold össze, hány pozitív osztója van 16 200-nak! 2. Bontsd fel a 60-at két szám összegére úgy, hogy az egyik szám hetede egyenlő legyen a másik szám nyolcadával! 3. Van
1991. évi verseny, 1. nap 1. Számold össze, hány pozitív osztója van 16 200-nak! 2. Bontsd fel a 60-at két szám összegére úgy, hogy az egyik szám hetede egyenlő legyen a másik szám nyolcadával! 3. Van
MATEMATIKAI KOMPETENCIATERÜLET A
 MATEMATIKAI KOMPETENCIATERÜLET A Matematika 2. évfolyam MÉRŐLAPOK 7. modul 6. melléklet 2. évfolyam 1. mérőlap tanuló/1. 1. Írd le a számokat egymás mellé! ; ; ; ; 2. Tedd a kapott számokat csökkenő sorrendbe!
MATEMATIKAI KOMPETENCIATERÜLET A Matematika 2. évfolyam MÉRŐLAPOK 7. modul 6. melléklet 2. évfolyam 1. mérőlap tanuló/1. 1. Írd le a számokat egymás mellé! ; ; ; ; 2. Tedd a kapott számokat csökkenő sorrendbe!
JÁTÉK KÖZÖSSÉG ÖNISMERET
 É N É S M Á S I K JÁTÉK KÖZÖSSÉG ÖNISMERET modul szerzôje: Nagy Erika SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK 3. ÉVFOLYM SZKB_103_13 124 SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK TNÁRI
É N É S M Á S I K JÁTÉK KÖZÖSSÉG ÖNISMERET modul szerzôje: Nagy Erika SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK 3. ÉVFOLYM SZKB_103_13 124 SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK TNÁRI
Matematika A 9. szakiskolai évfolyam. 7. modul EGYENES ARÁNYOSSÁG ÉS A LINEÁRIS FÜGGVÉNYEK
 Matematika A 9. szakiskolai évfolyam 7. modul EGYENES ARÁNYOSSÁG ÉS A LINEÁRIS FÜGGVÉNYEK Matematika A 9. szakiskolai évfolyam 7. modul: Egyenes arányosság és a lineáris függvények Tanári útmutató 2 A
Matematika A 9. szakiskolai évfolyam 7. modul EGYENES ARÁNYOSSÁG ÉS A LINEÁRIS FÜGGVÉNYEK Matematika A 9. szakiskolai évfolyam 7. modul: Egyenes arányosság és a lineáris függvények Tanári útmutató 2 A
Halmazok. A és B különbsége: A \ B. A és B metszete: A. A és B uniója: A
 Halmazok Érdekes feladat lehet, amikor bizonyos mennyiségű adatok között keressük az adott tulajdonsággal rendelkezők számát. A következőekben azt szeretném megmutatni, hogy a halmazábrák segítségével,
Halmazok Érdekes feladat lehet, amikor bizonyos mennyiségű adatok között keressük az adott tulajdonsággal rendelkezők számát. A következőekben azt szeretném megmutatni, hogy a halmazábrák segítségével,
ALGEBRAI KIFEJEZÉSEK, EGYENLETEK
 ALGEBRAI KIFEJEZÉSEK, EGYENLETEK AZ ALGEBRAI KIFEJEZÉS FOGALMÁNAK KIALAKÍTÁSA (7-9. OSZTÁLY) Racionális algebrai kifejezés (betűs kifejezés): betűket és számokat a négy alapművelet véges sokszori alkalmazásával
ALGEBRAI KIFEJEZÉSEK, EGYENLETEK AZ ALGEBRAI KIFEJEZÉS FOGALMÁNAK KIALAKÍTÁSA (7-9. OSZTÁLY) Racionális algebrai kifejezés (betűs kifejezés): betűket és számokat a négy alapművelet véges sokszori alkalmazásával
0645. MODUL SZÁMELMÉLET. Gyakorlás, mérés KÉSZÍTETTE: PINTÉR KLÁRA
 0645. MODUL SZÁMELMÉLET Gyakorlás, mérés KÉSZÍTETTE: PINTÉR KLÁRA 0645. Számelmélet Gyakorlás, mérés Tanári útmutató 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A
0645. MODUL SZÁMELMÉLET Gyakorlás, mérés KÉSZÍTETTE: PINTÉR KLÁRA 0645. Számelmélet Gyakorlás, mérés Tanári útmutató 2 MODULLEÍRÁS A modul célja Időkeret Ajánlott korosztály Modulkapcsolódási pontok A
KONFLIKTUSOK MEGJELENÉSE SZÓLÁSOKBAN, KÖZ - MONDÁSOKBAN
 É N É S M Á S I K KONFLIKTUSOK MEGJELENÉSE SZÓLÁSOKBN, KÖZ - MONDÁSOKBN modul szerzôje: Iván Márta SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK 3. ÉVFOLYM SZKB_103_12 114 SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI
É N É S M Á S I K KONFLIKTUSOK MEGJELENÉSE SZÓLÁSOKBN, KÖZ - MONDÁSOKBN modul szerzôje: Iván Márta SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI KOMPETENCIÁK 3. ÉVFOLYM SZKB_103_12 114 SZOCIÁLIS, ÉLETVITELI ÉS KÖRNYEZETI
